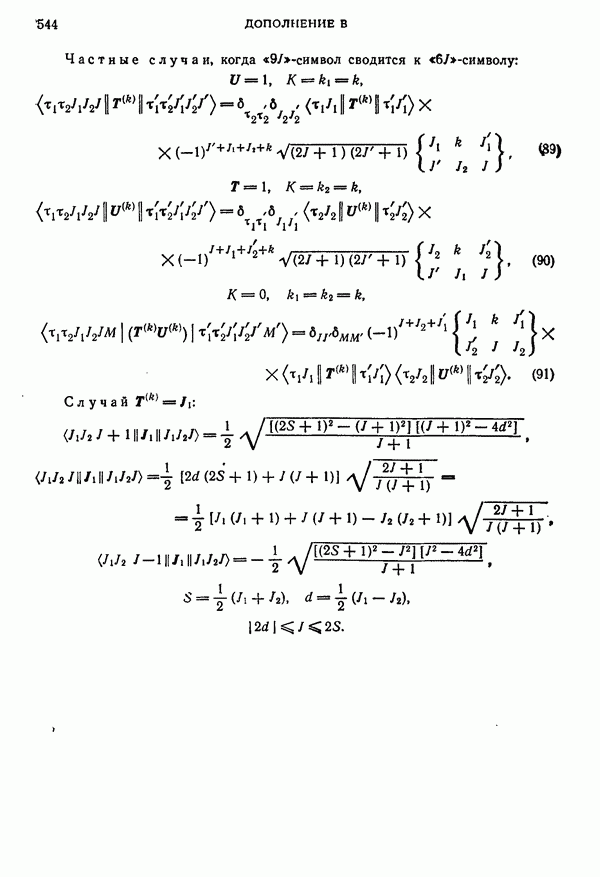| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
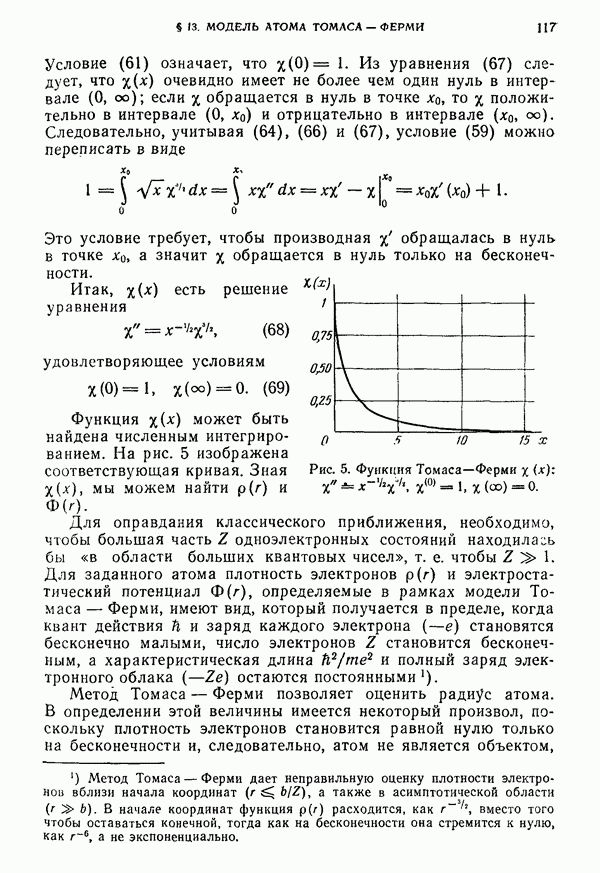
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
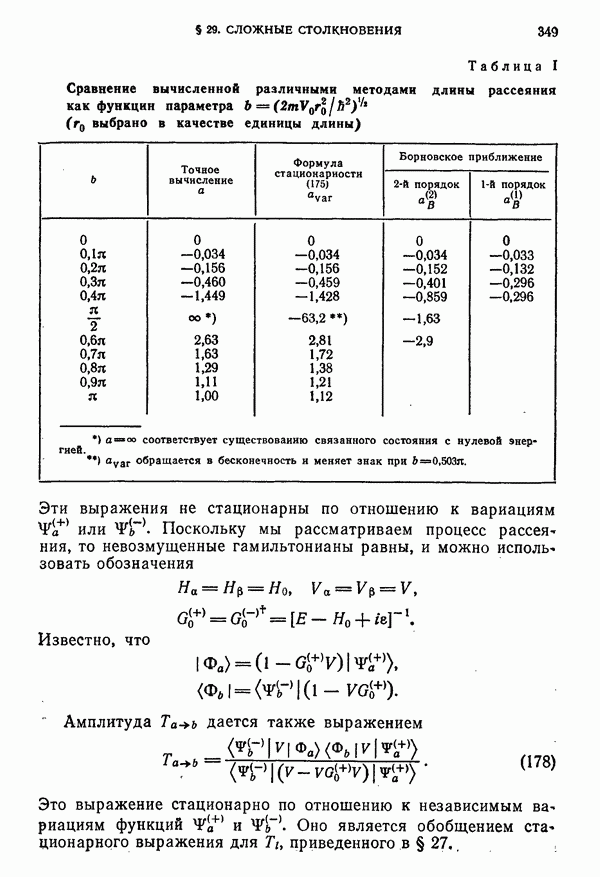
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
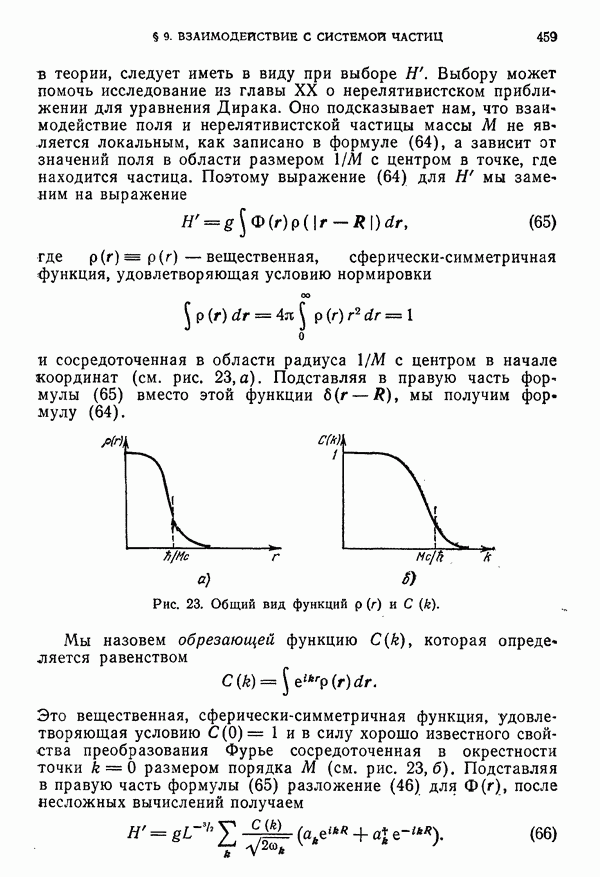
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
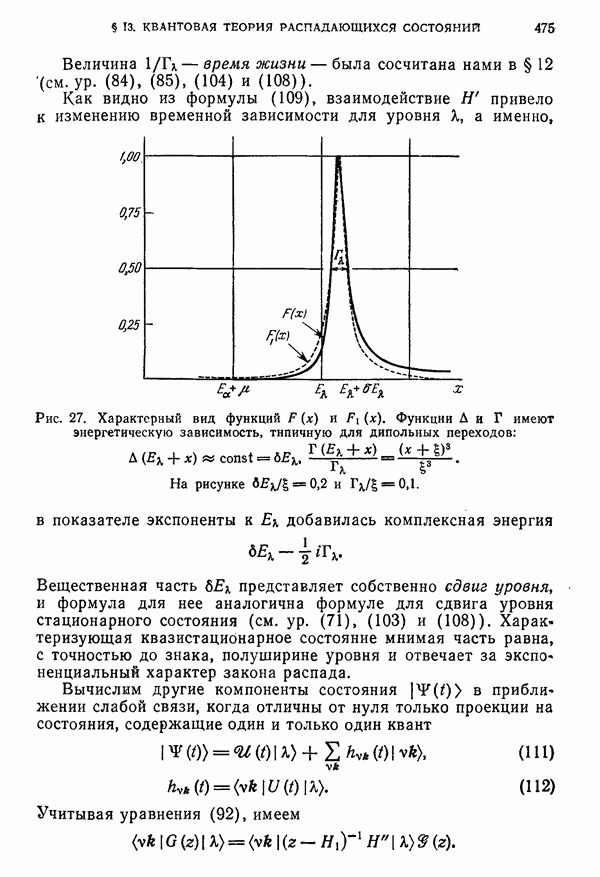
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 25. Простое рассеяние. Интерференция
В качестве первого приложения разложения (149) вычислим сечение упругого рассеяния частицы на двух атомах.
Допустим, что атомы находятся до и после рассеяния в основном состоянии  . Пусть
. Пусть  — волновые векторы падающей и рассеянной волн. Таким образом, мы рассматриваем переход
— волновые векторы падающей и рассеянной волн. Таким образом, мы рассматриваем переход  и имеем
и имеем

Чтобы вычислить амплитуду перехода, сохраним в разложении (149) только члены первого порядка

Принимая во внимание соотношения (150) и (151) и вводя обозначения

находим

Мы увидим, что это соотношение дает амплитуду рассеяния в рамках элементарной теории интерференции. Соотношение (153) позволяет связать сечение упругого рассеяния на двух атомах  с сечением
с сечением  такого же упругого рассеяния на одном атоме, т. е. с сечением процесса
такого же упругого рассеяния на одном атоме, т. е. с сечением процесса  Первое равно квадрату модуля элемента
Первое равно квадрату модуля элемента  умноженному на соответствующий множитель, а второе сечение равно квадрату модуля
умноженному на соответствующий множитель, а второе сечение равно квадрату модуля  умноженному на тот же множитель. Из соотношения (153) следует
умноженному на тот же множитель. Из соотношения (153) следует

Наличие в формуле (154) множителя  связано с явлением интерференции волн, рассеянных каждым атомом. Не будь интерференции мы имели бы равенство
связано с явлением интерференции волн, рассеянных каждым атомом. Не будь интерференции мы имели бы равенство  и сечение
и сечение  было бы просто суммой сечений рассеяния на каждом из атомов 1 и 2.
было бы просто суммой сечений рассеяния на каждом из атомов 1 и 2.
Мы получим обычные результаты, характерные для интерференции, если исследуем поведение  как функции угла рассеяния. Ограничимся обсуждением только двух предельных случаев, когда длина волны
как функции угла рассеяния. Ограничимся обсуждением только двух предельных случаев, когда длина волны  много больше или много меньше
много больше или много меньше 
Если  то
то  независимо от угла рассеяния и
независимо от угла рассеяния и  Следовательно, сечение рассеяния на двух атомах в четыре раза больше индивидуального сечения или в два раза больше того ответа, который мы получили бы, если бы не было явления интерференции.
Следовательно, сечение рассеяния на двух атомах в четыре раза больше индивидуального сечения или в два раза больше того ответа, который мы получили бы, если бы не было явления интерференции.
В случае  функция
функция  при изменении угла рассеяния быстро колеблется между значениями 0 и 2. Пусть углы, образованные векторами
при изменении угла рассеяния быстро колеблется между значениями 0 и 2. Пусть углы, образованные векторами  с вектором
с вектором  равны
равны  и а соответственно. Тогда
и а соответственно. Тогда

Следовательно,  обращается в нуль всякий раз, когда
обращается в нуль всякий раз, когда  равно произведению
равно произведению  на полуцелое число,
на полуцелое число,
и равно 2 всякий раз, когда  кратно
кратно  Соответствующие значения а определяют направления минимумов и максимумов интерференции. Ширина интерференционных полос имеет порядок
Соответствующие значения а определяют направления минимумов и максимумов интерференции. Ширина интерференционных полос имеет порядок  Возможность наблюдения этих эффектов зависит от угловой разрешающей способности детектирую-, щей аппаратуры. Последняя регистрирует частицы, рассеянный в некоторый телесный угол с конечными размерами
Возможность наблюдения этих эффектов зависит от угловой разрешающей способности детектирую-, щей аппаратуры. Последняя регистрирует частицы, рассеянный в некоторый телесный угол с конечными размерами  Полное число регистрируемых частиц равно интегралу
Полное число регистрируемых частиц равно интегралу  по этой конечной области. Зависимость от углов
по этой конечной области. Зависимость от углов  в этой области в основном определяется множителем
в этой области в основном определяется множителем  Если
Если  то функция
то функция  сильно осциллирует в области интегрирования и ее можно заменить средним значением, не меняя результата, т. е.
сильно осциллирует в области интегрирования и ее можно заменить средним значением, не меняя результата, т. е.  и ответ получается такой, как если бы рассеяние на двух атомах было некогерентным
и ответ получается такой, как если бы рассеяние на двух атомах было некогерентным  . Если же
. Если же  то
то  практически не меняется в области интегрирования и разрешающая способность детектора доста-точна для наблюдения явления интерференции.
практически не меняется в области интегрирования и разрешающая способность детектора доста-точна для наблюдения явления интерференции.
Рассмотрим теперь неупругое столкновение, при котором один из атомов переходит из основного состояния в возбужденное. Пусть  — волновой вектор рассеянной волны, тогда
— волновой вектор рассеянной волны, тогда

Сечение  есть сумма сечений
есть сумма сечений  которые соответствуют переходам
которые соответствуют переходам  . В приближении (152), когда мы сохраняем в разложении для Г только члены, отвечающие простому рассеянию, эти сечения легко вычисляются. При переходе
. В приближении (152), когда мы сохраняем в разложении для Г только члены, отвечающие простому рассеянию, эти сечения легко вычисляются. При переходе  атом 1 возбуждается, а атом 2 остается в основном состоянии. Вклад от
атом 1 возбуждается, а атом 2 остается в основном состоянии. Вклад от  очевидно обращается в нуль (см. ур. (151)), а вклад от
очевидно обращается в нуль (см. ур. (151)), а вклад от  дает
дает  — сечение процесса
— сечение процесса  неупругого рассеяния частицы на одном атоме. Переход
неупругого рассеяния частицы на одном атоме. Переход  отвечает противоположной ситуации: обращается в нуль вклад от
отвечает противоположной ситуации: обращается в нуль вклад от  , а вклад от
, а вклад от  равен
равен  Окончательно,
Окончательно,

В отличие от упругого рассеяния каждый атом действует так, как если бы он был один в этом процессе: волны, неупруго рассеянные атомом 1 и атомом 2, отвечают различным каналам и не могут интерферировать.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ III. СИММЕТРИИ И ИНВАРИАНТНОСТЬ
- Раздел I. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ МОМЕНТА ИМПУЛЬСА
- § 2. Определение момента импульса
- § 3. Основные алгебраические соотношения
- § 4. Спектр операторов
- § 5. Собственные векторы операторов. Построение инвариантных пространств
- § 6. Стандартное представление …
- § 7. Заключение
- Раздел II. ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА И СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 8. Спектр операторов l^2 и lz
- § 9. Определение и построение сферических функций
- Раздел III. МОМЕНТ ИМПУЛЬСА И ВРАЩЕНИЯ
- § 10. Определение вращений. Углы Эйлера
- § 11. Вращение физической системы. Оператор вращения
- § 12. Вращение наблюдаемых
- § 13. Момент импульса и инфинитезимальные вращения
- § 14. Построение оператора …
- § 15. Вращение на угол 2pi и полуцелый момент импульса
- § 16. Неприводимые инвариантные подпространства. Матрицы вращений
- § 17. Инвариантность относительно вращений и сохранение момента импульса
- Раздел IV. СПИН
- § 18. Гипотеза спина электрона
- § 19. Спин 1/2 и матрицы Паули
- § 20. Наблюдаемые и волновые функции частицы спина 1/2. Спинорные поля
- § 21. Векторные поля и частицы спина 1
- § 22. Зависящие от спина взаимодействия в атомах
- § 23. Зависящие от спина нуклол-нуклонные взаимодействия
- Раздел V. СЛОЖЕНИЕ МОМЕНТОВ ИМПУЛЬСА
- § 25. Теорема сложения двух моментов импульса
- § 26. Приложения и примеры
- § 27. Собственные векторы полного момента импульса. Коэффициенты Клебша—Гордана
- § 28. Приложение: система двух нуклонов
- § 29. Сложение трех и более моментов импульса. Коэффициенты Рака. «3sj»-символы
- Раздел VI. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ
- § 31. Неприводимые тензорные операторы. Определение
- § 32. Представление неприводимых тензорных операторов. Теорема Вигнера — Эккарта
- § 33. Приложения
- ГЛАВА XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ. ПРИНЦИП ЗАПРЕТА ПАУЛИ
- Раздел I. ПОСТУЛАТ СИММЕТРИЗАЦИИ
- § 2. Подобные частицы и симметрическое представление
- § 3. Операторы перестановки
- § 4. Алгебра операторов перестановки. Симметризаторы и антисимметризаторы
- § 5. Тождественные частицы и постулат симметризации
- § 6. Бозоны и статистика Бозе—Эйнштейна
- § 7. Фермионы и статистика Ферми — Дирака. Принцип запрета
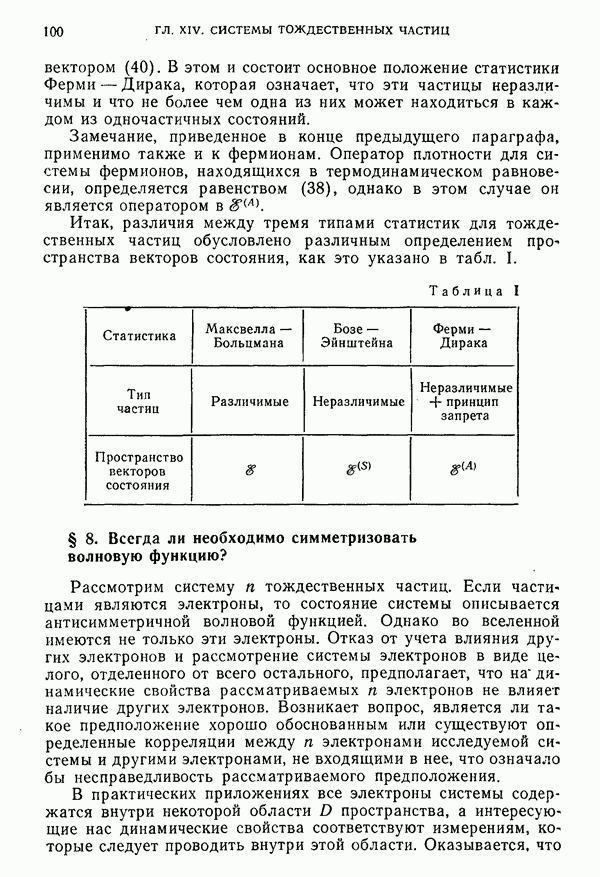
- § 8. Всегда ли необходимо симметризовать волновую функцию?
- Раздел II. ПРИЛОЖЕНИЯ
- § 9. Столкновение двух тождественных бесспиновых частиц
- § 10. Столкновение протонов
- § 11. Статистика атомных ядер
- § 12. Сложные атомы. Приближение центрального поля
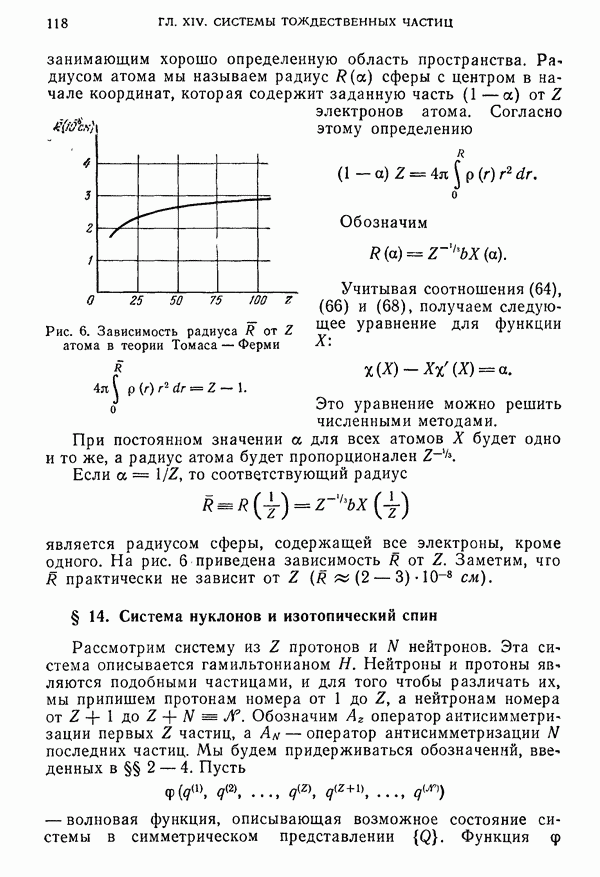
- § 13. Модель атома Томаса—Ферми
- § 14. Система нуклонов и изотопический спин
- § 15. Использование изотопического спина. Зарядовая независимость
- ГЛАВА XV. ИНВАРИАНТНОСТЬ И ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
- Раздел I. ДОПОЛНИТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СВЕДЕНИЯ. АНТИЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 3. Антилинейные операторы в гильбертовом пространстве
- § 4. Антиунитарные преобразования
- § 5. Антилинейные операторы и представления
- Раздел II. ПРЕОБРАЗОВАНИЯ И ГРУППЫ ПРЕОБРАЗОВАНИЙ
- § 6. Преобразования динамических переменных и динамических состояний системы
- § 7. Группы преобразований
- § 8. Группы операторов преобразований
- § 9. Непрерывные группы и инфинитезимальные преобразования. Трансляции. Вращения
- § 10. Конечные группы. Отражения
- Раздел III. ИНВАРИАНТНОСТЬ УРАВНЕНИИ ДВИЖЕНИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 12. Свойства инвариантности гамильтониана и законы сохранения
- § 13. Свойства инвариантности и эволюция динамических состояний
- § 14. Симметрии эффектов Штарка и Зеемана
- Раздел IV. ОБРАЩЕНИЕ ВРЕМЕНИ И ПРИНЦИП МИКРООБРАТИМОСТИ
- § 15. Сдвиги во времени и сохранение энергии
- § 16. Обращение времени в классической и квантовой механиках
- § 17. Обращение времени. Частица нулевого спина
- § 18. Общее определение обращения времени
- § 19. Обращение времени и комплексное сопряжение
- § 20. Принцип микрообратимости
- § 21. Следствие: вырождение Крамерса
- § 22. Вещественный гамильтониан, инвариантный относительно вращений
- ЧАСТЬ IV. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- ГЛАВА XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
- Раздел I. ВОЗМУЩЕНИЕ НЕВЫРОЖДЕННОГО УРОВНЯ
- § 2. Разложение по степеням возмущения
- § 3. Возмущение первого порядка
- § 4. Основное состояние атома гелия
- § 5. Кулоновская энергия атомных ядер
- § 6. Поправки высших порядков
- § 7. Эффект Штарка для жесткого ротатора
- Раздел II. ВОЗМУЩЕНИЕ ВЫРОЖДЕННОГО УРОВНЯ
- § 9. Атомные уровни без учета спин-орбитального взаимодействия
- § 10. Спин-орбитальное взаимодействие. LS- и jj-связь
- § 11. Атом с LS-связью. Расщепление за счет спии-орбитального взаимодействия
- § 12. Эффект Зеемана и эффект Пашена—Бака
- § 13. Симметрия Н и устранение вырождения
- § 14. Квазивырождение
- Раздел III. ЯВНЫЕ ВЫРАЖЕНИЯ ДЛЯ РАЗЛОЖЕНИЙ ПО ТЕОРИИ ВОЗМУЩЕНИЙ ВО ВСЕХ ПОРЯДКАХ
- § 15. Гамильтониан Н и его резольвента G(z)
- § 16. Разложение G(z), в ряд по степеням
- § 17. Вычисление собственных значений и собственных функций
- ГЛАВА XVII. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
- Раздел I. НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
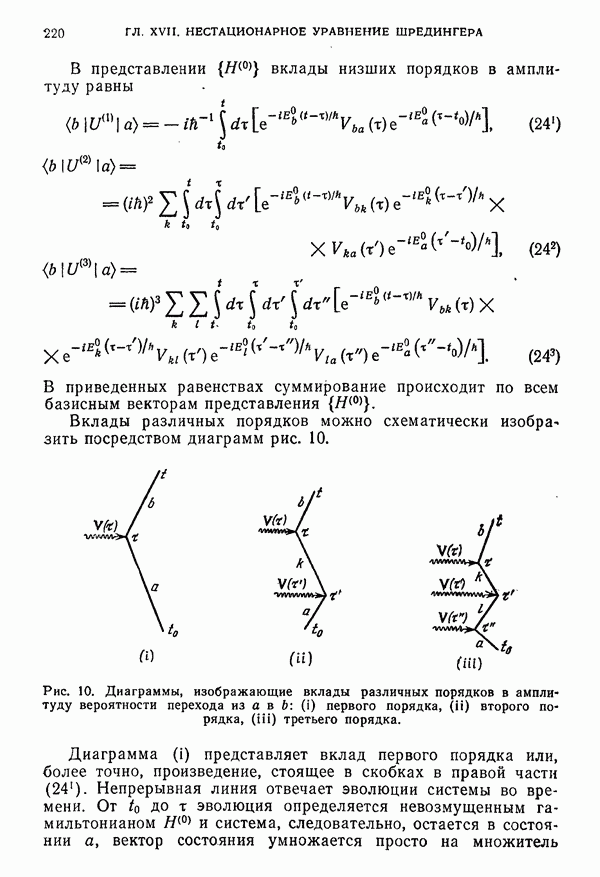
- § 2. Определение и вычисление по теории возмущений вероятностей переходов
- § 3. Полуклассическая теория кулоновского возбуждения ядер
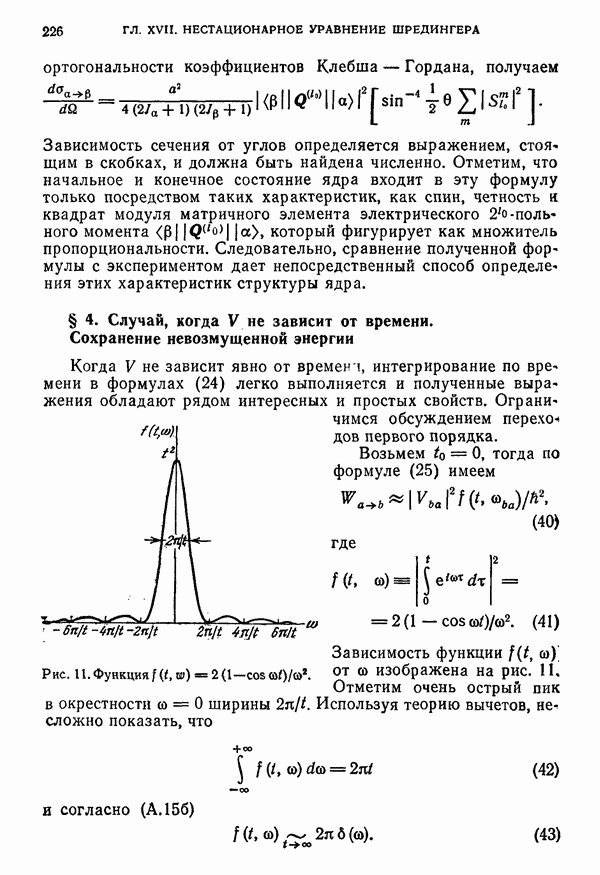
- § 4. Случай, когда V не зависит от времени. Сохранение невозмущенной энергии
- § 5. Приложение к вычислению сечений в борновском приближении
- § 6. Периодическое возмущение. Резонансы
- Раздел II. МГНОВЕННОЕ И АДИАБАТИЧЕСКОЕ ИЗМЕНЕНИЯ ГАМИЛЬТОНИАНА
- § 8. Быстрый переход и мгновенное приближение
- § 9. Мгновенное обращение магнитного поля
- § 10. Адиабатический переход. Общие положения. Тривиальный случай
- § 11. «Представление вращающихся осей»
- § 12. Доказательство адиабатической теоремы
- § 13. Адиабатическое приближение
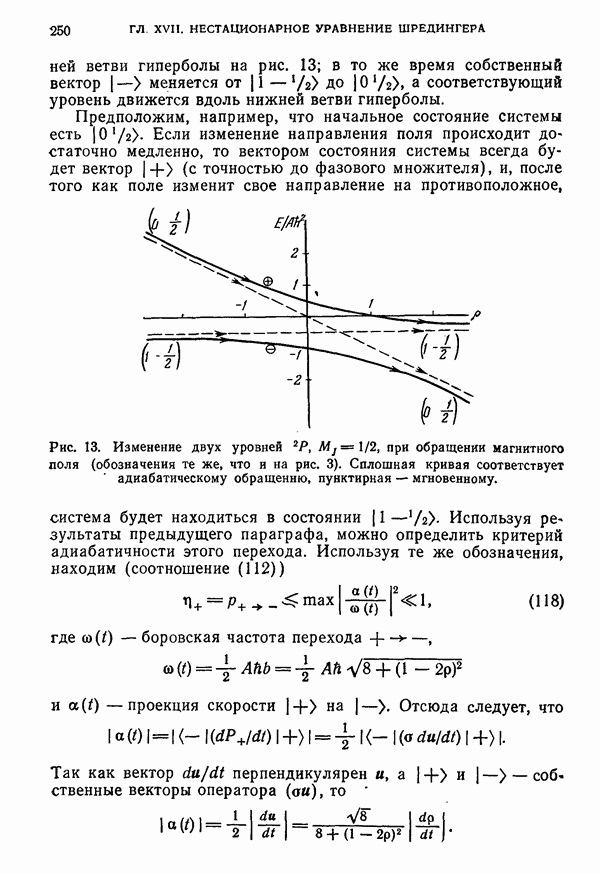
- § 14. Адиабатическое обращение магнитного поля
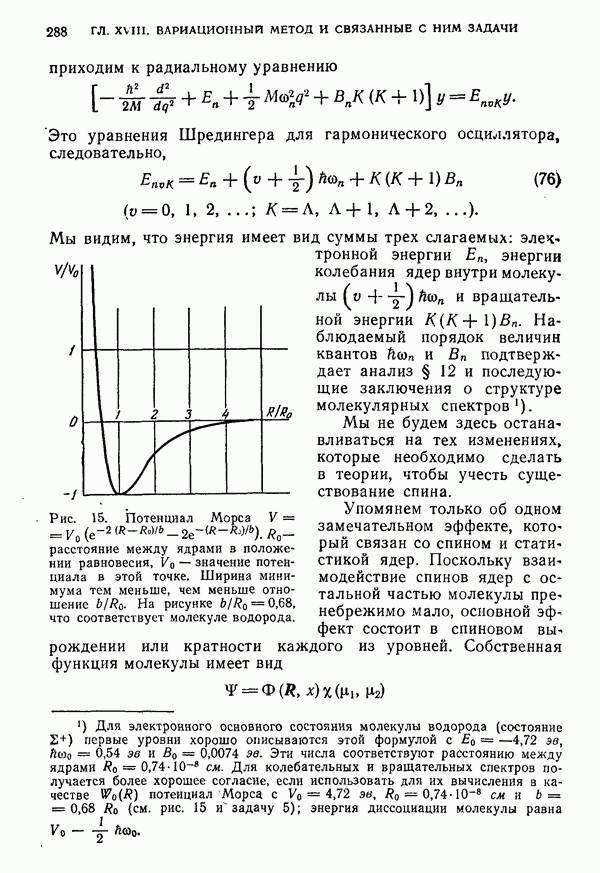
- ГЛАВА XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
- § 1. Вариационный метод Ритца
- Раздел I. ВАРИАЦИОННЫЙ МЕТОД ДЛЯ СВЯЗАННЫХ СОСТОЯНИЙ
- § 2. Вариационная форма задачи на собственные значения
- § 3. Вариационное вычисление дискретных уровней
- § 4. Простой пример: атом водорода
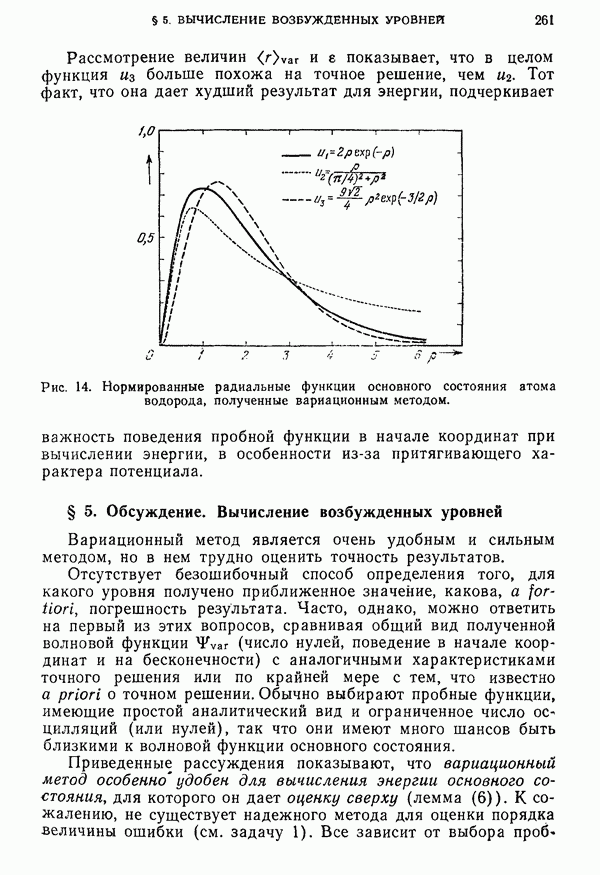
- § 5. Обсуждение. Вычисление возбужденных уровней
- § 6. Основное состояние атома гелия
- Раздел II. АТОМЫ ХАРТРИ И ФОКА—ДИРАКА
- § 7. Метод самосогласованного поля
- § 8. Вычисление Е[Ф]
- § 9. Уравнения Фока — Дирака
- § 10. Обсуждение результатов
- § 11. Уравнения Хартри
- § 12. Общие понятия. Разделение движения ядер и электронов
- § 13. Движение электронов в поле фиксированных ядер
- § 14. Адиабатическое приближение
- § 15. Гамильтониан ядер в адиабатическим приближении
- § 16. Метод Борна — Оппенгеймера
- § 17. Основные представления о двухатомных молекулах
- ГЛАВА XIX. ТЕОРИЯ РАССЕЯНИЯ
- Раздел I. СВОБОДНАЯ ФУНКЦИЯ ГРИНА И ПРИБЛИЖЕНИЕ БОРНА
- § 2. Интегральные представления амплитуды рассеяния
- § 3. Сечение рассеяния и T-матрица. Микрообратимость
- § 4. Борновское приближение
- § 5. Интегральное уравнение теории рассеяния
- § 6. Борновское разложение
- § 7. Критерий применимости борновского приближения
- § 8. Упругое рассеяние электронов на атоме
- § 9. Центральный потенциал. Вычисление сдвигов фаз
- § 10. Функция Грина как оператор. Связь с резольвентой оператора
- Раздел II. ОБОБЩЕНИЕ НА ИСКАЖЕННЫЕ ВОЛНЫ
- § 11. Обобщенное борновское приближение
- § 12. Обобщение борновского разложения
- § 13. Функция Грина искаженных волн
- § 14. Приложения. Определение и формальные свойства Т-матрицы
- § 15. Замечание о потенциалах 1/r
- Раздел III. СЛОЖНЫЕ СТОЛКНОВЕНИЯ И БОРНОВСКОЕ ПРИБЛИЖЕНИЕ
- § 17. Каналы
- § 18. Вычисление сечений. T-матрицы
- § 19. Интегральные представления амплитуды перехода
- § 20. Борновское приближение и его обобщения
- § 21. Рассеяние быстрых электронов атомом
- § 22. Кулоновское возбуждение ядер
- § 23. Функции Грина и интегральные уравнения для стационарных решений рассеяния
- § 24. Рассеяние частицы на двух центрах
- § 25. Простое рассеяние. Интерференция
- § 26. Многократное рассеяние
- Раздел IV. ВЫЧИСЛЕНИЕ АМПЛИТУД ПЕРЕХОДА ВАРИАЦИОННЫМ МЕТОДОМ
- § 27. Стационарные выражения сдвигов фаз. Обсуждение
- § 28. Вариационные вычисления сдвига фаз. Обсуждение
- § 29. Распространение метода на сложные столкновения
- Раздел V. ОБЩИЕ СВОЙСТВА МАТРИЦЫ ПЕРЕХОДА
- § 30. Сохранение потока. S-матрица
- § 31. Соотношение Бора—Пайерлса—Плачека (оптическая теорема)
- § 32. Микрообратимость
- § 33. Свойства инвариантности T-матрицы
- ЧАСТЬ V. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ КВАНТОВОЙ МЕХАНИКИ
- § 1. Релятивистская квантовая механика
- § 2. Обозначения и различные определения
- § 3. Группа Лоренца
- § 4. Классическая релятивистская динамика
- Раздел II. УРАВНЕНИЯ КЛЕЙНА — ГОРДОНА И ДИРАКА
- § 5. Уравнение Клейна—Гордона
- § 6. Уравнение Дирака
- § 7. Построение пространства. Представление Дирака
- § 8. Ковариантная форма уравнения Дирака
- § 9. Сопряженное уравнение. Определение тока
- Раздел III. СВОЙСТВА ИНВАРИАНТНОСТИ УРАВНЕНИЯ ДИРАКА
- § 10. Свойства матриц Дирака
- § 11. Инвариантность уравнения Дирака при ортохронных преобразованиях системы координат
- § 12. Преобразования собственной группы
- § 13. Пространственное отражение и ортохронная группа
- § 14. Построение ковариантных величин
- § 15. Другая формулировка свойств инвариантности: преобразование состояний
- § 16. Условие инвариантности уравнения движения
- § 17. Операторы преобразования. Импульс, момент импульса, четность
- § 18. Законы сохранения и интегралы движения
- § 19. Обращение времени и зарядовое сопряжение
- § 20. Калибровочная инвариантность
- Раздел IV. ИНТЕРПРЕТАЦИЯ ОПЕРАТОРОВ И ПРОСТЫЕ РЕШЕНИЯ
- § 21. Уравнение Дирака и принцип соответствия
- § 22. Динамические переменные частицы Дирака
- § 23. Свободный электрон. Плоские волны
- § 24. Построение плоских волн посредством преобразования Лоренца
- § 25. Центральный потенциал
- § 26. Свободные сферические волны
- § 27. Атом водорода
- Раздел V. НЕРЕЛЯТИВИСТСКИЙ ПРЕДЕЛ УРАВНЕНИЯ ДИРАКА
- § 29. Теория Паули как нерелятивистский предел теории Дирака
- § 30. Приложение: сверхтонкая структура и диполь-дипольная связь
- § 31. Поправки высших порядков и преобразование Фолди — Вотхойзена
- § 32. ФВ-преобразование для свободной частицы
- § 33. ФВ-преобразование для частицы во внешнем поле
- § 34. Электрон в центральном электростатистическом потенциале
- § 35. Обсуждения и выводы
- Раздел VI. РЕШЕНИЯ С ОТРИЦАТЕЛЬНОЙ ЭНЕРГИЕЙ И ТЕОРИЯ ПОЗИТРОНОВ
- § 36. Свойства зарядово-сопряженных решений
- § 37. Особое поведение решений с отрицательной энергией
- § 38. Изменение интерпретации состояний с отрицательной энергией. Теория дырок и позитронов
- § 39. Трудности теории дырок
- ГЛАВА XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
- Раздел I. КВАНТОВАНИЕ ВЕЩЕСТВЕННОГО СКАЛЯРНОГО ПОЛЯ
- § 2. Классические свободные поля. Нормальные колебания
- § 3. Квантование свободного поля
- § 4. Лагранжиан поля. Импульс, сопряженный к Ф(r)
- § 5. Комплексные базисные функции
- § 6. Плоские волны. Определение импульса
- § 7. Сферические волны. Определение момента импульса
- § 8. Пространственное отражение и обращение времени
- Раздел II. ВЗАИМОДЕЙСТВИЕ С АТОМНОЙ СИСТЕМОЙ
- § 9. Взаимодействие с системой частиц
- § 10. Слабая связь и рассмотрение по теории возмущений
- § 11. Сдвиги уровней
- § 12. Излучение квантов
- § 13. Квантовая теория распадающихся состояний. Ширина линии
- § 14. Упругое рассеяние. Дисперсионная формула
- § 15. Резонансное рассеяние. Образование метастабильного состояния
- § 16. Поглощение кванта (фотоэлектрический эффект). Радиационный захват
- Раздел III. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
- § 17. Уравнения классической теории Максвелла — Лоренца
- § 18. Инвариантность и законы сохранения классической теории
- § 19. Собственная энергия и классический радиус электрона
- § 20. Электромагнитный потенциал. Выбор калибровки
- § 21. Продольная и поперечная часть векторного поля
- § 22. Исключение продольного поля
- § 23. Энергия, импульс, момент импульса
- § 24. Гамильтониан свободного электромагнитного поля
- § 25. Гамильтониан излучения, взаимодействующего с частицами
- Раздел IV. КВАНТОВАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 26. Квантование свободного поля излучения. Фотоны
- § 27. Плоские волны. Импульс излучения
- § 28. Поляризация
- § 29. Разложение по мультиполям. Фотоны с определенным моментом импульса и четностью
- § 30. Взаимодействие с атомной системой
- § 31. Излучение фотона атомом. Дипольное излучение
- § 32. Комптоновское рассеяние при низких энергиях. Формула Томсона
- ДОПОЛНЕНИЕ В. КОЭФФИЦИЕНТЫ ВЕКТОРНОГО СЛОЖЕНИЯ И МАТРИЦЫ ВРАЩЕНИЯ
- § 1. Момент импульса. Основные обозначения и принятые соглашения
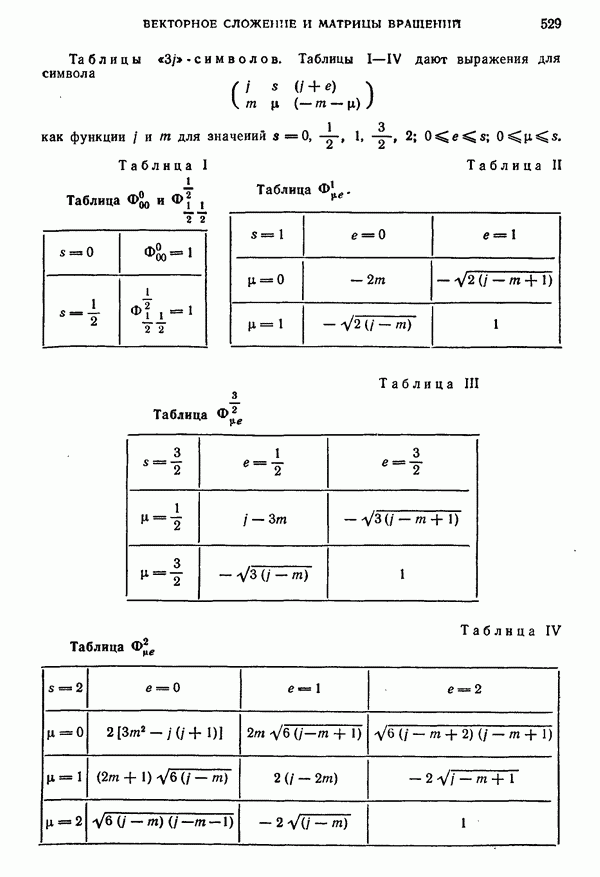
- Раздел I. КОЭФФИЦИЕНТЫ КЛЕБША — ГОРДАНА (К. — Г.) И «3j»-СИМВОЛЫ
- § 3. Основные свойства коэффициентов К. — Г.
- § 4. Методы вычисления
- § 5. Специальные значения и таблицы
- Раздел II. КОЭФФИЦИЕНТЫ РАКА И «6j»-СИМВОЛЫ
- § 6. Определение и основные обозначения
- § 7. Основные свойства «6j»-символов
- § 8. Формула Рака, таблицы
- Раздел III. «9j»-СИМВОЛЫ
- Раздел IV. МАТРИЦЫ ВРАЩЕНИЯ
- § 11. Основные свойства матриц R^J
- § 12. Вычисление матричных элементов
- § 13. Целые значения J (J=l) и преобразование сферических функций при вращениях
- Раздел V. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ
- § 15. Тензорное произведение неприводимых тензорных операторов
- ДОПОЛНЕНИЕ Г. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- Раздел I. ОСНОВНЫЕ ПОНЯТИЯ
- § 3. Классы сопряженных элементов
- § 4. Подгруппы
- § 5. Изоморфизм, гомоморфизм
- Раздел II. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ
- § 7. Операции над пространствами представлений. Приводимость
- § 8. Основные теоремы
- § 9. Приложения к квантовой механике
- Раздел III. КОНЕЧНЫЕ ГРУППЫ
- § 10. Основные понятия
- § 11. Представления
- § 12. Неприводимые компоненты представления
- § 13. Построение неприводимых инвариантных подпространств
- Раздел IV. ПЕРЕСТАНОВКИ
- § 14. Основные понятия. Циклы. Классы
- § 15. Разбиения
- § 16. «Симметризаторы» Юнга. Построение неприводимых представлений
- § 17. Основные свойства неприводимых представлений группы
- § 18. Система n фермионов спина 1/2