| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 24. Построение плоских волн посредством преобразования Лоренца
Если  то преобразование Лоренца переводит решение уравнения Дирака в решение того же уравнения. В частности, плоскую волну с импульсом
то преобразование Лоренца переводит решение уравнения Дирака в решение того же уравнения. В частности, плоскую волну с импульсом  можно получить преобразованием Лоренца из плоской волны с нулевым импульсом. На этом замечании основан метод, который позволит нам построить спиноры
можно получить преобразованием Лоренца из плоской волны с нулевым импульсом. На этом замечании основан метод, который позволит нам построить спиноры  приведенные в предыдущем параграфе.
приведенные в предыдущем параграфе.
Для нулевого импульса уравнение (150) принимает вид

Два возможных собственных значения равны  . Собственному значению вт.
. Собственному значению вт.  отвечает спинор
отвечает спинор  - собственный вектор оператора
- собственный вектор оператора  Будем предполагать, что этот спинор нормирован на единицу, направление спина фиксируем произвольным образом. Тогда
Будем предполагать, что этот спинор нормирован на единицу, направление спина фиксируем произвольным образом. Тогда  определен с точностью до фазы.
определен с точностью до фазы.
Плоская волна

есть решение уравнения Дирака, соответствующее нулевому импульсу и энергии  или
или  -вектору энергии-импульса
-вектору энергии-импульса  .
.
Рассмотрим то же решение в новой системе отсчета, движущейся по отношению к исходной со скоростью  . В новой системе отсчета
. В новой системе отсчета  -вектор энергии-импульса равен
-вектор энергии-импульса равен

Решением будет плоская волна

Таким образом, выражение в скобках пропорционально искомому спинору  который далее мы будем обозначать
который далее мы будем обозначать  Его норма равна временной компоненте соответствующего
Его норма равна временной компоненте соответствующего  -вектора потока, который можно получить посредством преобразования Лоренца из
-вектора потока, который можно получить посредством преобразования Лоренца из  -вектора потока, связанного с (0). Эта норма в результате равна
-вектора потока, связанного с (0). Эта норма в результате равна

Таким образом, мы определяем

Подставляя в это определение выражение (97) и приведенные выше значения  и
и  находим
находим

В частности, если и  — собственный вектор для
— собственный вектор для  то и
то и  — собственный вектор, который совпадает с одним из спиноров предыдущего параграфа. Если импульс
— собственный вектор, который совпадает с одним из спиноров предыдущего параграфа. Если импульс  направлен по оси
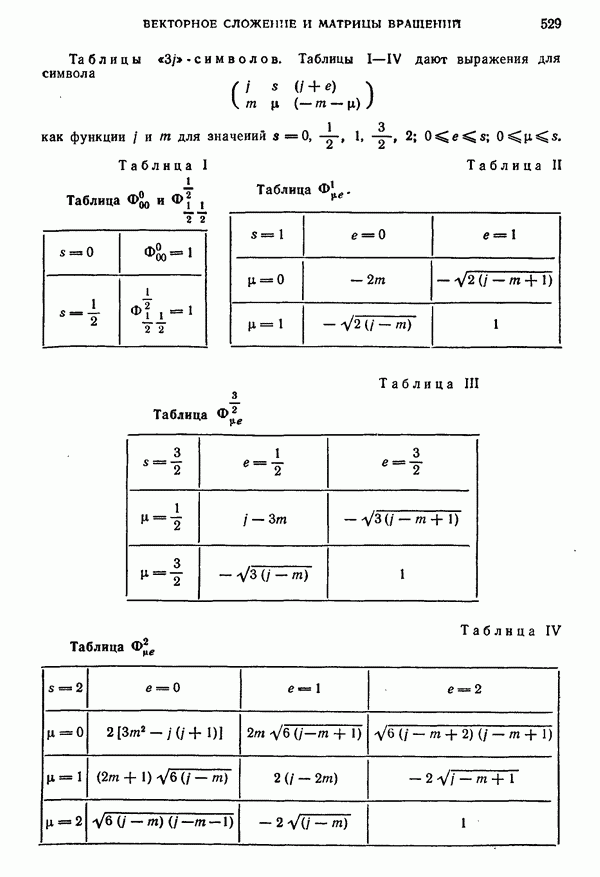
направлен по оси  то получаем результаты, приведенные в табл. IV.
то получаем результаты, приведенные в табл. IV.
Выражение (154) можно записать также в виде

где  — определенный формулой (153) 4-вектор энергии-импульса.
— определенный формулой (153) 4-вектор энергии-импульса.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ЧАСТЬ III. СИММЕТРИИ И ИНВАРИАНТНОСТЬ
- Раздел I. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ФУНКЦИИ МОМЕНТА ИМПУЛЬСА
- § 2. Определение момента импульса
- § 3. Основные алгебраические соотношения
- § 4. Спектр операторов
- § 5. Собственные векторы операторов. Построение инвариантных пространств
- § 6. Стандартное представление …
- § 7. Заключение
- Раздел II. ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА И СФЕРИЧЕСКИЕ ФУНКЦИИ
- § 8. Спектр операторов l^2 и lz
- § 9. Определение и построение сферических функций
- Раздел III. МОМЕНТ ИМПУЛЬСА И ВРАЩЕНИЯ
- § 10. Определение вращений. Углы Эйлера
- § 11. Вращение физической системы. Оператор вращения
- § 12. Вращение наблюдаемых
- § 13. Момент импульса и инфинитезимальные вращения
- § 14. Построение оператора …
- § 15. Вращение на угол 2pi и полуцелый момент импульса
- § 16. Неприводимые инвариантные подпространства. Матрицы вращений
- § 17. Инвариантность относительно вращений и сохранение момента импульса
- Раздел IV. СПИН
- § 18. Гипотеза спина электрона
- § 19. Спин 1/2 и матрицы Паули
- § 20. Наблюдаемые и волновые функции частицы спина 1/2. Спинорные поля
- § 21. Векторные поля и частицы спина 1
- § 22. Зависящие от спина взаимодействия в атомах
- § 23. Зависящие от спина нуклол-нуклонные взаимодействия
- Раздел V. СЛОЖЕНИЕ МОМЕНТОВ ИМПУЛЬСА
- § 25. Теорема сложения двух моментов импульса
- § 26. Приложения и примеры
- § 27. Собственные векторы полного момента импульса. Коэффициенты Клебша—Гордана
- § 28. Приложение: система двух нуклонов
- § 29. Сложение трех и более моментов импульса. Коэффициенты Рака. «3sj»-символы
- Раздел VI. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ
- § 31. Неприводимые тензорные операторы. Определение
- § 32. Представление неприводимых тензорных операторов. Теорема Вигнера — Эккарта
- § 33. Приложения
- ГЛАВА XIV. СИСТЕМЫ ТОЖДЕСТВЕННЫХ ЧАСТИЦ. ПРИНЦИП ЗАПРЕТА ПАУЛИ
- Раздел I. ПОСТУЛАТ СИММЕТРИЗАЦИИ
- § 2. Подобные частицы и симметрическое представление
- § 3. Операторы перестановки
- § 4. Алгебра операторов перестановки. Симметризаторы и антисимметризаторы
- § 5. Тождественные частицы и постулат симметризации
- § 6. Бозоны и статистика Бозе—Эйнштейна
- § 7. Фермионы и статистика Ферми — Дирака. Принцип запрета
- § 8. Всегда ли необходимо симметризовать волновую функцию?
- Раздел II. ПРИЛОЖЕНИЯ
- § 9. Столкновение двух тождественных бесспиновых частиц
- § 10. Столкновение протонов
- § 11. Статистика атомных ядер
- § 12. Сложные атомы. Приближение центрального поля
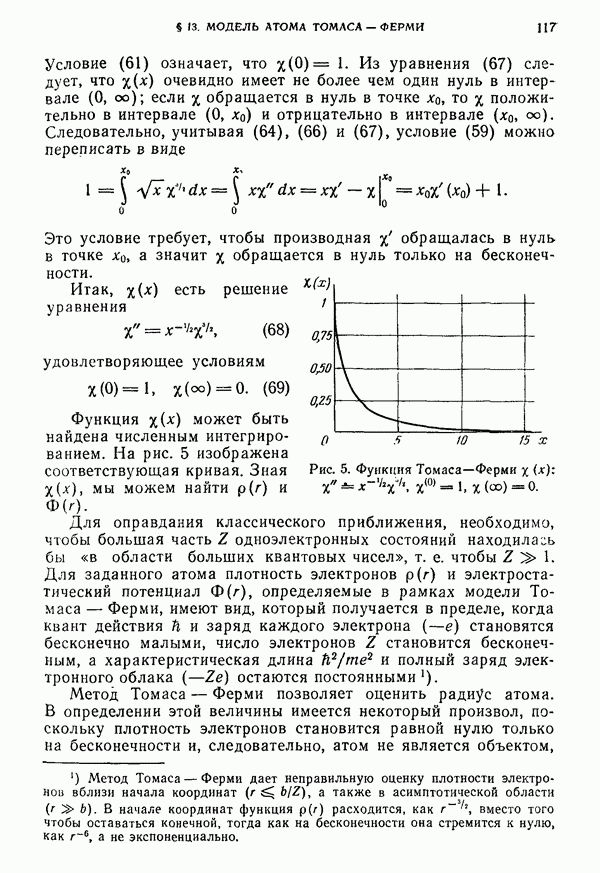
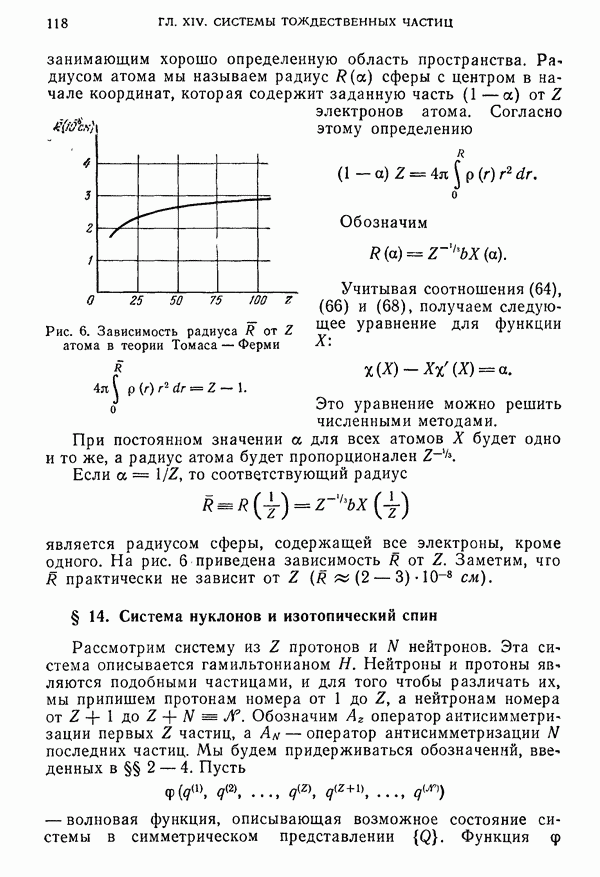
- § 13. Модель атома Томаса—Ферми
- § 14. Система нуклонов и изотопический спин
- § 15. Использование изотопического спина. Зарядовая независимость
- ГЛАВА XV. ИНВАРИАНТНОСТЬ И ЗАКОНЫ СОХРАНЕНИЯ. ОБРАЩЕНИЕ ВРЕМЕНИ
- Раздел I. ДОПОЛНИТЕЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СВЕДЕНИЯ. АНТИЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 3. Антилинейные операторы в гильбертовом пространстве
- § 4. Антиунитарные преобразования
- § 5. Антилинейные операторы и представления
- Раздел II. ПРЕОБРАЗОВАНИЯ И ГРУППЫ ПРЕОБРАЗОВАНИЙ
- § 6. Преобразования динамических переменных и динамических состояний системы
- § 7. Группы преобразований
- § 8. Группы операторов преобразований
- § 9. Непрерывные группы и инфинитезимальные преобразования. Трансляции. Вращения
- § 10. Конечные группы. Отражения
- Раздел III. ИНВАРИАНТНОСТЬ УРАВНЕНИИ ДВИЖЕНИЯ И ЗАКОНЫ СОХРАНЕНИЯ
- § 12. Свойства инвариантности гамильтониана и законы сохранения
- § 13. Свойства инвариантности и эволюция динамических состояний
- § 14. Симметрии эффектов Штарка и Зеемана
- Раздел IV. ОБРАЩЕНИЕ ВРЕМЕНИ И ПРИНЦИП МИКРООБРАТИМОСТИ
- § 15. Сдвиги во времени и сохранение энергии
- § 16. Обращение времени в классической и квантовой механиках
- § 17. Обращение времени. Частица нулевого спина
- § 18. Общее определение обращения времени
- § 19. Обращение времени и комплексное сопряжение
- § 20. Принцип микрообратимости
- § 21. Следствие: вырождение Крамерса
- § 22. Вещественный гамильтониан, инвариантный относительно вращений
- ЧАСТЬ IV. ПРИБЛИЖЕННЫЕ МЕТОДЫ
- ГЛАВА XVI. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
- Раздел I. ВОЗМУЩЕНИЕ НЕВЫРОЖДЕННОГО УРОВНЯ
- § 2. Разложение по степеням возмущения
- § 3. Возмущение первого порядка
- § 4. Основное состояние атома гелия
- § 5. Кулоновская энергия атомных ядер
- § 6. Поправки высших порядков
- § 7. Эффект Штарка для жесткого ротатора
- Раздел II. ВОЗМУЩЕНИЕ ВЫРОЖДЕННОГО УРОВНЯ
- § 9. Атомные уровни без учета спин-орбитального взаимодействия
- § 10. Спин-орбитальное взаимодействие. LS- и jj-связь
- § 11. Атом с LS-связью. Расщепление за счет спии-орбитального взаимодействия
- § 12. Эффект Зеемана и эффект Пашена—Бака
- § 13. Симметрия Н и устранение вырождения
- § 14. Квазивырождение
- Раздел III. ЯВНЫЕ ВЫРАЖЕНИЯ ДЛЯ РАЗЛОЖЕНИЙ ПО ТЕОРИИ ВОЗМУЩЕНИЙ ВО ВСЕХ ПОРЯДКАХ
- § 15. Гамильтониан Н и его резольвента G(z)
- § 16. Разложение G(z), в ряд по степеням
- § 17. Вычисление собственных значений и собственных функций
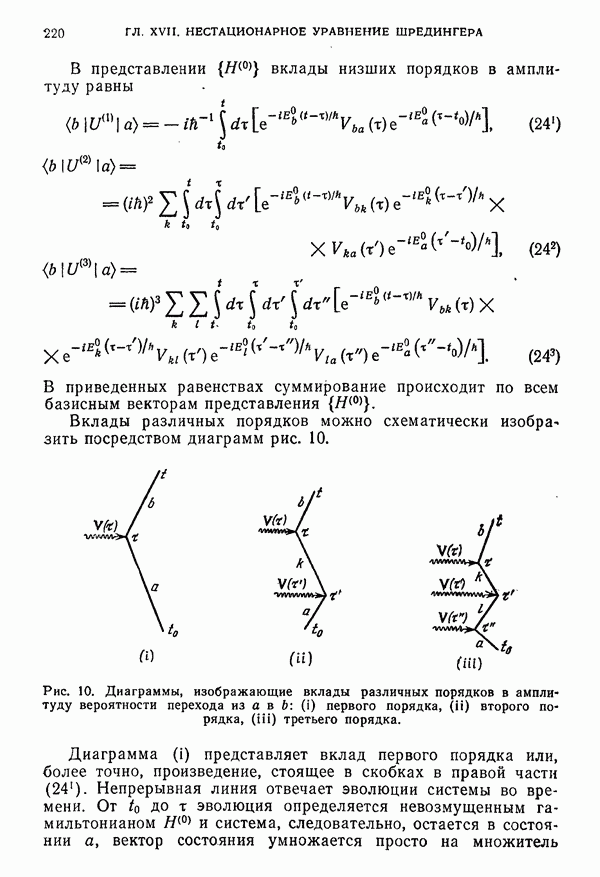
- ГЛАВА XVII. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСТАЦИОНАРНОГО УРАВНЕНИЯ ШРЕДИНГЕРА
- Раздел I. НЕСТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ
- § 2. Определение и вычисление по теории возмущений вероятностей переходов
- § 3. Полуклассическая теория кулоновского возбуждения ядер
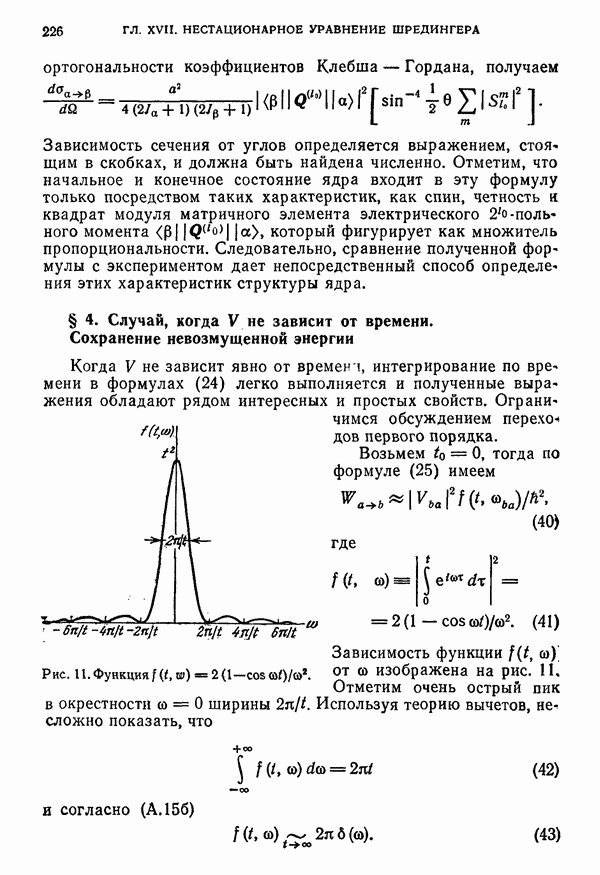
- § 4. Случай, когда V не зависит от времени. Сохранение невозмущенной энергии
- § 5. Приложение к вычислению сечений в борновском приближении
- § 6. Периодическое возмущение. Резонансы
- Раздел II. МГНОВЕННОЕ И АДИАБАТИЧЕСКОЕ ИЗМЕНЕНИЯ ГАМИЛЬТОНИАНА
- § 8. Быстрый переход и мгновенное приближение
- § 9. Мгновенное обращение магнитного поля
- § 10. Адиабатический переход. Общие положения. Тривиальный случай
- § 11. «Представление вращающихся осей»
- § 12. Доказательство адиабатической теоремы
- § 13. Адиабатическое приближение
- § 14. Адиабатическое обращение магнитного поля
- ГЛАВА XVIII. ВАРИАЦИОННЫЙ МЕТОД И СВЯЗАННЫЕ С НИМ ЗАДАЧИ
- § 1. Вариационный метод Ритца
- Раздел I. ВАРИАЦИОННЫЙ МЕТОД ДЛЯ СВЯЗАННЫХ СОСТОЯНИЙ
- § 2. Вариационная форма задачи на собственные значения
- § 3. Вариационное вычисление дискретных уровней
- § 4. Простой пример: атом водорода
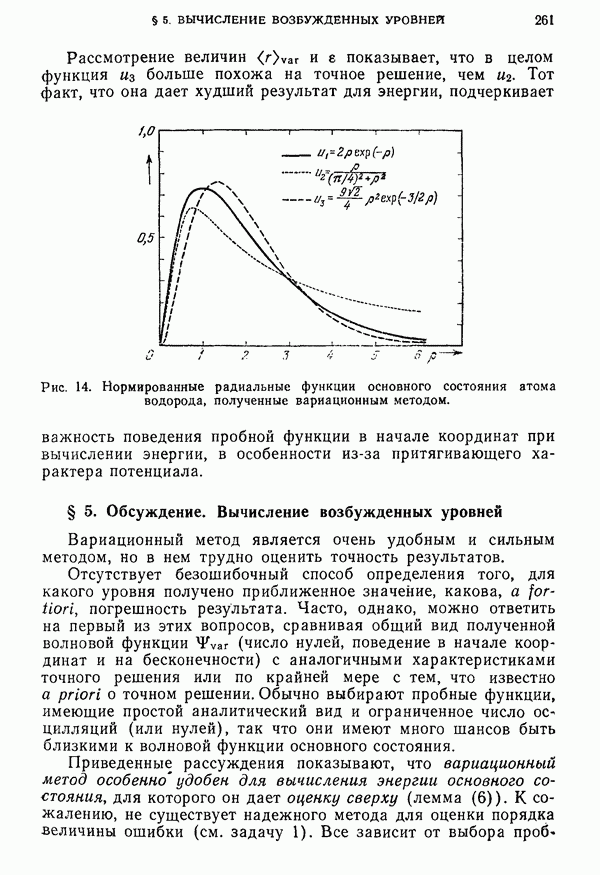
- § 5. Обсуждение. Вычисление возбужденных уровней
- § 6. Основное состояние атома гелия
- Раздел II. АТОМЫ ХАРТРИ И ФОКА—ДИРАКА
- § 7. Метод самосогласованного поля
- § 8. Вычисление Е[Ф]
- § 9. Уравнения Фока — Дирака
- § 10. Обсуждение результатов
- § 11. Уравнения Хартри
- § 12. Общие понятия. Разделение движения ядер и электронов
- § 13. Движение электронов в поле фиксированных ядер
- § 14. Адиабатическое приближение
- § 15. Гамильтониан ядер в адиабатическим приближении
- § 16. Метод Борна — Оппенгеймера
- § 17. Основные представления о двухатомных молекулах
- ГЛАВА XIX. ТЕОРИЯ РАССЕЯНИЯ
- Раздел I. СВОБОДНАЯ ФУНКЦИЯ ГРИНА И ПРИБЛИЖЕНИЕ БОРНА
- § 2. Интегральные представления амплитуды рассеяния
- § 3. Сечение рассеяния и T-матрица. Микрообратимость
- § 4. Борновское приближение
- § 5. Интегральное уравнение теории рассеяния
- § 6. Борновское разложение
- § 7. Критерий применимости борновского приближения
- § 8. Упругое рассеяние электронов на атоме
- § 9. Центральный потенциал. Вычисление сдвигов фаз
- § 10. Функция Грина как оператор. Связь с резольвентой оператора
- Раздел II. ОБОБЩЕНИЕ НА ИСКАЖЕННЫЕ ВОЛНЫ
- § 11. Обобщенное борновское приближение
- § 12. Обобщение борновского разложения
- § 13. Функция Грина искаженных волн
- § 14. Приложения. Определение и формальные свойства Т-матрицы
- § 15. Замечание о потенциалах 1/r
- Раздел III. СЛОЖНЫЕ СТОЛКНОВЕНИЯ И БОРНОВСКОЕ ПРИБЛИЖЕНИЕ
- § 17. Каналы
- § 18. Вычисление сечений. T-матрицы
- § 19. Интегральные представления амплитуды перехода
- § 20. Борновское приближение и его обобщения
- § 21. Рассеяние быстрых электронов атомом
- § 22. Кулоновское возбуждение ядер
- § 23. Функции Грина и интегральные уравнения для стационарных решений рассеяния
- § 24. Рассеяние частицы на двух центрах
- § 25. Простое рассеяние. Интерференция
- § 26. Многократное рассеяние
- Раздел IV. ВЫЧИСЛЕНИЕ АМПЛИТУД ПЕРЕХОДА ВАРИАЦИОННЫМ МЕТОДОМ
- § 27. Стационарные выражения сдвигов фаз. Обсуждение
- § 28. Вариационные вычисления сдвига фаз. Обсуждение
- § 29. Распространение метода на сложные столкновения
- Раздел V. ОБЩИЕ СВОЙСТВА МАТРИЦЫ ПЕРЕХОДА
- § 30. Сохранение потока. S-матрица
- § 31. Соотношение Бора—Пайерлса—Плачека (оптическая теорема)
- § 32. Микрообратимость
- § 33. Свойства инвариантности T-матрицы
- ЧАСТЬ V. ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ КВАНТОВОЙ МЕХАНИКИ
- § 1. Релятивистская квантовая механика
- § 2. Обозначения и различные определения
- § 3. Группа Лоренца
- § 4. Классическая релятивистская динамика
- Раздел II. УРАВНЕНИЯ КЛЕЙНА — ГОРДОНА И ДИРАКА
- § 5. Уравнение Клейна—Гордона
- § 6. Уравнение Дирака
- § 7. Построение пространства. Представление Дирака
- § 8. Ковариантная форма уравнения Дирака
- § 9. Сопряженное уравнение. Определение тока
- Раздел III. СВОЙСТВА ИНВАРИАНТНОСТИ УРАВНЕНИЯ ДИРАКА
- § 10. Свойства матриц Дирака
- § 11. Инвариантность уравнения Дирака при ортохронных преобразованиях системы координат
- § 12. Преобразования собственной группы
- § 13. Пространственное отражение и ортохронная группа
- § 14. Построение ковариантных величин
- § 15. Другая формулировка свойств инвариантности: преобразование состояний
- § 16. Условие инвариантности уравнения движения
- § 17. Операторы преобразования. Импульс, момент импульса, четность
- § 18. Законы сохранения и интегралы движения
- § 19. Обращение времени и зарядовое сопряжение
- § 20. Калибровочная инвариантность
- Раздел IV. ИНТЕРПРЕТАЦИЯ ОПЕРАТОРОВ И ПРОСТЫЕ РЕШЕНИЯ
- § 21. Уравнение Дирака и принцип соответствия
- § 22. Динамические переменные частицы Дирака
- § 23. Свободный электрон. Плоские волны
- § 24. Построение плоских волн посредством преобразования Лоренца
- § 25. Центральный потенциал
- § 26. Свободные сферические волны
- § 27. Атом водорода
- Раздел V. НЕРЕЛЯТИВИСТСКИЙ ПРЕДЕЛ УРАВНЕНИЯ ДИРАКА
- § 29. Теория Паули как нерелятивистский предел теории Дирака
- § 30. Приложение: сверхтонкая структура и диполь-дипольная связь
- § 31. Поправки высших порядков и преобразование Фолди — Вотхойзена
- § 32. ФВ-преобразование для свободной частицы
- § 33. ФВ-преобразование для частицы во внешнем поле
- § 34. Электрон в центральном электростатистическом потенциале
- § 35. Обсуждения и выводы
- Раздел VI. РЕШЕНИЯ С ОТРИЦАТЕЛЬНОЙ ЭНЕРГИЕЙ И ТЕОРИЯ ПОЗИТРОНОВ
- § 36. Свойства зарядово-сопряженных решений
- § 37. Особое поведение решений с отрицательной энергией
- § 38. Изменение интерпретации состояний с отрицательной энергией. Теория дырок и позитронов
- § 39. Трудности теории дырок
- ГЛАВА XXI. КВАНТОВЫЕ ПОЛЯ. ТЕОРИЯ ИЗЛУЧЕНИЯ
- Раздел I. КВАНТОВАНИЕ ВЕЩЕСТВЕННОГО СКАЛЯРНОГО ПОЛЯ
- § 2. Классические свободные поля. Нормальные колебания
- § 3. Квантование свободного поля
- § 4. Лагранжиан поля. Импульс, сопряженный к Ф(r)
- § 5. Комплексные базисные функции
- § 6. Плоские волны. Определение импульса
- § 7. Сферические волны. Определение момента импульса
- § 8. Пространственное отражение и обращение времени
- Раздел II. ВЗАИМОДЕЙСТВИЕ С АТОМНОЙ СИСТЕМОЙ
- § 9. Взаимодействие с системой частиц
- § 10. Слабая связь и рассмотрение по теории возмущений
- § 11. Сдвиги уровней
- § 12. Излучение квантов
- § 13. Квантовая теория распадающихся состояний. Ширина линии
- § 14. Упругое рассеяние. Дисперсионная формула
- § 15. Резонансное рассеяние. Образование метастабильного состояния
- § 16. Поглощение кванта (фотоэлектрический эффект). Радиационный захват
- Раздел III. КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ
- § 17. Уравнения классической теории Максвелла — Лоренца
- § 18. Инвариантность и законы сохранения классической теории
- § 19. Собственная энергия и классический радиус электрона
- § 20. Электромагнитный потенциал. Выбор калибровки
- § 21. Продольная и поперечная часть векторного поля
- § 22. Исключение продольного поля
- § 23. Энергия, импульс, момент импульса
- § 24. Гамильтониан свободного электромагнитного поля
- § 25. Гамильтониан излучения, взаимодействующего с частицами
- Раздел IV. КВАНТОВАЯ ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 26. Квантование свободного поля излучения. Фотоны
- § 27. Плоские волны. Импульс излучения
- § 28. Поляризация
- § 29. Разложение по мультиполям. Фотоны с определенным моментом импульса и четностью
- § 30. Взаимодействие с атомной системой
- § 31. Излучение фотона атомом. Дипольное излучение
- § 32. Комптоновское рассеяние при низких энергиях. Формула Томсона
- ДОПОЛНЕНИЕ В. КОЭФФИЦИЕНТЫ ВЕКТОРНОГО СЛОЖЕНИЯ И МАТРИЦЫ ВРАЩЕНИЯ
- § 1. Момент импульса. Основные обозначения и принятые соглашения
- Раздел I. КОЭФФИЦИЕНТЫ КЛЕБША — ГОРДАНА (К. — Г.) И «3j»-СИМВОЛЫ
- § 3. Основные свойства коэффициентов К. — Г.
- § 4. Методы вычисления
- § 5. Специальные значения и таблицы
- Раздел II. КОЭФФИЦИЕНТЫ РАКА И «6j»-СИМВОЛЫ
- § 6. Определение и основные обозначения
- § 7. Основные свойства «6j»-символов
- § 8. Формула Рака, таблицы
- Раздел III. «9j»-СИМВОЛЫ
- Раздел IV. МАТРИЦЫ ВРАЩЕНИЯ
- § 11. Основные свойства матриц R^J
- § 12. Вычисление матричных элементов
- § 13. Целые значения J (J=l) и преобразование сферических функций при вращениях
- Раздел V. НЕПРИВОДИМЫЕ ТЕНЗОРНЫЕ ОПЕРАТОРЫ
- § 15. Тензорное произведение неприводимых тензорных операторов
- ДОПОЛНЕНИЕ Г. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП
- Раздел I. ОСНОВНЫЕ ПОНЯТИЯ
- § 3. Классы сопряженных элементов
- § 4. Подгруппы
- § 5. Изоморфизм, гомоморфизм
- Раздел II. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ
- § 7. Операции над пространствами представлений. Приводимость
- § 8. Основные теоремы
- § 9. Приложения к квантовой механике
- Раздел III. КОНЕЧНЫЕ ГРУППЫ
- § 10. Основные понятия
- § 11. Представления
- § 12. Неприводимые компоненты представления
- § 13. Построение неприводимых инвариантных подпространств
- Раздел IV. ПЕРЕСТАНОВКИ
- § 14. Основные понятия. Циклы. Классы
- § 15. Разбиения
- § 16. «Симметризаторы» Юнга. Построение неприводимых представлений
- § 17. Основные свойства неприводимых представлений группы
- § 18. Система n фермионов спина 1/2