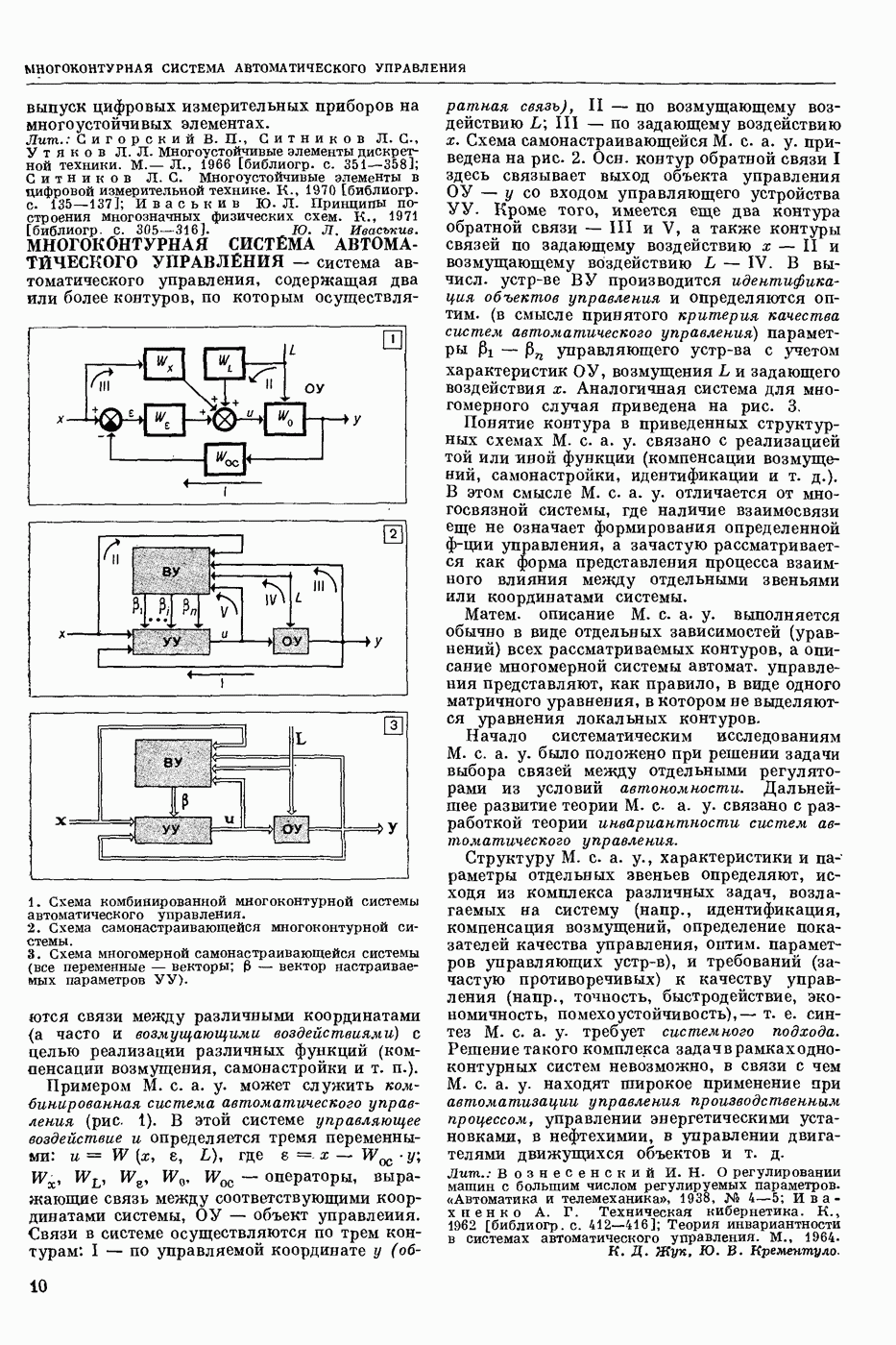
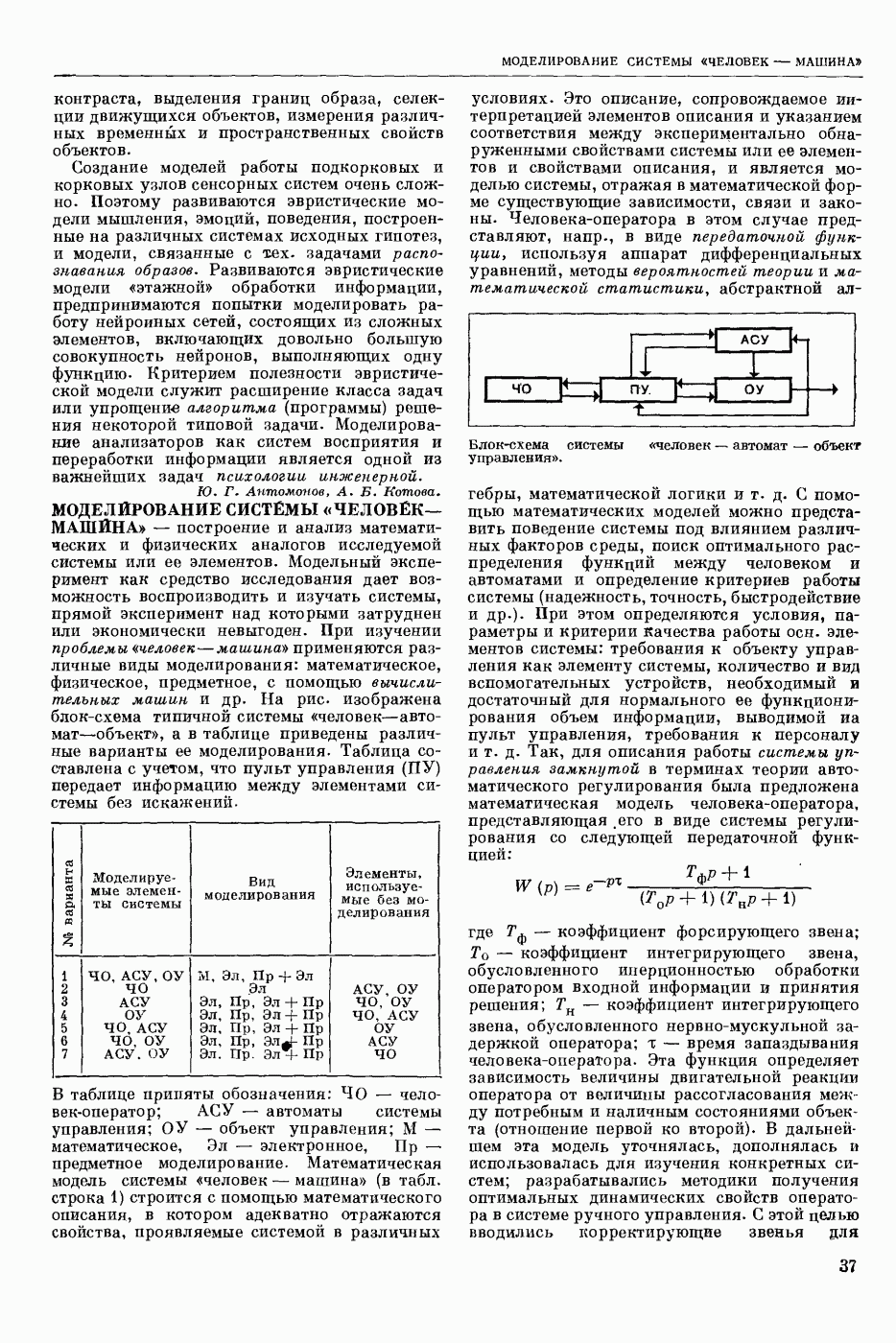
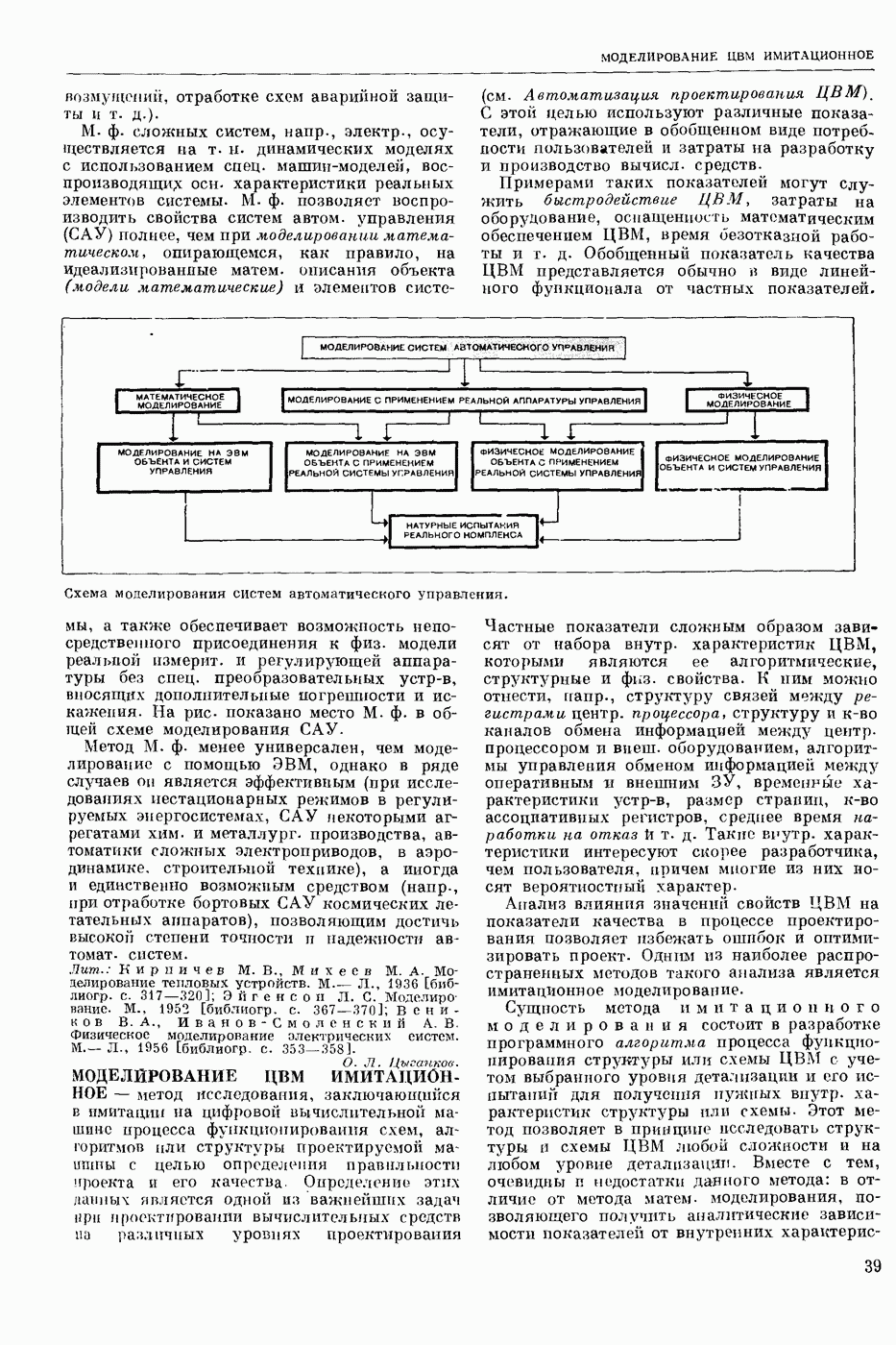
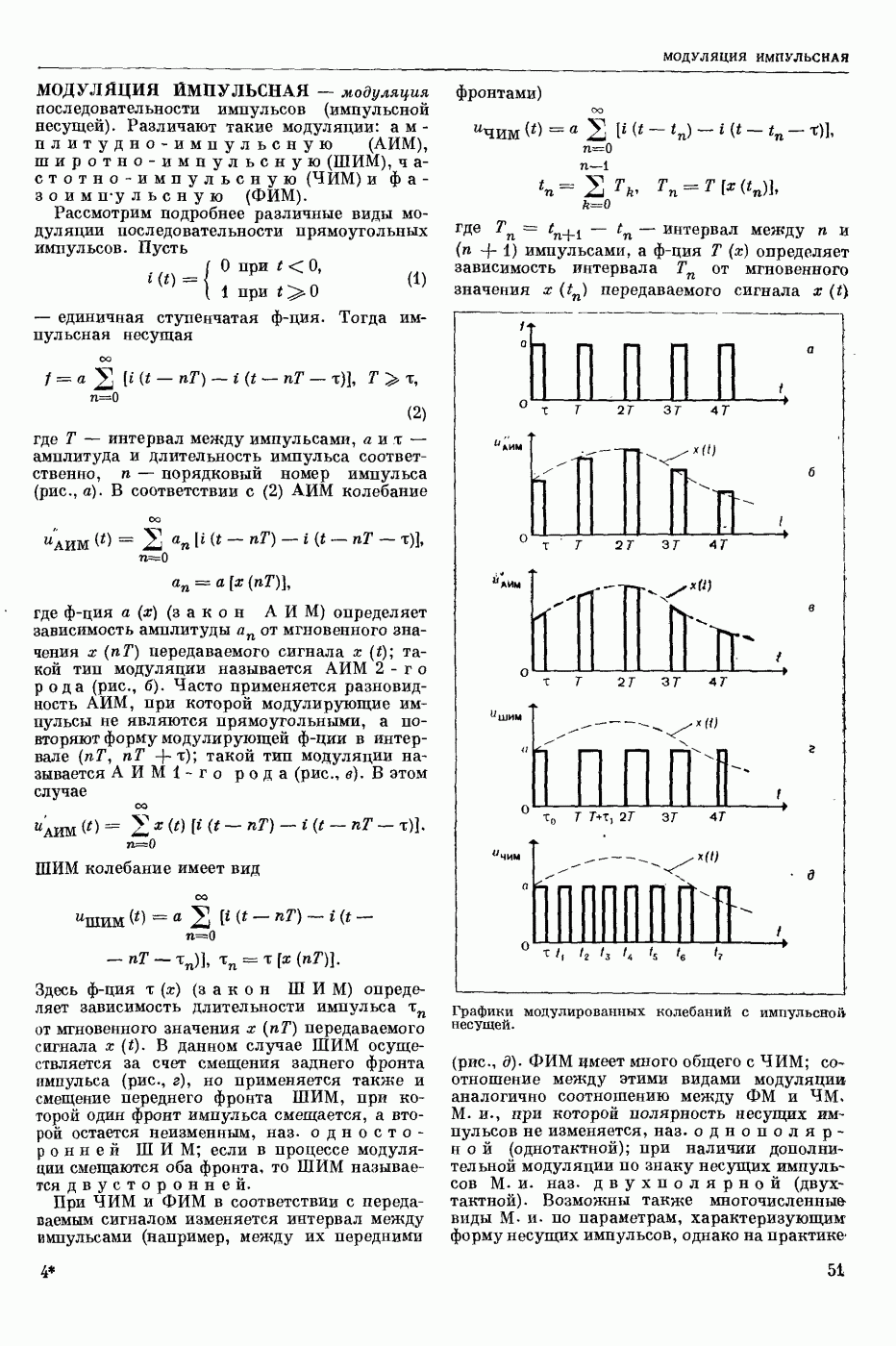
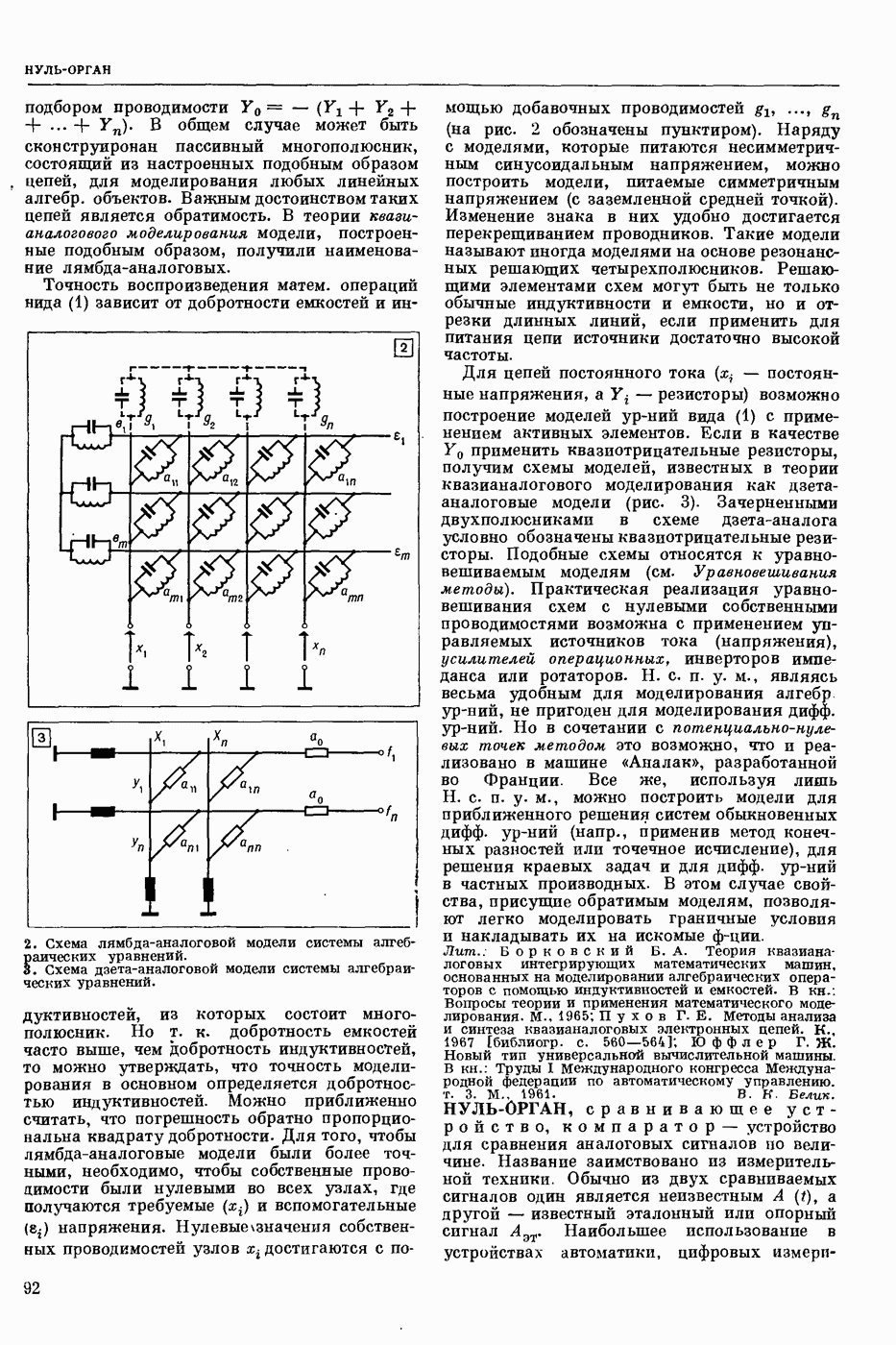
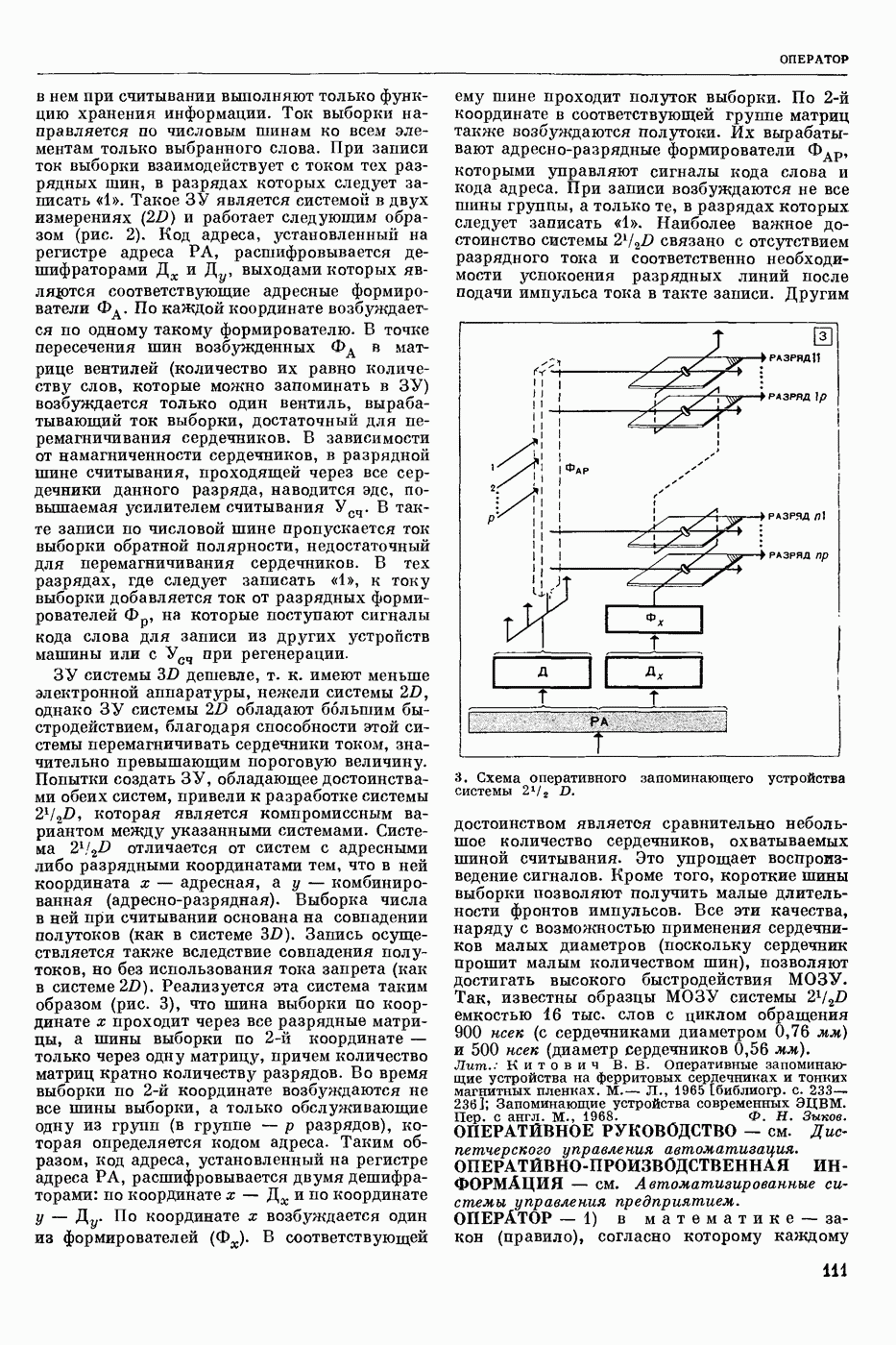
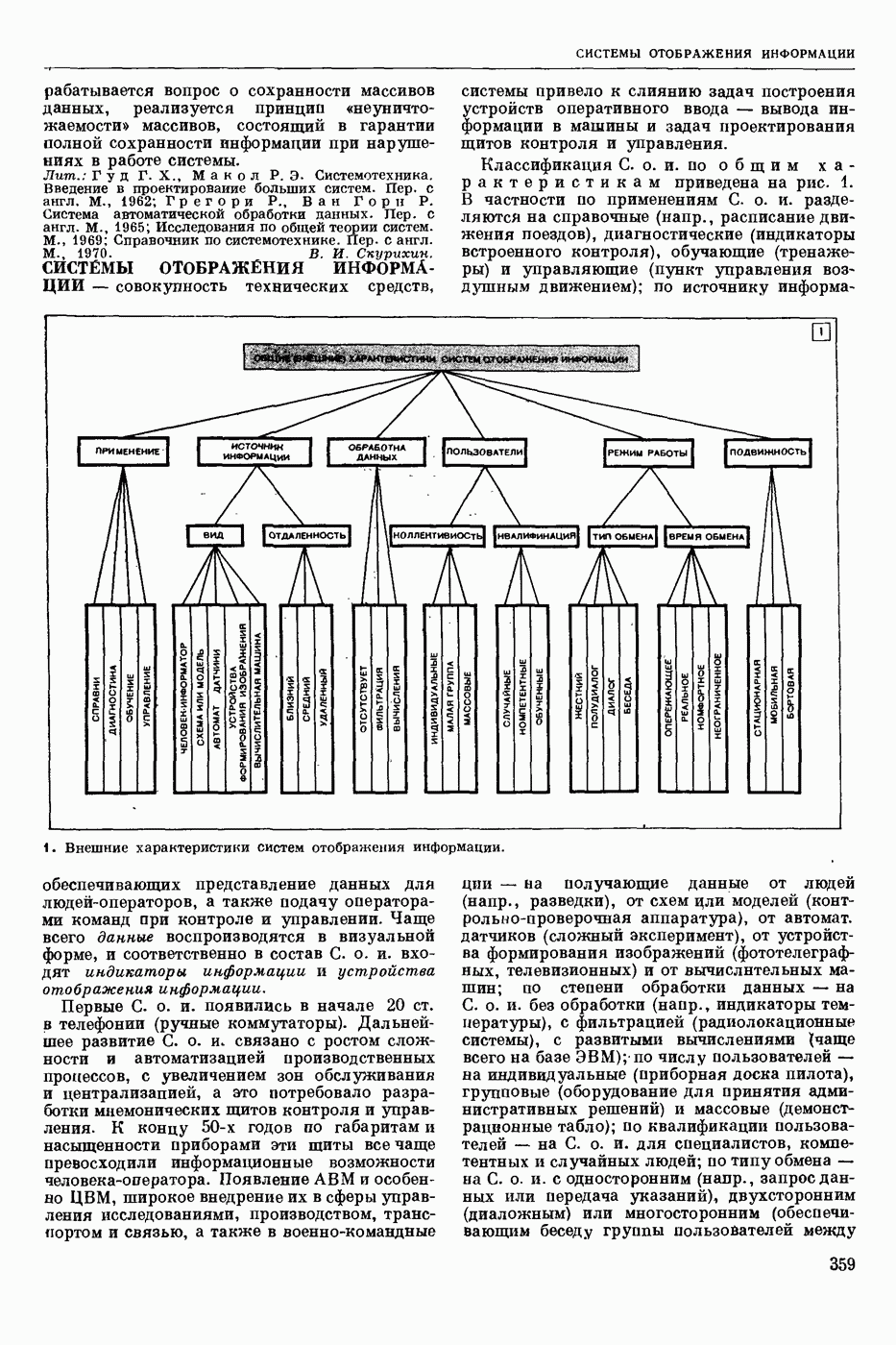
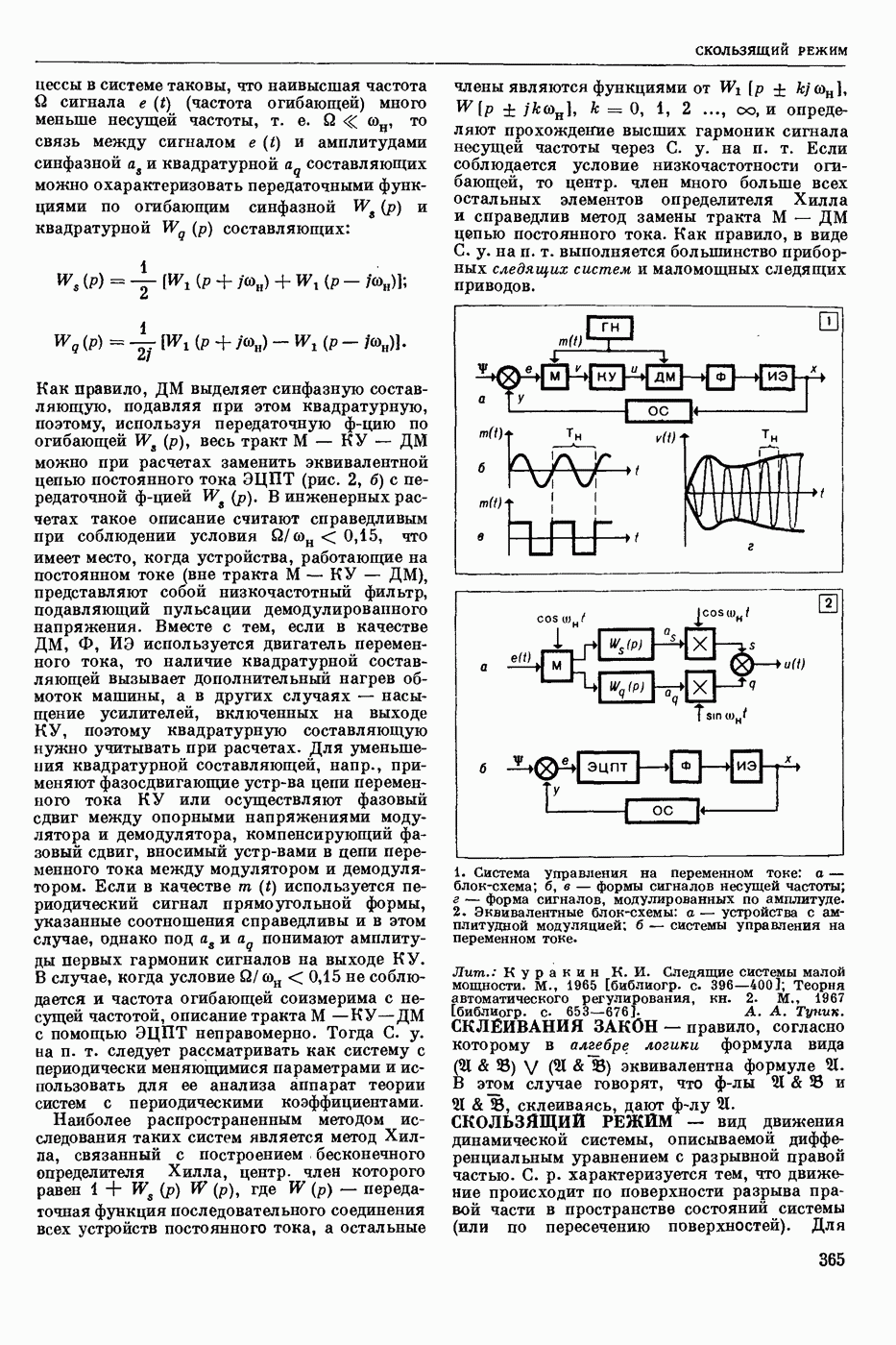
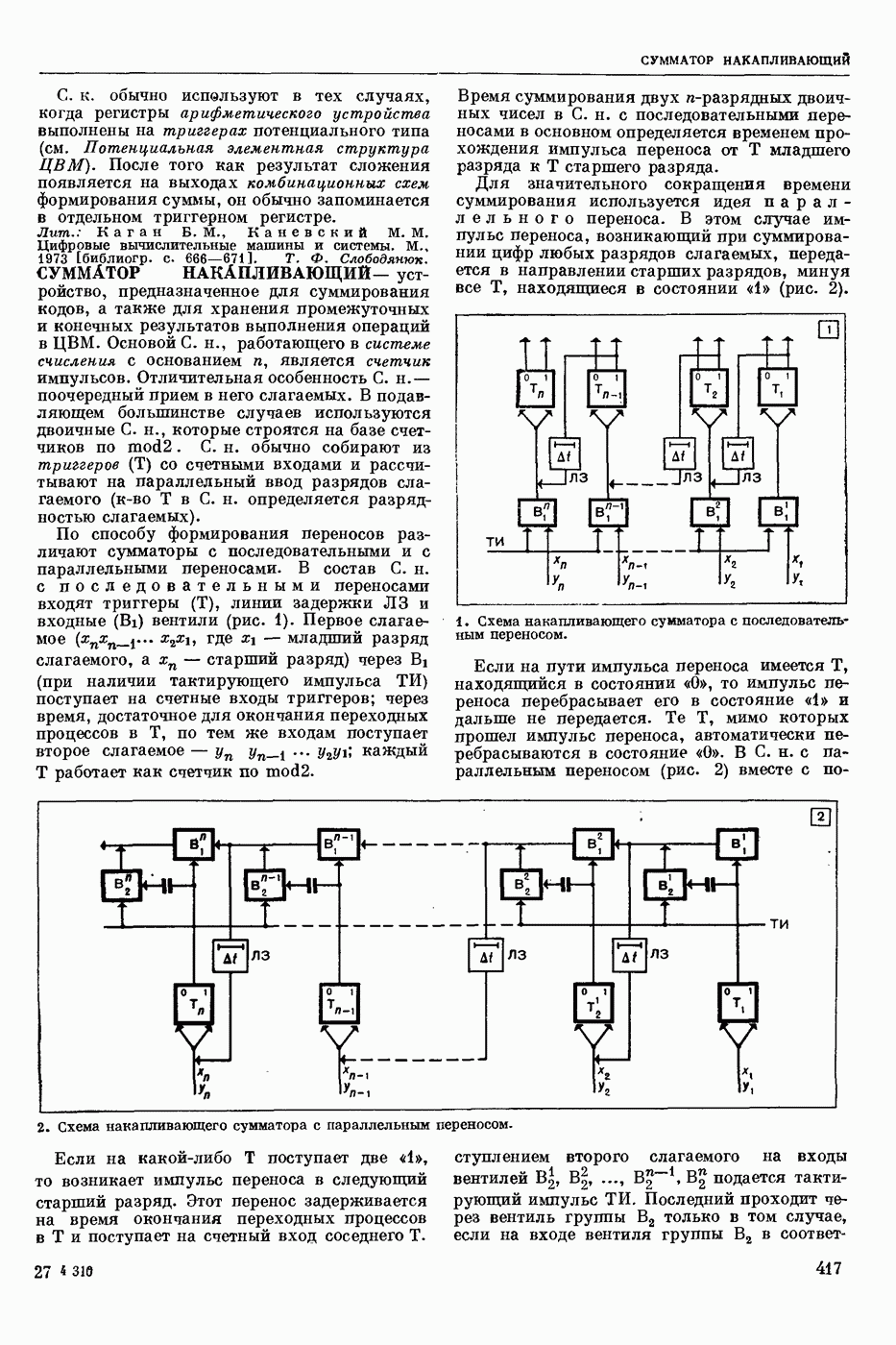
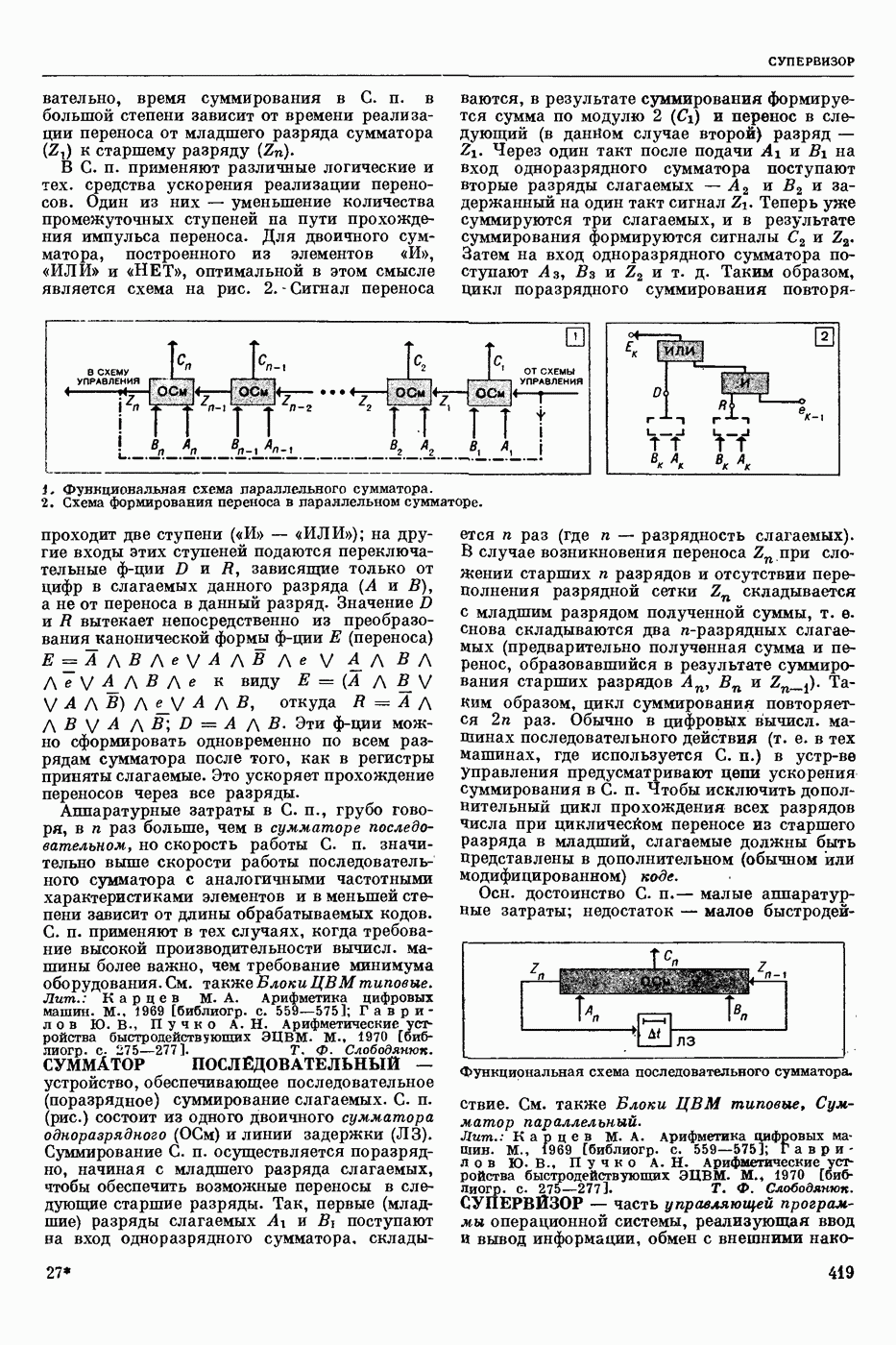
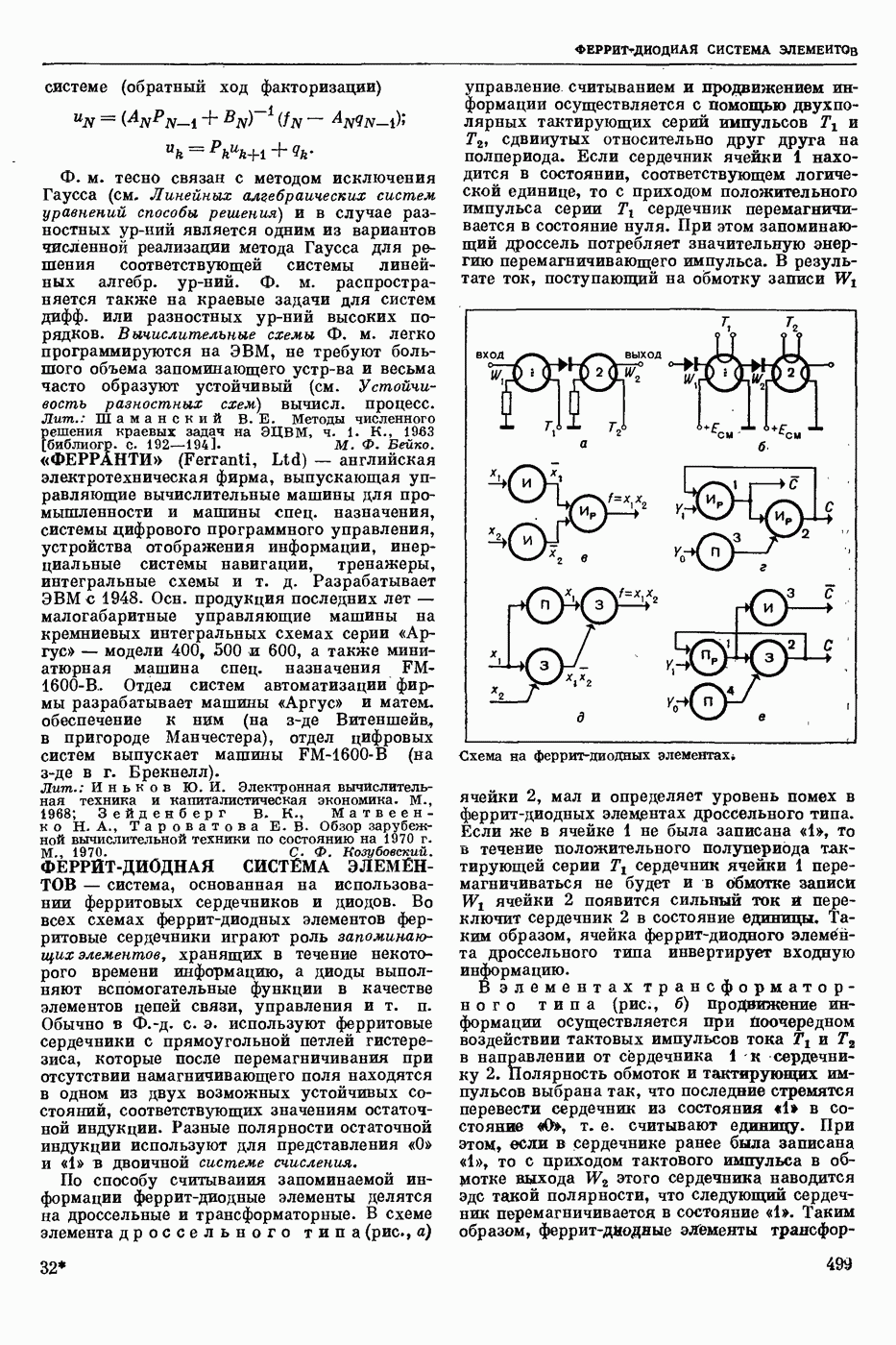
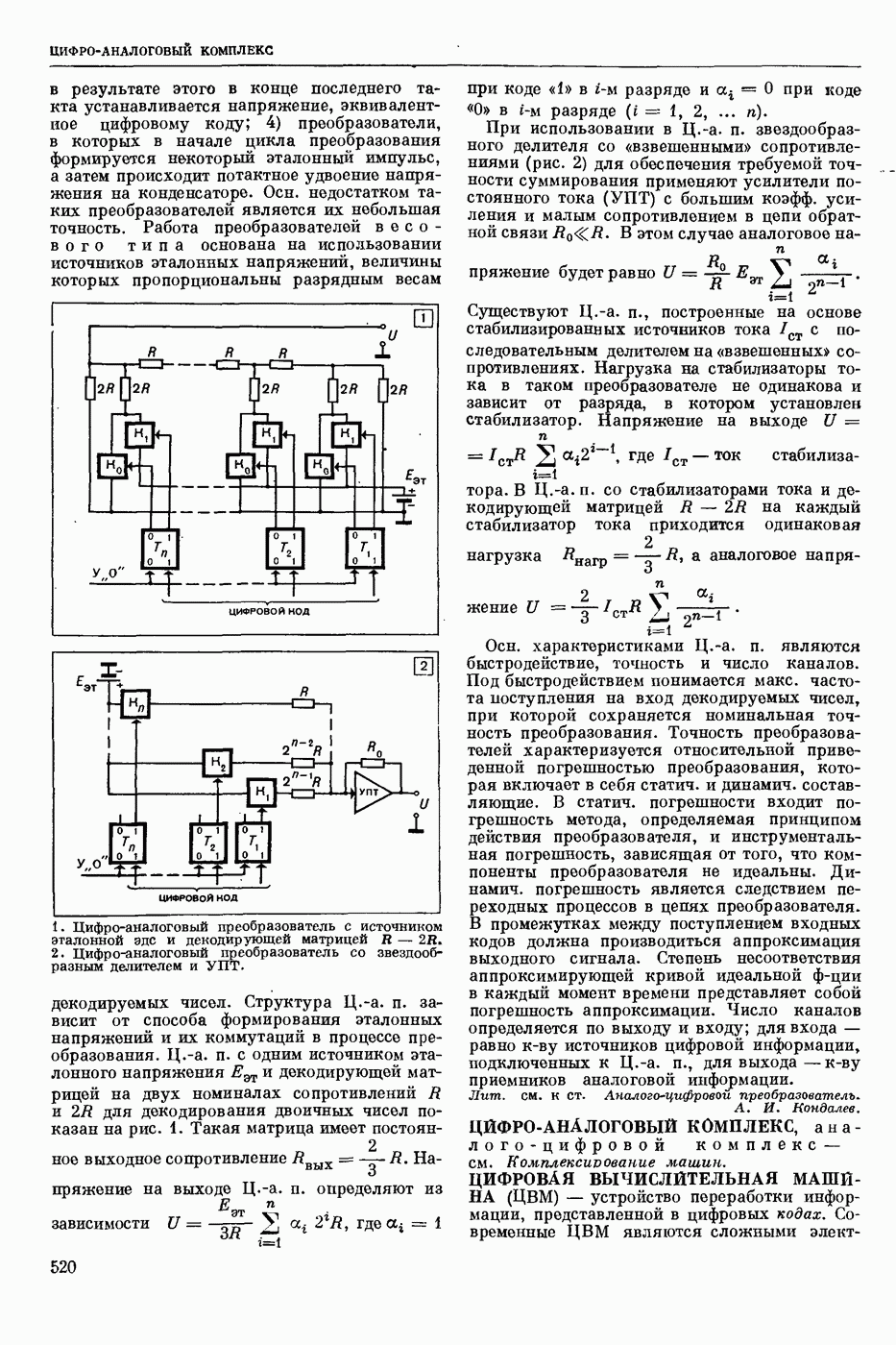
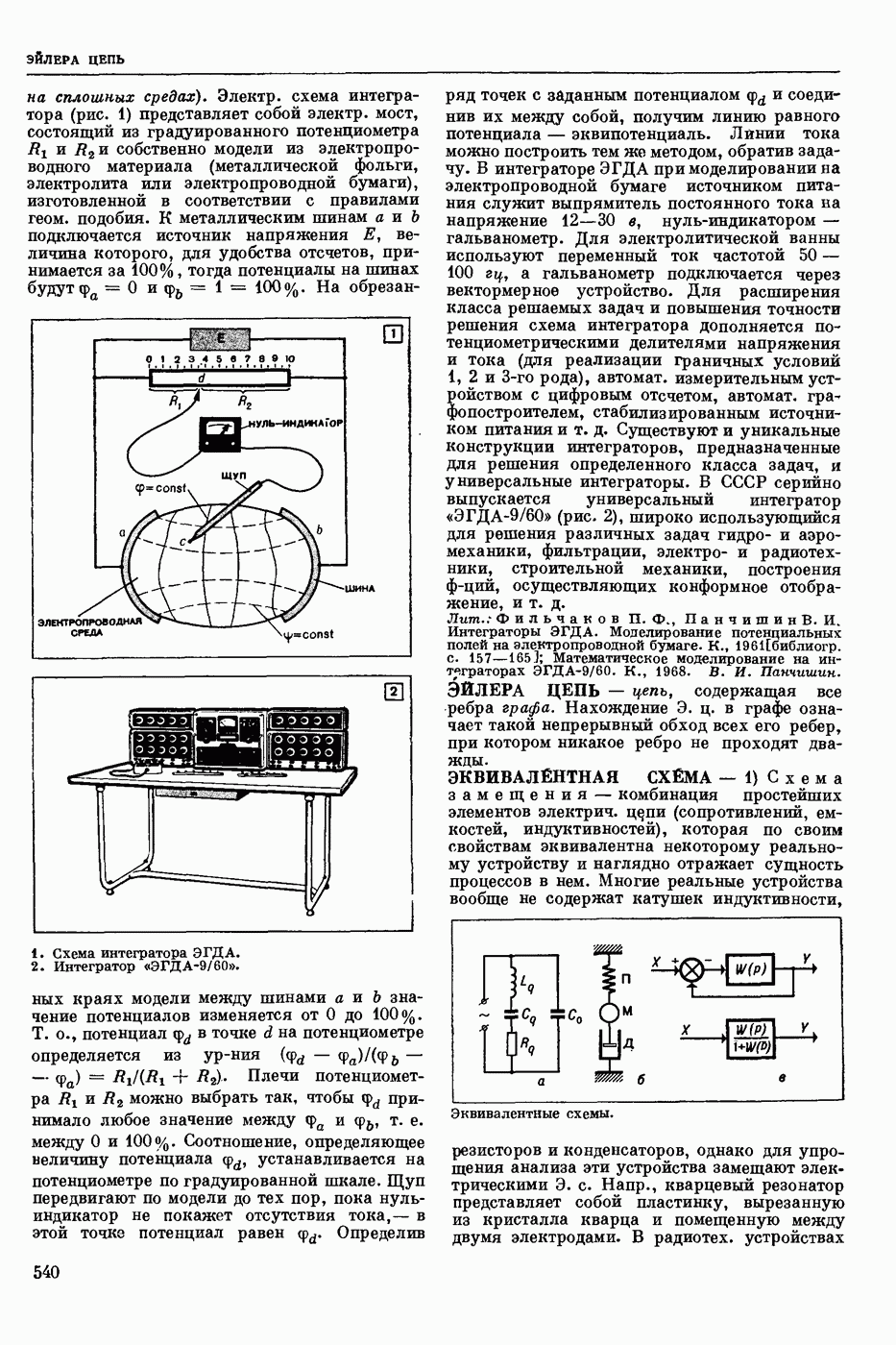
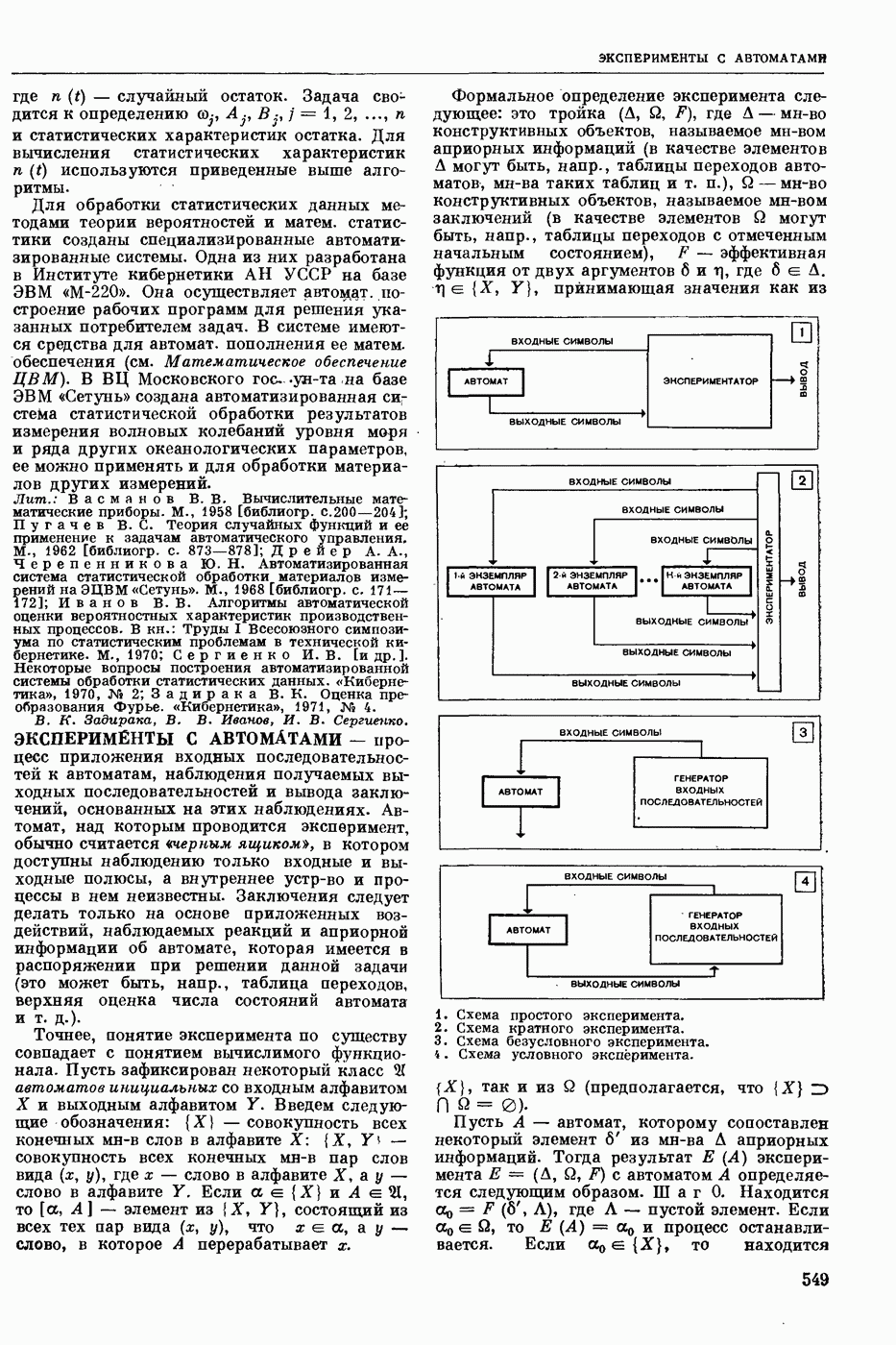
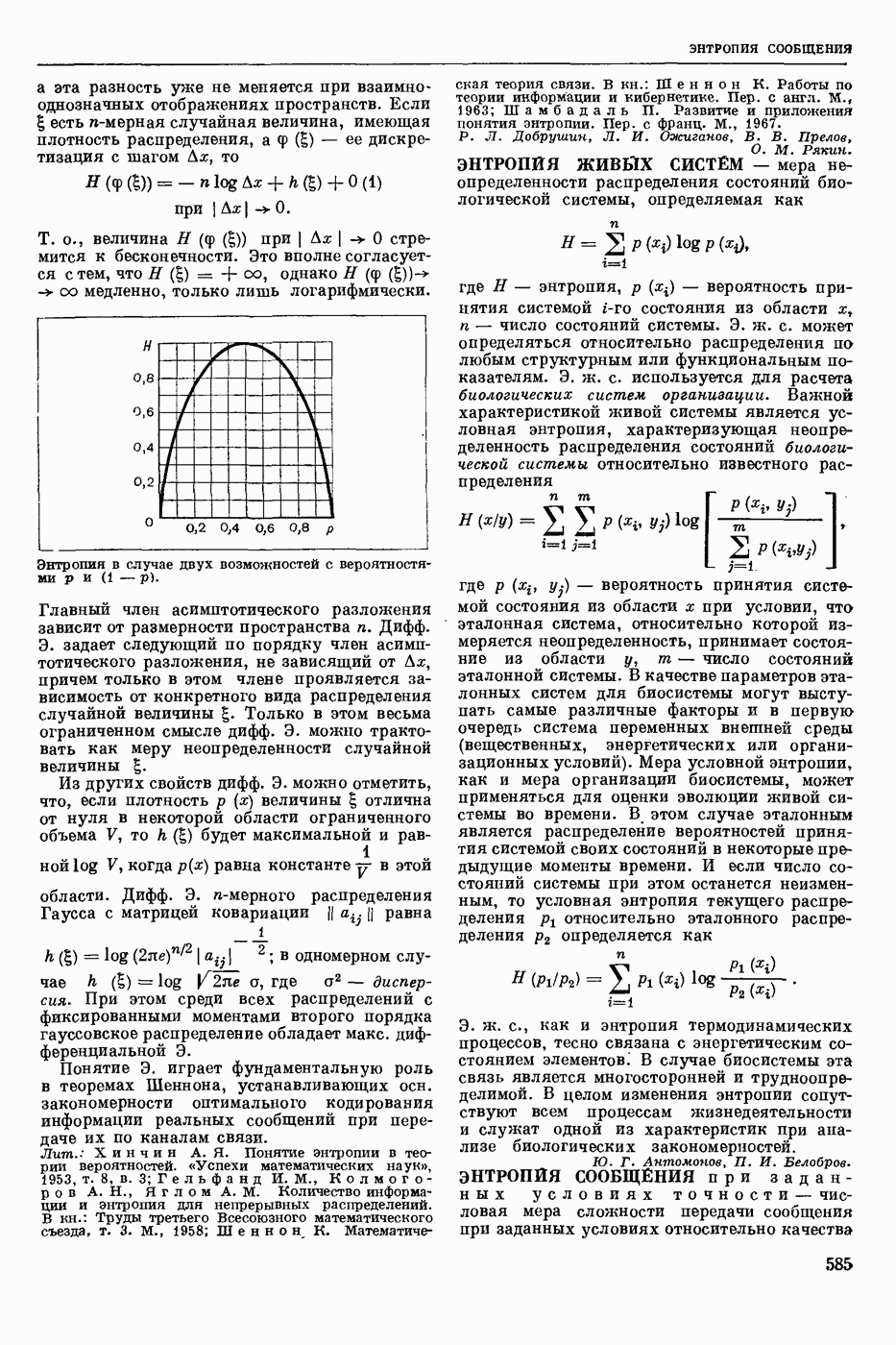
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ОПЕРАТОРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
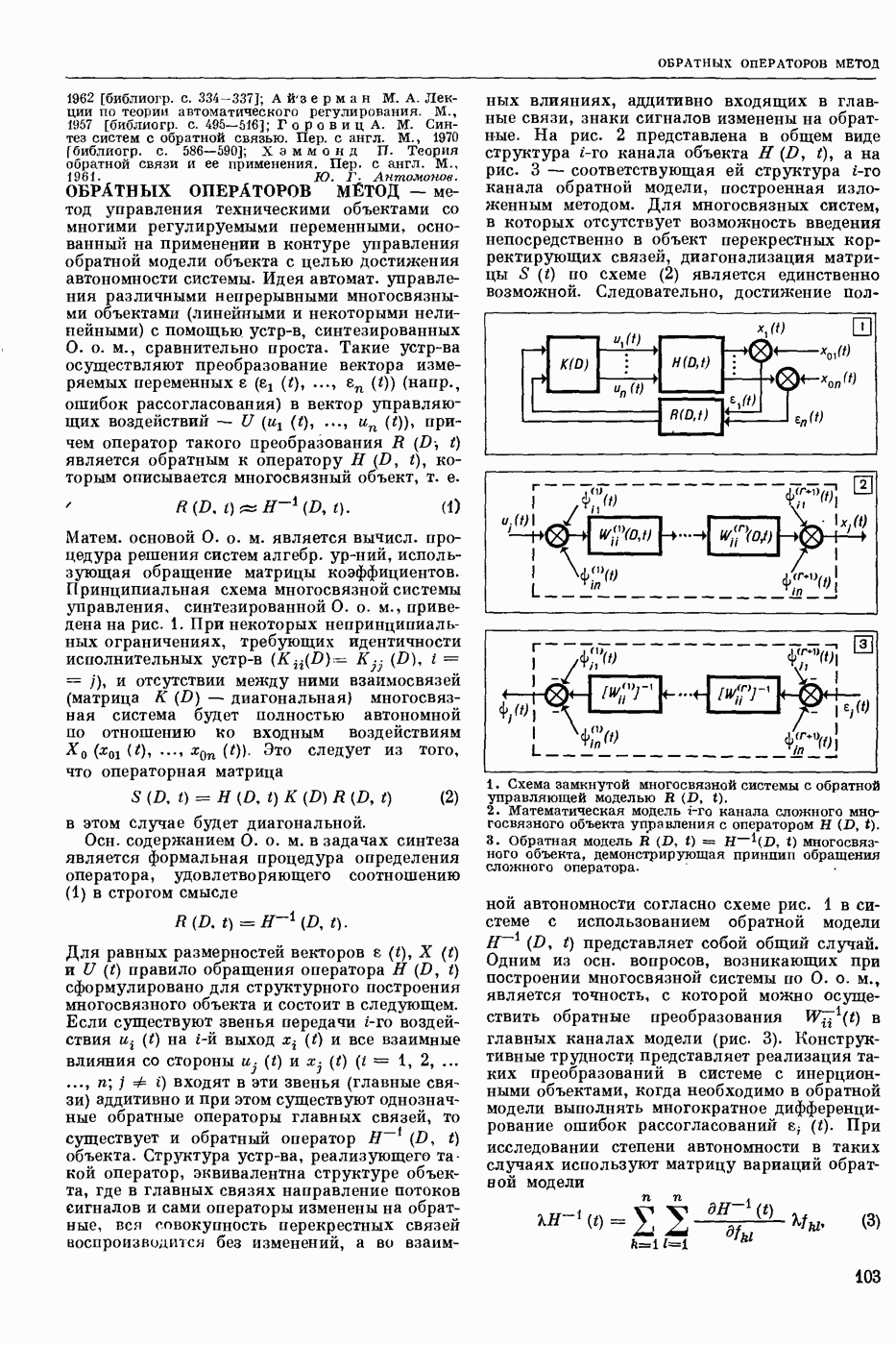
Многие задачи естествознания и техники сводятся к решению различных классов дифференциальных, интегральных, интегро-дифференциальных и др. уравнений. Методы функционального анализа дают возможность рассматривать эти ур-ния как частные случаи операторных ур-ний в функциональных пространствах (см. Пространство абстрактное в функциональном анализе), напр, в банаховых пространствах. Операторное ур-ние можно записать в виде:
где А — некоторый линейный или нелинейный оператор, действующий из банахова пространства X в банахово пространство Y, у — известный элемент пространства У, Решить ур-ние (1) — это значит найти такой элемент  , что
, что  . Частными случаями ур-ния (1) являются системы алгебр, и трансцендентных ур-ний, интегр. ур-ния, системы дифф. ур-ний и др. В настоящее время известно много различных методов, позволяющих с определенной степенью точности находить решения операторных ур-ний. К числу наиболее часто применяемых методов относятся итеративные, градиентные, проекционные, проекционно-итеративные и др.
. Частными случаями ур-ния (1) являются системы алгебр, и трансцендентных ур-ний, интегр. ур-ния, системы дифф. ур-ний и др. В настоящее время известно много различных методов, позволяющих с определенной степенью точности находить решения операторных ур-ний. К числу наиболее часто применяемых методов относятся итеративные, градиентные, проекционные, проекционно-итеративные и др.
1. Простейшим итеративным методом, который применяется для решения операторных ур-ний вида

где оператор Т действует из X в X (ур-ние (2) — частный случай ур-ния (1)), есть обычный вдтрд последовательных приближений. Он заключается в том, что исходя из некоторого начального приближения  последующие приближения
последующие приближения  определяют по ф-ле
определяют по ф-ле

Если оператор Т на некотором замкнутом мн-ве  является оператором сжатия, т. е. удовлетворяет условию Липшица
является оператором сжатия, т. е. удовлетворяет условию Липшица

с константой  и переводит М в М, то ур-ние (2) имеет в М единственное решение х, к которому сходятся последовательные приближения
и переводит М в М, то ур-ние (2) имеет в М единственное решение х, к которому сходятся последовательные приближения  При этом имеет место оценка погрешности
При этом имеет место оценка погрешности

Если  где В — линейный оператор,
где В — линейный оператор,  то по
то по  получаем
получаем

В данном случае необходимым и достаточным условием сходимости процесса (6) является условие

В качестве q можно взять  поэтому достаточным условием сходимости является условие
поэтому достаточным условием сходимости является условие 
Для решения систем операторных ур-ний можно применять метод Зейделя. Пусть задана система операторных ур-ний

где операторы  действуют из пространства
действуют из пространства  некоторые банаховы пространства). Последовательные приближения к решению системы (7) определяют по ф-лам
некоторые банаховы пространства). Последовательные приближения к решению системы (7) определяют по ф-лам

Если нелинейный оператор А в ур-нии (1) дифференцируем по Фреше, то для нахождения прибл. решения ур-ния (1) можно применять основной и модифицированный методы Ньютона — Канторовича.
Оператор А наз. дифференцируемым по Фреше в точке  если существует такой линейный оператор L, который может зависеть от х, что выполняется равенство
если существует такой линейный оператор L, который может зависеть от х, что выполняется равенство  , где
, где  при
при  Линейный оператор
Линейный оператор  производной Фреше оператора А и обозначается
производной Фреше оператора А и обозначается  Соответственно последовательные приближения
Соответственно последовательные приближения  определяют по ф-лам
определяют по ф-лам

Пусть для некоторого замкнутого шара  производная Фреше удовлетворяет условию
производная Фреше удовлетворяет условию  и имеют место оценки погрешности
и имеют место оценки погрешности

Тогда последовательные приближения (9) и (10) сходятся к решению  и соответственно справедливы оценки погрешности
и соответственно справедливы оценки погрешности

Рассмотрим применение градиентных методов для решения операторных ур-ний. Допустим, что пространство X совпадает с пространством Y и является гильбертовым. Пусть  и оператор А имеет производную
и оператор А имеет производную  которая является положительно определенным оператором для всех
которая является положительно определенным оператором для всех  то есть
то есть

Тогда задача нахождения решения ур-ния (1) эквивалентна задаче нахождения минимума функционала

Для нахождения минимума функционала (14) можно применить метод наискорейшего спуска, который заключается в том, что последовательные приближения определяют по ф-ле

где  определяют из условия минимума функционала
определяют из условия минимума функционала  . В случае, если А — линейный положительно определенный ограниченный оператор, параметры
. В случае, если А — линейный положительно определенный ограниченный оператор, параметры  определяют по формуле
определяют по формуле

Если  — соответственно нижняя и верхняя границы оператора А, то скорость сходимости характеризуется неравенством
— соответственно нижняя и верхняя границы оператора А, то скорость сходимости характеризуется неравенством

Метод минимальных невязок заключается в том, что последовательные приближения (15) определяют из условия

Если  дифференцируемая ф-ция, то
дифференцируемая ф-ция, то  определяют из ур-ния
определяют из ур-ния

В случае линейного ур-ния параметры  определяют по ф-ле
определяют по ф-ле

Скорость сходимости характеризуется неравенством (17). Рассмотрим отдельно случай, когда оператор А линейный, и построим итеративный процесс по ф-ле

где А — оператор, сопряженный с  . В этом случае
. В этом случае  можно определить из условия минимума нормы погрешности
можно определить из условия минимума нормы погрешности  тогда
тогда 

Процесс (21—22) сходится со скоростью геом. прогрессии со знаменателем  где
где  — соответственно нижняя и верхняя границы оператора АА.
— соответственно нижняя и верхняя границы оператора АА.
Проекционные методы составляют широкий класс прибл. методов решения операторных ур-ний. Эти методы состоят в  что прибл. решение ур-ния (1), принадлежащее некоторому подпространству
что прибл. решение ур-ния (1), принадлежащее некоторому подпространству  пространства X, определяется из ур-ния
пространства X, определяется из ур-ния

где  проекционный оператор, проектирующий начальное пространство Y на некоторое его подпространство
проекционный оператор, проектирующий начальное пространство Y на некоторое его подпространство  Частным случаем проекционного метода является метод Ритца решения ур-ния (1), в котором оператор А имеет производную, удовлетворяющую условию (13). Заключается он в том, что прибл. решение ищется в виде
Частным случаем проекционного метода является метод Ритца решения ур-ния (1), в котором оператор А имеет производную, удовлетворяющую условию (13). Заключается он в том, что прибл. решение ищется в виде

где  система линейно независимых элементов гильбертова пространства X, а постоянные
система линейно независимых элементов гильбертова пространства X, а постоянные  определяются из условия минимума функционала (14), т. е. из условия 1
определяются из условия минимума функционала (14), т. е. из условия 1

Если  дифференцируемая ф-ция аргументов
дифференцируемая ф-ция аргументов  то определяются из системы алгебр, или трансцендентных ур-ний
то определяются из системы алгебр, или трансцендентных ур-ний 

В случае, когда оператор А линейный, систему (26) — линейна и имеет вид

В силу того, что оператор А положительно определенный, определитель системы (27) является определителем Грама, следовательно, система имеет единственное решение.
Более общим, чем метод Ритца, является метод Бубнова — Галеркина. Этот метод можно применять также в случае, когда оператор А не обладает свойством (13). При пользовании методом Бубнова — Галеркина прибл. решение ур-ния (1) ищется в виде (24), а постоянные  определяются из условия ортогональности невязки
определяются из условия ортогональности невязки  к элементам
к элементам  т. е. из системы алгебр, или трансцендентных ур-ний
т. е. из системы алгебр, или трансцендентных ур-ний

Если А — линейный оператор, система (28) имеет вид (27).
Обобщением метода Бубнова—Галеркияа есть метод Галеркина — Петрова, согласно которому постоянные  определяют из системы
определяют из системы

где  — некоторая система линейных функционалов. В случае линейного оператора А система (29) принимает вид
— некоторая система линейных функционалов. В случае линейного оператора А система (29) принимает вид

По методу наименьших квадратов прибл. решение ур-ния (1), имеющее вид (24), определяют из условия минимума нормы невязки, т. е. из условия

Постоянные  находим из системы ур-ний
находим из системы ур-ний

Если оператор А линейный, то эту систему можно записать так:

Частным случаем метода Галеркина — Петрова является метод моментов, в котором  , где
, где  — некоторая система линейно независимых элементов. В данном случае
— некоторая система линейно независимых элементов. В данном случае  определяют из системы
определяют из системы

Для линейных ур-ний в гильбертовом пространстве можно применять метод минимальных погрешностей, согласно которому прибл. решение ур-ния вида (1) ищут в виде линейной комбинации

и постоянные  определяют из условия минимума величины
определяют из условия минимума величины  При этом для нахождения
При этом для нахождения  имеем систему линейных алгебр. ур-ний
имеем систему линейных алгебр. ур-ний 

Для решения операторных ур-ний применяют также проекционно-итеративные методы, сочетающие в себе идеи как проекционных, так и итеративных методов. Эти методы имеют более широкую область применимости и во многих случаях сходятся значительно быстрее, чем обычные итеративные методы.
Одним из проекционно-итеративных методов есть метод осреднения функциональных поправок Соколова, который состоит в том, что последовательные приближения  к решению ур-ния (2) определяются из ур-ний
к решению ур-ния (2) определяются из ур-ний

где Р — проекционный оператор, проектирующий пространство X на его подпространство X конечной или бесконечной размерности,  тождественный оператор). Другим вариантом проекционно-итеративного метода осреднения функциональных поправок является метод, по которому
тождественный оператор). Другим вариантом проекционно-итеративного метода осреднения функциональных поправок является метод, по которому  определяются как решения ур-ний
определяются как решения ур-ний

В случае, если X — конечномерное подпространство размерности к, решение ур-ний (37) и (38) на каждом шаге сводится к решению систем алгебр, или трансцендентных ур-ний порядка k. Если  , где В — линейный оператор, то получающиеся системы — линейны.
, где В — линейный оператор, то получающиеся системы — линейны.
Если существует обратный оператор  , то из ур-ний (37) и (38) получаем соответственно
, то из ур-ний (37) и (38) получаем соответственно

Достаточным условием сходимости алгоритмов (37) и (38) является

Условие (39) может выполняться и в случае, когда обычный метод последовательных приближений не сходится. Простейшим достаточным условием сходимости алгоритмов (37) и (38) для ур-ний в банаховом пространстве является условие  где
где  — соответственно константы Липшица операторов РТ и QT. Если ур-ние задано в гильбертовом пространстве и Р — оператор ортогонального проектирования, то простейшим условием сходимости алгоритмов (37) и (38) есть неравенство
— соответственно константы Липшица операторов РТ и QT. Если ур-ние задано в гильбертовом пространстве и Р — оператор ортогонального проектирования, то простейшим условием сходимости алгоритмов (37) и (38) есть неравенство  где I — константа Липшица оператора Т. В этом случае, если
где I — константа Липшица оператора Т. В этом случае, если  скорость сходимости характеризуется геометрической прогрессией со знаменателем
скорость сходимости характеризуется геометрической прогрессией со знаменателем

Существуют и менее ограничительные условия сходимости и оценки погрешности для различных классов операторов и пространств.
Алгоритмы (37) и (38) вкладываются в схему общего итеративного метода, согласно которому прибл. решения  к ур-нию
к ур-нию 
определяются из ур-ний

где операторы  определяются по рекуррентным ф-лам
определяются по рекуррентным ф-лам

Если  , то алгоритм (40) совпадает с (37), а если
, то алгоритм (40) совпадает с (37), а если  , то алгоритм (40) совпадает с алгоритмом (38).
, то алгоритм (40) совпадает с алгоритмом (38).
Для операторных ур-ний в частично упорядоченных пространствах часто удается построить две последовательности прибл. решений, которые монотонно (соответственно снизу и сверху) сходятся к искомому решению. Пусть X — частично упорядоченное банахово пространство, а оператор Т в ур-нии (2) можно представить в виде  , где
, где  при х, и обладает свойством
при х, и обладает свойством

Если при этом выполняются неравенства

то имеют место соотношения

где  определяются по рекуррентным формулам
определяются по рекуррентным формулам

x - решение ур-ния (2), принадлежащее отрезку  Оператор
Оператор  обладает свойством (41), напр., в случае, если
обладает свойством (41), напр., в случае, если  , где
, где  неубывающий, а
неубывающий, а  невозрастающий операторы. Элементы
невозрастающий операторы. Элементы  образуют соответственно неубывающую ограниченную сверху
образуют соответственно неубывающую ограниченную сверху  и невозрастающую ограниченную снизу
и невозрастающую ограниченную снизу  последовательности. Отсюда в некоторых случаях можно сделать вывод о сходимости их соответственно к пределам
последовательности. Отсюда в некоторых случаях можно сделать вывод о сходимости их соответственно к пределам  . Если
. Если  непрерывный оператор по
непрерывный оператор по  , то
, то  — решение ур-ния (2).
— решение ур-ния (2).
Рассмотренные методы широко используются в практике вычислений на ЭВМ.
Лит.:  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- МИХАЙЛОВА КРИТЕРИЙ
- МНОГОВАРИАНТНЫХ ЗАДАЧ РЕШЕНИЕ
- МНОГОГРАННОЕ МНОЖЕСТВО
- МНОГОГРАННЫЙ КОНУС
- МНОГОЗНАЧНЫЕ СХЕМЫ
- МНОГОКОНТУРНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОКРИТЕРИАЛЬНОСТИ ПРОБЛЕМА
- МНОГОМЕРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ РАЗДЕЛИТЕЛЬНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ УНИВЕРСАЛЬНЫЙ
- МНОГОПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ, мультипрограммная обработка информации
- МНОГОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- МНОГОШАГОВОГО ПРОЦЕССА ПРОИЗВОДСТВА МОДЕЛЬ
- МНОГОШАГОВОГО ПРОЦЕССА РАСПРЕДЕЛЕНИЯ МОДЕЛЬ
- МНОГОШАГОВЫЕ ЗАДАЧИ
- МНОГОЭТАПНОЕ ОБСЛУЖИВАНИЕ
- МНОЖЕСТВ ТЕОРИЯ
- МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- МОДЕЛИ ОБЪЕКТОВ РАСПОЗНАВАНИЯ
- МОДЕЛИ ПРОИЗВОДСТВА
- МОДЕЛИ РАВНОВЕСИЯ
- МОДЕЛИ РОСТА
- МОДЕЛИ ЭКОНОМИКИ
- МОДЕЛИРОВАНИЕ ВЕСТИБУЛЯРНОГО АНАЛИЗАТОРА
- МОДЕЛИРОВАНИЕ ВОСПРИЯТИЯ
- МОДЕЛИРОВАНИЕ ЖИВЫХ СИСТЕМ на молекулярном уровне
- МОДЕЛИРОВАНИЕ ИНЖЕНЕРНЫХ СЕТЕЙ НА АВМ
- МОДЕЛИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ МЫШЛЕНИЯ
- МОДЕЛИРОВАНИЕ НА СПЛОШНЫХ СРЕДАХ, электрическое моделирование
- МОДЕЛИРОВАНИЕ ПАМЯТИ
- МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАСПОЗНАВАНИЯ И ОБУЧЕНИЯ РАСПОЗНАВАНИЮ НА ЦВМ
- МОДЕЛИРОВАНИЕ ПСИХИЧЕСКИХ ФУНКЦИЙ
- МОДЕЛИРОВАНИЕ СЕНСОРНЫХ СИСТЕМ
- МОДЕЛИРОВАНИЕ СИСТЕМЫ «ЧЕЛОВЕК—МАШИНА»
- МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ ЦВМ ИМИТАЦИОННОЕ
- МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ НА ЦВМ
- МОДЕЛЬ ЗРИТЕЛЬНОГО АНАЛИЗАТОРА
- МОДЕЛЬ МАТЕМАТИЧЕСКАЯ
- МОДЕЛЬ НЕРВНОЙ КЛЕТКИ
- МОДЕЛЬ ПЕРЕМЕННОЙ СТРУКТУРЫ
- МОДЕЛЬ СЛУХОВОГО АНАЛИЗАТОРА
- МОДЕЛЬ «СМЫСЛ-ТЕКСТ»
- МОДЕЛЬ ФИЗИЧЕСКАЯ
- МОДЕЛЬ ЧУВСТВИТЕЛЬНОСТИ
- МОДУЛЯТОР
- МОДУЛЯЦИЯ ИМПУЛЬСНАЯ
- «МОЗГОВОЙ ШТУРМ»
- МОМЕНТОВ МЕТОД
- МОНИТОР
- МОНОТОННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- МОНТЕ-КАРЛО МЕТОД
- «МППИ-1», машина первичной переработки информации
- МУЛЬТИВИБРАТОР
- МУЛЬТИПРОГРАММИРОВАНИЕ
- МУЛЬТИПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- МУЛЬТИПРОЦЕССОРНЫЙ РЕЖИМ
- МУЛЬТИУСТОЙЧИВЫЕ СИСТЕМЫ
- МУРА АВТОМАТ
- МЫСЛИТЕЛЬНОЙ СПОСОБНОСТИ УСИЛИТЕЛЬ
- НАБЛЮДАЕМОСТИ И УПРАВЛЯЕМОСТИ УСЛОВИЯ
- НАБОРНОЕ ПОЛЕ
- НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НАДЁЖНОСТЬ КИБЕРНЕТИЧЕСКИХ СИСТЕМ
- НАДЁЖНОСТЬ РАСПОЗНАВАНИЯ
- НАИМЕНЬШИХ КВАДРАТОВ МЕТОД
- «НАИРИ»
- НАИСКОРЕЙШЕГО СПУСКА МЕТОД
- НАЙКВИСТА КРИТЕРИЙ
- НАКАПЛИВАЮЩИЕ СХЕМЫ
- НАКОПИТЕЛЬ, блок хранения информации
- НАКОПИТЕЛЬ НА МАГНИТНОЙ ЛЕНТЕ
- НАРАБОТКА НА ОТКАЗ
- НАРАБОТКА НА СБОЙ
- НАУКА УПРАВЛЕНИЯ
- НАУКОВЕДЕНИЕ
- НАУЧНАЯ ОРГАНИЗАЦИЯ ТРУДА (НОТ)
- НАУЧНО-ИНФОРМАЦИОННАЯ ДЕЯТЕЛЬНОСТЬ
- НАУЧНО-ТЕХНИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ
- НАУЧНО-ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ ОБРАБОТКА
- НАУЧНЫЙ СОВЕТ ПО КОМПЛЕКСНОЙ ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН СССР
- НАУЧНЫЙ СОВЕТ ПО ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН УССР
- НЕЗАВИСИМОСТЬ в теории вероятностей, статистическая независимость
- НЕЙРОБИОНИКА
- НЕЙРОКИБЕРНЕТИКА
- НЕЙРОН
- НЕЙРОН ФОРМАЛЬНЫЙ
- НЕЙРОННЫЕ СЕТИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫЕ ЗАДАЧИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- НЕЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ АВМ
- НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- НЕ НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НЕОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- НЕОДНОРОДНЫЙ ПОТОК В СЕТИ
- НЕОПРЕДЕЛЕННОСТЬ В УПРАВЛЕНИИ
- НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМЫ АКСИОМ, совместимость, корректность
- НЕРАЗРЕШИМЫЕ АЛГОРИТМИЧЕСКИЕ ПРОБЛЕМЫ
- «НИППОН ЭЛЕКТРИК КОМПАНИ» (Nippon Electric Company, Ltd)
- «ННБ», набор нелинейных блоков
- НОРМА ВЕКТОРА
- НОРМА МАТРИЦЫ
- НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- НОРМАЛЬНАЯ ФОРМА СОВЕРШЕННАЯ
- НОРМАЛЬНАЯ ФОРМА СОКРАЩЕННАЯ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- НОРМАЛЬНЫЕ АЛГОРИФМЫ, нормальные алгоритмы
- НОСИТЕЛЬ ИНФОРМАЦИИ
- НУЛЕВЫХ СОБСТВЕННЫХ ПРОВОДИМОСТЕЙ УЗЛОВ МЕТОД
- НУЛЬ-ОРГАН, сравнивающее устройство, компаратор
- НУМЕРАЦИЙ ТЕОРИЯ
- НЬЮТОНА ОБОБЩЕННЫЙ МЕТОД
- НЬЮТОНА ФОРМУЛЫ ИНТЕРПОЛИРОВАНИЯ
- ОБЛАСТЬ УПРАВЛЕНИЯ
- ОБЛЕГЧЁННОЕ РЕЗЕРВИРОВАНИЕ
- ОБОБЩЁННЫЕ ФУНКЦИИ
- ОБОБЩЕННЫХ ГРАДИЕНТОВ МЕТОД
- ОБРАБОТКА ДАННЫХ ПОСЛЕДОВАТЕЛЬНАЯ
- ОБРАБОТКА ДАННЫХ ПРОИЗВОЛЬНАЯ
- ОБРАБОТКА ИНФОРМАЦИИ В РЕАЛЬНОМ масштабе времени
- ОБРАБОТКА ИНФОРМАЦИИ В РЕЖИМЕ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- ОБРАБОТКИ ДАННЫХ СИСТЕМА
- ОБРАЗ, или распознаваемый класс, в кибернетике
- ОБРАТИМОСТИ ПРИНЦИП
- ОБРАТИМЫЕ ЭЛЕМЕНТЫ И МОДЕЛИ
- ОБРАТНАЯ СВЯЗЬ
- ОБРАТНЫХ ОПЕРАТОРОВ МЕТОД
- ОБУСЛОВЛЕННОСТИ ЧИСЛО
- ОБУЧАЮЩАЯ ВЫБОРКА
- ОБУЧАЮЩАЯ МАШИНА
- ОБУЧАЮЩАЯ ПРОГРАММА
- ОБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ОГРАНИЧЕНИЕ ФАЗОВЫХ КООРДИНАТ
- ОГРАНИЧИТЕЛЬ АМПЛИТУДЫ
- ОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- ОДНОРОДНЫЙ ПОТОК В СЕТИ
- ОДНОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ОКРУГЛЕНИЯ ПОГРЕШНОСТЬ
- ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ОЗУ)
- ОПЕРАТИВНОЕ РУКОВОДСТВО
- ОПЕРАТИВНО-ПРОИЗВОДСТВЕННАЯ ИНФОРМАЦИЯ
- ОПЕРАТОР
- ОПЕРАТОР АВТОМАТНЫЙ
- ОПЕРАТОР ЗАДЕРЖКИ
- ОПЕРАТОР ПРИСВАИВАНИЯ
- ОПЕРАТОР ЭЛЕМЕНТАРНЫЙ
- ОПЕРАТОР ЭЛЕМЕНТНЫЙ
- ОПЕРАТОРНАЯ СХЕМА
- ОПЕРАТОРНЫЕ УРАВНЕНИЯ
- ОПЕРАТОРНЫЙ МЕТОД ПРОГРАММИРОВАНИЯ
- ОПЕРАТОРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ОПЕРАТОРЫ ЛИНЕЙНЫЕ, линейные преобразования
- ОПЕРАЦИИ МАШИННЫЕ
- ОПЕРАЦИИ НАД МАССИВАМИ
- ОПЕРАЦИИ НАД СИМВОЛАМИ И СТРОКАМИ
- ОПЕРАЦИИ НАД ЧИСЛАМИ
- ОПЕРАЦИИ ИССЛЕДОВАНИЕ
- ОПЕРАЦИЙ СИСТЕМА
- ОПЕРАЦИОННАЯ СИСТЕМА
- ОПЕРАЦИЯ НАИМЕНЬШЕГО КОРНЯ
- ОПЕРАЦИЯ ПРИМИТИВНОЙ РЕКУРСИИ
- ОПИСАНИЕ ОБЪЕКТА РАСПОЗНАВАНИЯ
- ОПОРНОЕ НАПРЯЖЕНИЕ
- ОПОРНЫЙ ПЛАН
- ОПТИМАЛЬНАЯ ТОЧКА
- ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ТЕОРИЯ
- ОПТИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
- ОПТИМАЛЬНОСТИ НЕОБХОДИМЫЕ УСЛОВИЯ
- ОПТИМАЛЬНОСТИ ПРИНЦИП
- ОПТИМАЛЬНЫЙ ВЕКТОР
- ОПТИМАЛЬНЫХ ПАРАМЕТРОВ СИСТЕМЫ ВЫБОР
- ОПТИМАЛЬНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ОПТИМИЗАТОР АВТОМАТИЧЕСКИЙ
- ОПТИМИЗАЦИИ МЕТОДЫ численные
- «ОПТИМУМ»
- ОПТРОН
- ОРГАНИЗАЦИЯ ИНФОРМАЦИОННОГО МАССИВА
- ОРГАНИЗАЦИЯ УЧЕТА В АВТОМАТИЗИРОВАННЫХ СИСТЕМАХ УПРАВЛЕНИЯ
- ОРГАТЕХНИКА, организационная техника
- ОРДЕНА ЛЕНИНА ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- УПРАВЛЕНИЯ (АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ), ИАТ
- ОСТАНОВ
- ОСУЩЕСТВИМОСТИ ФИЗИЧЕСКОЙ КРИТЕРИИ
- ОСУЩЕСТВИМОСТИ ЦЕЛИ ПРИНЦИП
- ОТВЕТ РАСПОЗНАЮЩЕЙ СИСТЕМЫ
- ОТКАЗ ОТ РАСПОЗНАВАНИЯ
- ОТЛАДОЧНЫЕ ПРОГРАММЫ
- ОТНОШЕНИЕ
- ОТНОШЕНИЕ АНАЛИТИЧЕСКОЕ
- ОТНОШЕНИЕ БАЗИСНОЕ
- ОТНОШЕНИЕ ПАРАДИГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ ПРАВДОПОДОБИЯ
- ОТНОШЕНИЕ СИГНАЛ/ПОМЕХА
- ОТНОШЕНИЕ СИНТАГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ СИНТЕТИЧЕСКОЕ
- ОТНОШЕНИЕ ТЕКСТУАЛЬНОЕ
- ОТРИЦАНИЕ в алгебре логики
- ОЧЕРЕДЕЙ ТЕОРИЯ
- ОШИБКА В ПРИНЯТИИ ГИПОТЕЗ
- ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ОШИБОК ТЕОРИЯ
- ПАКЕТНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- ПАЛЬМА ПОТОК
- ПАМЯТИ ЗАЩИТА
- ПАМЯТИ РАСПРЕДЕЛЕНИЕ
- ПАМЯТЬ МАГАЗИННАЯ
- ПАМЯТЬ СТРАНИЧНАЯ
- ПАМЯТЬ ЦВМ
- ПАРАБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ
- ПАРАМЕТР ФАКТИЧЕСКИЙ
- ПАРАМЕТР ФОРМАЛЬНЫЙ
- ПАРАМЕТРОН
- ПАРЕТО ОПТИМУМ
- ПАЧКА ОШИБОК, пакет ошибок
- ПЕРЕВОД АВТОМАТИЧЕСКИЙ
- ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
- ПЕРЕДАЧИ ИНФОРМАЦИИ СКОРОСТЬ
- ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ПЕРЕРАБОТКА ИНФОРМАЦИИ В ЦВМ
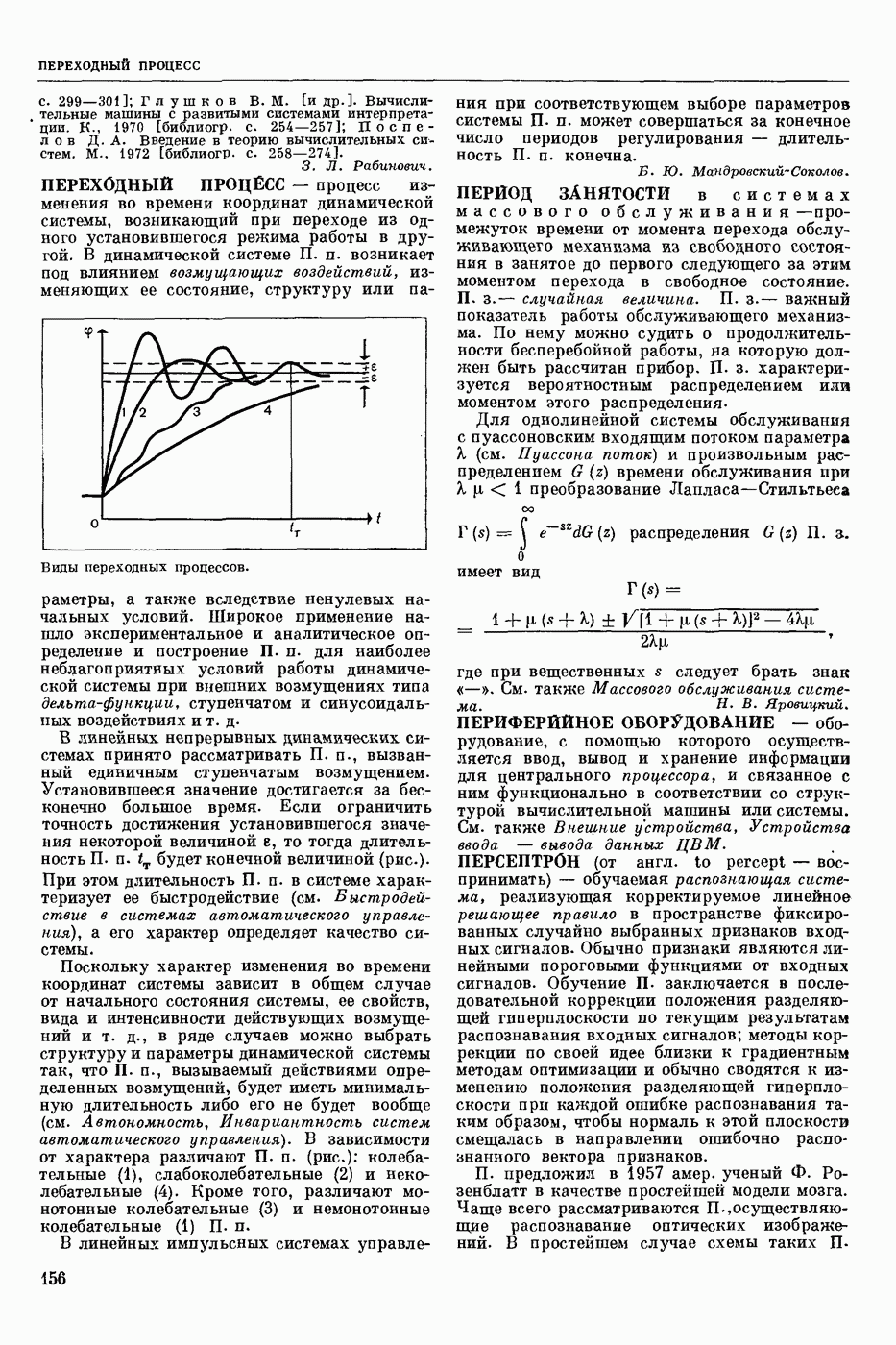
- ПЕРЕХОДНЫЙ ПРОЦЕСС
- ПЕРИОД ЗАНЯТОСТИ в системах массового обслуживания
- ПЕРИФЕРИЙНОЕ ОБОРУДОВАНИЕ
- ПЕРСЕПТРОН
- «ПЕРТ»
- ПЕРФОРАТОР
- ПЕРФОРАЦИОННАЯ КАРТА, перфокарта
- ПЕРФОРАЦИОННАЯ ЛЕНТА, перфолента
- ПЕЧАТНАЯ СХЕМА
- ПИРСА СТРЕЛКА, функция Вебба, отрицание дизъюнкции
- ПЛ-1
- ПЛАВАЮЩАЯ ЗАПЯТАЯ
- ПЛАН-ГРАФИК
- ПЛАТЕЖНАЯ МАТРИЦА
- ПЛАТЕЖНАЯ ФУНКЦИЯ
- ПЛЕНКА МАГНИТНАЯ
- ПНЕВМОНИКА, струйная пневмоавтоматика
- ПОВЕДЕНИЕ АВТОМАТОВ.
- ПОВЕДЕНИЕ АВТОМАТОВ В СЛУЧАЙНЫХ СРЕДАХ.
- ПОГЛОЩЕНИЯ ЗАКОН
- ПОГРЕШНОСТЕЙ ВЫЧИСЛЕНИЙ ТЕОРИЯ
- ПОГРЕШНОСТЬ
- ПОГРЕШНОСТЬ РЕШАЮЩЕГО ЭЛЕМЕНТА
- ПОДАВТОМАТ
- ПОДОБИЯ ТЕОРИЯ
- ПОДПРОГРАММА
- ПОДПРОГРАММА ЗАМКНУТАЯ
- ПОДПРОГРАММА ОТКРЫТАЯ
- ПОДПРОГРАММА СТАНДАРТНАЯ
- ПОДСИСТЕМА
- ПОИСК ИНФОРМАЦИИ АВТОМАТИЧЕСКИЙ
- ПОИСКА ЭКСТРЕМУМА ФУНКЦИЙ МЕТОДЫ
- ПОИСКОВОЕ ПРЕДПИСАНИЕ
- ПОИСКОВЫЙ МАССИВ
- ПОИСКОВЫЙ ОБРАЗ ДОКУМЕНТА
- ПОИСКОВЫЙ ОБРАЗ ЗАПРОСА
- ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ, экспоненциальное распределение
- ПОЛНОЙ ВЕРОЯТНОСТИ ФОРМУЛА
- ПОЛНОТА ФОРМАЛЬНОЙ ТЕОРИИ
- ПОЛНОТЫ ПРОБЛЕМА в теории автоматов
- ПОЛОС МЕТОД
- ПОЛУГРУППА, ассоциативная система
- ПОЛУМАРКОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- ПОЛУСУММАТОР
- ПОЛЬСКАЯ ЗАПИСЬ
- ПОМЕХИ
- ПОМЕХОУСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ
- ПОНТРЯГИНА ПРИНЦИП МАКСИМУМА
- ПОПОВА КРИТЕРИЙ
- ПОРОГ ЧУВСТВИТЕЛЬНОСТИ
- ПОРОГОВЫЙ ЭЛЕМЕНТ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
- ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ МЕТОД
- ПОСТА ИСЧИСЛЕНИЯ
- ПОСТА КОМБИНАТОРНАЯ ПРОБЛЕМА
- ПОСТА МАШИНА
- ПОТЕНЦИАЛОВ МЕТОД
- ПОТЕНЦИАЛЬНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-НУЛЕВАЯ ТОЧКА
- ПОТЕНЦИАЛЬНО-НУЛЕВЫХ ТОЧЕК МЕТОД
- ПОТЕНЦИАЛЬНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ МЕТОД
- ПОТЕРИ ИНФОРМАЦИИ при поиске
- ПОТОК БЕЗ ПОСЛЕДЕЙСТВИЯ
- ПОТОК В СЕТИ
- ПОТОК В СЕТИ НЕОДНОРОДНЫЙ
- ПОТОК ВЫХОДЯЩИЙ
- ПОТОК ГЕОМЕТРИЧЕСКИЙ
- ПОТОК ИНФОРМАЦИОННЫЙ ЗАМКНУТЫЙ
- ПОТОК НЕСТАЦИОНАРНЫЙ
- ПОТОК ПРОСТЕЙШИЙ
- ПОТОК РЕГУЛЯРНЫЙ
- ПОТОК С ОГРАНИЧЕННЫМ ПОСЛЕДЕЙСТВИЕМ
- ПОТОК СЛУЧАЙНЫЙ
- ПРАГМАТИКА
- ПРЕДИКАТ
- ПРЕДИКАТИВНОСТЬ
- ПРЕДСКАЗАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ПРЕДСКАЗЫВАЮЩИЙ ФИЛЬТР
- ПРЕДСТАВЛЕНИЙ ГРУПП ТЕОРИЯ
- ПРЕОБРАЗОВАНИЕ ПЕРИОДИЧЕСКИ-ОПРЕДЕЛЕННОЕ
- ПРЕОБРАЗОВАТЕЛИ ВОЛОКОННЫЕ
- ПРЕОБРАЗОВАТЕЛИ ДВУХ И БОЛЕЕ ПЕРЕМЕННЫХ
- ПРЕОБРАЗОВАТЕЛИ КОД-АНАЛОГ
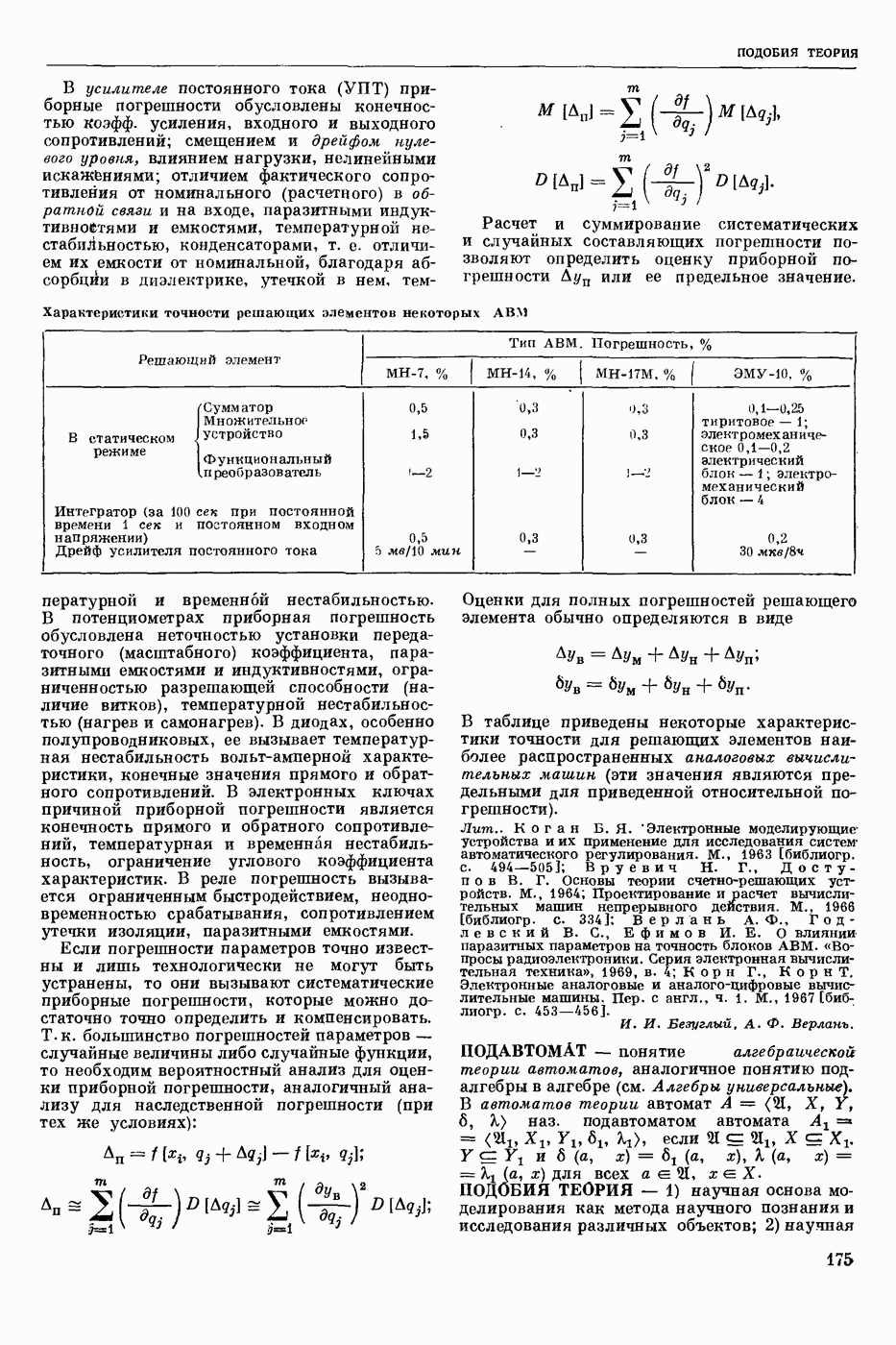
- ПРЕОБРАЗОВАТЕЛИ С ПОРАЗРЯДНЫМ КОДИРОВАНИЕМ
- ПРЕОБРАЗОВАТЕЛИ ФОРМЫ ИНФОРМАЦИИ
- ПРЕОБРАЗОВАТЕЛЬ ВРЕМЯ-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ИНТЕГРИРУЮЩЕГО ТИПА
- ПРЕОБРАЗОВАТЕЛЬ КОМБИНИРОВАННЫЙ
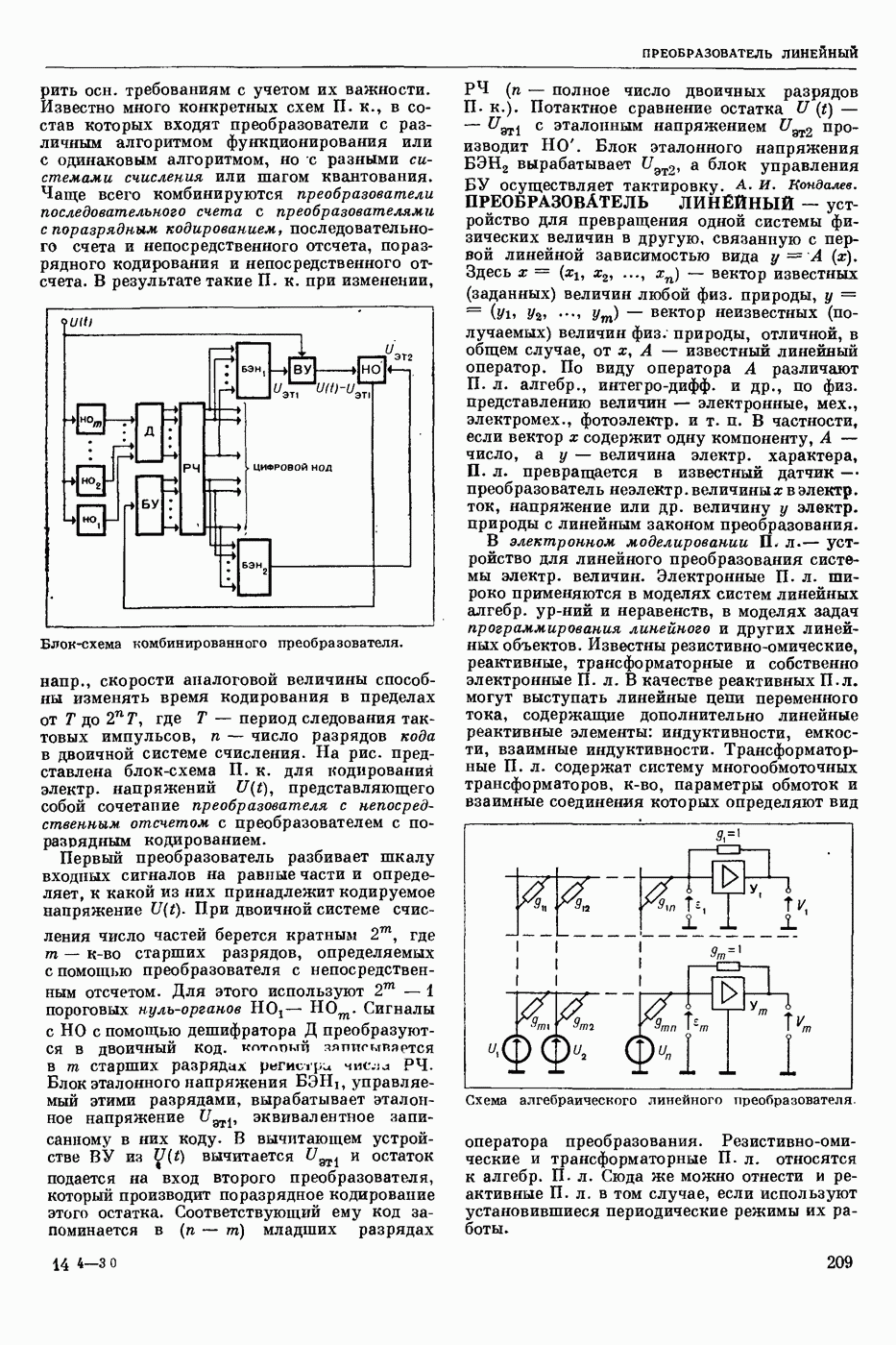
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ КВАЗИОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ ОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ НАКАПЛИВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ПРЕОБРАЗОВАТЕЛЬ РАЗВЕРТЫВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ С НЕПОСРЕДСТВЕННЫМ ОТСЧЕТОМ
- ПРЕОБРАЗОВАТЕЛЬ СЛЕДЯЩИЙ
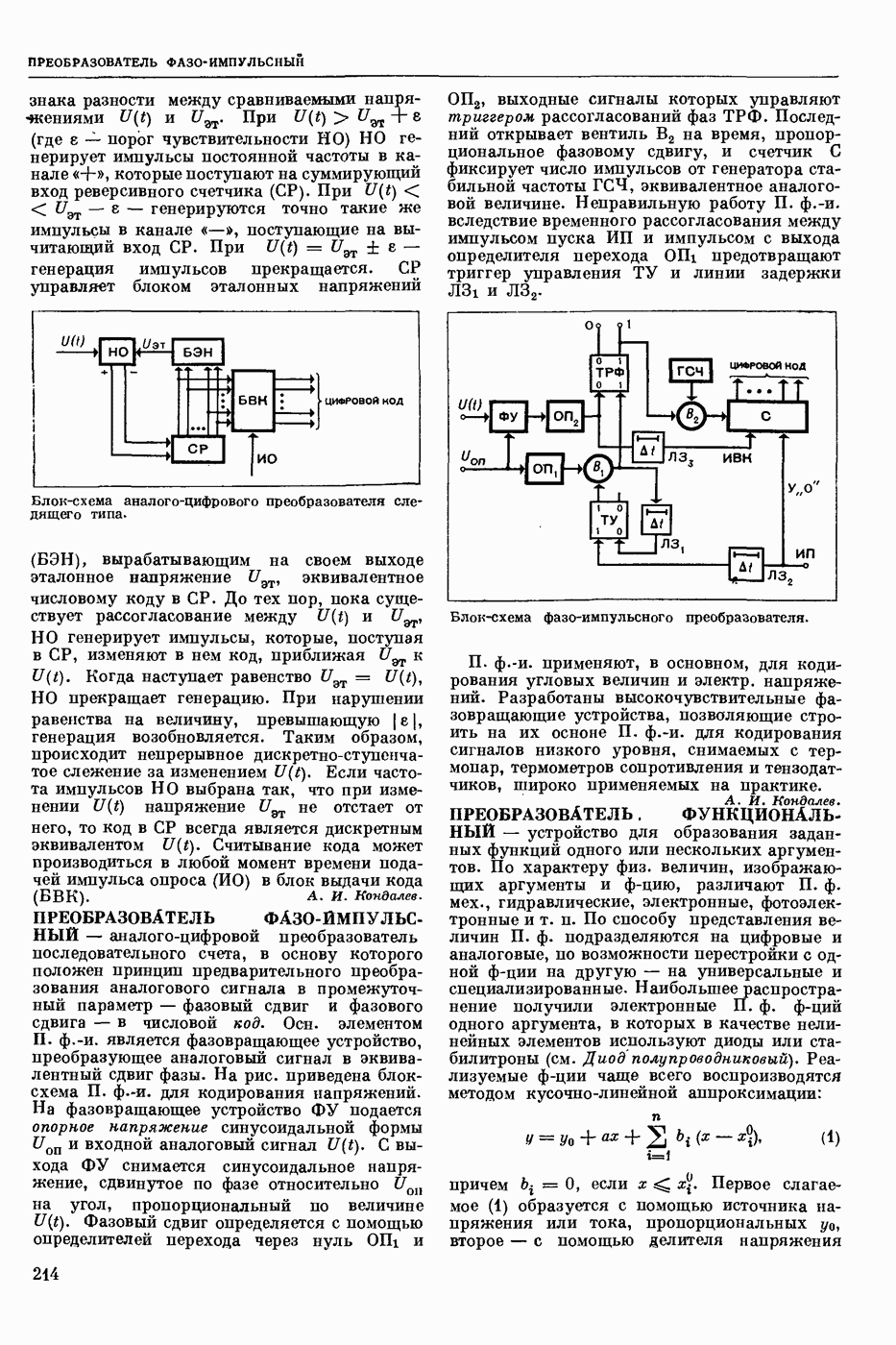
- ПРЕОБРАЗОВАТЕЛЬ ФАЗО-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ФУНКЦИОНАЛЬНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЦИКЛИЧЕСКИЙ
- ПРЕОБРАЗОВАТЕЛЬ ЧАСТОТНО-ИМПУЛЬСНЫЙ
- ПРЕСЛЕДОВАНИЯ ЗАДАЧА
- ПРИБЛИЖЕННЫХ МЕТОДОВ ОБЩАЯ ТЕОРИЯ
- ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- ПРИОРИТЕТ
- ПРИОРИТЕТОВ СИСТЕМА
- ПРОБЛЕМА «ЧЕЛОВЕК-МАШИНА»
- ПРОГОНКИ МЕТОД
- ПРОГРАММ СЕГМЕНТАЦИЯ
- ПРОГРАММА вычислительной машины
- ПРОГРАММА ДИАГНОСТИЧЕСКАЯ
- ПРОГРАММА ИСПЫТАТЕЛЬНАЯ
- ПРОГРАММА КОМПИЛИРУЮЩАЯ
- ПРОГРАММА УПРАВЛЯЮЩАЯ
- ПРОГРАММА-ДИСПЕТЧЕР
- ПРОГРАММИРОВАНИЕ АВМ
- ПРОГРАММИРОВАНИЕ ВЫПУКЛОЕ
- ПРОГРАММИРОВАНИЕ ДИНАМИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ДИСКРЕТНОЕ
- ПРОГРАММИРОВАНИЕ ДЛЯ ЦВМ
- ПРОГРАММИРОВАНИЕ КВАДРАТИЧНОЕ
- ПРОГРАММИРОВАНИЕ КУСОЧНО-ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ НЕЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ СТОХАСТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЧАСТИЧНО ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЭВРИСТИЧЕСКОЕ
- ПРОГРАММИРОВАННОЕ ОБУЧЕНИЕ
- ПРОГРАММИРОВАННЫЙ УЧЕБНИК
- ПРОГРАММИРУЮЩАЯ ПРОГРАММА
- ПРОГРАММНОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ в народном хозяйстве.
- ПРОГРАММЫ ОБСЛУЖИВАЮЩИЕ
- ПРОЕКТИРОВАНИЕ СЕТЕЙ И КОММУНИКАЦИЙ ОПТИМАЛЬНОЕ
- ПРОЕКЦИОННЫЕ МЕТОДЫ
- ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ
- «ПРОМIНЬ»
- ПРОПОЗИЦИОНАЛЬНЫЕ СВЯЗКИ, связки логические
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- ПРОСТОЙ ИТЕРАЦИИ МЕТОД
- ПРОСТРАНСТВО АБСТРАКТНОЕ в функциональном анализе
- ПРОСТРАНСТВО ИЗОБРАЖЕНИЙ
- ПРОЦЕДУРА в программировании
- ПРОЦЕДУРА РЕКУРСИВНАЯ
- ПРОЦЕСС КОНЕЧНОЙ ДЛИТЕЛЬНОСТИ
- ПРОЦЕСС УПРАВЛЯЕМЫЙ
- ПРОЦЕССОР
- ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
- ПРЯМЫЕ МЕТОДЫ решения задач прикладной математики
- ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА
- ПСИХОЛОГИЯ ИНЖЕНЕРНАЯ
- ПУАССОНА ПОТОК
- ПУАССОНА РАСПРЕДЕЛЕНИЕ
- ПУТЬ в теории графов
- РАВНОВЕСИЯ СИТУАЦИЯ
- «РАЗДАН»
- РАЗДЕЛЯЮЩАЯ ПОВЕРХНОСТЬ в распознавании образов
- РАЗМЕЩЕНИЯ ПРОИЗВОДСТВ МОДЕЛИ
- РАЗНОСТНАЯ СХЕМА
- РАЗРЯДНОСТЬ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- РАСПАРАЛЛЕЛИВАНИЕ АЛГОРИТМА
- РАСПОЗНАВАНИЕ ЗРИТЕЛЬНЫХ ОБРАЗОВ, распознавание изображений
- РАСПОЗНАВАНИЕ ОБРАЗОВ
- РАСПОЗНАВАНИЕ ПРОЦЕССОВ
- РАСПОЗНАВАНИЕ РЕЧЕВЫХ СИГНАЛОВ
- РАСПОЗНАЮЩАЯ СИСТЕМА
- РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- РАСПРЕДЕЛИТЕЛЬНАЯ ЗАДАЧА
- РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДЫ
- РАСЧЕТНЫЙ СТОЛ ПОСТОЯННОГО ТОКА, расчетная модель электрической системы
- РАСШИФРОВОЧНАЯ МАШИНА
- РАУСА КРИТЕРИЙ, Рауса — Гурвица критерий
- РЕАЛЬНЫЙ МАСШТАБ ВРЕМЕНИ
- РЕГЕНЕРАЦИЯ информации в вычислительных устройствах
- РЕГИСТР
- РЕГРЕССИЯ
- РЕГУЛИРОВАНИЕ ЗАПАСОВ
- РЕГУЛИРОВАНИЯ ЗАКОН
- РЕГУЛИРУЮЩИЕ СИСТЕМЫ ОРГАНИЗМА
- РЕГУЛЯРИЗАЦИИ МЕТОД
- РЕГУЛЯРНЫЕ СОБЫТИЯ И ВЫРАЖЕНИЯ
- РЕГУЛЯТОР ИМПУЛЬСНЫЙ
- РЕГУЛЯТОР ЭКСТРЕМАЛЬНЫЙ
- РЕГУЛЯТОРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- РЕГУЛЯТОРЫ ЦИФРОВЫЕ
- РЕДАКТИРОВАНИЕ ДАННЫХ
- РЕЖИМ ПЕРИОДИЗАЦИИ
- РЕЖИМ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- РЕКУРСИВНЫЕ ФУНКЦИИ
- РЕЛЕВАНТНОСТЬ ДОКУМЕНТА
- РЕЛЕЙНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
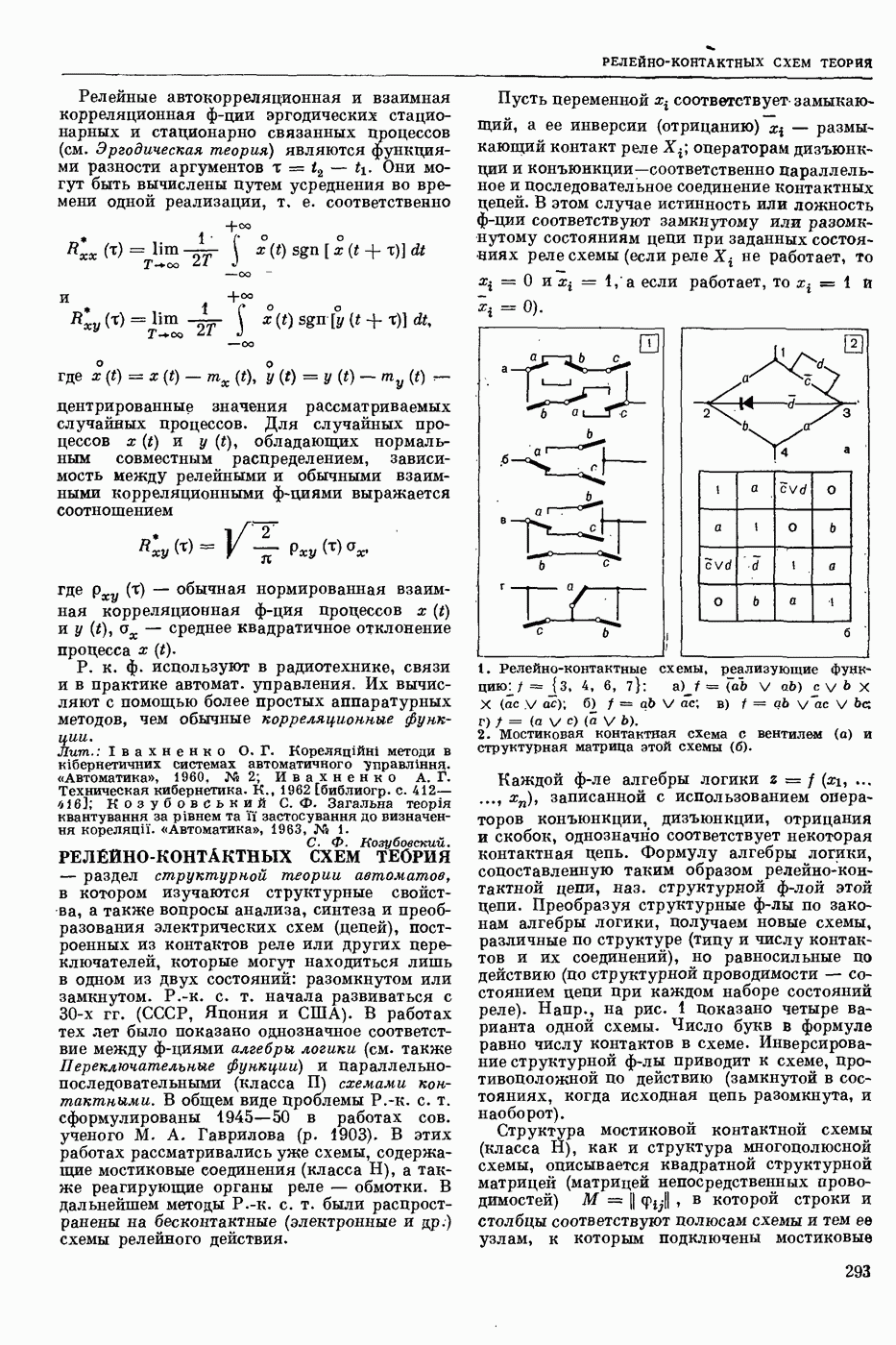
- РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ ТЕОРИЯ
- РЕФАЛ
- РЕФЕРАТ
- РЕФЕРИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- РЕФЛЕКСИВНОЕ УПРАВЛЕНИЕ
- РЕШАЮЩЕЕ ПРАВИЛО в распознавании образов
- РЕШАЮЩЕЕ УСТРОЙСТВО.
- РИСК РАСПОЗНАВАНИЯ
- РИСКА ПРОБЛЕМА
- РОБОТ
- РОБОТ ПРОМЫШЛЕННЫЙ
- РУНГЕ—КУТТЫ МЕТОД
- «РУТА-110»
- R-ФУНКЦИИ
- САМОДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- САМОКОРРЕКТИРУЮЩАЯСЯ СХЕМА
- САМОНАСТРАИВАЮЩАЯСЯ ПАРАМЕТРИЧЕСКАЯ СИСТЕМА
- САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА
- САМООБУЧАЮЩИЕСЯ СИСТЕМЫ
- САМООБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- СБОЙ ЦВМ
- СВЕРТКА РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН
- СВЕТОВОЙ КАРАНДАШ, световое перо
- СВОДИМОСТЬ в теории алгоритмов
- СВОЙСТВО ОТСУТСТВИЯ ПОСЛЕДЕЙСТВИЯ
- СВЯЗКИ ЛОГИЧЕСКИЕ
- СДВИГ
- «CDC-7600»
- СЕДЛОВЫЕ ТОЧКИ
- СЕКВЕНЦИЯ
- СЕМАНТИКА
- СЕМАНТИКА СТРУКТУРНАЯ
- СЕМАНТИЧЕСКИЙ АНАЛИЗ
- СЕМИОТИКА
- СЕРВОМОТОР
- СЕТЕВАЯ ЗАДАЧА
- СЕТЕВАЯ ЗАДАЧА НЕОДНОРОДНАЯ
- СЕТЕВАЯ МОДЕЛЬ
- СЕТЕВОЙ ГРАФИК
- СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
- «СЕТУНЬ»
- СЕТЧАТКА в распознавании образов
- СЕТЬ ИЗ НЕЙРОННЫХ ЭЛЕМЕНТОВ
- СЕТЬ ЛОГИЧЕСКАЯ
- СЕЧЕНИЙ ПРОСТРАНСТВА ПАРАМЕТРОВ МЕТОД
- СИГНАЛИЗИРУЮЩАЯ ФУНКЦИЯ
- СИЛЛОГИСТИКА
- «СИМЕНС» (Siemens Aktiengesellschaft)
- СИММЕТРИЧЕСКИЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- СИМПЛЕКС-МЕТОД
- СИМПСОНА ФОРМУЛА
- СИМСКРИПТ
- СИМУЛА
- «СИНТАКСИС»
- СИНТАКСИЧЕСКИЙ АНАЛИЗ АВТОМАТИЧЕСКИЙ естественных языков
- СИНТАКСИЧЕСКИЙ АНАЛИЗ ПРОГРАММ
- СИНТАКСИЧЕСКИЙ КОНТРОЛЬ ПРОГРАММ
- СИНТАКТИКА
- СИНТЕЗ АВТОМАТОВ АБСТРАКТНЫЙ
- СИНТЕЗ АВТОМАТОВ СТРУКТУРНЫЙ
- СИНТЕЗ АЛГОРИТМА УПРАВЛЕНИЯ
- СИНТЕЗ РЕЧЕВЫХ СИГНАЛОВ
- СИНХРОНИЗАЦИЯ РАБОТЫ ЦВМ
- «СИРИУС»
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СТАТИСТИЧЕСКАЯ ДИНАМИКА
- СИСТЕМ ОБЩАЯ ТЕОРИЯ
- СИСТЕМА АВТОМАТИЗИРОВАННАЯ
- СИСТЕМА АВТОМАТИЧЕСКАЯ
- СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ)
- СИСТЕМА АВТОМАТИЧЕСКОЙ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- СИСТЕМА АВТОНОМНАЯ
- СИСТЕМА АСТАТИЧЕСКАЯ
- СИСТЕМА ИНФОРМАЦИОННОГО ПОИСКА
- СИСТЕМА НЕАВТОНОМНАЯ
- СИСТЕМА НЕПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЕРЫВАНИЯ ЦВМ
- СИСТЕМА ПРОГРАММИРОВАНИЯ
- СИСТЕМА ПРОГРАММНОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА СЧИСЛЕНИЯ
- СИСТЕМА УПРАВЛЕНИЯ АДАПТИВНАЯ
- СИСТЕМА УПРАВЛЕНИЯ ЗАМКНУТАЯ, система управления по отклонению
- СИСТЕМА УПРАВЛЕНИЯ НАУЧНЫМ ЭКСПЕРИМЕНТОМ
- СИСТЕМА УПРАВЛЕНИЯ РАЗОМКНУТАЯ
- СИСТЕМА УПРАВЛЕНИЯ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
- СИСТЕМА УПРАВЛЕНИЯ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- СИСТЕМА УРАВНЕНИЙ В ВАРИАЦИЯХ
- СИСТЕМА УРАВНЕНИЙ СОПРЯЖЕННАЯ
- СИСТЕМА «ЧЕЛОВЕК — МАШИНА»
- СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- СИСТЕМНОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- СИСТЕМНЫЙ ПОДХОД
- СИСТЕМОТЕХНИКА
- СИСТЕМЫ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- СИСТЕМЫ С ВРЕМЕННЫМИ ОГРАНИЧЕНИЯМИ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ
- СИСТЕМЫ УПРАВЛЕНИЯ НА ПЕРЕМЕННОМ ТОКЕ
- СКЛЕИВАНИЯ ЗАКОН
- СКОЛЬЗЯЩИЙ РЕЖИМ
- СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЯ
- СЛЕДЯЩАЯ СИСТЕМА
- СЛОВАРНЫЙ ПОИСК
- СЛОВАРЬ АВТОМАТИЧЕСКИЙ
- СЛОВАРЬ ИНФОРМАЦИОННОГО ЯЗЫКА
- СЛОВАРЬ ЧАСТОТНЫЙ
- СЛОВО
- СЛОЖНОСТЬ ВЫЧИСЛЕНИЙ
- СЛОЖНОСТЬ ТЬЮРИНГОВЫХ ВЫЧИСЛЕНИЙ
- СЛОЖНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- СЛУЧАЙНАЯ ВЕЛИЧИНА
- СЛУЧАЙНАЯ ФУНКЦИЯ
- СЛУЧАЙНОГО ПОИСКА МЕТОДЫ
- СЛУЧАЙНОЕ ПОЛЕ
- СЛУЧАЙНОЕ СОБЫТИЕ
- СЛУЧАЙНЫЕ ЧИСЛА
- СЛУЧАЙНЫЙ ПРОЦЕСС, вероятностный процесс, стохастический процесс
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ ПРЕДСКАЗАНИЯ
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ ОБЫКНОВЕННЫХ УРАВНЕНИЙ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СОБЫТИЕ РЕГУЛЯРНОЕ
- СОБЫТИЯ ЦИКЛИЧЕСКАЯ ГЛУБИНА
- СОВМЕЩЕНИЕ ОПЕРАЦИЙ В МАШИНЕ
- «СОЛЯРТРОН ЭЛЕКТРОНИК ГРУП» (The Solartron Electronic Group, Ltd)
- СООБЩЕНИЕ в теории передачи информации
- СООБЩЕНИЙ ТЕОРИЯ
- СОПРОТИВЛЕНИЕ ОТРИЦАТЕЛЬНОЕ
- СОПРОТИВЛЕНИЕ ЦИФРОВОЕ УПРАВЛЯЕМОЕ
- СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- СОРТИРОВАЛЬНАЯ МАШИНА
- СОРТИРОВКА ДАННЫХ
- СОЦИОЛОГИЧЕСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ
- СПЕКТРАЛЬНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- СПЕКТРАЛЬНАЯ ФУНКЦИЯ стационарного в широком смысле случайного процесса
- СПЕЦИАЛИЗИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- СПЕЦИАЛЬНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СПЕЦИФИКАЦИЯ
- СПИСКОВАЯ СТРУКТУРА
- СПИСОК в программировании
- СПРАВОЧНО-ИНФОРМАЦИОННЫЙ ФОНД (СИФ)
- СТАБИЛИЗАЦИИ СИСТЕМА
- СТАНДАРТИЗИРОВАННАЯ ИСТОРИЯ БОЛЕЗНИ
- СТАНДАРТЫ ПО ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
- СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ МЕТОД
- СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- СТИЛТЬЕСА КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
- СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- СТОХАСТИЧЕСКИЙ ПРОЦЕСС
- СТОХАСТИЧЕСКИХ КВАЗИГРАДИЕНТОВ МЕТОД
- СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ МЕТОД
- СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ МЕТОДЫ
- СТРАТЕГИЯ ОПТИМАЛЬНАЯ
- СТРАТЕГИЯ ПОВЕДЕНИЯ
- СТРАТЕГИЯ СМЕШАННАЯ
- СТРАТЕГИЯ ЧИСТАЯ
- «СТРЕЛА»
- СТРУКТУРА, решетка.
- СТРУКТУРНАЯ ИНТЕРПРЕТАЦИЯ ЯЗЫКА
- СТРУКТУРНАЯ ПОЭТИКА
- СТРУКТУРНАЯ СХЕМА МОДЕЛИ
- СТРУКТУРНАЯ ТЕОРИЯ АВТОМАТОВ
- СТРУКТУРНОЕ СТИХОВЕДЕНИЕ
- СУММАТОР
- СУММАТОР КОМБИНАЦИОННЫЙ
- СУММАТОР НАКАПЛИВАЮЩИЙ
- СУММАТОР ОДНОРАЗРЯДНЫЙ
- СУММАТОР ПАРАЛЛЕЛЬНЫЙ
- СУММАТОР ПОСЛЕДОВАТЕЛЬНЫЙ
- СУПЕРВИЗОР
- СХЕМА ВЕНТИЛЬНАЯ
- СХЕМА КОНТАКТНАЯ
- СХЕМА КОНТАКТНАЯ БЕСПОВТОРНАЯ
- СХЕМА КОНТАКТНО-ВЕНТИЛЬНАЯ
- СХЕМА РЕЛЕЙНО-КОНТАКТНАЯ
- СХЕМА СРАВНЕНИЯ
- СХОДСТВА КРИТЕРИИ
- СЧЕТЧИК
- ТАБУЛИРОВАНИЕ ФУНКЦИЙ
- ТАБУЛЯТОР
- ТАЙПОТРОН
- ТАКТ
- ТАКТОВАЯ ЧАСТОТА
- ТВИСТОР
- ТЕЗАУРУС
- ТЕЛЕМЕХАНИКА
- ТЕЛЕТАЙП
- ТЕРМИНАЛ, абонентский пульт, оконечное устройство
- ТЕРМИНАЛЬНОЕ УПРАВЛЕНИЕ, управление конечным состоянием
- ТЕСТОВЫЕ ПРОГРАММЫ, тест-программы
- ТЕСТЫ
- ТЕХНИЧЕСКАЯ ДИАГНОСТИКА
- ТЕХНИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- ТЕХПРОМФИНПЛАН ПРЕДПРИЯТИЯ МАТРИЧНЫЙ
- ТОЖДЕСТВЕННО ИСТИННАЯ ФОРМУЛА, общезначимая формула
- ТОНКАЯ МАГНИТНАЯ ПЛЕНКА
- ТОПОЛОГИЯ
- «ТОСИБА» (Tokyo Shibaura Electric Company, Ltd)
- ТОЧКА РАВНОВЕСИЯ
- ТОЧКИ ПЕРЕКЛЮЧЕНИЯ
- ТОЧНОСТЬ ВОСПРОИЗВЕДЕНИЯ СООБЩЕНИЯ
- ТРАЕКТОРИЯ ДОПУСТИМАЯ
- ТРАЕКТОРИЯ ОПТИМАЛЬНАЯ
- ТРАЕКТОРИЯ ФАЗОВАЯ
- ТРАНЗИТИВНЫЙ ГРАФ
- ТРАНСЛЯТОР, компилирующая программа, программирующая программа
- ТРАНСЛЯТОР СИНТАКСИЧЕСКИ УПРАВЛЯЕМЫЙ
- ТРАНСПОРТНАЯ ЗАДАЧА
- ТРАНСПОРТНАЯ СЕТЬ
- ТРАНСФЛЮКСОР
- ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
- ТРИГГЕР
- ТРИГГЕР ДИНАМИЧЕСКИЙ
- ТРИГГЕР СТАТИЧЕСКИЙ
- ТРИОД ПОЛУПРОВОДНИКОВЫЙ, транзистор
- ТЬЮРИНГА МАШИНА
- УЗЛОВОЙ СПИСОК
- «УМ1-НХ»
- УНИВЕРСАЛЬНАЯ СИСТЕМА ЭЛЕМЕНТОВ ПРОМЫШЛЕННОЙ ПНЕВМОАВТОМАТИКИ (УСЭППА)
- UNCOL
- УПОРЯДОЧЕНИЕ МАССИВА
- УПРАВЛЕНИЕ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- УПРАВЛЕНИЕ ДАННЫМИ
- УПРАВЛЕНИЕ ЗАПАСАМИ
- УПРАВЛЕНИЕ КОМАНДАМИ
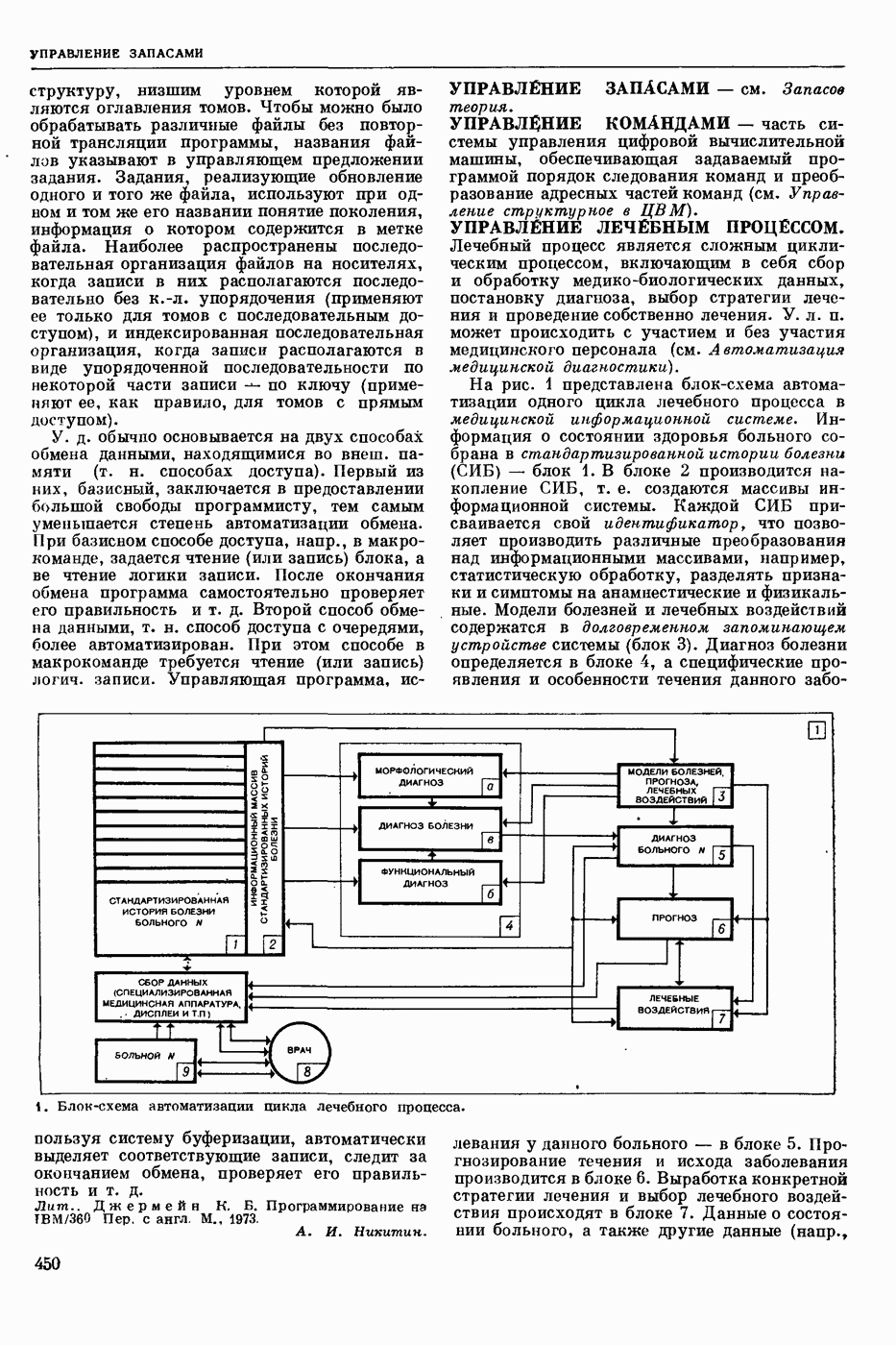
- УПРАВЛЕНИЕ ЛЕЧЕБНЫМ ПРОЦЕССОМ.
- УПРАВЛЕНИЕ ОПЕРАЦИЯМИ
- УПРАВЛЕНИЕ ОПТИМАЛЬНОЕ
- УПРАВЛЕНИЕ ПРОГРАММНОЕ
- УПРАВЛЕНИЕ С АДАПТАЦИЕЙ
- УПРАВЛЕНИЕ СТРУКТУРНОЕ В ЦВМ
- УПРАВЛЕНИЯ ОТНОШЕНИЕ, зависимости отношение
- УПРАВЛЕНИЯ СЛУЧАЙНЫМИ ПРОЦЕССАМИ ТЕОРИЯ
- УПРАВЛЯЮЩАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- УПРАВЛЯЮЩАЯ ПРОГРАММА
- УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, регулирующее воздействие
- «УПРАВЛЯЮЩИЕ СИСТЕМЫ И МАШИНЫ»
- УРАВНЕНИЙ КЛАССИФИКАЦИЯ.
- УРАВНОВЕШИВАНИЯ МЕТОДЫ
- «УРАЛ»
- УСИЛИТЕЛЬ
- УСИЛИТЕЛЬ ДИФФЕРЕНЦИАЛЬНЫЙ
- УСИЛИТЕЛЬ ОПЕРАЦИОННЫЙ, усилитель решающий
- УСИЛИТЕЛЬ ОТРАБАТЫВАЮЩИЙ
- УСИЛИТЕЛЬ РЕШАЮЩИЙ
- УСЛОВИЯ СТАЦИОНАРНОСТИ
- УСЛОВИЯ ТРАНСВЕРСАЛЬНОСТИ
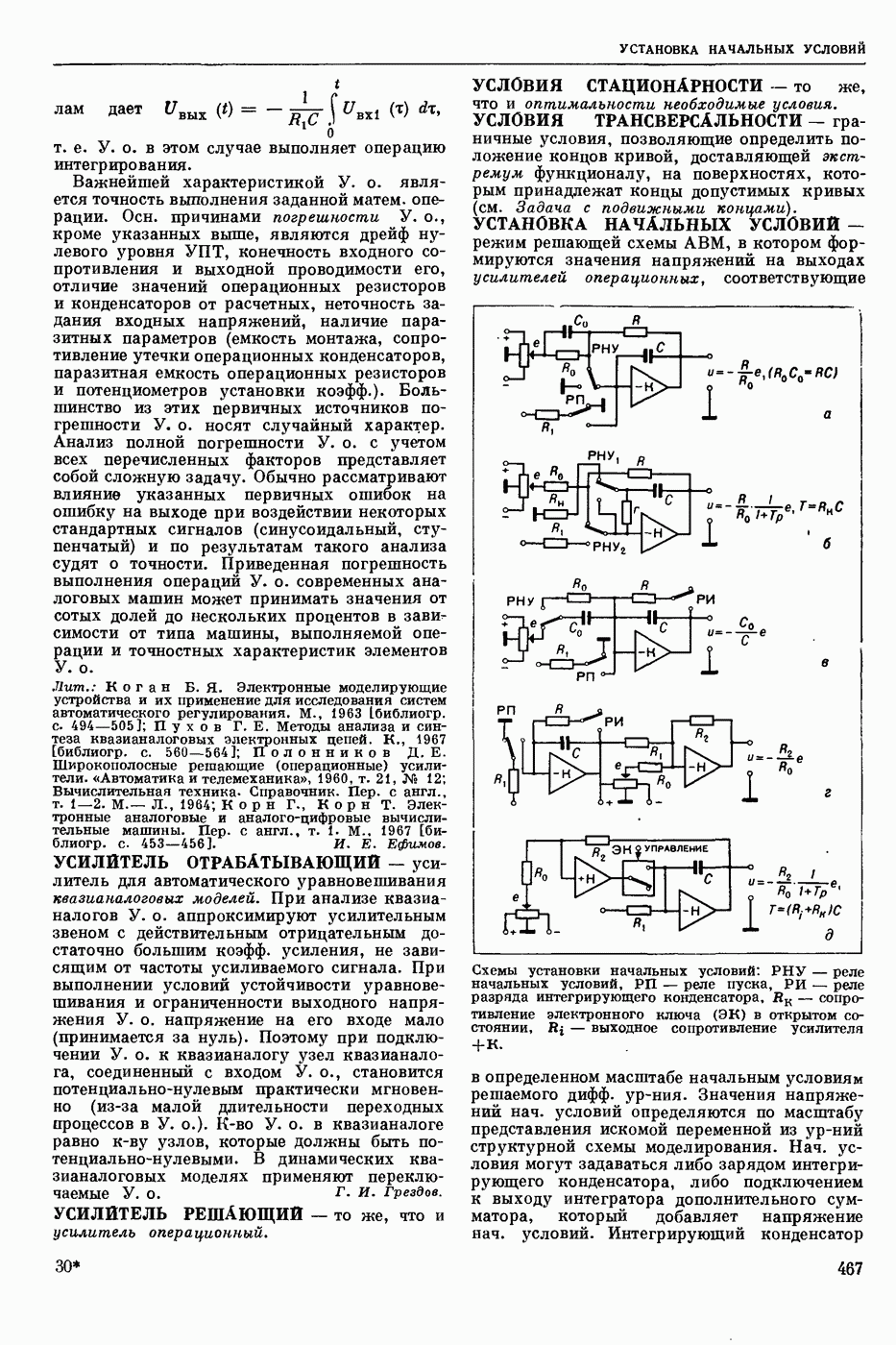
- УСТАНОВКА НАЧАЛЬНЫХ УСЛОВИЙ
- УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ КРИТЕРИИ
- УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
- УСТОЙЧИВОСТЬ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ
- УСТОЙЧИВОСТЬ МОДЕЛИ
- УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ
- УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ
- УСТОЙЧИВОСТЬ ЧИСЛЕННОГО МЕТОДА
- УСТРОЙСТВА ВВОДА—ВЫВОДА ДАННЫХ ЦВМ
- УСТРОЙСТВА ЗАПИСИ АНАЛОГОВОЙ ИНФОРМАЦИИ
- УСТРОЙСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- УСТРОЙСТВО ИНДИКАЦИИ ABM
- УСТРОЙСТВО ИНТЕГРИРУЮЩЕЕ, интегратор
- УСТРОЙСТВО ИНТЕГРО-ДИФФЕРЕНЦИРУЮЩЕЕ
- УСТРОЙСТВО ОБМЕНА ЦВМ
- УСТОЙСТВО ПЕРЕЗАПИСИ ДЛЯ ЦВМ
- УСТРОЙСТВО УПРАВЛЕНИЯ ЦВМ
- УСТРОЙСТВО ЦИФРОВОЙ РЕГИСТРАЦИИ
- ФАЗОВОГО ПРОСТРАНСТВА МЕТОД
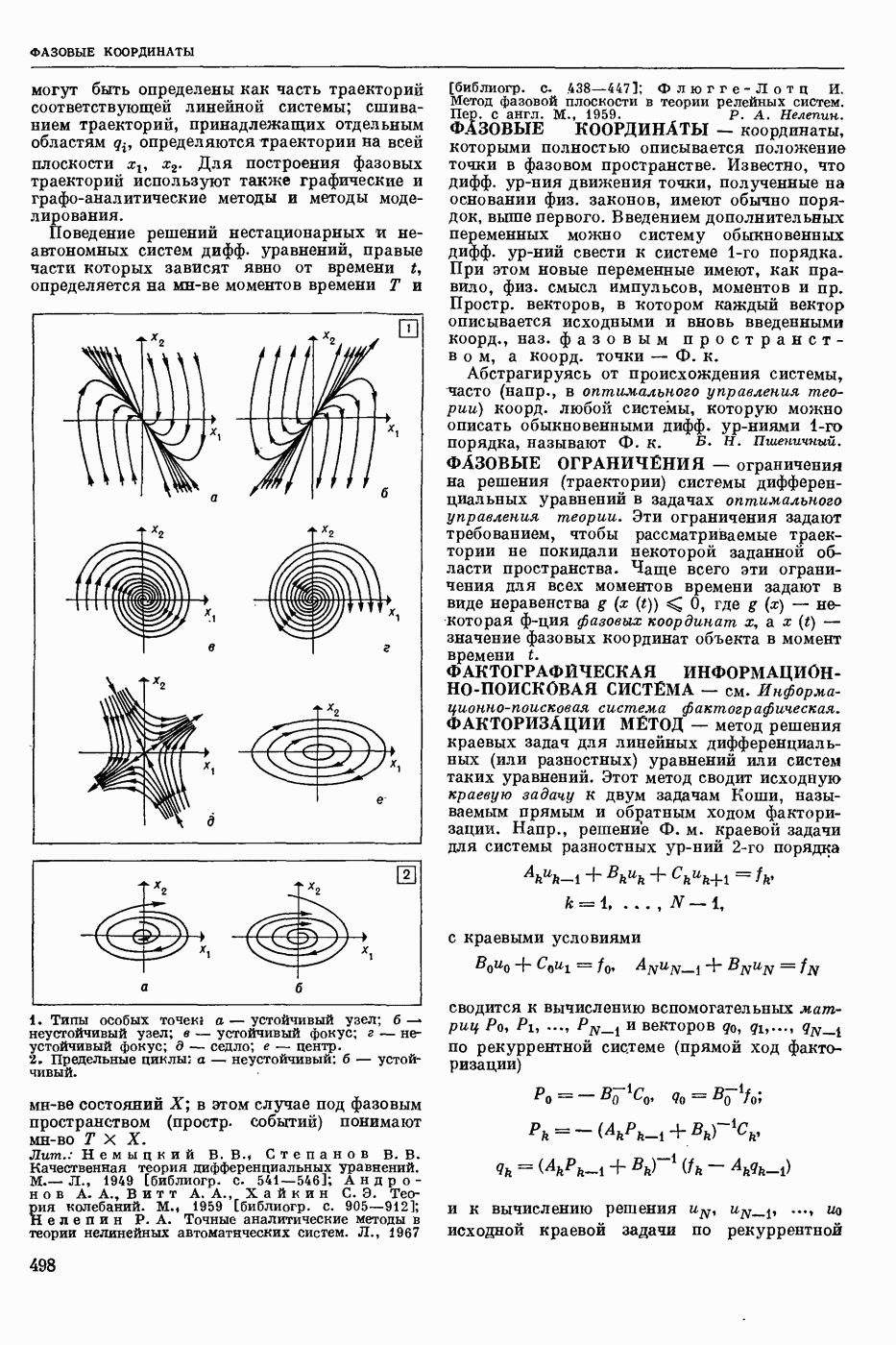
- ФАЗОВЫЕ КООРДИНАТЫ
- ФАЗОВЫЕ ОГРАНИЧЕНИЯ
- ФАКТОГРАФИЧЕСКАЯ ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ФАКТОРИЗАЦИИ МЕТОД
- «ФЕРРАНТИ» (Ferranti, Ltd)
- ФЕРРИТ-ДИОДНАЯ СИСТЕМА ЭЛЕМЕНТОВ
- ФЕРРИТ-ТРАНЗИСТОРНАЯ СИСТЕМА ЭЛЕ МЕНТОВ
- ФИКСАТОР, адрес второго ранга, косвенный адрес
- ФИКСИРОВАННАЯ ЗАПЯТАЯ
- ФИЛОСОФСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- ФИЛЬТР
- ФИЛЬТРАЦИЯ СЛУЧАЙНОГО ПРОЦЕССА
- ФОНД АЛГОРИТМОВ И ПРОГРАММ
- ФОНД СПРАВОЧНО-ИНФОРМАЦИОННЫЙ
- FORMAC
- ФОРМАЛИЗМ в математике
- ФОРТРАН
- «ФУДЗИЦУ» («Фудзи цусинки Сэйдзо», Fujitsu, Ltd)
- ФУНКЦИИ, СОХРАНЯЮЩИЕ КОНСТАНТУ
- ФУНКЦИИ, СОХРАНЯЮЩИЕ МНОЖЕСТВО
- ФУНКЦИИ, СОХРАНЯЮЩИЕ РАЗБИЕНИЕ
- ФУНКЦИОНАЛ
- ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ЭВМ
- ФУНКЦИОНАЛЬНЫЙ ЭЛЕМЕНТ ЭВМ
- ФУНКЦИЯ РАССТАНОВКИ
- ФУНКЦИЯ РЕШЕТЧАТАЯ
- ФУНКЦИЯ СТУПЕНЧАТАЯ
- ФУРЬЕ ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ФУРЬЕ ПРЕОБРАЗОВАНИЯ
- ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ в теории игр
- ХАРАКТРОН
- ХЕМИТРОН
- ХИНЧИНА-ПОЛАЧЕКА ФОРМУЛА
- «ХИТАЧИ» (Hitachi, Ltd)
- ХОМСКОГО ГРАММАТИКИ
- «ХОНИУЭЛЛ КОРПОРЕЙШЕН» (Honeywell Corporation)
- ХЭММИНГА КОД
- ЦВМ АСИНХРОННАЯ
- ЦВМ СИНХРОННАЯ
- ЦЕЛЕВАЯ ФУНКЦИЯ, функция цели
- ЦЕЛЕСООБРАЗНОСТЬ в кибернетике
- ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
- ЦЕНТРАЛЬНЫЙ ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ ИНСТИТУТ АКАДЕМИИ НАУК СССР
- ЦЕПИ СВЯЗАННЫЕ
- ЦЕПОЧКА
- ЦЕПЬ графа
- ЦЕПЬ ОКРУГЛЕНИЯ
- ЦЕПЬ ПЕРЕНОСА
- ЦИКЛ графа
- ЦИКЛ ПРОГРАММЫ
- ЦИКЛОМАТИЧЕСКОЕ ЧИСЛО
- ЦИПФА ЗАКОН
- ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ, преобразователи код
- ЦИФРО-АНАЛОГОВЫЙ КОМПЛЕКС, аналого-цифровой комплекс
- ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЦВМ)
- ЦИФРОВАЯ ИНТЕГРИРУЮЩАЯ МАШИНА
- ЦИФРОВАЯ МОДЕЛЬ СЕТЕВОГО ГРАФИКА
- ЦИФРОВОЙ ДИФФЕРЕНЦИАЛЬНЫЙ АНАЛИЗАТОР
- ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО
- ЧАСТПЧНО-РЕКУРСИВНЫЕ ФУНКЦИИ
- ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ЧЕБЫШЕВА ЗАДАЧА РАВНОМЕРНОГО ПРИБЛИЖЕНИЯ
- ЧЕЛОВЕК-ОПЕРАТОР
- ЧЕРЕДУЮЩАЯСЯ ЦЕПЬ
- ЧЕРНИЛА МАГНИТНЫЕ
- «ЧЕРНЫЙ ЯЩИК»
- ЧИРЧА ТЕЗИС
- ЧИСЛА ФОРМАТ
- ЧИСЛЕННЫЕ МЕТОДЫ
- ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
- ЧИТАЮЩИЙ АВТОМАТ, оптическое читающее устройство
- ЧИТАЮЩИЙ АВТОМАТ КОРРЕЛЯЦИОННЫЙ
- ЧУВСТВИТЕЛЬНОСТИ ТЕОРИЯ
- ШАГ КВАНТОВАНИЯ
- ШЕННОНА ЛАБИРИНТ
- ШЕННОНА МЫШЬ
- ШЕННОНА ФУНКЦИЯ
- ШЕПЛИ ВЕКТОР
- ШЕФФЕРА ШТРИХ, Шеффера функция, отрицание конъюнкции
- ШИНА
- ШИФРАТОР
- ШТРАФНАЯ ФУНКЦИЯ
- ШТРАФНЫХ ФУНКЦИЙ МЕТОД
- ШТРАФОВ МЕТОД
- ШУМ КВАНТОВАНИЯ
- ШУМ ПОИСКОВЫЙ
- ЭВРИСТИКА
- ЭВРИСТИЧЕСКИЕ МЕТОДЫ В РАСПОЗНАВАНИИ
- ЭЙЛЕРА ЦЕПЬ
- ЭКВИВАЛЕНТНАЯ СХЕМА
- ЭКВИВАЛЕНТНОСТИ ОТНОШЕНИЕ (эквивалентность, эквиваленци я) на множестве
- ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЭКВИВАЛЕНТНЫЕ СОСТОЯНИЯ АВТОМАТА
- ЭКВИВАЛЕНТНЫХ ВОЗМУЩЕНИЙ МЕТОД
- ЭКВИФИНАЛЬНОСТЬ СИСТЕМЫ УПРАВЛЕНИЯ
- ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ, в управлении народным хозяйством
- ЭКРАННЫЙ ПУЛЬТ
- ЭКСПЕРИМЕНТ БЕЗУСЛОВНЫЙ
- ЭКСПЕРИМЕНТ КРАТНЫЙ
- ЭКСПЕРИМЕНТ УСЛОВНЫЙ
- ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ СПОСОБЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
- ЭКСПЕРИМЕНТЫ С АВТОМАТАМИ
- ЭКСПЕРТНЫХ ОЦЕНОК МЕТОДЫ в прогнозировании
- ЭКСТРАПОЛИРОВАНИЕ В ОБУЧЕНИИ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ЭКСТРАПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ЭКСТРАПОЛИРОВАНИЕ ФУНКЦИЙ
- ЭКСТРЕМАЛЬ
- ЭКСТРЕМАЛЬНОЕ РЕГУЛИРОВАНИЕ
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ в теории графов
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ НА ГРАФАХ
- ЭКСТРЕМУМ
- ЭКСТРЕМУМ АБСОЛЮТНЫЙ
- ЭКСТРЕМУМ ГЛОБАЛЬНЫЙ
- ЭКСТРЕМУМ ЛОКАЛЬНЫЙ
- ЭКСТРЕМУМА ДРЕЙФ
- ЭЛЕКТРИЧЕСКИЕ МОДЕЛИРУЮЩИЕ СЕТКИ
- ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ТЕОРИЯ
- «ЭЛЕКТРОН»
- ЭЛЕКТРОННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЭВМ)
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЭЛЕМЕНТ ЗАДЕРЖКИ
- ЭЛЕМЕНТАРНАЯ СИСТЕМА
- ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ НАД СЛОВАМИ
- ЭЛЕМЕНТАРНЫЕ ТЕОРИИ.
- ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ЭЛЕМЕНТНЫЕ СТРУКТУРЫ НА ЛОГИЧЕСКИХ ЗАДЕРЖИВАЮЩИХ ЭЛЕМЕНТАХ
- ЭЛЕМЕНТНЫЙ СИНТЕЗ ЦВМ
- ЭЛИОНИКА
- ЭЛЛИПТИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- «ЭМИК-1»
- ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
- «ЭМСС»
- «ЭМУ»
- ЭНТРОПИЯ
- ЭНТРОПИЯ ЖИВЫХ СИСТЕМ
- ЭНТРОПИЯ СООБЩЕНИЯ при заданных условиях точности
- ЭПСИЛОН
- ЭПСИЛОН-ЭНТРОПИЯ
- ЭРГАТИЧЕСКАЯ СИСТЕМА
- ЭРГОДИЧЕСКАЯ ТЕОРИЯ
- ЭРГОДИЧЕСКОЕ СОСТОЯНИЕ
- ЭРЛАНГА ФОРМУЛЫ
- ЭТАЛОН в распознавании образов
- ЭТАЛОННОЕ НАПРЯЖЕНИЕ
- ЭФФЕКТИВНОСТЬ ИНФОРМАЦИОННОГО ПОИСКА техническая
- ЭШБИ ГОМЕОСТАТ
- «ЮНИВАК» (Univac)
- ЯДРО втеории игр
- ЯЗЫК АВТОМАТНЫЙ
- ЯЗЫК АЛГОРИТМИЧЕСКИЙ
- ЯЗЫК АНКЕТНЫЙ
- ЯЗЫК БЕСКОНТЕКСТНЫЙ, язык контекстно-свободный
- ЯЗЫК ДЕСКРИПТОРНЫЙ
- ЯЗЫК ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ
- ЯЗЫК ИНФОРМАЦИОННО-ПОИСКОВЫЙ
- ЯЗЫК ИНФОРМАЦИОННЫЙ
- ЯЗЫК ИСКУССТВЕННЫЙ
- ЯЗЫК КАТЕГОРИАЛЬНЫЙ
- ЯЗЫК ЛОГИЧЕСКИЙ для задания автоматов
- ЯЗЫК МАШИННО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК МАШИНЫ «МИР»
- ЯЗЫК ОПЕРАТОРНЫЙ
- ЯЗЫК ОПИСАНИЯ УСТРОЙСТВ ЦВМ
- ЯЗЫК ПРОМЕЖУТОЧНЫЙ
- ЯЗЫК ПРОЦЕДУРНО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК ТРАНСЛЯТОРА ВХОДНОЙ
- ЯЗЫК ЦВМ ВНУТРЕННИЙ
- ЯЗЫКА ИЗБЫТОЧНОСТЬ
- ЯЗЫКА ИНФОРМАЦИОННЫЕ ИЗМЕРЕНИЯ
- ЯЗЫКА МОДЕЛИ АНАЛИТИЧЕСКИЕ
- ЯЗЫКА МОДЕЛИ МАТЕМАТИЧЕСКИЕ
- ЯЗЫКА ЭНТРОПИЯ
- ЯЗЫКИ ЛОГИКО-МАТЕМАТИЧЕСКИЕ
- ЯЗЫКИ МАШИННЫЕ
- ЯЗЫКИ ПРОГРАММИРОВАНИЯ
- ЯЗЫКИ СПИСКОВЫЕ
- ЯЗЫКИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ
- ЯЗЫКИ ФОРМАЛЬНЫЕ
- ЯЗЫК — ПОСРЕДНИК
- ЯЧЕЙКА ЗАПОМИНАЮЩЕГО УСТРОЙСТВА