| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
СИСТЕМ ОБЩАЯ ТЕОРИЯ
— научное направление, связанное с разработкой совокупности философских, методологических, конкретно-научных и прикладных проблем анализа и синтеза сложных систем произвольной природы. Наиболее характерной чертой С. о. т., какую ей стремятся придать, создавая единую научную платформу, является ее междисциплинный характер. Основой для возможного единства принимают аналогичность (изоморфизм) процессов, протекающих в системах различного типа (тех., биол., эконом., социальных). Строго доказанный изоморфизм для систем различной природы дает возможность переносить знания из одной области в другую. Считают, что С. о. т. должна представлять собой область научных знаний, позволяющую изучать поведение, в т. ч. целенаправленное, систем любой сложности и любого назначения. Полагают также, что С. о. т. должна стать теоретическим фундаментом системотехники, т. к. (по мнению апологетов С. о. т.) системотехника еще не имеет своих научных методов и пользуется средствами и методами, заимствованными из других научных дисциплин. Амер. специалист в области создания С. о. т. М. Месарович сформулировал осн. требования, которым должна удовлетворять эта теория. Во-первых, она должна быть настолько общей, чтобы могла охватить многие уже существующие теории, касающиеся в том или ином разрезе теории систем. Как частные случаи из С. о. т. должны выводиться, напр., теория линейных динамических систем, теория автоматов конечных, алгоритмов теория и др. Во-вторых, С. о. т. должна иметь строго научный характер, ее термины и определения должны быть математически однозначны. Все это должно соответствовать ее назначению — изучать абстрактные модели соответствующих реальных систем. В-третьих, научное основание, на котором строится С. о. т., должно быть столь фундаментальным, чтобы ее выводы имели несомненную практическую ценность при изучении конкретных систем, встречающихся в жизни.Каждое из трех слов, входящих в название «систем общая теория», имеет свое определение, хотя по поводу слова «система» у ряда специалистов есть разногласия. 2-ое слово — «общая» — означает, что С. о. т. должна иметь дедуктивный характер и объединять другие теории — те, которые изучают системы в целом и те, которые рассматривают поведение систем (теорию управления, теорию адаптации, самоорганизации, обучения и т. д.). Считают, что объединение под названием С. о. т. всех этих научных теорий возможно только благодаря тому, что в С. о. т. используется более высокий уровень абстрагирования, чем в этих теория. Именно это обстоятельство дает возможность получить из С. о. т. все эти теории как частные случаи. Используемые в С. о. т. уровни абстрактного описания систем будут охарактеризованы как разъяснение термина «система». В С. о. т. используют наиболее абстрактные области математики (матем. ветвь семиотики, множеств теорию, абстрактную алгебру, общую топологию и др.). С. о. т. является в определенном отношении математической теорией, тесно связанной с теорией формальных систем, имея, однако, несоизмеримо более разноплановое назначение.
Слово «теория» в названии «С. о. т.» определяется в духе работ по математической логике и основаниям математики, в которых для введения термина «теория» предварительно дается понятие о классе элементарных высказываний — Р. «Теория» тогда определяется как подкласс  высказываний, которые считаются истинными.
высказываний, которые считаются истинными.
Различие между определением термина «теория» в названии С. о. т. и в работах по основаниям математики заключается только в том, что в С. о. т. не требуется, чтобы высказывания были правильными. При этом полагают, что истинность высказываний можно установить либо экспериментально — путем проверки следствий, вытекающих из «теории», либо на основании первично взятых аксиом.
По поводу слова «система» существовало много разногласий. Первоначально «систему» определяли как комплекс элементов, находящихся во взаимодействии (биолог-теоретик Л. Берталанфи в 1950), или как множество объектов вместе с отношениями между объектами и между их атрибутами (А. Холл и
Р. Ф. Фейджин) и т. д. Во всех такого рода определениях всегда подчеркивалось, что система представляет собой целостный комплекс взаимосвязанных элементов и что она имеет определенную структуру и взаимодействует с некоторой «средой».
Проблеме целостности в С. о. т. уделяется большое внимание. Само возникновение С. о. т. связано с известным спором между механистами и виталистами. Механисты утверждали, что все процессы в живом можно объяснить физ. и мех. законами без каких бы то ни было привлекаемых виталистами «жизненных сил», «энтилехии» и т. п. Особой остроты диспут достиг в связи с возможностью объяснить с общенаучных позиций целесообразное поведение живых организмов. Вся аргументация виталистов основывалась на том, что законы механики могут объяснить поведение динамической системы и определить ее конечное (финальное) состояние только при условии задания ее начального состояния. В живом же, говорили виталисты, проявляется принцип «эквифинальности», согласно которому вне зависимости от исходных начальных условий достигается интересующее, например, животного, конечное состояние. Целенаправленное поведение, утверждали они, характерно для живого, но отсутствует у машин и не объяснимо с позиций механики. Берталанфи подверг критике эти высказывания виталистов и на примерах из области хим. кинетики чисто математическим путем показал, что свойство «эквифинальности» может проявляться не только в живом (см. Эквифинальностъ системы управления). В период бурного развития кибернетики, когда были созданы разнообразные самонастраивающиеся, самоорганизующиеся и т. п. целесообразно действующие устройства, спор Берталанфи с виталистами стал выглядеть весьма наивным. Однако в свое время воззрения Берталанфи имели принципиальное значение и были весьма прогрессивными. Кроме вопроса об «эквифинальности», между виталистами и механистами возник спор и по поводу применимости к живым организмам второго начала термодинамики. Поскольку энтропия является в некоторой мере характеристикой «дезорганизованности» всякой системы, а живое существо, хотя бы в период своего роста и развития, повышает степень своей организации, то для живого второе начало термодинамики неприменимо, — утверждали виталисты и вновь приходили к заключению, что объяснить поведение живого лишь на основе законов физики и химии нельзя, т. е. нельзя обойтись без привлечения «жизненных сил», «энтилехии», или ч.-л. подобного. Берталанфи не трудно было доказать порочность подобных рассуждений, опираясь на тот, теперь общеизвестный, факт, что второе начало термодинамики справедливо только при изучении замкнутых систем (т. е. систем, не подверженных подводу к ним или отводу от них вещества и энергии), в то время как живые организмы — незамкнутые системы, При жизнедеятельности которых всегда происходит как подвод, так и отвод веществ и энергии.
Берталанфи выдвинул целую программу исследований незамкнутых систем, направленных на чисто научные методы доказательства существования определенных черт живого в системах, рассматриваемых как целое и состоящих из совокупности взаимодействующих элементов. Эту программу исследований он и назвал С. о. т. (общей теорией систем). К этим исходным посылкам, по мере развития других ветвей знаний, у Берталанфи и его последователей добавлялись и другие соображения. В настоящее время есть все основания говорить о тесном переплетении исследований по С. о. т. и кибернетике.
Обычно в усложнении научного анализа систем выделяют три этапа. Согласно этой градации, на первом этапе в науке рассматривалась «организованная простота» (механика), на втором — «беспорядочная сложность» (статистическая физика), на третьем - «организованная сложность» (С. о. т.). В поисках формального аппарата для С. о. т. в более поздний период ее развития (1962) обращались и к смежным дисциплинам. Сам Берталанфи включил в теоретическую часть С. о. т. — кибернетику, теорию информации игр теорию, теорию решений, топологию, факторный анализ, а в прикладную — системотехнику, операций исследование и психологию инженерную. В 1968 в теоретическую часть он еще добавил множеств теорию, теорию ячеек, графов теорию, теорию сетей, автоматов теорию, массового обслуживания теорию. Естественно, что при таком конгломеративном объединении многих дисциплин С. о. т. теряет свое научное лицо, и, ощущая это, Берталанфи вводит две трактовки для С. о. т. Первая из них именуется «С. о. т. в широком смысле», охватывая, по мнению Берталанфи, все перечисленные дисциплины. Вторая трактовка С. о. т. именуется «С. о. т. в узком понимании», ее стали называть абстрактной теорией систем (АТС).
Это второе направление является действительно специфичным для количественных исследований систем. Современное определение термина «система» связано именно с развитием АТС и им обусловлено. При этом следует учитывать, что определение термина «система» целиком вытекает из приведенного выше определения термина «теория» и полностью зависит от того, какая принята модель математическая реальной системы на базе постулированной «теории». Поскольку матем. моделей может быть сколь угодно много и все они определяются принятым уровнем абстрагирования, то нет и не может быть только одной формулировки для термина «система», т. к. определение этого термина в зависимости от принятого уровня абстрагирования является различным. Рассмотрение задач на каком-либо одном уровне абстракции позволяет дать ответы на определенную группу вопросов, а для получения ответов на другие вопросы необходимо провести исследование уже на другом уровне абстракции. Каждый из возможных
уровней АТС обладает ограниченными, присущими только данному уровню абстрагирования возможностями. Для достижения максимально возможной полноты сведений необходимо изучить одну и ту же систему на всех целесообразных для данного случая уровнях абстракции. С общефилософской точки зрения следует считать, что реальные системы неисчерпаемы в своих свойствах, и для познания действительности необходимо использовать те или иные уровни абстрагирования. Обзор современного состояния математики и работ по АТС позволяет утверждать, что наиболее пригодными являются следующие уровни абстрактного описания систем: 1) символический или, иначе, лингвистический; 2) теоретико-множественный; 3) абстрактно-алгебраический; 4) топологический; 5) логико-математический; 6) теоретико-информационный; 7) динамический; 8) эвристический. Поэтому построение АТС сводится к детальному рассмотрению тех формальных возможностей, какие представляются при изучении систем на соответствующем уровне абстрактного описания, и выяснению тех вопросов, на которые можно ответить при рассмотрении задач на каждом из уровней.
Лингвистический уровень описания — наиболее высокий уровень абстрагирования, из которого, как частные случаи, можно получить другие уровни абстрактного описания систем более низкого ранга. Процесс формализации в математике обычно понимают как отвлечение от изменчивости рассматриваемого объекта. Поэтому формальные построения тогда наиболее успешно могут быть использованы, когда удается с предметами или процессами данной области действительности каким-то образом сопоставить некоторые стабильные, неизменные понятия, в силу чего становится возможным выявить взаимоотношения, существующие между этими понятиями, а тем самым вскрыть связи, наблюдаемые в реальной действительности. Для обозначения вводимых понятий используют те или иные символы и устанавливают правила оперирования с ними, некоторая совокупность символов и правил пользования ими образуют абстрактный язык.
Понятие о высказывании на данном абстрактном языке означает, что имеется некоторое предложение (формула), построенное по грамматическим правилам данного языка, причем предполагается, что эта формула содержит варьируемые переменные, называемые конституэнтами, которые только при определенном их значении делают данное высказывание истинным. Если имеется множество К высказываний, но только М из них истинны, то говорят, что имеется теория Т относительно К множеств. Если же предполагается, что конституэнты в этих М высказываниях суть некоторые формально определяемые величины, то такие высказывания именуют правильными. С помощью этих понятий и дается определение термина «система». На лингвистическом уровне абстрактного описания, по М. Месаровичу, системой наз. множество правильных высказываний. Все высказывания делят обычно на два типа. К первому причисляют термы (имена предметов, члены предложения и т. д.), с помощью которых обозначают объекты исследования, а ко второму — функторы, определяющие отношения между термами. С помощью термов и функторов можно показать, как из лингвистического уровня абстрактного описания (уровня высшего ранга), как частный случай, возникает теоретико-множественный уровень абстрагирования (уровень более низкого ранга), еслиуюлагать, что термы суть некоторые множества S, с помощью которых перечисляют элементы или, иначе, подсистемы изучаемых систем, а функторы устанавливают характер отношений между введенными в описании множествами. По Н. Бурбаки (псевдоним группы франц. математиков), множество образуется из элементов, обладающих некоторыми свойствами и находящимися в некоторых отношениях между собой и с элементами других множеств. Сложные системы управления вполне подходят под такого рода определение понятия «множество», и это убеждает в том, что построение АТС на теоретикомножественном уровне абстракции вполне уместно и целесообразно. На теоретико-множественном языке определение термина «система» дается следующим образом. Система есть собственное подмножество  , где X — прямое (декартово) произведение множеств
, где X — прямое (декартово) произведение множеств  Как известно, декартовым произведением рнда множеств наз. множество конечных наборов таких элементов
Как известно, декартовым произведением рнда множеств наз. множество конечных наборов таких элементов  что
что  . Это и записывается в виде выражения
. Это и записывается в виде выражения  Каждый элемент
Каждый элемент  множества
множества  в свою очередь, может быть множеством, что позволяет описывать весьма сложные системы. Как на пример реальной системы, изученной на теоретико-множественном языке, можно указать на кибернетическую систему управления предприятием, которую описал англ. ученый С. Бир. Он пытался установить аналогию, существующую, по его мнению, между структурой естественного мозга и «искусственного мозга», создаваемого для целей кибернетического управления производством. Не отрицая безусловной полезности такого рода исследований, следует осознавать, что на теоретико-множественном уровне абстрагирования можно получить только общие сведения о реальных системах, а для более конкретных целей необходимы другие абстрактные модели, которые бы позволяли производить более тонкий анализ различных свойств реальных систем. Это и вызвало к жизни появление многих других способов описания систем, использующих различные иные способы абстрактного описания. Эти, более низкого ранга, уровни абстрагирования, в свою очередь, являются уже частными случаями по отношению к теоретико-множественному уровню абстрактного описания систем. Так, напр., если связи между элементами рассматриваемых мн-в устанавливаются с помощью некоторых однозначных функций, отображающих элементы
в свою очередь, может быть множеством, что позволяет описывать весьма сложные системы. Как на пример реальной системы, изученной на теоретико-множественном языке, можно указать на кибернетическую систему управления предприятием, которую описал англ. ученый С. Бир. Он пытался установить аналогию, существующую, по его мнению, между структурой естественного мозга и «искусственного мозга», создаваемого для целей кибернетического управления производством. Не отрицая безусловной полезности такого рода исследований, следует осознавать, что на теоретико-множественном уровне абстрагирования можно получить только общие сведения о реальных системах, а для более конкретных целей необходимы другие абстрактные модели, которые бы позволяли производить более тонкий анализ различных свойств реальных систем. Это и вызвало к жизни появление многих других способов описания систем, использующих различные иные способы абстрактного описания. Эти, более низкого ранга, уровни абстрагирования, в свою очередь, являются уже частными случаями по отношению к теоретико-множественному уровню абстрактного описания систем. Так, напр., если связи между элементами рассматриваемых мн-в устанавливаются с помощью некоторых однозначных функций, отображающих элементы
мн-ва в само исходное мн-во, то приходим к абстрактно-алгебраическому уровню описания систем. В таких случаях говорят, что между элементами мн-в установлены нульарные, унарные, бинарные, тернарные и т. д. отношения.
Если же на элементах рассматриваемых множеств определены некоторые топологические структуры, то в этом случае приходим к топологическому уровню абстрактного описания систем, причем может быть использован язык общей топологии или ее ветвей, именуемых гомологической топологией, алгебраической топологией и т. д. Выбор подходящего уровня абстрактного описания при изучении той или иной реальной системы является всегда наиболее ответственным и трудным шагом в теоретико-системных построениях. Эта часть исследования почти не поддается формализации и во многом зависит от эрудиции исследователя, его профессиональной принадлежности, целей исследования и т. д. Наибольшее значение в АТС придается именно абстрактно-алгебраическому уровню описания систем. На этом языке термин «система» определяют как «некоторое отношение R, определенное на декартовом произведении множеств X». Следовательно, система определяется заданием  , где
, где  и семейством отношений (напр., бинарных, тернарных и т. д.)
и семейством отношений (напр., бинарных, тернарных и т. д.)

Если затем эти отношения подвергаются еще и дополнительным ограничениям, то приходят к тем или иным абстрактно-алгебр. структурам — группам, полугруппам, кольцам, модулям и пр., с помощью которых описываются соответствующие системы. Показано, что существенное продвижение в деле построения АТС возможно на основе использования модулей над кольцом полиномов. При использовании их удается построить общую теорию, которая с единой точки зрения охватывает такие ранее развивавшиеся совершенно порознь ветви знаний, как теория конечных автоматов и теория линейных динамических систем. Достигается это путем введения более обобщенного понятия о динамической системе, чем то, которое ранее использовалось в науке. Чтобы дать строгое матем. определение понятию «динамическая система», ее наделяют свойством иметь «входы» и «выходы», т. е. определяют как некоторый структуированный объект, куда в определенные моменты времени можно вводить вещество, энергию и информацию, а в другие моменты времени — выводить их. Динамические системы можно представить и как системы, где процессы протекают непрерывно, и как системы, в которых все процессы совершаются только в дискретные моменты времени. При этом в обоих случаях предполагают, что поведение системы можно анализировать на некотором интервале времени, а это непосредственно и определяет прилагательное «динамическая» в термине «динамическая система». Предполагают также, что в системе 2 вход и  не может быть произвольным (напр., бесконечно большим), а должен принадлежать ограниченному мн-ву значений, так что всегда и
не может быть произвольным (напр., бесконечно большим), а должен принадлежать ограниченному мн-ву значений, так что всегда и  . Аналогичным образом определяют и выходы у (t). они все также должны принадлежать фиксированному мн-ву, т. е.
. Аналогичным образом определяют и выходы у (t). они все также должны принадлежать фиксированному мн-ву, т. е.  . Более того, предполагают, что выходы не могут быть произвольными и по характеру своего изменения, а должны входить в ограниченный и вполне определенный класс ф-ций Q, действующих на заданном интервале времени
. Более того, предполагают, что выходы не могут быть произвольными и по характеру своего изменения, а должны входить в ограниченный и вполне определенный класс ф-ций Q, действующих на заданном интервале времени  . Кроме того, вводится понятие «состояние системы», характеризующее ее внутреннее свойство. Знание его как
. Кроме того, вводится понятие «состояние системы», характеризующее ее внутреннее свойство. Знание его как  в совокупности со знанием входного сигнала и
в совокупности со знанием входного сигнала и  , действующего в момент времени
, действующего в момент времени  определяют выходной сигнал
определяют выходной сигнал  в некоторый последующий момент времени t, т. е.
в некоторый последующий момент времени t, т. е.

 — заданная функциональная связь между переменными, указанными в скобках. Заданием
— заданная функциональная связь между переменными, указанными в скобках. Заданием  предопределяется мн-во Г возможных значений выходных ф-ций у (t). В определение термина «динамическая система» входит и способ определения нового состояния системы
предопределяется мн-во Г возможных значений выходных ф-ций у (t). В определение термина «динамическая система» входит и способ определения нового состояния системы  в последующий момент времени
в последующий момент времени  на основе знания состояния системы
на основе знания состояния системы  в предшествующий момент времени и знания выходного сигнала и
в предшествующий момент времени и знания выходного сигнала и  т. е.
т. е.

где  - также заданная функциональная связь между указанными переменными.
- также заданная функциональная связь между указанными переменными.
Следовательно, определение термина «динамическая система» сводится к заданию восьмерки величин

Как видим, оно весьма похоже на определение «конечного автомата», но в действительности шире, т. к. позволяет получить, как частные случаи, и теорию конечных автоматов, и теорию линейных непрерывных динамических систем. Приведенное определение является весьма общим, и для того, чтобы можно было проводить плодотворный анализ, необходимо ввести соответствующие доопределения (конечномерность, линейность, стационарность и др.). Однако все задачи можно решать для определенной выше динамической системы, а затем лишь указывать связи между соответствующими величинами, при которых динамическая система становится либо конечным автоматом, либо линейной непрерывной динамической системой, обычно изучаемой в классической теории управления. Задачи, рассматриваемые для подобной динамической системы — традиционны, это — вопросы устойчивости, идентификации объектов и состояний, автономности, инвариантности, оптимальности, наблюдаемости и управляемости условия и т. д. Есть, однако, и новые задачи, например, задача реализуемости, связанная с проблемой принципиальной осуществимости абстрактной динамической реальной системы, определенной выше. Специфика развиваемой в АТС теории заключается прежде всего в том,
что различные множества, входящие в определение динамической системы (X, U и др.), наделены свойствами топологических пространств, а ф-ции отображения  непрерывны относительно соответствующих топологий. Это позволило вскрыть много ранее неизвестных фактов и сделать ряд обобщенных интерпретаций для некоторых известных понятий. Так, в совершенно иной трактовке можно представить хорошо известные из теории автоматического регулирования понятия: передаточная функция, свойство наблюдаемости для конечных автоматов и нелинейных непрерывных динамических систем и т. д. Особо же значимым является результат, показывающий, что язык теории модулей, возникающий на базе обобщения теории полугрупп путем введения двух дополнительных операций (свертывания и суммирования), позволяет заменить изучение динамической системы изучением соответствующей алгебраической структуры. Все это свидетельствует о том, что АТС позволяет получать новые результаты для вполне четко очерченного класса систем, делать соответствующие обобщения, и это в полной мере подтверждает плодотворность построения абстрактных теорий для изучения сложных систем произвольной природы. Язык теории отношений и абстрактной алгебры позволяет формализовать и такие понятия, как цель, принятие решений, целенаправленное поведение, адаптация, обучение, самообучение, самоорганизация и пр. (об информационном уровне абстрактного описания систем см. Семиотика, Информации теория; о логикоматематическом уровне — см. Логика математическая, Семантика логическая; об эвристическом уровне абстрактного описания систем см. Эвристика, Программирование эвристическое, Кибернетика техническая).
непрерывны относительно соответствующих топологий. Это позволило вскрыть много ранее неизвестных фактов и сделать ряд обобщенных интерпретаций для некоторых известных понятий. Так, в совершенно иной трактовке можно представить хорошо известные из теории автоматического регулирования понятия: передаточная функция, свойство наблюдаемости для конечных автоматов и нелинейных непрерывных динамических систем и т. д. Особо же значимым является результат, показывающий, что язык теории модулей, возникающий на базе обобщения теории полугрупп путем введения двух дополнительных операций (свертывания и суммирования), позволяет заменить изучение динамической системы изучением соответствующей алгебраической структуры. Все это свидетельствует о том, что АТС позволяет получать новые результаты для вполне четко очерченного класса систем, делать соответствующие обобщения, и это в полной мере подтверждает плодотворность построения абстрактных теорий для изучения сложных систем произвольной природы. Язык теории отношений и абстрактной алгебры позволяет формализовать и такие понятия, как цель, принятие решений, целенаправленное поведение, адаптация, обучение, самообучение, самоорганизация и пр. (об информационном уровне абстрактного описания систем см. Семиотика, Информации теория; о логикоматематическом уровне — см. Логика математическая, Семантика логическая; об эвристическом уровне абстрактного описания систем см. Эвристика, Программирование эвристическое, Кибернетика техническая).
АТС является еще молодой ветвью кибернетики, и ее становление происходит только в вастоящее время, хотя С. о. т. зародилась еще в 30-х годах 20 ст. и в 50-е годы сформировалась в самостоятельное широкое направление.
После первичных публикаций и периода «заговора молчания», когда, по собственному выражению основоположника С. о. т. Берталанфи, интеллектуальный климат в науке еще не содействовал развитию идей С. о. т., к 1954 положение дел изменилось в лучшую сторону. В то время в США было организовано «Общество исследований в области общей теории систем» («Society for General Systems Research»). Его организаторами были: биологи Л. Берталанфи, Р. Жерар и А. Раппопорт — специалист по матем. проблемам в области биологии и психологии, К. Боулдинг — экономист. Целью создания общества было: 1) исследовать изоморфизмы понятий, законов и моделей в различных областях науки с тем, чтобы переносить их из одной дисциплины в другую; 2) способствовать построению адекватных теоретических моделей для тех областей науки, в которых их нет; 3) минимизировать дублирование теоретических исследований в различных научных областях; 4) содействовать выявлению единства науки путем установления связей между специалистами различных научных направлений. Начиная с 1956 общество издает под редакцией Берталанфи и Раппопорта ежегодники «General Systems», в которых публикуются исследования, как правило, принципиального для С. о. т. характера. Несколько позже (1959) при Кейсовском технологическом институте (США) создан «Центр системных исследований». Корпорация «Интернейшенал бизнес машинз корпорейшет) в 1963 организовала Институт системных исследований (Systems Research Institute). Примерно в этот же период в США были организованы соответствующие отделы в таких организациях, как «RAND Corporation», «Systems Development Corporation» и др. Уже прошли десятки международных симпозиумов, специально посвященных С. о. т. (в США, Японии, СССР, Польше, Болгарии). Выходит целый ряд спец. изданий, таких как: «Mathematical systems theory», «IEEE transaction on systems science and cybernetics» (издание Американского ин-та радиоинженеров). Начиная с 1969 в СССР также издается ежегодник «Системные исследования», специально посвященный проблема тике С. о. т. Все это свидетельствует о том, что проблеме С. о. т. во всем мире уделяется большое внимание, хотя она еще и не продемонстрировала своих подлинных успехов в практических применениях.
Лит.: Системные исследования. М., 1969; Кухтенко А. И. Обзор основных направлений развития общей теории систем. В кн.: Материалы координационного совещания секции технической кибернетики Научного Совета по кибернетике АН УССР. К., 1969; Общая теория систем. Пер. с англ. М., 1966; Исследования по общей теории систем. М., 1969; System theory. New York, 1969; Bertalanffуl. von. General system theory. New York, 1969; Калман P., Фалб П., Арбиб М. Очерки по математической теории систем. Пер. с англ. М., 1971 [библиогр. с. 386—393]. А. И. Кухтенко.
| << Предыдущий параграф | Следующий параграф >> |
- МИХАЙЛОВА КРИТЕРИЙ
- МНОГОВАРИАНТНЫХ ЗАДАЧ РЕШЕНИЕ
- МНОГОГРАННОЕ МНОЖЕСТВО
- МНОГОГРАННЫЙ КОНУС
- МНОГОЗНАЧНЫЕ СХЕМЫ
- МНОГОКОНТУРНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОКРИТЕРИАЛЬНОСТИ ПРОБЛЕМА
- МНОГОМЕРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ РАЗДЕЛИТЕЛЬНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ УНИВЕРСАЛЬНЫЙ
- МНОГОПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ, мультипрограммная обработка информации
- МНОГОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- МНОГОШАГОВОГО ПРОЦЕССА ПРОИЗВОДСТВА МОДЕЛЬ
- МНОГОШАГОВОГО ПРОЦЕССА РАСПРЕДЕЛЕНИЯ МОДЕЛЬ
- МНОГОШАГОВЫЕ ЗАДАЧИ
- МНОГОЭТАПНОЕ ОБСЛУЖИВАНИЕ
- МНОЖЕСТВ ТЕОРИЯ
- МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- МОДЕЛИ ОБЪЕКТОВ РАСПОЗНАВАНИЯ
- МОДЕЛИ ПРОИЗВОДСТВА
- МОДЕЛИ РАВНОВЕСИЯ
- МОДЕЛИ РОСТА
- МОДЕЛИ ЭКОНОМИКИ
- МОДЕЛИРОВАНИЕ ВЕСТИБУЛЯРНОГО АНАЛИЗАТОРА
- МОДЕЛИРОВАНИЕ ВОСПРИЯТИЯ
- МОДЕЛИРОВАНИЕ ЖИВЫХ СИСТЕМ на молекулярном уровне
- МОДЕЛИРОВАНИЕ ИНЖЕНЕРНЫХ СЕТЕЙ НА АВМ
- МОДЕЛИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ МЫШЛЕНИЯ
- МОДЕЛИРОВАНИЕ НА СПЛОШНЫХ СРЕДАХ, электрическое моделирование
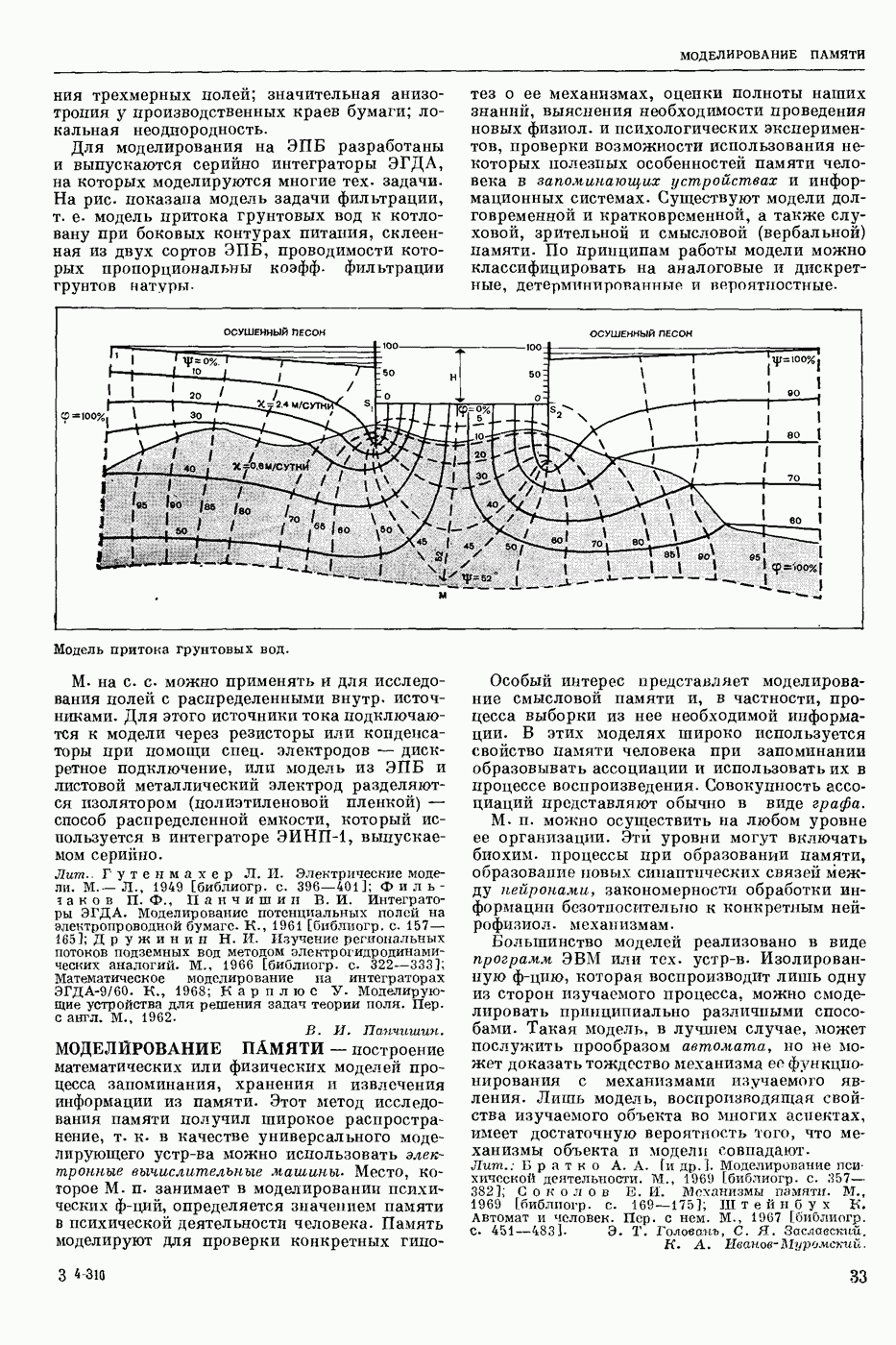
- МОДЕЛИРОВАНИЕ ПАМЯТИ
- МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАСПОЗНАВАНИЯ И ОБУЧЕНИЯ РАСПОЗНАВАНИЮ НА ЦВМ
- МОДЕЛИРОВАНИЕ ПСИХИЧЕСКИХ ФУНКЦИЙ
- МОДЕЛИРОВАНИЕ СЕНСОРНЫХ СИСТЕМ
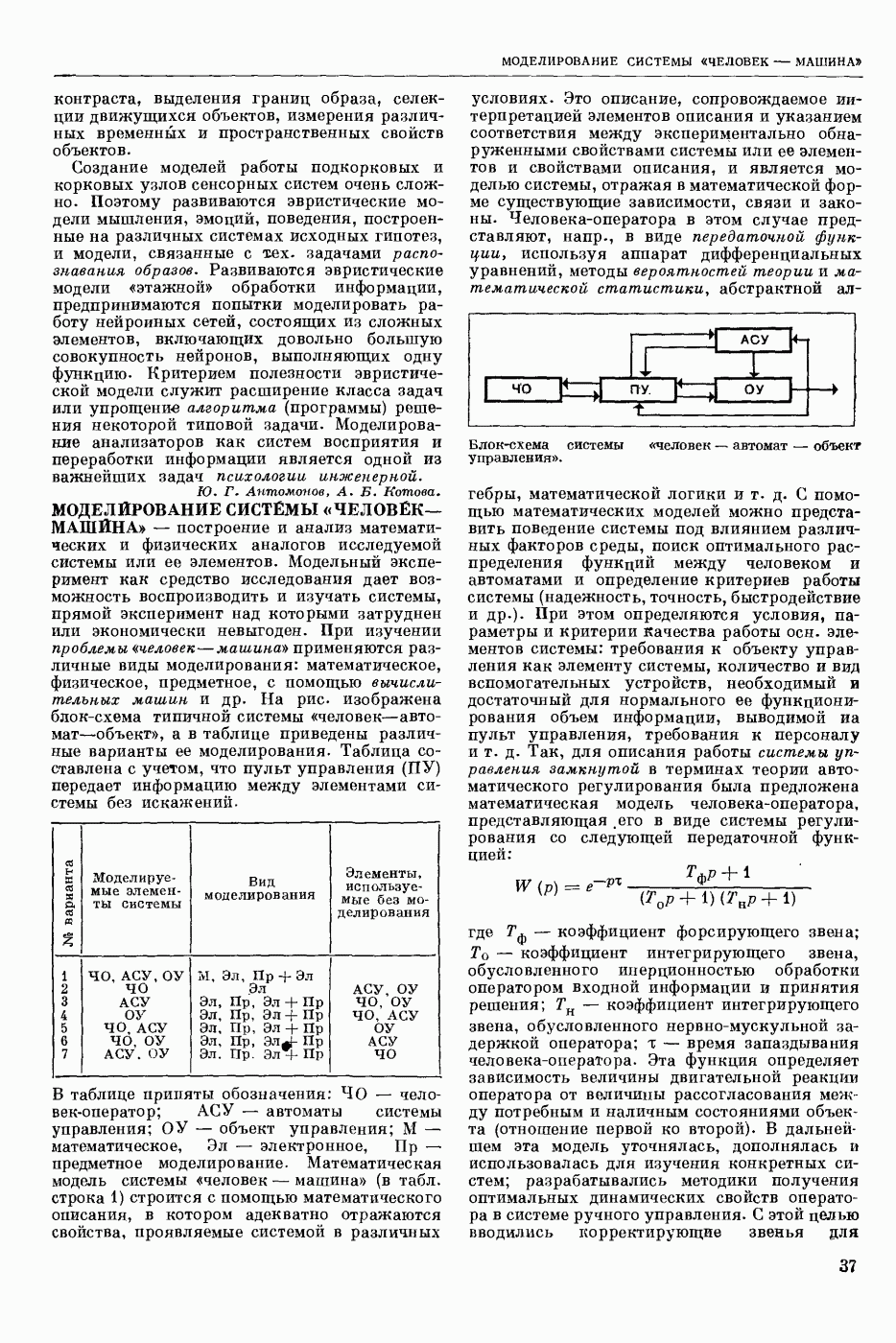
- МОДЕЛИРОВАНИЕ СИСТЕМЫ «ЧЕЛОВЕК—МАШИНА»
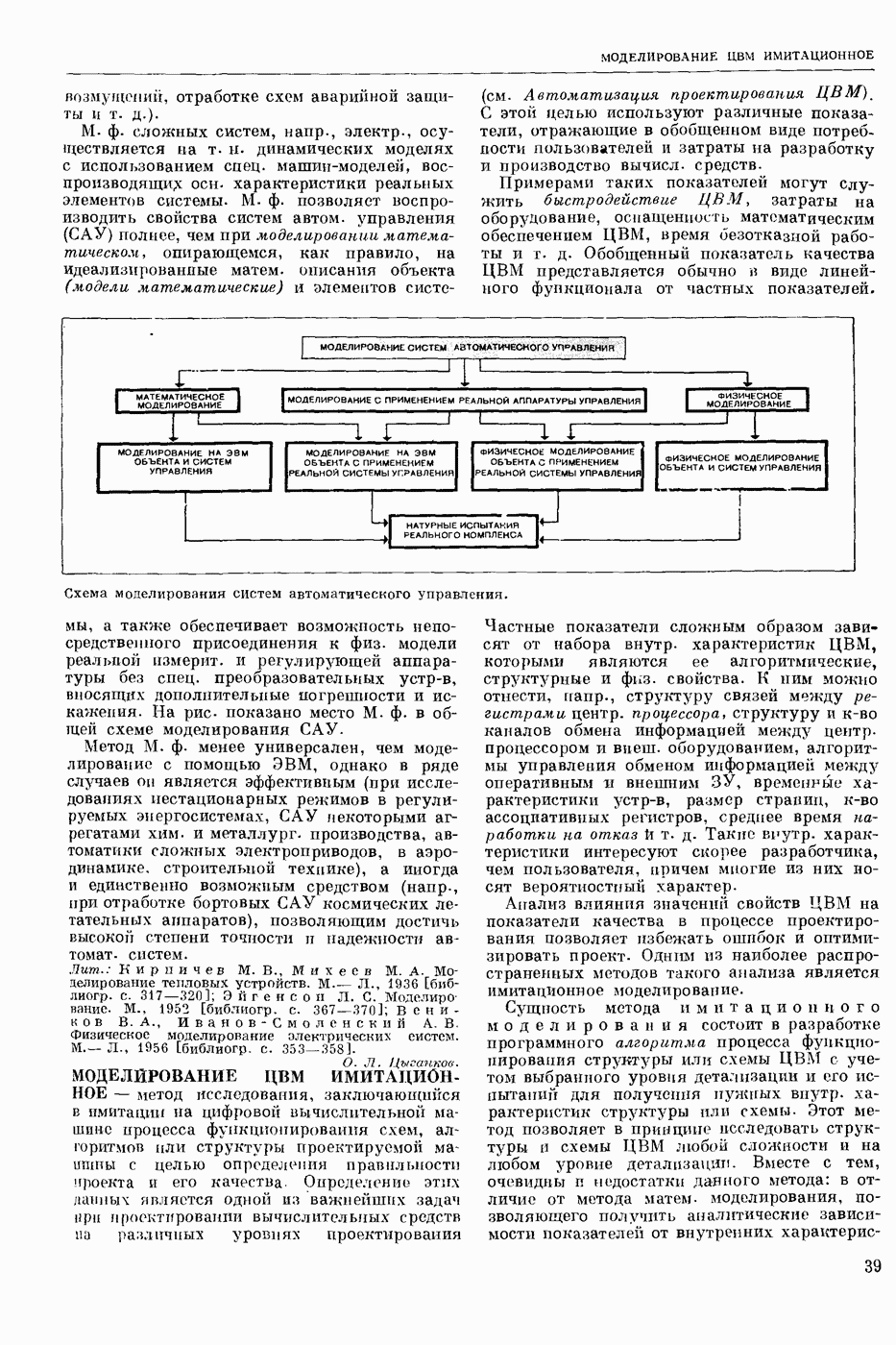
- МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ ЦВМ ИМИТАЦИОННОЕ
- МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ НА ЦВМ
- МОДЕЛЬ ЗРИТЕЛЬНОГО АНАЛИЗАТОРА
- МОДЕЛЬ МАТЕМАТИЧЕСКАЯ
- МОДЕЛЬ НЕРВНОЙ КЛЕТКИ
- МОДЕЛЬ ПЕРЕМЕННОЙ СТРУКТУРЫ
- МОДЕЛЬ СЛУХОВОГО АНАЛИЗАТОРА
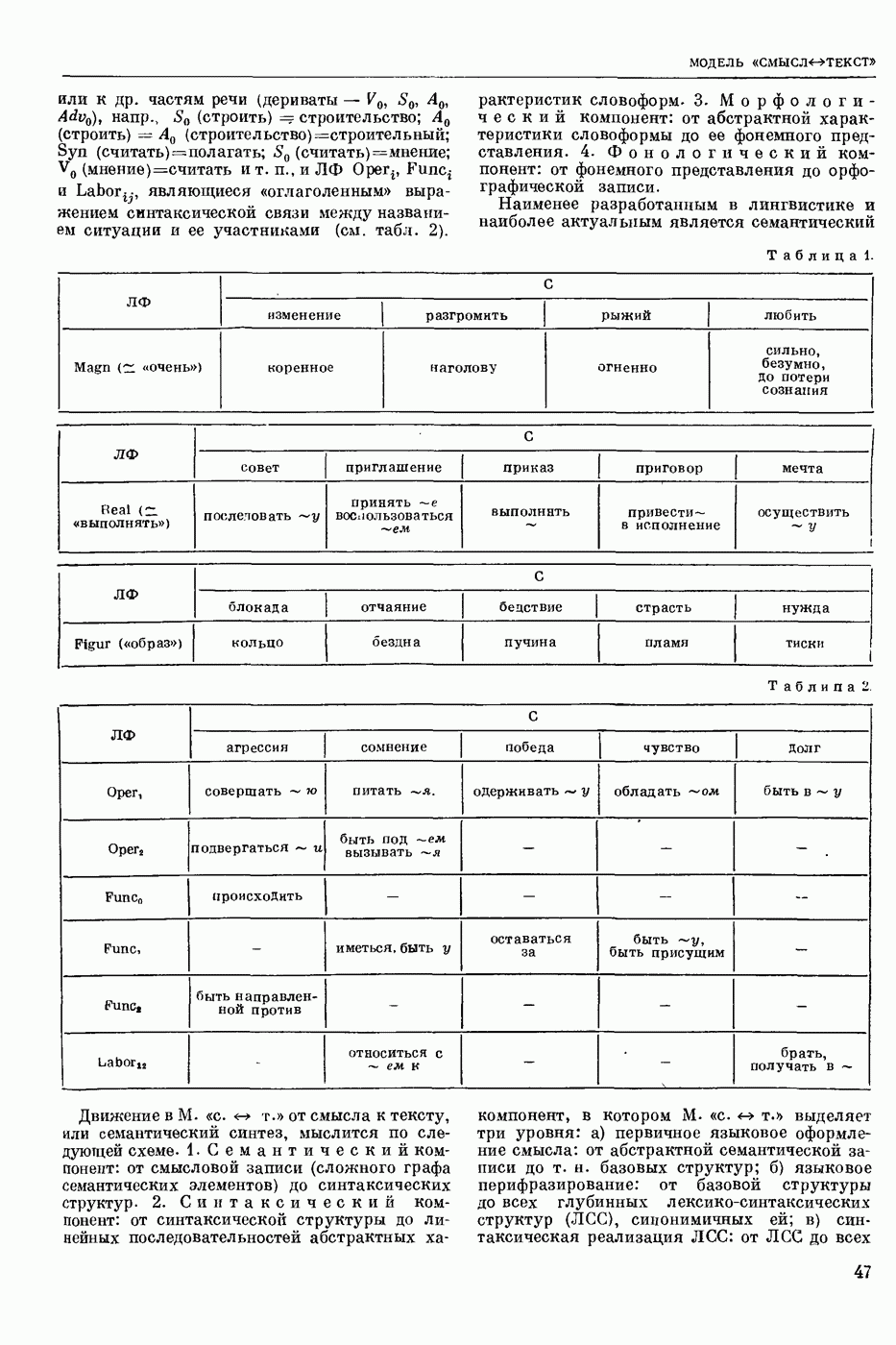
- МОДЕЛЬ «СМЫСЛ-ТЕКСТ»
- МОДЕЛЬ ФИЗИЧЕСКАЯ
- МОДЕЛЬ ЧУВСТВИТЕЛЬНОСТИ
- МОДУЛЯТОР
- МОДУЛЯЦИЯ ИМПУЛЬСНАЯ
- «МОЗГОВОЙ ШТУРМ»
- МОМЕНТОВ МЕТОД
- МОНИТОР
- МОНОТОННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- МОНТЕ-КАРЛО МЕТОД
- «МППИ-1», машина первичной переработки информации
- МУЛЬТИВИБРАТОР
- МУЛЬТИПРОГРАММИРОВАНИЕ
- МУЛЬТИПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- МУЛЬТИПРОЦЕССОРНЫЙ РЕЖИМ
- МУЛЬТИУСТОЙЧИВЫЕ СИСТЕМЫ
- МУРА АВТОМАТ
- МЫСЛИТЕЛЬНОЙ СПОСОБНОСТИ УСИЛИТЕЛЬ
- НАБЛЮДАЕМОСТИ И УПРАВЛЯЕМОСТИ УСЛОВИЯ
- НАБОРНОЕ ПОЛЕ
- НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НАДЁЖНОСТЬ КИБЕРНЕТИЧЕСКИХ СИСТЕМ
- НАДЁЖНОСТЬ РАСПОЗНАВАНИЯ
- НАИМЕНЬШИХ КВАДРАТОВ МЕТОД
- «НАИРИ»
- НАИСКОРЕЙШЕГО СПУСКА МЕТОД
- НАЙКВИСТА КРИТЕРИЙ
- НАКАПЛИВАЮЩИЕ СХЕМЫ
- НАКОПИТЕЛЬ, блок хранения информации
- НАКОПИТЕЛЬ НА МАГНИТНОЙ ЛЕНТЕ
- НАРАБОТКА НА ОТКАЗ
- НАРАБОТКА НА СБОЙ
- НАУКА УПРАВЛЕНИЯ
- НАУКОВЕДЕНИЕ
- НАУЧНАЯ ОРГАНИЗАЦИЯ ТРУДА (НОТ)
- НАУЧНО-ИНФОРМАЦИОННАЯ ДЕЯТЕЛЬНОСТЬ
- НАУЧНО-ТЕХНИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ
- НАУЧНО-ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ ОБРАБОТКА
- НАУЧНЫЙ СОВЕТ ПО КОМПЛЕКСНОЙ ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН СССР
- НАУЧНЫЙ СОВЕТ ПО ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН УССР
- НЕЗАВИСИМОСТЬ в теории вероятностей, статистическая независимость
- НЕЙРОБИОНИКА
- НЕЙРОКИБЕРНЕТИКА
- НЕЙРОН
- НЕЙРОН ФОРМАЛЬНЫЙ
- НЕЙРОННЫЕ СЕТИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫЕ ЗАДАЧИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- НЕЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ АВМ
- НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- НЕ НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НЕОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- НЕОДНОРОДНЫЙ ПОТОК В СЕТИ
- НЕОПРЕДЕЛЕННОСТЬ В УПРАВЛЕНИИ
- НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМЫ АКСИОМ, совместимость, корректность
- НЕРАЗРЕШИМЫЕ АЛГОРИТМИЧЕСКИЕ ПРОБЛЕМЫ
- «НИППОН ЭЛЕКТРИК КОМПАНИ» (Nippon Electric Company, Ltd)
- «ННБ», набор нелинейных блоков
- НОРМА ВЕКТОРА
- НОРМА МАТРИЦЫ
- НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- НОРМАЛЬНАЯ ФОРМА СОВЕРШЕННАЯ
- НОРМАЛЬНАЯ ФОРМА СОКРАЩЕННАЯ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- НОРМАЛЬНЫЕ АЛГОРИФМЫ, нормальные алгоритмы
- НОСИТЕЛЬ ИНФОРМАЦИИ
- НУЛЕВЫХ СОБСТВЕННЫХ ПРОВОДИМОСТЕЙ УЗЛОВ МЕТОД
- НУЛЬ-ОРГАН, сравнивающее устройство, компаратор
- НУМЕРАЦИЙ ТЕОРИЯ
- НЬЮТОНА ОБОБЩЕННЫЙ МЕТОД
- НЬЮТОНА ФОРМУЛЫ ИНТЕРПОЛИРОВАНИЯ
- ОБЛАСТЬ УПРАВЛЕНИЯ
- ОБЛЕГЧЁННОЕ РЕЗЕРВИРОВАНИЕ
- ОБОБЩЁННЫЕ ФУНКЦИИ
- ОБОБЩЕННЫХ ГРАДИЕНТОВ МЕТОД
- ОБРАБОТКА ДАННЫХ ПОСЛЕДОВАТЕЛЬНАЯ
- ОБРАБОТКА ДАННЫХ ПРОИЗВОЛЬНАЯ
- ОБРАБОТКА ИНФОРМАЦИИ В РЕАЛЬНОМ масштабе времени
- ОБРАБОТКА ИНФОРМАЦИИ В РЕЖИМЕ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- ОБРАБОТКИ ДАННЫХ СИСТЕМА
- ОБРАЗ, или распознаваемый класс, в кибернетике
- ОБРАТИМОСТИ ПРИНЦИП
- ОБРАТИМЫЕ ЭЛЕМЕНТЫ И МОДЕЛИ
- ОБРАТНАЯ СВЯЗЬ
- ОБРАТНЫХ ОПЕРАТОРОВ МЕТОД
- ОБУСЛОВЛЕННОСТИ ЧИСЛО
- ОБУЧАЮЩАЯ ВЫБОРКА
- ОБУЧАЮЩАЯ МАШИНА
- ОБУЧАЮЩАЯ ПРОГРАММА
- ОБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ОГРАНИЧЕНИЕ ФАЗОВЫХ КООРДИНАТ
- ОГРАНИЧИТЕЛЬ АМПЛИТУДЫ
- ОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- ОДНОРОДНЫЙ ПОТОК В СЕТИ
- ОДНОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ОКРУГЛЕНИЯ ПОГРЕШНОСТЬ
- ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ОЗУ)
- ОПЕРАТИВНОЕ РУКОВОДСТВО
- ОПЕРАТИВНО-ПРОИЗВОДСТВЕННАЯ ИНФОРМАЦИЯ
- ОПЕРАТОР
- ОПЕРАТОР АВТОМАТНЫЙ
- ОПЕРАТОР ЗАДЕРЖКИ
- ОПЕРАТОР ПРИСВАИВАНИЯ
- ОПЕРАТОР ЭЛЕМЕНТАРНЫЙ
- ОПЕРАТОР ЭЛЕМЕНТНЫЙ
- ОПЕРАТОРНАЯ СХЕМА
- ОПЕРАТОРНЫЕ УРАВНЕНИЯ
- ОПЕРАТОРНЫЙ МЕТОД ПРОГРАММИРОВАНИЯ
- ОПЕРАТОРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ОПЕРАТОРЫ ЛИНЕЙНЫЕ, линейные преобразования
- ОПЕРАЦИИ МАШИННЫЕ
- ОПЕРАЦИИ НАД МАССИВАМИ
- ОПЕРАЦИИ НАД СИМВОЛАМИ И СТРОКАМИ
- ОПЕРАЦИИ НАД ЧИСЛАМИ
- ОПЕРАЦИИ ИССЛЕДОВАНИЕ
- ОПЕРАЦИЙ СИСТЕМА
- ОПЕРАЦИОННАЯ СИСТЕМА
- ОПЕРАЦИЯ НАИМЕНЬШЕГО КОРНЯ
- ОПЕРАЦИЯ ПРИМИТИВНОЙ РЕКУРСИИ
- ОПИСАНИЕ ОБЪЕКТА РАСПОЗНАВАНИЯ
- ОПОРНОЕ НАПРЯЖЕНИЕ
- ОПОРНЫЙ ПЛАН
- ОПТИМАЛЬНАЯ ТОЧКА
- ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ТЕОРИЯ
- ОПТИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
- ОПТИМАЛЬНОСТИ НЕОБХОДИМЫЕ УСЛОВИЯ
- ОПТИМАЛЬНОСТИ ПРИНЦИП
- ОПТИМАЛЬНЫЙ ВЕКТОР
- ОПТИМАЛЬНЫХ ПАРАМЕТРОВ СИСТЕМЫ ВЫБОР
- ОПТИМАЛЬНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ОПТИМИЗАТОР АВТОМАТИЧЕСКИЙ
- ОПТИМИЗАЦИИ МЕТОДЫ численные
- «ОПТИМУМ»
- ОПТРОН
- ОРГАНИЗАЦИЯ ИНФОРМАЦИОННОГО МАССИВА
- ОРГАНИЗАЦИЯ УЧЕТА В АВТОМАТИЗИРОВАННЫХ СИСТЕМАХ УПРАВЛЕНИЯ
- ОРГАТЕХНИКА, организационная техника
- ОРДЕНА ЛЕНИНА ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- УПРАВЛЕНИЯ (АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ), ИАТ
- ОСТАНОВ
- ОСУЩЕСТВИМОСТИ ФИЗИЧЕСКОЙ КРИТЕРИИ
- ОСУЩЕСТВИМОСТИ ЦЕЛИ ПРИНЦИП
- ОТВЕТ РАСПОЗНАЮЩЕЙ СИСТЕМЫ
- ОТКАЗ ОТ РАСПОЗНАВАНИЯ
- ОТЛАДОЧНЫЕ ПРОГРАММЫ
- ОТНОШЕНИЕ
- ОТНОШЕНИЕ АНАЛИТИЧЕСКОЕ
- ОТНОШЕНИЕ БАЗИСНОЕ
- ОТНОШЕНИЕ ПАРАДИГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ ПРАВДОПОДОБИЯ
- ОТНОШЕНИЕ СИГНАЛ/ПОМЕХА
- ОТНОШЕНИЕ СИНТАГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ СИНТЕТИЧЕСКОЕ
- ОТНОШЕНИЕ ТЕКСТУАЛЬНОЕ
- ОТРИЦАНИЕ в алгебре логики
- ОЧЕРЕДЕЙ ТЕОРИЯ
- ОШИБКА В ПРИНЯТИИ ГИПОТЕЗ
- ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ОШИБОК ТЕОРИЯ
- ПАКЕТНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- ПАЛЬМА ПОТОК
- ПАМЯТИ ЗАЩИТА
- ПАМЯТИ РАСПРЕДЕЛЕНИЕ
- ПАМЯТЬ МАГАЗИННАЯ
- ПАМЯТЬ СТРАНИЧНАЯ
- ПАМЯТЬ ЦВМ
- ПАРАБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ
- ПАРАМЕТР ФАКТИЧЕСКИЙ
- ПАРАМЕТР ФОРМАЛЬНЫЙ
- ПАРАМЕТРОН
- ПАРЕТО ОПТИМУМ
- ПАЧКА ОШИБОК, пакет ошибок
- ПЕРЕВОД АВТОМАТИЧЕСКИЙ
- ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
- ПЕРЕДАЧИ ИНФОРМАЦИИ СКОРОСТЬ
- ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ПЕРЕРАБОТКА ИНФОРМАЦИИ В ЦВМ
- ПЕРЕХОДНЫЙ ПРОЦЕСС
- ПЕРИОД ЗАНЯТОСТИ в системах массового обслуживания
- ПЕРИФЕРИЙНОЕ ОБОРУДОВАНИЕ
- ПЕРСЕПТРОН
- «ПЕРТ»
- ПЕРФОРАТОР
- ПЕРФОРАЦИОННАЯ КАРТА, перфокарта
- ПЕРФОРАЦИОННАЯ ЛЕНТА, перфолента
- ПЕЧАТНАЯ СХЕМА
- ПИРСА СТРЕЛКА, функция Вебба, отрицание дизъюнкции
- ПЛ-1
- ПЛАВАЮЩАЯ ЗАПЯТАЯ
- ПЛАН-ГРАФИК
- ПЛАТЕЖНАЯ МАТРИЦА
- ПЛАТЕЖНАЯ ФУНКЦИЯ
- ПЛЕНКА МАГНИТНАЯ
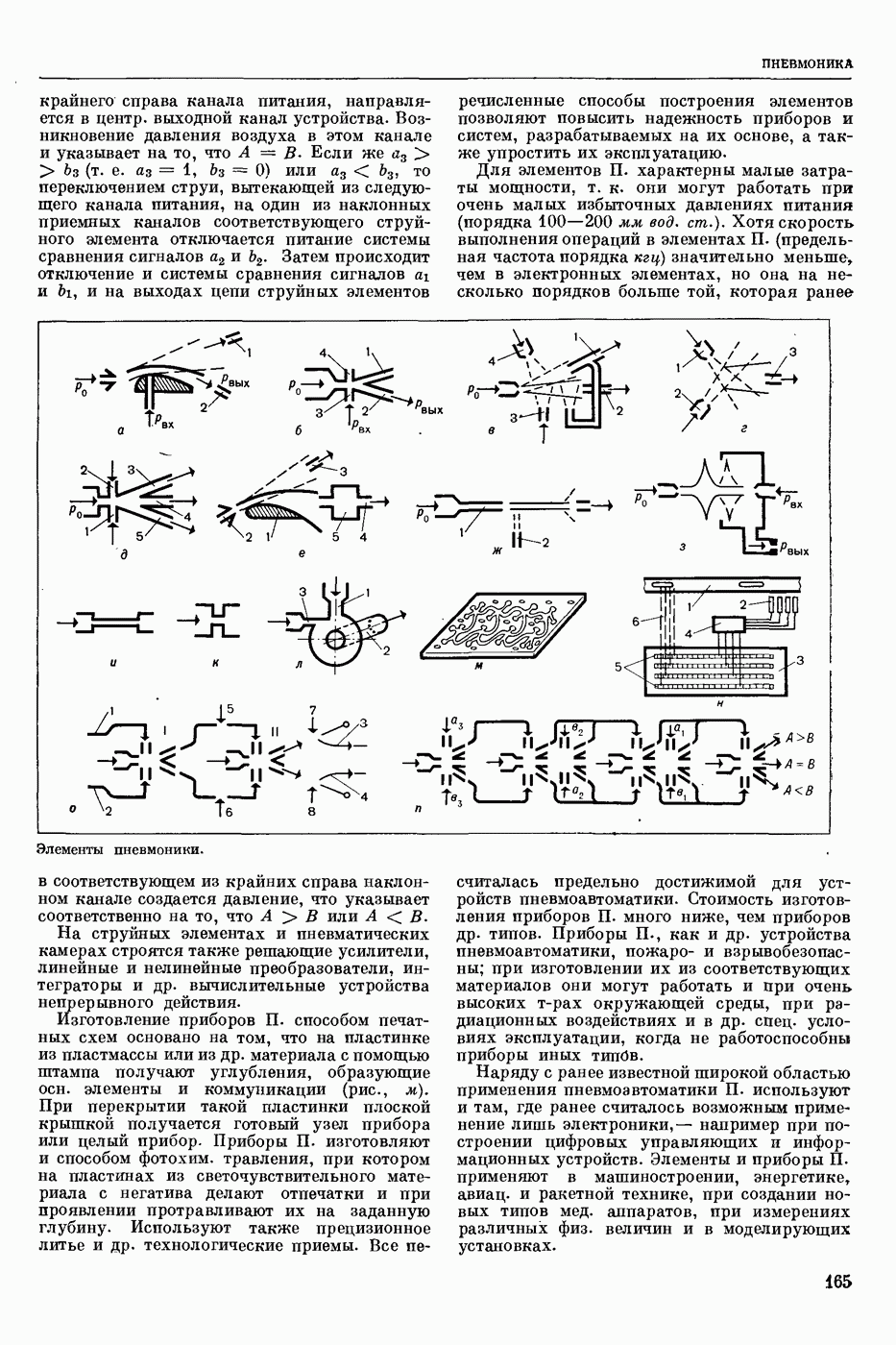
- ПНЕВМОНИКА, струйная пневмоавтоматика
- ПОВЕДЕНИЕ АВТОМАТОВ.
- ПОВЕДЕНИЕ АВТОМАТОВ В СЛУЧАЙНЫХ СРЕДАХ.
- ПОГЛОЩЕНИЯ ЗАКОН
- ПОГРЕШНОСТЕЙ ВЫЧИСЛЕНИЙ ТЕОРИЯ
- ПОГРЕШНОСТЬ
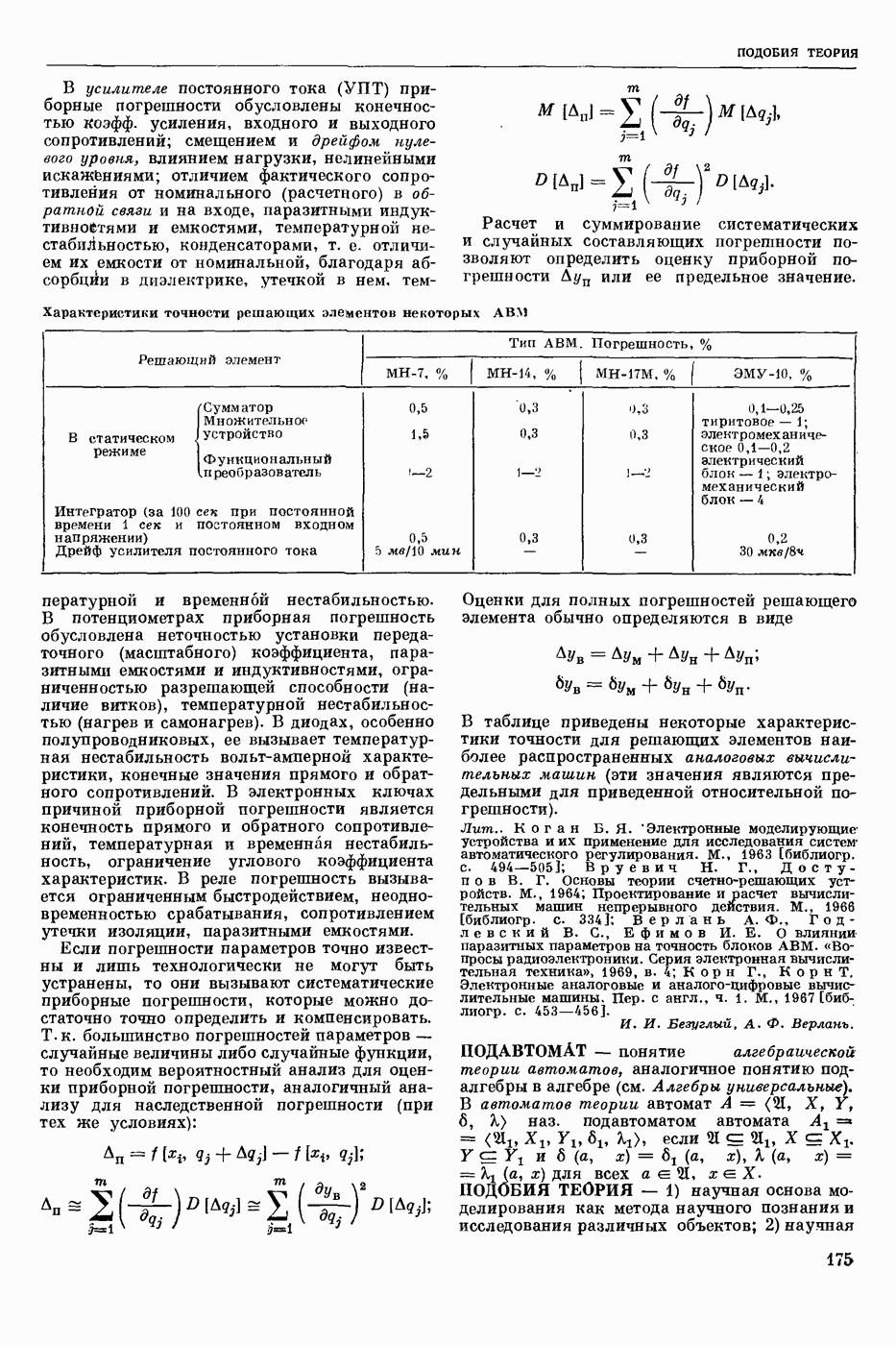
- ПОГРЕШНОСТЬ РЕШАЮЩЕГО ЭЛЕМЕНТА
- ПОДАВТОМАТ
- ПОДОБИЯ ТЕОРИЯ
- ПОДПРОГРАММА
- ПОДПРОГРАММА ЗАМКНУТАЯ
- ПОДПРОГРАММА ОТКРЫТАЯ
- ПОДПРОГРАММА СТАНДАРТНАЯ
- ПОДСИСТЕМА
- ПОИСК ИНФОРМАЦИИ АВТОМАТИЧЕСКИЙ
- ПОИСКА ЭКСТРЕМУМА ФУНКЦИЙ МЕТОДЫ
- ПОИСКОВОЕ ПРЕДПИСАНИЕ
- ПОИСКОВЫЙ МАССИВ
- ПОИСКОВЫЙ ОБРАЗ ДОКУМЕНТА
- ПОИСКОВЫЙ ОБРАЗ ЗАПРОСА
- ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ, экспоненциальное распределение
- ПОЛНОЙ ВЕРОЯТНОСТИ ФОРМУЛА
- ПОЛНОТА ФОРМАЛЬНОЙ ТЕОРИИ
- ПОЛНОТЫ ПРОБЛЕМА в теории автоматов
- ПОЛОС МЕТОД
- ПОЛУГРУППА, ассоциативная система
- ПОЛУМАРКОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
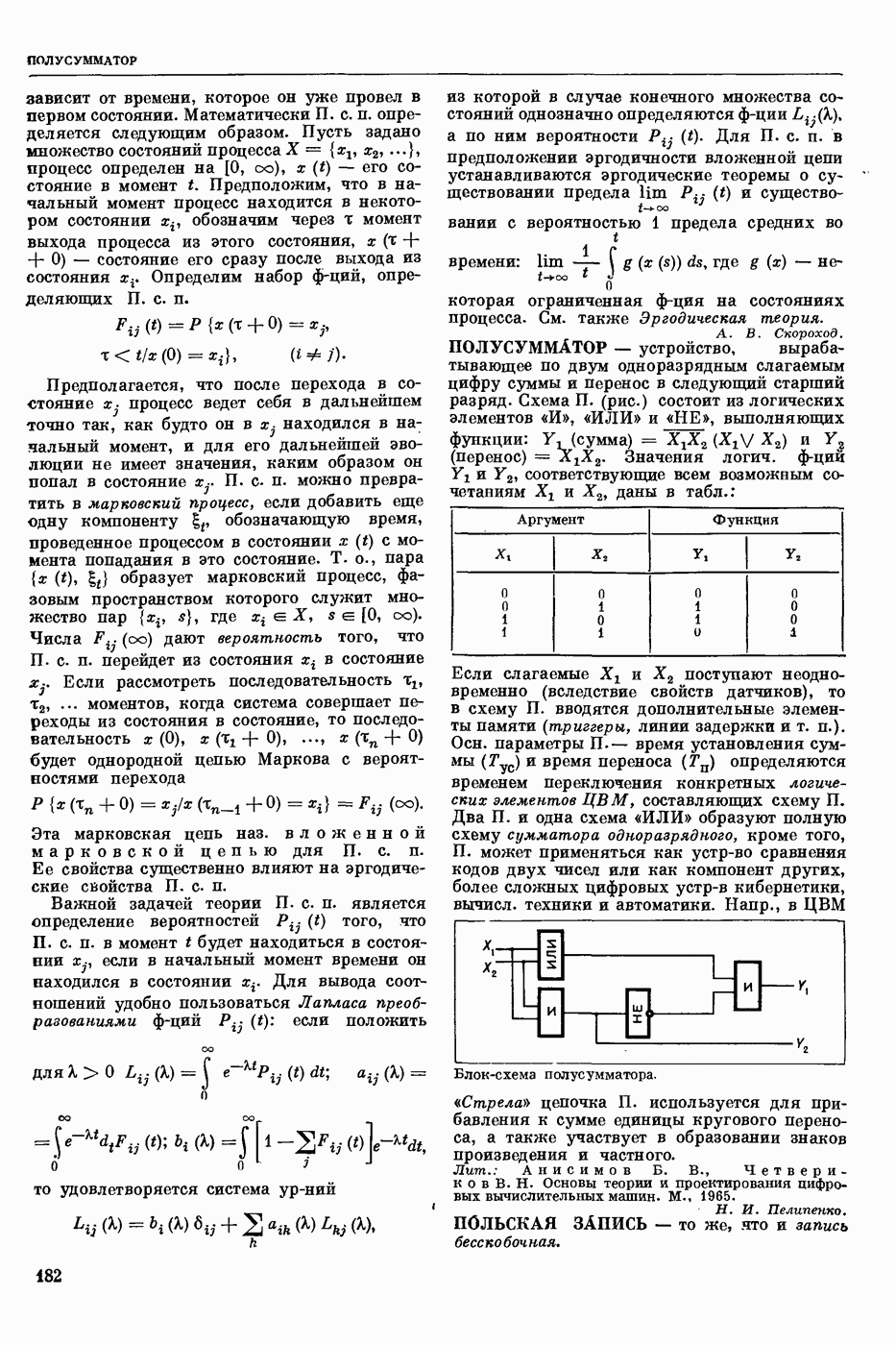
- ПОЛУСУММАТОР
- ПОЛЬСКАЯ ЗАПИСЬ
- ПОМЕХИ
- ПОМЕХОУСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ
- ПОНТРЯГИНА ПРИНЦИП МАКСИМУМА
- ПОПОВА КРИТЕРИЙ
- ПОРОГ ЧУВСТВИТЕЛЬНОСТИ
- ПОРОГОВЫЙ ЭЛЕМЕНТ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
- ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ МЕТОД
- ПОСТА ИСЧИСЛЕНИЯ
- ПОСТА КОМБИНАТОРНАЯ ПРОБЛЕМА
- ПОСТА МАШИНА
- ПОТЕНЦИАЛОВ МЕТОД
- ПОТЕНЦИАЛЬНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
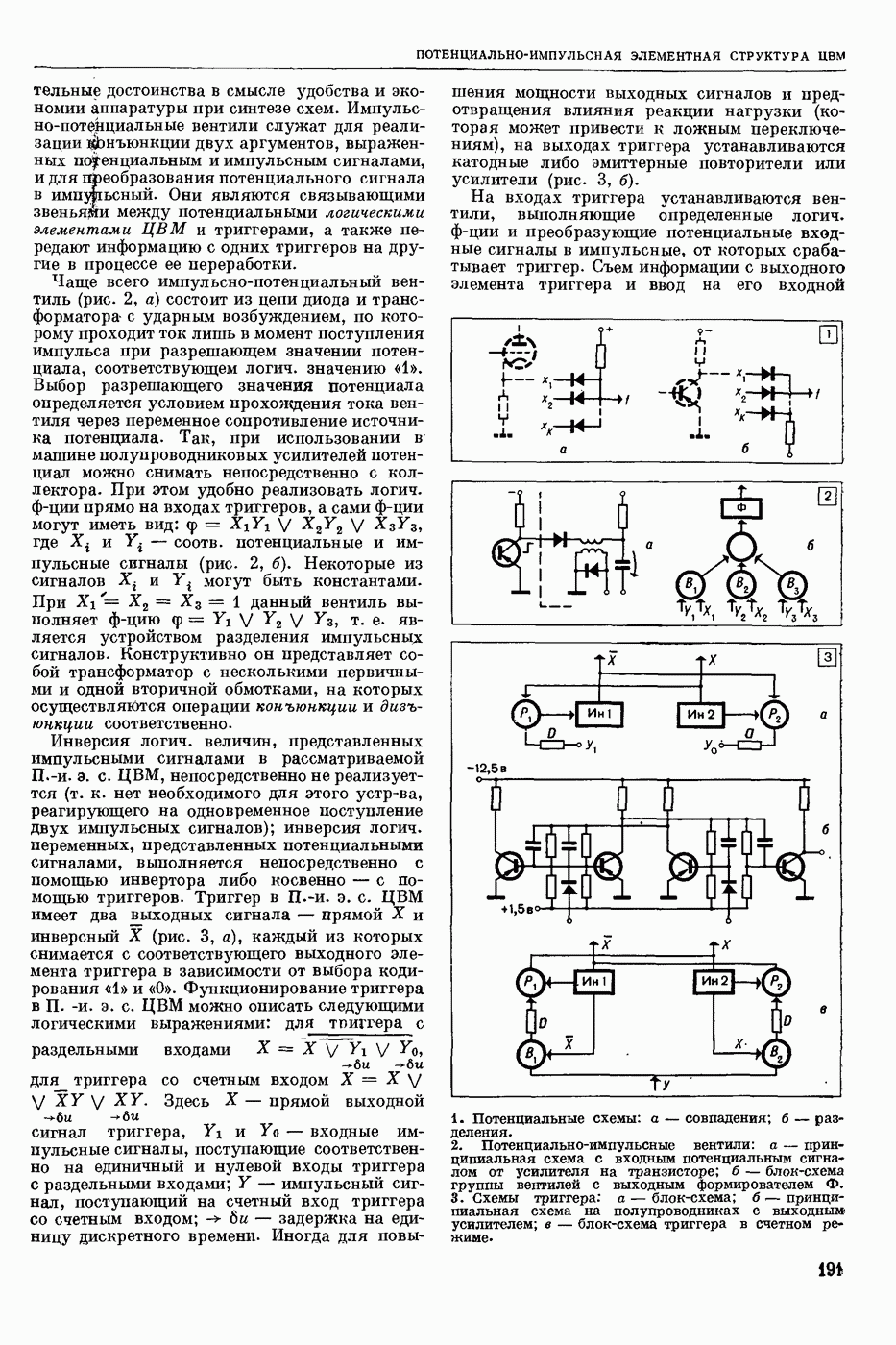
- ПОТЕНЦИАЛЬНО-ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-НУЛЕВАЯ ТОЧКА
- ПОТЕНЦИАЛЬНО-НУЛЕВЫХ ТОЧЕК МЕТОД
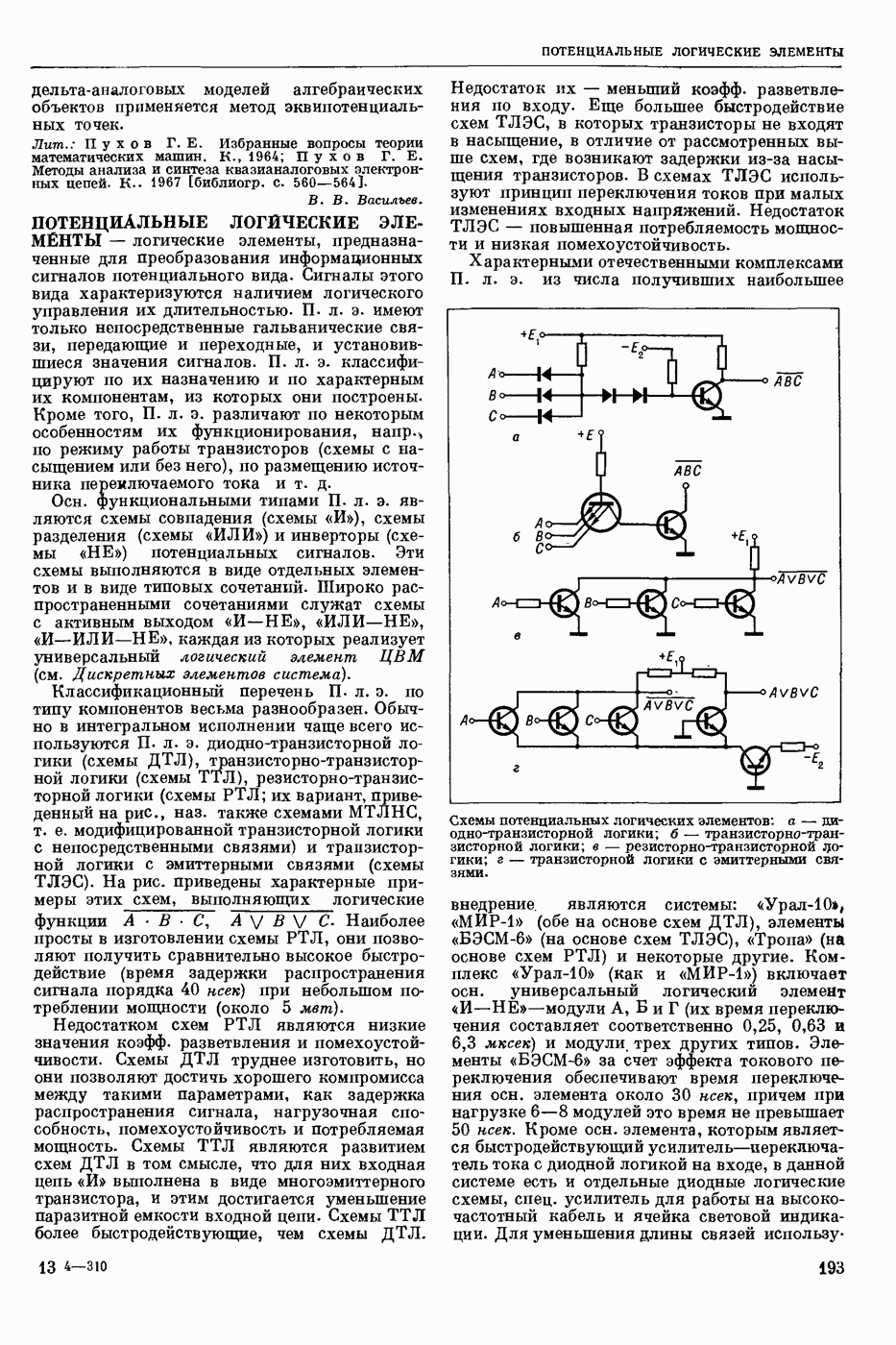
- ПОТЕНЦИАЛЬНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ МЕТОД
- ПОТЕРИ ИНФОРМАЦИИ при поиске
- ПОТОК БЕЗ ПОСЛЕДЕЙСТВИЯ
- ПОТОК В СЕТИ
- ПОТОК В СЕТИ НЕОДНОРОДНЫЙ
- ПОТОК ВЫХОДЯЩИЙ
- ПОТОК ГЕОМЕТРИЧЕСКИЙ
- ПОТОК ИНФОРМАЦИОННЫЙ ЗАМКНУТЫЙ
- ПОТОК НЕСТАЦИОНАРНЫЙ
- ПОТОК ПРОСТЕЙШИЙ
- ПОТОК РЕГУЛЯРНЫЙ
- ПОТОК С ОГРАНИЧЕННЫМ ПОСЛЕДЕЙСТВИЕМ
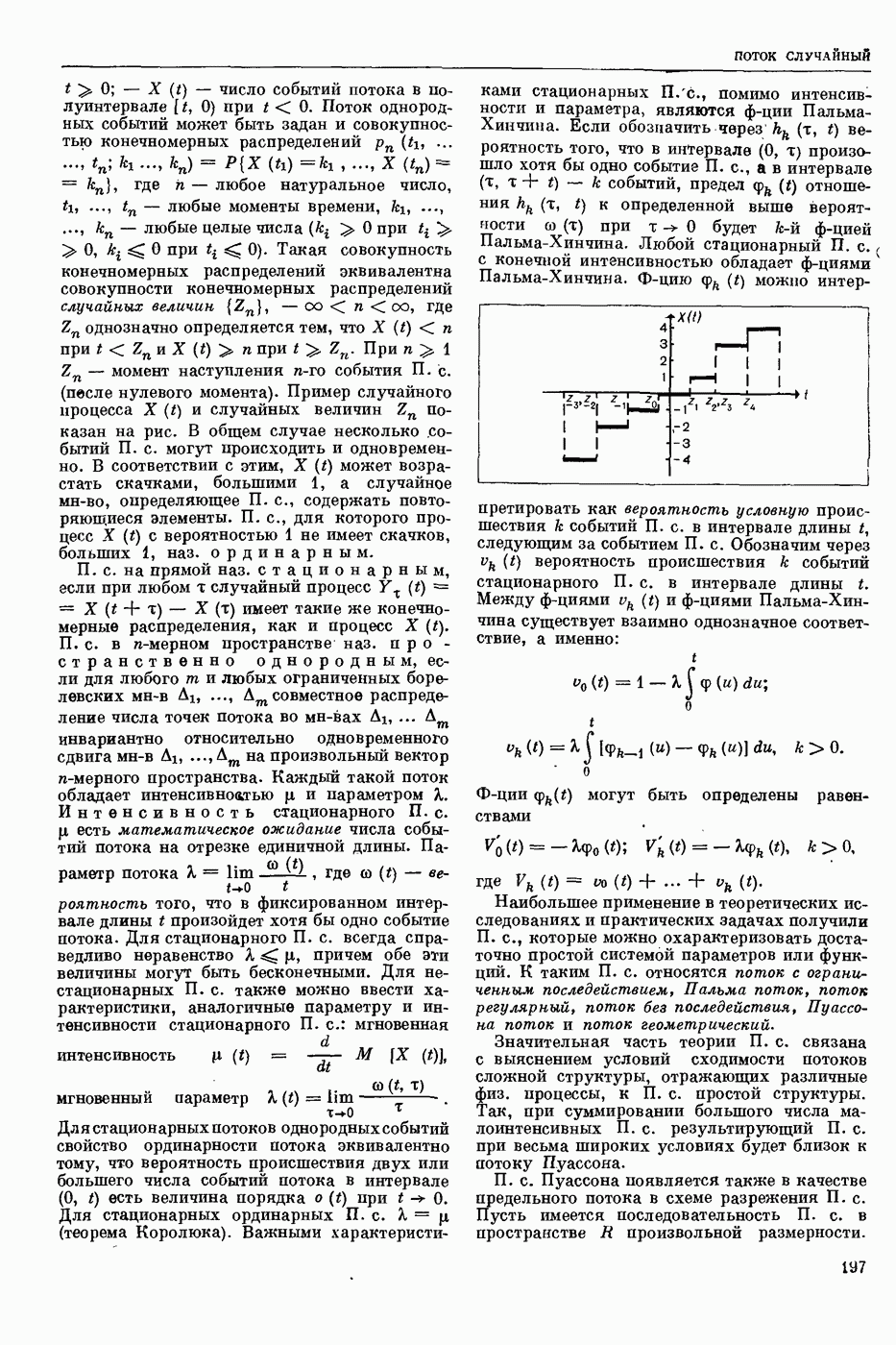
- ПОТОК СЛУЧАЙНЫЙ
- ПРАГМАТИКА
- ПРЕДИКАТ
- ПРЕДИКАТИВНОСТЬ
- ПРЕДСКАЗАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ПРЕДСКАЗЫВАЮЩИЙ ФИЛЬТР
- ПРЕДСТАВЛЕНИЙ ГРУПП ТЕОРИЯ
- ПРЕОБРАЗОВАНИЕ ПЕРИОДИЧЕСКИ-ОПРЕДЕЛЕННОЕ
- ПРЕОБРАЗОВАТЕЛИ ВОЛОКОННЫЕ
- ПРЕОБРАЗОВАТЕЛИ ДВУХ И БОЛЕЕ ПЕРЕМЕННЫХ
- ПРЕОБРАЗОВАТЕЛИ КОД-АНАЛОГ
- ПРЕОБРАЗОВАТЕЛИ С ПОРАЗРЯДНЫМ КОДИРОВАНИЕМ
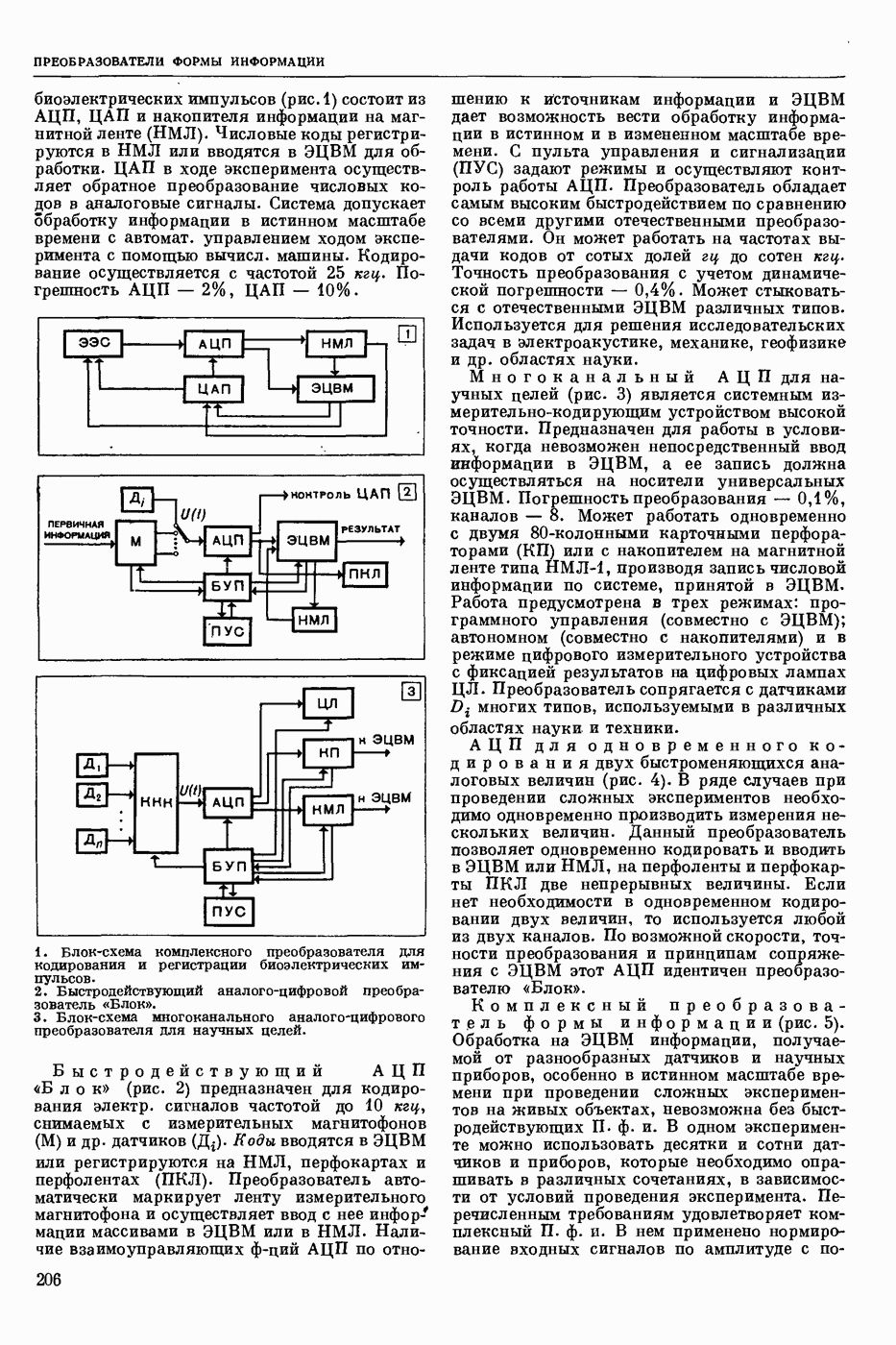
- ПРЕОБРАЗОВАТЕЛИ ФОРМЫ ИНФОРМАЦИИ
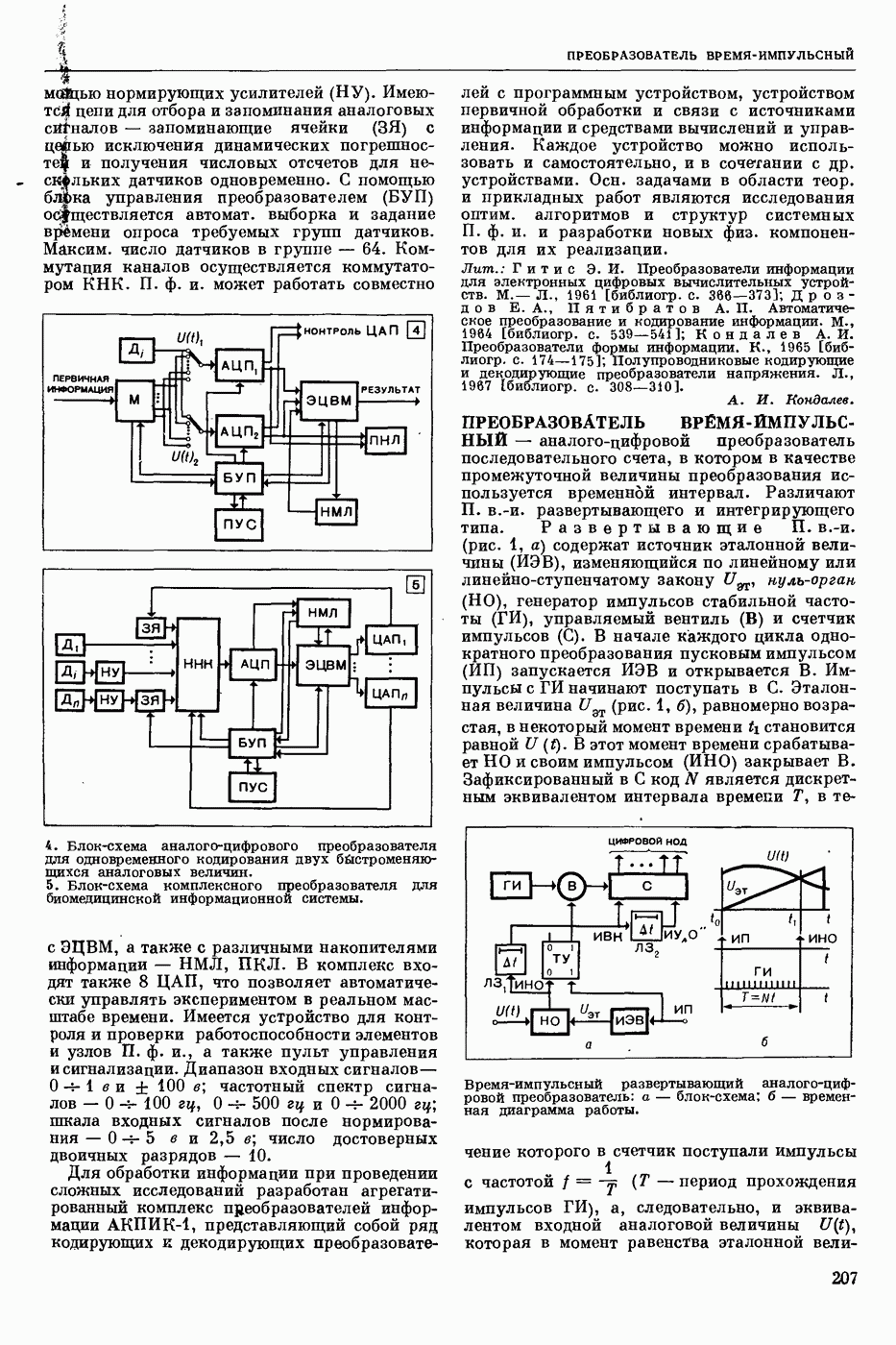
- ПРЕОБРАЗОВАТЕЛЬ ВРЕМЯ-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ИНТЕГРИРУЮЩЕГО ТИПА
- ПРЕОБРАЗОВАТЕЛЬ КОМБИНИРОВАННЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ КВАЗИОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ ОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ НАКАПЛИВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ПРЕОБРАЗОВАТЕЛЬ РАЗВЕРТЫВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ С НЕПОСРЕДСТВЕННЫМ ОТСЧЕТОМ
- ПРЕОБРАЗОВАТЕЛЬ СЛЕДЯЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ФАЗО-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ФУНКЦИОНАЛЬНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЦИКЛИЧЕСКИЙ
- ПРЕОБРАЗОВАТЕЛЬ ЧАСТОТНО-ИМПУЛЬСНЫЙ
- ПРЕСЛЕДОВАНИЯ ЗАДАЧА
- ПРИБЛИЖЕННЫХ МЕТОДОВ ОБЩАЯ ТЕОРИЯ
- ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- ПРИОРИТЕТ
- ПРИОРИТЕТОВ СИСТЕМА
- ПРОБЛЕМА «ЧЕЛОВЕК-МАШИНА»
- ПРОГОНКИ МЕТОД
- ПРОГРАММ СЕГМЕНТАЦИЯ
- ПРОГРАММА вычислительной машины
- ПРОГРАММА ДИАГНОСТИЧЕСКАЯ
- ПРОГРАММА ИСПЫТАТЕЛЬНАЯ
- ПРОГРАММА КОМПИЛИРУЮЩАЯ
- ПРОГРАММА УПРАВЛЯЮЩАЯ
- ПРОГРАММА-ДИСПЕТЧЕР
- ПРОГРАММИРОВАНИЕ АВМ
- ПРОГРАММИРОВАНИЕ ВЫПУКЛОЕ
- ПРОГРАММИРОВАНИЕ ДИНАМИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ДИСКРЕТНОЕ
- ПРОГРАММИРОВАНИЕ ДЛЯ ЦВМ
- ПРОГРАММИРОВАНИЕ КВАДРАТИЧНОЕ
- ПРОГРАММИРОВАНИЕ КУСОЧНО-ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ НЕЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ СТОХАСТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЧАСТИЧНО ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЭВРИСТИЧЕСКОЕ
- ПРОГРАММИРОВАННОЕ ОБУЧЕНИЕ
- ПРОГРАММИРОВАННЫЙ УЧЕБНИК
- ПРОГРАММИРУЮЩАЯ ПРОГРАММА
- ПРОГРАММНОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ в народном хозяйстве.
- ПРОГРАММЫ ОБСЛУЖИВАЮЩИЕ
- ПРОЕКТИРОВАНИЕ СЕТЕЙ И КОММУНИКАЦИЙ ОПТИМАЛЬНОЕ
- ПРОЕКЦИОННЫЕ МЕТОДЫ
- ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ
- «ПРОМIНЬ»
- ПРОПОЗИЦИОНАЛЬНЫЕ СВЯЗКИ, связки логические
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- ПРОСТОЙ ИТЕРАЦИИ МЕТОД
- ПРОСТРАНСТВО АБСТРАКТНОЕ в функциональном анализе
- ПРОСТРАНСТВО ИЗОБРАЖЕНИЙ
- ПРОЦЕДУРА в программировании
- ПРОЦЕДУРА РЕКУРСИВНАЯ
- ПРОЦЕСС КОНЕЧНОЙ ДЛИТЕЛЬНОСТИ
- ПРОЦЕСС УПРАВЛЯЕМЫЙ
- ПРОЦЕССОР
- ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
- ПРЯМЫЕ МЕТОДЫ решения задач прикладной математики
- ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА
- ПСИХОЛОГИЯ ИНЖЕНЕРНАЯ
- ПУАССОНА ПОТОК
- ПУАССОНА РАСПРЕДЕЛЕНИЕ
- ПУТЬ в теории графов
- РАВНОВЕСИЯ СИТУАЦИЯ
- «РАЗДАН»
- РАЗДЕЛЯЮЩАЯ ПОВЕРХНОСТЬ в распознавании образов
- РАЗМЕЩЕНИЯ ПРОИЗВОДСТВ МОДЕЛИ
- РАЗНОСТНАЯ СХЕМА
- РАЗРЯДНОСТЬ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- РАСПАРАЛЛЕЛИВАНИЕ АЛГОРИТМА
- РАСПОЗНАВАНИЕ ЗРИТЕЛЬНЫХ ОБРАЗОВ, распознавание изображений
- РАСПОЗНАВАНИЕ ОБРАЗОВ
- РАСПОЗНАВАНИЕ ПРОЦЕССОВ
- РАСПОЗНАВАНИЕ РЕЧЕВЫХ СИГНАЛОВ
- РАСПОЗНАЮЩАЯ СИСТЕМА
- РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- РАСПРЕДЕЛИТЕЛЬНАЯ ЗАДАЧА
- РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДЫ
- РАСЧЕТНЫЙ СТОЛ ПОСТОЯННОГО ТОКА, расчетная модель электрической системы
- РАСШИФРОВОЧНАЯ МАШИНА
- РАУСА КРИТЕРИЙ, Рауса — Гурвица критерий
- РЕАЛЬНЫЙ МАСШТАБ ВРЕМЕНИ
- РЕГЕНЕРАЦИЯ информации в вычислительных устройствах
- РЕГИСТР
- РЕГРЕССИЯ
- РЕГУЛИРОВАНИЕ ЗАПАСОВ
- РЕГУЛИРОВАНИЯ ЗАКОН
- РЕГУЛИРУЮЩИЕ СИСТЕМЫ ОРГАНИЗМА
- РЕГУЛЯРИЗАЦИИ МЕТОД
- РЕГУЛЯРНЫЕ СОБЫТИЯ И ВЫРАЖЕНИЯ
- РЕГУЛЯТОР ИМПУЛЬСНЫЙ
- РЕГУЛЯТОР ЭКСТРЕМАЛЬНЫЙ
- РЕГУЛЯТОРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- РЕГУЛЯТОРЫ ЦИФРОВЫЕ
- РЕДАКТИРОВАНИЕ ДАННЫХ
- РЕЖИМ ПЕРИОДИЗАЦИИ
- РЕЖИМ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- РЕКУРСИВНЫЕ ФУНКЦИИ
- РЕЛЕВАНТНОСТЬ ДОКУМЕНТА
- РЕЛЕЙНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ ТЕОРИЯ
- РЕФАЛ
- РЕФЕРАТ
- РЕФЕРИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- РЕФЛЕКСИВНОЕ УПРАВЛЕНИЕ
- РЕШАЮЩЕЕ ПРАВИЛО в распознавании образов
- РЕШАЮЩЕЕ УСТРОЙСТВО.
- РИСК РАСПОЗНАВАНИЯ
- РИСКА ПРОБЛЕМА
- РОБОТ
- РОБОТ ПРОМЫШЛЕННЫЙ
- РУНГЕ—КУТТЫ МЕТОД
- «РУТА-110»
- R-ФУНКЦИИ
- САМОДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- САМОКОРРЕКТИРУЮЩАЯСЯ СХЕМА
- САМОНАСТРАИВАЮЩАЯСЯ ПАРАМЕТРИЧЕСКАЯ СИСТЕМА
- САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА
- САМООБУЧАЮЩИЕСЯ СИСТЕМЫ
- САМООБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- СБОЙ ЦВМ
- СВЕРТКА РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН
- СВЕТОВОЙ КАРАНДАШ, световое перо
- СВОДИМОСТЬ в теории алгоритмов
- СВОЙСТВО ОТСУТСТВИЯ ПОСЛЕДЕЙСТВИЯ
- СВЯЗКИ ЛОГИЧЕСКИЕ
- СДВИГ
- «CDC-7600»
- СЕДЛОВЫЕ ТОЧКИ
- СЕКВЕНЦИЯ
- СЕМАНТИКА
- СЕМАНТИКА СТРУКТУРНАЯ
- СЕМАНТИЧЕСКИЙ АНАЛИЗ
- СЕМИОТИКА
- СЕРВОМОТОР
- СЕТЕВАЯ ЗАДАЧА
- СЕТЕВАЯ ЗАДАЧА НЕОДНОРОДНАЯ
- СЕТЕВАЯ МОДЕЛЬ
- СЕТЕВОЙ ГРАФИК
- СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
- «СЕТУНЬ»
- СЕТЧАТКА в распознавании образов
- СЕТЬ ИЗ НЕЙРОННЫХ ЭЛЕМЕНТОВ
- СЕТЬ ЛОГИЧЕСКАЯ
- СЕЧЕНИЙ ПРОСТРАНСТВА ПАРАМЕТРОВ МЕТОД
- СИГНАЛИЗИРУЮЩАЯ ФУНКЦИЯ
- СИЛЛОГИСТИКА
- «СИМЕНС» (Siemens Aktiengesellschaft)
- СИММЕТРИЧЕСКИЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- СИМПЛЕКС-МЕТОД
- СИМПСОНА ФОРМУЛА
- СИМСКРИПТ
- СИМУЛА
- «СИНТАКСИС»
- СИНТАКСИЧЕСКИЙ АНАЛИЗ АВТОМАТИЧЕСКИЙ естественных языков
- СИНТАКСИЧЕСКИЙ АНАЛИЗ ПРОГРАММ
- СИНТАКСИЧЕСКИЙ КОНТРОЛЬ ПРОГРАММ
- СИНТАКТИКА
- СИНТЕЗ АВТОМАТОВ АБСТРАКТНЫЙ
- СИНТЕЗ АВТОМАТОВ СТРУКТУРНЫЙ
- СИНТЕЗ АЛГОРИТМА УПРАВЛЕНИЯ
- СИНТЕЗ РЕЧЕВЫХ СИГНАЛОВ
- СИНХРОНИЗАЦИЯ РАБОТЫ ЦВМ
- «СИРИУС»
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СТАТИСТИЧЕСКАЯ ДИНАМИКА
- СИСТЕМ ОБЩАЯ ТЕОРИЯ
- СИСТЕМА АВТОМАТИЗИРОВАННАЯ
- СИСТЕМА АВТОМАТИЧЕСКАЯ
- СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ)
- СИСТЕМА АВТОМАТИЧЕСКОЙ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- СИСТЕМА АВТОНОМНАЯ
- СИСТЕМА АСТАТИЧЕСКАЯ
- СИСТЕМА ИНФОРМАЦИОННОГО ПОИСКА
- СИСТЕМА НЕАВТОНОМНАЯ
- СИСТЕМА НЕПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЕРЫВАНИЯ ЦВМ
- СИСТЕМА ПРОГРАММИРОВАНИЯ
- СИСТЕМА ПРОГРАММНОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА СЧИСЛЕНИЯ
- СИСТЕМА УПРАВЛЕНИЯ АДАПТИВНАЯ
- СИСТЕМА УПРАВЛЕНИЯ ЗАМКНУТАЯ, система управления по отклонению
- СИСТЕМА УПРАВЛЕНИЯ НАУЧНЫМ ЭКСПЕРИМЕНТОМ
- СИСТЕМА УПРАВЛЕНИЯ РАЗОМКНУТАЯ
- СИСТЕМА УПРАВЛЕНИЯ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
- СИСТЕМА УПРАВЛЕНИЯ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- СИСТЕМА УРАВНЕНИЙ В ВАРИАЦИЯХ
- СИСТЕМА УРАВНЕНИЙ СОПРЯЖЕННАЯ
- СИСТЕМА «ЧЕЛОВЕК — МАШИНА»
- СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- СИСТЕМНОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- СИСТЕМНЫЙ ПОДХОД
- СИСТЕМОТЕХНИКА
- СИСТЕМЫ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- СИСТЕМЫ С ВРЕМЕННЫМИ ОГРАНИЧЕНИЯМИ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ
- СИСТЕМЫ УПРАВЛЕНИЯ НА ПЕРЕМЕННОМ ТОКЕ
- СКЛЕИВАНИЯ ЗАКОН
- СКОЛЬЗЯЩИЙ РЕЖИМ
- СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЯ
- СЛЕДЯЩАЯ СИСТЕМА
- СЛОВАРНЫЙ ПОИСК
- СЛОВАРЬ АВТОМАТИЧЕСКИЙ
- СЛОВАРЬ ИНФОРМАЦИОННОГО ЯЗЫКА
- СЛОВАРЬ ЧАСТОТНЫЙ
- СЛОВО
- СЛОЖНОСТЬ ВЫЧИСЛЕНИЙ
- СЛОЖНОСТЬ ТЬЮРИНГОВЫХ ВЫЧИСЛЕНИЙ
- СЛОЖНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- СЛУЧАЙНАЯ ВЕЛИЧИНА
- СЛУЧАЙНАЯ ФУНКЦИЯ
- СЛУЧАЙНОГО ПОИСКА МЕТОДЫ
- СЛУЧАЙНОЕ ПОЛЕ
- СЛУЧАЙНОЕ СОБЫТИЕ
- СЛУЧАЙНЫЕ ЧИСЛА
- СЛУЧАЙНЫЙ ПРОЦЕСС, вероятностный процесс, стохастический процесс
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ ПРЕДСКАЗАНИЯ
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ ОБЫКНОВЕННЫХ УРАВНЕНИЙ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СОБЫТИЕ РЕГУЛЯРНОЕ
- СОБЫТИЯ ЦИКЛИЧЕСКАЯ ГЛУБИНА
- СОВМЕЩЕНИЕ ОПЕРАЦИЙ В МАШИНЕ
- «СОЛЯРТРОН ЭЛЕКТРОНИК ГРУП» (The Solartron Electronic Group, Ltd)
- СООБЩЕНИЕ в теории передачи информации
- СООБЩЕНИЙ ТЕОРИЯ
- СОПРОТИВЛЕНИЕ ОТРИЦАТЕЛЬНОЕ
- СОПРОТИВЛЕНИЕ ЦИФРОВОЕ УПРАВЛЯЕМОЕ
- СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- СОРТИРОВАЛЬНАЯ МАШИНА
- СОРТИРОВКА ДАННЫХ
- СОЦИОЛОГИЧЕСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ
- СПЕКТРАЛЬНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- СПЕКТРАЛЬНАЯ ФУНКЦИЯ стационарного в широком смысле случайного процесса
- СПЕЦИАЛИЗИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- СПЕЦИАЛЬНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СПЕЦИФИКАЦИЯ
- СПИСКОВАЯ СТРУКТУРА
- СПИСОК в программировании
- СПРАВОЧНО-ИНФОРМАЦИОННЫЙ ФОНД (СИФ)
- СТАБИЛИЗАЦИИ СИСТЕМА
- СТАНДАРТИЗИРОВАННАЯ ИСТОРИЯ БОЛЕЗНИ
- СТАНДАРТЫ ПО ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
- СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ МЕТОД
- СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- СТИЛТЬЕСА КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
- СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- СТОХАСТИЧЕСКИЙ ПРОЦЕСС
- СТОХАСТИЧЕСКИХ КВАЗИГРАДИЕНТОВ МЕТОД
- СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ МЕТОД
- СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ МЕТОДЫ
- СТРАТЕГИЯ ОПТИМАЛЬНАЯ
- СТРАТЕГИЯ ПОВЕДЕНИЯ
- СТРАТЕГИЯ СМЕШАННАЯ
- СТРАТЕГИЯ ЧИСТАЯ
- «СТРЕЛА»
- СТРУКТУРА, решетка.
- СТРУКТУРНАЯ ИНТЕРПРЕТАЦИЯ ЯЗЫКА
- СТРУКТУРНАЯ ПОЭТИКА
- СТРУКТУРНАЯ СХЕМА МОДЕЛИ
- СТРУКТУРНАЯ ТЕОРИЯ АВТОМАТОВ
- СТРУКТУРНОЕ СТИХОВЕДЕНИЕ
- СУММАТОР
- СУММАТОР КОМБИНАЦИОННЫЙ
- СУММАТОР НАКАПЛИВАЮЩИЙ
- СУММАТОР ОДНОРАЗРЯДНЫЙ
- СУММАТОР ПАРАЛЛЕЛЬНЫЙ
- СУММАТОР ПОСЛЕДОВАТЕЛЬНЫЙ
- СУПЕРВИЗОР
- СХЕМА ВЕНТИЛЬНАЯ
- СХЕМА КОНТАКТНАЯ
- СХЕМА КОНТАКТНАЯ БЕСПОВТОРНАЯ
- СХЕМА КОНТАКТНО-ВЕНТИЛЬНАЯ
- СХЕМА РЕЛЕЙНО-КОНТАКТНАЯ
- СХЕМА СРАВНЕНИЯ
- СХОДСТВА КРИТЕРИИ
- СЧЕТЧИК
- ТАБУЛИРОВАНИЕ ФУНКЦИЙ
- ТАБУЛЯТОР
- ТАЙПОТРОН
- ТАКТ
- ТАКТОВАЯ ЧАСТОТА
- ТВИСТОР
- ТЕЗАУРУС
- ТЕЛЕМЕХАНИКА
- ТЕЛЕТАЙП
- ТЕРМИНАЛ, абонентский пульт, оконечное устройство
- ТЕРМИНАЛЬНОЕ УПРАВЛЕНИЕ, управление конечным состоянием
- ТЕСТОВЫЕ ПРОГРАММЫ, тест-программы
- ТЕСТЫ
- ТЕХНИЧЕСКАЯ ДИАГНОСТИКА
- ТЕХНИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- ТЕХПРОМФИНПЛАН ПРЕДПРИЯТИЯ МАТРИЧНЫЙ
- ТОЖДЕСТВЕННО ИСТИННАЯ ФОРМУЛА, общезначимая формула
- ТОНКАЯ МАГНИТНАЯ ПЛЕНКА
- ТОПОЛОГИЯ
- «ТОСИБА» (Tokyo Shibaura Electric Company, Ltd)
- ТОЧКА РАВНОВЕСИЯ
- ТОЧКИ ПЕРЕКЛЮЧЕНИЯ
- ТОЧНОСТЬ ВОСПРОИЗВЕДЕНИЯ СООБЩЕНИЯ
- ТРАЕКТОРИЯ ДОПУСТИМАЯ
- ТРАЕКТОРИЯ ОПТИМАЛЬНАЯ
- ТРАЕКТОРИЯ ФАЗОВАЯ
- ТРАНЗИТИВНЫЙ ГРАФ
- ТРАНСЛЯТОР, компилирующая программа, программирующая программа
- ТРАНСЛЯТОР СИНТАКСИЧЕСКИ УПРАВЛЯЕМЫЙ
- ТРАНСПОРТНАЯ ЗАДАЧА
- ТРАНСПОРТНАЯ СЕТЬ
- ТРАНСФЛЮКСОР
- ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
- ТРИГГЕР
- ТРИГГЕР ДИНАМИЧЕСКИЙ
- ТРИГГЕР СТАТИЧЕСКИЙ
- ТРИОД ПОЛУПРОВОДНИКОВЫЙ, транзистор
- ТЬЮРИНГА МАШИНА
- УЗЛОВОЙ СПИСОК
- «УМ1-НХ»
- УНИВЕРСАЛЬНАЯ СИСТЕМА ЭЛЕМЕНТОВ ПРОМЫШЛЕННОЙ ПНЕВМОАВТОМАТИКИ (УСЭППА)
- UNCOL
- УПОРЯДОЧЕНИЕ МАССИВА
- УПРАВЛЕНИЕ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- УПРАВЛЕНИЕ ДАННЫМИ
- УПРАВЛЕНИЕ ЗАПАСАМИ
- УПРАВЛЕНИЕ КОМАНДАМИ
- УПРАВЛЕНИЕ ЛЕЧЕБНЫМ ПРОЦЕССОМ.
- УПРАВЛЕНИЕ ОПЕРАЦИЯМИ
- УПРАВЛЕНИЕ ОПТИМАЛЬНОЕ
- УПРАВЛЕНИЕ ПРОГРАММНОЕ
- УПРАВЛЕНИЕ С АДАПТАЦИЕЙ
- УПРАВЛЕНИЕ СТРУКТУРНОЕ В ЦВМ
- УПРАВЛЕНИЯ ОТНОШЕНИЕ, зависимости отношение
- УПРАВЛЕНИЯ СЛУЧАЙНЫМИ ПРОЦЕССАМИ ТЕОРИЯ
- УПРАВЛЯЮЩАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- УПРАВЛЯЮЩАЯ ПРОГРАММА
- УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, регулирующее воздействие
- «УПРАВЛЯЮЩИЕ СИСТЕМЫ И МАШИНЫ»
- УРАВНЕНИЙ КЛАССИФИКАЦИЯ.
- УРАВНОВЕШИВАНИЯ МЕТОДЫ
- «УРАЛ»
- УСИЛИТЕЛЬ
- УСИЛИТЕЛЬ ДИФФЕРЕНЦИАЛЬНЫЙ
- УСИЛИТЕЛЬ ОПЕРАЦИОННЫЙ, усилитель решающий
- УСИЛИТЕЛЬ ОТРАБАТЫВАЮЩИЙ
- УСИЛИТЕЛЬ РЕШАЮЩИЙ
- УСЛОВИЯ СТАЦИОНАРНОСТИ
- УСЛОВИЯ ТРАНСВЕРСАЛЬНОСТИ
- УСТАНОВКА НАЧАЛЬНЫХ УСЛОВИЙ
- УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ КРИТЕРИИ
- УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
- УСТОЙЧИВОСТЬ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ
- УСТОЙЧИВОСТЬ МОДЕЛИ
- УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ
- УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ
- УСТОЙЧИВОСТЬ ЧИСЛЕННОГО МЕТОДА
- УСТРОЙСТВА ВВОДА—ВЫВОДА ДАННЫХ ЦВМ
- УСТРОЙСТВА ЗАПИСИ АНАЛОГОВОЙ ИНФОРМАЦИИ
- УСТРОЙСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- УСТРОЙСТВО ИНДИКАЦИИ ABM
- УСТРОЙСТВО ИНТЕГРИРУЮЩЕЕ, интегратор
- УСТРОЙСТВО ИНТЕГРО-ДИФФЕРЕНЦИРУЮЩЕЕ
- УСТРОЙСТВО ОБМЕНА ЦВМ
- УСТОЙСТВО ПЕРЕЗАПИСИ ДЛЯ ЦВМ
- УСТРОЙСТВО УПРАВЛЕНИЯ ЦВМ
- УСТРОЙСТВО ЦИФРОВОЙ РЕГИСТРАЦИИ
- ФАЗОВОГО ПРОСТРАНСТВА МЕТОД
- ФАЗОВЫЕ КООРДИНАТЫ
- ФАЗОВЫЕ ОГРАНИЧЕНИЯ
- ФАКТОГРАФИЧЕСКАЯ ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ФАКТОРИЗАЦИИ МЕТОД
- «ФЕРРАНТИ» (Ferranti, Ltd)
- ФЕРРИТ-ДИОДНАЯ СИСТЕМА ЭЛЕМЕНТОВ
- ФЕРРИТ-ТРАНЗИСТОРНАЯ СИСТЕМА ЭЛЕ МЕНТОВ
- ФИКСАТОР, адрес второго ранга, косвенный адрес
- ФИКСИРОВАННАЯ ЗАПЯТАЯ
- ФИЛОСОФСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
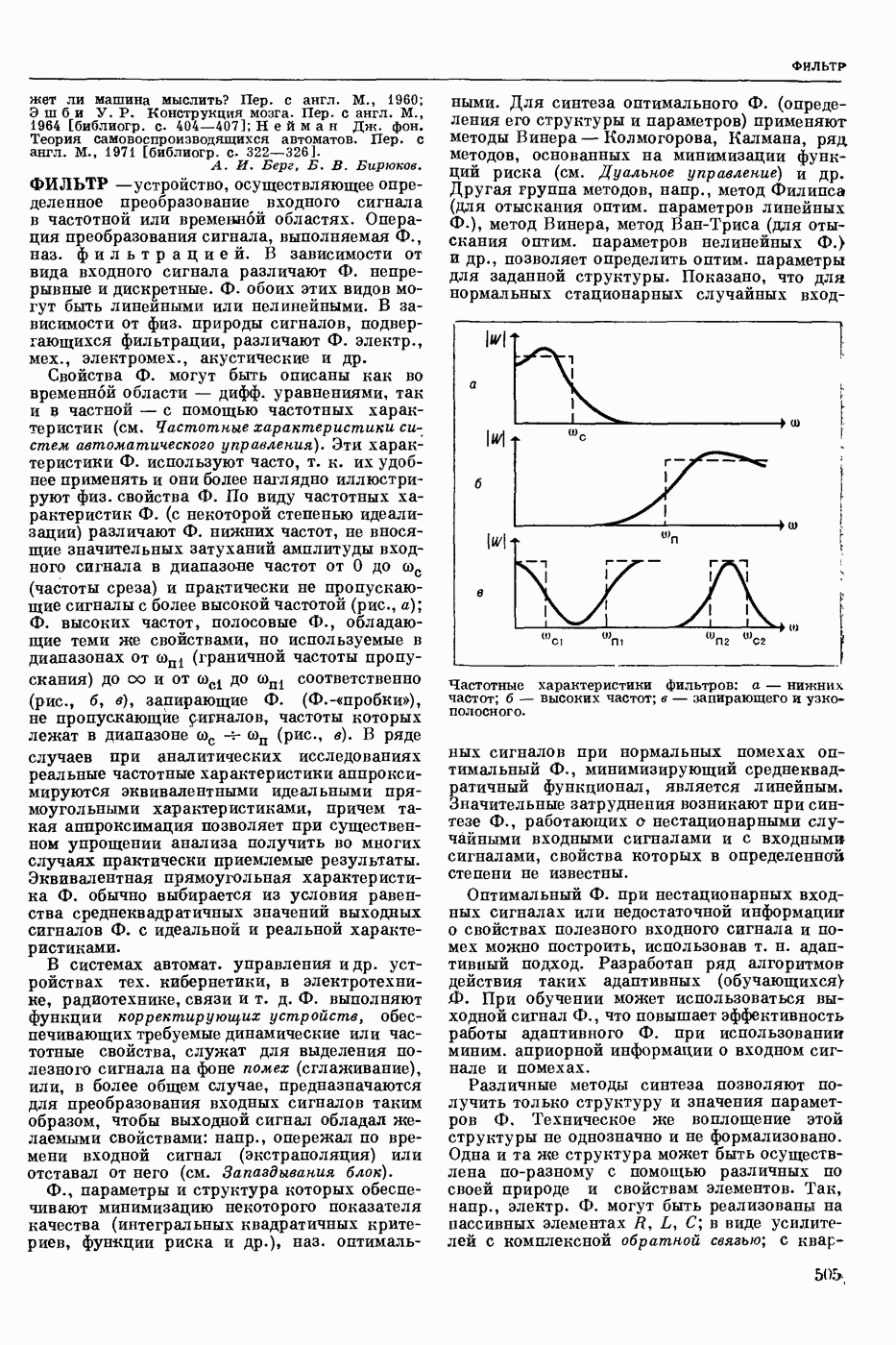
- ФИЛЬТР
- ФИЛЬТРАЦИЯ СЛУЧАЙНОГО ПРОЦЕССА
- ФОНД АЛГОРИТМОВ И ПРОГРАММ
- ФОНД СПРАВОЧНО-ИНФОРМАЦИОННЫЙ
- FORMAC
- ФОРМАЛИЗМ в математике
- ФОРТРАН
- «ФУДЗИЦУ» («Фудзи цусинки Сэйдзо», Fujitsu, Ltd)
- ФУНКЦИИ, СОХРАНЯЮЩИЕ КОНСТАНТУ
- ФУНКЦИИ, СОХРАНЯЮЩИЕ МНОЖЕСТВО
- ФУНКЦИИ, СОХРАНЯЮЩИЕ РАЗБИЕНИЕ
- ФУНКЦИОНАЛ
- ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ЭВМ
- ФУНКЦИОНАЛЬНЫЙ ЭЛЕМЕНТ ЭВМ
- ФУНКЦИЯ РАССТАНОВКИ
- ФУНКЦИЯ РЕШЕТЧАТАЯ
- ФУНКЦИЯ СТУПЕНЧАТАЯ
- ФУРЬЕ ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ФУРЬЕ ПРЕОБРАЗОВАНИЯ
- ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ в теории игр
- ХАРАКТРОН
- ХЕМИТРОН
- ХИНЧИНА-ПОЛАЧЕКА ФОРМУЛА
- «ХИТАЧИ» (Hitachi, Ltd)
- ХОМСКОГО ГРАММАТИКИ
- «ХОНИУЭЛЛ КОРПОРЕЙШЕН» (Honeywell Corporation)
- ХЭММИНГА КОД
- ЦВМ АСИНХРОННАЯ
- ЦВМ СИНХРОННАЯ
- ЦЕЛЕВАЯ ФУНКЦИЯ, функция цели
- ЦЕЛЕСООБРАЗНОСТЬ в кибернетике
- ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
- ЦЕНТРАЛЬНЫЙ ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ ИНСТИТУТ АКАДЕМИИ НАУК СССР
- ЦЕПИ СВЯЗАННЫЕ
- ЦЕПОЧКА
- ЦЕПЬ графа
- ЦЕПЬ ОКРУГЛЕНИЯ
- ЦЕПЬ ПЕРЕНОСА
- ЦИКЛ графа
- ЦИКЛ ПРОГРАММЫ
- ЦИКЛОМАТИЧЕСКОЕ ЧИСЛО
- ЦИПФА ЗАКОН
- ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ, преобразователи код
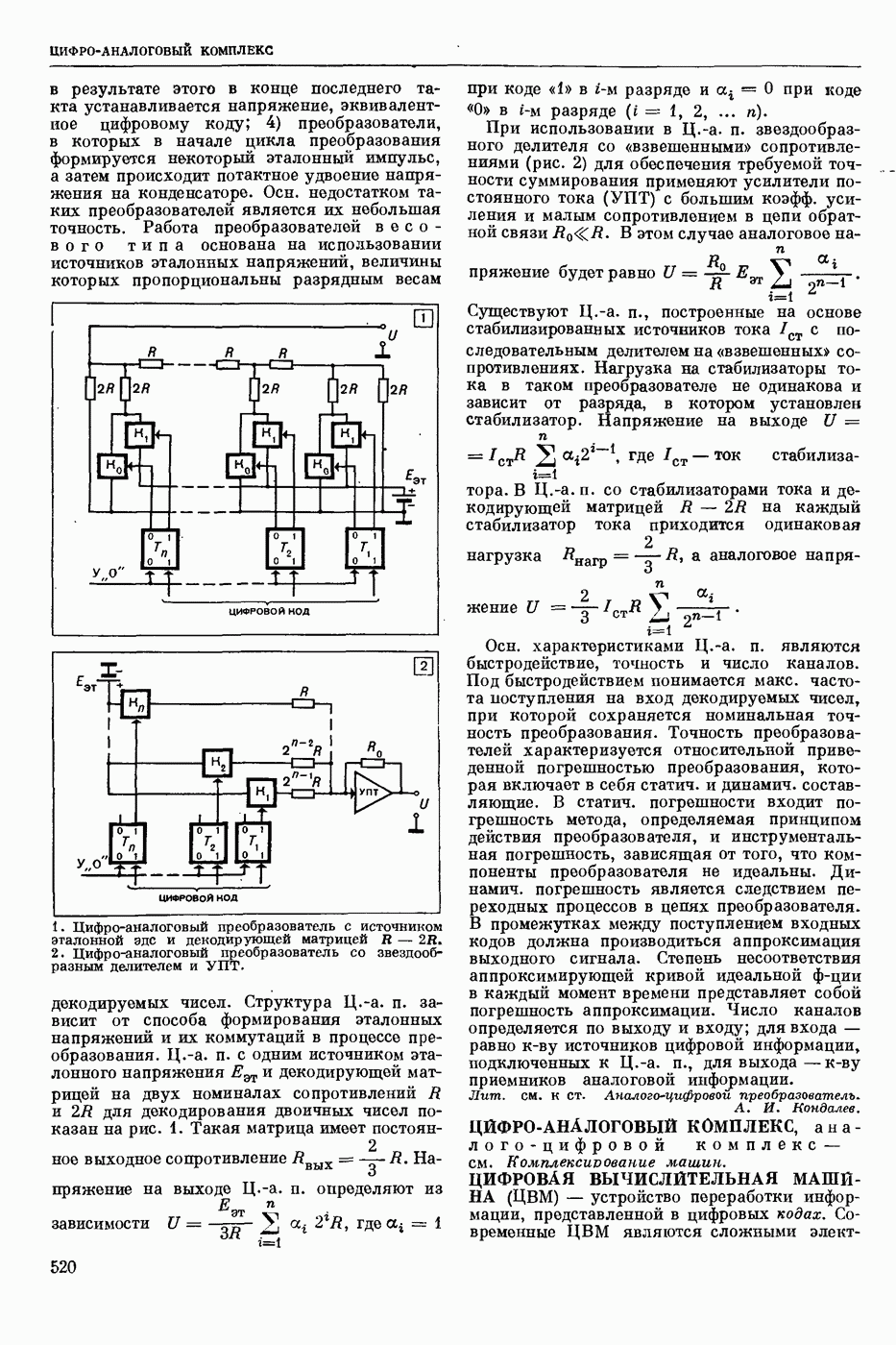
- ЦИФРО-АНАЛОГОВЫЙ КОМПЛЕКС, аналого-цифровой комплекс
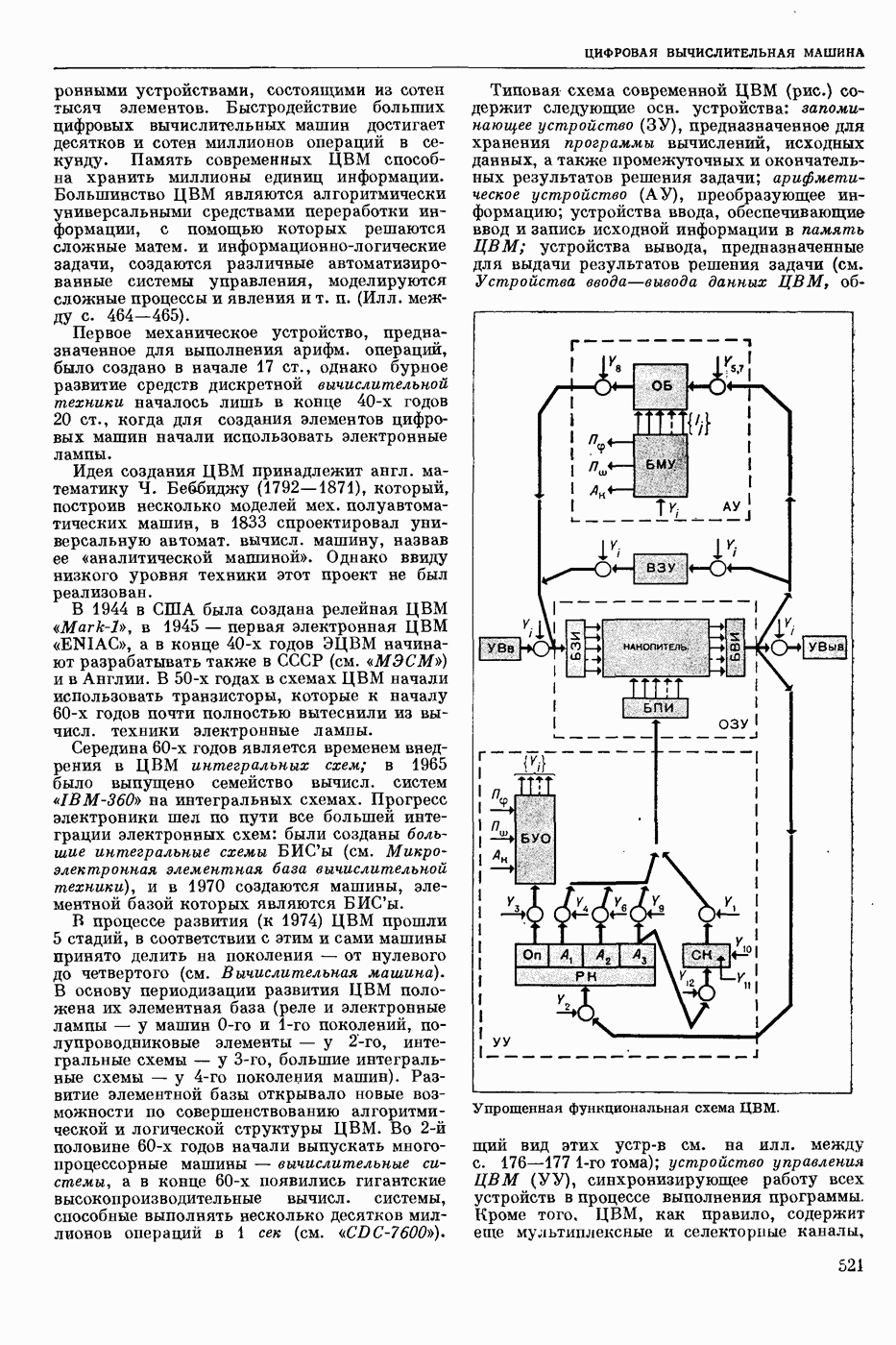
- ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЦВМ)
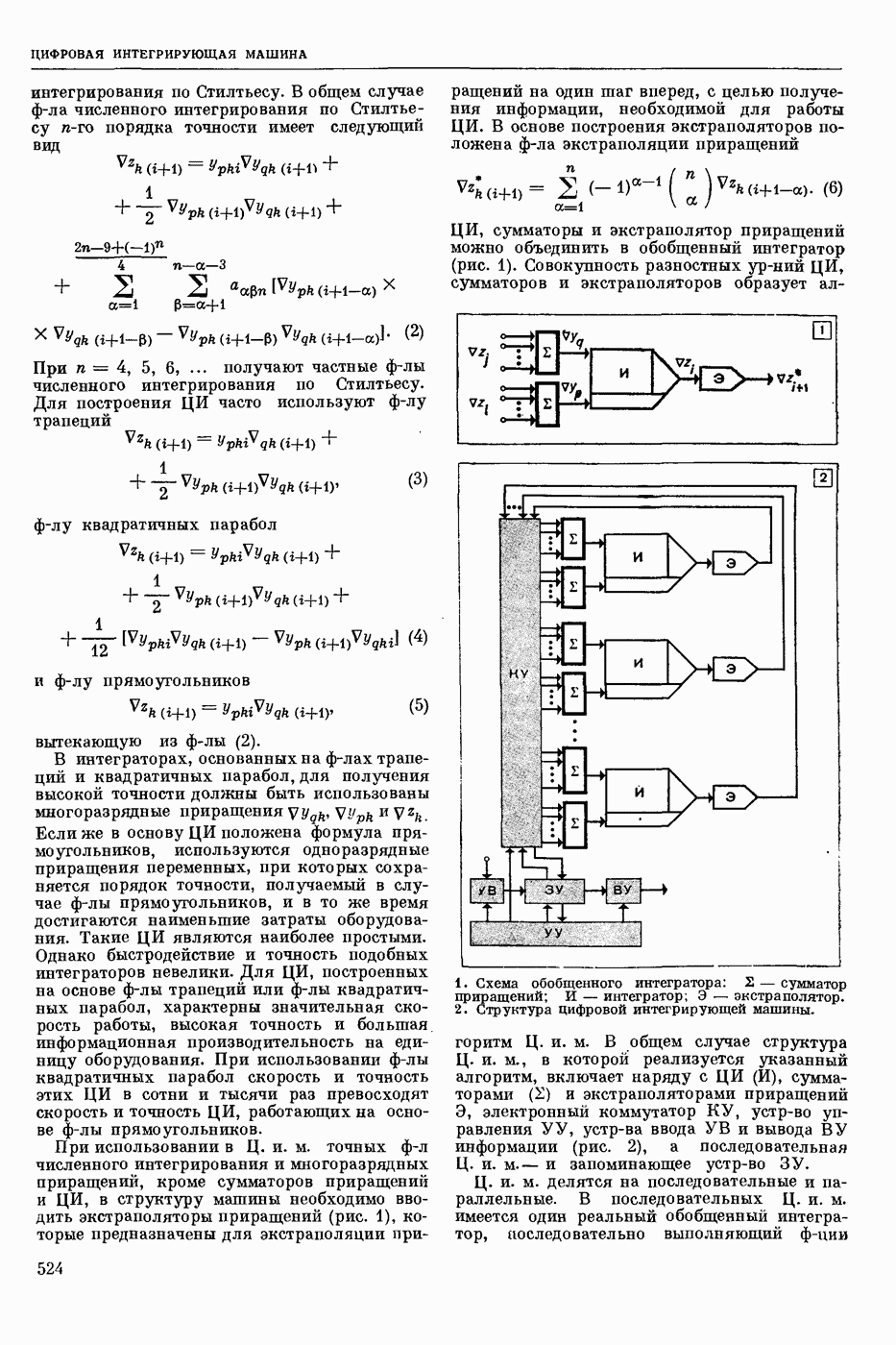
- ЦИФРОВАЯ ИНТЕГРИРУЮЩАЯ МАШИНА
- ЦИФРОВАЯ МОДЕЛЬ СЕТЕВОГО ГРАФИКА
- ЦИФРОВОЙ ДИФФЕРЕНЦИАЛЬНЫЙ АНАЛИЗАТОР
- ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО
- ЧАСТПЧНО-РЕКУРСИВНЫЕ ФУНКЦИИ
- ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ЧЕБЫШЕВА ЗАДАЧА РАВНОМЕРНОГО ПРИБЛИЖЕНИЯ
- ЧЕЛОВЕК-ОПЕРАТОР
- ЧЕРЕДУЮЩАЯСЯ ЦЕПЬ
- ЧЕРНИЛА МАГНИТНЫЕ
- «ЧЕРНЫЙ ЯЩИК»
- ЧИРЧА ТЕЗИС
- ЧИСЛА ФОРМАТ
- ЧИСЛЕННЫЕ МЕТОДЫ
- ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
- ЧИТАЮЩИЙ АВТОМАТ, оптическое читающее устройство
- ЧИТАЮЩИЙ АВТОМАТ КОРРЕЛЯЦИОННЫЙ
- ЧУВСТВИТЕЛЬНОСТИ ТЕОРИЯ
- ШАГ КВАНТОВАНИЯ
- ШЕННОНА ЛАБИРИНТ
- ШЕННОНА МЫШЬ
- ШЕННОНА ФУНКЦИЯ
- ШЕПЛИ ВЕКТОР
- ШЕФФЕРА ШТРИХ, Шеффера функция, отрицание конъюнкции
- ШИНА
- ШИФРАТОР
- ШТРАФНАЯ ФУНКЦИЯ
- ШТРАФНЫХ ФУНКЦИЙ МЕТОД
- ШТРАФОВ МЕТОД
- ШУМ КВАНТОВАНИЯ
- ШУМ ПОИСКОВЫЙ
- ЭВРИСТИКА
- ЭВРИСТИЧЕСКИЕ МЕТОДЫ В РАСПОЗНАВАНИИ
- ЭЙЛЕРА ЦЕПЬ
- ЭКВИВАЛЕНТНАЯ СХЕМА
- ЭКВИВАЛЕНТНОСТИ ОТНОШЕНИЕ (эквивалентность, эквиваленци я) на множестве
- ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЭКВИВАЛЕНТНЫЕ СОСТОЯНИЯ АВТОМАТА
- ЭКВИВАЛЕНТНЫХ ВОЗМУЩЕНИЙ МЕТОД
- ЭКВИФИНАЛЬНОСТЬ СИСТЕМЫ УПРАВЛЕНИЯ
- ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ, в управлении народным хозяйством
- ЭКРАННЫЙ ПУЛЬТ
- ЭКСПЕРИМЕНТ БЕЗУСЛОВНЫЙ
- ЭКСПЕРИМЕНТ КРАТНЫЙ
- ЭКСПЕРИМЕНТ УСЛОВНЫЙ
- ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ СПОСОБЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
- ЭКСПЕРИМЕНТЫ С АВТОМАТАМИ
- ЭКСПЕРТНЫХ ОЦЕНОК МЕТОДЫ в прогнозировании
- ЭКСТРАПОЛИРОВАНИЕ В ОБУЧЕНИИ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ЭКСТРАПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ЭКСТРАПОЛИРОВАНИЕ ФУНКЦИЙ
- ЭКСТРЕМАЛЬ
- ЭКСТРЕМАЛЬНОЕ РЕГУЛИРОВАНИЕ
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ в теории графов
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ НА ГРАФАХ
- ЭКСТРЕМУМ
- ЭКСТРЕМУМ АБСОЛЮТНЫЙ
- ЭКСТРЕМУМ ГЛОБАЛЬНЫЙ
- ЭКСТРЕМУМ ЛОКАЛЬНЫЙ
- ЭКСТРЕМУМА ДРЕЙФ
- ЭЛЕКТРИЧЕСКИЕ МОДЕЛИРУЮЩИЕ СЕТКИ
- ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ТЕОРИЯ
- «ЭЛЕКТРОН»
- ЭЛЕКТРОННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЭВМ)
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ
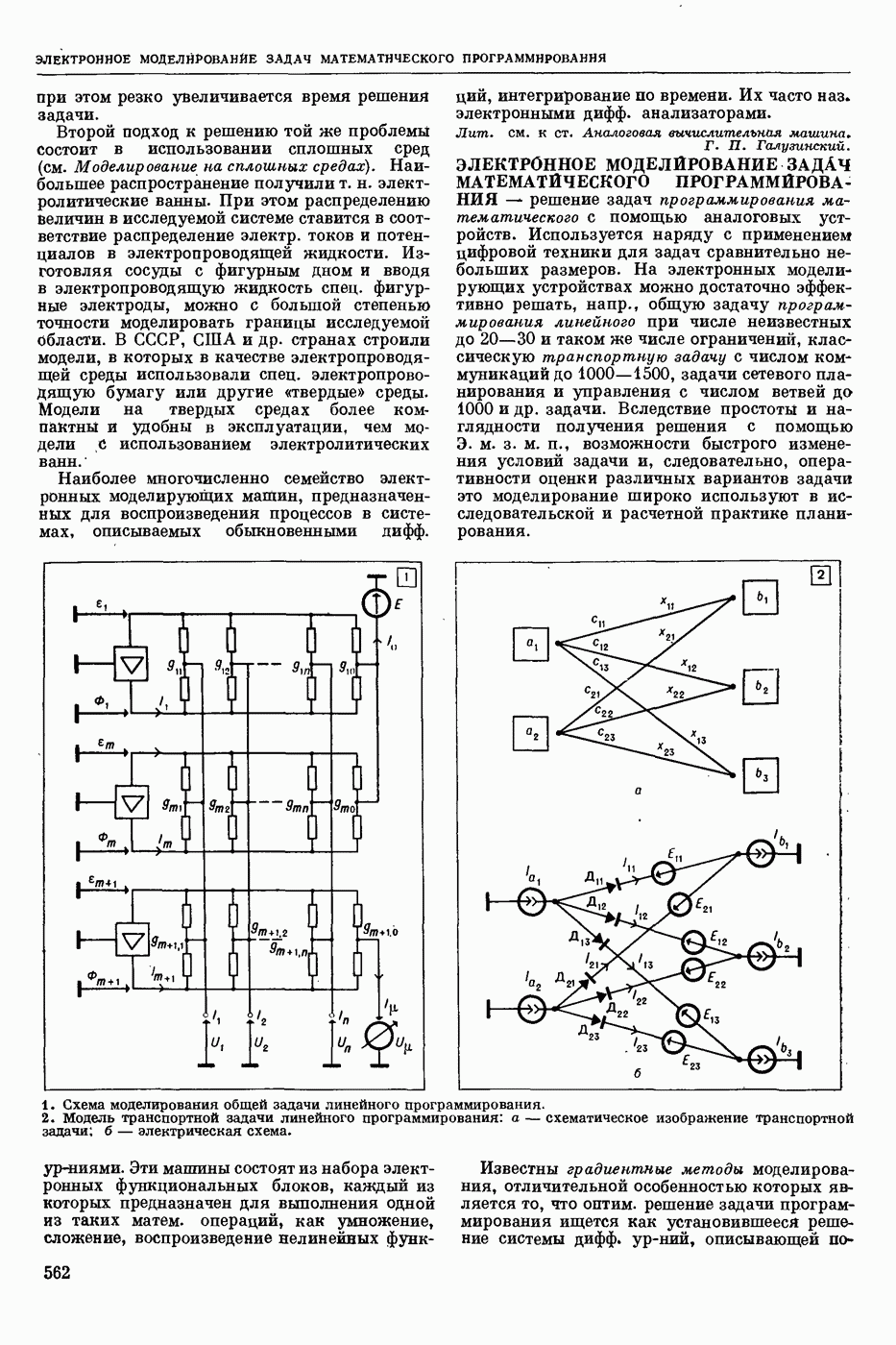
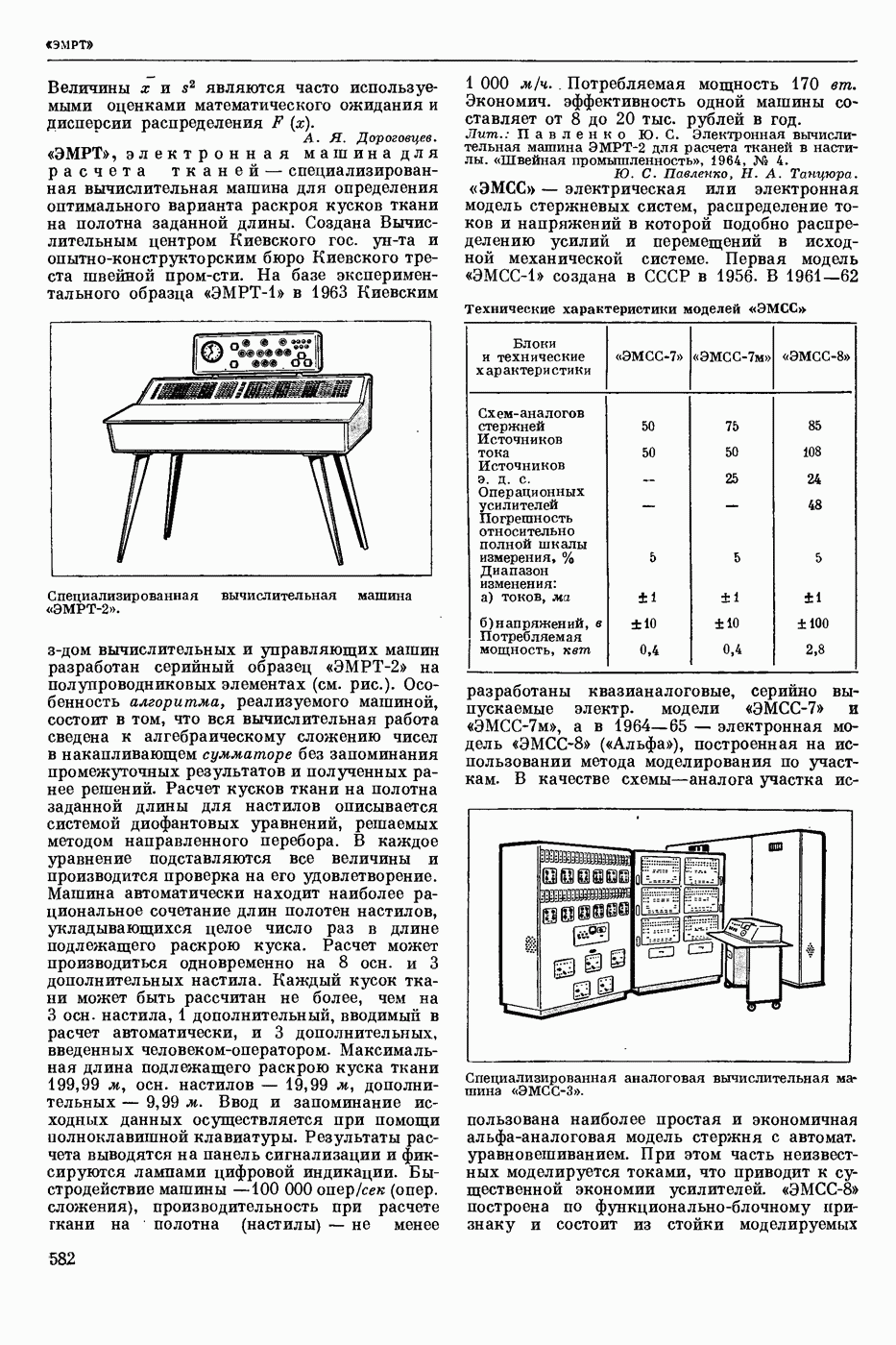
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЭЛЕМЕНТ ЗАДЕРЖКИ
- ЭЛЕМЕНТАРНАЯ СИСТЕМА
- ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ НАД СЛОВАМИ
- ЭЛЕМЕНТАРНЫЕ ТЕОРИИ.
- ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ЭЛЕМЕНТНЫЕ СТРУКТУРЫ НА ЛОГИЧЕСКИХ ЗАДЕРЖИВАЮЩИХ ЭЛЕМЕНТАХ
- ЭЛЕМЕНТНЫЙ СИНТЕЗ ЦВМ
- ЭЛИОНИКА
- ЭЛЛИПТИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- «ЭМИК-1»
- ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
- «ЭМСС»
- «ЭМУ»
- ЭНТРОПИЯ
- ЭНТРОПИЯ ЖИВЫХ СИСТЕМ
- ЭНТРОПИЯ СООБЩЕНИЯ при заданных условиях точности
- ЭПСИЛОН
- ЭПСИЛОН-ЭНТРОПИЯ
- ЭРГАТИЧЕСКАЯ СИСТЕМА
- ЭРГОДИЧЕСКАЯ ТЕОРИЯ
- ЭРГОДИЧЕСКОЕ СОСТОЯНИЕ
- ЭРЛАНГА ФОРМУЛЫ
- ЭТАЛОН в распознавании образов
- ЭТАЛОННОЕ НАПРЯЖЕНИЕ
- ЭФФЕКТИВНОСТЬ ИНФОРМАЦИОННОГО ПОИСКА техническая
- ЭШБИ ГОМЕОСТАТ
- «ЮНИВАК» (Univac)
- ЯДРО втеории игр
- ЯЗЫК АВТОМАТНЫЙ
- ЯЗЫК АЛГОРИТМИЧЕСКИЙ
- ЯЗЫК АНКЕТНЫЙ
- ЯЗЫК БЕСКОНТЕКСТНЫЙ, язык контекстно-свободный
- ЯЗЫК ДЕСКРИПТОРНЫЙ
- ЯЗЫК ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ
- ЯЗЫК ИНФОРМАЦИОННО-ПОИСКОВЫЙ
- ЯЗЫК ИНФОРМАЦИОННЫЙ
- ЯЗЫК ИСКУССТВЕННЫЙ
- ЯЗЫК КАТЕГОРИАЛЬНЫЙ
- ЯЗЫК ЛОГИЧЕСКИЙ для задания автоматов
- ЯЗЫК МАШИННО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК МАШИНЫ «МИР»
- ЯЗЫК ОПЕРАТОРНЫЙ
- ЯЗЫК ОПИСАНИЯ УСТРОЙСТВ ЦВМ
- ЯЗЫК ПРОМЕЖУТОЧНЫЙ
- ЯЗЫК ПРОЦЕДУРНО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК ТРАНСЛЯТОРА ВХОДНОЙ
- ЯЗЫК ЦВМ ВНУТРЕННИЙ
- ЯЗЫКА ИЗБЫТОЧНОСТЬ
- ЯЗЫКА ИНФОРМАЦИОННЫЕ ИЗМЕРЕНИЯ
- ЯЗЫКА МОДЕЛИ АНАЛИТИЧЕСКИЕ
- ЯЗЫКА МОДЕЛИ МАТЕМАТИЧЕСКИЕ
- ЯЗЫКА ЭНТРОПИЯ
- ЯЗЫКИ ЛОГИКО-МАТЕМАТИЧЕСКИЕ
- ЯЗЫКИ МАШИННЫЕ
- ЯЗЫКИ ПРОГРАММИРОВАНИЯ
- ЯЗЫКИ СПИСКОВЫЕ
- ЯЗЫКИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ
- ЯЗЫКИ ФОРМАЛЬНЫЕ
- ЯЗЫК — ПОСРЕДНИК
- ЯЧЕЙКА ЗАПОМИНАЮЩЕГО УСТРОЙСТВА