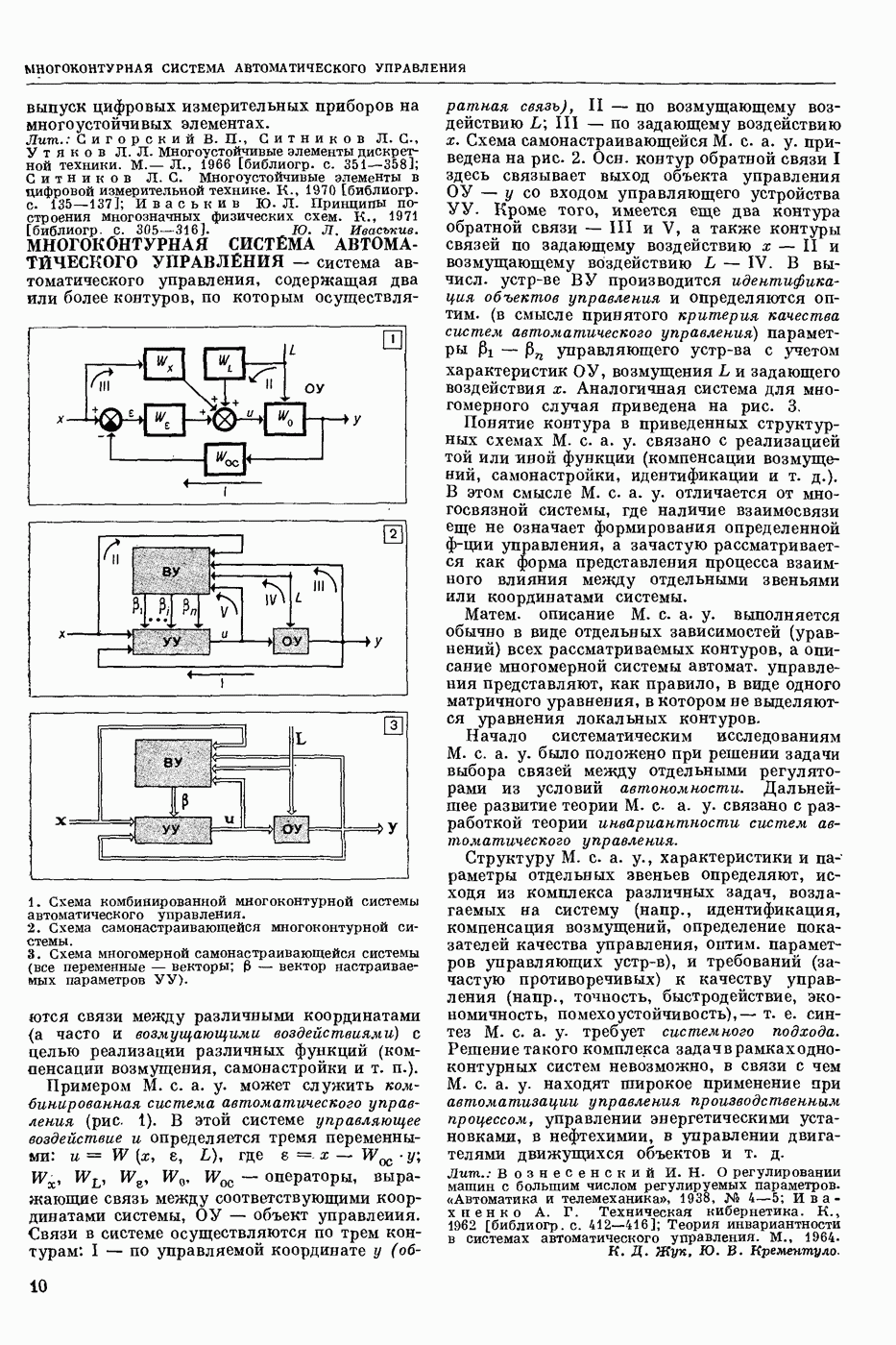
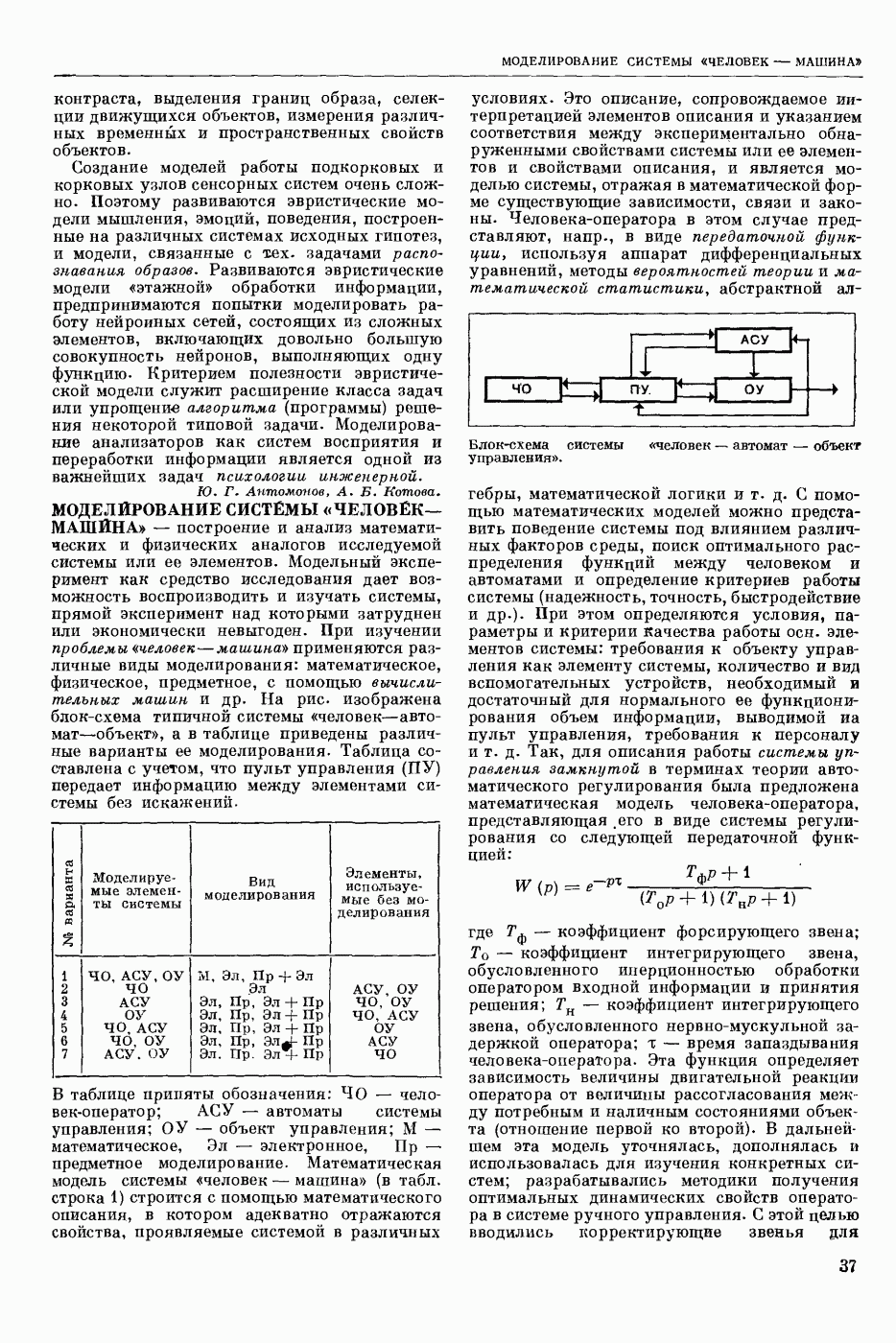
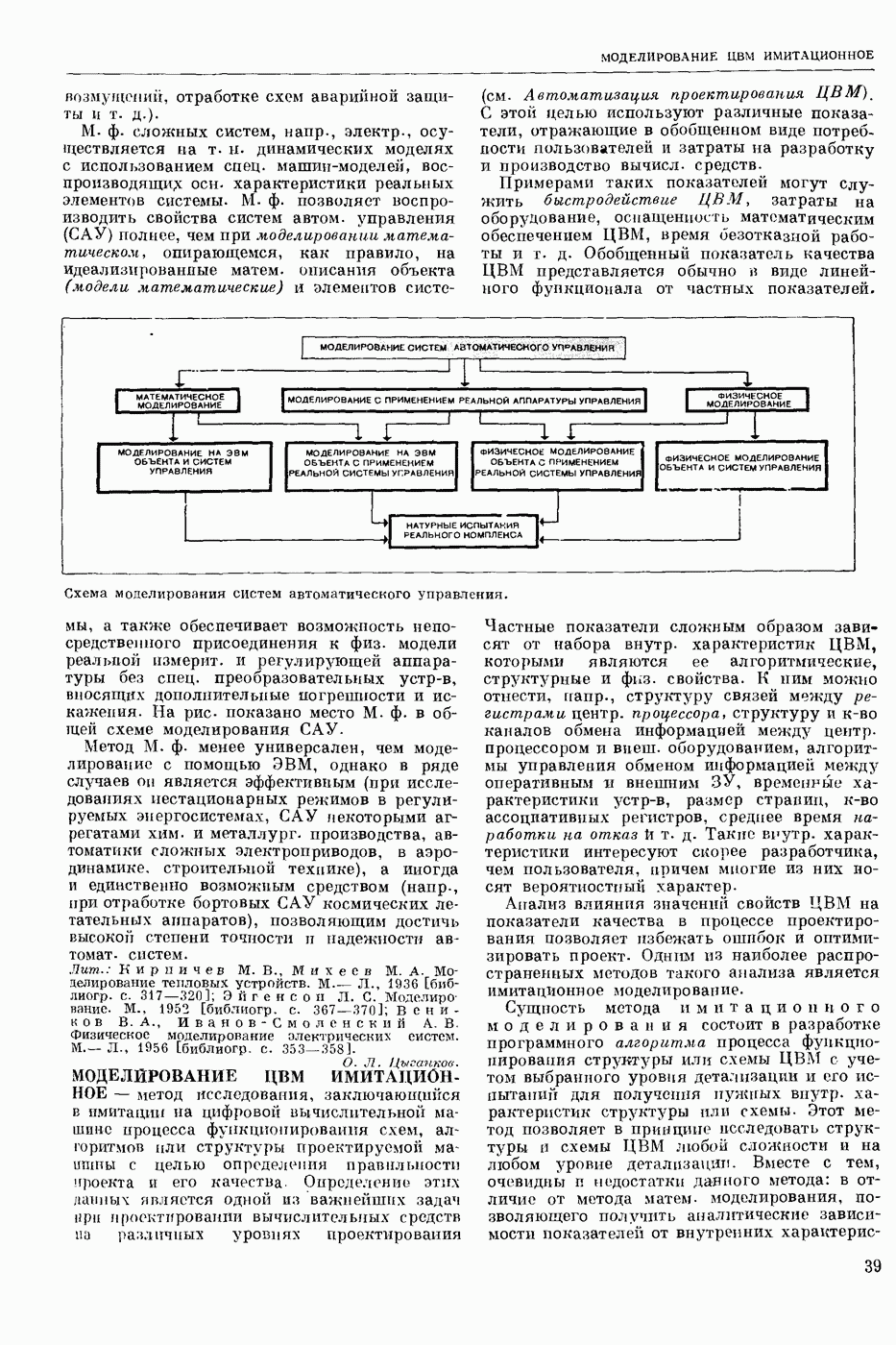
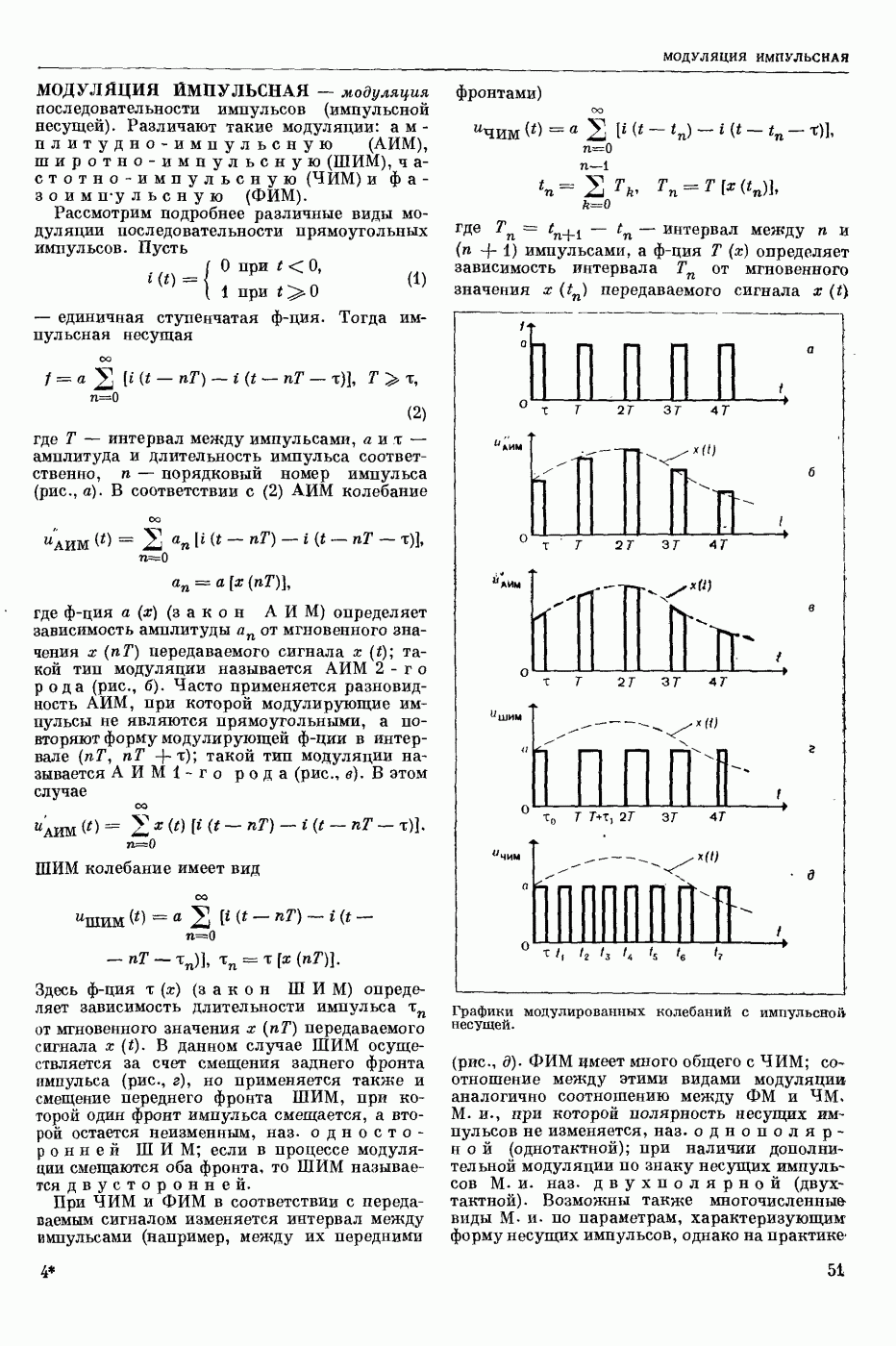
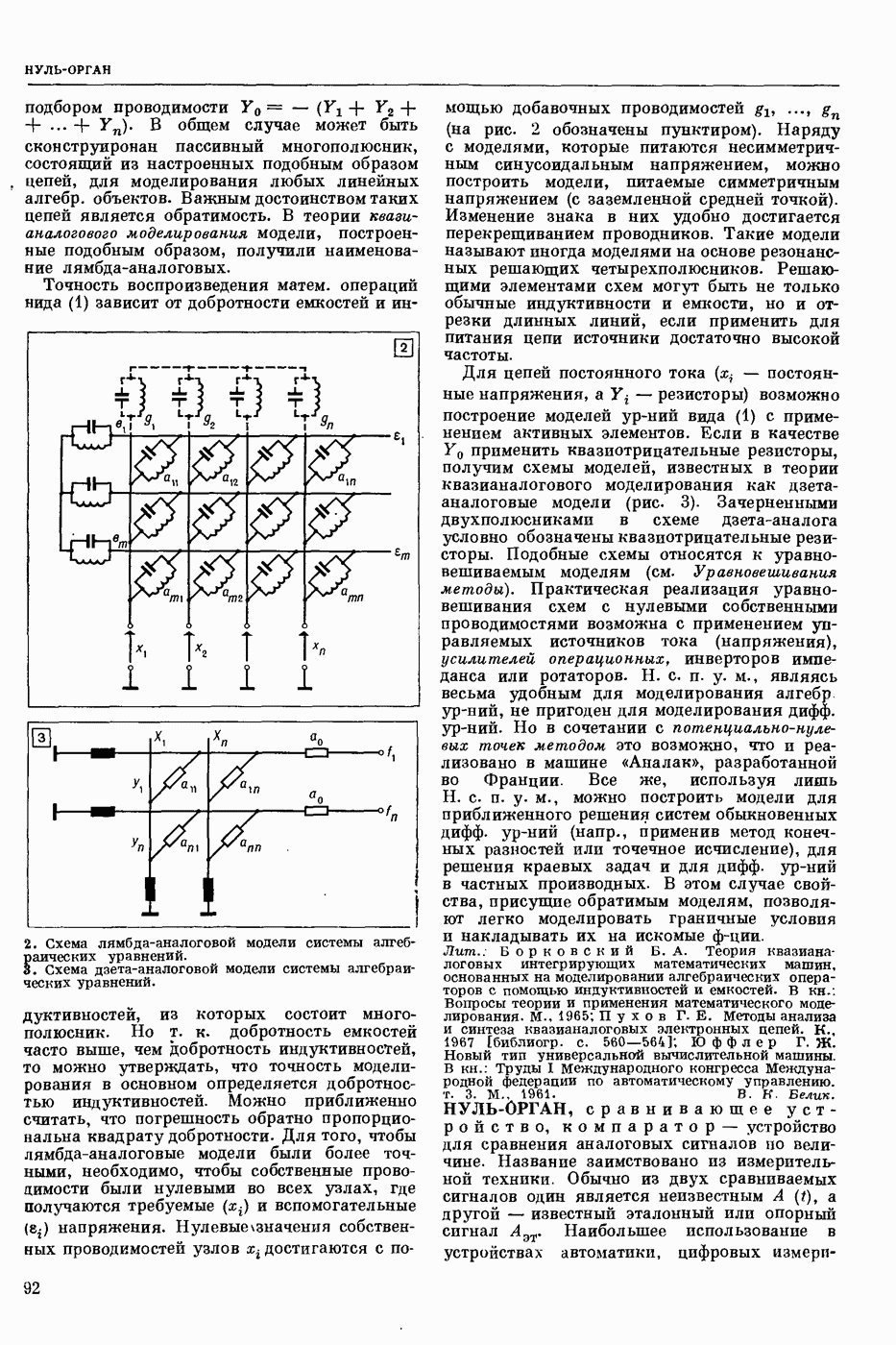
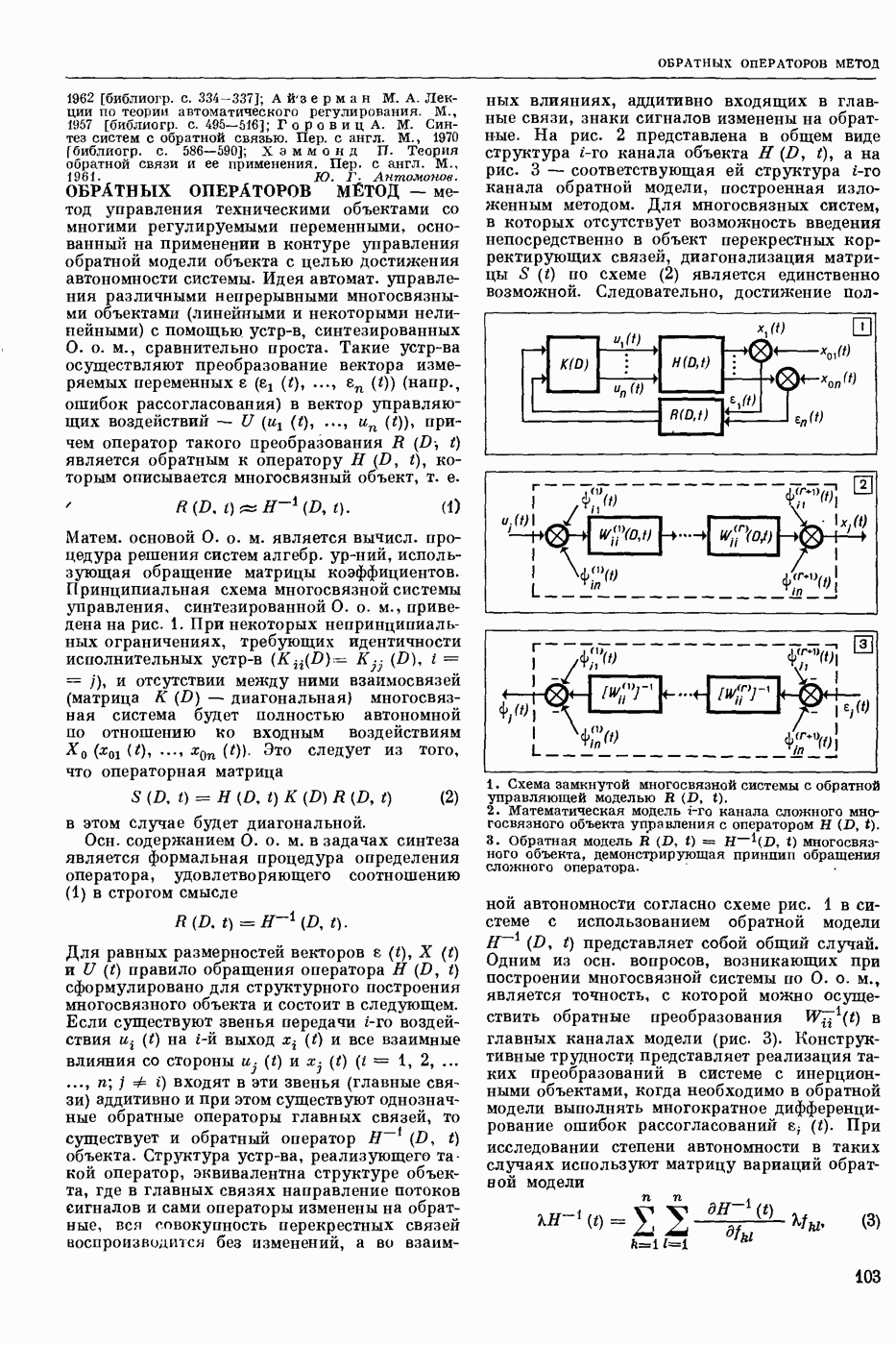
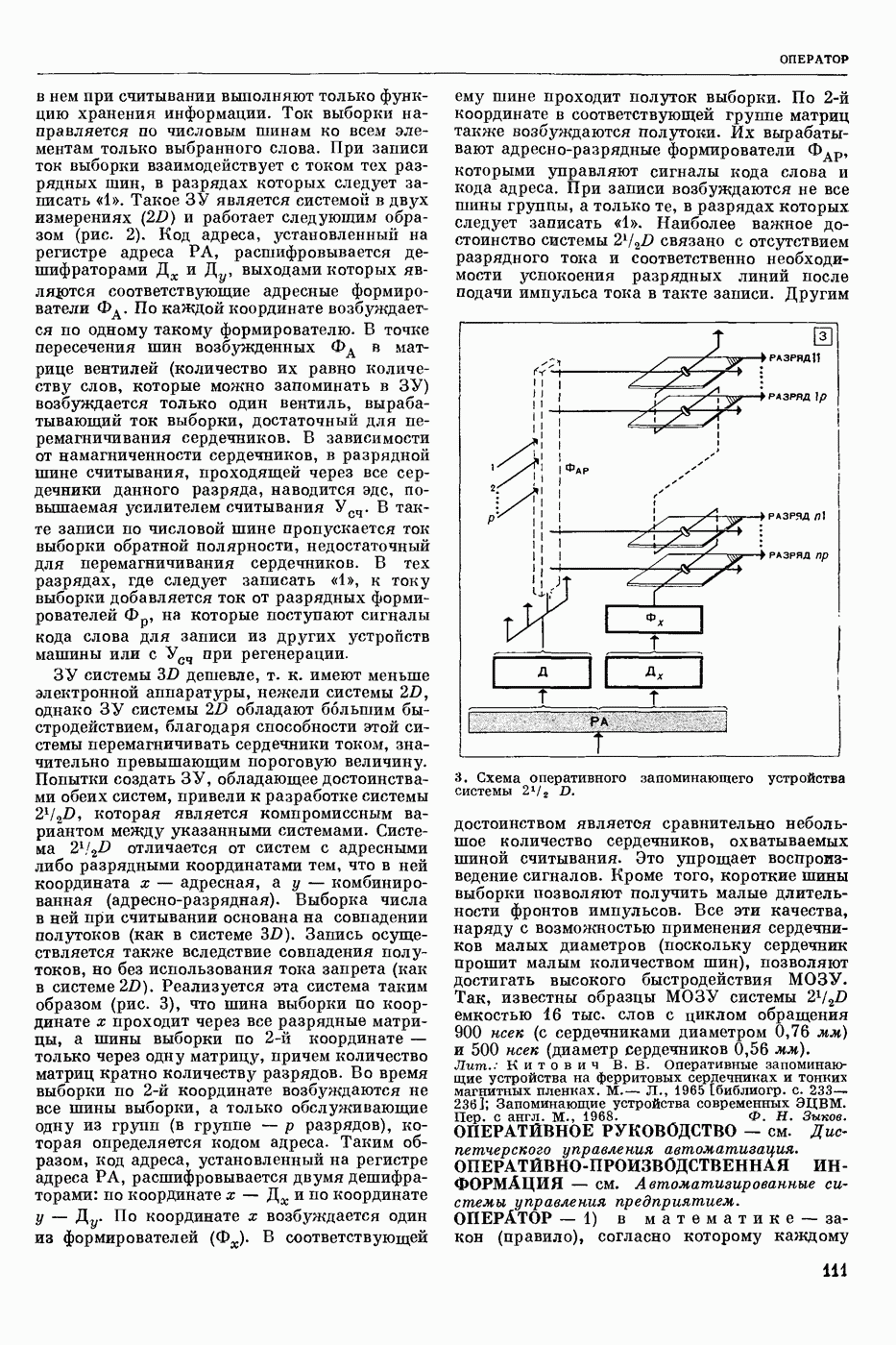
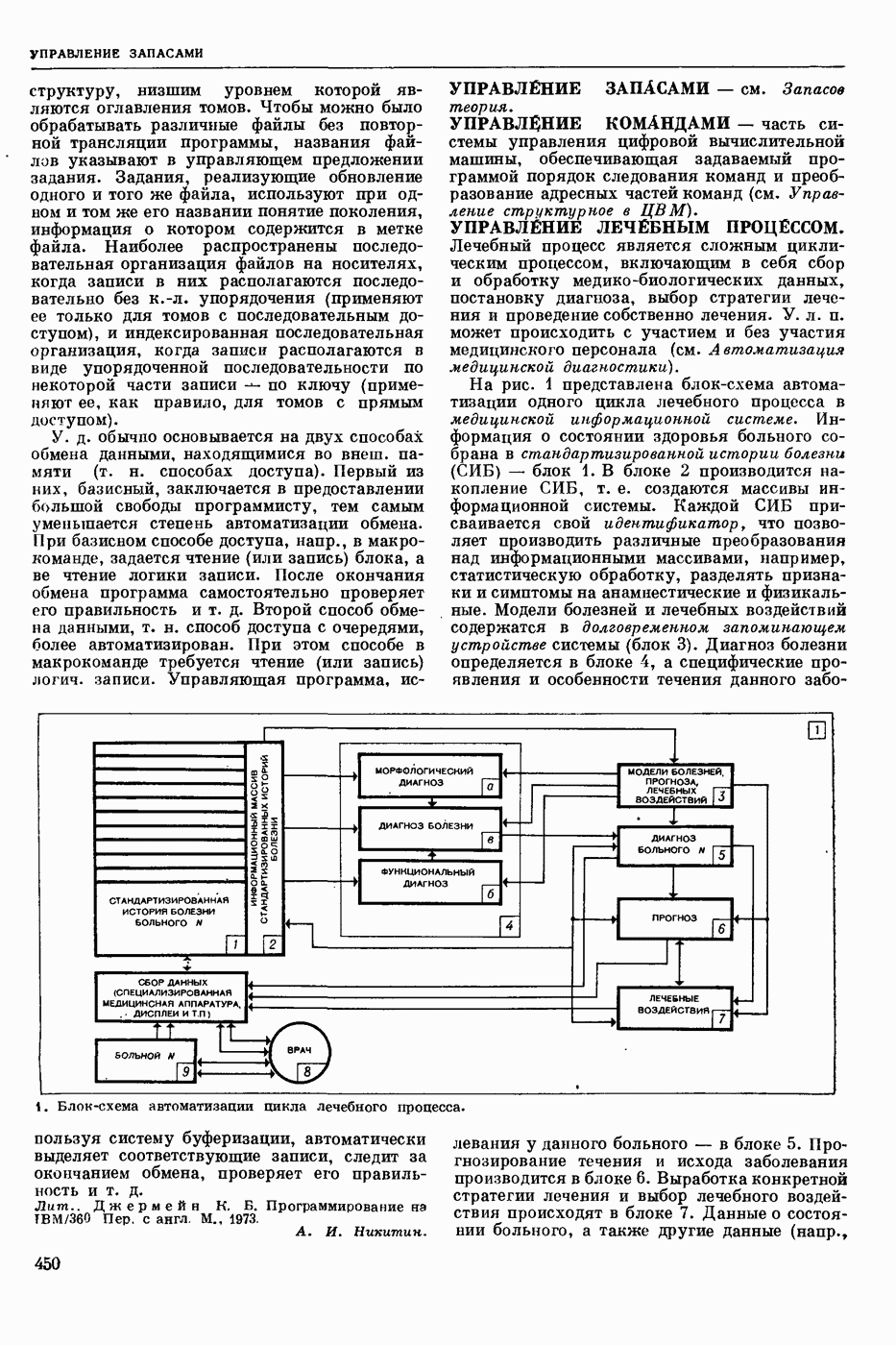
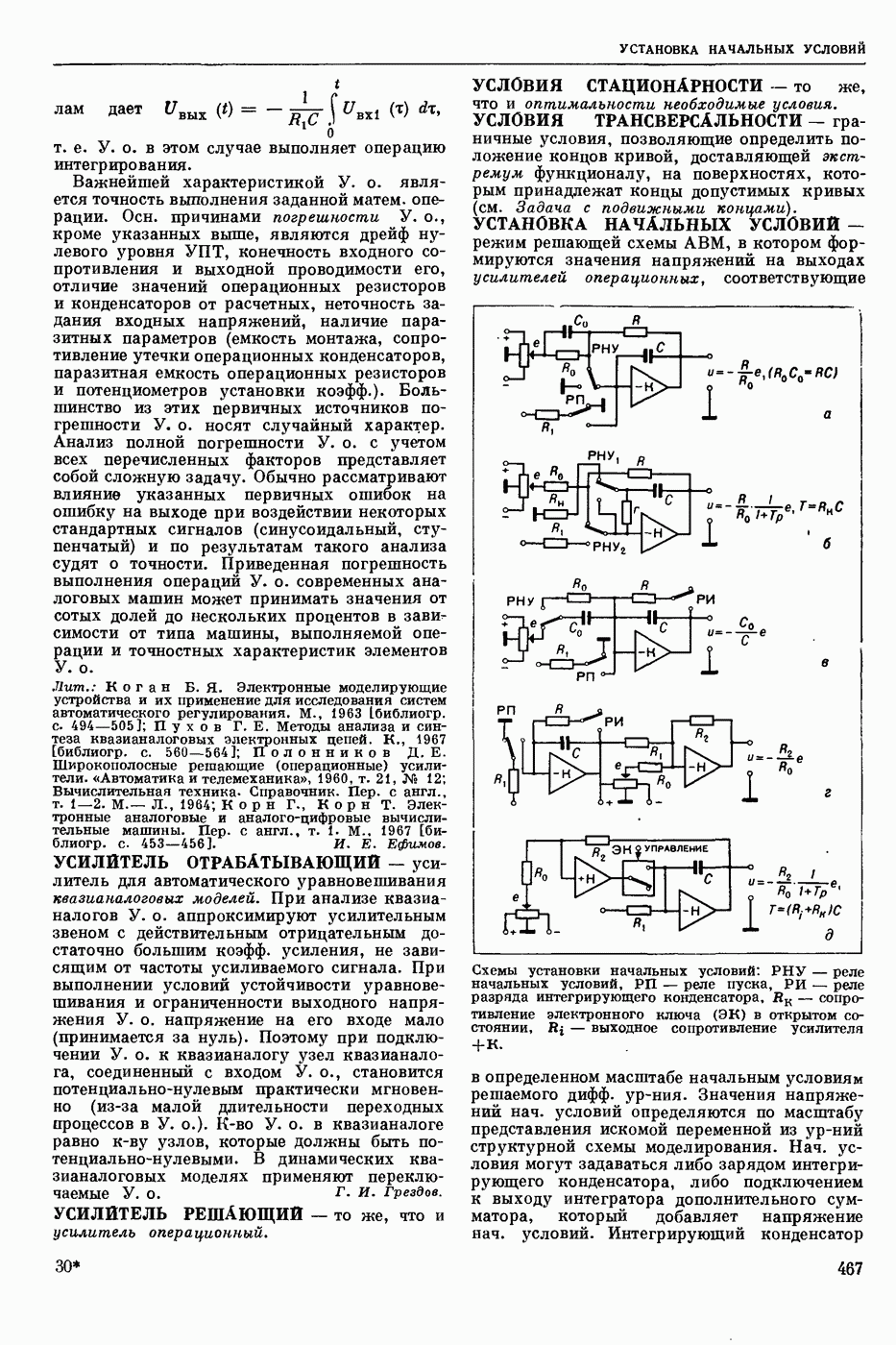
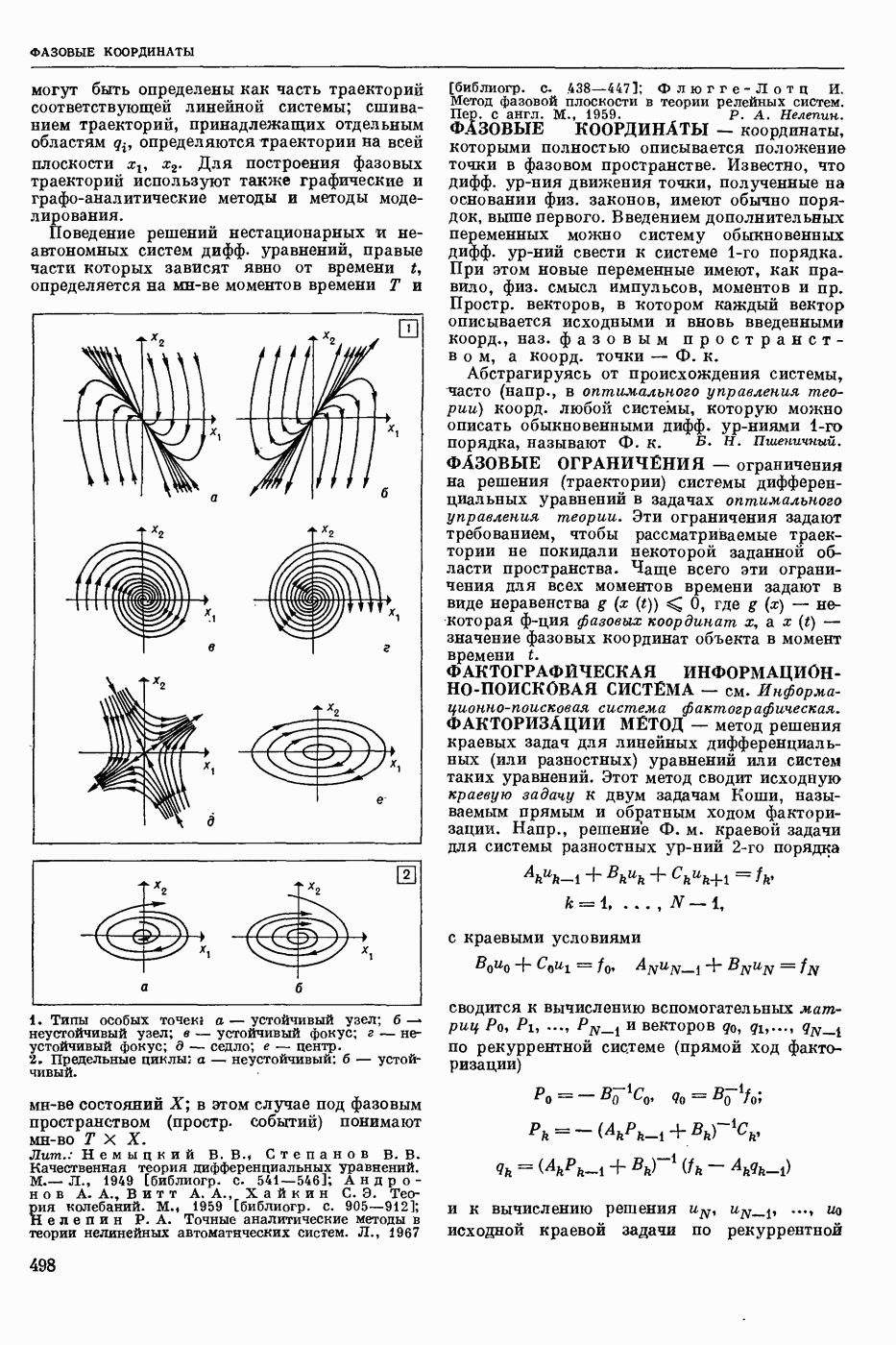
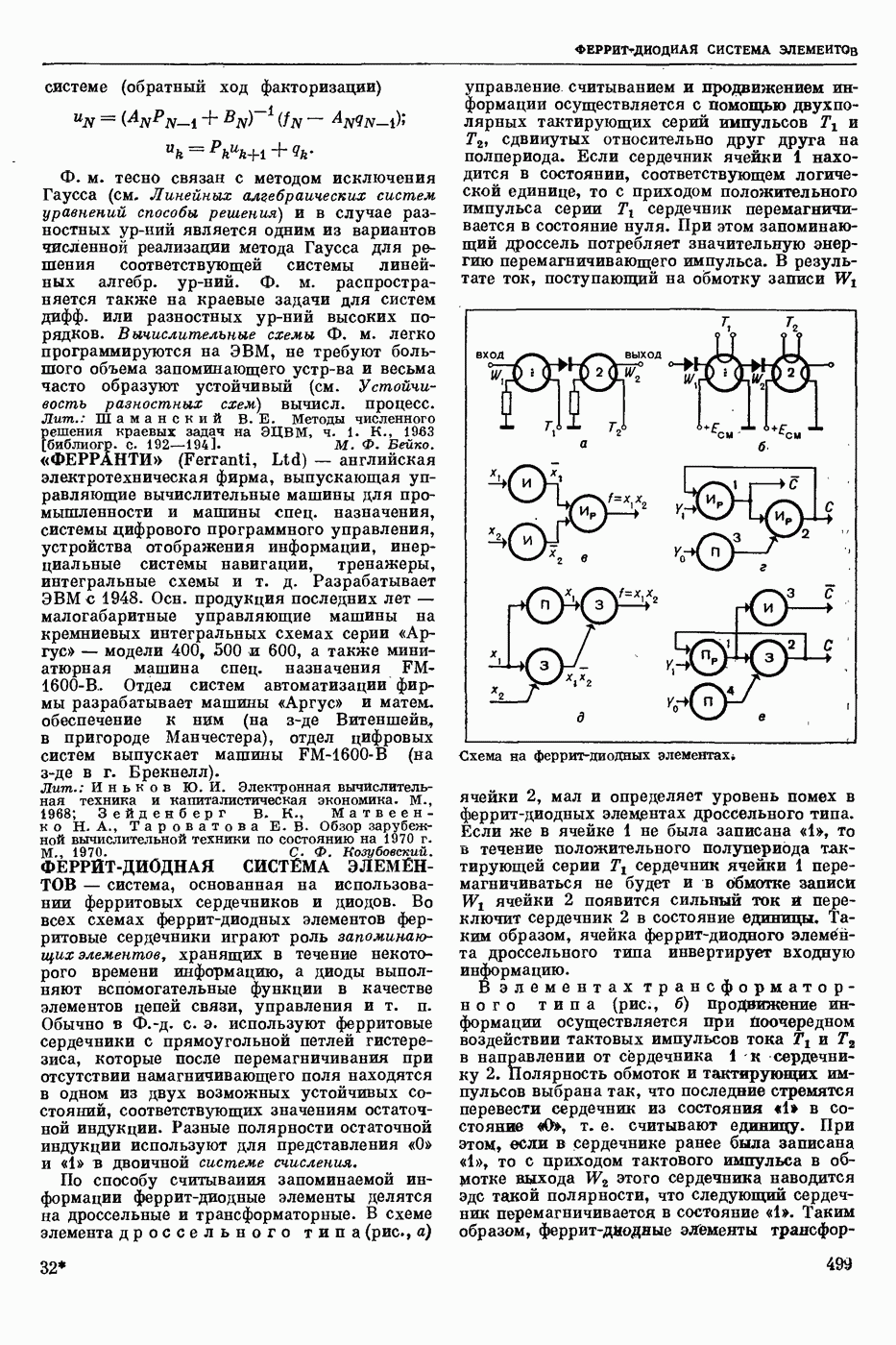
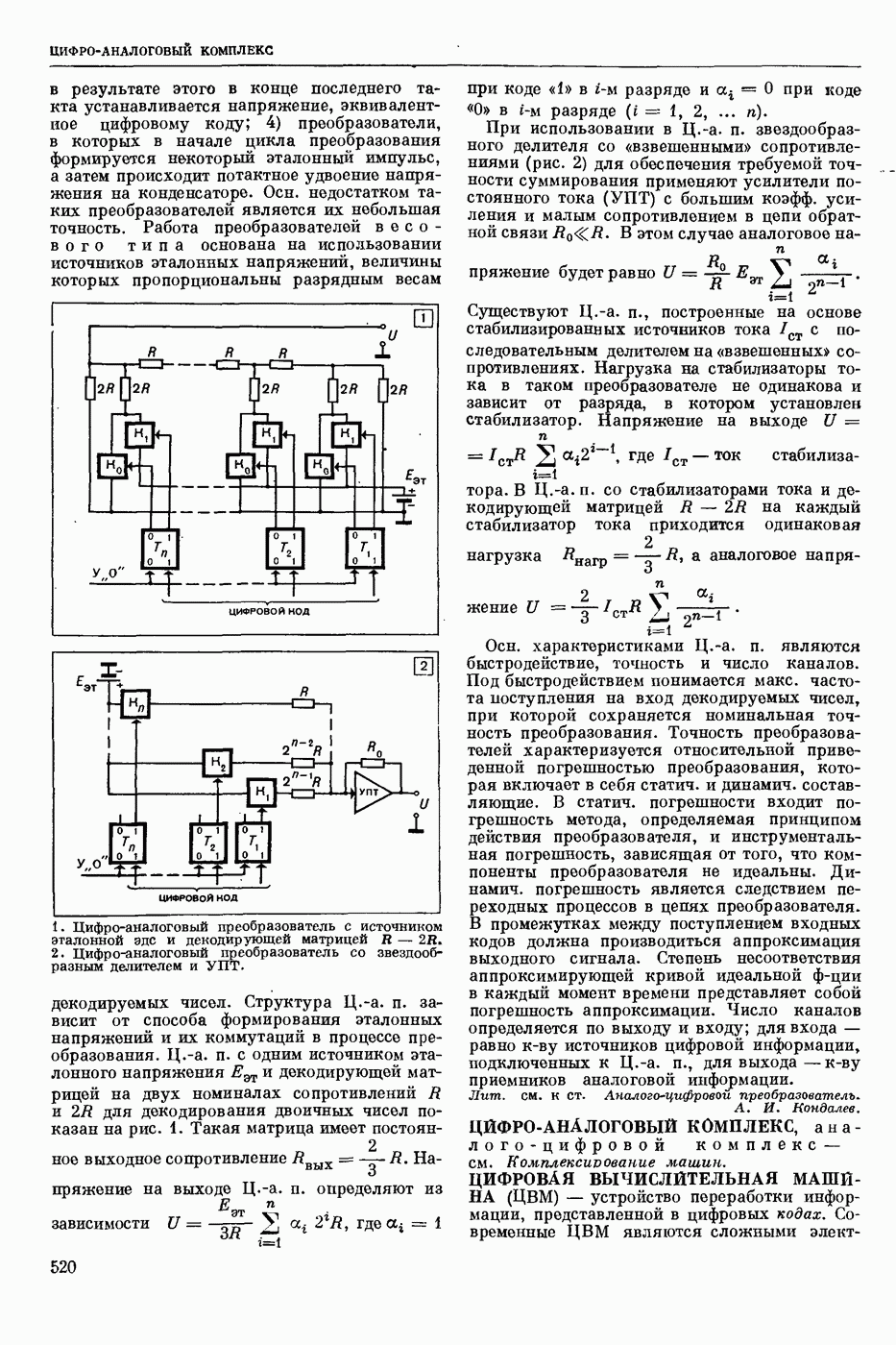
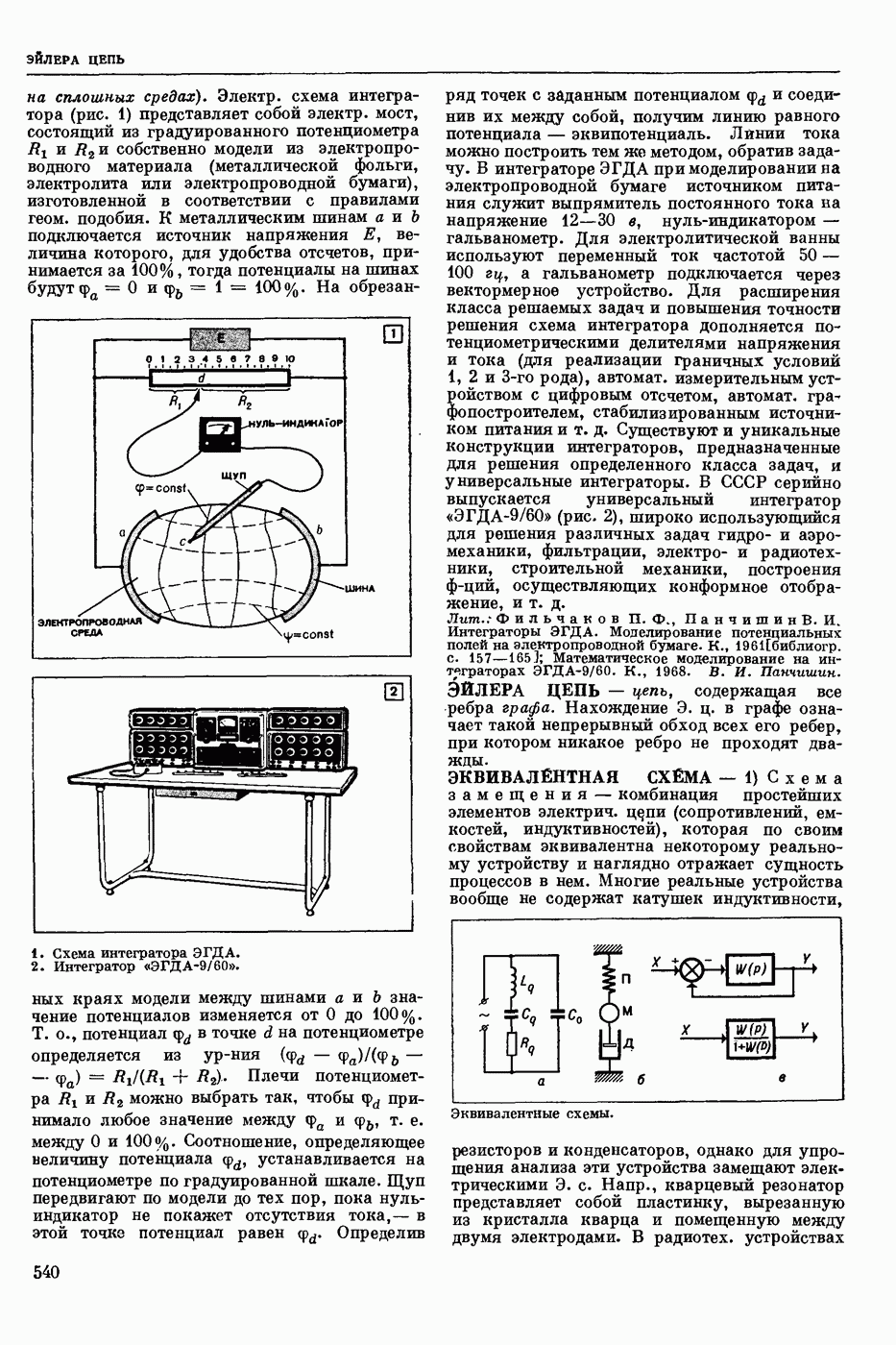
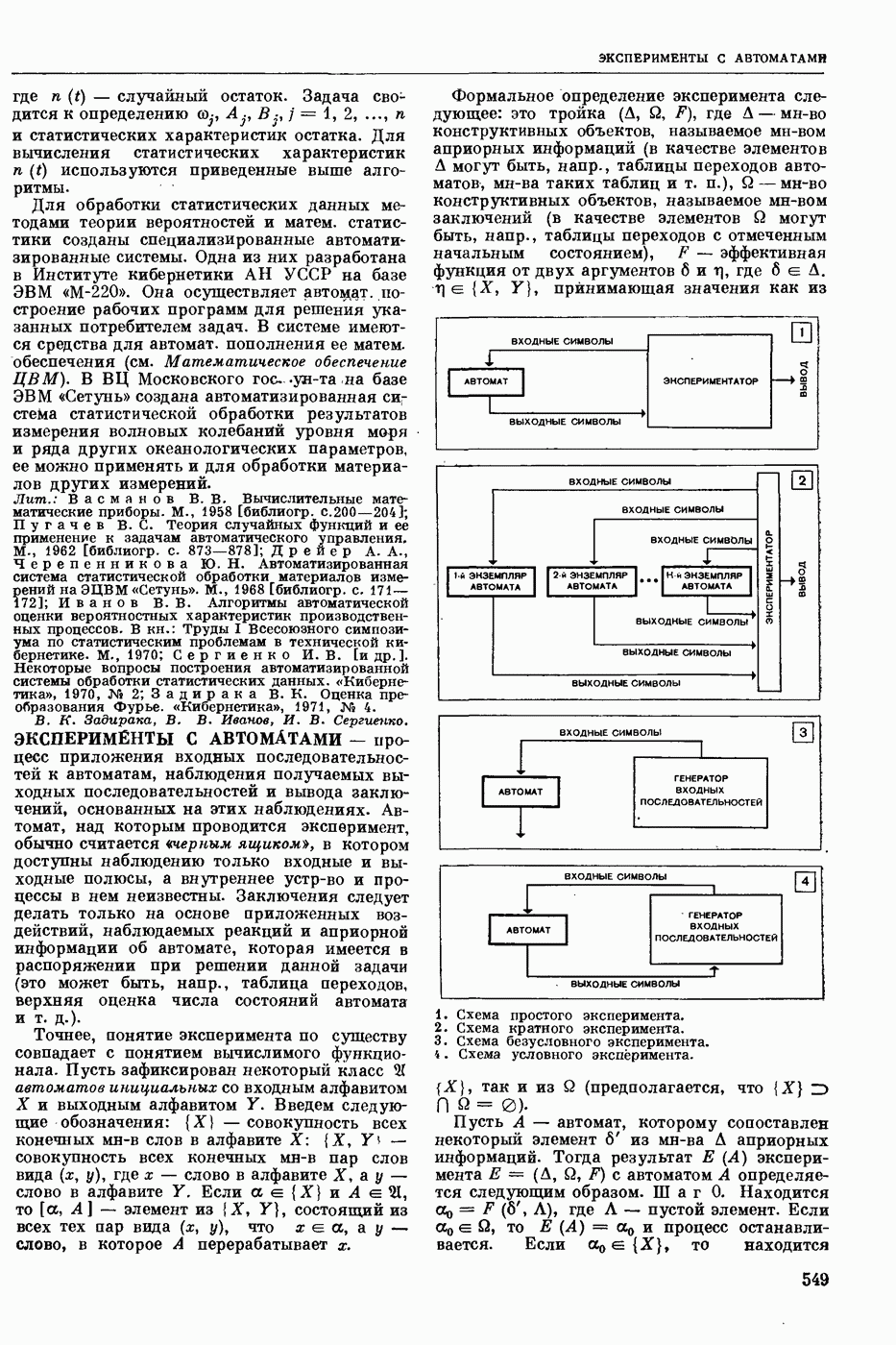
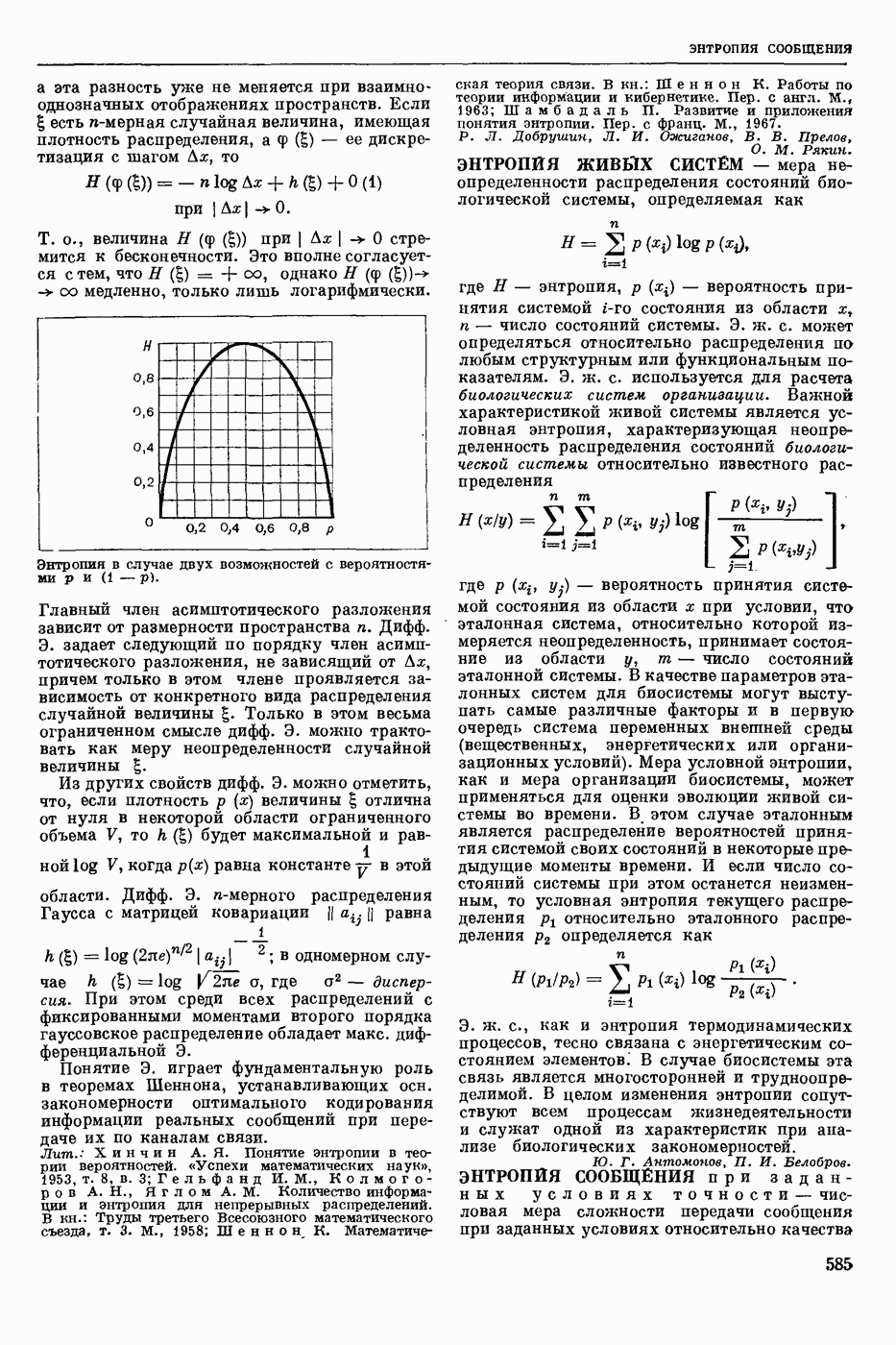
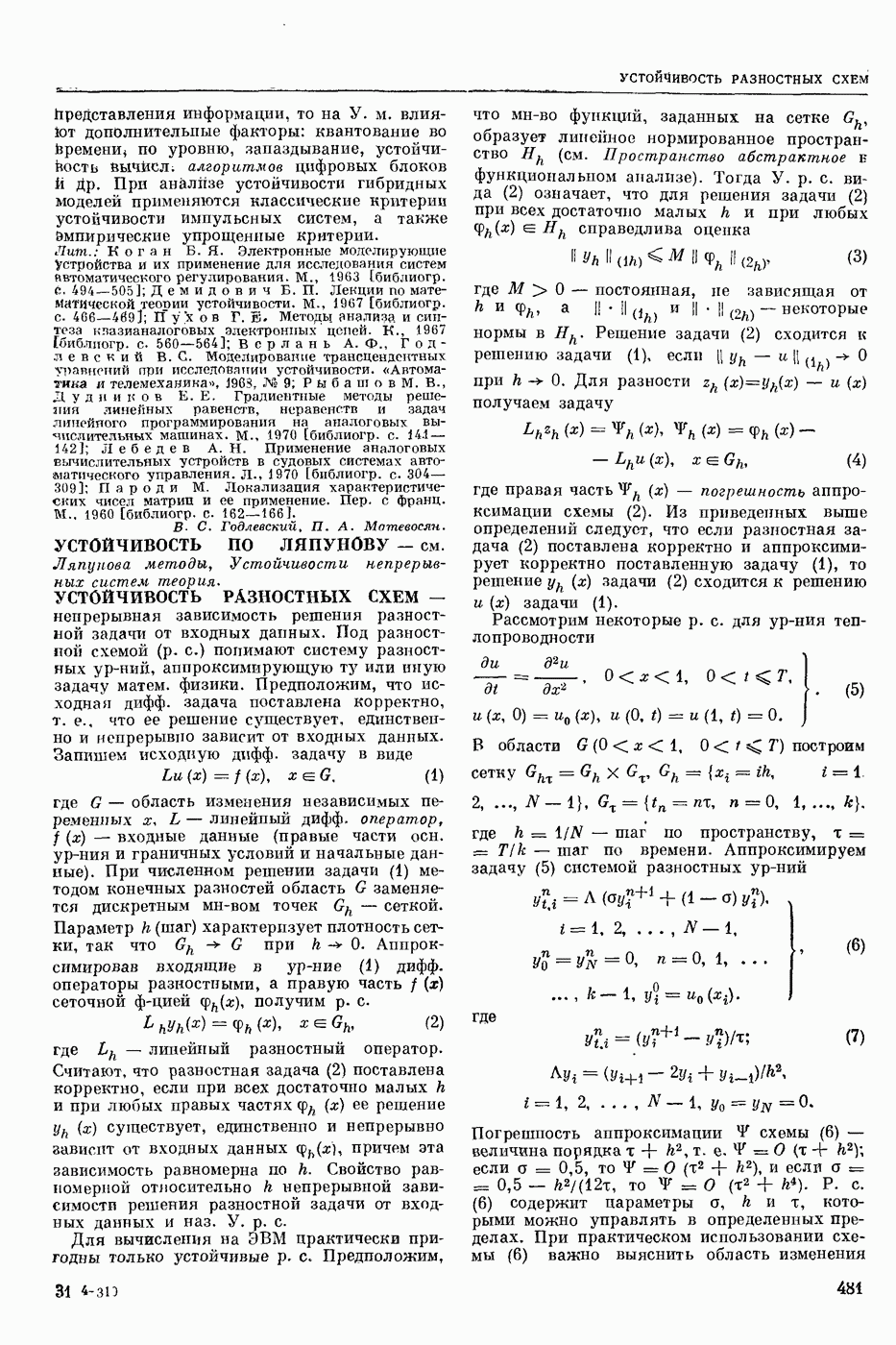| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
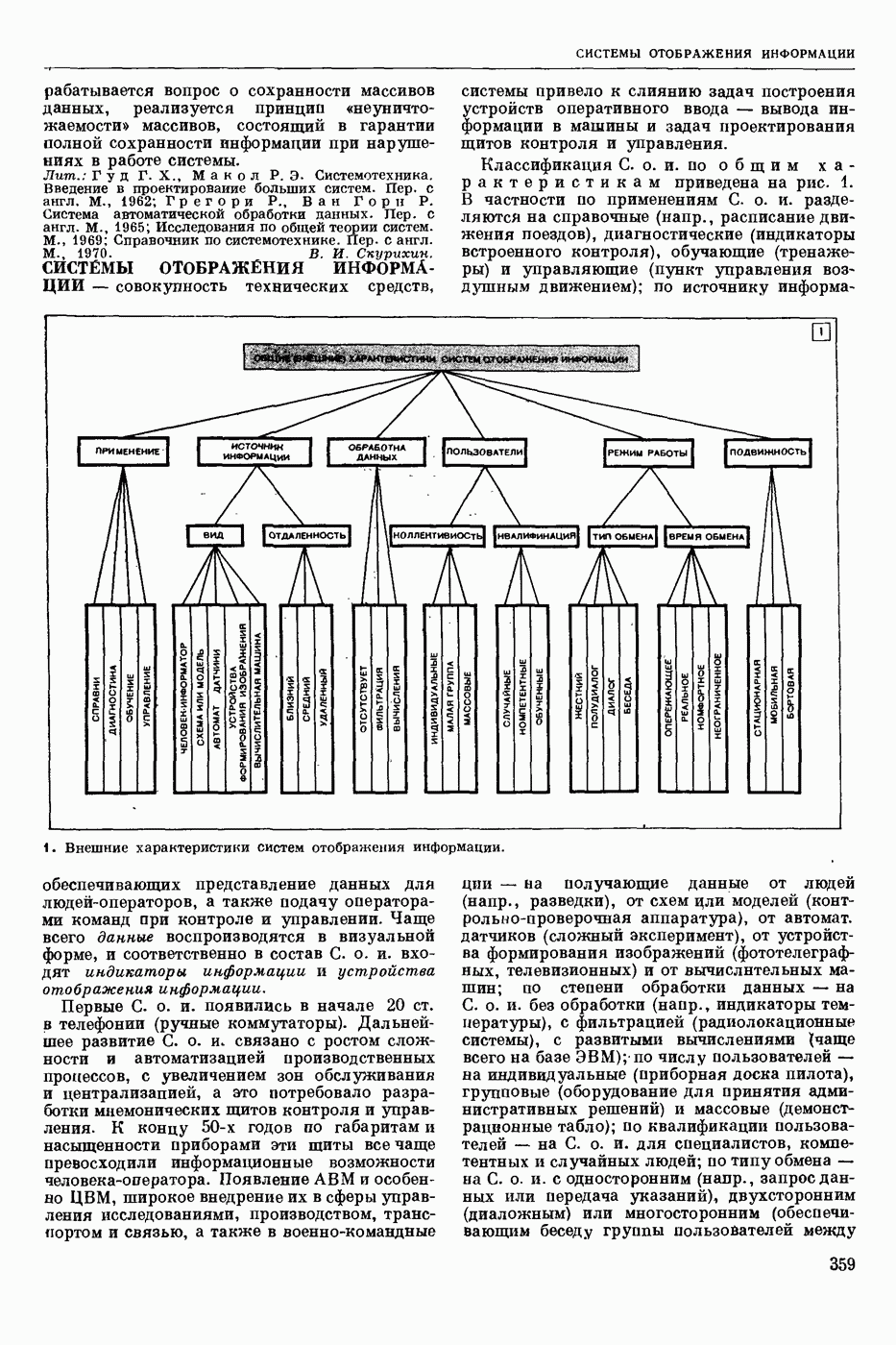
ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО
— множество М, в котором введено отношение порядка, т. е. для некоторых пар элементов х, у установлено абстрактное отношение х < у (х предшествует у); при этом ни для какого х не должно быть х < х, и из должно следовать х < z (иногда Ч. у. м. называют упорядоченными). В алгебре Ч. у. м. обычно определяют как мн-во, на котором задано рефлексивное, антисимметричное и транзитивное отношение называемое также порядком. С отношением
должно следовать х < z (иногда Ч. у. м. называют упорядоченными). В алгебре Ч. у. м. обычно определяют как мн-во, на котором задано рефлексивное, антисимметричное и транзитивное отношение называемое также порядком. С отношением  , введенным выше (тогда его называют строгим порядком), отношение
, введенным выше (тогда его называют строгим порядком), отношение  связано следующим образом:
связано следующим образом:  или
или 
Примеры. 1. Мн-во действительных чисел с обычным упорядочением;  означает, что число
означает, что число  положительно. В этом случае для любой пары элементов
положительно. В этом случае для любой пары элементов  либо
либо  у, либо
у, либо 
Мн-во всех матриц  с действительными элементами;
с действительными элементами;  означает, что
означает, что  для всех
для всех  но
но  . Очевидно, что существуют «несравнимые» матрицы
. Очевидно, что существуют «несравнимые» матрицы  , для которых ни
, для которых ни  ни
ни 
Мн-во всех непрерывных ф-ций  на отрезке
на отрезке  означает, что для всех
означает, что для всех  но
но 
В этом случае также существуют пары  для которых ни
для которых ни  ни
ни 
Понятие частичной упорядоченности важно в сочетании с алгебраическими структурами (напр., абелевой группой), или алгебраическими и топологическими (в теории частично упорядоченных линейных пространств). Частичная упорядоченность в киберн. системах часто имеет характер иерархического подчинения. Простейшей моделью такого подчинения является отношение подчинения между гранями симплекса:  означает, что грань х является собственной гранью грани у.
означает, что грань х является собственной гранью грани у.
Если М — Ч. у. м. с порядком  то положив а -К b в том и только том случае, когда
то положив а -К b в том и только том случае, когда  определим на М новый порядок. Возникающее при этом Ч. у.
определим на М новый порядок. Возникающее при этом Ч. у.  двойственным (или дуальным) к М. Для всякого высказывания о Ч. у. м. существует двойственное высказывание, получаемое заменой символа
двойственным (или дуальным) к М. Для всякого высказывания о Ч. у. м. существует двойственное высказывание, получаемое заменой символа  Напр., нижний конус
Напр., нижний конус  подмн-ва А в Ч. у. м. М определяется условием
подмн-ва А в Ч. у. м. М определяется условием  а для всех
а для всех  а верхний конус
а верхний конус  условием:
условием:  для всех
для всех  Элемент
Элемент  максимальным, если
максимальным, если  или минимальным, если
или минимальным, если  а. Элемент а в Ч. у.
а. Элемент а в Ч. у.  наибольшим (или единицей), если а
наибольшим (или единицей), если а  для всех
для всех  . Двойственным образом определяется наименьший элемент (или нуль). Конечно, всякий наибольший (наименьший) элемент максимален (минимален), но не наоборот. Если среди элементов нижнего конуса
. Двойственным образом определяется наименьший элемент (или нуль). Конечно, всякий наибольший (наименьший) элемент максимален (минимален), но не наоборот. Если среди элементов нижнего конуса  отличных от а, существует наибольший элемент b, то говорят, что а покрывает b (или что b непосредственно предшествует а, или а непосредственно следует за b). Если Ч. у. м. М имеет «0» и «1», то ряд
отличных от а, существует наибольший элемент b, то говорят, что а покрывает b (или что b непосредственно предшествует а, или а непосредственно следует за b). Если Ч. у. м. М имеет «0» и «1», то ряд  где покрывает наз. композиционным рядом.
где покрывает наз. композиционным рядом.
В исследовании Ч. у. м. и их применений чрезвычайно полезен принцип двойственности: если справедлива какая-либо теорема о Ч. у.  сформулированная в общелогических терминах и терминах порядка, то справедлива и двойственная ей теорема.
сформулированная в общелогических терминах и терминах порядка, то справедлива и двойственная ей теорема.
Если для любых элементов х и у из Ч. у. м. М имеет место одно и только одно из трех утверждений:  то множество М наз. линейно упорядоченным (или совершенно упорядоченным, а также цепью). Всякий минимальный (максимальный) элемент линейно упорядоченного мн-ва является наименьшим (наибольшим). Вообще говоря, подмножества линейно упорядоченного мн-ва не имеют миним. элементов; напр., во мн-ве
то множество М наз. линейно упорядоченным (или совершенно упорядоченным, а также цепью). Всякий минимальный (максимальный) элемент линейно упорядоченного мн-ва является наименьшим (наибольшим). Вообще говоря, подмножества линейно упорядоченного мн-ва не имеют миним. элементов; напр., во мн-ве  упорядоченном обычным отношением «меньше», часть
упорядоченном обычным отношением «меньше», часть  не имеет миним. элемента. Если каждая часть М имеет миним. элемент, М. наз. вполне упорядоченным множеством. Напр., мн-во натуральных чисел
не имеет миним. элемента. Если каждая часть М имеет миним. элемент, М. наз. вполне упорядоченным множеством. Напр., мн-во натуральных чисел  вполне упорядочено, а мн-во Z всех целых чисел — нет. По теореме Цермело (1904), любое мн-во может быть вполне упорядочено, т. е. в нем можно ввести отношение порядка, обладающее описанным выше свойством. Ч. у.
вполне упорядочено, а мн-во Z всех целых чисел — нет. По теореме Цермело (1904), любое мн-во может быть вполне упорядочено, т. е. в нем можно ввести отношение порядка, обладающее описанным выше свойством. Ч. у.  изоморфными, если существует такое биективное отображение
изоморфными, если существует такое биективное отображение  что из
что из  следует
следует  Если М частично упорядочено, то для любого
Если М частично упорядочено, то для любого  подмножество
подмножество  отрезком М. Для двух вполне упорядоченных мн-в М и N можно показать, что либо М изоморфно отрезку N, либо
отрезком М. Для двух вполне упорядоченных мн-в М и N можно показать, что либо М изоморфно отрезку N, либо  — отрезку М: если верно то и другое, то М изоморфно N. Изоморфизм есть эквивалентности отношение между вполне упорядоченными мн-вами; классы эквивалентности наз. ординальными (порядковыми) числами.
— отрезку М: если верно то и другое, то М изоморфно N. Изоморфизм есть эквивалентности отношение между вполне упорядоченными мн-вами; классы эквивалентности наз. ординальными (порядковыми) числами.  обозначает ординальное число, соответствующее М. Для ординальных чисел вводится отношение
обозначает ординальное число, соответствующее М. Для ординальных чисел вводится отношение  если М изоморфно отрезку N, но не N. Конечное ординальное число есть класс эквивалентности, содержащий отрезок натурального ряда
если М изоморфно отрезку N, но не N. Конечное ординальное число есть класс эквивалентности, содержащий отрезок натурального ряда  , с
, с
естественным упорядочением. Наименьшее бесконечное ординальное число со есть класс, содержащий весь натуральный ряд  с естественным упорядочением. Порядковые числа важны как средство доказательства по методу трансфинитной индукции, который является естественным обобщением обычного метода полной индукции. Пусть требуется доказать предложение Р (а), формулировка которого содержит произвольное ординальное число а. Принцип трансфинитной индукции состоит в том, что если верно Р (1) и из справедливости
с естественным упорядочением. Порядковые числа важны как средство доказательства по методу трансфинитной индукции, который является естественным обобщением обычного метода полной индукции. Пусть требуется доказать предложение Р (а), формулировка которого содержит произвольное ординальное число а. Принцип трансфинитной индукции состоит в том, что если верно Р (1) и из справедливости  для
для  следует справедливость Р (а), то Р (а) верно для всех а. Этот принцип можно доказать как теорему в рамках аксиоматической теории
следует справедливость Р (а), то Р (а) верно для всех а. Этот принцип можно доказать как теорему в рамках аксиоматической теории  Применение его требует предварительного полного упорядочения мн-ва объектов, для которых доказывается предложение, что приводит к их трансфинитной нумерации; такое упорядочение возможно в силу аксиомы выбора Цермело. С помощью трансфинитной индукции доказывается ряд важных теорем математики, напр., теорема Хана—Банаха в функциональном анализе. Важным является также построение различных матем. объектов с помощью трансфинитной индукции. Применение трансфинитной индукции часто заменяется подходом, основанным на теореме Цорна. Пусть М — Ч. у. м., X; если
Применение его требует предварительного полного упорядочения мн-ва объектов, для которых доказывается предложение, что приводит к их трансфинитной нумерации; такое упорядочение возможно в силу аксиомы выбора Цермело. С помощью трансфинитной индукции доказывается ряд важных теорем математики, напр., теорема Хана—Банаха в функциональном анализе. Важным является также построение различных матем. объектов с помощью трансфинитной индукции. Применение трансфинитной индукции часто заменяется подходом, основанным на теореме Цорна. Пусть М — Ч. у. м., X; если  и для всех
и для всех  , то у наз. мажорантой X. Если всякое линейно упорядоченное подмножество
, то у наз. мажорантой X. Если всякое линейно упорядоченное подмножество  имеет мажоранту, М наз. индуктивным. Теорема Цорна о том, что всякое индуктивное упорядоченное мн-во обладает по крайней мере одним максимальным элементом, широко применяется в алгебре, функциональном анализе и др. областях математики. Наглядное представление об этой теореме дает упорядочение подмножеств данного мн-ва «по вложению»
имеет мажоранту, М наз. индуктивным. Теорема Цорна о том, что всякое индуктивное упорядоченное мн-во обладает по крайней мере одним максимальным элементом, широко применяется в алгебре, функциональном анализе и др. областях математики. Наглядное представление об этой теореме дает упорядочение подмножеств данного мн-ва «по вложению»  означает
означает  .
.
Доказательства с помощью теоремы Цорна состоят в том, что ищется макс. подмножество  данного мн-ва М, обладающее некоторым свойством, а затем доказывается, что предположение
данного мн-ва М, обладающее некоторым свойством, а затем доказывается, что предположение  приводит к противоречию; отсюда заключают, что требуемым свойством обладает все мн-во М.
приводит к противоречию; отсюда заключают, что требуемым свойством обладает все мн-во М.
Лит.: Alexandroff P. Diskrete Raume. «Математический сборник», 1937, т. 2, в. 3; Канторович Л. В., Вулих Б. 3., Пинскер А. Г. Функциональный анализ в полуупорядоченных пространствах. М.- Л., 1950 [библиогр. с. 543—546]; Курош А. Г. Лекции по общей алгебре. М., 1962 [библиогр. с. 383—387]; Скорняков Л. А. Элементы теории структур. М., 1970 [библиогр. с. 145]; Риге Ж. Бинарные отношения, замыкания, соответствия Галуа. В кн.; Кибернетический сборник, в. 7. М., 1963; Бурбаки Н. Начала математики, ч. 1. Основные структуры анализа, кн. 2. Теория множеств. Пер. с франц. М., 1965. А. В. Гладкий.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- МИХАЙЛОВА КРИТЕРИЙ
- МНОГОВАРИАНТНЫХ ЗАДАЧ РЕШЕНИЕ
- МНОГОГРАННОЕ МНОЖЕСТВО
- МНОГОГРАННЫЙ КОНУС
- МНОГОЗНАЧНЫЕ СХЕМЫ
- МНОГОКОНТУРНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОКРИТЕРИАЛЬНОСТИ ПРОБЛЕМА
- МНОГОМЕРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ РАЗДЕЛИТЕЛЬНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ УНИВЕРСАЛЬНЫЙ
- МНОГОПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ, мультипрограммная обработка информации
- МНОГОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- МНОГОШАГОВОГО ПРОЦЕССА ПРОИЗВОДСТВА МОДЕЛЬ
- МНОГОШАГОВОГО ПРОЦЕССА РАСПРЕДЕЛЕНИЯ МОДЕЛЬ
- МНОГОШАГОВЫЕ ЗАДАЧИ
- МНОГОЭТАПНОЕ ОБСЛУЖИВАНИЕ
- МНОЖЕСТВ ТЕОРИЯ
- МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- МОДЕЛИ ОБЪЕКТОВ РАСПОЗНАВАНИЯ
- МОДЕЛИ ПРОИЗВОДСТВА
- МОДЕЛИ РАВНОВЕСИЯ
- МОДЕЛИ РОСТА
- МОДЕЛИ ЭКОНОМИКИ
- МОДЕЛИРОВАНИЕ ВЕСТИБУЛЯРНОГО АНАЛИЗАТОРА
- МОДЕЛИРОВАНИЕ ВОСПРИЯТИЯ
- МОДЕЛИРОВАНИЕ ЖИВЫХ СИСТЕМ на молекулярном уровне
- МОДЕЛИРОВАНИЕ ИНЖЕНЕРНЫХ СЕТЕЙ НА АВМ
- МОДЕЛИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ МЫШЛЕНИЯ
- МОДЕЛИРОВАНИЕ НА СПЛОШНЫХ СРЕДАХ, электрическое моделирование
- МОДЕЛИРОВАНИЕ ПАМЯТИ
- МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАСПОЗНАВАНИЯ И ОБУЧЕНИЯ РАСПОЗНАВАНИЮ НА ЦВМ
- МОДЕЛИРОВАНИЕ ПСИХИЧЕСКИХ ФУНКЦИЙ
- МОДЕЛИРОВАНИЕ СЕНСОРНЫХ СИСТЕМ
- МОДЕЛИРОВАНИЕ СИСТЕМЫ «ЧЕЛОВЕК—МАШИНА»
- МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ ЦВМ ИМИТАЦИОННОЕ
- МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ НА ЦВМ
- МОДЕЛЬ ЗРИТЕЛЬНОГО АНАЛИЗАТОРА
- МОДЕЛЬ МАТЕМАТИЧЕСКАЯ
- МОДЕЛЬ НЕРВНОЙ КЛЕТКИ
- МОДЕЛЬ ПЕРЕМЕННОЙ СТРУКТУРЫ
- МОДЕЛЬ СЛУХОВОГО АНАЛИЗАТОРА
- МОДЕЛЬ «СМЫСЛ-ТЕКСТ»
- МОДЕЛЬ ФИЗИЧЕСКАЯ
- МОДЕЛЬ ЧУВСТВИТЕЛЬНОСТИ
- МОДУЛЯТОР
- МОДУЛЯЦИЯ ИМПУЛЬСНАЯ
- «МОЗГОВОЙ ШТУРМ»
- МОМЕНТОВ МЕТОД
- МОНИТОР
- МОНОТОННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- МОНТЕ-КАРЛО МЕТОД
- «МППИ-1», машина первичной переработки информации
- МУЛЬТИВИБРАТОР
- МУЛЬТИПРОГРАММИРОВАНИЕ
- МУЛЬТИПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- МУЛЬТИПРОЦЕССОРНЫЙ РЕЖИМ
- МУЛЬТИУСТОЙЧИВЫЕ СИСТЕМЫ
- МУРА АВТОМАТ
- МЫСЛИТЕЛЬНОЙ СПОСОБНОСТИ УСИЛИТЕЛЬ
- НАБЛЮДАЕМОСТИ И УПРАВЛЯЕМОСТИ УСЛОВИЯ
- НАБОРНОЕ ПОЛЕ
- НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НАДЁЖНОСТЬ КИБЕРНЕТИЧЕСКИХ СИСТЕМ
- НАДЁЖНОСТЬ РАСПОЗНАВАНИЯ
- НАИМЕНЬШИХ КВАДРАТОВ МЕТОД
- «НАИРИ»
- НАИСКОРЕЙШЕГО СПУСКА МЕТОД
- НАЙКВИСТА КРИТЕРИЙ
- НАКАПЛИВАЮЩИЕ СХЕМЫ
- НАКОПИТЕЛЬ, блок хранения информации
- НАКОПИТЕЛЬ НА МАГНИТНОЙ ЛЕНТЕ
- НАРАБОТКА НА ОТКАЗ
- НАРАБОТКА НА СБОЙ
- НАУКА УПРАВЛЕНИЯ
- НАУКОВЕДЕНИЕ
- НАУЧНАЯ ОРГАНИЗАЦИЯ ТРУДА (НОТ)
- НАУЧНО-ИНФОРМАЦИОННАЯ ДЕЯТЕЛЬНОСТЬ
- НАУЧНО-ТЕХНИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ
- НАУЧНО-ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ ОБРАБОТКА
- НАУЧНЫЙ СОВЕТ ПО КОМПЛЕКСНОЙ ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН СССР
- НАУЧНЫЙ СОВЕТ ПО ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН УССР
- НЕЗАВИСИМОСТЬ в теории вероятностей, статистическая независимость
- НЕЙРОБИОНИКА
- НЕЙРОКИБЕРНЕТИКА
- НЕЙРОН
- НЕЙРОН ФОРМАЛЬНЫЙ
- НЕЙРОННЫЕ СЕТИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫЕ ЗАДАЧИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- НЕЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ АВМ
- НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- НЕ НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НЕОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- НЕОДНОРОДНЫЙ ПОТОК В СЕТИ
- НЕОПРЕДЕЛЕННОСТЬ В УПРАВЛЕНИИ
- НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМЫ АКСИОМ, совместимость, корректность
- НЕРАЗРЕШИМЫЕ АЛГОРИТМИЧЕСКИЕ ПРОБЛЕМЫ
- «НИППОН ЭЛЕКТРИК КОМПАНИ» (Nippon Electric Company, Ltd)
- «ННБ», набор нелинейных блоков
- НОРМА ВЕКТОРА
- НОРМА МАТРИЦЫ
- НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- НОРМАЛЬНАЯ ФОРМА СОВЕРШЕННАЯ
- НОРМАЛЬНАЯ ФОРМА СОКРАЩЕННАЯ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- НОРМАЛЬНЫЕ АЛГОРИФМЫ, нормальные алгоритмы
- НОСИТЕЛЬ ИНФОРМАЦИИ
- НУЛЕВЫХ СОБСТВЕННЫХ ПРОВОДИМОСТЕЙ УЗЛОВ МЕТОД
- НУЛЬ-ОРГАН, сравнивающее устройство, компаратор
- НУМЕРАЦИЙ ТЕОРИЯ
- НЬЮТОНА ОБОБЩЕННЫЙ МЕТОД
- НЬЮТОНА ФОРМУЛЫ ИНТЕРПОЛИРОВАНИЯ
- ОБЛАСТЬ УПРАВЛЕНИЯ
- ОБЛЕГЧЁННОЕ РЕЗЕРВИРОВАНИЕ
- ОБОБЩЁННЫЕ ФУНКЦИИ
- ОБОБЩЕННЫХ ГРАДИЕНТОВ МЕТОД
- ОБРАБОТКА ДАННЫХ ПОСЛЕДОВАТЕЛЬНАЯ
- ОБРАБОТКА ДАННЫХ ПРОИЗВОЛЬНАЯ
- ОБРАБОТКА ИНФОРМАЦИИ В РЕАЛЬНОМ масштабе времени
- ОБРАБОТКА ИНФОРМАЦИИ В РЕЖИМЕ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- ОБРАБОТКИ ДАННЫХ СИСТЕМА
- ОБРАЗ, или распознаваемый класс, в кибернетике
- ОБРАТИМОСТИ ПРИНЦИП
- ОБРАТИМЫЕ ЭЛЕМЕНТЫ И МОДЕЛИ
- ОБРАТНАЯ СВЯЗЬ
- ОБРАТНЫХ ОПЕРАТОРОВ МЕТОД
- ОБУСЛОВЛЕННОСТИ ЧИСЛО
- ОБУЧАЮЩАЯ ВЫБОРКА
- ОБУЧАЮЩАЯ МАШИНА
- ОБУЧАЮЩАЯ ПРОГРАММА
- ОБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ОГРАНИЧЕНИЕ ФАЗОВЫХ КООРДИНАТ
- ОГРАНИЧИТЕЛЬ АМПЛИТУДЫ
- ОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- ОДНОРОДНЫЙ ПОТОК В СЕТИ
- ОДНОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ОКРУГЛЕНИЯ ПОГРЕШНОСТЬ
- ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ОЗУ)
- ОПЕРАТИВНОЕ РУКОВОДСТВО
- ОПЕРАТИВНО-ПРОИЗВОДСТВЕННАЯ ИНФОРМАЦИЯ
- ОПЕРАТОР
- ОПЕРАТОР АВТОМАТНЫЙ
- ОПЕРАТОР ЗАДЕРЖКИ
- ОПЕРАТОР ПРИСВАИВАНИЯ
- ОПЕРАТОР ЭЛЕМЕНТАРНЫЙ
- ОПЕРАТОР ЭЛЕМЕНТНЫЙ
- ОПЕРАТОРНАЯ СХЕМА
- ОПЕРАТОРНЫЕ УРАВНЕНИЯ
- ОПЕРАТОРНЫЙ МЕТОД ПРОГРАММИРОВАНИЯ
- ОПЕРАТОРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ОПЕРАТОРЫ ЛИНЕЙНЫЕ, линейные преобразования
- ОПЕРАЦИИ МАШИННЫЕ
- ОПЕРАЦИИ НАД МАССИВАМИ
- ОПЕРАЦИИ НАД СИМВОЛАМИ И СТРОКАМИ
- ОПЕРАЦИИ НАД ЧИСЛАМИ
- ОПЕРАЦИИ ИССЛЕДОВАНИЕ
- ОПЕРАЦИЙ СИСТЕМА
- ОПЕРАЦИОННАЯ СИСТЕМА
- ОПЕРАЦИЯ НАИМЕНЬШЕГО КОРНЯ
- ОПЕРАЦИЯ ПРИМИТИВНОЙ РЕКУРСИИ
- ОПИСАНИЕ ОБЪЕКТА РАСПОЗНАВАНИЯ
- ОПОРНОЕ НАПРЯЖЕНИЕ
- ОПОРНЫЙ ПЛАН
- ОПТИМАЛЬНАЯ ТОЧКА
- ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ТЕОРИЯ
- ОПТИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
- ОПТИМАЛЬНОСТИ НЕОБХОДИМЫЕ УСЛОВИЯ
- ОПТИМАЛЬНОСТИ ПРИНЦИП
- ОПТИМАЛЬНЫЙ ВЕКТОР
- ОПТИМАЛЬНЫХ ПАРАМЕТРОВ СИСТЕМЫ ВЫБОР
- ОПТИМАЛЬНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ОПТИМИЗАТОР АВТОМАТИЧЕСКИЙ
- ОПТИМИЗАЦИИ МЕТОДЫ численные
- «ОПТИМУМ»
- ОПТРОН
- ОРГАНИЗАЦИЯ ИНФОРМАЦИОННОГО МАССИВА
- ОРГАНИЗАЦИЯ УЧЕТА В АВТОМАТИЗИРОВАННЫХ СИСТЕМАХ УПРАВЛЕНИЯ
- ОРГАТЕХНИКА, организационная техника
- ОРДЕНА ЛЕНИНА ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- УПРАВЛЕНИЯ (АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ), ИАТ
- ОСТАНОВ
- ОСУЩЕСТВИМОСТИ ФИЗИЧЕСКОЙ КРИТЕРИИ
- ОСУЩЕСТВИМОСТИ ЦЕЛИ ПРИНЦИП
- ОТВЕТ РАСПОЗНАЮЩЕЙ СИСТЕМЫ
- ОТКАЗ ОТ РАСПОЗНАВАНИЯ
- ОТЛАДОЧНЫЕ ПРОГРАММЫ
- ОТНОШЕНИЕ
- ОТНОШЕНИЕ АНАЛИТИЧЕСКОЕ
- ОТНОШЕНИЕ БАЗИСНОЕ
- ОТНОШЕНИЕ ПАРАДИГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ ПРАВДОПОДОБИЯ
- ОТНОШЕНИЕ СИГНАЛ/ПОМЕХА
- ОТНОШЕНИЕ СИНТАГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ СИНТЕТИЧЕСКОЕ
- ОТНОШЕНИЕ ТЕКСТУАЛЬНОЕ
- ОТРИЦАНИЕ в алгебре логики
- ОЧЕРЕДЕЙ ТЕОРИЯ
- ОШИБКА В ПРИНЯТИИ ГИПОТЕЗ
- ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ОШИБОК ТЕОРИЯ
- ПАКЕТНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- ПАЛЬМА ПОТОК
- ПАМЯТИ ЗАЩИТА
- ПАМЯТИ РАСПРЕДЕЛЕНИЕ
- ПАМЯТЬ МАГАЗИННАЯ
- ПАМЯТЬ СТРАНИЧНАЯ
- ПАМЯТЬ ЦВМ
- ПАРАБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ
- ПАРАМЕТР ФАКТИЧЕСКИЙ
- ПАРАМЕТР ФОРМАЛЬНЫЙ
- ПАРАМЕТРОН
- ПАРЕТО ОПТИМУМ
- ПАЧКА ОШИБОК, пакет ошибок
- ПЕРЕВОД АВТОМАТИЧЕСКИЙ
- ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
- ПЕРЕДАЧИ ИНФОРМАЦИИ СКОРОСТЬ
- ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ПЕРЕРАБОТКА ИНФОРМАЦИИ В ЦВМ
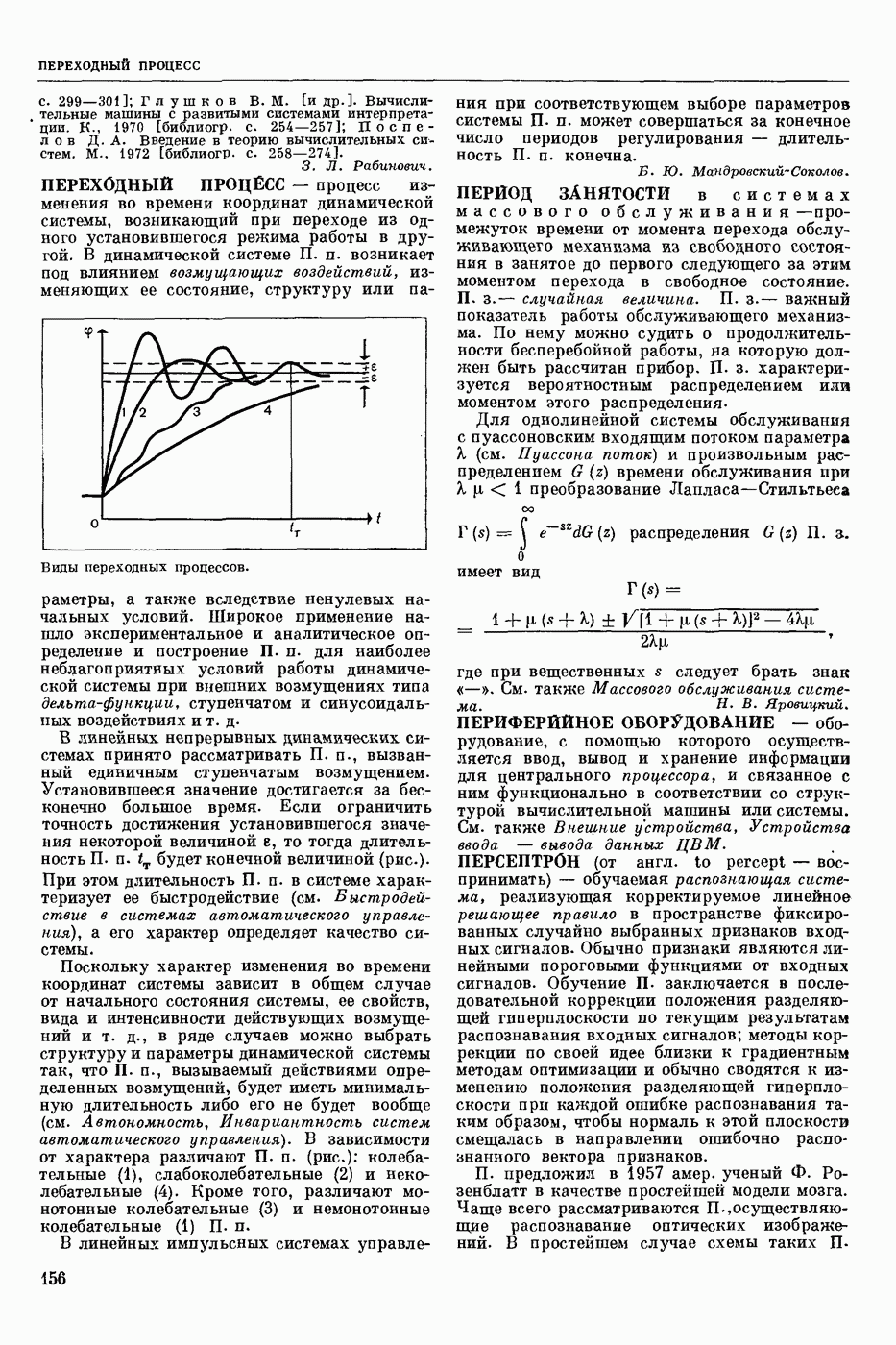
- ПЕРЕХОДНЫЙ ПРОЦЕСС
- ПЕРИОД ЗАНЯТОСТИ в системах массового обслуживания
- ПЕРИФЕРИЙНОЕ ОБОРУДОВАНИЕ
- ПЕРСЕПТРОН
- «ПЕРТ»
- ПЕРФОРАТОР
- ПЕРФОРАЦИОННАЯ КАРТА, перфокарта
- ПЕРФОРАЦИОННАЯ ЛЕНТА, перфолента
- ПЕЧАТНАЯ СХЕМА
- ПИРСА СТРЕЛКА, функция Вебба, отрицание дизъюнкции
- ПЛ-1
- ПЛАВАЮЩАЯ ЗАПЯТАЯ
- ПЛАН-ГРАФИК
- ПЛАТЕЖНАЯ МАТРИЦА
- ПЛАТЕЖНАЯ ФУНКЦИЯ
- ПЛЕНКА МАГНИТНАЯ
- ПНЕВМОНИКА, струйная пневмоавтоматика
- ПОВЕДЕНИЕ АВТОМАТОВ.
- ПОВЕДЕНИЕ АВТОМАТОВ В СЛУЧАЙНЫХ СРЕДАХ.
- ПОГЛОЩЕНИЯ ЗАКОН
- ПОГРЕШНОСТЕЙ ВЫЧИСЛЕНИЙ ТЕОРИЯ
- ПОГРЕШНОСТЬ
- ПОГРЕШНОСТЬ РЕШАЮЩЕГО ЭЛЕМЕНТА
- ПОДАВТОМАТ
- ПОДОБИЯ ТЕОРИЯ
- ПОДПРОГРАММА
- ПОДПРОГРАММА ЗАМКНУТАЯ
- ПОДПРОГРАММА ОТКРЫТАЯ
- ПОДПРОГРАММА СТАНДАРТНАЯ
- ПОДСИСТЕМА
- ПОИСК ИНФОРМАЦИИ АВТОМАТИЧЕСКИЙ
- ПОИСКА ЭКСТРЕМУМА ФУНКЦИЙ МЕТОДЫ
- ПОИСКОВОЕ ПРЕДПИСАНИЕ
- ПОИСКОВЫЙ МАССИВ
- ПОИСКОВЫЙ ОБРАЗ ДОКУМЕНТА
- ПОИСКОВЫЙ ОБРАЗ ЗАПРОСА
- ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ, экспоненциальное распределение
- ПОЛНОЙ ВЕРОЯТНОСТИ ФОРМУЛА
- ПОЛНОТА ФОРМАЛЬНОЙ ТЕОРИИ
- ПОЛНОТЫ ПРОБЛЕМА в теории автоматов
- ПОЛОС МЕТОД
- ПОЛУГРУППА, ассоциативная система
- ПОЛУМАРКОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- ПОЛУСУММАТОР
- ПОЛЬСКАЯ ЗАПИСЬ
- ПОМЕХИ
- ПОМЕХОУСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ
- ПОНТРЯГИНА ПРИНЦИП МАКСИМУМА
- ПОПОВА КРИТЕРИЙ
- ПОРОГ ЧУВСТВИТЕЛЬНОСТИ
- ПОРОГОВЫЙ ЭЛЕМЕНТ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
- ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ МЕТОД
- ПОСТА ИСЧИСЛЕНИЯ
- ПОСТА КОМБИНАТОРНАЯ ПРОБЛЕМА
- ПОСТА МАШИНА
- ПОТЕНЦИАЛОВ МЕТОД
- ПОТЕНЦИАЛЬНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-НУЛЕВАЯ ТОЧКА
- ПОТЕНЦИАЛЬНО-НУЛЕВЫХ ТОЧЕК МЕТОД
- ПОТЕНЦИАЛЬНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ МЕТОД
- ПОТЕРИ ИНФОРМАЦИИ при поиске
- ПОТОК БЕЗ ПОСЛЕДЕЙСТВИЯ
- ПОТОК В СЕТИ
- ПОТОК В СЕТИ НЕОДНОРОДНЫЙ
- ПОТОК ВЫХОДЯЩИЙ
- ПОТОК ГЕОМЕТРИЧЕСКИЙ
- ПОТОК ИНФОРМАЦИОННЫЙ ЗАМКНУТЫЙ
- ПОТОК НЕСТАЦИОНАРНЫЙ
- ПОТОК ПРОСТЕЙШИЙ
- ПОТОК РЕГУЛЯРНЫЙ
- ПОТОК С ОГРАНИЧЕННЫМ ПОСЛЕДЕЙСТВИЕМ
- ПОТОК СЛУЧАЙНЫЙ
- ПРАГМАТИКА
- ПРЕДИКАТ
- ПРЕДИКАТИВНОСТЬ
- ПРЕДСКАЗАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ПРЕДСКАЗЫВАЮЩИЙ ФИЛЬТР
- ПРЕДСТАВЛЕНИЙ ГРУПП ТЕОРИЯ
- ПРЕОБРАЗОВАНИЕ ПЕРИОДИЧЕСКИ-ОПРЕДЕЛЕННОЕ
- ПРЕОБРАЗОВАТЕЛИ ВОЛОКОННЫЕ
- ПРЕОБРАЗОВАТЕЛИ ДВУХ И БОЛЕЕ ПЕРЕМЕННЫХ
- ПРЕОБРАЗОВАТЕЛИ КОД-АНАЛОГ
- ПРЕОБРАЗОВАТЕЛИ С ПОРАЗРЯДНЫМ КОДИРОВАНИЕМ
- ПРЕОБРАЗОВАТЕЛИ ФОРМЫ ИНФОРМАЦИИ
- ПРЕОБРАЗОВАТЕЛЬ ВРЕМЯ-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ИНТЕГРИРУЮЩЕГО ТИПА
- ПРЕОБРАЗОВАТЕЛЬ КОМБИНИРОВАННЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ КВАЗИОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ ОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ НАКАПЛИВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ПРЕОБРАЗОВАТЕЛЬ РАЗВЕРТЫВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ С НЕПОСРЕДСТВЕННЫМ ОТСЧЕТОМ
- ПРЕОБРАЗОВАТЕЛЬ СЛЕДЯЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ФАЗО-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ФУНКЦИОНАЛЬНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЦИКЛИЧЕСКИЙ
- ПРЕОБРАЗОВАТЕЛЬ ЧАСТОТНО-ИМПУЛЬСНЫЙ
- ПРЕСЛЕДОВАНИЯ ЗАДАЧА
- ПРИБЛИЖЕННЫХ МЕТОДОВ ОБЩАЯ ТЕОРИЯ
- ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- ПРИОРИТЕТ
- ПРИОРИТЕТОВ СИСТЕМА
- ПРОБЛЕМА «ЧЕЛОВЕК-МАШИНА»
- ПРОГОНКИ МЕТОД
- ПРОГРАММ СЕГМЕНТАЦИЯ
- ПРОГРАММА вычислительной машины
- ПРОГРАММА ДИАГНОСТИЧЕСКАЯ
- ПРОГРАММА ИСПЫТАТЕЛЬНАЯ
- ПРОГРАММА КОМПИЛИРУЮЩАЯ
- ПРОГРАММА УПРАВЛЯЮЩАЯ
- ПРОГРАММА-ДИСПЕТЧЕР
- ПРОГРАММИРОВАНИЕ АВМ
- ПРОГРАММИРОВАНИЕ ВЫПУКЛОЕ
- ПРОГРАММИРОВАНИЕ ДИНАМИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ДИСКРЕТНОЕ
- ПРОГРАММИРОВАНИЕ ДЛЯ ЦВМ
- ПРОГРАММИРОВАНИЕ КВАДРАТИЧНОЕ
- ПРОГРАММИРОВАНИЕ КУСОЧНО-ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ НЕЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ СТОХАСТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЧАСТИЧНО ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЭВРИСТИЧЕСКОЕ
- ПРОГРАММИРОВАННОЕ ОБУЧЕНИЕ
- ПРОГРАММИРОВАННЫЙ УЧЕБНИК
- ПРОГРАММИРУЮЩАЯ ПРОГРАММА
- ПРОГРАММНОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ в народном хозяйстве.
- ПРОГРАММЫ ОБСЛУЖИВАЮЩИЕ
- ПРОЕКТИРОВАНИЕ СЕТЕЙ И КОММУНИКАЦИЙ ОПТИМАЛЬНОЕ
- ПРОЕКЦИОННЫЕ МЕТОДЫ
- ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ
- «ПРОМIНЬ»
- ПРОПОЗИЦИОНАЛЬНЫЕ СВЯЗКИ, связки логические
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- ПРОСТОЙ ИТЕРАЦИИ МЕТОД
- ПРОСТРАНСТВО АБСТРАКТНОЕ в функциональном анализе
- ПРОСТРАНСТВО ИЗОБРАЖЕНИЙ
- ПРОЦЕДУРА в программировании
- ПРОЦЕДУРА РЕКУРСИВНАЯ
- ПРОЦЕСС КОНЕЧНОЙ ДЛИТЕЛЬНОСТИ
- ПРОЦЕСС УПРАВЛЯЕМЫЙ
- ПРОЦЕССОР
- ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
- ПРЯМЫЕ МЕТОДЫ решения задач прикладной математики
- ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА
- ПСИХОЛОГИЯ ИНЖЕНЕРНАЯ
- ПУАССОНА ПОТОК
- ПУАССОНА РАСПРЕДЕЛЕНИЕ
- ПУТЬ в теории графов
- РАВНОВЕСИЯ СИТУАЦИЯ
- «РАЗДАН»
- РАЗДЕЛЯЮЩАЯ ПОВЕРХНОСТЬ в распознавании образов
- РАЗМЕЩЕНИЯ ПРОИЗВОДСТВ МОДЕЛИ
- РАЗНОСТНАЯ СХЕМА
- РАЗРЯДНОСТЬ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- РАСПАРАЛЛЕЛИВАНИЕ АЛГОРИТМА
- РАСПОЗНАВАНИЕ ЗРИТЕЛЬНЫХ ОБРАЗОВ, распознавание изображений
- РАСПОЗНАВАНИЕ ОБРАЗОВ
- РАСПОЗНАВАНИЕ ПРОЦЕССОВ
- РАСПОЗНАВАНИЕ РЕЧЕВЫХ СИГНАЛОВ
- РАСПОЗНАЮЩАЯ СИСТЕМА
- РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- РАСПРЕДЕЛИТЕЛЬНАЯ ЗАДАЧА
- РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДЫ
- РАСЧЕТНЫЙ СТОЛ ПОСТОЯННОГО ТОКА, расчетная модель электрической системы
- РАСШИФРОВОЧНАЯ МАШИНА
- РАУСА КРИТЕРИЙ, Рауса — Гурвица критерий
- РЕАЛЬНЫЙ МАСШТАБ ВРЕМЕНИ
- РЕГЕНЕРАЦИЯ информации в вычислительных устройствах
- РЕГИСТР
- РЕГРЕССИЯ
- РЕГУЛИРОВАНИЕ ЗАПАСОВ
- РЕГУЛИРОВАНИЯ ЗАКОН
- РЕГУЛИРУЮЩИЕ СИСТЕМЫ ОРГАНИЗМА
- РЕГУЛЯРИЗАЦИИ МЕТОД
- РЕГУЛЯРНЫЕ СОБЫТИЯ И ВЫРАЖЕНИЯ
- РЕГУЛЯТОР ИМПУЛЬСНЫЙ
- РЕГУЛЯТОР ЭКСТРЕМАЛЬНЫЙ
- РЕГУЛЯТОРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- РЕГУЛЯТОРЫ ЦИФРОВЫЕ
- РЕДАКТИРОВАНИЕ ДАННЫХ
- РЕЖИМ ПЕРИОДИЗАЦИИ
- РЕЖИМ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- РЕКУРСИВНЫЕ ФУНКЦИИ
- РЕЛЕВАНТНОСТЬ ДОКУМЕНТА
- РЕЛЕЙНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ ТЕОРИЯ
- РЕФАЛ
- РЕФЕРАТ
- РЕФЕРИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- РЕФЛЕКСИВНОЕ УПРАВЛЕНИЕ
- РЕШАЮЩЕЕ ПРАВИЛО в распознавании образов
- РЕШАЮЩЕЕ УСТРОЙСТВО.
- РИСК РАСПОЗНАВАНИЯ
- РИСКА ПРОБЛЕМА
- РОБОТ
- РОБОТ ПРОМЫШЛЕННЫЙ
- РУНГЕ—КУТТЫ МЕТОД
- «РУТА-110»
- R-ФУНКЦИИ
- САМОДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- САМОКОРРЕКТИРУЮЩАЯСЯ СХЕМА
- САМОНАСТРАИВАЮЩАЯСЯ ПАРАМЕТРИЧЕСКАЯ СИСТЕМА
- САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА
- САМООБУЧАЮЩИЕСЯ СИСТЕМЫ
- САМООБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- СБОЙ ЦВМ
- СВЕРТКА РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН
- СВЕТОВОЙ КАРАНДАШ, световое перо
- СВОДИМОСТЬ в теории алгоритмов
- СВОЙСТВО ОТСУТСТВИЯ ПОСЛЕДЕЙСТВИЯ
- СВЯЗКИ ЛОГИЧЕСКИЕ
- СДВИГ
- «CDC-7600»
- СЕДЛОВЫЕ ТОЧКИ
- СЕКВЕНЦИЯ
- СЕМАНТИКА
- СЕМАНТИКА СТРУКТУРНАЯ
- СЕМАНТИЧЕСКИЙ АНАЛИЗ
- СЕМИОТИКА
- СЕРВОМОТОР
- СЕТЕВАЯ ЗАДАЧА
- СЕТЕВАЯ ЗАДАЧА НЕОДНОРОДНАЯ
- СЕТЕВАЯ МОДЕЛЬ
- СЕТЕВОЙ ГРАФИК
- СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
- «СЕТУНЬ»
- СЕТЧАТКА в распознавании образов
- СЕТЬ ИЗ НЕЙРОННЫХ ЭЛЕМЕНТОВ
- СЕТЬ ЛОГИЧЕСКАЯ
- СЕЧЕНИЙ ПРОСТРАНСТВА ПАРАМЕТРОВ МЕТОД
- СИГНАЛИЗИРУЮЩАЯ ФУНКЦИЯ
- СИЛЛОГИСТИКА
- «СИМЕНС» (Siemens Aktiengesellschaft)
- СИММЕТРИЧЕСКИЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- СИМПЛЕКС-МЕТОД
- СИМПСОНА ФОРМУЛА
- СИМСКРИПТ
- СИМУЛА
- «СИНТАКСИС»
- СИНТАКСИЧЕСКИЙ АНАЛИЗ АВТОМАТИЧЕСКИЙ естественных языков
- СИНТАКСИЧЕСКИЙ АНАЛИЗ ПРОГРАММ
- СИНТАКСИЧЕСКИЙ КОНТРОЛЬ ПРОГРАММ
- СИНТАКТИКА
- СИНТЕЗ АВТОМАТОВ АБСТРАКТНЫЙ
- СИНТЕЗ АВТОМАТОВ СТРУКТУРНЫЙ
- СИНТЕЗ АЛГОРИТМА УПРАВЛЕНИЯ
- СИНТЕЗ РЕЧЕВЫХ СИГНАЛОВ
- СИНХРОНИЗАЦИЯ РАБОТЫ ЦВМ
- «СИРИУС»
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СТАТИСТИЧЕСКАЯ ДИНАМИКА
- СИСТЕМ ОБЩАЯ ТЕОРИЯ
- СИСТЕМА АВТОМАТИЗИРОВАННАЯ
- СИСТЕМА АВТОМАТИЧЕСКАЯ
- СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ)
- СИСТЕМА АВТОМАТИЧЕСКОЙ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- СИСТЕМА АВТОНОМНАЯ
- СИСТЕМА АСТАТИЧЕСКАЯ
- СИСТЕМА ИНФОРМАЦИОННОГО ПОИСКА
- СИСТЕМА НЕАВТОНОМНАЯ
- СИСТЕМА НЕПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЕРЫВАНИЯ ЦВМ
- СИСТЕМА ПРОГРАММИРОВАНИЯ
- СИСТЕМА ПРОГРАММНОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА СЧИСЛЕНИЯ
- СИСТЕМА УПРАВЛЕНИЯ АДАПТИВНАЯ
- СИСТЕМА УПРАВЛЕНИЯ ЗАМКНУТАЯ, система управления по отклонению
- СИСТЕМА УПРАВЛЕНИЯ НАУЧНЫМ ЭКСПЕРИМЕНТОМ
- СИСТЕМА УПРАВЛЕНИЯ РАЗОМКНУТАЯ
- СИСТЕМА УПРАВЛЕНИЯ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
- СИСТЕМА УПРАВЛЕНИЯ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- СИСТЕМА УРАВНЕНИЙ В ВАРИАЦИЯХ
- СИСТЕМА УРАВНЕНИЙ СОПРЯЖЕННАЯ
- СИСТЕМА «ЧЕЛОВЕК — МАШИНА»
- СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- СИСТЕМНОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- СИСТЕМНЫЙ ПОДХОД
- СИСТЕМОТЕХНИКА
- СИСТЕМЫ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- СИСТЕМЫ С ВРЕМЕННЫМИ ОГРАНИЧЕНИЯМИ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ
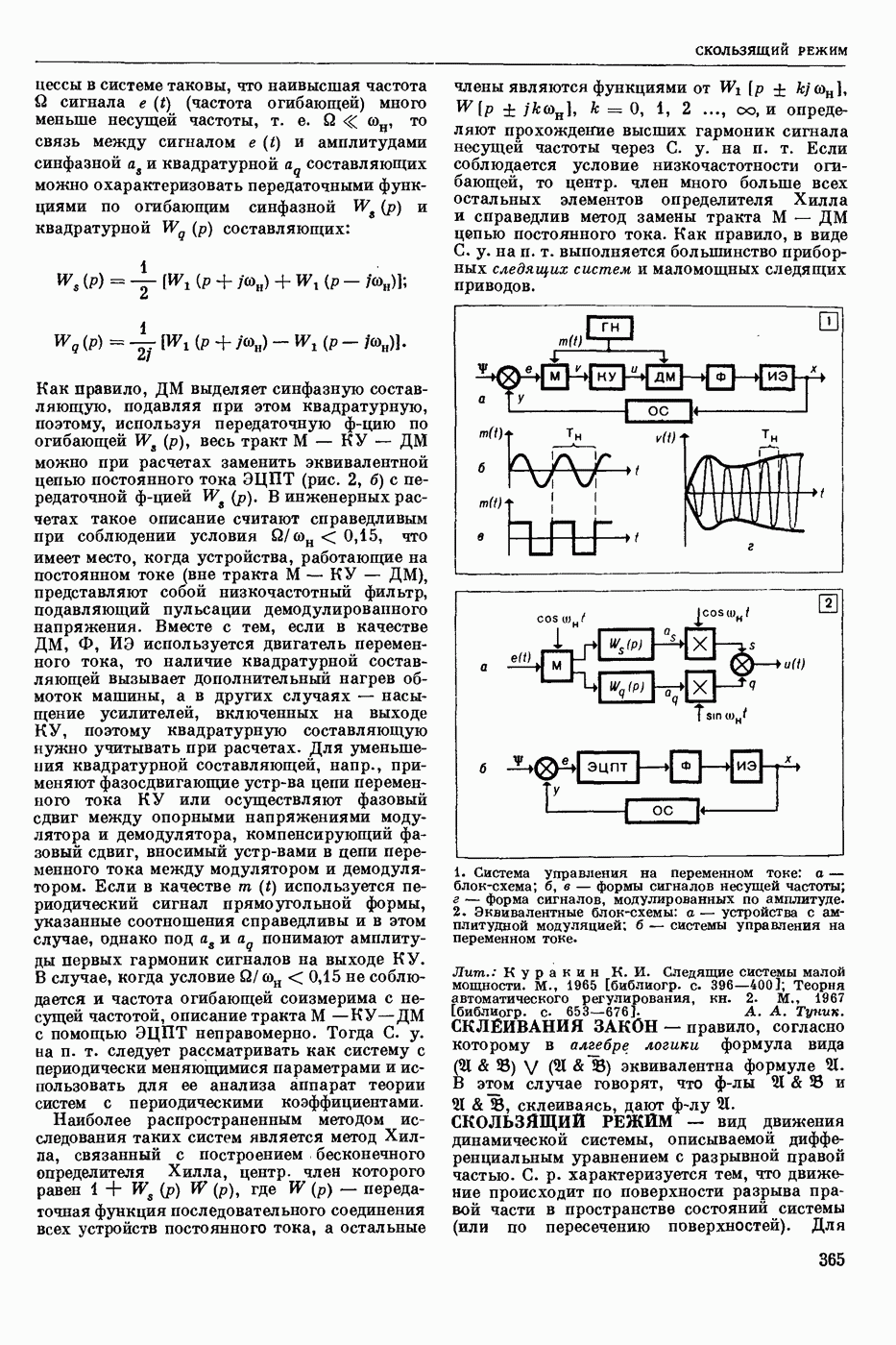
- СИСТЕМЫ УПРАВЛЕНИЯ НА ПЕРЕМЕННОМ ТОКЕ
- СКЛЕИВАНИЯ ЗАКОН
- СКОЛЬЗЯЩИЙ РЕЖИМ
- СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЯ
- СЛЕДЯЩАЯ СИСТЕМА
- СЛОВАРНЫЙ ПОИСК
- СЛОВАРЬ АВТОМАТИЧЕСКИЙ
- СЛОВАРЬ ИНФОРМАЦИОННОГО ЯЗЫКА
- СЛОВАРЬ ЧАСТОТНЫЙ
- СЛОВО
- СЛОЖНОСТЬ ВЫЧИСЛЕНИЙ
- СЛОЖНОСТЬ ТЬЮРИНГОВЫХ ВЫЧИСЛЕНИЙ
- СЛОЖНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- СЛУЧАЙНАЯ ВЕЛИЧИНА
- СЛУЧАЙНАЯ ФУНКЦИЯ
- СЛУЧАЙНОГО ПОИСКА МЕТОДЫ
- СЛУЧАЙНОЕ ПОЛЕ
- СЛУЧАЙНОЕ СОБЫТИЕ
- СЛУЧАЙНЫЕ ЧИСЛА
- СЛУЧАЙНЫЙ ПРОЦЕСС, вероятностный процесс, стохастический процесс
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ ПРЕДСКАЗАНИЯ
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ ОБЫКНОВЕННЫХ УРАВНЕНИЙ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СОБЫТИЕ РЕГУЛЯРНОЕ
- СОБЫТИЯ ЦИКЛИЧЕСКАЯ ГЛУБИНА
- СОВМЕЩЕНИЕ ОПЕРАЦИЙ В МАШИНЕ
- «СОЛЯРТРОН ЭЛЕКТРОНИК ГРУП» (The Solartron Electronic Group, Ltd)
- СООБЩЕНИЕ в теории передачи информации
- СООБЩЕНИЙ ТЕОРИЯ
- СОПРОТИВЛЕНИЕ ОТРИЦАТЕЛЬНОЕ
- СОПРОТИВЛЕНИЕ ЦИФРОВОЕ УПРАВЛЯЕМОЕ
- СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- СОРТИРОВАЛЬНАЯ МАШИНА
- СОРТИРОВКА ДАННЫХ
- СОЦИОЛОГИЧЕСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ
- СПЕКТРАЛЬНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- СПЕКТРАЛЬНАЯ ФУНКЦИЯ стационарного в широком смысле случайного процесса
- СПЕЦИАЛИЗИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- СПЕЦИАЛЬНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СПЕЦИФИКАЦИЯ
- СПИСКОВАЯ СТРУКТУРА
- СПИСОК в программировании
- СПРАВОЧНО-ИНФОРМАЦИОННЫЙ ФОНД (СИФ)
- СТАБИЛИЗАЦИИ СИСТЕМА
- СТАНДАРТИЗИРОВАННАЯ ИСТОРИЯ БОЛЕЗНИ
- СТАНДАРТЫ ПО ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
- СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ МЕТОД
- СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- СТИЛТЬЕСА КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
- СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- СТОХАСТИЧЕСКИЙ ПРОЦЕСС
- СТОХАСТИЧЕСКИХ КВАЗИГРАДИЕНТОВ МЕТОД
- СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ МЕТОД
- СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ МЕТОДЫ
- СТРАТЕГИЯ ОПТИМАЛЬНАЯ
- СТРАТЕГИЯ ПОВЕДЕНИЯ
- СТРАТЕГИЯ СМЕШАННАЯ
- СТРАТЕГИЯ ЧИСТАЯ
- «СТРЕЛА»
- СТРУКТУРА, решетка.
- СТРУКТУРНАЯ ИНТЕРПРЕТАЦИЯ ЯЗЫКА
- СТРУКТУРНАЯ ПОЭТИКА
- СТРУКТУРНАЯ СХЕМА МОДЕЛИ
- СТРУКТУРНАЯ ТЕОРИЯ АВТОМАТОВ
- СТРУКТУРНОЕ СТИХОВЕДЕНИЕ
- СУММАТОР
- СУММАТОР КОМБИНАЦИОННЫЙ
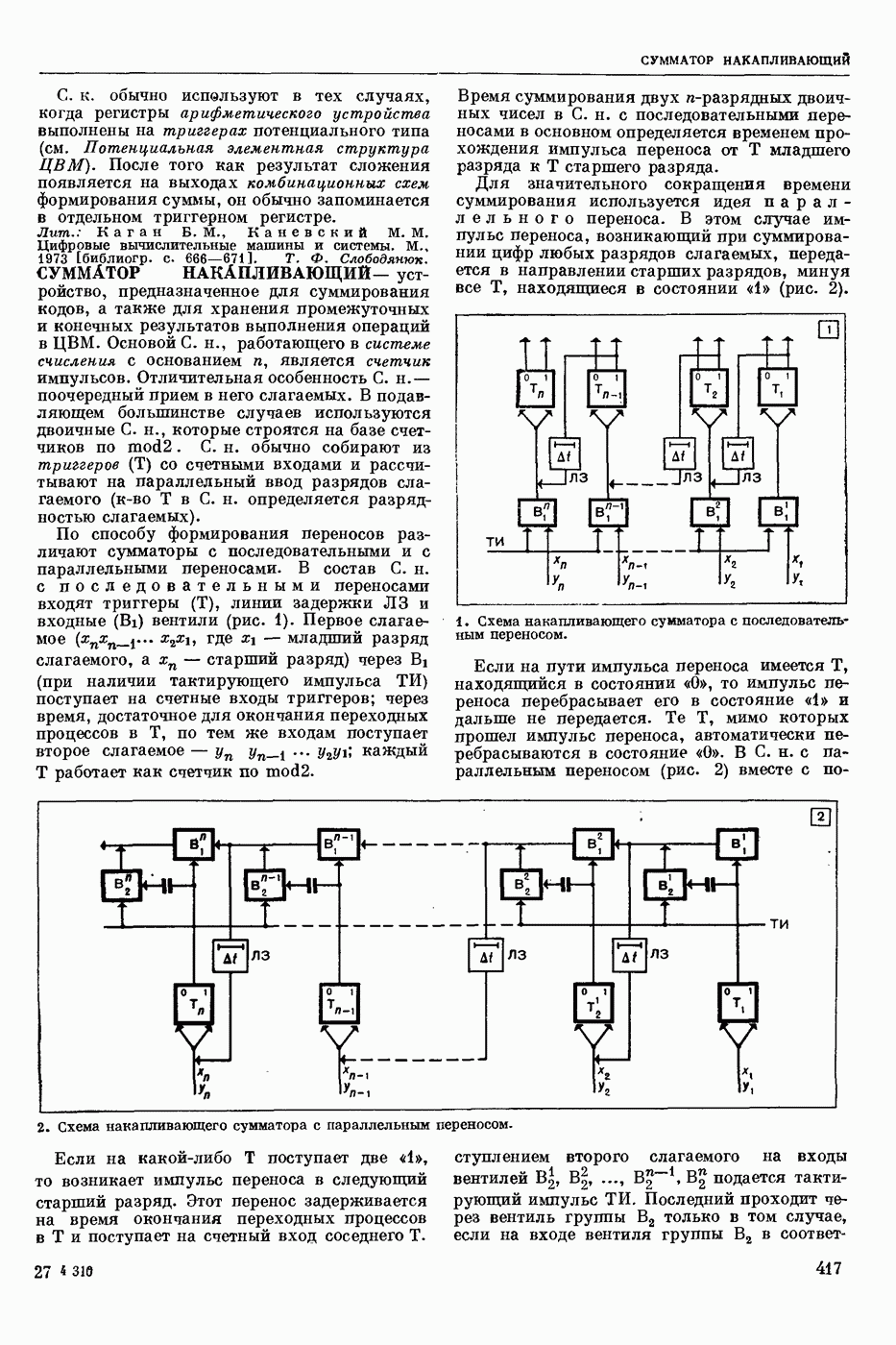
- СУММАТОР НАКАПЛИВАЮЩИЙ
- СУММАТОР ОДНОРАЗРЯДНЫЙ
- СУММАТОР ПАРАЛЛЕЛЬНЫЙ
- СУММАТОР ПОСЛЕДОВАТЕЛЬНЫЙ
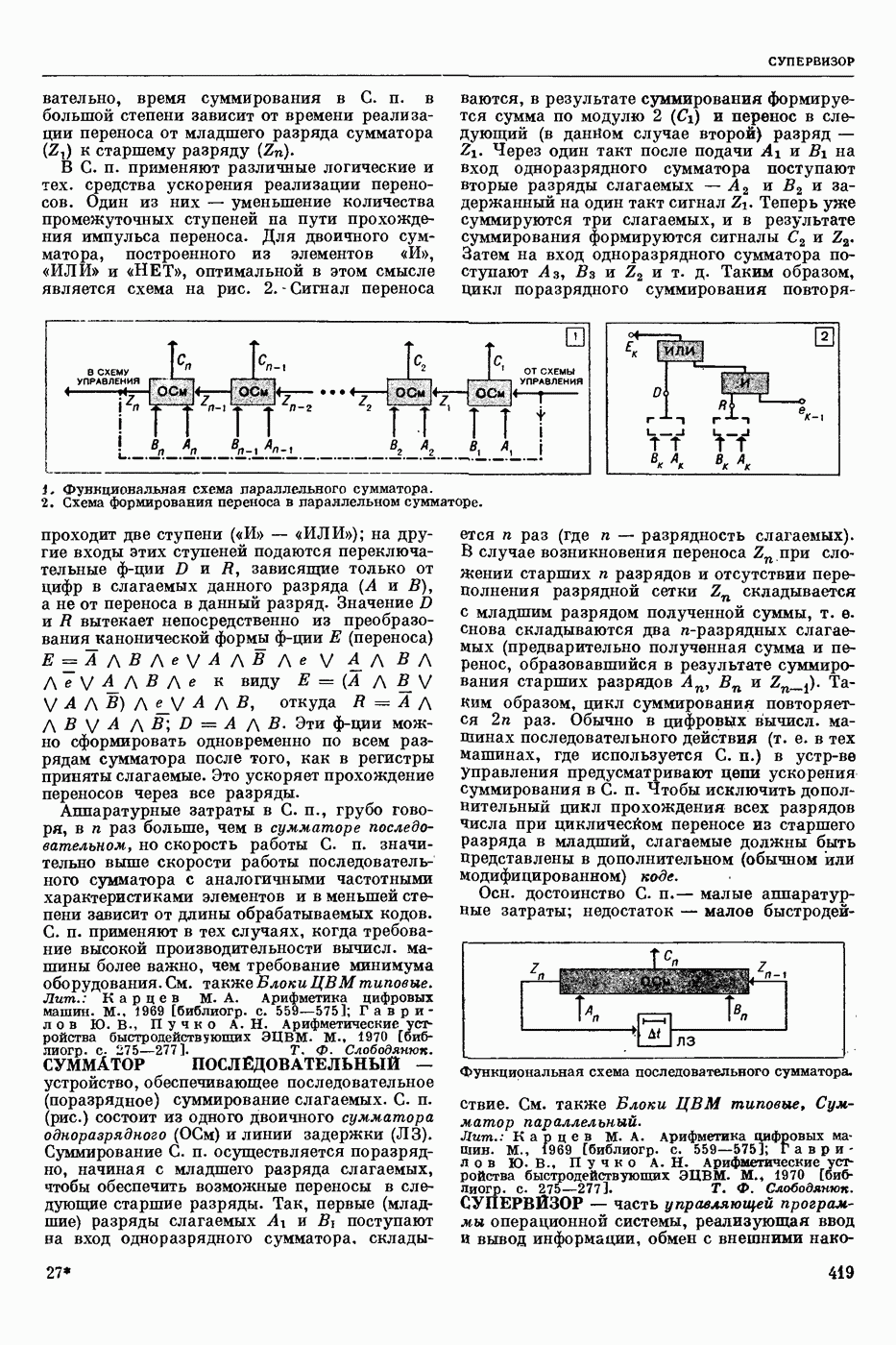
- СУПЕРВИЗОР
- СХЕМА ВЕНТИЛЬНАЯ
- СХЕМА КОНТАКТНАЯ
- СХЕМА КОНТАКТНАЯ БЕСПОВТОРНАЯ
- СХЕМА КОНТАКТНО-ВЕНТИЛЬНАЯ
- СХЕМА РЕЛЕЙНО-КОНТАКТНАЯ
- СХЕМА СРАВНЕНИЯ
- СХОДСТВА КРИТЕРИИ
- СЧЕТЧИК
- ТАБУЛИРОВАНИЕ ФУНКЦИЙ
- ТАБУЛЯТОР
- ТАЙПОТРОН
- ТАКТ
- ТАКТОВАЯ ЧАСТОТА
- ТВИСТОР
- ТЕЗАУРУС
- ТЕЛЕМЕХАНИКА
- ТЕЛЕТАЙП
- ТЕРМИНАЛ, абонентский пульт, оконечное устройство
- ТЕРМИНАЛЬНОЕ УПРАВЛЕНИЕ, управление конечным состоянием
- ТЕСТОВЫЕ ПРОГРАММЫ, тест-программы
- ТЕСТЫ
- ТЕХНИЧЕСКАЯ ДИАГНОСТИКА
- ТЕХНИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- ТЕХПРОМФИНПЛАН ПРЕДПРИЯТИЯ МАТРИЧНЫЙ
- ТОЖДЕСТВЕННО ИСТИННАЯ ФОРМУЛА, общезначимая формула
- ТОНКАЯ МАГНИТНАЯ ПЛЕНКА
- ТОПОЛОГИЯ
- «ТОСИБА» (Tokyo Shibaura Electric Company, Ltd)
- ТОЧКА РАВНОВЕСИЯ
- ТОЧКИ ПЕРЕКЛЮЧЕНИЯ
- ТОЧНОСТЬ ВОСПРОИЗВЕДЕНИЯ СООБЩЕНИЯ
- ТРАЕКТОРИЯ ДОПУСТИМАЯ
- ТРАЕКТОРИЯ ОПТИМАЛЬНАЯ
- ТРАЕКТОРИЯ ФАЗОВАЯ
- ТРАНЗИТИВНЫЙ ГРАФ
- ТРАНСЛЯТОР, компилирующая программа, программирующая программа
- ТРАНСЛЯТОР СИНТАКСИЧЕСКИ УПРАВЛЯЕМЫЙ
- ТРАНСПОРТНАЯ ЗАДАЧА
- ТРАНСПОРТНАЯ СЕТЬ
- ТРАНСФЛЮКСОР
- ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
- ТРИГГЕР
- ТРИГГЕР ДИНАМИЧЕСКИЙ
- ТРИГГЕР СТАТИЧЕСКИЙ
- ТРИОД ПОЛУПРОВОДНИКОВЫЙ, транзистор
- ТЬЮРИНГА МАШИНА
- УЗЛОВОЙ СПИСОК
- «УМ1-НХ»
- УНИВЕРСАЛЬНАЯ СИСТЕМА ЭЛЕМЕНТОВ ПРОМЫШЛЕННОЙ ПНЕВМОАВТОМАТИКИ (УСЭППА)
- UNCOL
- УПОРЯДОЧЕНИЕ МАССИВА
- УПРАВЛЕНИЕ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- УПРАВЛЕНИЕ ДАННЫМИ
- УПРАВЛЕНИЕ ЗАПАСАМИ
- УПРАВЛЕНИЕ КОМАНДАМИ
- УПРАВЛЕНИЕ ЛЕЧЕБНЫМ ПРОЦЕССОМ.
- УПРАВЛЕНИЕ ОПЕРАЦИЯМИ
- УПРАВЛЕНИЕ ОПТИМАЛЬНОЕ
- УПРАВЛЕНИЕ ПРОГРАММНОЕ
- УПРАВЛЕНИЕ С АДАПТАЦИЕЙ
- УПРАВЛЕНИЕ СТРУКТУРНОЕ В ЦВМ
- УПРАВЛЕНИЯ ОТНОШЕНИЕ, зависимости отношение
- УПРАВЛЕНИЯ СЛУЧАЙНЫМИ ПРОЦЕССАМИ ТЕОРИЯ
- УПРАВЛЯЮЩАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- УПРАВЛЯЮЩАЯ ПРОГРАММА
- УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, регулирующее воздействие
- «УПРАВЛЯЮЩИЕ СИСТЕМЫ И МАШИНЫ»
- УРАВНЕНИЙ КЛАССИФИКАЦИЯ.
- УРАВНОВЕШИВАНИЯ МЕТОДЫ
- «УРАЛ»
- УСИЛИТЕЛЬ
- УСИЛИТЕЛЬ ДИФФЕРЕНЦИАЛЬНЫЙ
- УСИЛИТЕЛЬ ОПЕРАЦИОННЫЙ, усилитель решающий
- УСИЛИТЕЛЬ ОТРАБАТЫВАЮЩИЙ
- УСИЛИТЕЛЬ РЕШАЮЩИЙ
- УСЛОВИЯ СТАЦИОНАРНОСТИ
- УСЛОВИЯ ТРАНСВЕРСАЛЬНОСТИ
- УСТАНОВКА НАЧАЛЬНЫХ УСЛОВИЙ
- УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ КРИТЕРИИ
- УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
- УСТОЙЧИВОСТЬ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ
- УСТОЙЧИВОСТЬ МОДЕЛИ
- УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ
- УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ
- УСТОЙЧИВОСТЬ ЧИСЛЕННОГО МЕТОДА
- УСТРОЙСТВА ВВОДА—ВЫВОДА ДАННЫХ ЦВМ
- УСТРОЙСТВА ЗАПИСИ АНАЛОГОВОЙ ИНФОРМАЦИИ
- УСТРОЙСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- УСТРОЙСТВО ИНДИКАЦИИ ABM
- УСТРОЙСТВО ИНТЕГРИРУЮЩЕЕ, интегратор
- УСТРОЙСТВО ИНТЕГРО-ДИФФЕРЕНЦИРУЮЩЕЕ
- УСТРОЙСТВО ОБМЕНА ЦВМ
- УСТОЙСТВО ПЕРЕЗАПИСИ ДЛЯ ЦВМ
- УСТРОЙСТВО УПРАВЛЕНИЯ ЦВМ
- УСТРОЙСТВО ЦИФРОВОЙ РЕГИСТРАЦИИ
- ФАЗОВОГО ПРОСТРАНСТВА МЕТОД
- ФАЗОВЫЕ КООРДИНАТЫ
- ФАЗОВЫЕ ОГРАНИЧЕНИЯ
- ФАКТОГРАФИЧЕСКАЯ ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ФАКТОРИЗАЦИИ МЕТОД
- «ФЕРРАНТИ» (Ferranti, Ltd)
- ФЕРРИТ-ДИОДНАЯ СИСТЕМА ЭЛЕМЕНТОВ
- ФЕРРИТ-ТРАНЗИСТОРНАЯ СИСТЕМА ЭЛЕ МЕНТОВ
- ФИКСАТОР, адрес второго ранга, косвенный адрес
- ФИКСИРОВАННАЯ ЗАПЯТАЯ
- ФИЛОСОФСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- ФИЛЬТР
- ФИЛЬТРАЦИЯ СЛУЧАЙНОГО ПРОЦЕССА
- ФОНД АЛГОРИТМОВ И ПРОГРАММ
- ФОНД СПРАВОЧНО-ИНФОРМАЦИОННЫЙ
- FORMAC
- ФОРМАЛИЗМ в математике
- ФОРТРАН
- «ФУДЗИЦУ» («Фудзи цусинки Сэйдзо», Fujitsu, Ltd)
- ФУНКЦИИ, СОХРАНЯЮЩИЕ КОНСТАНТУ
- ФУНКЦИИ, СОХРАНЯЮЩИЕ МНОЖЕСТВО
- ФУНКЦИИ, СОХРАНЯЮЩИЕ РАЗБИЕНИЕ
- ФУНКЦИОНАЛ
- ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ЭВМ
- ФУНКЦИОНАЛЬНЫЙ ЭЛЕМЕНТ ЭВМ
- ФУНКЦИЯ РАССТАНОВКИ
- ФУНКЦИЯ РЕШЕТЧАТАЯ
- ФУНКЦИЯ СТУПЕНЧАТАЯ
- ФУРЬЕ ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ФУРЬЕ ПРЕОБРАЗОВАНИЯ
- ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ в теории игр
- ХАРАКТРОН
- ХЕМИТРОН
- ХИНЧИНА-ПОЛАЧЕКА ФОРМУЛА
- «ХИТАЧИ» (Hitachi, Ltd)
- ХОМСКОГО ГРАММАТИКИ
- «ХОНИУЭЛЛ КОРПОРЕЙШЕН» (Honeywell Corporation)
- ХЭММИНГА КОД
- ЦВМ АСИНХРОННАЯ
- ЦВМ СИНХРОННАЯ
- ЦЕЛЕВАЯ ФУНКЦИЯ, функция цели
- ЦЕЛЕСООБРАЗНОСТЬ в кибернетике
- ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
- ЦЕНТРАЛЬНЫЙ ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ ИНСТИТУТ АКАДЕМИИ НАУК СССР
- ЦЕПИ СВЯЗАННЫЕ
- ЦЕПОЧКА
- ЦЕПЬ графа
- ЦЕПЬ ОКРУГЛЕНИЯ
- ЦЕПЬ ПЕРЕНОСА
- ЦИКЛ графа
- ЦИКЛ ПРОГРАММЫ
- ЦИКЛОМАТИЧЕСКОЕ ЧИСЛО
- ЦИПФА ЗАКОН
- ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ, преобразователи код
- ЦИФРО-АНАЛОГОВЫЙ КОМПЛЕКС, аналого-цифровой комплекс
- ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЦВМ)
- ЦИФРОВАЯ ИНТЕГРИРУЮЩАЯ МАШИНА
- ЦИФРОВАЯ МОДЕЛЬ СЕТЕВОГО ГРАФИКА
- ЦИФРОВОЙ ДИФФЕРЕНЦИАЛЬНЫЙ АНАЛИЗАТОР
- ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО
- ЧАСТПЧНО-РЕКУРСИВНЫЕ ФУНКЦИИ
- ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ЧЕБЫШЕВА ЗАДАЧА РАВНОМЕРНОГО ПРИБЛИЖЕНИЯ
- ЧЕЛОВЕК-ОПЕРАТОР
- ЧЕРЕДУЮЩАЯСЯ ЦЕПЬ
- ЧЕРНИЛА МАГНИТНЫЕ
- «ЧЕРНЫЙ ЯЩИК»
- ЧИРЧА ТЕЗИС
- ЧИСЛА ФОРМАТ
- ЧИСЛЕННЫЕ МЕТОДЫ
- ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
- ЧИТАЮЩИЙ АВТОМАТ, оптическое читающее устройство
- ЧИТАЮЩИЙ АВТОМАТ КОРРЕЛЯЦИОННЫЙ
- ЧУВСТВИТЕЛЬНОСТИ ТЕОРИЯ
- ШАГ КВАНТОВАНИЯ
- ШЕННОНА ЛАБИРИНТ
- ШЕННОНА МЫШЬ
- ШЕННОНА ФУНКЦИЯ
- ШЕПЛИ ВЕКТОР
- ШЕФФЕРА ШТРИХ, Шеффера функция, отрицание конъюнкции
- ШИНА
- ШИФРАТОР
- ШТРАФНАЯ ФУНКЦИЯ
- ШТРАФНЫХ ФУНКЦИЙ МЕТОД
- ШТРАФОВ МЕТОД
- ШУМ КВАНТОВАНИЯ
- ШУМ ПОИСКОВЫЙ
- ЭВРИСТИКА
- ЭВРИСТИЧЕСКИЕ МЕТОДЫ В РАСПОЗНАВАНИИ
- ЭЙЛЕРА ЦЕПЬ
- ЭКВИВАЛЕНТНАЯ СХЕМА
- ЭКВИВАЛЕНТНОСТИ ОТНОШЕНИЕ (эквивалентность, эквиваленци я) на множестве
- ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЭКВИВАЛЕНТНЫЕ СОСТОЯНИЯ АВТОМАТА
- ЭКВИВАЛЕНТНЫХ ВОЗМУЩЕНИЙ МЕТОД
- ЭКВИФИНАЛЬНОСТЬ СИСТЕМЫ УПРАВЛЕНИЯ
- ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ, в управлении народным хозяйством
- ЭКРАННЫЙ ПУЛЬТ
- ЭКСПЕРИМЕНТ БЕЗУСЛОВНЫЙ
- ЭКСПЕРИМЕНТ КРАТНЫЙ
- ЭКСПЕРИМЕНТ УСЛОВНЫЙ
- ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ СПОСОБЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
- ЭКСПЕРИМЕНТЫ С АВТОМАТАМИ
- ЭКСПЕРТНЫХ ОЦЕНОК МЕТОДЫ в прогнозировании
- ЭКСТРАПОЛИРОВАНИЕ В ОБУЧЕНИИ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ЭКСТРАПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ЭКСТРАПОЛИРОВАНИЕ ФУНКЦИЙ
- ЭКСТРЕМАЛЬ
- ЭКСТРЕМАЛЬНОЕ РЕГУЛИРОВАНИЕ
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ в теории графов
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ НА ГРАФАХ
- ЭКСТРЕМУМ
- ЭКСТРЕМУМ АБСОЛЮТНЫЙ
- ЭКСТРЕМУМ ГЛОБАЛЬНЫЙ
- ЭКСТРЕМУМ ЛОКАЛЬНЫЙ
- ЭКСТРЕМУМА ДРЕЙФ
- ЭЛЕКТРИЧЕСКИЕ МОДЕЛИРУЮЩИЕ СЕТКИ
- ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ТЕОРИЯ
- «ЭЛЕКТРОН»
- ЭЛЕКТРОННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЭВМ)
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЭЛЕМЕНТ ЗАДЕРЖКИ
- ЭЛЕМЕНТАРНАЯ СИСТЕМА
- ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ НАД СЛОВАМИ
- ЭЛЕМЕНТАРНЫЕ ТЕОРИИ.
- ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ЭЛЕМЕНТНЫЕ СТРУКТУРЫ НА ЛОГИЧЕСКИХ ЗАДЕРЖИВАЮЩИХ ЭЛЕМЕНТАХ
- ЭЛЕМЕНТНЫЙ СИНТЕЗ ЦВМ
- ЭЛИОНИКА
- ЭЛЛИПТИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- «ЭМИК-1»
- ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
- «ЭМСС»
- «ЭМУ»
- ЭНТРОПИЯ
- ЭНТРОПИЯ ЖИВЫХ СИСТЕМ
- ЭНТРОПИЯ СООБЩЕНИЯ при заданных условиях точности
- ЭПСИЛОН
- ЭПСИЛОН-ЭНТРОПИЯ
- ЭРГАТИЧЕСКАЯ СИСТЕМА
- ЭРГОДИЧЕСКАЯ ТЕОРИЯ
- ЭРГОДИЧЕСКОЕ СОСТОЯНИЕ
- ЭРЛАНГА ФОРМУЛЫ
- ЭТАЛОН в распознавании образов
- ЭТАЛОННОЕ НАПРЯЖЕНИЕ
- ЭФФЕКТИВНОСТЬ ИНФОРМАЦИОННОГО ПОИСКА техническая
- ЭШБИ ГОМЕОСТАТ
- «ЮНИВАК» (Univac)
- ЯДРО втеории игр
- ЯЗЫК АВТОМАТНЫЙ
- ЯЗЫК АЛГОРИТМИЧЕСКИЙ
- ЯЗЫК АНКЕТНЫЙ
- ЯЗЫК БЕСКОНТЕКСТНЫЙ, язык контекстно-свободный
- ЯЗЫК ДЕСКРИПТОРНЫЙ
- ЯЗЫК ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ
- ЯЗЫК ИНФОРМАЦИОННО-ПОИСКОВЫЙ
- ЯЗЫК ИНФОРМАЦИОННЫЙ
- ЯЗЫК ИСКУССТВЕННЫЙ
- ЯЗЫК КАТЕГОРИАЛЬНЫЙ
- ЯЗЫК ЛОГИЧЕСКИЙ для задания автоматов
- ЯЗЫК МАШИННО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК МАШИНЫ «МИР»
- ЯЗЫК ОПЕРАТОРНЫЙ
- ЯЗЫК ОПИСАНИЯ УСТРОЙСТВ ЦВМ
- ЯЗЫК ПРОМЕЖУТОЧНЫЙ
- ЯЗЫК ПРОЦЕДУРНО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК ТРАНСЛЯТОРА ВХОДНОЙ
- ЯЗЫК ЦВМ ВНУТРЕННИЙ
- ЯЗЫКА ИЗБЫТОЧНОСТЬ
- ЯЗЫКА ИНФОРМАЦИОННЫЕ ИЗМЕРЕНИЯ
- ЯЗЫКА МОДЕЛИ АНАЛИТИЧЕСКИЕ
- ЯЗЫКА МОДЕЛИ МАТЕМАТИЧЕСКИЕ
- ЯЗЫКА ЭНТРОПИЯ
- ЯЗЫКИ ЛОГИКО-МАТЕМАТИЧЕСКИЕ
- ЯЗЫКИ МАШИННЫЕ
- ЯЗЫКИ ПРОГРАММИРОВАНИЯ
- ЯЗЫКИ СПИСКОВЫЕ
- ЯЗЫКИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ
- ЯЗЫКИ ФОРМАЛЬНЫЕ
- ЯЗЫК — ПОСРЕДНИК
- ЯЧЕЙКА ЗАПОМИНАЮЩЕГО УСТРОЙСТВА