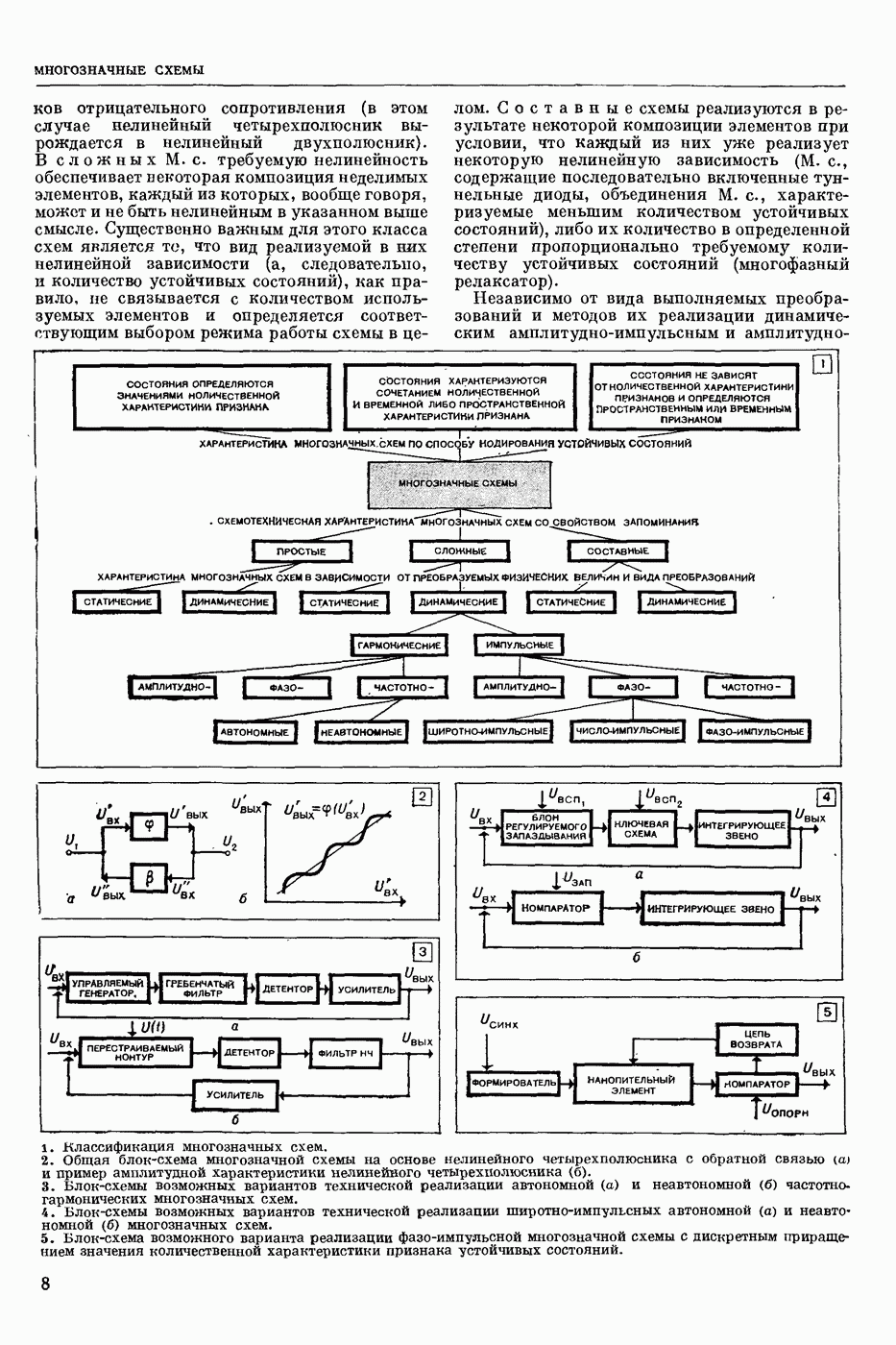
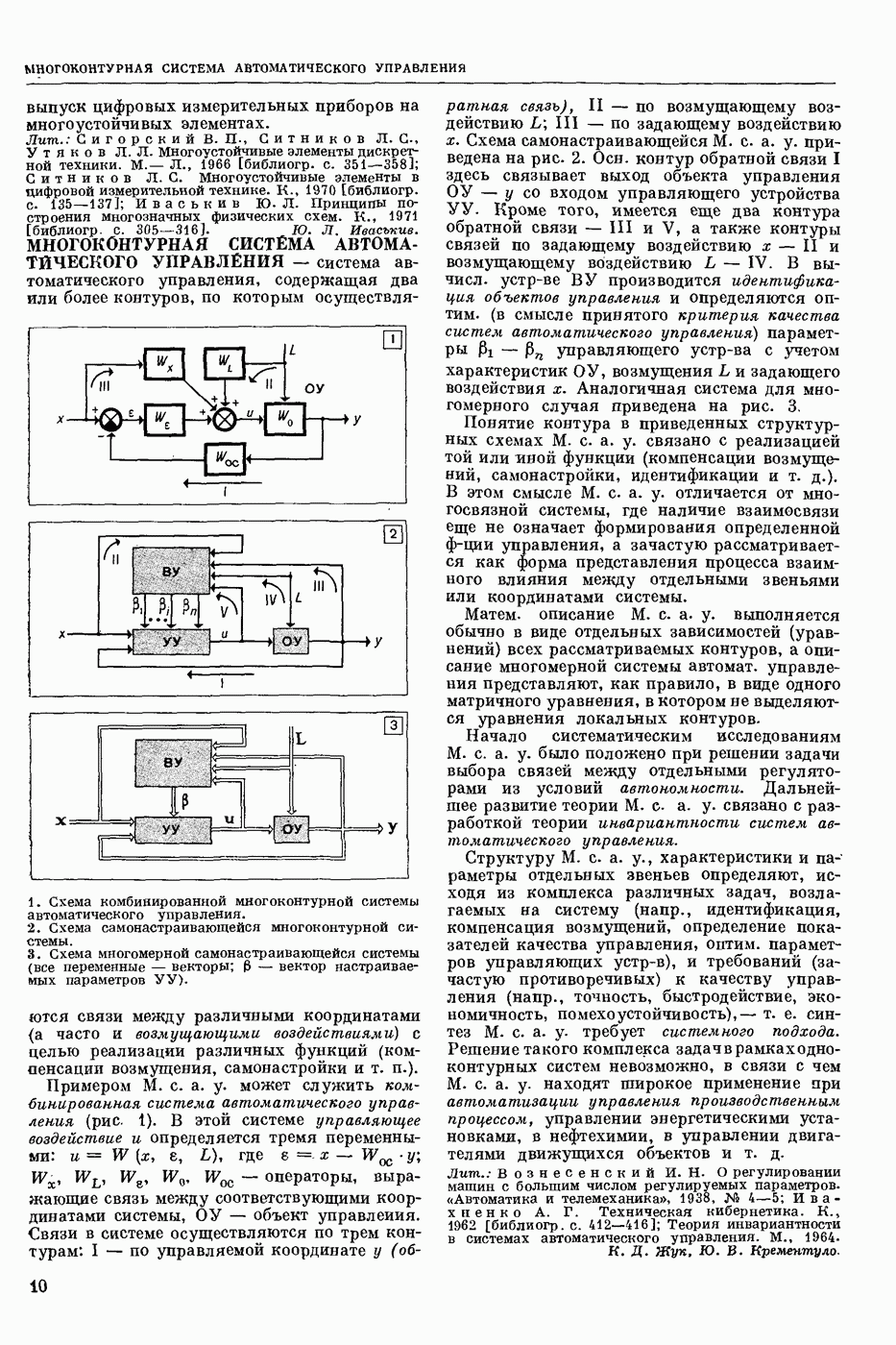
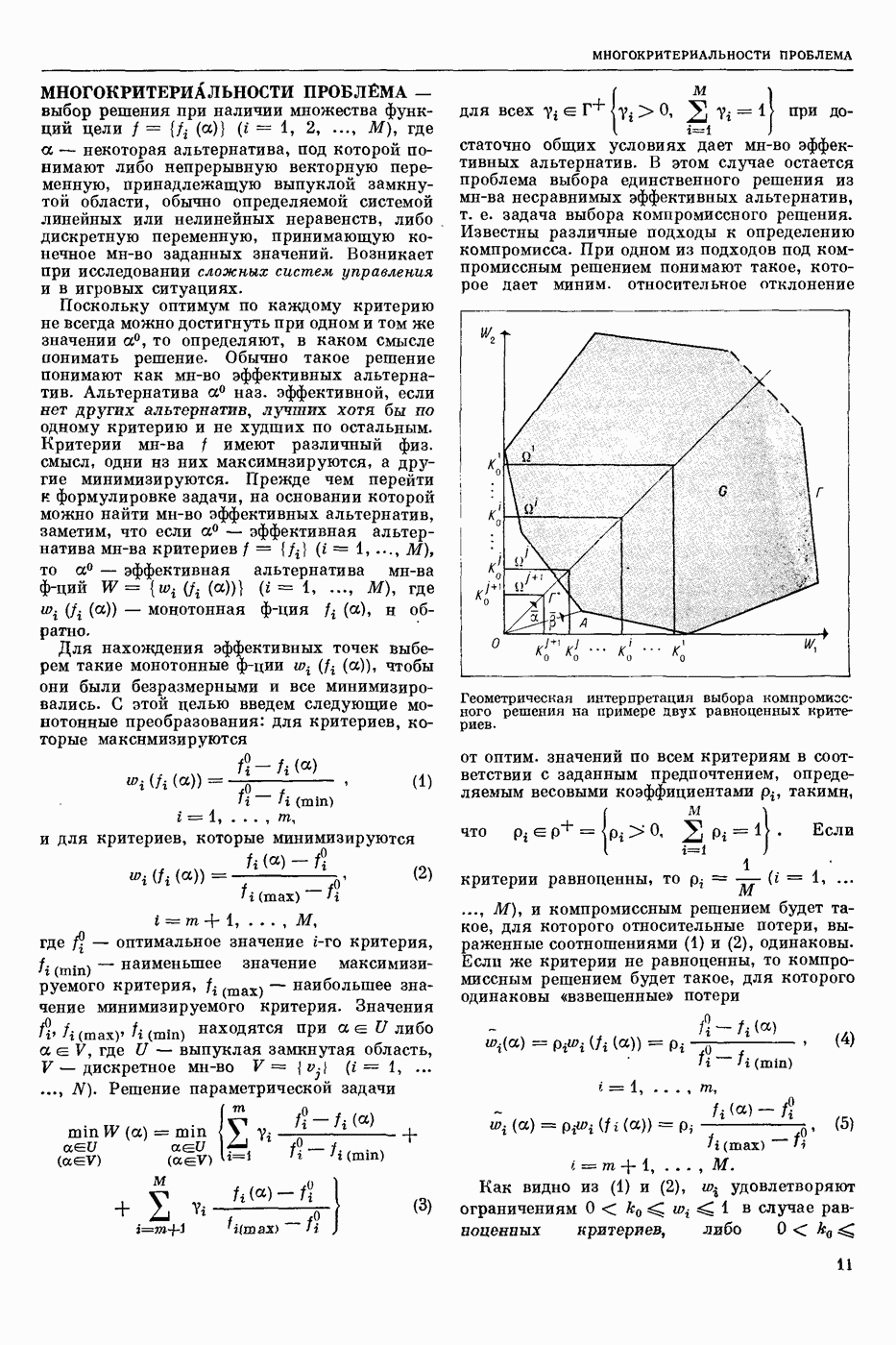
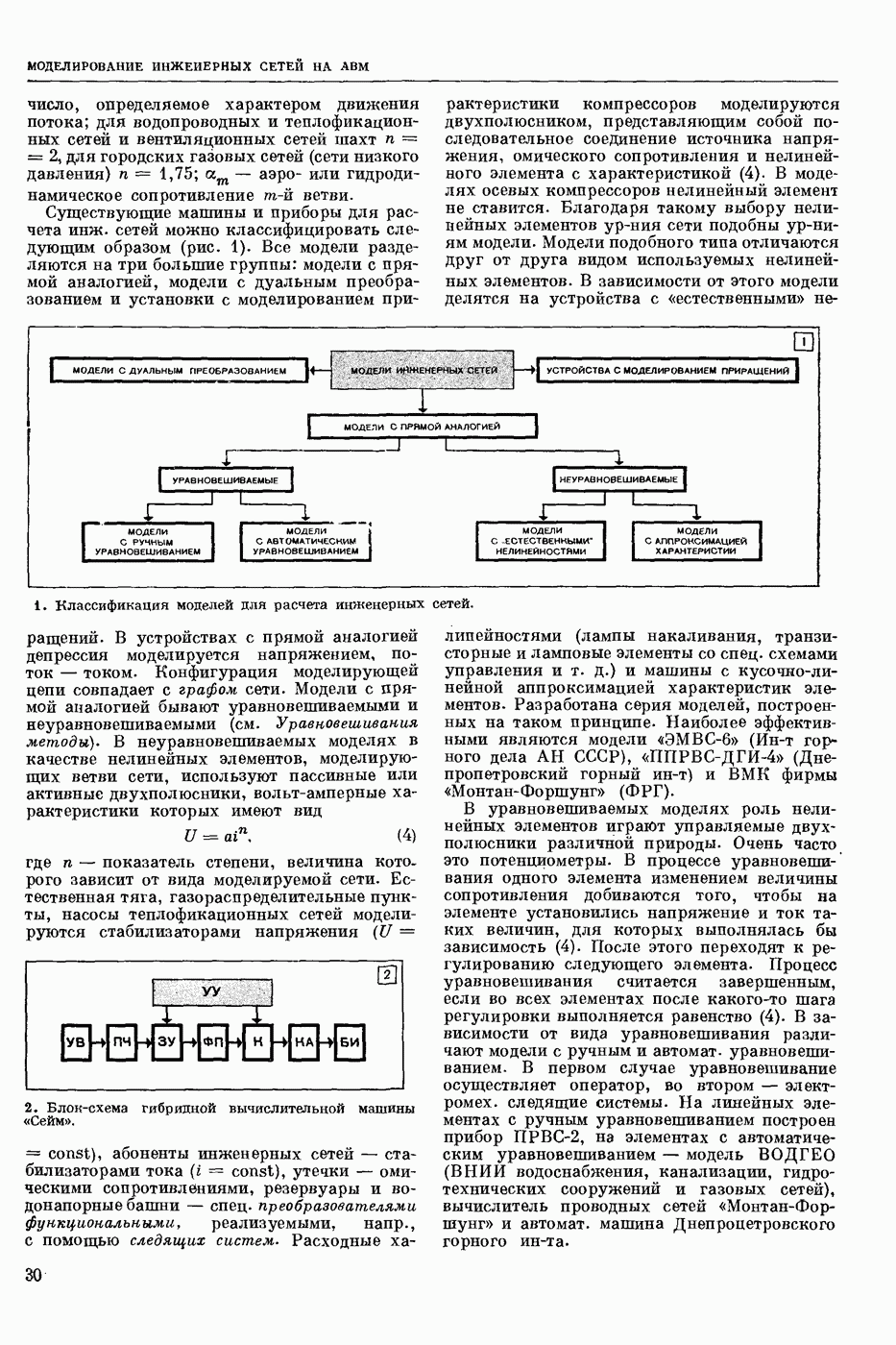
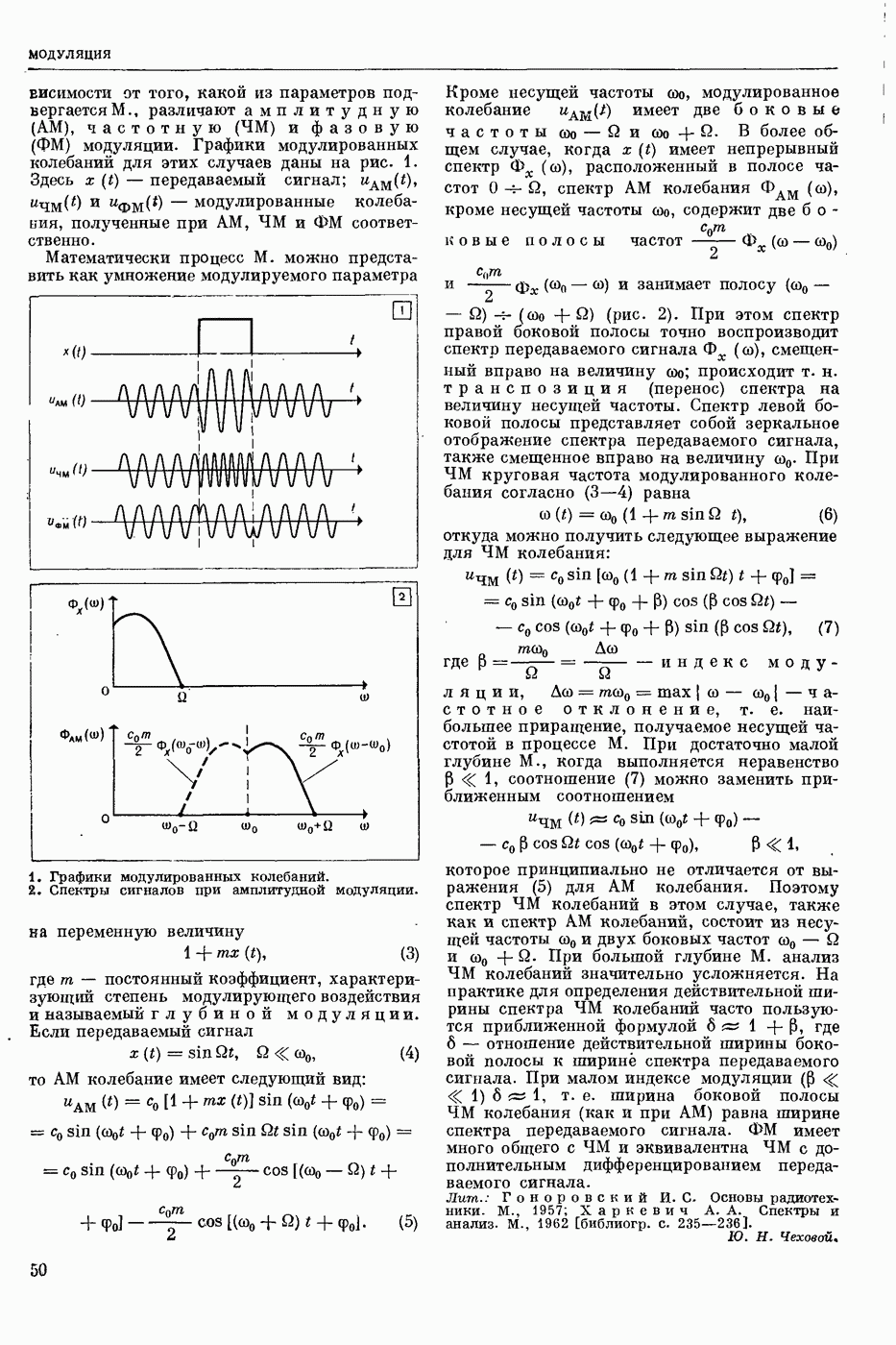
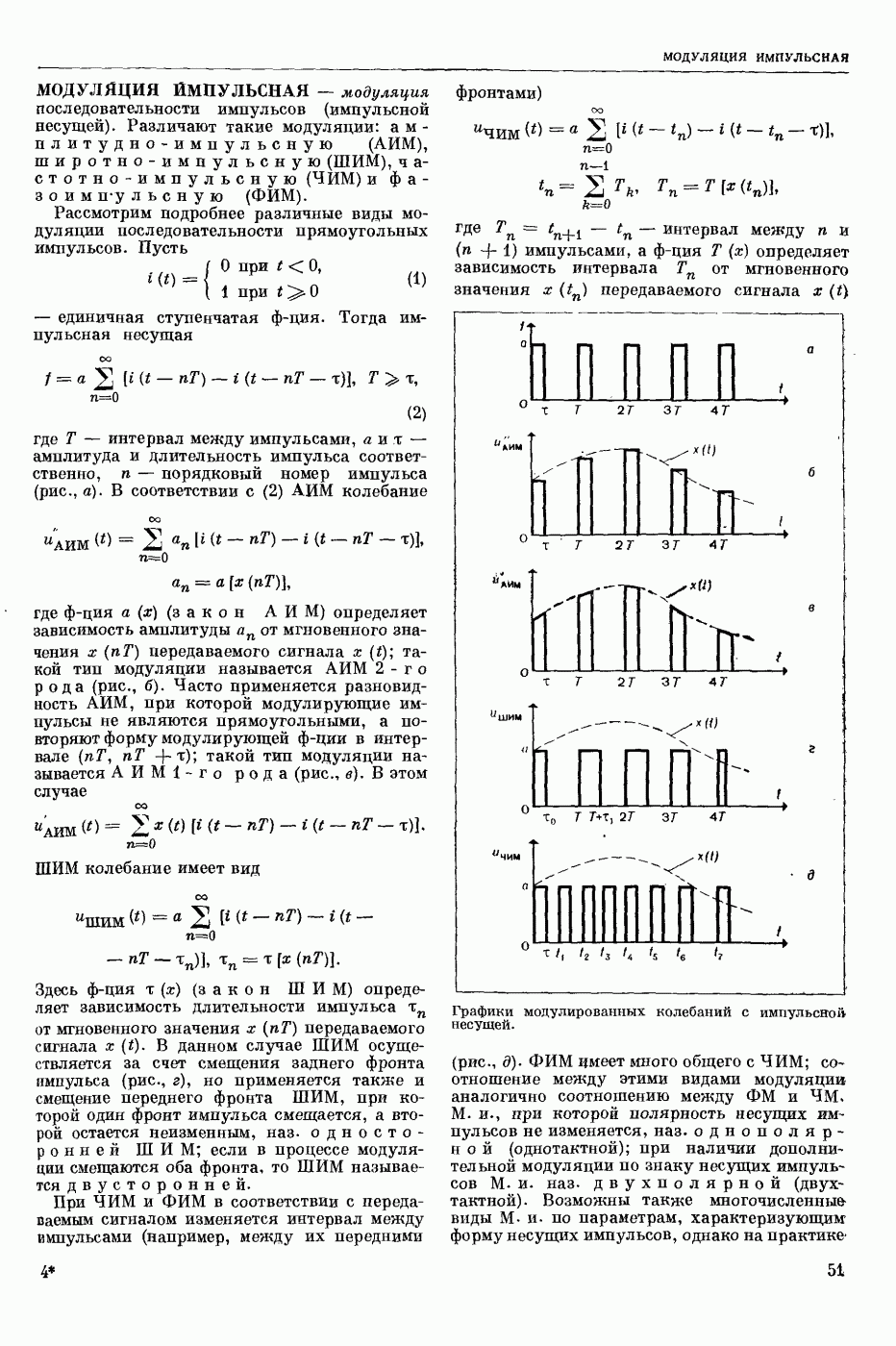
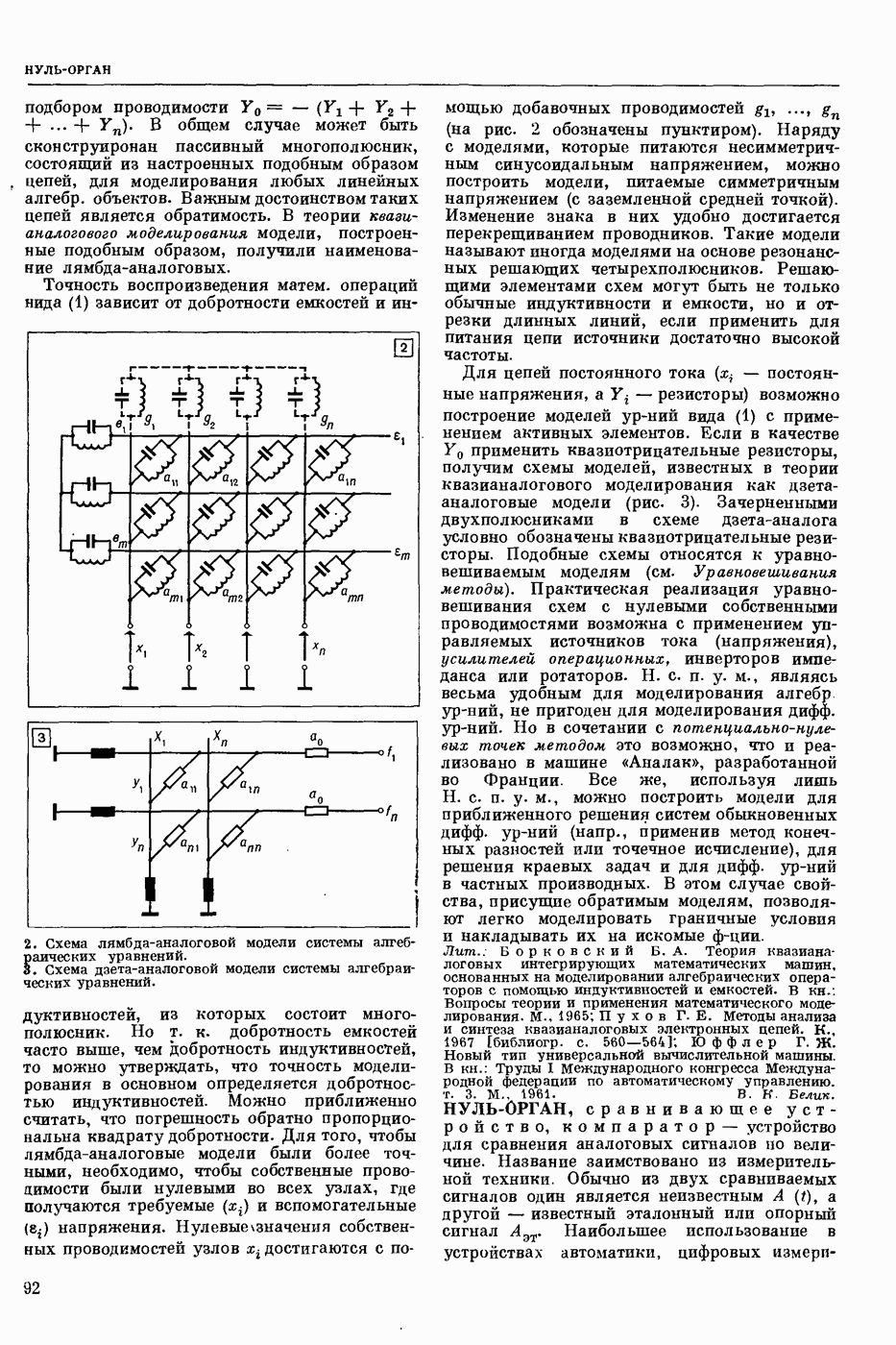
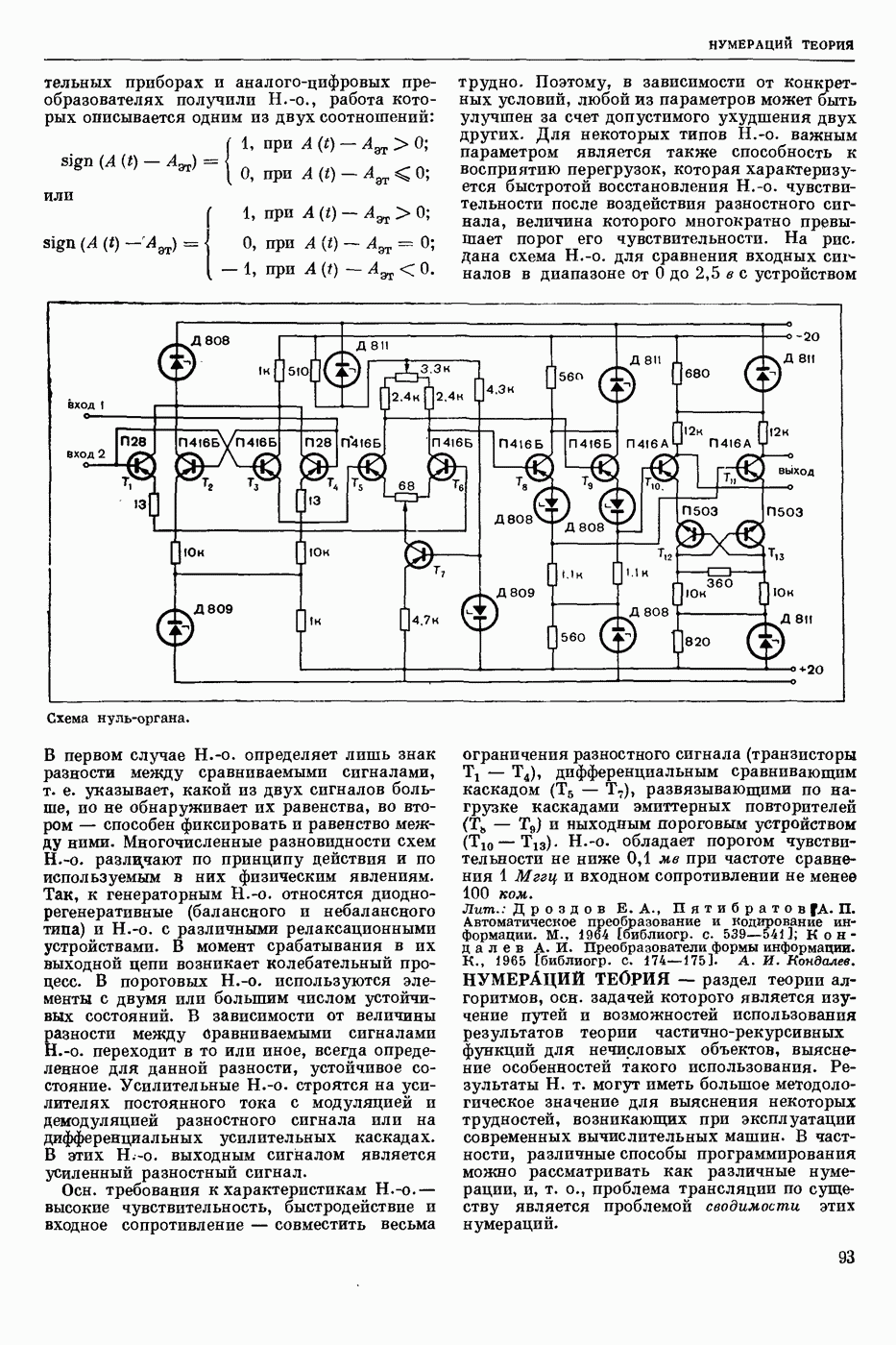
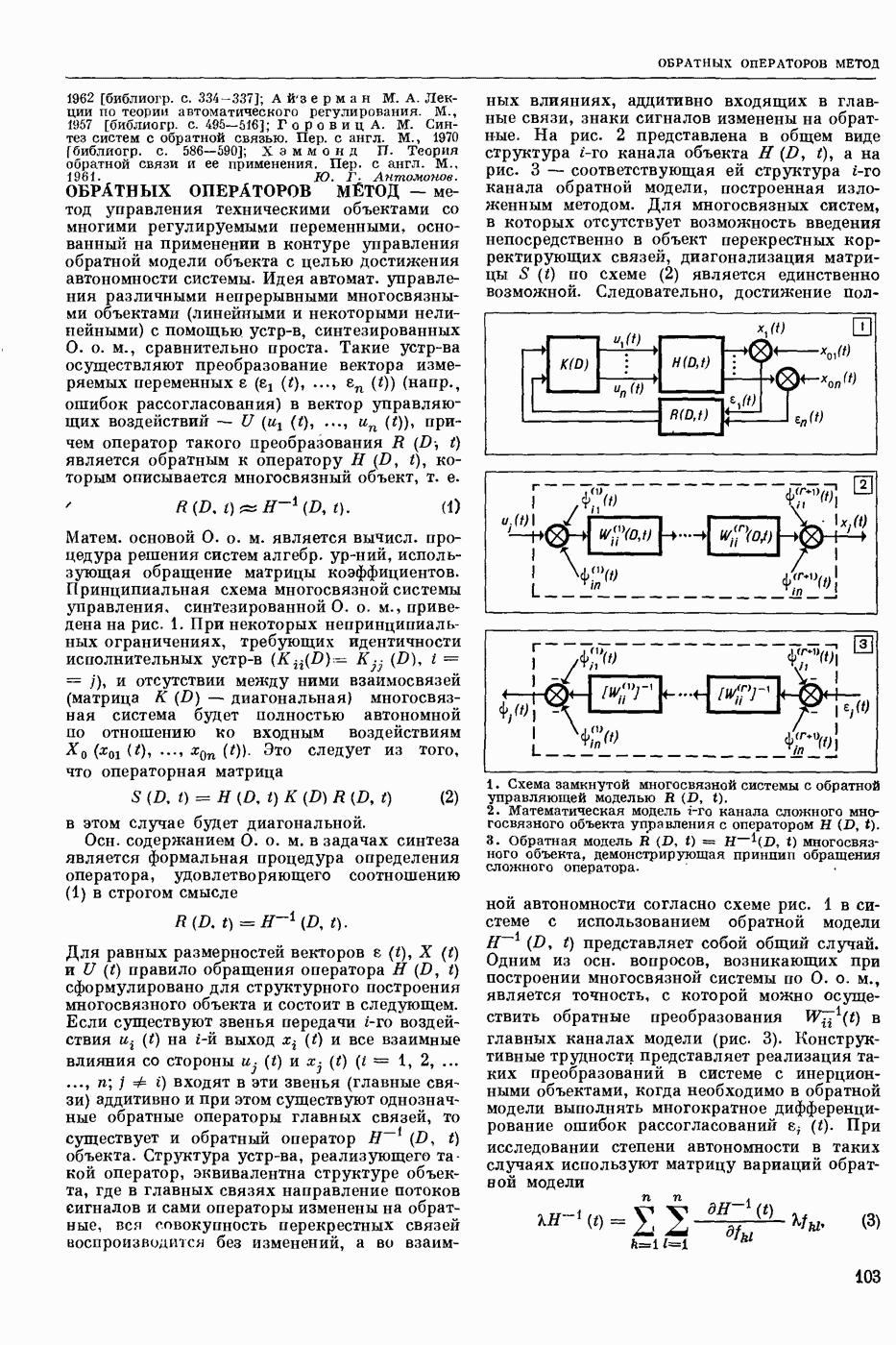
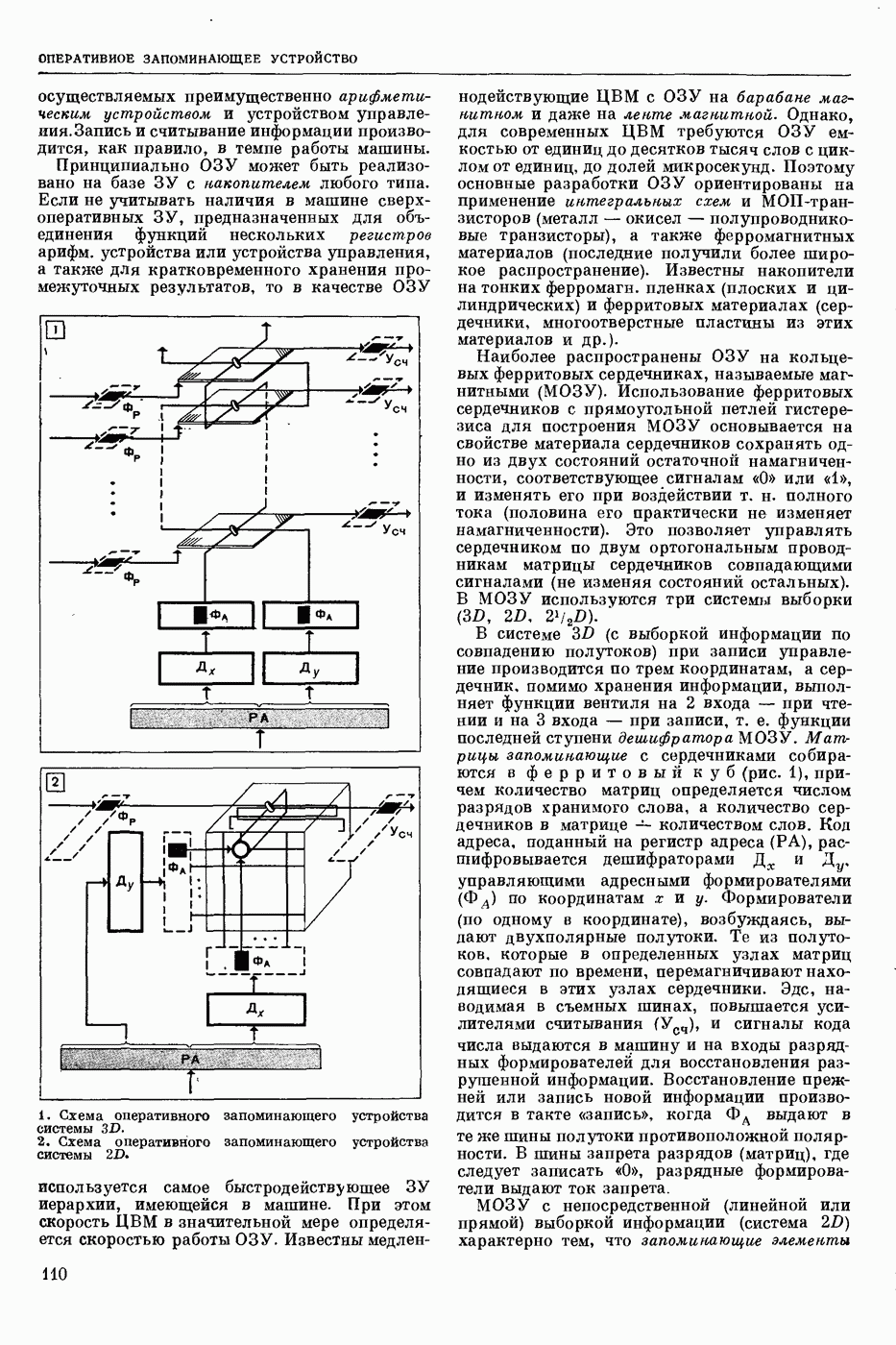
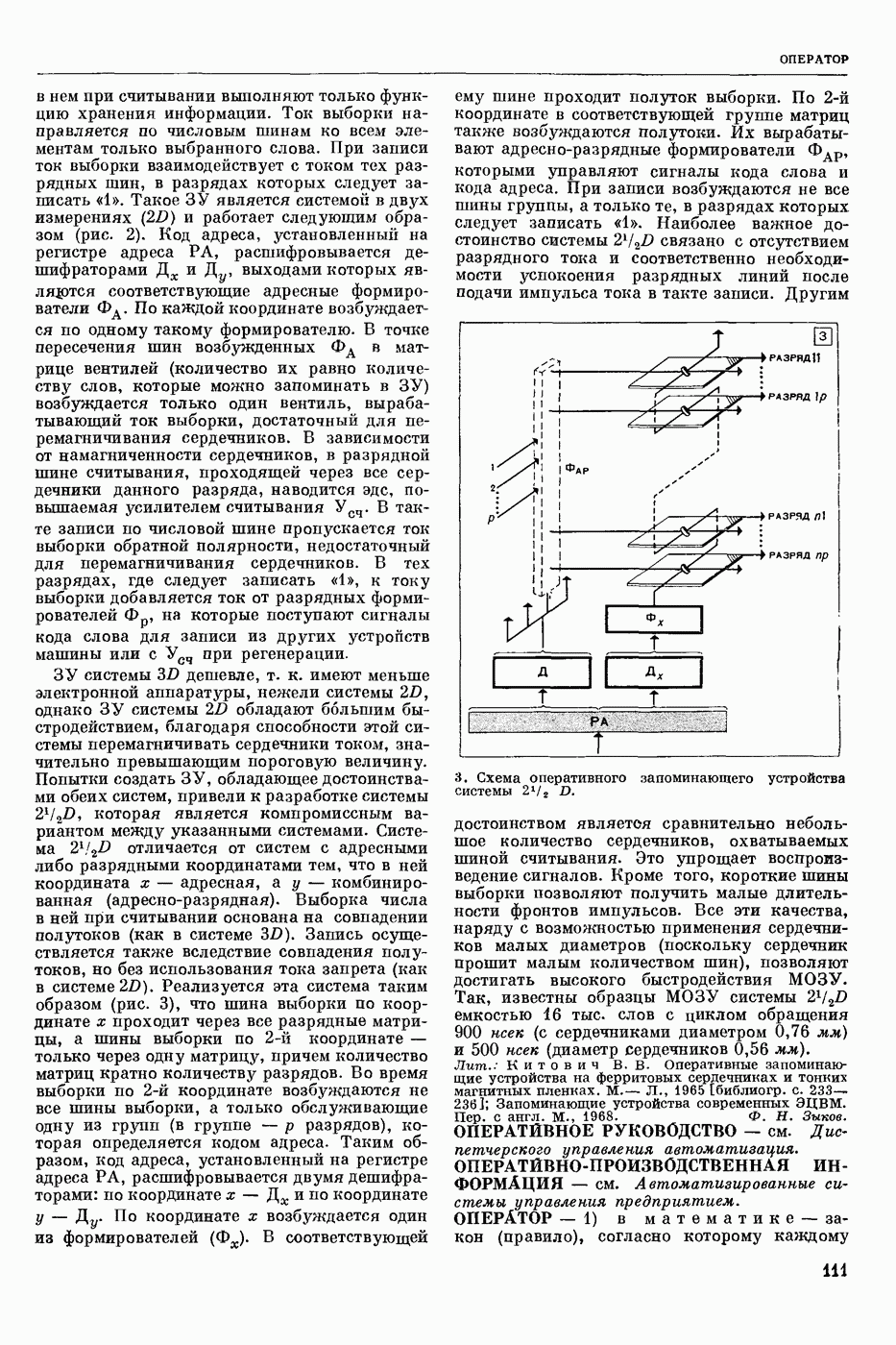
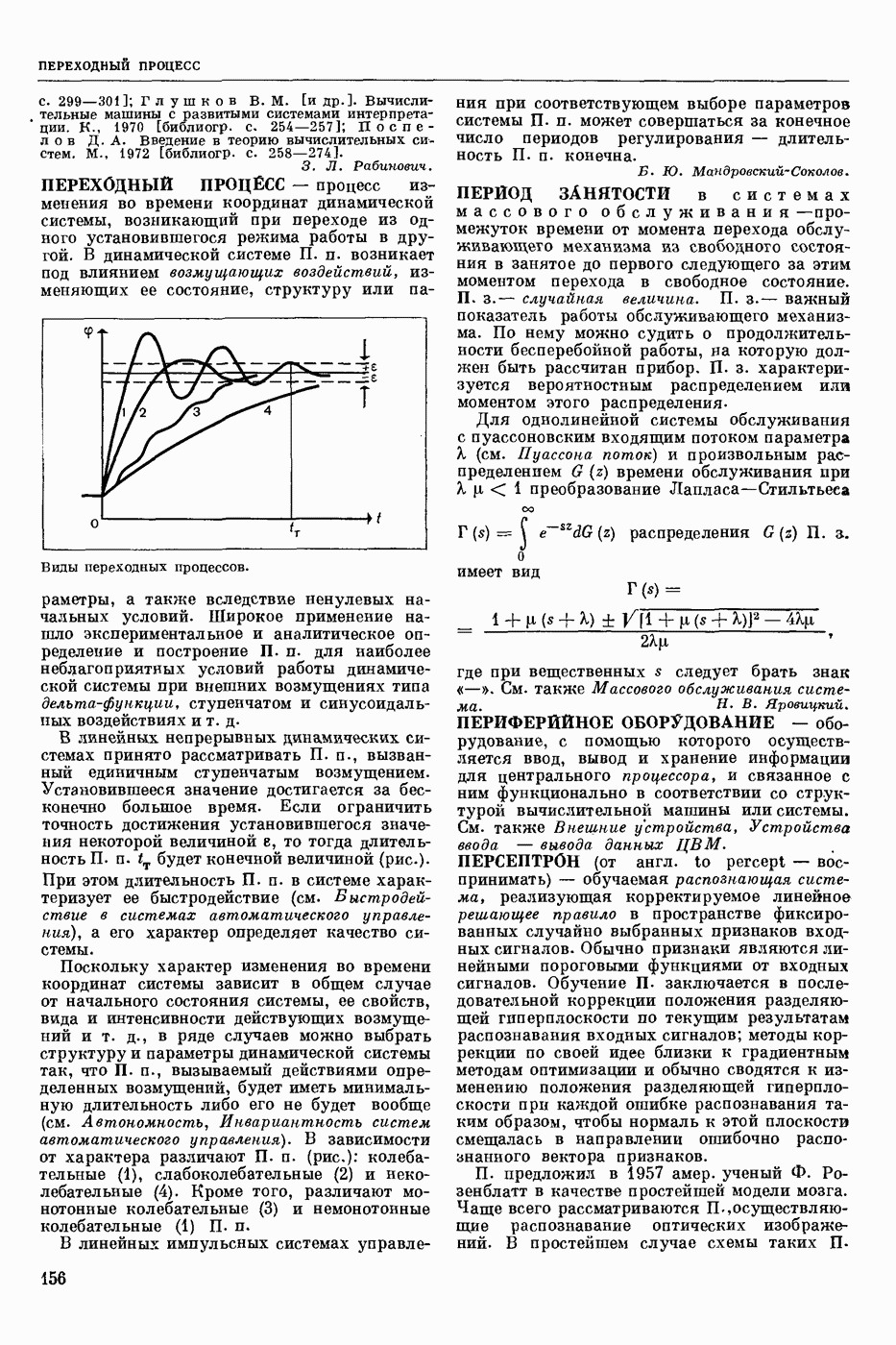
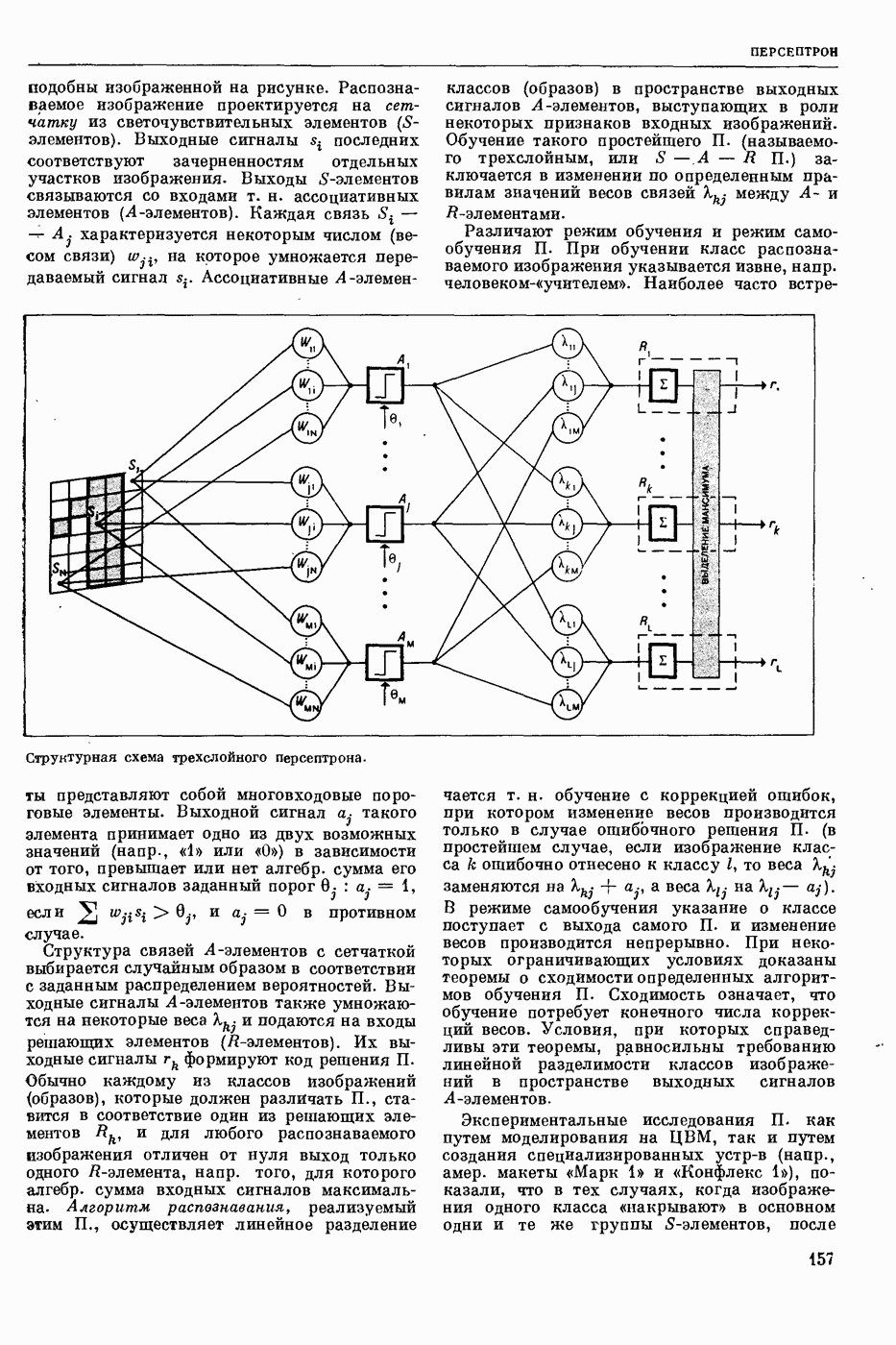
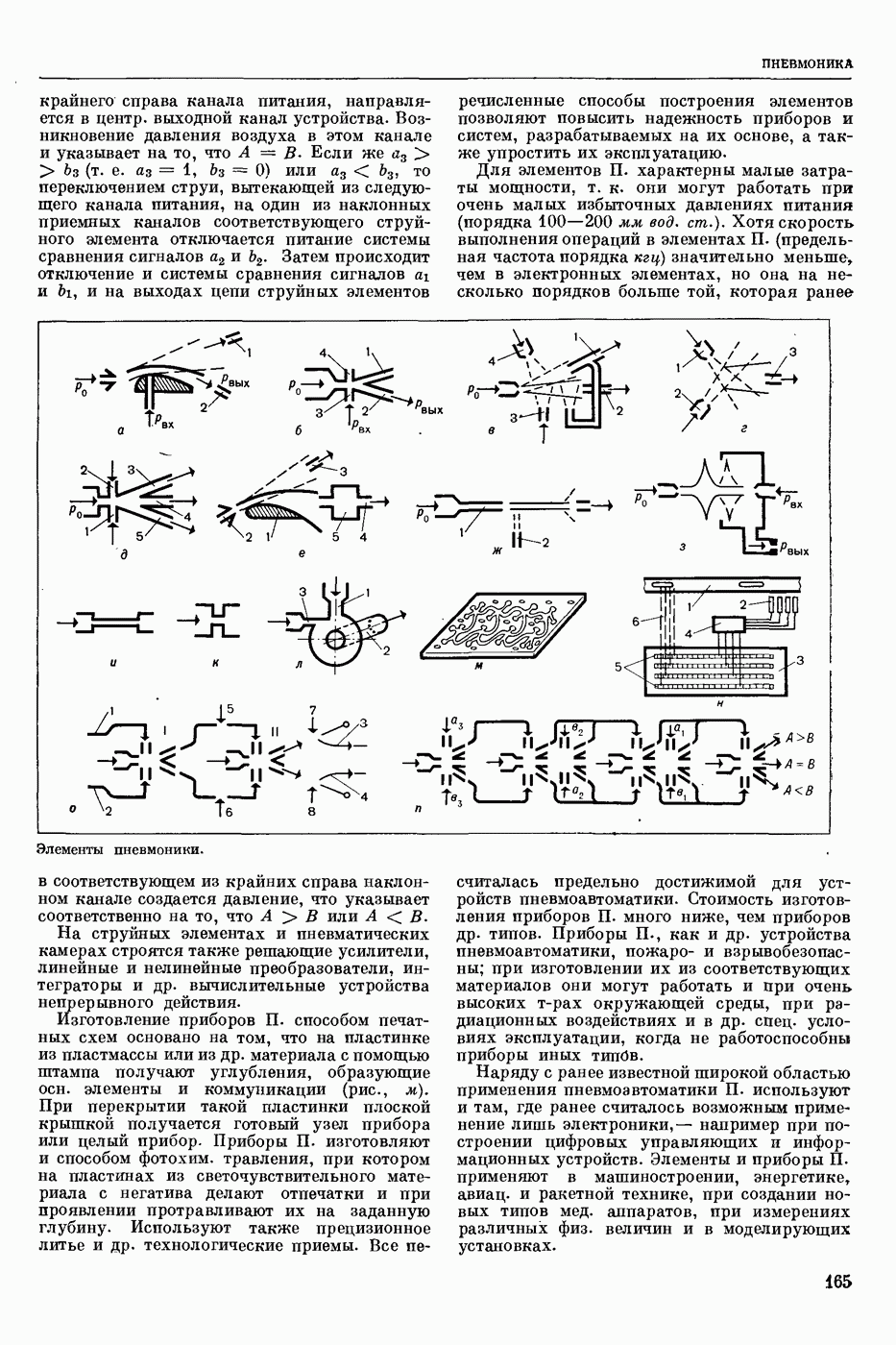
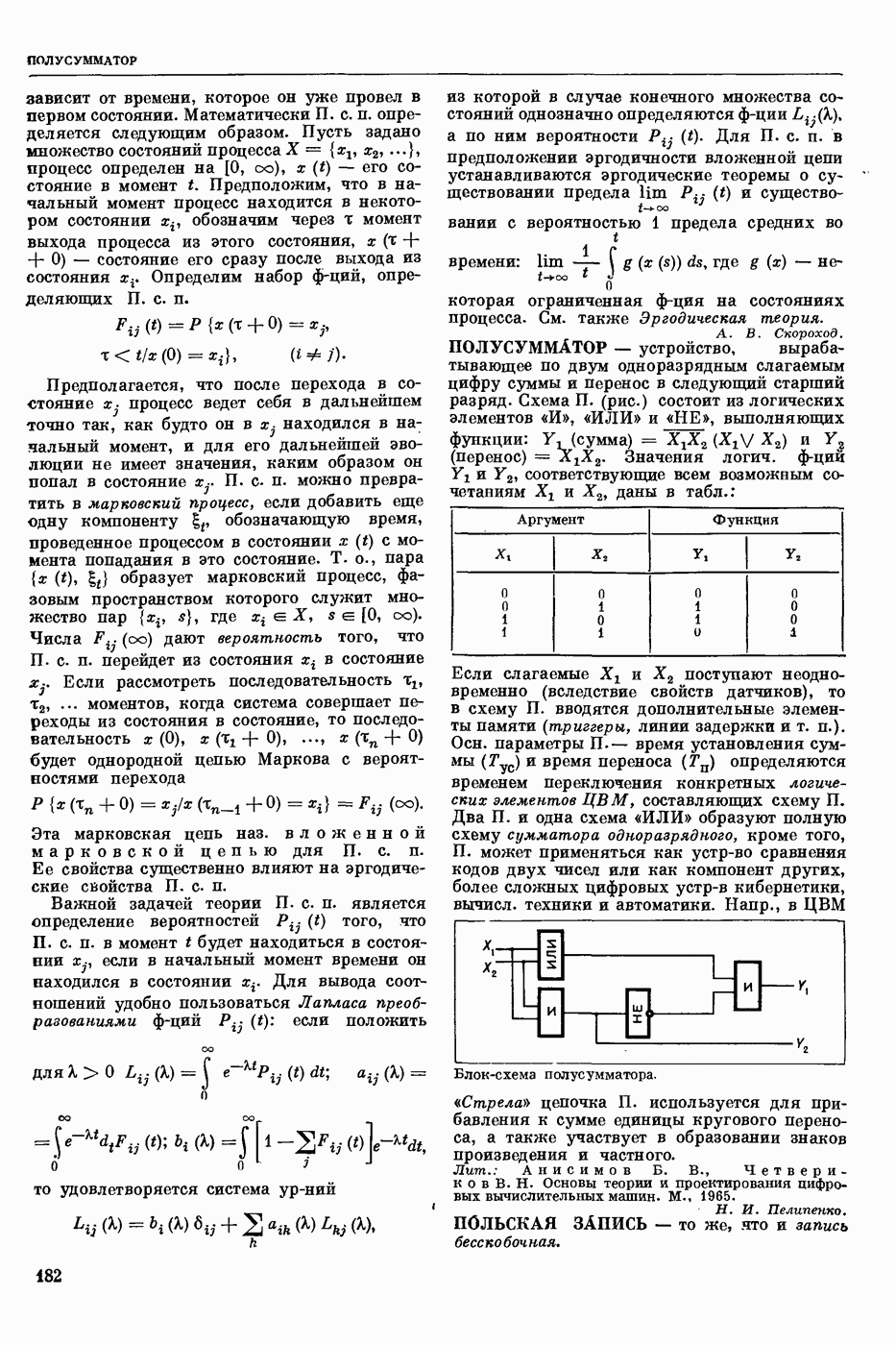
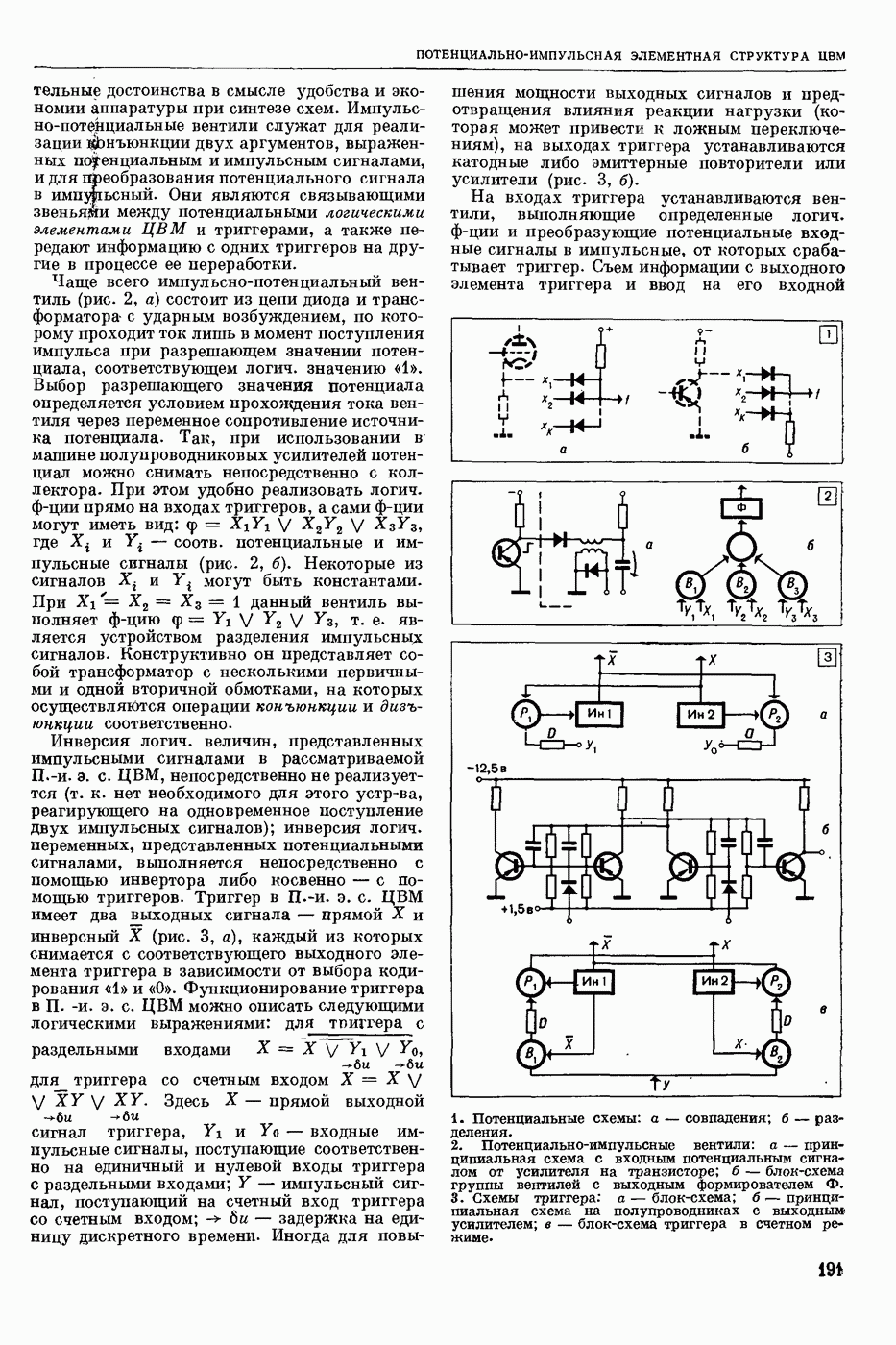
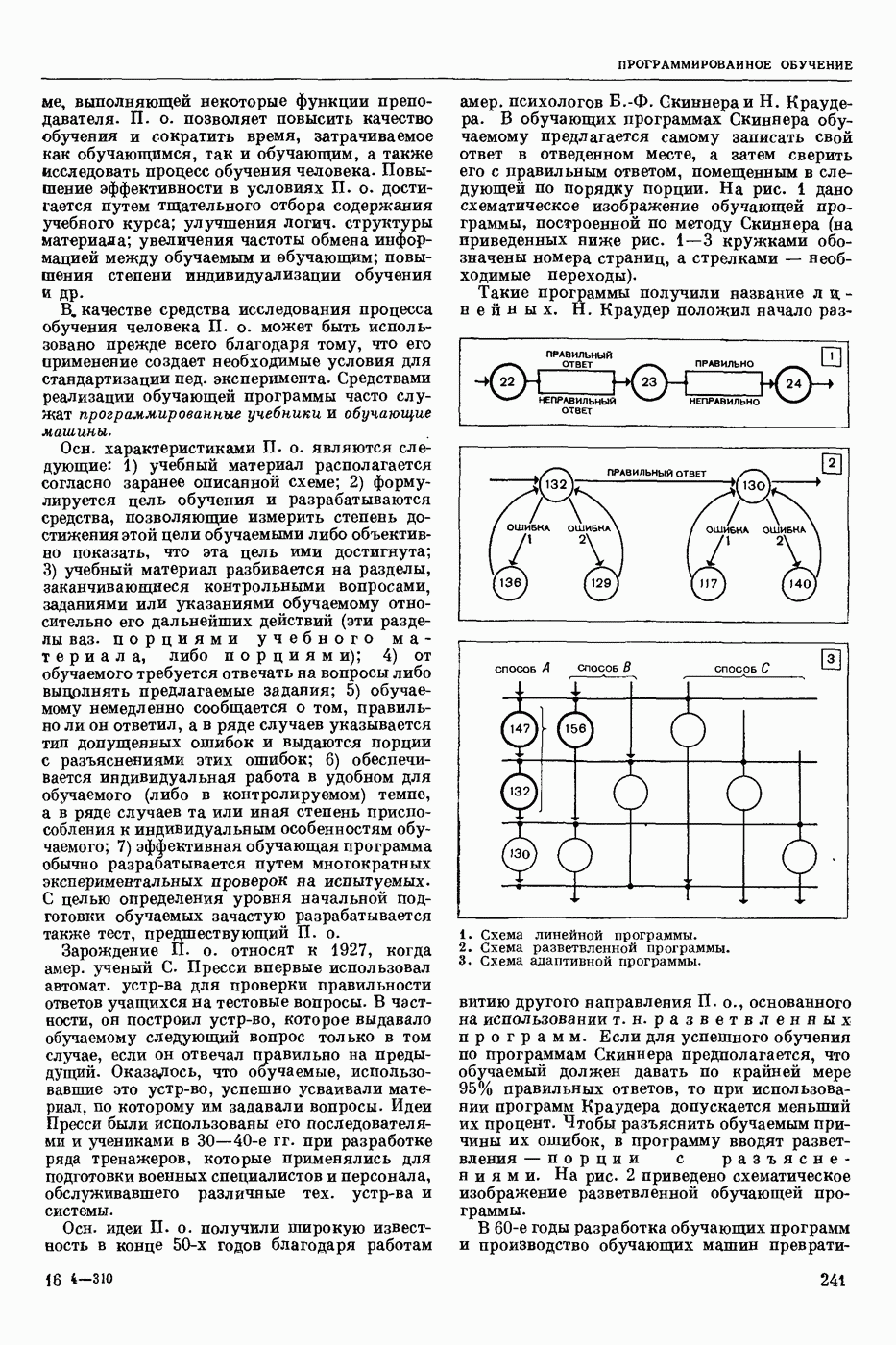
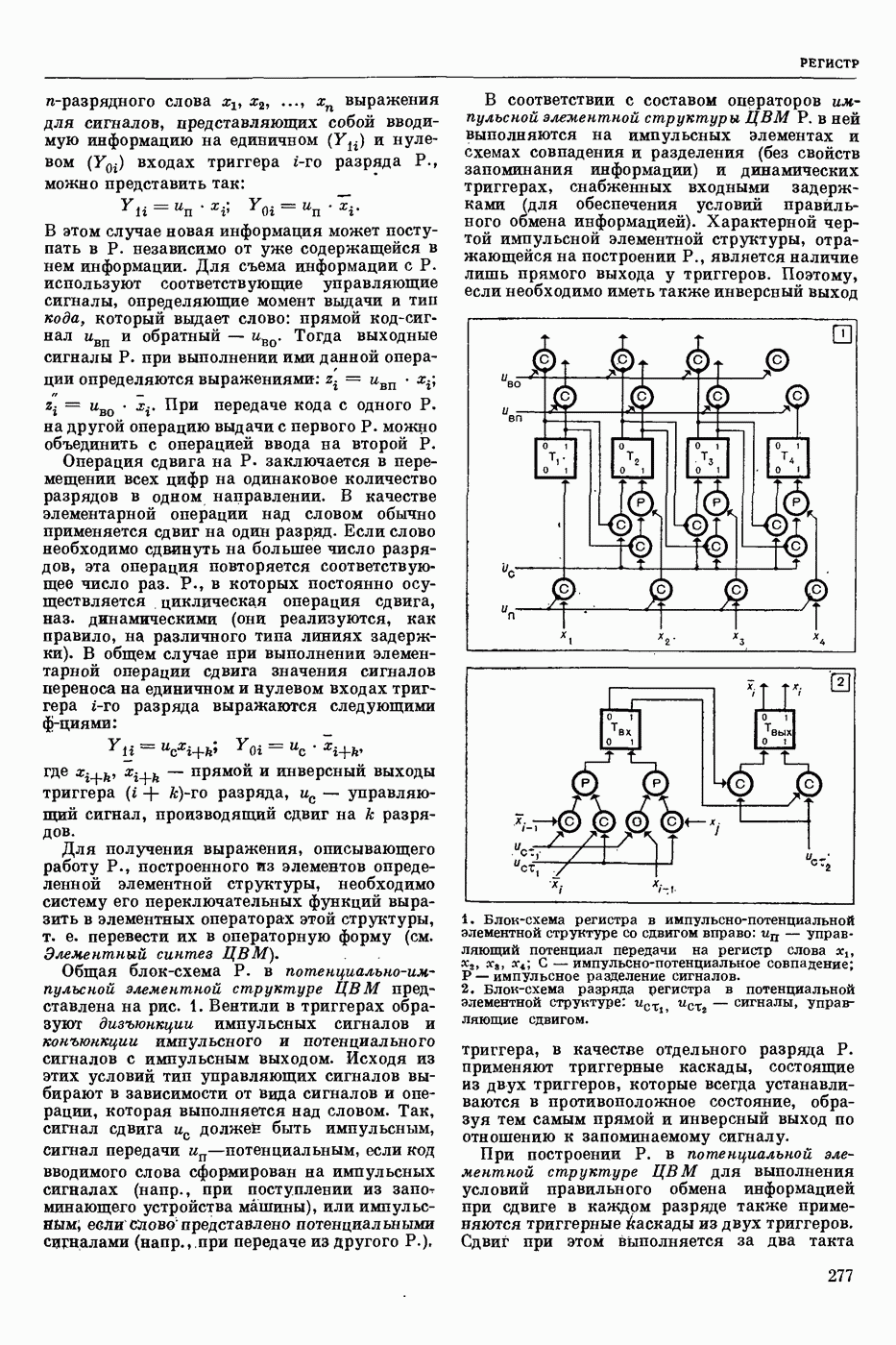
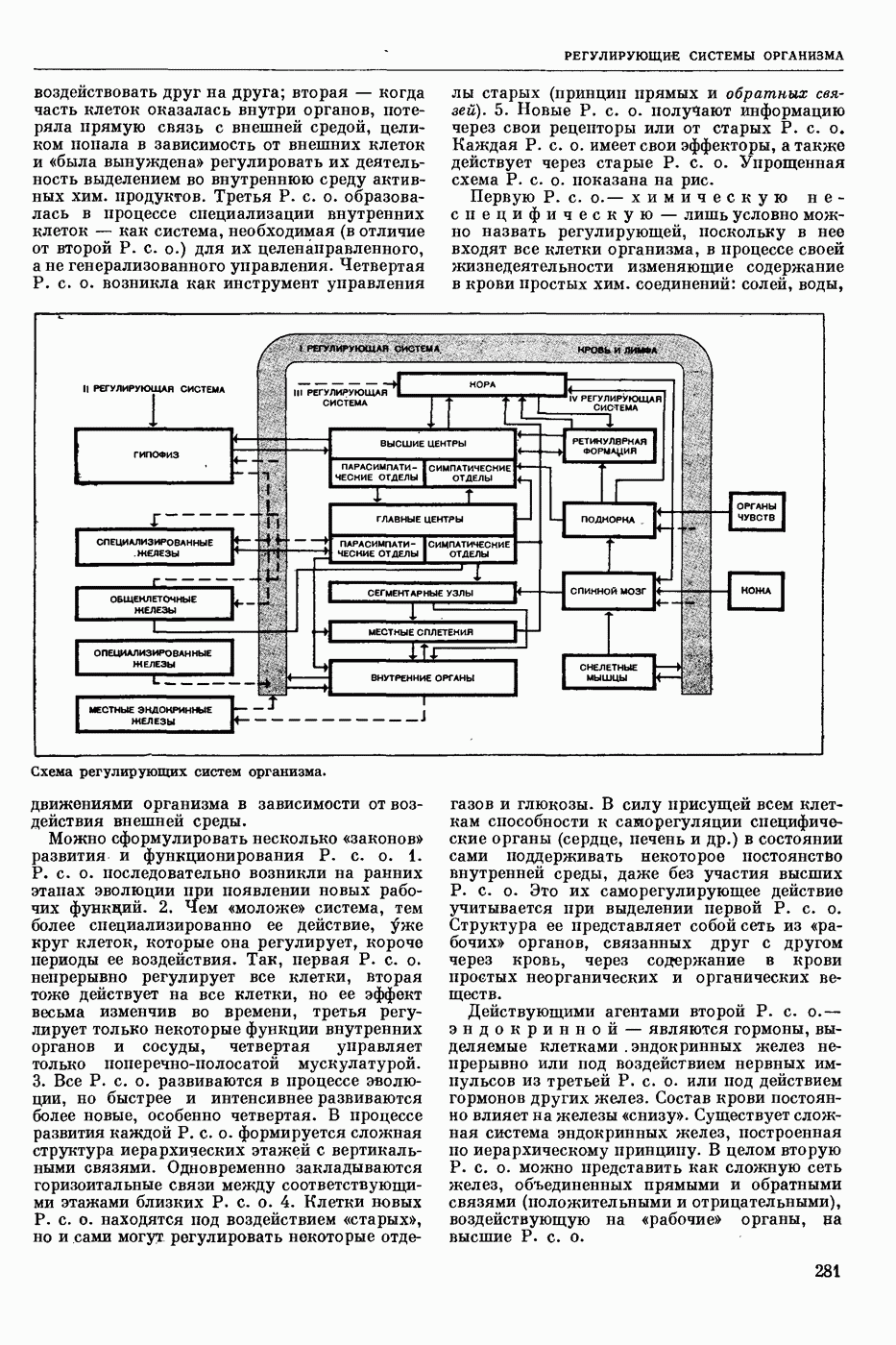
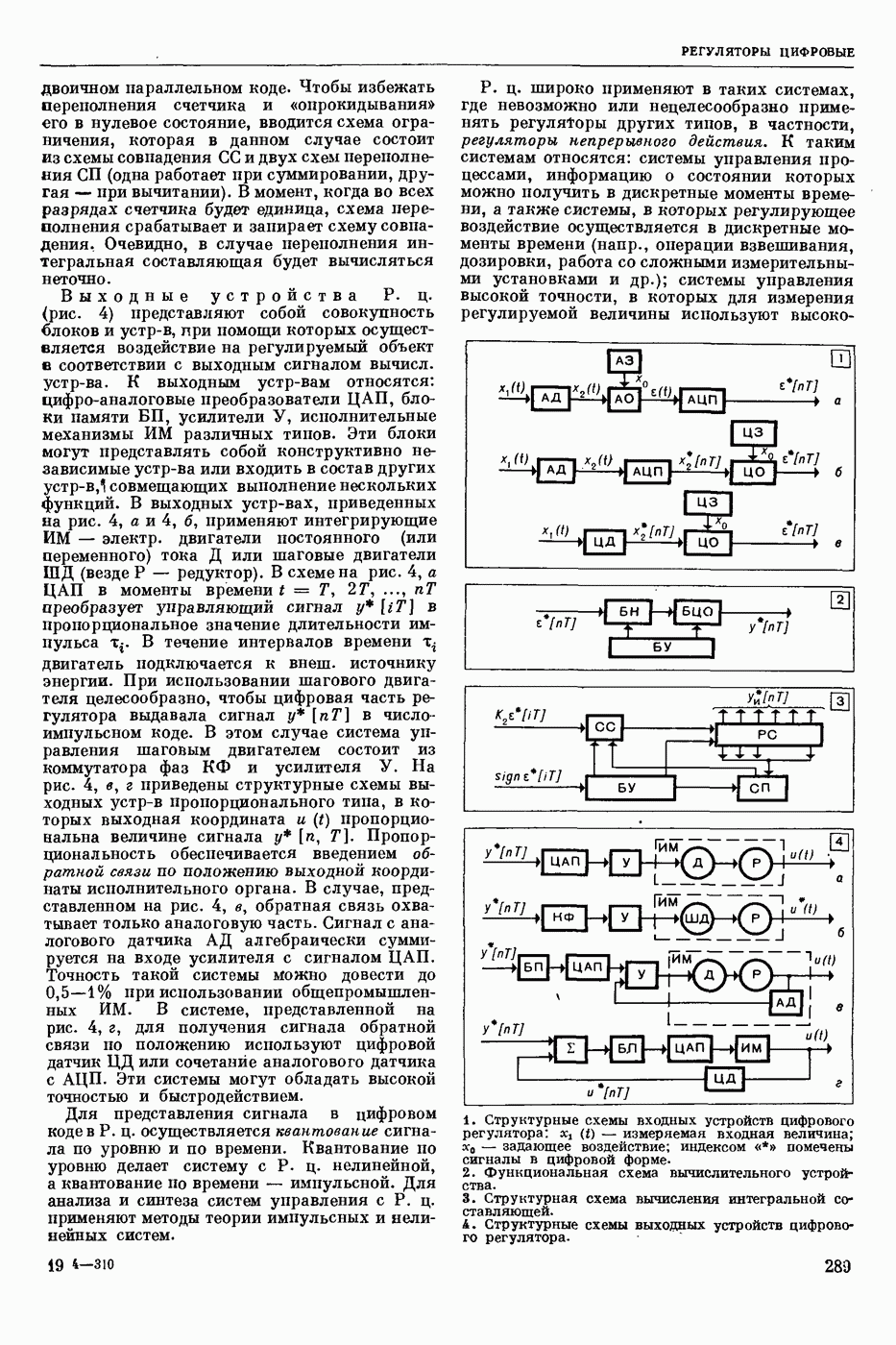
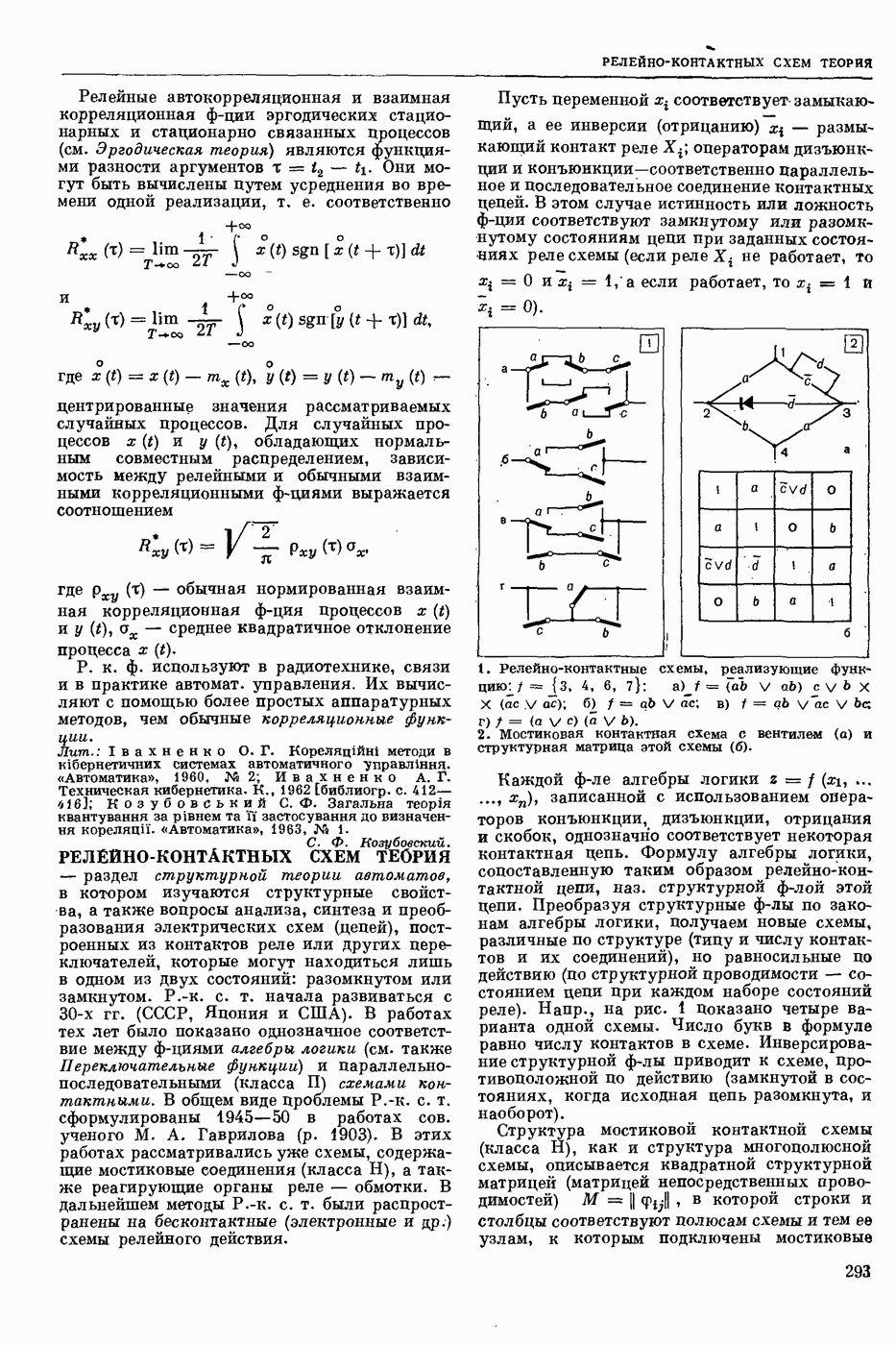
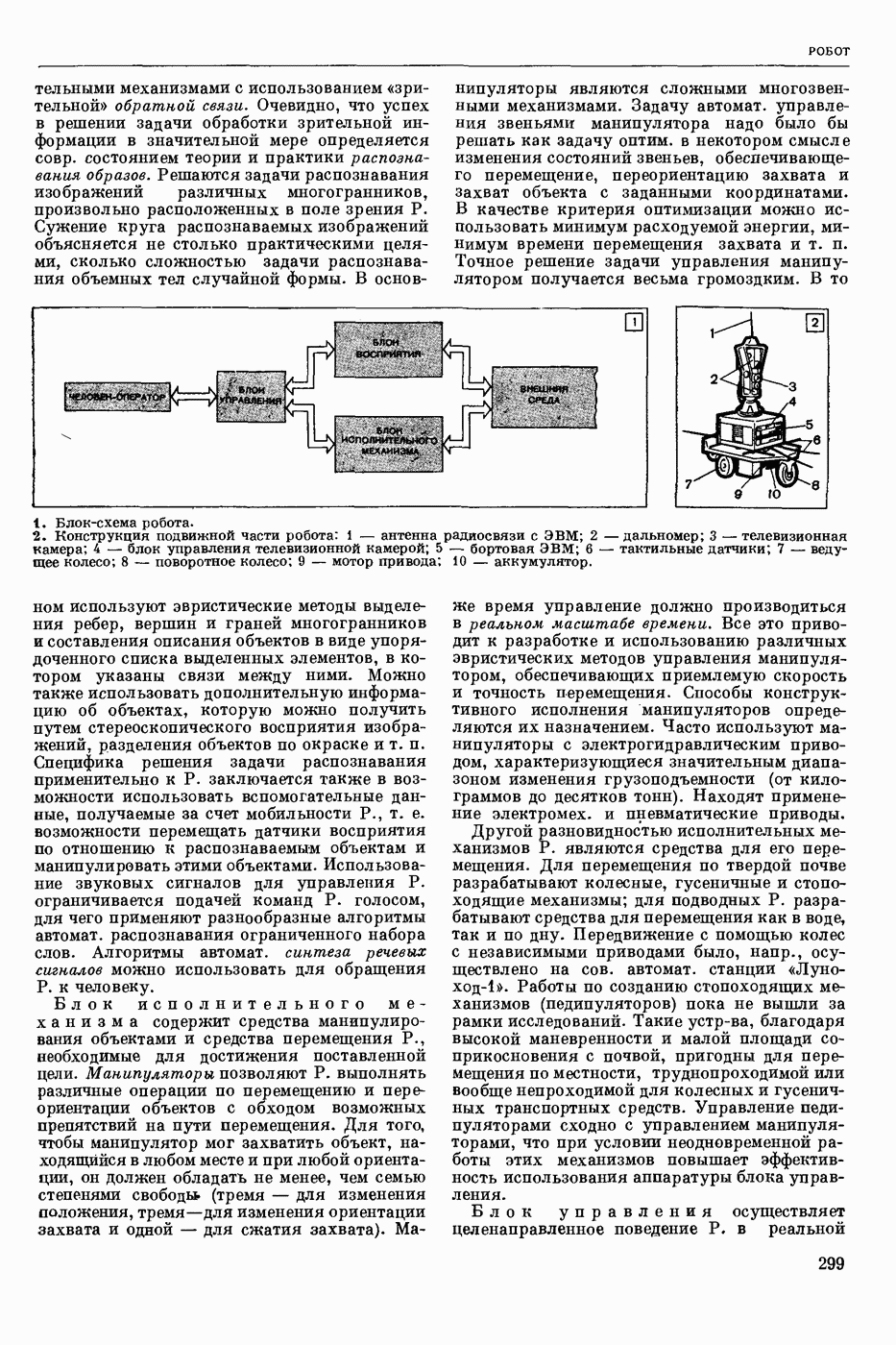
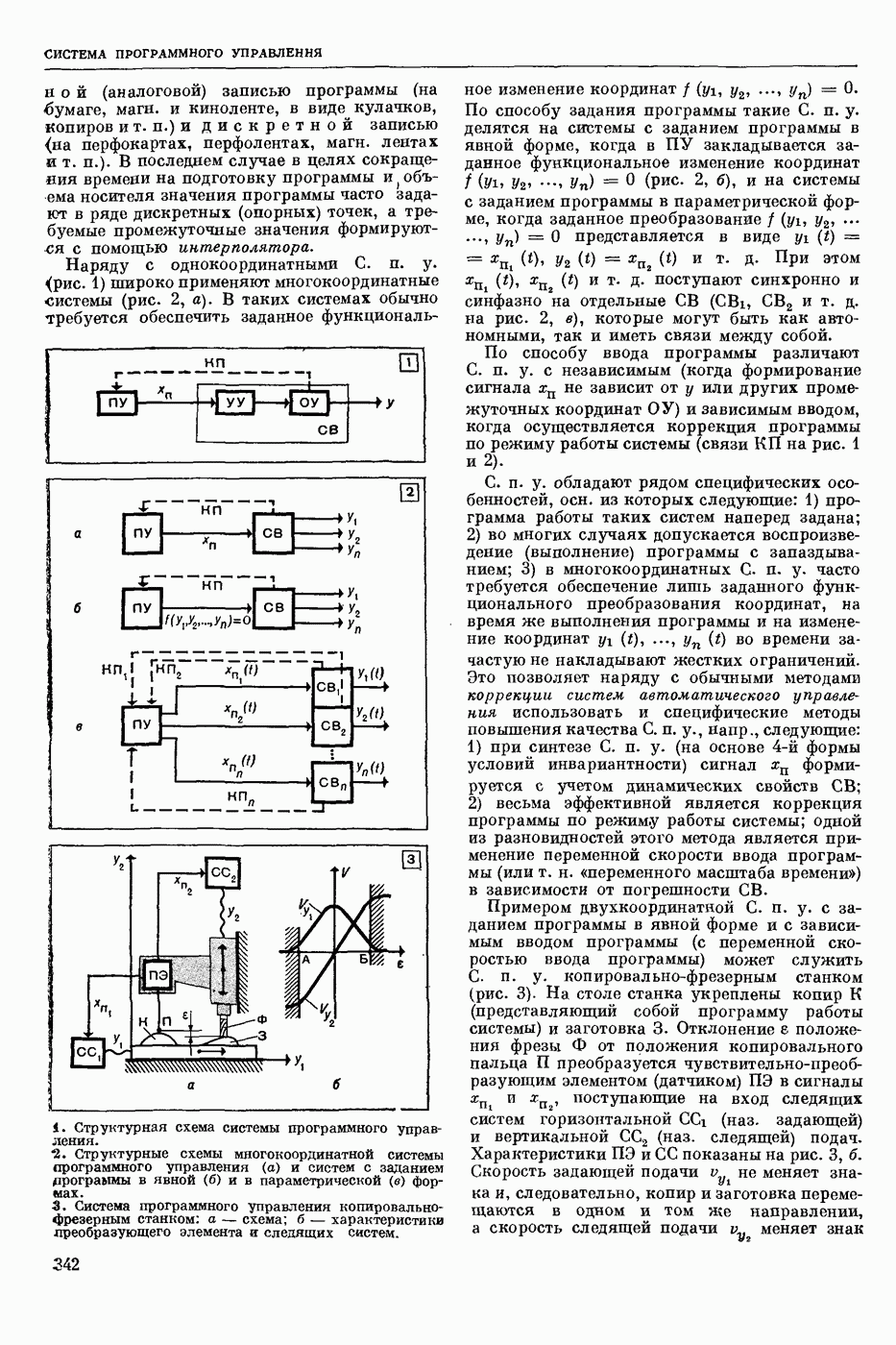
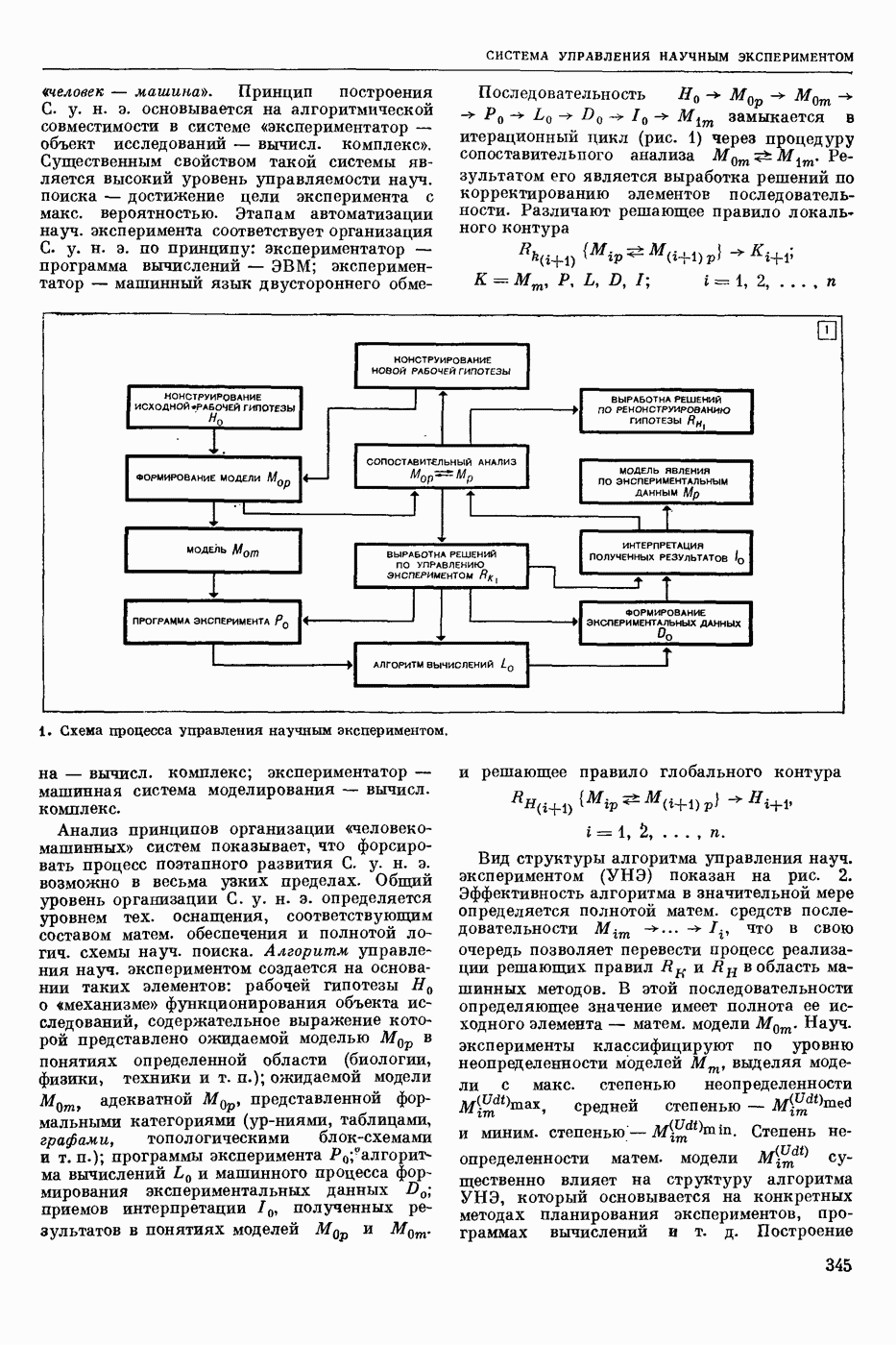
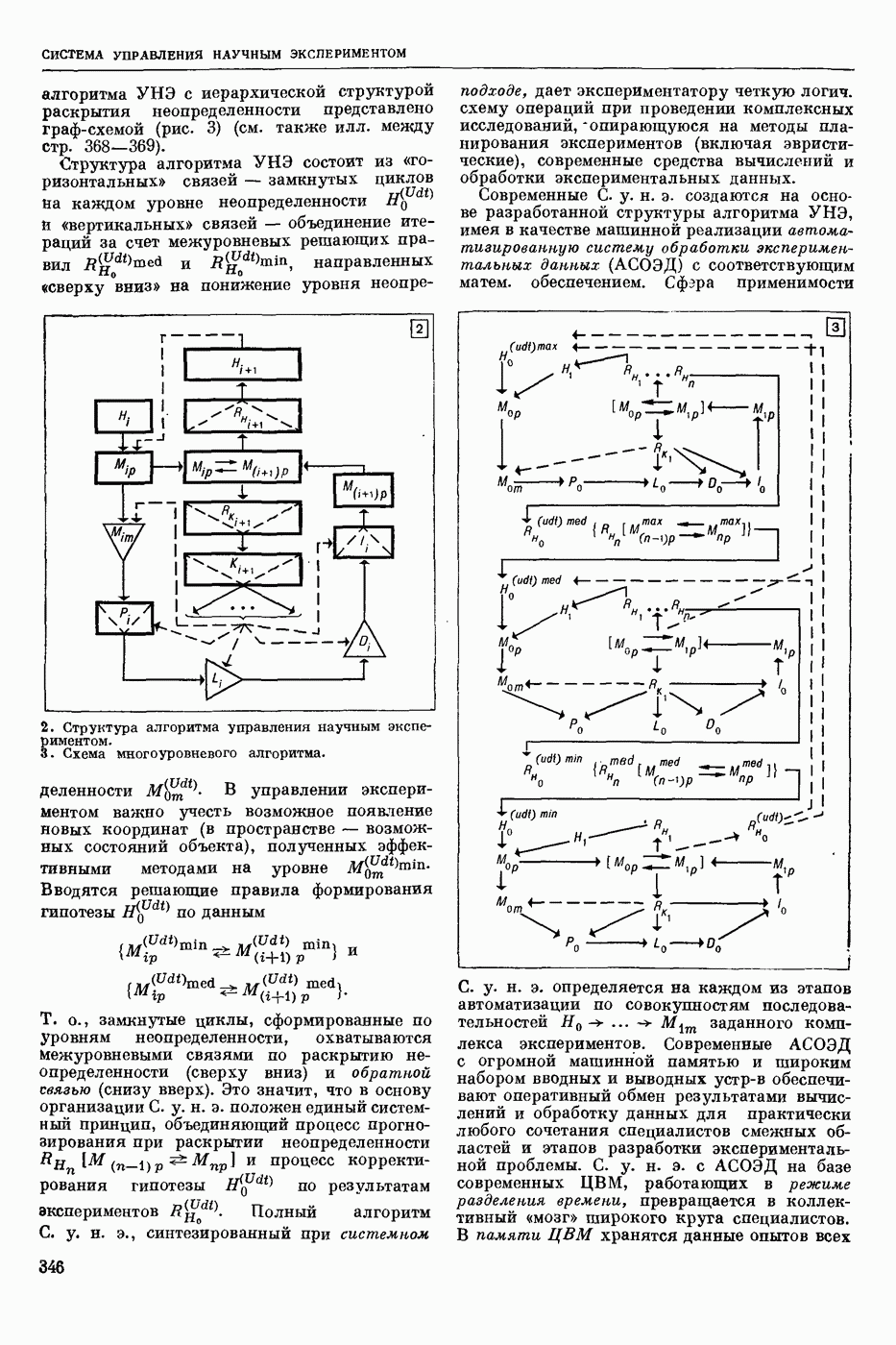
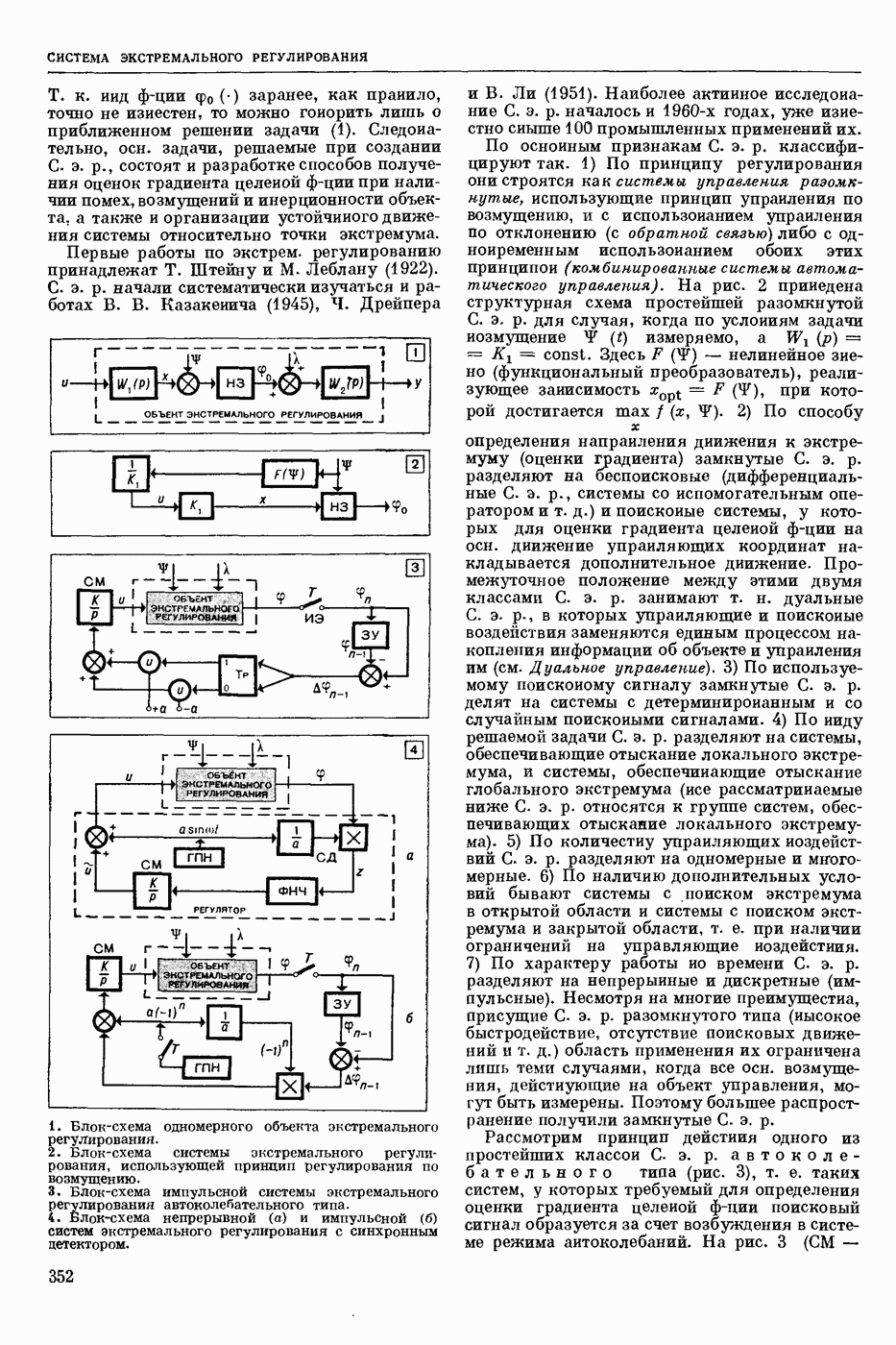
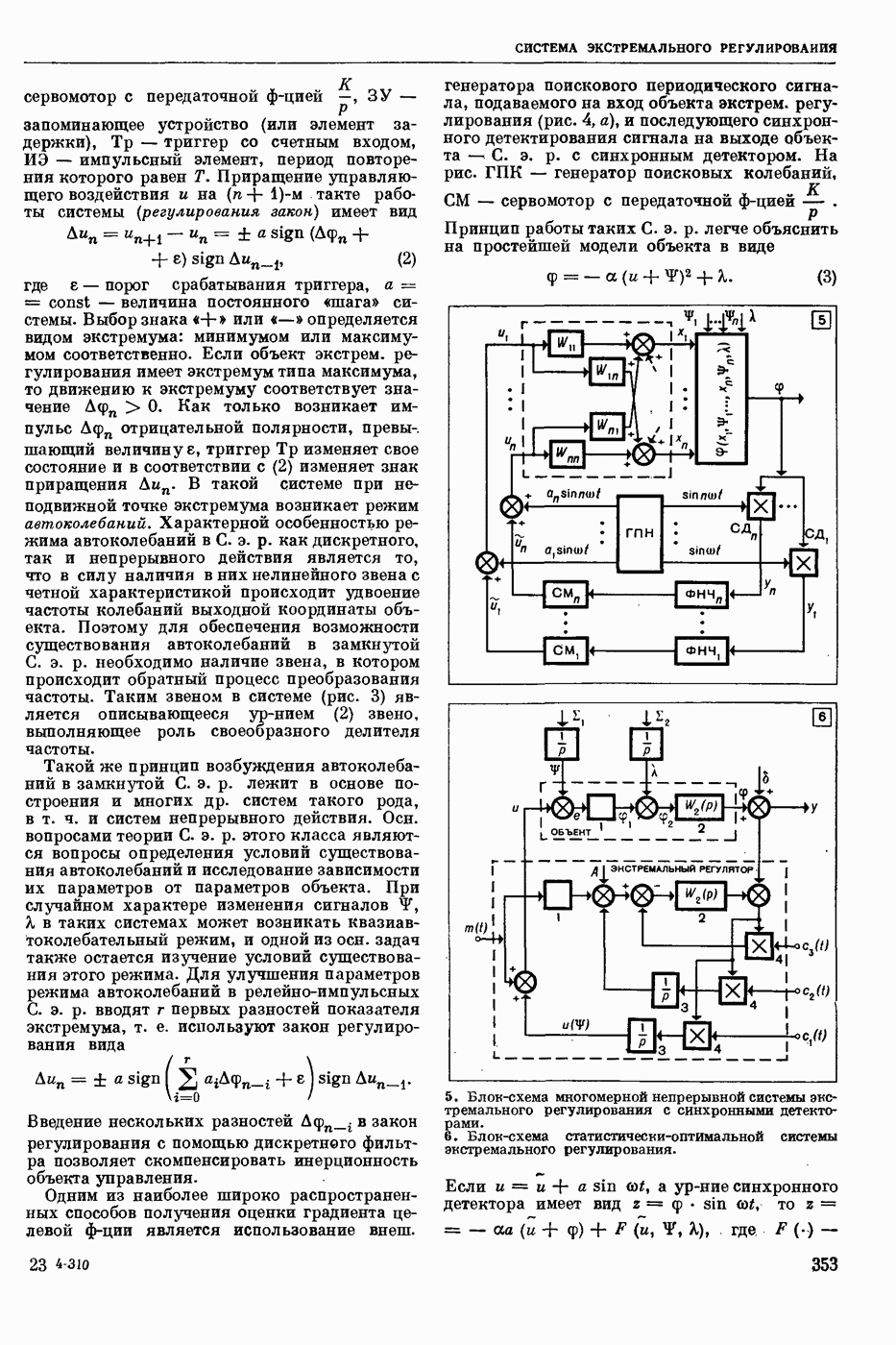
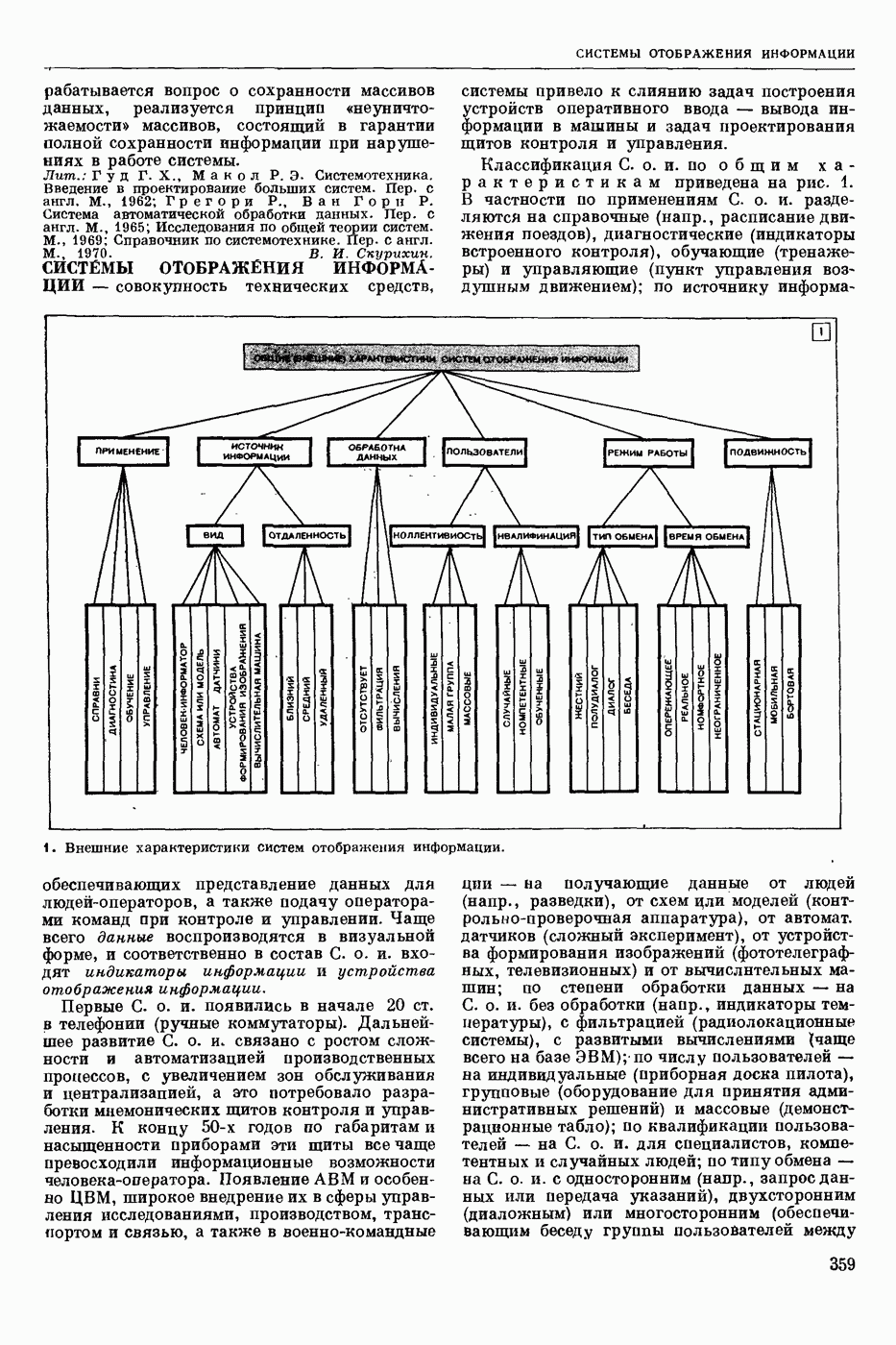
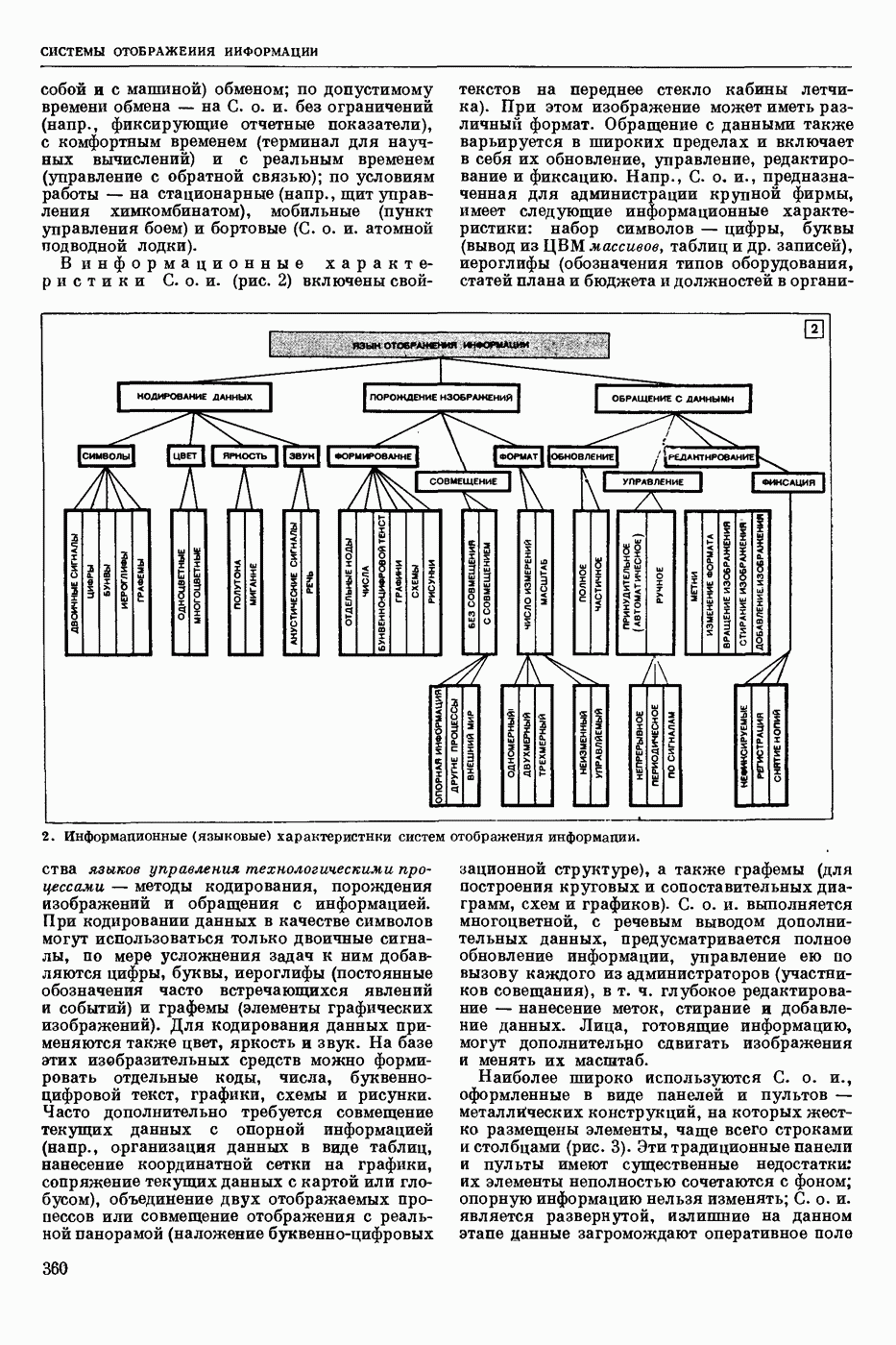
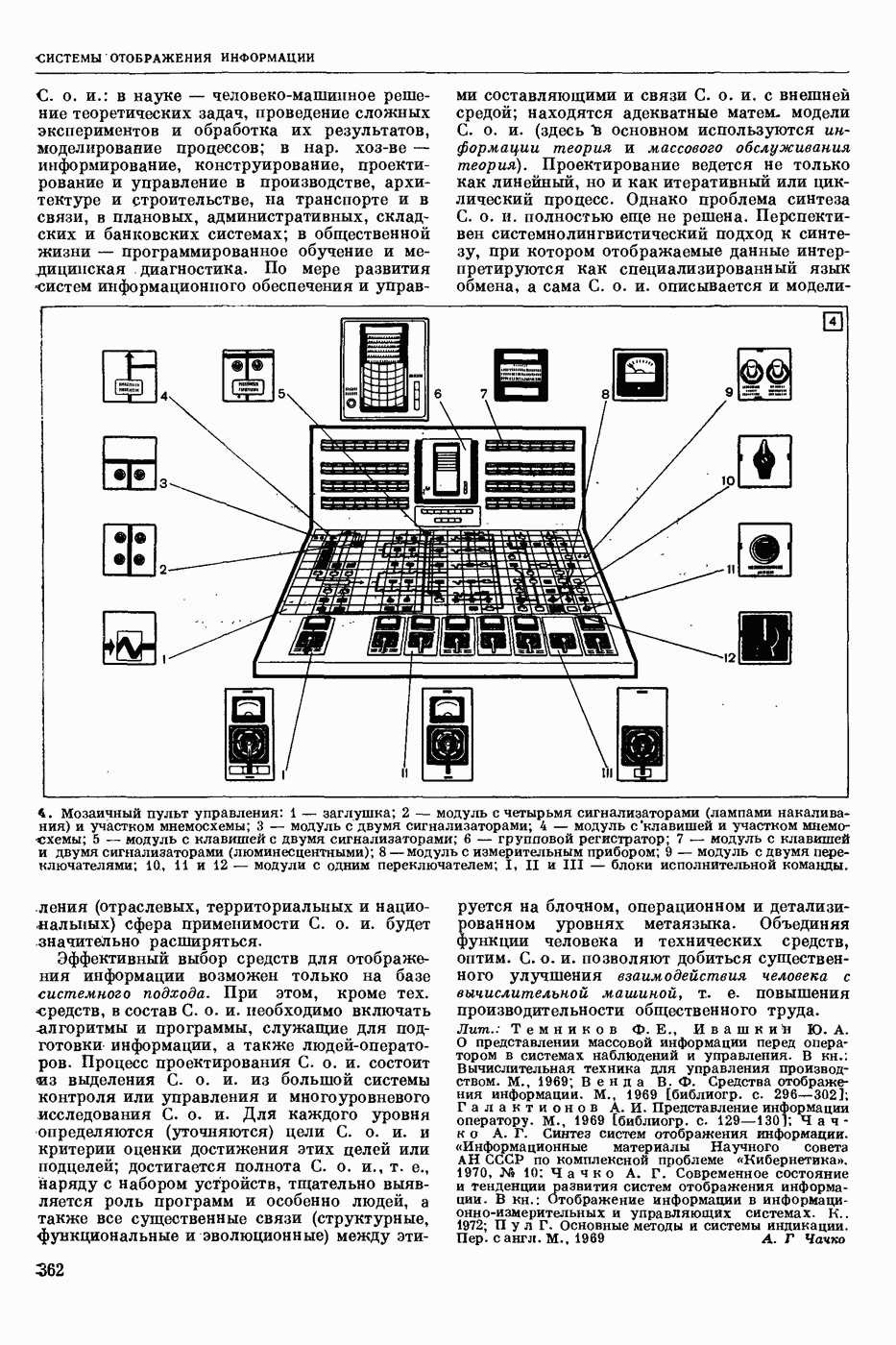
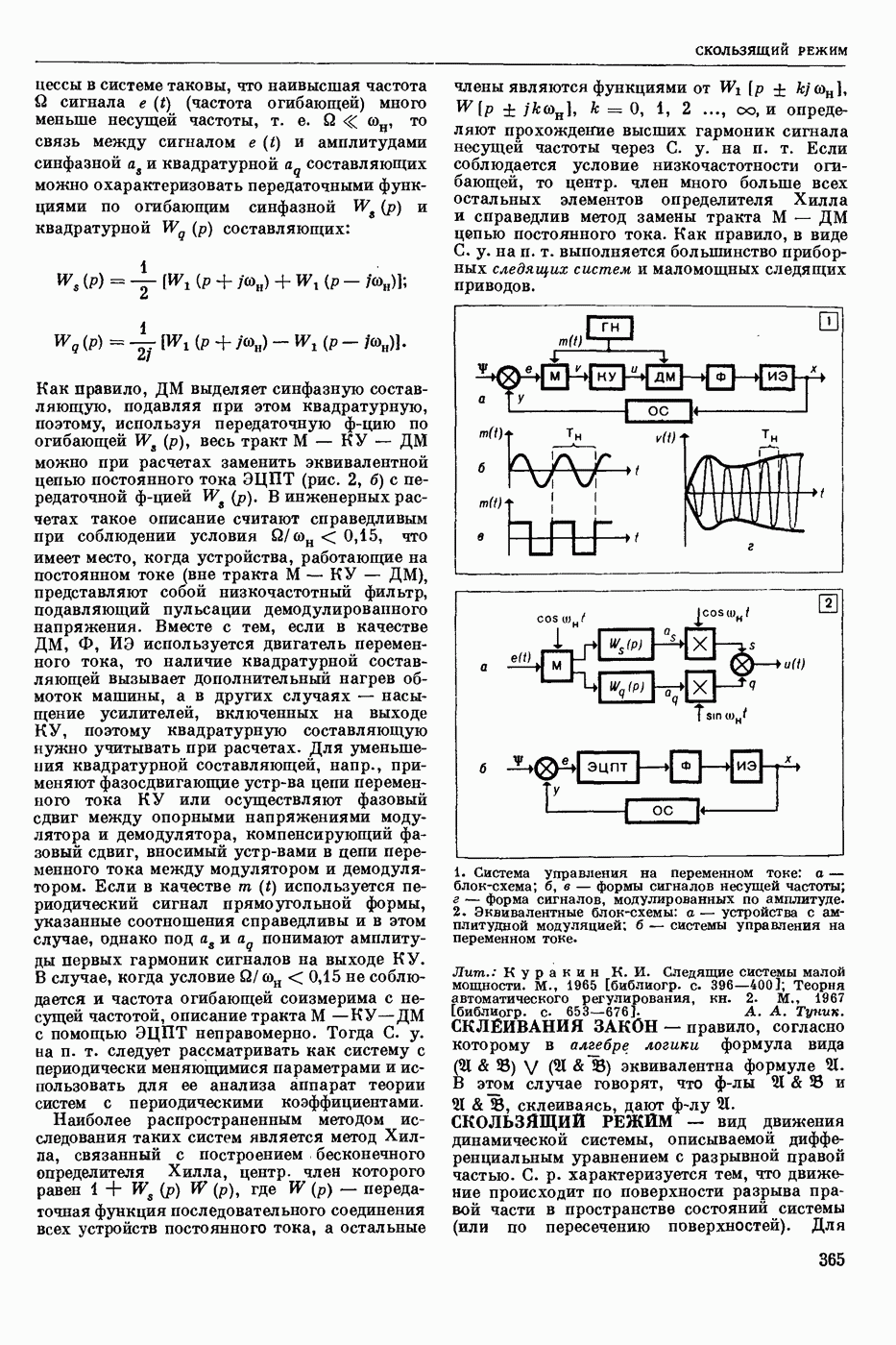
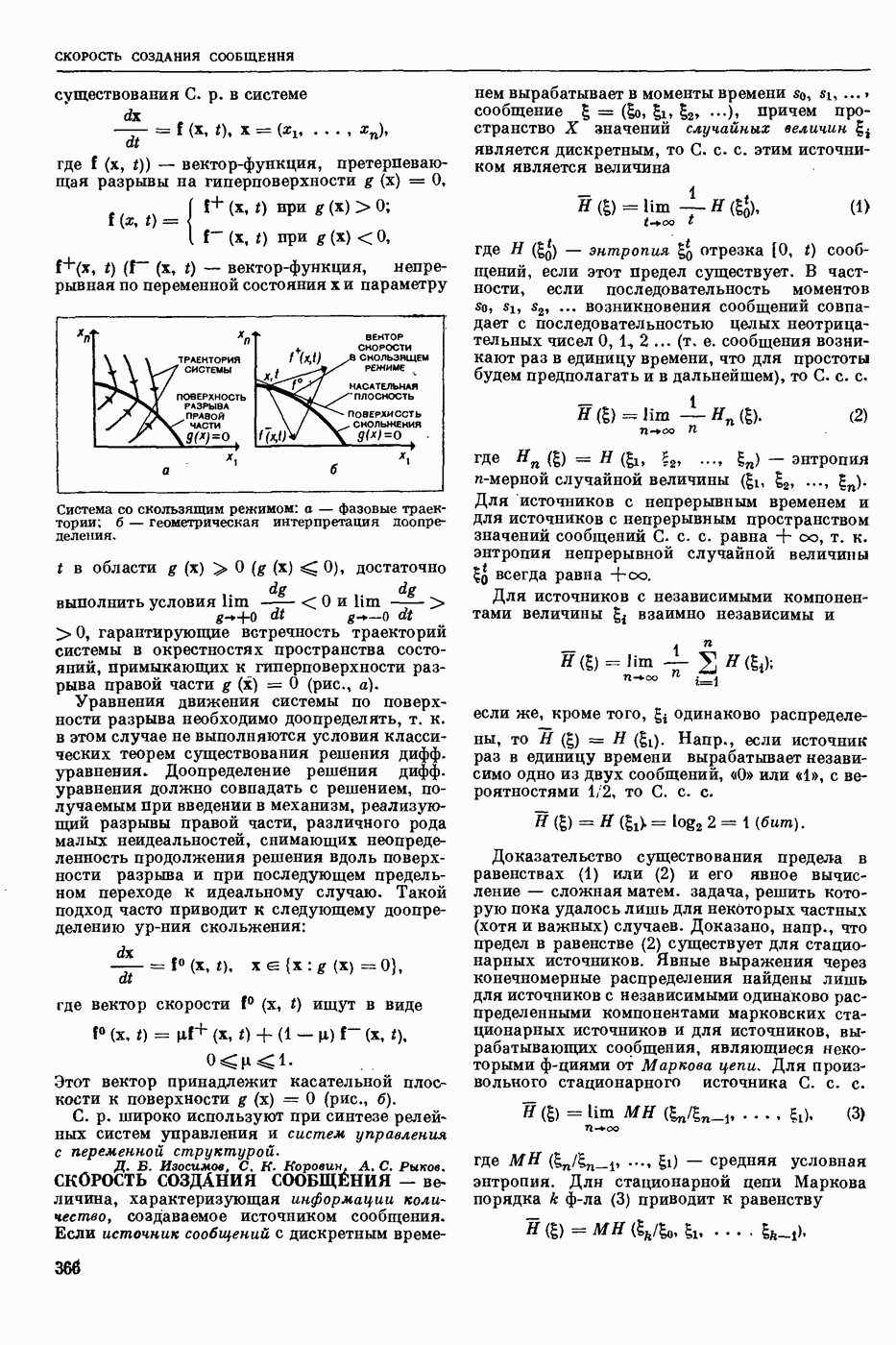
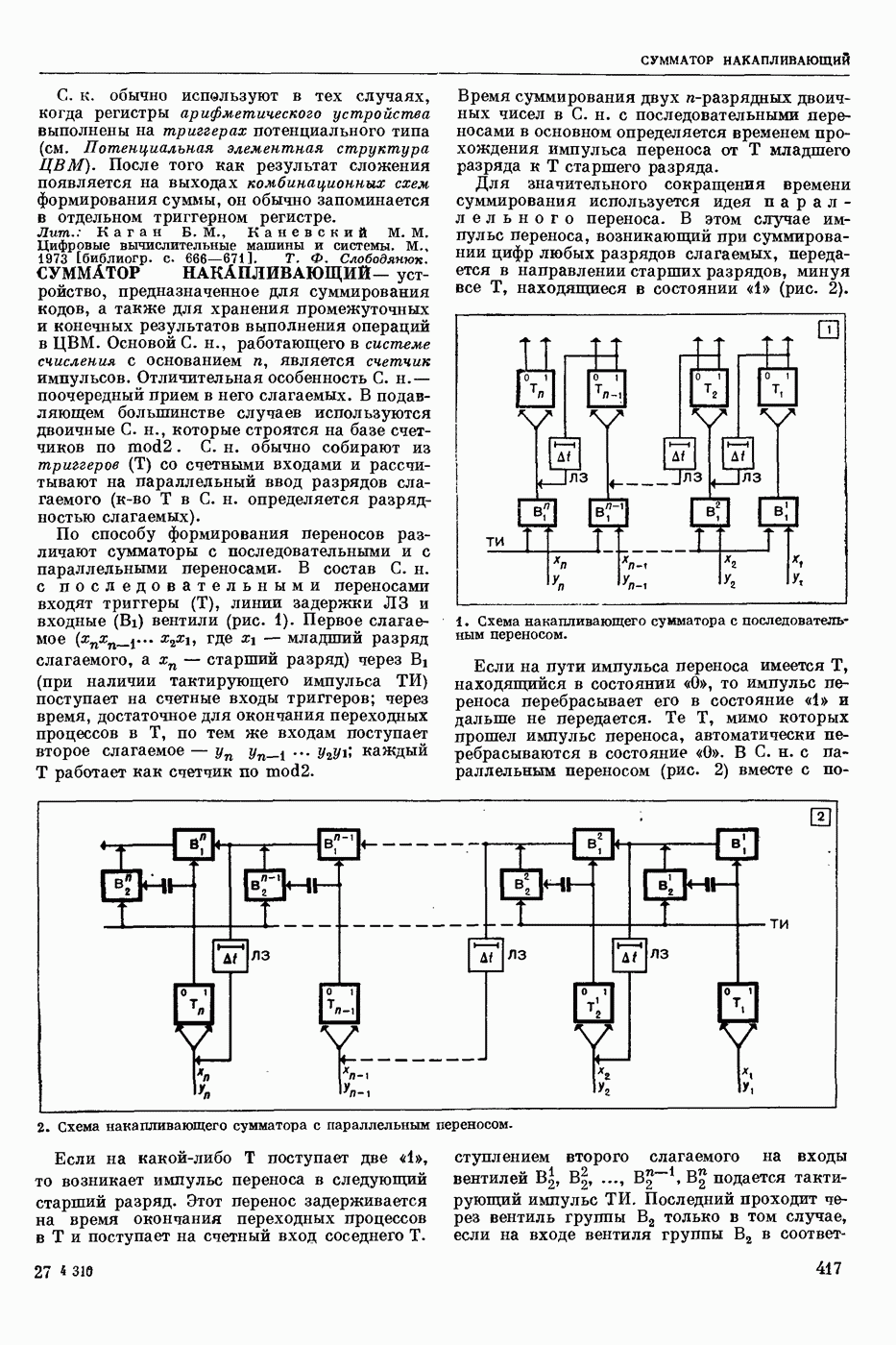
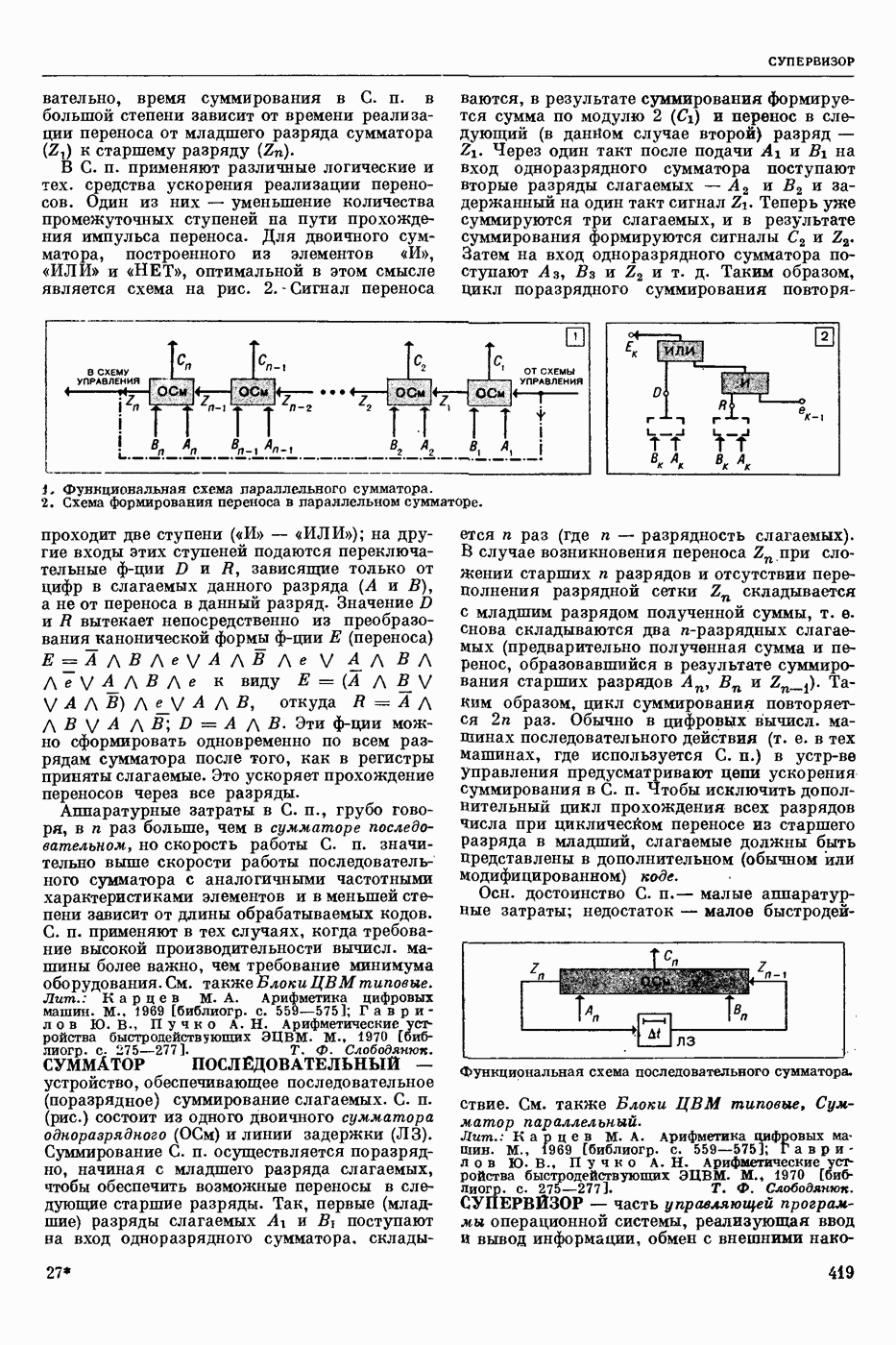
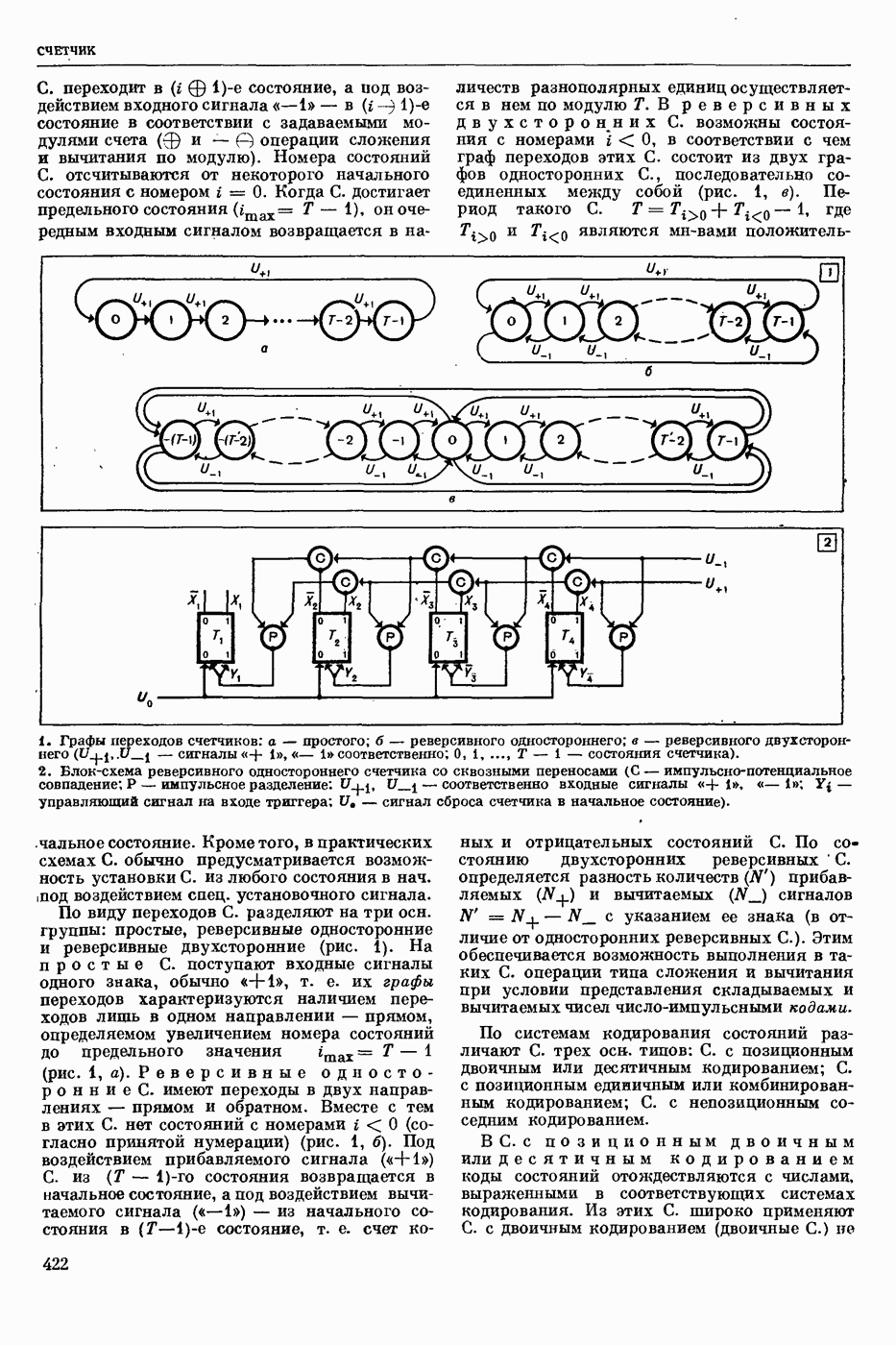
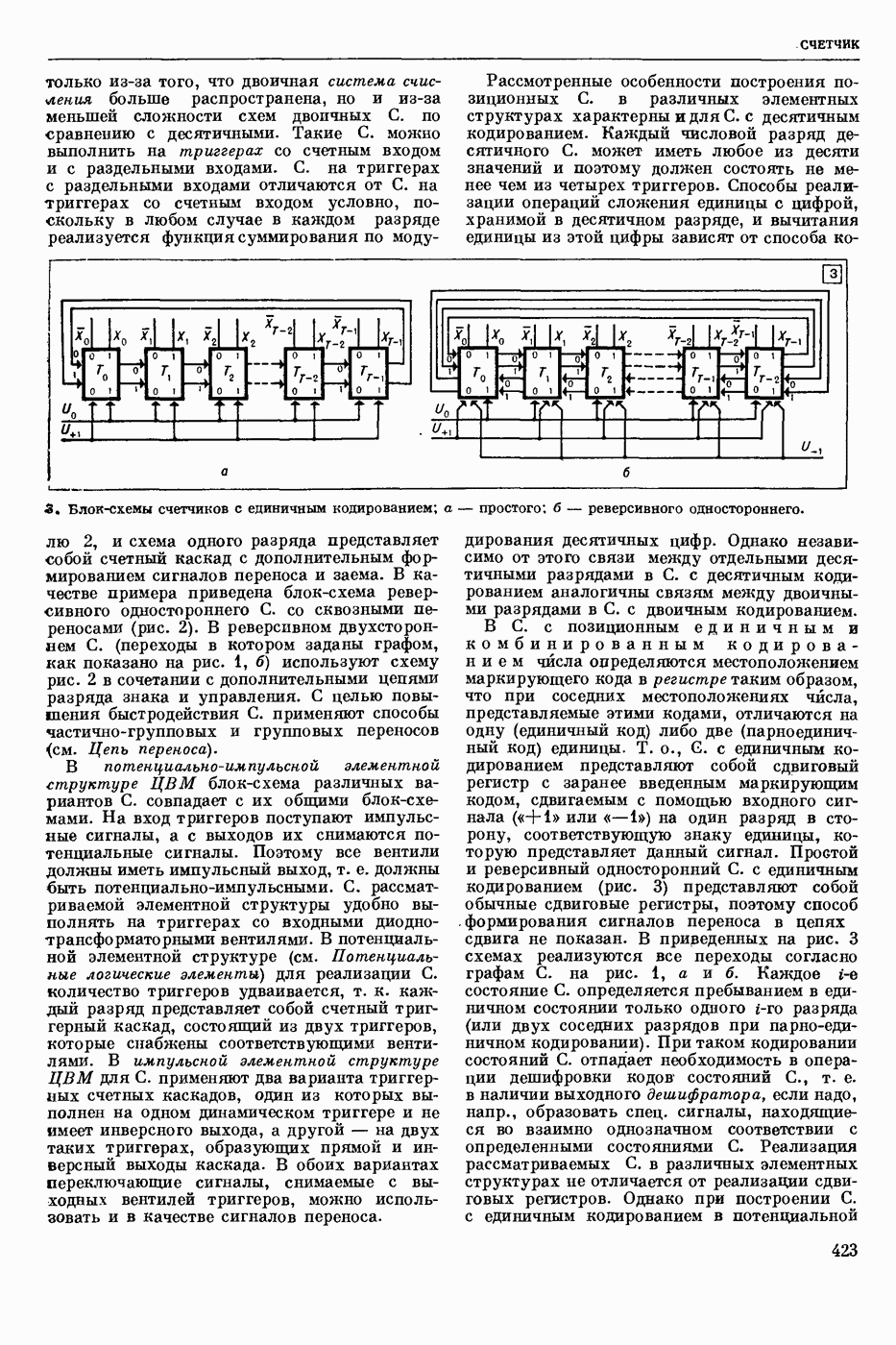
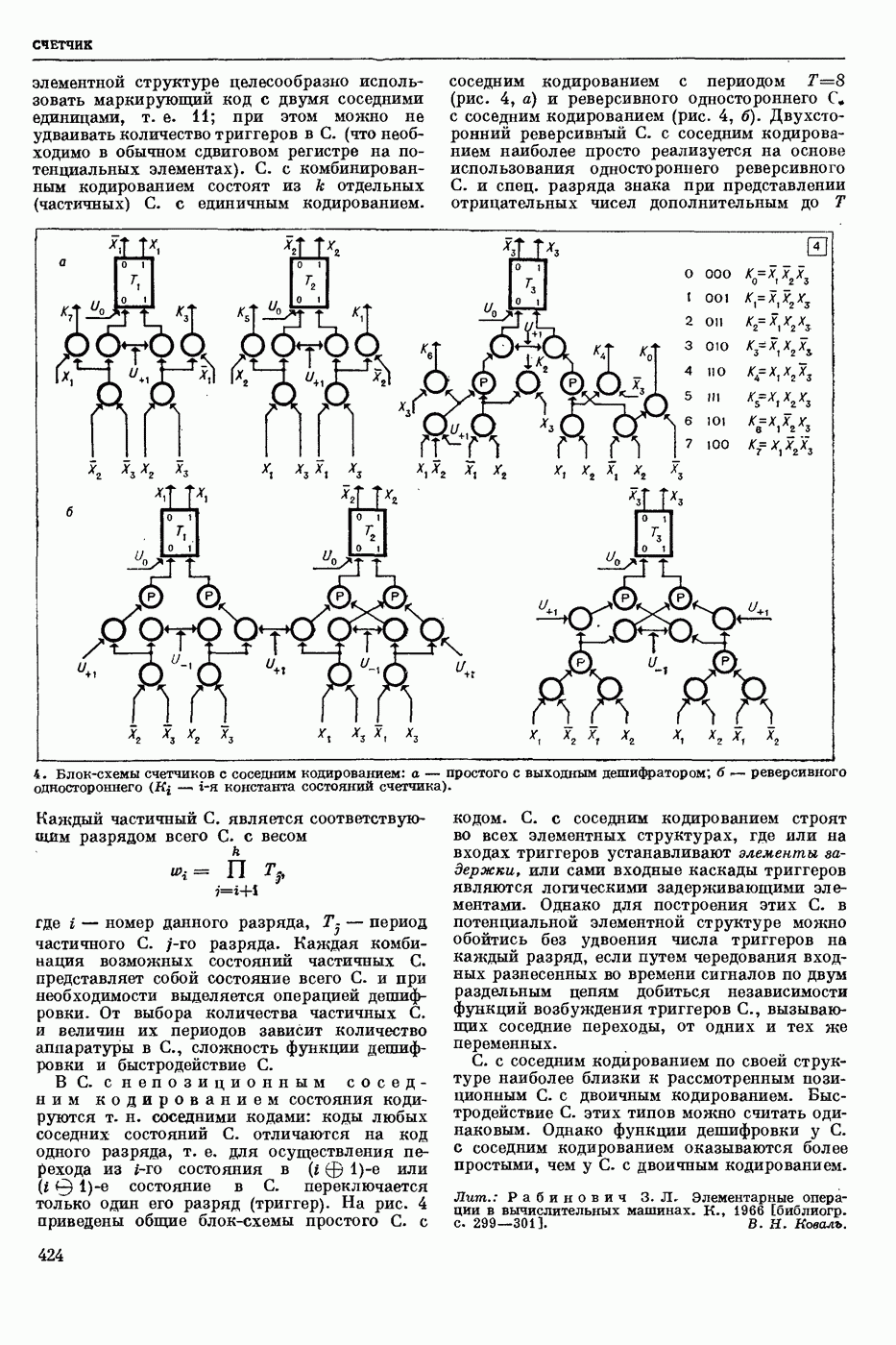
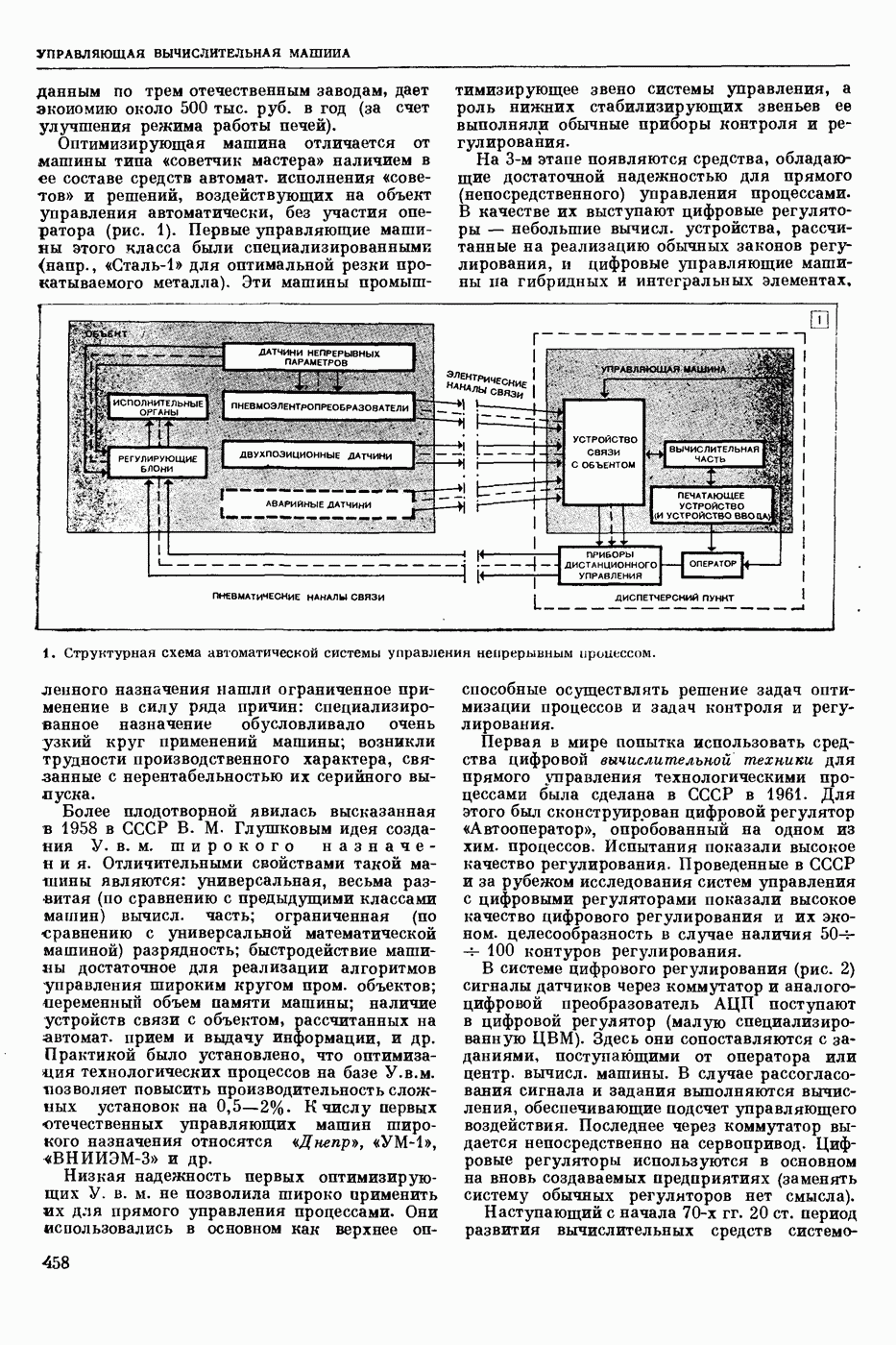
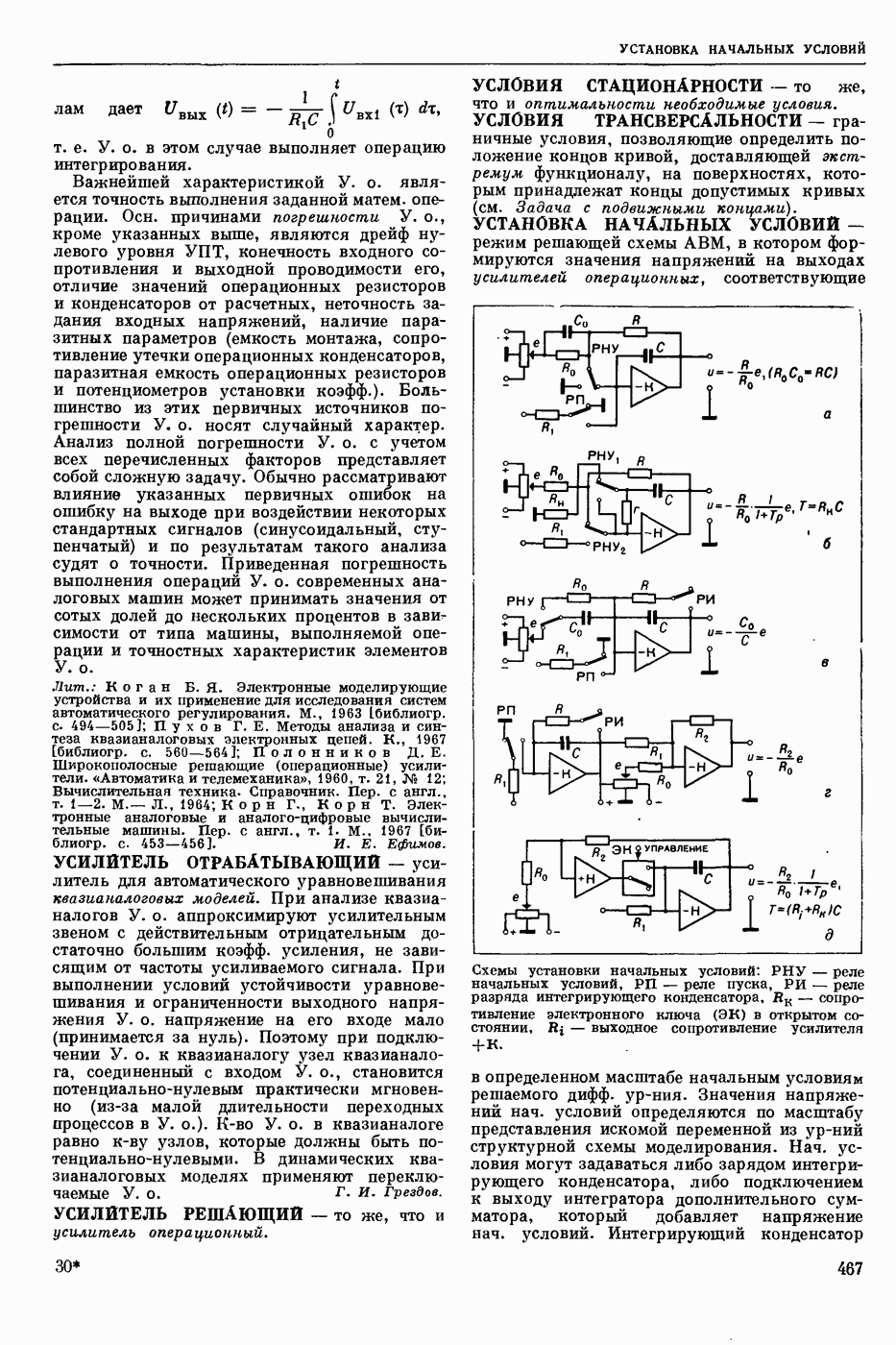
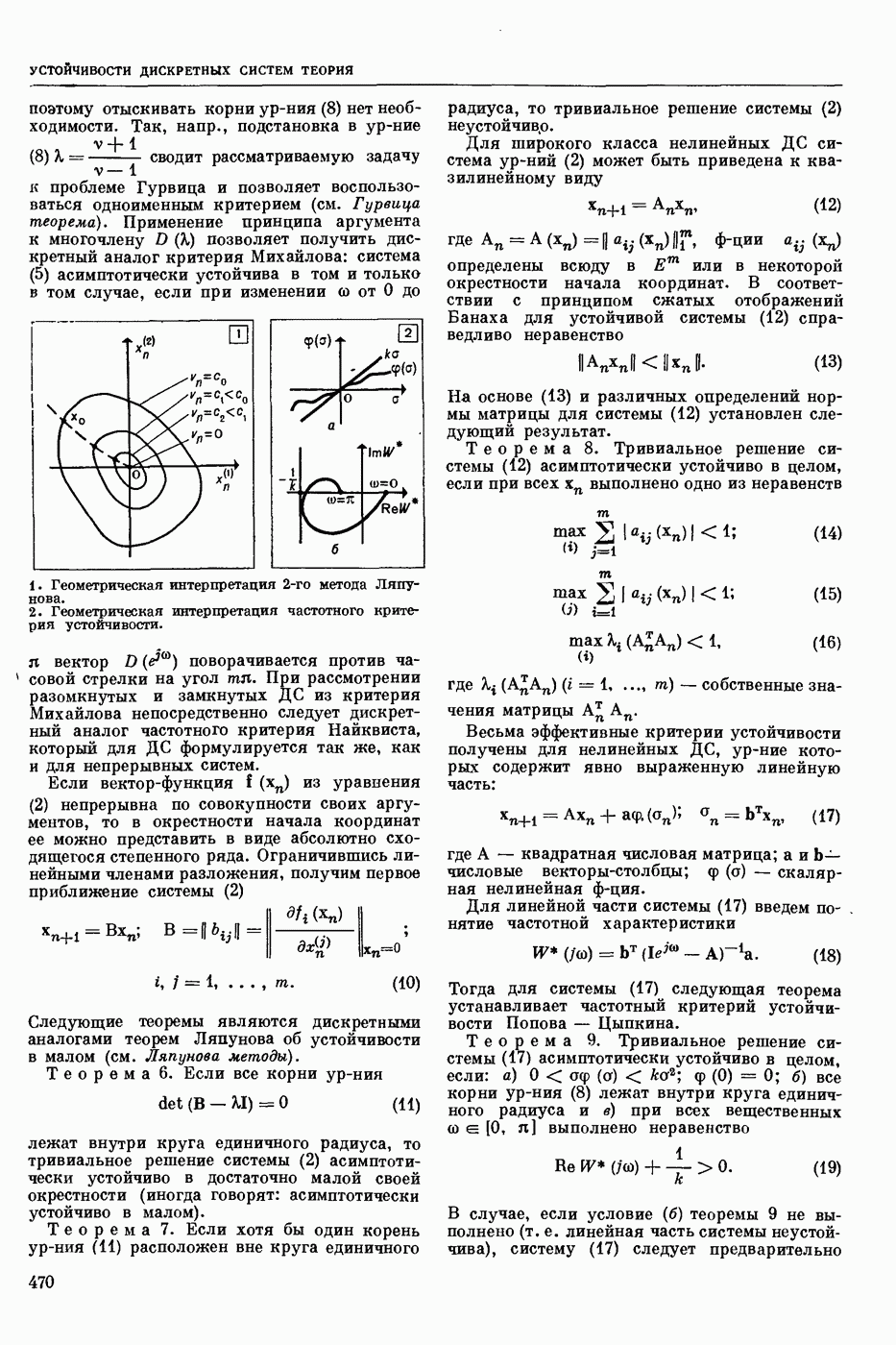
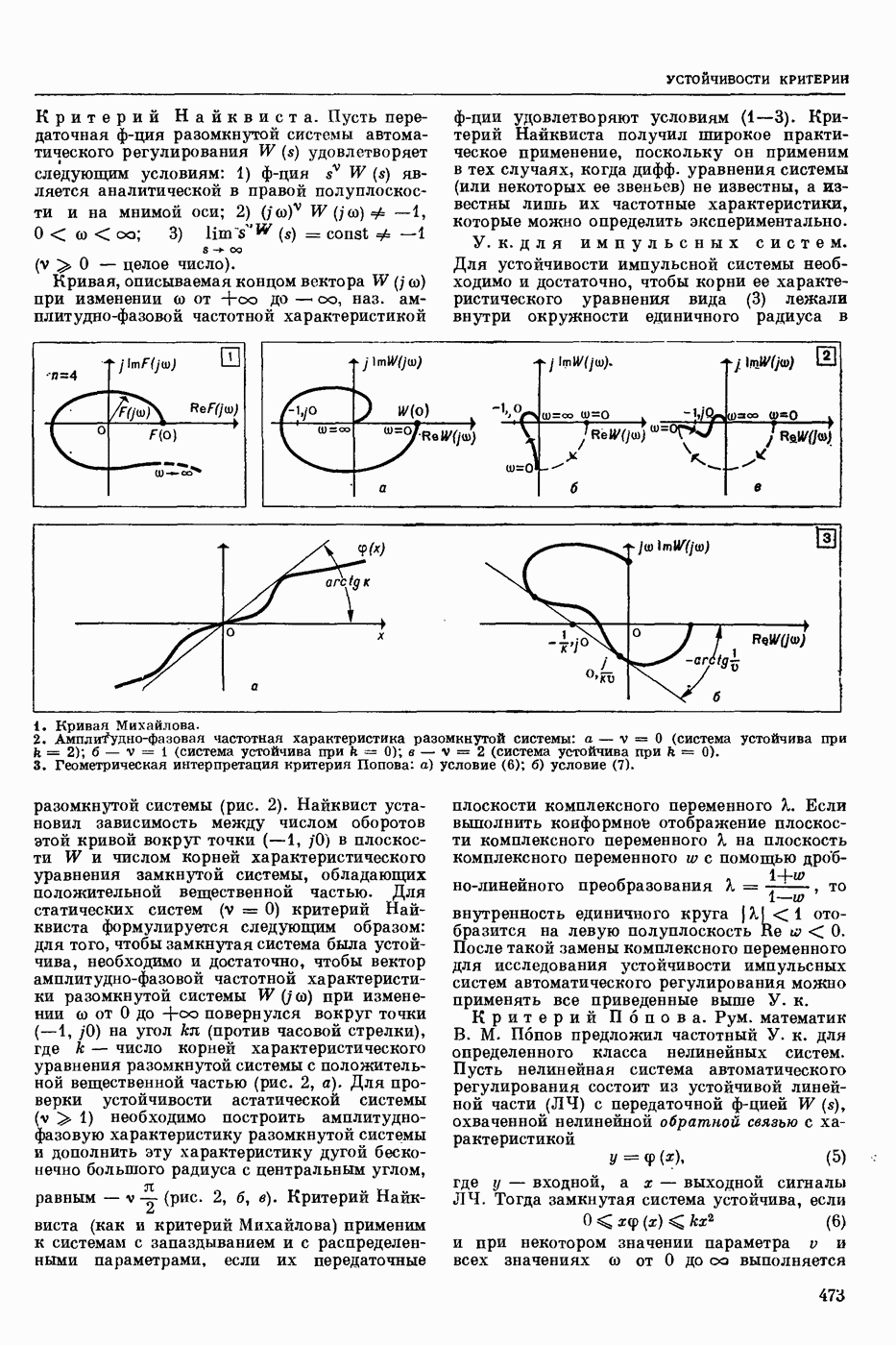
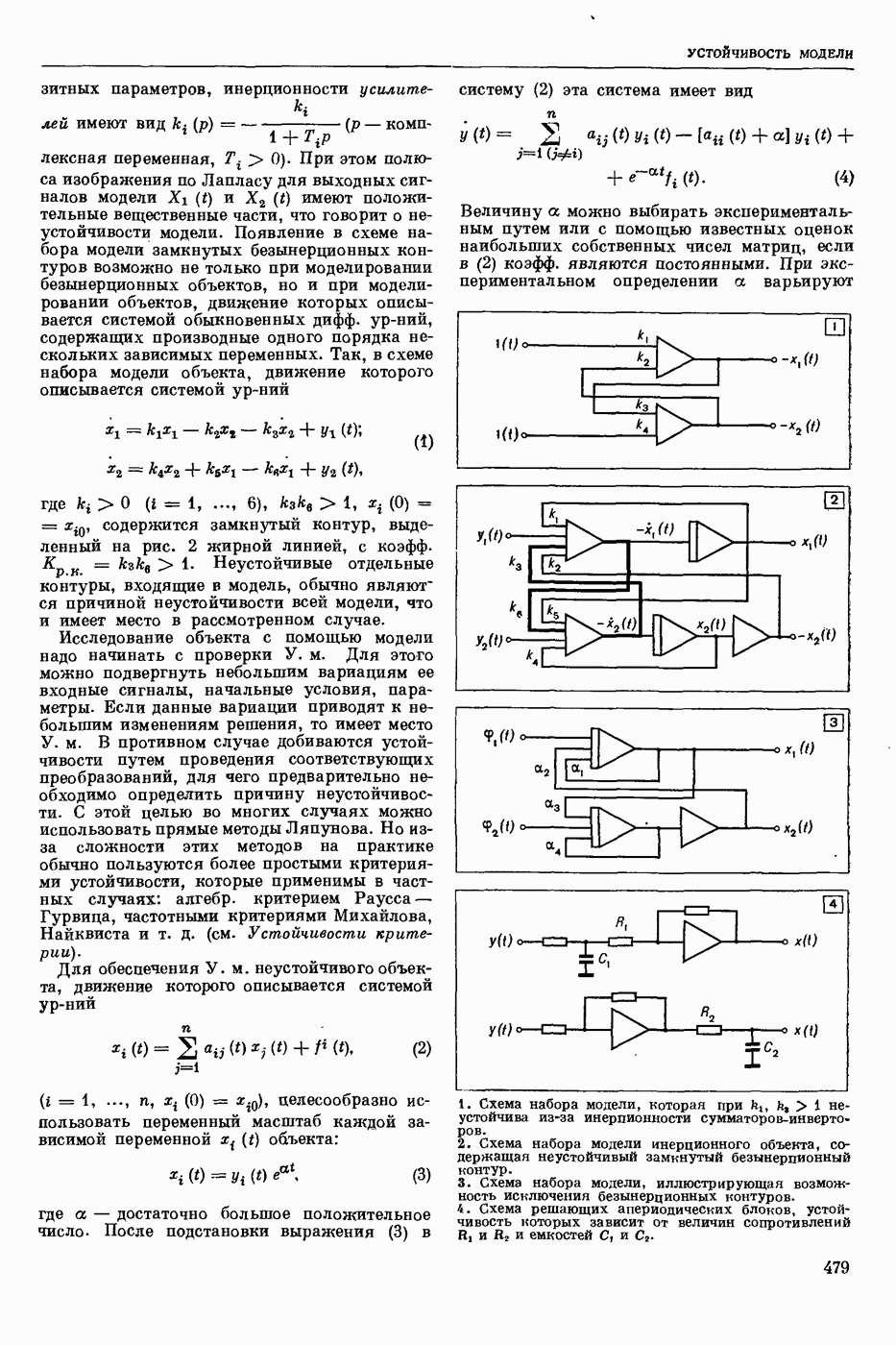
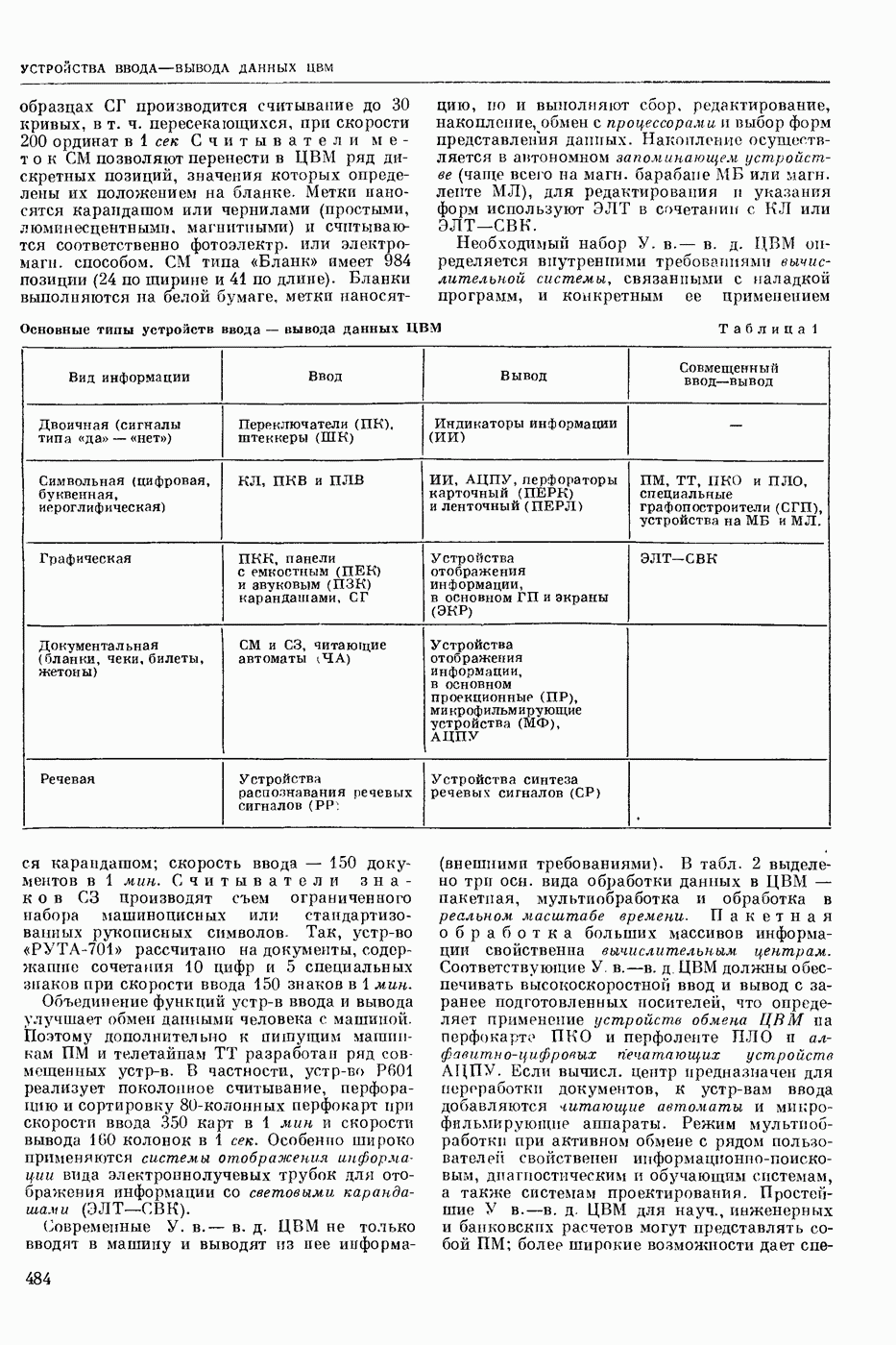
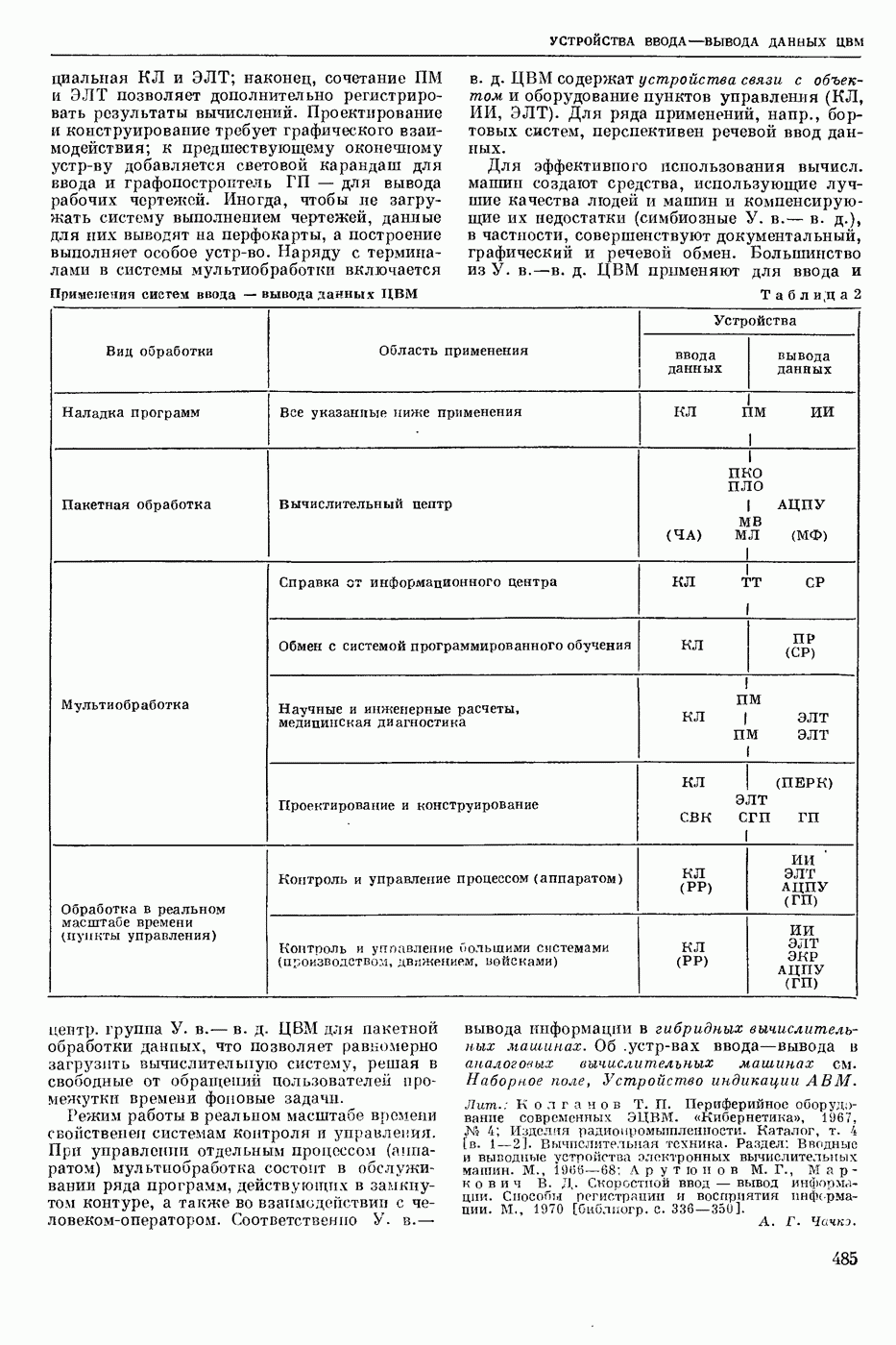
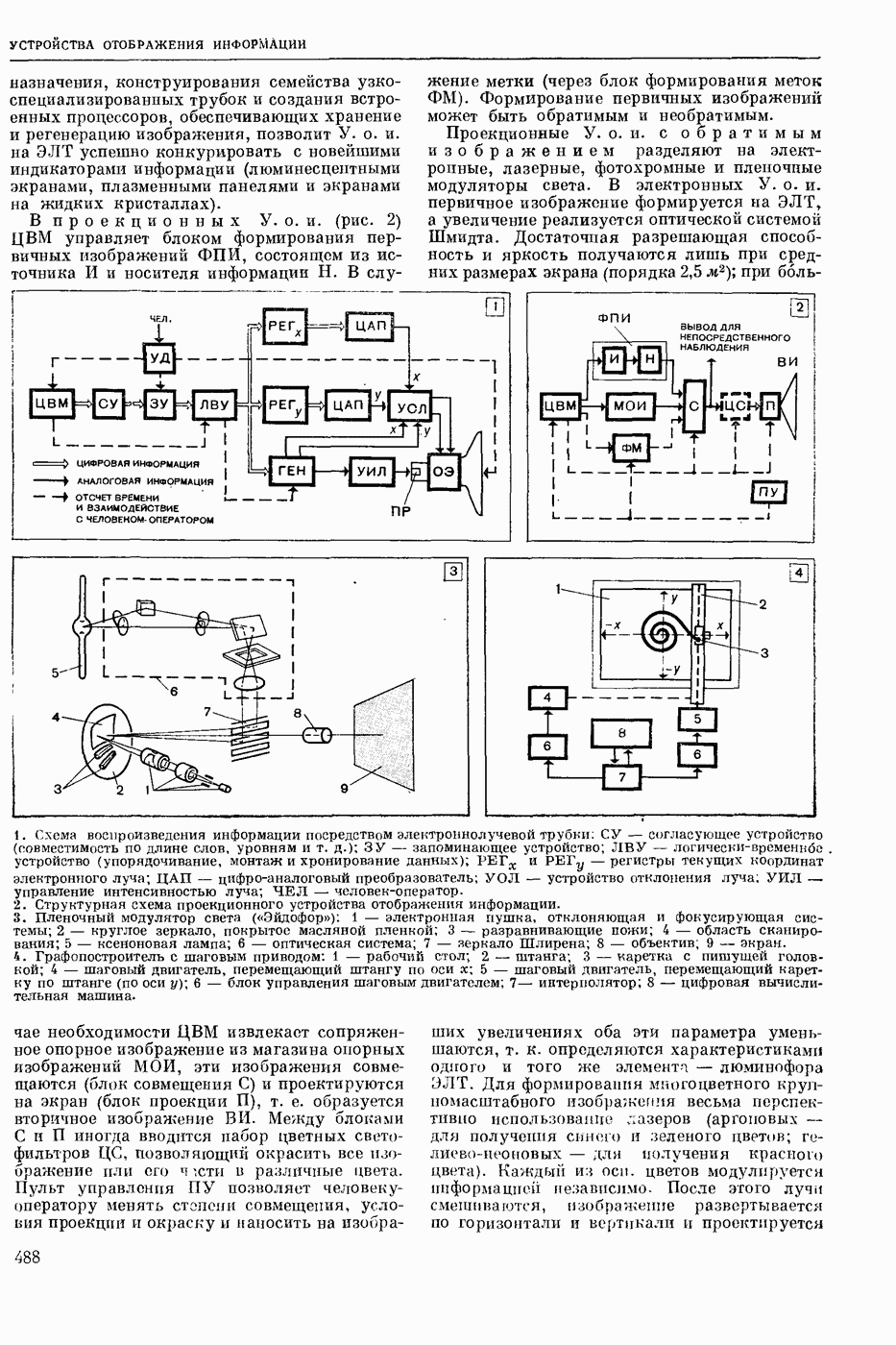
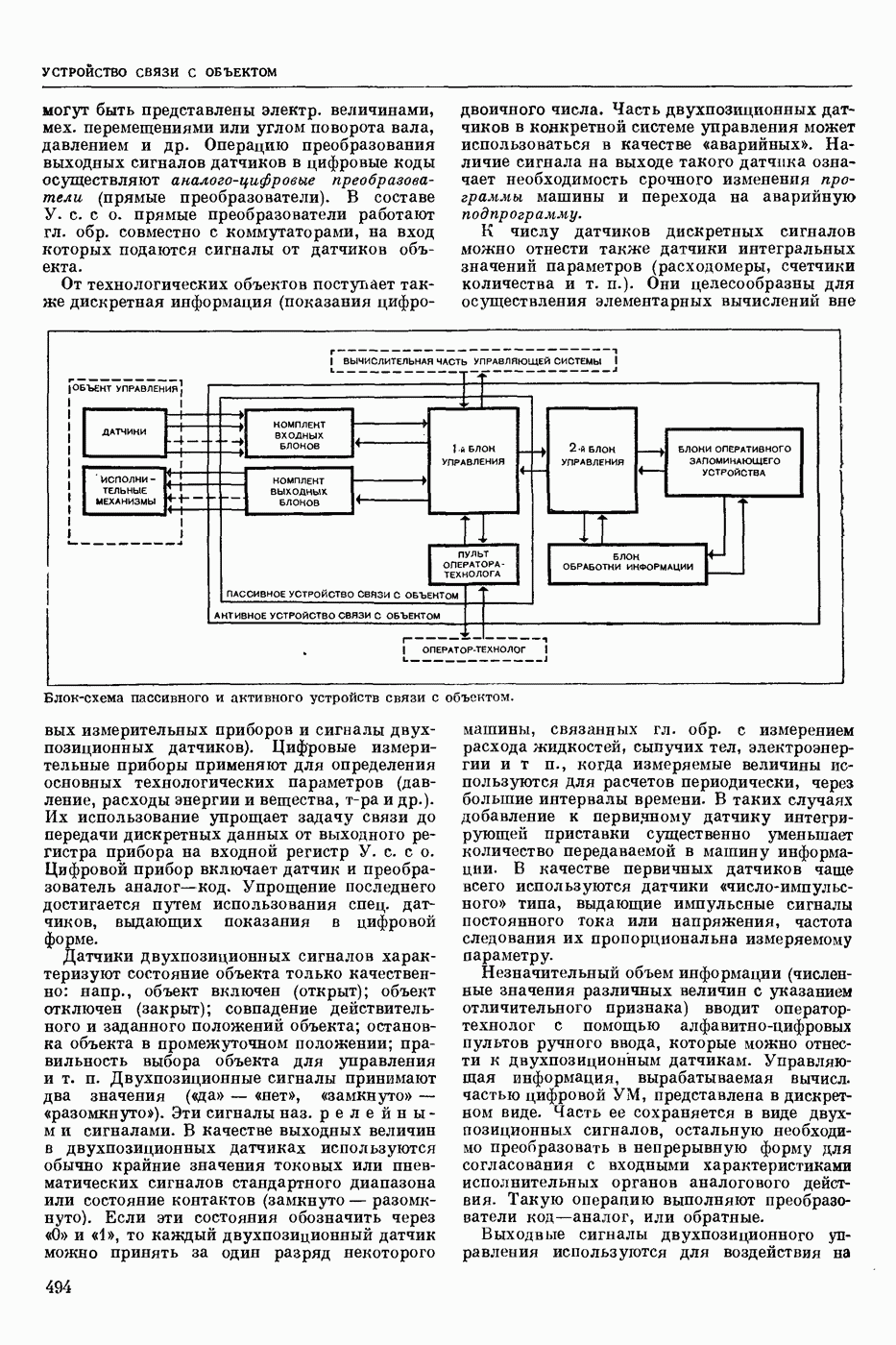
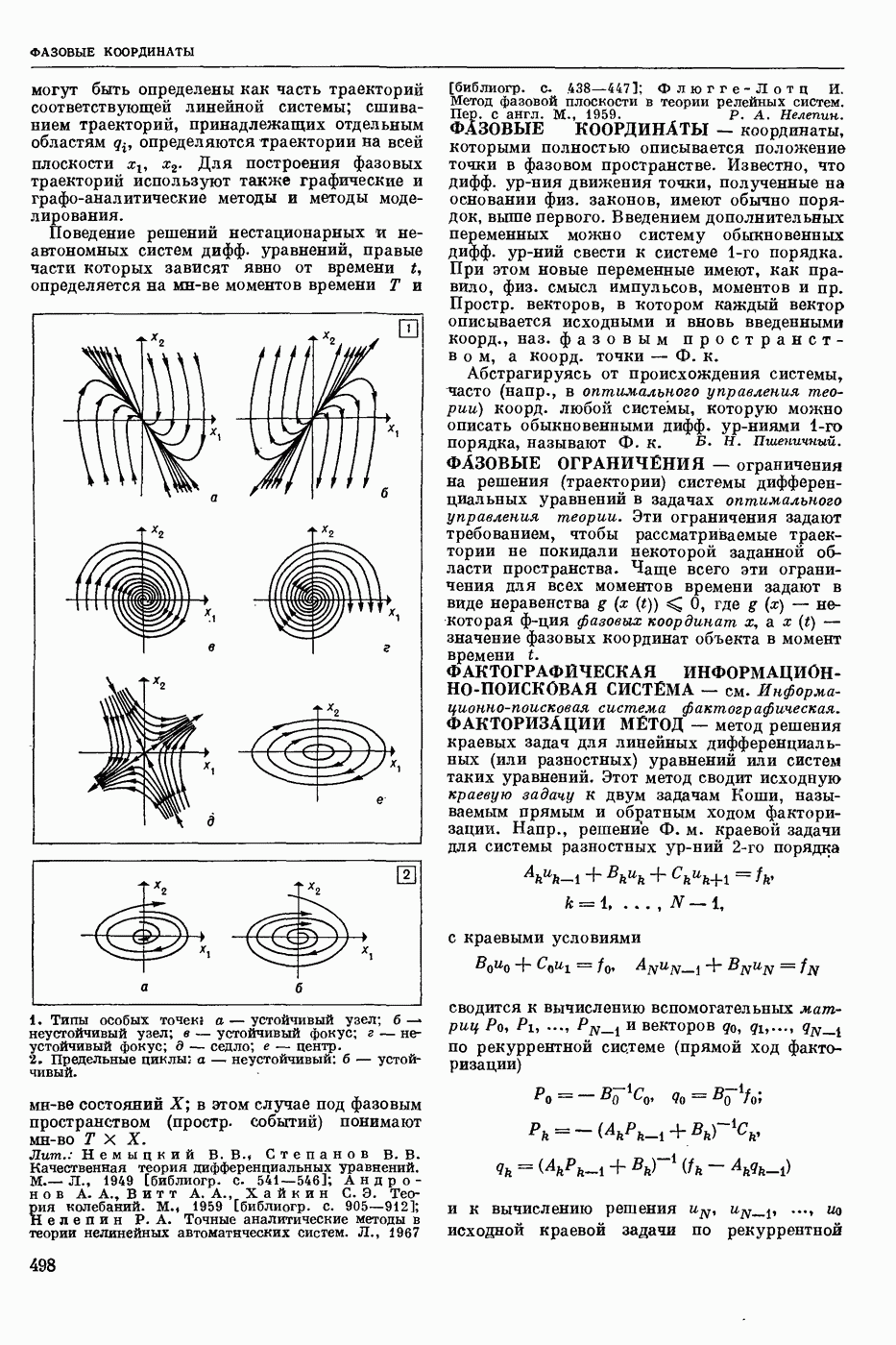
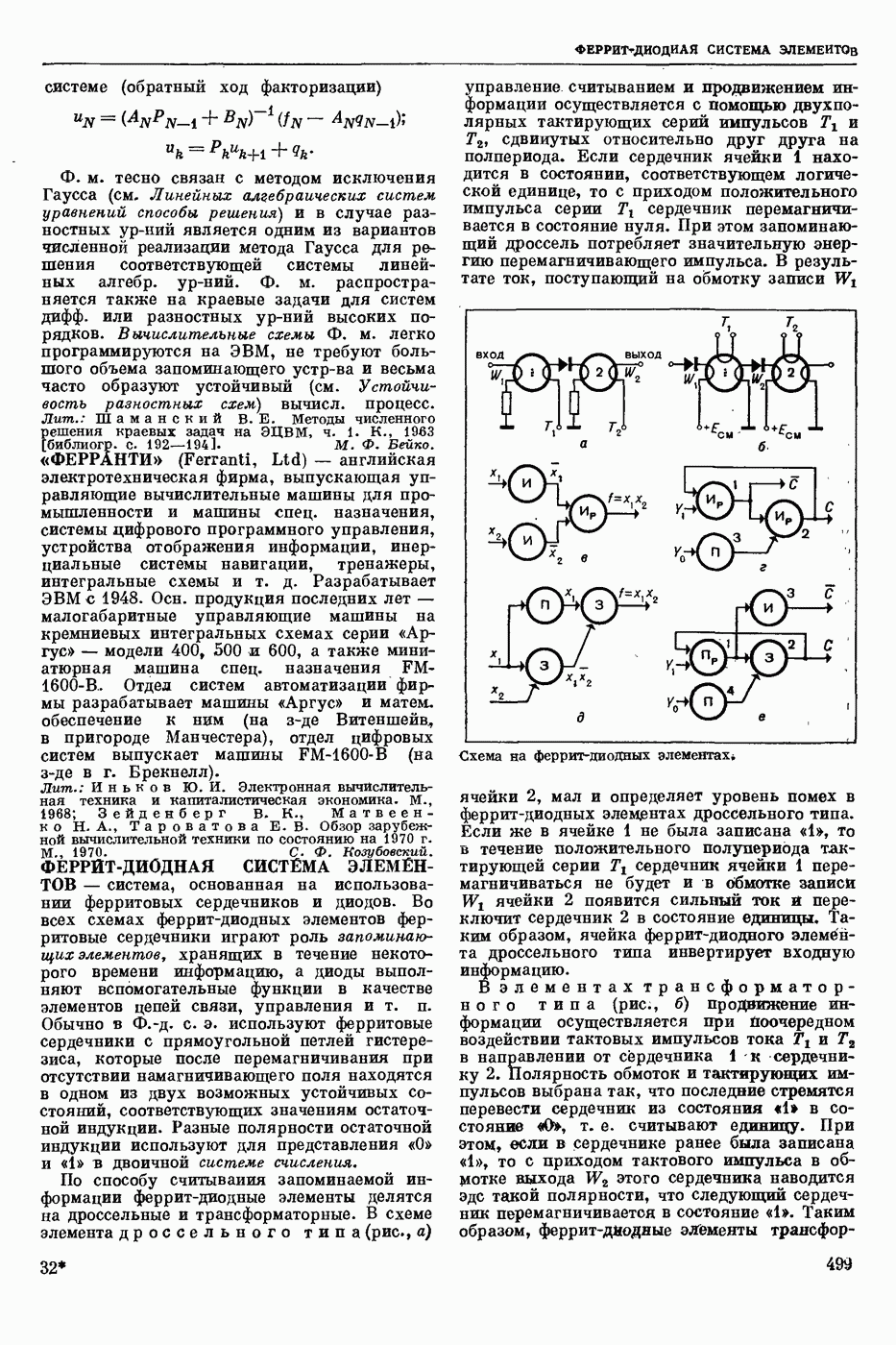
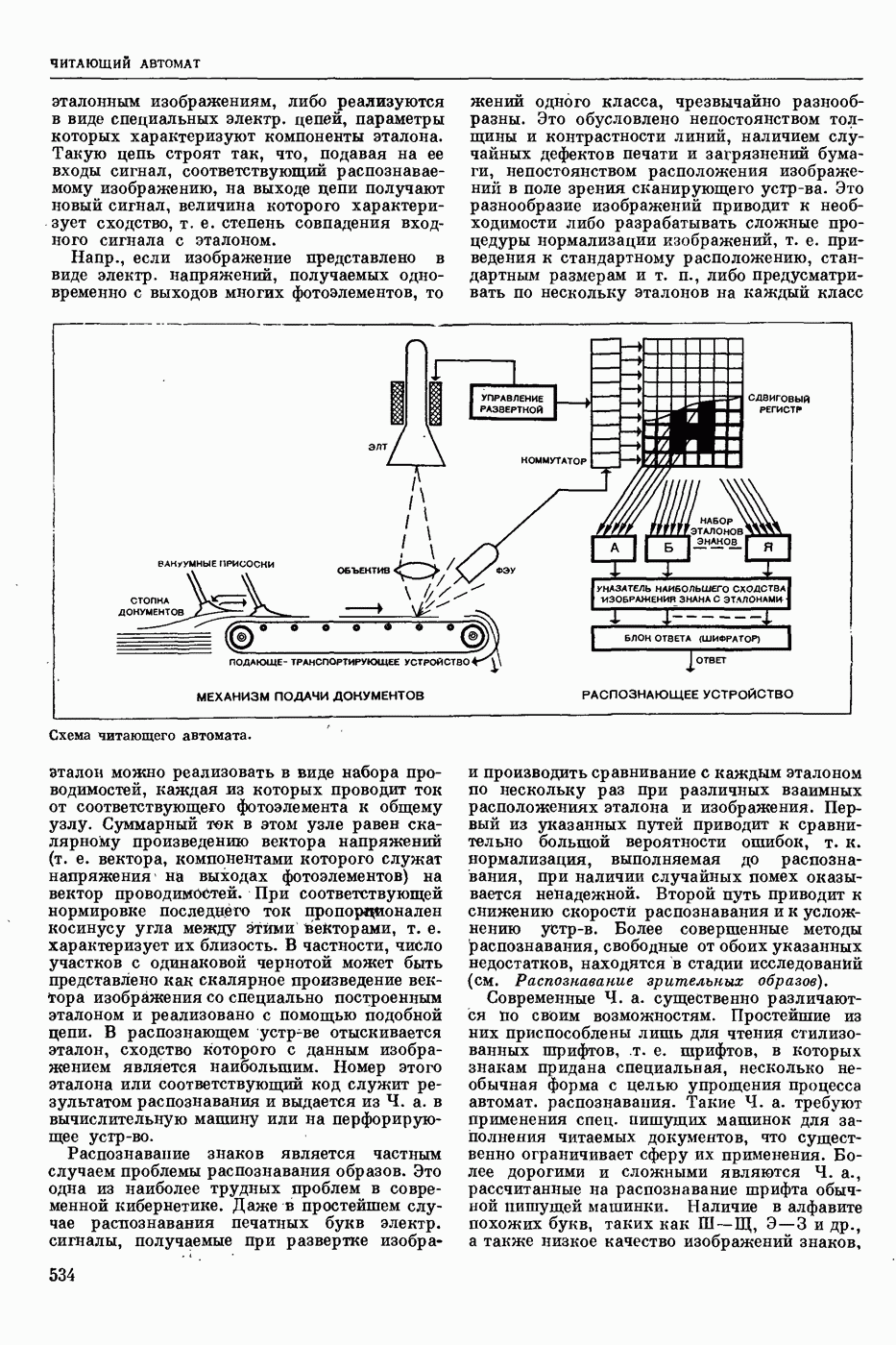
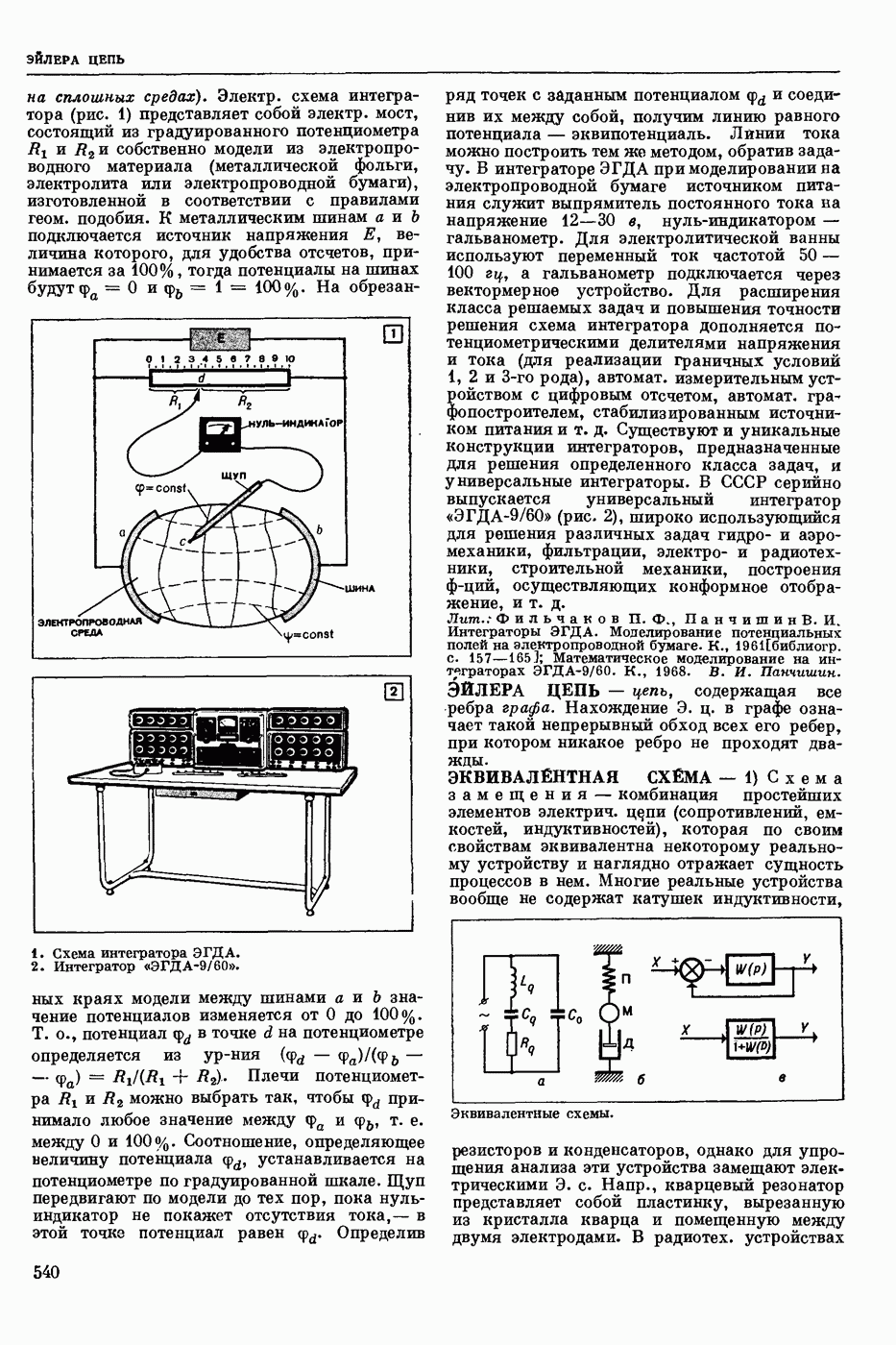
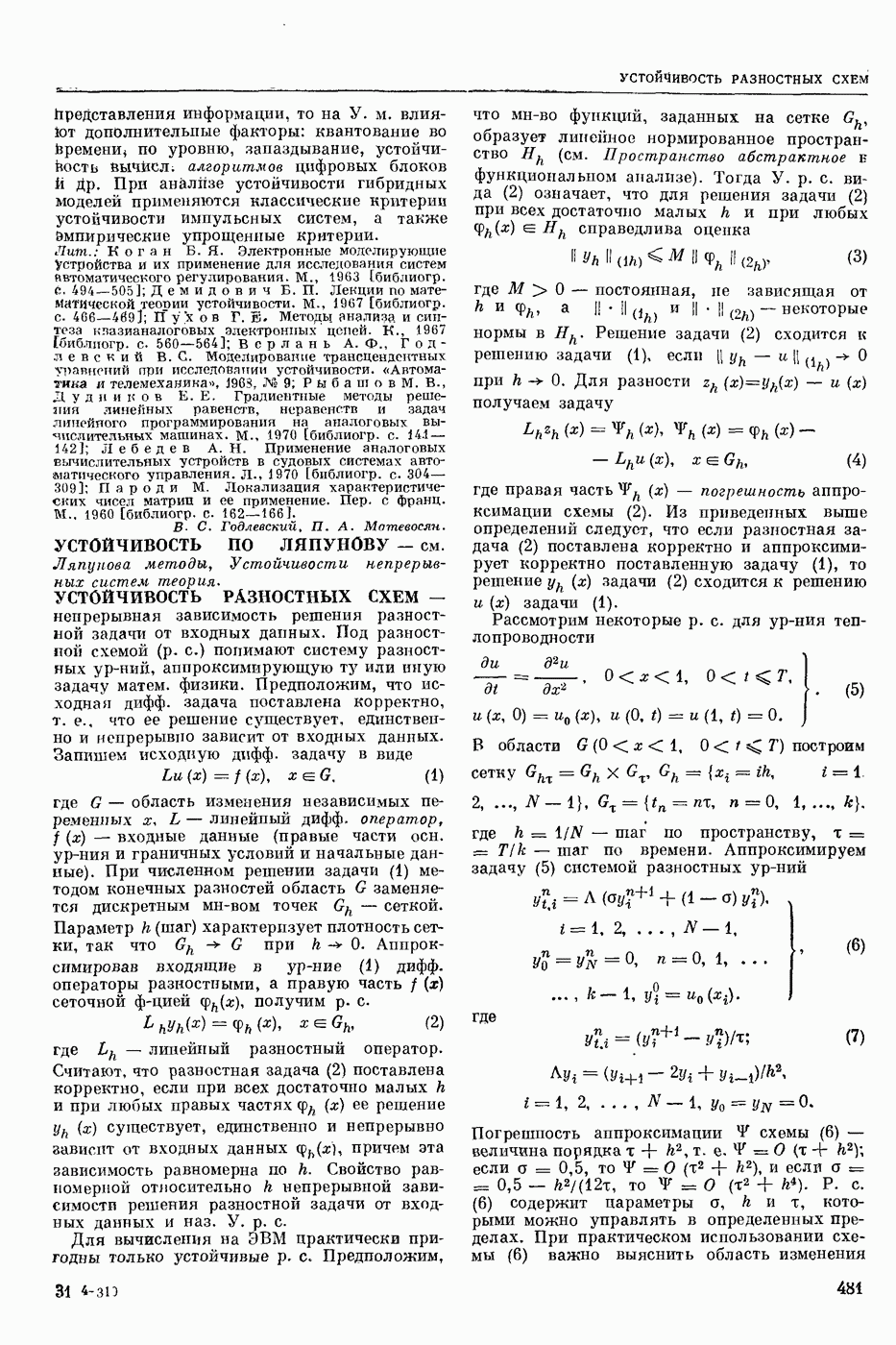| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
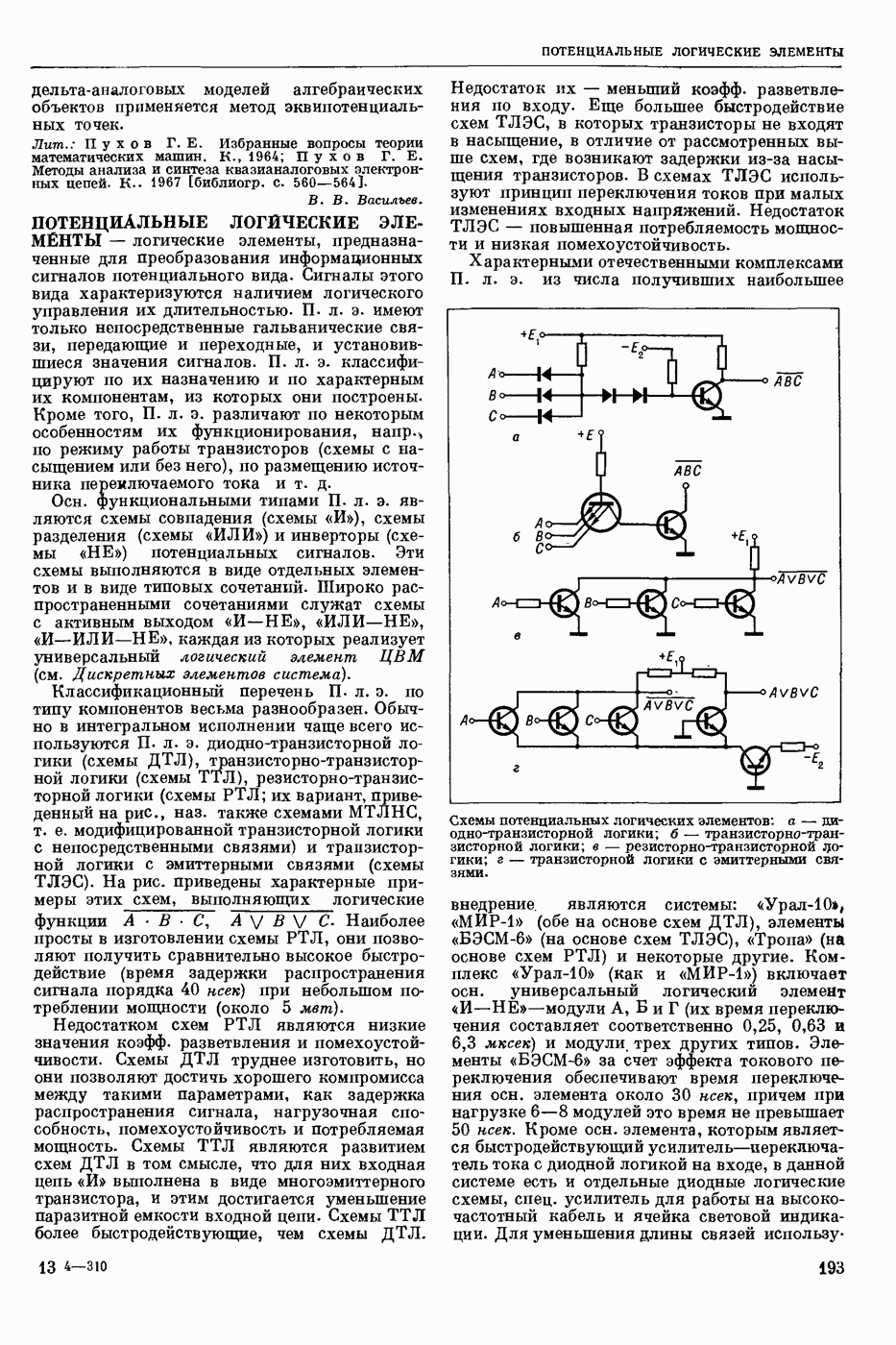
УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ ТЕОРИЯ
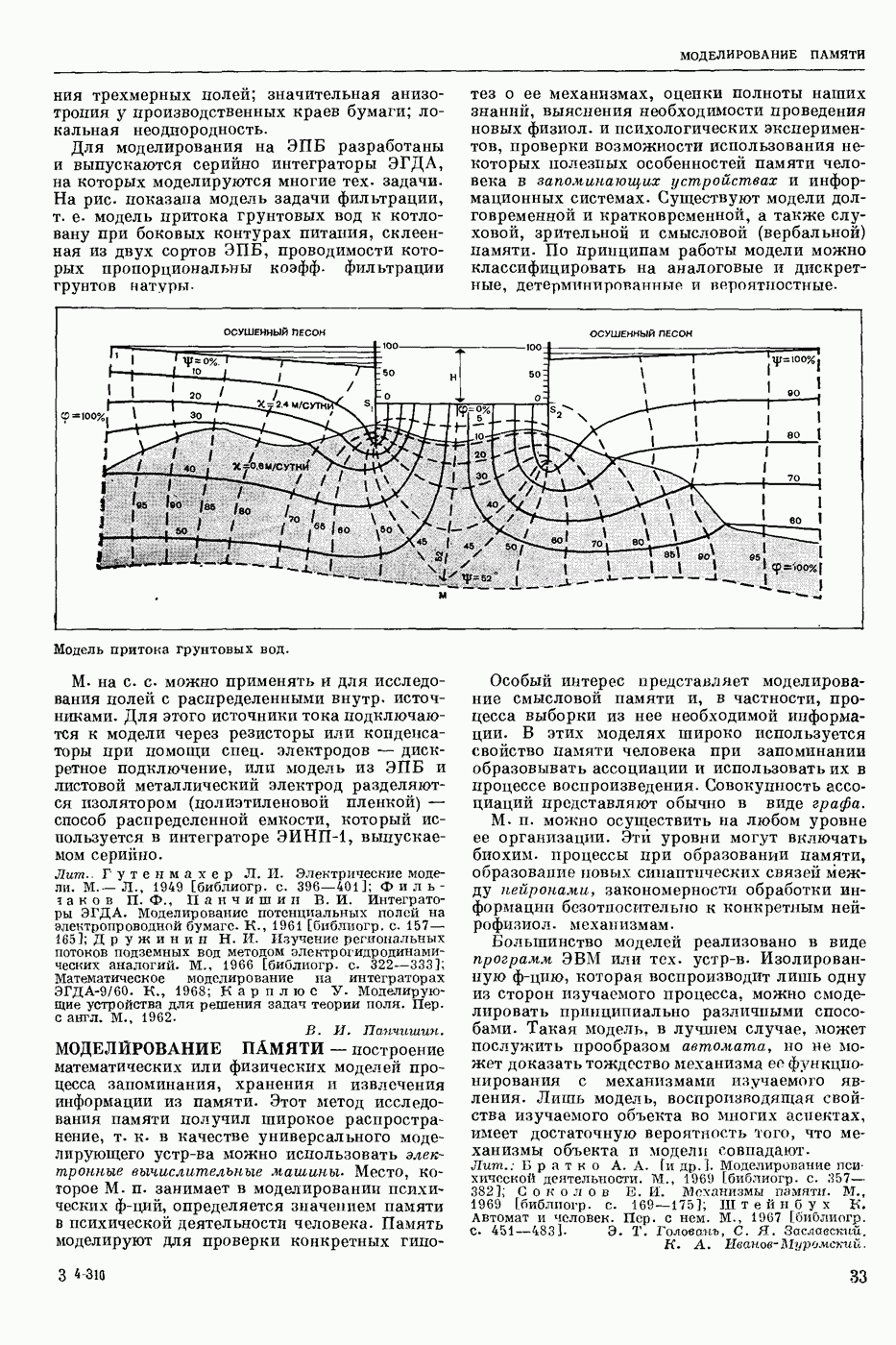
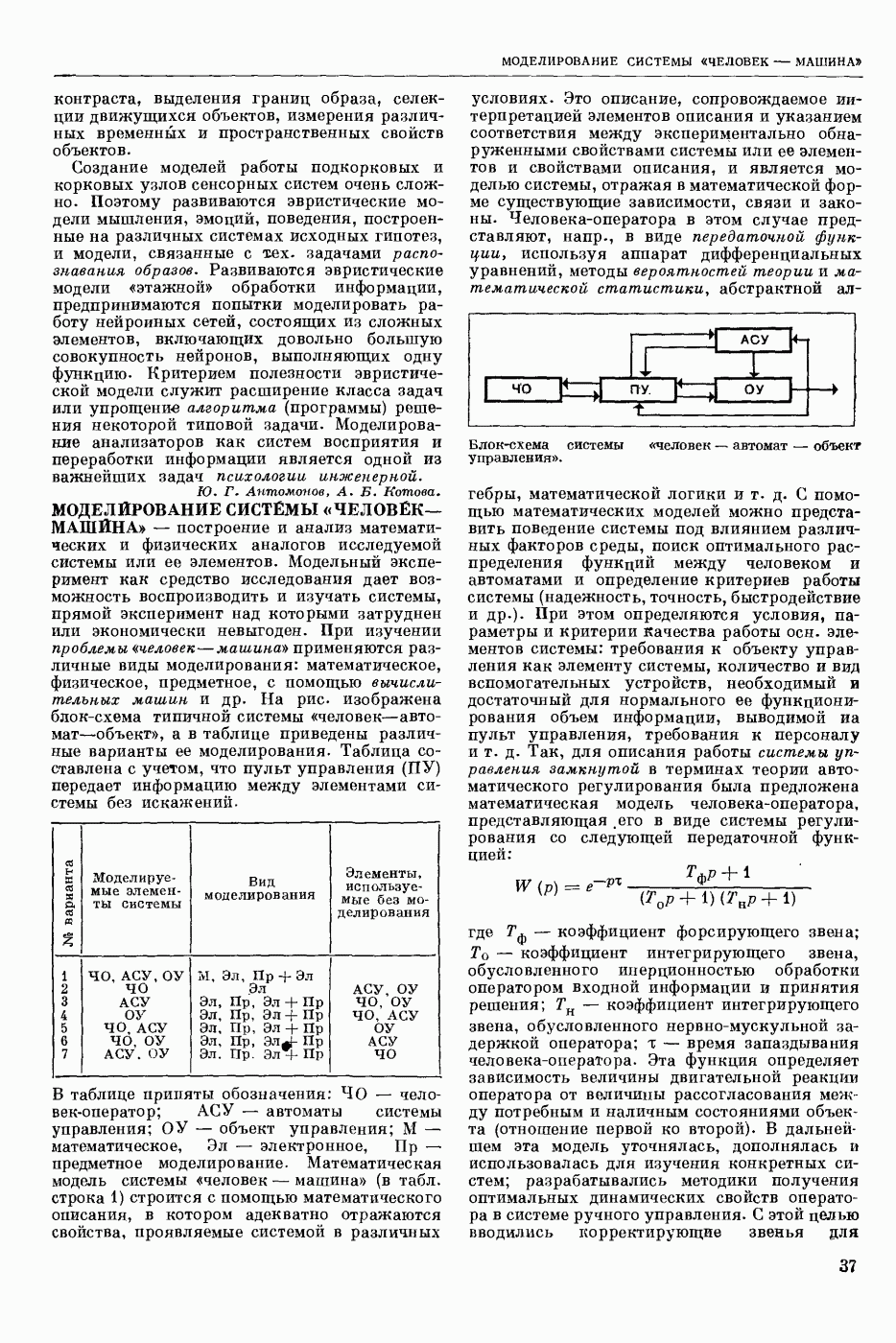
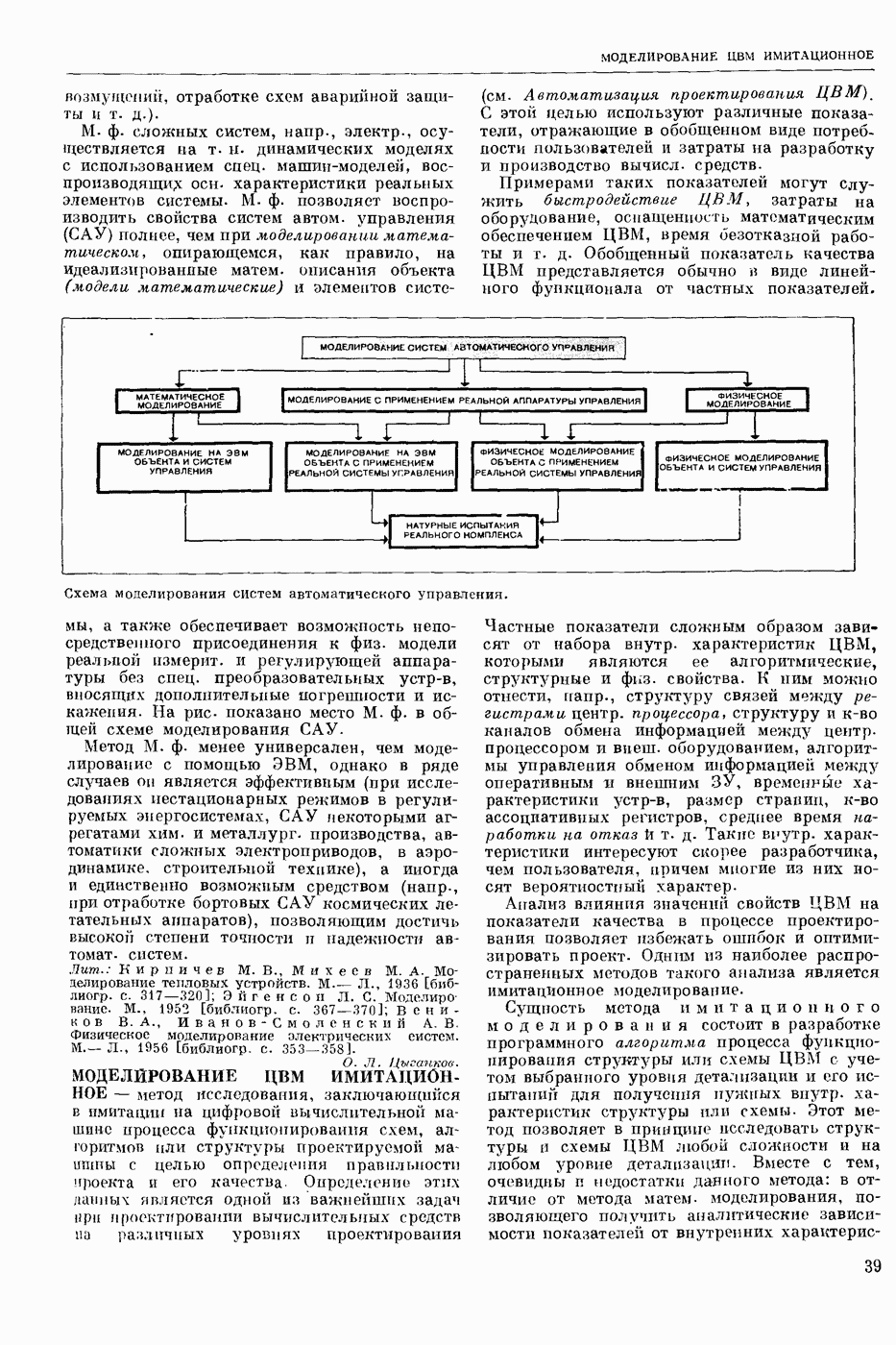
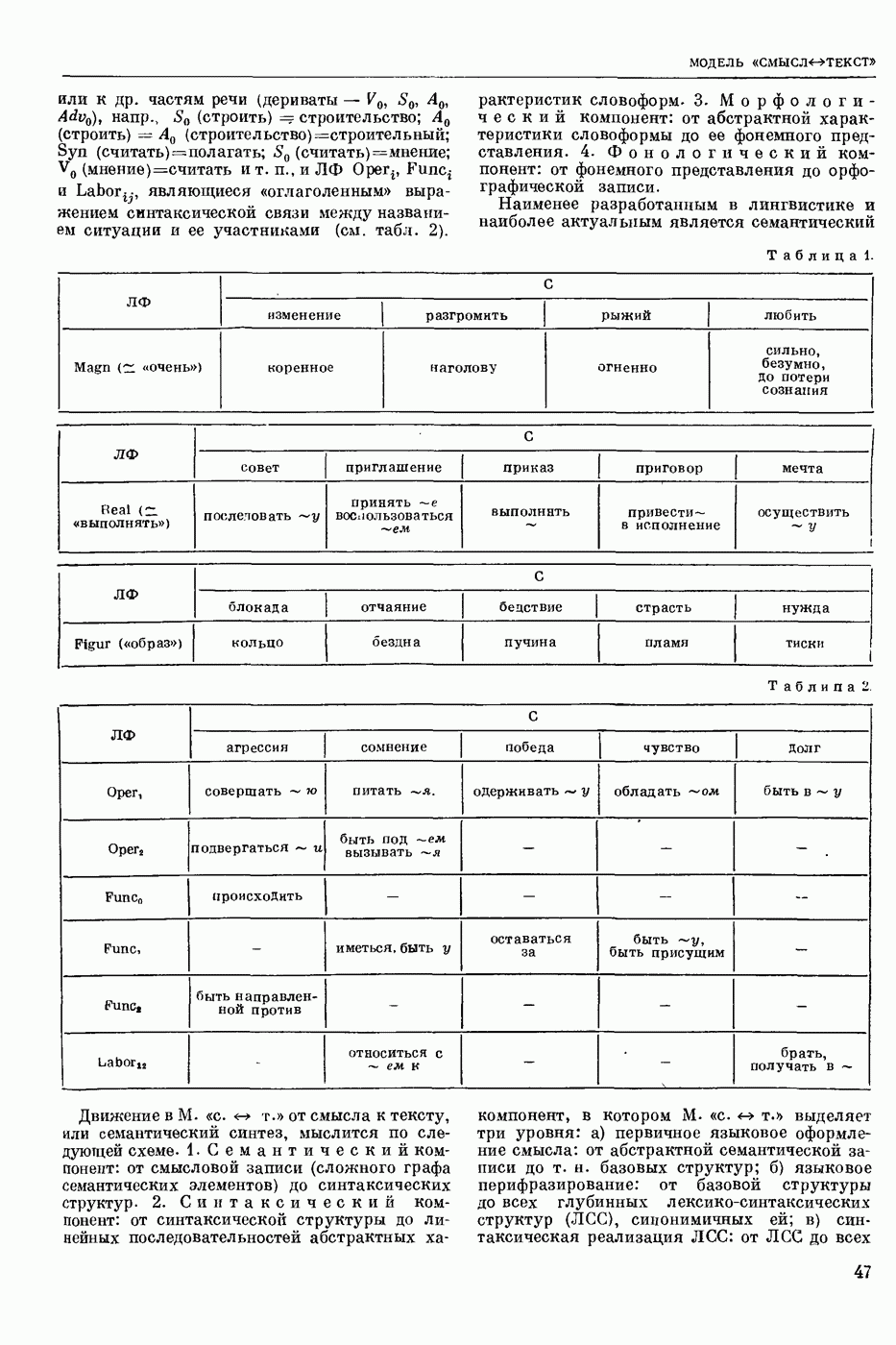
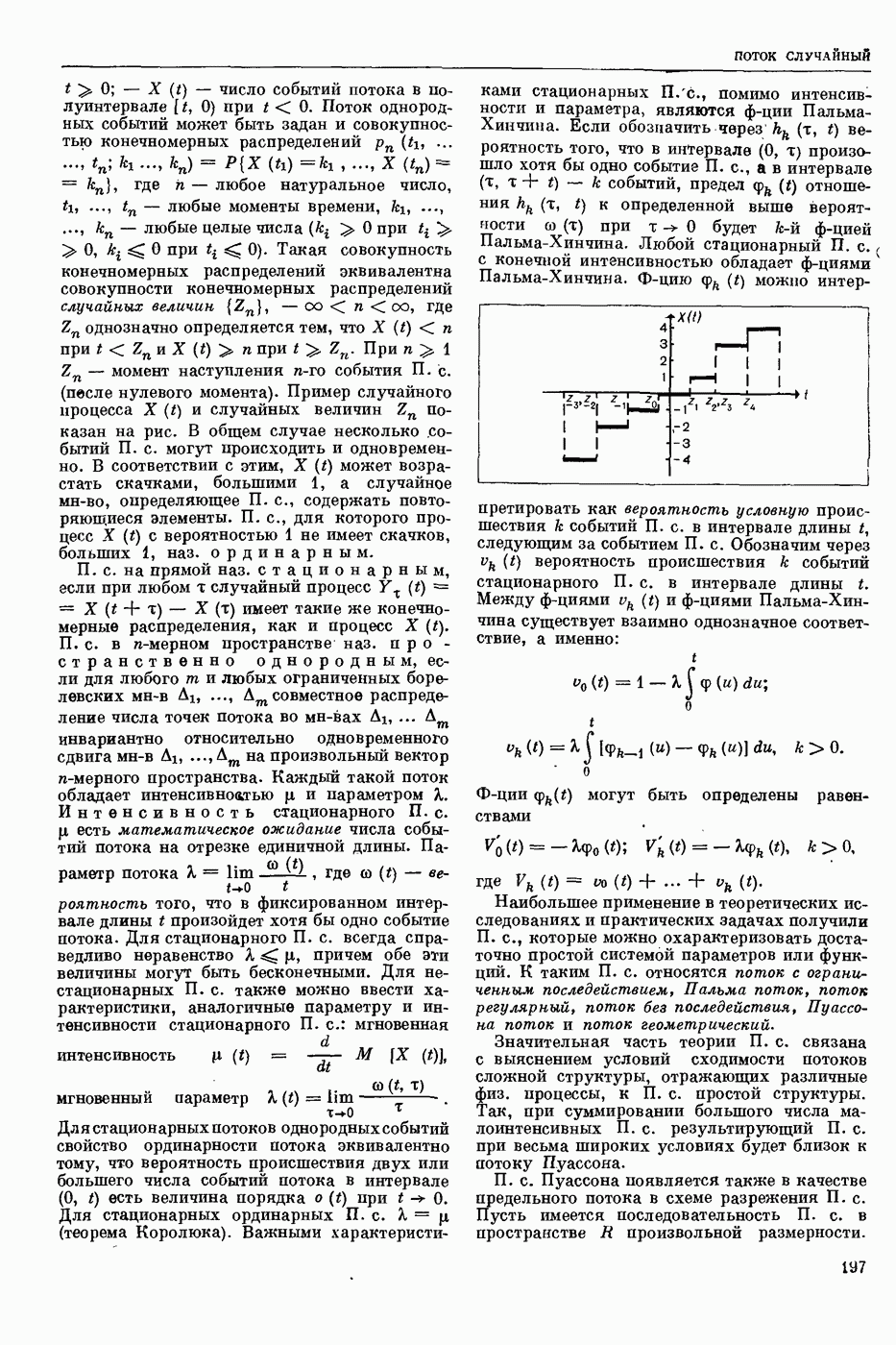
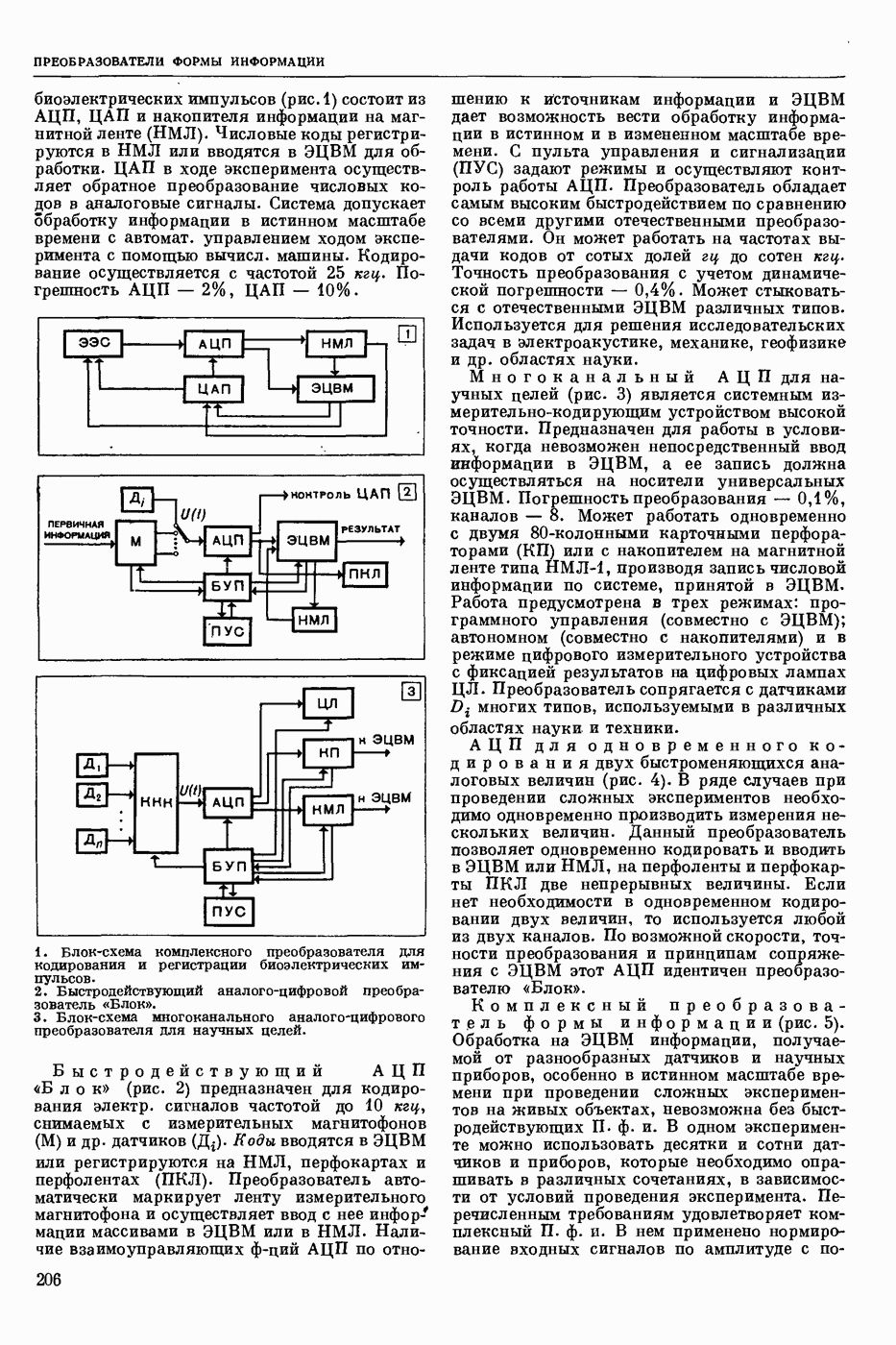
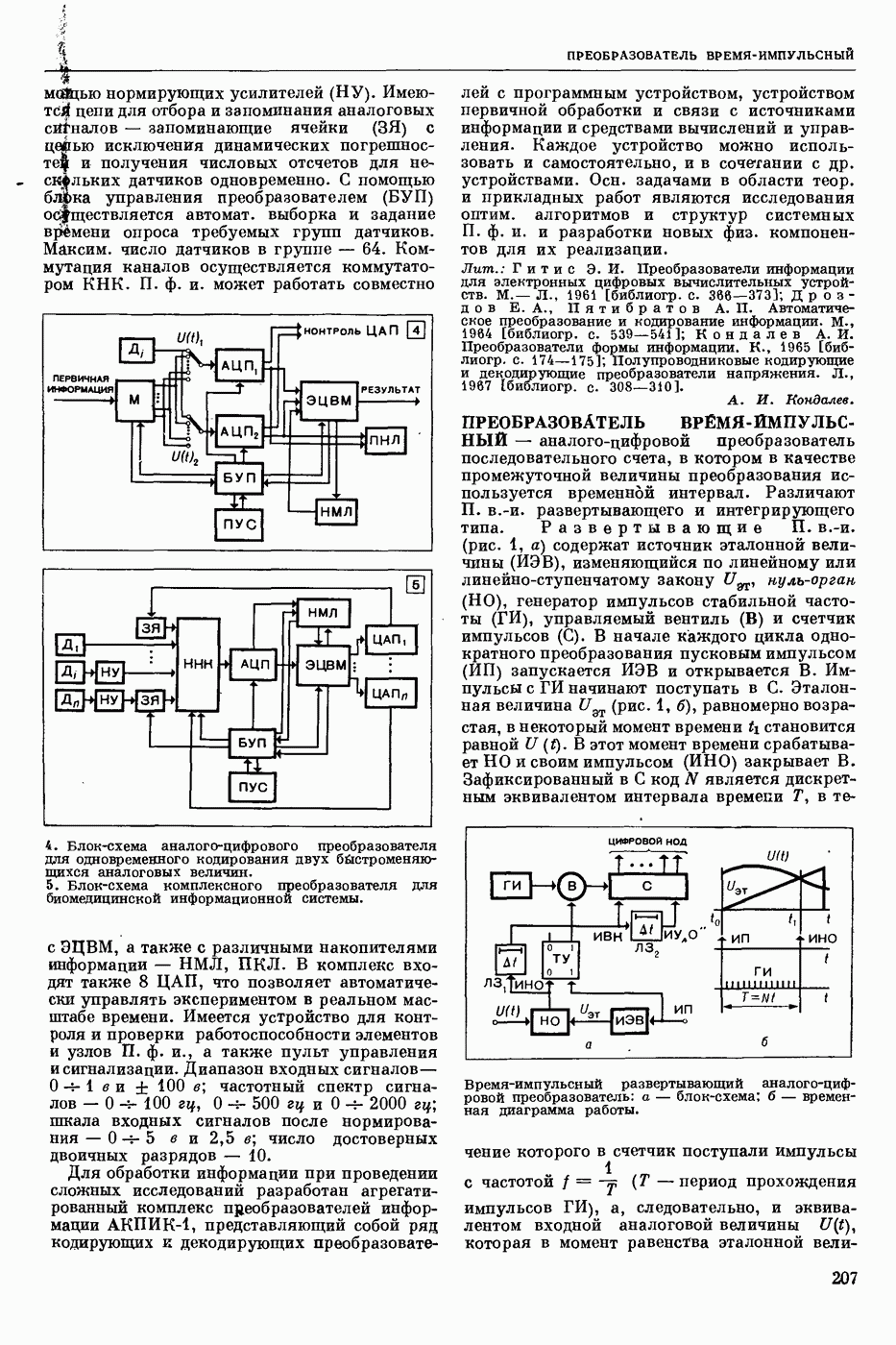
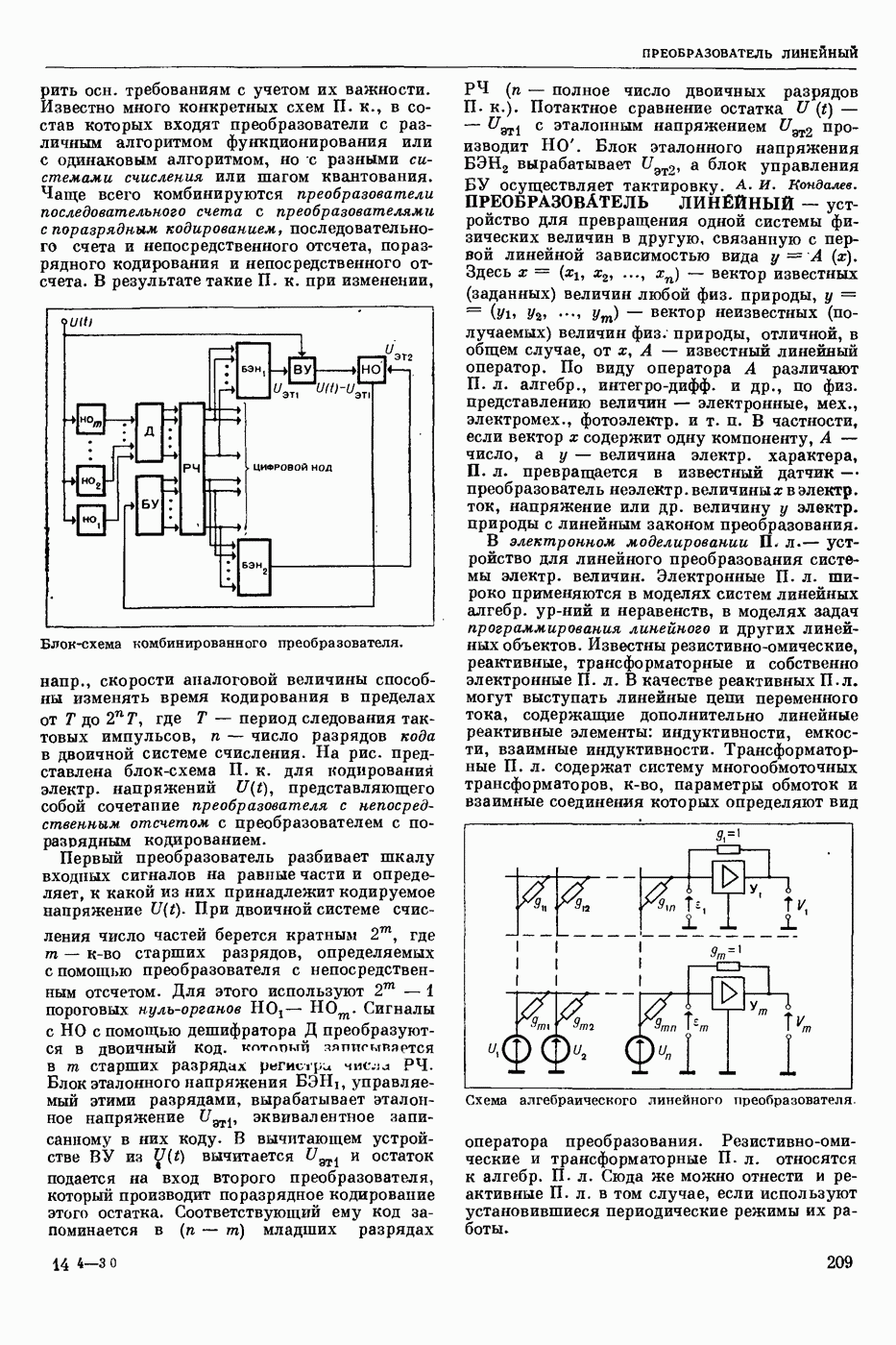
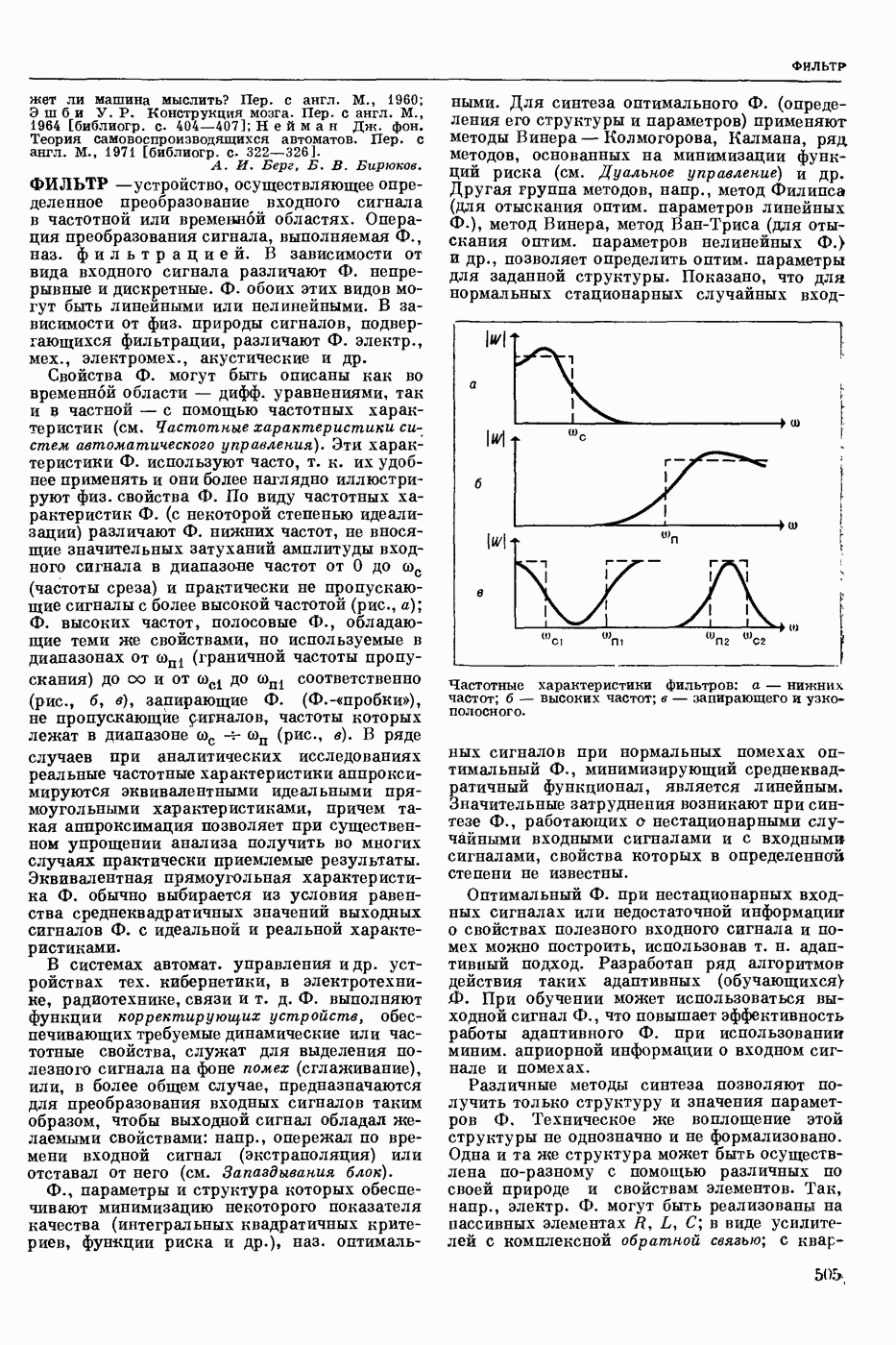
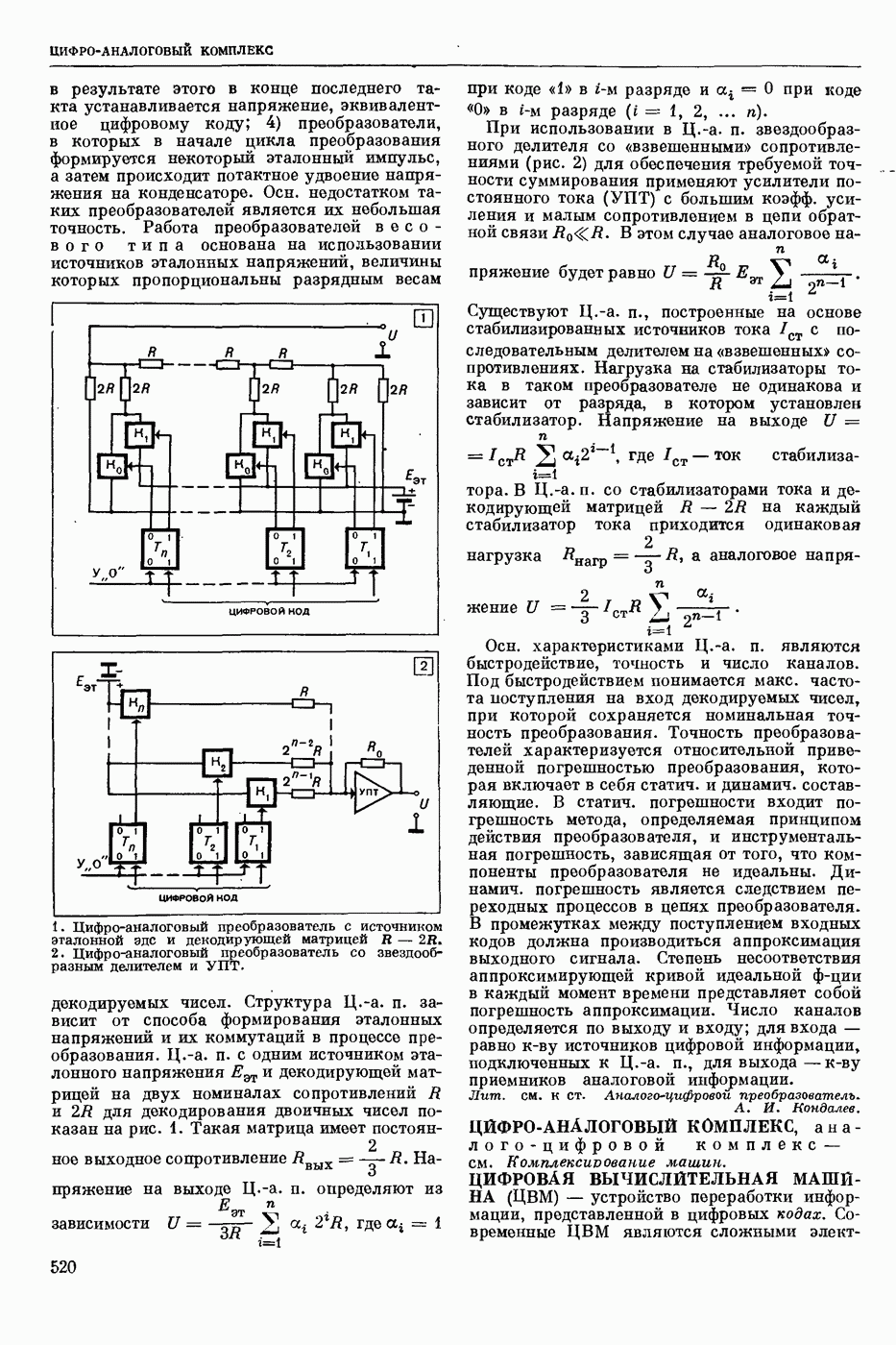
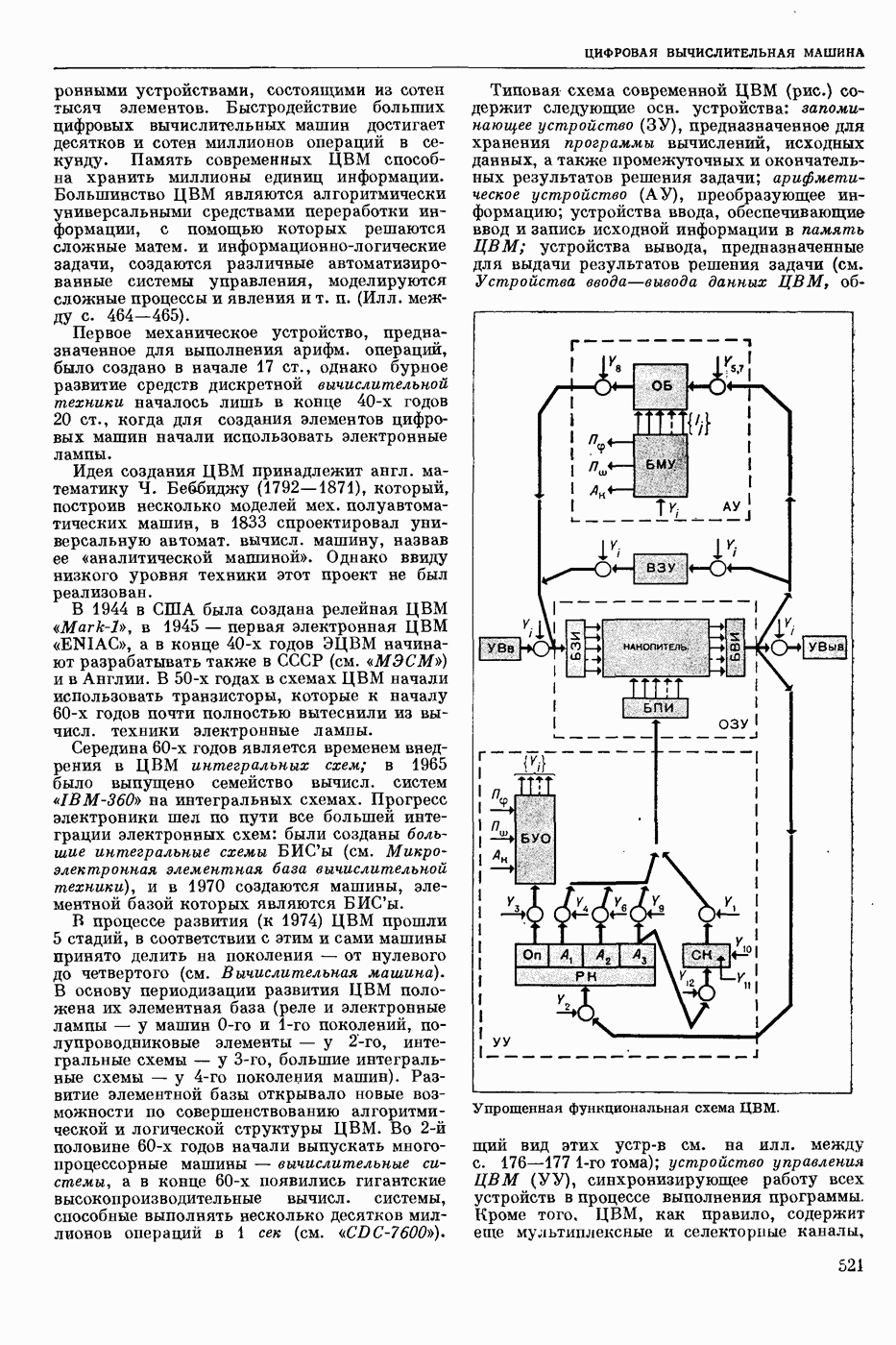
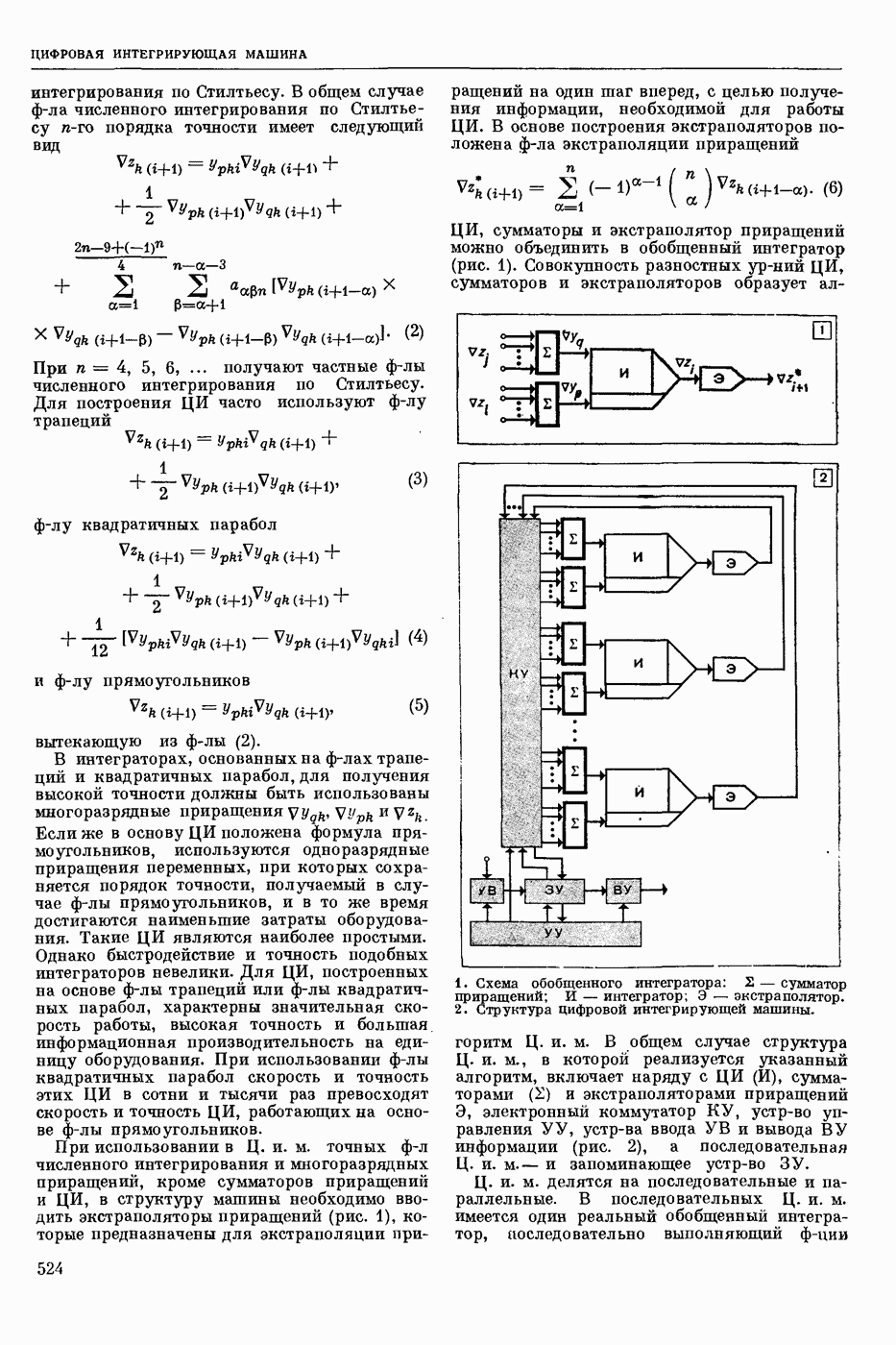
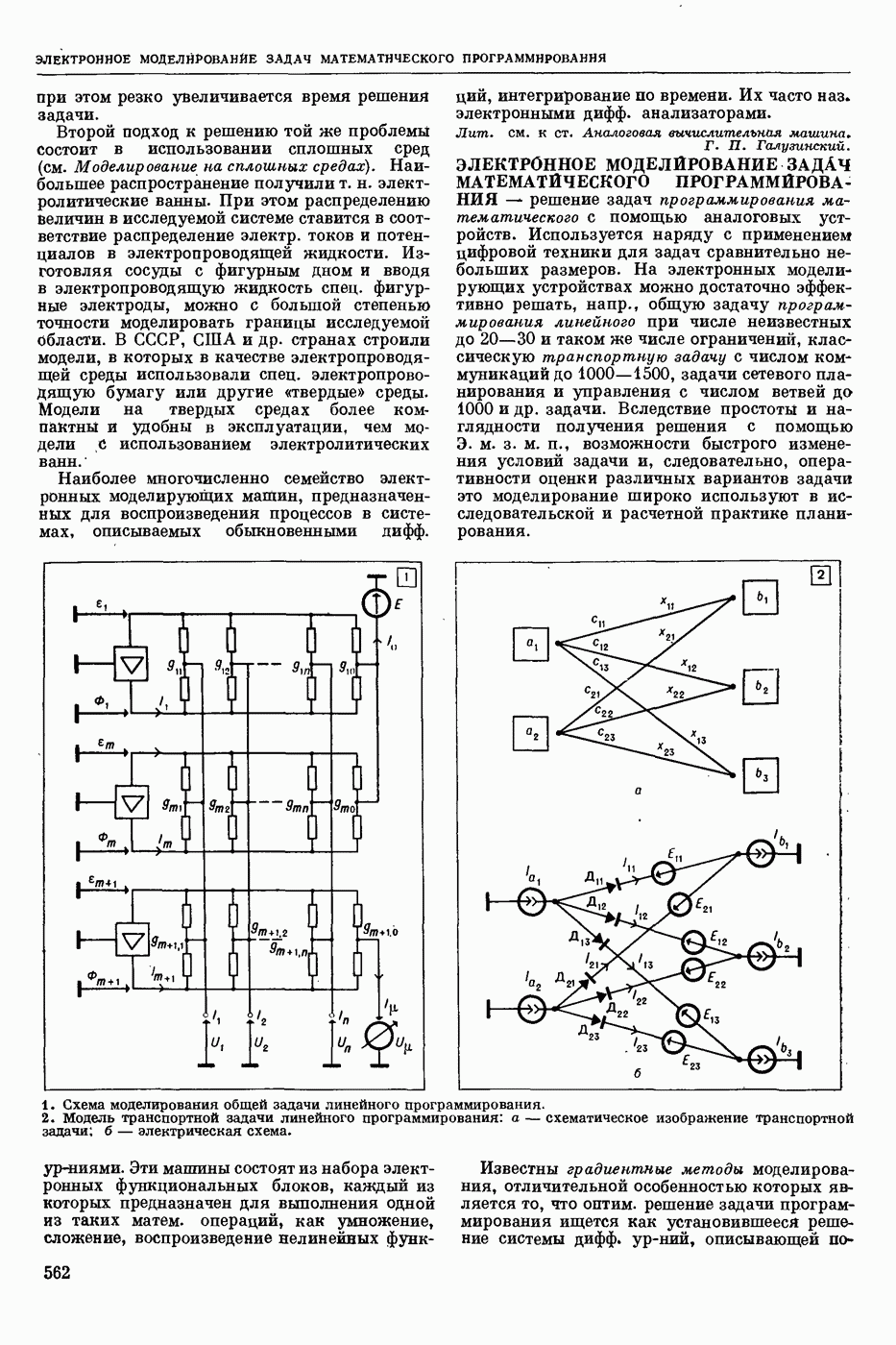
— раздел прикладной математики и автоматического управления теории (кибернетики технической), изучающий условия, при которых непрерывная система (НС) обладает устойчивостью. Устойчивость (в широком смысле) — это свойство системы возвращаться в исходный или близкий к нему установившийся режим из различных начальных состояний. Достаточно широкий и наиболее изученный класс НС, т. н. системы с сосредоточенными параметрами, можно описать в виде нормальной системы обыкновенных дифф. уравнений
где  переменные, описывающие состояние
переменные, описывающие состояние  , t — время, или в векторно-матричной форме
, t — время, или в векторно-матричной форме

где  n-мерные векторы-столбцы. Пусть
n-мерные векторы-столбцы. Пусть  некоторое наперед заданное частное решение ур-ния (2) (невозмущенное движение), устойчивость которого требуется исследовать. Разность
некоторое наперед заданное частное решение ур-ния (2) (невозмущенное движение), устойчивость которого требуется исследовать. Разность  есть отклонение решения
есть отклонение решения  от
от  Переменные
Переменные  удовлетворяют ураинениям возмущенного движения
удовлетворяют ураинениям возмущенного движения

где  или в векторно-матричной форме
или в векторно-матричной форме

где  векторы-столбцы, причем
векторы-столбцы, причем  Предположим, что ф-ции
Предположим, что ф-ции  удовлетворяют условиям существования и единственности решения системы (3).
удовлетворяют условиям существования и единственности решения системы (3).
Определение 1. Невозмущенное движение системы  устойчивым по Ляпунову при
устойчивым по Ляпунову при  короче, устойчивым), если для любых
короче, устойчивым), если для любых  существует
существует  такое, что для всех возмущенных движений, удовлетворяющих условию
такое, что для всех возмущенных движений, удовлетворяющих условию  справедливо неравенство
справедливо неравенство  при всех
при всех  . В противном случае оно называется неустойчивым. Под нормой вектора х здесь и далее понимаем евклидову норму
. В противном случае оно называется неустойчивым. Под нормой вектора х здесь и далее понимаем евклидову норму 
Определение 2. Невозмущенное движение  асимптотически устойчивым при
асимптотически устойчивым при  если оно устойчиво по Ляпунову и для любого
если оно устойчиво по Ляпунову и для любого  существует
существует  такое, что для всех возмущенных движений, удовлетворяющих условию
такое, что для всех возмущенных движений, удовлетворяющих условию  существует предел
существует предел  Сфера
Сфера  при фиксированном
при фиксированном  является областью притяжения невозмущенного движения. Если областью притяжения является все пространство
является областью притяжения невозмущенного движения. Если областью притяжения является все пространство  то невозмущенное движение наз. асимптотически устойчивым в целом. Кроме этих осн. определений устойчивости существует много других (устойчивость по Лагранжу, орбитальная устойчивость,
то невозмущенное движение наз. асимптотически устойчивым в целом. Кроме этих осн. определений устойчивости существует много других (устойчивость по Лагранжу, орбитальная устойчивость,  -устойчивость, устойчивость инвариантного множества и др.). Понятие устойчивости относится к движению, а не к системе, но для краткости говорят об устойчивых и неустойчивых системах, подразумевая под устойчивостью НС устойчивость их невозмущенного движения.
-устойчивость, устойчивость инвариантного множества и др.). Понятие устойчивости относится к движению, а не к системе, но для краткости говорят об устойчивых и неустойчивых системах, подразумевая под устойчивостью НС устойчивость их невозмущенного движения.
Важный класс НС составляют линейные НС (ЛНС), для которых уравнение (4) имеет вид

где  -
-  -матрица, элементы которой в общем случае являются функциями времени. Для случая, когда
-матрица, элементы которой в общем случае являются функциями времени. Для случая, когда  постоянная матрица, верна следующая теорема.
постоянная матрица, верна следующая теорема.
Теорема 1. ЛHC (5) с постоянной матрицей А устойчива тогда и только тогда, когда все характеристические числа (собственные значения)  матрицы А обладают неположительными вещественными частями
матрицы А обладают неположительными вещественными частями

причем характеристические числа с нулевой вещественной частью допускают лишь простые элементарные делители. Если  то линейная система асимптотически устойчива.
то линейная система асимптотически устойчива.
Характеристические числа матрицы А являются корнями ее характеристического (векового) уравнения

где I — единичная матрица.
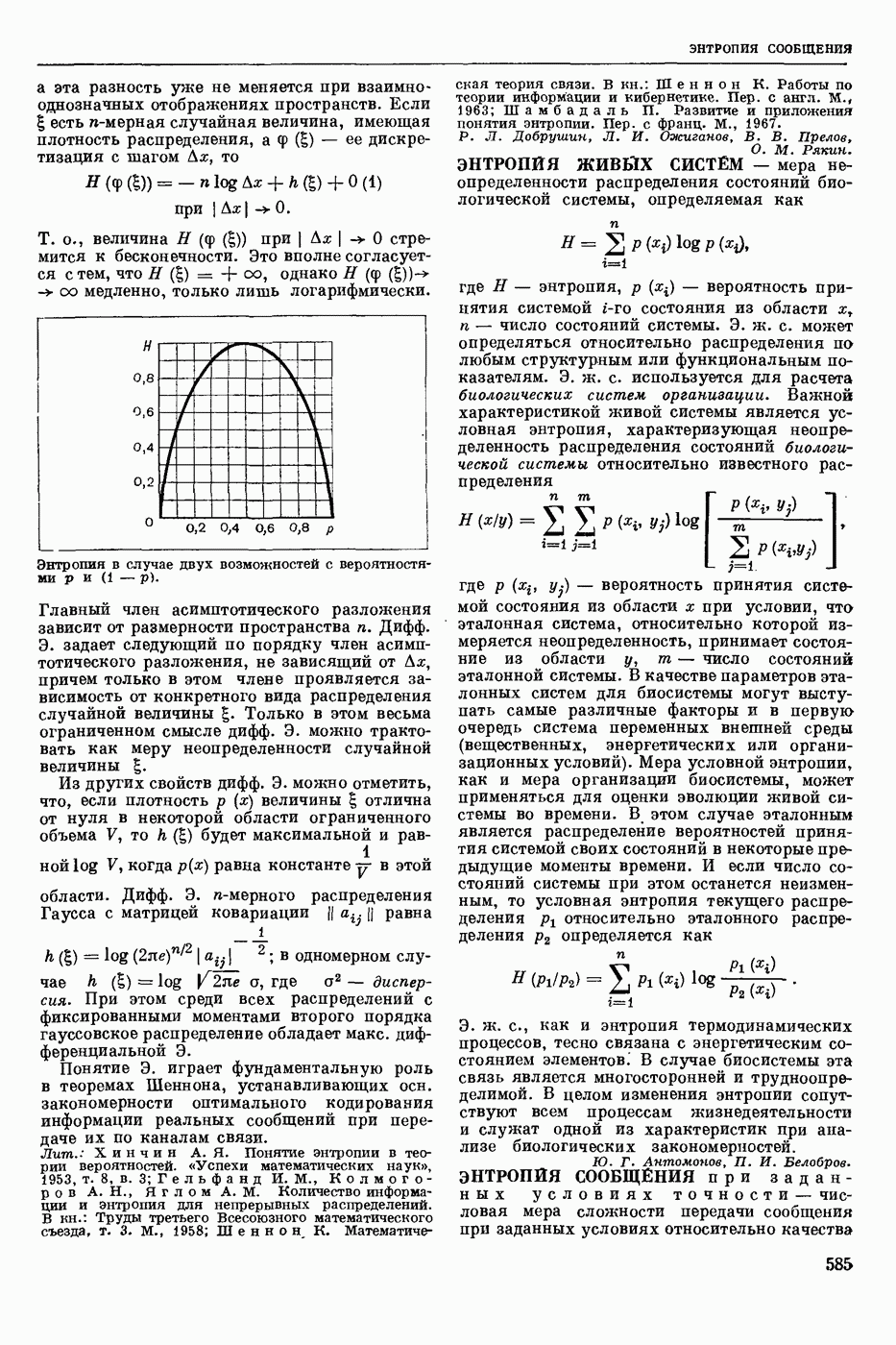
Поскольку уравнения высоких степеней не имеют общих выражений для корней, то важное значение приобретают правила, по которым можно судить о знаках действительных частей корней уравнения (7), не решая его. Эти правила являются устойчивости критериями для системы (5) с постоянной матрицей. Критериями такого типа являются, напр., критерии Рауса, Гурвица, Михайлова, Найквиста.
Среди  с переменными параметрами более всего изучены системы с периодической матрицей
с переменными параметрами более всего изучены системы с периодической матрицей

К этому классу относятся, напр., системы управления на переменном токе.
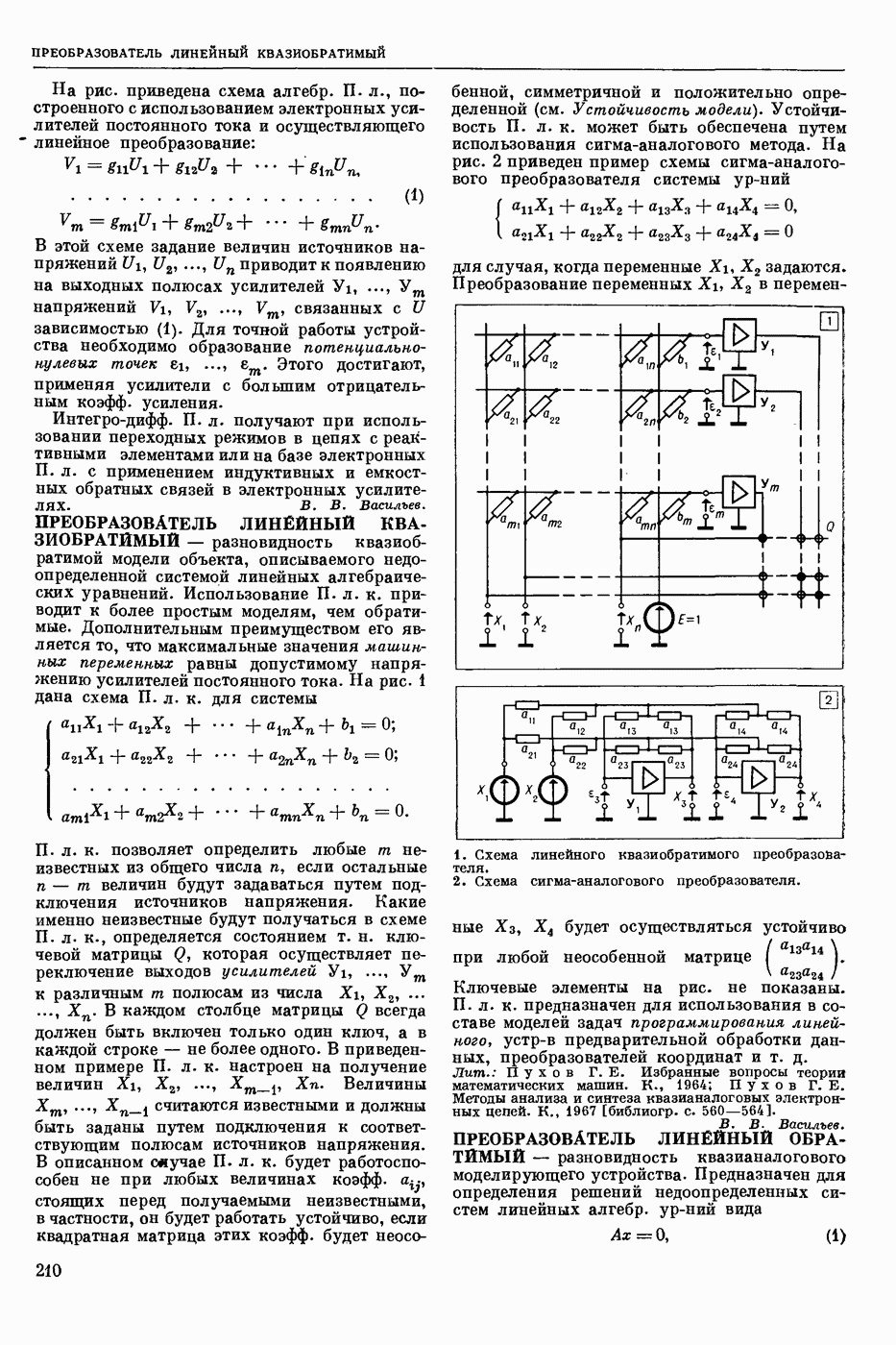
Теорема 2 (Флоке). Для ЛHC (5) с сопериодической матрицей, нормированная при  фундаментальная матрица решений (матрицам) имеет вид
фундаментальная матрица решений (матрицам) имеет вид

где  кусочно-гладкая сопериодическая неособенная матрица, причем
кусочно-гладкая сопериодическая неособенная матрица, причем  — постоянная матрица.
— постоянная матрица.
Матрицу  матрицей монодромии. Собственные значения
матрицей монодромии. Собственные значения  матрицы монодромии, т. е. корни характеристического уравнения
матрицы монодромии, т. е. корни характеристического уравнения

называются мультипликаторами.
Теорема 3. ЛHC (5) с  -периодической непрерывной матрицей устойчива тогда и только тогда, когда все характеристические числа матрицы монодромии (мультипликаторы)
-периодической непрерывной матрицей устойчива тогда и только тогда, когда все характеристические числа матрицы монодромии (мультипликаторы)  -расположены внутри замкнутого единичного круга
-расположены внутри замкнутого единичного круга  причем мультипликаторы, лежащие на окружности
причем мультипликаторы, лежащие на окружности  допускают лишь простые элементарные делители.
допускают лишь простые элементарные делители.
Для асимптотической устойчивости системы необходимо и достаточно, чтобы все мультипликаторы находились строго внутри единичного круга 
Поскольку в общем случае не существует метода определения мультипликаторов, изложим один из приближенных способов их вычисления. С помощью точек  разобъем интервал
разобъем интервал  на
на  равных частей, и пусть
равных частей, и пусть

В дифф. уравнении 

заменим сопериодическую матрицу  кусочно-постоянной матрицей
кусочно-постоянной матрицей

где  . Обозначим символом
. Обозначим символом  непрерывную матрицу, удовлетворяющую в точках непрерывности матрицы (11) дифф. уравнению
непрерывную матрицу, удовлетворяющую в точках непрерывности матрицы (11) дифф. уравнению 

Тогда 

и

Так как корни  характеристического уравнения
характеристического уравнения

являются непрерывными функциями параметра h, то в силу соотношения (14) имеем

Таким образом, выбрав h достаточно малым, из уравнения (15) можно определить мультипликаторы  с любой степенью точности.
с любой степенью точности.
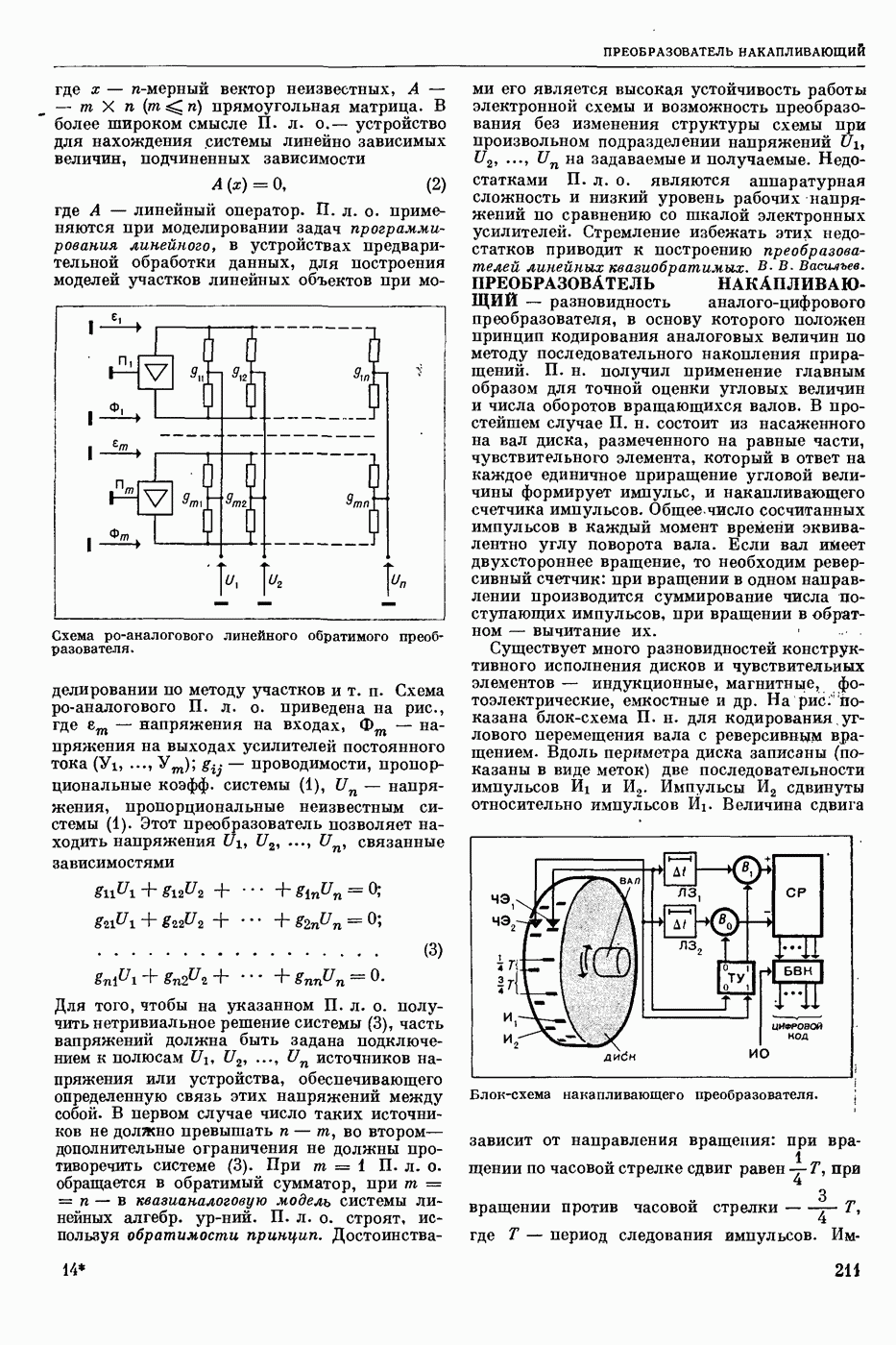
Нелинейные НС (ННС) вида (4) исследованы значительно меньше, чем ЛHC. Для исследования устойчивости системы (4) рус. математик А. М. Ляпунов (1857— 1918) выяснил условия, при которых задача об устойчивости решается по первому приближению. Для этого правые части уравнений (3) раскладывают в ряд по степеням  и уравнение (4) записывают в виде
и уравнение (4) записывают в виде 

где  непрерывная вектор-функция от высших степеней х.
непрерывная вектор-функция от высших степеней х.
Пусть для случая  — постоянная матрица) выполняется условие
— постоянная матрица) выполняется условие

равномерно по 
Теорема 3. Если система первого приближения  асимптотически устоичива, то тривиальное решение
асимптотически устоичива, то тривиальное решение  системы (17) асимптотически устойчиво по Ляпунову при
системы (17) асимптотически устойчиво по Ляпунову при  . Если же хотя бы одно собственное значение матрицы А обладает положительной вещественной частью, то оно неустойчиво по Ляпунову при
. Если же хотя бы одно собственное значение матрицы А обладает положительной вещественной частью, то оно неустойчиво по Ляпунову при  . Аналогичные теоремы доказаны и для общего случая
. Аналогичные теоремы доказаны и для общего случая 
В критических случаях (когда вещественная часть хотя бы одного собственного значения матрицы А равна нулю) уравнения первого приближения не всегда дают ответ на вопрос об устойчивости полной системы. Одним из существенных результатов в области исследования критических случаев является теорема Андронова—Витта. Пусть автономная система

допускает сопериодические решения  . Тогда система первого приближения имеет вид
. Тогда система первого приближения имеет вид

где  .
.
Теорема 4 (Андронова — Витта). Пусть система первого приближения (20) имеет один простой мультипликатор, равный 1, а остальные ее мультипликаторы находятся строго внутри единичного круга  . Тогда
. Тогда  -периодическое решение
-периодическое решение  системы (19) устойчиво по Ляпунову при
системы (19) устойчиво по Ляпунову при 
Метод исследования устойчивости ННС по первому приближению гарантирует лишь асимптотическую устойчивость в малом (т. е. для достаточно малых начальных отклонений) и не охватывает полностью критических случаев, а также не применим к системам, для которых не выполнено условие (18).
Осн. универсальным методом решения задач теории устойчивости ННС, позволяющим получать условия асимптотической устойчивости в некоторой области и даже в целом, является прямой метод Ляпунова, который сводится к построению спец. вспомогательных функций (см. Ляпунова методы). Основу этого метода составляют теоремы, которые наиболее просто формулируются для автономных систем.
Теорема 5 (1-я теорема Ляпунова). Если для дифф. уравнений (4) существует такая функция  обращающаяся в нуль лишь в начале координат, что ее полная производная по времени
обращающаяся в нуль лишь в начале координат, что ее полная производная по времени  полученная в силу уравнений (4), неположительна или тождественно равна нулю, то невозмущенное движение
полученная в силу уравнений (4), неположительна или тождественно равна нулю, то невозмущенное движение  системы (2) устойчиво.
системы (2) устойчиво.
Теорема 6 (2-я теорема Ляпунова). Если выполнены условия теоремы 5 и функции  обращаются в нуль только в начале координат, то невозмущенное движение
обращаются в нуль только в начале координат, то невозмущенное движение  системы (2) устойчиво асимптотически.
системы (2) устойчиво асимптотически.
Теор  теорема Ляпунова). Если для дифф. уравнений (4) существует такая функция
теорема Ляпунова). Если для дифф. уравнений (4) существует такая функция  что ее полная производная по времени
что ее полная производная по времени  составленная в силу уравнений (4), удовлетворяет условиям теоремы 6-й и в сколь угодно малой окрестности начала координат функция
составленная в силу уравнений (4), удовлетворяет условиям теоремы 6-й и в сколь угодно малой окрестности начала координат функция  может принимать отрицательные значения, то невозмущенное движение
может принимать отрицательные значения, то невозмущенное движение  системы (2) неустойчиво.
системы (2) неустойчиво.
Практическое применение этих теорем затруднено тем, что общего метода построения функций  Ляпунова) не существует.
Ляпунова) не существует.
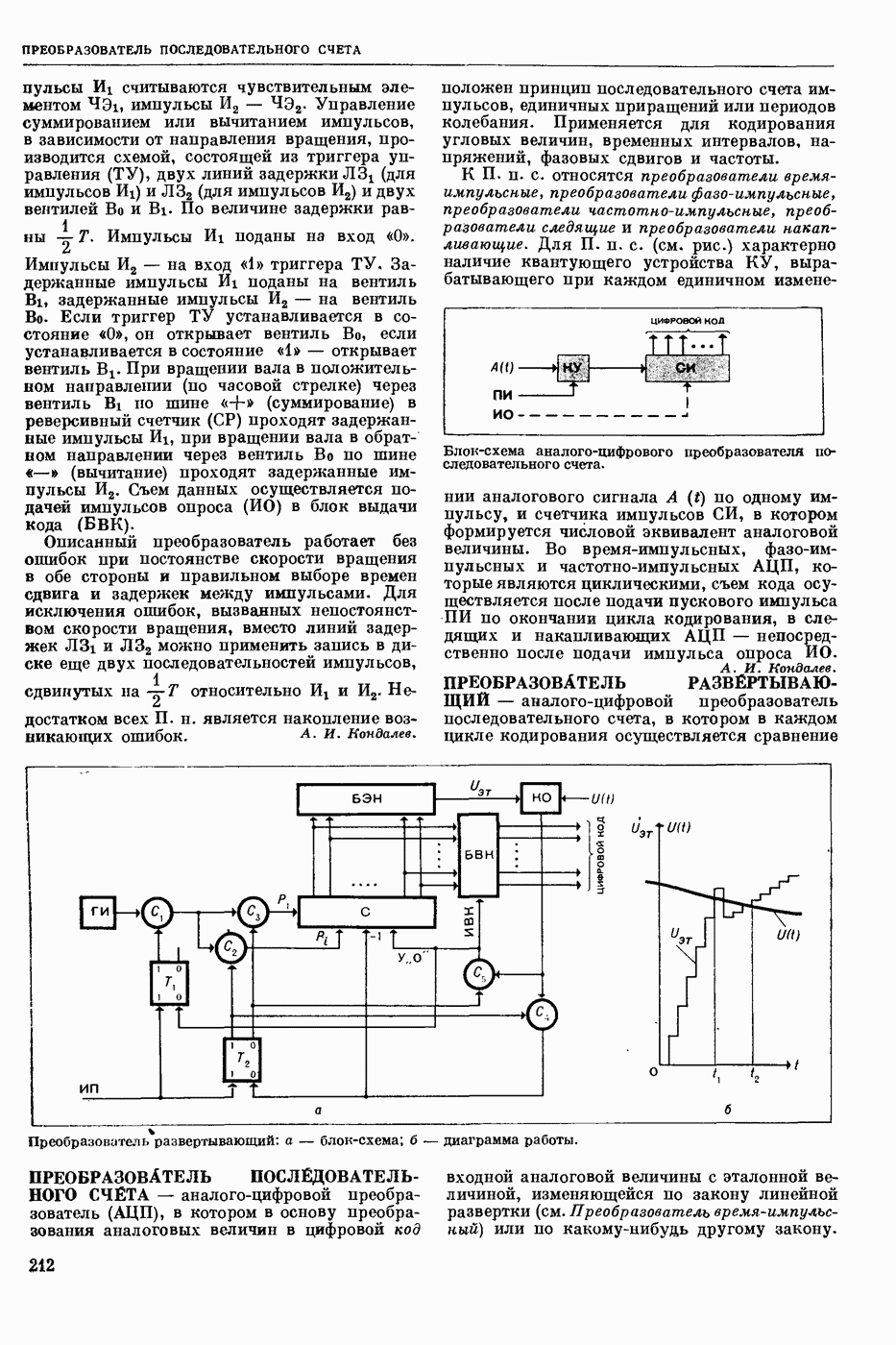
Наиболее исследованным является класс ННС, описываемый векторно-матричным уравнением вида 

где А — постоянная ( -матрица, b и с —
-матрица, b и с —  -мерные постоянные векторы (знак означает эрмитово сопряжение),
-мерные постоянные векторы (знак означает эрмитово сопряжение),  нелинейная ф-ция
нелинейная ф-ция  .
.
Осн. результаты для абсолютной устойчивости таких систем получены с помощью т. н. частотных методов.
Определение 3. Абсолютная устойчивость системы (21) — это асимптотическая устойчивость в целом для некоторого класса нелинейностей 
Классы функций  задаются квадратичными неравенствами вида
задаются квадратичными неравенствами вида

где  — некоторые числа. Напр., наиболее распространенный (и наиболее изученный) класс
— некоторые числа. Напр., наиболее распространенный (и наиболее изученный) класс  задается так:
задается так:

или

При исследовании абсолютной устойчивости применяют два подхода: прямой метод Ляпунова в сочетании с методом матричных неравенств Якубовича—Калмана и метод интегр. оценок Попова. При первом подходе используется ф-ция Ляпунова вида

где  постоянная (
постоянная ( -матрица и
-матрица и  некоторая постоянная, которые выбираются из условия
некоторая постоянная, которые выбираются из условия  для заданного класса нелинейностей
для заданного класса нелинейностей  ). При решении задачи выбора матрицы
). При решении задачи выбора матрицы  и параметра Ф применяется спец. прием (
и параметра Ф применяется спец. прием ( -процедура), состоящий в том, что условие
-процедура), состоящий в том, что условие  заменяется условием
заменяется условием  что в данном случае
что в данном случае  -процедура не приводит к «ухудшению» результата). Проблема выбора
-процедура не приводит к «ухудшению» результата). Проблема выбора  сводится к нахождению условий существования решения
сводится к нахождению условий существования решения
некоторых матричных неравенств. Эти условия следуют из спец. алгебр, леммы Якубовича — Калмана и имеют вид частотных неравенств, которые накладывают ограничения на параметры системы.
При втором подходе уравнение системы записывается в интегр. форме

где  реакция линейной части системы на ненулевые начальные условия, и
реакция линейной части системы на ненулевые начальные условия, и  составляющая решения
составляющая решения  обусловленная наличием обратной связи (нелинейного регулятора), к
обусловленная наличием обратной связи (нелинейного регулятора), к  импульсная переходная характеристика линейной части системы. Предполагается, что она удовлетворяет условиям
импульсная переходная характеристика линейной части системы. Предполагается, что она удовлетворяет условиям

При  выражения (21) и (24) совпадают. Однако уравнение (24) является более общим, т. к. оно охватывает случай линейной части системы с распределенными параметрами. Метод интегр. оценок Попова (назван по имени рум. матем. В. М. Попова, который впервые применил его для решения задачи об абсолютной устойчивости) основан на совместном изучении уравнения (24) и положительных функционалов следующего вида:
выражения (21) и (24) совпадают. Однако уравнение (24) является более общим, т. к. оно охватывает случай линейной части системы с распределенными параметрами. Метод интегр. оценок Попова (назван по имени рум. матем. В. М. Попова, который впервые применил его для решения задачи об абсолютной устойчивости) основан на совместном изучении уравнения (24) и положительных функционалов следующего вида: 

где  квадратичная форма, при составлении которой исходят из квадратичных связей, которым удовлетворяют входы и выходы нелинейностей. Так, для класса нелинейностей, заданного условием (23), рассматривается форма
квадратичная форма, при составлении которой исходят из квадратичных связей, которым удовлетворяют входы и выходы нелинейностей. Так, для класса нелинейностей, заданного условием (23), рассматривается форма  где
где  — некоторая положительная постоянная.
— некоторая положительная постоянная.
Аргументами формы  являются вещественные величины
являются вещественные величины  . Считая
. Считая  независимыми переменными, распространим (с сохранением эрмитовости) форму
независимыми переменными, распространим (с сохранением эрмитовости) форму  на комплексные значения
на комплексные значения  . Положим
. Положим

где  . Здесь
. Здесь  комплексная величина,
комплексная величина,  — чисто мнимый параметр и
— чисто мнимый параметр и  передаточная функция линейной части системы
передаточная функция линейной части системы  обозначает операцию преобразования по Лапласу).
обозначает операцию преобразования по Лапласу).
Теорема 8. Предположим, что выполнемо условие (25). Тогда, если а) Характерно, что для одних и тех же классов нелинейностей оба подхода в большинстве случаев дают одни и те же условия абсолютной устойчивости. Хотя второй подход охватывает более широкий класс систем, вида (24), первый подход не утратил своего значения. Его аппарат позднее был применен к исследованию асимптотической устойчивости в области (определение области притяжения), к получению условий диссипативности и изучению других свойств системы (21).
Центральным результатом, полученным при использовании частотных методов, является следующая теорема.
Теорема 9 (частотный критерий Попова). Система (21) или (24) абсолютно устойчива, если а) где Эти подходы были обобщены на случай систем со многими нелинейностями
где А, В, С — постоянные соответственно Теорема 10. Система (23) абсолютно устойчива, если а) б) линейная часть системы асимптотически устойчива; в) при всех  где
где  некоторая постоянная, зависящая от начальных условий
некоторая постоянная, зависящая от начальных условий  и такая, что
и такая, что  при
при  форма
форма  является неотрицательной формой
является неотрицательной формой  ; в) форма
; в) форма  то система (24) абсолютно устойчива. Условие (в) накладывает ограничения на частотную характеристику линейной части системы
то система (24) абсолютно устойчива. Условие (в) накладывает ограничения на частотную характеристику линейной части системы  в виде частотного неравенства, при выполнении которого гарантируется абсолютная устойчивость системы для заданного класса нелинейностей.
в виде частотного неравенства, при выполнении которого гарантируется абсолютная устойчивость системы для заданного класса нелинейностей.
 однозначная непрерывная функция, принадлежащая классу нелинейностей, выделяемому условием (23); б) линейная часть системы асимптотически устойчива; в) при всех 0 со
однозначная непрерывная функция, принадлежащая классу нелинейностей, выделяемому условием (23); б) линейная часть системы асимптотически устойчива; в) при всех 0 со  выполнено неравенство
выполнено неравенство

 передаточная функция линейной части системы
передаточная функция линейной части системы  для системы
для системы  произвольная постоянная, выбираемая из условия выполнения (28).
произвольная постоянная, выбираемая из условия выполнения (28).

 матрицы,
матрицы,  —
—  -мерный вектор нелинейностей.
-мерный вектор нелинейностей.
 однозначные непрерывные ф-ции, удовлетворяющие условиям
однозначные непрерывные ф-ции, удовлетворяющие условиям

 выполнено неравенство
выполнено неравенство

где  диагональная матрица,
диагональная матрица,  — диагональные матрицы, выбираемые из условия выполнения неравенства
— диагональные матрицы, выбираемые из условия выполнения неравенства  передаточная матрица линейной части системы, под
передаточная матрица линейной части системы, под  подразумевается
подразумевается  U Как и в предыдущей теореме, утверждения теоремы 7 справедливы и для случая линейной части системы с распределенными параметрами. В дальнейшем были получены условия абсолютной устойчивости для систем (в т. ч.- в некоторых критических случаях) с нестационарными, неоднозначными (гистерезисными) и разрывными нелинейностями, а также для систем, обладающих множеством равновесных состояний. Получены критерии устойчивости, учитывающие более тонкие свойства нелинейностей, как, напр., ограниченность производной, монотонность, нечетность и т. д. Для этого были рассмотрены функции Ляпунова вида
U Как и в предыдущей теореме, утверждения теоремы 7 справедливы и для случая линейной части системы с распределенными параметрами. В дальнейшем были получены условия абсолютной устойчивости для систем (в т. ч.- в некоторых критических случаях) с нестационарными, неоднозначными (гистерезисными) и разрывными нелинейностями, а также для систем, обладающих множеством равновесных состояний. Получены критерии устойчивости, учитывающие более тонкие свойства нелинейностей, как, напр., ограниченность производной, монотонность, нечетность и т. д. Для этого были рассмотрены функции Ляпунова вида

где  или функционалы
или функционалы

где  квадратичная форма
квадратичная форма  .
.
Достаточно общий формализованный метод получения частотных критериев абсолютной устойчивости предложил сов. математик В. А. Якубович.
Лит.: Гантмахер Ф. Р., Якубович В. А. Абсолютная устойчивость нелинейных регулируемых систем. В кн.: Труды II Всесоюзного съезда по теоретической и прикладной механике, в. 1. М., 1965; Малкин И. Г. Теория устойчивости движения. М., 1966; Якубович В. А. Частотные условия абсолютной устойчивости систем управления с несколькими нелинейными или линейными нестационарными блоками. «Автоматика и телемеханика», 1967, т. 28, № 6; Демидович Б. П. Лекции по математической теории устойчивости. М., 1967 [библиогр. с. 466—469]; Чезари Л. Асимптотическое поведение и устойчивость решений обыкновенных дифференциальных уравнений. Пер. с англ. М., 1964 [библиогр. с. 324—465]; Попов В. М. Гиперустойчивость автоматических систем. Пер. с рум. М., 1970 [библиогр. с. 435.-453]. М. М. Лычак, О. С. Яковлев.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- МИХАЙЛОВА КРИТЕРИЙ
- МНОГОВАРИАНТНЫХ ЗАДАЧ РЕШЕНИЕ
- МНОГОГРАННОЕ МНОЖЕСТВО
- МНОГОГРАННЫЙ КОНУС
- МНОГОЗНАЧНЫЕ СХЕМЫ
- МНОГОКОНТУРНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОКРИТЕРИАЛЬНОСТИ ПРОБЛЕМА
- МНОГОМЕРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ РАЗДЕЛИТЕЛЬНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ УНИВЕРСАЛЬНЫЙ
- МНОГОПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ, мультипрограммная обработка информации
- МНОГОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- МНОГОШАГОВОГО ПРОЦЕССА ПРОИЗВОДСТВА МОДЕЛЬ
- МНОГОШАГОВОГО ПРОЦЕССА РАСПРЕДЕЛЕНИЯ МОДЕЛЬ
- МНОГОШАГОВЫЕ ЗАДАЧИ
- МНОГОЭТАПНОЕ ОБСЛУЖИВАНИЕ
- МНОЖЕСТВ ТЕОРИЯ
- МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- МОДЕЛИ ОБЪЕКТОВ РАСПОЗНАВАНИЯ
- МОДЕЛИ ПРОИЗВОДСТВА
- МОДЕЛИ РАВНОВЕСИЯ
- МОДЕЛИ РОСТА
- МОДЕЛИ ЭКОНОМИКИ
- МОДЕЛИРОВАНИЕ ВЕСТИБУЛЯРНОГО АНАЛИЗАТОРА
- МОДЕЛИРОВАНИЕ ВОСПРИЯТИЯ
- МОДЕЛИРОВАНИЕ ЖИВЫХ СИСТЕМ на молекулярном уровне
- МОДЕЛИРОВАНИЕ ИНЖЕНЕРНЫХ СЕТЕЙ НА АВМ
- МОДЕЛИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ МЫШЛЕНИЯ
- МОДЕЛИРОВАНИЕ НА СПЛОШНЫХ СРЕДАХ, электрическое моделирование
- МОДЕЛИРОВАНИЕ ПАМЯТИ
- МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАСПОЗНАВАНИЯ И ОБУЧЕНИЯ РАСПОЗНАВАНИЮ НА ЦВМ
- МОДЕЛИРОВАНИЕ ПСИХИЧЕСКИХ ФУНКЦИЙ
- МОДЕЛИРОВАНИЕ СЕНСОРНЫХ СИСТЕМ
- МОДЕЛИРОВАНИЕ СИСТЕМЫ «ЧЕЛОВЕК—МАШИНА»
- МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ ЦВМ ИМИТАЦИОННОЕ
- МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ НА ЦВМ
- МОДЕЛЬ ЗРИТЕЛЬНОГО АНАЛИЗАТОРА
- МОДЕЛЬ МАТЕМАТИЧЕСКАЯ
- МОДЕЛЬ НЕРВНОЙ КЛЕТКИ
- МОДЕЛЬ ПЕРЕМЕННОЙ СТРУКТУРЫ
- МОДЕЛЬ СЛУХОВОГО АНАЛИЗАТОРА
- МОДЕЛЬ «СМЫСЛ-ТЕКСТ»
- МОДЕЛЬ ФИЗИЧЕСКАЯ
- МОДЕЛЬ ЧУВСТВИТЕЛЬНОСТИ
- МОДУЛЯТОР
- МОДУЛЯЦИЯ ИМПУЛЬСНАЯ
- «МОЗГОВОЙ ШТУРМ»
- МОМЕНТОВ МЕТОД
- МОНИТОР
- МОНОТОННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- МОНТЕ-КАРЛО МЕТОД
- «МППИ-1», машина первичной переработки информации
- МУЛЬТИВИБРАТОР
- МУЛЬТИПРОГРАММИРОВАНИЕ
- МУЛЬТИПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- МУЛЬТИПРОЦЕССОРНЫЙ РЕЖИМ
- МУЛЬТИУСТОЙЧИВЫЕ СИСТЕМЫ
- МУРА АВТОМАТ
- МЫСЛИТЕЛЬНОЙ СПОСОБНОСТИ УСИЛИТЕЛЬ
- НАБЛЮДАЕМОСТИ И УПРАВЛЯЕМОСТИ УСЛОВИЯ
- НАБОРНОЕ ПОЛЕ
- НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НАДЁЖНОСТЬ КИБЕРНЕТИЧЕСКИХ СИСТЕМ
- НАДЁЖНОСТЬ РАСПОЗНАВАНИЯ
- НАИМЕНЬШИХ КВАДРАТОВ МЕТОД
- «НАИРИ»
- НАИСКОРЕЙШЕГО СПУСКА МЕТОД
- НАЙКВИСТА КРИТЕРИЙ
- НАКАПЛИВАЮЩИЕ СХЕМЫ
- НАКОПИТЕЛЬ, блок хранения информации
- НАКОПИТЕЛЬ НА МАГНИТНОЙ ЛЕНТЕ
- НАРАБОТКА НА ОТКАЗ
- НАРАБОТКА НА СБОЙ
- НАУКА УПРАВЛЕНИЯ
- НАУКОВЕДЕНИЕ
- НАУЧНАЯ ОРГАНИЗАЦИЯ ТРУДА (НОТ)
- НАУЧНО-ИНФОРМАЦИОННАЯ ДЕЯТЕЛЬНОСТЬ
- НАУЧНО-ТЕХНИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ
- НАУЧНО-ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ ОБРАБОТКА
- НАУЧНЫЙ СОВЕТ ПО КОМПЛЕКСНОЙ ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН СССР
- НАУЧНЫЙ СОВЕТ ПО ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН УССР
- НЕЗАВИСИМОСТЬ в теории вероятностей, статистическая независимость
- НЕЙРОБИОНИКА
- НЕЙРОКИБЕРНЕТИКА
- НЕЙРОН
- НЕЙРОН ФОРМАЛЬНЫЙ
- НЕЙРОННЫЕ СЕТИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫЕ ЗАДАЧИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- НЕЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ АВМ
- НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- НЕ НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НЕОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- НЕОДНОРОДНЫЙ ПОТОК В СЕТИ
- НЕОПРЕДЕЛЕННОСТЬ В УПРАВЛЕНИИ
- НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМЫ АКСИОМ, совместимость, корректность
- НЕРАЗРЕШИМЫЕ АЛГОРИТМИЧЕСКИЕ ПРОБЛЕМЫ
- «НИППОН ЭЛЕКТРИК КОМПАНИ» (Nippon Electric Company, Ltd)
- «ННБ», набор нелинейных блоков
- НОРМА ВЕКТОРА
- НОРМА МАТРИЦЫ
- НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- НОРМАЛЬНАЯ ФОРМА СОВЕРШЕННАЯ
- НОРМАЛЬНАЯ ФОРМА СОКРАЩЕННАЯ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- НОРМАЛЬНЫЕ АЛГОРИФМЫ, нормальные алгоритмы
- НОСИТЕЛЬ ИНФОРМАЦИИ
- НУЛЕВЫХ СОБСТВЕННЫХ ПРОВОДИМОСТЕЙ УЗЛОВ МЕТОД
- НУЛЬ-ОРГАН, сравнивающее устройство, компаратор
- НУМЕРАЦИЙ ТЕОРИЯ
- НЬЮТОНА ОБОБЩЕННЫЙ МЕТОД
- НЬЮТОНА ФОРМУЛЫ ИНТЕРПОЛИРОВАНИЯ
- ОБЛАСТЬ УПРАВЛЕНИЯ
- ОБЛЕГЧЁННОЕ РЕЗЕРВИРОВАНИЕ
- ОБОБЩЁННЫЕ ФУНКЦИИ
- ОБОБЩЕННЫХ ГРАДИЕНТОВ МЕТОД
- ОБРАБОТКА ДАННЫХ ПОСЛЕДОВАТЕЛЬНАЯ
- ОБРАБОТКА ДАННЫХ ПРОИЗВОЛЬНАЯ
- ОБРАБОТКА ИНФОРМАЦИИ В РЕАЛЬНОМ масштабе времени
- ОБРАБОТКА ИНФОРМАЦИИ В РЕЖИМЕ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- ОБРАБОТКИ ДАННЫХ СИСТЕМА
- ОБРАЗ, или распознаваемый класс, в кибернетике
- ОБРАТИМОСТИ ПРИНЦИП
- ОБРАТИМЫЕ ЭЛЕМЕНТЫ И МОДЕЛИ
- ОБРАТНАЯ СВЯЗЬ
- ОБРАТНЫХ ОПЕРАТОРОВ МЕТОД
- ОБУСЛОВЛЕННОСТИ ЧИСЛО
- ОБУЧАЮЩАЯ ВЫБОРКА
- ОБУЧАЮЩАЯ МАШИНА
- ОБУЧАЮЩАЯ ПРОГРАММА
- ОБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ОГРАНИЧЕНИЕ ФАЗОВЫХ КООРДИНАТ
- ОГРАНИЧИТЕЛЬ АМПЛИТУДЫ
- ОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- ОДНОРОДНЫЙ ПОТОК В СЕТИ
- ОДНОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ОКРУГЛЕНИЯ ПОГРЕШНОСТЬ
- ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ОЗУ)
- ОПЕРАТИВНОЕ РУКОВОДСТВО
- ОПЕРАТИВНО-ПРОИЗВОДСТВЕННАЯ ИНФОРМАЦИЯ
- ОПЕРАТОР
- ОПЕРАТОР АВТОМАТНЫЙ
- ОПЕРАТОР ЗАДЕРЖКИ
- ОПЕРАТОР ПРИСВАИВАНИЯ
- ОПЕРАТОР ЭЛЕМЕНТАРНЫЙ
- ОПЕРАТОР ЭЛЕМЕНТНЫЙ
- ОПЕРАТОРНАЯ СХЕМА
- ОПЕРАТОРНЫЕ УРАВНЕНИЯ
- ОПЕРАТОРНЫЙ МЕТОД ПРОГРАММИРОВАНИЯ
- ОПЕРАТОРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ОПЕРАТОРЫ ЛИНЕЙНЫЕ, линейные преобразования
- ОПЕРАЦИИ МАШИННЫЕ
- ОПЕРАЦИИ НАД МАССИВАМИ
- ОПЕРАЦИИ НАД СИМВОЛАМИ И СТРОКАМИ
- ОПЕРАЦИИ НАД ЧИСЛАМИ
- ОПЕРАЦИИ ИССЛЕДОВАНИЕ
- ОПЕРАЦИЙ СИСТЕМА
- ОПЕРАЦИОННАЯ СИСТЕМА
- ОПЕРАЦИЯ НАИМЕНЬШЕГО КОРНЯ
- ОПЕРАЦИЯ ПРИМИТИВНОЙ РЕКУРСИИ
- ОПИСАНИЕ ОБЪЕКТА РАСПОЗНАВАНИЯ
- ОПОРНОЕ НАПРЯЖЕНИЕ
- ОПОРНЫЙ ПЛАН
- ОПТИМАЛЬНАЯ ТОЧКА
- ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ТЕОРИЯ
- ОПТИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
- ОПТИМАЛЬНОСТИ НЕОБХОДИМЫЕ УСЛОВИЯ
- ОПТИМАЛЬНОСТИ ПРИНЦИП
- ОПТИМАЛЬНЫЙ ВЕКТОР
- ОПТИМАЛЬНЫХ ПАРАМЕТРОВ СИСТЕМЫ ВЫБОР
- ОПТИМАЛЬНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ОПТИМИЗАТОР АВТОМАТИЧЕСКИЙ
- ОПТИМИЗАЦИИ МЕТОДЫ численные
- «ОПТИМУМ»
- ОПТРОН
- ОРГАНИЗАЦИЯ ИНФОРМАЦИОННОГО МАССИВА
- ОРГАНИЗАЦИЯ УЧЕТА В АВТОМАТИЗИРОВАННЫХ СИСТЕМАХ УПРАВЛЕНИЯ
- ОРГАТЕХНИКА, организационная техника
- ОРДЕНА ЛЕНИНА ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- УПРАВЛЕНИЯ (АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ), ИАТ
- ОСТАНОВ
- ОСУЩЕСТВИМОСТИ ФИЗИЧЕСКОЙ КРИТЕРИИ
- ОСУЩЕСТВИМОСТИ ЦЕЛИ ПРИНЦИП
- ОТВЕТ РАСПОЗНАЮЩЕЙ СИСТЕМЫ
- ОТКАЗ ОТ РАСПОЗНАВАНИЯ
- ОТЛАДОЧНЫЕ ПРОГРАММЫ
- ОТНОШЕНИЕ
- ОТНОШЕНИЕ АНАЛИТИЧЕСКОЕ
- ОТНОШЕНИЕ БАЗИСНОЕ
- ОТНОШЕНИЕ ПАРАДИГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ ПРАВДОПОДОБИЯ
- ОТНОШЕНИЕ СИГНАЛ/ПОМЕХА
- ОТНОШЕНИЕ СИНТАГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ СИНТЕТИЧЕСКОЕ
- ОТНОШЕНИЕ ТЕКСТУАЛЬНОЕ
- ОТРИЦАНИЕ в алгебре логики
- ОЧЕРЕДЕЙ ТЕОРИЯ
- ОШИБКА В ПРИНЯТИИ ГИПОТЕЗ
- ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ОШИБОК ТЕОРИЯ
- ПАКЕТНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- ПАЛЬМА ПОТОК
- ПАМЯТИ ЗАЩИТА
- ПАМЯТИ РАСПРЕДЕЛЕНИЕ
- ПАМЯТЬ МАГАЗИННАЯ
- ПАМЯТЬ СТРАНИЧНАЯ
- ПАМЯТЬ ЦВМ
- ПАРАБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ
- ПАРАМЕТР ФАКТИЧЕСКИЙ
- ПАРАМЕТР ФОРМАЛЬНЫЙ
- ПАРАМЕТРОН
- ПАРЕТО ОПТИМУМ
- ПАЧКА ОШИБОК, пакет ошибок
- ПЕРЕВОД АВТОМАТИЧЕСКИЙ
- ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
- ПЕРЕДАЧИ ИНФОРМАЦИИ СКОРОСТЬ
- ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ПЕРЕРАБОТКА ИНФОРМАЦИИ В ЦВМ
- ПЕРЕХОДНЫЙ ПРОЦЕСС
- ПЕРИОД ЗАНЯТОСТИ в системах массового обслуживания
- ПЕРИФЕРИЙНОЕ ОБОРУДОВАНИЕ
- ПЕРСЕПТРОН
- «ПЕРТ»
- ПЕРФОРАТОР
- ПЕРФОРАЦИОННАЯ КАРТА, перфокарта
- ПЕРФОРАЦИОННАЯ ЛЕНТА, перфолента
- ПЕЧАТНАЯ СХЕМА
- ПИРСА СТРЕЛКА, функция Вебба, отрицание дизъюнкции
- ПЛ-1
- ПЛАВАЮЩАЯ ЗАПЯТАЯ
- ПЛАН-ГРАФИК
- ПЛАТЕЖНАЯ МАТРИЦА
- ПЛАТЕЖНАЯ ФУНКЦИЯ
- ПЛЕНКА МАГНИТНАЯ
- ПНЕВМОНИКА, струйная пневмоавтоматика
- ПОВЕДЕНИЕ АВТОМАТОВ.
- ПОВЕДЕНИЕ АВТОМАТОВ В СЛУЧАЙНЫХ СРЕДАХ.
- ПОГЛОЩЕНИЯ ЗАКОН
- ПОГРЕШНОСТЕЙ ВЫЧИСЛЕНИЙ ТЕОРИЯ
- ПОГРЕШНОСТЬ
- ПОГРЕШНОСТЬ РЕШАЮЩЕГО ЭЛЕМЕНТА
- ПОДАВТОМАТ
- ПОДОБИЯ ТЕОРИЯ
- ПОДПРОГРАММА
- ПОДПРОГРАММА ЗАМКНУТАЯ
- ПОДПРОГРАММА ОТКРЫТАЯ
- ПОДПРОГРАММА СТАНДАРТНАЯ
- ПОДСИСТЕМА
- ПОИСК ИНФОРМАЦИИ АВТОМАТИЧЕСКИЙ
- ПОИСКА ЭКСТРЕМУМА ФУНКЦИЙ МЕТОДЫ
- ПОИСКОВОЕ ПРЕДПИСАНИЕ
- ПОИСКОВЫЙ МАССИВ
- ПОИСКОВЫЙ ОБРАЗ ДОКУМЕНТА
- ПОИСКОВЫЙ ОБРАЗ ЗАПРОСА
- ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ, экспоненциальное распределение
- ПОЛНОЙ ВЕРОЯТНОСТИ ФОРМУЛА
- ПОЛНОТА ФОРМАЛЬНОЙ ТЕОРИИ
- ПОЛНОТЫ ПРОБЛЕМА в теории автоматов
- ПОЛОС МЕТОД
- ПОЛУГРУППА, ассоциативная система
- ПОЛУМАРКОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- ПОЛУСУММАТОР
- ПОЛЬСКАЯ ЗАПИСЬ
- ПОМЕХИ
- ПОМЕХОУСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ
- ПОНТРЯГИНА ПРИНЦИП МАКСИМУМА
- ПОПОВА КРИТЕРИЙ
- ПОРОГ ЧУВСТВИТЕЛЬНОСТИ
- ПОРОГОВЫЙ ЭЛЕМЕНТ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
- ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ МЕТОД
- ПОСТА ИСЧИСЛЕНИЯ
- ПОСТА КОМБИНАТОРНАЯ ПРОБЛЕМА
- ПОСТА МАШИНА
- ПОТЕНЦИАЛОВ МЕТОД
- ПОТЕНЦИАЛЬНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-НУЛЕВАЯ ТОЧКА
- ПОТЕНЦИАЛЬНО-НУЛЕВЫХ ТОЧЕК МЕТОД
- ПОТЕНЦИАЛЬНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ МЕТОД
- ПОТЕРИ ИНФОРМАЦИИ при поиске
- ПОТОК БЕЗ ПОСЛЕДЕЙСТВИЯ
- ПОТОК В СЕТИ
- ПОТОК В СЕТИ НЕОДНОРОДНЫЙ
- ПОТОК ВЫХОДЯЩИЙ
- ПОТОК ГЕОМЕТРИЧЕСКИЙ
- ПОТОК ИНФОРМАЦИОННЫЙ ЗАМКНУТЫЙ
- ПОТОК НЕСТАЦИОНАРНЫЙ
- ПОТОК ПРОСТЕЙШИЙ
- ПОТОК РЕГУЛЯРНЫЙ
- ПОТОК С ОГРАНИЧЕННЫМ ПОСЛЕДЕЙСТВИЕМ
- ПОТОК СЛУЧАЙНЫЙ
- ПРАГМАТИКА
- ПРЕДИКАТ
- ПРЕДИКАТИВНОСТЬ
- ПРЕДСКАЗАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ПРЕДСКАЗЫВАЮЩИЙ ФИЛЬТР
- ПРЕДСТАВЛЕНИЙ ГРУПП ТЕОРИЯ
- ПРЕОБРАЗОВАНИЕ ПЕРИОДИЧЕСКИ-ОПРЕДЕЛЕННОЕ
- ПРЕОБРАЗОВАТЕЛИ ВОЛОКОННЫЕ
- ПРЕОБРАЗОВАТЕЛИ ДВУХ И БОЛЕЕ ПЕРЕМЕННЫХ
- ПРЕОБРАЗОВАТЕЛИ КОД-АНАЛОГ
- ПРЕОБРАЗОВАТЕЛИ С ПОРАЗРЯДНЫМ КОДИРОВАНИЕМ
- ПРЕОБРАЗОВАТЕЛИ ФОРМЫ ИНФОРМАЦИИ
- ПРЕОБРАЗОВАТЕЛЬ ВРЕМЯ-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ИНТЕГРИРУЮЩЕГО ТИПА
- ПРЕОБРАЗОВАТЕЛЬ КОМБИНИРОВАННЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ КВАЗИОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ ОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ НАКАПЛИВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ПРЕОБРАЗОВАТЕЛЬ РАЗВЕРТЫВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ С НЕПОСРЕДСТВЕННЫМ ОТСЧЕТОМ
- ПРЕОБРАЗОВАТЕЛЬ СЛЕДЯЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ФАЗО-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ФУНКЦИОНАЛЬНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЦИКЛИЧЕСКИЙ
- ПРЕОБРАЗОВАТЕЛЬ ЧАСТОТНО-ИМПУЛЬСНЫЙ
- ПРЕСЛЕДОВАНИЯ ЗАДАЧА
- ПРИБЛИЖЕННЫХ МЕТОДОВ ОБЩАЯ ТЕОРИЯ
- ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- ПРИОРИТЕТ
- ПРИОРИТЕТОВ СИСТЕМА
- ПРОБЛЕМА «ЧЕЛОВЕК-МАШИНА»
- ПРОГОНКИ МЕТОД
- ПРОГРАММ СЕГМЕНТАЦИЯ
- ПРОГРАММА вычислительной машины
- ПРОГРАММА ДИАГНОСТИЧЕСКАЯ
- ПРОГРАММА ИСПЫТАТЕЛЬНАЯ
- ПРОГРАММА КОМПИЛИРУЮЩАЯ
- ПРОГРАММА УПРАВЛЯЮЩАЯ
- ПРОГРАММА-ДИСПЕТЧЕР
- ПРОГРАММИРОВАНИЕ АВМ
- ПРОГРАММИРОВАНИЕ ВЫПУКЛОЕ
- ПРОГРАММИРОВАНИЕ ДИНАМИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ДИСКРЕТНОЕ
- ПРОГРАММИРОВАНИЕ ДЛЯ ЦВМ
- ПРОГРАММИРОВАНИЕ КВАДРАТИЧНОЕ
- ПРОГРАММИРОВАНИЕ КУСОЧНО-ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ НЕЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ СТОХАСТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЧАСТИЧНО ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЭВРИСТИЧЕСКОЕ
- ПРОГРАММИРОВАННОЕ ОБУЧЕНИЕ
- ПРОГРАММИРОВАННЫЙ УЧЕБНИК
- ПРОГРАММИРУЮЩАЯ ПРОГРАММА
- ПРОГРАММНОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ в народном хозяйстве.
- ПРОГРАММЫ ОБСЛУЖИВАЮЩИЕ
- ПРОЕКТИРОВАНИЕ СЕТЕЙ И КОММУНИКАЦИЙ ОПТИМАЛЬНОЕ
- ПРОЕКЦИОННЫЕ МЕТОДЫ
- ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ
- «ПРОМIНЬ»
- ПРОПОЗИЦИОНАЛЬНЫЕ СВЯЗКИ, связки логические
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- ПРОСТОЙ ИТЕРАЦИИ МЕТОД
- ПРОСТРАНСТВО АБСТРАКТНОЕ в функциональном анализе
- ПРОСТРАНСТВО ИЗОБРАЖЕНИЙ
- ПРОЦЕДУРА в программировании
- ПРОЦЕДУРА РЕКУРСИВНАЯ
- ПРОЦЕСС КОНЕЧНОЙ ДЛИТЕЛЬНОСТИ
- ПРОЦЕСС УПРАВЛЯЕМЫЙ
- ПРОЦЕССОР
- ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
- ПРЯМЫЕ МЕТОДЫ решения задач прикладной математики
- ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА
- ПСИХОЛОГИЯ ИНЖЕНЕРНАЯ
- ПУАССОНА ПОТОК
- ПУАССОНА РАСПРЕДЕЛЕНИЕ
- ПУТЬ в теории графов
- РАВНОВЕСИЯ СИТУАЦИЯ
- «РАЗДАН»
- РАЗДЕЛЯЮЩАЯ ПОВЕРХНОСТЬ в распознавании образов
- РАЗМЕЩЕНИЯ ПРОИЗВОДСТВ МОДЕЛИ
- РАЗНОСТНАЯ СХЕМА
- РАЗРЯДНОСТЬ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- РАСПАРАЛЛЕЛИВАНИЕ АЛГОРИТМА
- РАСПОЗНАВАНИЕ ЗРИТЕЛЬНЫХ ОБРАЗОВ, распознавание изображений
- РАСПОЗНАВАНИЕ ОБРАЗОВ
- РАСПОЗНАВАНИЕ ПРОЦЕССОВ
- РАСПОЗНАВАНИЕ РЕЧЕВЫХ СИГНАЛОВ
- РАСПОЗНАЮЩАЯ СИСТЕМА
- РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- РАСПРЕДЕЛИТЕЛЬНАЯ ЗАДАЧА
- РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДЫ
- РАСЧЕТНЫЙ СТОЛ ПОСТОЯННОГО ТОКА, расчетная модель электрической системы
- РАСШИФРОВОЧНАЯ МАШИНА
- РАУСА КРИТЕРИЙ, Рауса — Гурвица критерий
- РЕАЛЬНЫЙ МАСШТАБ ВРЕМЕНИ
- РЕГЕНЕРАЦИЯ информации в вычислительных устройствах
- РЕГИСТР
- РЕГРЕССИЯ
- РЕГУЛИРОВАНИЕ ЗАПАСОВ
- РЕГУЛИРОВАНИЯ ЗАКОН
- РЕГУЛИРУЮЩИЕ СИСТЕМЫ ОРГАНИЗМА
- РЕГУЛЯРИЗАЦИИ МЕТОД
- РЕГУЛЯРНЫЕ СОБЫТИЯ И ВЫРАЖЕНИЯ
- РЕГУЛЯТОР ИМПУЛЬСНЫЙ
- РЕГУЛЯТОР ЭКСТРЕМАЛЬНЫЙ
- РЕГУЛЯТОРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- РЕГУЛЯТОРЫ ЦИФРОВЫЕ
- РЕДАКТИРОВАНИЕ ДАННЫХ
- РЕЖИМ ПЕРИОДИЗАЦИИ
- РЕЖИМ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- РЕКУРСИВНЫЕ ФУНКЦИИ
- РЕЛЕВАНТНОСТЬ ДОКУМЕНТА
- РЕЛЕЙНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
- РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ ТЕОРИЯ
- РЕФАЛ
- РЕФЕРАТ
- РЕФЕРИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- РЕФЛЕКСИВНОЕ УПРАВЛЕНИЕ
- РЕШАЮЩЕЕ ПРАВИЛО в распознавании образов
- РЕШАЮЩЕЕ УСТРОЙСТВО.
- РИСК РАСПОЗНАВАНИЯ
- РИСКА ПРОБЛЕМА
- РОБОТ
- РОБОТ ПРОМЫШЛЕННЫЙ
- РУНГЕ—КУТТЫ МЕТОД
- «РУТА-110»
- R-ФУНКЦИИ
- САМОДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- САМОКОРРЕКТИРУЮЩАЯСЯ СХЕМА
- САМОНАСТРАИВАЮЩАЯСЯ ПАРАМЕТРИЧЕСКАЯ СИСТЕМА
- САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА
- САМООБУЧАЮЩИЕСЯ СИСТЕМЫ
- САМООБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- СБОЙ ЦВМ
- СВЕРТКА РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН
- СВЕТОВОЙ КАРАНДАШ, световое перо
- СВОДИМОСТЬ в теории алгоритмов
- СВОЙСТВО ОТСУТСТВИЯ ПОСЛЕДЕЙСТВИЯ
- СВЯЗКИ ЛОГИЧЕСКИЕ
- СДВИГ
- «CDC-7600»
- СЕДЛОВЫЕ ТОЧКИ
- СЕКВЕНЦИЯ
- СЕМАНТИКА
- СЕМАНТИКА СТРУКТУРНАЯ
- СЕМАНТИЧЕСКИЙ АНАЛИЗ
- СЕМИОТИКА
- СЕРВОМОТОР
- СЕТЕВАЯ ЗАДАЧА
- СЕТЕВАЯ ЗАДАЧА НЕОДНОРОДНАЯ
- СЕТЕВАЯ МОДЕЛЬ
- СЕТЕВОЙ ГРАФИК
- СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
- «СЕТУНЬ»
- СЕТЧАТКА в распознавании образов
- СЕТЬ ИЗ НЕЙРОННЫХ ЭЛЕМЕНТОВ
- СЕТЬ ЛОГИЧЕСКАЯ
- СЕЧЕНИЙ ПРОСТРАНСТВА ПАРАМЕТРОВ МЕТОД
- СИГНАЛИЗИРУЮЩАЯ ФУНКЦИЯ
- СИЛЛОГИСТИКА
- «СИМЕНС» (Siemens Aktiengesellschaft)
- СИММЕТРИЧЕСКИЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- СИМПЛЕКС-МЕТОД
- СИМПСОНА ФОРМУЛА
- СИМСКРИПТ
- СИМУЛА
- «СИНТАКСИС»
- СИНТАКСИЧЕСКИЙ АНАЛИЗ АВТОМАТИЧЕСКИЙ естественных языков
- СИНТАКСИЧЕСКИЙ АНАЛИЗ ПРОГРАММ
- СИНТАКСИЧЕСКИЙ КОНТРОЛЬ ПРОГРАММ
- СИНТАКТИКА
- СИНТЕЗ АВТОМАТОВ АБСТРАКТНЫЙ
- СИНТЕЗ АВТОМАТОВ СТРУКТУРНЫЙ
- СИНТЕЗ АЛГОРИТМА УПРАВЛЕНИЯ
- СИНТЕЗ РЕЧЕВЫХ СИГНАЛОВ
- СИНХРОНИЗАЦИЯ РАБОТЫ ЦВМ
- «СИРИУС»
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СТАТИСТИЧЕСКАЯ ДИНАМИКА
- СИСТЕМ ОБЩАЯ ТЕОРИЯ
- СИСТЕМА АВТОМАТИЗИРОВАННАЯ
- СИСТЕМА АВТОМАТИЧЕСКАЯ
- СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ)
- СИСТЕМА АВТОМАТИЧЕСКОЙ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- СИСТЕМА АВТОНОМНАЯ
- СИСТЕМА АСТАТИЧЕСКАЯ
- СИСТЕМА ИНФОРМАЦИОННОГО ПОИСКА
- СИСТЕМА НЕАВТОНОМНАЯ
- СИСТЕМА НЕПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЕРЫВАНИЯ ЦВМ
- СИСТЕМА ПРОГРАММИРОВАНИЯ
- СИСТЕМА ПРОГРАММНОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА СЧИСЛЕНИЯ
- СИСТЕМА УПРАВЛЕНИЯ АДАПТИВНАЯ
- СИСТЕМА УПРАВЛЕНИЯ ЗАМКНУТАЯ, система управления по отклонению
- СИСТЕМА УПРАВЛЕНИЯ НАУЧНЫМ ЭКСПЕРИМЕНТОМ
- СИСТЕМА УПРАВЛЕНИЯ РАЗОМКНУТАЯ
- СИСТЕМА УПРАВЛЕНИЯ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
- СИСТЕМА УПРАВЛЕНИЯ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- СИСТЕМА УРАВНЕНИЙ В ВАРИАЦИЯХ
- СИСТЕМА УРАВНЕНИЙ СОПРЯЖЕННАЯ
- СИСТЕМА «ЧЕЛОВЕК — МАШИНА»
- СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- СИСТЕМНОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- СИСТЕМНЫЙ ПОДХОД
- СИСТЕМОТЕХНИКА
- СИСТЕМЫ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- СИСТЕМЫ С ВРЕМЕННЫМИ ОГРАНИЧЕНИЯМИ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ
- СИСТЕМЫ УПРАВЛЕНИЯ НА ПЕРЕМЕННОМ ТОКЕ
- СКЛЕИВАНИЯ ЗАКОН
- СКОЛЬЗЯЩИЙ РЕЖИМ
- СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЯ
- СЛЕДЯЩАЯ СИСТЕМА
- СЛОВАРНЫЙ ПОИСК
- СЛОВАРЬ АВТОМАТИЧЕСКИЙ
- СЛОВАРЬ ИНФОРМАЦИОННОГО ЯЗЫКА
- СЛОВАРЬ ЧАСТОТНЫЙ
- СЛОВО
- СЛОЖНОСТЬ ВЫЧИСЛЕНИЙ
- СЛОЖНОСТЬ ТЬЮРИНГОВЫХ ВЫЧИСЛЕНИЙ
- СЛОЖНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- СЛУЧАЙНАЯ ВЕЛИЧИНА
- СЛУЧАЙНАЯ ФУНКЦИЯ
- СЛУЧАЙНОГО ПОИСКА МЕТОДЫ
- СЛУЧАЙНОЕ ПОЛЕ
- СЛУЧАЙНОЕ СОБЫТИЕ
- СЛУЧАЙНЫЕ ЧИСЛА
- СЛУЧАЙНЫЙ ПРОЦЕСС, вероятностный процесс, стохастический процесс
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ ПРЕДСКАЗАНИЯ
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ ОБЫКНОВЕННЫХ УРАВНЕНИЙ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СОБЫТИЕ РЕГУЛЯРНОЕ
- СОБЫТИЯ ЦИКЛИЧЕСКАЯ ГЛУБИНА
- СОВМЕЩЕНИЕ ОПЕРАЦИЙ В МАШИНЕ
- «СОЛЯРТРОН ЭЛЕКТРОНИК ГРУП» (The Solartron Electronic Group, Ltd)
- СООБЩЕНИЕ в теории передачи информации
- СООБЩЕНИЙ ТЕОРИЯ
- СОПРОТИВЛЕНИЕ ОТРИЦАТЕЛЬНОЕ
- СОПРОТИВЛЕНИЕ ЦИФРОВОЕ УПРАВЛЯЕМОЕ
- СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- СОРТИРОВАЛЬНАЯ МАШИНА
- СОРТИРОВКА ДАННЫХ
- СОЦИОЛОГИЧЕСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ
- СПЕКТРАЛЬНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- СПЕКТРАЛЬНАЯ ФУНКЦИЯ стационарного в широком смысле случайного процесса
- СПЕЦИАЛИЗИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- СПЕЦИАЛЬНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СПЕЦИФИКАЦИЯ
- СПИСКОВАЯ СТРУКТУРА
- СПИСОК в программировании
- СПРАВОЧНО-ИНФОРМАЦИОННЫЙ ФОНД (СИФ)
- СТАБИЛИЗАЦИИ СИСТЕМА
- СТАНДАРТИЗИРОВАННАЯ ИСТОРИЯ БОЛЕЗНИ
- СТАНДАРТЫ ПО ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
- СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ МЕТОД
- СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- СТИЛТЬЕСА КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
- СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- СТОХАСТИЧЕСКИЙ ПРОЦЕСС
- СТОХАСТИЧЕСКИХ КВАЗИГРАДИЕНТОВ МЕТОД
- СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ МЕТОД
- СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ МЕТОДЫ
- СТРАТЕГИЯ ОПТИМАЛЬНАЯ
- СТРАТЕГИЯ ПОВЕДЕНИЯ
- СТРАТЕГИЯ СМЕШАННАЯ
- СТРАТЕГИЯ ЧИСТАЯ
- «СТРЕЛА»
- СТРУКТУРА, решетка.
- СТРУКТУРНАЯ ИНТЕРПРЕТАЦИЯ ЯЗЫКА
- СТРУКТУРНАЯ ПОЭТИКА
- СТРУКТУРНАЯ СХЕМА МОДЕЛИ
- СТРУКТУРНАЯ ТЕОРИЯ АВТОМАТОВ
- СТРУКТУРНОЕ СТИХОВЕДЕНИЕ
- СУММАТОР
- СУММАТОР КОМБИНАЦИОННЫЙ
- СУММАТОР НАКАПЛИВАЮЩИЙ
- СУММАТОР ОДНОРАЗРЯДНЫЙ
- СУММАТОР ПАРАЛЛЕЛЬНЫЙ
- СУММАТОР ПОСЛЕДОВАТЕЛЬНЫЙ
- СУПЕРВИЗОР
- СХЕМА ВЕНТИЛЬНАЯ
- СХЕМА КОНТАКТНАЯ
- СХЕМА КОНТАКТНАЯ БЕСПОВТОРНАЯ
- СХЕМА КОНТАКТНО-ВЕНТИЛЬНАЯ
- СХЕМА РЕЛЕЙНО-КОНТАКТНАЯ
- СХЕМА СРАВНЕНИЯ
- СХОДСТВА КРИТЕРИИ
- СЧЕТЧИК
- ТАБУЛИРОВАНИЕ ФУНКЦИЙ
- ТАБУЛЯТОР
- ТАЙПОТРОН
- ТАКТ
- ТАКТОВАЯ ЧАСТОТА
- ТВИСТОР
- ТЕЗАУРУС
- ТЕЛЕМЕХАНИКА
- ТЕЛЕТАЙП
- ТЕРМИНАЛ, абонентский пульт, оконечное устройство
- ТЕРМИНАЛЬНОЕ УПРАВЛЕНИЕ, управление конечным состоянием
- ТЕСТОВЫЕ ПРОГРАММЫ, тест-программы
- ТЕСТЫ
- ТЕХНИЧЕСКАЯ ДИАГНОСТИКА
- ТЕХНИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- ТЕХПРОМФИНПЛАН ПРЕДПРИЯТИЯ МАТРИЧНЫЙ
- ТОЖДЕСТВЕННО ИСТИННАЯ ФОРМУЛА, общезначимая формула
- ТОНКАЯ МАГНИТНАЯ ПЛЕНКА
- ТОПОЛОГИЯ
- «ТОСИБА» (Tokyo Shibaura Electric Company, Ltd)
- ТОЧКА РАВНОВЕСИЯ
- ТОЧКИ ПЕРЕКЛЮЧЕНИЯ
- ТОЧНОСТЬ ВОСПРОИЗВЕДЕНИЯ СООБЩЕНИЯ
- ТРАЕКТОРИЯ ДОПУСТИМАЯ
- ТРАЕКТОРИЯ ОПТИМАЛЬНАЯ
- ТРАЕКТОРИЯ ФАЗОВАЯ
- ТРАНЗИТИВНЫЙ ГРАФ
- ТРАНСЛЯТОР, компилирующая программа, программирующая программа
- ТРАНСЛЯТОР СИНТАКСИЧЕСКИ УПРАВЛЯЕМЫЙ
- ТРАНСПОРТНАЯ ЗАДАЧА
- ТРАНСПОРТНАЯ СЕТЬ
- ТРАНСФЛЮКСОР
- ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
- ТРИГГЕР
- ТРИГГЕР ДИНАМИЧЕСКИЙ
- ТРИГГЕР СТАТИЧЕСКИЙ
- ТРИОД ПОЛУПРОВОДНИКОВЫЙ, транзистор
- ТЬЮРИНГА МАШИНА
- УЗЛОВОЙ СПИСОК
- «УМ1-НХ»
- УНИВЕРСАЛЬНАЯ СИСТЕМА ЭЛЕМЕНТОВ ПРОМЫШЛЕННОЙ ПНЕВМОАВТОМАТИКИ (УСЭППА)
- UNCOL
- УПОРЯДОЧЕНИЕ МАССИВА
- УПРАВЛЕНИЕ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- УПРАВЛЕНИЕ ДАННЫМИ
- УПРАВЛЕНИЕ ЗАПАСАМИ
- УПРАВЛЕНИЕ КОМАНДАМИ
- УПРАВЛЕНИЕ ЛЕЧЕБНЫМ ПРОЦЕССОМ.
- УПРАВЛЕНИЕ ОПЕРАЦИЯМИ
- УПРАВЛЕНИЕ ОПТИМАЛЬНОЕ
- УПРАВЛЕНИЕ ПРОГРАММНОЕ
- УПРАВЛЕНИЕ С АДАПТАЦИЕЙ
- УПРАВЛЕНИЕ СТРУКТУРНОЕ В ЦВМ
- УПРАВЛЕНИЯ ОТНОШЕНИЕ, зависимости отношение
- УПРАВЛЕНИЯ СЛУЧАЙНЫМИ ПРОЦЕССАМИ ТЕОРИЯ
- УПРАВЛЯЮЩАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- УПРАВЛЯЮЩАЯ ПРОГРАММА
- УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, регулирующее воздействие
- «УПРАВЛЯЮЩИЕ СИСТЕМЫ И МАШИНЫ»
- УРАВНЕНИЙ КЛАССИФИКАЦИЯ.
- УРАВНОВЕШИВАНИЯ МЕТОДЫ
- «УРАЛ»
- УСИЛИТЕЛЬ
- УСИЛИТЕЛЬ ДИФФЕРЕНЦИАЛЬНЫЙ
- УСИЛИТЕЛЬ ОПЕРАЦИОННЫЙ, усилитель решающий
- УСИЛИТЕЛЬ ОТРАБАТЫВАЮЩИЙ
- УСИЛИТЕЛЬ РЕШАЮЩИЙ
- УСЛОВИЯ СТАЦИОНАРНОСТИ
- УСЛОВИЯ ТРАНСВЕРСАЛЬНОСТИ
- УСТАНОВКА НАЧАЛЬНЫХ УСЛОВИЙ
- УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ КРИТЕРИИ
- УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
- УСТОЙЧИВОСТЬ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ
- УСТОЙЧИВОСТЬ МОДЕЛИ
- УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ
- УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ
- УСТОЙЧИВОСТЬ ЧИСЛЕННОГО МЕТОДА
- УСТРОЙСТВА ВВОДА—ВЫВОДА ДАННЫХ ЦВМ
- УСТРОЙСТВА ЗАПИСИ АНАЛОГОВОЙ ИНФОРМАЦИИ
- УСТРОЙСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- УСТРОЙСТВО ИНДИКАЦИИ ABM
- УСТРОЙСТВО ИНТЕГРИРУЮЩЕЕ, интегратор
- УСТРОЙСТВО ИНТЕГРО-ДИФФЕРЕНЦИРУЮЩЕЕ
- УСТРОЙСТВО ОБМЕНА ЦВМ
- УСТОЙСТВО ПЕРЕЗАПИСИ ДЛЯ ЦВМ
- УСТРОЙСТВО УПРАВЛЕНИЯ ЦВМ
- УСТРОЙСТВО ЦИФРОВОЙ РЕГИСТРАЦИИ
- ФАЗОВОГО ПРОСТРАНСТВА МЕТОД
- ФАЗОВЫЕ КООРДИНАТЫ
- ФАЗОВЫЕ ОГРАНИЧЕНИЯ
- ФАКТОГРАФИЧЕСКАЯ ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ФАКТОРИЗАЦИИ МЕТОД
- «ФЕРРАНТИ» (Ferranti, Ltd)
- ФЕРРИТ-ДИОДНАЯ СИСТЕМА ЭЛЕМЕНТОВ
- ФЕРРИТ-ТРАНЗИСТОРНАЯ СИСТЕМА ЭЛЕ МЕНТОВ
- ФИКСАТОР, адрес второго ранга, косвенный адрес
- ФИКСИРОВАННАЯ ЗАПЯТАЯ
- ФИЛОСОФСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- ФИЛЬТР
- ФИЛЬТРАЦИЯ СЛУЧАЙНОГО ПРОЦЕССА
- ФОНД АЛГОРИТМОВ И ПРОГРАММ
- ФОНД СПРАВОЧНО-ИНФОРМАЦИОННЫЙ
- FORMAC
- ФОРМАЛИЗМ в математике
- ФОРТРАН
- «ФУДЗИЦУ» («Фудзи цусинки Сэйдзо», Fujitsu, Ltd)
- ФУНКЦИИ, СОХРАНЯЮЩИЕ КОНСТАНТУ
- ФУНКЦИИ, СОХРАНЯЮЩИЕ МНОЖЕСТВО
- ФУНКЦИИ, СОХРАНЯЮЩИЕ РАЗБИЕНИЕ
- ФУНКЦИОНАЛ
- ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ЭВМ
- ФУНКЦИОНАЛЬНЫЙ ЭЛЕМЕНТ ЭВМ
- ФУНКЦИЯ РАССТАНОВКИ
- ФУНКЦИЯ РЕШЕТЧАТАЯ
- ФУНКЦИЯ СТУПЕНЧАТАЯ
- ФУРЬЕ ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ФУРЬЕ ПРЕОБРАЗОВАНИЯ
- ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ в теории игр
- ХАРАКТРОН
- ХЕМИТРОН
- ХИНЧИНА-ПОЛАЧЕКА ФОРМУЛА
- «ХИТАЧИ» (Hitachi, Ltd)
- ХОМСКОГО ГРАММАТИКИ
- «ХОНИУЭЛЛ КОРПОРЕЙШЕН» (Honeywell Corporation)
- ХЭММИНГА КОД
- ЦВМ АСИНХРОННАЯ
- ЦВМ СИНХРОННАЯ
- ЦЕЛЕВАЯ ФУНКЦИЯ, функция цели
- ЦЕЛЕСООБРАЗНОСТЬ в кибернетике
- ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
- ЦЕНТРАЛЬНЫЙ ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ ИНСТИТУТ АКАДЕМИИ НАУК СССР
- ЦЕПИ СВЯЗАННЫЕ
- ЦЕПОЧКА
- ЦЕПЬ графа
- ЦЕПЬ ОКРУГЛЕНИЯ
- ЦЕПЬ ПЕРЕНОСА
- ЦИКЛ графа
- ЦИКЛ ПРОГРАММЫ
- ЦИКЛОМАТИЧЕСКОЕ ЧИСЛО
- ЦИПФА ЗАКОН
- ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ, преобразователи код
- ЦИФРО-АНАЛОГОВЫЙ КОМПЛЕКС, аналого-цифровой комплекс
- ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЦВМ)
- ЦИФРОВАЯ ИНТЕГРИРУЮЩАЯ МАШИНА
- ЦИФРОВАЯ МОДЕЛЬ СЕТЕВОГО ГРАФИКА
- ЦИФРОВОЙ ДИФФЕРЕНЦИАЛЬНЫЙ АНАЛИЗАТОР
- ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО
- ЧАСТПЧНО-РЕКУРСИВНЫЕ ФУНКЦИИ
- ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ЧЕБЫШЕВА ЗАДАЧА РАВНОМЕРНОГО ПРИБЛИЖЕНИЯ
- ЧЕЛОВЕК-ОПЕРАТОР
- ЧЕРЕДУЮЩАЯСЯ ЦЕПЬ
- ЧЕРНИЛА МАГНИТНЫЕ
- «ЧЕРНЫЙ ЯЩИК»
- ЧИРЧА ТЕЗИС
- ЧИСЛА ФОРМАТ
- ЧИСЛЕННЫЕ МЕТОДЫ
- ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
- ЧИТАЮЩИЙ АВТОМАТ, оптическое читающее устройство
- ЧИТАЮЩИЙ АВТОМАТ КОРРЕЛЯЦИОННЫЙ
- ЧУВСТВИТЕЛЬНОСТИ ТЕОРИЯ
- ШАГ КВАНТОВАНИЯ
- ШЕННОНА ЛАБИРИНТ
- ШЕННОНА МЫШЬ
- ШЕННОНА ФУНКЦИЯ
- ШЕПЛИ ВЕКТОР
- ШЕФФЕРА ШТРИХ, Шеффера функция, отрицание конъюнкции
- ШИНА
- ШИФРАТОР
- ШТРАФНАЯ ФУНКЦИЯ
- ШТРАФНЫХ ФУНКЦИЙ МЕТОД
- ШТРАФОВ МЕТОД
- ШУМ КВАНТОВАНИЯ
- ШУМ ПОИСКОВЫЙ
- ЭВРИСТИКА
- ЭВРИСТИЧЕСКИЕ МЕТОДЫ В РАСПОЗНАВАНИИ
- ЭЙЛЕРА ЦЕПЬ
- ЭКВИВАЛЕНТНАЯ СХЕМА
- ЭКВИВАЛЕНТНОСТИ ОТНОШЕНИЕ (эквивалентность, эквиваленци я) на множестве
- ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЭКВИВАЛЕНТНЫЕ СОСТОЯНИЯ АВТОМАТА
- ЭКВИВАЛЕНТНЫХ ВОЗМУЩЕНИЙ МЕТОД
- ЭКВИФИНАЛЬНОСТЬ СИСТЕМЫ УПРАВЛЕНИЯ
- ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ, в управлении народным хозяйством
- ЭКРАННЫЙ ПУЛЬТ
- ЭКСПЕРИМЕНТ БЕЗУСЛОВНЫЙ
- ЭКСПЕРИМЕНТ КРАТНЫЙ
- ЭКСПЕРИМЕНТ УСЛОВНЫЙ
- ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ СПОСОБЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
- ЭКСПЕРИМЕНТЫ С АВТОМАТАМИ
- ЭКСПЕРТНЫХ ОЦЕНОК МЕТОДЫ в прогнозировании
- ЭКСТРАПОЛИРОВАНИЕ В ОБУЧЕНИИ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ЭКСТРАПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ЭКСТРАПОЛИРОВАНИЕ ФУНКЦИЙ
- ЭКСТРЕМАЛЬ
- ЭКСТРЕМАЛЬНОЕ РЕГУЛИРОВАНИЕ
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ в теории графов
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ НА ГРАФАХ
- ЭКСТРЕМУМ
- ЭКСТРЕМУМ АБСОЛЮТНЫЙ
- ЭКСТРЕМУМ ГЛОБАЛЬНЫЙ
- ЭКСТРЕМУМ ЛОКАЛЬНЫЙ
- ЭКСТРЕМУМА ДРЕЙФ
- ЭЛЕКТРИЧЕСКИЕ МОДЕЛИРУЮЩИЕ СЕТКИ
- ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ТЕОРИЯ
- «ЭЛЕКТРОН»
- ЭЛЕКТРОННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЭВМ)
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЭЛЕМЕНТ ЗАДЕРЖКИ
- ЭЛЕМЕНТАРНАЯ СИСТЕМА
- ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ НАД СЛОВАМИ
- ЭЛЕМЕНТАРНЫЕ ТЕОРИИ.
- ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ЭЛЕМЕНТНЫЕ СТРУКТУРЫ НА ЛОГИЧЕСКИХ ЗАДЕРЖИВАЮЩИХ ЭЛЕМЕНТАХ
- ЭЛЕМЕНТНЫЙ СИНТЕЗ ЦВМ
- ЭЛИОНИКА
- ЭЛЛИПТИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- «ЭМИК-1»
- ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
- «ЭМСС»
- «ЭМУ»
- ЭНТРОПИЯ
- ЭНТРОПИЯ ЖИВЫХ СИСТЕМ
- ЭНТРОПИЯ СООБЩЕНИЯ при заданных условиях точности
- ЭПСИЛОН
- ЭПСИЛОН-ЭНТРОПИЯ
- ЭРГАТИЧЕСКАЯ СИСТЕМА
- ЭРГОДИЧЕСКАЯ ТЕОРИЯ
- ЭРГОДИЧЕСКОЕ СОСТОЯНИЕ
- ЭРЛАНГА ФОРМУЛЫ
- ЭТАЛОН в распознавании образов
- ЭТАЛОННОЕ НАПРЯЖЕНИЕ
- ЭФФЕКТИВНОСТЬ ИНФОРМАЦИОННОГО ПОИСКА техническая
- ЭШБИ ГОМЕОСТАТ
- «ЮНИВАК» (Univac)
- ЯДРО втеории игр
- ЯЗЫК АВТОМАТНЫЙ
- ЯЗЫК АЛГОРИТМИЧЕСКИЙ
- ЯЗЫК АНКЕТНЫЙ
- ЯЗЫК БЕСКОНТЕКСТНЫЙ, язык контекстно-свободный
- ЯЗЫК ДЕСКРИПТОРНЫЙ
- ЯЗЫК ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ
- ЯЗЫК ИНФОРМАЦИОННО-ПОИСКОВЫЙ
- ЯЗЫК ИНФОРМАЦИОННЫЙ
- ЯЗЫК ИСКУССТВЕННЫЙ
- ЯЗЫК КАТЕГОРИАЛЬНЫЙ
- ЯЗЫК ЛОГИЧЕСКИЙ для задания автоматов
- ЯЗЫК МАШИННО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК МАШИНЫ «МИР»
- ЯЗЫК ОПЕРАТОРНЫЙ
- ЯЗЫК ОПИСАНИЯ УСТРОЙСТВ ЦВМ
- ЯЗЫК ПРОМЕЖУТОЧНЫЙ
- ЯЗЫК ПРОЦЕДУРНО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК ТРАНСЛЯТОРА ВХОДНОЙ
- ЯЗЫК ЦВМ ВНУТРЕННИЙ
- ЯЗЫКА ИЗБЫТОЧНОСТЬ
- ЯЗЫКА ИНФОРМАЦИОННЫЕ ИЗМЕРЕНИЯ
- ЯЗЫКА МОДЕЛИ АНАЛИТИЧЕСКИЕ
- ЯЗЫКА МОДЕЛИ МАТЕМАТИЧЕСКИЕ
- ЯЗЫКА ЭНТРОПИЯ
- ЯЗЫКИ ЛОГИКО-МАТЕМАТИЧЕСКИЕ
- ЯЗЫКИ МАШИННЫЕ
- ЯЗЫКИ ПРОГРАММИРОВАНИЯ
- ЯЗЫКИ СПИСКОВЫЕ
- ЯЗЫКИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ
- ЯЗЫКИ ФОРМАЛЬНЫЕ
- ЯЗЫК — ПОСРЕДНИК
- ЯЧЕЙКА ЗАПОМИНАЮЩЕГО УСТРОЙСТВА