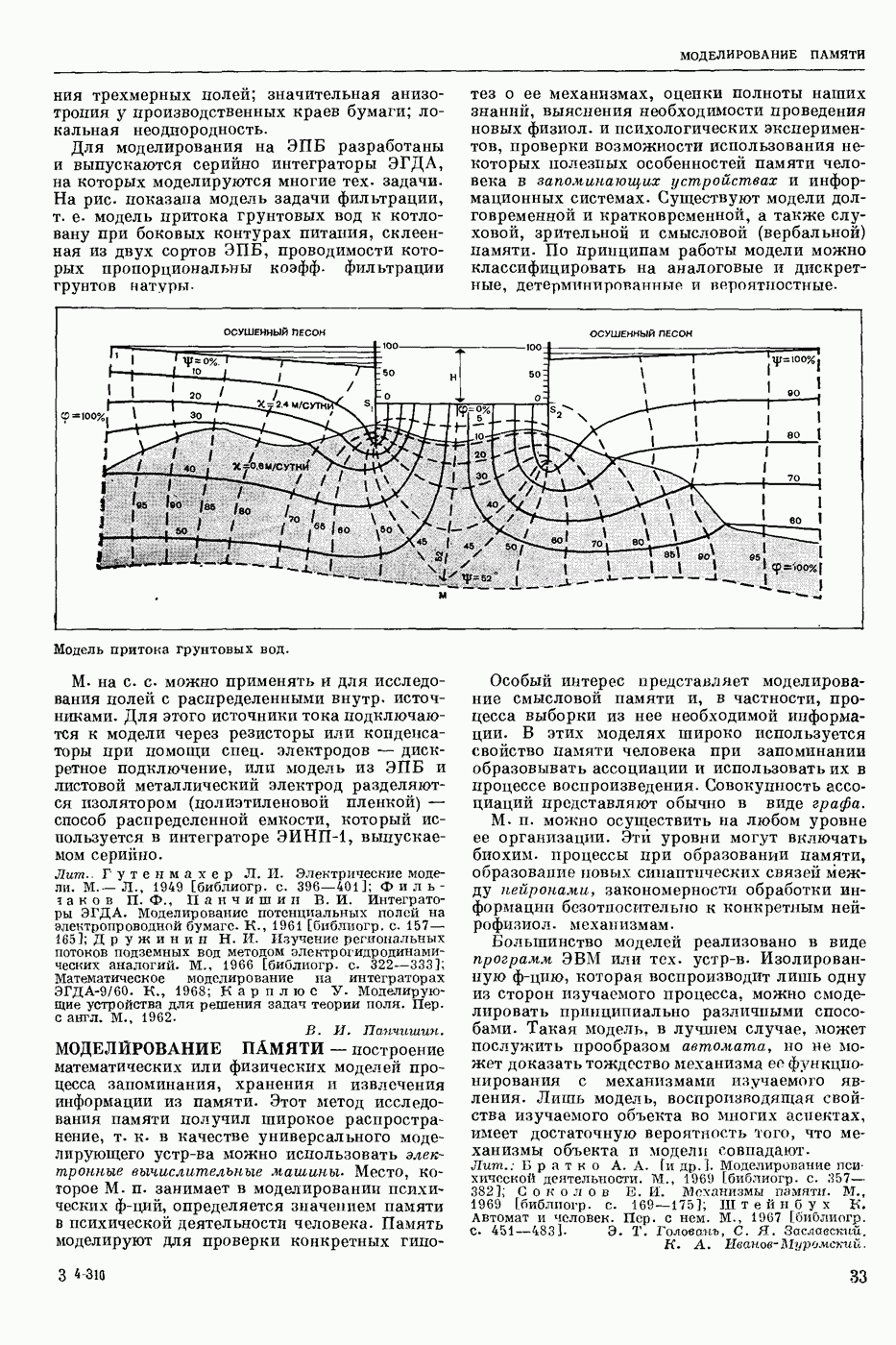
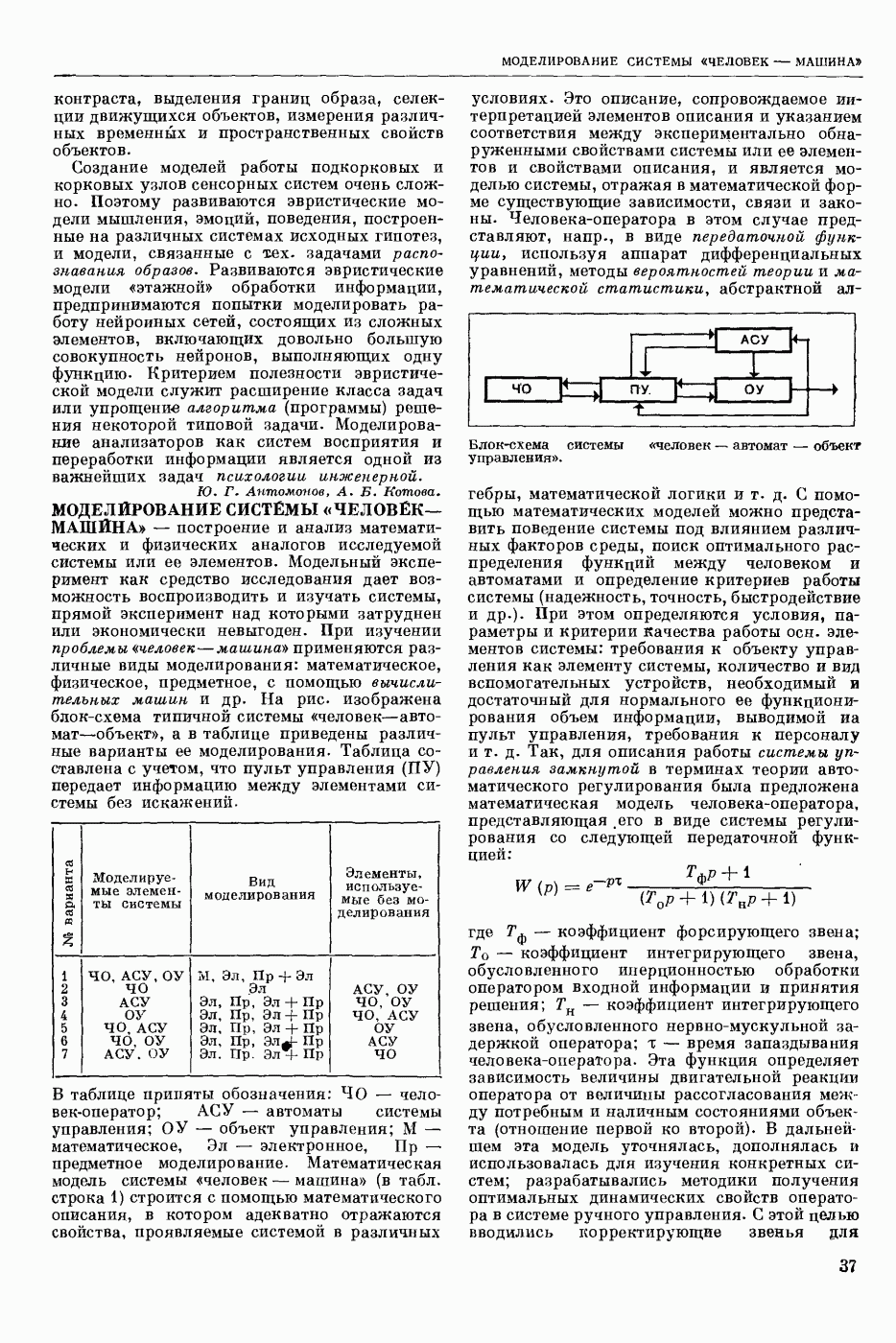
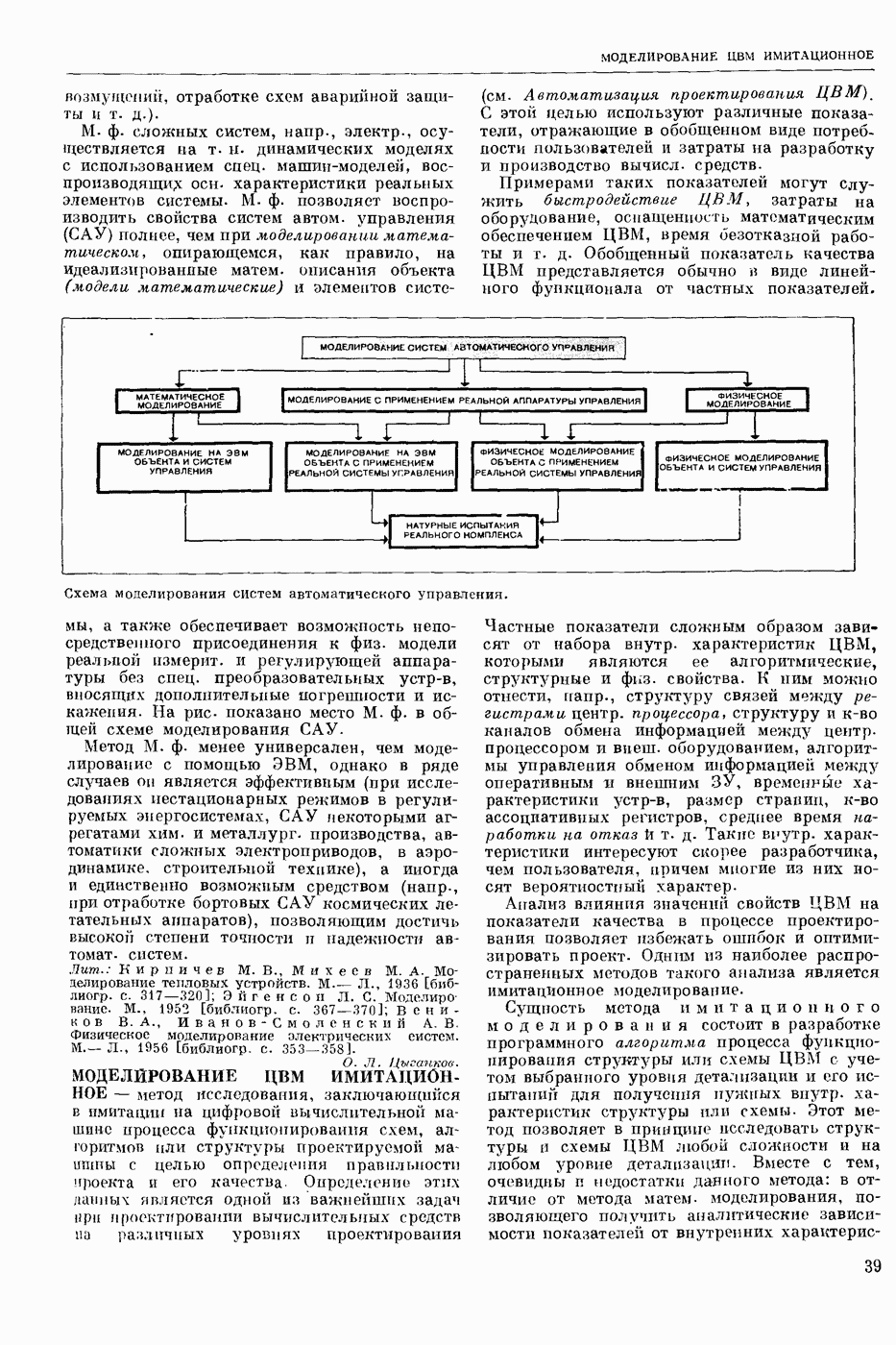
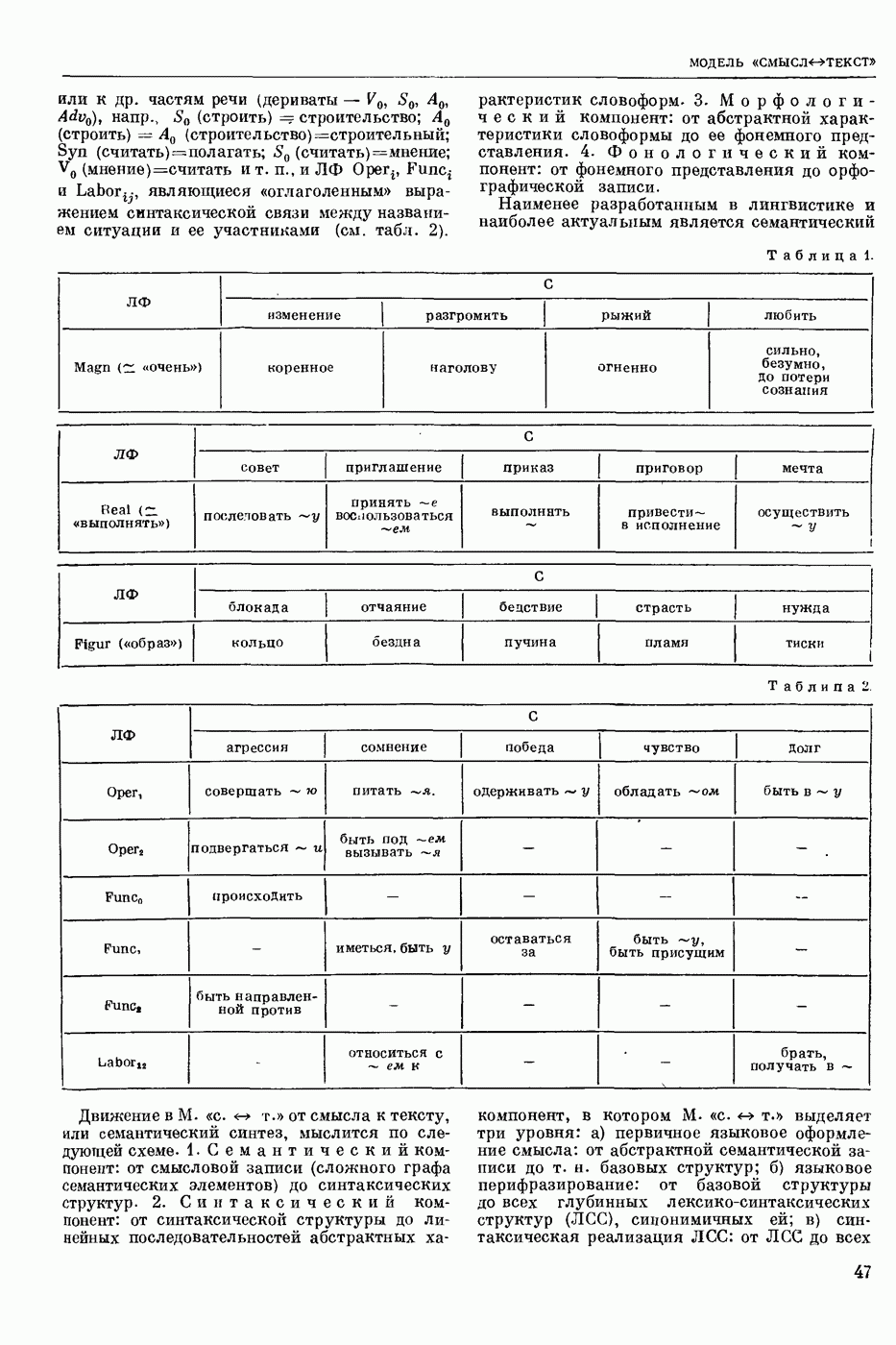
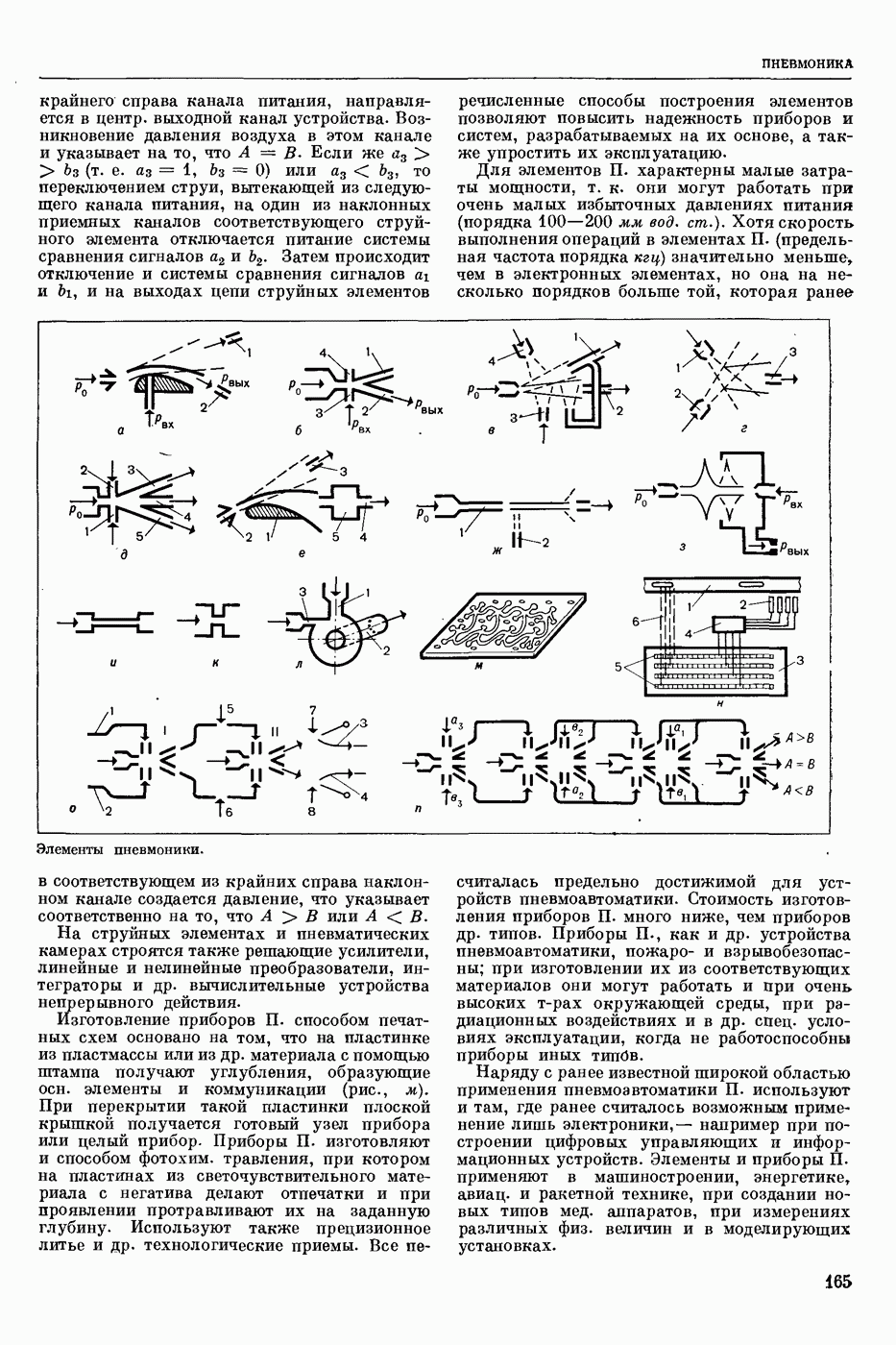
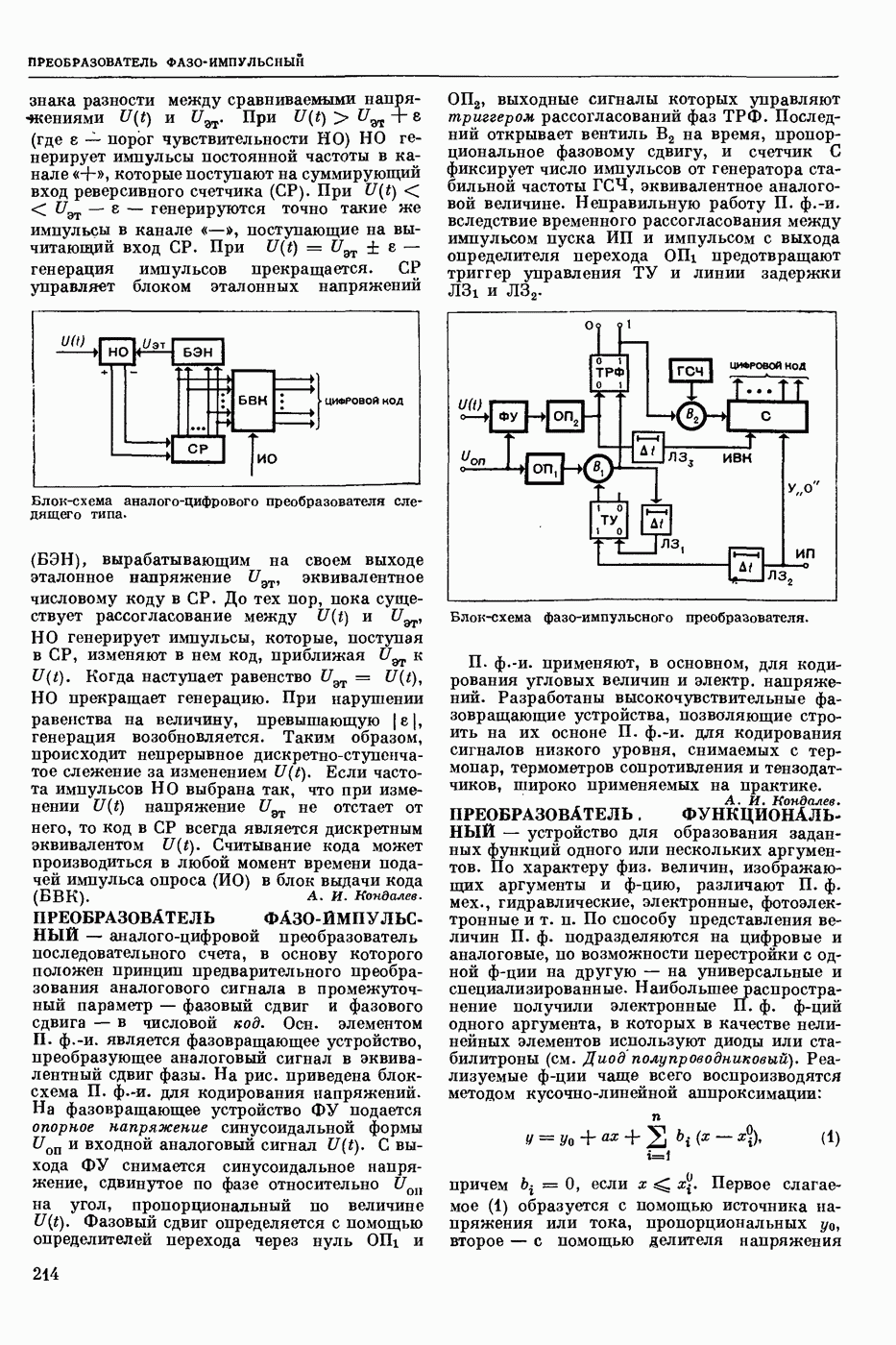
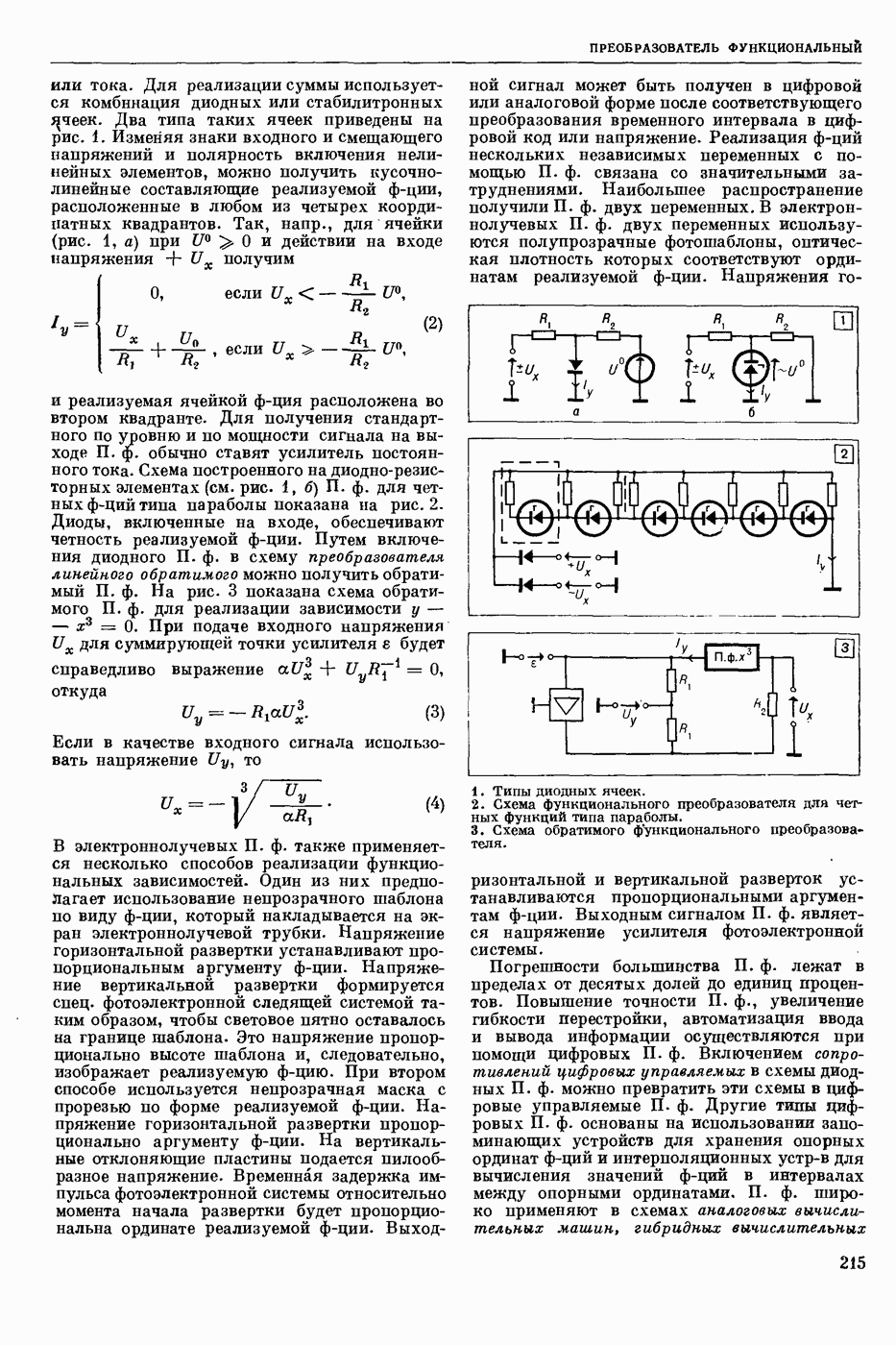
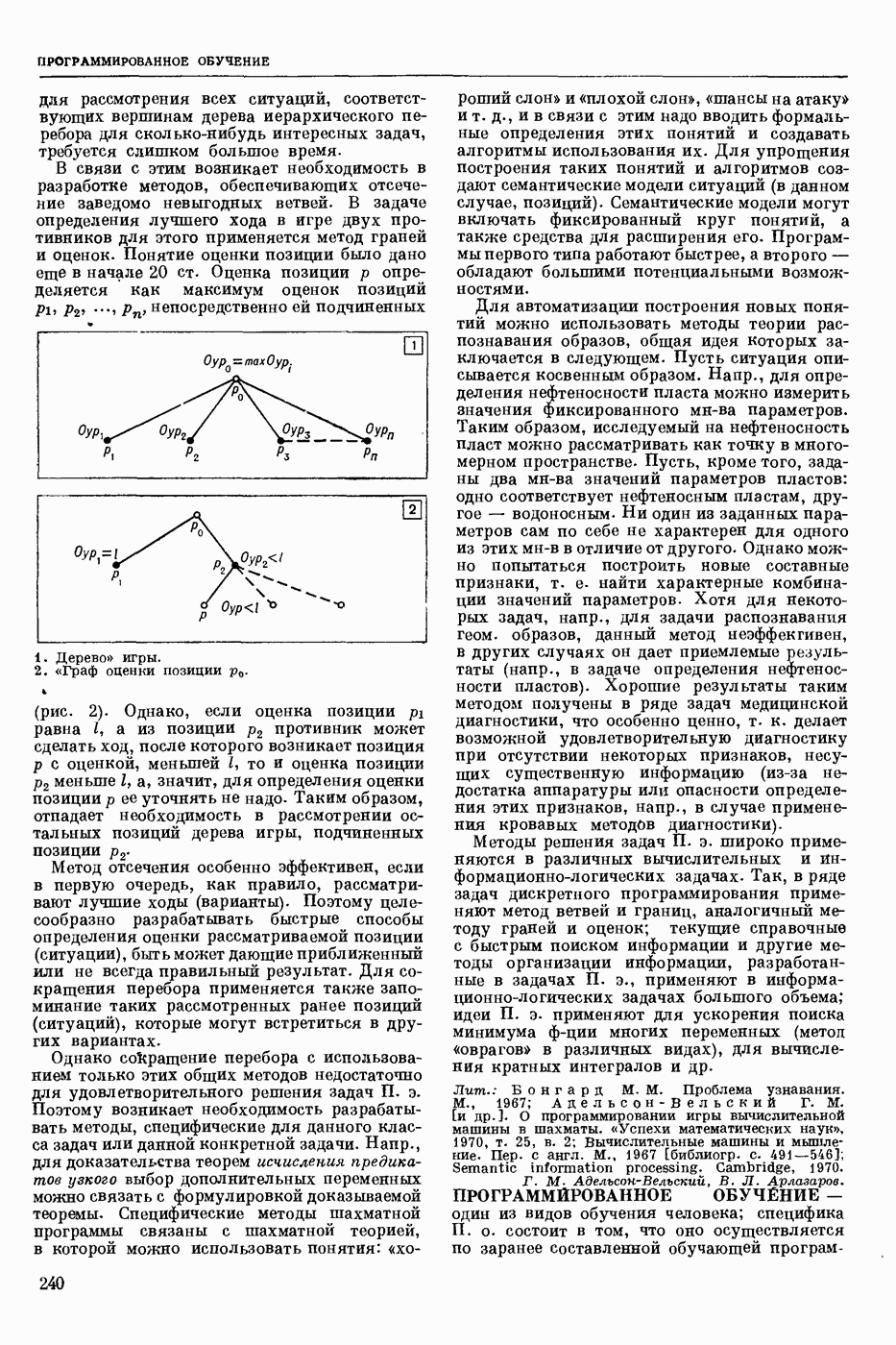
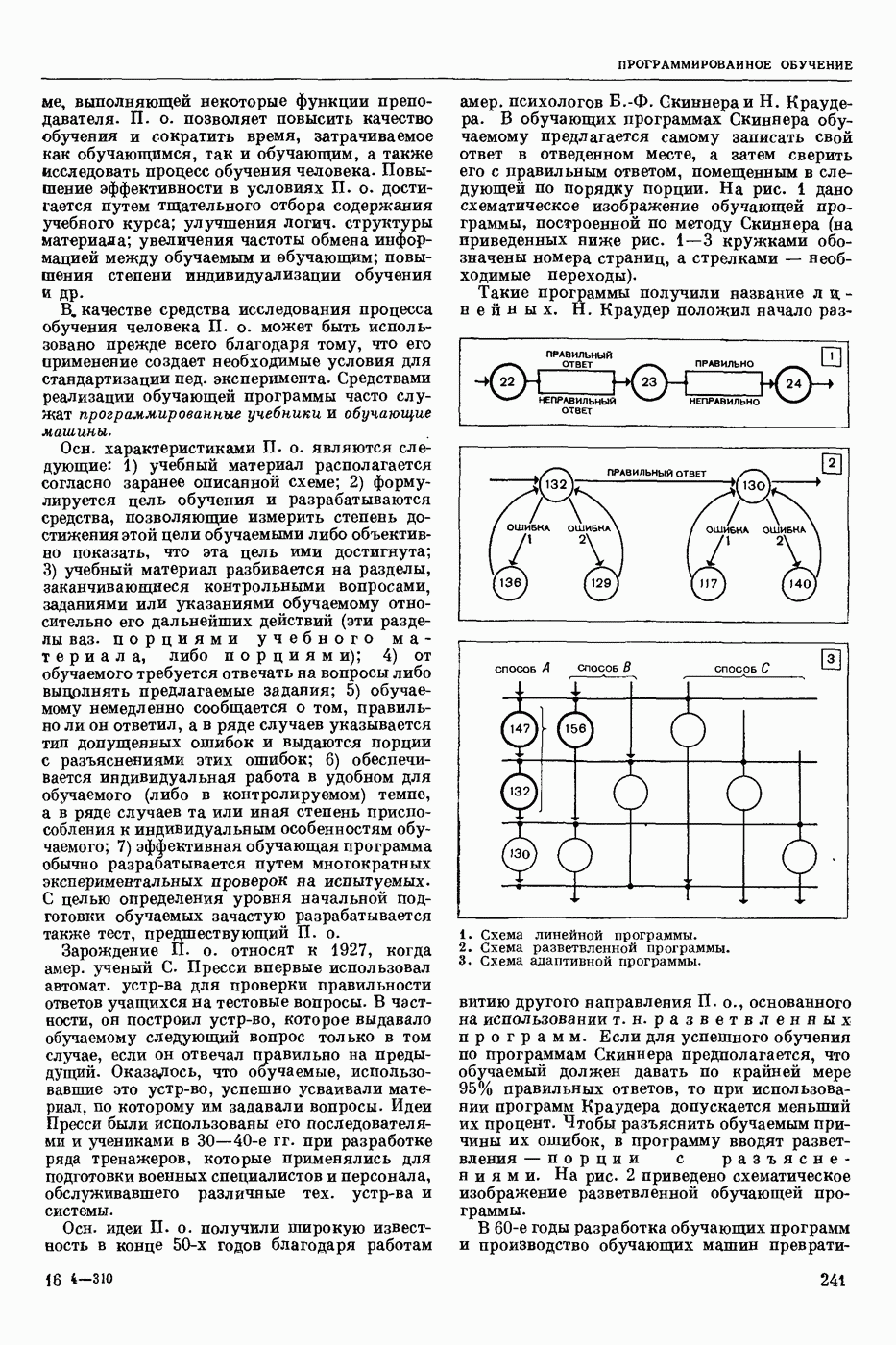
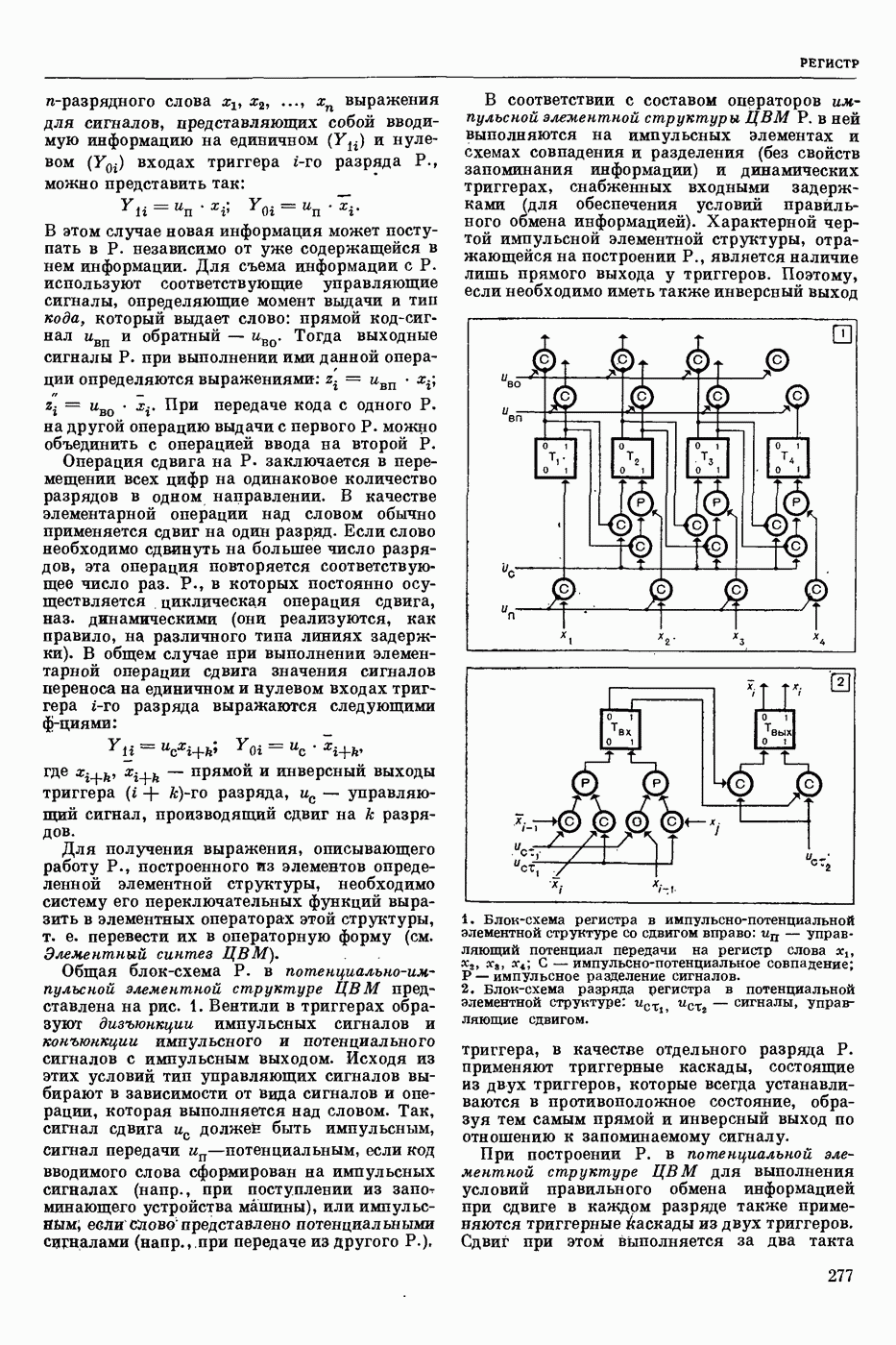
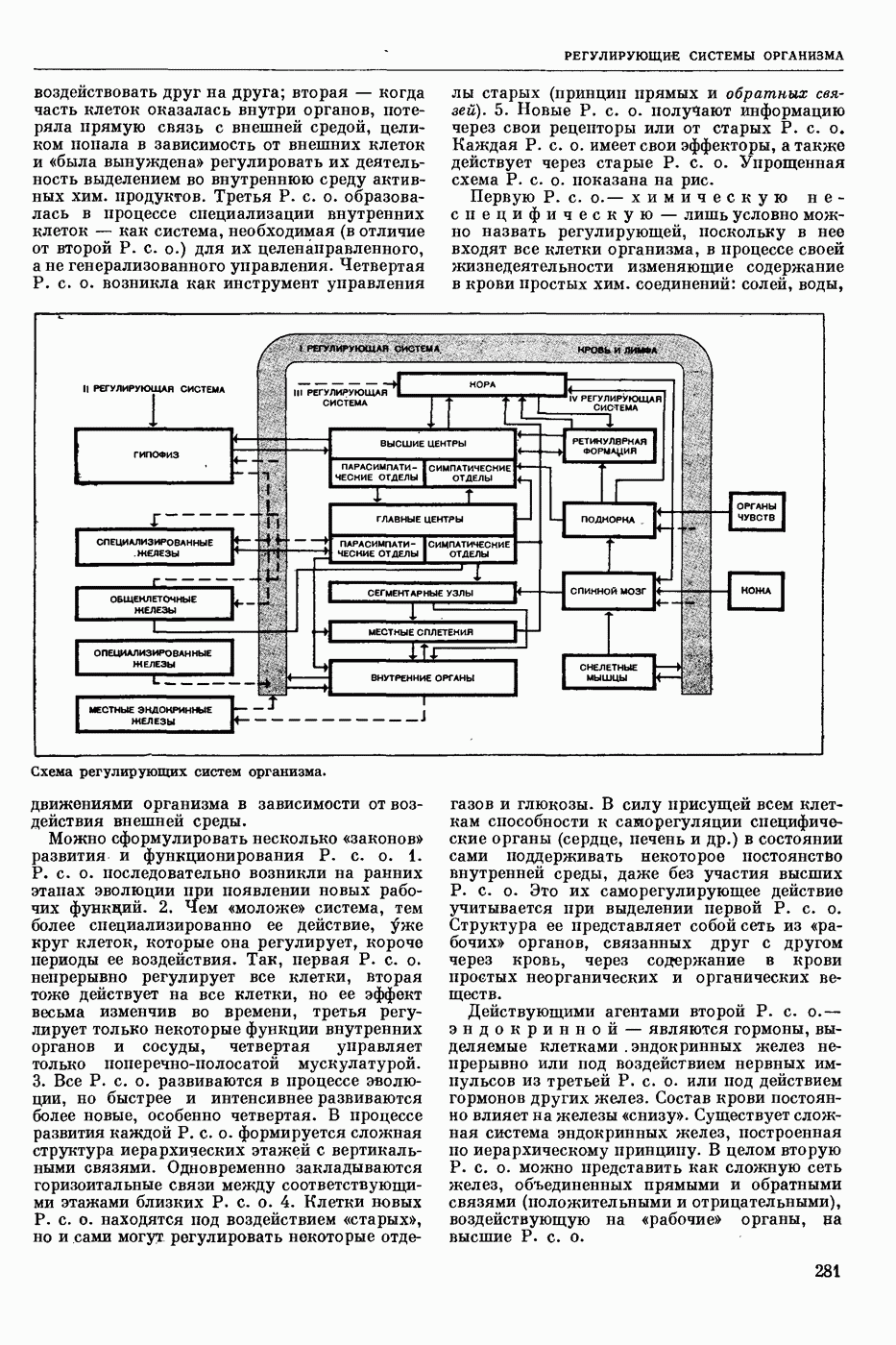
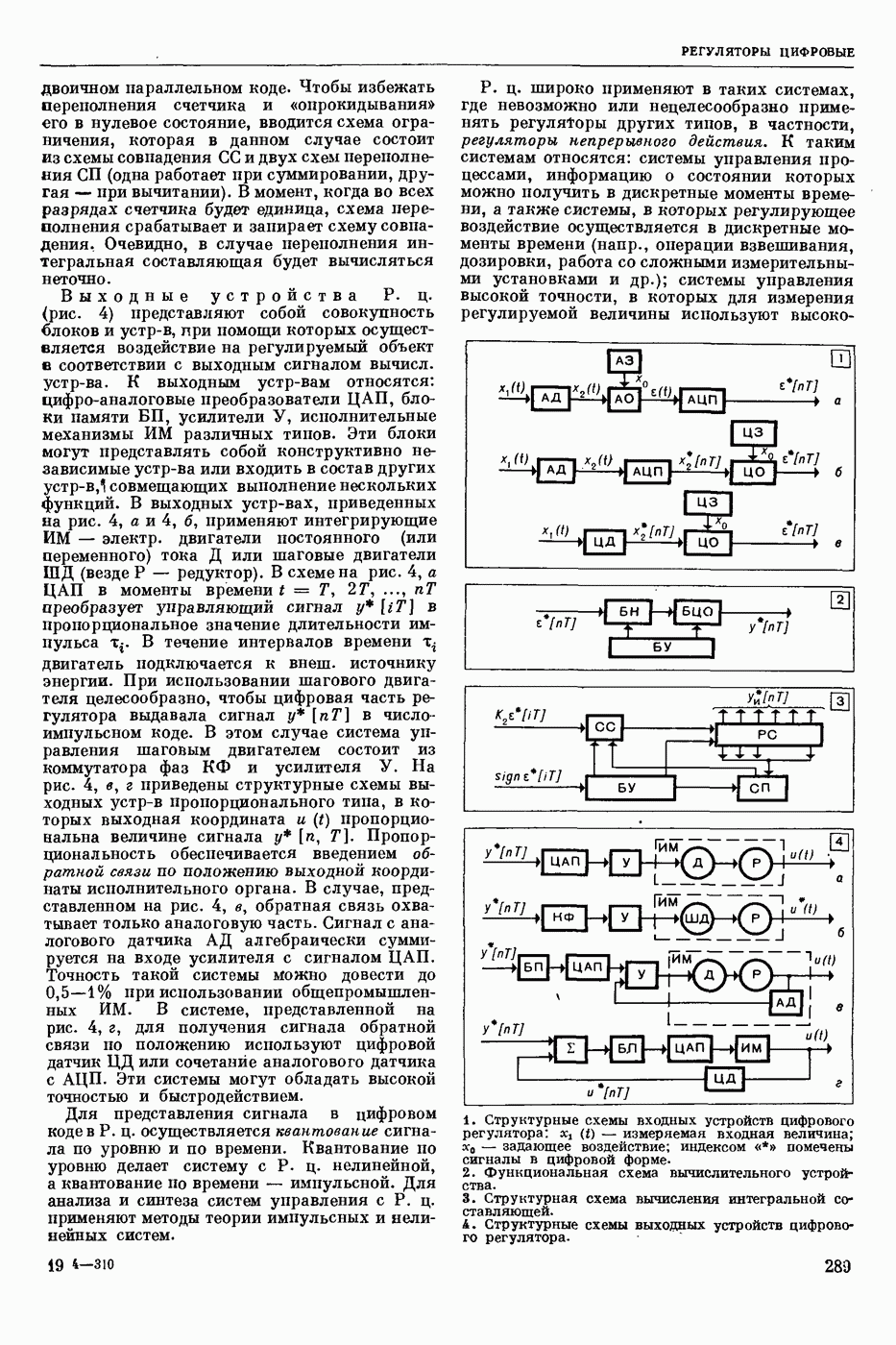
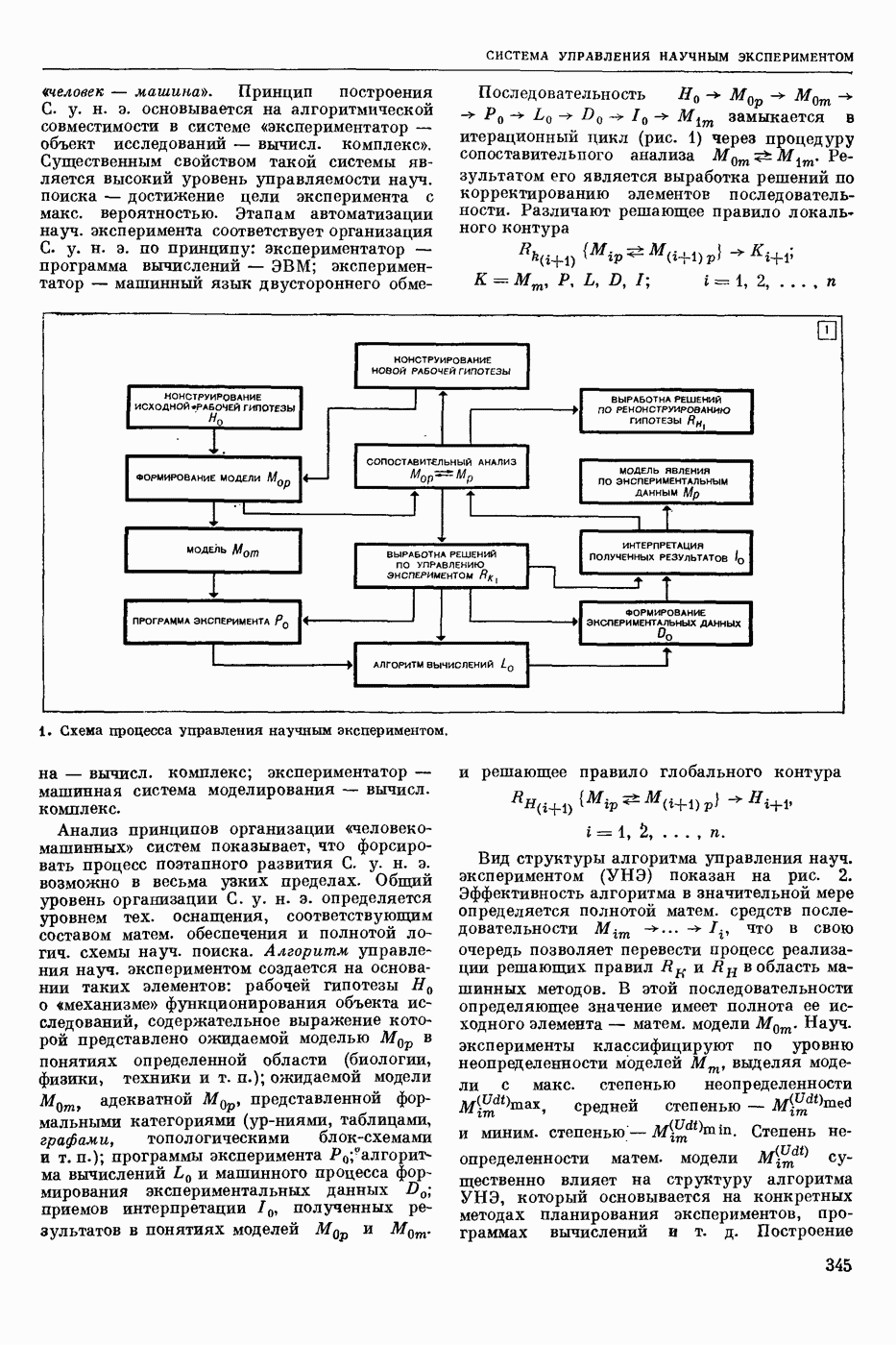
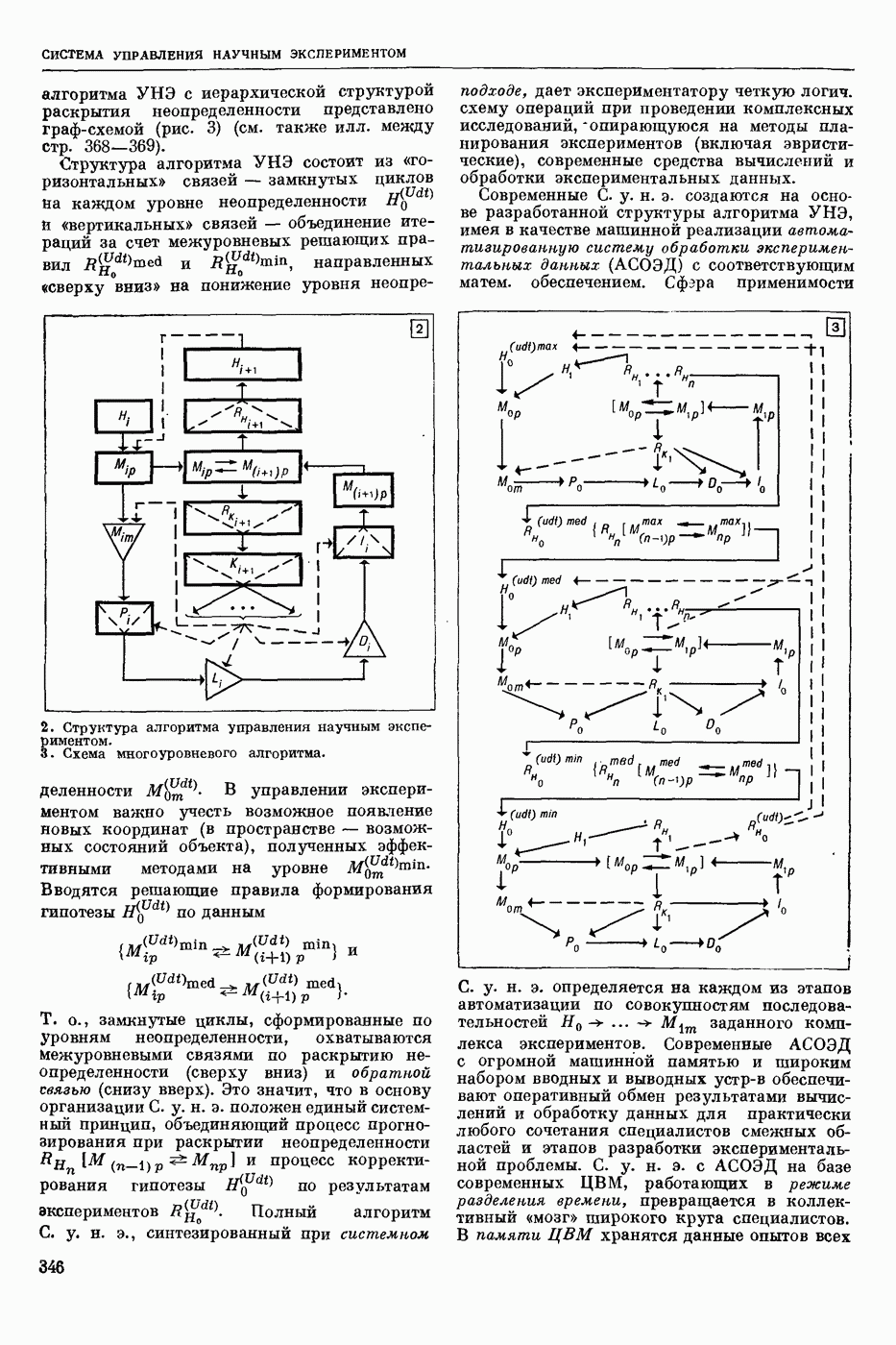
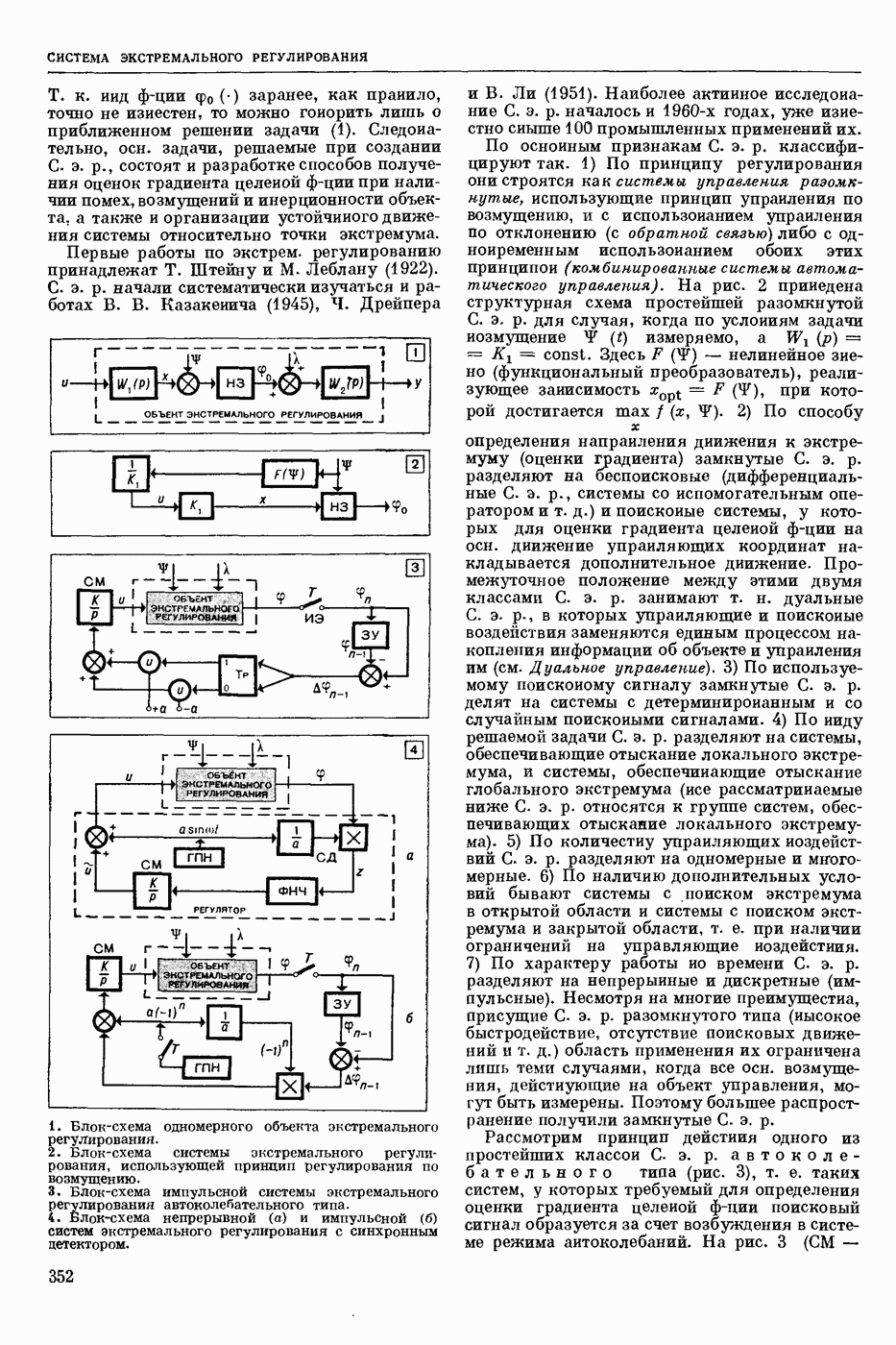
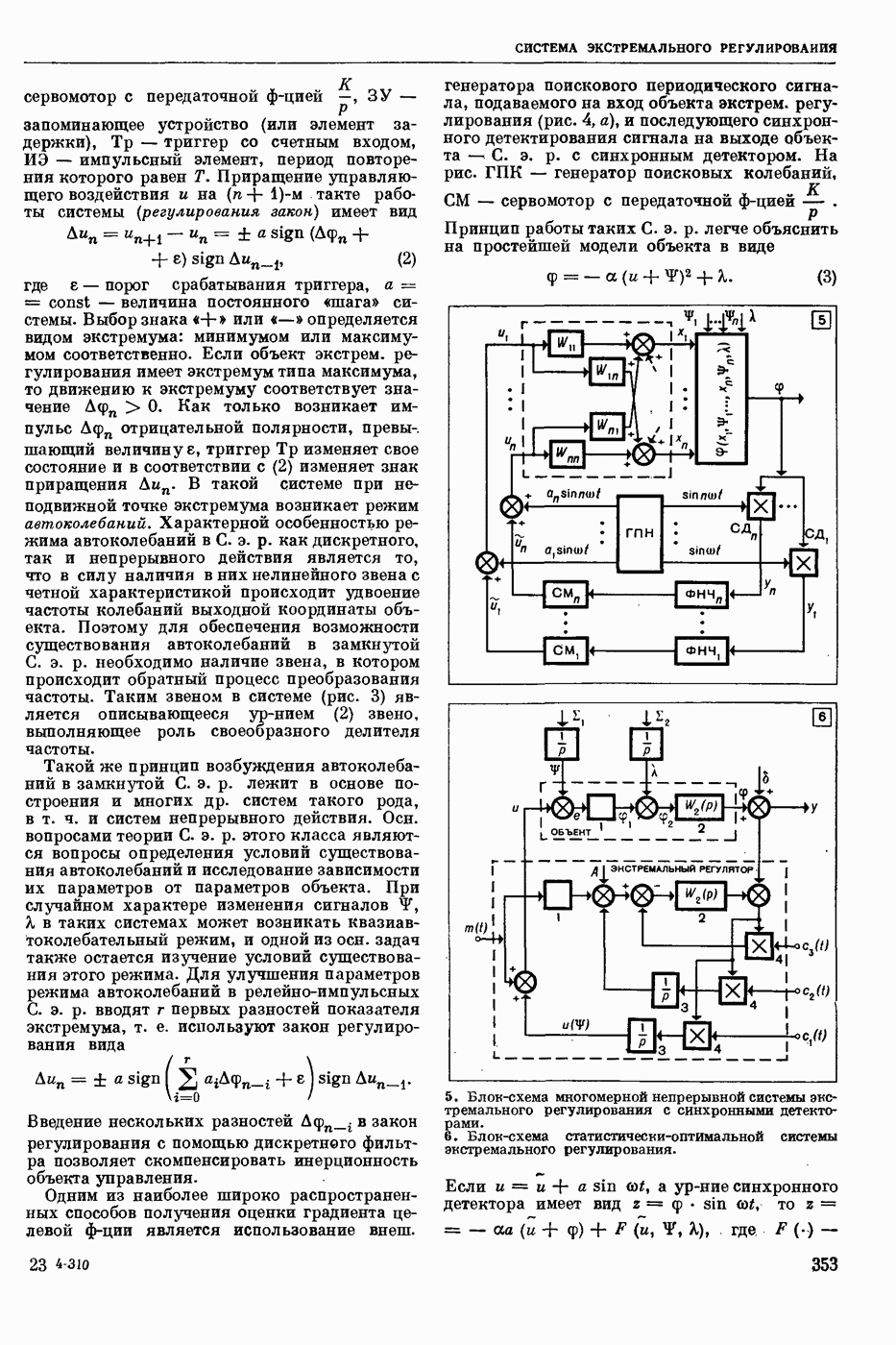
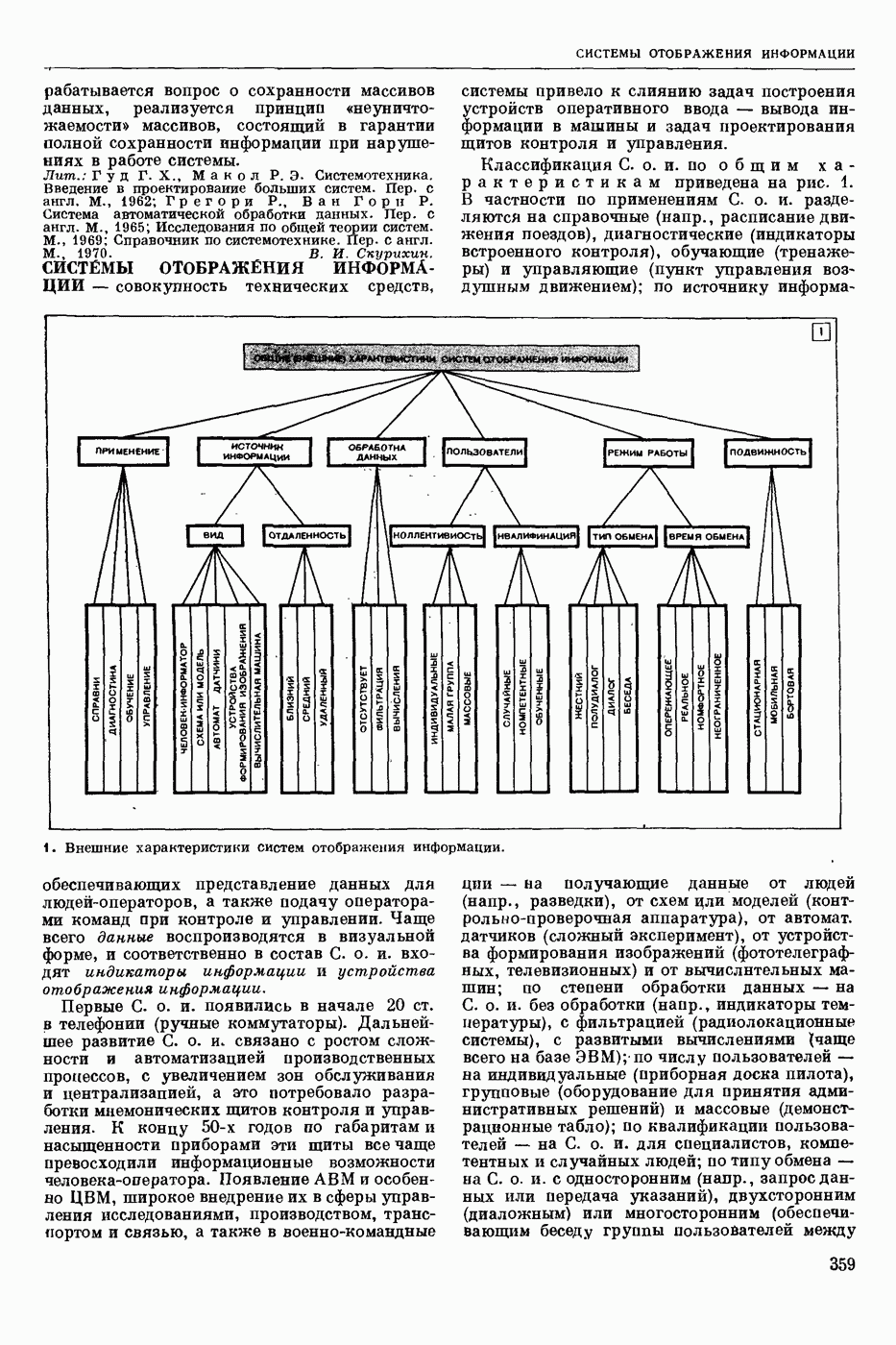
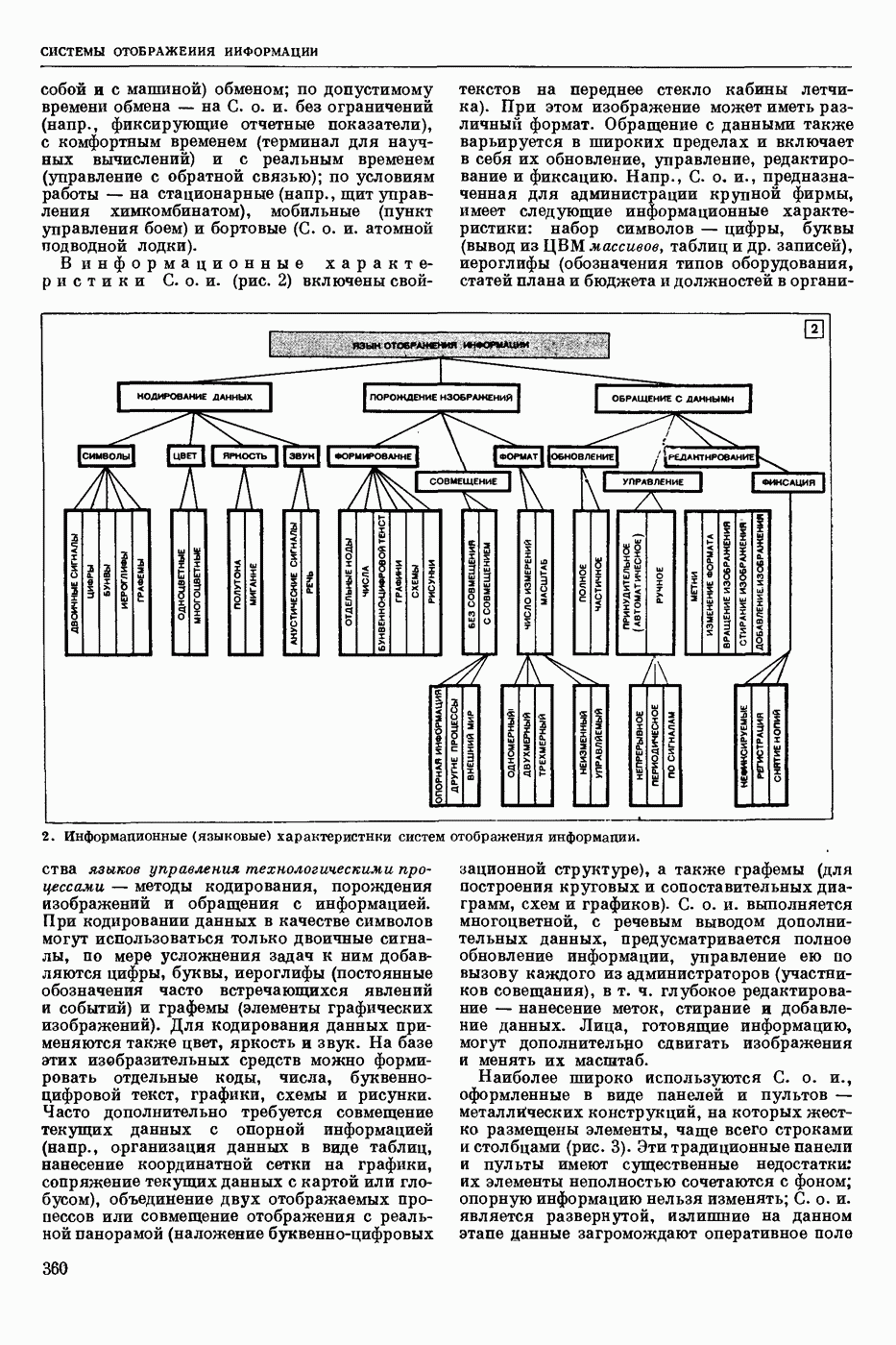
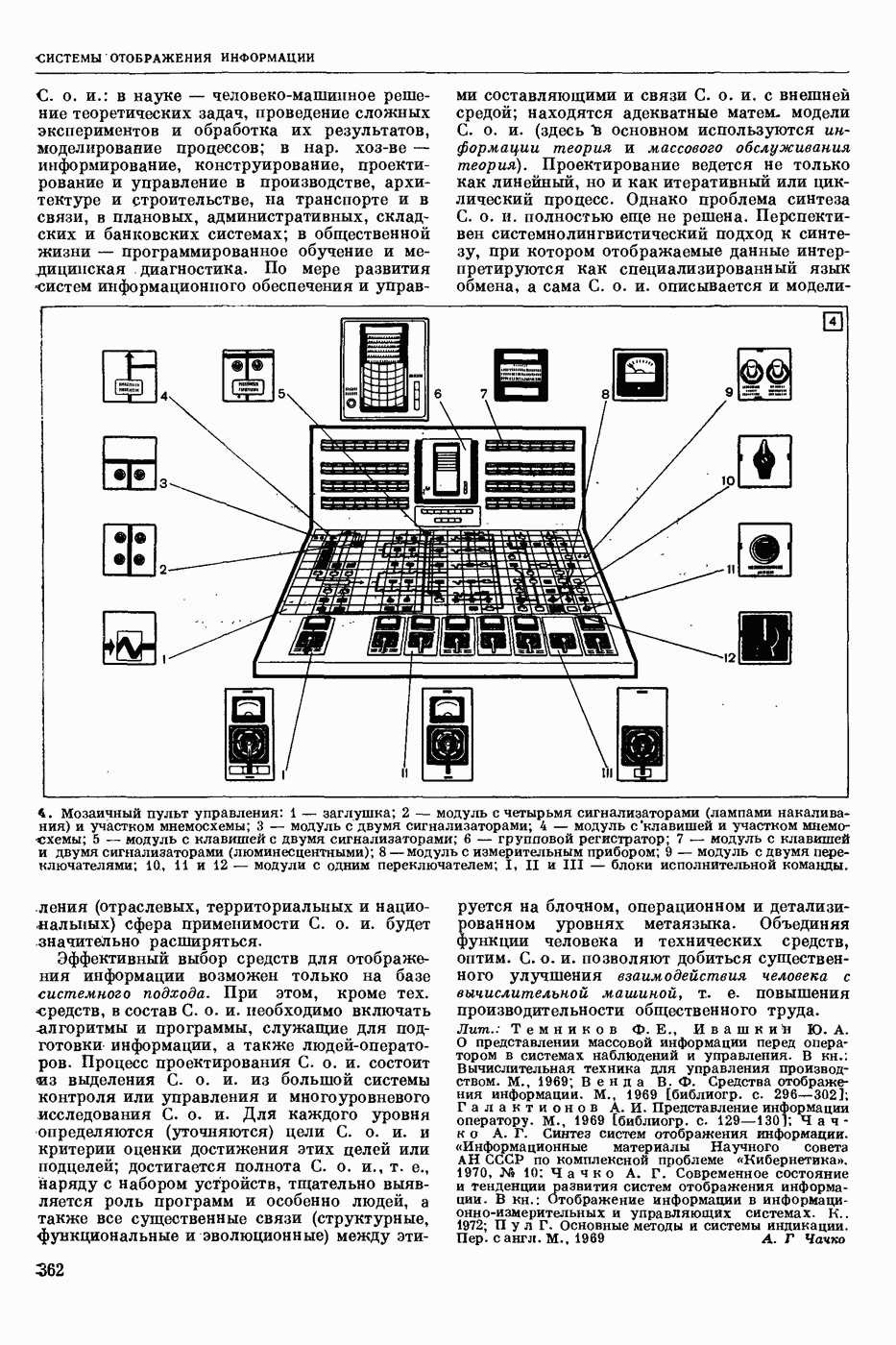
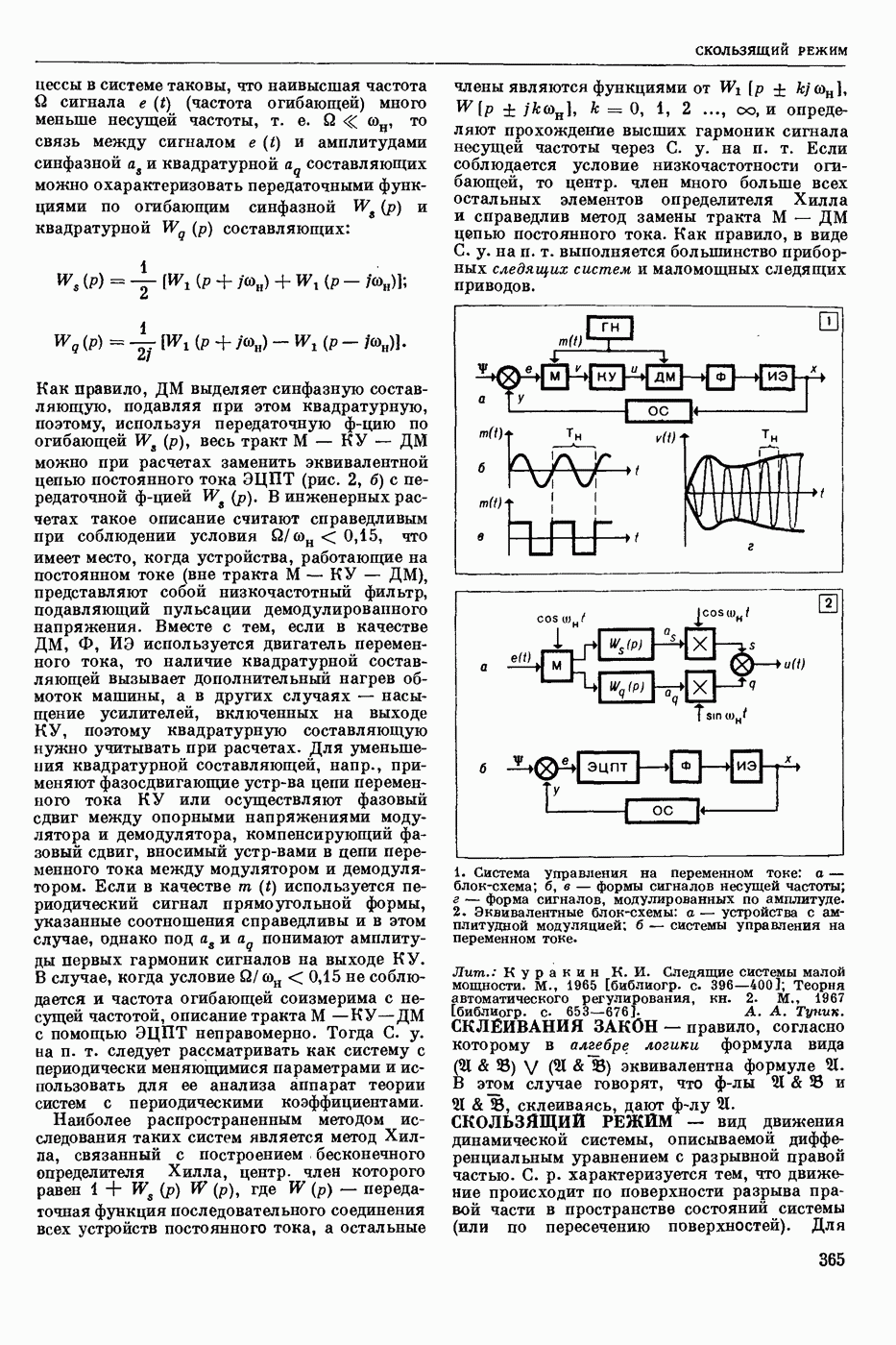
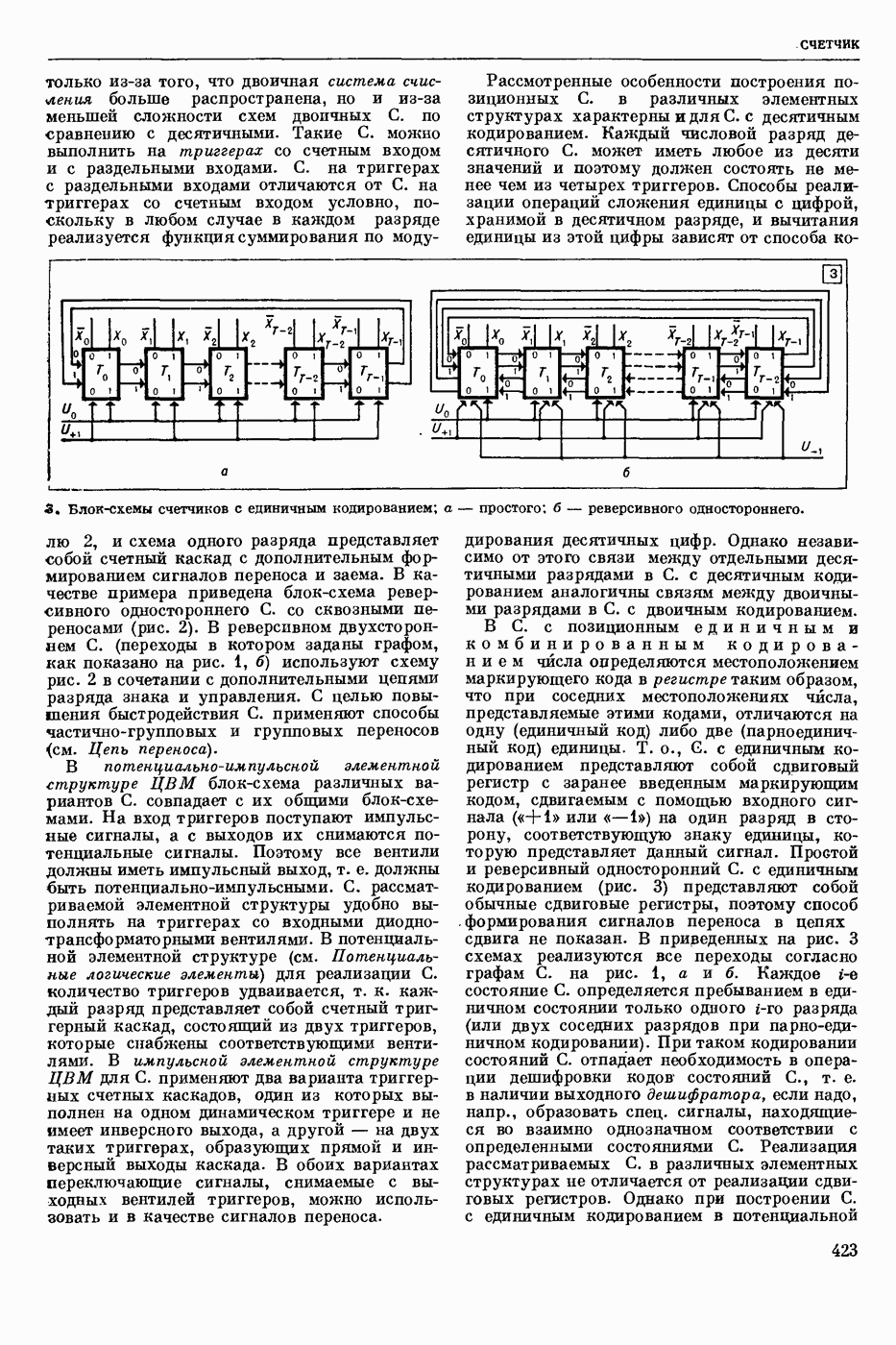
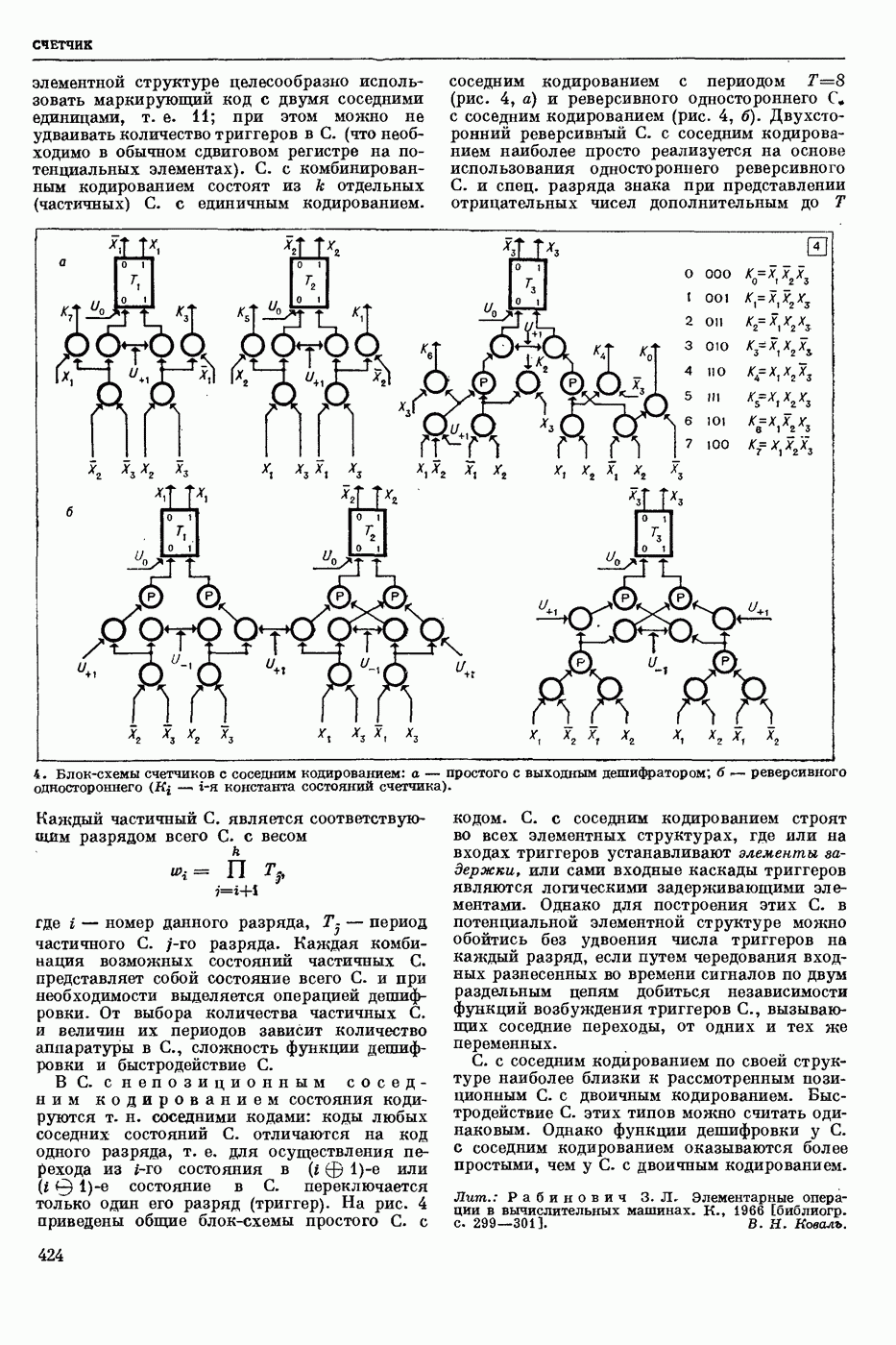
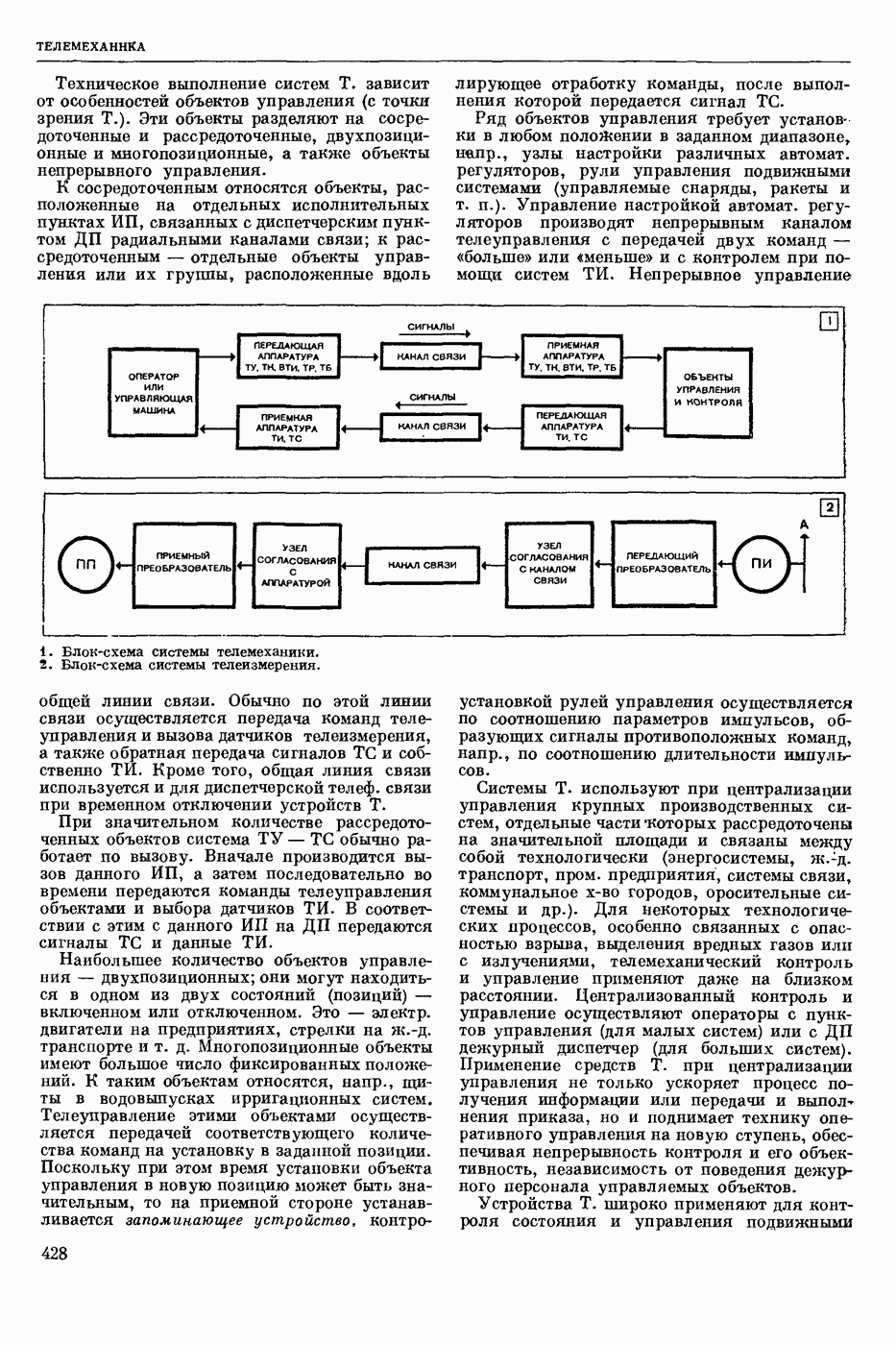
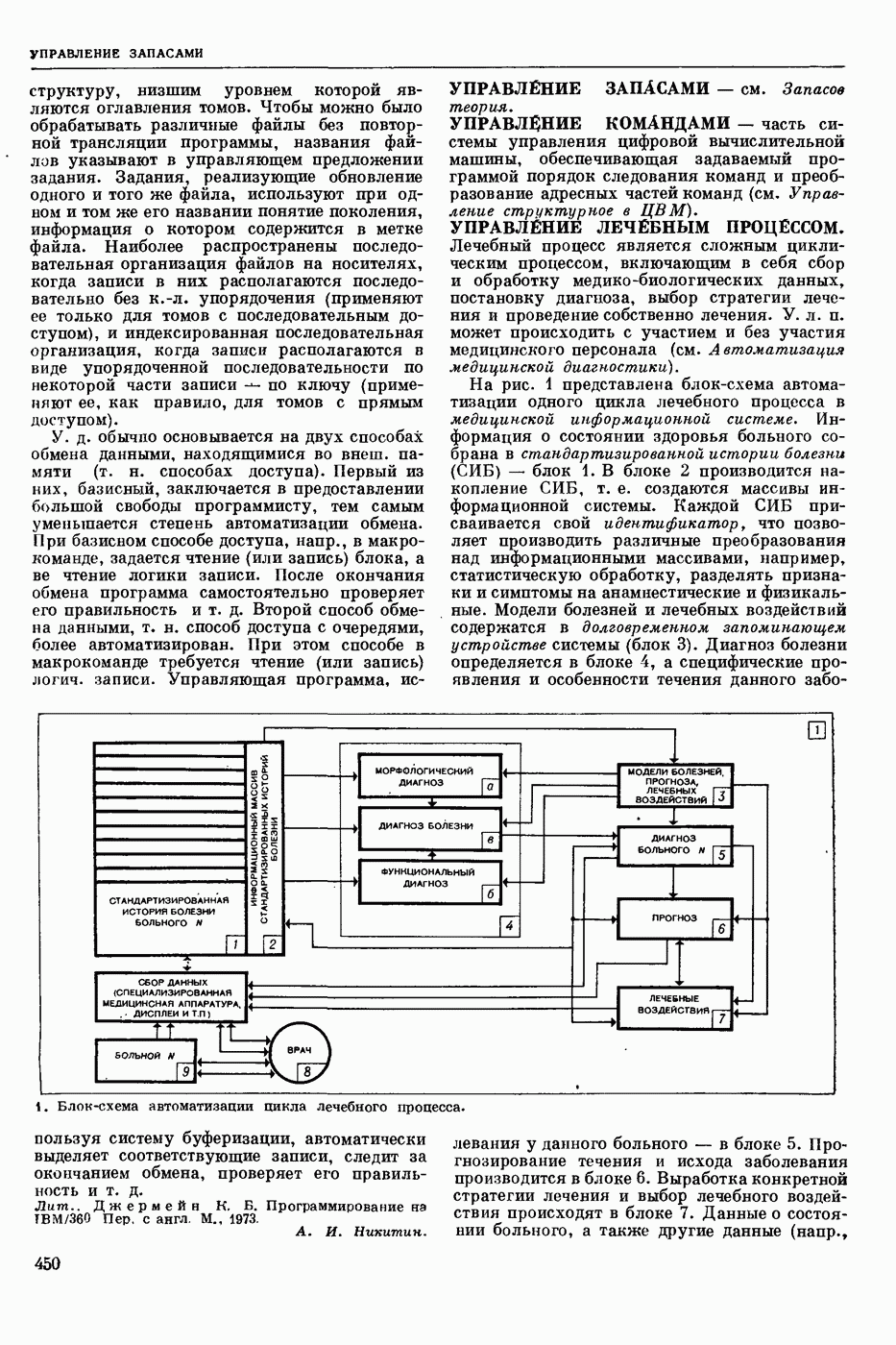
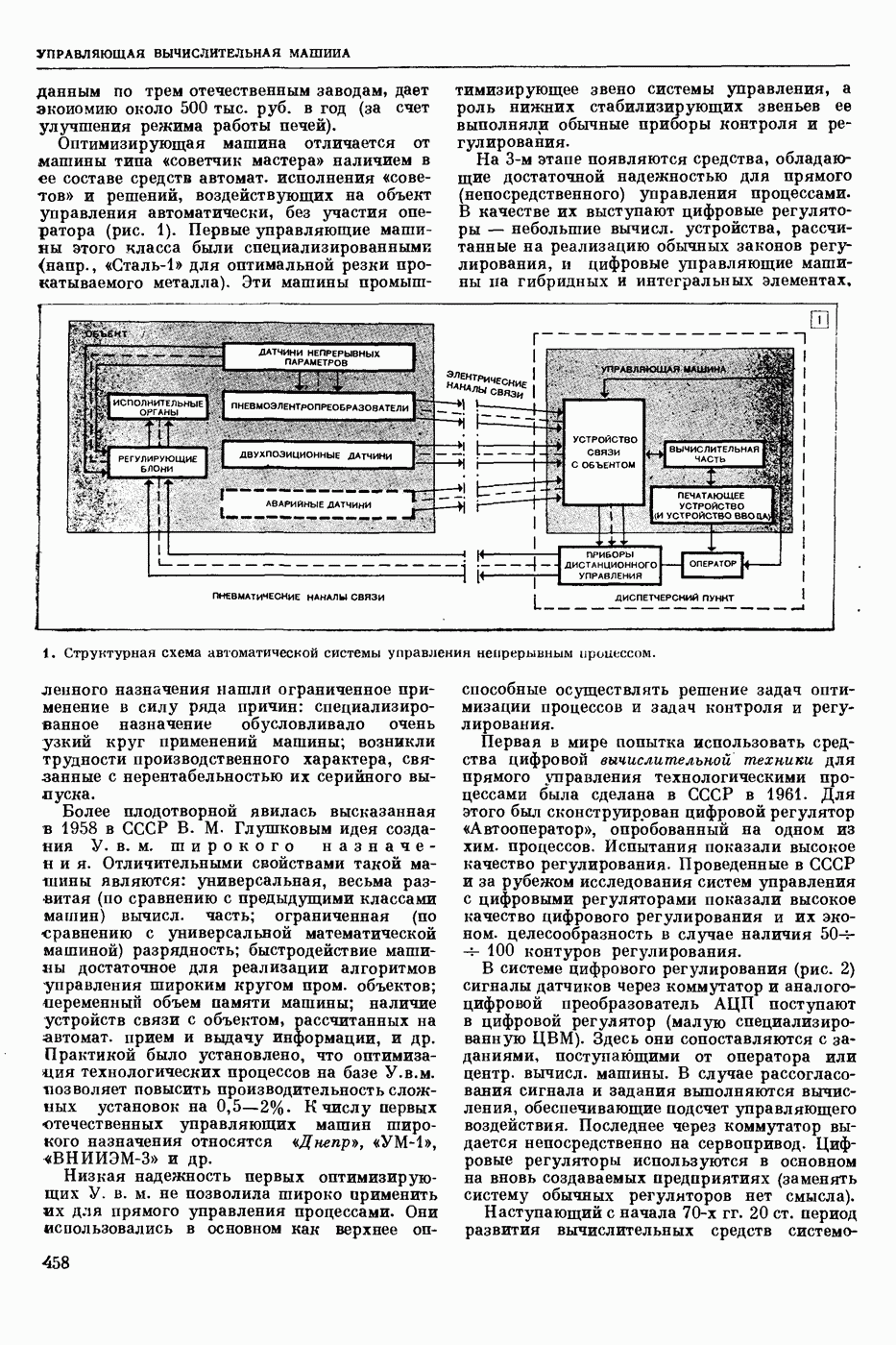
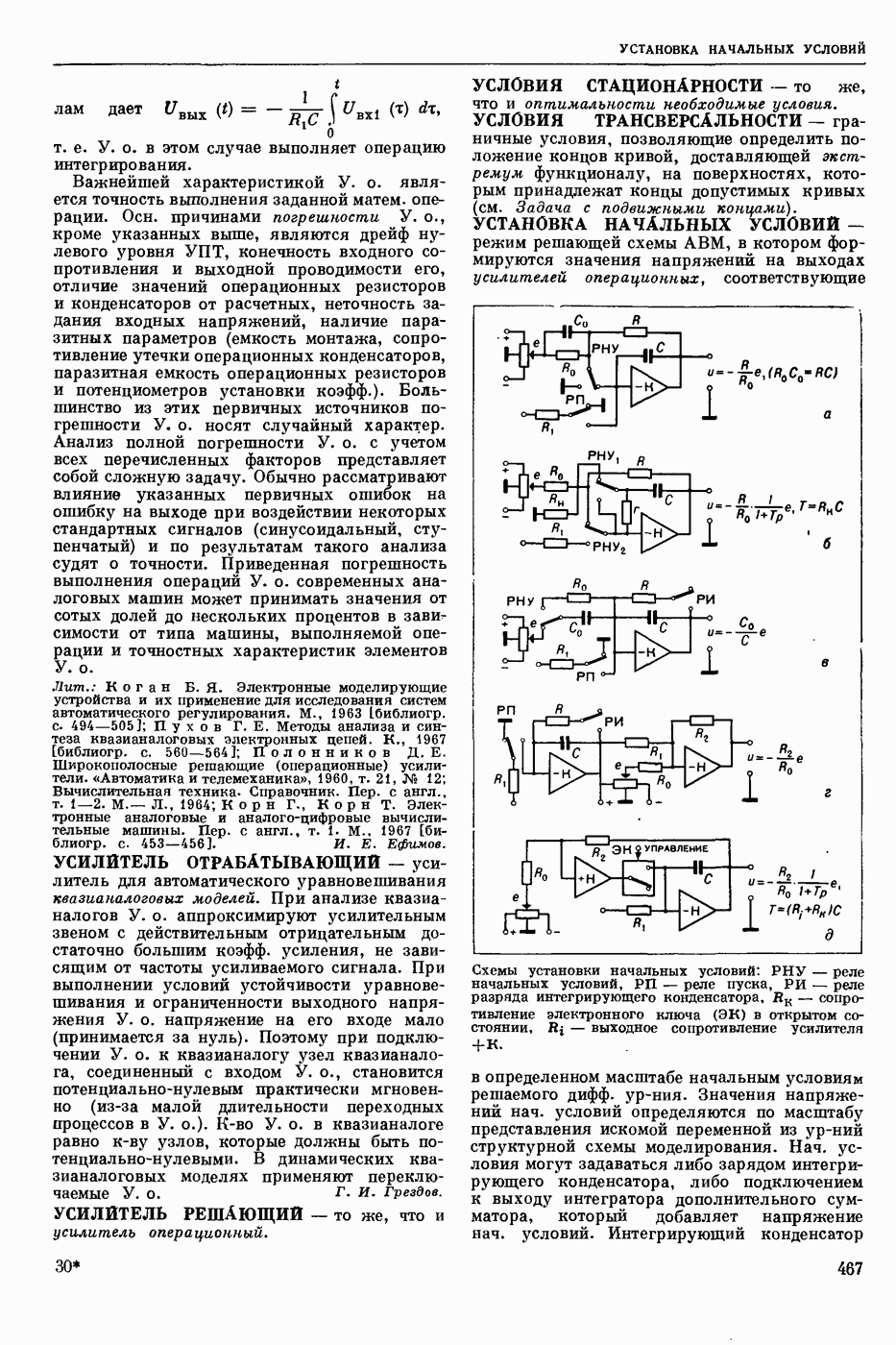
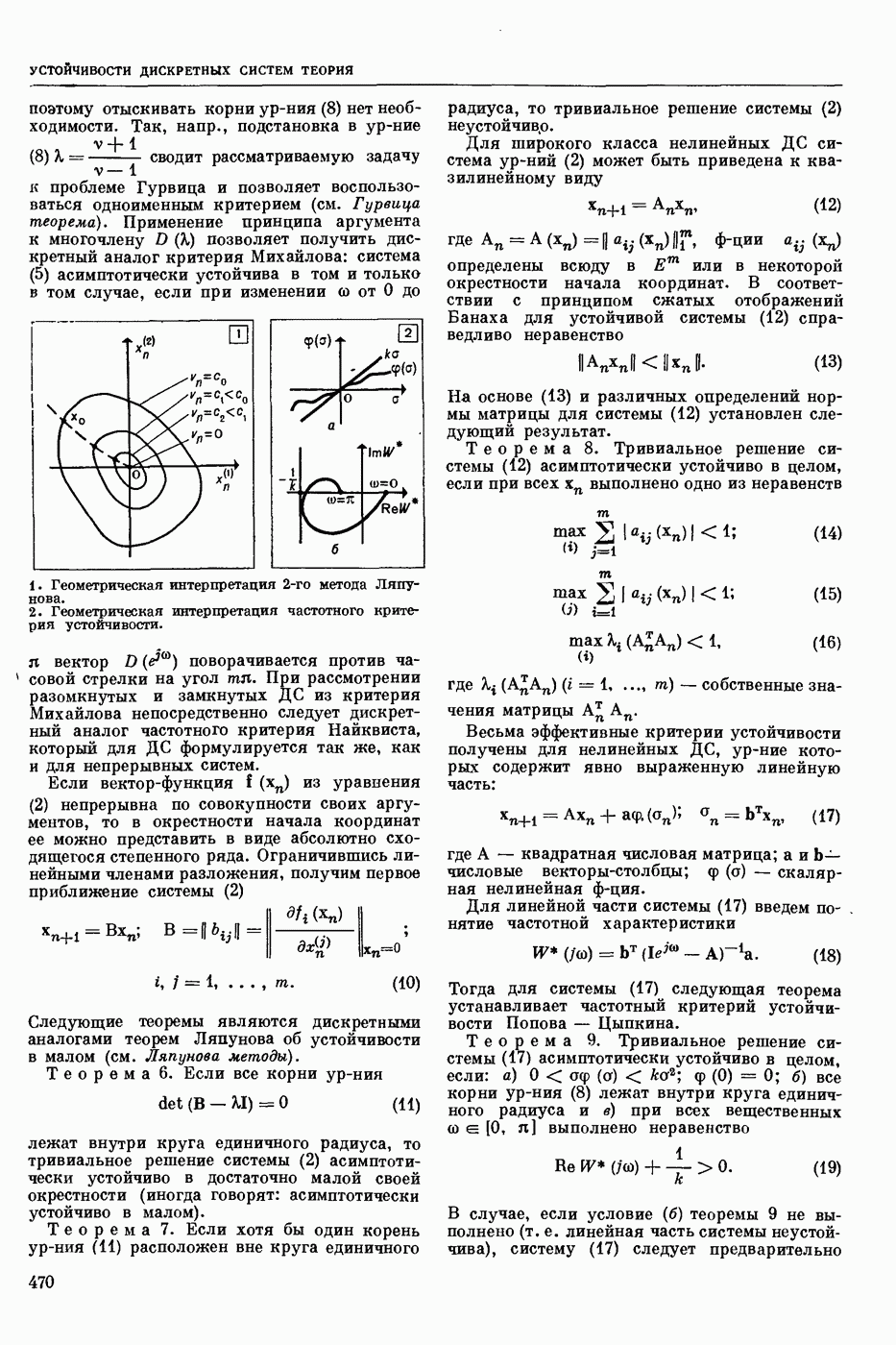
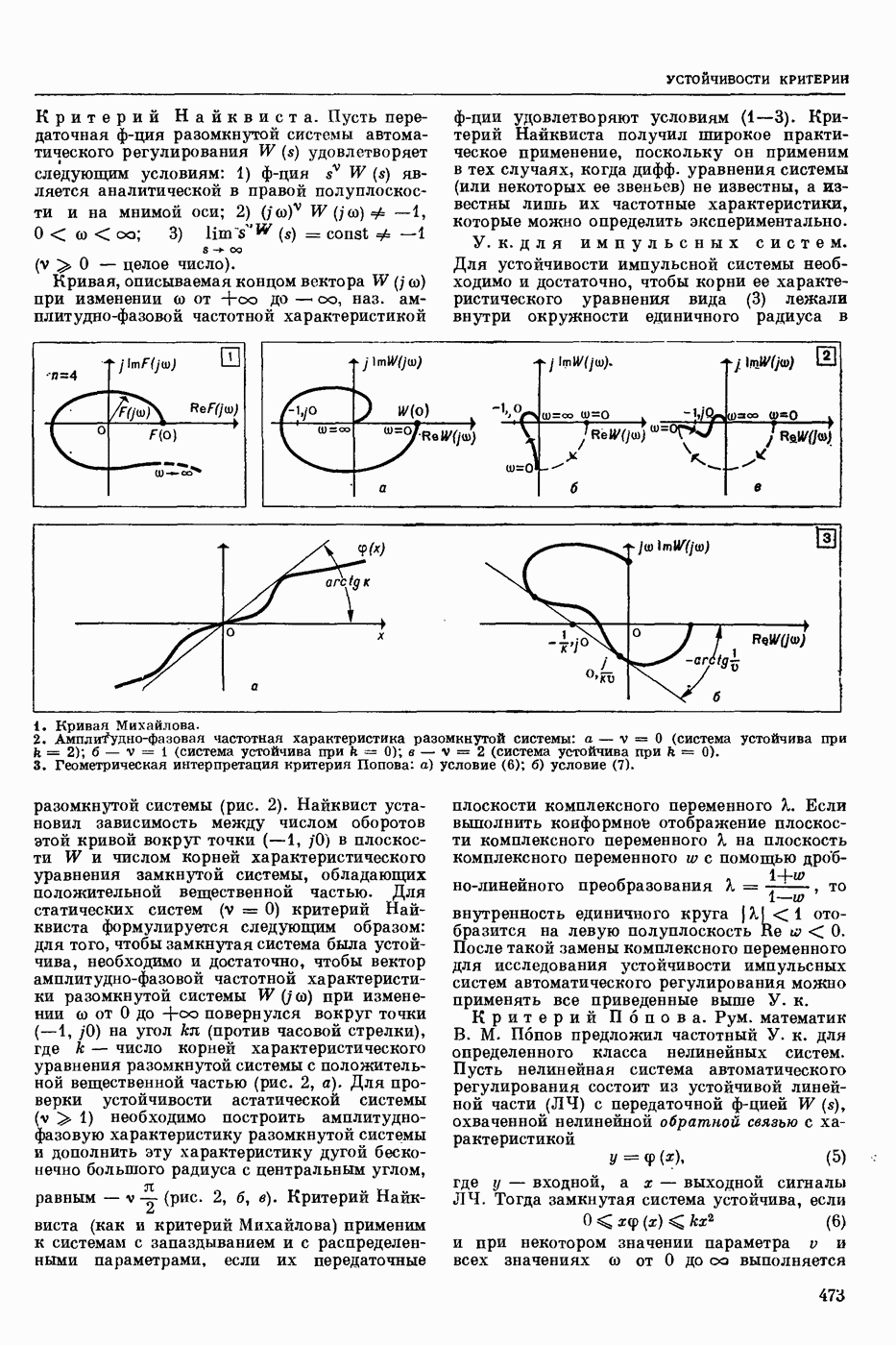
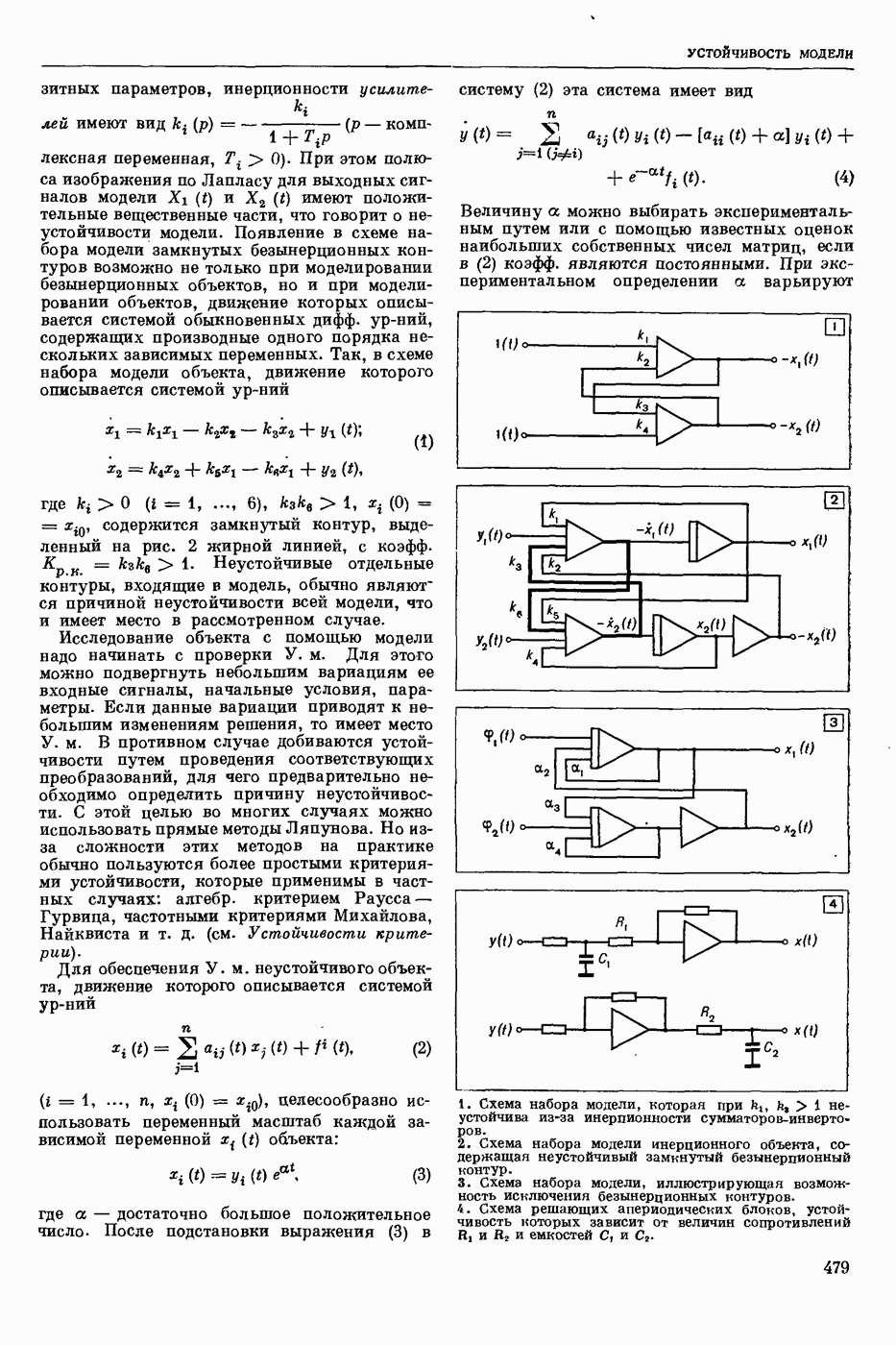
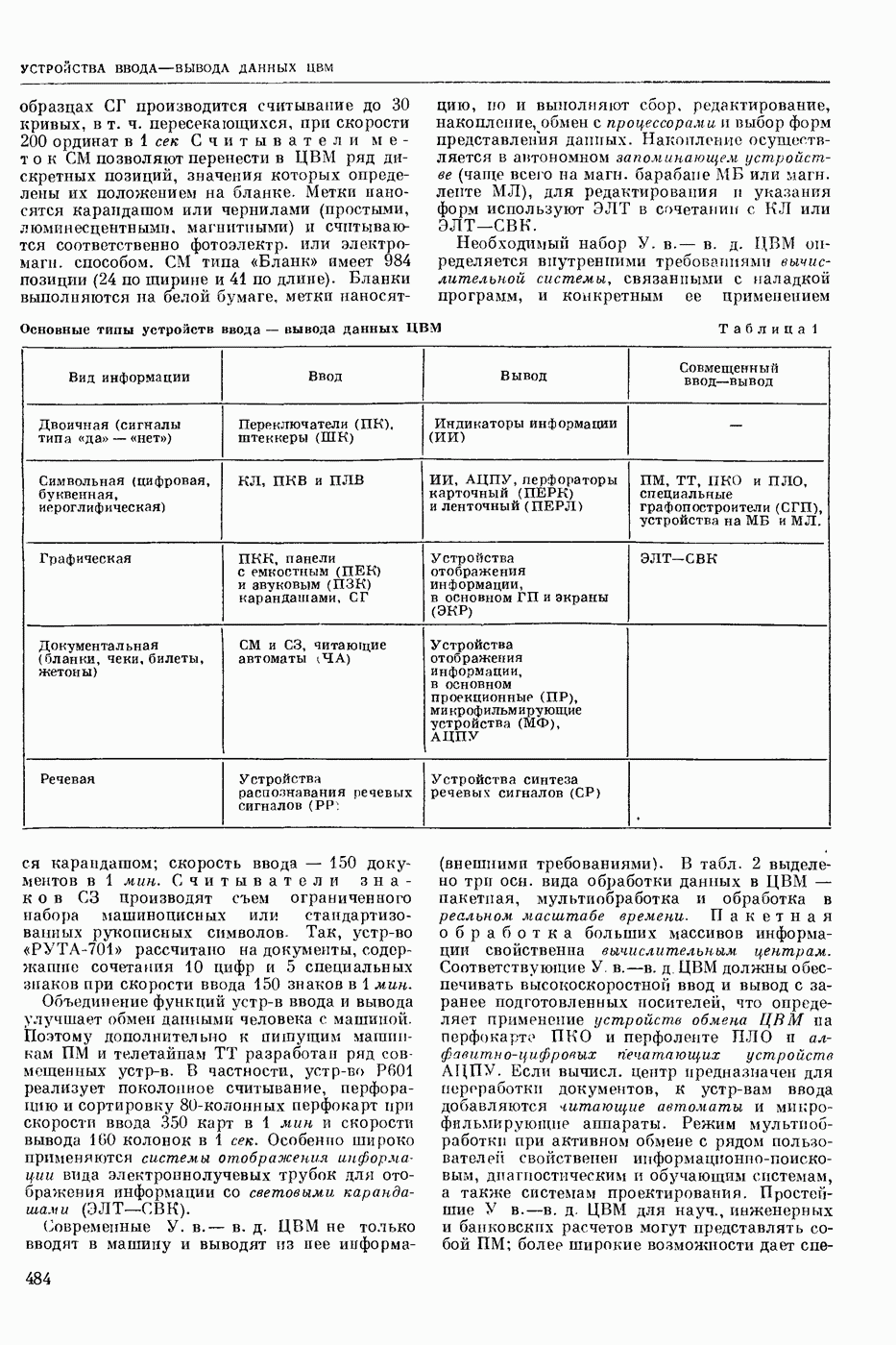
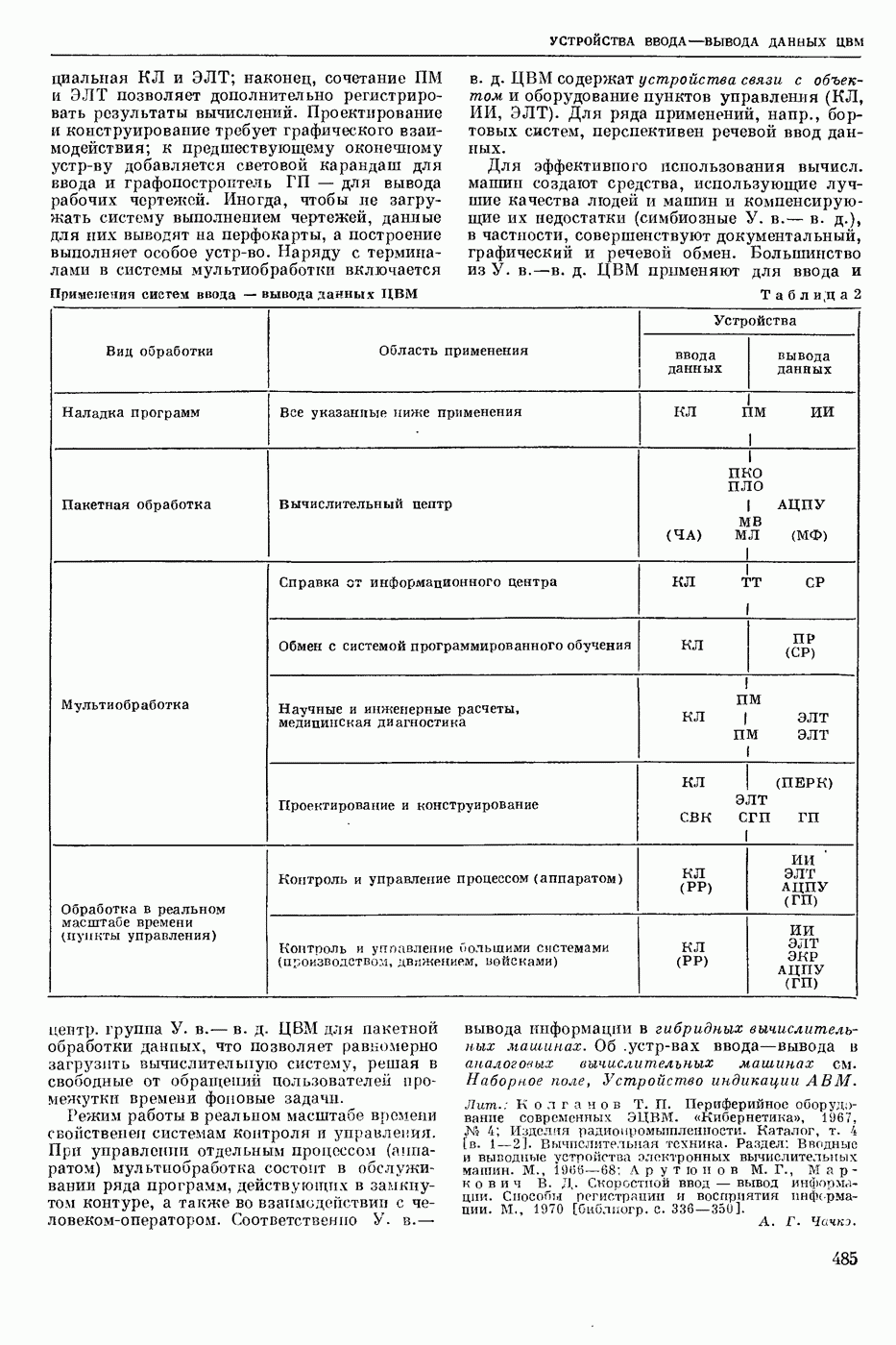
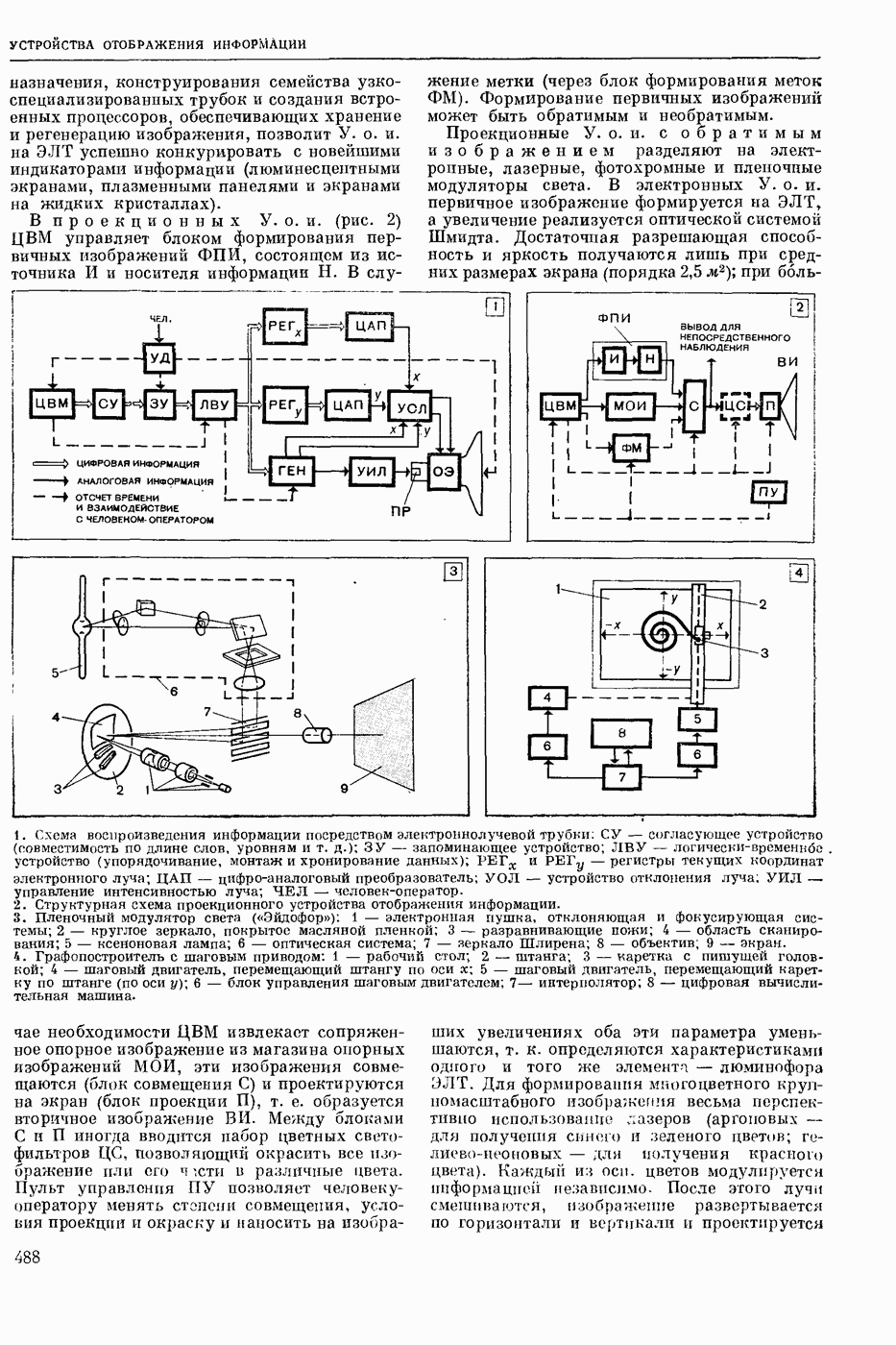
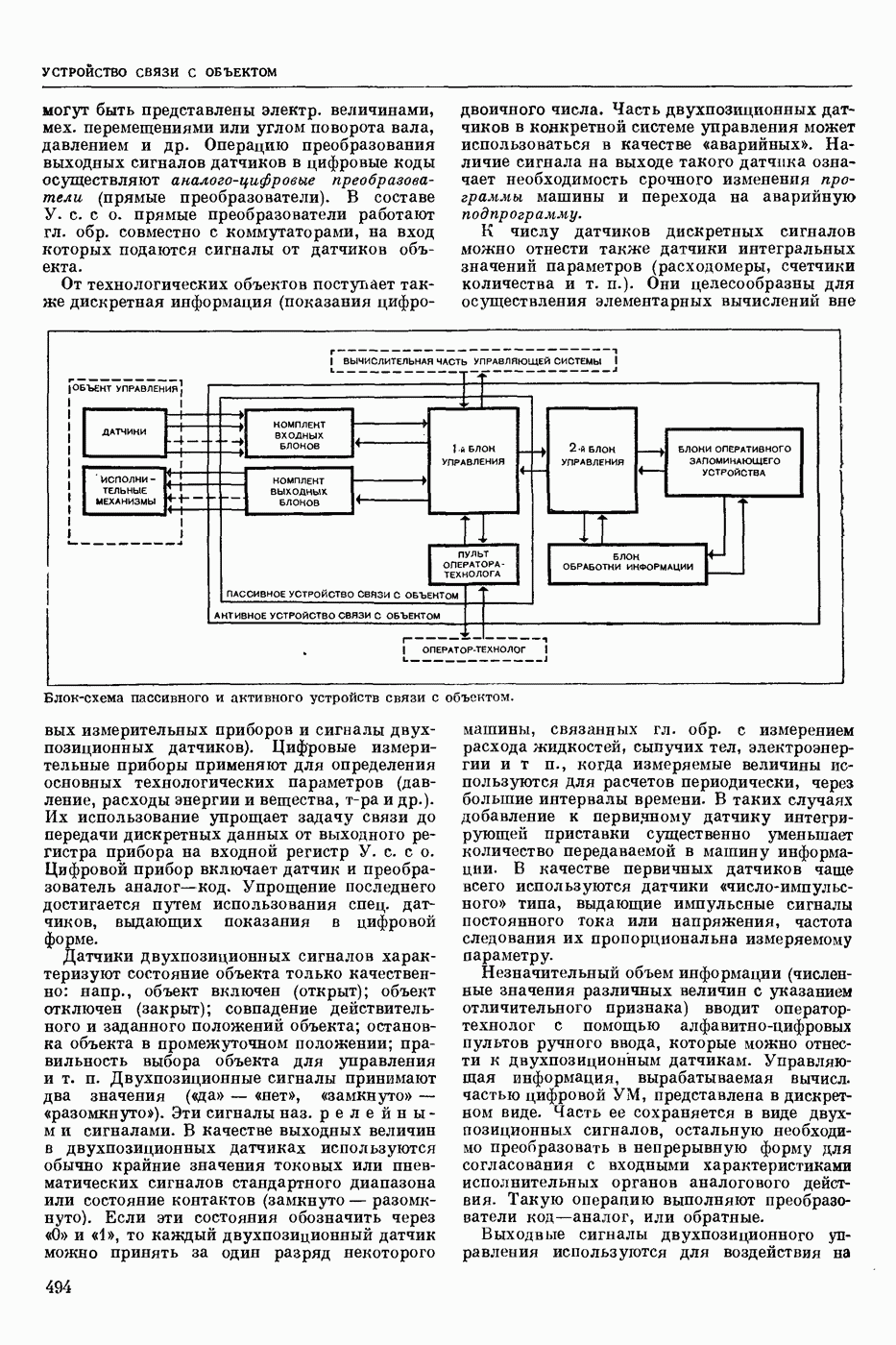
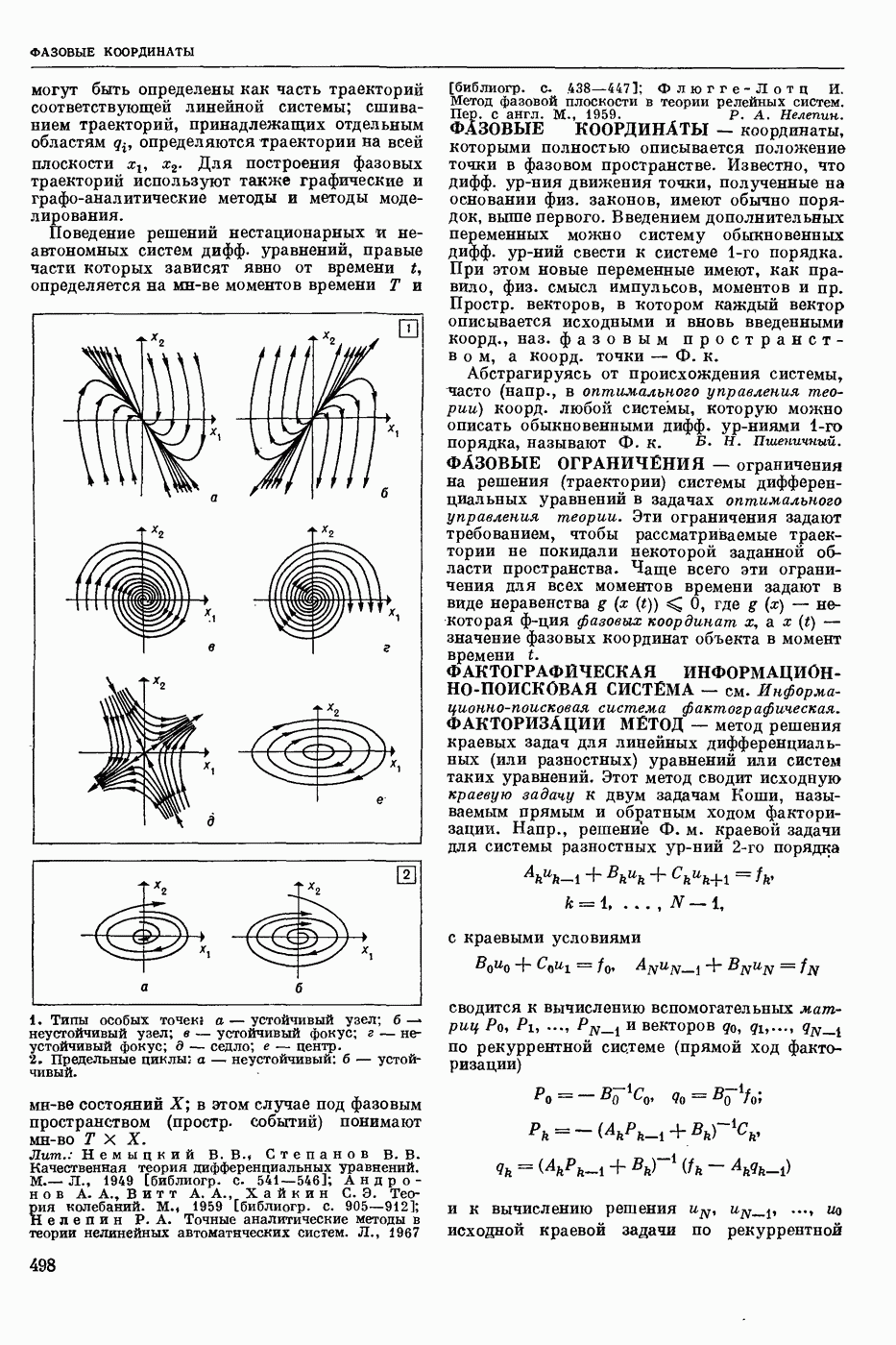
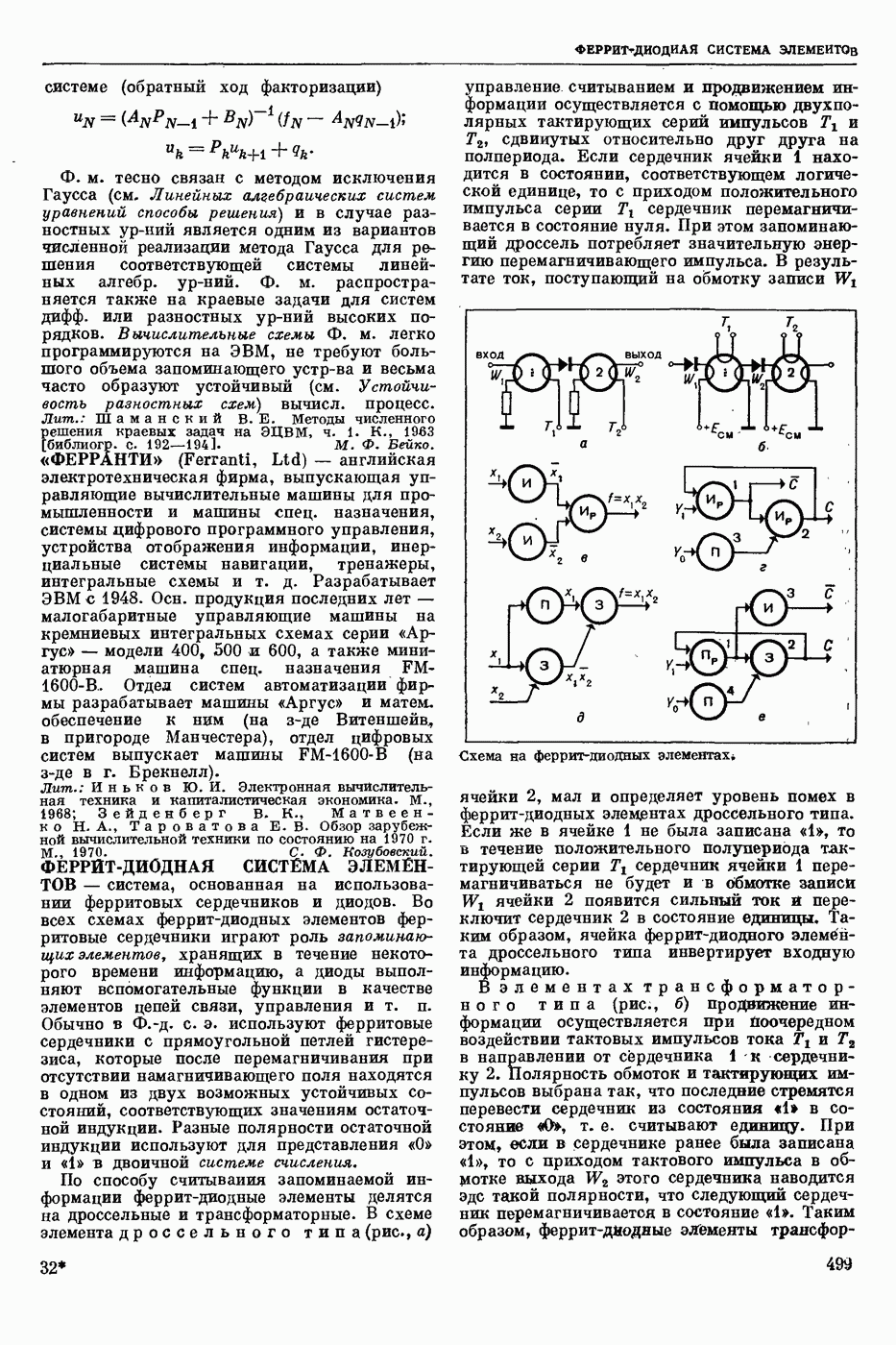
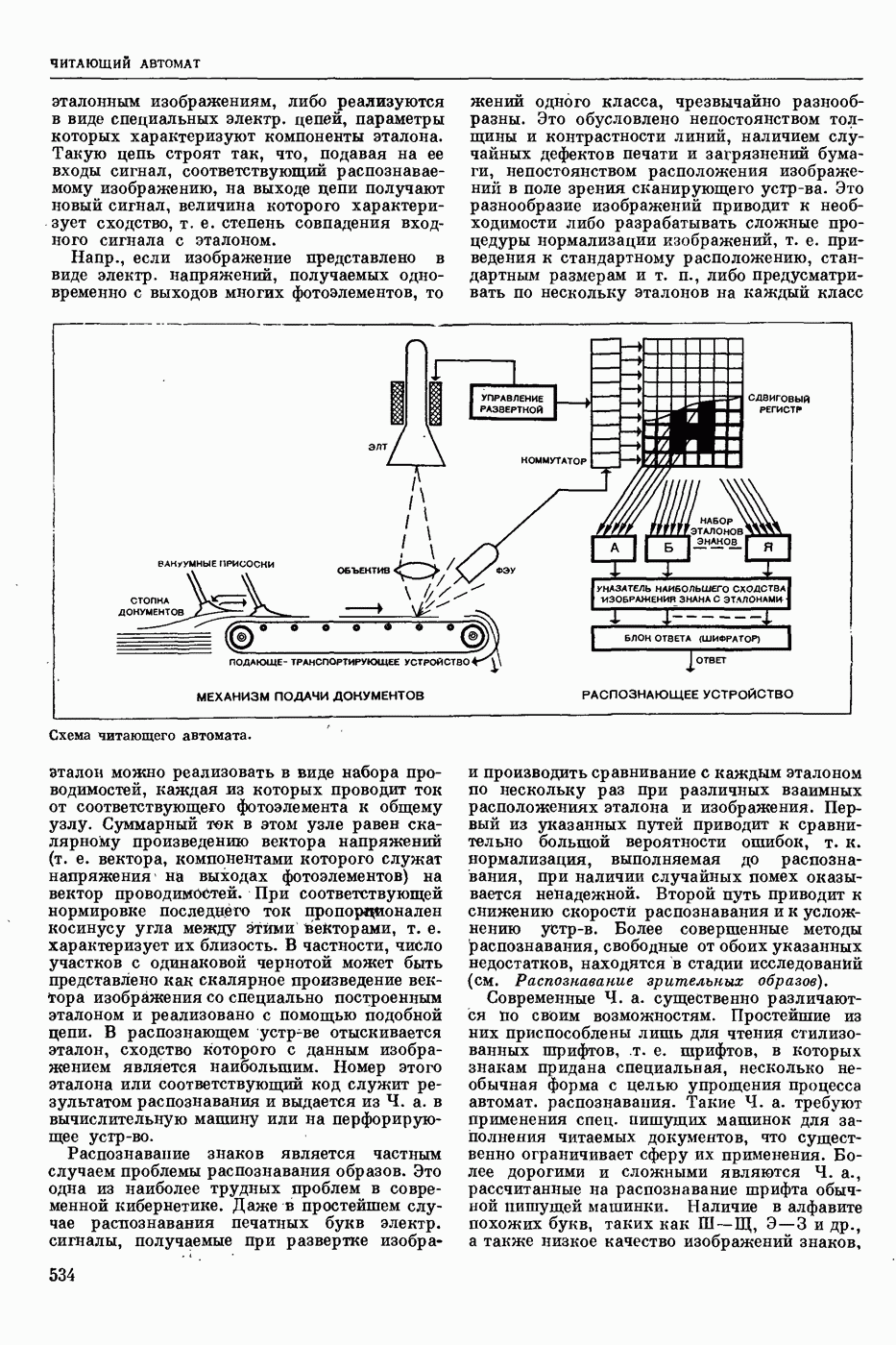
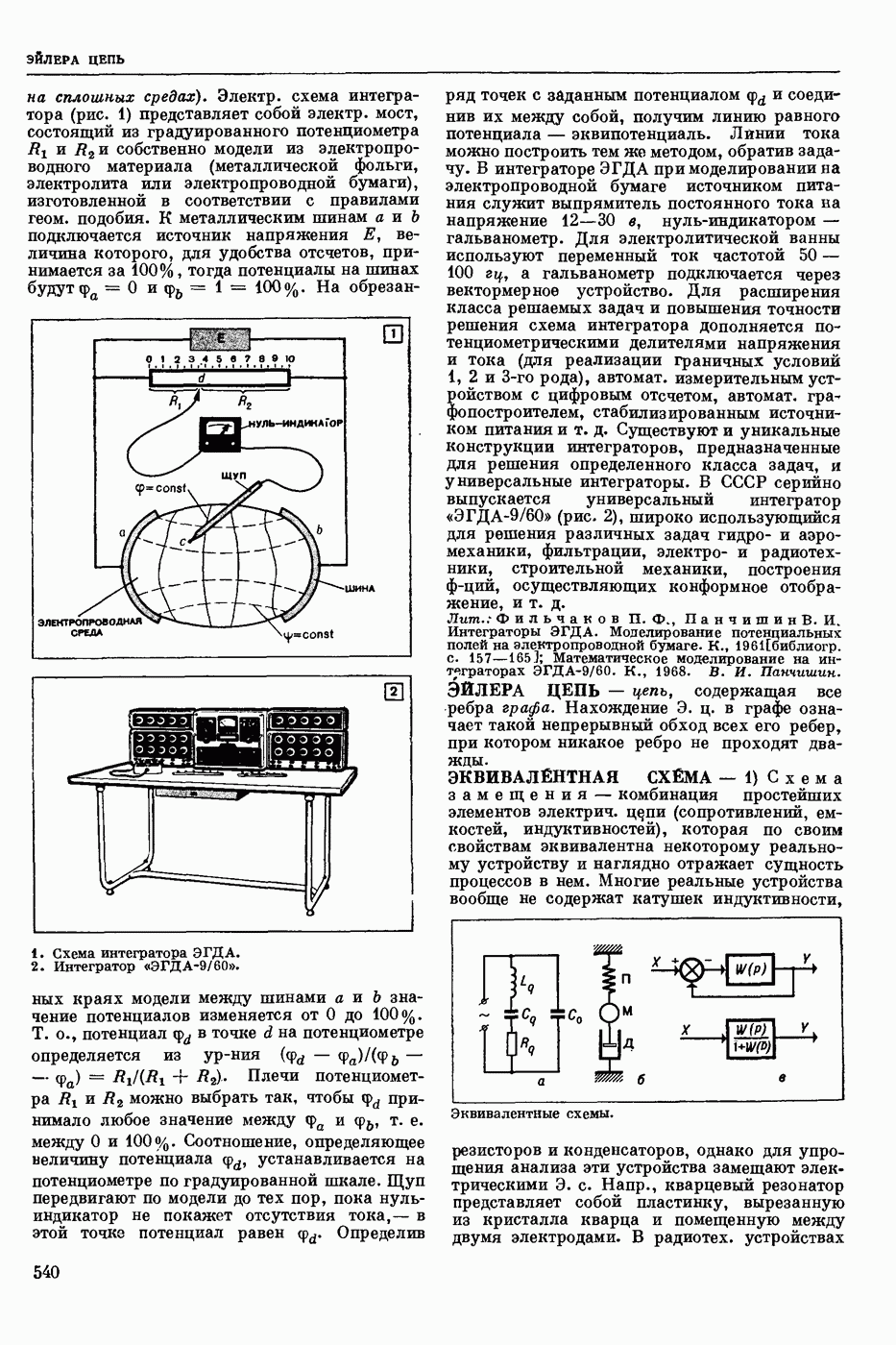
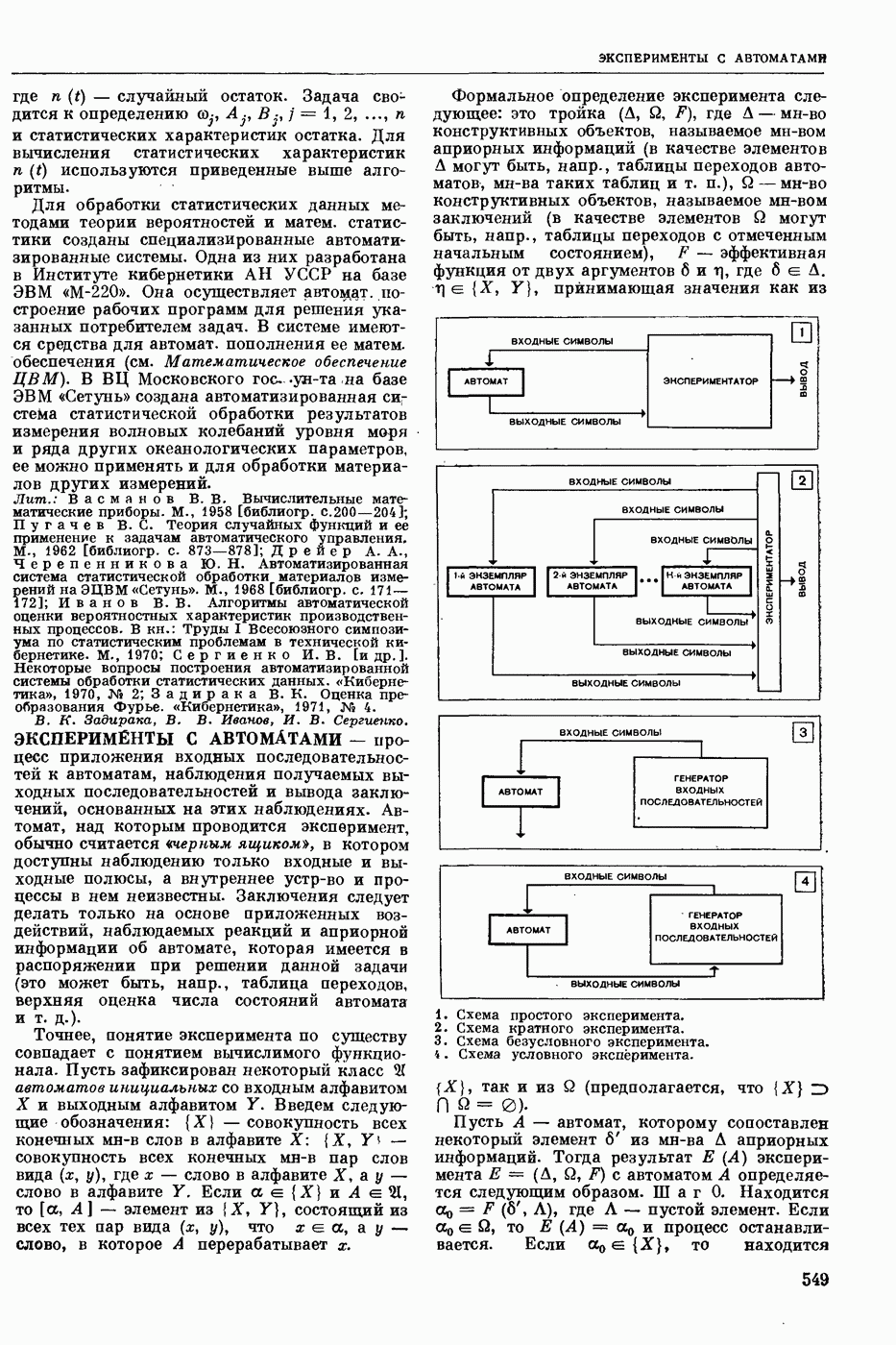
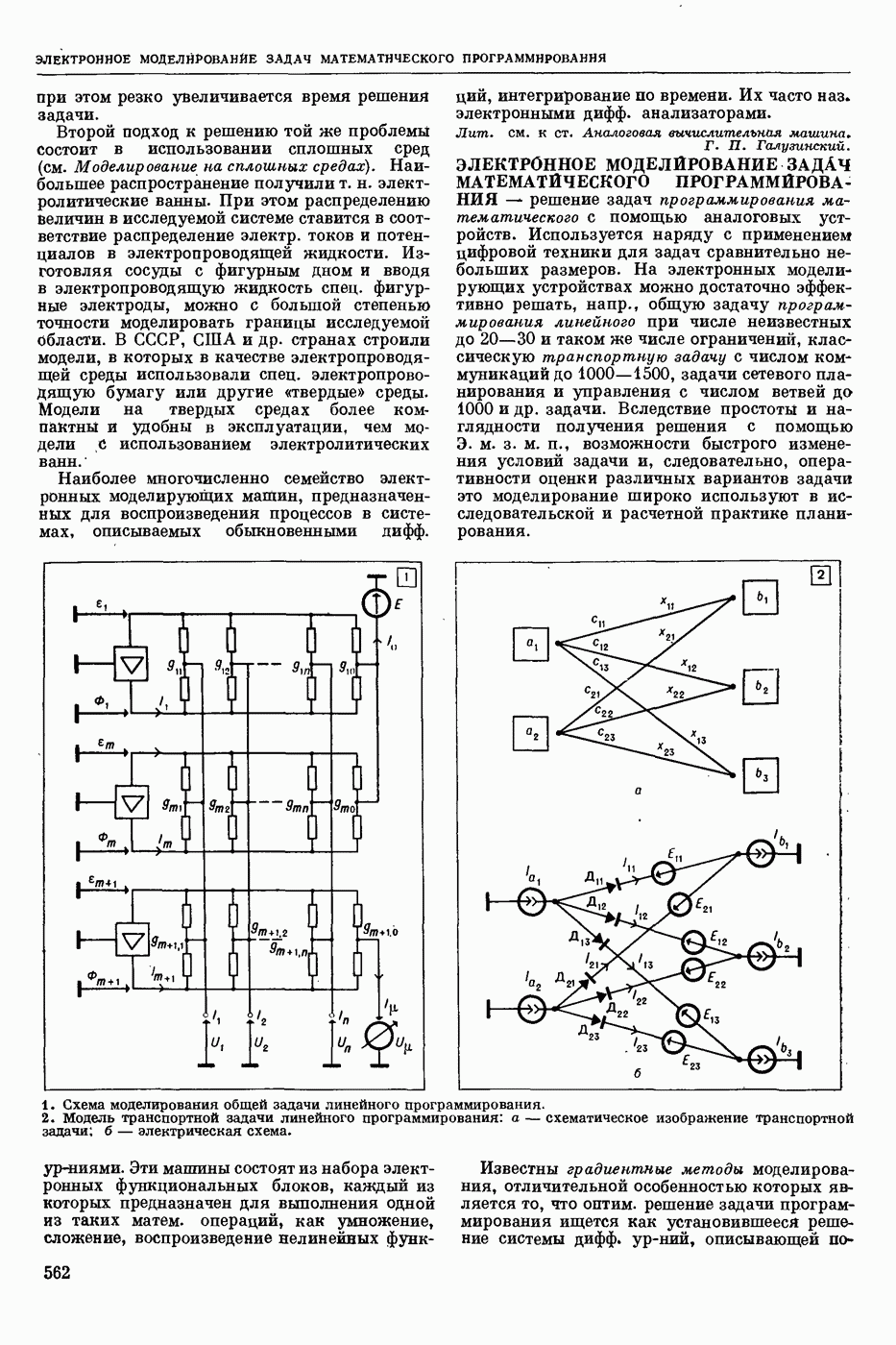
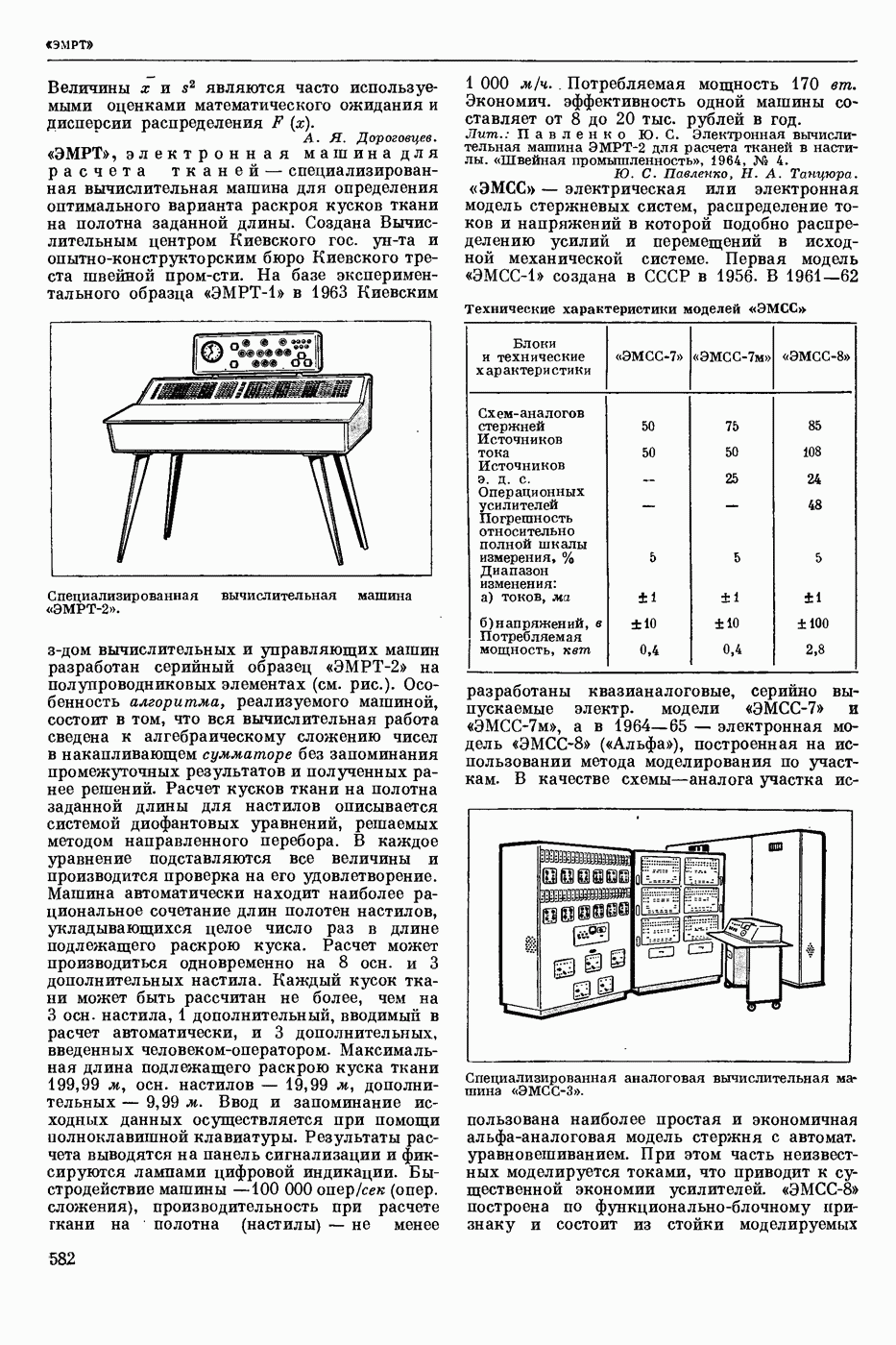
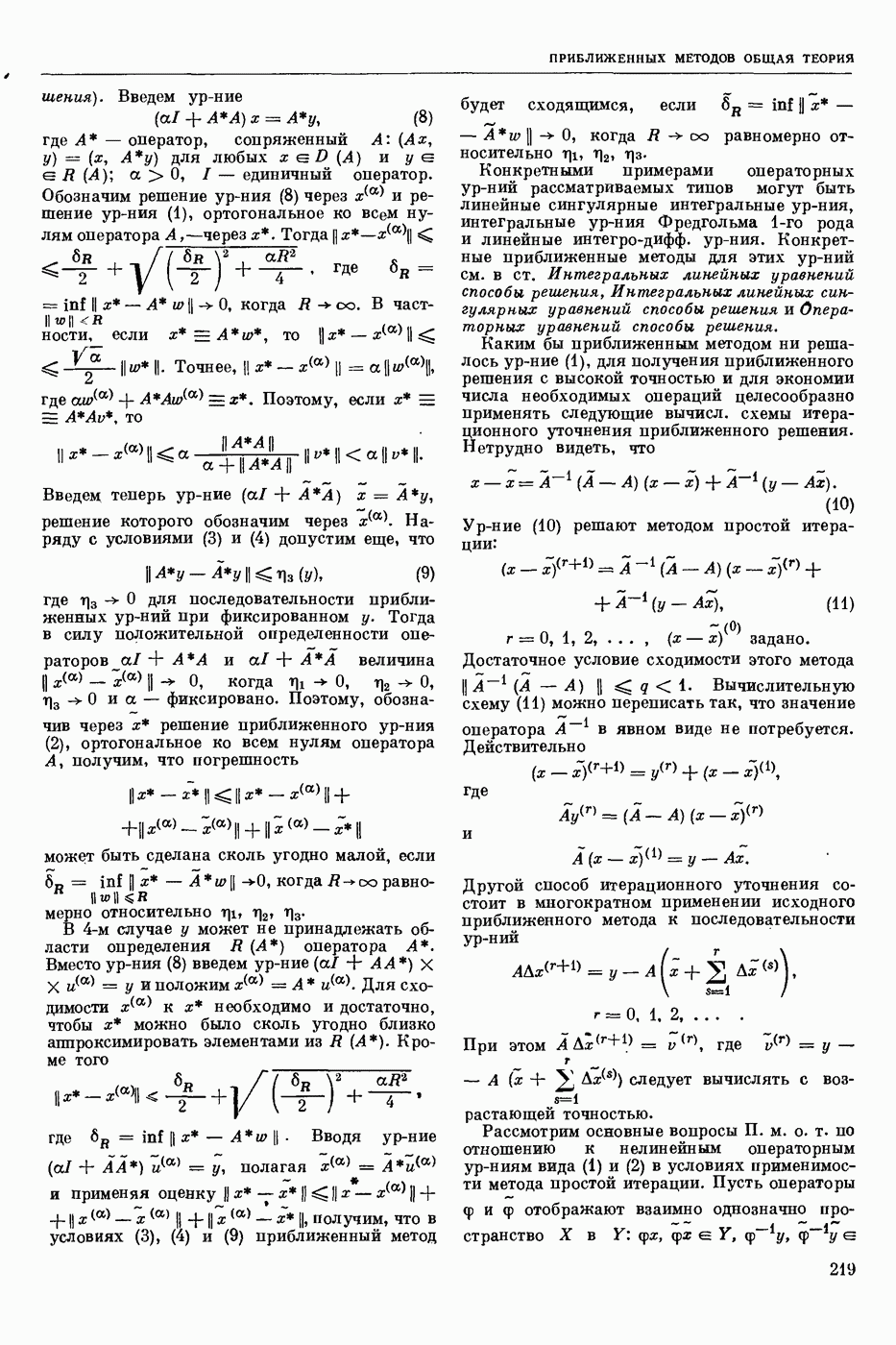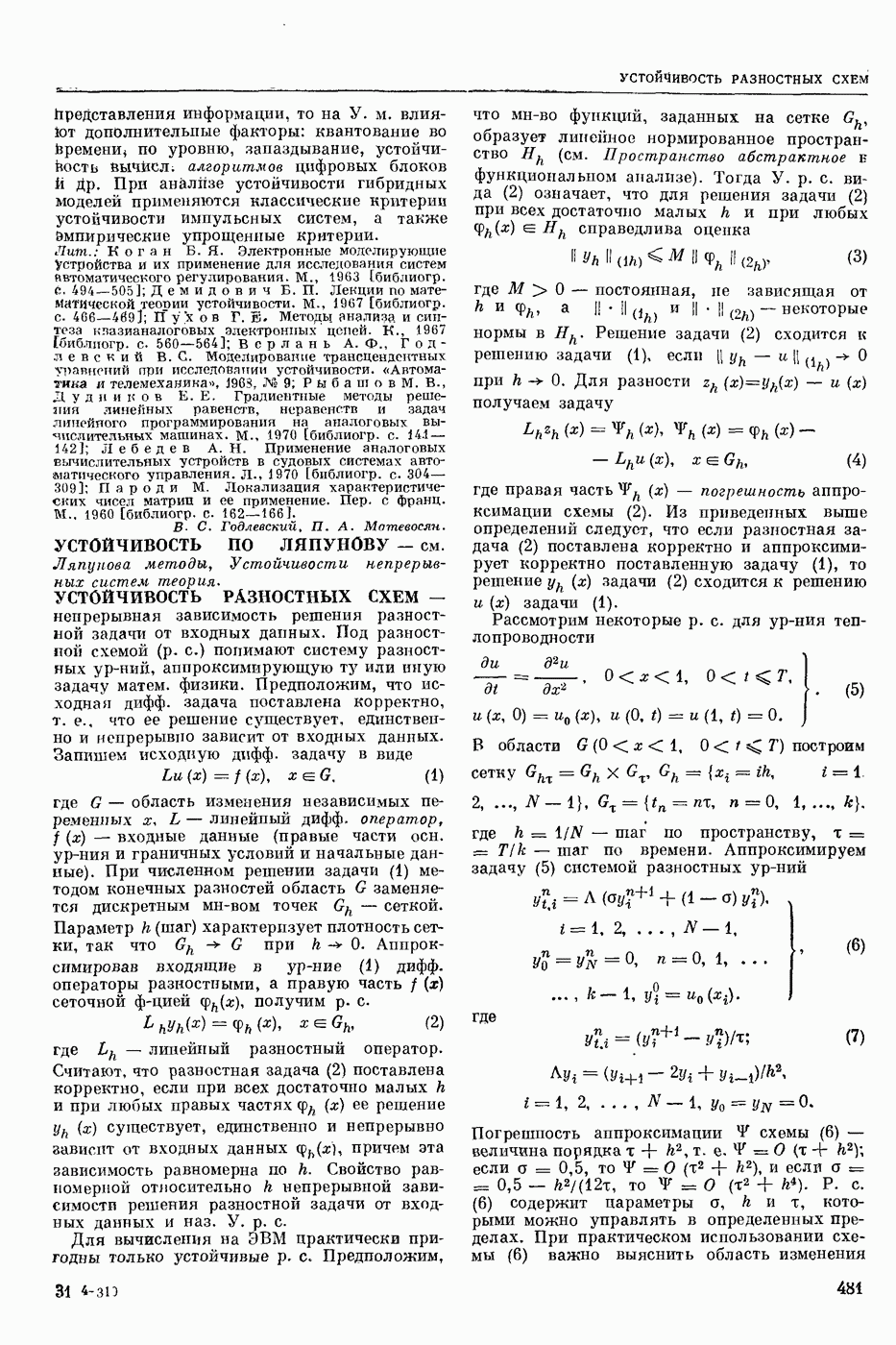| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ТОЖДЕСТВЕННО ИСТИННАЯ ФОРМУЛА, общезначимая формула
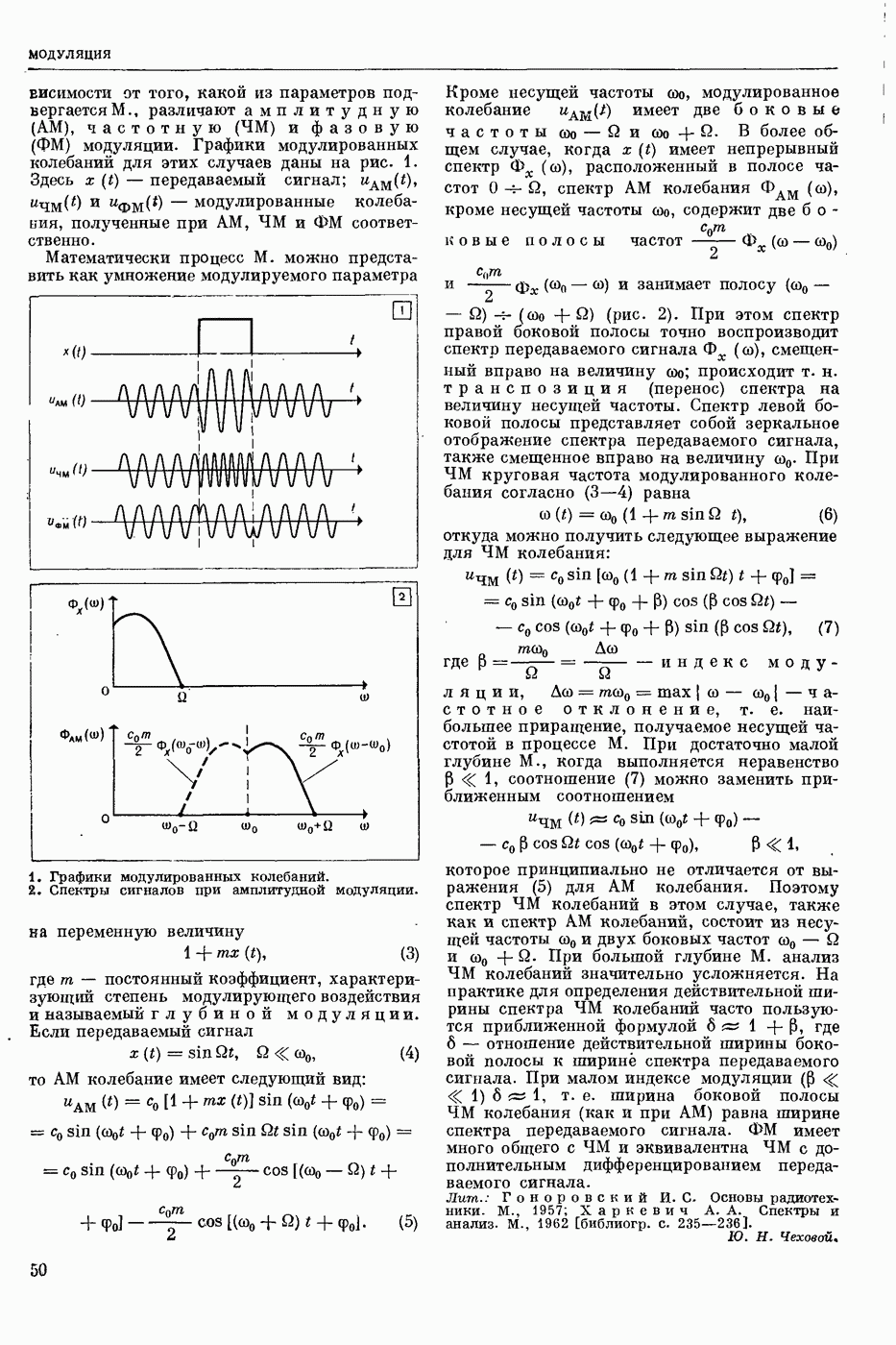
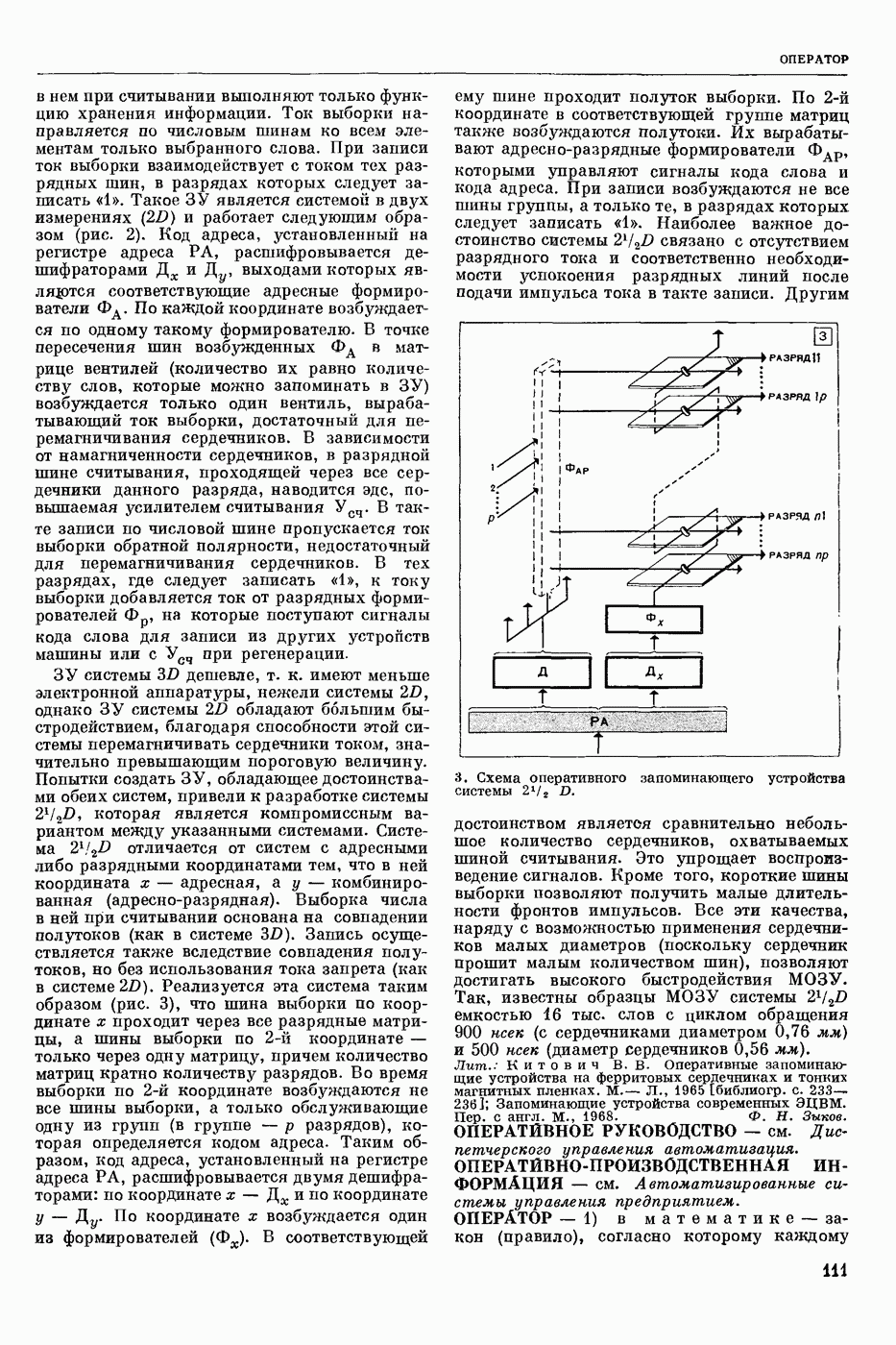
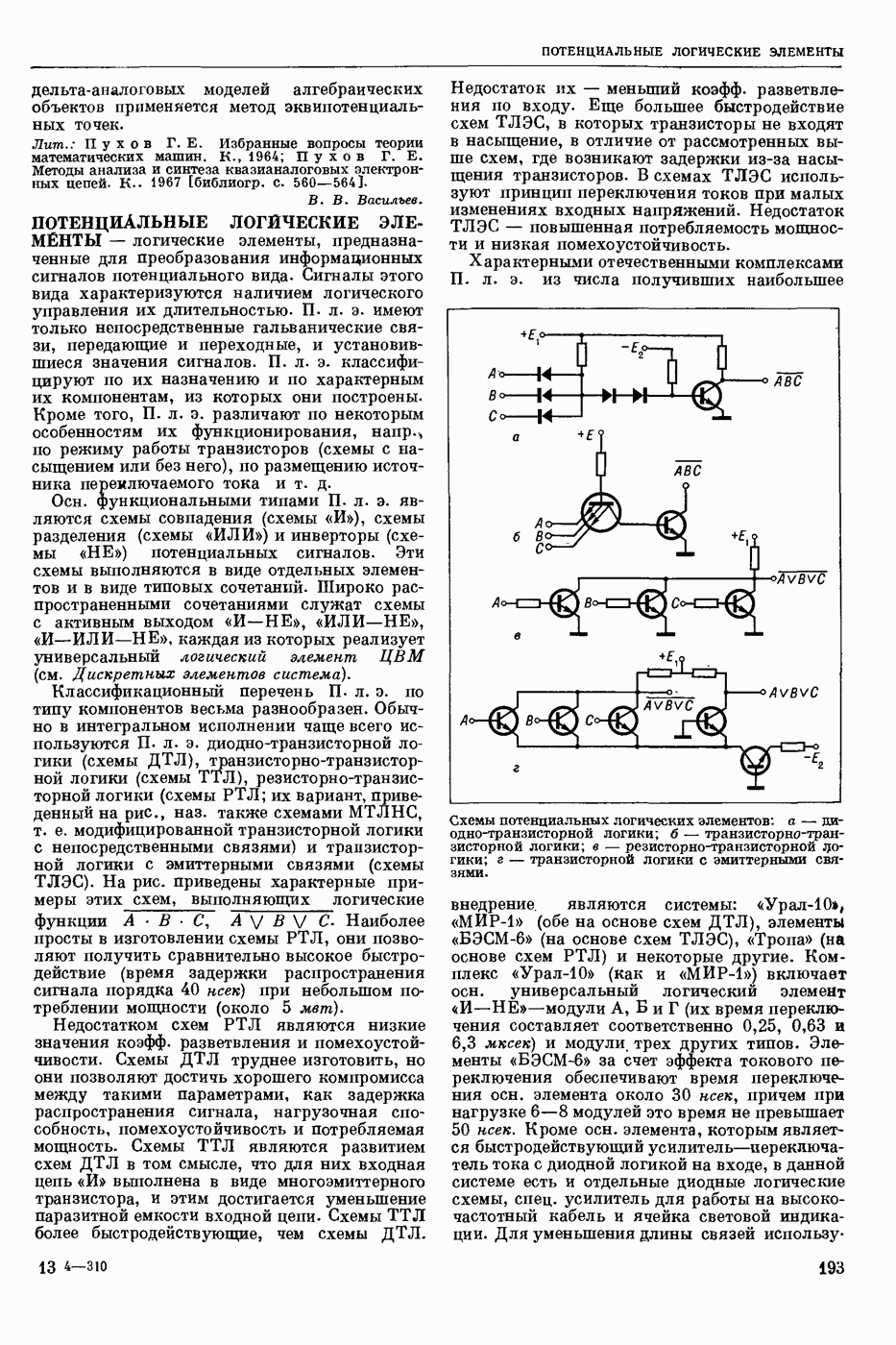
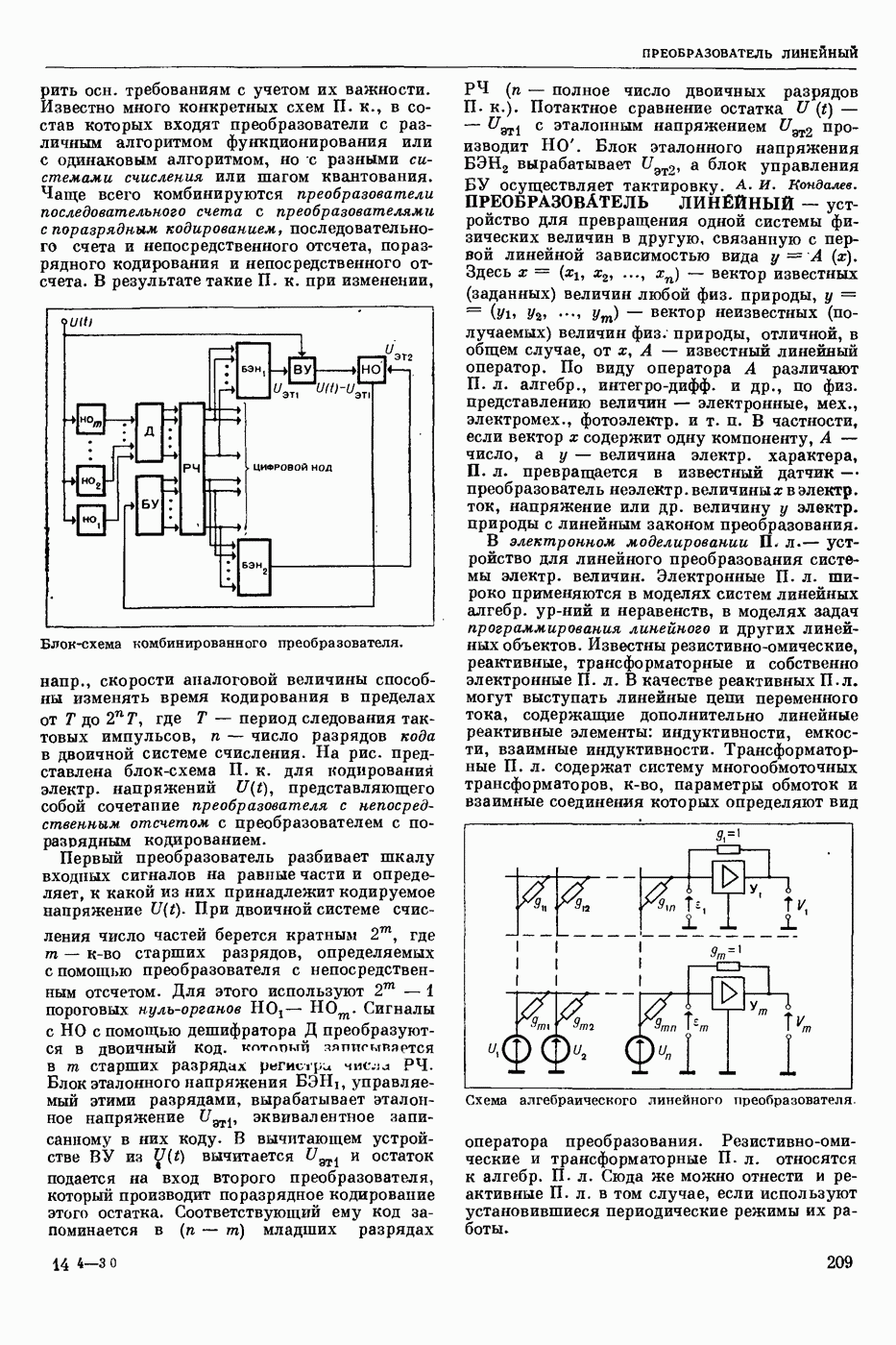
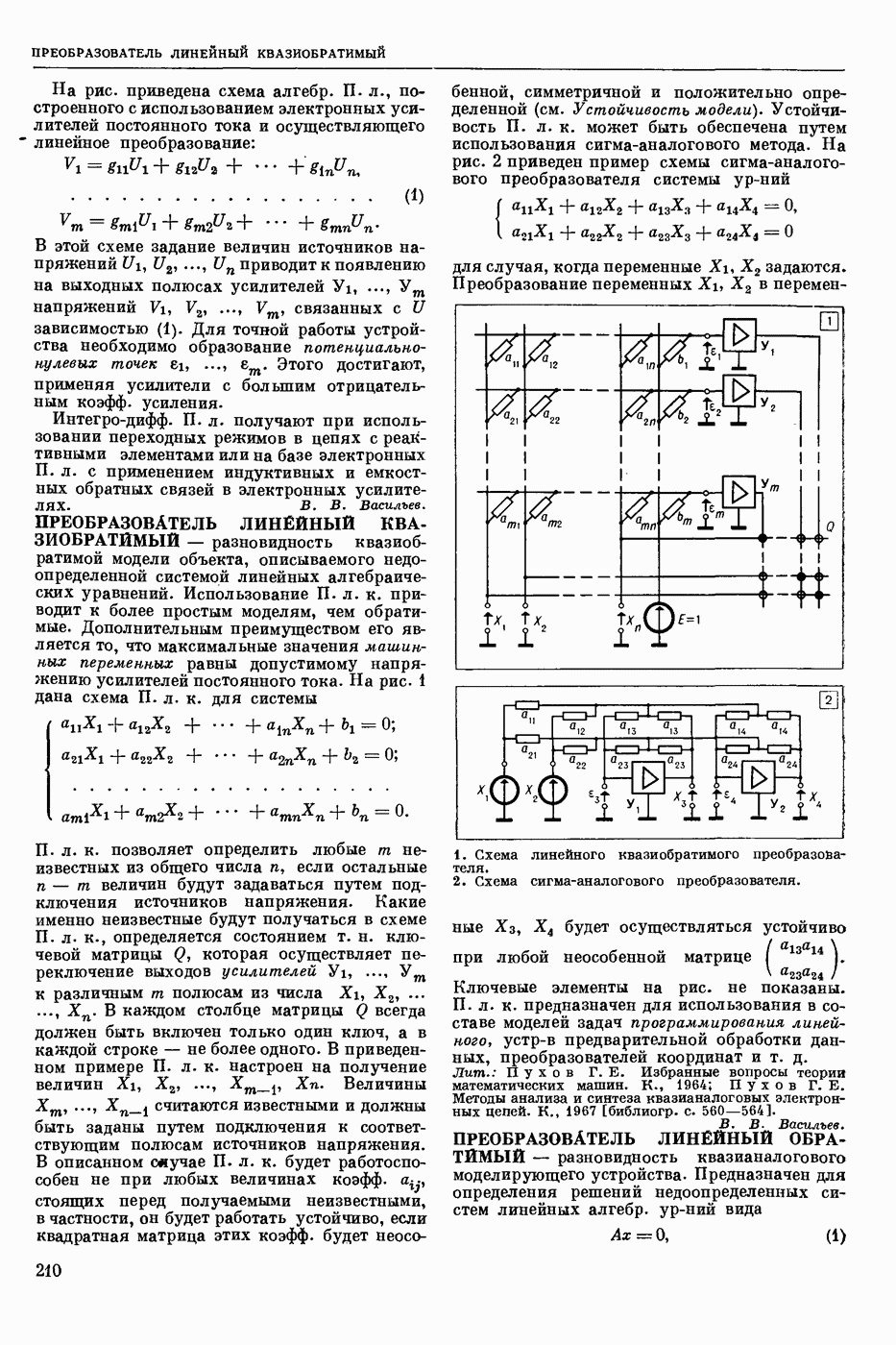
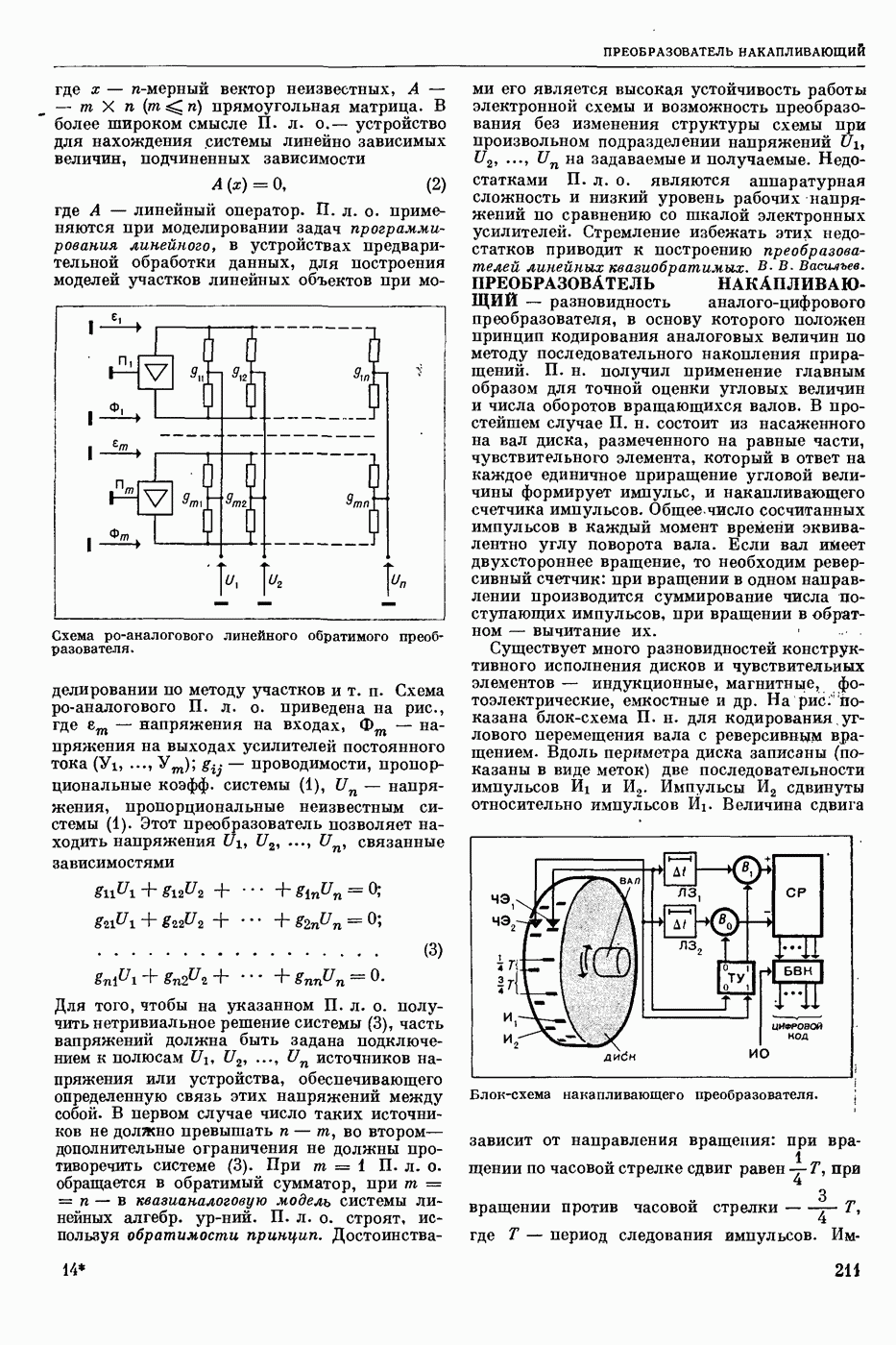
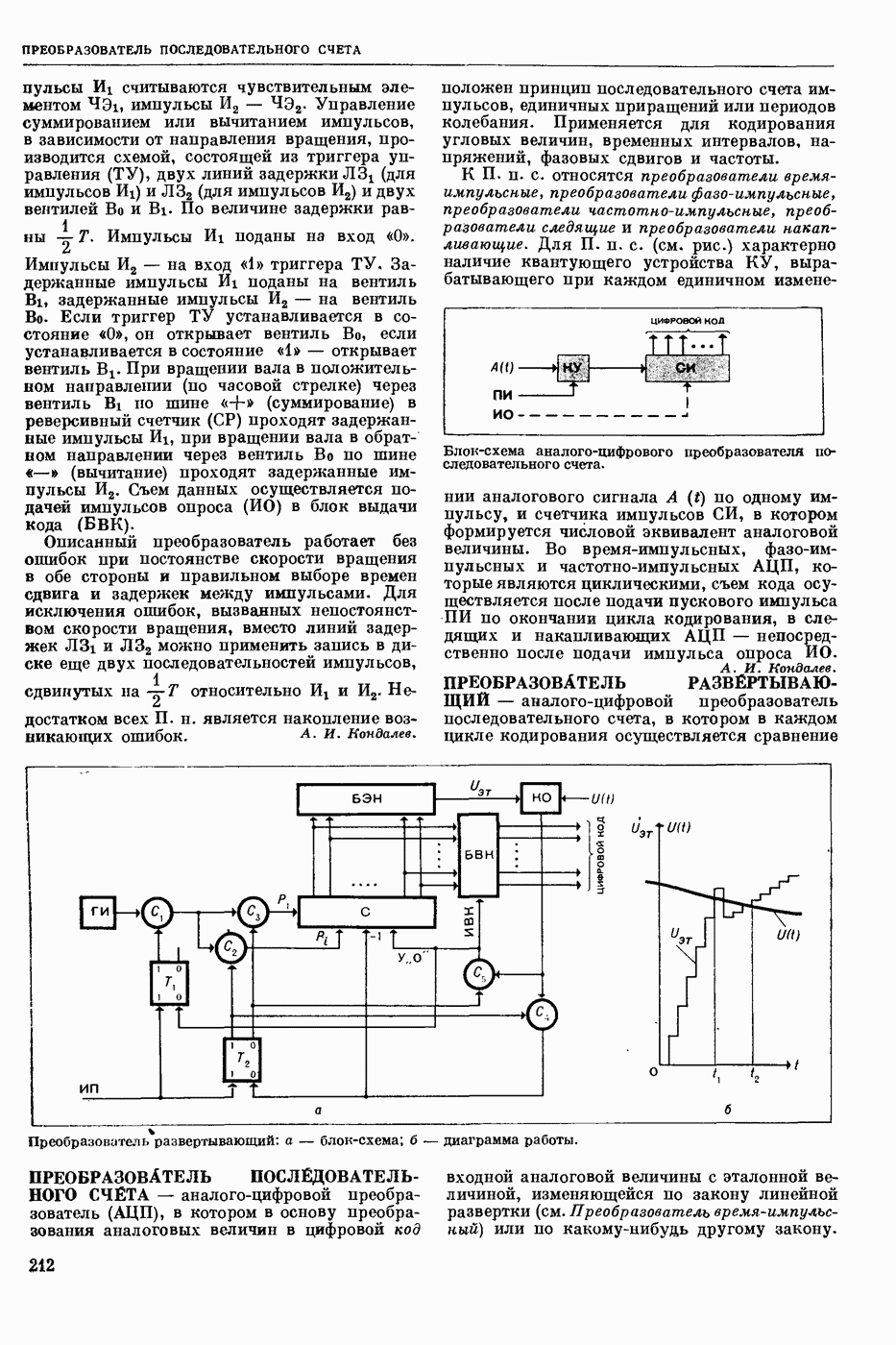
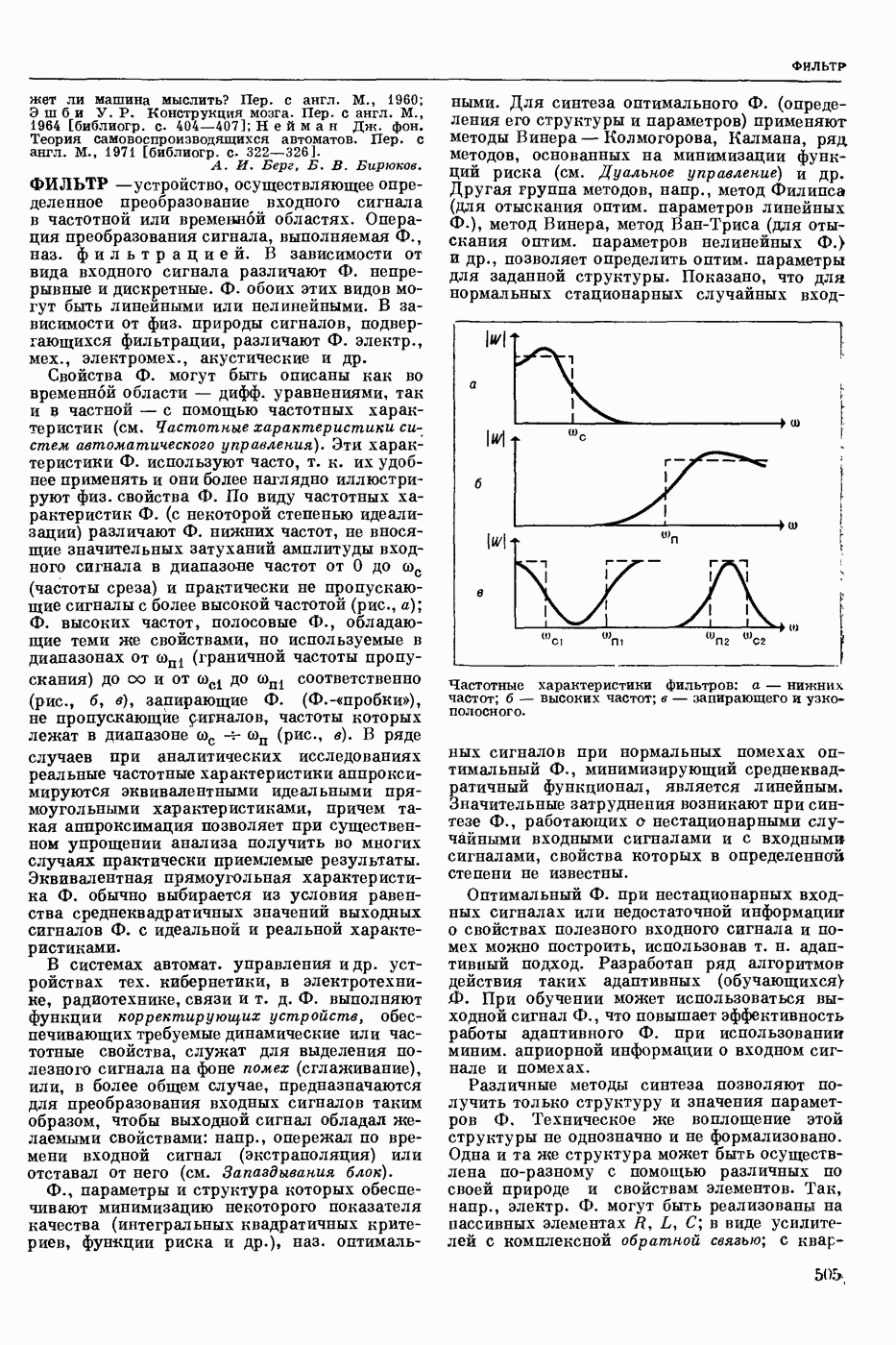
— формула того или иного логического языка (см. Языки логико-математические) истинная (при обычном понимании содержания входящих в нее логических операций) на любом непустом множестве М при любых значениях на М всех входящих в нее свободных переменных и постоянных (предметных, функциональных и предикатных). Напр., в исчислении высказываний Т. и. ф. является ф-ла , в исчислении предикатов узком
, в исчислении предикатов узком  в логике предикатов второй ступени
в логике предикатов второй ступени  выполнимой, если существуют такое непустое мн-во М и такие значения на М для всех входящих в
выполнимой, если существуют такое непустое мн-во М и такие значения на М для всех входящих в  свободных переменных и постоянных, при которых ф-ла становится истинной, в противном случае ее наз. невыполнимой или тождественно ложной. Формула тождественно истинна тогда и только тогда, когда ее отрицание тождественно ложно.
свободных переменных и постоянных, при которых ф-ла становится истинной, в противном случае ее наз. невыполнимой или тождественно ложной. Формула тождественно истинна тогда и только тогда, когда ее отрицание тождественно ложно.  логическим следствием из
логическим следствием из  , если
, если  истинна всегда, когда истинна ф-ла
истинна всегда, когда истинна ф-ла  . Если
. Если  является логич. следствием из
является логич. следствием из  , то
, то  является Т. и. ф.
является Т. и. ф.
Мн-во всех Т. и. ф. исчисления высказываний разрешимо; мн-во всех Т. и. ф. узкого исчисления предикатов не разрешимо, но эффективно аксиоматизируемо и, следовательно, рекурсивно перечислимо. Мн-во всех Т. и. ф. языка второй ступени и вообще языка любой высшей ступени (см. Логика предикатов высших ступеней) уже не является рекурсивно перечислимым, и, тем более, не эффективно аксиоматизируемо. в. Ф. Костырко.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- МИХАЙЛОВА КРИТЕРИЙ
- МНОГОВАРИАНТНЫХ ЗАДАЧ РЕШЕНИЕ
- МНОГОГРАННОЕ МНОЖЕСТВО
- МНОГОГРАННЫЙ КОНУС
- МНОГОЗНАЧНЫЕ СХЕМЫ
- МНОГОКОНТУРНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОКРИТЕРИАЛЬНОСТИ ПРОБЛЕМА
- МНОГОМЕРНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ РАЗДЕЛИТЕЛЬНЫЙ
- МНОГОПОЛЮСНИК КОНТАКТНЫЙ УНИВЕРСАЛЬНЫЙ
- МНОГОПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ, мультипрограммная обработка информации
- МНОГОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- МНОГОШАГОВОГО ПРОЦЕССА ПРОИЗВОДСТВА МОДЕЛЬ
- МНОГОШАГОВОГО ПРОЦЕССА РАСПРЕДЕЛЕНИЯ МОДЕЛЬ
- МНОГОШАГОВЫЕ ЗАДАЧИ
- МНОГОЭТАПНОЕ ОБСЛУЖИВАНИЕ
- МНОЖЕСТВ ТЕОРИЯ
- МНОЖИТЕЛЬНО-ДЕЛИТЕЛЬНЫЕ УСТРОЙСТВА
- МОДЕЛИ ОБЪЕКТОВ РАСПОЗНАВАНИЯ
- МОДЕЛИ ПРОИЗВОДСТВА
- МОДЕЛИ РАВНОВЕСИЯ
- МОДЕЛИ РОСТА
- МОДЕЛИ ЭКОНОМИКИ
- МОДЕЛИРОВАНИЕ ВЕСТИБУЛЯРНОГО АНАЛИЗАТОРА
- МОДЕЛИРОВАНИЕ ВОСПРИЯТИЯ
- МОДЕЛИРОВАНИЕ ЖИВЫХ СИСТЕМ на молекулярном уровне
- МОДЕЛИРОВАНИЕ ИНЖЕНЕРНЫХ СЕТЕЙ НА АВМ
- МОДЕЛИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ МЫШЛЕНИЯ
- МОДЕЛИРОВАНИЕ НА СПЛОШНЫХ СРЕДАХ, электрическое моделирование
- МОДЕЛИРОВАНИЕ ПАМЯТИ
- МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАСПОЗНАВАНИЯ И ОБУЧЕНИЯ РАСПОЗНАВАНИЮ НА ЦВМ
- МОДЕЛИРОВАНИЕ ПСИХИЧЕСКИХ ФУНКЦИЙ
- МОДЕЛИРОВАНИЕ СЕНСОРНЫХ СИСТЕМ
- МОДЕЛИРОВАНИЕ СИСТЕМЫ «ЧЕЛОВЕК—МАШИНА»
- МОДЕЛИРОВАНИЕ ФИЗИЧЕСКОЕ
- МОДЕЛИРОВАНИЕ ЦВМ ИМИТАЦИОННОЕ
- МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ НА ЦВМ
- МОДЕЛЬ ЗРИТЕЛЬНОГО АНАЛИЗАТОРА
- МОДЕЛЬ МАТЕМАТИЧЕСКАЯ
- МОДЕЛЬ НЕРВНОЙ КЛЕТКИ
- МОДЕЛЬ ПЕРЕМЕННОЙ СТРУКТУРЫ
- МОДЕЛЬ СЛУХОВОГО АНАЛИЗАТОРА
- МОДЕЛЬ «СМЫСЛ-ТЕКСТ»
- МОДЕЛЬ ФИЗИЧЕСКАЯ
- МОДЕЛЬ ЧУВСТВИТЕЛЬНОСТИ
- МОДУЛЯТОР
- МОДУЛЯЦИЯ ИМПУЛЬСНАЯ
- «МОЗГОВОЙ ШТУРМ»
- МОМЕНТОВ МЕТОД
- МОНИТОР
- МОНОТОННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- МОНТЕ-КАРЛО МЕТОД
- «МППИ-1», машина первичной переработки информации
- МУЛЬТИВИБРАТОР
- МУЛЬТИПРОГРАММИРОВАНИЕ
- МУЛЬТИПРОГРАММНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- МУЛЬТИПРОЦЕССОРНЫЙ РЕЖИМ
- МУЛЬТИУСТОЙЧИВЫЕ СИСТЕМЫ
- МУРА АВТОМАТ
- МЫСЛИТЕЛЬНОЙ СПОСОБНОСТИ УСИЛИТЕЛЬ
- НАБЛЮДАЕМОСТИ И УПРАВЛЯЕМОСТИ УСЛОВИЯ
- НАБОРНОЕ ПОЛЕ
- НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НАДЁЖНОСТЬ КИБЕРНЕТИЧЕСКИХ СИСТЕМ
- НАДЁЖНОСТЬ РАСПОЗНАВАНИЯ
- НАИМЕНЬШИХ КВАДРАТОВ МЕТОД
- «НАИРИ»
- НАИСКОРЕЙШЕГО СПУСКА МЕТОД
- НАЙКВИСТА КРИТЕРИЙ
- НАКАПЛИВАЮЩИЕ СХЕМЫ
- НАКОПИТЕЛЬ, блок хранения информации
- НАКОПИТЕЛЬ НА МАГНИТНОЙ ЛЕНТЕ
- НАРАБОТКА НА ОТКАЗ
- НАРАБОТКА НА СБОЙ
- НАУКА УПРАВЛЕНИЯ
- НАУКОВЕДЕНИЕ
- НАУЧНАЯ ОРГАНИЗАЦИЯ ТРУДА (НОТ)
- НАУЧНО-ИНФОРМАЦИОННАЯ ДЕЯТЕЛЬНОСТЬ
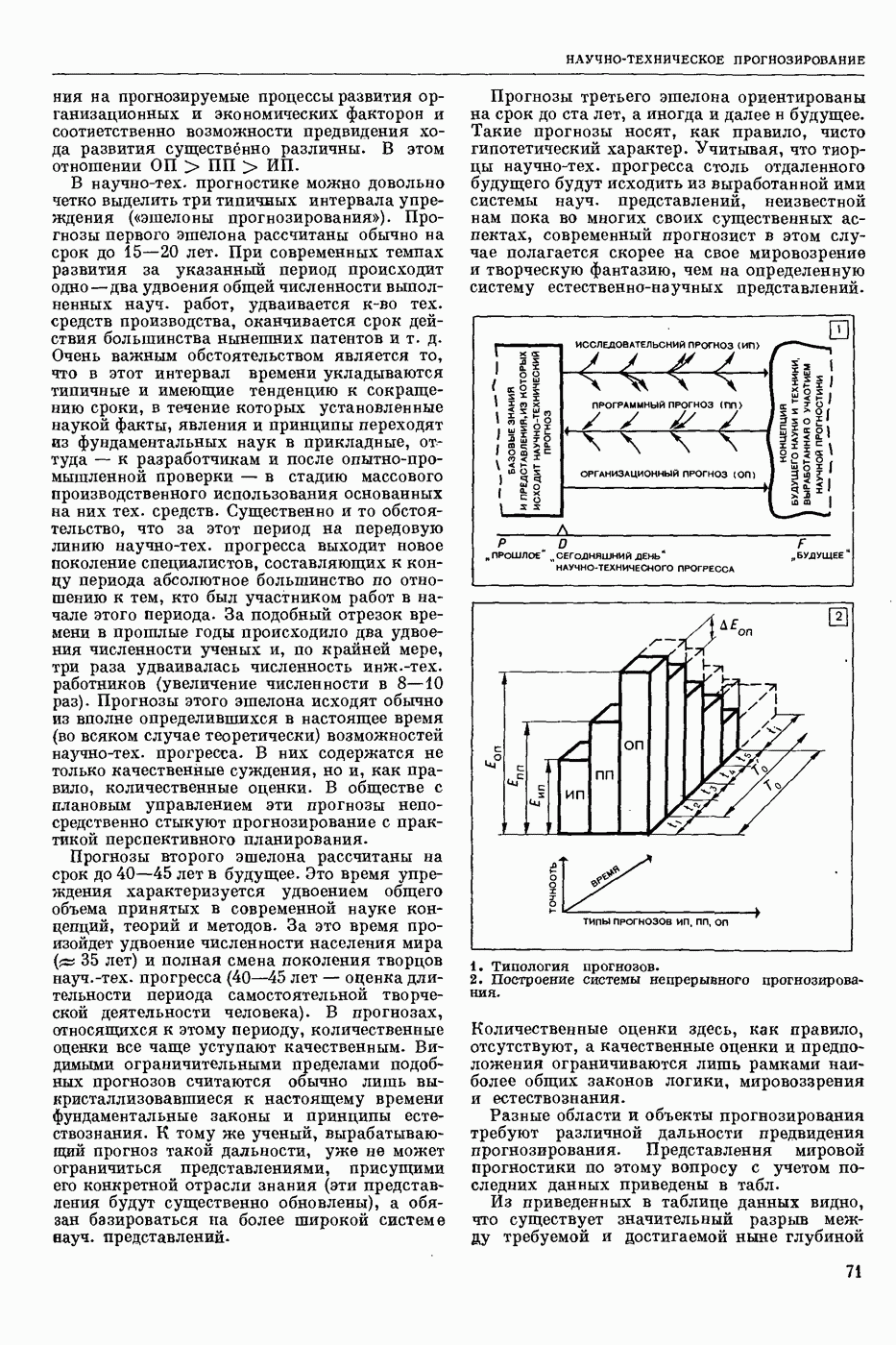
- НАУЧНО-ТЕХНИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ
- НАУЧНО-ТЕХНИЧЕСКОЙ ИНФОРМАЦИИ ОБРАБОТКА
- НАУЧНЫЙ СОВЕТ ПО КОМПЛЕКСНОЙ ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН СССР
- НАУЧНЫЙ СОВЕТ ПО ПРОБЛЕМЕ «КИБЕРНЕТИКА» АН УССР
- НЕЗАВИСИМОСТЬ в теории вероятностей, статистическая независимость
- НЕЙРОБИОНИКА
- НЕЙРОКИБЕРНЕТИКА
- НЕЙРОН
- НЕЙРОН ФОРМАЛЬНЫЙ
- НЕЙРОННЫЕ СЕТИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫЕ ЗАДАЧИ
- НЕКОРРЕКТНО ПОСТАВЛЕННЫХ ЗАДАЧ СПОСОБЫ РЕШЕНИЯ.
- НЕЛИНЕЙНАЯ СИСТЕМА УПРАВЛЕНИЯ
- НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ АВМ
- НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- НЕ НАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ
- НЕОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- НЕОДНОРОДНЫЙ ПОТОК В СЕТИ
- НЕОПРЕДЕЛЕННОСТЬ В УПРАВЛЕНИИ
- НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- НЕПРОТИВОРЕЧИВОСТЬ СИСТЕМЫ АКСИОМ, совместимость, корректность
- НЕРАЗРЕШИМЫЕ АЛГОРИТМИЧЕСКИЕ ПРОБЛЕМЫ
- «НИППОН ЭЛЕКТРИК КОМПАНИ» (Nippon Electric Company, Ltd)
- «ННБ», набор нелинейных блоков
- НОРМА ВЕКТОРА
- НОРМА МАТРИЦЫ
- НОРМАЛЬНАЯ ФОРМА МИНИМАЛЬНАЯ
- НОРМАЛЬНАЯ ФОРМА СОВЕРШЕННАЯ
- НОРМАЛЬНАЯ ФОРМА СОКРАЩЕННАЯ
- НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
- НОРМАЛЬНЫЕ АЛГОРИФМЫ, нормальные алгоритмы
- НОСИТЕЛЬ ИНФОРМАЦИИ
- НУЛЕВЫХ СОБСТВЕННЫХ ПРОВОДИМОСТЕЙ УЗЛОВ МЕТОД
- НУЛЬ-ОРГАН, сравнивающее устройство, компаратор
- НУМЕРАЦИЙ ТЕОРИЯ
- НЬЮТОНА ОБОБЩЕННЫЙ МЕТОД
- НЬЮТОНА ФОРМУЛЫ ИНТЕРПОЛИРОВАНИЯ
- ОБЛАСТЬ УПРАВЛЕНИЯ
- ОБЛЕГЧЁННОЕ РЕЗЕРВИРОВАНИЕ
- ОБОБЩЁННЫЕ ФУНКЦИИ
- ОБОБЩЕННЫХ ГРАДИЕНТОВ МЕТОД
- ОБРАБОТКА ДАННЫХ ПОСЛЕДОВАТЕЛЬНАЯ
- ОБРАБОТКА ДАННЫХ ПРОИЗВОЛЬНАЯ
- ОБРАБОТКА ИНФОРМАЦИИ В РЕАЛЬНОМ масштабе времени
- ОБРАБОТКА ИНФОРМАЦИИ В РЕЖИМЕ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- ОБРАБОТКИ ДАННЫХ СИСТЕМА
- ОБРАЗ, или распознаваемый класс, в кибернетике
- ОБРАТИМОСТИ ПРИНЦИП
- ОБРАТИМЫЕ ЭЛЕМЕНТЫ И МОДЕЛИ
- ОБРАТНАЯ СВЯЗЬ
- ОБРАТНЫХ ОПЕРАТОРОВ МЕТОД
- ОБУСЛОВЛЕННОСТИ ЧИСЛО
- ОБУЧАЮЩАЯ ВЫБОРКА
- ОБУЧАЮЩАЯ МАШИНА
- ОБУЧАЮЩАЯ ПРОГРАММА
- ОБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ОГРАНИЧЕНИЕ ФАЗОВЫХ КООРДИНАТ
- ОГРАНИЧИТЕЛЬ АМПЛИТУДЫ
- ОДНОРОДНАЯ СЕТЕВАЯ ЗАДАЧА
- ОДНОРОДНЫЙ ПОТОК В СЕТИ
- ОДНОТОЧЕЧНАЯ КРАЕВАЯ ЗАДАЧА
- ОКРУГЛЕНИЯ ПОГРЕШНОСТЬ
- ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО (ОЗУ)
- ОПЕРАТИВНОЕ РУКОВОДСТВО
- ОПЕРАТИВНО-ПРОИЗВОДСТВЕННАЯ ИНФОРМАЦИЯ
- ОПЕРАТОР
- ОПЕРАТОР АВТОМАТНЫЙ
- ОПЕРАТОР ЗАДЕРЖКИ
- ОПЕРАТОР ПРИСВАИВАНИЯ
- ОПЕРАТОР ЭЛЕМЕНТАРНЫЙ
- ОПЕРАТОР ЭЛЕМЕНТНЫЙ
- ОПЕРАТОРНАЯ СХЕМА
- ОПЕРАТОРНЫЕ УРАВНЕНИЯ
- ОПЕРАТОРНЫЙ МЕТОД ПРОГРАММИРОВАНИЯ
- ОПЕРАТОРНЫХ УРАВНЕНИЙ СПОСОБЫ РЕШЕНИЯ.
- ОПЕРАТОРЫ ЛИНЕЙНЫЕ, линейные преобразования
- ОПЕРАЦИИ МАШИННЫЕ
- ОПЕРАЦИИ НАД МАССИВАМИ
- ОПЕРАЦИИ НАД СИМВОЛАМИ И СТРОКАМИ
- ОПЕРАЦИИ НАД ЧИСЛАМИ
- ОПЕРАЦИИ ИССЛЕДОВАНИЕ
- ОПЕРАЦИЙ СИСТЕМА
- ОПЕРАЦИОННАЯ СИСТЕМА
- ОПЕРАЦИЯ НАИМЕНЬШЕГО КОРНЯ
- ОПЕРАЦИЯ ПРИМИТИВНОЙ РЕКУРСИИ
- ОПИСАНИЕ ОБЪЕКТА РАСПОЗНАВАНИЯ
- ОПОРНОЕ НАПРЯЖЕНИЕ
- ОПОРНЫЙ ПЛАН
- ОПТИМАЛЬНАЯ ТОЧКА
- ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ТЕОРИЯ
- ОПТИМАЛЬНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
- ОПТИМАЛЬНОСТИ НЕОБХОДИМЫЕ УСЛОВИЯ
- ОПТИМАЛЬНОСТИ ПРИНЦИП
- ОПТИМАЛЬНЫЙ ВЕКТОР
- ОПТИМАЛЬНЫХ ПАРАМЕТРОВ СИСТЕМЫ ВЫБОР
- ОПТИМАЛЬНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ОПТИМИЗАТОР АВТОМАТИЧЕСКИЙ
- ОПТИМИЗАЦИИ МЕТОДЫ численные
- «ОПТИМУМ»
- ОПТРОН
- ОРГАНИЗАЦИЯ ИНФОРМАЦИОННОГО МАССИВА
- ОРГАНИЗАЦИЯ УЧЕТА В АВТОМАТИЗИРОВАННЫХ СИСТЕМАХ УПРАВЛЕНИЯ
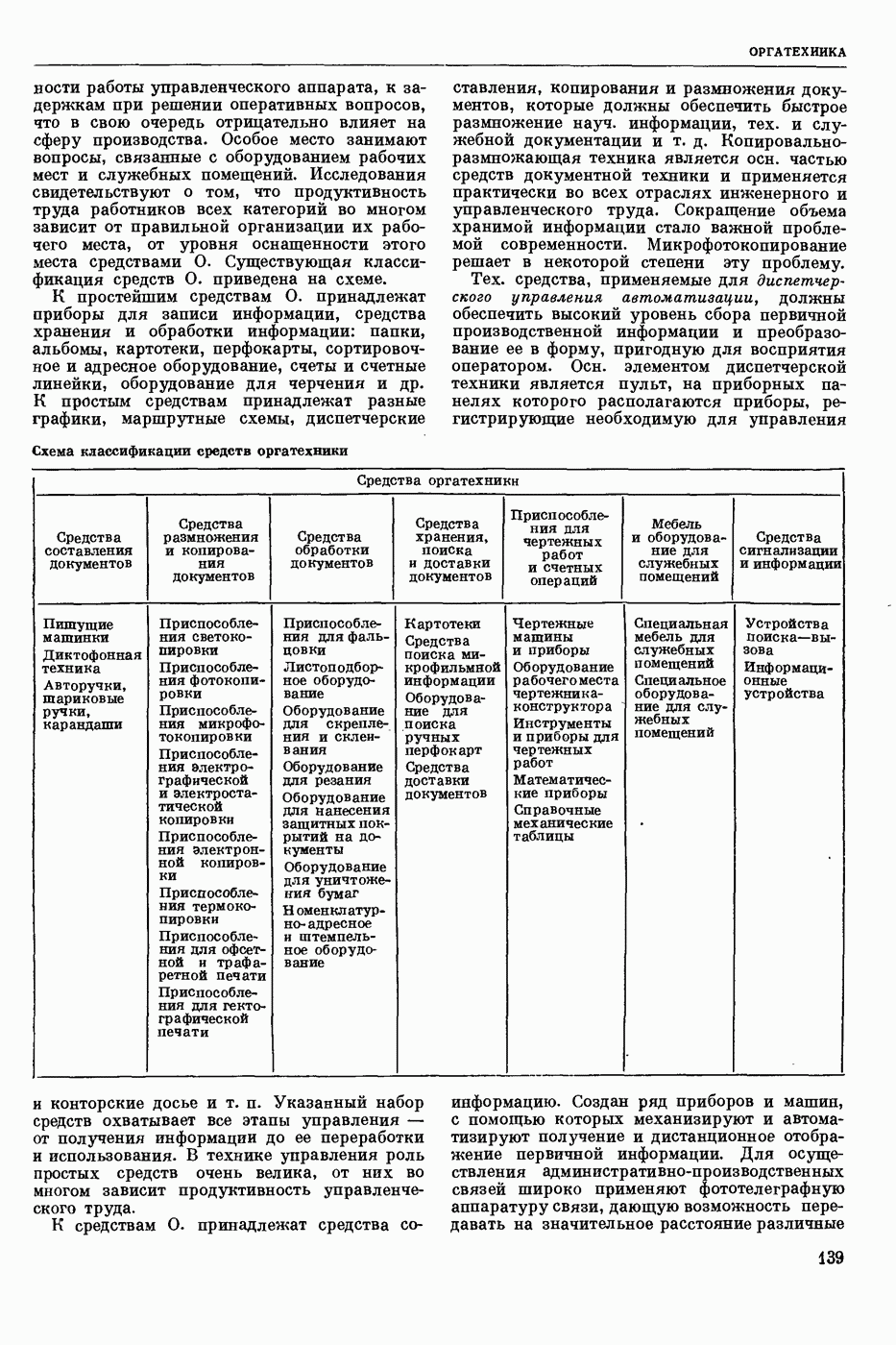
- ОРГАТЕХНИКА, организационная техника
- ОРДЕНА ЛЕНИНА ИНСТИТУТ КИБЕРНЕТИКИ АКАДЕМИИ НАУК УКРАИНСКОЙ ССР
- УПРАВЛЕНИЯ (АВТОМАТИКИ И ТЕЛЕМЕХАНИКИ), ИАТ
- ОСТАНОВ
- ОСУЩЕСТВИМОСТИ ФИЗИЧЕСКОЙ КРИТЕРИИ
- ОСУЩЕСТВИМОСТИ ЦЕЛИ ПРИНЦИП
- ОТВЕТ РАСПОЗНАЮЩЕЙ СИСТЕМЫ
- ОТКАЗ ОТ РАСПОЗНАВАНИЯ
- ОТЛАДОЧНЫЕ ПРОГРАММЫ
- ОТНОШЕНИЕ
- ОТНОШЕНИЕ АНАЛИТИЧЕСКОЕ
- ОТНОШЕНИЕ БАЗИСНОЕ
- ОТНОШЕНИЕ ПАРАДИГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ ПРАВДОПОДОБИЯ
- ОТНОШЕНИЕ СИГНАЛ/ПОМЕХА
- ОТНОШЕНИЕ СИНТАГМАТИЧЕСКОЕ
- ОТНОШЕНИЕ СИНТЕТИЧЕСКОЕ
- ОТНОШЕНИЕ ТЕКСТУАЛЬНОЕ
- ОТРИЦАНИЕ в алгебре логики
- ОЧЕРЕДЕЙ ТЕОРИЯ
- ОШИБКА В ПРИНЯТИИ ГИПОТЕЗ
- ОШИБКИ В СИСТЕМАХ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ОШИБОК ТЕОРИЯ
- ПАКЕТНАЯ ОБРАБОТКА ИНФОРМАЦИИ
- ПАЛЬМА ПОТОК
- ПАМЯТИ ЗАЩИТА
- ПАМЯТИ РАСПРЕДЕЛЕНИЕ
- ПАМЯТЬ МАГАЗИННАЯ
- ПАМЯТЬ СТРАНИЧНАЯ
- ПАМЯТЬ ЦВМ
- ПАРАБОЛИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- ПАРАЛЛЕЛЬНЫЙ АЛГОРИТМ
- ПАРАМЕТР ФАКТИЧЕСКИЙ
- ПАРАМЕТР ФОРМАЛЬНЫЙ
- ПАРАМЕТРОН
- ПАРЕТО ОПТИМУМ
- ПАЧКА ОШИБОК, пакет ошибок
- ПЕРЕВОД АВТОМАТИЧЕСКИЙ
- ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
- ПЕРЕДАЧИ ИНФОРМАЦИИ СКОРОСТЬ
- ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИ
- ПЕРЕМЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- ПЕРЕРАБОТКА ИНФОРМАЦИИ В ЦВМ
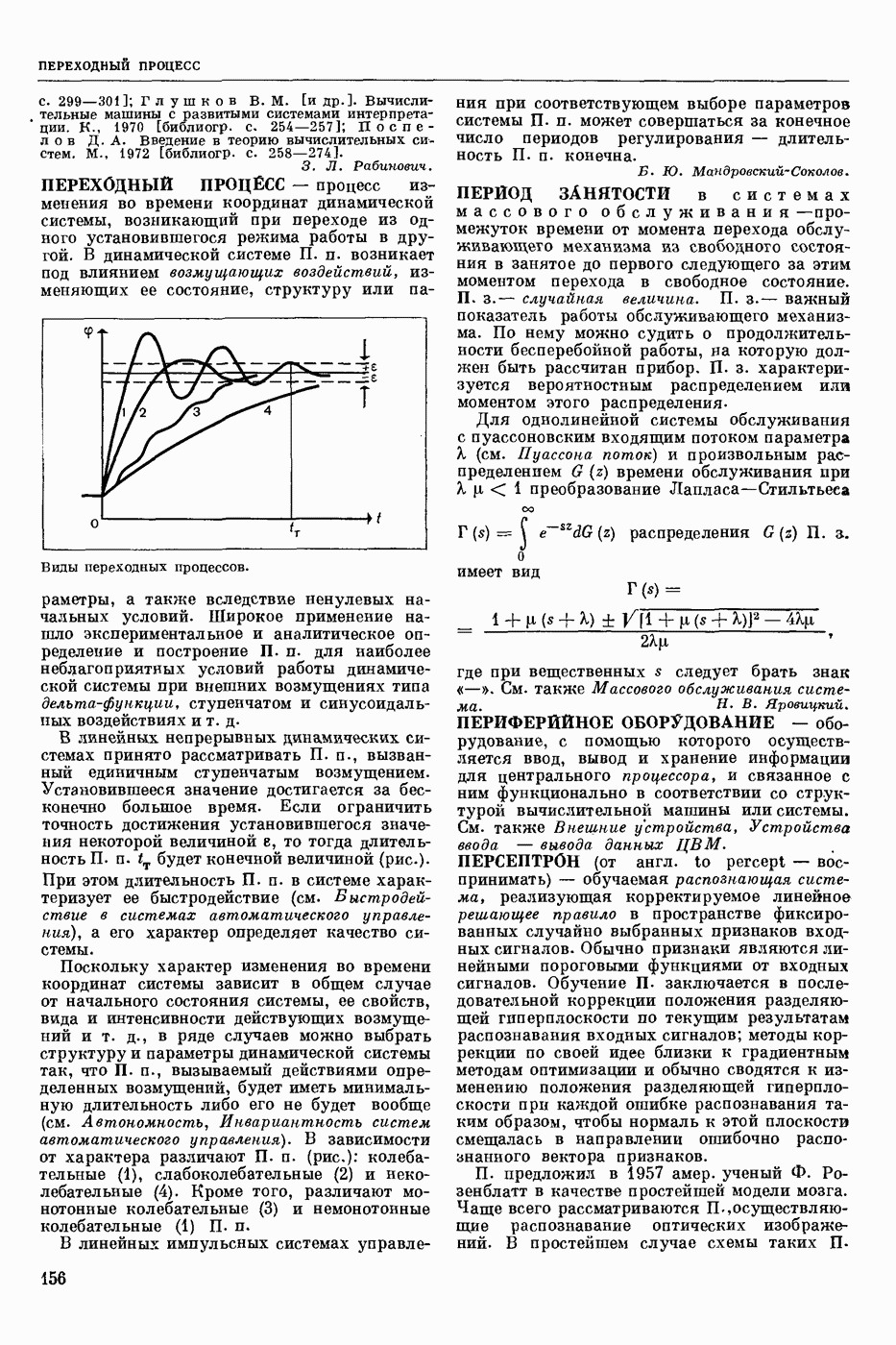
- ПЕРЕХОДНЫЙ ПРОЦЕСС
- ПЕРИОД ЗАНЯТОСТИ в системах массового обслуживания
- ПЕРИФЕРИЙНОЕ ОБОРУДОВАНИЕ
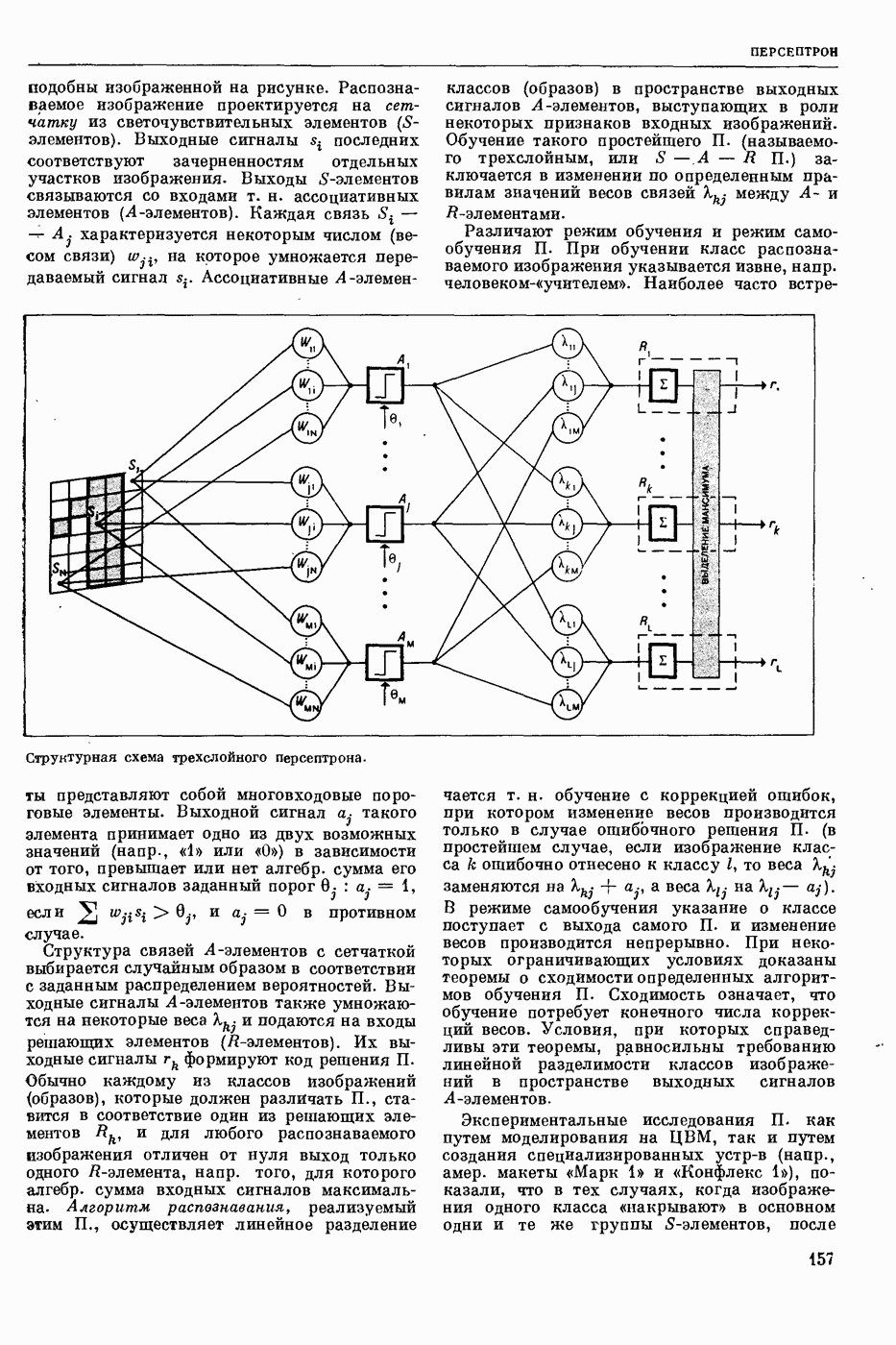
- ПЕРСЕПТРОН
- «ПЕРТ»
- ПЕРФОРАТОР
- ПЕРФОРАЦИОННАЯ КАРТА, перфокарта
- ПЕРФОРАЦИОННАЯ ЛЕНТА, перфолента
- ПЕЧАТНАЯ СХЕМА
- ПИРСА СТРЕЛКА, функция Вебба, отрицание дизъюнкции
- ПЛ-1
- ПЛАВАЮЩАЯ ЗАПЯТАЯ
- ПЛАН-ГРАФИК
- ПЛАТЕЖНАЯ МАТРИЦА
- ПЛАТЕЖНАЯ ФУНКЦИЯ
- ПЛЕНКА МАГНИТНАЯ
- ПНЕВМОНИКА, струйная пневмоавтоматика
- ПОВЕДЕНИЕ АВТОМАТОВ.
- ПОВЕДЕНИЕ АВТОМАТОВ В СЛУЧАЙНЫХ СРЕДАХ.
- ПОГЛОЩЕНИЯ ЗАКОН
- ПОГРЕШНОСТЕЙ ВЫЧИСЛЕНИЙ ТЕОРИЯ
- ПОГРЕШНОСТЬ
- ПОГРЕШНОСТЬ РЕШАЮЩЕГО ЭЛЕМЕНТА
- ПОДАВТОМАТ
- ПОДОБИЯ ТЕОРИЯ
- ПОДПРОГРАММА
- ПОДПРОГРАММА ЗАМКНУТАЯ
- ПОДПРОГРАММА ОТКРЫТАЯ
- ПОДПРОГРАММА СТАНДАРТНАЯ
- ПОДСИСТЕМА
- ПОИСК ИНФОРМАЦИИ АВТОМАТИЧЕСКИЙ
- ПОИСКА ЭКСТРЕМУМА ФУНКЦИЙ МЕТОДЫ
- ПОИСКОВОЕ ПРЕДПИСАНИЕ
- ПОИСКОВЫЙ МАССИВ
- ПОИСКОВЫЙ ОБРАЗ ДОКУМЕНТА
- ПОИСКОВЫЙ ОБРАЗ ЗАПРОСА
- ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ, экспоненциальное распределение
- ПОЛНОЙ ВЕРОЯТНОСТИ ФОРМУЛА
- ПОЛНОТА ФОРМАЛЬНОЙ ТЕОРИИ
- ПОЛНОТЫ ПРОБЛЕМА в теории автоматов
- ПОЛОС МЕТОД
- ПОЛУГРУППА, ассоциативная система
- ПОЛУМАРКОВСКИЙ СЛУЧАЙНЫЙ ПРОЦЕСС
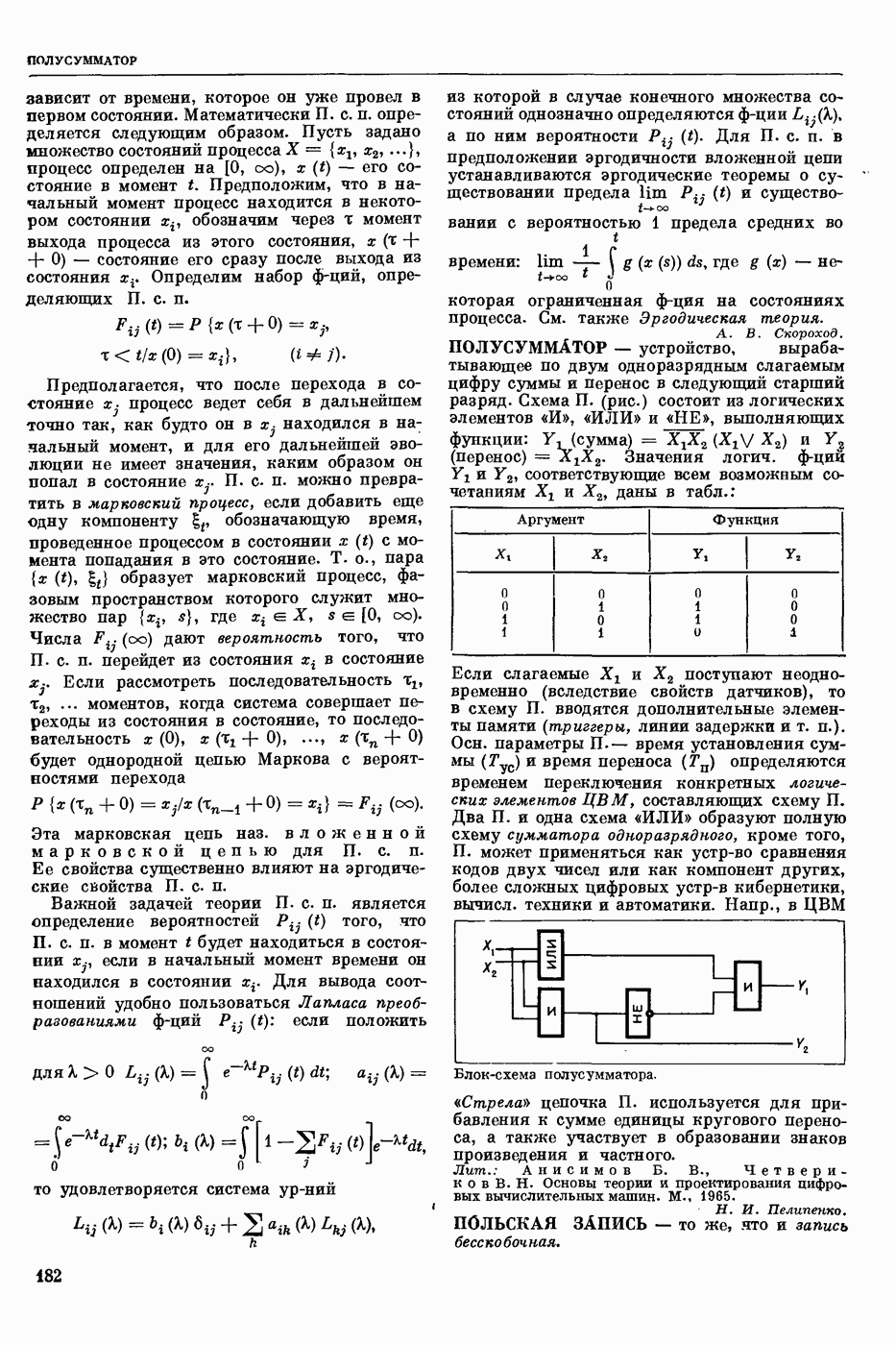
- ПОЛУСУММАТОР
- ПОЛЬСКАЯ ЗАПИСЬ
- ПОМЕХИ
- ПОМЕХОУСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ
- ПОНТРЯГИНА ПРИНЦИП МАКСИМУМА
- ПОПОВА КРИТЕРИЙ
- ПОРОГ ЧУВСТВИТЕЛЬНОСТИ
- ПОРОГОВЫЙ ЭЛЕМЕНТ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ
- ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ ВАРИАНТОВ
- ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИИ МЕТОД
- ПОСТА ИСЧИСЛЕНИЯ
- ПОСТА КОМБИНАТОРНАЯ ПРОБЛЕМА
- ПОСТА МАШИНА
- ПОТЕНЦИАЛОВ МЕТОД
- ПОТЕНЦИАЛЬНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
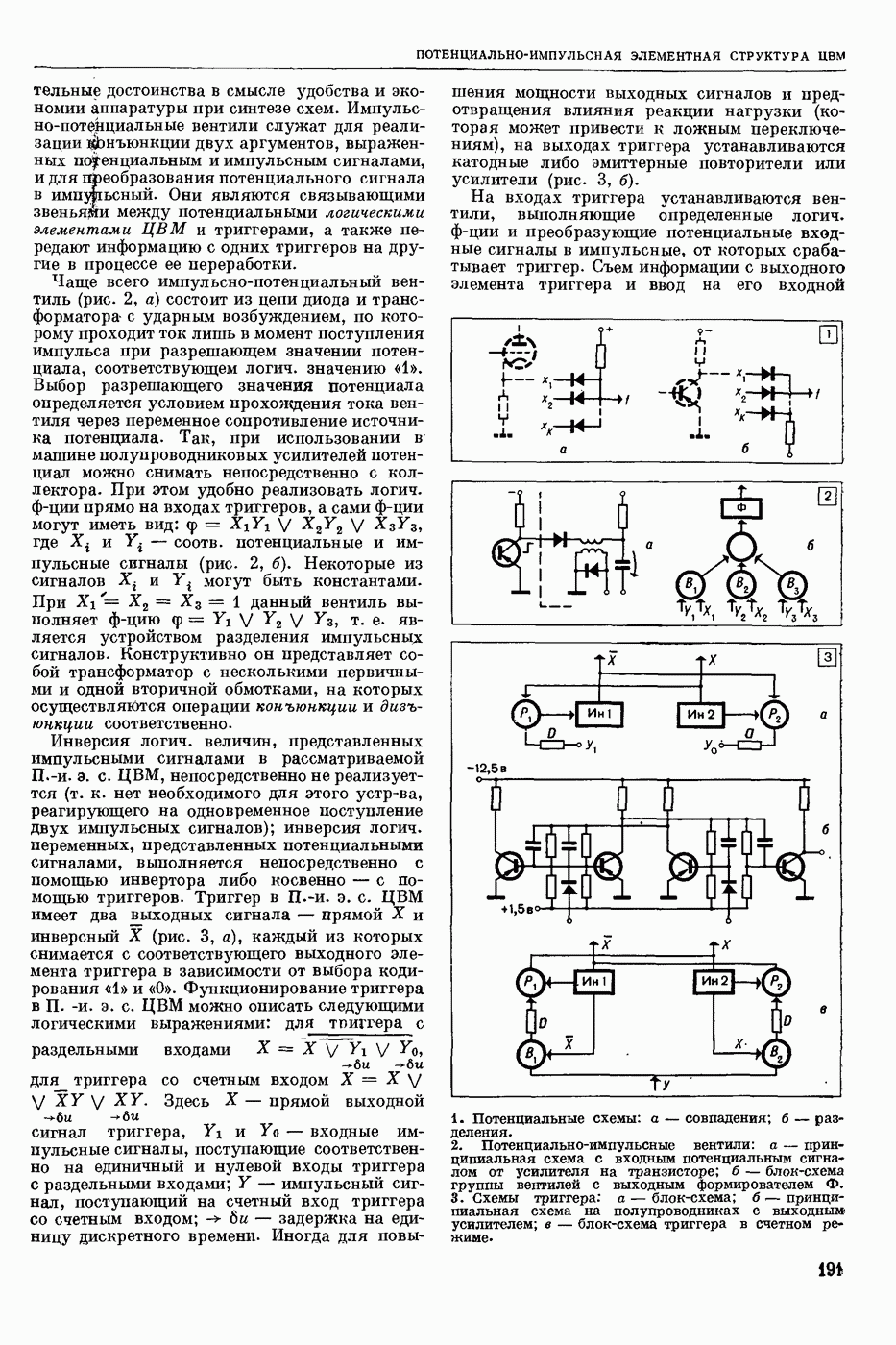
- ПОТЕНЦИАЛЬНО-ИМПУЛЬСНАЯ ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ПОТЕНЦИАЛЬНО-НУЛЕВАЯ ТОЧКА
- ПОТЕНЦИАЛЬНО-НУЛЕВЫХ ТОЧЕК МЕТОД
- ПОТЕНЦИАЛЬНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ МЕТОД
- ПОТЕРИ ИНФОРМАЦИИ при поиске
- ПОТОК БЕЗ ПОСЛЕДЕЙСТВИЯ
- ПОТОК В СЕТИ
- ПОТОК В СЕТИ НЕОДНОРОДНЫЙ
- ПОТОК ВЫХОДЯЩИЙ
- ПОТОК ГЕОМЕТРИЧЕСКИЙ
- ПОТОК ИНФОРМАЦИОННЫЙ ЗАМКНУТЫЙ
- ПОТОК НЕСТАЦИОНАРНЫЙ
- ПОТОК ПРОСТЕЙШИЙ
- ПОТОК РЕГУЛЯРНЫЙ
- ПОТОК С ОГРАНИЧЕННЫМ ПОСЛЕДЕЙСТВИЕМ
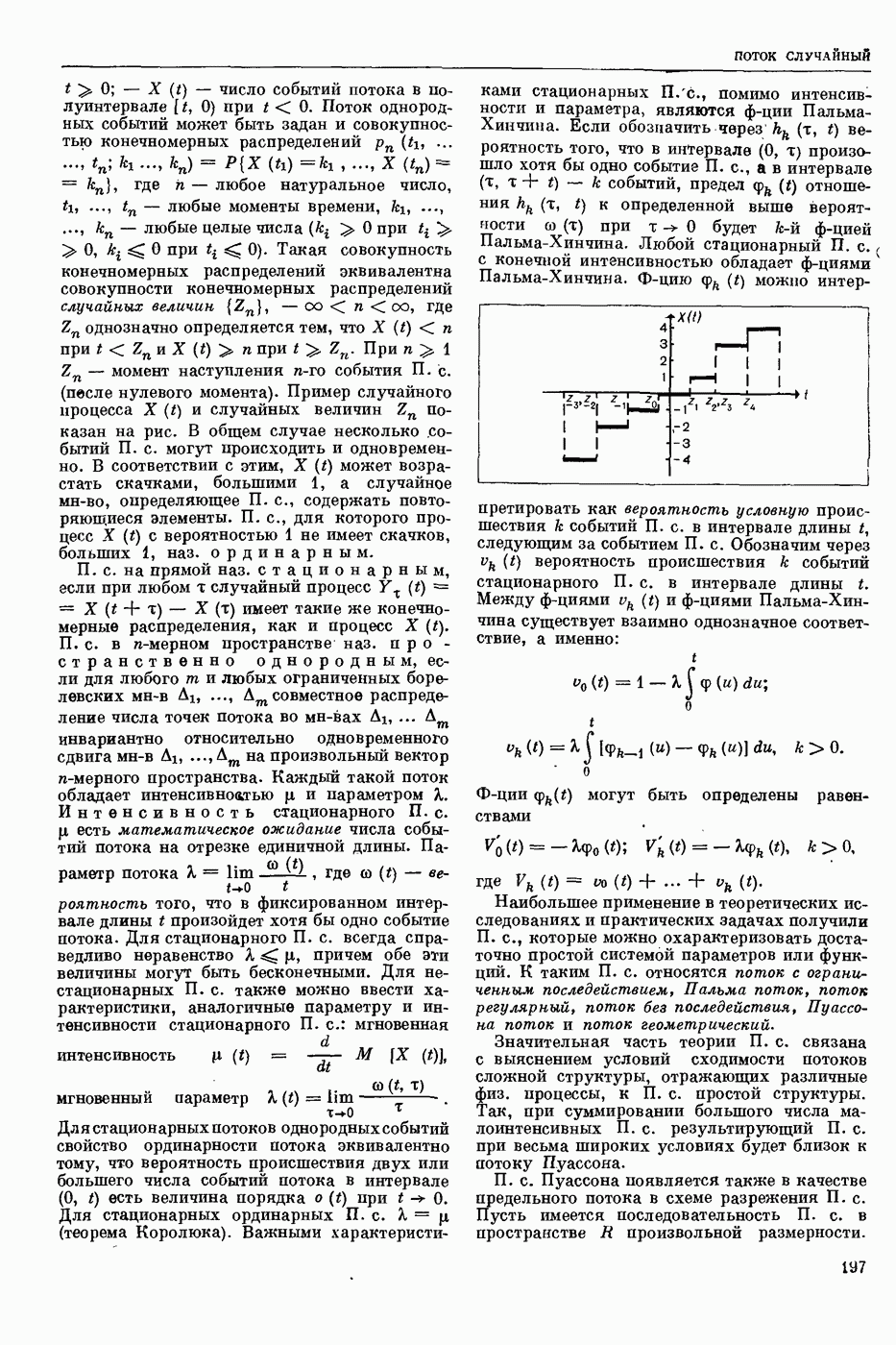
- ПОТОК СЛУЧАЙНЫЙ
- ПРАГМАТИКА
- ПРЕДИКАТ
- ПРЕДИКАТИВНОСТЬ
- ПРЕДСКАЗАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- ПРЕДСКАЗЫВАЮЩИЙ ФИЛЬТР
- ПРЕДСТАВЛЕНИЙ ГРУПП ТЕОРИЯ
- ПРЕОБРАЗОВАНИЕ ПЕРИОДИЧЕСКИ-ОПРЕДЕЛЕННОЕ
- ПРЕОБРАЗОВАТЕЛИ ВОЛОКОННЫЕ
- ПРЕОБРАЗОВАТЕЛИ ДВУХ И БОЛЕЕ ПЕРЕМЕННЫХ
- ПРЕОБРАЗОВАТЕЛИ КОД-АНАЛОГ
- ПРЕОБРАЗОВАТЕЛИ С ПОРАЗРЯДНЫМ КОДИРОВАНИЕМ
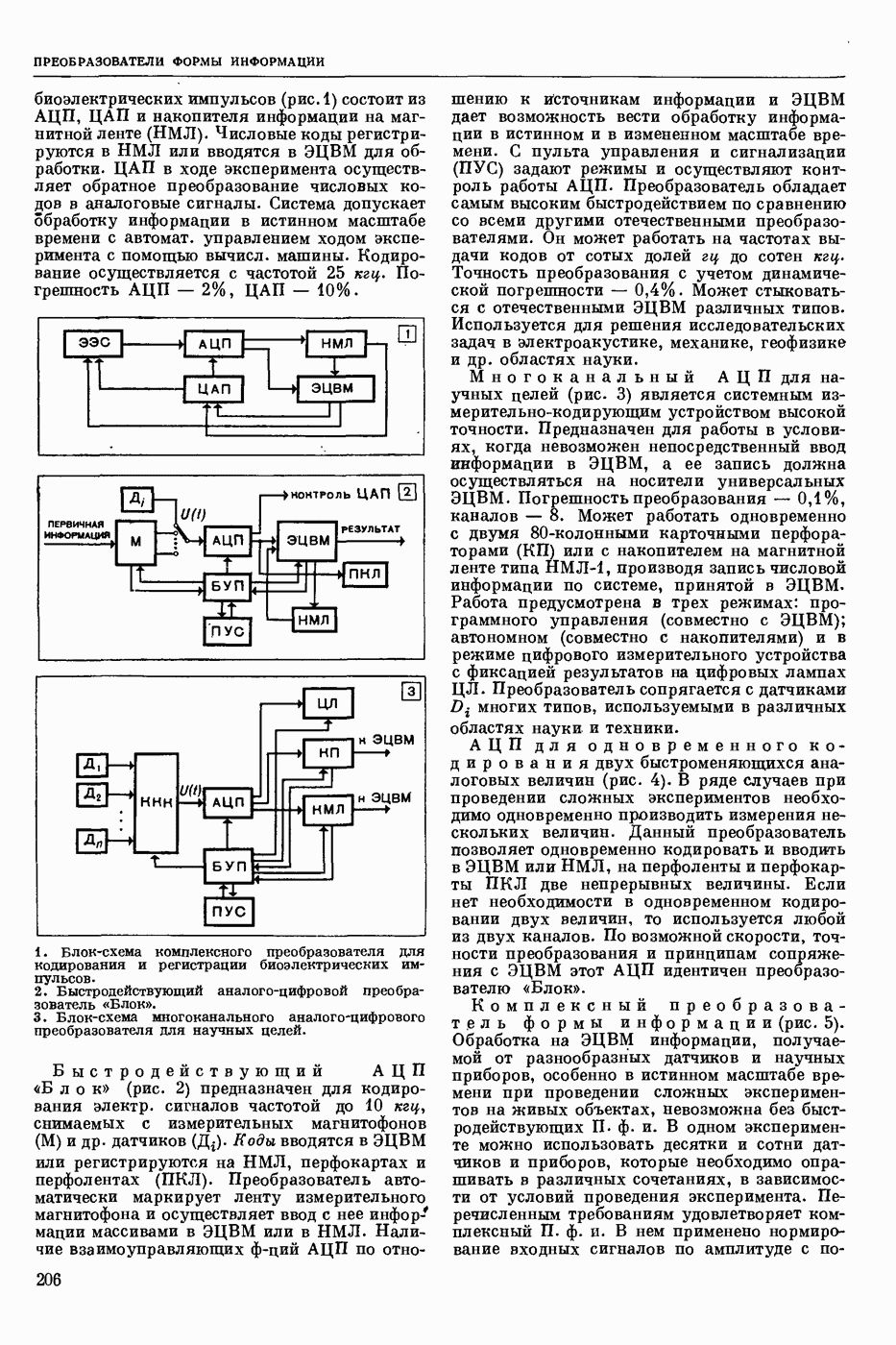
- ПРЕОБРАЗОВАТЕЛИ ФОРМЫ ИНФОРМАЦИИ
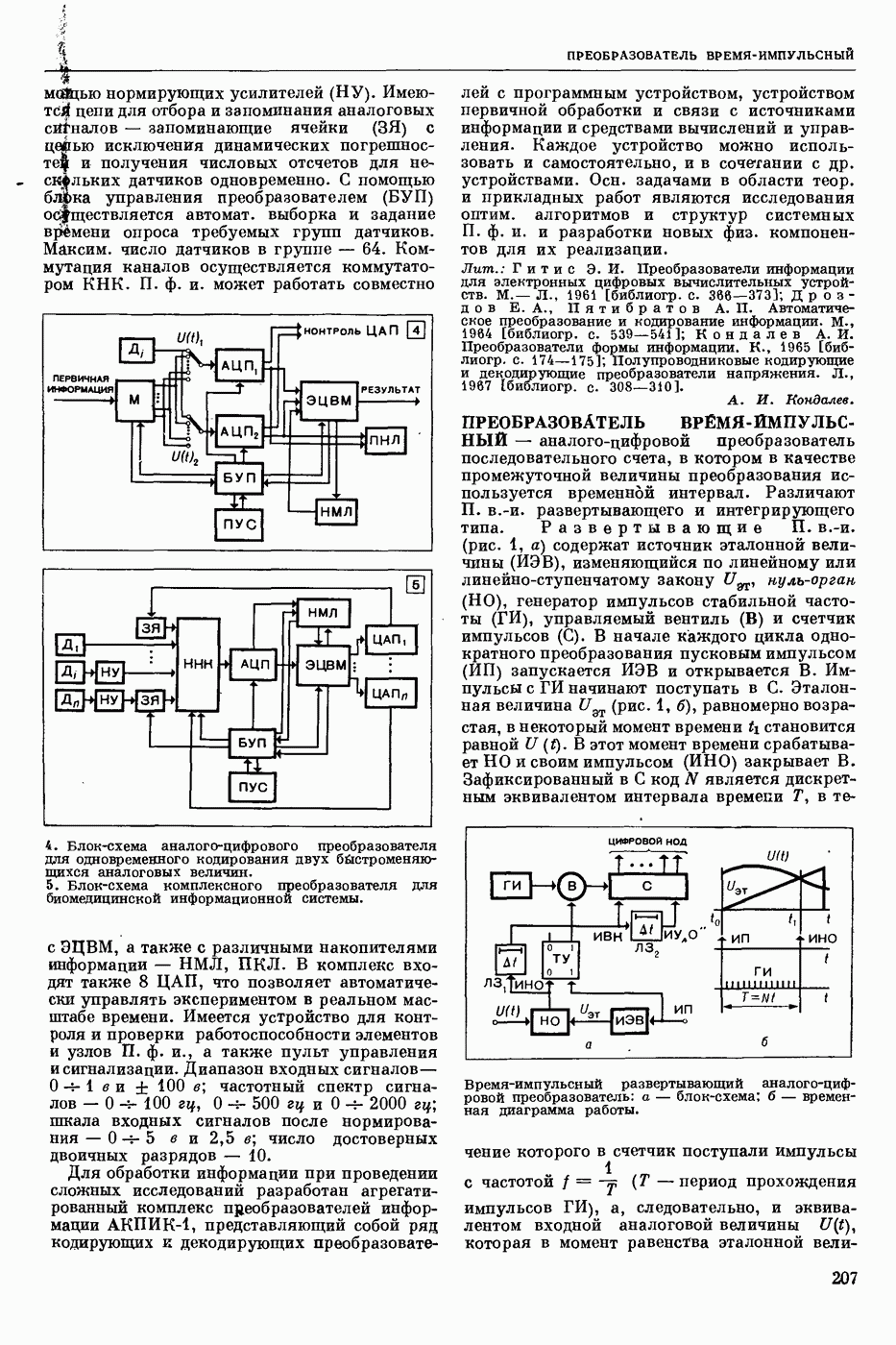
- ПРЕОБРАЗОВАТЕЛЬ ВРЕМЯ-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ИНТЕГРИРУЮЩЕГО ТИПА
- ПРЕОБРАЗОВАТЕЛЬ КОМБИНИРОВАННЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ КВАЗИОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЛИНЕЙНЫЙ ОБРАТИМЫЙ
- ПРЕОБРАЗОВАТЕЛЬ НАКАПЛИВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО СЧЕТА
- ПРЕОБРАЗОВАТЕЛЬ РАЗВЕРТЫВАЮЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ С НЕПОСРЕДСТВЕННЫМ ОТСЧЕТОМ
- ПРЕОБРАЗОВАТЕЛЬ СЛЕДЯЩИЙ
- ПРЕОБРАЗОВАТЕЛЬ ФАЗО-ИМПУЛЬСНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ФУНКЦИОНАЛЬНЫЙ
- ПРЕОБРАЗОВАТЕЛЬ ЦИКЛИЧЕСКИЙ
- ПРЕОБРАЗОВАТЕЛЬ ЧАСТОТНО-ИМПУЛЬСНЫЙ
- ПРЕСЛЕДОВАНИЯ ЗАДАЧА
- ПРИБЛИЖЕННЫХ МЕТОДОВ ОБЩАЯ ТЕОРИЯ
- ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- ПРИОРИТЕТ
- ПРИОРИТЕТОВ СИСТЕМА
- ПРОБЛЕМА «ЧЕЛОВЕК-МАШИНА»
- ПРОГОНКИ МЕТОД
- ПРОГРАММ СЕГМЕНТАЦИЯ
- ПРОГРАММА вычислительной машины
- ПРОГРАММА ДИАГНОСТИЧЕСКАЯ
- ПРОГРАММА ИСПЫТАТЕЛЬНАЯ
- ПРОГРАММА КОМПИЛИРУЮЩАЯ
- ПРОГРАММА УПРАВЛЯЮЩАЯ
- ПРОГРАММА-ДИСПЕТЧЕР
- ПРОГРАММИРОВАНИЕ АВМ
- ПРОГРАММИРОВАНИЕ ВЫПУКЛОЕ
- ПРОГРАММИРОВАНИЕ ДИНАМИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ДИСКРЕТНОЕ
- ПРОГРАММИРОВАНИЕ ДЛЯ ЦВМ
- ПРОГРАММИРОВАНИЕ КВАДРАТИЧНОЕ
- ПРОГРАММИРОВАНИЕ КУСОЧНО-ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ ЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ МАТЕМАТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ НЕЛИНЕЙНОЕ
- ПРОГРАММИРОВАНИЕ СТОХАСТИЧЕСКОЕ
- ПРОГРАММИРОВАНИЕ ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЧАСТИЧНО ЦЕЛОЧИСЛЕННОЕ
- ПРОГРАММИРОВАНИЕ ЭВРИСТИЧЕСКОЕ
- ПРОГРАММИРОВАННОЕ ОБУЧЕНИЕ
- ПРОГРАММИРОВАННЫЙ УЧЕБНИК
- ПРОГРАММИРУЮЩАЯ ПРОГРАММА
- ПРОГРАММНОЕ ПЛАНИРОВАНИЕ И УПРАВЛЕНИЕ в народном хозяйстве.
- ПРОГРАММЫ ОБСЛУЖИВАЮЩИЕ
- ПРОЕКТИРОВАНИЕ СЕТЕЙ И КОММУНИКАЦИЙ ОПТИМАЛЬНОЕ
- ПРОЕКЦИОННЫЕ МЕТОДЫ
- ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ
- «ПРОМIНЬ»
- ПРОПОЗИЦИОНАЛЬНЫЕ СВЯЗКИ, связки логические
- ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА
- ПРОСТОЙ ИТЕРАЦИИ МЕТОД
- ПРОСТРАНСТВО АБСТРАКТНОЕ в функциональном анализе
- ПРОСТРАНСТВО ИЗОБРАЖЕНИЙ
- ПРОЦЕДУРА в программировании
- ПРОЦЕДУРА РЕКУРСИВНАЯ
- ПРОЦЕСС КОНЕЧНОЙ ДЛИТЕЛЬНОСТИ
- ПРОЦЕСС УПРАВЛЯЕМЫЙ
- ПРОЦЕССОР
- ПРОЦЕССЫ С НЕЗАВИСИМЫМИ ПРИРАЩЕНИЯМИ
- ПРЯМЫЕ МЕТОДЫ решения задач прикладной математики
- ПСЕВДОСЛУЧАЙНЫЕ ЧИСЛА
- ПСИХОЛОГИЯ ИНЖЕНЕРНАЯ
- ПУАССОНА ПОТОК
- ПУАССОНА РАСПРЕДЕЛЕНИЕ
- ПУТЬ в теории графов
- РАВНОВЕСИЯ СИТУАЦИЯ
- «РАЗДАН»
- РАЗДЕЛЯЮЩАЯ ПОВЕРХНОСТЬ в распознавании образов
- РАЗМЕЩЕНИЯ ПРОИЗВОДСТВ МОДЕЛИ
- РАЗНОСТНАЯ СХЕМА
- РАЗРЯДНОСТЬ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
- РАСПАРАЛЛЕЛИВАНИЕ АЛГОРИТМА
- РАСПОЗНАВАНИЕ ЗРИТЕЛЬНЫХ ОБРАЗОВ, распознавание изображений
- РАСПОЗНАВАНИЕ ОБРАЗОВ
- РАСПОЗНАВАНИЕ ПРОЦЕССОВ
- РАСПОЗНАВАНИЕ РЕЧЕВЫХ СИГНАЛОВ
- РАСПОЗНАЮЩАЯ СИСТЕМА
- РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- РАСПРЕДЕЛИТЕЛЬНАЯ ЗАДАЧА
- РАСЧЕТА ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ МЕТОДЫ
- РАСЧЕТНЫЙ СТОЛ ПОСТОЯННОГО ТОКА, расчетная модель электрической системы
- РАСШИФРОВОЧНАЯ МАШИНА
- РАУСА КРИТЕРИЙ, Рауса — Гурвица критерий
- РЕАЛЬНЫЙ МАСШТАБ ВРЕМЕНИ
- РЕГЕНЕРАЦИЯ информации в вычислительных устройствах
- РЕГИСТР
- РЕГРЕССИЯ
- РЕГУЛИРОВАНИЕ ЗАПАСОВ
- РЕГУЛИРОВАНИЯ ЗАКОН
- РЕГУЛИРУЮЩИЕ СИСТЕМЫ ОРГАНИЗМА
- РЕГУЛЯРИЗАЦИИ МЕТОД
- РЕГУЛЯРНЫЕ СОБЫТИЯ И ВЫРАЖЕНИЯ
- РЕГУЛЯТОР ИМПУЛЬСНЫЙ
- РЕГУЛЯТОР ЭКСТРЕМАЛЬНЫЙ
- РЕГУЛЯТОРЫ НЕПРЕРЫВНОГО ДЕЙСТВИЯ
- РЕГУЛЯТОРЫ ЦИФРОВЫЕ
- РЕДАКТИРОВАНИЕ ДАННЫХ
- РЕЖИМ ПЕРИОДИЗАЦИИ
- РЕЖИМ РАЗДЕЛЕНИЯ ВРЕМЕНИ
- РЕКУРСИВНЫЕ ФУНКЦИИ
- РЕЛЕВАНТНОСТЬ ДОКУМЕНТА
- РЕЛЕЙНАЯ КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ
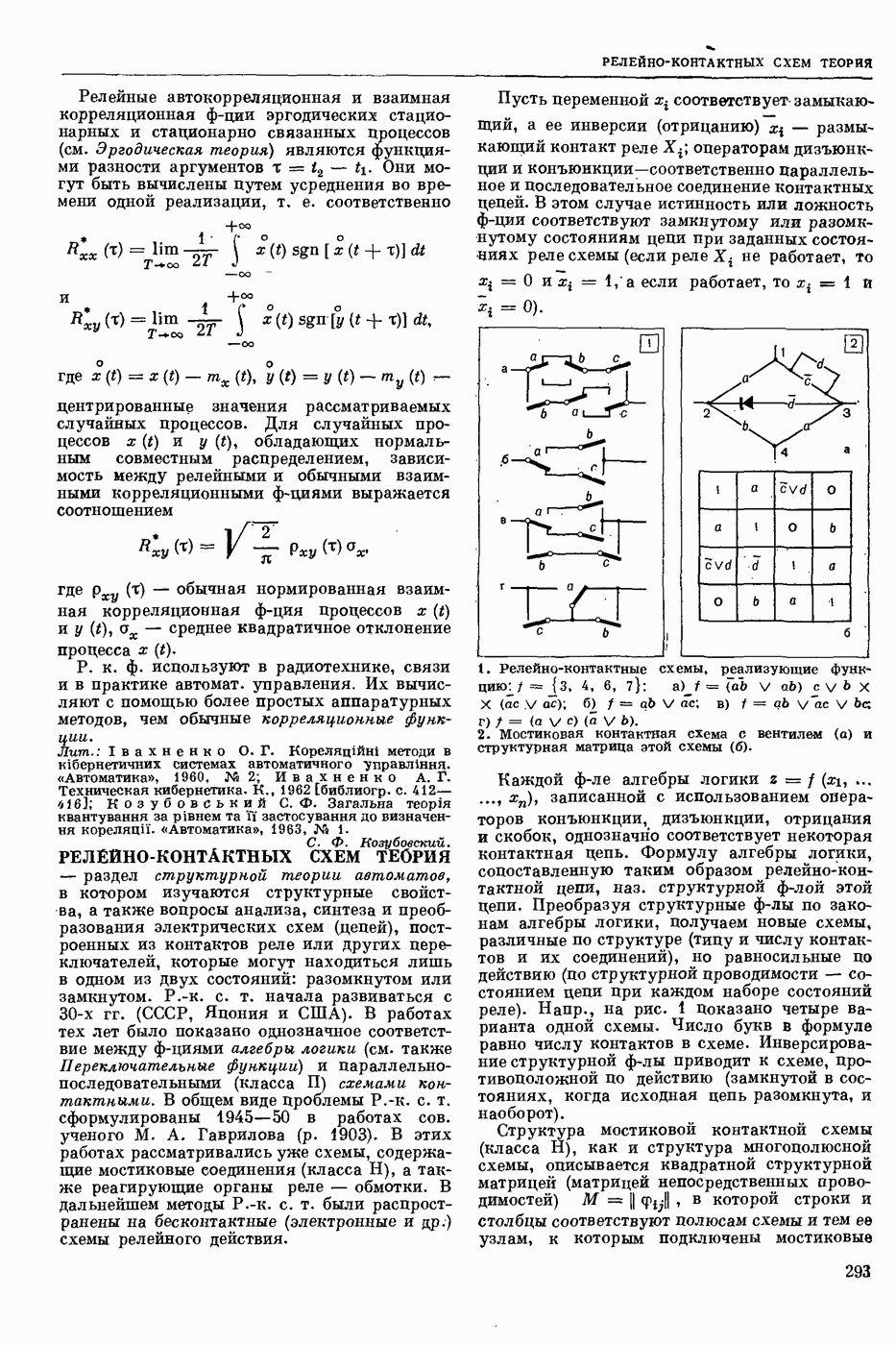
- РЕЛЕЙНО-КОНТАКТНЫХ СХЕМ ТЕОРИЯ
- РЕФАЛ
- РЕФЕРАТ
- РЕФЕРИРОВАНИЕ АВТОМАТИЧЕСКОЕ
- РЕФЛЕКСИВНОЕ УПРАВЛЕНИЕ
- РЕШАЮЩЕЕ ПРАВИЛО в распознавании образов
- РЕШАЮЩЕЕ УСТРОЙСТВО.
- РИСК РАСПОЗНАВАНИЯ
- РИСКА ПРОБЛЕМА
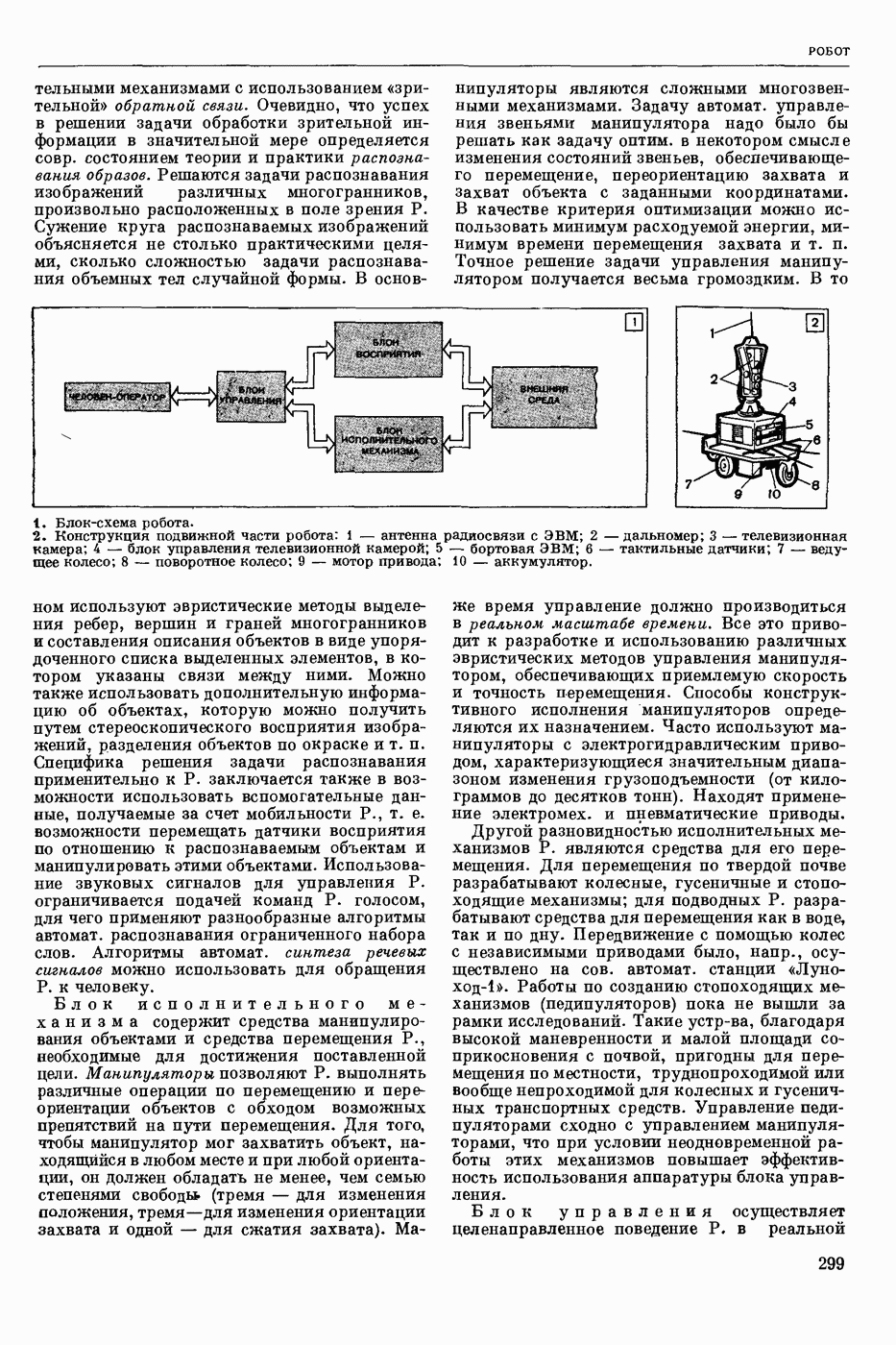
- РОБОТ
- РОБОТ ПРОМЫШЛЕННЫЙ
- РУНГЕ—КУТТЫ МЕТОД
- «РУТА-110»
- R-ФУНКЦИИ
- САМОДВОЙСТВЕННЫЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- САМОКОРРЕКТИРУЮЩАЯСЯ СХЕМА
- САМОНАСТРАИВАЮЩАЯСЯ ПАРАМЕТРИЧЕСКАЯ СИСТЕМА
- САМОНАСТРАИВАЮЩАЯСЯ СИСТЕМА
- САМООБУЧАЮЩИЕСЯ СИСТЕМЫ
- САМООБУЧЕНИЕ РАСПОЗНАВАНИЮ ОБРАЗОВ
- СБОЙ ЦВМ
- СВЕРТКА РАСПРЕДЕЛЕНИЙ СЛУЧАЙНЫХ ВЕЛИЧИН
- СВЕТОВОЙ КАРАНДАШ, световое перо
- СВОДИМОСТЬ в теории алгоритмов
- СВОЙСТВО ОТСУТСТВИЯ ПОСЛЕДЕЙСТВИЯ
- СВЯЗКИ ЛОГИЧЕСКИЕ
- СДВИГ
- «CDC-7600»
- СЕДЛОВЫЕ ТОЧКИ
- СЕКВЕНЦИЯ
- СЕМАНТИКА
- СЕМАНТИКА СТРУКТУРНАЯ
- СЕМАНТИЧЕСКИЙ АНАЛИЗ
- СЕМИОТИКА
- СЕРВОМОТОР
- СЕТЕВАЯ ЗАДАЧА
- СЕТЕВАЯ ЗАДАЧА НЕОДНОРОДНАЯ
- СЕТЕВАЯ МОДЕЛЬ
- СЕТЕВОЙ ГРАФИК
- СЕТЕВЫЕ МЕТОДЫ ПЛАНИРОВАНИЯ И УПРАВЛЕНИЯ
- «СЕТУНЬ»
- СЕТЧАТКА в распознавании образов
- СЕТЬ ИЗ НЕЙРОННЫХ ЭЛЕМЕНТОВ
- СЕТЬ ЛОГИЧЕСКАЯ
- СЕЧЕНИЙ ПРОСТРАНСТВА ПАРАМЕТРОВ МЕТОД
- СИГНАЛИЗИРУЮЩАЯ ФУНКЦИЯ
- СИЛЛОГИСТИКА
- «СИМЕНС» (Siemens Aktiengesellschaft)
- СИММЕТРИЧЕСКИЕ ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ
- СИМПЛЕКС-МЕТОД
- СИМПСОНА ФОРМУЛА
- СИМСКРИПТ
- СИМУЛА
- «СИНТАКСИС»
- СИНТАКСИЧЕСКИЙ АНАЛИЗ АВТОМАТИЧЕСКИЙ естественных языков
- СИНТАКСИЧЕСКИЙ АНАЛИЗ ПРОГРАММ
- СИНТАКСИЧЕСКИЙ КОНТРОЛЬ ПРОГРАММ
- СИНТАКТИКА
- СИНТЕЗ АВТОМАТОВ АБСТРАКТНЫЙ
- СИНТЕЗ АВТОМАТОВ СТРУКТУРНЫЙ
- СИНТЕЗ АЛГОРИТМА УПРАВЛЕНИЯ
- СИНТЕЗ РЕЧЕВЫХ СИГНАЛОВ
- СИНХРОНИЗАЦИЯ РАБОТЫ ЦВМ
- «СИРИУС»
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ АНАЛИЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СИНТЕЗ
- СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ СТАТИСТИЧЕСКАЯ ДИНАМИКА
- СИСТЕМ ОБЩАЯ ТЕОРИЯ
- СИСТЕМА АВТОМАТИЗИРОВАННАЯ
- СИСТЕМА АВТОМАТИЧЕСКАЯ
- СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ)
- СИСТЕМА АВТОМАТИЧЕСКОЙ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
- СИСТЕМА АВТОНОМНАЯ
- СИСТЕМА АСТАТИЧЕСКАЯ
- СИСТЕМА ИНФОРМАЦИОННОГО ПОИСКА
- СИСТЕМА НЕАВТОНОМНАЯ
- СИСТЕМА НЕПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЕРЫВАНИЯ ЦВМ
- СИСТЕМА ПРОГРАММИРОВАНИЯ
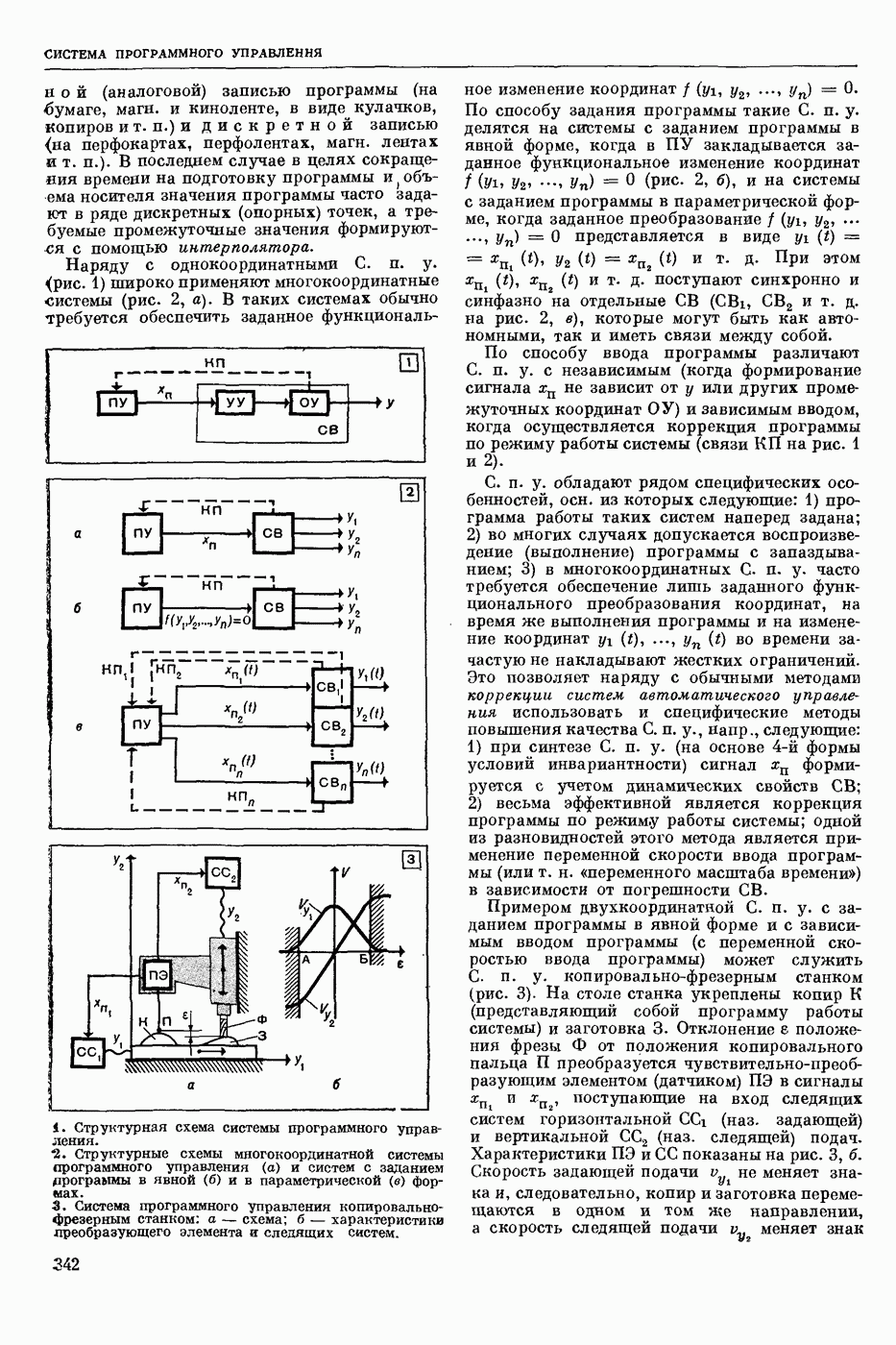
- СИСТЕМА ПРОГРАММНОГО УПРАВЛЕНИЯ
- СИСТЕМА ПРЯМОГО УПРАВЛЕНИЯ
- СИСТЕМА СЧИСЛЕНИЯ
- СИСТЕМА УПРАВЛЕНИЯ АДАПТИВНАЯ
- СИСТЕМА УПРАВЛЕНИЯ ЗАМКНУТАЯ, система управления по отклонению
- СИСТЕМА УПРАВЛЕНИЯ НАУЧНЫМ ЭКСПЕРИМЕНТОМ
- СИСТЕМА УПРАВЛЕНИЯ РАЗОМКНУТАЯ
- СИСТЕМА УПРАВЛЕНИЯ С ПЕРЕМЕННОЙ СТРУКТУРОЙ
- СИСТЕМА УПРАВЛЕНИЯ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- СИСТЕМА УРАВНЕНИЙ В ВАРИАЦИЯХ
- СИСТЕМА УРАВНЕНИЙ СОПРЯЖЕННАЯ
- СИСТЕМА «ЧЕЛОВЕК — МАШИНА»
- СИСТЕМА ЭКСТРЕМАЛЬНОГО РЕГУЛИРОВАНИЯ
- СИСТЕМНОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- СИСТЕМНЫЙ ПОДХОД
- СИСТЕМОТЕХНИКА
- СИСТЕМЫ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- СИСТЕМЫ С ВРЕМЕННЫМИ ОГРАНИЧЕНИЯМИ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ
- СИСТЕМЫ С ОГРАНИЧЕННЫМ ВРЕМЕНЕМ ПРЕБЫВАНИЯ
- СИСТЕМЫ УПРАВЛЕНИЯ НА ПЕРЕМЕННОМ ТОКЕ
- СКЛЕИВАНИЯ ЗАКОН
- СКОЛЬЗЯЩИЙ РЕЖИМ
- СКОРОСТЬ СОЗДАНИЯ СООБЩЕНИЯ
- СЛЕДЯЩАЯ СИСТЕМА
- СЛОВАРНЫЙ ПОИСК
- СЛОВАРЬ АВТОМАТИЧЕСКИЙ
- СЛОВАРЬ ИНФОРМАЦИОННОГО ЯЗЫКА
- СЛОВАРЬ ЧАСТОТНЫЙ
- СЛОВО
- СЛОЖНОСТЬ ВЫЧИСЛЕНИЙ
- СЛОЖНОСТЬ ТЬЮРИНГОВЫХ ВЫЧИСЛЕНИЙ
- СЛОЖНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
- СЛУЧАЙНАЯ ВЕЛИЧИНА
- СЛУЧАЙНАЯ ФУНКЦИЯ
- СЛУЧАЙНОГО ПОИСКА МЕТОДЫ
- СЛУЧАЙНОЕ ПОЛЕ
- СЛУЧАЙНОЕ СОБЫТИЕ
- СЛУЧАЙНЫЕ ЧИСЛА
- СЛУЧАЙНЫЙ ПРОЦЕСС, вероятностный процесс, стохастический процесс
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ
- СЛУЧАЙНЫХ ПРОЦЕССОВ ТЕОРИЯ ПРЕДСКАЗАНИЯ
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ ОБЫКНОВЕННЫХ УРАВНЕНИЙ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ ВЫЧИСЛЕНИЙ.
- СОБСТВЕННЫХ ЗНАЧЕНИЙ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СОБЫТИЕ РЕГУЛЯРНОЕ
- СОБЫТИЯ ЦИКЛИЧЕСКАЯ ГЛУБИНА
- СОВМЕЩЕНИЕ ОПЕРАЦИЙ В МАШИНЕ
- «СОЛЯРТРОН ЭЛЕКТРОНИК ГРУП» (The Solartron Electronic Group, Ltd)
- СООБЩЕНИЕ в теории передачи информации
- СООБЩЕНИЙ ТЕОРИЯ
- СОПРОТИВЛЕНИЕ ОТРИЦАТЕЛЬНОЕ
- СОПРОТИВЛЕНИЕ ЦИФРОВОЕ УПРАВЛЯЕМОЕ
- СОПРЯЖЕННЫХ НАПРАВЛЕНИЙ МЕТОД
- СОРТИРОВАЛЬНАЯ МАШИНА
- СОРТИРОВКА ДАННЫХ
- СОЦИОЛОГИЧЕСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ
- СПЕКТРАЛЬНАЯ ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
- СПЕКТРАЛЬНАЯ ФУНКЦИЯ стационарного в широком смысле случайного процесса
- СПЕЦИАЛИЗИРОВАННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- СПЕЦИАЛЬНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- СПЕЦИФИКАЦИЯ
- СПИСКОВАЯ СТРУКТУРА
- СПИСОК в программировании
- СПРАВОЧНО-ИНФОРМАЦИОННЫЙ ФОНД (СИФ)
- СТАБИЛИЗАЦИИ СИСТЕМА
- СТАНДАРТИЗИРОВАННАЯ ИСТОРИЯ БОЛЕЗНИ
- СТАНДАРТЫ ПО ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКЕ
- СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
- СТАТИСТИЧЕСКИЕ МЕТОДЫ РАСПОЗНАВАНИЯ
- СТАТИСТИЧЕСКИЕ ОЦЕНКИ
- СТАТИСТИЧЕСКИХ ИСПЫТАНИЙ МЕТОД
- СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ МЕТОД
- СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- СТИЛТЬЕСА КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ
- СТОХАСТИЧЕСКИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- СТОХАСТИЧЕСКИЙ ПРОЦЕСС
- СТОХАСТИЧЕСКИХ КВАЗИГРАДИЕНТОВ МЕТОД
- СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ МЕТОД
- СТОХАСТИЧЕСКОЙ ОПТИМИЗАЦИИ МЕТОДЫ
- СТРАТЕГИЯ ОПТИМАЛЬНАЯ
- СТРАТЕГИЯ ПОВЕДЕНИЯ
- СТРАТЕГИЯ СМЕШАННАЯ
- СТРАТЕГИЯ ЧИСТАЯ
- «СТРЕЛА»
- СТРУКТУРА, решетка.
- СТРУКТУРНАЯ ИНТЕРПРЕТАЦИЯ ЯЗЫКА
- СТРУКТУРНАЯ ПОЭТИКА
- СТРУКТУРНАЯ СХЕМА МОДЕЛИ
- СТРУКТУРНАЯ ТЕОРИЯ АВТОМАТОВ
- СТРУКТУРНОЕ СТИХОВЕДЕНИЕ
- СУММАТОР
- СУММАТОР КОМБИНАЦИОННЫЙ
- СУММАТОР НАКАПЛИВАЮЩИЙ
- СУММАТОР ОДНОРАЗРЯДНЫЙ
- СУММАТОР ПАРАЛЛЕЛЬНЫЙ
- СУММАТОР ПОСЛЕДОВАТЕЛЬНЫЙ
- СУПЕРВИЗОР
- СХЕМА ВЕНТИЛЬНАЯ
- СХЕМА КОНТАКТНАЯ
- СХЕМА КОНТАКТНАЯ БЕСПОВТОРНАЯ
- СХЕМА КОНТАКТНО-ВЕНТИЛЬНАЯ
- СХЕМА РЕЛЕЙНО-КОНТАКТНАЯ
- СХЕМА СРАВНЕНИЯ
- СХОДСТВА КРИТЕРИИ
- СЧЕТЧИК
- ТАБУЛИРОВАНИЕ ФУНКЦИЙ
- ТАБУЛЯТОР
- ТАЙПОТРОН
- ТАКТ
- ТАКТОВАЯ ЧАСТОТА
- ТВИСТОР
- ТЕЗАУРУС
- ТЕЛЕМЕХАНИКА
- ТЕЛЕТАЙП
- ТЕРМИНАЛ, абонентский пульт, оконечное устройство
- ТЕРМИНАЛЬНОЕ УПРАВЛЕНИЕ, управление конечным состоянием
- ТЕСТОВЫЕ ПРОГРАММЫ, тест-программы
- ТЕСТЫ
- ТЕХНИЧЕСКАЯ ДИАГНОСТИКА
- ТЕХНИЧЕСКОЕ ПРОЕКТИРОВАНИЕ ЦВМ
- ТЕХПРОМФИНПЛАН ПРЕДПРИЯТИЯ МАТРИЧНЫЙ
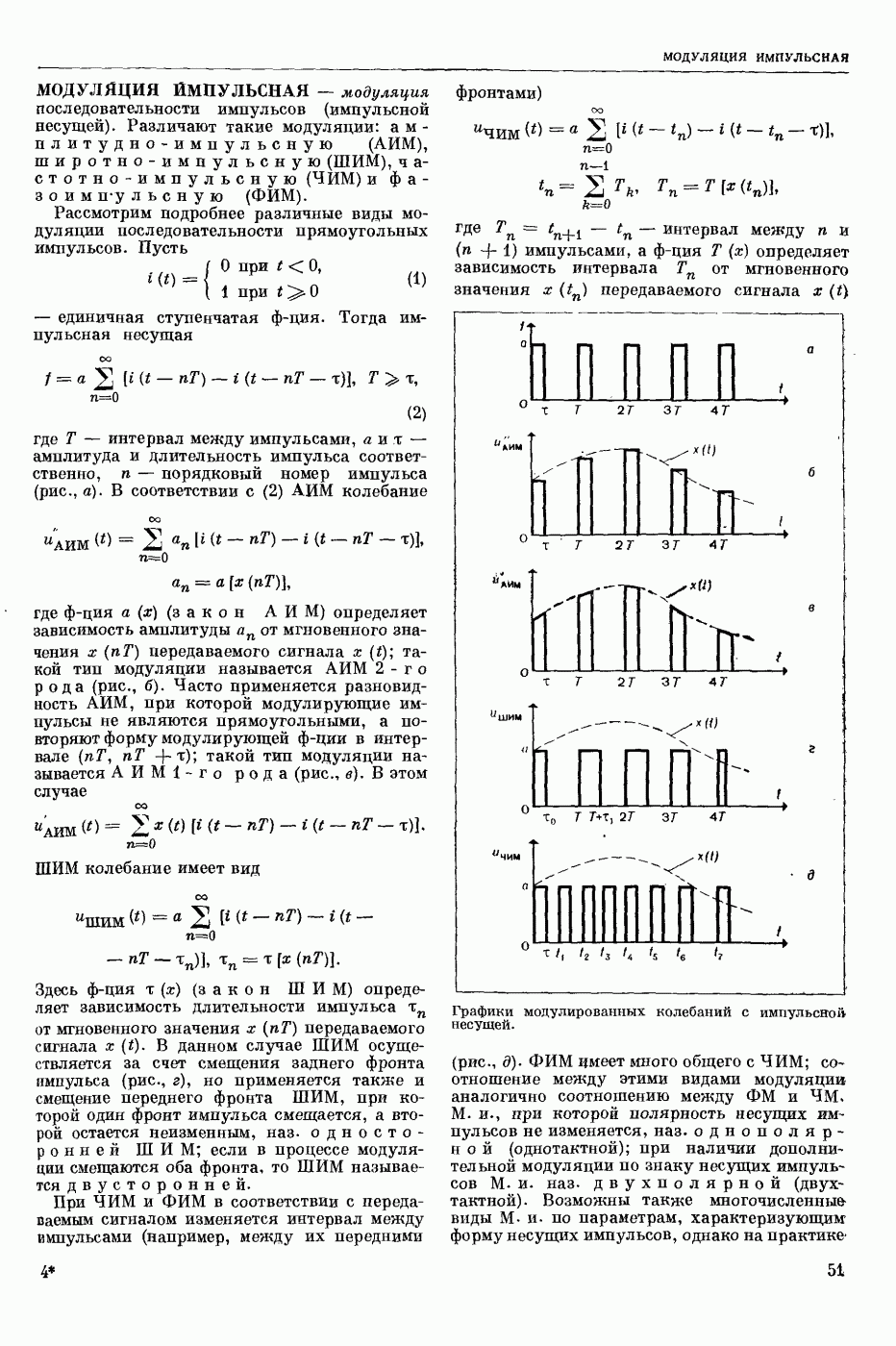
- ТОЖДЕСТВЕННО ИСТИННАЯ ФОРМУЛА, общезначимая формула
- ТОНКАЯ МАГНИТНАЯ ПЛЕНКА
- ТОПОЛОГИЯ
- «ТОСИБА» (Tokyo Shibaura Electric Company, Ltd)
- ТОЧКА РАВНОВЕСИЯ
- ТОЧКИ ПЕРЕКЛЮЧЕНИЯ
- ТОЧНОСТЬ ВОСПРОИЗВЕДЕНИЯ СООБЩЕНИЯ
- ТРАЕКТОРИЯ ДОПУСТИМАЯ
- ТРАЕКТОРИЯ ОПТИМАЛЬНАЯ
- ТРАЕКТОРИЯ ФАЗОВАЯ
- ТРАНЗИТИВНЫЙ ГРАФ
- ТРАНСЛЯТОР, компилирующая программа, программирующая программа
- ТРАНСЛЯТОР СИНТАКСИЧЕСКИ УПРАВЛЯЕМЫЙ
- ТРАНСПОРТНАЯ ЗАДАЧА
- ТРАНСПОРТНАЯ СЕТЬ
- ТРАНСФЛЮКСОР
- ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
- ТРИГГЕР
- ТРИГГЕР ДИНАМИЧЕСКИЙ
- ТРИГГЕР СТАТИЧЕСКИЙ
- ТРИОД ПОЛУПРОВОДНИКОВЫЙ, транзистор
- ТЬЮРИНГА МАШИНА
- УЗЛОВОЙ СПИСОК
- «УМ1-НХ»
- УНИВЕРСАЛЬНАЯ СИСТЕМА ЭЛЕМЕНТОВ ПРОМЫШЛЕННОЙ ПНЕВМОАВТОМАТИКИ (УСЭППА)
- UNCOL
- УПОРЯДОЧЕНИЕ МАССИВА
- УПРАВЛЕНИЕ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- УПРАВЛЕНИЕ ДАННЫМИ
- УПРАВЛЕНИЕ ЗАПАСАМИ
- УПРАВЛЕНИЕ КОМАНДАМИ
- УПРАВЛЕНИЕ ЛЕЧЕБНЫМ ПРОЦЕССОМ.
- УПРАВЛЕНИЕ ОПЕРАЦИЯМИ
- УПРАВЛЕНИЕ ОПТИМАЛЬНОЕ
- УПРАВЛЕНИЕ ПРОГРАММНОЕ
- УПРАВЛЕНИЕ С АДАПТАЦИЕЙ
- УПРАВЛЕНИЕ СТРУКТУРНОЕ В ЦВМ
- УПРАВЛЕНИЯ ОТНОШЕНИЕ, зависимости отношение
- УПРАВЛЕНИЯ СЛУЧАЙНЫМИ ПРОЦЕССАМИ ТЕОРИЯ
- УПРАВЛЯЮЩАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
- УПРАВЛЯЮЩАЯ ПРОГРАММА
- УПРАВЛЯЮЩЕЕ ВОЗДЕЙСТВИЕ, регулирующее воздействие
- «УПРАВЛЯЮЩИЕ СИСТЕМЫ И МАШИНЫ»
- УРАВНЕНИЙ КЛАССИФИКАЦИЯ.
- УРАВНОВЕШИВАНИЯ МЕТОДЫ
- «УРАЛ»
- УСИЛИТЕЛЬ
- УСИЛИТЕЛЬ ДИФФЕРЕНЦИАЛЬНЫЙ
- УСИЛИТЕЛЬ ОПЕРАЦИОННЫЙ, усилитель решающий
- УСИЛИТЕЛЬ ОТРАБАТЫВАЮЩИЙ
- УСИЛИТЕЛЬ РЕШАЮЩИЙ
- УСЛОВИЯ СТАЦИОНАРНОСТИ
- УСЛОВИЯ ТРАНСВЕРСАЛЬНОСТИ
- УСТАНОВКА НАЧАЛЬНЫХ УСЛОВИЙ
- УСТОЙЧИВОСТИ ДИСКРЕТНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ КРИТЕРИИ
- УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ СИСТЕМ ТЕОРИЯ
- УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ТЕОРИЯ
- УСТОЙЧИВОСТЬ ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМОВ
- УСТОЙЧИВОСТЬ МОДЕЛИ
- УСТОЙЧИВОСТЬ ПО ЛЯПУНОВУ
- УСТОЙЧИВОСТЬ РАЗНОСТНЫХ СХЕМ
- УСТОЙЧИВОСТЬ ЧИСЛЕННОГО МЕТОДА
- УСТРОЙСТВА ВВОДА—ВЫВОДА ДАННЫХ ЦВМ
- УСТРОЙСТВА ЗАПИСИ АНАЛОГОВОЙ ИНФОРМАЦИИ
- УСТРОЙСТВА ОТОБРАЖЕНИЯ ИНФОРМАЦИИ
- УСТРОЙСТВО ИНДИКАЦИИ ABM
- УСТРОЙСТВО ИНТЕГРИРУЮЩЕЕ, интегратор
- УСТРОЙСТВО ИНТЕГРО-ДИФФЕРЕНЦИРУЮЩЕЕ
- УСТРОЙСТВО ОБМЕНА ЦВМ
- УСТОЙСТВО ПЕРЕЗАПИСИ ДЛЯ ЦВМ
- УСТРОЙСТВО УПРАВЛЕНИЯ ЦВМ
- УСТРОЙСТВО ЦИФРОВОЙ РЕГИСТРАЦИИ
- ФАЗОВОГО ПРОСТРАНСТВА МЕТОД
- ФАЗОВЫЕ КООРДИНАТЫ
- ФАЗОВЫЕ ОГРАНИЧЕНИЯ
- ФАКТОГРАФИЧЕСКАЯ ИНФОРМАЦИОННО-ПОИСКОВАЯ СИСТЕМА
- ФАКТОРИЗАЦИИ МЕТОД
- «ФЕРРАНТИ» (Ferranti, Ltd)
- ФЕРРИТ-ДИОДНАЯ СИСТЕМА ЭЛЕМЕНТОВ
- ФЕРРИТ-ТРАНЗИСТОРНАЯ СИСТЕМА ЭЛЕ МЕНТОВ
- ФИКСАТОР, адрес второго ранга, косвенный адрес
- ФИКСИРОВАННАЯ ЗАПЯТАЯ
- ФИЛОСОФСКИЕ ВОПРОСЫ КИБЕРНЕТИКИ
- ФИЛЬТР
- ФИЛЬТРАЦИЯ СЛУЧАЙНОГО ПРОЦЕССА
- ФОНД АЛГОРИТМОВ И ПРОГРАММ
- ФОНД СПРАВОЧНО-ИНФОРМАЦИОННЫЙ
- FORMAC
- ФОРМАЛИЗМ в математике
- ФОРТРАН
- «ФУДЗИЦУ» («Фудзи цусинки Сэйдзо», Fujitsu, Ltd)
- ФУНКЦИИ, СОХРАНЯЮЩИЕ КОНСТАНТУ
- ФУНКЦИИ, СОХРАНЯЮЩИЕ МНОЖЕСТВО
- ФУНКЦИИ, СОХРАНЯЮЩИЕ РАЗБИЕНИЕ
- ФУНКЦИОНАЛ
- ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ЭВМ
- ФУНКЦИОНАЛЬНЫЙ ЭЛЕМЕНТ ЭВМ
- ФУНКЦИЯ РАССТАНОВКИ
- ФУНКЦИЯ РЕШЕТЧАТАЯ
- ФУНКЦИЯ СТУПЕНЧАТАЯ
- ФУРЬЕ ИНТЕГРАЛОВ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ФУРЬЕ ПРЕОБРАЗОВАНИЯ
- ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ в теории игр
- ХАРАКТРОН
- ХЕМИТРОН
- ХИНЧИНА-ПОЛАЧЕКА ФОРМУЛА
- «ХИТАЧИ» (Hitachi, Ltd)
- ХОМСКОГО ГРАММАТИКИ
- «ХОНИУЭЛЛ КОРПОРЕЙШЕН» (Honeywell Corporation)
- ХЭММИНГА КОД
- ЦВМ АСИНХРОННАЯ
- ЦВМ СИНХРОННАЯ
- ЦЕЛЕВАЯ ФУНКЦИЯ, функция цели
- ЦЕЛЕСООБРАЗНОСТЬ в кибернетике
- ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
- ЦЕНТРАЛЬНЫЙ ЭКОНОМИКО-МАТЕМАТИЧЕСКИЙ ИНСТИТУТ АКАДЕМИИ НАУК СССР
- ЦЕПИ СВЯЗАННЫЕ
- ЦЕПОЧКА
- ЦЕПЬ графа
- ЦЕПЬ ОКРУГЛЕНИЯ
- ЦЕПЬ ПЕРЕНОСА
- ЦИКЛ графа
- ЦИКЛ ПРОГРАММЫ
- ЦИКЛОМАТИЧЕСКОЕ ЧИСЛО
- ЦИПФА ЗАКОН
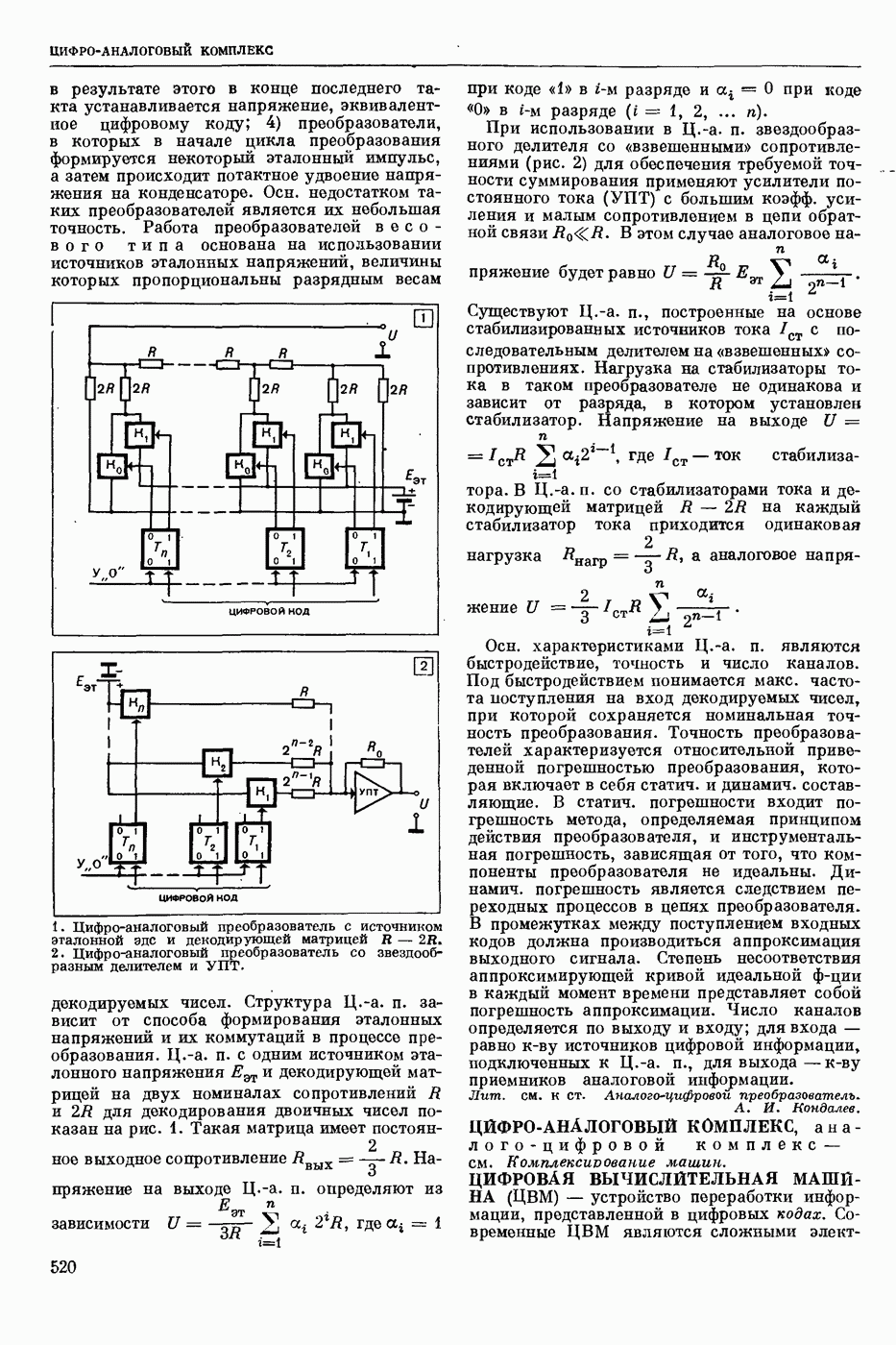
- ЦИФРО-АНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ, преобразователи код
- ЦИФРО-АНАЛОГОВЫЙ КОМПЛЕКС, аналого-цифровой комплекс
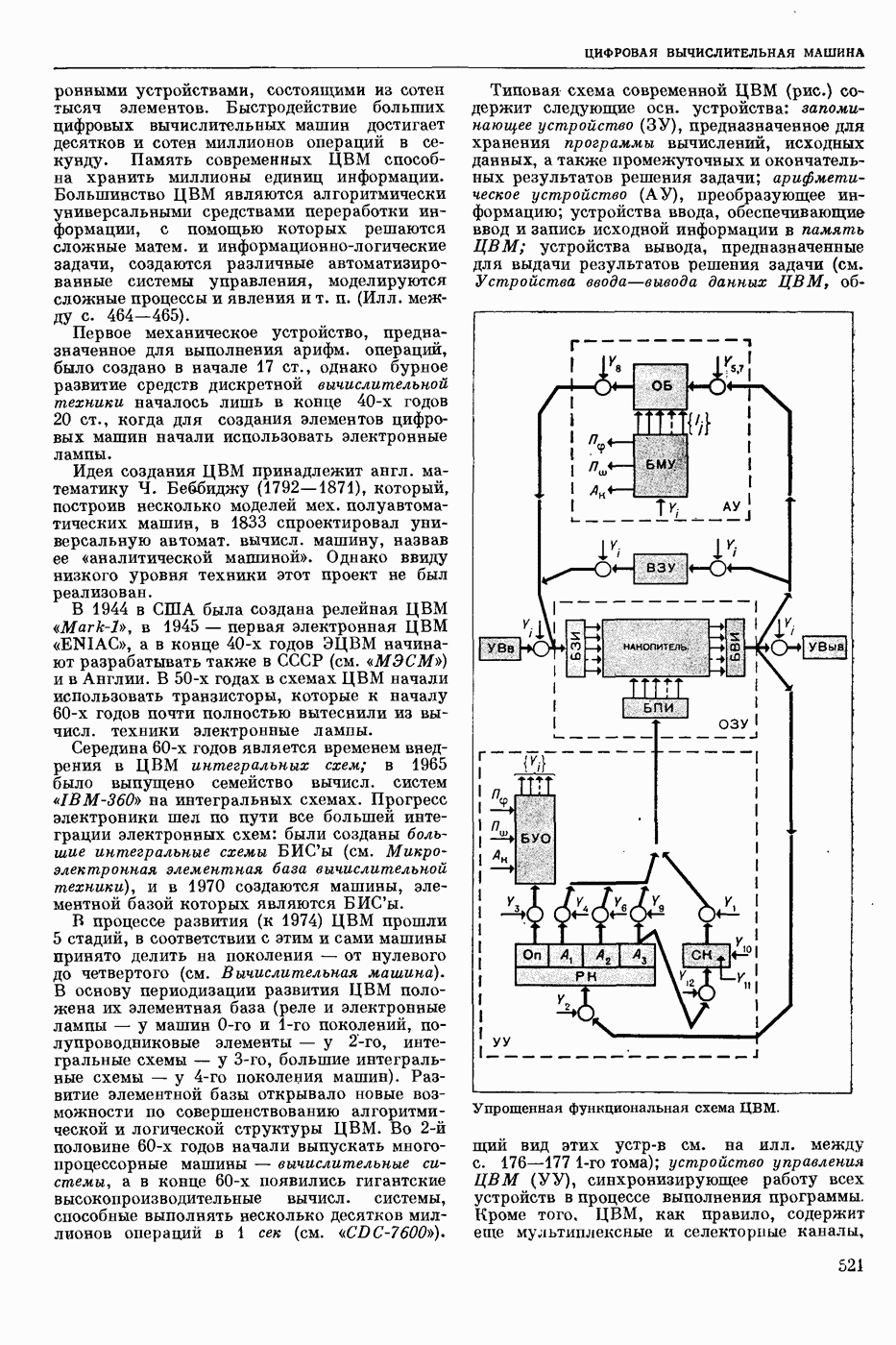
- ЦИФРОВАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЦВМ)
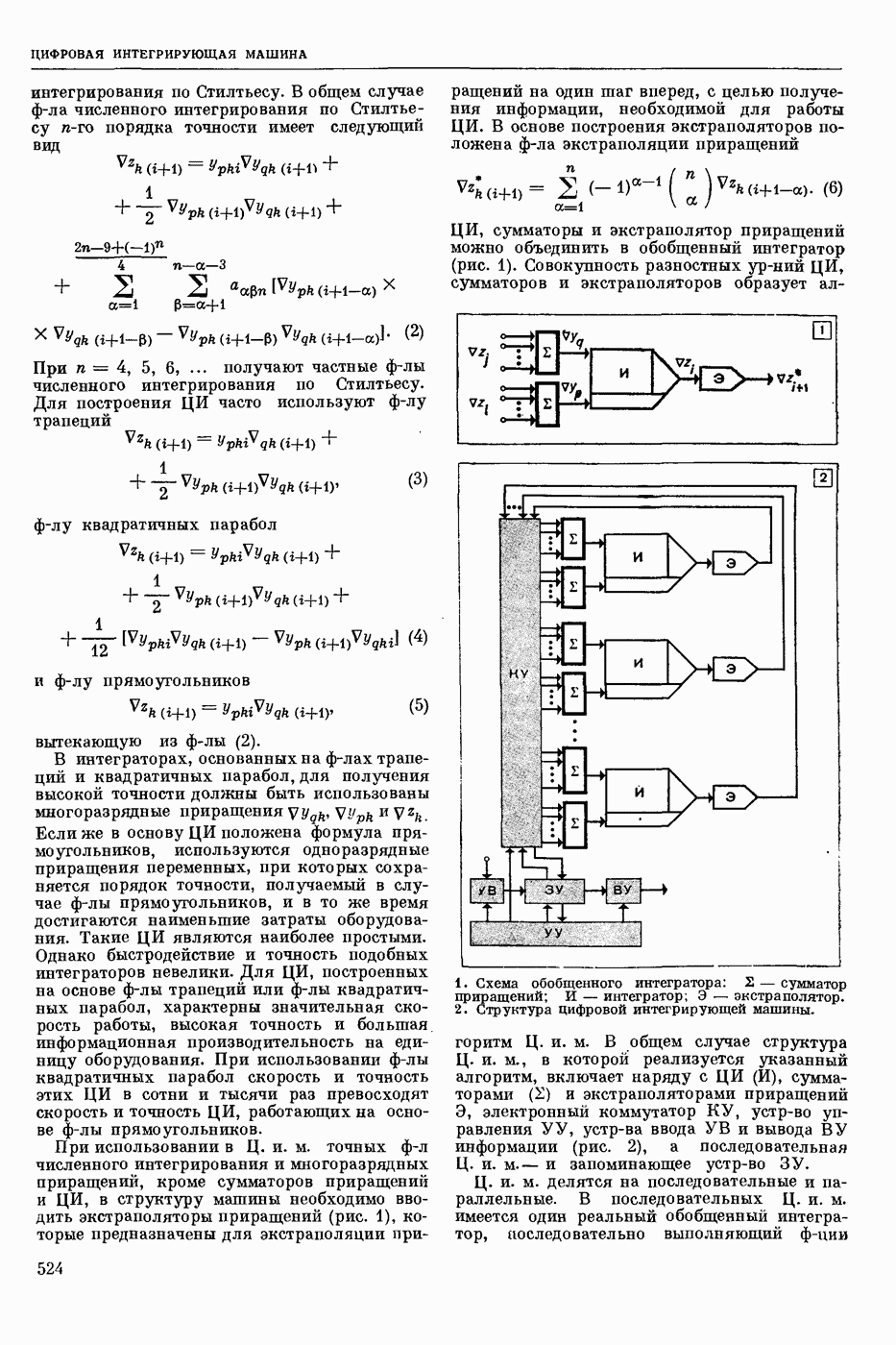
- ЦИФРОВАЯ ИНТЕГРИРУЮЩАЯ МАШИНА
- ЦИФРОВАЯ МОДЕЛЬ СЕТЕВОГО ГРАФИКА
- ЦИФРОВОЙ ДИФФЕРЕНЦИАЛЬНЫЙ АНАЛИЗАТОР
- ЧАСТИЧНО УПОРЯДОЧЕННОЕ МНОЖЕСТВО
- ЧАСТПЧНО-РЕКУРСИВНЫЕ ФУНКЦИИ
- ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
- ЧЕБЫШЕВА ЗАДАЧА РАВНОМЕРНОГО ПРИБЛИЖЕНИЯ
- ЧЕЛОВЕК-ОПЕРАТОР
- ЧЕРЕДУЮЩАЯСЯ ЦЕПЬ
- ЧЕРНИЛА МАГНИТНЫЕ
- «ЧЕРНЫЙ ЯЩИК»
- ЧИРЧА ТЕЗИС
- ЧИСЛА ФОРМАТ
- ЧИСЛЕННЫЕ МЕТОДЫ
- ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
- ЧИТАЮЩИЙ АВТОМАТ, оптическое читающее устройство
- ЧИТАЮЩИЙ АВТОМАТ КОРРЕЛЯЦИОННЫЙ
- ЧУВСТВИТЕЛЬНОСТИ ТЕОРИЯ
- ШАГ КВАНТОВАНИЯ
- ШЕННОНА ЛАБИРИНТ
- ШЕННОНА МЫШЬ
- ШЕННОНА ФУНКЦИЯ
- ШЕПЛИ ВЕКТОР
- ШЕФФЕРА ШТРИХ, Шеффера функция, отрицание конъюнкции
- ШИНА
- ШИФРАТОР
- ШТРАФНАЯ ФУНКЦИЯ
- ШТРАФНЫХ ФУНКЦИЙ МЕТОД
- ШТРАФОВ МЕТОД
- ШУМ КВАНТОВАНИЯ
- ШУМ ПОИСКОВЫЙ
- ЭВРИСТИКА
- ЭВРИСТИЧЕСКИЕ МЕТОДЫ В РАСПОЗНАВАНИИ
- ЭЙЛЕРА ЦЕПЬ
- ЭКВИВАЛЕНТНАЯ СХЕМА
- ЭКВИВАЛЕНТНОСТИ ОТНОШЕНИЕ (эквивалентность, эквиваленци я) на множестве
- ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ
- ЭКВИВАЛЕНТНЫЕ СОСТОЯНИЯ АВТОМАТА
- ЭКВИВАЛЕНТНЫХ ВОЗМУЩЕНИЙ МЕТОД
- ЭКВИФИНАЛЬНОСТЬ СИСТЕМЫ УПРАВЛЕНИЯ
- ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ МЕТОДЫ, в управлении народным хозяйством
- ЭКРАННЫЙ ПУЛЬТ
- ЭКСПЕРИМЕНТ БЕЗУСЛОВНЫЙ
- ЭКСПЕРИМЕНТ КРАТНЫЙ
- ЭКСПЕРИМЕНТ УСЛОВНЫЙ
- ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ СПОСОБЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ
- ЭКСПЕРИМЕНТЫ С АВТОМАТАМИ
- ЭКСПЕРТНЫХ ОЦЕНОК МЕТОДЫ в прогнозировании
- ЭКСТРАПОЛИРОВАНИЕ В ОБУЧЕНИИ РАСПОЗНАВАНИЮ ОБРАЗОВ
- ЭКСТРАПОЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
- ЭКСТРАПОЛИРОВАНИЕ ФУНКЦИЙ
- ЭКСТРЕМАЛЬ
- ЭКСТРЕМАЛЬНОЕ РЕГУЛИРОВАНИЕ
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ в теории графов
- ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ НА ГРАФАХ
- ЭКСТРЕМУМ
- ЭКСТРЕМУМ АБСОЛЮТНЫЙ
- ЭКСТРЕМУМ ГЛОБАЛЬНЫЙ
- ЭКСТРЕМУМ ЛОКАЛЬНЫЙ
- ЭКСТРЕМУМА ДРЕЙФ
- ЭЛЕКТРИЧЕСКИЕ МОДЕЛИРУЮЩИЕ СЕТКИ
- ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ТЕОРИЯ
- «ЭЛЕКТРОН»
- ЭЛЕКТРОННАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА (ЭВМ)
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ
- ЭЛЕКТРОННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- ЭЛЕМЕНТ ЗАДЕРЖКИ
- ЭЛЕМЕНТАРНАЯ СИСТЕМА
- ЭЛЕМЕНТАРНЫЕ ОПЕРАЦИИ НАД СЛОВАМИ
- ЭЛЕМЕНТАРНЫЕ ТЕОРИИ.
- ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ СПОСОБЫ ВЫЧИСЛЕНИЯ.
- ЭЛЕМЕНТНАЯ СТРУКТУРА ЦВМ
- ЭЛЕМЕНТНЫЕ СТРУКТУРЫ НА ЛОГИЧЕСКИХ ЗАДЕРЖИВАЮЩИХ ЭЛЕМЕНТАХ
- ЭЛЕМЕНТНЫЙ СИНТЕЗ ЦВМ
- ЭЛИОНИКА
- ЭЛЛИПТИЧЕСКОГО ТИПА ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ СПОСОБЫ РЕШЕНИЯ.
- «ЭМИК-1»
- ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
- «ЭМСС»
- «ЭМУ»
- ЭНТРОПИЯ
- ЭНТРОПИЯ ЖИВЫХ СИСТЕМ
- ЭНТРОПИЯ СООБЩЕНИЯ при заданных условиях точности
- ЭПСИЛОН
- ЭПСИЛОН-ЭНТРОПИЯ
- ЭРГАТИЧЕСКАЯ СИСТЕМА
- ЭРГОДИЧЕСКАЯ ТЕОРИЯ
- ЭРГОДИЧЕСКОЕ СОСТОЯНИЕ
- ЭРЛАНГА ФОРМУЛЫ
- ЭТАЛОН в распознавании образов
- ЭТАЛОННОЕ НАПРЯЖЕНИЕ
- ЭФФЕКТИВНОСТЬ ИНФОРМАЦИОННОГО ПОИСКА техническая
- ЭШБИ ГОМЕОСТАТ
- «ЮНИВАК» (Univac)
- ЯДРО втеории игр
- ЯЗЫК АВТОМАТНЫЙ
- ЯЗЫК АЛГОРИТМИЧЕСКИЙ
- ЯЗЫК АНКЕТНЫЙ
- ЯЗЫК БЕСКОНТЕКСТНЫЙ, язык контекстно-свободный
- ЯЗЫК ДЕСКРИПТОРНЫЙ
- ЯЗЫК ИНФОРМАЦИОННО-ЛОГИЧЕСКИЙ
- ЯЗЫК ИНФОРМАЦИОННО-ПОИСКОВЫЙ
- ЯЗЫК ИНФОРМАЦИОННЫЙ
- ЯЗЫК ИСКУССТВЕННЫЙ
- ЯЗЫК КАТЕГОРИАЛЬНЫЙ
- ЯЗЫК ЛОГИЧЕСКИЙ для задания автоматов
- ЯЗЫК МАШИННО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК МАШИНЫ «МИР»
- ЯЗЫК ОПЕРАТОРНЫЙ
- ЯЗЫК ОПИСАНИЯ УСТРОЙСТВ ЦВМ
- ЯЗЫК ПРОМЕЖУТОЧНЫЙ
- ЯЗЫК ПРОЦЕДУРНО-ОРИЕНТИРОВАННЫЙ
- ЯЗЫК ТРАНСЛЯТОРА ВХОДНОЙ
- ЯЗЫК ЦВМ ВНУТРЕННИЙ
- ЯЗЫКА ИЗБЫТОЧНОСТЬ
- ЯЗЫКА ИНФОРМАЦИОННЫЕ ИЗМЕРЕНИЯ
- ЯЗЫКА МОДЕЛИ АНАЛИТИЧЕСКИЕ
- ЯЗЫКА МОДЕЛИ МАТЕМАТИЧЕСКИЕ
- ЯЗЫКА ЭНТРОПИЯ
- ЯЗЫКИ ЛОГИКО-МАТЕМАТИЧЕСКИЕ
- ЯЗЫКИ МАШИННЫЕ
- ЯЗЫКИ ПРОГРАММИРОВАНИЯ
- ЯЗЫКИ СПИСКОВЫЕ
- ЯЗЫКИ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ
- ЯЗЫКИ ФОРМАЛЬНЫЕ
- ЯЗЫК — ПОСРЕДНИК
- ЯЧЕЙКА ЗАПОМИНАЮЩЕГО УСТРОЙСТВА