ГЛАВА XIII. УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ. ПРОДОЛЬНЫЙ ИЗГИБ СТЕРЖНЕЙ (СТОЕК)

Критические силы и формы продольного изгиба для стержней с постоянной жесткостью при изгибе

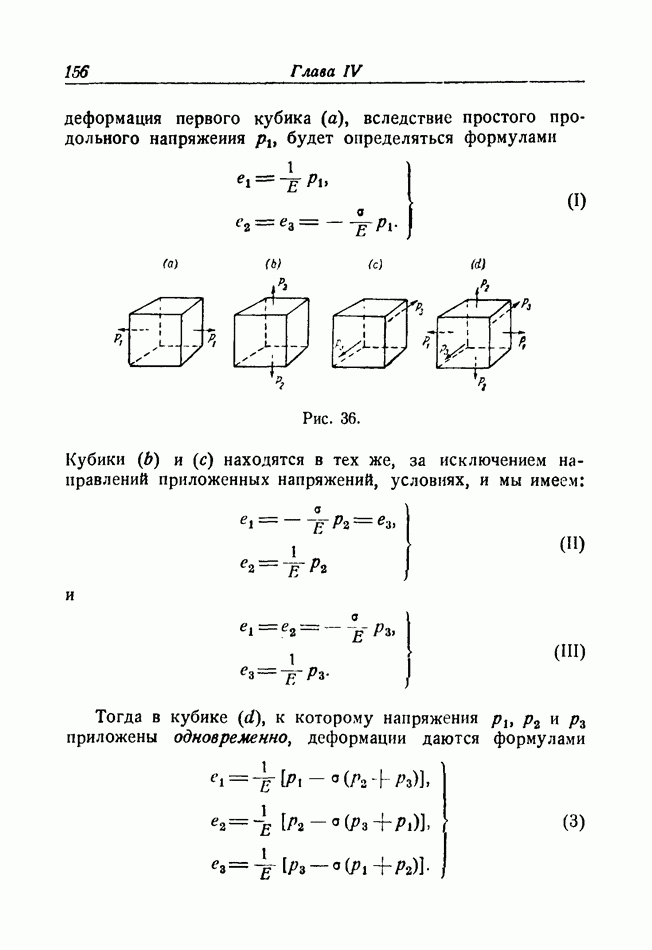
466. В главе VI, §§ 197—201, мы рассмотрели формы продольного изгиба для первоначально прямого стержня с постоянной жесткостью при изгибе, возникающие в результате действия на него осевой сжимающей силы

Как было показано, уравнение, определяющее форму изогнутой оси стержня, записывается так:

где через обозначена жесткость при изгибе. Если I — длина стержня, любое целое число, то выражение

в котором величины не определены, является решением уравнения (1), удовлетворяющим условиям шарнирного закрепления на концах при силе осевого сжатия величины

Таким образом для каждого стержня с постоянным поперечным сечением существует ряд «критических» значений Р:

таких, что, если сила сжатия принимает одно из значений этого ряда, то стержень может сохранять равновесие в некоторой конфигурации, для которой прогиб определен по

форме, но не определен по величине. Если же сила сжатия имеет значение, не принадлежащее этому ряду, то единственной возможной конфигурацией равновесия является тхрямолинейная форма называется критической силой для стержня, а уравнение (2) при определяет так называемую форму продольного изгиба. Ряд (4), определяющий значения критических сил, совпадает с (21) § 200.

В этой главе мы распространим аналитические методы решения задачи на стержни с переменной жесткостью при изгибе (5), а также рассмотрим новые методы оценки критических сил. Начнем с того, что покажем практическое значение уже полученных результатов.