| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Энергетические соображения
509. Уравнение (17) можно интерпретировать с точки зрения уравнения энергии. При любом свободном колебании должно осуществляться следующее энергетическое условие:

в нашей задаче, когда у дается выражением (16), получаем (индекс  опущен), что:
опущен), что:

Подставив полученные выражения в условие (18), мы увидим, что величина

не должна зависеть от  Откуда следует, что выражение, стоящее в фигурных скобках, должно обращаться в нуль, т. е. мы получаем уравнение (17)
Откуда следует, что выражение, стоящее в фигурных скобках, должно обращаться в нуль, т. е. мы получаем уравнение (17)
510. Аналогичные соображения применимы к любой задаче, относящейся к свободным колебаниям упругой системы. Рассматривая колебания только «нормальной» формы, мы принимаем, что изменение прогиба со временем в каждой точке характеризуется формулой (16), т. е. фаза и частота колебаний не меняются от точки к точке. Тогда полную упругую энергию можно выразить в виде некоторого интеграла.
умноженного на  а полную кинетическую энергию в виде другого интеграла, умноженного на
а полную кинетическую энергию в виде другого интеграла, умноженного на  Уравнение энергии (18), как и выше, дает возможность выразить
Уравнение энергии (18), как и выше, дает возможность выразить  с помощью отношения этих двух интегралов. Это отношение дает точное значение
с помощью отношения этих двух интегралов. Это отношение дает точное значение  когда в него подставлена истинная форма нормального колебания. Согласно методу Рэлея это отношение дает хорошее приближение к наименьшей частоте
когда в него подставлена истинная форма нормального колебания. Согласно методу Рэлея это отношение дает хорошее приближение к наименьшей частоте  после подстановки во входящие в него интегралы формы прогиба, наиболее близкой к истинной форме нормального колебания основного тона, т. е. форме первого нормального колебания.
после подстановки во входящие в него интегралы формы прогиба, наиболее близкой к истинной форме нормального колебания основного тона, т. е. форме первого нормального колебания.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ АВТОРА К ПЕРВОМУ АНГЛИЙСКОМУ ИЗДАНИЮ
- ГЛАВА I. ЗАКОН ГУНА И СЛЕДСТВИЯ ИЗ НЕГО ДЛЯ УПРУГИХ ТЕЛ, НАХОДЯЩИХСЯ В РАВНОВЕСИИ ПОД ДЕЙСТВИЕМ ПРИЛОЖЕННЫХ К НИМ ВНЕШНИХ СИЛ
- Закон Гука и принцип суперпозиции
- «Соответствующие» силы и перемещения
- Работа, совершаемая силами, приложенными к упругому телу
- Упругая энергия деформации. Соотношения между коэффициентами влияния
- Теорема взаимности
- Полная упругая энергия деформации, выраженная как функция приложенных сил
- Теорема Кирхгофа о единственности решения
- Первая теорема Кастилиано
- Теорема, взаимная с первой теоремой Кастилиано
- Связь с общей теоремой механики
- РЕЗЮМЕ
- Пример механической системы, подчиняющейся закону Гука
- Замечания по поводу определений «соответствующих» сил и перемещений
- Обобщение теорем
- Условия, при которых упругие энергии деформации можно складывать
- «Деформометр» Беггса
- ГЛАВА II. ПРИМЕРЫ ПРОСТЕЙШИХ УПРУГИХ СИСТЕМ, ПОДЧИНЯЮЩИХСЯ ЗАКОНУ ГУКА
- Прямые стержни, подверженные действию сил растяжения или сжатия
- Некоторые приложения теоремы, взаимной с первой теоремой Кастилиано
- Полное удлинение, выраженное через составляющие перемещения
- Пример пространственной задачи
- Приложение первой теоремы Кастилиано
- Упругая энергия изогнутого стержня или арки
- Применение первой теоремы Кастилиано к задачам об изгибе прямых балок
- Применение первой теоремы Кастилиано к задачам об изгибе первоначально искривленных балок
- Арки
- Двухшарнирная арка
- Бесшарнирная арка
- Пологие арки постоянного поперечного сечения
- Влияние повышения температуры
- Учет упругой энергии сжатия
- Вычисление вертикальных перемещений
- Спиральные пружины
- Прямоугольные рамы
- Теорема трех моментов Клапейрона
- ГЛАВА III. ТЕЛА С «НАЧАЛЬНЫМИ НАПРЯЖЕНИЯМИ». ВТОРАЯ ТЕОРЕМА КАСТИЛИАНО И ПРИНЦИП СЕН-ВЕНАНА
- Пример тела с «начальными напряжениями»
- Применение принципа суперпозиции к телам с начальными напряжениями
- Начальные напряжения иного происхождения. Температурные напряжения
- Другие примеры тел с начальными напряжениями
- Первая теорема о минимуме упругой энергии
- Применение к упругой энергии, запасенной «начальными напряжениями»
- Теорема о влиянии связей
- Вторая теорема о минимуме упругой энергии («вторая теорема Кастилиано»)
- Принцип Сен-Венана
- Обоснование нашей формулы изгиба и т. д.
- ДОПОЛНЕНИЕ К ГЛАВЕ III. Вычисление напряжений в фермах
- Простые и статически неопределимые фермы
- Определение напряжений в простых фермах. (1) Графические методы
- «Метод сечений» Риттера
- «Метод замены» Геннеберга
- Определение напряжений в простых фермах. (2) Аналитические методы
- Коэффициенты растяжения
- Определение напряжений в статически неопределимых фермах
- Методы последовательных приближений
- Метод «релаксации»
- «Метод распределения момента» профессора Гарди Кросса
- ГЛАВА IV. ЭЛЕМЕНТАРНЫЕ ТЕОРИИ НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
- Экспериментальные основания теории внутренних деформаций
- Простое и сложное напряжение
- Упругая энергия, запасенная при сложном напряжении. Удельная упругая энергия деформации
- «Объемное расширение» и «модуль объемного сжатия»
- Касательное напряжение, сдвиг и «модуль сдвига»
- Соотношения между упругими постоянными. Пределы для «сигма»
- Следствия сопротивления боковому расширению
- Соотношения между напряжениями и деформациями в общем случае
- Касательное напряжение не может пересекать свободную от нагрузки поверхность тела
- Сложение нормальных и касательных напряжений
- Преобразования напряжений и деформаций. Главные плоскости напряжений и главные напряжения
- Главные плоскости деформаций и главные деформации
- Стационарные значения касательного напряжения и сдвига
- Разложение напряженного состояния на касательное напряжение, сопровождаемое равными нормальными напряжениями
- ДОПОЛНЕНИЕ К ГЛАВЕ IV
- Поведение материала за пределом пропорциональности. Теории прочности
- ГЛАВА V. ПРОСТЫЕ ТИПЫ НАПРЯЖЕННЫХ СОСТОЯНИЙ: ТОНКОСТЕННЫЕ КРУГЛЫЕ ТРУБЫ ПОД ДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ, КРУЧЕНИЕ ТОНКОСТЕННЫХ ТРУБ И КРУГЛЫХ ВАЛОВ, ЧИСТЫЙ ИЗГИБ ЦИЛИНДРИЧЕСКИХ СТЕРЖНЕЙ
- Тонкостенная круглая труба под действием внутреннего гидростатического давления
- Кручение тонкостенных круглых труб
- Кручение круглых валов
- Тонкостенные трубы некругового поперечного сечения
- Чистый изгиб цилиндрических стержней или балок
- Искажение поперечного сечения. «Антикластическая» кривизна
- Совместное действие изгиба и растяжения (или сжатия)
- Косой изгиб
- Упругая энергия изгиба
- Общая (приближенная) теория изгиба
- Составные балки
- Железобетонные балки
- ГЛАВА VI. ЗАДАЧИ, СВЯЗАННЫЕ С ДЕФОРМАЦИЯМИ БАЛОК ПРИ ИЗГИБЕ
- Уравнения, определяющие прогиб прямой балки
- Графические методы решения
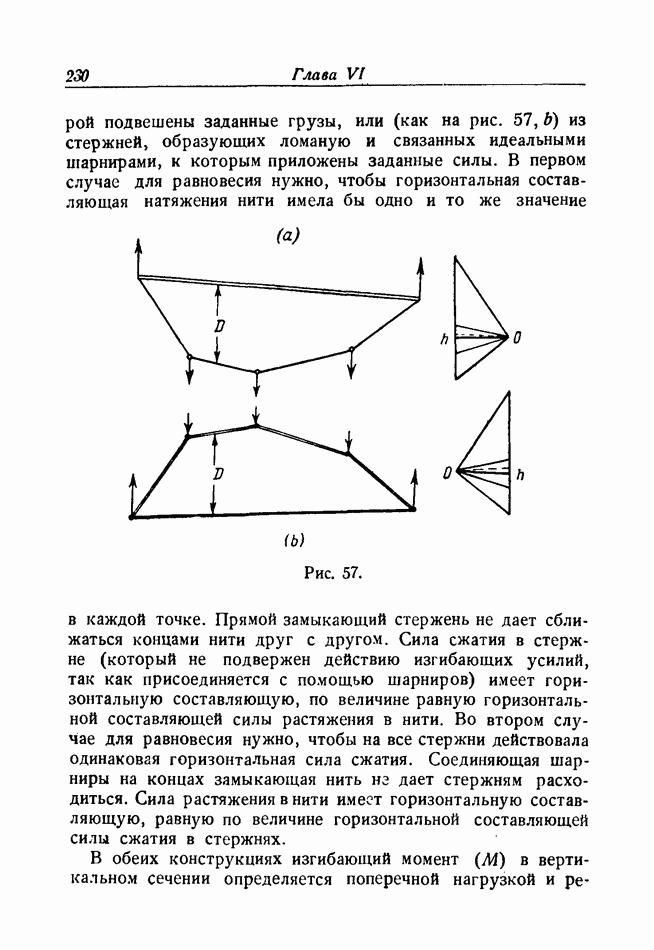
- Использование «веревочной» аналогии
- Неразрезные балки
- Использование «безразмерных» уравнений
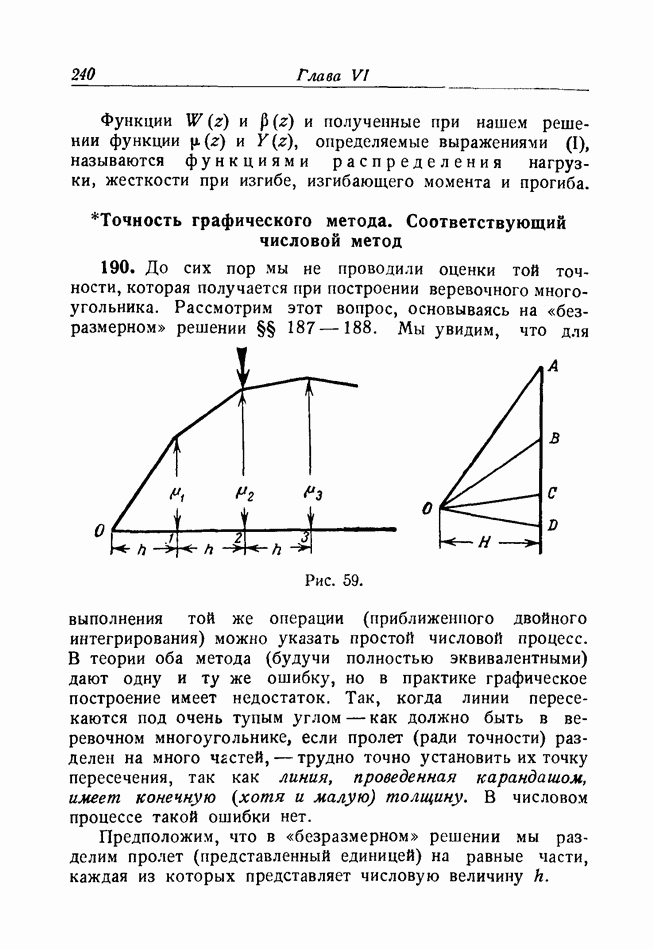
- Точность графического метода. Соответствующий числовой метод
- «Начальная модификация» заданной нагрузки
- Аналитические методы решения
- Метод Маколея
- Учет сосредоточенных изгибающих моментов
- Устойчивость сжатых стержней (стоек)
- Другие типы условий на концах
- Стойки переменного поперечного сечения
- Прямые стержни, подверженные действию силы осевого сжатия совместно с действием поперечной нагрузки
- Круговая диаграмма Говарда
- Критические скорости вращающихся валов
- Поперечные колебания стержней или валов
- Собственные частоты и формы нормальных колебаний
- Собственные колебания стержня постоянного поперечного сечения
- Балка на упругом основании
- Длинный стержень, подверженный действию сосредоточенной силы, приложенной посредине
- ГЛАВА VII. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ПРИБЛИЖЕННЫХ ТЕОРИЙ ИЗГИБА И КРУЧЕНИЯ
- Напряжения при изгибе балки, вызванные перерезывающей силой
- Касательное напряжение в балке узкого прямоугольного сечения
- Касательное напряжение в стенке балки двутаврового сечения
- Упругая энергия сдвига
- ПРИБЛИЖЕННАЯ ТЕОРИЯ ИЗГИБА ТОНКИХ ПЛАСТИНОК
- Упругая энергия изгиба пластинок
- Общий случай изогнутой пластинки. Компоненты упругого момента
- Условия равновесия под действием поперечной нагрузки
- Изгиб круглых пластинок
- Круглая пластинка под действием равномерной поперечной нагрузки
- Свободные поперечные колебания однородной круглой пластинки
- Круглая пластинка с заделанным краем
- ЦИЛИНДРИЧЕСКИЕ ПРУЖИНЫ
- Пружины малого шага под действием осевой нагрузки
- Пружины большого шага под действием осевой нагрузки
- Действие осевого момента
- НАПРЯЖЕНИЯ И ПРОГИБЫ КОЛЕНЧАТЫХ ВАЛОВ
- Прогиб консольного коленчатого вала
- Напряжения в коленчатых валах
- Тонкостенные сосуды под действием внутреннего давления
- ДОПОЛНЕНИЕ К ГЛАВЕ VII
- Граничные условия в теории пластинок
- ГЛАВА VIII. ОБЩАЯ ТЕОРИЯ НАПРЯЖЕНИЙ
- Напряжения в непрерывных материалах
- Шесть независимых компонентов напряжения
- Преобразование компонентов напряжения
- Главные напряжения и главные плоскости напряжений
- Поверхность напряжений
- Круговая диаграмма Мора
- Стационарные значения касательного напряжения
- Разложение любого напряженного состояния на равномерное растягивающее и касательные напряжения
- Уравнение движения в напряжениях
- Граничные условия
- Функции напряжений
- ДОПОЛНЕНИЕ К ГЛАВЕ VIII. Применение круговой диаграммы Мора к вопросу о прочности материала
- ГЛАВА IX. ОБЩАЯ ТЕОРИЯ ДЕФОРМАЦИЙ
- Преобразование компонентов деформации
- Главные удлинения
- Компоненты деформации, выраженные как функции главных удлинений
- Компоненты вращения
- Тождественные соотношения между компонентами деформации
- Смещения, соответствующие заданной деформации
- ГЛАВА X. СООТНОШЕНИЯ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ И ОБЩИЕ УРАВНЕНИЯ ТЕОРИИ УПРУГОСТИ
- Обобщенный закон Гука
- Соотношения между напряжениями и деформациями в изотропных телах
- Модуль сдвига
- Модуль объемного сжатия
- Модуль Юнга и коэффициент Пуассона
- Соотношения между упругими постоянными. Обозначения
- Общие уравнения для изотропных тел
- Термоупругие уравнения
- Различные методы решения
- Упругая энергия деформации, запасенная изотропным телом
- Упругая энергия, запасенная анизотропными телами
- ГЛАВА XI. РЕШЕНИЯ ОБЩИХ УРАВНЕНИЙ
- ПОЛУОБРАТНЫЙ МЕТОД СЕН-ВЕНАНА
- Задача Сен-Венана
- Кручение цилиндрического тела
- Простое растяжение
- Чистый изгиб
- Однородный цилиндр под действием собственного веса
- Постоянная перерезывающая сила
- РЕЗЮМЕ
- ЗАДАЧИ С ЧИСТО РАДИАЛЬНЫМИ СМЕЩЕНИЯМИ
- Сферическая оболочка под действием давлений
- Напряжения от сил притяжения
- Напряжения, являющиеся следствием неравномерного нагрева
- Радиальные колебания сплошного изотропного шара
- Распространение радиальных колебаний в шаре или сферической оболочке
- «Отражение» от закрепленной сферической поверхности
- РАСПРОСТРАНЕНИЕ КГУТИЛЬНЫХ КОЛЕБАНИЙ В КРУГЛЫХ ВАЛАХ И ТРУБАХ
- Отражение от закрепленного конца
- Отражение на свободном конце
- Графическое изображение явлений отражения
- Распространение продольных волн в цилиндрических стержнях
- ДОПОЛНЕНИЕ К ГЛАВЕ XI
- Приближенные решения задан кручения и изгиба
- ГЛАВА XII. ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ. ТОЛСТОСТЕННЫЕ ТРУБЫ И ВРАЩАЮЩИЕСЯ ВАЛЫ
- Плоское напряженное состояние
- РЕЗЮМЕ
- Обобщенное плоское напряженное состояние
- Исследование напряжений оптическим методом
- Применение Ден-Гартогом способа мыльной пленки
- Консоль с узким прямоугольным поперечным сечением под действием равномерно распределенной нагрузки
- Соотношения между функциями напряжений для плоской деформации и для плоского напряженного состояния
- Цилиндрические координаты
- Типовые решения для функции напряжений плоской деформации или плоского напряженного состояния
- Компоненты напряжения
- Влияние малого круглого отверстия на напряжения в пластинке, подверженной равномерному растяжению
- Напряжения в крюке узкого прямоугольного поперечного сечения
- Чистый изгиб кругового бруса
- ОСЕСИММЕТРИЧНЫЕ НАПРЯЖЕННЫЕ СОСТОЯНИЯ
- Деформации вследствие радиальных смещений в круговом цилиндре
- Выражения для радиального, тангенциального и продольного напряжений
- Уравнения равновесия
- Решение уравнений
- Напряжение в длинном цилиндрическом вале (или трубе), вращающемся с постоянной угловой скоростью
- Влияние малого осевого отверстия
- Соотношение между функциями напряжений для плоской деформации и для плоского напряжённого состояния
- Напряжения в тонком вращающемся диске
- Температурные напряжения в длинном цилиндре круглого поперечного сечения
- Случай отсутствия массовых сил. Толстостенная труба под действием постоянного давления
- Замкнутый цилиндрический сосуд
- Горячая и прессовая посадки
- ДОПОЛНЕНИЕ К ГЛАВЕ XII. Задачи, относящиеся к конструированию стволов артиллерийских орудий
- Общая теория проектирования составных труб
- Теоретические пределы прочности
- Максимальная прочность при наиболее эффективном использовании материала
- Бесконечно толстая труба как труба с максимальной прочностью
- Проволочный бандаж
- Постоянная разность напряжений в бандаже
- Заданные натяжения бандажа
- Постоянное натяжение в бандаже
- ГЛАВА XIII. УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ. ПРОДОЛЬНЫЙ ИЗГИБ СТЕРЖНЕЙ (СТОЕК)
- Влияние эксцентриситета точки приложения силы и начальной кривизны
- Экспериментальные наблюдения
- Точность приближенного исследования. Теория «эластики»
- Устойчивость эластики
- Значение приближенного исследования
- Напряжения, вызванные совместным действием поперечной нагрузки и силы осевого сжатия
- Применение теоремы энергии к задаче о продольном изгибе стержня постоянного поперечного сечения
- Приближенное вычисление наименьшей критической силы методом Рэлея
- Стойки переменной жесткости при изгибе. Сопряженные соотношения
- Применение метода Рэлея к стойкам с переменным поперечным сечением
- Условия на концах, отличающиеся от условий шарнирного закрепления
- Вывод основного уравнения вариационным методом из энергетического соотношения
- УСТОЙЧИВОСТЬ УПРУГОЙ ПЛАСТИНКИ, ПОДВЕРЖЕННОЙ ДЕЙСТВИЮ СИЛ, ЛЕЖАЩИХ В ЕЕ ПЛОСКОСТИ
- Устойчивость прямоугольной пластинки, подверженной на сторонах действию сил сжатия
- Применение методов релаксации к задачам устойчивости упругих систем
- ГЛАВА XIV. УСТОЙЧИВОСТЬ УПРУГИХ СИСТЕМ (ПРОДОЛЖЕНИЕ) И ТЕОРИЯ КОЛЕБАНИЙ
- Применение метода Рэлея к определению критических скоростей вращающихся валов
- Сопряженные соотношения
- Приближенная формула, полученная методом Рэлея
- Применение метода Рэлея к свободным колебаниям упругой системы
- Энергетические соображения
- Свободные поперечные колебания упругой нити, подверженной действию растягивающих сил
- Свободные поперечные колебания стержня, подверженного действию растягивающих сил
- Обобщение метода Рэлея
- Поперечные колебания тяжелой вращающейся нити или стержня (лопасть воздушного винта)
- Дальнейшее обобщение метода Рэлея
- Стержень постоянного поперечного сечения, нагруженный посредине сосредоточенной массой
- «Метод переменного параметра»
- Колебания круглой пластинки
- Общие замечания о «методе Рэлея»
- Выражение заданной функции в виде ряда по собственным функциям
- Вынужденные колебания балки постоянного поперечного сечения с шарнирно опертыми концами
- Влияние на балку постоянного поперечного сечения двигающегося по ней груза постоянной величины
- Влияние на балку постоянного поперечного сечения пульсирующей, движущейся нагрузки
- Применение методов релаксации к задачам о колебаниях