| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
176. Новые доказательства основных теорем.
1° 1-я теорема Вейерштрасса. Функция  предположена непрерывной в ограниченной замкнутой области
предположена непрерывной в ограниченной замкнутой области  Следовательно, каждую точку
Следовательно, каждую точку
 этой области можно окружить такой окрестностью а, что в ее пределах (если через
этой области можно окружить такой окрестностью а, что в ее пределах (если через  обозначено наперед взятое число)
обозначено наперед взятое число)

или

Таким образом, в области  функция оказывается ограниченной.
функция оказывается ограниченной.
Применяя лемму Бореля к системе  этих окрестностей, можно выделить из конечное число окрестностей,
этих окрестностей, можно выделить из конечное число окрестностей,  которые в совокупности покрывают всю область
которые в совокупности покрывают всю область  . Если
. Если

то, взяв в качестве  наименьшее из
наименьшее из  , а в качестве М - наибольшее из
, а в качестве М - наибольшее из  будем иметь в
будем иметь в 

2° Теорема Кантора. Задавшись произвольным числом  каждую точку
каждую точку  окружим такой окрестностью
окружим такой окрестностью

что для любой принадлежащей ей точки  будет
будет

Если  есть другая подобная же точка, так что и
есть другая подобная же точка, так что и

то в результате

Заменим каждый прямоугольник а вчетверо меньшим прямоугольником, с тем же центром,

Система  этих открытых прямоугольников покрывает область
этих открытых прямоугольников покрывает область  . По лемме Бореля, из нее выделяем конечную систему прямоугольников
. По лемме Бореля, из нее выделяем конечную систему прямоугольников

с тем же свойством. Наконец, обозначим через 8 наименьшее из всех чисел 
Пусть  - любые две точки области
- любые две точки области  для которых
для которых

Точка  принадлежит одной из окрестностей
принадлежит одной из окрестностей  например, окрестности
например, окрестности

так что

Из (10), так как  следует, что
следует, что  Отсюда
Отсюда

и точки  обе оказываются лежащими в одной из первоначально определенных окрестностей
обе оказываются лежащими в одной из первоначально определенных окрестностей

а тогда, по доказанному, для них выполняется (9).
Итак, удалось по  выбрать
выбрать  независимо от положения точки
независимо от положения точки  чем и доказано, что функция
чем и доказано, что функция  равномерно непрерывна.
равномерно непрерывна.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Упорядочение области рациональных чисел.
- 3. Сложение и вычитание рациональных чисел.
- 4. Умножение и деление рациональных чисел.
- 5. Аксиома Архимеда.
- § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
- 7. Упорядочение области вещественных чисел.
- 8. Вспомогательные предложения.
- 9. Представление вещественного числа бесконечной десятичной дробью.
- 10. Непрерывность области вещественных чисел.
- 11. Границы числовых множеств.
- § 3. Арифметические действия над вещественными числами
- 13. Свойства сложения.
- 14. Определение произведения вещественных чисел.
- 15. Свойства умножения.
- 16. Заключение.
- 17. Абсолютные величины.
- § 4. Дальнейшие свойства и приложения вещественных чисел
- 19. Степень с любым вещественным показателем.
- 20. Логарифмы.
- 21. Измерение отрезков.
- ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. Варианта и ее предел
- 23. Предел варианты.
- 24. Бесконечно малые величины.
- 25. Примеры.
- 26. Некоторые теоремы о варианте, имеющей предел.
- 27. Бесконечно большие величины.
- § 2. Теоремы о пределах, облегчающие нахождение пределов
- 29. Леммы о бесконечно малых.
- 30. Арифметические операция над переменными.
- 31. Неопределенные выражения.
- 32. Примеры на нахождение пределов.
- 33. Теорема Штольца и ее применения.
- § 3. Монотонная варианта
- 35. Примеры.
- 36. Число е.
- 37. Приближенное вычисление числа е.
- 38. Лемма о вложенных промежутках.
- § 4. Принцип сходимости. Частичные пределы
- 40. Частичные последовательности и частичные пределы.
- 41. Лемма Больцано — Вейерштрасса
- 42. Наибольший и наименьший пределы.
- ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. Понятие функции
- 44. Функциональная зависимость между переменными. Примеры.
- 45. Определение понятия функции.
- 46. Аналитический способ задания функции.
- 47. График функции.
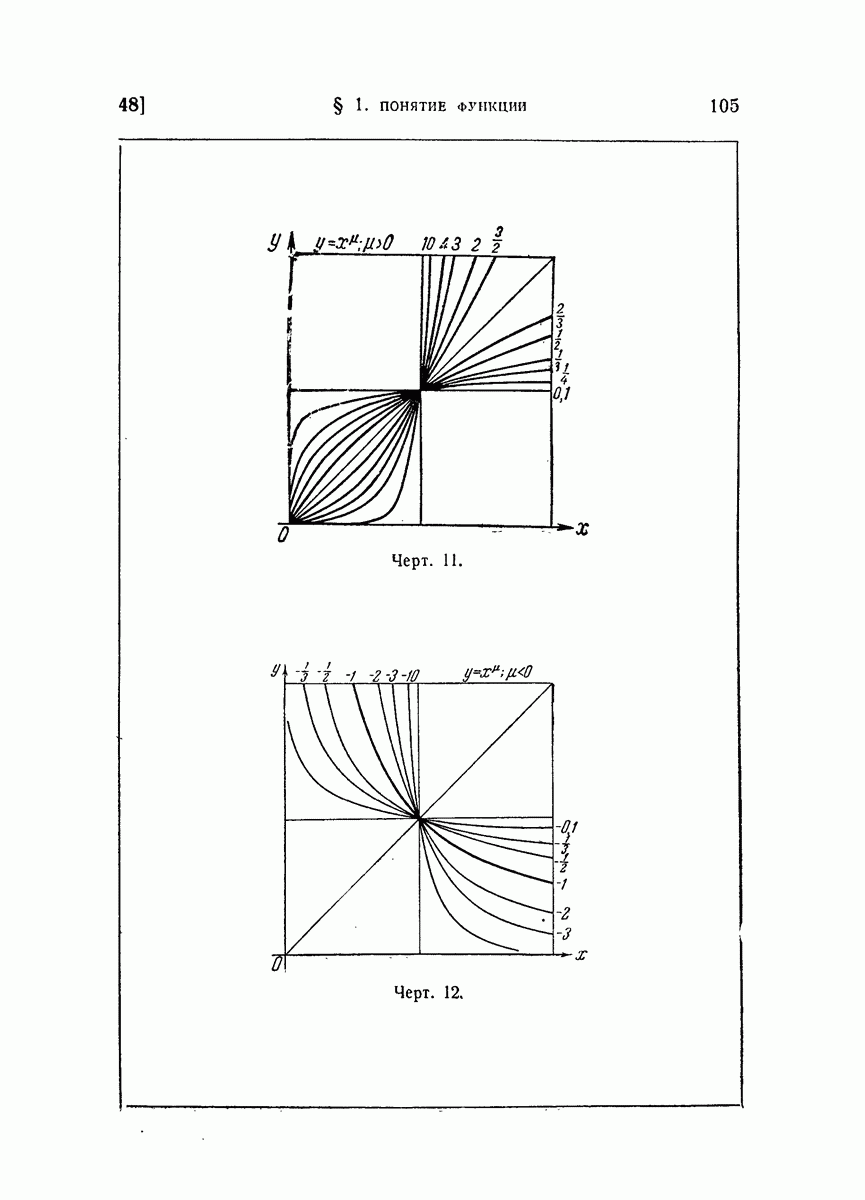
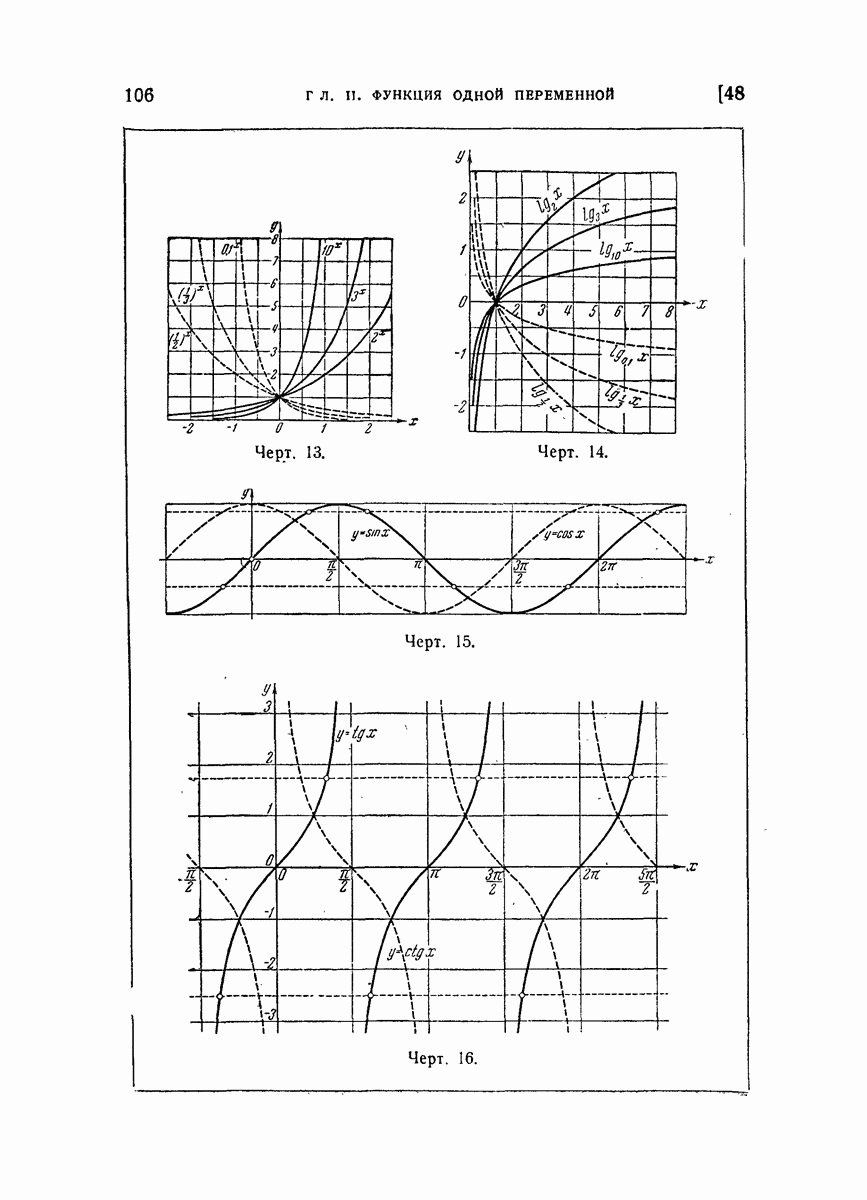
- 48. Важнейшие классы функций.
- 49. Понятие обратной функции.
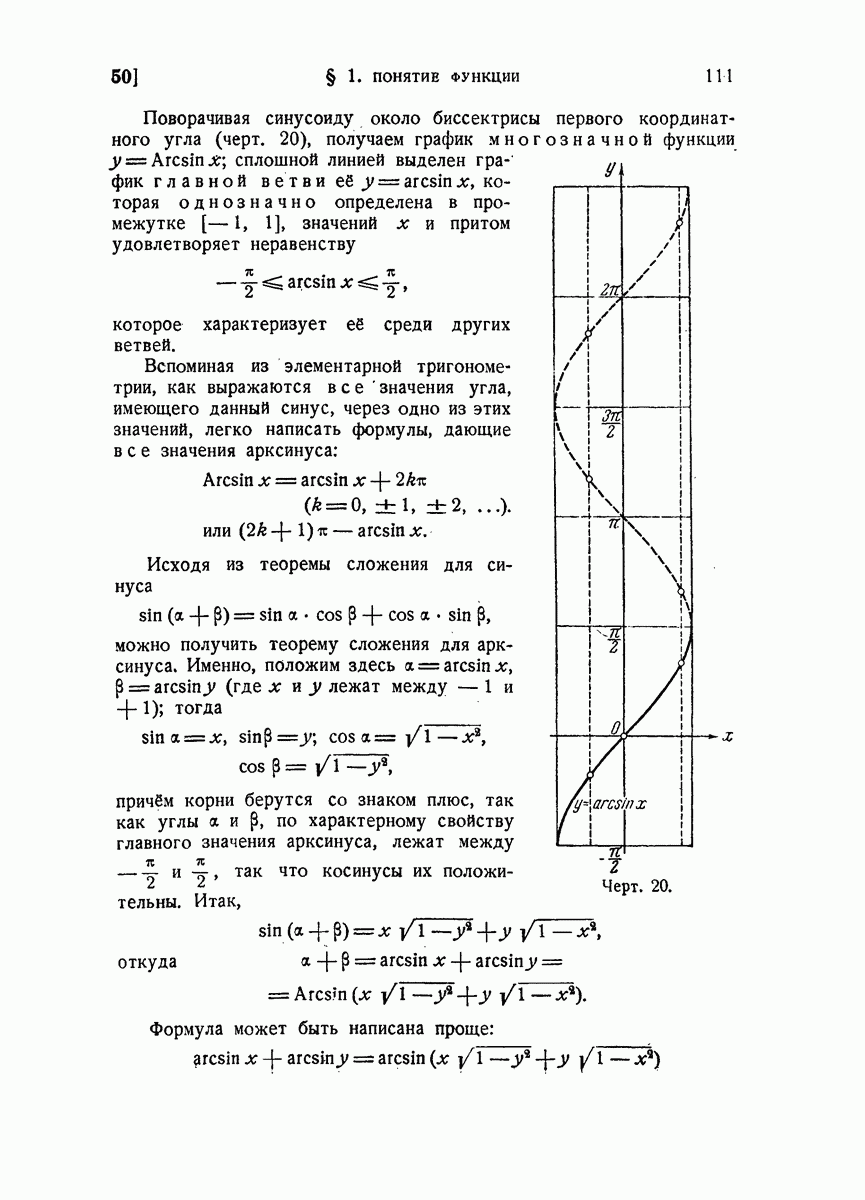
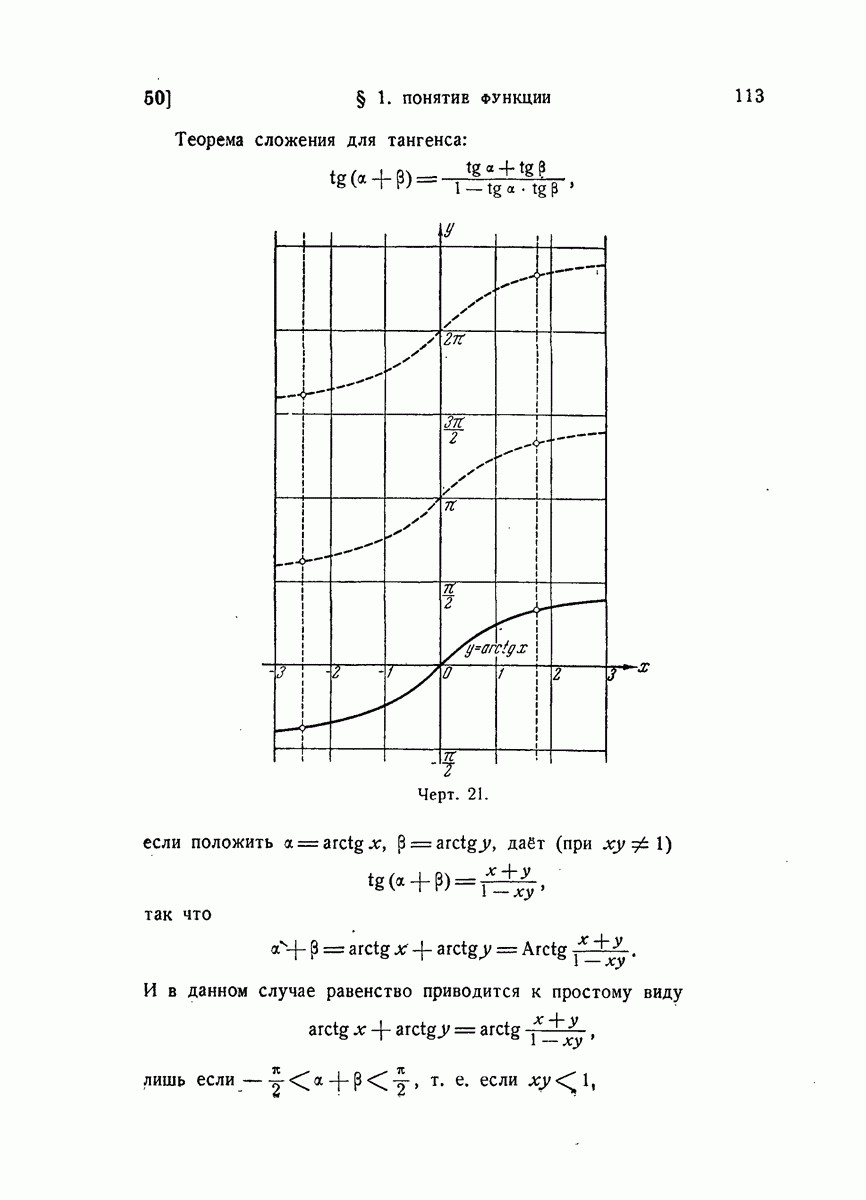
- 50. Обратные тригонометрические функции.
- 51. Суперпозиция функций. Заключительные замечания.
- § 2. Предел функции
- 53. Сведение к случаю варианты.
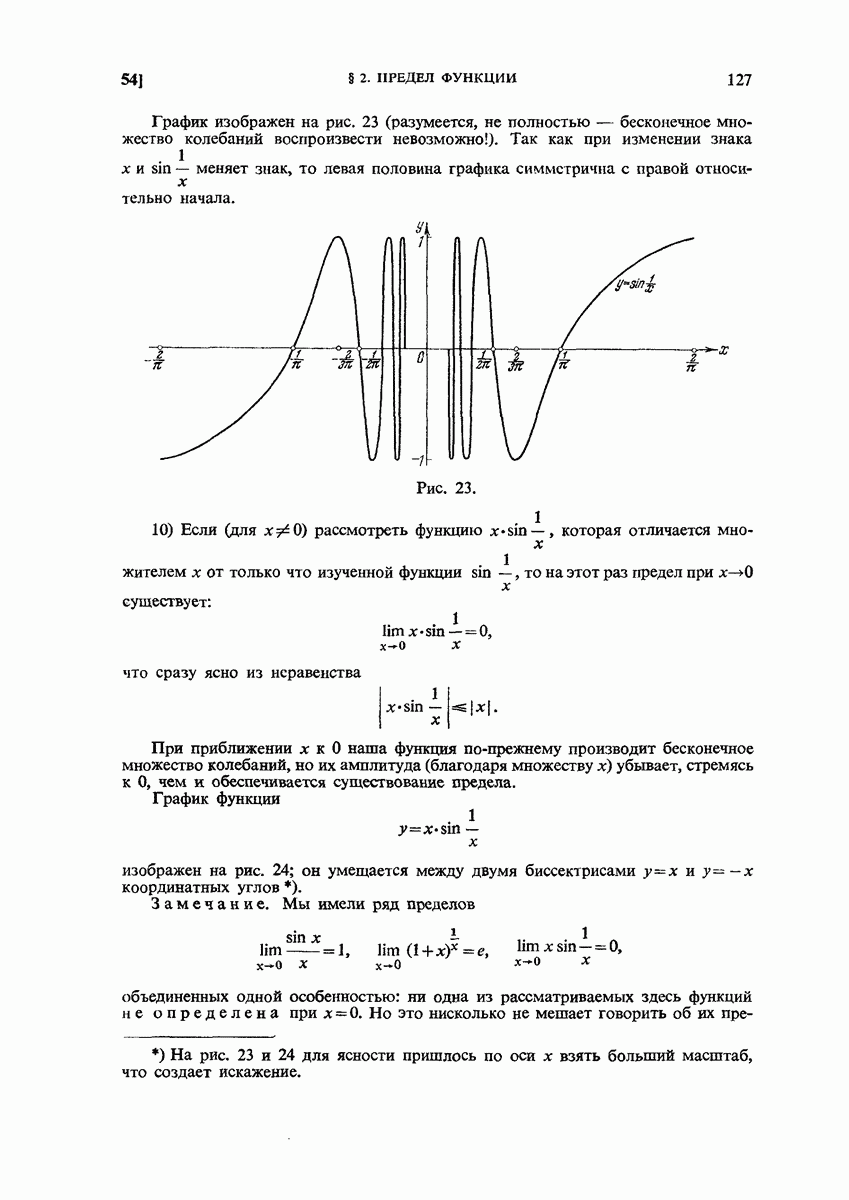
- 54. Примеры.
- 55. Распространение теории пределов.
- 56. Примеры.
- 57. Предел монотонной функции.
- 58. Общий признак Больцано—Коши.
- 59. Наибольший и наименьший пределы функции.
- § 3. Классификация бесконечно малых и бесконечно больших величин
- 61. Шкала бесконечно малых.
- 62. Эквивалентные бесконечно малые.
- 63. Выделение главной части.
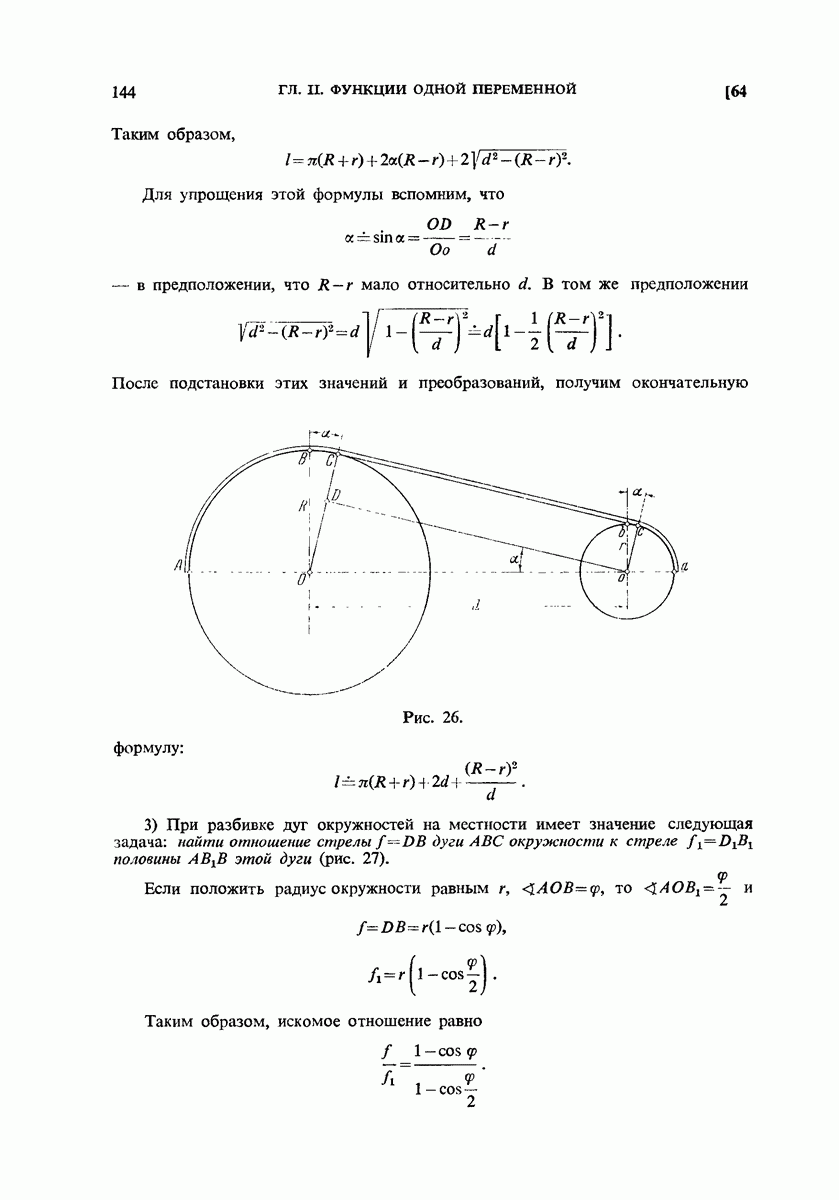
- 64. Задачи.
- 65. Классификация бесконечно больших.
- § 4. Непрерывность (и разрывы) функций
- 67. Арифметические операции над непрерывными функциями.
- 68. Примеры непрерывных функций.
- 69. Односторонняя непрерывность. Классификация разрывов.
- 70. Примеры разрывных функций.
- 71. Непрерывность и разрывы монотонной функции.
- 72. Непрерывность элементарных функций.
- 73. Суперпозиция непрерывных функций.
- 74. Решение одного функционального уравнения.
- 75. Функциональная характеристика показательной, логарифмической и степенной функций.
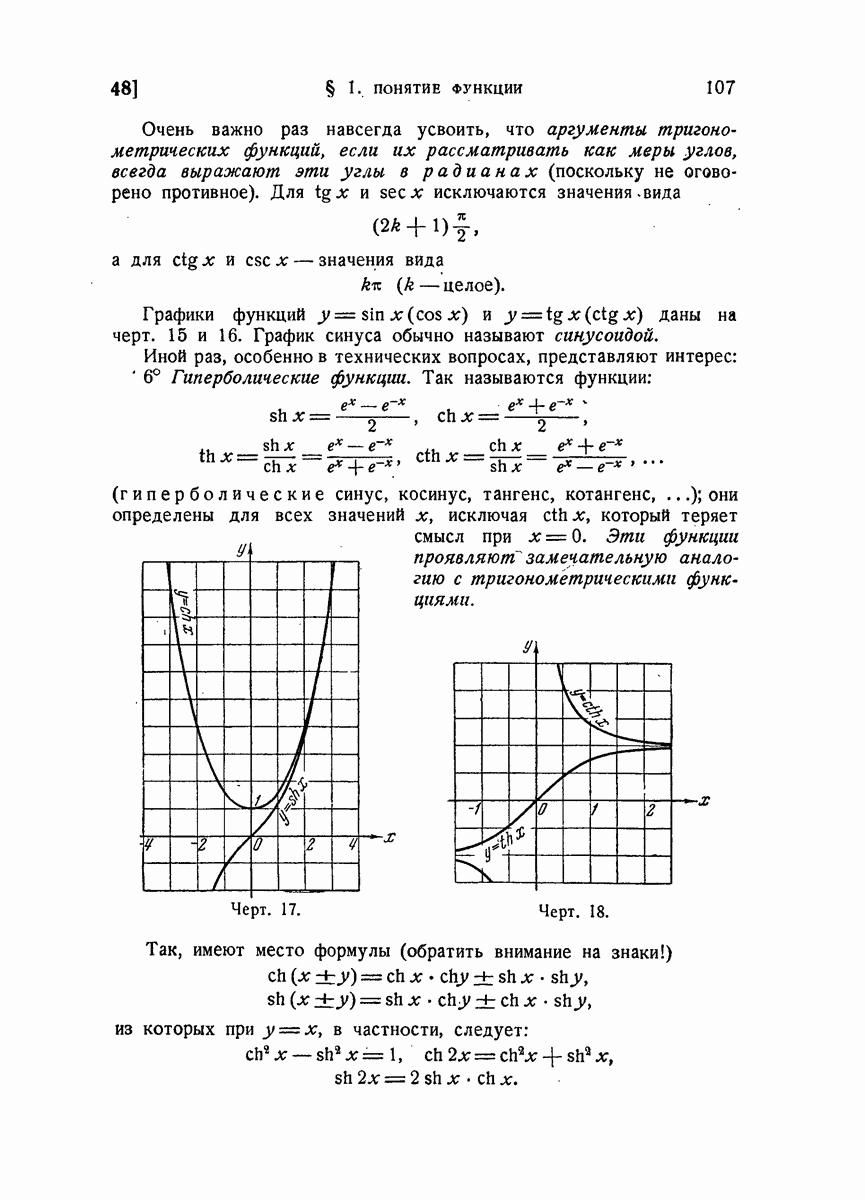
- 76. Функциональная характеристика тригонометрического и гиперболического косинусов.
- 77. Использование непрерывности функций для вычисления пределов.
- 78. Степенно-показательные выражения.
- 79. Примеры.
- § 5. Свойства непрерывных функций
- 81. Применение к решению уравнений.
- 82. Теорема о промежуточном значении.
- 83. Существование обратной функции.
- 84. Теорема об ограниченности функции.
- 85. Наибольшее и наименьшее значения функции.
- 86. Понятие равномерной непрерывности.
- 87. Теорема Кантора.
- 88. Лемма Бореля.
- 89. Новые доказательства основных теорем.
- ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная и ее вычисление
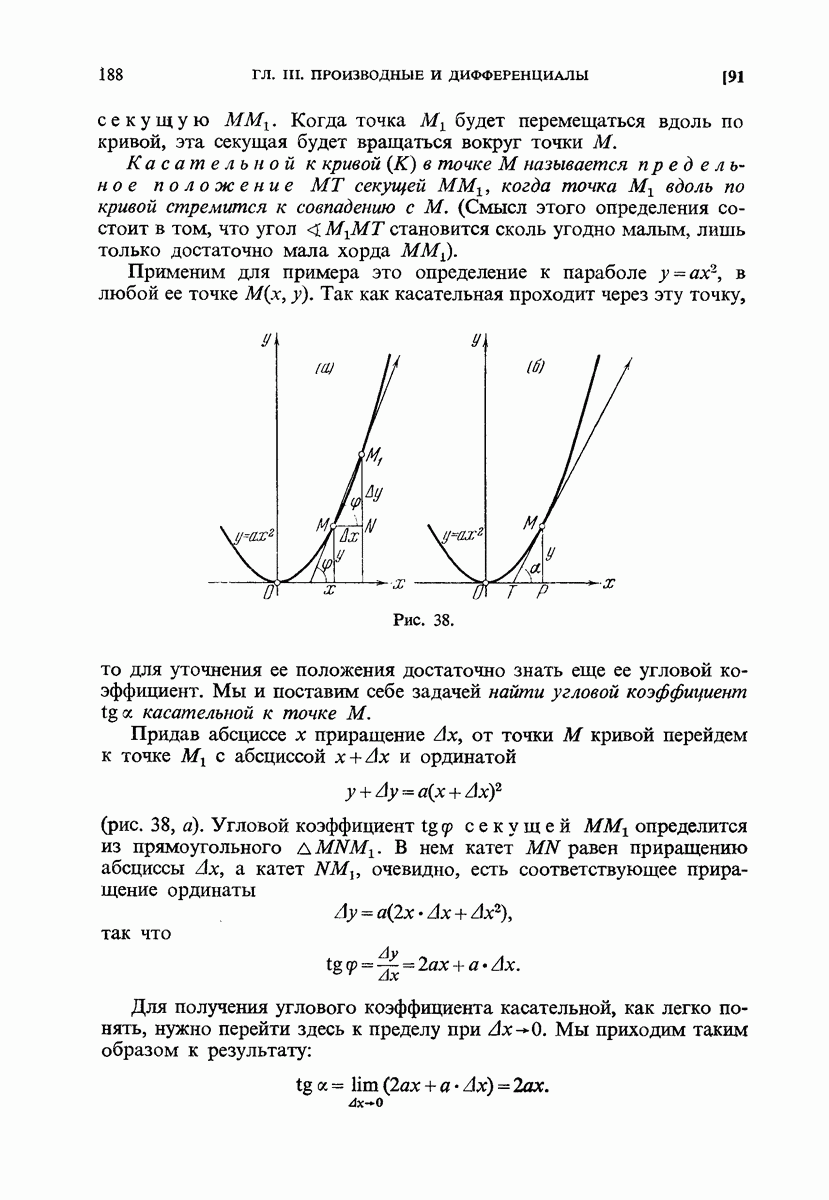
- 91. Задача о проведении касательной к кривой.
- 92. Определение производной.
- 93. Примеры вычисления производных.
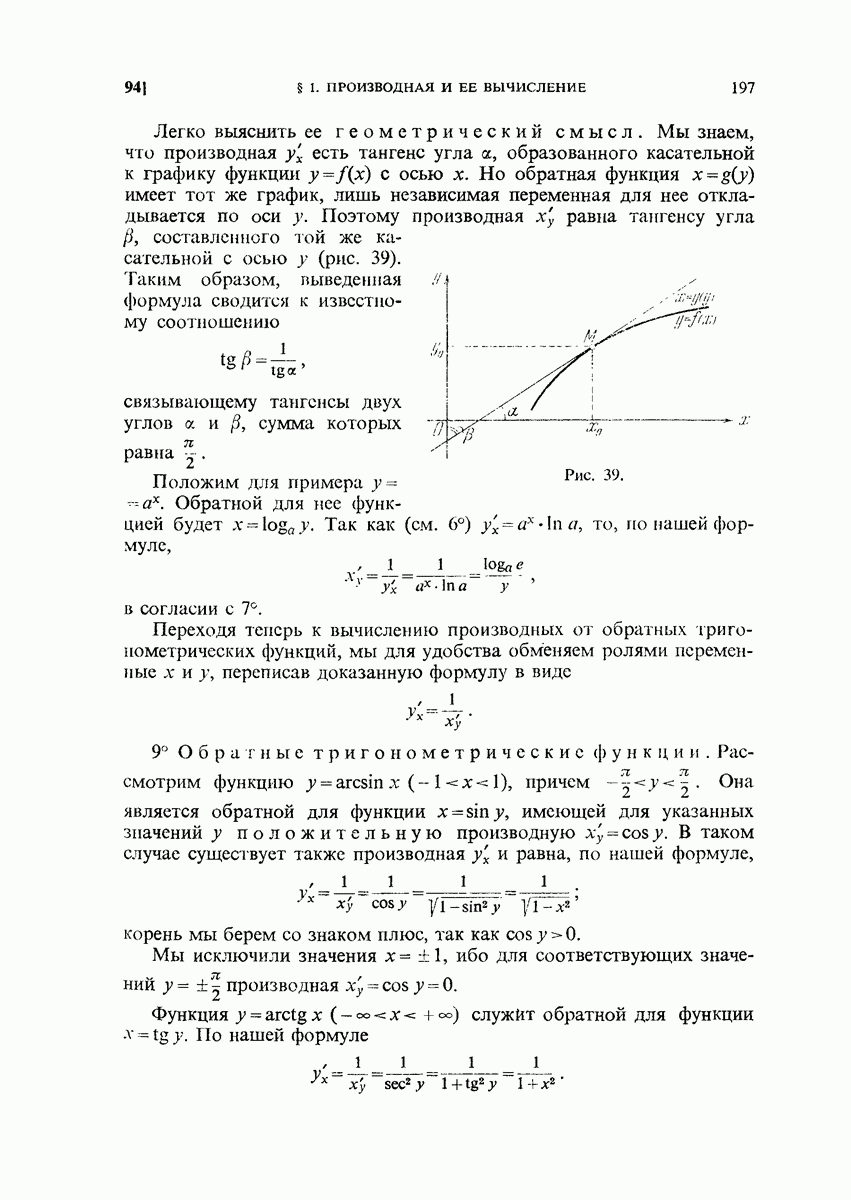
- 94. Производная обратной функции.
- 95. Сводка формул для производных.
- 96. Формула для превращения функции.
- 97. Простейшие правила вычисления производных.
- 98. Производная сложной функции.
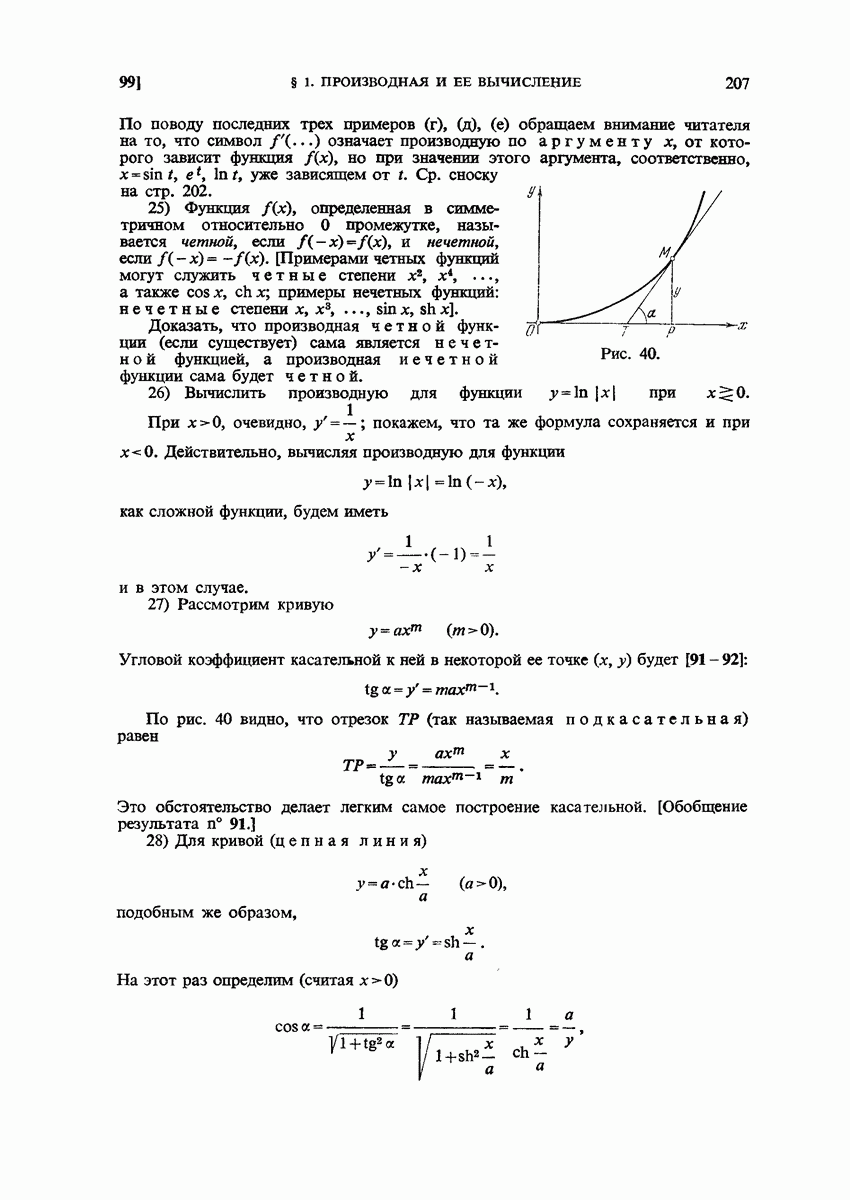
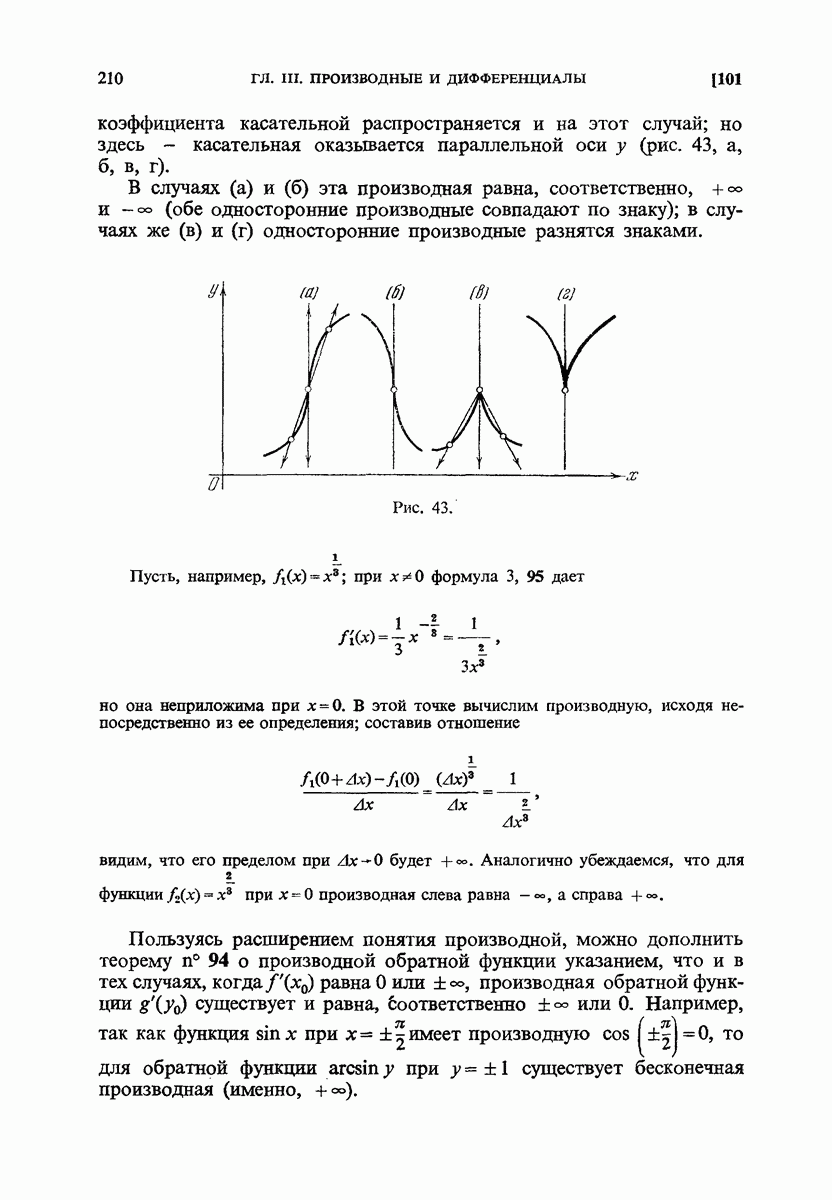
- 100. Односторонние производные.
- 101. Бесконечные производные.
- 102. Дальнейшие примеры особых случаев.
- § 2. Дифференциал
- 104. Связь между диффереицируемостью и существованием производной.
- 105. Основные формулы и правила дифференцирования.
- 106. Инвариантность формы дифференциала.
- 107. Дифференциалы как источник приближенных формул.
- 108. Применение дифференциалов при оценке погрешностей.
- § 3. Основные теоремы дифференциального исчисления
- 110. Теорема Дарбу
- 111. Теорема Ролля.
- 112. Формула Лагранжа.
- 113. Предел производной.
- 114. Формула Коши.
- § 4. Производные и дифференциалы высших порядков
- 116. Общие формулы для производных любого порядка.
- 117. Формула Лейбница.
- 118. Примеры.
- 119. Дифференциалы высших порядков.
- 120. Нарушение инвариантности формы для дифференциалов высших порядков.
- 121. Параметрическое дифференцирование.
- 122. Конечные разности.
- § 5. Формула Тейлора
- 124. Разложение произвольной функции; дополнительный член в форме Пеано.
- 125. Примеры.
- 126. Другие формы дополнительного члена.
- 127. Приближенные формулы.
- § 6. Интерполирование
- 129. Дополнительный члеп формулы Лагранжа.
- 130. Интерполирование с кратными узлами. Формула Эрмита.
- ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
- § 1. Изучение хода изменения функции
- 132. Условие монотонности функции.
- 133. Доказательство неравенств.
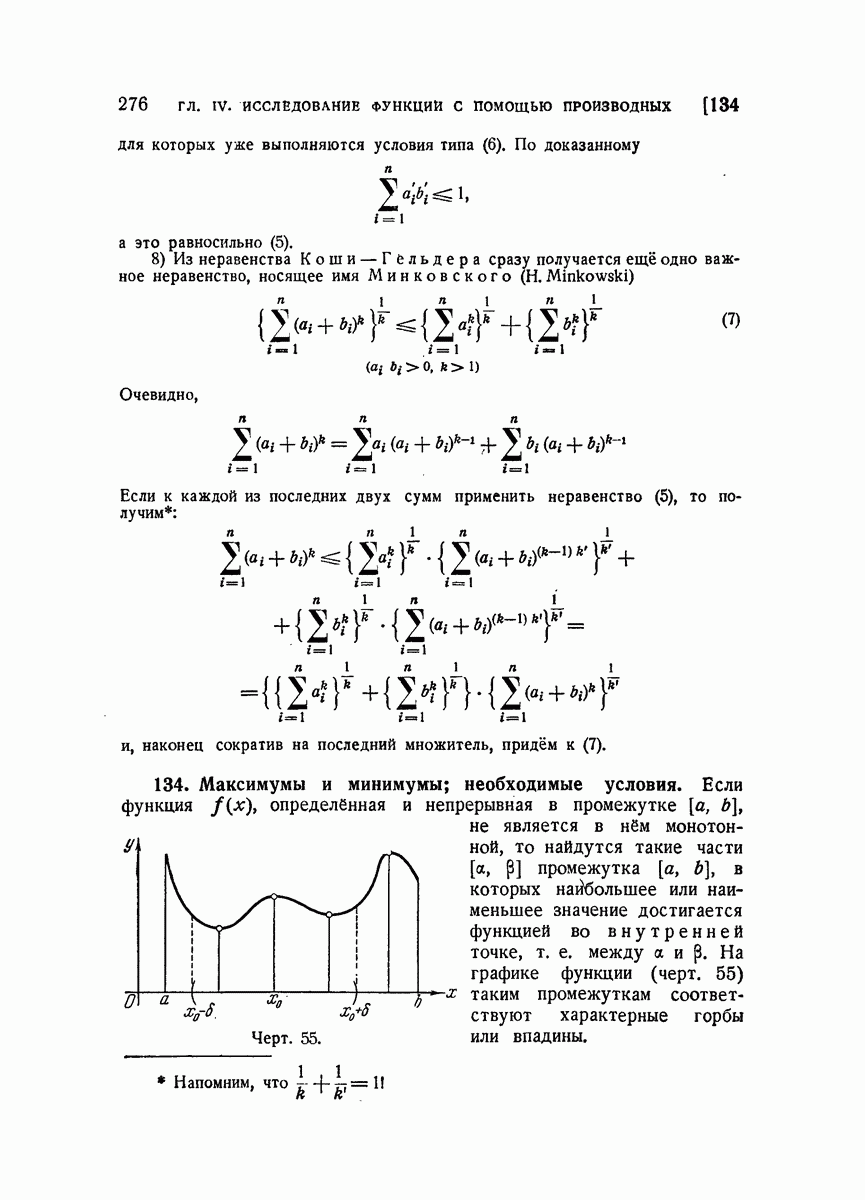
- 134. Максимумы и минимумы; необходимые условия.
- 136. Достаточные условия. Первое правило.
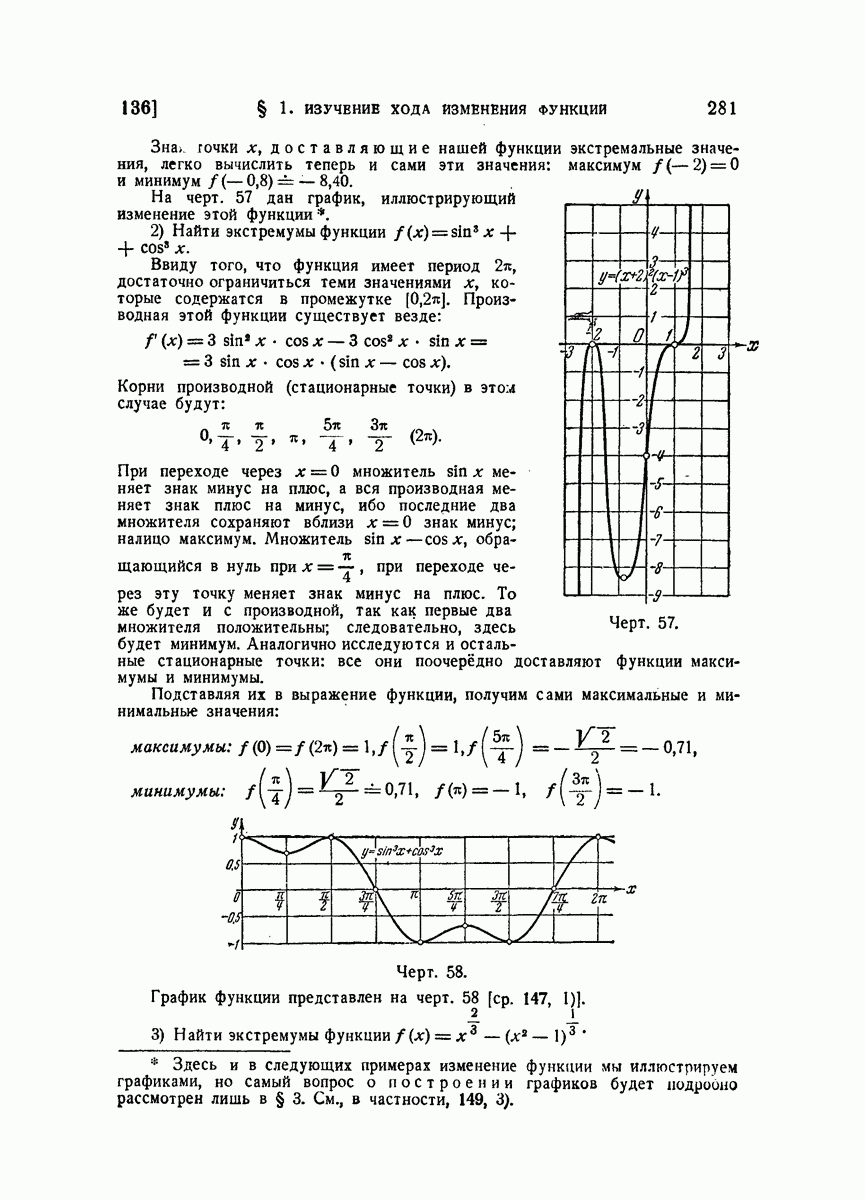
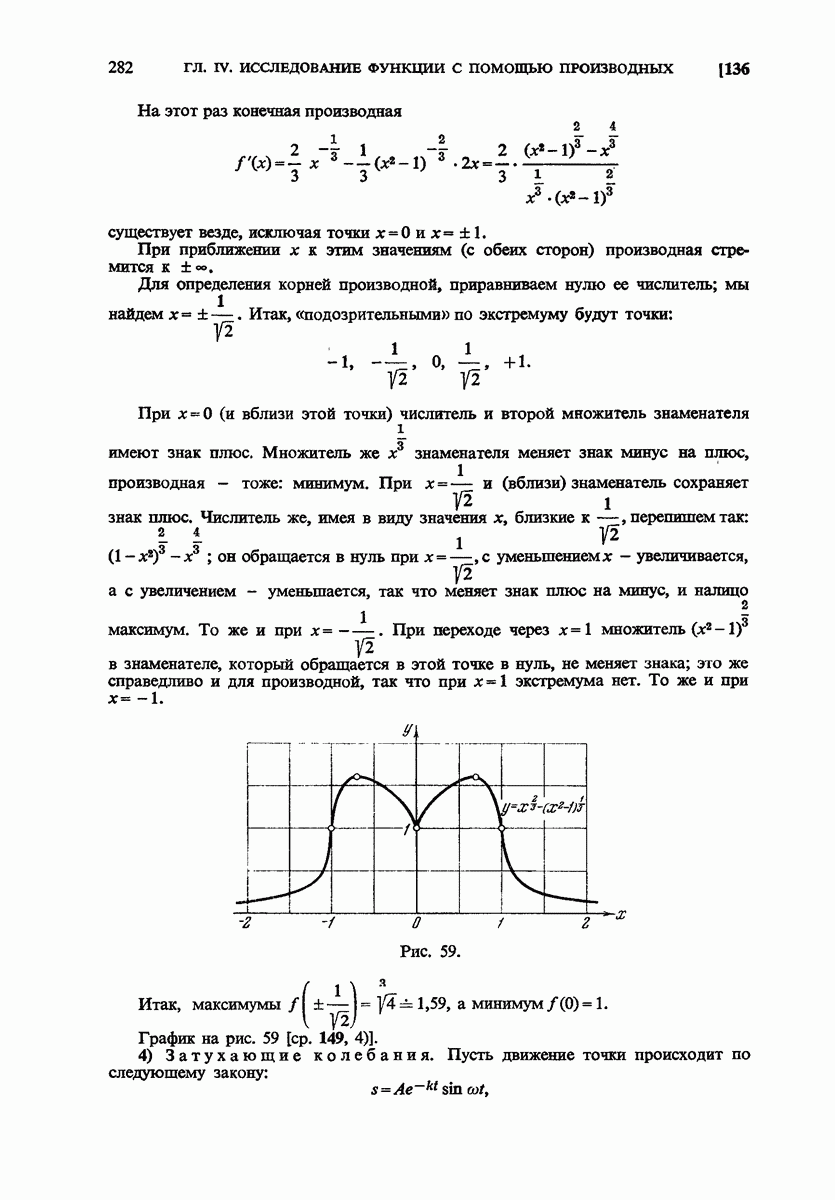
- 136. Примеры.
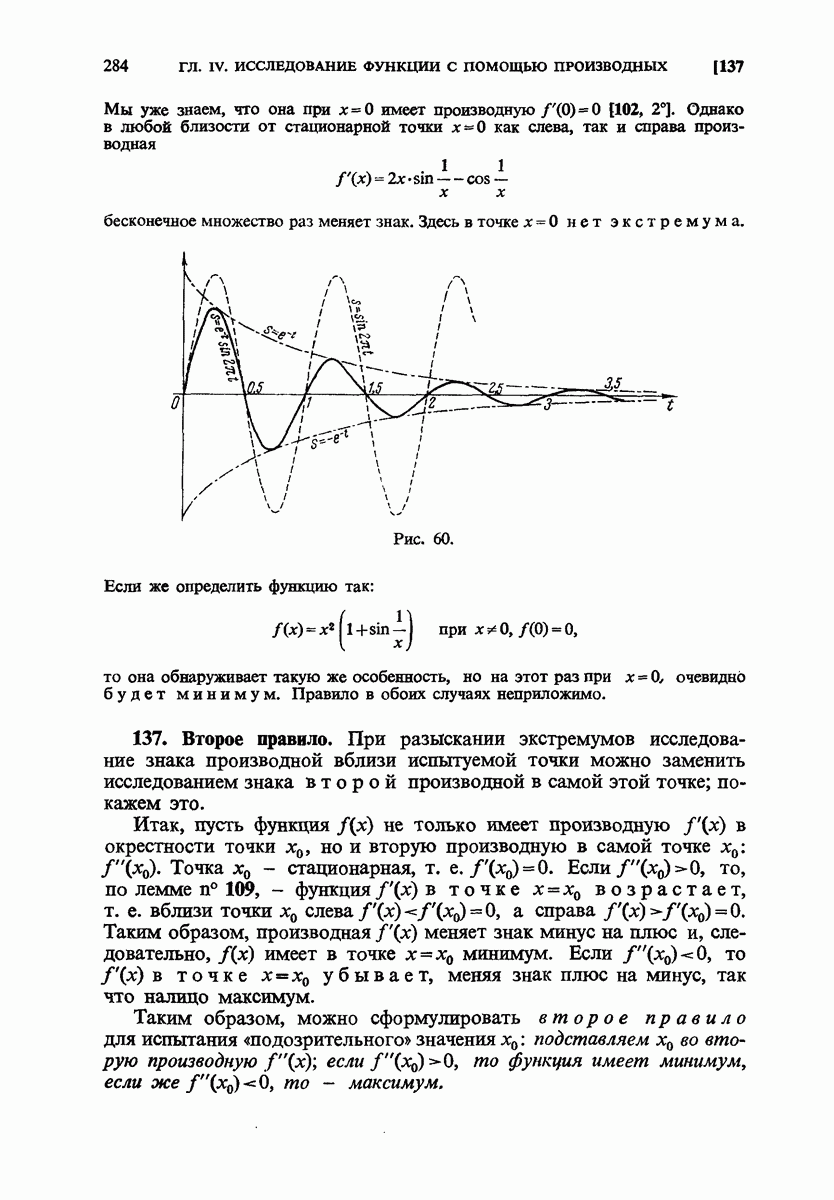
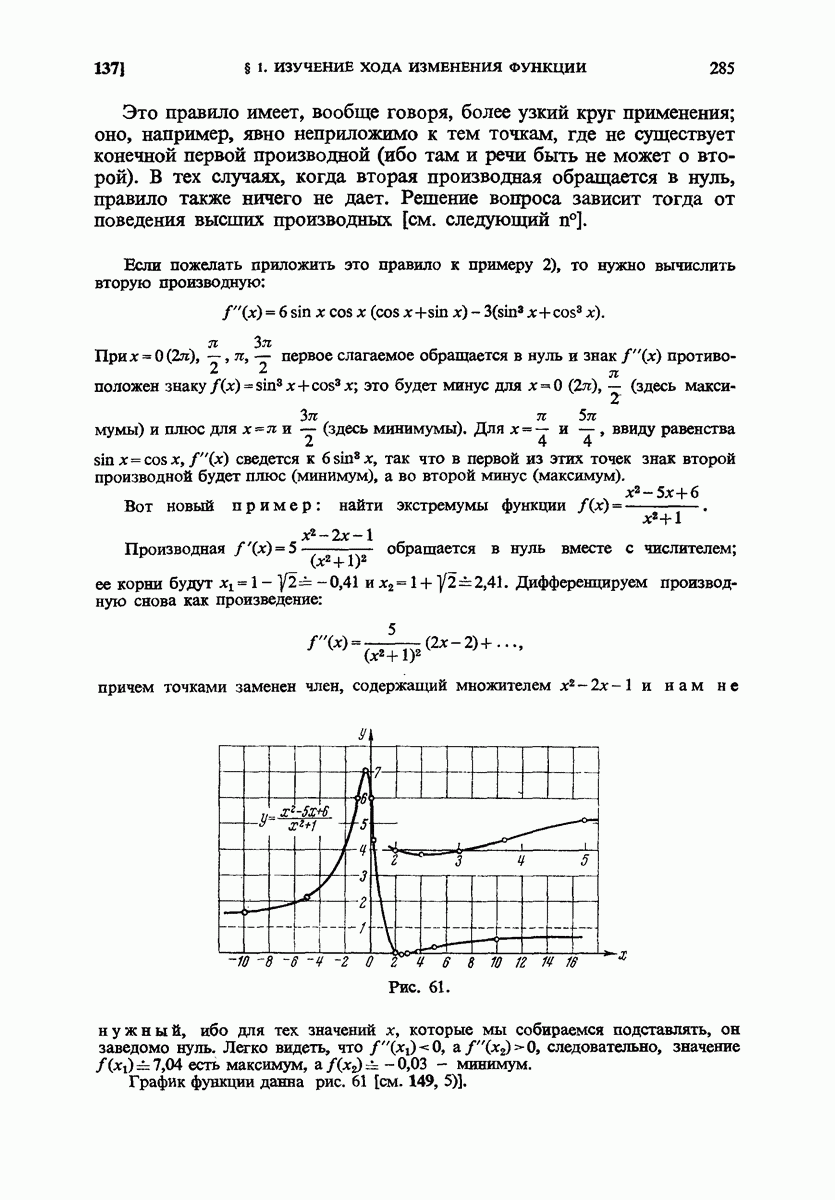
- 137. Второе правило.
- 138. Использование высших производных.
- 139. Разыскание наибольших и наименьших значений.
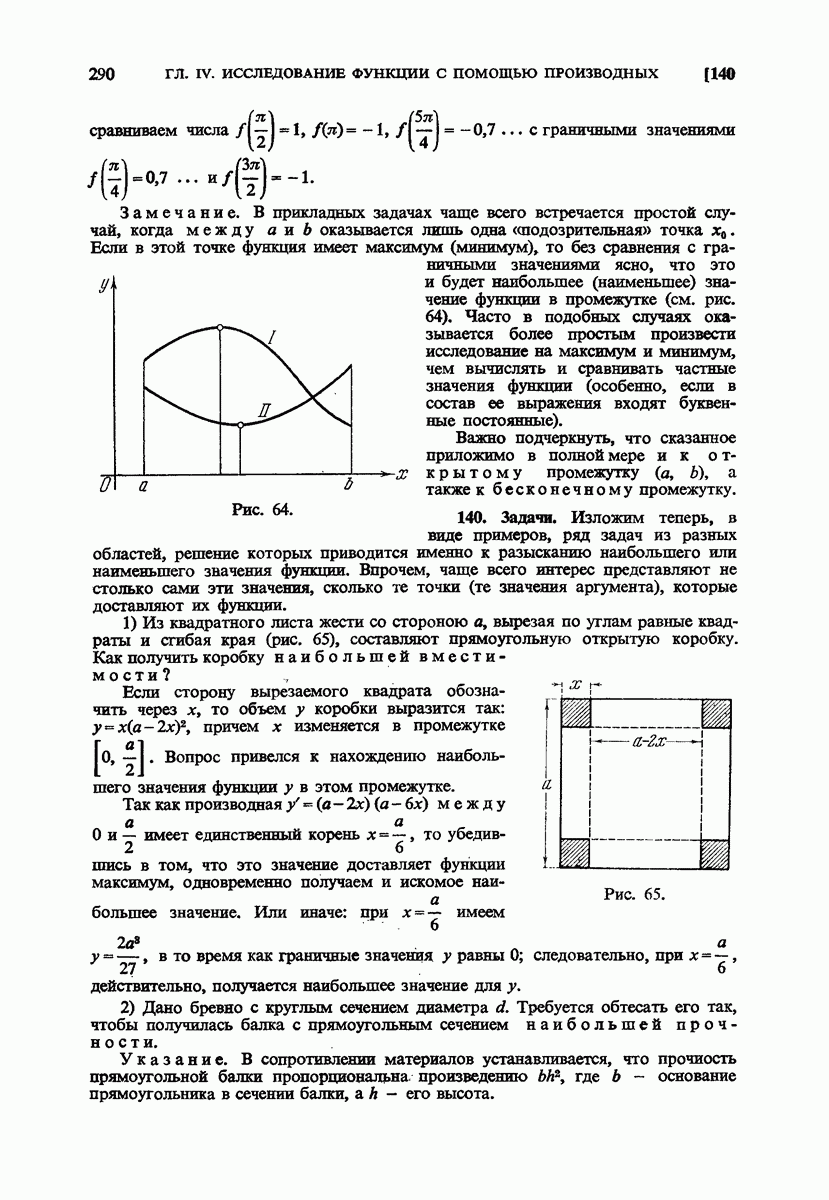
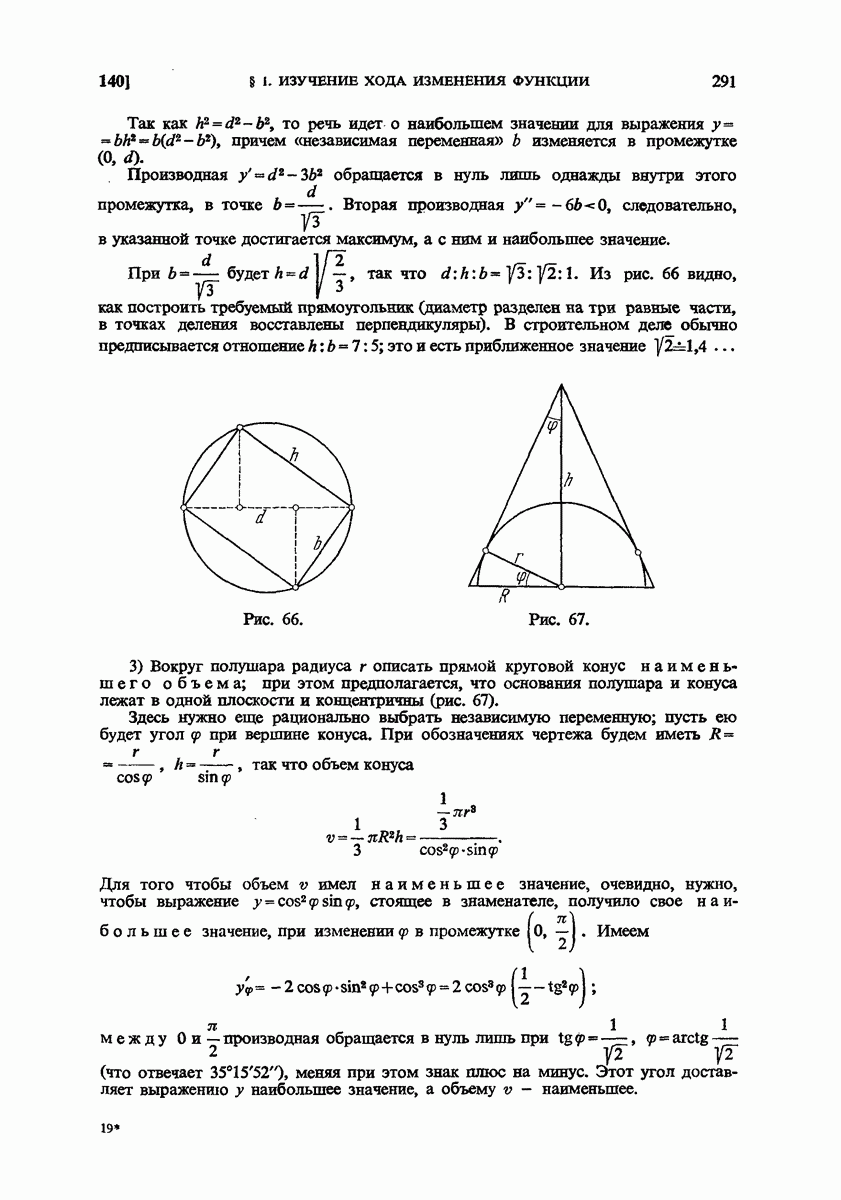
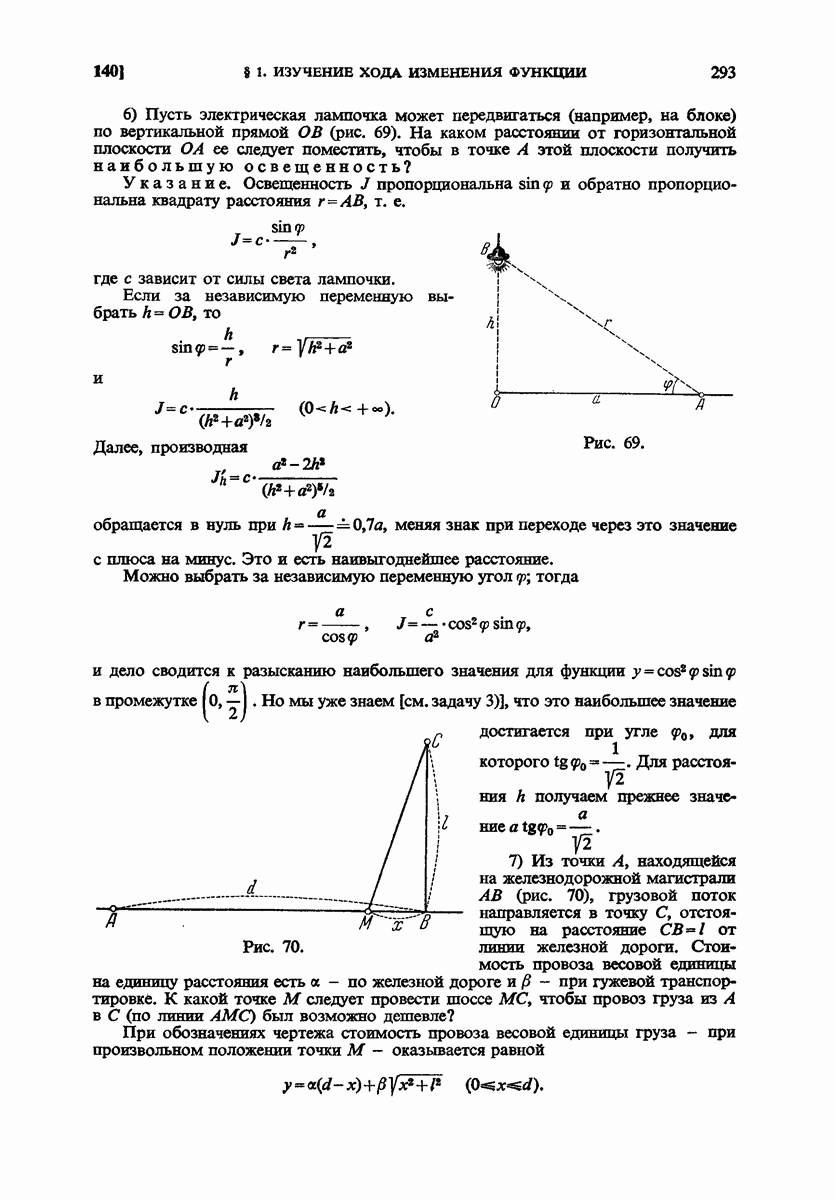
- 140. Задачи.
- § 2. Выпуклые (и вогнутые) функции
- 142. Простейшие предложения о выпуклых функциях.
- 143. Условия выпуклости функции.
- 144. Неравенство Иенсена и его приложения.
- 145. Точки перегиба.
- § 3. Построение графиков функций
- 147. Схема построения графика. Примеры.
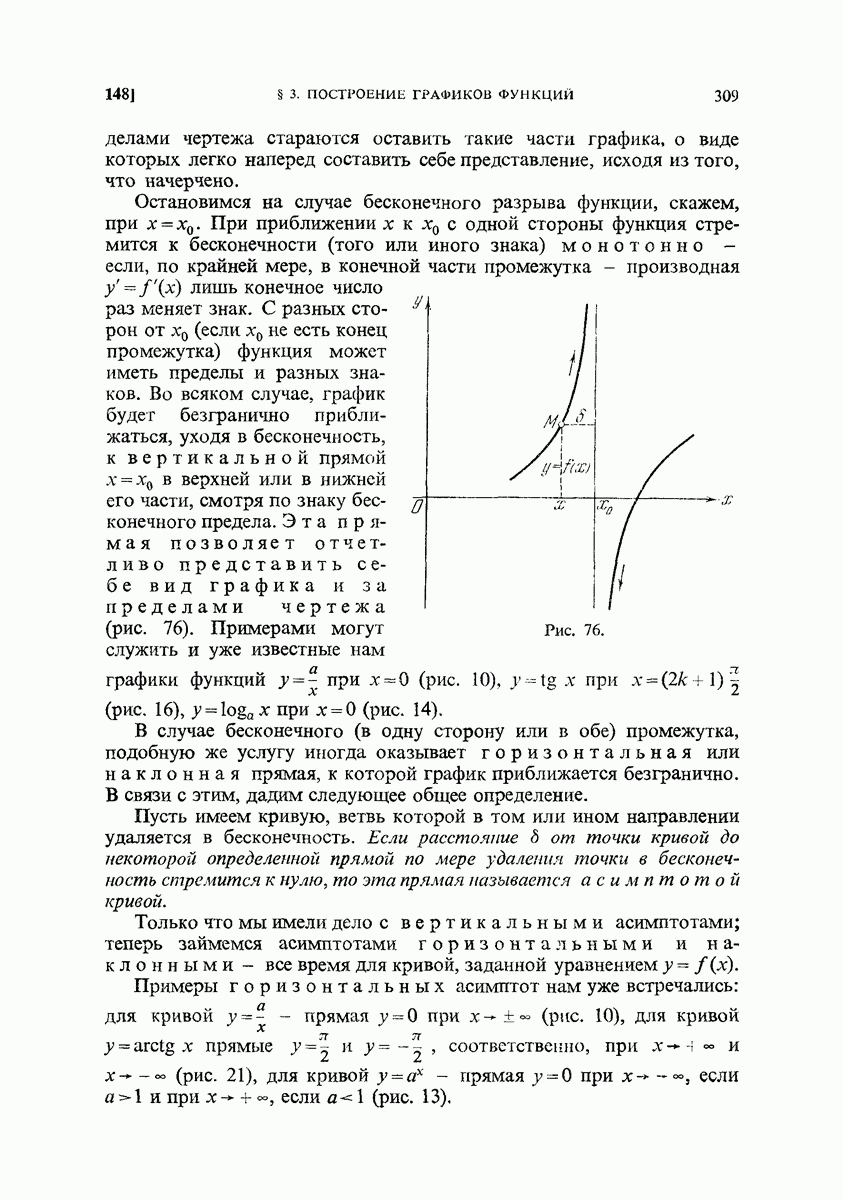
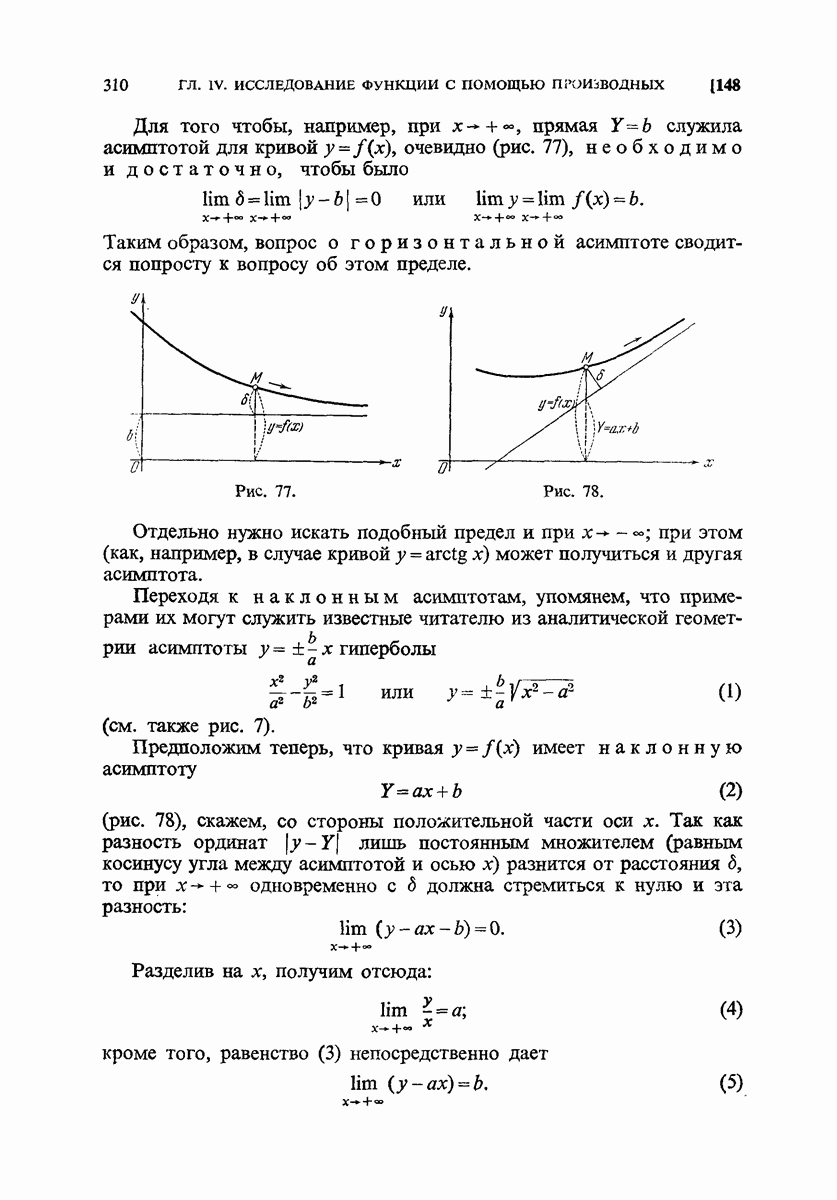
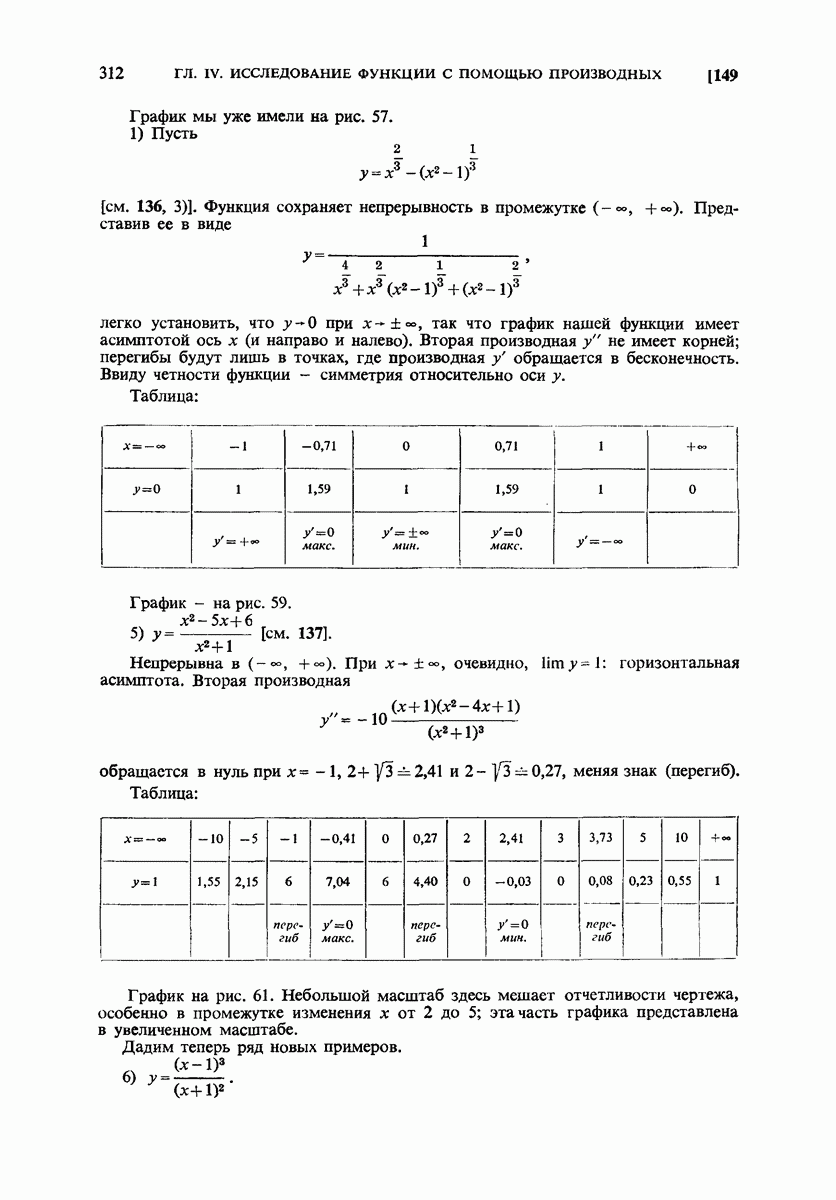
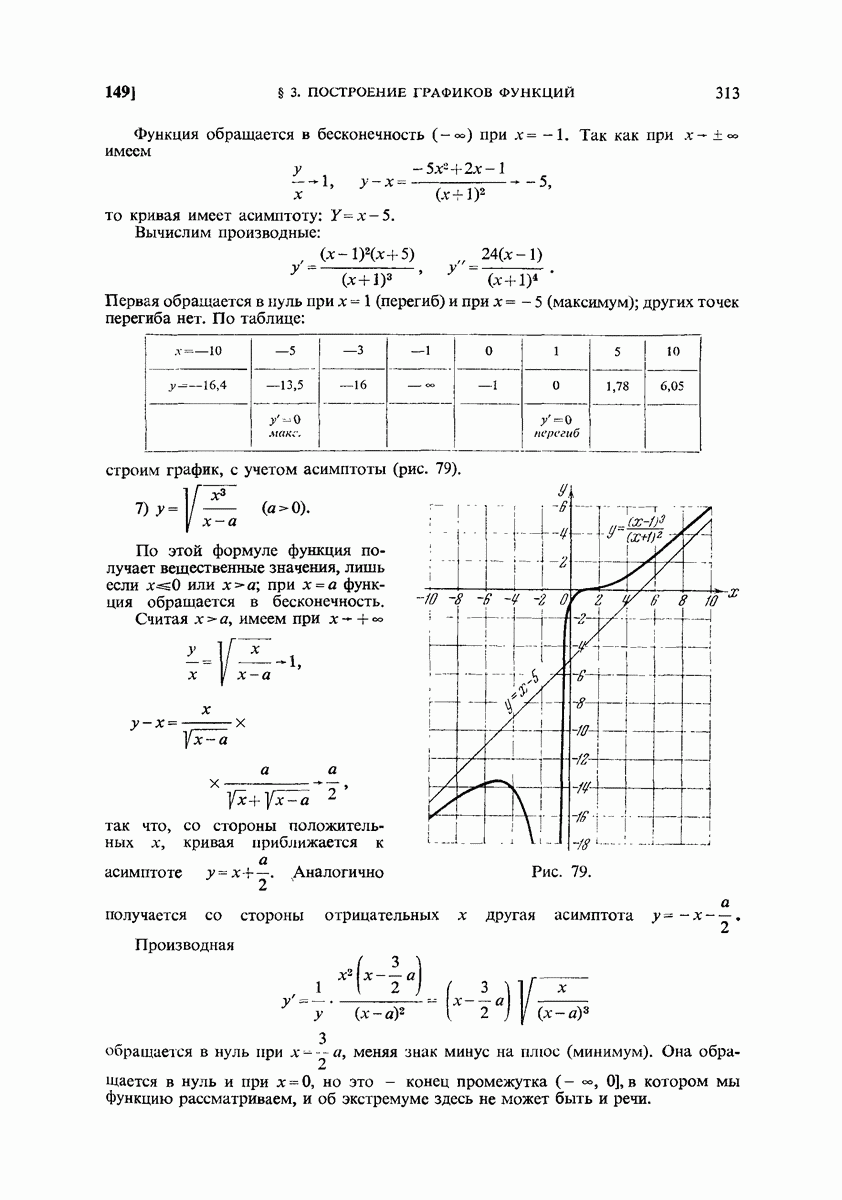
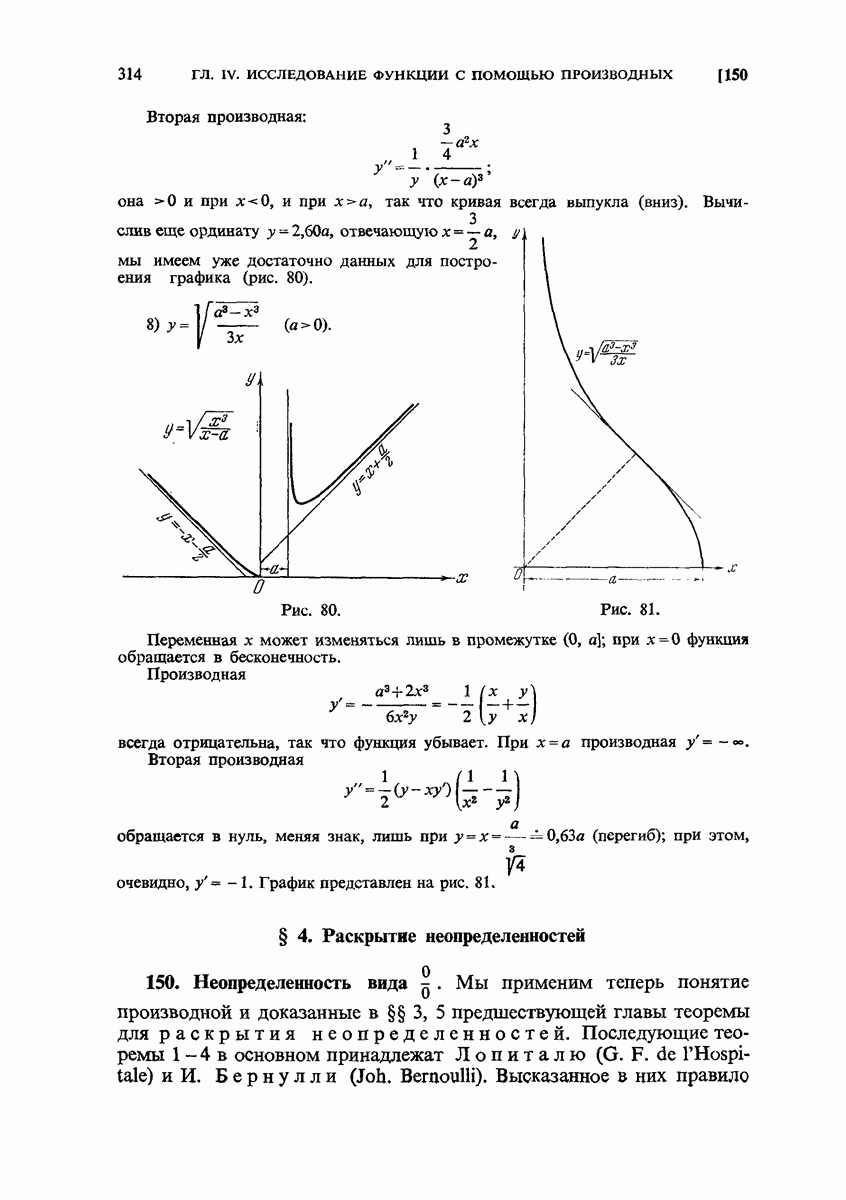
- 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
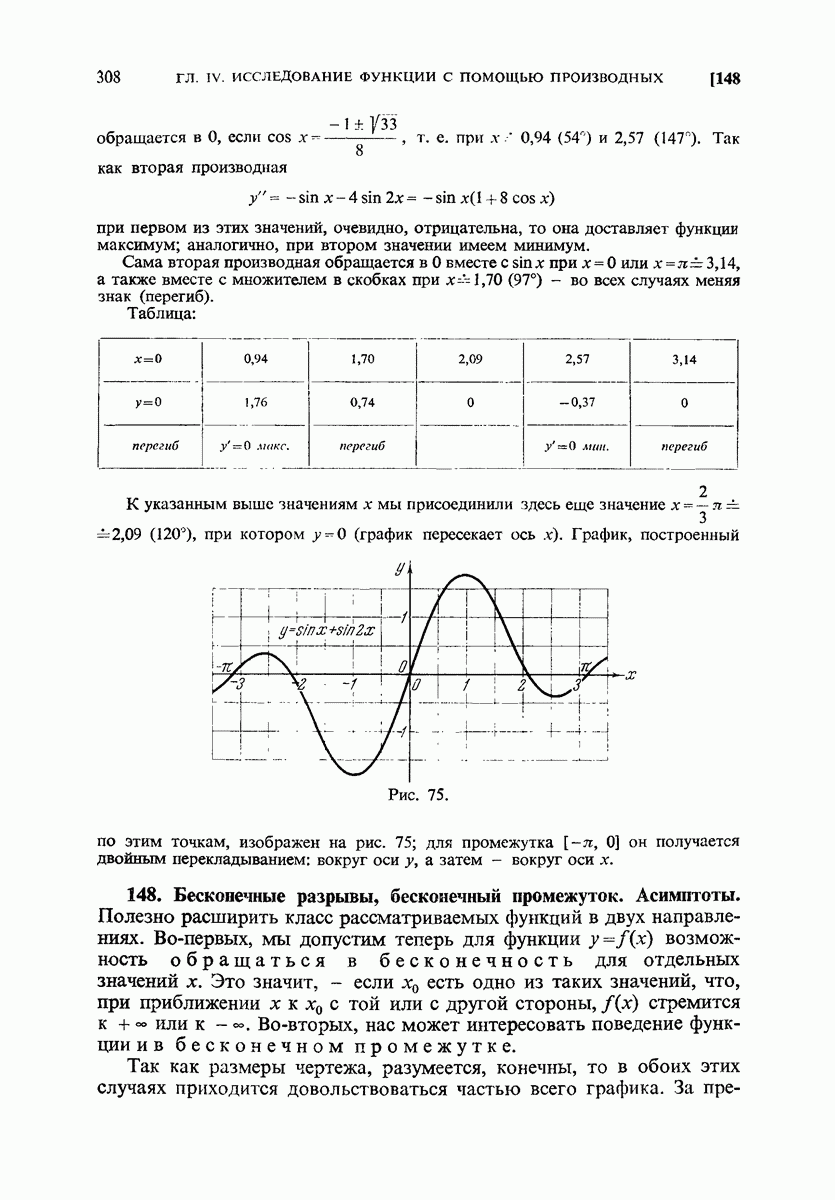
- 149. Примеры.
- § 4. Раскрытие неопределенностей
- 151. Неопределенность вида oo/oo
- 152. Другие виды неопределенностей.
- § 5. Приближенное решение уравнений
- 154. Правило пропорциональных частей (метод хорд).
- 155. Правило Ньютона (метод касательных).
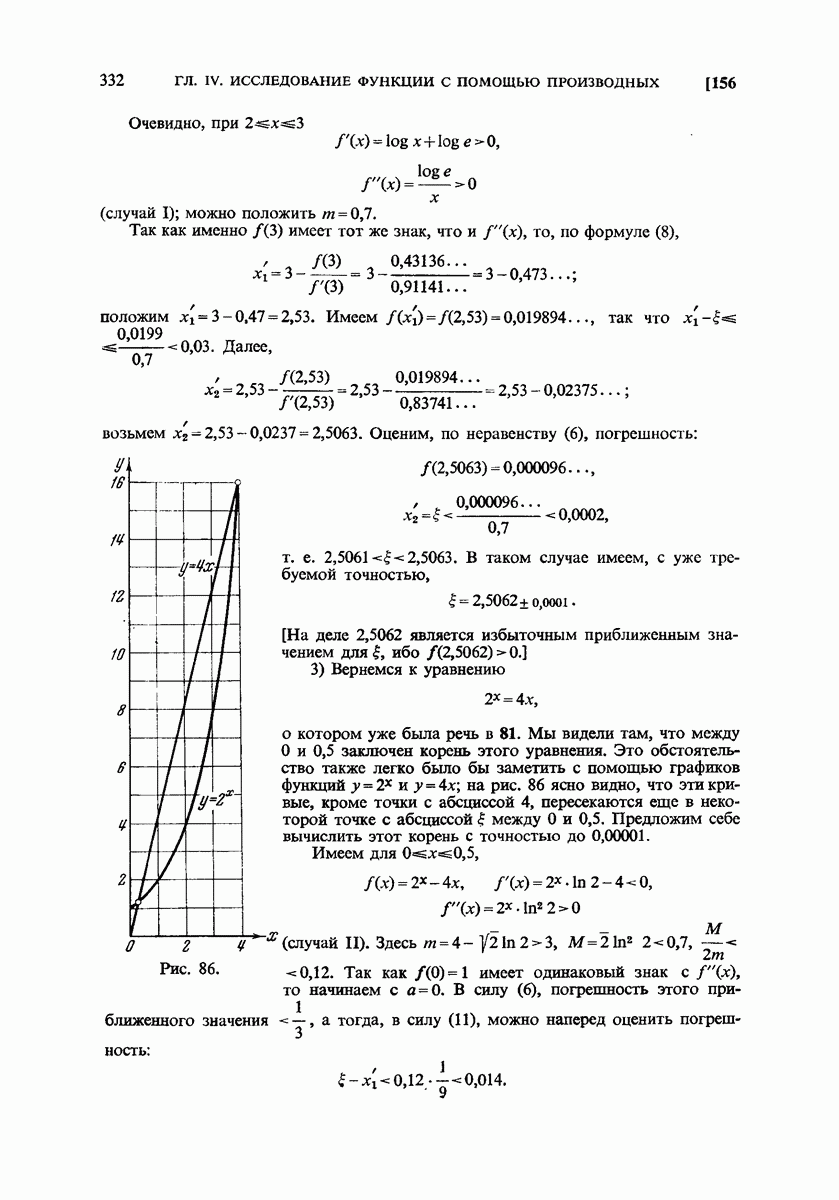
- 156. Примеры в упражнения.
- 157. Комбинированный метод.
- 158. Примеры и упражнения.
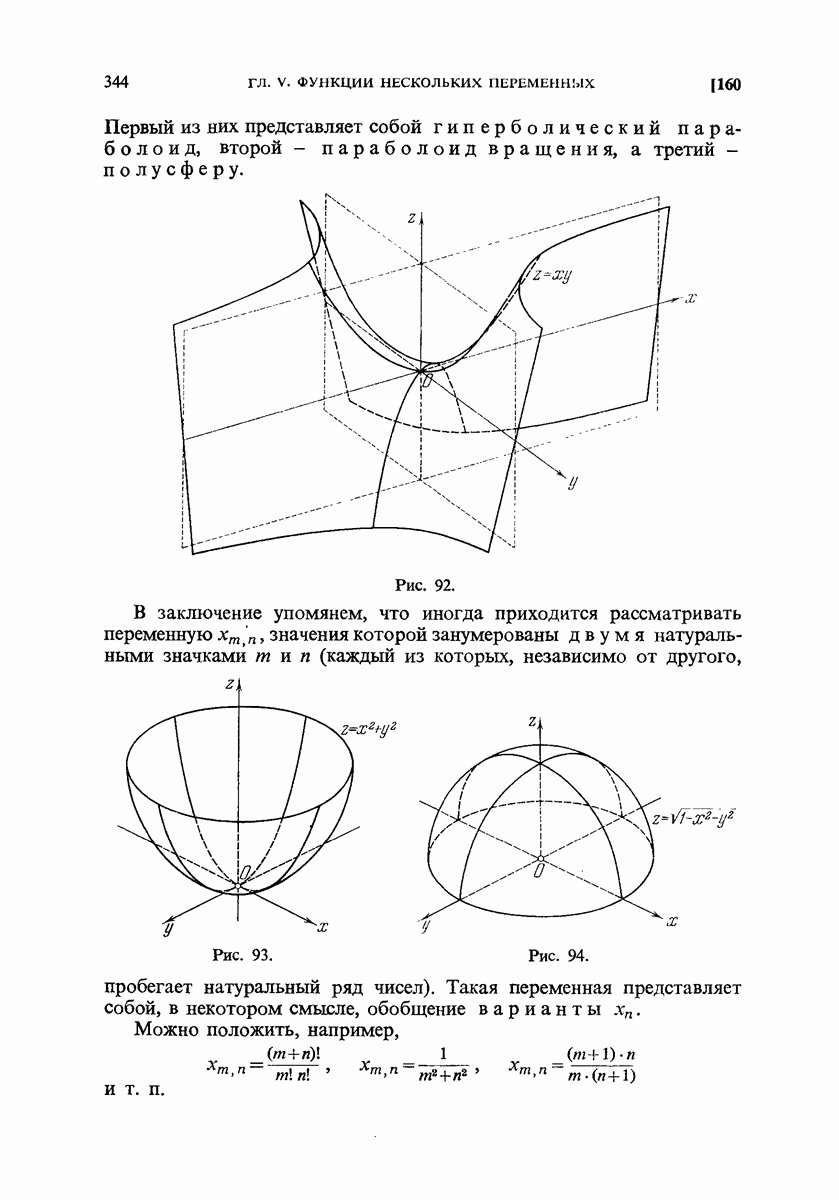
- ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 159. Функциональная зависимость между переменными. Примеры.
- 160. Функции двух переменных и области их определения.
- 161. Арифметическое n-мерное пространство.
- 162. Примеры областей в n-мерном пространстве.
- 163. Общее определение открытой и замкнутой области.
- 164. Функции n переменных.
- 165. Предел функции нескольких переменных.
- 166. Сведение к случаю варианты.
- 167. Примеры.
- 168. Повторные пределы.
- § 2. Непрерывные функции
- 170. Операции над непрерывными функциями.
- 171. Функции, непрерывные в области. Теоремы Больцано—Коши.
- 172. Лемма Больцано—Вейерштрасса.
- 173. Теоремы Вейерштрасса.
- 174. Равномерная непрерывность.
- 175. Лемма Бореля.
- 176. Новые доказательства основных теорем.
- § 3. Производные и дифференциалы функций нескольких переменных
- 178. Полное приращение функции.
- 179. Полный дифференциал.
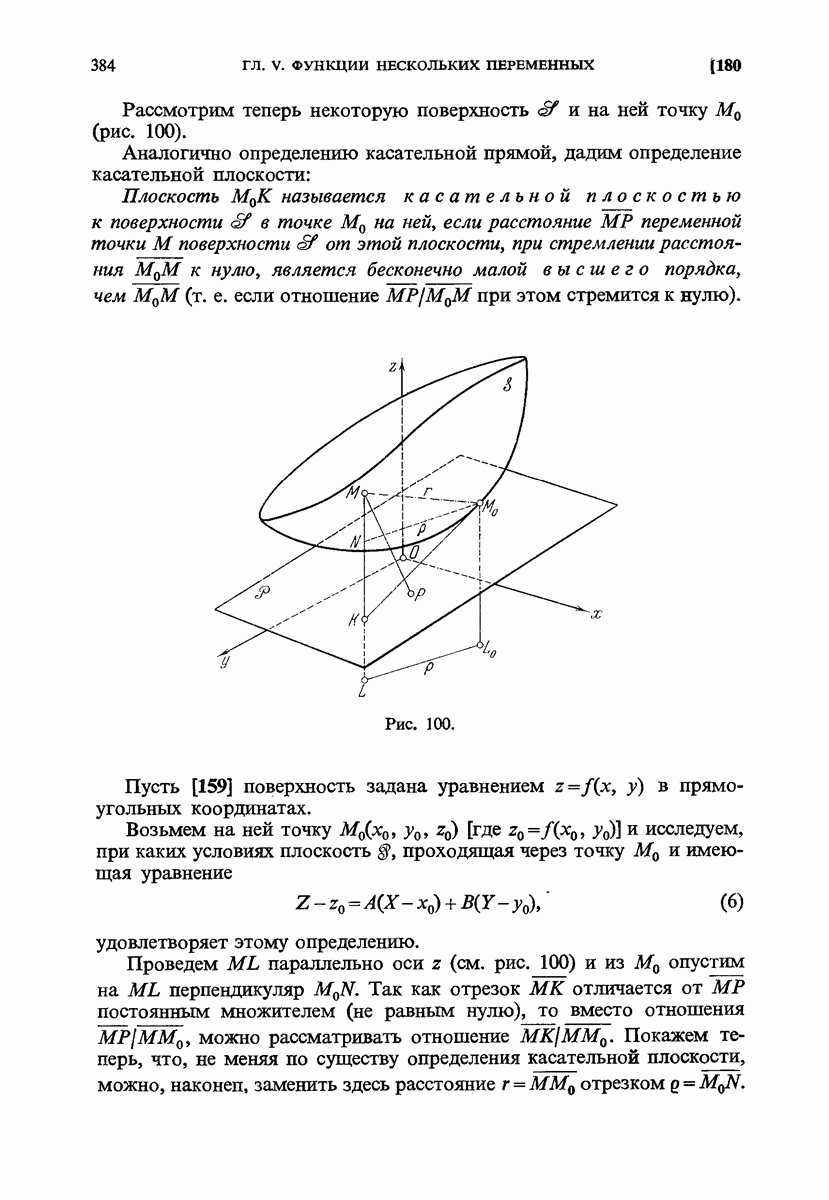
- 180. Геометрическая интерпретация для случая функции двух переменных.
- 181. Производные от сложных функций.
- 182. Примеры.
- 183. Формула конечных приращений.
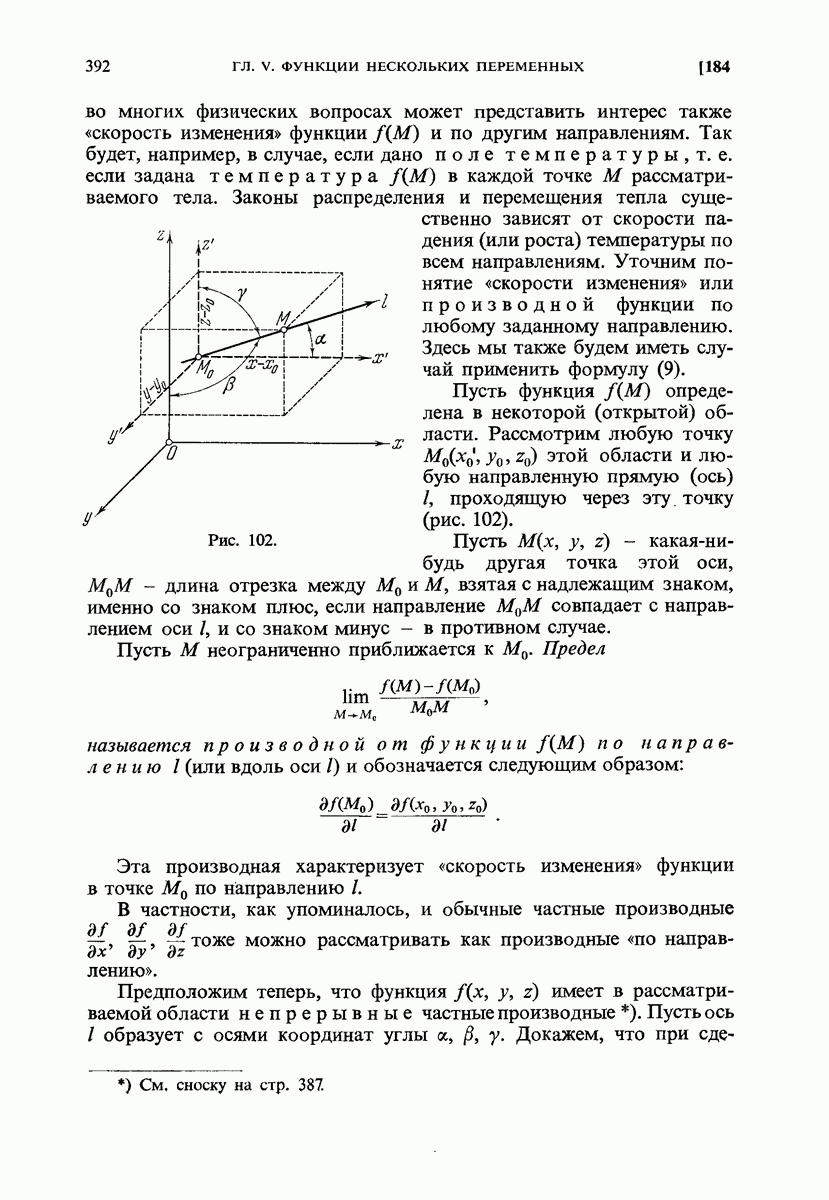
- 184. Производная по заданному направлению.
- 185. Инвариантность формы (первого) дифференциала.
- 186. Применение полного дифференциала в приближенных вычислениях.
- 187. Однородные функции.
- 188. Формула Эйлера.
- § 4. Производные и дифференциалы высших порядков
- 190. Теорема о смешанных производных.
- 191. Обобщение.
- 192. Производные высших порядков от сложной функции.
- 193. Дифференциалы высших порядков.
- 194. Дифференциалы сложных функций.
- 195. Формула Тейлора.
- § 5. Экстремумы, наибольшие и наименьшие значения
- 197. Достаточные условия (случай функции двух переменных).
- 198. Достаточные условия (общий случай).
- 199. Условия отсутствия экстремума.
- 200. Наибольшее и наименьшее значения функции. Примеры.
- 201. Задачи.
- ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
- § 1. Формальные свойства функциональных определителей
- 203. Умножение якобианов.
- 204. Умножение функциональных матриц (матриц Якоби).
- § 2. Неявные функции
- 206. Существование неявной функции.
- 207. Дифференцируемость неявной функции.
- 208. Неявные функции от нескольких переменных.
- 209. Вычисление производных неявных функций.
- 210. Примеры.
- § 3. Некоторые приложения теории неявных функций
- 212. Метод неопределенных множителей Лагранжа.
- 213. Достаточные для относительного экстремума условия.
- 214. Примеры и задачи.
- 215. Понятие независимости функций.
- 216. Ранг матрицы Якоби.
- § 4. Замена переменных
- 218. Примеры.
- 219. Функции нескольких переменных. Замена независимых переменных.
- 220. Метод вычисления дифференциалов.
- 221. Общий случай замены переменных.
- 222. Примеры.
- ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
- § 1. Аналитическое представление кривых и поверхностей
- 224. Примеры.
- 225. Кривые механического происхождения.
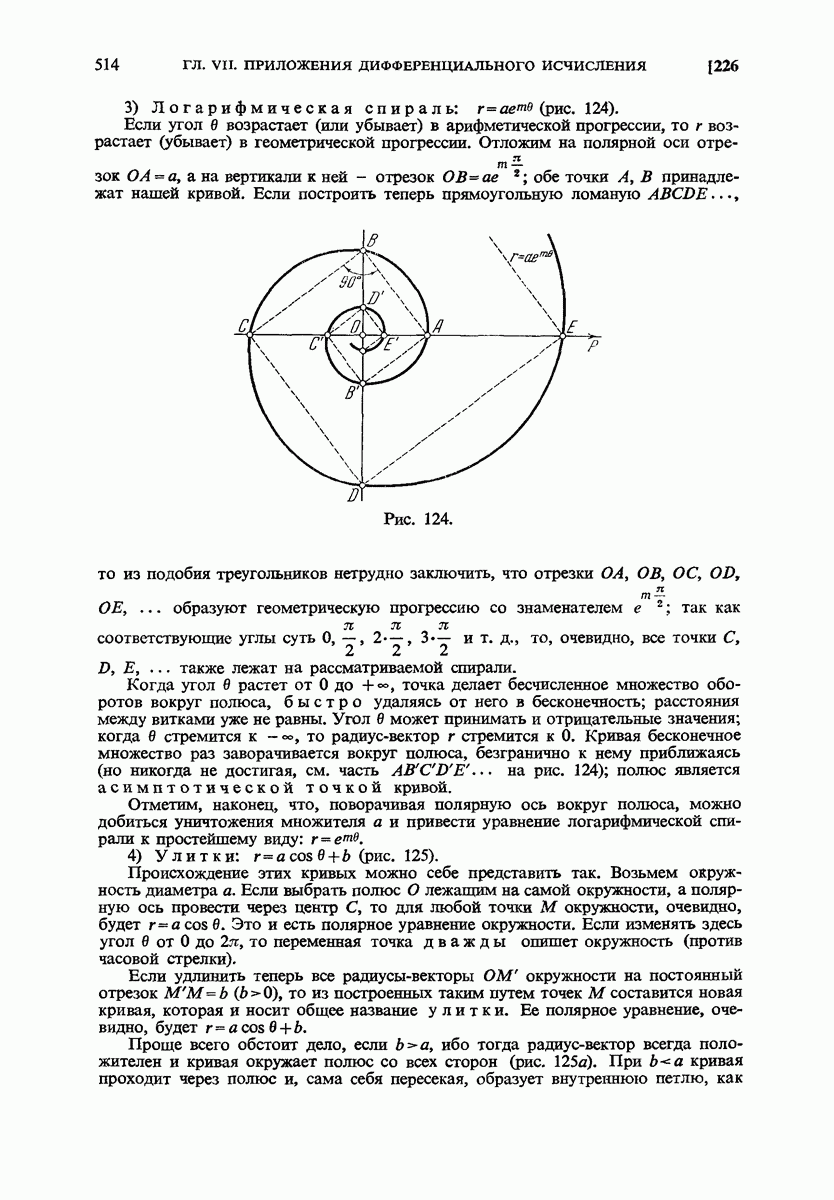
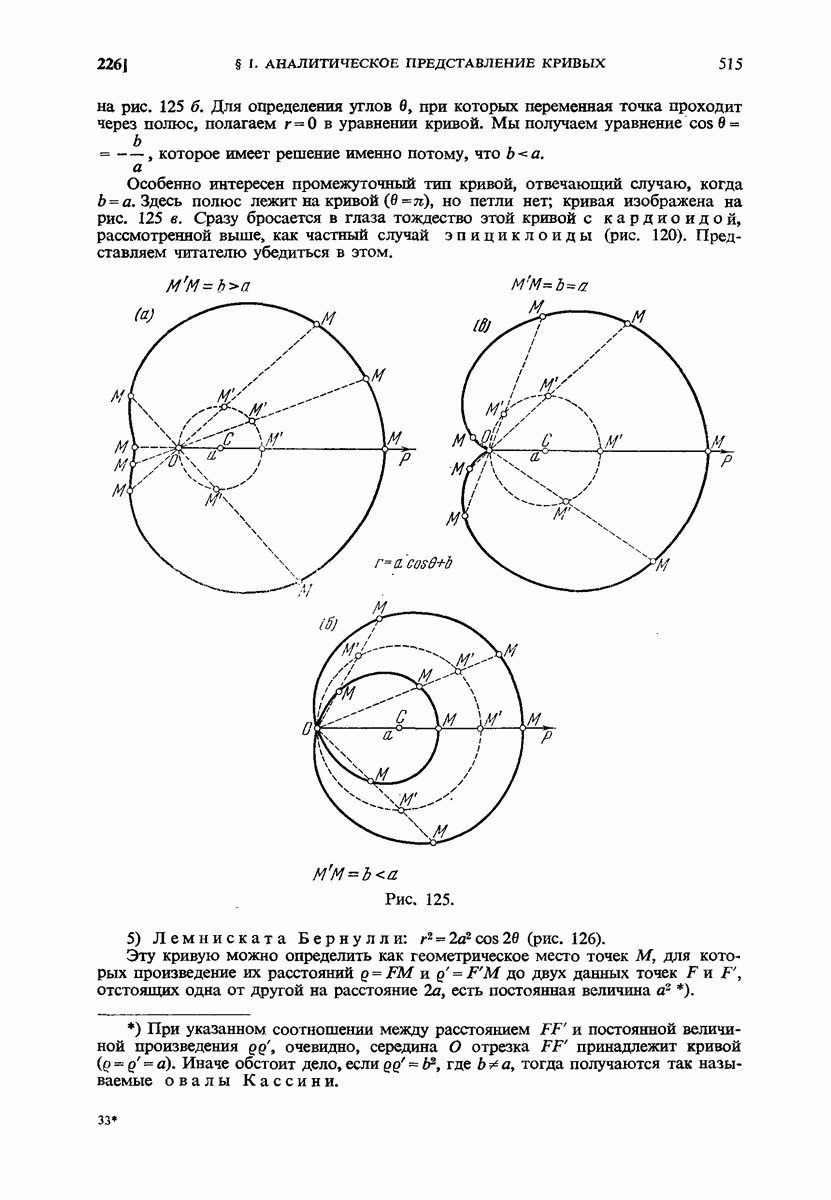
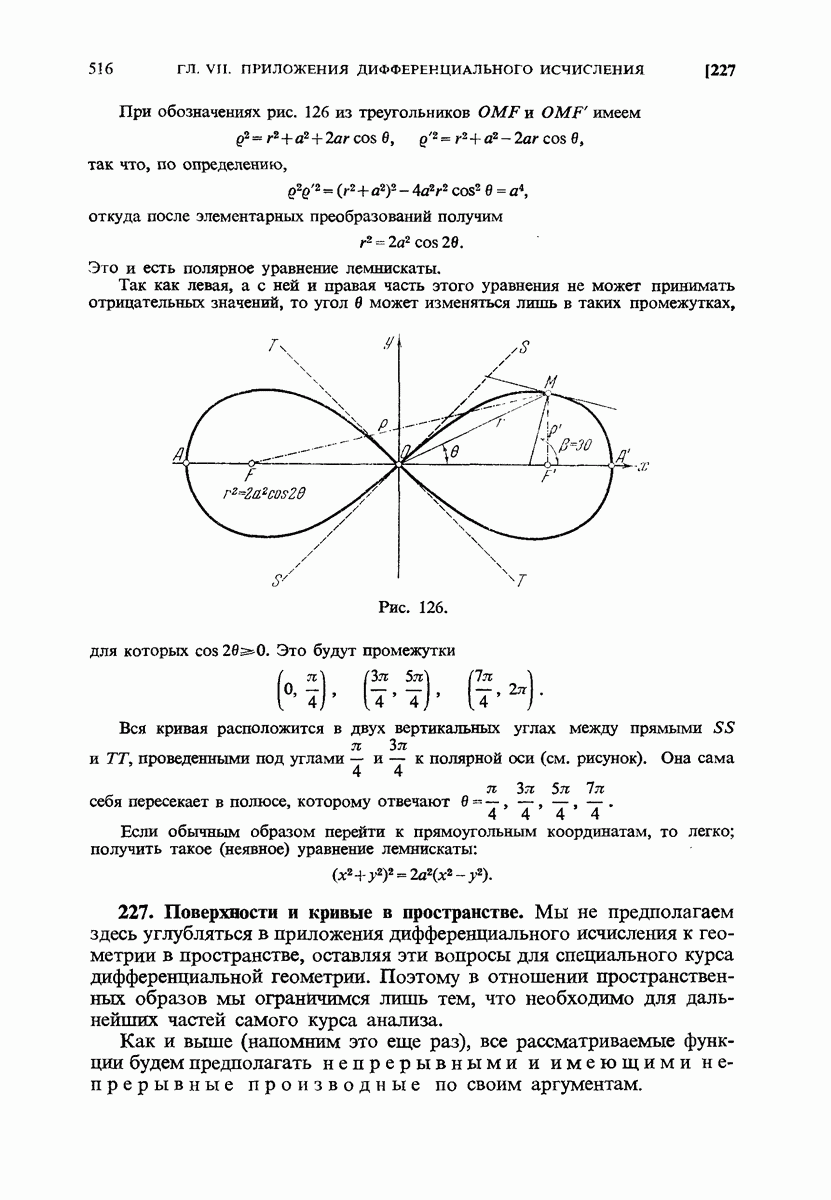
- 226. Кривые на плоскости (в полярных координатах). Примеры.
- 227. Поверхности и кривые в пространстве.
- 228. Параметрическое представление.
- 229. Примеры.
- § 2. Касательная и касательная плоскость
- 231. Примеры.
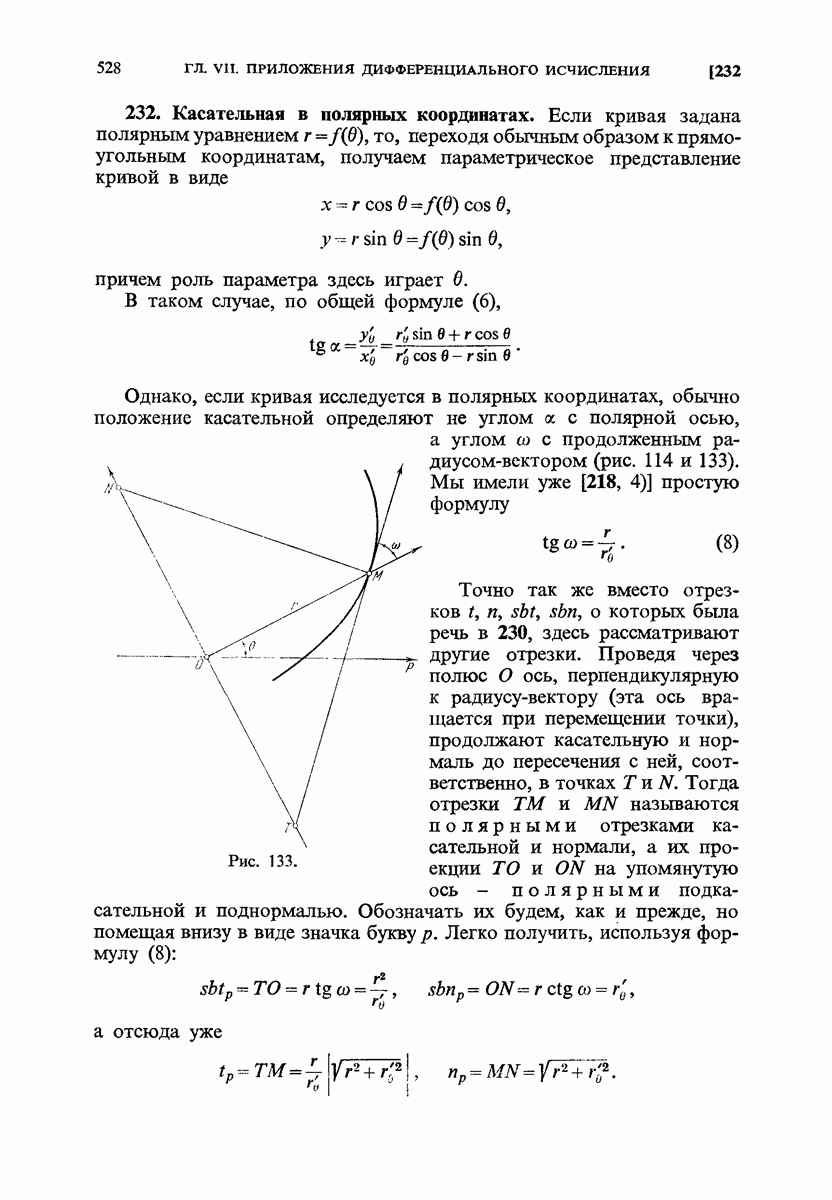
- 232. Касательная в полярных координатах.
- 233. Примеры.
- 234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
- 235. Примеры.
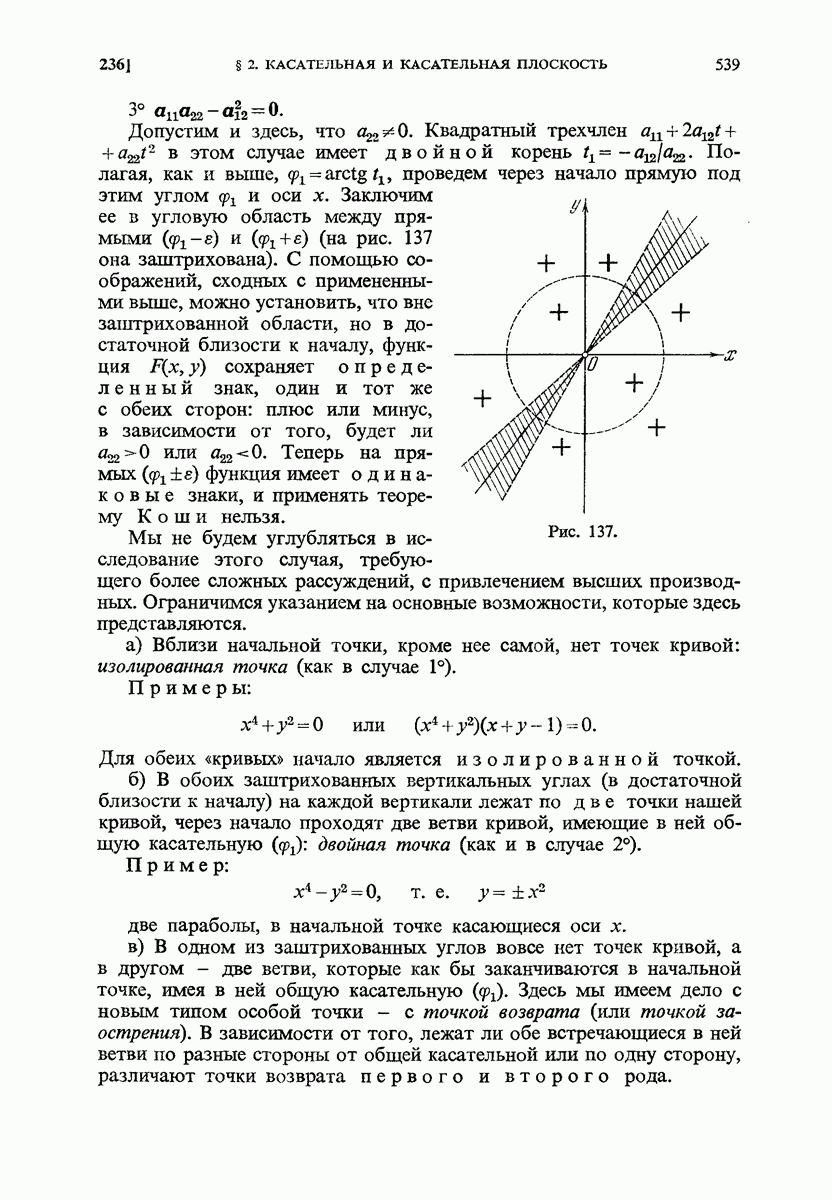
- 236. Особые точки плоских кривых.
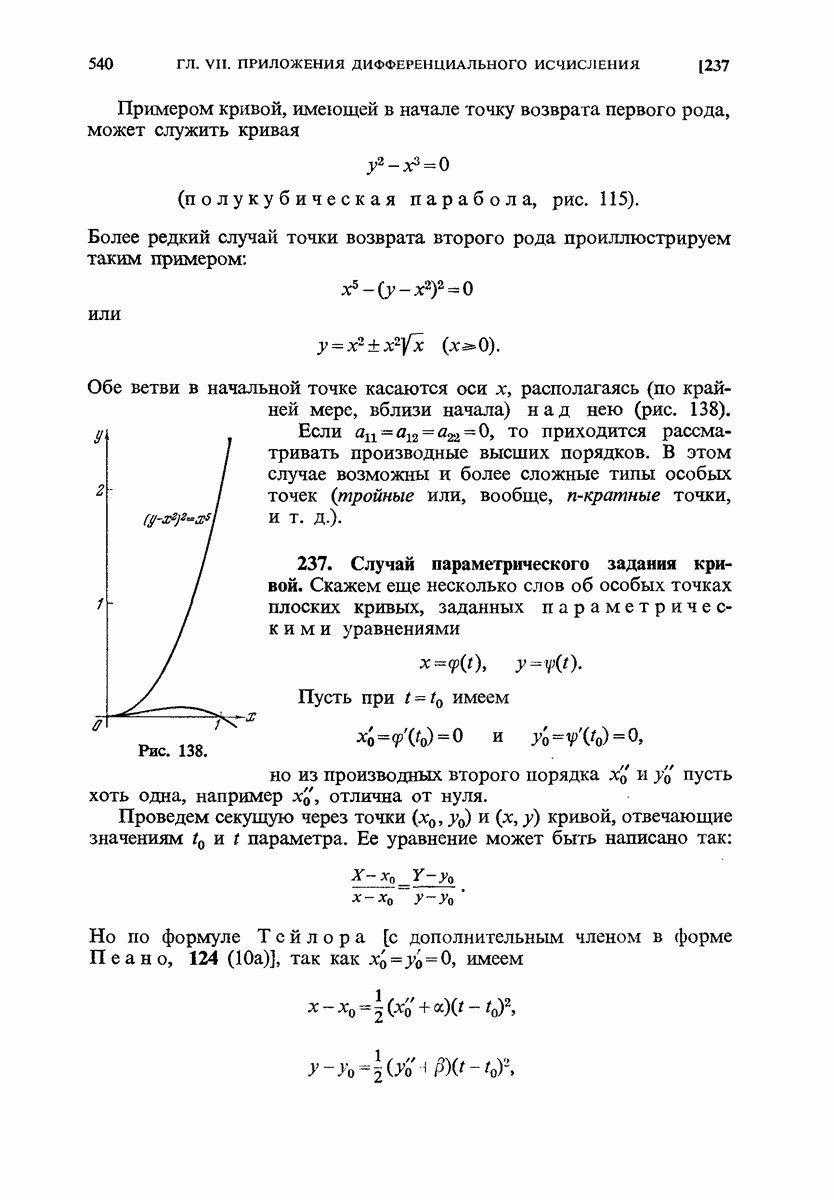
- 237. Случай параметрического задания кривой.
- § 3. Касание кривых между собой
- 239. Примеры.
- 240. Характеристические точки.
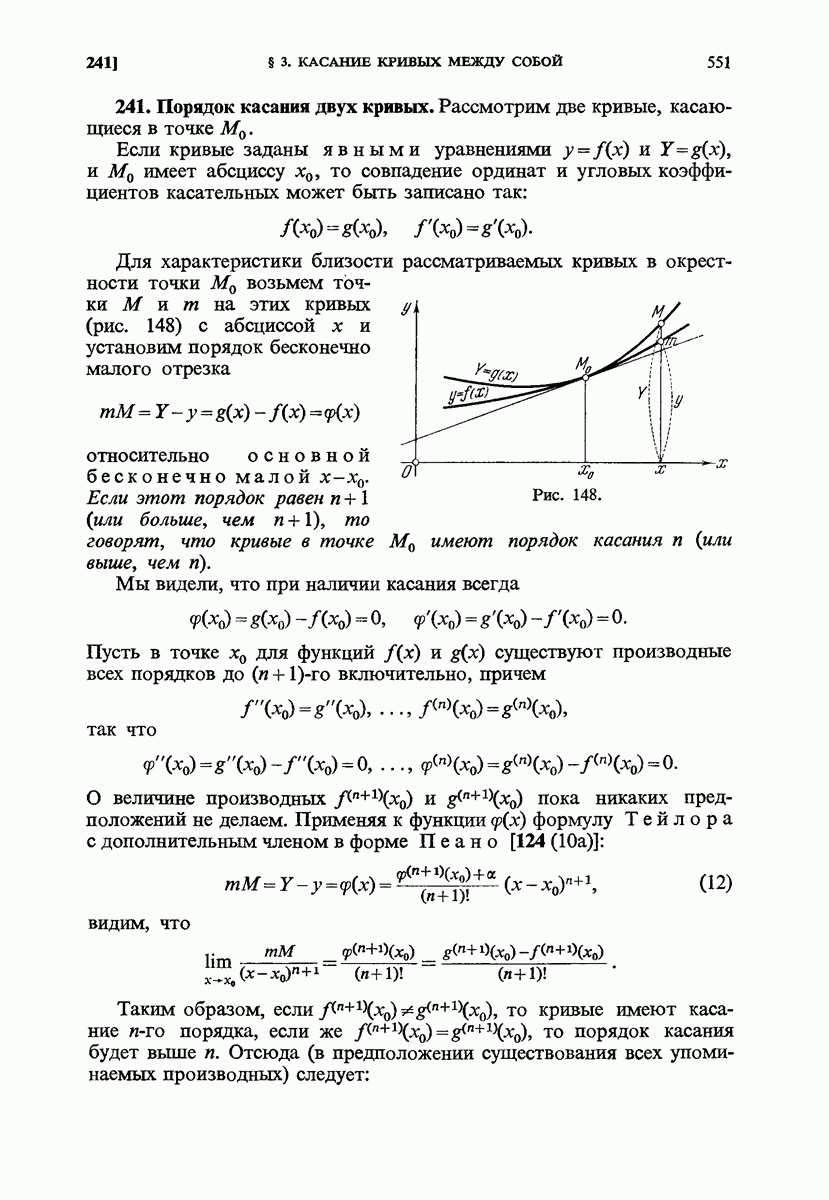
- 241. Порядок касания двух кривых.
- 242. Случай неявного задания одной из кривых.
- 243. Соприкасающаяся кривая.
- 244. Другой подход к соприкасающимся кривым.
- § 4. Длина плоской кривой
- 246. Направление на кривой.
- 247. Длина кривой. Аддитивность длины дуги.
- 248. Достаточные условия спрямляемости. Дифференциал дуги.
- 249. Дуга в роли параметра. Положительное направление касательной.
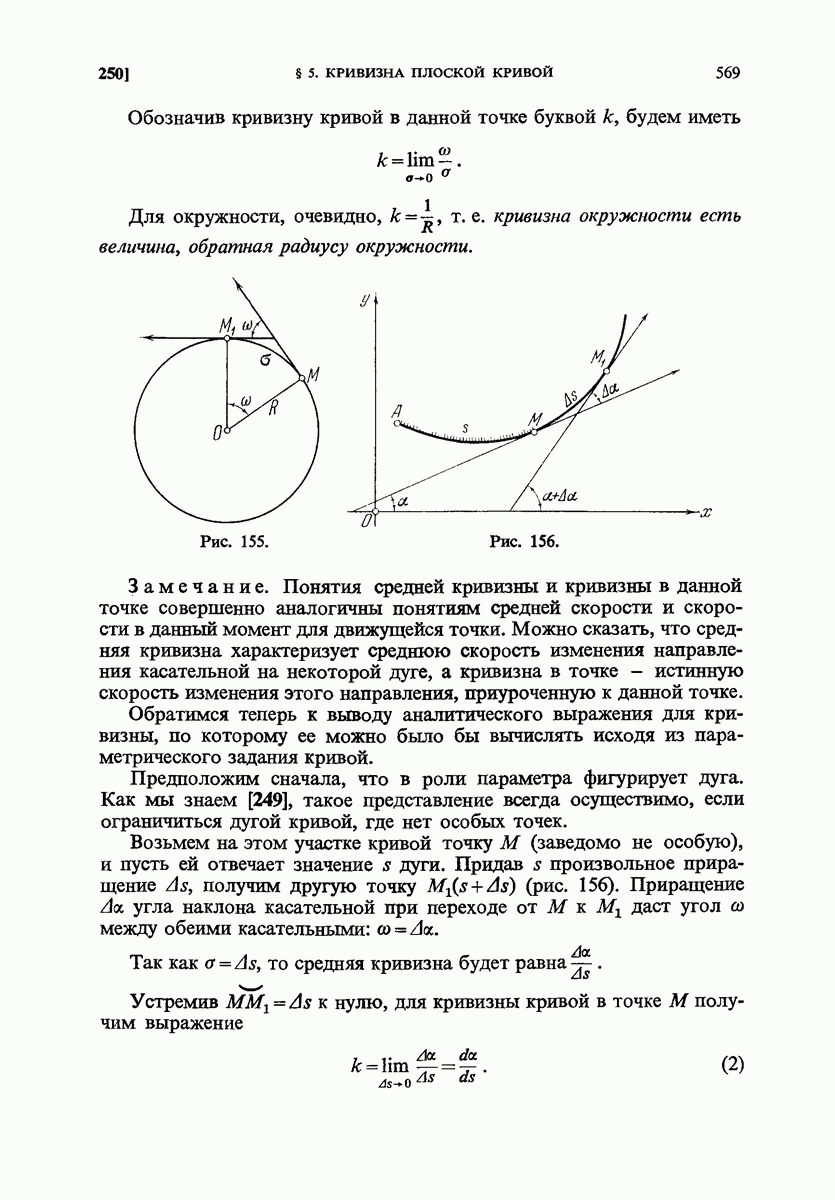
- § 5. Кривизна плоской кривой
- 251. Круг кривизны и радиус кривизны.
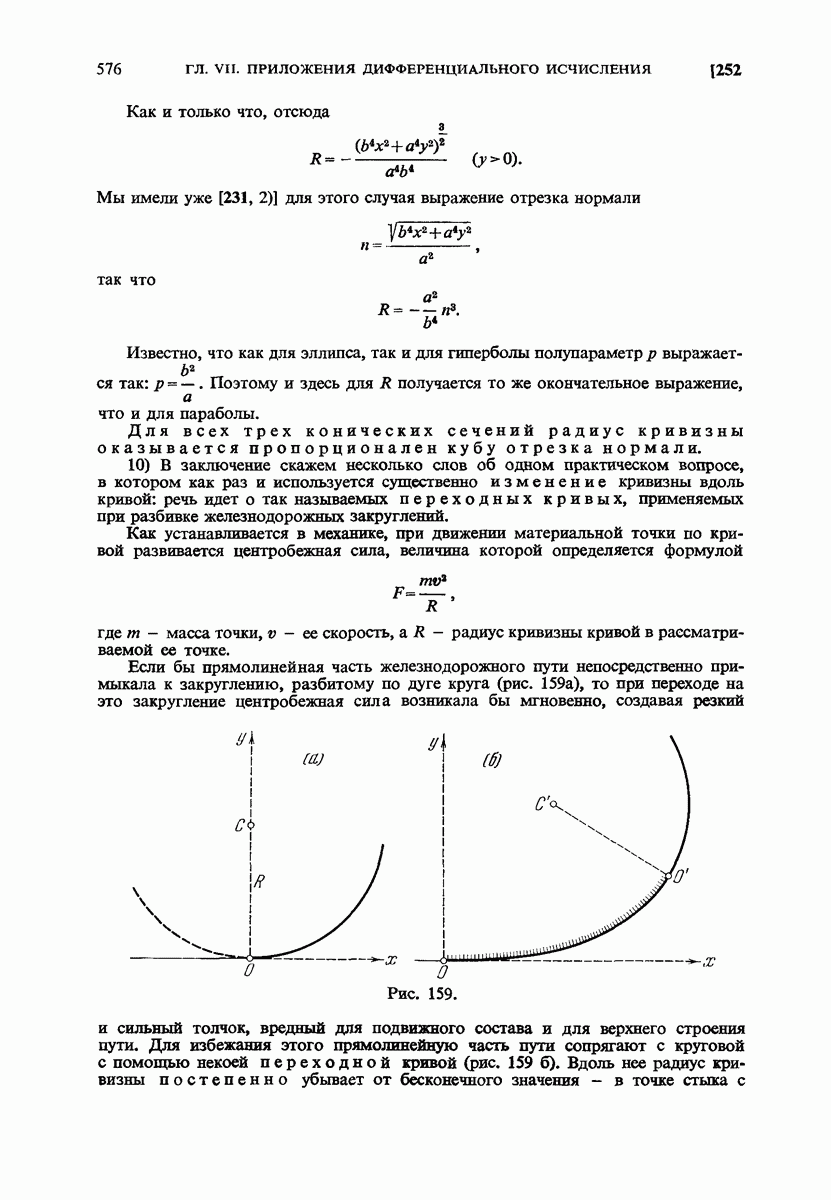
- 252. Примеры.
- 253. Координаты центра кривизны.
- 254. Определение эволюты и эвольвенты; разыскание эволюты.
- 255. Свойства эволют и эвольвент.
- 256. Разыскание эвольвент.
- ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ