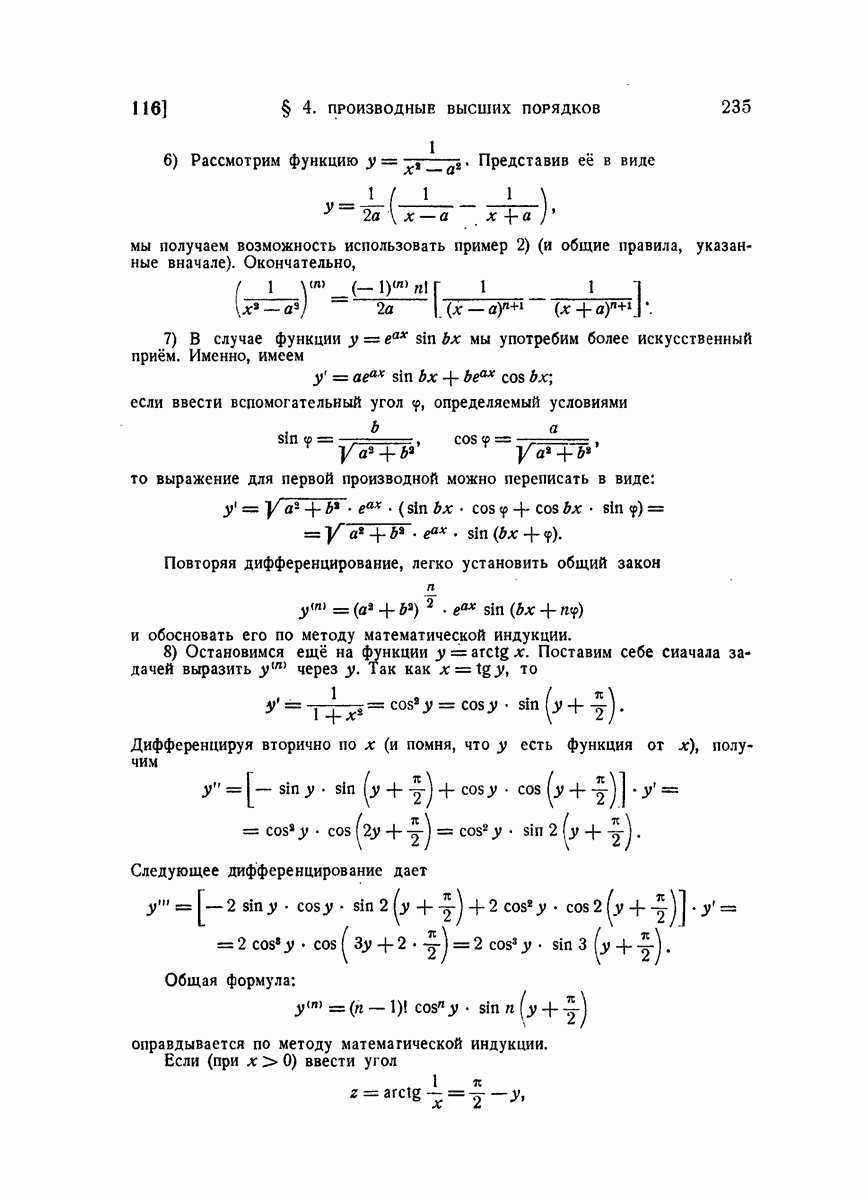| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
61. Шкала бесконечно малых.
Иной раз встречается надобность в более точной сравнительной характеристике поведения бесконечно малых, в выражении их порядков числами. В этом случае, прежде всего, в качестве своего рода «эталона» выбирают одну из фигурирующих в данном исследовании бесконечно малых (скажем, а); ее называют основной. Конечно, выбор основной бесконечно малой в известной мере произволен, но обычно берут простейшую из всех. Если рассматриваемые величины, как мы предположили, являются функциями от х и становятся бесконечно малыми при стремлении х к а, то в зависимости от того, будет ли а нулем, конечным и отличным от нуля числом или бесконечностью, естественно за основную бесконечно малую взять, соответственно

Далее, из степеней основной бесконечно малой а (мы будем считать  с различными положительными показателями,
с различными положительными показателями,  составляют как бы шкалу для оценки бесконечно малых более сложной природы.
составляют как бы шкалу для оценки бесконечно малых более сложной природы.
III. Уславливаются считать бесконечно малую  величиной
величиной  порядка (относительно основной бесконечно малой
порядка (относительно основной бесконечно малой  если
если  будут величинами одного порядка, т. е. если отношение
будут величинами одного порядка, т. е. если отношение  имеет конечный и отличный от нуля предел.
имеет конечный и отличный от нуля предел.
Теперь, например, можно, не довольствуясь утверждением, что бесконечно малые  будут величинами высшего порядка, чем
будут величинами высшего порядка, чем  сказать точно, что первые две из них суть бесконечно малые второго порядка, а последняя — третьего порядка относительно
сказать точно, что первые две из них суть бесконечно малые второго порядка, а последняя — третьего порядка относительно  ибо [56, 4); 5), (а) и (б)]
ибо [56, 4); 5), (а) и (б)]

Чтобы взять более сложный пример, рассмотрим выражение

при  оно будет бесконечно малым, что становится ясным, если представить его в виде
оно будет бесконечно малым, что становится ясным, если представить его в виде

Продолжая это преобразование, найдем:

Полагая  теперь уже нетрудно сообразить, что
теперь уже нетрудно сообразить, что 

Таким образом, здесь порядок выражается числом 
Не следует думать, конечно, что для всякой бесконечно малой  (даже сравнимой со всеми степенями
(даже сравнимой со всеми степенями  может быть установлен определенный порядок.
может быть установлен определенный порядок.
Любопытные примеры, относящиеся сюда, можно получить из формул, установленных в 54, 4) и 

Прежде всего, отсюда

Заменив теперь здесь х на — и положив еще в первом из этих соотношений  мы получим:
мы получим:

Таким образом, бесконечно малая  будет высшего порядка, чем все степени
будет высшего порядка, чем все степени  в то время как бесконечно малая
в то время как бесконечно малая  оказывается низшего порядка, чем все эти степени.
оказывается низшего порядка, чем все эти степени.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Упорядочение области рациональных чисел.
- 3. Сложение и вычитание рациональных чисел.
- 4. Умножение и деление рациональных чисел.
- 5. Аксиома Архимеда.
- § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
- 7. Упорядочение области вещественных чисел.
- 8. Вспомогательные предложения.
- 9. Представление вещественного числа бесконечной десятичной дробью.
- 10. Непрерывность области вещественных чисел.
- 11. Границы числовых множеств.
- § 3. Арифметические действия над вещественными числами
- 13. Свойства сложения.
- 14. Определение произведения вещественных чисел.
- 15. Свойства умножения.
- 16. Заключение.
- 17. Абсолютные величины.
- § 4. Дальнейшие свойства и приложения вещественных чисел
- 19. Степень с любым вещественным показателем.
- 20. Логарифмы.
- 21. Измерение отрезков.
- ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. Варианта и ее предел
- 23. Предел варианты.
- 24. Бесконечно малые величины.
- 25. Примеры.
- 26. Некоторые теоремы о варианте, имеющей предел.
- 27. Бесконечно большие величины.
- § 2. Теоремы о пределах, облегчающие нахождение пределов
- 29. Леммы о бесконечно малых.
- 30. Арифметические операция над переменными.
- 31. Неопределенные выражения.
- 32. Примеры на нахождение пределов.
- 33. Теорема Штольца и ее применения.
- § 3. Монотонная варианта
- 35. Примеры.
- 36. Число е.
- 37. Приближенное вычисление числа е.
- 38. Лемма о вложенных промежутках.
- § 4. Принцип сходимости. Частичные пределы
- 40. Частичные последовательности и частичные пределы.
- 41. Лемма Больцано — Вейерштрасса
- 42. Наибольший и наименьший пределы.
- ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. Понятие функции
- 44. Функциональная зависимость между переменными. Примеры.
- 45. Определение понятия функции.
- 46. Аналитический способ задания функции.
- 47. График функции.
- 48. Важнейшие классы функций.
- 49. Понятие обратной функции.
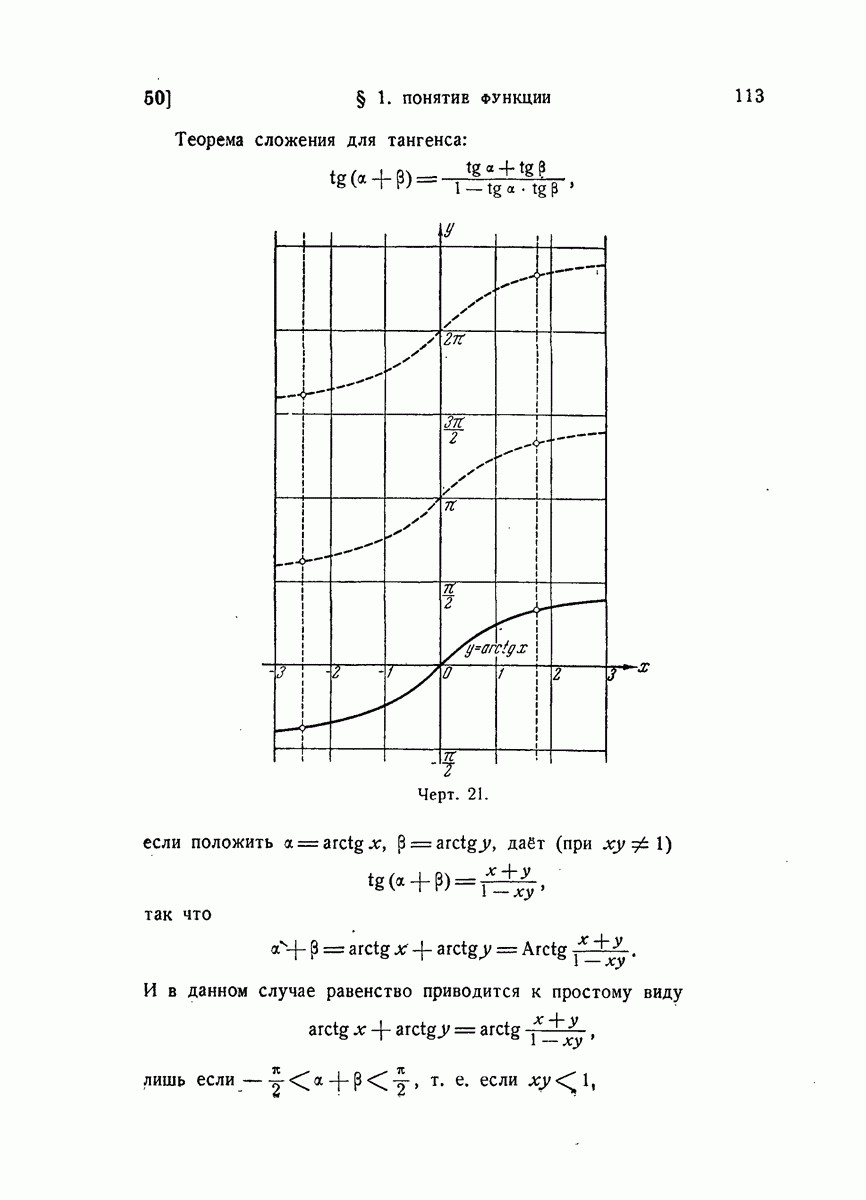
- 50. Обратные тригонометрические функции.
- 51. Суперпозиция функций. Заключительные замечания.
- § 2. Предел функции
- 53. Сведение к случаю варианты.
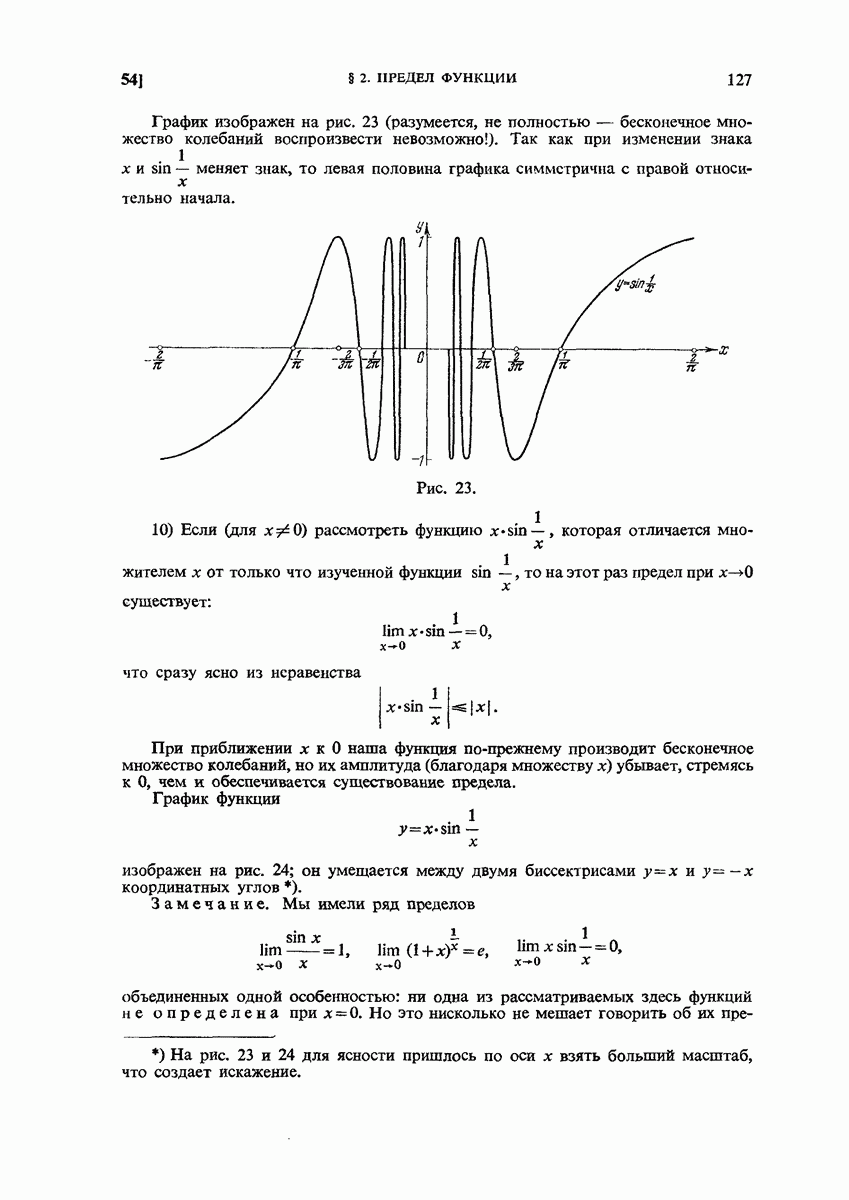
- 54. Примеры.
- 55. Распространение теории пределов.
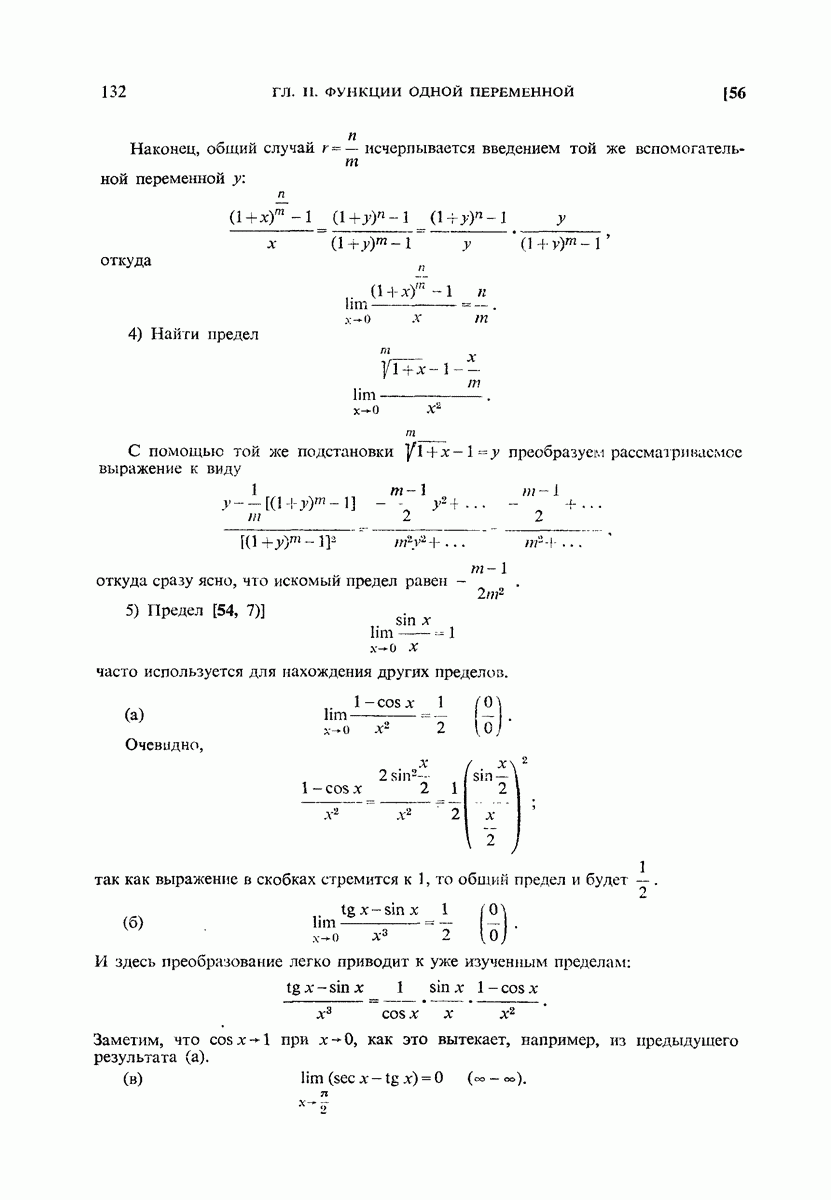
- 56. Примеры.
- 57. Предел монотонной функции.
- 58. Общий признак Больцано—Коши.
- 59. Наибольший и наименьший пределы функции.
- § 3. Классификация бесконечно малых и бесконечно больших величин
- 61. Шкала бесконечно малых.
- 62. Эквивалентные бесконечно малые.
- 63. Выделение главной части.
- 64. Задачи.
- 65. Классификация бесконечно больших.
- § 4. Непрерывность (и разрывы) функций
- 67. Арифметические операции над непрерывными функциями.
- 68. Примеры непрерывных функций.
- 69. Односторонняя непрерывность. Классификация разрывов.
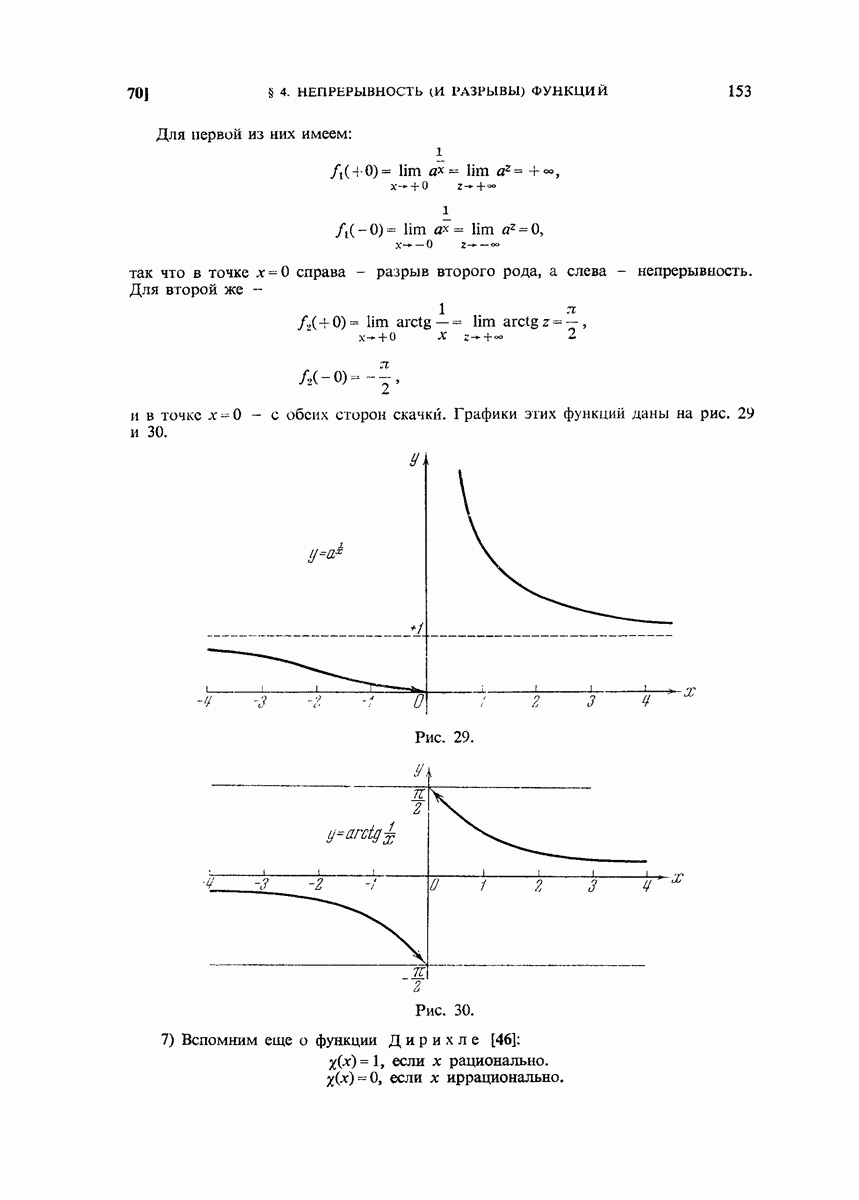
- 70. Примеры разрывных функций.
- 71. Непрерывность и разрывы монотонной функции.
- 72. Непрерывность элементарных функций.
- 73. Суперпозиция непрерывных функций.
- 74. Решение одного функционального уравнения.
- 75. Функциональная характеристика показательной, логарифмической и степенной функций.
- 76. Функциональная характеристика тригонометрического и гиперболического косинусов.
- 77. Использование непрерывности функций для вычисления пределов.
- 78. Степенно-показательные выражения.
- 79. Примеры.
- § 5. Свойства непрерывных функций
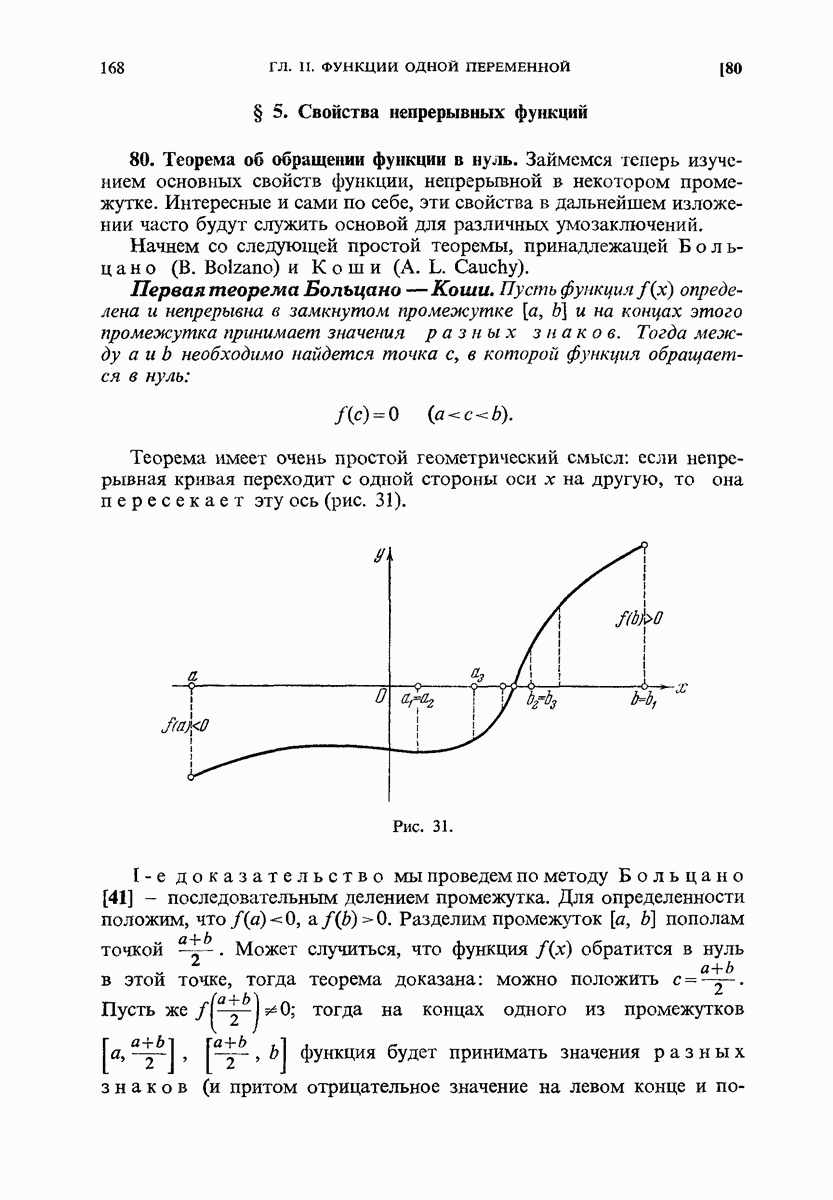
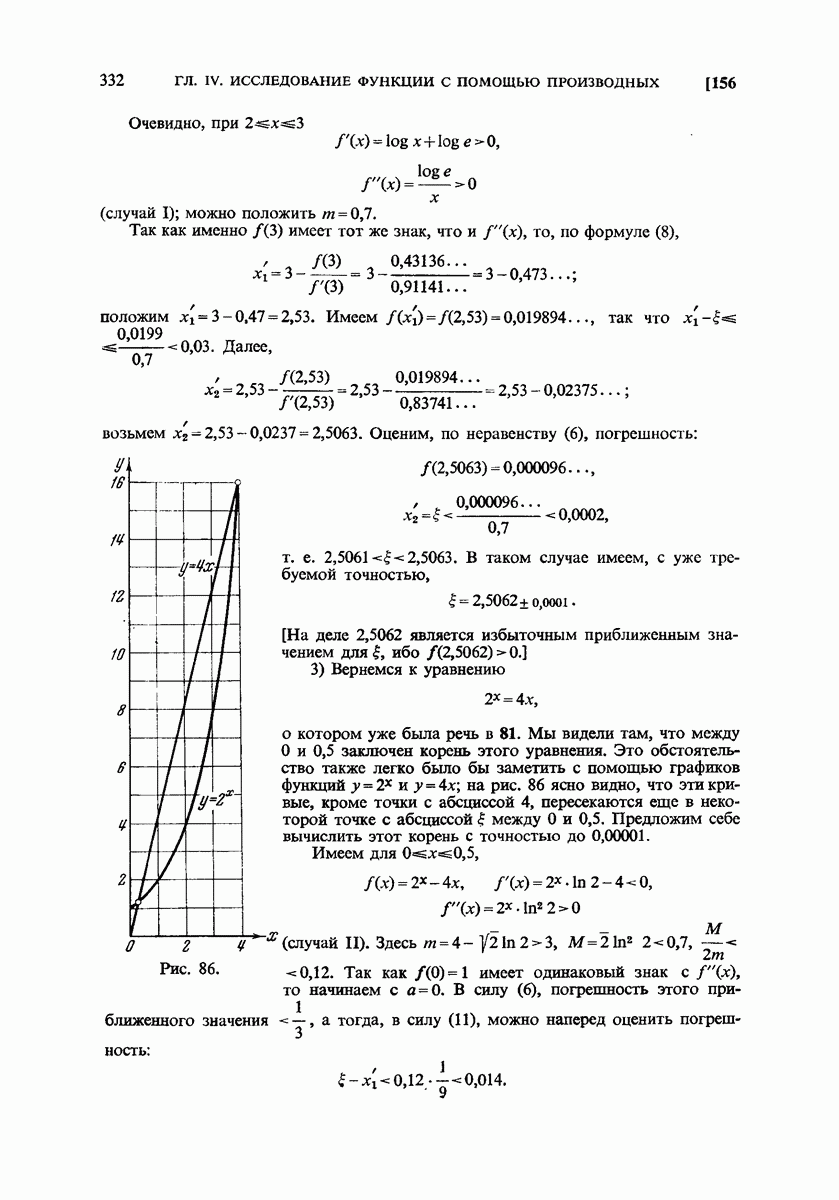
- 81. Применение к решению уравнений.
- 82. Теорема о промежуточном значении.
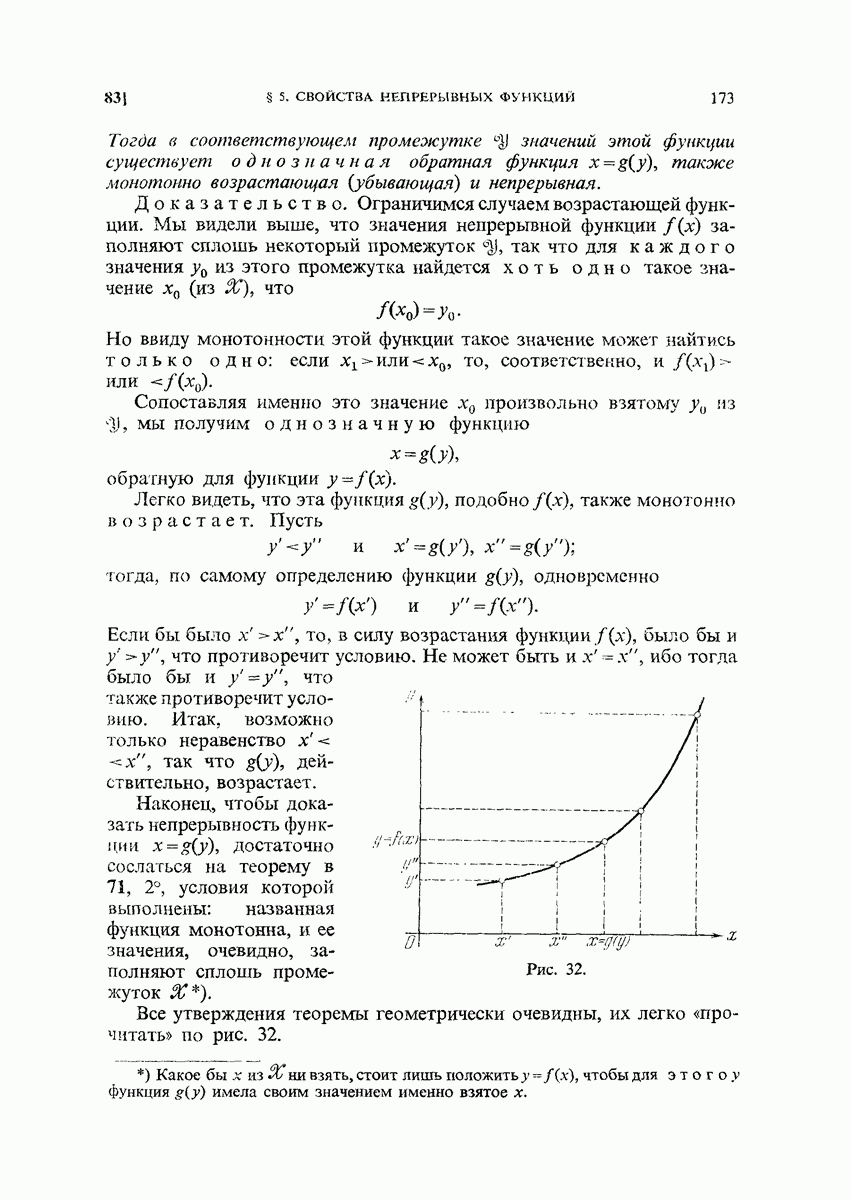
- 83. Существование обратной функции.
- 84. Теорема об ограниченности функции.
- 85. Наибольшее и наименьшее значения функции.
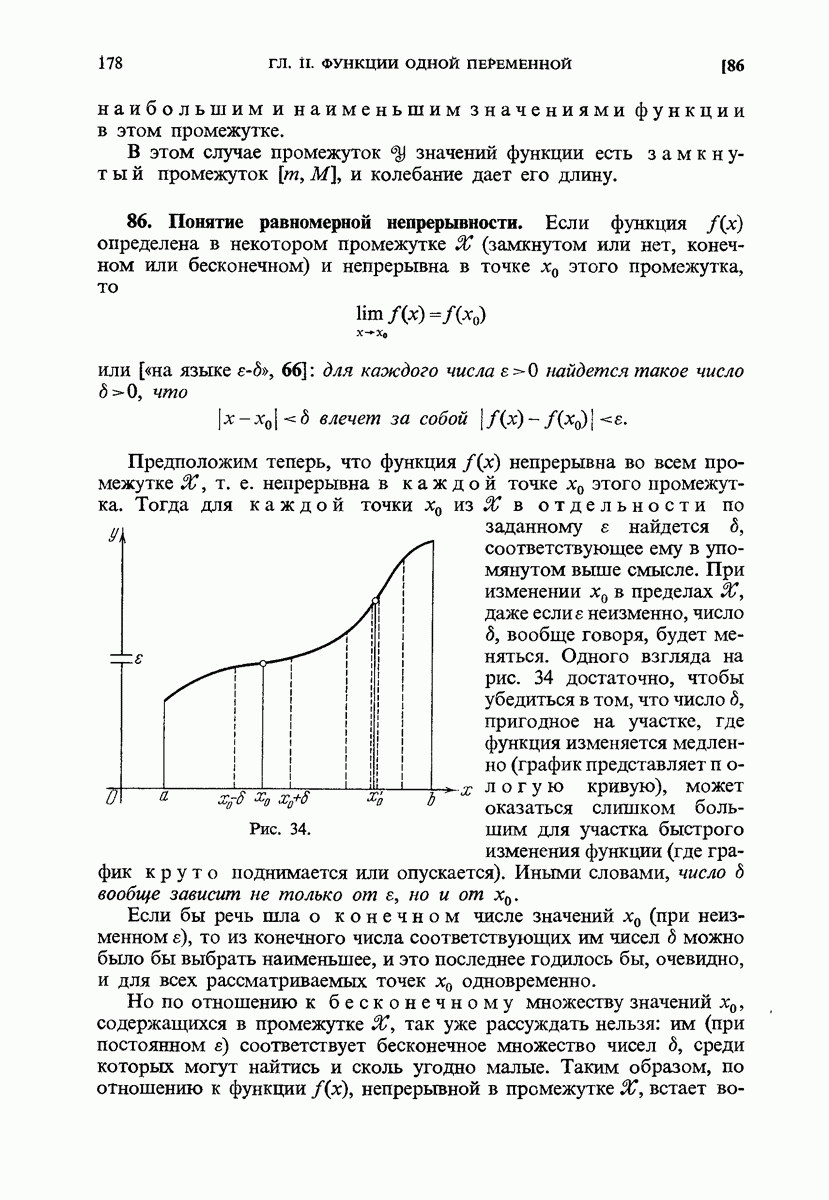
- 86. Понятие равномерной непрерывности.
- 87. Теорема Кантора.
- 88. Лемма Бореля.
- 89. Новые доказательства основных теорем.
- ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная и ее вычисление
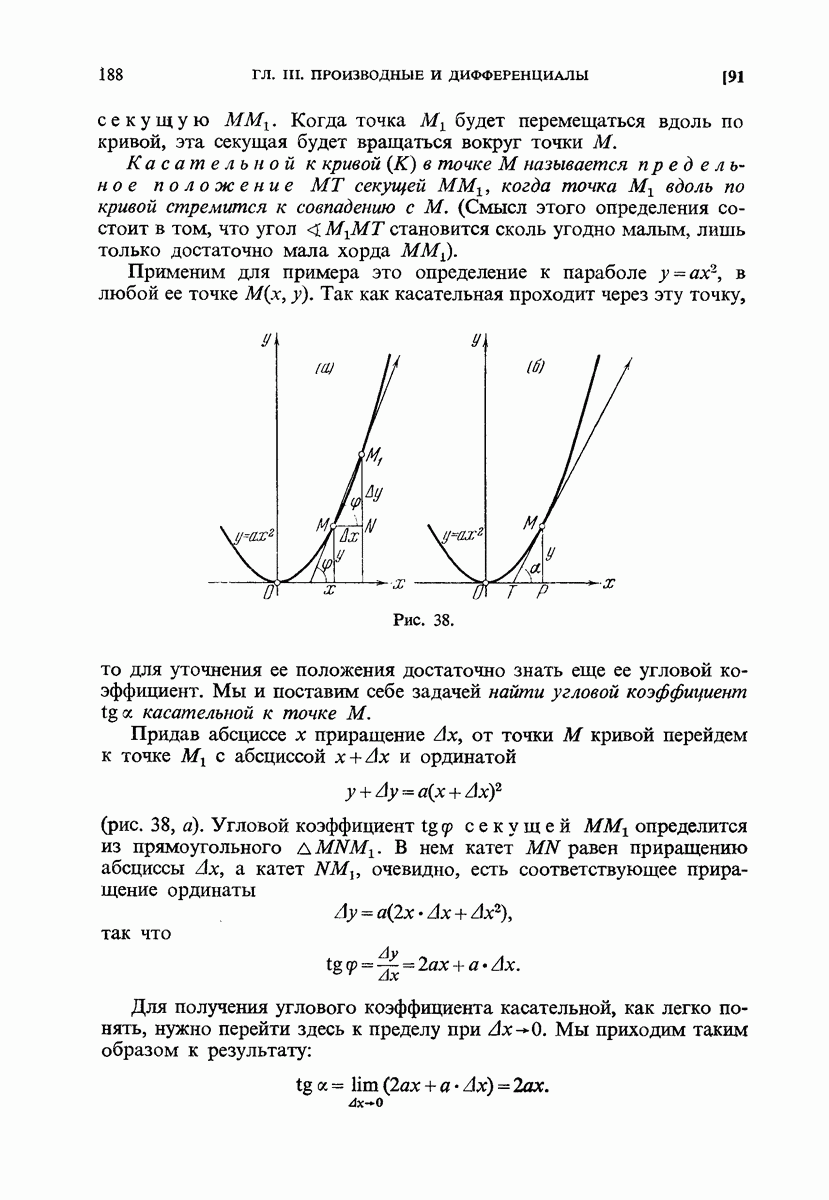
- 91. Задача о проведении касательной к кривой.
- 92. Определение производной.
- 93. Примеры вычисления производных.
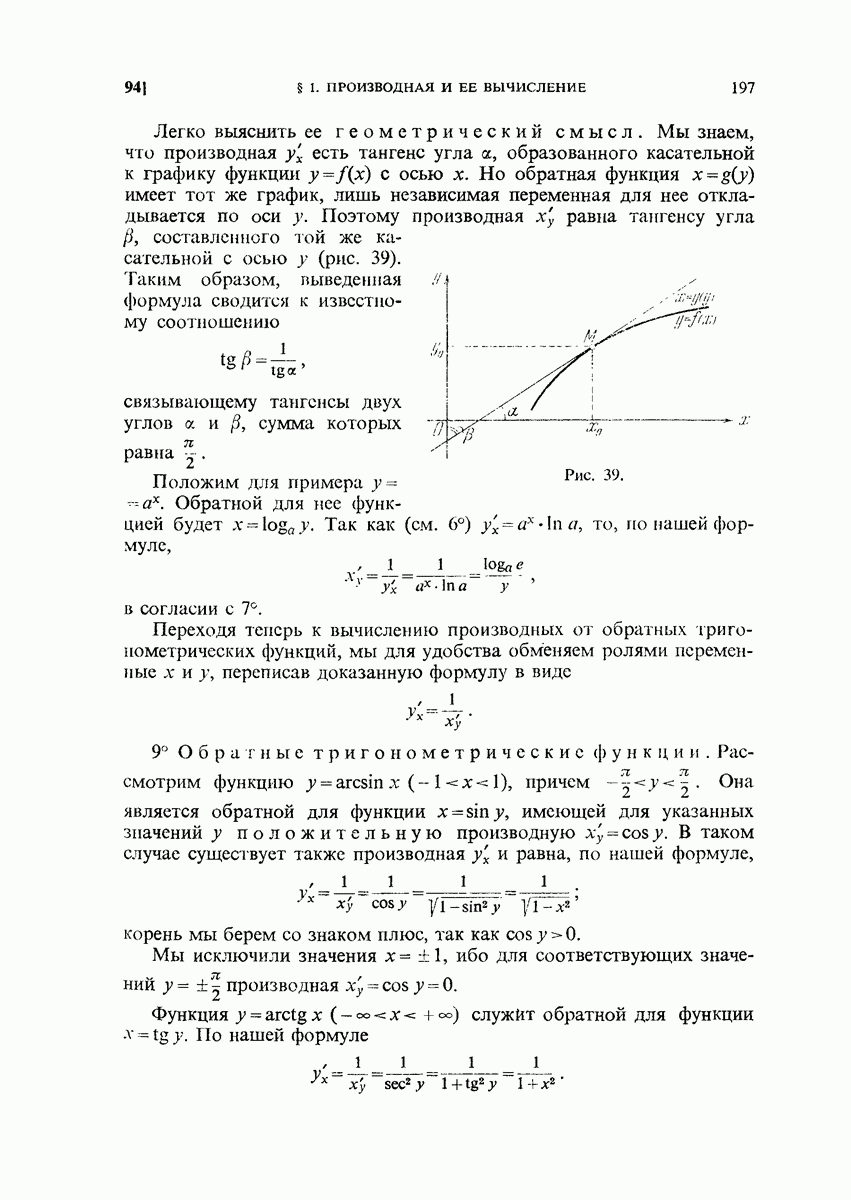
- 94. Производная обратной функции.
- 95. Сводка формул для производных.
- 96. Формула для превращения функции.
- 97. Простейшие правила вычисления производных.
- 98. Производная сложной функции.
- 100. Односторонние производные.
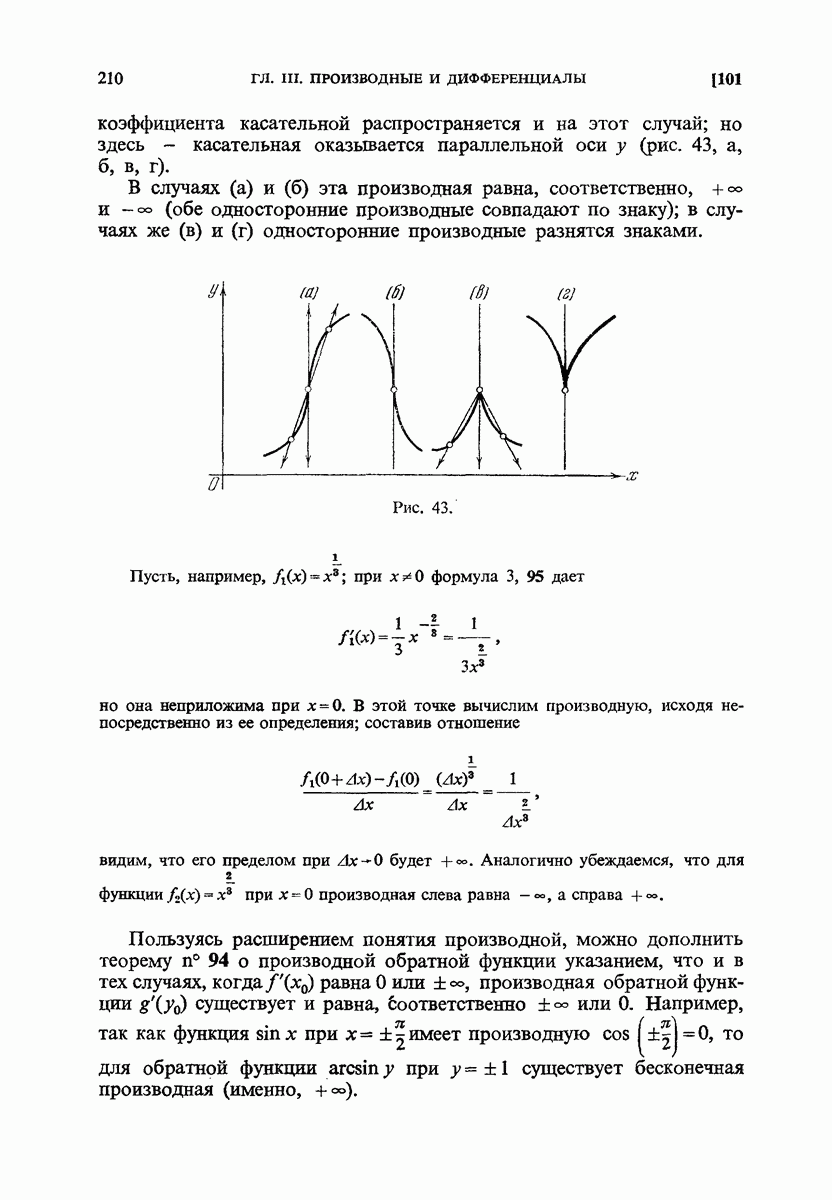
- 101. Бесконечные производные.
- 102. Дальнейшие примеры особых случаев.
- § 2. Дифференциал
- 104. Связь между диффереицируемостью и существованием производной.
- 105. Основные формулы и правила дифференцирования.
- 106. Инвариантность формы дифференциала.
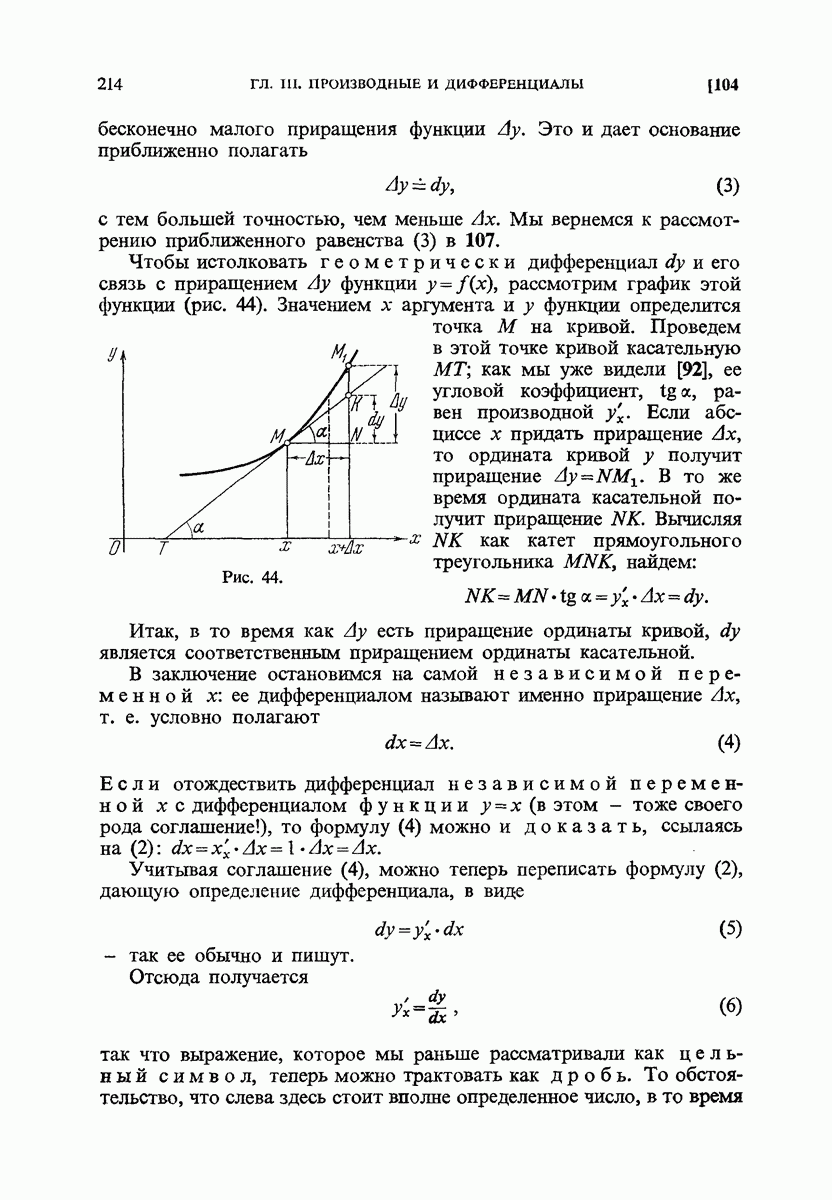
- 107. Дифференциалы как источник приближенных формул.
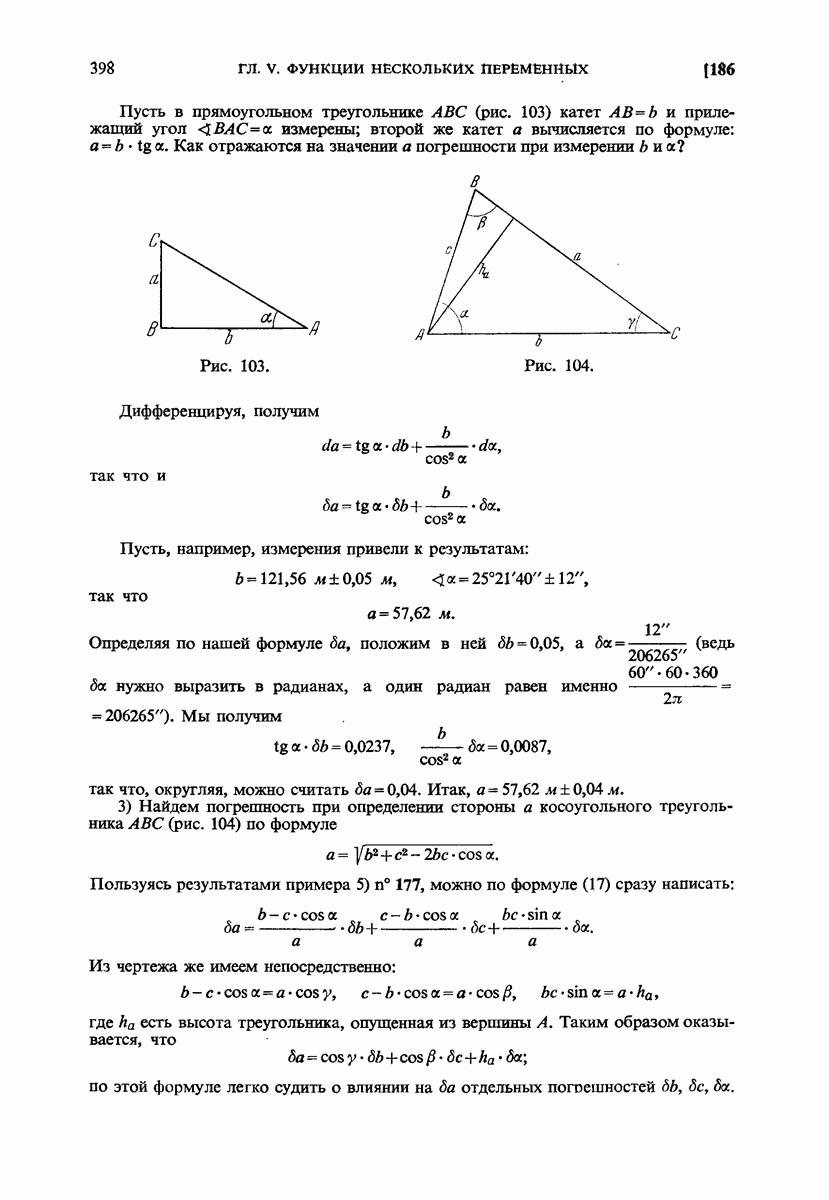
- 108. Применение дифференциалов при оценке погрешностей.
- § 3. Основные теоремы дифференциального исчисления
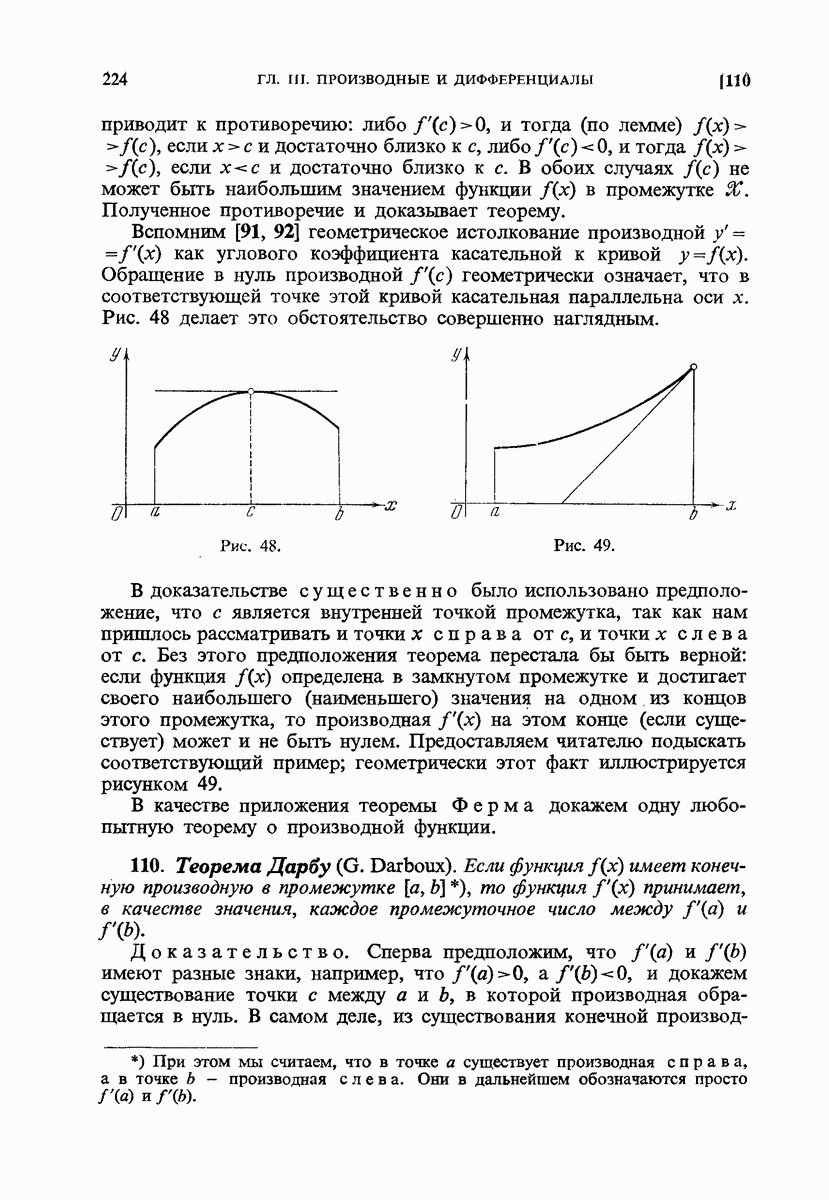
- 110. Теорема Дарбу
- 111. Теорема Ролля.
- 112. Формула Лагранжа.
- 113. Предел производной.
- 114. Формула Коши.
- § 4. Производные и дифференциалы высших порядков
- 116. Общие формулы для производных любого порядка.
- 117. Формула Лейбница.
- 118. Примеры.
- 119. Дифференциалы высших порядков.
- 120. Нарушение инвариантности формы для дифференциалов высших порядков.
- 121. Параметрическое дифференцирование.
- 122. Конечные разности.
- § 5. Формула Тейлора
- 124. Разложение произвольной функции; дополнительный член в форме Пеано.
- 125. Примеры.
- 126. Другие формы дополнительного члена.
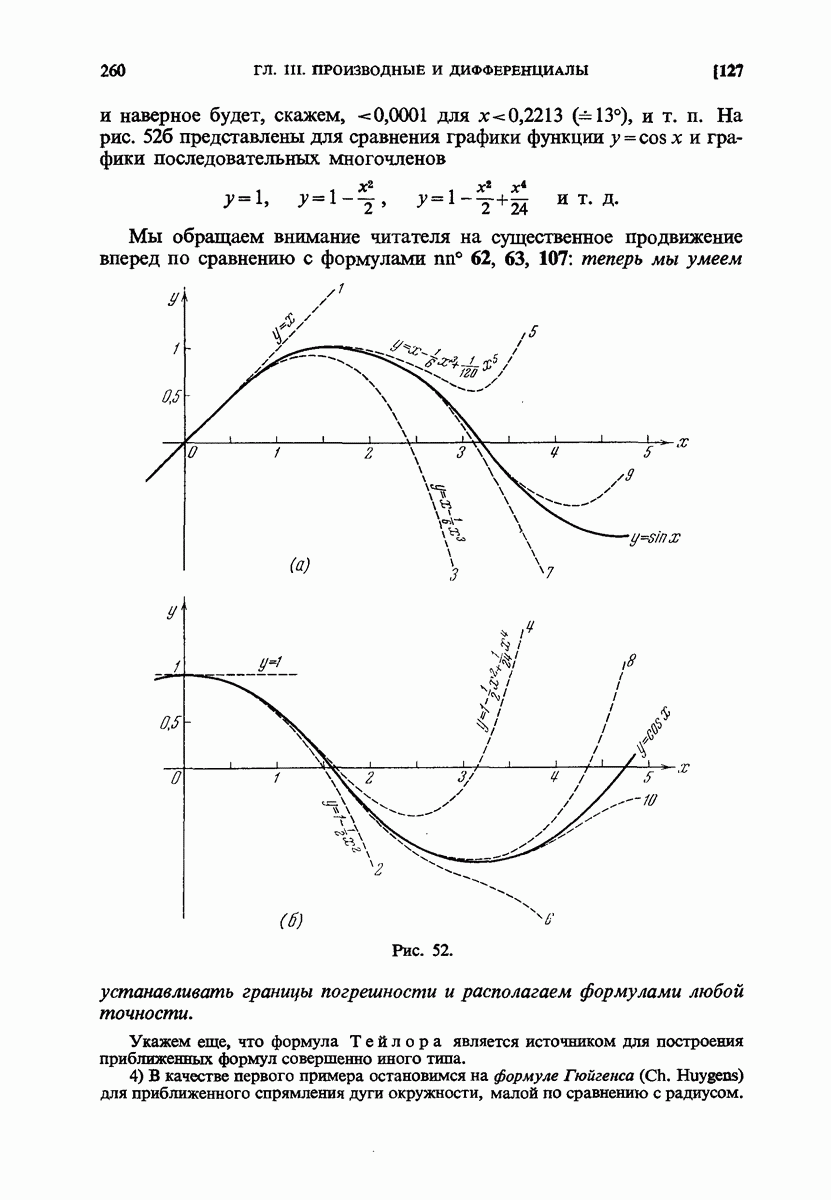
- 127. Приближенные формулы.
- § 6. Интерполирование
- 129. Дополнительный члеп формулы Лагранжа.
- 130. Интерполирование с кратными узлами. Формула Эрмита.
- ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
- § 1. Изучение хода изменения функции
- 132. Условие монотонности функции.
- 133. Доказательство неравенств.
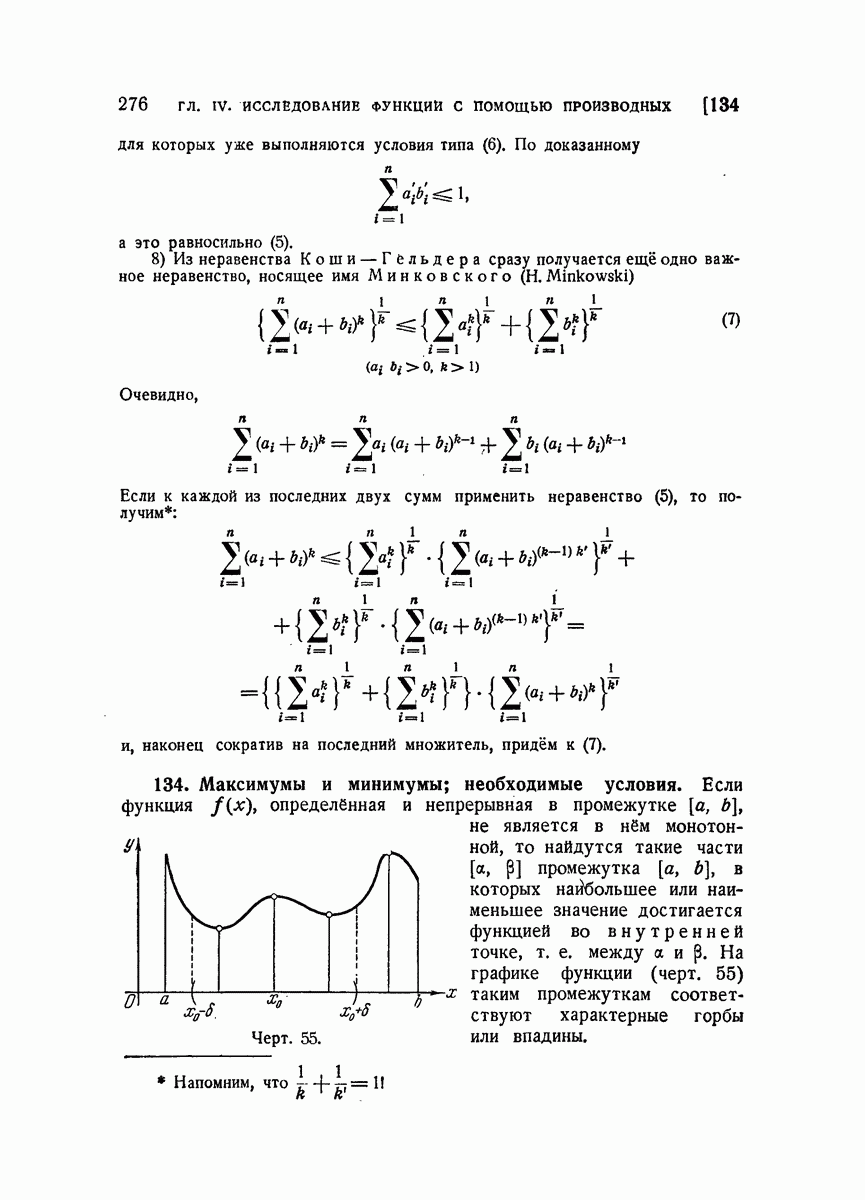
- 134. Максимумы и минимумы; необходимые условия.
- 136. Достаточные условия. Первое правило.
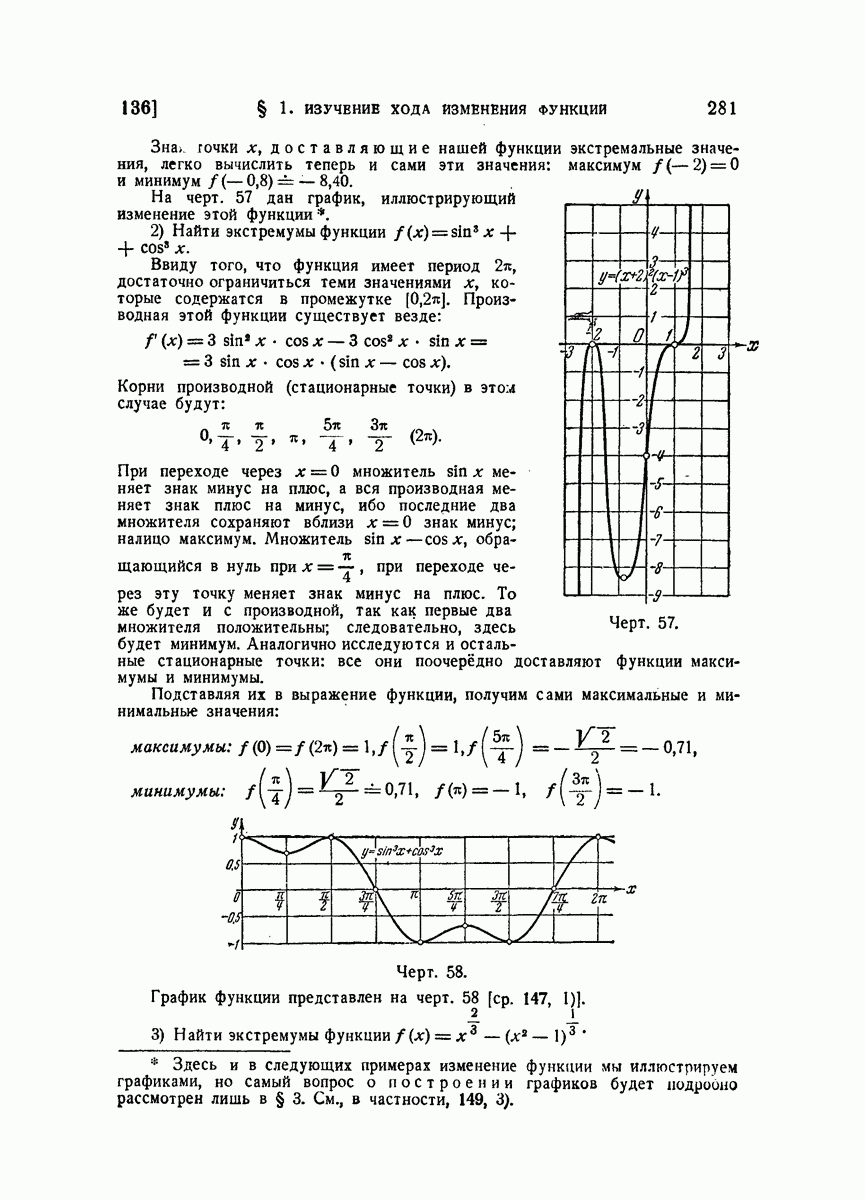
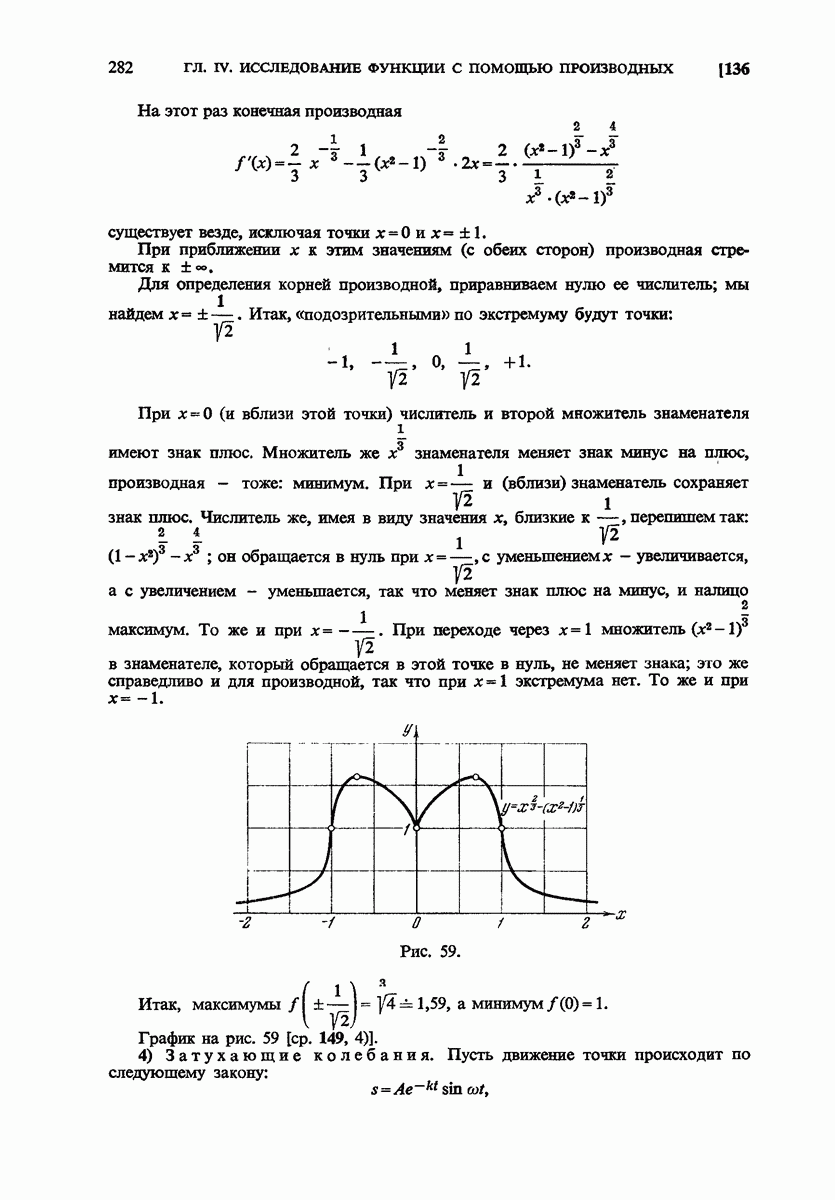
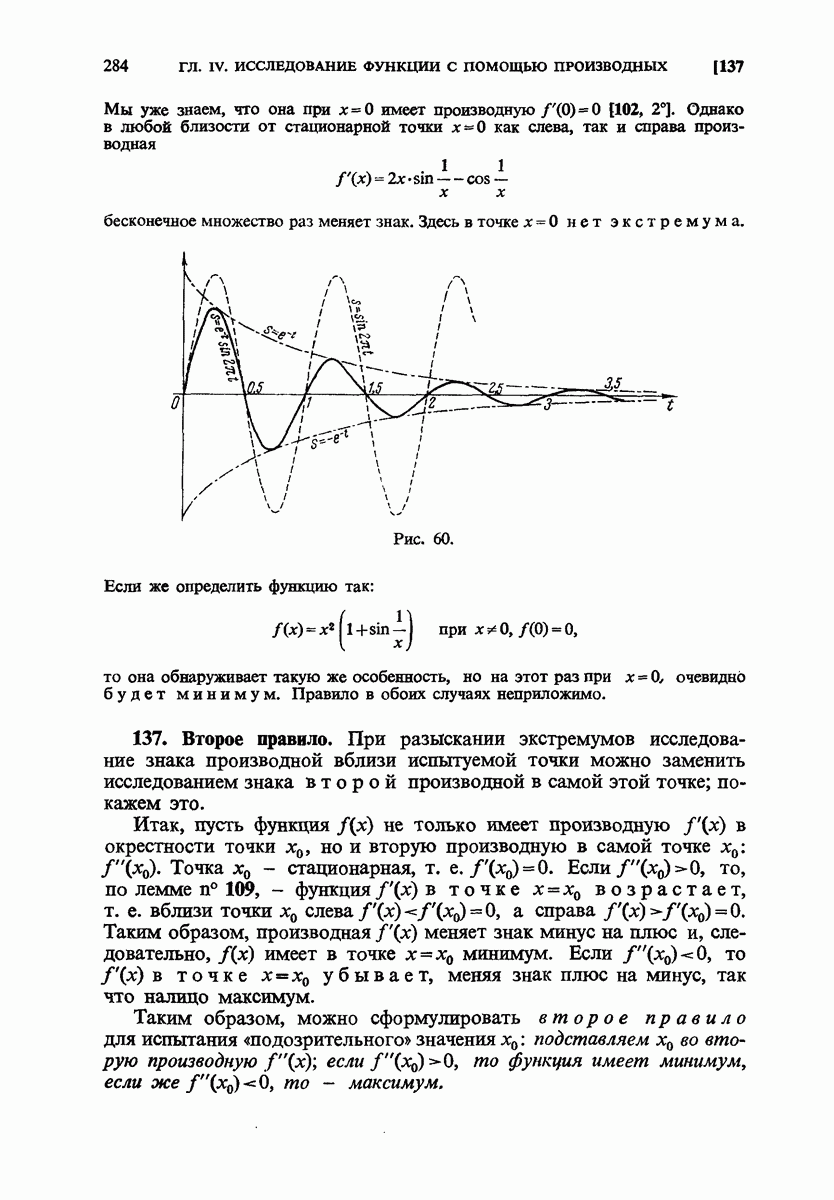
- 136. Примеры.
- 137. Второе правило.
- 138. Использование высших производных.
- 139. Разыскание наибольших и наименьших значений.
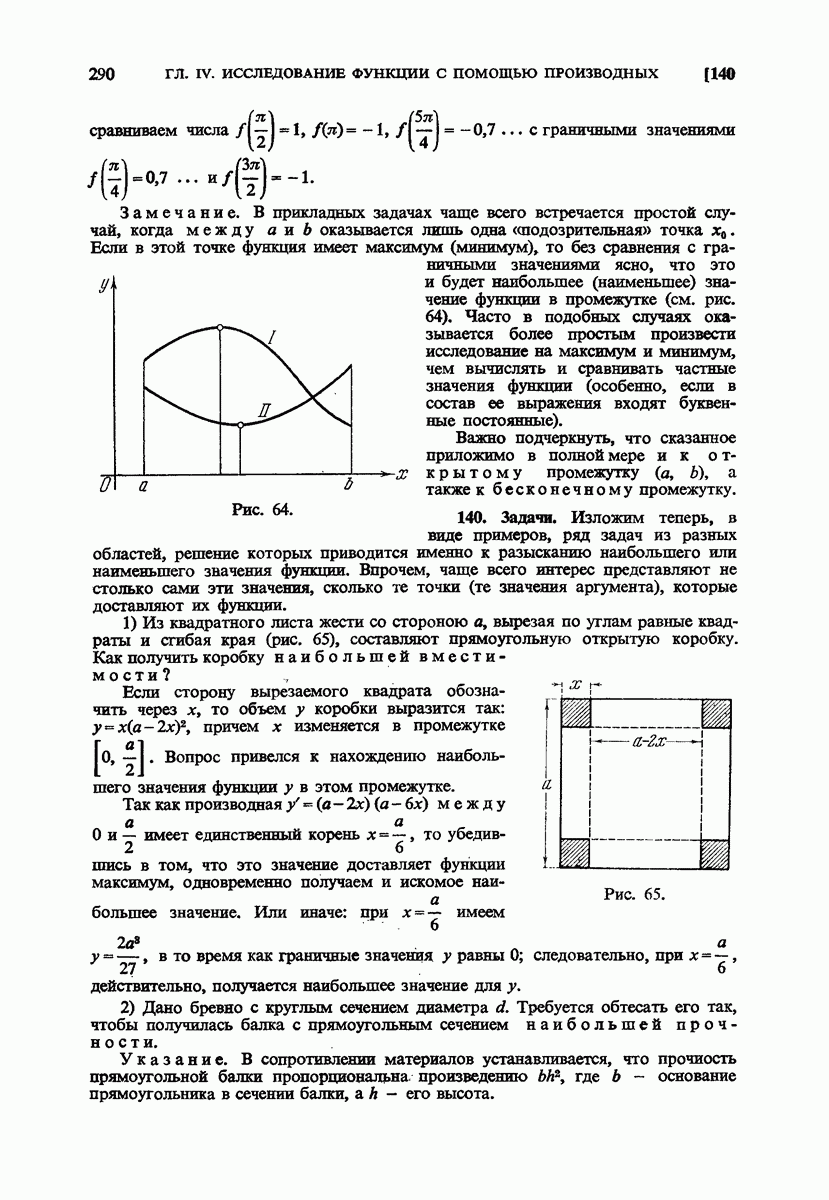
- 140. Задачи.
- § 2. Выпуклые (и вогнутые) функции
- 142. Простейшие предложения о выпуклых функциях.
- 143. Условия выпуклости функции.
- 144. Неравенство Иенсена и его приложения.
- 145. Точки перегиба.
- § 3. Построение графиков функций
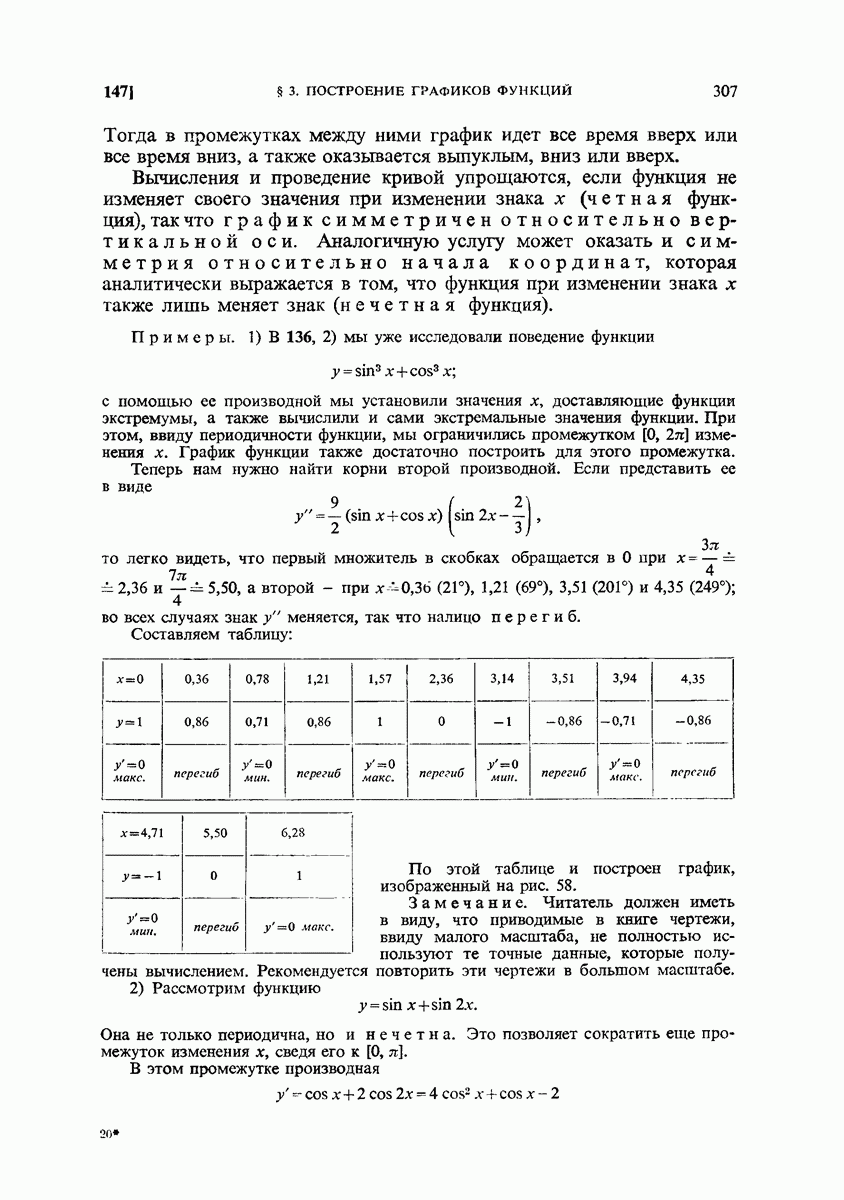
- 147. Схема построения графика. Примеры.
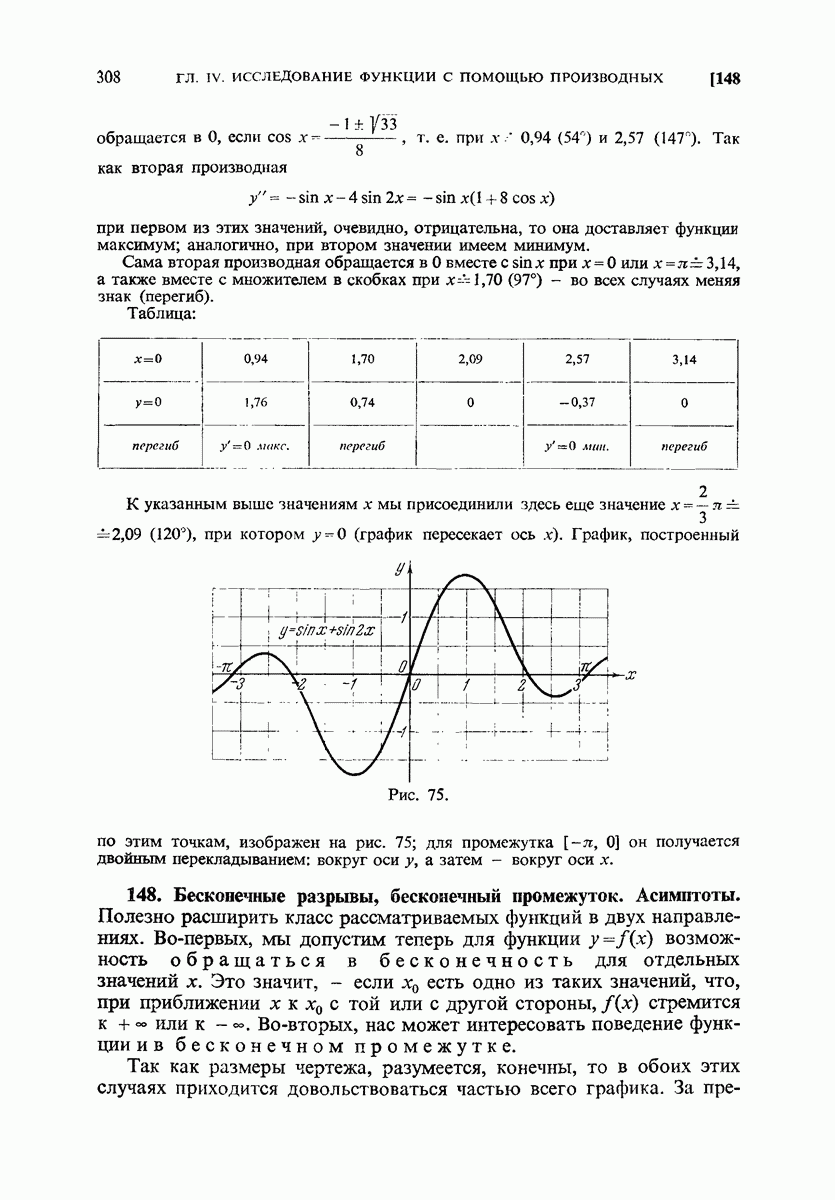
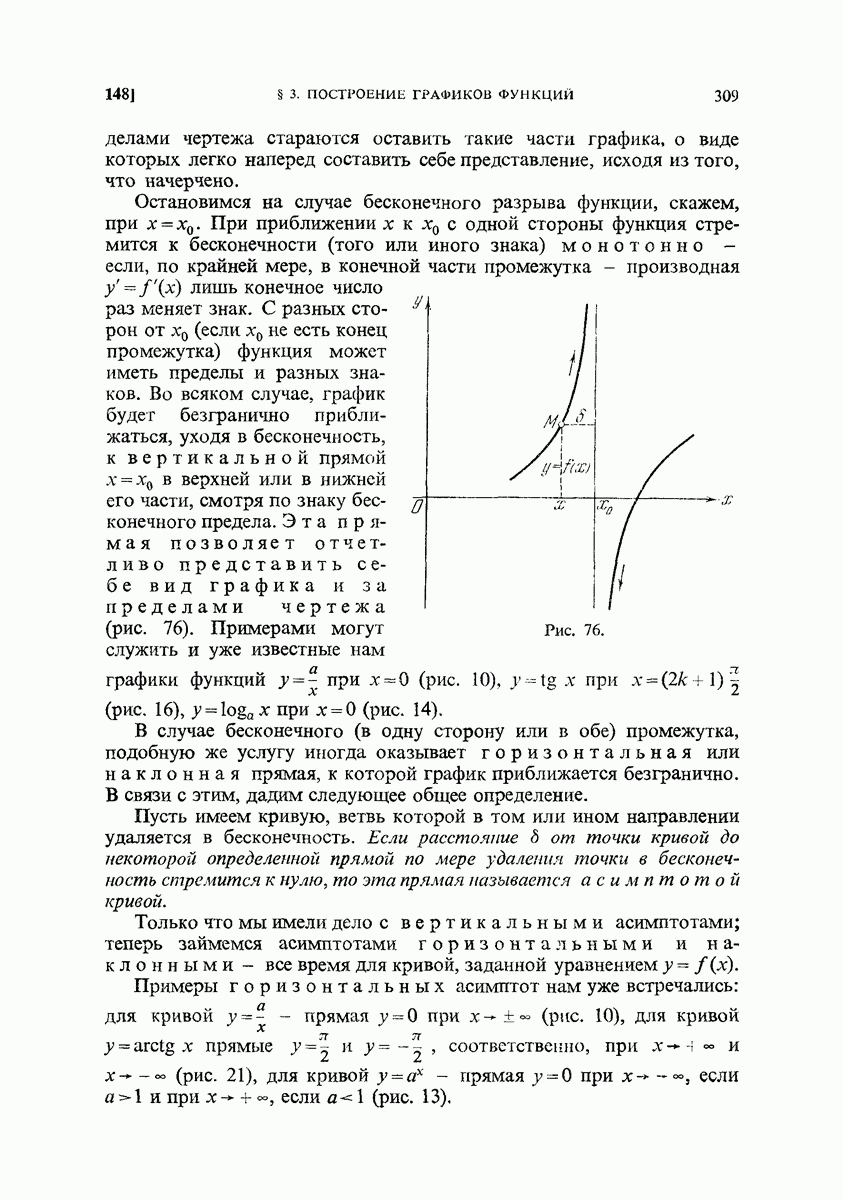
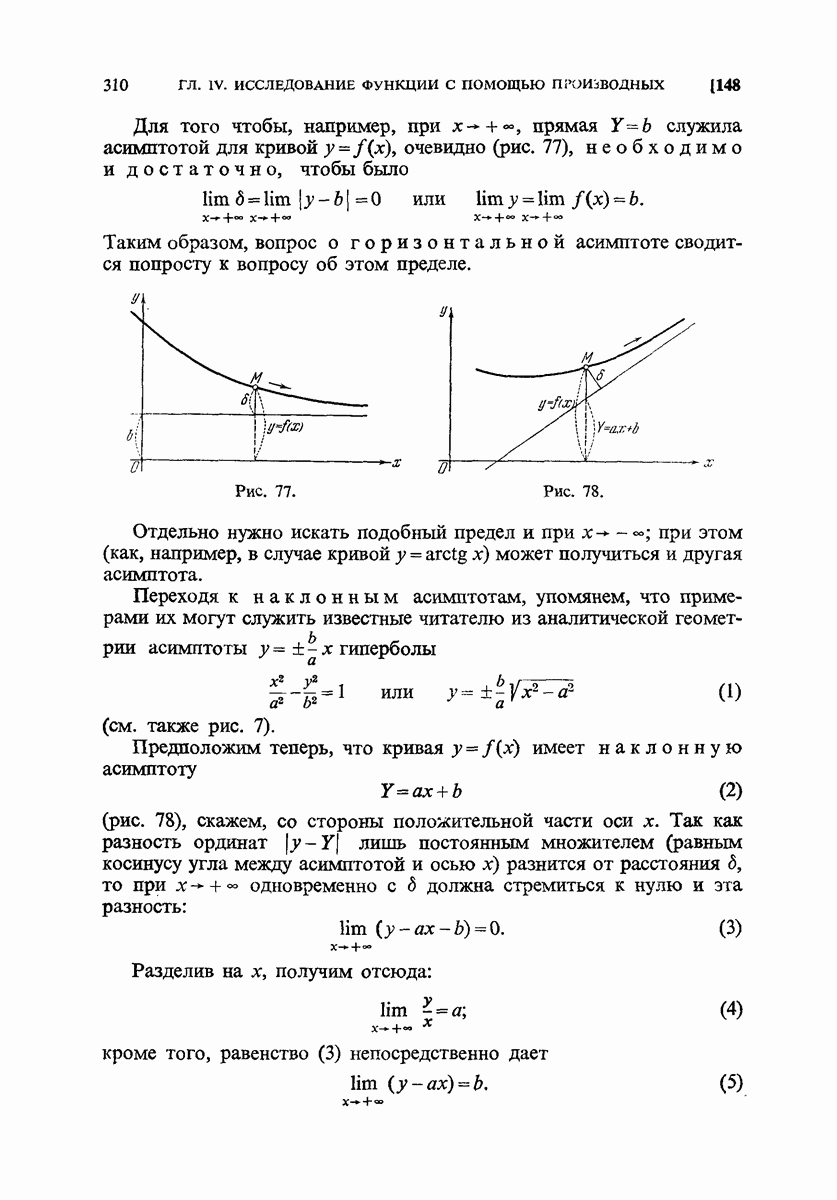
- 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
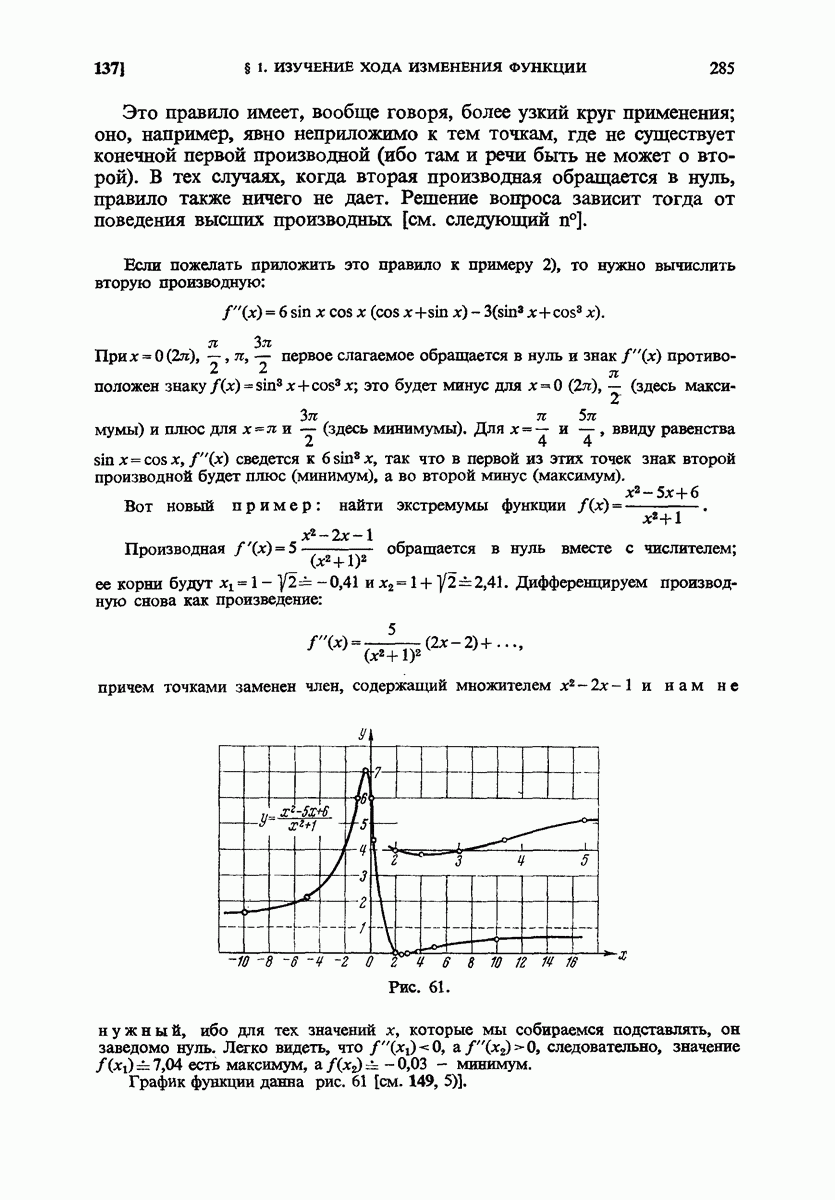
- 149. Примеры.
- § 4. Раскрытие неопределенностей
- 151. Неопределенность вида oo/oo
- 152. Другие виды неопределенностей.
- § 5. Приближенное решение уравнений
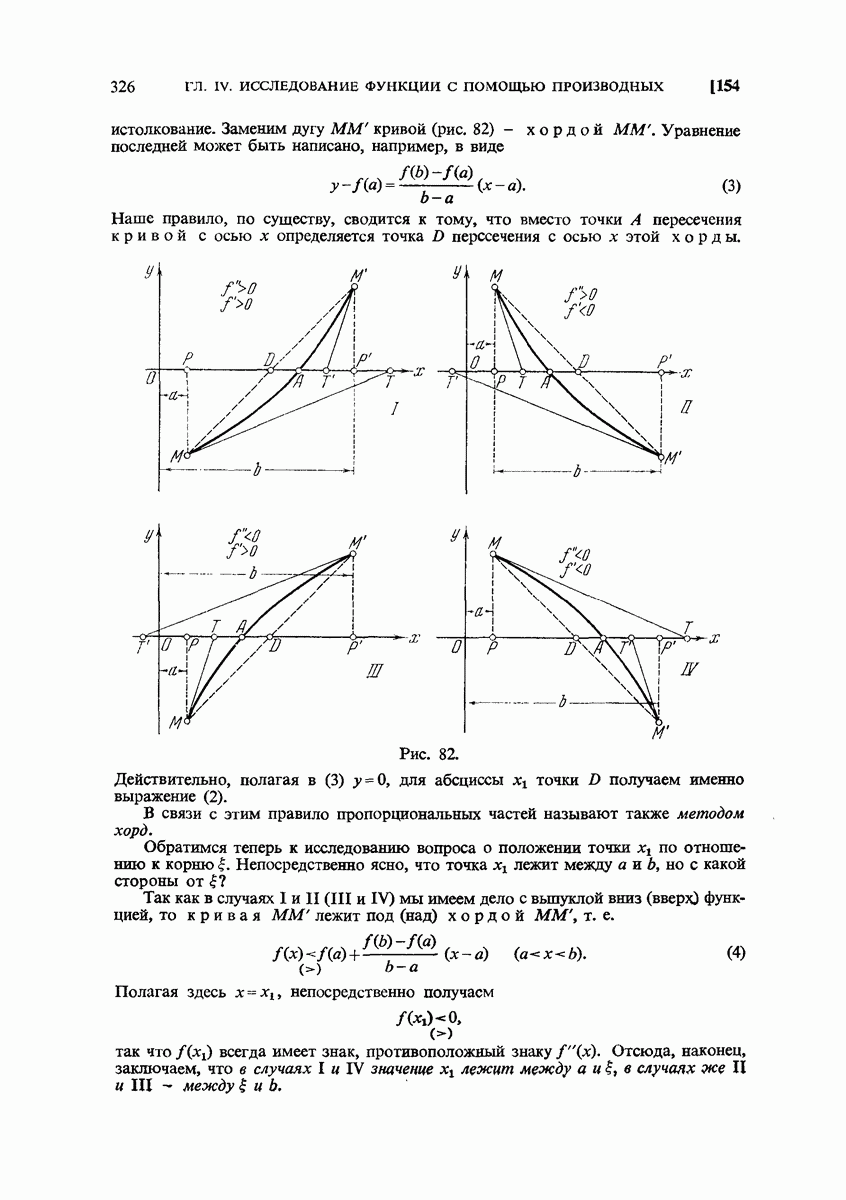
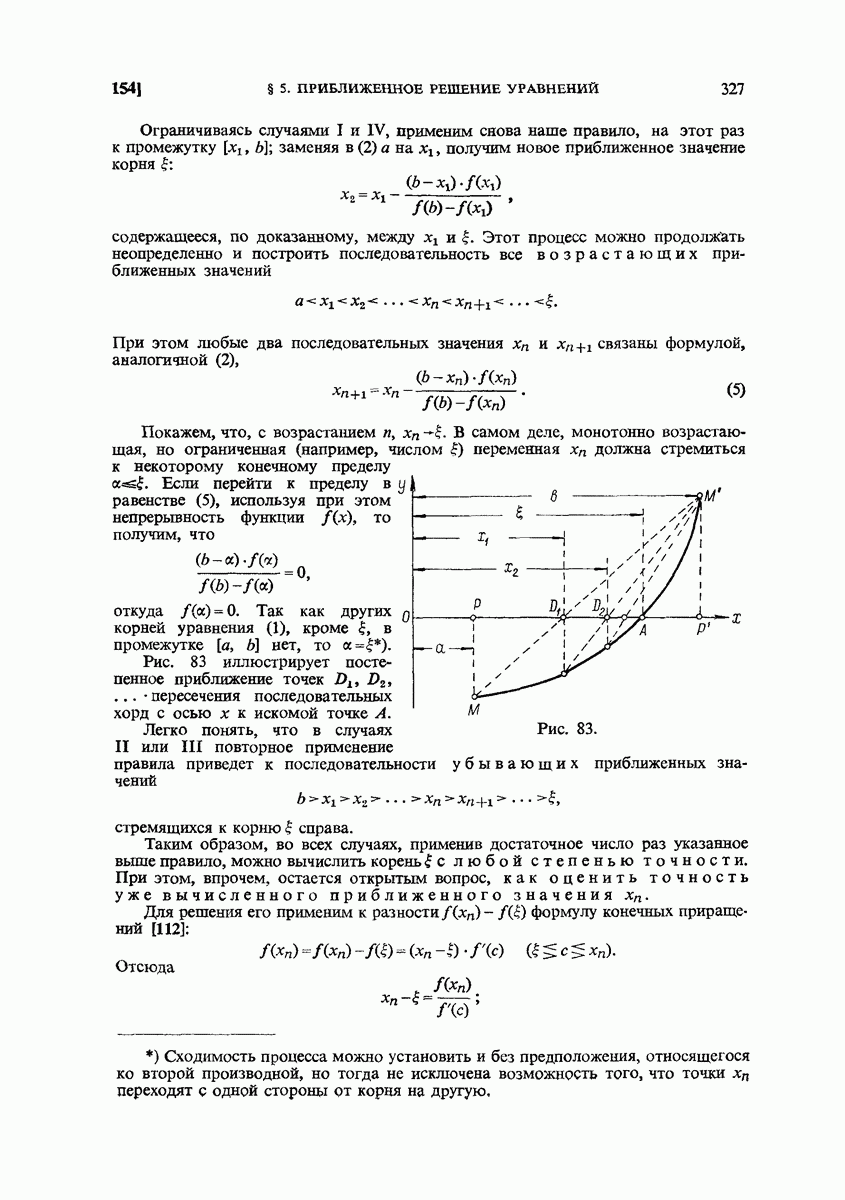
- 154. Правило пропорциональных частей (метод хорд).
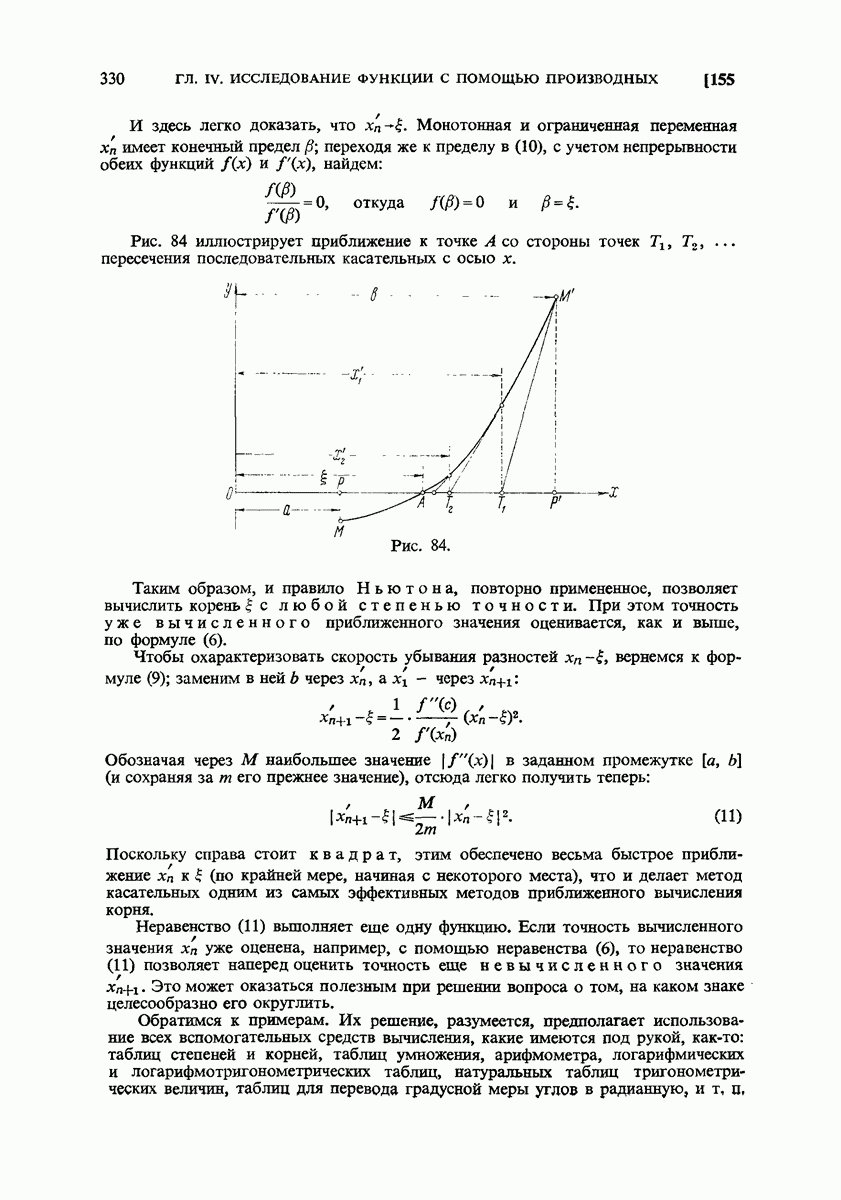
- 155. Правило Ньютона (метод касательных).
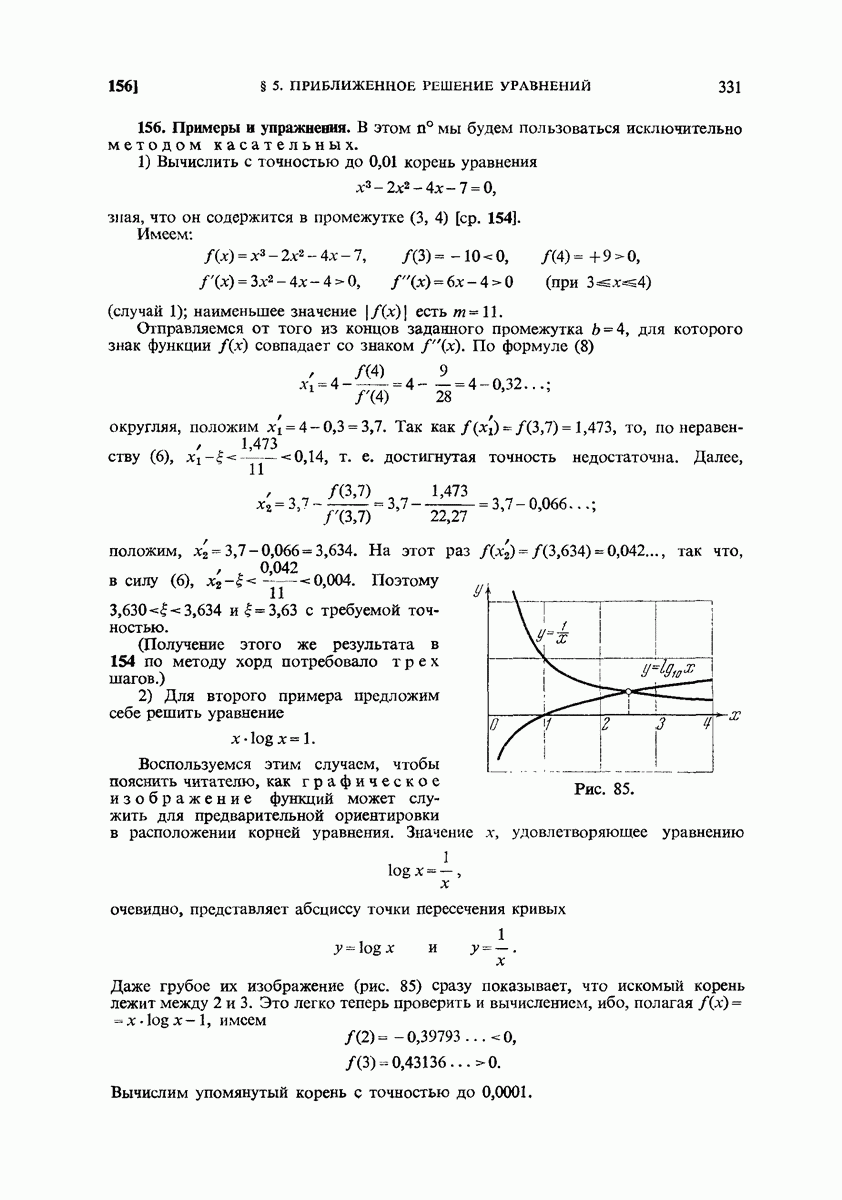
- 156. Примеры в упражнения.
- 157. Комбинированный метод.
- 158. Примеры и упражнения.
- ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 159. Функциональная зависимость между переменными. Примеры.
- 160. Функции двух переменных и области их определения.
- 161. Арифметическое n-мерное пространство.
- 162. Примеры областей в n-мерном пространстве.
- 163. Общее определение открытой и замкнутой области.
- 164. Функции n переменных.
- 165. Предел функции нескольких переменных.
- 166. Сведение к случаю варианты.
- 167. Примеры.
- 168. Повторные пределы.
- § 2. Непрерывные функции
- 170. Операции над непрерывными функциями.
- 171. Функции, непрерывные в области. Теоремы Больцано—Коши.
- 172. Лемма Больцано—Вейерштрасса.
- 173. Теоремы Вейерштрасса.
- 174. Равномерная непрерывность.
- 175. Лемма Бореля.
- 176. Новые доказательства основных теорем.
- § 3. Производные и дифференциалы функций нескольких переменных
- 178. Полное приращение функции.
- 179. Полный дифференциал.
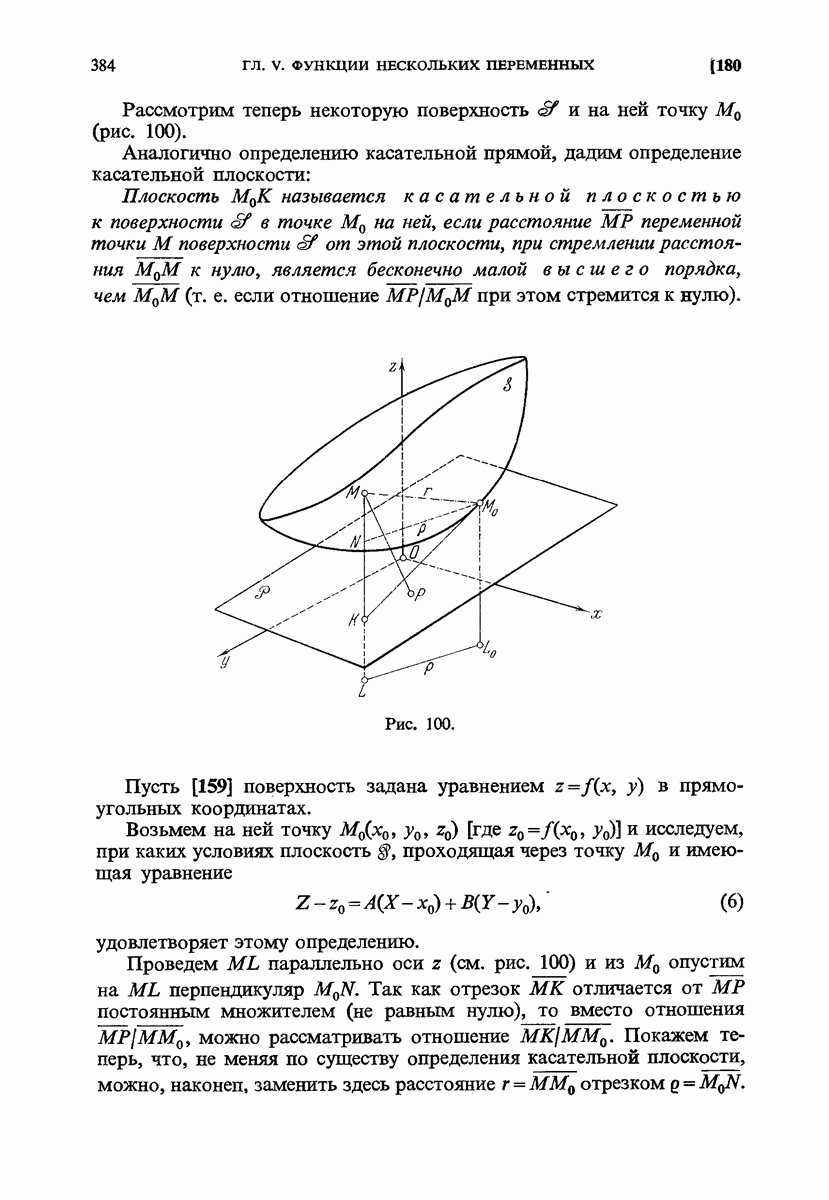
- 180. Геометрическая интерпретация для случая функции двух переменных.
- 181. Производные от сложных функций.
- 182. Примеры.
- 183. Формула конечных приращений.
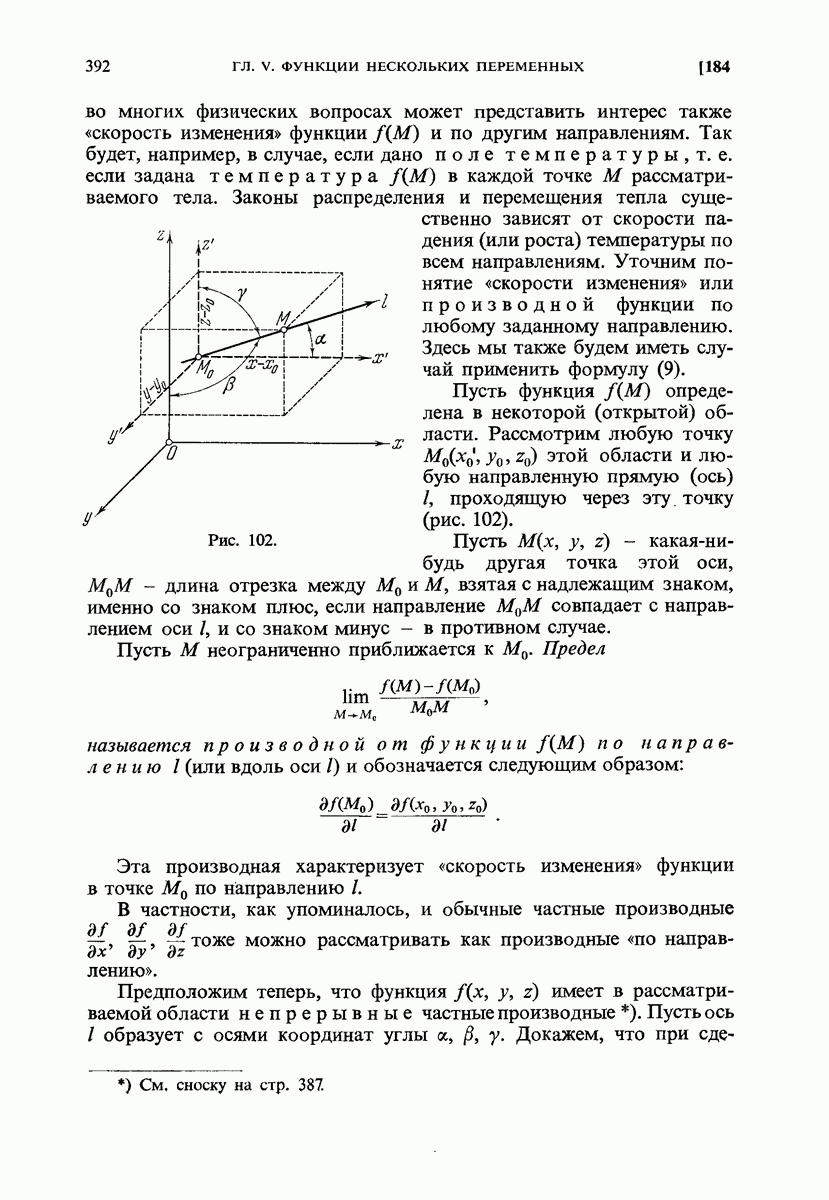
- 184. Производная по заданному направлению.
- 185. Инвариантность формы (первого) дифференциала.
- 186. Применение полного дифференциала в приближенных вычислениях.
- 187. Однородные функции.
- 188. Формула Эйлера.
- § 4. Производные и дифференциалы высших порядков
- 190. Теорема о смешанных производных.
- 191. Обобщение.
- 192. Производные высших порядков от сложной функции.
- 193. Дифференциалы высших порядков.
- 194. Дифференциалы сложных функций.
- 195. Формула Тейлора.
- § 5. Экстремумы, наибольшие и наименьшие значения
- 197. Достаточные условия (случай функции двух переменных).
- 198. Достаточные условия (общий случай).
- 199. Условия отсутствия экстремума.
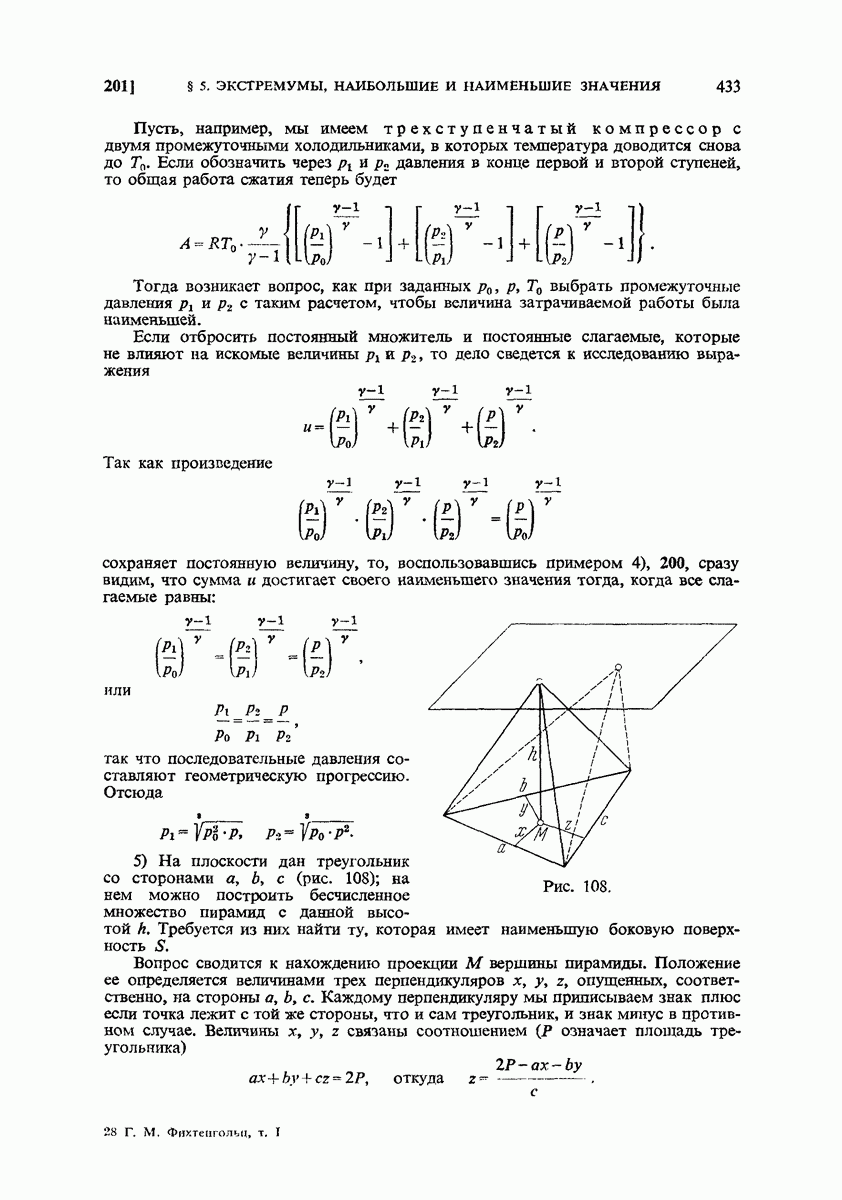
- 200. Наибольшее и наименьшее значения функции. Примеры.
- 201. Задачи.
- ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
- § 1. Формальные свойства функциональных определителей
- 203. Умножение якобианов.
- 204. Умножение функциональных матриц (матриц Якоби).
- § 2. Неявные функции
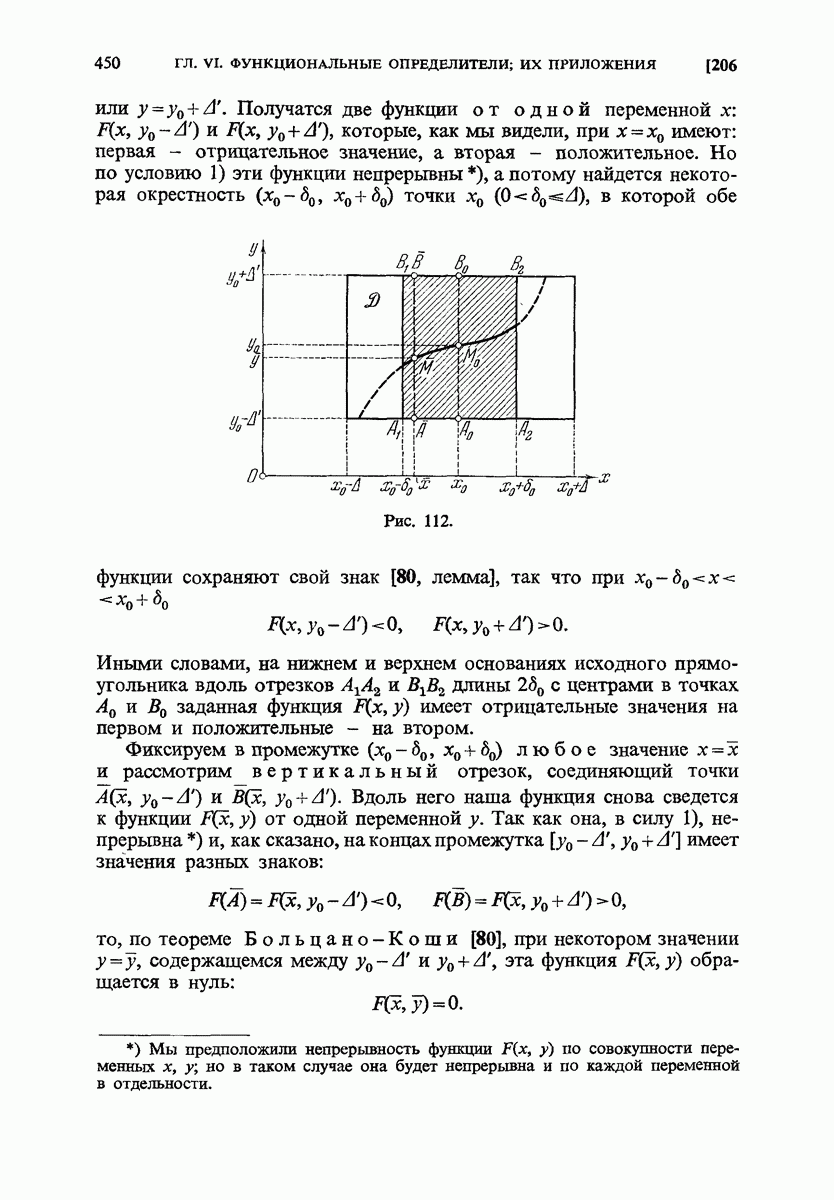
- 206. Существование неявной функции.
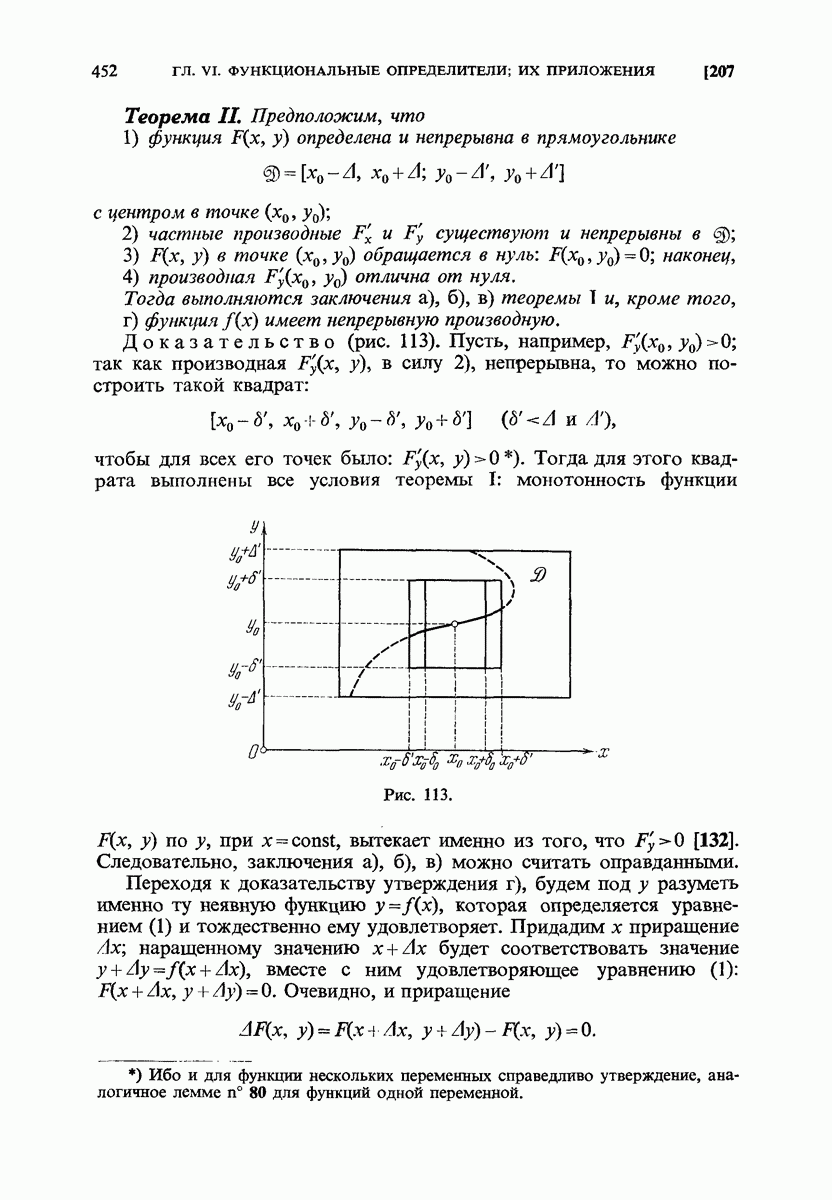
- 207. Дифференцируемость неявной функции.
- 208. Неявные функции от нескольких переменных.
- 209. Вычисление производных неявных функций.
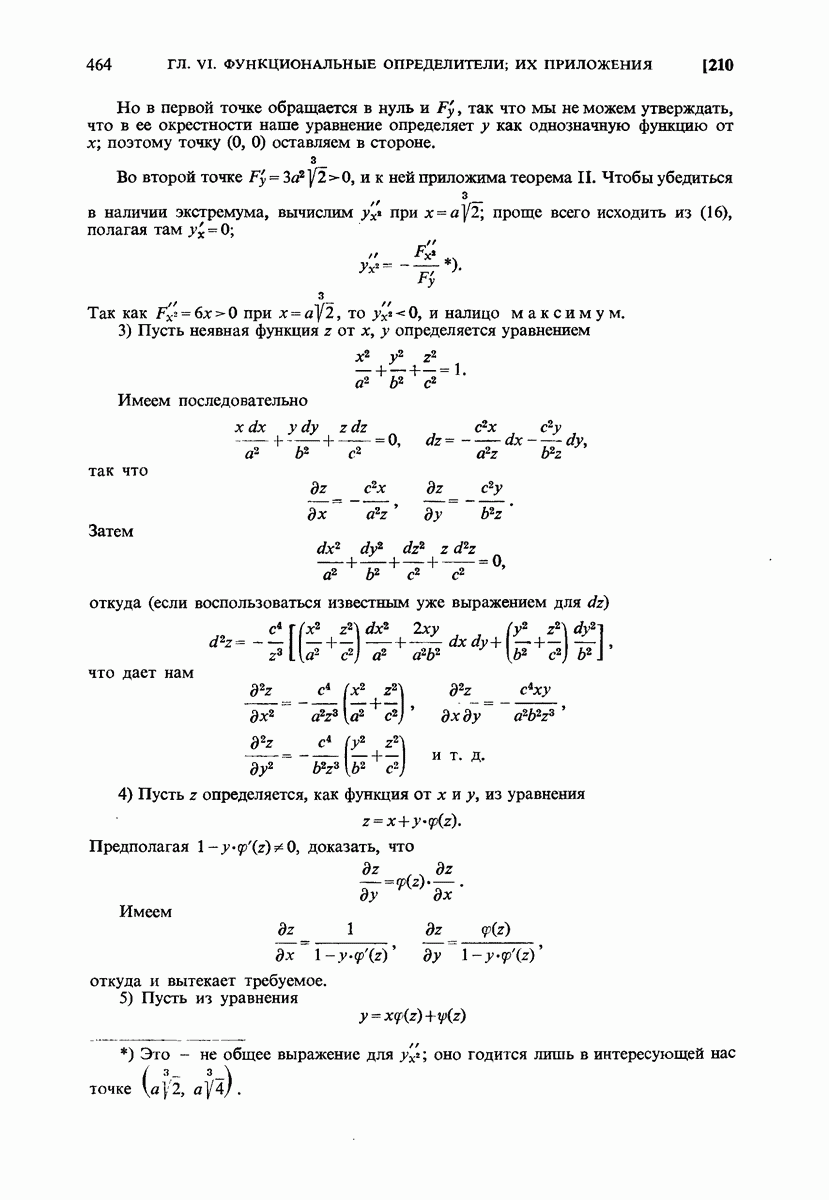
- 210. Примеры.
- § 3. Некоторые приложения теории неявных функций
- 212. Метод неопределенных множителей Лагранжа.
- 213. Достаточные для относительного экстремума условия.
- 214. Примеры и задачи.
- 215. Понятие независимости функций.
- 216. Ранг матрицы Якоби.
- § 4. Замена переменных
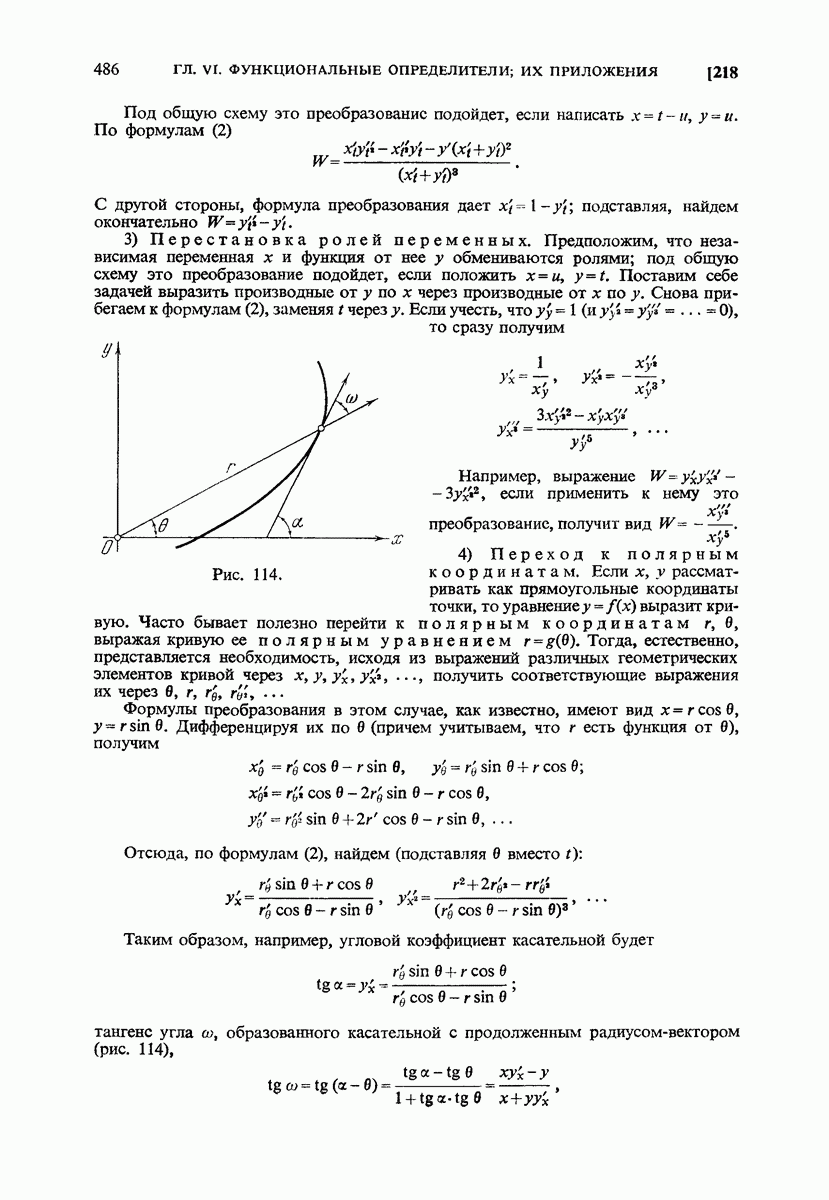
- 218. Примеры.
- 219. Функции нескольких переменных. Замена независимых переменных.
- 220. Метод вычисления дифференциалов.
- 221. Общий случай замены переменных.
- 222. Примеры.
- ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
- § 1. Аналитическое представление кривых и поверхностей
- 224. Примеры.
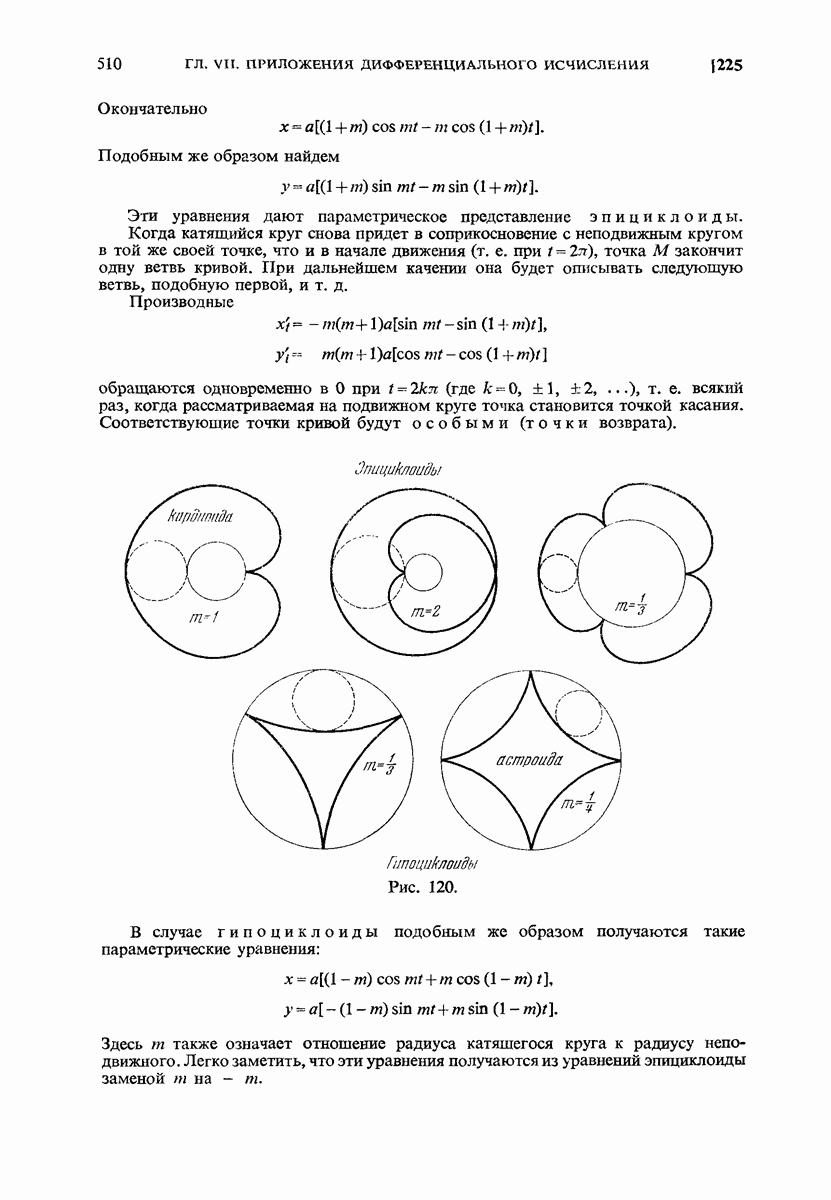
- 225. Кривые механического происхождения.
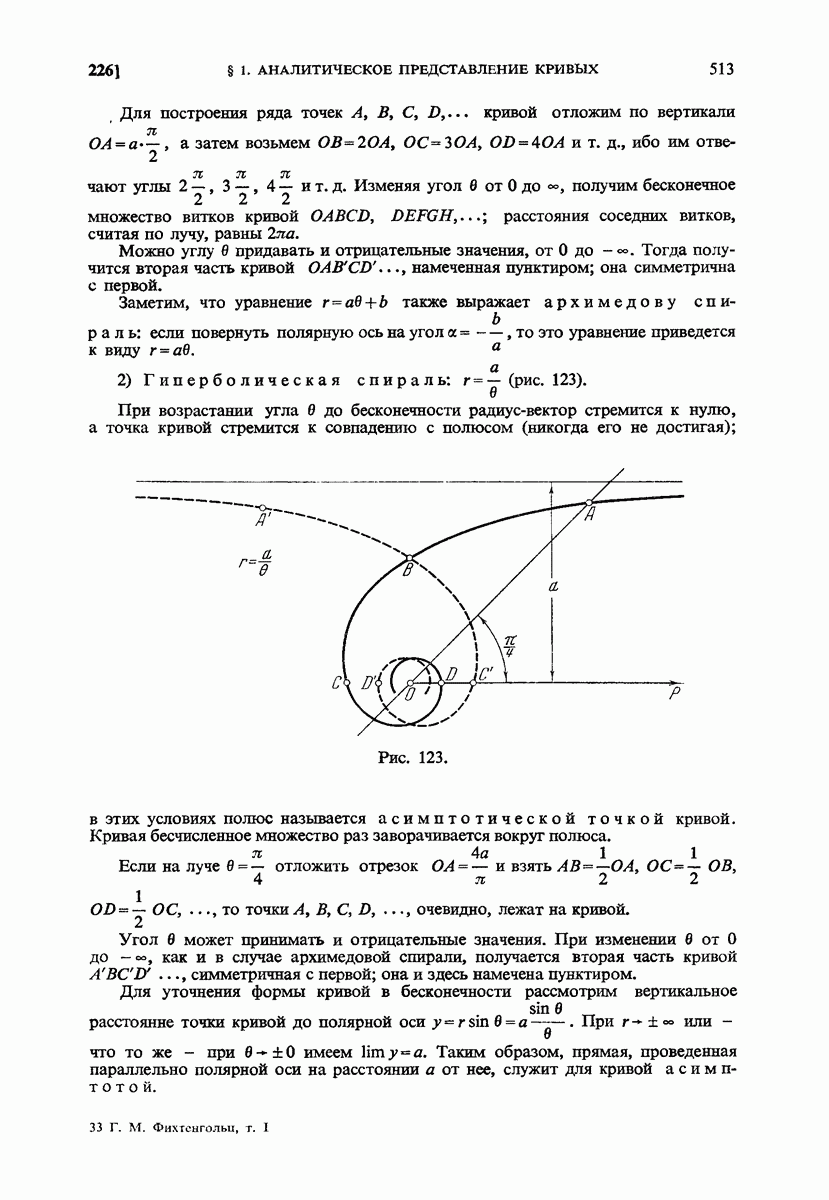
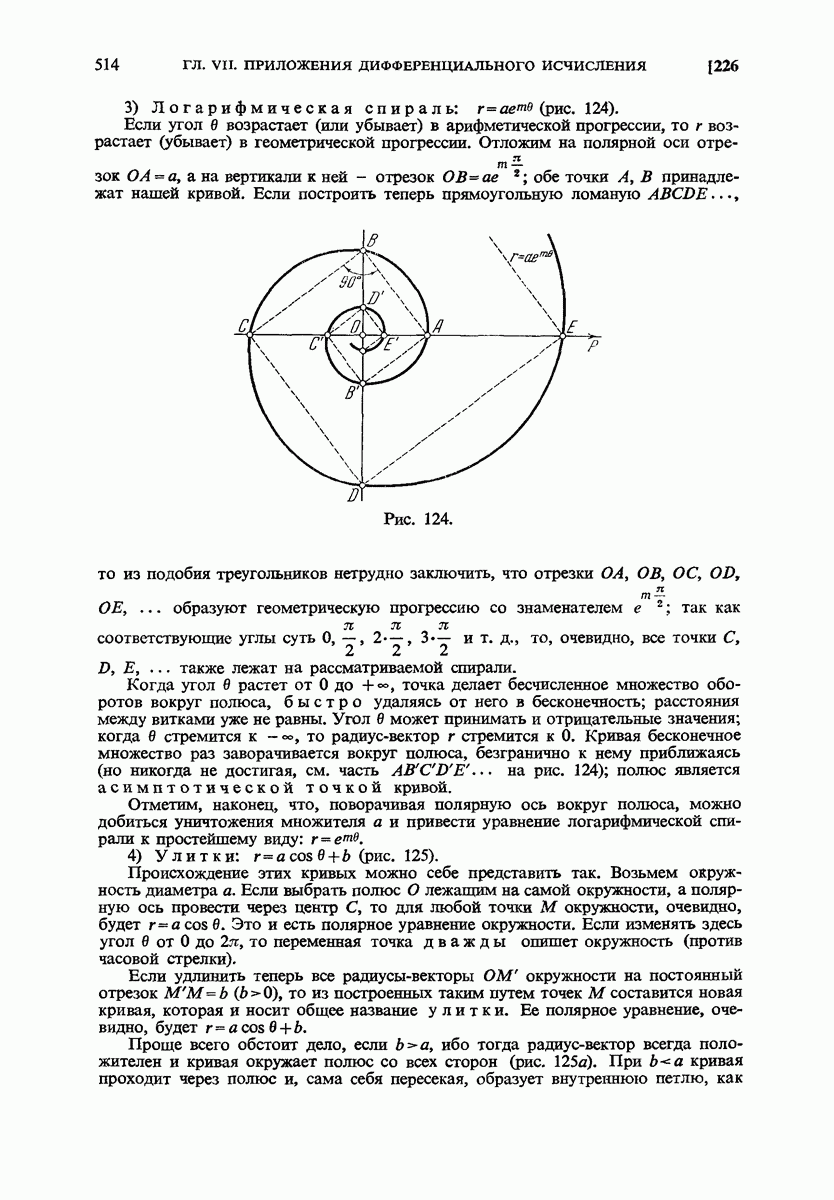
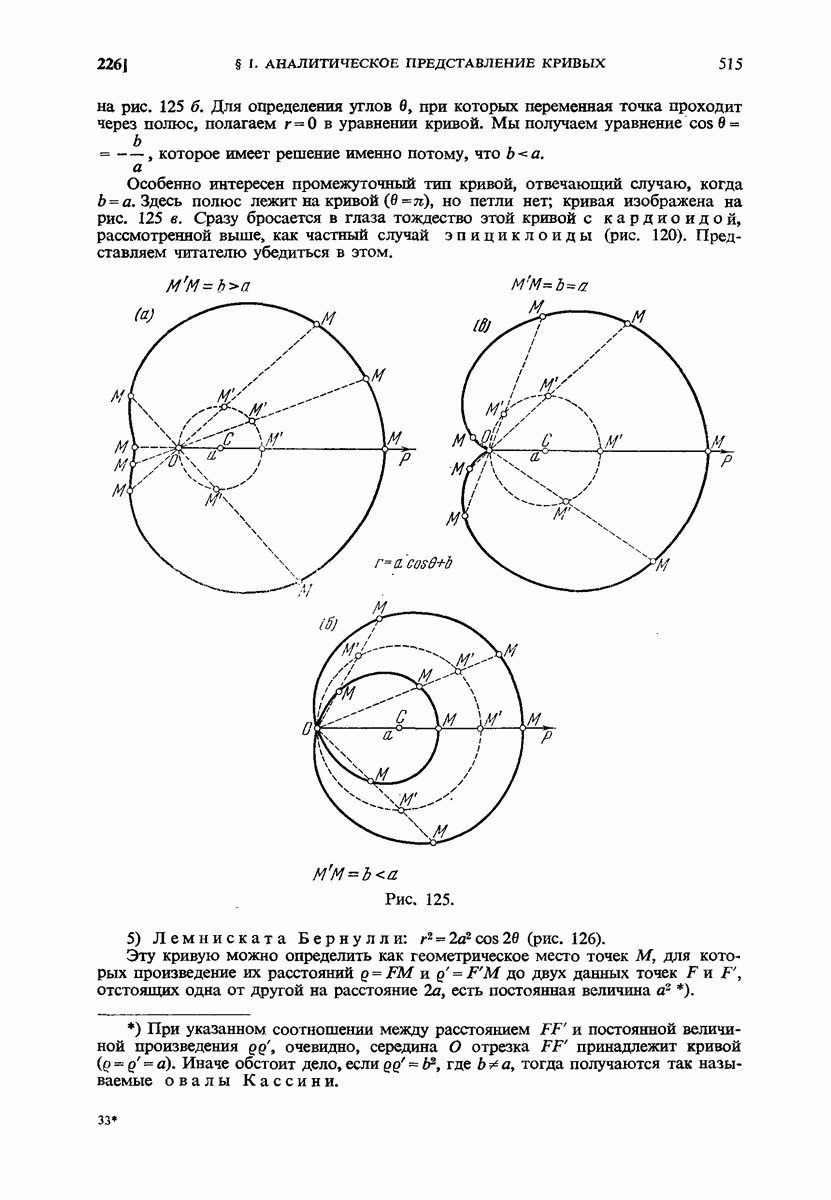
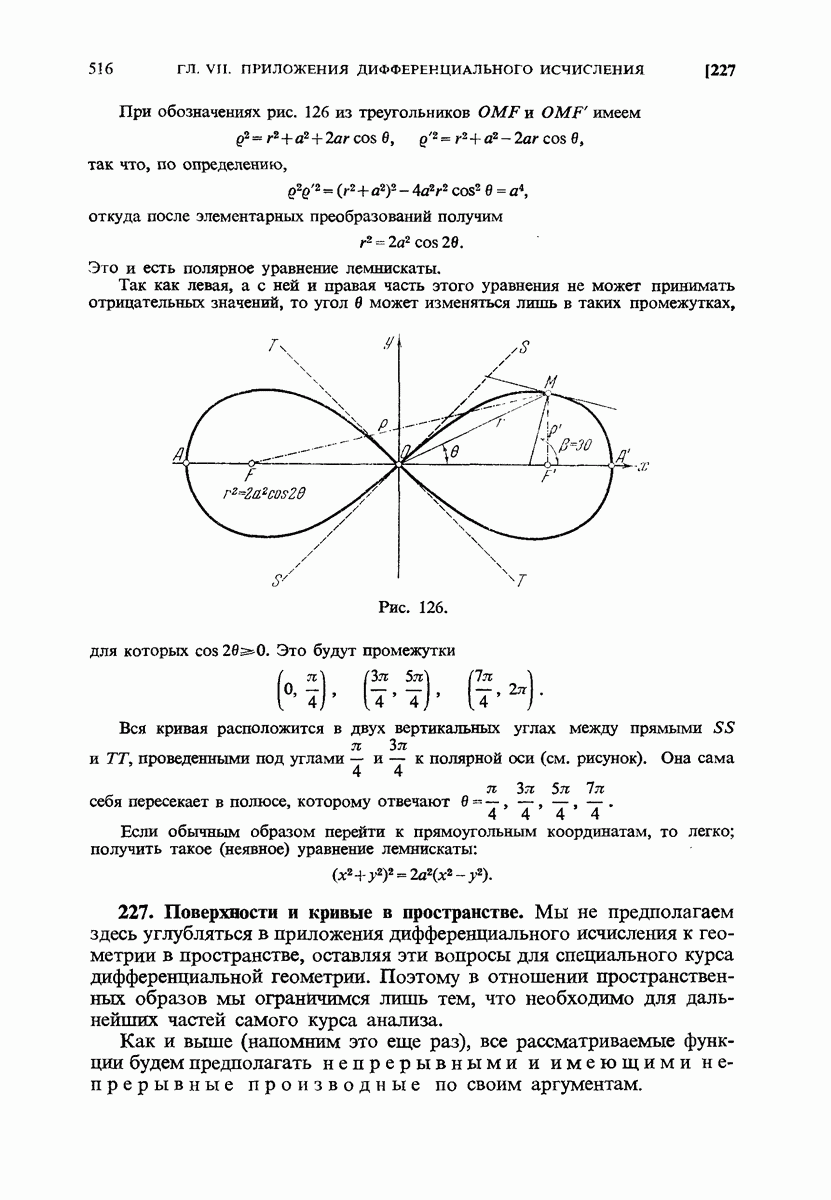
- 226. Кривые на плоскости (в полярных координатах). Примеры.
- 227. Поверхности и кривые в пространстве.
- 228. Параметрическое представление.
- 229. Примеры.
- § 2. Касательная и касательная плоскость
- 231. Примеры.
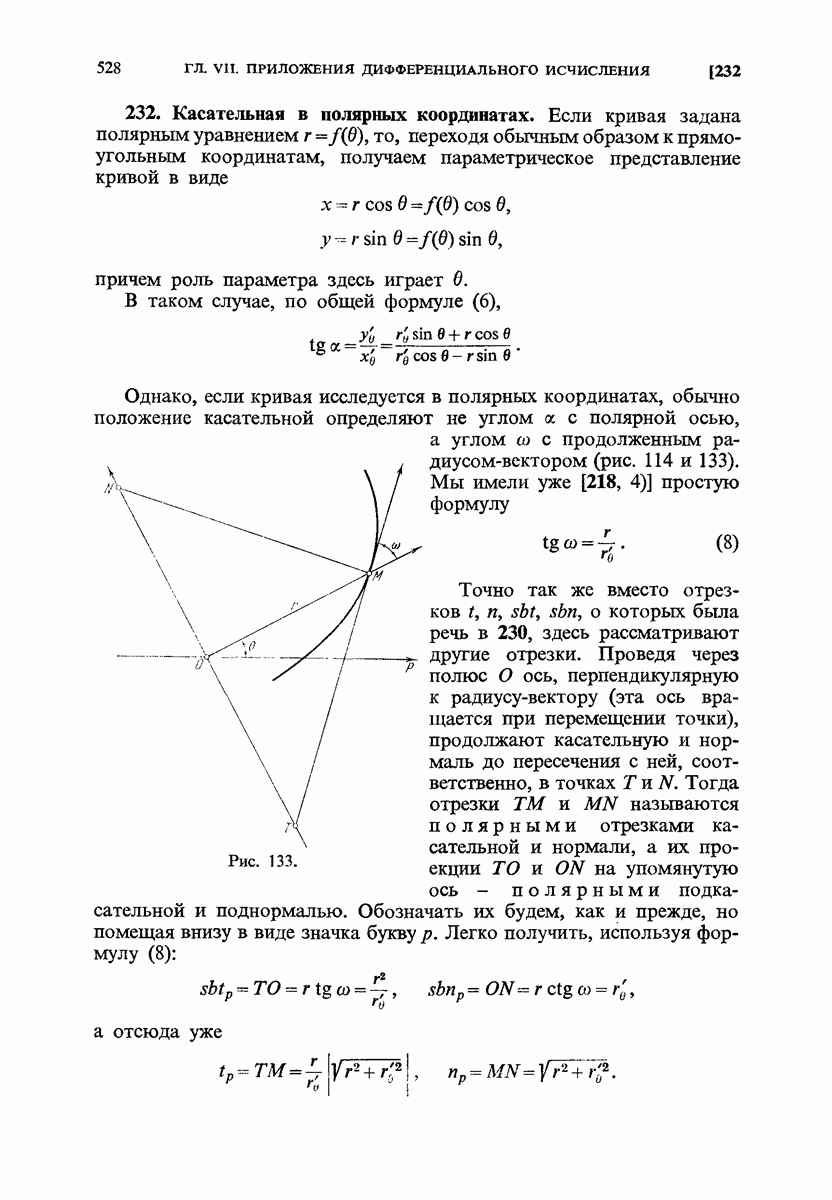
- 232. Касательная в полярных координатах.
- 233. Примеры.
- 234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
- 235. Примеры.
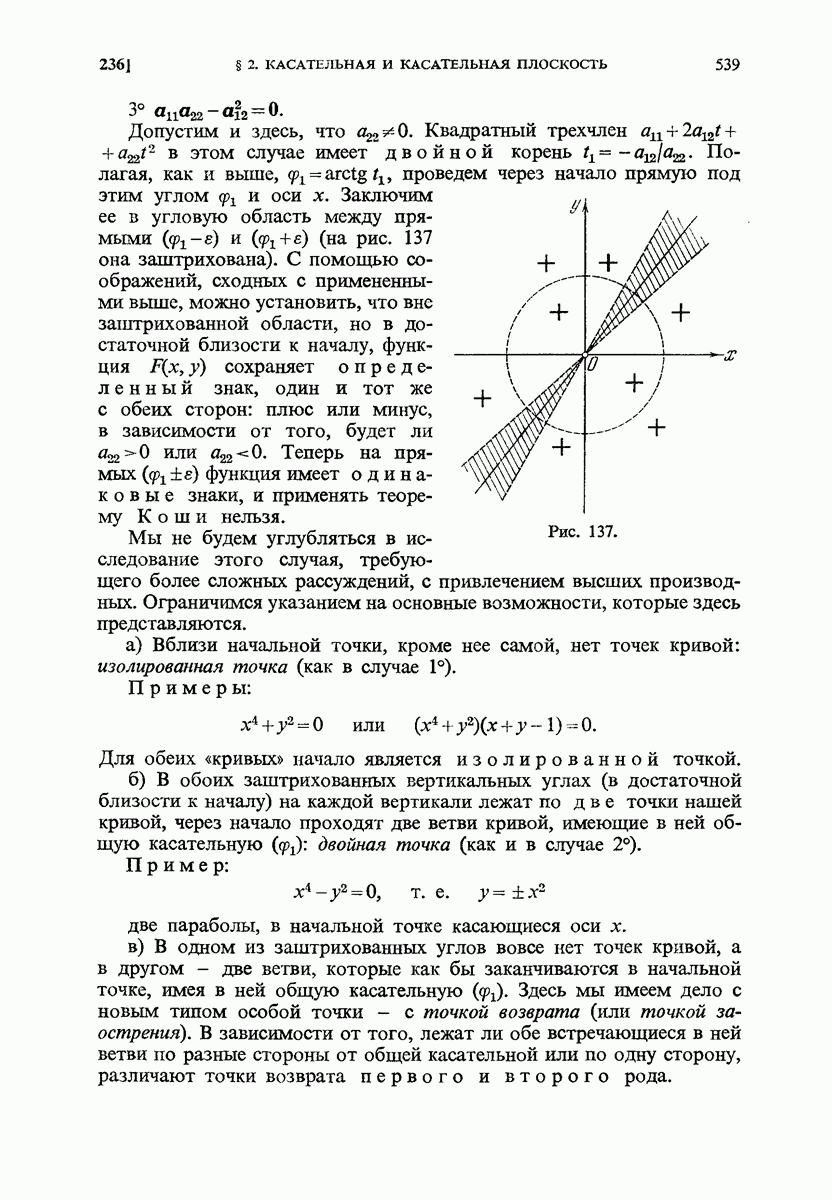
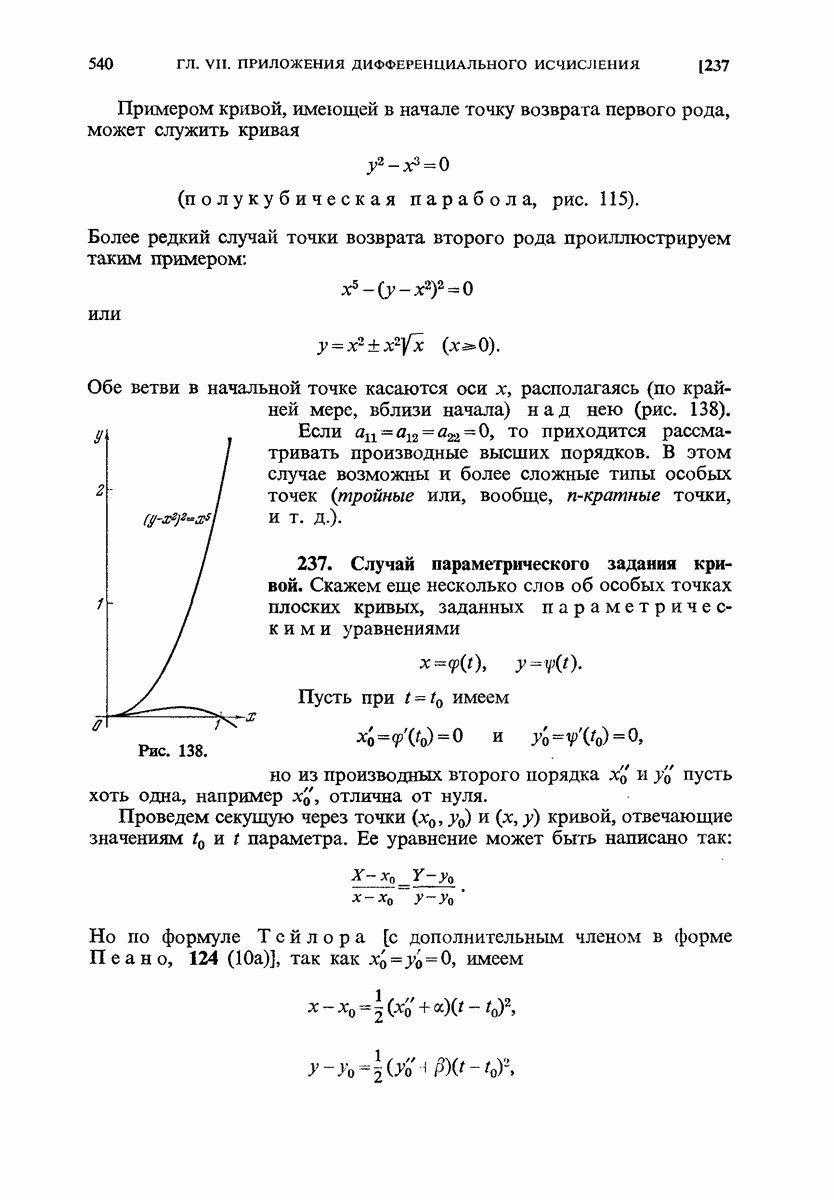
- 236. Особые точки плоских кривых.
- 237. Случай параметрического задания кривой.
- § 3. Касание кривых между собой
- 239. Примеры.
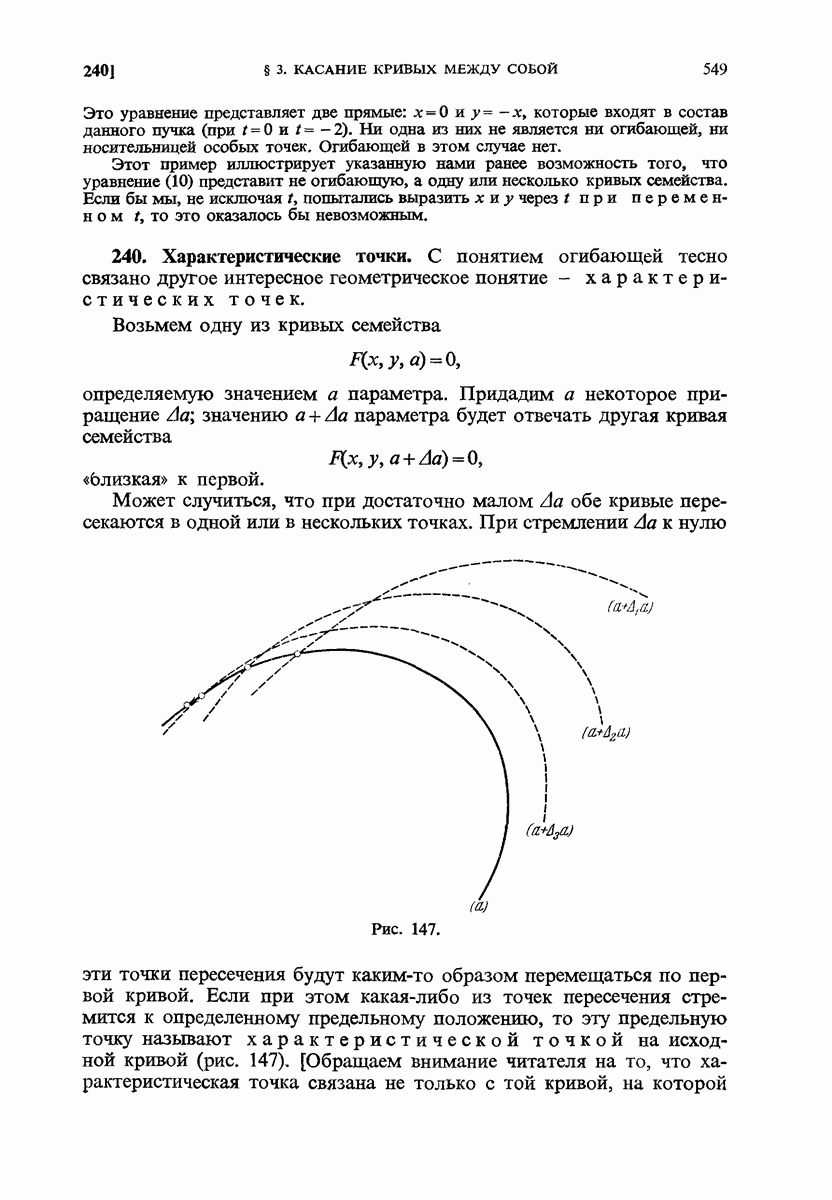
- 240. Характеристические точки.
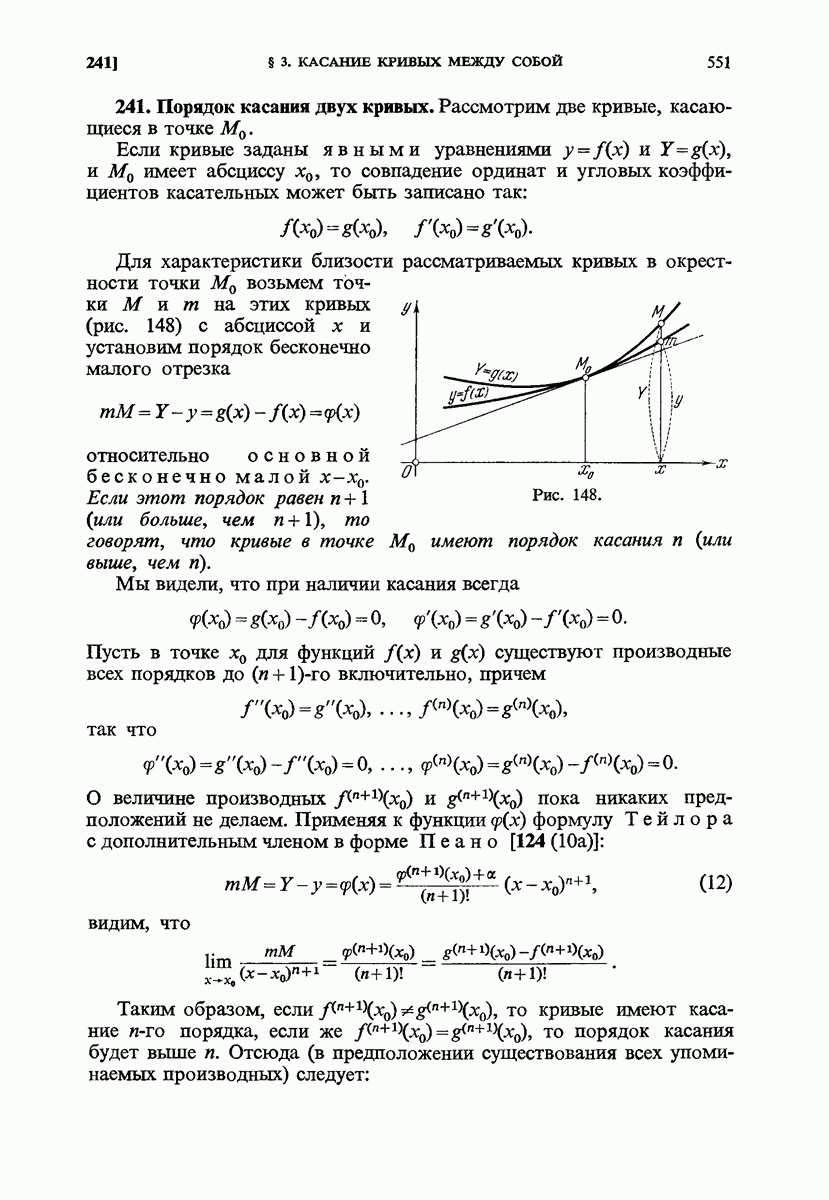
- 241. Порядок касания двух кривых.
- 242. Случай неявного задания одной из кривых.
- 243. Соприкасающаяся кривая.
- 244. Другой подход к соприкасающимся кривым.
- § 4. Длина плоской кривой
- 246. Направление на кривой.
- 247. Длина кривой. Аддитивность длины дуги.
- 248. Достаточные условия спрямляемости. Дифференциал дуги.
- 249. Дуга в роли параметра. Положительное направление касательной.
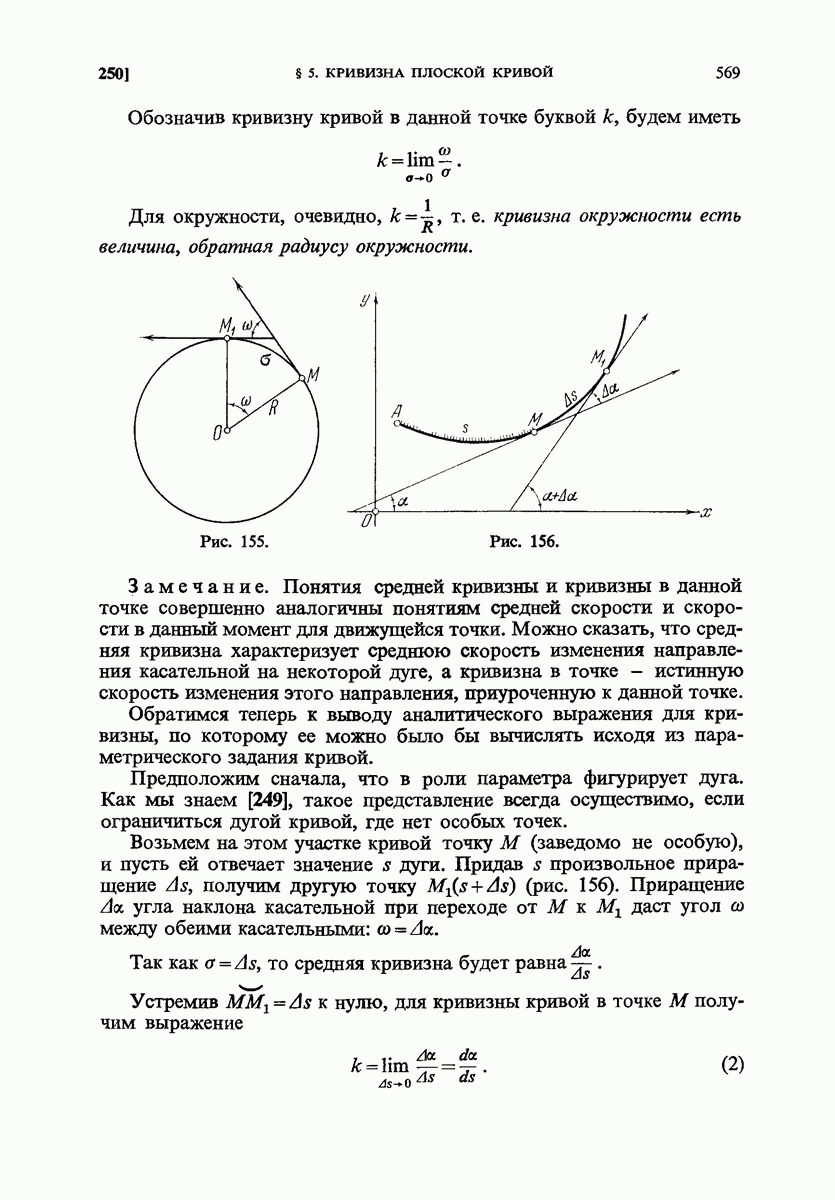
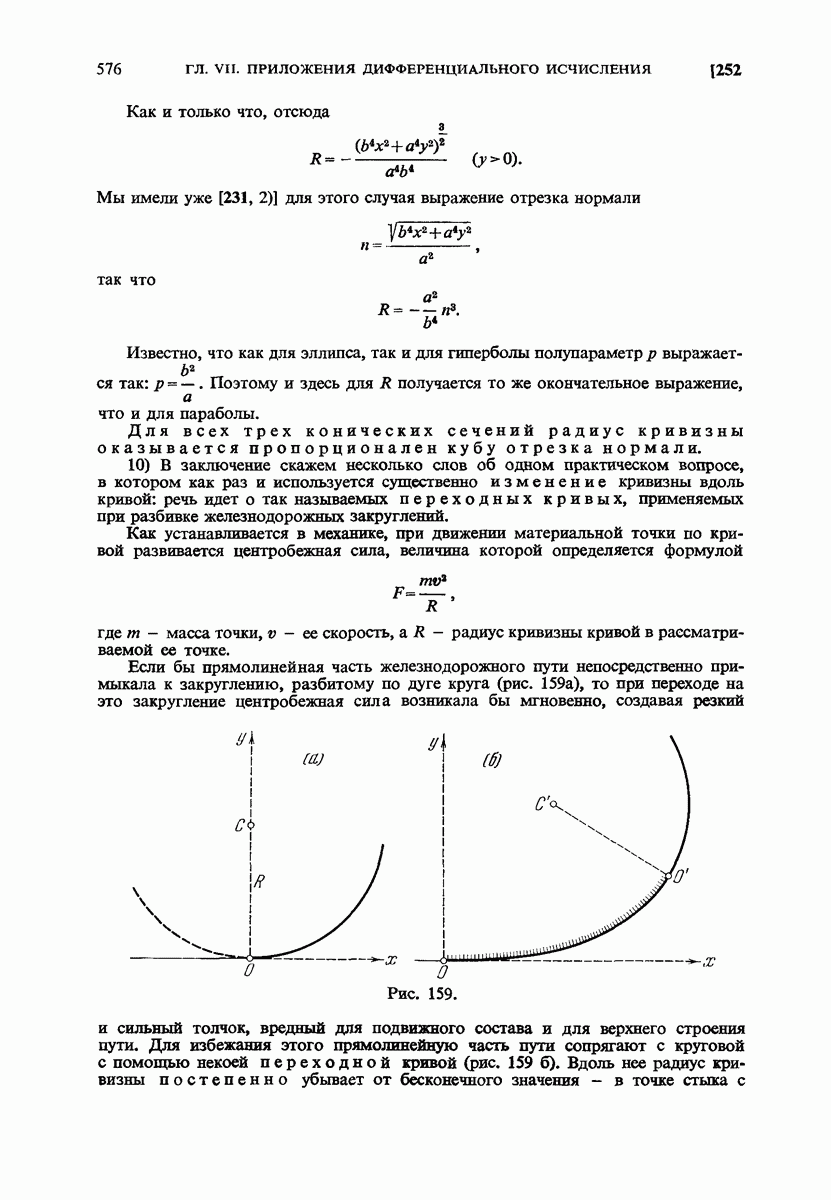
- § 5. Кривизна плоской кривой
- 251. Круг кривизны и радиус кривизны.
- 252. Примеры.
- 253. Координаты центра кривизны.
- 254. Определение эволюты и эвольвенты; разыскание эволюты.
- 255. Свойства эволют и эвольвент.
- 256. Разыскание эвольвент.
- ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ