| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
222. Примеры.
1) Переход к полярным координатам. Пусть z есть функция точки на плоскости  Обыкновенно положение точки определяется ее прямоугольными координатами
Обыкновенно положение точки определяется ее прямоугольными координатами  так что z является функцией от переменных х и у. Часто, однако, оказывается более удобным характеризовать положение точки полярными координатами
так что z является функцией от переменных х и у. Часто, однако, оказывается более удобным характеризовать положение точки полярными координатами  и тогда возникает необходимость преобразования к новым переменным. Проделаем этот переход различными методами.
и тогда возникает необходимость преобразования к новым переменным. Проделаем этот переход различными методами.
Прямой метод: независимыми переменными считаются  Исходя из формул преобразования
Исходя из формул преобразования

по образцу формул (10) имеем

откуда

так что выражения  играют здесь роль коэффициентов
играют здесь роль коэффициентов  Затем,
Затем,

Аналогично находим

Обратный метод: независимыми переменными считаются х, у. Для того чтобы воспользоваться формулами (11), нужно знать производные 
Их можно найти, разрешив предварительно уравнения, связывающие старые переменные с новыми, относительно последних. Но можно воспользоваться методами дифференцирования неявных функций, не разрешая уравнений. Если продифференцировать формулы преобразования по х и по у, считая  функциями от х и у, то получим
функциями от х и у, то получим

и

Отсюда

и по формулам (11) - мы возвращаемся к выражению (25), и т. д.
Метод вычисления дифференциалов. Пусть, как и только что, независимыми переменными будут х, у.
Дифференцируем полным образом формулы преобразования

отсюда

так что

что снова приводит к выражениям (25).
Вторичное дифференцирование формул для  дает:
дает:

Тогда для  будем иметь:
будем иметь:

откуда для вторых производных  получатся те же выражения, что и выше.
получатся те же выражения, что и выше.
Рассмотрим, для примера, выражения

С помощью найденных формул они преобразуются так:

2) Переход к сферическим координатам. В пространстве роль, аналогичную полярным координатам на плоскости, играют так называемые сферические координаты  в, с которыми прямоугольные координаты х, у, z связаны с помощью формул
в, с которыми прямоугольные координаты х, у, z связаны с помощью формул

Пусть требуется преобразовать к переменным  выражения
выражения

где и есть некоторая функция точки в пространстве.
Если преобразование произвести в два приема, полагая сначала  (и оставляя z неизменным), а затем
(и оставляя z неизменным), а затем  (оставляя 0 неизменным), то можно будет воспользоваться результатами примера 1). Например, для второго выражения имеем
(оставляя 0 неизменным), то можно будет воспользоваться результатами примера 1). Например, для второго выражения имеем

Выражение в скобках, на основании того же примера 1), перепишется так:

наконец,

Подставляя все это, окончательно найдем

Аналогично,

3) Показать, что выражения  сохраняют свою форму при любом преобразовании прямоугольных координат в прямоугольные же
сохраняют свою форму при любом преобразовании прямоугольных координат в прямоугольные же

где коэффициенты  с удовлетворяют известным соотношениям
с удовлетворяют известным соотношениям

Метод вычисления дифференциалов. Считая х, у, z независимыми переменными, имеем

Тогда

откуда

возводя в квадрат и складывая, в силу (26), получим

Затем,

Выражение  есть сумма коэффициентов при
есть сумма коэффициентов при  с помощью (26) нетрудно установить, что
с помощью (26) нетрудно установить, что

4) Преобразовать уравнение

к новым переменным t, по формулам 
Прямой метод. Считая независимыми переменными t, будем иметь

Отсюда

Далее,

и т. д. Сложив все подобные выражения (и отбросив числовой множитель), получим преобразованное уравнение в виде

До сих пор заменялись лишь независимые переменные; приведем примеры, где замене подвергается и функция.
5) Преобразовать уравнение  полагая
полагая

Прямой метод. Независимые переменные:  . Дифференцируем третью из формул преобразования по t и по и, рассматривая переменные z и
. Дифференцируем третью из формул преобразования по t и по и, рассматривая переменные z и  как функции от t, и (первую - через посредство
как функции от t, и (первую - через посредство 

Отсюда

Преобразованное уравнение после сокращения будет иметь вид:

Решим ту же задачу иначе.
Обратный метод. Выразим из формул преобразования новые переменные через старые:

и будем считать независимыми переменными х, у. Дифференцируя третью формулу по х и по  зависит от них через посредство
зависит от них через посредство  , найдем:
, найдем:

или

6) Выражение 

преобразовать к переменным 
Метод вычисления дифференциалов. Независимые переменные: х, у. Дифференцируем формулы преобразования:

Если  рассматривать, как функцию от х, у через посредство t, и, то дифференциал
рассматривать, как функцию от х, у через посредство t, и, то дифференциал  напишется так:
напишется так:

Сопоставляя два выражения для  находим
находим

Составим теперь вторые дифференциалы от новых переменных:

С другой стороны,

Приравнивая оба выражения для  и заменяя
и заменяя  полученным выше его выражением, придем к равенству, из которого определится
полученным выше его выражением, придем к равенству, из которого определится 

Отсюда можно определить производные  — как коэффициенты при
— как коэффициенты при  Но нужный нам результат можно получить проще, заметив, что
Но нужный нам результат можно получить проще, заметив, что  переходит в
переходит в  если взять
если взять  Таким путем находим:
Таким путем находим:

7) Преобразование Лежандра. Наподобие 5), 218 мы и здесь приведем преобразование Лежандра как пример более общего преобразования, когда уже формулы, связывающие старые и новые переменные, содержат производные. Положим

Разумея под z некоторую определенную функцию от  будем предполагать ее такой, что
будем предполагать ее такой, что

Дифференцируя третью из формул преобразования по х и по у (причем  рассматриваем как функцию от х, у через посредство
рассматриваем как функцию от х, у через посредство  , получим
, получим

откуда

т. e. преобразование имеет взаимный характер.
Дифференцируя первые две из полученных формул (28) сначала по х, а затем по у, придем к уравнениям

и

Так как [203 (4)]

то из этих уравнений

Если x, у, z и t, u, v трактовать как координаты некоторых точек пространства, то преобразование Лежандра можно рассматривать как преобразование пространства (но не точечное). Поверхность, характеризуемая зависимостью между z и  переходит при этом в поверхность, определяемую зависимостью между
переходит при этом в поверхность, определяемую зависимостью между  . Так как
. Так как  — зависят только от
— зависят только от  то преобразование Лежандра сохраняет касание.
то преобразование Лежандра сохраняет касание.
8) Легко обобщить преобразование Лежандра на случай пространства любого числа измерений. Пусть, скажем, z есть функция от  Положим
Положим

здесь  есть новая функция от новых переменных
есть новая функция от новых переменных 
Будем предполагать и здесь определитель

отличным от нуля.
Продифференцируем формулу, определяющую  по
по  (рассматривая при этом
(рассматривая при этом  как функцию от
как функцию от  через посредство
через посредство 

Ввиду  , отсюда следует
, отсюда следует

Таким образом, и

так что в общем случае преобразование также имеет взаимный характер.
9) Наконец, рассмотрим еще один пример преобразования, представляющий некоторое своеобразие. Пусть

будет функция от  переменных, однородная 2-й степени относительно переменных
переменных, однородная 2-й степени относительно переменных  Предполагая определитель
Предполагая определитель

отличным от нуля, положим

и введем  в качестве новых независимых переменных вместо
в качестве новых независимых переменных вместо  . Тогда функция
. Тогда функция  преобразуется в некоторую функцию
преобразуется в некоторую функцию

Доказать, что

Дифференцируя  по
по  рассматривая
рассматривая  как функцию от
как функцию от  через посредство
через посредство 

С другой стороны, производная будет однородной функцией первой степени относительно переменных  Тогда по формуле Эйлера [188]
Тогда по формуле Эйлера [188]

Сопоставляя полученные два разложения для  ввиду О, заключаем о справедливости соотношений (а).
ввиду О, заключаем о справедливости соотношений (а).
Дифференцируя же по  получим
получим

Но  очевидно, однородная функция второй степени относительно
очевидно, однородная функция второй степени относительно  Снова применяя формулу Эйлера, видим, что последняя сумма дает нам
Снова применяя формулу Эйлера, видим, что последняя сумма дает нам

Отсюда и следуют соотношения (б).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Упорядочение области рациональных чисел.
- 3. Сложение и вычитание рациональных чисел.
- 4. Умножение и деление рациональных чисел.
- 5. Аксиома Архимеда.
- § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
- 7. Упорядочение области вещественных чисел.
- 8. Вспомогательные предложения.
- 9. Представление вещественного числа бесконечной десятичной дробью.
- 10. Непрерывность области вещественных чисел.
- 11. Границы числовых множеств.
- § 3. Арифметические действия над вещественными числами
- 13. Свойства сложения.
- 14. Определение произведения вещественных чисел.
- 15. Свойства умножения.
- 16. Заключение.
- 17. Абсолютные величины.
- § 4. Дальнейшие свойства и приложения вещественных чисел
- 19. Степень с любым вещественным показателем.
- 20. Логарифмы.
- 21. Измерение отрезков.
- ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. Варианта и ее предел
- 23. Предел варианты.
- 24. Бесконечно малые величины.
- 25. Примеры.
- 26. Некоторые теоремы о варианте, имеющей предел.
- 27. Бесконечно большие величины.
- § 2. Теоремы о пределах, облегчающие нахождение пределов
- 29. Леммы о бесконечно малых.
- 30. Арифметические операция над переменными.
- 31. Неопределенные выражения.
- 32. Примеры на нахождение пределов.
- 33. Теорема Штольца и ее применения.
- § 3. Монотонная варианта
- 35. Примеры.
- 36. Число е.
- 37. Приближенное вычисление числа е.
- 38. Лемма о вложенных промежутках.
- § 4. Принцип сходимости. Частичные пределы
- 40. Частичные последовательности и частичные пределы.
- 41. Лемма Больцано — Вейерштрасса
- 42. Наибольший и наименьший пределы.
- ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. Понятие функции
- 44. Функциональная зависимость между переменными. Примеры.
- 45. Определение понятия функции.
- 46. Аналитический способ задания функции.
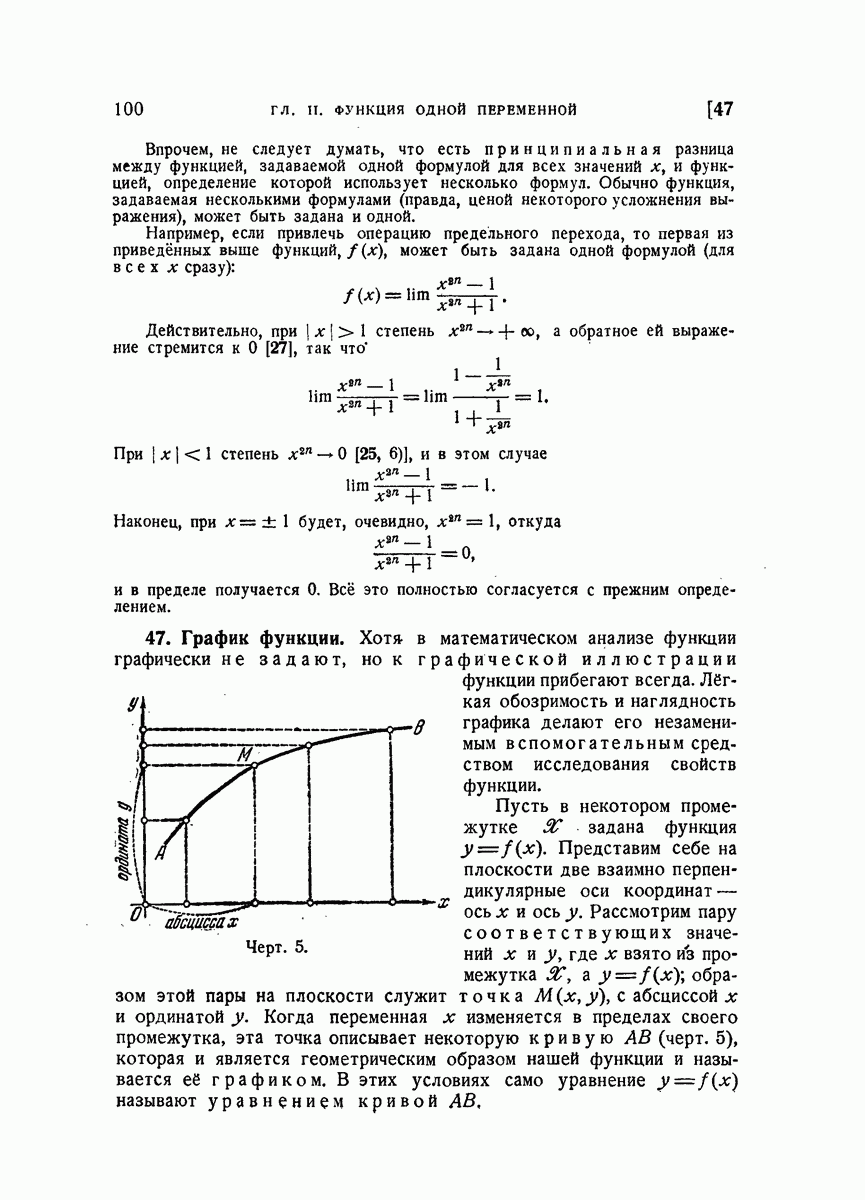
- 47. График функции.
- 48. Важнейшие классы функций.
- 49. Понятие обратной функции.
- 50. Обратные тригонометрические функции.
- 51. Суперпозиция функций. Заключительные замечания.
- § 2. Предел функции
- 53. Сведение к случаю варианты.
- 54. Примеры.
- 55. Распространение теории пределов.
- 56. Примеры.
- 57. Предел монотонной функции.
- 58. Общий признак Больцано—Коши.
- 59. Наибольший и наименьший пределы функции.
- § 3. Классификация бесконечно малых и бесконечно больших величин
- 61. Шкала бесконечно малых.
- 62. Эквивалентные бесконечно малые.
- 63. Выделение главной части.
- 64. Задачи.
- 65. Классификация бесконечно больших.
- § 4. Непрерывность (и разрывы) функций
- 67. Арифметические операции над непрерывными функциями.
- 68. Примеры непрерывных функций.
- 69. Односторонняя непрерывность. Классификация разрывов.
- 70. Примеры разрывных функций.
- 71. Непрерывность и разрывы монотонной функции.
- 72. Непрерывность элементарных функций.
- 73. Суперпозиция непрерывных функций.
- 74. Решение одного функционального уравнения.
- 75. Функциональная характеристика показательной, логарифмической и степенной функций.
- 76. Функциональная характеристика тригонометрического и гиперболического косинусов.
- 77. Использование непрерывности функций для вычисления пределов.
- 78. Степенно-показательные выражения.
- 79. Примеры.
- § 5. Свойства непрерывных функций
- 81. Применение к решению уравнений.
- 82. Теорема о промежуточном значении.
- 83. Существование обратной функции.
- 84. Теорема об ограниченности функции.
- 85. Наибольшее и наименьшее значения функции.
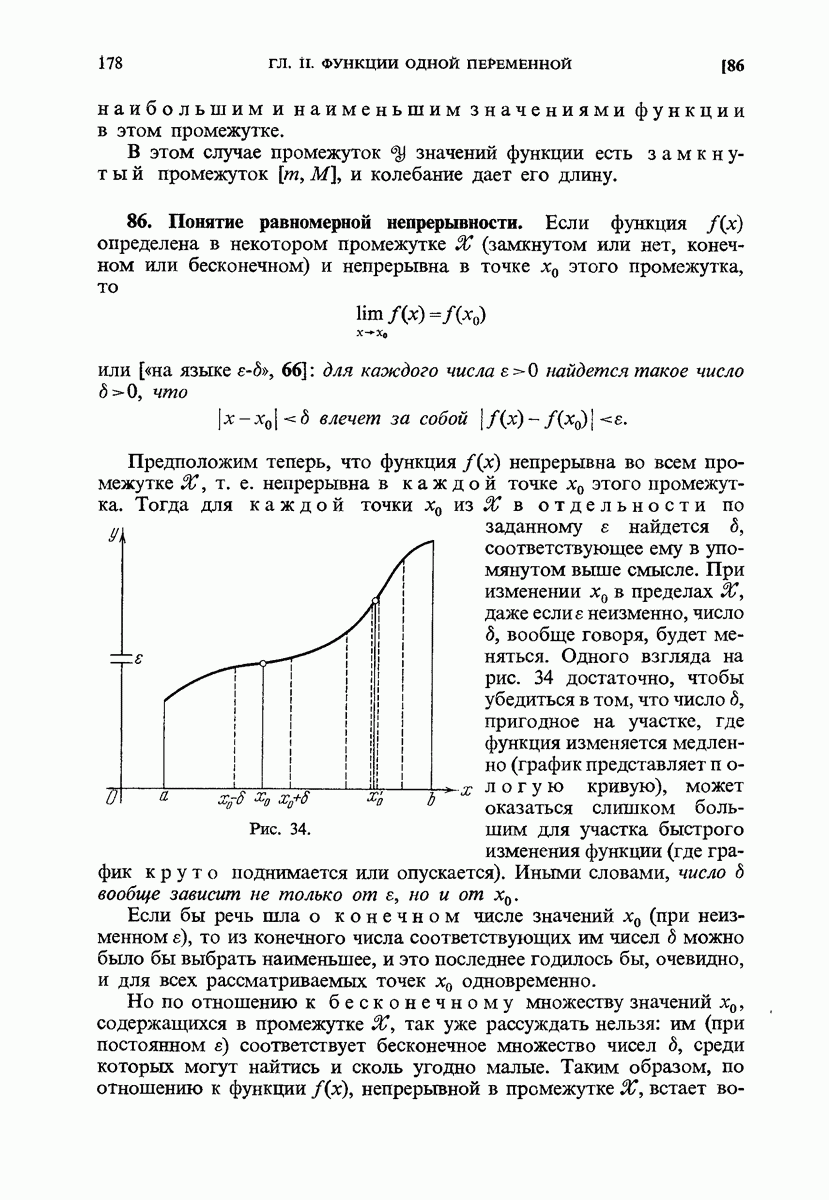
- 86. Понятие равномерной непрерывности.
- 87. Теорема Кантора.
- 88. Лемма Бореля.
- 89. Новые доказательства основных теорем.
- ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная и ее вычисление
- 91. Задача о проведении касательной к кривой.
- 92. Определение производной.
- 93. Примеры вычисления производных.
- 94. Производная обратной функции.
- 95. Сводка формул для производных.
- 96. Формула для превращения функции.
- 97. Простейшие правила вычисления производных.
- 98. Производная сложной функции.
- 100. Односторонние производные.
- 101. Бесконечные производные.
- 102. Дальнейшие примеры особых случаев.
- § 2. Дифференциал
- 104. Связь между диффереицируемостью и существованием производной.
- 105. Основные формулы и правила дифференцирования.
- 106. Инвариантность формы дифференциала.
- 107. Дифференциалы как источник приближенных формул.
- 108. Применение дифференциалов при оценке погрешностей.
- § 3. Основные теоремы дифференциального исчисления
- 110. Теорема Дарбу
- 111. Теорема Ролля.
- 112. Формула Лагранжа.
- 113. Предел производной.
- 114. Формула Коши.
- § 4. Производные и дифференциалы высших порядков
- 116. Общие формулы для производных любого порядка.
- 117. Формула Лейбница.
- 118. Примеры.
- 119. Дифференциалы высших порядков.
- 120. Нарушение инвариантности формы для дифференциалов высших порядков.
- 121. Параметрическое дифференцирование.
- 122. Конечные разности.
- § 5. Формула Тейлора
- 124. Разложение произвольной функции; дополнительный член в форме Пеано.
- 125. Примеры.
- 126. Другие формы дополнительного члена.
- 127. Приближенные формулы.
- § 6. Интерполирование
- 129. Дополнительный члеп формулы Лагранжа.
- 130. Интерполирование с кратными узлами. Формула Эрмита.
- ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
- § 1. Изучение хода изменения функции
- 132. Условие монотонности функции.
- 133. Доказательство неравенств.
- 134. Максимумы и минимумы; необходимые условия.
- 136. Достаточные условия. Первое правило.
- 136. Примеры.
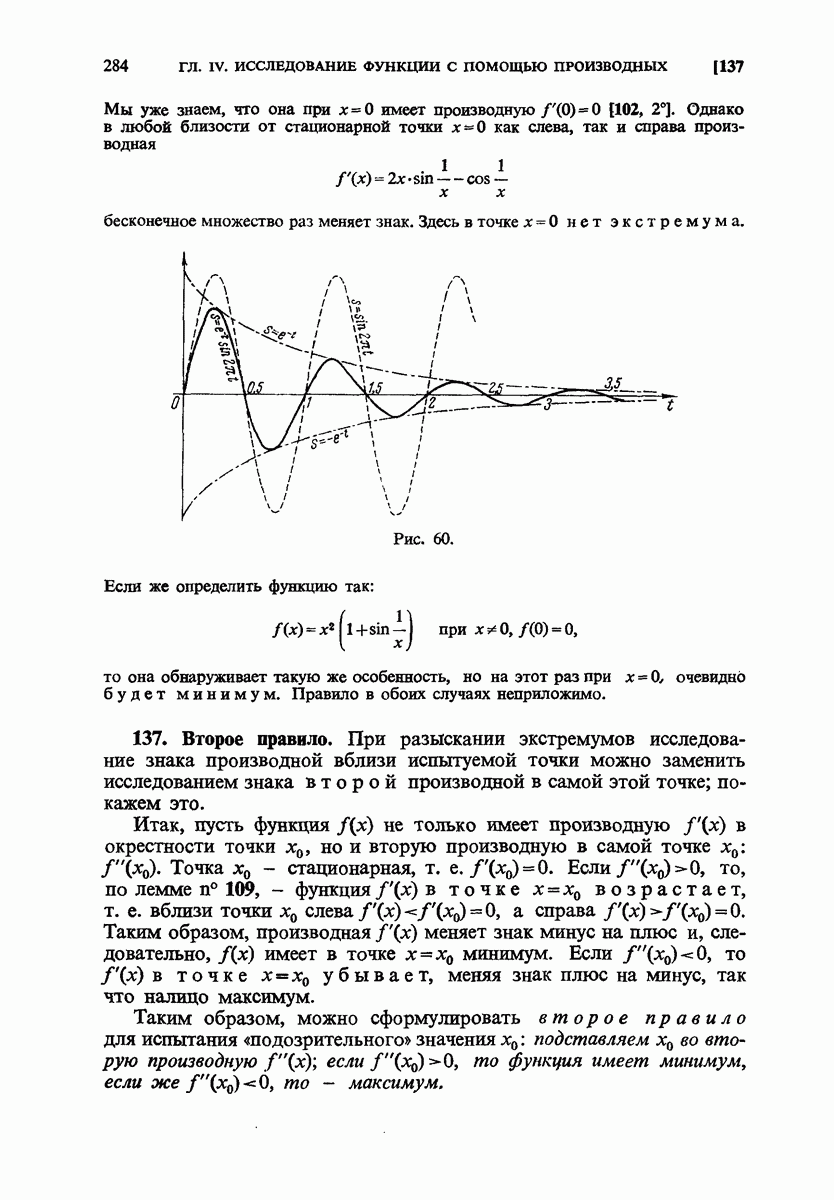
- 137. Второе правило.
- 138. Использование высших производных.
- 139. Разыскание наибольших и наименьших значений.
- 140. Задачи.
- § 2. Выпуклые (и вогнутые) функции
- 142. Простейшие предложения о выпуклых функциях.
- 143. Условия выпуклости функции.
- 144. Неравенство Иенсена и его приложения.
- 145. Точки перегиба.
- § 3. Построение графиков функций
- 147. Схема построения графика. Примеры.
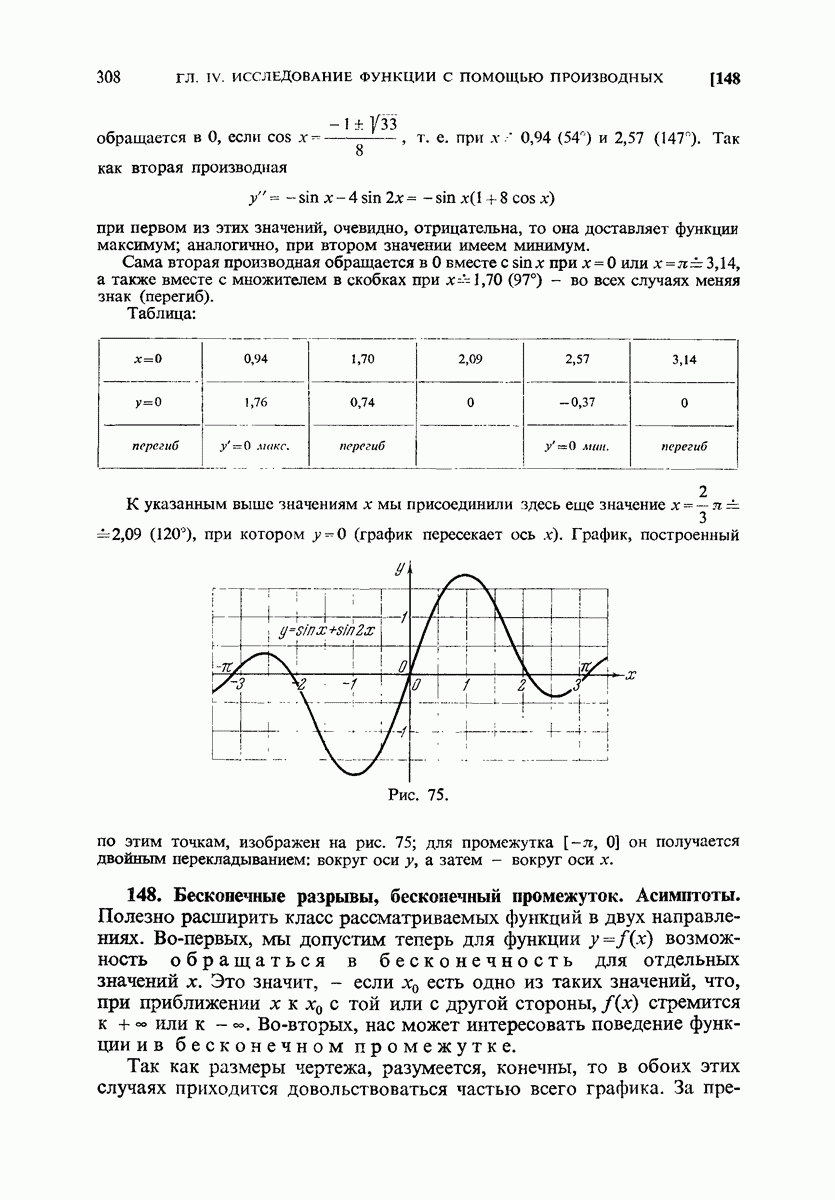
- 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
- 149. Примеры.
- § 4. Раскрытие неопределенностей
- 151. Неопределенность вида oo/oo
- 152. Другие виды неопределенностей.
- § 5. Приближенное решение уравнений
- 154. Правило пропорциональных частей (метод хорд).
- 155. Правило Ньютона (метод касательных).
- 156. Примеры в упражнения.
- 157. Комбинированный метод.
- 158. Примеры и упражнения.
- ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 159. Функциональная зависимость между переменными. Примеры.
- 160. Функции двух переменных и области их определения.
- 161. Арифметическое n-мерное пространство.
- 162. Примеры областей в n-мерном пространстве.
- 163. Общее определение открытой и замкнутой области.
- 164. Функции n переменных.
- 165. Предел функции нескольких переменных.
- 166. Сведение к случаю варианты.
- 167. Примеры.
- 168. Повторные пределы.
- § 2. Непрерывные функции
- 170. Операции над непрерывными функциями.
- 171. Функции, непрерывные в области. Теоремы Больцано—Коши.
- 172. Лемма Больцано—Вейерштрасса.
- 173. Теоремы Вейерштрасса.
- 174. Равномерная непрерывность.
- 175. Лемма Бореля.
- 176. Новые доказательства основных теорем.
- § 3. Производные и дифференциалы функций нескольких переменных
- 178. Полное приращение функции.
- 179. Полный дифференциал.
- 180. Геометрическая интерпретация для случая функции двух переменных.
- 181. Производные от сложных функций.
- 182. Примеры.
- 183. Формула конечных приращений.
- 184. Производная по заданному направлению.
- 185. Инвариантность формы (первого) дифференциала.
- 186. Применение полного дифференциала в приближенных вычислениях.
- 187. Однородные функции.
- 188. Формула Эйлера.
- § 4. Производные и дифференциалы высших порядков
- 190. Теорема о смешанных производных.
- 191. Обобщение.
- 192. Производные высших порядков от сложной функции.
- 193. Дифференциалы высших порядков.
- 194. Дифференциалы сложных функций.
- 195. Формула Тейлора.
- § 5. Экстремумы, наибольшие и наименьшие значения
- 197. Достаточные условия (случай функции двух переменных).
- 198. Достаточные условия (общий случай).
- 199. Условия отсутствия экстремума.
- 200. Наибольшее и наименьшее значения функции. Примеры.
- 201. Задачи.
- ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
- § 1. Формальные свойства функциональных определителей
- 203. Умножение якобианов.
- 204. Умножение функциональных матриц (матриц Якоби).
- § 2. Неявные функции
- 206. Существование неявной функции.
- 207. Дифференцируемость неявной функции.
- 208. Неявные функции от нескольких переменных.
- 209. Вычисление производных неявных функций.
- 210. Примеры.
- § 3. Некоторые приложения теории неявных функций
- 212. Метод неопределенных множителей Лагранжа.
- 213. Достаточные для относительного экстремума условия.
- 214. Примеры и задачи.
- 215. Понятие независимости функций.
- 216. Ранг матрицы Якоби.
- § 4. Замена переменных
- 218. Примеры.
- 219. Функции нескольких переменных. Замена независимых переменных.
- 220. Метод вычисления дифференциалов.
- 221. Общий случай замены переменных.
- 222. Примеры.
- ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
- § 1. Аналитическое представление кривых и поверхностей
- 224. Примеры.
- 225. Кривые механического происхождения.
- 226. Кривые на плоскости (в полярных координатах). Примеры.
- 227. Поверхности и кривые в пространстве.
- 228. Параметрическое представление.
- 229. Примеры.
- § 2. Касательная и касательная плоскость
- 231. Примеры.
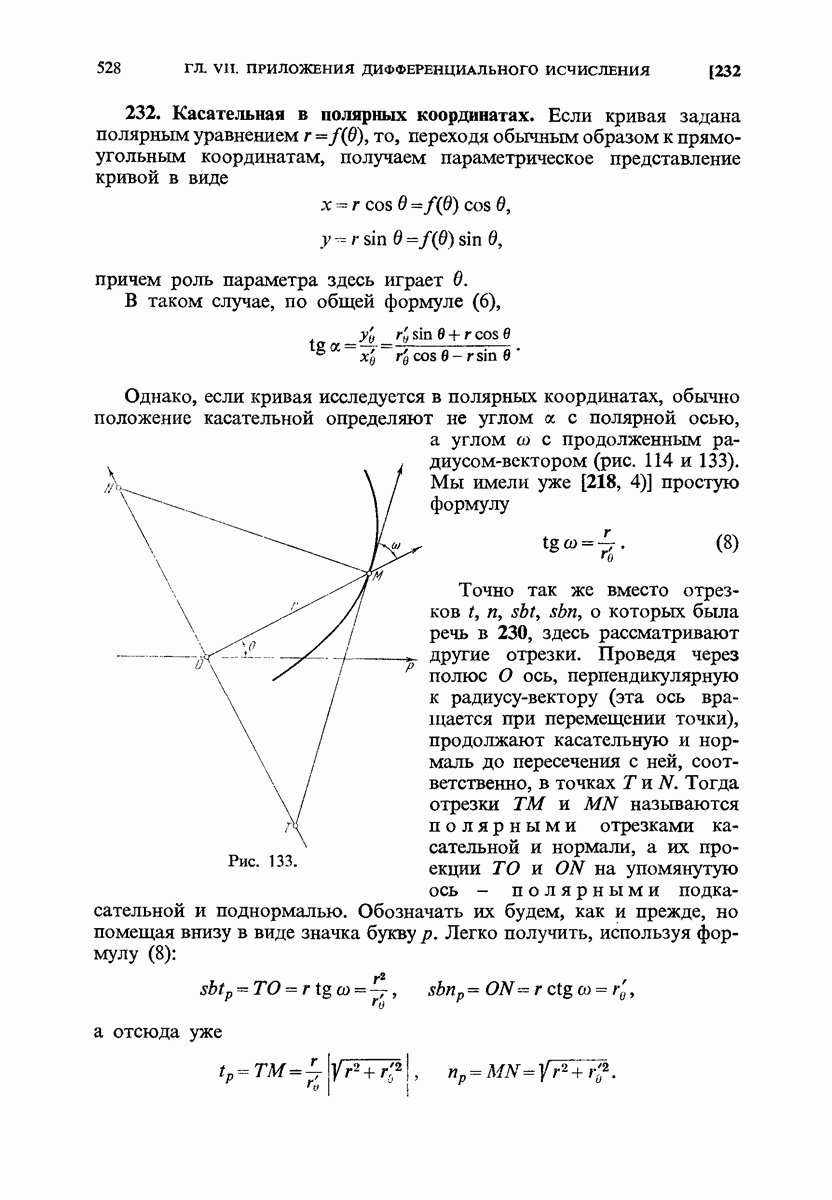
- 232. Касательная в полярных координатах.
- 233. Примеры.
- 234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
- 235. Примеры.
- 236. Особые точки плоских кривых.
- 237. Случай параметрического задания кривой.
- § 3. Касание кривых между собой
- 239. Примеры.
- 240. Характеристические точки.
- 241. Порядок касания двух кривых.
- 242. Случай неявного задания одной из кривых.
- 243. Соприкасающаяся кривая.
- 244. Другой подход к соприкасающимся кривым.
- § 4. Длина плоской кривой
- 246. Направление на кривой.
- 247. Длина кривой. Аддитивность длины дуги.
- 248. Достаточные условия спрямляемости. Дифференциал дуги.
- 249. Дуга в роли параметра. Положительное направление касательной.
- § 5. Кривизна плоской кривой
- 251. Круг кривизны и радиус кривизны.
- 252. Примеры.
- 253. Координаты центра кривизны.
- 254. Определение эволюты и эвольвенты; разыскание эволюты.
- 255. Свойства эволют и эвольвент.
- 256. Разыскание эвольвент.
- ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ