| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
201. Задачи.
Многие задачи — как из области математики, так и из других областей науки и техники - приводят к вопросу о нахождении наибольшего или наименьшего значения некоторой функции.
Решение задач  связано с уже рассмотренными в предыдущем п° примерами.
связано с уже рассмотренными в предыдущем п° примерами.
1) Среди всех вписанных в данный круг радиуса  треугольников найти тот, площадь которого наибольшая (рис. 107).
треугольников найти тот, площадь которого наибольшая (рис. 107).
Если через  обозначить центральные углы, опирающиеся на стороны треугольника, то они связаны зависимостью
обозначить центральные углы, опирающиеся на стороны треугольника, то они связаны зависимостью

откуда

Площадь треугольника Р через них выражается так:

Область изменения переменных х и у здесь определяется условиями:  Нужно найти те значения переменных, которые сообщают выражению в скобках наибольшую величину.
Нужно найти те значения переменных, которые сообщают выражению в скобках наибольшую величину.
Мы уже знаем [200, пример 1)], что это будут  так что и
так что и  получается равносторонний треугольник.
получается равносторонний треугольник.
2) Среди всех треугольников данного периметра  найти тот, площадь которого Р наибольшая.
найти тот, площадь которого Р наибольшая.
Пусть х, у, z означают стороны треугольника; тогда по формуле Герона

Можно было бы, подставив сюда  преобразовать Р к виду
преобразовать Р к виду

и искать наибольшее значение этой функции в треугольной области, о которой уже была речь в 160, 6).
Мы поступим иначе: задача сводится к нахождению наибольшего значения для произведения положительных чисел

- при условии, что их сумма постоянна:

А мы уже знаем [200, пример 3)], что для этого все множители должны быть равны,  так что
так что  Снова получается равносторонний треугольник.
Снова получается равносторонний треугольник.
3) Среди вписанных в данный эллипсоид

прямоугольных параллелепипедов (с ребрами, параллельными осям его) найти тот, который имеет наибольший объем.
Если через х, у, z обозначить коор динаты той из вершин, которая лежит в первом координатном трехгранном угле, то объем  Вместо
Вместо  можно рассмотреть величину
можно рассмотреть величину

ибо они, очевидно, достигают своих наибольших значений при одних и тех же х, у, z. По отношению же к и вопрос снова приводится к примеру 3) предыдущего п°, Ответ:

4) Предположим, что какой-нибудь газ (например, воздух) сжимается в поршневом компрессоре от атмосферного давления  до давления
до давления  Работа, затрачиваемая при этом на сжатие 1 моля газа, выразится так:
Работа, затрачиваемая при этом на сжатие 1 моля газа, выразится так:

здесь  есть «газовая постоянная»,
есть «газовая постоянная»,  - абсолютная температура газа до сжатия, а у есть некоторое число
- абсолютная температура газа до сжатия, а у есть некоторое число  зависящее от конструкции компрессора. Работа А, очевидно, тем меньше, чем меньше начальная температура
зависящее от конструкции компрессора. Работа А, очевидно, тем меньше, чем меньше начальная температура  При больших степенях сжатия, когда экономия в затрачиваемой работе представляет важность, разбивают весь процесс сжатия на несколько ступеней, в промежутках подвергая сжатый (и нагревающийся вместе с тем) газ - охлаждению.
При больших степенях сжатия, когда экономия в затрачиваемой работе представляет важность, разбивают весь процесс сжатия на несколько ступеней, в промежутках подвергая сжатый (и нагревающийся вместе с тем) газ - охлаждению.
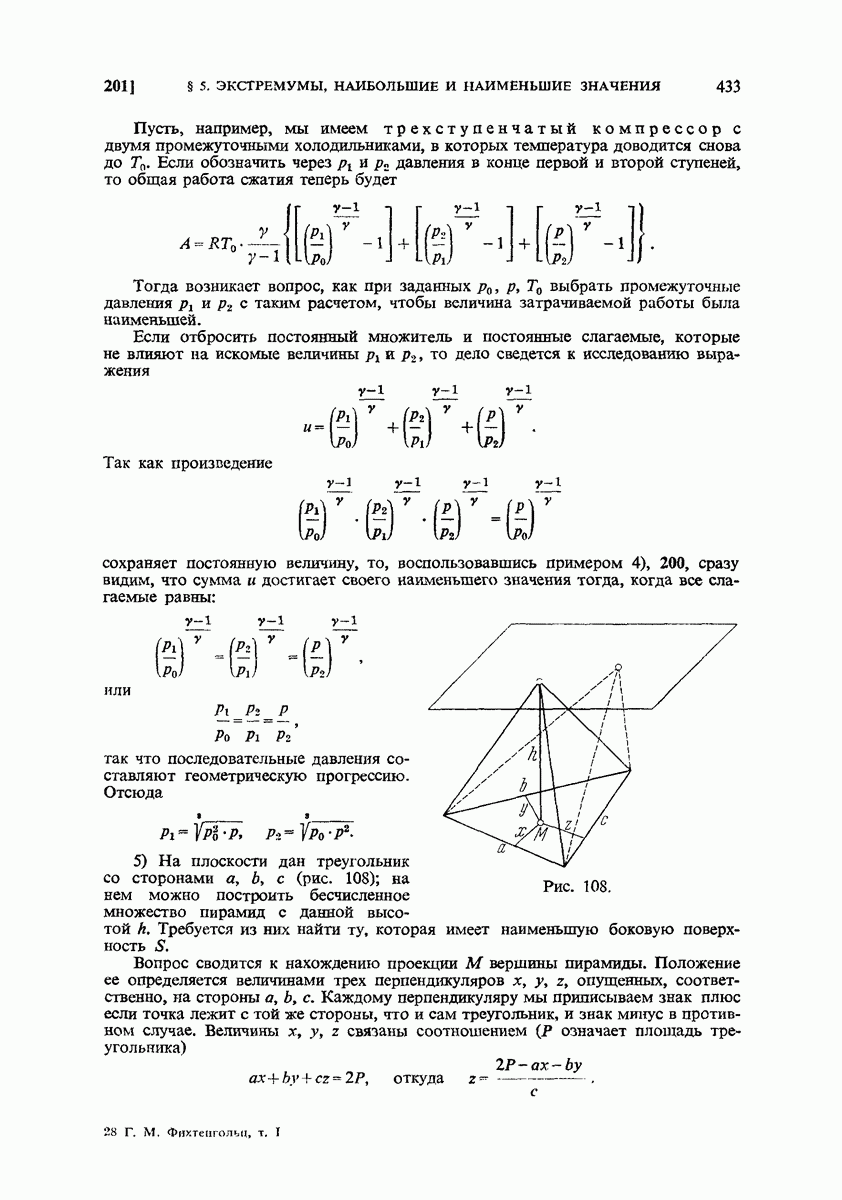
Пусть, например, мы имеем трехступенчатый компрессор с двумя промежуточными холодильниками, в которых температура доводится снова до  Если обозначить через
Если обозначить через  давления в конце первой и второй ступеней, то общая работа сжатия теперь будет
давления в конце первой и второй ступеней, то общая работа сжатия теперь будет

Тогда возникает вопрос, как при заданных  выбрать промежуточные давления
выбрать промежуточные давления  с таким расчетом, чтобы величина затрачиваемой работы была наименьшей.
с таким расчетом, чтобы величина затрачиваемой работы была наименьшей.
Если отбросить постоянный множитель и постоянные слагаемые, которые не влияют на искомые величины  то дело сведется к исследованию выражения
то дело сведется к исследованию выражения

Так как произведение

сохраняет постоянную величину, то, воспользовавшись примером 4), 200, сразу видим, что сумма и достигает своего наименьшего значения тогда, когда все слагаемые равны:

или

так что последовательные давления составляют геометрическую прогрессию.

Рис. 108.
Отсюда

5) На плоскости дан треугольник со сторонами  с (рис. 108); на нем можно построить бесчисленное множество пирамид с данной высотой А. Требуется из них найти ту, которая имеет наименьшую боковую поверхность
с (рис. 108); на нем можно построить бесчисленное множество пирамид с данной высотой А. Требуется из них найти ту, которая имеет наименьшую боковую поверхность 
Вопрос сводится к нахождению проекции М вершины пирамиды. Положение ее определяется величинами трех перпендикуляров х, у, z, опущенных, соответственно, на стороны  с. Каждому перпендикуляру мы приписываем знак плюс если точка лежит с той же стороны, что и сам треугольник, и знак минус в противном случае. Величины х, у, z связаны соотношением (Р означает площадь треугольника)
с. Каждому перпендикуляру мы приписываем знак плюс если точка лежит с той же стороны, что и сам треугольник, и знак минус в противном случае. Величины х, у, z связаны соотношением (Р означает площадь треугольника)

Интересующая нас боковая поверхность S выразится теперь так:

где  должно быть заменено найденным выражением; областью изменения независимых переменных х, у является вся плоскость
должно быть заменено найденным выражением; областью изменения независимых переменных х, у является вся плоскость  . Имеем
. Имеем

или

Соответствующая точка М есть центр вписанного в треугольник круга.
Что этим значениям х и у отвечает наименьшее значение для  легко показать как в примере 4) предыдущего п°, опираясь на то, что - при безграничном возрастании х или у - и S растет до бесконечности.
легко показать как в примере 4) предыдущего п°, опираясь на то, что - при безграничном возрастании х или у - и S растет до бесконечности.
6) Пусть даны на плоскости три точки  не лежащие на одной прямой. Требуется найти в этой плоскости такую точку, чтобы сумма ее расстояний до данных точек была наименьшей.
не лежащие на одной прямой. Требуется найти в этой плоскости такую точку, чтобы сумма ее расстояний до данных точек была наименьшей.
Взяв любую точку  положим
положим

Тогда исследованию подлежит функция

Для нее существуют - везде, кроме данных точек, - частные производные

где  означает угол прямой
означает угол прямой  с осью х.
с осью х.
«Подозрительными» по экстремуму точками являются, таким образом, прежде всего точки  в которых производных нет, а затем та точка
в которых производных нет, а затем та точка  (мы увидим, что она не всегда существует), в которой производные зараз обращаются в 0. Так как при бесконечном возрастании х или у наша функция и, очевидно, также бесконечно растет, то наименьшего значения она достигает в одной из упомянутых точек.
(мы увидим, что она не всегда существует), в которой производные зараз обращаются в 0. Так как при бесконечном возрастании х или у наша функция и, очевидно, также бесконечно растет, то наименьшего значения она достигает в одной из упомянутых точек.
Чтобы разыскать стационарную точку  приравняем нулю обе частные производные; это даст нам условия:
приравняем нулю обе частные производные; это даст нам условия:

Умножим первое на  а второе на
а второе на  и вычтем; мы получим
и вычтем; мы получим

Аналогично найдем, что

Таким образом, углы между прямыми  взятыми попарно, все должны быть равны
взятыми попарно, все должны быть равны  и точка
и точка  получается в пересечении дуг, построенных на сторонах треугольника и вмещающих угол
получается в пересечении дуг, построенных на сторонах треугольника и вмещающих угол 

Рис. 109.
Если в этом треугольнике нет угла, большего или равного  то названные дуги, действительно, пересекаются внутри треугольника и определяют точку
то названные дуги, действительно, пересекаются внутри треугольника и определяют точку  из которой стороны его видны под углами, равными — (рис. 109). В этом случае надлежит сравнить значения, которые и получает в названных четырех точках.
из которой стороны его видны под углами, равными — (рис. 109). В этом случае надлежит сравнить значения, которые и получает в названных четырех точках.
Мы докажем, что значение и в стационарной точке  будет меньше других (а значит, и вообще наименьшим). Действительно, по «теореме косинусов»
будет меньше других (а значит, и вообще наименьшим). Действительно, по «теореме косинусов»

так что

Аналогично

Складывая, получим

т. е.

Очевидно, точка  здесь может быть заменена точкой
здесь может быть заменена точкой  или
или  что и завершает доказательство.
что и завершает доказательство.
Иначе обстоит дело, если один из углов треугольника  равен или больше —
равен или больше —  Тогда стационарной точки вовсе не существует и наименьшее значение функции и доставляется одной из данных точек
Тогда стационарной точки вовсе не существует и наименьшее значение функции и доставляется одной из данных точек  - именно той, которая служит вершиной тупого угла.
- именно той, которая служит вершиной тупого угла.
Любопытной особенностью этой задачи является именно то, что в ней приходится, кроме стационарной точки, считаться и с точками, в которых производных не существует [ср. 196, замечание II].
7) Обобщим задачу 1): станем искать вписанный в данный круг (радиуса R) ( -угольник с наибольшей площадью Р.
-угольник с наибольшей площадью Р.
Обозначим через  центральные углы, которые опираются на стороны многоугольника; тогда
центральные углы, которые опираются на стороны многоугольника; тогда

откуда

Площадь Р равна

если подставить вместо  его выражение, то вопрос сведется к разысканию наибольшего значения для функции
его выражение, то вопрос сведется к разысканию наибольшего значения для функции

причем область  изменения независимых переменных
изменения независимых переменных  определяется неравенством
определяется неравенством

т. е. представляет собой  -мерный симплекс [162].
-мерный симплекс [162].
По общему правилу вычисляем производные и приравниваем их нулю:

единственной внутренней точкой области, в которой выполняются эти условия, будет точка

ей отвечает  .
.
Для того чтобы доказать, что это, действительно, будет наибольшим значением и, воспользуемся методом математической индукции. При  наше утверждение уже установлено в примере 1) предыдущего п°. Допустим, что оно верно для случая
наше утверждение уже установлено в примере 1) предыдущего п°. Допустим, что оно верно для случая  слагаемых синусов (так что для их суммы наибольшим значением будет
слагаемых синусов (так что для их суммы наибольшим значением будет  и докажем верность его и для нашей суммы
и докажем верность его и для нашей суммы  синусов.
синусов.
Согласно общим указаниям, сделанным выше, надлежит сравнить значение  значениями, которые функция принимает на границе области
значениями, которые функция принимает на границе области  Возьмем, например, «грань симплекса»
Возьмем, например, «грань симплекса»  на ней и будет функцией лишь от
на ней и будет функцией лишь от  переменных:
переменных:

и, по допущению, наибольшим значением здесь будет  То же можно установить и для других «граней». Но так как
То же можно установить и для других «граней». Но так как

то наше утверждение доказано. Наибольшую площадь будет иметь правильный многоугольник.
8) Рассмотрим электрическую питательную сеть с параллельным включением. На рис. 110 представлена схема сети причем А и В - зажимы источника тока и  — приемники тока, потребляющие, соответственно, токи
— приемники тока, потребляющие, соответственно, токи  Требуется, при наперед заданном допустимом общем падении потенциала в цепи
Требуется, при наперед заданном допустимом общем падении потенциала в цепи  , определить сечения проводов так, чтобы на всю магистраль пошло наименьшее количество меди.
, определить сечения проводов так, чтобы на всю магистраль пошло наименьшее количество меди.
Очевидно, достаточно ограничиться рассмотрением одного из проводов, скажем  так как другой провод находится в совершенно аналогичных условиях. Обозначим через
так как другой провод находится в совершенно аналогичных условиях. Обозначим через  длины частей
длины частей  через
через  площади их поперечных сечений
площади их поперечных сечений  Тогда выражение
Тогда выражение

как раз и представит объем всей затраченной меди (в  для него нам нужно добиться наименьшей величины, принимая во внимание, что общее падение потенциала в проводе
для него нам нужно добиться наименьшей величины, принимая во внимание, что общее падение потенциала в проводе  должно равняться е.
должно равняться е.

Рис. 110.
Легко подсчитать, какие токи  будут протекать в отрезках
будут протекать в отрезках  цепи:
цепи:

Ваш обозначить через о сопротивление медной проволоки длиной в  с сечением в
с сечением в  то сопротивления этих отрезков будут
то сопротивления этих отрезков будут

так что соответствующие падения потенциала в этих отрезках, согласно закону Ома, выразятся так:

Чтобы избежать сложных выкладок, мы, вместо переменных  введем именно эти величины
введем именно эти величины  связанные простым условием
связанные простым условием

Тогда, в свою очередь,

и

причем область изменения независимых переменных  определяется неравенствами
определяется неравенствами

(открытый симплекс).
Приравнивания нулю производные и по всем переменным, получим систему уравнений

откуда (снова вводя 

Удобно обозначить общую величину всех этих отношений через  . Тогда
. Тогда

причем  легко определяется из условия
легко определяется из условия 

Так как, при приближении точки  к границе области, и растет до бесконечности, то найденные значения
к границе области, и растет до бесконечности, то найденные значения  действительно доставляют функции и наименьшее значение.
действительно доставляют функции и наименьшее значение.
Наконец, возвращаясь к нашим основным переменным ди  находим
находим

так что наивыгоднейшие сечения проводов оказываются пропорциональными корням квадратным из соответствующих сил тока.
9) Метод наименьших квадратов. Так называется очень распространенный метод обработки наблюдений, суть которого заключается в следующем.
Пусть требуется определить значения трех величин х, у, z, если для них установлено  линейных уравнений
линейных уравнений

причем некоторые из коэффициентов  получены опытным путем и известны лишь по приближению. При этом мы предположим, что хоть какие-нибудь три из этих уравнений имеют определитель, отличный от нуля: например, пусть
получены опытным путем и известны лишь по приближению. При этом мы предположим, что хоть какие-нибудь три из этих уравнений имеют определитель, отличный от нуля: например, пусть

Однако вычисленные из первых трех уравнений значения х, у, z, вообще говоря, не будут точно удовлетворять остальным (либо ввиду неизбежных погрешностей в коэффициентах уравнений, либо вследствие того, что сами равенства оказываются лишь приближенными). Не имея оснований предпочесть одни уравнения другим и считаясь с неизбежностью погрешностей

какие бы ни брать значения х, у, z, стараются достичь лишь того, чтобы сумма квадратов этих погрешностей

была наименьшей (отсюда и название метода). Иными словами, наилучше согласующимися с результатами опыта считаются те значения х, у, z, которые доставляют наименьшую величину функции 
По общему правилу, чтобы найти эти значения, приравниваем нулю производные от  по
по 

Гаусс (С. F. Gauss) ввел другие обозначения сумм однотипных слагаемых, разнящихся лишь указателями; именно, он пишет

В обозначениях Гаусса полученные для определения значений х, у, z уравнения перепишутся так:

их называют нормальными уравнениями.
Для того чтобы быть уверенными, что этими уравнениями однозначно определятся значения х, у, z, нужно установить, что определитель системы отличен от нуля. Но по известной теореме алгебры, квадрат этого определителя представляется в виде

причем суммирование распространяется на всевозможные сочетания  из
из  значков
значков  по три. Так как из всех определителей справа, по нашему предположению, хоть один отличен от нуля, то отсюда и следует, что определитель слева также не нуль.
по три. Так как из всех определителей справа, по нашему предположению, хоть один отличен от нуля, то отсюда и следует, что определитель слева также не нуль.
Остается еще убедиться в том, что определяемые из нормальных уравнений значения переменных действительно доставляют функции  наименьшее значение. Для этого достаточно, например, установить, что вне сферы достаточно большого радиуса
наименьшее значение. Для этого достаточно, например, установить, что вне сферы достаточно большого радиуса  будет сколь угодно велико.
будет сколь угодно велико.
С этой целью рассмотрим значения первых трех скобок в выражении 

Ввиду (14) через эти значения, в свою очередь, линейно выражаются, с вполне определенными постоянными коэффициентами, и х, у, z, так что, пока все три величины  остаются ограниченными, ограниченными необходимо будут сами х, у, z. Отсюда уже ясно, что при бесконечном возрастании
остаются ограниченными, ограниченными необходимо будут сами х, у, z. Отсюда уже ясно, что при бесконечном возрастании  также растет до бесконечности и
также растет до бесконечности и  (а следовательно, и W).
(а следовательно, и W).
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Упорядочение области рациональных чисел.
- 3. Сложение и вычитание рациональных чисел.
- 4. Умножение и деление рациональных чисел.
- 5. Аксиома Архимеда.
- § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
- 7. Упорядочение области вещественных чисел.
- 8. Вспомогательные предложения.
- 9. Представление вещественного числа бесконечной десятичной дробью.
- 10. Непрерывность области вещественных чисел.
- 11. Границы числовых множеств.
- § 3. Арифметические действия над вещественными числами
- 13. Свойства сложения.
- 14. Определение произведения вещественных чисел.
- 15. Свойства умножения.
- 16. Заключение.
- 17. Абсолютные величины.
- § 4. Дальнейшие свойства и приложения вещественных чисел
- 19. Степень с любым вещественным показателем.
- 20. Логарифмы.
- 21. Измерение отрезков.
- ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. Варианта и ее предел
- 23. Предел варианты.
- 24. Бесконечно малые величины.
- 25. Примеры.
- 26. Некоторые теоремы о варианте, имеющей предел.
- 27. Бесконечно большие величины.
- § 2. Теоремы о пределах, облегчающие нахождение пределов
- 29. Леммы о бесконечно малых.
- 30. Арифметические операция над переменными.
- 31. Неопределенные выражения.
- 32. Примеры на нахождение пределов.
- 33. Теорема Штольца и ее применения.
- § 3. Монотонная варианта
- 35. Примеры.
- 36. Число е.
- 37. Приближенное вычисление числа е.
- 38. Лемма о вложенных промежутках.
- § 4. Принцип сходимости. Частичные пределы
- 40. Частичные последовательности и частичные пределы.
- 41. Лемма Больцано — Вейерштрасса
- 42. Наибольший и наименьший пределы.
- ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. Понятие функции
- 44. Функциональная зависимость между переменными. Примеры.
- 45. Определение понятия функции.
- 46. Аналитический способ задания функции.
- 47. График функции.
- 48. Важнейшие классы функций.
- 49. Понятие обратной функции.
- 50. Обратные тригонометрические функции.
- 51. Суперпозиция функций. Заключительные замечания.
- § 2. Предел функции
- 53. Сведение к случаю варианты.
- 54. Примеры.
- 55. Распространение теории пределов.
- 56. Примеры.
- 57. Предел монотонной функции.
- 58. Общий признак Больцано—Коши.
- 59. Наибольший и наименьший пределы функции.
- § 3. Классификация бесконечно малых и бесконечно больших величин
- 61. Шкала бесконечно малых.
- 62. Эквивалентные бесконечно малые.
- 63. Выделение главной части.
- 64. Задачи.
- 65. Классификация бесконечно больших.
- § 4. Непрерывность (и разрывы) функций
- 67. Арифметические операции над непрерывными функциями.
- 68. Примеры непрерывных функций.
- 69. Односторонняя непрерывность. Классификация разрывов.
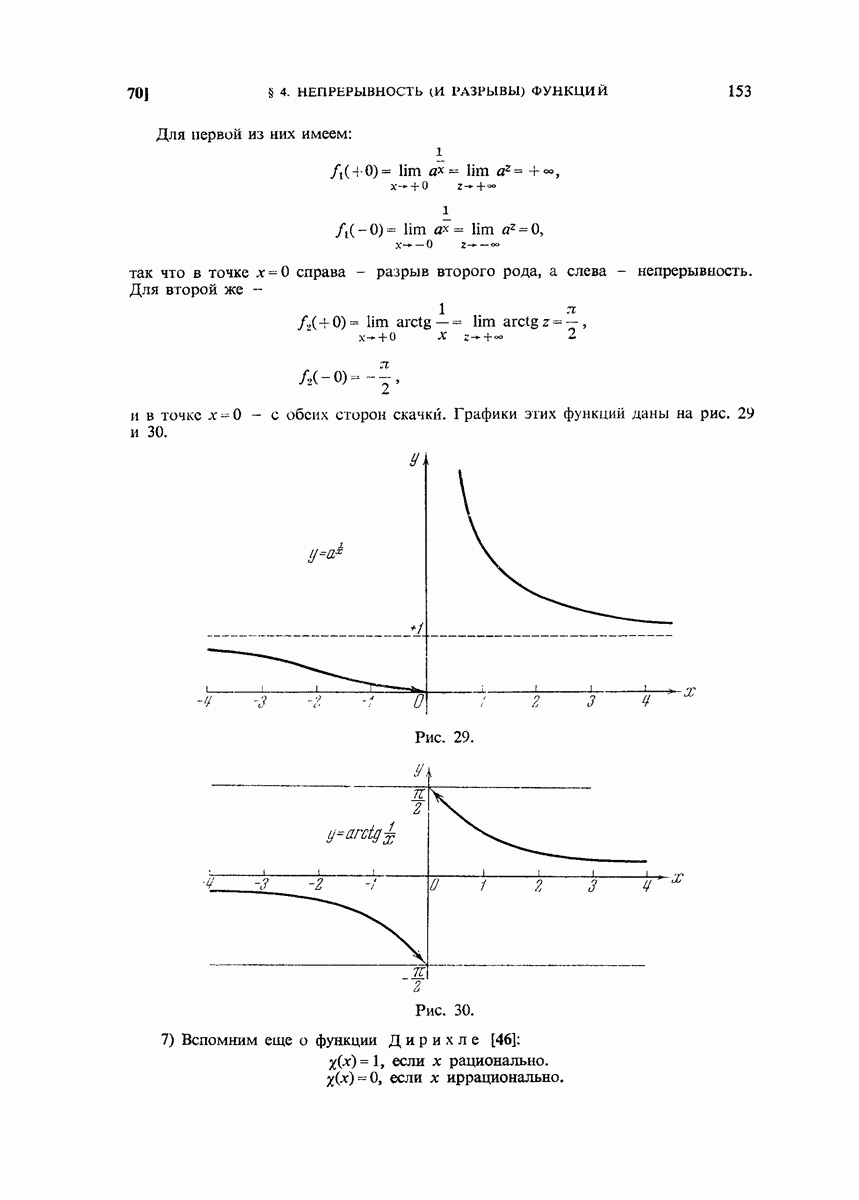
- 70. Примеры разрывных функций.
- 71. Непрерывность и разрывы монотонной функции.
- 72. Непрерывность элементарных функций.
- 73. Суперпозиция непрерывных функций.
- 74. Решение одного функционального уравнения.
- 75. Функциональная характеристика показательной, логарифмической и степенной функций.
- 76. Функциональная характеристика тригонометрического и гиперболического косинусов.
- 77. Использование непрерывности функций для вычисления пределов.
- 78. Степенно-показательные выражения.
- 79. Примеры.
- § 5. Свойства непрерывных функций
- 81. Применение к решению уравнений.
- 82. Теорема о промежуточном значении.
- 83. Существование обратной функции.
- 84. Теорема об ограниченности функции.
- 85. Наибольшее и наименьшее значения функции.
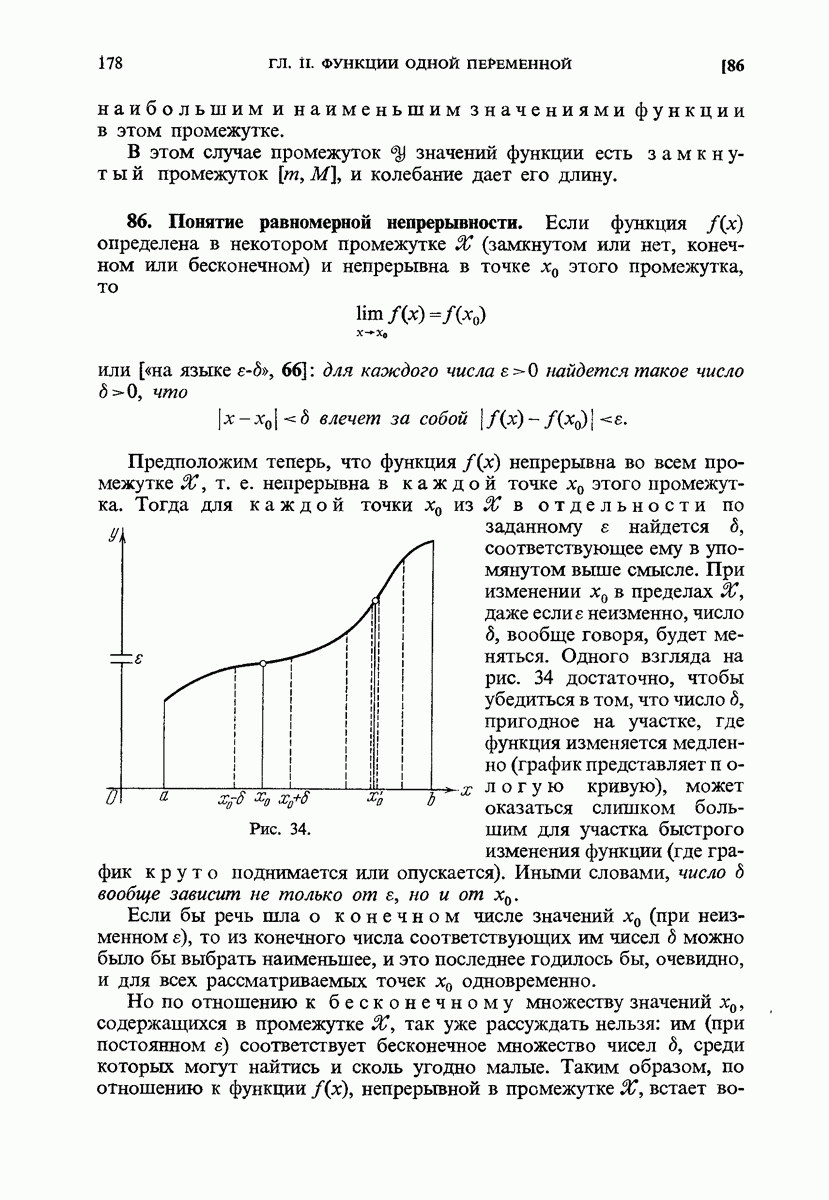
- 86. Понятие равномерной непрерывности.
- 87. Теорема Кантора.
- 88. Лемма Бореля.
- 89. Новые доказательства основных теорем.
- ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная и ее вычисление
- 91. Задача о проведении касательной к кривой.
- 92. Определение производной.
- 93. Примеры вычисления производных.
- 94. Производная обратной функции.
- 95. Сводка формул для производных.
- 96. Формула для превращения функции.
- 97. Простейшие правила вычисления производных.
- 98. Производная сложной функции.
- 100. Односторонние производные.
- 101. Бесконечные производные.
- 102. Дальнейшие примеры особых случаев.
- § 2. Дифференциал
- 104. Связь между диффереицируемостью и существованием производной.
- 105. Основные формулы и правила дифференцирования.
- 106. Инвариантность формы дифференциала.
- 107. Дифференциалы как источник приближенных формул.
- 108. Применение дифференциалов при оценке погрешностей.
- § 3. Основные теоремы дифференциального исчисления
- 110. Теорема Дарбу
- 111. Теорема Ролля.
- 112. Формула Лагранжа.
- 113. Предел производной.
- 114. Формула Коши.
- § 4. Производные и дифференциалы высших порядков
- 116. Общие формулы для производных любого порядка.
- 117. Формула Лейбница.
- 118. Примеры.
- 119. Дифференциалы высших порядков.
- 120. Нарушение инвариантности формы для дифференциалов высших порядков.
- 121. Параметрическое дифференцирование.
- 122. Конечные разности.
- § 5. Формула Тейлора
- 124. Разложение произвольной функции; дополнительный член в форме Пеано.
- 125. Примеры.
- 126. Другие формы дополнительного члена.
- 127. Приближенные формулы.
- § 6. Интерполирование
- 129. Дополнительный члеп формулы Лагранжа.
- 130. Интерполирование с кратными узлами. Формула Эрмита.
- ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
- § 1. Изучение хода изменения функции
- 132. Условие монотонности функции.
- 133. Доказательство неравенств.
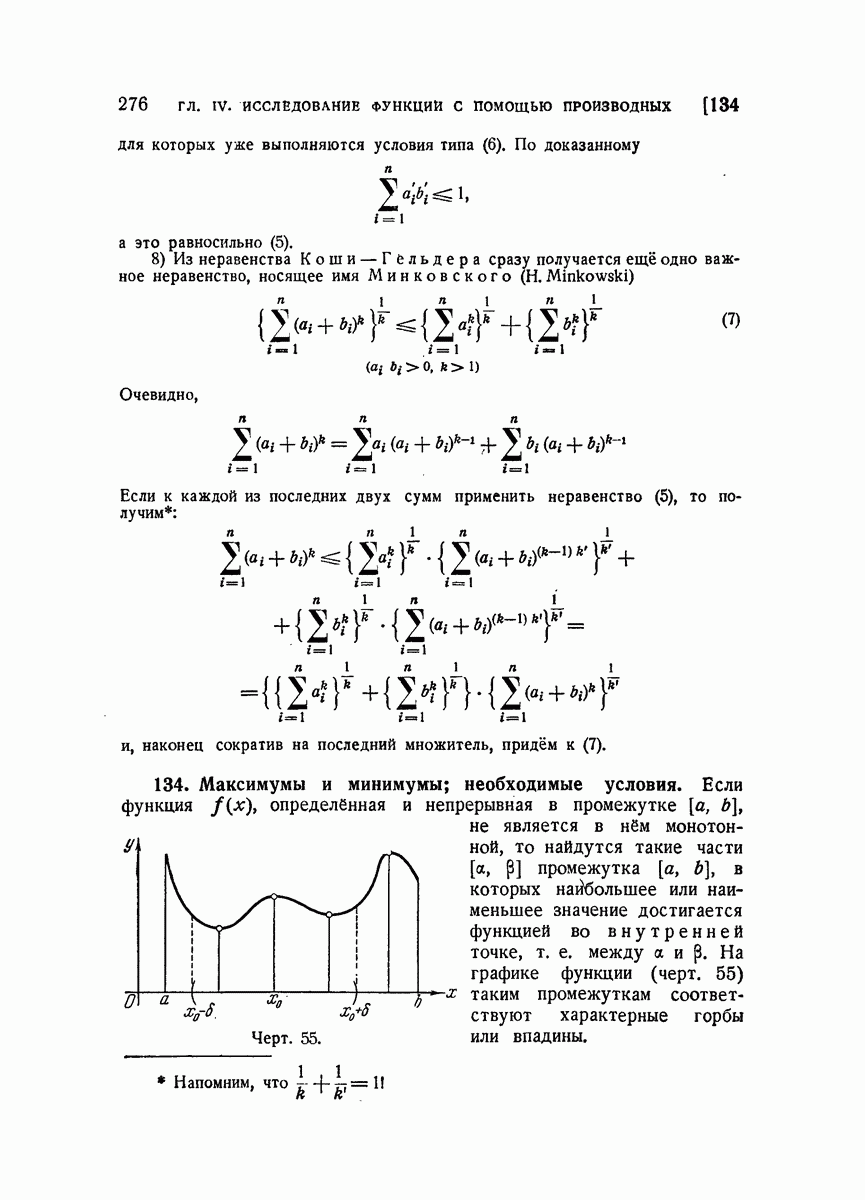
- 134. Максимумы и минимумы; необходимые условия.
- 136. Достаточные условия. Первое правило.
- 136. Примеры.
- 137. Второе правило.
- 138. Использование высших производных.
- 139. Разыскание наибольших и наименьших значений.
- 140. Задачи.
- § 2. Выпуклые (и вогнутые) функции
- 142. Простейшие предложения о выпуклых функциях.
- 143. Условия выпуклости функции.
- 144. Неравенство Иенсена и его приложения.
- 145. Точки перегиба.
- § 3. Построение графиков функций
- 147. Схема построения графика. Примеры.
- 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
- 149. Примеры.
- § 4. Раскрытие неопределенностей
- 151. Неопределенность вида oo/oo
- 152. Другие виды неопределенностей.
- § 5. Приближенное решение уравнений
- 154. Правило пропорциональных частей (метод хорд).
- 155. Правило Ньютона (метод касательных).
- 156. Примеры в упражнения.
- 157. Комбинированный метод.
- 158. Примеры и упражнения.
- ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 159. Функциональная зависимость между переменными. Примеры.
- 160. Функции двух переменных и области их определения.
- 161. Арифметическое n-мерное пространство.
- 162. Примеры областей в n-мерном пространстве.
- 163. Общее определение открытой и замкнутой области.
- 164. Функции n переменных.
- 165. Предел функции нескольких переменных.
- 166. Сведение к случаю варианты.
- 167. Примеры.
- 168. Повторные пределы.
- § 2. Непрерывные функции
- 170. Операции над непрерывными функциями.
- 171. Функции, непрерывные в области. Теоремы Больцано—Коши.
- 172. Лемма Больцано—Вейерштрасса.
- 173. Теоремы Вейерштрасса.
- 174. Равномерная непрерывность.
- 175. Лемма Бореля.
- 176. Новые доказательства основных теорем.
- § 3. Производные и дифференциалы функций нескольких переменных
- 178. Полное приращение функции.
- 179. Полный дифференциал.
- 180. Геометрическая интерпретация для случая функции двух переменных.
- 181. Производные от сложных функций.
- 182. Примеры.
- 183. Формула конечных приращений.
- 184. Производная по заданному направлению.
- 185. Инвариантность формы (первого) дифференциала.
- 186. Применение полного дифференциала в приближенных вычислениях.
- 187. Однородные функции.
- 188. Формула Эйлера.
- § 4. Производные и дифференциалы высших порядков
- 190. Теорема о смешанных производных.
- 191. Обобщение.
- 192. Производные высших порядков от сложной функции.
- 193. Дифференциалы высших порядков.
- 194. Дифференциалы сложных функций.
- 195. Формула Тейлора.
- § 5. Экстремумы, наибольшие и наименьшие значения
- 197. Достаточные условия (случай функции двух переменных).
- 198. Достаточные условия (общий случай).
- 199. Условия отсутствия экстремума.
- 200. Наибольшее и наименьшее значения функции. Примеры.
- 201. Задачи.
- ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
- § 1. Формальные свойства функциональных определителей
- 203. Умножение якобианов.
- 204. Умножение функциональных матриц (матриц Якоби).
- § 2. Неявные функции
- 206. Существование неявной функции.
- 207. Дифференцируемость неявной функции.
- 208. Неявные функции от нескольких переменных.
- 209. Вычисление производных неявных функций.
- 210. Примеры.
- § 3. Некоторые приложения теории неявных функций
- 212. Метод неопределенных множителей Лагранжа.
- 213. Достаточные для относительного экстремума условия.
- 214. Примеры и задачи.
- 215. Понятие независимости функций.
- 216. Ранг матрицы Якоби.
- § 4. Замена переменных
- 218. Примеры.
- 219. Функции нескольких переменных. Замена независимых переменных.
- 220. Метод вычисления дифференциалов.
- 221. Общий случай замены переменных.
- 222. Примеры.
- ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
- § 1. Аналитическое представление кривых и поверхностей
- 224. Примеры.
- 225. Кривые механического происхождения.
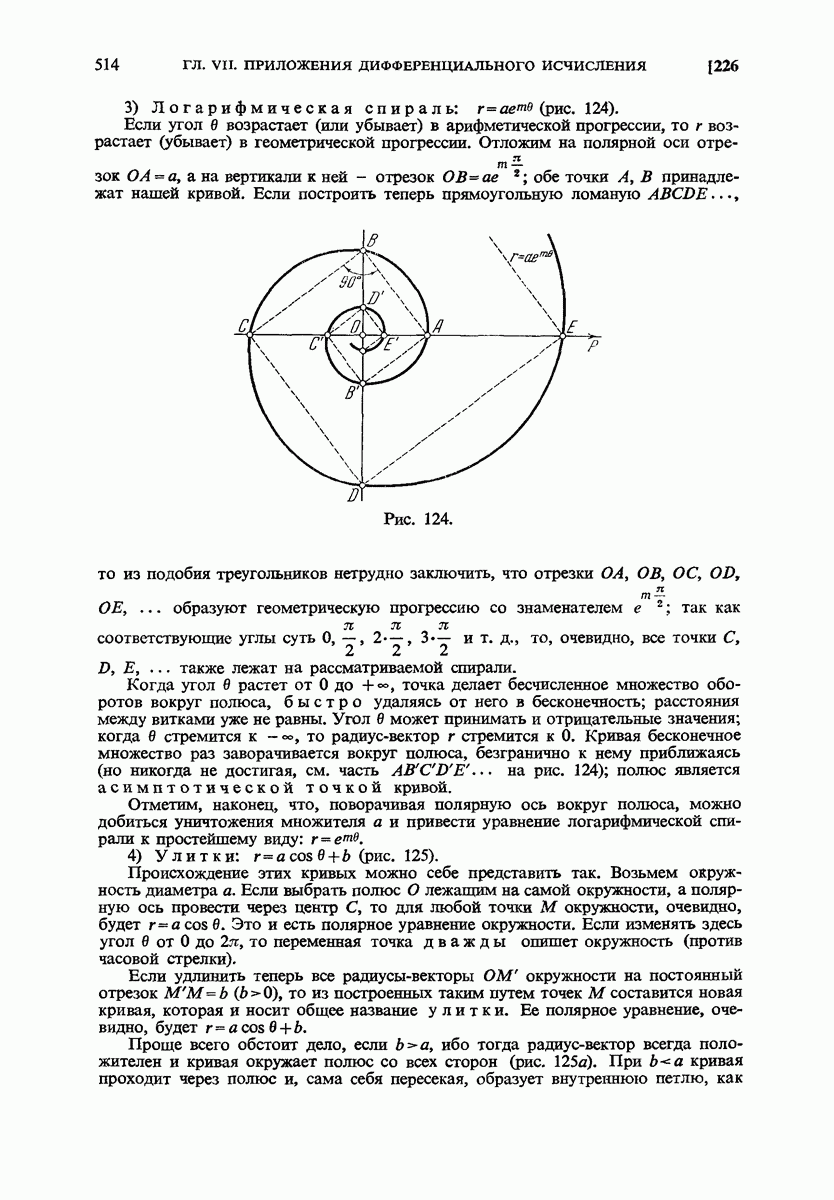
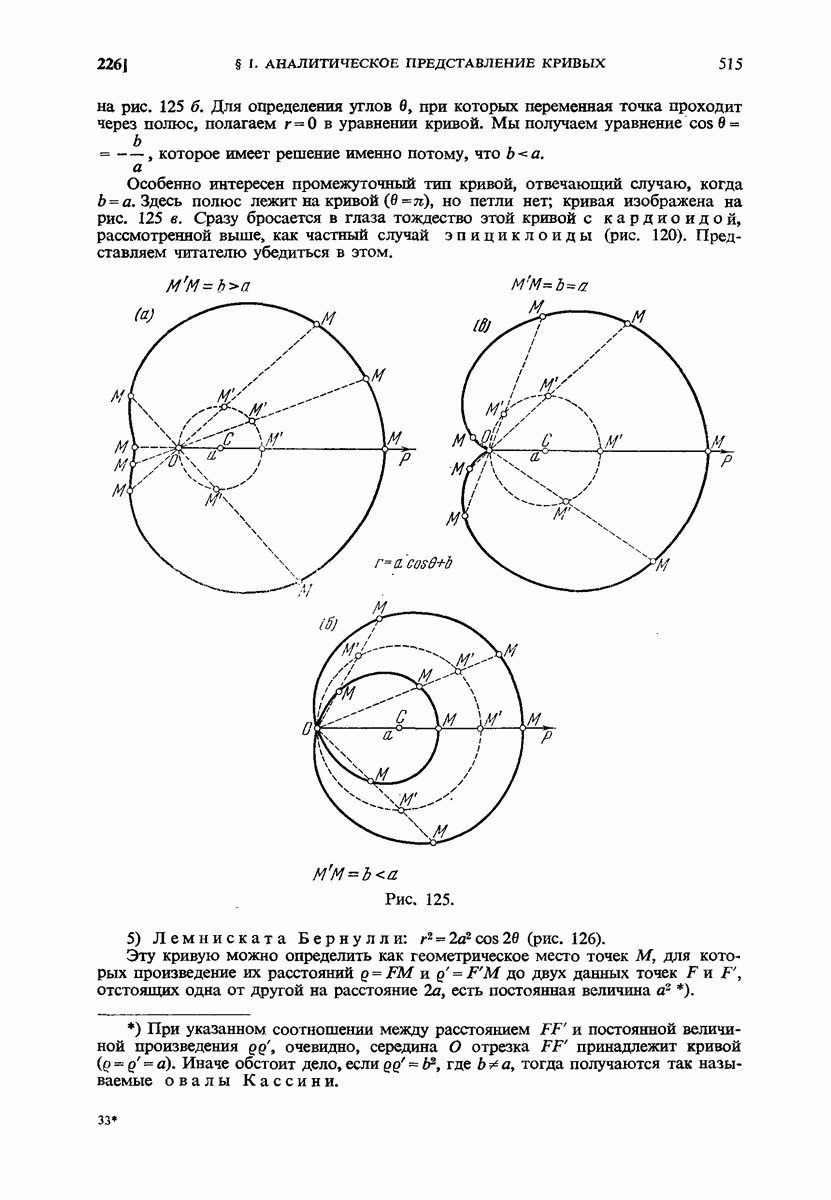
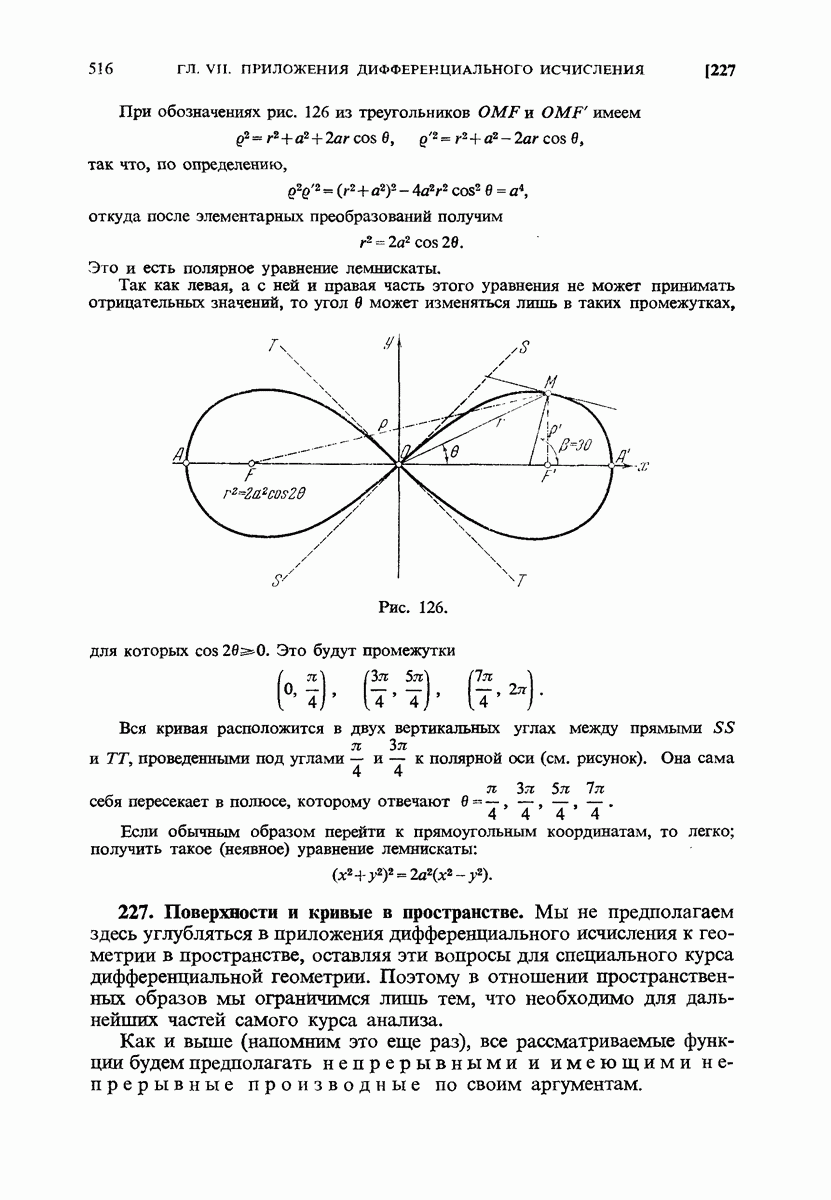
- 226. Кривые на плоскости (в полярных координатах). Примеры.
- 227. Поверхности и кривые в пространстве.
- 228. Параметрическое представление.
- 229. Примеры.
- § 2. Касательная и касательная плоскость
- 231. Примеры.
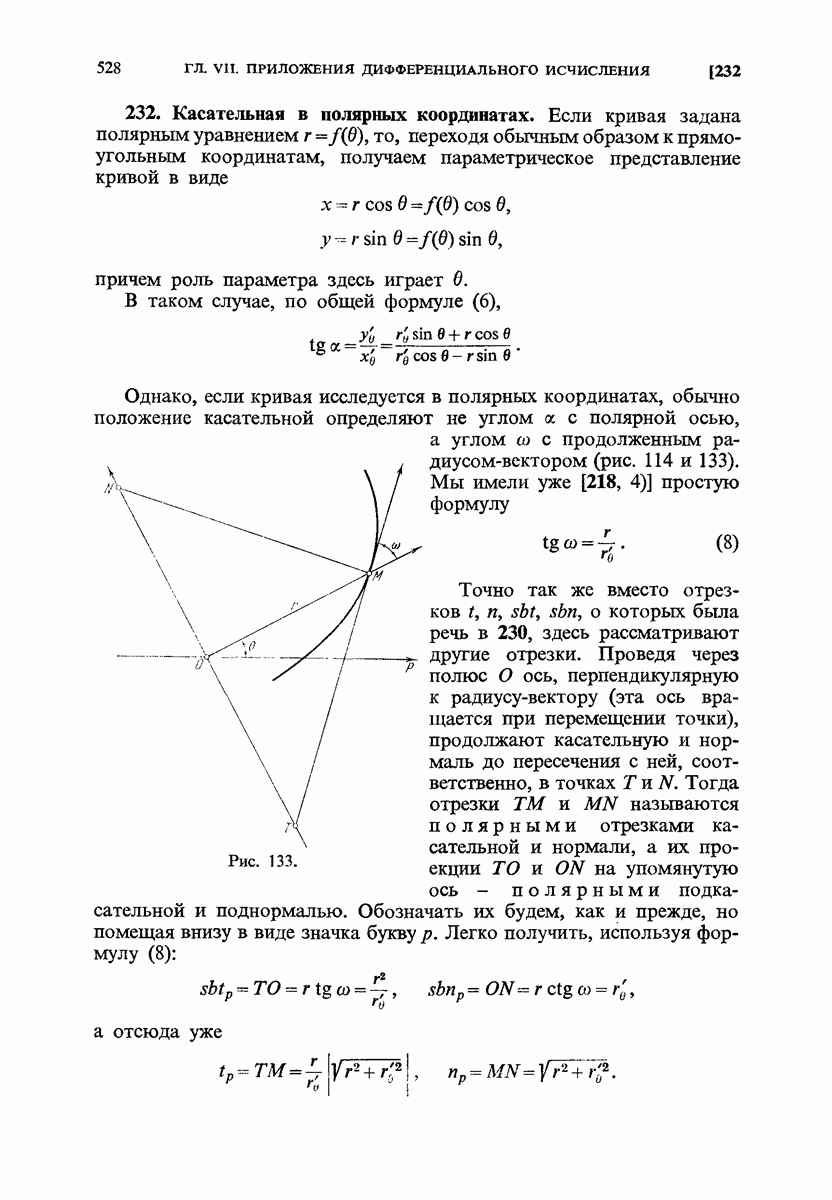
- 232. Касательная в полярных координатах.
- 233. Примеры.
- 234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
- 235. Примеры.
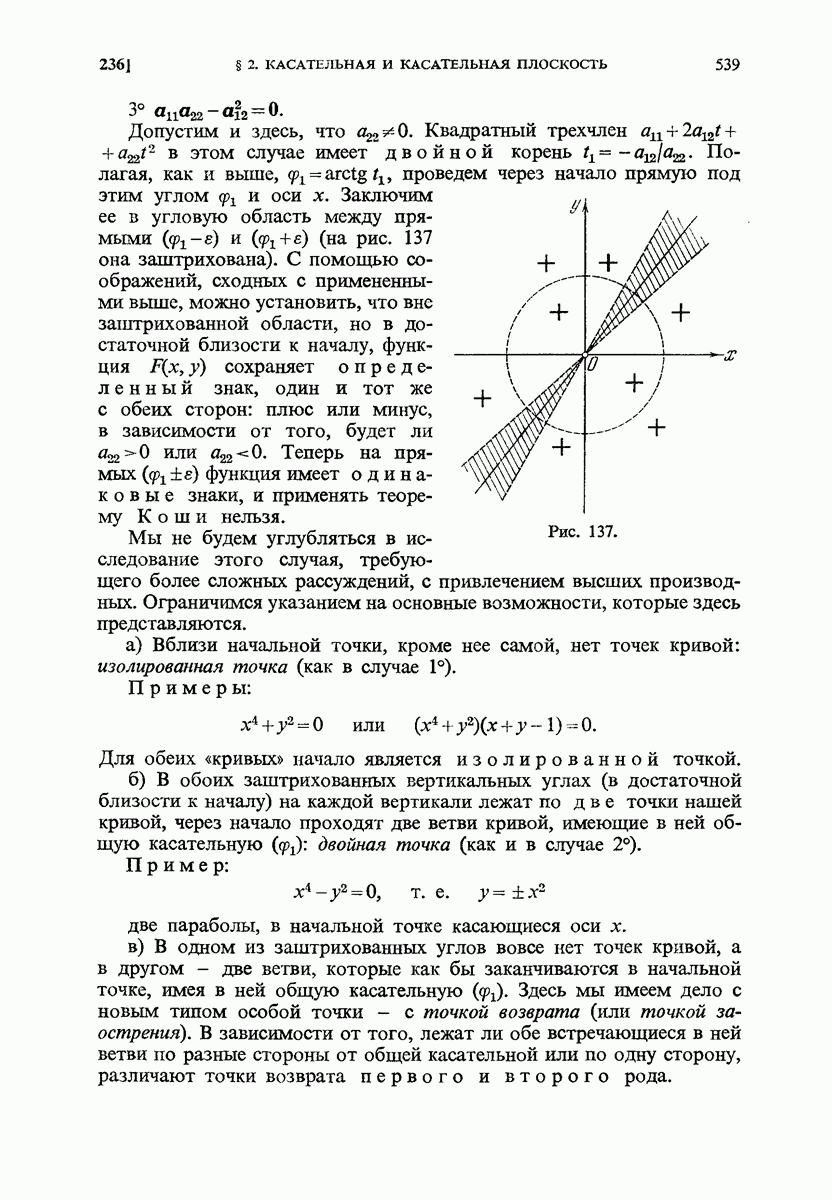
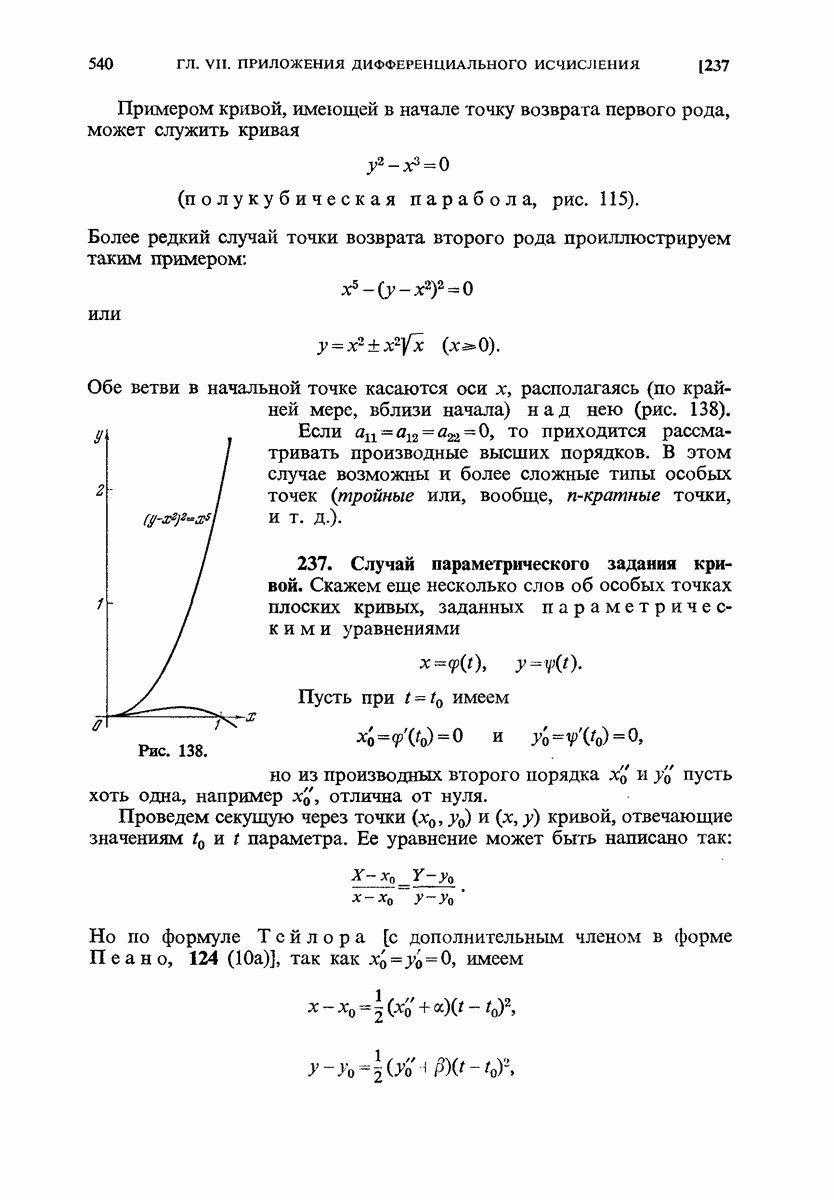
- 236. Особые точки плоских кривых.
- 237. Случай параметрического задания кривой.
- § 3. Касание кривых между собой
- 239. Примеры.
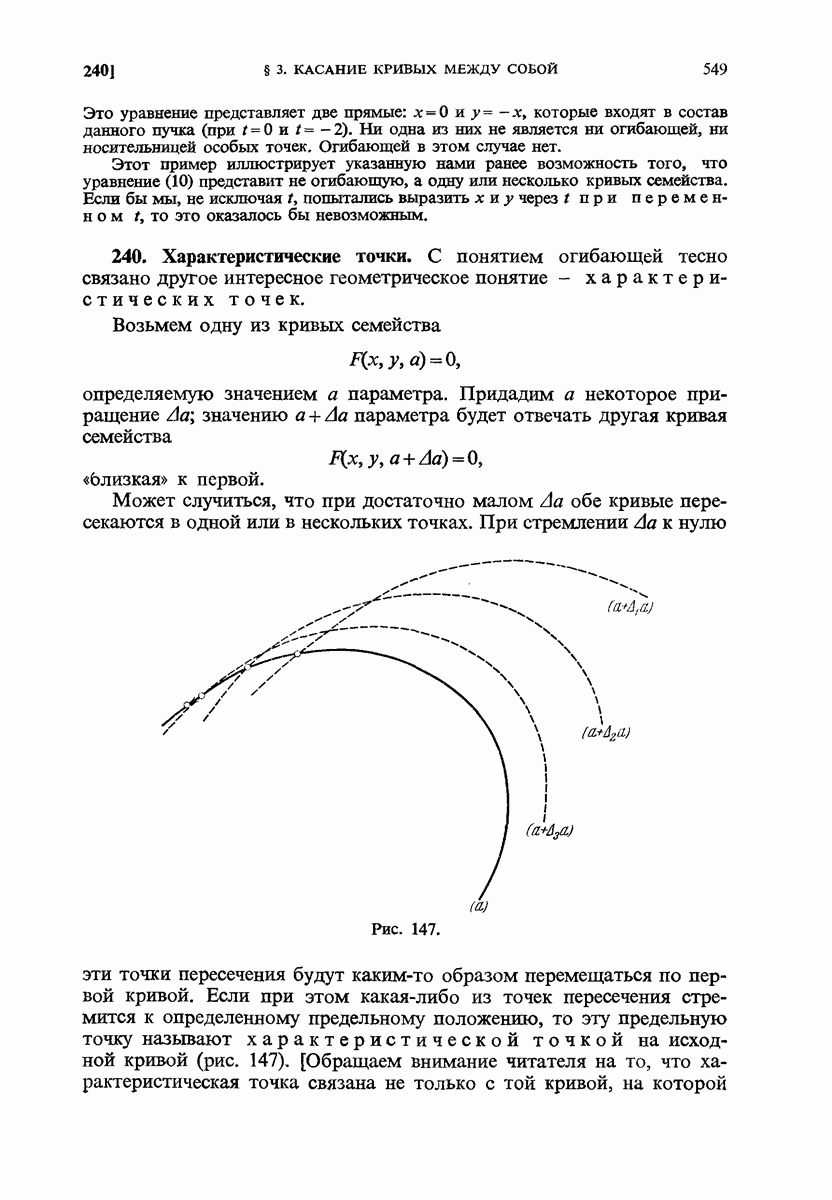
- 240. Характеристические точки.
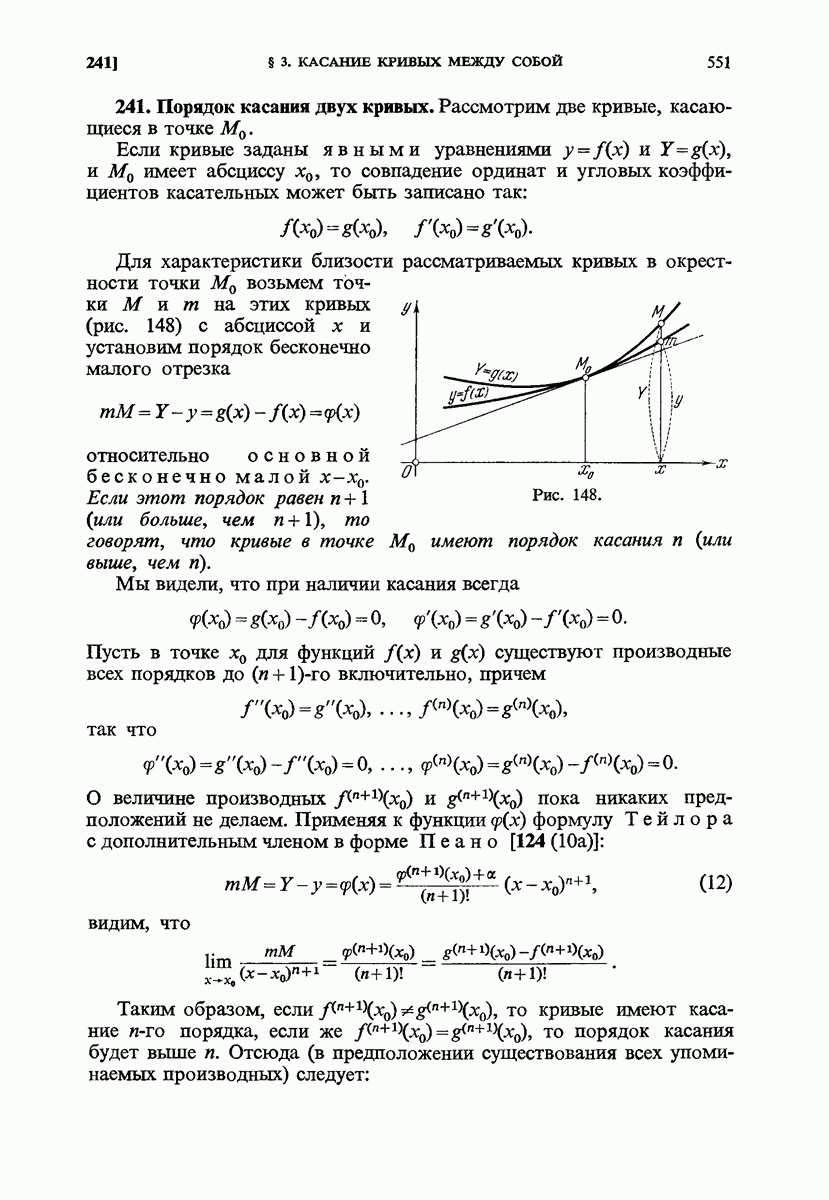
- 241. Порядок касания двух кривых.
- 242. Случай неявного задания одной из кривых.
- 243. Соприкасающаяся кривая.
- 244. Другой подход к соприкасающимся кривым.
- § 4. Длина плоской кривой
- 246. Направление на кривой.
- 247. Длина кривой. Аддитивность длины дуги.
- 248. Достаточные условия спрямляемости. Дифференциал дуги.
- 249. Дуга в роли параметра. Положительное направление касательной.
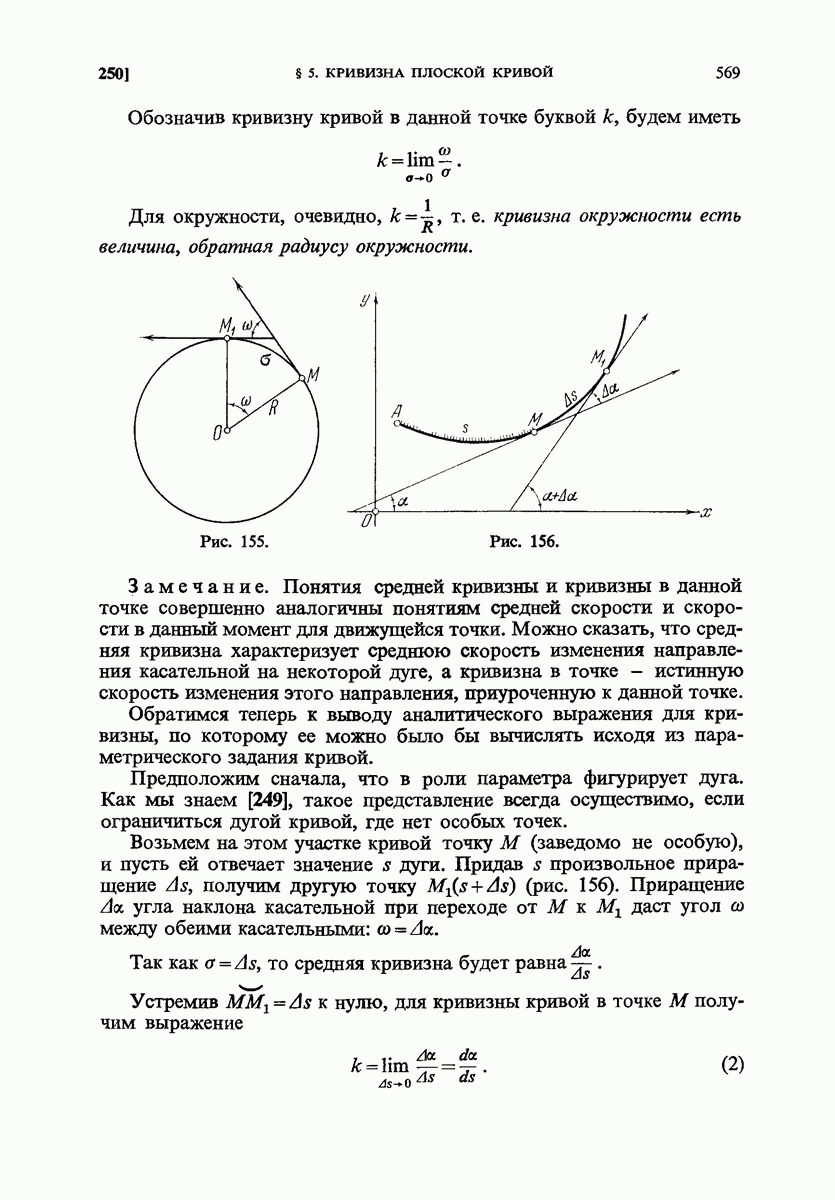
- § 5. Кривизна плоской кривой
- 251. Круг кривизны и радиус кривизны.
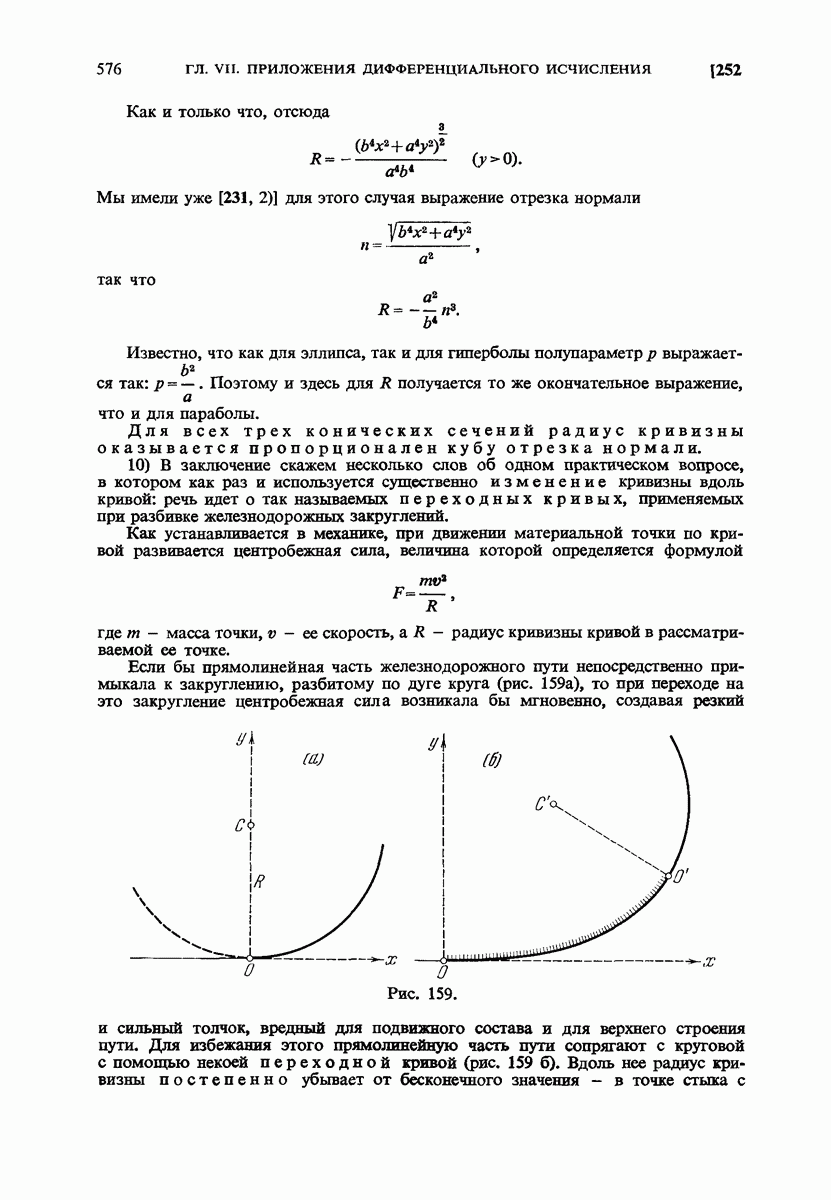
- 252. Примеры.
- 253. Координаты центра кривизны.
- 254. Определение эволюты и эвольвенты; разыскание эволюты.
- 255. Свойства эволют и эвольвент.
- 256. Разыскание эвольвент.
- ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ