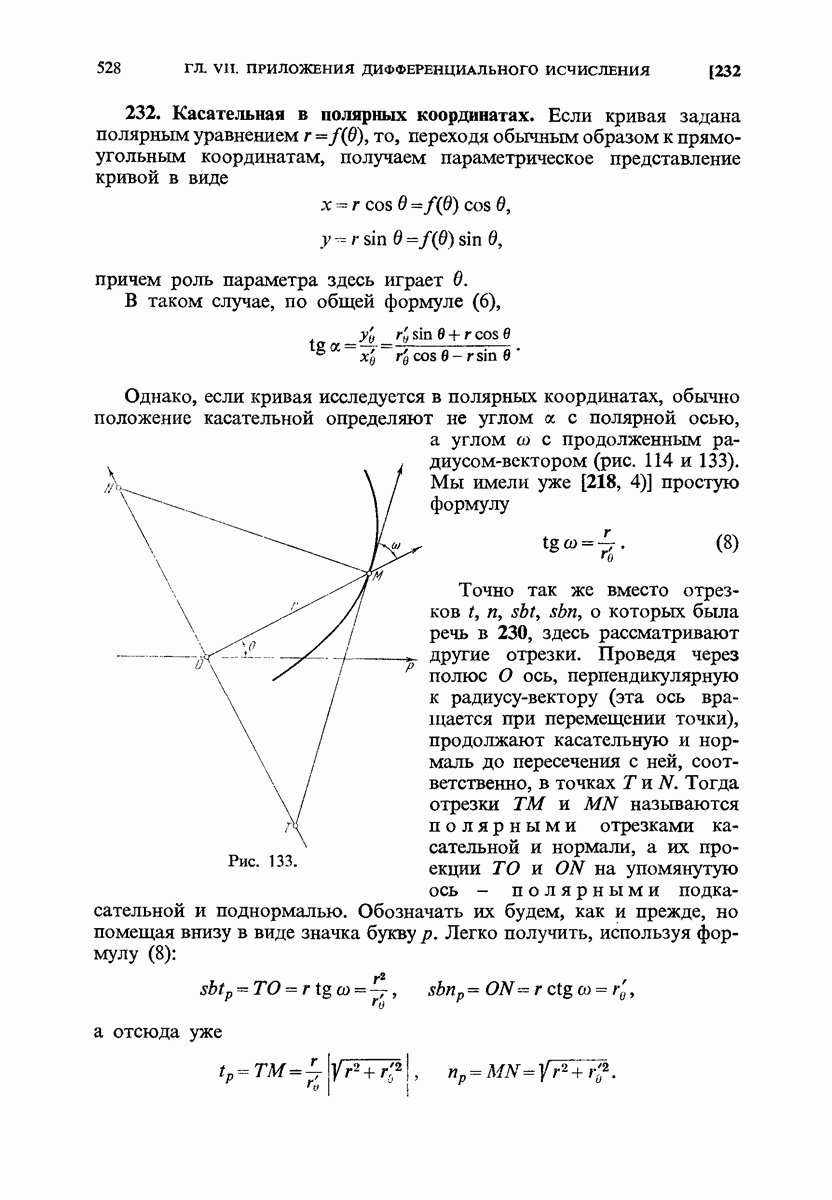
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
252. Примеры.
1) Цепная линия: (рис. 41)
В этом случае [ср. 99, 28)]

с другой стороны,

Поэтому [см. (7а)]

Так как то же выражение, как нетрудно видеть, имеет и отрезок нормали  то приходим к такому способу построения центра кривизны С: отрезок нормали
то приходим к такому способу построения центра кривизны С: отрезок нормали  (см. рис.) нужно отложить по нормали же, но в обратную (положительную) сторону.
(см. рис.) нужно отложить по нормали же, но в обратную (положительную) сторону.
2) Астроида: (рис. 116)

Производные  можно найти, не разрешая уравнения, по методу дифференцирования неявных функций:
можно найти, не разрешая уравнения, по методу дифференцирования неявных функций:

откуда

затем:

откуда

Подставляя значения у и у" в формулу (7а), получим

3) Циклоида:

(рис. 118).
Так как [231, 4)]  то
то  с другой же стороны, как легко вычислить,
с другой же стороны, как легко вычислить,

так что

В таком случае для вычисления  можно воспользоваться основной формулой (6):
можно воспользоваться основной формулой (6):

Если вспомнить выведенное нами в 231, 4) выражение для отрезка нормали и, то окажется, что

Отсюда - построение центра кривизны С, ясное из чертежа.
4) Эвольвента круга:

(рис. 121).
Здесь  [231, 6)], так что
[231, 6)], так что  . С другой стороны,
. С другой стороны,

отсюда

Поэтому также получаем просто

Таким образом, точка касания В (точка схода нити с круга) и будет центром кривизны для траектории конца М нити. Геометрическим местом центров кривизны нашей кривой оказывается исхо дный круг.
[Здесь мы сталкиваемся с частным осуществлением одного факта, который в общем виде будет рассмотрен нами ниже, в 255.]
5) Логарифмическая спираль:  (рис. 134).
(рис. 134).
Имеем  Подставляя это в формулу (76), найдем:
Подставляя это в формулу (76), найдем:

Но  так что выражение для
так что выражение для  можно написать в виде
можно написать в виде

а тогда непосредственно из чертежа ясно, что полярный отрезок нормали  . Следовательно, центром кривизны будет точка
. Следовательно, центром кривизны будет точка  это дает легкий способ построения центра кривизны для логарифмической спирали.
это дает легкий способ построения центра кривизны для логарифмической спирали.
6) Кардиоида:  (рис. 135).
(рис. 135).
Здесь  Легко подсчитать, что
Легко подсчитать, что

остается еще вычислить

а тогда, по формуле (76), сразу получаем

Вспоминая [233, 4)] выражение полярного отрезка нормали для кардиоиды, видим, что

7) Лемниската:  (рис. 126).
(рис. 126).
Мы видели в 233, 5), что в этом случае  так что
так что  Но тогда по формуле (6) сразу получаем
Но тогда по формуле (6) сразу получаем

Так как нормаль к лемнискате мы строить умеем, то отсюда получается и способ построения центра кривизны.
8) Парабола: 
Пользуясь здесь методами дифференцирования неявных функций, найдем последовательно

Теперь, по формуле (7а),

Вспоминая [231, 1)], что отрезок нормали  получаем
получаем

9) Эллипс и гипербола: 
Дифференцируем это равенство дважды:

далее,

Как и только что, отсюда

Мы имели уже [231, 2)] для этого случая выражение отрезка нормали

так что

Известно, что как для эллипса, так и для гиперболы полупараметр  выражается так:
выражается так:  . Поэтому и здесь для
. Поэтому и здесь для  получается то же окончательное выражение, что и для параболы.
получается то же окончательное выражение, что и для параболы.
Для всех трех конических сечений радиус кривизны оказывается пропорционален кубу отрезка нормали.
10) В заключение скажем несколько слов об одном практическом вопросе, в котором как раз и используется существенно изменение кривизны вдоль кривой: речь идет о так называемых переходных кривых, применяемых при разбивке железнодорожных закруглений.
Как устанавливается в механике, при движении материальной точки по кривой развивается центробежная сила, величина которой определяется формулой

где  - масса точки,
- масса точки,  - ее скорость,
- ее скорость,  радиус кривизны кривой в рассматриваемой ее точке.
радиус кривизны кривой в рассматриваемой ее точке.
Если бы прямолинейная часть железнодорожного пути непосредственно примыкала к закруглению, разбитому по дуге круга (рис. 159 а), то при переходе на это закругление центробежная сила возникала бы мгновенно, создавая резкий и сильный толчок, вредный для подвижного состава и для верхнего строения пути.

Рис. 159.
Для избежания этого прямолинейную часть пути сопрягают с круговой с помощью некоей переходной кривой (рис. 159 б). Вдоль нее радиус кривизны постепенно убывает от бесконечного значения - в точке стыка с
прямолинейной частью - до величины радиуса круга - в точке стыка с круговой дугой, и соответственно этому постепенно нарастает центробежная сила. В качестве переходной кривой чаще всего используется кубическая парабола  . В этом случае, очевидно, имеем
. В этом случае, очевидно, имеем 

так что для радиуса кривизны получается выражение

При  имеем
имеем  наша кривая в начале координат касается оси х и имеет нулевую кривизну
наша кривая в начале координат касается оси х и имеет нулевую кривизну 
Иногда в роли переходной кривой применяется и лемниската.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Упорядочение области рациональных чисел.
- 3. Сложение и вычитание рациональных чисел.
- 4. Умножение и деление рациональных чисел.
- 5. Аксиома Архимеда.
- § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
- 7. Упорядочение области вещественных чисел.
- 8. Вспомогательные предложения.
- 9. Представление вещественного числа бесконечной десятичной дробью.
- 10. Непрерывность области вещественных чисел.
- 11. Границы числовых множеств.
- § 3. Арифметические действия над вещественными числами
- 13. Свойства сложения.
- 14. Определение произведения вещественных чисел.
- 15. Свойства умножения.
- 16. Заключение.
- 17. Абсолютные величины.
- § 4. Дальнейшие свойства и приложения вещественных чисел
- 19. Степень с любым вещественным показателем.
- 20. Логарифмы.
- 21. Измерение отрезков.
- ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. Варианта и ее предел
- 23. Предел варианты.
- 24. Бесконечно малые величины.
- 25. Примеры.
- 26. Некоторые теоремы о варианте, имеющей предел.
- 27. Бесконечно большие величины.
- § 2. Теоремы о пределах, облегчающие нахождение пределов
- 29. Леммы о бесконечно малых.
- 30. Арифметические операция над переменными.
- 31. Неопределенные выражения.
- 32. Примеры на нахождение пределов.
- 33. Теорема Штольца и ее применения.
- § 3. Монотонная варианта
- 35. Примеры.
- 36. Число е.
- 37. Приближенное вычисление числа е.
- 38. Лемма о вложенных промежутках.
- § 4. Принцип сходимости. Частичные пределы
- 40. Частичные последовательности и частичные пределы.
- 41. Лемма Больцано — Вейерштрасса
- 42. Наибольший и наименьший пределы.
- ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. Понятие функции
- 44. Функциональная зависимость между переменными. Примеры.
- 45. Определение понятия функции.
- 46. Аналитический способ задания функции.
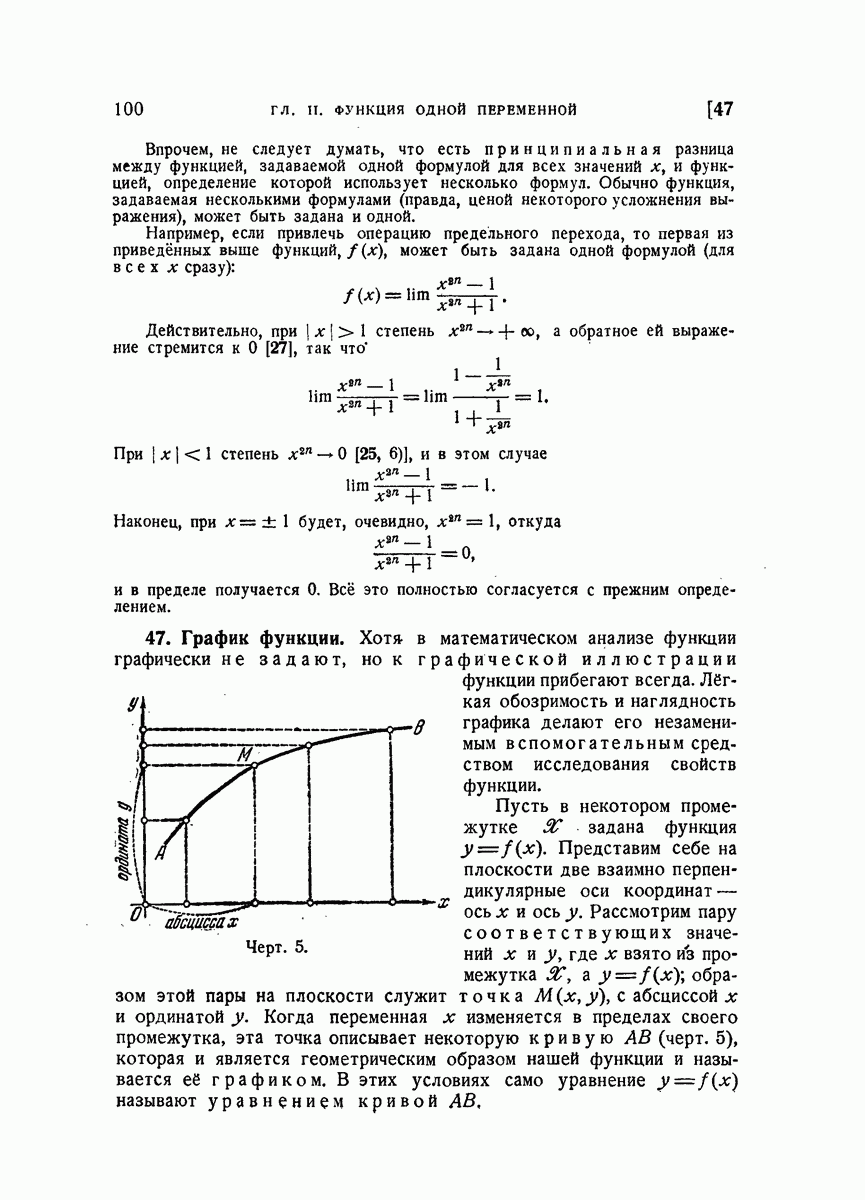
- 47. График функции.
- 48. Важнейшие классы функций.
- 49. Понятие обратной функции.
- 50. Обратные тригонометрические функции.
- 51. Суперпозиция функций. Заключительные замечания.
- § 2. Предел функции
- 53. Сведение к случаю варианты.
- 54. Примеры.
- 55. Распространение теории пределов.
- 56. Примеры.
- 57. Предел монотонной функции.
- 58. Общий признак Больцано—Коши.
- 59. Наибольший и наименьший пределы функции.
- § 3. Классификация бесконечно малых и бесконечно больших величин
- 61. Шкала бесконечно малых.
- 62. Эквивалентные бесконечно малые.
- 63. Выделение главной части.
- 64. Задачи.
- 65. Классификация бесконечно больших.
- § 4. Непрерывность (и разрывы) функций
- 67. Арифметические операции над непрерывными функциями.
- 68. Примеры непрерывных функций.
- 69. Односторонняя непрерывность. Классификация разрывов.
- 70. Примеры разрывных функций.
- 71. Непрерывность и разрывы монотонной функции.
- 72. Непрерывность элементарных функций.
- 73. Суперпозиция непрерывных функций.
- 74. Решение одного функционального уравнения.
- 75. Функциональная характеристика показательной, логарифмической и степенной функций.
- 76. Функциональная характеристика тригонометрического и гиперболического косинусов.
- 77. Использование непрерывности функций для вычисления пределов.
- 78. Степенно-показательные выражения.
- 79. Примеры.
- § 5. Свойства непрерывных функций
- 81. Применение к решению уравнений.
- 82. Теорема о промежуточном значении.
- 83. Существование обратной функции.
- 84. Теорема об ограниченности функции.
- 85. Наибольшее и наименьшее значения функции.
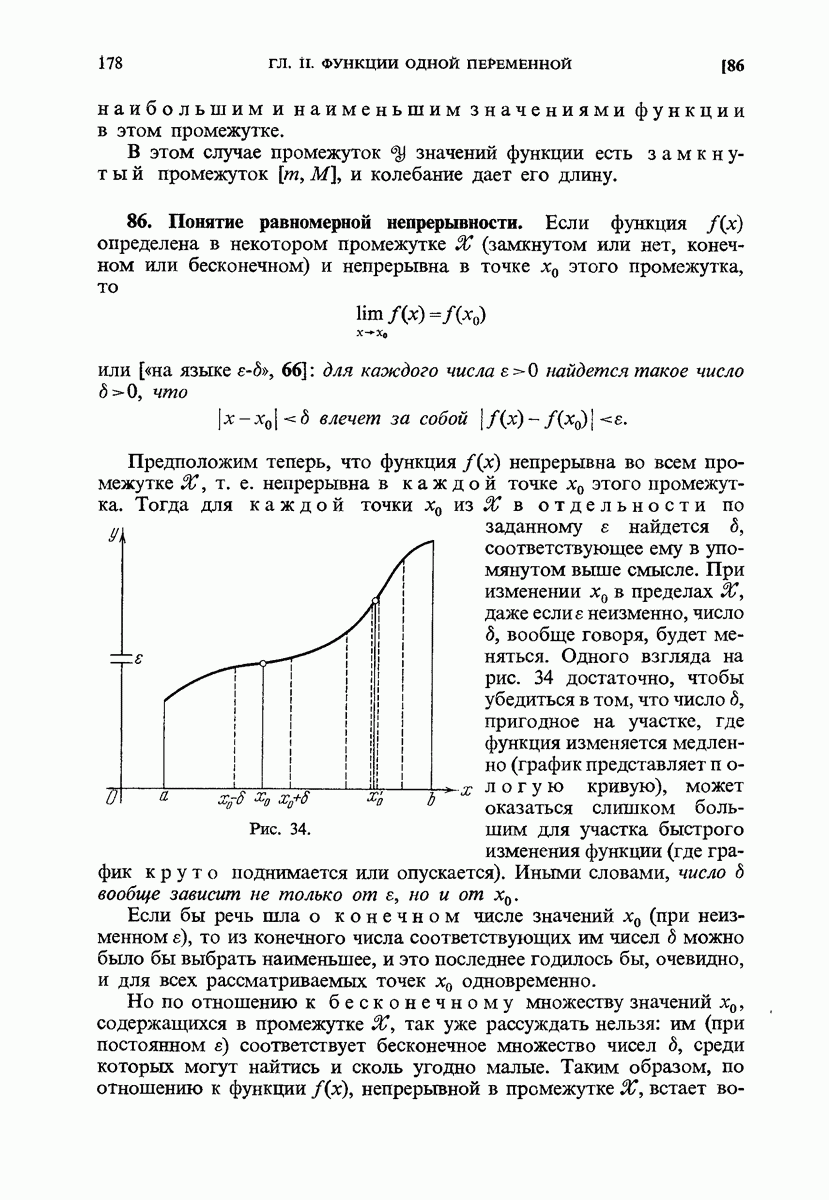
- 86. Понятие равномерной непрерывности.
- 87. Теорема Кантора.
- 88. Лемма Бореля.
- 89. Новые доказательства основных теорем.
- ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная и ее вычисление
- 91. Задача о проведении касательной к кривой.
- 92. Определение производной.
- 93. Примеры вычисления производных.
- 94. Производная обратной функции.
- 95. Сводка формул для производных.
- 96. Формула для превращения функции.
- 97. Простейшие правила вычисления производных.
- 98. Производная сложной функции.
- 100. Односторонние производные.
- 101. Бесконечные производные.
- 102. Дальнейшие примеры особых случаев.
- § 2. Дифференциал
- 104. Связь между диффереицируемостью и существованием производной.
- 105. Основные формулы и правила дифференцирования.
- 106. Инвариантность формы дифференциала.
- 107. Дифференциалы как источник приближенных формул.
- 108. Применение дифференциалов при оценке погрешностей.
- § 3. Основные теоремы дифференциального исчисления
- 110. Теорема Дарбу
- 111. Теорема Ролля.
- 112. Формула Лагранжа.
- 113. Предел производной.
- 114. Формула Коши.
- § 4. Производные и дифференциалы высших порядков
- 116. Общие формулы для производных любого порядка.
- 117. Формула Лейбница.
- 118. Примеры.
- 119. Дифференциалы высших порядков.
- 120. Нарушение инвариантности формы для дифференциалов высших порядков.
- 121. Параметрическое дифференцирование.
- 122. Конечные разности.
- § 5. Формула Тейлора
- 124. Разложение произвольной функции; дополнительный член в форме Пеано.
- 125. Примеры.
- 126. Другие формы дополнительного члена.
- 127. Приближенные формулы.
- § 6. Интерполирование
- 129. Дополнительный члеп формулы Лагранжа.
- 130. Интерполирование с кратными узлами. Формула Эрмита.
- ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
- § 1. Изучение хода изменения функции
- 132. Условие монотонности функции.
- 133. Доказательство неравенств.
- 134. Максимумы и минимумы; необходимые условия.
- 136. Достаточные условия. Первое правило.
- 136. Примеры.
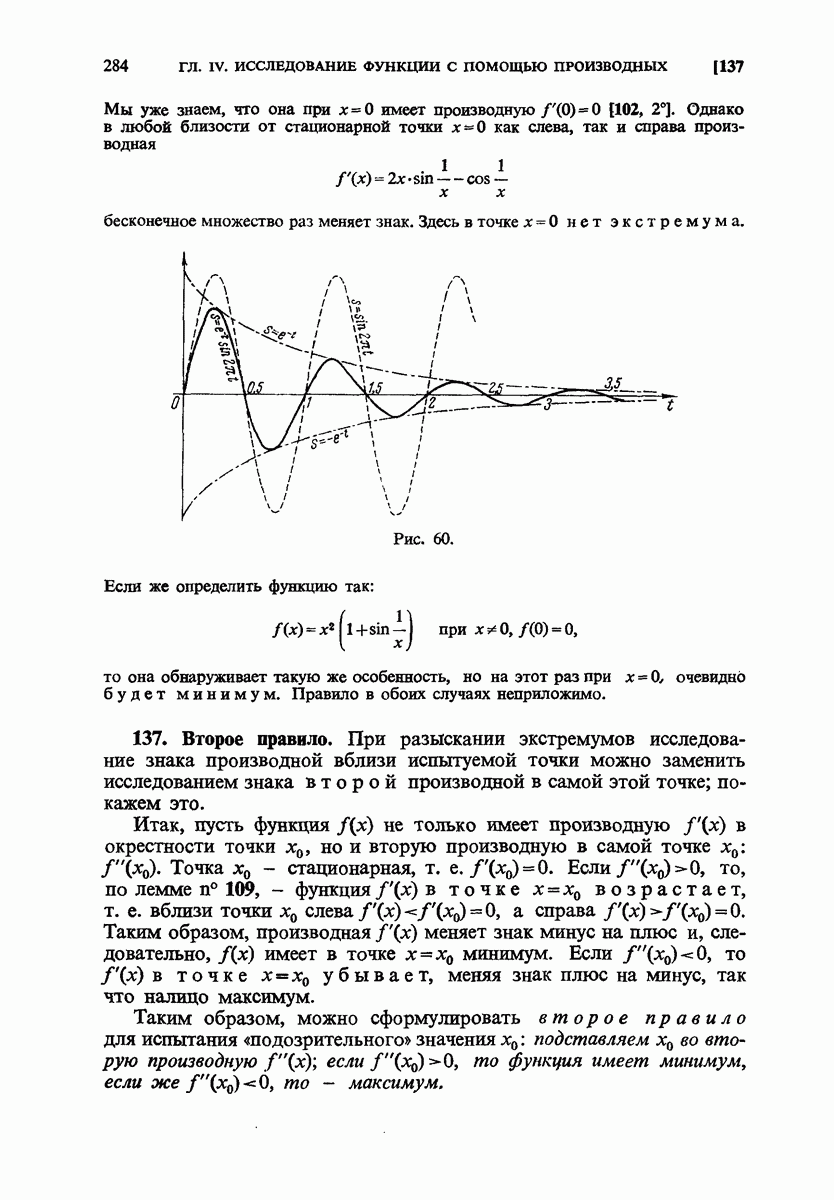
- 137. Второе правило.
- 138. Использование высших производных.
- 139. Разыскание наибольших и наименьших значений.
- 140. Задачи.
- § 2. Выпуклые (и вогнутые) функции
- 142. Простейшие предложения о выпуклых функциях.
- 143. Условия выпуклости функции.
- 144. Неравенство Иенсена и его приложения.
- 145. Точки перегиба.
- § 3. Построение графиков функций
- 147. Схема построения графика. Примеры.
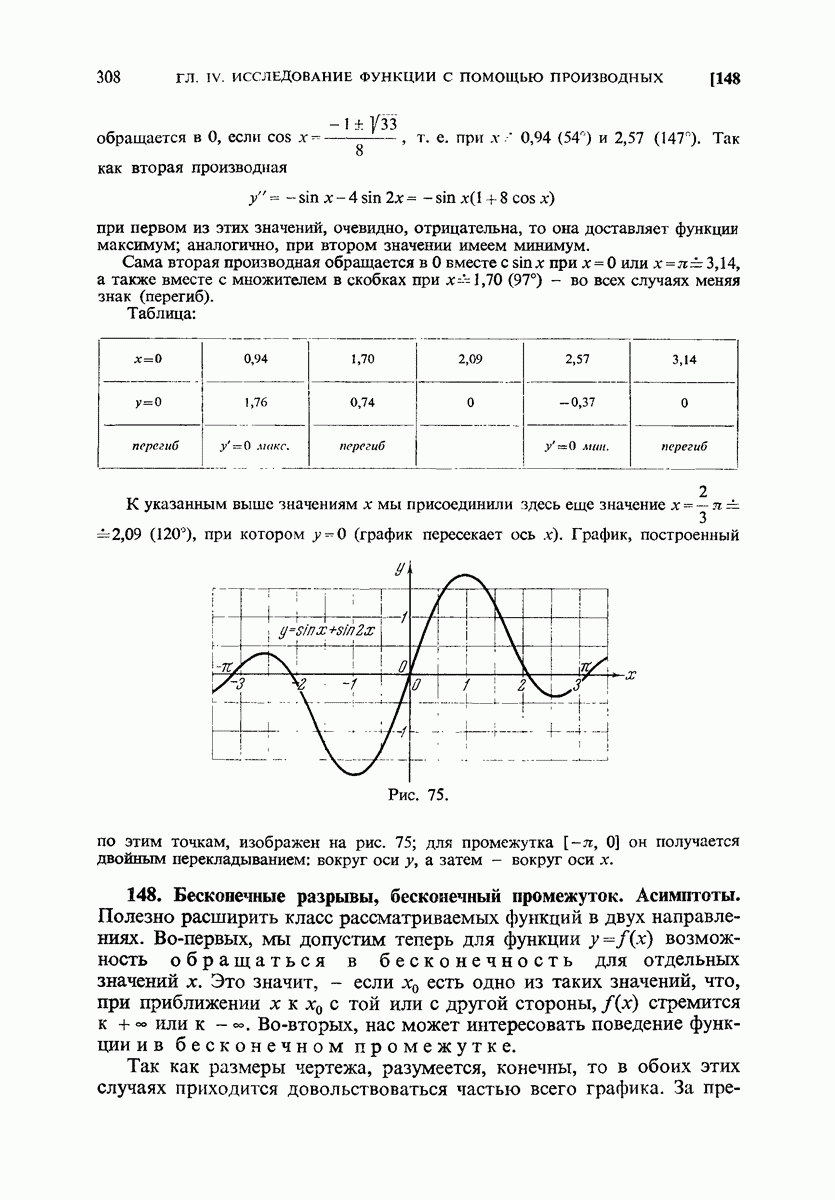
- 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
- 149. Примеры.
- § 4. Раскрытие неопределенностей
- 151. Неопределенность вида oo/oo
- 152. Другие виды неопределенностей.
- § 5. Приближенное решение уравнений
- 154. Правило пропорциональных частей (метод хорд).
- 155. Правило Ньютона (метод касательных).
- 156. Примеры в упражнения.
- 157. Комбинированный метод.
- 158. Примеры и упражнения.
- ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 159. Функциональная зависимость между переменными. Примеры.
- 160. Функции двух переменных и области их определения.
- 161. Арифметическое n-мерное пространство.
- 162. Примеры областей в n-мерном пространстве.
- 163. Общее определение открытой и замкнутой области.
- 164. Функции n переменных.
- 165. Предел функции нескольких переменных.
- 166. Сведение к случаю варианты.
- 167. Примеры.
- 168. Повторные пределы.
- § 2. Непрерывные функции
- 170. Операции над непрерывными функциями.
- 171. Функции, непрерывные в области. Теоремы Больцано—Коши.
- 172. Лемма Больцано—Вейерштрасса.
- 173. Теоремы Вейерштрасса.
- 174. Равномерная непрерывность.
- 175. Лемма Бореля.
- 176. Новые доказательства основных теорем.
- § 3. Производные и дифференциалы функций нескольких переменных
- 178. Полное приращение функции.
- 179. Полный дифференциал.
- 180. Геометрическая интерпретация для случая функции двух переменных.
- 181. Производные от сложных функций.
- 182. Примеры.
- 183. Формула конечных приращений.
- 184. Производная по заданному направлению.
- 185. Инвариантность формы (первого) дифференциала.
- 186. Применение полного дифференциала в приближенных вычислениях.
- 187. Однородные функции.
- 188. Формула Эйлера.
- § 4. Производные и дифференциалы высших порядков
- 190. Теорема о смешанных производных.
- 191. Обобщение.
- 192. Производные высших порядков от сложной функции.
- 193. Дифференциалы высших порядков.
- 194. Дифференциалы сложных функций.
- 195. Формула Тейлора.
- § 5. Экстремумы, наибольшие и наименьшие значения
- 197. Достаточные условия (случай функции двух переменных).
- 198. Достаточные условия (общий случай).
- 199. Условия отсутствия экстремума.
- 200. Наибольшее и наименьшее значения функции. Примеры.
- 201. Задачи.
- ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
- § 1. Формальные свойства функциональных определителей
- 203. Умножение якобианов.
- 204. Умножение функциональных матриц (матриц Якоби).
- § 2. Неявные функции
- 206. Существование неявной функции.
- 207. Дифференцируемость неявной функции.
- 208. Неявные функции от нескольких переменных.
- 209. Вычисление производных неявных функций.
- 210. Примеры.
- § 3. Некоторые приложения теории неявных функций
- 212. Метод неопределенных множителей Лагранжа.
- 213. Достаточные для относительного экстремума условия.
- 214. Примеры и задачи.
- 215. Понятие независимости функций.
- 216. Ранг матрицы Якоби.
- § 4. Замена переменных
- 218. Примеры.
- 219. Функции нескольких переменных. Замена независимых переменных.
- 220. Метод вычисления дифференциалов.
- 221. Общий случай замены переменных.
- 222. Примеры.
- ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
- § 1. Аналитическое представление кривых и поверхностей
- 224. Примеры.
- 225. Кривые механического происхождения.
- 226. Кривые на плоскости (в полярных координатах). Примеры.
- 227. Поверхности и кривые в пространстве.
- 228. Параметрическое представление.
- 229. Примеры.
- § 2. Касательная и касательная плоскость
- 231. Примеры.
- 232. Касательная в полярных координатах.
- 233. Примеры.
- 234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
- 235. Примеры.
- 236. Особые точки плоских кривых.
- 237. Случай параметрического задания кривой.
- § 3. Касание кривых между собой
- 239. Примеры.
- 240. Характеристические точки.
- 241. Порядок касания двух кривых.
- 242. Случай неявного задания одной из кривых.
- 243. Соприкасающаяся кривая.
- 244. Другой подход к соприкасающимся кривым.
- § 4. Длина плоской кривой
- 246. Направление на кривой.
- 247. Длина кривой. Аддитивность длины дуги.
- 248. Достаточные условия спрямляемости. Дифференциал дуги.
- 249. Дуга в роли параметра. Положительное направление касательной.
- § 5. Кривизна плоской кривой
- 251. Круг кривизны и радиус кривизны.
- 252. Примеры.
- 253. Координаты центра кривизны.
- 254. Определение эволюты и эвольвенты; разыскание эволюты.
- 255. Свойства эволют и эвольвент.
- 256. Разыскание эвольвент.
- ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ