| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
45. Определение понятия функции.
Отвлечемся теперь, как обычно, от физического смысла рассматриваемых величин и дадим точное общее определение понятия функции - одного из основных понятий математического анализа.
Пусть даны две переменные х и у с областями изменения X и Предположим, что по условиям вопроса переменной х может быть приписано произвольное значение из области X без каких-либо ограничений. Тогда переменная у называется функцией от переменной х в области ее изменения X, если по некоторому правилу или закону каждому значению х из X ставится в соответствие одно определенное значение у (из 
Независимая переменная х называется также аргументом функции.
В этом определении существенны два момента: во-первых, указание области X изменения аргумента х (её называют областью определения функции) и, во-вторых, установление правила или закона соответствия между значениями х и у. (Область  изменения функции у обычно не указывается, поскольку самый закон соответствия уже определяет множество принимаемых функцией значений.)
изменения функции у обычно не указывается, поскольку самый закон соответствия уже определяет множество принимаемых функцией значений.)
Можно в определении понятия функции стать на более общую точку зрения, допуская, чтобы каждому значению х из X отвечало
не одно, а несколько значений у (и даже бесконечное множество их). В подобных случаях функцию называют многозначной, в отличие от однозначной функции, определенной выше. Впрочем, в курсе анализа, стоящем на точке зрения вещественной переменной, избегают многозначных функций, и впредь говоря о функции, если не оговорено противное, мы будем разуметь однозначную функцию.
Для указания того факта, что у есть функция от х, пишут:

Буквы  характеризуют именно то правило, по которому получается значение у, отвечающее заданному х. Поэтому, если одновременно рассматриваются различные функции от одного и того же аргумента х, связанные с различными законами соответствия, их не следует обозначать одной и той же буквой.
характеризуют именно то правило, по которому получается значение у, отвечающее заданному х. Поэтому, если одновременно рассматриваются различные функции от одного и того же аргумента х, связанные с различными законами соответствия, их не следует обозначать одной и той же буквой.
Хотя именно буква  (в различных алфавитах) связана со словом «функция», но для обозначения функциональной зависимости, разумеется, может применяться и любая другая буква; иногда даже повторяют ту же букву у:
(в различных алфавитах) связана со словом «функция», но для обозначения функциональной зависимости, разумеется, может применяться и любая другая буква; иногда даже повторяют ту же букву у: 
В некоторых случаях пишут аргумент и в виде значка при функции, например,  Под этот тип подходит привычное нам обозначение варианты
Под этот тип подходит привычное нам обозначение варианты  которая является (как мы теперь можем сказать) функцией от «независимой переменной»
которая является (как мы теперь можем сказать) функцией от «независимой переменной»  пробегающей ряд натуральных чисел
пробегающей ряд натуральных чисел  Аналогично и обозначение
Аналогично и обозначение  для номера
для номера  (в определении предела варианты, 23), которое подчеркивает его зависимость от
(в определении предела варианты, 23), которое подчеркивает его зависимость от  и т. д.
и т. д.
Если, рассматривая функцию, скажем,  мы хотим отметить ее частное значение, которое отвечает выбранному частному значению х, равному
мы хотим отметить ее частное значение, которое отвечает выбранному частному значению х, равному  то для обозначения его употребляют символ:
то для обозначения его употребляют символ:  Например, если
Например, если

то  означает численное значение функции
означает численное значение функции  при
при  т. е. попросту число
т. е. попросту число  аналогично,
аналогично,  означает число
означает число  число
число  и т. п.
и т. п.
Обратимся теперь к самому правилу или закону соответствия между значениями переменных, которое составляет сущность понятия функциональной зависимости. Правило это может быть весьма разнообразной природы, поскольку оно ничем не было ограничено.
Наиболее простым и естественным представляется осуществление этого правила в виде аналитического выражения или
формулы, содержащих указание на те операции или действия над постоянными числами и над значением х, которые надо произвести, чтобы получить соответствующее значение у. Этот аналитический способ задания функции является наиболее важным для математического анализа (мы еще вернемся к нему в следующем п°). С ним читатель всего лучше знаком из школьного курса математики; наконец, именно аналитическим способом мы пользовались в приведенных в 44 примерах.
Однако было бы ошибочным думать, что это - единственный способ, которым может быть задана функция. В самой математике нередки случаи, когда функция определяется без помощи формулы. Такова, например, функция  - «целая часть числа
- «целая часть числа  . Легко сообразить, что
. Легко сообразить, что

хотя никакой формулы, выражающей  нас нет.
нас нет.
Таковы также и многочисленные «арифметические функции», т. е., функции от натурального аргумента, принимающие лишь натуральные же значения. В виде примера упомянем «о факториале числа и»:

а также о функции  представляющей число делителей числа и, или о функции
представляющей число делителей числа и, или о функции  указывающей, сколько в ряду
указывающей, сколько в ряду  имеется чисел, взаимно простых с и. Несмотря на своеобразный характер правил, которыми задаются эти функции, они позволяют вычислять значения функций с такой же определенностью, как и формулы. Например, имеем:
имеется чисел, взаимно простых с и. Несмотря на своеобразный характер правил, которыми задаются эти функции, они позволяют вычислять значения функций с такой же определенностью, как и формулы. Например, имеем:

В естественных науках и в технике зависимость между величинами часто устанавливается экспериментально или путем наблюдений. Например, если подвергнуть воду произвольно выбранному давлению  (атм), то на опыте можно определить соответствующую ему температуру
(атм), то на опыте можно определить соответствующую ему температуру  кипения воды: в есть функция от
кипения воды: в есть функция от  . Однако эта функциональная зависимость задается не какой-либо формулой, а лишь таблицей, где просто сопоставлены полученные из опыта данные. Примеры табличного способа задания функции легко найти в любом техническом справочнике.
. Однако эта функциональная зависимость задается не какой-либо формулой, а лишь таблицей, где просто сопоставлены полученные из опыта данные. Примеры табличного способа задания функции легко найти в любом техническом справочнике.
Наконец, упомянем еще, что в некоторых случаях - при помощи самопишущих приборов - функциональная зависимость между физическими величинами задается непосредственно графиком. Например, «индикаторная диаграмма», снимаемая при помощи индикатора,
тора, дает зависимость между объемом V и давлением  пара в цилиндре работающей паровой машины; «барограмма», доставляемая барографом, представляет суточный ход атмосферного давления, и т. п.
пара в цилиндре работающей паровой машины; «барограмма», доставляемая барографом, представляет суточный ход атмосферного давления, и т. п.
Мы не входим в подробности относительно табличного и графического способов задания функциональной зависимости, так как ими в математическом анализе не приходится пользоваться.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Упорядочение области рациональных чисел.
- 3. Сложение и вычитание рациональных чисел.
- 4. Умножение и деление рациональных чисел.
- 5. Аксиома Архимеда.
- § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
- 7. Упорядочение области вещественных чисел.
- 8. Вспомогательные предложения.
- 9. Представление вещественного числа бесконечной десятичной дробью.
- 10. Непрерывность области вещественных чисел.
- 11. Границы числовых множеств.
- § 3. Арифметические действия над вещественными числами
- 13. Свойства сложения.
- 14. Определение произведения вещественных чисел.
- 15. Свойства умножения.
- 16. Заключение.
- 17. Абсолютные величины.
- § 4. Дальнейшие свойства и приложения вещественных чисел
- 19. Степень с любым вещественным показателем.
- 20. Логарифмы.
- 21. Измерение отрезков.
- ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. Варианта и ее предел
- 23. Предел варианты.
- 24. Бесконечно малые величины.
- 25. Примеры.
- 26. Некоторые теоремы о варианте, имеющей предел.
- 27. Бесконечно большие величины.
- § 2. Теоремы о пределах, облегчающие нахождение пределов
- 29. Леммы о бесконечно малых.
- 30. Арифметические операция над переменными.
- 31. Неопределенные выражения.
- 32. Примеры на нахождение пределов.
- 33. Теорема Штольца и ее применения.
- § 3. Монотонная варианта
- 35. Примеры.
- 36. Число е.
- 37. Приближенное вычисление числа е.
- 38. Лемма о вложенных промежутках.
- § 4. Принцип сходимости. Частичные пределы
- 40. Частичные последовательности и частичные пределы.
- 41. Лемма Больцано — Вейерштрасса
- 42. Наибольший и наименьший пределы.
- ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. Понятие функции
- 44. Функциональная зависимость между переменными. Примеры.
- 45. Определение понятия функции.
- 46. Аналитический способ задания функции.
- 47. График функции.
- 48. Важнейшие классы функций.
- 49. Понятие обратной функции.
- 50. Обратные тригонометрические функции.
- 51. Суперпозиция функций. Заключительные замечания.
- § 2. Предел функции
- 53. Сведение к случаю варианты.
- 54. Примеры.
- 55. Распространение теории пределов.
- 56. Примеры.
- 57. Предел монотонной функции.
- 58. Общий признак Больцано—Коши.
- 59. Наибольший и наименьший пределы функции.
- § 3. Классификация бесконечно малых и бесконечно больших величин
- 61. Шкала бесконечно малых.
- 62. Эквивалентные бесконечно малые.
- 63. Выделение главной части.
- 64. Задачи.
- 65. Классификация бесконечно больших.
- § 4. Непрерывность (и разрывы) функций
- 67. Арифметические операции над непрерывными функциями.
- 68. Примеры непрерывных функций.
- 69. Односторонняя непрерывность. Классификация разрывов.
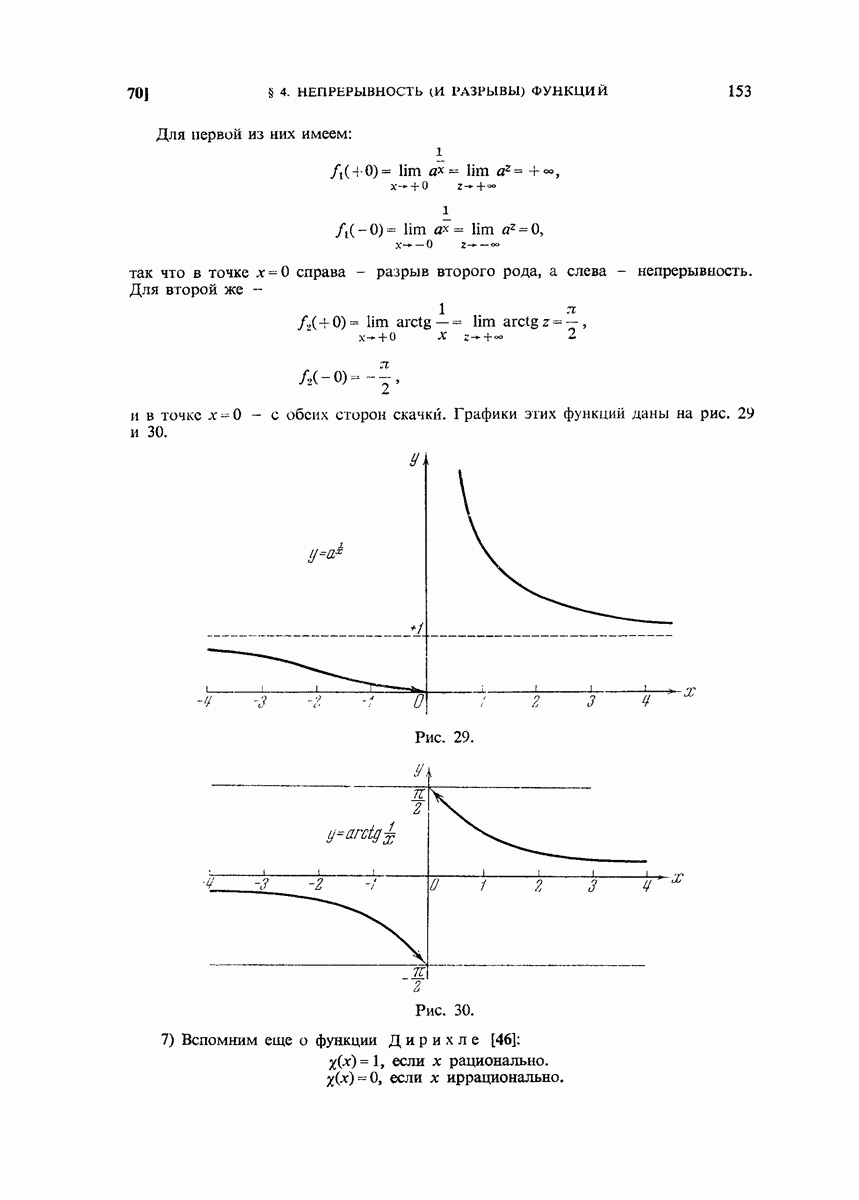
- 70. Примеры разрывных функций.
- 71. Непрерывность и разрывы монотонной функции.
- 72. Непрерывность элементарных функций.
- 73. Суперпозиция непрерывных функций.
- 74. Решение одного функционального уравнения.
- 75. Функциональная характеристика показательной, логарифмической и степенной функций.
- 76. Функциональная характеристика тригонометрического и гиперболического косинусов.
- 77. Использование непрерывности функций для вычисления пределов.
- 78. Степенно-показательные выражения.
- 79. Примеры.
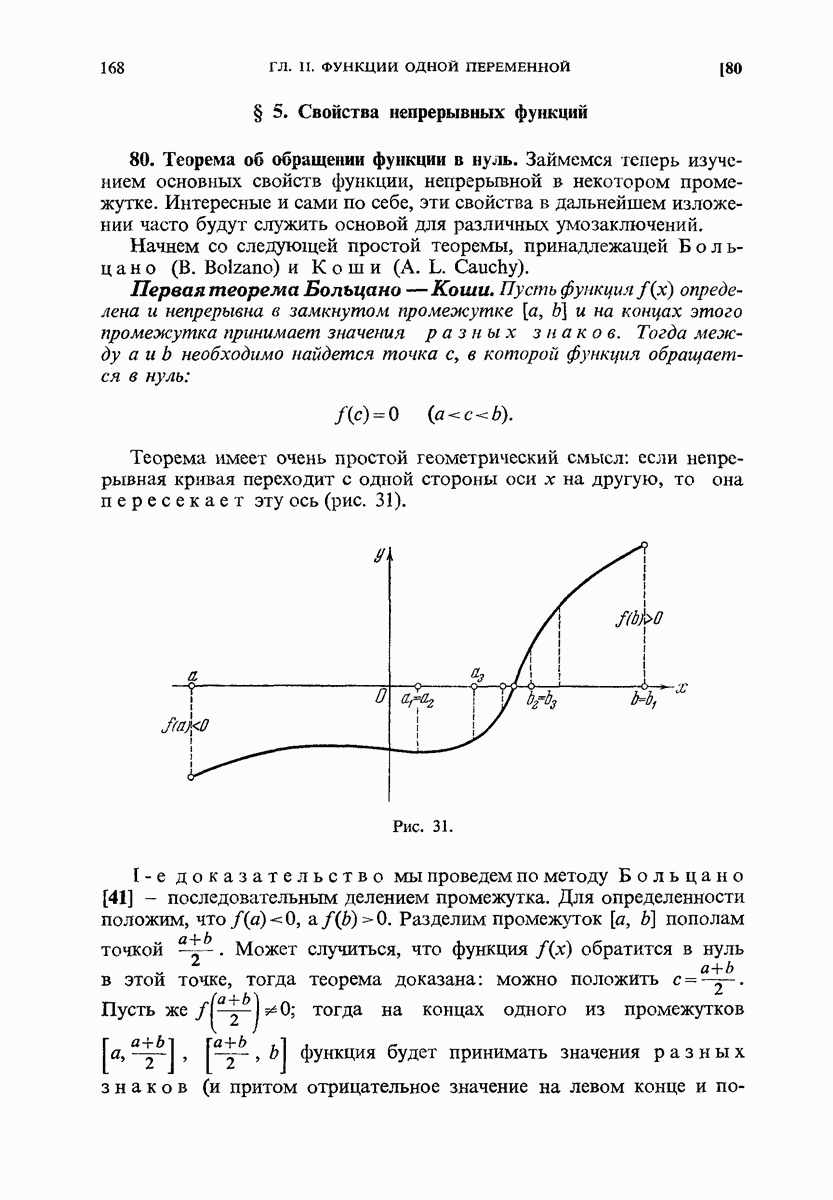
- § 5. Свойства непрерывных функций
- 81. Применение к решению уравнений.
- 82. Теорема о промежуточном значении.
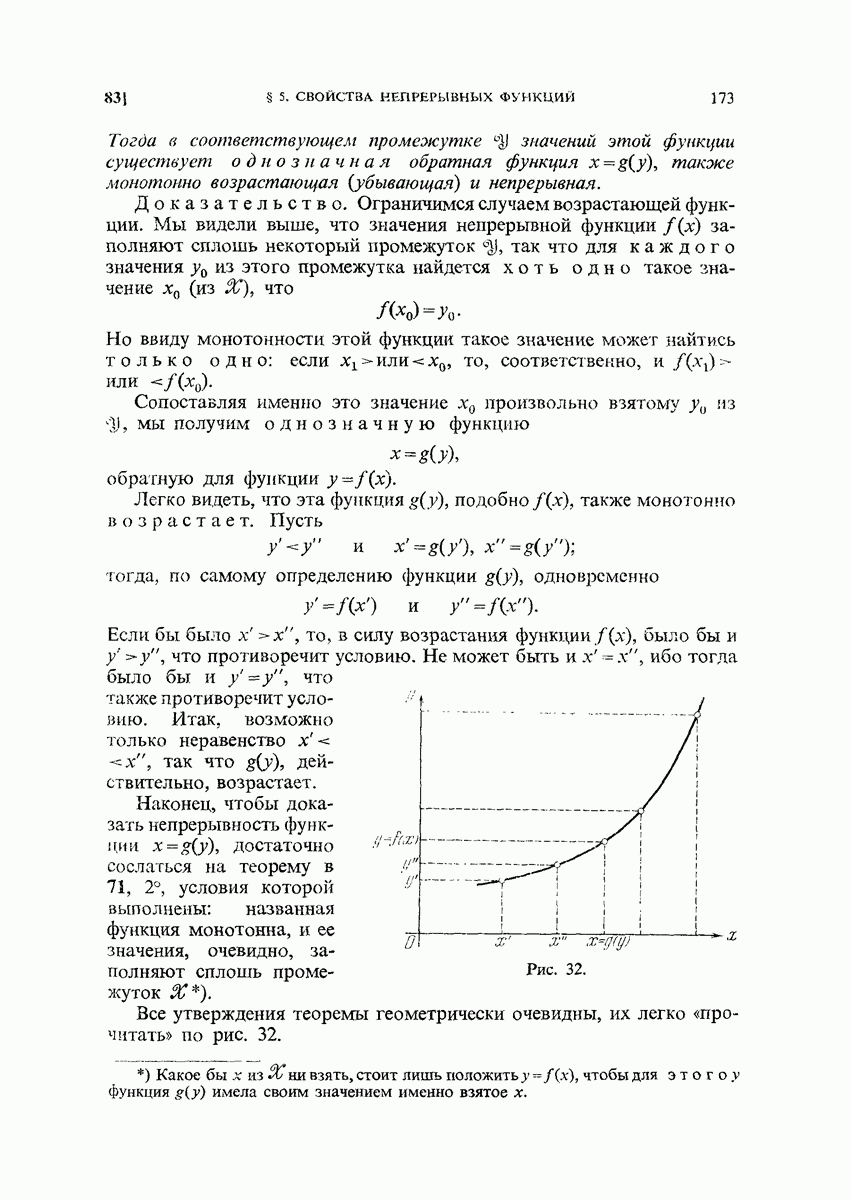
- 83. Существование обратной функции.
- 84. Теорема об ограниченности функции.
- 85. Наибольшее и наименьшее значения функции.
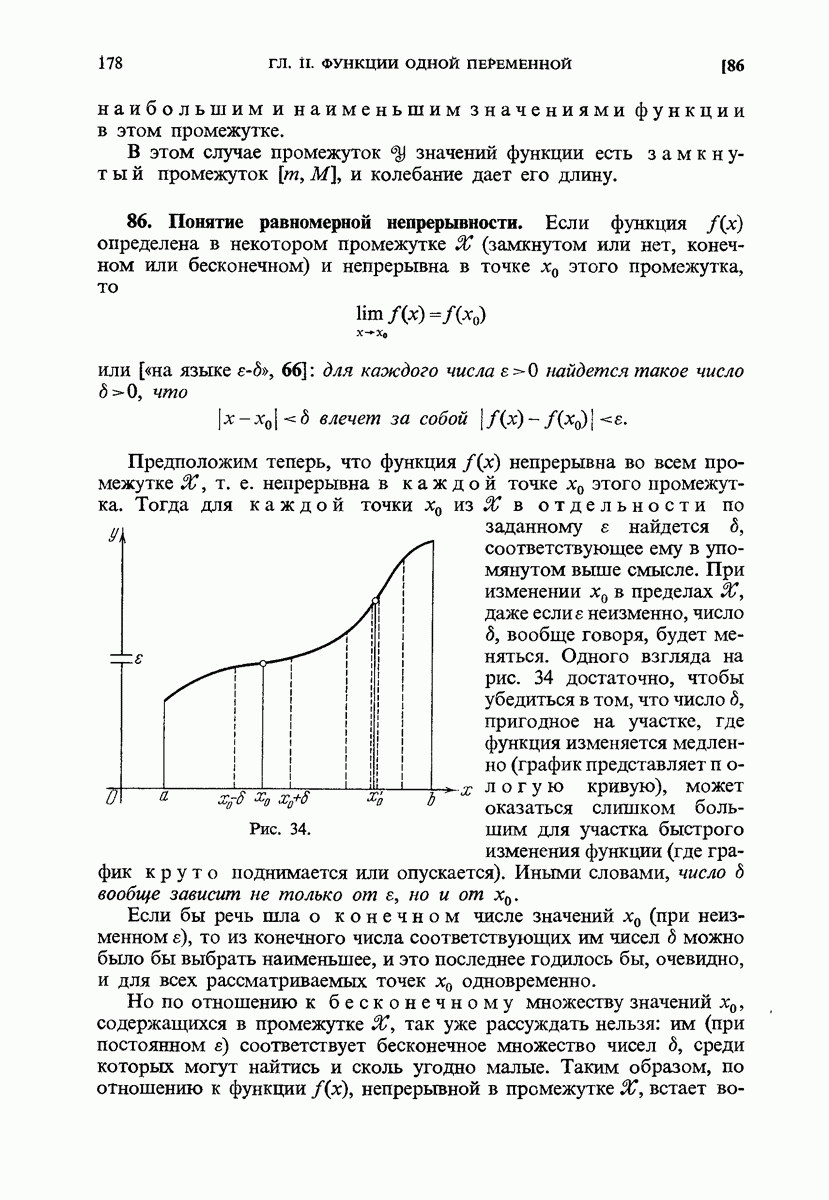
- 86. Понятие равномерной непрерывности.
- 87. Теорема Кантора.
- 88. Лемма Бореля.
- 89. Новые доказательства основных теорем.
- ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная и ее вычисление
- 91. Задача о проведении касательной к кривой.
- 92. Определение производной.
- 93. Примеры вычисления производных.
- 94. Производная обратной функции.
- 95. Сводка формул для производных.
- 96. Формула для превращения функции.
- 97. Простейшие правила вычисления производных.
- 98. Производная сложной функции.
- 100. Односторонние производные.
- 101. Бесконечные производные.
- 102. Дальнейшие примеры особых случаев.
- § 2. Дифференциал
- 104. Связь между диффереицируемостью и существованием производной.
- 105. Основные формулы и правила дифференцирования.
- 106. Инвариантность формы дифференциала.
- 107. Дифференциалы как источник приближенных формул.
- 108. Применение дифференциалов при оценке погрешностей.
- § 3. Основные теоремы дифференциального исчисления
- 110. Теорема Дарбу
- 111. Теорема Ролля.
- 112. Формула Лагранжа.
- 113. Предел производной.
- 114. Формула Коши.
- § 4. Производные и дифференциалы высших порядков
- 116. Общие формулы для производных любого порядка.
- 117. Формула Лейбница.
- 118. Примеры.
- 119. Дифференциалы высших порядков.
- 120. Нарушение инвариантности формы для дифференциалов высших порядков.
- 121. Параметрическое дифференцирование.
- 122. Конечные разности.
- § 5. Формула Тейлора
- 124. Разложение произвольной функции; дополнительный член в форме Пеано.
- 125. Примеры.
- 126. Другие формы дополнительного члена.
- 127. Приближенные формулы.
- § 6. Интерполирование
- 129. Дополнительный члеп формулы Лагранжа.
- 130. Интерполирование с кратными узлами. Формула Эрмита.
- ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
- § 1. Изучение хода изменения функции
- 132. Условие монотонности функции.
- 133. Доказательство неравенств.
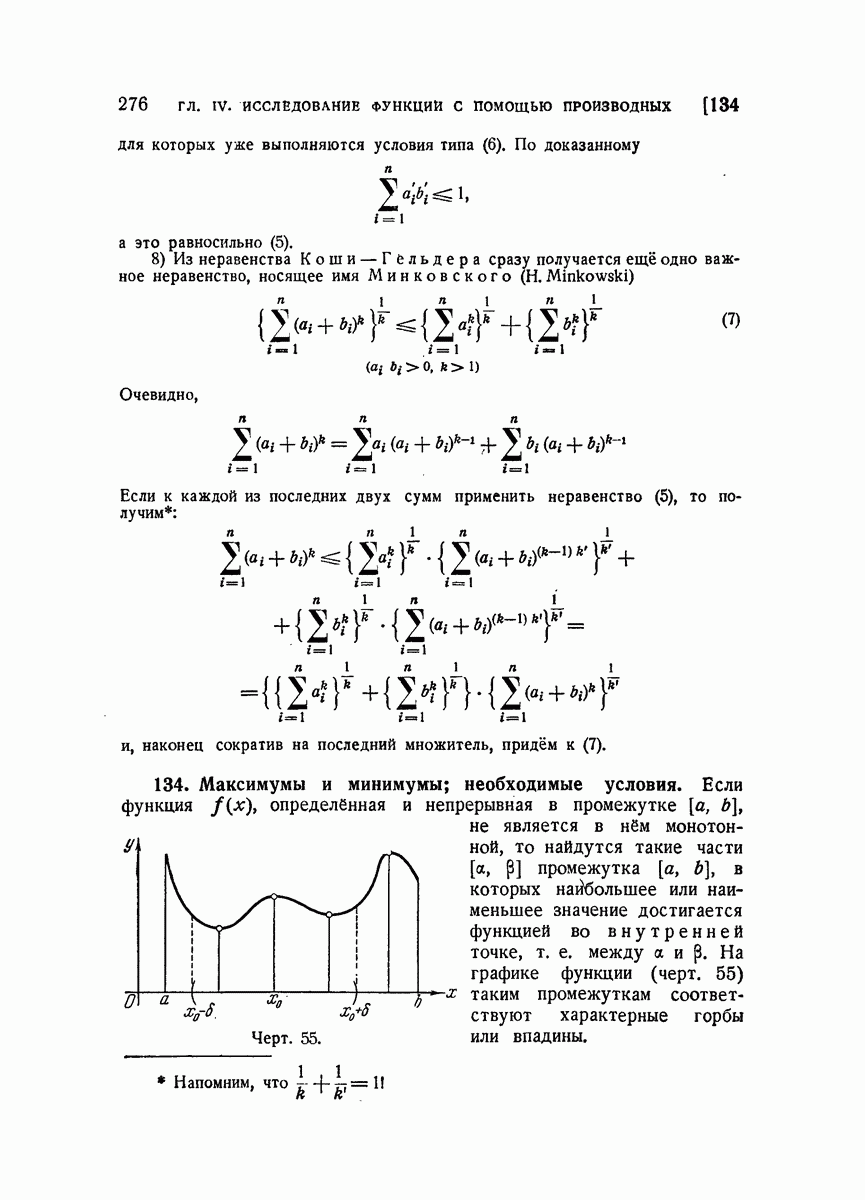
- 134. Максимумы и минимумы; необходимые условия.
- 136. Достаточные условия. Первое правило.
- 136. Примеры.
- 137. Второе правило.
- 138. Использование высших производных.
- 139. Разыскание наибольших и наименьших значений.
- 140. Задачи.
- § 2. Выпуклые (и вогнутые) функции
- 142. Простейшие предложения о выпуклых функциях.
- 143. Условия выпуклости функции.
- 144. Неравенство Иенсена и его приложения.
- 145. Точки перегиба.
- § 3. Построение графиков функций
- 147. Схема построения графика. Примеры.
- 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
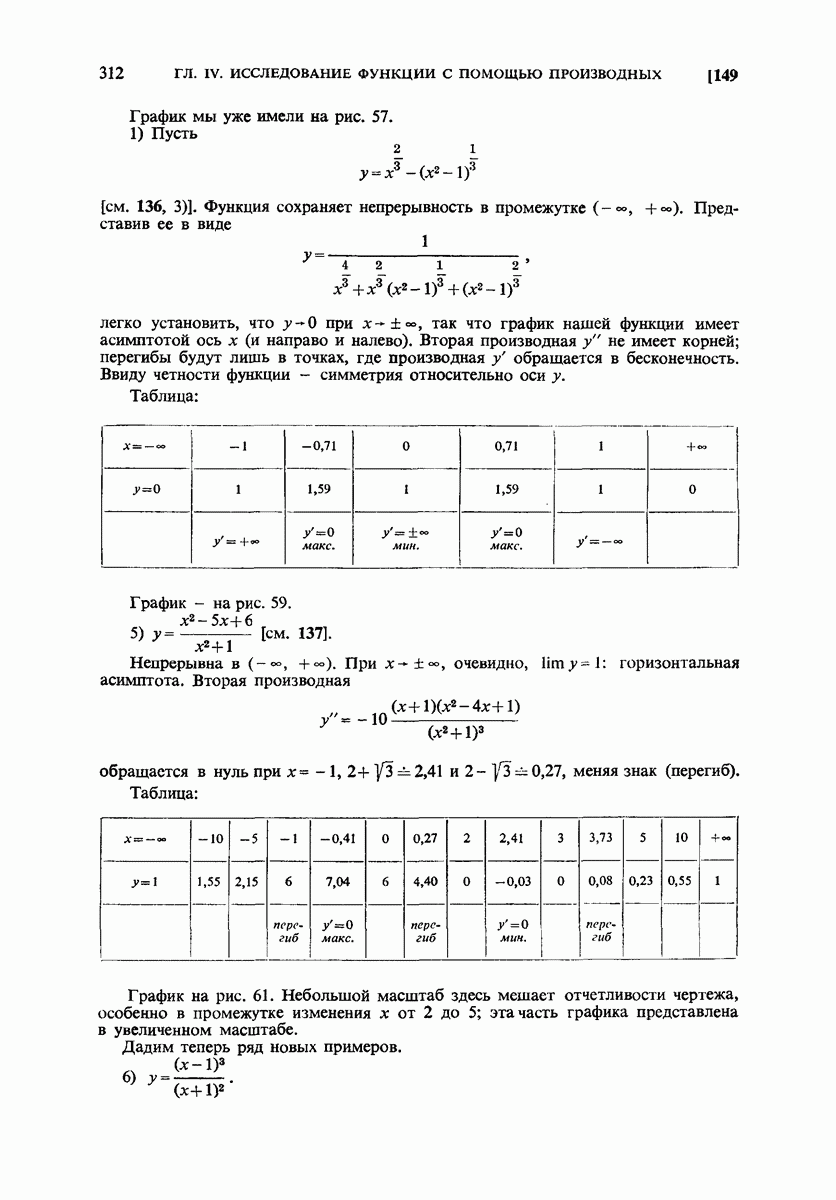
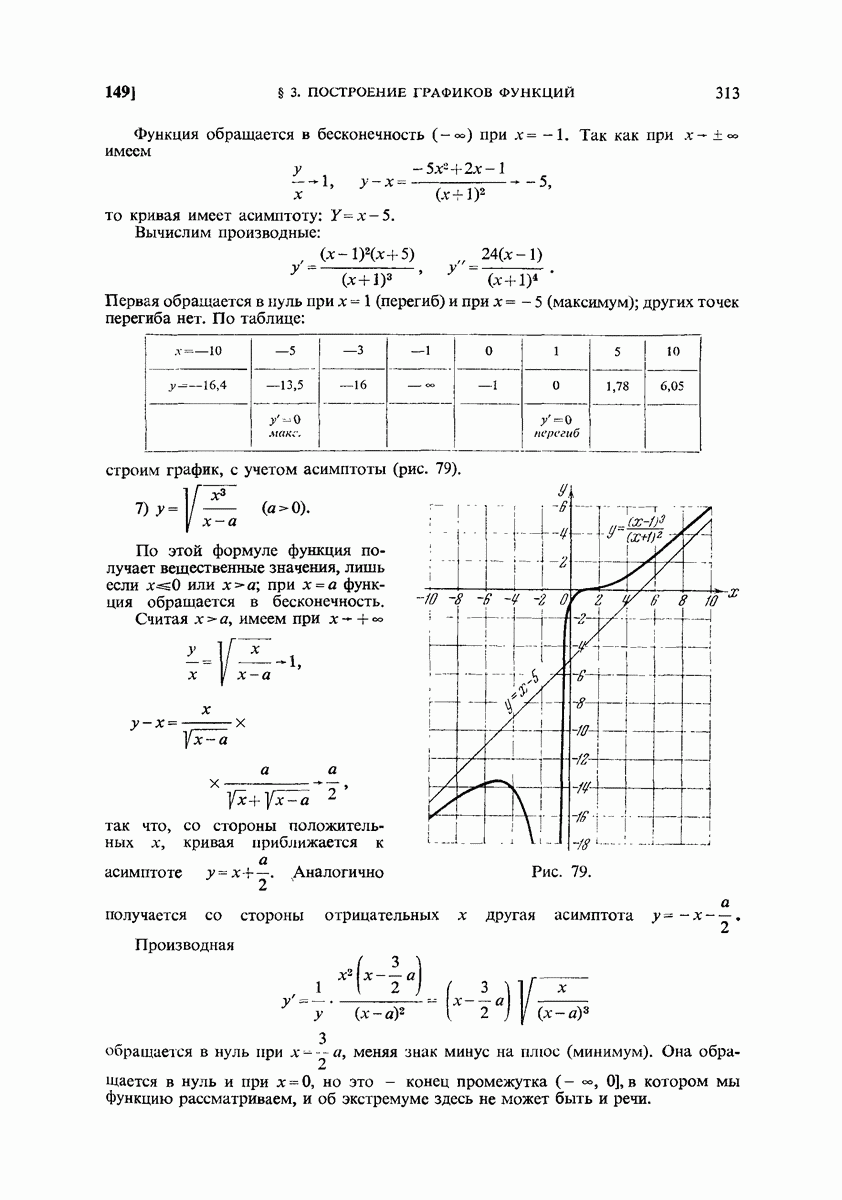
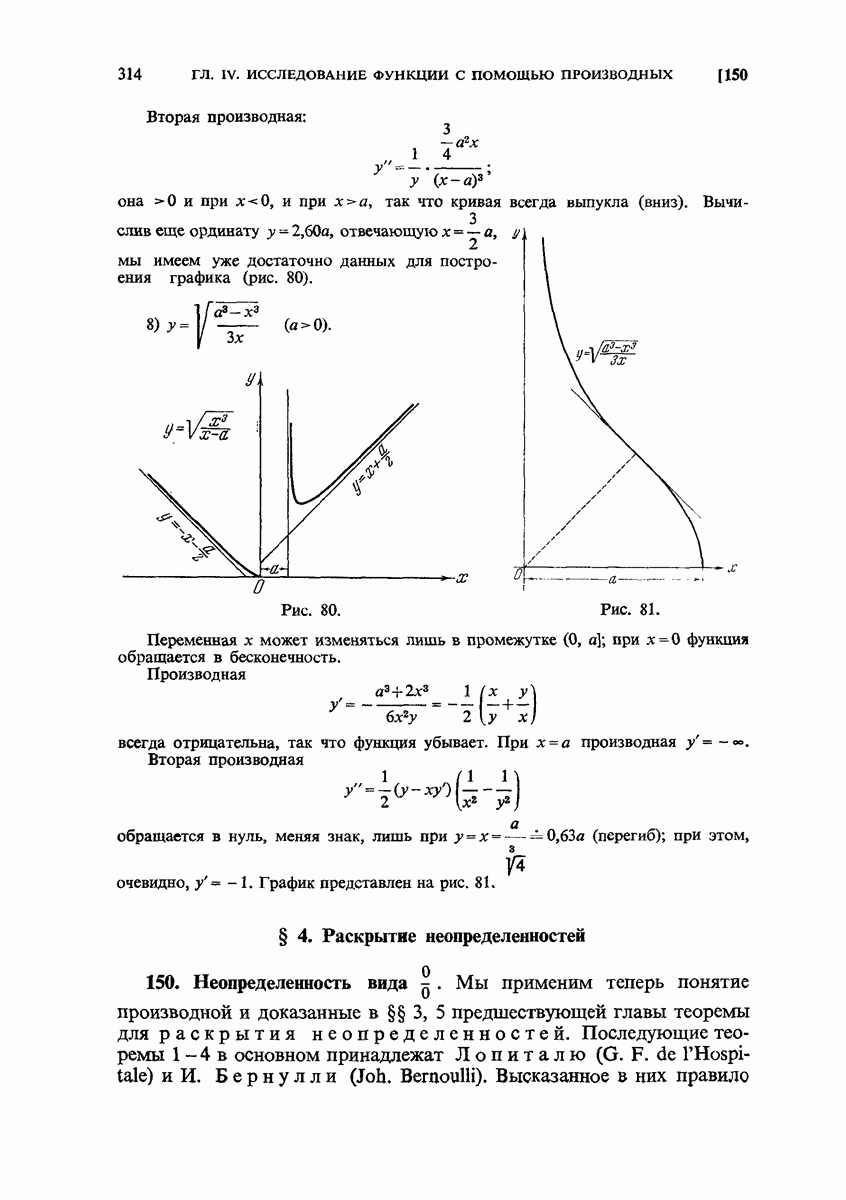
- 149. Примеры.
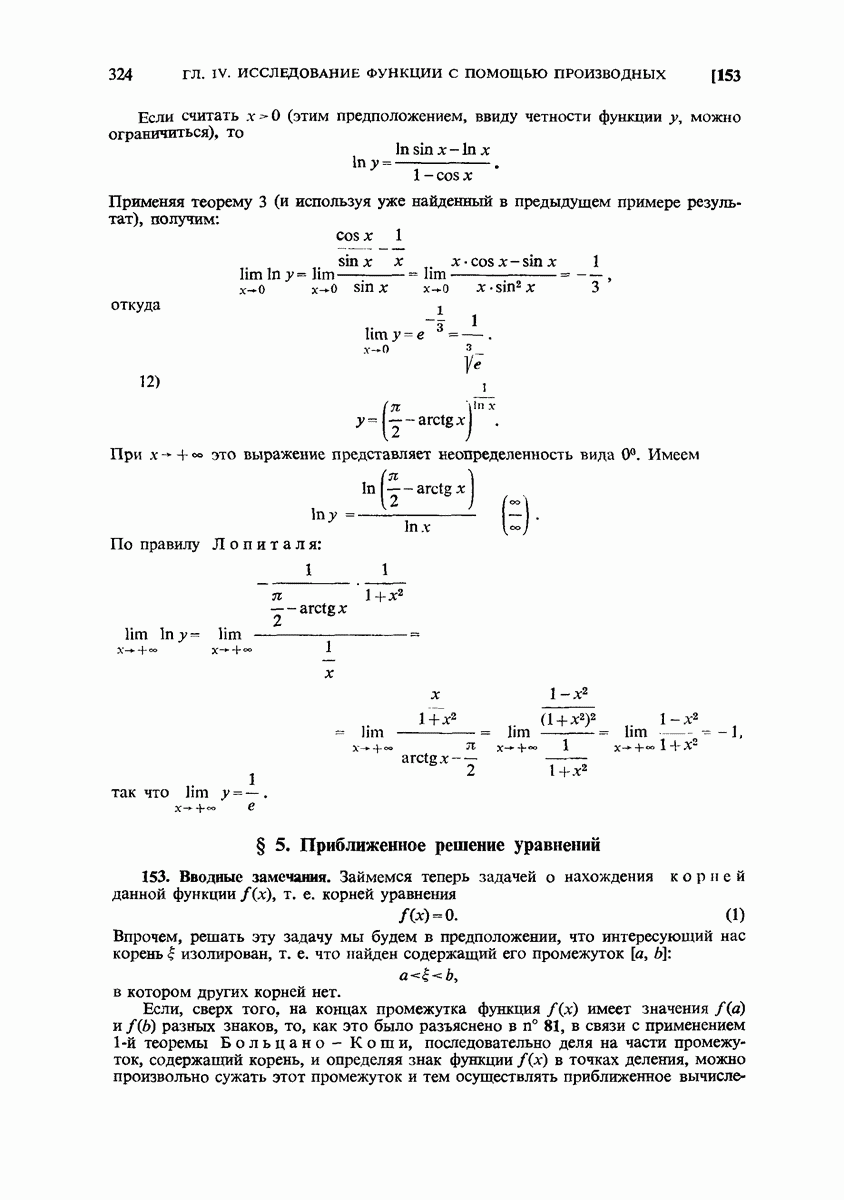
- § 4. Раскрытие неопределенностей
- 151. Неопределенность вида oo/oo
- 152. Другие виды неопределенностей.
- § 5. Приближенное решение уравнений
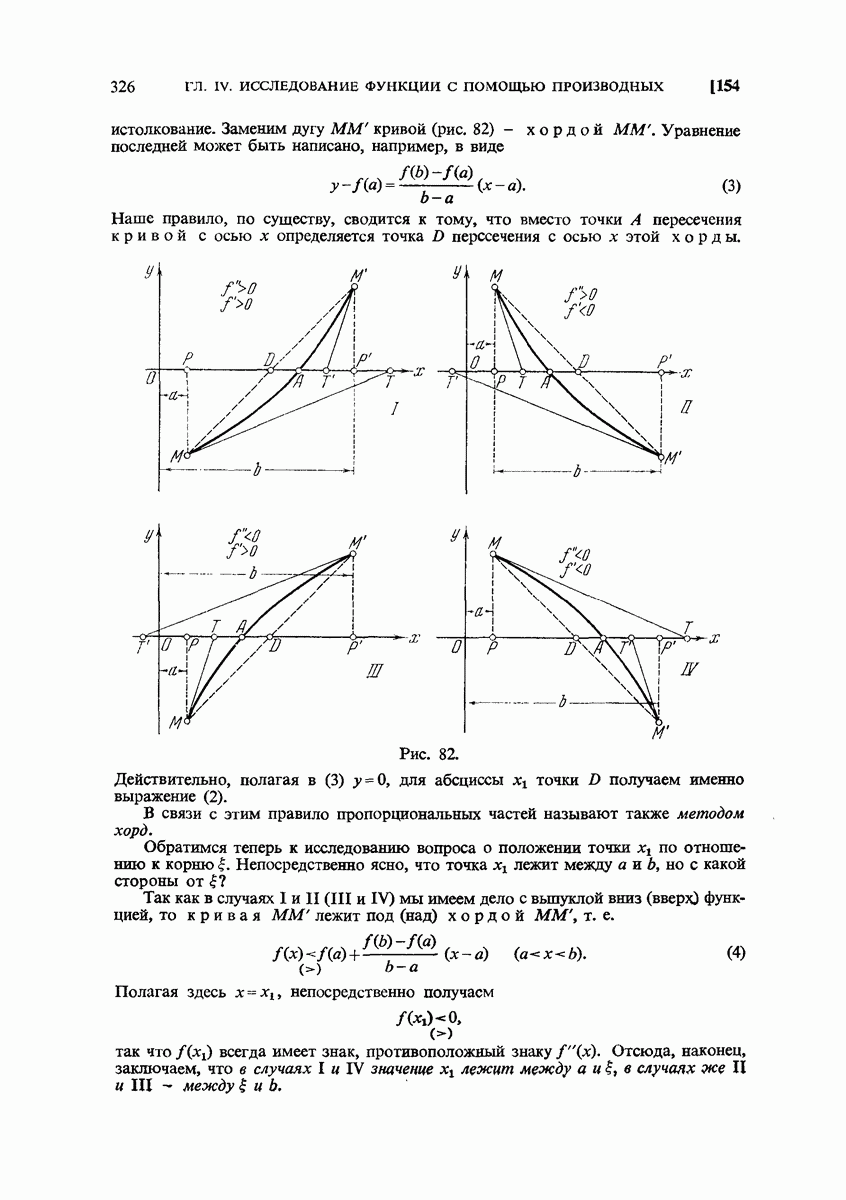
- 154. Правило пропорциональных частей (метод хорд).
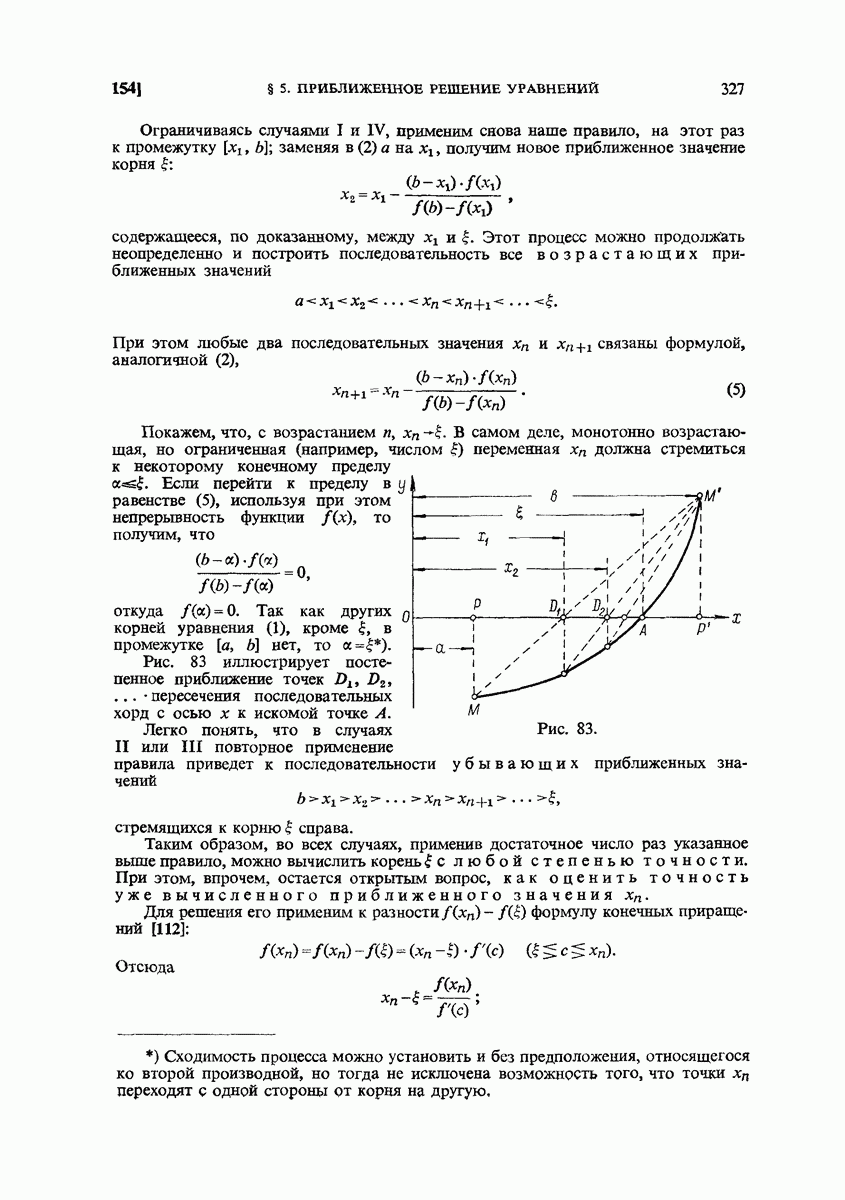
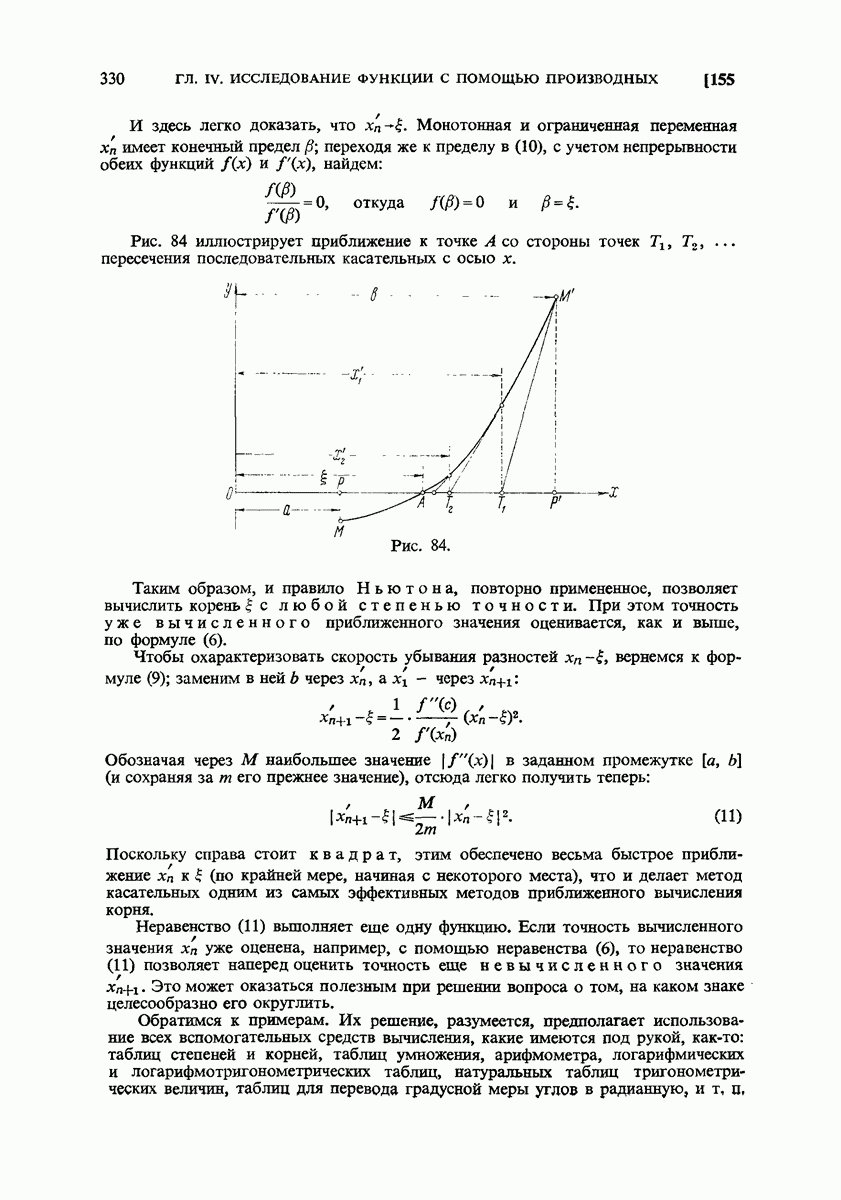
- 155. Правило Ньютона (метод касательных).
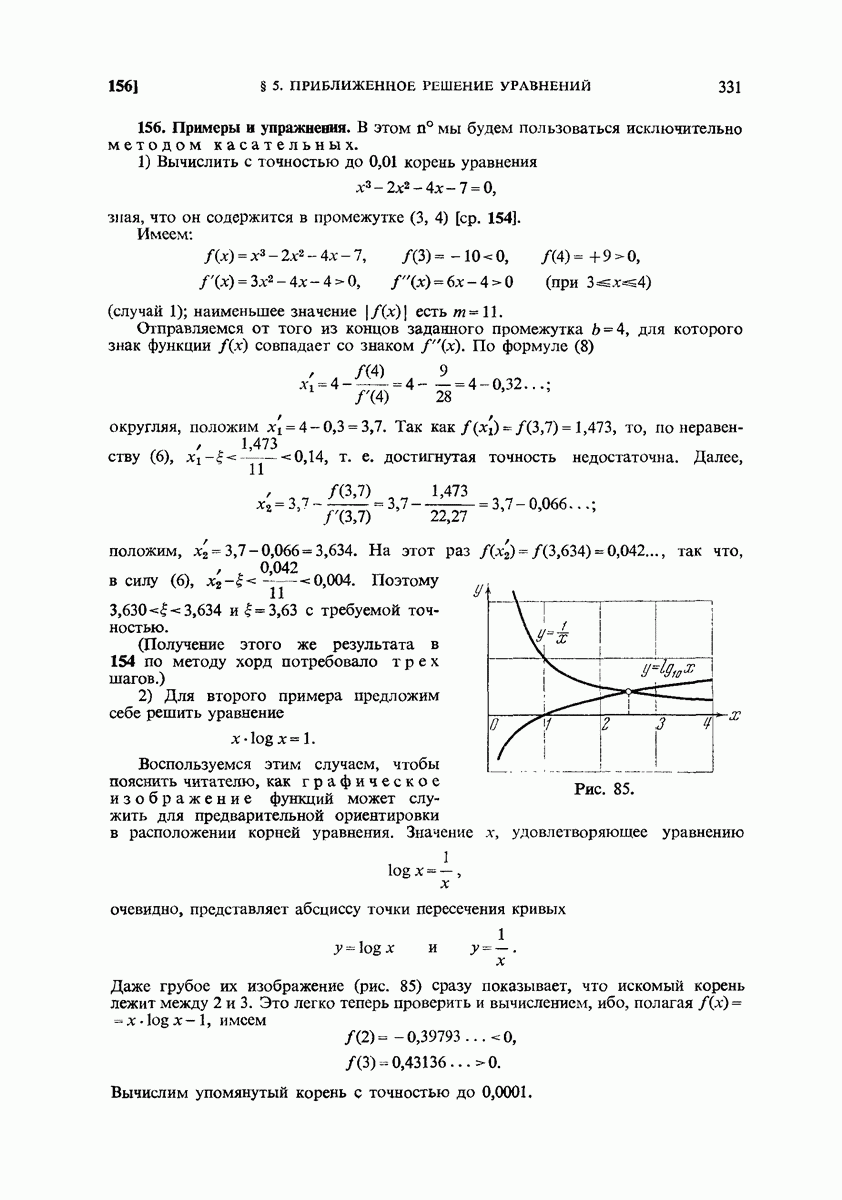
- 156. Примеры в упражнения.
- 157. Комбинированный метод.
- 158. Примеры и упражнения.
- ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 159. Функциональная зависимость между переменными. Примеры.
- 160. Функции двух переменных и области их определения.
- 161. Арифметическое n-мерное пространство.
- 162. Примеры областей в n-мерном пространстве.
- 163. Общее определение открытой и замкнутой области.
- 164. Функции n переменных.
- 165. Предел функции нескольких переменных.
- 166. Сведение к случаю варианты.
- 167. Примеры.
- 168. Повторные пределы.
- § 2. Непрерывные функции
- 170. Операции над непрерывными функциями.
- 171. Функции, непрерывные в области. Теоремы Больцано—Коши.
- 172. Лемма Больцано—Вейерштрасса.
- 173. Теоремы Вейерштрасса.
- 174. Равномерная непрерывность.
- 175. Лемма Бореля.
- 176. Новые доказательства основных теорем.
- § 3. Производные и дифференциалы функций нескольких переменных
- 178. Полное приращение функции.
- 179. Полный дифференциал.
- 180. Геометрическая интерпретация для случая функции двух переменных.
- 181. Производные от сложных функций.
- 182. Примеры.
- 183. Формула конечных приращений.
- 184. Производная по заданному направлению.
- 185. Инвариантность формы (первого) дифференциала.
- 186. Применение полного дифференциала в приближенных вычислениях.
- 187. Однородные функции.
- 188. Формула Эйлера.
- § 4. Производные и дифференциалы высших порядков
- 190. Теорема о смешанных производных.
- 191. Обобщение.
- 192. Производные высших порядков от сложной функции.
- 193. Дифференциалы высших порядков.
- 194. Дифференциалы сложных функций.
- 195. Формула Тейлора.
- § 5. Экстремумы, наибольшие и наименьшие значения
- 197. Достаточные условия (случай функции двух переменных).
- 198. Достаточные условия (общий случай).
- 199. Условия отсутствия экстремума.
- 200. Наибольшее и наименьшее значения функции. Примеры.
- 201. Задачи.
- ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
- § 1. Формальные свойства функциональных определителей
- 203. Умножение якобианов.
- 204. Умножение функциональных матриц (матриц Якоби).
- § 2. Неявные функции
- 206. Существование неявной функции.
- 207. Дифференцируемость неявной функции.
- 208. Неявные функции от нескольких переменных.
- 209. Вычисление производных неявных функций.
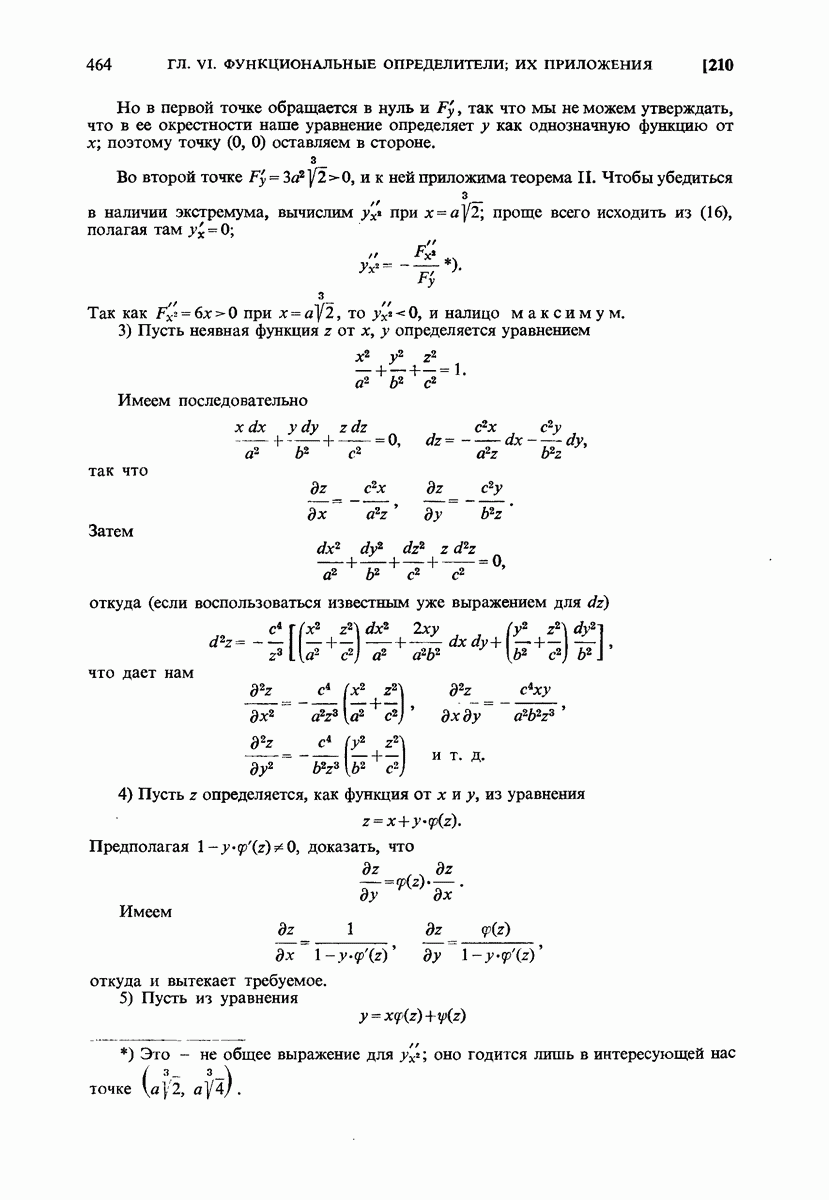
- 210. Примеры.
- § 3. Некоторые приложения теории неявных функций
- 212. Метод неопределенных множителей Лагранжа.
- 213. Достаточные для относительного экстремума условия.
- 214. Примеры и задачи.
- 215. Понятие независимости функций.
- 216. Ранг матрицы Якоби.
- § 4. Замена переменных
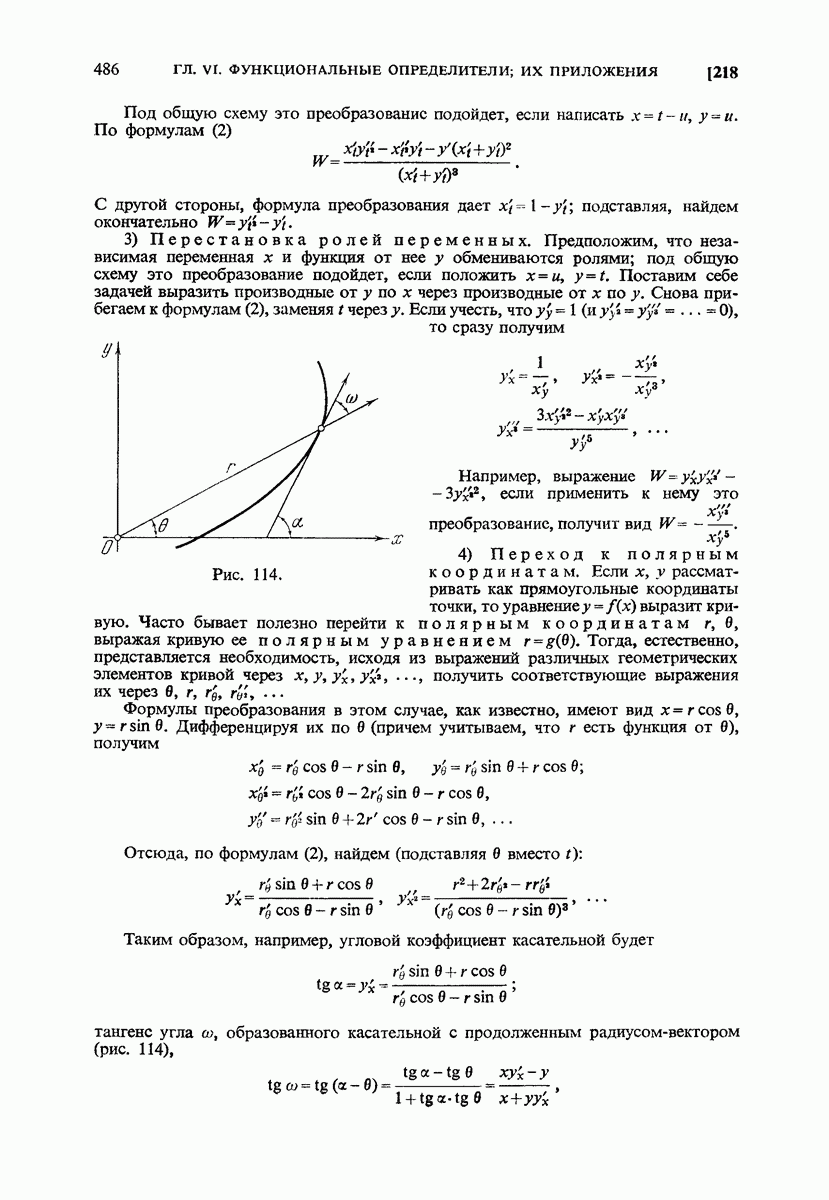
- 218. Примеры.
- 219. Функции нескольких переменных. Замена независимых переменных.
- 220. Метод вычисления дифференциалов.
- 221. Общий случай замены переменных.
- 222. Примеры.
- ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
- § 1. Аналитическое представление кривых и поверхностей
- 224. Примеры.
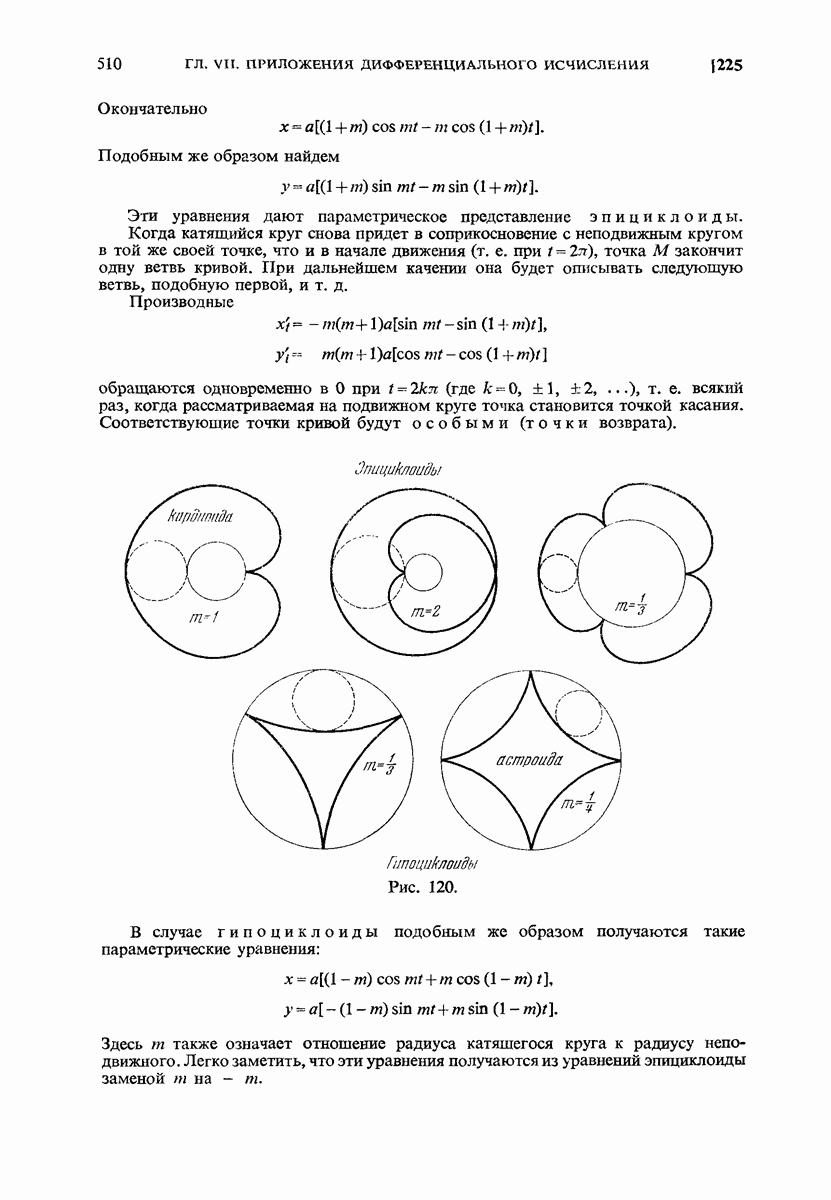
- 225. Кривые механического происхождения.
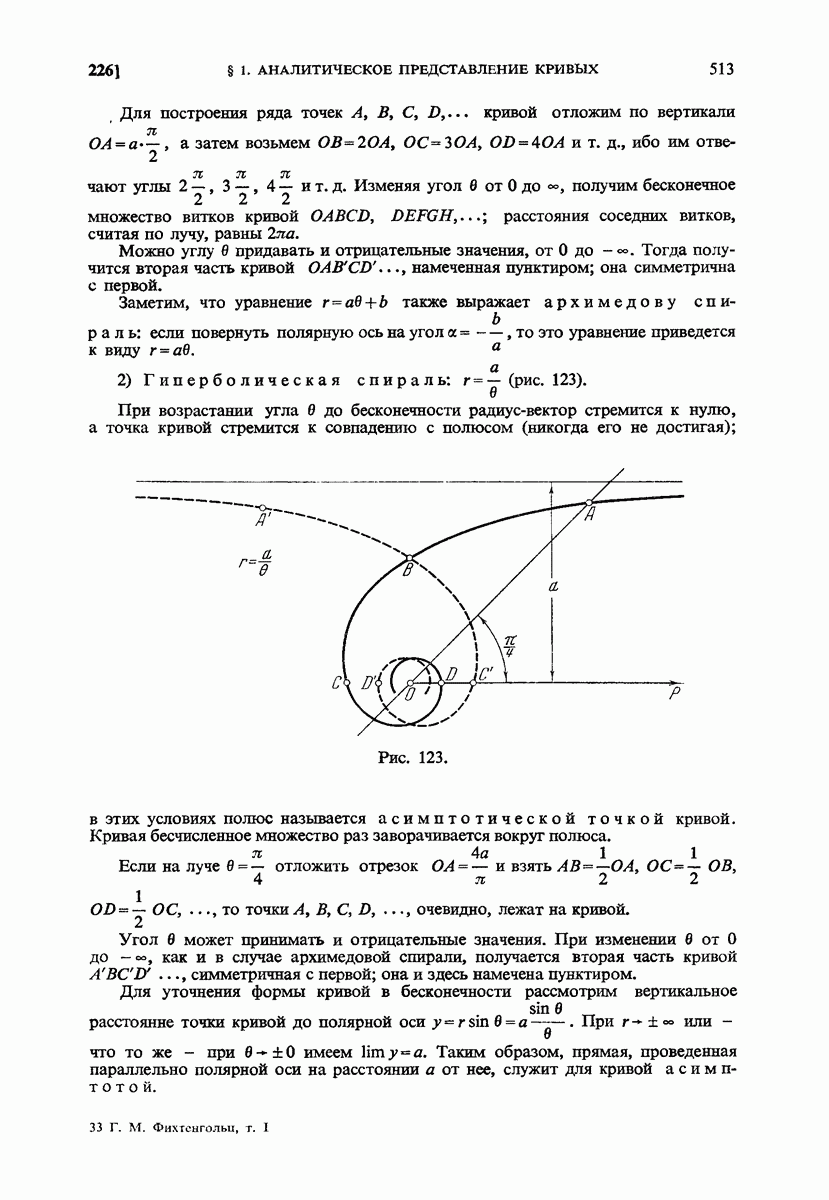
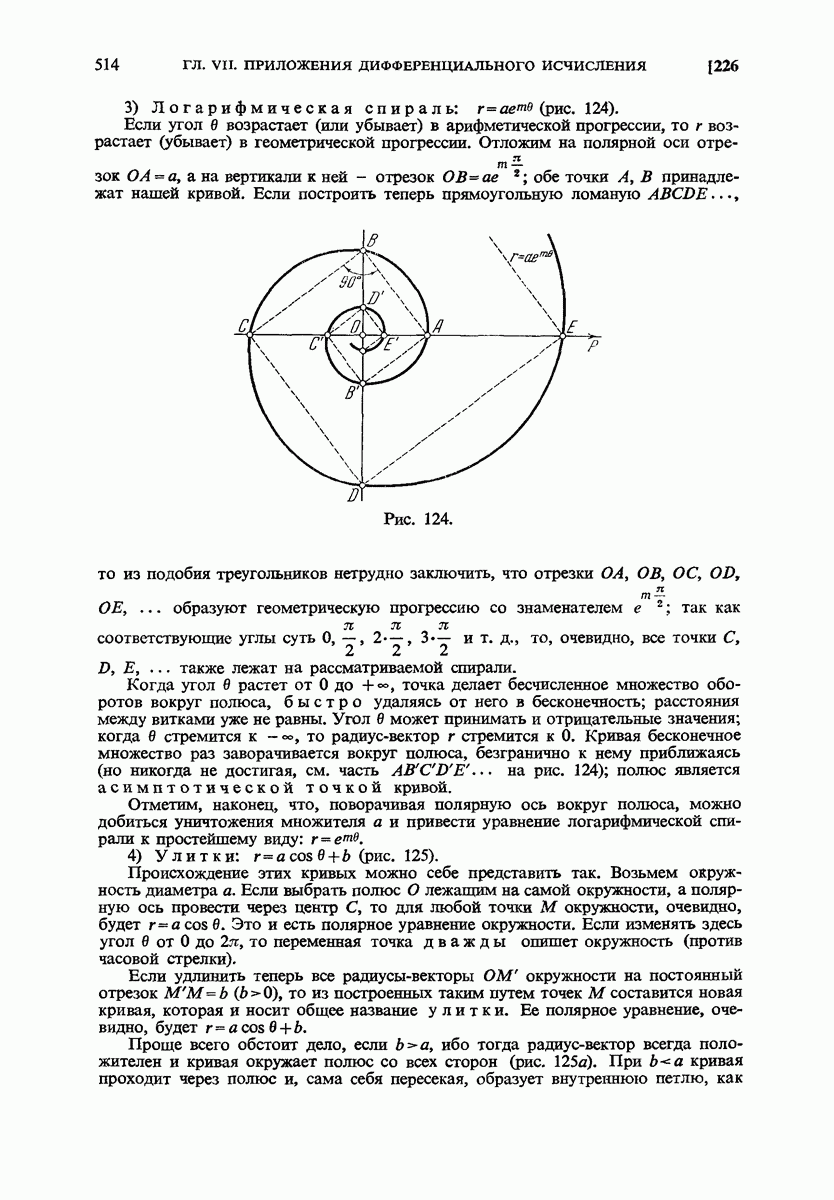
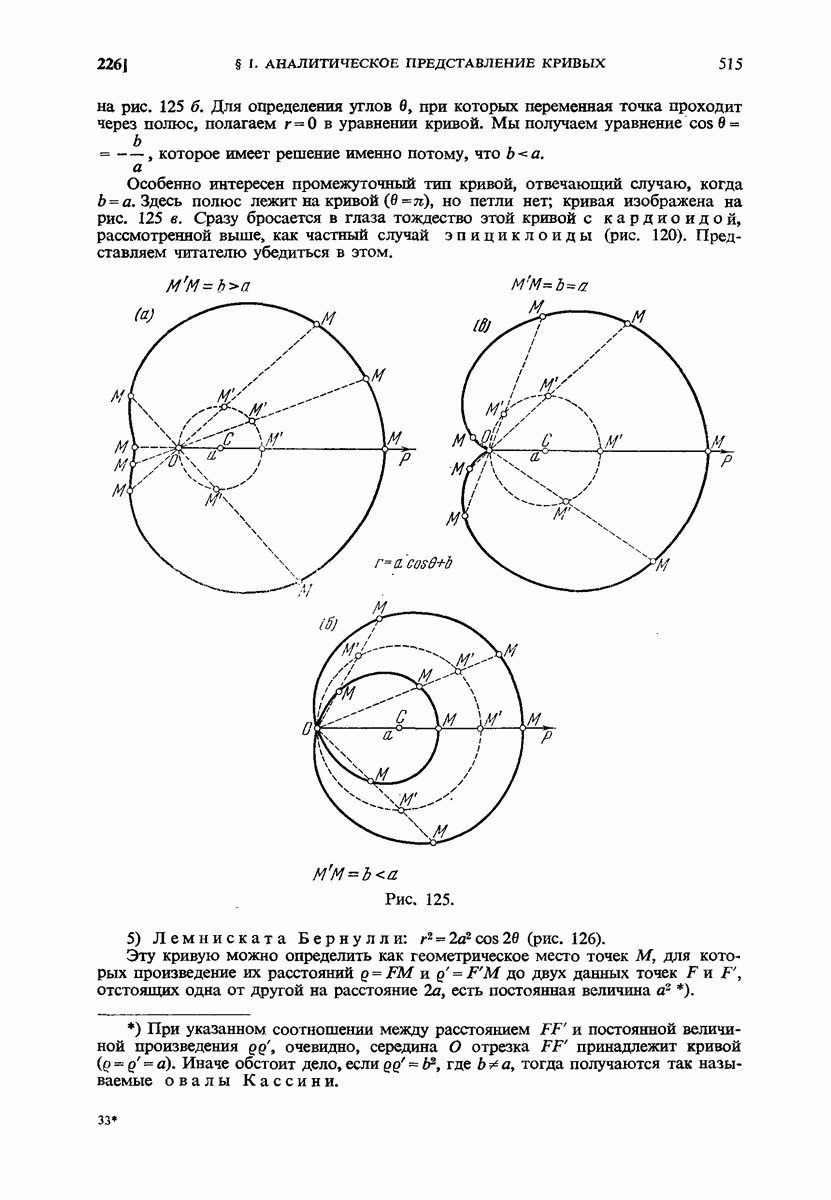
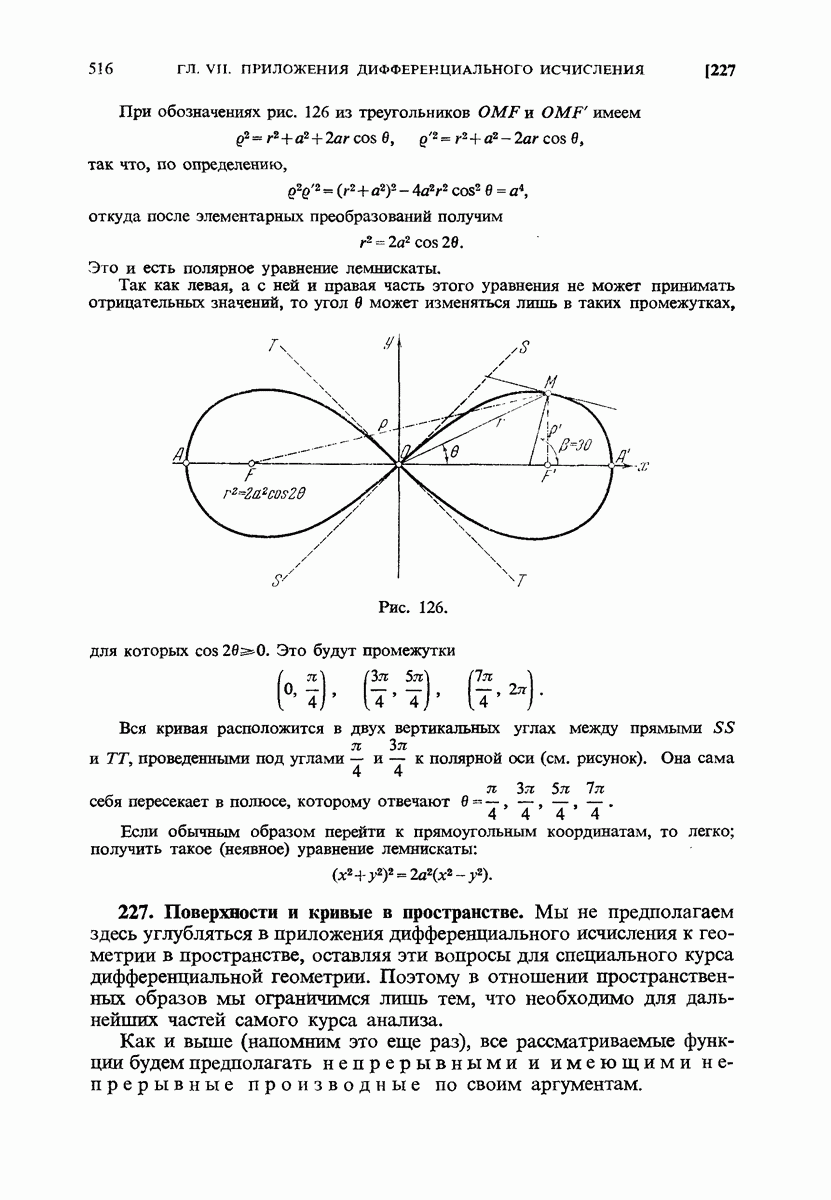
- 226. Кривые на плоскости (в полярных координатах). Примеры.
- 227. Поверхности и кривые в пространстве.
- 228. Параметрическое представление.
- 229. Примеры.
- § 2. Касательная и касательная плоскость
- 231. Примеры.
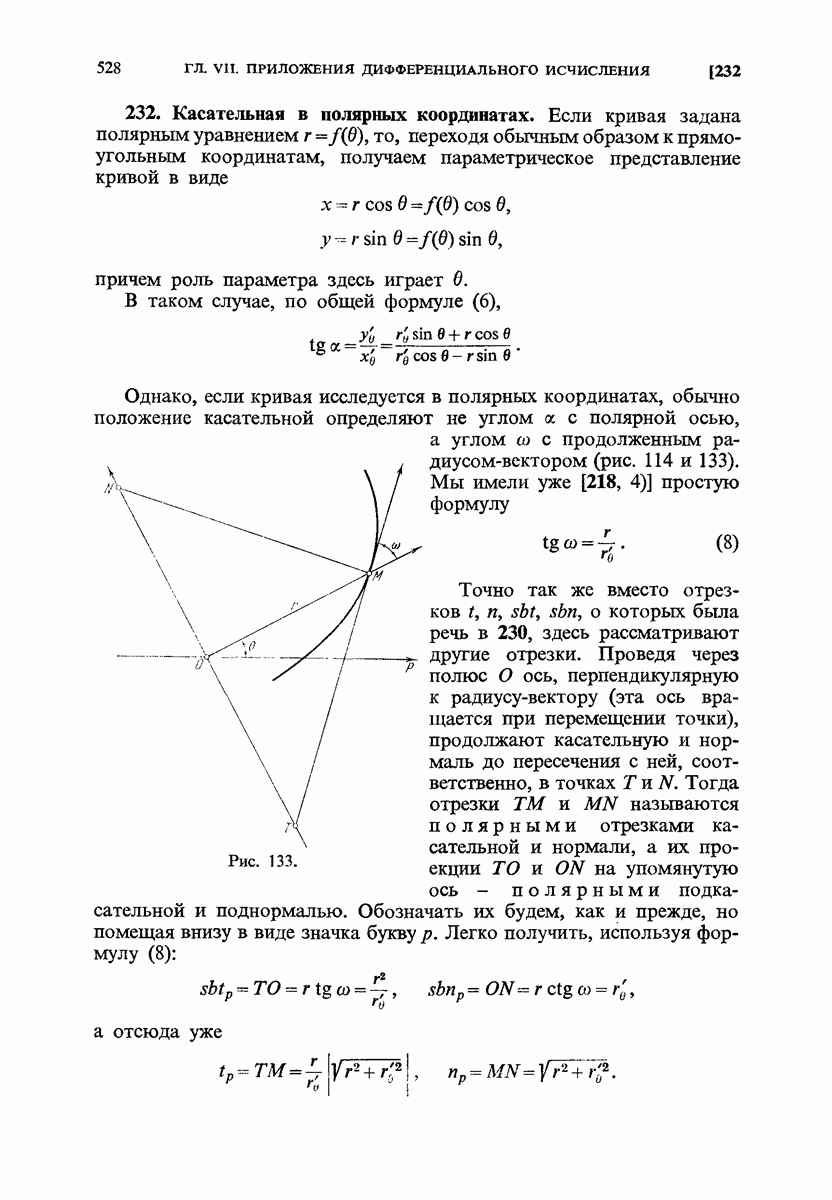
- 232. Касательная в полярных координатах.
- 233. Примеры.
- 234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
- 235. Примеры.
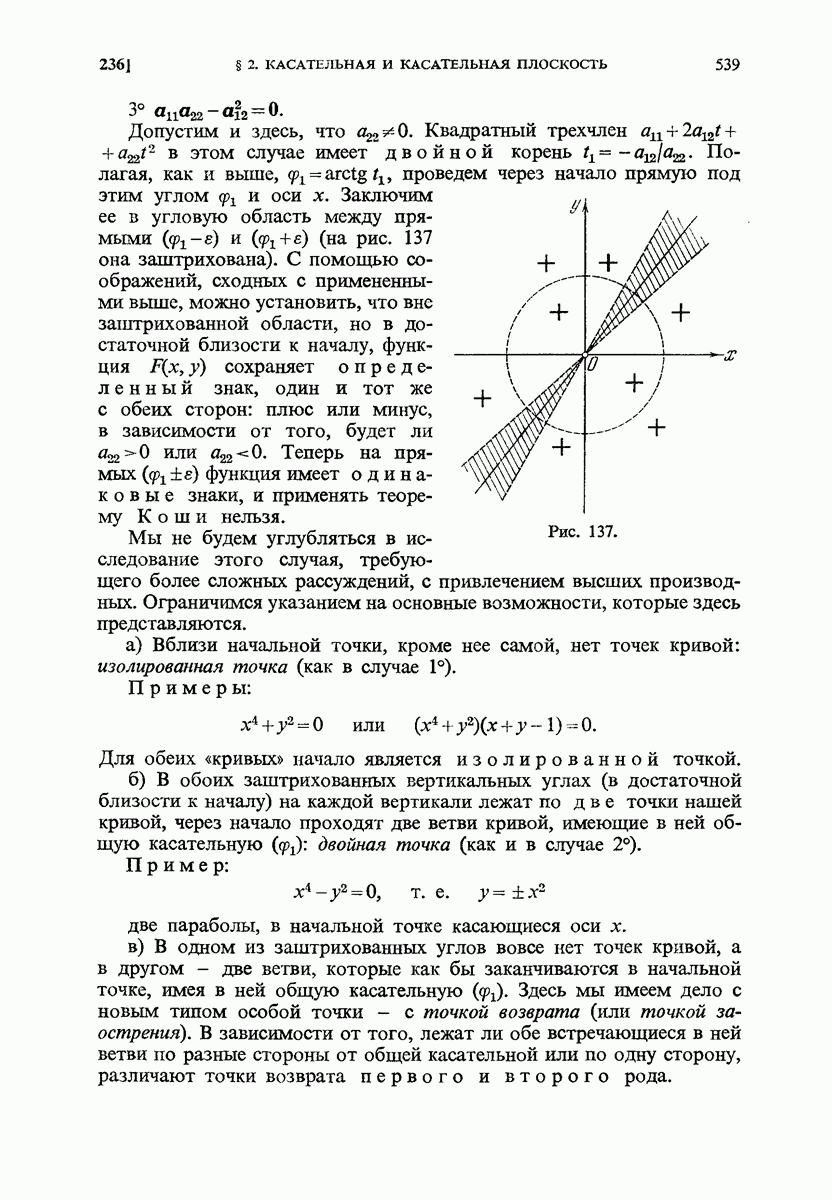
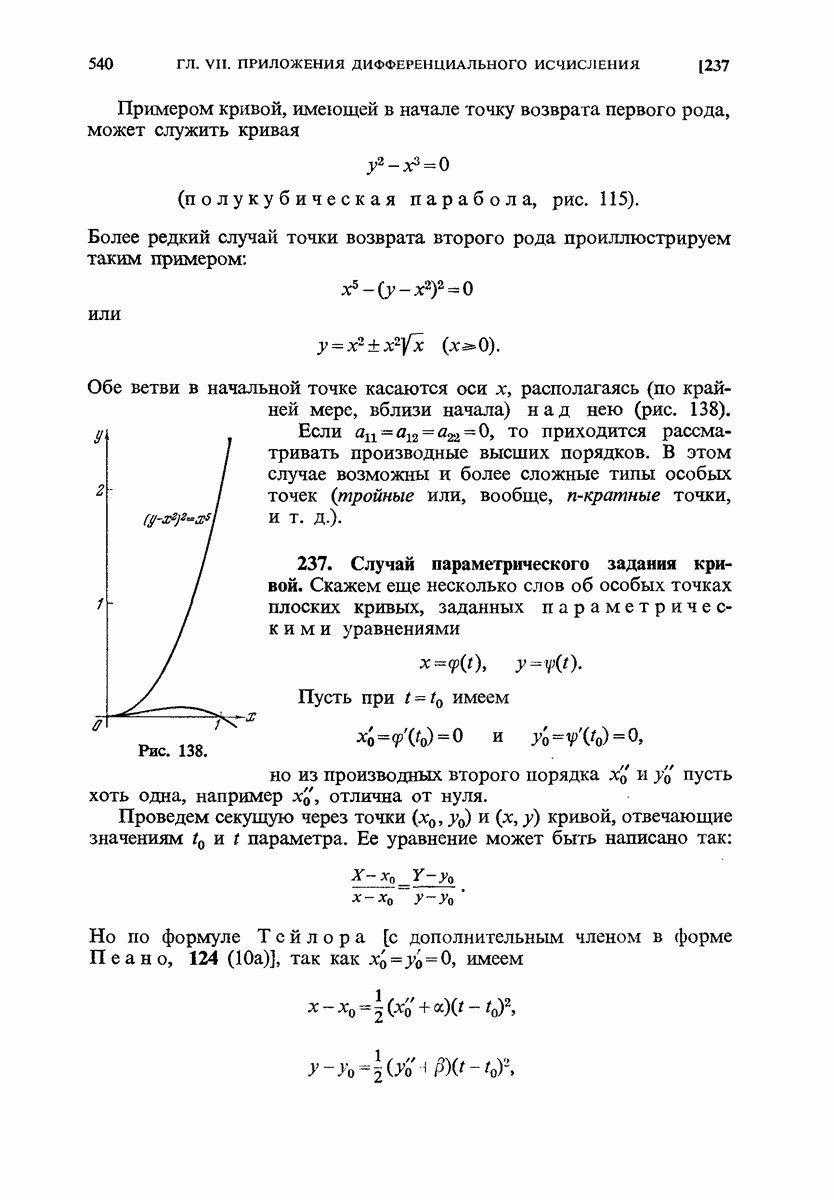
- 236. Особые точки плоских кривых.
- 237. Случай параметрического задания кривой.
- § 3. Касание кривых между собой
- 239. Примеры.
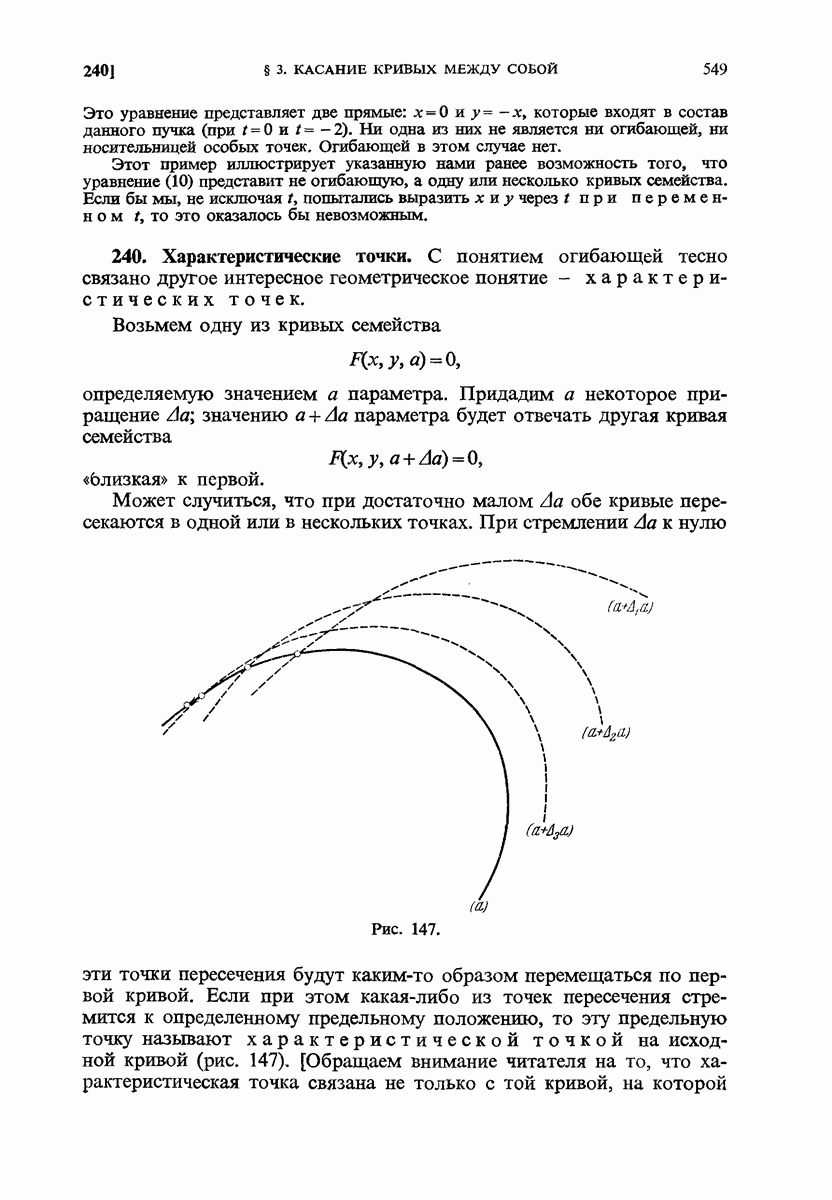
- 240. Характеристические точки.
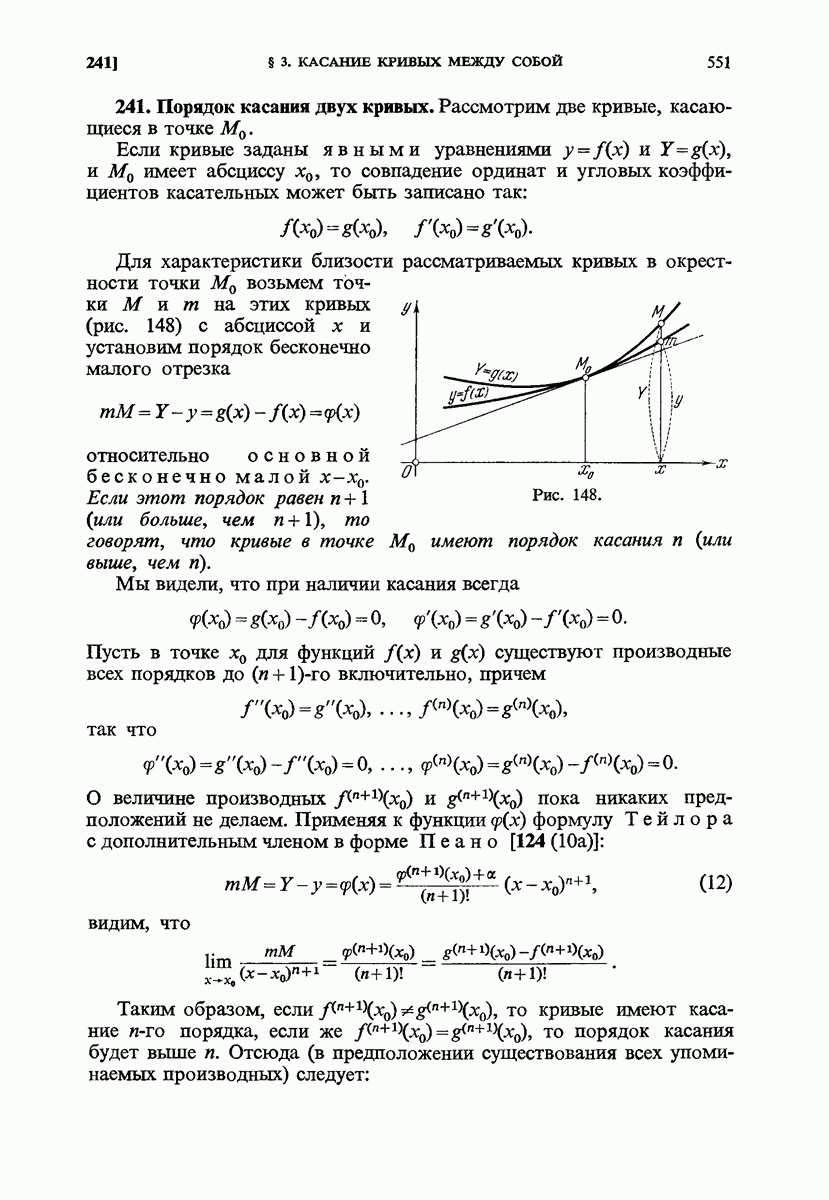
- 241. Порядок касания двух кривых.
- 242. Случай неявного задания одной из кривых.
- 243. Соприкасающаяся кривая.
- 244. Другой подход к соприкасающимся кривым.
- § 4. Длина плоской кривой
- 246. Направление на кривой.
- 247. Длина кривой. Аддитивность длины дуги.
- 248. Достаточные условия спрямляемости. Дифференциал дуги.
- 249. Дуга в роли параметра. Положительное направление касательной.
- § 5. Кривизна плоской кривой
- 251. Круг кривизны и радиус кривизны.
- 252. Примеры.
- 253. Координаты центра кривизны.
- 254. Определение эволюты и эвольвенты; разыскание эволюты.
- 255. Свойства эволют и эвольвент.
- 256. Разыскание эвольвент.
- ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ