| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
248. Достаточные условия спрямляемости. Дифференциал дуги.
До сих пор мы рассматривали общий случай непрерывной простой кривой (1). Желая дать удобные достаточные условия ее спрямляемости и изучить дальнейшие свойства длины дуги, мы вернемся к обычным в этой главе предположениям о существовании непрерывных производных  Докажем, что при сделанных предположениях кривая (1) спрямляема.
Докажем, что при сделанных предположениях кривая (1) спрямляема.
Рассмотрим ломаную с вершинами в точках (2), определяемых значениями параметра (3). Координатами точки  будут
будут

Тогда периметр  ломаной запишется так:
ломаной запишется так:

Но по формуле конечных приращений [112]

так что, окончательно,

Если через  обозначить, соответственно, наибольшие значения функций
обозначить, соответственно, наибольшие значения функций  в промежутке
в промежутке  , то из (7) нетрудно получить оценку:
, то из (7) нетрудно получить оценку:

Множество  оказывается ограниченным сверху, значит, кривая имеет конечную длину
оказывается ограниченным сверху, значит, кривая имеет конечную длину  , т. е. спрямляема, что и требовалось доказать.
, т. е. спрямляема, что и требовалось доказать.
Так как  то из (8) попутно получаем и оценку для S сверху:
то из (8) попутно получаем и оценку для S сверху:

которая нам сейчас понадобится. Впрочем, нам нужна будет и оценка снизу; если ввести наименьшие значения  и Т функций
и Т функций  в промежутке
в промежутке  то из (7), аналогично (8), найдем, что
то из (7), аналогично (8), найдем, что

а тогда тем более

Если изменить  ним вместе и положение точки
ним вместе и положение точки  на кривой, то длина переменной дуги
на кривой, то длина переменной дуги  окажется функцией от параметра
окажется функцией от параметра  мы будем обозначать ее через
мы будем обозначать ее через

Придадим переменной t положительное приращение  точка М переместится вдоль по кривой, по направлению к В, в положение М (рис. 151). Величина S получит положительное же приращение
точка М переместится вдоль по кривой, по направлению к В, в положение М (рис. 151). Величина S получит положительное же приращение  равное длине дуги
равное длине дуги  (по аддитивности длины дуги, доказанной в предыдущем п°). Таким образом, функция
(по аддитивности длины дуги, доказанной в предыдущем п°). Таким образом, функция  оказывается возрастающей.
оказывается возрастающей.

Рис. 151.
Рассмотрим теперь, вместо промежутка  , промежуток
, промежуток  и применим к дуге
и применим к дуге  длины
длины  оценки (9) и (9:
оценки (9) и (9:

но здесь под  мы вправе разуметь наименьшее и наибольшее значения функции
мы вправе разуметь наименьшее и наибольшее значения функции  уже в промежутке
уже в промежутке  Отсюда
Отсюда

и, так как - по непрерывности производных - при  оба числа
оба числа  а оба числа
а оба числа  то оба корня в предшествующем неравенстве стремятся к общему пределу
то оба корня в предшествующем неравенстве стремятся к общему пределу

Следовательно, к тому же пределу стремится и отношение  как легко видеть, это справедливо и для
как легко видеть, это справедливо и для  Итак, имеем окончательно: длина переменной дуги
Итак, имеем окончательно: длина переменной дуги  оказывается дифференцируемой функцией от параметра
оказывается дифференцируемой функцией от параметра  ее производная по параметру выражается формулой:
ее производная по параметру выражается формулой:

или, короче,

Если возвести это равенство в квадрат и умножить почленно на  то получим замечательную по простоте формулу
то получим замечательную по простоте формулу

которая к тому же обладает геометрической наглядностью. На рис. 152 в (криволинейном) прямоугольном треугольнике  «катетами» служат приращения координат точки
«катетами» служат приращения координат точки  а «гипотенузой» - дуга
а «гипотенузой» - дуга  , которая является приращением дуги
, которая является приращением дуги  Оказывается, что если не для самих приращений, то для их главных частей - дифференциалов - имеет место своеобразная «теорема Пифагора».
Оказывается, что если не для самих приращений, то для их главных частей - дифференциалов - имеет место своеобразная «теорема Пифагора».

Рис. 152.
Полезно отметить частные случаи важной формулы (10), отвечающие различным частным типам задания кривой. Так, если кривая задана явным уравнением в декартовых координатах  то в роли «параметра» оказывается х, дуга s зависит от
то в роли «параметра» оказывается х, дуга s зависит от  и формула (10) принимает вид
и формула (10) принимает вид

Если же кривая задана полярным уравнением  то это, как мы знаем, равносильно заданию ее параметрическими уравнениями
то это, как мы знаем, равносильно заданию ее параметрическими уравнениями

где параметром будет в; дуга на этот раз будет функцией от  Так как, очевидно,
Так как, очевидно,

то

и формула (10) преобразуется так:

Часто представляется удобным взять в качестве начальной точки А для отсчета дуг не один из концов дуги, а какую-либо внутреннюю точку ее. В этом случае естественно дуги, откладываемые от нее в направлении возрастания параметра, считать положительными, а в другом - отрицательными и, соответственно этому, длину дуги в первом случае снабжать знаком плюс, а во втором - знаком минус. Вот эту величину s дуги со знаком мы для краткости будем называть просто дугой. Формулы (10), (11), (10а), (106) имеют место во всех случаях.
[Заметим, что если положительное направление для отсчета дуг выбирать не в сторону возрастания периметра, как это делается
обычно, а в сторону его убывания, то в формулах (10), (10а), (106) пришлось бы перед радикалом поставить знак минус.]
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Упорядочение области рациональных чисел.
- 3. Сложение и вычитание рациональных чисел.
- 4. Умножение и деление рациональных чисел.
- 5. Аксиома Архимеда.
- § 2. Введение иррациональных чисел. Упорядочение области вещественных чисел
- 7. Упорядочение области вещественных чисел.
- 8. Вспомогательные предложения.
- 9. Представление вещественного числа бесконечной десятичной дробью.
- 10. Непрерывность области вещественных чисел.
- 11. Границы числовых множеств.
- § 3. Арифметические действия над вещественными числами
- 13. Свойства сложения.
- 14. Определение произведения вещественных чисел.
- 15. Свойства умножения.
- 16. Заключение.
- 17. Абсолютные величины.
- § 4. Дальнейшие свойства и приложения вещественных чисел
- 19. Степень с любым вещественным показателем.
- 20. Логарифмы.
- 21. Измерение отрезков.
- ГЛАВА ПЕРВАЯ. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. Варианта и ее предел
- 23. Предел варианты.
- 24. Бесконечно малые величины.
- 25. Примеры.
- 26. Некоторые теоремы о варианте, имеющей предел.
- 27. Бесконечно большие величины.
- § 2. Теоремы о пределах, облегчающие нахождение пределов
- 29. Леммы о бесконечно малых.
- 30. Арифметические операция над переменными.
- 31. Неопределенные выражения.
- 32. Примеры на нахождение пределов.
- 33. Теорема Штольца и ее применения.
- § 3. Монотонная варианта
- 35. Примеры.
- 36. Число е.
- 37. Приближенное вычисление числа е.
- 38. Лемма о вложенных промежутках.
- § 4. Принцип сходимости. Частичные пределы
- 40. Частичные последовательности и частичные пределы.
- 41. Лемма Больцано — Вейерштрасса
- 42. Наибольший и наименьший пределы.
- ГЛАВА ВТОРАЯ. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
- § 1. Понятие функции
- 44. Функциональная зависимость между переменными. Примеры.
- 45. Определение понятия функции.
- 46. Аналитический способ задания функции.
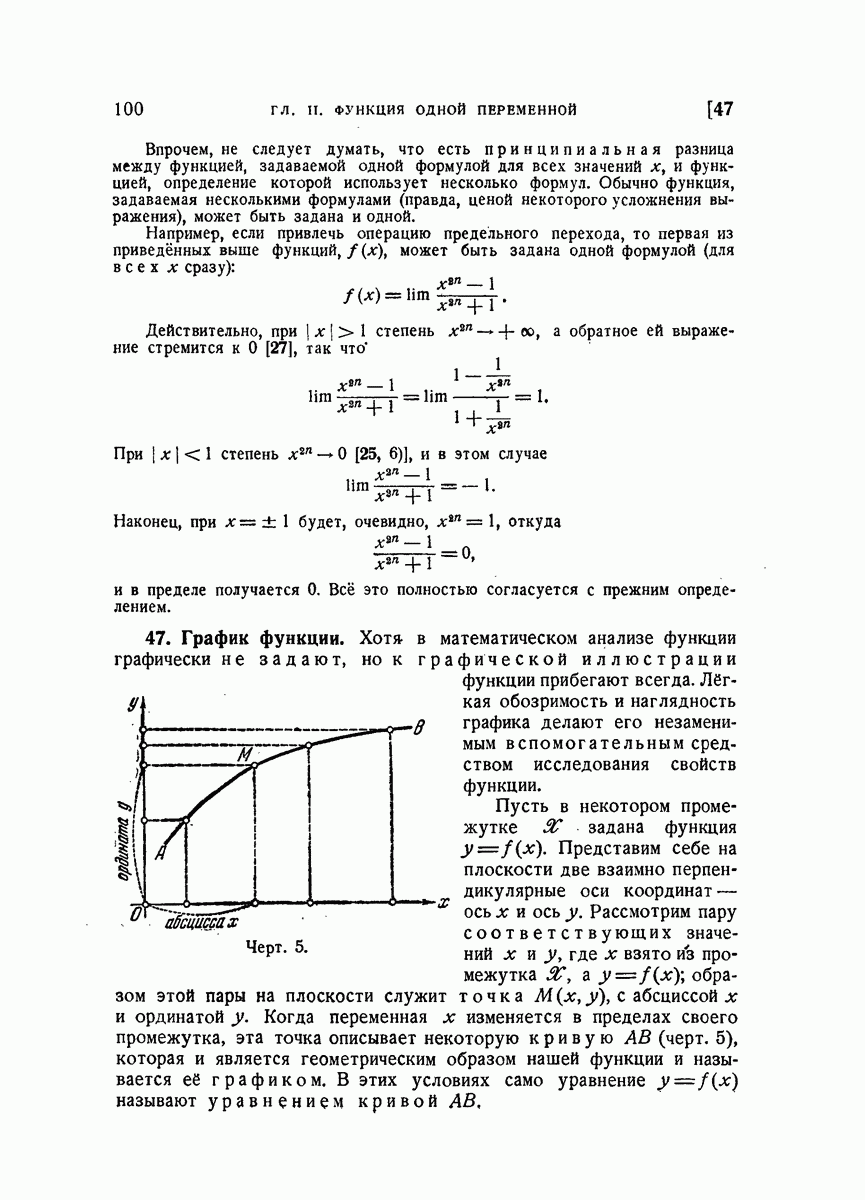
- 47. График функции.
- 48. Важнейшие классы функций.
- 49. Понятие обратной функции.
- 50. Обратные тригонометрические функции.
- 51. Суперпозиция функций. Заключительные замечания.
- § 2. Предел функции
- 53. Сведение к случаю варианты.
- 54. Примеры.
- 55. Распространение теории пределов.
- 56. Примеры.
- 57. Предел монотонной функции.
- 58. Общий признак Больцано—Коши.
- 59. Наибольший и наименьший пределы функции.
- § 3. Классификация бесконечно малых и бесконечно больших величин
- 61. Шкала бесконечно малых.
- 62. Эквивалентные бесконечно малые.
- 63. Выделение главной части.
- 64. Задачи.
- 65. Классификация бесконечно больших.
- § 4. Непрерывность (и разрывы) функций
- 67. Арифметические операции над непрерывными функциями.
- 68. Примеры непрерывных функций.
- 69. Односторонняя непрерывность. Классификация разрывов.
- 70. Примеры разрывных функций.
- 71. Непрерывность и разрывы монотонной функции.
- 72. Непрерывность элементарных функций.
- 73. Суперпозиция непрерывных функций.
- 74. Решение одного функционального уравнения.
- 75. Функциональная характеристика показательной, логарифмической и степенной функций.
- 76. Функциональная характеристика тригонометрического и гиперболического косинусов.
- 77. Использование непрерывности функций для вычисления пределов.
- 78. Степенно-показательные выражения.
- 79. Примеры.
- § 5. Свойства непрерывных функций
- 81. Применение к решению уравнений.
- 82. Теорема о промежуточном значении.
- 83. Существование обратной функции.
- 84. Теорема об ограниченности функции.
- 85. Наибольшее и наименьшее значения функции.
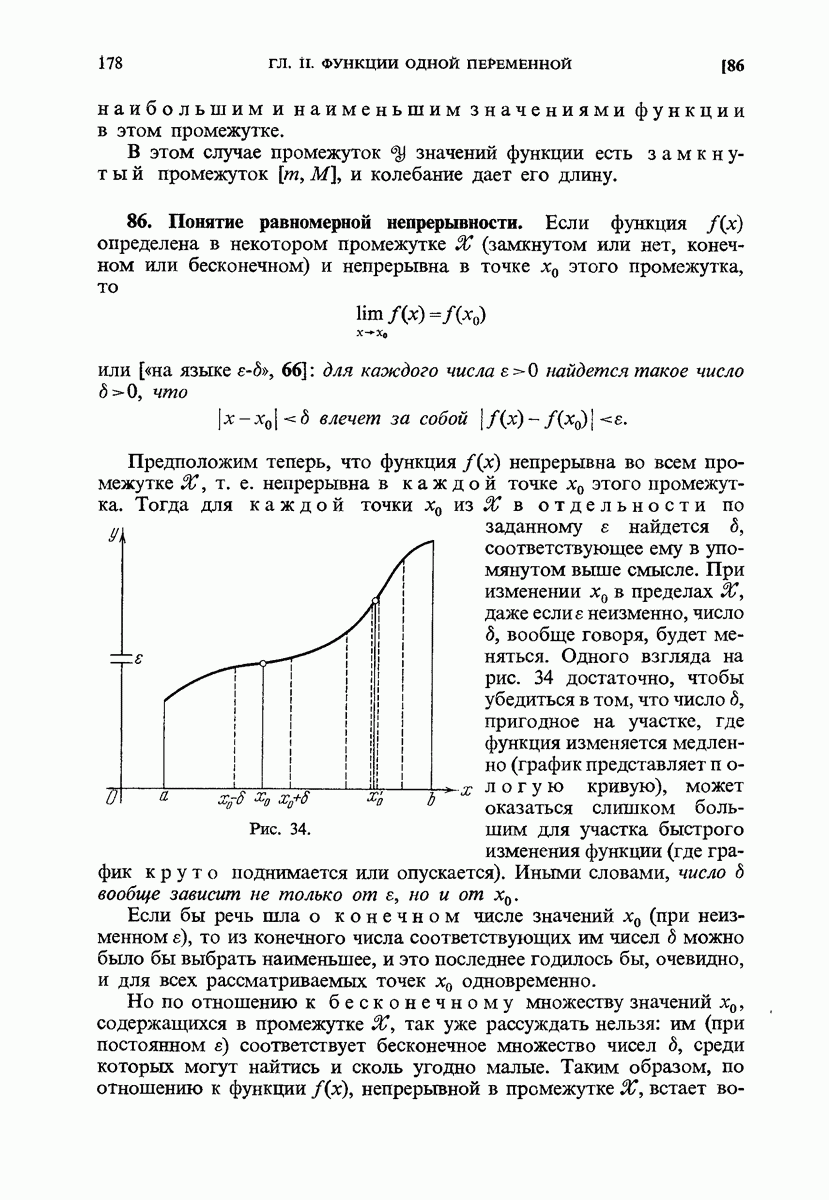
- 86. Понятие равномерной непрерывности.
- 87. Теорема Кантора.
- 88. Лемма Бореля.
- 89. Новые доказательства основных теорем.
- ГЛАВА ТРЕТЬЯ. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
- § 1. Производная и ее вычисление
- 91. Задача о проведении касательной к кривой.
- 92. Определение производной.
- 93. Примеры вычисления производных.
- 94. Производная обратной функции.
- 95. Сводка формул для производных.
- 96. Формула для превращения функции.
- 97. Простейшие правила вычисления производных.
- 98. Производная сложной функции.
- 100. Односторонние производные.
- 101. Бесконечные производные.
- 102. Дальнейшие примеры особых случаев.
- § 2. Дифференциал
- 104. Связь между диффереицируемостью и существованием производной.
- 105. Основные формулы и правила дифференцирования.
- 106. Инвариантность формы дифференциала.
- 107. Дифференциалы как источник приближенных формул.
- 108. Применение дифференциалов при оценке погрешностей.
- § 3. Основные теоремы дифференциального исчисления
- 110. Теорема Дарбу
- 111. Теорема Ролля.
- 112. Формула Лагранжа.
- 113. Предел производной.
- 114. Формула Коши.
- § 4. Производные и дифференциалы высших порядков
- 116. Общие формулы для производных любого порядка.
- 117. Формула Лейбница.
- 118. Примеры.
- 119. Дифференциалы высших порядков.
- 120. Нарушение инвариантности формы для дифференциалов высших порядков.
- 121. Параметрическое дифференцирование.
- 122. Конечные разности.
- § 5. Формула Тейлора
- 124. Разложение произвольной функции; дополнительный член в форме Пеано.
- 125. Примеры.
- 126. Другие формы дополнительного члена.
- 127. Приближенные формулы.
- § 6. Интерполирование
- 129. Дополнительный члеп формулы Лагранжа.
- 130. Интерполирование с кратными узлами. Формула Эрмита.
- ГЛАВА ЧЕТВЕРТАЯ. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
- § 1. Изучение хода изменения функции
- 132. Условие монотонности функции.
- 133. Доказательство неравенств.
- 134. Максимумы и минимумы; необходимые условия.
- 136. Достаточные условия. Первое правило.
- 136. Примеры.
- 137. Второе правило.
- 138. Использование высших производных.
- 139. Разыскание наибольших и наименьших значений.
- 140. Задачи.
- § 2. Выпуклые (и вогнутые) функции
- 142. Простейшие предложения о выпуклых функциях.
- 143. Условия выпуклости функции.
- 144. Неравенство Иенсена и его приложения.
- 145. Точки перегиба.
- § 3. Построение графиков функций
- 147. Схема построения графика. Примеры.
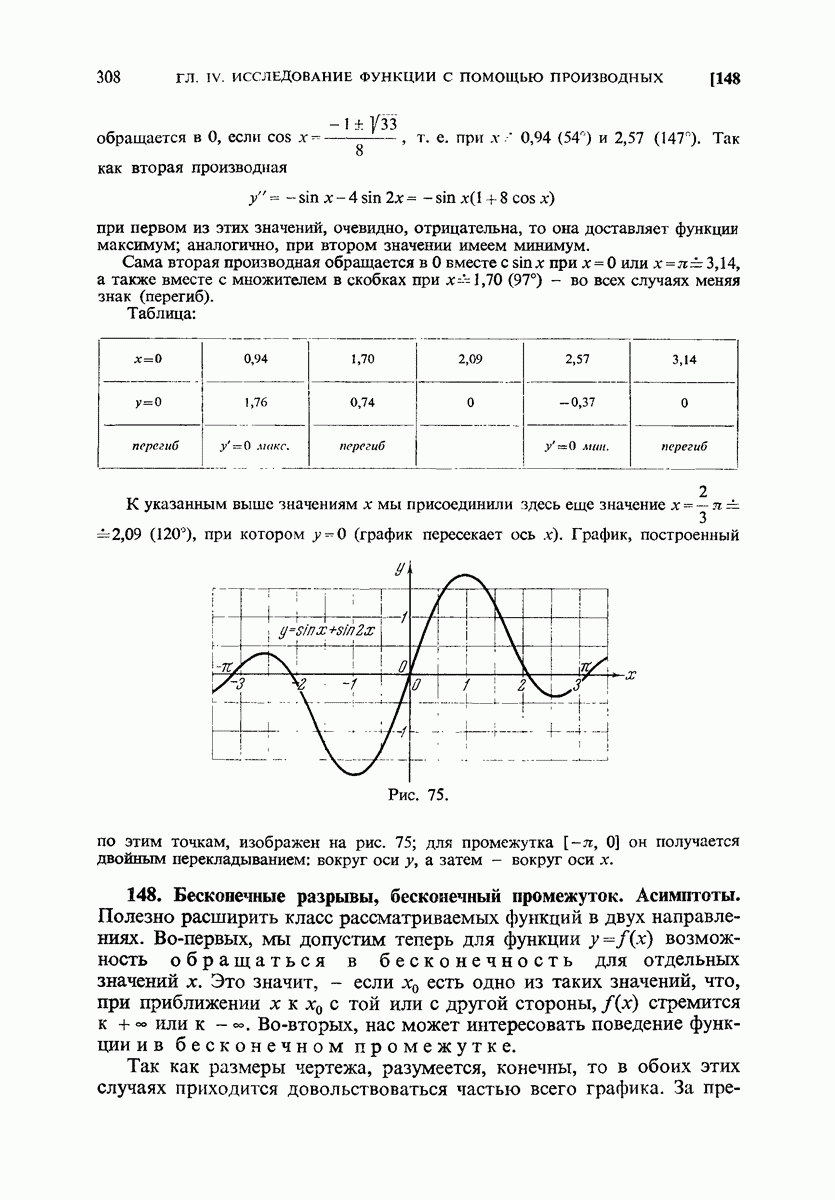
- 148. Бесконечные разрывы, бесконечный промежуток. Асимптоты.
- 149. Примеры.
- § 4. Раскрытие неопределенностей
- 151. Неопределенность вида oo/oo
- 152. Другие виды неопределенностей.
- § 5. Приближенное решение уравнений
- 154. Правило пропорциональных частей (метод хорд).
- 155. Правило Ньютона (метод касательных).
- 156. Примеры в упражнения.
- 157. Комбинированный метод.
- 158. Примеры и упражнения.
- ГЛАВА ПЯТАЯ. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 159. Функциональная зависимость между переменными. Примеры.
- 160. Функции двух переменных и области их определения.
- 161. Арифметическое n-мерное пространство.
- 162. Примеры областей в n-мерном пространстве.
- 163. Общее определение открытой и замкнутой области.
- 164. Функции n переменных.
- 165. Предел функции нескольких переменных.
- 166. Сведение к случаю варианты.
- 167. Примеры.
- 168. Повторные пределы.
- § 2. Непрерывные функции
- 170. Операции над непрерывными функциями.
- 171. Функции, непрерывные в области. Теоремы Больцано—Коши.
- 172. Лемма Больцано—Вейерштрасса.
- 173. Теоремы Вейерштрасса.
- 174. Равномерная непрерывность.
- 175. Лемма Бореля.
- 176. Новые доказательства основных теорем.
- § 3. Производные и дифференциалы функций нескольких переменных
- 178. Полное приращение функции.
- 179. Полный дифференциал.
- 180. Геометрическая интерпретация для случая функции двух переменных.
- 181. Производные от сложных функций.
- 182. Примеры.
- 183. Формула конечных приращений.
- 184. Производная по заданному направлению.
- 185. Инвариантность формы (первого) дифференциала.
- 186. Применение полного дифференциала в приближенных вычислениях.
- 187. Однородные функции.
- 188. Формула Эйлера.
- § 4. Производные и дифференциалы высших порядков
- 190. Теорема о смешанных производных.
- 191. Обобщение.
- 192. Производные высших порядков от сложной функции.
- 193. Дифференциалы высших порядков.
- 194. Дифференциалы сложных функций.
- 195. Формула Тейлора.
- § 5. Экстремумы, наибольшие и наименьшие значения
- 197. Достаточные условия (случай функции двух переменных).
- 198. Достаточные условия (общий случай).
- 199. Условия отсутствия экстремума.
- 200. Наибольшее и наименьшее значения функции. Примеры.
- 201. Задачи.
- ГЛАВА ШЕСТАЯ. ФУНКЦИОНАЛЬНЫЕ ОПРЕДЕЛИТЕЛИ; ИХ ПРИЛОЖЕНИЯ
- § 1. Формальные свойства функциональных определителей
- 203. Умножение якобианов.
- 204. Умножение функциональных матриц (матриц Якоби).
- § 2. Неявные функции
- 206. Существование неявной функции.
- 207. Дифференцируемость неявной функции.
- 208. Неявные функции от нескольких переменных.
- 209. Вычисление производных неявных функций.
- 210. Примеры.
- § 3. Некоторые приложения теории неявных функций
- 212. Метод неопределенных множителей Лагранжа.
- 213. Достаточные для относительного экстремума условия.
- 214. Примеры и задачи.
- 215. Понятие независимости функций.
- 216. Ранг матрицы Якоби.
- § 4. Замена переменных
- 218. Примеры.
- 219. Функции нескольких переменных. Замена независимых переменных.
- 220. Метод вычисления дифференциалов.
- 221. Общий случай замены переменных.
- 222. Примеры.
- ГЛАВА СЕДЬМАЯ. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ
- § 1. Аналитическое представление кривых и поверхностей
- 224. Примеры.
- 225. Кривые механического происхождения.
- 226. Кривые на плоскости (в полярных координатах). Примеры.
- 227. Поверхности и кривые в пространстве.
- 228. Параметрическое представление.
- 229. Примеры.
- § 2. Касательная и касательная плоскость
- 231. Примеры.
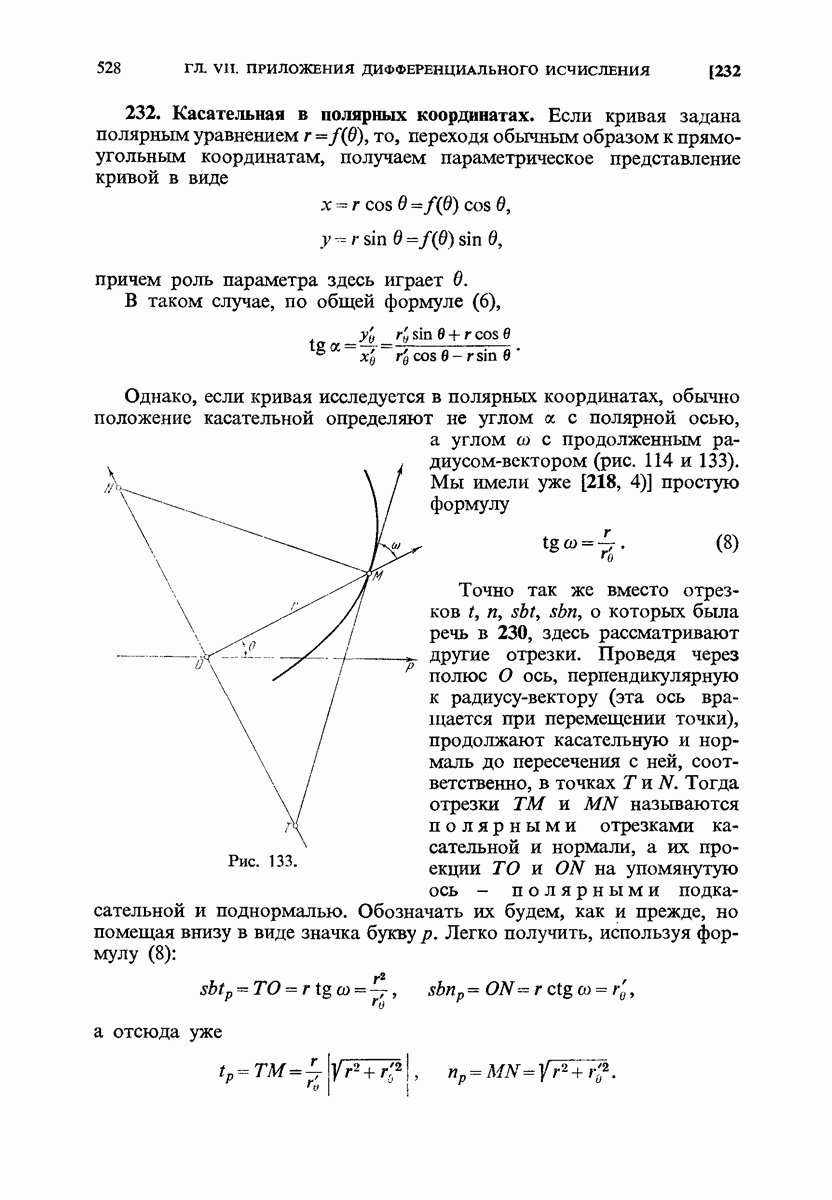
- 232. Касательная в полярных координатах.
- 233. Примеры.
- 234. Касательная к пространственной кривой. Касательная плоскость к поверхности.
- 235. Примеры.
- 236. Особые точки плоских кривых.
- 237. Случай параметрического задания кривой.
- § 3. Касание кривых между собой
- 239. Примеры.
- 240. Характеристические точки.
- 241. Порядок касания двух кривых.
- 242. Случай неявного задания одной из кривых.
- 243. Соприкасающаяся кривая.
- 244. Другой подход к соприкасающимся кривым.
- § 4. Длина плоской кривой
- 246. Направление на кривой.
- 247. Длина кривой. Аддитивность длины дуги.
- 248. Достаточные условия спрямляемости. Дифференциал дуги.
- 249. Дуга в роли параметра. Положительное направление касательной.
- § 5. Кривизна плоской кривой
- 251. Круг кривизны и радиус кривизны.
- 252. Примеры.
- 253. Координаты центра кривизны.
- 254. Определение эволюты и эвольвенты; разыскание эволюты.
- 255. Свойства эволют и эвольвент.
- 256. Разыскание эвольвент.
- ДОПОЛНЕНИЕ. ЗАДАЧА РАСПРОСТРАНЕНИЯ ФУНКЦИЙ