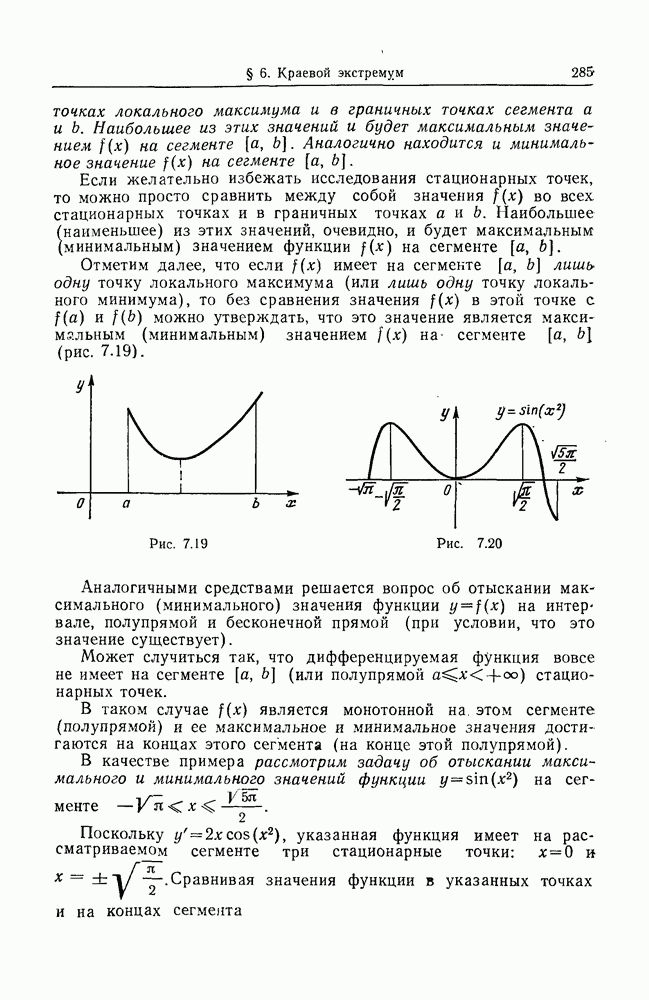
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
1. Теорема о разрешимости системы функциональных уравнений.
В предыдущем параграфе мы рассматривали вопрос о существовании и дифференцируемости неявной функции, определяемой посредством одного функционального уравнения. В этом параграфе мы рассмотрим аналогичный вопрос для совокупности  (m — любое натуральное число) неявных функций, определяемых: посредством системы функциональных уравнений.
(m — любое натуральное число) неявных функций, определяемых: посредством системы функциональных уравнений.
Итак, предположим, что  функций
функций

ищутся как решение системы  функциональных уравнений
функциональных уравнений

Изучим вопрос о разрешимости системы функциональных уравнений (13.14) относительно  . Под термином «решение системы (13.14)» мы в дальнейшем будем понимать совокупность
. Под термином «решение системы (13.14)» мы в дальнейшем будем понимать совокупность  функций (13.13) таких, что при подстановке этих функцию в систему
функций (13.13) таких, что при подстановке этих функцию в систему  все уравнения этой системы обращаются в тождества. Это решение мы будем называть непрерывным и дифференцируемым в некоторрй области D изменения переменных
все уравнения этой системы обращаются в тождества. Это решение мы будем называть непрерывным и дифференцируемым в некоторрй области D изменения переменных  если каждая из функций (13.13) непрерывна
если каждая из функций (13.13) непрерывна 
дифференцируема в области  Договоримся обозначать символом
Договоримся обозначать символом  пространство
пространство  переменных
переменных  а символом
а символом  пространство
пространство  переменных
переменных 
Рассмотрим  функций
функций  стоящих в левых частях системы (13.14), и составим из частных производных этих функций следующий определитель:
стоящих в левых частях системы (13.14), и составим из частных производных этих функций следующий определитель:

Будем называть определитель вида (13.15) определителем Якоби (или кратко якобианом) функций  по переменным
по переменным  и кратко обозначать символом
и кратко обозначать символом 

Имеет место следующее замечательное утверждение.
Теорема 13.2 (обобщение теоремы 13.1). Пусть  функций
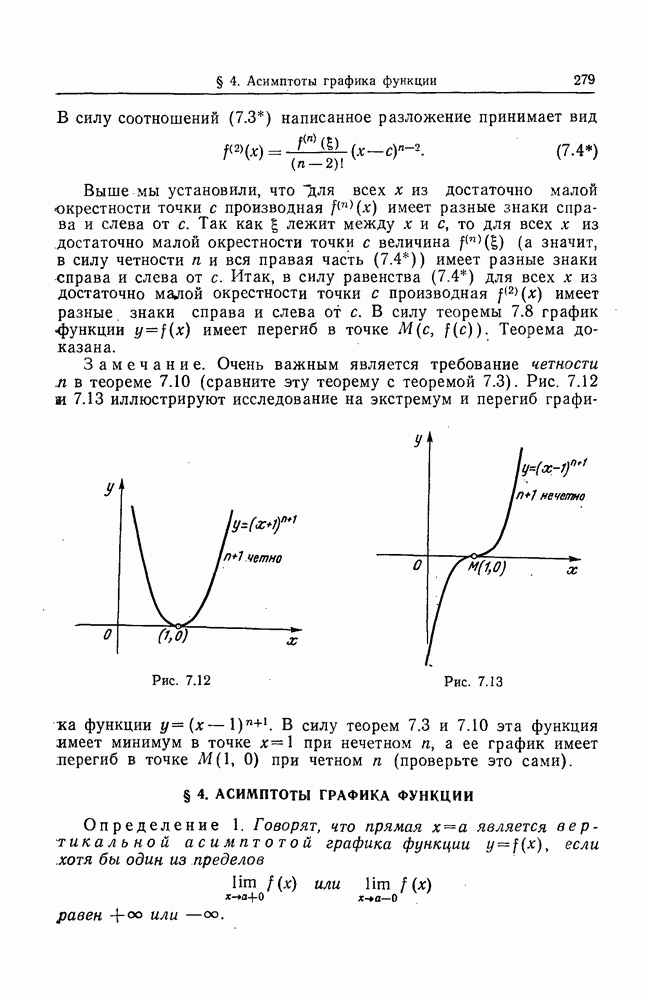
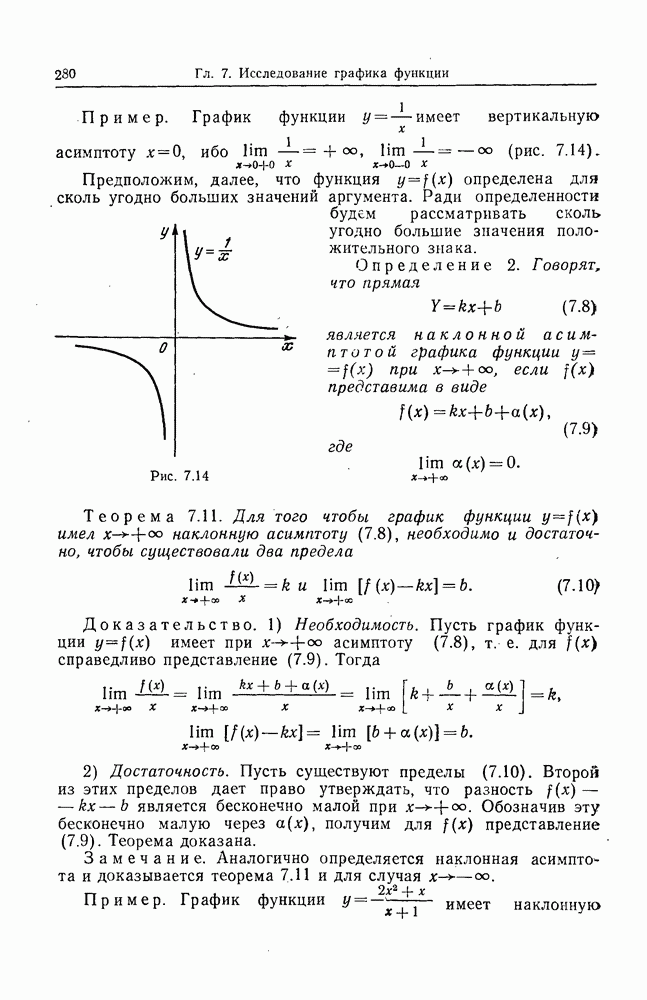
функций

дифференцируемы в некоторой окрестности точки  пространства
пространства  причем частные производные этих функций по переменным
причем частные производные этих функций по переменным  непрерывны в точке
непрерывны в точке  Тогда если в точке
Тогда если в точке  все функции (13.16) обращаются в нуль, а якобиан
все функции (13.16) обращаются в нуль, а якобиан  отличен от нуля в
отличен от нуля в  то для достаточно
то для достаточно  малых положительных чисел
малых положительных чисел  найдется такая окрестность точки
найдется такая окрестность точки  пространства
пространства  что в пределах этой окрестности существуют единственные
что в пределах этой окрестности существуют единственные  функций (13.13), которые удовлетворяют условиям
функций (13.13), которые удовлетворяют условиям  и являются решением системы уравнений (13.14), причем это решение непрерывно и дифференцируемо в указанной окрестности точки
и являются решением системы уравнений (13.14), причем это решение непрерывно и дифференцируемо в указанной окрестности точки 
Замечание. При  теорема 13.2 переходит в доказанную выше теорему 13.1, ибо в этом случае якобиан (13.15) обращается в частную производную
теорема 13.2 переходит в доказанную выше теорему 13.1, ибо в этом случае якобиан (13.15) обращается в частную производную 
Доказательство теоремы 13.2 проведем методом математической индукции. При  теорема уже доказана. Поэтому достаточно, предположив теорему 13.2 справедливой для системы
теорема уже доказана. Поэтому достаточно, предположив теорему 13.2 справедливой для системы  функциональных уравнений, доказать справедливость этой теоремы и для системы
функциональных уравнений, доказать справедливость этой теоремы и для системы  функциональных уравнений. Поскольку, по предположению, якобиан
функциональных уравнений. Поскольку, по предположению, якобиан

отличен от нуля в точке  то хотя бы один из миноров
то хотя бы один из миноров  порядка этого якобиана отличен от нуля в точке
порядка этого якобиана отличен от нуля в точке  Не ограничивая общности, будем считать, что в точке
Не ограничивая общности, будем считать, что в точке  отличен от нуля обведенный пунктиром минор, стоящий в левом верхнем углу. Тогда в силу предположения индукции первые
отличен от нуля обведенный пунктиром минор, стоящий в левом верхнем углу. Тогда в силу предположения индукции первые  уравнений системы (13.14) разрешимы относительно
уравнений системы (13.14) разрешимы относительно  . Точнее, для достаточно малых положительных чисел
. Точнее, для достаточно малых положительных чисел  найдется такая окрестность точки
найдется такая окрестность точки  пространства
пространства  переменных
переменных  что в пределах этой окрестности определены
что в пределах этой окрестности определены  функций
функций

которые удовлетворяют условиям  и являются при наличии этих условий единственным и дифференцируемым решением системы первых
и являются при наличии этих условий единственным и дифференцируемым решением системы первых  уравнений (13.14).
уравнений (13.14).
Подставим найденные функции (13.18) в левую часть последнего из уравнений (13.14). При этом левая часть последнего из уравнений (13.14) превращается в функцию, зависящую только от

(эту функцию мы обозначили символом  Таким образом, последнее из уравнений системы (13.14) приводит нас к уравнению
Таким образом, последнее из уравнений системы (13.14) приводит нас к уравнению

В силу равенства (13.19)  можно рассматривать как сложную функцию своих аргументов. Тогда, применяя теорему о дифференцируемости сложной функции, мы можем утверждать, что функция
можно рассматривать как сложную функцию своих аргументов. Тогда, применяя теорему о дифференцируемости сложной функции, мы можем утверждать, что функция  дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки  пространства
пространства  Равенство (13.19) и последнее из уравнений (13.14) позволяют утверждать, что
Равенство (13.19) и последнее из уравнений (13.14) позволяют утверждать, что  Поэтому, для того чтобы доказать, что к уравнению (13.20) применима теорема 13.1 и это, уравнение разрешимо относительно
Поэтому, для того чтобы доказать, что к уравнению (13.20) применима теорема 13.1 и это, уравнение разрешимо относительно  достаточно установить, что частная производная
достаточно установить, что частная производная  непрерывна и отлична от нуля в точке
непрерывна и отлична от нуля в точке  Для того чтобы сделать это, вычислим указанную частную производную. Подставим в первые
Для того чтобы сделать это, вычислим указанную частную производную. Подставим в первые  уравнений системы (13.14) функции (13.18), являющиеся решением этих уравнений, и продифференцируем полученные при этом тождества
уравнений системы (13.14) функции (13.18), являющиеся решением этих уравнений, и продифференцируем полученные при этом тождества  Получим
Получим

Далее продифференцируем по  равенство (13.19). Получим
равенство (13.19). Получим

Умножим теперь равенства  на соответствующие алгебраические дополнения
на соответствующие алгебраические дополнения  элементов последнего столбца якобиана (13.17) и после этого сложим эти равенства. Получим
элементов последнего столбца якобиана (13.17) и после этого сложим эти равенства. Получим

Так как сумма произведений элементов данного столбца определителя на соответствующие алгебраические дополнения элементов этого (другого) столбца равна определителю (нулю), то каждая квадратная скобка равна нулю, а круглая скобка равна якобиану (13.17).
Таким образом, мы получим, что

Здесь символом А обозначен якобиан (13.17), а  — алгебраическое дополнение последнего элемента последнего столбца, которое совпадает с минором, обведенным пунктиром и, по предположению, отличным от
— алгебраическое дополнение последнего элемента последнего столбца, которое совпадает с минором, обведенным пунктиром и, по предположению, отличным от  в точке
в точке  Поделив равенство (13.22) на
Поделив равенство (13.22) на  окончательно найдем
окончательно найдем

Формула (13.23), справедливая в точке  доказывает непрерывность частной производной
доказывает непрерывность частной производной  в тдчке
в тдчке  (ибо А и
(ибо А и  состоят из частных производных функций (13.16) по
состоят из частных производных функций (13.16) по  непрерывных в точке
непрерывных в точке  Кроме того, из формулы (13.23) вытекает, что
Кроме того, из формулы (13.23) вытекает, что  в точке
в точке  отлична от нуля (ибо
отлична от нуля (ибо  отличен от нуля в точке
отличен от нуля в точке  Тем самым мы доказали, что к уравнению (13.20) можно применить теорему 13.1.
Тем самым мы доказали, что к уравнению (13.20) можно применить теорему 13.1.
Согласно этой теореме для достаточно малого положительного числа  найдется такая окрестность точки
найдется такая окрестность точки  пространства
пространства  что всюду в пределах этой окрестности определена функция
что всюду в пределах этой окрестности определена функция

которая удовлетворяет условию  и является
и является  наличии этого условия единственным, непрерывным и дифференцируемым решением уравнения (13.20). Имея в виду, что функции 13.18) являются решениями первых
наличии этого условия единственным, непрерывным и дифференцируемым решением уравнения (13.20). Имея в виду, что функции 13.18) являются решениями первых  уравнений (13.14) при любых
уравнений (13.14) при любых  из окрестности точки
из окрестности точки  и вставляя найденную функцию (13.24) в
и вставляя найденную функцию (13.24) в  мы получим функции, зависящие только от переменных
мы получим функции, зависящие только от переменных 

(Эти функции мы обозначили символами  Теорема о дифференцируемости сложной функции дает право утверждать, что каждая из функций
Теорема о дифференцируемости сложной функции дает право утверждать, что каждая из функций  дифференцируема в окрестности точки
дифференцируема в окрестности точки  Таким образом, мы доказали, что
Таким образом, мы доказали, что  функций
функций

удовлетворяют в окрестности точки  условиям
условиям 
 и представляют собой при наличии этих условий непрерывное и дифференцируемое в некоторой окрестности точка
и представляют собой при наличии этих условий непрерывное и дифференцируемое в некоторой окрестности точка  решение системы (13.14).
решение системы (13.14).
Остается доказать, что функции (13.25) представляют собой единственное решение системы (13.14), удовлетворяющее условиям  (при достаточно малых положительных
(при достаточно малых положительных 
Предположим что кроме функций (13.25) существуют еще т. функций

также являющихся решением системы (13.14) и удовлетворяющих условиям 
Тогда в силу предположения индукции первые  функций. (13.25) представляют собой при заданном
функций. (13.25) представляют собой при заданном  единственное и, дифференцируемое решение системы первых
единственное и, дифференцируемое решение системы первых  уравнений. (13.14). Но при заданном
уравнений. (13.14). Но при заданном  единственное решение системы первых
единственное решение системы первых  уравнений (13.14) дается равенствами (13.18). Таким образом, справедливы соотношения
уравнений (13.14) дается равенствами (13.18). Таким образом, справедливы соотношения

в которых  — те же функции, что и (13.18).
— те же функции, что и (13.18).
В таком случае последнее уравнение (13.14) и соотношение (13.19) позволяют нам утверждать, что  является единственным решением уравнения (13.20), т. е.
является единственным решением уравнения (13.20), т. е. 
При наличии равенства  из соотношений (13.18) и (13.18) сразу же вытекает,
из соотношений (13.18) и (13.18) сразу же вытекает, 
Теорема 13.2 полностью доказана.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРА
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- Глава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Недостаточность рациональных чисел для измерения отрезков числовой оси.
- 3. Упорядочение множества бесконечных десятичных дробей.
- § 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
- 2. Существование точных граней.
- § 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
- § 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Существование и единственность суммы и произведения вещественных чисел.
- § 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Некоторые часто употребляемые соотношения.
- 3. Некоторые конкретные множества вещественных чисел.
- § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Аксиоматическое введение множества вещественных чисел.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
- 2. Операции над множествами.
- 3. Счетные и несчетные множества. Несчетность сегмента [0, 1]. Мощность множества.
- 4. Свойства операций над множествами. Отображение множеств.
- Глава 3. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
- 2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- 3. Основные свойства бесконечно малых последовательностей.
- 4. Сходящиеся последовательности и их свойства.
- § 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Теорема о сходимости монотонной ограниченной последовательности.
- 4. Примеры сходящихся монотонных последовательностей.
- § 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Расширение понятий предельной точки и верхнего и нижнего пределов.
- 3. Критерий Коши сходимости последовательности.
- § 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ
- 2. Предел функции по Гейне и по Коши.
- 3. Критерий Коши существования предела функции.
- 4. Арифметические операции над функциями, имеющими предел.
- 5. Бесконечно малые и бесконечно большие функции.
- § 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ
- Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
- 2. Арифметические операции над непрерывными функциями.
- 3. Сложная функция и ее непрерывность.
- § 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ
- 2. Понятие обратной функции.
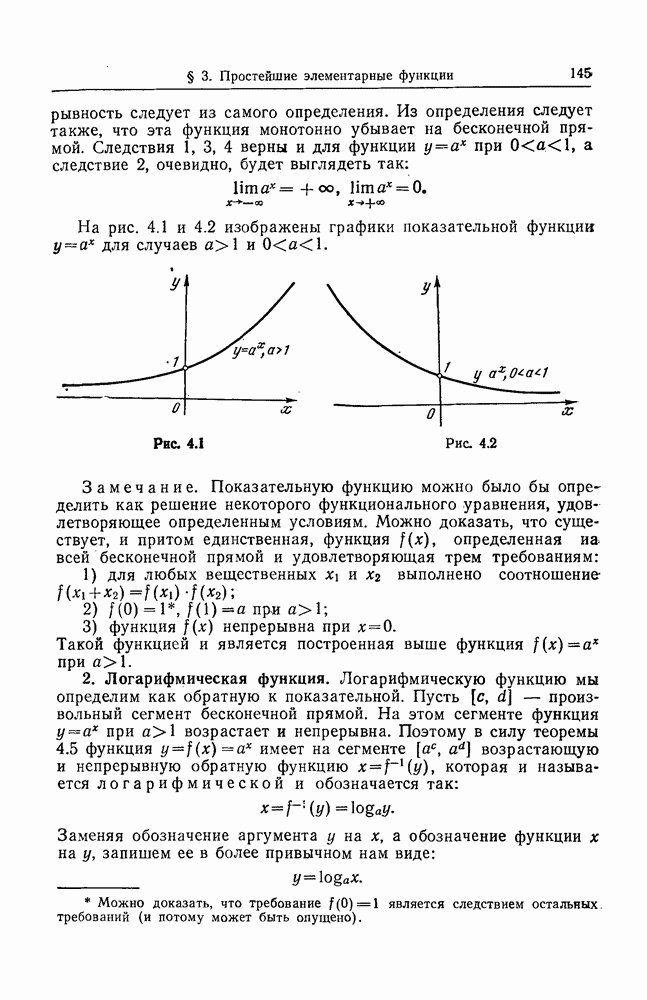
- § 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
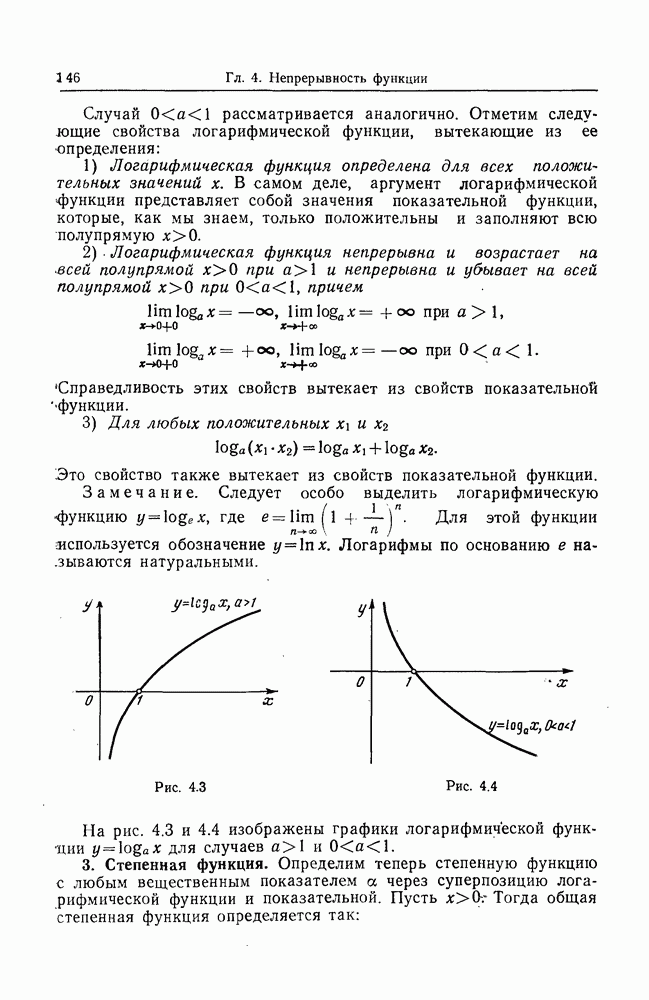
- 2. Логарифмическая функция.
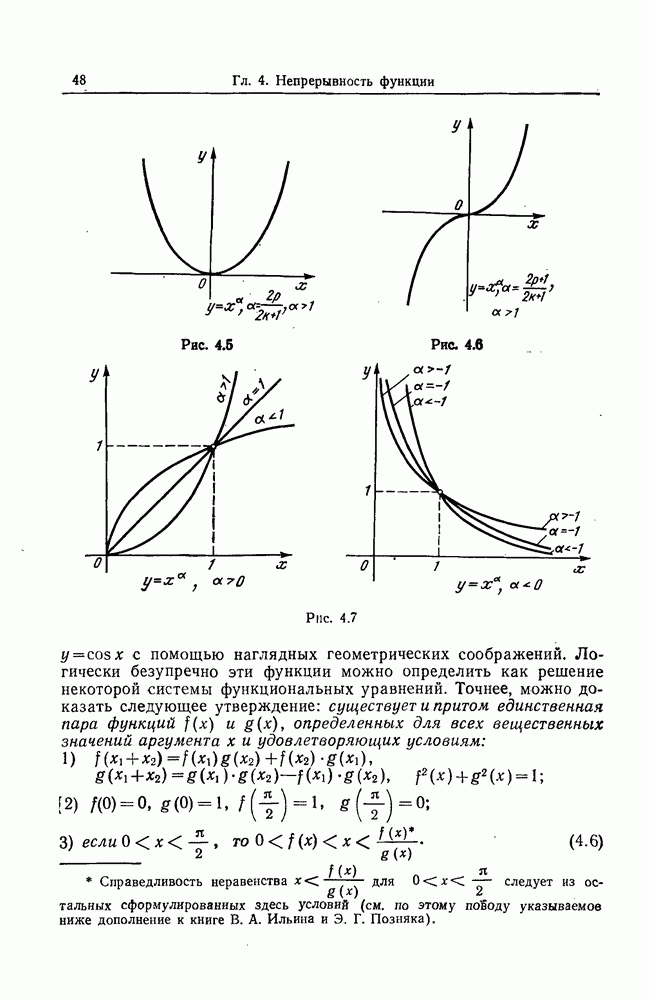
- 3. Степенная функция.
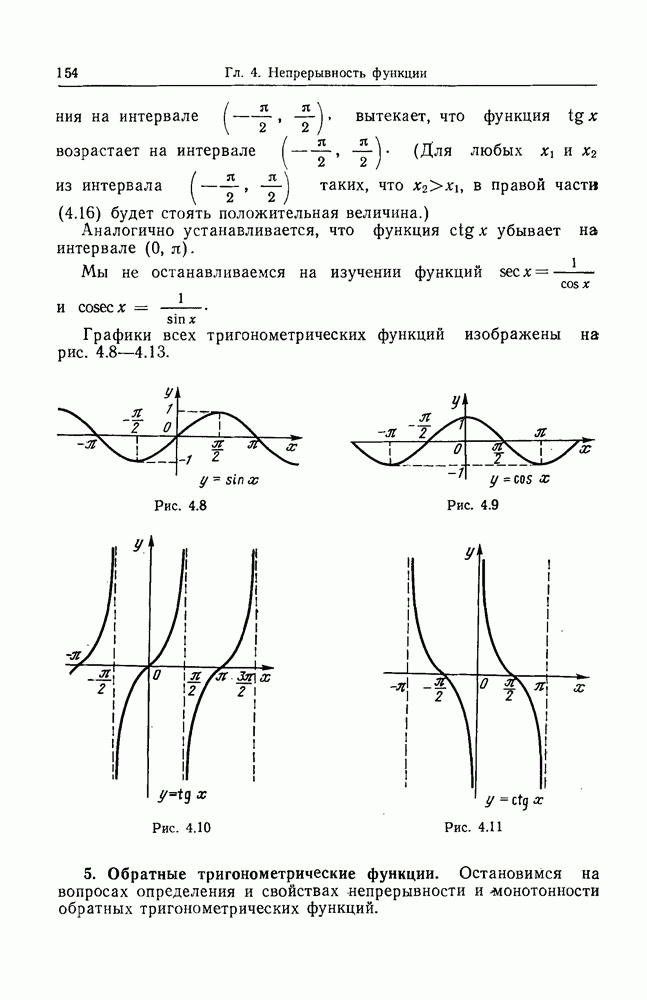
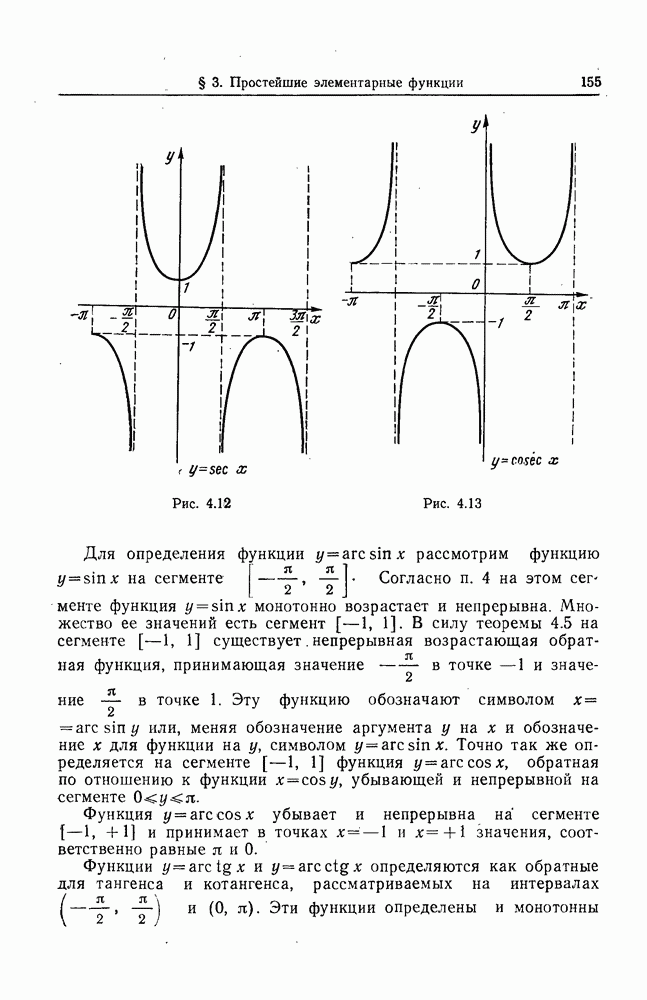
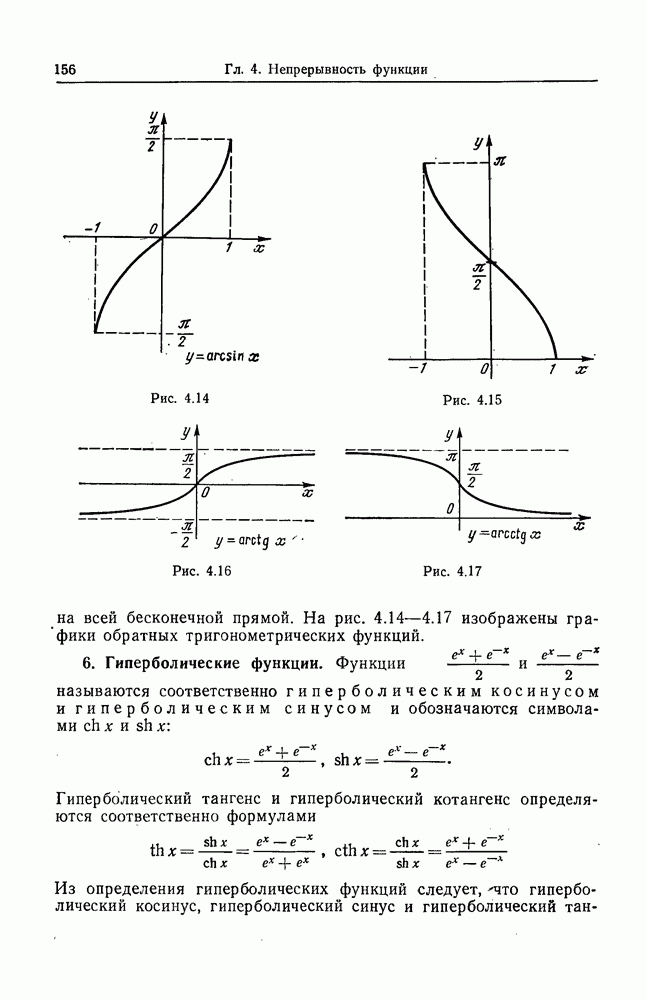
- 4. Тригонометрические функции.
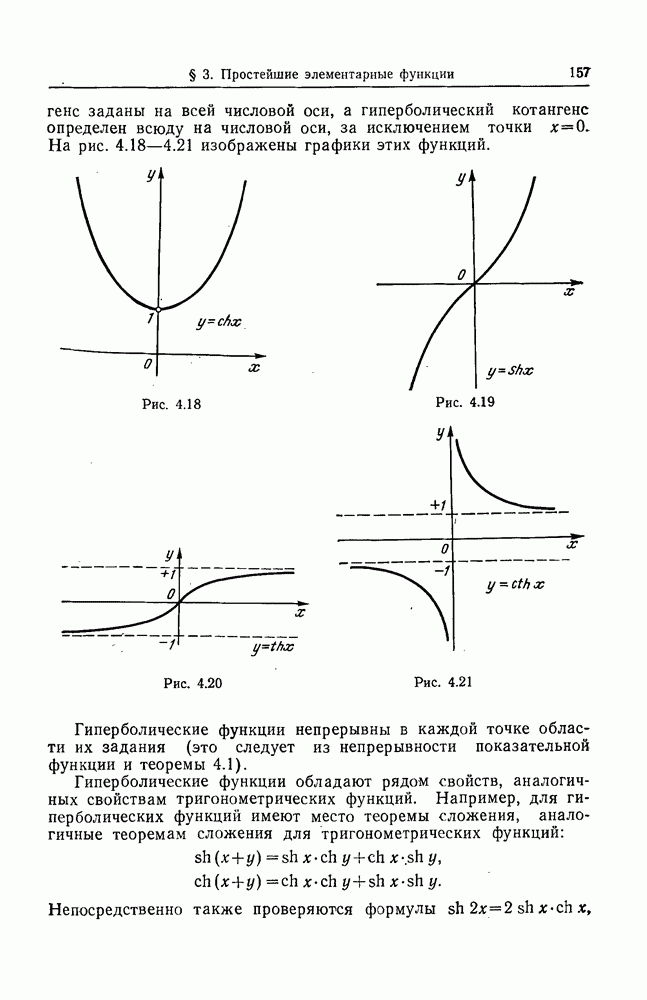
- 5. Обратные тригонометрические функции.
- 6. Гиперболические функции.
- § 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА
- 2. Второй замечательный предел.
- § 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ
- 2. О точках разрыва монотонной функции.
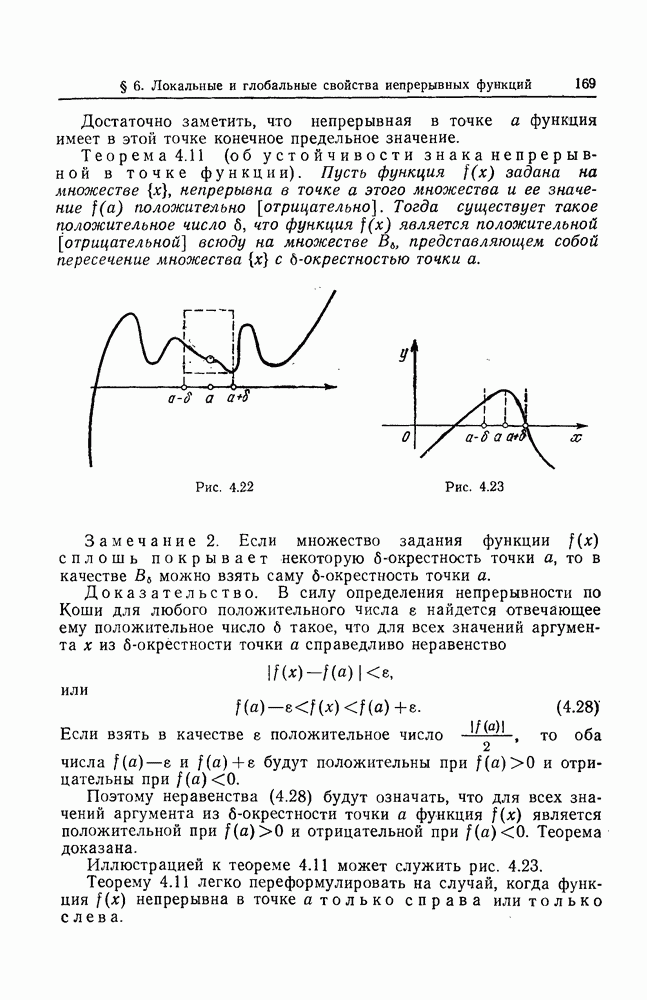
- § 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
- 2. Глобальные свойства непрерывных функций.
- 3. Понятие равномерной непрерывности функции.
- 4. Понятие модуля непрерывности функции.
- § 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА
- 2. О покрытиях множества системой открытых множеств.
- 3. Понятие компактности множества.
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. ПОНЯТИЕ ПРОИЗВОДНОЙ
- 2. Определение производной.
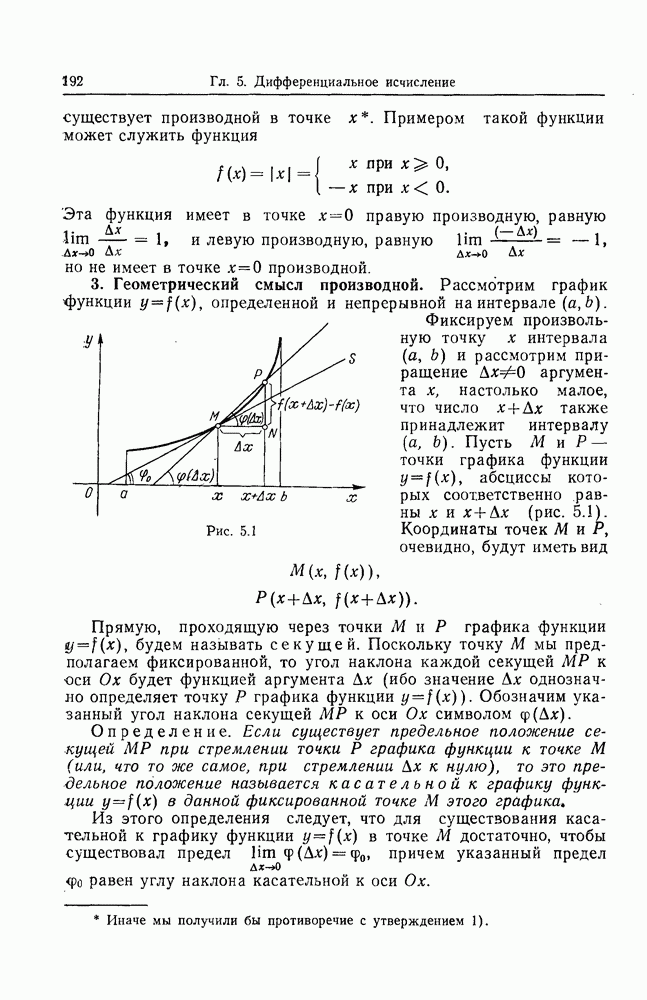
- 3. Геометрический смысл производной.
- § 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
- 2. Дифференцируемость и непрерывность.
- 3. Понятие дифференциала функции.
- § 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ
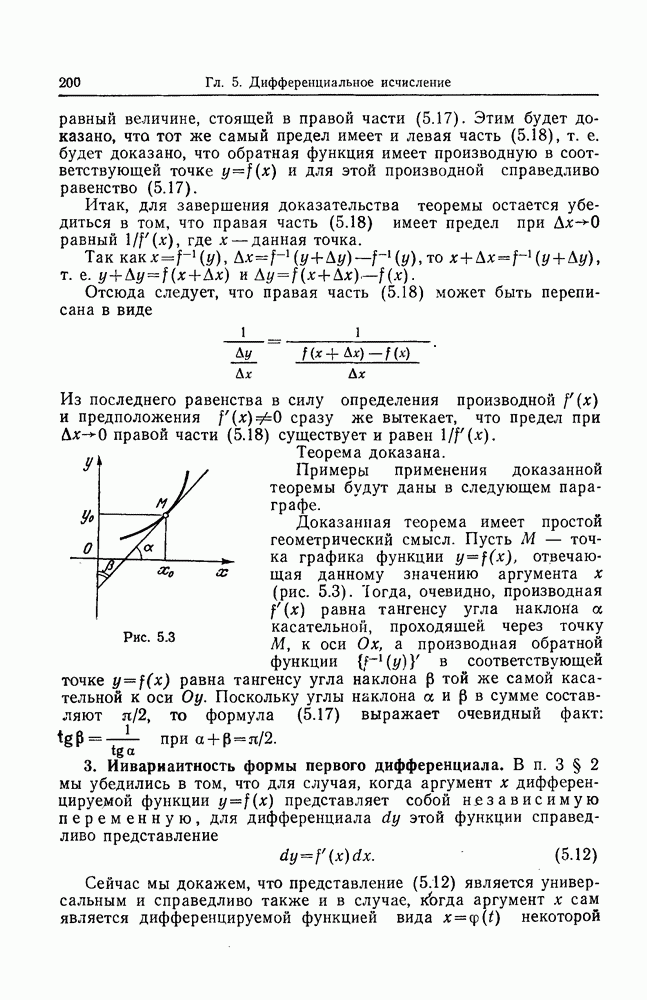
- 2. Дифференцирование обратной функции.
- 3. Инвариантность формы первого дифференциала.
- 4. Применение дифференциала для установления приближенных формул.
- § 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ
- § 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Производная логарифмической функции.
- 3. Производные показательной и обратных тригонометрических функций.
- 4. Производная степенной функции.
- 5. Таблица производных простейших элементарных функций.
- 6. Таблица дифференциалов простейших элементарных функций.
- 7. Логарифмическая производная. Производная степенно-показательной функции.
- § 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. n-ые производные некоторых функций.
- 3. Формула Лейбница для n-й производной произведения двух функций.
- 4. Дифференциалы высших порядков.
- § 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
- § 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ
- Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
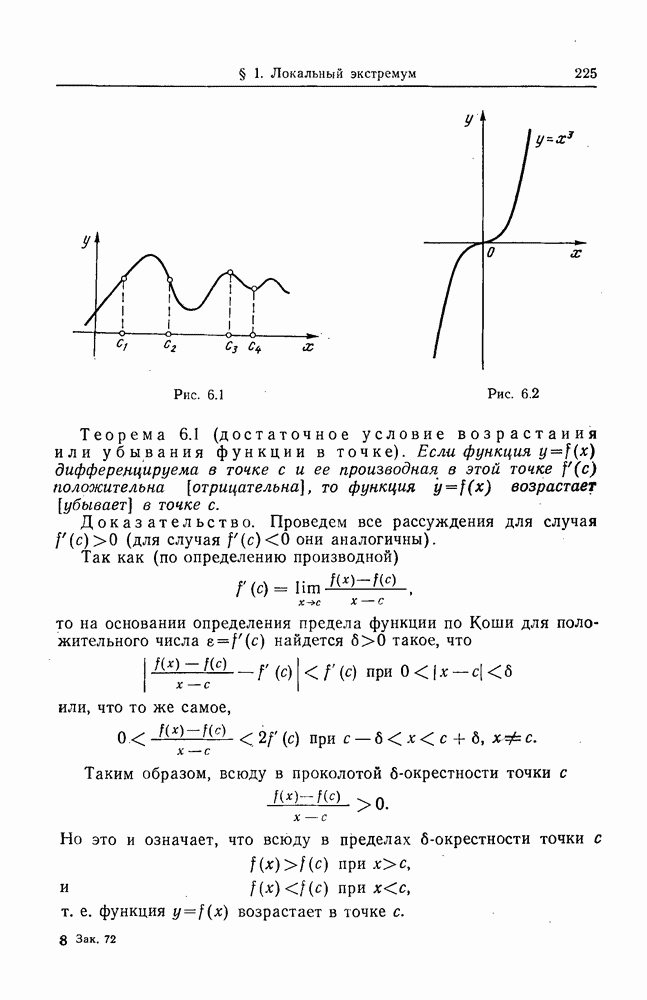
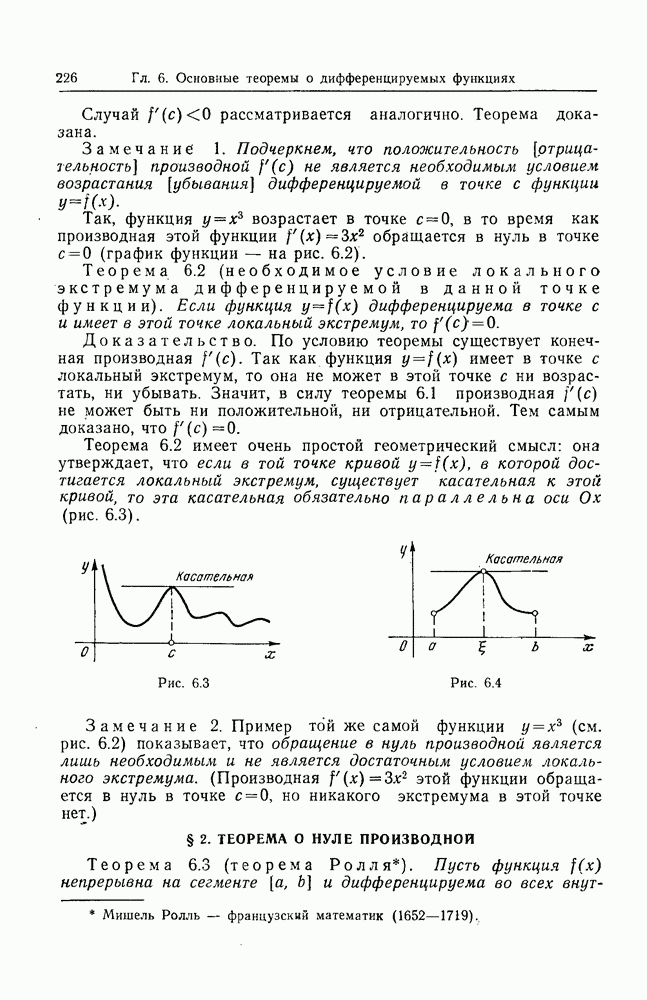
- § 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
- § 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ
- § 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА)
- § 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА
- 2. Условия монотонности функции на интервале.
- 3. Отсутствие разрывов первого рода и устранимых разрывов у производной.
- 4. Вывод некоторых неравенств.
- § 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ)
- § 6. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ)
- 2. Раскрытие неопределенности вида oo/oo
- 3. Раскрытие неопределенностей других видов.
- § 7. ФОРМУЛА ТЕЙЛОРА
- § 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА
- 2. Другая запись формулы Тейлора.
- 3. Формула Маклорена.
- § 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Разложение по формуле Маклорена некоторых элементарных функций.
- § 10. ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА
- 2. Доказательство иррациональности числа е.
- 3. Вычисление значений тригонометрических функций.
- 4. Асимптотическая оценка элементарных функций и вычисление пределов.
- Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ
- § 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК
- 2. Отыскание стационарных точек.
- 3. Первое достаточное условие экстремума.
- 4. Второе достаточное условие экстремума.
- 5. Третье достаточное условие, экстремума.
- 6. Экстремум функции, недифференцируемой в данной точке.
- 7. Общая схема отыскания экстремумов.
- § 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ
- § 3. ТОЧКИ ПЕРЕГИБА
- 2. Первое достаточное условие перегиба.
- 3. Некоторые обобщения первого достаточного условия перегиба.
- 4. Второе достаточное условие перегиба.
- 5. Третье достаточное условие перегиба.
- § 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
- § 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ
- 2. Краевой экстремум.
- 3. Теорема Дарбу.
- ДОПОЛНЕНИЕ
- Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции
- Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Неопределенный интеграл.
- 3. Основные свойства неопределенного интеграла.
- 4. Таблица основных неопределенных интегралов.
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование по частям.
- § 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Краткие сведения о корнях алгебраических многочленов.
- 3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей.
- 4. Разложение правильной рациональной дроби на сумму простейших дробей.
- 5. Интегрируемость рациональной дроби в элементарных функциях.
- 6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА
- 2. Основные свойства верхних и нижних сумм.
- § 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- 2. Классы интегрируемых функций.
- § 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ
- 2. Оценки интегралов.
- § 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ
- 2. Основная формула интегрального исчисления.
- 3. Важные правила, позволяющие вычислять определенные интегралы.
- 4. Остаточный член формулы Тейлора в интегральной форме.
- § 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ
- 2. Неравенство Гёльдера для сумм.
- 3. Неравенство Минковского для сумм.
- 4. Неравенство Гёльдера для интегралов.
- 5. Неравенство Минковского для интегралов.
- § 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА
- 2. Критерий интегрируемости Лебега.
- ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Критерий Коши сходимости несобственного интеграла первого рода.
- 3. Абсолютная и условная сходимость несобственных интегралов.
- 4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям.
- § 2. Несобственные интегралы второго рода
- § 3. Главное значение несобственного интеграла
- ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса
- 2. Свойства интеграла Стилтьеса.
- Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. ДЛИНА ДУГИ КРИВОЙ
- 2. Понятие параметризуемой кривой.
- 3. Длина дуги кривой. Понятие спрямляемой кривой.
- 4. Критерий спрямляемости кривой. Вычисление длины дуги кривой.
- 5. Дифференциал дуги.
- 6. Примеры.
- § 2. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
- 2. Площадь плоской фигуры.
- 3. Площадь криволинейной трапеции и криволинейного сектора.
- 4. Примеры вычисления площадей.
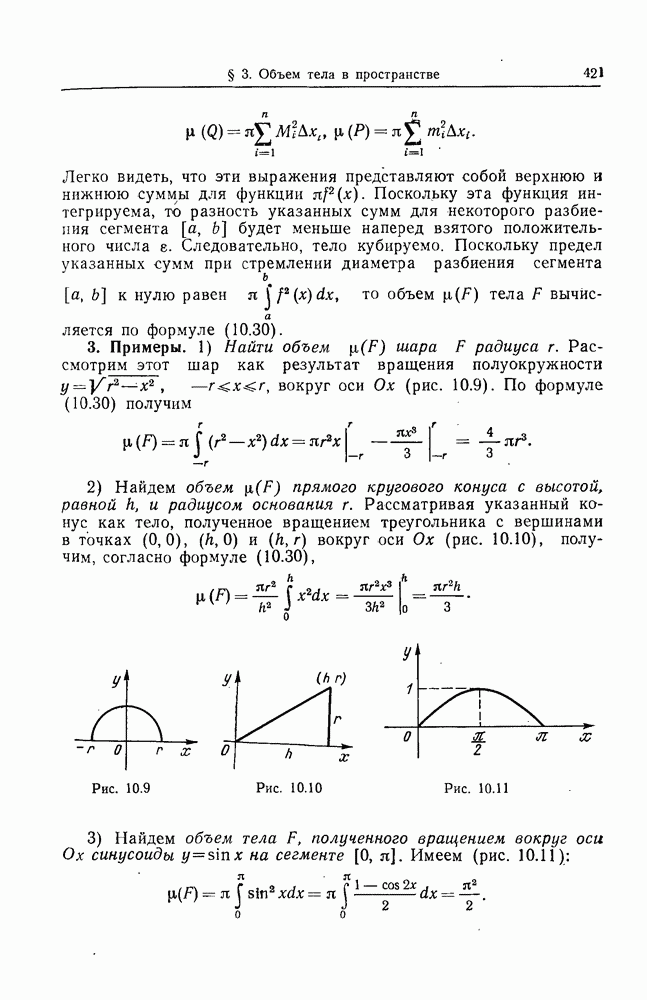
- § 3. ОБЪЕМ ТЕЛА В ПРОСТРАНСТВЕ
- 2. Некоторые классы кубируемых тел.
- 3. Примеры.
- Глава 11. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
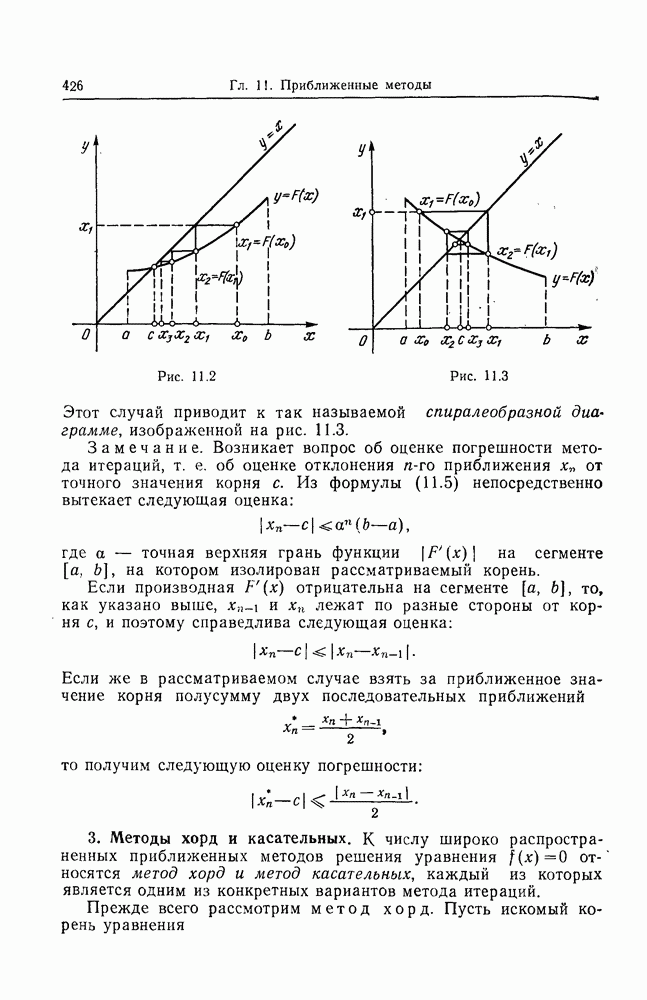
- § 1. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ
- 2. Метод итераций.
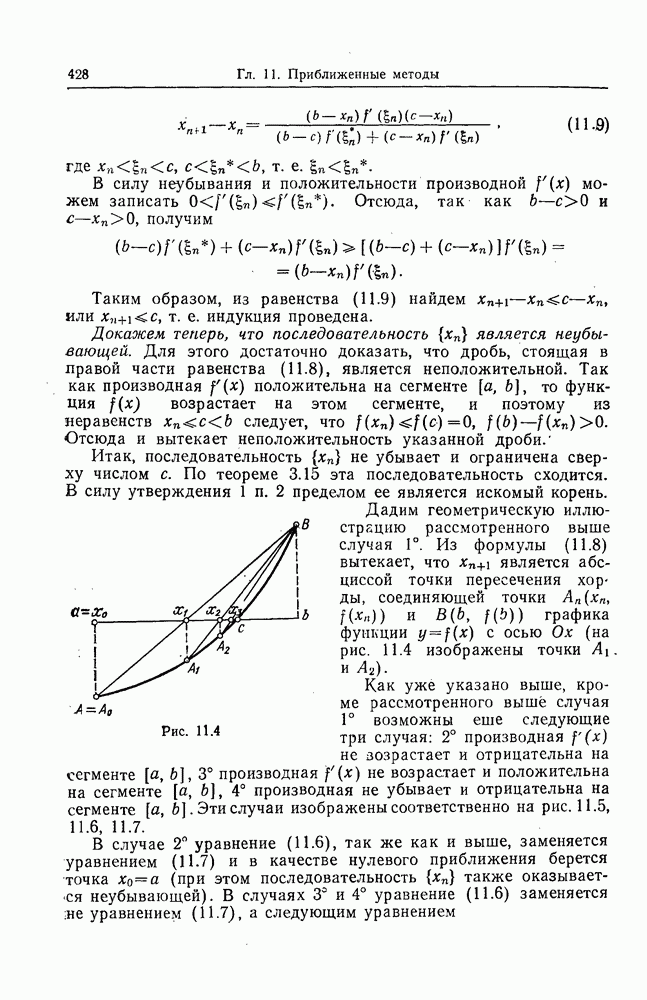
- 3. Методы хорд и касательных.
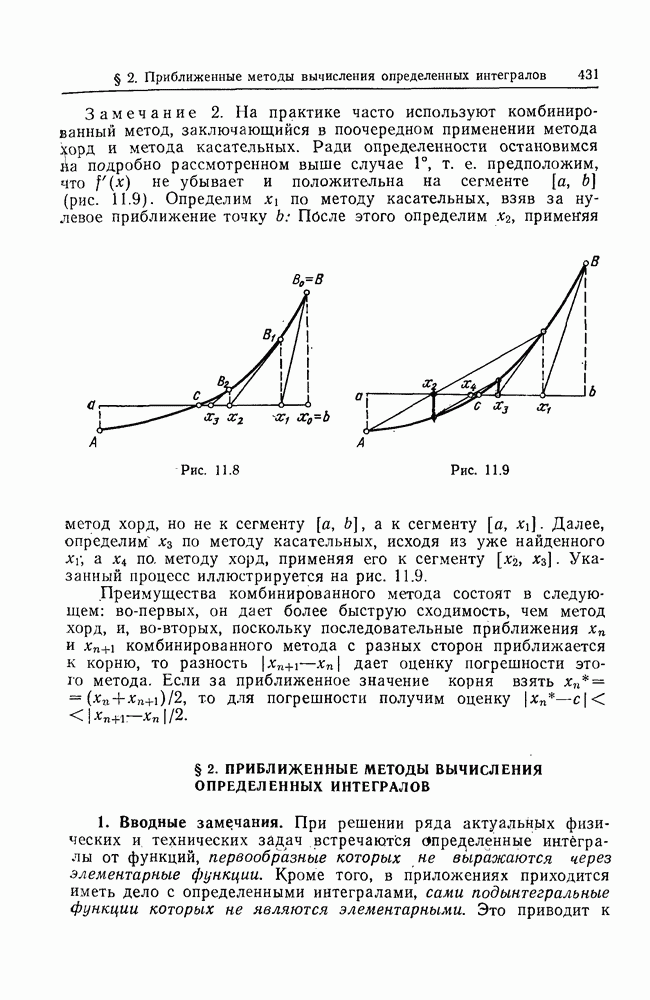
- § 2. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- 2. Метод прямоугольников.
- 3. Метод трапеций.
- 4. Метод парабол.
- Глава 12. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ПОНЯТИЕ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Множества точек m-мерного евклидова пространства.
- 3. Понятие функции m переменных.
- § 2. ПРЕДЕЛ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Свойство ограниченной последовательности точек E^m.
- 3. Предел функции m переменных.
- 4. Бесконечно малые функции m переменных.
- 5. Повторные пределы.
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Непрерывность функции m переменных по одной переменной.
- 3. Основные свойства непрерывных функций нескольких переменных.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Дифференцируемость функции нескольких переменных.
- 3. Геометрический смысл условия дифференцируемости функции двух переменных.
- 4. Достаточные условия дифференцируемости.
- 5. Дифференциал функции нескольких переменных.
- 6. Дифференцирование сложной функции.
- 7. Инвариантность формы первого дифференциала.
- 8. Производная по направлению. Градиент.
- § 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. Дифференциалы высших порядков.
- 3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме.
- 4. Формула Тейлора с остаточным членом в форме Пеано.
- § 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Достаточные условия локального экстремума функции m переменных.
- 3. Случай функции двух переменных.
- ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции
- 1. Выпуклые множества и выпуклые функции.
- 2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции.
- 3. Поиск минимума сильно выпуклой функции.
- ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства
- 2. Открытые и замкнутые множества.
- 3. Прямое произведение метрических пространств.
- 4. Всюду плотные и совершенные множества.
- 5. Сходимость. Непрерывные отображения.
- 6. Компактность.
- 7. Базис пространства.
- Топологические пространства
- Линейные нормированные пространства, линейные операторы
- ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах
- 2. Формула Лагранжа конечных приращений.
- 3. Связь между слабой и сильной дифференцируемостью.
- 4. Дифференцируемость функционалов.
- 5. Интеграл от абстрактных функций.
- 6. Формула Ньютона — Лейбница для абстрактных функций.
- 7. Производные второго порядка.
- 8. Отображение m-мерного евклидова пространства в n-мерное.
- 9. Производные и дифференциалы высших порядков.
- 10. Формула Тейлора для отображений одного нормированного пространства в другое.
- Исследование на экстремум функционалов в нормированных пространствах
- 2. Достаточные условия экстремума.
- Глава 13. НЕЯВНЫЕ ФУНКЦИИ
- § 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ
- 2. Вычисление частных производных неявно заданной функции.
- 3. Особые точки поверхности и плоской кривой.
- 4. Условия, обеспечивающие существование для функции y=f(x) обратной функции.
- § 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
- 2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений.
- 3. Взаимно однозначное отображение двух множеств m-мерного пространства.
- § 3. ЗАВИСИМОСТЬ ФУНКЦИЙ
- 2. Функциональные матрицы и их приложения.
- § 4. УСЛОВНЫЙ ЭКСТРЕМУМ
- 2. Метод неопределенных множителей Лагранжа.
- 3. Достаточные условия.
- 4. Пример.
- ДОПОЛНЕНИЕ
- Отображения банаховых пространств. Аналог теоремы о неявной функции
- 2. Случай конечномерных пространств.
- 3. Особые точки поверхности в пространстве n измерений. Обратное отображение.
- 4. Условный экстремум в случае отображений нормированных пространств.