| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Арифметические операции над непрерывными функциями.
Убедимся в том, что арифметические операции над непрерывными функциями приводят снова к непрерывным функциям. Справедлива следующая теорема.
Основная теорема 4.1. Пусть на одном и том же множестве заданы функции  непрерывные в точке а. Тогда функции
непрерывные в точке а. Тогда функции  и непрерывны в точке а (в случае частного нужно дополнительно требовать
и непрерывны в точке а (в случае частного нужно дополнительно требовать 
Доказательство. Так как непрерывные в точке а функции  имеют в точке а пределы, соответственно равны
имеют в точке а пределы, соответственно равны  то в силу теоремы 3.21 из гл. 3 пределы функций
то в силу теоремы 3.21 из гл. 3 пределы функций  существуют и равны соответственно
существуют и равны соответственно  Но как раз
Но как раз  величины равны частным значениям перечисленных функций в точке а. По определению эти функции непрерывны в точке а, что и требовалось доказать.
величины равны частным значениям перечисленных функций в точке а. По определению эти функции непрерывны в точке а, что и требовалось доказать.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРА
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- Глава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Недостаточность рациональных чисел для измерения отрезков числовой оси.
- 3. Упорядочение множества бесконечных десятичных дробей.
- § 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
- 2. Существование точных граней.
- § 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
- § 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Существование и единственность суммы и произведения вещественных чисел.
- § 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Некоторые часто употребляемые соотношения.
- 3. Некоторые конкретные множества вещественных чисел.
- § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Аксиоматическое введение множества вещественных чисел.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
- 2. Операции над множествами.
- 3. Счетные и несчетные множества. Несчетность сегмента [0, 1]. Мощность множества.
- 4. Свойства операций над множествами. Отображение множеств.
- Глава 3. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
- 2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- 3. Основные свойства бесконечно малых последовательностей.
- 4. Сходящиеся последовательности и их свойства.
- § 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Теорема о сходимости монотонной ограниченной последовательности.
- 4. Примеры сходящихся монотонных последовательностей.
- § 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Расширение понятий предельной точки и верхнего и нижнего пределов.
- 3. Критерий Коши сходимости последовательности.
- § 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ
- 2. Предел функции по Гейне и по Коши.
- 3. Критерий Коши существования предела функции.
- 4. Арифметические операции над функциями, имеющими предел.
- 5. Бесконечно малые и бесконечно большие функции.
- § 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ
- Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
- 2. Арифметические операции над непрерывными функциями.
- 3. Сложная функция и ее непрерывность.
- § 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ
- 2. Понятие обратной функции.
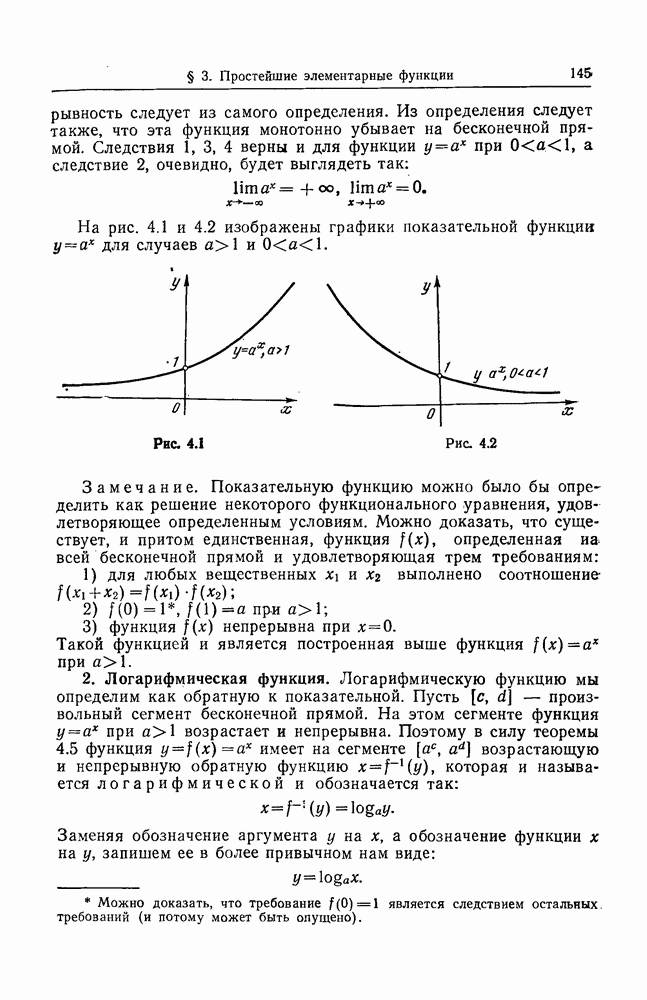
- § 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
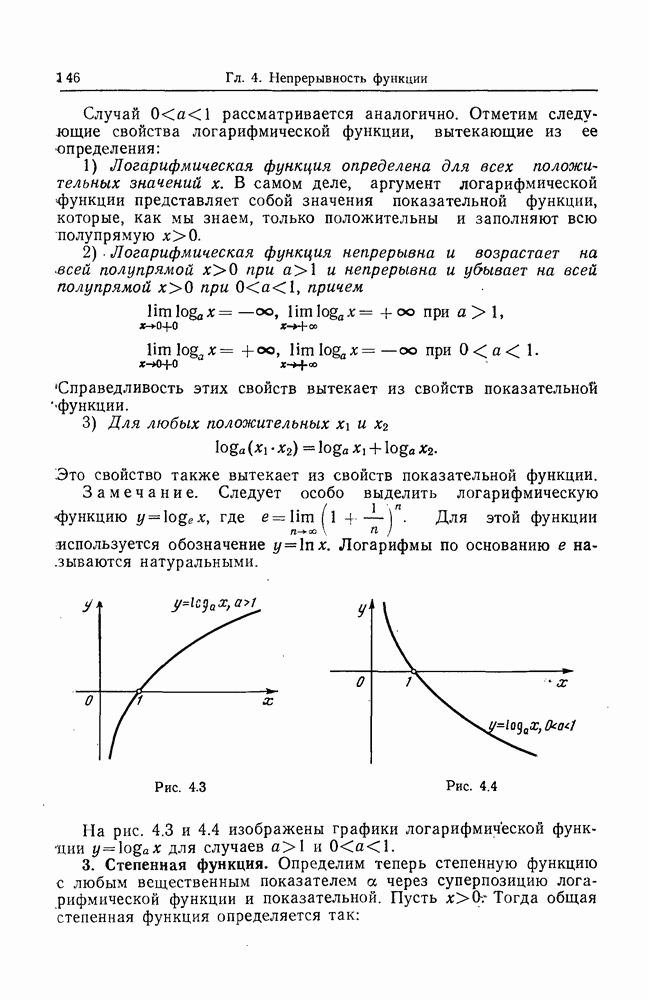
- 2. Логарифмическая функция.
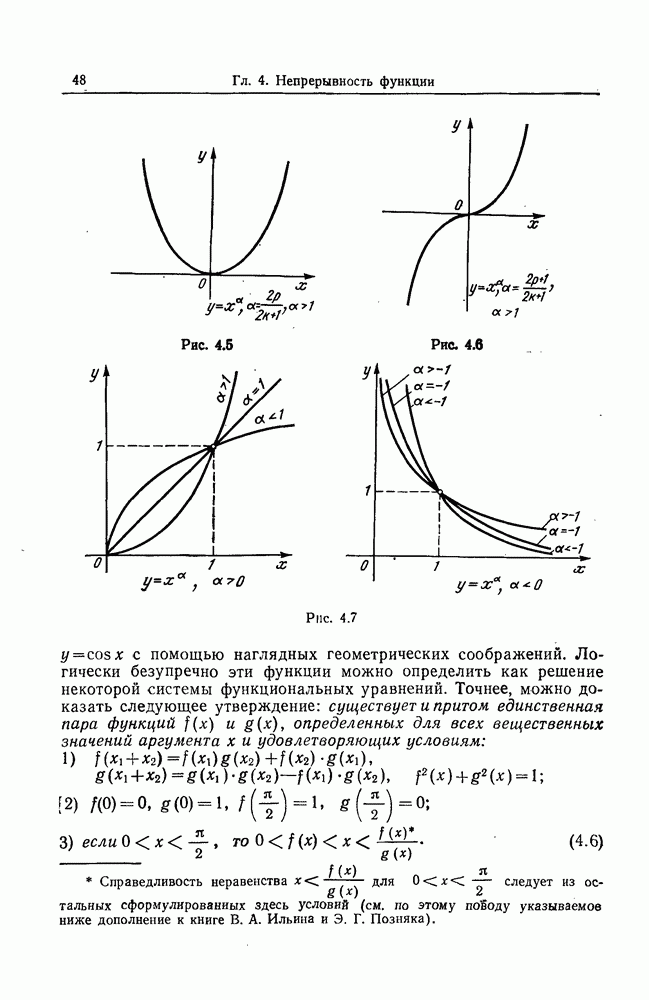
- 3. Степенная функция.
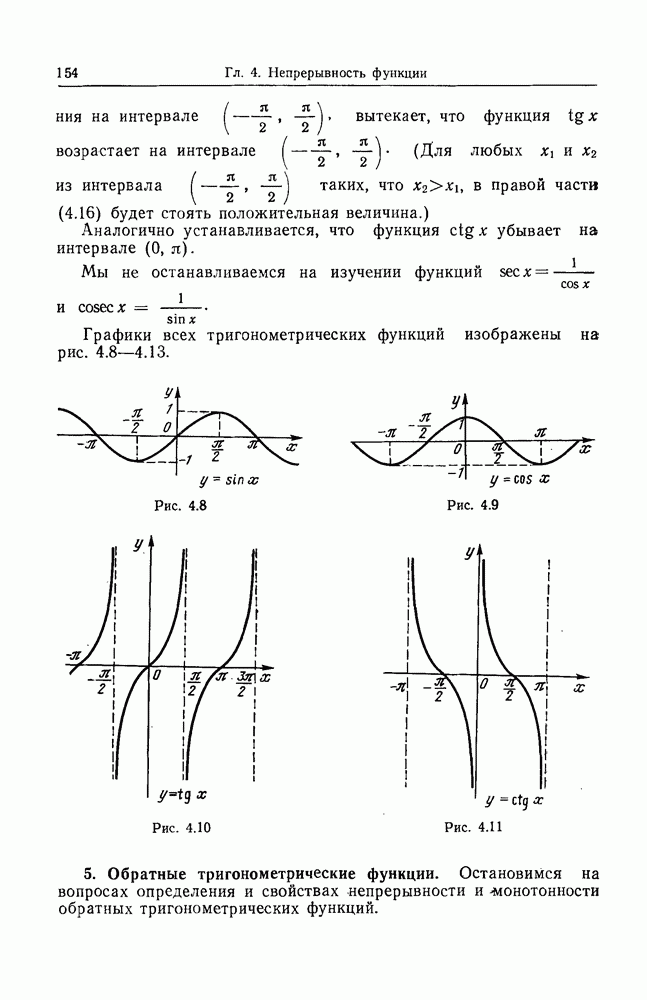
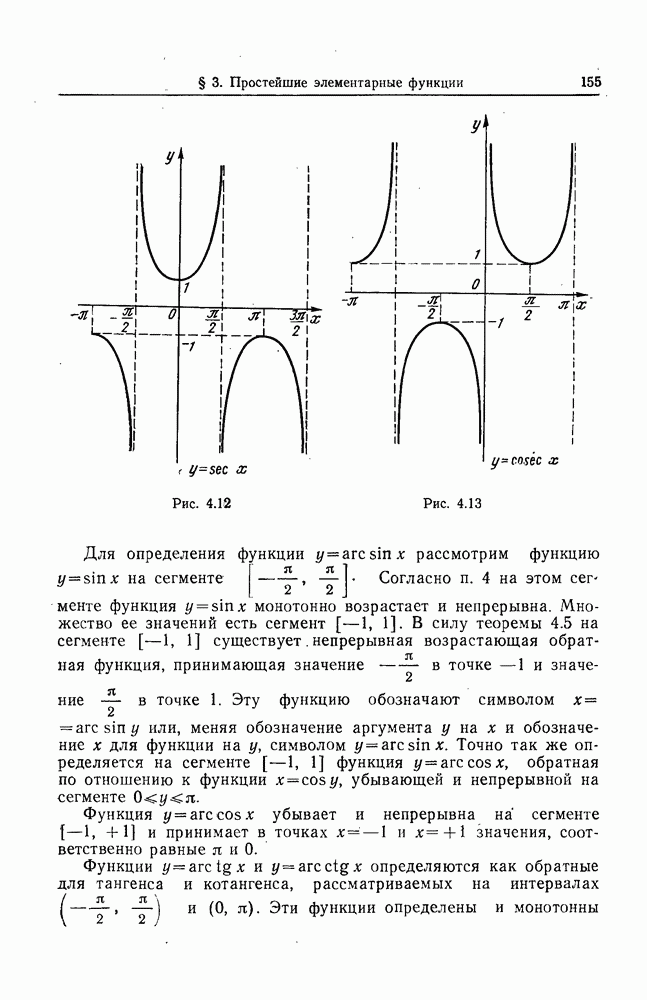
- 4. Тригонометрические функции.
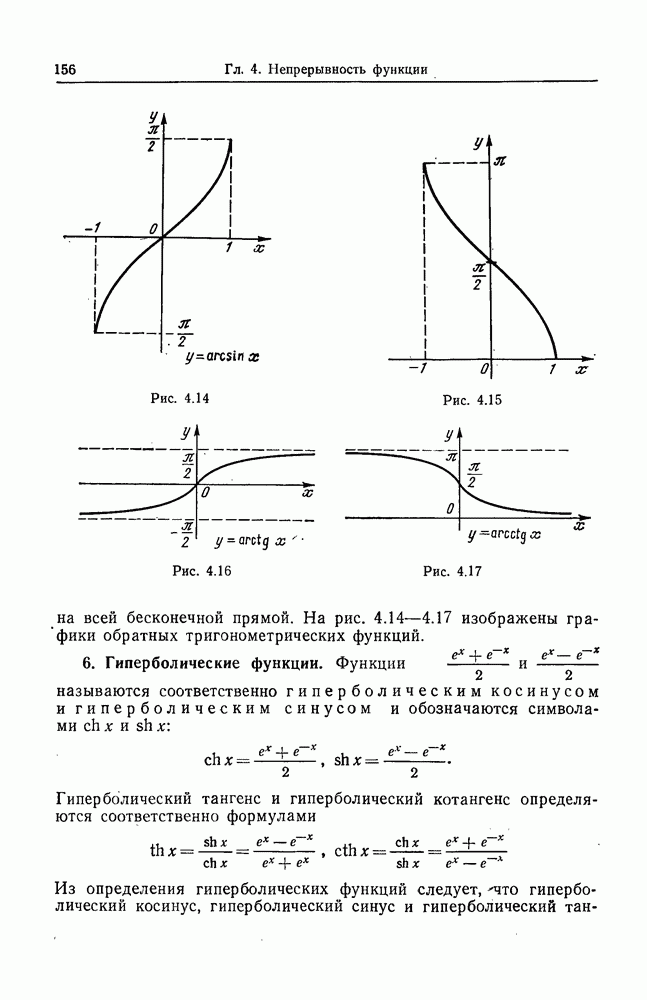
- 5. Обратные тригонометрические функции.
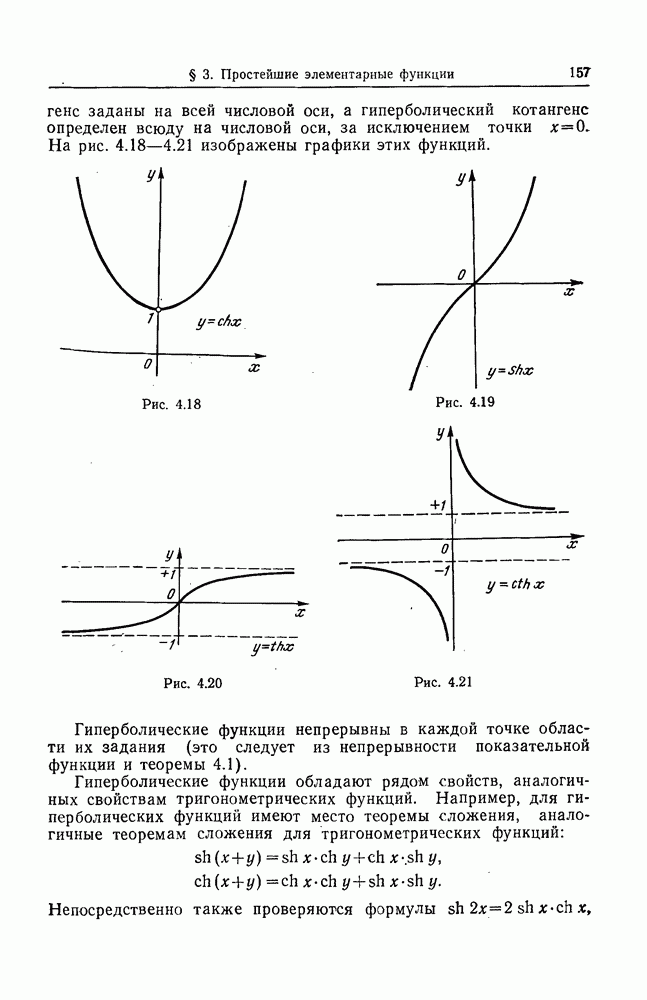
- 6. Гиперболические функции.
- § 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА
- 2. Второй замечательный предел.
- § 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ
- 2. О точках разрыва монотонной функции.
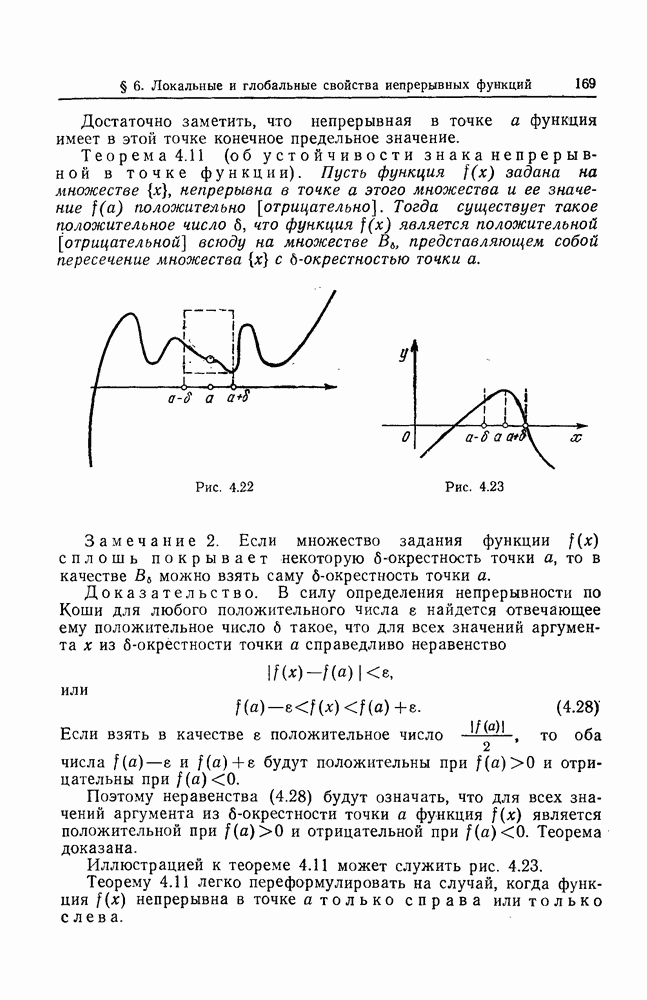
- § 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
- 2. Глобальные свойства непрерывных функций.
- 3. Понятие равномерной непрерывности функции.
- 4. Понятие модуля непрерывности функции.
- § 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА
- 2. О покрытиях множества системой открытых множеств.
- 3. Понятие компактности множества.
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. ПОНЯТИЕ ПРОИЗВОДНОЙ
- 2. Определение производной.
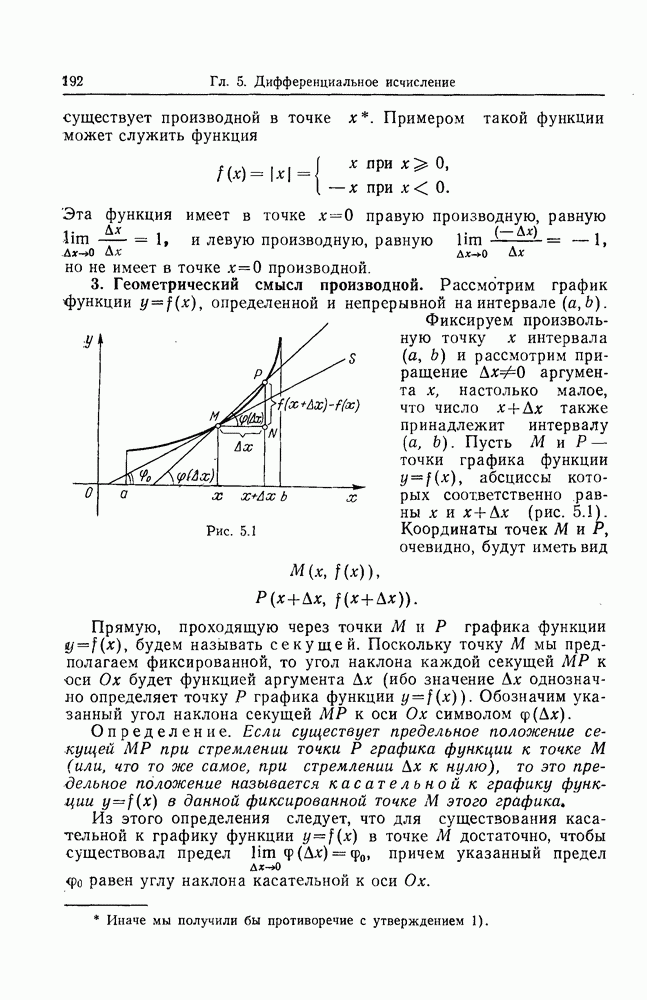
- 3. Геометрический смысл производной.
- § 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
- 2. Дифференцируемость и непрерывность.
- 3. Понятие дифференциала функции.
- § 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ
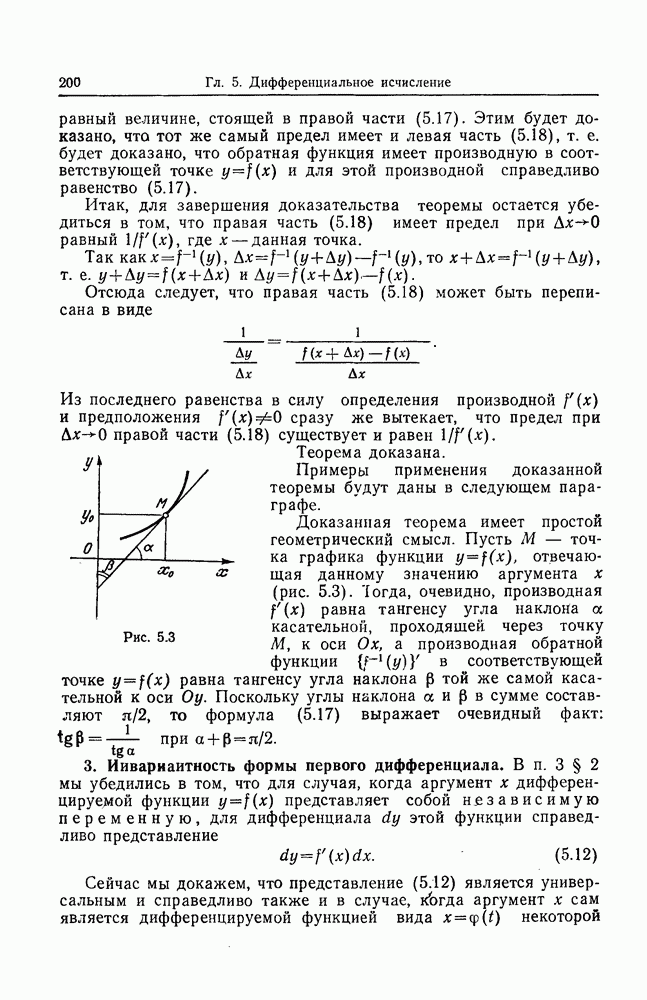
- 2. Дифференцирование обратной функции.
- 3. Инвариантность формы первого дифференциала.
- 4. Применение дифференциала для установления приближенных формул.
- § 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ
- § 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Производная логарифмической функции.
- 3. Производные показательной и обратных тригонометрических функций.
- 4. Производная степенной функции.
- 5. Таблица производных простейших элементарных функций.
- 6. Таблица дифференциалов простейших элементарных функций.
- 7. Логарифмическая производная. Производная степенно-показательной функции.
- § 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. n-ые производные некоторых функций.
- 3. Формула Лейбница для n-й производной произведения двух функций.
- 4. Дифференциалы высших порядков.
- § 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
- § 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ
- Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
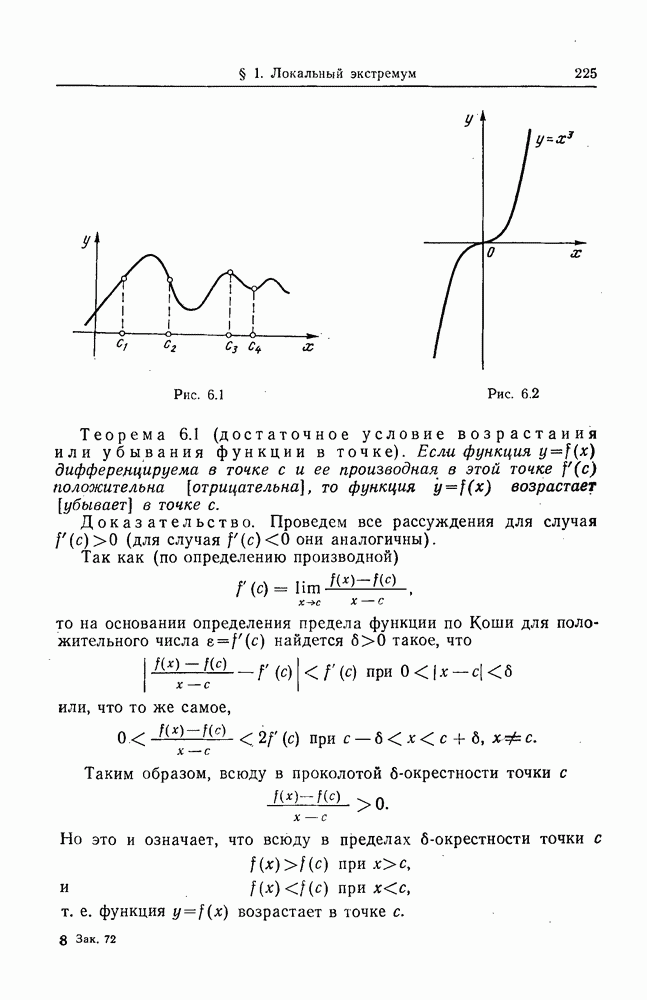
- § 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
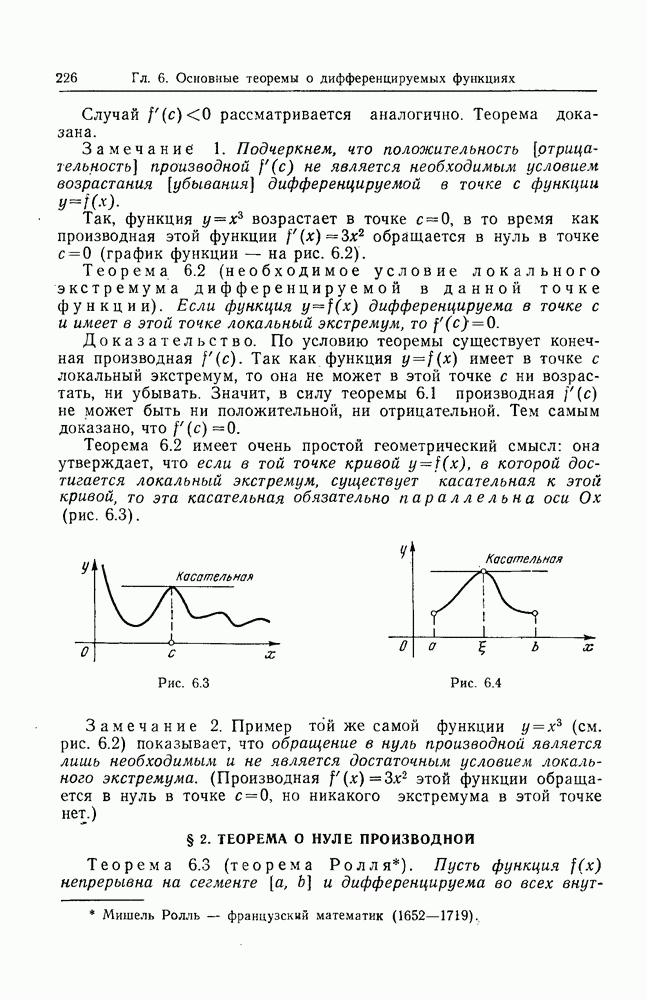
- § 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ
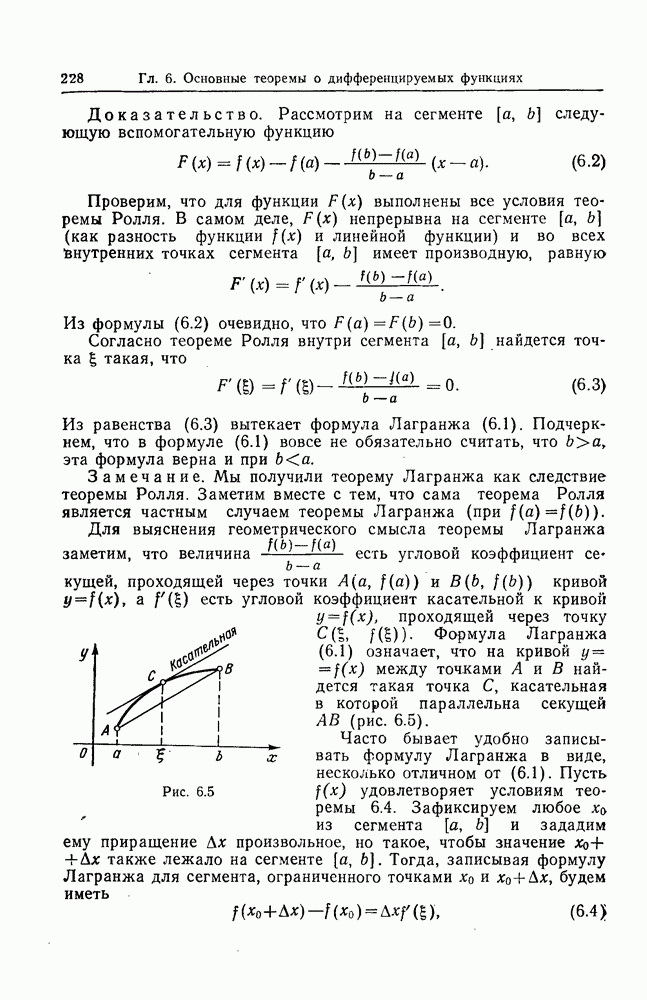
- § 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА)
- § 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА
- 2. Условия монотонности функции на интервале.
- 3. Отсутствие разрывов первого рода и устранимых разрывов у производной.
- 4. Вывод некоторых неравенств.
- § 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ)
- § 6. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ)
- 2. Раскрытие неопределенности вида oo/oo
- 3. Раскрытие неопределенностей других видов.
- § 7. ФОРМУЛА ТЕЙЛОРА
- § 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА
- 2. Другая запись формулы Тейлора.
- 3. Формула Маклорена.
- § 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Разложение по формуле Маклорена некоторых элементарных функций.
- § 10. ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА
- 2. Доказательство иррациональности числа е.
- 3. Вычисление значений тригонометрических функций.
- 4. Асимптотическая оценка элементарных функций и вычисление пределов.
- Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ
- § 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК
- 2. Отыскание стационарных точек.
- 3. Первое достаточное условие экстремума.
- 4. Второе достаточное условие экстремума.
- 5. Третье достаточное условие, экстремума.
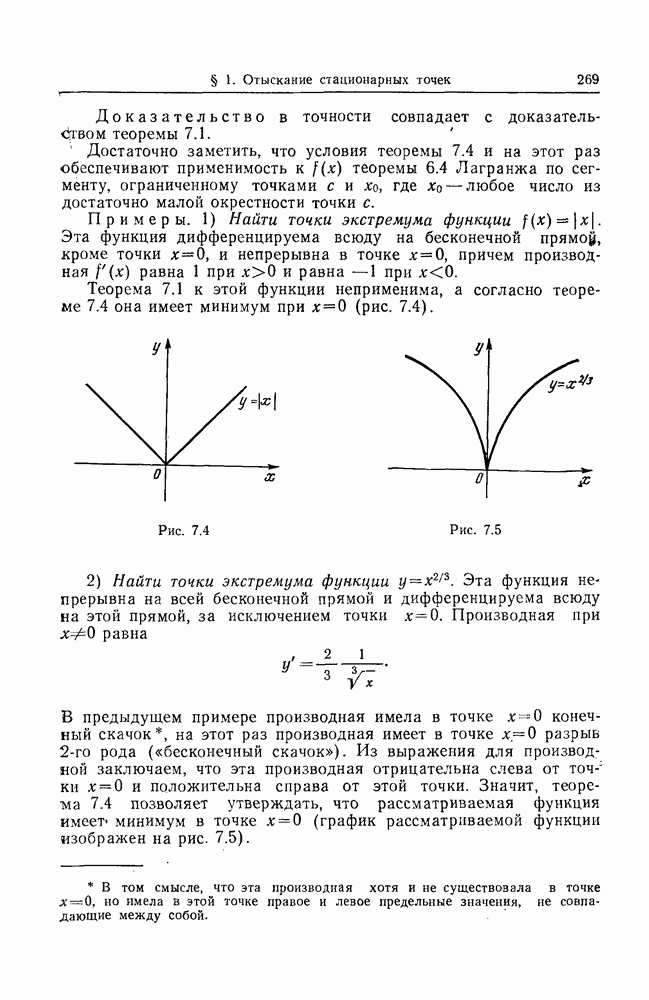
- 6. Экстремум функции, недифференцируемой в данной точке.
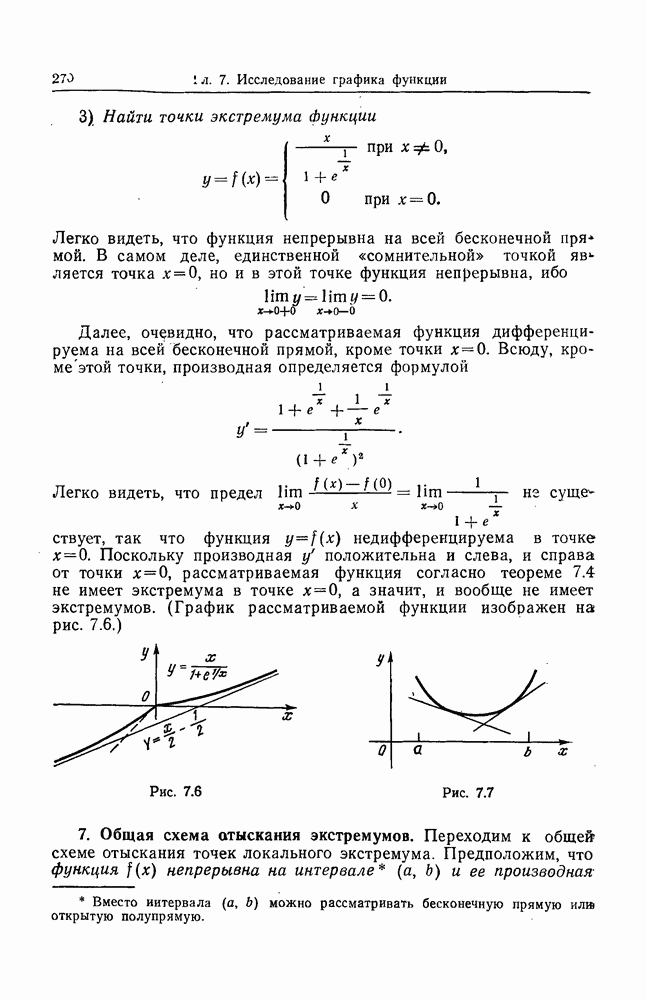
- 7. Общая схема отыскания экстремумов.
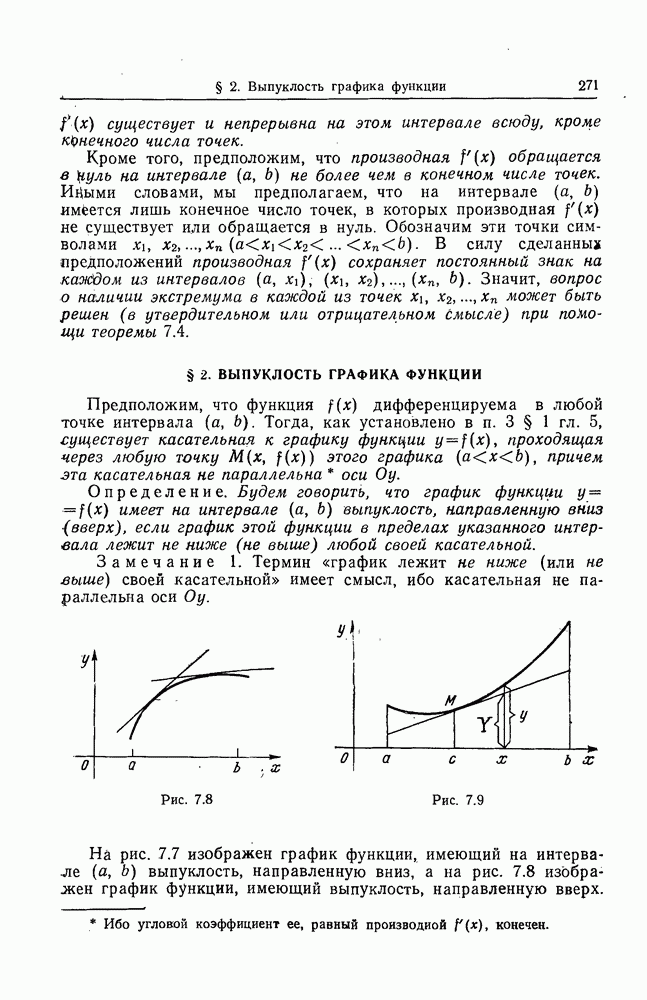
- § 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ
- § 3. ТОЧКИ ПЕРЕГИБА
- 2. Первое достаточное условие перегиба.
- 3. Некоторые обобщения первого достаточного условия перегиба.
- 4. Второе достаточное условие перегиба.
- 5. Третье достаточное условие перегиба.
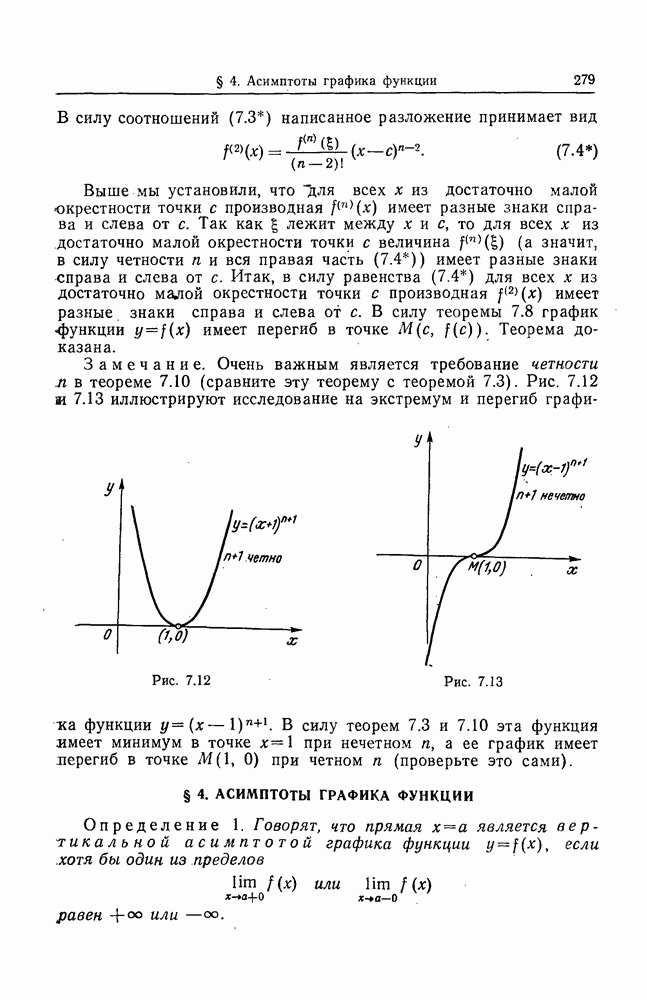
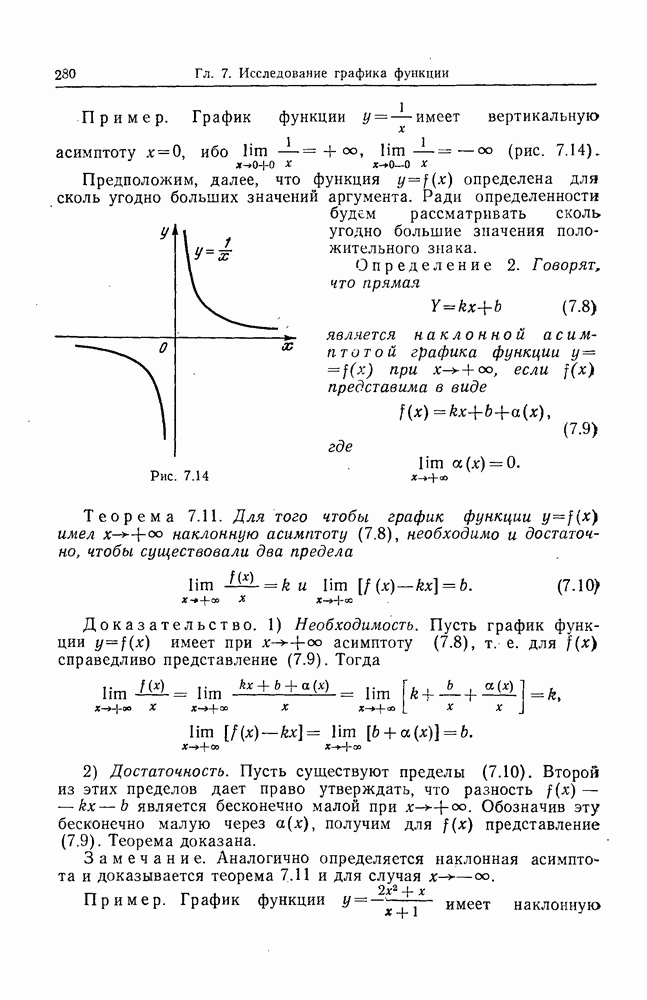
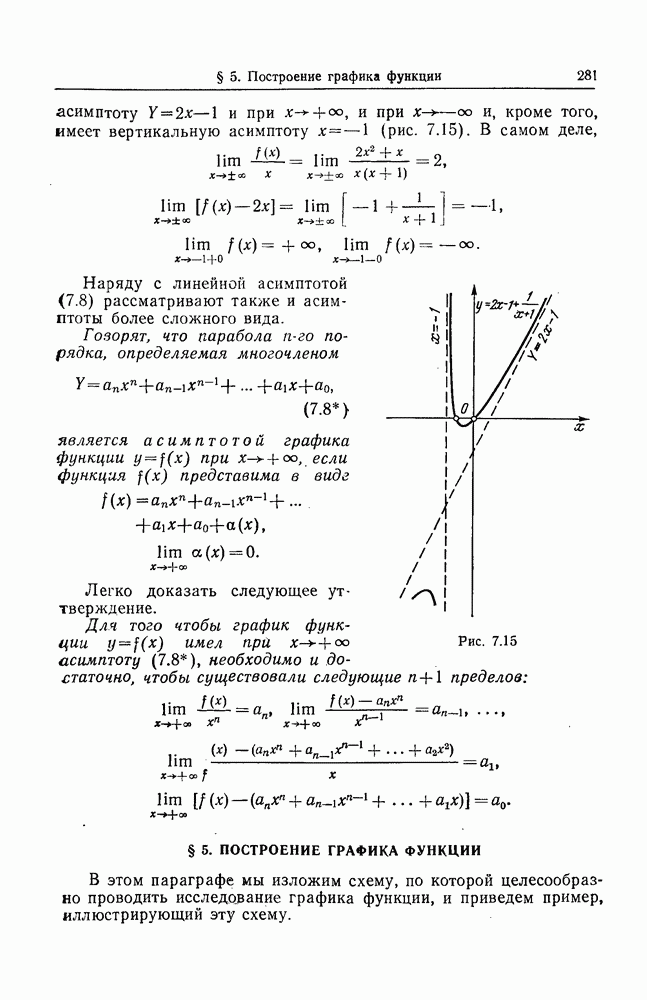
- § 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
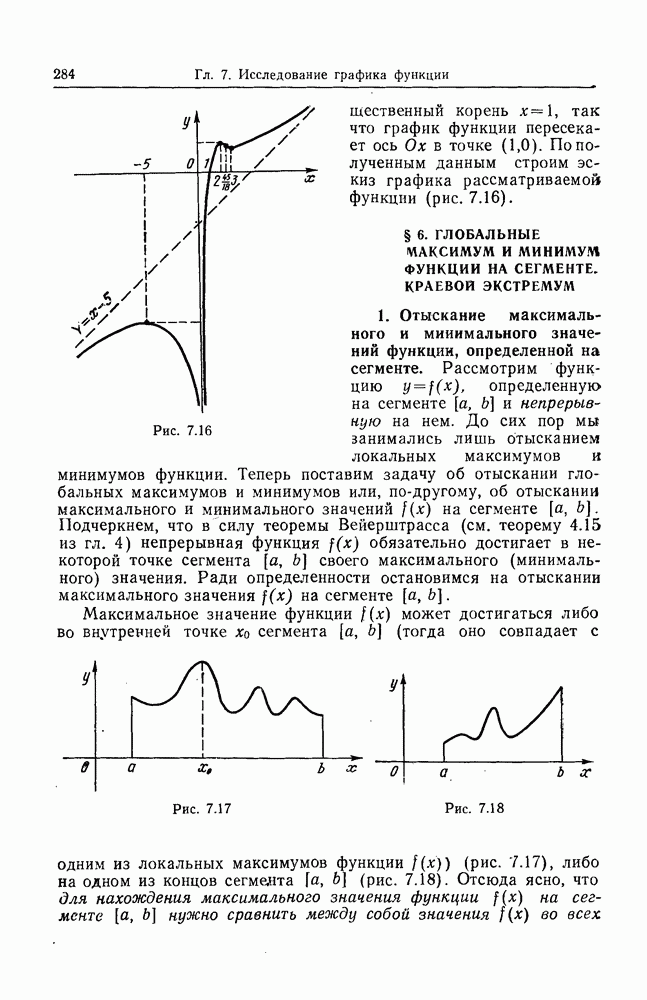
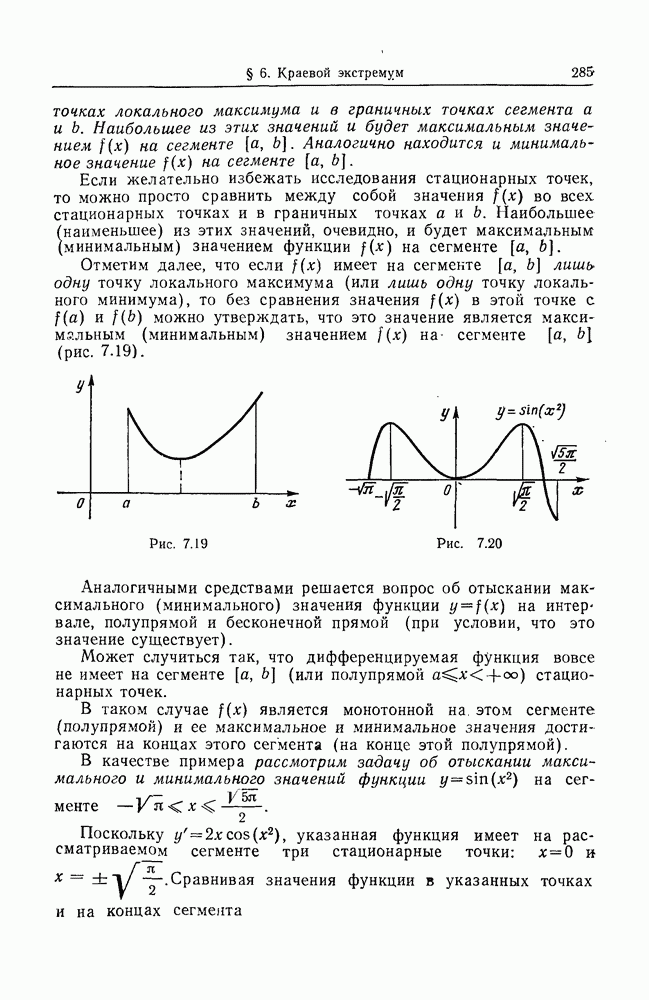
- § 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ
- 2. Краевой экстремум.
- 3. Теорема Дарбу.
- ДОПОЛНЕНИЕ
- Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции
- Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Неопределенный интеграл.
- 3. Основные свойства неопределенного интеграла.
- 4. Таблица основных неопределенных интегралов.
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование по частям.
- § 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Краткие сведения о корнях алгебраических многочленов.
- 3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей.
- 4. Разложение правильной рациональной дроби на сумму простейших дробей.
- 5. Интегрируемость рациональной дроби в элементарных функциях.
- 6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
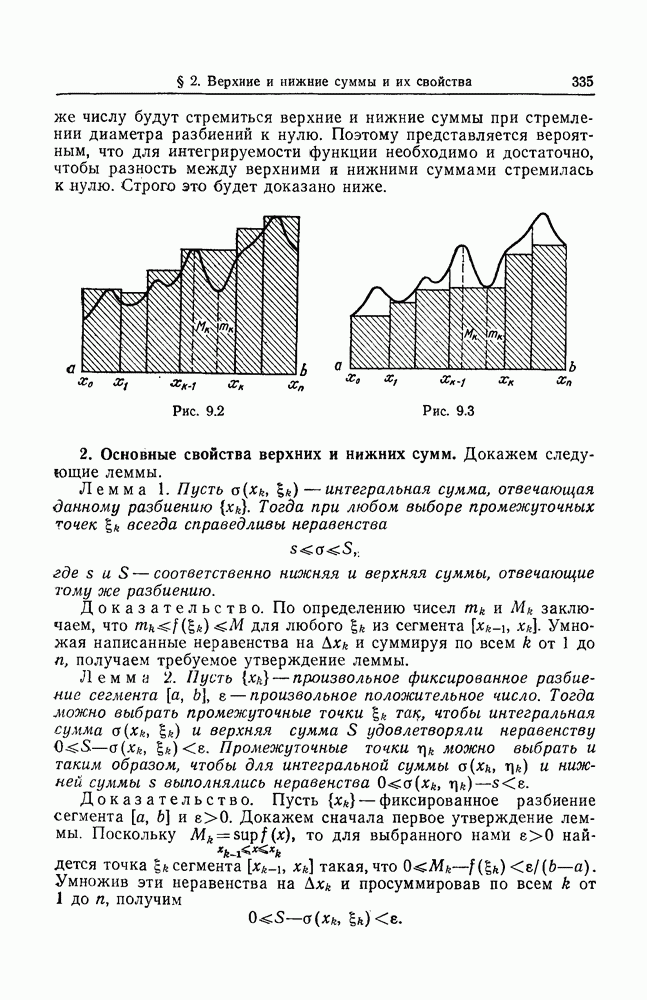
- ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА
- 2. Основные свойства верхних и нижних сумм.
- § 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- 2. Классы интегрируемых функций.
- § 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ
- 2. Оценки интегралов.
- § 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ
- 2. Основная формула интегрального исчисления.
- 3. Важные правила, позволяющие вычислять определенные интегралы.
- 4. Остаточный член формулы Тейлора в интегральной форме.
- § 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ
- 2. Неравенство Гёльдера для сумм.
- 3. Неравенство Минковского для сумм.
- 4. Неравенство Гёльдера для интегралов.
- 5. Неравенство Минковского для интегралов.
- § 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА
- 2. Критерий интегрируемости Лебега.
- ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Критерий Коши сходимости несобственного интеграла первого рода.
- 3. Абсолютная и условная сходимость несобственных интегралов.
- 4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям.
- § 2. Несобственные интегралы второго рода
- § 3. Главное значение несобственного интеграла
- ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса
- 2. Свойства интеграла Стилтьеса.
- Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. ДЛИНА ДУГИ КРИВОЙ
- 2. Понятие параметризуемой кривой.
- 3. Длина дуги кривой. Понятие спрямляемой кривой.
- 4. Критерий спрямляемости кривой. Вычисление длины дуги кривой.
- 5. Дифференциал дуги.
- 6. Примеры.
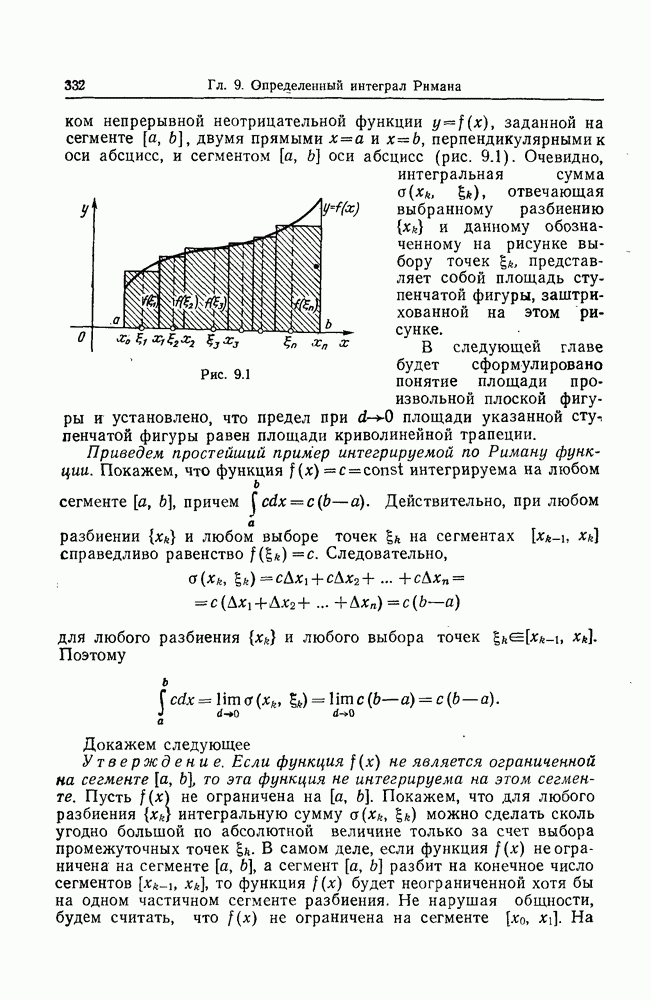
- § 2. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
- 2. Площадь плоской фигуры.
- 3. Площадь криволинейной трапеции и криволинейного сектора.
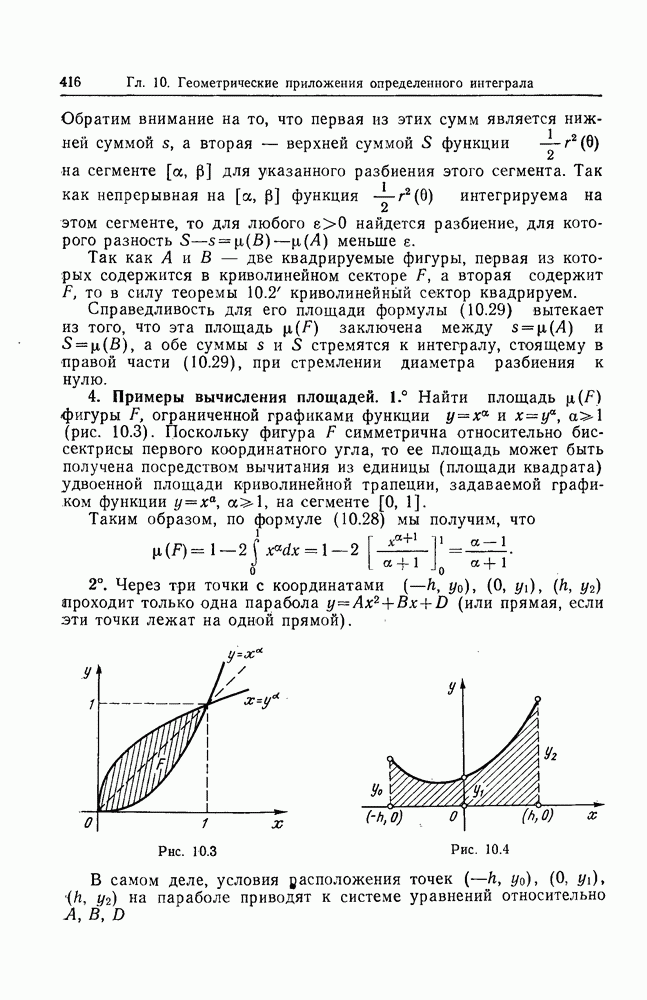
- 4. Примеры вычисления площадей.
- § 3. ОБЪЕМ ТЕЛА В ПРОСТРАНСТВЕ
- 2. Некоторые классы кубируемых тел.
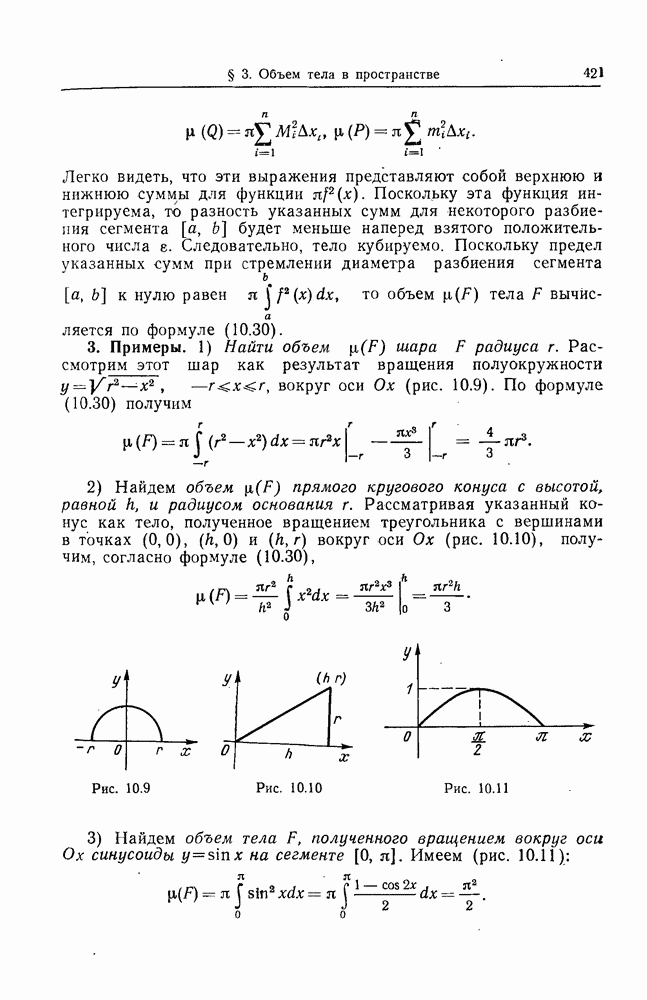
- 3. Примеры.
- Глава 11. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- § 1. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ
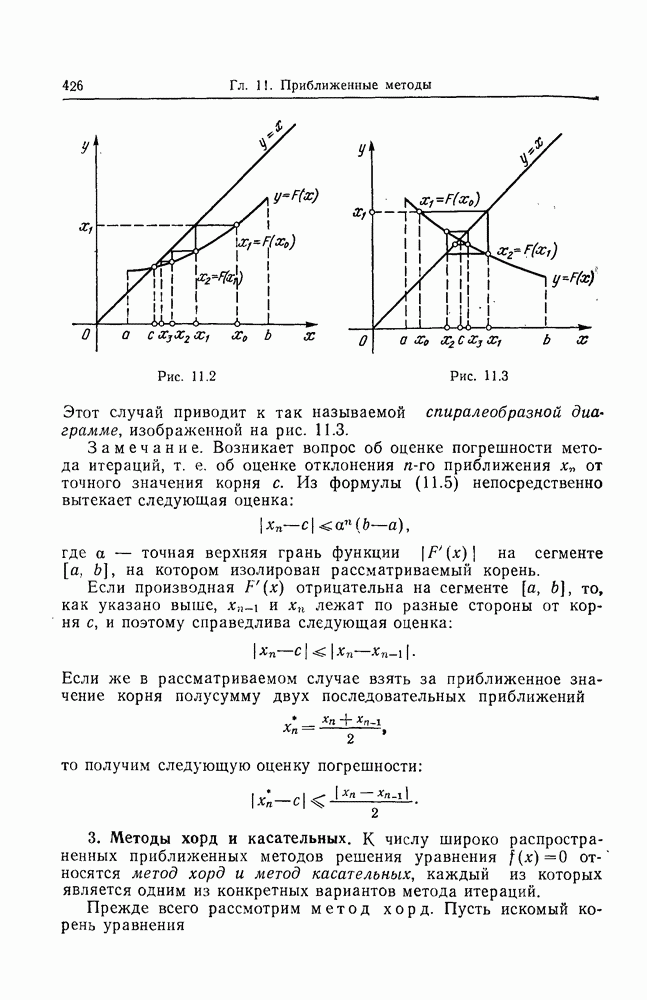
- 2. Метод итераций.
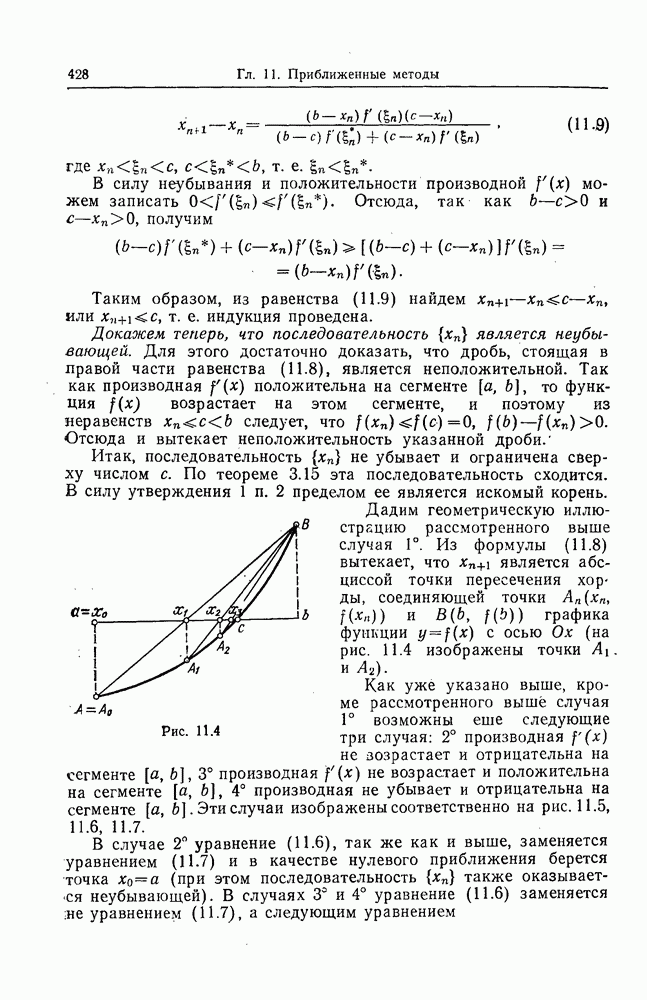
- 3. Методы хорд и касательных.
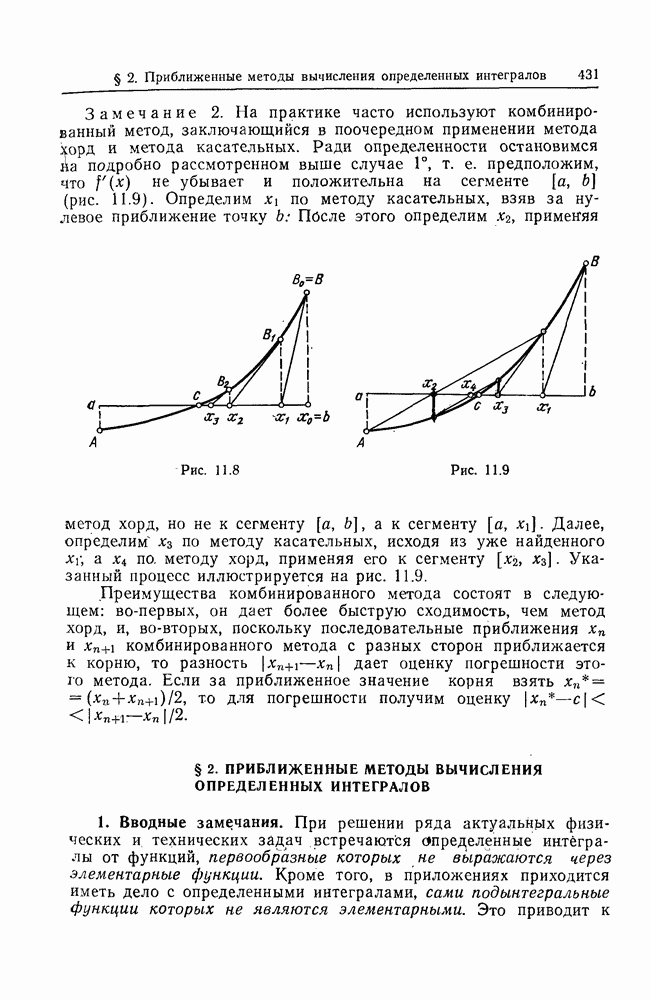
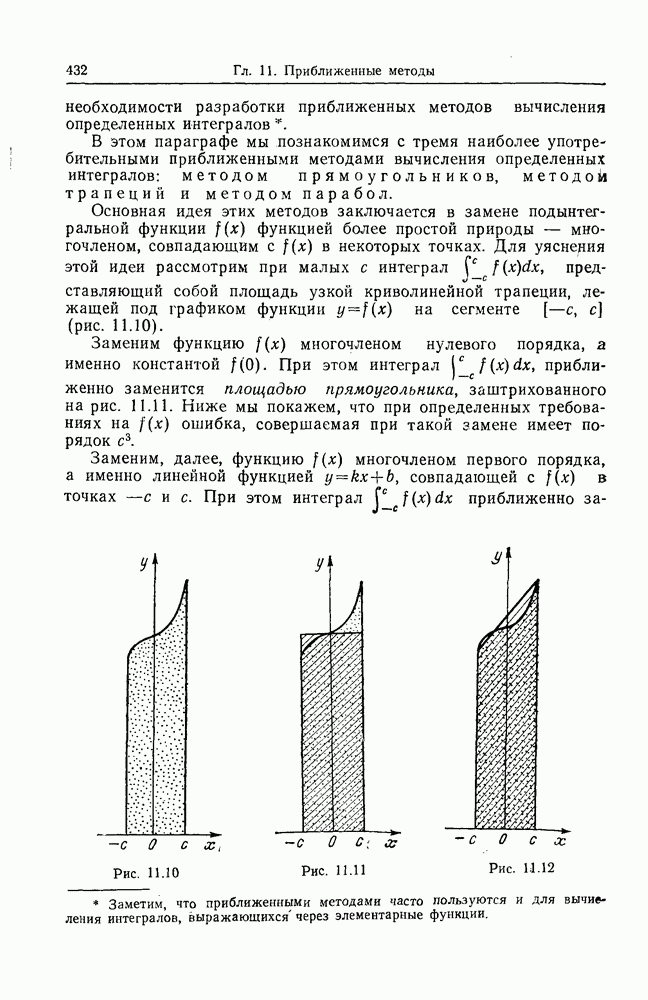
- § 2. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
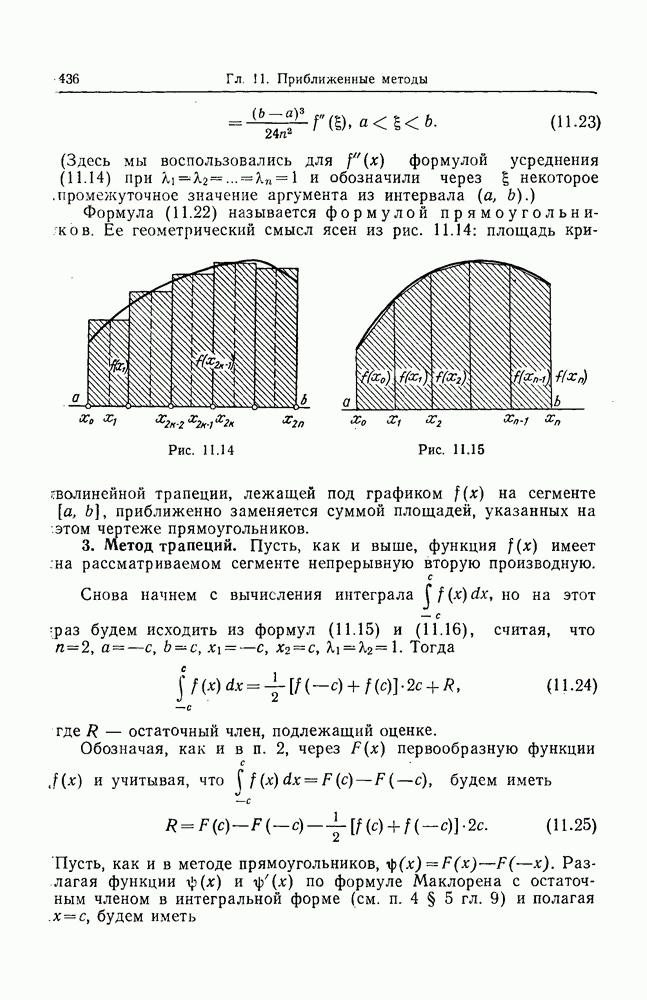
- 2. Метод прямоугольников.
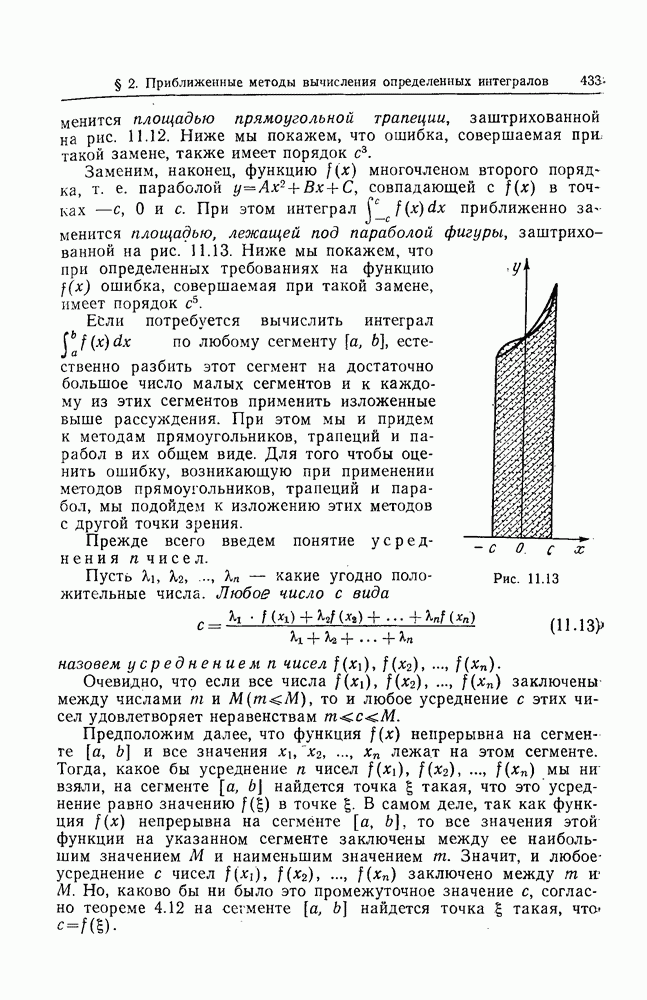
- 3. Метод трапеций.
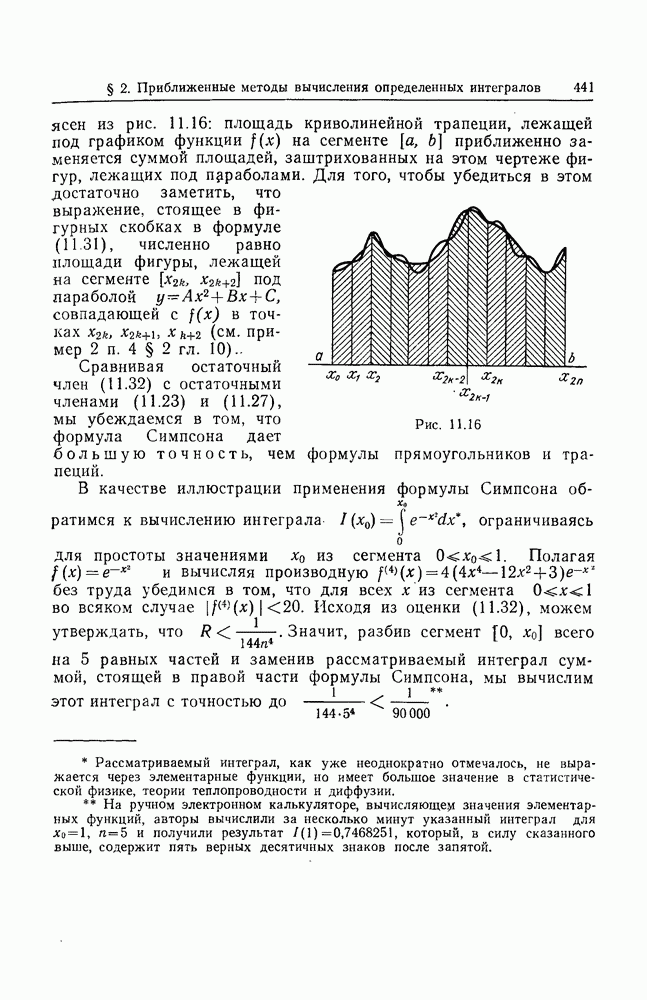
- 4. Метод парабол.
- Глава 12. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ПОНЯТИЕ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Множества точек m-мерного евклидова пространства.
- 3. Понятие функции m переменных.
- § 2. ПРЕДЕЛ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Свойство ограниченной последовательности точек E^m.
- 3. Предел функции m переменных.
- 4. Бесконечно малые функции m переменных.
- 5. Повторные пределы.
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Непрерывность функции m переменных по одной переменной.
- 3. Основные свойства непрерывных функций нескольких переменных.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Дифференцируемость функции нескольких переменных.
- 3. Геометрический смысл условия дифференцируемости функции двух переменных.
- 4. Достаточные условия дифференцируемости.
- 5. Дифференциал функции нескольких переменных.
- 6. Дифференцирование сложной функции.
- 7. Инвариантность формы первого дифференциала.
- 8. Производная по направлению. Градиент.
- § 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. Дифференциалы высших порядков.
- 3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме.
- 4. Формула Тейлора с остаточным членом в форме Пеано.
- § 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Достаточные условия локального экстремума функции m переменных.
- 3. Случай функции двух переменных.
- ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции
- 1. Выпуклые множества и выпуклые функции.
- 2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции.
- 3. Поиск минимума сильно выпуклой функции.
- ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства
- 2. Открытые и замкнутые множества.
- 3. Прямое произведение метрических пространств.
- 4. Всюду плотные и совершенные множества.
- 5. Сходимость. Непрерывные отображения.
- 6. Компактность.
- 7. Базис пространства.
- Топологические пространства
- Линейные нормированные пространства, линейные операторы
- ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах
- 2. Формула Лагранжа конечных приращений.
- 3. Связь между слабой и сильной дифференцируемостью.
- 4. Дифференцируемость функционалов.
- 5. Интеграл от абстрактных функций.
- 6. Формула Ньютона — Лейбница для абстрактных функций.
- 7. Производные второго порядка.
- 8. Отображение m-мерного евклидова пространства в n-мерное.
- 9. Производные и дифференциалы высших порядков.
- 10. Формула Тейлора для отображений одного нормированного пространства в другое.
- Исследование на экстремум функционалов в нормированных пространствах
- 2. Достаточные условия экстремума.
- Глава 13. НЕЯВНЫЕ ФУНКЦИИ
- § 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ
- 2. Вычисление частных производных неявно заданной функции.
- 3. Особые точки поверхности и плоской кривой.
- 4. Условия, обеспечивающие существование для функции y=f(x) обратной функции.
- § 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
- 2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений.
- 3. Взаимно однозначное отображение двух множеств m-мерного пространства.
- § 3. ЗАВИСИМОСТЬ ФУНКЦИЙ
- 2. Функциональные матрицы и их приложения.
- § 4. УСЛОВНЫЙ ЭКСТРЕМУМ
- 2. Метод неопределенных множителей Лагранжа.
- 3. Достаточные условия.
- 4. Пример.
- ДОПОЛНЕНИЕ
- Отображения банаховых пространств. Аналог теоремы о неявной функции
- 2. Случай конечномерных пространств.
- 3. Особые точки поверхности в пространстве n измерений. Обратное отображение.
- 4. Условный экстремум в случае отображений нормированных пространств.