| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
В настоящей главе, не претендуя на точность формулировок и отправляясь от простейших задач механики, мы постараемся обрисовать основной круг понятий и проблем математического анализа.
1. Начнем наше рассмотрение с выяснения тех математических понятий, которые неизбежно возникают при описании самого простейшего вида движения — движения материальной точки вдоль прямой линии.
Если материальная точка движется вдоль оси  обозначает время, отсчитываемое от некоторого начального момента, то для описания указанного движения необходимо знать правило, посредством которого каждому значению времени х ставится в соответствие координата у движущейся точки в момент времени х.
обозначает время, отсчитываемое от некоторого начального момента, то для описания указанного движения необходимо знать правило, посредством которого каждому значению времени х ставится в соответствие координата у движущейся точки в момент времени х.
В механике такое правило называют законом движения. Абстрагируясь от конкретного механического смысла переменных х и у и рассматривая в качестве х и у две совершенно произвольные переменные величины, мы придем к понятию функции, являющемуся одним из важнейших понятий математического анализа.
Если известно правило, посредством которого каждому значению одной переменной х ставится в соответствие определенное значение другой переменной у, то говорят, что переменная у является функцией переменной х, и пишут  или
или 
При этом переменную х называют аргументом или независимой переменной, а переменную у — функцией аргумента х.
Букву  в записи
в записи  обычно называют характеристикой рассматриваемой функции, а значение
обычно называют характеристикой рассматриваемой функции, а значение  называют частным значением функции в точке х. Совокупность всех частных значений функции принято называть областью изменения этой функции.
называют частным значением функции в точке х. Совокупность всех частных значений функции принято называть областью изменения этой функции.
Отметим сразу же, что приведенная формулировка понятия функции требует уточнения, ибо в этой формулировке ничего не говорится о том, из какого множества берутся значения независимой переменной х.
Множество, состоящее из тех и только тех чисел, которые являются значениями независимой переменной х, обычно называют
областью задания функции. Описание областей задания функции требует развития теории числовых множеств.
Отметим еще, что понятие функции (так же, как и понятие числа, множества и переменной величины) естественно считать начальным понятием (т. е. таким понятием, которое можно описать, но нельзя строго определить, ибо любая попытка дать строгое определение указанного понятия неизбежно сведется к замене определяемого понятия ему эквивалентным). Таким образом, вместо термина «определение функции» естественнее употреблять термин «понятие функции».
Отметим, наконец, что для обозначения аргумента функции и ее характеристики могут употребляться различные буквы. Так, например, запись  обозначает, что переменная х является функцией аргумента
обозначает, что переменная х является функцией аргумента  причем характеристика этой функции обозначена через
причем характеристика этой функции обозначена через  При одновременном рассмотрении нескольких функций одного аргумента t для обозначения характеристик этих функций необходимо употреблять различные символы.
При одновременном рассмотрении нескольких функций одного аргумента t для обозначения характеристик этих функций необходимо употреблять различные символы.
2. Часто приходится рассматривать такую функцию  аргумент х которой сам является функцией вида
аргумент х которой сам является функцией вида  некоторой новой переменной
некоторой новой переменной  . В таком случае говорят, что переменная у представляет собой сложную функцию аргумента
. В таком случае говорят, что переменная у представляет собой сложную функцию аргумента  а переменную х называют промежуточным аргументом. Указанную сложную функцию называют также суперпозицией функций
а переменную х называют промежуточным аргументом. Указанную сложную функцию называют также суперпозицией функций  Для обозначения указанной сложной функции естественно использовать символ
Для обозначения указанной сложной функции естественно использовать символ 
Рассмотрим простой пример, иллюстрирующий возникновение понятия сложной функции. Предположим, что материальная точка М равномерно с постоянной угловой скоростью со вращается но окружности радиуса 

Рис. 1.1
Найдем закон движения проекции М точки М на некоторую ось  проходящую через центр О окружности и лежащую в ее плоскости (рис. 1.1). При этом естественно предположить, что в начальный момент времени
проходящую через центр О окружности и лежащую в ее плоскости (рис. 1.1). При этом естественно предположить, что в начальный момент времени  движущаяся точка М находилась в точке
движущаяся точка М находилась в точке  пересечения окружности с осью
пересечения окружности с осью 
Обозначим через у координату проекции М точки М на ось  а через х угол
а через х угол  на который повернется точка М за время
на который повернется точка М за время  Очевидно, что
Очевидно, что  и мы получим, что координата у проекции М представляет собой сложную функцию времени t вида
и мы получим, что координата у проекции М представляет собой сложную функцию времени t вида  где
где  Эту сложную функцию можно записать в виде
Эту сложную функцию можно записать в виде  Отметим, что движение по закону
Отметим, что движение по закону  в механике принято называть гармоническим колебанием.
в механике принято называть гармоническим колебанием.
3. Из курса физики известно, что важной характеристикой движения материальной точки является ее мгновенная скорость в каждый момент времени х. Если материальная точка движется вдоль оси  по закону
по закону  то, фиксировав произвольный момент времени х и какое угодно приращение времени
то, фиксировав произвольный момент времени х и какое угодно приращение времени  мы можем утверждать, что в момент времени х движущаяся точка имеет координату
мы можем утверждать, что в момент времени х движущаяся точка имеет координату  а в момент времени
а в момент времени  координату
координату 
Таким образом, число  представляет собой путь, пройденный движущейся точкой за промежуток времени от х до
представляет собой путь, пройденный движущейся точкой за промежуток времени от х до 
Отсюда вытекает, что отношение

обычно называемое разностным отношением, представляет собой среднюю скорость движущейся точки за промежуток времени от х до 
Мгновенной скоростью (или просто скоростью) движущейся точки называется предел, к которому стремится средняя скорость (1.1) при стремлении к нулю промежутка времени 
Если использовать известный из курса средней школы символ предела, то можно записать следующее соотношение для мгновенной скорости  в момент времени
в момент времени 

Физическое понятие мгновенной скорости приводит к фундаментальному математическому понятию производной. Абстрагируясь от механического смысла рассмотренной выше функции  мы назовем производной произвольной функции
мы назовем производной произвольной функции  в данной фиксированной точке х предел, стоящий в правой части (1.2) (при условии, конечно, что этот предел существует).
в данной фиксированной точке х предел, стоящий в правой части (1.2) (при условии, конечно, что этот предел существует).
Используя для обозначения производной функции  в точке х символ
в точке х символ  или
или  мы можем по определению записать следующее равенство:
мы можем по определению записать следующее равенство:

Операцию нахождения производной договоримся называть дифференцированием.
Наше рассмотрение показывает, что при вычислении производной фундаментальную роль играет понятие предела функции.
Предварительное представление о понятии предела функции (да и осамом понятии производной) дается в курсе средней школы. Однако строгое и последовательное изучение понятия предела возможно лишь на базе строгой теории вещественных чисел. Так, например, без строгой теории вещественных чисел невозможно установить существование двух следующих важных пределов:

неизбежно возникающих, как мы увидим ниже, при вычислении производных функций 
Итак, проведенное нами рассмотрение показывает, что вопрос о существовании и вычислении производной упирается в необходимость развития строгой теории вещественных чисел и на ее базе теории пределов.
4. Займемся теперь вычислением производных двух конкретных элементарных функций  и выясним, какие математические проблемы неизбежно возникают при этом.
и выясним, какие математические проблемы неизбежно возникают при этом.
Сначала вычислим производную функцию  в любой фиксированной точке х. Для этой функции разностное отношение (1.1), очевидно, имеет вид
в любой фиксированной точке х. Для этой функции разностное отношение (1.1), очевидно, имеет вид

Таким образом, производная функции  в точке х по определению равна пределу
в точке х по определению равна пределу

(при условии, что этот предел существует).
Можно ожидать, что

Заметим, однако, что не для всякой функции  справедливо равенство
справедливо равенство

Функция  для которой в данной точке х справедливо равенство (1.5), называется непрерывной (в точке
для которой в данной точке х справедливо равенство (1.5), называется непрерывной (в точке  Понятие
Понятие
непрерывности функции является одним из важнейших математических понятий и будет основательно изучаться в систематическом курсе математического анализа. В частности, в систематическом курсе будет доказано, что функция  является непрерывной в каждой точке х, т. е. в каждой точке х справедливо равенство (1.4).
является непрерывной в каждой точке х, т. е. в каждой точке х справедливо равенство (1.4).
Заметим теперь, что для вычисления предела (1.3) недостаточно доказать справедливость соотношения (1.4). Для этого необходимо еще вычислить следующий предел:

В систематическом курсе анализа будет строго доказано, что предел (1.6), часто называемый первым замечательным пределом, существует и равен единице.
Только после того, как будет установлена непрерывность функции  (т. е. равенство
(т. е. равенство  и вычислен первый за мечательный предел (1.6), мы сможем, опираясь еще на то, что предел произведения равен произведению пределов сомножителей, строго утверждать, что предел (1.3) существует и равен
и вычислен первый за мечательный предел (1.6), мы сможем, опираясь еще на то, что предел произведения равен произведению пределов сомножителей, строго утверждать, что предел (1.3) существует и равен  или, что то же самое, производная функции
или, что то же самое, производная функции  существует и равна
существует и равна 
Перейдем теперь к вычислению производной функции  считая, что
считая, что  и фиксировав произвольную точку
и фиксировав произвольную точку  Для этой функции разностное отношение (1.1) имеет вид
Для этой функции разностное отношение (1.1) имеет вид

 и выбирается так, что
и выбирается так, что  Таким образом, производная функции
Таким образом, производная функции  в любой точке
в любой точке  по определению равна пределу
по определению равна пределу

(при условии, что этот предел существует). Преобразуем дробь, стоящую в (1.7), проделав следующие операции: 1) заменим разность логарифмов логарифмом частного; 2) произведем умножение и деление на одну и ту же величину  внесем множитель, стоящий перед логарифмом, под знак логарифма, сделав его показателем степени. В результате получим, что предел
внесем множитель, стоящий перед логарифмом, под знак логарифма, сделав его показателем степени. В результате получим, что предел  равен
равен


Рассмотрим отдельно предел при  выражения, заключенного в правой части последнего равенства в квадратные скобки:
выражения, заключенного в правой части последнего равенства в квадратные скобки:

Этот предел часто называют вторым замечательным пределом. В систематическом курсе анализа будет установлено, что этот предел равен иррациональному числу  которое с точностью до пятнадцати знаков после запятой имеет вид
которое с точностью до пятнадцати знаков после запятой имеет вид 
Кроме того, в систематическом курсе будет доказана непрерывность функции  в каждой точке
в каждой точке  и, в частности, в точке х=е. Но тогда из существования равного
и, в частности, в точке х=е. Но тогда из существования равного  предела (1.9) будет следовать, что
предела (1.9) будет следовать, что

Последнее соотношение и соотношение (1.8) позволяют утверждать, что предел (1.7) равен

Таким образом, после того как будет вычислен второй замечательный предел и установлена непрерывность функции  в точке
в точке  мы сможем строго утверждать, что логарифмическая функция имеет производную, причем
мы сможем строго утверждать, что логарифмическая функция имеет производную, причем

5. В курсе средней школы кроме двух рассмотренных нами функций  изучались еще следующие функции:
изучались еще следующие функции:  — вещественное число),
— вещественное число), 
Все перечисленные функции принято называть простейшими элементарными.
Замечательным является тот факт, что при вычислении производных всех простейших элементарных функций не возникает никаких новых трудностей, кроме тех, с которыми мы встретились при вычислении производных функций  Нетрудно
Нетрудно
проверить, что для вычисления производных всех простейших элементарных функций требуются лишь арифметические свойства операции предельного перехода, два замечательных предела и факт непрерывности каждой из этих функций в точках областей их задания.
Отмеченное обстоятельство дает нам право без дальнейших разъяснений привести таблицу производных всех простейших элементарных функций.

В частности, при 

В частности, при 

Строгое обоснование приведенной таблицы является одной из важных задач той части математического анализа, которую принято называть дифференциальным исчислением.
Традиционной задачей классического дифференциального исчисления является и несколько более общая задача — вычисление производной любой функции  которая получается из перечисленных выше простейших элементарных функций путем конечного числа суперпозиций и конечного числа четырех арифметических действий (сложения, умножения, вычитания и деления). Такую функцию
которая получается из перечисленных выше простейших элементарных функций путем конечного числа суперпозиций и конечного числа четырех арифметических действий (сложения, умножения, вычитания и деления). Такую функцию  принято называть просто элементарной.
принято называть просто элементарной.
Итак, элементарной называется функция, которая получается из простейших элементарных функций путем конечного числа суперпозиций и четырех арифметических действий.
Примером элементарной функции может служить функция

Для вычисления производной любой элементарной функции следует присоединить к выписанной нами таблице производных простейших элементарных функций два правила: 1) правило дифференцирования сложной функции, 2) правило дифференцирования суммы, разности, произведения и частного функций.
Правило дифференцирования сложной функции  где
где  имеет следующий вид: если функция
имеет следующий вид: если функция  имеет производную в данной точке
имеет производную в данной точке  а функция
а функция  имеет производную в соответствующей точке
имеет производную в соответствующей точке  то сложная функция
то сложная функция  имеет производную в точке
имеет производную в точке  причем эта производная (обозначим ее через
причем эта производная (обозначим ее через  равна
равна

т. е. равна произведению производной функции  в точке
в точке  на производную функции
на производную функции  в точке
в точке 
Справедливость для производной сложной функции формулы (1.10) легко оправдать с помощью наводящих соображений,  строгий вывод формулы (1.10) не является простым и будет приведен в систематическом курсе математического анализа.
строгий вывод формулы (1.10) не является простым и будет приведен в систематическом курсе математического анализа.
Гораздо проще устанавливаются правила дифференцирования суммы, разности, произведения и частного двух функций, которые имеют вид

(в последней формуле требуется необращение в нуль функции  в рассматриваемой точке
в рассматриваемой точке 
Подводя итог, мы можем заключить, что одной из важных задач части математического анализа, называемой дифференциальным исчислением, является строгое обоснование таблицы производных простейших элементарных функций и правил дифференцирования сложной функции, а также суммы, разности, произведения и частного функций.
Это обоснование позволит вычислить производную любой элементарной функции  т. е. любой функции
т. е. любой функции  получающейся из простейших элементарных путем конечного числа суперпозиций и четырех арифметических действий. При этом оказывается, что производная любой элементарной функции представляет собой также элементарную функцию, т. е. операция дифференцирования не выводит нас из класса элементарных функций.
получающейся из простейших элементарных путем конечного числа суперпозиций и четырех арифметических действий. При этом оказывается, что производная любой элементарной функции представляет собой также элементарную функцию, т. е. операция дифференцирования не выводит нас из класса элементарных функций.
Отмеченное обстоятельство оправдывает введение класса элементарных функций как традиционного объекта классического анализа.
6. Еще раз обратимся к рассмотрению механической задачи о движении материальной точки вдоль прямой линии — оси  но на этот раз предположим, что для любого момента времени х нам задана мгновенная скорость
но на этот раз предположим, что для любого момента времени х нам задана мгновенная скорость  движущейся точки и требуется найти закон движения этой точки.
движущейся точки и требуется найти закон движения этой точки.
Поскольку мгновенная скорость  является производной функции
является производной функции  определяющей закон движения, то задача сводится к разысканию по данной функции
определяющей закон движения, то задача сводится к разысканию по данной функции  такой функции
такой функции  производная
производная  которой равна
которой равна  Отвлекаясь от механического смысла функций
Отвлекаясь от механического смысла функций  мы придем к математическим понятиям первообразной и неопределенного интеграла.
мы придем к математическим понятиям первообразной и неопределенного интеграла.
Первообразной функции  называется такая функция
называется такая функция  производная которой
производная которой  равна
равна 
Это определение требует уточнения: следует четко оговорить, «а каком множестве должно быть справедливо равенство  Отмеченное обстоятельство еще раз подчеркивает необходимость развития теории множеств. Уточнение понятия первообразной будет дано в систематическом курсе.
Отмеченное обстоятельство еще раз подчеркивает необходимость развития теории множеств. Уточнение понятия первообразной будет дано в систематическом курсе.
Заметим, что если функция  является первообразной функции
является первообразной функции  то и функция
то и функция  где С — произвольная постоянная, также является первообразной функции
где С — произвольная постоянная, также является первообразной функции  (в силу того, что производная постоянной С равна нулю).
(в силу того, что производная постоянной С равна нулю).
Более трудным является обратное утверждение: любые две первообразные одной и той же функции  на интервале
на интервале  могут отличаться лишь постоянным слагаемым. Доказательство этого утверждения требует развитого аппарата математического анализа и будет проведено в систематическом курсе анализа.
могут отличаться лишь постоянным слагаемым. Доказательство этого утверждения требует развитого аппарата математического анализа и будет проведено в систематическом курсе анализа.
Опираясь на указанное утверждение, мы можем констатировать следующий факт: если функция  является одной из первообразных функции
является одной из первообразных функции  то любая первообразная функции
то любая первообразная функции  имеет вид
имеет вид  где С — постоянная.
где С — постоянная.
Совокупность всех первообразных данной функции  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом

Только что отмеченный нами факт позволяет утверждать, что если  — одна из первообразных функции
— одна из первообразных функции  то неопределенный интеграл от функции
то неопределенный интеграл от функции  равен
равен

где С — любая постоянная.
Возвратимся к поставленной нами задаче об отыскании закона движения материальной точки вдоль оси  по известной
по известной
мгновенной скорости  этой точки. Мы теперь можем утверждать, что искомый закон движения определяется функцией
этой точки. Мы теперь можем утверждать, что искомый закон движения определяется функцией  где
где  - любая первообразная функция
- любая первообразная функция  постоянная. Как мы видим, без дополнительных условий закон движения по мгновенной скорости определяется неоднозначно: с: точностью до постоянного слагаемого С. Для определения постоянной С должно быть привлечено дополнительное условие, обычно заключающееся в задании координаты
постоянная. Как мы видим, без дополнительных условий закон движения по мгновенной скорости определяется неоднозначно: с: точностью до постоянного слагаемого С. Для определения постоянной С должно быть привлечено дополнительное условие, обычно заключающееся в задании координаты  движущейся точки в некоторый момент времени
движущейся точки в некоторый момент времени  Используя это условие, мы
Используя это условие, мы  -лучим соотношение
-лучим соотношение  из которого
из которого  так что окончательно искомый закон движения имеет вид
так что окончательно искомый закон движения имеет вид

7. Рассмотрим вопрос об отыскании первообразных и неопределенных интегралов от некоторых элементарных функций. Так как функция  является производной функции
является производной функции  то функция
то функция  является одной из первообразных функции
является одной из первообразных функции  и потому любая первообразная функции
и потому любая первообразная функции  имеет вид
имеет вид  где С — постоянная. Таким образом,
где С — постоянная. Таким образом,

Только что проведенное рассуждение имеет общий характер. Можно утверждать, что любая формула дифференциального исчисления  утверждающая, что функция
утверждающая, что функция  является: производной функции
является: производной функции  порождает эквивалентную ей формулу интегрального исчисления
порождает эквивалентную ей формулу интегрального исчисления  , утверждающую, что неопределенный интеграл от функции
, утверждающую, что неопределенный интеграл от функции  равен
равен  где С — любая постоянная.
где С — любая постоянная.
Таким образом, выписанная выше таблица производных простейших элементарных функций порождает эквивалентную ей таблицу важных неопределенных интегралов, которую мы приводим ниже.

В частности, при 


Приведенная таблица в систематическом курсе анализа будет дополнена двумя важнейшими правилами интегрирования (интегрированием посредством замены переменной и интегрированием по частям).
Здесь мы не будем приводить формулировку этих правил, а лишь отметим, что написанная таблица вместе с этими правилами составляет важный вычислительный аппарат той части математического анализа, которую принято называть интегральным исчислением.
Следует, однако, сразу же подчеркнуть, что для вычисления многих важных неопределенных интегралов этого аппарата оказывается недостаточно. Например, этого аппарата недостаточно для вычисления неопределенного интеграла

играющего важную роль в теории вероятностей и в других разделах точных наук.
Интеграл (1.11) служит примером интеграла от элементарной функции, не являющегося элементарной функцией. Таким образом, в отличие от операции дифференцирования, операция интегрирования выводит нас из класса элементарных функций. Это обстоятельство подчеркивает условность самого понятия элементарной функции как традиционного объекта классического анализа.
Недостаточность описанного нами аппарата ставит на повестку дня задачу о существовании и о вычислении первообразной и неопределенного интеграла от любой функции  только непрерывной в каждой точке х области своего задания.
только непрерывной в каждой точке х области своего задания.
Оказывается, такую задачу можно решить при помощи другого подхода к проблеме интегрирования функции, К выяснейию которого мы сейчас и перейдем:
8. Снова предположим, что функция  представляет собой мгновенную скорость движущейся вдоль оси
представляет собой мгновенную скорость движущейся вдоль оси  материальной точки. Поставим цель — вычислить путь, пройденный этой точкой за промежуток времени от
материальной точки. Поставим цель — вычислить путь, пройденный этой точкой за промежуток времени от  до
до 
Для облегчения рассуждений будем считать, что скорость  неотрицательна для всех значений времени х.
неотрицательна для всех значений времени х.
Для решения поставленной задачи разобьем промежуток времени на малые промежутки, ограниченные моментами времени

Естественно считать, что на каждом малом промежутке времени от  до
до  скорость
скорость  меняется мало (что заведомо будет иметь место всякий раз, когда
меняется мало (что заведомо будет иметь место всякий раз, когда  является непрерывной в каждой точке
является непрерывной в каждой точке  Но тогда приближенно можно считать скорость
Но тогда приближенно можно считать скорость  постоянной на каждом промежутке
постоянной на каждом промежутке  и равной значению где — некоторое значение времени из промежутка
и равной значению где — некоторое значение времени из промежутка 
Таким образом, путь  пройденный движущейся точкой за промежуток времени от
пройденный движущейся точкой за промежуток времени от  до
до  приближенно можно считать равным произведению
приближенно можно считать равным произведению  на длину
на длину  промежутка
промежутка  Итак,
Итак,

В таком случае путь  пройденный материальной точкой за весь промежуток времени от
пройденный материальной точкой за весь промежуток времени от  до
до  будет приближенно равен сумме
будет приближенно равен сумме

Сумму, стоящую в правой части (1.12), принято называть интегральной суммой.
Естественно ожидать, что точное значение пути  мы получим, переходя в интегральной сумме, стоящей в правой части (1.12), к пределу при стремлении к нулю наибольшей из длин
мы получим, переходя в интегральной сумме, стоящей в правой части (1.12), к пределу при стремлении к нулю наибольшей из длин  (при этом, конечно, общее число
(при этом, конечно, общее число  частичных промежутков будет неограниченно возрастать).
частичных промежутков будет неограниченно возрастать).
Используя символ предела и обозначая через  наибольшее из чисел
наибольшее из чисел  получим, что
получим, что

Разумеется, требует уточнения вопрос о том, что мы понимаем под пределом интегральной суммы, стоящим в правой части (1.13). На этот раз операция предельного перехода встречается в новой и более сложной форме, чем при вычислении обычного предела функции 
Строгое определение и изучение свойств предела вида (1.13) будет дано в систематическом курсе анализа. Здесь же мы укажем, что в математике предел, стоящий в правой части (1.13),
называется определенным интегралом от функции  в пределах от а до Ь и обозначается символом
в пределах от а до Ь и обозначается символом

Итак, определенный интеграл (1.14) равен пути  пройденному движущейся со скоростью
пройденному движущейся со скоростью  материальной точкой за? промежуток времени от
материальной точкой за? промежуток времени от  до
до 
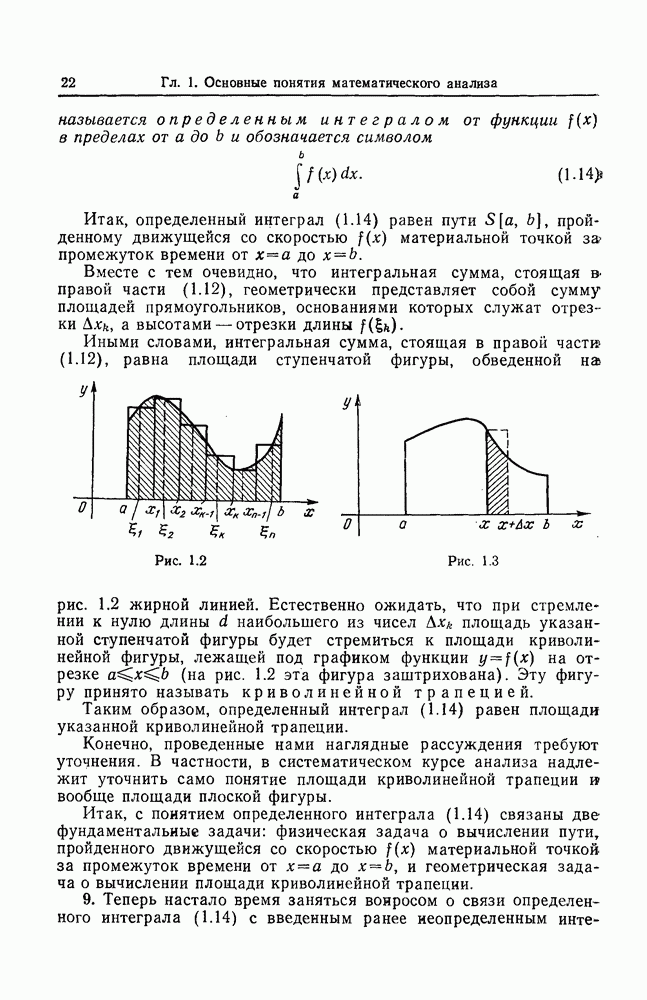
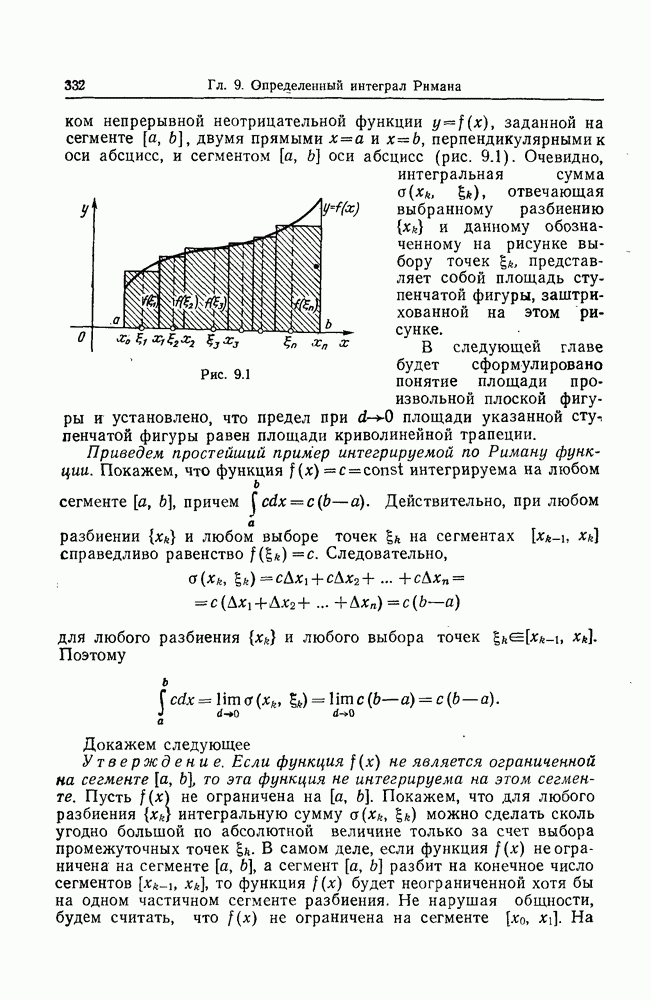
Вместе с тем очевидно, что интегральная сумма, стоящая в правой части (1.12), геометрически представляет собой сумму площадей прямоугольников, основаниями которых служат отрезки  а высотами — отрезки длины
а высотами — отрезки длины 
Иными словами, интегральная сумма, стоящая в правой части (1.12), равна площади ступенчатой фигуры, обведенной на рис. 1.2 жирной линией.

Рис. 1.2

Рис. 1.3
Естественно ожидать, что при стремлении к нулю длины  наибольшего из чисел
наибольшего из чисел  площадь указанной ступенчатой фигуры будет стремиться к площади криволинейной фигуры, лежащей под графиком функции
площадь указанной ступенчатой фигуры будет стремиться к площади криволинейной фигуры, лежащей под графиком функции  на отрезке
на отрезке  (на рис. 1.2 эта фигура заштрихована). Эту фигуру принято называть криволинейной трапецией.
(на рис. 1.2 эта фигура заштрихована). Эту фигуру принято называть криволинейной трапецией.
Таким образом, определенный интеграл (1.14) равен площади указанной криволинейной трапеции.
Конечно, проведенные нами наглядные рассуждения требуют уточнения. В частности, в систематическом курсе анализа надлежит уточнить само понятие площади криволинейной трапеции и вообще площади плоской фигуры.
Итак, с понятием определенного интеграла (1.14) связаны две фундаментальные задачи: физическая задача о вычислении пути, пройденного движущейся со скоростью  материальной точкой за промежуток времени от х — а до
материальной точкой за промежуток времени от х — а до  и геометрическая задача о вычислении площади криволинейной трапеции.
и геометрическая задача о вычислении площади криволинейной трапеции.
9. Теперь настало время заняться вонросом о связи определенного интеграла (1.14) с введенным ранее неопределенным интегралом
(или с первообразной), а также вопросом о способах вычисления определенного интеграла.
Обозначим через  определенный интеграл от функции
определенный интеграл от функции  в пределах от а до х, где а — некоторое фиксированное значение аргумента,
в пределах от а до х, где а — некоторое фиксированное значение аргумента,  — переменное значение. Иными словами, положим
— переменное значение. Иными словами, положим

С геометрической точки зрения этот интеграл, как это показывает проведенное выше рассмотрение, равен площади криволинейной трапеции, лежащей под графиком функции  на сегменте
на сегменте  На рис. 1.3 эта криволинейная трапеция обведена жирной линией.
На рис. 1.3 эта криволинейная трапеция обведена жирной линией.
Используя наглядные геометрические соображения, убедимся в том, что введенная нами фуркция (1.15) является одной из первообразных функции  т. е. убедимся в том, что
т. е. убедимся в том, что 
Пусть  некоторое достаточно малое приращение аргумента х. Очевидно, разность
некоторое достаточно малое приращение аргумента х. Очевидно, разность  представляет собой площадь «узкой» криволинейной трапеции, заштрихованной на рис. 1.3. С другой стороны, если функция
представляет собой площадь «узкой» криволинейной трапеции, заштрихованной на рис. 1.3. С другой стороны, если функция  непрерывна в каждой точке х, т. е. если значение этой функции при малом изменении аргумента меняется мало, то указанная площадь «узкой» криволинейной трапеции мало отличается от площади
непрерывна в каждой точке х, т. е. если значение этой функции при малом изменении аргумента меняется мало, то указанная площадь «узкой» криволинейной трапеции мало отличается от площади  прямоугольника с основанием
прямоугольника с основанием  и высотой
и высотой 
Отсюда следует, что при малом  разностное отношение
разностное отношение

мало отличается от высоты  указанного прямоугольника, т. е. предел при
указанного прямоугольника, т. е. предел при  разностного отношения (1.16) обязан быть равен
разностного отношения (1.16) обязан быть равен  Вместе с тем, по определению, указанный предел равен производной
Вместе с тем, по определению, указанный предел равен производной 
Итак, мы убедились в том, что  т. е. функция (1.15) является одной из первообразных функции
т. е. функция (1.15) является одной из первообразных функции  Но тогда любая первообразная функции
Но тогда любая первообразная функции  равна
равна

где С — постоянная.
Проведенные нами рассуждения имеют предварительный характер, но при наличии развитого аппарата математического
анализа им легко придать строгий характер и строго доказать, что у любой функции  только непрерывной в каждой точке х, существует первообразная (а значит, и неопределенный интеграл), причем любая первообразная этой функции определяется равенством (1.17).
только непрерывной в каждой точке х, существует первообразная (а значит, и неопределенный интеграл), причем любая первообразная этой функции определяется равенством (1.17).
Равенство (1.17), в свою очередь, позволяет установить связь между определенным интегралом  и любой первообразной
и любой первообразной  функции
функции 
Для установления такой связи возьмем в равенстве (1.17) в качестве верхнего предела интегрирования сначала число  , а затем число а. При этом получим
, а затем число а. При этом получим

(ибо интеграл  очевидно, равен нулю).
очевидно, равен нулю).
Вычитая из равенства (1.18) равенство (1.19), мы получим, знаменитую формулу Ньютона — Лейбница

сводящую вопрос о вычислении - определенного интеграла  к вычислению разности значений любой первообразной
к вычислению разности значений любой первообразной  функции
функции  в точках
в точках 
Строгое обоснование формулы Ньютона — Лейбница является одной из важных задач математического анализа.
10. Заметим, однако, что точное аналитическое выражение для первообразной можно получить лишь для узкого класса функций. Поэтому наличие формулы Ньютона — Лейбница не снимает вопроса о приближенных способах вычисления определенного интеграла.
Простейший способ приближенного вычисления определенного интеграла (так называемый метод прямоугольников) основан на замене вычисляемого интеграла  интегральной суммой, стоящей в правой части (1.12), у которой все точки
интегральной суммой, стоящей в правой части (1.12), у которой все точки
 являются серединами соответствующих сегментов
являются серединами соответствующих сегментов  а длины всех указанных сегментов, т. е. все числа
а длины всех указанных сегментов, т. е. все числа  равны друг другу.
равны друг другу.
В систематическом курсе анализа будет доказано, что при определенных требованиях на функцию  ошибка, совершаемая при замене интеграла
ошибка, совершаемая при замене интеграла  указанной специальной интетральной суммой, имеет порядок
указанной специальной интетральной суммой, имеет порядок  где
где  — число частичных сегментов.
— число частичных сегментов.
Замечательным является то обстоятельство, что метод прямоугольников (как и многие другие методы приближенного вычисления определенного интеграла) допускает удобную реализацию на ЭВМ. Это обстоятельство и равенство (1.17) делают эти методы эффективным средством вычисления первообразных и неопределенных интегралов.
Ниже мы приводим результат вычисления на ЭВМ по методу прямоугольников так называемого интеграла Пуассона

для значения х из сегмента 
Результаты вычислений собраны нами в табл. 1, в которой в первой колонке стоит аргумент х интеграла Пуассона, во второй колонке указана длина  частичного сегмента (или шага), в третьей колонке приведен результат вычисления, а в четвертой колонке указано число
частичного сегмента (или шага), в третьей колонке приведен результат вычисления, а в четвертой колонке указано число  частичных сегментов.
частичных сегментов.
Таким образом, для интеграла Пуассона, не являющегося, как указано выше, элементарной функцией, с помощью ЭВМ и простейших приближенных методов без труда могут быть составлены таблицы его значений, делающие использование этого интеграла столь же доступным, как и использование любой элементарной функции.
11. Наряду с приближенными методами вычисления интегралов важную роль в современной математике играют приближенные методы отыскания корней различных уравнений.
Рассмотрим простейшее уравнение

В систематическом курсе анализа будет доказано, что при определенных
Таблица 1 (см. скан)
деленных требованиях, налагаемых на функцию  корень
корень  уравнения (1.20) может быть найден как предел последовательности итераций
уравнения (1.20) может быть найден как предел последовательности итераций  первая из которых
первая из которых  берется из некоторого достаточно широкого диапазона, а все последующие шаг за шагом определяются по формуле
берется из некоторого достаточно широкого диапазона, а все последующие шаг за шагом определяются по формуле

Указанный метод приближенного вычисления корня уравнения (1.20) называется методом Ньютона (или методом касательных). Этот метод допускает очень удобную реализацию на ЭВМ.
В качестве конкретного примера рассмотрим уравнение (1.20) с функцией  вида
вида  где а — положительное вещественное число,
где а — положительное вещественное число,  — целое положительное число. Для такой функции
— целое положительное число. Для такой функции  положительным корнем уравнения (1.20) будет являться число
положительным корнем уравнения (1.20) будет являться число  (т. е. корень степени
(т. е. корень степени  из положительного вещественного числа а).
из положительного вещественного числа а).
Формула (1.21), определяющая последовательные приближения метода Ньютона, на этот раз принимает вид

(Чтобы убедиться в этом, достаточно учесть, что 
Формула (1.22) представляет собой эффективный легко реализуемый на ЭВМ алгоритм вычисления корня степени  из положительного числа а.
из положительного числа а.
Приведем пример вычислений, проведенных на ЭВМ по этой формуле.
Всякое положительное вещественное число а представимо (и притом единственным способом) в виде  где I — целое число, а х удовлетворяет неравенствам
где I — целое число, а х удовлетворяет неравенствам  Будем каждый раз выбирать за первое приближение
Будем каждый раз выбирать за первое приближение  число
число  где
где  — степень извлекаемого корня, а символ
— степень извлекаемого корня, а символ  обозначает целую часть числа
обозначает целую часть числа 
Результаты вычислений собраны нами в приводимую ниже табл. 2, в которой в первой колонке стоят числа а, из которых извлекается корень, во второй колонке указаны степени  извлекаемых корней, в третьей колонке приведен результат вычислений, а в четвертой колонке указано число сделанных итераций.
извлекаемых корней, в третьей колонке приведен результат вычислений, а в четвертой колонке указано число сделанных итераций.
Таблица 2

12. Мы рассмотрели постановку важнейших задач математического анализа, отправляясь от простейшей механической модели движения материальной точки вдоль прямой линии. Такая модель естественно привела нас к необходимости построения дифференциального и интегрального исчисления функции  одной независимой переменной.
одной независимой переменной.
При описании более сложных задач естествознания возникает понятие функции нескольких независимых переменных  Так, например, температура и нагреваемого тела представляет собой функцию четырех независимых переменных: трех координат
Так, например, температура и нагреваемого тела представляет собой функцию четырех независимых переменных: трех координат  точки этого тела и времени
точки этого тела и времени  Эту функцию естественно обозначить символом
Эту функцию естественно обозначить символом 
Для функции нескольких независимых переменных естественно ввести понятие производной по каждой из переменных (такую производную называют частной производной по данной переменной).
Важной задачей для последующего развития математического анализа является построение дифференциального и интегрального исчислений функций нескольких переменных.
Наконец, математический анализ, понимаемый в совсем широком смысле, включает в себя теорию так называемых дифференциальных уравнений (т. е. уравнений, содержащих искомые функции под знаками производных).
В последние десятилетия широкое развитие получили теории, исходящие из обобщенной трактовки самого понятия функции, понятия производной и понятия решения дифференциального уравнения, связывающего производные функции.
Создание математического анализа является одним из величайших достижений человеческого разума. Оно позволило от рассмотрения отдельных разрозненных физических и геометрических задач (таких, как падение тела под действием силы тяжести, вычисление площади, лежащей под параболой) перейти к развитию общих методов решения больших классов задач. Развитие математического анализа, в свою очередь, оказало огромное влияние на прогресс науки и техники.
Классический математический анализ представляет собой очень удобную идеализированную модель, основанную на том, что мы располагаем точными значениями всех исходных величин и можем найти точные значения всех вычисляемых величин.
Заметим вместе с тем, что, отправляясь от этой модели, мы, как правило, можем оценить погрешность, возникающую вследствие того, что исходные величины заданы нам с некоторой ошибкой и все вычисления могут быть проведены лишь с определенной точностью.
Таким образом, аппарат математического анализа может быть использован для построения численных методов и оценки погрешностей.
Подводя итог, систематизируем первоочередные и наиболее важные проблемы, выявившиеся в результате проведенного нами предварительного рассмотрения.
1. Уточнение понятий вещественного числа, множества и функции.
2. Развитие теории пределов и связанного с этой теорией понятия непрерывности функции.
3. Построение аппарата дифференциального и интегрального исчислений.
4. Построение теории определенного интеграла как предела сумм специального вида.
5. Развитие приближенных методов вычисления определенных интегралов и приближенных методов решения уравнений.
6. Выяснение некоторых геометрических понятий (таких, как площадь плоской фигуры, длина дуги).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ ТИТУЛЬНОГО РЕДАКТОРА
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- Глава 2. ВЕЩЕСТВЕННЫЕ ЧИСЛА
- 2. Недостаточность рациональных чисел для измерения отрезков числовой оси.
- 3. Упорядочение множества бесконечных десятичных дробей.
- § 2. ОГРАНИЧЕННЫЕ СВЕРХУ (ИЛИ СНИЗУ) МНОЖЕСТВА ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
- 2. Существование точных граней.
- § 3. ПРИБЛИЖЕНИЕ ЧИСЕЛ, ПРЕДСТАВИМЫХ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ, РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
- § 4. ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ. ОПИСАНИЕ МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Существование и единственность суммы и произведения вещественных чисел.
- § 5. СВОЙСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Некоторые часто употребляемые соотношения.
- 3. Некоторые конкретные множества вещественных чисел.
- § 6. ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ТЕОРИИ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
- 2. Аксиоматическое введение множества вещественных чисел.
- § 7. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
- 2. Операции над множествами.
- 3. Счетные и несчетные множества. Несчетность сегмента [0, 1]. Мощность множества.
- 4. Свойства операций над множествами. Отображение множеств.
- Глава 3. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. ПОСЛЕДОВАТЕЛЬНОСТЬ И ЕЕ ПРЕДЕЛ
- 2. Ограниченные, неограниченные, бесконечно малые и бесконечно большие последовательности.
- 3. Основные свойства бесконечно малых последовательностей.
- 4. Сходящиеся последовательности и их свойства.
- § 2. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Теорема о сходимости монотонной ограниченной последовательности.
- 4. Примеры сходящихся монотонных последовательностей.
- § 3. ПРОИЗВОЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
- 2. Расширение понятий предельной точки и верхнего и нижнего пределов.
- 3. Критерий Коши сходимости последовательности.
- § 4. ПРЕДЕЛ (ИЛИ ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ) ФУНКЦИИ
- 2. Предел функции по Гейне и по Коши.
- 3. Критерий Коши существования предела функции.
- 4. Арифметические операции над функциями, имеющими предел.
- 5. Бесконечно малые и бесконечно большие функции.
- § 5. ОБЩЕЕ ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ
- Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
- § 1. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
- 2. Арифметические операции над непрерывными функциями.
- 3. Сложная функция и ее непрерывность.
- § 2. СВОЙСТВА МОНОТОННЫХ ФУНКЦИЙ
- 2. Понятие обратной функции.
- § 3. ПРОСТЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
- 2. Логарифмическая функция.
- 3. Степенная функция.
- 4. Тригонометрические функции.
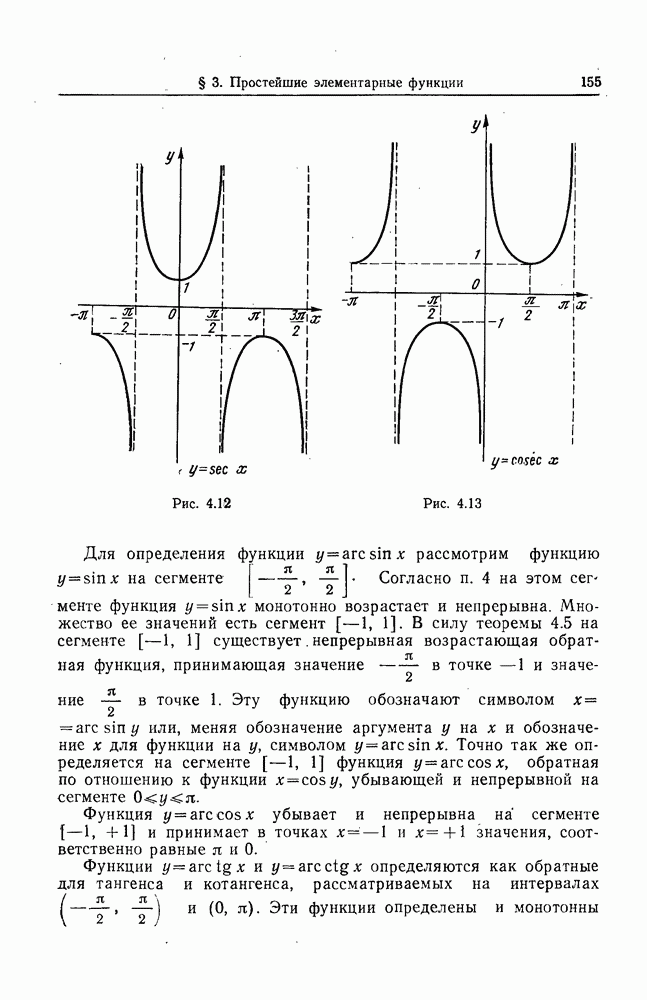
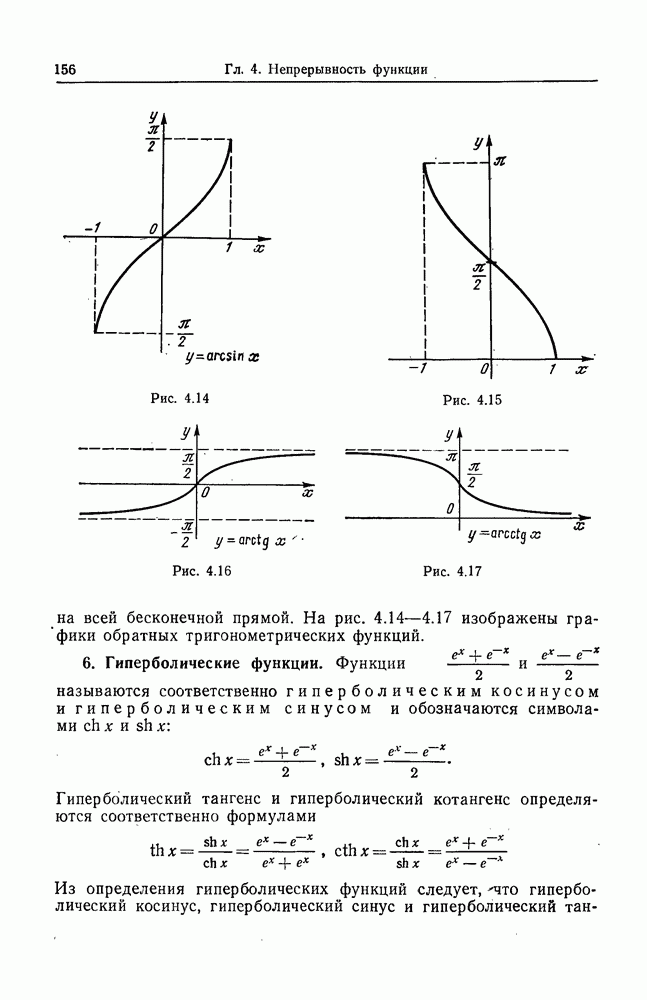
- 5. Обратные тригонометрические функции.
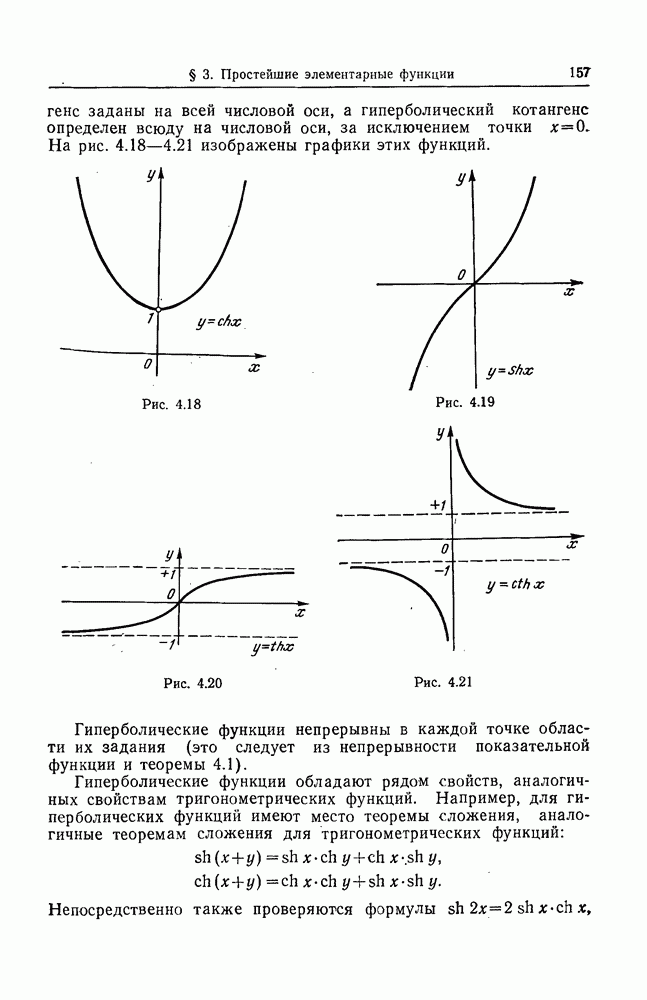
- 6. Гиперболические функции.
- § 4. ДВА ЗАМЕЧАТЕЛЬНЫХ ПРЕДЕЛА
- 2. Второй замечательный предел.
- § 5. ТОЧКИ РАЗРЫВА ФУНКЦИИ И ИХ КЛАССИФИКАЦИЯ
- 2. О точках разрыва монотонной функции.
- § 6. ЛОКАЛЬНЫЕ И ГЛОБАЛЬНЫЕ СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ
- 2. Глобальные свойства непрерывных функций.
- 3. Понятие равномерной непрерывности функции.
- 4. Понятие модуля непрерывности функции.
- § 7. ПОНЯТИЕ КОМПАКТНОСТИ МНОЖЕСТВА
- 2. О покрытиях множества системой открытых множеств.
- 3. Понятие компактности множества.
- Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 1. ПОНЯТИЕ ПРОИЗВОДНОЙ
- 2. Определение производной.
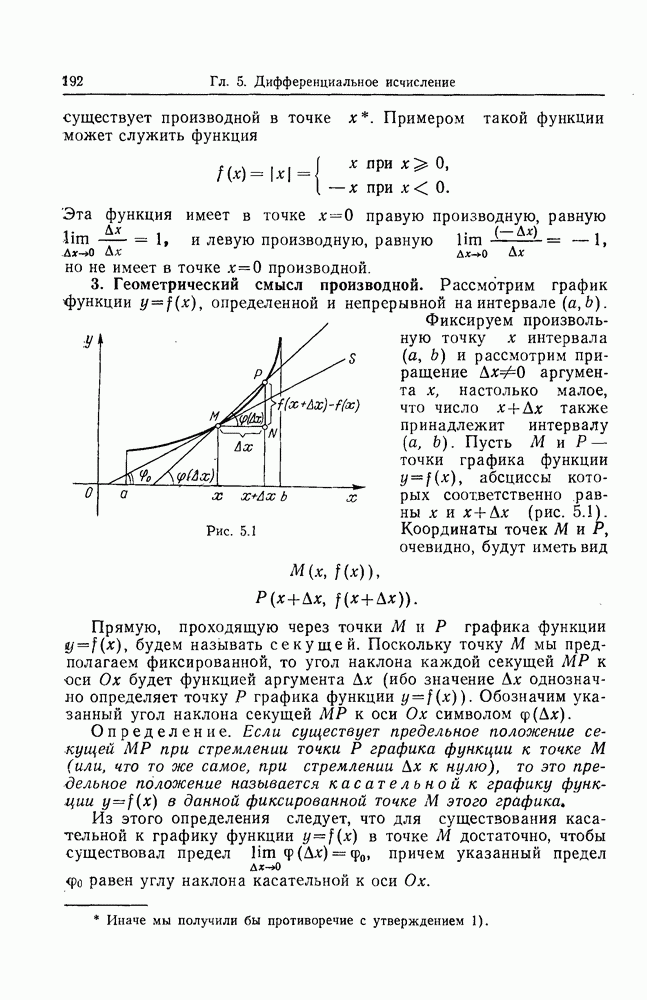
- 3. Геометрический смысл производной.
- § 2. ПОНЯТИЕ ДИФФЕРЕНЦИРУЕМОСТИ ФУНКЦИИ
- 2. Дифференцируемость и непрерывность.
- 3. Понятие дифференциала функции.
- § 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ И ОБРАТНОЙ ФУНКЦИИ
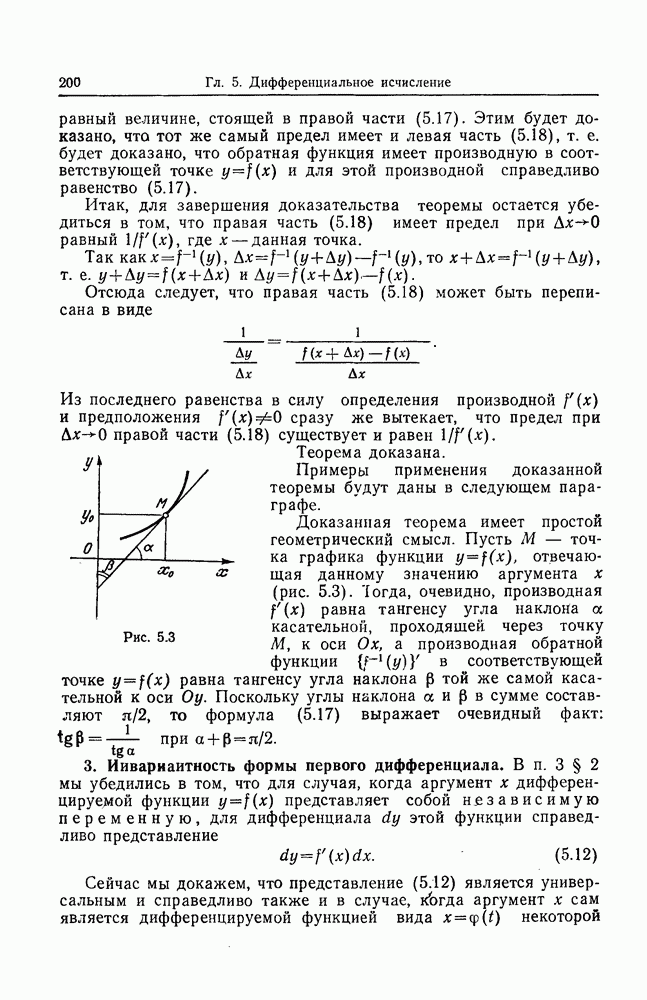
- 2. Дифференцирование обратной функции.
- 3. Инвариантность формы первого дифференциала.
- 4. Применение дифференциала для установления приближенных формул.
- § 4. ДИФФЕРЕНЦИРОВАНИЕ СУММЫ, РАЗНОСТИ, ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ФУНКЦИЙ
- § 5. ПРОИЗВОДНЫЕ ПРОСТЕЙШИХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Производная логарифмической функции.
- 3. Производные показательной и обратных тригонометрических функций.
- 4. Производная степенной функции.
- 5. Таблица производных простейших элементарных функций.
- 6. Таблица дифференциалов простейших элементарных функций.
- 7. Логарифмическая производная. Производная степенно-показательной функции.
- § 6. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. n-ые производные некоторых функций.
- 3. Формула Лейбница для n-й производной произведения двух функций.
- 4. Дифференциалы высших порядков.
- § 7. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
- § 8. ПРОИЗВОДНАЯ ВЕКТОРНОЙ ФУНКЦИИ
- Глава 6. ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
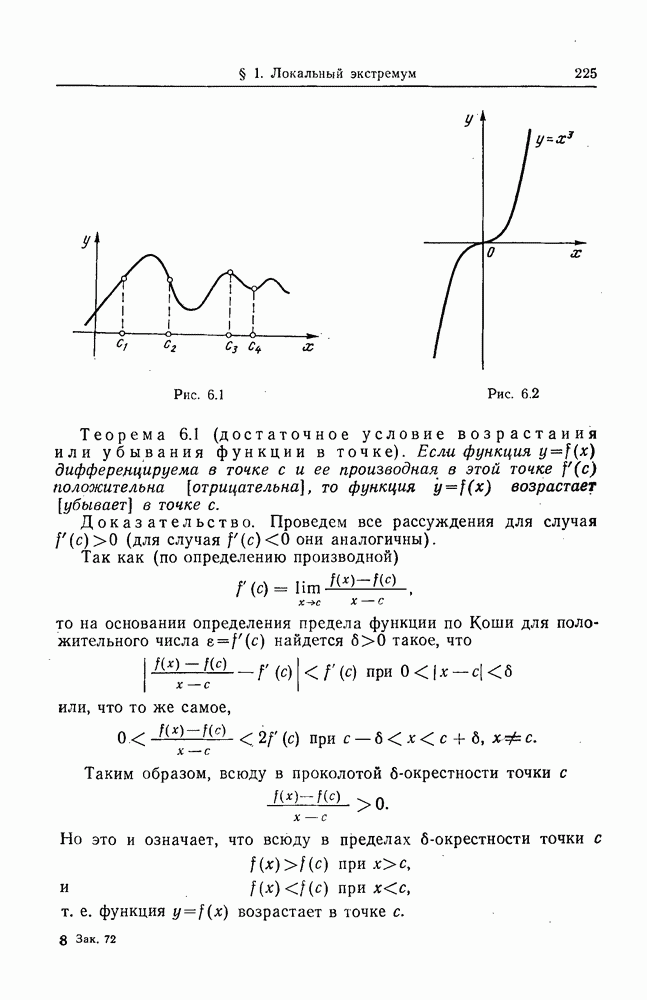
- § 1. ВОЗРАСТАНИЕ (УБЫВАНИЕ) ФУНКЦИИ В ТОЧКЕ. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
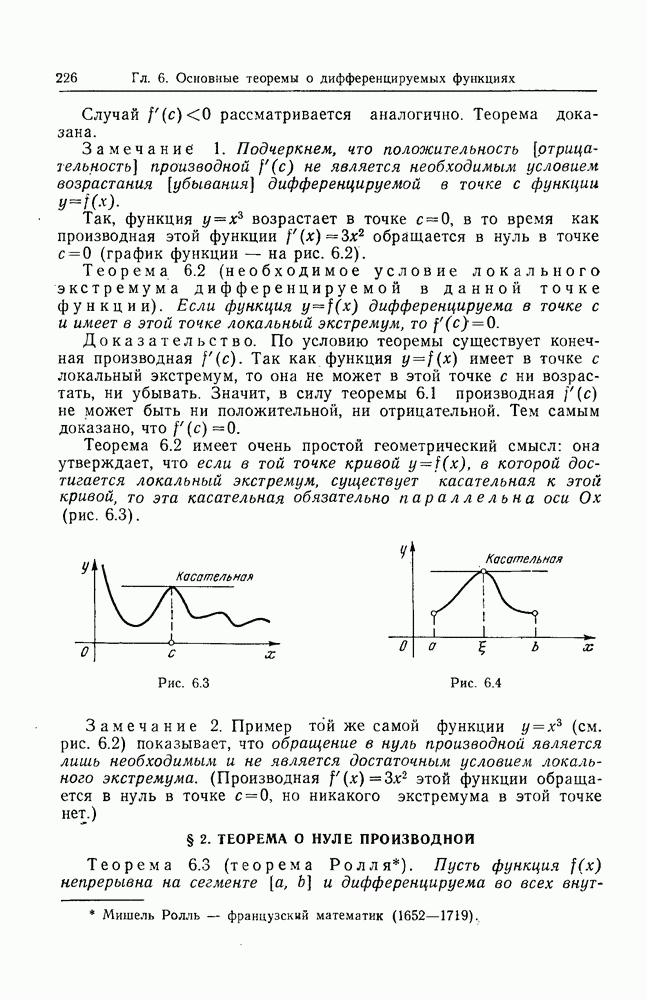
- § 2. ТЕОРЕМА О НУЛЕ ПРОИЗВОДНОЙ
- § 3. ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА ЛАГРАНЖА)
- § 4. НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ЛАГРАНЖА
- 2. Условия монотонности функции на интервале.
- 3. Отсутствие разрывов первого рода и устранимых разрывов у производной.
- 4. Вывод некоторых неравенств.
- § 5. ОБОБЩЕННАЯ ФОРМУЛА КОНЕЧНЫХ ПРИРАЩЕНИЙ (ФОРМУЛА КОШИ)
- § 6. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ (ПРАВИЛО ЛОПИТАЛЯ)
- 2. Раскрытие неопределенности вида oo/oo
- 3. Раскрытие неопределенностей других видов.
- § 7. ФОРМУЛА ТЕЙЛОРА
- § 8. РАЗЛИЧНЫЕ ФОРМЫ ОСТАТОЧНОГО ЧЛЕНА. ФОРМУЛА МАКЛОРЕНА
- 2. Другая запись формулы Тейлора.
- 3. Формула Маклорена.
- § 9. ОЦЕНКА ОСТАТОЧНОГО ЧЛЕНА. РАЗЛОЖЕНИЕ НЕКОТОРЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
- 2. Разложение по формуле Маклорена некоторых элементарных функций.
- § 10. ПРИМЕРЫ ПРИЛОЖЕНИЙ ФОРМУЛЫ МАКЛОРЕНА
- 2. Доказательство иррациональности числа е.
- 3. Вычисление значений тригонометрических функций.
- 4. Асимптотическая оценка элементарных функций и вычисление пределов.
- Глава 7. ИССЛЕДОВАНИЕ ГРАФИКА ФУНКЦИИ И ОТЫСКАНИЕ ЭКСТРЕМАЛЬНЫХ ЗНАЧЕНИИ
- § 1. ОТЫСКАНИЕ СТАЦИОНАРНЫХ ТОЧЕК
- 2. Отыскание стационарных точек.
- 3. Первое достаточное условие экстремума.
- 4. Второе достаточное условие экстремума.
- 5. Третье достаточное условие, экстремума.
- 6. Экстремум функции, недифференцируемой в данной точке.
- 7. Общая схема отыскания экстремумов.
- § 2. ВЫПУКЛОСТЬ ГРАФИКА ФУНКЦИИ
- § 3. ТОЧКИ ПЕРЕГИБА
- 2. Первое достаточное условие перегиба.
- 3. Некоторые обобщения первого достаточного условия перегиба.
- 4. Второе достаточное условие перегиба.
- 5. Третье достаточное условие перегиба.
- § 4. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ
- § 6. ГЛОБАЛЬНЫЕ МАКСИМУМ И МИНИМУМ ФУНКЦИИ НА СЕГМЕНТЕ. КРАЕВОЙ ЭКСТРЕМУМ
- 2. Краевой экстремум.
- 3. Теорема Дарбу.
- ДОПОЛНЕНИЕ
- Алгоритм отыскания экстремальных значений функции, использующий только значения этой функции
- Глава 8. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ И НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Неопределенный интеграл.
- 3. Основные свойства неопределенного интеграла.
- 4. Таблица основных неопределенных интегралов.
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование по частям.
- § 3. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ в ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Краткие сведения о корнях алгебраических многочленов.
- 3. Разложение алгебраического многочлена с вещественными коэффициентами на произведение неприводимых множителей.
- 4. Разложение правильной рациональной дроби на сумму простейших дробей.
- 5. Интегрируемость рациональной дроби в элементарных функциях.
- 6. Интегрируемость в элементарных функциях некоторых тригонометрических и иррациональных выражений.
- § 4. ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
- Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА
- ИНТЕГРАЛ РИМАНА: § 2. ВЕРХНИЕ И НИЖНИЕ СУММЫ И ИХ СВОЙСТВА
- 2. Основные свойства верхних и нижних сумм.
- § 3. ТЕОРЕМЫ О НЕОБХОДИМЫХ И ДОСТАТОЧНЫХ УСЛОВИЯХ ИНТЕГРИРУЕМОСТИ ФУНКЦИЙ. КЛАССЫ ИНТЕГРИРУЕМЫХ ФУНКЦИЙ
- 2. Классы интегрируемых функций.
- § 4. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА. ОЦЕНКИ ИНТЕГРАЛОВ. ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ
- 2. Оценки интегралов.
- § 5. ПЕРВООБРАЗНАЯ НЕПРЕРЫВНОЙ ФУНКЦИИ. ПРАВИЛА ИНТЕГРИРОВАНИЯ ФУНКЦИЙ
- 2. Основная формула интегрального исчисления.
- 3. Важные правила, позволяющие вычислять определенные интегралы.
- 4. Остаточный член формулы Тейлора в интегральной форме.
- § 6. НЕРАВЕНСТВА ДЛЯ СУММ И ИНТЕГРАЛОВ
- 2. Неравенство Гёльдера для сумм.
- 3. Неравенство Минковского для сумм.
- 4. Неравенство Гёльдера для интегралов.
- 5. Неравенство Минковского для интегралов.
- § 7. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ РИМАНА
- 2. Критерий интегрируемости Лебега.
- ДОПОЛНЕНИЕ 1. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Критерий Коши сходимости несобственного интеграла первого рода.
- 3. Абсолютная и условная сходимость несобственных интегралов.
- 4. Замена переменных под знаком несобственного интеграла и формула интегрирования по частям.
- § 2. Несобственные интегралы второго рода
- § 3. Главное значение несобственного интеграла
- ДОПОЛНЕНИЕ 2. Интеграл Стилтьеса
- 2. Свойства интеграла Стилтьеса.
- Глава 10. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- § 1. ДЛИНА ДУГИ КРИВОЙ
- 2. Понятие параметризуемой кривой.
- 3. Длина дуги кривой. Понятие спрямляемой кривой.
- 4. Критерий спрямляемости кривой. Вычисление длины дуги кривой.
- 5. Дифференциал дуги.
- 6. Примеры.
- § 2. ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
- 2. Площадь плоской фигуры.
- 3. Площадь криволинейной трапеции и криволинейного сектора.
- 4. Примеры вычисления площадей.
- § 3. ОБЪЕМ ТЕЛА В ПРОСТРАНСТВЕ
- 2. Некоторые классы кубируемых тел.
- 3. Примеры.
- Глава 11. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ И ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- § 1. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ КОРНЕЙ УРАВНЕНИЙ
- 2. Метод итераций.
- 3. Методы хорд и касательных.
- § 2. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- 2. Метод прямоугольников.
- 3. Метод трапеций.
- 4. Метод парабол.
- Глава 12. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ПОНЯТИЕ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Множества точек m-мерного евклидова пространства.
- 3. Понятие функции m переменных.
- § 2. ПРЕДЕЛ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Свойство ограниченной последовательности точек E^m.
- 3. Предел функции m переменных.
- 4. Бесконечно малые функции m переменных.
- 5. Повторные пределы.
- § 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Непрерывность функции m переменных по одной переменной.
- 3. Основные свойства непрерывных функций нескольких переменных.
- § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Дифференцируемость функции нескольких переменных.
- 3. Геометрический смысл условия дифференцируемости функции двух переменных.
- 4. Достаточные условия дифференцируемости.
- 5. Дифференциал функции нескольких переменных.
- 6. Дифференцирование сложной функции.
- 7. Инвариантность формы первого дифференциала.
- 8. Производная по направлению. Градиент.
- § 5. ЧАСТНЫЕ ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
- 2. Дифференциалы высших порядков.
- 3. Формула Тейлора с остаточным членом в форме Лагранжа и в интегральной форме.
- 4. Формула Тейлора с остаточным членом в форме Пеано.
- § 6. ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ m ПЕРЕМЕННЫХ
- 2. Достаточные условия локального экстремума функции m переменных.
- 3. Случай функции двух переменных.
- ДОПОЛНЕНИЕ 1. Градиентный метод поиска экстремума сильно выпуклой функции
- 1. Выпуклые множества и выпуклые функции.
- 2. Существование минимума у сильно выпуклой функции и единственность минимума у строго выпуклой функции.
- 3. Поиск минимума сильно выпуклой функции.
- ДОПОЛНЕНИЕ 2. Метрические, нормированные пространства
- 2. Открытые и замкнутые множества.
- 3. Прямое произведение метрических пространств.
- 4. Всюду плотные и совершенные множества.
- 5. Сходимость. Непрерывные отображения.
- 6. Компактность.
- 7. Базис пространства.
- Топологические пространства
- Линейные нормированные пространства, линейные операторы
- ДОПОЛНЕНИЕ 3. Дифференциальное исчисление в линейных нормированных пространствах
- 2. Формула Лагранжа конечных приращений.
- 3. Связь между слабой и сильной дифференцируемостью.
- 4. Дифференцируемость функционалов.
- 5. Интеграл от абстрактных функций.
- 6. Формула Ньютона — Лейбница для абстрактных функций.
- 7. Производные второго порядка.
- 8. Отображение m-мерного евклидова пространства в n-мерное.
- 9. Производные и дифференциалы высших порядков.
- 10. Формула Тейлора для отображений одного нормированного пространства в другое.
- Исследование на экстремум функционалов в нормированных пространствах
- 2. Достаточные условия экстремума.
- Глава 13. НЕЯВНЫЕ ФУНКЦИИ
- § 1. СУЩЕСТВОВАНИЕ И ДИФФЕРЕНЦИРУЕМОСТЬ НЕЯВНО ЗАДАННОЙ ФУНКЦИИ
- 2. Вычисление частных производных неявно заданной функции.
- 3. Особые точки поверхности и плоской кривой.
- 4. Условия, обеспечивающие существование для функции y=f(x) обратной функции.
- § 2. НЕЯВНЫЕ ФУНКЦИИ, ОПРЕДЕЛЯЕМЫЕ СИСТЕМОЙ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
- 2. Вычисление частных производных функций, неявно определяемых посредством системы функциональных уравнений.
- 3. Взаимно однозначное отображение двух множеств m-мерного пространства.
- § 3. ЗАВИСИМОСТЬ ФУНКЦИЙ
- 2. Функциональные матрицы и их приложения.
- § 4. УСЛОВНЫЙ ЭКСТРЕМУМ
- 2. Метод неопределенных множителей Лагранжа.
- 3. Достаточные условия.
- 4. Пример.
- ДОПОЛНЕНИЕ
- Отображения банаховых пространств. Аналог теоремы о неявной функции
- 2. Случай конечномерных пространств.
- 3. Особые точки поверхности в пространстве n измерений. Обратное отображение.
- 4. Условный экстремум в случае отображений нормированных пространств.