| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. ФУНКЦИЯ ГРИНА
В предыдущем параграфе мы дали определение фундаментального решения уравнения Лапласа. Легко видеть, что фундаментальное решение определяется неоднозначно. Действительно, наряду с построенным выше фундаментальным решением (4.2.6) рассмотрим функцию

где  — произвольная функция пары точек х и гладкая и гармоническая по х при каждом
— произвольная функция пары точек х и гладкая и гармоническая по х при каждом  Если
Если  — гладкая финитная функция, то имеет место равенство
— гладкая финитная функция, то имеет место равенство

в чем легко убедиться, перебросив дифференцирование с и на у. Отсюда и из равенства (4.2.1) получаем

Таким образом,  есть также фундаментальное решение уравнения Лапласа.
есть также фундаментальное решение уравнения Лапласа.
Наличие произвольной гармонической функции  в качестве слагаемого в
в качестве слагаемого в  дает возможность строить такое фундаментальное решение, которое удовлетворяет однородным граничным условиям рассматривавшихся выше граничных задач. Такое фундаментальное решение называется функцией Грина граничной задачи. Ниже мы дадим точное определение функции Грина, изучим ее свойства и покажем, как каждое решение граничной задачи может быть представлено с помощью функции Грина.
дает возможность строить такое фундаментальное решение, которое удовлетворяет однородным граничным условиям рассматривавшихся выше граничных задач. Такое фундаментальное решение называется функцией Грина граничной задачи. Ниже мы дадим точное определение функции Грина, изучим ее свойства и покажем, как каждое решение граничной задачи может быть представлено с помощью функции Грина.
1. Функция Грина.
Прежде чем дать точное определение, мы приведем некоторые наводящие соображения. Рассмотрим задачу А в той классической ее постановке, которая была приведена в п. 1.2. Предположим, что мы хотим построить фундаментальное решение, которое удовлетворяло бы однородным граничным условиям этой задачи:

Здесь и в дальнейшем в этом пункте мы будем считать  заданной и фиксированной точкой множества
заданной и фиксированной точкой множества 
Ясно, как нужно подбирать функцию  входящую в равенство (1), чтобы выполнялись граничные условия (1.1). Для этого нужно решить следующую граничную задачу: найти функцию
входящую в равенство (1), чтобы выполнялись граничные условия (1.1). Для этого нужно решить следующую граничную задачу: найти функцию  удовлетворяющую уравнению Лапласа
удовлетворяющую уравнению Лапласа

в области  и граничному условию
и граничному условию

Мы определим у как обобщенное решение задачи (1.2) - (1.4). В дальнейшем будет показано, что решение является гладкой (и даже неограниченно дифференцируемой) функцией по обеим точкам  в области
в области  Нарушение гладкости может происходить на границе, что вполне естественно, так как никакие условия гладкости на границу налагаться не будут.
Нарушение гладкости может происходить на границе, что вполне естественно, так как никакие условия гладкости на границу налагаться не будут.
Перейдем к точным определениям. Как и в п. 2.2, мы будем предполагать, что  есть ограниченное открытое связное множество с конечным периметром;
есть ограниченное открытое связное множество с конечным периметром;  его существенная граница;
его существенная граница;  ее подмножества, измеримые по
ее подмножества, измеримые по  -мерной мере Хаусдорфа, причем
-мерной мере Хаусдорфа, причем 
Мы будем рассматривать задачу А в той постановке, в какой она сформулирована в п. 2.2, но только применительно к уравнению Лапласа. Поэтому функционал  (см. (2.1.3)) имеет вид
(см. (2.1.3)) имеет вид

Мы сохраним предположение, что задача А является сильноэллиптической (см. п. 2.3).
Мы будем, далее, предполагать, что соответствующая однородная задача имеет только нулевое решение. Это условие необходимо для 
ществования функции Грина, в чем можно будет убедиться, выражая решения через функцию Грина, как это делается ниже.
Для определения функции  как решения задачи А в той постановке, в какой она приведена в п. 2.2, требуется указать функционал
как решения задачи А в той постановке, в какой она приведена в п. 2.2, требуется указать функционал  соответствующий граничному условию (1.4). Этот функционал имеет вид
соответствующий граничному условию (1.4). Этот функционал имеет вид

Теперь мы можем дать определение функции Грина.
Определение. Функцией Грина задачи А называется функция

где  - фундаментальное решение (4.2.6) уравнения Лапласа,
- фундаментальное решение (4.2.6) уравнения Лапласа,  есть функция, принадлежащая пространству
есть функция, принадлежащая пространству  удовлетворяющая граничному условию
удовлетворяющая граничному условию

и уравнению

при всех  где
где  задаются равенствами (1.5) и (1.6).
задаются равенствами (1.5) и (1.6).
Естественно возникает вопрос, существует ли такая функция  т. е. существует ли решение граничной задачи (1.8), (1.9). Заметим, что формально здесь не выполняются условия, которые требовались при постановке задачи А в п. 2.2. Именно там требовалось, чтобы функция
т. е. существует ли решение граничной задачи (1.8), (1.9). Заметим, что формально здесь не выполняются условия, которые требовались при постановке задачи А в п. 2.2. Именно там требовалось, чтобы функция  входящая в равенство (2.2.4), принадлежала пространству
входящая в равенство (2.2.4), принадлежала пространству  Соответствующая функция
Соответствующая функция  входящая в условие (1.8), не удовлетворяет этому требованию. Однако в действительности это не существенно, так как в постановке граничной задачи участвует только след функции
входящая в условие (1.8), не удовлетворяет этому требованию. Однако в действительности это не существенно, так как в постановке граничной задачи участвует только след функции  на 5, по точке х, а точка
на 5, по точке х, а точка  является внутренней точкой множества
является внутренней точкой множества  Поэтому ясно, что функцию
Поэтому ясно, что функцию  можно так изменить в окрестности точки
можно так изменить в окрестности точки  что она станет гладкой, а ее след не изменится.
что она станет гладкой, а ее след не изменится.
Существование решения задачи (1.8), (1.9) следует из первой теоремы Фредгольма, так как мы предположили, что соответствующая однородная задача имеет только нулевое решение. Последнее, в частности, имеет место, если функционал  положительно-определенный. Для этого, как показано в п. 2.8, достаточно, чтобы выполнялись следующие условия:
положительно-определенный. Для этого, как показано в п. 2.8, достаточно, чтобы выполнялись следующие условия:  и либо
и либо  либо
либо  на множестве положительной
на множестве положительной  -мерной меры.
-мерной меры.
Для любой финитной в  функции
функции  равенство (1.9) принимает вид
равенство (1.9) принимает вид

Следовательно, по определению обобщенного решения эллиптического уравнения (см. п. 2.2) функция  является обобщенным решением уравнения Лапласа на множестве
является обобщенным решением уравнения Лапласа на множестве  Поэтому по теореме 1 п. 4.6 функция
Поэтому по теореме 1 п. 4.6 функция  непрерывна и неограниченно дифференцируема по координатам точки х.
непрерывна и неограниченно дифференцируема по координатам точки х.
2. Симметричность.
Теорема. Функция  является симметричной, т. е. имеет место равенство
является симметричной, т. е. имеет место равенство

для всех точек 
Доказательство. Обозначим

где  функция, определенная равенством (4.4.5), — «срезка» функции
функция, определенная равенством (4.4.5), — «срезка» функции  непрерывна и имеет ограниченные производные.
непрерывна и имеет ограниченные производные.
Пусть  некоторая точка множества
некоторая точка множества  отличная от
отличная от  Тогда при достаточно большом
Тогда при достаточно большом  имеет место равенство
имеет место равенство

Поэтому  может быть взята в качестве функции
может быть взята в качестве функции  входящей в равенство (1.9). Это равенство примет вид
входящей в равенство (1.9). Это равенство примет вид

Далее, интеграл

существует, так как стоящие под знаком этого интеграла производные суммируемы в квадрате. Интегрирование по частям дает следующее равенство:

При этом мы считаем  столь большим, что
столь большим, что  при
при  Первый из интегралов есть среднее значение функции
Первый из интегралов есть среднее значение функции  по сфере
по сфере  (см. равенство (4.3.10)). Так как функция
(см. равенство (4.3.10)). Так как функция  является гармонической в окрестности точки
является гармонической в окрестности точки  то по теореме о среднем значении (см. п. 4.7) мы получаем из (2.6)
то по теореме о среднем значении (см. п. 4.7) мы получаем из (2.6)

Вычтем отсюда равенство (2.4). Получим

Левая часть этого равенства не изменится, если поменять местами точки  Поэтому
Поэтому  Теорема доказана.
Теорема доказана.
Следствие. Функция  симметрична, непрерывна и неограниченно дифференцируема по каждой из точек
симметрична, непрерывна и неограниченно дифференцируема по каждой из точек 
Доказательство. Симметричность функции  следует из теоремы и симметричности функции
следует из теоремы и симметричности функции  Неограниченная дифференцируемость по точке х доказана в п. 1, по точке
Неограниченная дифференцируемость по точке х доказана в п. 1, по точке  следует отсюда и из симметричности.
следует отсюда и из симметричности.
3. Решение задачи А.
Мы покажем, что если известна функция Грина, то решение задачи А для уравнения Пуассона может быть записано явно в виде интеграла. В некоторых случаях (например, в случае первой краевой задачи для шара) известны аналитические выражения функции Грина (см., например, [29]). В этих случаях решение граничной задачи сводится просто к вычислению интеграла. Однако выражение решения через функцию Грина важно не только в вычислительном аспекте. Его можно существенно использовать для изучения свойств и поведения решений.
Мы ограничимся для простоты случаем, когда рассматривается уравнение Пуассона с однородными граничными условиями. Заметим,
что для неоднородных граничных условий выражение решения с помощью функции Грина в виде интеграла также возможно.
Итак, рассмотрим граничную задачу, которая в классической постановке выглядит следующим образом:

В обобщенной постановке она состоит в нахождении решения и  уравнения
уравнения

для всех  Здесь
Здесь  функционал (1.5). В дальнейшем, говоря о решении задачи (3.1), мы будем иметь в виду решение именно в этом смысле. Мы предполагаем выполненными условия, сформулированные в п. 1.
функционал (1.5). В дальнейшем, говоря о решении задачи (3.1), мы будем иметь в виду решение именно в этом смысле. Мы предполагаем выполненными условия, сформулированные в п. 1.
Теорема. Пусть  решение задачи (3.1). Тогда в каждой точке
решение задачи (3.1). Тогда в каждой точке  в которой выполняется условие
в которой выполняется условие

для функции  существует шаровое среднее
существует шаровое среднее  и имеет место равенство
и имеет место равенство

Таким образом, почти всюду в 

Для любой функции  интеграл (3.5) является решением задачи (3.1).
интеграл (3.5) является решением задачи (3.1).
Доказательство. Для любой точки  мы можем в качестве функции
мы можем в качестве функции  входящей в (3.2), взять функцию
входящей в (3.2), взять функцию  определенную равенством (2.2), при достаточно большом
определенную равенством (2.2), при достаточно большом  Получим
Получим

Так как  то эта функция может быть взята в качестве функции
то эта функция может быть взята в качестве функции  входящей в уравнение (1.9). Тогда будем иметь
входящей в уравнение (1.9). Тогда будем иметь

где  задается равенством (1.6).
задается равенством (1.6).
Подставляя в функционал  функцию
функцию  вместо
вместо  и интегрируя по частям, получим
и интегрируя по частям, получим

где  внешний след функции
внешний след функции  на сфере
на сфере 
Вычтем (3.7) из (3.8). Тогда из (3.6), учитывая, что  получим
получим

Заметим, что при выполнении условия (3.3) имеет место равенство

причем интеграл, стоящий справа, существует. Действительно, так как функция  принадлежит пространству
принадлежит пространству  то существование интеграла зависит только от функции
то существование интеграла зависит только от функции  Учитывая вид
Учитывая вид  (см. 4.2.6)), мы заключаем, что условие (3.3) гарантирует существование интеграла (3.10). При этом нужно заметить, что при
(см. 4.2.6)), мы заключаем, что условие (3.3) гарантирует существование интеграла (3.10). При этом нужно заметить, что при  никаких условий не нужно, так как в этом случае
никаких условий не нужно, так как в этом случае  Ввиду неравенства
Ввиду неравенства  предельный переход в (3.10) возможен.
предельный переход в (3.10) возможен.
В левой части равенства (3.9) стоит среднее значение функции  по сфере
по сфере  (см. (4.3.10)). Воспользуемся леммой п. 4.3.
(см. (4.3.10)). Воспользуемся леммой п. 4.3.
Согласно этой лемме из равенства (3.10) следуют существование шарового среднего  и равенство (3.4).
и равенство (3.4).
Для полного доказательства теоремы остается только показать, что для любой функции  интеграл (3.5) дает решение граничной задачи (3.1). Но на основании условий, сформулированных в п. 1, задача (3.1) имеет решение и, а по доказанному выше это решение имеет вид (3.5). Теорема доказана.
интеграл (3.5) дает решение граничной задачи (3.1). Но на основании условий, сформулированных в п. 1, задача (3.1) имеет решение и, а по доказанному выше это решение имеет вид (3.5). Теорема доказана.
Заметим, что в важных для приложений случаях  и трехмерного пространств
и трехмерного пространств  условие (3.3) выполняется в каждой точке
условие (3.3) выполняется в каждой точке  так как в этих случаях функция
так как в этих случаях функция  суммируема в квадрате.
суммируема в квадрате.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ ПЕРВЫЙ. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА И ТЕОРИИ МЕРЫ
- § 1. МНОЖЕСТВА
- 2. Действия над множествами.
- 3. Ограниченные множества.
- 4. Функции.
- § 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 1. Двумерное векторное пространство как пример линейного пространства.
- 2. Определение линейного пространства.
- 3. Примеры линейных пространств.
- 4. Действия над векторами.
- 5. Линейная комбинация векторов.
- 6. Линейная зависимость и независимость векторов.
- 7. Размерность пространства.
- 8. Подпространства.
- 9. Линейная оболочка.
- 10. Линейно-независимые последовательности.
- § 3. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- 2. Свойства скалярного произведения.
- 3. Норма вектора.
- 4. Неравенство Коши-Буняковского.
- 5. Неравенство треугольника.
- § 4. НОРМИРОВАННЫЕ ПРОСТРАНСТВА
- 2. Свойства нормы.
- 3. Сходимость.
- 4. Сходимость в пространстве Rn.
- 5. Открытые и замкнутые множества.
- 6. Подпространства нормированного пространства.
- 7. Сепарабельные пространства.
- 8. Полные пространства.
- 9. Полнота пространства Rn.
- 10. Пространство (М) ограниченных функций.
- 11. Пространство (С) ограниченных непрерывных функций.
- 12. Понятие о компактности.
- § 5. ОРТОНОРМИРОВАННЫЙ БАЗИС ЕВКЛИДОВА ПРОСТРАНСТВА
- 2. Ортогонализация последовательности векторов.
- 3. Ортонормированный базис конечномерного пространства.
- 4. Проекция вектора на подпространство.
- 5. Ряды Фурье.
- 6. Ортонормированный базис сепарабельного пространства.
- 7. Разложение по ортогональным системам.
- 8. Ортогональные дополнения.
- § 6. КОМПЛЕКСНЫЕ ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 2. Комплексные евклидовы и нормированные пространства.
- Приложение к главе I. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- § 7. МАТРИЦЫ
- 2. Действия над матрицами.
- 3. Обратимые матрицы.
- 4. Транспонирование матриц.
- § 8. ОПРЕДЕЛИТЕЛИ
- 3. Свойства определителя.
- 4. Обратные матрицы.
- § 9. РАНГ МАТРИЦЫ
- 3. Базис конечномерного пространства.
- Глава II. МЕРА И ИНТЕГРАЛ
- 1. Аддитивные функции множества.
- 2. Мера.
- 3. Полная вариация меры.
- 4. Пространство мер.
- 5. Абсолютная непрерывность.
- 6. Регулярные меры.
- 7. Мера Лебега.
- 8. Мера Хаусдорфа.
- § 2. ИЗМЕРИМЫЕ ФУНКЦИИ
- 2. Простые измеримые функции.
- 3. Измеримые функции.
- § 3. ИНТЕГРАЛ
- 1. Интегрирование простых измеримых функций.
- 2. Суммируемые функции. Интеграл.
- 3. Основные свойства интеграла.
- 4. Предельный переход под знаком интеграла.
- 5. Критерий суммируемости функций.
- 6. Интеграл Лебега.
- 7. Произведение мер. Теорема Фубини.
- § 4. Пространство Lp
- 1. Функции, суммируемые в степени р.
- 2. Пространство Lp.
- 3. Критерий компактности.
- Глава III. ОПЕРАТОРЫ И ФУНКЦИОНАЛЫ
- § 1. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 2. Примеры линейных операторов.
- 3. Ограниченные операторы.
- 4. Примеры ограниченных операторов.
- 5. Пример неограниченного оператора.
- 6. Непрерывность линейных операторов.
- 7. Действия над операторами.
- § 2. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
- 2 Примеры линейных функционалов.
- 3. Сопряженное пространство.
- 4. Линейные функционалы в гильбертовом пространстве.
- 5. Линейные функционалы в пространстве непрерывных функций.
- § 3. СОПРЯЖЕННЫЕ ОПЕРАТОРЫ
- 2. Примеры сопряженных операторов.
- 3. Свойства сопряженных операторов.
- 4. Самосопряженные операторы.
- 5. Квадратичные формы.
- § 4. КОНЕЧНОМЕРНЫЕ И ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
- 2. Вполне непрерывные операторы.
- § 5. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ
- 2. Самосопряженные операторы.
- 3. Самосопряженные вполне непрерывные операторы.
- 4. Самосопряженные операторы в конечномерных пространствах, матрицы и квадратичные формы.
- § 6. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
- 2. Метод последовательных приближений.
- 3. Операторы сжатия.
- 4. Линейные уравнения.
- РАЗДЕЛ ВТОРОЙ. АНАЛИЗ В ПРОСТРАНСТВАХ BV
- Глава IV. ДИФФЕРЕНЦИРОВАНИЕ
- § 1. ОБОБЩЕННЫЕ ПРОИЗВОДНЫЕ
- 2. Обобщенная производная как функционал.
- § 2. МНОЖЕСТВА С КОНЕЧНЫМ ПЕРИМЕТРОМ
- 2. Множества ограниченной вариации.
- 3. Алгебра множеств с конечным периметром.
- 4. Периметр множества.
- § 3. ПРОСТРАНСТВО BV
- 2. Функции ограниченной вариации.
- 3. Интегральное условие.
- 4. Полная вариация градиента.
- § 4. АППРОКСИМАТИВНЫЙ ПРЕДЕЛ ФУНКЦИИ
- 2. Аппроксимативный предел.
- 3. Основные теоремы о пределах.
- 4. Регулярные точки.
- § 5. СТРУКТУРА ФУНКЦИЙ, ПРИНАДЛЕЖАЩИХ ПРОСТРАНСТВУ BV
- 5. Структура функций, принадлежащих пространству BV.
- 6. Среднее значение.
- § 6. ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
- 2. Усредненная суперпозиция.
- 3. Дифференцирование суперпозиции.
- 4. Дифференцирование произведения.
- Глава V. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ
- § 1. ФОРМУЛА ГРИНА
- 2. След функции на границе.
- 3. Дифференцирование произведения функции на характеристическую функцию множества.
- 4. Формула Грина.
- 5. Множества класса Г.
- 6. Полный скачок.
- 7. Интегрирование по частям.
- 8. Формулы векторного анализа.
- § 2. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- 3. Аналитические функции. Теорема Коши.
- 4. Разрывные аналитические функции.
- 5. Полный скачок.
- 6. Выражение аналитической функции через скачок.
- § 3. ПРОСТРАНСТВО BV2
- 6. Полная непрерывность оператора вложения.
- 7. Регулярные точки границы.
- § 4. ЗАКОНЫ СОХРАНЕНИЯ
- 1. Дифференциальная форма законов сохранения.
- 2. Условия на разрывах.
- РАЗДЕЛ ТРЕТИЙ. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- Глава VI. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 2. Основная теорема.
- 3. Скалярное уравнение.
- 4. Априорная оценка и нелокальная разрешимость.
- § 2. ЛИНЕЙНЫЕ УРАВНЕНИЯ
- 2. Системы с постоянными коэффициентами.
- 3. Скалярное уравнение высшего порядка.
- § 3. ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Метод функций Ляпунова.
- 3. Некоторые примеры функции Ляпунова.
- 4. Метод линеаризации.
- § 4. ПОЛОЖЕНИЕ РАВНОВЕСИЯ СИСТЕМЫ ДВУХ УРАВНЕНИЙ. ПОНЯТИЕ О ПРЕДЕЛЬНОМ ЦИКЛЕ
- 2. Некоторые замечания.
- 3. Понятие о предельном цикле.
- § 5. УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХ
- 2. Теорема Тихонова.
- 3. Теорема Понтрягина-Родыгина.
- Глава VII. ЛИНЕЙНЫЕ ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ И ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Граничные задачи.
- 3. Формулы Грина.
- 4. Сопряженная задача.
- § 2. ИССЛЕДОВАНИЕ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Задача А.
- 3. Сильная эллиптичность.
- 4. Пространство, порожденное задачей А.
- 5. Младшие члены.
- 6. О разрешимости и единственности решения граничных задач.
- 7. Теоремы Фредгольма.
- 8. Положительно-определенные функционалы.
- § 3. СОБСТВЕННЫЕ ФУНКЦИИ
- 2. Связь с собственными функциями вполне непрерывного симметричного оператора.
- 3. Экстремальные свойства собственных значений.
- 4. Разложение по сойственным функциям.
- 5. Тригонометрические ряды Фурье.
- 6. Критерий положительной определенности функционалов.
- § 4. ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕ
- 1. Оператор Лапласа на сферически-симметричных функциях.
- 2. Фундаментальное решение.
- 3. Интегральные формулы.
- 4. Решение уравнения Пуассона.
- 5. Объемные потенциалы.
- 6. О гладкости обобщенных решений.
- 7. Теорема о среднем значении.
- § 5. ФУНКЦИЯ ГРИНА
- § 6. ПОЛОЖИТЕЛЬНОСТЬ РЕШЕНИЙ
- 1. Об одном свойстве билинейных функционалов в пространстве BV2.
- 2. Дифференциальные неравенства.
- 3. Строгая положительность решений.
- 4. Принцип максимума.
- 5. Свойства первой собственной функции.
- 6. Ограниченность решений.
- Приложение к главе VII. РАЗРЕШИМОСТЬ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1. Уравнения в евклидовых пространствах.
- 2. Линейные алгебраические системы.
- 3. Конечномерные операторы.
- 4. Теоремы Фредгольма.
- § 8. УРАВНЕНИЯ С ВПОЛНЕ НЕПРЕРЫВНЫМ ОПЕРАТОРОМ
- Глава VIII. ПАРАБОЛИЧЕСКИЕ УРАВНЕНИЯ
- § 1. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 2. Основные пространства функций. Обобщенное решение.
- 3. Интегральная оценка. Единственность.
- 4. Положительность решений.
- § 2. РАЗРЕШИМОСТЬ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Неоднородное уравнение.
- § 3. ГРАНИЧНАЯ ЗАДАЧА ДЛЯ КВАЗИЛИНЕЙНОГО УРАВНЕНИЯ
- 2. Теорема о разрешимости.
- § 4. ЗАДАЧА КОШИ
- 2. Уравнение теплопроводности.
- 4. Квазилинейное уравнение.
- Глава IX. КВАЗИЛИНЕЙНЫЕ ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. РАЗРЕШИМОСТЬ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Установление решения параболического уравнения.
- 3. Верхняя и нижняя функции.
- 4. Теорема о разрешимости.
- § 2. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ С ПАРАМЕТРОМ
- 2. Существование критического значения. Оценка сверху.
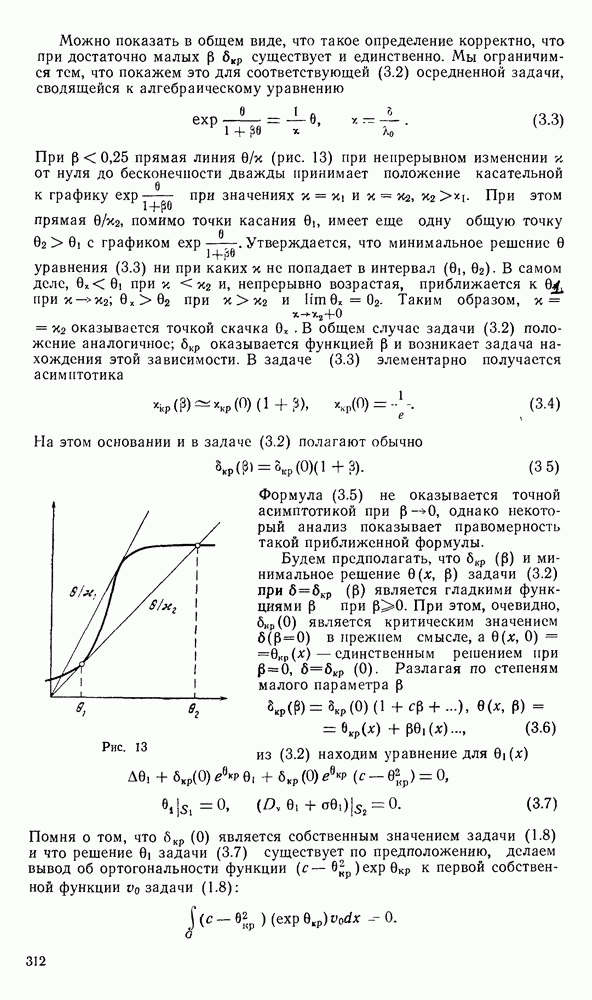
- 3. Асимптотическая формула для …
- § 3. ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Критерии устойчивости.
- 3. Некоторые следствия критериев устойчивости.
- 4. Задача с параметром.
- 5. Случай … Единственность.
- 6. Случай … Разрешимость.
- § 4. ОСРЕДНЕНИЕ УРАВНЕНИЙ
- 2. Анализ осредненного уравнения.
- РАЗДЕЛ ЧЕТВЕРТЫЙ. МАТЕМАТИЧЕСКИЕ ВОПРОСЫ ХИМИЧЕСКОЙ ФИЗИКИ
- Глава X. МАТЕМАТИЧЕСКИЕ ЗАДАЧИ МАКРОКИНЕТИКИ
- § 1. ПРОСТЕЙШАЯ МОДЕЛЬ НЕИЗОТЕРМИЧЕСКОГО ПРОТЕКАНИЯ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2. Тепловое самовоспламенение.
- 3. Зажигание.
- 4. Распространение пламени.
- § 2. МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОВОГО ВЗРЫВА
- 3. Условие воспламенения в случае ограниченного источника.
- § 3. ВЫЧИСЛЕНИЕ КРИТИЧЕСКИХ УСЛОВИЙ
- 3. Расчет предвзрывного разогрева.
- § 4. СТАЦИОНАРНАЯ ЗАДАЧА ТЕОРИИ ЗАЖИГАНИЯ
- 2. Зажигание с торца полубесконечного цилиндра.
- 3. Анализ осредненного уравнения.
- 4. Приближенная формула для …
- § 5. СФЕРИЧЕСКИ-СИММЕТРИЧНАЯ СТАЦИОНАРНАЯ ЗАДАЧА С РАСПРЕДЕЛЕННЫМИ ИСТОЧНИКАМИ
- Глава XI. КАЧЕСТВЕННЫЕ МЕТОДЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 1. СТАЦИОНАРНАЯ ЗАДАЧА О РАСПРОСТРАНЕНИИ ПЛАМЕНИ
- § 2. СФЕРИЧЕСКИ-СИММЕТРИЧНАЯ ЗАДАЧА О ТЕПЛОВОМ ВЗРЫВЕ
- § 3. КВАЗИСТАЦИОНАРНАЯ ТЕОРИЯ ТЕПЛОВОГО ВЗРЫВА
- 2. Теория Мержанова-Дубовицкого.
- 3. Метод равномерного выгорания.
- § 4. НЕИЗОТЕРМИЧЕСКОЕ ТЕЧЕНИЕ ВЯЗКОУПРУГОЙ ЖИДКОСТИ ПРИ ОДНОРОДНОМ ДЕФОРМИРОВАНИИ
- 2. Сдвиговое течение.
- 3. Растяжение.
- Глава XII. УРАВНЕНИЯ ХИМИЧЕСКОЙ КИНЕТИКИ
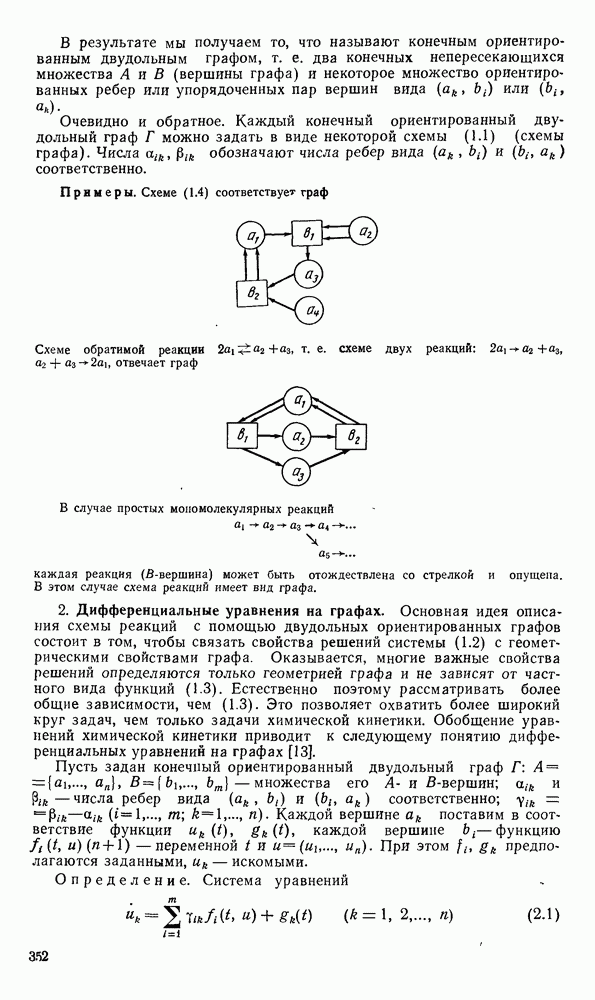
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ НА ГРАФАХ
- 2. Дифференциальные уравнения на графах.
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЙ НА ГРАФАХ
- 2. Индексация вершин графа.
- 3. Строгая положительность.
- 4. Поведение в нуле.
- 5. Априорные оценки. Нелокальная разрешимость.
- 6. Балансные неравенства в случае ациклического графа.
- § 3. ПОВЕДЕНИЕ РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ
- 2. Случай ациклического графа.
- 3. Обратимые реакции. Детальное равновесие.
- 4. Обратимые реакции. Выход на стационарный режим.
- § 4. О ПОКАЗАТЕЛЯХ ЛЯПУНОВА
- § 5. О МЕТОДЕ КВАЗИСТАЦИОНАРНЫХ КОНЦЕНТРАЦИЙ