| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5. Абсолютная непрерывность.
Определение. Мера  называется абсолютно непрерывной относительно меры
называется абсолютно непрерывной относительно меры  если для любого числа
если для любого числа  можно указать такое число
можно указать такое число  что
что

для любого множества  такого, что
такого, что

Теорема. Для того чтобы мера К была абсолютно непрерывной относительно меры  необходимо и достаточно, чтобы из равенства
необходимо и достаточно, чтобы из равенства  следовало
следовало 
Доказательство. Необходимость. Пусть  абсолютно непрерывна относительно
абсолютно непрерывна относительно  и пусть для некоторого множества
и пусть для некоторого множества  Тогда из определения абсолютной непрерывности следует, что
Тогда из определения абсолютной непрерывности следует, что  для любого
для любого  Это значит, что
Это значит, что 
Достаточность. Пусть из равенства  следует, что
следует, что  Покажем, что
Покажем, что  абсолютно непрерывна относительно
абсолютно непрерывна относительно  Предположим противное. Тогда найдется такое число
Предположим противное. Тогда найдется такое число  что для любого натурального числа
что для любого натурального числа  существует множество
существует множество  такое, что
такое, что

Обозначим:

Так как  то из (5.2) следует, что
то из (5.2) следует, что  а так как
а так как  образуют монотонно убывающую последовательность, сходящуюся к
образуют монотонно убывающую последовательность, сходящуюся к  то
то

Далее, из (5.1) и (5.3), пользуясь свойством (3.9) полной вариации, получаем

Отсюда

Неравенства (5.4) и (5.5) противоречат предположению. Это противоречие устанавливает абсолютную непрерывность меры  относительно меры
относительно меры  Теорема доказана.
Теорема доказана.
Следствие. Множество всех абсолютно непрерывных мер относительно заданной меры  образует подпространство в
образует подпространство в 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ ПЕРВЫЙ. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА И ТЕОРИИ МЕРЫ
- § 1. МНОЖЕСТВА
- 2. Действия над множествами.
- 3. Ограниченные множества.
- 4. Функции.
- § 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 1. Двумерное векторное пространство как пример линейного пространства.
- 2. Определение линейного пространства.
- 3. Примеры линейных пространств.
- 4. Действия над векторами.
- 5. Линейная комбинация векторов.
- 6. Линейная зависимость и независимость векторов.
- 7. Размерность пространства.
- 8. Подпространства.
- 9. Линейная оболочка.
- 10. Линейно-независимые последовательности.
- § 3. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- 2. Свойства скалярного произведения.
- 3. Норма вектора.
- 4. Неравенство Коши-Буняковского.
- 5. Неравенство треугольника.
- § 4. НОРМИРОВАННЫЕ ПРОСТРАНСТВА
- 2. Свойства нормы.
- 3. Сходимость.
- 4. Сходимость в пространстве Rn.
- 5. Открытые и замкнутые множества.
- 6. Подпространства нормированного пространства.
- 7. Сепарабельные пространства.
- 8. Полные пространства.
- 9. Полнота пространства Rn.
- 10. Пространство (М) ограниченных функций.
- 11. Пространство (С) ограниченных непрерывных функций.
- 12. Понятие о компактности.
- § 5. ОРТОНОРМИРОВАННЫЙ БАЗИС ЕВКЛИДОВА ПРОСТРАНСТВА
- 2. Ортогонализация последовательности векторов.
- 3. Ортонормированный базис конечномерного пространства.
- 4. Проекция вектора на подпространство.
- 5. Ряды Фурье.
- 6. Ортонормированный базис сепарабельного пространства.
- 7. Разложение по ортогональным системам.
- 8. Ортогональные дополнения.
- § 6. КОМПЛЕКСНЫЕ ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 2. Комплексные евклидовы и нормированные пространства.
- Приложение к главе I. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- § 7. МАТРИЦЫ
- 2. Действия над матрицами.
- 3. Обратимые матрицы.
- 4. Транспонирование матриц.
- § 8. ОПРЕДЕЛИТЕЛИ
- 3. Свойства определителя.
- 4. Обратные матрицы.
- § 9. РАНГ МАТРИЦЫ
- 3. Базис конечномерного пространства.
- Глава II. МЕРА И ИНТЕГРАЛ
- 1. Аддитивные функции множества.
- 2. Мера.
- 3. Полная вариация меры.
- 4. Пространство мер.
- 5. Абсолютная непрерывность.
- 6. Регулярные меры.
- 7. Мера Лебега.
- 8. Мера Хаусдорфа.
- § 2. ИЗМЕРИМЫЕ ФУНКЦИИ
- 2. Простые измеримые функции.
- 3. Измеримые функции.
- § 3. ИНТЕГРАЛ
- 1. Интегрирование простых измеримых функций.
- 2. Суммируемые функции. Интеграл.
- 3. Основные свойства интеграла.
- 4. Предельный переход под знаком интеграла.
- 5. Критерий суммируемости функций.
- 6. Интеграл Лебега.
- 7. Произведение мер. Теорема Фубини.
- § 4. Пространство Lp
- 1. Функции, суммируемые в степени р.
- 2. Пространство Lp.
- 3. Критерий компактности.
- Глава III. ОПЕРАТОРЫ И ФУНКЦИОНАЛЫ
- § 1. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 2. Примеры линейных операторов.
- 3. Ограниченные операторы.
- 4. Примеры ограниченных операторов.
- 5. Пример неограниченного оператора.
- 6. Непрерывность линейных операторов.
- 7. Действия над операторами.
- § 2. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
- 2 Примеры линейных функционалов.
- 3. Сопряженное пространство.
- 4. Линейные функционалы в гильбертовом пространстве.
- 5. Линейные функционалы в пространстве непрерывных функций.
- § 3. СОПРЯЖЕННЫЕ ОПЕРАТОРЫ
- 2. Примеры сопряженных операторов.
- 3. Свойства сопряженных операторов.
- 4. Самосопряженные операторы.
- 5. Квадратичные формы.
- § 4. КОНЕЧНОМЕРНЫЕ И ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
- 2. Вполне непрерывные операторы.
- § 5. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ
- 2. Самосопряженные операторы.
- 3. Самосопряженные вполне непрерывные операторы.
- 4. Самосопряженные операторы в конечномерных пространствах, матрицы и квадратичные формы.
- § 6. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
- 2. Метод последовательных приближений.
- 3. Операторы сжатия.
- 4. Линейные уравнения.
- РАЗДЕЛ ВТОРОЙ. АНАЛИЗ В ПРОСТРАНСТВАХ BV
- Глава IV. ДИФФЕРЕНЦИРОВАНИЕ
- § 1. ОБОБЩЕННЫЕ ПРОИЗВОДНЫЕ
- 2. Обобщенная производная как функционал.
- § 2. МНОЖЕСТВА С КОНЕЧНЫМ ПЕРИМЕТРОМ
- 2. Множества ограниченной вариации.
- 3. Алгебра множеств с конечным периметром.
- 4. Периметр множества.
- § 3. ПРОСТРАНСТВО BV
- 2. Функции ограниченной вариации.
- 3. Интегральное условие.
- 4. Полная вариация градиента.
- § 4. АППРОКСИМАТИВНЫЙ ПРЕДЕЛ ФУНКЦИИ
- 2. Аппроксимативный предел.
- 3. Основные теоремы о пределах.
- 4. Регулярные точки.
- § 5. СТРУКТУРА ФУНКЦИЙ, ПРИНАДЛЕЖАЩИХ ПРОСТРАНСТВУ BV
- 5. Структура функций, принадлежащих пространству BV.
- 6. Среднее значение.
- § 6. ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
- 2. Усредненная суперпозиция.
- 3. Дифференцирование суперпозиции.
- 4. Дифференцирование произведения.
- Глава V. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ
- § 1. ФОРМУЛА ГРИНА
- 2. След функции на границе.
- 3. Дифференцирование произведения функции на характеристическую функцию множества.
- 4. Формула Грина.
- 5. Множества класса Г.
- 6. Полный скачок.
- 7. Интегрирование по частям.
- 8. Формулы векторного анализа.
- § 2. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- 3. Аналитические функции. Теорема Коши.
- 4. Разрывные аналитические функции.
- 5. Полный скачок.
- 6. Выражение аналитической функции через скачок.
- § 3. ПРОСТРАНСТВО BV2
- 6. Полная непрерывность оператора вложения.
- 7. Регулярные точки границы.
- § 4. ЗАКОНЫ СОХРАНЕНИЯ
- 1. Дифференциальная форма законов сохранения.
- 2. Условия на разрывах.
- РАЗДЕЛ ТРЕТИЙ. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- Глава VI. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 2. Основная теорема.
- 3. Скалярное уравнение.
- 4. Априорная оценка и нелокальная разрешимость.
- § 2. ЛИНЕЙНЫЕ УРАВНЕНИЯ
- 2. Системы с постоянными коэффициентами.
- 3. Скалярное уравнение высшего порядка.
- § 3. ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Метод функций Ляпунова.
- 3. Некоторые примеры функции Ляпунова.
- 4. Метод линеаризации.
- § 4. ПОЛОЖЕНИЕ РАВНОВЕСИЯ СИСТЕМЫ ДВУХ УРАВНЕНИЙ. ПОНЯТИЕ О ПРЕДЕЛЬНОМ ЦИКЛЕ
- 2. Некоторые замечания.
- 3. Понятие о предельном цикле.
- § 5. УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХ
- 2. Теорема Тихонова.
- 3. Теорема Понтрягина-Родыгина.
- Глава VII. ЛИНЕЙНЫЕ ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ И ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Граничные задачи.
- 3. Формулы Грина.
- 4. Сопряженная задача.
- § 2. ИССЛЕДОВАНИЕ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Задача А.
- 3. Сильная эллиптичность.
- 4. Пространство, порожденное задачей А.
- 5. Младшие члены.
- 6. О разрешимости и единственности решения граничных задач.
- 7. Теоремы Фредгольма.
- 8. Положительно-определенные функционалы.
- § 3. СОБСТВЕННЫЕ ФУНКЦИИ
- 2. Связь с собственными функциями вполне непрерывного симметричного оператора.
- 3. Экстремальные свойства собственных значений.
- 4. Разложение по сойственным функциям.
- 5. Тригонометрические ряды Фурье.
- 6. Критерий положительной определенности функционалов.
- § 4. ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕ
- 1. Оператор Лапласа на сферически-симметричных функциях.
- 2. Фундаментальное решение.
- 3. Интегральные формулы.
- 4. Решение уравнения Пуассона.
- 5. Объемные потенциалы.
- 6. О гладкости обобщенных решений.
- 7. Теорема о среднем значении.
- § 5. ФУНКЦИЯ ГРИНА
- § 6. ПОЛОЖИТЕЛЬНОСТЬ РЕШЕНИЙ
- 1. Об одном свойстве билинейных функционалов в пространстве BV2.
- 2. Дифференциальные неравенства.
- 3. Строгая положительность решений.
- 4. Принцип максимума.
- 5. Свойства первой собственной функции.
- 6. Ограниченность решений.
- Приложение к главе VII. РАЗРЕШИМОСТЬ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1. Уравнения в евклидовых пространствах.
- 2. Линейные алгебраические системы.
- 3. Конечномерные операторы.
- 4. Теоремы Фредгольма.
- § 8. УРАВНЕНИЯ С ВПОЛНЕ НЕПРЕРЫВНЫМ ОПЕРАТОРОМ
- Глава VIII. ПАРАБОЛИЧЕСКИЕ УРАВНЕНИЯ
- § 1. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 2. Основные пространства функций. Обобщенное решение.
- 3. Интегральная оценка. Единственность.
- 4. Положительность решений.
- § 2. РАЗРЕШИМОСТЬ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Неоднородное уравнение.
- § 3. ГРАНИЧНАЯ ЗАДАЧА ДЛЯ КВАЗИЛИНЕЙНОГО УРАВНЕНИЯ
- 2. Теорема о разрешимости.
- § 4. ЗАДАЧА КОШИ
- 2. Уравнение теплопроводности.
- 4. Квазилинейное уравнение.
- Глава IX. КВАЗИЛИНЕЙНЫЕ ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. РАЗРЕШИМОСТЬ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Установление решения параболического уравнения.
- 3. Верхняя и нижняя функции.
- 4. Теорема о разрешимости.
- § 2. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ С ПАРАМЕТРОМ
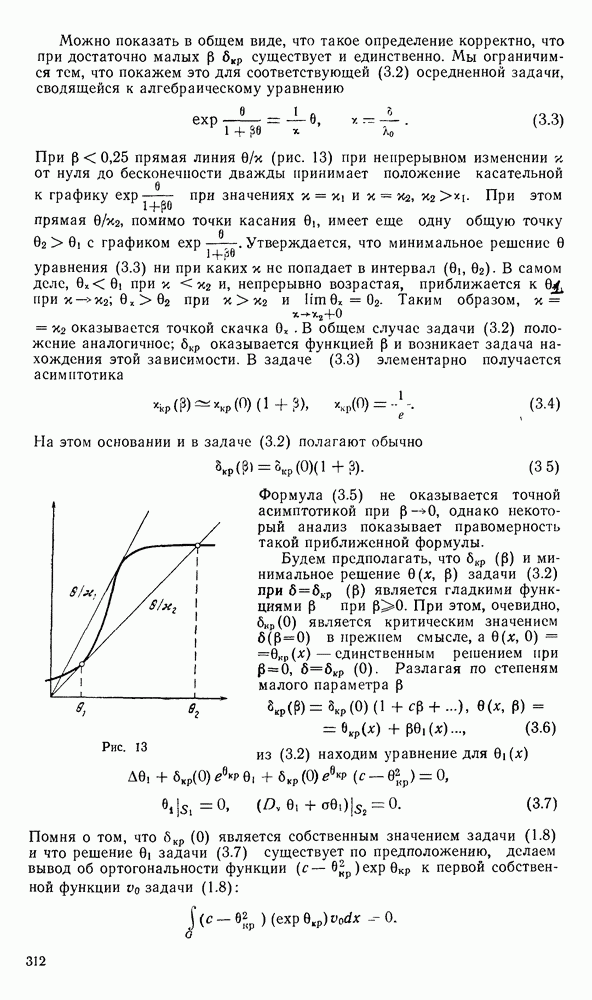
- 2. Существование критического значения. Оценка сверху.
- 3. Асимптотическая формула для …
- § 3. ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Критерии устойчивости.
- 3. Некоторые следствия критериев устойчивости.
- 4. Задача с параметром.
- 5. Случай … Единственность.
- 6. Случай … Разрешимость.
- § 4. ОСРЕДНЕНИЕ УРАВНЕНИЙ
- 2. Анализ осредненного уравнения.
- РАЗДЕЛ ЧЕТВЕРТЫЙ. МАТЕМАТИЧЕСКИЕ ВОПРОСЫ ХИМИЧЕСКОЙ ФИЗИКИ
- Глава X. МАТЕМАТИЧЕСКИЕ ЗАДАЧИ МАКРОКИНЕТИКИ
- § 1. ПРОСТЕЙШАЯ МОДЕЛЬ НЕИЗОТЕРМИЧЕСКОГО ПРОТЕКАНИЯ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2. Тепловое самовоспламенение.
- 3. Зажигание.
- 4. Распространение пламени.
- § 2. МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОВОГО ВЗРЫВА
- 3. Условие воспламенения в случае ограниченного источника.
- § 3. ВЫЧИСЛЕНИЕ КРИТИЧЕСКИХ УСЛОВИЙ
- 3. Расчет предвзрывного разогрева.
- § 4. СТАЦИОНАРНАЯ ЗАДАЧА ТЕОРИИ ЗАЖИГАНИЯ
- 2. Зажигание с торца полубесконечного цилиндра.
- 3. Анализ осредненного уравнения.
- 4. Приближенная формула для …
- § 5. СФЕРИЧЕСКИ-СИММЕТРИЧНАЯ СТАЦИОНАРНАЯ ЗАДАЧА С РАСПРЕДЕЛЕННЫМИ ИСТОЧНИКАМИ
- Глава XI. КАЧЕСТВЕННЫЕ МЕТОДЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 1. СТАЦИОНАРНАЯ ЗАДАЧА О РАСПРОСТРАНЕНИИ ПЛАМЕНИ
- § 2. СФЕРИЧЕСКИ-СИММЕТРИЧНАЯ ЗАДАЧА О ТЕПЛОВОМ ВЗРЫВЕ
- § 3. КВАЗИСТАЦИОНАРНАЯ ТЕОРИЯ ТЕПЛОВОГО ВЗРЫВА
- 2. Теория Мержанова-Дубовицкого.
- 3. Метод равномерного выгорания.
- § 4. НЕИЗОТЕРМИЧЕСКОЕ ТЕЧЕНИЕ ВЯЗКОУПРУГОЙ ЖИДКОСТИ ПРИ ОДНОРОДНОМ ДЕФОРМИРОВАНИИ
- 2. Сдвиговое течение.
- 3. Растяжение.
- Глава XII. УРАВНЕНИЯ ХИМИЧЕСКОЙ КИНЕТИКИ
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ НА ГРАФАХ
- 2. Дифференциальные уравнения на графах.
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЙ НА ГРАФАХ
- 2. Индексация вершин графа.
- 3. Строгая положительность.
- 4. Поведение в нуле.
- 5. Априорные оценки. Нелокальная разрешимость.
- 6. Балансные неравенства в случае ациклического графа.
- § 3. ПОВЕДЕНИЕ РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ
- 2. Случай ациклического графа.
- 3. Обратимые реакции. Детальное равновесие.
- 4. Обратимые реакции. Выход на стационарный режим.
- § 4. О ПОКАЗАТЕЛЯХ ЛЯПУНОВА
- § 5. О МЕТОДЕ КВАЗИСТАЦИОНАРНЫХ КОНЦЕНТРАЦИЙ