| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
РАЗДЕЛ ТРЕТИЙ. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Этот раздел содержит в основном теорию граничных (краевых) задач для эллиптических и параболических уравнений. При изложении этой теории мы последовательно придерживаемся концепции обобщенного решения, что не только позволяет ставить и решать краевые задачи при весьма слабых ограничениях на область и коэффициенты уравнений, но и существенно упрощает их исследование, избавляя от необходимости доказывать гладкость решений. Тонкие вопросы о гладкости решений на этом пути отделяются от вопросов о разрешимости и единственности и, когда это необходимо, могут быть исследованы независимо.
Новое определение обобщенного решения как функции класса  излагаемое здесь впервые, позволяет обобщать и усиливать известные результаты для этих уравнений. При этом не требуется никакой гладкости от границ рассматриваемых областей. Краевые задачи рассматриваются в областях, являющихся открытыми множествами с конечным периметром. Коэффициенты линейных уравнений, как правило, — ограниченные измеримые функции, а правые части — функции, суммируемые с квадратом. Нужно отметить, Что на практике нередко приходится иметь дело как с негладкой границей области, так и с разрывными коэффициентами, так что концепция обобщенною решения имеет не только теоретические удобства, по и вызвана потребностями прак тики
излагаемое здесь впервые, позволяет обобщать и усиливать известные результаты для этих уравнений. При этом не требуется никакой гладкости от границ рассматриваемых областей. Краевые задачи рассматриваются в областях, являющихся открытыми множествами с конечным периметром. Коэффициенты линейных уравнений, как правило, — ограниченные измеримые функции, а правые части — функции, суммируемые с квадратом. Нужно отметить, Что на практике нередко приходится иметь дело как с негладкой границей области, так и с разрывными коэффициентами, так что концепция обобщенною решения имеет не только теоретические удобства, по и вызвана потребностями прак тики
При исследовании нелинейных уравнений весьма полезными оказываются теоремы о монотонной зависимости решений от граничных условий и правых частей, которые доказываются непосредственно для обобщенных решений. Это позволяет последовательно пользоваться техни кой верхних и нижних функций и формулировать основные теоремы о разрешимости в терминах этих функций. Удобство такого подхода состоит в том, что не требуется специальных ограничений (типа ограничений роста функций), которые обычно накладываются для получения априорной оценки модуля решения. Во всех случаях подобного рода ограничений верхняя и нижняя функции легко строятся.
Несколько в стороне от основного материала этого раздела оказался материал главы VI, где излагаются некоторые вопросы теории обыкновенных дифференциальных уравнений. Хотя она представляет собой самостоятельную область математики и обычно не включается в раздел уравнений математической физики, мы сочли уместным дать в форме справочника минимум сведений из этой теории, необходимых для понимания последнего раздела книги. Эта глава не опирается на предыдущие разделы книги. Изложение в ней носит в основном конспективный характер. Особенно это относится к последним двум параграфам. В частности, изложение понятия предельного цикла и связанных с ним вопросов является чисто описательным. Применение излагаемых
понятий и методов иллюстрируется на примерах. Ряд таких примеров читатель найдет в главе XI. Многие понятия и методы находят применение в главе  при исследовании уравнений химической кинетики
при исследовании уравнений химической кинетики
Глава VII посвящепа теории граничных задач для линейных эллиптических уравнений В § 2, 3 доказаны теоремы о разрешимости (типа теорем Фредгольма) для сопряженной пары граничных задач и установлена полнота системы собственных функций. При этом используется георема о, полной непрерывности оператора вложения пространства  в пространство
в пространство  доказанная в предыдущем разделе, с помощью которой граничные задачи сводятся к эквивалентным уравнениям с вполне непрерывными операторами. Эти результаты справедливы также и для систем уравнений при выполнении определенных условий, которые легко могут быть сформулированы. Для понимания теорем о разрешимости граничных задач требуется знание теории Фредгольма для уравнений с вполне непрерывными операторами в гильбертовом пространстве. Для удобства читателя эта теория включена в виде приложения к главе VII.
доказанная в предыдущем разделе, с помощью которой граничные задачи сводятся к эквивалентным уравнениям с вполне непрерывными операторами. Эти результаты справедливы также и для систем уравнений при выполнении определенных условий, которые легко могут быть сформулированы. Для понимания теорем о разрешимости граничных задач требуется знание теории Фредгольма для уравнений с вполне непрерывными операторами в гильбертовом пространстве. Для удобства читателя эта теория включена в виде приложения к главе VII.
В § 4 с помощью фундаментального решения для уравнения Лапласа получено потенциальное представление функций из  в том числе разрывных, выражающее эти функции через их первые обобщенные производные. Показано, что на множестве точек скачка рассматриваемой функции это представление имеет вид потенциала двойного слоя. В остальной части этого параграфа излагаются известные методы доказательства гладкости обобщенных решений с помощью фундаментального решения В этом месте рассмотрения ведутся строго внутри области, и аппарат анализа в классах
в том числе разрывных, выражающее эти функции через их первые обобщенные производные. Показано, что на множестве точек скачка рассматриваемой функции это представление имеет вид потенциала двойного слоя. В остальной части этого параграфа излагаются известные методы доказательства гладкости обобщенных решений с помощью фундаментального решения В этом месте рассмотрения ведутся строго внутри области, и аппарат анализа в классах  не используется. Он применяется по существу в следующем параграфе (§ 5) при изучении функции Грина граничной задачи и выражении решения через нее, так как здесь приходится учитывать влияние границы и граничных условий.
не используется. Он применяется по существу в следующем параграфе (§ 5) при изучении функции Грина граничной задачи и выражении решения через нее, так как здесь приходится учитывать влияние границы и граничных условий.
Важным свойством решений эллиптических граничных задач является свойство положительности решения при положительных правых частях. Из него следуют, в частности, оценки решений в равномерных нормах. В § 6 доказана положительность обобщенных решений, принадлежащих пространству  без каких бы то ни было дополнительных условий гладкости решений, а также строгая положительность первой собственной функции. Эти результаты дают возможность в дальнейшем (глава IX) проводить исследование граничных задач для квазилинейных эллиптических уравнений, систематически используя аппарат верхних и нижних функций непосредственно для обобщенных решений, не заботясь об их гладкости.
без каких бы то ни было дополнительных условий гладкости решений, а также строгая положительность первой собственной функции. Эти результаты дают возможность в дальнейшем (глава IX) проводить исследование граничных задач для квазилинейных эллиптических уравнений, систематически используя аппарат верхних и нижних функций непосредственно для обобщенных решений, не заботясь об их гладкости.
Теория параболических уравнений (глава VIII) излагается для уравнений дивергентного вида. Это непринципиальное ограничение вызвано применяемым методом построения решений. Не желая дальнейшего увеличения объема книги, мы ограничиваемся построением решений с помощью разложения но собственным функциям (метод Фурье) и принципа сжатых отображений, изложенных в предыдущих главах.
В § 1 вводятся понятие обобщенного решения краевой задачи для линейного уравнения и необходимые для этого функциональные пространства. Доказаны интегральная априорная оценка решения и теорема единственности. Кроме того, доказана важная при исследовании нелинейных уравнений теорема о положительности решения.
Изложению метода Фурье посвящен § 2.
В § 3 вводится понятие верхней и нижней функций краевой задачи для квазилинейного уравнения и доказывается теорема о разрешимости задачи при наличии верхней и нижней функций. Требование о наличии таких функций менее ограничительно, чем различные условия (см. 130, 37]), служащие для оценки модуля решения Следует отметить, что
локальная разрешимость различных задач для параболических уравнений [54, 61] имеет безусловный характер, т. е. не требует каких бы то ни было дополнительных ограничений.
В § 4 рассматривается задача Коши для простейшего вида линейных и квазилинейных параболических уравнений.
Решение краевой задачи для квазилинейного эллиптического уравнения (глава IX) мы рассматриваем как установившееся решение соответствующего параболического уравнения и строим его как предел при  решения подходящей краевой задачи для параболического уравнения. Основная теорема о разрешимости (§ 1) состоит в том, что при. наличии верхней и нижней функций, связанных естественным неравенством
решения подходящей краевой задачи для параболического уравнения. Основная теорема о разрешимости (§ 1) состоит в том, что при. наличии верхней и нижней функций, связанных естественным неравенством  задача разрешима и существует хотя бы одно решение, лежащее между нижней и верхней функциями. При этом выше нижней функции всегда оказывается наименьшее решение, а ниже верхней функции — наибольшее. Единственность решения, вообще говоря, не имеет места.
задача разрешима и существует хотя бы одно решение, лежащее между нижней и верхней функциями. При этом выше нижней функции всегда оказывается наименьшее решение, а ниже верхней функции — наибольшее. Единственность решения, вообще говоря, не имеет места.
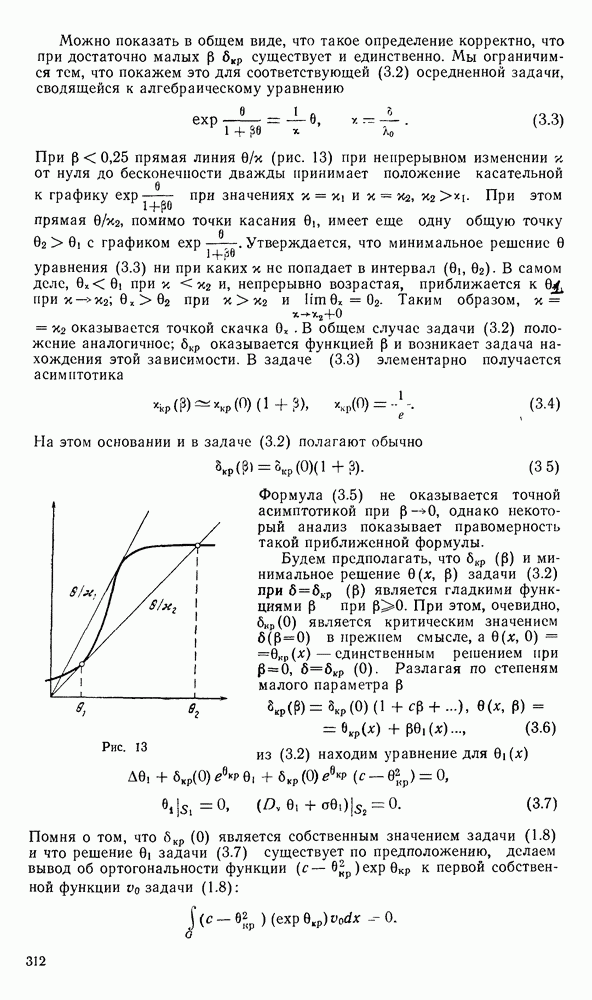
На основе этой теоремы в § 2 строится теория критического значения (аналог собственного значения в линейном случае). Получены условия существования и важные количественные оценки для критического значения. Эти результаты находят приложения, например, в теории теплового взрыва (глава X).
В § 3 рассматриваются вопросы устойчивости решения. Понятие устойчивости, используемое при этом, является естественным обобщением понятия асимптотической устойчивости стационарной точки обыкновенного дифференциального уравнения Вводится понятие отделимости решения, которое оказывается эквивалентным понятию устойчивости и является удобным критерием устойчивости Получены простые достаточные условия устойчивости и единственности устойчивого решения.
В § 4 обосновывается некоторый метод приближенного решения нелинейных эллиптических и параболических уравнений — метод весового осреднения, который находит многочисленные приложения в задачах макрокинетики. Некоторые из них приведены в главе 
Глава IX написана в основном по материалам работ [55, 56, 58]. Однако изложение с точки зрения обобщенных решений и примененный при этом новый подход к понятию обобщенного решения позволили существенно упростить изложение и расширить класс рассматриваемых областей и граничных условий. Хотя изложение ведется для уравнений с линейной и дивергентной главной частью, однако многие результаты переносятся на широкий класс квазилинейных эллиптических уравнений (ср. [55]). По поводу других результатов и методов теории эллиптических и параболических уравнений, а также имеющейся обширной литературы авторы отсылают читателя к фундаментальным работам [1, 21, 30, 31,37,49,61].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- РАЗДЕЛ ПЕРВЫЙ. ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА И ТЕОРИИ МЕРЫ
- § 1. МНОЖЕСТВА
- 2. Действия над множествами.
- 3. Ограниченные множества.
- 4. Функции.
- § 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 1. Двумерное векторное пространство как пример линейного пространства.
- 2. Определение линейного пространства.
- 3. Примеры линейных пространств.
- 4. Действия над векторами.
- 5. Линейная комбинация векторов.
- 6. Линейная зависимость и независимость векторов.
- 7. Размерность пространства.
- 8. Подпространства.
- 9. Линейная оболочка.
- 10. Линейно-независимые последовательности.
- § 3. ЕВКЛИДОВЫ ПРОСТРАНСТВА
- 2. Свойства скалярного произведения.
- 3. Норма вектора.
- 4. Неравенство Коши-Буняковского.
- 5. Неравенство треугольника.
- § 4. НОРМИРОВАННЫЕ ПРОСТРАНСТВА
- 2. Свойства нормы.
- 3. Сходимость.
- 4. Сходимость в пространстве Rn.
- 5. Открытые и замкнутые множества.
- 6. Подпространства нормированного пространства.
- 7. Сепарабельные пространства.
- 8. Полные пространства.
- 9. Полнота пространства Rn.
- 10. Пространство (М) ограниченных функций.
- 11. Пространство (С) ограниченных непрерывных функций.
- 12. Понятие о компактности.
- § 5. ОРТОНОРМИРОВАННЫЙ БАЗИС ЕВКЛИДОВА ПРОСТРАНСТВА
- 2. Ортогонализация последовательности векторов.
- 3. Ортонормированный базис конечномерного пространства.
- 4. Проекция вектора на подпространство.
- 5. Ряды Фурье.
- 6. Ортонормированный базис сепарабельного пространства.
- 7. Разложение по ортогональным системам.
- 8. Ортогональные дополнения.
- § 6. КОМПЛЕКСНЫЕ ЛИНЕЙНЫЕ ПРОСТРАНСТВА
- 2. Комплексные евклидовы и нормированные пространства.
- Приложение к главе I. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- § 7. МАТРИЦЫ
- 2. Действия над матрицами.
- 3. Обратимые матрицы.
- 4. Транспонирование матриц.
- § 8. ОПРЕДЕЛИТЕЛИ
- 3. Свойства определителя.
- 4. Обратные матрицы.
- § 9. РАНГ МАТРИЦЫ
- 3. Базис конечномерного пространства.
- Глава II. МЕРА И ИНТЕГРАЛ
- 1. Аддитивные функции множества.
- 2. Мера.
- 3. Полная вариация меры.
- 4. Пространство мер.
- 5. Абсолютная непрерывность.
- 6. Регулярные меры.
- 7. Мера Лебега.
- 8. Мера Хаусдорфа.
- § 2. ИЗМЕРИМЫЕ ФУНКЦИИ
- 2. Простые измеримые функции.
- 3. Измеримые функции.
- § 3. ИНТЕГРАЛ
- 1. Интегрирование простых измеримых функций.
- 2. Суммируемые функции. Интеграл.
- 3. Основные свойства интеграла.
- 4. Предельный переход под знаком интеграла.
- 5. Критерий суммируемости функций.
- 6. Интеграл Лебега.
- 7. Произведение мер. Теорема Фубини.
- § 4. Пространство Lp
- 1. Функции, суммируемые в степени р.
- 2. Пространство Lp.
- 3. Критерий компактности.
- Глава III. ОПЕРАТОРЫ И ФУНКЦИОНАЛЫ
- § 1. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
- 2. Примеры линейных операторов.
- 3. Ограниченные операторы.
- 4. Примеры ограниченных операторов.
- 5. Пример неограниченного оператора.
- 6. Непрерывность линейных операторов.
- 7. Действия над операторами.
- § 2. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
- 2 Примеры линейных функционалов.
- 3. Сопряженное пространство.
- 4. Линейные функционалы в гильбертовом пространстве.
- 5. Линейные функционалы в пространстве непрерывных функций.
- § 3. СОПРЯЖЕННЫЕ ОПЕРАТОРЫ
- 2. Примеры сопряженных операторов.
- 3. Свойства сопряженных операторов.
- 4. Самосопряженные операторы.
- 5. Квадратичные формы.
- § 4. КОНЕЧНОМЕРНЫЕ И ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
- 2. Вполне непрерывные операторы.
- § 5. СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ
- 2. Самосопряженные операторы.
- 3. Самосопряженные вполне непрерывные операторы.
- 4. Самосопряженные операторы в конечномерных пространствах, матрицы и квадратичные формы.
- § 6. МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ
- 2. Метод последовательных приближений.
- 3. Операторы сжатия.
- 4. Линейные уравнения.
- РАЗДЕЛ ВТОРОЙ. АНАЛИЗ В ПРОСТРАНСТВАХ BV
- Глава IV. ДИФФЕРЕНЦИРОВАНИЕ
- § 1. ОБОБЩЕННЫЕ ПРОИЗВОДНЫЕ
- 2. Обобщенная производная как функционал.
- § 2. МНОЖЕСТВА С КОНЕЧНЫМ ПЕРИМЕТРОМ
- 2. Множества ограниченной вариации.
- 3. Алгебра множеств с конечным периметром.
- 4. Периметр множества.
- § 3. ПРОСТРАНСТВО BV
- 2. Функции ограниченной вариации.
- 3. Интегральное условие.
- 4. Полная вариация градиента.
- § 4. АППРОКСИМАТИВНЫЙ ПРЕДЕЛ ФУНКЦИИ
- 2. Аппроксимативный предел.
- 3. Основные теоремы о пределах.
- 4. Регулярные точки.
- § 5. СТРУКТУРА ФУНКЦИЙ, ПРИНАДЛЕЖАЩИХ ПРОСТРАНСТВУ BV
- 5. Структура функций, принадлежащих пространству BV.
- 6. Среднее значение.
- § 6. ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ
- 2. Усредненная суперпозиция.
- 3. Дифференцирование суперпозиции.
- 4. Дифференцирование произведения.
- Глава V. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ
- § 1. ФОРМУЛА ГРИНА
- 2. След функции на границе.
- 3. Дифференцирование произведения функции на характеристическую функцию множества.
- 4. Формула Грина.
- 5. Множества класса Г.
- 6. Полный скачок.
- 7. Интегрирование по частям.
- 8. Формулы векторного анализа.
- § 2. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- 3. Аналитические функции. Теорема Коши.
- 4. Разрывные аналитические функции.
- 5. Полный скачок.
- 6. Выражение аналитической функции через скачок.
- § 3. ПРОСТРАНСТВО BV2
- 6. Полная непрерывность оператора вложения.
- 7. Регулярные точки границы.
- § 4. ЗАКОНЫ СОХРАНЕНИЯ
- 1. Дифференциальная форма законов сохранения.
- 2. Условия на разрывах.
- РАЗДЕЛ ТРЕТИЙ. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
- Глава VI. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- 2. Основная теорема.
- 3. Скалярное уравнение.
- 4. Априорная оценка и нелокальная разрешимость.
- § 2. ЛИНЕЙНЫЕ УРАВНЕНИЯ
- 2. Системы с постоянными коэффициентами.
- 3. Скалярное уравнение высшего порядка.
- § 3. ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Метод функций Ляпунова.
- 3. Некоторые примеры функции Ляпунова.
- 4. Метод линеаризации.
- § 4. ПОЛОЖЕНИЕ РАВНОВЕСИЯ СИСТЕМЫ ДВУХ УРАВНЕНИЙ. ПОНЯТИЕ О ПРЕДЕЛЬНОМ ЦИКЛЕ
- 2. Некоторые замечания.
- 3. Понятие о предельном цикле.
- § 5. УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХ
- 2. Теорема Тихонова.
- 3. Теорема Понтрягина-Родыгина.
- Глава VII. ЛИНЕЙНЫЕ ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ И ГРАНИЧНЫЕ ЗАДАЧИ
- 2. Граничные задачи.
- 3. Формулы Грина.
- 4. Сопряженная задача.
- § 2. ИССЛЕДОВАНИЕ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Задача А.
- 3. Сильная эллиптичность.
- 4. Пространство, порожденное задачей А.
- 5. Младшие члены.
- 6. О разрешимости и единственности решения граничных задач.
- 7. Теоремы Фредгольма.
- 8. Положительно-определенные функционалы.
- § 3. СОБСТВЕННЫЕ ФУНКЦИИ
- 2. Связь с собственными функциями вполне непрерывного симметричного оператора.
- 3. Экстремальные свойства собственных значений.
- 4. Разложение по сойственным функциям.
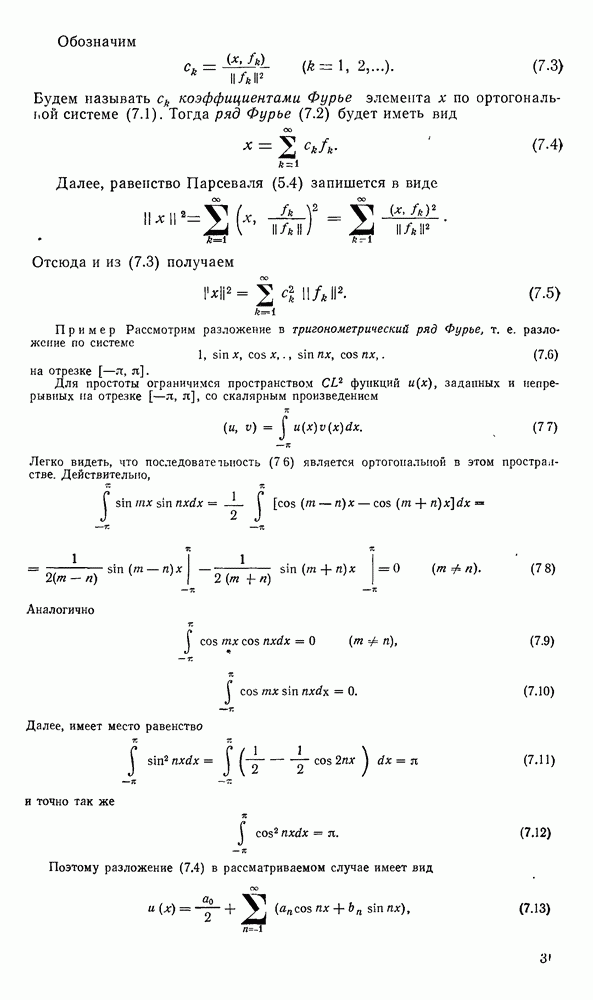
- 5. Тригонометрические ряды Фурье.
- 6. Критерий положительной определенности функционалов.
- § 4. ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕ
- 1. Оператор Лапласа на сферически-симметричных функциях.
- 2. Фундаментальное решение.
- 3. Интегральные формулы.
- 4. Решение уравнения Пуассона.
- 5. Объемные потенциалы.
- 6. О гладкости обобщенных решений.
- 7. Теорема о среднем значении.
- § 5. ФУНКЦИЯ ГРИНА
- § 6. ПОЛОЖИТЕЛЬНОСТЬ РЕШЕНИЙ
- 1. Об одном свойстве билинейных функционалов в пространстве BV2.
- 2. Дифференциальные неравенства.
- 3. Строгая положительность решений.
- 4. Принцип максимума.
- 5. Свойства первой собственной функции.
- 6. Ограниченность решений.
- Приложение к главе VII. РАЗРЕШИМОСТЬ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 1. Уравнения в евклидовых пространствах.
- 2. Линейные алгебраические системы.
- 3. Конечномерные операторы.
- 4. Теоремы Фредгольма.
- § 8. УРАВНЕНИЯ С ВПОЛНЕ НЕПРЕРЫВНЫМ ОПЕРАТОРОМ
- Глава VIII. ПАРАБОЛИЧЕСКИЕ УРАВНЕНИЯ
- § 1. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ ЛИНЕЙНЫХ УРАВНЕНИЙ
- 2. Основные пространства функций. Обобщенное решение.
- 3. Интегральная оценка. Единственность.
- 4. Положительность решений.
- § 2. РАЗРЕШИМОСТЬ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Неоднородное уравнение.
- § 3. ГРАНИЧНАЯ ЗАДАЧА ДЛЯ КВАЗИЛИНЕЙНОГО УРАВНЕНИЯ
- 2. Теорема о разрешимости.
- § 4. ЗАДАЧА КОШИ
- 2. Уравнение теплопроводности.
- 4. Квазилинейное уравнение.
- Глава IX. КВАЗИЛИНЕЙНЫЕ ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ
- § 1. РАЗРЕШИМОСТЬ ГРАНИЧНОЙ ЗАДАЧИ
- 2. Установление решения параболического уравнения.
- 3. Верхняя и нижняя функции.
- 4. Теорема о разрешимости.
- § 2. ЭЛЛИПТИЧЕСКИЕ УРАВНЕНИЯ С ПАРАМЕТРОМ
- 2. Существование критического значения. Оценка сверху.
- 3. Асимптотическая формула для …
- § 3. ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Критерии устойчивости.
- 3. Некоторые следствия критериев устойчивости.
- 4. Задача с параметром.
- 5. Случай … Единственность.
- 6. Случай … Разрешимость.
- § 4. ОСРЕДНЕНИЕ УРАВНЕНИЙ
- 2. Анализ осредненного уравнения.
- РАЗДЕЛ ЧЕТВЕРТЫЙ. МАТЕМАТИЧЕСКИЕ ВОПРОСЫ ХИМИЧЕСКОЙ ФИЗИКИ
- Глава X. МАТЕМАТИЧЕСКИЕ ЗАДАЧИ МАКРОКИНЕТИКИ
- § 1. ПРОСТЕЙШАЯ МОДЕЛЬ НЕИЗОТЕРМИЧЕСКОГО ПРОТЕКАНИЯ ХИМИЧЕСКОЙ РЕАКЦИИ
- 2. Тепловое самовоспламенение.
- 3. Зажигание.
- 4. Распространение пламени.
- § 2. МАТЕМАТИЧЕСКАЯ ТЕОРИЯ ТЕПЛОВОГО ВЗРЫВА
- 3. Условие воспламенения в случае ограниченного источника.
- § 3. ВЫЧИСЛЕНИЕ КРИТИЧЕСКИХ УСЛОВИЙ
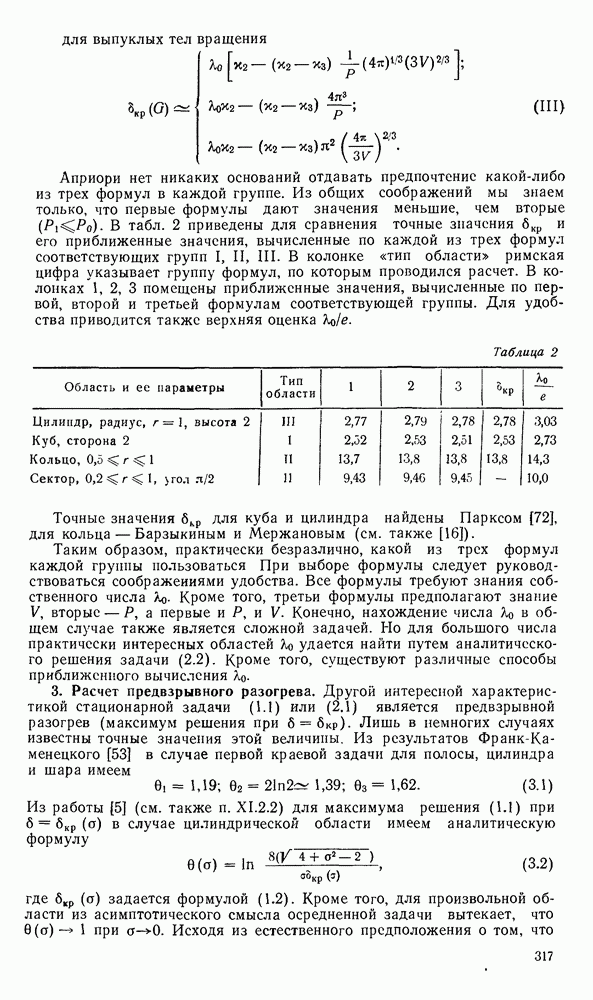
- 3. Расчет предвзрывного разогрева.
- § 4. СТАЦИОНАРНАЯ ЗАДАЧА ТЕОРИИ ЗАЖИГАНИЯ
- 2. Зажигание с торца полубесконечного цилиндра.
- 3. Анализ осредненного уравнения.
- 4. Приближенная формула для …
- § 5. СФЕРИЧЕСКИ-СИММЕТРИЧНАЯ СТАЦИОНАРНАЯ ЗАДАЧА С РАСПРЕДЕЛЕННЫМИ ИСТОЧНИКАМИ
- Глава XI. КАЧЕСТВЕННЫЕ МЕТОДЫ ТЕОРИИ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 1. СТАЦИОНАРНАЯ ЗАДАЧА О РАСПРОСТРАНЕНИИ ПЛАМЕНИ
- § 2. СФЕРИЧЕСКИ-СИММЕТРИЧНАЯ ЗАДАЧА О ТЕПЛОВОМ ВЗРЫВЕ
- § 3. КВАЗИСТАЦИОНАРНАЯ ТЕОРИЯ ТЕПЛОВОГО ВЗРЫВА
- 2. Теория Мержанова-Дубовицкого.
- 3. Метод равномерного выгорания.
- § 4. НЕИЗОТЕРМИЧЕСКОЕ ТЕЧЕНИЕ ВЯЗКОУПРУГОЙ ЖИДКОСТИ ПРИ ОДНОРОДНОМ ДЕФОРМИРОВАНИИ
- 2. Сдвиговое течение.
- 3. Растяжение.
- Глава XII. УРАВНЕНИЯ ХИМИЧЕСКОЙ КИНЕТИКИ
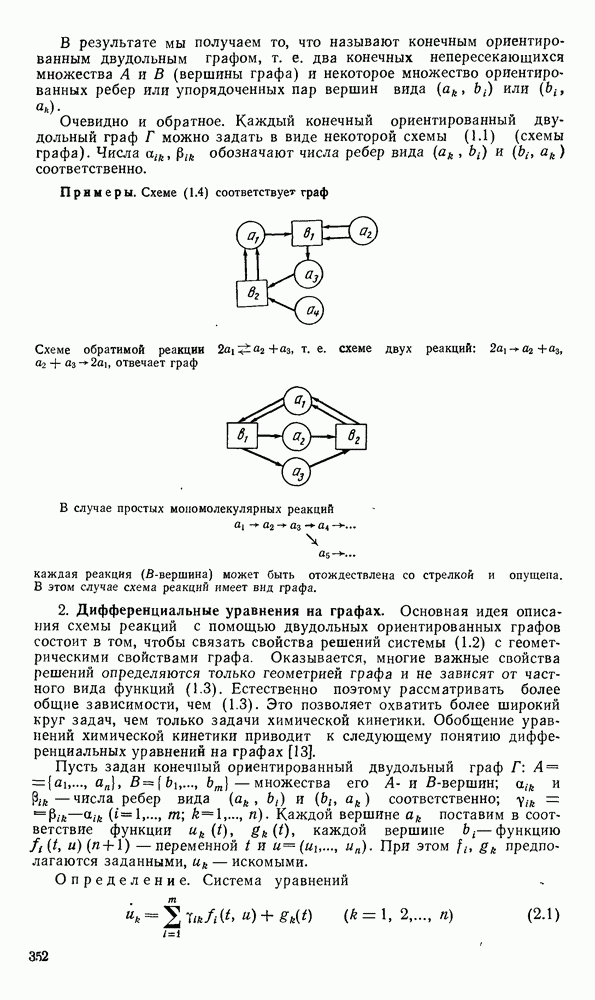
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ НА ГРАФАХ
- 2. Дифференциальные уравнения на графах.
- § 2. СВОЙСТВА РЕШЕНИЙ УРАВНЕНИЙ НА ГРАФАХ
- 2. Индексация вершин графа.
- 3. Строгая положительность.
- 4. Поведение в нуле.
- 5. Априорные оценки. Нелокальная разрешимость.
- 6. Балансные неравенства в случае ациклического графа.
- § 3. ПОВЕДЕНИЕ РЕШЕНИЙ ПРИ БОЛЬШИХ ВРЕМЕНАХ
- 2. Случай ациклического графа.
- 3. Обратимые реакции. Детальное равновесие.
- 4. Обратимые реакции. Выход на стационарный режим.
- § 4. О ПОКАЗАТЕЛЯХ ЛЯПУНОВА
- § 5. О МЕТОДЕ КВАЗИСТАЦИОНАРНЫХ КОНЦЕНТРАЦИЙ