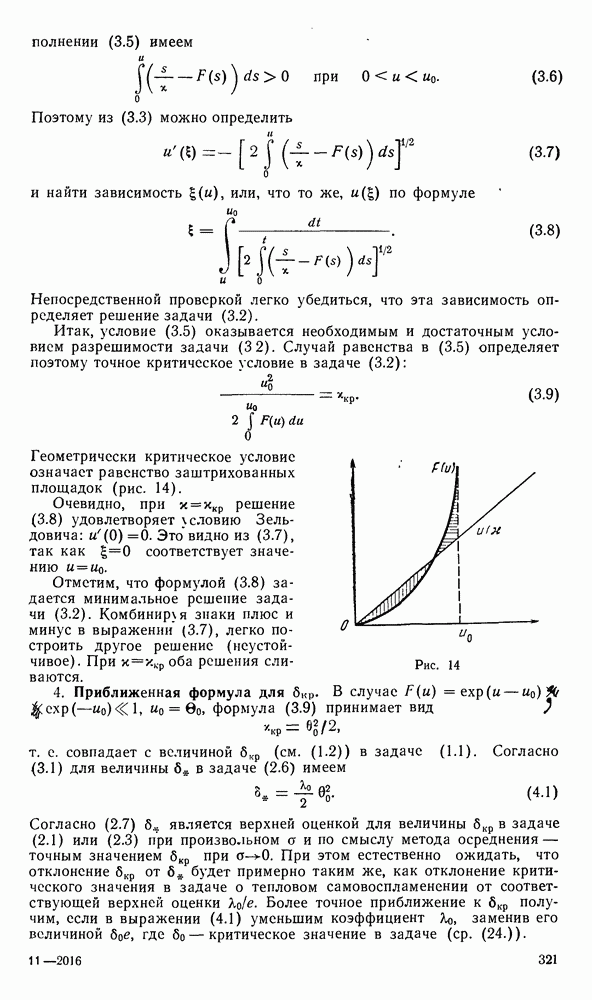
§ 2. СФЕРИЧЕСКИ-СИММЕТРИЧНАЯ ЗАДАЧА О ТЕПЛОВОМ ВЗРЫВЕ

1. Введение параметра ...

Настоящий параграф посвящен качественному исследованию сферически-симметричной задачи (ср.

Выражение

представляет собой радиальную часть оператора Лапласа в пространстве размерности Случаи относятся соответственно к плоскопараллельной полосе, цилиндру и шару. Общетеоретический интерес представляет рассмотрение задачи (1.1) при произвольном (даже нецелом) Кроме того, в § 5 предыдущей главы мы видели, что многие задачи с распределенными источниками сводятся к задаче (1.1) с произвольным, вообще говоря, нецелым Удобно поэтому считать непрерывно меняющимся параметром.

Во многих отношениях оказывается более удобным задаваться не величиной а величиной и находить как функцию Такой подход позволяет легко свести исследование третьей краевой задачи к случаю первой краевой задачи т. е. избавиться от одного параметра а. Совершенно очевидно, что решение задачи (1.1), удовлетворяющее условию имеет вид

где оказываются решением задачи

которая уже не содержит параметра Конечно, по двум условиям (1.3) нельзя однозначно найти и 9, и Здесь имеется ввиду еще одно дополнительное условие. Обычно накладываемое условие симметрии

в соответствии с теорией обобщенного решения естественно заменить более слабым (при —1) условием

При этом интересно выяснить, вытекает ли из (1.5) условие (1.4).

Перейдем в задаче (1.3) к новым переменным:

Уравнение (1.3) дает тождество

Дифференцируя это тождество по и, имеем

Из (1.4), (1.6) — (1.7) следует, что при имеем Кроме того,

С учетом этого нахождение функции сводится к решению задачи

Граничные условия при дают согласно (1.6), (1.7)

Таким образом, искомая связь между определяется формулой

где определяется из задачи (1.10). Так как задача (1.10) не содержит параметров и и связь между определяется тем же самым уравнением

Это соотношение было получено впервые Энигом [64]. Из него следует, что достигает своего максимального значения при так что оказывается критическим значением параметра выше которого решение задачи (1.3) уже невозможно ни при каком Несколько иначе обстоит дело в задаче (1.1). В этом случае согласно формулам (1.2) и (1.11)

и этот максимум достигается, вообще говоря, при Из (1.12) вытекает любопытный результат: независимо от если решение задачи (1.1) при существует.

2. Случай ...

Все уравнения элементарно интегрируются при отвечающем случаю бесконечного круглого цилиндра. Из (1 10) имеем

Последнее соотношение (1.6) с учетом и при дает

Непосредственно из (1.7) или интегрируя соотношение

получаем решение задачи (1.3):

Эти формулы определяют ограниченное вещественное решение задачи (1.3) в интервале Исключая параметр мы получаем решение первой краевой задачи единственное при и два решения, отвечающие двум корням

при Подставив в выражение эти корни, получим

При

Из формул (1.2) и (2.1) мы получаем параметрическое представление решения задачи (11) при произвольном а:

Легко вычислить по формуле (1.13). Максимум достигается при

Подставляя это значение в выражение для имеем

Эта формула впервые получена Барзыкиным и Мержановым [5]. Очевидно, при монотонно возрастает и

3. Исследование особых точек.

В общем случае при уравнение (1.10) имеет две особые точки:

1) ; 2) , причем ввиду того, что является решением, входящим в точку эта точка может быть либо «седлом», либо «узлом». Из вида матрицы коэффициентов при линейных членах числителя и знаменателя

легко заключить, что точка является «седлом» при «узлом» при Решение является одной из сепаратрис этой точки. Наклон другой, ненулевой сепаратрисы задается равенством

Интегральная кривая, а также особая точка уравнения (1.10) определяет, вообще говоря, решение задачи (1.3). Так, особой точке отвечает согласно (1.6), (1.7) решение при Из (1.6), (1.7) при находим решение

отвечающее особой точке и Сепаратрисе отвечает

функция (3.2) является неограниченным решением (1.3) при при произвольном значении Условие (1.4) для нее не имеет леста. Однако, как легко видеть, при имеет место (1.5). Так что 13 (1.5) не следует (1.4), и задача (1.3) может иметь неограниченное при решение.

Функция (3.3) не удовлетворяет условию (1.5) ни при каком если Можно показать, что условию (1.5) не удовлетворяют и решения задачи (1.3), отвечающие интегральным кривым уравнения (1.10) при («узел»), касающимся при одной из сепаратрис. При пучок решений (1.10) касается сепаратрисы Соответствующие решения (1.3) имеют при тот же характер, что и функция (3.3). При переходе через значение (вырожденный узел») сепаратрисы меняются ролями: касательной к пучку решений становится сепаратриса с наклоном (3.1).

Таким образом, при задача (1.3), (1.5) вообще не имеет оешения, кроме тривиального случая При стается исследовать только ненулевую сепаратрису с наклоном 3.1).

Отметим прежде всего, что при эта сепаратриса неограниченно продолжается в область причем при Это легко следует из уравнения 1.10). Поведение при определяется характером особой точке Впрочем, при эта точка попадает в область и не влияет на ход сепаратрисы, поскольку отделяется от ее другой сепаратрисой При как нетрудно видеть, эпаратриса также неограниченно продолжается в область походит через максимум в точке затем убывает, приближаясь к сепаратрисе со стороны области

При точка лежит в области и существенно лияет на поведение сепаратрисы. Линеаризуя числитель и знаменатель правой части (1.10) в окрестности получим

Матрица коэффициентов

имеет собственные значения

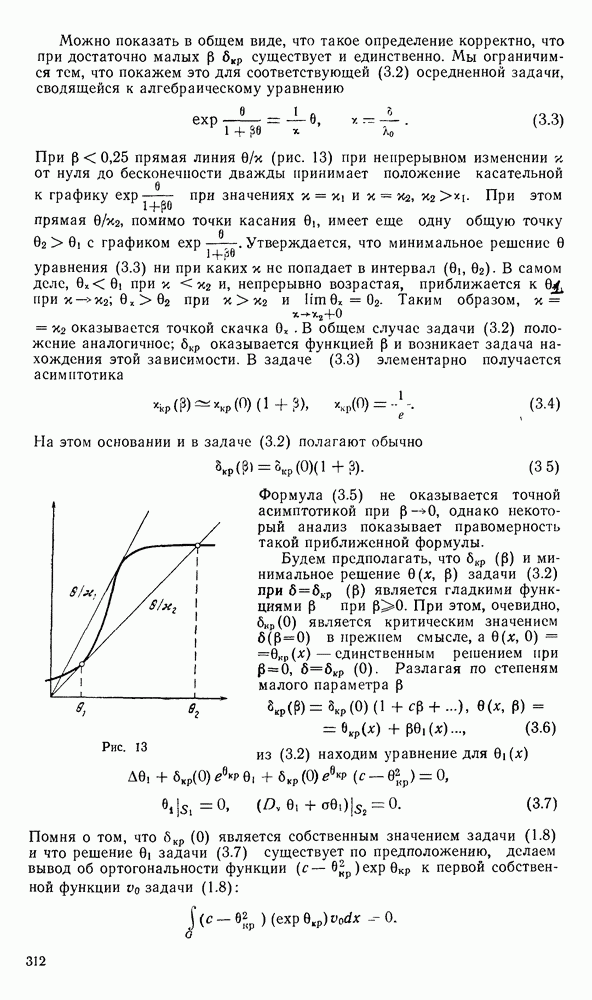
Рис. 16

Таким образом, при мы имеем «фокус», а при — «узел» в точке При сепаратриса монотонно возрастает в интервале оставаясь выше прямой линии бесконечных наклонов при достигает максимума и, как и все интегральные кривые, закручивается спиралью вокруг точки совершая бесконечное число витков. При этом

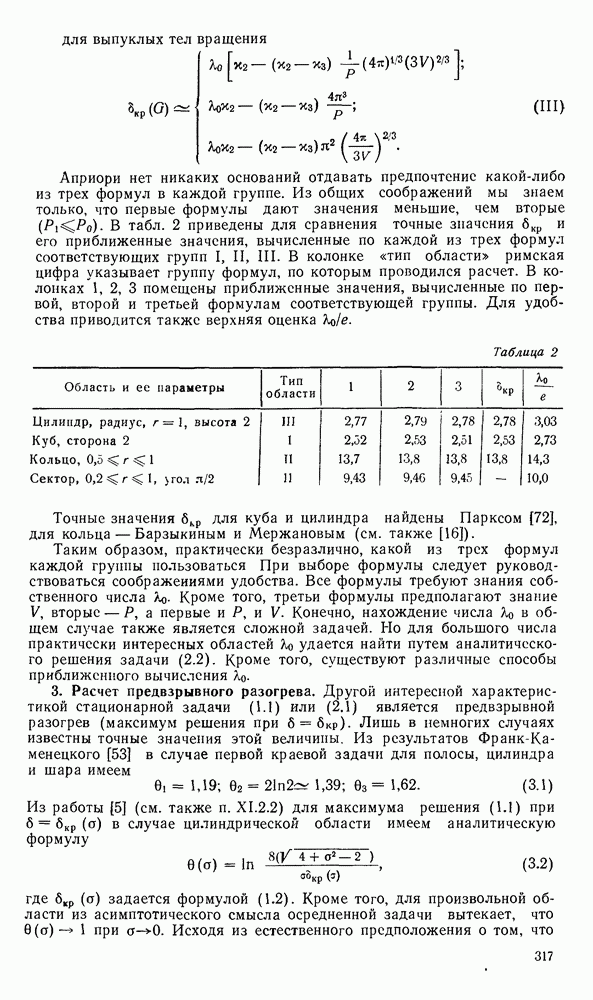
вся траектория лежит выше разделяющей линии На рис. 16 кривая 1 схематически изображает ход сепаратрисы при Пунктирные линии изображают линию нулевых наклонов и линию бесконечных наклонов В этом случае кривая определена лишь в ограниченной области изменения и является многозначной функцией и в некоторой окрестности точки

В случае «узла» в точке существуют сепаратрисы, наклоны которых

согласно (3.4) находятся из квадратного уравнения

Оба наклона, как видим, положительны, В плоскости рассмотрим прямую линию

проходящую через особую точку и имеющую наклон Очевидно, Покажем, что для исследуемой сепаратрисы в интервале имеют место неравенства

Первое неравенство очевидно. При любом сепаратриса проходит в интервале выше линии бесконечных наклонов Второе из неравенств (3.9) ввиду имеет место по крайней мере в некотором интервале Оценим поле наклонов уравнения (1.10) вдоль прямой

Здесь использовано условие и свойства корней уравнения Таким образом, вдоль прямой (3.8)

т. е. интегральные кривые уравнения (1.10) при возрастании и могут пересекать прямую (3.8) лишь со стороны области А так как при малых и имеем то это неравенство имеет место во всем интервале Неравенства (3.9) установлены.

Из (3.9) следует важный вывод о том, что сепаратриса монотонно возрастая в интервале входит в особую точку и дальше не продолжается. При этом, очевидно, как и все интегральные кривые, касается при прямой т. е.

а рис. 16 ход кривой схематически изображен кривой 2.

4. Некоторые выводы.

Можно показать, что каждой точке лежащей на траектории, описываемой сепаратрисой в плоскости ( однозначно соответствует решение задачи (1.3), (1.5). В том случае, когда является однозначной функцией это решение легко построить с учетом (1.7) и интегрированием соотношений (1.6). Полагая при имеем

Эти формулы дают параметрическое представление решения задачи (1.3), (1.5). Они остаются в силе и для точек лежащих на однозначной ветви кривой проходящей через точку В частности, критическое значение есть всегда имеется в виду указанная однозначная ветвь), а число решений задачи (1.3), (1.5) при фиксированном есть число корней уравнения

Из анализа поведения можно сделать следующие выводы:

При существует единственный корень уравнения (4.2), а следовательно, единственное решение задачи (1.3), (1.5). При существуют два решения задачи (1.3), (1.5), отвечающие двум корням уравнения (4.2). При эти решения сливаются и задача (1.3), (15) имеет единственное решение. Любое решение может быть построено по формулам (4.1).

Существует такое что при каждом уравнений (4.2), а значит и задача (1.3), (1.5), имеет единственное решение. Для любого натурального числа можно указать такое из интервала что при нем уравнение (4.2) и задача (1.3), (1.5) имеют ровно решений. При число решений бесконечно. При существует единственное решение задачи (1.3), (1.5).

Функция определена при однозначна и монотонна. Причем При любом из интервала — задача (1.3), (1.5) имеет единственное решение, отвечающее единственному корню уравнения (4.2). Любое решение имеет вид (4 1). Решение при задается формулой (3.2) и не ограничено.

Эти выводы переносятся и на случай задачи (1.1), (1.5) при При определении числа решений вместо уравнения (4.2) согласно формулам (1.2) следует рассматривать уравнение

Структура множества решений при остается той же, что и в случае Согласно (1.13) критическое значение достигается в некоторой точке

Некоторые отличия возникают при Теперь кривая может и не быть монотонной по Однако она имеет не более одной точки максимума при и является монотонной функцией в том и только в том случае, когда

Согласно (3.10) условие (4.4) имеет место в области

Следовательно, при выполнении (4.5)

При любом задача (11), (1.5) имеет единственное решение. При решение становится неограниченным. Согласно (1.2), (3.2)

В области

кривая достигает максимума при а затем убывает до величины Поэтому при

существует два решения задачи (1.1), (1.5), соответствующие двум корням уравнения (4.3). При решение единственно и ограничено.

Особо подчеркнем следующие выводы наших исследований:

I. Задача нахождения зависимости и величины решается независимо от исходной задачи (1.1), (1.5) и сводится к решению задачи (1.12), которая легко решается численно. Следует выйти из особой точки вдоль сепаратрисы, т. е. положить где достаточно малое положительное число, и решать уравнение (1.12) до максимума т. е. до при и до максимума при . В области (4.5) изменения параметров и а значение задается формулой (4.6), а соответствующее решение задачи (1.1), (1.5) — формулой (4.7), так что решение не ограничено. Неограниченное решение задачи (1.1), (1.5) может существовать и при Та же формула (4.7) определяет решение при и в случае причем в этом случае

В области (4.5) и только в ней решение задачи (1.1), (1.5) единственно при каждом Вне области является точкой ветвления решения. При решение единственно и ограничено.

III. Неединственность решения задачи (1.1), (1.5) при является скорее правилом, чем исключением. Причем структура множества всех решений при весьма сложна. Однако устойчивым при согласно по крайней мере при целых значениях , оказывается только одно, наименьшее решение. Оно определяется формулами (4.1), (1.2) при подходящем значении являющемся наименьшим корнем уравнения (4.3).