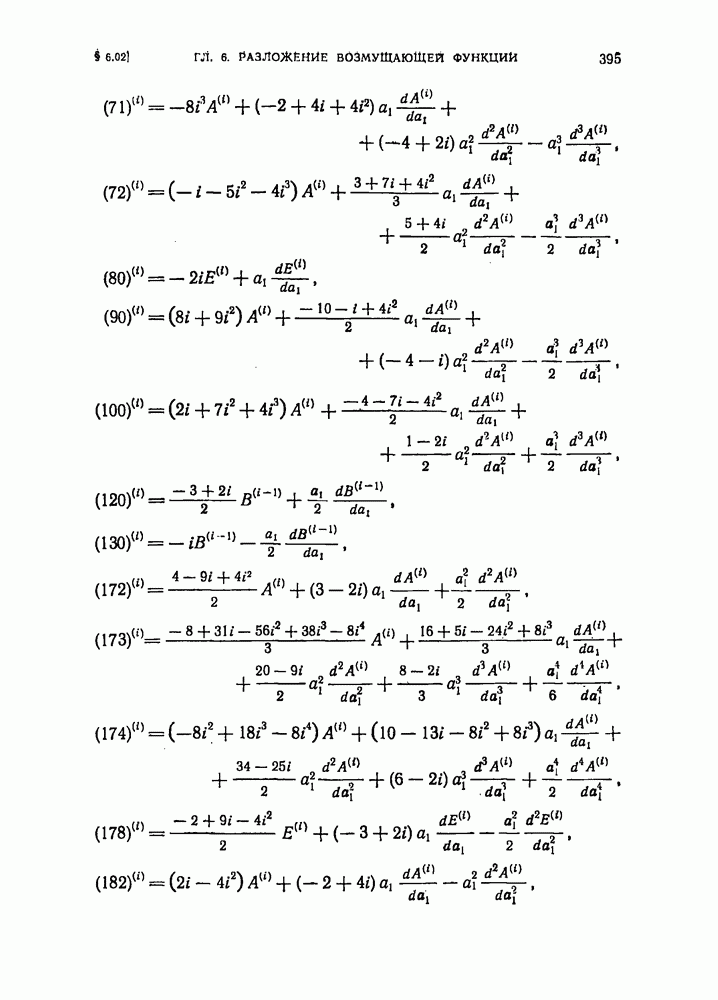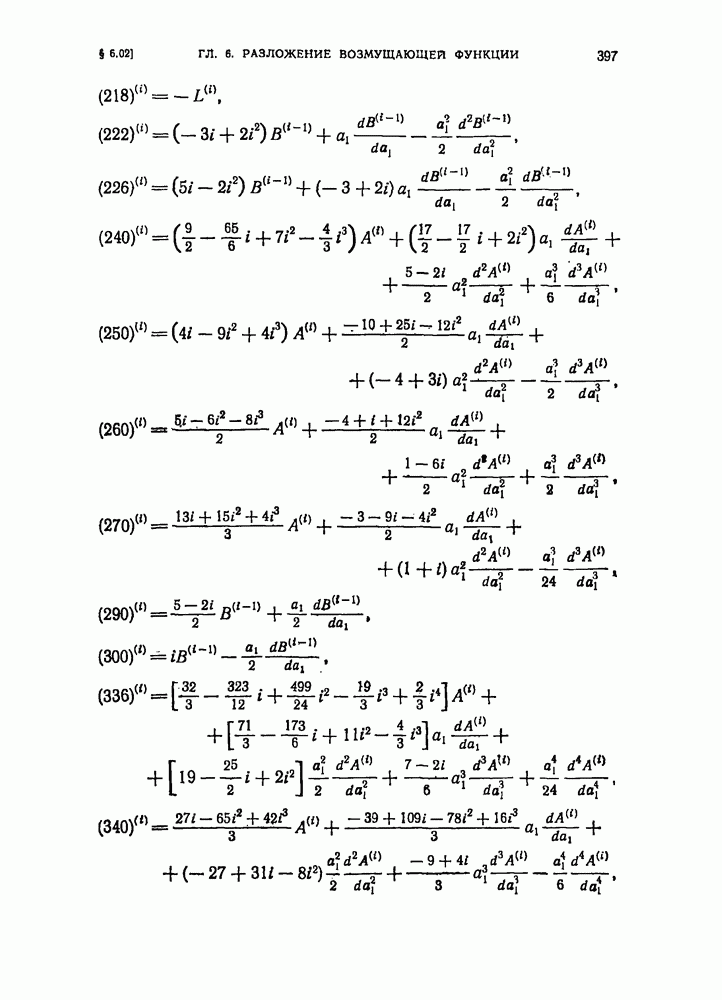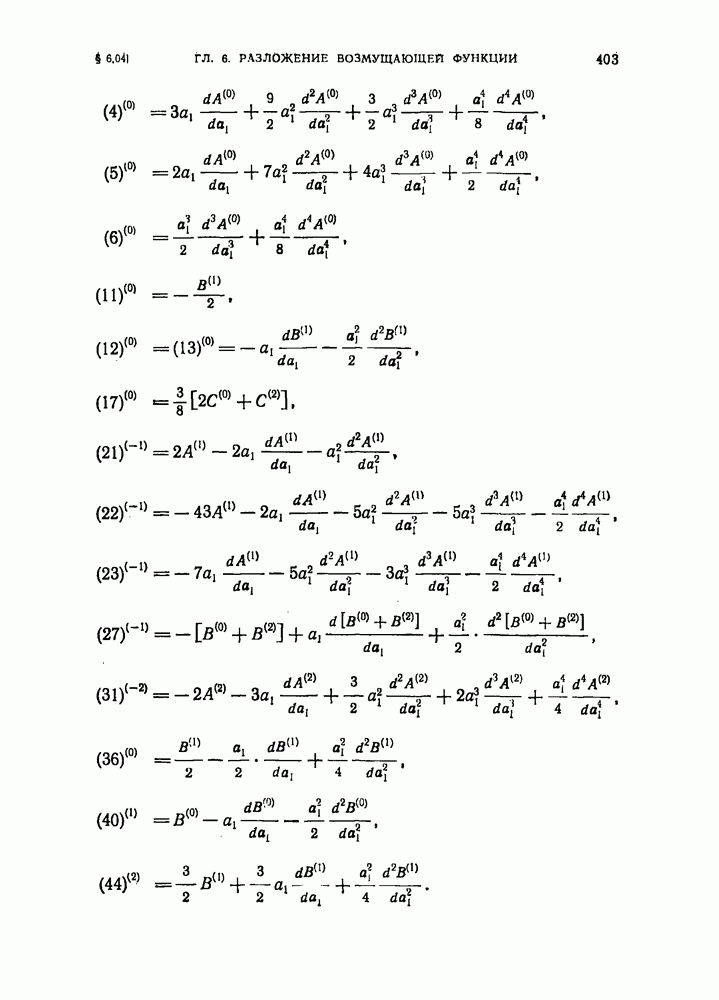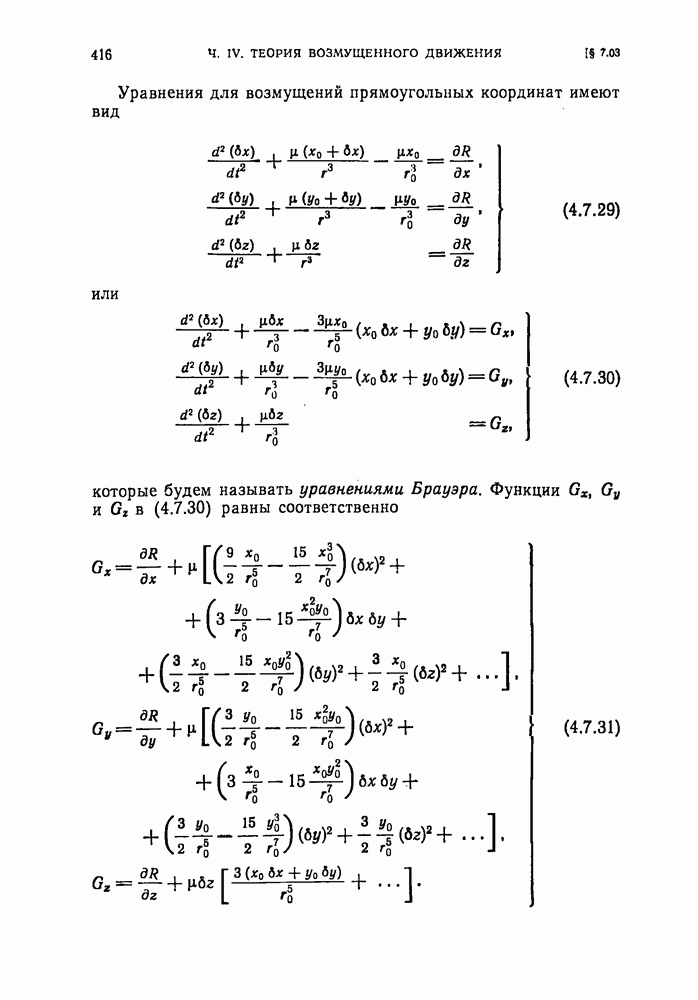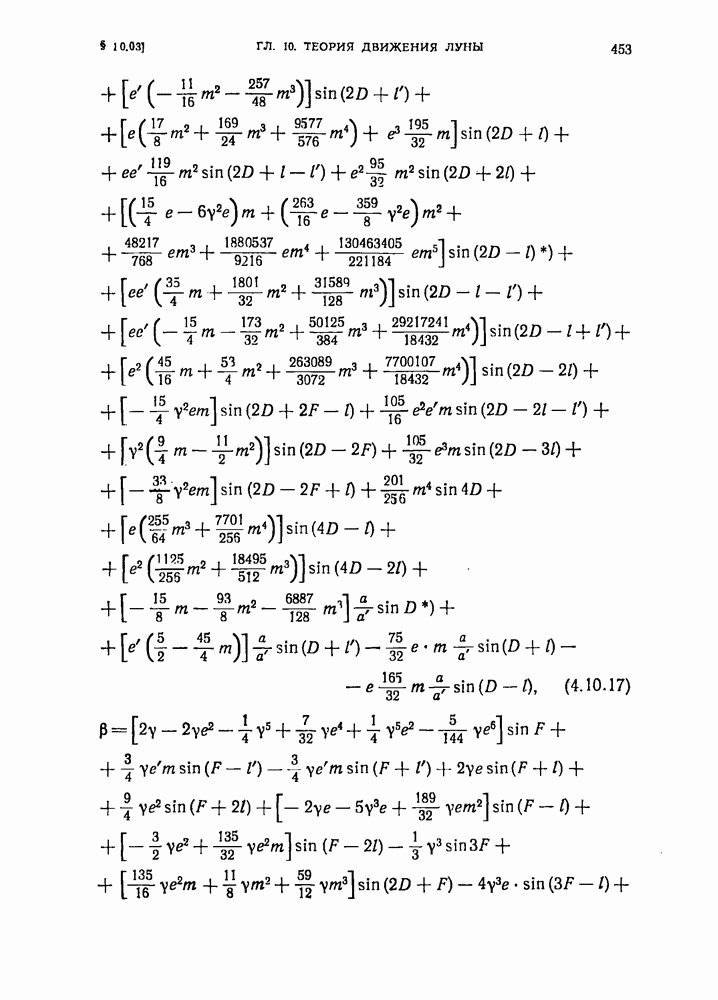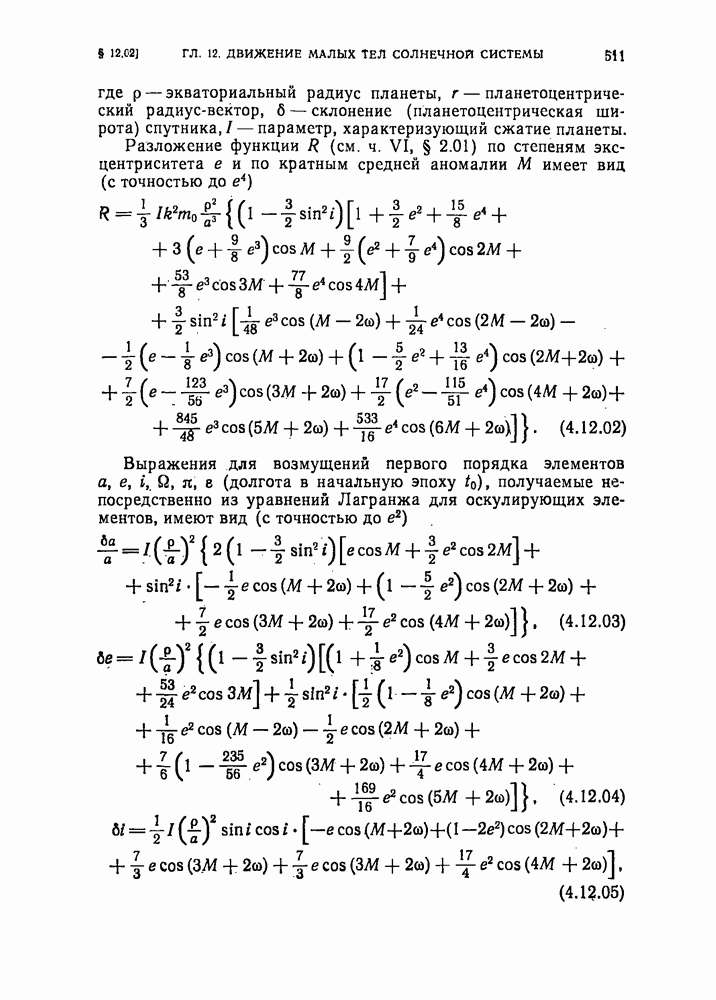| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 3. УЛУЧШЕНИЕ ПЕРВОНАЧАЛЬНОЙ ОРБИТЫ
Способы, изложенные в предыдущей главе, позволяют получить лишь предварительную орбиту. Ошибки элементов такой орбиты обусловлены недостаточной точностью наблюдений, потерей точности при вычислениях. Кроме того, поскольку фактическая орбита любого небесного тела не является невозмущенной (кеплеровой), элементы предварительной орбиты представляют собой, по существу, некоторые средние элементы кеплеровой орбиты, приближенно представляющей возмущенное движение, наблюдаемое на данном интервале времени.
Методы улучшения первоначальной орбиты небесного тела преследуют цель или уточнения предварительных элементов кеплеровой орбиты в предположении, что движение остается невозмущенным, или нахождения как можно более точных значений оскулирующих элементов орбиты на тот или иной момент времени в предположении, что имеет место возмущенное движение.
Наряду с учебными пособиями [1], [2] для более подробного ознакомления со способами улучшения орбит можно рекомендовать [7], [8].
§ 3.01. Дифференциальное исправление орбит. Постановка задачи
В настоящее время для улучшения первоначальной орбиты наиболее эффективным является так называемый дифференциальный метод исправления элементов орбиты, рассчитанный на применение современной вычислительной техники и позволяющий использовать всю совокупность наблюдений данного небесного тела.
Пусть имеются наблюденные значения геоцентрических экваториальных координат  на моменты
на моменты  Пусть имеется таблица значений
Пусть имеется таблица значений  геоцентрических расстояний
геоцентрических расстояний  а также прямоугольных экваториальных гелиоцентрических координат
а также прямоугольных экваториальных гелиоцентрических координат  вычисленных на эти
вычисленных на эти
же моменты по элементам предварительной орбиты, отнесенной к моменту 
Обозначим через  ошибки вычисленных координат, так что
ошибки вычисленных координат, так что

где  — значения
— значения  точно соответствующие наблюденным
точно соответствующие наблюденным  Предполагается, что ошибки
Предполагается, что ошибки  малы и зависят только от погрешностей элементов предварительной орбиты на момент
малы и зависят только от погрешностей элементов предварительной орбиты на момент 
Зависимость  от
от  выражается с точностью до членов первого порядка формулами
выражается с точностью до членов первого порядка формулами

где  — вычисленные значения (индекс
— вычисленные значения (индекс  для сокращения записи опускаем).
для сокращения записи опускаем).
В свою очередь зависимость  от поправок к элементам предварительной орбиты выражается с точностью до членов первого порядка формулами
от поправок к элементам предварительной орбиты выражается с точностью до членов первого порядка формулами

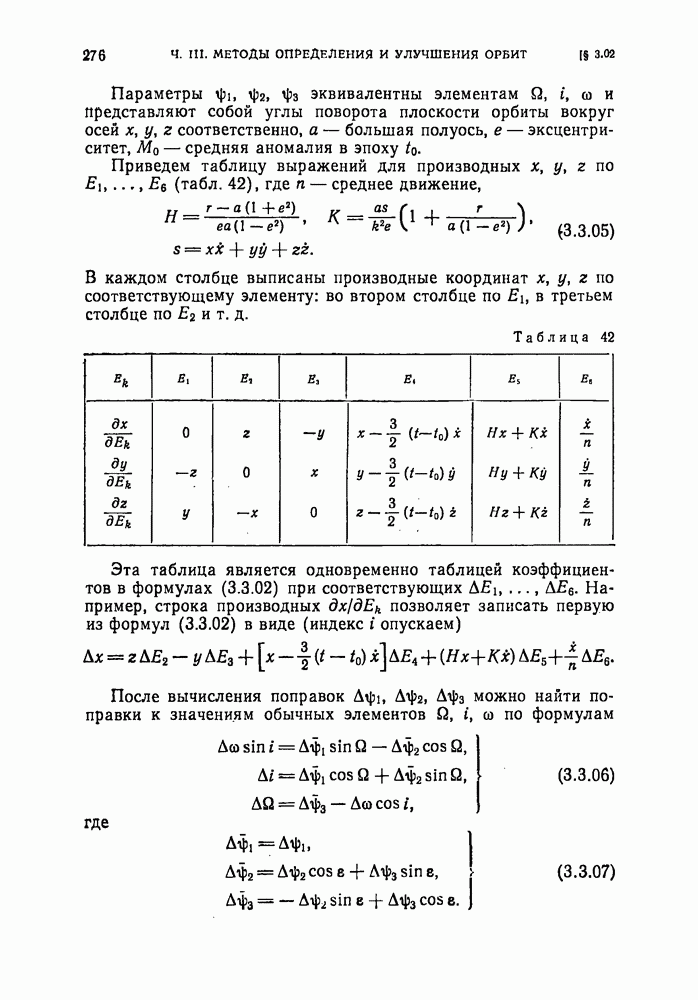
где  — элементы орбиты, а
— элементы орбиты, а  — значения частных производных
— значения частных производных  по
по  на момент
на момент  Членами порядка выше первого в формулах (3.3.01), (3.3.02) относительно
Членами порядка выше первого в формулах (3.3.01), (3.3.02) относительно  пренебрегают. В формулах (3.3.02) часто для
пренебрегают. В формулах (3.3.02) часто для
удобства вычислений в качестве  принимают некоторые функции элементов.
принимают некоторые функции элементов.
Вычисление координат  может производиться по формулам невозмущенного движения. Тогда ошибки
может производиться по формулам невозмущенного движения. Тогда ошибки  обусловлены отклонением фактического движения от невозмущенного, и
обусловлены отклонением фактического движения от невозмущенного, и  надо рассматривать как поправки к элементам (или функциям от элементов) невозмущенной орбиты, учет которых позволит получить невозмущенную орбиту, достаточно хорошо описывающую фактическое движение. Однако чаще всего координаты
надо рассматривать как поправки к элементам (или функциям от элементов) невозмущенной орбиты, учет которых позволит получить невозмущенную орбиту, достаточно хорошо описывающую фактическое движение. Однако чаще всего координаты  вычисляются с учетом возмущений. Тогда
вычисляются с учетом возмущений. Тогда  рассматривают как погрешности начальных значений элементов (или функций элементов) оскулирующей орбиты на момент
рассматривают как погрешности начальных значений элементов (или функций элементов) оскулирующей орбиты на момент  учет которых позволит вычислить более точно возмущения. Члены, обусловленные изменениями
учет которых позволит вычислить более точно возмущения. Члены, обусловленные изменениями  с течением времени и неточностью метода вычисления возмущений, считаются имеющими более высокий порядок малости и при составлении соотношений (3.3.02) не учитываются.
с течением времени и неточностью метода вычисления возмущений, считаются имеющими более высокий порядок малости и при составлении соотношений (3.3.02) не учитываются.
После нахождения численных значений производных  подставляют выражения (3.3.02) для
подставляют выражения (3.3.02) для  в (3.3.01) и получают соотношения вида
в (3.3.01) и получают соотношения вида

где  — численные коэффициенты. Эти соотношения представляют собой так называемые условные уравнения относительно
— численные коэффициенты. Эти соотношения представляют собой так называемые условные уравнения относительно  решаемые по способу наименьших квадратов (с применением ЭВМ, если число наблюдений достаточно велико). См. ч. VII, гл. 4.
решаемые по способу наименьших квадратов (с применением ЭВМ, если число наблюдений достаточно велико). См. ч. VII, гл. 4.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Часть I. СФЕРИЧЕСКАЯ И ЭФЕМЕРИДНАЯ АСТРОНОМИЯ, ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
- Глава 1. СИСТЕМЫ КООРДИНАТ
- § 1.02. Главные круги, линии и точки небесной сферы
- § 1.03. Горизонтальная система координат
- § 1.04. Экваториальные системы координат
- § 1.05. Эклиптическая система координат
- § 1.06. Галактическая система координат
- § 1.07. Основные формулы сферической тригонометрии
- § 1.08. Соотношения между различными астрономическими координатами
- § 1.09. Прямоугольные системы координат
- § 1.10. Системы географических координат
- § 1.11. Соотношения между астрономическими и геодезическими координатами
- § 1.12. Планетоцентрические системы координат [25]
- § 1.13. Марсоцентрическая и ареографическая системы координат
- § 1.14. Юпитероцентрическая и зенографическая системы координат
- § 1.15. Сатурноцентрическая система координат
- § 1.16. Системы координат, определяемые осевым вращением Солнца, Венеры, Урана и Нептуна
- § 1.17. Луноцентрическая и селенографическая системы координат
- § 1.18. Орбитальная система координат
- § 1.19. Объектоцентрическая система координат
- Глава 2. РЕДУКЦИОННЫЕ ВЫЧИСЛЕНИЯ
- § 2.01. Прецессия
- § 2.02. Редукция звездных положений с учетом прецессии и собственного движения
- § 2.03. Нутация
- § 2.04. Годичная аберрация
- § 2.05. Сводка основных формул редукции звездных положений
- § 2.06. Учет влияния членов второго порядка
- § 2.07. Годичный параллакс
- § 2.08. Точные формулы для учета прецессии
- § 2.09. Формулы учета прецессии в прямоугольных экваториальных координатах
- § 2.10. Формулы учета прецессии в прямоугольных эклиптических координатах
- § 2.11. Совместный учет прецессии и нутации в прямоугольных экваториальных координатах
- § 2.12. Формулы учета прецессии в координатах и элементах орбит при умеренных и малых разностях эпох
- § 2.13. Аберрация света
- § 2.14. Приведение звезды на видимое место в прямоугольных координатах
- § 2.15. Об учете орбитального движения компонент двойных звезд
- § 2.16. Параллакс
- § 2.17. Учет суточного параллакса в горизонтальной системе координат
- § 2.18. Формулы учета суточного параллакса в экваториальной системе координат
- § 2.19. Формулы учета суточного параллакса в координатах Солнца и планет
- § 2.20. Формулы учета суточного параллакса в системе эклиптических координат
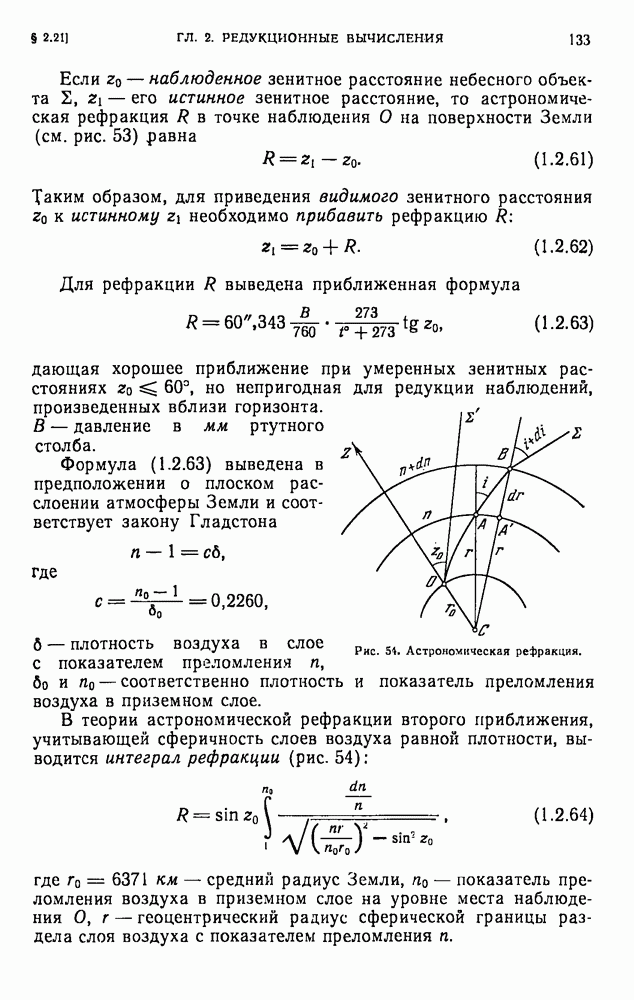
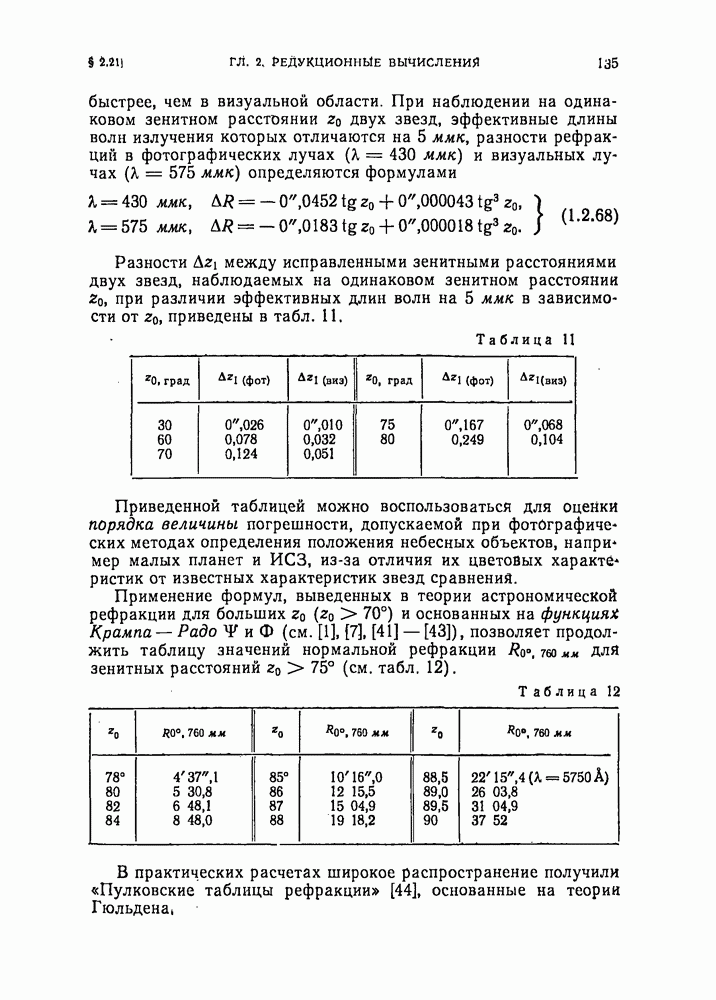
- § 2.21. Астрономическая рефракция
- § 2.22. Формулы учета рефракции в координатах небесных объектов
- § 2.23. Рефракция при наблюдении небесных объектов, расположенных на конечных расстояниях от Земли
- § 2.24. Дифференциальная прецессия и нутация. Дифференциальная аберрация и дифференциальный параллакс
- § 2.25. Сравнение теории с наблюдениями
- § 2.26. Каталоги звездных положений
- § 2.27. Геоцентрические координаты нуль-пункта селенографической системы отсчета
- § 2.28. Вычисление топоцентрических расстояний до точек лунной поверхности
- Глава 3. ВРЕМЯ И ЕГО ИЗМЕРЕНИЕ
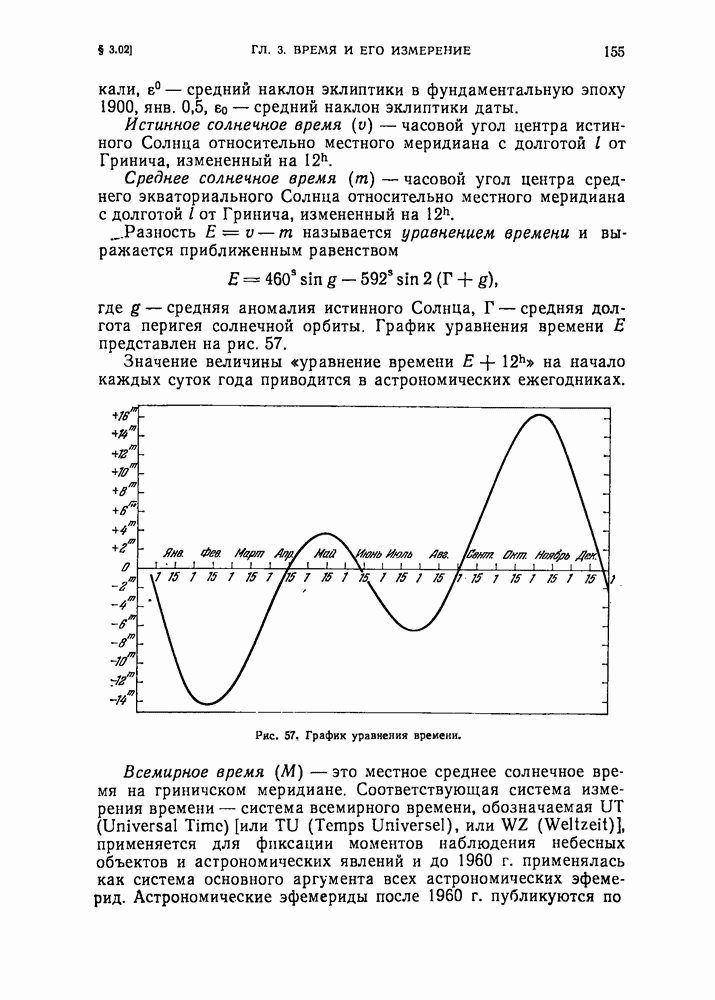
- § 3.02. Звездное и солнечное время. Всемирное время
- § 3.03. Квазиравномерное всемирное время
- § 3.04. Связь между всемирным временем и звездным гриничским временем
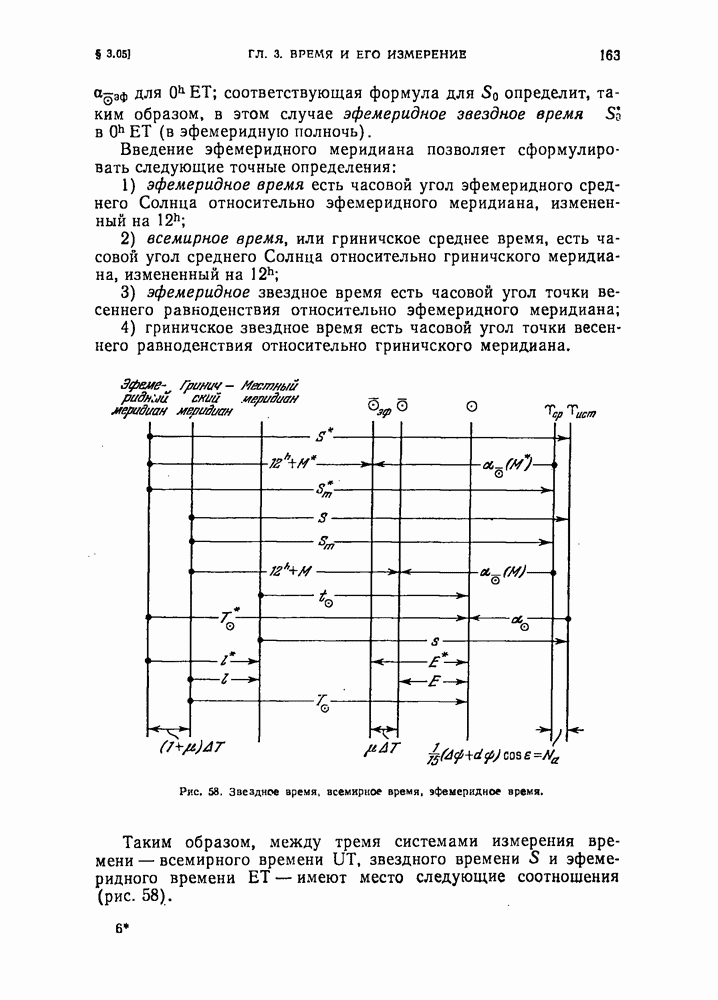
- § 3.05. Эфемеридное время
- § 3.06. Поправка за эфемеридное время
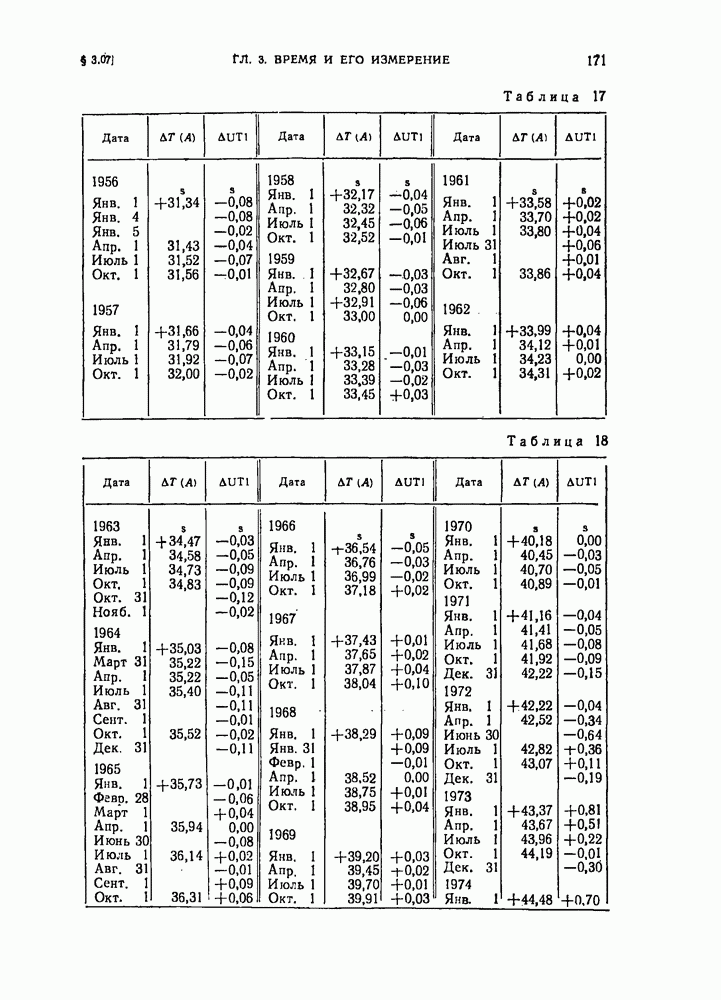
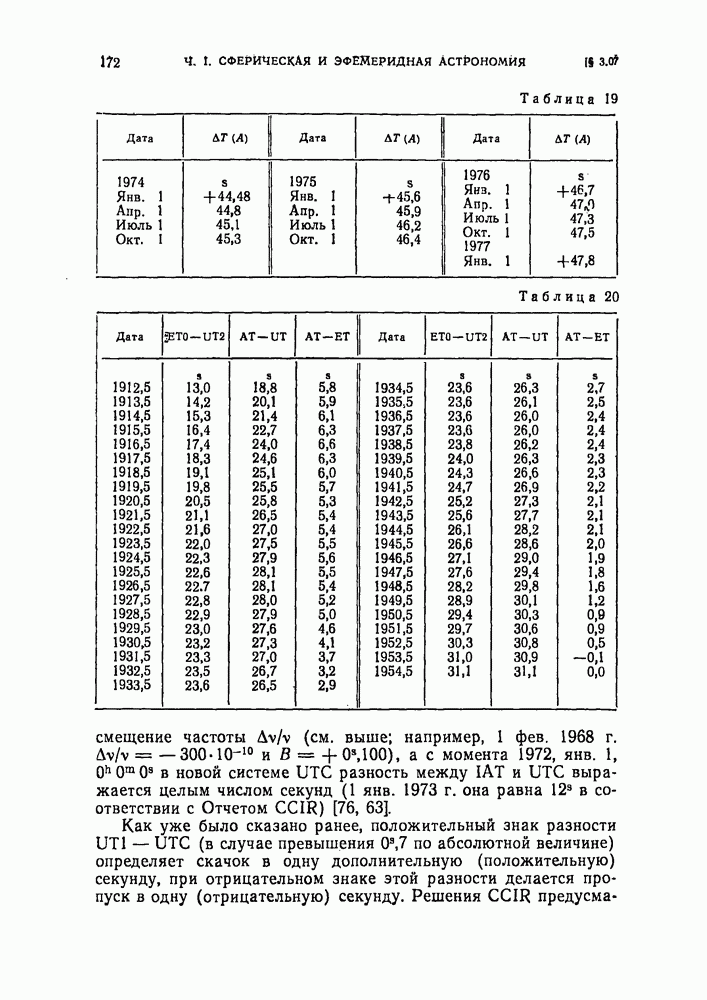
- § 3.07. Атомное время
- § 3.08. Юлианский период. Юлианские дни
- Глава 4. АСТРОНОМИЧЕСКИЕ ПОСТОЯННЫЕ
- § 4.02. Задачи астродинамики и астрономические постоянные
- § 4.03. Результаты радиолокационных определений астрономической единицы в км
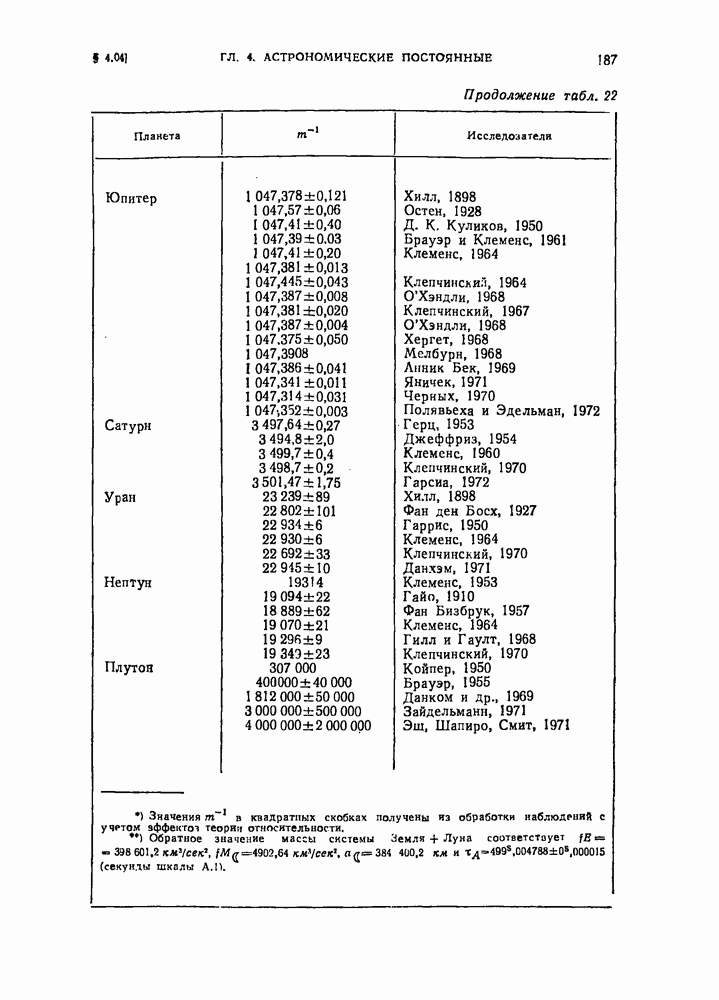
- § 4.04. Значения масс больших планет
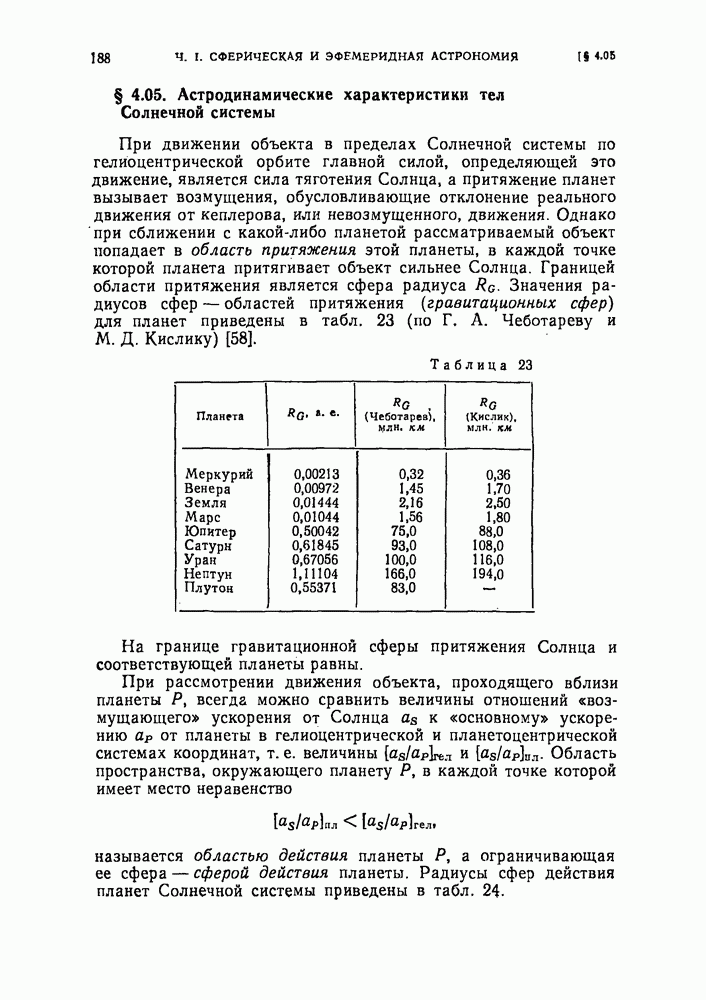
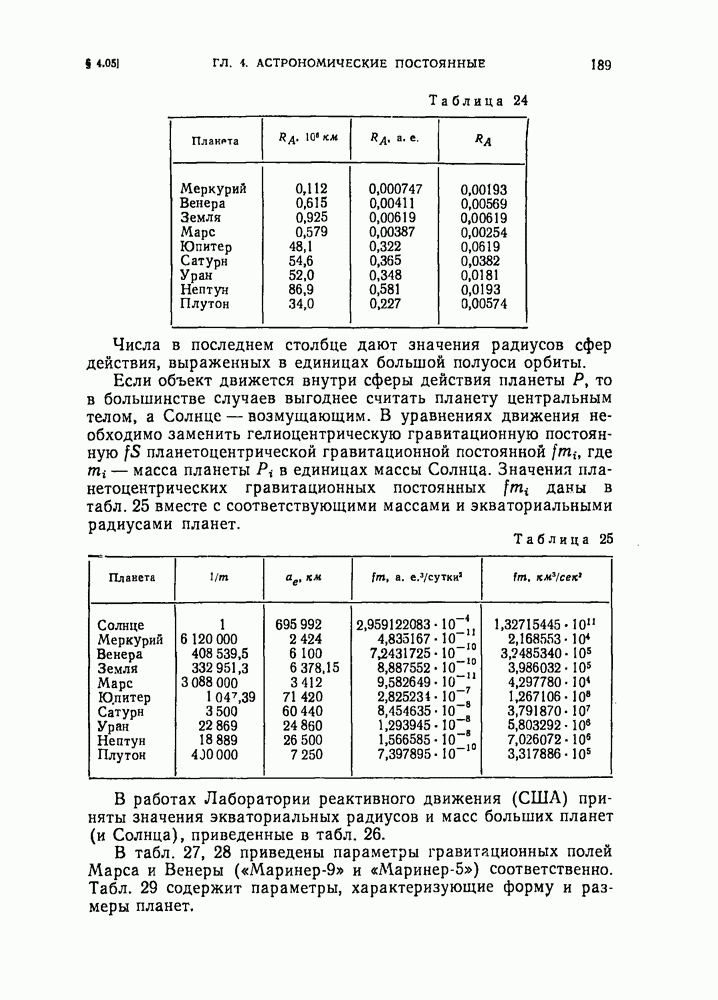
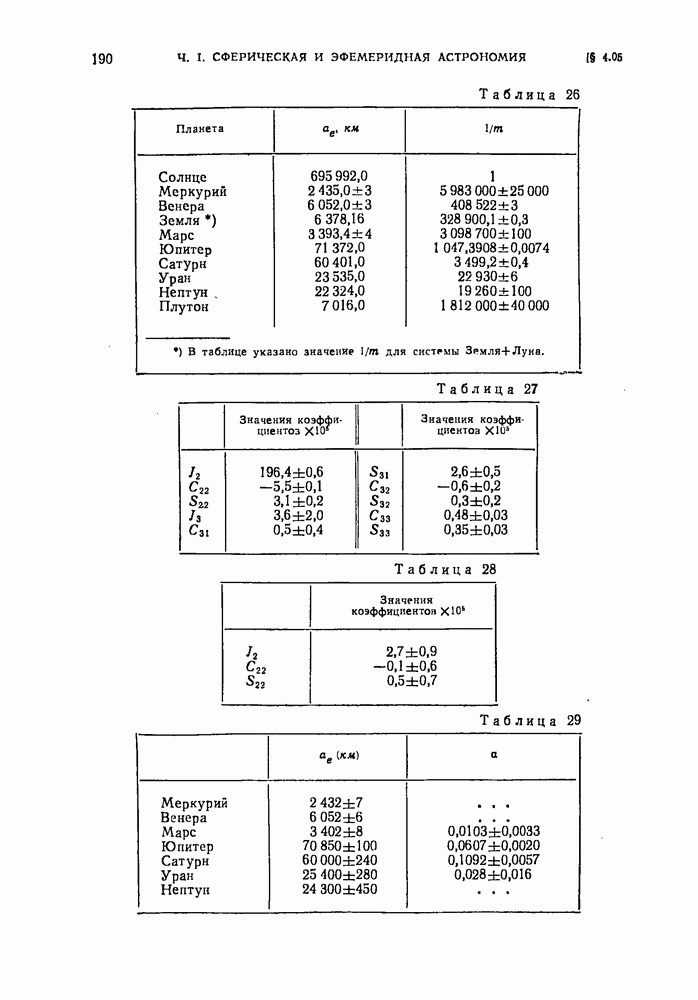
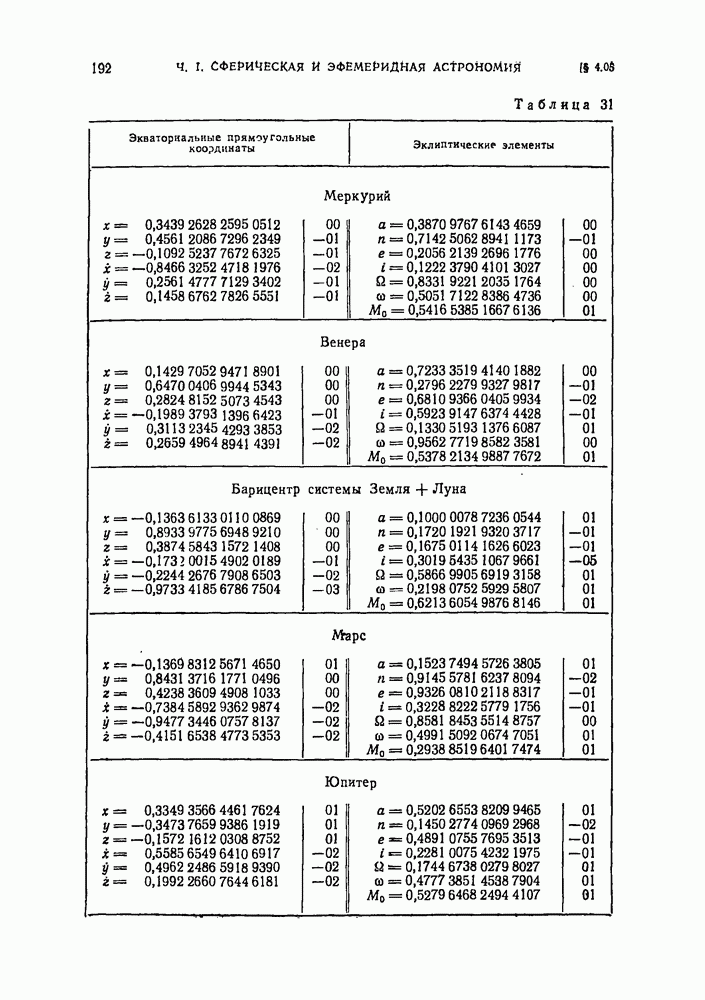
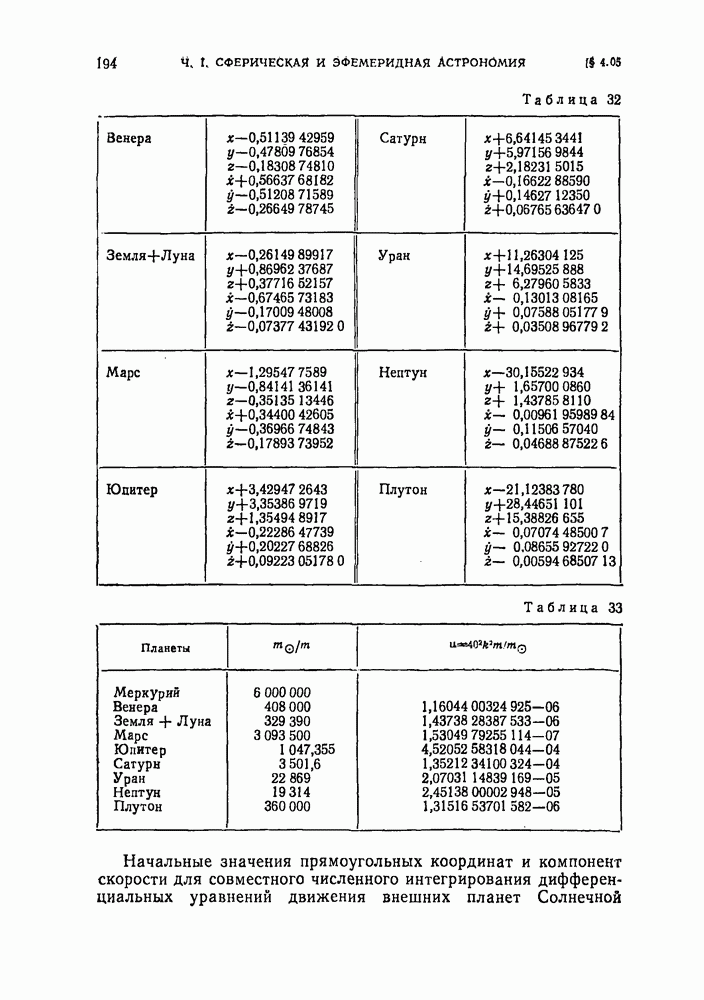
- § 4.05. Астродинамические характеристики тел Солнечной системы
- § 4.06. Астродинамические постоянные, связанные с Землей
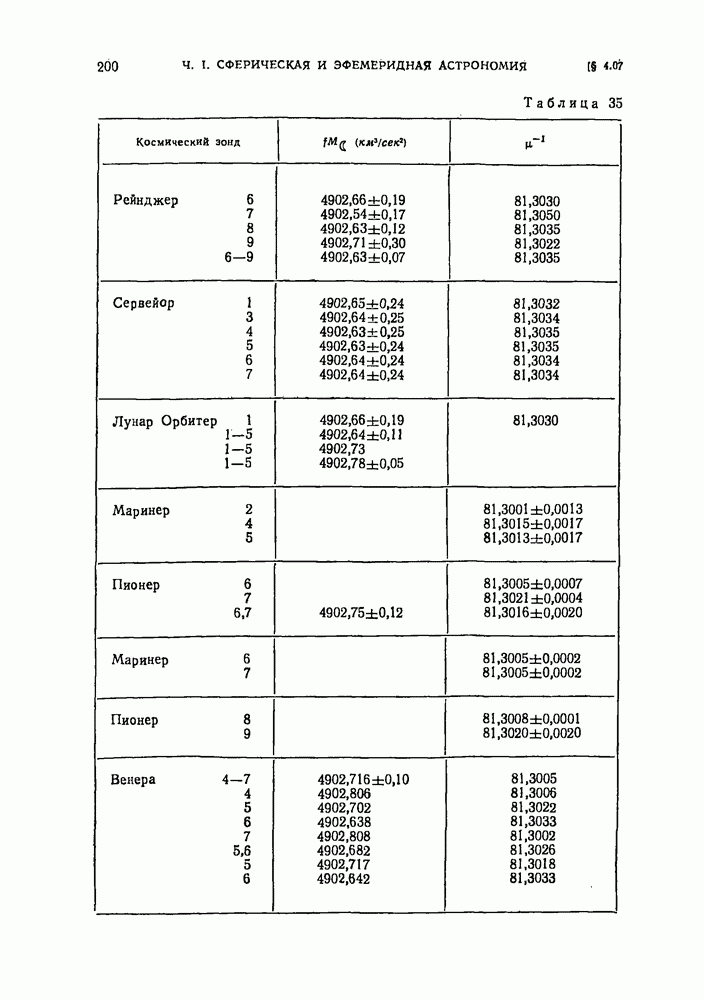
- § 4.07. Астродинамические постоянные, связанные с Луной
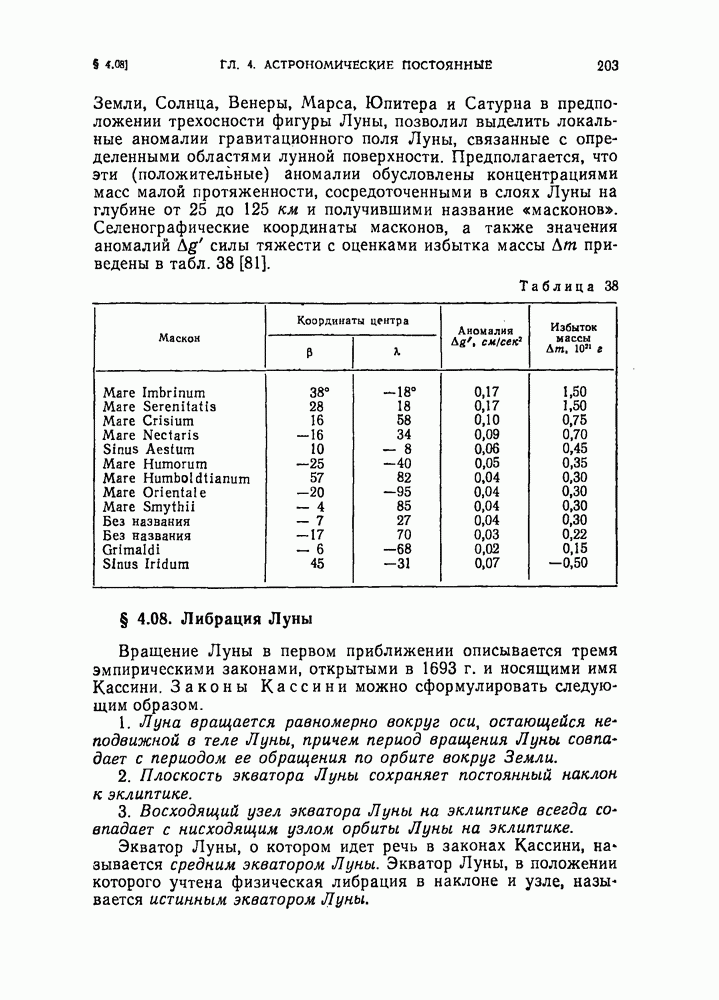
- § 4.08. Либрация Луны
- Часть II. ЗАДАЧА ДВУХ ТЕЛ
- Глава 1. ОБЩАЯ ТЕОРИЯ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ
- § 1.02. Первые интегралы уравнений невозмущенного кеплеровского движения
- § 1.03. Типы невозмущенного кеплеровского движения
- § 1.04. Элементы орбиты
- § 1.05. Формулы, связывающие постоянные интегрирования и элементы орбиты
- Глава 2. ОСНОВНЫЕ ФОРМУЛЫ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ
- § 2.02. Круговое движение
- § 2.03. Гиперболическое движение
- § 2.04. Параболическое движение
- § 2.05. Прямолинейное движение
- § 2.06. Вычисление эфемерид планет и комет
- Глава 3. РАЗЛОЖЕНИЕ КООРДИНАТ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ В РЯДЫ
- § 3.02. Разложение функций истинной аномалии в тригонометрические ряды по кратным средней аномалии
- § 3.03. Первые члены рядов по кратным средней аномалии для некоторых функций
- § 3.04. Формула Лагранжа
- § 3.05. Ряды по степеням эксцентриситета
- § 3.06. Тригонометрические ряды по кратным эксцентрической аномалии
- § 3.07. Ряды по кратным истинной аномалии
- § 3.08. Разложения координат невозмущенного кеплеровского движения в ряды по степеням времени
- § 3.09. Степенные ряды в случае эллиптического движения
- Часть III. МЕТОДЫ ОПРЕДЕЛЕНИЯ И УЛУЧШЕНИЯ ОРБИТ
- Глава 1. ВЫЧИСЛЕНИЕ КООРДИНАТ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ ПО ЭЛЕМЕНТАМ ОРБИТЫ
- § 1.02. Вычисление орбитальных координат в случае параболической орбиты
- § 1.03. Вычисление орбитальных координат в случае орбит, эксцентриситет которых близок к единице
- § 1.04. Вычисление гелиоцентрических прямоугольных эклиптических и экваториальных координат
- Глава 2. ОПРЕДЕЛЕНИЕ ОРБИТ
- § 2.02. Особые случаи, встречающиеся при вычислении гелиоцентрических координат
- § 2.03. Определение гелиоцентрических положений по четырем геоцентрическим наблюдениям в случае эллиптической или гиперболической орбит
- § 2.04. Определение гелиоцентрических положений по трем геоцентрическим наблюдениям в случае параболической орбиты
- § 2.05. Вычисление элементов эллиптической орбиты по двум гелиоцентрическим положениям
- § 2.06. Определение элементов гиперболической орбиты по двум гелиоцентрическим положениям
- § 2.07. Определение элементов параболической орбиты по двум гелиоцентрическим положениям
- § 2.08. Уравнения Ламберта и Эйлера
- § 2.09. Определение элементов эллиптической или гиперболической орбиты по двум гелиоцентрическим положениям с помощью уравнения Ламберта
- § 2.10. Определение элементов круговой орбиты по двум наблюдениям
- § 2.11. Вычисление элементов гелиоцентрической орбиты по положению и скорости в начальный момент
- Глава 3. УЛУЧШЕНИЕ ПЕРВОНАЧАЛЬНОЙ ОРБИТЫ
- § 3.01. Дифференциальное исправление орбит. Постановка задачи
- § 3.02. Выражения для производных от координат по элементам (или по функциям элементов)
- § 3.03. Условные уравнения, составляемые по наблюдениям долготы и широты небесного тела
- Глава 4. ОПРЕДЕЛЕНИЕ И УЛУЧШЕНИЕ ЭЛЕМЕНТОВ ОРБИТ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- § 4.01. Определение элементов орбит ИСЗ по положению и скорости в момент выхода на орбиту
- § 4.02. Определение предварительных элементов орбиты ИСЗ по наблюдениям
- § 4.03. Улучшение орбит ИСЗ
- Часть IV. ТЕОРИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ
- Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ЗАДАЧИ n ТЕЛ В КООРДИНАТАХ
- § 1.02. Уравнение Лагранжа — Якоби
- § 1.03. Уравнения движения в барицентрических прямоугольных координатах
- § 1.04. Уравнения движения в координатах Якоби
- § 1.05. Уравнения относительного движения в прямоугольных координатах
- § 1.06. Уравнения движения в идеальных прямоугольных координатах Ганзена
- § 1.07. Уравнения абсолютного движения в цилиндрических координатах
- § 1.08. Уравнения относительного движения в цилиндрических координатах
- § 1.09. Уравнения абсолютного движения в сферических координатах
- § 1.10. Уравнения относительного движения в сферических координатах
- § 1.11. Уравнения движения в полярных координатах Ганзена
- § 1.12. Уравнения Клеро — Лапласа
- § 1.13. Общее правило составления канонических уравнений
- § 1.14. Первая каноническая форма уравнений абсолютного движения
- § 1.15. Вторая каноническая форма уравнений абсолютного движения
- § 1.16. Третья каноническая форма уравнений абсолютного движения
- § 1.17. Первая каноническая форма уравнений относительного движения
- § 1.18. Вторая каноническая форма уравнений относительного движения
- § 1.19. Третья каноническая форма уравнений относительного движения
- § 1.20. Уравнение Гамильтона — Якоби. Метод Гамильтона — Якоби
- § 1.21. Уравнения движения системы в векторной форме
- Глава 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПОСТУПАТЕЛЬНО-ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ
- § 2.02. Силовая функция системы тел
- § 2.03. Разложение силовой функции двух тел
- § 2.04. Уравнения поступательно-вращательного движения системы тел в абсолютной прямоугольной системе координат
- § 2.05. Уравнения поступательно-вращательного движения системы тел в относительной прямоугольной системе координат
- § 2.06. Каноническая форма уравнений поступательно-вращательного движения системы тел
- Глава 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ТЕЛА ДЛЯ РАЗЛИЧНЫХ СИСТЕМ ОСКУЛИРУЮЩИХ ЭЛЕМЕНТОВ
- § 3.01. Метод Лагранжа вариации произвольных постоянных
- § 3.02. Уравнения Ньютона для кеплеровских оскулирующих элементов (общий случай)
- § 3.03. Уравнения Ньютона для эллиптических кеплеровских оскулирующих элементов
- § 3.04. Уравнения Лагранжа для кеплеровских оскулирующих элементов (общий случай)
- § 3.05. Уравнения Лагранжа для эллиптических кеплеровских оскулирующих элементов
- § 3.06. Уравнения возмущенного движения для канонических элементов Якоби
- § 3.07. Уравнения возмущенного движения для канонических элементов Делоне
- § 3.08. Две системы канонических элементов Пуанкаре
- § 3.09. Уравнения возмущенного движения в переменных Лагранжа для случая малых эксцентриситетов
- § 3.10. Уравнения в переменных Лагранжа для случая малых наклонов
- § 3.11. Уравнения возмущенного движения в переменных Лагранжа (общий случай)
- § 3.12. Связь между прямоугольными координатами движущейся точки и различными системами канонических элементов
- Глава 4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ЗАДАЧИ n ТЕЛ ДЛЯ РАЗЛИЧНЫХ СИСТЕМ ОСКУЛИРУЮЩИХ ЭЛЕМЕНТОВ
- § 4.01. Уравнения Ньютона для кеплеровских оскулирующих элементов (общий случай)
- § 4.02. Уравнения Ньютона для эллиптических кеплеровских оскулирующих элементов
- § 4.03. Уравнения Лагранжа для кеплеровских оскулирующих элементов (общий случай)
- § 4.04. Уравнения Лагранжа для эллиптических кеплеровских оскулирующих элементов
- § 4.05. Уравнения возмущенного движения в канонических элементах Якоби
- § 4.06. Уравнения возмущенного движения в канонических элементах Делоне
- § 4.07. Две системы канонических элементов Пуанкаре
- § 4.08. Уравнения возмущенного движения в переменных Лагранжа для случая малых эксцентриситетов
- § 4.09. Уравнения в переменных Лагранжа для случая малых наклонов
- § 4.10. Уравнения возмущенного движения в переменных Лагранжа (общий случай)
- Глава 5. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 5.01. Эллиптические интегралы и эллиптические функции
- § 5.02. Гипергеометрический ряд и гипергеометрическая функция
- § 5.03. Полиномы Лежандра. Функции Лежандра
- § 5.04. Присоединенные функции Лежандра
- § 5.05. Сферические функции
- § 5.06. Цилиндрические функции. Функции Бесселя
- § 5.07. Функции Ламе
- § 5.08. Полиномы Гегенбауэра. Коэффициенты Лапласа
- § 5.09. Числа Коши
- Глава 6. РАЗЛОЖЕНИЕ ВОЗМУЩАЮЩЕЙ ФУНКЦИИ
- § 6.01. Разложение возмущающей функции в задаче о движении двух планет (случай круговых орбит)
- § 6.02. Разложение возмущающей функции в задаче о движении двух планет (случай малых эксцентриситетов и взаимного наклона)
- § 6.03. Разложение возмущающей функции в случае произвольного взаимного наклона
- § 6.04. Вековая часть возмущающей функции в двухпланетной задаче
- § 6.05. Численные методы разложения возмущающей функции
- § 6.06. Полуаналитический метод Брауэра — Клеменса разложения возмущающей функции
- Глава 7. АНАЛИТИЧЕСКИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ВОЗМУЩЕНИЙ КООРДИНАТ
- § 7.02. Метод Ганзена
- § 7.03. Метод Брауэра
- § 7.04. Метод Лапласа — Ньюкома
- Глава 8. АНАЛИТИЧЕСКИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ВОЗМУЩЕНИЙ ЭЛЕМЕНТОВ
- § 8.01. Общий вид возмущений элементов. Порядок, степень, ранг и класс возмущений
- § 8.02. Метод Гаусса вычисления вековых возмущений первого порядка
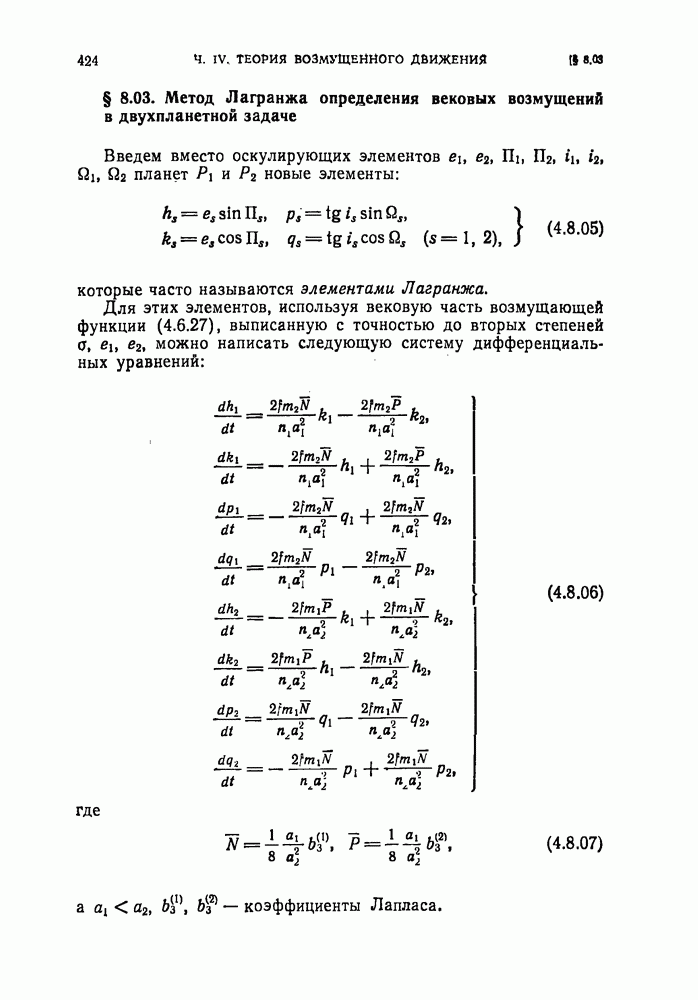
- § 8.03. Метод Лагранжа определения вековых возмущений в двухпланетной задаче
- § 8.04. Основы метода Делоне
- § 8.05. Связь между возмущениями координат и возмущениями элементов
- Глава 9. МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ, ОСНОВАННЫЕ НА СХЕМАХ ОСРЕДНЕНИЯ
- § 9.01. Основные схемы осреднения возмущающей функции в двухпланетной задаче
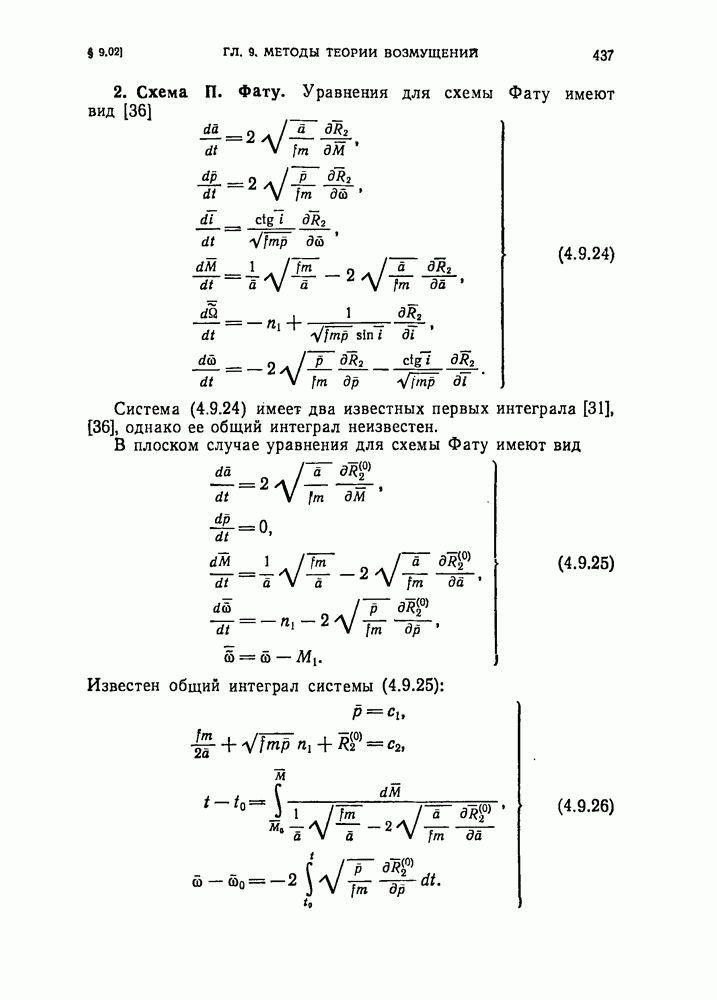
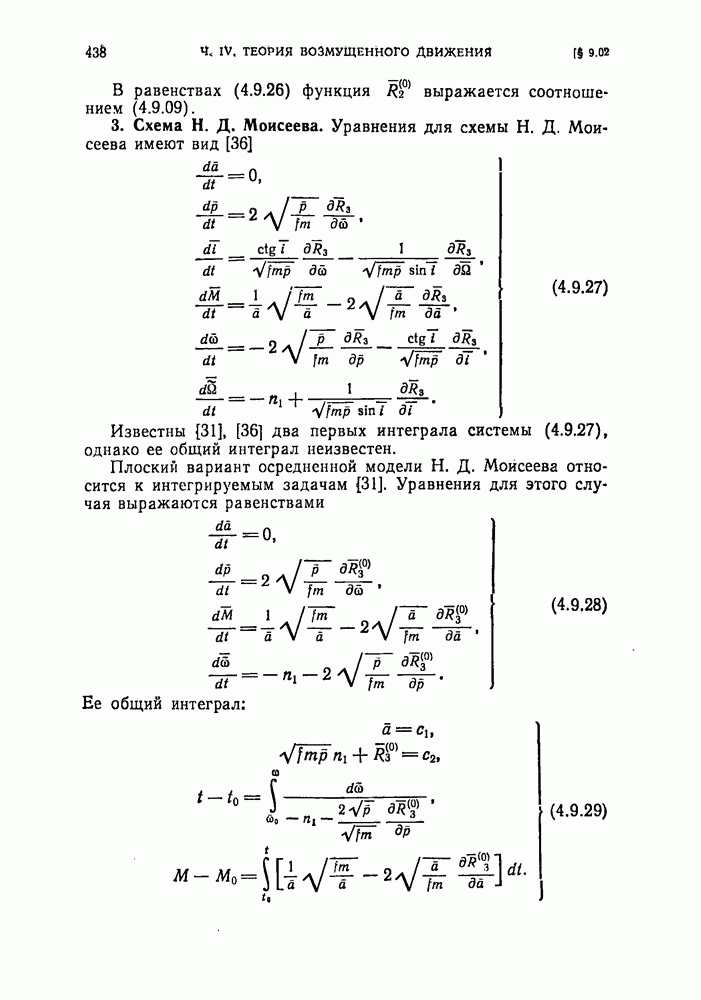
- § 9.02. Уравнения осредненных схем ограниченной круговой задачи трех тел, определяющие промежуточную орбиту (нулевое приближение). Их первые интегралы
- § 9.03. Разложение возмущающей функции для схем осреднения
- § 9.04. Основы метода теории возмущений
- Глава 10. ТЕОРИЯ ДВИЖЕНИЯ ЛУНЫ
- § 10.01. Уравнения основной проблемы в теории движения Луны
- § 10.02. Разложение возмущающей функции в основной проблеме теории движения Луны
- § 10.03. Решение Делоне основной проблемы в теории движения Луны
- § 10.04. Основные этапы построения теории Хилла—Брауна движения Луны
- § 10.05. Промежуточная орбита в теории Хилла — Брауна
- § 10.06. Общее решение уравнений основной проблемы в теории Хилла—Брауна
- § 10.07. Переход к сферическим координатам
- § 10.08. Численные значения постоянных интегрирования и параметров в теории Хилла — Брауна
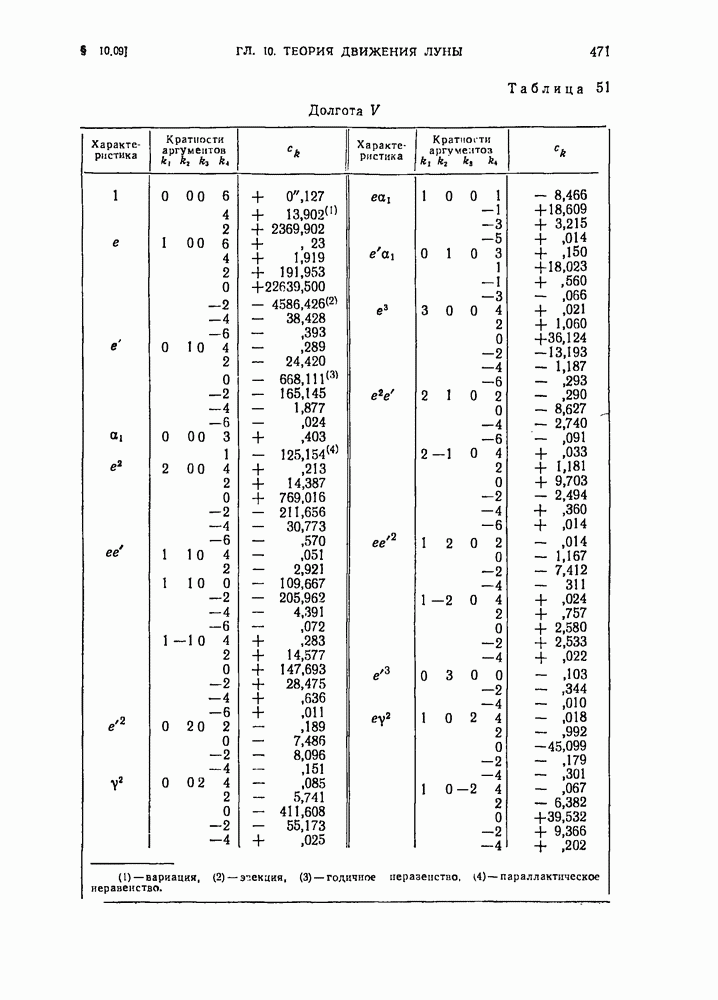
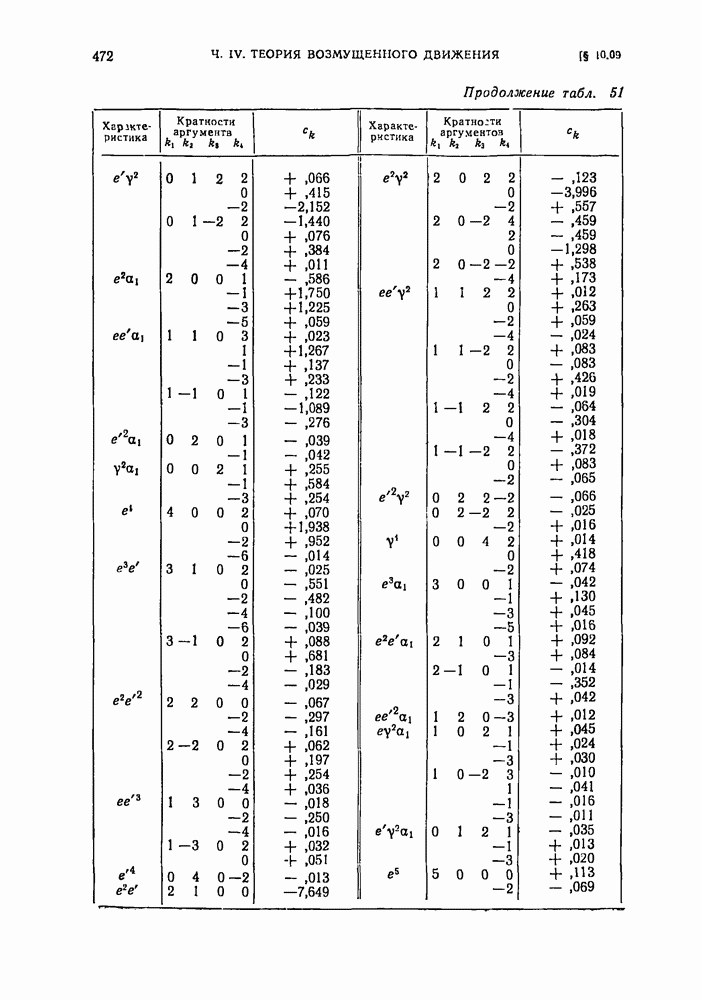
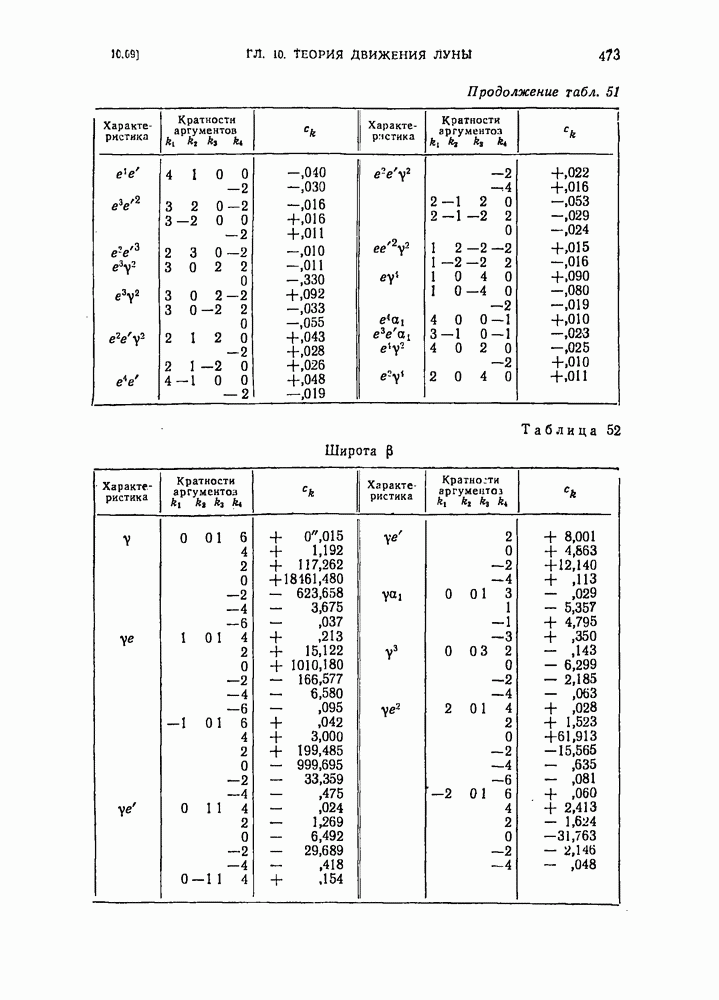
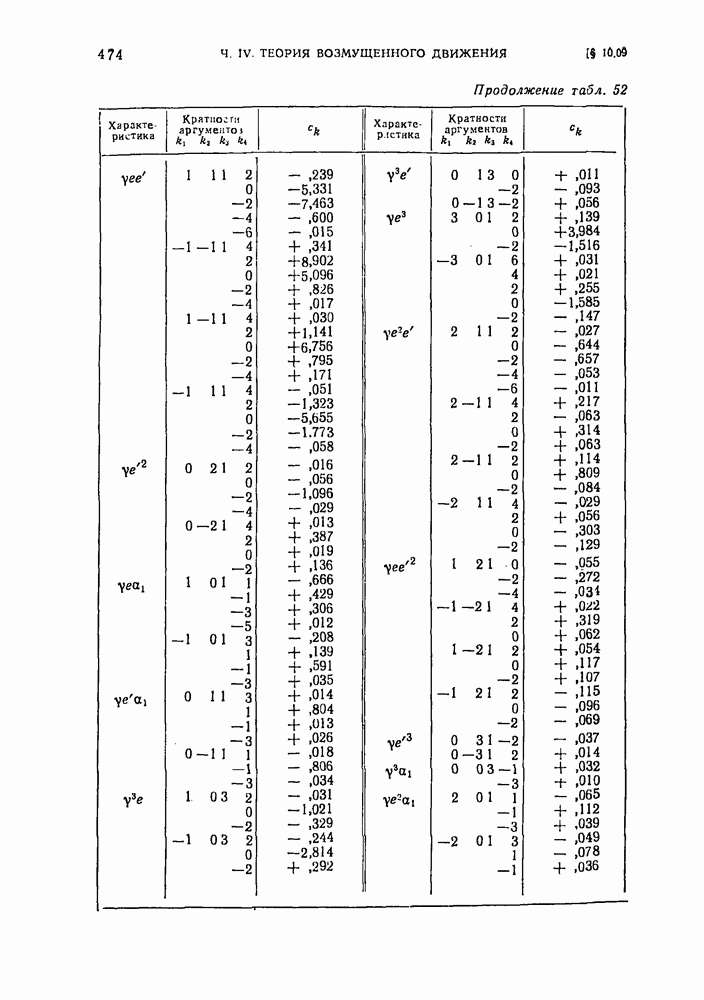
- § 10.09. Окончательные выражения для долготы, широты и синуса параллакса, соответствующие решению основной проблемы
- § 10.10. Возмущения Луны, обусловленные притяжением планет, фигурами Земли и Луны
- § 10.11. Уточнение теории движения Луны Хилла—Брауна
- Глава 11. ТЕОРИЯ ДВИЖЕНИЯ БОЛЬШИХ ПЛАНЕТ
- § 11.01. Внутренние планеты
- § 11.02. Внешние планеты
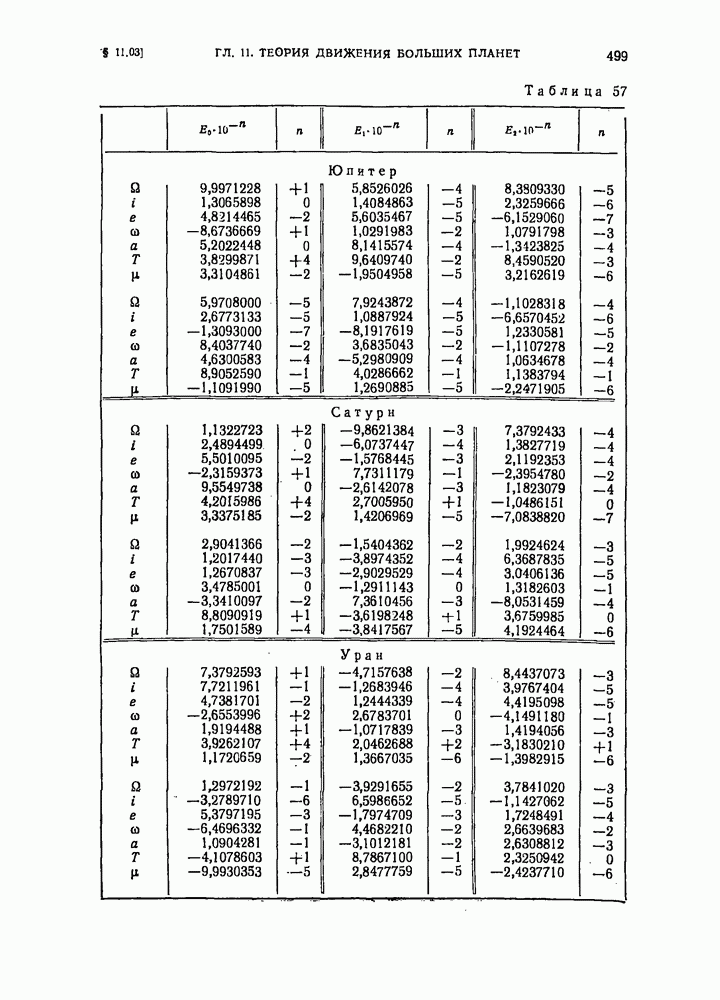
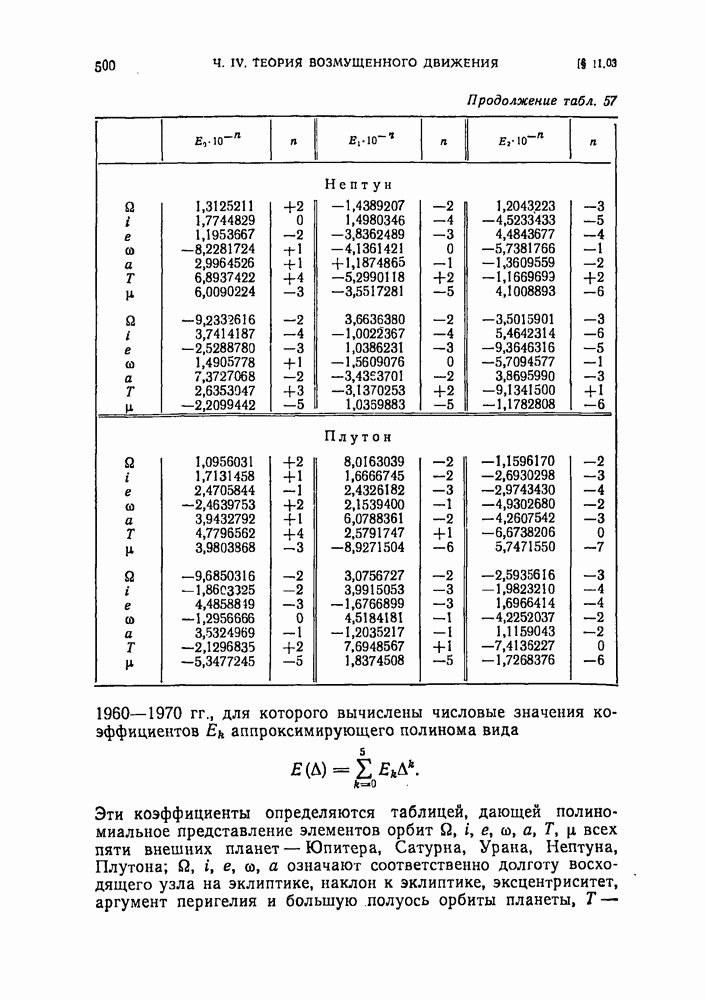
- § 11.03. Полиномиальное представление оскулирующих элементов орбит внешних планет
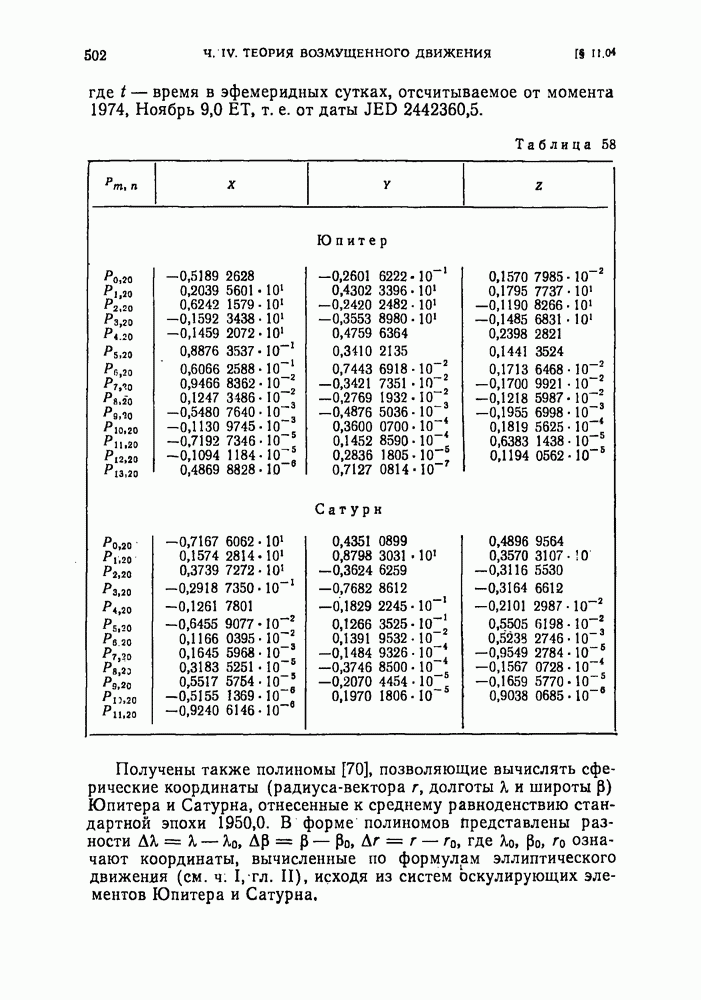
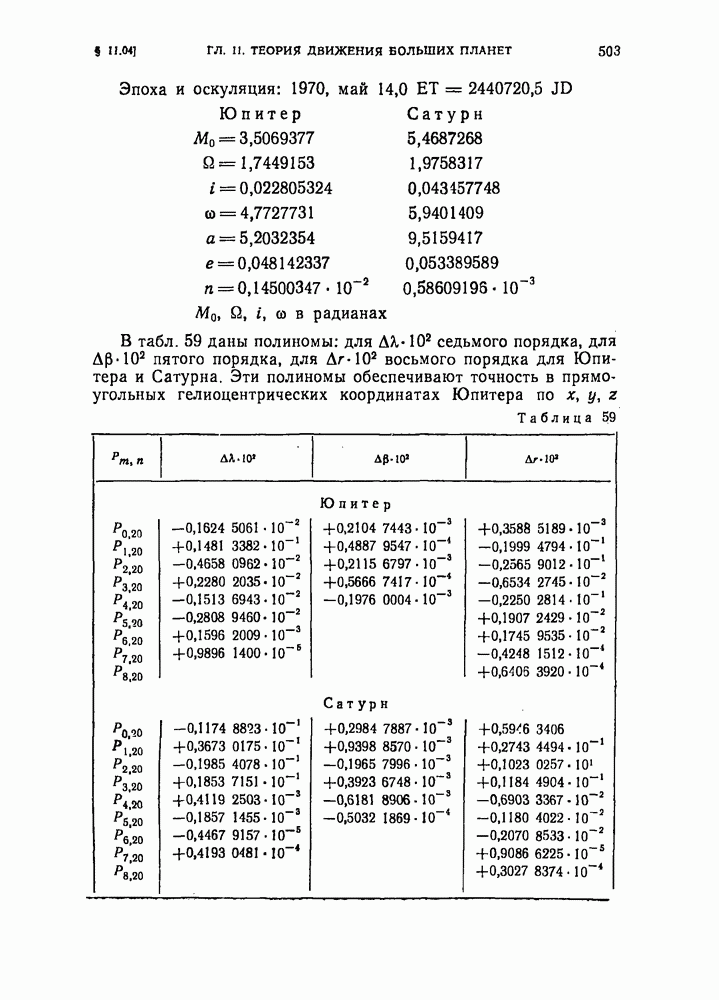
- § 11.04. Полиномиальное представление прямоугольных гелиоцентрических координат Юпитера и Сатурна
- § 11.05. Тригонометрическая теория вековых возмущений орбит больших планет
- Глава 12. ДВИЖЕНИЕ МАЛЫХ ТЕЛ СОЛНЕЧНОЙ СИСТЕМЫ
- § 12.01. Невозмущенное движение спутников
- § 12.02. Возмущения оскулирующих элементов орбит спутников, вызываемые сжатием планеты
- § 12.03. Возмущения в движении спутников, вызываемые притяжением Солнца
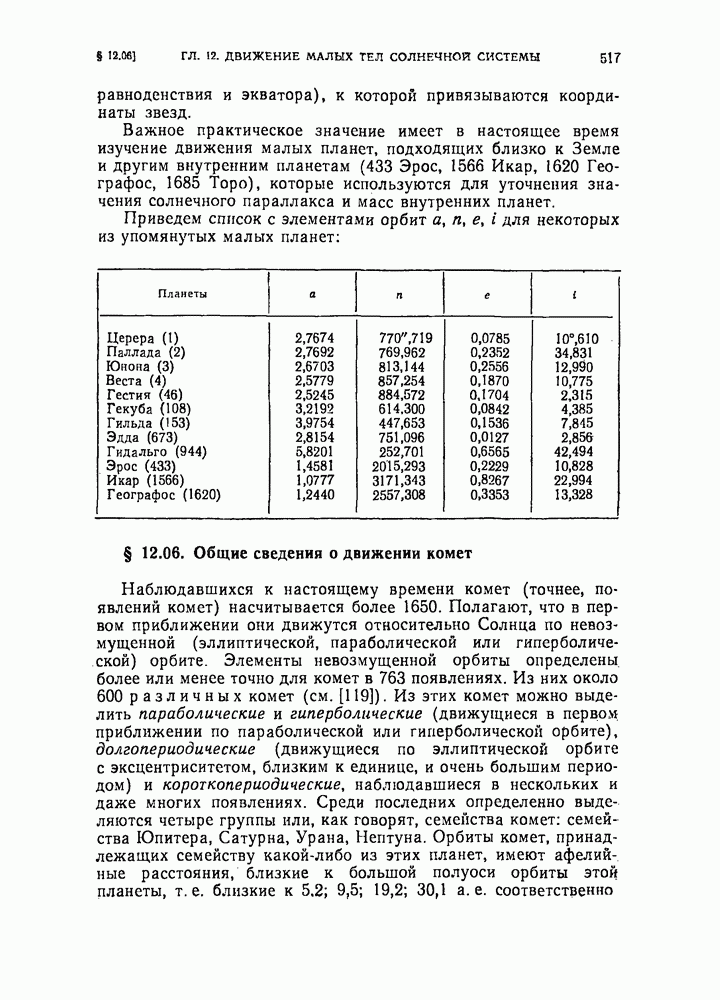
- § 12.04. Общие сведения о характере движения малых планет
- § 12.05. Возмущенное движение малых планет
- § 12.06. Общие сведения о движении комет
- § 12.07. Возмущенное движение комет
- Часть V. ЗАДАЧА ТРЕХ ТЕЛ
- Глава 1. НЕОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 1.02. Лагранжевы решения. Точки либрации
- Глава 2. ОГРАНИЧЕННАЯ КРУГОВАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 2.01. Дифференциальные уравнения движения. Интеграл Якоби
- § 2.02. Поверхность нулевой относительной скорости
- § 2.03. Лагранжевы решения ограниченной круговой задачи трех тел. Точки либрации
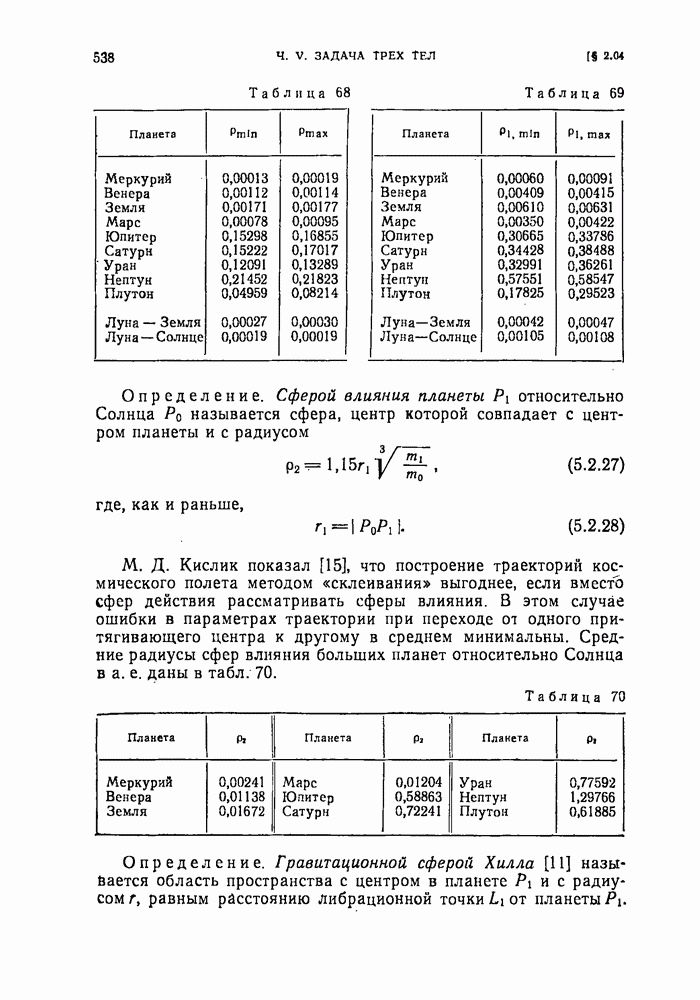
- § 2.04. Различные гравитационные сферы
- § 2.05. Периодические решения ограниченной круговой задачи трех тел
- § 2.06. Критерий Тиссерана
- § 2.07. Уравнения ограниченной круговой задачи в эллипсоидальных переменных
- § 2.08. Уравнение Гамильтона—Якоби в эллипсоидальных переменных
- § 2.09. Понижение порядка системы уравнений плоской ограниченной круговой задачи трех тел
- Глава 3. ДРУГИЕ ОГРАНИЧЕННЫЕ ЗАДАЧИ ТРЕХ ТЕЛ
- § 3.01. Общий случай ограниченной задачи трех тел
- § 3.02. Задача двух неподвижных центров
- § 3.03. Задача Хилла
- Часть VI. ДВИЖЕНИЕ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- Глава 1. ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИСКУССТВЕННОГО СПУТНИКА
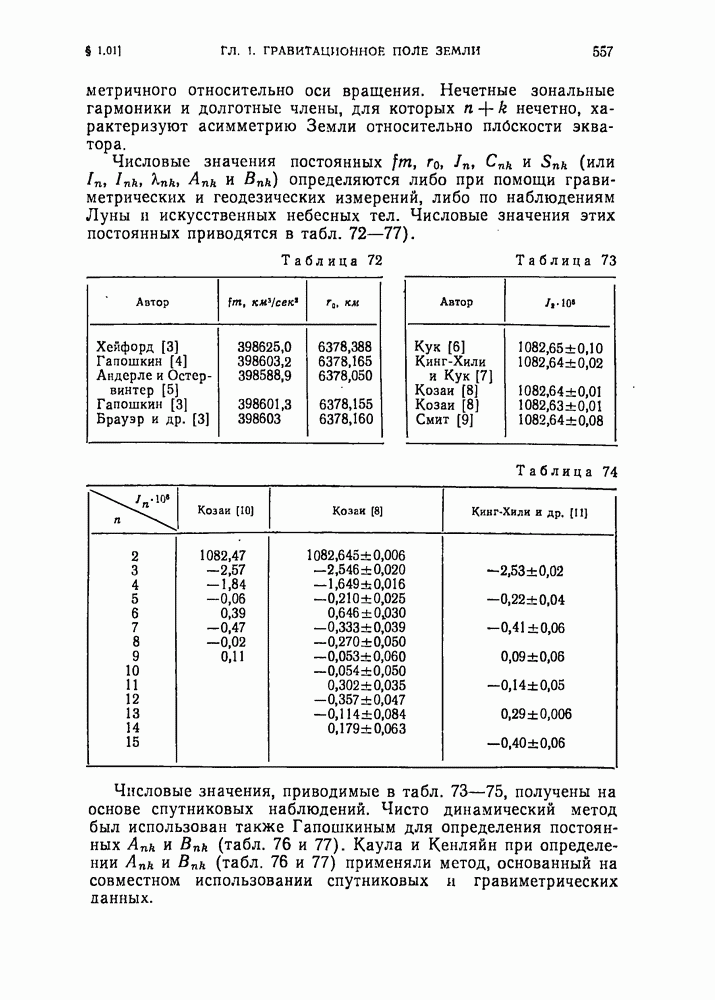
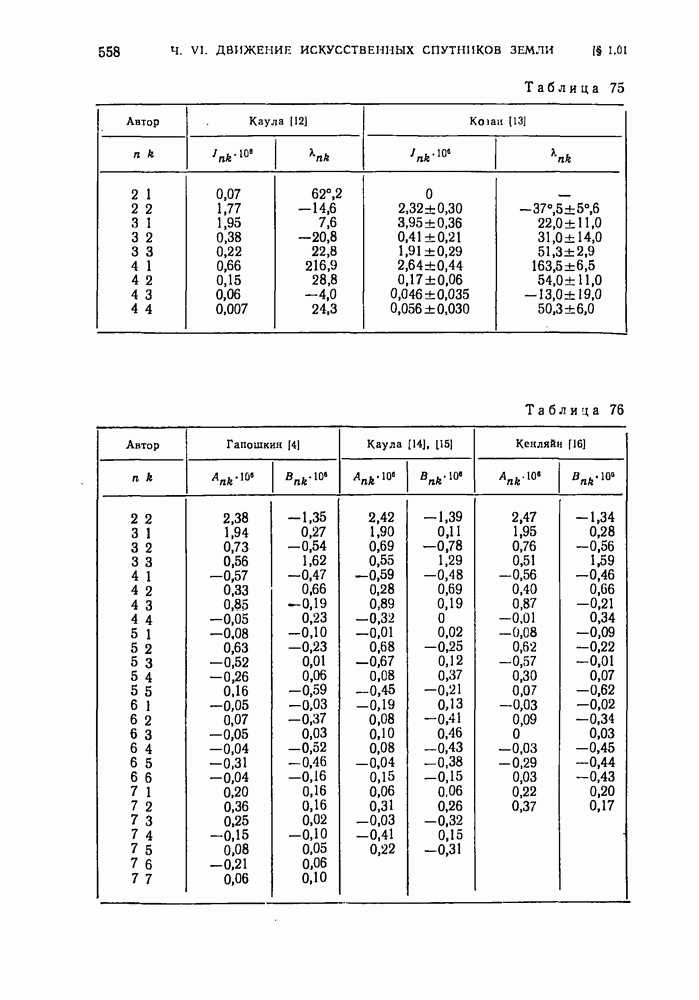
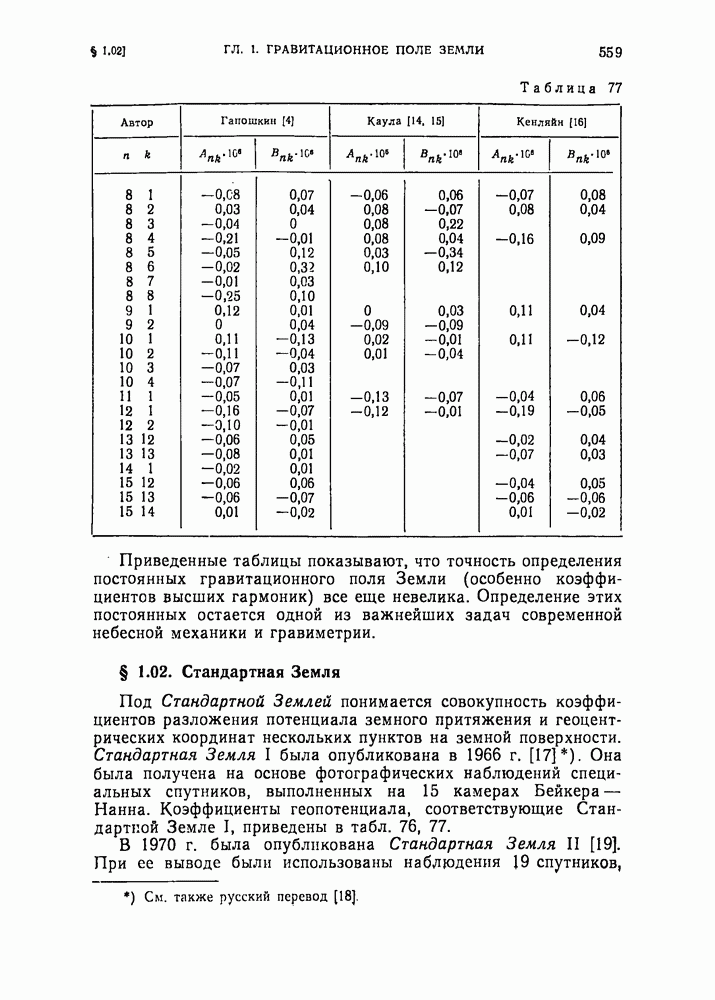
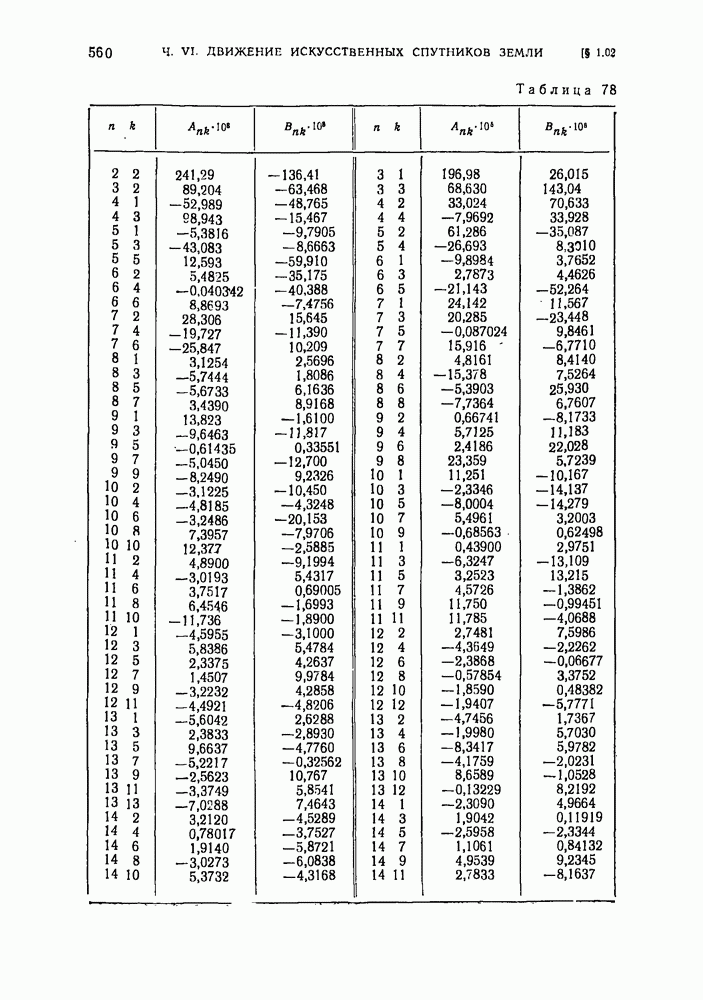
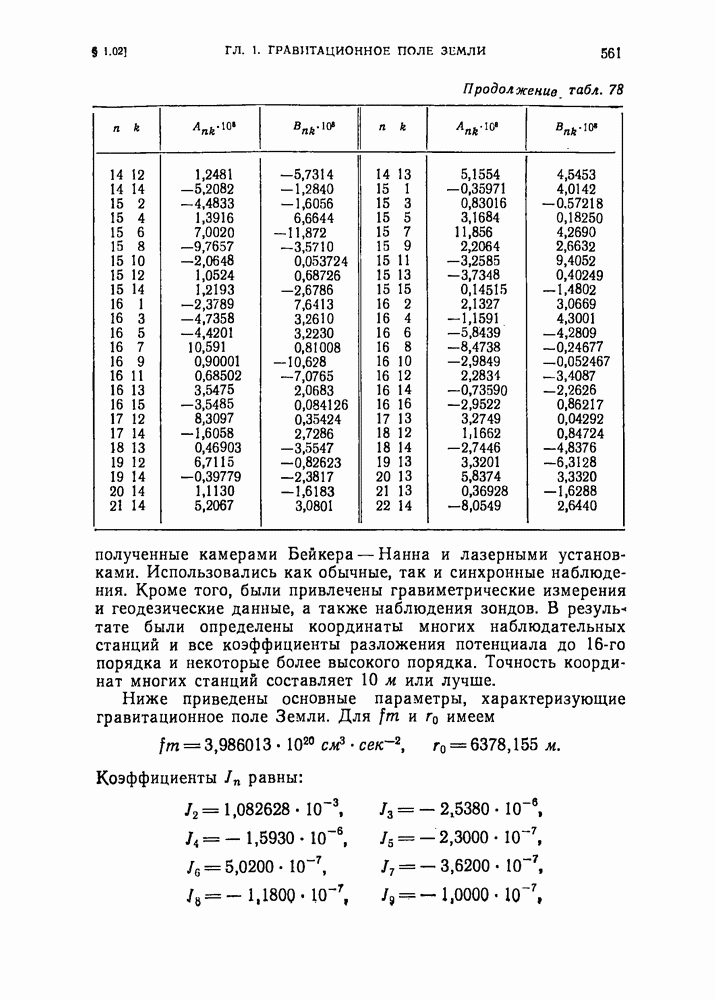
- § 1.02. Стандартная Земля
- § 1.03. Дифференциальные уравнения движения спутника
- § 1.04. Элементы орбиты ИСЗ. Дифференциальные уравнения для оскулирующих элементов
- Глава 2. ВОЗМУЩЕНИЯ, ВЫЗЫВАЕМЫЕ ВТОРОЙ ЗОНАЛЬНОЙ ГАРМОНИКОЙ ГЕОПОТЕНЦИАЛА
- § 2.01. Возмущения от второй зональной гармоники как функции средней аномалии
- § 2.02. Возмущения от второй зональной гармоники как функции истинной аномалии
- § 2.03. Случай орбит с малыми эксцентриситетами
- Глава 3. ТЕОРИЯ ПРОМЕЖУТОЧНЫХ ОРБИТ ИСЗ
- § 3.01. Задачи Штерна, Гарфинкеля и Акснеса
- § 3.02. Задачи Баррара, Винти и Кислика
- § 3.03. Обобщенная задача двух неподвижных центров
- § 3.04. Промежуточная орбита, основанная на обобщенной задаче двух неподвижных центров
- § 3.05. Дифференциальные уравнения для элементов промежуточной орбиты
- Глава 4. ВОЗМУЩЕНИЯ ГРАВИТАЦИОННОИ ПРИРОДЫ
- § 4.01. Возмущения от зональных гармоник высших порядков
- § 4.02. Возмущения от зональной гармоники произвольного порядка
- § 4.03. Возмущения от тессеральных и секториальных гармоник
- § 4.04. Лунно-солнечные возмущения
- § 4.05. Определение постоянных интегрирования
- § 4.06. Вычисление возмущенных координат спутника
- Глава 5. ВОЗМУЩЕНИЯ, ВЫЗЫВАЕМЫЕ СОПРОТИВЛЕНИЕМ АТМОСФЕРЫ И СВЕТОВЫМ ДАВЛЕНИЕМ
- § 5.02. Стандартная атмосфера
- § 5.03. Сила сопротивления атмосферы
- § 5.04. Основные возмущения от сопротивления атмосферы
- § 5.05. Продолжительность жизни спутника
- § 5.06. Эволюция орбиты на больших промежутках времени
- § 5.07. Сила светового давления
- § 5.08. Возмущения от светового давления (без учета тени)
- § 5.09. Возмущения от светового давления (с учетом тени)
- § 5.10. Теневая функция
- Глава 6. ДРУГИЕ ВОЗМУЩЕНИЯ В ДВИЖЕНИИ ИСЗ
- § 6.01. Возмущения, вызываемые прецессией и нутацией экваториальной плоскости Земли
- § 6.02. Возмущения, вызываемые приливной деформацией Земли
- § 6.03. Релятивистские эффекты. Влияние электромагнитных сил и притяжения атмосферы
- Часть VII. ЧИСЛЕННЫЕ МЕТОДЫ
- Глава 1. ИНТЕРПОЛИРОВАНИЕ И ПРИБЛИЖЕНИЕ ФУНКЦИЙ
- § 1.02. Интерполяционные формулы
- § 1.03. Остаточные члены интерполяционных формул
- § 1.04. Обратное интерполирование
- § 1.05. Интерполирование функции двух переменных
- § 1.06. Приближение функций с помощью сплайнов
- § 1.07. Среднеквадратичные приближения функций
- § 1.08. Сглаживание табличных значений функций
- § 1.09. Равномерные приближения
- § 1.10. Аппроксимация периодических функций с известным периодом тригонометрическими полиномами по методу наименьших квадратов
- § 1.11. Аппроксимация условно-периодических функций с известными частотами полиномом Фурье по методу наименьших квадратов
- § 1.12. Определение неизвестных частот периодической или условно-периодической функции по совокупности табличных данных
- § 1.13. Выделение «вековой части» функции по совокупности табличных значений
- Глава 2. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
- § 2.01. Численное дифференцирование с помощью интерполяционных формул
- § 2.02. Другие формулы численного дифференцирования
- § 2.03. Численное интегрирование функции по таблице ее значений с постоянным шагом
- § 2.04. Квадратурные формулы Гаусса
- § 2.05. Численное интегрирование сильно осциллирующих функций
- § 2.06. Правило Рунге практической оценки погрешности квадратурных формул
- § 2.07. Квадратурные формулы для несобственных интегралов
- Глава 3. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 3.01. Метод Рунге—Кутта
- § 3.02. Метод Адамса
- § 3.03. Метод Коуэлла
- § 3.04. Метод Штермера (для уравнений второго порядка)
- § 3.05. Метод Коуэлла (1-й вариант)
- § 3.06. Метод Коуэлла (2-й вариант)
- § 3.07. Накопление погрешностей при численном интегрировании
- § 3.08. Метод Энке численного интегрирования уравнений возмущенного движения
- § 3.09. Общая постановка краевой задачи для обыкновенных дифференциальных уравнений. Случай линейной краевой задачи
- § 3.10. Метод стрельбы при нахождении решения линейной двухточечной краевой задачи
- § 3.11. Краевая задача для квазилинейной системы с линейными краевыми условиями
- § 3.12. Краевая задача для системы, близкой к нелинейной невозмущенной системе
- § 3.13. Применение метода градиентного спуска для решения нелинейной краевой задачи общего вида
- § 3.14. Разностный метод решений краевых задач
- Глава 4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- § 4.02. Линейные и равноточные условные уравнения
- § 4.03. Вероятностные оценки погрешности решения
- § 4.04. Неравноточные условные уравнения
- § 4.05. Линеаризация условных уравнений общего вида
- Часть VIII. ОПТИМАЛЬНЫЕ И КРАЕВЫЕ ЗАДАЧИ АСТРОДИНАМИКИ
- Глава 1. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ И МАТЕМАТИЧЕСКОЙ ТЕОРИИ ОПТИМАЛЬНЫХ ПРОЦЕССОВ
- § 1.01. Понятие функционала
- § 1.02. Задача Лагранжа. Множители Лагранжа. Уравнения Эйлера
- § 1.03. Первая формулировка задачи Майера
- § 1.04. Вторая формулировка задачи Майера
- § 1.05. Изопериметрическая задача
- § 1.06. Задача Больца
- § 1.07. Третья формулировка задачи Майера. Обобщение теоремы Лагранжа. Характеристические уравнения (обобщенные уравнения Эйлера — Лагранжа)
- § 1.08. Свойство множителей Лагранжа на ломаных экстремалях. Условие Вейерштрасса — Эрдмана
- § 1.09. Принцип максимума Понтрягина
- § 1.10. Принцип оптимальности Беллмана
- Глава 2. ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ ТЕЛ ПЕРЕМЕННОЙ МАССЫ
- § 2.01. Основное уравнение динамики точки переменной массы (уравнение Мещерского)
- § 2.02. Обобщенное уравнение Мещерского
- § 2.03. Уравнения движения тела переменной массы в обобщенных координатах (уравнения Лагранжа второго рода)
- § 2.04. Канонические уравнения движения тела переменной массы
- Глава 3. НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ЗАДАЧИ ДИНАМИКИ ПОЛЕТА В ОКОЛОЗЕМНОМ ПРОСТРАНСТВЕ
- § 3.01. Уравнения движения ракеты. Формула Циолковского
- § 3.02. Развернутая форма характеристических уравнений для задачи о движении ракеты
- § 3.03. Определение базис-вектора и p-траектории. Определение функций переключения
- § 3.04. Определение импульсной тяги. Точки соединения на оптимальных траекториях
- § 3.05. Максимизация высоты вертикального подъема ракеты в однородном поле тяжести
- § 3.06. Максимизация горизонтальной дальности полета ракеты в однородном поле тяжести при заданной программе расхода топлива
- § 3.07. Общая вариационная задача для движения ракеты в однородном поле тяжести
- § 3.08. Общая вариационная задача для движения ракеты в однородном поле тяжести при наличии аэродинамического сопротивления
- § 3.09. Определение оптимальной программы тяги при вертикальном подъеме ракеты в неоднородном поле тяготения в сопротивляющейся атмосфере
- § 3.10. Задача о максимизации полной энергии космического аппарата
- § 3.11. Задача о минимизации характеристической скорости маневра
- Глава 4. МЕЖОРБИТАЛЬНЫЕ ПЕРЕЛЕТЫ
- § 4.02. Уравнение для базиса-вектора на участке нулевой тяги при движении ракеты в ньютоновском поле тяготения
- § 4.03. Уравнение для базиса-вектора на участке промежуточной тяги при движении ракеты в ньютоновском поле тяготения
- § 4.04. Уравнение для базиса-вектора на участке максимальной тяги при движении ракеты в ньютоновском поле тяготения
- § 4.05. Метод p-траекторий. Структура оптимальной траектории
- § 4.06. Связь между величиной импульса и элементами эллиптической орбиты
- § 4.07. Оптимальный n-импульсный переход между двумя заданными компланарными эллиптическими орбитами
- § 4.08. Оптимальный переход между двумя компланарными круговыми орбитами
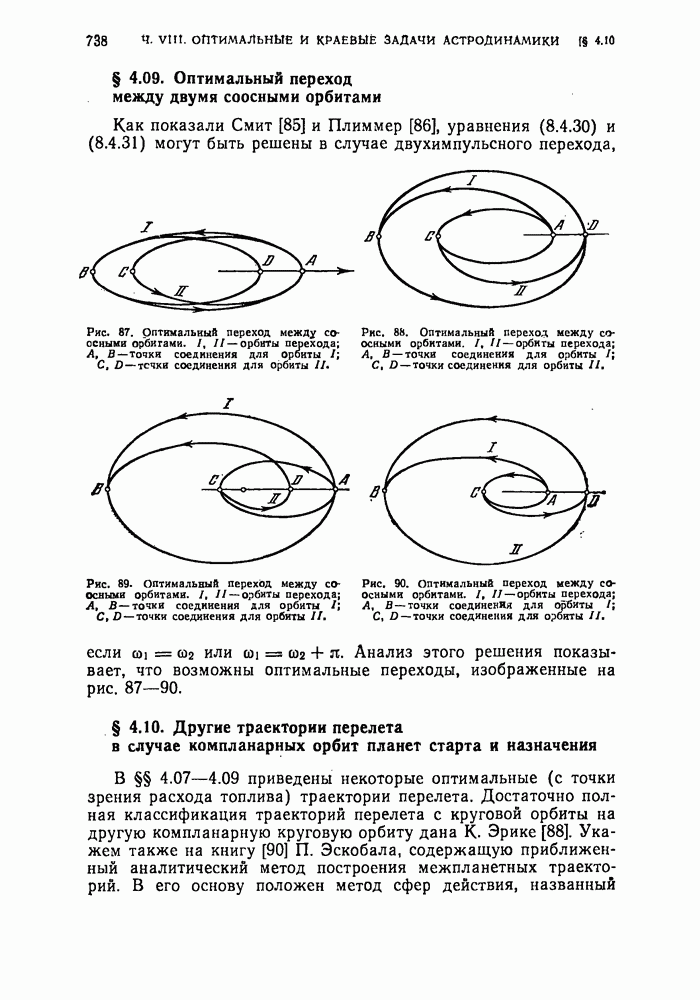
- § 4.09. Оптимальный переход между двумя соосными орбитами
- § 4.10. Другие траектории перелета в случае компланарных орбит планет старта и назначения
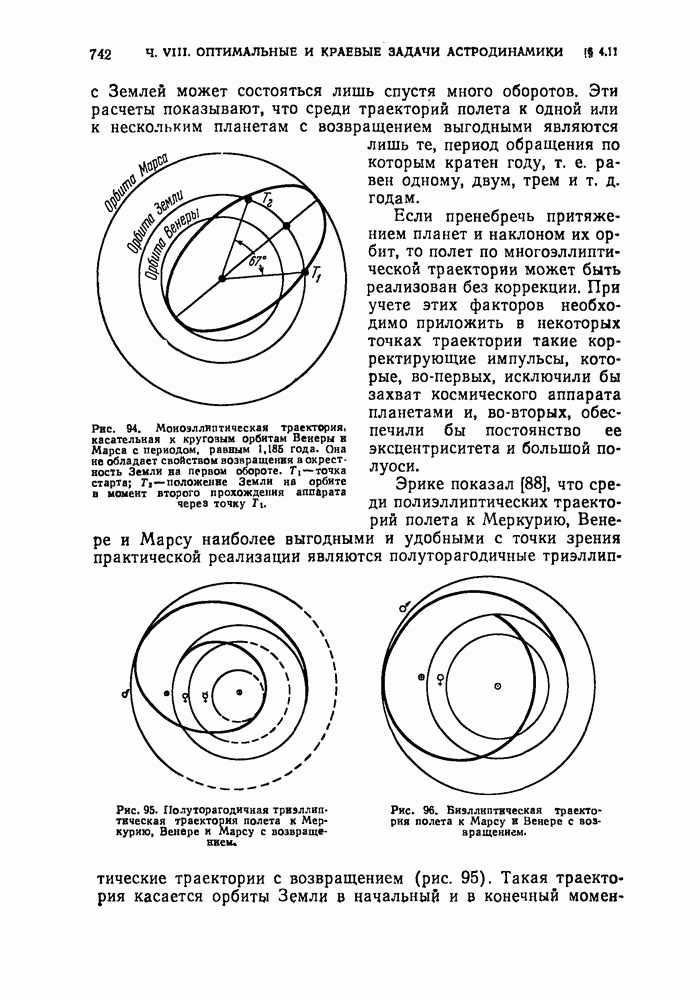
- § 4.11. Траектории полета вблизи нескольких планет
- § 4.12. Начальный этап (запуск и уход) межпланетной траектории
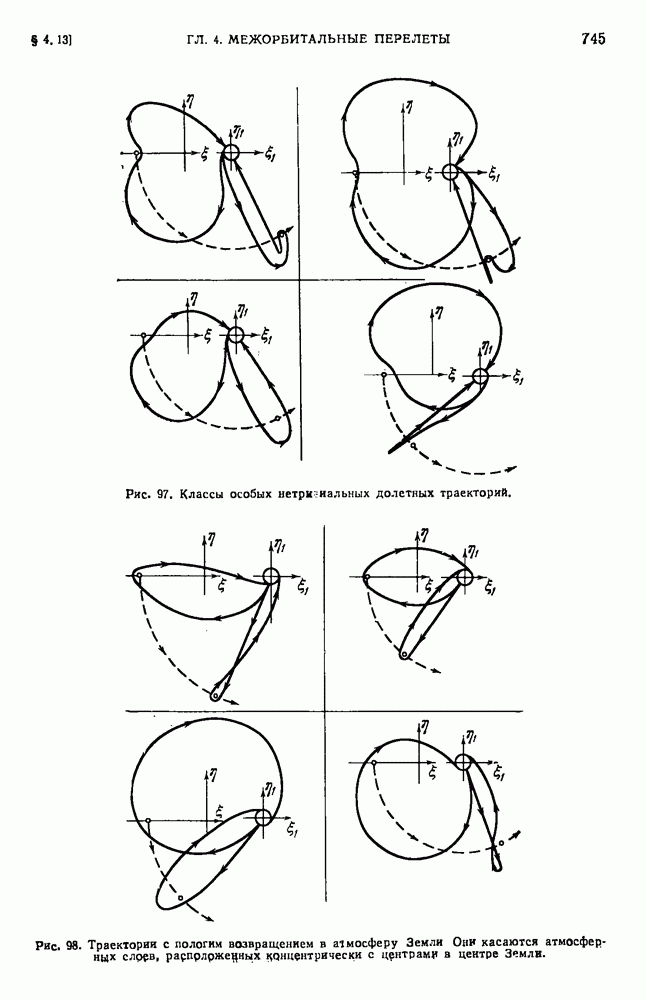
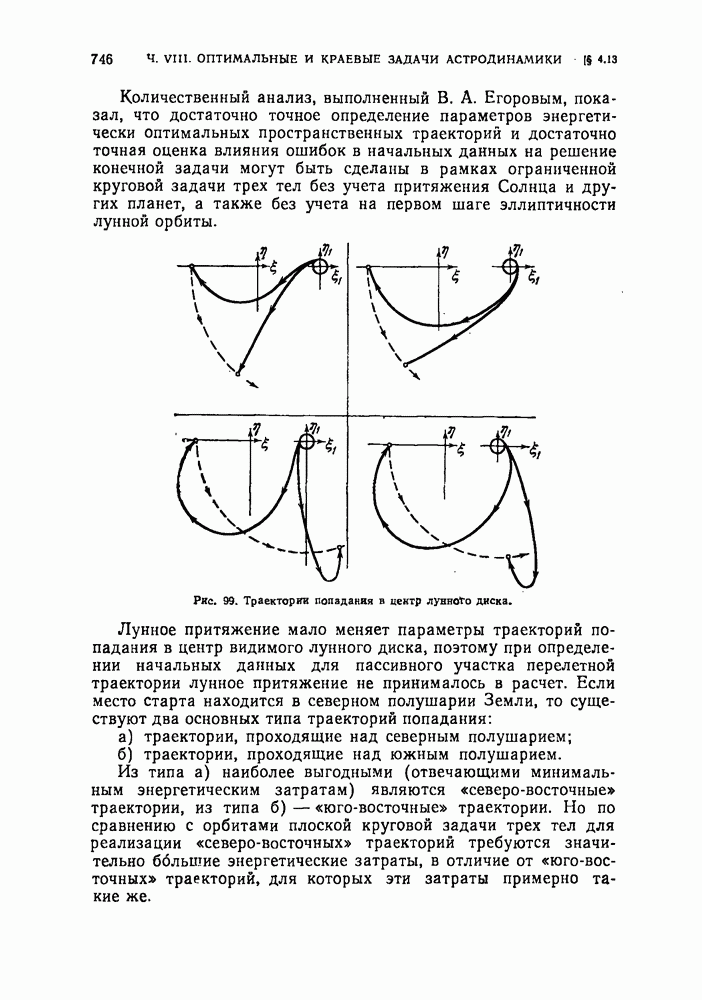
- § 4.13. Полеты к Луне
- Часть IX. ДВИЖЕНИЕ ЕСТЕСТВЕННЫХ И ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
- Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
- § 1.02. Канонические уравнения вращательного движения небесных тел
- § 1.03. Астродинамические дифференциальные уравнения возмущенного движения спутника относительно центра масс
- § 1.04. Моменты сил, действующих на спутник
- § 1.05. Движение спутника относительно центра масс в центральном ньютоновском поле
- § 1.06. Задача о поступательно-вращательном движении двух гравитирующих динамически симметричных тел
- § 1.07. Вращение Луны
- § 1.08. Дифференциальные уравнения движения деформируемого небесного тела
- § 1.09. Теория фигур небесных тел
- Глава 2. УСТОЙЧИВОСТЬ И СТАБИЛИЗАЦИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ
- § 2.01. Устойчивость движения спутников в гравитационном поле сил
- § 2.02. Устойчивость движения спутников под действием моментов сил различной природы
- § 2.03. Стабилизация движения спутников и космических аппаратов
- Часть X. КАЧЕСТВЕННАЯ НЕБЕСНАЯ МЕХАНИКА
- Глава 1. ПЕРИОДИЧЕСКИЕ И УСЛОВНО-ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ. ФИНАЛЬНЫЕ ДВИЖЕНИЯ
- § 1.02. Метод Ляпунова
- § 1.03. Периодические решения, полученные методом Пуанкаре
- § 1.04. Периодические решения, полученные методом Ляпунова
- § 1.05. Периодические решения, полученные качественными методами
- § 1.06. Почти периодические функции и их свойства. Условно-периодические функции
- § 1.07. Теорема Арнольда о существовании условно-периодических решений гамильтоновых систем
- § 1.08. Условно-периодические решения в небесной механике. Геометрическая интерпретация
- § 1.09. Финальные движения в задаче трех тел. Захват и обмен в задаче трех тел
- Глава 2. ПРОБЛЕМА ИНТЕГРИРУЕМОСТИ И СХОДИМОСТЬ РЯДОВ В НЕБЕСНОЙ МЕХАНИКЕ
- § 2.01. Теорема Пуассона об интеграле гамильтоновой системы
- § 2.02. Теорема Брунса о несуществовании алгебраических первых интегралов задачи трех тел, отличных от классических
- § 2.03. Теорема Пуанкаре о несуществовании однозначных аналитических первых интегралов гамильтоновой системы
- § 2.04. Случаи интегрируемости уравнения Гамильтона — Якоби методом разделения переменных
- § 2.05. Теорема о неприводимости уравнения Гамильтона — Якоби для плоской ограниченной круговой задачи трех тел к уравнению типа Штеккеля
- § 2.06. Соударения
- § 2.07. Решение задачи трех тел в виде рядов, сходящихся для всех вещественных значений времени. Теорема Зундмана
- § 2.08. Сходимость рядов Хилла в основной проблеме теории движения Луны
- § 2.09. Характер сходимости рядов классической теории возмущений
- § 2.10. Теоремы Пуанкаре о ранге и классе возмущений
- § 2.11. Поиск частных, первых и общих интегралов заданной аналитической структуры обыкновенных дифференциальных уравнений на ЭВМ. Приложение к ограниченной задаче трех тел
- § 2.12. Поиск решений уравнения Гамильтона — Якоби на ЭВМ. Приложение к ограниченной задаче трех тел
- Глава 3. ПРОБЛЕМА УСТОЙЧИВОСТИ В НЕБЕСНОЙ МЕХАНИКЕ
- § 3.01. Определение устойчивости по Ляпунову
- § 3.02. Определение орбитальной устойчивости
- § 3.03. Другие определения устойчивости
- § 3.04. Знакопостоянные и знакоопределенные функции. Полная производная в силу системы
- § 3.05. Теоремы Ляпунова об устойчивости
- § 3.06. Устойчивость по отношению к части переменных. Теорема В. В. Румянцева
- § 3.07. Связка первых интегралов. Способ Н. Г. Четаева
- § 3.08. Устойчивость при постоянно действующих возмущениях. Теорема И. Г. Малкина
- § 3.09. Теоремы Лапласа — Лагранжа и Пуассона об отсутствии вековых возмущений больших полуосей
- § 3.10. Теоремы об устойчивости планетных орбит
- § 3.11. Теоремы Арнольда об устойчивости решения гамильтоновой системы в общем эллиптическом случае
- § 3.12. Устойчивость лагранжевых равновесных решений задачи трех тел
- § 3.13. Устойчивость других решений задачи трех тел
- § 3.14. Устойчивость орбитальных движений искусственных спутников