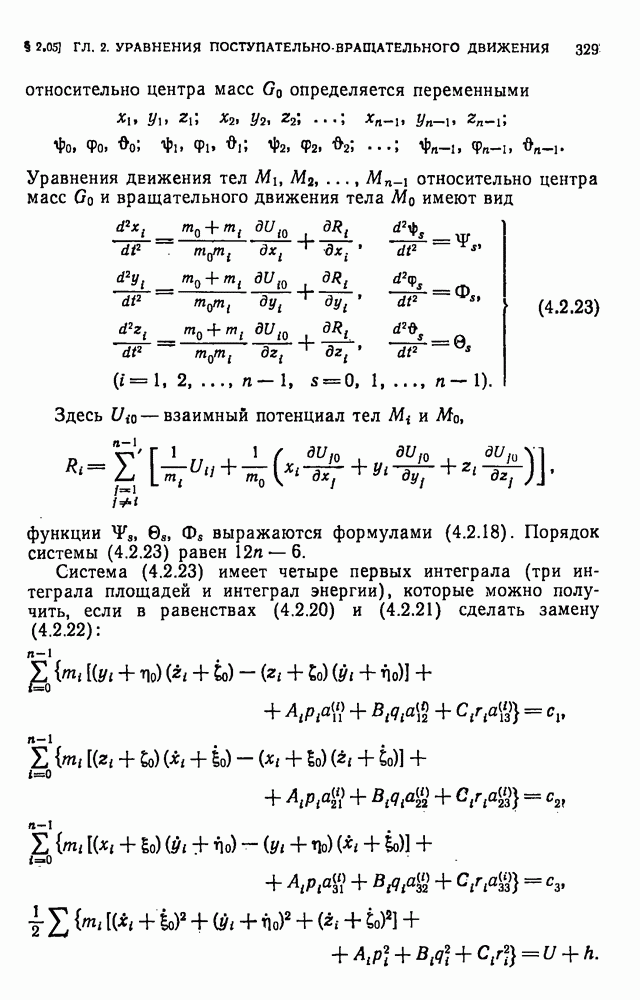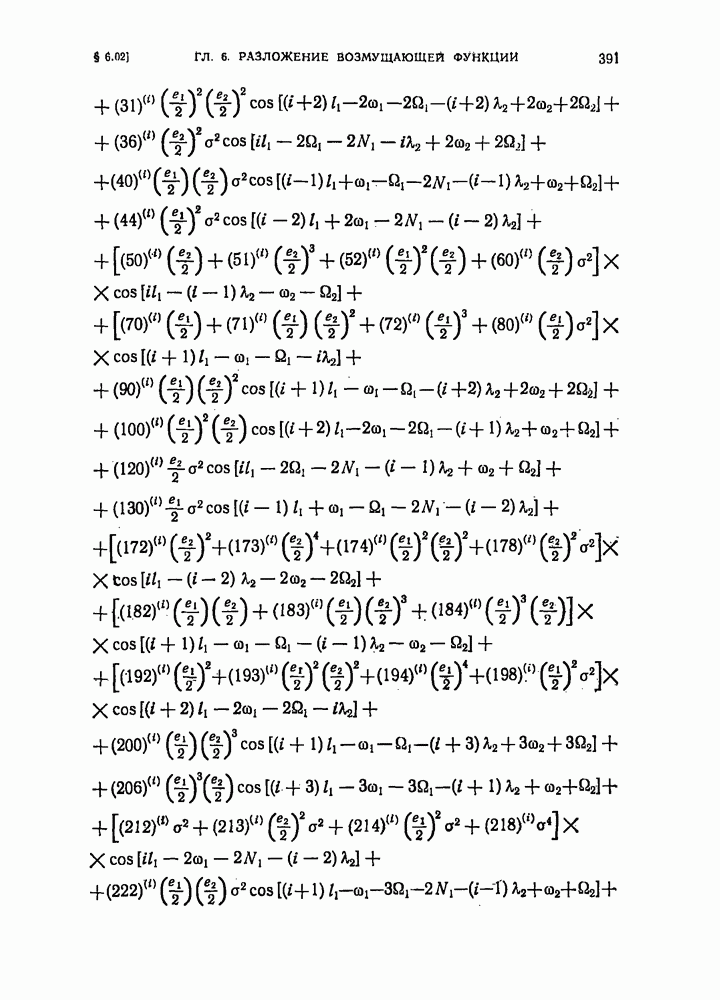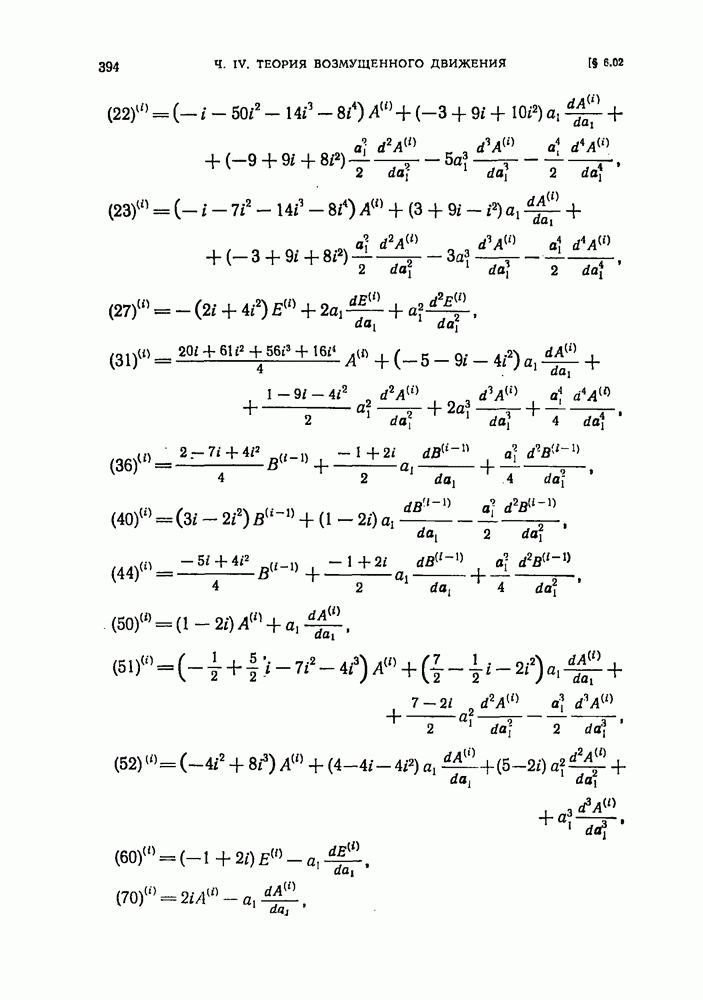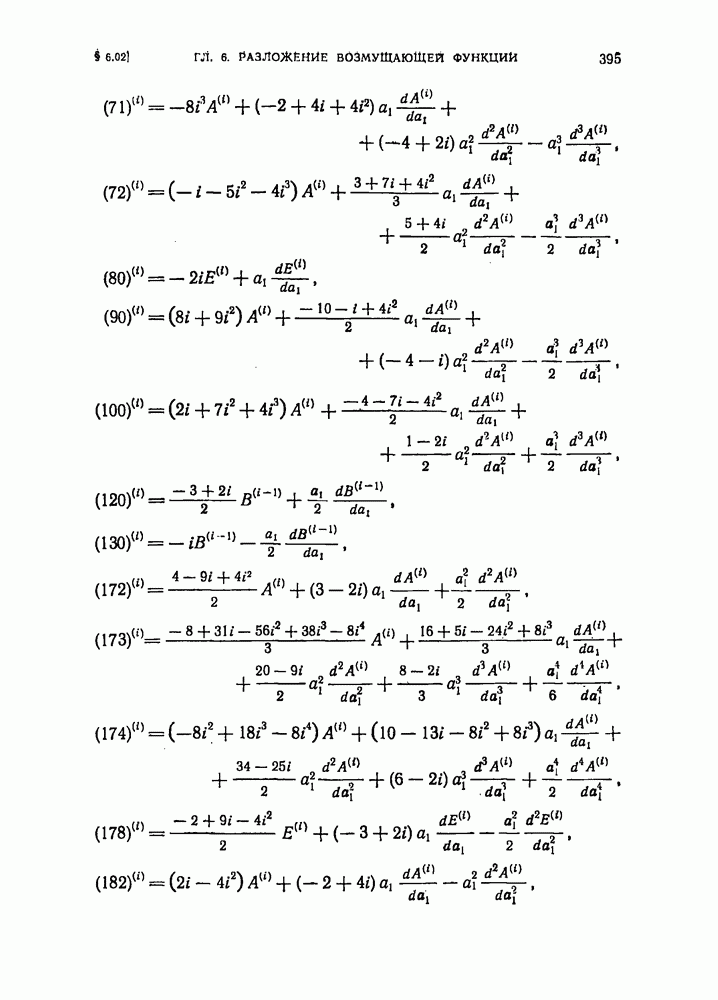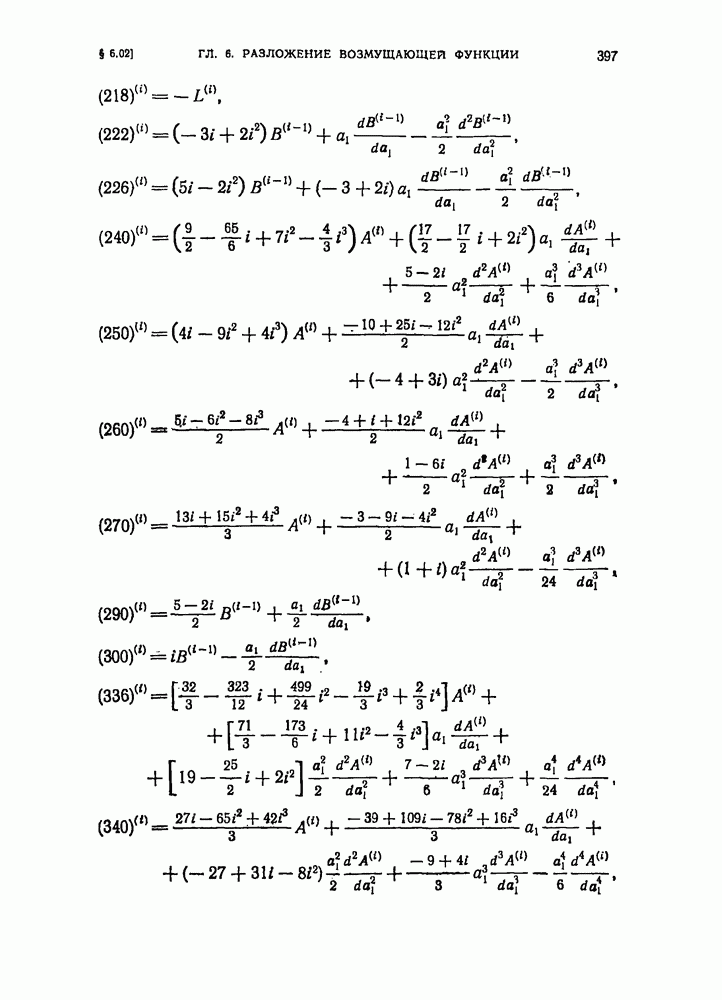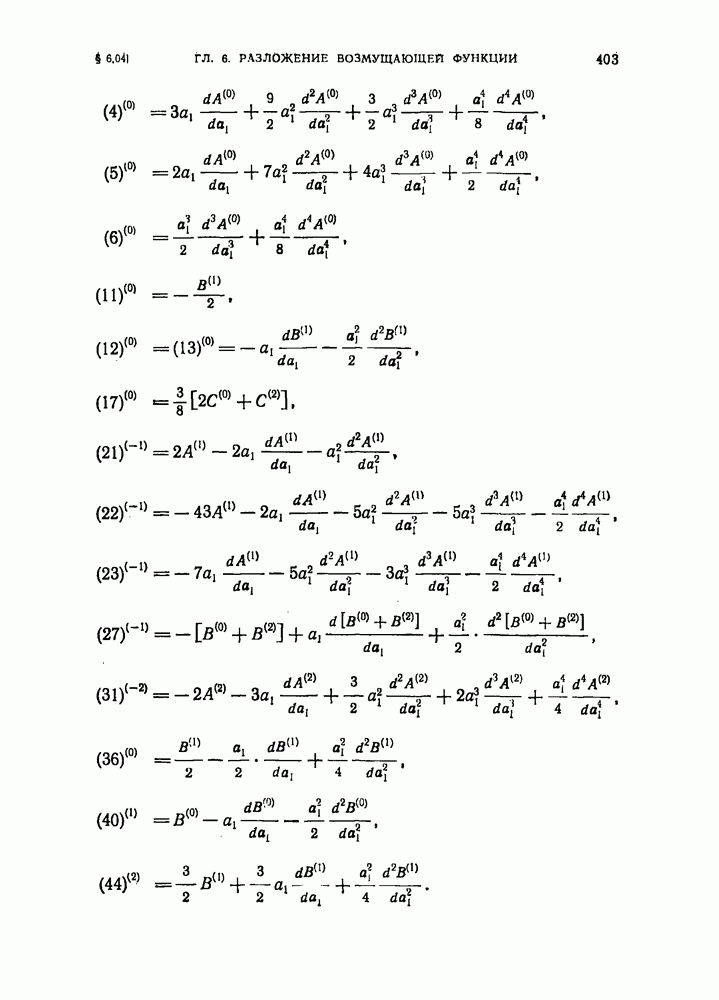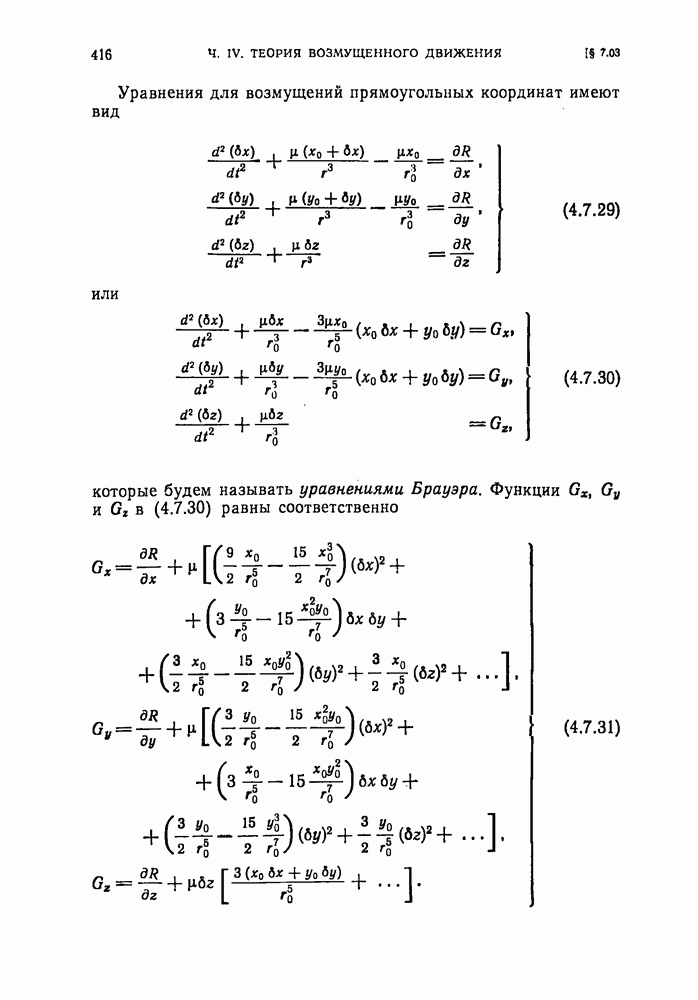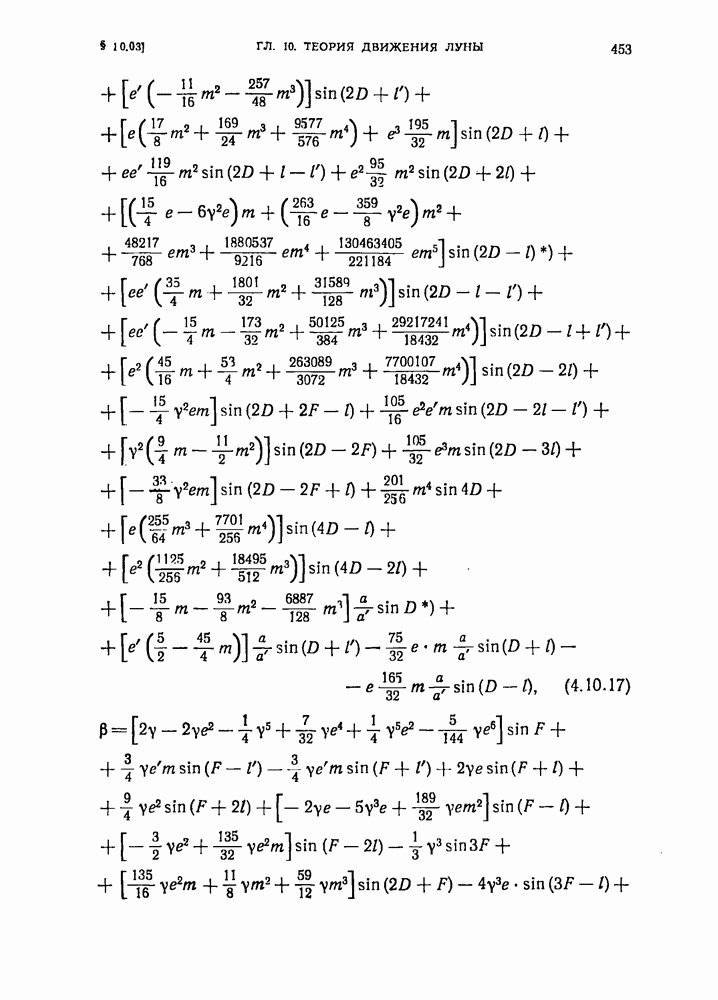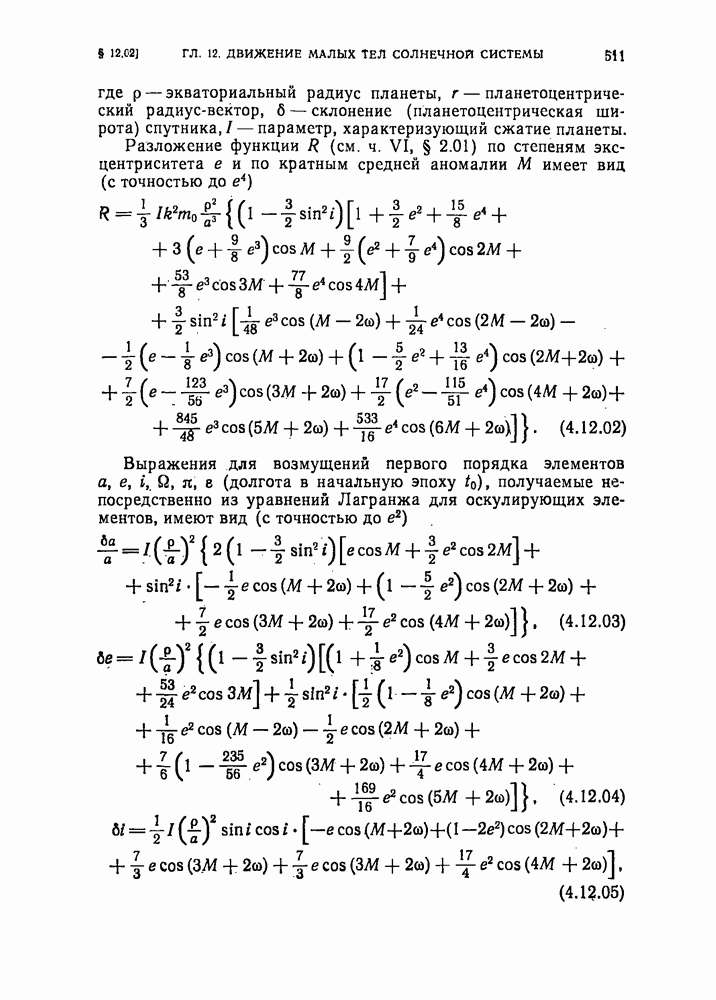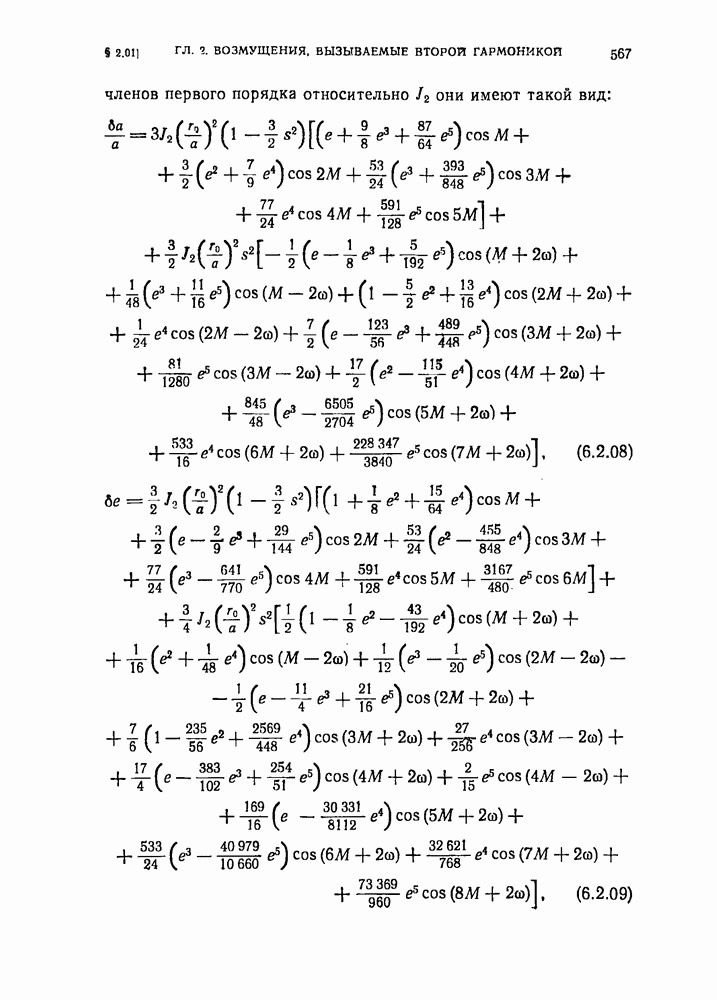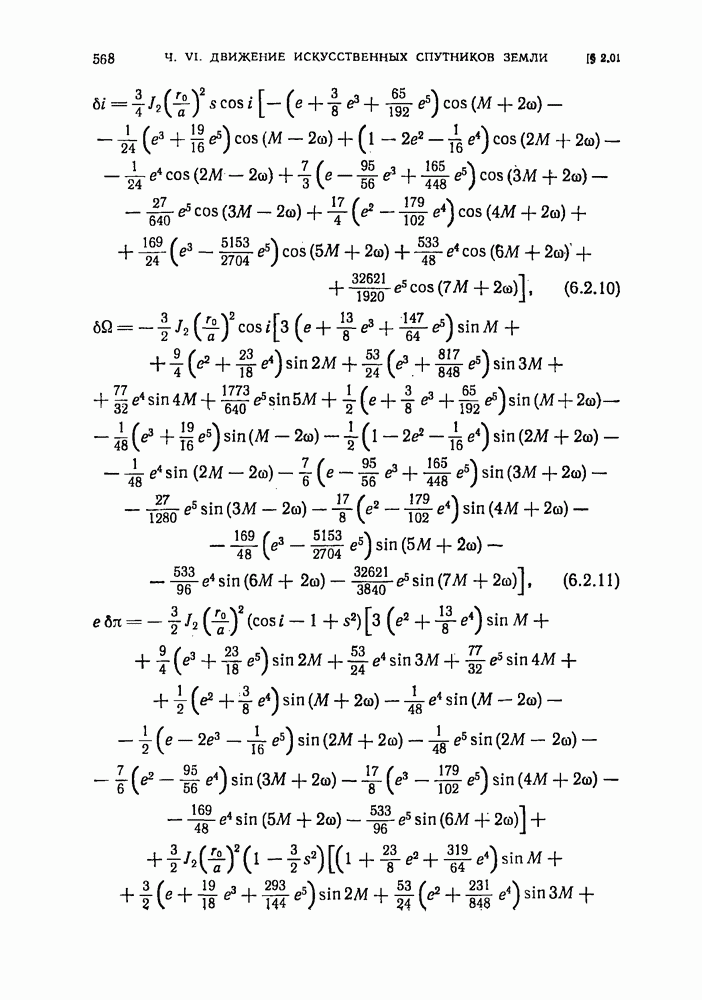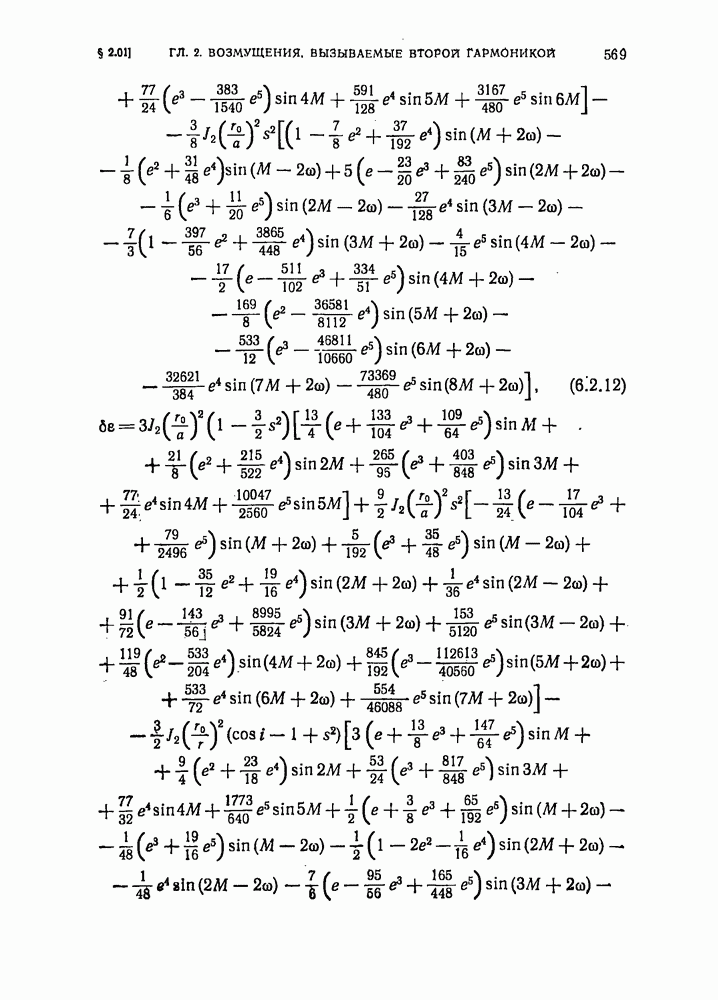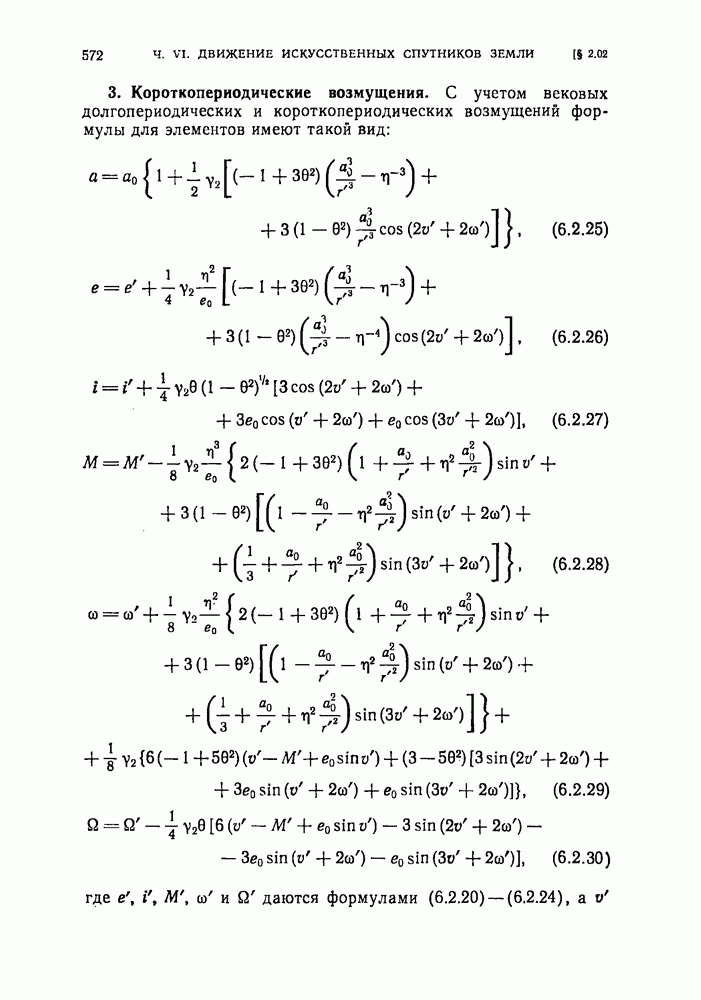| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
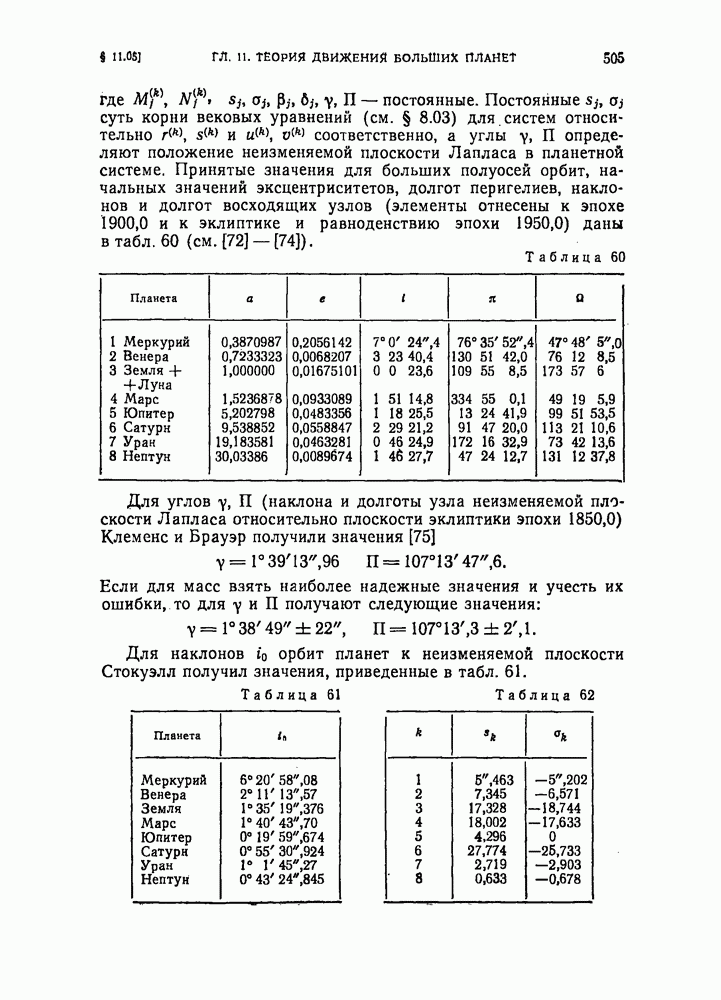
505
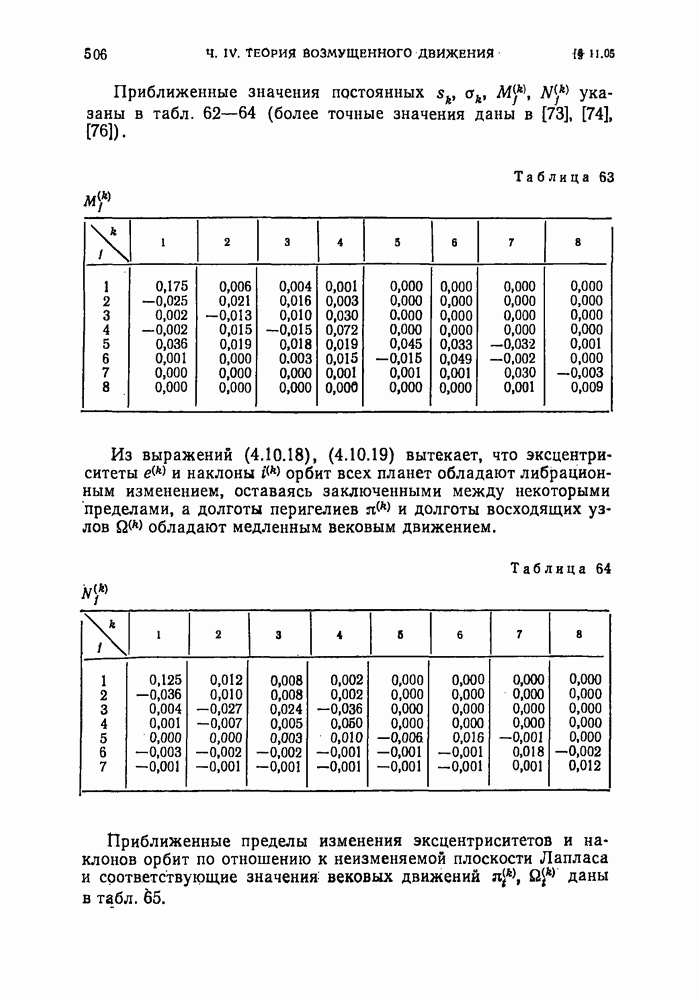
506
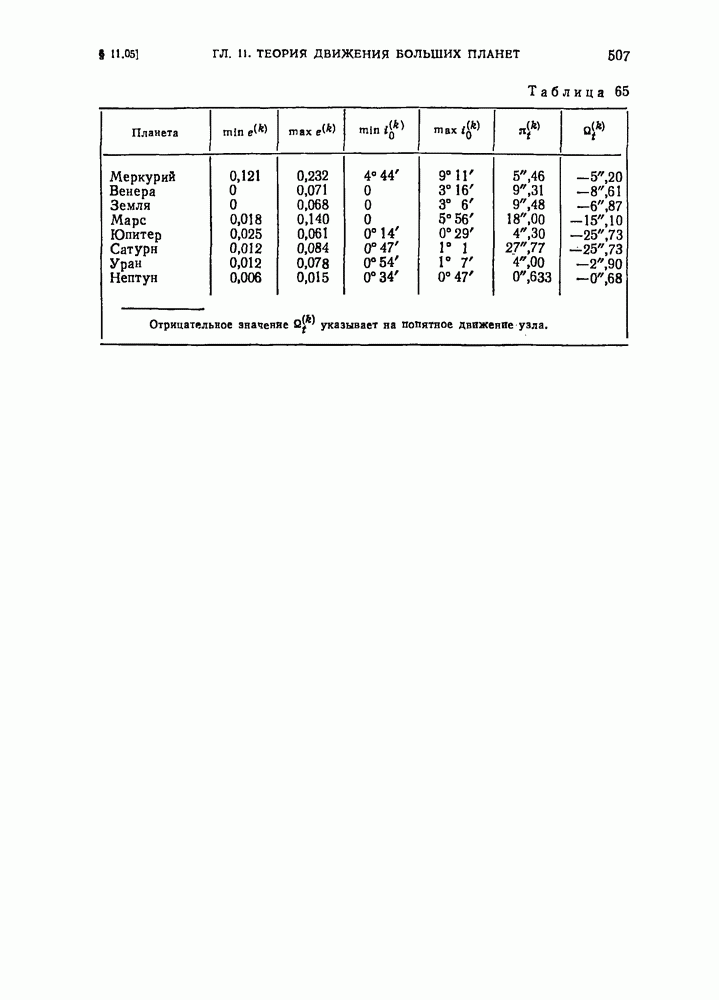
507
508
509
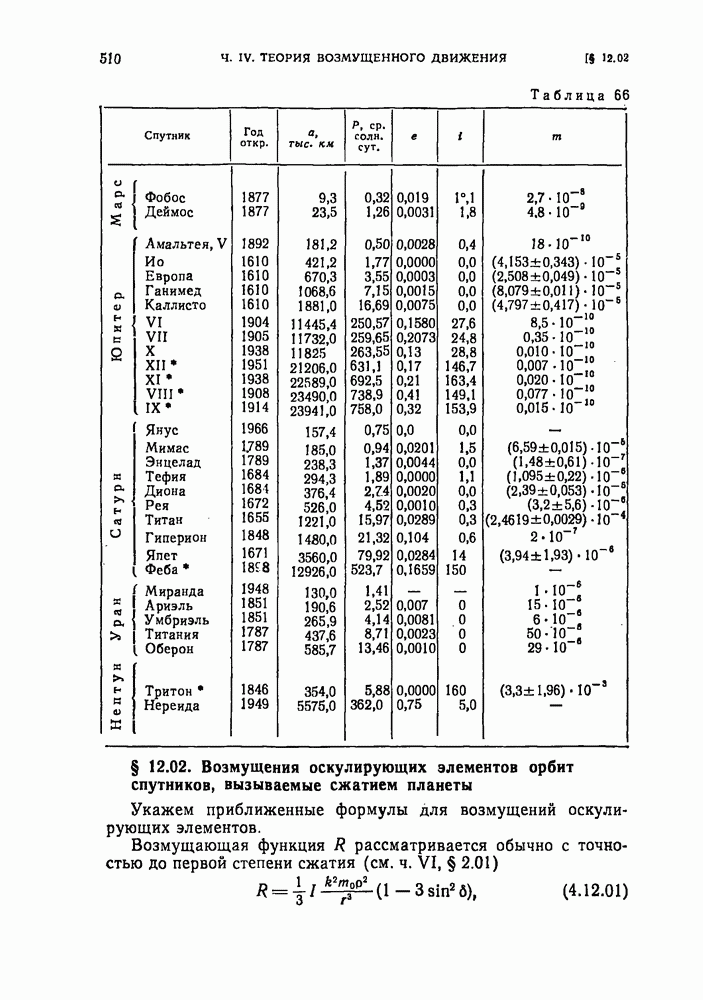
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
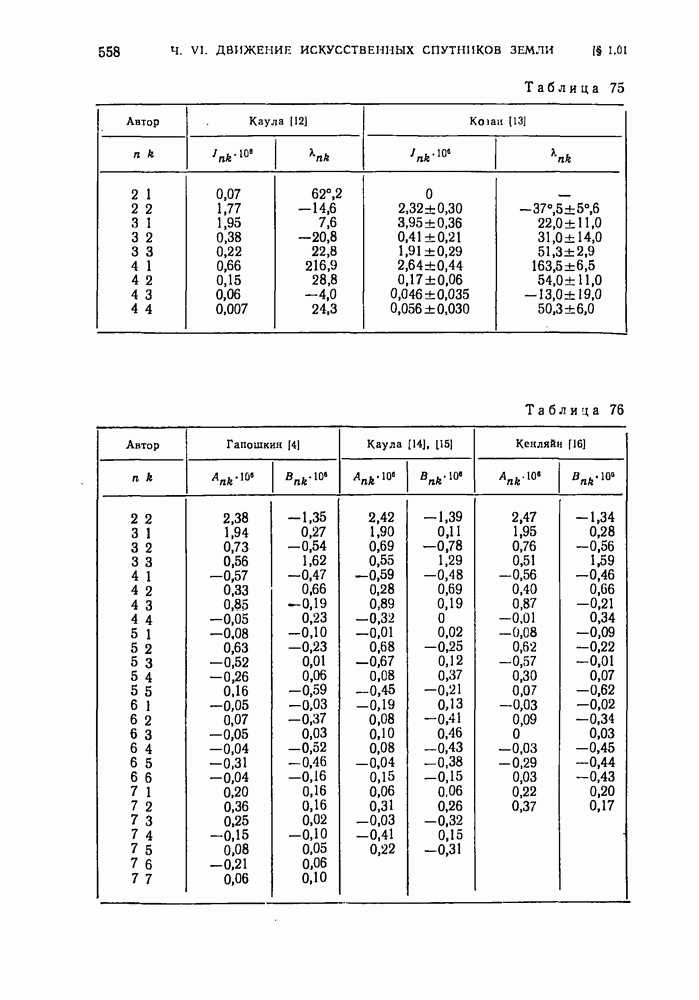
558
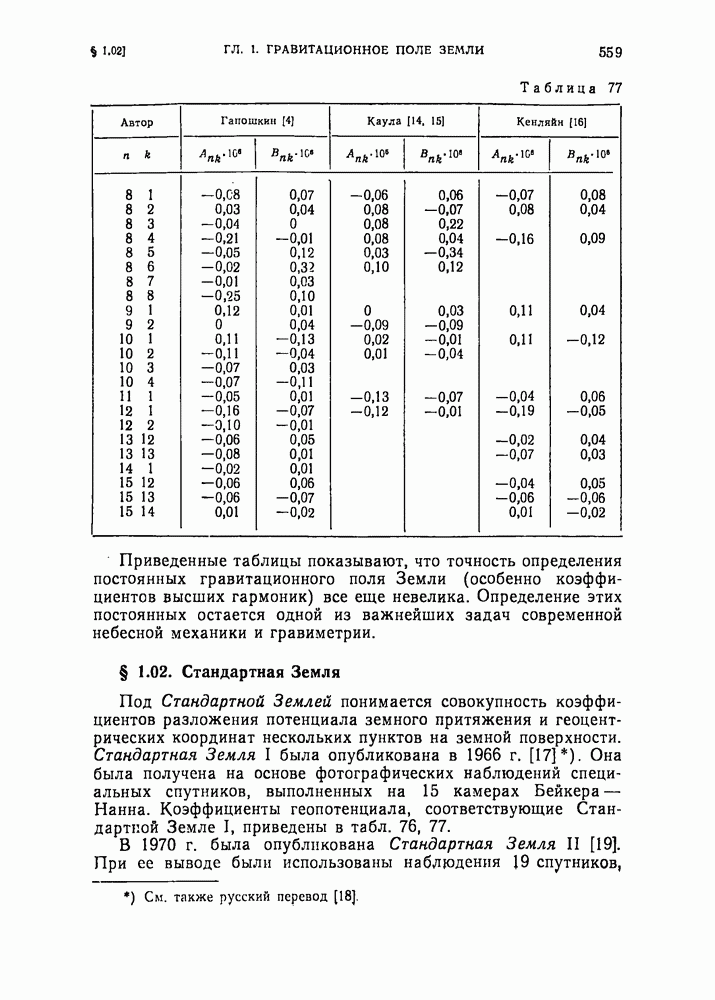
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
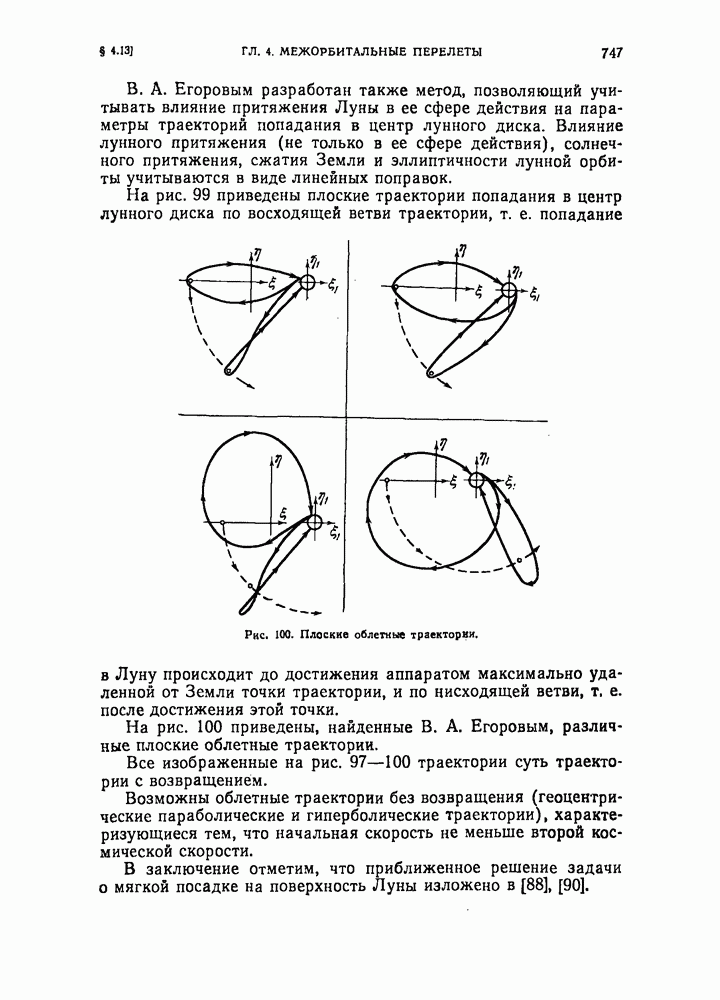
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
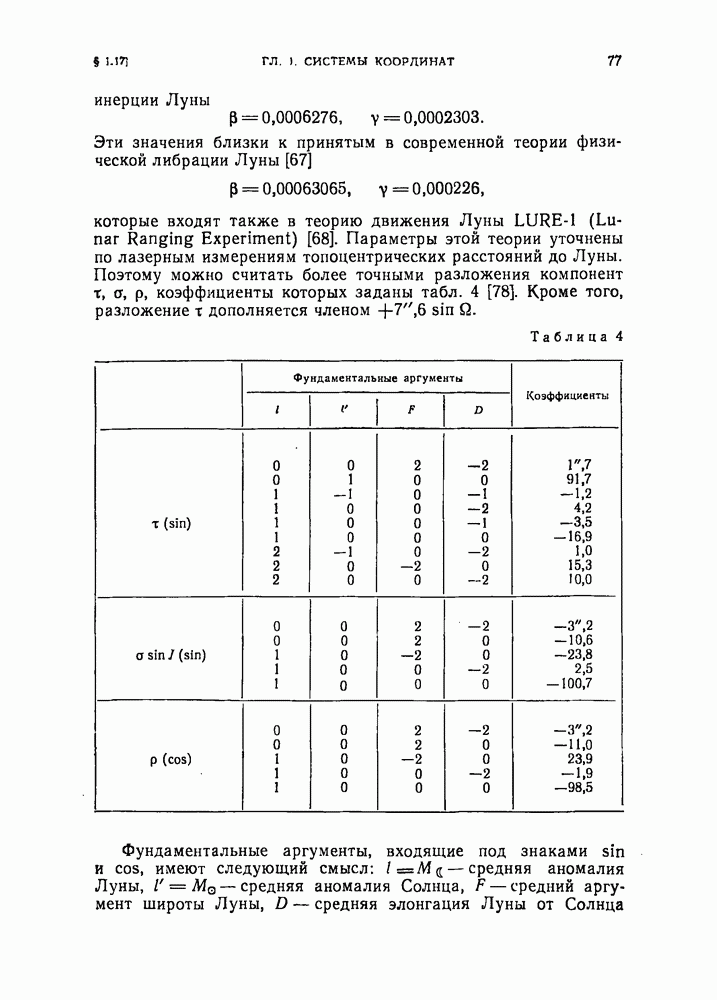
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Часть I. СФЕРИЧЕСКАЯ И ЭФЕМЕРИДНАЯ АСТРОНОМИЯ, ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
Изучение движения небесных объектов в Солнечной системе связано в той или иной степени с двумя проблемами астрономии — проблемой точного предвычисления положения небесного объекта в определенной системе координат на заданный момент времени и проблемой обработки наблюдений этого объекта. Для правильного решения этих проблем необходимо знать не только закон движения небесного объекта, но и законы изменения ориентировки в пространстве систем координат, относительно которых происходит рассматриваемое движение, необходимо уметь найти путем подходящего преобразования координат такую систему отсчета, в которой уравнения движения имеют наиболее выгодную для поставленных целей форму.
С необходимостью учета изменений положения основных элементов координатных систем во времени связана также задача сравнения наблюденных положений объекта с теоретически предвычисленными, особенно при больших промежутках времени наблюдения. К ней тесно примыкают вопросы фиксации физических моментов наблюдений в различных системах измерения времени и перехода от одной системы к другой.
Наконец, совершенствование теории движения небесного объекта, сопутствующее повышению точности наблюдений, требует улучшения числовых значений параметров теории, к которым относятся астрономические постоянные — универсальные величины, соотношения между которыми следуют из основных законов механики неба.
Изложению этих вопросов с конечной целью дать читателю возможность применения рабочих формул в конкретных случаях посвящена эта часть настоящего «Справочного руководства».
Глава 1. СИСТЕМЫ КООРДИНАТ
§ 1.01. Небесная сфера
Наблюдения и предвычисления положений небесных тел, а также изучение их движения, всегда связаны с определенной системой отсчета (системой координат и системой измерения времени).
Все системы астрономических (и аэродинамических) координат строятся по одному и тому же принципу: всегда выбирают основную (фундаментальную) плоскость и указывают направление основной (главной) оси системы координат.
За начало координат принимают обычно либо точку наблюдения на земной поверхности, либо центр Земли, Солнца или планеты и т. д.
В основу сферической астрономии положено понятие небесной сферы, центр которой совпадает с началом рассматриваемой системы отсчета, а радиус может быть выбран совершенно произвольным (обычно его полагают равным единице). Таким образом, вводится понятие топоцентрической небесной сферы с центром в точке наблюдения (в топоцентре), геоцентрической небесной сферы с центром, совпадающим с центром масс Земли, гелиоцентрической небесной сферы с центром в центре масс Солнца, планетоцентрической небесной сферы с центром в центре масс планеты. Аналогично вводятся соответствующие различные системы координат: топоцентрическая, геоцентрическая, гелиоцентрическая, планетоцентрическая и т. д. Иногда вводят барицентрическую систему координат, начало которой совпадает с центром масс (барицентром) системы нескольких небесных тел (например, системы Солнце + внутренние планеты).
Необходимо всегда иметь в виду, что термином «планетоцентрическая (селено-, или луноцентрическая) система координат» обозначается система, основная плоскость которой параллельна плоскости небесного экватора для Земли, и проводить четкое различие между этим термином и термином «планетографическая (селенографическая) система координат», относящимся к системам, основной плоскостью которых является плоскость экватора собственного осевого вращения планеты (Луны). В случае планетографических систем координат латинское название небесного тела заменяется в наименовании координат соответствующим греческим эквивалентом (например, юпитероцентрические координаты, но зенографические координаты, марсоцентрические координаты, но ареографические координаты и т. д.). Планетографические системы координат применяются большей частью для определения положений точек и деталей поверхности соответствующих планет [1].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Часть I. СФЕРИЧЕСКАЯ И ЭФЕМЕРИДНАЯ АСТРОНОМИЯ, ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
- Глава 1. СИСТЕМЫ КООРДИНАТ
- § 1.02. Главные круги, линии и точки небесной сферы
- § 1.03. Горизонтальная система координат
- § 1.04. Экваториальные системы координат
- § 1.05. Эклиптическая система координат
- § 1.06. Галактическая система координат
- § 1.07. Основные формулы сферической тригонометрии
- § 1.08. Соотношения между различными астрономическими координатами
- § 1.09. Прямоугольные системы координат
- § 1.10. Системы географических координат
- § 1.11. Соотношения между астрономическими и геодезическими координатами
- § 1.12. Планетоцентрические системы координат [25]
- § 1.13. Марсоцентрическая и ареографическая системы координат
- § 1.14. Юпитероцентрическая и зенографическая системы координат
- § 1.15. Сатурноцентрическая система координат
- § 1.16. Системы координат, определяемые осевым вращением Солнца, Венеры, Урана и Нептуна
- § 1.17. Луноцентрическая и селенографическая системы координат
- § 1.18. Орбитальная система координат
- § 1.19. Объектоцентрическая система координат
- Глава 2. РЕДУКЦИОННЫЕ ВЫЧИСЛЕНИЯ
- § 2.01. Прецессия
- § 2.02. Редукция звездных положений с учетом прецессии и собственного движения
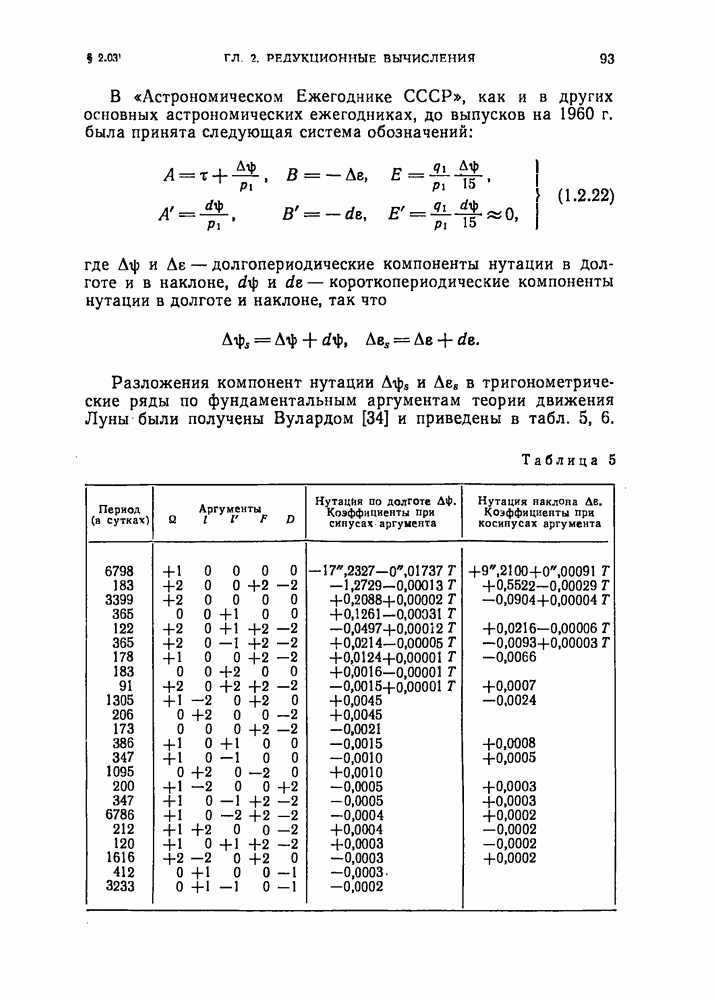
- § 2.03. Нутация
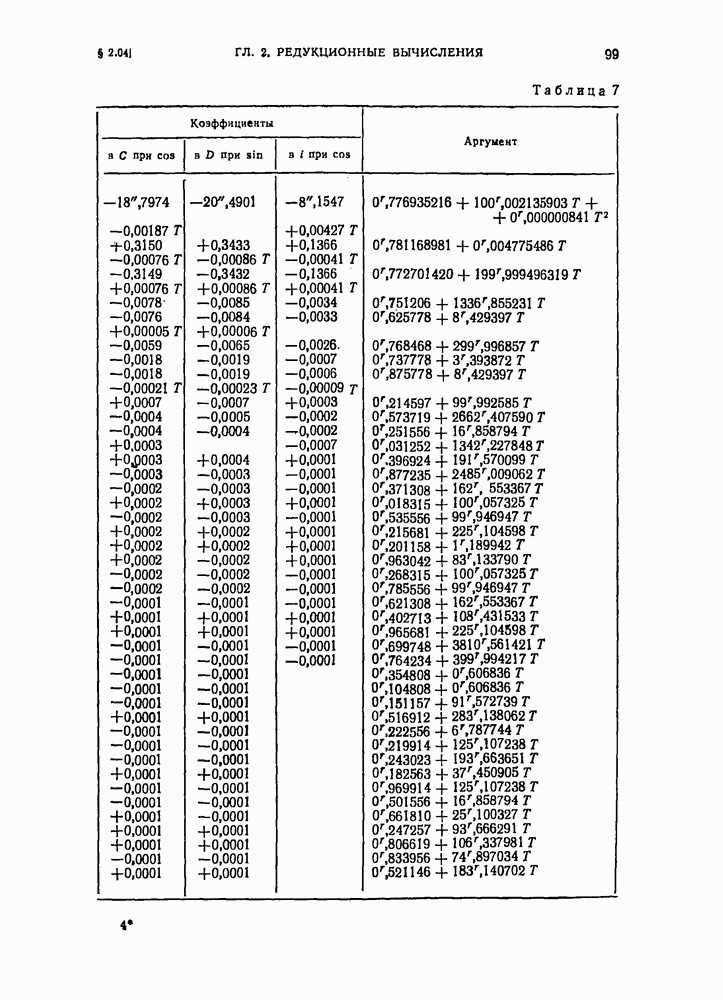
- § 2.04. Годичная аберрация
- § 2.05. Сводка основных формул редукции звездных положений
- § 2.06. Учет влияния членов второго порядка
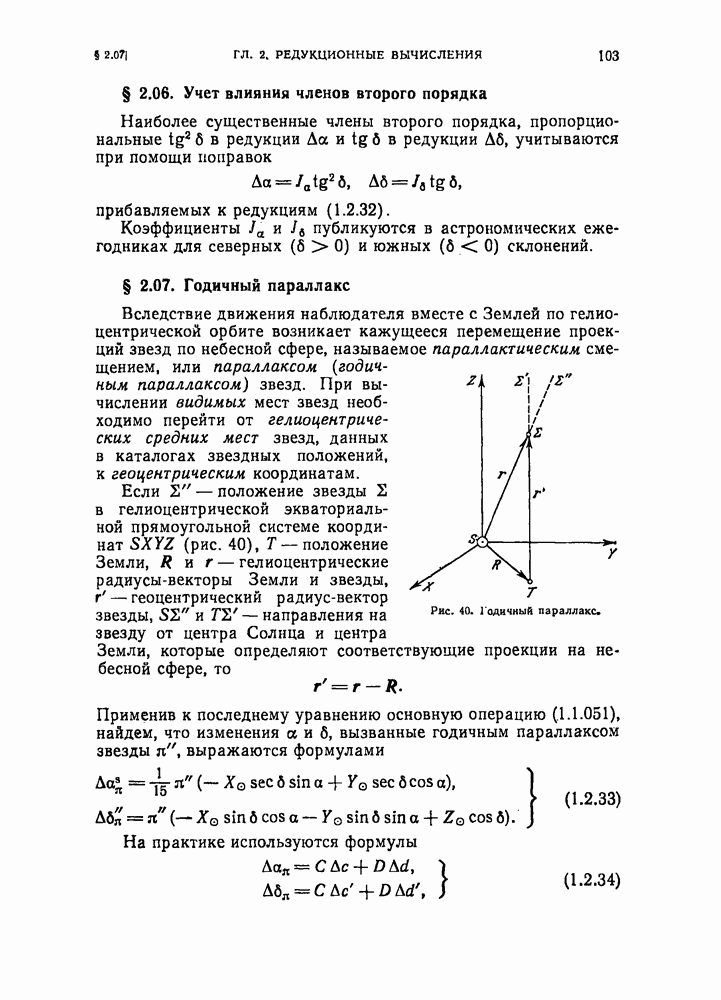
- § 2.07. Годичный параллакс
- § 2.08. Точные формулы для учета прецессии
- § 2.09. Формулы учета прецессии в прямоугольных экваториальных координатах
- § 2.10. Формулы учета прецессии в прямоугольных эклиптических координатах
- § 2.11. Совместный учет прецессии и нутации в прямоугольных экваториальных координатах
- § 2.12. Формулы учета прецессии в координатах и элементах орбит при умеренных и малых разностях эпох
- § 2.13. Аберрация света
- § 2.14. Приведение звезды на видимое место в прямоугольных координатах
- § 2.15. Об учете орбитального движения компонент двойных звезд
- § 2.16. Параллакс
- § 2.17. Учет суточного параллакса в горизонтальной системе координат
- § 2.18. Формулы учета суточного параллакса в экваториальной системе координат
- § 2.19. Формулы учета суточного параллакса в координатах Солнца и планет
- § 2.20. Формулы учета суточного параллакса в системе эклиптических координат
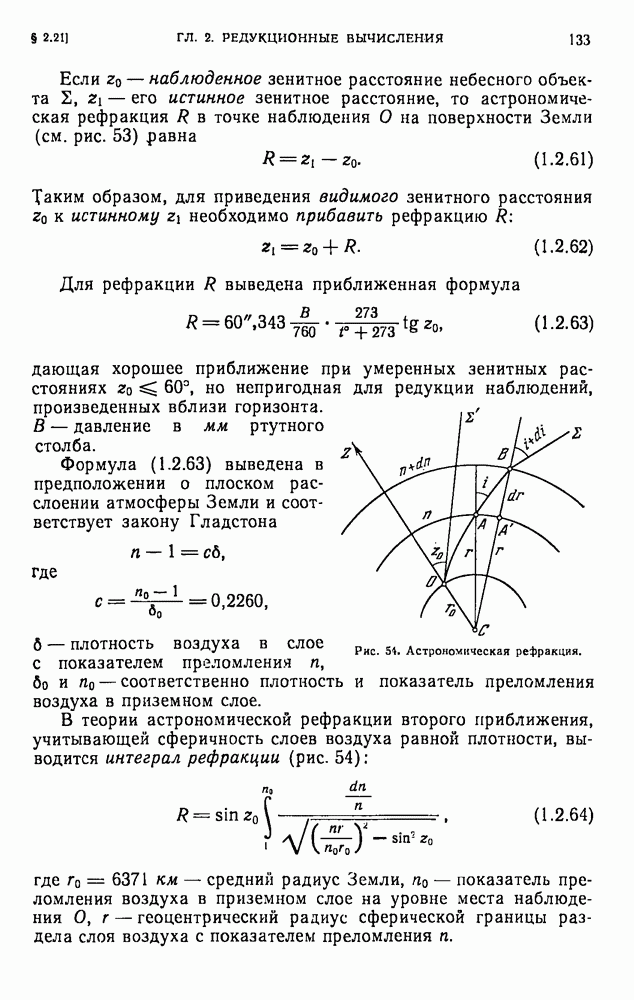
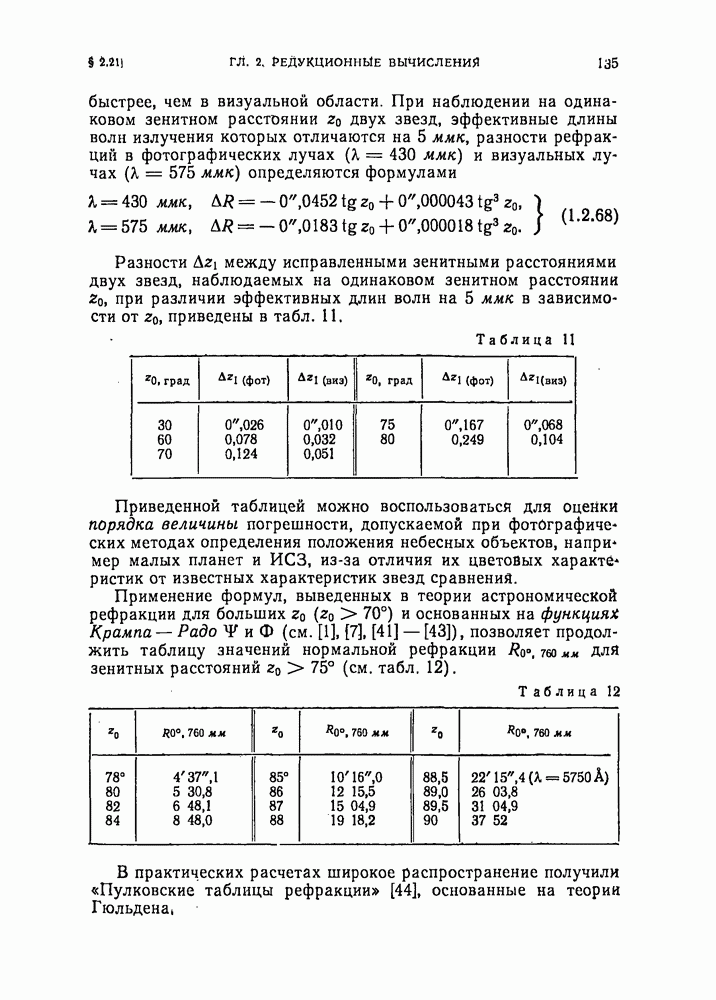
- § 2.21. Астрономическая рефракция
- § 2.22. Формулы учета рефракции в координатах небесных объектов
- § 2.23. Рефракция при наблюдении небесных объектов, расположенных на конечных расстояниях от Земли
- § 2.24. Дифференциальная прецессия и нутация. Дифференциальная аберрация и дифференциальный параллакс
- § 2.25. Сравнение теории с наблюдениями
- § 2.26. Каталоги звездных положений
- § 2.27. Геоцентрические координаты нуль-пункта селенографической системы отсчета
- § 2.28. Вычисление топоцентрических расстояний до точек лунной поверхности
- Глава 3. ВРЕМЯ И ЕГО ИЗМЕРЕНИЕ
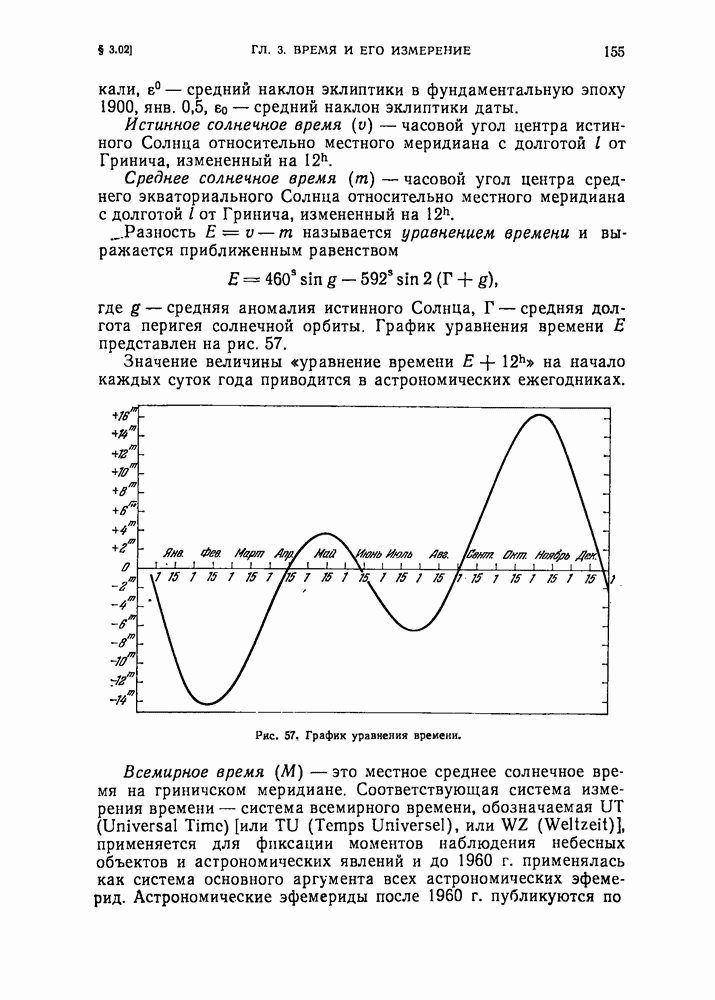
- § 3.02. Звездное и солнечное время. Всемирное время
- § 3.03. Квазиравномерное всемирное время
- § 3.04. Связь между всемирным временем и звездным гриничским временем
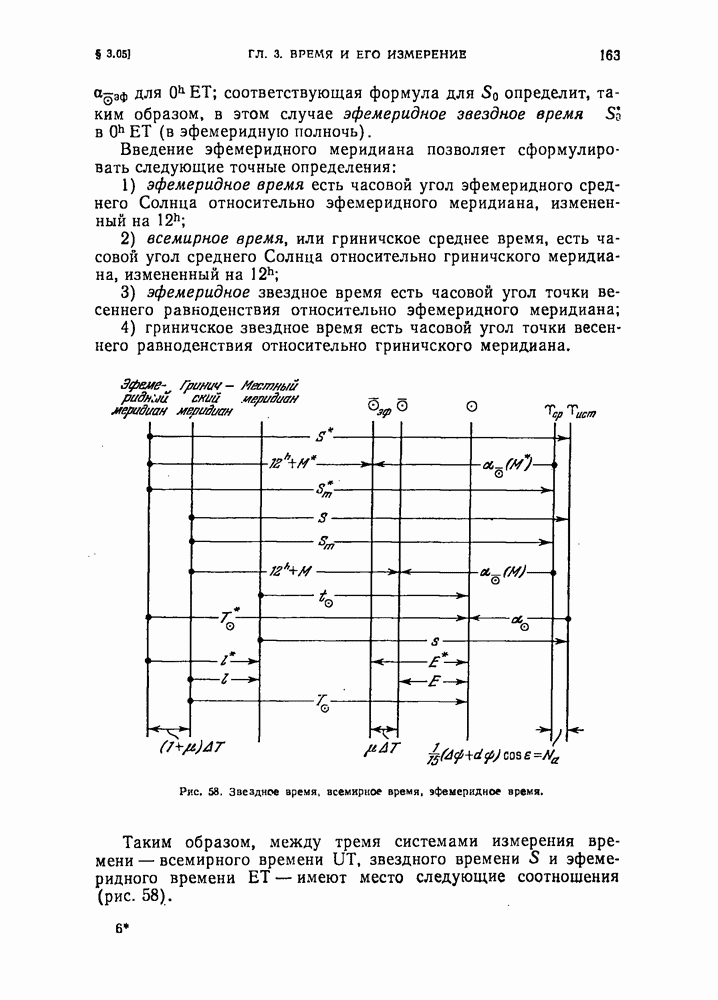
- § 3.05. Эфемеридное время
- § 3.06. Поправка за эфемеридное время
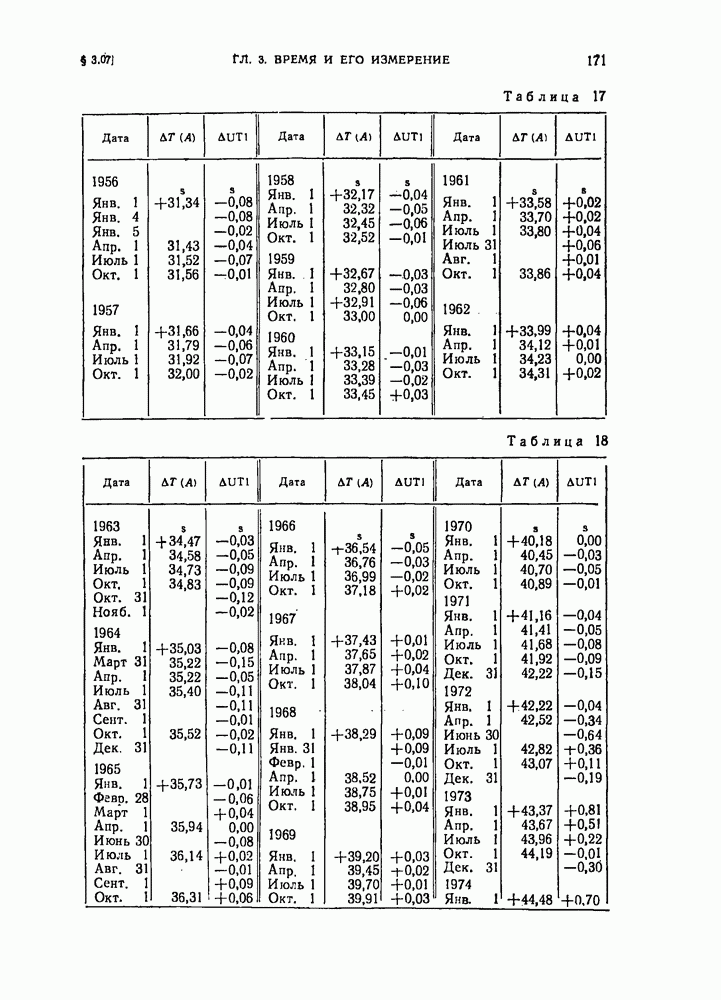
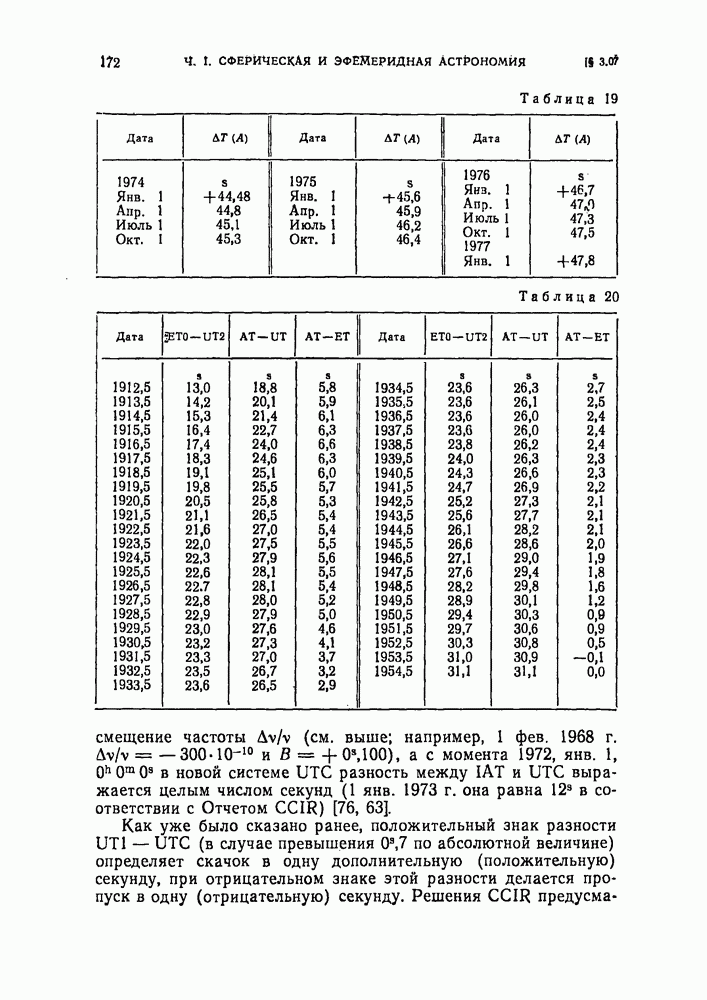
- § 3.07. Атомное время
- § 3.08. Юлианский период. Юлианские дни
- Глава 4. АСТРОНОМИЧЕСКИЕ ПОСТОЯННЫЕ
- § 4.02. Задачи астродинамики и астрономические постоянные
- § 4.03. Результаты радиолокационных определений астрономической единицы в км
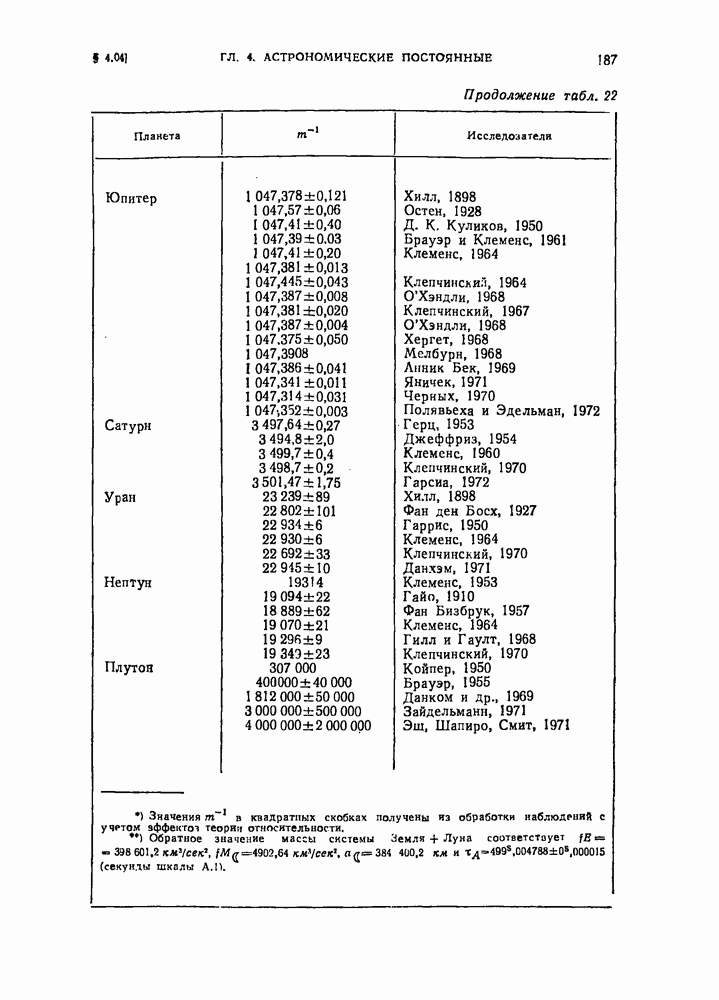
- § 4.04. Значения масс больших планет
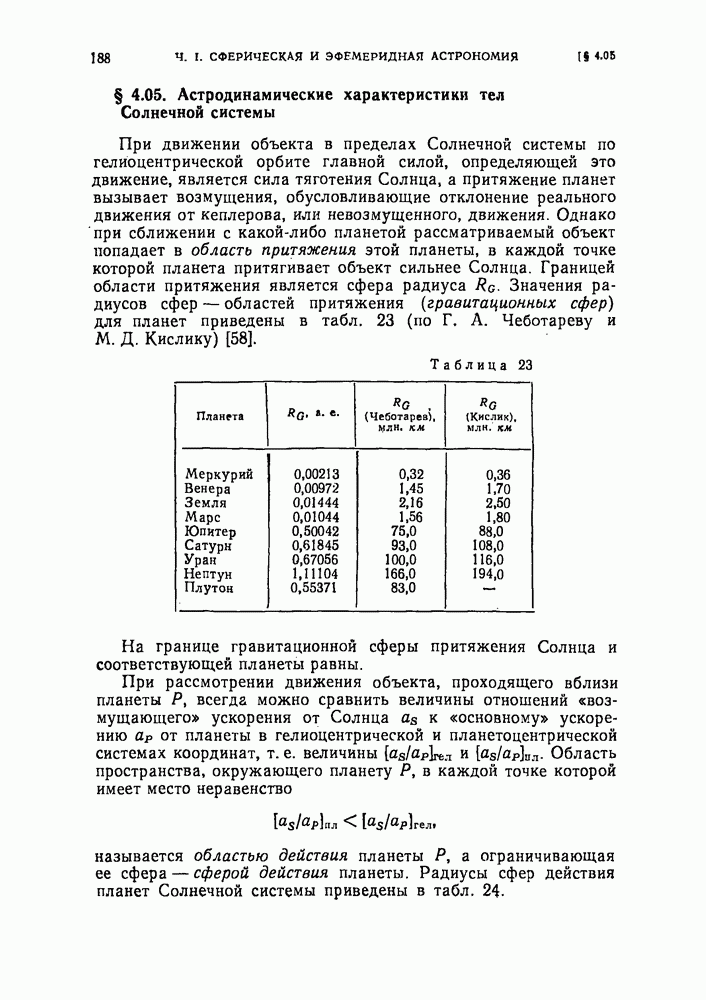
- § 4.05. Астродинамические характеристики тел Солнечной системы
- § 4.06. Астродинамические постоянные, связанные с Землей
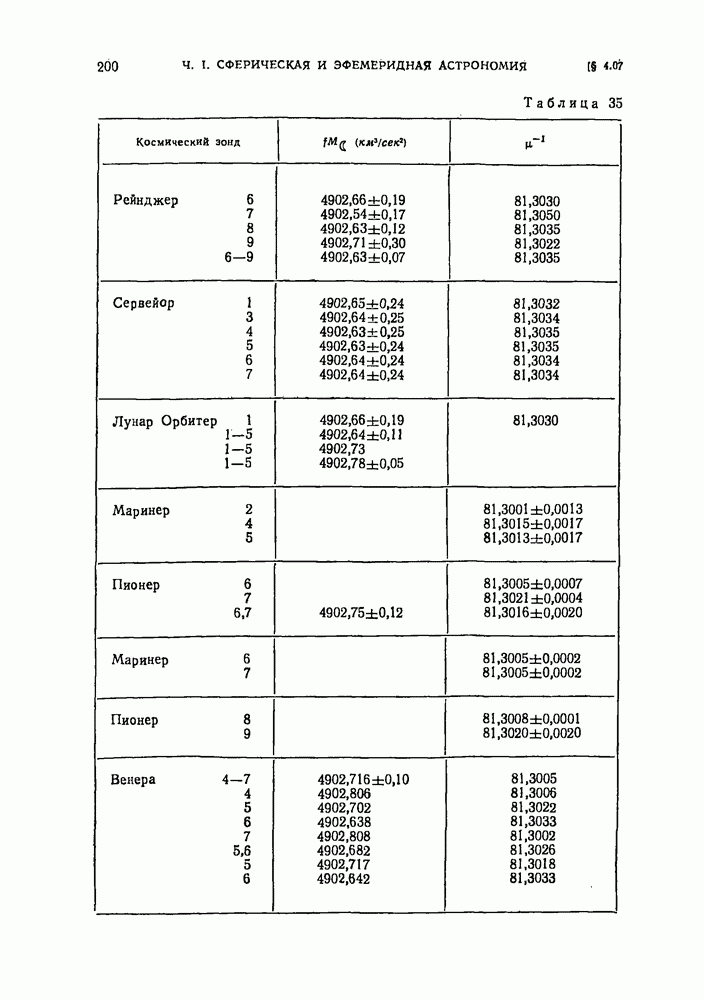
- § 4.07. Астродинамические постоянные, связанные с Луной
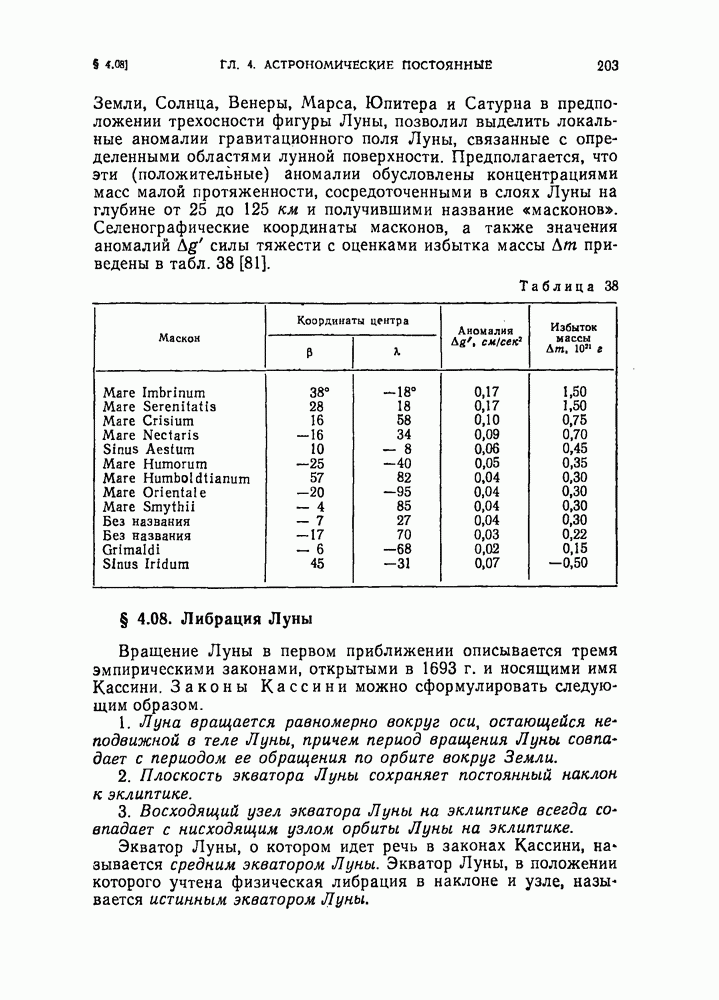
- § 4.08. Либрация Луны
- Часть II. ЗАДАЧА ДВУХ ТЕЛ
- Глава 1. ОБЩАЯ ТЕОРИЯ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ
- § 1.02. Первые интегралы уравнений невозмущенного кеплеровского движения
- § 1.03. Типы невозмущенного кеплеровского движения
- § 1.04. Элементы орбиты
- § 1.05. Формулы, связывающие постоянные интегрирования и элементы орбиты
- Глава 2. ОСНОВНЫЕ ФОРМУЛЫ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ
- § 2.02. Круговое движение
- § 2.03. Гиперболическое движение
- § 2.04. Параболическое движение
- § 2.05. Прямолинейное движение
- § 2.06. Вычисление эфемерид планет и комет
- Глава 3. РАЗЛОЖЕНИЕ КООРДИНАТ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ В РЯДЫ
- § 3.02. Разложение функций истинной аномалии в тригонометрические ряды по кратным средней аномалии
- § 3.03. Первые члены рядов по кратным средней аномалии для некоторых функций
- § 3.04. Формула Лагранжа
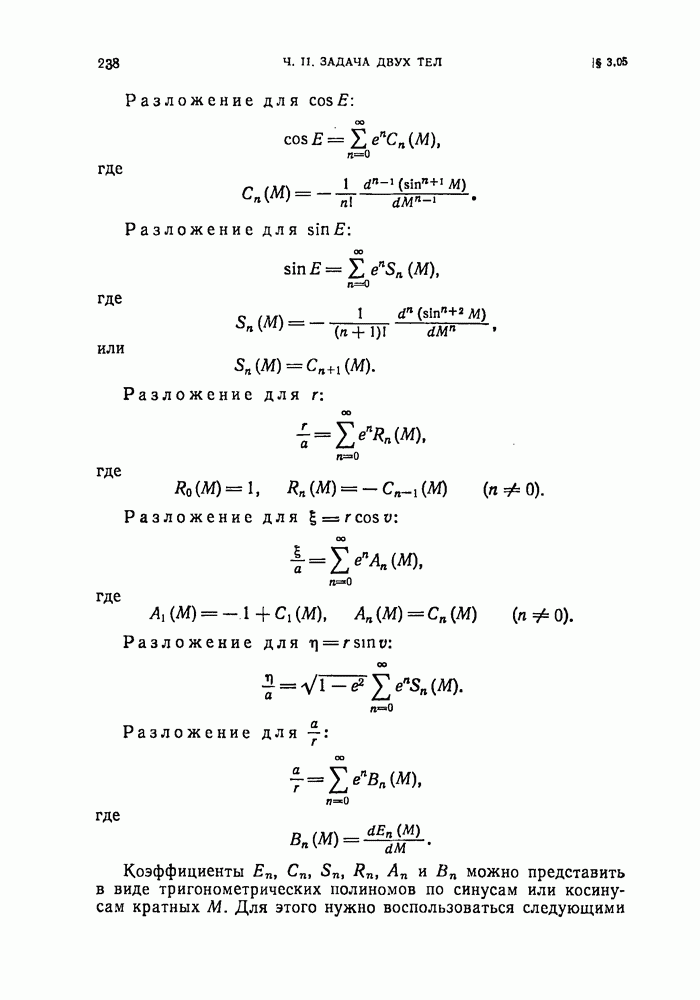
- § 3.05. Ряды по степеням эксцентриситета
- § 3.06. Тригонометрические ряды по кратным эксцентрической аномалии
- § 3.07. Ряды по кратным истинной аномалии
- § 3.08. Разложения координат невозмущенного кеплеровского движения в ряды по степеням времени
- § 3.09. Степенные ряды в случае эллиптического движения
- Часть III. МЕТОДЫ ОПРЕДЕЛЕНИЯ И УЛУЧШЕНИЯ ОРБИТ
- Глава 1. ВЫЧИСЛЕНИЕ КООРДИНАТ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ ПО ЭЛЕМЕНТАМ ОРБИТЫ
- § 1.02. Вычисление орбитальных координат в случае параболической орбиты
- § 1.03. Вычисление орбитальных координат в случае орбит, эксцентриситет которых близок к единице
- § 1.04. Вычисление гелиоцентрических прямоугольных эклиптических и экваториальных координат
- Глава 2. ОПРЕДЕЛЕНИЕ ОРБИТ
- § 2.02. Особые случаи, встречающиеся при вычислении гелиоцентрических координат
- § 2.03. Определение гелиоцентрических положений по четырем геоцентрическим наблюдениям в случае эллиптической или гиперболической орбит
- § 2.04. Определение гелиоцентрических положений по трем геоцентрическим наблюдениям в случае параболической орбиты
- § 2.05. Вычисление элементов эллиптической орбиты по двум гелиоцентрическим положениям
- § 2.06. Определение элементов гиперболической орбиты по двум гелиоцентрическим положениям
- § 2.07. Определение элементов параболической орбиты по двум гелиоцентрическим положениям
- § 2.08. Уравнения Ламберта и Эйлера
- § 2.09. Определение элементов эллиптической или гиперболической орбиты по двум гелиоцентрическим положениям с помощью уравнения Ламберта
- § 2.10. Определение элементов круговой орбиты по двум наблюдениям
- § 2.11. Вычисление элементов гелиоцентрической орбиты по положению и скорости в начальный момент
- Глава 3. УЛУЧШЕНИЕ ПЕРВОНАЧАЛЬНОЙ ОРБИТЫ
- § 3.01. Дифференциальное исправление орбит. Постановка задачи
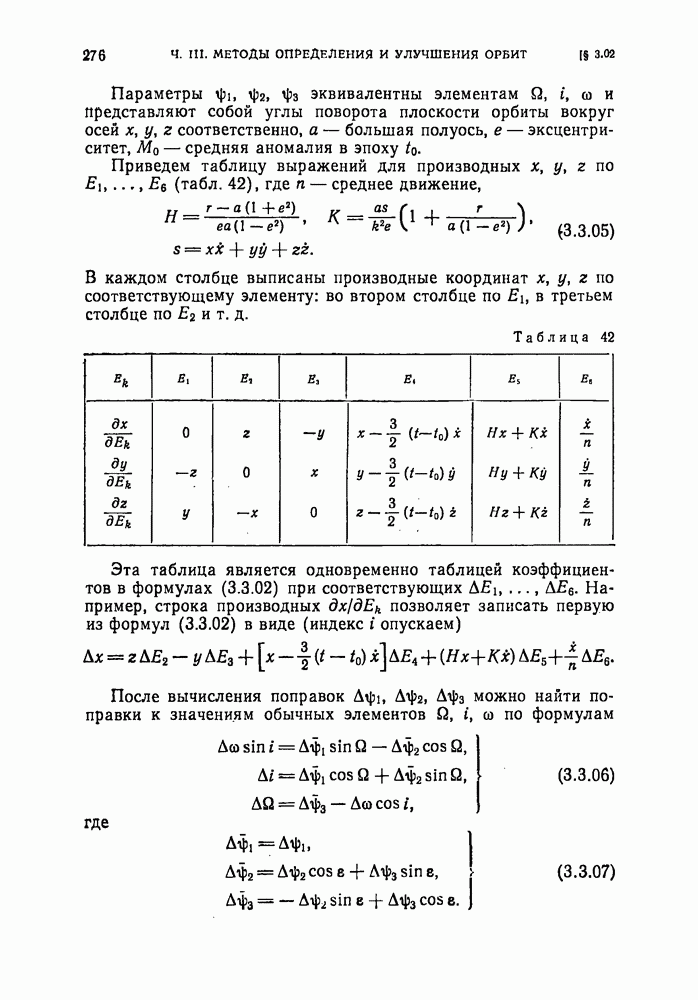
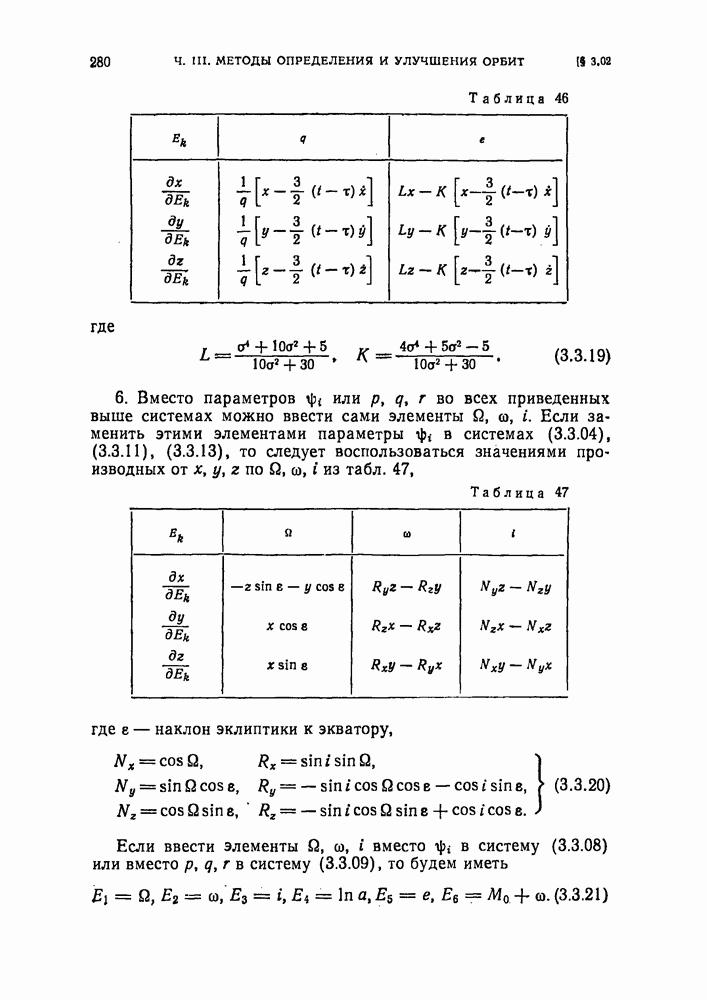
- § 3.02. Выражения для производных от координат по элементам (или по функциям элементов)
- § 3.03. Условные уравнения, составляемые по наблюдениям долготы и широты небесного тела
- Глава 4. ОПРЕДЕЛЕНИЕ И УЛУЧШЕНИЕ ЭЛЕМЕНТОВ ОРБИТ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- § 4.01. Определение элементов орбит ИСЗ по положению и скорости в момент выхода на орбиту
- § 4.02. Определение предварительных элементов орбиты ИСЗ по наблюдениям
- § 4.03. Улучшение орбит ИСЗ
- Часть IV. ТЕОРИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ
- Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ЗАДАЧИ n ТЕЛ В КООРДИНАТАХ
- § 1.02. Уравнение Лагранжа — Якоби
- § 1.03. Уравнения движения в барицентрических прямоугольных координатах
- § 1.04. Уравнения движения в координатах Якоби
- § 1.05. Уравнения относительного движения в прямоугольных координатах
- § 1.06. Уравнения движения в идеальных прямоугольных координатах Ганзена
- § 1.07. Уравнения абсолютного движения в цилиндрических координатах
- § 1.08. Уравнения относительного движения в цилиндрических координатах
- § 1.09. Уравнения абсолютного движения в сферических координатах
- § 1.10. Уравнения относительного движения в сферических координатах
- § 1.11. Уравнения движения в полярных координатах Ганзена
- § 1.12. Уравнения Клеро — Лапласа
- § 1.13. Общее правило составления канонических уравнений
- § 1.14. Первая каноническая форма уравнений абсолютного движения
- § 1.15. Вторая каноническая форма уравнений абсолютного движения
- § 1.16. Третья каноническая форма уравнений абсолютного движения
- § 1.17. Первая каноническая форма уравнений относительного движения
- § 1.18. Вторая каноническая форма уравнений относительного движения
- § 1.19. Третья каноническая форма уравнений относительного движения
- § 1.20. Уравнение Гамильтона — Якоби. Метод Гамильтона — Якоби
- § 1.21. Уравнения движения системы в векторной форме
- Глава 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПОСТУПАТЕЛЬНО-ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ
- § 2.02. Силовая функция системы тел
- § 2.03. Разложение силовой функции двух тел
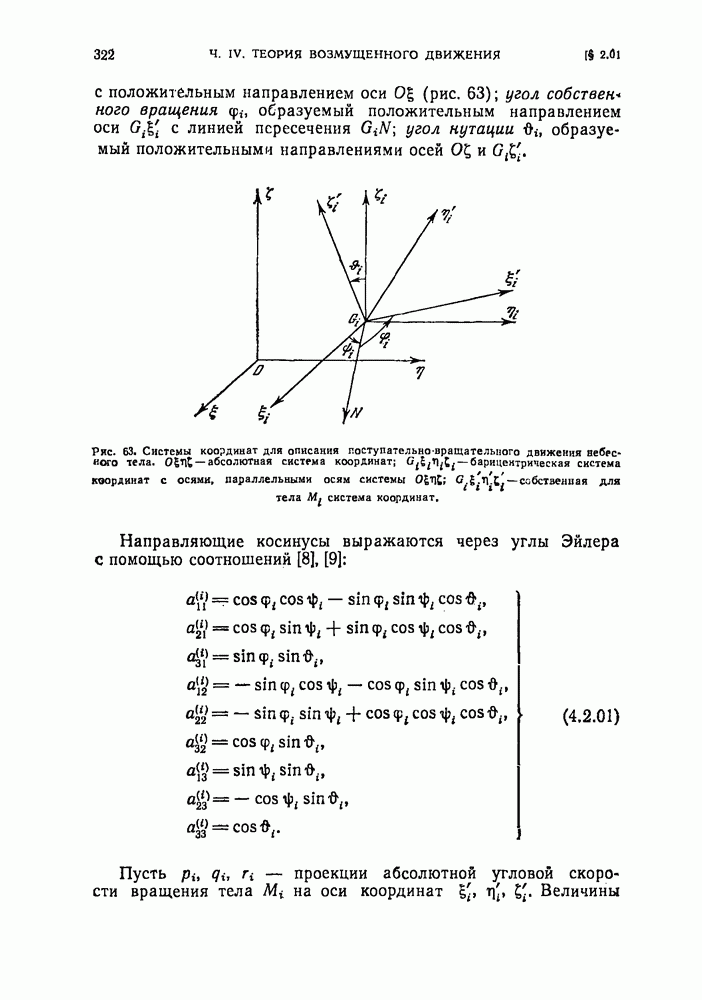
- § 2.04. Уравнения поступательно-вращательного движения системы тел в абсолютной прямоугольной системе координат
- § 2.05. Уравнения поступательно-вращательного движения системы тел в относительной прямоугольной системе координат
- § 2.06. Каноническая форма уравнений поступательно-вращательного движения системы тел
- Глава 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ТЕЛА ДЛЯ РАЗЛИЧНЫХ СИСТЕМ ОСКУЛИРУЮЩИХ ЭЛЕМЕНТОВ
- § 3.01. Метод Лагранжа вариации произвольных постоянных
- § 3.02. Уравнения Ньютона для кеплеровских оскулирующих элементов (общий случай)
- § 3.03. Уравнения Ньютона для эллиптических кеплеровских оскулирующих элементов
- § 3.04. Уравнения Лагранжа для кеплеровских оскулирующих элементов (общий случай)
- § 3.05. Уравнения Лагранжа для эллиптических кеплеровских оскулирующих элементов
- § 3.06. Уравнения возмущенного движения для канонических элементов Якоби
- § 3.07. Уравнения возмущенного движения для канонических элементов Делоне
- § 3.08. Две системы канонических элементов Пуанкаре
- § 3.09. Уравнения возмущенного движения в переменных Лагранжа для случая малых эксцентриситетов
- § 3.10. Уравнения в переменных Лагранжа для случая малых наклонов
- § 3.11. Уравнения возмущенного движения в переменных Лагранжа (общий случай)
- § 3.12. Связь между прямоугольными координатами движущейся точки и различными системами канонических элементов
- Глава 4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ЗАДАЧИ n ТЕЛ ДЛЯ РАЗЛИЧНЫХ СИСТЕМ ОСКУЛИРУЮЩИХ ЭЛЕМЕНТОВ
- § 4.01. Уравнения Ньютона для кеплеровских оскулирующих элементов (общий случай)
- § 4.02. Уравнения Ньютона для эллиптических кеплеровских оскулирующих элементов
- § 4.03. Уравнения Лагранжа для кеплеровских оскулирующих элементов (общий случай)
- § 4.04. Уравнения Лагранжа для эллиптических кеплеровских оскулирующих элементов
- § 4.05. Уравнения возмущенного движения в канонических элементах Якоби
- § 4.06. Уравнения возмущенного движения в канонических элементах Делоне
- § 4.07. Две системы канонических элементов Пуанкаре
- § 4.08. Уравнения возмущенного движения в переменных Лагранжа для случая малых эксцентриситетов
- § 4.09. Уравнения в переменных Лагранжа для случая малых наклонов
- § 4.10. Уравнения возмущенного движения в переменных Лагранжа (общий случай)
- Глава 5. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 5.01. Эллиптические интегралы и эллиптические функции
- § 5.02. Гипергеометрический ряд и гипергеометрическая функция
- § 5.03. Полиномы Лежандра. Функции Лежандра
- § 5.04. Присоединенные функции Лежандра
- § 5.05. Сферические функции
- § 5.06. Цилиндрические функции. Функции Бесселя
- § 5.07. Функции Ламе
- § 5.08. Полиномы Гегенбауэра. Коэффициенты Лапласа
- § 5.09. Числа Коши
- Глава 6. РАЗЛОЖЕНИЕ ВОЗМУЩАЮЩЕЙ ФУНКЦИИ
- § 6.01. Разложение возмущающей функции в задаче о движении двух планет (случай круговых орбит)
- § 6.02. Разложение возмущающей функции в задаче о движении двух планет (случай малых эксцентриситетов и взаимного наклона)
- § 6.03. Разложение возмущающей функции в случае произвольного взаимного наклона
- § 6.04. Вековая часть возмущающей функции в двухпланетной задаче
- § 6.05. Численные методы разложения возмущающей функции
- § 6.06. Полуаналитический метод Брауэра — Клеменса разложения возмущающей функции
- Глава 7. АНАЛИТИЧЕСКИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ВОЗМУЩЕНИЙ КООРДИНАТ
- § 7.02. Метод Ганзена
- § 7.03. Метод Брауэра
- § 7.04. Метод Лапласа — Ньюкома
- Глава 8. АНАЛИТИЧЕСКИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ВОЗМУЩЕНИЙ ЭЛЕМЕНТОВ
- § 8.01. Общий вид возмущений элементов. Порядок, степень, ранг и класс возмущений
- § 8.02. Метод Гаусса вычисления вековых возмущений первого порядка
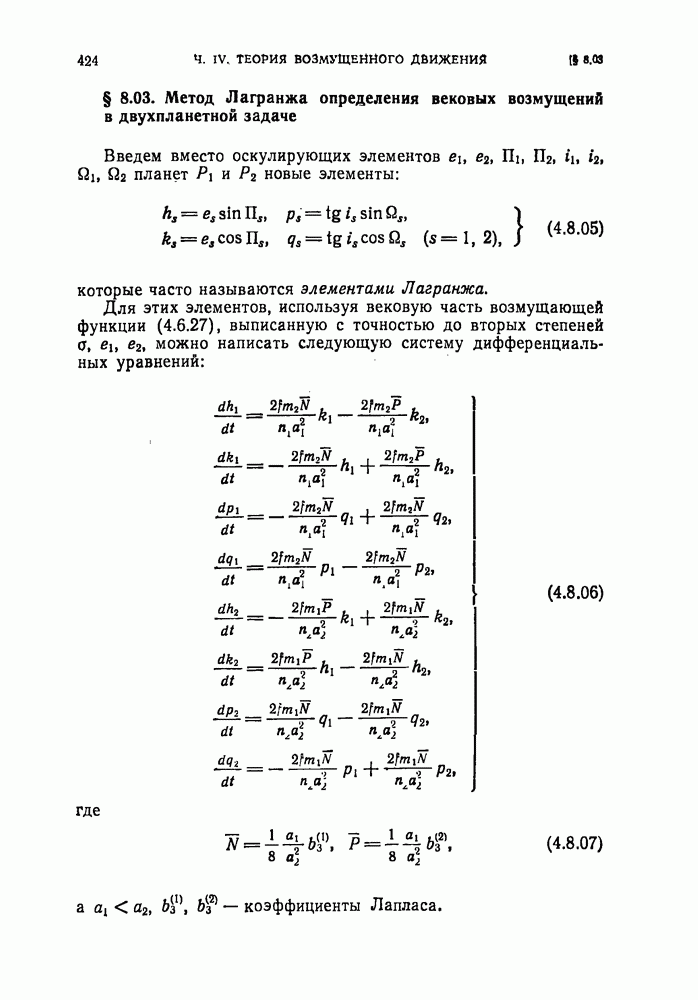
- § 8.03. Метод Лагранжа определения вековых возмущений в двухпланетной задаче
- § 8.04. Основы метода Делоне
- § 8.05. Связь между возмущениями координат и возмущениями элементов
- Глава 9. МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ, ОСНОВАННЫЕ НА СХЕМАХ ОСРЕДНЕНИЯ
- § 9.01. Основные схемы осреднения возмущающей функции в двухпланетной задаче
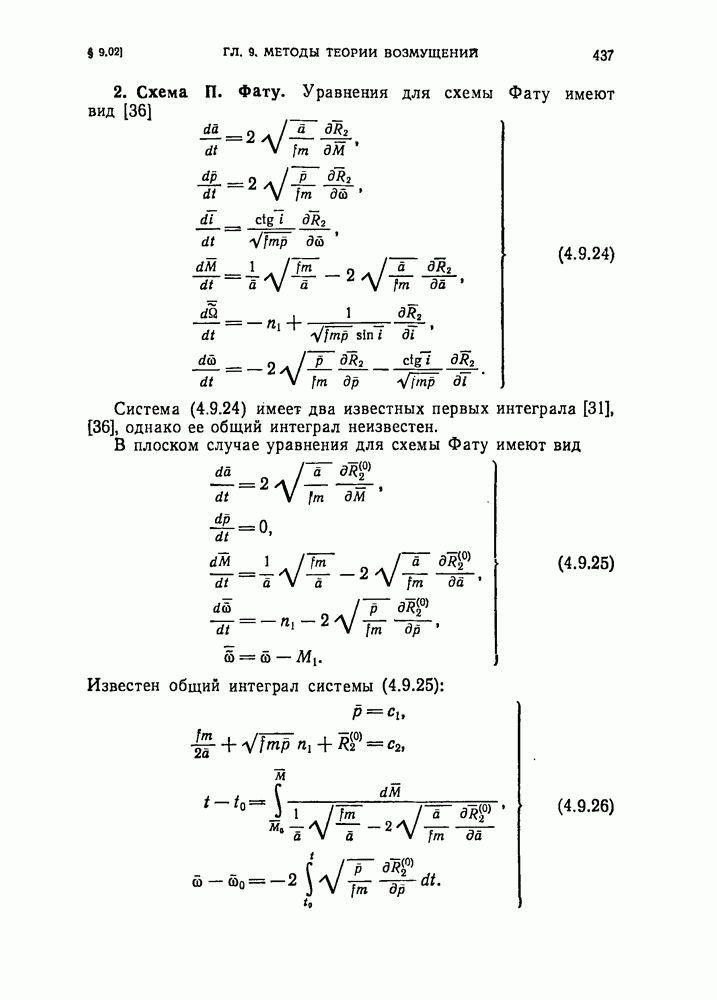
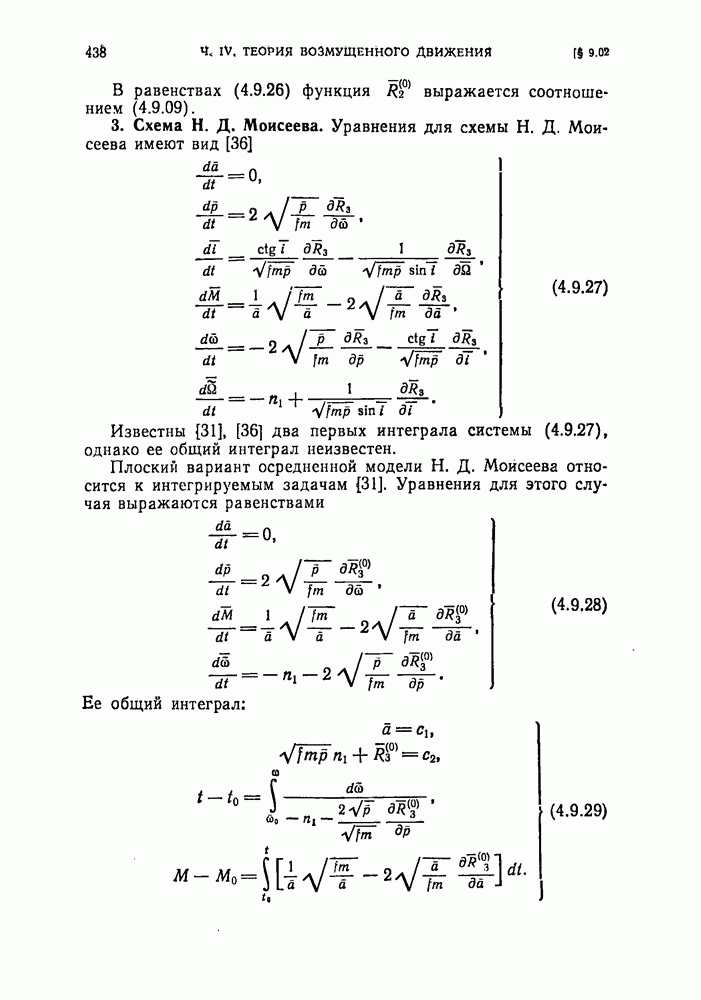
- § 9.02. Уравнения осредненных схем ограниченной круговой задачи трех тел, определяющие промежуточную орбиту (нулевое приближение). Их первые интегралы
- § 9.03. Разложение возмущающей функции для схем осреднения
- § 9.04. Основы метода теории возмущений
- Глава 10. ТЕОРИЯ ДВИЖЕНИЯ ЛУНЫ
- § 10.01. Уравнения основной проблемы в теории движения Луны
- § 10.02. Разложение возмущающей функции в основной проблеме теории движения Луны
- § 10.03. Решение Делоне основной проблемы в теории движения Луны
- § 10.04. Основные этапы построения теории Хилла—Брауна движения Луны
- § 10.05. Промежуточная орбита в теории Хилла — Брауна
- § 10.06. Общее решение уравнений основной проблемы в теории Хилла—Брауна
- § 10.07. Переход к сферическим координатам
- § 10.08. Численные значения постоянных интегрирования и параметров в теории Хилла — Брауна
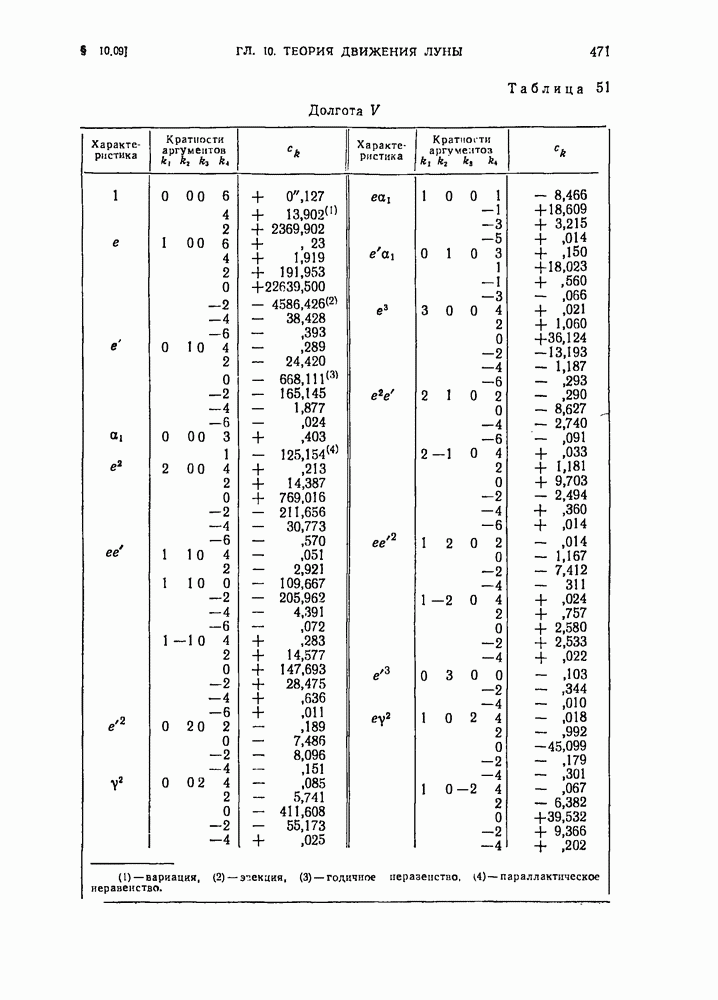
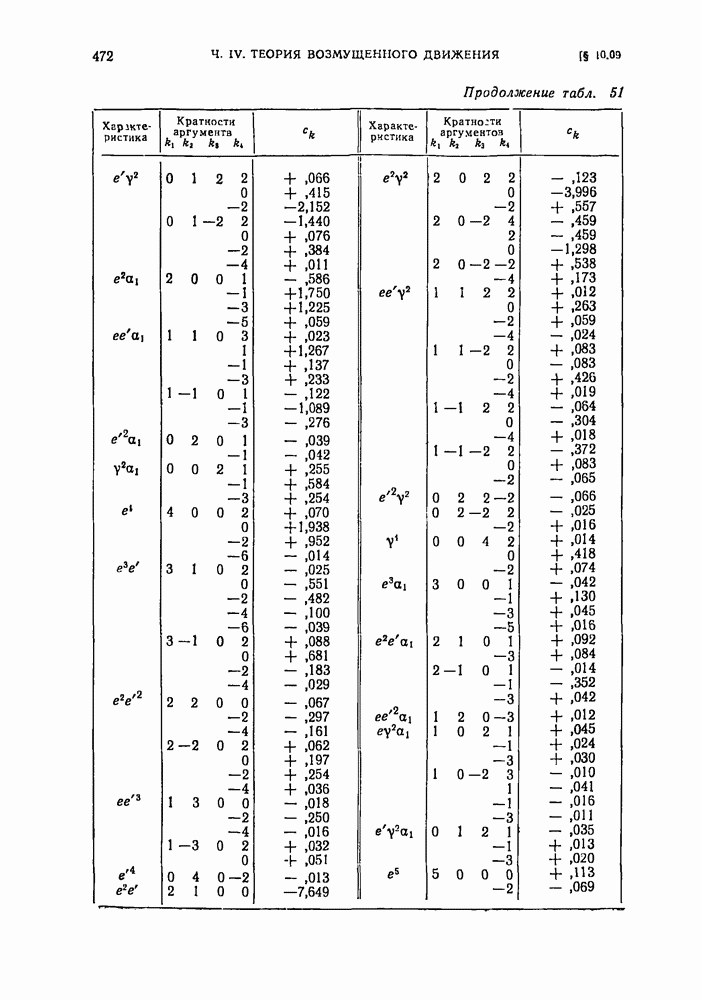
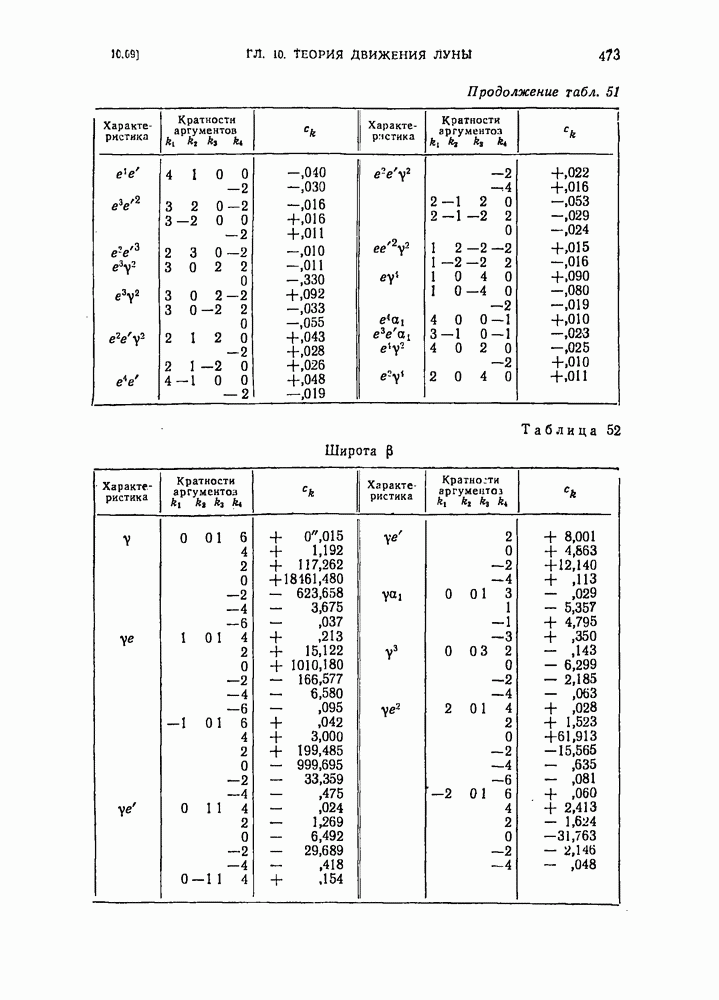
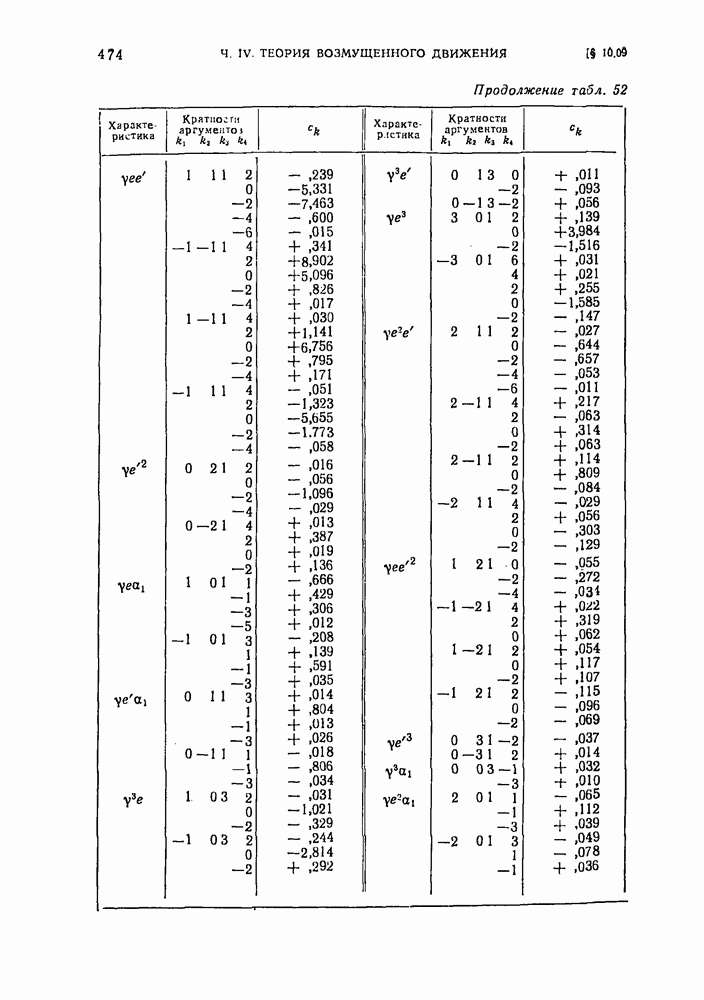
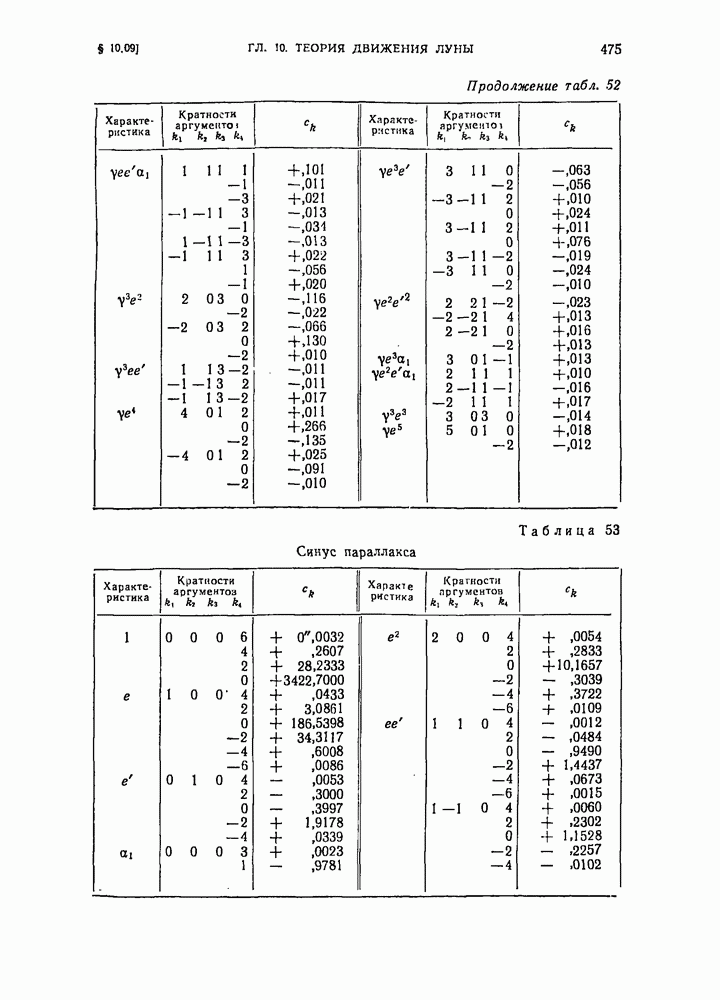
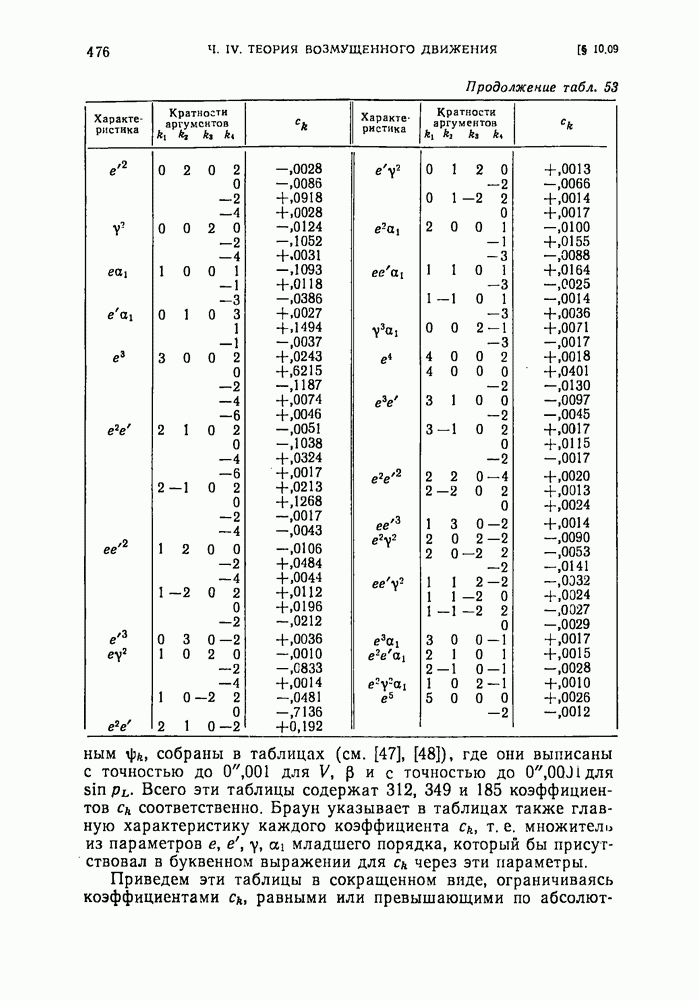
- § 10.09. Окончательные выражения для долготы, широты и синуса параллакса, соответствующие решению основной проблемы
- § 10.10. Возмущения Луны, обусловленные притяжением планет, фигурами Земли и Луны
- § 10.11. Уточнение теории движения Луны Хилла—Брауна
- Глава 11. ТЕОРИЯ ДВИЖЕНИЯ БОЛЬШИХ ПЛАНЕТ
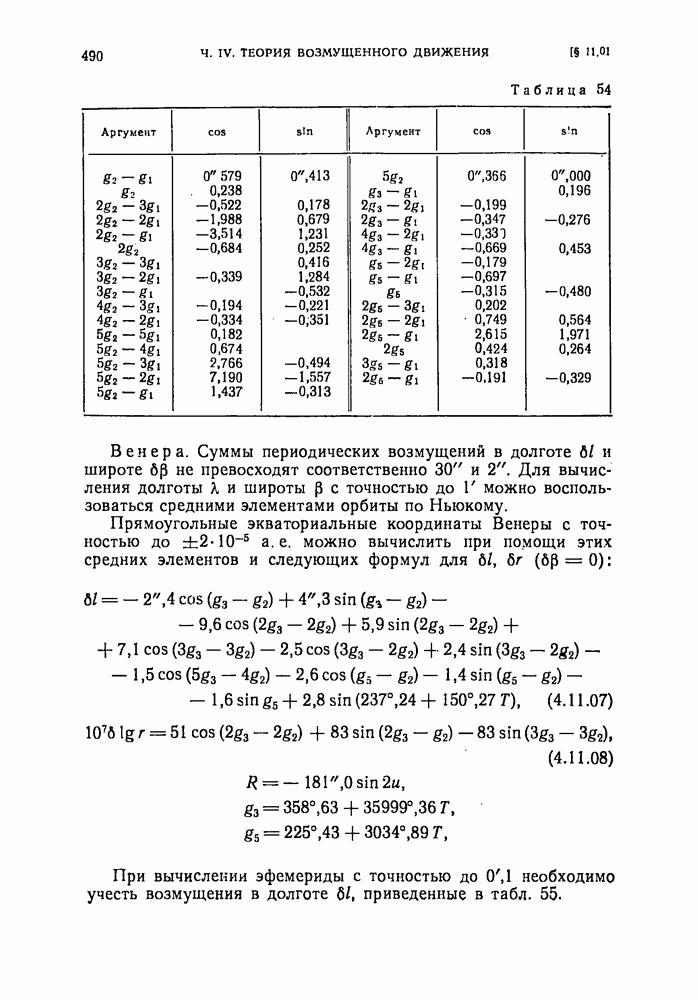
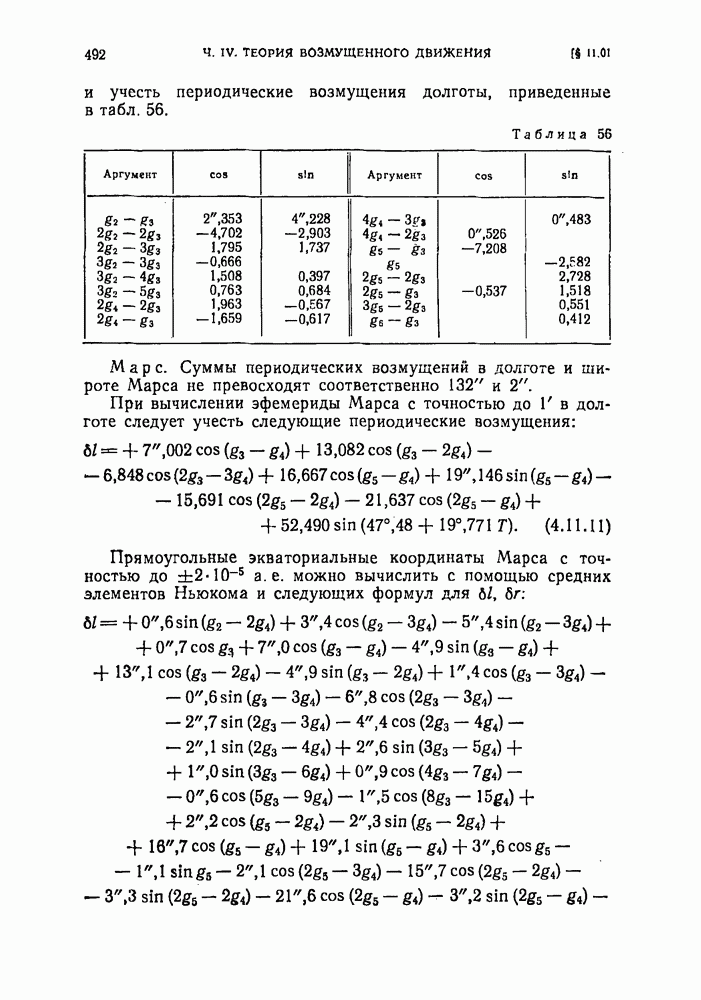
- § 11.01. Внутренние планеты
- § 11.02. Внешние планеты
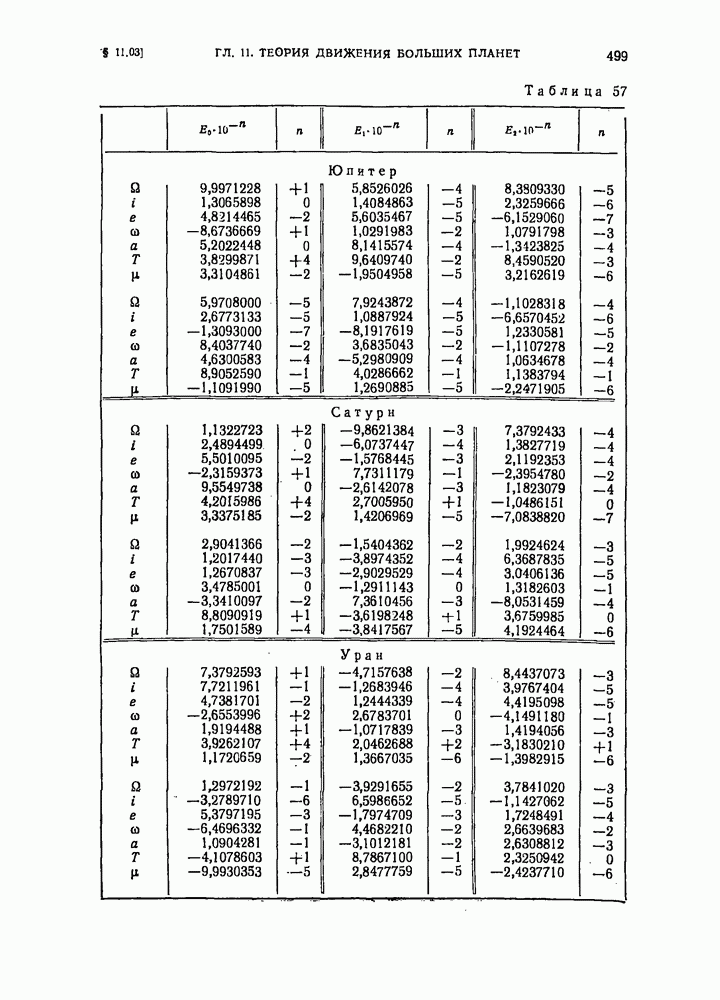
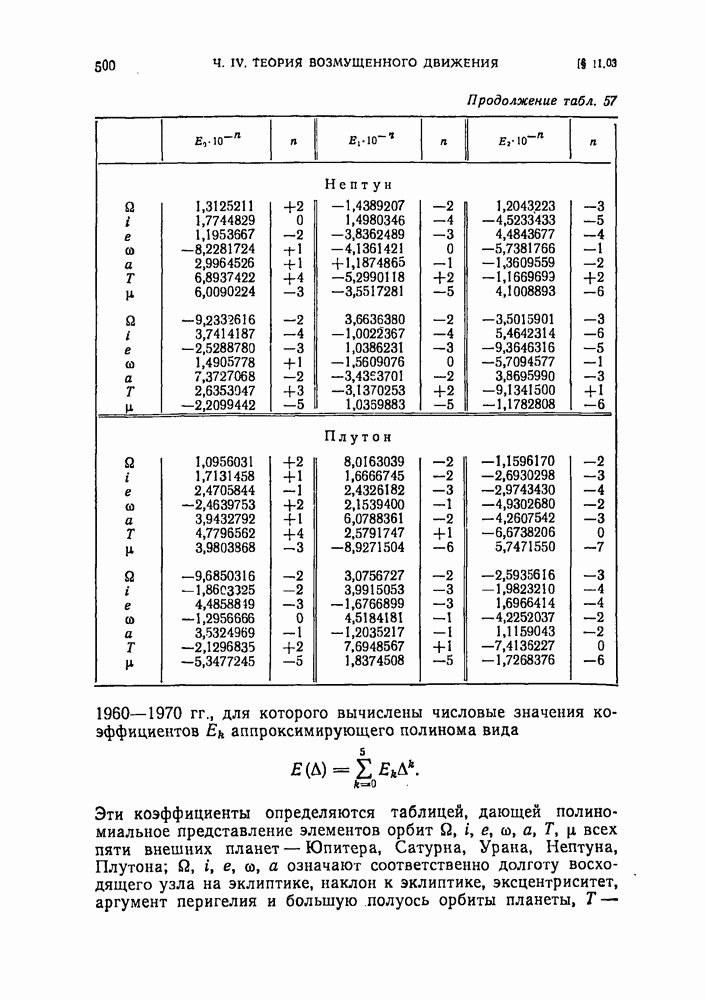
- § 11.03. Полиномиальное представление оскулирующих элементов орбит внешних планет
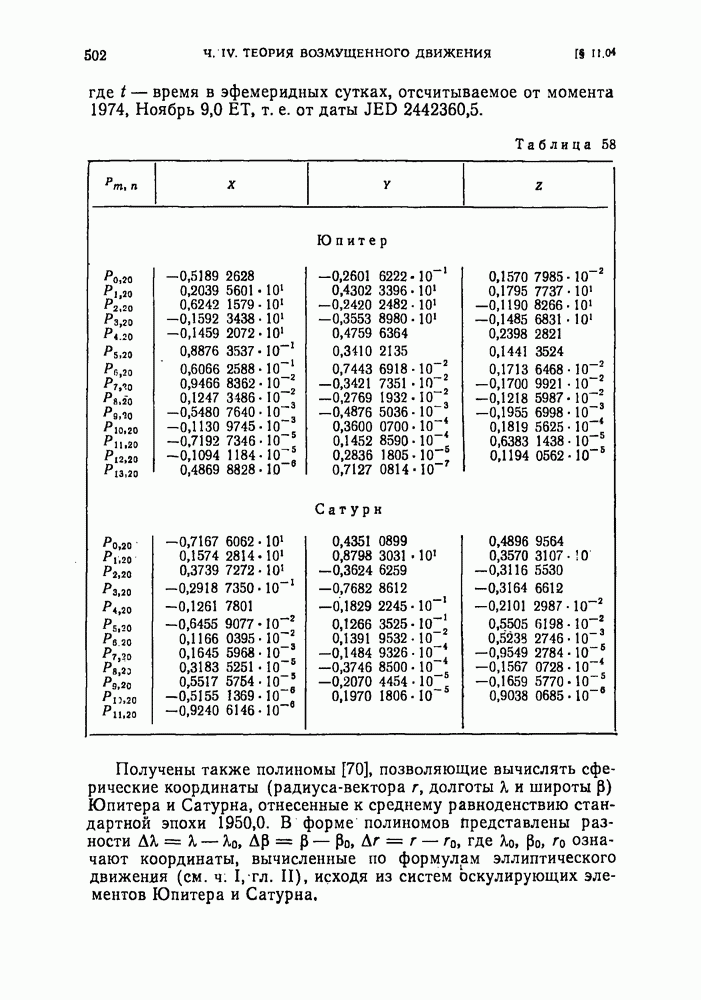
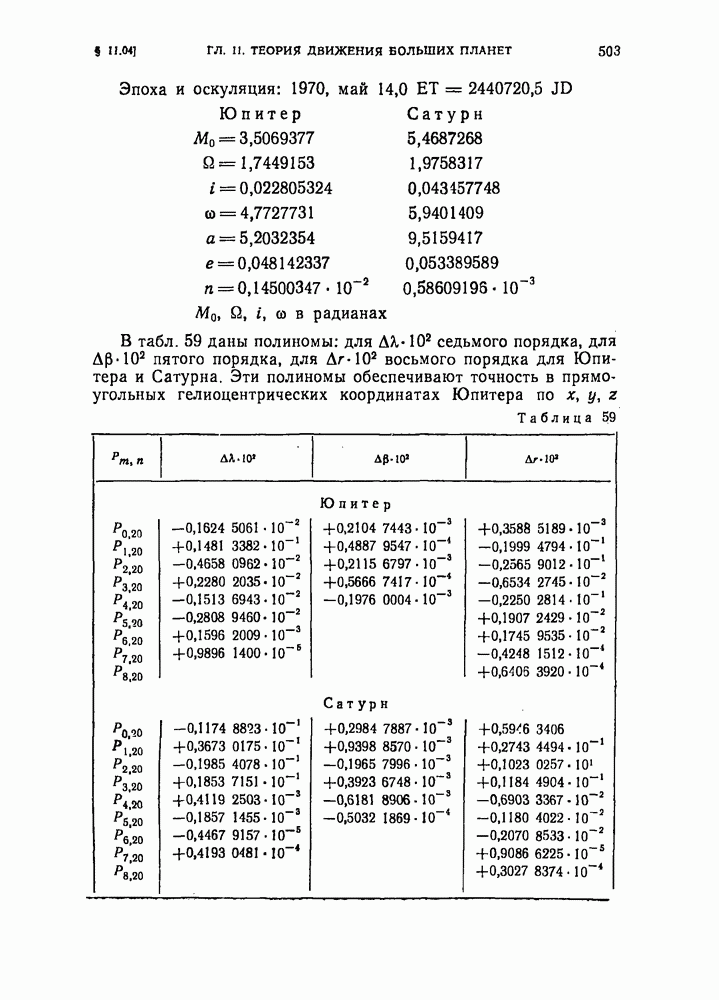
- § 11.04. Полиномиальное представление прямоугольных гелиоцентрических координат Юпитера и Сатурна
- § 11.05. Тригонометрическая теория вековых возмущений орбит больших планет
- Глава 12. ДВИЖЕНИЕ МАЛЫХ ТЕЛ СОЛНЕЧНОЙ СИСТЕМЫ
- § 12.01. Невозмущенное движение спутников
- § 12.02. Возмущения оскулирующих элементов орбит спутников, вызываемые сжатием планеты
- § 12.03. Возмущения в движении спутников, вызываемые притяжением Солнца
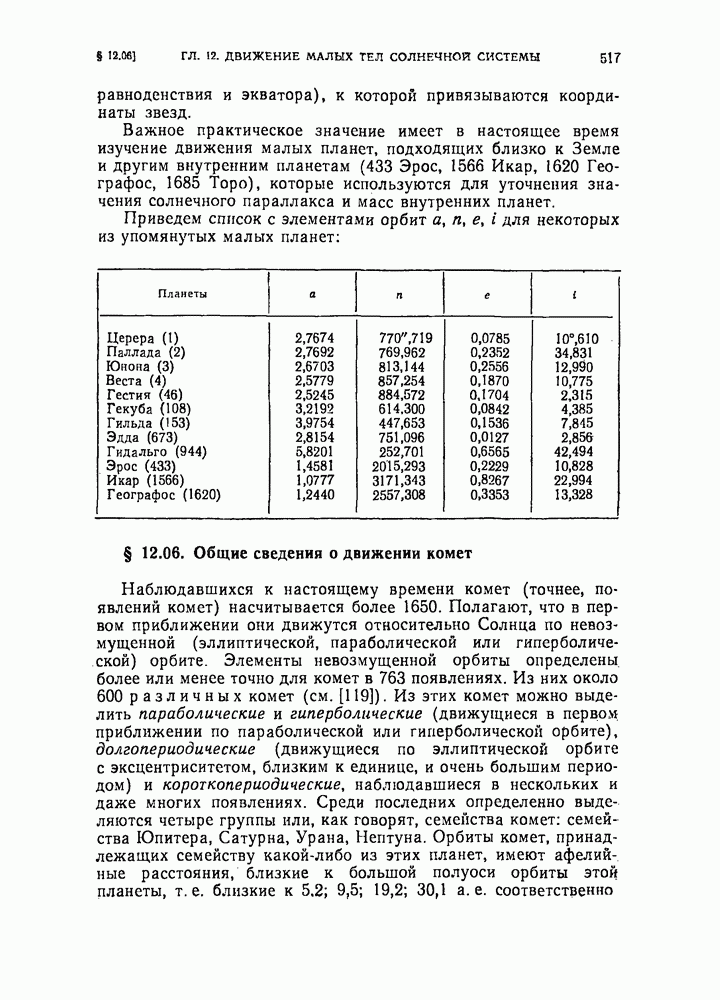
- § 12.04. Общие сведения о характере движения малых планет
- § 12.05. Возмущенное движение малых планет
- § 12.06. Общие сведения о движении комет
- § 12.07. Возмущенное движение комет
- Часть V. ЗАДАЧА ТРЕХ ТЕЛ
- Глава 1. НЕОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 1.02. Лагранжевы решения. Точки либрации
- Глава 2. ОГРАНИЧЕННАЯ КРУГОВАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 2.01. Дифференциальные уравнения движения. Интеграл Якоби
- § 2.02. Поверхность нулевой относительной скорости
- § 2.03. Лагранжевы решения ограниченной круговой задачи трех тел. Точки либрации
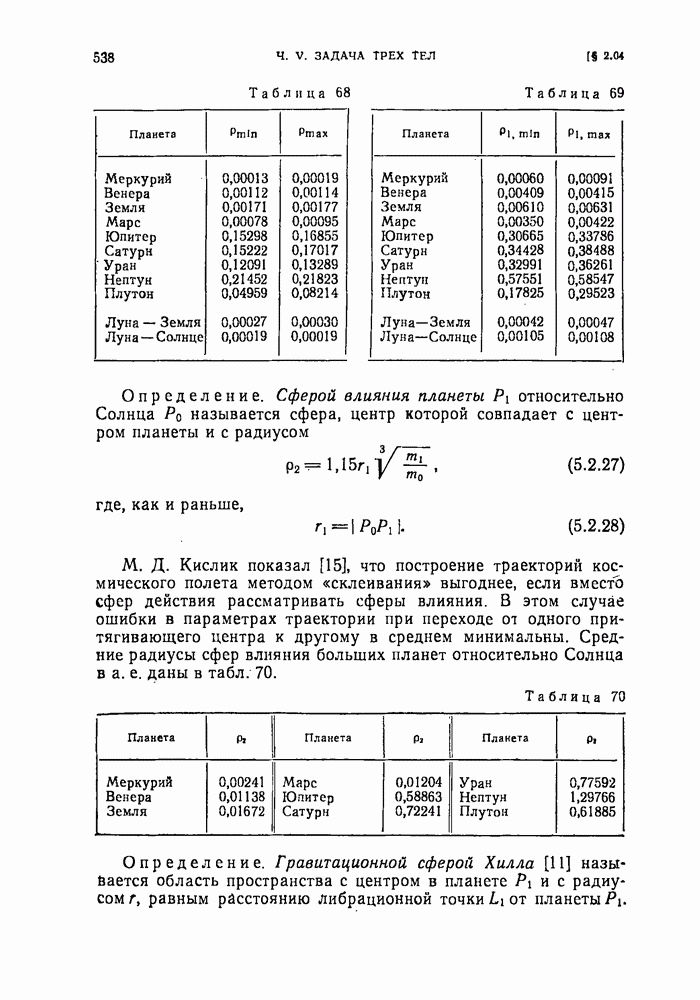
- § 2.04. Различные гравитационные сферы
- § 2.05. Периодические решения ограниченной круговой задачи трех тел
- § 2.06. Критерий Тиссерана
- § 2.07. Уравнения ограниченной круговой задачи в эллипсоидальных переменных
- § 2.08. Уравнение Гамильтона—Якоби в эллипсоидальных переменных
- § 2.09. Понижение порядка системы уравнений плоской ограниченной круговой задачи трех тел
- Глава 3. ДРУГИЕ ОГРАНИЧЕННЫЕ ЗАДАЧИ ТРЕХ ТЕЛ
- § 3.01. Общий случай ограниченной задачи трех тел
- § 3.02. Задача двух неподвижных центров
- § 3.03. Задача Хилла
- Часть VI. ДВИЖЕНИЕ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
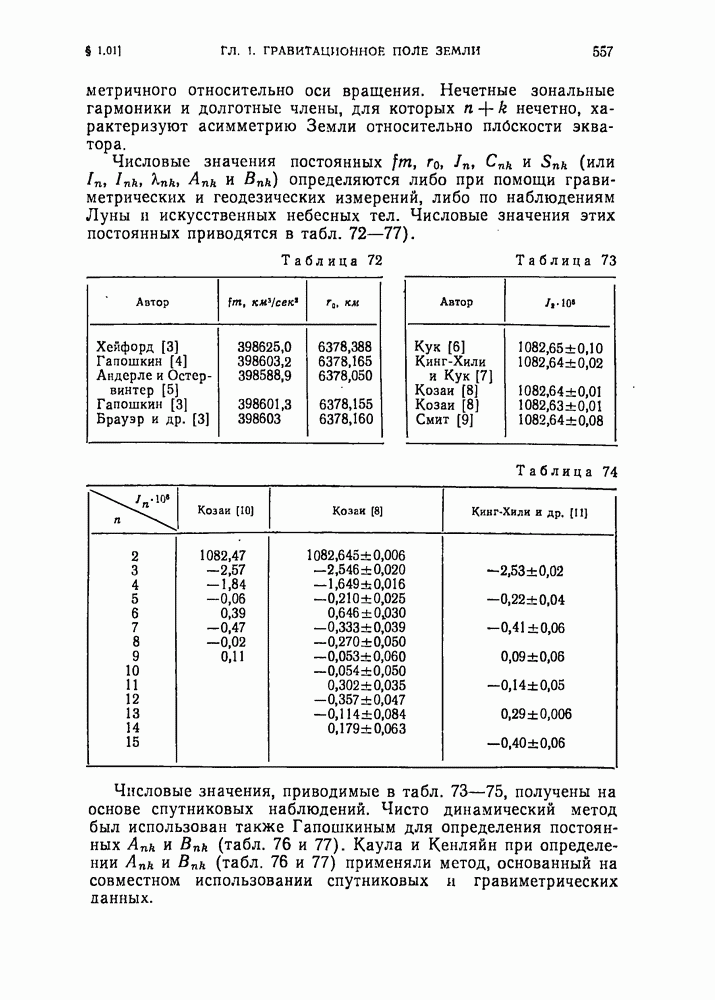
- Глава 1. ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИСКУССТВЕННОГО СПУТНИКА
- § 1.02. Стандартная Земля
- § 1.03. Дифференциальные уравнения движения спутника
- § 1.04. Элементы орбиты ИСЗ. Дифференциальные уравнения для оскулирующих элементов
- Глава 2. ВОЗМУЩЕНИЯ, ВЫЗЫВАЕМЫЕ ВТОРОЙ ЗОНАЛЬНОЙ ГАРМОНИКОЙ ГЕОПОТЕНЦИАЛА
- § 2.01. Возмущения от второй зональной гармоники как функции средней аномалии
- § 2.02. Возмущения от второй зональной гармоники как функции истинной аномалии
- § 2.03. Случай орбит с малыми эксцентриситетами
- Глава 3. ТЕОРИЯ ПРОМЕЖУТОЧНЫХ ОРБИТ ИСЗ
- § 3.01. Задачи Штерна, Гарфинкеля и Акснеса
- § 3.02. Задачи Баррара, Винти и Кислика
- § 3.03. Обобщенная задача двух неподвижных центров
- § 3.04. Промежуточная орбита, основанная на обобщенной задаче двух неподвижных центров
- § 3.05. Дифференциальные уравнения для элементов промежуточной орбиты
- Глава 4. ВОЗМУЩЕНИЯ ГРАВИТАЦИОННОИ ПРИРОДЫ
- § 4.01. Возмущения от зональных гармоник высших порядков
- § 4.02. Возмущения от зональной гармоники произвольного порядка
- § 4.03. Возмущения от тессеральных и секториальных гармоник
- § 4.04. Лунно-солнечные возмущения
- § 4.05. Определение постоянных интегрирования
- § 4.06. Вычисление возмущенных координат спутника
- Глава 5. ВОЗМУЩЕНИЯ, ВЫЗЫВАЕМЫЕ СОПРОТИВЛЕНИЕМ АТМОСФЕРЫ И СВЕТОВЫМ ДАВЛЕНИЕМ
- § 5.02. Стандартная атмосфера
- § 5.03. Сила сопротивления атмосферы
- § 5.04. Основные возмущения от сопротивления атмосферы
- § 5.05. Продолжительность жизни спутника
- § 5.06. Эволюция орбиты на больших промежутках времени
- § 5.07. Сила светового давления
- § 5.08. Возмущения от светового давления (без учета тени)
- § 5.09. Возмущения от светового давления (с учетом тени)
- § 5.10. Теневая функция
- Глава 6. ДРУГИЕ ВОЗМУЩЕНИЯ В ДВИЖЕНИИ ИСЗ
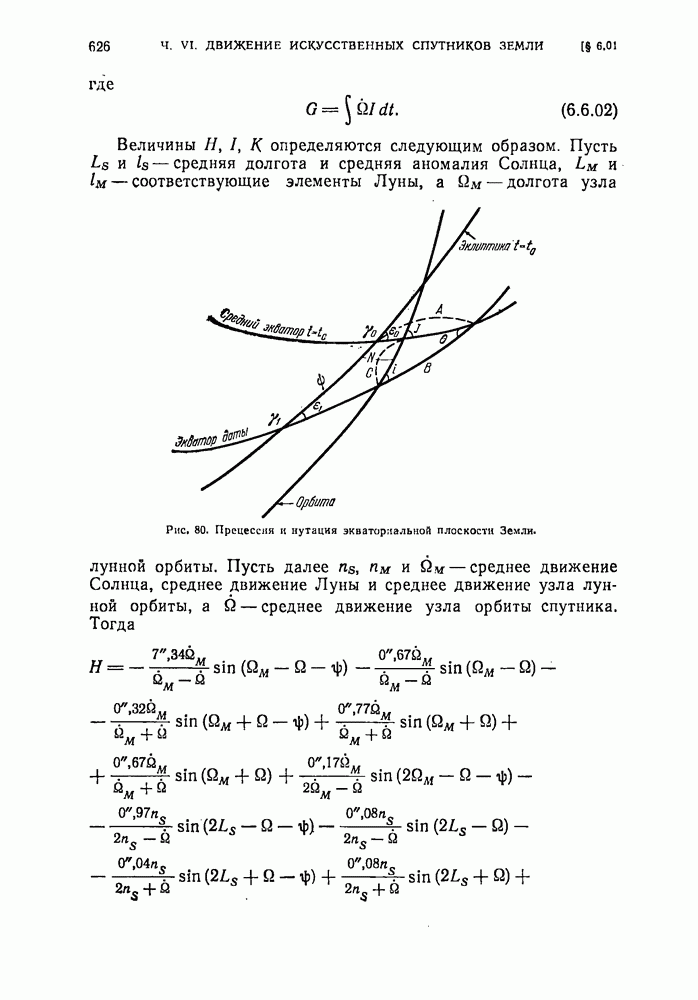
- § 6.01. Возмущения, вызываемые прецессией и нутацией экваториальной плоскости Земли
- § 6.02. Возмущения, вызываемые приливной деформацией Земли
- § 6.03. Релятивистские эффекты. Влияние электромагнитных сил и притяжения атмосферы
- Часть VII. ЧИСЛЕННЫЕ МЕТОДЫ
- Глава 1. ИНТЕРПОЛИРОВАНИЕ И ПРИБЛИЖЕНИЕ ФУНКЦИЙ
- § 1.02. Интерполяционные формулы
- § 1.03. Остаточные члены интерполяционных формул
- § 1.04. Обратное интерполирование
- § 1.05. Интерполирование функции двух переменных
- § 1.06. Приближение функций с помощью сплайнов
- § 1.07. Среднеквадратичные приближения функций
- § 1.08. Сглаживание табличных значений функций
- § 1.09. Равномерные приближения
- § 1.10. Аппроксимация периодических функций с известным периодом тригонометрическими полиномами по методу наименьших квадратов
- § 1.11. Аппроксимация условно-периодических функций с известными частотами полиномом Фурье по методу наименьших квадратов
- § 1.12. Определение неизвестных частот периодической или условно-периодической функции по совокупности табличных данных
- § 1.13. Выделение «вековой части» функции по совокупности табличных значений
- Глава 2. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
- § 2.01. Численное дифференцирование с помощью интерполяционных формул
- § 2.02. Другие формулы численного дифференцирования
- § 2.03. Численное интегрирование функции по таблице ее значений с постоянным шагом
- § 2.04. Квадратурные формулы Гаусса
- § 2.05. Численное интегрирование сильно осциллирующих функций
- § 2.06. Правило Рунге практической оценки погрешности квадратурных формул
- § 2.07. Квадратурные формулы для несобственных интегралов
- Глава 3. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 3.01. Метод Рунге—Кутта
- § 3.02. Метод Адамса
- § 3.03. Метод Коуэлла
- § 3.04. Метод Штермера (для уравнений второго порядка)
- § 3.05. Метод Коуэлла (1-й вариант)
- § 3.06. Метод Коуэлла (2-й вариант)
- § 3.07. Накопление погрешностей при численном интегрировании
- § 3.08. Метод Энке численного интегрирования уравнений возмущенного движения
- § 3.09. Общая постановка краевой задачи для обыкновенных дифференциальных уравнений. Случай линейной краевой задачи
- § 3.10. Метод стрельбы при нахождении решения линейной двухточечной краевой задачи
- § 3.11. Краевая задача для квазилинейной системы с линейными краевыми условиями
- § 3.12. Краевая задача для системы, близкой к нелинейной невозмущенной системе
- § 3.13. Применение метода градиентного спуска для решения нелинейной краевой задачи общего вида
- § 3.14. Разностный метод решений краевых задач
- Глава 4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- § 4.02. Линейные и равноточные условные уравнения
- § 4.03. Вероятностные оценки погрешности решения
- § 4.04. Неравноточные условные уравнения
- § 4.05. Линеаризация условных уравнений общего вида
- Часть VIII. ОПТИМАЛЬНЫЕ И КРАЕВЫЕ ЗАДАЧИ АСТРОДИНАМИКИ
- Глава 1. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ И МАТЕМАТИЧЕСКОЙ ТЕОРИИ ОПТИМАЛЬНЫХ ПРОЦЕССОВ
- § 1.01. Понятие функционала
- § 1.02. Задача Лагранжа. Множители Лагранжа. Уравнения Эйлера
- § 1.03. Первая формулировка задачи Майера
- § 1.04. Вторая формулировка задачи Майера
- § 1.05. Изопериметрическая задача
- § 1.06. Задача Больца
- § 1.07. Третья формулировка задачи Майера. Обобщение теоремы Лагранжа. Характеристические уравнения (обобщенные уравнения Эйлера — Лагранжа)
- § 1.08. Свойство множителей Лагранжа на ломаных экстремалях. Условие Вейерштрасса — Эрдмана
- § 1.09. Принцип максимума Понтрягина
- § 1.10. Принцип оптимальности Беллмана
- Глава 2. ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ ТЕЛ ПЕРЕМЕННОЙ МАССЫ
- § 2.01. Основное уравнение динамики точки переменной массы (уравнение Мещерского)
- § 2.02. Обобщенное уравнение Мещерского
- § 2.03. Уравнения движения тела переменной массы в обобщенных координатах (уравнения Лагранжа второго рода)
- § 2.04. Канонические уравнения движения тела переменной массы
- Глава 3. НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ЗАДАЧИ ДИНАМИКИ ПОЛЕТА В ОКОЛОЗЕМНОМ ПРОСТРАНСТВЕ
- § 3.01. Уравнения движения ракеты. Формула Циолковского
- § 3.02. Развернутая форма характеристических уравнений для задачи о движении ракеты
- § 3.03. Определение базис-вектора и p-траектории. Определение функций переключения
- § 3.04. Определение импульсной тяги. Точки соединения на оптимальных траекториях
- § 3.05. Максимизация высоты вертикального подъема ракеты в однородном поле тяжести
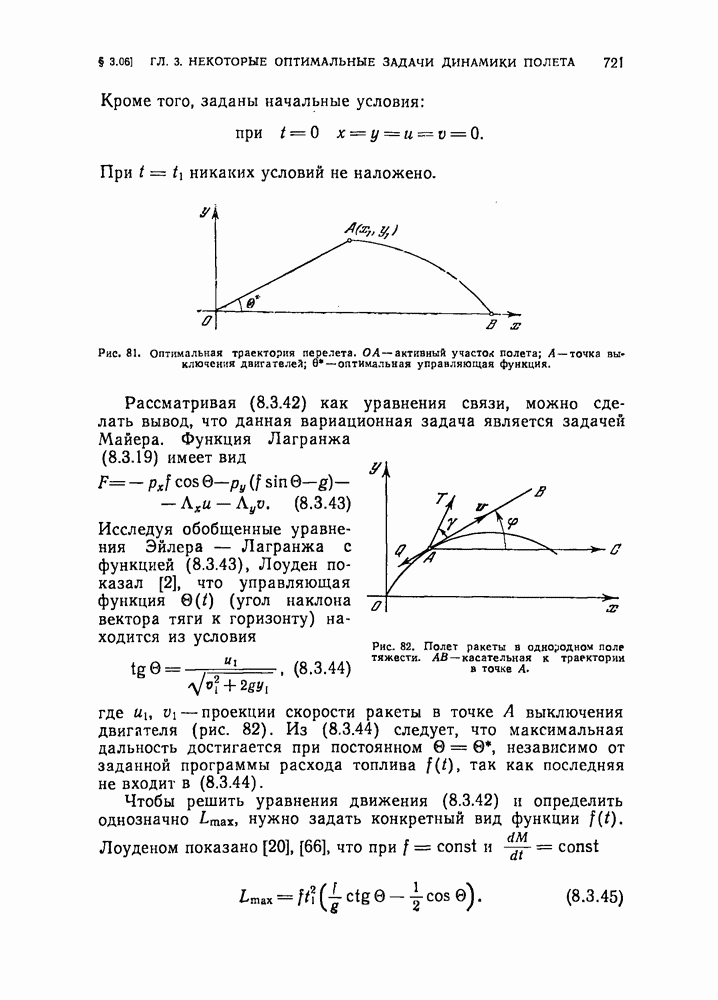
- § 3.06. Максимизация горизонтальной дальности полета ракеты в однородном поле тяжести при заданной программе расхода топлива
- § 3.07. Общая вариационная задача для движения ракеты в однородном поле тяжести
- § 3.08. Общая вариационная задача для движения ракеты в однородном поле тяжести при наличии аэродинамического сопротивления
- § 3.09. Определение оптимальной программы тяги при вертикальном подъеме ракеты в неоднородном поле тяготения в сопротивляющейся атмосфере
- § 3.10. Задача о максимизации полной энергии космического аппарата
- § 3.11. Задача о минимизации характеристической скорости маневра
- Глава 4. МЕЖОРБИТАЛЬНЫЕ ПЕРЕЛЕТЫ
- § 4.02. Уравнение для базиса-вектора на участке нулевой тяги при движении ракеты в ньютоновском поле тяготения
- § 4.03. Уравнение для базиса-вектора на участке промежуточной тяги при движении ракеты в ньютоновском поле тяготения
- § 4.04. Уравнение для базиса-вектора на участке максимальной тяги при движении ракеты в ньютоновском поле тяготения
- § 4.05. Метод p-траекторий. Структура оптимальной траектории
- § 4.06. Связь между величиной импульса и элементами эллиптической орбиты
- § 4.07. Оптимальный n-импульсный переход между двумя заданными компланарными эллиптическими орбитами
- § 4.08. Оптимальный переход между двумя компланарными круговыми орбитами
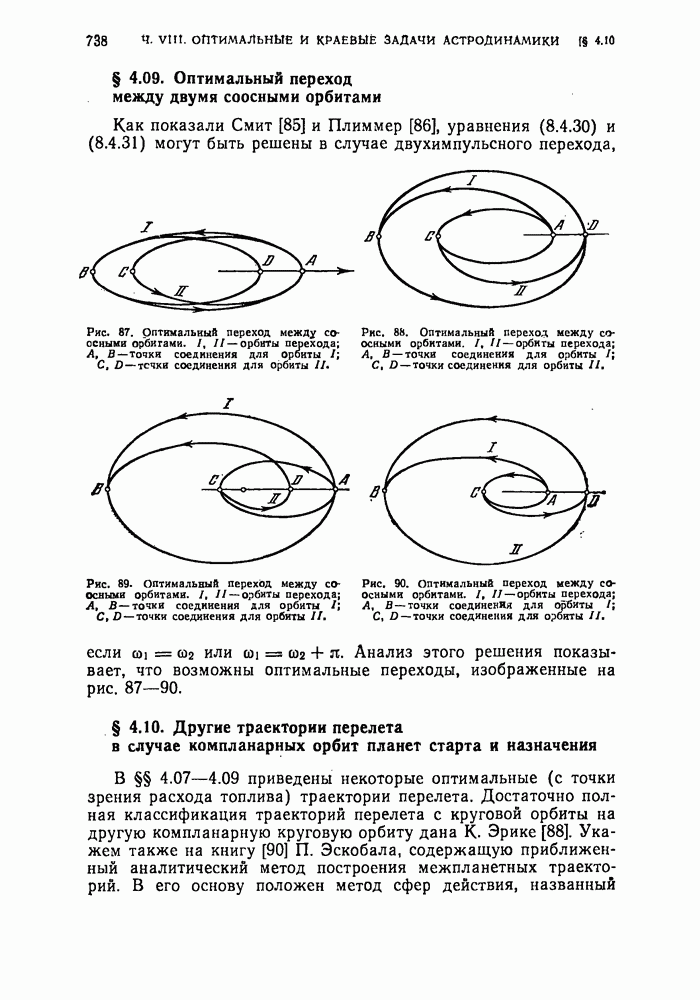
- § 4.09. Оптимальный переход между двумя соосными орбитами
- § 4.10. Другие траектории перелета в случае компланарных орбит планет старта и назначения
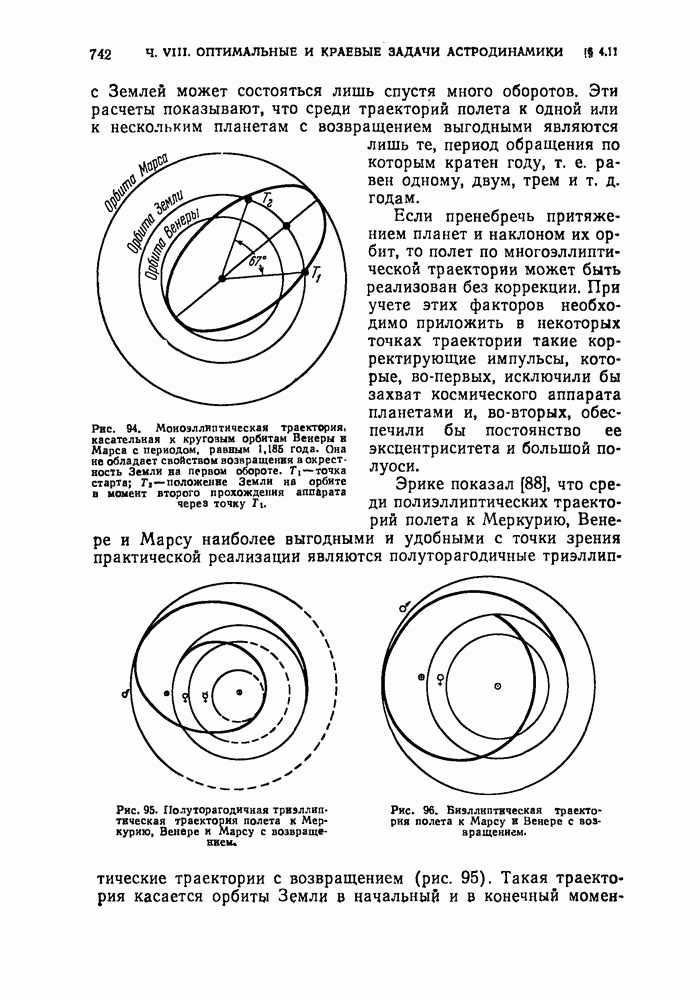
- § 4.11. Траектории полета вблизи нескольких планет
- § 4.12. Начальный этап (запуск и уход) межпланетной траектории
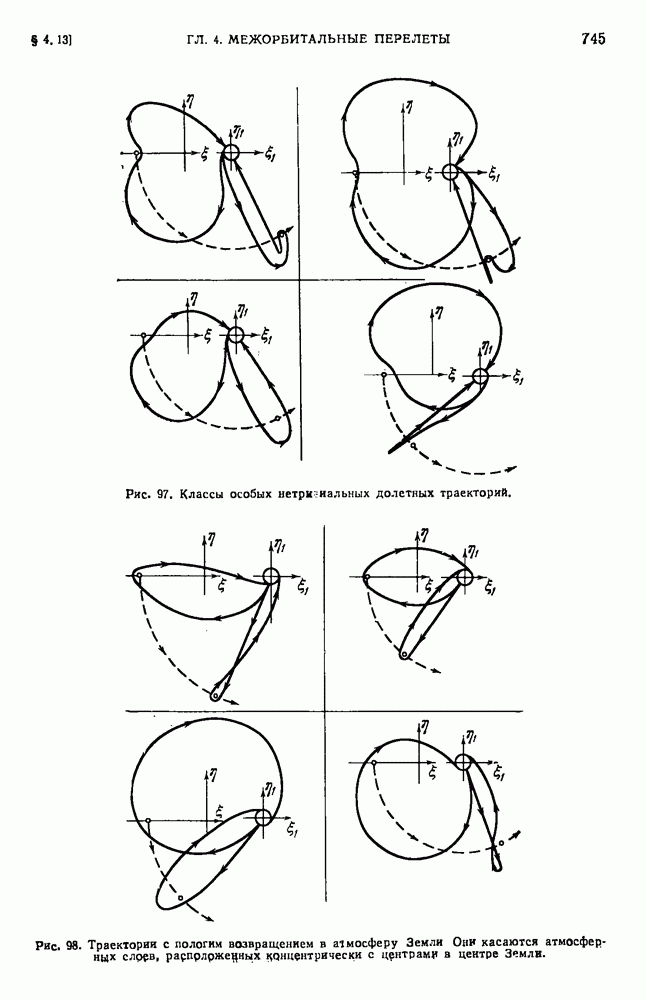
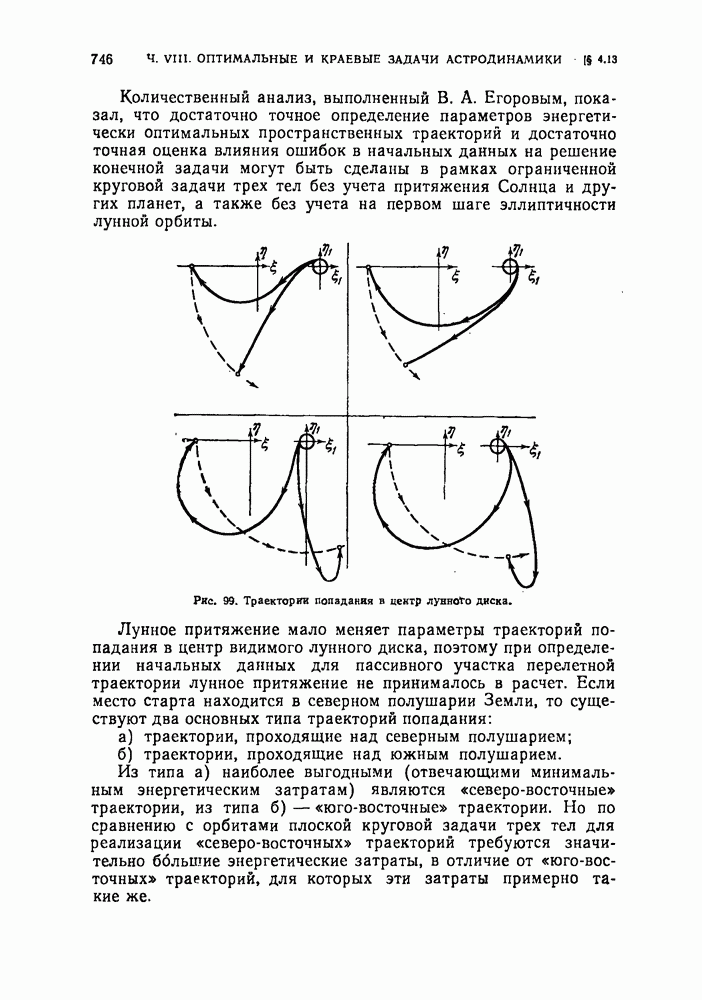
- § 4.13. Полеты к Луне
- Часть IX. ДВИЖЕНИЕ ЕСТЕСТВЕННЫХ И ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
- Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
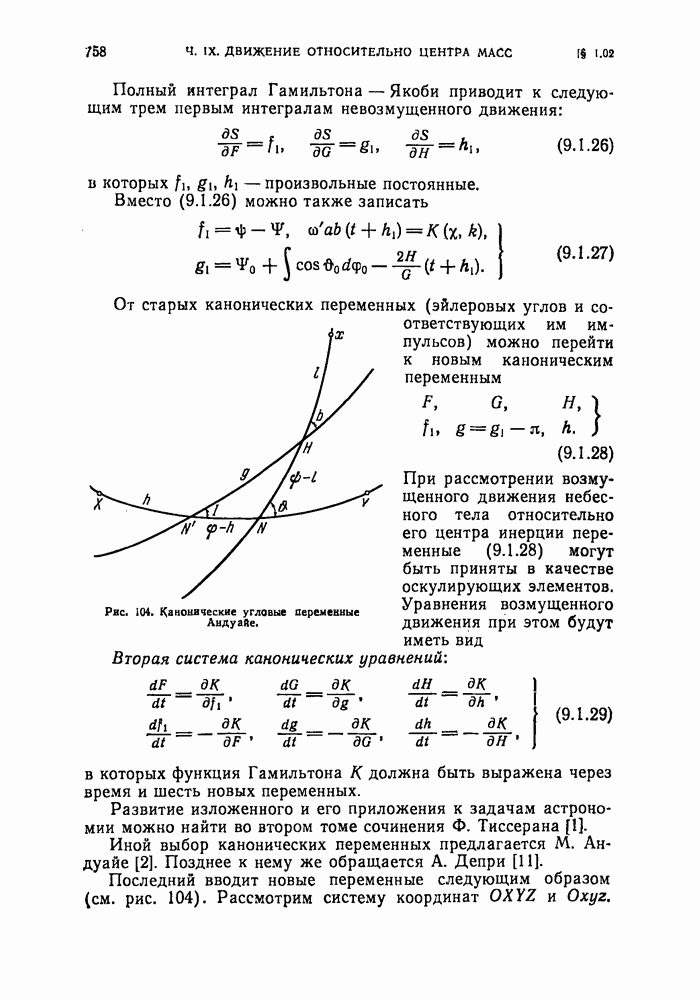
- § 1.02. Канонические уравнения вращательного движения небесных тел
- § 1.03. Астродинамические дифференциальные уравнения возмущенного движения спутника относительно центра масс
- § 1.04. Моменты сил, действующих на спутник
- § 1.05. Движение спутника относительно центра масс в центральном ньютоновском поле
- § 1.06. Задача о поступательно-вращательном движении двух гравитирующих динамически симметричных тел
- § 1.07. Вращение Луны
- § 1.08. Дифференциальные уравнения движения деформируемого небесного тела
- § 1.09. Теория фигур небесных тел
- Глава 2. УСТОЙЧИВОСТЬ И СТАБИЛИЗАЦИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ
- § 2.01. Устойчивость движения спутников в гравитационном поле сил
- § 2.02. Устойчивость движения спутников под действием моментов сил различной природы
- § 2.03. Стабилизация движения спутников и космических аппаратов
- Часть X. КАЧЕСТВЕННАЯ НЕБЕСНАЯ МЕХАНИКА
- Глава 1. ПЕРИОДИЧЕСКИЕ И УСЛОВНО-ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ. ФИНАЛЬНЫЕ ДВИЖЕНИЯ
- § 1.02. Метод Ляпунова
- § 1.03. Периодические решения, полученные методом Пуанкаре
- § 1.04. Периодические решения, полученные методом Ляпунова
- § 1.05. Периодические решения, полученные качественными методами
- § 1.06. Почти периодические функции и их свойства. Условно-периодические функции
- § 1.07. Теорема Арнольда о существовании условно-периодических решений гамильтоновых систем
- § 1.08. Условно-периодические решения в небесной механике. Геометрическая интерпретация
- § 1.09. Финальные движения в задаче трех тел. Захват и обмен в задаче трех тел
- Глава 2. ПРОБЛЕМА ИНТЕГРИРУЕМОСТИ И СХОДИМОСТЬ РЯДОВ В НЕБЕСНОЙ МЕХАНИКЕ
- § 2.01. Теорема Пуассона об интеграле гамильтоновой системы
- § 2.02. Теорема Брунса о несуществовании алгебраических первых интегралов задачи трех тел, отличных от классических
- § 2.03. Теорема Пуанкаре о несуществовании однозначных аналитических первых интегралов гамильтоновой системы
- § 2.04. Случаи интегрируемости уравнения Гамильтона — Якоби методом разделения переменных
- § 2.05. Теорема о неприводимости уравнения Гамильтона — Якоби для плоской ограниченной круговой задачи трех тел к уравнению типа Штеккеля
- § 2.06. Соударения
- § 2.07. Решение задачи трех тел в виде рядов, сходящихся для всех вещественных значений времени. Теорема Зундмана
- § 2.08. Сходимость рядов Хилла в основной проблеме теории движения Луны
- § 2.09. Характер сходимости рядов классической теории возмущений
- § 2.10. Теоремы Пуанкаре о ранге и классе возмущений
- § 2.11. Поиск частных, первых и общих интегралов заданной аналитической структуры обыкновенных дифференциальных уравнений на ЭВМ. Приложение к ограниченной задаче трех тел
- § 2.12. Поиск решений уравнения Гамильтона — Якоби на ЭВМ. Приложение к ограниченной задаче трех тел
- Глава 3. ПРОБЛЕМА УСТОЙЧИВОСТИ В НЕБЕСНОЙ МЕХАНИКЕ
- § 3.01. Определение устойчивости по Ляпунову
- § 3.02. Определение орбитальной устойчивости
- § 3.03. Другие определения устойчивости
- § 3.04. Знакопостоянные и знакоопределенные функции. Полная производная в силу системы
- § 3.05. Теоремы Ляпунова об устойчивости
- § 3.06. Устойчивость по отношению к части переменных. Теорема В. В. Румянцева
- § 3.07. Связка первых интегралов. Способ Н. Г. Четаева
- § 3.08. Устойчивость при постоянно действующих возмущениях. Теорема И. Г. Малкина
- § 3.09. Теоремы Лапласа — Лагранжа и Пуассона об отсутствии вековых возмущений больших полуосей
- § 3.10. Теоремы об устойчивости планетных орбит
- § 3.11. Теоремы Арнольда об устойчивости решения гамильтоновой системы в общем эллиптическом случае
- § 3.12. Устойчивость лагранжевых равновесных решений задачи трех тел
- § 3.13. Устойчивость других решений задачи трех тел
- § 3.14. Устойчивость орбитальных движений искусственных спутников