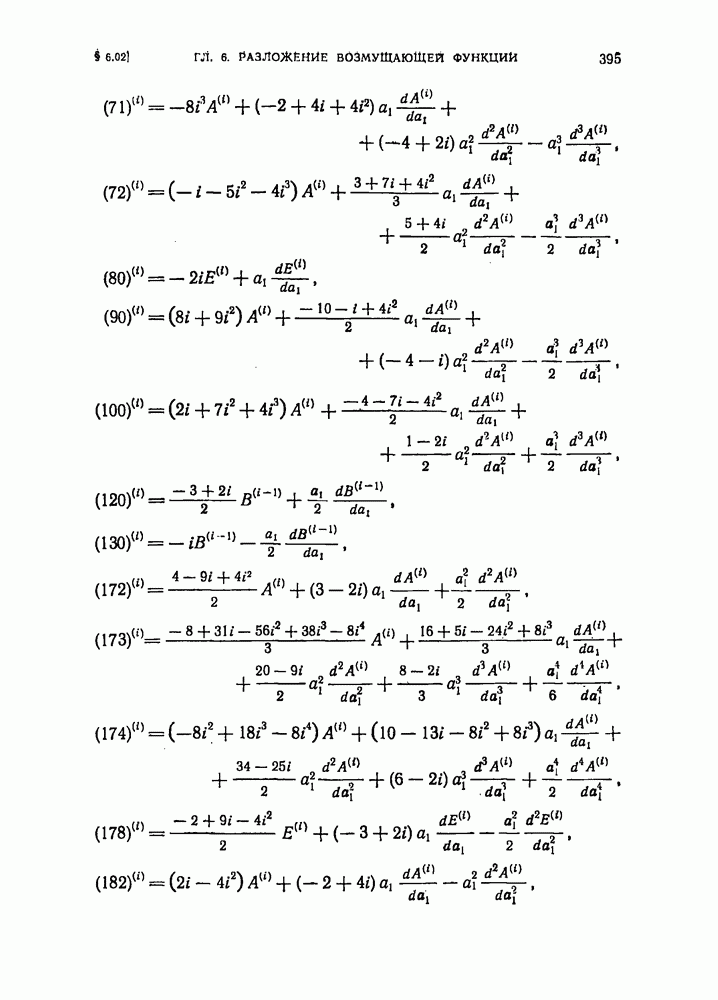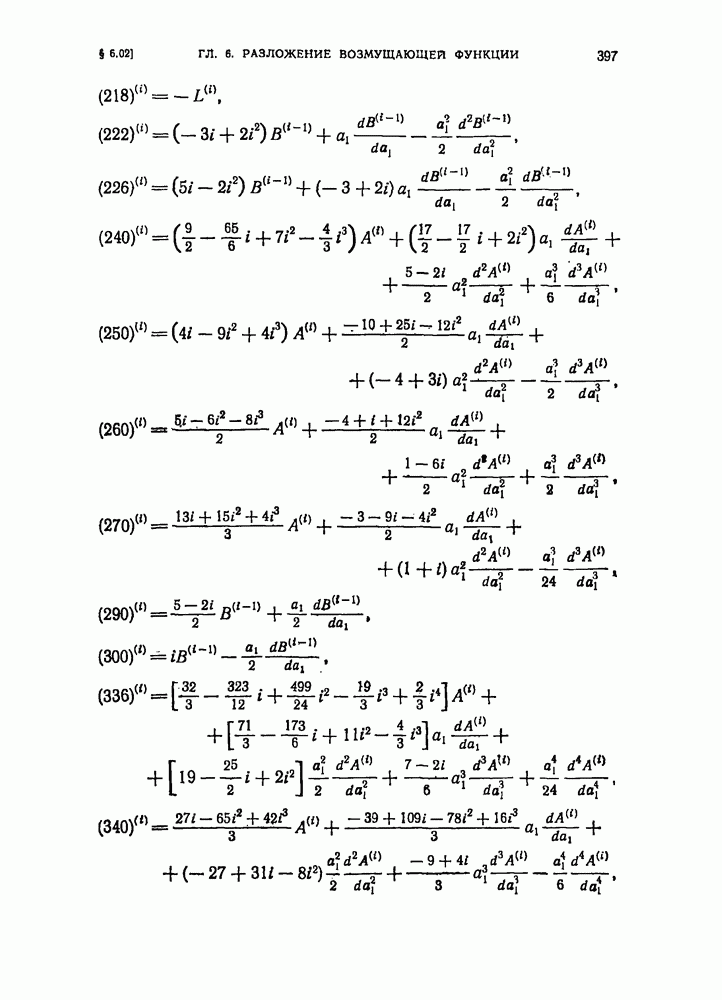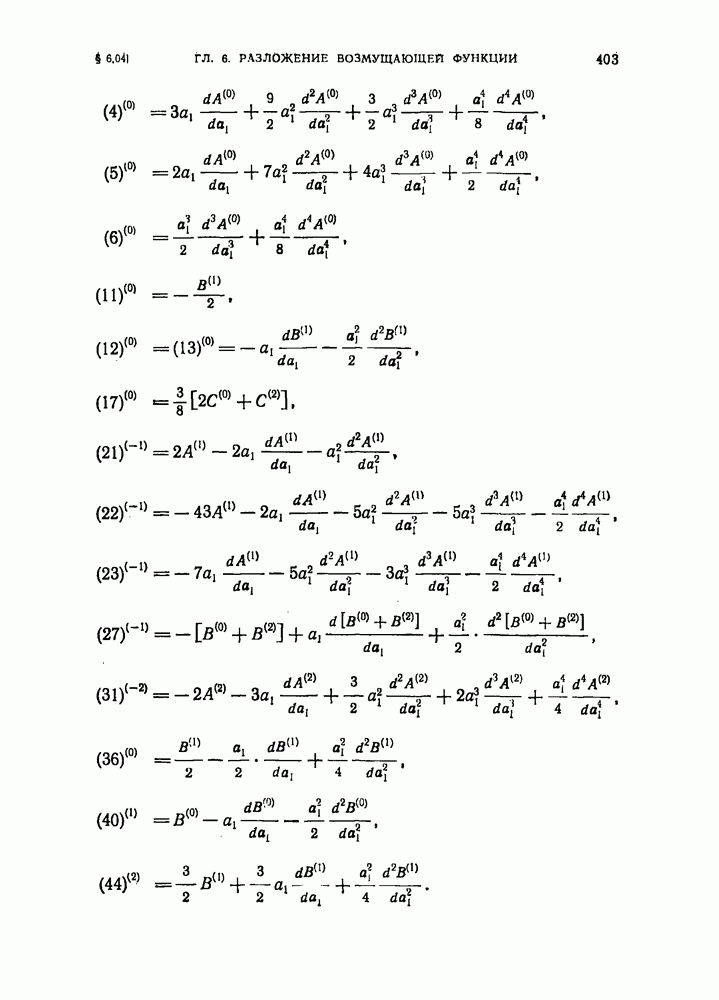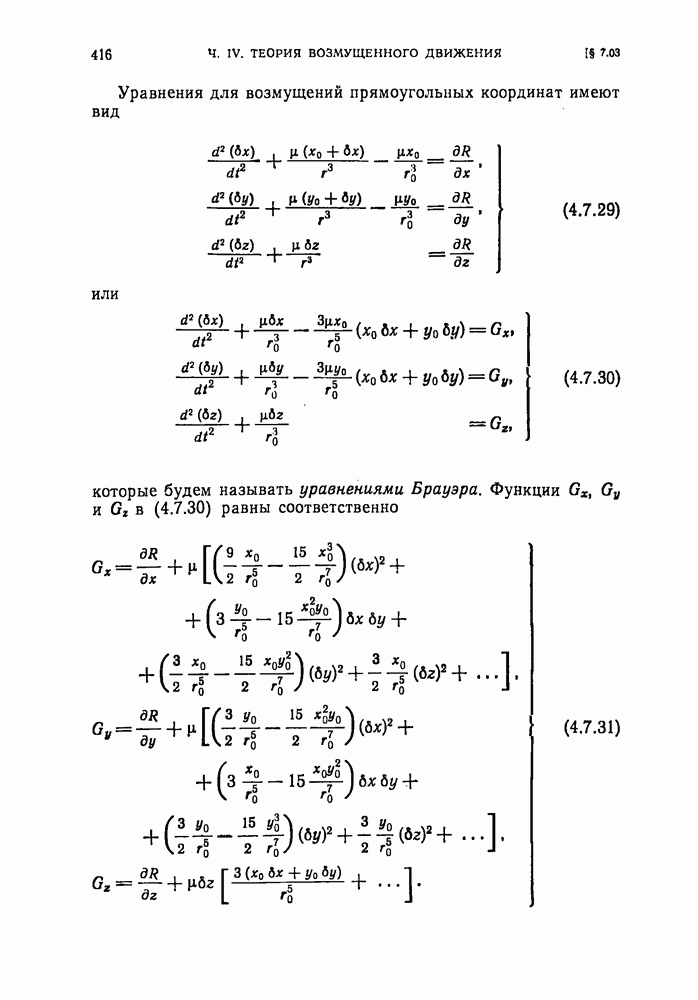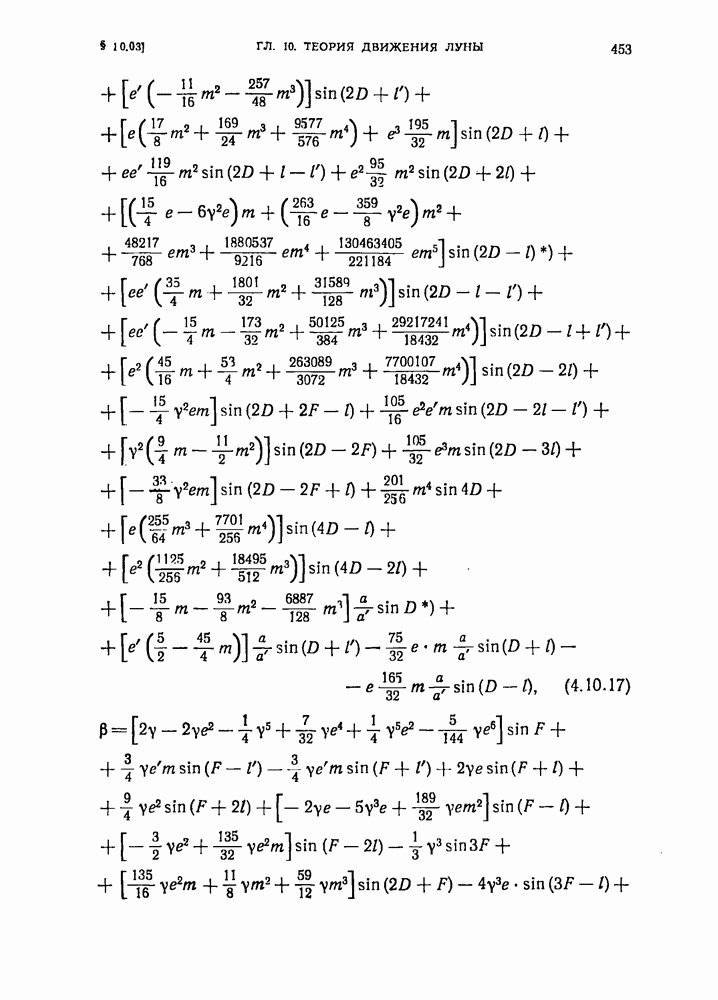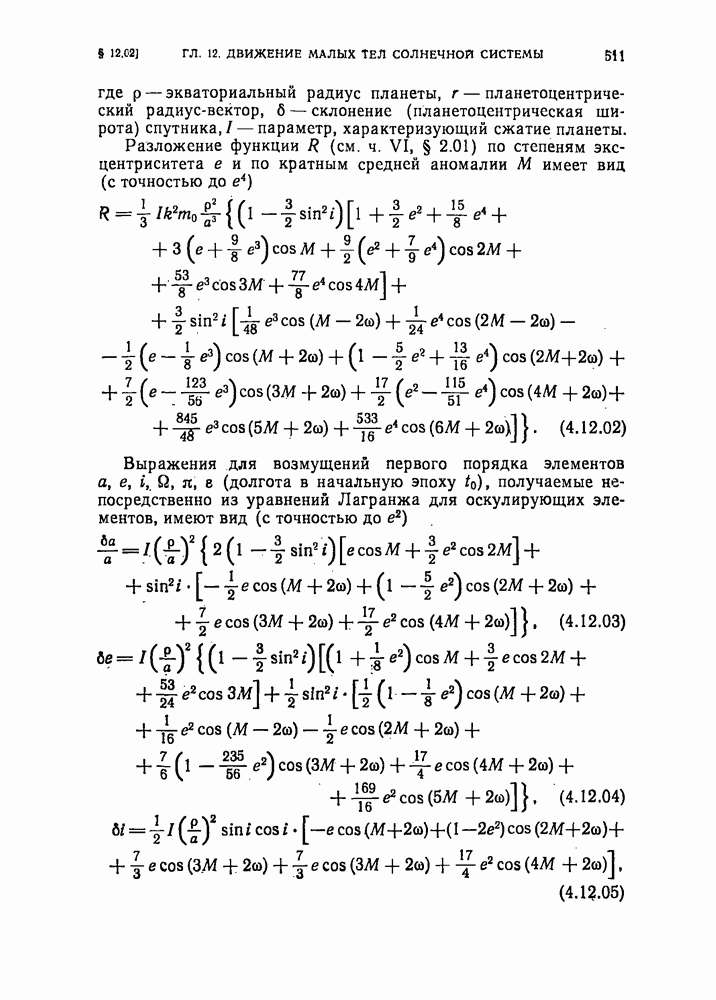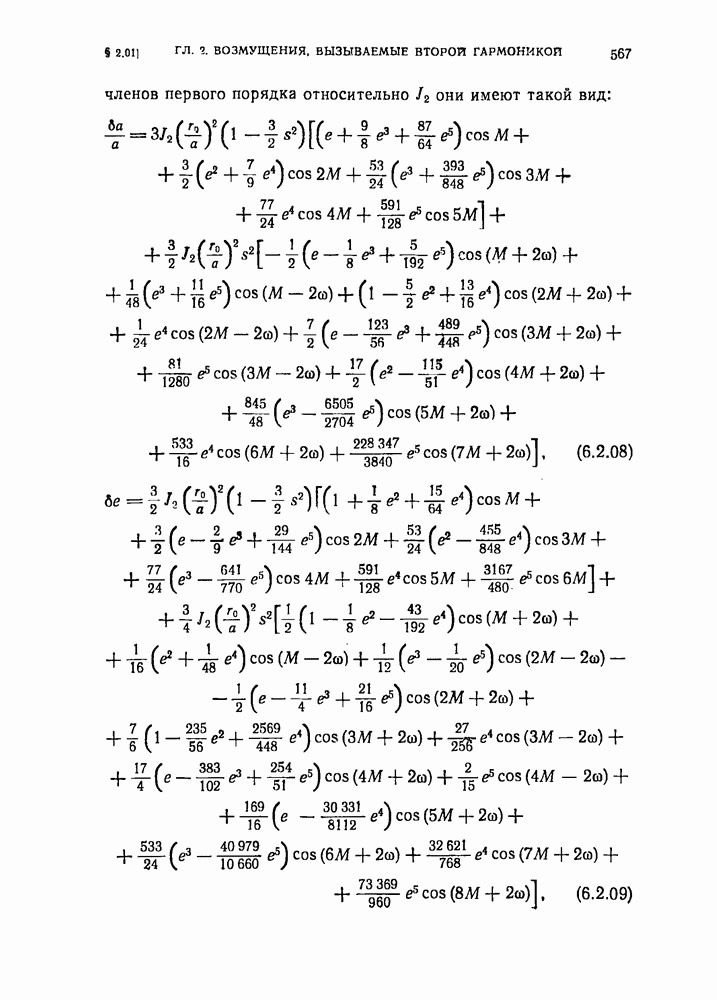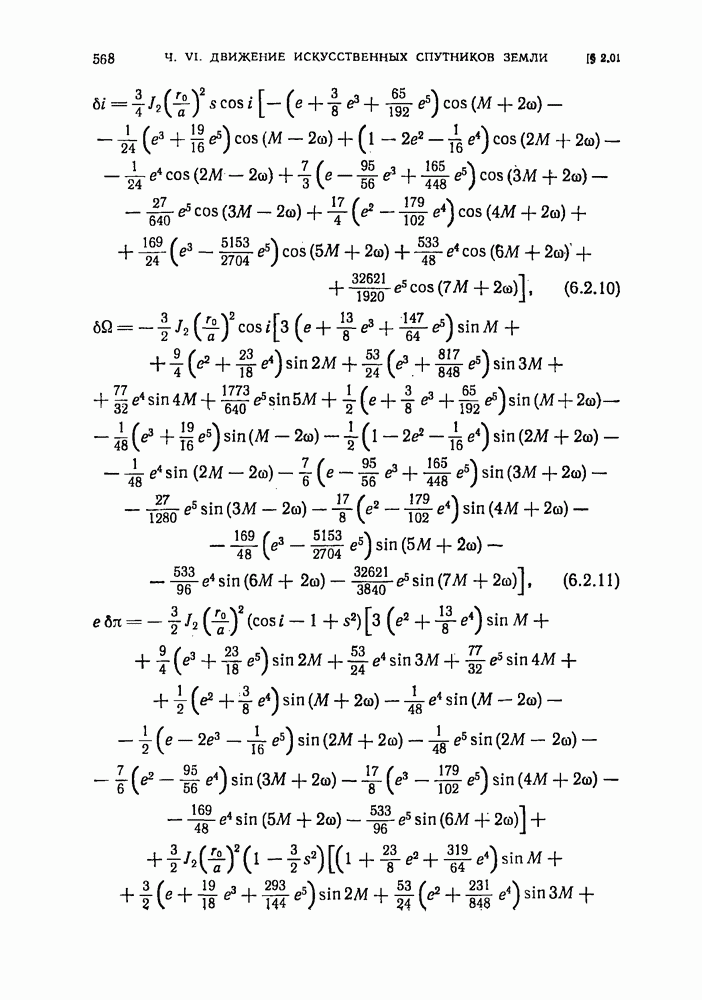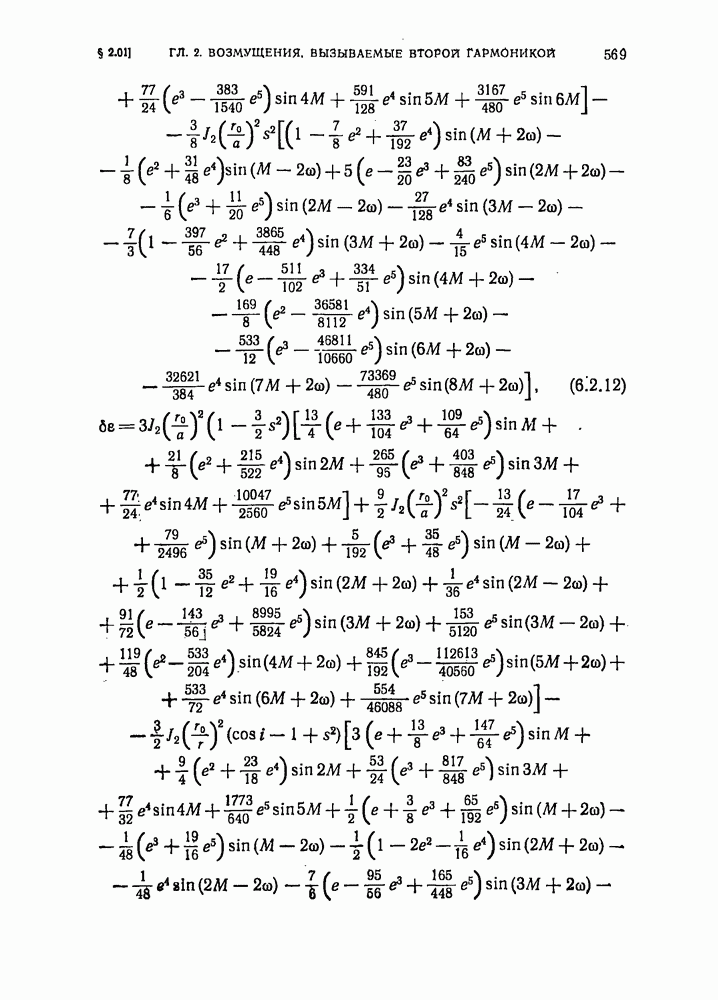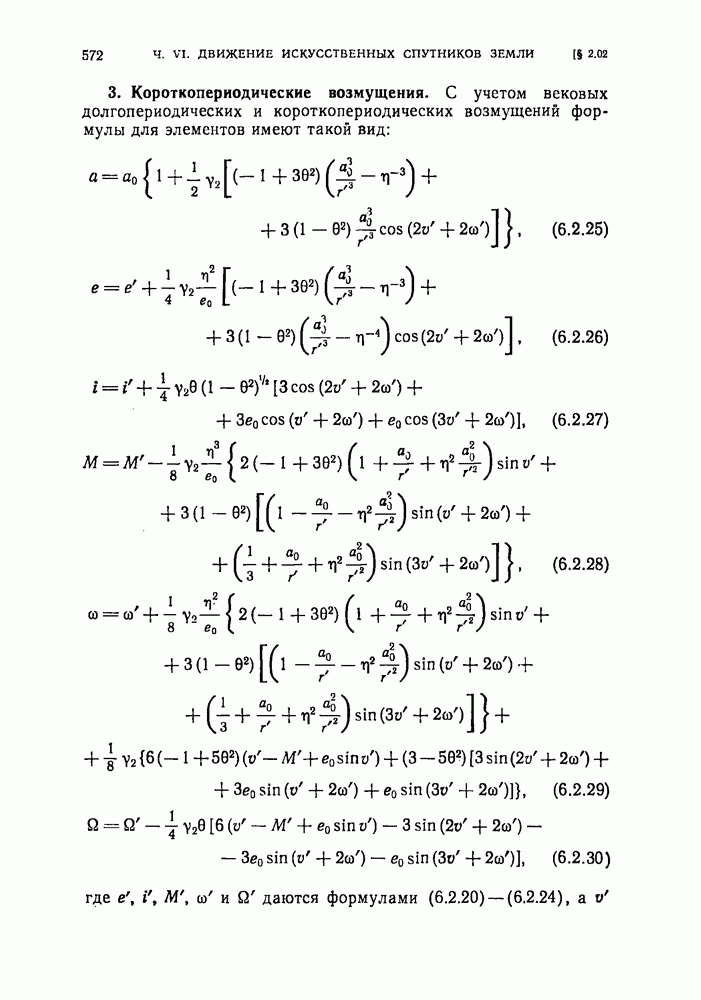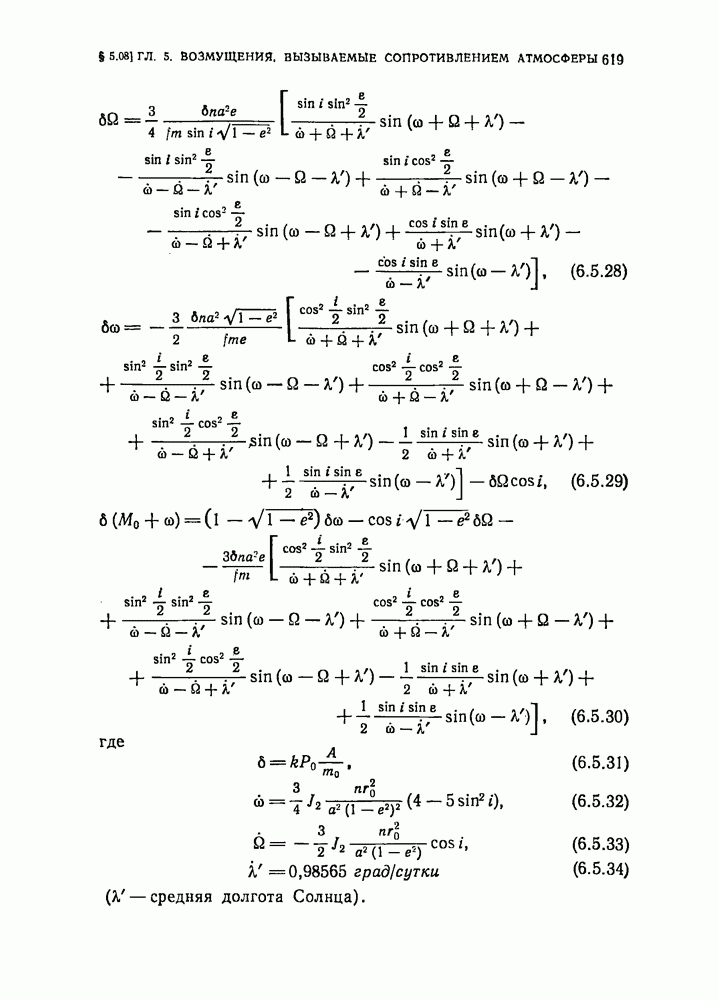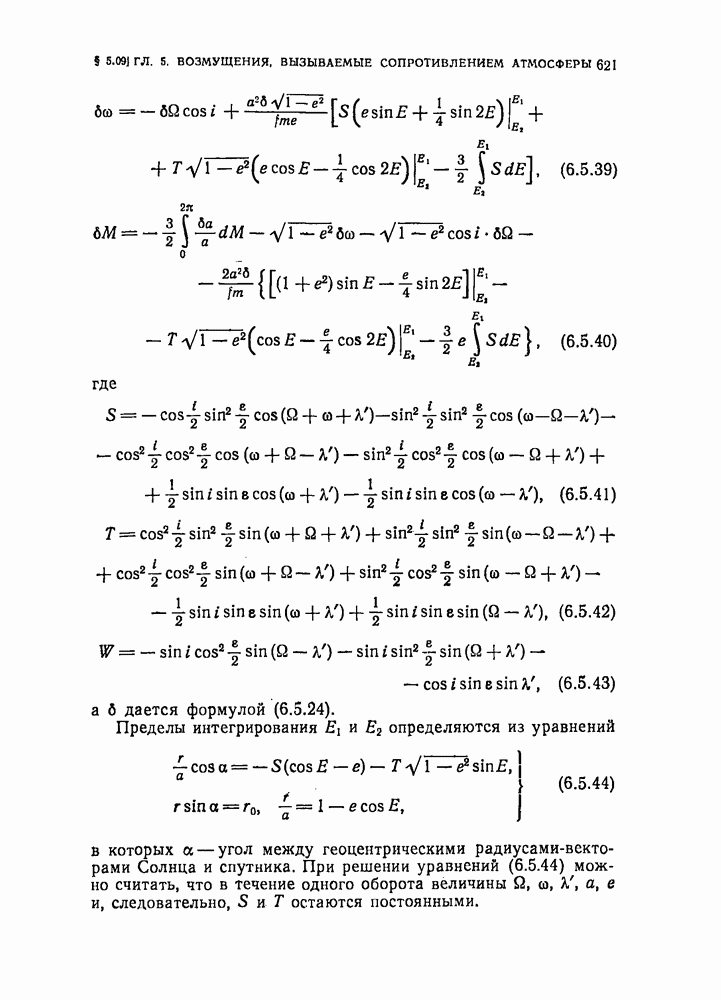| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 1.04. Обратное интерполирование
Обратное интерполирование заключается в нахождении значения аргумента, соответствующего заданному значению табличной функции.
Обозначим последнее через  а искомое значение аргумента
а искомое значение аргумента  — через Ближайшее табличное значение функции обозначим через
— через Ближайшее табличное значение функции обозначим через  пронумеруем соответствующим образом предшествующие и последующие значения функции и составим таблицу разностей. Положим
пронумеруем соответствующим образом предшествующие и последующие значения функции и составим таблицу разностей. Положим  где
где  — неизвестное, так что
— неизвестное, так что 
Вычисление  целесообразно выполнить следующим образом.
целесообразно выполнить следующим образом.
Перепишем, например, интерполяционную формулу Бесселя (7.1.08) в виде

Эта формула рассматривается далее как уравнение относительно неизвестного  и его решение ищется методом
и его решение ищется методом
последовательных приближений. В первом приближении полагают

а последующие приближения  ищутся по формуле
ищутся по формуле

Аналогичным образом можно применить формулу Стирлинга
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- Часть I. СФЕРИЧЕСКАЯ И ЭФЕМЕРИДНАЯ АСТРОНОМИЯ, ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
- Глава 1. СИСТЕМЫ КООРДИНАТ
- § 1.02. Главные круги, линии и точки небесной сферы
- § 1.03. Горизонтальная система координат
- § 1.04. Экваториальные системы координат
- § 1.05. Эклиптическая система координат
- § 1.06. Галактическая система координат
- § 1.07. Основные формулы сферической тригонометрии
- § 1.08. Соотношения между различными астрономическими координатами
- § 1.09. Прямоугольные системы координат
- § 1.10. Системы географических координат
- § 1.11. Соотношения между астрономическими и геодезическими координатами
- § 1.12. Планетоцентрические системы координат [25]
- § 1.13. Марсоцентрическая и ареографическая системы координат
- § 1.14. Юпитероцентрическая и зенографическая системы координат
- § 1.15. Сатурноцентрическая система координат
- § 1.16. Системы координат, определяемые осевым вращением Солнца, Венеры, Урана и Нептуна
- § 1.17. Луноцентрическая и селенографическая системы координат
- § 1.18. Орбитальная система координат
- § 1.19. Объектоцентрическая система координат
- Глава 2. РЕДУКЦИОННЫЕ ВЫЧИСЛЕНИЯ
- § 2.01. Прецессия
- § 2.02. Редукция звездных положений с учетом прецессии и собственного движения
- § 2.03. Нутация
- § 2.04. Годичная аберрация
- § 2.05. Сводка основных формул редукции звездных положений
- § 2.06. Учет влияния членов второго порядка
- § 2.07. Годичный параллакс
- § 2.08. Точные формулы для учета прецессии
- § 2.09. Формулы учета прецессии в прямоугольных экваториальных координатах
- § 2.10. Формулы учета прецессии в прямоугольных эклиптических координатах
- § 2.11. Совместный учет прецессии и нутации в прямоугольных экваториальных координатах
- § 2.12. Формулы учета прецессии в координатах и элементах орбит при умеренных и малых разностях эпох
- § 2.13. Аберрация света
- § 2.14. Приведение звезды на видимое место в прямоугольных координатах
- § 2.15. Об учете орбитального движения компонент двойных звезд
- § 2.16. Параллакс
- § 2.17. Учет суточного параллакса в горизонтальной системе координат
- § 2.18. Формулы учета суточного параллакса в экваториальной системе координат
- § 2.19. Формулы учета суточного параллакса в координатах Солнца и планет
- § 2.20. Формулы учета суточного параллакса в системе эклиптических координат
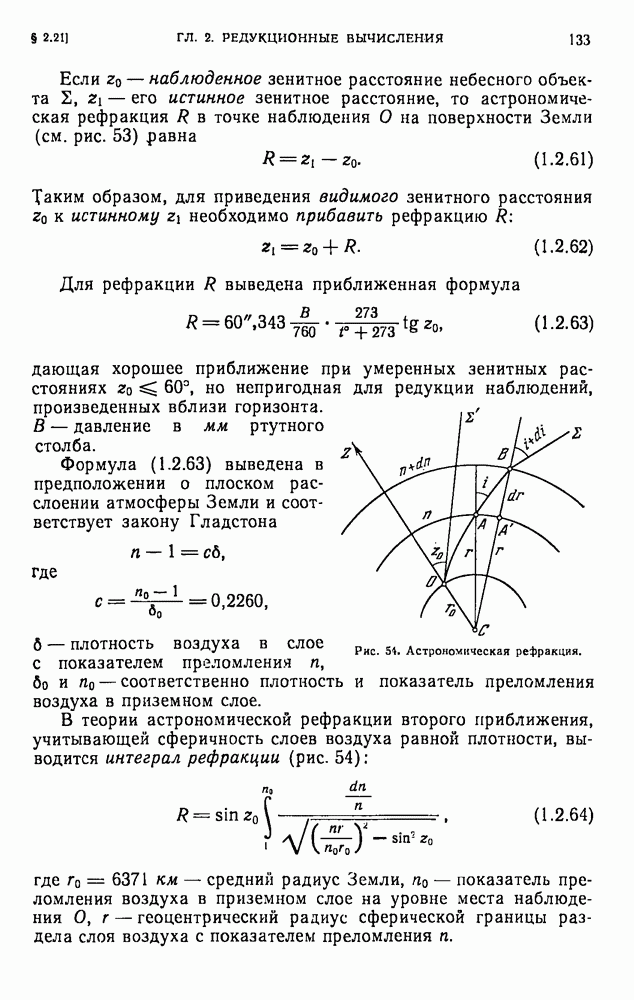
- § 2.21. Астрономическая рефракция
- § 2.22. Формулы учета рефракции в координатах небесных объектов
- § 2.23. Рефракция при наблюдении небесных объектов, расположенных на конечных расстояниях от Земли
- § 2.24. Дифференциальная прецессия и нутация. Дифференциальная аберрация и дифференциальный параллакс
- § 2.25. Сравнение теории с наблюдениями
- § 2.26. Каталоги звездных положений
- § 2.27. Геоцентрические координаты нуль-пункта селенографической системы отсчета
- § 2.28. Вычисление топоцентрических расстояний до точек лунной поверхности
- Глава 3. ВРЕМЯ И ЕГО ИЗМЕРЕНИЕ
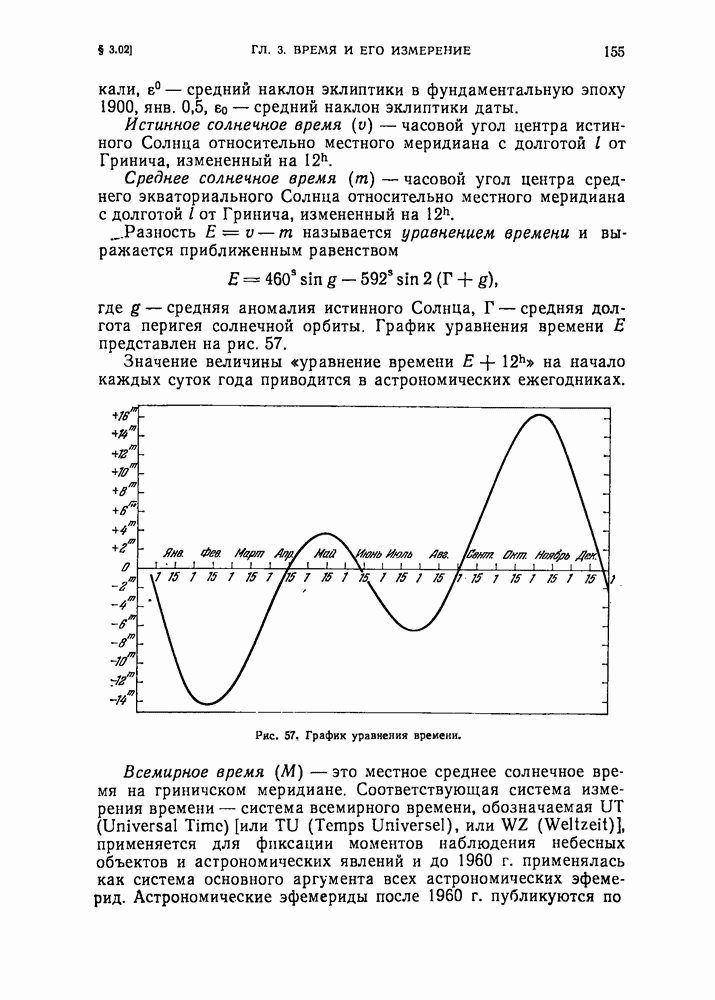
- § 3.02. Звездное и солнечное время. Всемирное время
- § 3.03. Квазиравномерное всемирное время
- § 3.04. Связь между всемирным временем и звездным гриничским временем
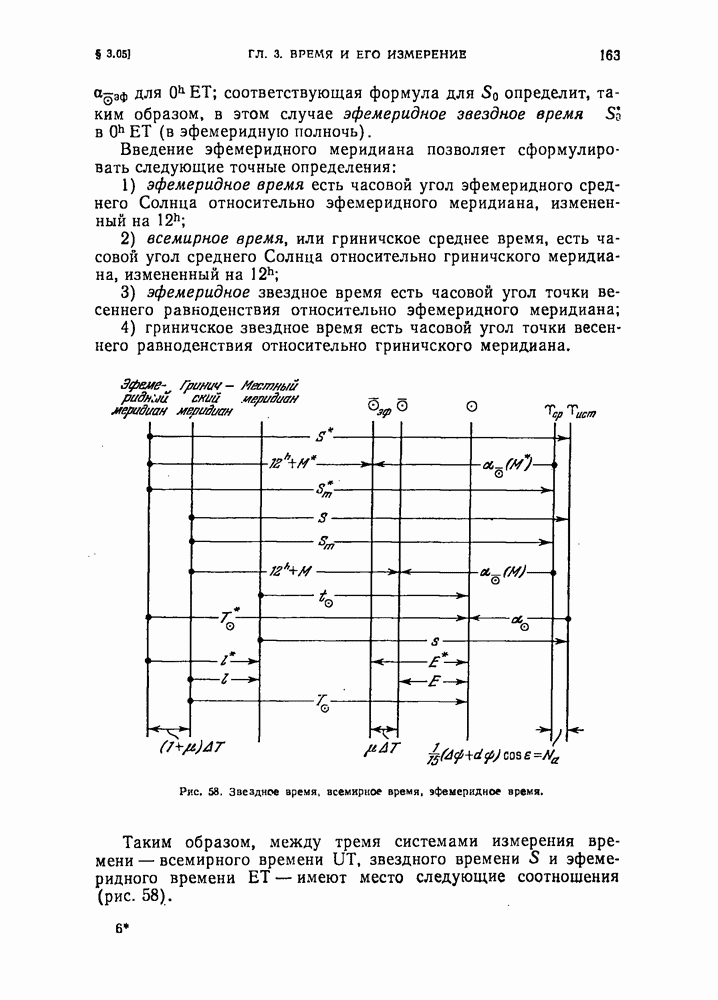
- § 3.05. Эфемеридное время
- § 3.06. Поправка за эфемеридное время
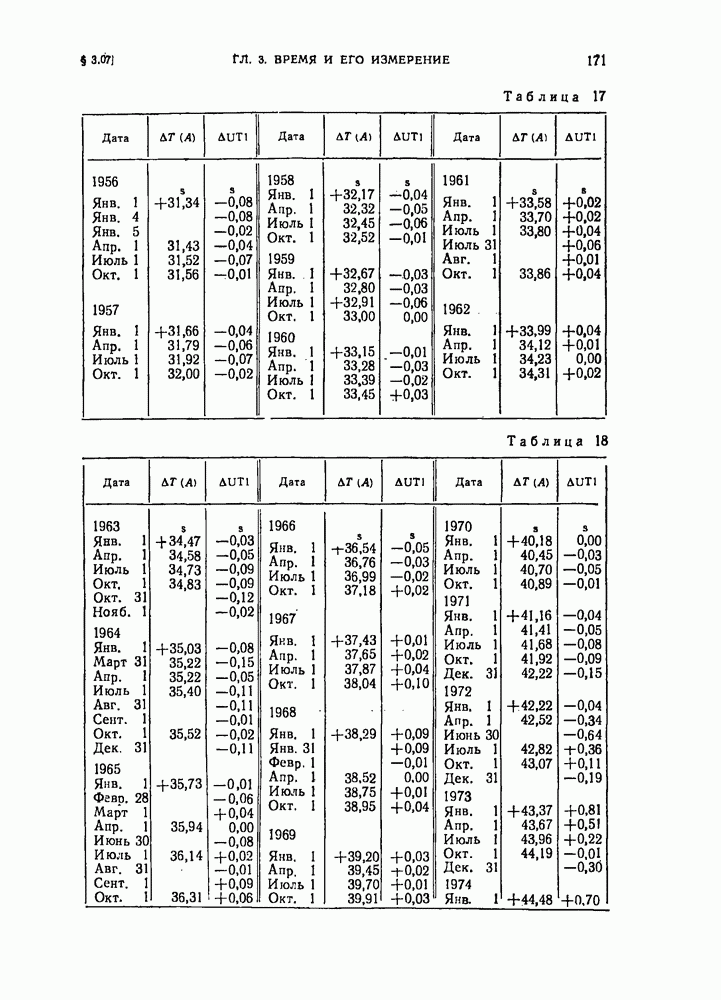
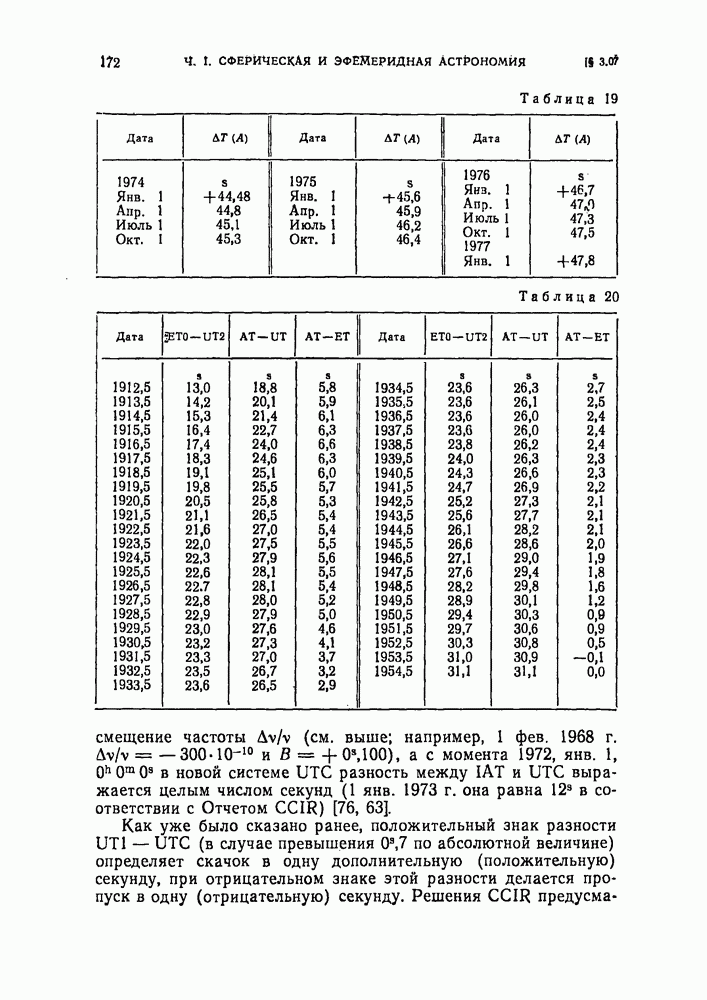
- § 3.07. Атомное время
- § 3.08. Юлианский период. Юлианские дни
- Глава 4. АСТРОНОМИЧЕСКИЕ ПОСТОЯННЫЕ
- § 4.02. Задачи астродинамики и астрономические постоянные
- § 4.03. Результаты радиолокационных определений астрономической единицы в км
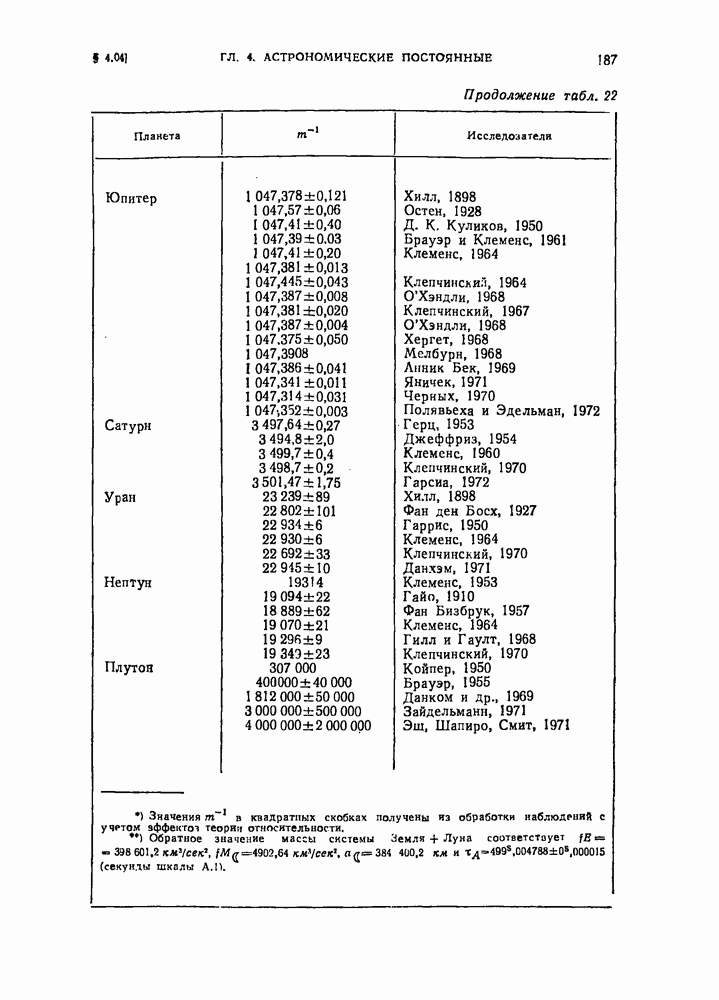
- § 4.04. Значения масс больших планет
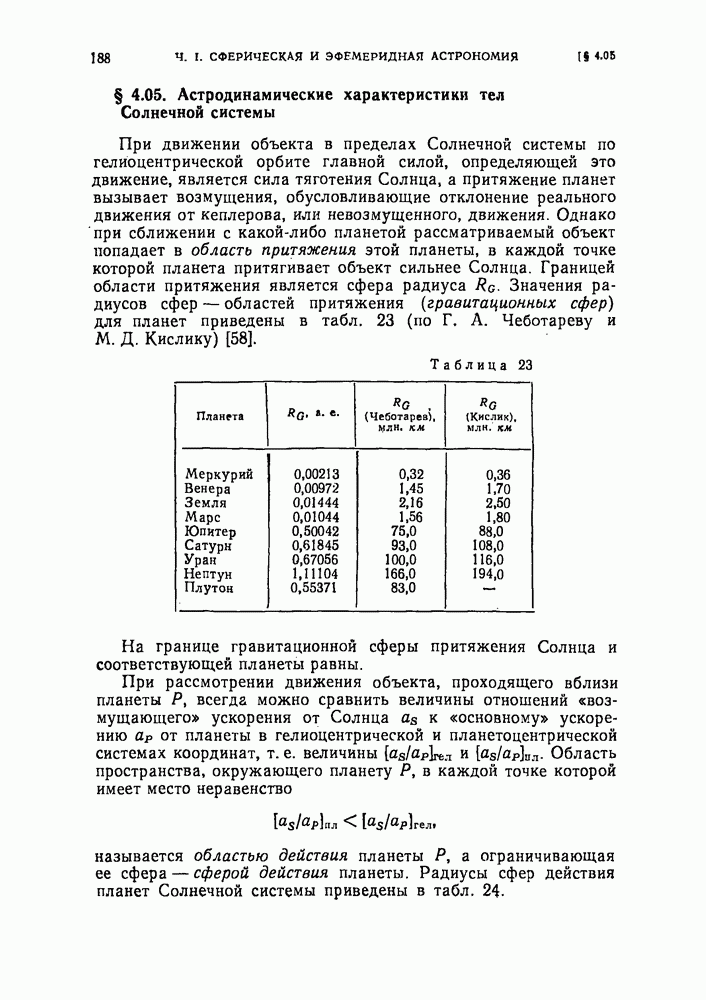
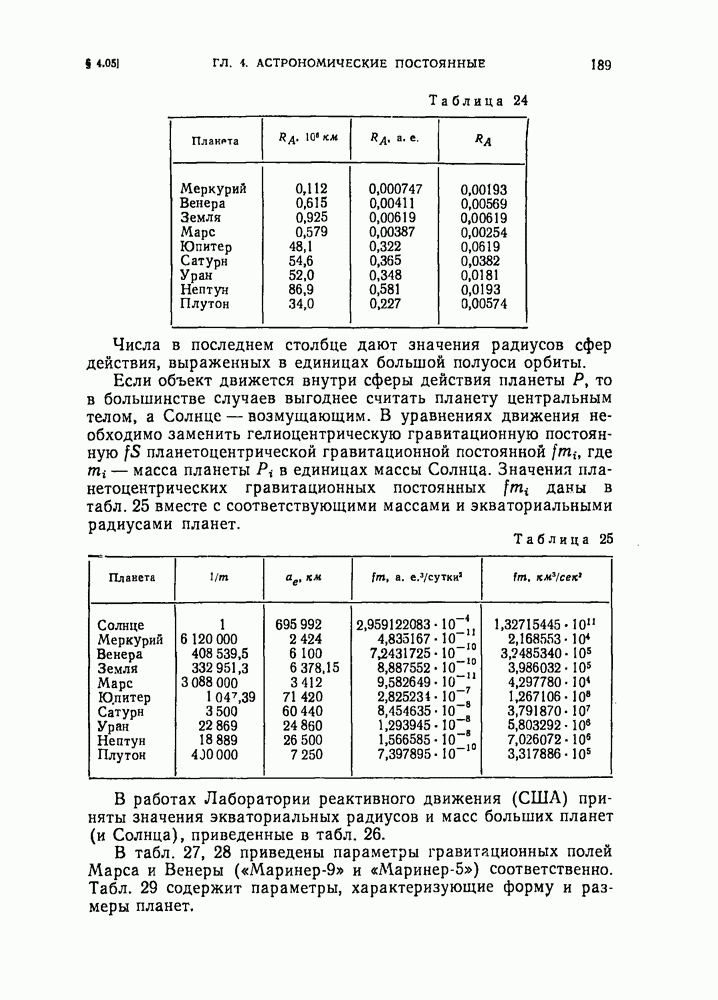
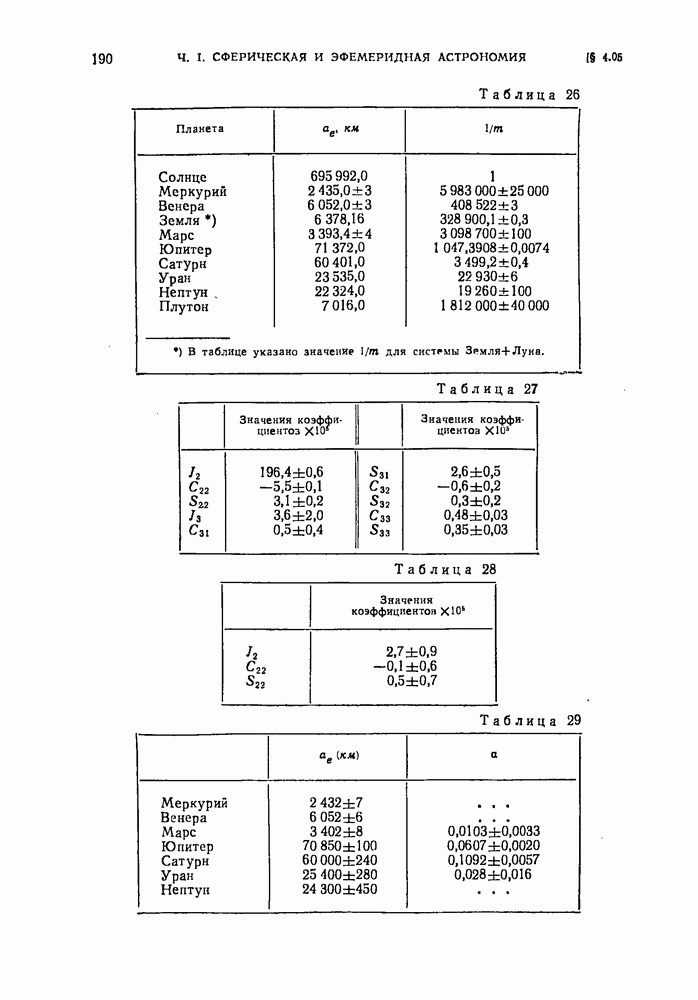
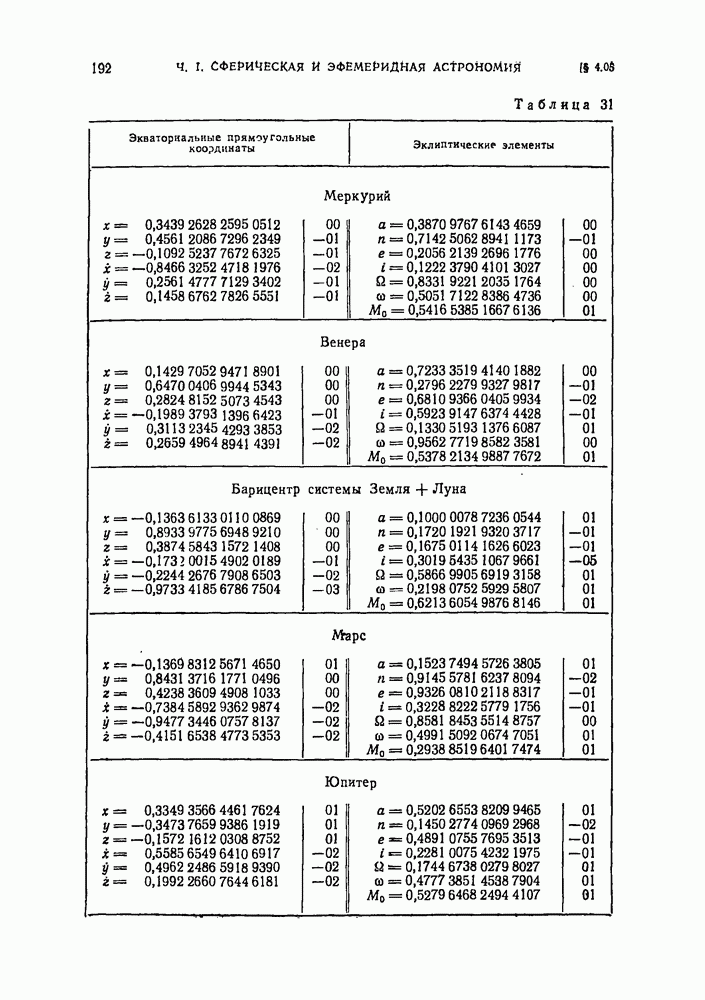
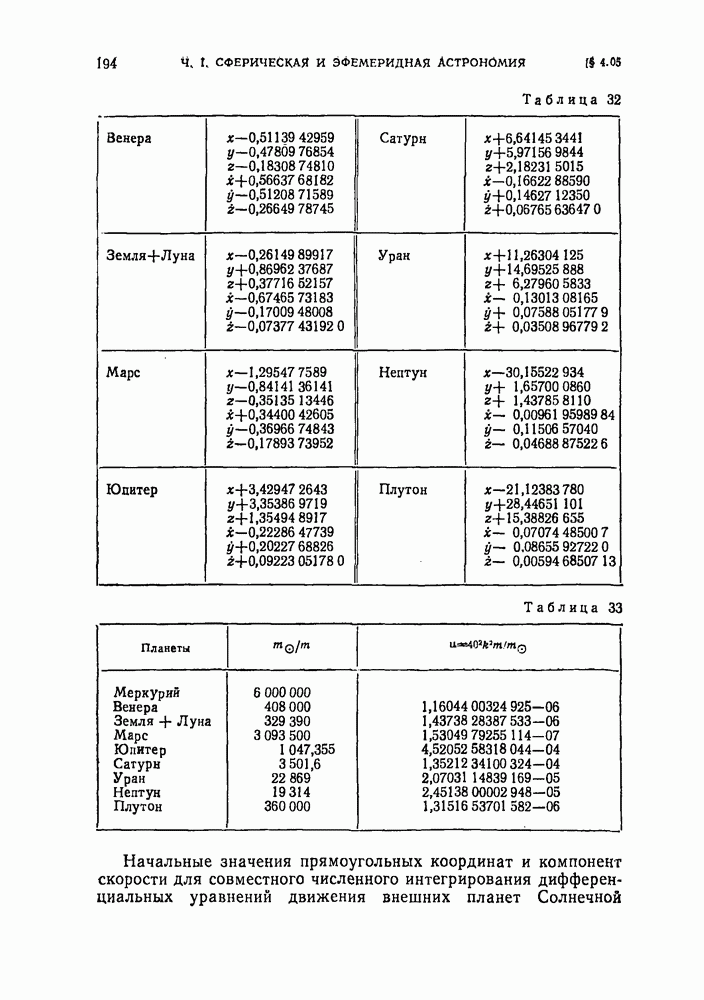
- § 4.05. Астродинамические характеристики тел Солнечной системы
- § 4.06. Астродинамические постоянные, связанные с Землей
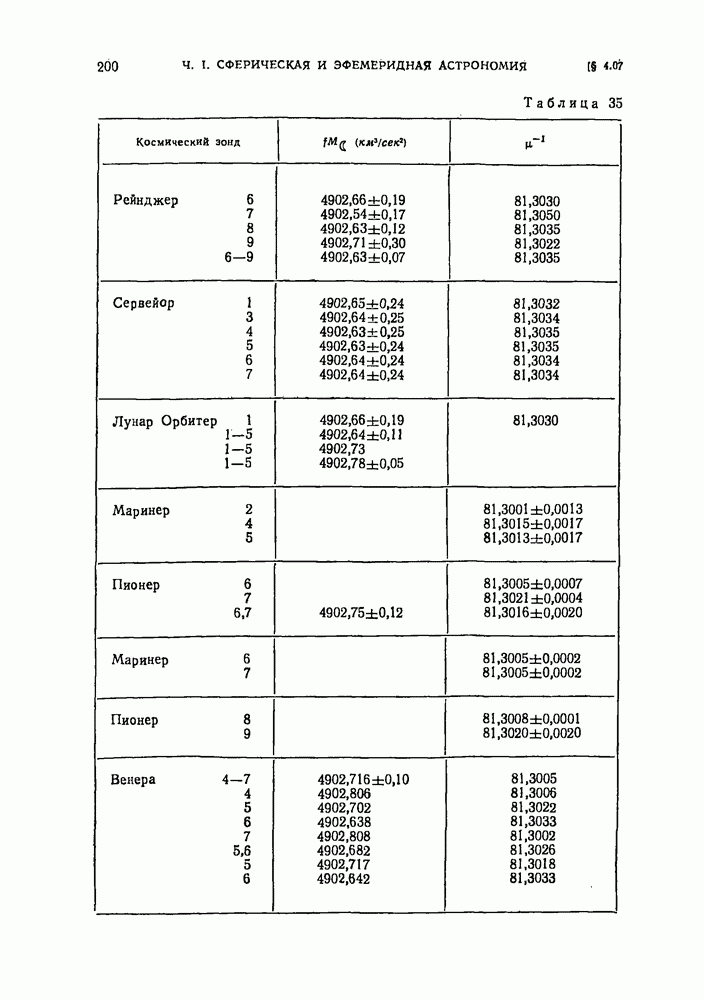
- § 4.07. Астродинамические постоянные, связанные с Луной
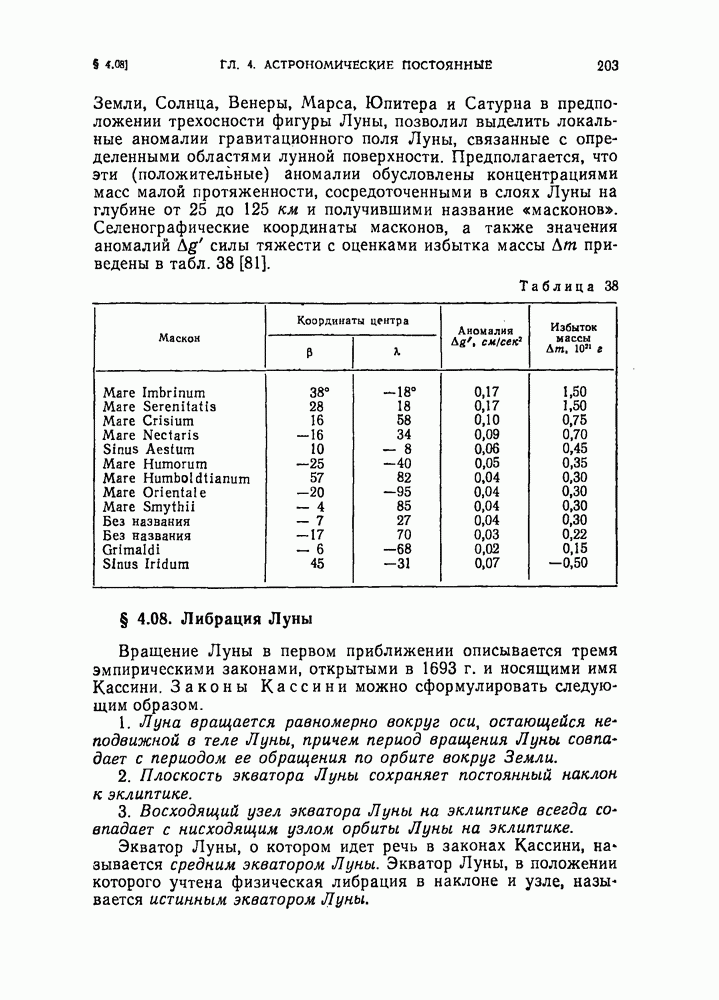
- § 4.08. Либрация Луны
- Часть II. ЗАДАЧА ДВУХ ТЕЛ
- Глава 1. ОБЩАЯ ТЕОРИЯ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ
- § 1.02. Первые интегралы уравнений невозмущенного кеплеровского движения
- § 1.03. Типы невозмущенного кеплеровского движения
- § 1.04. Элементы орбиты
- § 1.05. Формулы, связывающие постоянные интегрирования и элементы орбиты
- Глава 2. ОСНОВНЫЕ ФОРМУЛЫ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ
- § 2.02. Круговое движение
- § 2.03. Гиперболическое движение
- § 2.04. Параболическое движение
- § 2.05. Прямолинейное движение
- § 2.06. Вычисление эфемерид планет и комет
- Глава 3. РАЗЛОЖЕНИЕ КООРДИНАТ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ В РЯДЫ
- § 3.02. Разложение функций истинной аномалии в тригонометрические ряды по кратным средней аномалии
- § 3.03. Первые члены рядов по кратным средней аномалии для некоторых функций
- § 3.04. Формула Лагранжа
- § 3.05. Ряды по степеням эксцентриситета
- § 3.06. Тригонометрические ряды по кратным эксцентрической аномалии
- § 3.07. Ряды по кратным истинной аномалии
- § 3.08. Разложения координат невозмущенного кеплеровского движения в ряды по степеням времени
- § 3.09. Степенные ряды в случае эллиптического движения
- Часть III. МЕТОДЫ ОПРЕДЕЛЕНИЯ И УЛУЧШЕНИЯ ОРБИТ
- Глава 1. ВЫЧИСЛЕНИЕ КООРДИНАТ НЕВОЗМУЩЕННОГО КЕПЛЕРОВСКОГО ДВИЖЕНИЯ ПО ЭЛЕМЕНТАМ ОРБИТЫ
- § 1.02. Вычисление орбитальных координат в случае параболической орбиты
- § 1.03. Вычисление орбитальных координат в случае орбит, эксцентриситет которых близок к единице
- § 1.04. Вычисление гелиоцентрических прямоугольных эклиптических и экваториальных координат
- Глава 2. ОПРЕДЕЛЕНИЕ ОРБИТ
- § 2.02. Особые случаи, встречающиеся при вычислении гелиоцентрических координат
- § 2.03. Определение гелиоцентрических положений по четырем геоцентрическим наблюдениям в случае эллиптической или гиперболической орбит
- § 2.04. Определение гелиоцентрических положений по трем геоцентрическим наблюдениям в случае параболической орбиты
- § 2.05. Вычисление элементов эллиптической орбиты по двум гелиоцентрическим положениям
- § 2.06. Определение элементов гиперболической орбиты по двум гелиоцентрическим положениям
- § 2.07. Определение элементов параболической орбиты по двум гелиоцентрическим положениям
- § 2.08. Уравнения Ламберта и Эйлера
- § 2.09. Определение элементов эллиптической или гиперболической орбиты по двум гелиоцентрическим положениям с помощью уравнения Ламберта
- § 2.10. Определение элементов круговой орбиты по двум наблюдениям
- § 2.11. Вычисление элементов гелиоцентрической орбиты по положению и скорости в начальный момент
- Глава 3. УЛУЧШЕНИЕ ПЕРВОНАЧАЛЬНОЙ ОРБИТЫ
- § 3.01. Дифференциальное исправление орбит. Постановка задачи
- § 3.02. Выражения для производных от координат по элементам (или по функциям элементов)
- § 3.03. Условные уравнения, составляемые по наблюдениям долготы и широты небесного тела
- Глава 4. ОПРЕДЕЛЕНИЕ И УЛУЧШЕНИЕ ЭЛЕМЕНТОВ ОРБИТ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- § 4.01. Определение элементов орбит ИСЗ по положению и скорости в момент выхода на орбиту
- § 4.02. Определение предварительных элементов орбиты ИСЗ по наблюдениям
- § 4.03. Улучшение орбит ИСЗ
- Часть IV. ТЕОРИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ
- Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ЗАДАЧИ n ТЕЛ В КООРДИНАТАХ
- § 1.02. Уравнение Лагранжа — Якоби
- § 1.03. Уравнения движения в барицентрических прямоугольных координатах
- § 1.04. Уравнения движения в координатах Якоби
- § 1.05. Уравнения относительного движения в прямоугольных координатах
- § 1.06. Уравнения движения в идеальных прямоугольных координатах Ганзена
- § 1.07. Уравнения абсолютного движения в цилиндрических координатах
- § 1.08. Уравнения относительного движения в цилиндрических координатах
- § 1.09. Уравнения абсолютного движения в сферических координатах
- § 1.10. Уравнения относительного движения в сферических координатах
- § 1.11. Уравнения движения в полярных координатах Ганзена
- § 1.12. Уравнения Клеро — Лапласа
- § 1.13. Общее правило составления канонических уравнений
- § 1.14. Первая каноническая форма уравнений абсолютного движения
- § 1.15. Вторая каноническая форма уравнений абсолютного движения
- § 1.16. Третья каноническая форма уравнений абсолютного движения
- § 1.17. Первая каноническая форма уравнений относительного движения
- § 1.18. Вторая каноническая форма уравнений относительного движения
- § 1.19. Третья каноническая форма уравнений относительного движения
- § 1.20. Уравнение Гамильтона — Якоби. Метод Гамильтона — Якоби
- § 1.21. Уравнения движения системы в векторной форме
- Глава 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПОСТУПАТЕЛЬНО-ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ
- § 2.02. Силовая функция системы тел
- § 2.03. Разложение силовой функции двух тел
- § 2.04. Уравнения поступательно-вращательного движения системы тел в абсолютной прямоугольной системе координат
- § 2.05. Уравнения поступательно-вращательного движения системы тел в относительной прямоугольной системе координат
- § 2.06. Каноническая форма уравнений поступательно-вращательного движения системы тел
- Глава 3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ТЕЛА ДЛЯ РАЗЛИЧНЫХ СИСТЕМ ОСКУЛИРУЮЩИХ ЭЛЕМЕНТОВ
- § 3.01. Метод Лагранжа вариации произвольных постоянных
- § 3.02. Уравнения Ньютона для кеплеровских оскулирующих элементов (общий случай)
- § 3.03. Уравнения Ньютона для эллиптических кеплеровских оскулирующих элементов
- § 3.04. Уравнения Лагранжа для кеплеровских оскулирующих элементов (общий случай)
- § 3.05. Уравнения Лагранжа для эллиптических кеплеровских оскулирующих элементов
- § 3.06. Уравнения возмущенного движения для канонических элементов Якоби
- § 3.07. Уравнения возмущенного движения для канонических элементов Делоне
- § 3.08. Две системы канонических элементов Пуанкаре
- § 3.09. Уравнения возмущенного движения в переменных Лагранжа для случая малых эксцентриситетов
- § 3.10. Уравнения в переменных Лагранжа для случая малых наклонов
- § 3.11. Уравнения возмущенного движения в переменных Лагранжа (общий случай)
- § 3.12. Связь между прямоугольными координатами движущейся точки и различными системами канонических элементов
- Глава 4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВОЗМУЩЕННОГО ДВИЖЕНИЯ ЗАДАЧИ n ТЕЛ ДЛЯ РАЗЛИЧНЫХ СИСТЕМ ОСКУЛИРУЮЩИХ ЭЛЕМЕНТОВ
- § 4.01. Уравнения Ньютона для кеплеровских оскулирующих элементов (общий случай)
- § 4.02. Уравнения Ньютона для эллиптических кеплеровских оскулирующих элементов
- § 4.03. Уравнения Лагранжа для кеплеровских оскулирующих элементов (общий случай)
- § 4.04. Уравнения Лагранжа для эллиптических кеплеровских оскулирующих элементов
- § 4.05. Уравнения возмущенного движения в канонических элементах Якоби
- § 4.06. Уравнения возмущенного движения в канонических элементах Делоне
- § 4.07. Две системы канонических элементов Пуанкаре
- § 4.08. Уравнения возмущенного движения в переменных Лагранжа для случая малых эксцентриситетов
- § 4.09. Уравнения в переменных Лагранжа для случая малых наклонов
- § 4.10. Уравнения возмущенного движения в переменных Лагранжа (общий случай)
- Глава 5. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
- § 5.01. Эллиптические интегралы и эллиптические функции
- § 5.02. Гипергеометрический ряд и гипергеометрическая функция
- § 5.03. Полиномы Лежандра. Функции Лежандра
- § 5.04. Присоединенные функции Лежандра
- § 5.05. Сферические функции
- § 5.06. Цилиндрические функции. Функции Бесселя
- § 5.07. Функции Ламе
- § 5.08. Полиномы Гегенбауэра. Коэффициенты Лапласа
- § 5.09. Числа Коши
- Глава 6. РАЗЛОЖЕНИЕ ВОЗМУЩАЮЩЕЙ ФУНКЦИИ
- § 6.01. Разложение возмущающей функции в задаче о движении двух планет (случай круговых орбит)
- § 6.02. Разложение возмущающей функции в задаче о движении двух планет (случай малых эксцентриситетов и взаимного наклона)
- § 6.03. Разложение возмущающей функции в случае произвольного взаимного наклона
- § 6.04. Вековая часть возмущающей функции в двухпланетной задаче
- § 6.05. Численные методы разложения возмущающей функции
- § 6.06. Полуаналитический метод Брауэра — Клеменса разложения возмущающей функции
- Глава 7. АНАЛИТИЧЕСКИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ВОЗМУЩЕНИЙ КООРДИНАТ
- § 7.02. Метод Ганзена
- § 7.03. Метод Брауэра
- § 7.04. Метод Лапласа — Ньюкома
- Глава 8. АНАЛИТИЧЕСКИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ВОЗМУЩЕНИЙ ЭЛЕМЕНТОВ
- § 8.01. Общий вид возмущений элементов. Порядок, степень, ранг и класс возмущений
- § 8.02. Метод Гаусса вычисления вековых возмущений первого порядка
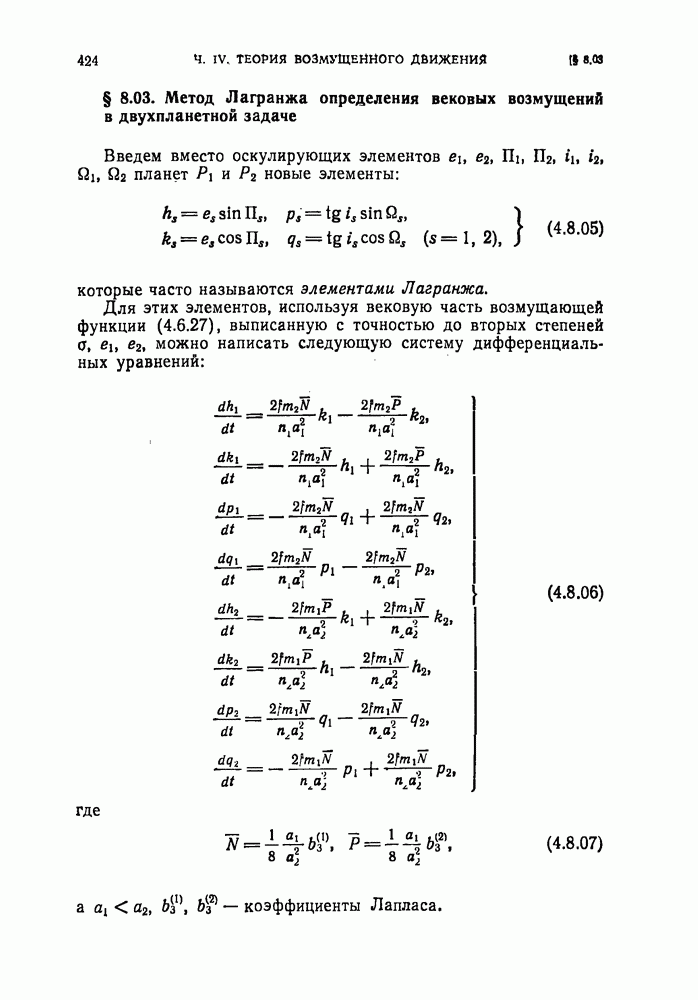
- § 8.03. Метод Лагранжа определения вековых возмущений в двухпланетной задаче
- § 8.04. Основы метода Делоне
- § 8.05. Связь между возмущениями координат и возмущениями элементов
- Глава 9. МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ, ОСНОВАННЫЕ НА СХЕМАХ ОСРЕДНЕНИЯ
- § 9.01. Основные схемы осреднения возмущающей функции в двухпланетной задаче
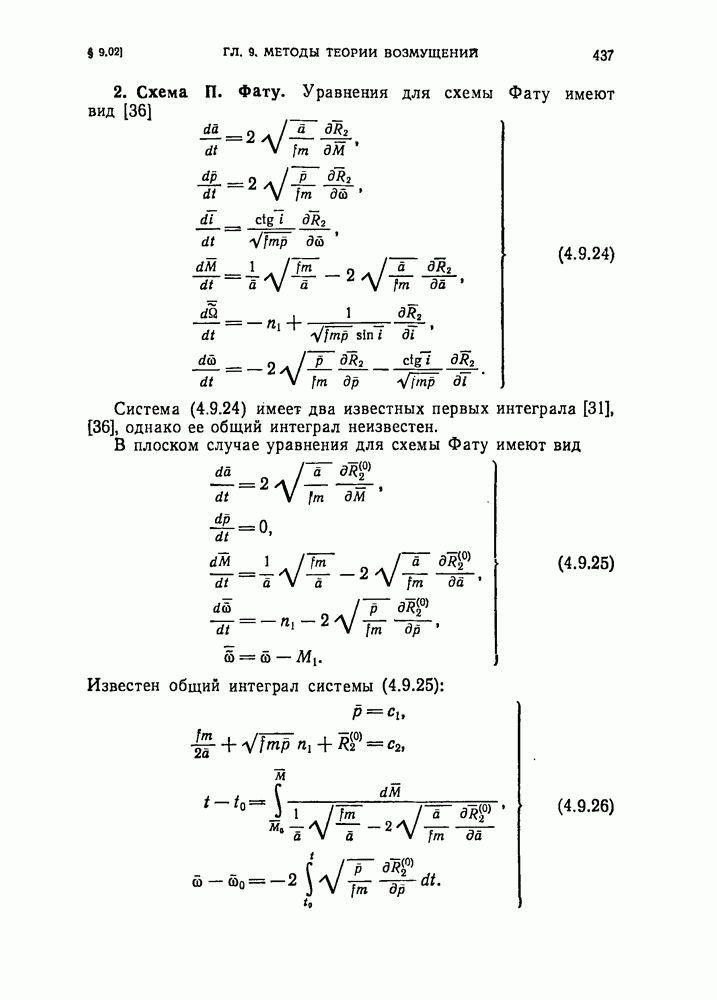
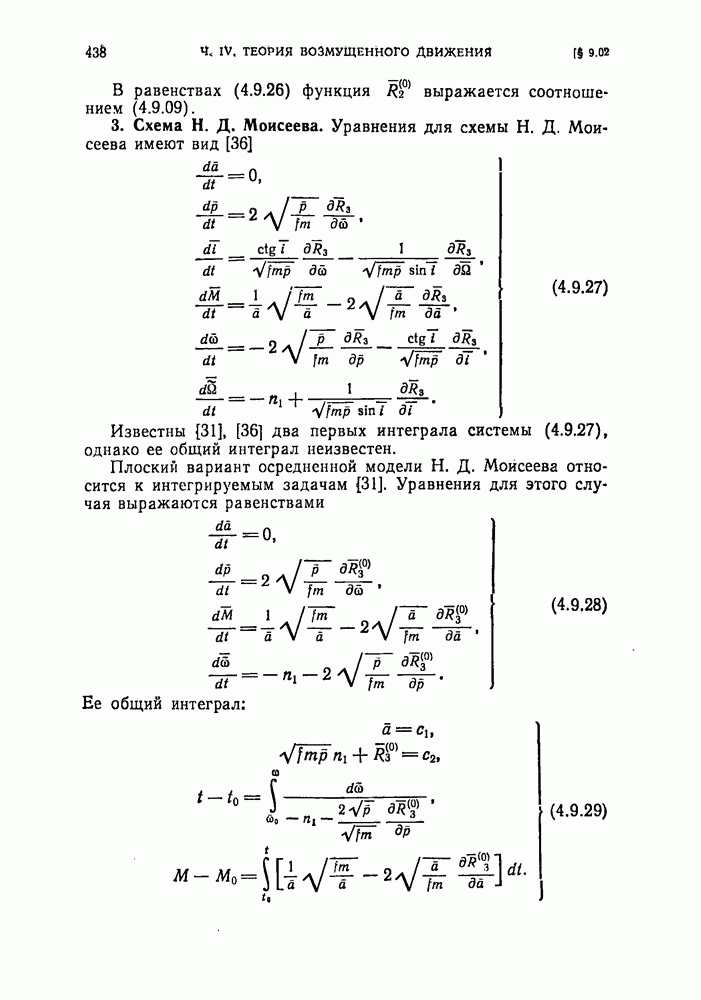
- § 9.02. Уравнения осредненных схем ограниченной круговой задачи трех тел, определяющие промежуточную орбиту (нулевое приближение). Их первые интегралы
- § 9.03. Разложение возмущающей функции для схем осреднения
- § 9.04. Основы метода теории возмущений
- Глава 10. ТЕОРИЯ ДВИЖЕНИЯ ЛУНЫ
- § 10.01. Уравнения основной проблемы в теории движения Луны
- § 10.02. Разложение возмущающей функции в основной проблеме теории движения Луны
- § 10.03. Решение Делоне основной проблемы в теории движения Луны
- § 10.04. Основные этапы построения теории Хилла—Брауна движения Луны
- § 10.05. Промежуточная орбита в теории Хилла — Брауна
- § 10.06. Общее решение уравнений основной проблемы в теории Хилла—Брауна
- § 10.07. Переход к сферическим координатам
- § 10.08. Численные значения постоянных интегрирования и параметров в теории Хилла — Брауна
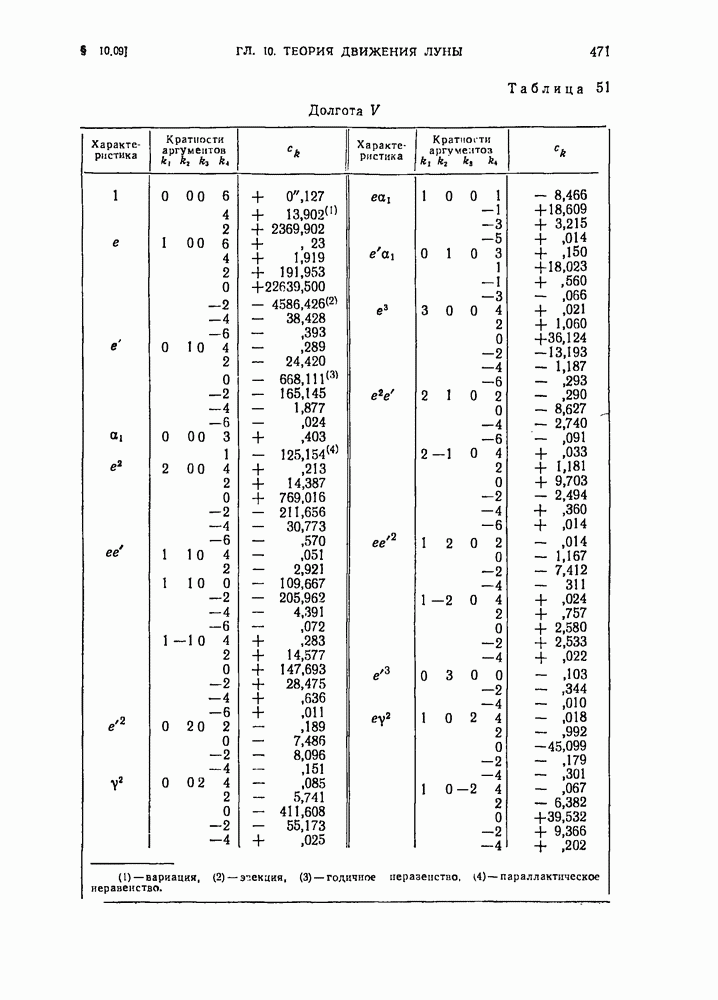
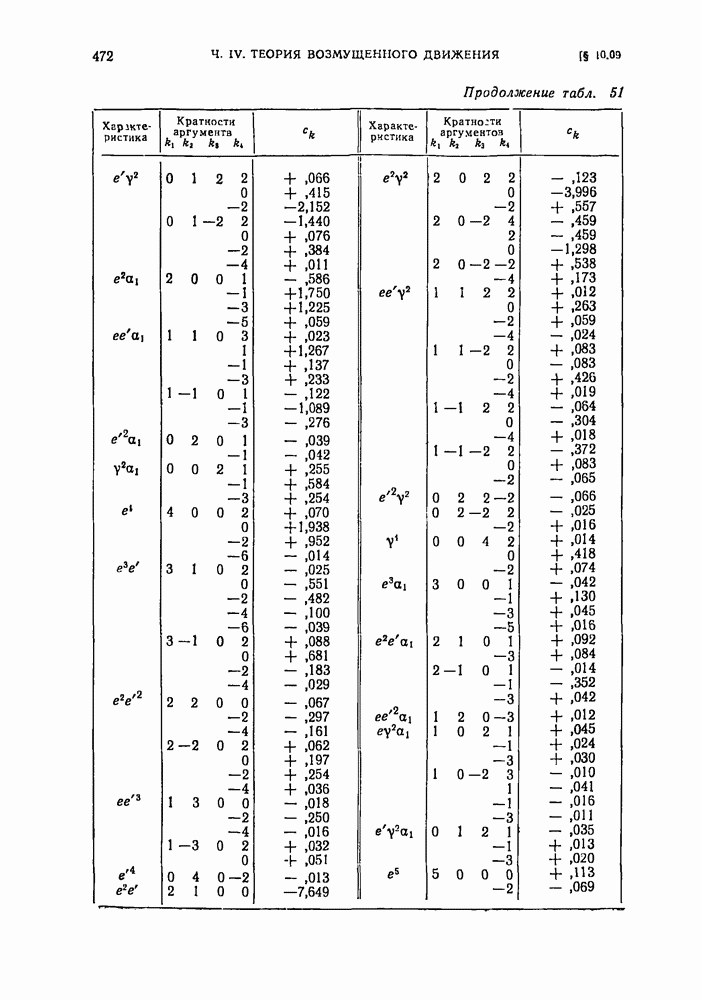
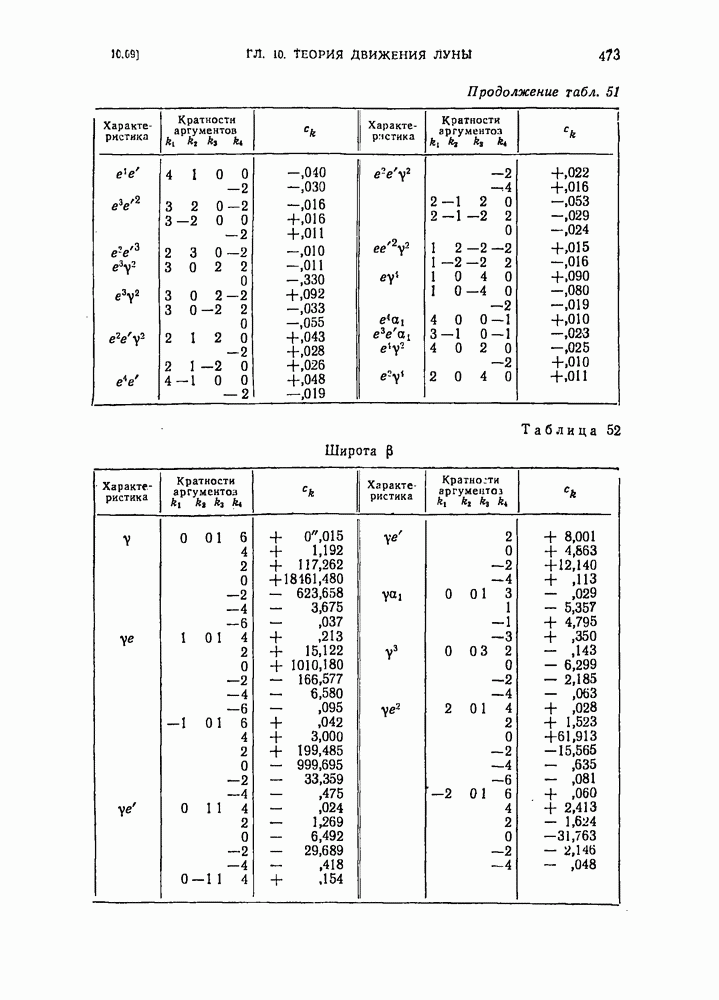
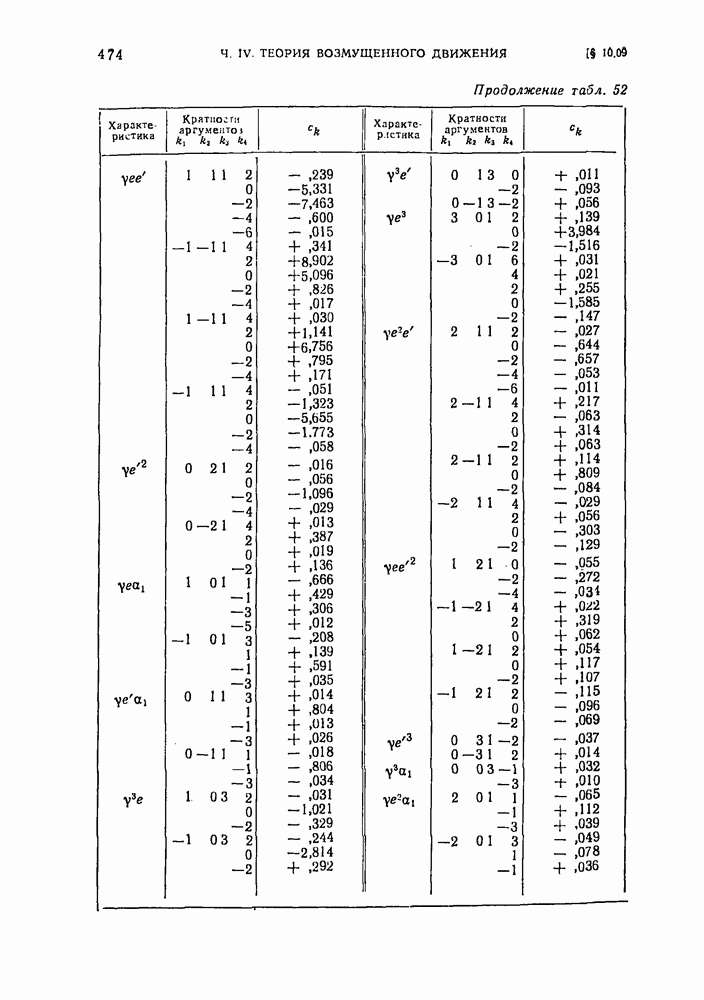
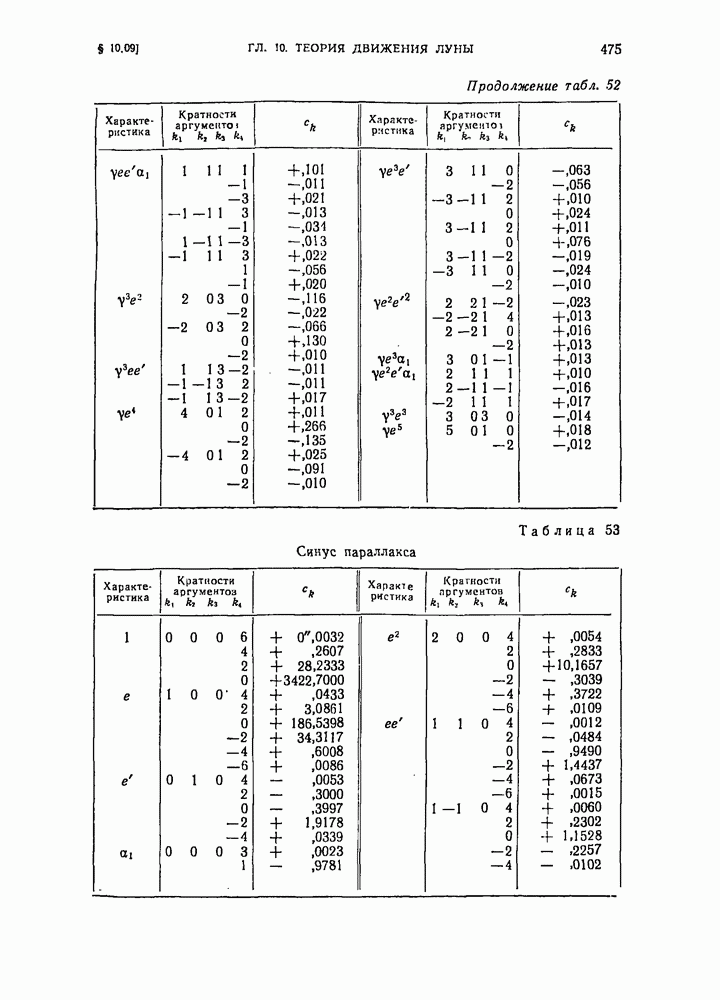
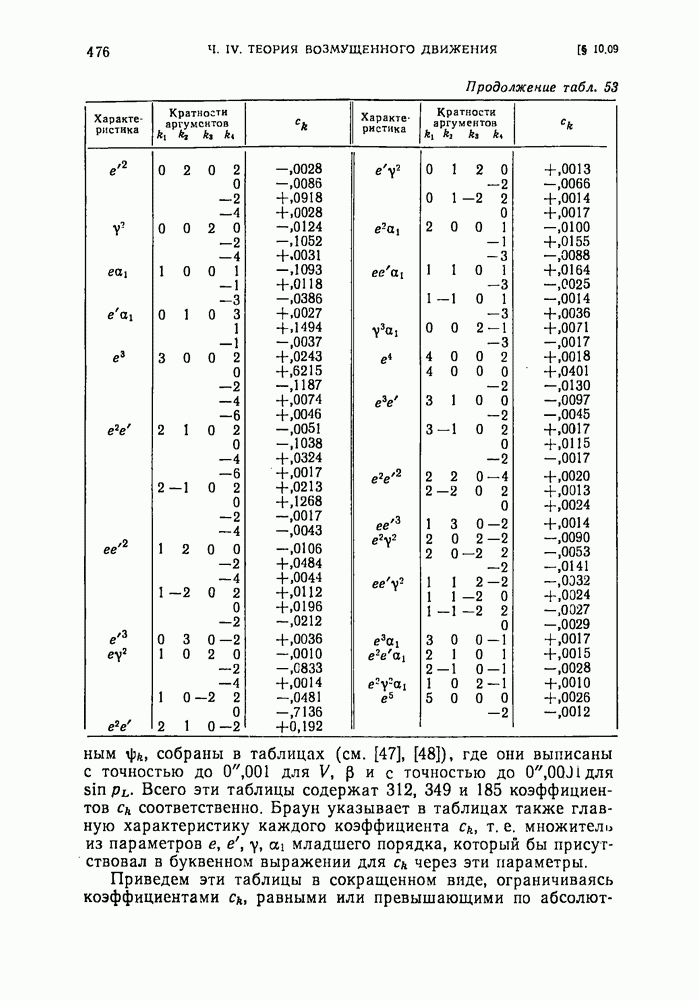
- § 10.09. Окончательные выражения для долготы, широты и синуса параллакса, соответствующие решению основной проблемы
- § 10.10. Возмущения Луны, обусловленные притяжением планет, фигурами Земли и Луны
- § 10.11. Уточнение теории движения Луны Хилла—Брауна
- Глава 11. ТЕОРИЯ ДВИЖЕНИЯ БОЛЬШИХ ПЛАНЕТ
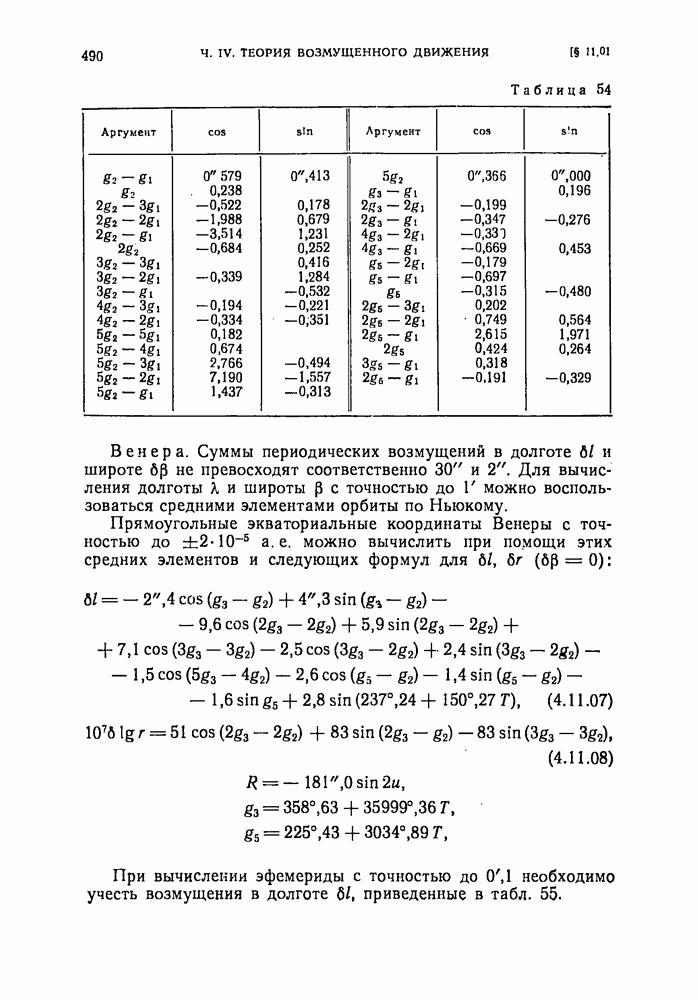
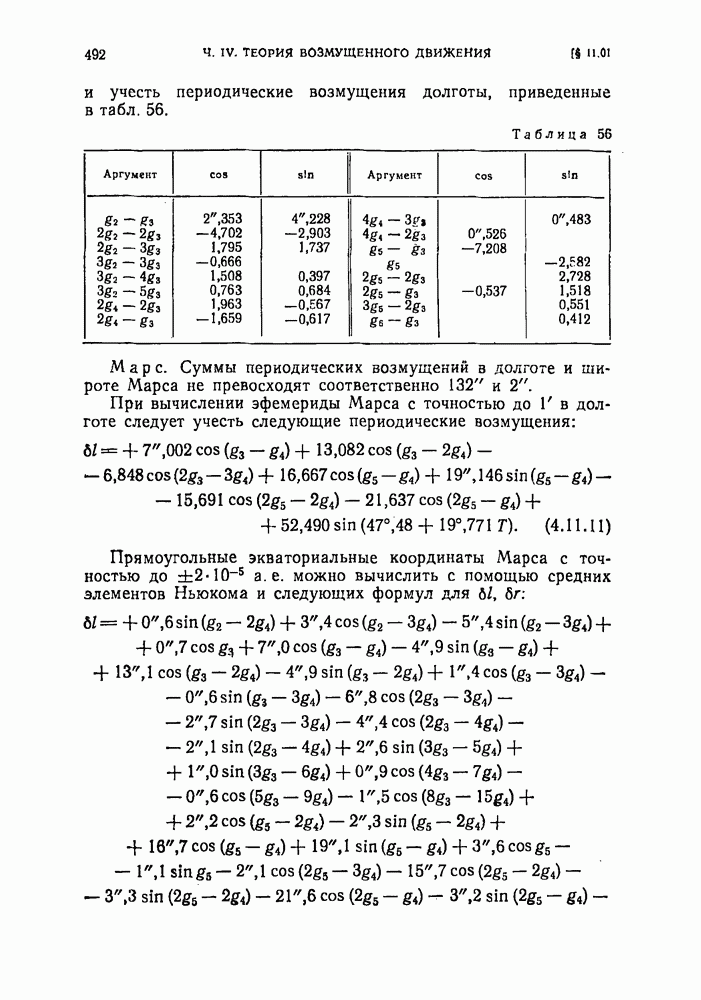
- § 11.01. Внутренние планеты
- § 11.02. Внешние планеты
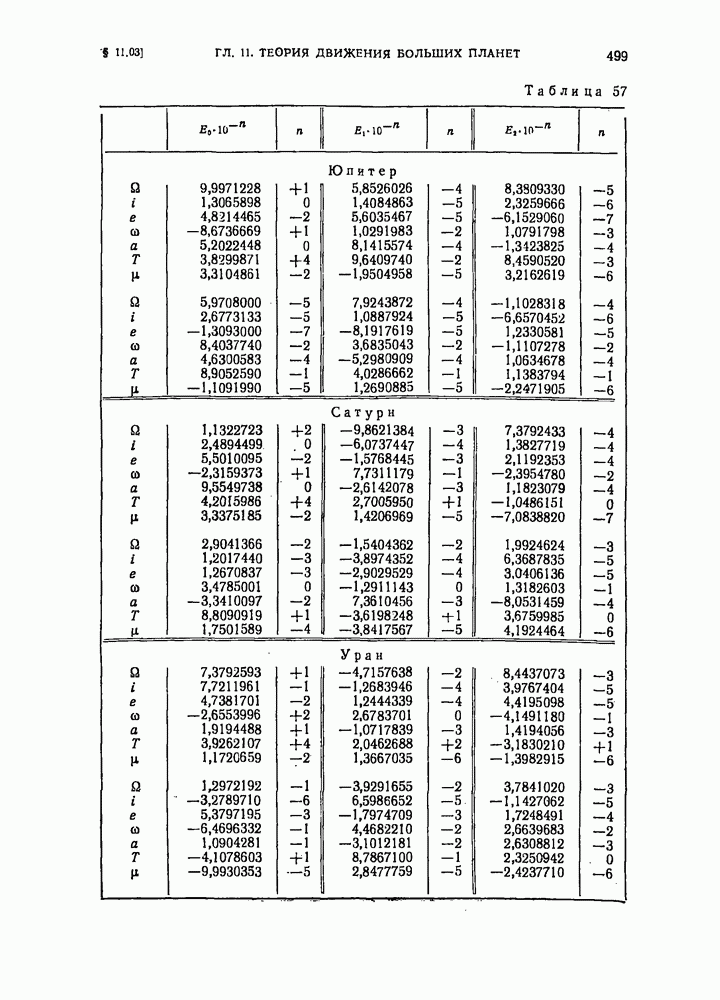
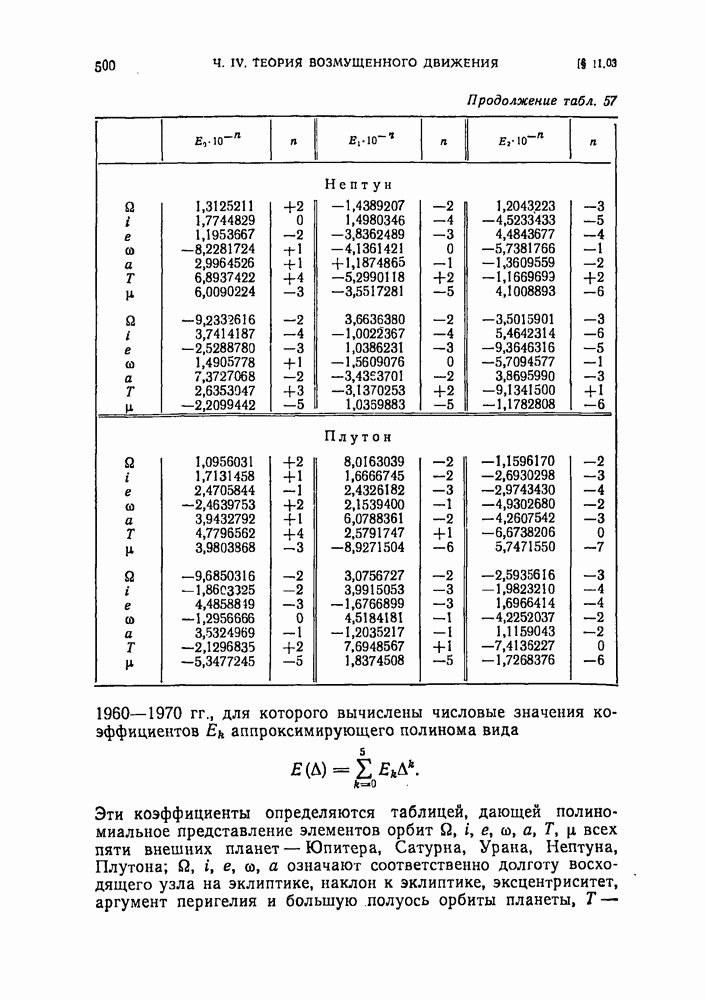
- § 11.03. Полиномиальное представление оскулирующих элементов орбит внешних планет
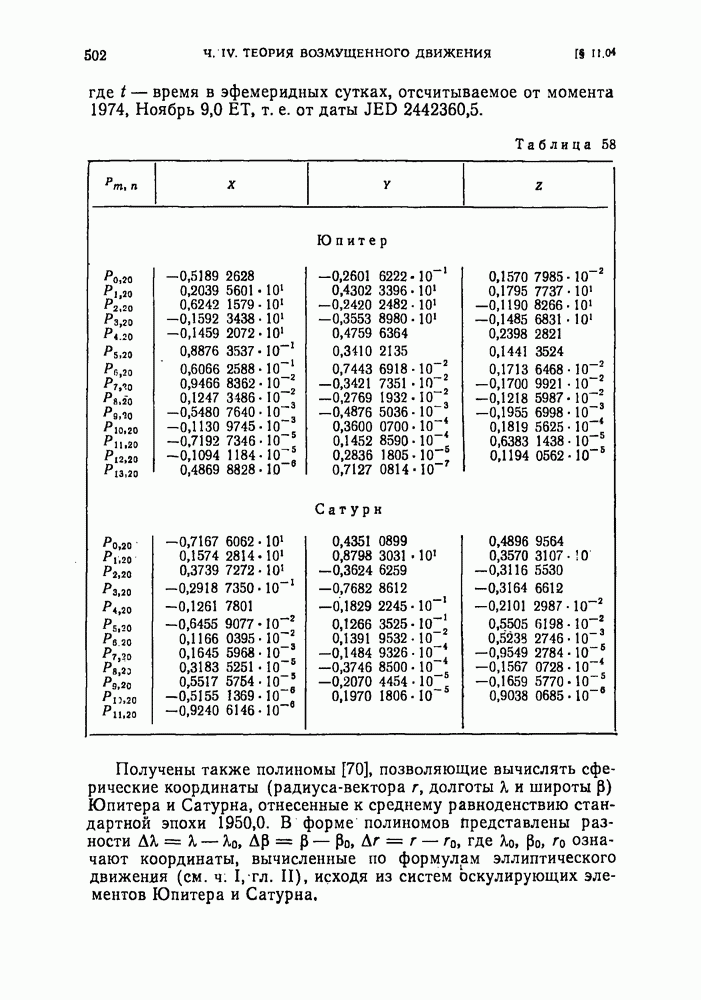
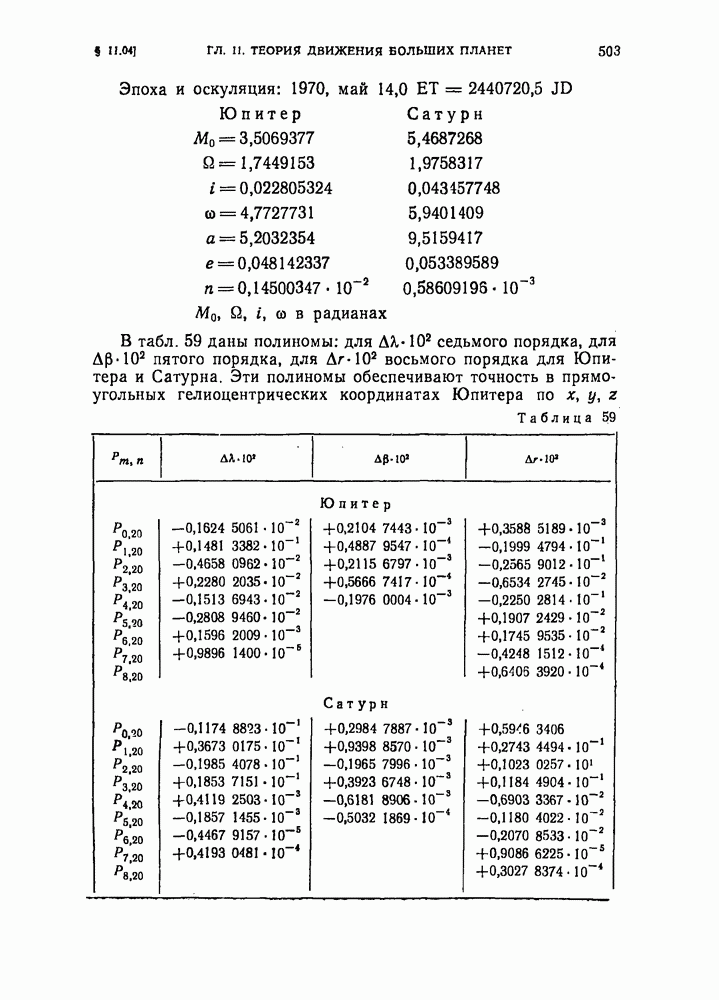
- § 11.04. Полиномиальное представление прямоугольных гелиоцентрических координат Юпитера и Сатурна
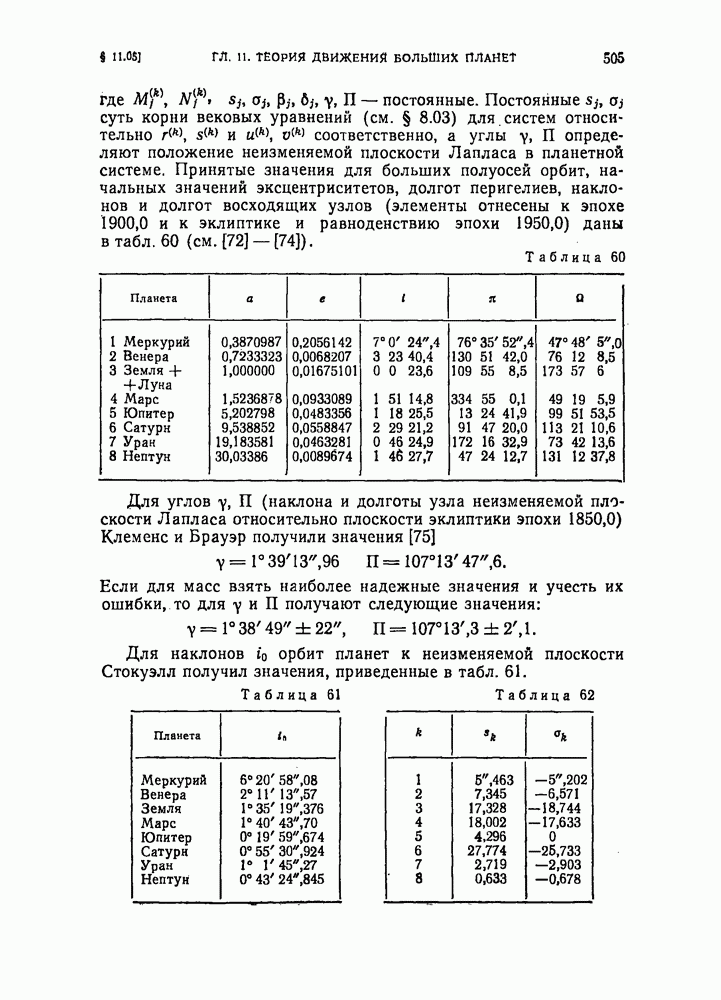
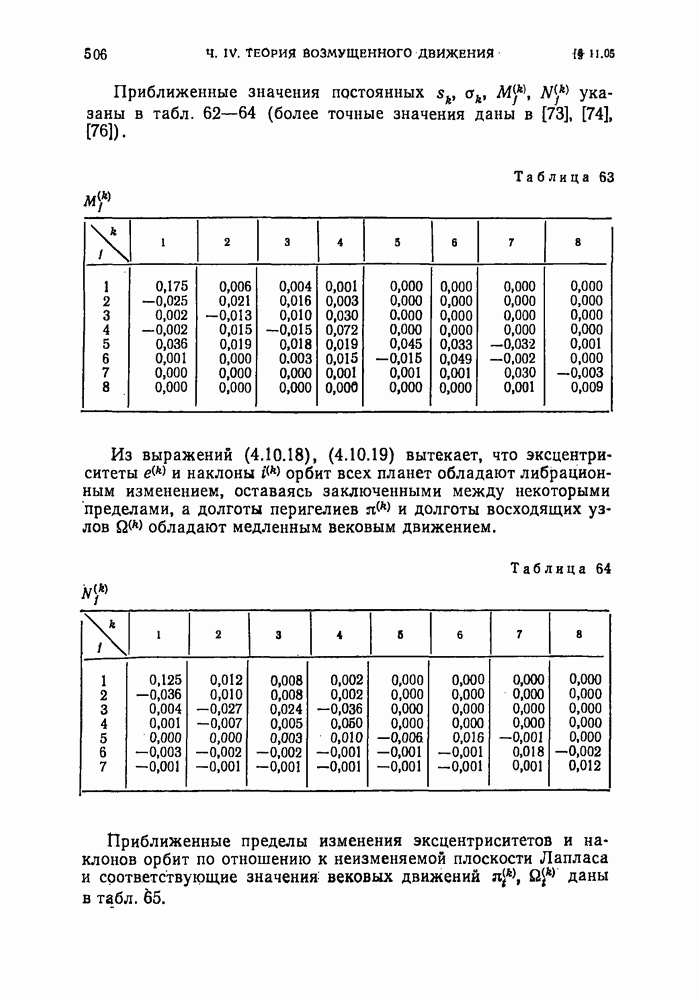
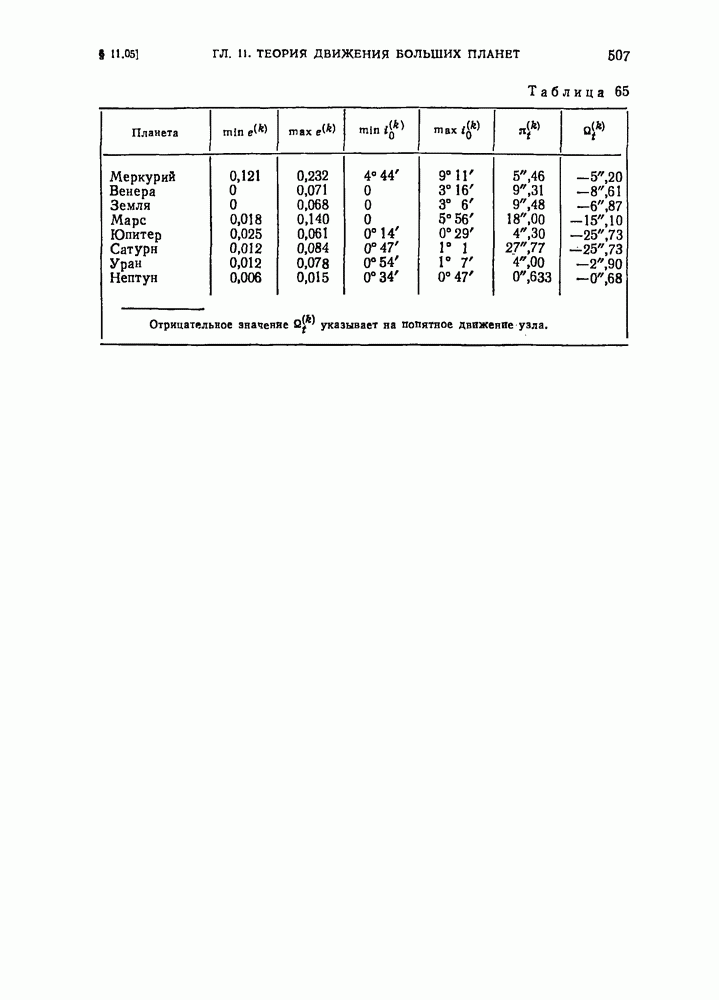
- § 11.05. Тригонометрическая теория вековых возмущений орбит больших планет
- Глава 12. ДВИЖЕНИЕ МАЛЫХ ТЕЛ СОЛНЕЧНОЙ СИСТЕМЫ
- § 12.01. Невозмущенное движение спутников
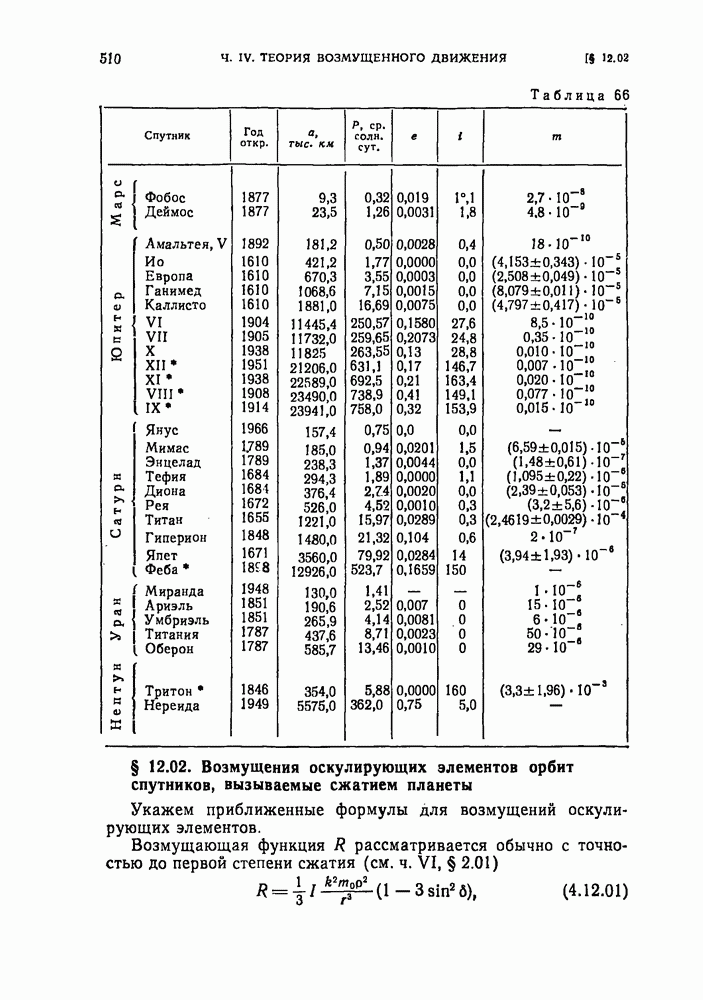
- § 12.02. Возмущения оскулирующих элементов орбит спутников, вызываемые сжатием планеты
- § 12.03. Возмущения в движении спутников, вызываемые притяжением Солнца
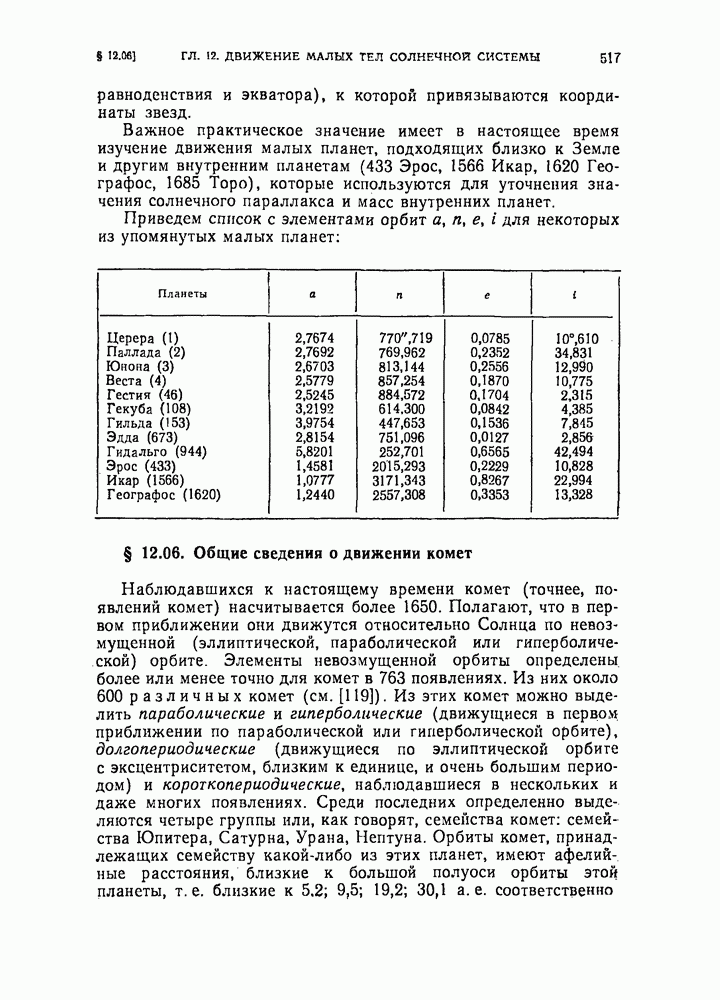
- § 12.04. Общие сведения о характере движения малых планет
- § 12.05. Возмущенное движение малых планет
- § 12.06. Общие сведения о движении комет
- § 12.07. Возмущенное движение комет
- Часть V. ЗАДАЧА ТРЕХ ТЕЛ
- Глава 1. НЕОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 1.02. Лагранжевы решения. Точки либрации
- Глава 2. ОГРАНИЧЕННАЯ КРУГОВАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 2.01. Дифференциальные уравнения движения. Интеграл Якоби
- § 2.02. Поверхность нулевой относительной скорости
- § 2.03. Лагранжевы решения ограниченной круговой задачи трех тел. Точки либрации
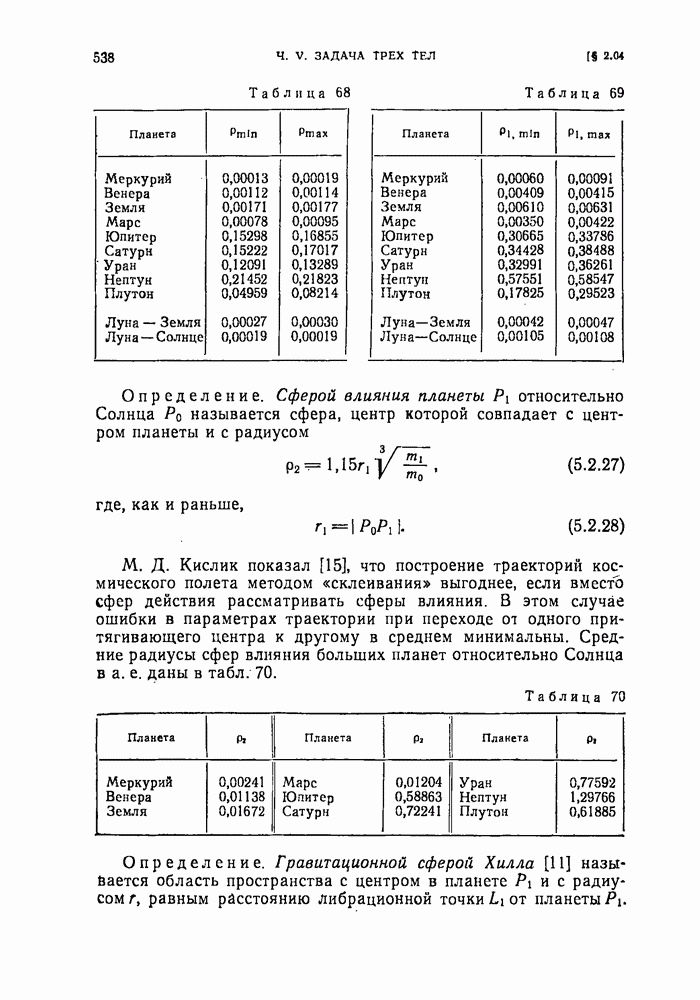
- § 2.04. Различные гравитационные сферы
- § 2.05. Периодические решения ограниченной круговой задачи трех тел
- § 2.06. Критерий Тиссерана
- § 2.07. Уравнения ограниченной круговой задачи в эллипсоидальных переменных
- § 2.08. Уравнение Гамильтона—Якоби в эллипсоидальных переменных
- § 2.09. Понижение порядка системы уравнений плоской ограниченной круговой задачи трех тел
- Глава 3. ДРУГИЕ ОГРАНИЧЕННЫЕ ЗАДАЧИ ТРЕХ ТЕЛ
- § 3.01. Общий случай ограниченной задачи трех тел
- § 3.02. Задача двух неподвижных центров
- § 3.03. Задача Хилла
- Часть VI. ДВИЖЕНИЕ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- Глава 1. ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИСКУССТВЕННОГО СПУТНИКА
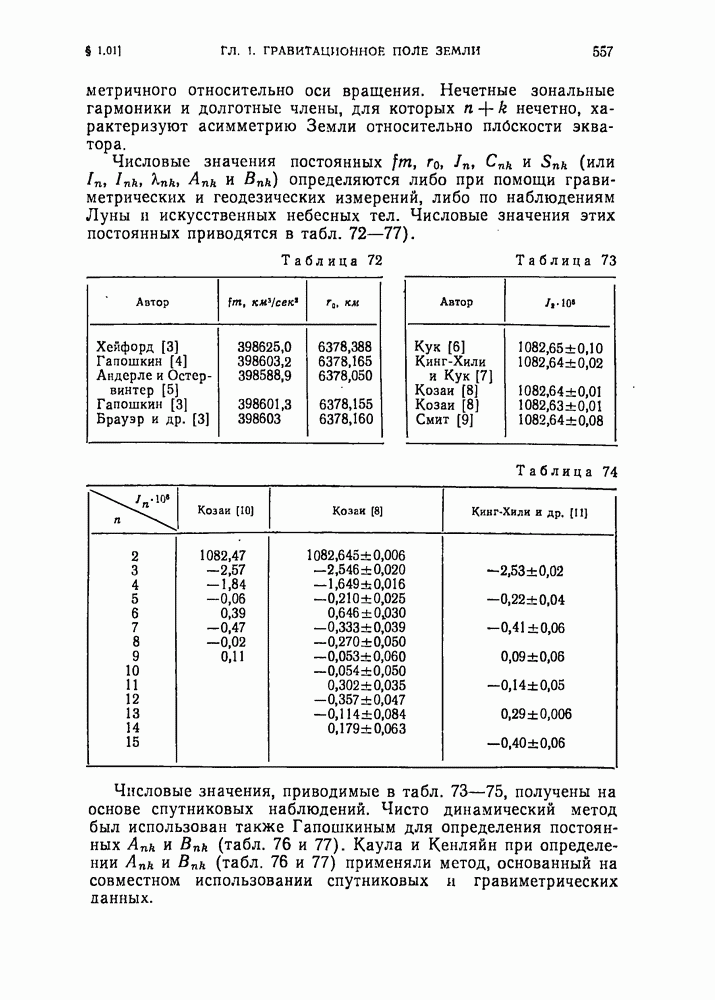
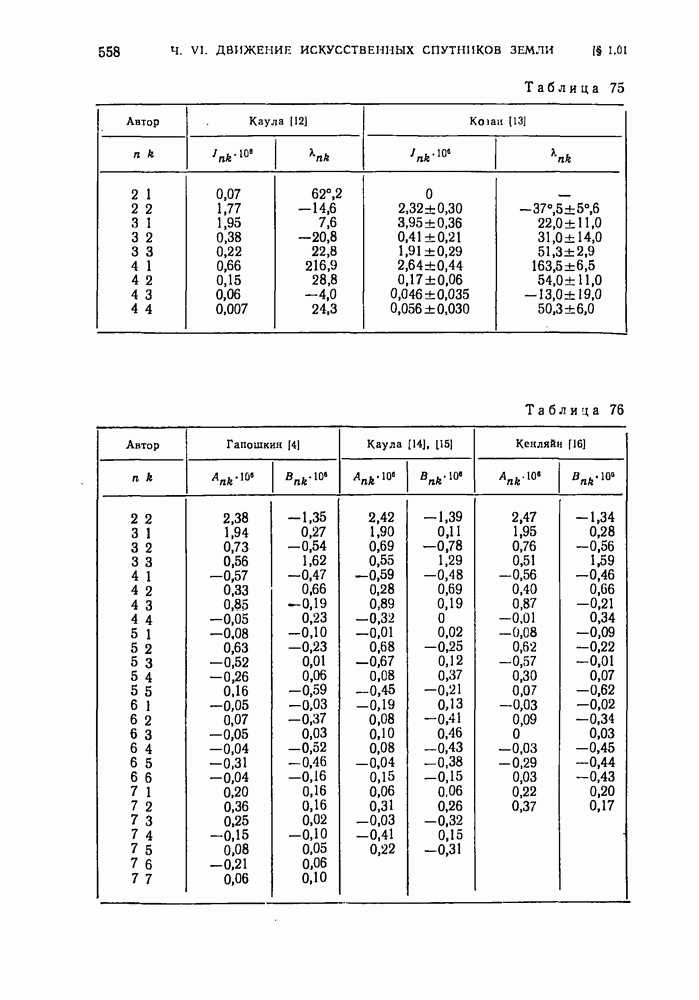
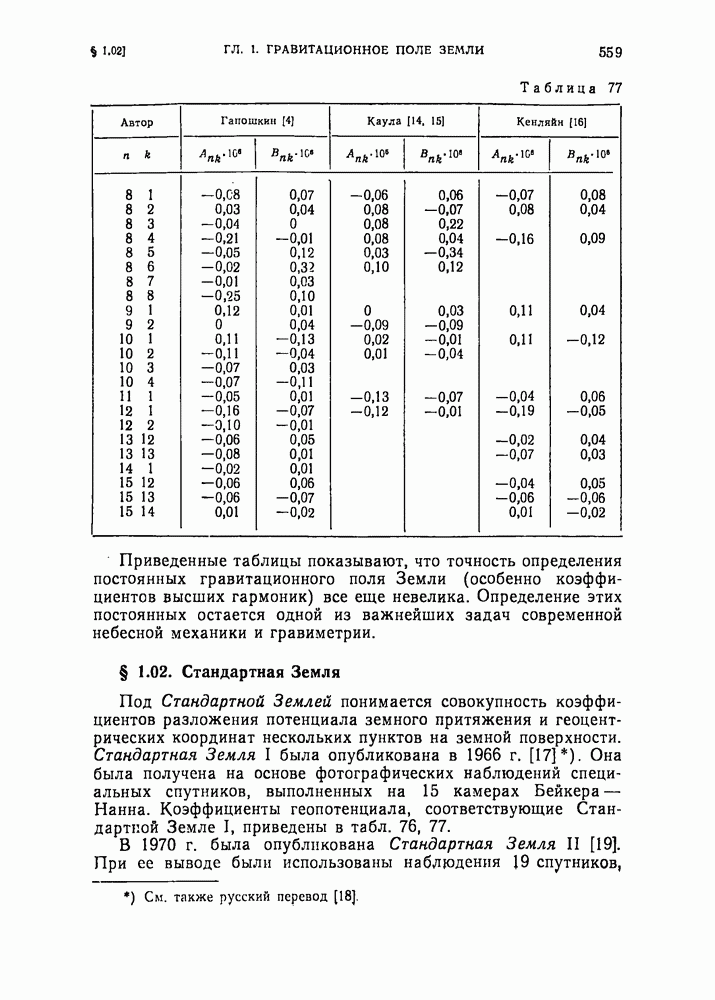
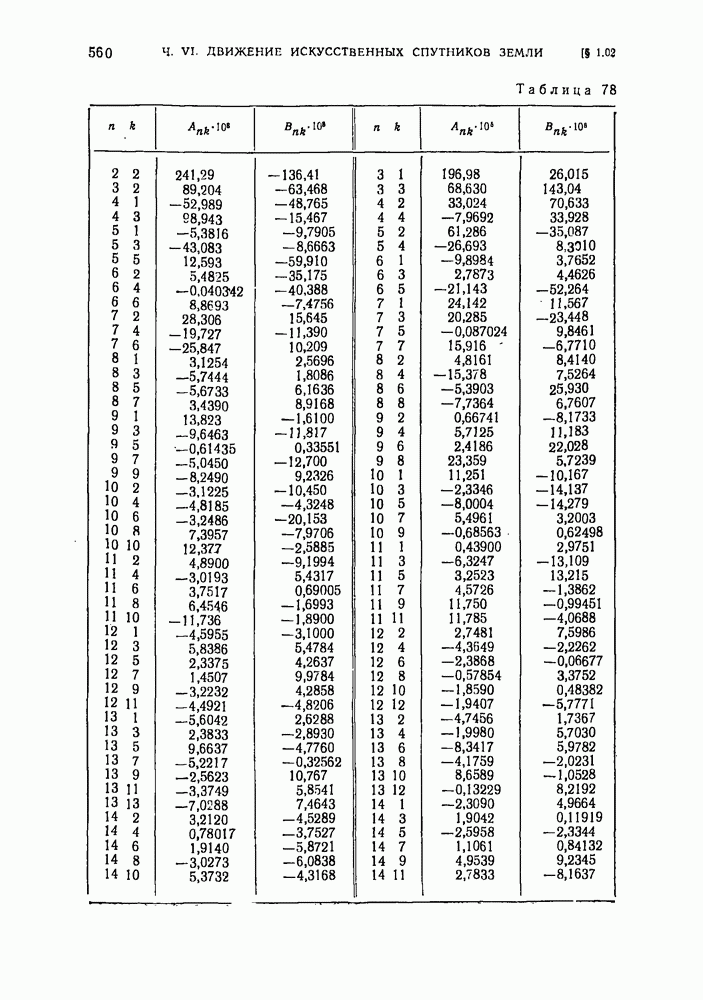
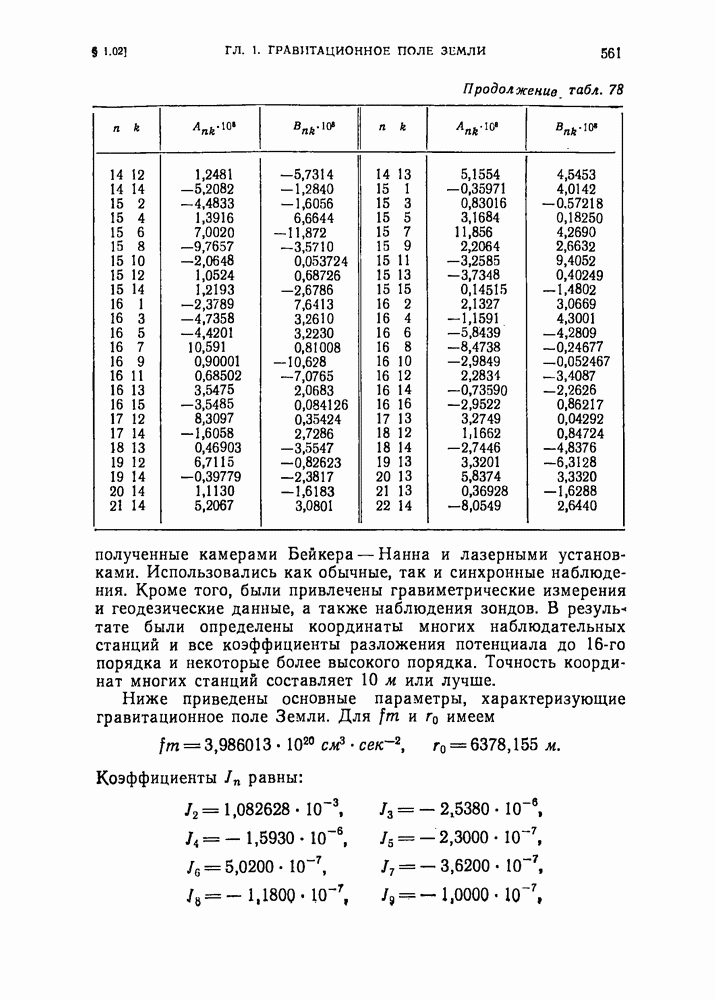
- § 1.02. Стандартная Земля
- § 1.03. Дифференциальные уравнения движения спутника
- § 1.04. Элементы орбиты ИСЗ. Дифференциальные уравнения для оскулирующих элементов
- Глава 2. ВОЗМУЩЕНИЯ, ВЫЗЫВАЕМЫЕ ВТОРОЙ ЗОНАЛЬНОЙ ГАРМОНИКОЙ ГЕОПОТЕНЦИАЛА
- § 2.01. Возмущения от второй зональной гармоники как функции средней аномалии
- § 2.02. Возмущения от второй зональной гармоники как функции истинной аномалии
- § 2.03. Случай орбит с малыми эксцентриситетами
- Глава 3. ТЕОРИЯ ПРОМЕЖУТОЧНЫХ ОРБИТ ИСЗ
- § 3.01. Задачи Штерна, Гарфинкеля и Акснеса
- § 3.02. Задачи Баррара, Винти и Кислика
- § 3.03. Обобщенная задача двух неподвижных центров
- § 3.04. Промежуточная орбита, основанная на обобщенной задаче двух неподвижных центров
- § 3.05. Дифференциальные уравнения для элементов промежуточной орбиты
- Глава 4. ВОЗМУЩЕНИЯ ГРАВИТАЦИОННОИ ПРИРОДЫ
- § 4.01. Возмущения от зональных гармоник высших порядков
- § 4.02. Возмущения от зональной гармоники произвольного порядка
- § 4.03. Возмущения от тессеральных и секториальных гармоник
- § 4.04. Лунно-солнечные возмущения
- § 4.05. Определение постоянных интегрирования
- § 4.06. Вычисление возмущенных координат спутника
- Глава 5. ВОЗМУЩЕНИЯ, ВЫЗЫВАЕМЫЕ СОПРОТИВЛЕНИЕМ АТМОСФЕРЫ И СВЕТОВЫМ ДАВЛЕНИЕМ
- § 5.02. Стандартная атмосфера
- § 5.03. Сила сопротивления атмосферы
- § 5.04. Основные возмущения от сопротивления атмосферы
- § 5.05. Продолжительность жизни спутника
- § 5.06. Эволюция орбиты на больших промежутках времени
- § 5.07. Сила светового давления
- § 5.08. Возмущения от светового давления (без учета тени)
- § 5.09. Возмущения от светового давления (с учетом тени)
- § 5.10. Теневая функция
- Глава 6. ДРУГИЕ ВОЗМУЩЕНИЯ В ДВИЖЕНИИ ИСЗ
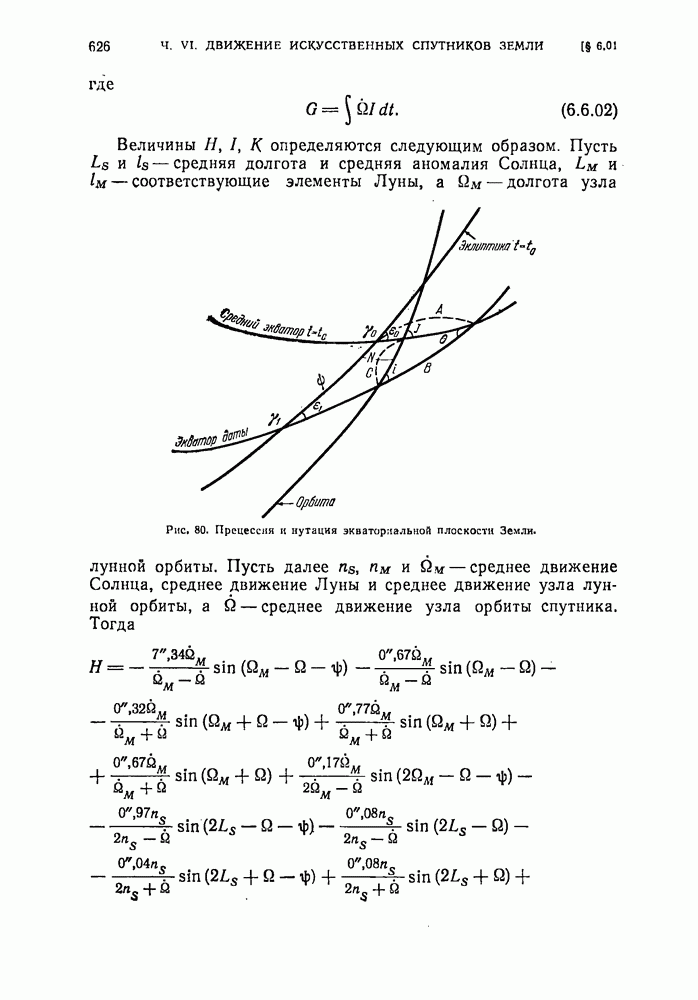
- § 6.01. Возмущения, вызываемые прецессией и нутацией экваториальной плоскости Земли
- § 6.02. Возмущения, вызываемые приливной деформацией Земли
- § 6.03. Релятивистские эффекты. Влияние электромагнитных сил и притяжения атмосферы
- Часть VII. ЧИСЛЕННЫЕ МЕТОДЫ
- Глава 1. ИНТЕРПОЛИРОВАНИЕ И ПРИБЛИЖЕНИЕ ФУНКЦИЙ
- § 1.02. Интерполяционные формулы
- § 1.03. Остаточные члены интерполяционных формул
- § 1.04. Обратное интерполирование
- § 1.05. Интерполирование функции двух переменных
- § 1.06. Приближение функций с помощью сплайнов
- § 1.07. Среднеквадратичные приближения функций
- § 1.08. Сглаживание табличных значений функций
- § 1.09. Равномерные приближения
- § 1.10. Аппроксимация периодических функций с известным периодом тригонометрическими полиномами по методу наименьших квадратов
- § 1.11. Аппроксимация условно-периодических функций с известными частотами полиномом Фурье по методу наименьших квадратов
- § 1.12. Определение неизвестных частот периодической или условно-периодической функции по совокупности табличных данных
- § 1.13. Выделение «вековой части» функции по совокупности табличных значений
- Глава 2. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ
- § 2.01. Численное дифференцирование с помощью интерполяционных формул
- § 2.02. Другие формулы численного дифференцирования
- § 2.03. Численное интегрирование функции по таблице ее значений с постоянным шагом
- § 2.04. Квадратурные формулы Гаусса
- § 2.05. Численное интегрирование сильно осциллирующих функций
- § 2.06. Правило Рунге практической оценки погрешности квадратурных формул
- § 2.07. Квадратурные формулы для несобственных интегралов
- Глава 3. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 3.01. Метод Рунге—Кутта
- § 3.02. Метод Адамса
- § 3.03. Метод Коуэлла
- § 3.04. Метод Штермера (для уравнений второго порядка)
- § 3.05. Метод Коуэлла (1-й вариант)
- § 3.06. Метод Коуэлла (2-й вариант)
- § 3.07. Накопление погрешностей при численном интегрировании
- § 3.08. Метод Энке численного интегрирования уравнений возмущенного движения
- § 3.09. Общая постановка краевой задачи для обыкновенных дифференциальных уравнений. Случай линейной краевой задачи
- § 3.10. Метод стрельбы при нахождении решения линейной двухточечной краевой задачи
- § 3.11. Краевая задача для квазилинейной системы с линейными краевыми условиями
- § 3.12. Краевая задача для системы, близкой к нелинейной невозмущенной системе
- § 3.13. Применение метода градиентного спуска для решения нелинейной краевой задачи общего вида
- § 3.14. Разностный метод решений краевых задач
- Глава 4. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
- § 4.02. Линейные и равноточные условные уравнения
- § 4.03. Вероятностные оценки погрешности решения
- § 4.04. Неравноточные условные уравнения
- § 4.05. Линеаризация условных уравнений общего вида
- Часть VIII. ОПТИМАЛЬНЫЕ И КРАЕВЫЕ ЗАДАЧИ АСТРОДИНАМИКИ
- Глава 1. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ И МАТЕМАТИЧЕСКОЙ ТЕОРИИ ОПТИМАЛЬНЫХ ПРОЦЕССОВ
- § 1.01. Понятие функционала
- § 1.02. Задача Лагранжа. Множители Лагранжа. Уравнения Эйлера
- § 1.03. Первая формулировка задачи Майера
- § 1.04. Вторая формулировка задачи Майера
- § 1.05. Изопериметрическая задача
- § 1.06. Задача Больца
- § 1.07. Третья формулировка задачи Майера. Обобщение теоремы Лагранжа. Характеристические уравнения (обобщенные уравнения Эйлера — Лагранжа)
- § 1.08. Свойство множителей Лагранжа на ломаных экстремалях. Условие Вейерштрасса — Эрдмана
- § 1.09. Принцип максимума Понтрягина
- § 1.10. Принцип оптимальности Беллмана
- Глава 2. ОСНОВНЫЕ УРАВНЕНИЯ ДИНАМИКИ ТЕЛ ПЕРЕМЕННОЙ МАССЫ
- § 2.01. Основное уравнение динамики точки переменной массы (уравнение Мещерского)
- § 2.02. Обобщенное уравнение Мещерского
- § 2.03. Уравнения движения тела переменной массы в обобщенных координатах (уравнения Лагранжа второго рода)
- § 2.04. Канонические уравнения движения тела переменной массы
- Глава 3. НЕКОТОРЫЕ ОПТИМАЛЬНЫЕ ЗАДАЧИ ДИНАМИКИ ПОЛЕТА В ОКОЛОЗЕМНОМ ПРОСТРАНСТВЕ
- § 3.01. Уравнения движения ракеты. Формула Циолковского
- § 3.02. Развернутая форма характеристических уравнений для задачи о движении ракеты
- § 3.03. Определение базис-вектора и p-траектории. Определение функций переключения
- § 3.04. Определение импульсной тяги. Точки соединения на оптимальных траекториях
- § 3.05. Максимизация высоты вертикального подъема ракеты в однородном поле тяжести
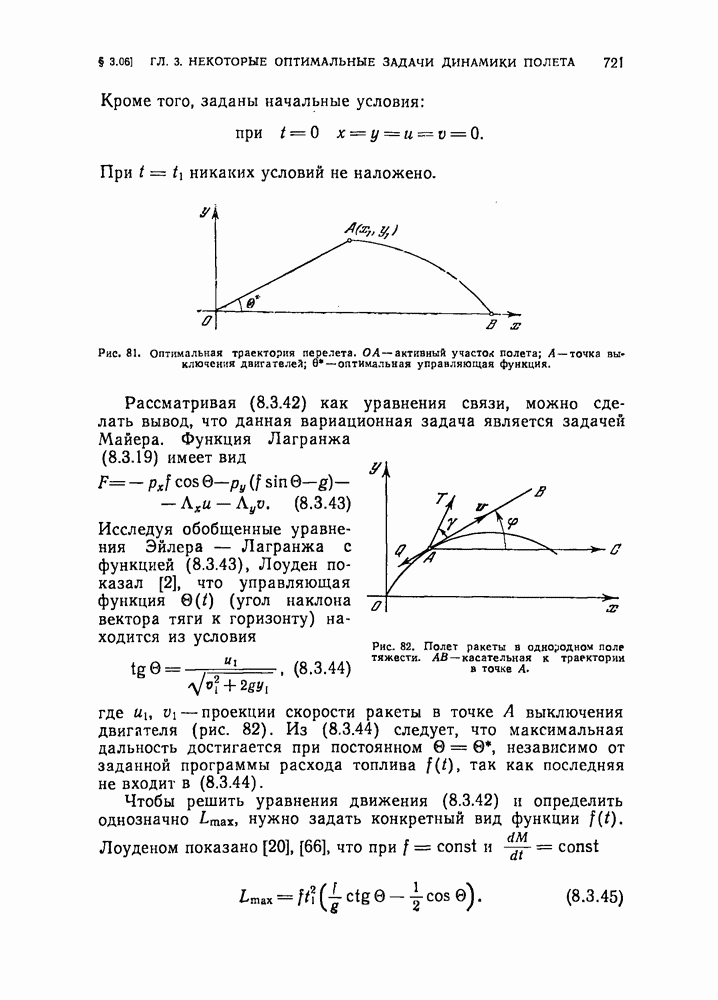
- § 3.06. Максимизация горизонтальной дальности полета ракеты в однородном поле тяжести при заданной программе расхода топлива
- § 3.07. Общая вариационная задача для движения ракеты в однородном поле тяжести
- § 3.08. Общая вариационная задача для движения ракеты в однородном поле тяжести при наличии аэродинамического сопротивления
- § 3.09. Определение оптимальной программы тяги при вертикальном подъеме ракеты в неоднородном поле тяготения в сопротивляющейся атмосфере
- § 3.10. Задача о максимизации полной энергии космического аппарата
- § 3.11. Задача о минимизации характеристической скорости маневра
- Глава 4. МЕЖОРБИТАЛЬНЫЕ ПЕРЕЛЕТЫ
- § 4.02. Уравнение для базиса-вектора на участке нулевой тяги при движении ракеты в ньютоновском поле тяготения
- § 4.03. Уравнение для базиса-вектора на участке промежуточной тяги при движении ракеты в ньютоновском поле тяготения
- § 4.04. Уравнение для базиса-вектора на участке максимальной тяги при движении ракеты в ньютоновском поле тяготения
- § 4.05. Метод p-траекторий. Структура оптимальной траектории
- § 4.06. Связь между величиной импульса и элементами эллиптической орбиты
- § 4.07. Оптимальный n-импульсный переход между двумя заданными компланарными эллиптическими орбитами
- § 4.08. Оптимальный переход между двумя компланарными круговыми орбитами
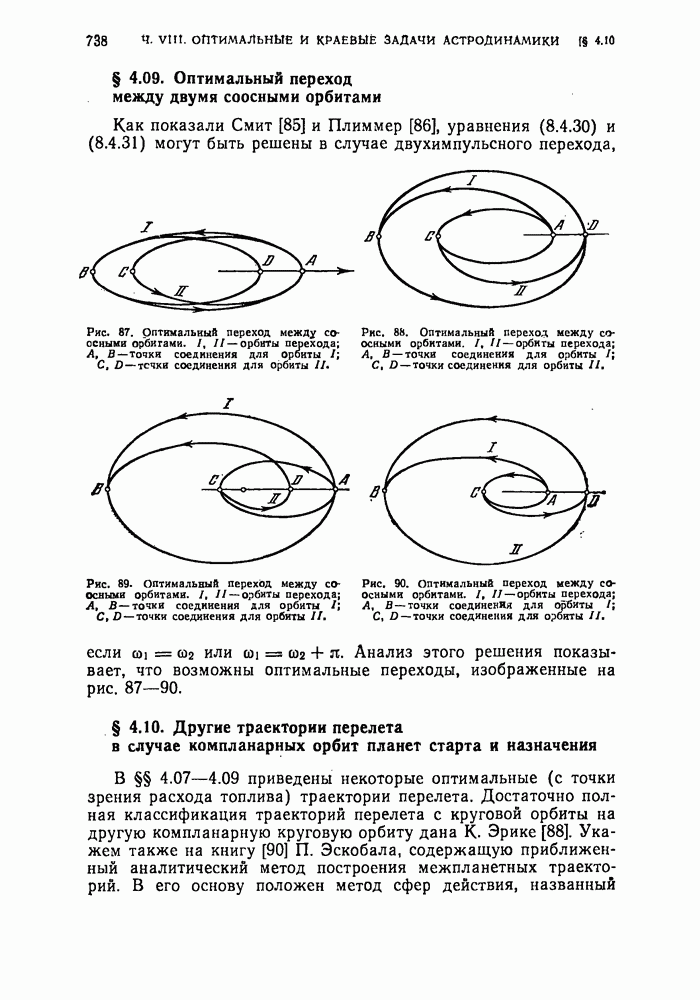
- § 4.09. Оптимальный переход между двумя соосными орбитами
- § 4.10. Другие траектории перелета в случае компланарных орбит планет старта и назначения
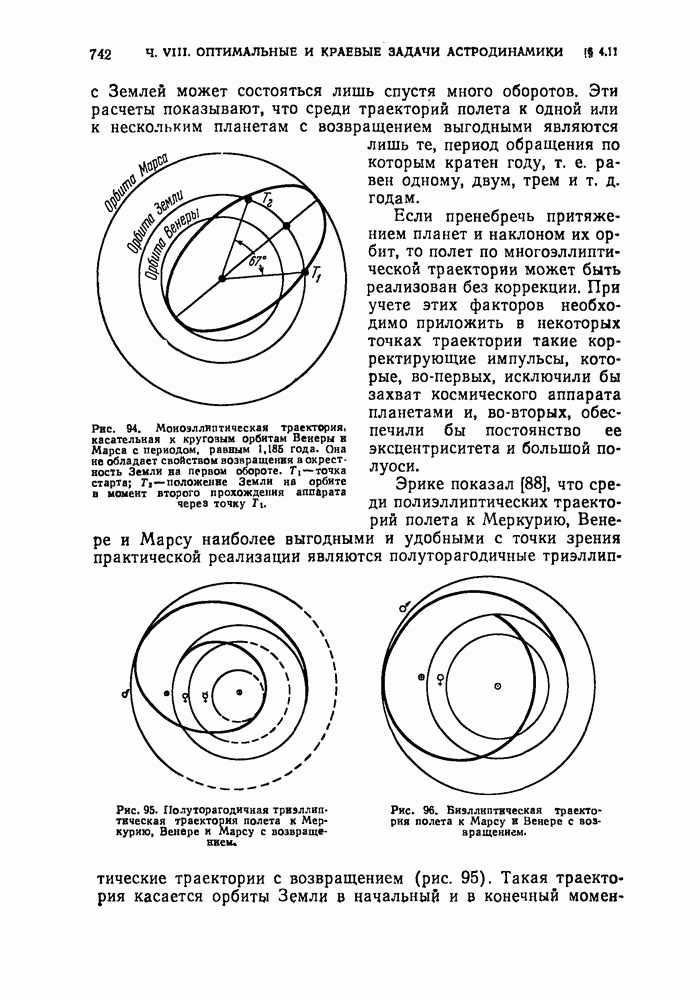
- § 4.11. Траектории полета вблизи нескольких планет
- § 4.12. Начальный этап (запуск и уход) межпланетной траектории
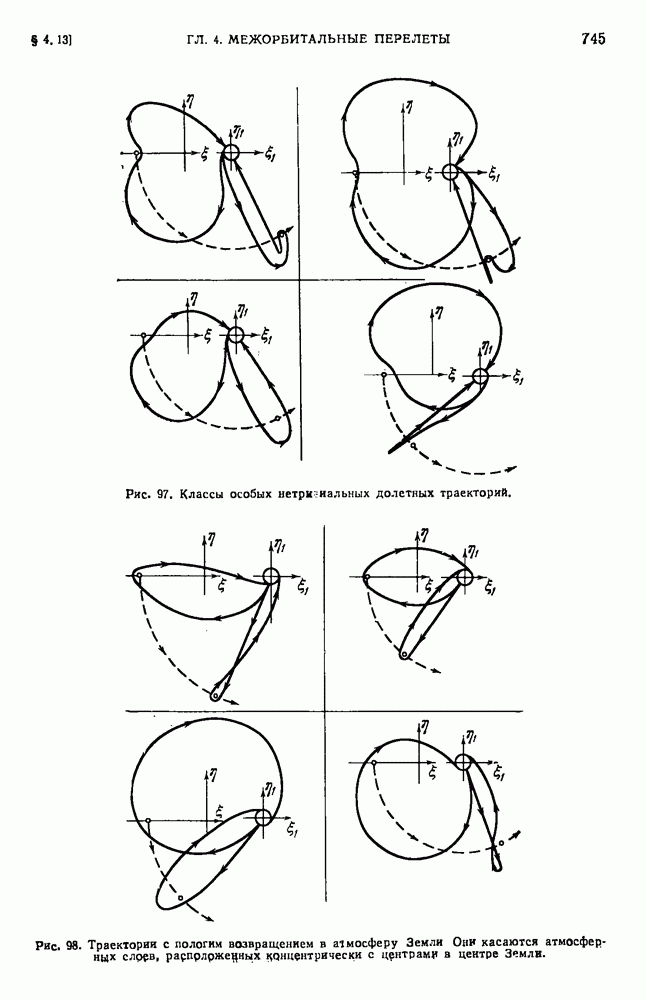
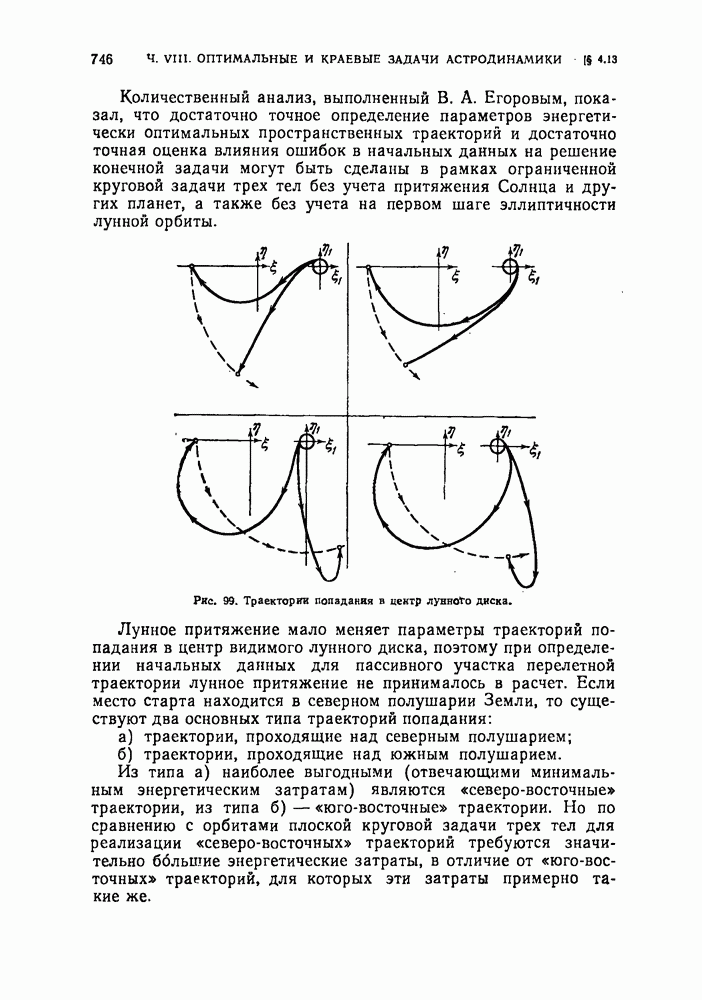
- § 4.13. Полеты к Луне
- Часть IX. ДВИЖЕНИЕ ЕСТЕСТВЕННЫХ И ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
- Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ НЕБЕСНЫХ ТЕЛ ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
- § 1.02. Канонические уравнения вращательного движения небесных тел
- § 1.03. Астродинамические дифференциальные уравнения возмущенного движения спутника относительно центра масс
- § 1.04. Моменты сил, действующих на спутник
- § 1.05. Движение спутника относительно центра масс в центральном ньютоновском поле
- § 1.06. Задача о поступательно-вращательном движении двух гравитирующих динамически симметричных тел
- § 1.07. Вращение Луны
- § 1.08. Дифференциальные уравнения движения деформируемого небесного тела
- § 1.09. Теория фигур небесных тел
- Глава 2. УСТОЙЧИВОСТЬ И СТАБИЛИЗАЦИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ИСКУССТВЕННЫХ НЕБЕСНЫХ ТЕЛ
- § 2.01. Устойчивость движения спутников в гравитационном поле сил
- § 2.02. Устойчивость движения спутников под действием моментов сил различной природы
- § 2.03. Стабилизация движения спутников и космических аппаратов
- Часть X. КАЧЕСТВЕННАЯ НЕБЕСНАЯ МЕХАНИКА
- Глава 1. ПЕРИОДИЧЕСКИЕ И УСЛОВНО-ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ. ФИНАЛЬНЫЕ ДВИЖЕНИЯ
- § 1.02. Метод Ляпунова
- § 1.03. Периодические решения, полученные методом Пуанкаре
- § 1.04. Периодические решения, полученные методом Ляпунова
- § 1.05. Периодические решения, полученные качественными методами
- § 1.06. Почти периодические функции и их свойства. Условно-периодические функции
- § 1.07. Теорема Арнольда о существовании условно-периодических решений гамильтоновых систем
- § 1.08. Условно-периодические решения в небесной механике. Геометрическая интерпретация
- § 1.09. Финальные движения в задаче трех тел. Захват и обмен в задаче трех тел
- Глава 2. ПРОБЛЕМА ИНТЕГРИРУЕМОСТИ И СХОДИМОСТЬ РЯДОВ В НЕБЕСНОЙ МЕХАНИКЕ
- § 2.01. Теорема Пуассона об интеграле гамильтоновой системы
- § 2.02. Теорема Брунса о несуществовании алгебраических первых интегралов задачи трех тел, отличных от классических
- § 2.03. Теорема Пуанкаре о несуществовании однозначных аналитических первых интегралов гамильтоновой системы
- § 2.04. Случаи интегрируемости уравнения Гамильтона — Якоби методом разделения переменных
- § 2.05. Теорема о неприводимости уравнения Гамильтона — Якоби для плоской ограниченной круговой задачи трех тел к уравнению типа Штеккеля
- § 2.06. Соударения
- § 2.07. Решение задачи трех тел в виде рядов, сходящихся для всех вещественных значений времени. Теорема Зундмана
- § 2.08. Сходимость рядов Хилла в основной проблеме теории движения Луны
- § 2.09. Характер сходимости рядов классической теории возмущений
- § 2.10. Теоремы Пуанкаре о ранге и классе возмущений
- § 2.11. Поиск частных, первых и общих интегралов заданной аналитической структуры обыкновенных дифференциальных уравнений на ЭВМ. Приложение к ограниченной задаче трех тел
- § 2.12. Поиск решений уравнения Гамильтона — Якоби на ЭВМ. Приложение к ограниченной задаче трех тел
- Глава 3. ПРОБЛЕМА УСТОЙЧИВОСТИ В НЕБЕСНОЙ МЕХАНИКЕ
- § 3.01. Определение устойчивости по Ляпунову
- § 3.02. Определение орбитальной устойчивости
- § 3.03. Другие определения устойчивости
- § 3.04. Знакопостоянные и знакоопределенные функции. Полная производная в силу системы
- § 3.05. Теоремы Ляпунова об устойчивости
- § 3.06. Устойчивость по отношению к части переменных. Теорема В. В. Румянцева
- § 3.07. Связка первых интегралов. Способ Н. Г. Четаева
- § 3.08. Устойчивость при постоянно действующих возмущениях. Теорема И. Г. Малкина
- § 3.09. Теоремы Лапласа — Лагранжа и Пуассона об отсутствии вековых возмущений больших полуосей
- § 3.10. Теоремы об устойчивости планетных орбит
- § 3.11. Теоремы Арнольда об устойчивости решения гамильтоновой системы в общем эллиптическом случае
- § 3.12. Устойчивость лагранжевых равновесных решений задачи трех тел
- § 3.13. Устойчивость других решений задачи трех тел
- § 3.14. Устойчивость орбитальных движений искусственных спутников