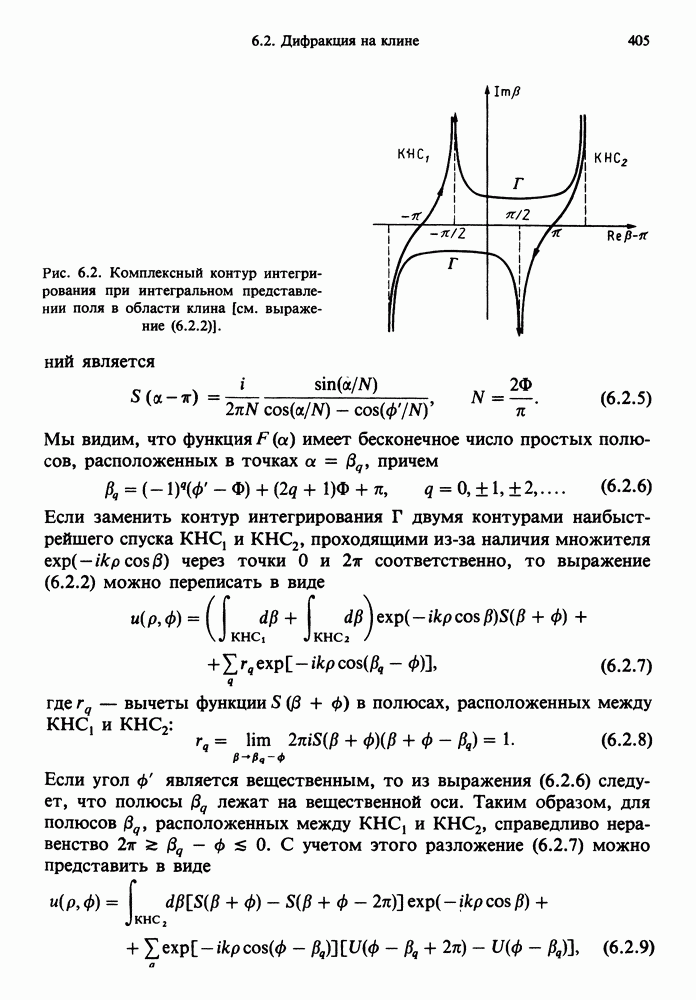
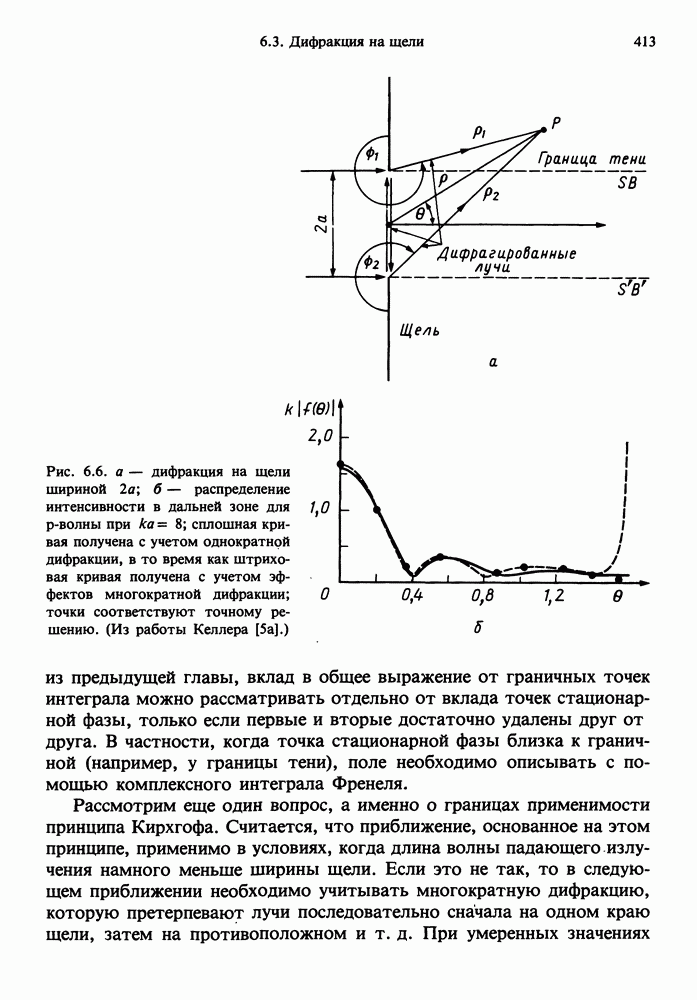
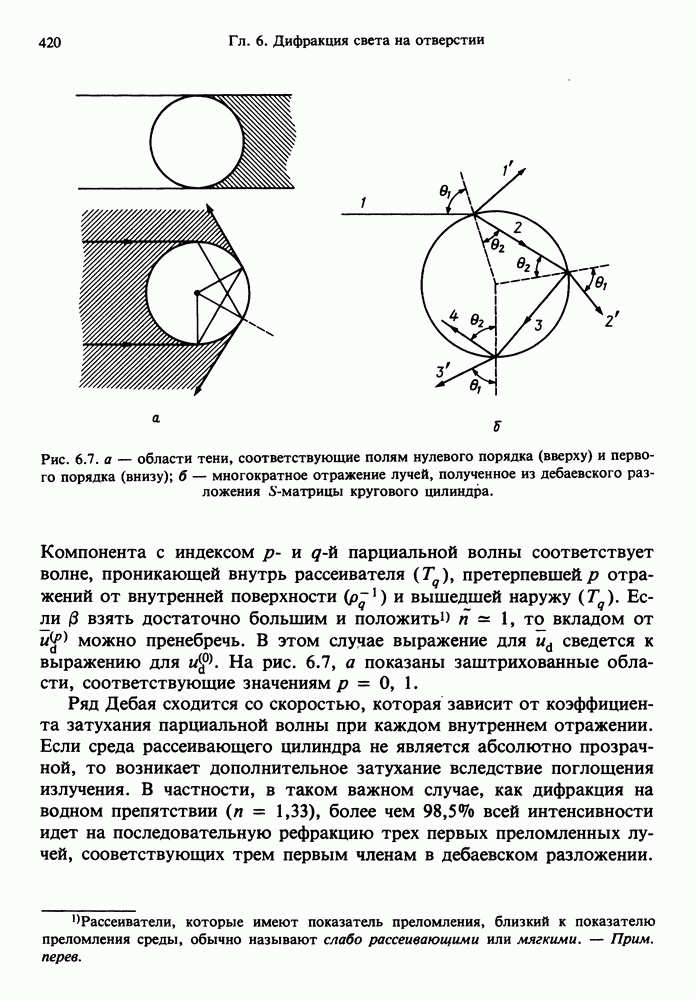
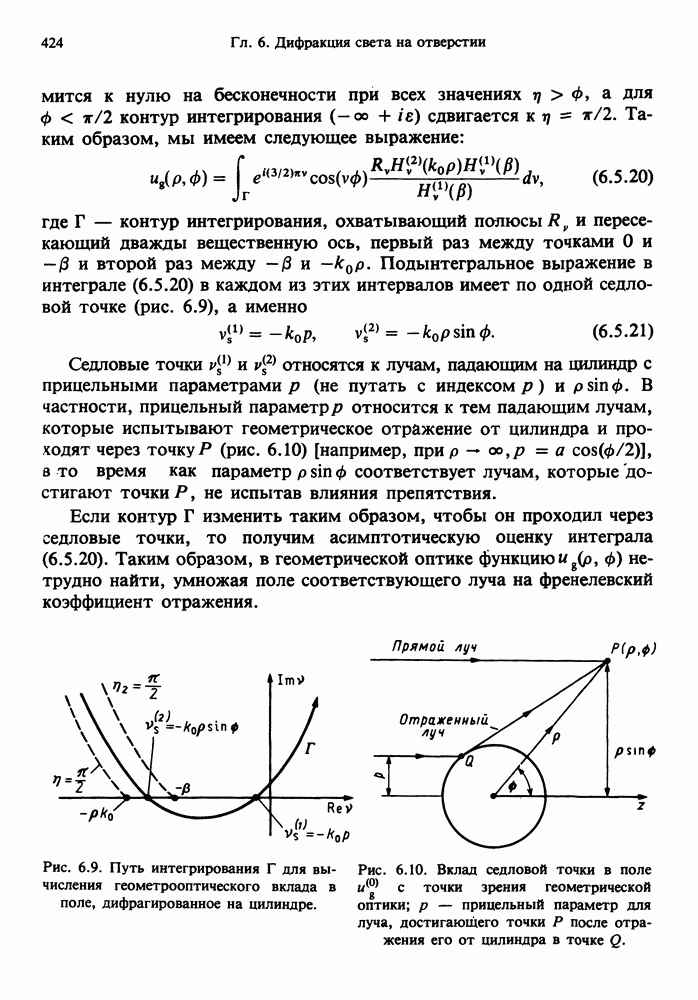
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.2.2.В. Общий случай
Для получения решения в общем случае, описываемом интегродифференциальными уравнениями (1.2.30) и (1.2.31), приходится, как правило, использовать численные методы. С этой целью уравнения удобно представить в дифференциальной форме. Точнее говоря, с помощью определяющих выражений (1.2.28) и (1.2.29) можно показать, что при  (см. разд. 1.2.2.а) эти уравнения эквивалентны системе уравнений, одним из которых является (1.2.26), а два других имеют соответственно вид
(см. разд. 1.2.2.а) эти уравнения эквивалентны системе уравнений, одним из которых является (1.2.26), а два других имеют соответственно вид

Эту систему необходимо дополнить условиями 
Такая система уравнений описывает распространение очень коротких импульсов  не) в лазерах высокой мощности, используемых в экспериментах по инерциональному удержанию плазмы.
не) в лазерах высокой мощности, используемых в экспериментах по инерциональному удержанию плазмы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ОСНОВНЫЕ СВОЙСТВА РАСПРОСТРАНЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 1.1. УРАВНЕНИЯ МАКСВЕЛЛА
- 1.1.1. Векторный и скалярный потенциалы
- 1.2. РАСПРОСТРАНЕНИЕ ИЗЛУЧЕНИЯ В СРЕДЕ С ЧАСТОТНОЙ ДИСПЕРСИЕЙ
- 1.2.1. Нелинейное распространение волн
- 1.2.2. Распространение импульса в двухуровневой резонансной среде
- 1.2.2.а. Режим скоростных уравнений для длинных импульсов
- 1.2.2.б. Самоиндуцированная прозрачность
- 1.2.2.В. Общий случай
- 1.2.3. Соотношение Крамерса — Кронига и монохроматические волны
- 1.2.3.а. Диэлектрическая восприимчивость в резонансной двухуровневой среде
- 1.2.3.б. Распространение монохроматической волны в однородной среде
- 1.3. СОСТОЯНИЕ ПОЛЯРИЗАЦИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 1.3.1. Параметры Стокса и матрица Джонса
- 1.3.2. Поляризация затухающих волн
- 1.4. РАСПРОСТРАНЕНИЕ ВОЛН В АНИЗОТРОПНОЙ СРЕДЕ
- 1.4.1. Двойное лучепреломление
- 1.4.1.а. Электрооптический эффект
- 1.5. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ
- 1.5.1. Естественная оптическая активность
- 1.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 1.6.1. Соотношения Пойнтинга для квазимонохроматического пучка в среде с пространственной дисперсией
- 1.7. РАСПРОСТРАНЕНИЕ ВОЛН В ДВИЖУЩЕЙСЯ СРЕДЕ
- 1.8. СВОЙСТВА КОГЕРЕНТНОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ГЛАВА 2. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2.1. ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 2.2. АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ СКАЛЯРНОГО ВОЛНОВОГО УРАВНЕНИЯ
- 2.3. УРАВНЕНИЕ ЭЙКОНАЛА
- 2.4. УРАВНЕНИЕ ДЛЯ ЛУЧЕЙ
- 2.4.1. Теорема Малюса — Дюпина
- 2.4.2. Кривизна и закручивание лучей
- 2.4.3. Построение луча
- 2.5. ТРАНСПОРТНОЕ УРАВНЕНИЕ ДЛЯ А0
- 2.6. ТРАНСПОРТНЫЕ УРАВНЕНИЯ ДЛЯ Аm
- 2.6.1. Параболическое волновое уравнение Фока — Леонтовича
- 2.7. ЗАТУХАЮЩИЕ ВОЛНЫ И КОМПЛЕКСНЫЕ ЭЙКОНАЛЫ
- 2.7.1. Двумерные затухающие поля
- 2.8. ГЕОМЕТРИЧЕСКАЯ ОПТИКА МАКСВЕЛЛОВСКИХ ВЕКТОРНЫХ ПОЛЕЙ
- 2.8.2. Асимптотическое разложение магнитного поля
- 2.8.3. Асимптотическое разложение вектора Пойнтинга
- 2.8.4. Ряд Лунеберга — Клейна на поверхности раздела двух сред
- 2.9. ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА ВОЛНОВЫХ ФРОНТОВ
- 2.10. КАУСТИКИ И ВОЛНОВЫЕ ФРОНТЫ
- 2.10.1. Аналитические свойства конгруэнции, лучей, волновых фронтов и каустик
- 2.10.1.а. Волновые фронты
- 2.10.1.б. Каустики
- 2.11. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛНОВОГО ФРОНТА НА НЕПЛОСКОЙ ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
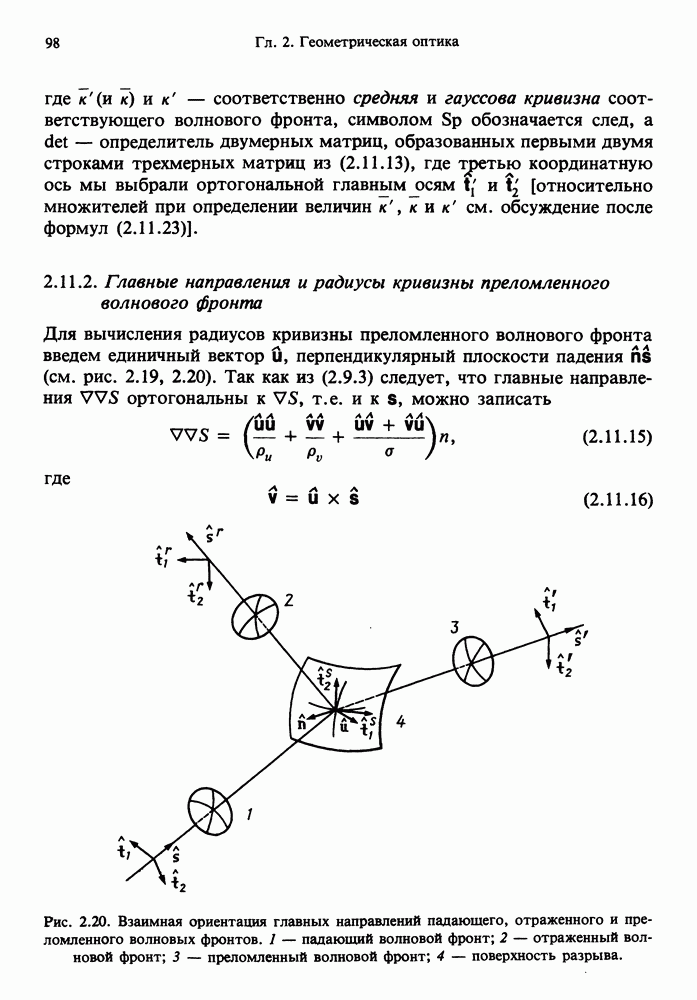
- 2.11.2. Главные направления и радиусы кривизны преломленного волнового фронта
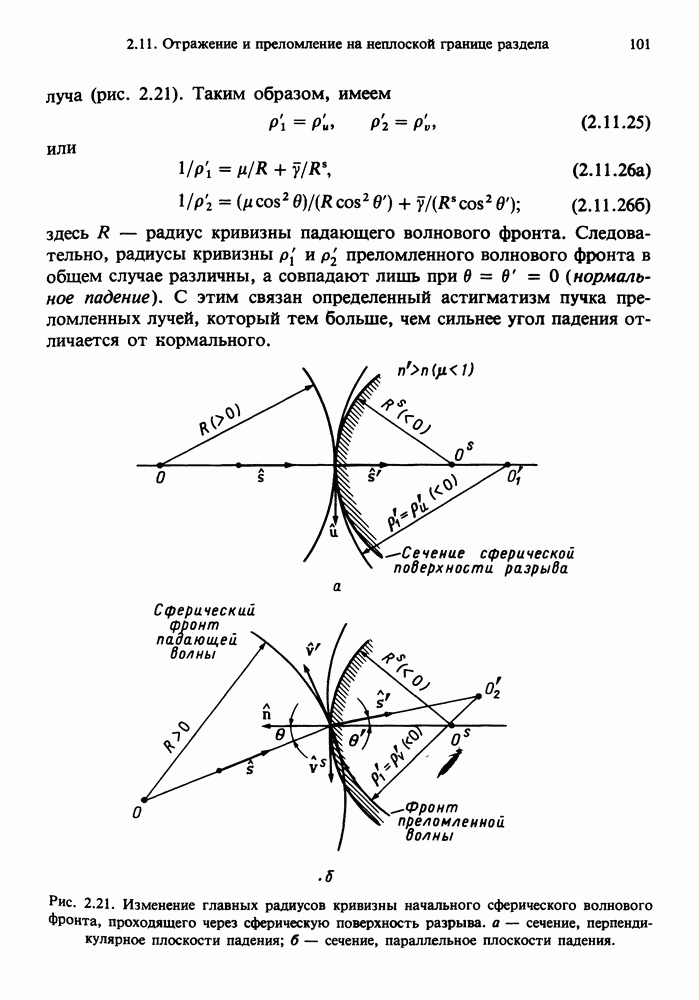
- 2.11.3. Сферические преломляющие поверхности
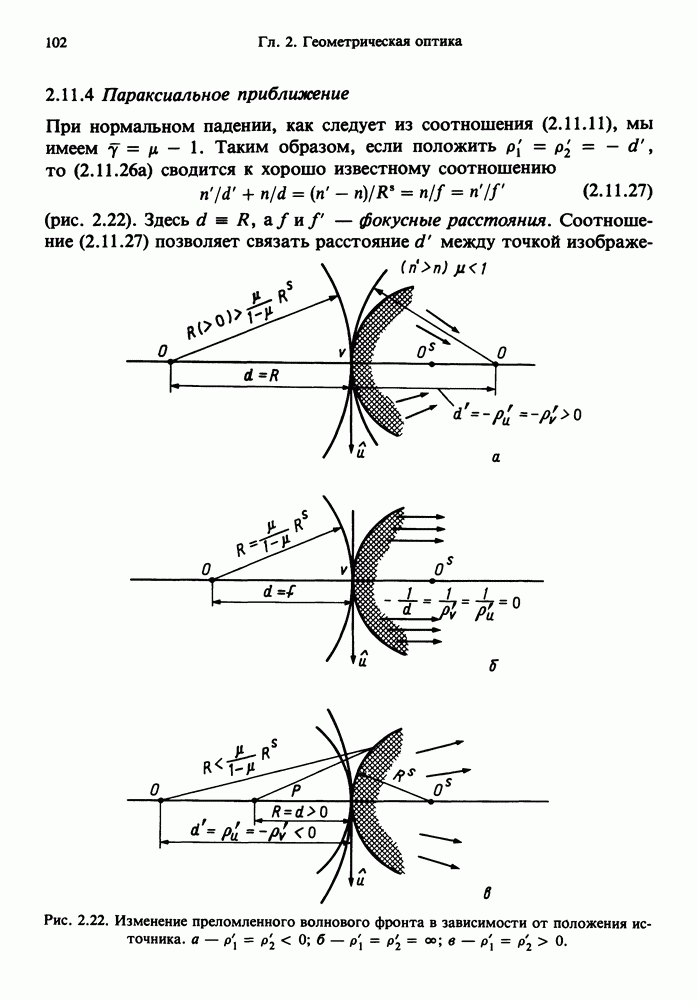
- 2.11.4 Параксиальное приближение
- 2.11.5. Сферические отражающие поверхности
- 2.12. РЕШЕНИЕ УРАВНЕНИЯ ЭЙКОНАЛА МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
- 2.12.1.а. Аксиально-симметричное распределение показателя преломления
- 2.12.1.б. Линзоподобные среды
- 2.12.1.в. Физические свойства комплексных эйконалов
- 2.12.2. Цилиндрические координаты
- 2.12.2.а. Аксиально-симметричный профиль показателя преломления
- 2.12.3. Сферические координаты
- 2.13. ВЫЧИСЛЕНИЕ ТРАЕКТОРИЙ ЛУЧЕЙ МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
- 2.13.2. Сферически-симметричные среды
- 2.13.3. Градиентные оптические элементы
- 2.14. СКАЛЯРНЫЕ УРАВНЕНИЯ ДЛЯ ЛУЧЕЙ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ; ПРИНЦИП ФЕРМА
- 2.14.1. Анизотропные среды
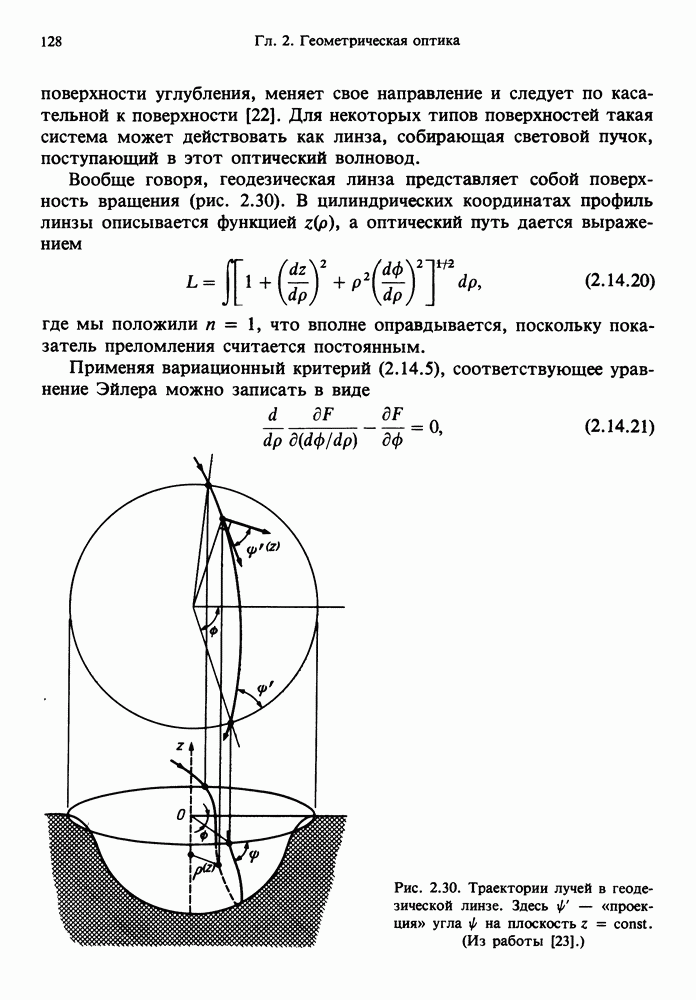
- 2.14.2. Геодезические линзы
- 2.14.3. Метод ковариантного дифференцирования
- 2.15. ЭЛЕМЕНТЫ ГАМИЛЬТОНОВОЙ ОПТИКИ
- 2.15.1. Точечные, угловые и смешанные характеристики
- 2.15.2. Угловая характеристика поверхности вращения
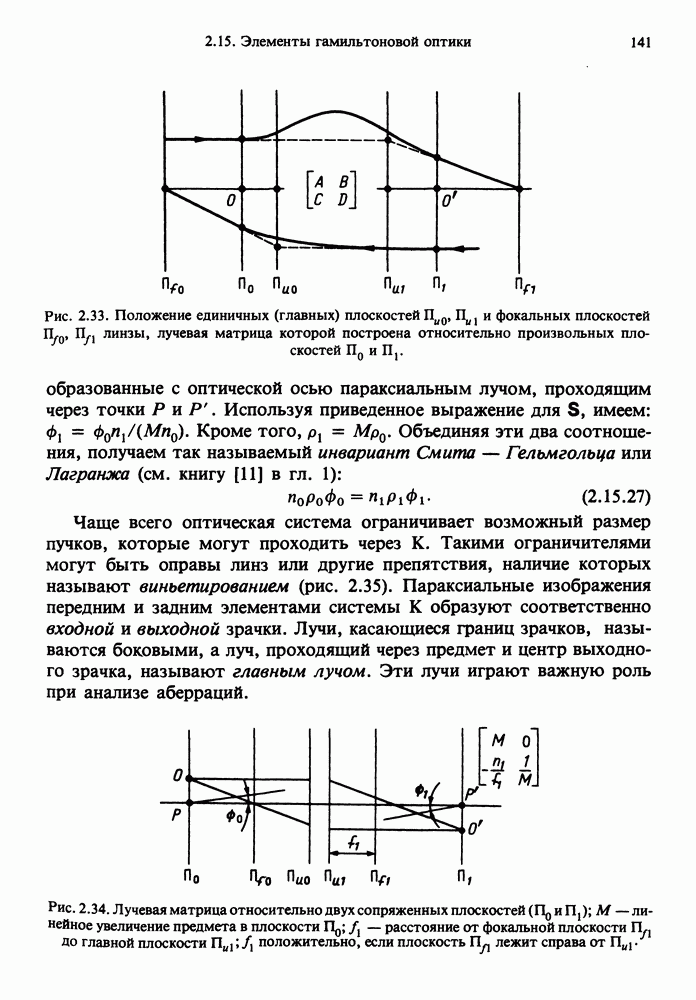
- 2.15.3. Лучевая матрица
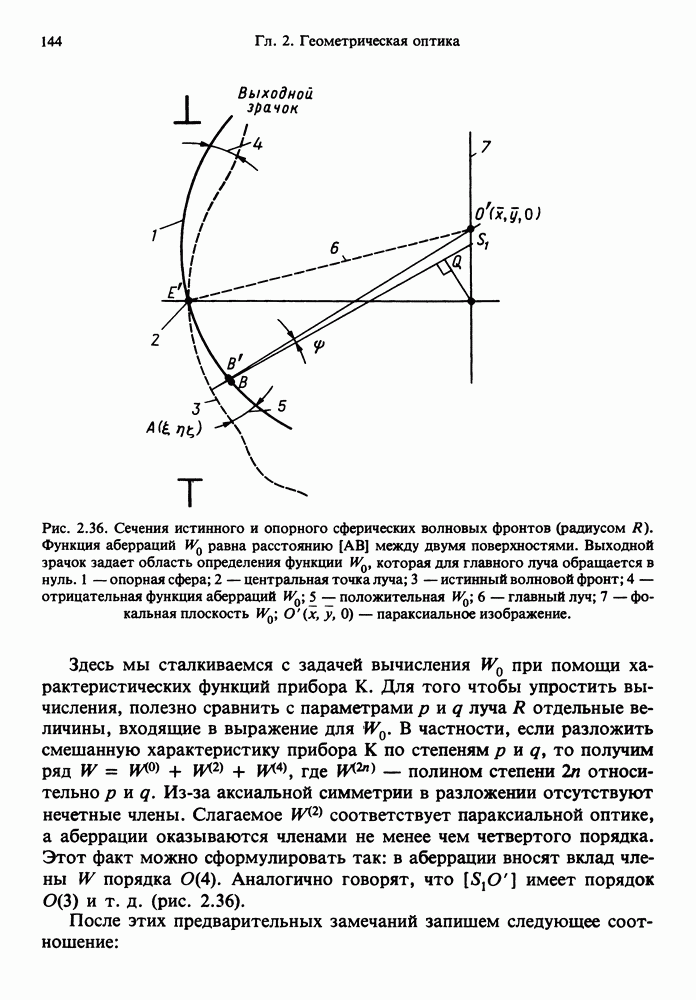
- 2.15.4. Аберрации волнового фронта
- ГЛАВА 3. ПЛОСКИЕ МНОГОСЛОЙНЫЕ СРЕДЫ
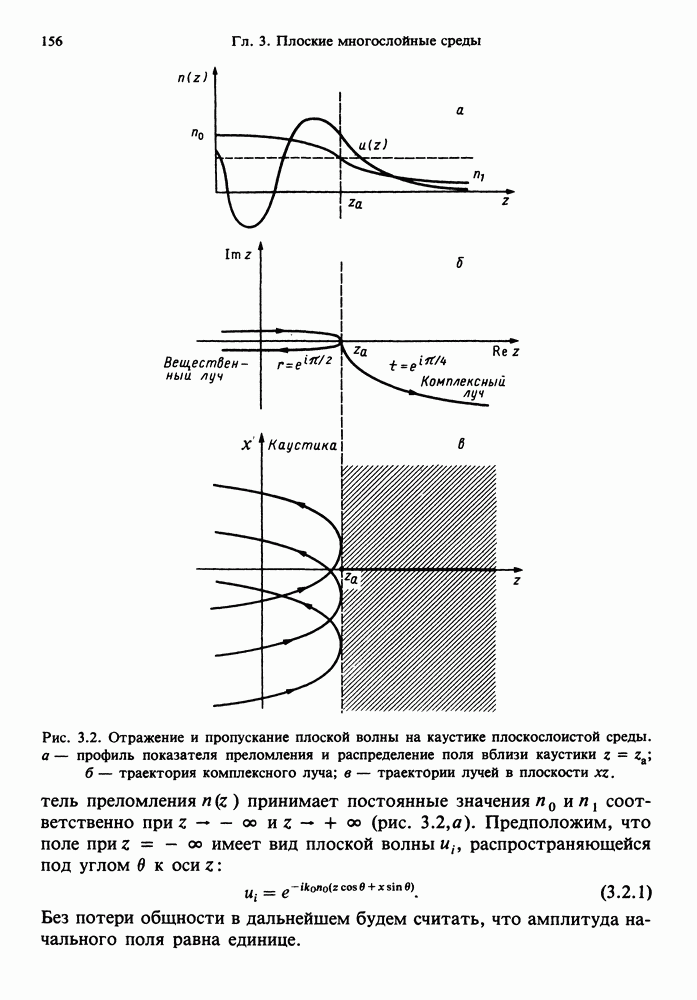
- 3.2. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СЛОИСТЫХ СРЕДАХ
- 3.3. СШИВКА АСИМПТОТИЧЕСКИХ РАЗЛОЖЕНИЙ; МЕТОД ЛАНГЕРА
- 3.3.1. Прошедшие и отраженные волны
- 3.3.2. Переход из запрещенной зоны в разрешенную
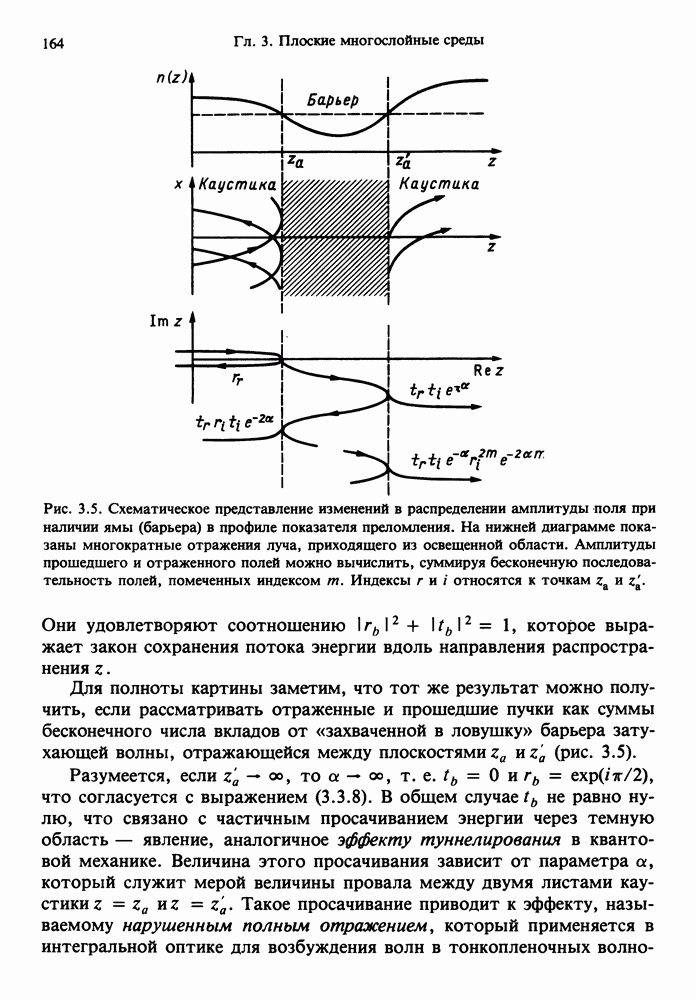
- 3.3.3. Темный барьер
- 3.3.4. Канал
- 3.4. ОТРАЖЕНИЕ И ПРОПУСКАНИЕ ПРОИЗВОЛЬНОЙ НЕОДНОРОДНОЙ СРЕДОЙ
- 3.5. ТОЧНОЕ РЕШЕНИЕ ДЛЯ СЛОЯ С ЛИНЕЙНО УВЕЛИЧИВАЮЩИМСЯ ПОКАЗАТЕЛЕМ ПРЕЛОМЛЕНИЯ
- 3.6. МНОГОСЛОЙНЫЕ СРЕДЫ С КУСОЧНО-ПОСТОЯННЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
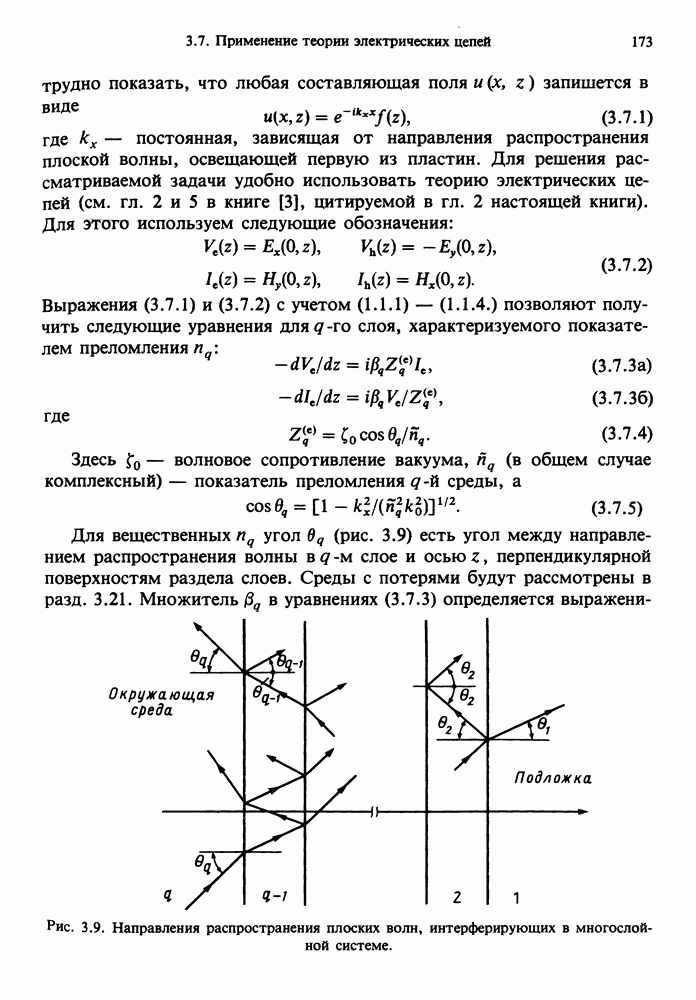
- 3.7. ПРИМЕНЕНИЕ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
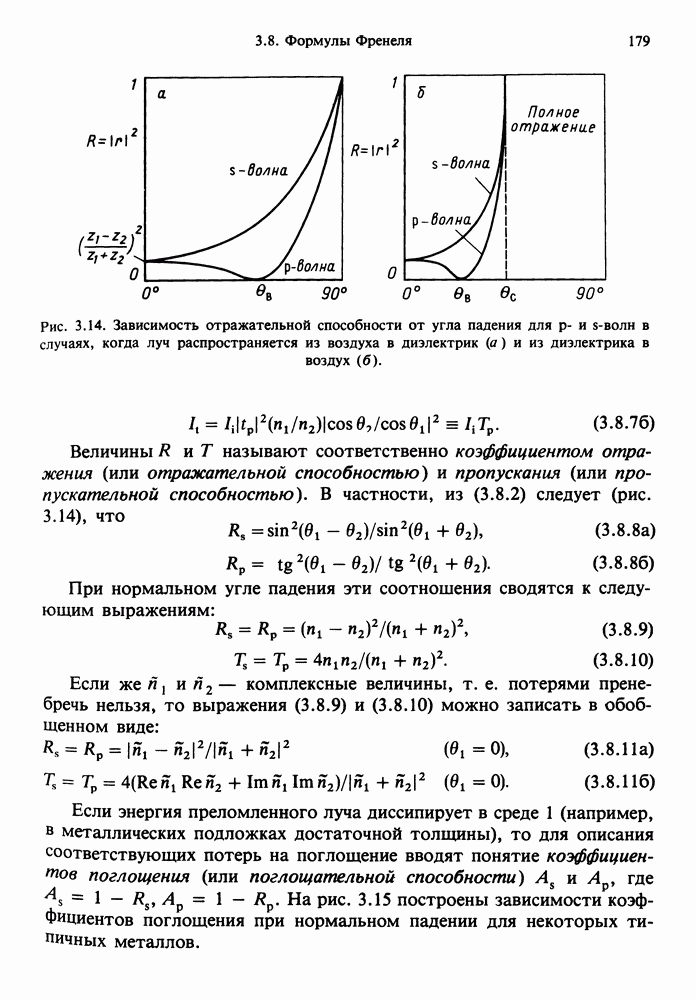
- 3.8. ФОРМУЛЫ ФРЕНЕЛЯ
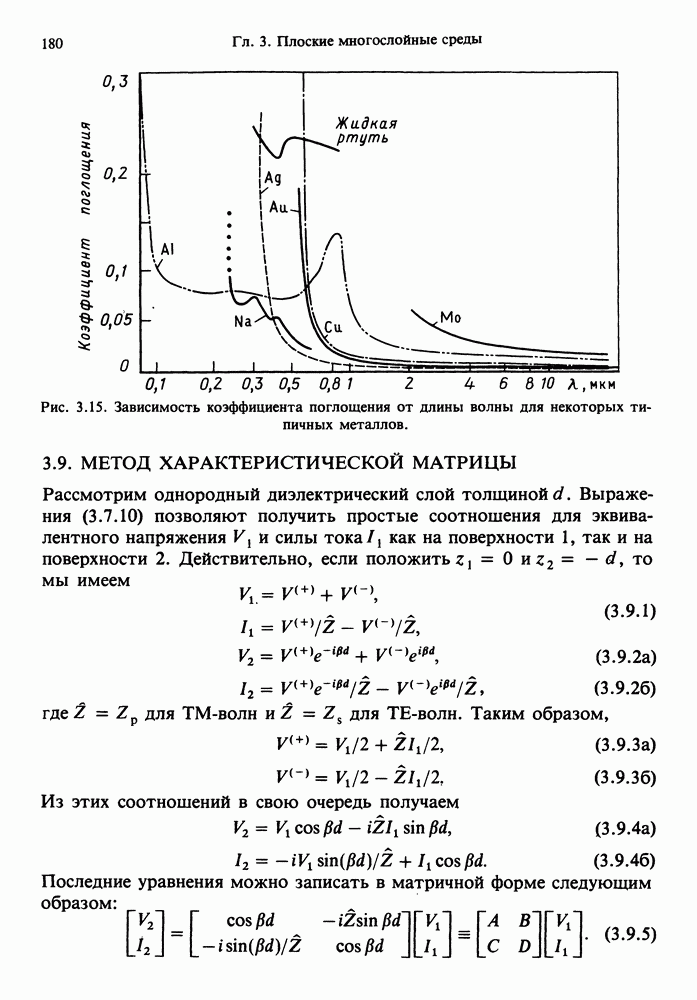
- 3.9. МЕТОД ХАРАКТЕРИСТИЧЕСКОЙ МАТРИЦЫ
- 3.9.1. Уравнение для М-матрицы
- 3.9.2. Вычисление М-матрицы для мультислоя
- 3.10. БЛОХОВСКИЕ ВОЛНЫ
- 3.11. ПОЛОСЫ ПРОПУСКАНИЯ И НЕПРОЗРАЧНОСТИ СТОПЫ ЧЕТВЕРТЬВОЛНОВЫХ ПЛАСТИНОК
- 3.12. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ МУЛЬТИСЛОЯ
- 3.12.1. Формула Эйри
- 3.12.2. Четвертьволновые стопы
- 3.12.3. Однослойные покрытия
- 3.12.4. Отражение от сдоя со слабо изменяющимся профилем
- 3.13. МЕТАЛЛИЧЕСКИЕ И ДИЭЛЕКТРИЧЕСКИЕ ОТРАЖАТЕЛИ
- 3.13.1. Отражение при наклонном падении
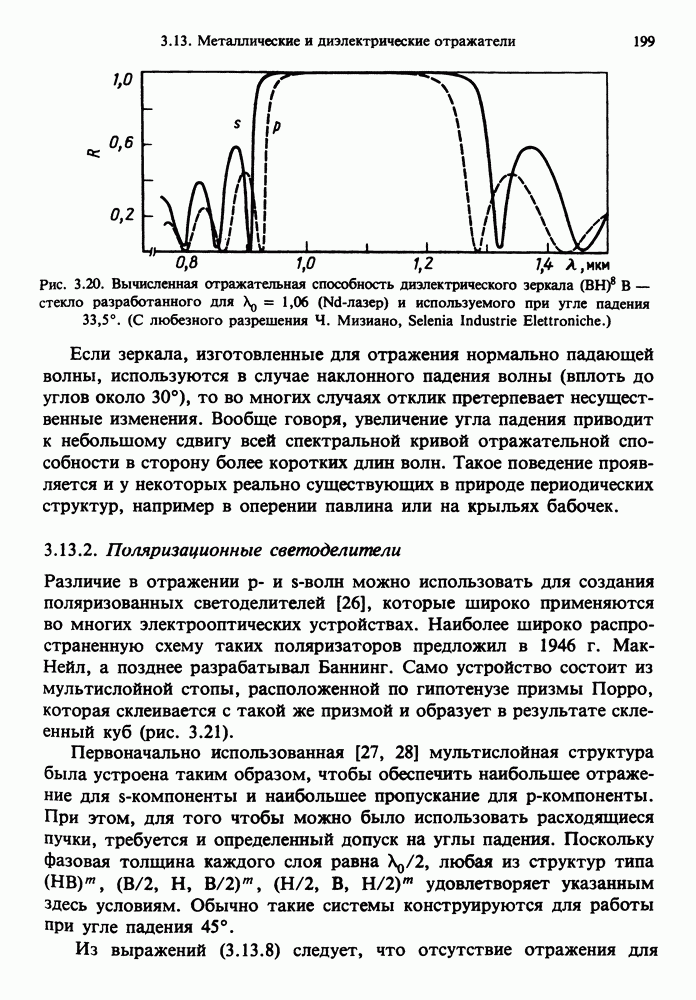
- 3.13.2. Поляризационные светоделители
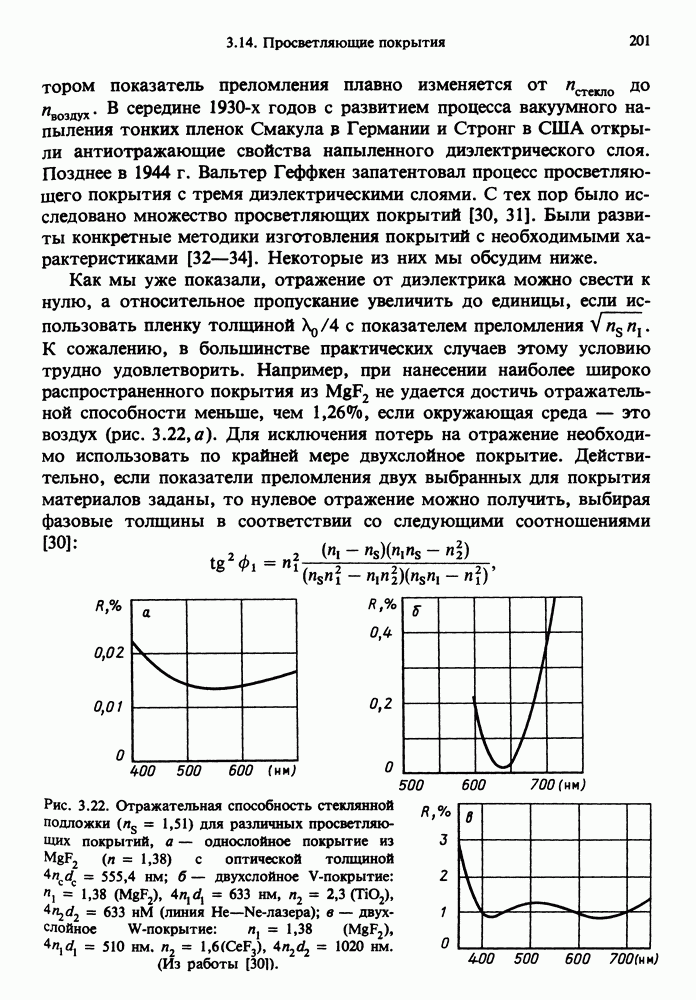
- 3.14. ПРОСВЕТЛЯЮЩИЕ ПОКРЫТИЯ
- 3.15. ИНТЕРФЕРЕНЦИОННЫЕ ФИЛЬТРЫ
- 3.16. АНИЗОТРОПНЫЕ СЛОИСТЫЕ СРЕДЫ
- 3.16.2. Коэффициенты отражения и пропускания мультислоя
- 3.17. РАСПРОСТРАНЕНИЕ ВОЛН В ПЕРИОДИЧЕСКОЙ СРЕДЕ
- 3.17.1. Теорема Флоке
- 3.17.2. Детерминант Хилла
- 3.17.3. Теория связанных мод
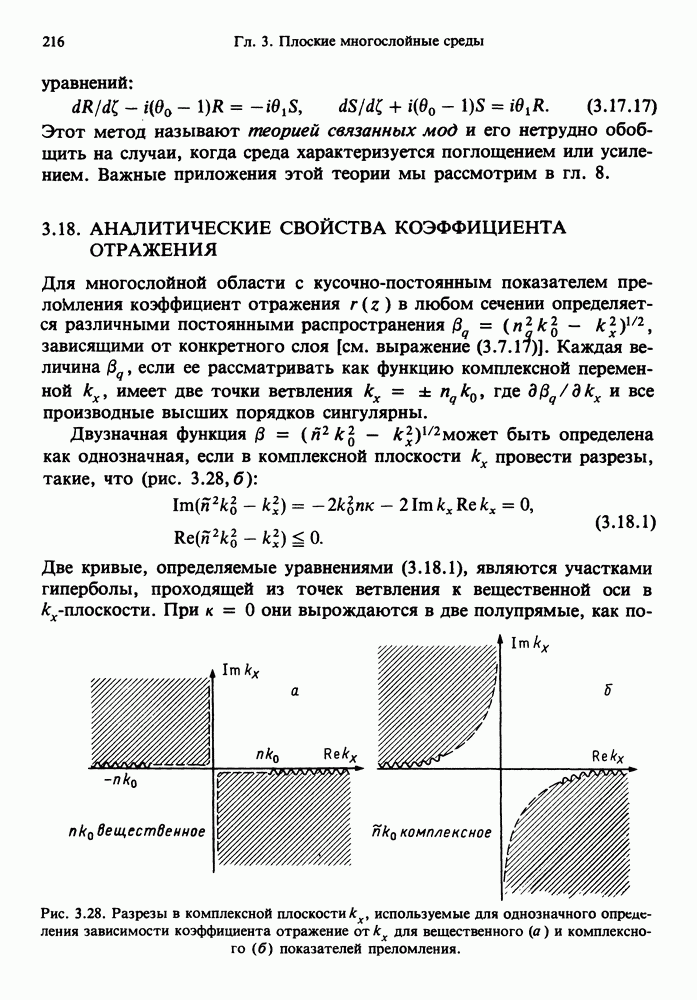
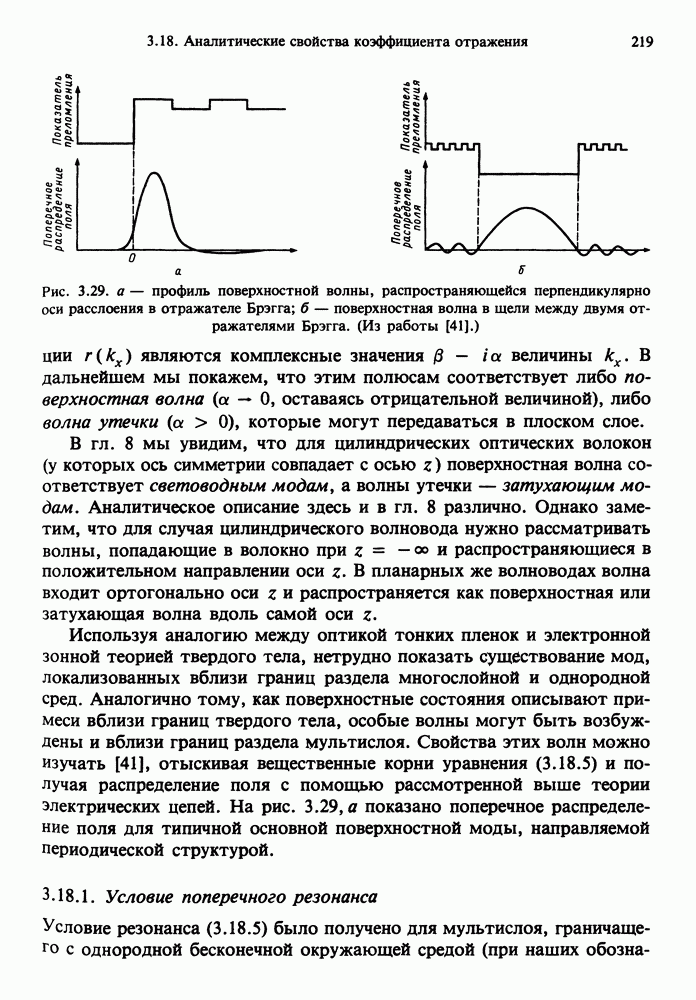
- 3.18. АНАЛИТИЧЕСКИЕ СВОЙСТВА КОЭФФИЦИЕНТА ОТРАЖЕНИЯ
- 3.18.1. Условие поперечного резонанса
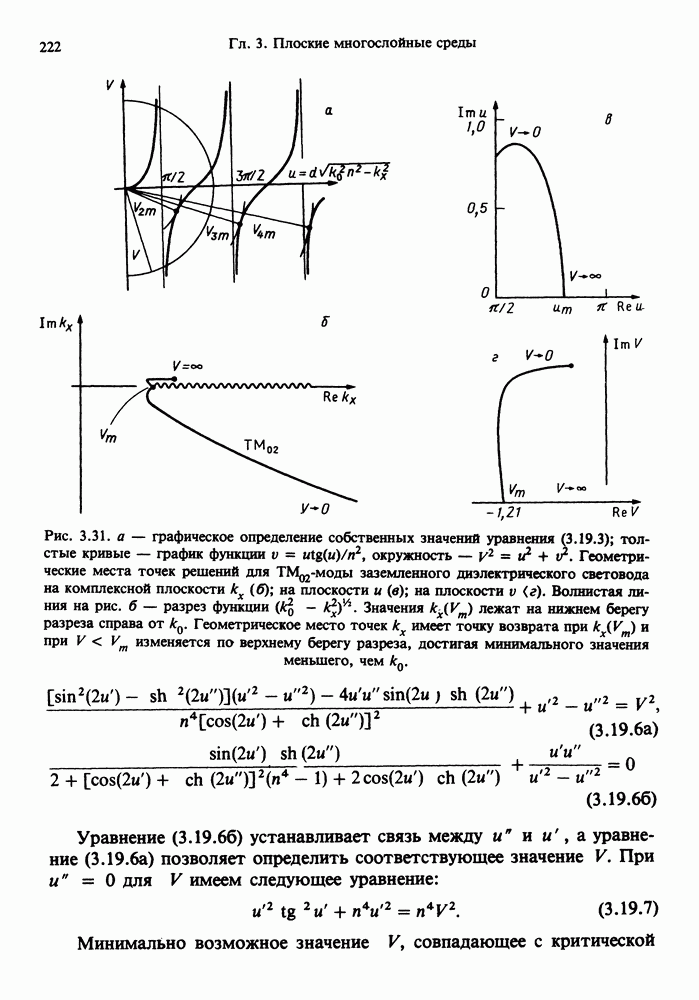
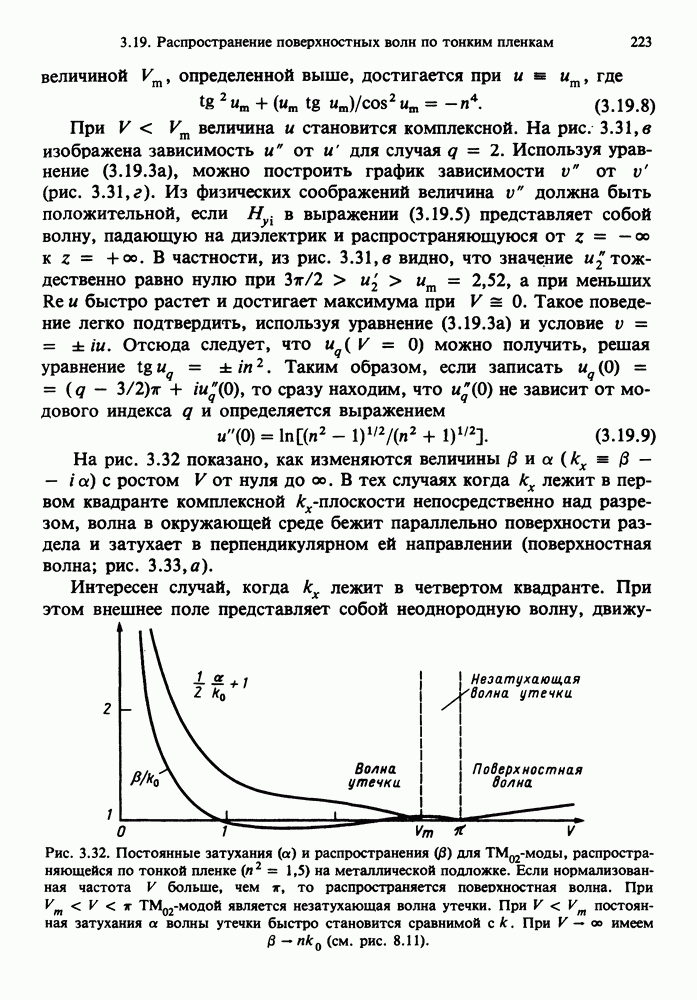
- 3.19. РАСПРОСТРАНЕНИЕ ПОВЕРХНОСТНЫХ И ЗАТУХАЮЩИХ ВОЛН ПО ТОНКИМ ПЛЕНКАМ
- 3.20. ОСВЕЩЕНИЕ ПОД УГЛОМ, БОЛЬШИМ КРИТИЧЕСКОГО
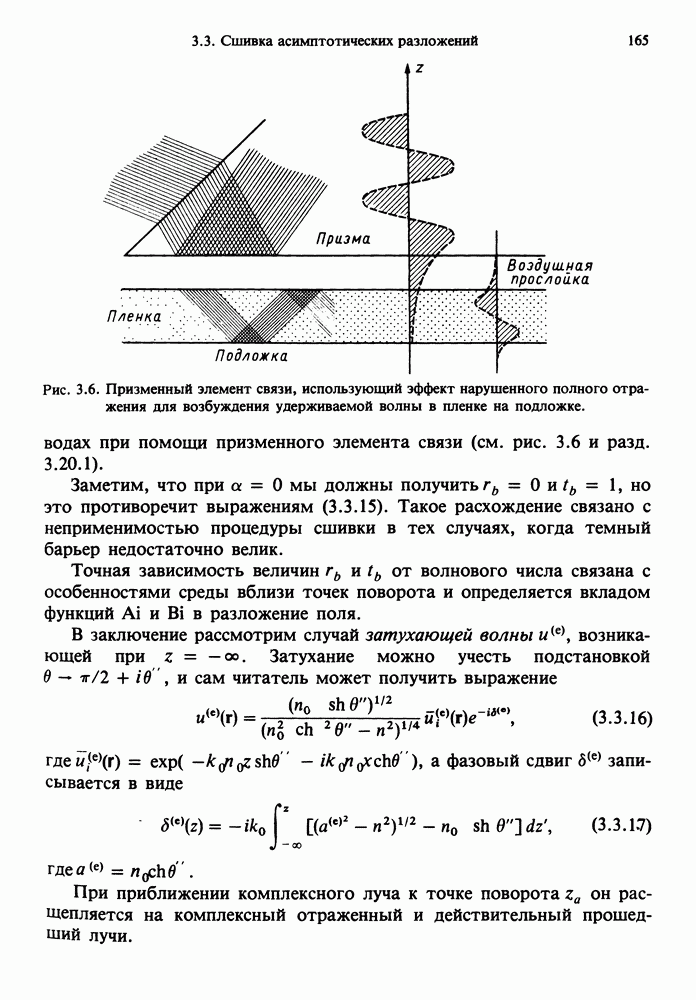
- 3.20.1. Нарушенное полное отражение
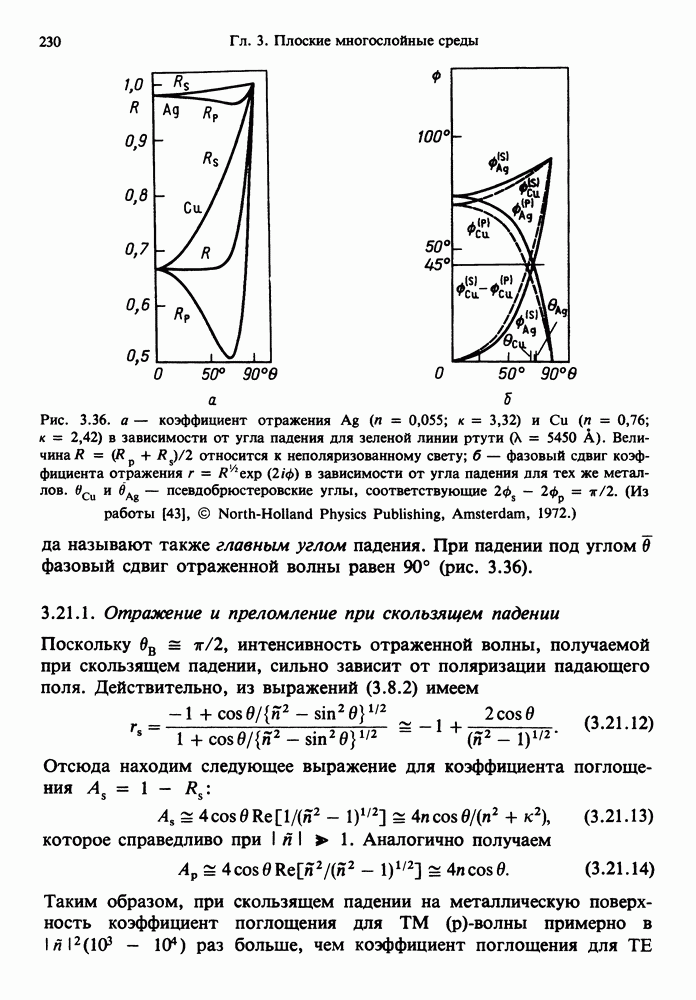
- 3.21. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ГРАНИЦЕ РАЗДЕЛА МЕЖДУ ДИЭЛЕКТРИКОМ И СРЕДОЙ С ПОТЕРЯМИ
- 3.21.1. Отражение и преломление при скользящем падении
- 3.21.2. Отражение и преломление при нормальном падении
- 3.21.3. Отражение при произвольном угле падения
- 3.22. ПОВЕРХНОСТНЫЕ ВОЛНЫ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
- 3.22.1. Поверхностные волны в металлах
- 3.23. ИМПЕДАНСНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
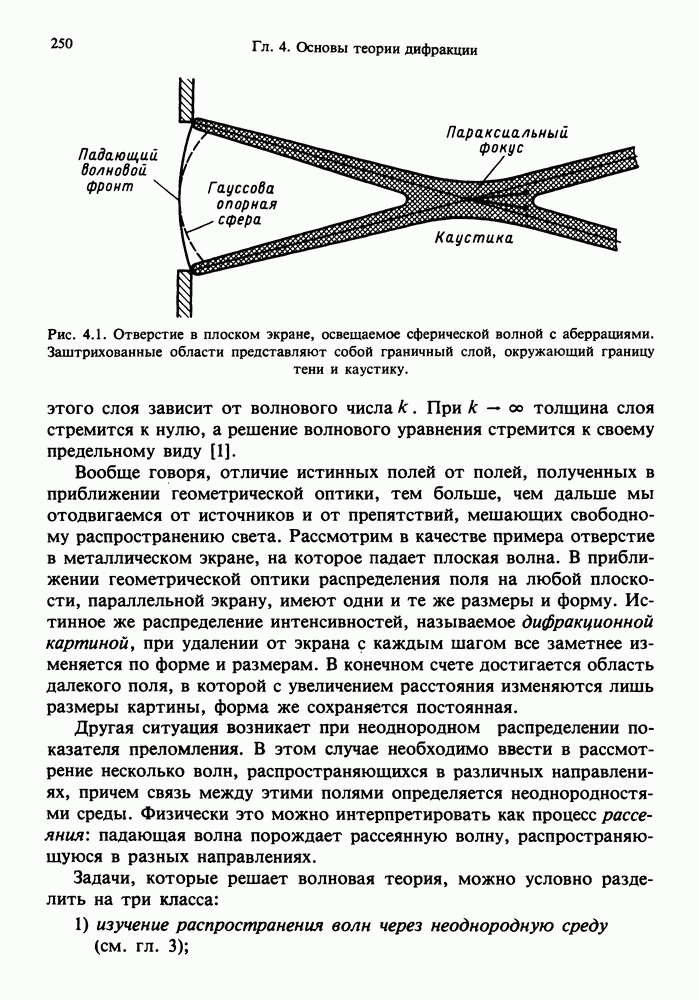
- ГЛАВА 4. ОСНОВЫ ТЕОРИИ ДИФРАКЦИИ
- 4.1.2. Математический аппарат
- 4.2. МЕТОД ФУНКЦИИ ГРИНА
- 4.2.1. Интегральная теорема Гелъмгольца — Кирхгофа
- 4.2.2. Принцип Гюйгенса
- 4.3. ПРИНЦИП ГЮЙГЕНСА В ФОРМУЛИРОВКЕ КИРХГОФА — КОТТЛЕРА
- 4.4. УСЛОВИЕ ЗОММЕРФЕЛЬДА НА ПОЛЕ ИЗЛУЧЕНИЯ
- 4.5. ДИФРАКЦИОННЫЕ ИНТЕГРАЛЫ РЭЛЕЯ ДЛЯ ПЛОСКИХ ЭКРАНОВ
- 4.6. ПРИНЦИП БАБИНЕ
- 4.7. ДИФРАКЦИОННЫЕ ИНТЕГРАЛЫ ДЛЯ ДВУМЕРНЫХ ПОЛЕЙ
- 4.8. РАЗЛОЖЕНИЕ ПОЛЯ ПО ПЛОСКИМ ВОЛНАМ
- 4.9. УГЛОВОЙ СПЕКТР
- 4.9.1. Угловой спектр двумерных волн
- 4.9.2. Угловой спектр в комплексной области
- 4.9.3. Полюсные сингулярности
- 4.9.4. Точки ветвления
- 4.10. ДИФРАКЦИОННЫЕ ФОРМУЛЫ ФРЕНЕЛЯ И ФРАУНГОФЕРА
- 4.10.2. Формула Фраунгофера
- 4.10.3. Обобщение на двумерные поля
- 4.10.4. Дифракция периодических полей
- 4.11. РАЗЛОЖЕНИЕ ПОЛЯ ПО ЦИЛИНДРИЧЕСКИМ ВОЛНАМ
- 4.11.1. Приближение Френеля
- 4.11.2. Разложение плоской волны по цилиндрическим волнам
- 4.11.3. Апертурно ограниченные вращательно-симметричные поля
- 4.11.3.а. Разложение в ряды Буавена
- 4.12. ЦИЛИНДРИЧЕСКИЕ ВОЛНЫ КОМПЛЕКСНОГО ПОРЯДКА И ПРЕОБРАЗОВАНИЕ ВАТСОНА
- 4.12.1. Нули функции … в верхней полуплоскости
- 4.12.2. Ползущие волны
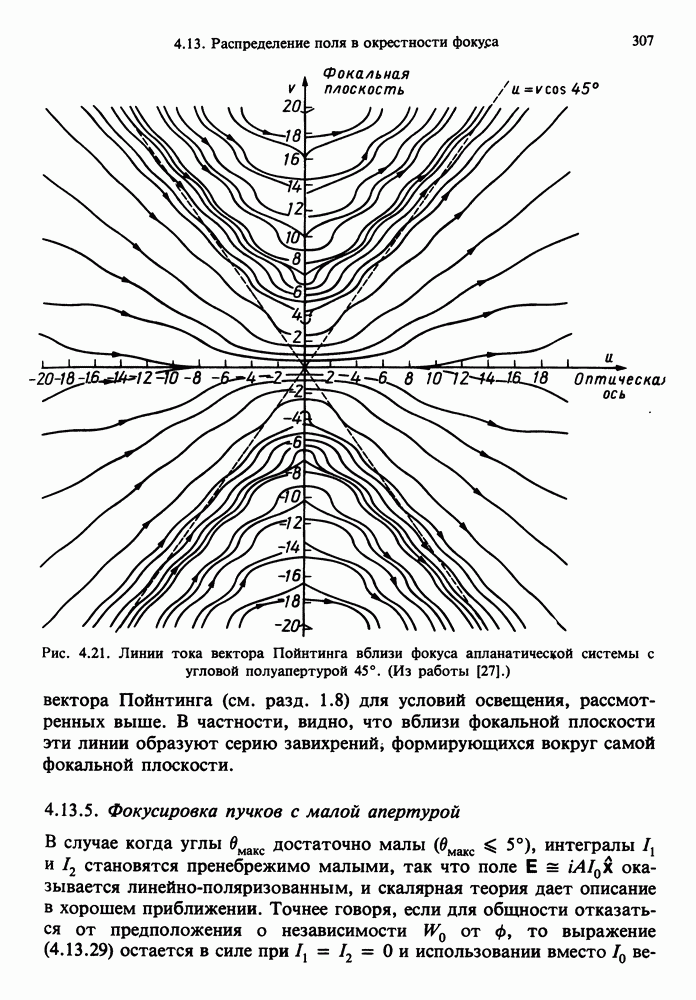
- 4.13. РАСПРЕДЕЛЕНИЕ ПОЛЯ В ОКРЕСТНОСТИ ФОКУСА
- 4.13.1. Точечные источники электромагнитного поля
- 4.13.2. Перенос векторных полей из пространства предмета к выходному зрачку
- 4.13.3. Дифракционный интеграл Лунеберга — Дебая
- 4.13.4. Фокусировка линейно-поляризованных плоских волн
- 4.13.5. Фокусировка пучков с малой апертурой
- 4.13.6. Распределение поля вдоль оптической оси для гауссова пучка с ограниченной апертурой
- 4.13.7. Распределение поля в фокальной плоскости для гауссова пучка с ограниченной апертурой
- 4.13.8. Разрешающая способность
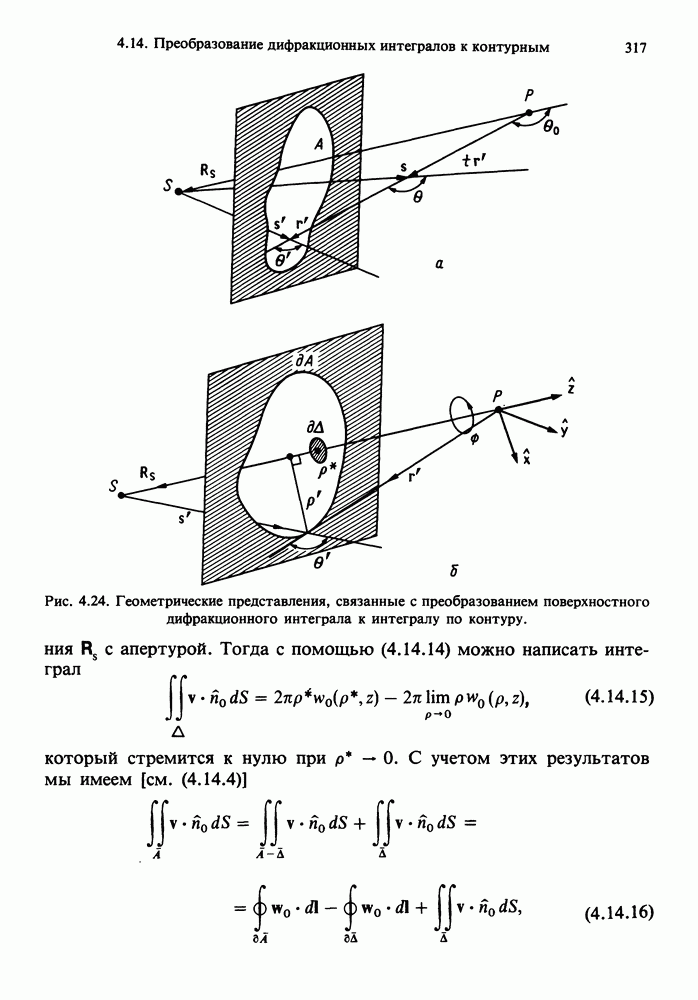
- 4.14. ПРЕОБРАЗОВАНИЕ ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ К КОНТУРНЫМ
- 4.14.2. Векторный потенциал сферических волн
- 4.15. ИЗОБРАЖЕНИЕ ПРИ КОГЕРЕНТНОМ И НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 4.15.1. Импульсный отклик и передаточная функция точки
- 4.15.2. Когерентное изображение протяженных источников
- 4.15.3. Распространение взаимной интенсивности; теорема Ван-Циттерта — Цернике
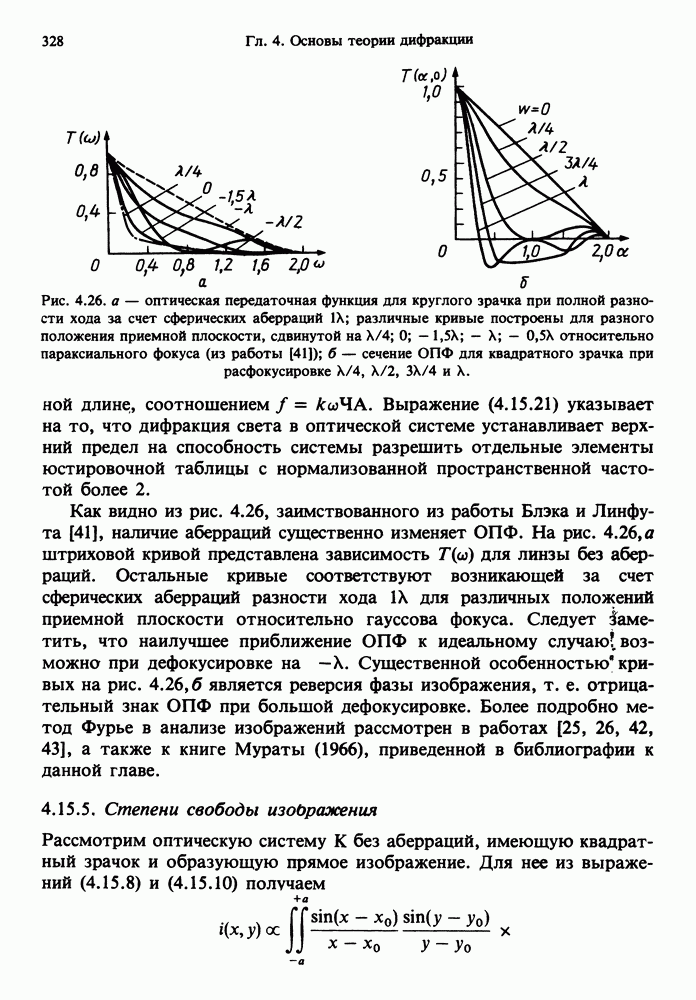
- 4.15.4. Исследование оптических систем с помощью оптической передаточной функции (ОПФ)
- 4.15.5. Степени свободы изображения
- ГЛАВА 5. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ
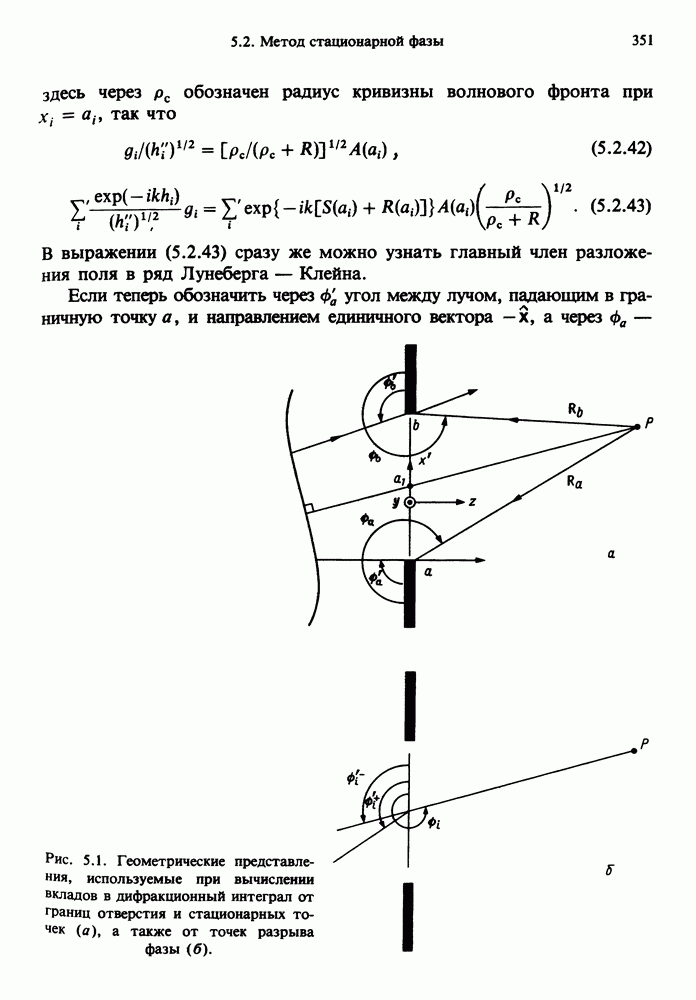
- 5.2. МЕТОД СТАЦИОНАРНОЙ ФАЗЫ
- 5.2.1. Асимптотическое разложение интегралов типа преобразования Фурье с монотонной фазой
- 5.2.2. Обобщение метода СФ на дифракционные интегралы с несколькими стационарными и сингулярными точками
- 5.2.3. Вклады стационарных точек
- 5.2.4. Вклады граничных точек
- 5.2.5. Вклады точек разрыва
- 5.2.6 Асимптотическое выражение для дифракционных интегралов
- 5.2.7. Устранение СФ-сингулярностей с помощью сравнительных интегралов
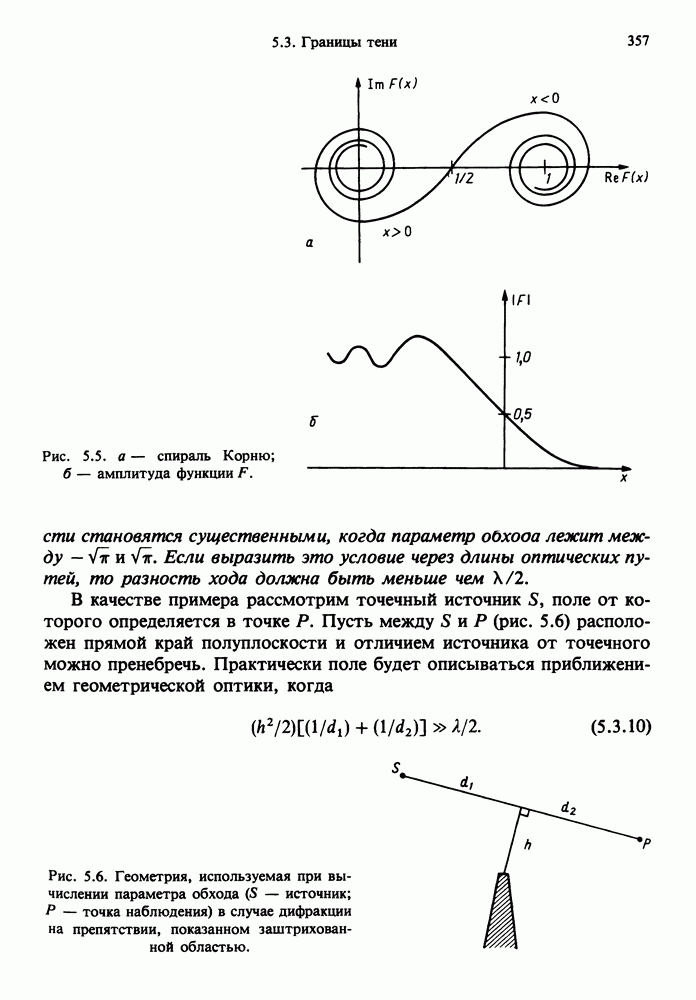
- 5.3. ГРАНИЦЫ ТЕНИ; СТАЦИОНАРНАЯ ТОЧКА ВБЛИЗИ ГРАНИЧНОЙ
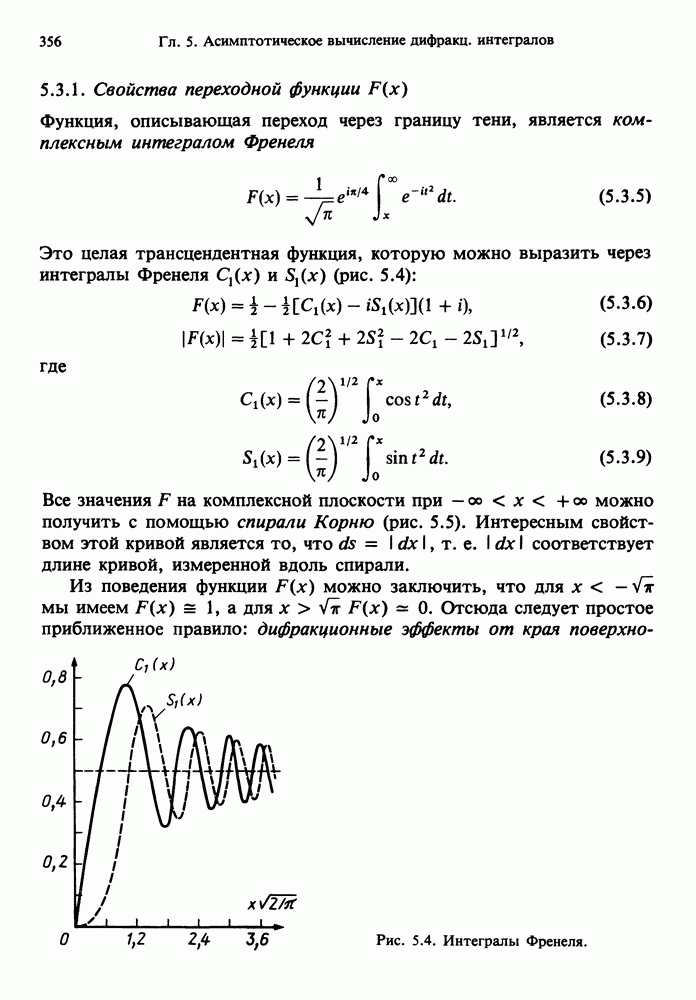
- 5.3.1. Свойства переходной функции F(x)
- 5.3.2. Асимптотическое поведение функции F(x)
- 5.3.3. Асимптотическое представление поля
- 5.3.4. F(x) при малых аргументах
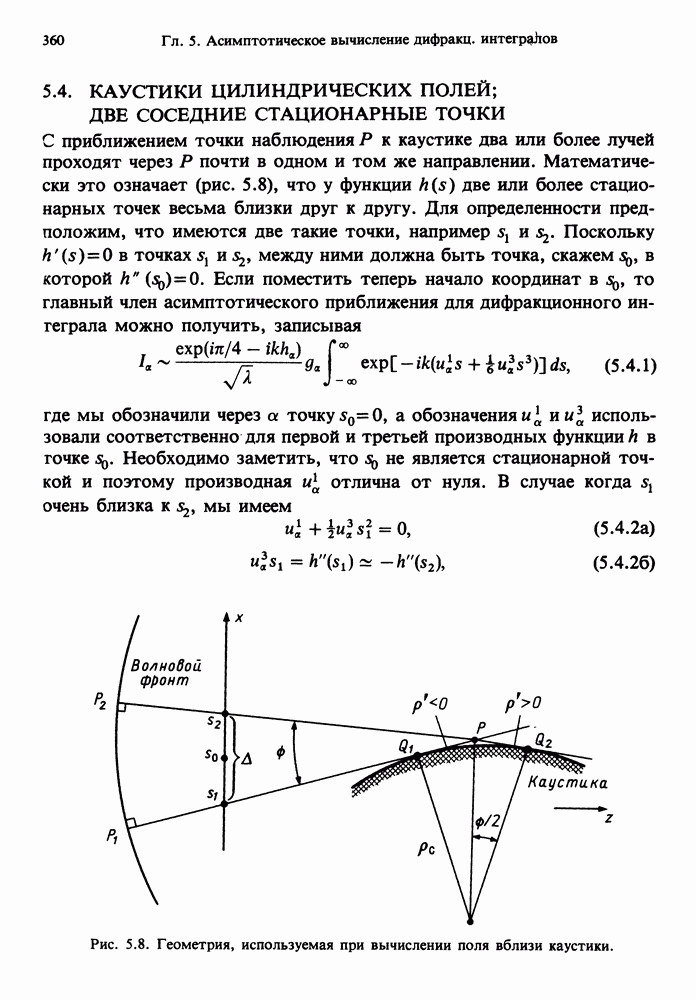
- 5.4. КАУСТИКИ ЦИЛИНДРИЧЕСКИХ ПОЛЕЙ; ДВЕ СОСЕДНИЕ СТАЦИОНАРНЫЕ ТОЧКИ
- 5.5. ПОЛЕ ВБЛИЗИ ДВУМЕРНОГО ОСТРИЯ КАУСТИКИ; МОДЕЛЬ ДЛЯ ИМПУЛЬСНОГО ОТКЛИКА ПРИ НАЛИЧИИ ДЕФОКУСИРОВКИ И АБЕРРАЦИЙ ТРЕТЬЕГО ПОРЯДКА
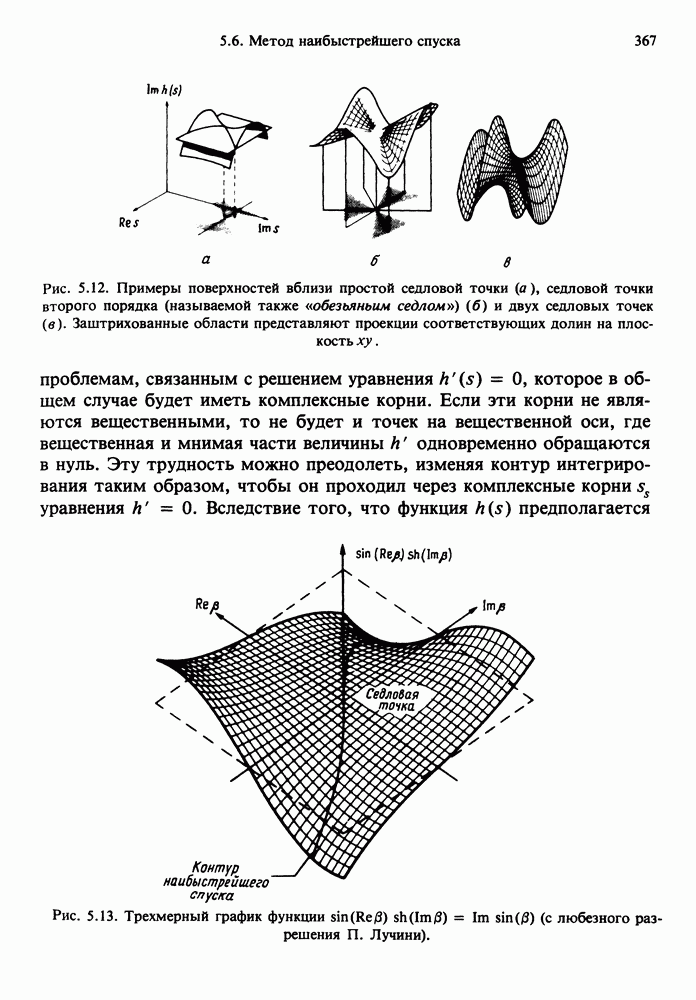
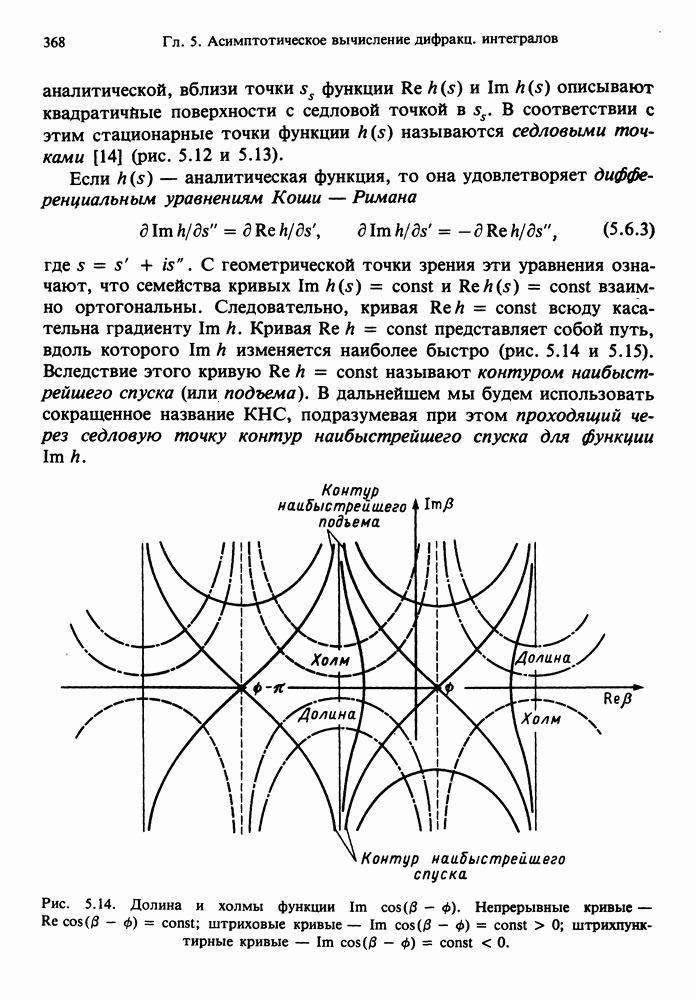
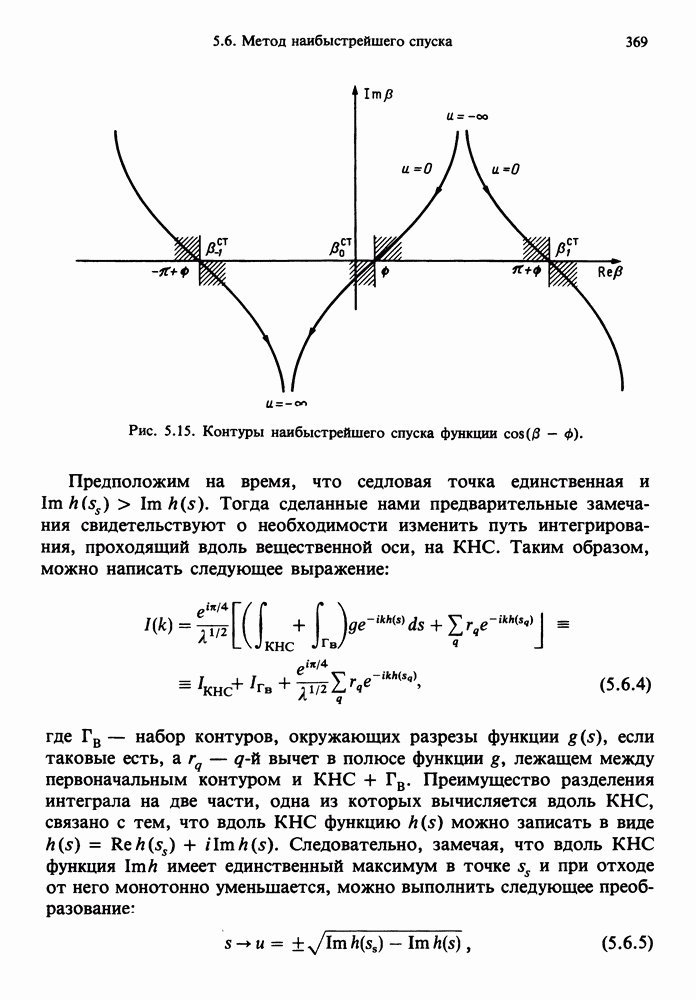
- 5.6. МЕТОД НАИБЫСТРЕЙШЕГО СПУСКА
- 5.6.1. Полюс вблизи седловой точки
- 5.6.2. Точка ветвления вблизи седловой точки
- 5.7. ДИФРАКЦИОННЫЕ ЭФФЕКТЫ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ ДИЭЛЕКТРИКОВ
- 5.7.1. Боковые волны
- 5.7.2. Эффект Гуса — Хенхена
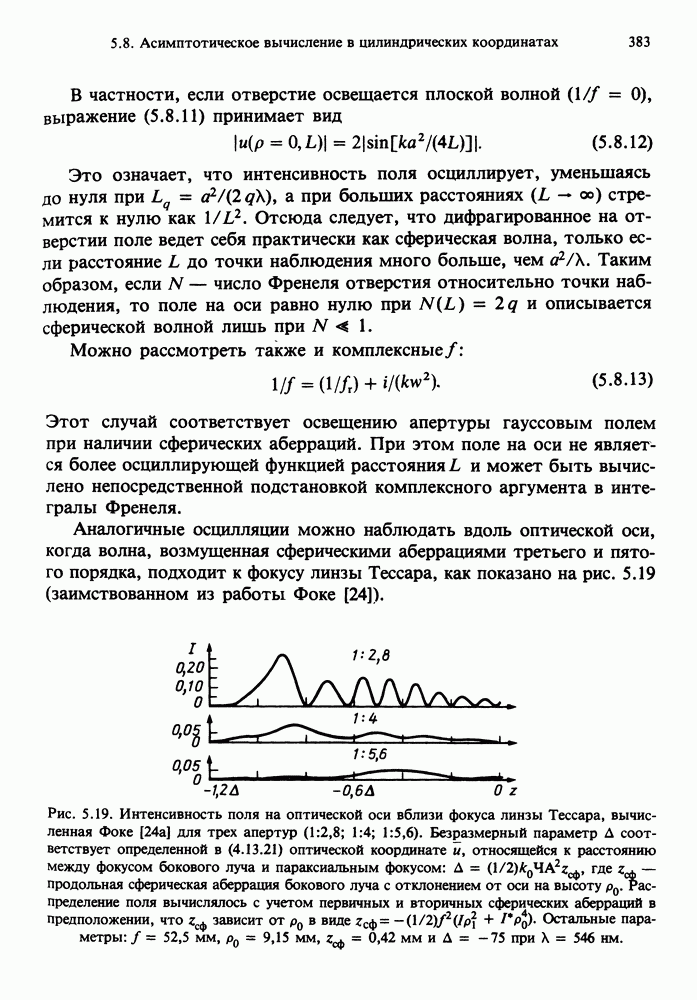
- 5.8. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- 5.9 ВЫВОД АСИМПТОТИЧЕСКИХ РЯДОВ ИЗ СРАВНИТЕЛЬНЫХ ИНТЕГРАЛОВ; МЕТОД ЧЕСТЕРА — ФРИДМАНА — УРСЕЛЛА (ЧФУ)
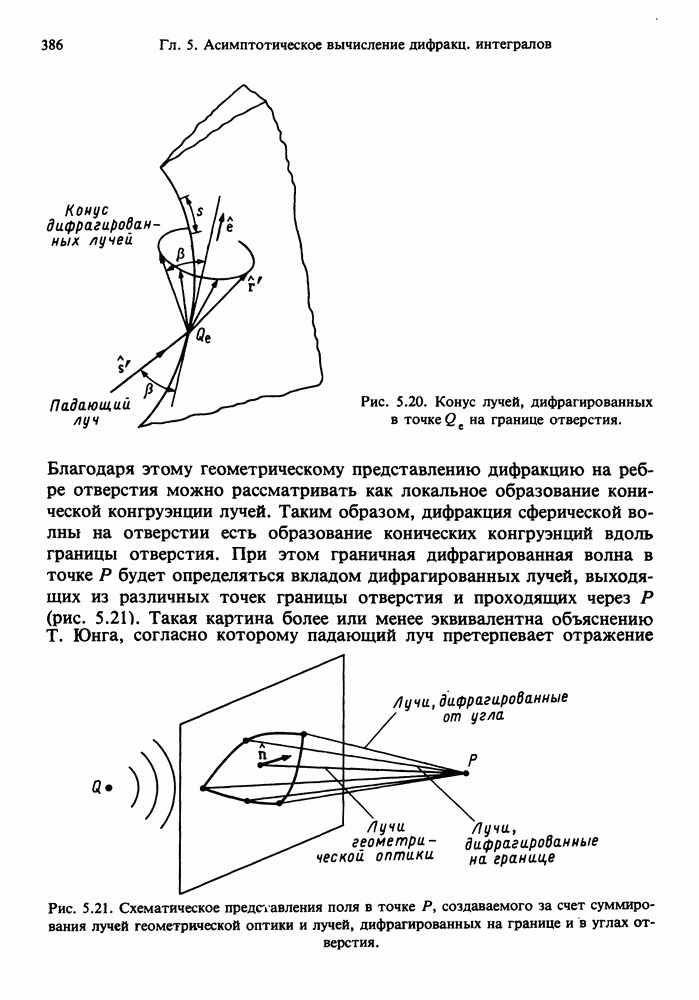
- 5.10. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ПОЛЯ, ДИФРАГИРОВАННОГО НА ОТВЕРСТИИ
- 5.10.1. Каустика дифрагированных лучей
- 5.10.2. Дифракция на острие
- 5.10.3. Дифракция от угла
- 5.11. АСИМПТОТИЧЕСКАЯ ФОРМА РАЗЛОЖЕНИЯ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ
- 5.12. ФОРМУЛА УИЛЛИСА
- ГЛАВА 6. ДИФРАКЦИЯ СВЕТА НА ОТВЕРСТИИ И РАССЕЯНИЕ НА МЕТАЛЛИЧЕСКИХ И ДИЭЛЕКТРИЧЕСКИХ ПРЕДМЕТАХ
- 6.2. ДИФРАКЦИЯ НА КЛИНЕ
- 6.2.1. Клин с конечным импедансом
- 6.2.2. Дифракционная матрица для искривленной кромки
- 6.2.3. Дифракция на диэлектрическом клине
- 6.3. ДИФРАКЦИЯ НА ЩЕЛИ
- 6.4. ДИФРАКЦИЯ НА ДИЭЛЕКТРИЧЕСКОМ ЦИЛИНДРЕ
- 6.4.1. Дифракция на круговом диэлектрическом цилиндре
- 6.5. S-МАТРИЦА И ПРЕДСТАВЛЕНИЕ ВАТСОНА — РЕДЖЕ
- 6.5.1. Дебаевское разложение
- 6.5.2. Представление Ватсона — Редже
- 6.5.3. Первый член дебаевского разложения
- 6.6. ПОВЕРХНОСТНЫЕ ДИФРАКЦИОННЫЕ ВОЛНЫ
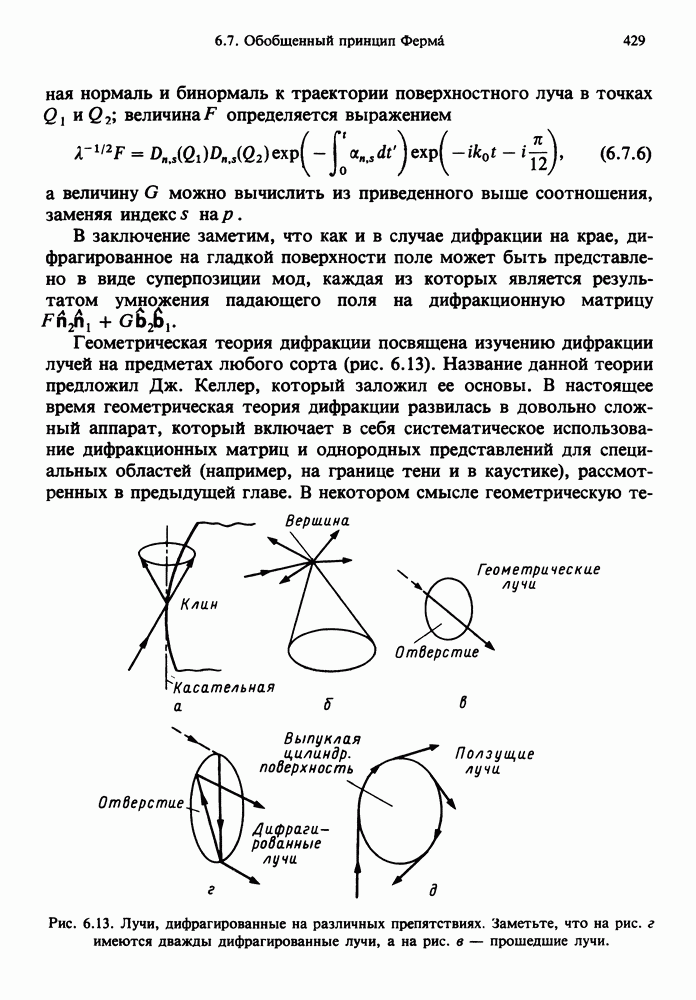
- 6.7. ОБОБЩЕННЫЙ ПРИНЦИП ФЕРМА И ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ДИФРАКЦИИ
- 6.8. РАССЕЯНИЕ СВЕТА ДИЭЛЕКТРИЧЕСКИМИ ТЕЛАМИ
- 6.9. ПРИБЛИЖЕНИЕ ФИЗИЧЕСКОЙ ОПТИКИ ДЛЯ ИДЕАЛЬНО ПРОВОДЯЩЕГО ТЕЛА
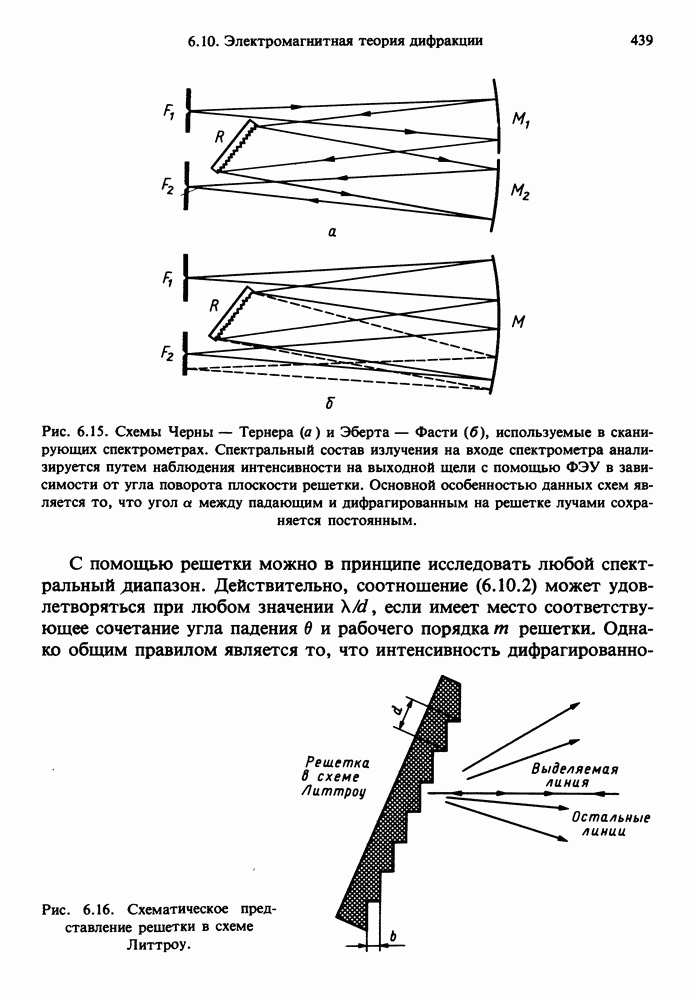
- 6.10. ЭЛЕКТРОМАГНИТНАЯ ТЕОРИЯ ДИФРАКЦИИ НА ИДЕАЛЬНО ПРОВОДЯЩИХ И ДИЭЛЕКТРИЧЕСКИХ ДИФРАКЦИОННЫХ РЕШЕТКАХ
- 6.10.1. Применения дифракционных решеток
- 6.10.2. Поле, дифрагированное на решетке
- 6.10.3. Представление Рэлея для металлической решетки
- 6.10.4. Интегральный метод
- 6.10.5. Разрешающая способность
- 6.10.6. Эффективность решетки и аномалии Вуда
- 6.11. РАССЕЯНИЕ НА ТЕЛАХ КОНЕЧНЫХ РАЗМЕРОВ
- 6.11.1. Сечение экстинкции и оптическая теорема
- 6.12. РАЗЛОЖЕНИЕ РАССЕЯННОГО ПОЛЯ ПО СФЕРИЧЕСКИМ ГАРМОНИКАМ
- 6.12.1. Радиальное волновое уравнение
- 6.12.2. Векторные сферические гармоники
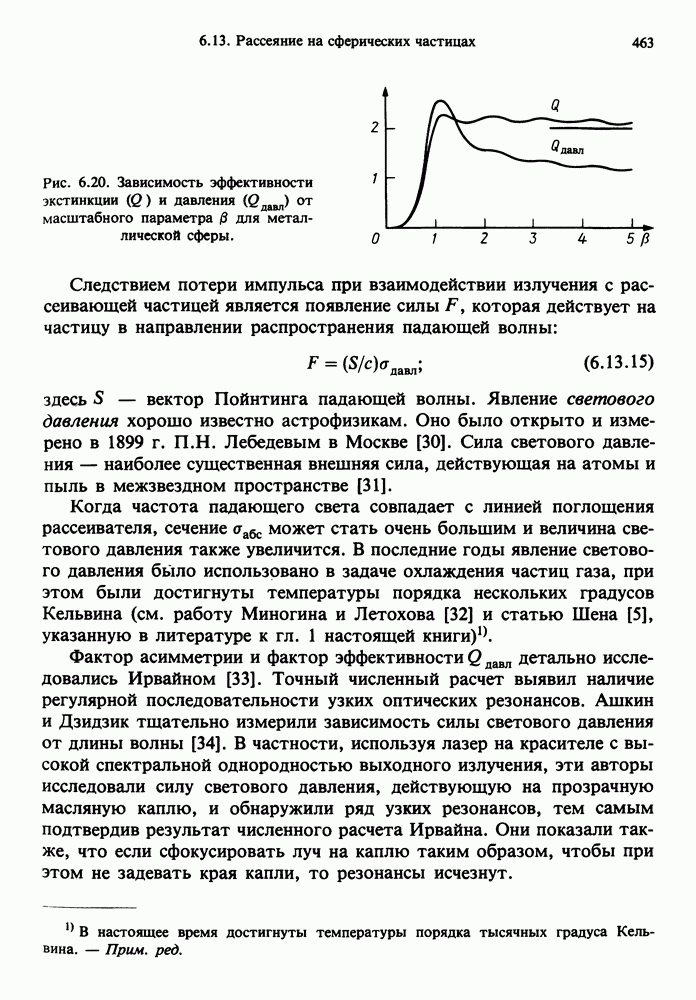
- 6.13. РАССЕЯНИЕ НА СФЕРИЧЕСКИХ ЧАСТИЦАХ
- 6.13.1. Разложение рассеянного поля по парциальным волнам
- 6.13.2. Амплитуды рассеяния S и фактор эффективности Q
- 6.13.3. Параметры Стокса для рассеянного поля
- 6.13.4. Малые сферы
- 6.13.5. Собственные моды диэлектрической сферы
- 6.13.6. Теория ван де Хюлста для сферы очень большого размера
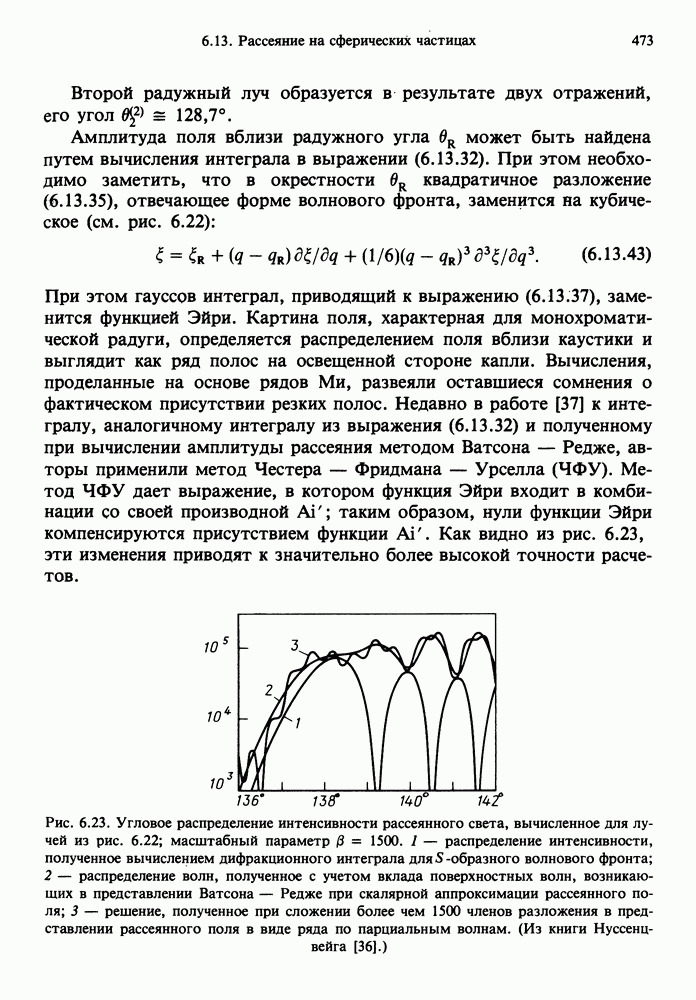
- 6.13.7. Теория глории и радуги в приближении геометрической оптики
- ГЛАВА 7. ОПТИЧЕСКИЕ РЕЗОНАТОРЫ И ИНТЕРФЕРОМЕТРЫ ФАБРИ — ПЕРО
- 7.1. ОБЩИЕ СВОЙСТВА РЕЗОНАТОРОВ ДЛЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 7.1.2. Микроволновые (СВЧ) и оптические генераторы
- 7.2. ОБЩИЕ СВОЙСТВА ОПТИЧЕСКИХ РЕЗОНАТОРОВ
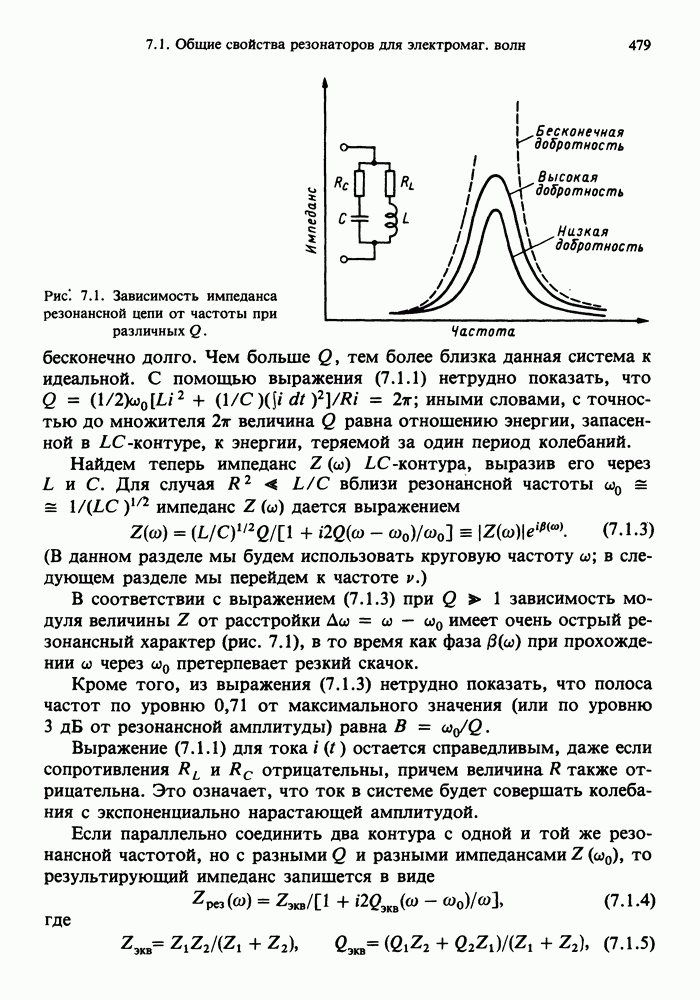
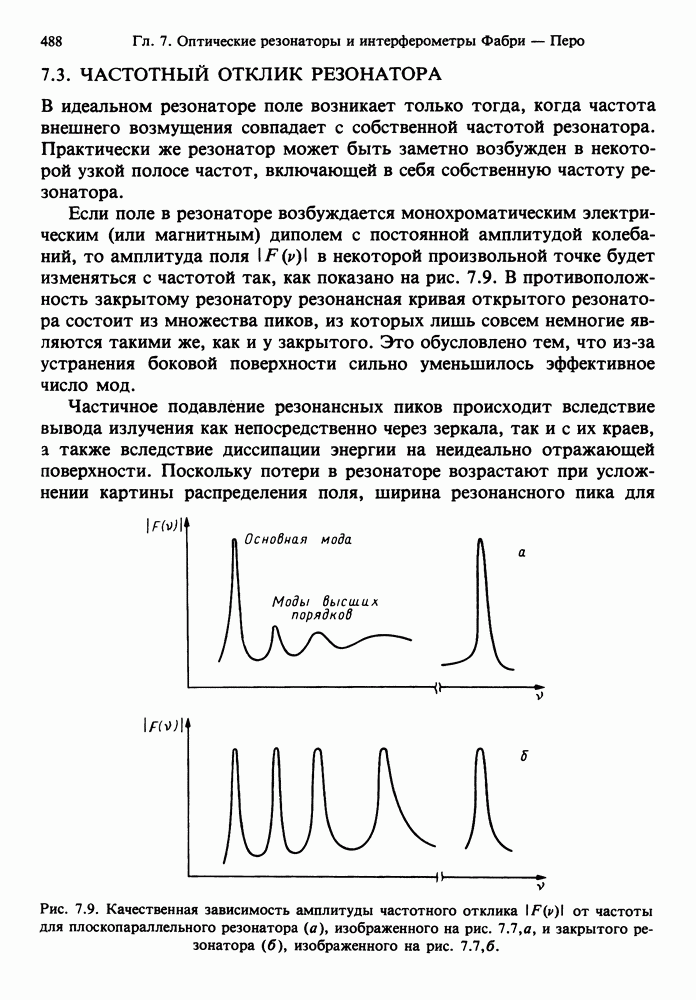
- 7.3. ЧАСТОТНЫЙ ОТКЛИК РЕЗОНАТОРА
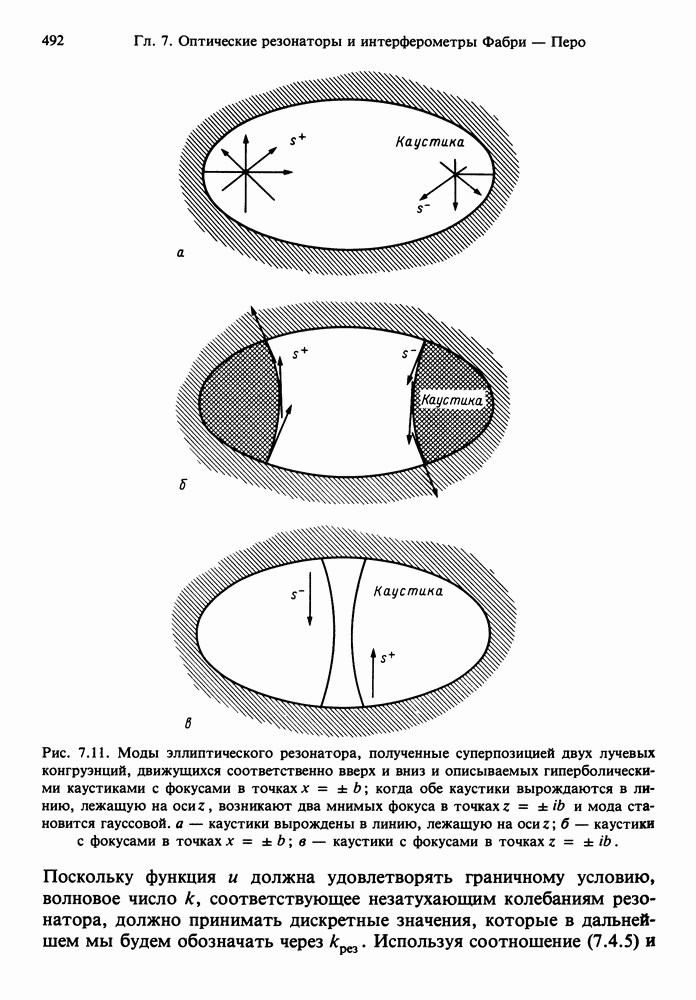
- 7.4. РАССМОТРЕНИЕ ЗАКРЫТОГО ЭЛЛИПТИЧЕСКОГО РЕЗОНАТОРА В РАМКАХ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
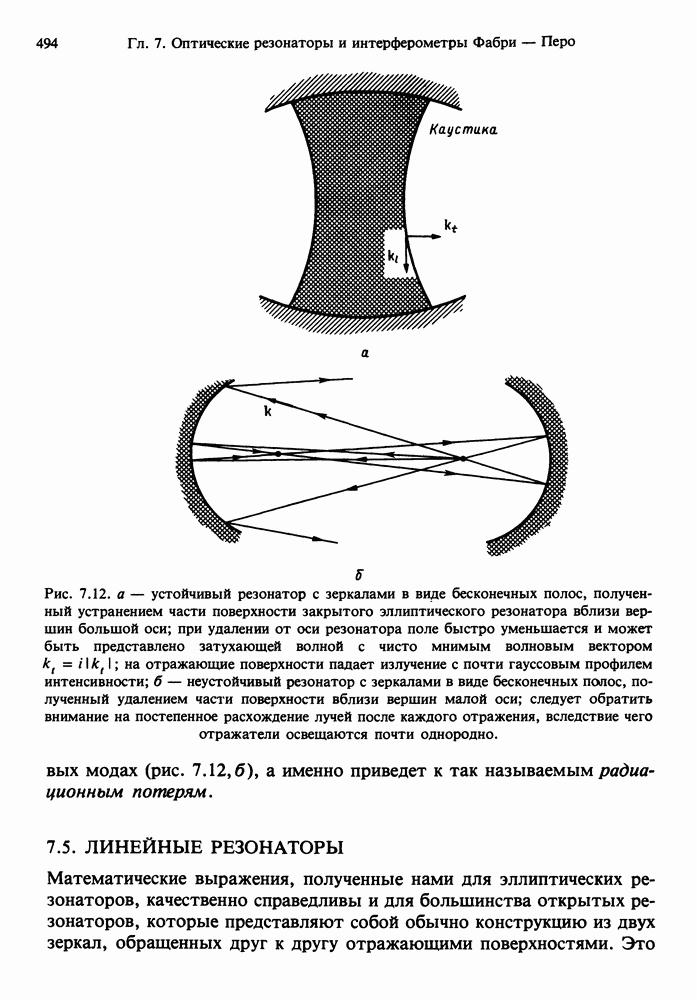
- 7.5. ЛИНЕЙНЫЕ РЕЗОНАТОРЫ
- 7.6. РАССМОТРЕНИЕ РЕЗОНАТОРА КАК ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЗ
- 7.7. ПОЛЯ ОТ ИСТОЧНИКОВ, РАСПОЛОЖЕННЫХ В КОМПЛЕКСНОЙ ПЛОСКОСТИ
- 7.8. ЭРМИТ-ГАУССОВЫ И ЛАГЕРР-ГАУССОВЫ ПУЧКИ
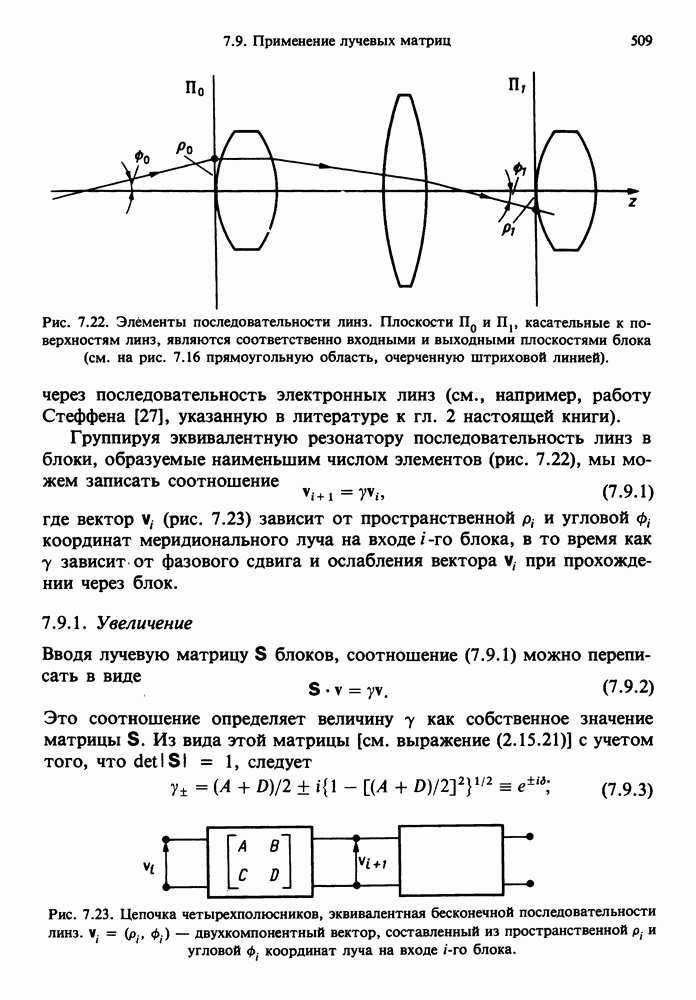
- 7.9. ПРИМЕНЕНИЕ ЛУЧЕВЫХ МАТРИЦ ДЛЯ ОПИСАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЗ, ЭКВИВАЛЕНТНОЙ РЕЗОНАТОРУ
- 7.9.1. Увеличение
- 7.9.2. Комплексная кривизна волнового фронта
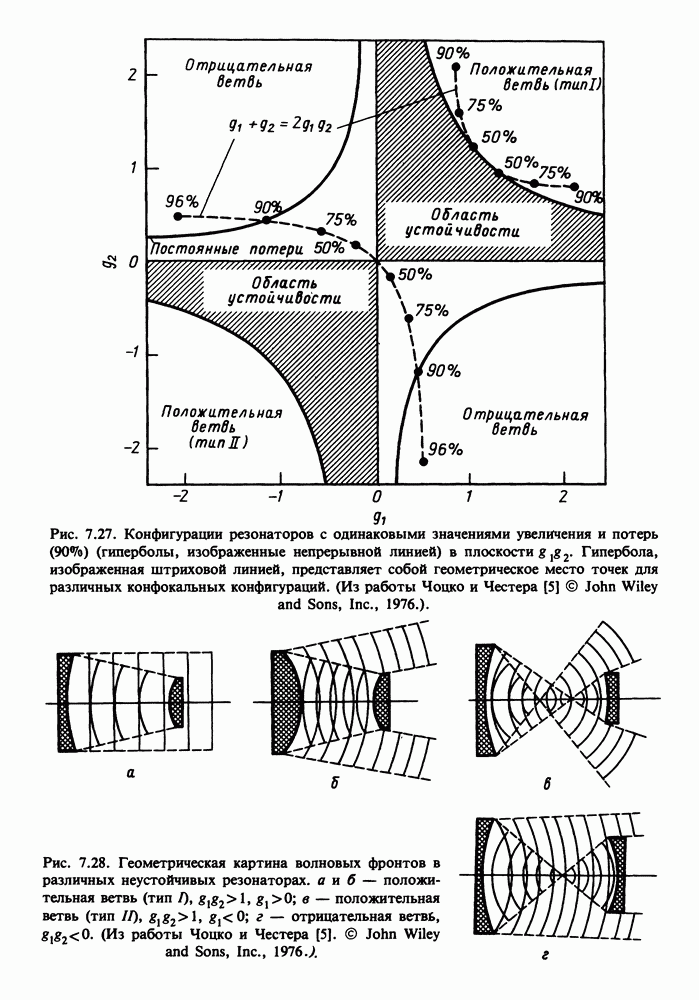
- 7.9.3. Диаграмма устойчивости Бойда — Когельника
- 7.10. МОДОВОЕ ПРЕДСТАВЛЕНИЕ ПОЛЯ ВНУТРИ УСТОЙЧИВОГО РЕЗОНАТОРА, НЕ ИМЕЮЩЕГО ДИФРАКЦИОННЫХ ПОТЕРЬ
- 7.10.1. Приближение медленноменяющейся амплитуды
- 7.11. УСТОЙЧИВЫЕ РЕЗОНАТОРЫ
- 7.11.1. Дифракционные потери и расходимость
- 7.11.2. Влияние разъюстировки резонатора
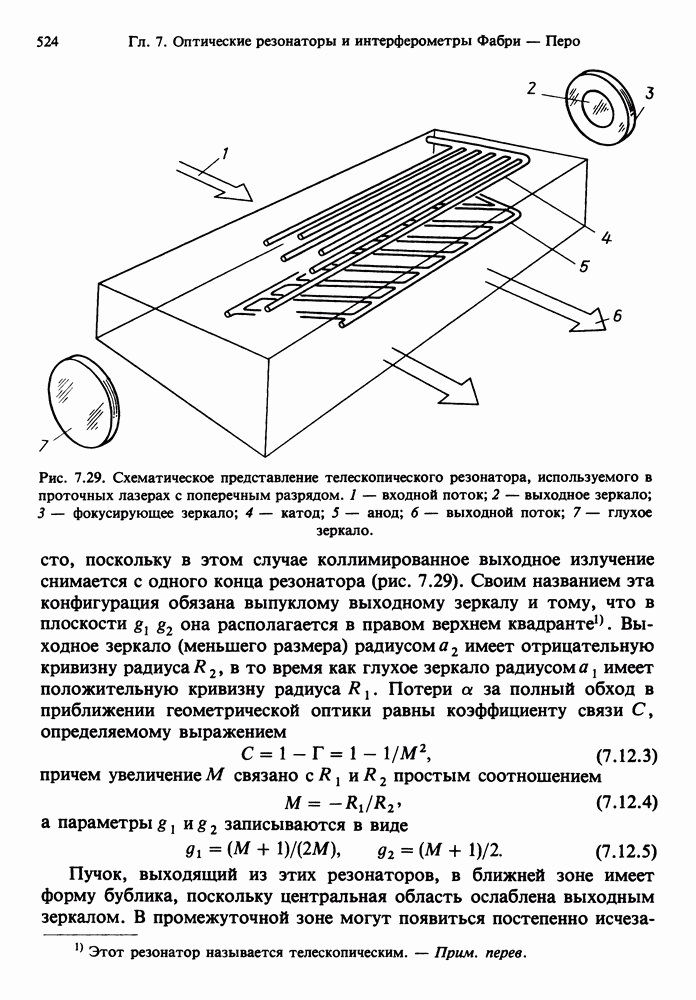
- 7.12. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
- 7.13. ВОЛНОВАЯ ТЕОРИЯ ПУСТЫХ РЕЗОНАТОРОВ
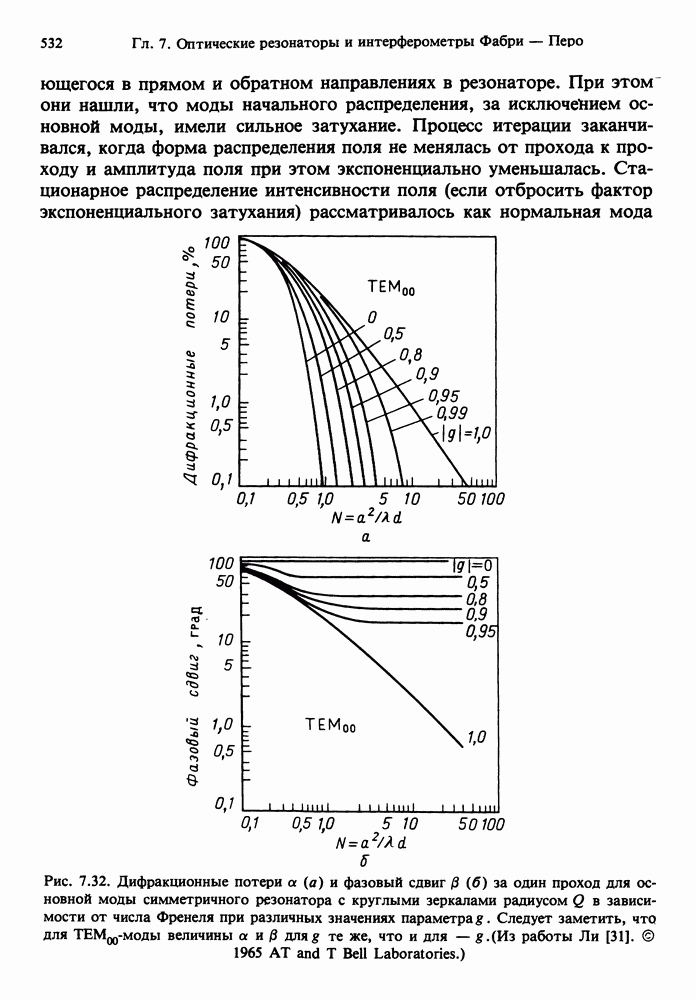
- 7.14. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФОКСА — ЛИ
- 7.14.1. Потери за полный проход
- 7.14.2. Фазовый сдвиг
- 7.14.3 Симметричные резонаторы
- 7.14.4. Соотношения подобия
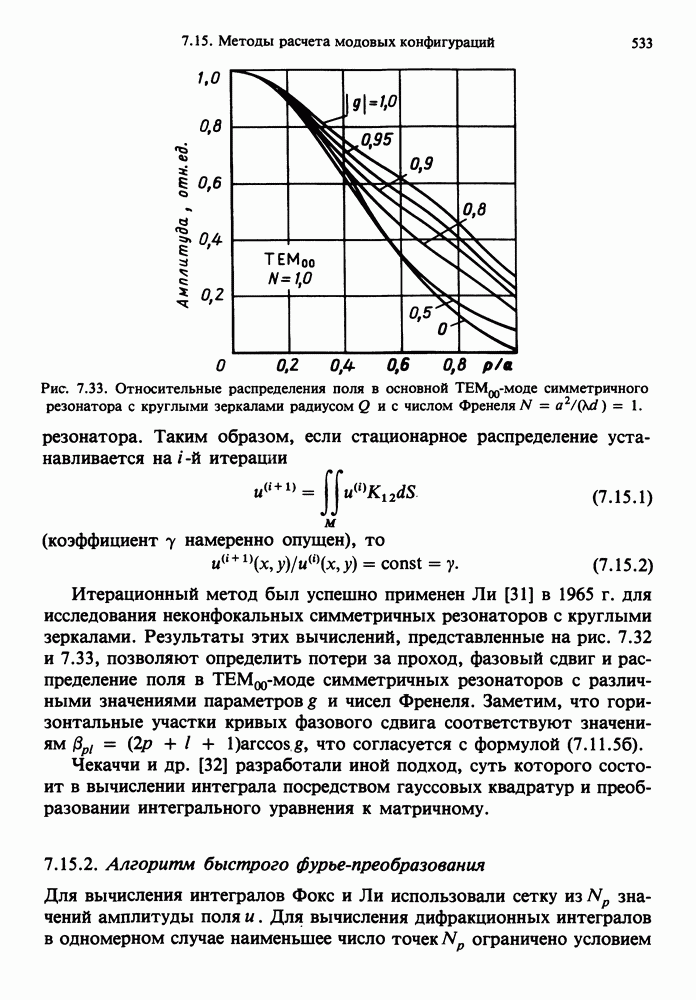
- 7.15. МЕТОДЫ РАСЧЕТА МОДОВЫХ КОНФИГУРАЦИЙ
- 7.15.2. Алгоритм быстрого фурье-преобразования
- 7.15.3. Вычисление мод высокого порядка
- 7.16. УСТОЙЧИВЫЕ РЕЗОНАТОРЫ С ПРЯМОУГОЛЬНЫМИ ЗЕРКАЛАМИ
- 7.16.1. Конфокальный резонатор
- 7.16.2. Теория Вайнилтейна для концентрических и плоскопараллельных резонаторов
- 7.17. РЕЗОНАТОРЫ С АКСИАЛЬНОЙ СИММЕТРИЕЙ
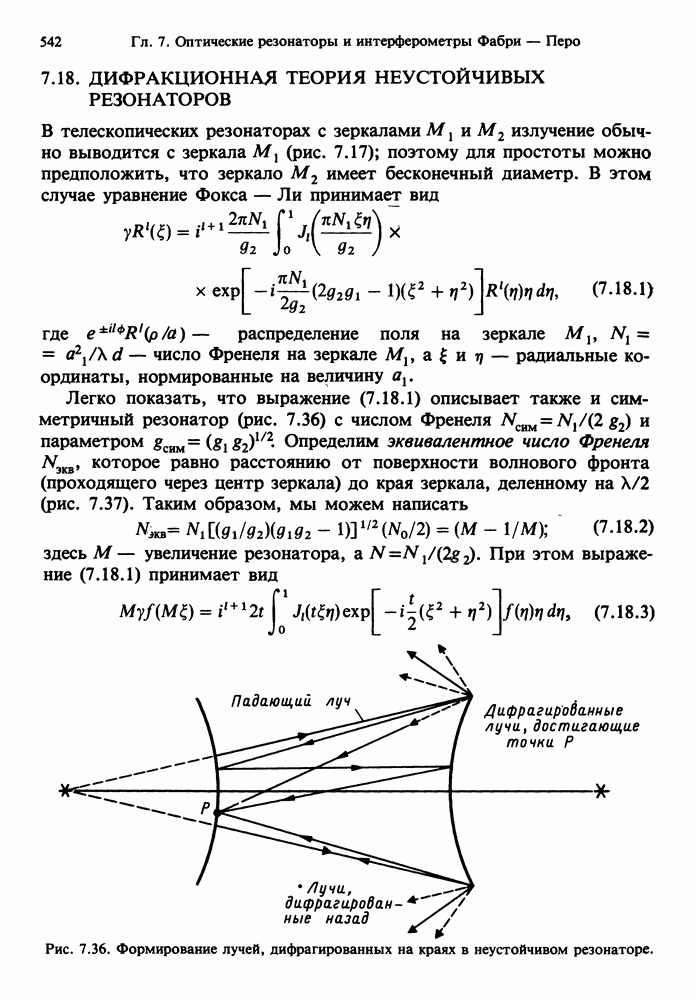
- 7.18. ДИФРАКЦИОННАЯ ТЕОРИЯ НЕУСТОЙЧИВЫХ РЕЗОНАТОРОВ
- 7.19. РЕЗОНАТОРЫ С АКТИВНОЙ СРЕДОЙ
- 7.19.1 Нелинейная диэлектрическая восприимчивость лазерной среды
- 7.19.2. Одномодовый режим
- 7.19.3. Одночастотная многомодовая генерация
- 7.19.4. Уравнения Ригрода
- 7.19.5. Выходная мощность
- 7.20. ПЕРЕСТРОЙКА ЧАСТОТЫ
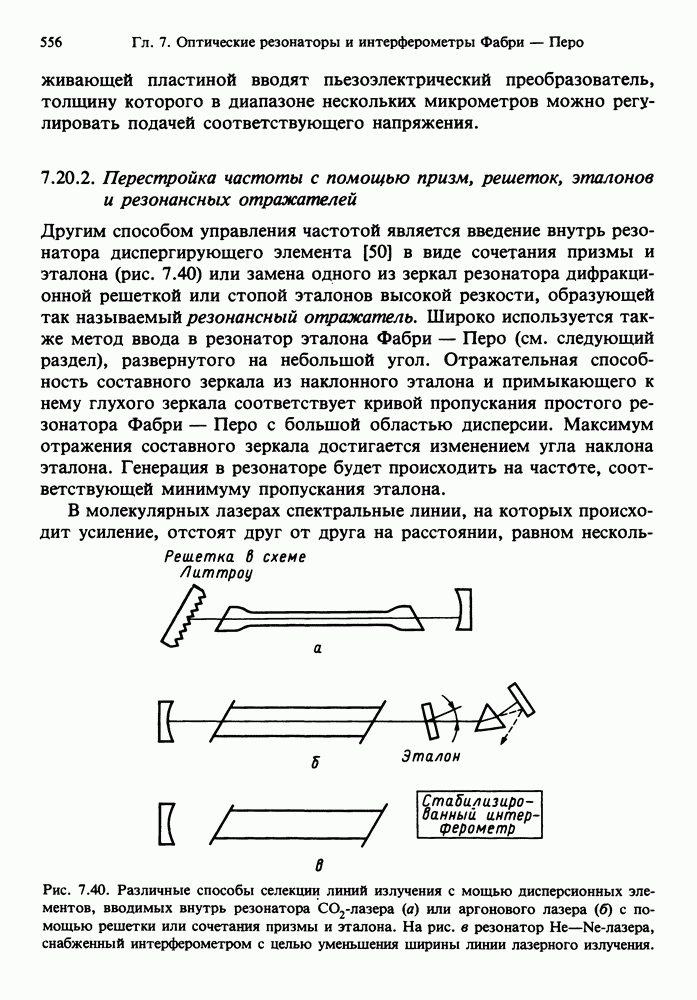
- 7.20.2. Перестройка частоты с помощью призм, решеток, эталонов и резонансных отражателей
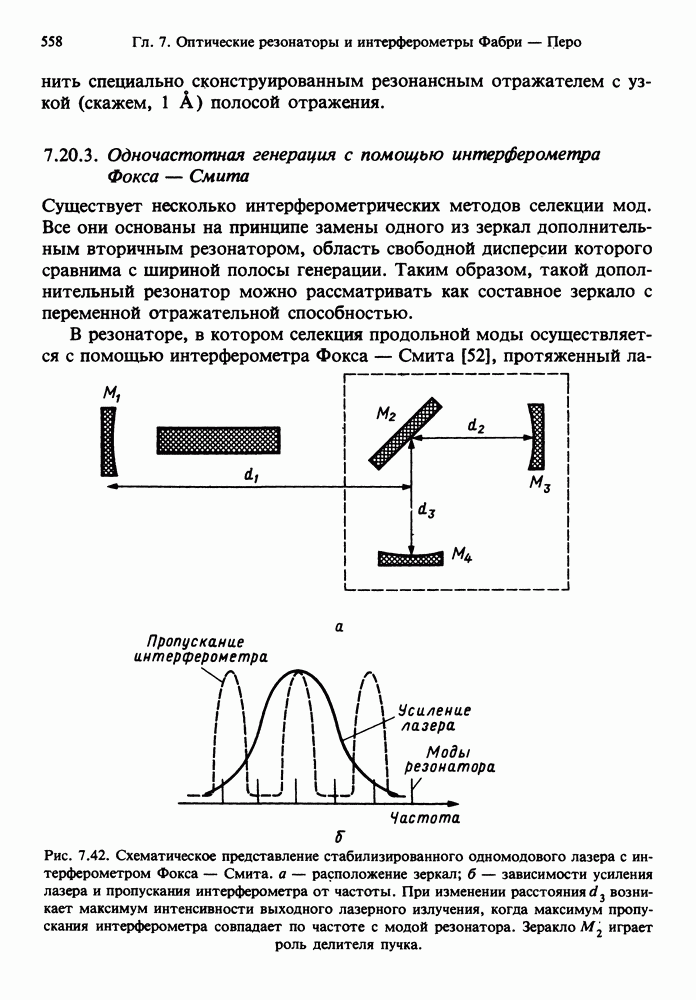
- 7.20.3. Одночастотная генерация с помощью интерферометра Фокса — Смита
- 7.20.4. Стабилизация частоты с помощью инжекции внешнего сигнала
- 7.21. ИНТЕРФЕРОМЕТРЫ ФАБРИ — ПЕРО
- 7.21.1. Коэффициент пропускания идеального интерферометра Фабри — Перо
- 7.21.2. Применение интерферометра Фабри — Перо
- 7.21.3 Составные интерферометры Фабри — Перо
- 7.21.4. Аппаратная функция интерферометра
- ГЛАВА 8. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 8.1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 8.2. ВОЛОКНА СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
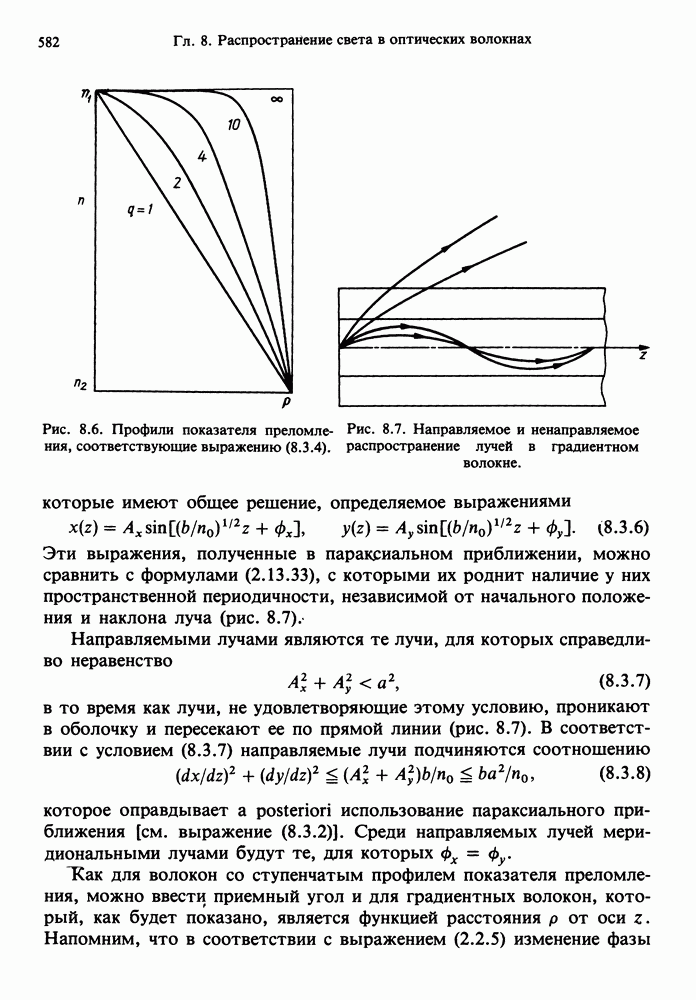
- 8.3. ГРАДИЕНТНЫЕ ВОЛОКНА
- 8.4. МОДОВАЯ ТЕОРИЯ
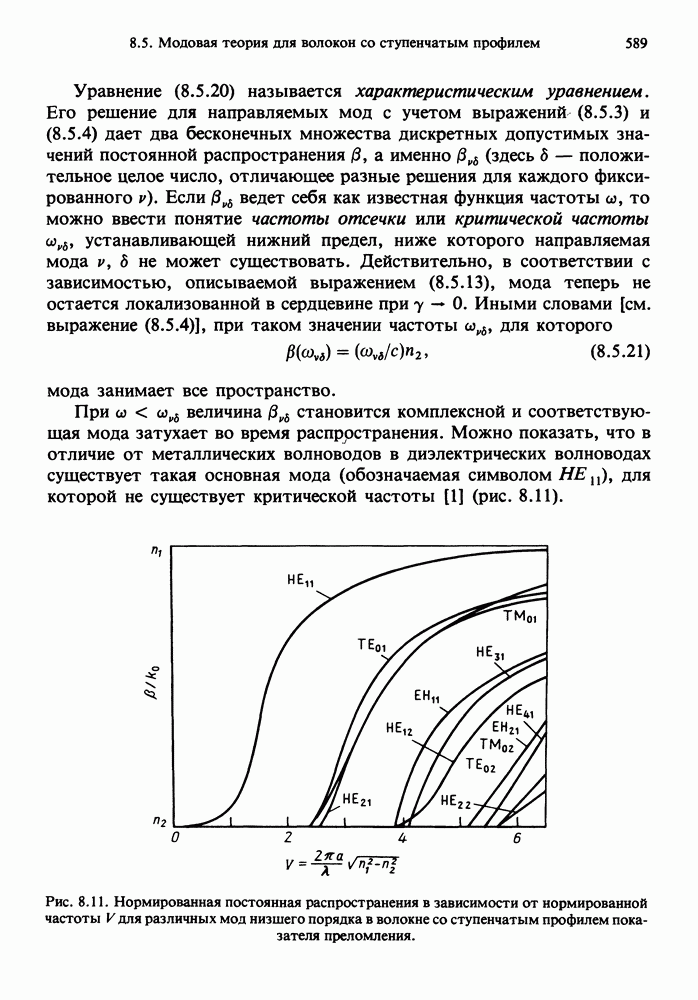
- 8.5. МОДОВАЯ ТЕОРИЯ ДЛЯ ВОЛОКОН СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- 8.6. СЛАБОНАПРАВЛЯЮЩИЕ ВОЛОКНА СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- 8.7. ВОЛОКНА С ПАРАБОЛИЧЕСКИМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- 8.8. НЕНАПРАВЛЯЕМЫЕ МОДЫ
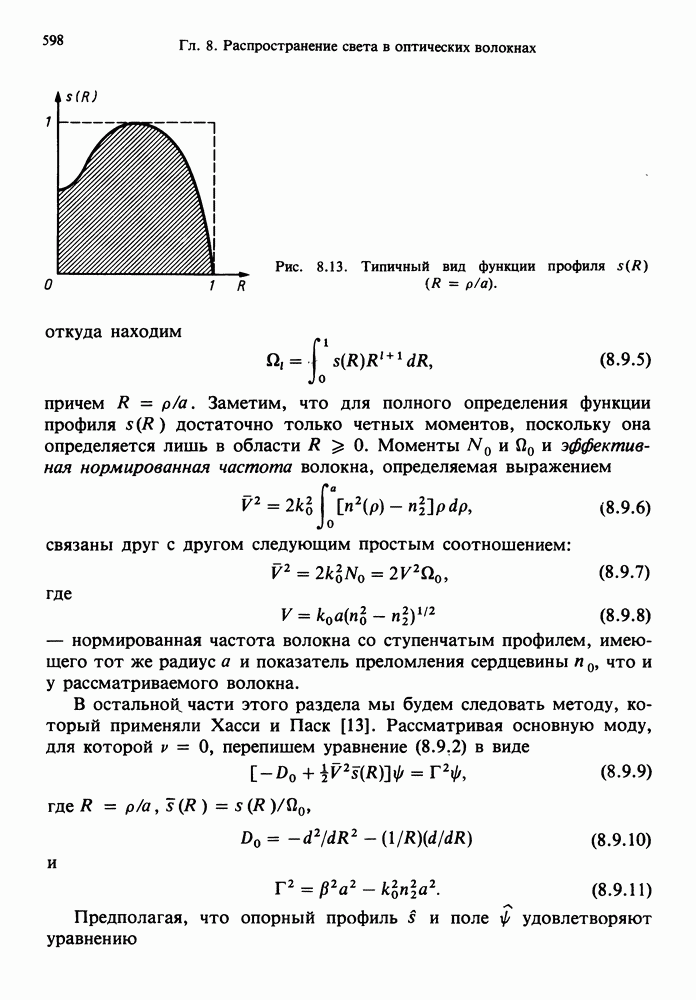
- 8.9. ОДНОМОДОВЫЕ ВОЛОКНА
- 8.10. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ВНУТРИ ВОЛОКНА
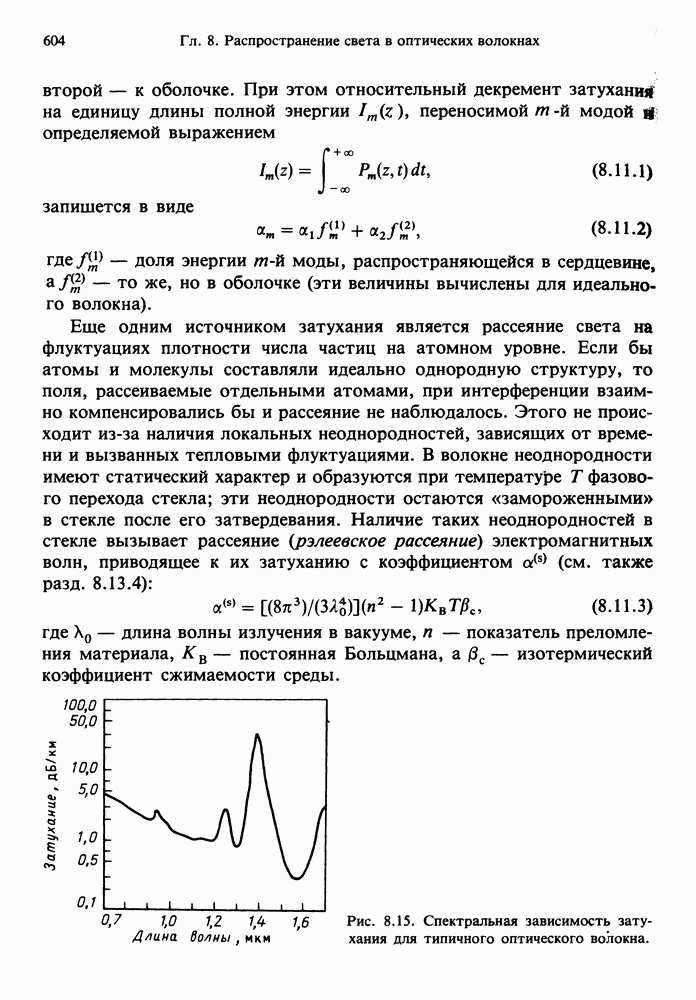
- 8.11. ЗАТУХАНИЕ
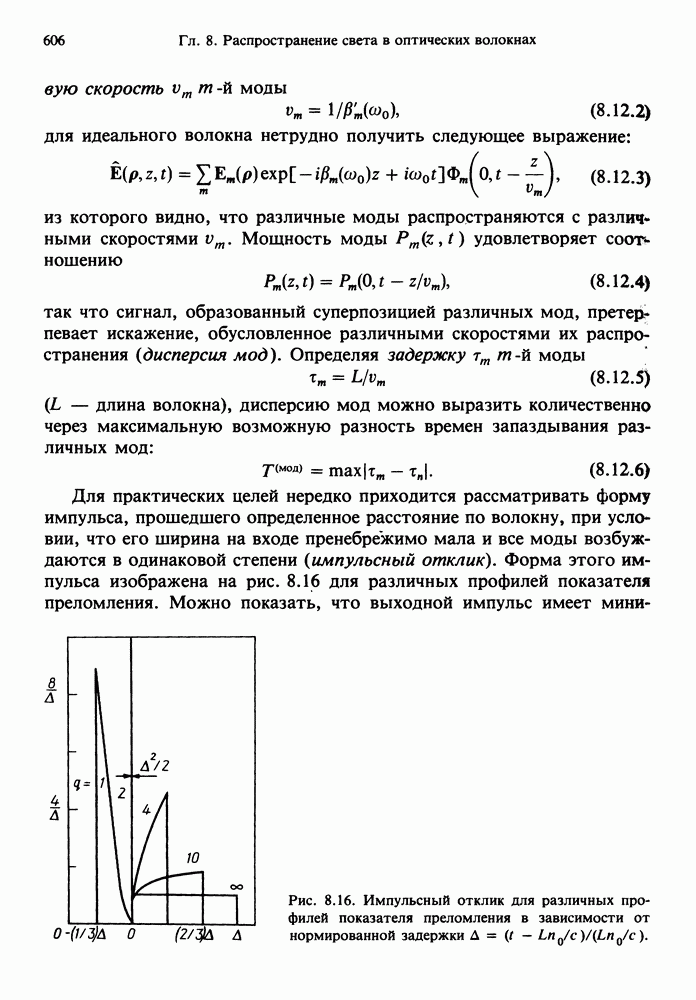
- 8.12. ДИСПЕРСИЯ МОД
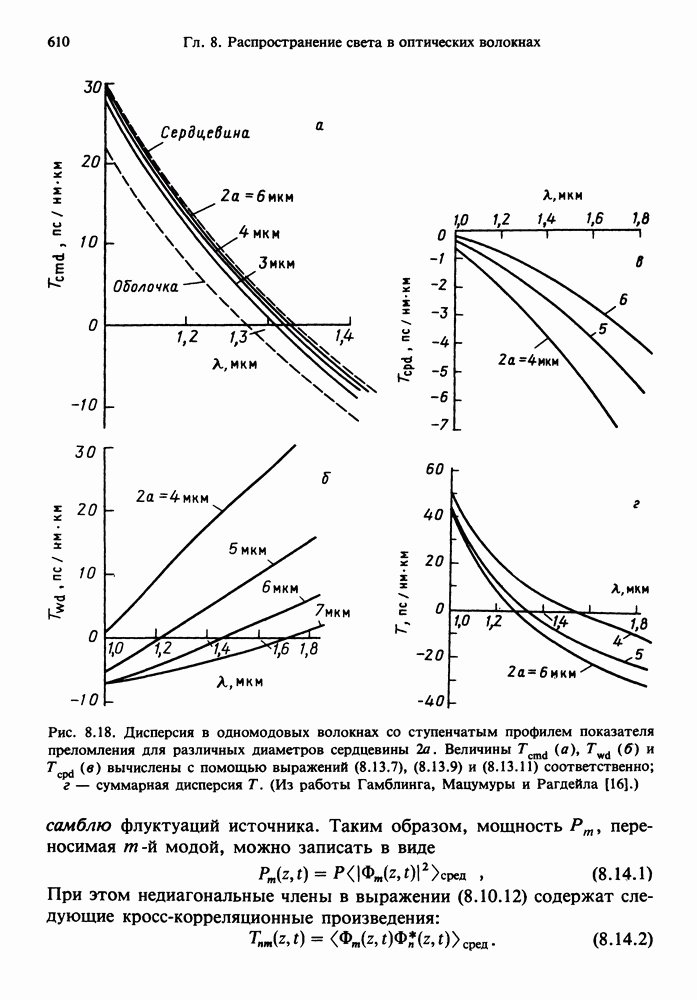
- 8.13. ХРОМАТИЧЕСКАЯ ДИСПЕРСИЯ
- 8.14. МОДОВЫЙ ШУМ
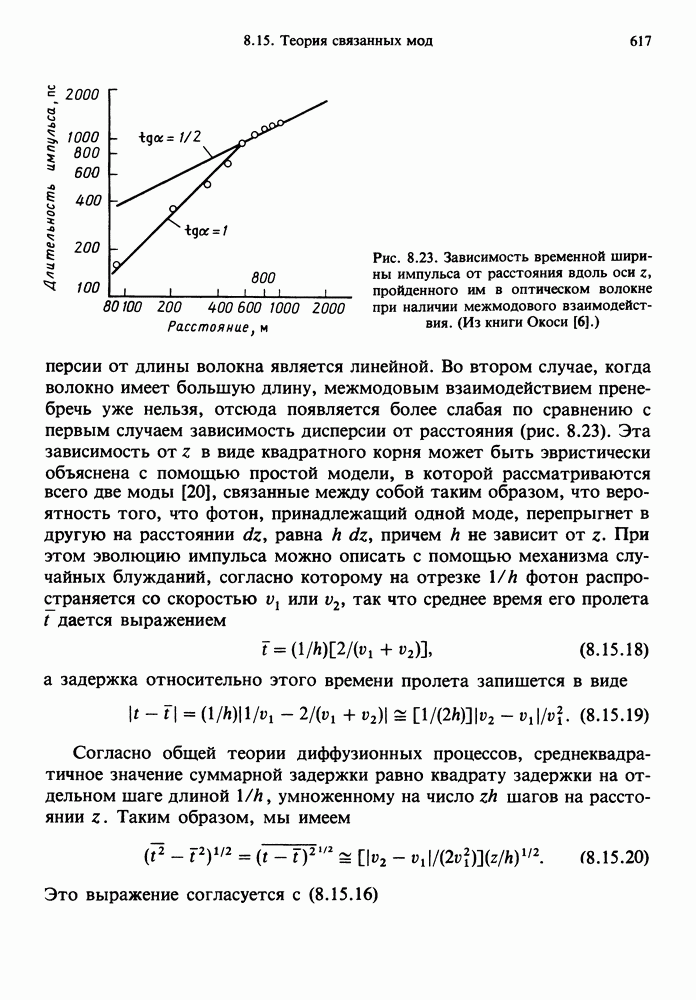
- 8.15. ТЕОРИЯ СВЯЗАННЫХ МОД
- 8.16. СТАТИСТИЧЕСКАЯ ТЕОРИЯ РАСПРОСТРАНЕНИЯ В СИСТЕМЕ ОПТИЧЕСКИХ ВОЛОКОН
- 8.17. ОПТИЧЕСКИЕ ВОЛОКНА, СОХРАНЯЮЩИЕ ПОЛЯРИЗАЦИЮ ИЗЛУЧЕНИЯ
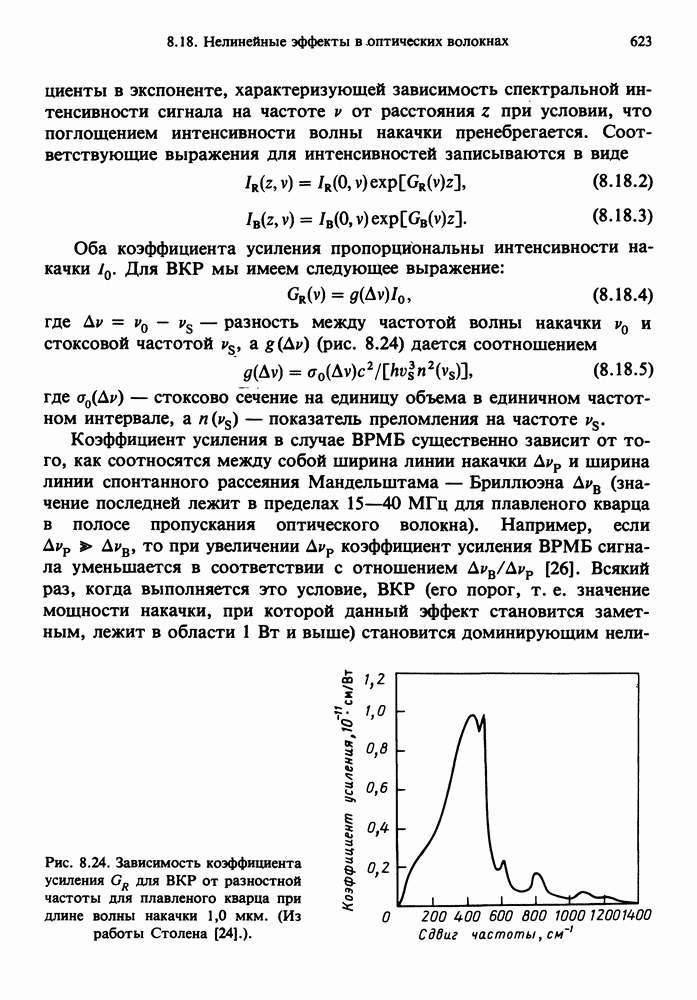
- 8.18. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 8.19. САМОИНДУЦИРОВАННЫЕ НЕЛИНЕЙНЫЕ ЭФФЕКТЫ
- 8.19.1. Фазовая самомодуляция
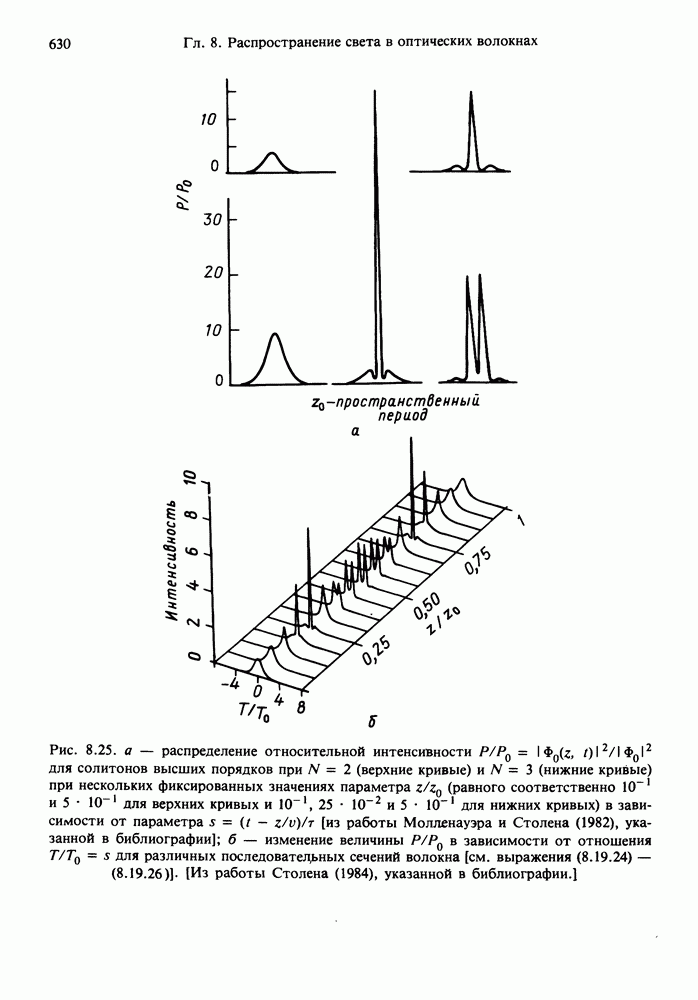
- 8.19.2. Солитоны
- 8.19.3. Вырожденное четырехволновое смешение