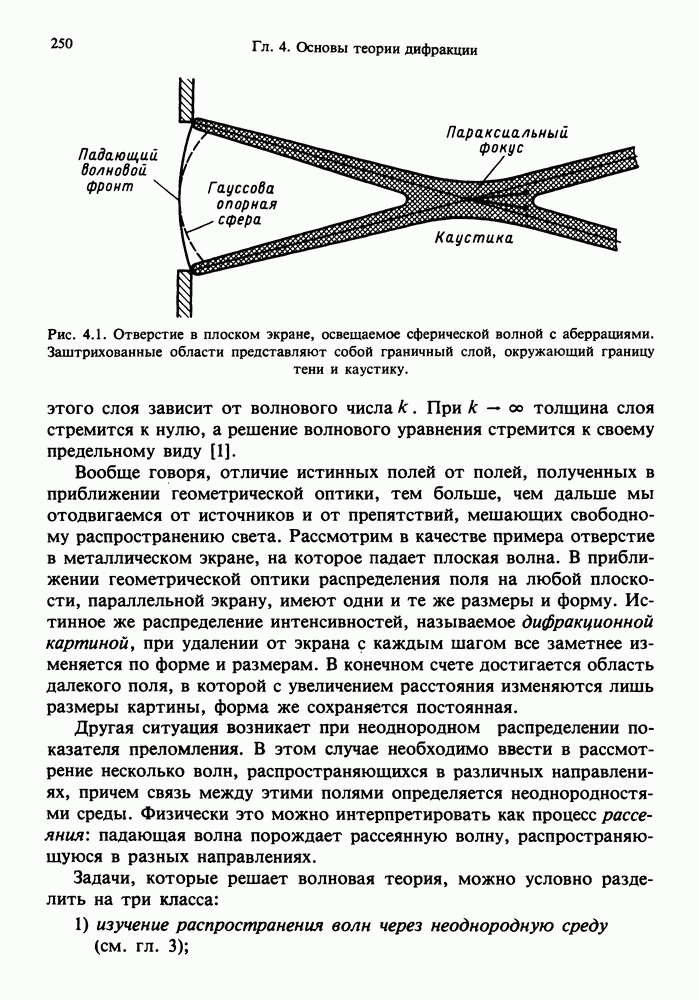
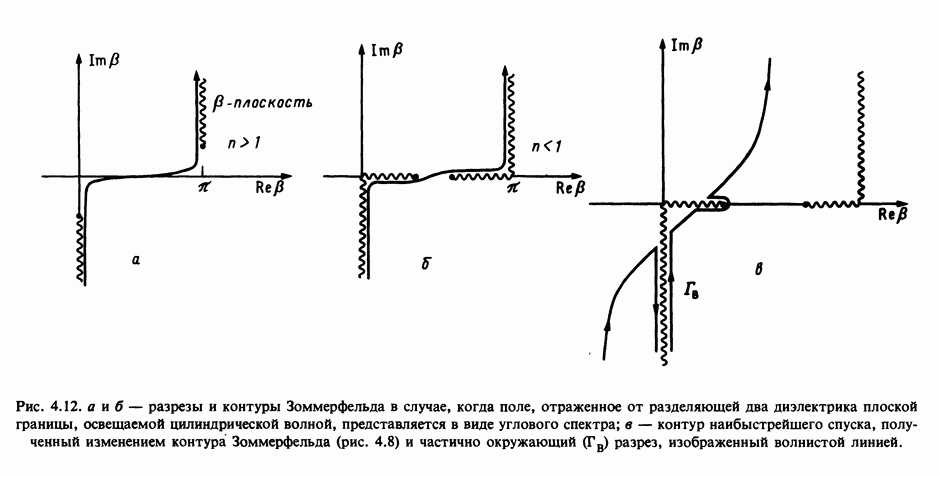
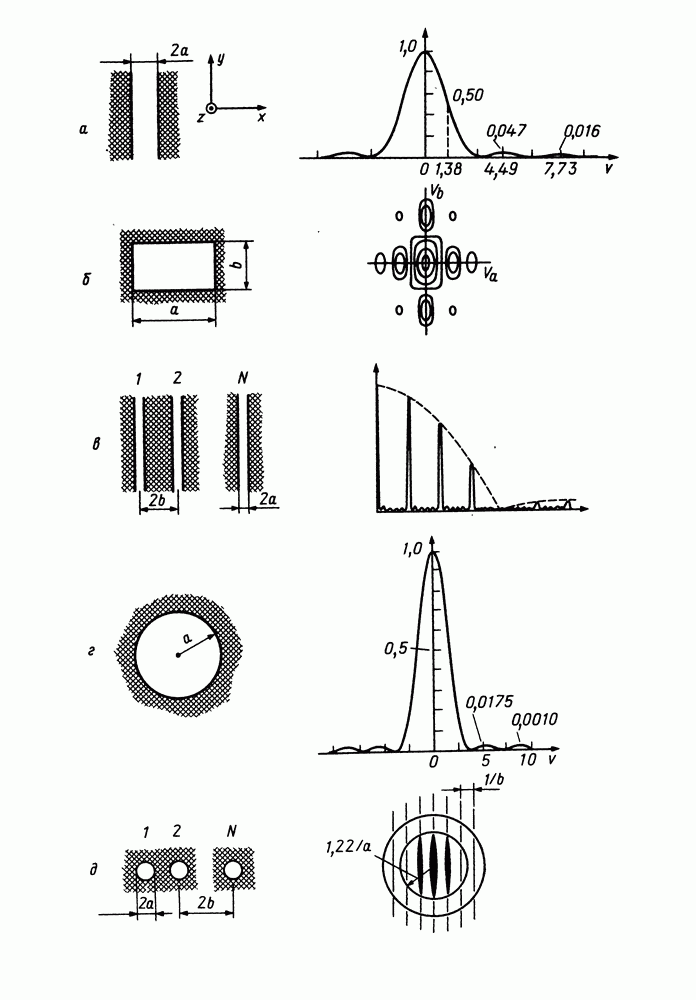
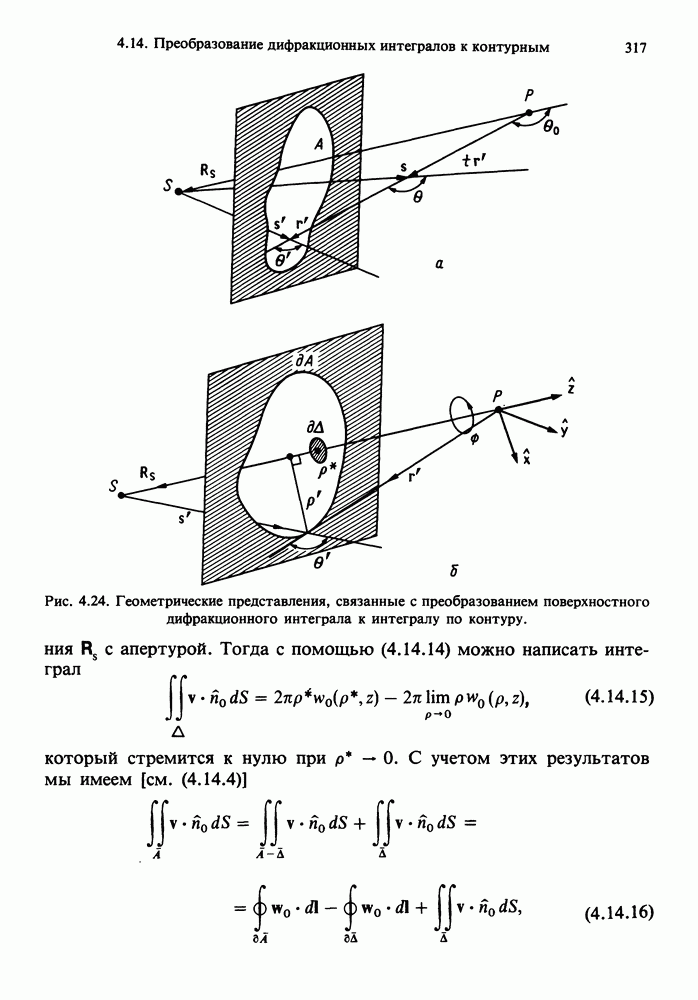
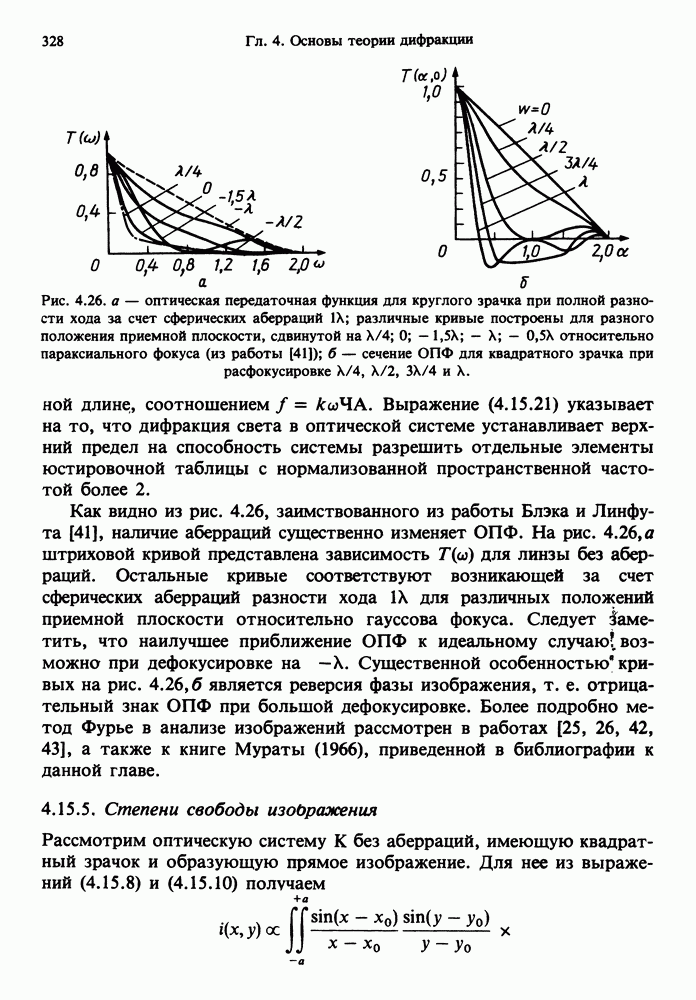
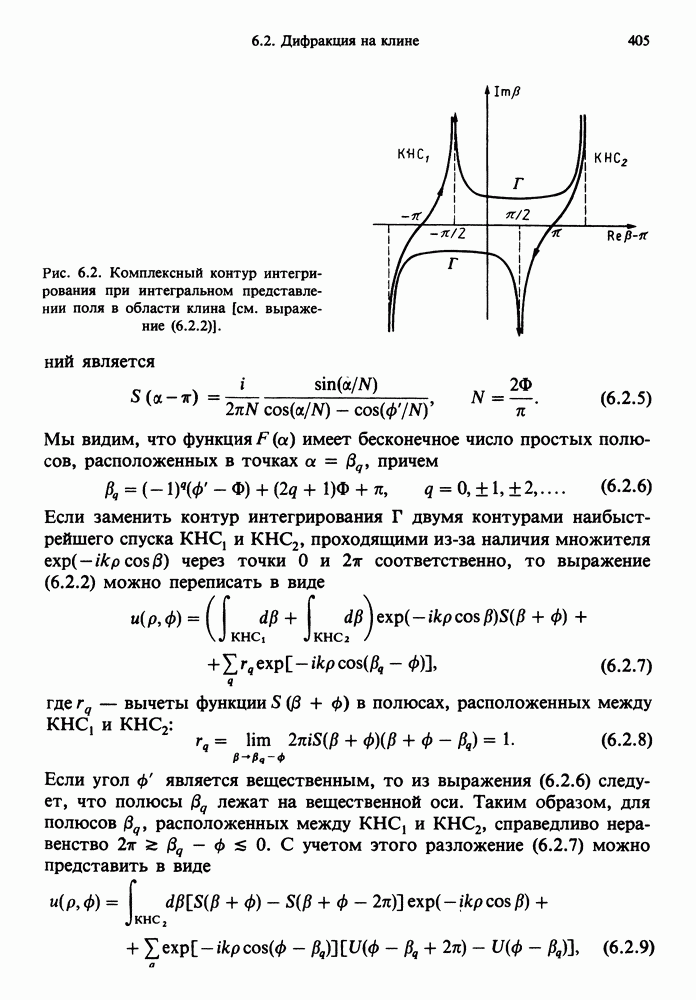
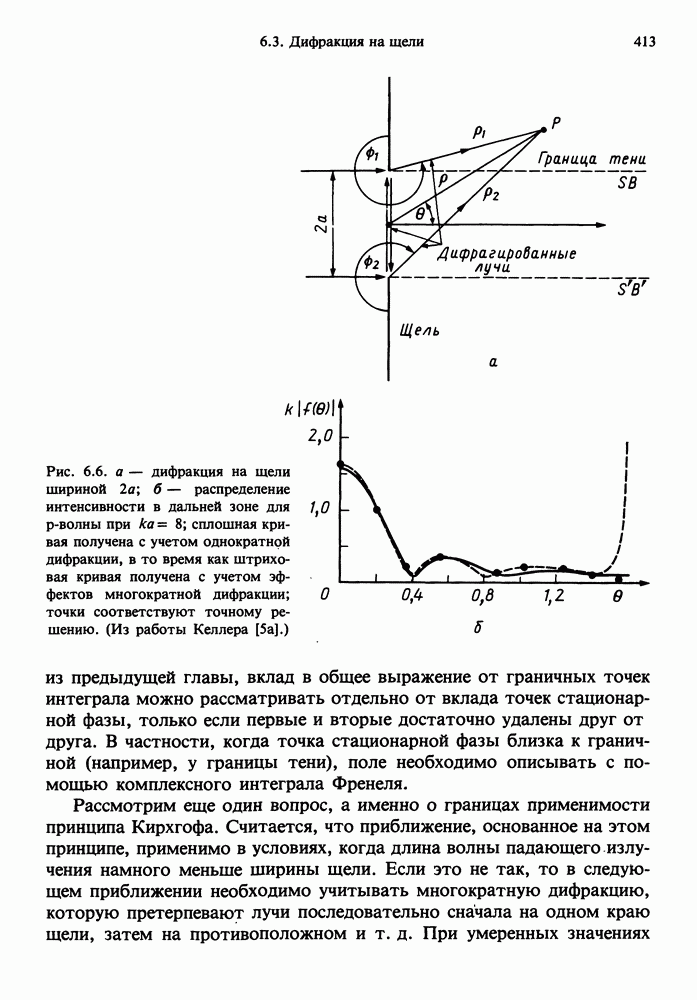
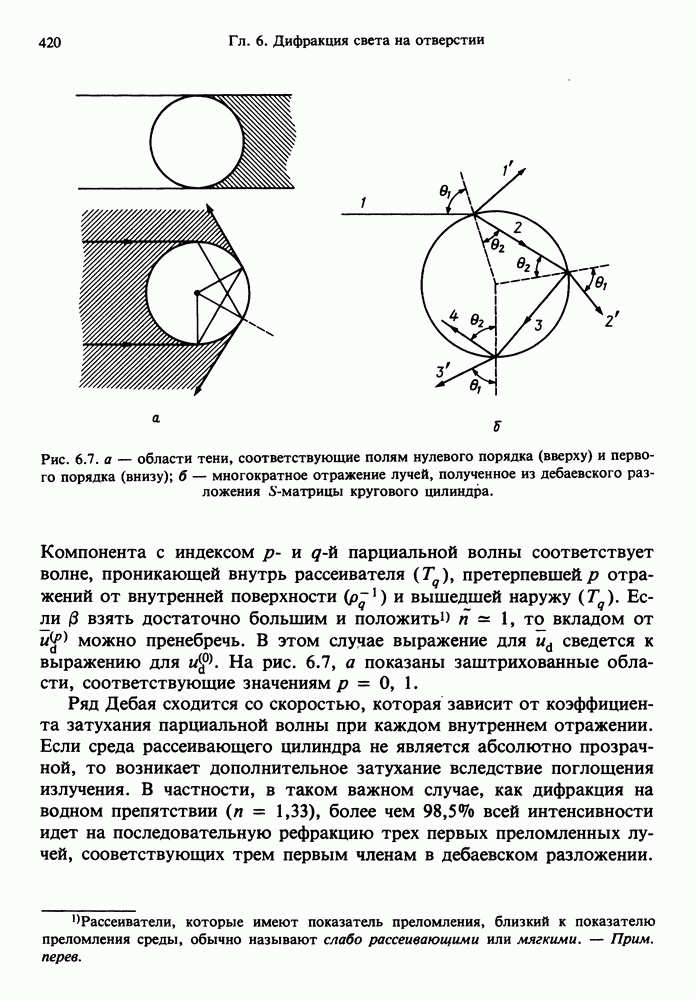
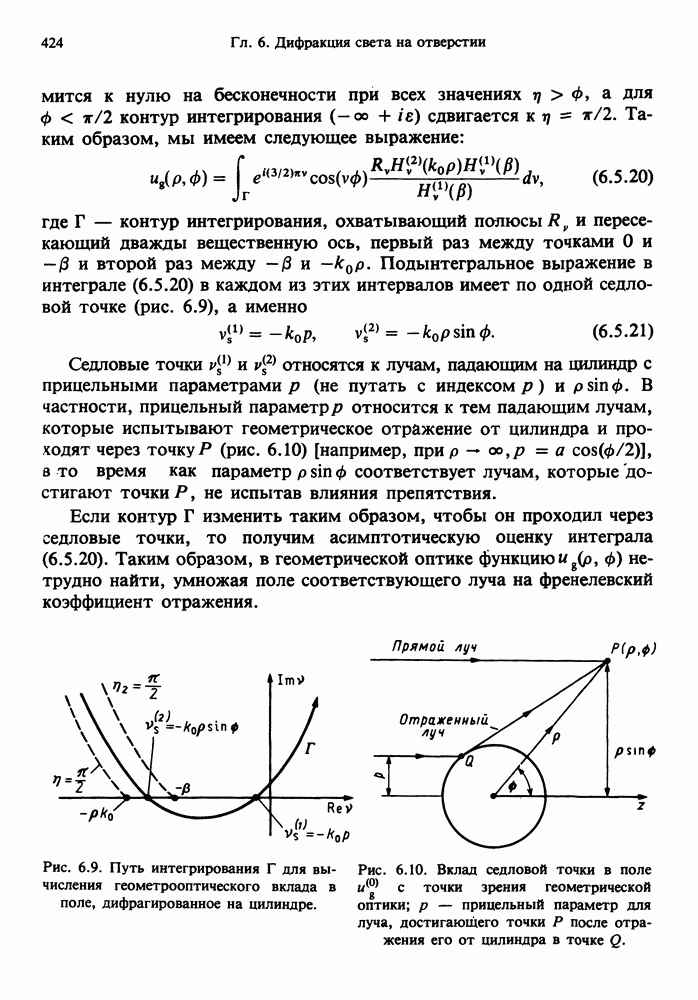
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2.14. СКАЛЯРНЫЕ УРАВНЕНИЯ ДЛЯ ЛУЧЕЙ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ; ПРИНЦИП ФЕРМА
Метод разделения переменных можно с успехом использовать для определения траекторий лучей, если распределение показателя преломления  обладает некоторой симметрией по отношению к криволинейной системе координат. Здесь мы хотим доказать важное следствие уравнения (2.4.6), позволяющее определить траектории для произвольного распределения
обладает некоторой симметрией по отношению к криволинейной системе координат. Здесь мы хотим доказать важное следствие уравнения (2.4.6), позволяющее определить траектории для произвольного распределения 
Для этого напомним, что геодезической линией метрического пространства называется траектория, длина которой стационарна при бесконечно малых изменениях траектории с фиксированными конечными точками. Рассмотрим метрическое пространство, точки которого совпадают с точками обычного пространства, но метрика изменяется в соответствии с функцией  так что длина произвольной кривой между точками
так что длина произвольной кривой между точками  определяется как
определяется как

Величину  обычно называют оптической длиной. Докажем теперь, что кривые, для которых величина
обычно называют оптической длиной. Докажем теперь, что кривые, для которых величина  стационарна при фиксированных точках
стационарна при фиксированных точках  или (что эквивалентно) геодезические линии рассматриваемого пространства совпадают со всеми возможными решениями уравнения (2.4.6), т. е. со всеми возможными лучами. Если через
или (что эквивалентно) геодезические линии рассматриваемого пространства совпадают со всеми возможными решениями уравнения (2.4.6), т. е. со всеми возможными лучами. Если через  (сопряженные точки) проходит большее число лучей, то в большинстве случаев эти лучи имеют одинаковую оптическую длину
(сопряженные точки) проходит большее число лучей, то в большинстве случаев эти лучи имеют одинаковую оптическую длину  так что мы можем определить функцию
так что мы можем определить функцию  совпадающую с оптической длиной лучей. Эту функцию называют точечной характеристикой среды, и ее свойства мы рассмотрим более подробно в разд. 2.15.
совпадающую с оптической длиной лучей. Эту функцию называют точечной характеристикой среды, и ее свойства мы рассмотрим более подробно в разд. 2.15.
На языке вариационного исчисления сформулированное выше свойство означает, что оптический путь является экстремальным по отношению ко всем другим кривым, которые не удовлетворяют законам
оптики. Для доказательства этого вычислим вариацию 5 величины  используя для простоты математических выкладок в качестве переменной интегрирования декартову координату (например, z):
используя для простоты математических выкладок в качестве переменной интегрирования декартову координату (например, z):

Здесь точки над буквами означают дифференцирование по  Любая кривая, соединяющая две фиксированные точки
Любая кривая, соединяющая две фиксированные точки  соответствует одной из возможных выборок пар непрерывных функций
соответствует одной из возможных выборок пар непрерывных функций  принимающих определенные значения на концах интервала
принимающих определенные значения на концах интервала  Вариация длин соответствует следующему изменению этих функций:
Вариация длин соответствует следующему изменению этих функций:  так что
так что

Интегрируя по частям второй и четвертый члены в правой части этого выражения и учитывая возможную разрывность показателя преломления  получаем
получаем

В правой части уравнения (2.14.4) второй член является суммой по поверхности  разрывов функции
разрывов функции  связано с резкими изменениями
связано с резкими изменениями  при увеличении
при увеличении  а третий член является суммой вкладов от областей, в которых
а третий член является суммой вкладов от областей, в которых  непрерывна. Одинаковыми индексами в каждом из членов обозначено суммирование по х и у. Так как
непрерывна. Одинаковыми индексами в каждом из членов обозначено суммирование по х и у. Так как  фиксированы,
фиксированы,  Поэтому первый член в правой части (2.14.4) равен нулю. Однако мы ищем геодезические линии, удовлетворяющие условию
Поэтому первый член в правой части (2.14.4) равен нулю. Однако мы ищем геодезические линии, удовлетворяющие условию

при любых  Из уравнения (2.14.4) следует, что это возможно, только если удовлетворяются следующие уравнения:
Из уравнения (2.14.4) следует, что это возможно, только если удовлетворяются следующие уравнения:

(уравнения Эйлера), дополненные условиями скачка на каждой поверхности разрыва:

Если использовать соотношения  то сразу выяснится, что уравнения (2.14.6) совпадают со скалярными компонентами уравнения лучей (2.4.5) вдоль осей х и у. Очевидно, что то же самое верно и для оси
то сразу выяснится, что уравнения (2.14.6) совпадают со скалярными компонентами уравнения лучей (2.4.5) вдоль осей х и у. Очевидно, что то же самое верно и для оси  Доказательство совпадения лучей с геодезическими линиями можно считать завершенным, если заметить, что уравнение (2.14.7) эквивалентно закону Снеллиуса. Это легко показать, выбирая, например, ось
Доказательство совпадения лучей с геодезическими линиями можно считать завершенным, если заметить, что уравнение (2.14.7) эквивалентно закону Снеллиуса. Это легко показать, выбирая, например, ось  перпендикулярно поверхности разрыва, а плоскость
перпендикулярно поверхности разрыва, а плоскость  в качестве плоскости падения. Более строгий вывод закона Снеллиуса из вариационных принципов содержится в работе Зацкиса [19].
в качестве плоскости падения. Более строгий вывод закона Снеллиуса из вариационных принципов содержится в работе Зацкиса [19].
Обычно соотношения (2.14.5) называют принципом Ферма. Согласно этому принципу, оптическая длина луча, соединяющего точки  меньше оптической длины любой другой кривой, соединяющей эти точки и расположенной вблизи луча. Строго говоря, принцип Ферма справедлив лишь в том случае, когда точки
меньше оптической длины любой другой кривой, соединяющей эти точки и расположенной вблизи луча. Строго говоря, принцип Ферма справедлив лишь в том случае, когда точки  расположены достаточно близко друг от друга. Покажем это на примере вогнутого сферического зеркала [1] (рис. 2.28). Пусть луч
расположены достаточно близко друг от друга. Покажем это на примере вогнутого сферического зеркала [1] (рис. 2.28). Пусть луч  соединяет точки
соединяет точки  расположенные симметрично на прямой, проходящей через центр О сферического зеркала у. Эллипс
расположенные симметрично на прямой, проходящей через центр О сферического зеркала у. Эллипс  с фокусами в точках
с фокусами в точках  лежит правее у, поэтому
лежит правее у, поэтому  Следовательно, длина
Следовательно, длина  является относительным максимумом при смещении точки
является относительным максимумом при смещении точки  по поверхности зеркала. Обратная ситуация возникает, если рассматриваемые две точки
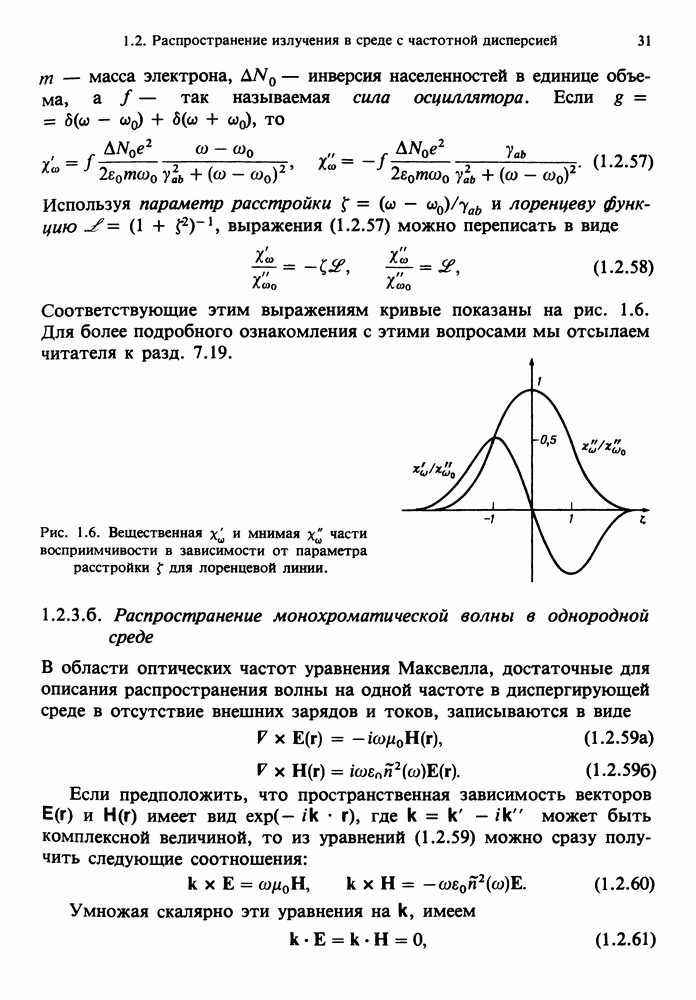
по поверхности зеркала. Обратная ситуация возникает, если рассматриваемые две точки  располагаются достаточно близко к точке
располагаются достаточно близко к точке  Из-за своей ограниченной применимости
Из-за своей ограниченной применимости

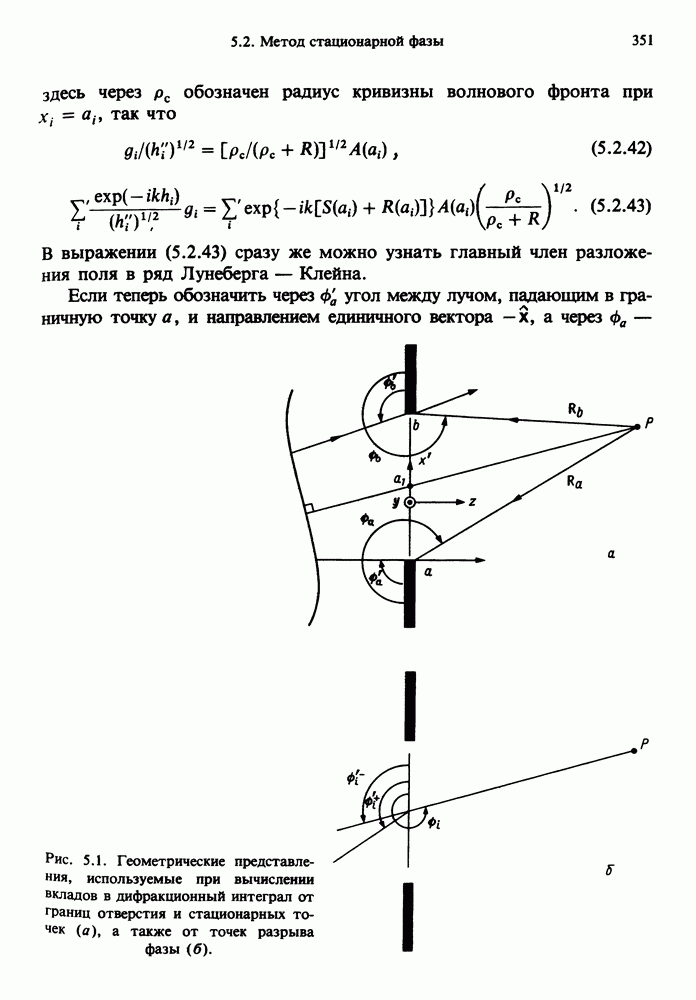
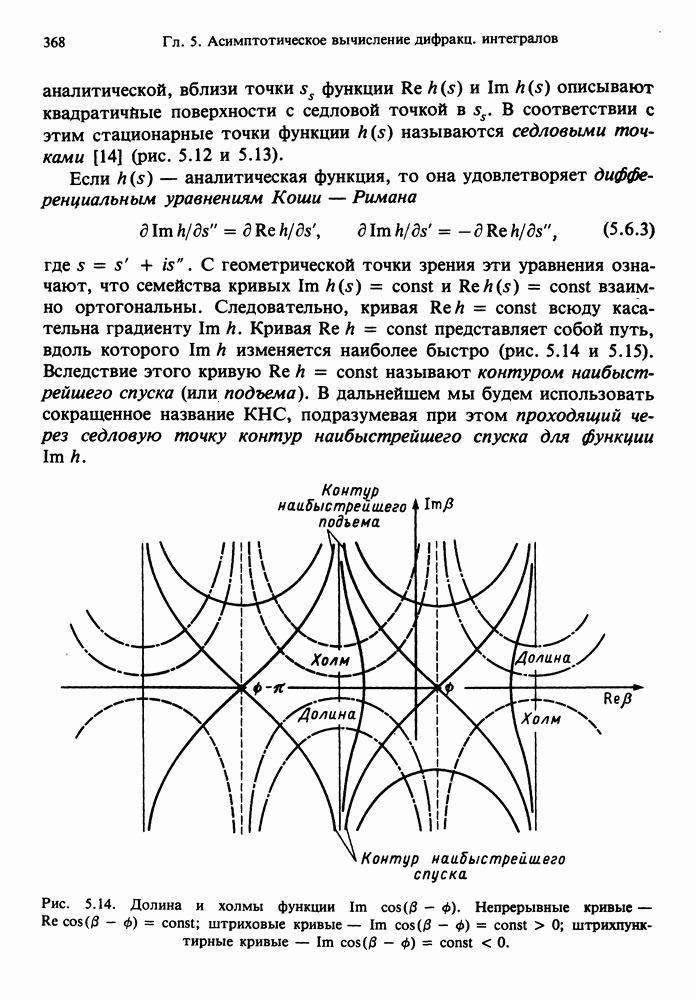
Рис. 2.28. Иллюстрация к формулировке Каратеодори принципа Ферма [1].
принцип Ферма нуждается в уточнении. Каратеодори сформулировал его следующим образом: для каждой точки светового луча существует конечная окрестность, в которой принцип Ферма справедлив. (Обобщение принципа Ферма для дифрагированных лучей см. в разд. 6.7.)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. ОСНОВНЫЕ СВОЙСТВА РАСПРОСТРАНЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 1.1. УРАВНЕНИЯ МАКСВЕЛЛА
- 1.1.1. Векторный и скалярный потенциалы
- 1.2. РАСПРОСТРАНЕНИЕ ИЗЛУЧЕНИЯ В СРЕДЕ С ЧАСТОТНОЙ ДИСПЕРСИЕЙ
- 1.2.1. Нелинейное распространение волн
- 1.2.2. Распространение импульса в двухуровневой резонансной среде
- 1.2.2.а. Режим скоростных уравнений для длинных импульсов
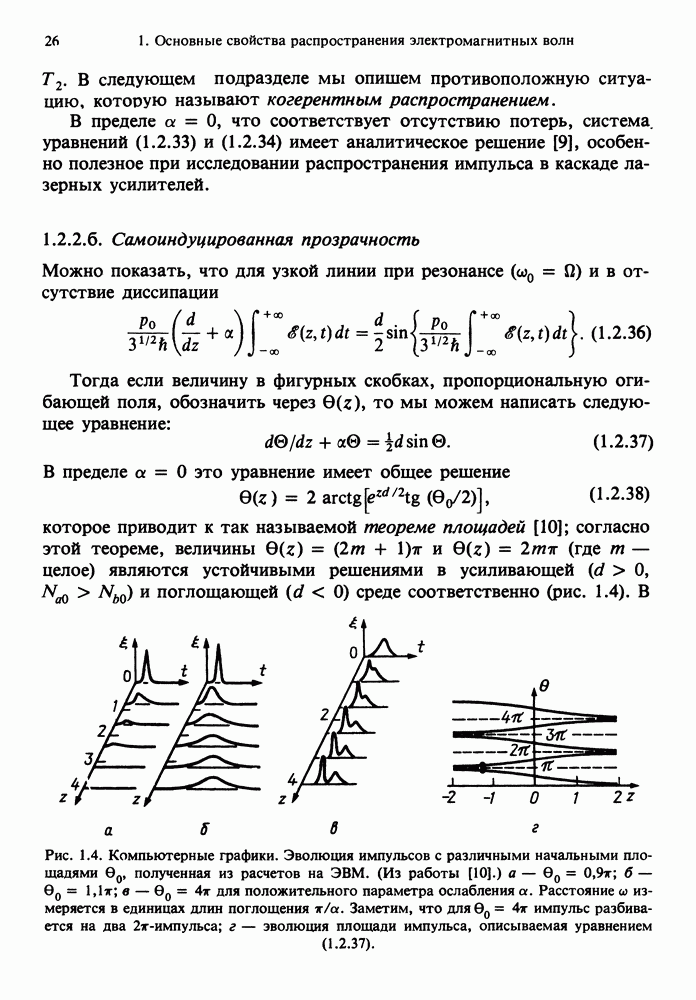
- 1.2.2.б. Самоиндуцированная прозрачность
- 1.2.2.В. Общий случай
- 1.2.3. Соотношение Крамерса — Кронига и монохроматические волны
- 1.2.3.а. Диэлектрическая восприимчивость в резонансной двухуровневой среде
- 1.2.3.б. Распространение монохроматической волны в однородной среде
- 1.3. СОСТОЯНИЕ ПОЛЯРИЗАЦИИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 1.3.1. Параметры Стокса и матрица Джонса
- 1.3.2. Поляризация затухающих волн
- 1.4. РАСПРОСТРАНЕНИЕ ВОЛН В АНИЗОТРОПНОЙ СРЕДЕ
- 1.4.1. Двойное лучепреломление
- 1.4.1.а. Электрооптический эффект
- 1.5. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ПРОСТРАНСТВЕННОЙ ДИСПЕРСИЕЙ
- 1.5.1. Естественная оптическая активность
- 1.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
- 1.6.1. Соотношения Пойнтинга для квазимонохроматического пучка в среде с пространственной дисперсией
- 1.7. РАСПРОСТРАНЕНИЕ ВОЛН В ДВИЖУЩЕЙСЯ СРЕДЕ
- 1.8. СВОЙСТВА КОГЕРЕНТНОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- ГЛАВА 2. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 2.1. ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 2.2. АСИМПТОТИЧЕСКОЕ РЕШЕНИЕ СКАЛЯРНОГО ВОЛНОВОГО УРАВНЕНИЯ
- 2.3. УРАВНЕНИЕ ЭЙКОНАЛА
- 2.4. УРАВНЕНИЕ ДЛЯ ЛУЧЕЙ
- 2.4.1. Теорема Малюса — Дюпина
- 2.4.2. Кривизна и закручивание лучей
- 2.4.3. Построение луча
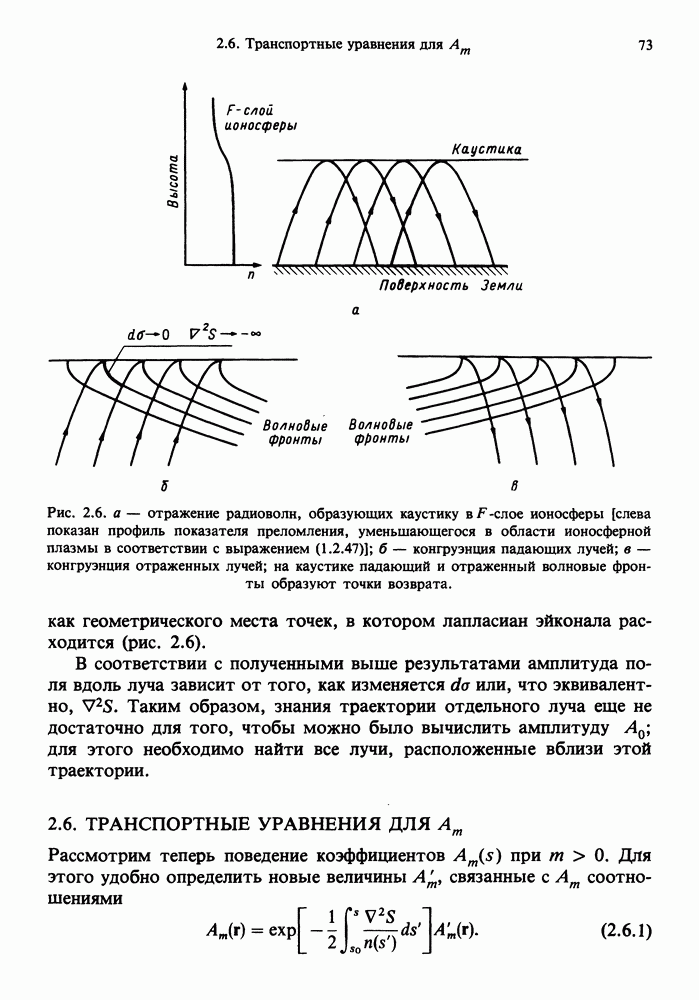
- 2.5. ТРАНСПОРТНОЕ УРАВНЕНИЕ ДЛЯ А0
- 2.6. ТРАНСПОРТНЫЕ УРАВНЕНИЯ ДЛЯ Аm
- 2.6.1. Параболическое волновое уравнение Фока — Леонтовича
- 2.7. ЗАТУХАЮЩИЕ ВОЛНЫ И КОМПЛЕКСНЫЕ ЭЙКОНАЛЫ
- 2.7.1. Двумерные затухающие поля
- 2.8. ГЕОМЕТРИЧЕСКАЯ ОПТИКА МАКСВЕЛЛОВСКИХ ВЕКТОРНЫХ ПОЛЕЙ
- 2.8.2. Асимптотическое разложение магнитного поля
- 2.8.3. Асимптотическое разложение вектора Пойнтинга
- 2.8.4. Ряд Лунеберга — Клейна на поверхности раздела двух сред
- 2.9. ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА ВОЛНОВЫХ ФРОНТОВ
- 2.10. КАУСТИКИ И ВОЛНОВЫЕ ФРОНТЫ
- 2.10.1. Аналитические свойства конгруэнции, лучей, волновых фронтов и каустик
- 2.10.1.а. Волновые фронты
- 2.10.1.б. Каустики
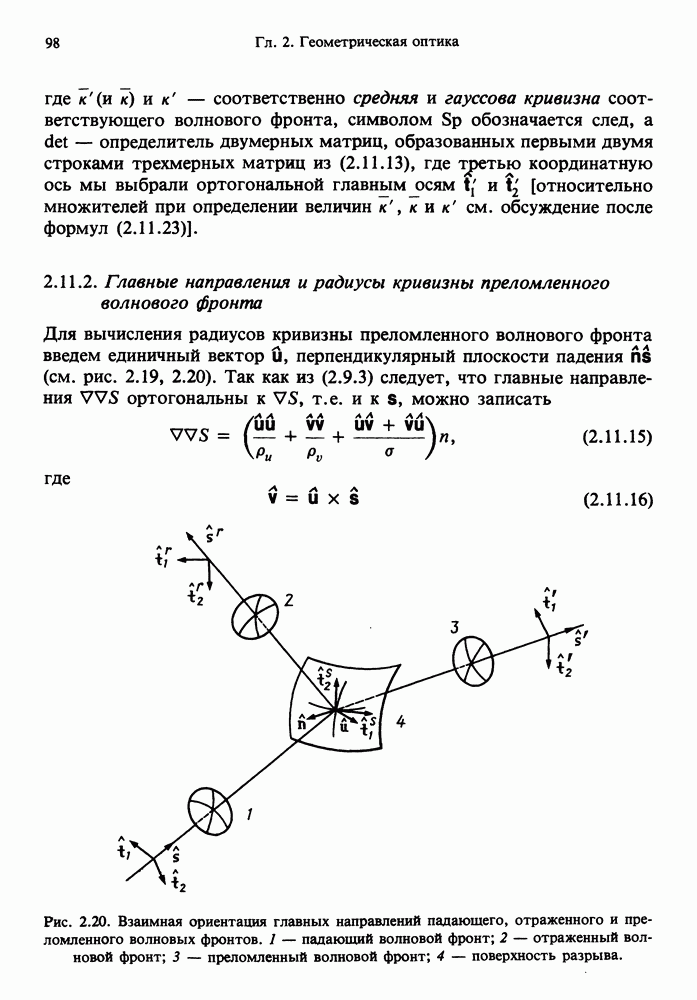
- 2.11. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ВОЛНОВОГО ФРОНТА НА НЕПЛОСКОЙ ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
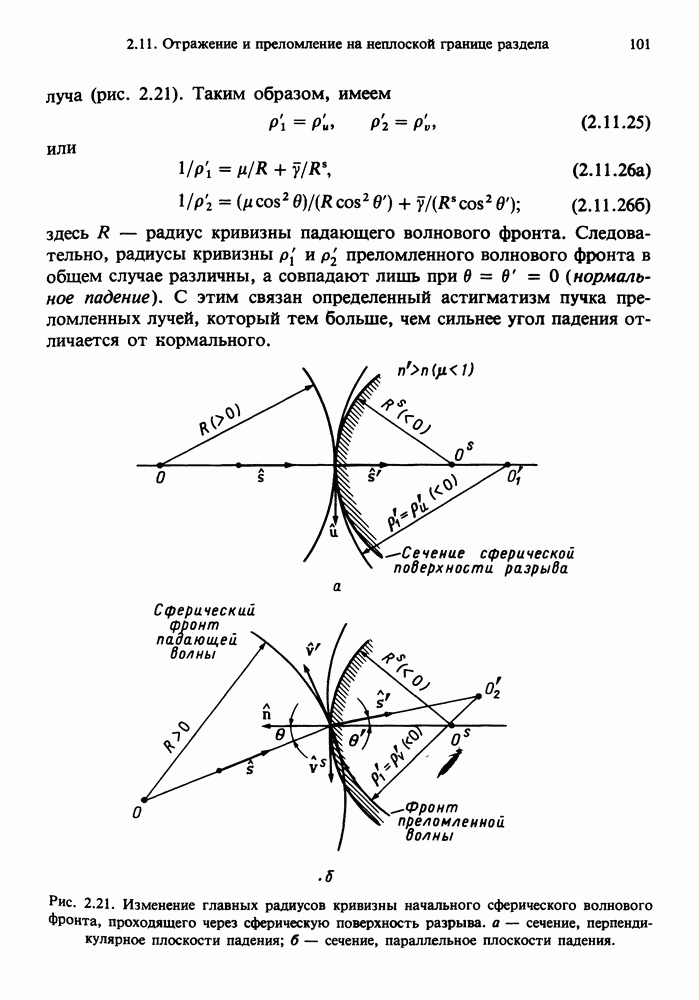
- 2.11.2. Главные направления и радиусы кривизны преломленного волнового фронта
- 2.11.3. Сферические преломляющие поверхности
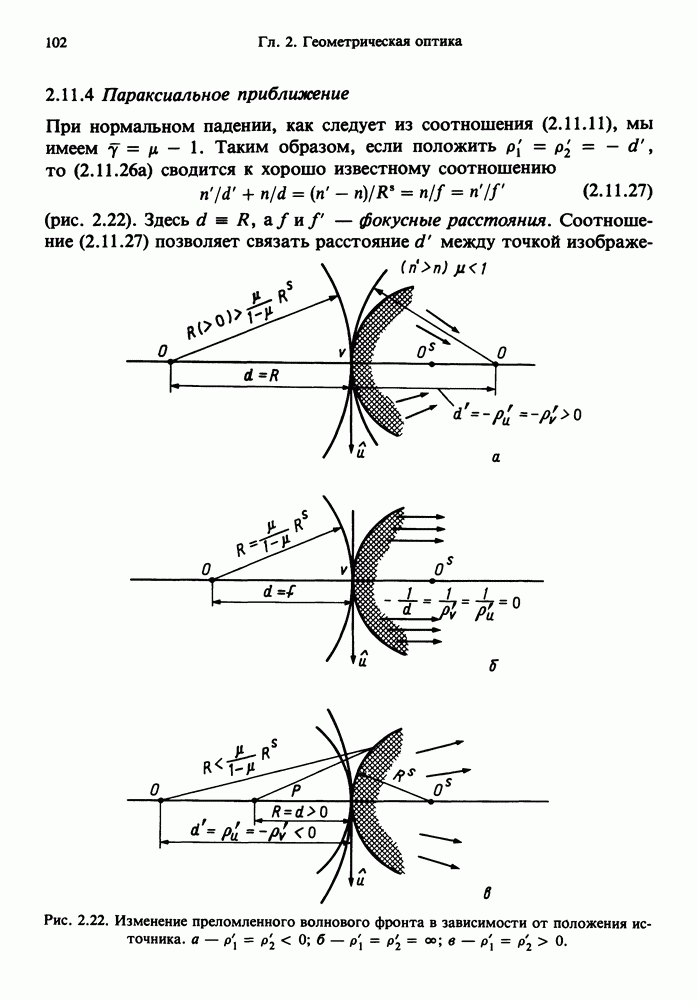
- 2.11.4 Параксиальное приближение
- 2.11.5. Сферические отражающие поверхности
- 2.12. РЕШЕНИЕ УРАВНЕНИЯ ЭЙКОНАЛА МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
- 2.12.1.а. Аксиально-симметричное распределение показателя преломления
- 2.12.1.б. Линзоподобные среды
- 2.12.1.в. Физические свойства комплексных эйконалов
- 2.12.2. Цилиндрические координаты
- 2.12.2.а. Аксиально-симметричный профиль показателя преломления
- 2.12.3. Сферические координаты
- 2.13. ВЫЧИСЛЕНИЕ ТРАЕКТОРИЙ ЛУЧЕЙ МЕТОДОМ РАЗДЕЛЕНИЯ ПЕРЕМЕННЫХ
- 2.13.2. Сферически-симметричные среды
- 2.13.3. Градиентные оптические элементы
- 2.14. СКАЛЯРНЫЕ УРАВНЕНИЯ ДЛЯ ЛУЧЕЙ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ; ПРИНЦИП ФЕРМА
- 2.14.1. Анизотропные среды
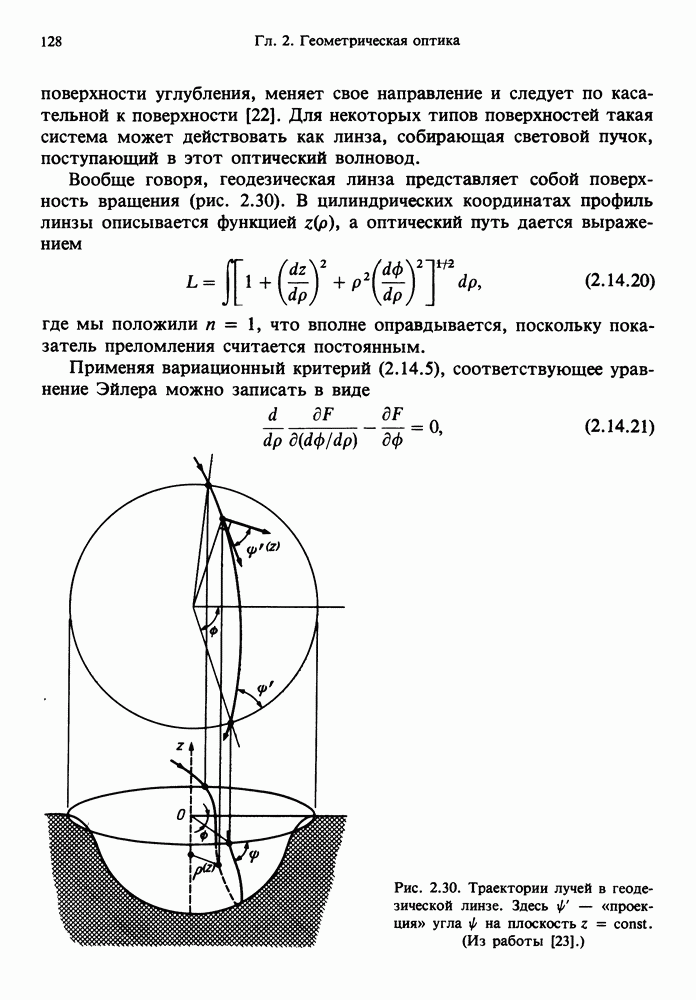
- 2.14.2. Геодезические линзы
- 2.14.3. Метод ковариантного дифференцирования
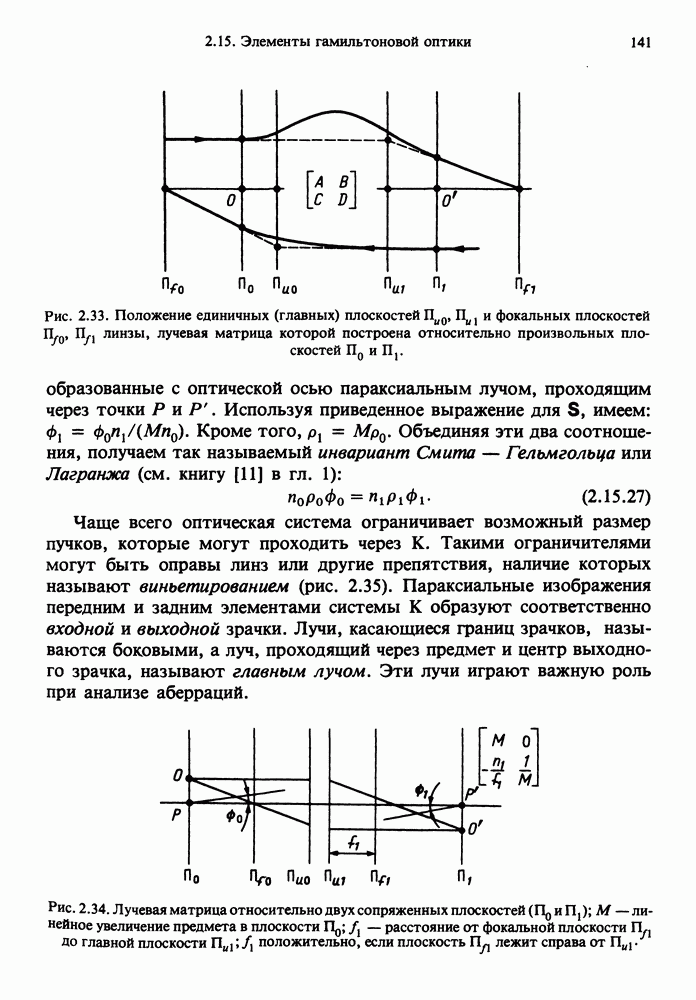
- 2.15. ЭЛЕМЕНТЫ ГАМИЛЬТОНОВОЙ ОПТИКИ
- 2.15.1. Точечные, угловые и смешанные характеристики
- 2.15.2. Угловая характеристика поверхности вращения
- 2.15.3. Лучевая матрица
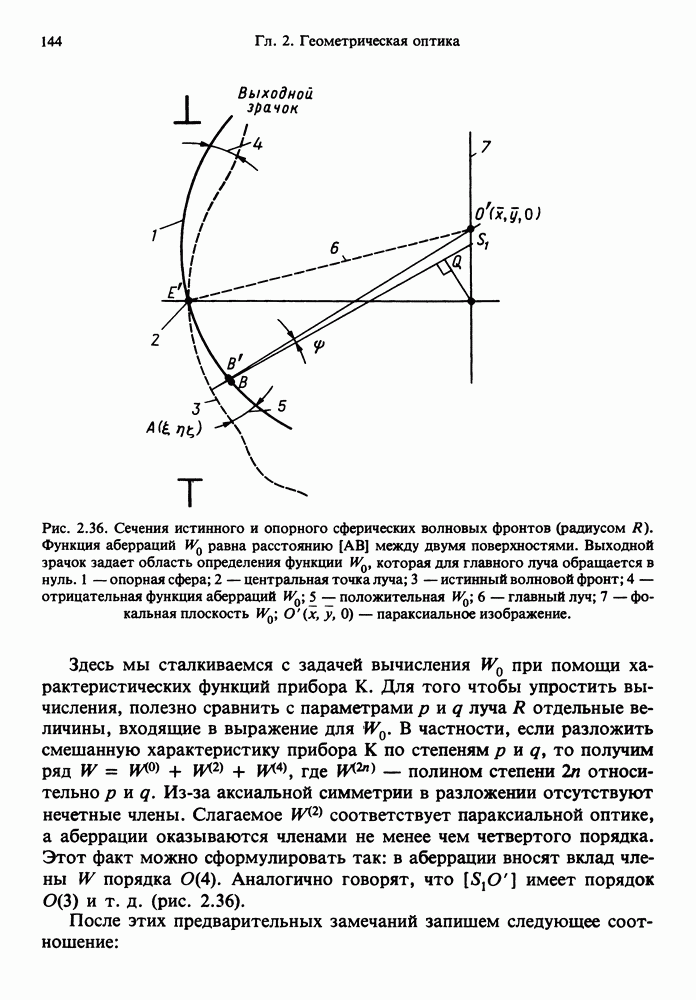
- 2.15.4. Аберрации волнового фронта
- ГЛАВА 3. ПЛОСКИЕ МНОГОСЛОЙНЫЕ СРЕДЫ
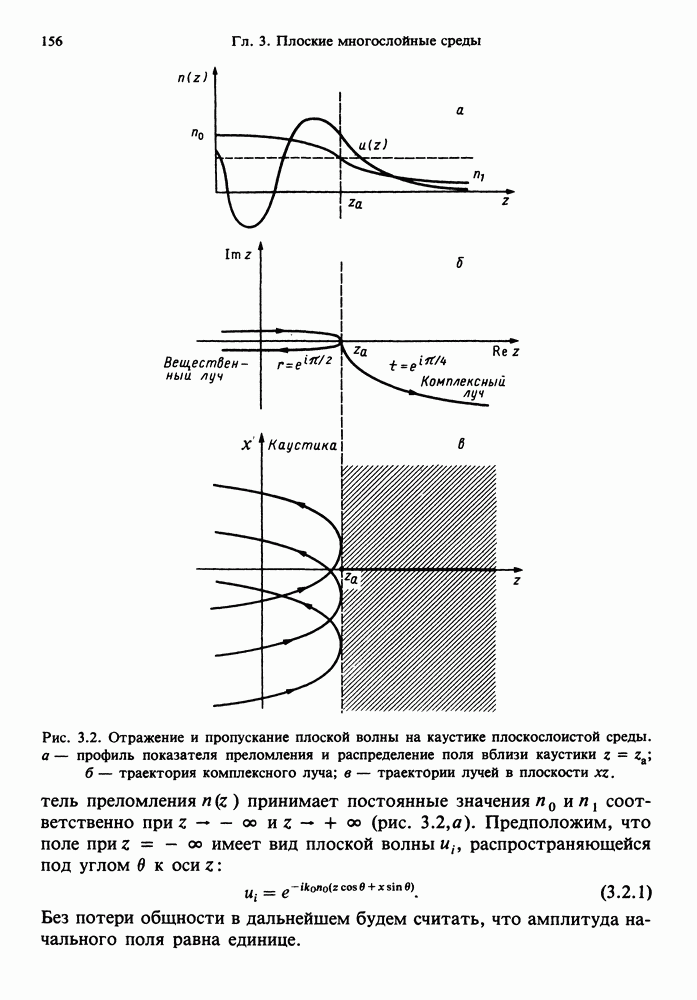
- 3.2. ГЕОМЕТРИЧЕСКАЯ ОПТИКА В СЛОИСТЫХ СРЕДАХ
- 3.3. СШИВКА АСИМПТОТИЧЕСКИХ РАЗЛОЖЕНИЙ; МЕТОД ЛАНГЕРА
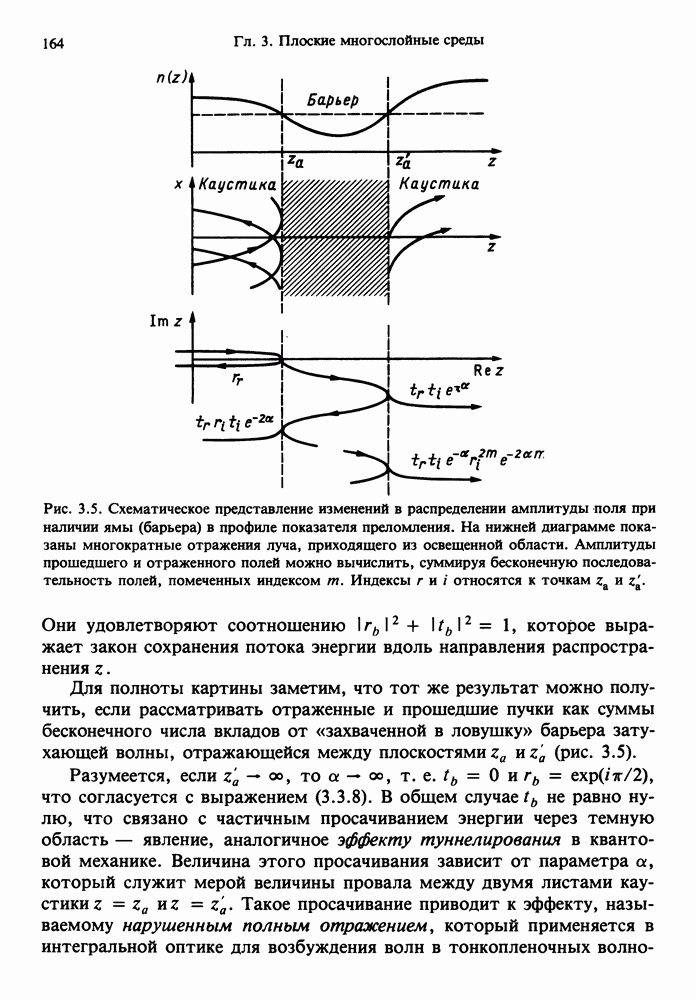
- 3.3.1. Прошедшие и отраженные волны
- 3.3.2. Переход из запрещенной зоны в разрешенную
- 3.3.3. Темный барьер
- 3.3.4. Канал
- 3.4. ОТРАЖЕНИЕ И ПРОПУСКАНИЕ ПРОИЗВОЛЬНОЙ НЕОДНОРОДНОЙ СРЕДОЙ
- 3.5. ТОЧНОЕ РЕШЕНИЕ ДЛЯ СЛОЯ С ЛИНЕЙНО УВЕЛИЧИВАЮЩИМСЯ ПОКАЗАТЕЛЕМ ПРЕЛОМЛЕНИЯ
- 3.6. МНОГОСЛОЙНЫЕ СРЕДЫ С КУСОЧНО-ПОСТОЯННЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
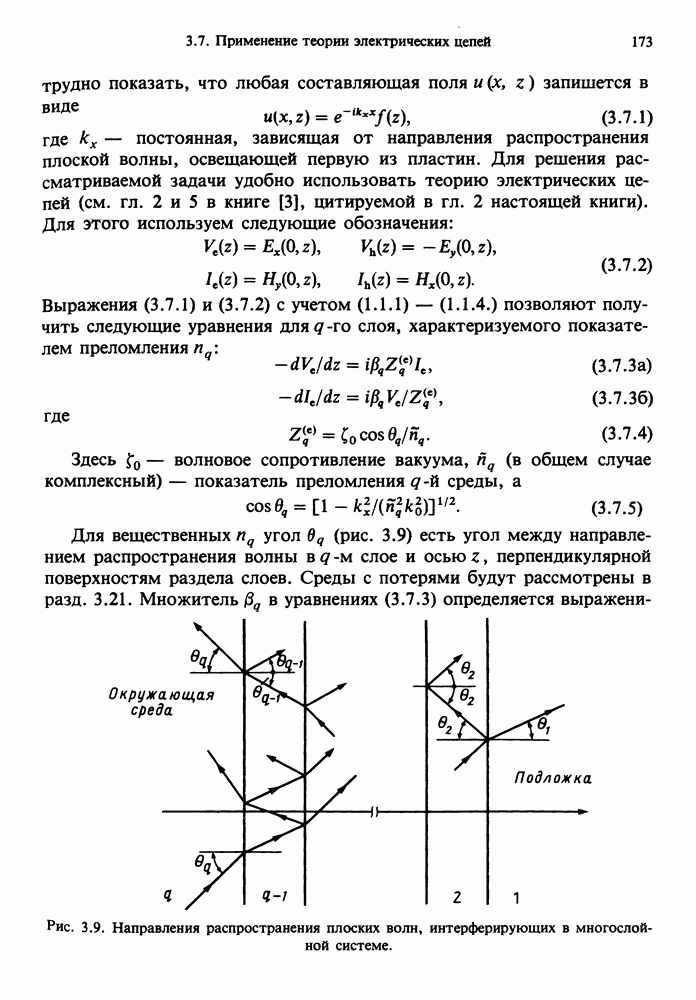
- 3.7. ПРИМЕНЕНИЕ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
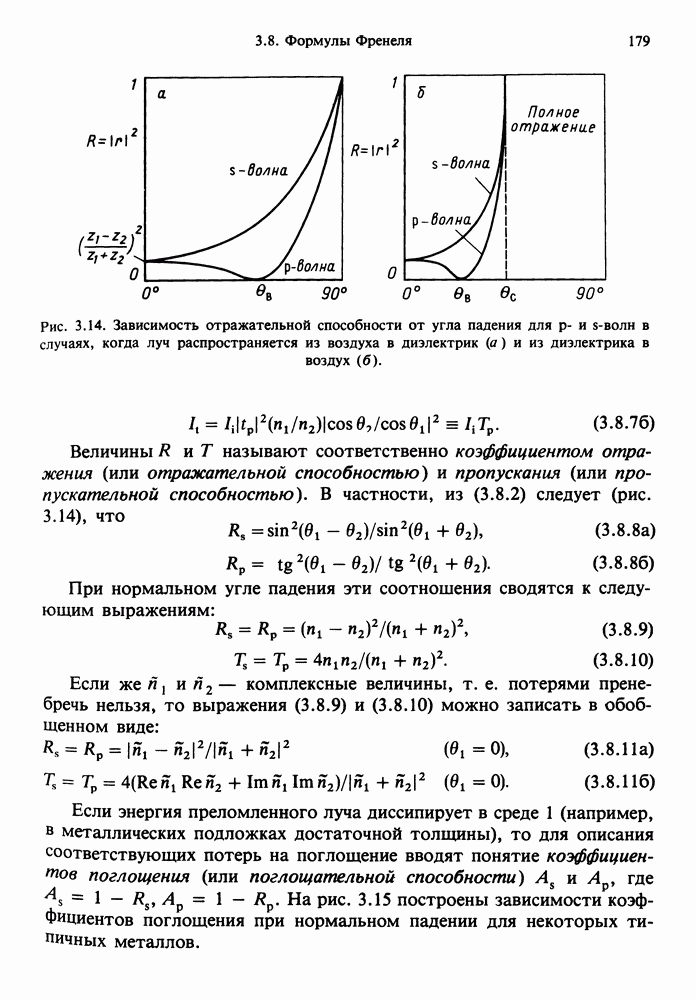
- 3.8. ФОРМУЛЫ ФРЕНЕЛЯ
- 3.9. МЕТОД ХАРАКТЕРИСТИЧЕСКОЙ МАТРИЦЫ
- 3.9.1. Уравнение для М-матрицы
- 3.9.2. Вычисление М-матрицы для мультислоя
- 3.10. БЛОХОВСКИЕ ВОЛНЫ
- 3.11. ПОЛОСЫ ПРОПУСКАНИЯ И НЕПРОЗРАЧНОСТИ СТОПЫ ЧЕТВЕРТЬВОЛНОВЫХ ПЛАСТИНОК
- 3.12. КОЭФФИЦИЕНТ ОТРАЖЕНИЯ МУЛЬТИСЛОЯ
- 3.12.1. Формула Эйри
- 3.12.2. Четвертьволновые стопы
- 3.12.3. Однослойные покрытия
- 3.12.4. Отражение от сдоя со слабо изменяющимся профилем
- 3.13. МЕТАЛЛИЧЕСКИЕ И ДИЭЛЕКТРИЧЕСКИЕ ОТРАЖАТЕЛИ
- 3.13.1. Отражение при наклонном падении
- 3.13.2. Поляризационные светоделители
- 3.14. ПРОСВЕТЛЯЮЩИЕ ПОКРЫТИЯ
- 3.15. ИНТЕРФЕРЕНЦИОННЫЕ ФИЛЬТРЫ
- 3.16. АНИЗОТРОПНЫЕ СЛОИСТЫЕ СРЕДЫ
- 3.16.2. Коэффициенты отражения и пропускания мультислоя
- 3.17. РАСПРОСТРАНЕНИЕ ВОЛН В ПЕРИОДИЧЕСКОЙ СРЕДЕ
- 3.17.1. Теорема Флоке
- 3.17.2. Детерминант Хилла
- 3.17.3. Теория связанных мод
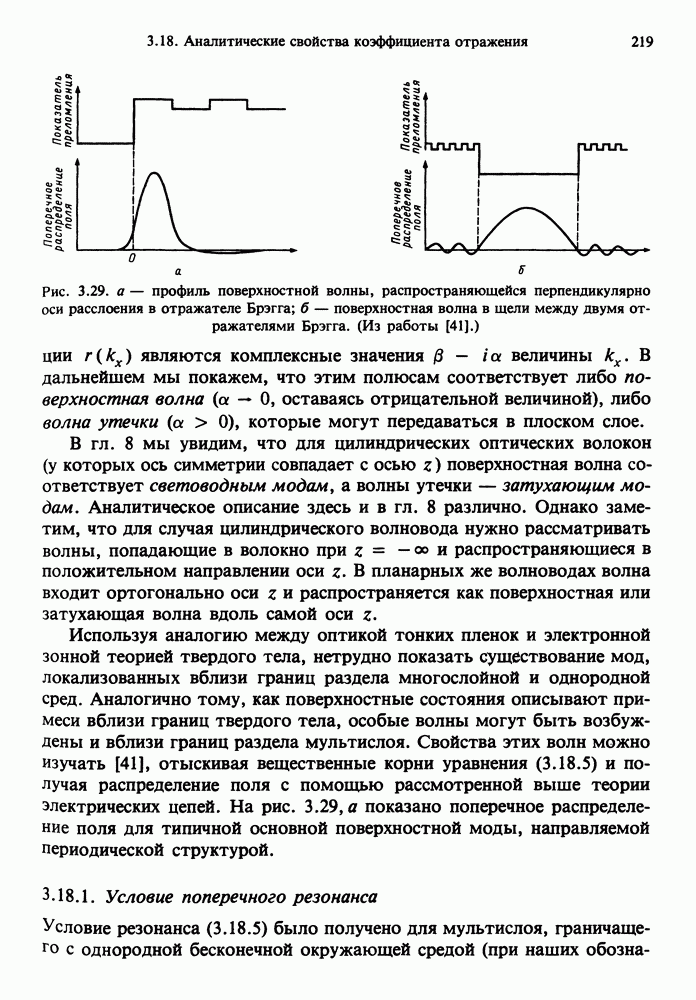
- 3.18. АНАЛИТИЧЕСКИЕ СВОЙСТВА КОЭФФИЦИЕНТА ОТРАЖЕНИЯ
- 3.18.1. Условие поперечного резонанса
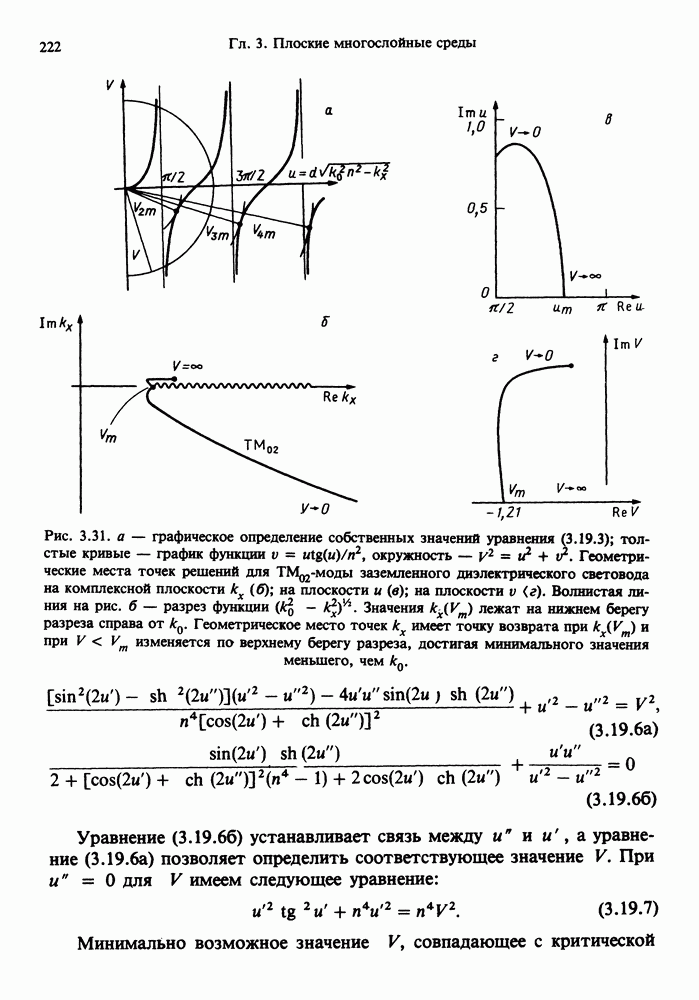
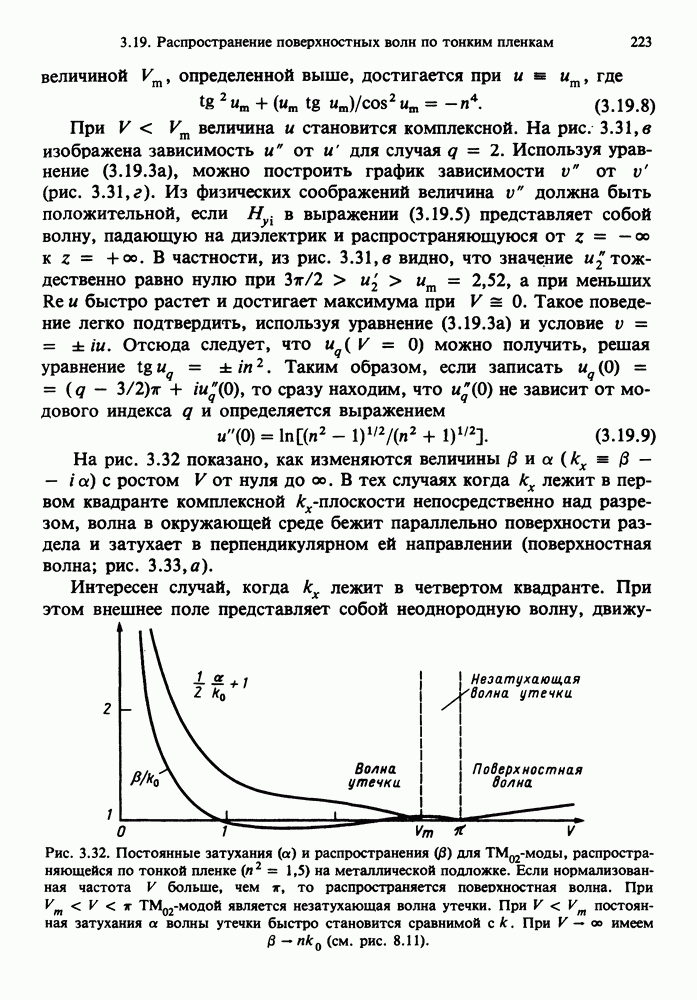
- 3.19. РАСПРОСТРАНЕНИЕ ПОВЕРХНОСТНЫХ И ЗАТУХАЮЩИХ ВОЛН ПО ТОНКИМ ПЛЕНКАМ
- 3.20. ОСВЕЩЕНИЕ ПОД УГЛОМ, БОЛЬШИМ КРИТИЧЕСКОГО
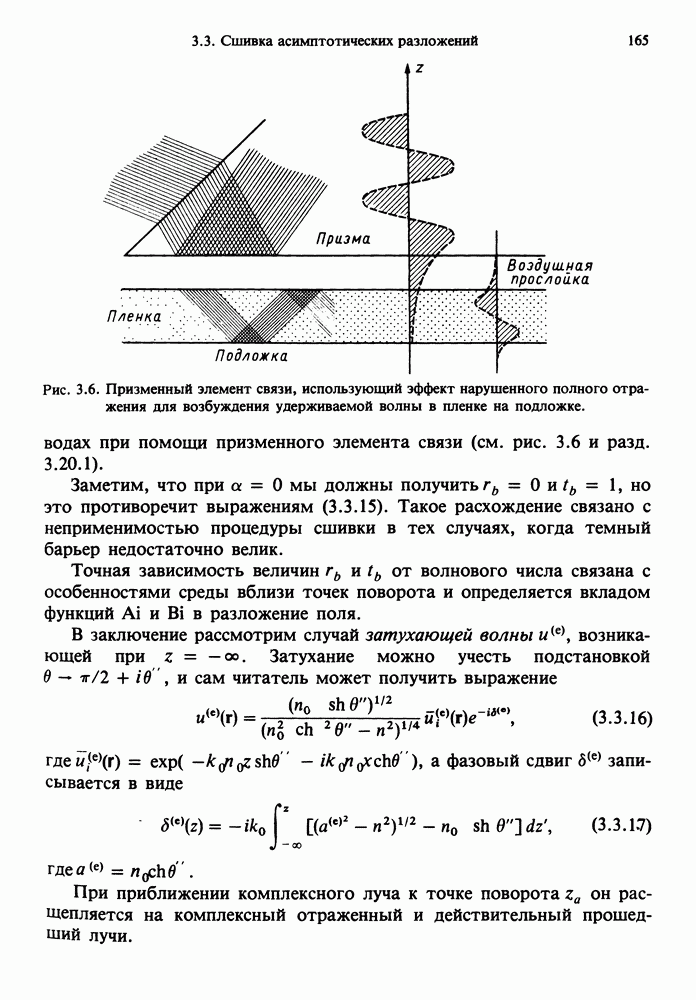
- 3.20.1. Нарушенное полное отражение
- 3.21. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ГРАНИЦЕ РАЗДЕЛА МЕЖДУ ДИЭЛЕКТРИКОМ И СРЕДОЙ С ПОТЕРЯМИ
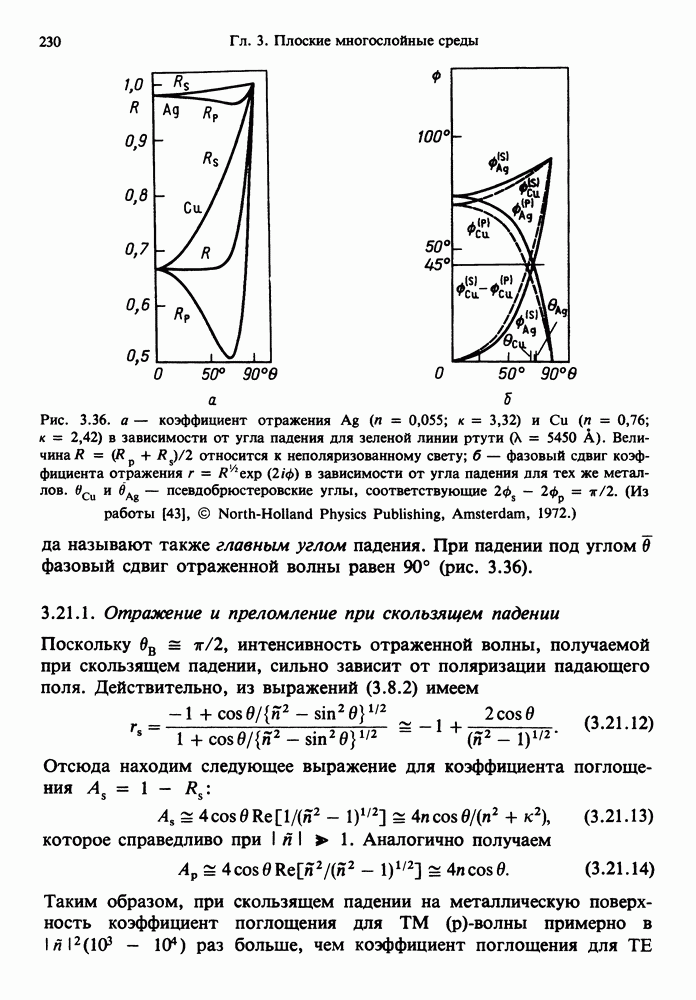
- 3.21.1. Отражение и преломление при скользящем падении
- 3.21.2. Отражение и преломление при нормальном падении
- 3.21.3. Отражение при произвольном угле падения
- 3.22. ПОВЕРХНОСТНЫЕ ВОЛНЫ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД
- 3.22.1. Поверхностные волны в металлах
- 3.23. ИМПЕДАНСНЫЕ ГРАНИЧНЫЕ УСЛОВИЯ
- ГЛАВА 4. ОСНОВЫ ТЕОРИИ ДИФРАКЦИИ
- 4.1.2. Математический аппарат
- 4.2. МЕТОД ФУНКЦИИ ГРИНА
- 4.2.1. Интегральная теорема Гелъмгольца — Кирхгофа
- 4.2.2. Принцип Гюйгенса
- 4.3. ПРИНЦИП ГЮЙГЕНСА В ФОРМУЛИРОВКЕ КИРХГОФА — КОТТЛЕРА
- 4.4. УСЛОВИЕ ЗОММЕРФЕЛЬДА НА ПОЛЕ ИЗЛУЧЕНИЯ
- 4.5. ДИФРАКЦИОННЫЕ ИНТЕГРАЛЫ РЭЛЕЯ ДЛЯ ПЛОСКИХ ЭКРАНОВ
- 4.6. ПРИНЦИП БАБИНЕ
- 4.7. ДИФРАКЦИОННЫЕ ИНТЕГРАЛЫ ДЛЯ ДВУМЕРНЫХ ПОЛЕЙ
- 4.8. РАЗЛОЖЕНИЕ ПОЛЯ ПО ПЛОСКИМ ВОЛНАМ
- 4.9. УГЛОВОЙ СПЕКТР
- 4.9.1. Угловой спектр двумерных волн
- 4.9.2. Угловой спектр в комплексной области
- 4.9.3. Полюсные сингулярности
- 4.9.4. Точки ветвления
- 4.10. ДИФРАКЦИОННЫЕ ФОРМУЛЫ ФРЕНЕЛЯ И ФРАУНГОФЕРА
- 4.10.2. Формула Фраунгофера
- 4.10.3. Обобщение на двумерные поля
- 4.10.4. Дифракция периодических полей
- 4.11. РАЗЛОЖЕНИЕ ПОЛЯ ПО ЦИЛИНДРИЧЕСКИМ ВОЛНАМ
- 4.11.1. Приближение Френеля
- 4.11.2. Разложение плоской волны по цилиндрическим волнам
- 4.11.3. Апертурно ограниченные вращательно-симметричные поля
- 4.11.3.а. Разложение в ряды Буавена
- 4.12. ЦИЛИНДРИЧЕСКИЕ ВОЛНЫ КОМПЛЕКСНОГО ПОРЯДКА И ПРЕОБРАЗОВАНИЕ ВАТСОНА
- 4.12.1. Нули функции … в верхней полуплоскости
- 4.12.2. Ползущие волны
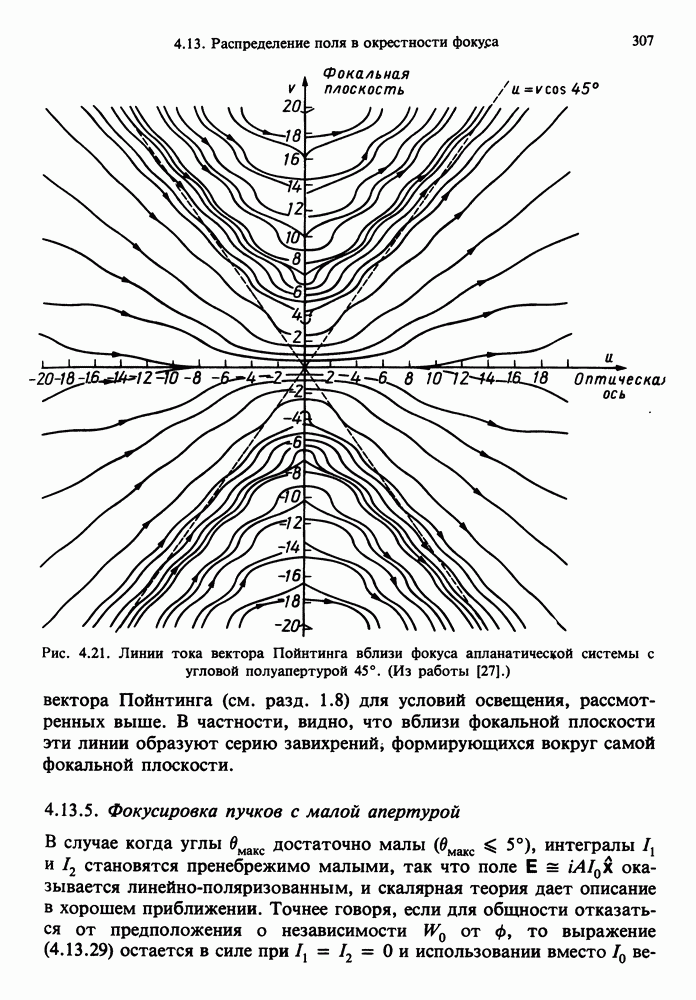
- 4.13. РАСПРЕДЕЛЕНИЕ ПОЛЯ В ОКРЕСТНОСТИ ФОКУСА
- 4.13.1. Точечные источники электромагнитного поля
- 4.13.2. Перенос векторных полей из пространства предмета к выходному зрачку
- 4.13.3. Дифракционный интеграл Лунеберга — Дебая
- 4.13.4. Фокусировка линейно-поляризованных плоских волн
- 4.13.5. Фокусировка пучков с малой апертурой
- 4.13.6. Распределение поля вдоль оптической оси для гауссова пучка с ограниченной апертурой
- 4.13.7. Распределение поля в фокальной плоскости для гауссова пучка с ограниченной апертурой
- 4.13.8. Разрешающая способность
- 4.14. ПРЕОБРАЗОВАНИЕ ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ К КОНТУРНЫМ
- 4.14.2. Векторный потенциал сферических волн
- 4.15. ИЗОБРАЖЕНИЕ ПРИ КОГЕРЕНТНОМ И НЕКОГЕРЕНТНОМ ОСВЕЩЕНИИ
- 4.15.1. Импульсный отклик и передаточная функция точки
- 4.15.2. Когерентное изображение протяженных источников
- 4.15.3. Распространение взаимной интенсивности; теорема Ван-Циттерта — Цернике
- 4.15.4. Исследование оптических систем с помощью оптической передаточной функции (ОПФ)
- 4.15.5. Степени свободы изображения
- ГЛАВА 5. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ
- 5.2. МЕТОД СТАЦИОНАРНОЙ ФАЗЫ
- 5.2.1. Асимптотическое разложение интегралов типа преобразования Фурье с монотонной фазой
- 5.2.2. Обобщение метода СФ на дифракционные интегралы с несколькими стационарными и сингулярными точками
- 5.2.3. Вклады стационарных точек
- 5.2.4. Вклады граничных точек
- 5.2.5. Вклады точек разрыва
- 5.2.6 Асимптотическое выражение для дифракционных интегралов
- 5.2.7. Устранение СФ-сингулярностей с помощью сравнительных интегралов
- 5.3. ГРАНИЦЫ ТЕНИ; СТАЦИОНАРНАЯ ТОЧКА ВБЛИЗИ ГРАНИЧНОЙ
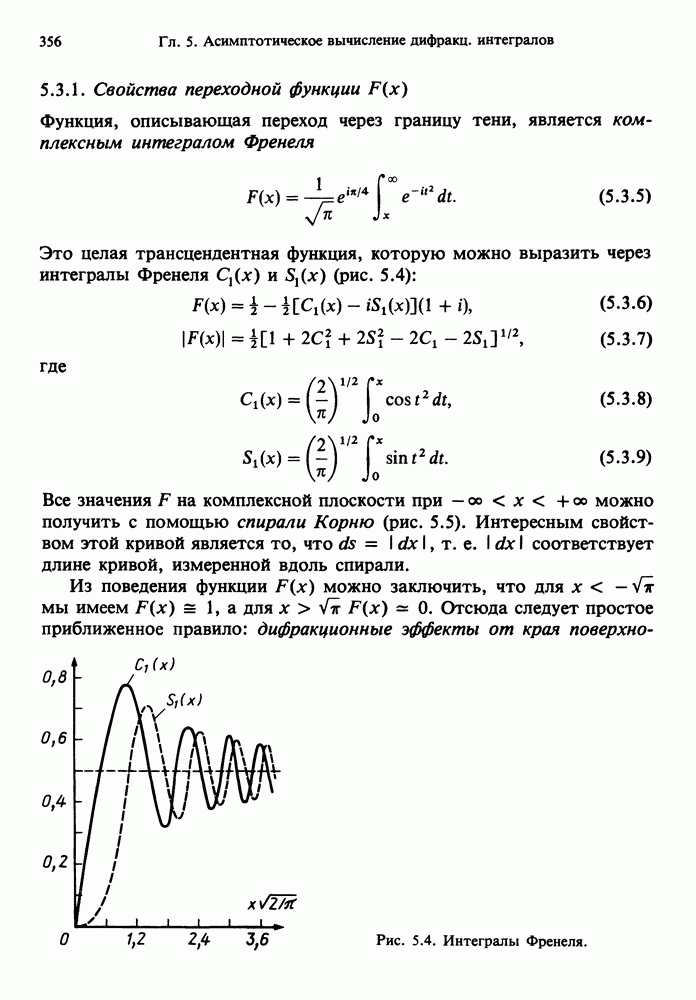
- 5.3.1. Свойства переходной функции F(x)
- 5.3.2. Асимптотическое поведение функции F(x)
- 5.3.3. Асимптотическое представление поля
- 5.3.4. F(x) при малых аргументах
- 5.4. КАУСТИКИ ЦИЛИНДРИЧЕСКИХ ПОЛЕЙ; ДВЕ СОСЕДНИЕ СТАЦИОНАРНЫЕ ТОЧКИ
- 5.5. ПОЛЕ ВБЛИЗИ ДВУМЕРНОГО ОСТРИЯ КАУСТИКИ; МОДЕЛЬ ДЛЯ ИМПУЛЬСНОГО ОТКЛИКА ПРИ НАЛИЧИИ ДЕФОКУСИРОВКИ И АБЕРРАЦИЙ ТРЕТЬЕГО ПОРЯДКА
- 5.6. МЕТОД НАИБЫСТРЕЙШЕГО СПУСКА
- 5.6.1. Полюс вблизи седловой точки
- 5.6.2. Точка ветвления вблизи седловой точки
- 5.7. ДИФРАКЦИОННЫЕ ЭФФЕКТЫ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ ДИЭЛЕКТРИКОВ
- 5.7.1. Боковые волны
- 5.7.2. Эффект Гуса — Хенхена
- 5.8. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ДИФРАКЦИОННЫХ ИНТЕГРАЛОВ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
- 5.9 ВЫВОД АСИМПТОТИЧЕСКИХ РЯДОВ ИЗ СРАВНИТЕЛЬНЫХ ИНТЕГРАЛОВ; МЕТОД ЧЕСТЕРА — ФРИДМАНА — УРСЕЛЛА (ЧФУ)
- 5.10. АСИМПТОТИЧЕСКОЕ ВЫЧИСЛЕНИЕ ПОЛЯ, ДИФРАГИРОВАННОГО НА ОТВЕРСТИИ
- 5.10.1. Каустика дифрагированных лучей
- 5.10.2. Дифракция на острие
- 5.10.3. Дифракция от угла
- 5.11. АСИМПТОТИЧЕСКАЯ ФОРМА РАЗЛОЖЕНИЯ ПОЛЕЙ ПО ПЛОСКИМ ВОЛНАМ
- 5.12. ФОРМУЛА УИЛЛИСА
- ГЛАВА 6. ДИФРАКЦИЯ СВЕТА НА ОТВЕРСТИИ И РАССЕЯНИЕ НА МЕТАЛЛИЧЕСКИХ И ДИЭЛЕКТРИЧЕСКИХ ПРЕДМЕТАХ
- 6.2. ДИФРАКЦИЯ НА КЛИНЕ
- 6.2.1. Клин с конечным импедансом
- 6.2.2. Дифракционная матрица для искривленной кромки
- 6.2.3. Дифракция на диэлектрическом клине
- 6.3. ДИФРАКЦИЯ НА ЩЕЛИ
- 6.4. ДИФРАКЦИЯ НА ДИЭЛЕКТРИЧЕСКОМ ЦИЛИНДРЕ
- 6.4.1. Дифракция на круговом диэлектрическом цилиндре
- 6.5. S-МАТРИЦА И ПРЕДСТАВЛЕНИЕ ВАТСОНА — РЕДЖЕ
- 6.5.1. Дебаевское разложение
- 6.5.2. Представление Ватсона — Редже
- 6.5.3. Первый член дебаевского разложения
- 6.6. ПОВЕРХНОСТНЫЕ ДИФРАКЦИОННЫЕ ВОЛНЫ
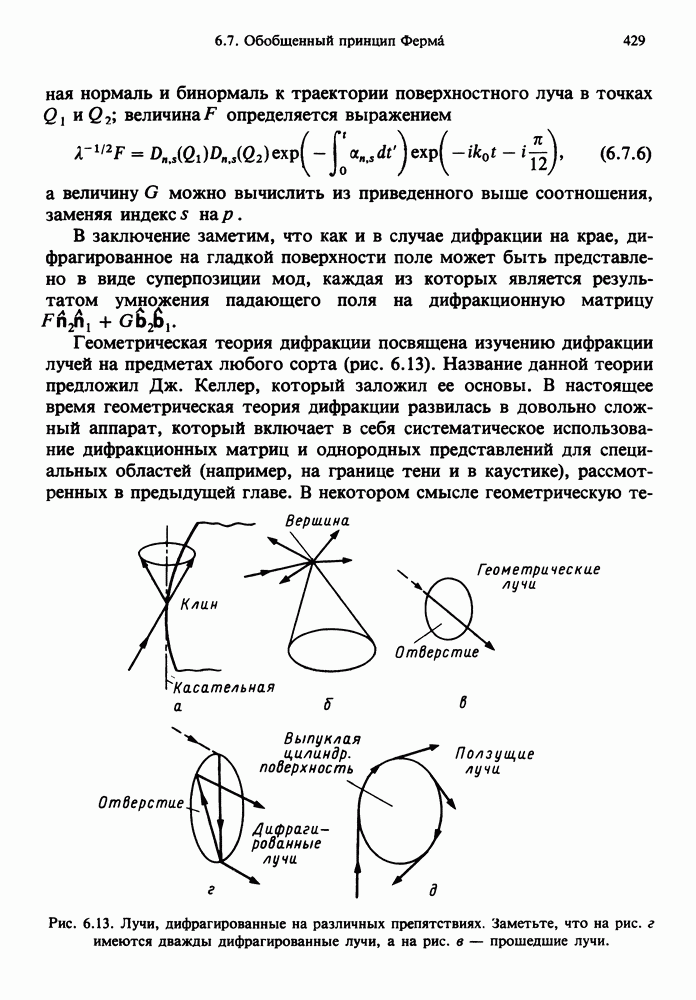
- 6.7. ОБОБЩЕННЫЙ ПРИНЦИП ФЕРМА И ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ДИФРАКЦИИ
- 6.8. РАССЕЯНИЕ СВЕТА ДИЭЛЕКТРИЧЕСКИМИ ТЕЛАМИ
- 6.9. ПРИБЛИЖЕНИЕ ФИЗИЧЕСКОЙ ОПТИКИ ДЛЯ ИДЕАЛЬНО ПРОВОДЯЩЕГО ТЕЛА
- 6.10. ЭЛЕКТРОМАГНИТНАЯ ТЕОРИЯ ДИФРАКЦИИ НА ИДЕАЛЬНО ПРОВОДЯЩИХ И ДИЭЛЕКТРИЧЕСКИХ ДИФРАКЦИОННЫХ РЕШЕТКАХ
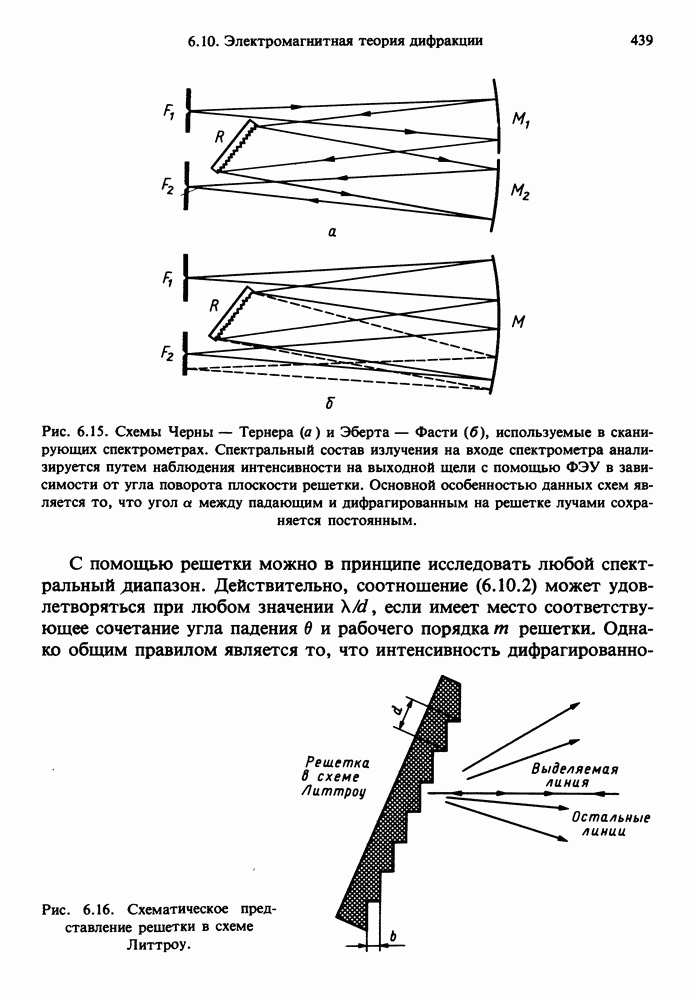
- 6.10.1. Применения дифракционных решеток
- 6.10.2. Поле, дифрагированное на решетке
- 6.10.3. Представление Рэлея для металлической решетки
- 6.10.4. Интегральный метод
- 6.10.5. Разрешающая способность
- 6.10.6. Эффективность решетки и аномалии Вуда
- 6.11. РАССЕЯНИЕ НА ТЕЛАХ КОНЕЧНЫХ РАЗМЕРОВ
- 6.11.1. Сечение экстинкции и оптическая теорема
- 6.12. РАЗЛОЖЕНИЕ РАССЕЯННОГО ПОЛЯ ПО СФЕРИЧЕСКИМ ГАРМОНИКАМ
- 6.12.1. Радиальное волновое уравнение
- 6.12.2. Векторные сферические гармоники
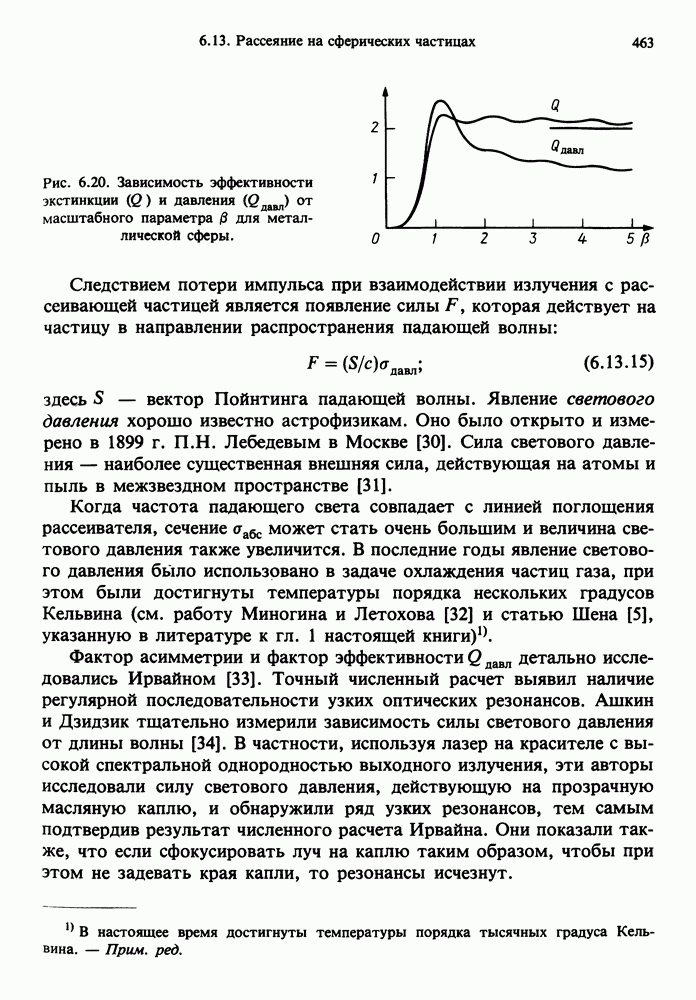
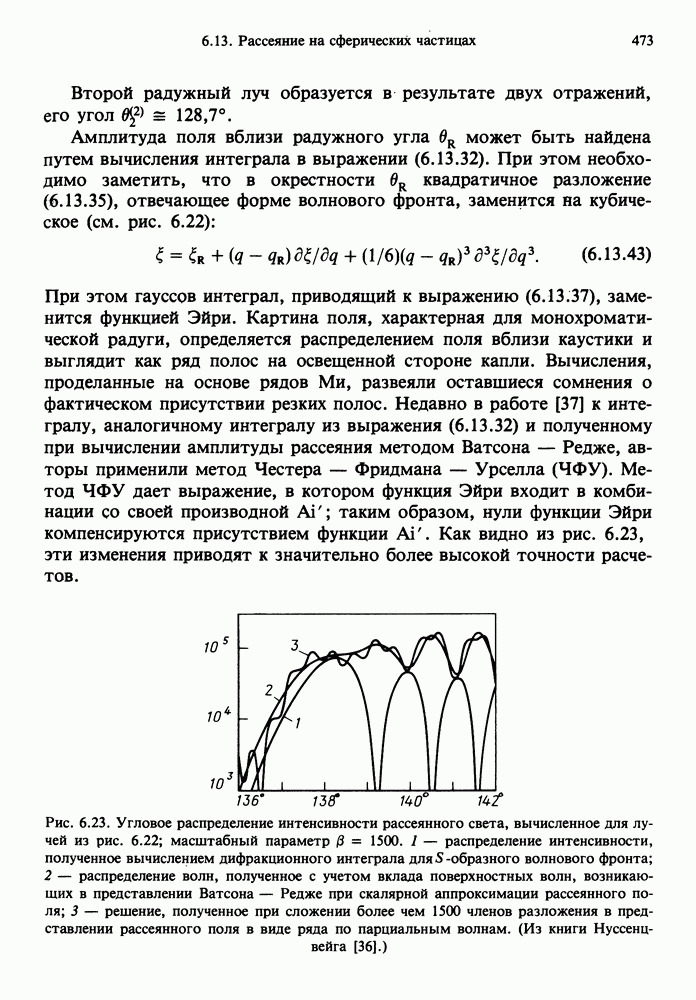
- 6.13. РАССЕЯНИЕ НА СФЕРИЧЕСКИХ ЧАСТИЦАХ
- 6.13.1. Разложение рассеянного поля по парциальным волнам
- 6.13.2. Амплитуды рассеяния S и фактор эффективности Q
- 6.13.3. Параметры Стокса для рассеянного поля
- 6.13.4. Малые сферы
- 6.13.5. Собственные моды диэлектрической сферы
- 6.13.6. Теория ван де Хюлста для сферы очень большого размера
- 6.13.7. Теория глории и радуги в приближении геометрической оптики
- ГЛАВА 7. ОПТИЧЕСКИЕ РЕЗОНАТОРЫ И ИНТЕРФЕРОМЕТРЫ ФАБРИ — ПЕРО
- 7.1. ОБЩИЕ СВОЙСТВА РЕЗОНАТОРОВ ДЛЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- 7.1.2. Микроволновые (СВЧ) и оптические генераторы
- 7.2. ОБЩИЕ СВОЙСТВА ОПТИЧЕСКИХ РЕЗОНАТОРОВ
- 7.3. ЧАСТОТНЫЙ ОТКЛИК РЕЗОНАТОРА
- 7.4. РАССМОТРЕНИЕ ЗАКРЫТОГО ЭЛЛИПТИЧЕСКОГО РЕЗОНАТОРА В РАМКАХ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
- 7.5. ЛИНЕЙНЫЕ РЕЗОНАТОРЫ
- 7.6. РАССМОТРЕНИЕ РЕЗОНАТОРА КАК ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЗ
- 7.7. ПОЛЯ ОТ ИСТОЧНИКОВ, РАСПОЛОЖЕННЫХ В КОМПЛЕКСНОЙ ПЛОСКОСТИ
- 7.8. ЭРМИТ-ГАУССОВЫ И ЛАГЕРР-ГАУССОВЫ ПУЧКИ
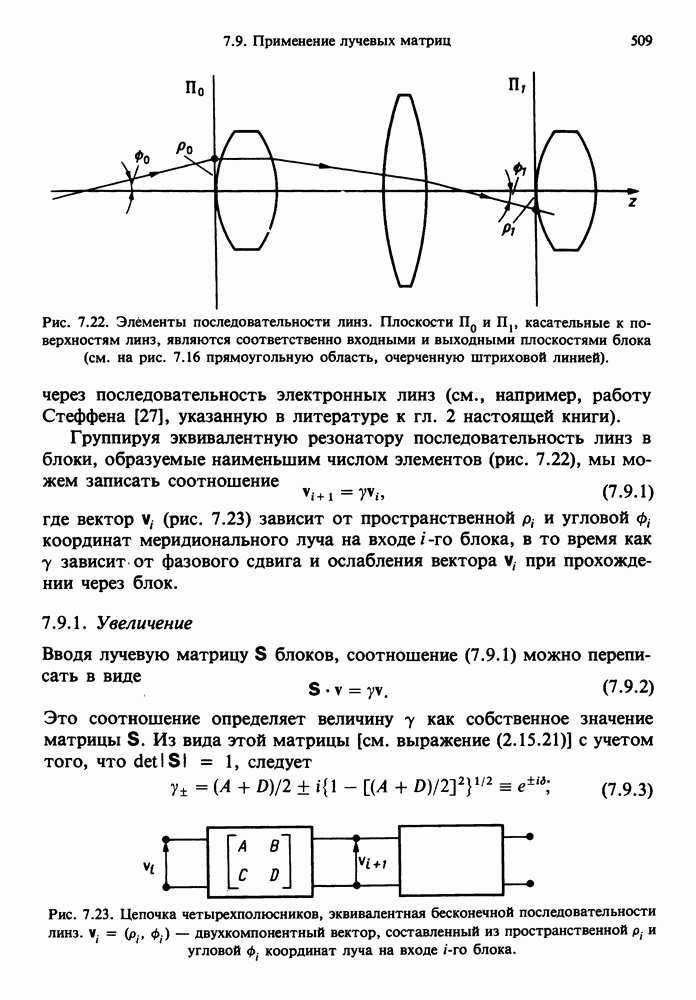
- 7.9. ПРИМЕНЕНИЕ ЛУЧЕВЫХ МАТРИЦ ДЛЯ ОПИСАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЗ, ЭКВИВАЛЕНТНОЙ РЕЗОНАТОРУ
- 7.9.1. Увеличение
- 7.9.2. Комплексная кривизна волнового фронта
- 7.9.3. Диаграмма устойчивости Бойда — Когельника
- 7.10. МОДОВОЕ ПРЕДСТАВЛЕНИЕ ПОЛЯ ВНУТРИ УСТОЙЧИВОГО РЕЗОНАТОРА, НЕ ИМЕЮЩЕГО ДИФРАКЦИОННЫХ ПОТЕРЬ
- 7.10.1. Приближение медленноменяющейся амплитуды
- 7.11. УСТОЙЧИВЫЕ РЕЗОНАТОРЫ
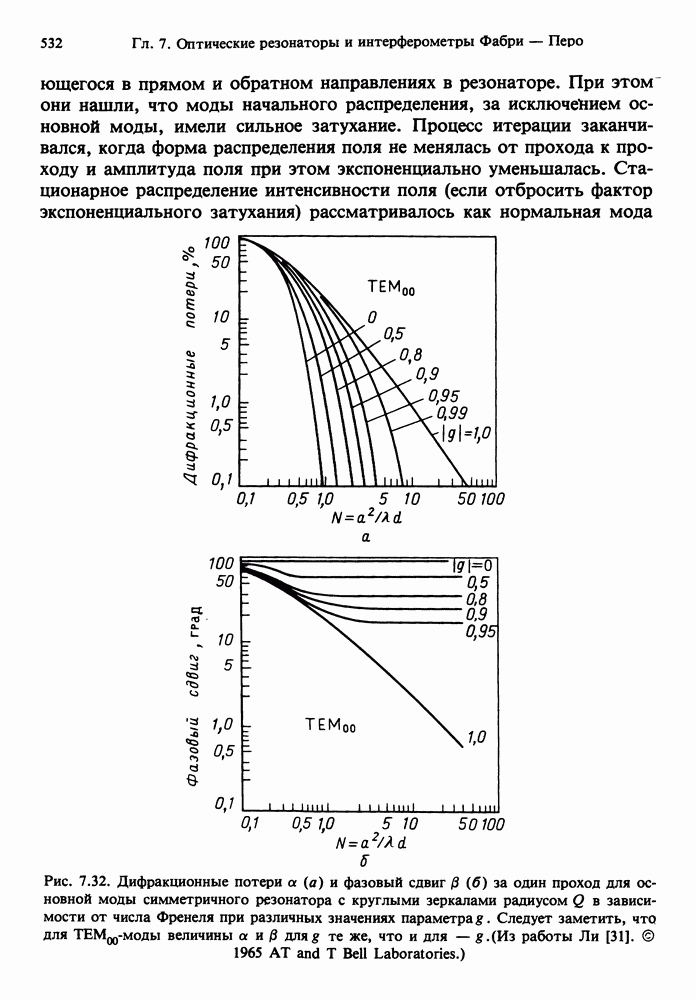
- 7.11.1. Дифракционные потери и расходимость
- 7.11.2. Влияние разъюстировки резонатора
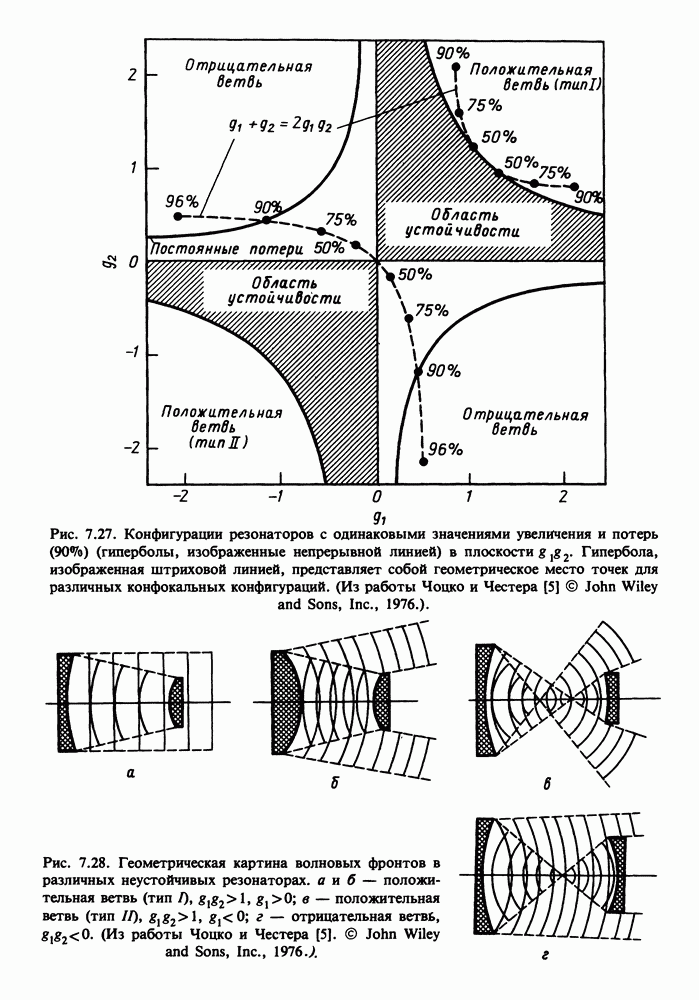
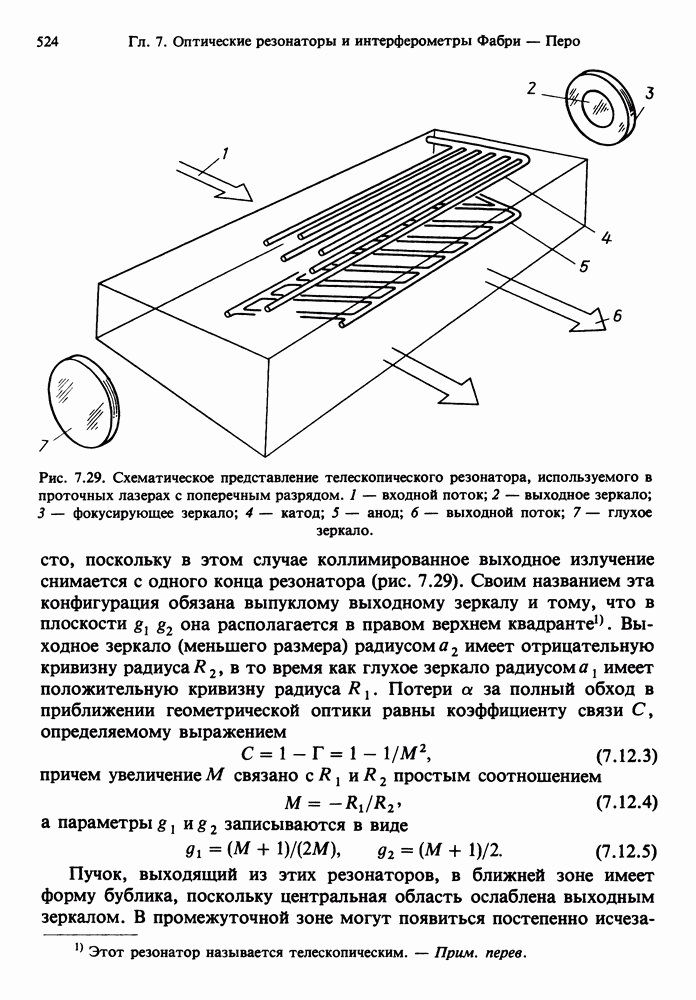
- 7.12. НЕУСТОЙЧИВЫЕ РЕЗОНАТОРЫ
- 7.13. ВОЛНОВАЯ ТЕОРИЯ ПУСТЫХ РЕЗОНАТОРОВ
- 7.14. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФОКСА — ЛИ
- 7.14.1. Потери за полный проход
- 7.14.2. Фазовый сдвиг
- 7.14.3 Симметричные резонаторы
- 7.14.4. Соотношения подобия
- 7.15. МЕТОДЫ РАСЧЕТА МОДОВЫХ КОНФИГУРАЦИЙ
- 7.15.2. Алгоритм быстрого фурье-преобразования
- 7.15.3. Вычисление мод высокого порядка
- 7.16. УСТОЙЧИВЫЕ РЕЗОНАТОРЫ С ПРЯМОУГОЛЬНЫМИ ЗЕРКАЛАМИ
- 7.16.1. Конфокальный резонатор
- 7.16.2. Теория Вайнилтейна для концентрических и плоскопараллельных резонаторов
- 7.17. РЕЗОНАТОРЫ С АКСИАЛЬНОЙ СИММЕТРИЕЙ
- 7.18. ДИФРАКЦИОННАЯ ТЕОРИЯ НЕУСТОЙЧИВЫХ РЕЗОНАТОРОВ
- 7.19. РЕЗОНАТОРЫ С АКТИВНОЙ СРЕДОЙ
- 7.19.1 Нелинейная диэлектрическая восприимчивость лазерной среды
- 7.19.2. Одномодовый режим
- 7.19.3. Одночастотная многомодовая генерация
- 7.19.4. Уравнения Ригрода
- 7.19.5. Выходная мощность
- 7.20. ПЕРЕСТРОЙКА ЧАСТОТЫ
- 7.20.2. Перестройка частоты с помощью призм, решеток, эталонов и резонансных отражателей
- 7.20.3. Одночастотная генерация с помощью интерферометра Фокса — Смита
- 7.20.4. Стабилизация частоты с помощью инжекции внешнего сигнала
- 7.21. ИНТЕРФЕРОМЕТРЫ ФАБРИ — ПЕРО
- 7.21.1. Коэффициент пропускания идеального интерферометра Фабри — Перо
- 7.21.2. Применение интерферометра Фабри — Перо
- 7.21.3 Составные интерферометры Фабри — Перо
- 7.21.4. Аппаратная функция интерферометра
- ГЛАВА 8. РАСПРОСТРАНЕНИЕ СВЕТА В ОПТИЧЕСКИХ ВОЛОКНАХ
- 8.1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- 8.2. ВОЛОКНА СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- 8.3. ГРАДИЕНТНЫЕ ВОЛОКНА
- 8.4. МОДОВАЯ ТЕОРИЯ
- 8.5. МОДОВАЯ ТЕОРИЯ ДЛЯ ВОЛОКОН СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- 8.6. СЛАБОНАПРАВЛЯЮЩИЕ ВОЛОКНА СО СТУПЕНЧАТЫМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- 8.7. ВОЛОКНА С ПАРАБОЛИЧЕСКИМ ПРОФИЛЕМ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ
- 8.8. НЕНАПРАВЛЯЕМЫЕ МОДЫ
- 8.9. ОДНОМОДОВЫЕ ВОЛОКНА
- 8.10. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ ВНУТРИ ВОЛОКНА
- 8.11. ЗАТУХАНИЕ
- 8.12. ДИСПЕРСИЯ МОД
- 8.13. ХРОМАТИЧЕСКАЯ ДИСПЕРСИЯ
- 8.14. МОДОВЫЙ ШУМ
- 8.15. ТЕОРИЯ СВЯЗАННЫХ МОД
- 8.16. СТАТИСТИЧЕСКАЯ ТЕОРИЯ РАСПРОСТРАНЕНИЯ В СИСТЕМЕ ОПТИЧЕСКИХ ВОЛОКОН
- 8.17. ОПТИЧЕСКИЕ ВОЛОКНА, СОХРАНЯЮЩИЕ ПОЛЯРИЗАЦИЮ ИЗЛУЧЕНИЯ
- 8.18. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ В ОПТИЧЕСКИХ ВОЛОКНАХ
- 8.19. САМОИНДУЦИРОВАННЫЕ НЕЛИНЕЙНЫЕ ЭФФЕКТЫ
- 8.19.1. Фазовая самомодуляция
- 8.19.2. Солитоны
- 8.19.3. Вырожденное четырехволновое смешение