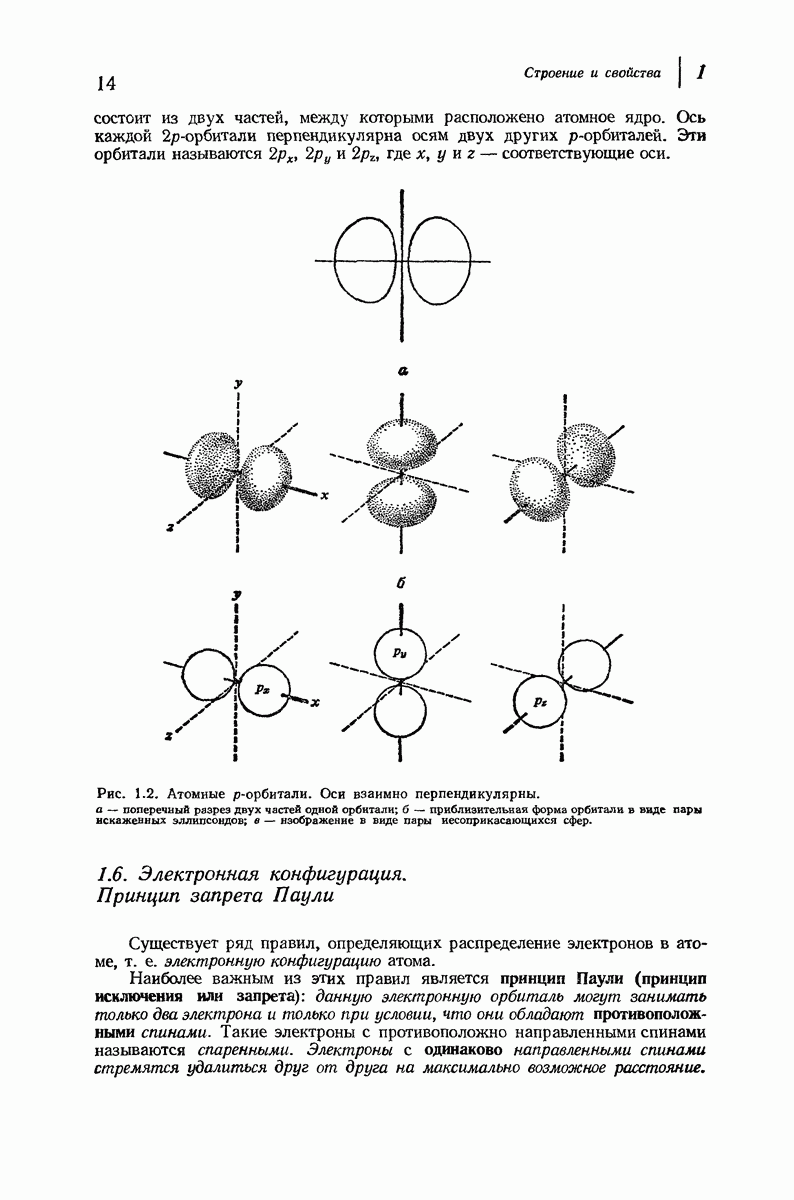
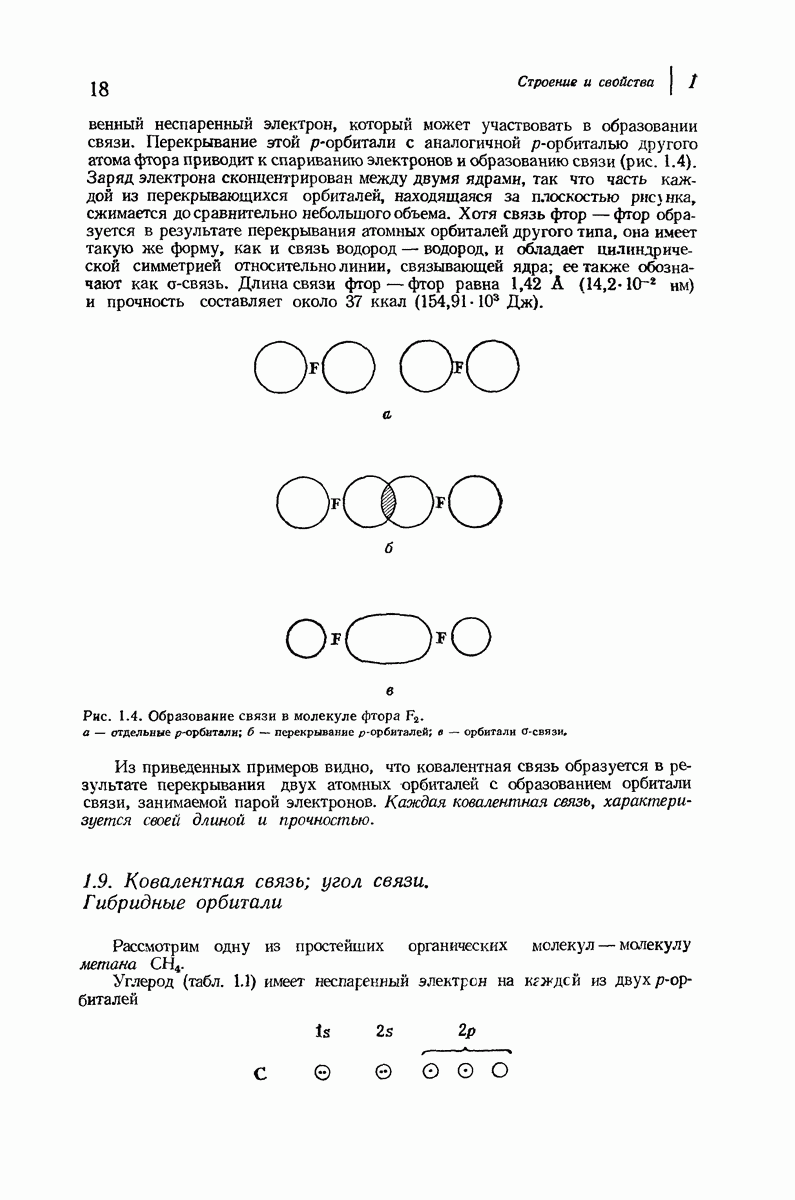
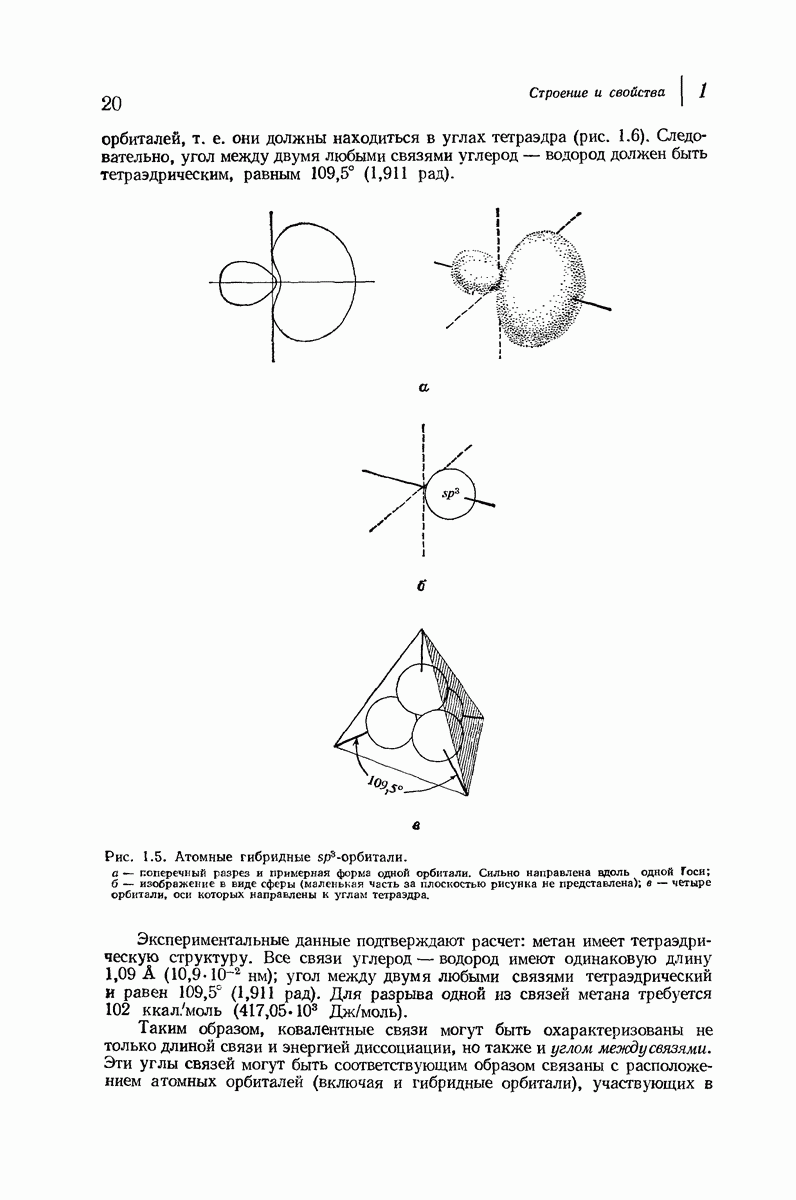
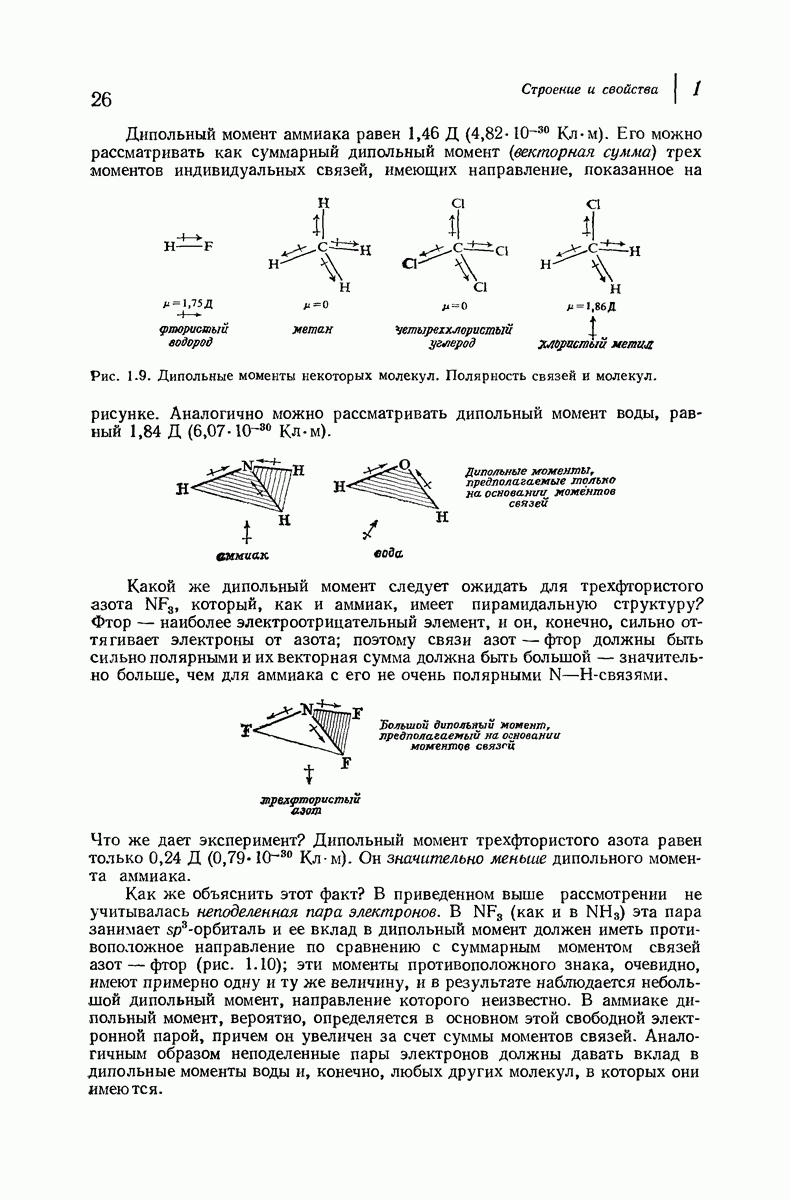
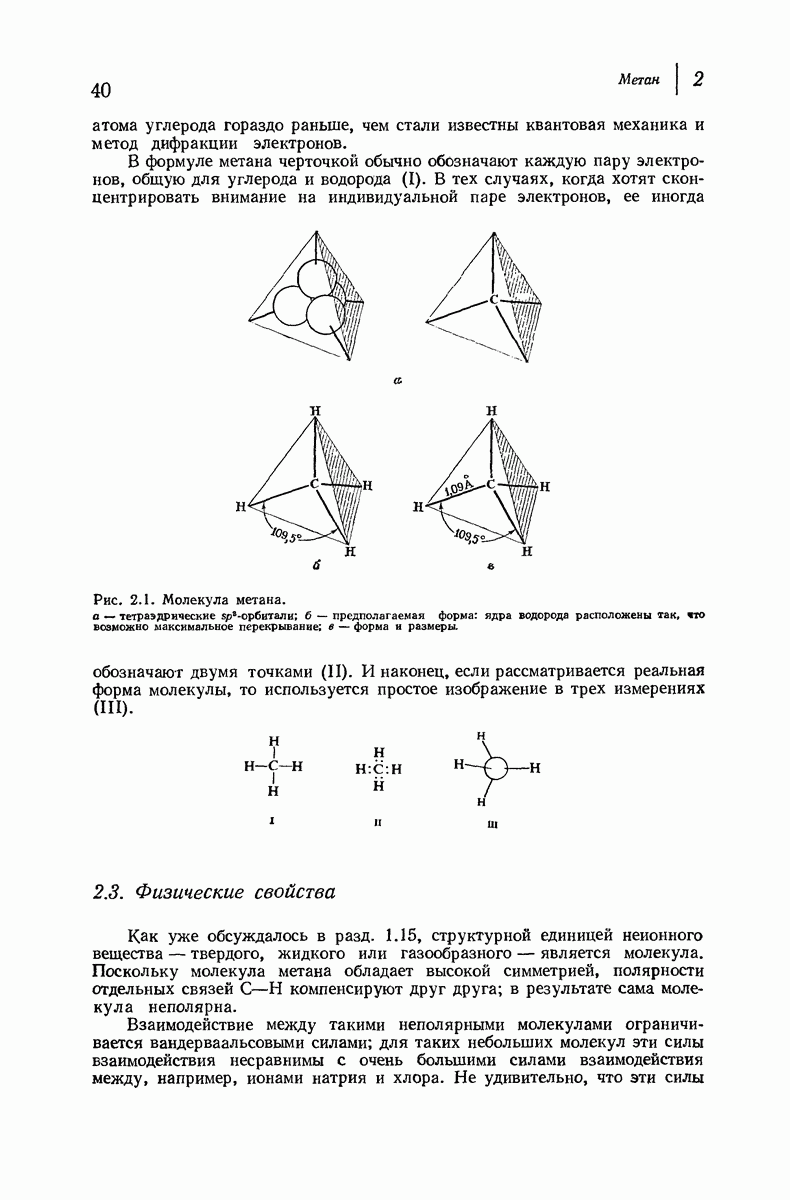
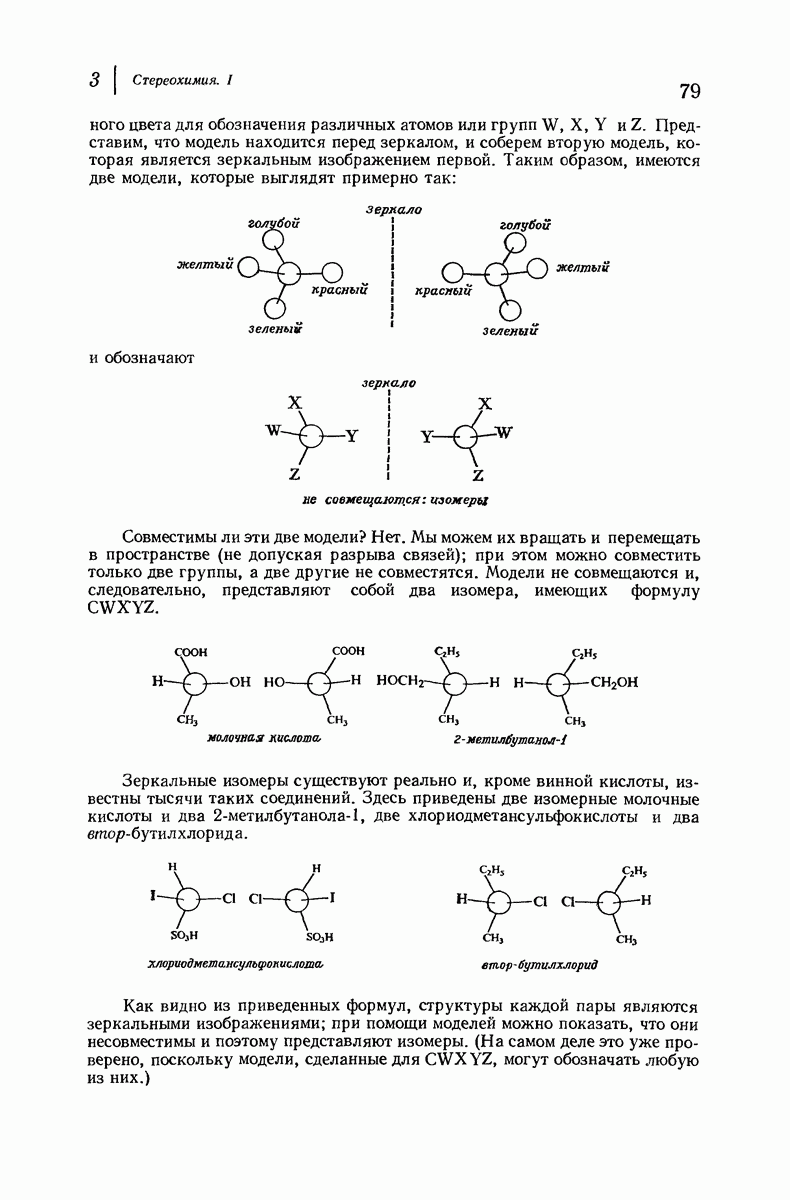
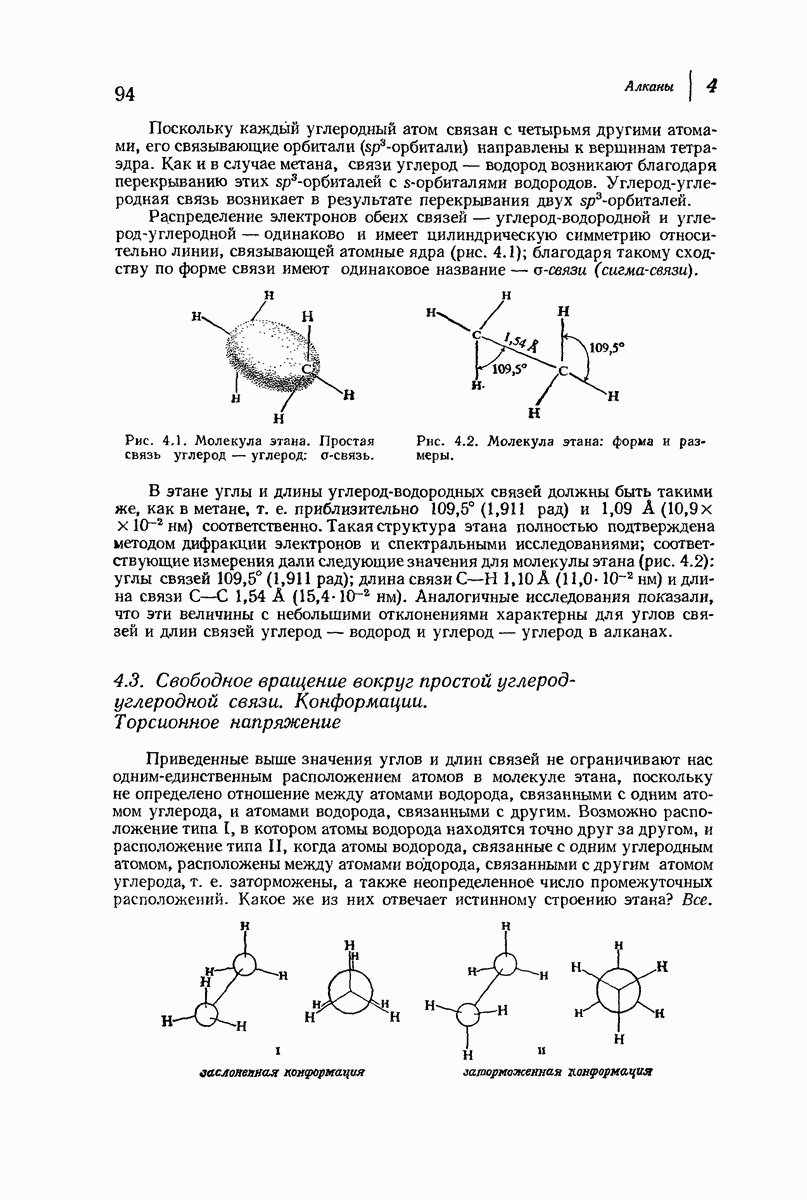
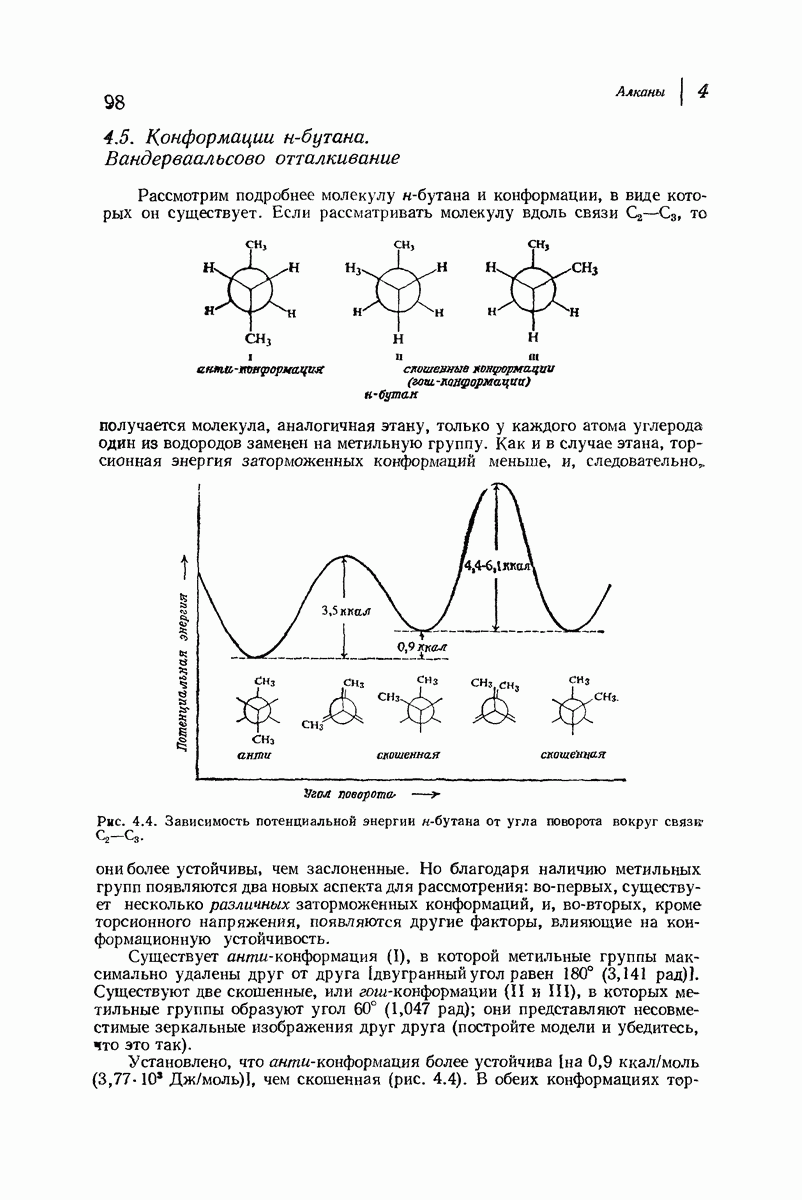
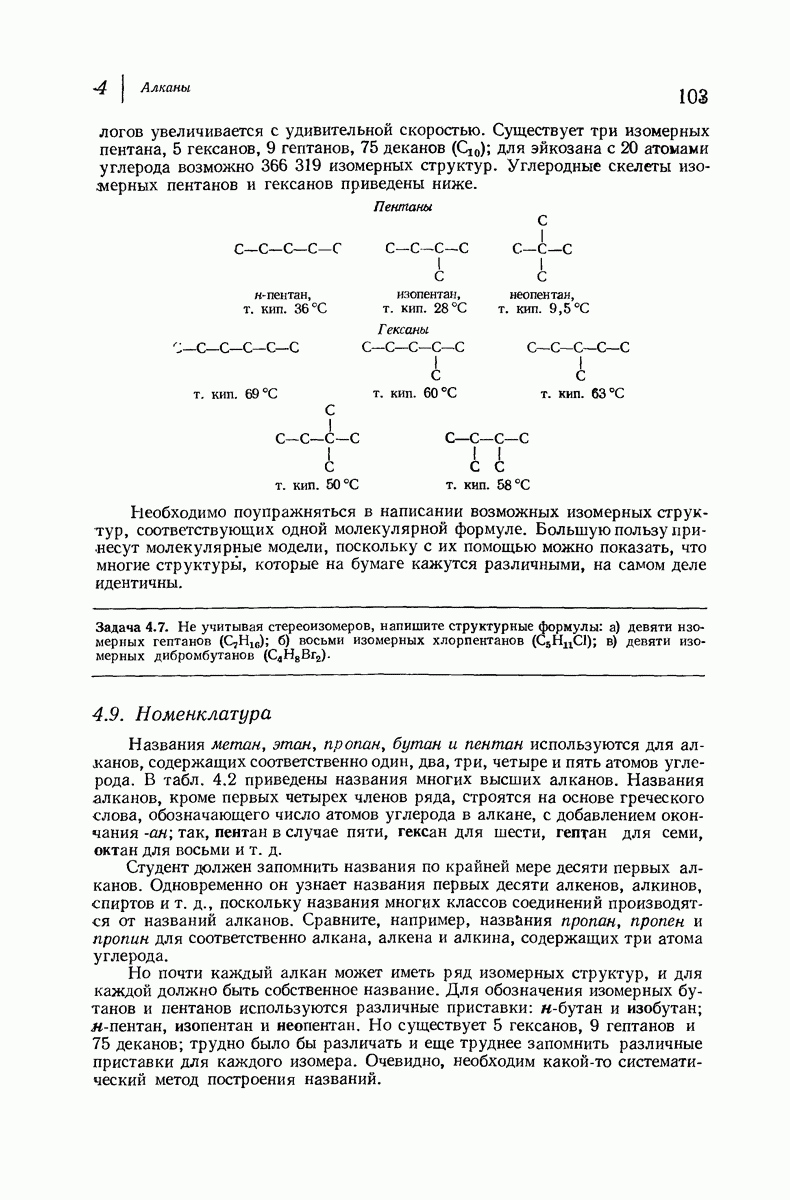
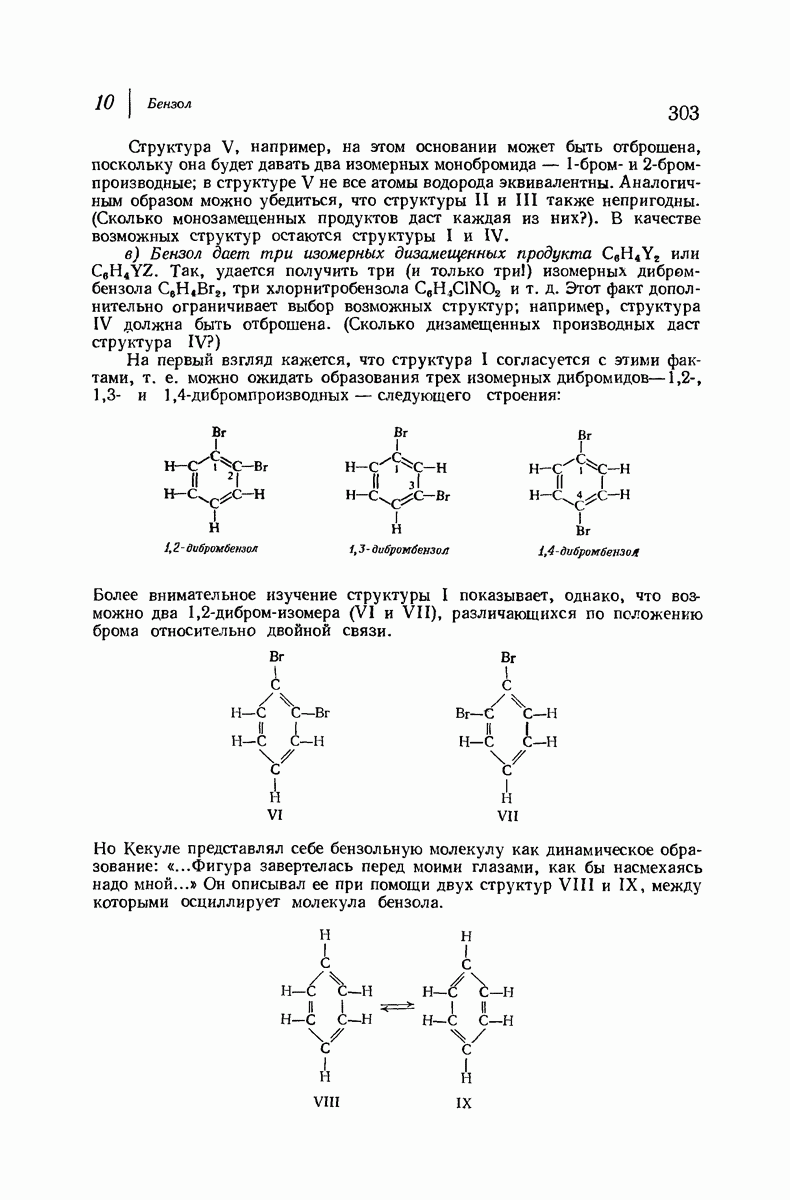
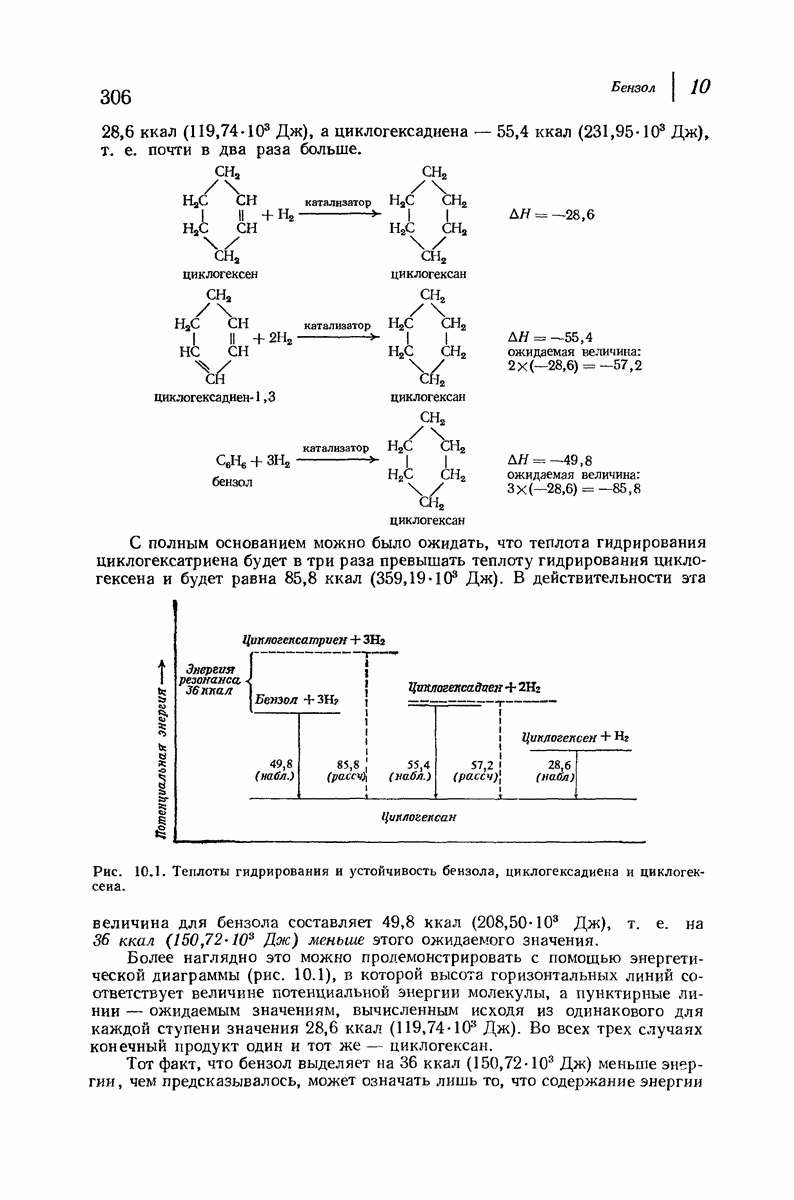
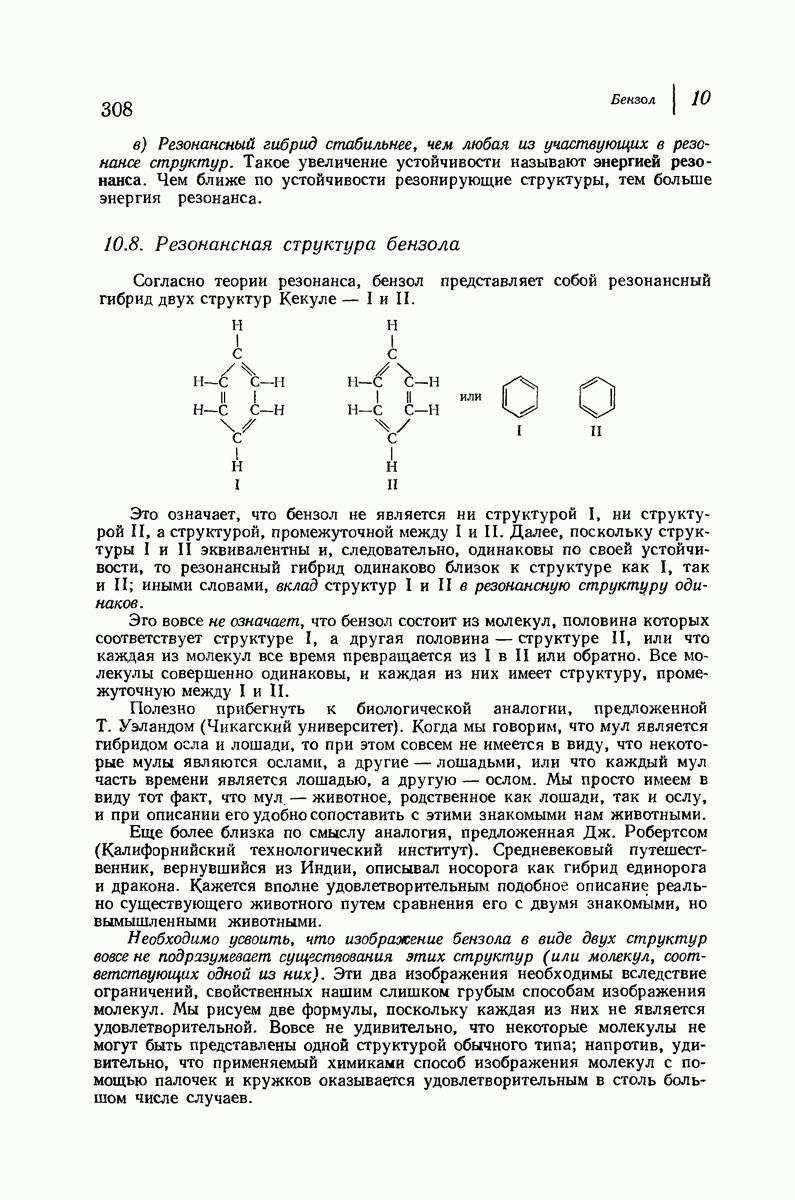
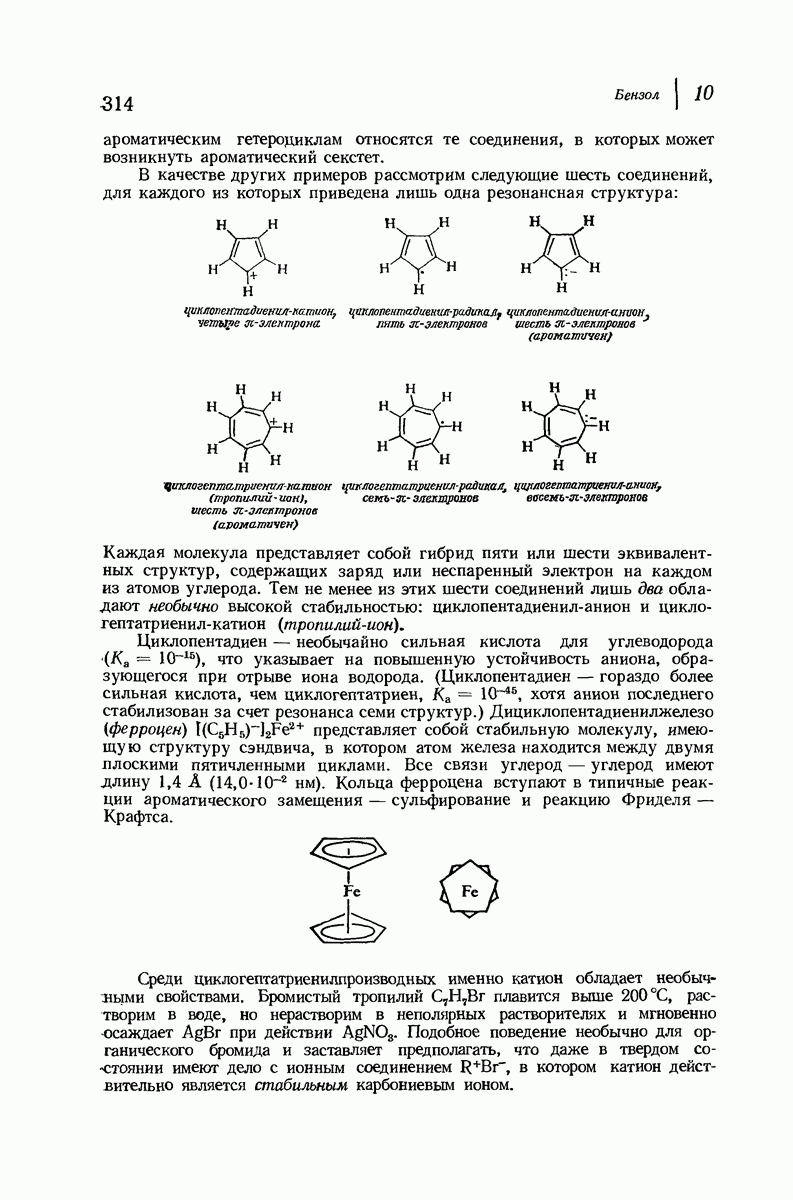
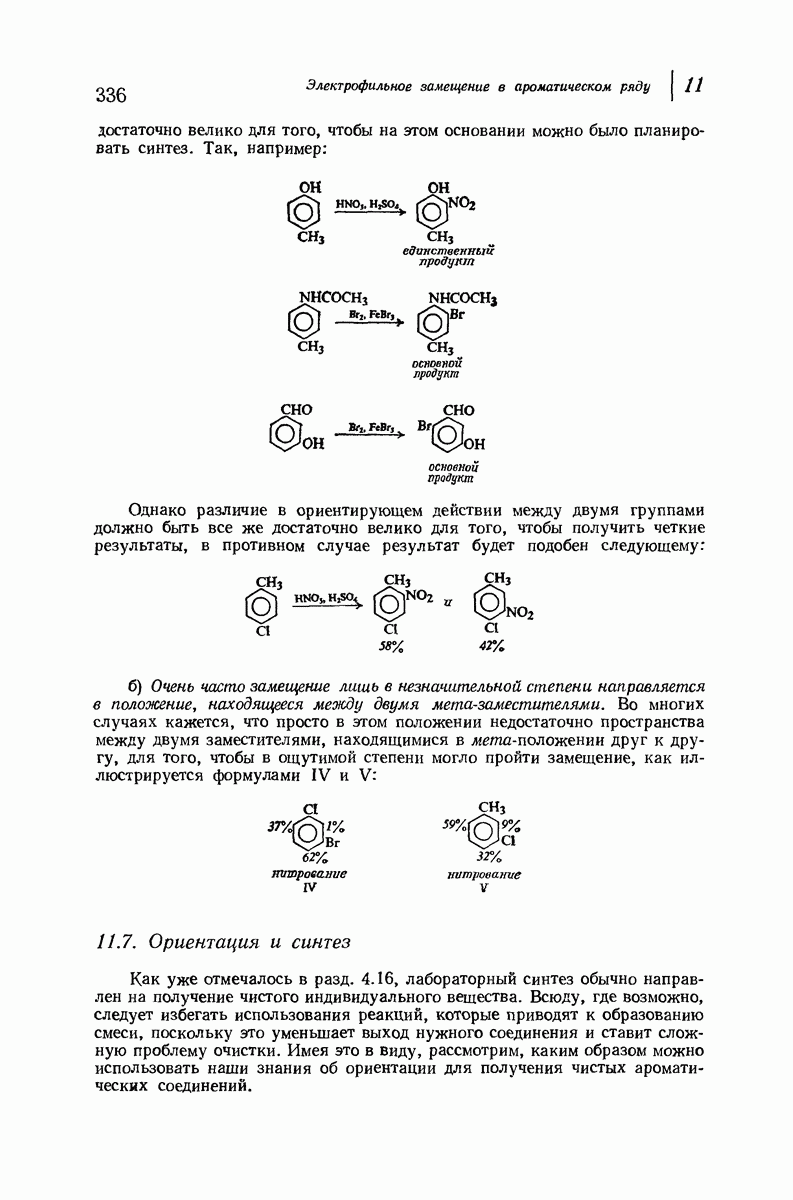
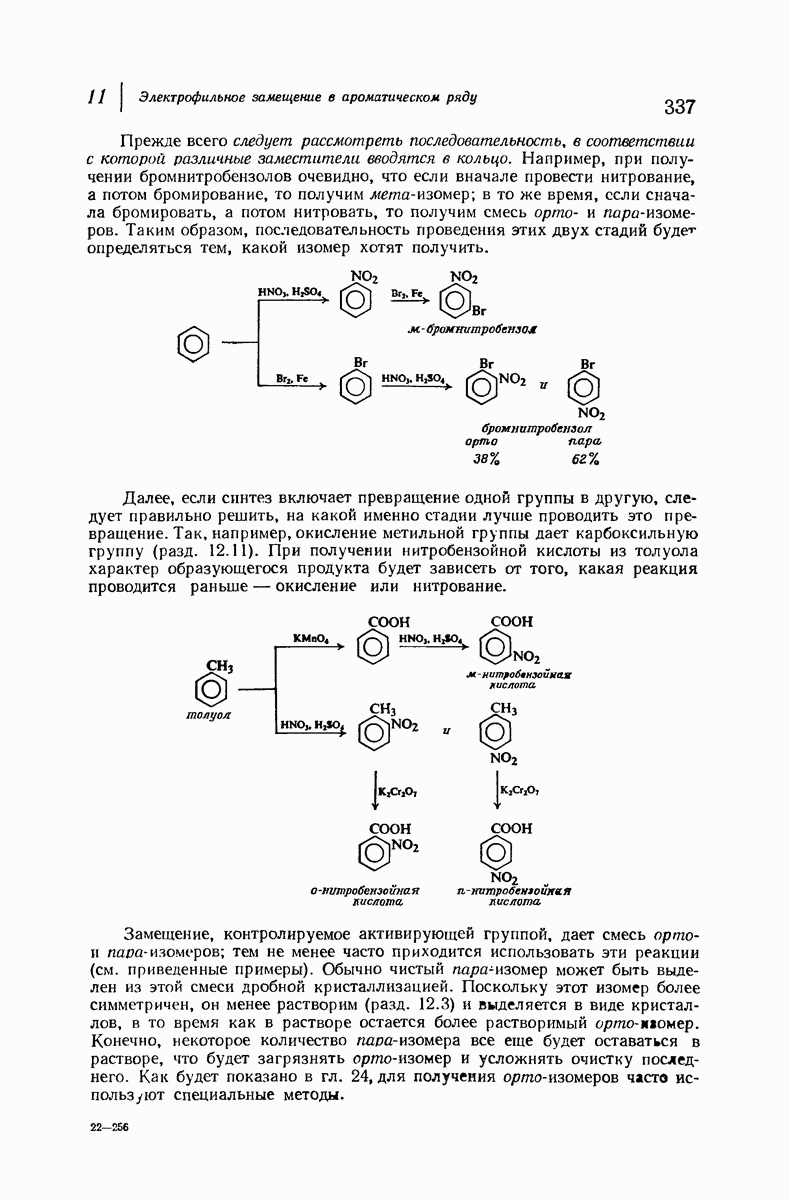
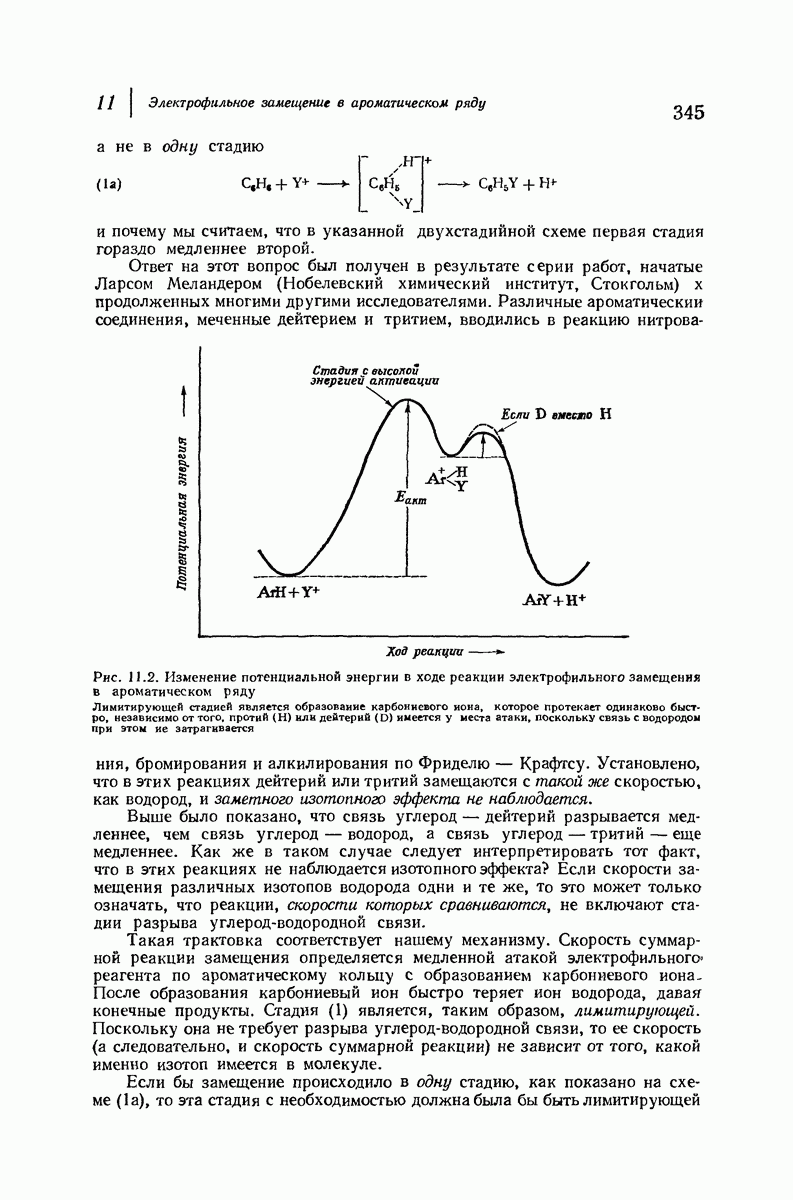
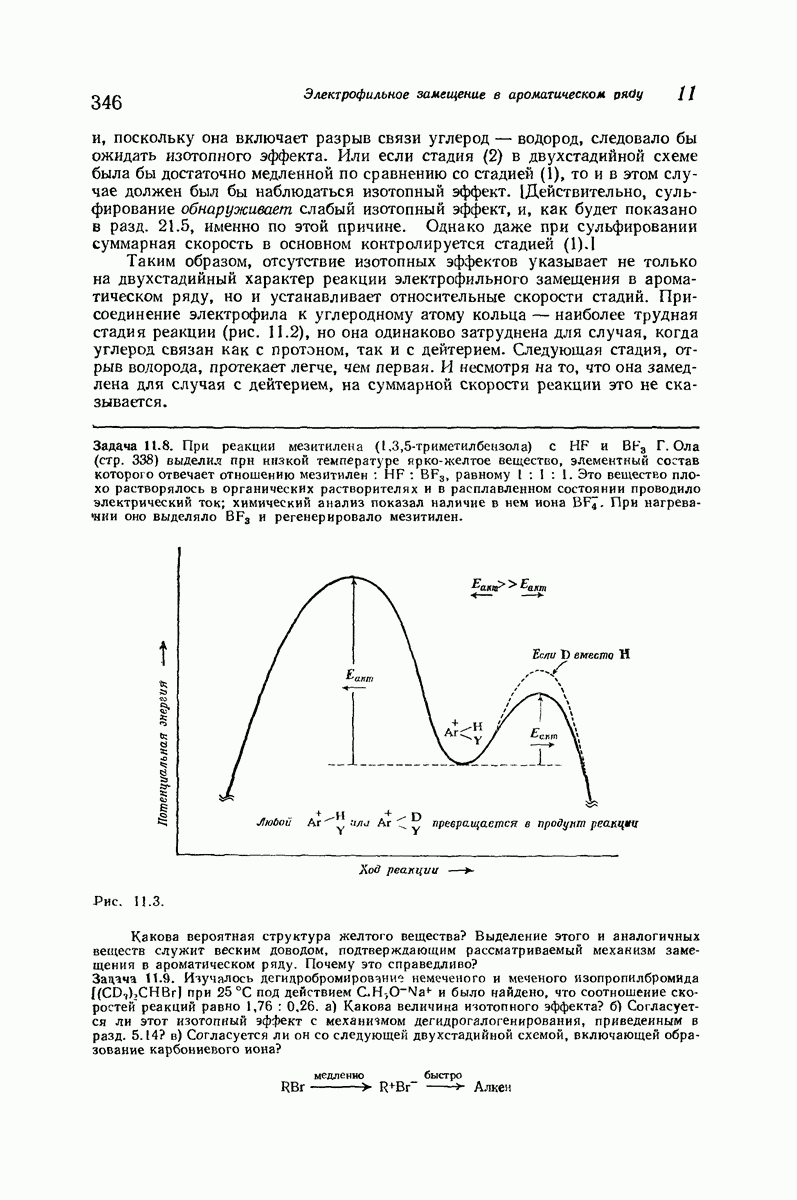
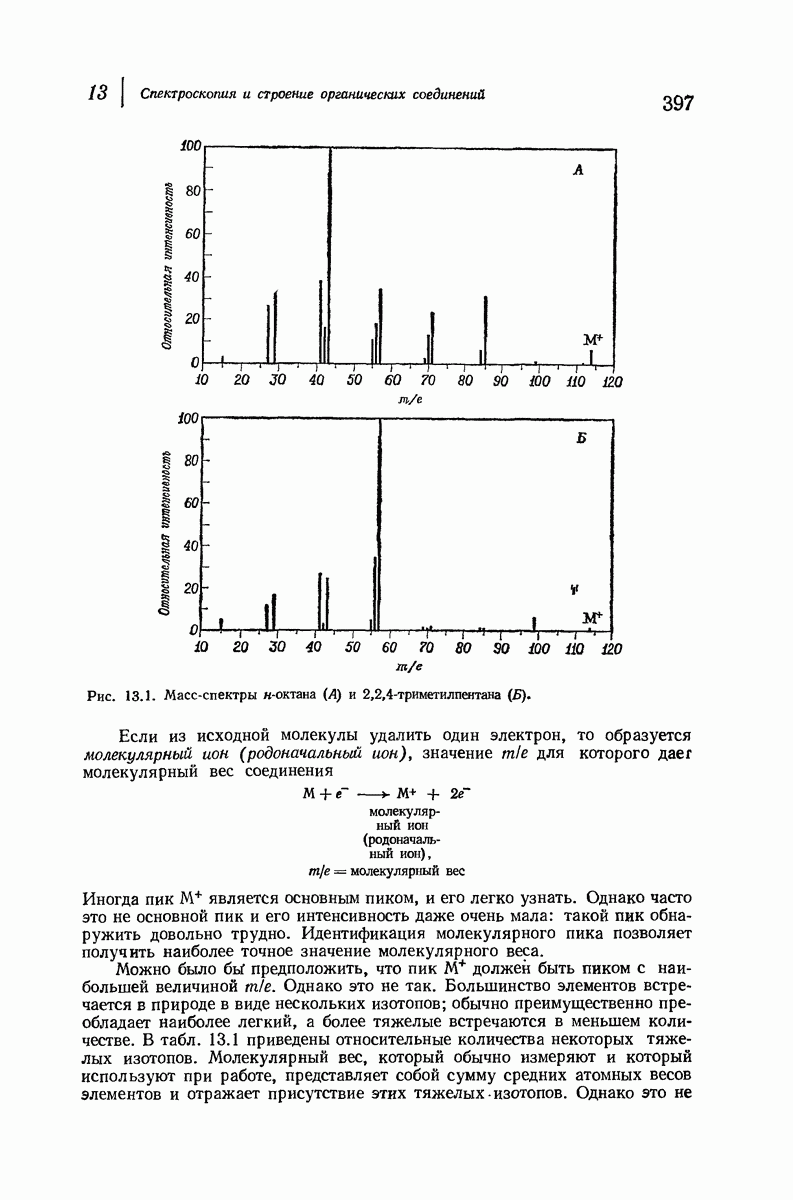
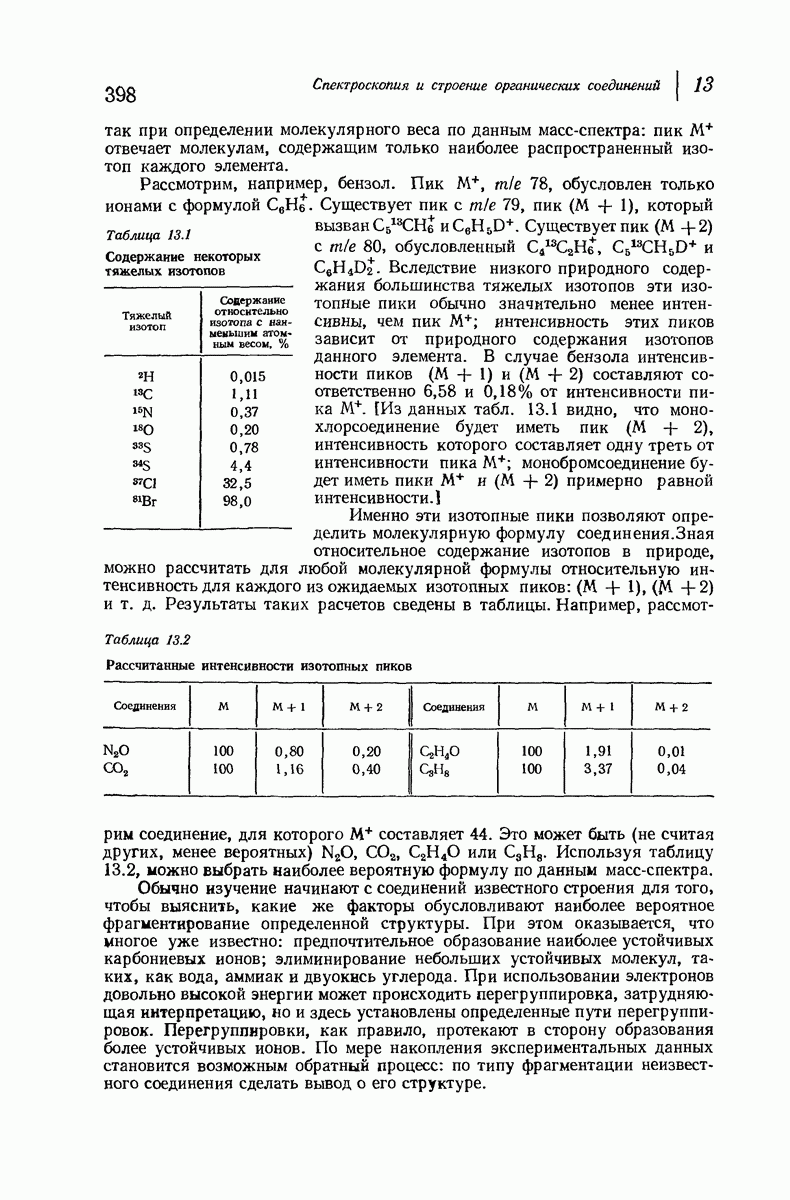
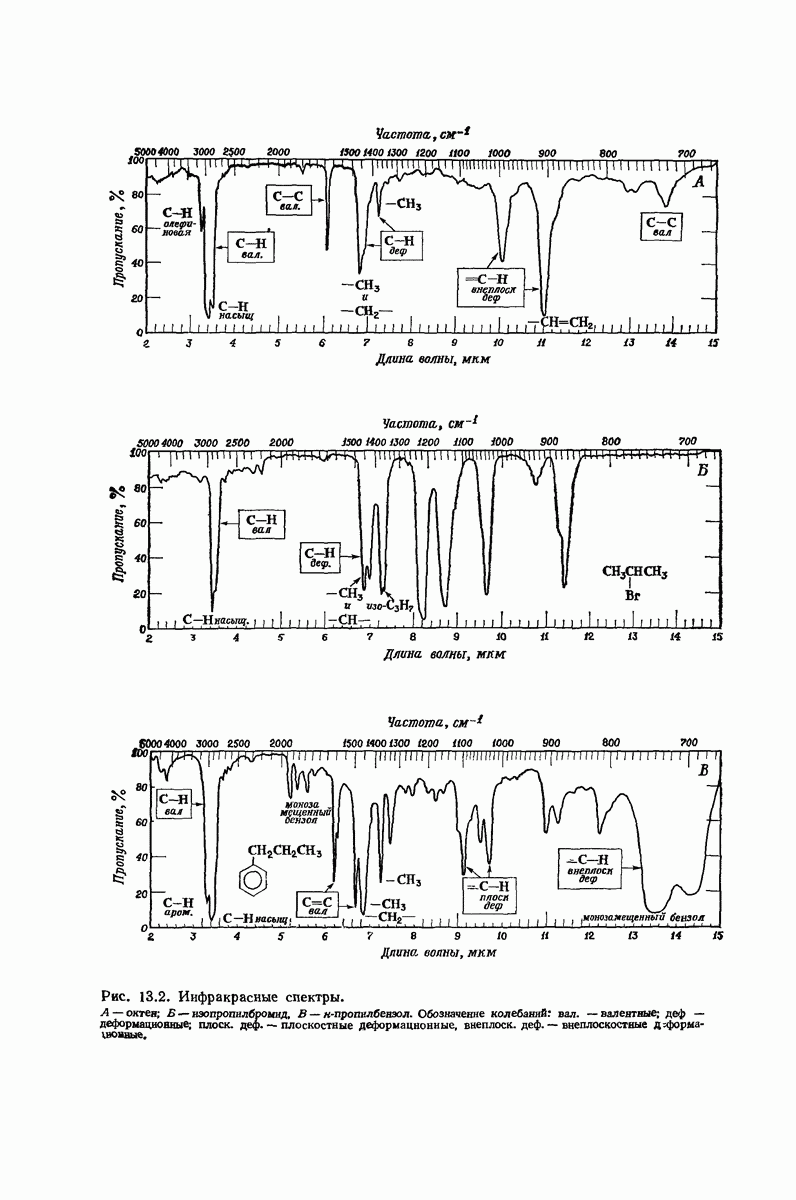
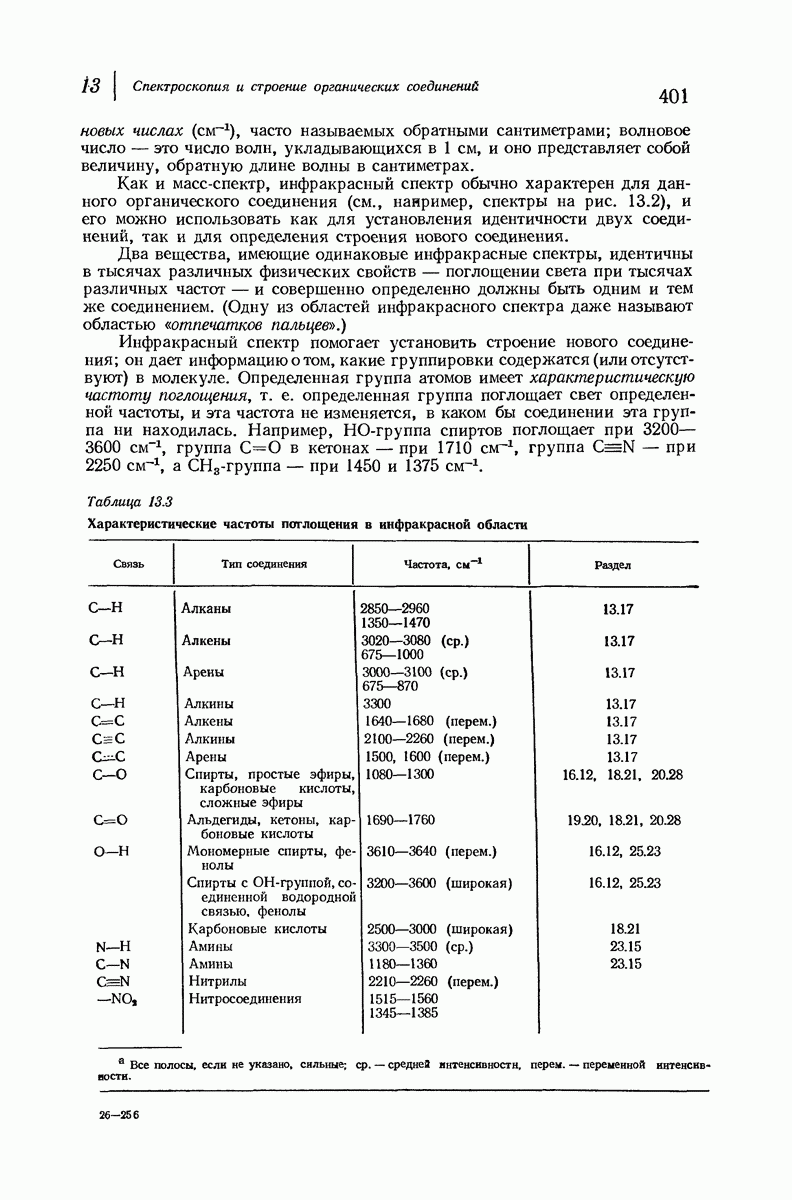
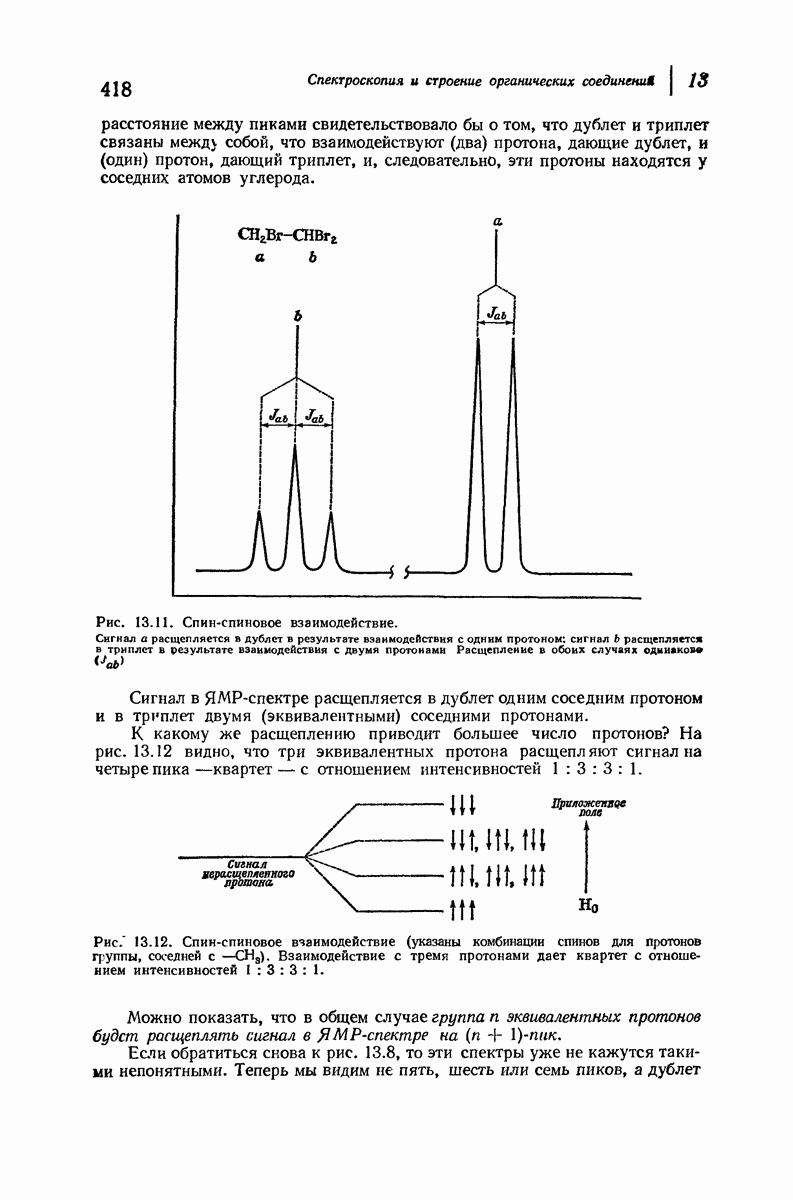
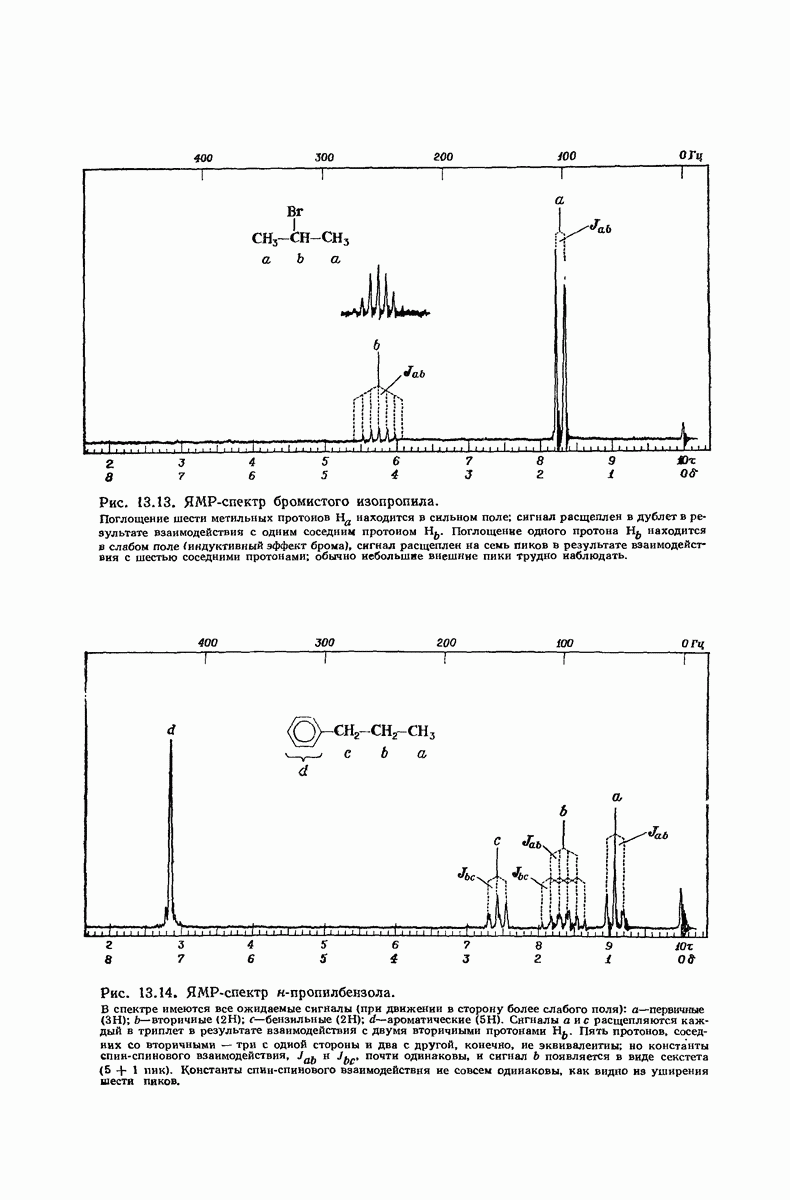
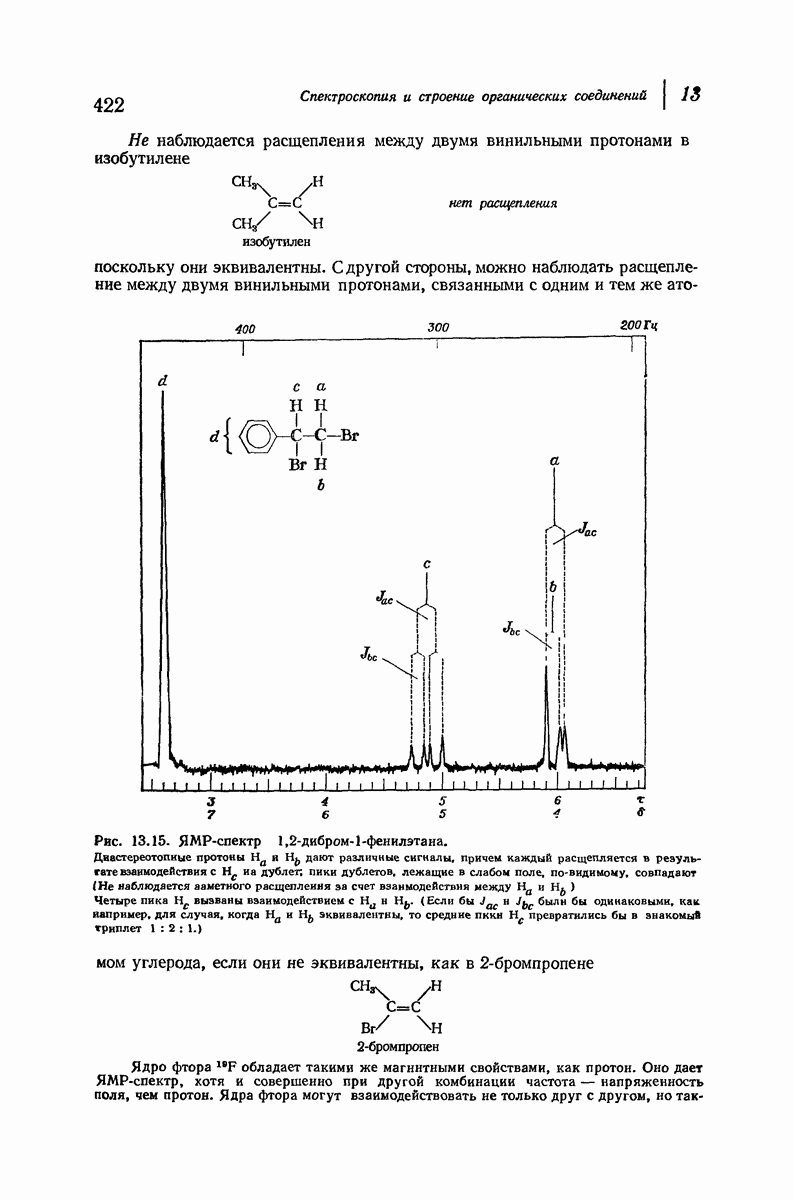
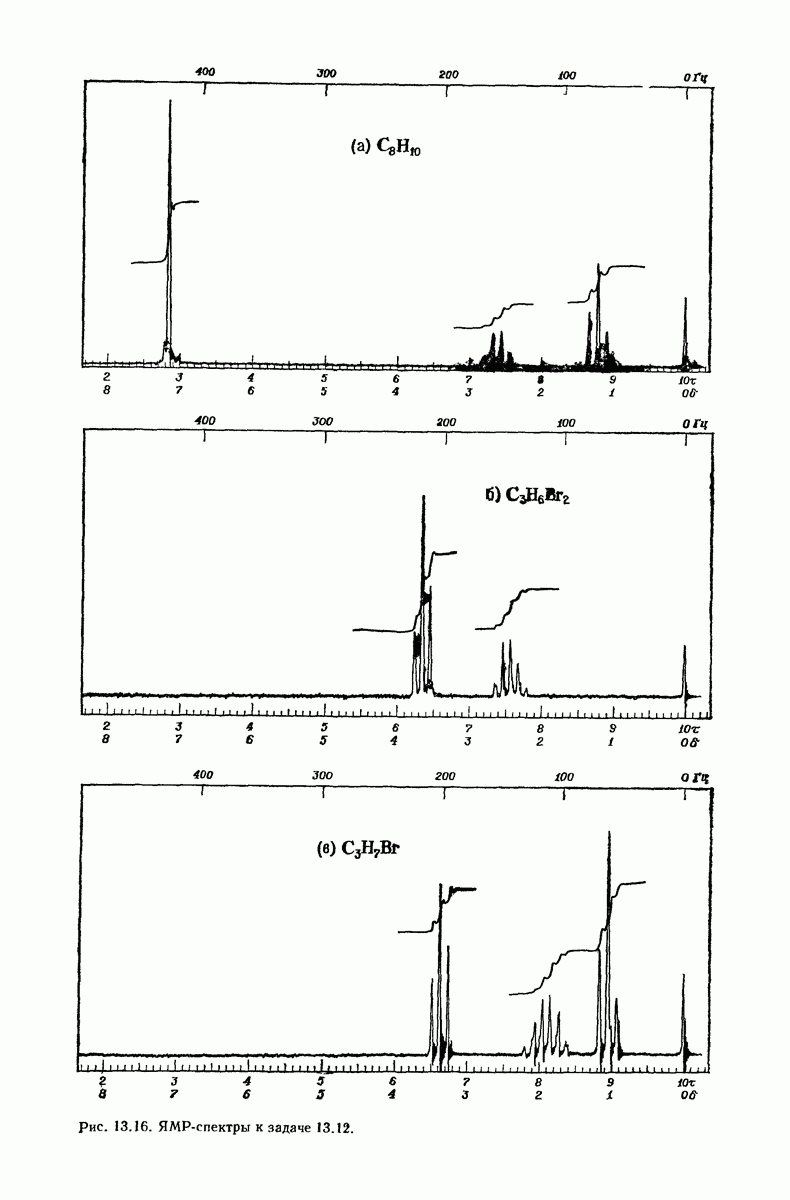
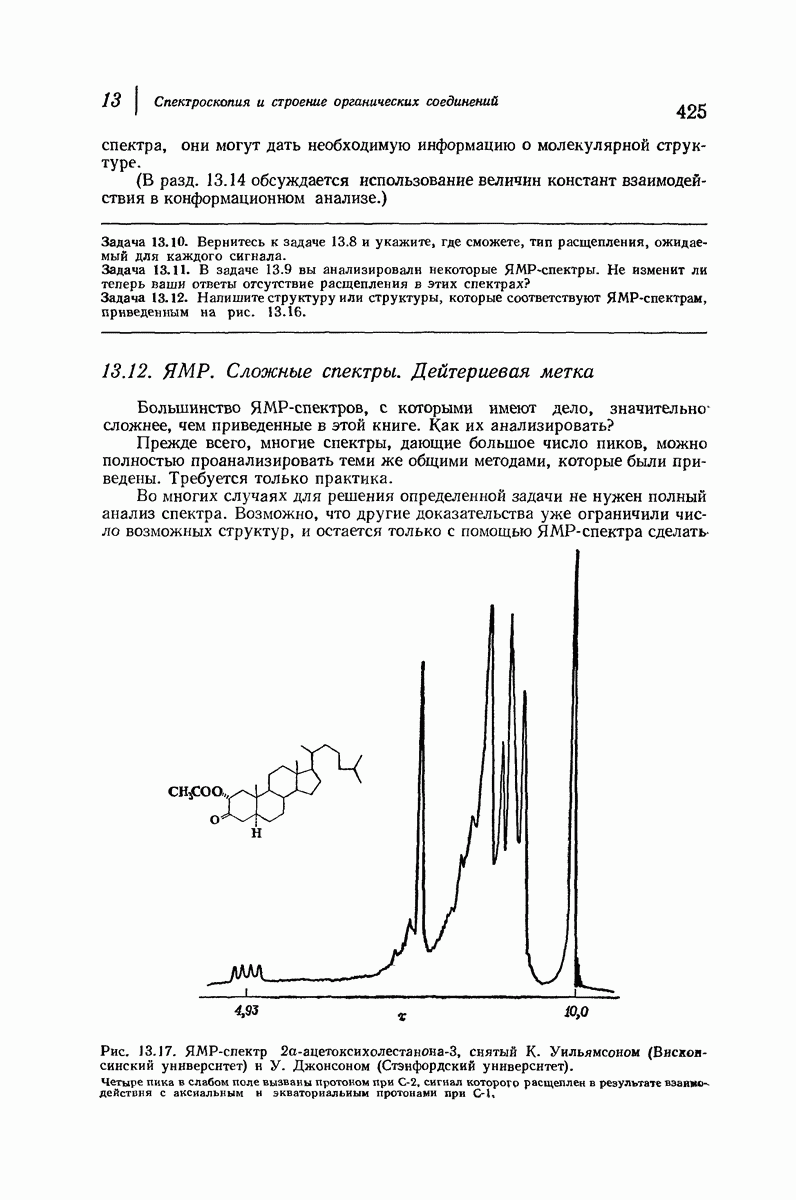
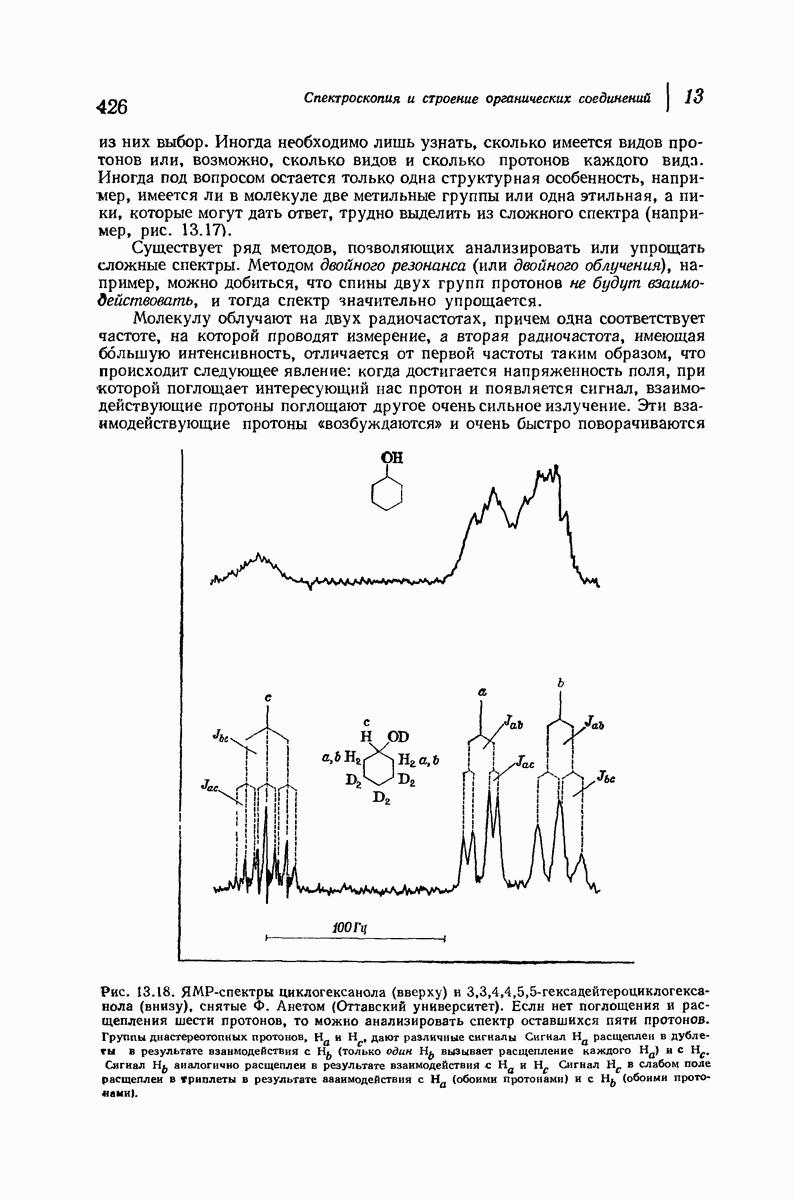
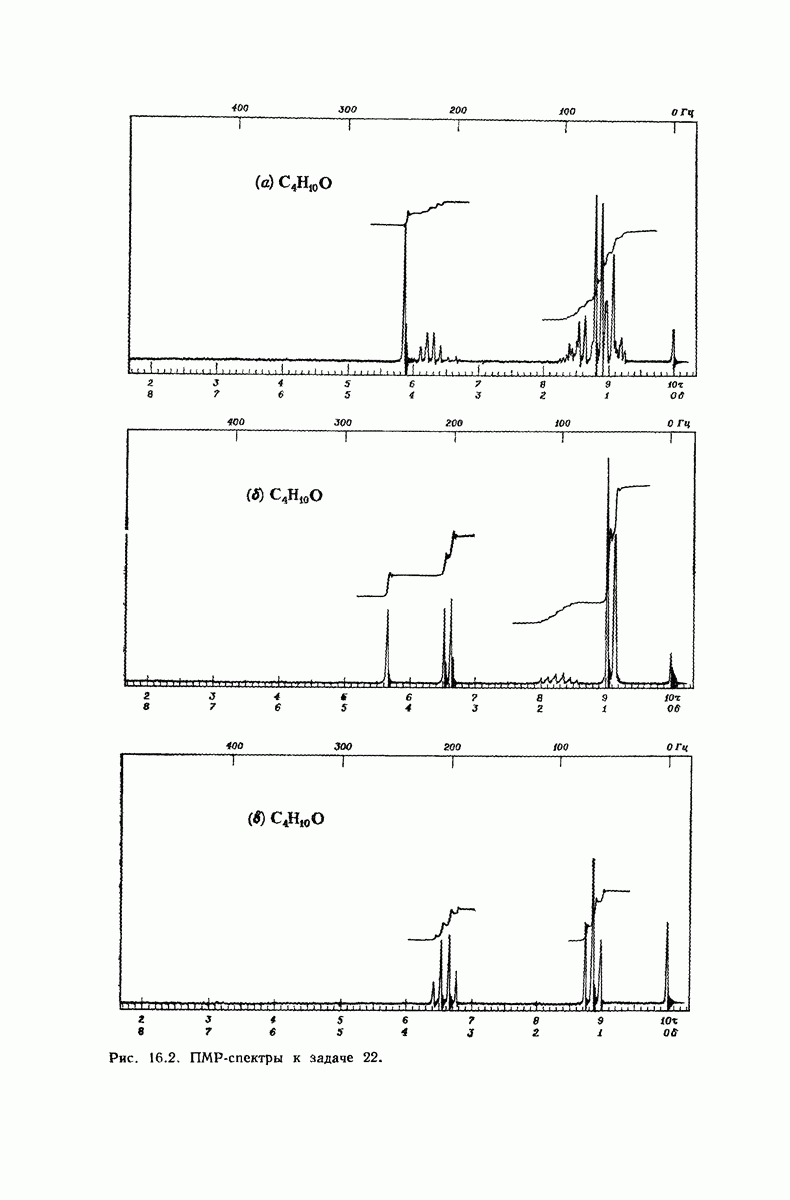
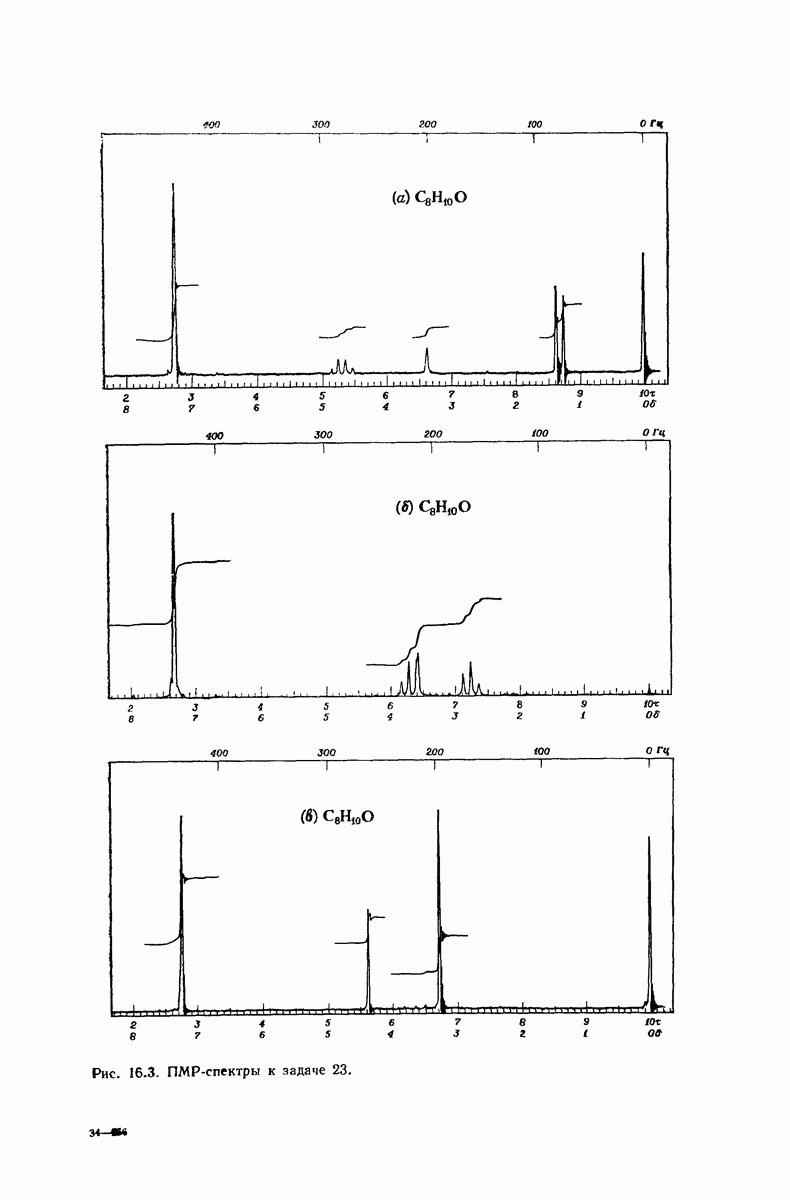
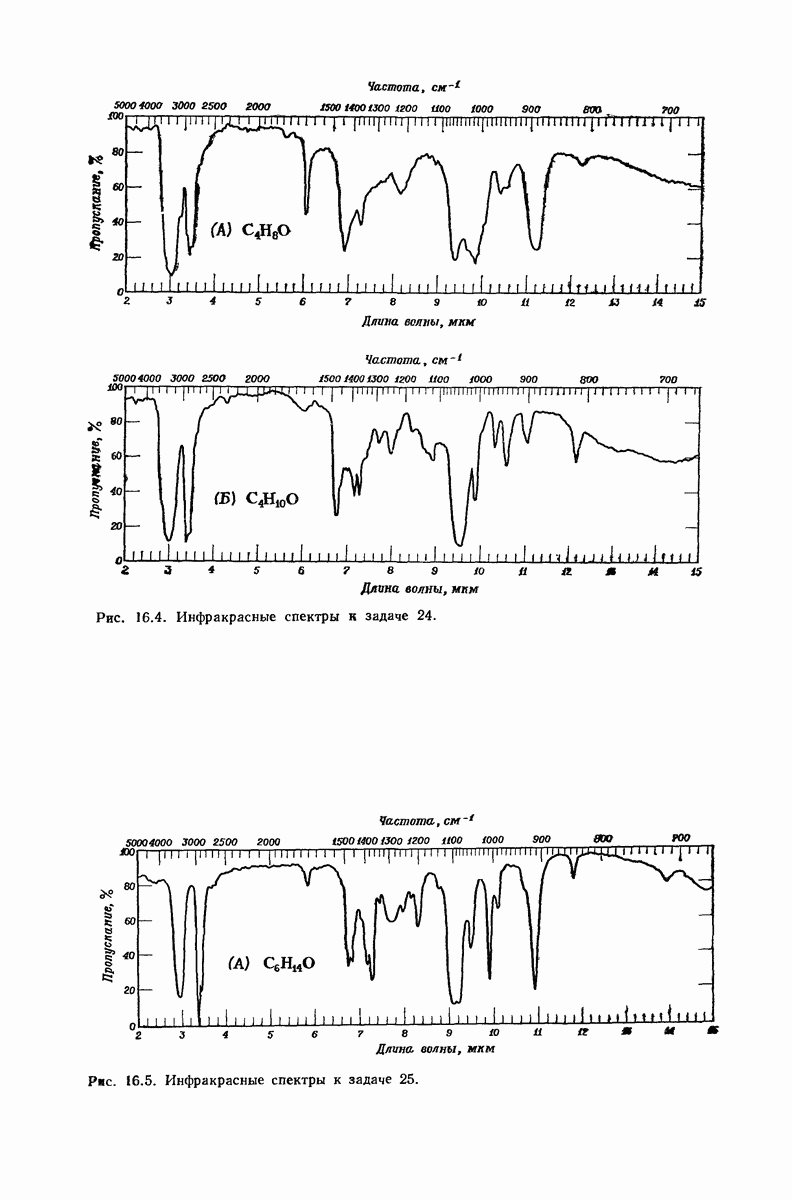
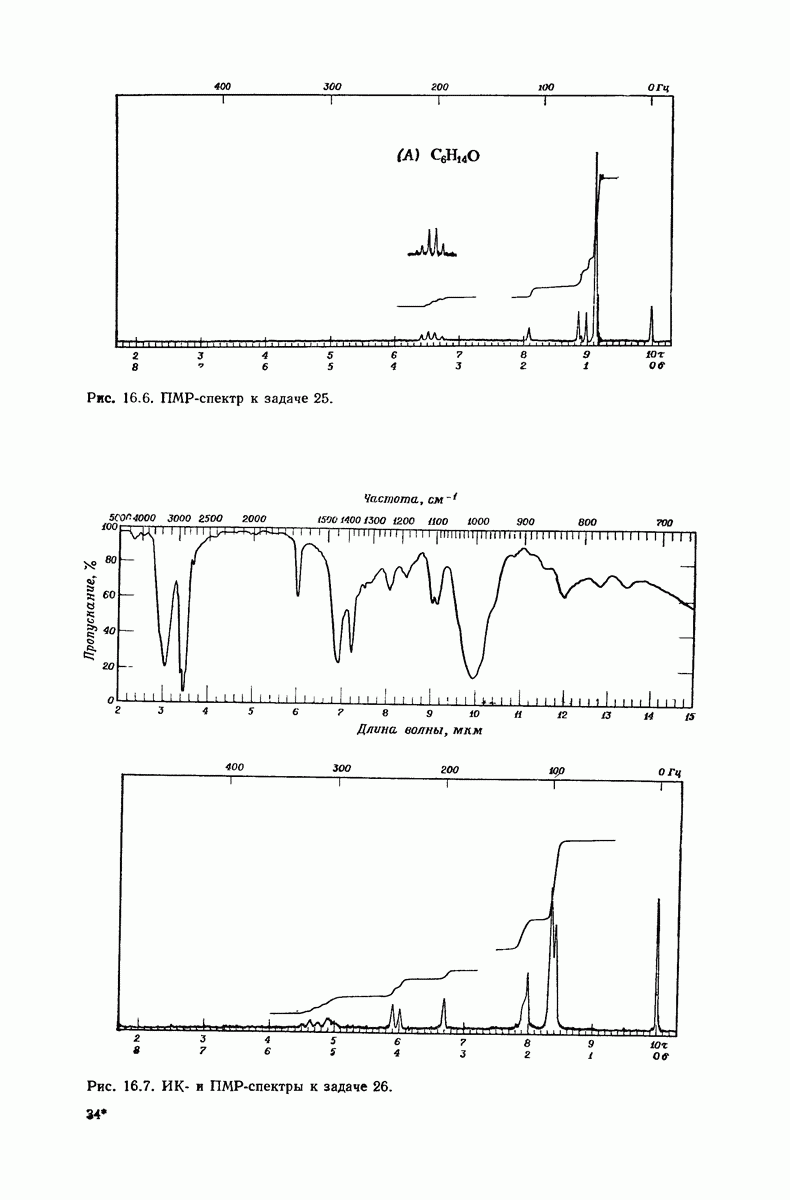
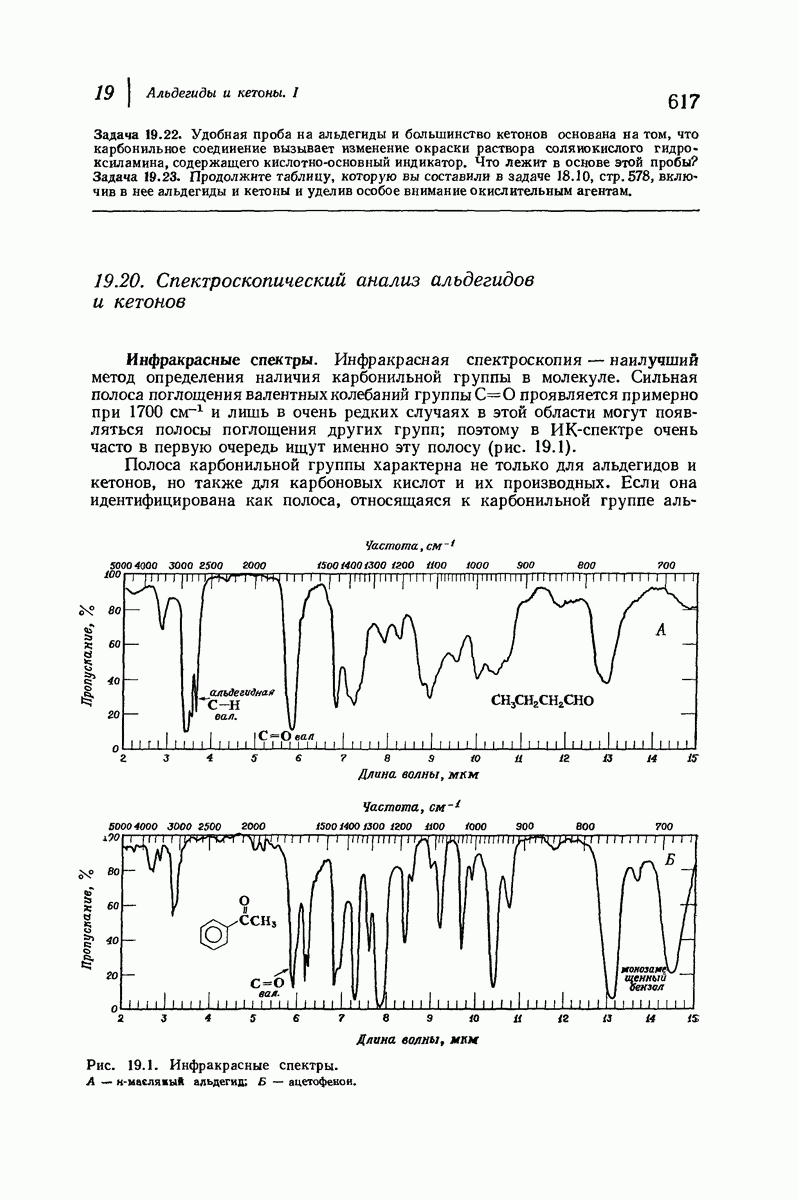
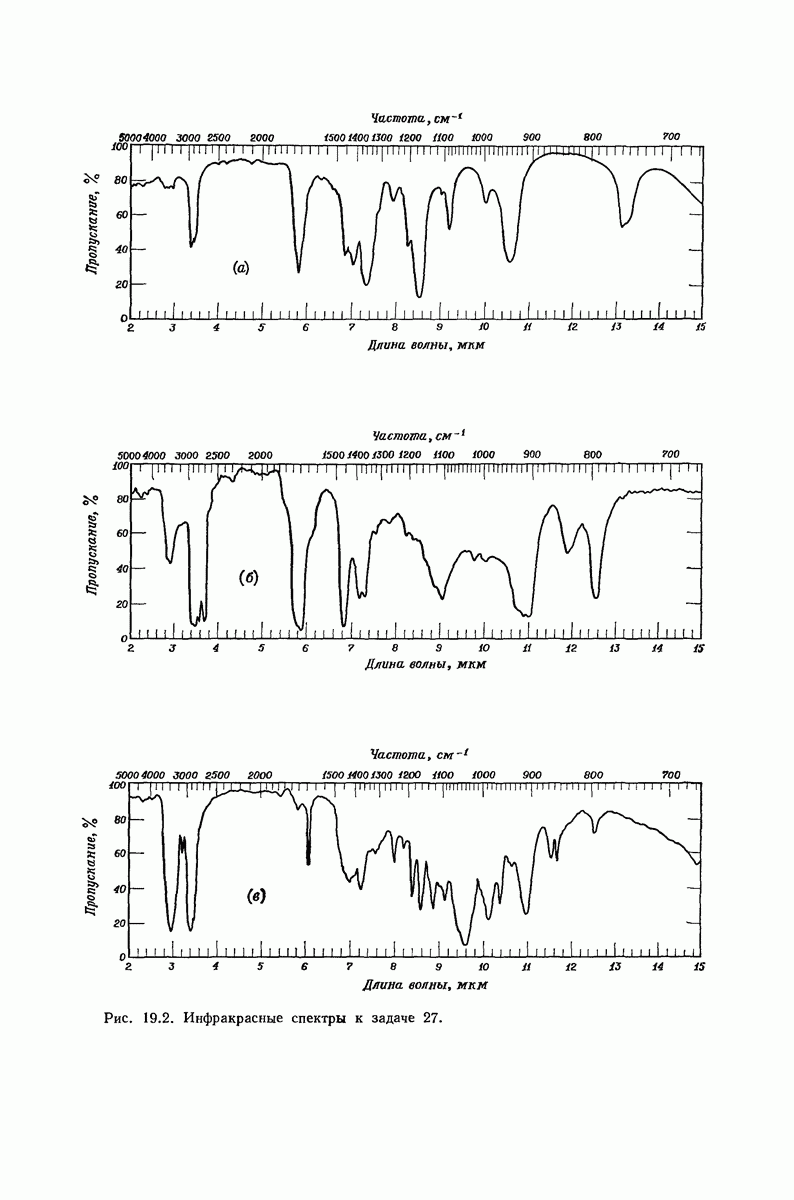
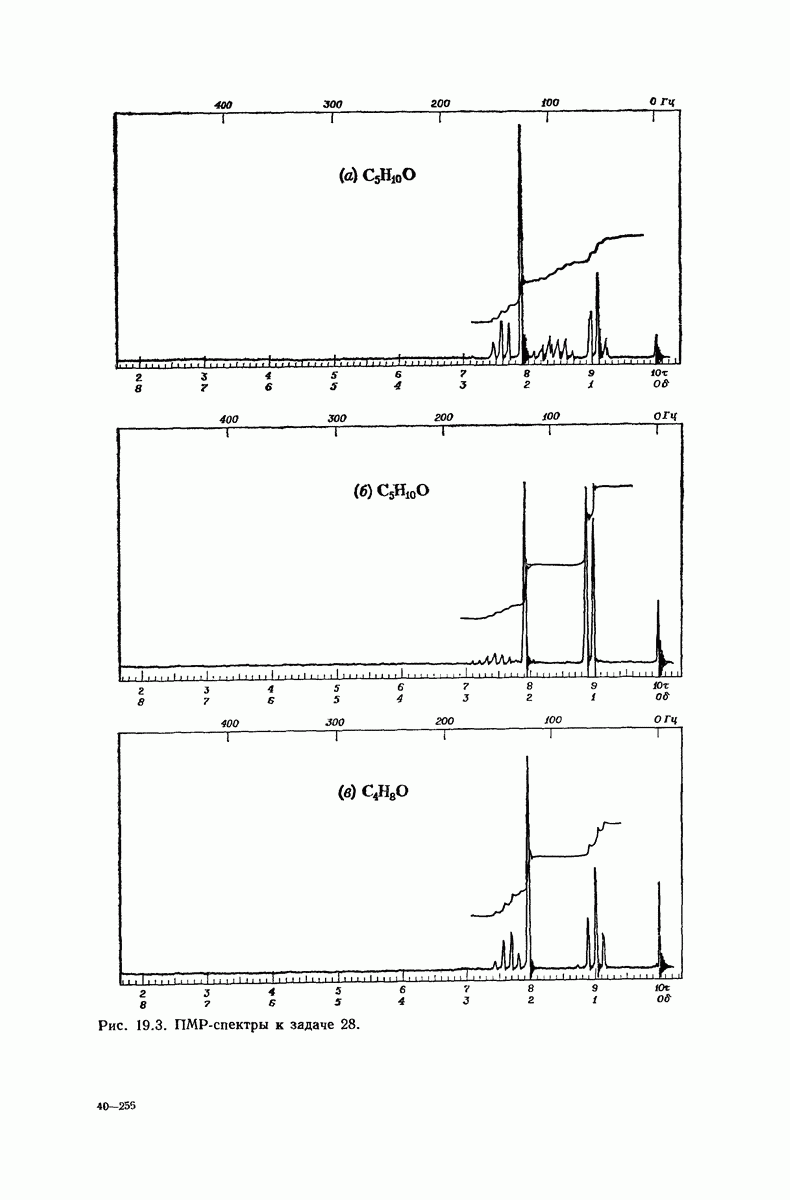
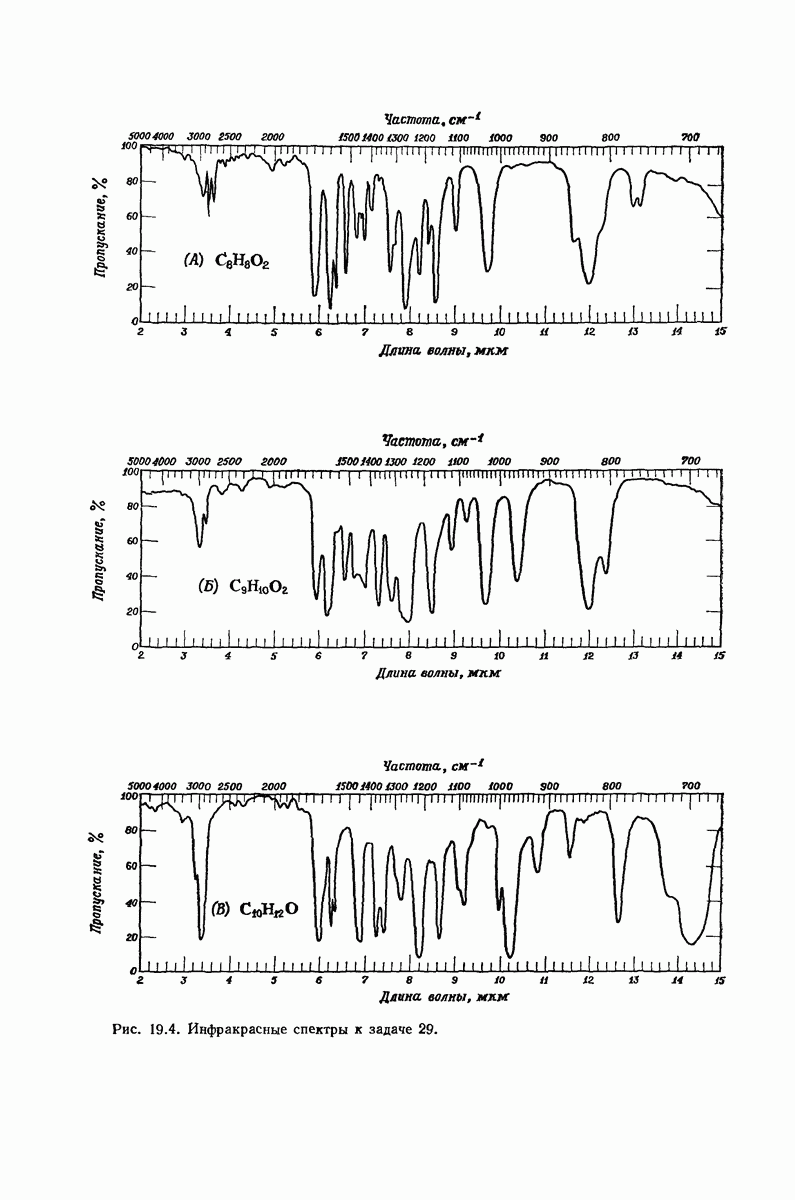
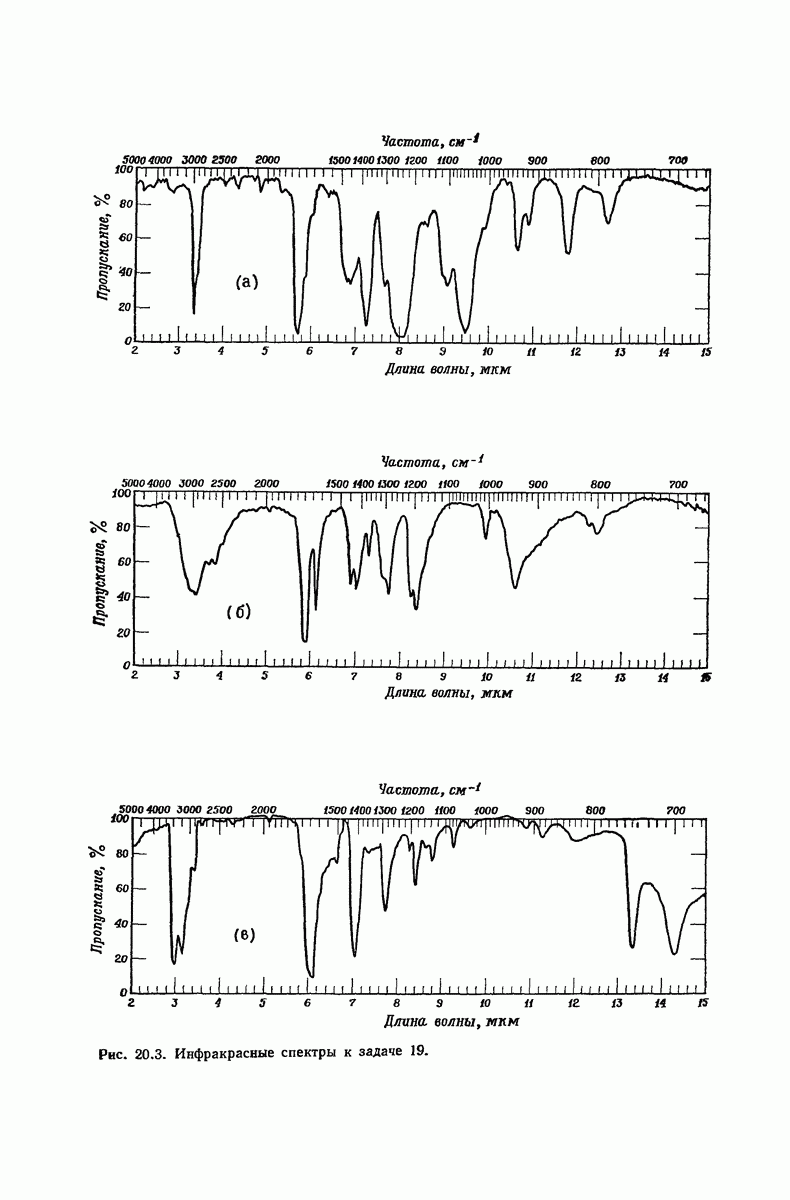
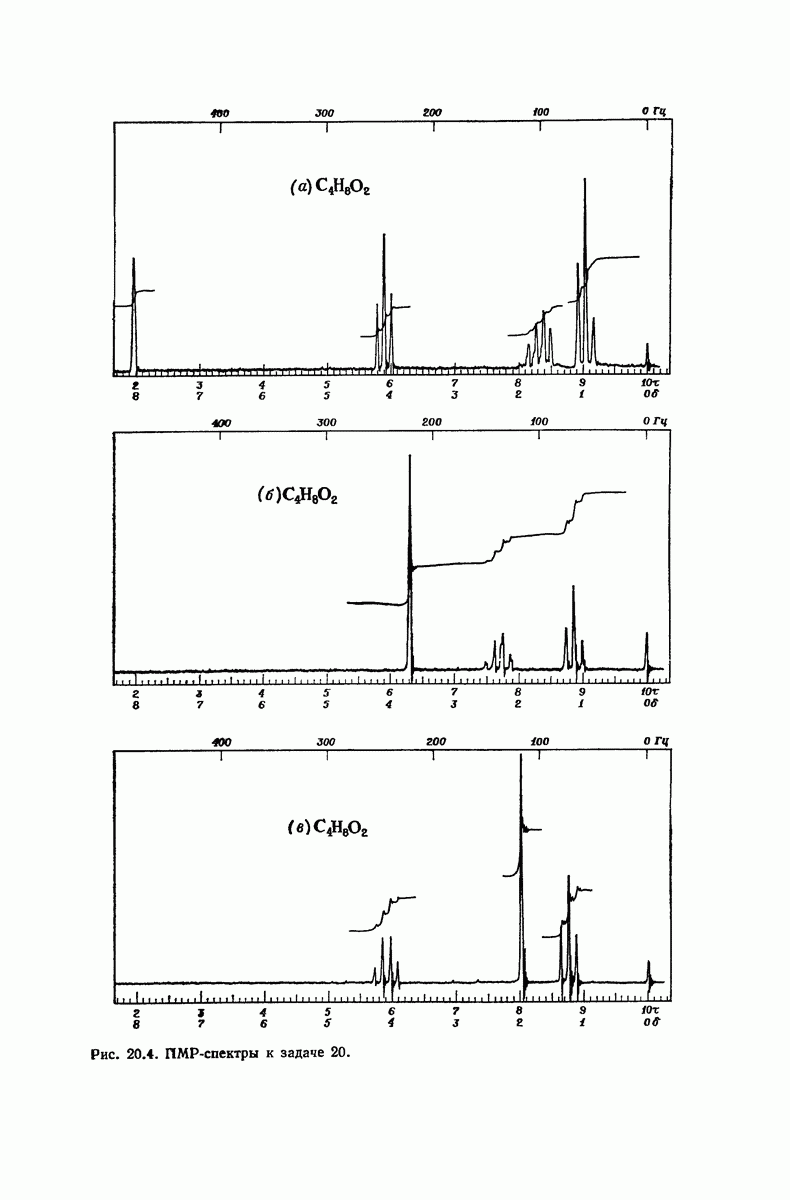
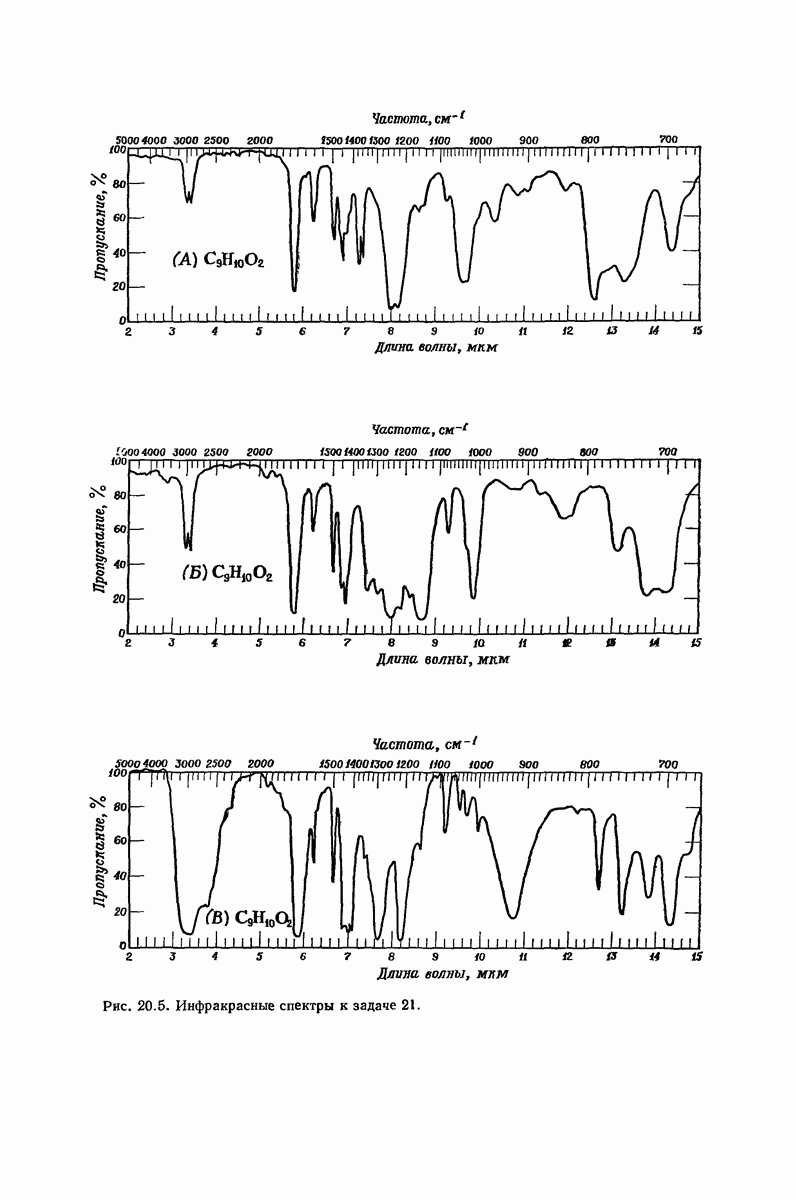
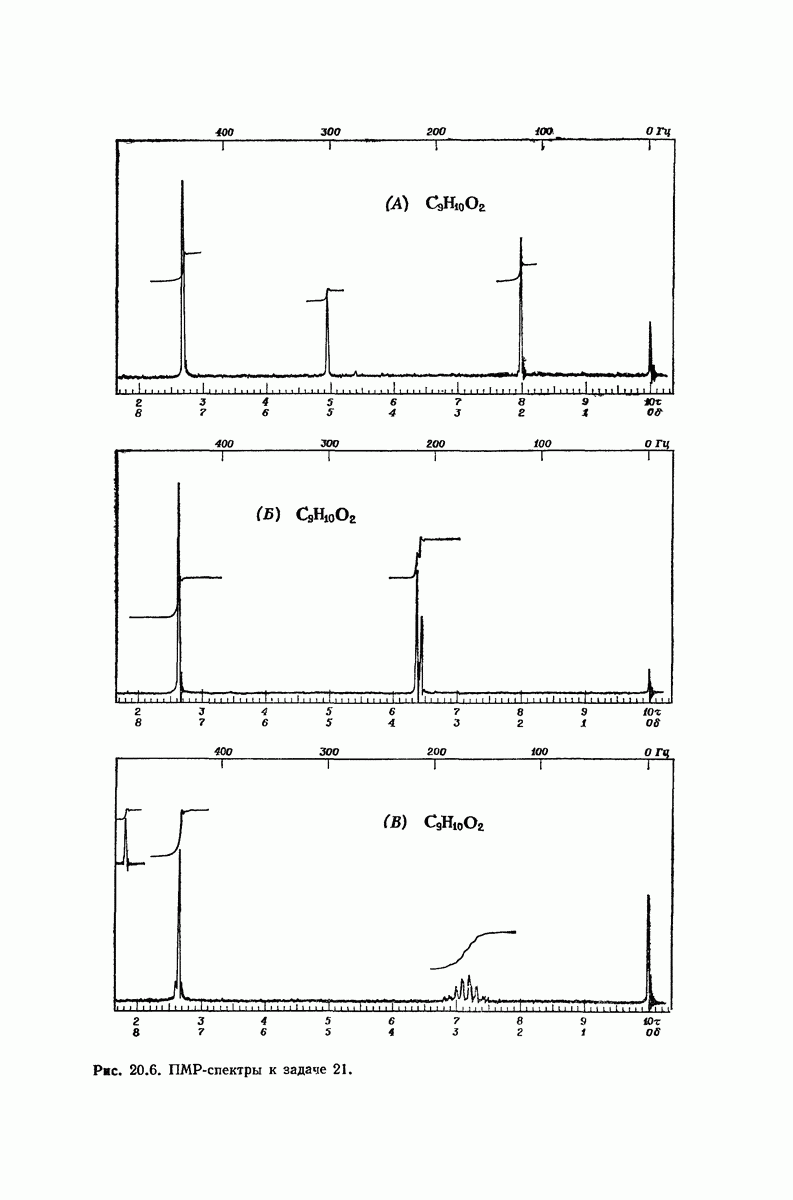
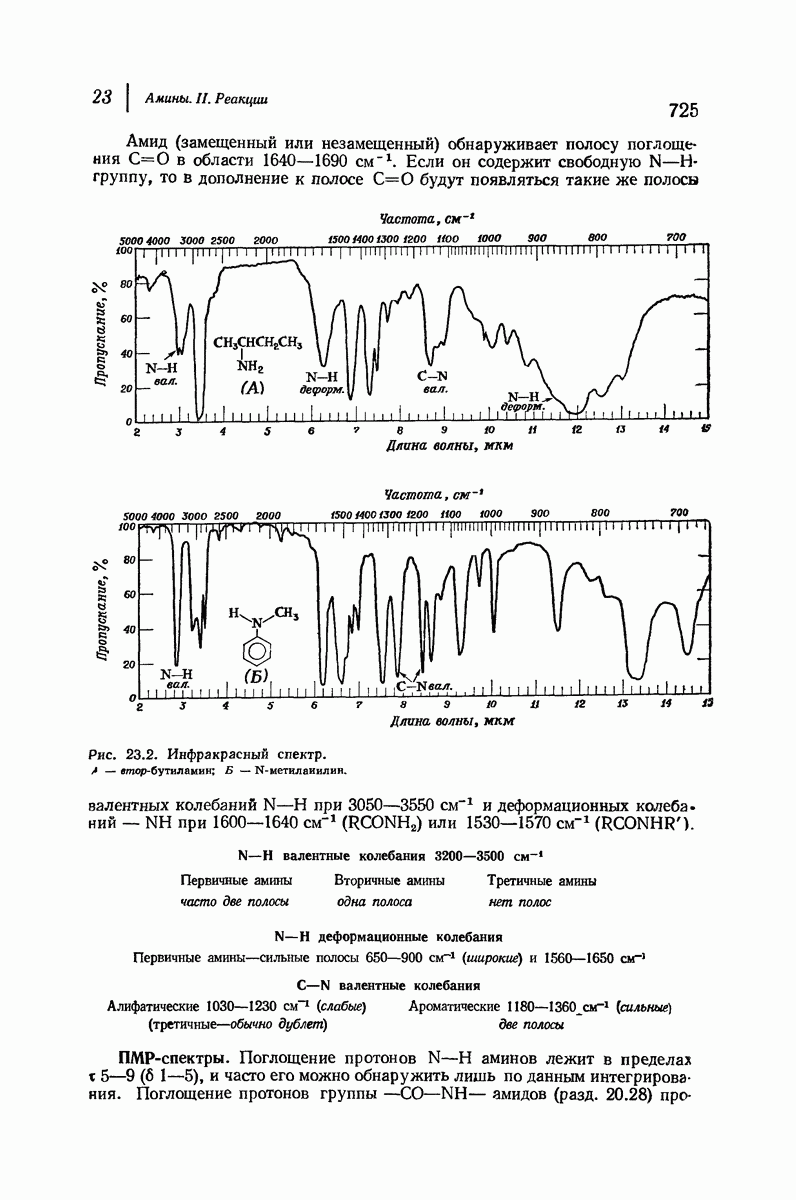
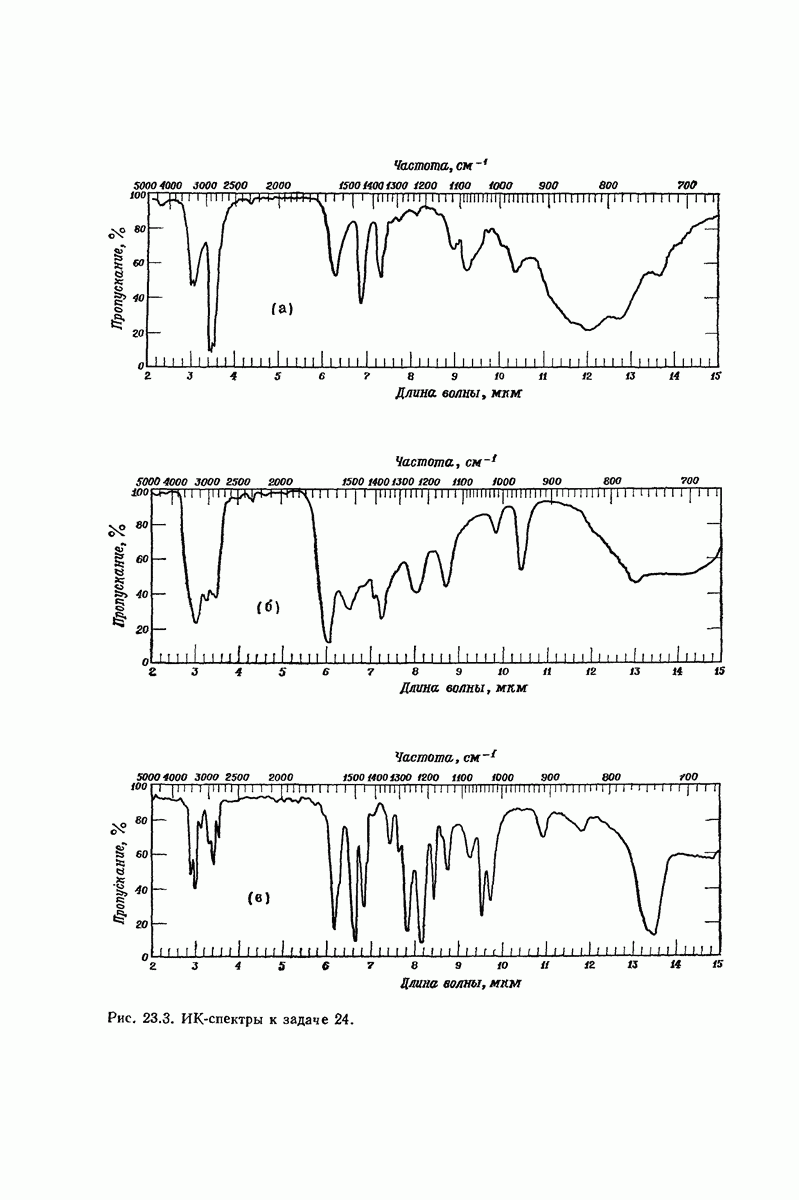
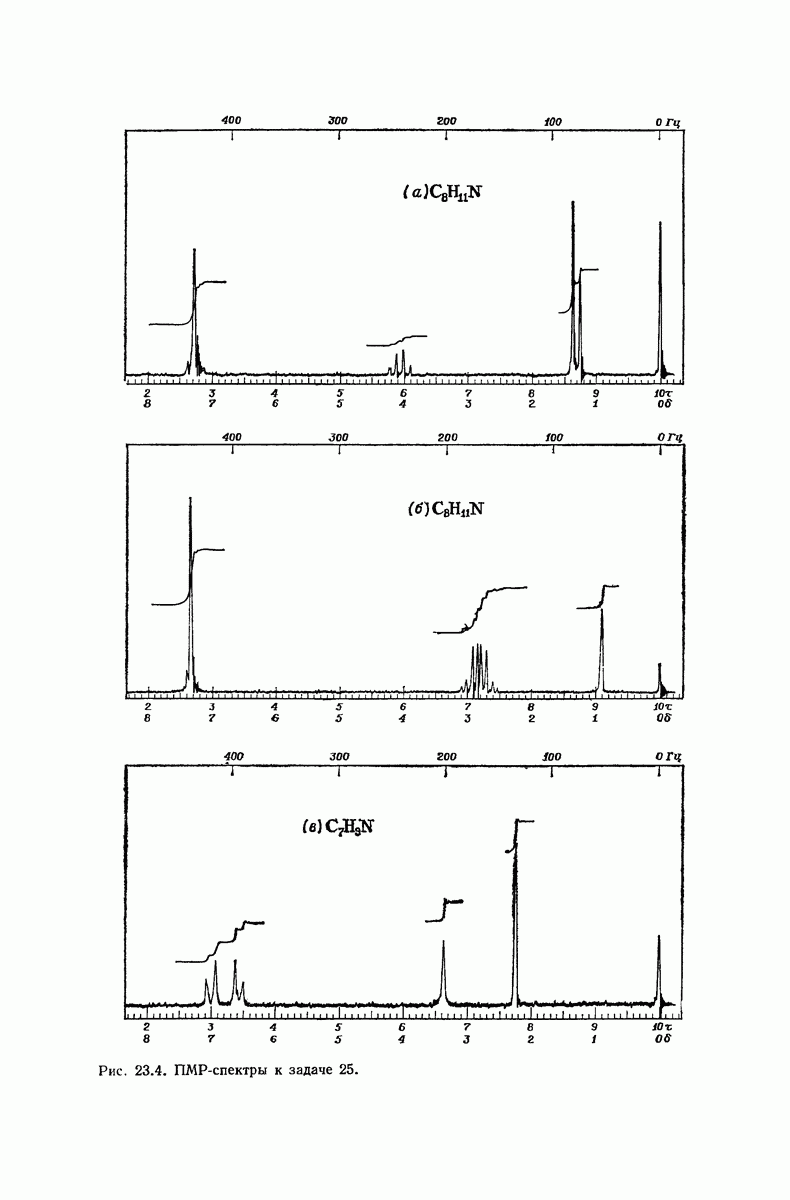
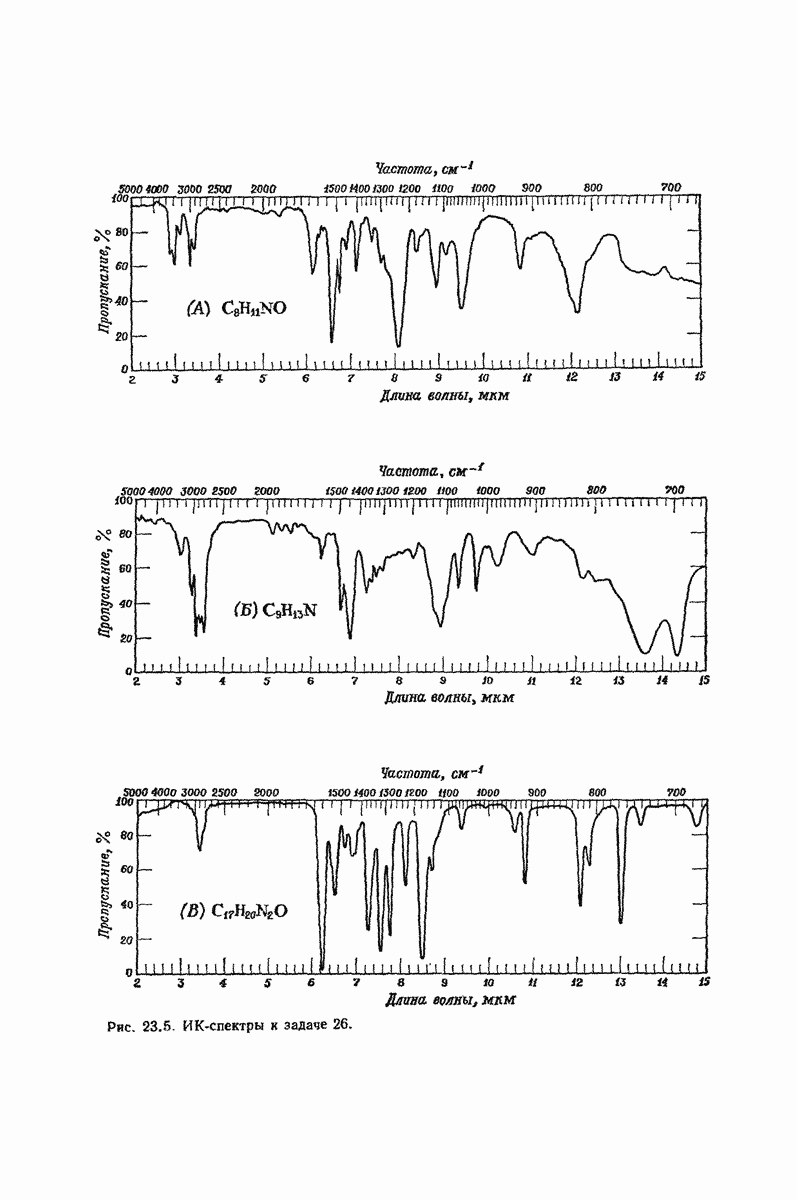
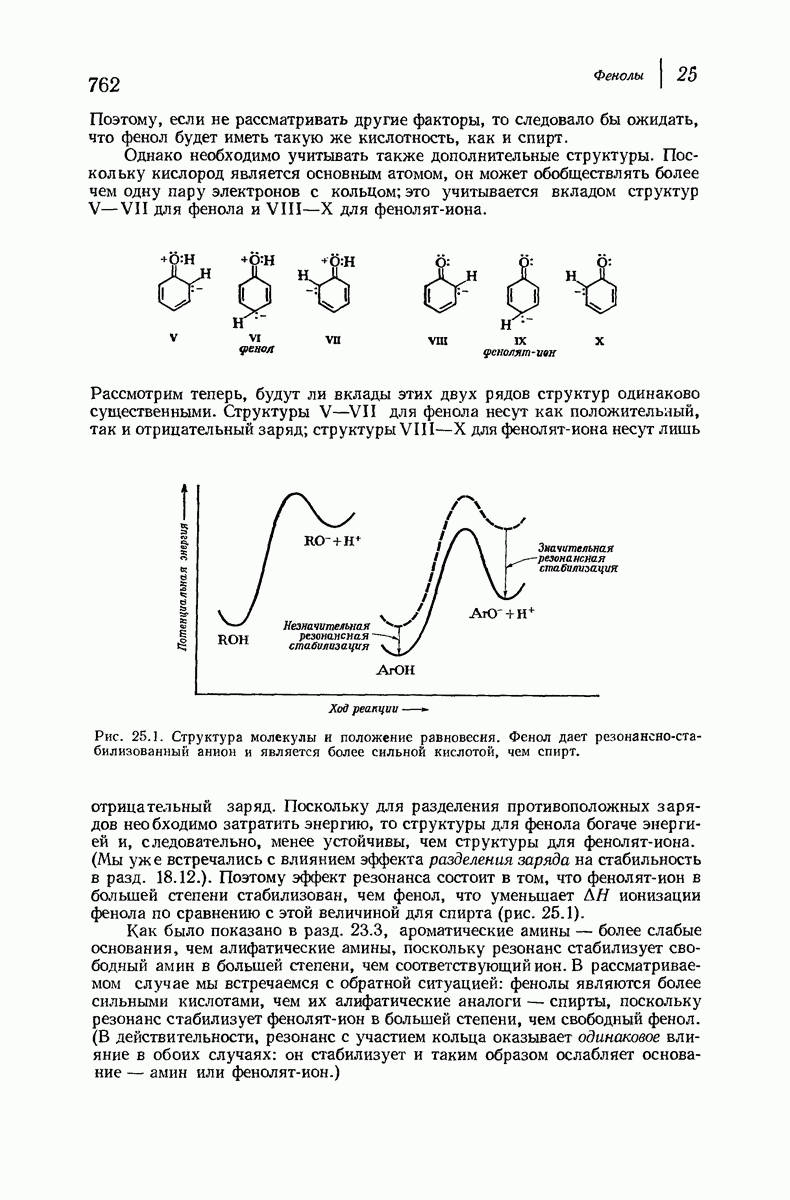
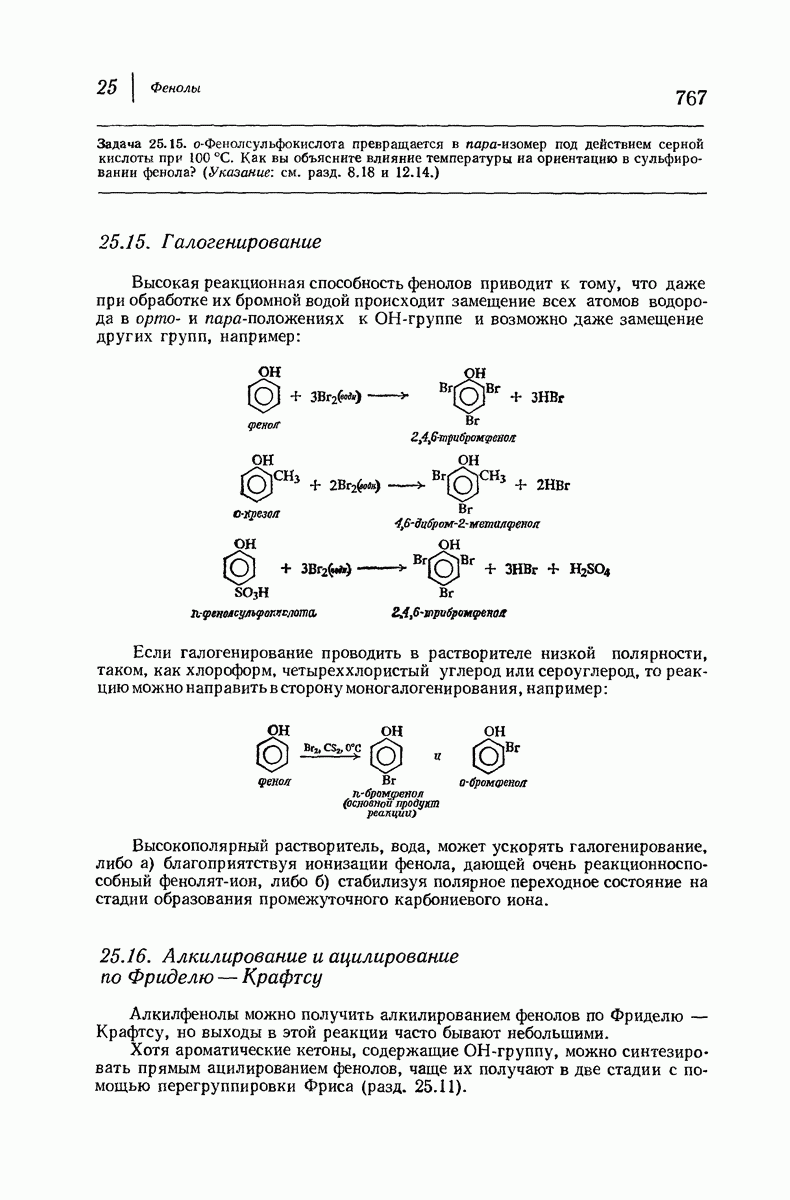
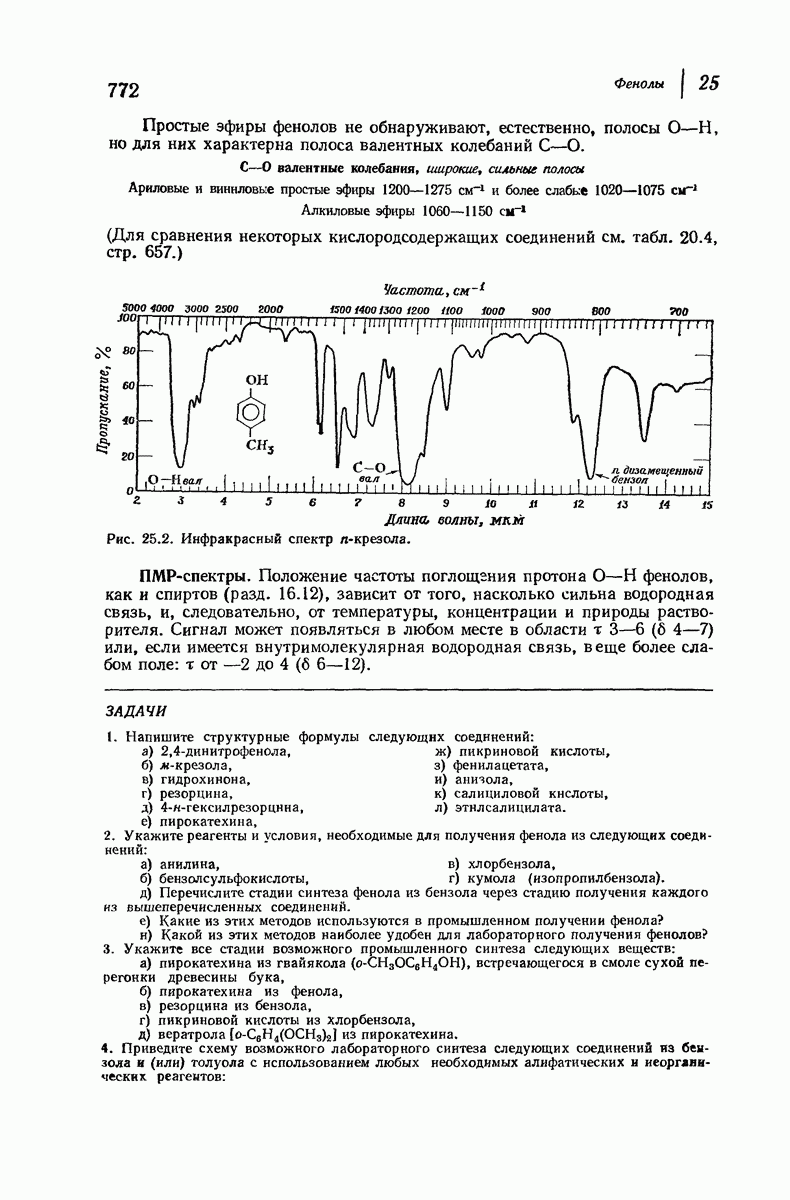
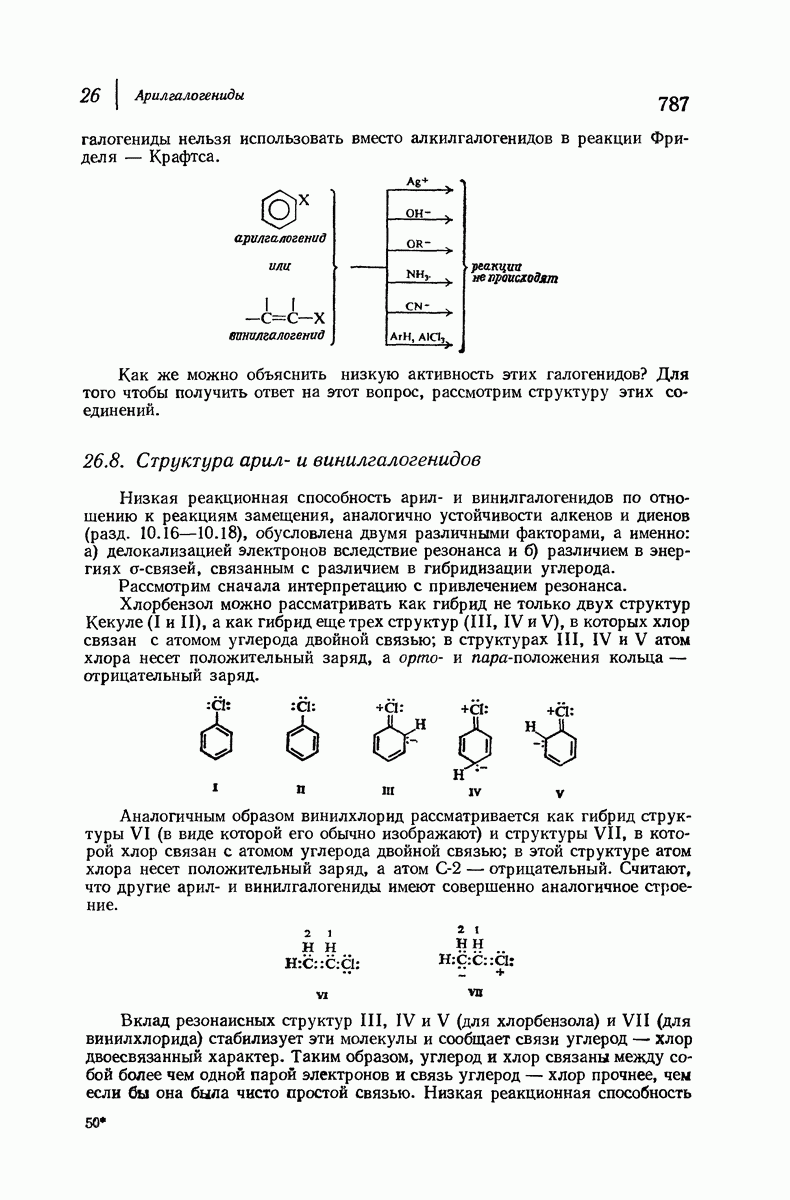
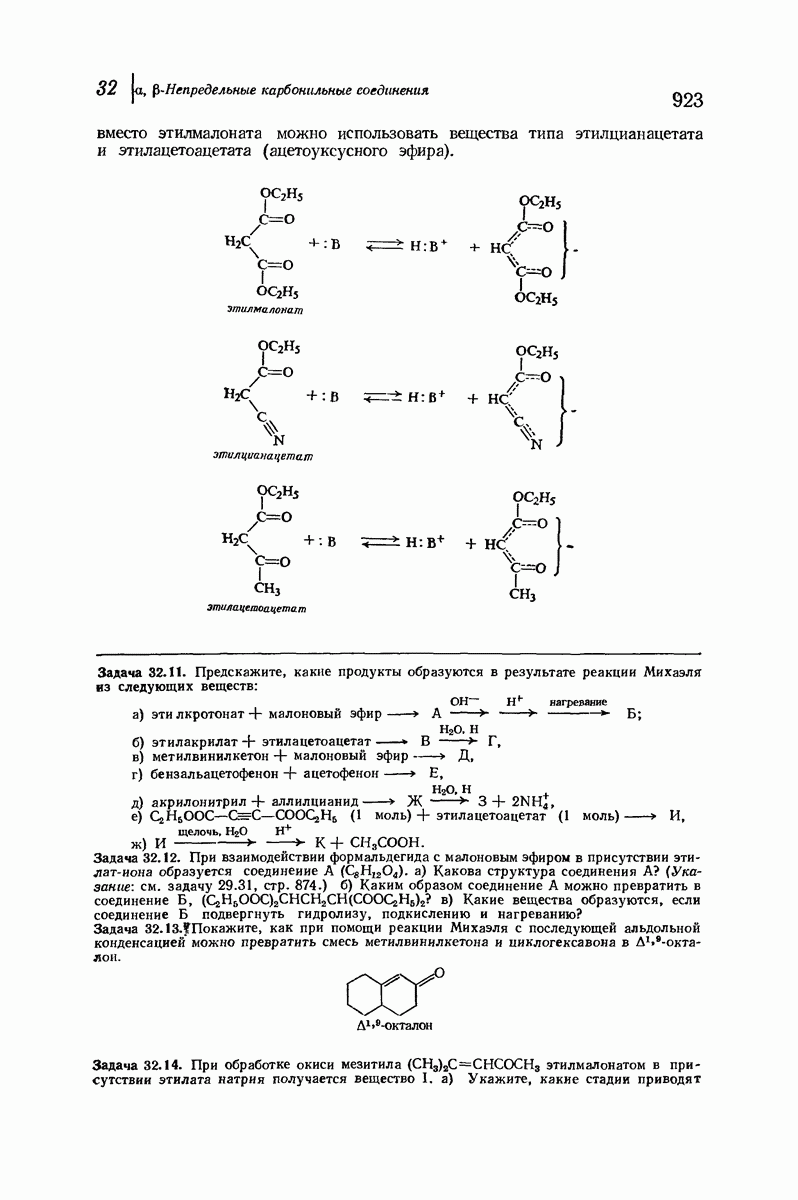
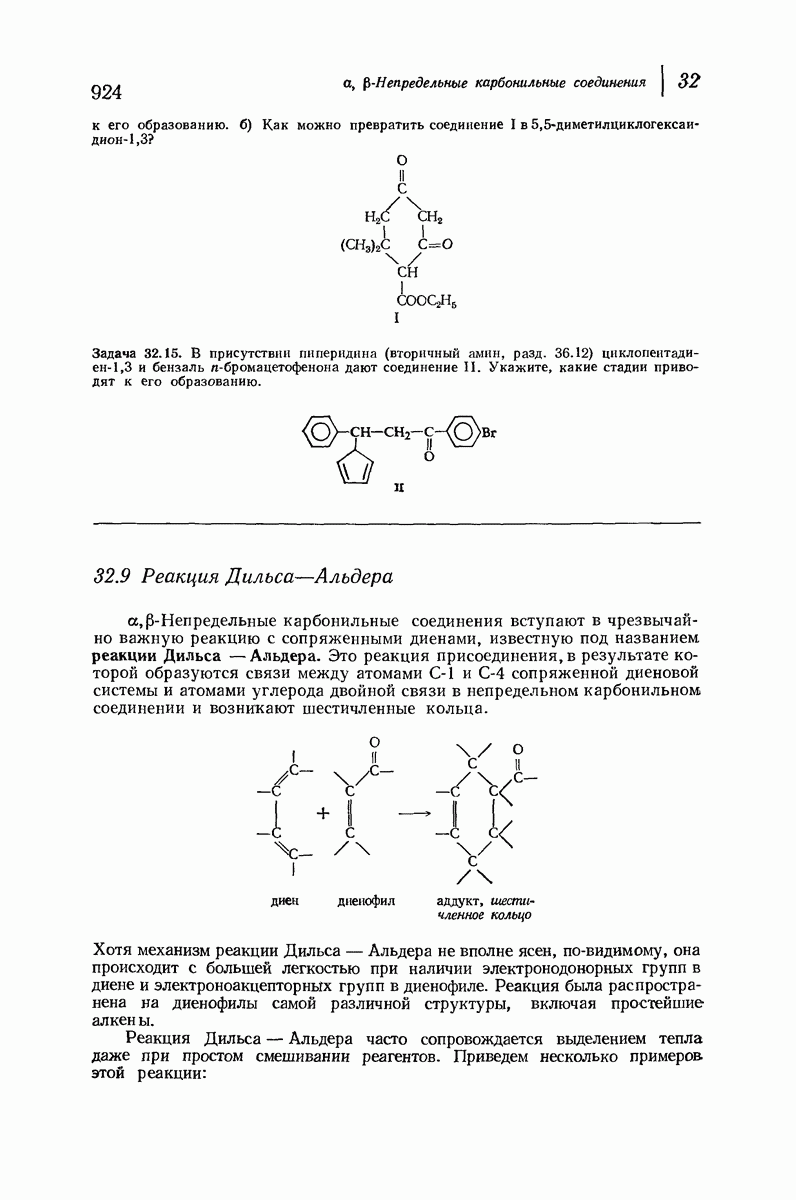
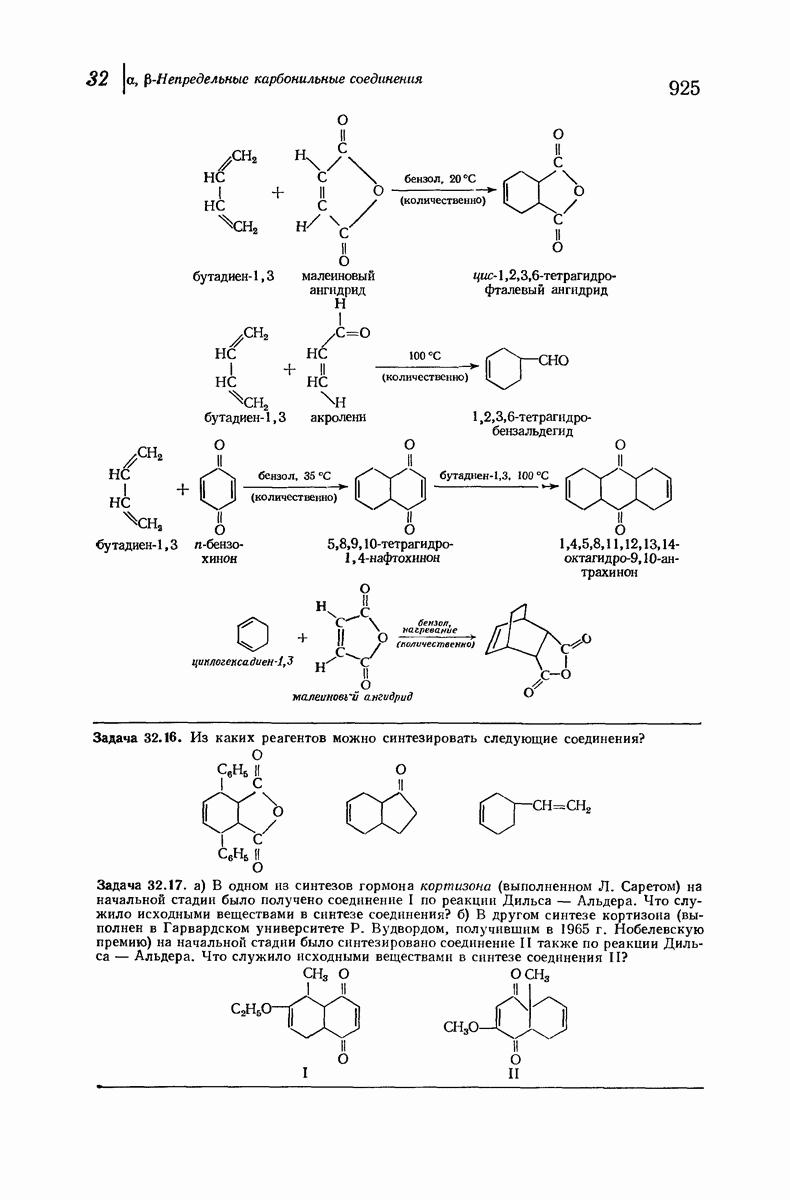
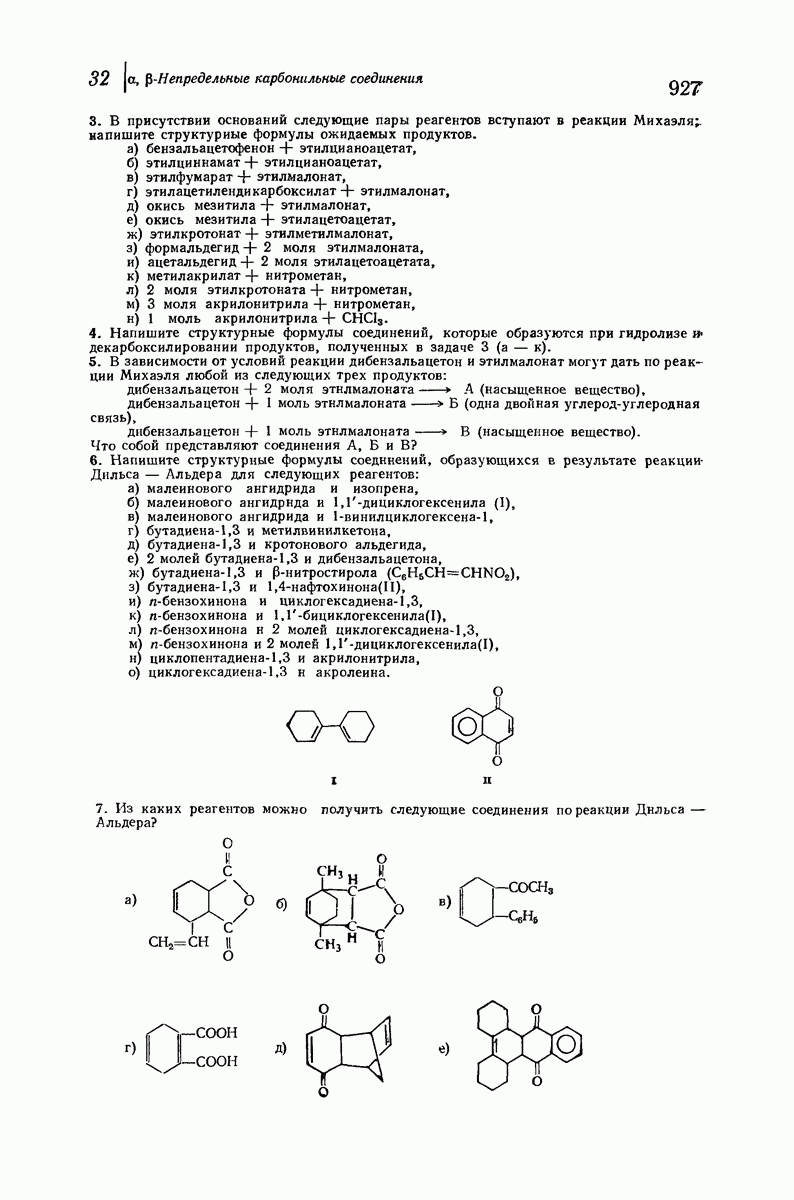
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
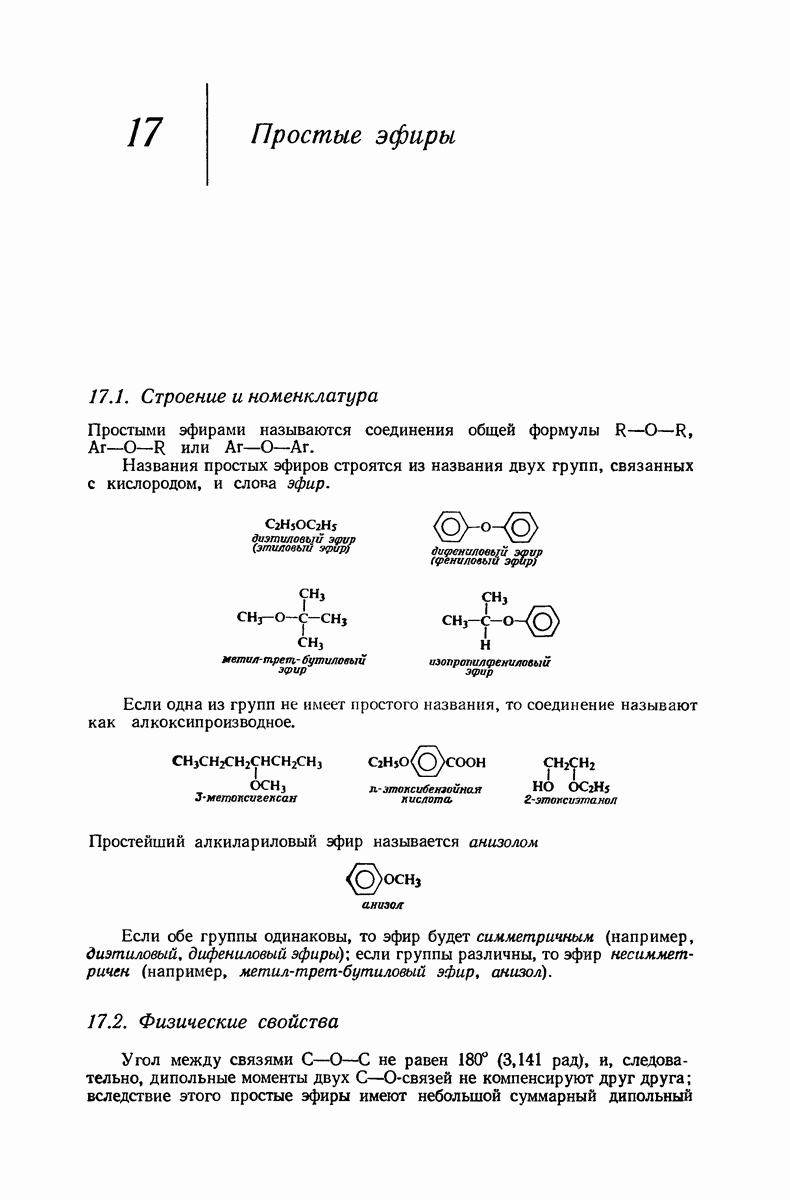
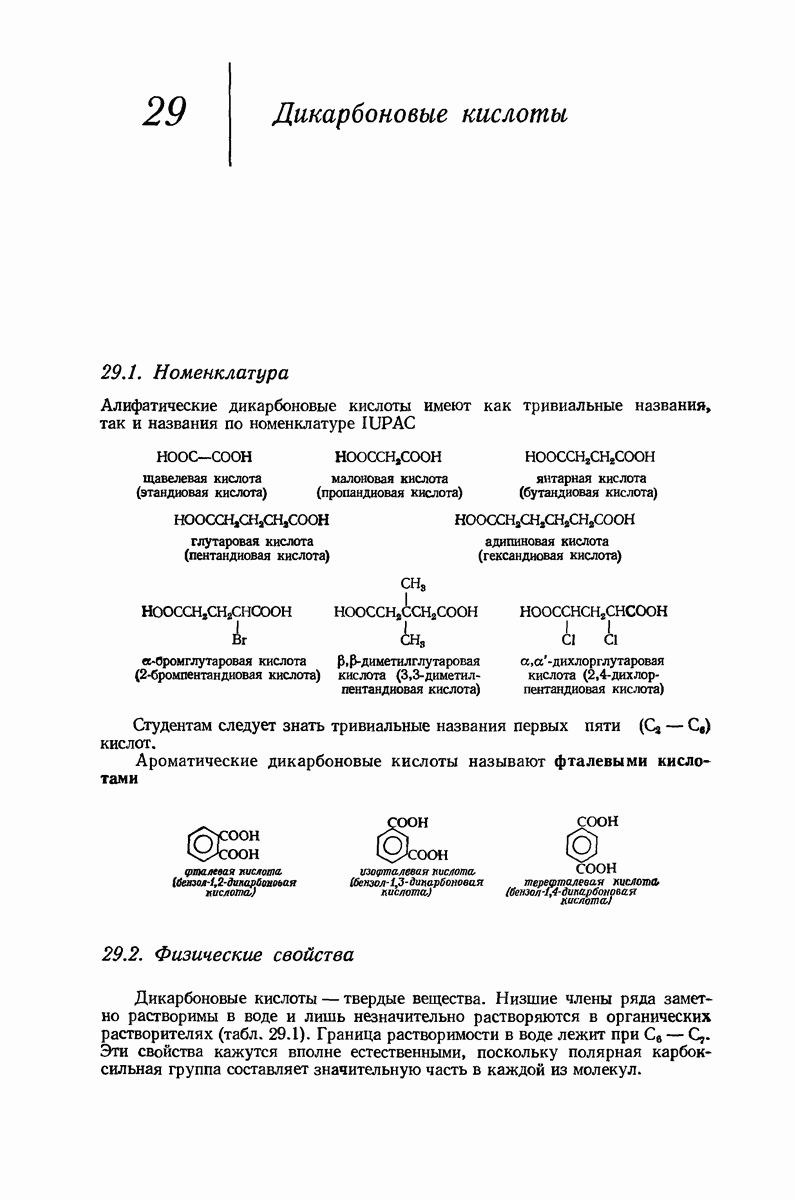
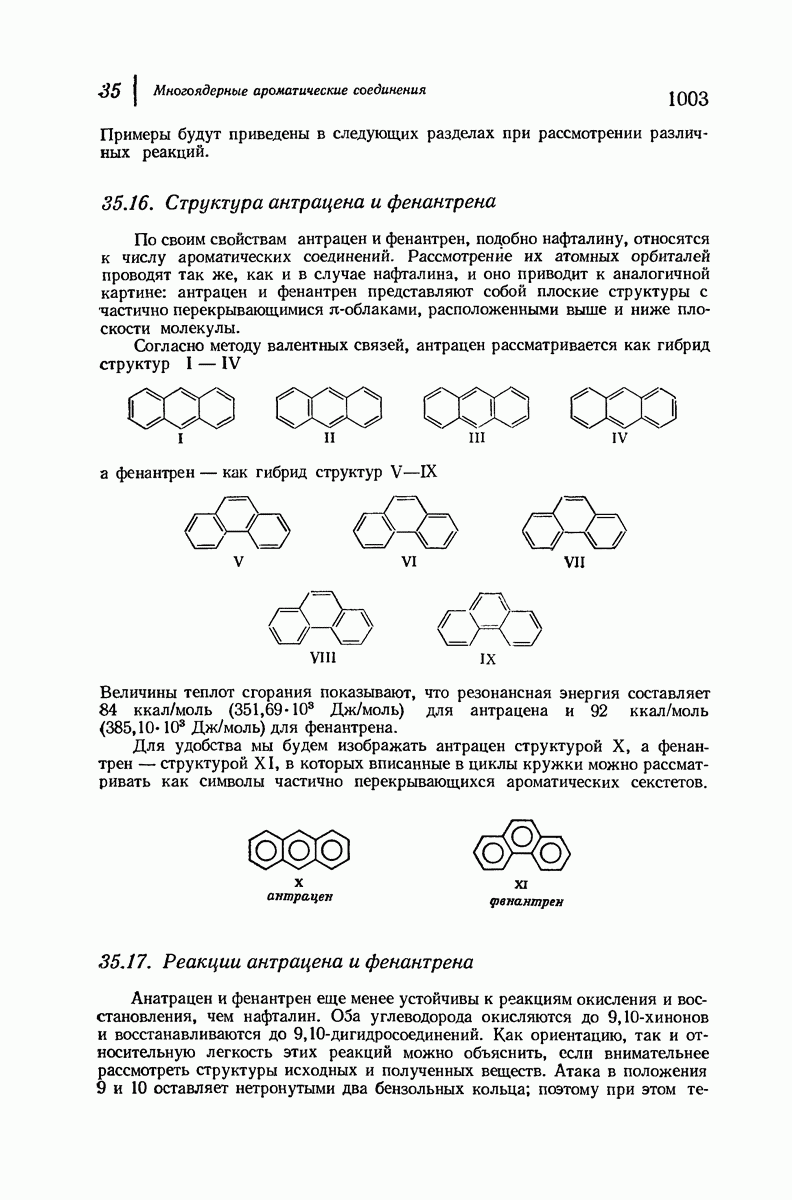
9.12. Конформация циклоалканов
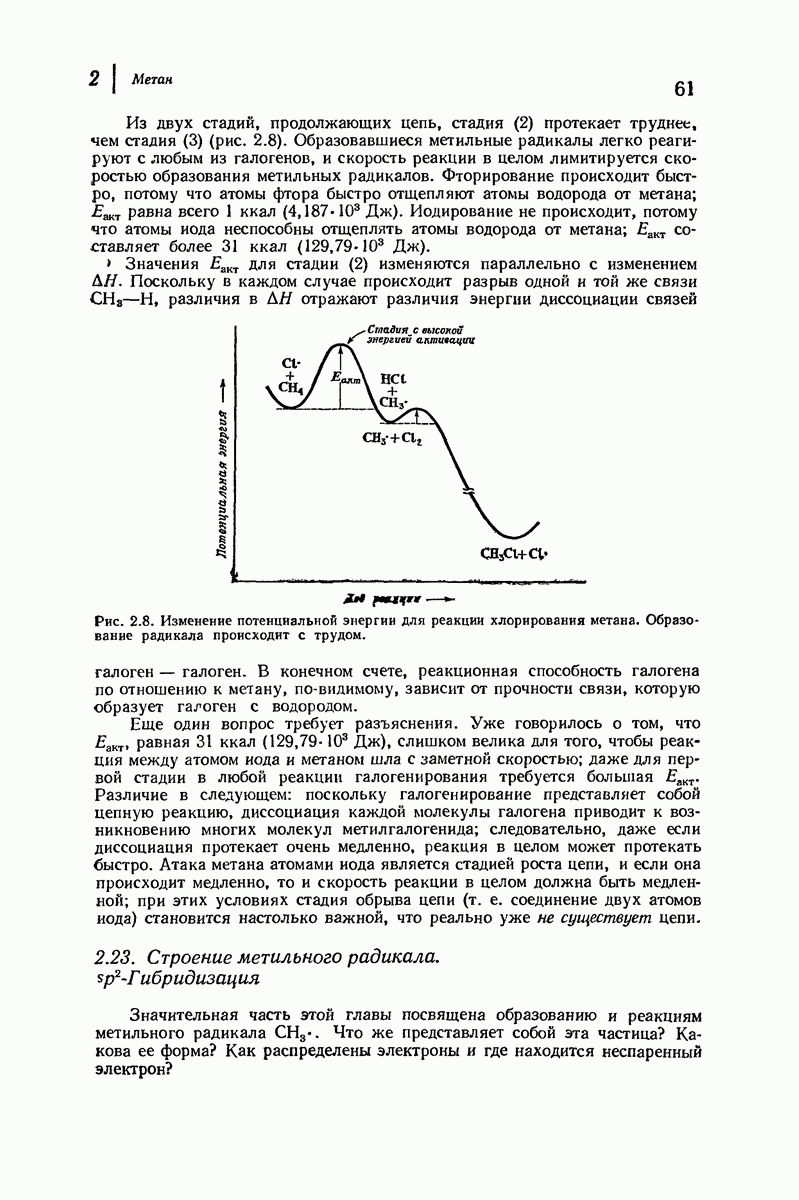
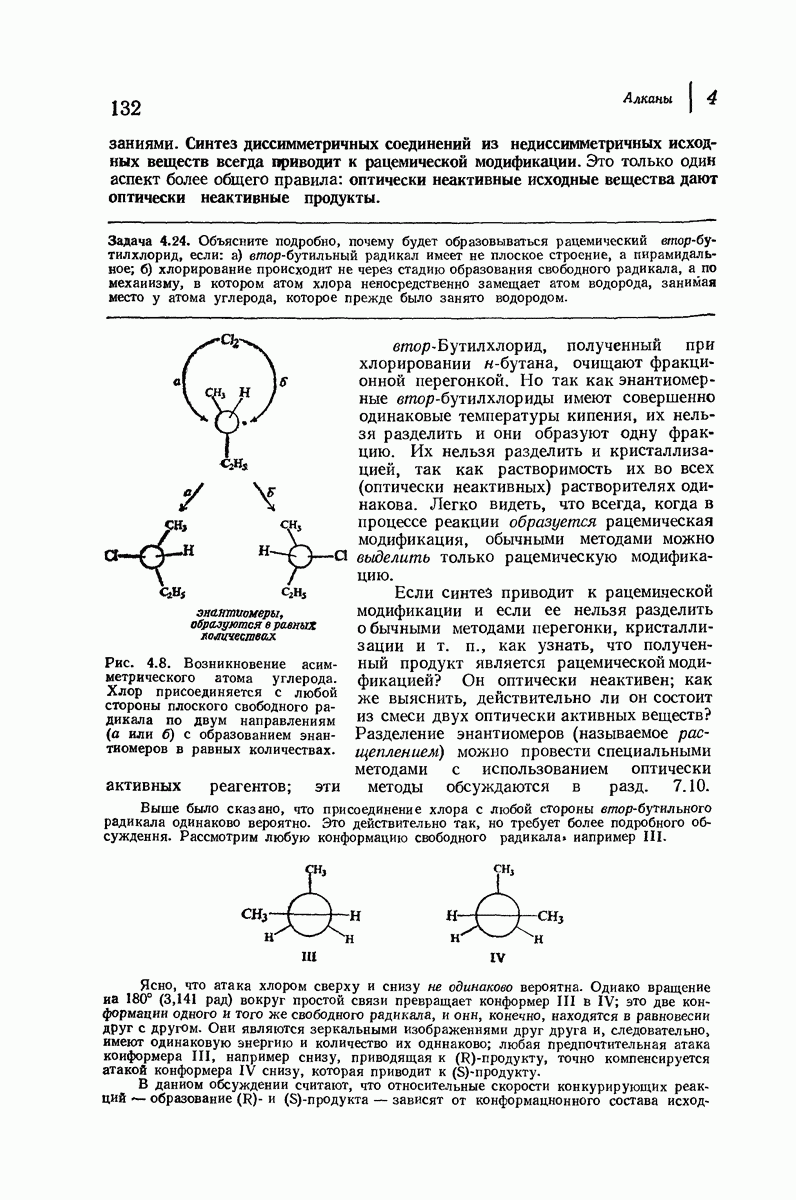
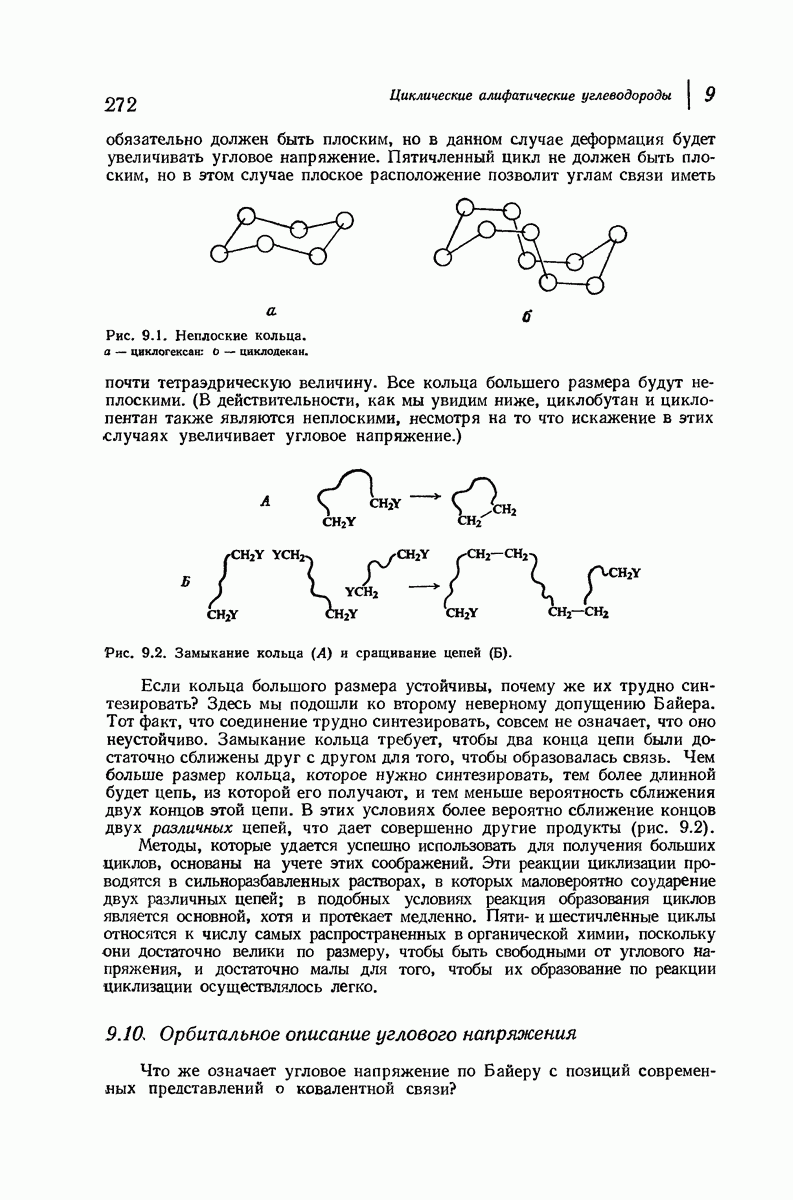
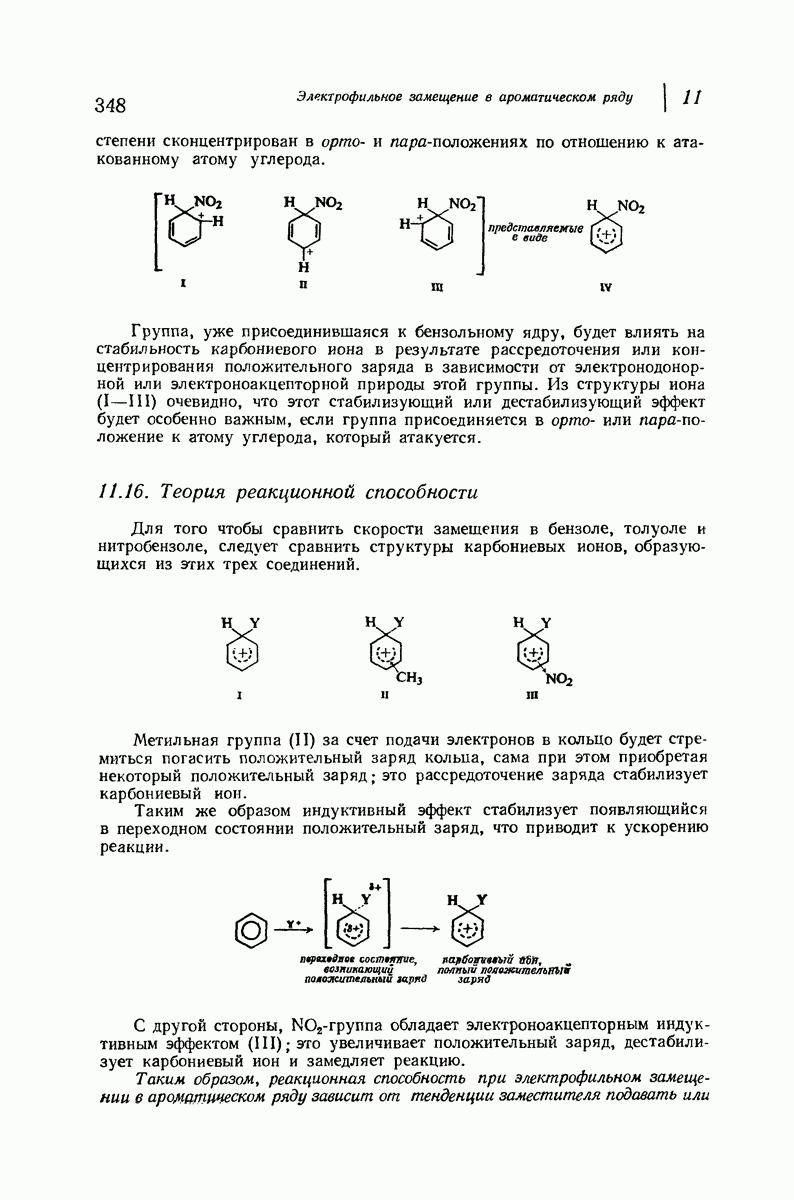
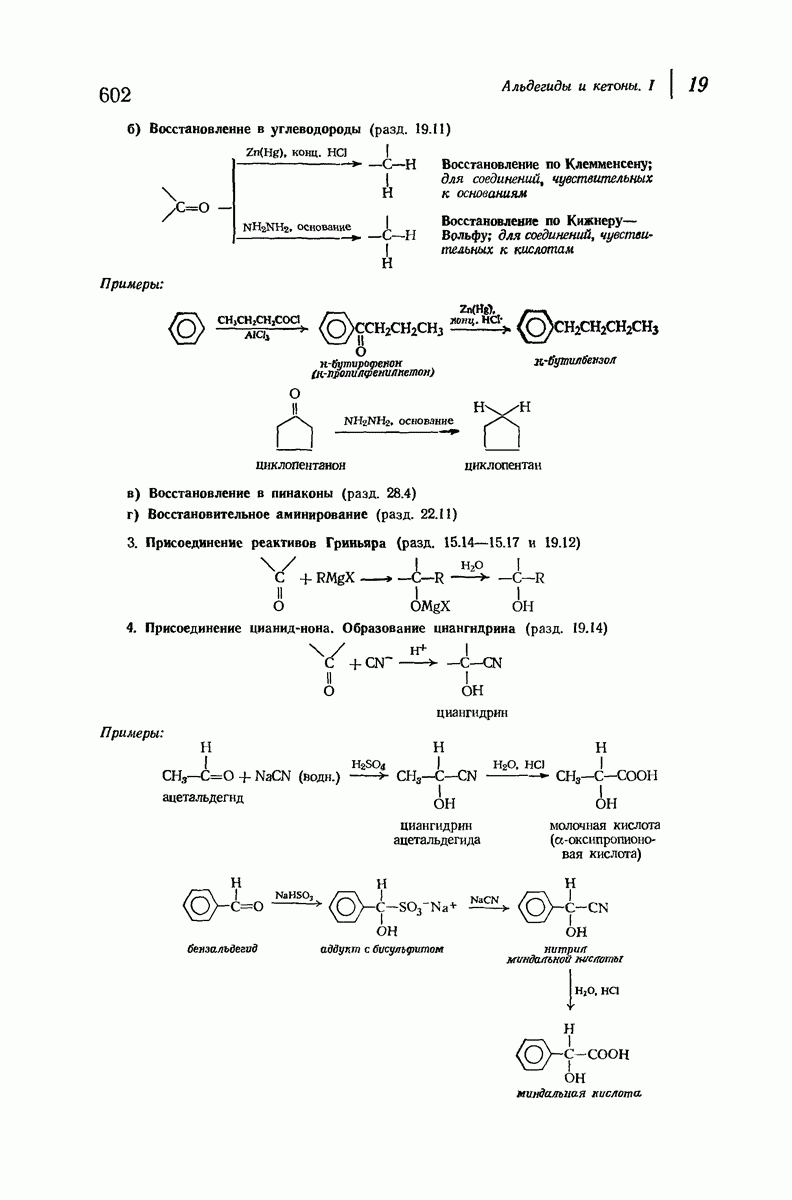
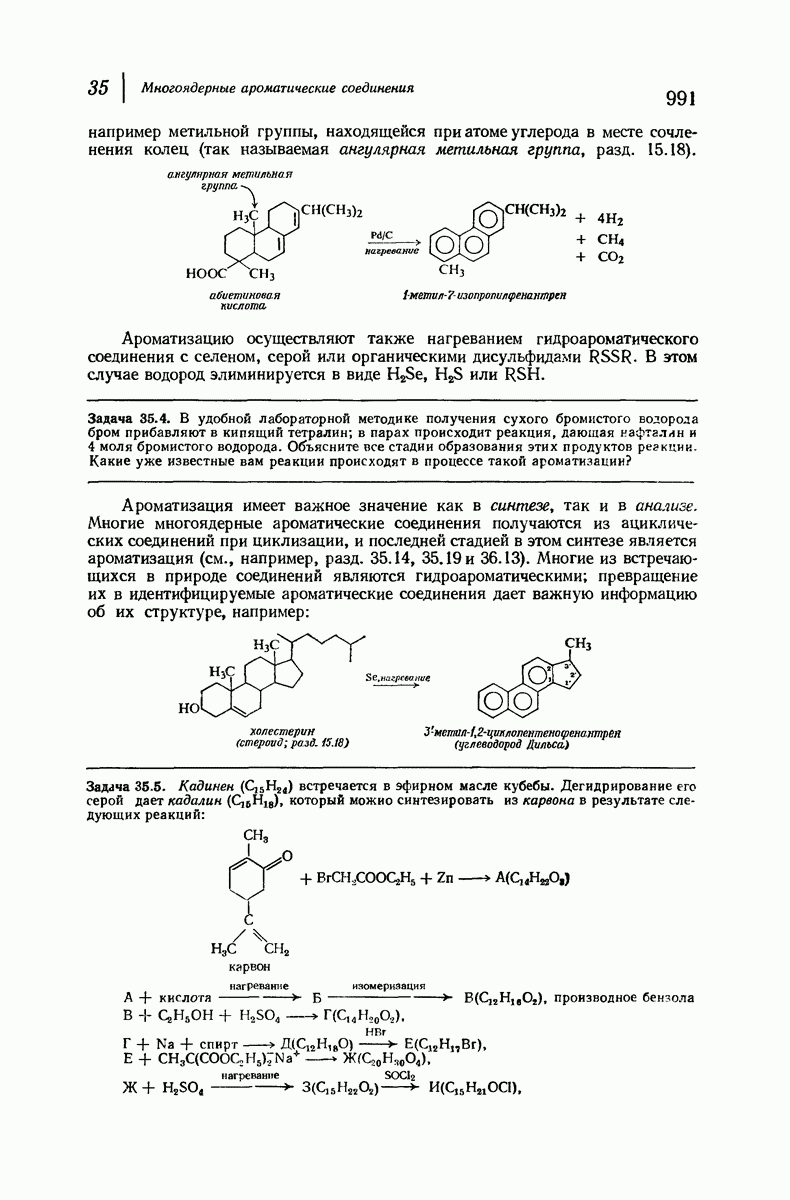
Рассмотрим внимательнее неплоские кольца, начнем с циклогексана, наиболее важного циклоалкана. Построим модель молекулы и изучим конформации, свободные от углового напряжения.
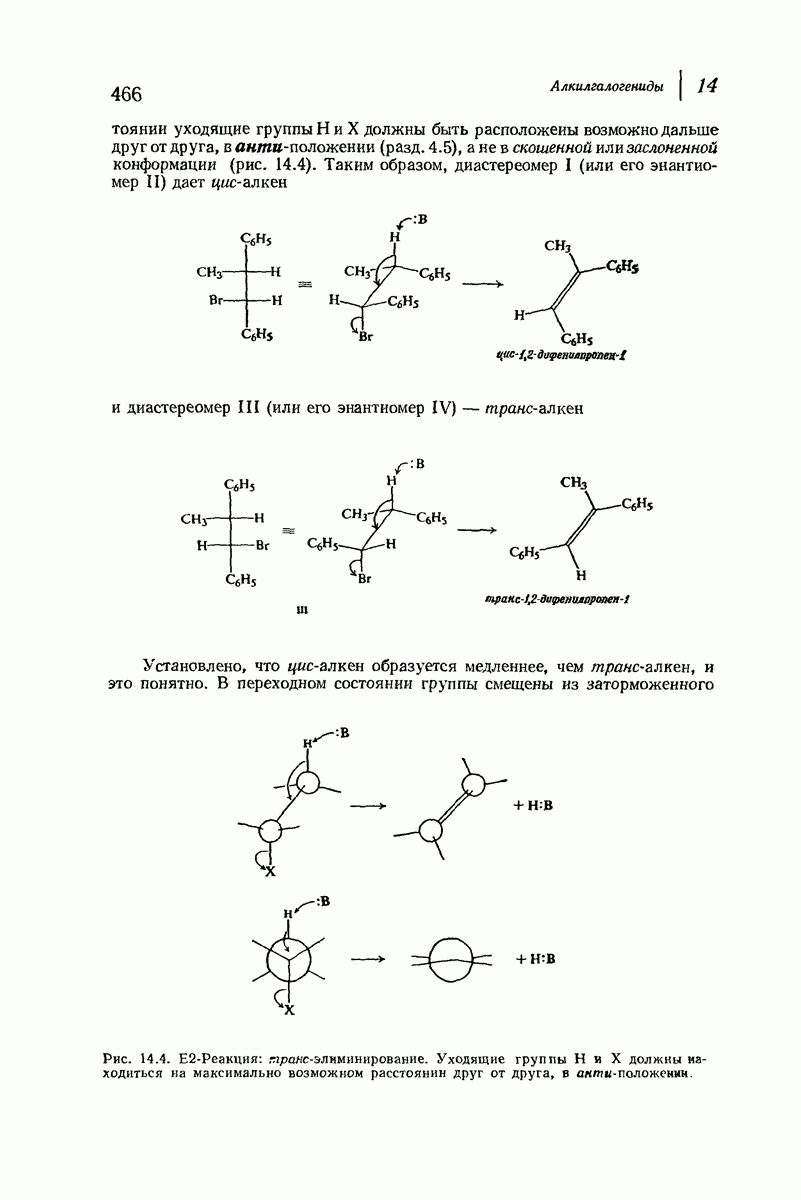
В первую очередь рассмотрим форму кресла (рис. 9.4). Если посмотреть вдоль любой из углерод-углеродных связей, то увидим, что в каждом случае имеется идеальная заторможенная конформация

Таким образом, эта конформация свободна не только от углового, но также и от торсионного напряжения. Она имеет минимальный запас энергии и поэтому является конформационным изомером. Форма кресла — наиболее устойчивая конформация для циклогексана и почти всех его производных.
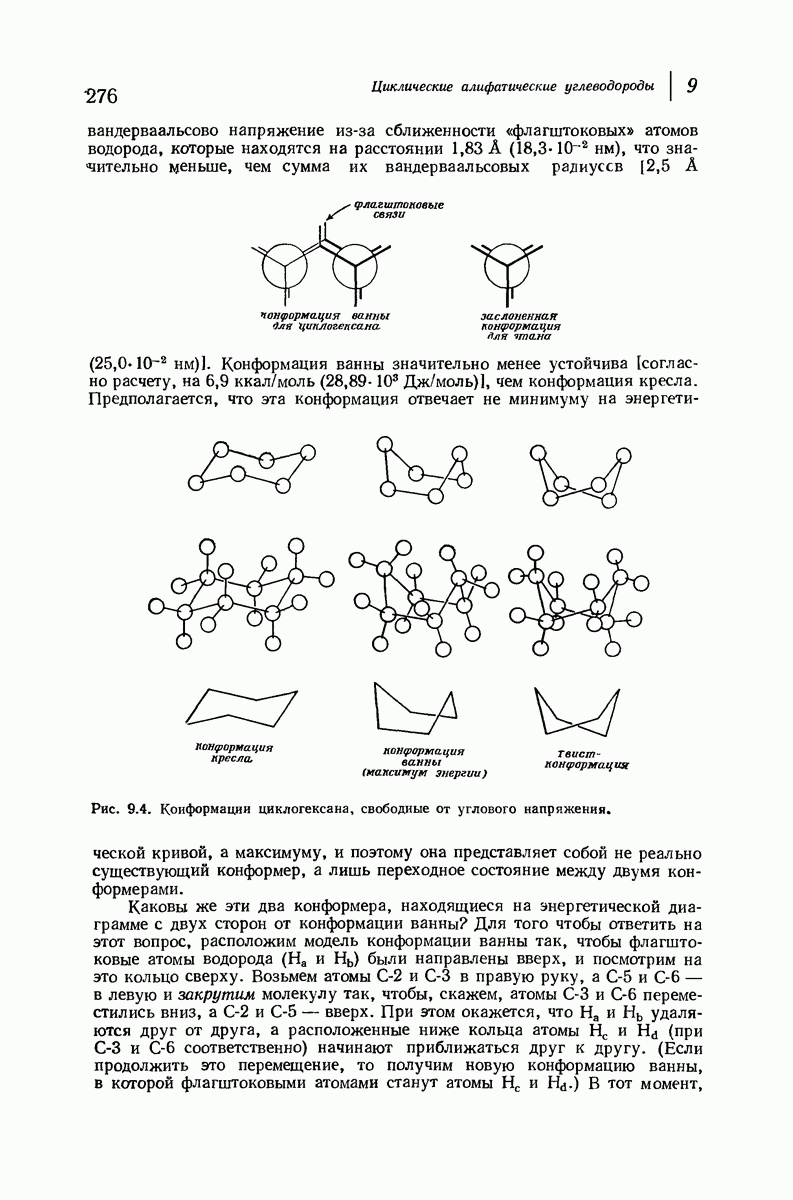
Теперь «поднимем» левый конец молекулы (рис. 9.4) так, чтобы получить конформацию ванны. (Как и все другие превращения, которые мы будем осуществлять в этом разделе, указанное превращение сопряжено лишь с поворотом вокруг простых связей, т. е. является конформационным превращением.) Это расположение атомов не кажется очень благоприятным. Если взглянуть вдоль любой из двух углерод-углеродных связей, то увидим, что в каждом случае имеется набор заслоненных связей. Поэтому можно ожидать значительного торсионного напряжения, по величине соответствующего напряжению в двух молекулах этана. Кроме того, имеется еще
вандерваальсово напряжение из-за сближенности «флагштоковых» атомов водорода, которые находятся на расстоянии  что значительно меньше, чем сумма их вандерваальсовых радиуссв
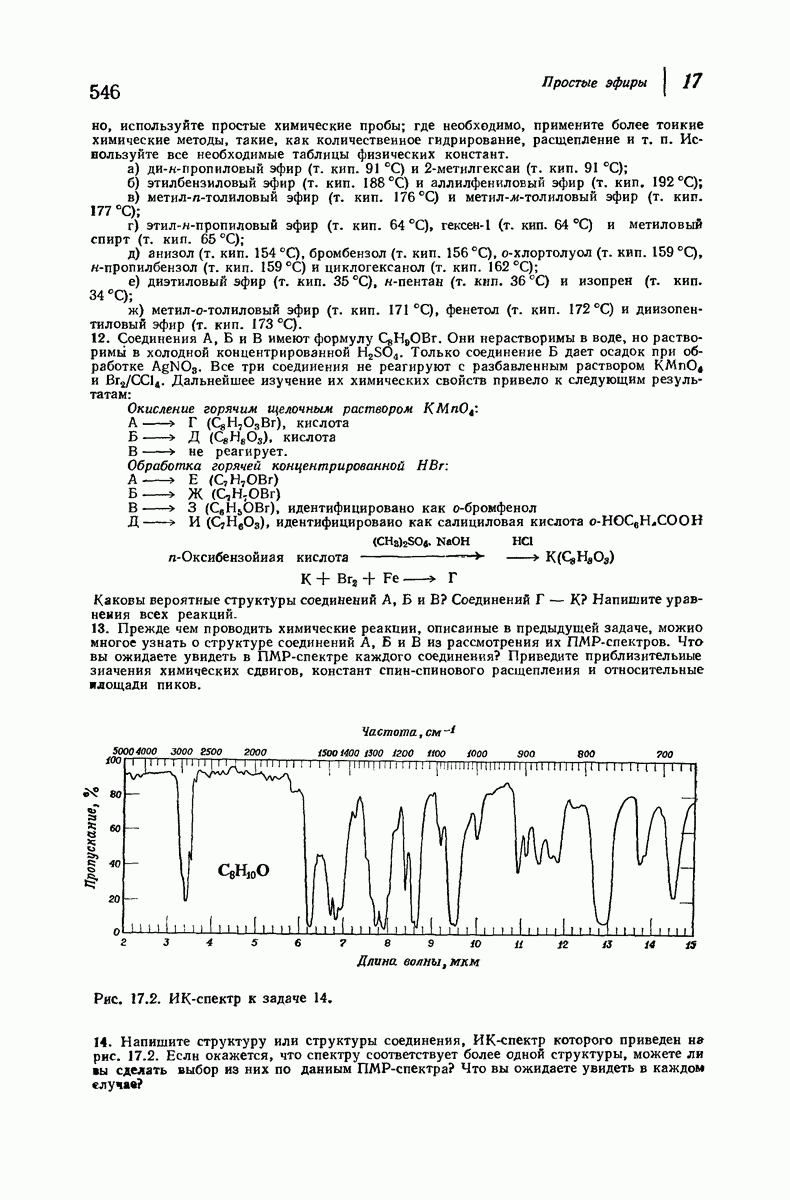
что значительно меньше, чем сумма их вандерваальсовых радиуссв 

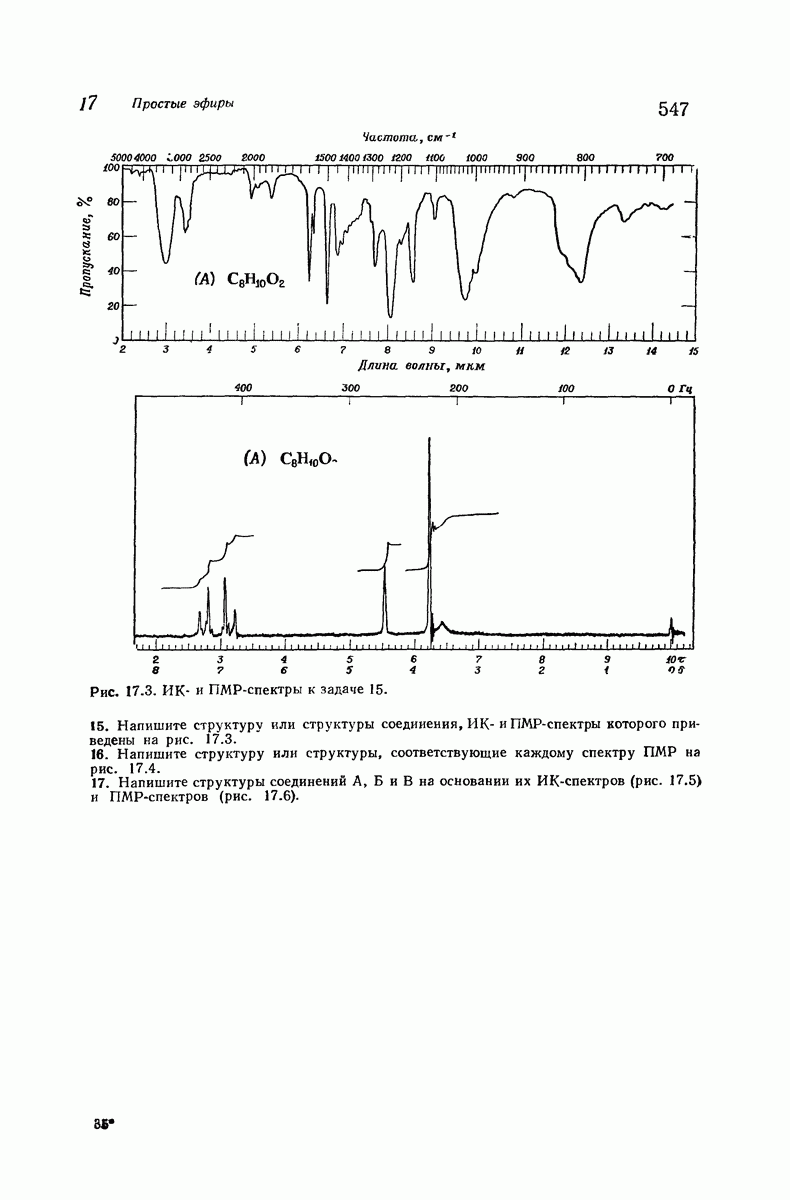
 Конформация ванны значительно менее устойчива [согласно расчету, на 6,9 ккал/моль
Конформация ванны значительно менее устойчива [согласно расчету, на 6,9 ккал/моль  чем конформация кресла.
чем конформация кресла.

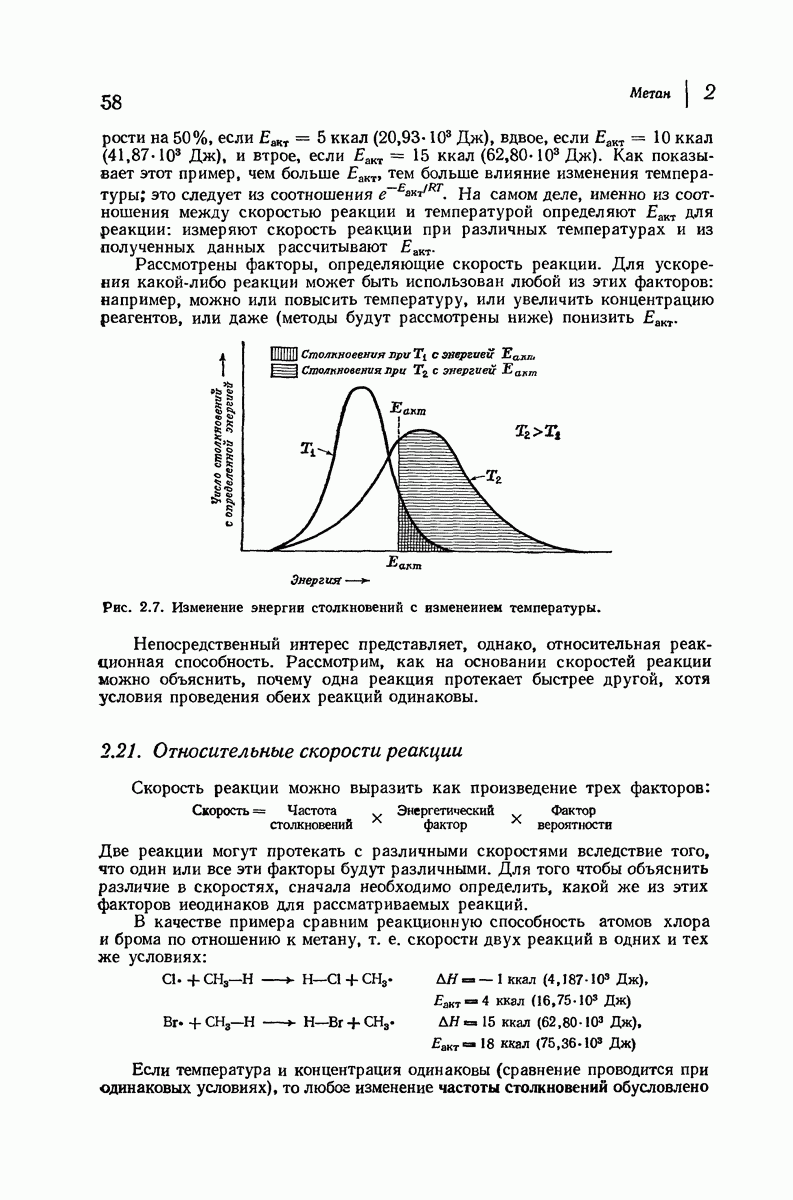
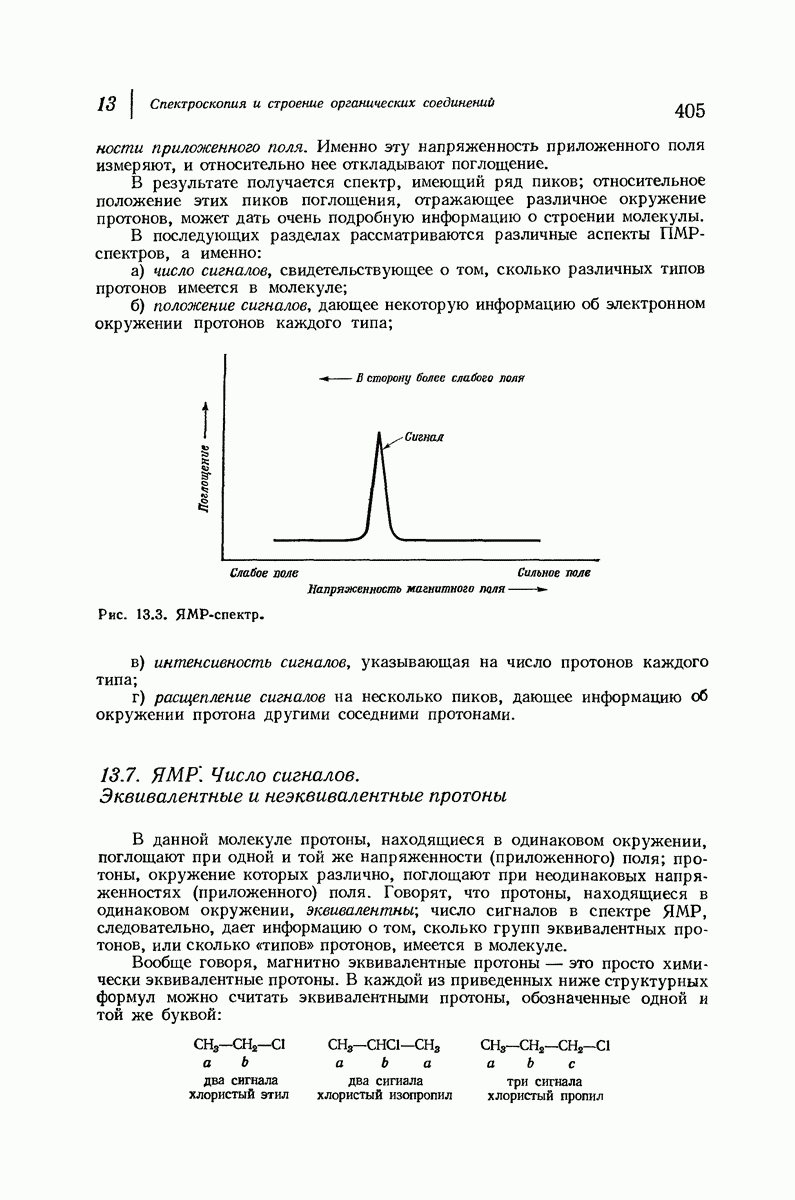
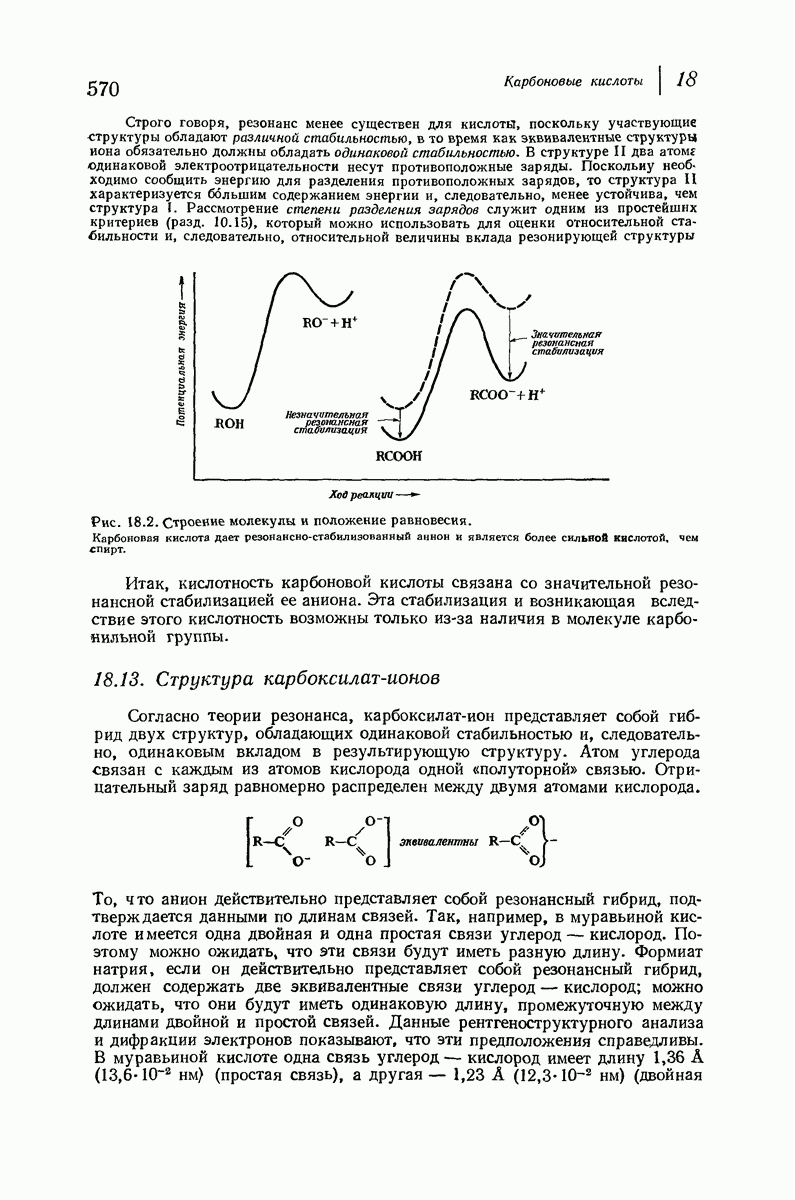
Рис. 9.4. Конформации циклогексана, свободные от углового напряжения.
Предполагается, что эта конформация отвечает не минимуму на энергетической кривой, а максимуму, и поэтому она представляет собой не реально существующий конформер, а лишь переходное состояние между двумя конформерами.
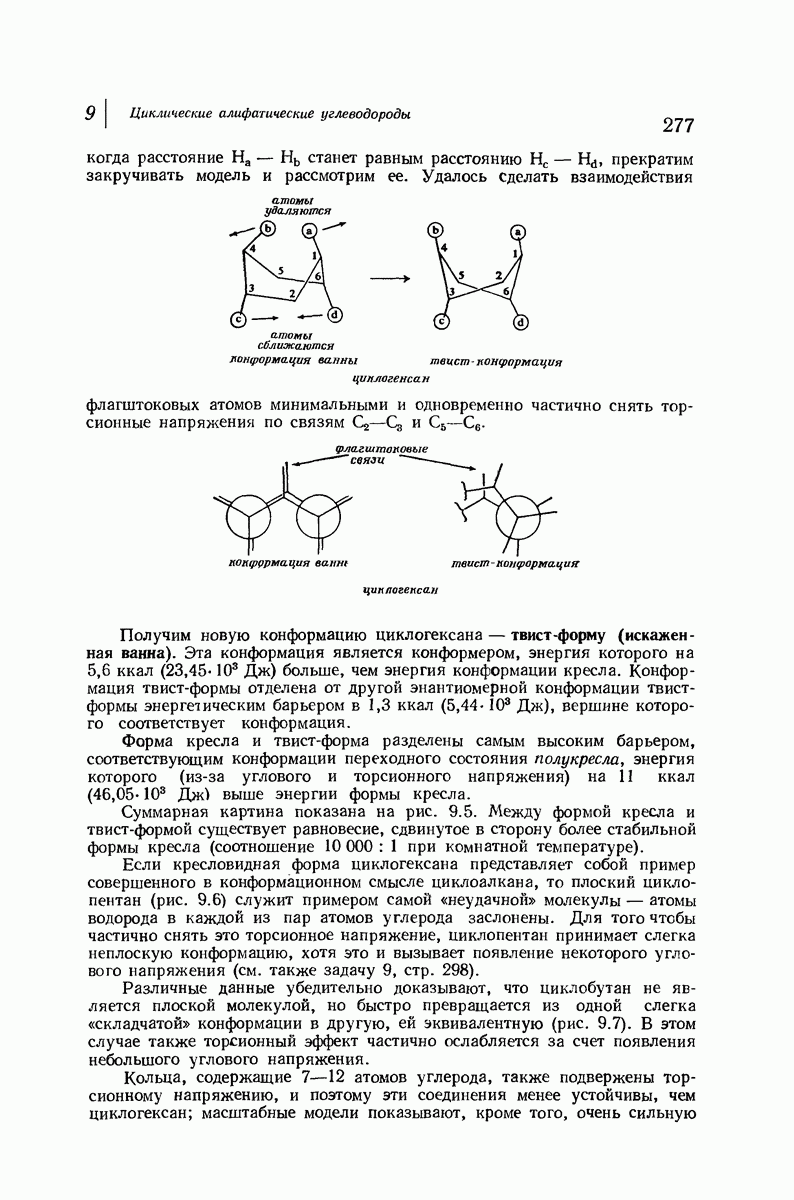
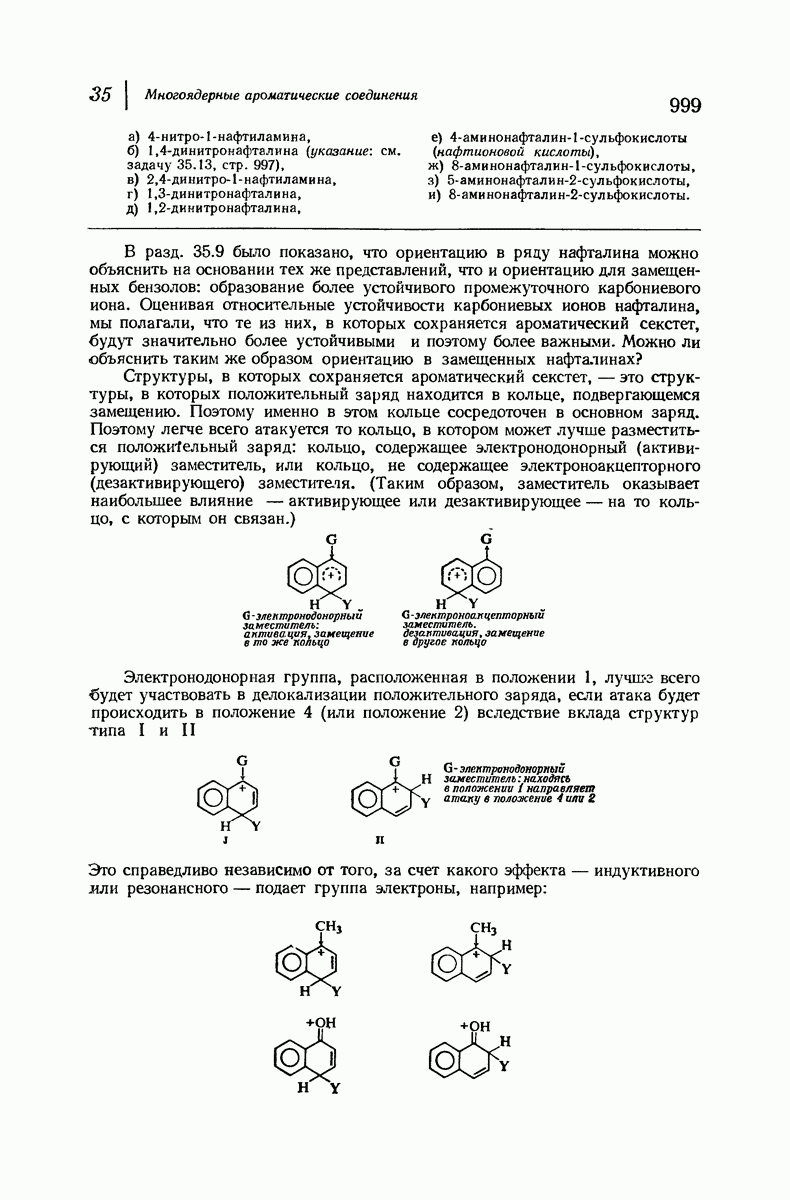
Каковы же эти два конформера, находящиеся на энергетической диаграмме с двух сторон от конформации ванны? Для того чтобы ответить на этот вопрос, расположим модель конформации ванны так, чтобы флагштоковые атомы водорода (На и  были направлены вверх, и посмотрим на это кольцо сверху. Возьмем атомы
были направлены вверх, и посмотрим на это кольцо сверху. Возьмем атомы  в правую руку, а
в правую руку, а  в левую и закрутим молекулу так, чтобы, скажем, атомы
в левую и закрутим молекулу так, чтобы, скажем, атомы  переместились вниз, а
переместились вниз, а  вверх. При этом окажется, что На и
вверх. При этом окажется, что На и  удаляются друг от друга, а расположенные ниже кольца атомы
удаляются друг от друга, а расположенные ниже кольца атомы  и На (при
и На (при  соответственно) начинают приближаться друг к другу. (Если продолжить это перемещение, то получим новую конформацию ванны, в которой флагштоковыми атомами станут атомы
соответственно) начинают приближаться друг к другу. (Если продолжить это перемещение, то получим новую конформацию ванны, в которой флагштоковыми атомами станут атомы  и
и  .) В тот момент,
.) В тот момент,
когда расстояние  станет равным расстоянию
станет равным расстоянию  прекратим закручивать модель и рассмотрим ее. Удалось Сделать взаимодействия
прекратим закручивать модель и рассмотрим ее. Удалось Сделать взаимодействия

флагштоковых атомов минимальными и одновременно частично снять торсионные напряжения по связям 

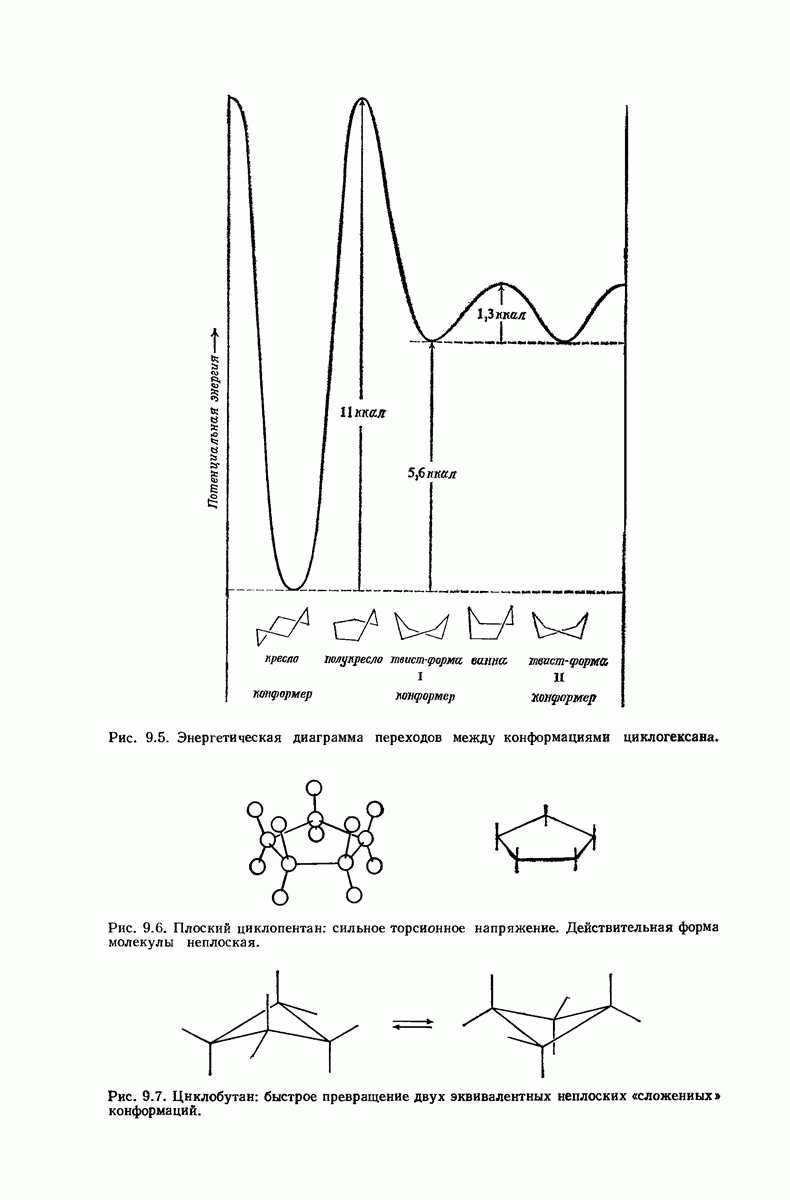
Получим новую конформацию циклогексана — твист-форму (искаженная ванна). Эта конформация является конформером, энергия которого на 5,6 ккал  больше, чем энергия конформации кресла. Конформация твист-формы отделена от другой энантиомерной конформации твист-формы энергетическим барьером в 1,3 ккал
больше, чем энергия конформации кресла. Конформация твист-формы отделена от другой энантиомерной конформации твист-формы энергетическим барьером в 1,3 ккал  вершине которого соответствует конформация.
вершине которого соответствует конформация.
Форма кресла и твист-форма разделены самым высоким барьером, соответствующим конформации переходного состояния полукресла, энергия которого (из-за углового и торсионного напряжения) на 11 ккал  выше энергии формы кресла.
выше энергии формы кресла.
Суммарная картина показана на рис. 9.5. Между формой кресла и твист-формой существует равновесие, сдвинутое в сторону более стабильной формы кресла (соотношение  при комнатной температуре).
при комнатной температуре).
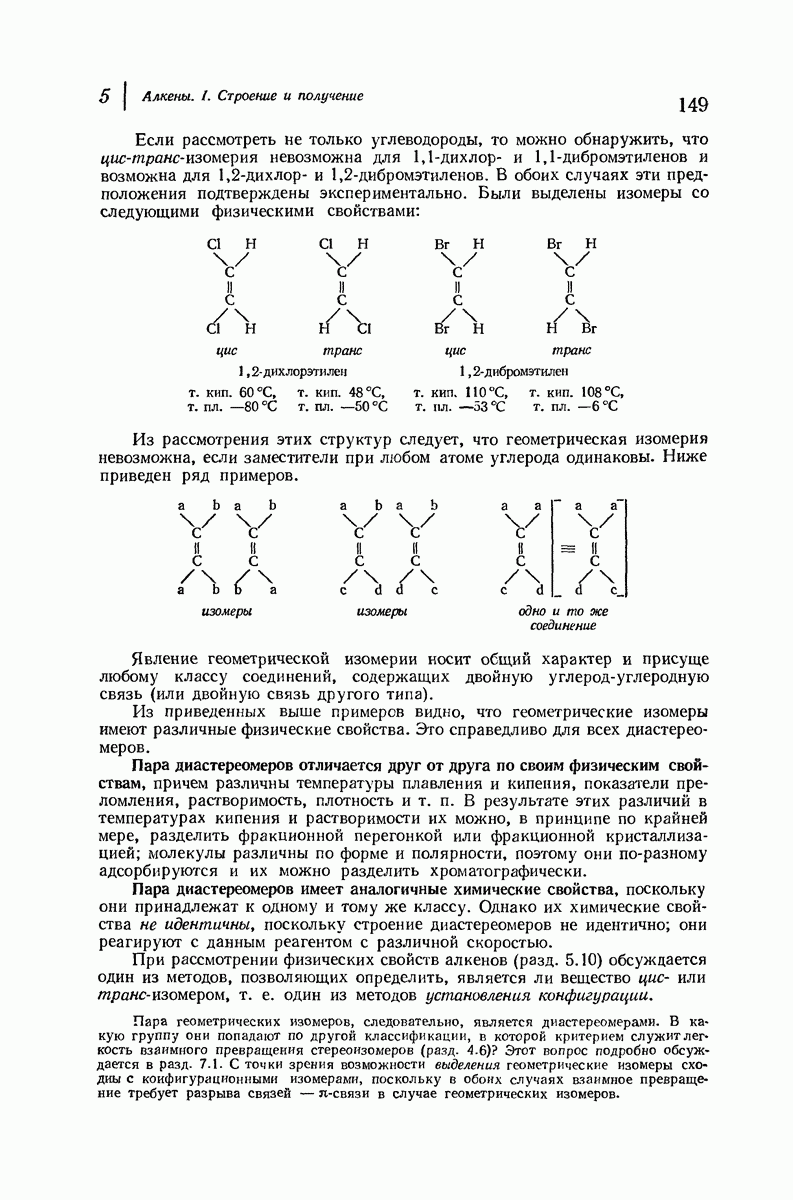
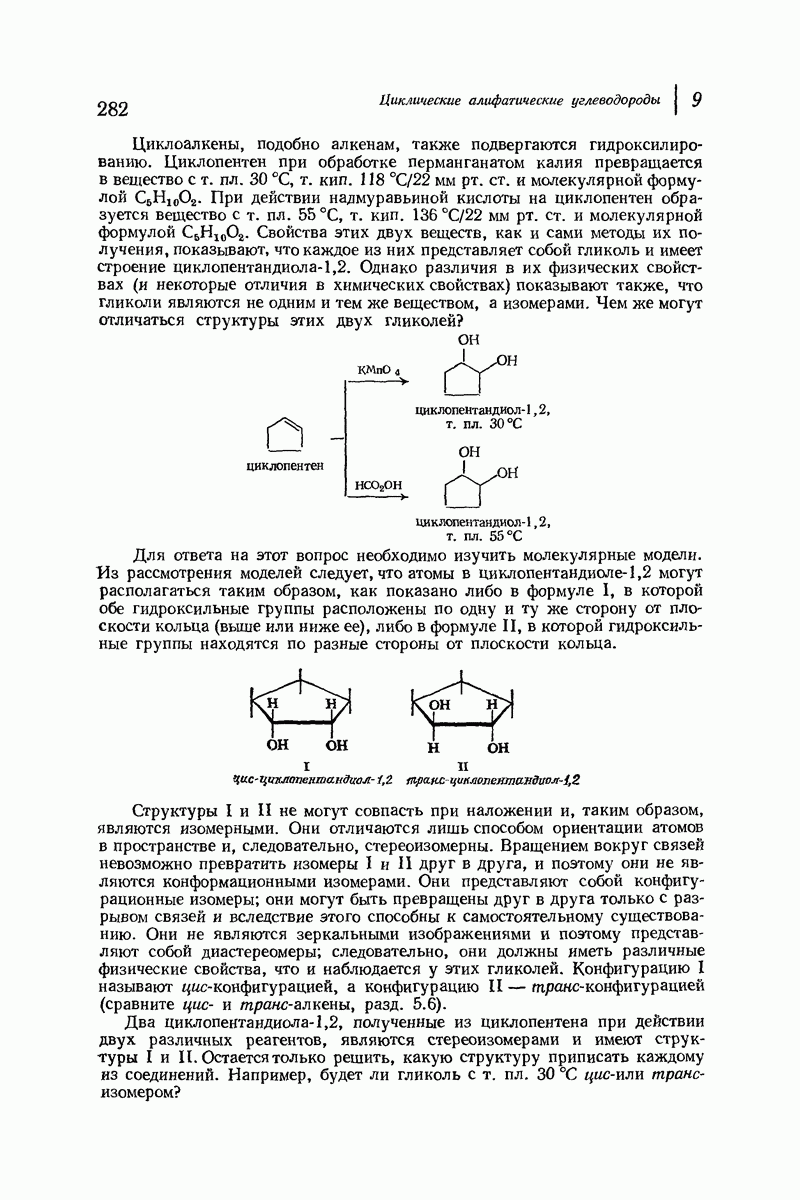
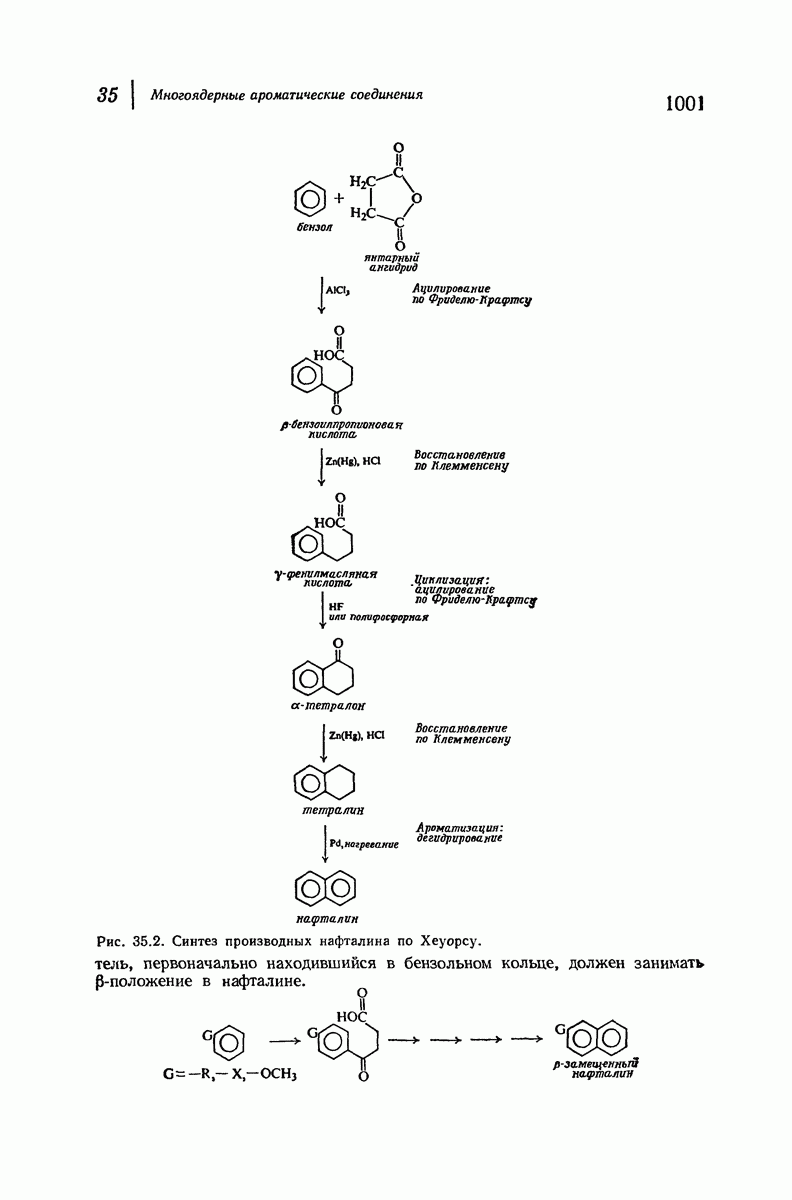
Если кресловидная форма циклогексана представляет собой пример совершенного в конформационном смысле циклоалкана, то плоский цикло-пентан (рис. 9.6) служит примером самой «неудачной» молекулы — атомы водорода в каждой из пар атомов углерода заслонены. Для того чтобы частично снять это торсионное напряжение, циклопентан принимает слегка неплоскую конформацию, хотя это и вызывает появление некоторого углового напряжения (см. также задачу 9, стр. 298).
Различные данные убедительно доказывают, что циклобутан не является плоской молекулой, но быстро превращается из одной слегка «складчатой» конформации в другую, ей эквивалентную (рис. 9.7). В этом случае также торсионный эффект частично ослабляется за счет появления небольшого углового напряжения.
Кольца, содержащие 7—12 атомов углерода, также подвержены торсионному напряжению, и поэтому эти соединения менее устойчивы, чем циклогексан; масштабные модели показывают, кроме того, очень сильную

(кликните для просмотра скана)
сближенность атомов водорода внутри этих циклов. Лишь циклы с довольно большим числом звеньев, по-видимому, столь же устойчивы, как и циклогексан.
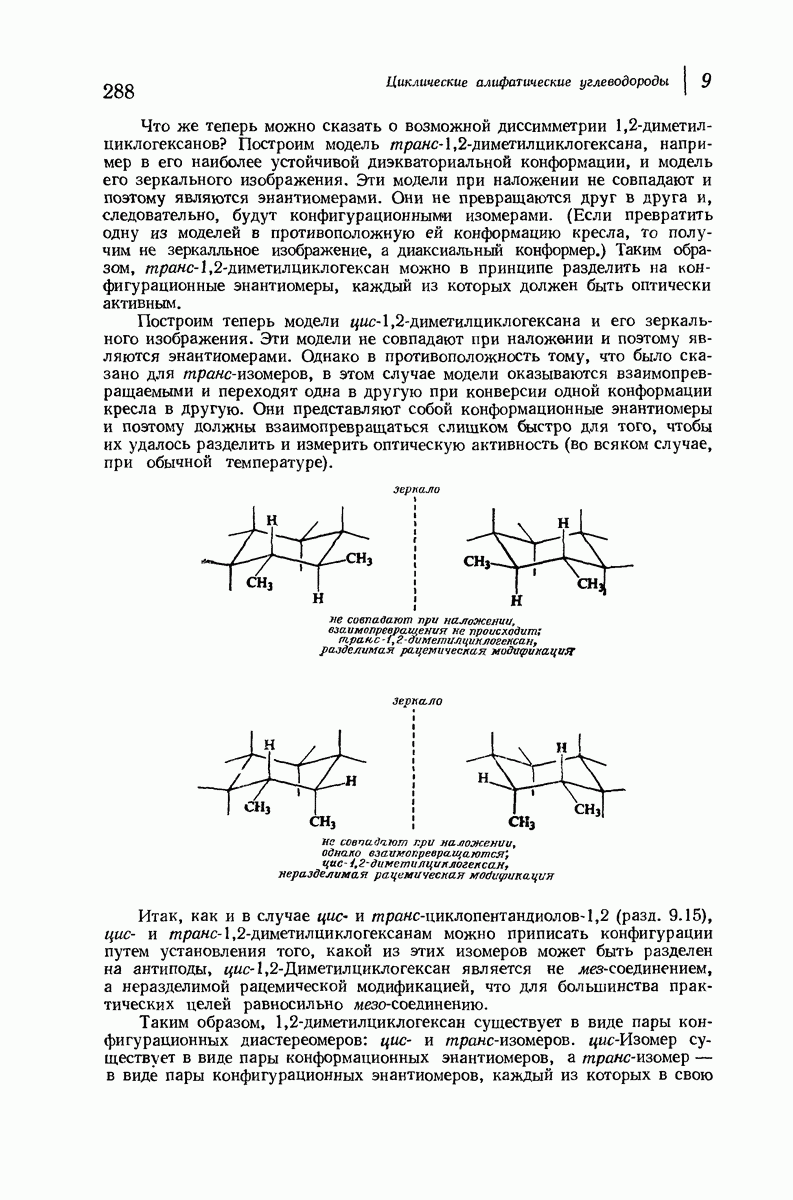
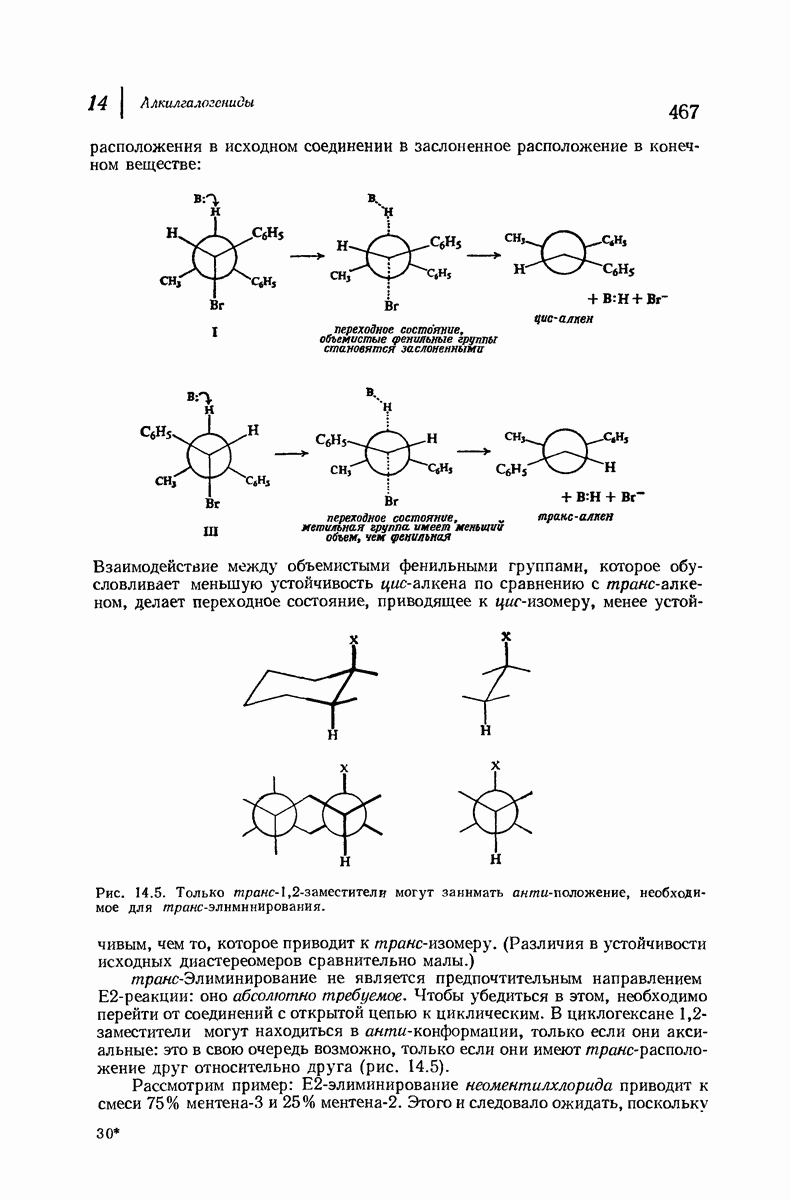
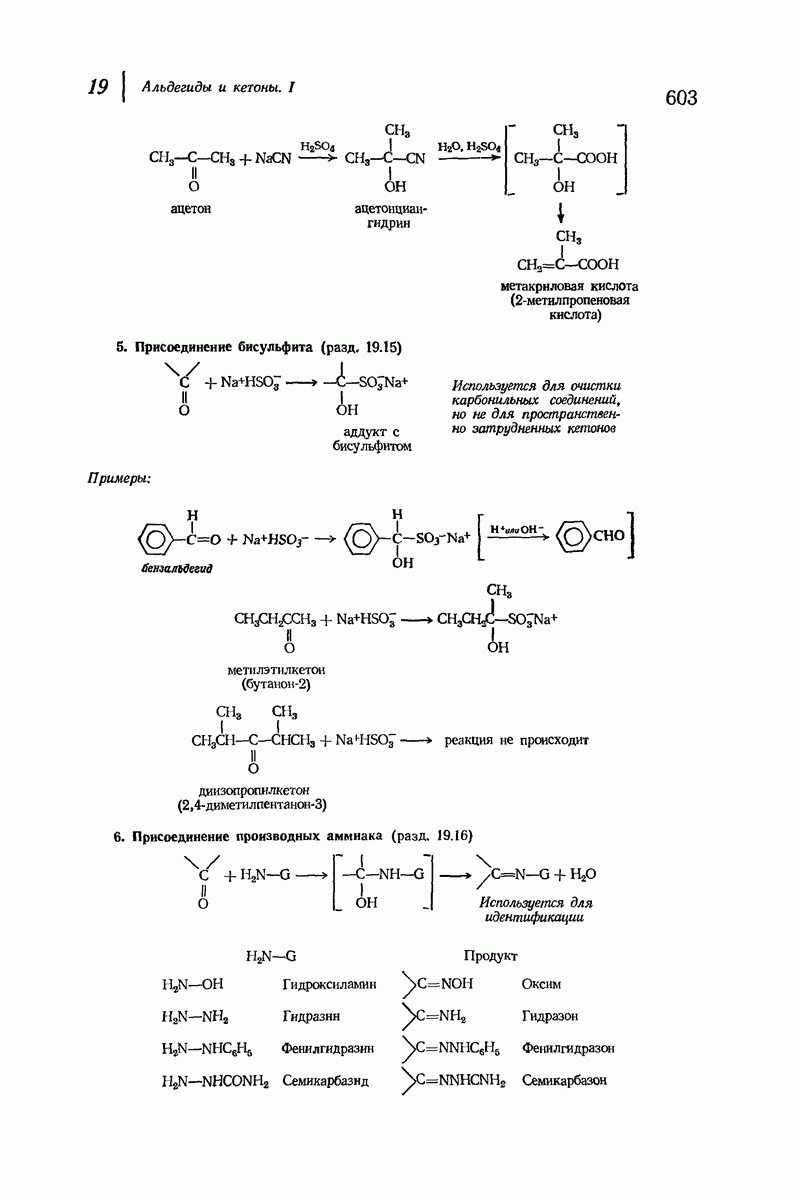
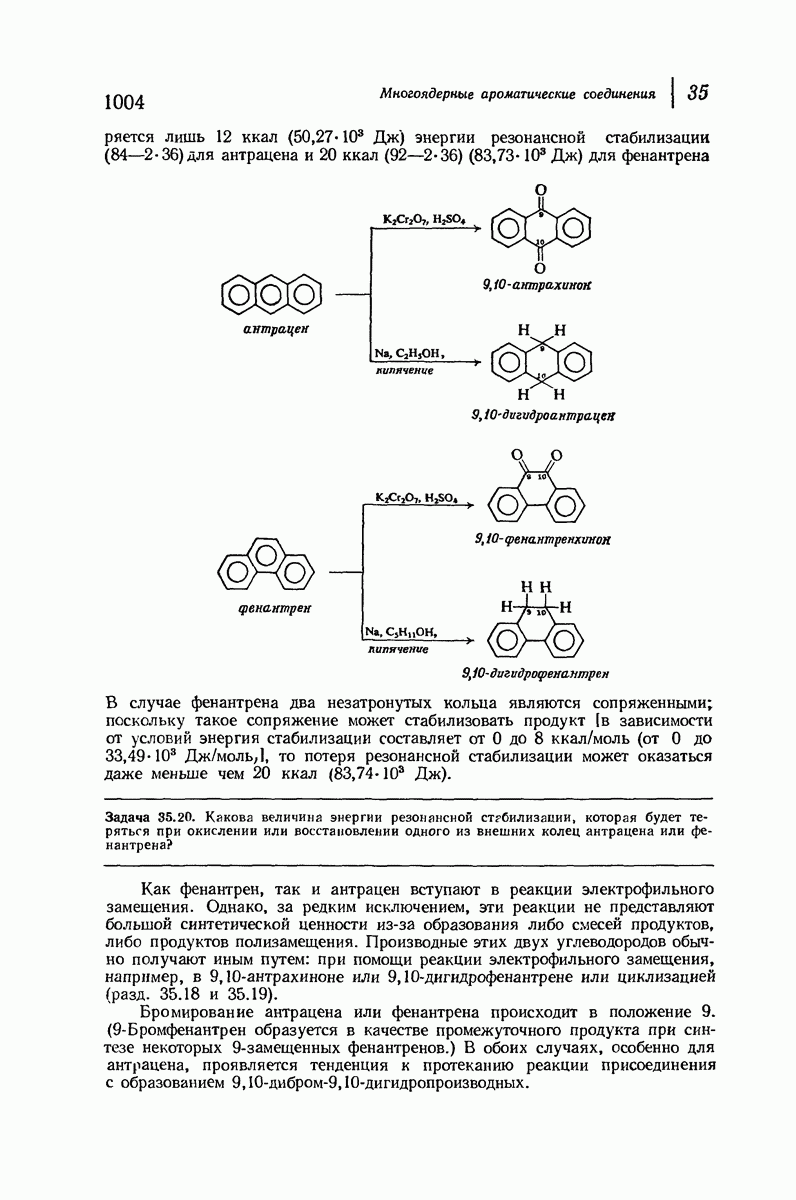
9.13. Экваториальные и аксиальные связи в циклогексане
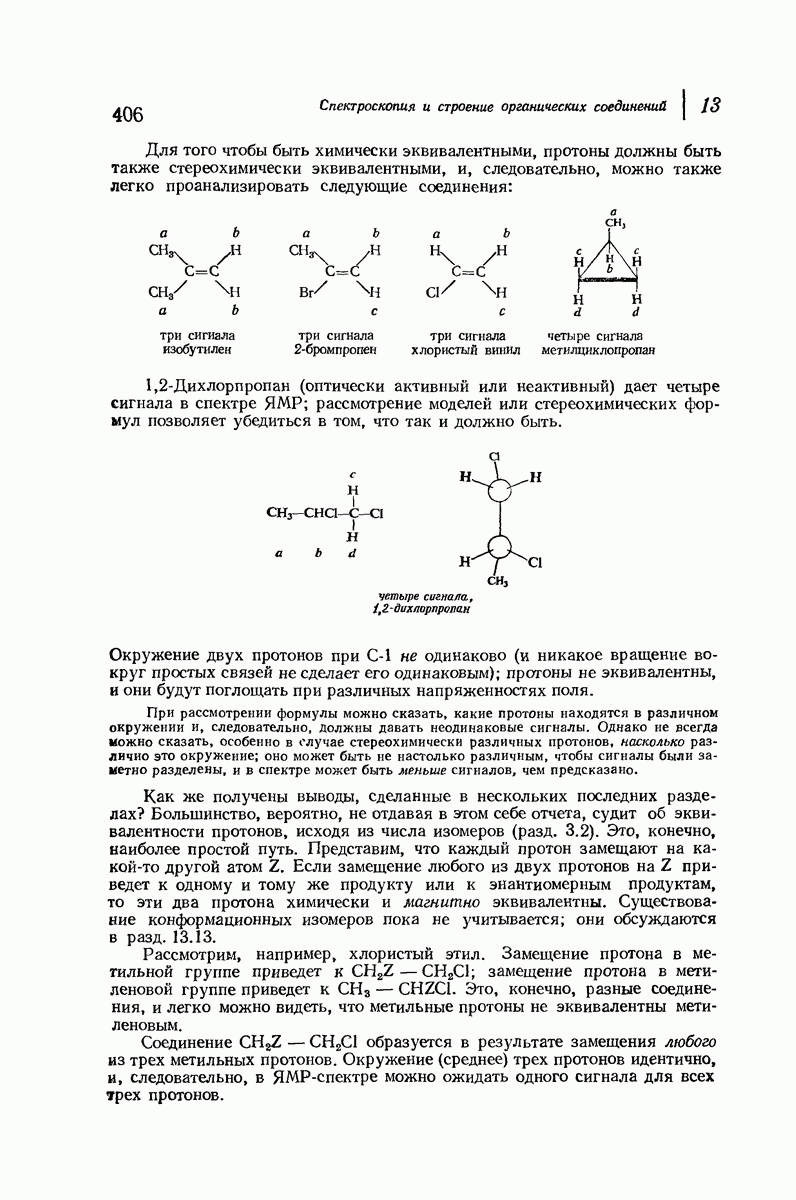
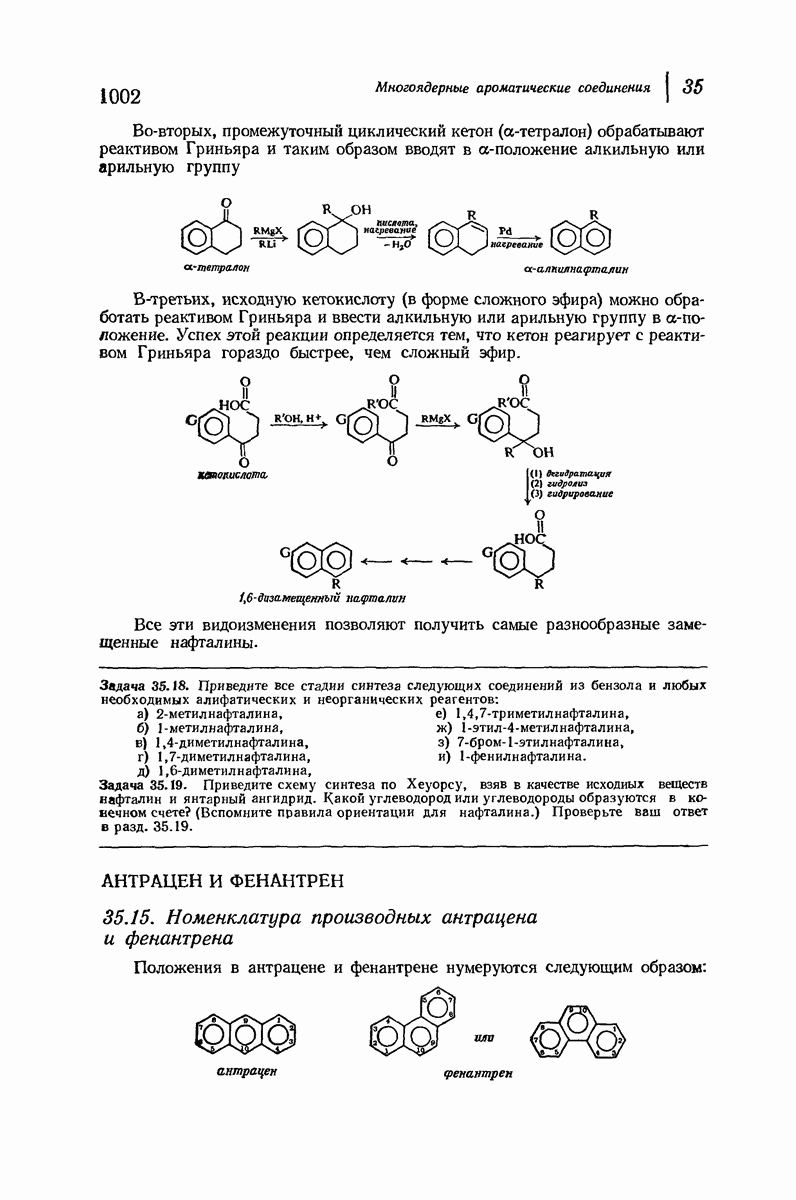
Вернемся к модели циклогексана в конформации кресла (рис. 9.8). Хотя его кольцо неплоское, можно считать, что атомы углерода находятся приблизительно в одной плоскости.

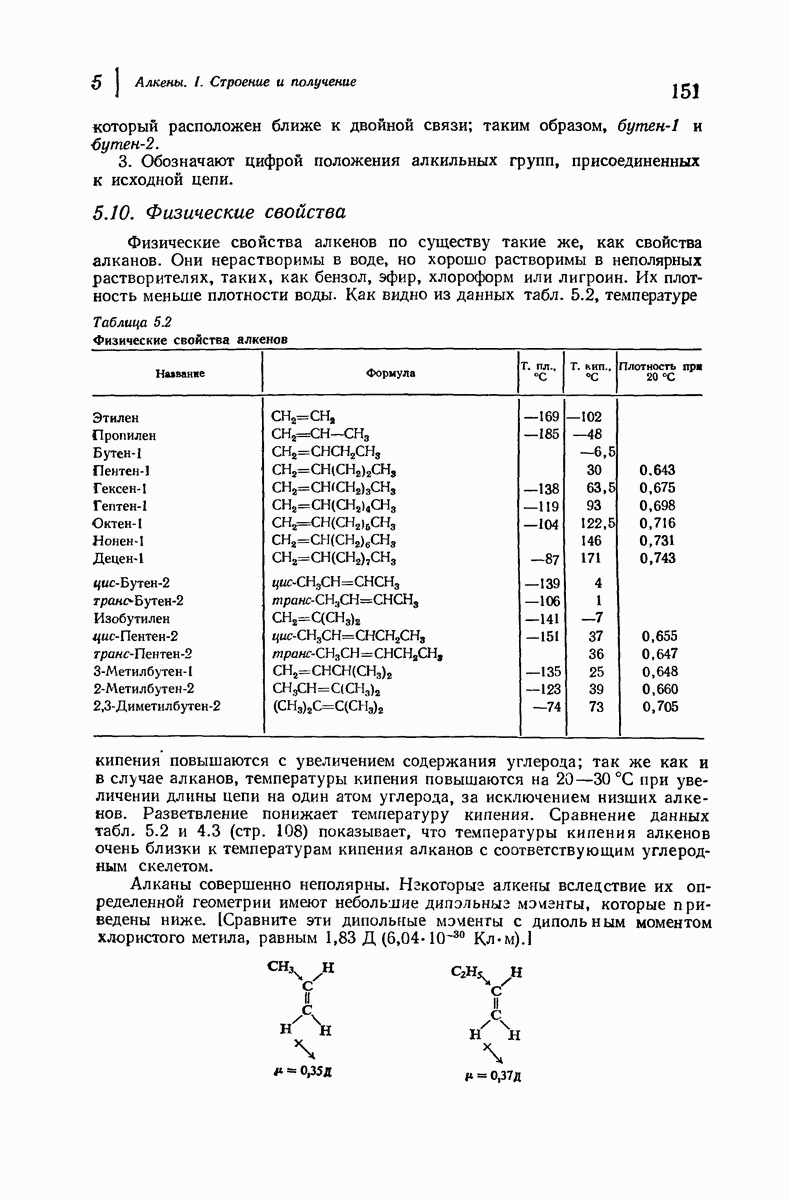
Рис. 9.8. Экваториальные и аксиальные связи в циклогексане.
Если рассматривать молекулу таким образом, то заметим, что атомы водорода занимают положения двух типов; шесть атомов лежат в плоскости атомов углерода, а шесть других — над или под нею. Связи шести атомов первого типа лежат в поясе, обрамляющем «экватор» кольца, и их называют экваториальными. Связи других шести атомов направлены вдоль оси  перпендикулярной плоскости кольца, и их называют аксиальными. В конформации кресла каждый из атомов углерода имеет одну экваториальную и одну аксиальную связь.
перпендикулярной плоскости кольца, и их называют аксиальными. В конформации кресла каждый из атомов углерода имеет одну экваториальную и одну аксиальную связь.
Сам циклогексан, в котором атомы углерода связаны лишь с атомами водорода, свободен не только от углового и торсионного напряжения, но и от вандерваальсова напряжения. Атомы водорода у соседних атомов углерода находятся на таком же расстоянии друг от друга  , как и в затороженной конформации этана, и если они и испытывают взаимодействие между собой, то это слабое вандерваальсово притяжение. Отметим также, что три аксиальных атома водорода, находящихся с одной из сторон кольца, несколько сближены, хотя они и не находятся у соседних атомов углерода; в действительности расстояние между ними оказывается таким же благоприятным, как расстояние между другими атомами водорода
, как и в затороженной конформации этана, и если они и испытывают взаимодействие между собой, то это слабое вандерваальсово притяжение. Отметим также, что три аксиальных атома водорода, находящихся с одной из сторон кольца, несколько сближены, хотя они и не находятся у соседних атомов углерода; в действительности расстояние между ними оказывается таким же благоприятным, как расстояние между другими атомами водорода 
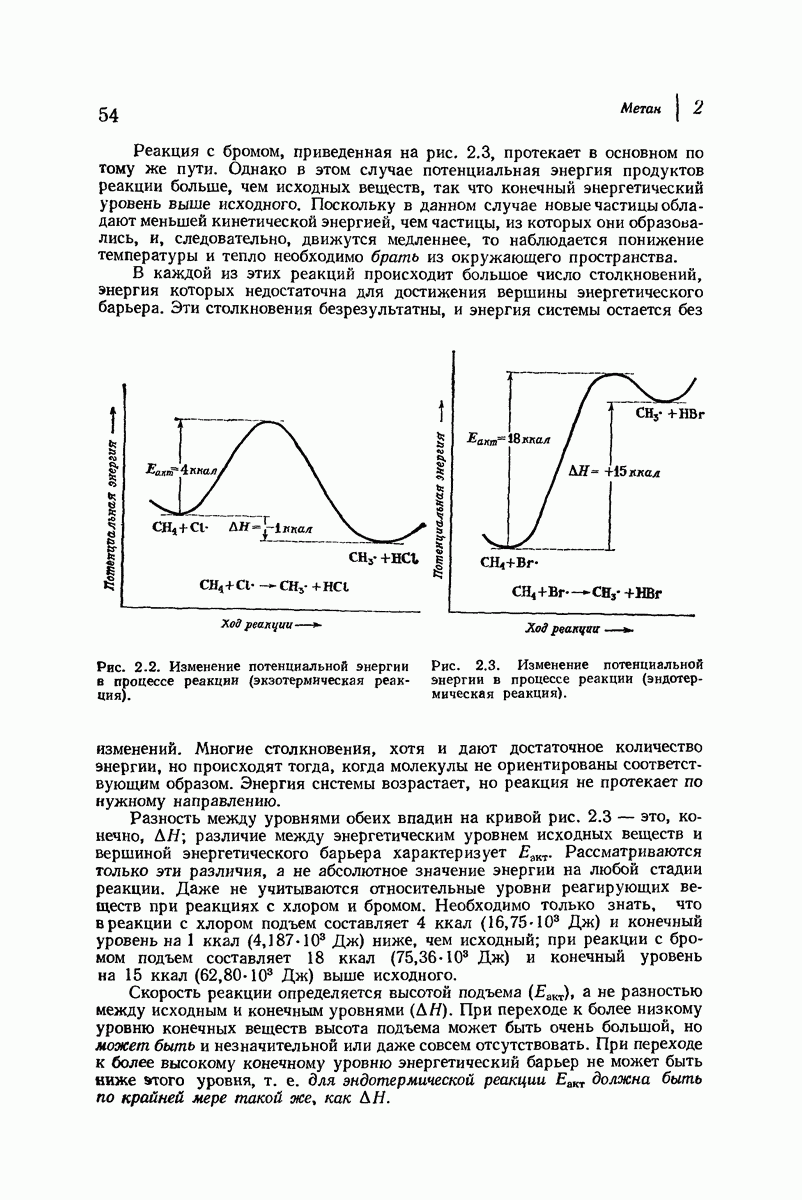
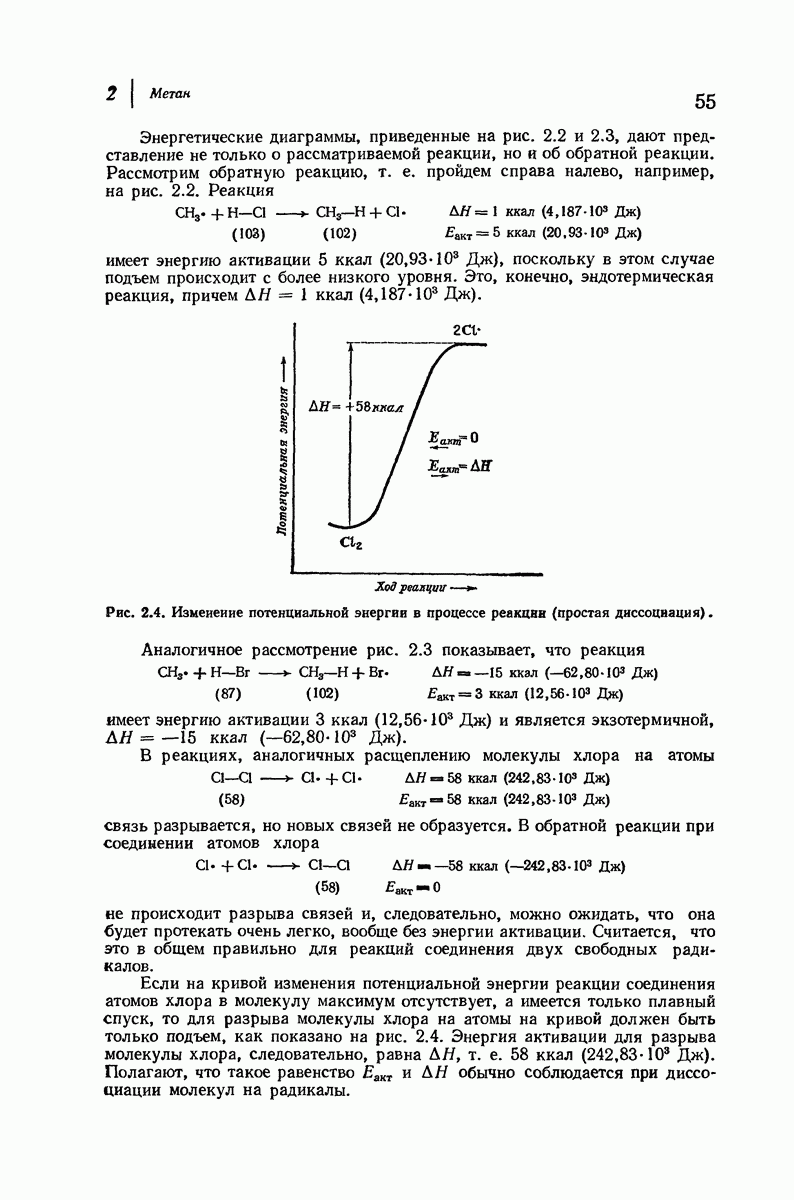
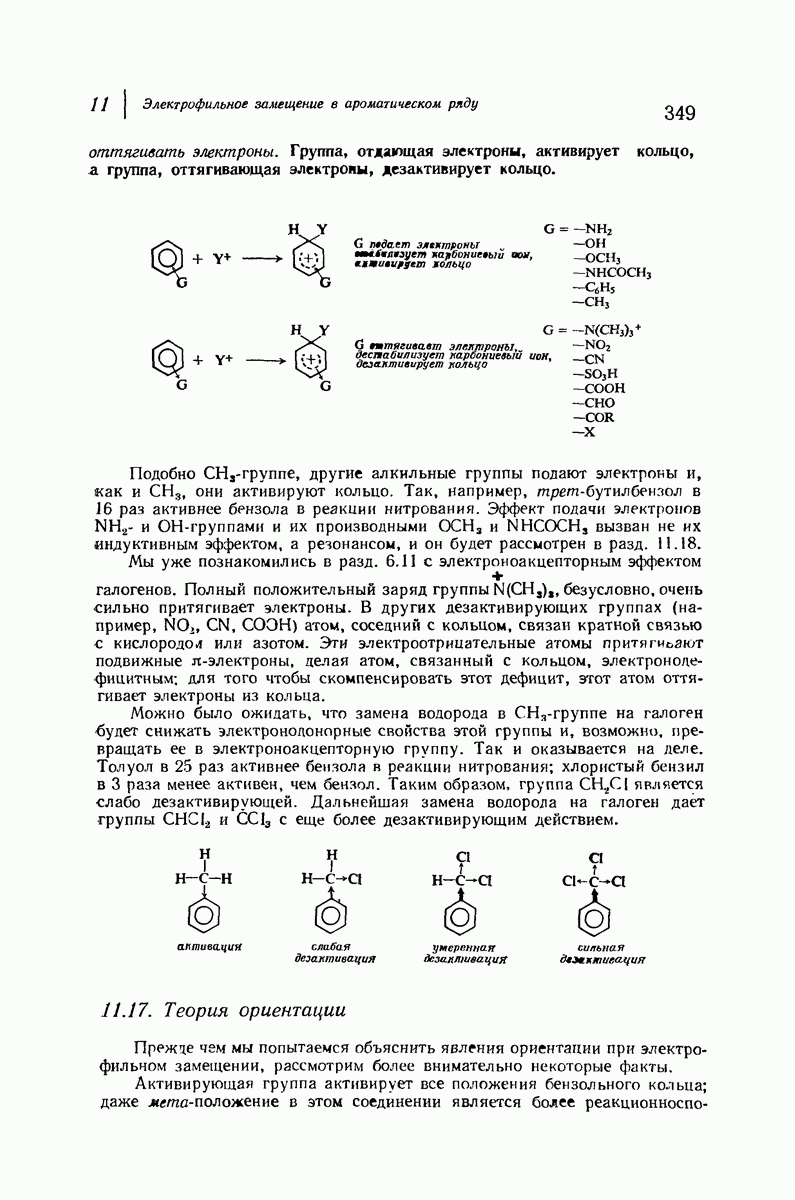
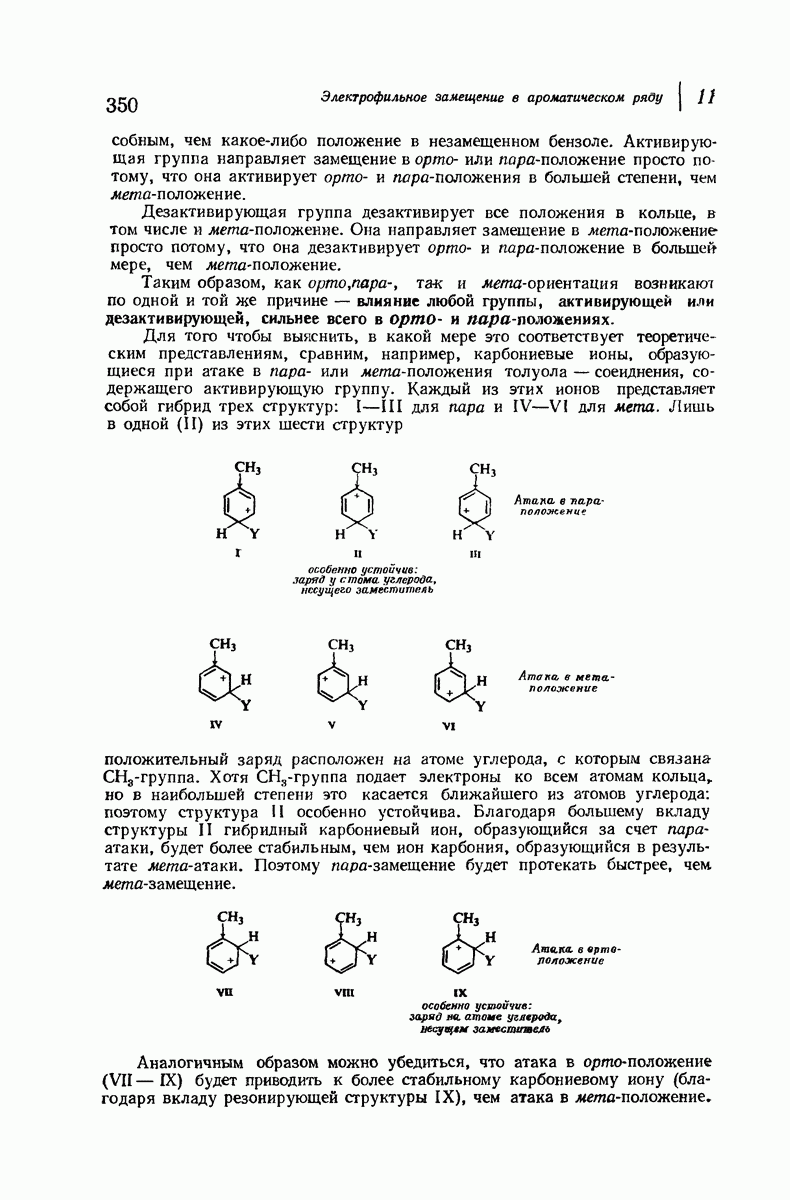
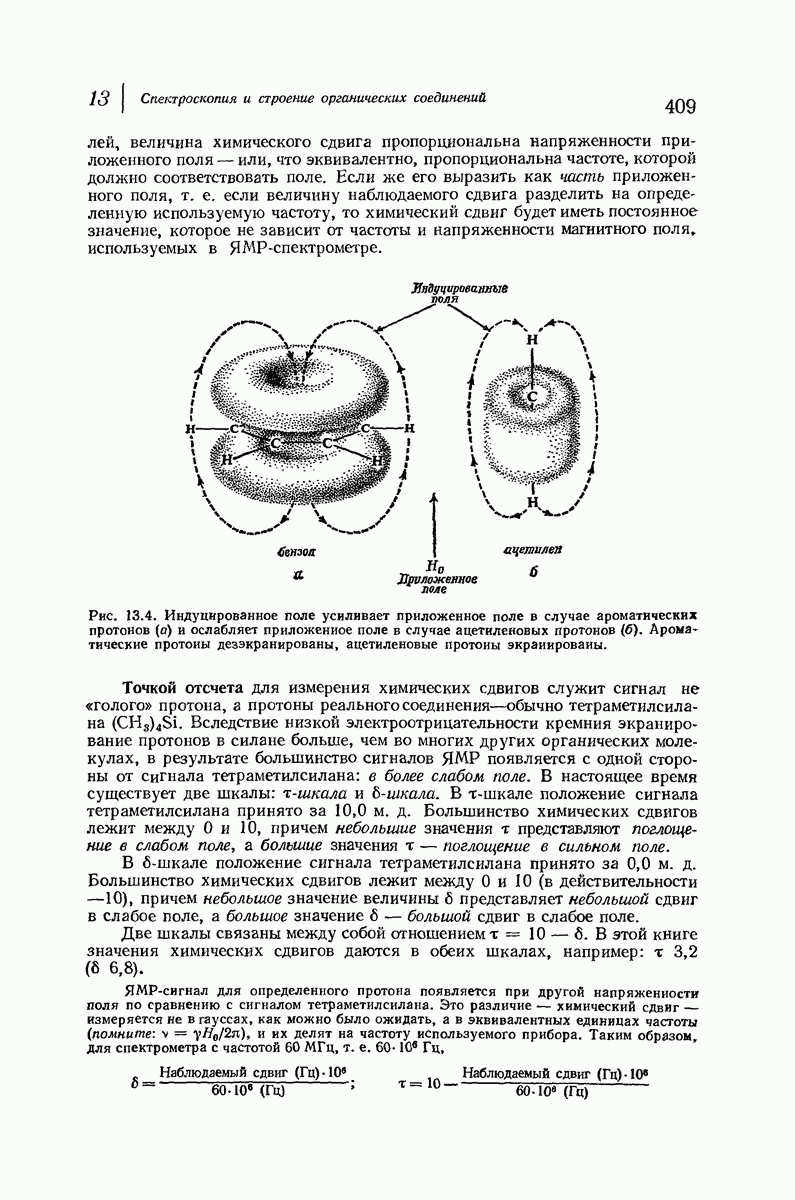
Если водород заместить на атом или группу большего размера, то наблюдается перекрывание атомов. Оно наиболее сильно для атомов, связанных с кольцом тремя аксиальными связями и находящихся на одной стороне молекулы. Возникающее взаимодействие называют 1,3-диаксиальным взаимодействием. За исключением водорода, все остальные экваториальные атомы или группы находятся в менее стесненном положении, чем аксиальные.
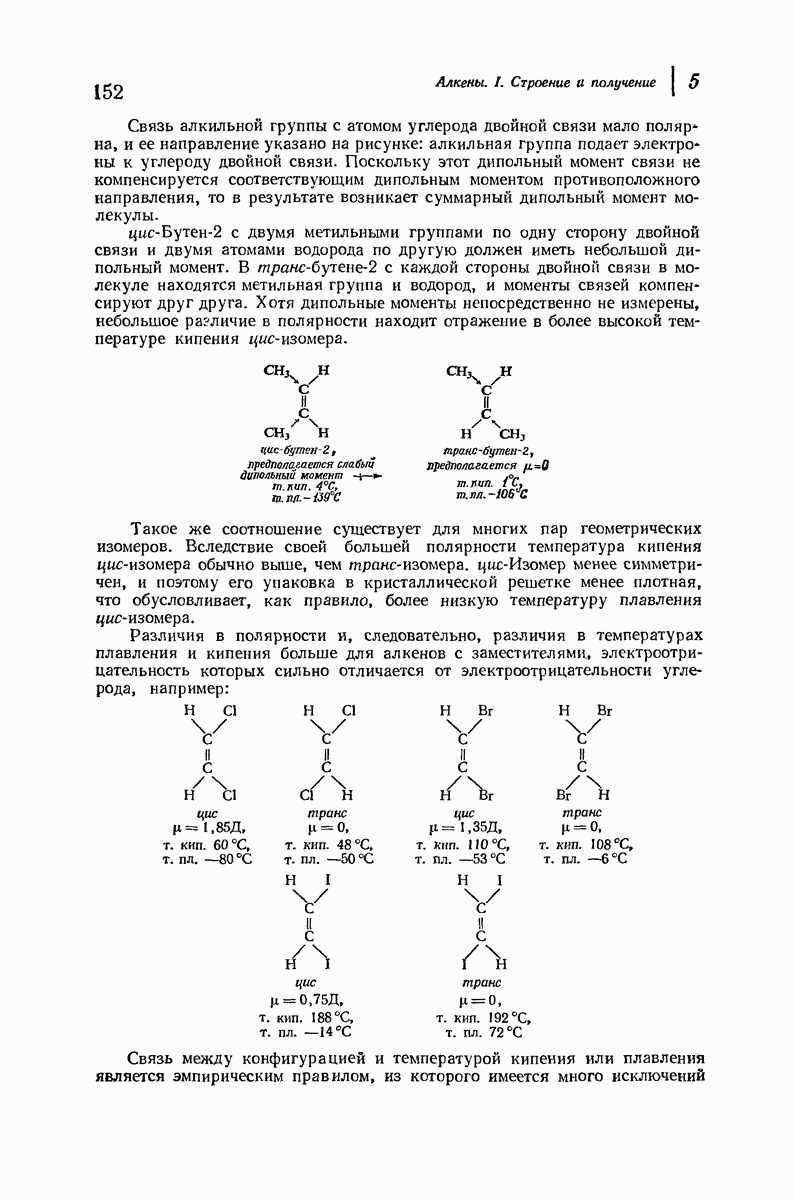
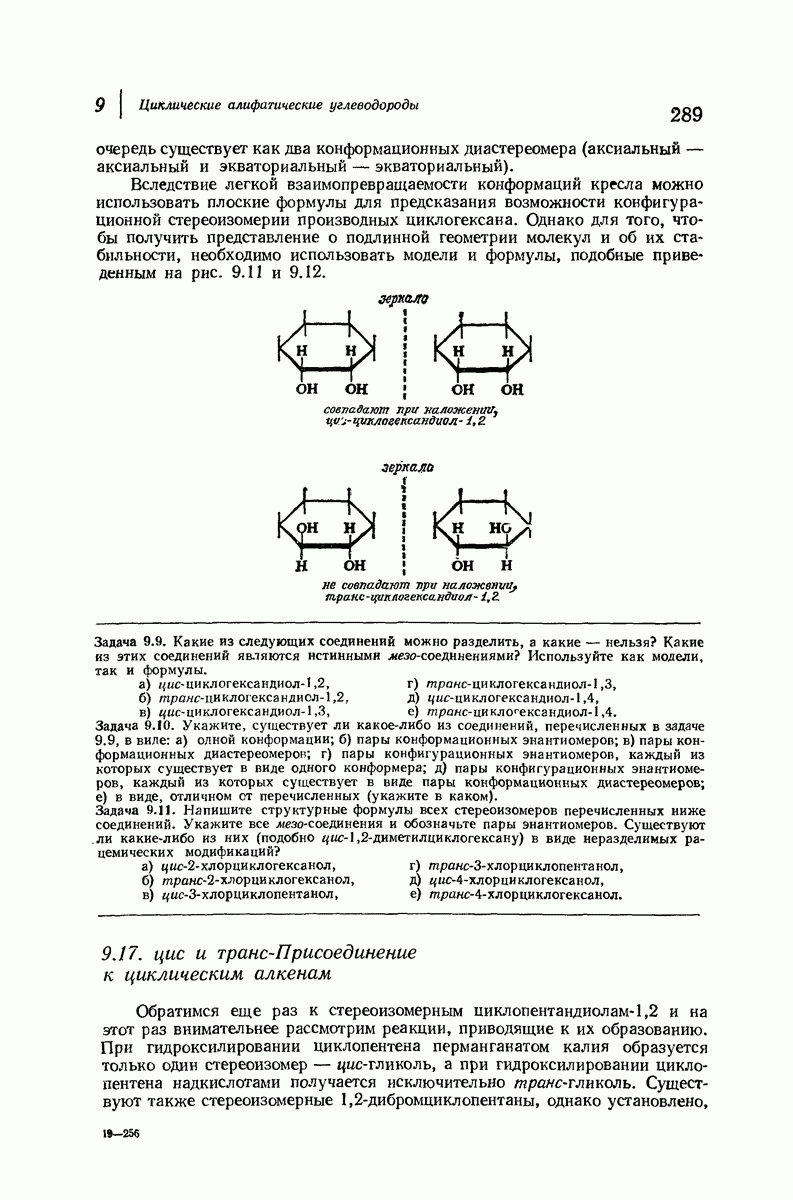
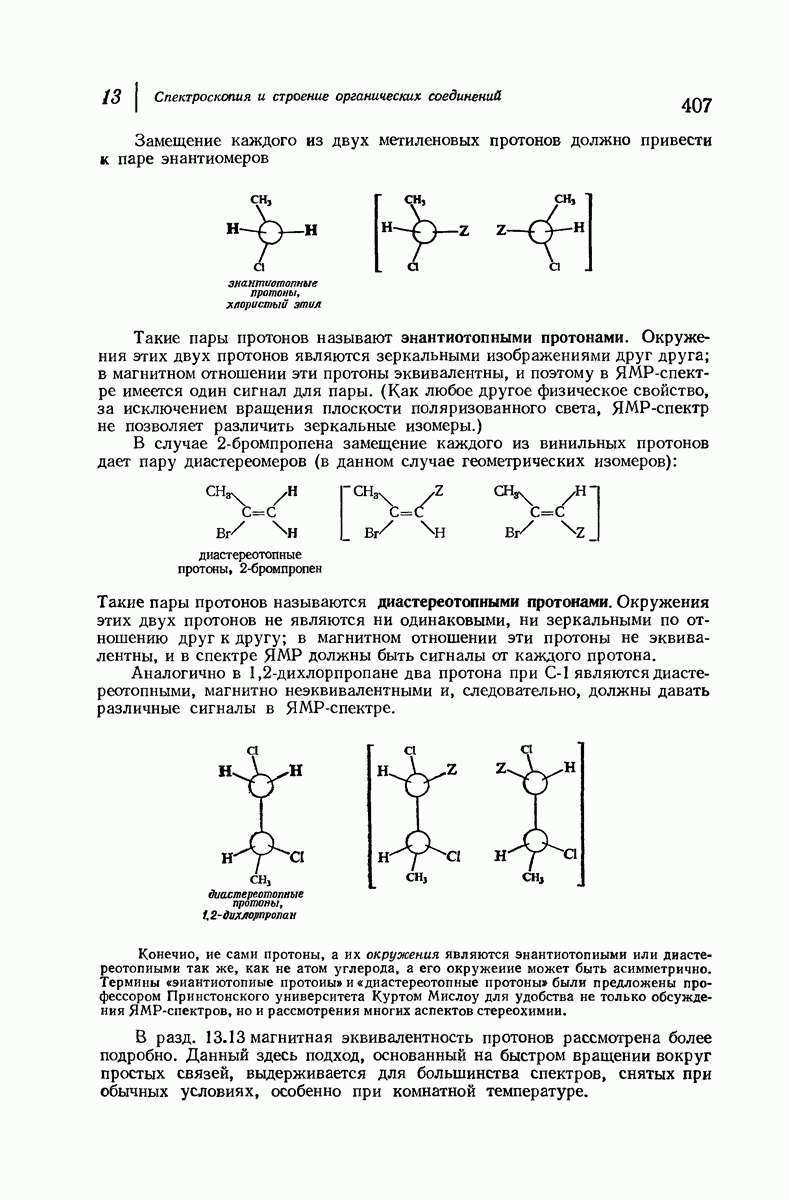
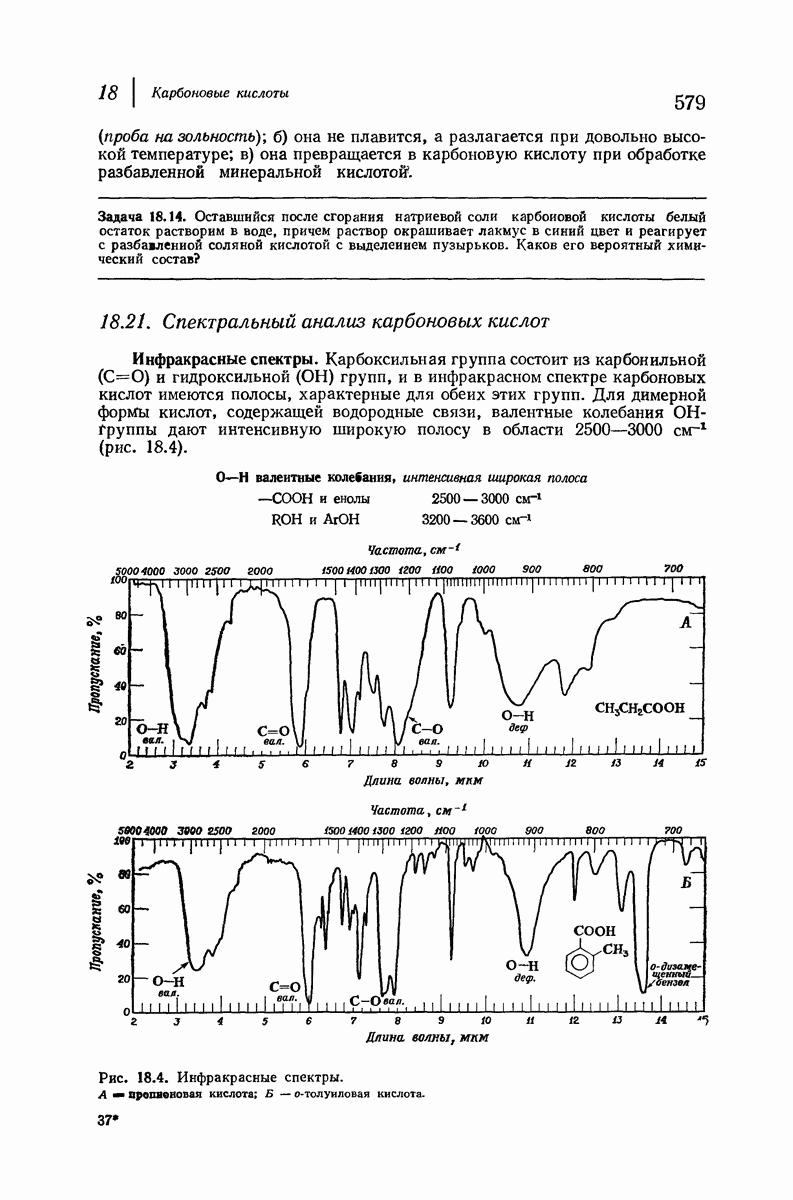
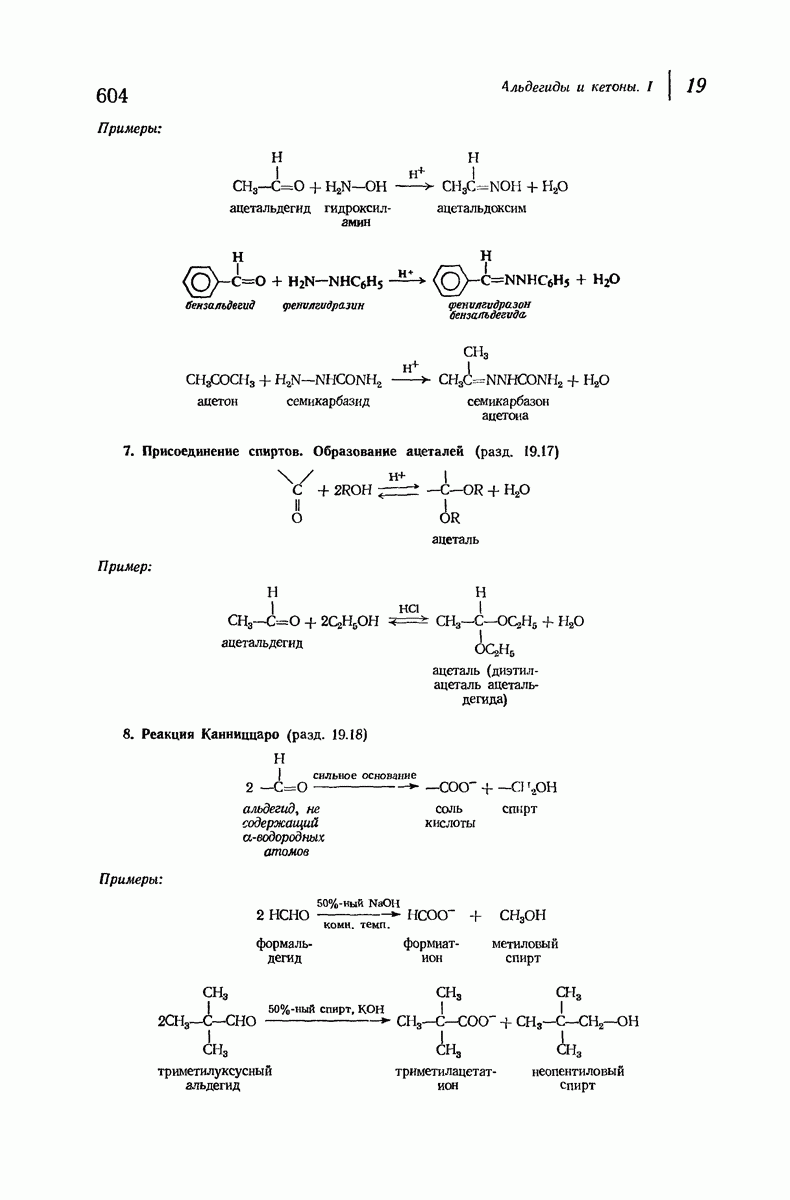
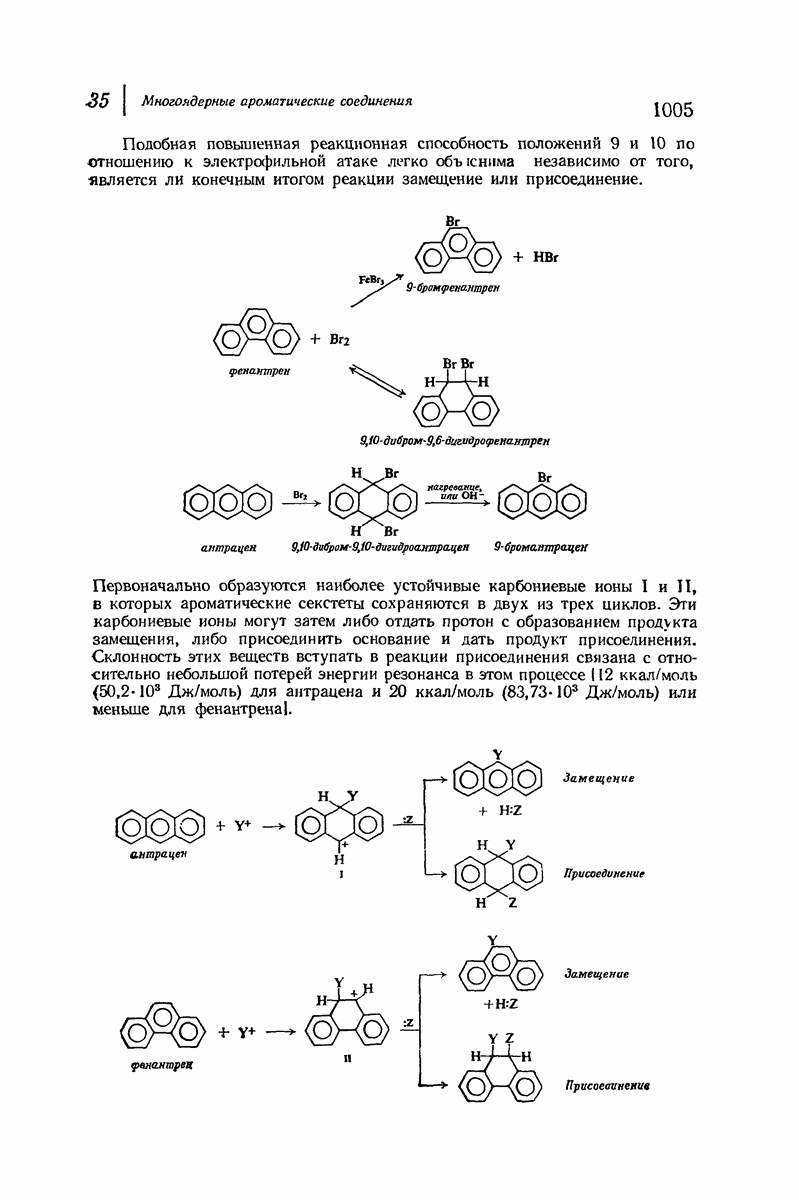
В качестве простого примера важности 1,3-диаксиальных взаимодействий рассмотрим метилциклогексан. Основное внимание при оценке устойчивости различных конформаций этого соединения будет уделено метильной группе, поскольку она — самый большой заместитель в кольце, наиболее чувствительный к пространственному сближению групп. Возможны две кресловидные конформации для этого соединения (рис. 9.9), в одной из которых метильная группа находится в экваториальном положении, а в
другой — в аксиальном. Как показано на рис. 9.10, два аксиальных атома водорода  ближе находятся к аксиальной метильной группе
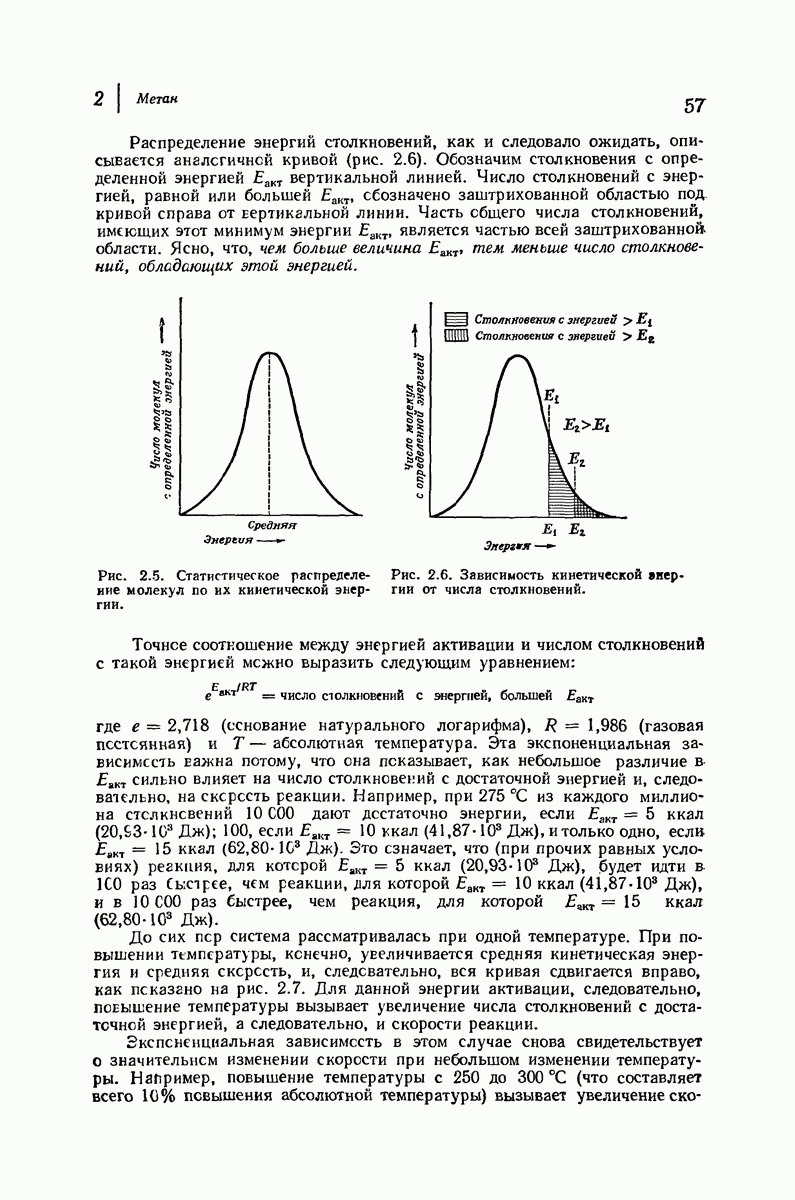
ближе находятся к аксиальной метильной группе  чем любые из атомов водорода к экваториальной
чем любые из атомов водорода к экваториальной  -группе.
-группе.

Рис. 9.9. Конформации кресла метилциклогексана.
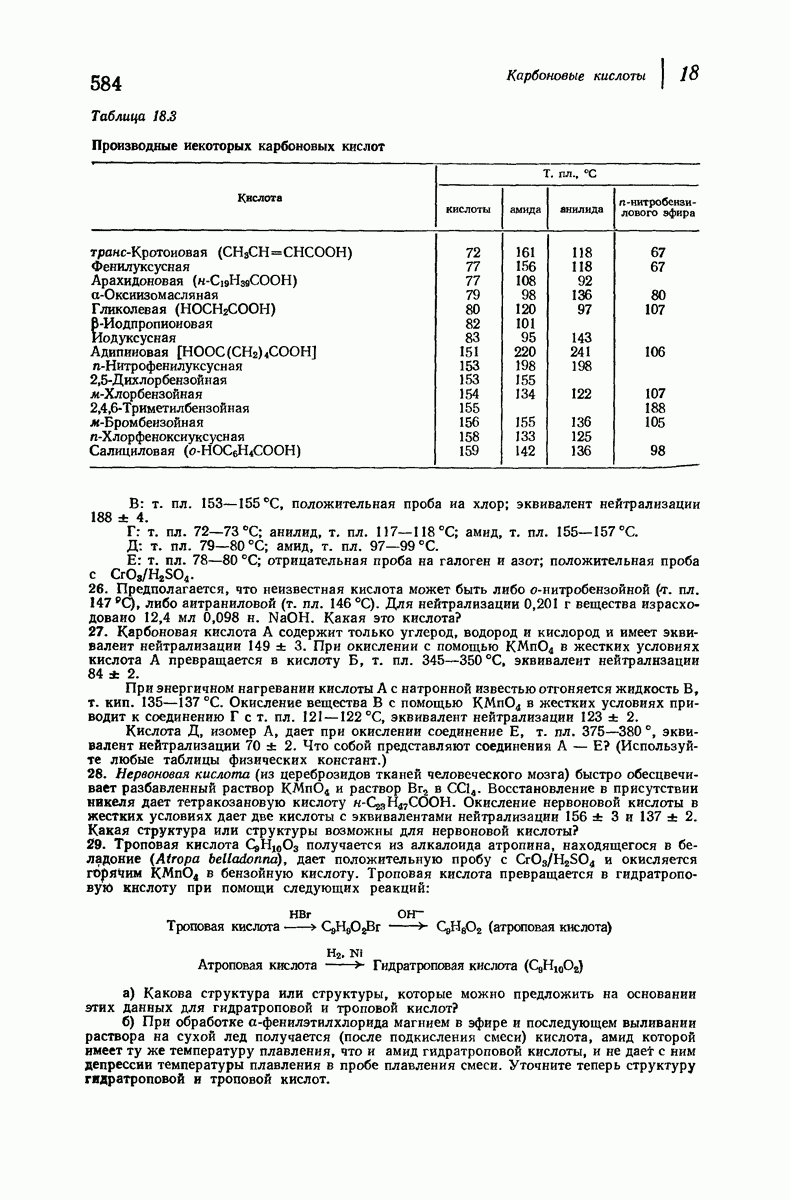
Можно ожидать, что экваториальная конформация будет более устойчивой, и она оказывается таковой, причем различие в энергии составляет примерно 1,8 ккал  При комнатной температуре большая часть молекул (примерно 95%) находится в конформации с метильной группой в незатрудненном экваториальном положении.
При комнатной температуре большая часть молекул (примерно 95%) находится в конформации с метильной группой в незатрудненном экваториальном положении.

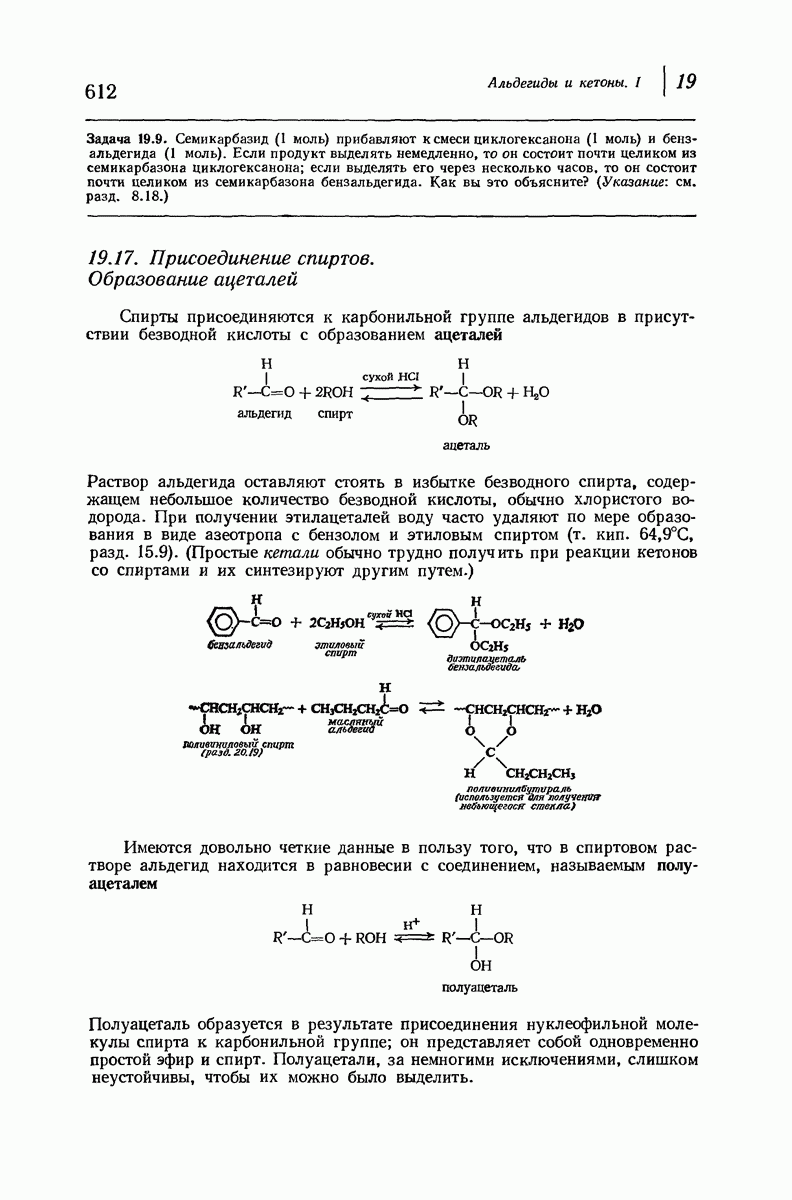
Рис. 9.10. 1,3-Диаксиальные взаимодействия. Аксиальная  -группа более затруднена, чем экваториальная.
-группа более затруднена, чем экваториальная.
Таким образом, в экваториальном положении  -группа направлена в сторону от ближайших соседей — двух атомов водорода (аксиального и экваториального) у соседних атомов углерода. Иначе обстоит дело при аксиальном положении
-группа направлена в сторону от ближайших соседей — двух атомов водорода (аксиального и экваториального) у соседних атомов углерода. Иначе обстоит дело при аксиальном положении  поскольку в этом случае связь
поскольку в этом случае связь  параллельна связям, удерживающим ближайшие соседние атомы — два аксиальных атома водорода.
параллельна связям, удерживающим ближайшие соседние атомы — два аксиальных атома водорода.
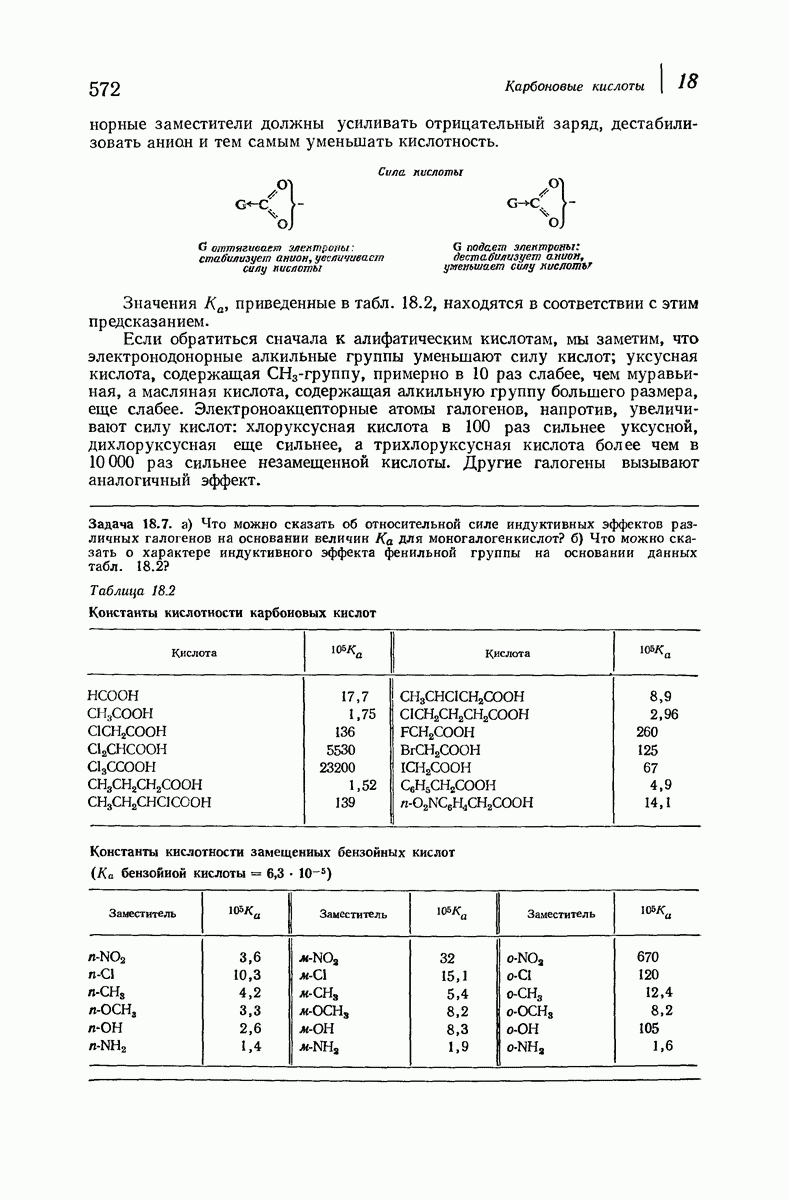
Конформационный анализ в состоянии не только объяснить, почему одна конформация более устойчива, чем другая, но часто также дает возможность вычислить с удовлетворительной степенью точности, насколько она более стабильна.
Различие в 1,8 ккал  в устойчивости двух конформаций метилциклогексана обусловлено 1,3-диаксиальным взаимодействием метильной группы и двух атомов водорода. Если на основании этого принять, что величина 0,9 ккал
в устойчивости двух конформаций метилциклогексана обусловлено 1,3-диаксиальным взаимодействием метильной группы и двух атомов водорода. Если на основании этого принять, что величина 0,9 ккал  соответствует каждому 1,3-диаксиаль-ному взаимодействию
соответствует каждому 1,3-диаксиаль-ному взаимодействию  водород, то обнаруживается, что удается с удивительной степенью точности рассчитывать различия в энергии конформаций для различных циклогексанов, содержащих более одной метильной группы.
водород, то обнаруживается, что удается с удивительной степенью точности рассчитывать различия в энергии конформаций для различных циклогексанов, содержащих более одной метильной группы.
Отметим, что величина 0,9 ккал  это то же самое значение, которое в разд. 4.5 было приписано скошенному взаимодействию в н-бутане; изучение моделей показывает, что это совпадение не случайно.
это то же самое значение, которое в разд. 4.5 было приписано скошенному взаимодействию в н-бутане; изучение моделей показывает, что это совпадение не случайно.
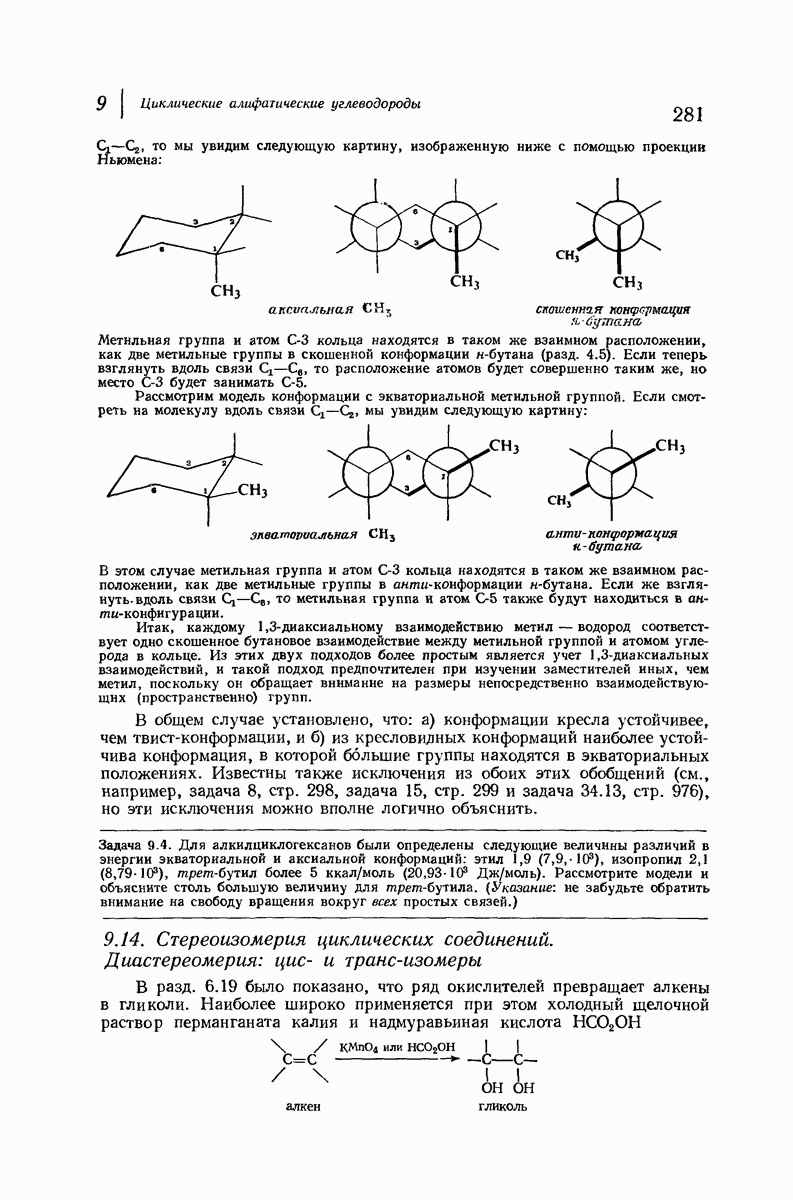
Рассмотрим модель конформации метилциклогексана с аксиальной метильной группой. Если держать эту модель так, чтобы можно было рассматривать ее вдоль связи
 то мы увидим следующую картину, изображенную ниже с помощью проекции Ньюмена:
то мы увидим следующую картину, изображенную ниже с помощью проекции Ньюмена:

Метальная группа и атом  кольца находятся в таком же взаимном расположении, как две метильные группы в скошенной конформации н-бутана (разд. 4.5). Если теперь взглянуть вдоль связи
кольца находятся в таком же взаимном расположении, как две метильные группы в скошенной конформации н-бутана (разд. 4.5). Если теперь взглянуть вдоль связи  то расположение атомов будет совершенно таким же, но место
то расположение атомов будет совершенно таким же, но место  будет занимать
будет занимать 
Рассмотрим модель конформации с экваториальной метильной группой. Если смотреть на молекулу вдоль связи  мы увидим следующую картину:
мы увидим следующую картину:

В этом случае метильная группа и атом  кольца находятся в таком же взаимном расположении, как две метильные группы в акти-конформации н-бутана. Если же взглянуть вдоль связи
кольца находятся в таком же взаимном расположении, как две метильные группы в акти-конформации н-бутана. Если же взглянуть вдоль связи  то метильная группа и атом
то метильная группа и атом  также будут находиться в анти-конфигурации.
также будут находиться в анти-конфигурации.
Итак, каждому 1,3-диаксиальному взаимодействию метил — водород соответствует одно скошенное бутановое взаимодействие между метильной группой и атомом углерода в кольце. Из этих двух подходов более простым является учет 1,3-диаксиальных взаимодействий, и такой подход предпочтителен при изучении заместителей иных, чем метил, поскольку он обращает внимание на размеры непосредственно взаимодействующих (пространственно) групп.
В общем случае установлено, что: а) конформации кресла устойчивее, чем твист-конформации, и б) из кресловидных конформаций наиболее устойчива конформация, в которой большие группы находятся в экваториальных положениях. Известны также исключения из обоих этих обобщений (см., например, задача 8, стр. 298, задача 15, стр. 299 и задача 34.13, стр. 976), но эти исключения можно вполне логично объяснить.
Задача 9.4. Для алкилциклогексанов были определены следующие величины различий в энергии экваториальной и аксиальной конформаций: этил  изопропил
изопропил  трет-бутил более 5 ккал/моль
трет-бутил более 5 ккал/моль  Рассмотрите модели и объясните столь большую величину для трет-бутила. (Указание: не забудьте обратить внимание на свободу вращения вокруг всех простых связей.)
Рассмотрите модели и объясните столь большую величину для трет-бутила. (Указание: не забудьте обратить внимание на свободу вращения вокруг всех простых связей.)
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- 1 Строение и свойства
- 1.1. Органическая химия
- 1.2. Теория строения
- 1.3. Представление о химической связи до 1926 г.
- 1.4. Квантовая механика
- 1.5. Атомные орбитали
- 1.6. Электронная конфигурация. Принцип запрета Паули
- 1.7. Молекулярные орбитали
- 1.8. Ковалентная связь
- 1.10. Неподеленные пары электронов
- 1.11. Внутримолекулярные силы
- 1.12. Полярность связей
- 1.13. Полярность молекул
- 1.14. Строение и физические свойства
- 1.15. Температура плавления
- 1.16. Межмолекулярные силы
- 1.17. Температура кипения
- 1.18. Растворимость
- 1.19. Кислоты и основания
- 1.20. Изомерия
- 2. Метан. ЭНЕРГИЯ АКТИВАЦИИ. ПЕРЕХОДНОЕ СОСТОЯНИЕ
- 2.1. Углеводороды
- 2.2. Строение метана
- 2.3. Физические свойства
- 2.4. Источники
- 2.5. Реакции
- 2.6. Окисление. Теплота сгорания
- 2.7. Хлорирование: реакция замещения
- 2.8. Контроль за реакцией хлорирования
- 2.9. Реакции с другими галогенами: галогенирование
- 2.10. Относительная реакционная способность
- 2.11. Механизм реакции
- 2.12. Механизм хлорирования. Свободные радикалы
- 2.13. Цепные реакции
- 2.14. Ингибиторы
- 2.15. Проверка механизма хлорирования
- 2.16. Энергия диссоциации связей
- 2.17. Теплота реакции
- 2.18. Энергия активации
- 2.19. Течение реакции: изменение энергии
- 2.20. Скорость реакции
- 2.21. Относительные скорости реакции
- 2.22. Реакционная способность галогенов по отношению к метану
- 2.23. Строение метильного радикала. sp2-Гибридизация
- 2.24. Переходное состояние
- 2.25. Реакционная способность и переходное состояние
- 2.26. Молекулярная формула: ее фундаментальное значение
- 2.27. Качественный элементный анализ: углерод, водород и галоген
- 2.28. Количественный элементный анализ: углерод, водород и галоген
- 2.29. Эмпирическая формула
- 2.30. Определение молекулярного веса: метод определения плотности пара. Молекулярная формула
- 3. Стереохимия. I
- 3.1. Стереохимия и стереоизомерия
- 3.2. Число стереоизомеров и тетраэдрический атом углерода
- 3.3. Оптическая активность. Плоскополяризованный свет
- 3.4. Поляриметр
- 3.5. Удельное вращение
- 3.6. Открытие энантиомерии
- 3.7. Энантиомерия и тетраэдрический атом углерода
- 3.8. Энантиомерия и оптическая активность
- 3.9. Предсказание энантиомерии. Диссимметрия
- 3.10. Асимметрический атом углерода
- 3.11. Энантиомеры
- 3.12. Рацемическая модификация
- 3.13. Оптическая активность: более подробное рассмотрение
- 3.14. Конфигурация
- 3.15. Обозначения конфигурации: R и S
- 3.16. Правила старшинства
- 3.17. Обозначение конфигурации соединений с несколькими асимметрическими атомами
- 4. Алканы. Свободнорадикальное замещение
- 4.2. Строение этана
- 4.3. Свободное вращение вокруг простой углерод-углеродной связи. Конформации. Торсионное напряжение
- 4.4. Пропан и бутаны
- 4.5. Конформации н-бутана. Вандерваальсово отталкивание
- 4.6. Конформационные изомеры
- 4.7. Конформационный анализ. Диполь-дипольные взаимодействия
- 4.8. Высшие алканы. Гомологический ряд
- 4.9. Номенклатура
- 4.10. Алкильные группы
- 4.11. Тривиальные названия
- 4.12. Номенклатура IUPAC
- 4.13. Типы углеродных и водородных атомов
- 4.14. Физические свойства
- 4.15. Промышленные источники
- 4.16. Получение в промышленности и в лаборатории
- 4.17. Методы синтеза
- 4.18. Реактив Гриньяра
- 4.19. Реакция Вюрца
- 4.20. Реакции
- 4.21. Галогенирование
- 4.22 Механизм галогенирования
- 4.23. Ориентация при галогенировании
- 4.24. Относительная реакционная способность алканов в реакциях галогенирования
- 4.25. Легкость отщепления атомов водорода. Энергия активации
- 4.26. Устойчивость свободных радикалов
- 4.27. Легкость образования свободных радикалов
- 4.28. Переходное состояние при галогенировании
- 4.29. Направление реакции и реакционная способность
- 4.30. Реакционная способность и избирательность
- 4.31. Отсутствие перегруппировок свободных радикалов. Изотопные метки
- 4.32 Синтез и оптическая активность. Возникновение асимметрического атома углерода
- 4.33. Метилен (карбен). Внедрение
- 4.34. Горение
- 4.35. Пиролиз: крекинг
- 4.36. Определение строения
- 4.37. Анализ алканов
- 5. Алкены. I. Строение и получение
- 5.1. Ненасыщенные углеводороды
- 5.2. Строение этилена. Двойная углерод-углеродная связь
- 5.3. Гибридизация и размер орбиталей
- 5.4. Пропилен
- 5.5. Бутилены
- 5.6. Диастереомерия: геометрическая изомерия
- 5.7. Высшие алкены
- 5.8. Общие названия
- 5.9. Номенклатура IUPAC
- 5.10. Физические свойства
- 5.11. Промышленные источники
- 5.12. Методы синтеза
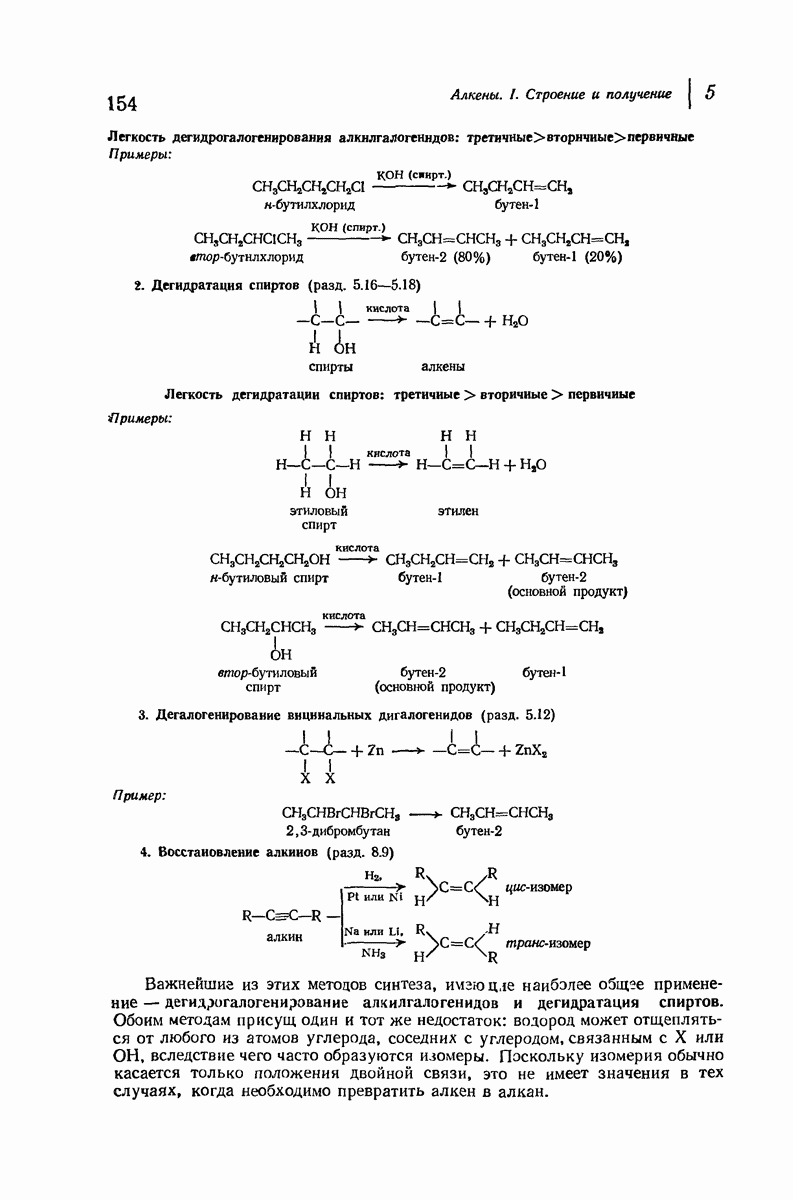
- 5.13. Дегидрогалогенирование алкилгалогенидов
- 5.14. Механизм дегидрогалогенирования
- 5.15. Направление реакции и реакционная способность при дегидрогалогенировании
- 5.16. Дегидратация спиртов
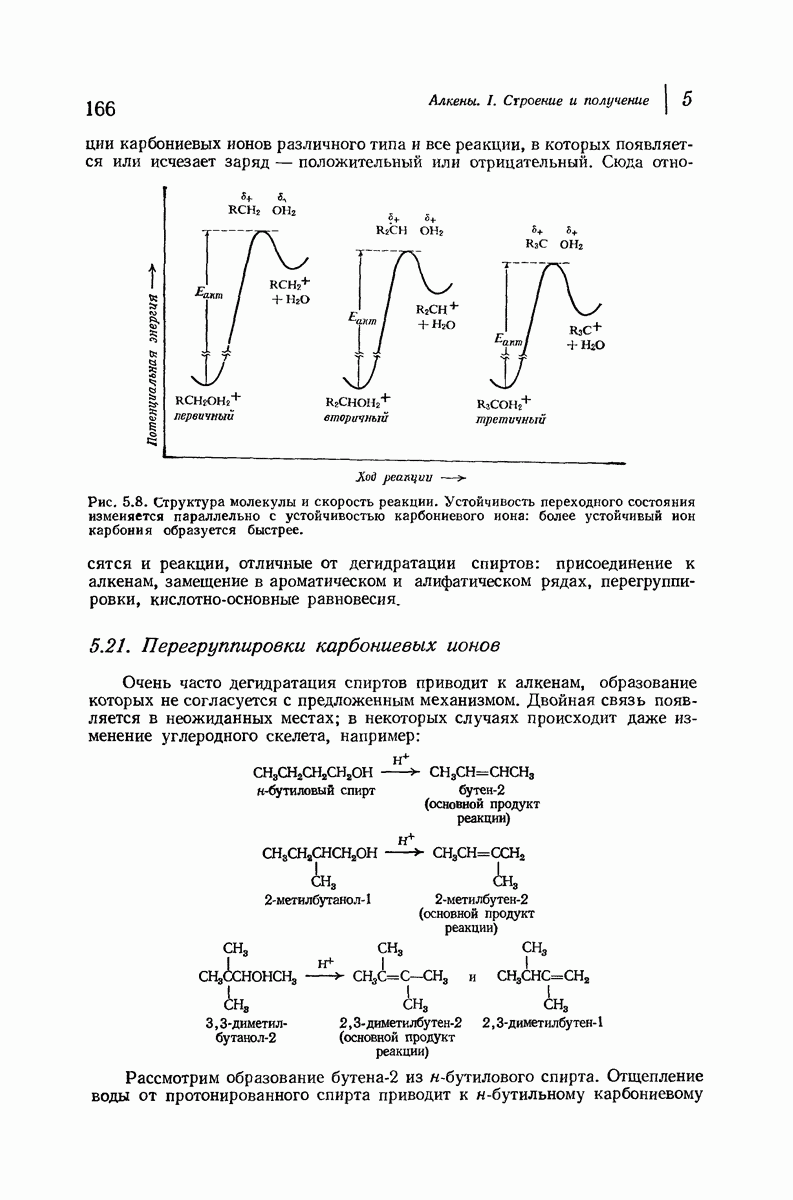
- 5.17. Теория карбониевых ионов
- 5.18. Механизм дегидратации спиртов
- 5.19. Устойчивость карбониевых ионов. Распределение заряда
- 5.20. Легкость образования карбониевых ионов
- 5.21. Перегруппировки карбониевых ионов
- 5.22. Направление реакции и реакционная способность при дегидратации
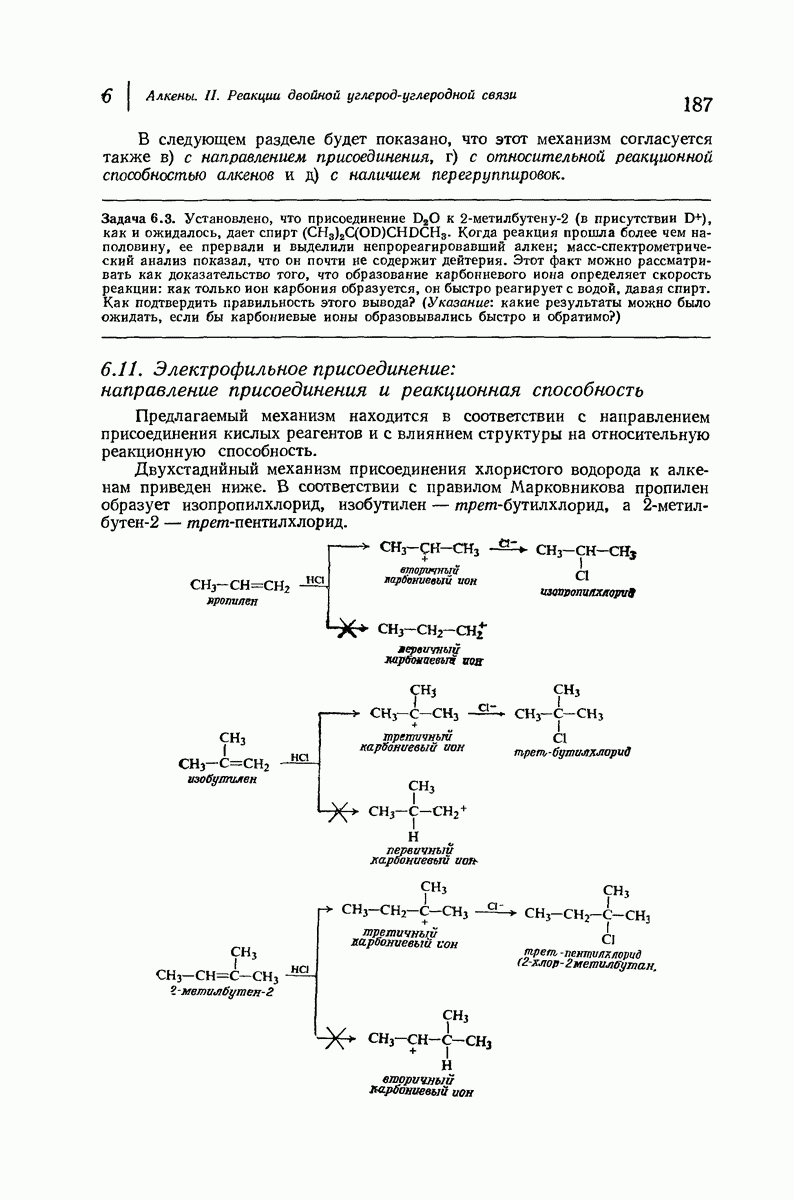
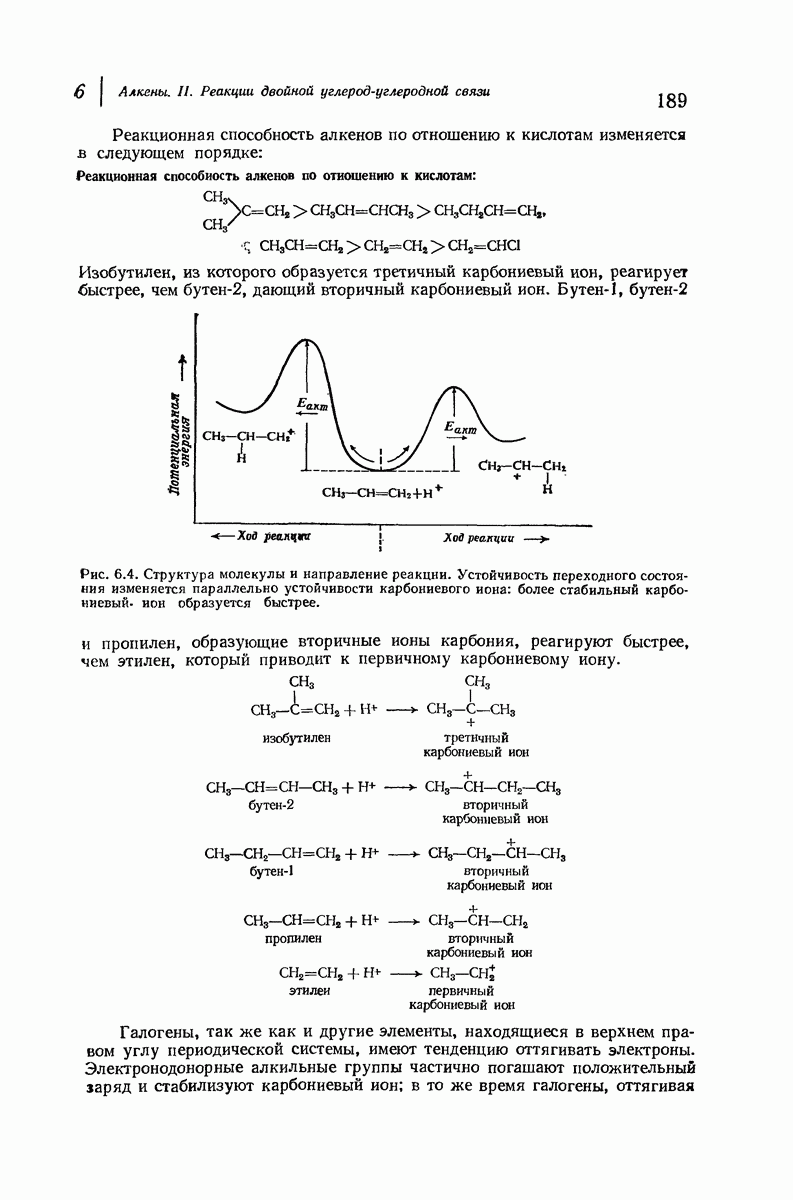
- 6 Алкены II. Реакции двойной углерод-углеродной связи
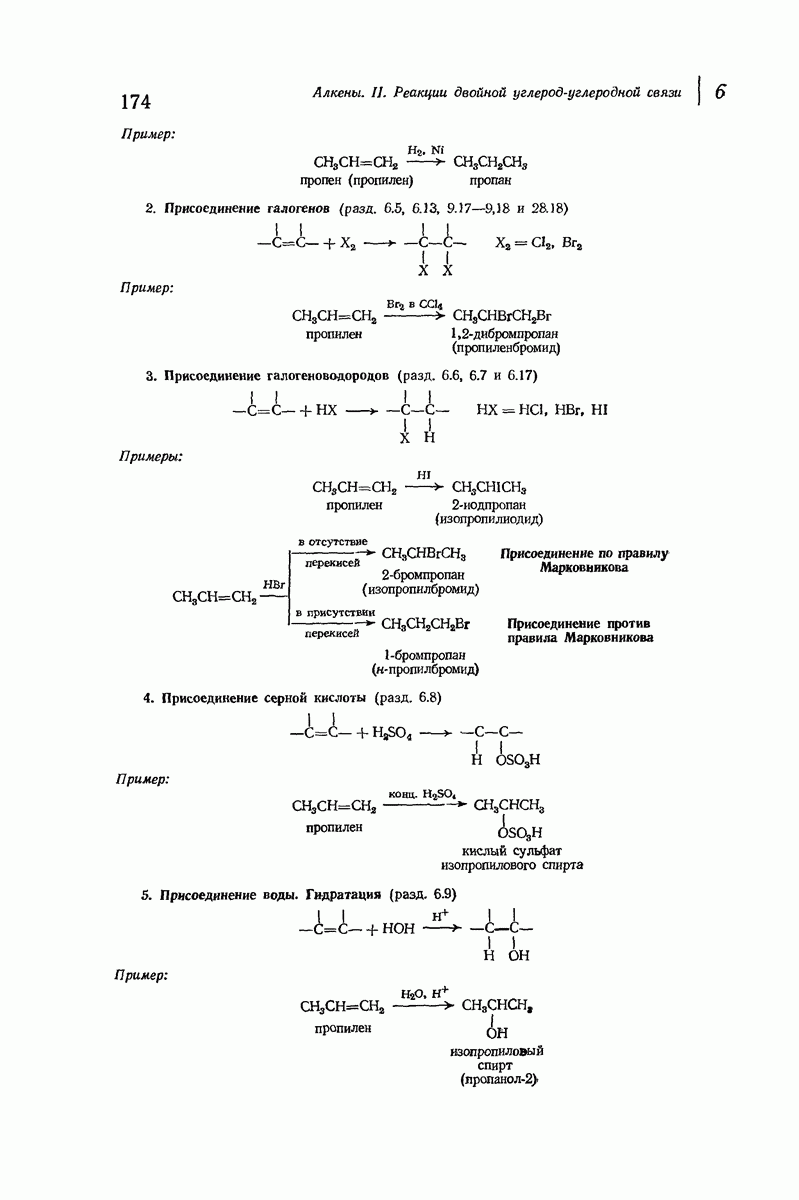
- 6.2. Реакции двойной углерод-углеродной связи: присоединение
- 6.3. Гидрирование. Теплота гидрирования
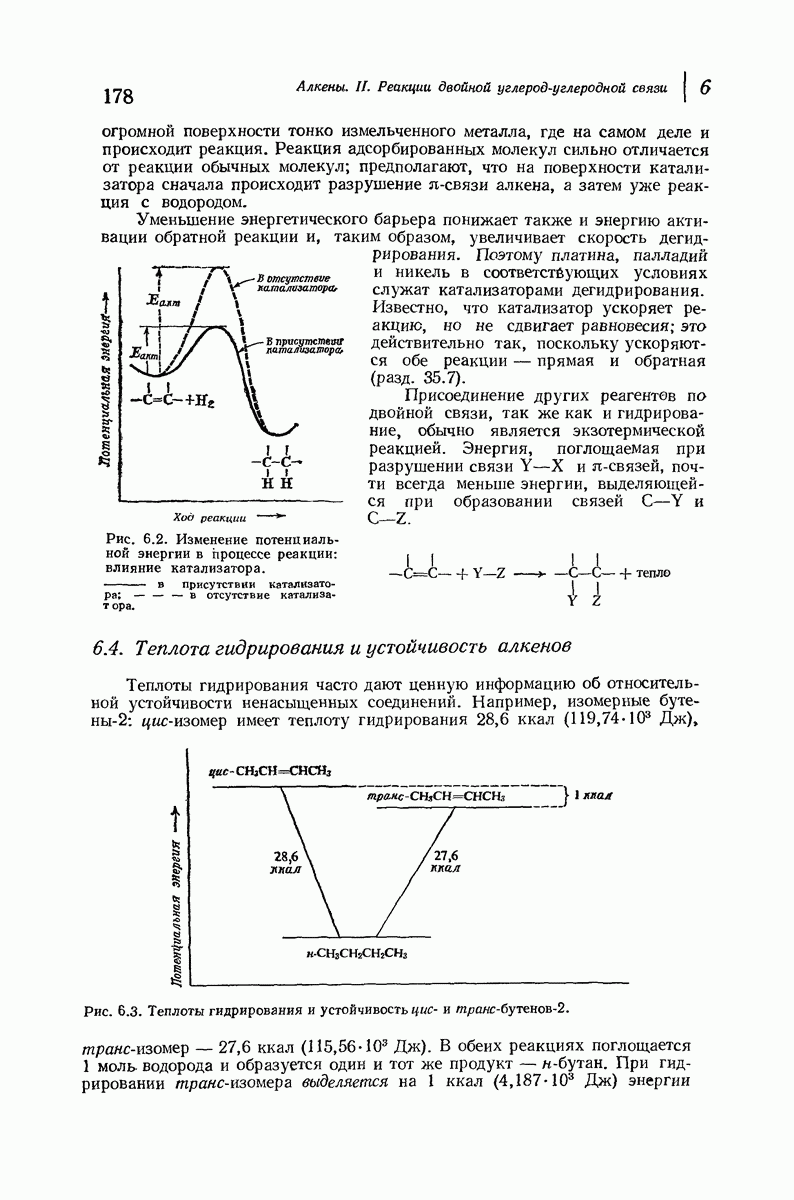
- 6.4. Теплота гидрирования и устойчивость алкенов
- 6.5. Присоединение галогенов
- 6.6. Присоединение галогеноводородов. Правило Марковникова
- 6.7. Присоединение бромистого водорода. Влияние перекисей
- 6.8. Присоединение серной кислоты
- 6.9. Присоединение воды. Гидратация
- 6.10. Электрофильное присоединение: механизм
- 6.11. Электрофильное присоединение: направление присоединения и реакционная способность
- 6.12. Электрофильное присоединение: перегруппировки
- 6.13. Механизм присоединения галогенов
- 6.14. Образование галогенгидринов
- 6.15. Присоединение алкенов. Димеризация
- 6.16. Присоединение алканов. Алкилирование
- 6.17. Свободнорадикальное присоединение. Механизм присоединения бромистого водорода, инициируемый перекисями
- 6.18. Другие реакции свободнорадикального присоединения
- 6.19. Гидроксилирование. Образование гликолей
- 6.20. Реакции замещения. Галогенирование. Аллильный водород
- 6.21. Ориентация и реакционная способность при замещении
- 6.22. Озонолиз. Определение структуры методом расщепления
- 6.23. Анализ алкенов
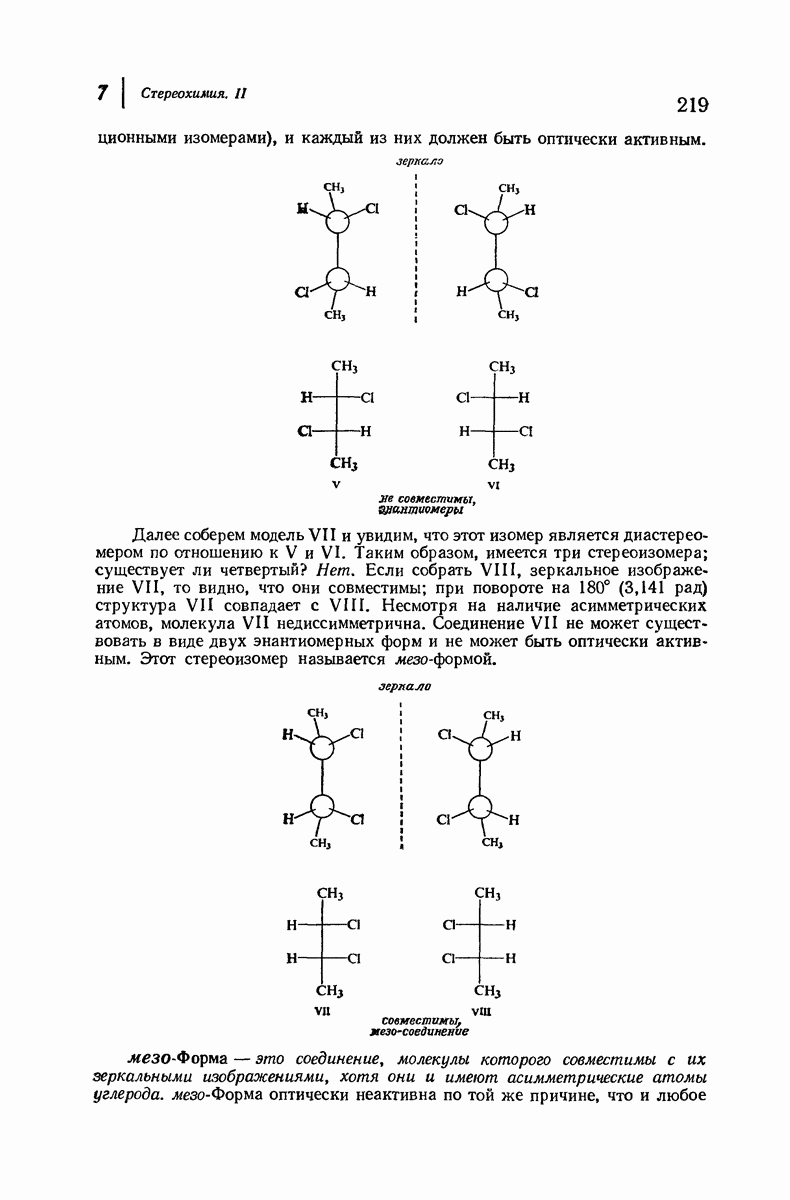
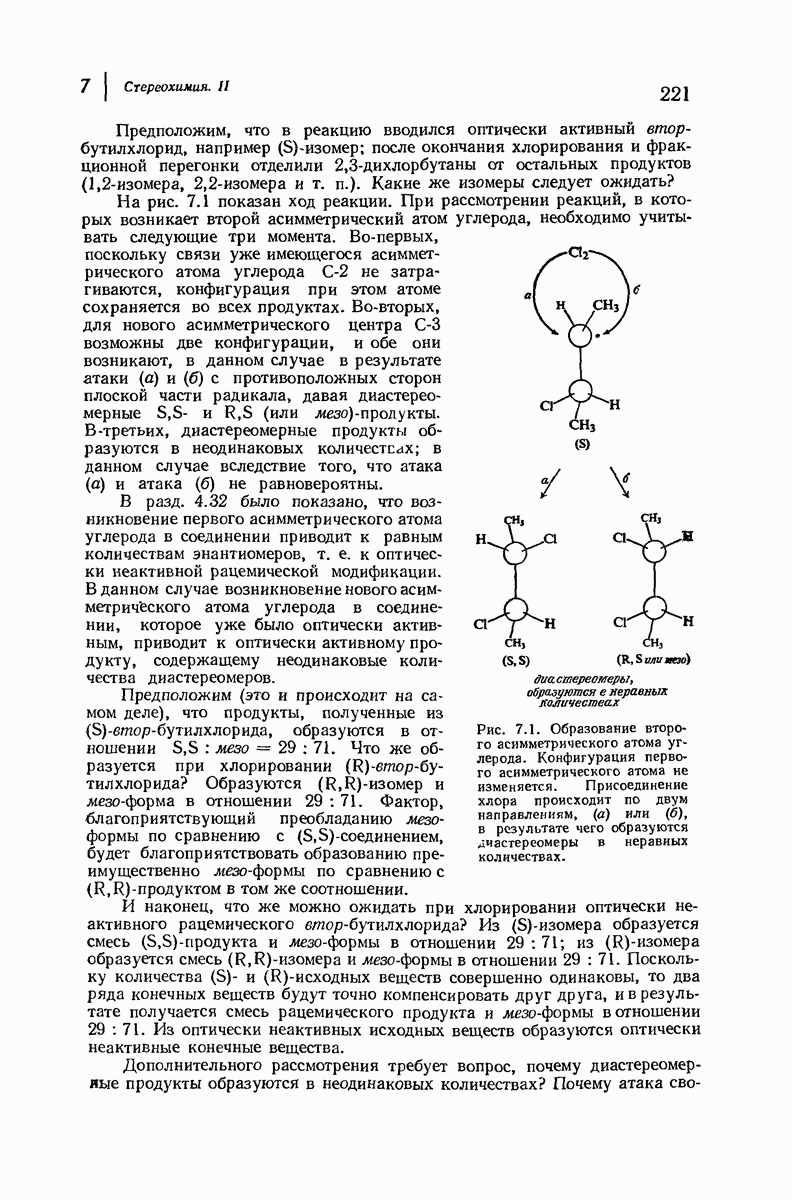
- 7. Стереохимия. II
- 7.1. Классификация стереоизомеров
- 7.2. Реакции стереоизомеров
- 7.3. Реакции диссимметричных молекул. Разрыв связи
- 7.4. Реакции диссимметричных молекул. Относительные конфигурации
- 7.5. Оптическая чистота
- 7.6. Стереоизомеры: диастереомеры
- 7.7. Стереоизомеры: мезо-формы
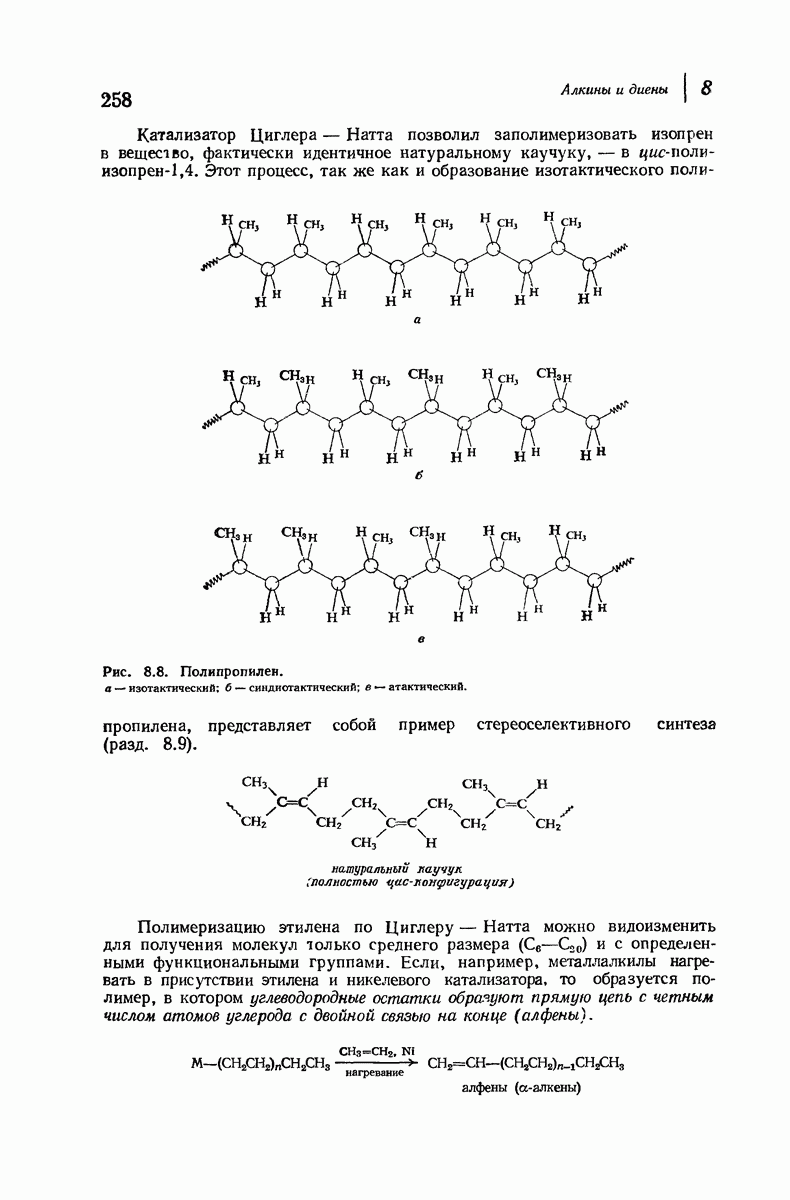
- 7.8. Реакции диссимметричных молекул. Образование второго асимметрического атома углерода
- 7.9. Реакции диссимметричных молекул. Механизм свободнорадикального хлорирования
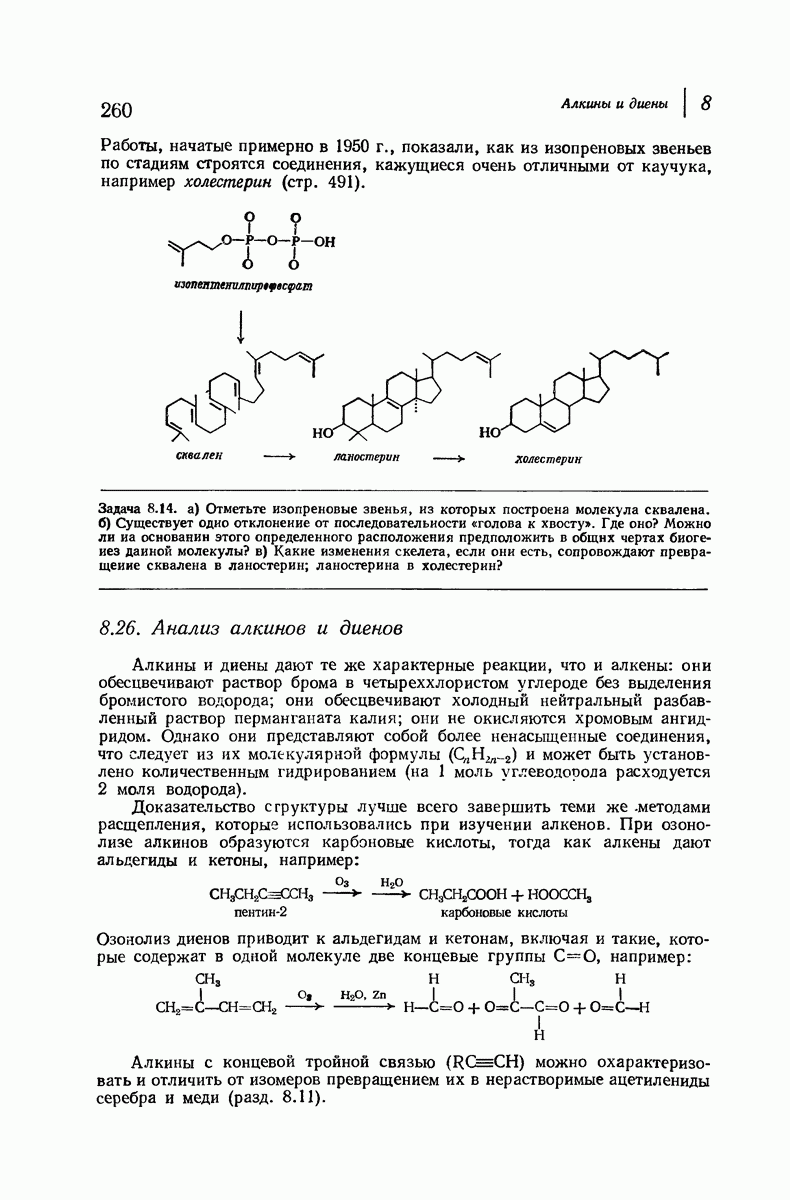
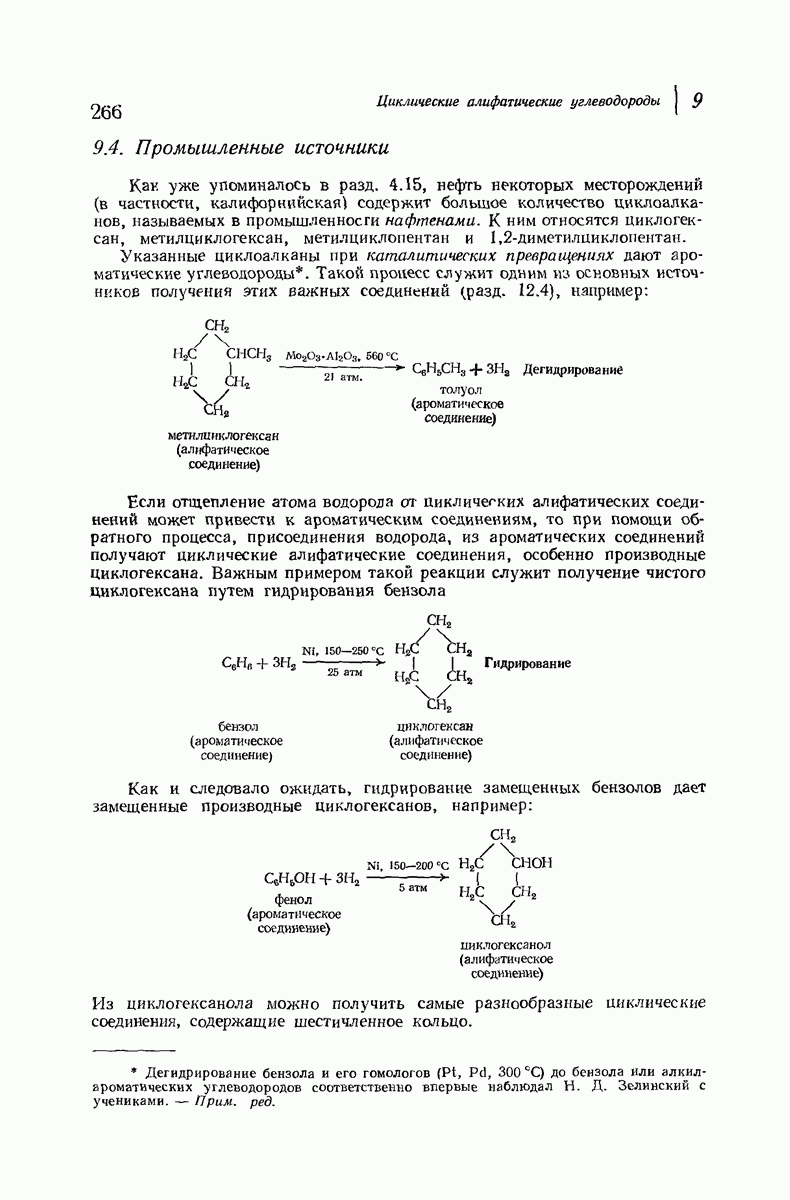
- 7.10. Реакции диссимметричных молекул с оптически активным реагентами. Расщепление
- 8. Алкины и диены
- 8.3. Высшие алкины. Номенклатура
- 8.4. Физические свойства алкинов
- 8.5. Промышленный источник ацетилена
- 8.6. Методы синтеза алкинов
- 8.7. Реакции алкинов
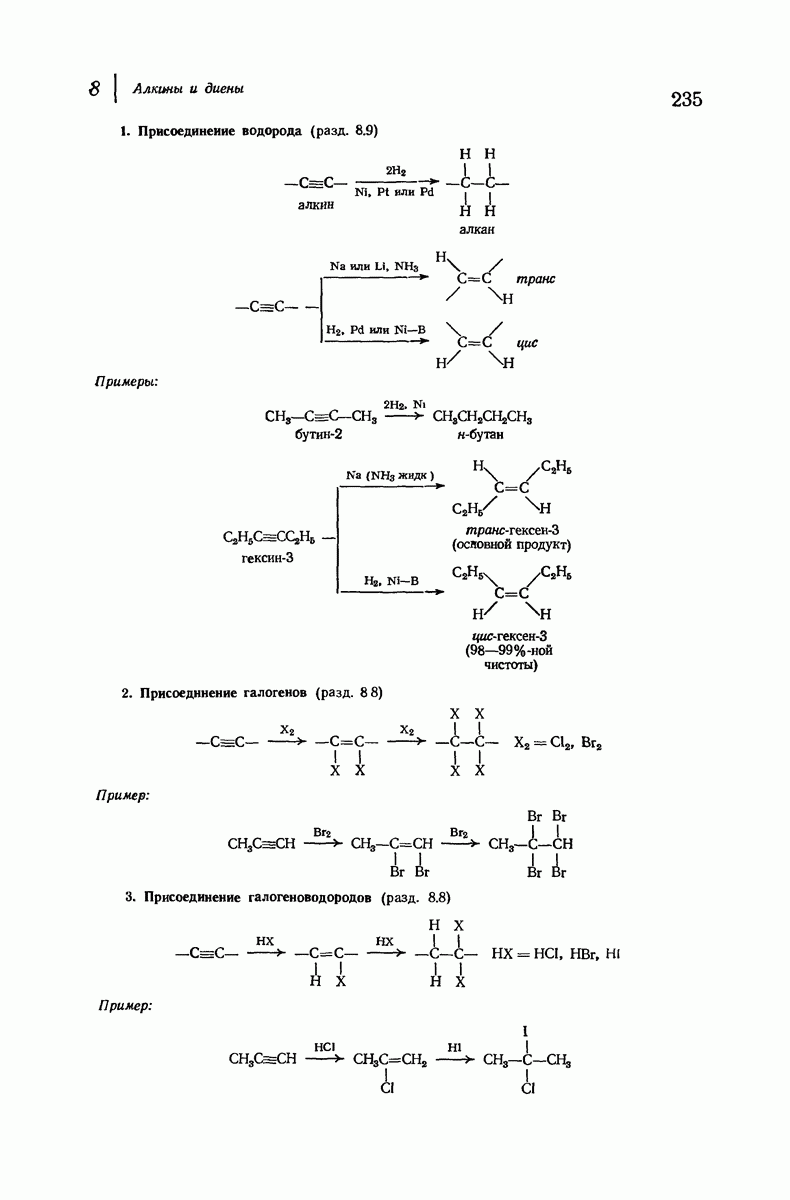
- 8.8. Реакции присоединения алкинов
- 8.9. Восстановление алкинов в алкены. Стереоселективные реакции
- 8.10. Кислотность алкинов. Очень слабые кислоты
- 8.11. Образование ацетиленидов тяжелых металлов
- 8.12. Реакция ацетиленидов натрия с алкилгалогенидами. Сравнение реакций замещения и элиминирования
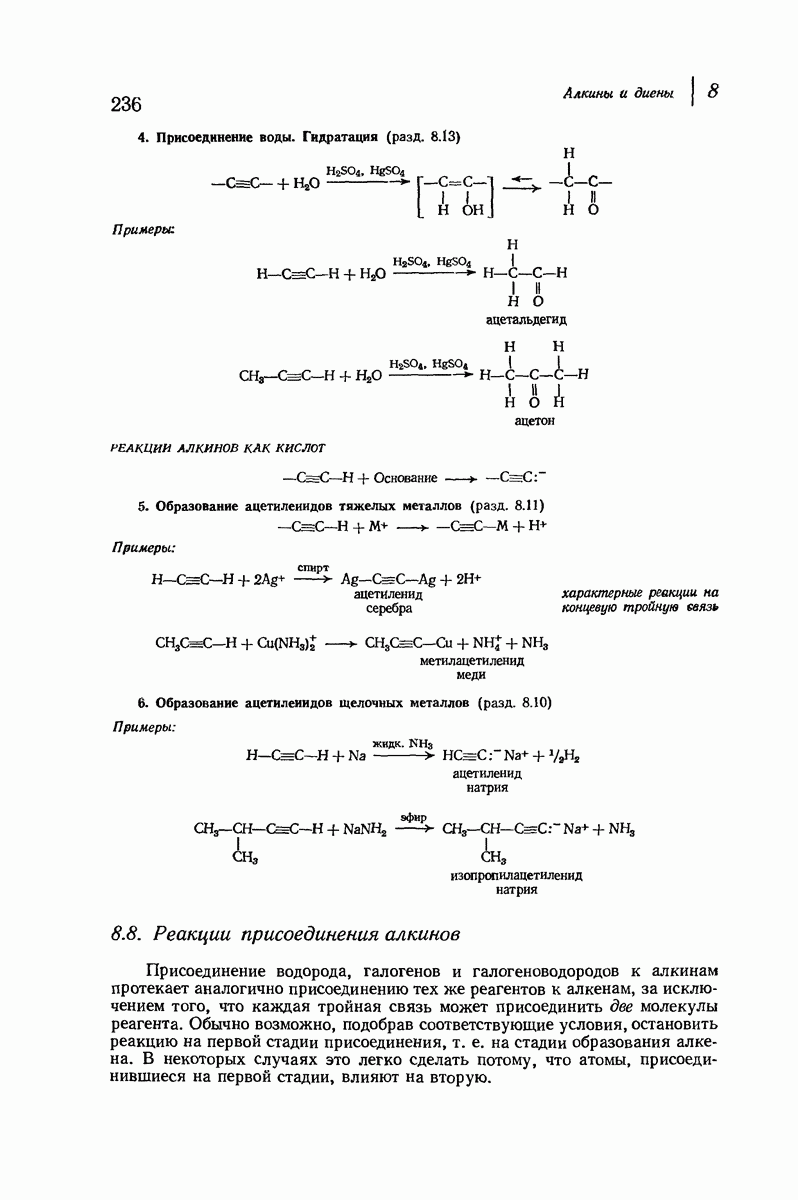
- 8.13. Гидратация алкинов. Таутомерия
- 8.14. Строение и номенклатура диенов
- 8.15. Методы синтеза и свойства диенов
- 8.16. Устойчивость сопряженных диенов
- 8.17. Электрофильное присоединение к сопряженным диенам. 1,4-Присоединение
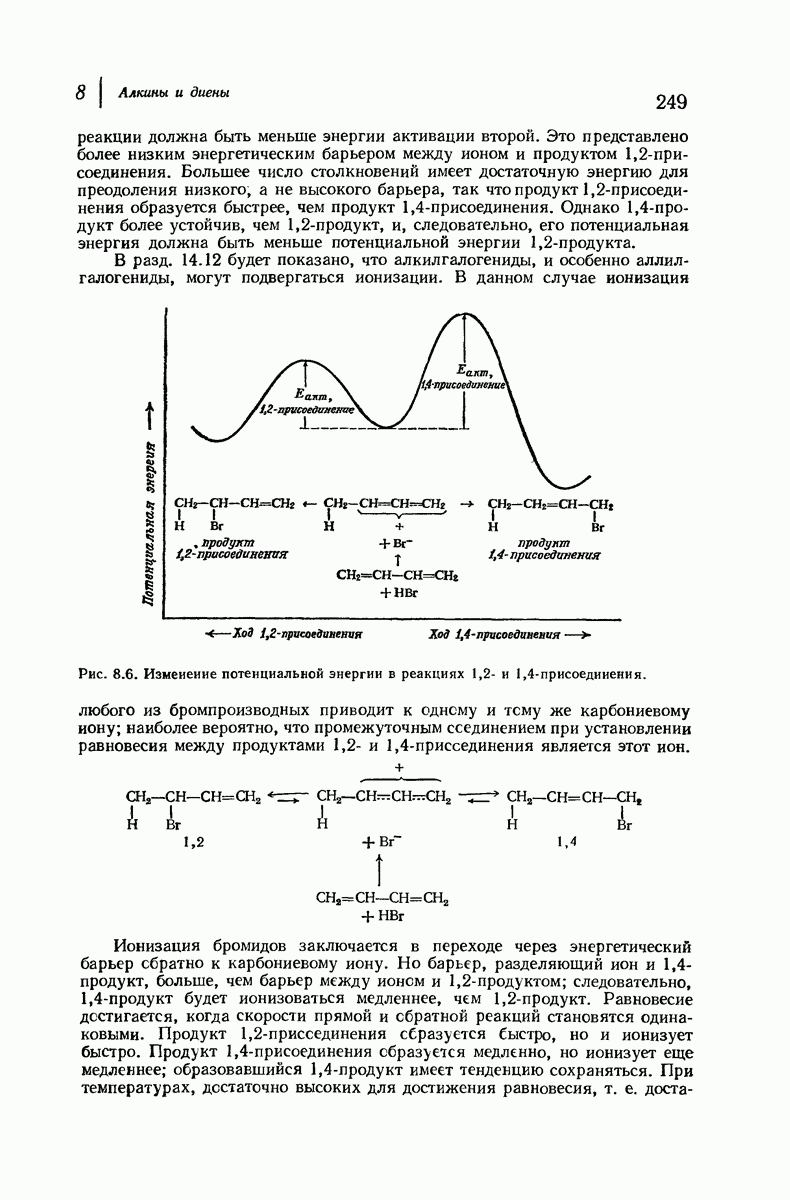
- 8.18. 1,2- и 1,4-Присоединение. Скорость и равновесие
- 8.19. Свободнорадикальное присоединение к сопряженным диенам: направление присоединения
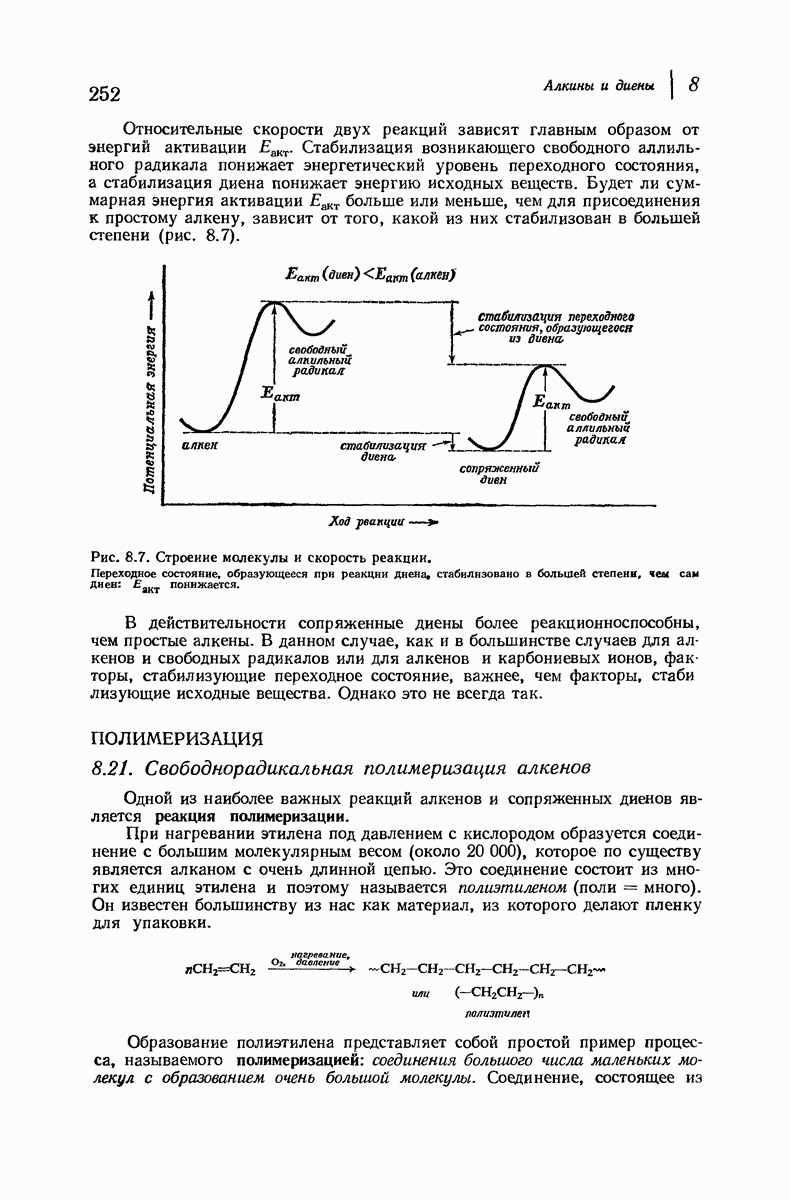
- 8.20. Свободнорадикальное присоединение к сопряженным диеном: реакционная способность
- ПОЛИМЕРИЗАЦИЯ
- 8.21. Свободнорадикальная полимеризация алкенов
- 8.22. Свободнорадикальная полимеризация диенов. Натуральный каучук и его заменители
- 8.23. Сополимеризация
- 8.24. Ионная полимеризация
- 8.25. Изопрен и изопреновое правило
- 8.26. Анализ алкинов и диенов
- 9. Циклические алифатические углеводороды
- 9.1. Ациклические и циклические соединения
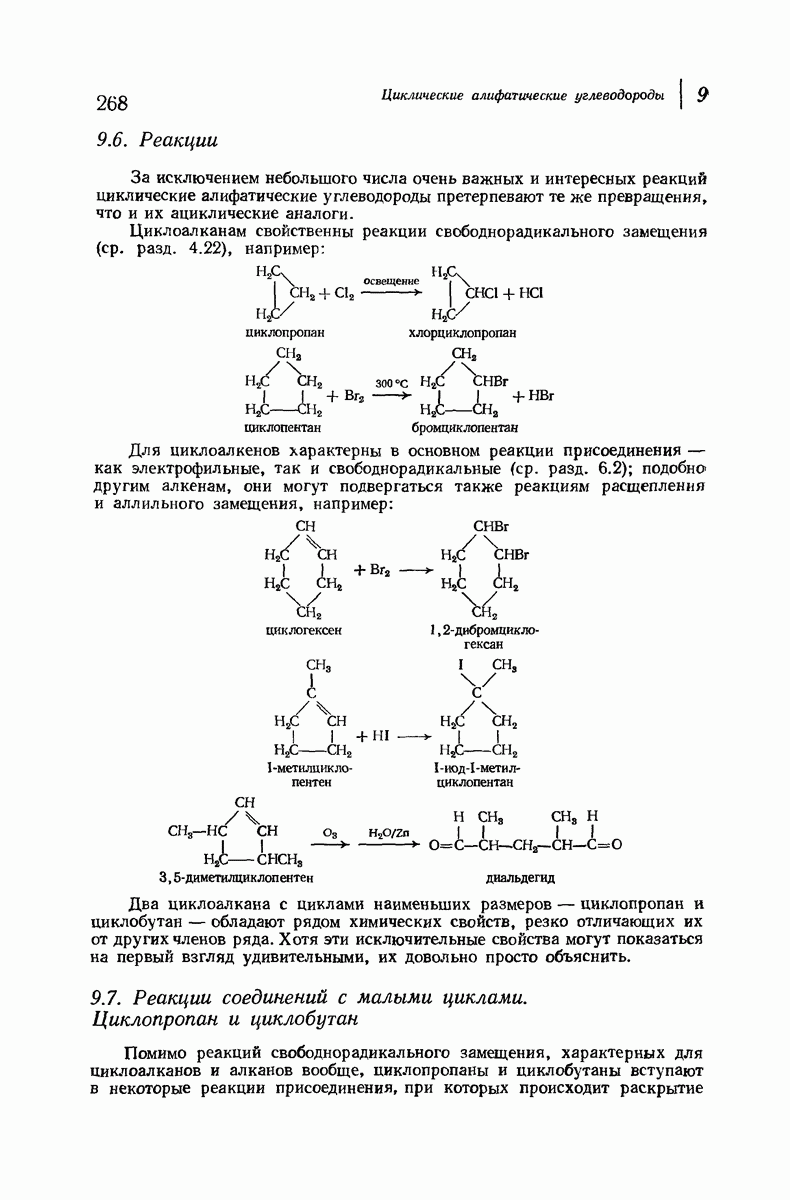
- 9.7. Реакции соединений с малыми циклами. Циклопропан и циклобутан
- 9.8. Теория напряжения Байера
- 9.9. Теплоты сгорания и относительная стабильность циклоалканов
- 9.10. Орбитальное описание углового напряжения
- 9.11. Факторы, влияющие на устойчивость конформаций
- 9.12. Конформация циклоалканов
- 9.14. Стереоизомерия циклических соединений. Диастереомерия: цис- и транс-изомеры
- 9.15. Стереоизомерия циклических соединений. Энантиомерия
- 9.16. Стереоизомерия циклических соединений. Конформационный анализ
- 9.17. цис и транс-Присоединение к циклическим алкенам
- 9.18. цис и транс-Присоединение к ациклическим алкенам. Стереоспецифические реакции
- 9.19. Присоединение метиленов
- 9.20. Замещенные метилены. а-Эламинирование
- 9.21. Анализ циклических алифатических углеводородов
- 10. Бензол. РЕЗОНАНС. АРОМАТИЧНОСТЬ
- 10.1. Алифатические и ароматические соединения
- 10.2. Структура бензола
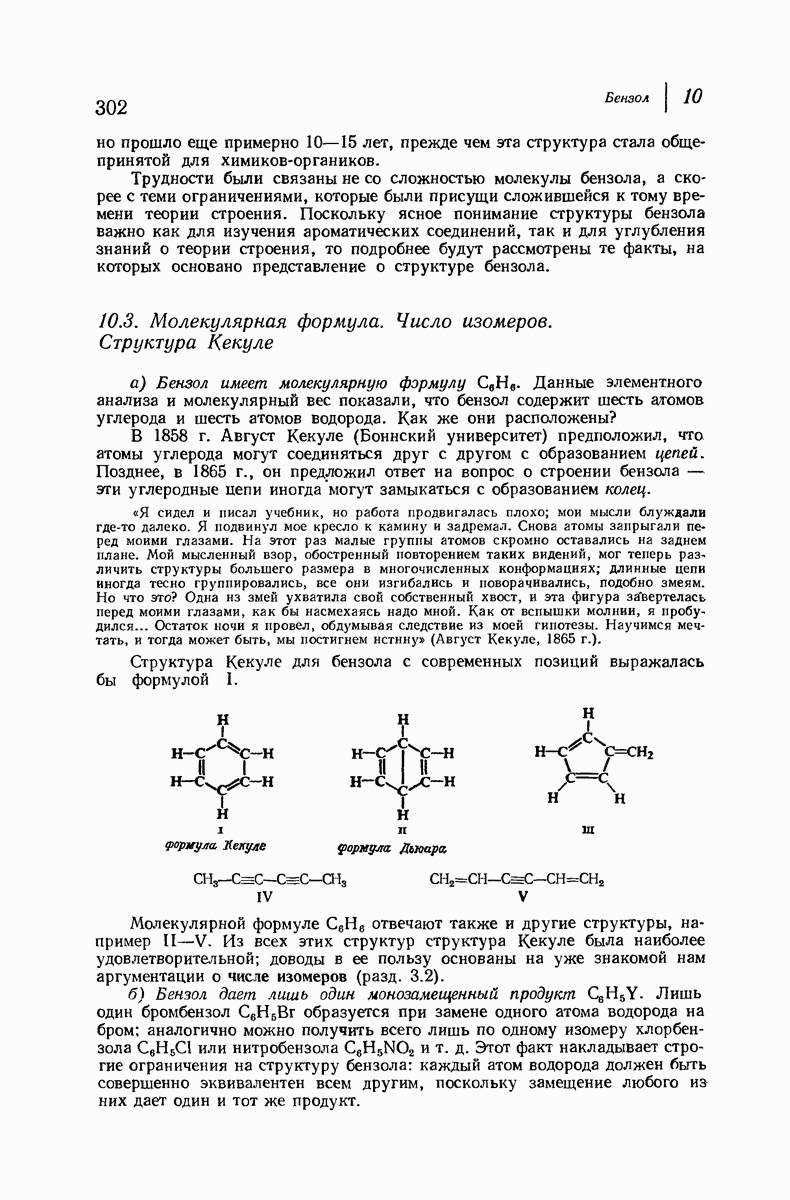
- 10.3. Молекулярная формула. Число изомеров. Структура Кекуле
- 10.4. Стабильность бензольного кольца. Реакции бензола
- 10.5. Устойчивость бензольного кольца. Теплоты гидрирования и сгорания
- 10.6. Длины углерод-углеродных связей в бензоле
- 10.7. Теория резонанса
- 10.8. Резонансная структура бензола
- 10.9. Длины связей в бензоле
- 10.10. Число изомеров
- 10.11. Стабильность бензола
- 10.12. Орбитальное представление структуры бензола
- 10.13. Изображение бензольного кольца
- 10.14. Ароматические свойства. (4n+2)-Правило Хюккеля
- 10.15. Применение теории резонанса
- 10.16. Резонанс в сопряженных диенах
- 10.13. Изображение бензольного кольца
- 10.18. Стабильность диенов и алкенов: альтернативная интерпретация
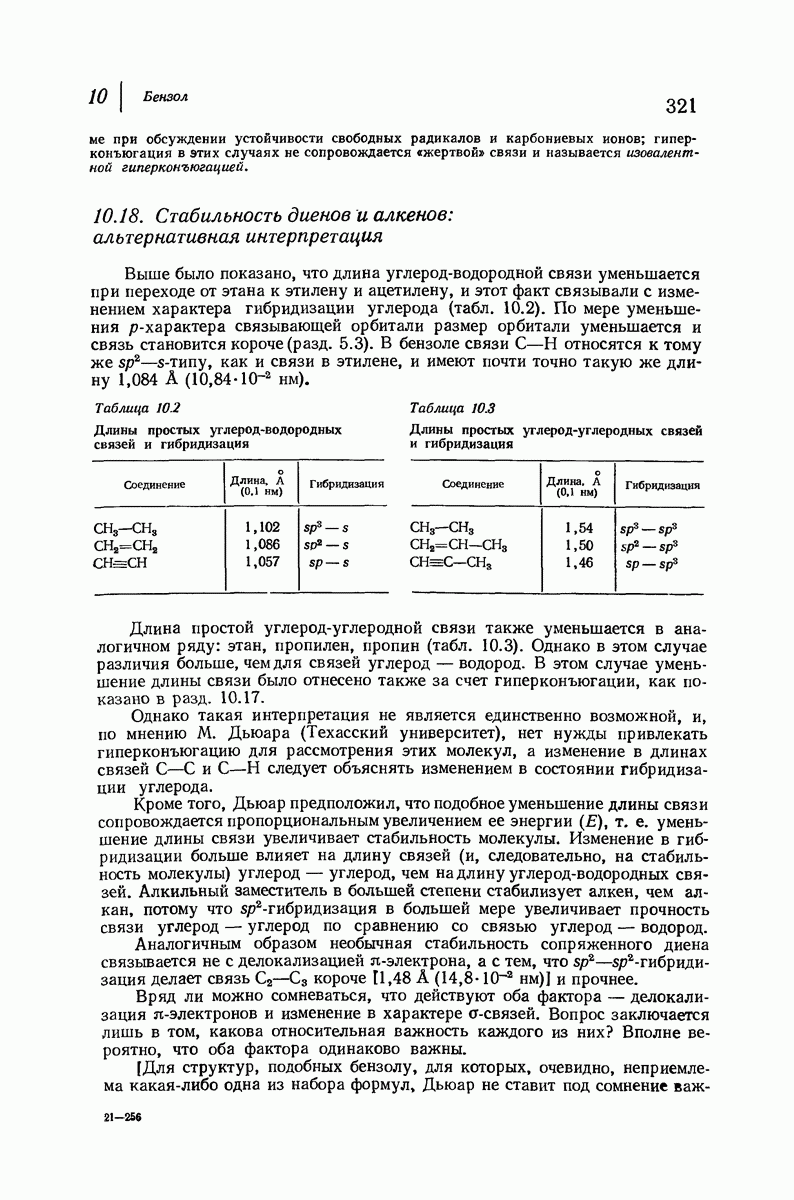
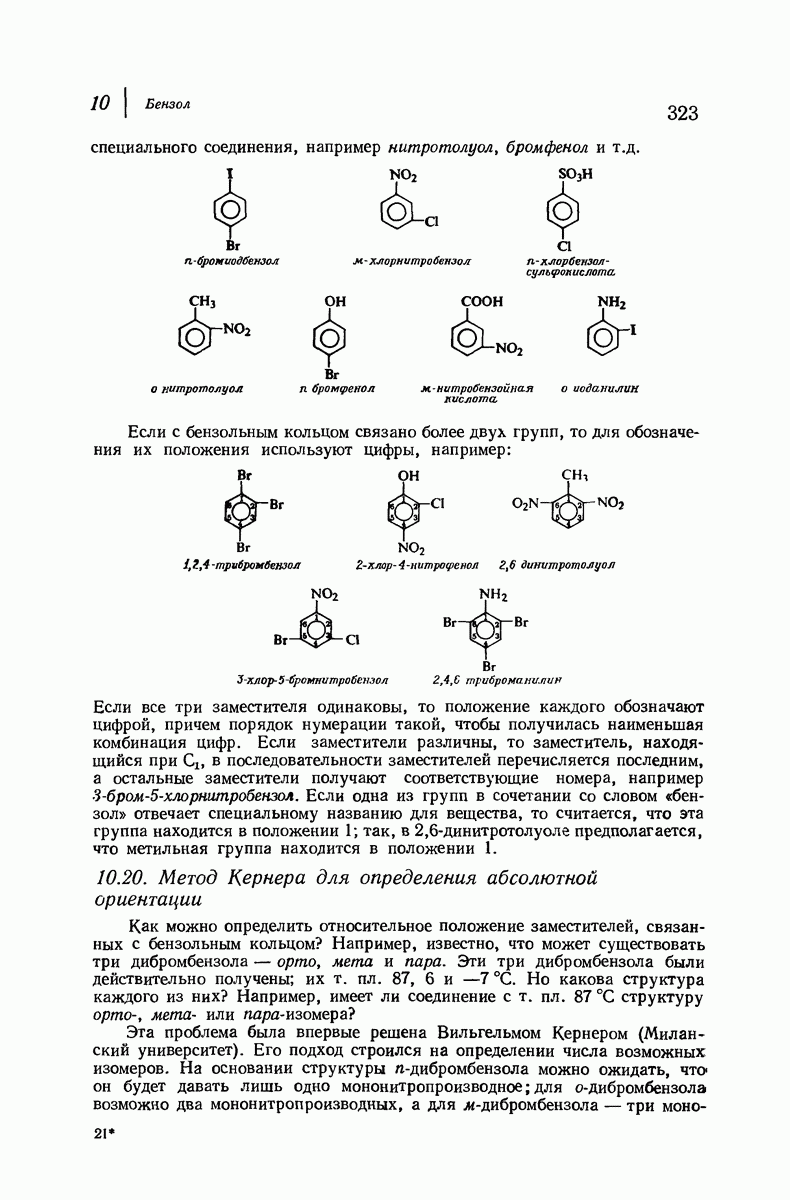
- 10.19. Номенклатура производных бензола
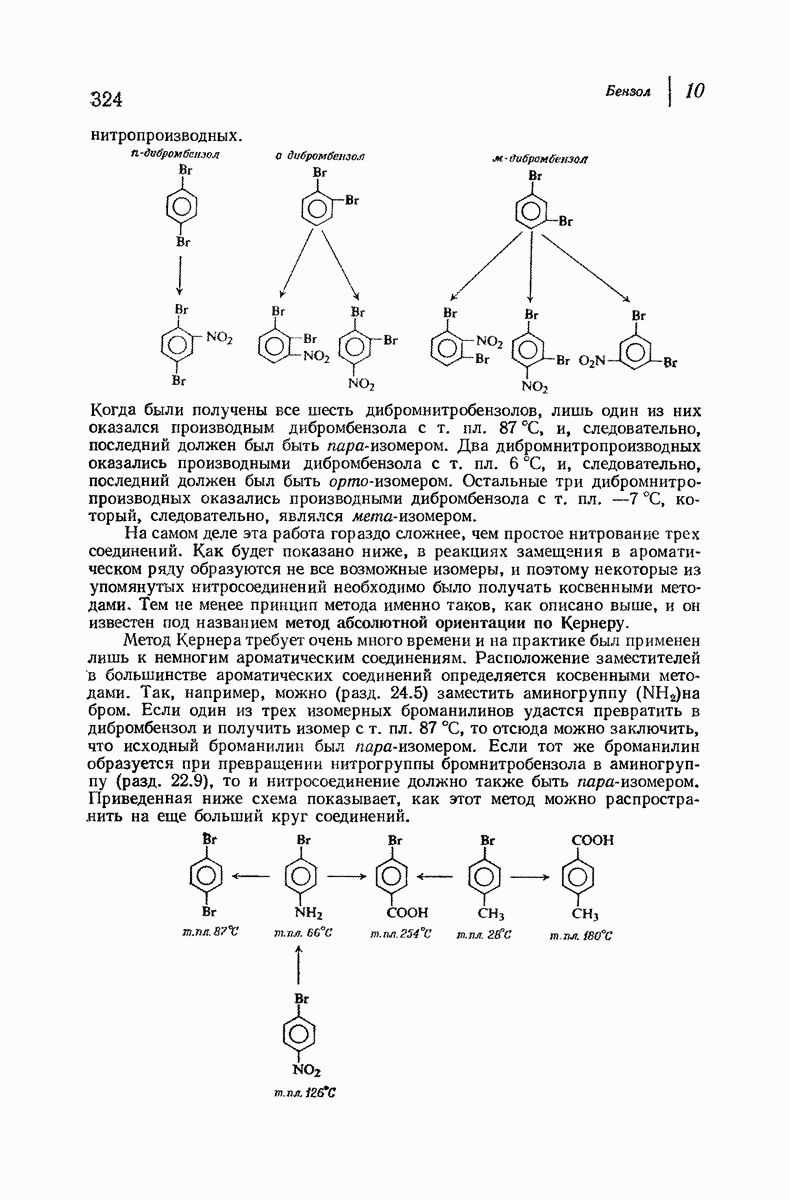
- 10.20. Метод Кернера для определения абсолютной ориентации
- 10.21. Качественный элементный анализ: азот и сера
- 10.22. Количественный элементный анализ: азот и сера
- 10.23. Определение молекулярного веса: понижение температуры замерзания. Метод Раста
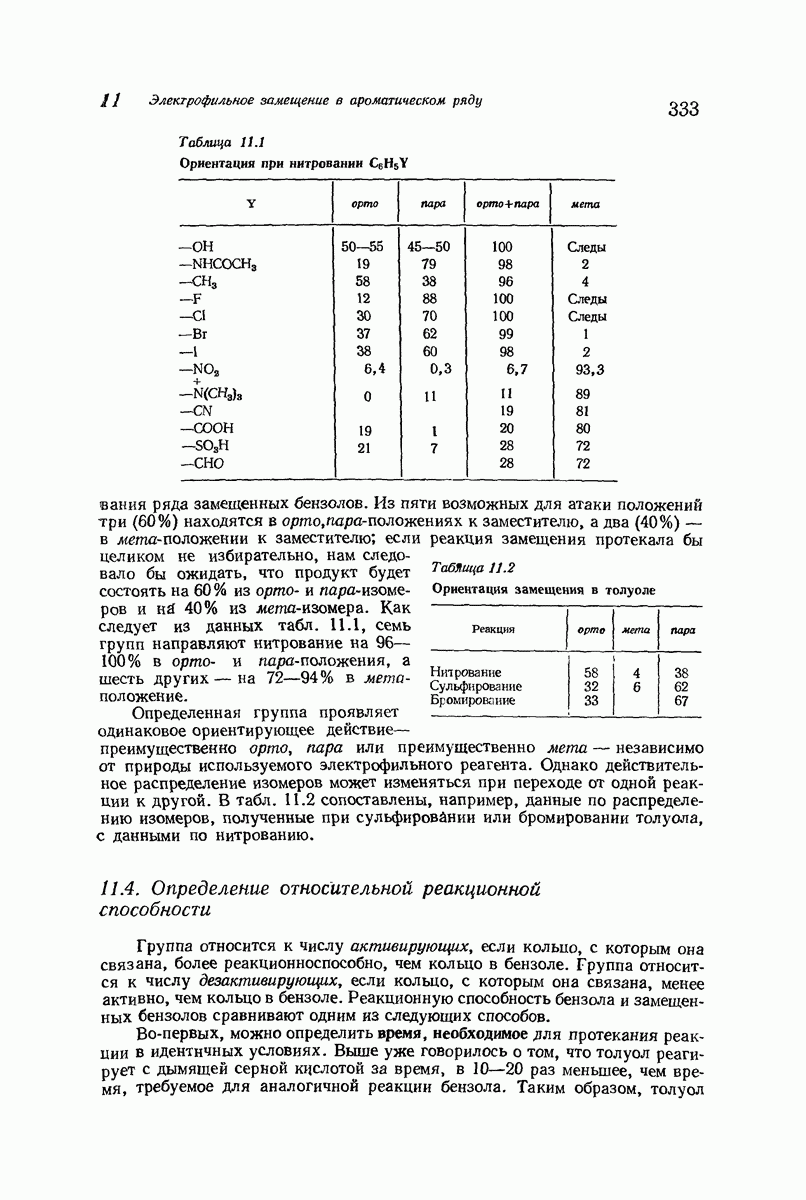
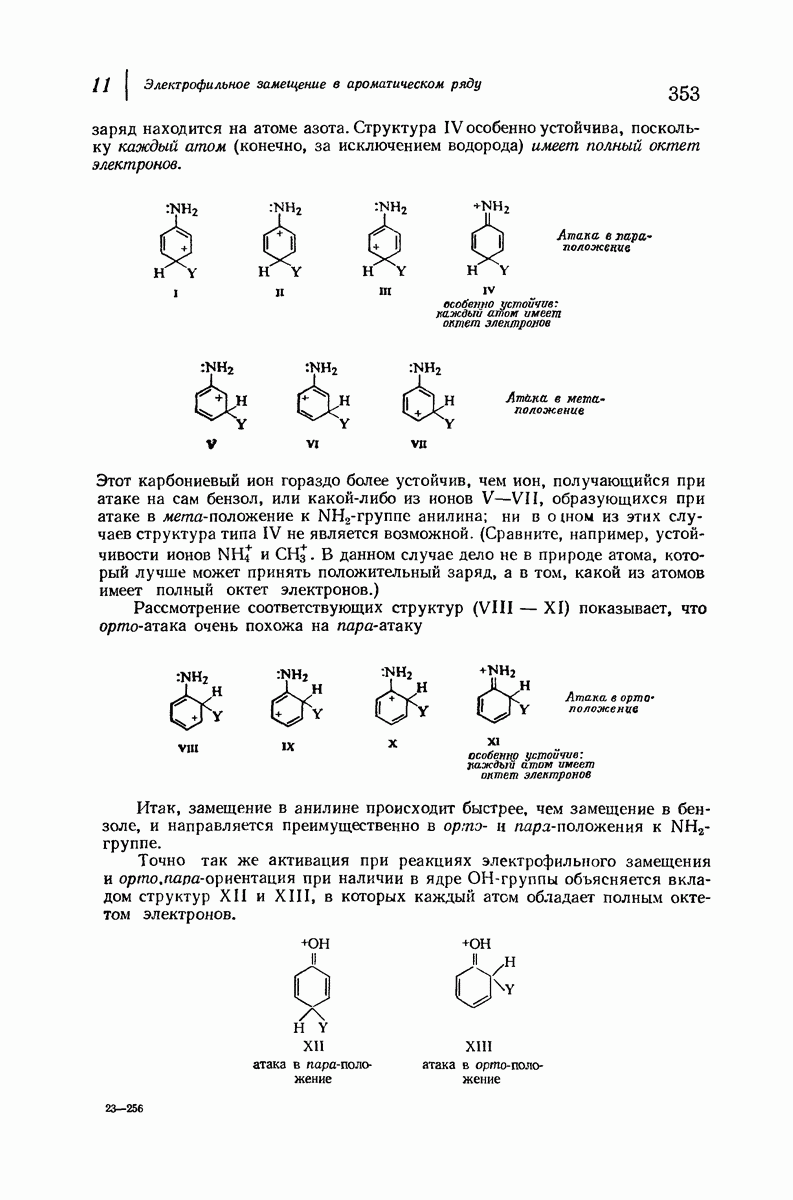
- 11. Электрофильное замещение в ароматическом ряду
- 11.6. Ориентация в дизамещенных бензолах
- 11.7. Ориентация и синтез
- 11.8. Механизм нитрования
- 11.9. Механизм сульфирования
- 11.10. Механизм галогенирования
- 11.11. Механизм алкилирования по Фриделю-Крафтсу
- 11.12. Механизм электрофильного замещения в ароматическом ряду: общие положения
- 11.13. Изотопный эффект
- 11.14. Механизм электрофильного замещения в ароматическом ряду: две стадии
- 11.15. Реакционная способность и ориентация
- 11.16. Теория реакционной способности
- 11.17. Теория ориентации
- 11.18. Подача электронов за счет эффекта резонанса
- 11.19. Связь с другими реакциями карбониевых ионов
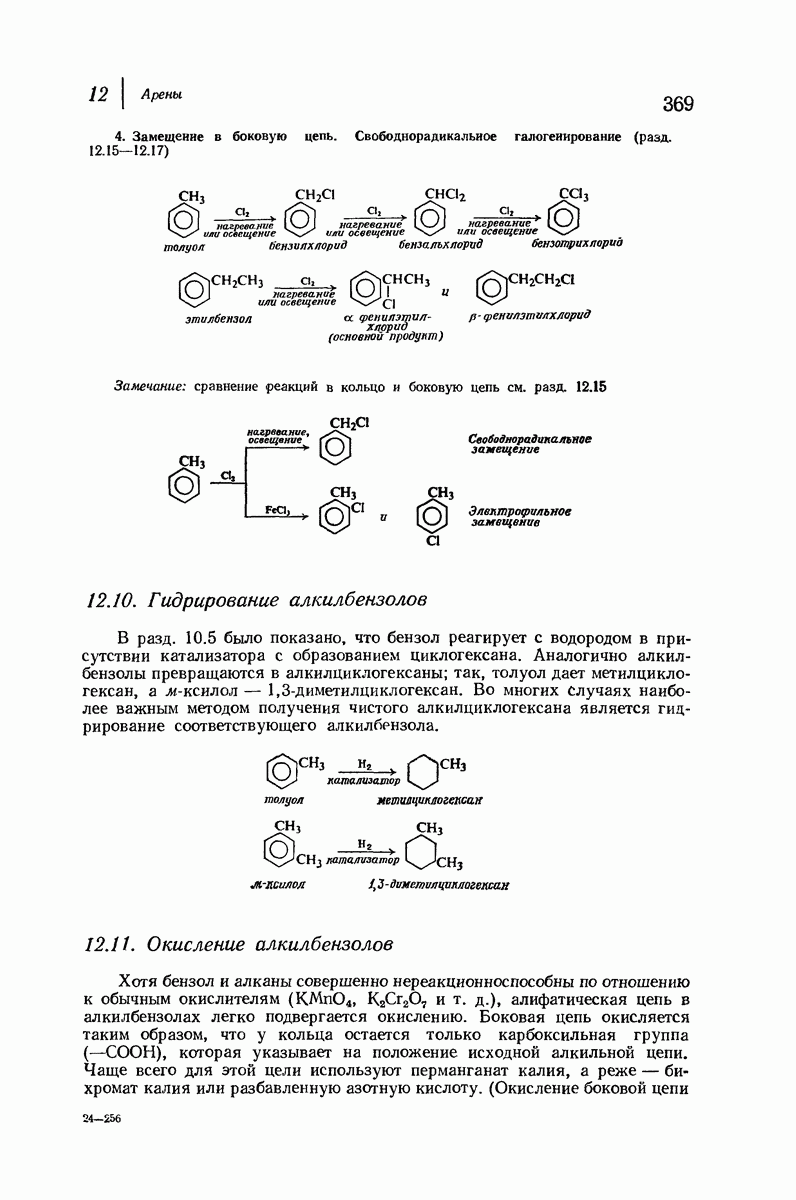
- 12. Арены
- 12.1. Жирноароматические углеводороды
- 12.4. Промышленные источники алкилбензолов
- 12.5. Методы синтеза алкилбензолов
- 12.6. Алкилирование по Фриделю-Крафтсу
- 12.7. Механизм алкилирования по Фриделю-Крафтсу
- 12.8. Ограничения для реакции алкилирования по Фриделю-Крафтсу
- 12.9. Реакции алкилбензолов
- 12.10. Гидрирование алкилбензолов
- 12.11. Окисление алкилбензолов
- 12.12. Нитрование алкилбензолов
- 12.13. Сульфирование алкилбензолов
- 12.14. Алкилирование алкилбензолов по Фриделю-Крафтсу
- 12.15. Галогенирование алкилбензолов в кольцо и в боковую цепь
- 12.16. Бромирование алкилбензолов в боковую цепь: ориентация и реакционная способность
- 12.17. Хлорирование алкилбензолов в боковую цепь: ориентация и реакционная способность. Полярные факторы при свободнорадикальных реакциях
- 12.18. Резонансная стабилизация свободного аллильного радикала
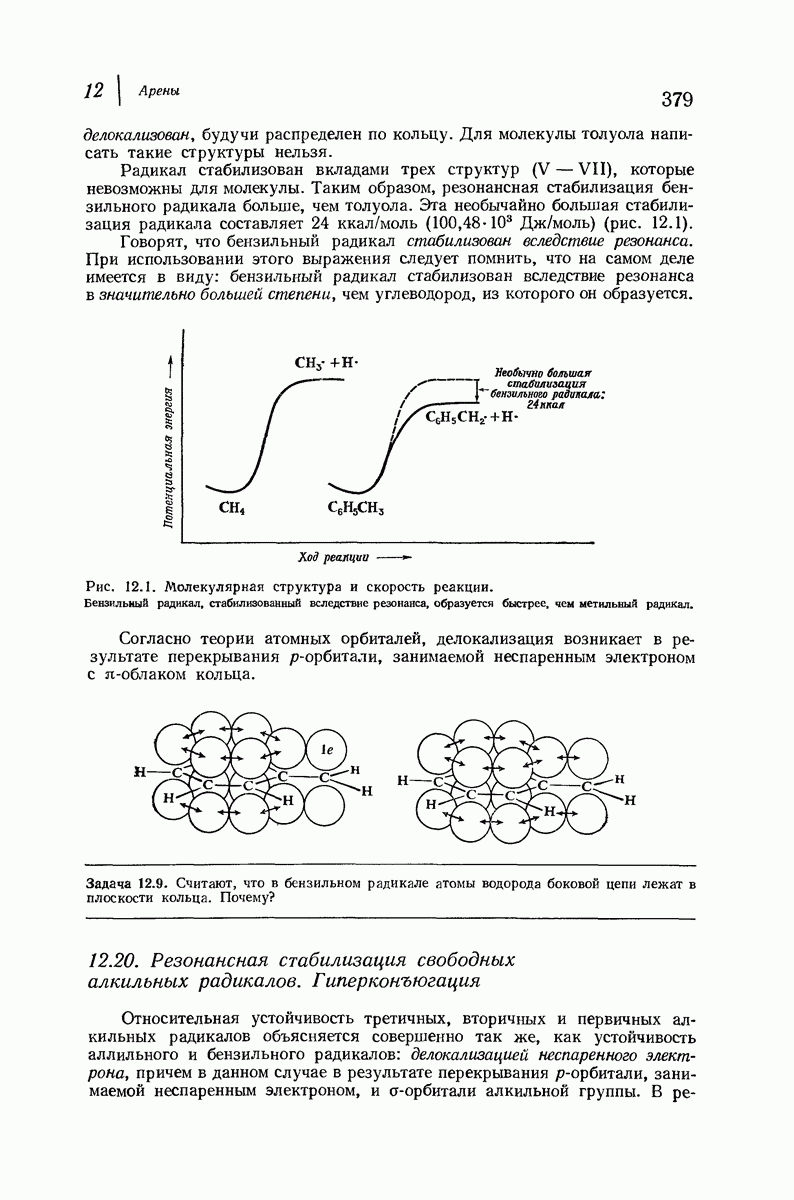
- 12.19. Резонансная стабилизация свободного бензильного радикала
- 12.20. Резонансная стабилизация свободных алкильных радикалов. Гиперконъюгация
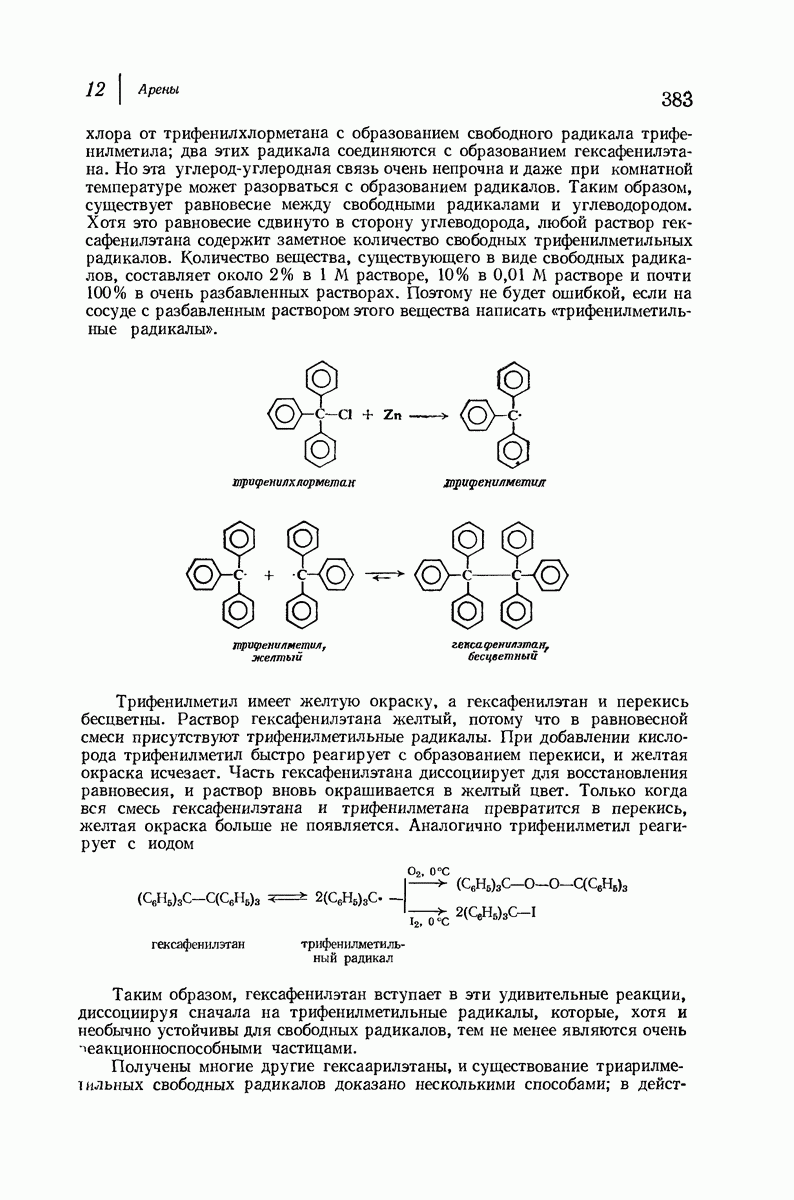
- 12.21. Трифенилметил: устойчивый свободный радикал
- 12.22. Получение алкилбензолов. Сопряжение с кольцом
- 12.23. Реакции алкенилбензолов
- 12.24. Присоединение к сопряженным алкенилбензолам: ориентация. Устойчивость бензильного карбониевого иона
- 12.25. Присоединение к сопряженным алкенилбензолам: реакционная способность
- 12.26. Полимеризация стирола
- 12.27. Алкинилбензолы
- 12.28. Анализ алкилбензолов
- 12.29. Анализ алкенил- и алкинилбензолов
- 13. Спектроскопия и строение органических соединений
- 13.2. Масс-спектры
- 13.3. Электромагнитный спектр
- 13.4. Инфракрасный спектр
- 13.5. Ультрафиолетовый спектр
- 13.6. Спектр ядерного магнитного резонанса (ЯMP)
- 13.7. ЯМР. Число сигналов. Эквивалентные и неэквивалентные протоны
- 13.8. ЯМР. Положение сигналов. Химический сдвиг
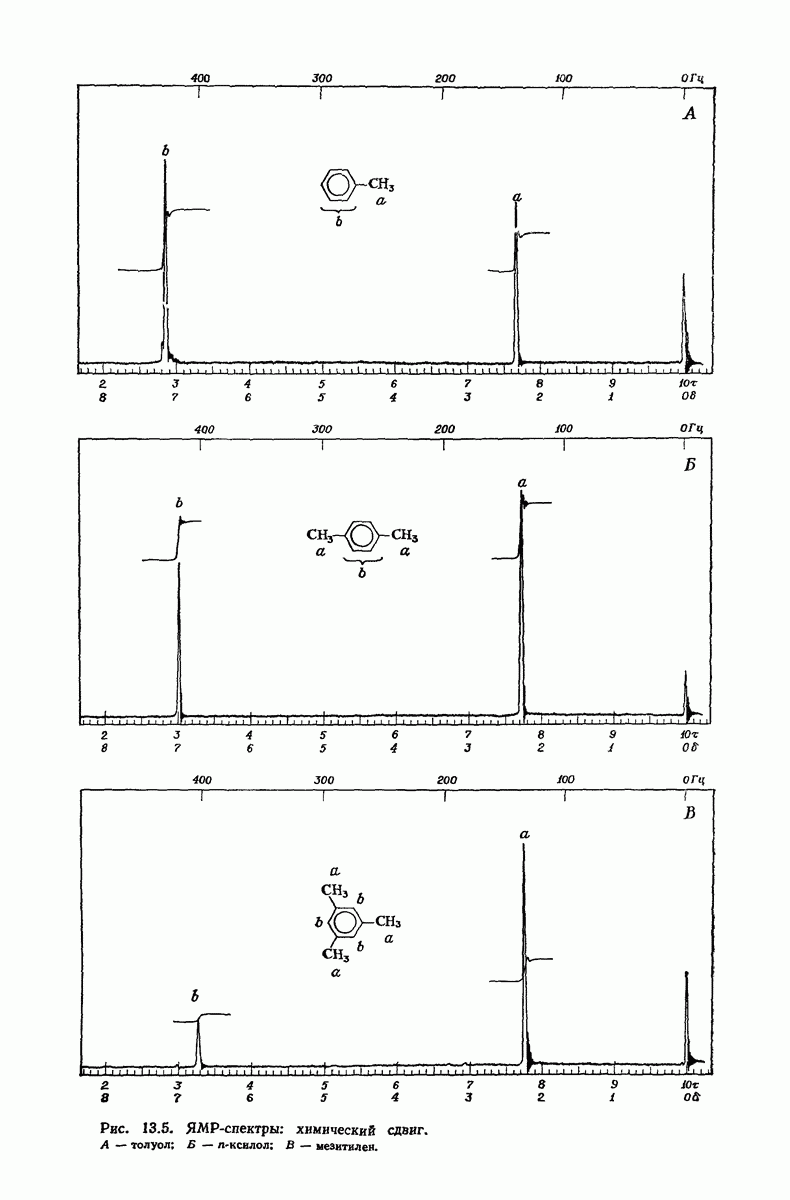
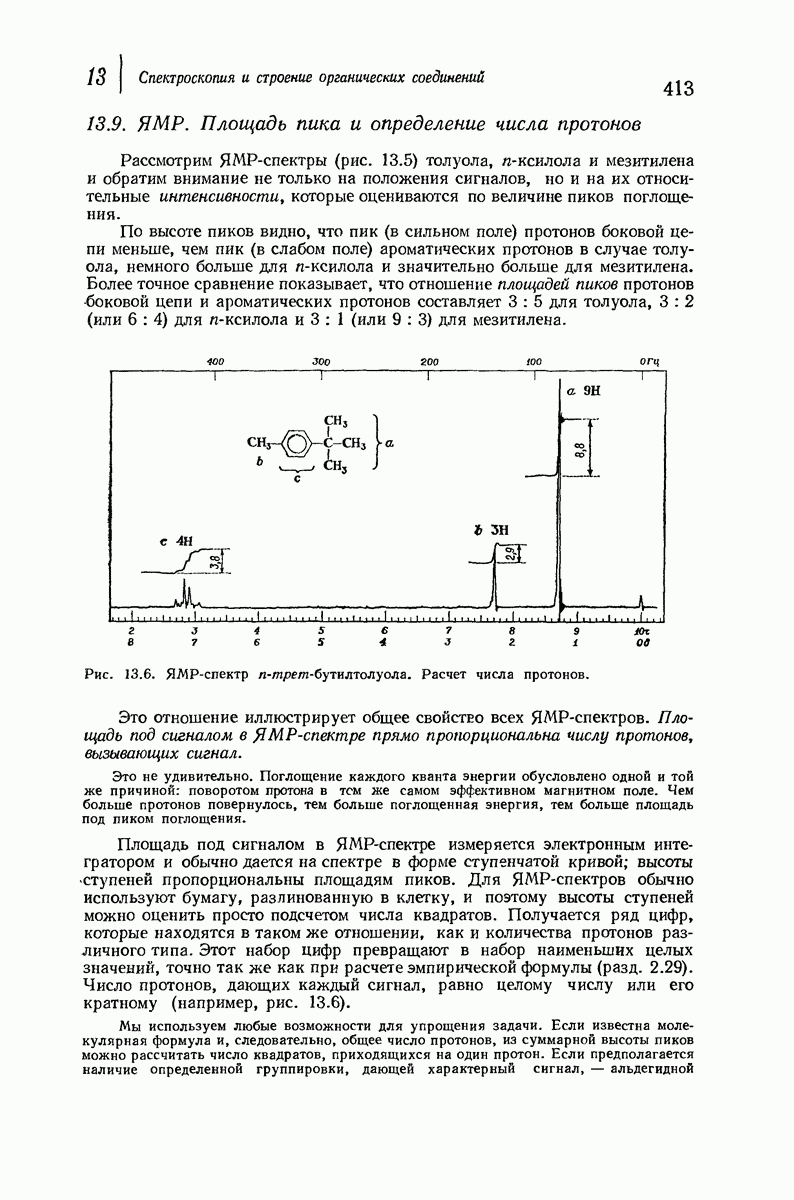
- 13.9. ЯМР. Площадь пика и определение числа протонов
- 13.10. ЯМР. Расщепление сигналов. Спин-спиновое взаимодействие
- 13.11. ЯМР. Константы взаимодействия
- 13.12. ЯМР. Сложные спектры. Дейтериееая метка
- 13.13. Магнитная эквивалентность протонов: более подробное рассмотрение
- 13.14. ЯМР и конформационный анализ
- 13.15. Спектр электронного парамагнитного резонанса (ЭПР)
- 13.16. Спектральный анализ углеводородов. Масс-спектры
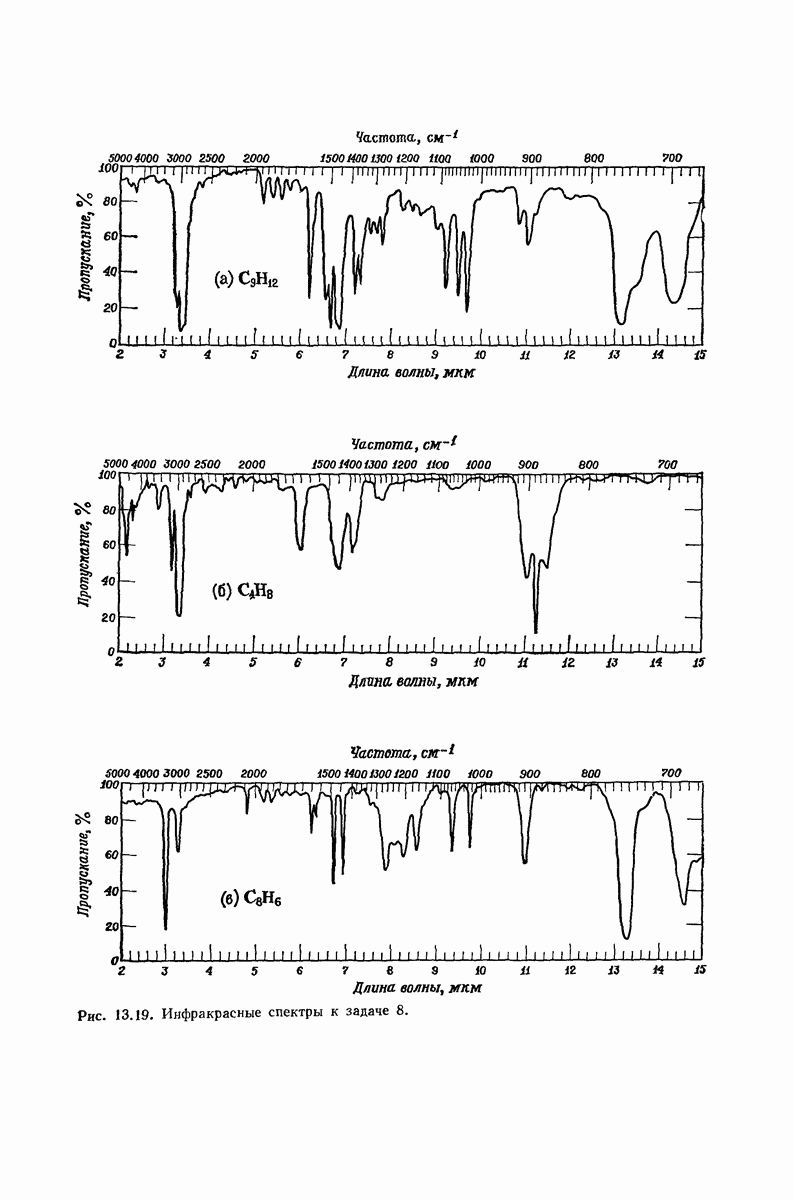
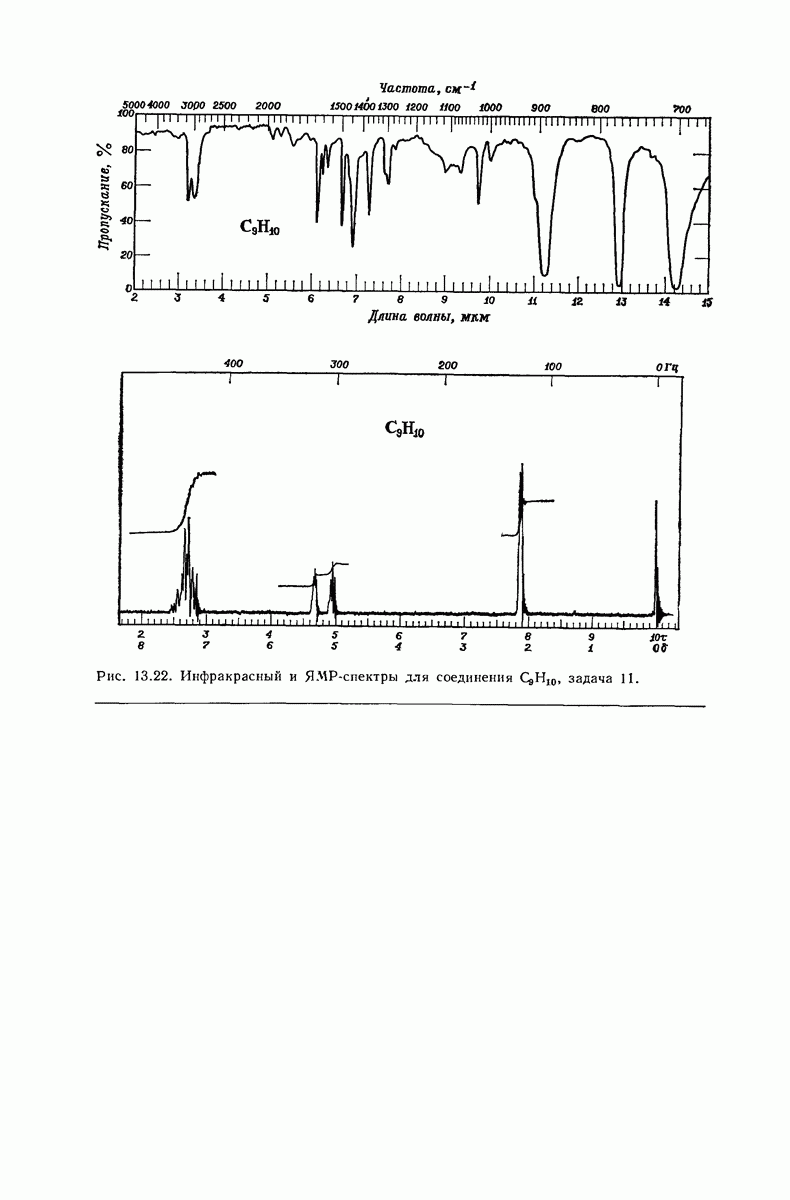
- 13.17. Спектральный анализ углеводородов. Инфракрасные спектры
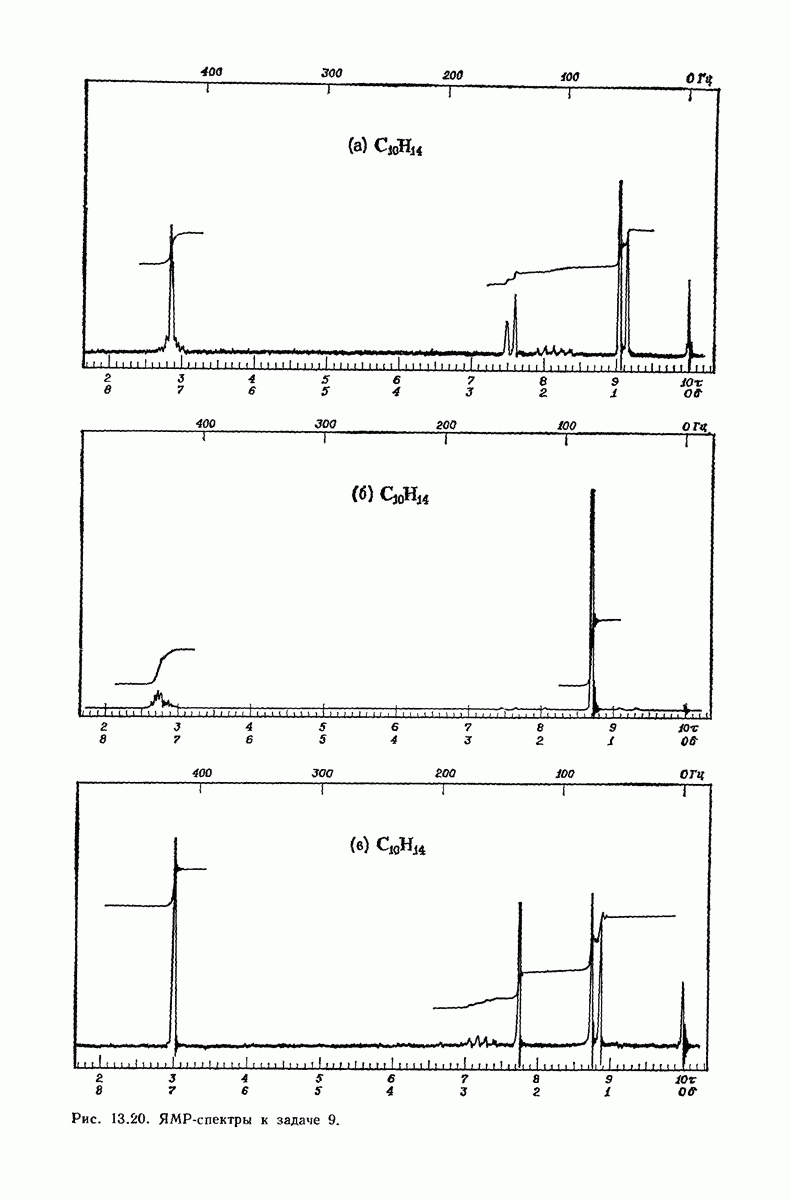
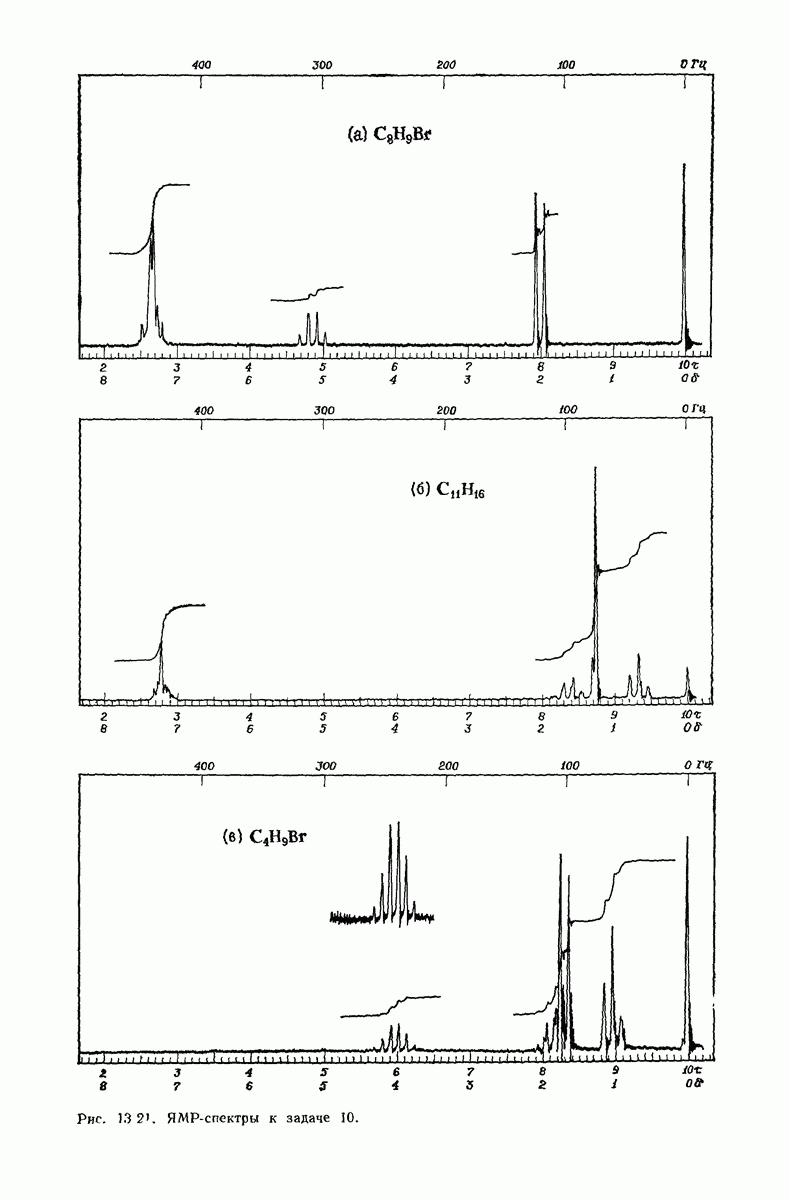
- 13.18. Спектральный анализ углеводородов. ЯМР-спектры
- 14. Алкилгалогениды. НУКЛЕОФИЛЬНОЕ ЗАМЕЩЕНИЕ В АЛИФАТИЧЕСКОМ РЯДУ
- 14.8. Кинетика реакции нуклеофильного замещения в алифатическом ряду. Реакции первого и второго порядка
- 14.9. SN2-Реакция: механизм и кинетика
- 14.10. SN2-Реакция: стереохимия
- 14.11. SN2-Реакция: реакционная способность
- 14.12. SN1-Реакция: механизм и кинетика. Стадия, определяющая скорость
- 14.13. Стереохимия SN1-реакций
- 14.14. SN1-Реакция: реакционная способность
- 14.15. SN1-Реакция: перегруппировки
- 14.16. Сравнение SN1- и SN2-реакций
- 14.17. Элиминирование (отщепление): Е2 и Е1
- 14.18. Доказательства Е1-механизма
- 14.19. Доказательства E2-механизма
- 14.20. Сравнение реакций элиминирования и замещения
- 14.21. Апротонные растворители
- 14.22 Анализ алкилгалогенидов
- 14.23. Спектральный анализ алкилгалогенидов
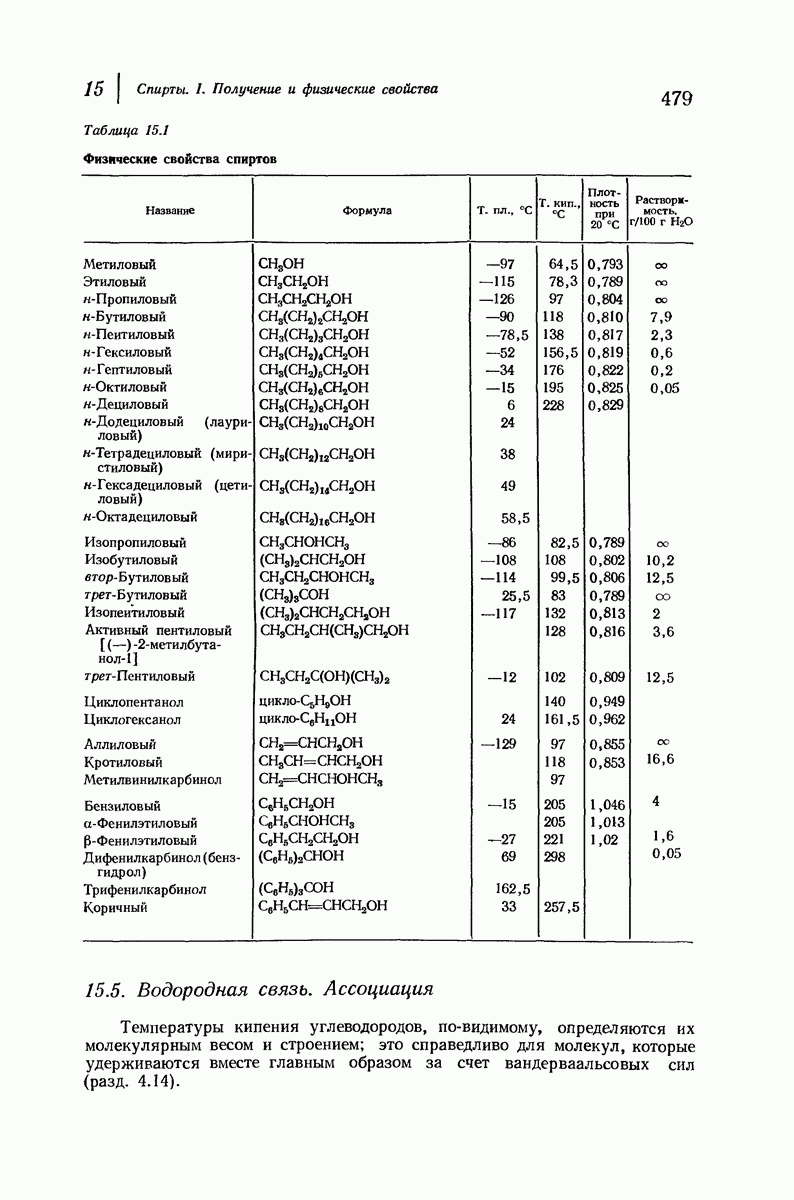
- 15. Спирты. I. Получение и физические свойства
- 15.5. Водородная связь. Ассоциация
- 15.6. Промышленные источники
- 15.7. Этиловый спирт
- 15.8. 95%-ный спирт: азеотропная смесь
- 15.9. Абсолютный спирт
- 15.10. Методы синтеза
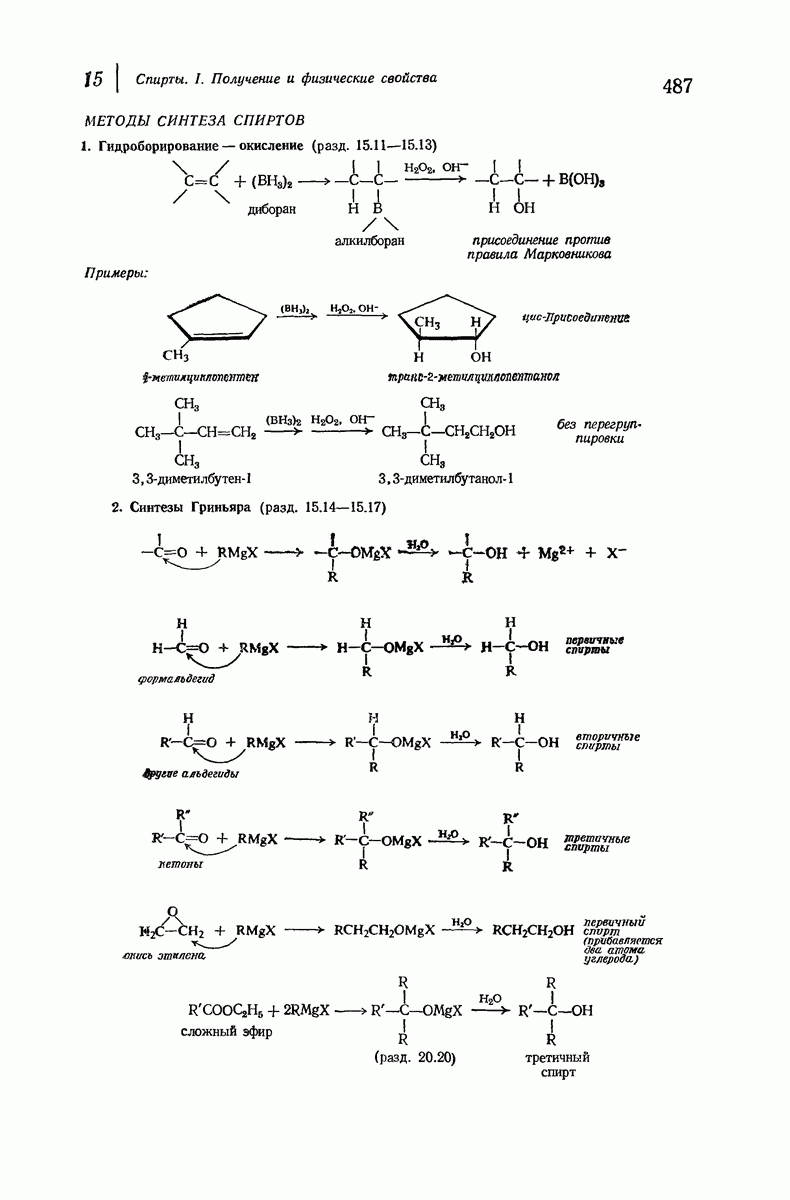
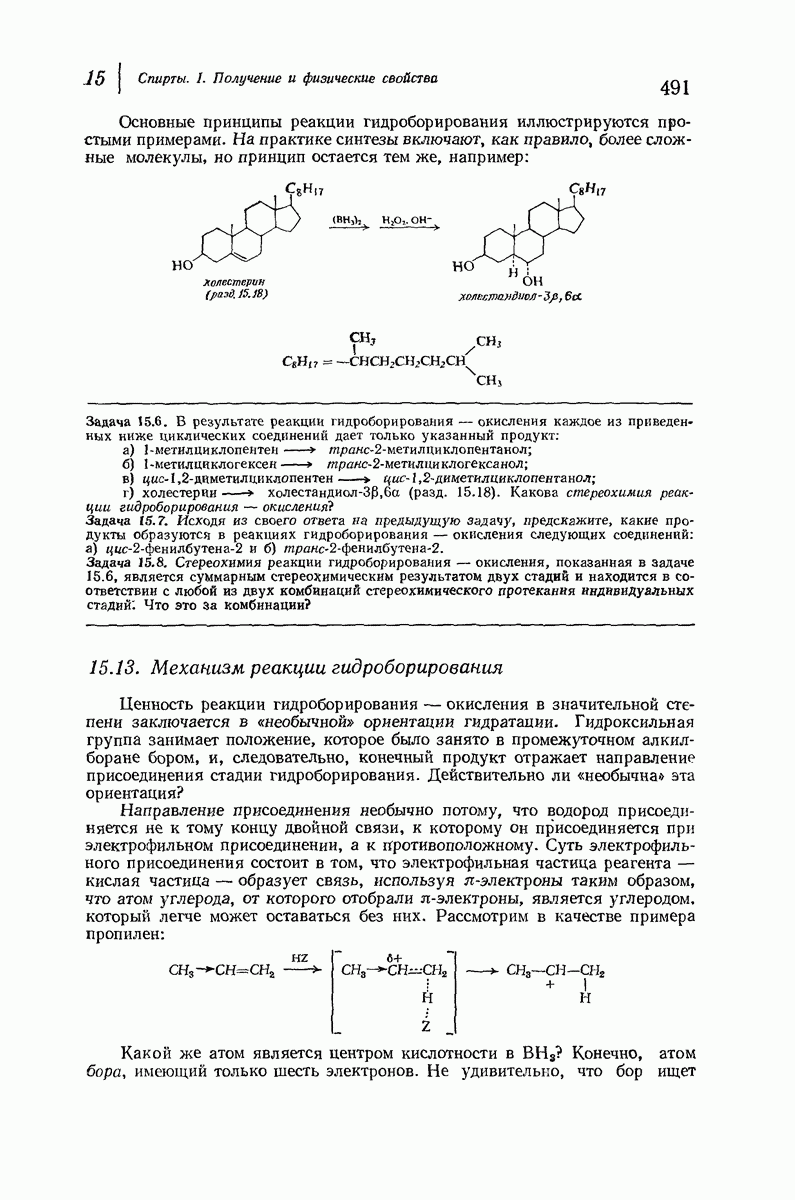
- 15.11. Гидроборирование — окисление
- 15.12. Направление присоединения в реакции гидроборирования
- 15.13. Механизм реакции гидроборирования
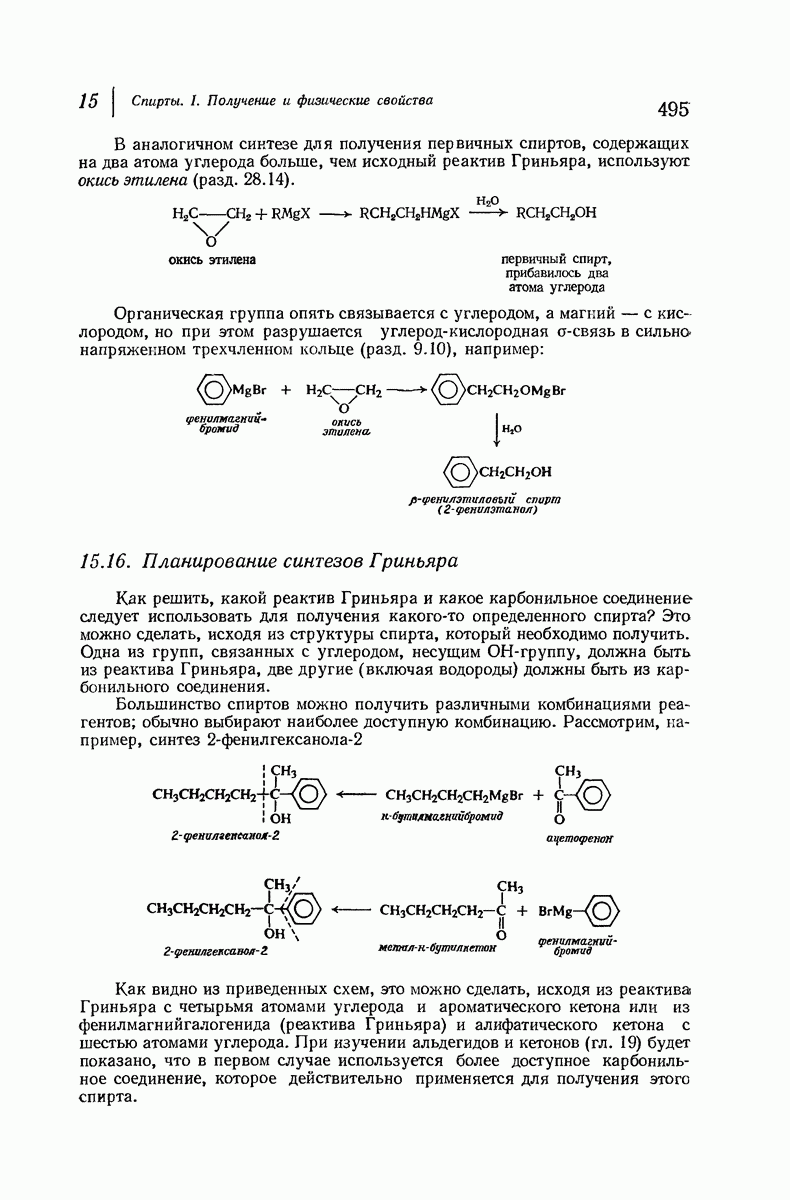
- 15.14. Синтез спиртов с помощью реактивов Гриньяра
- 15.15. Продукты синтезов Гриньяра
- 15.16. Планирование синтезов Гриньяра
- 15.17. Ограничения синтеза Гриньяра
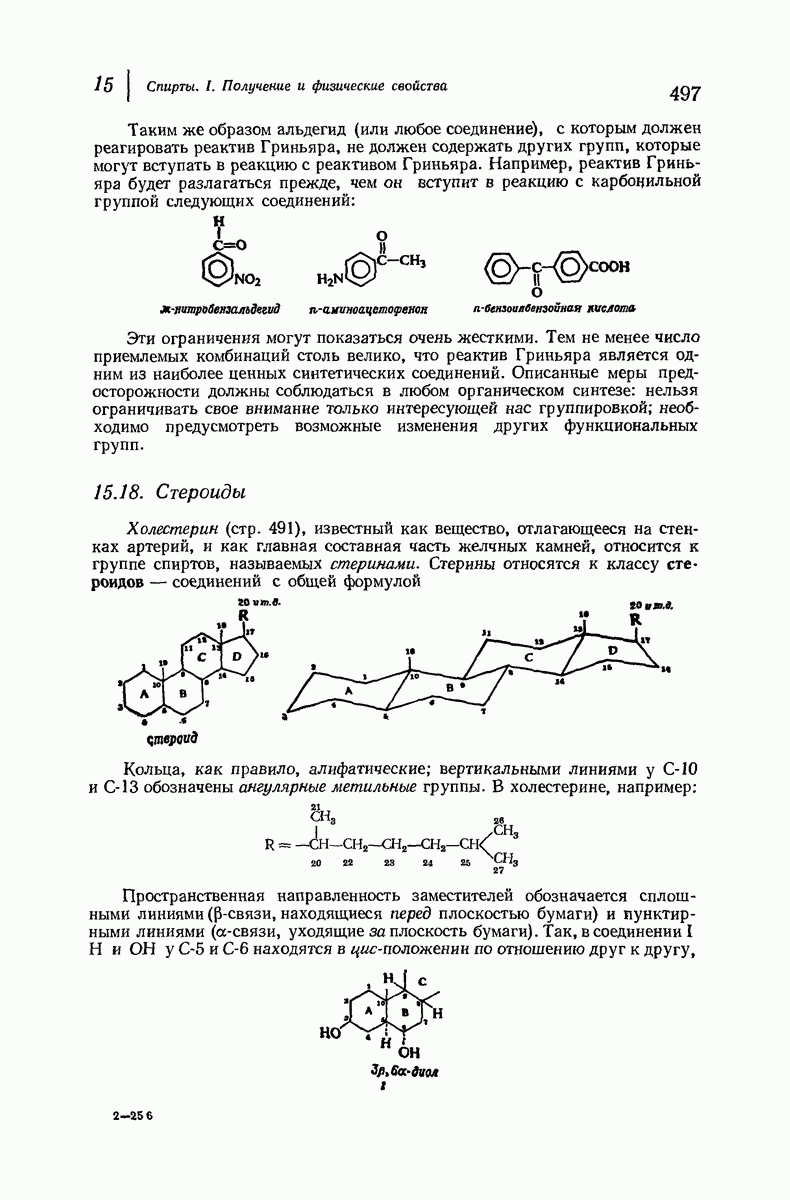
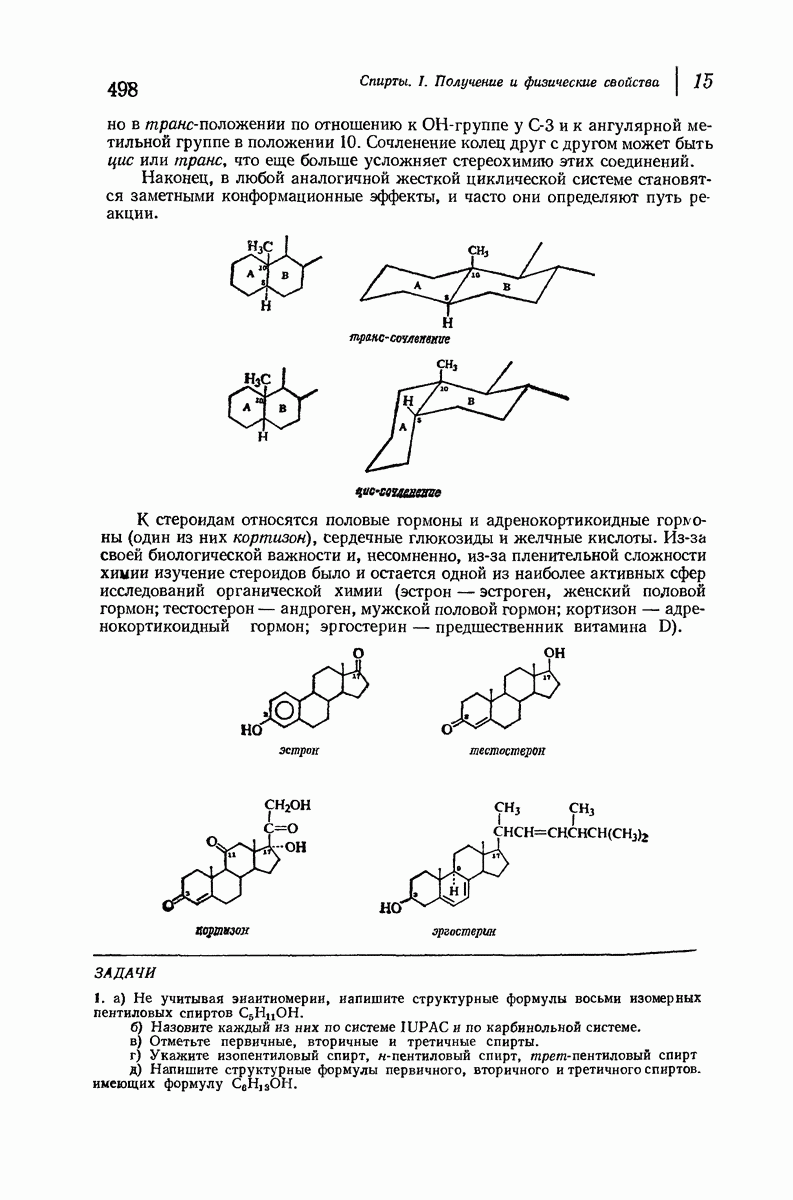
- 15.18. Стероиды
- 16. Спирты. II. Реакции
- 16.4. Реакции с галогеноводородами
- 16.5. Реакция с галогеноводородами: механизм
- 16.6. Спирты как кислоты
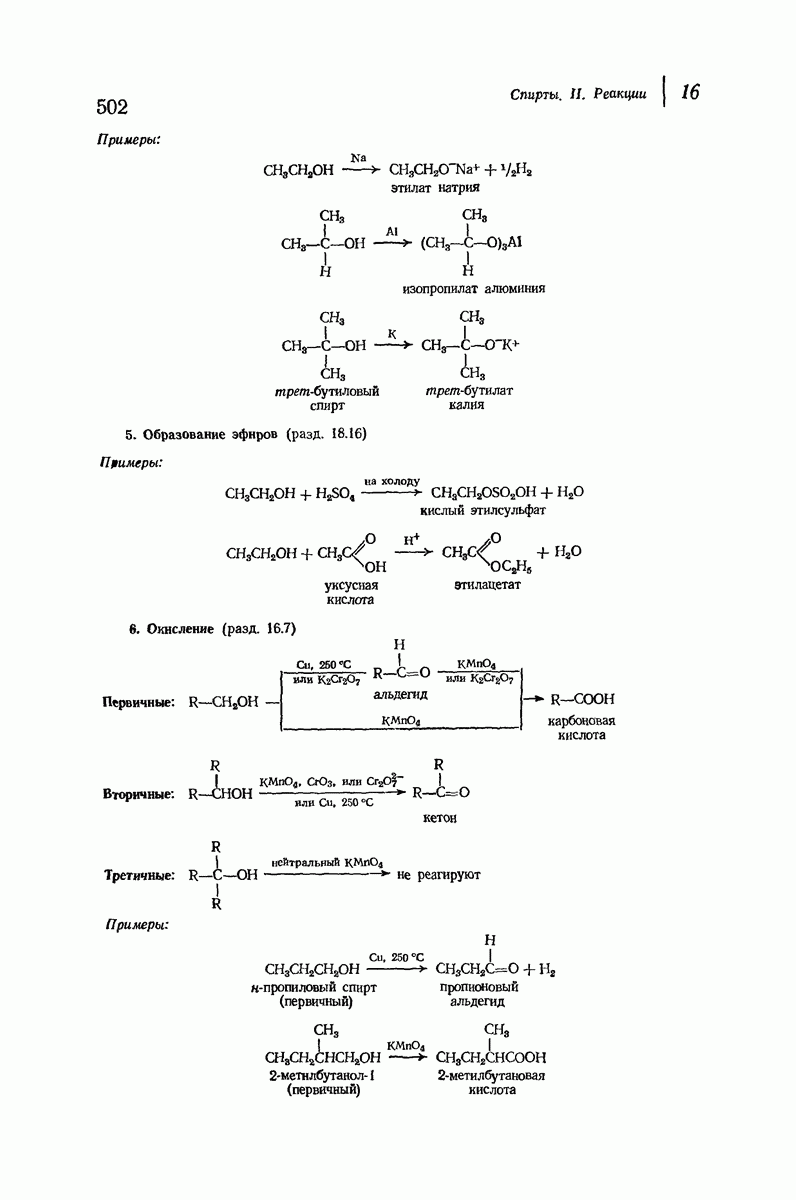
- 16.7. Окисление спиртов
- 16.8. Уравнивание окислительно-восстановительных реакций
- 16.9. Методы синтеза
- 16.10. Синтезы с использованием спиртов
- 16.11. Анализ спиртов. Характерные реакции. Проба Лукаса. Иодоформная реакция
- 16.12. Спектральный анализ
- 17. Простые эфиры
- 17.4. Перекиси в эфирах
- 17.5. Абсолютный эфир
- 17.6. Опасности при работе с диэтиловым эфиром
- 17.7. Синтез Вильямсона
- 17.8. Получение замещенных эфиров
- 17.9. Реакции простых эфиров. Расщепление кислотами
- 17.10. Электрофильное замещение в ароматических эфирах
- 17.11. Циклические эфиры
- 17.12. Анализ простых эфиров
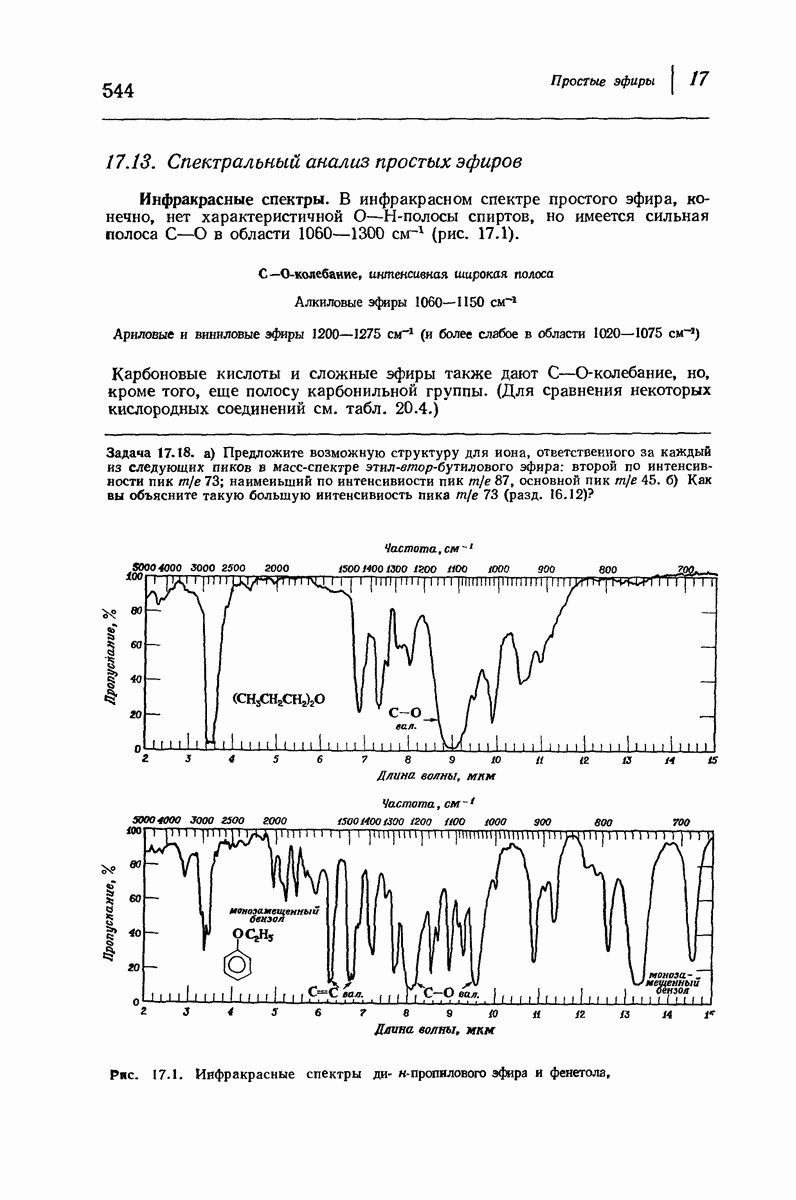
- 17.13. Спектральный анализ простых эфиров
- 18. Карбоновые кислоты
- 18.4. Соли карболовых кислот
- 18.7. Синтез Гриньяра
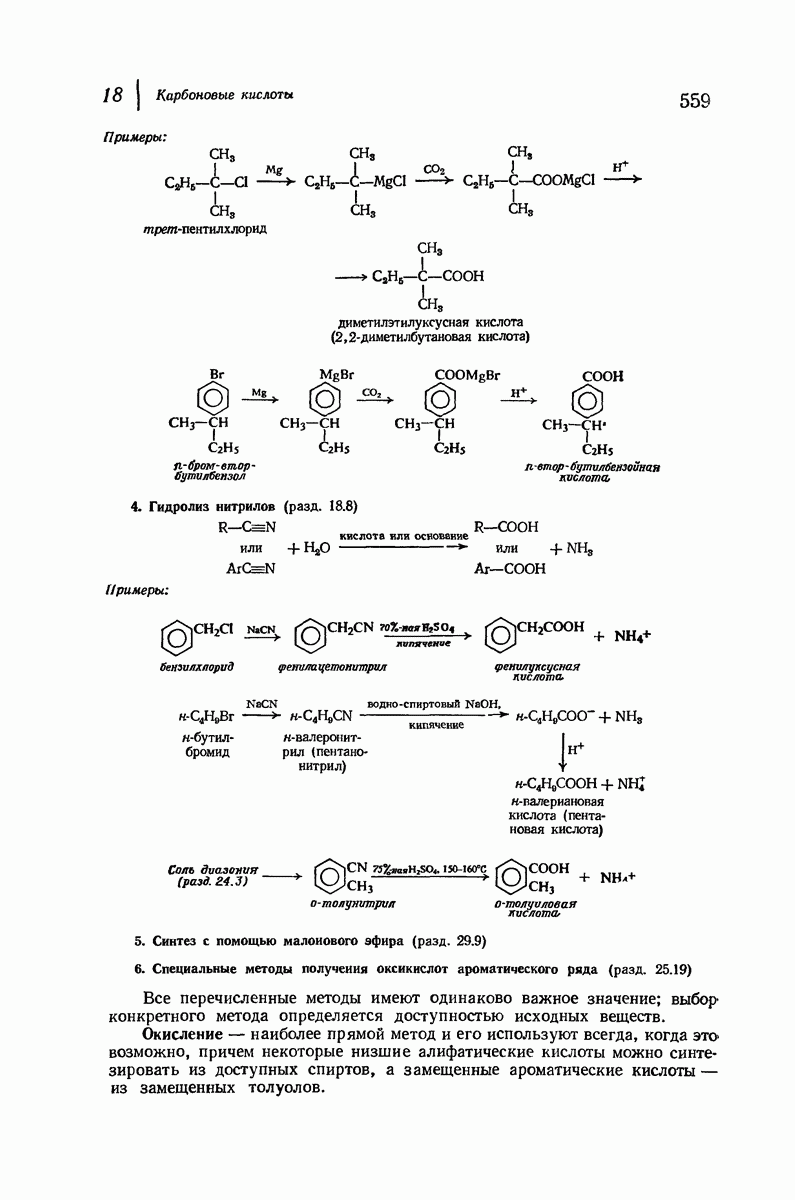
- 18.8. Нитрильный синтез
- 18.9. Реакции
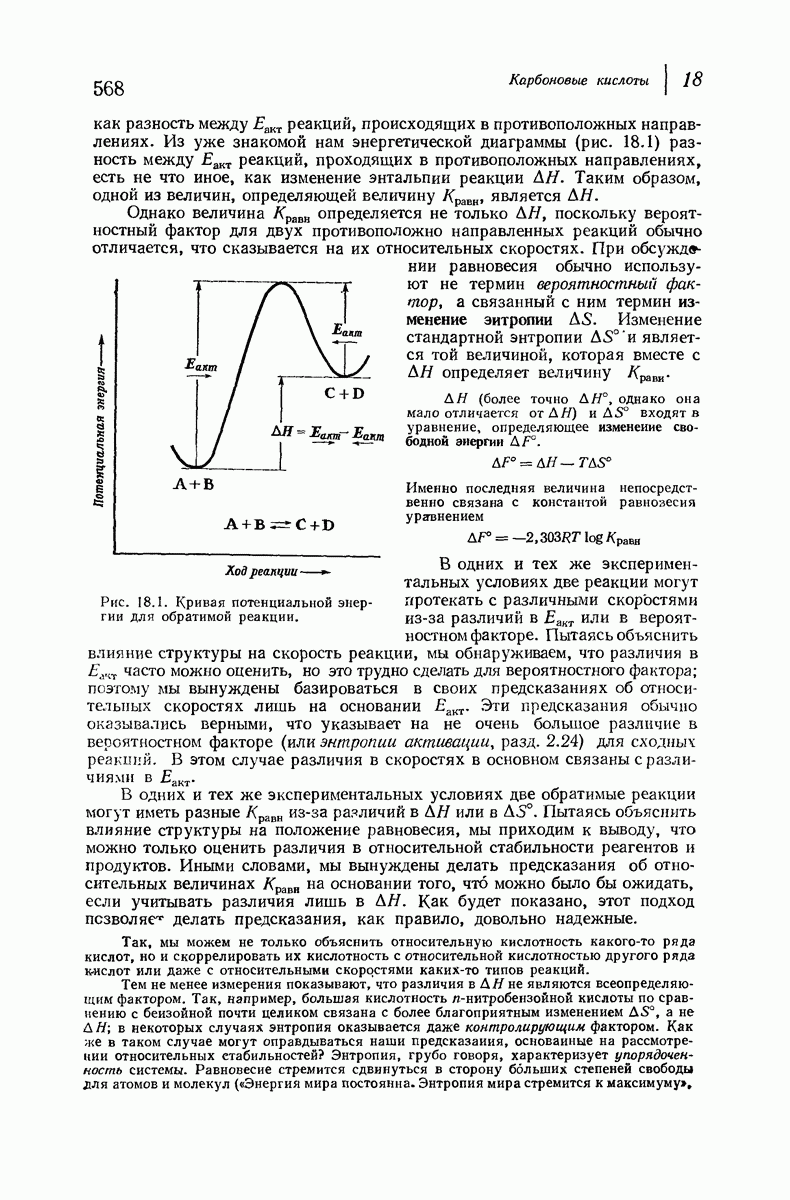
- 18.10. Ионизация карбоновых кислот. Константа кислотности
- 18.11. Равновесие
- 18.12. Кислотность карбоновых кислот
- 18.13. Структура карбоксилат-ионов
- 18.14. Влияние заместителей на кислотность
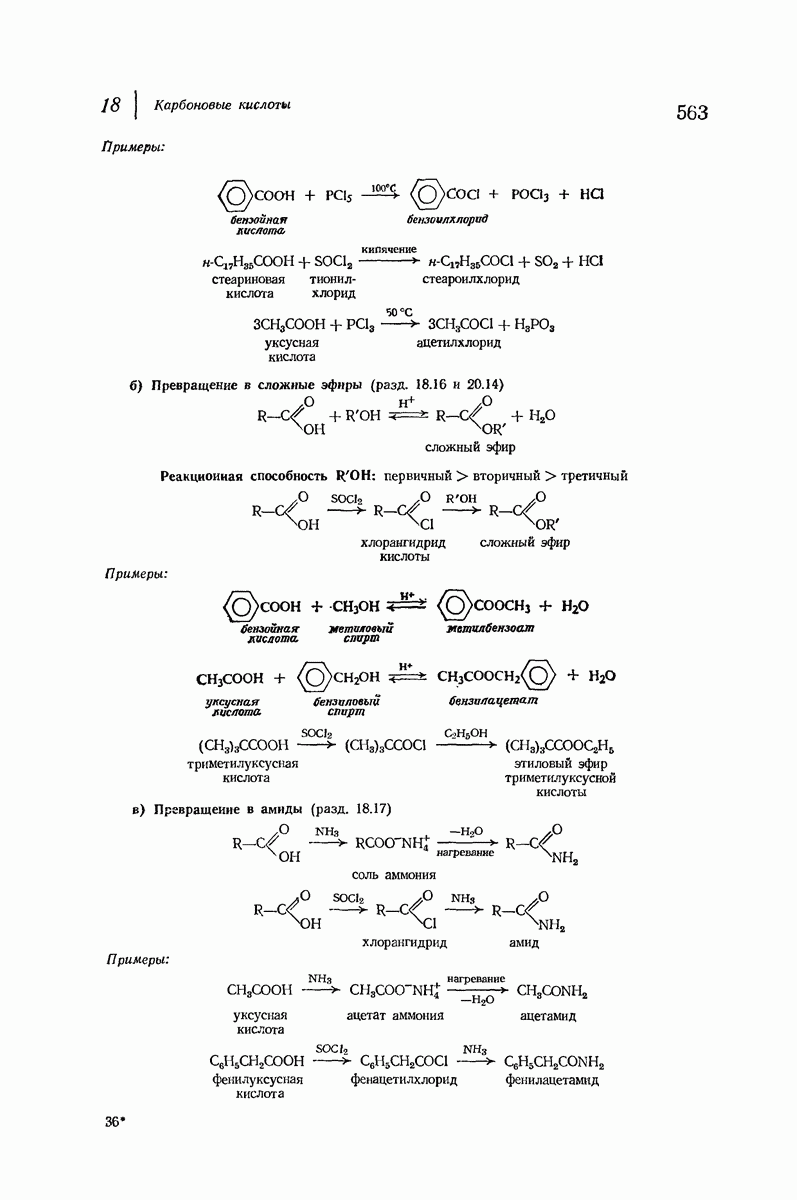
- 18.15. Превращение в хлорангидриды кислот
- 18.16. Превращение в сложные эфиры
- 18.17. Превращение в амиды
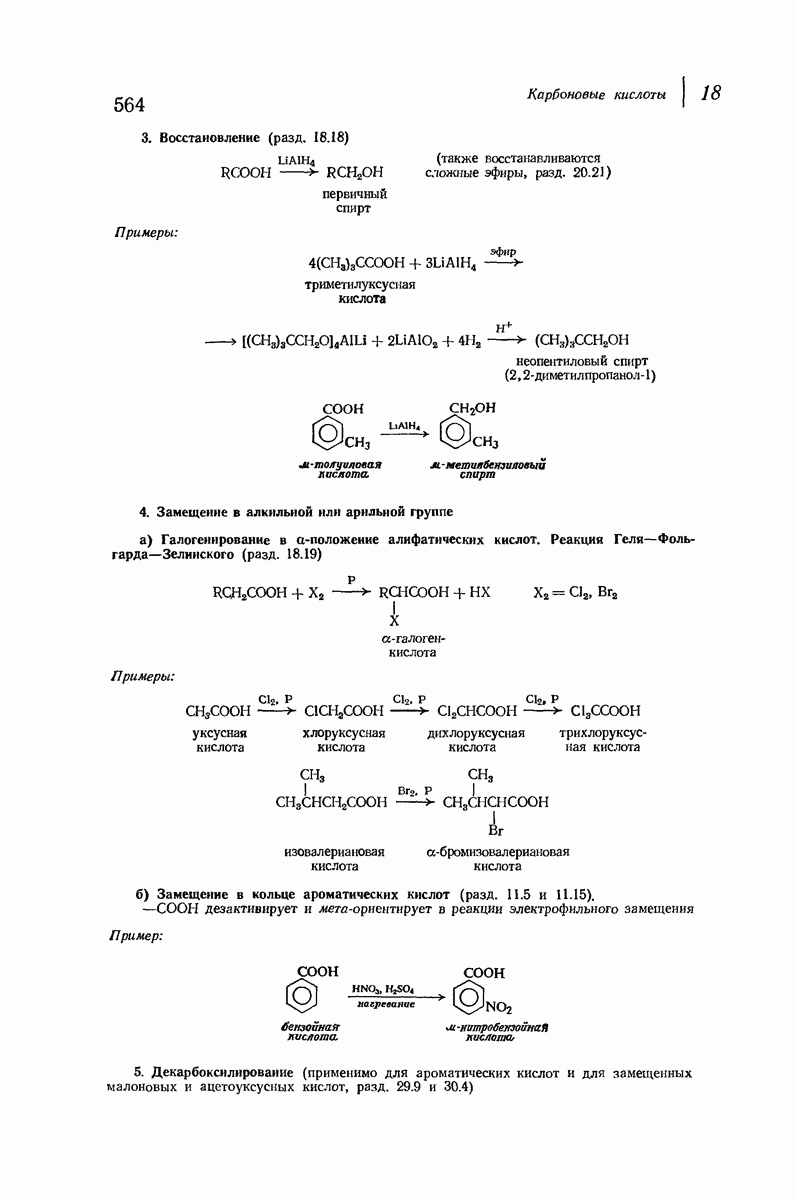
- 18.18. Восстановление кислот в спирты
- 18.19. Галогенирование алифатических кислот. Реакция Геля — Фольгарда — Зелинского
- 18.20. Анализ карбоновых кислот. Эквивалент нейтрализации
- 18.21. Спектральный анализ карбоновых кислот
- 19. Альдегиды и кетоны. I НУКЛЕОФИЛЬНОЕ ПРИСОЕДИНЕНИЕ
- 19.6. Синтез альдегидов окислением
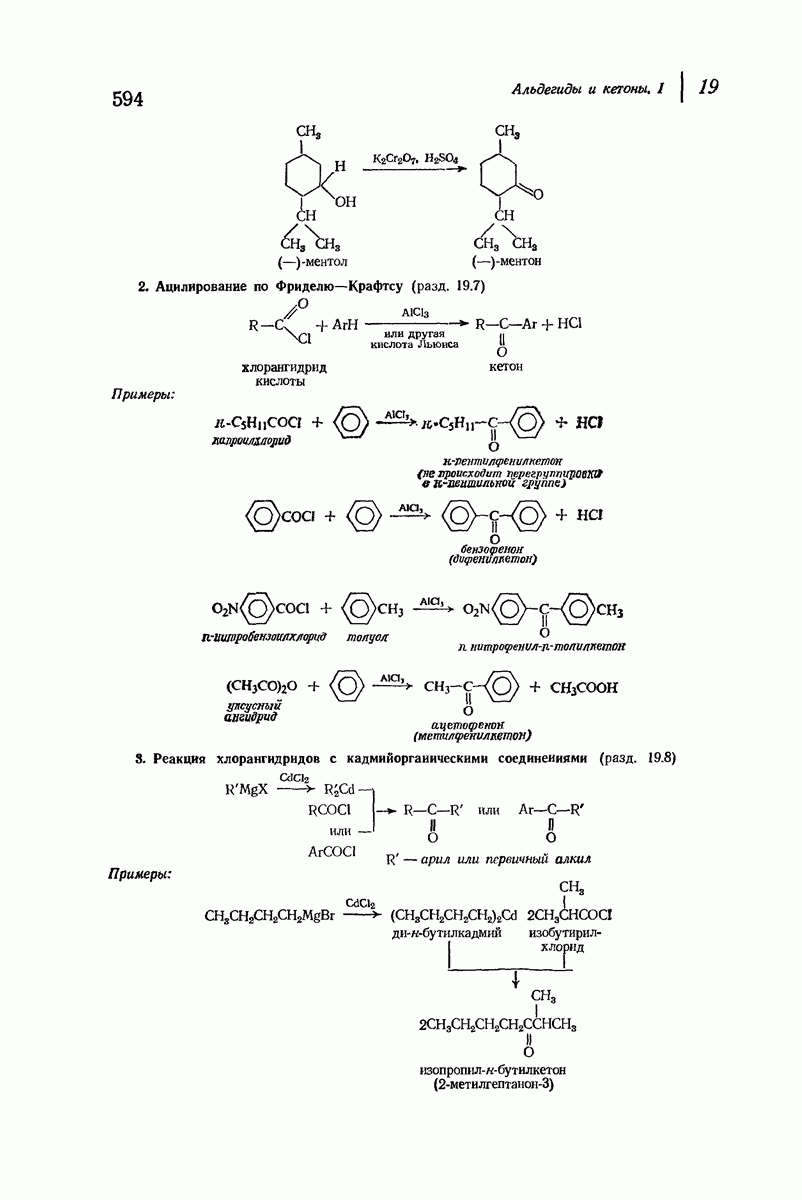
- 19.7. Синтез кетонов ацилированием по Фриделю — Крафтсу
- 19.8. Синтез кетонов с использованием кадмийорганических соединений
- 19.9. Реакции. Нуклеофильное присоединение
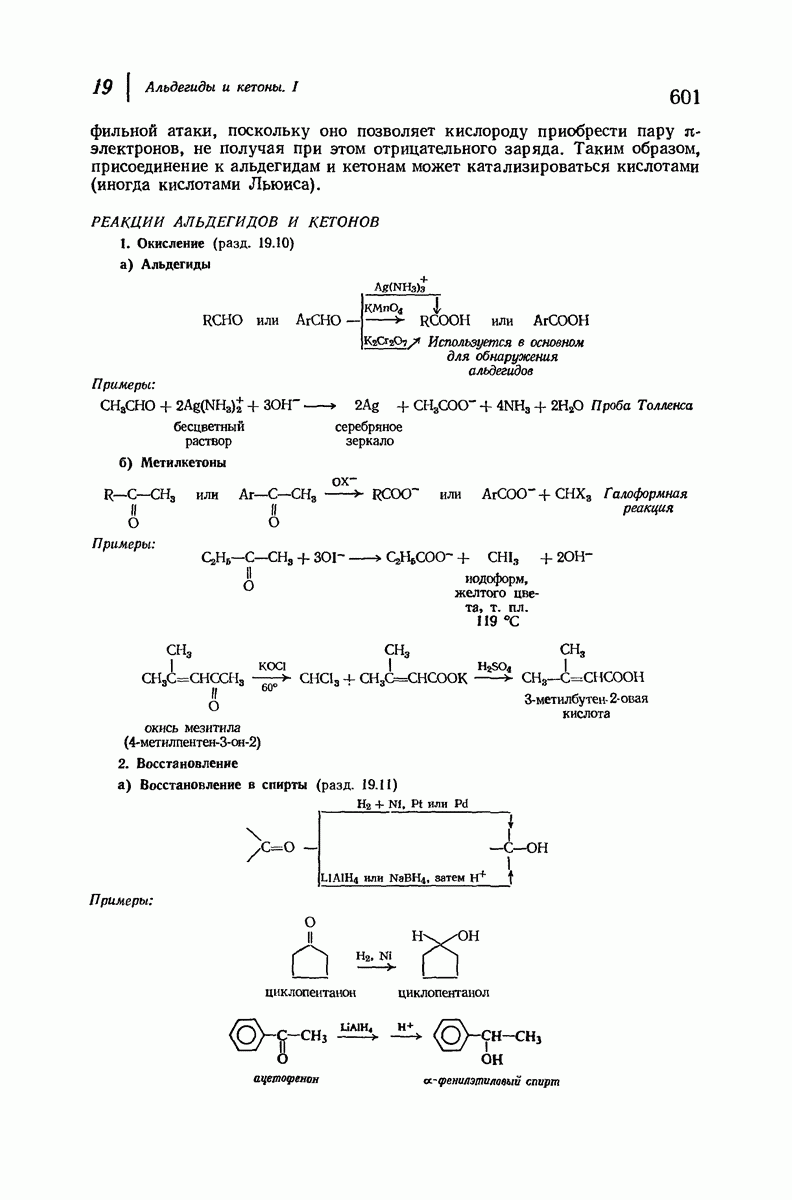
- 19.10. Окисление
- 19.11. Восстановление
- 19.12. Присоединение реактивов Гриньяра
- 19.13. Восстановление гидридами металлов
- 19.14. Присоединение цианид-иона
- 19.15. Присоединение бисульфита
- 19.16. Присоединение производных аммиака
- 19.17. Присоединение спиртов. Образование ацеталей
- 19.18. Реакция Канниццаро
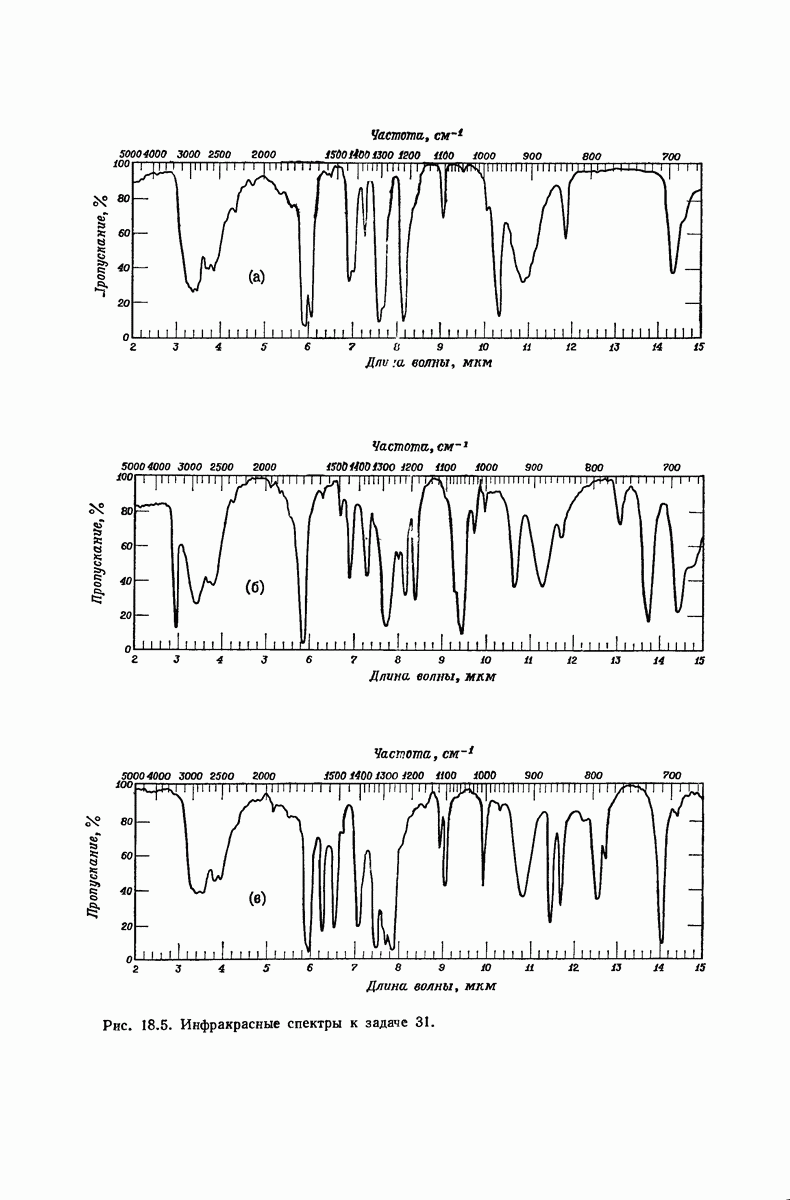
- 19.19. Анализ альдегидов и кетонов
- 19.20. Спектроскопический анализ альдегидов и кетонов
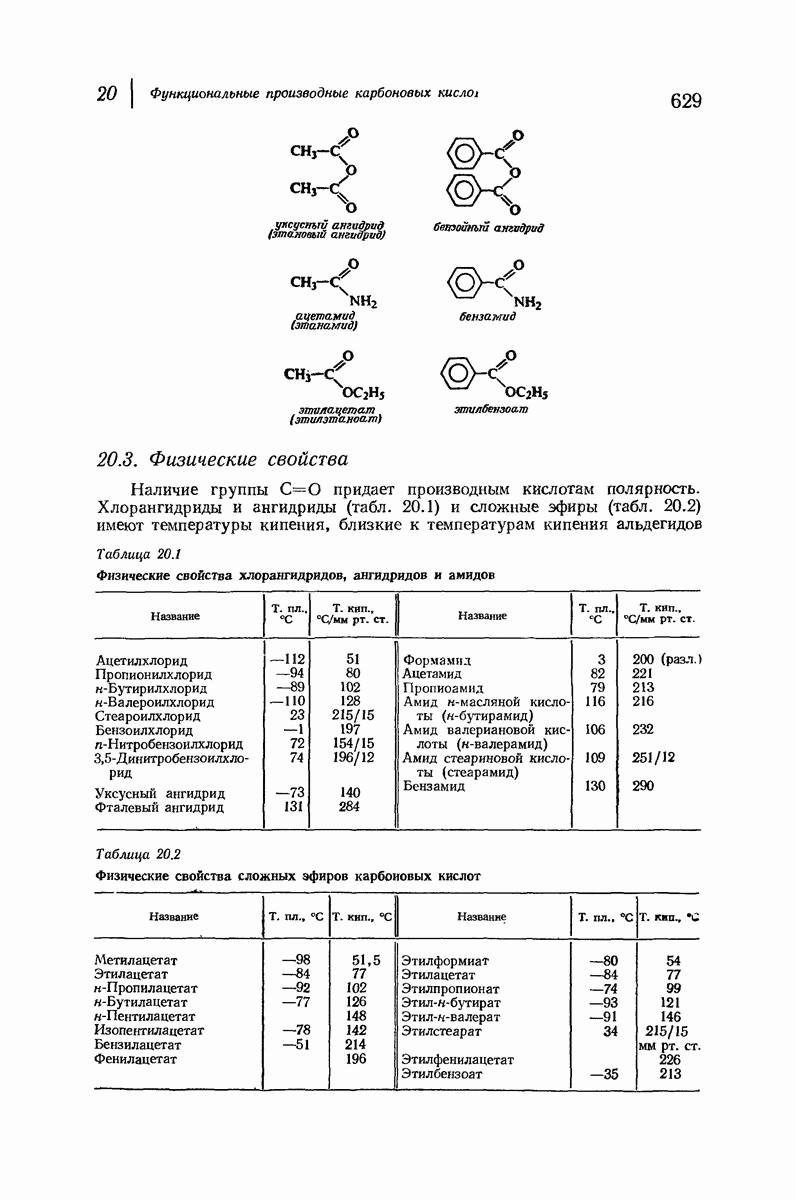
- 20. Функциональные производные карбоновых кислот. НУКЛЕОФИЛЬНОЕ ЗАМЕЩЕНИЕ В АЦИЛЬНОИ ГРУППЕ
- 20.4. Нуклеофильное замещение в ацильной группе. Роль карбонильной группы
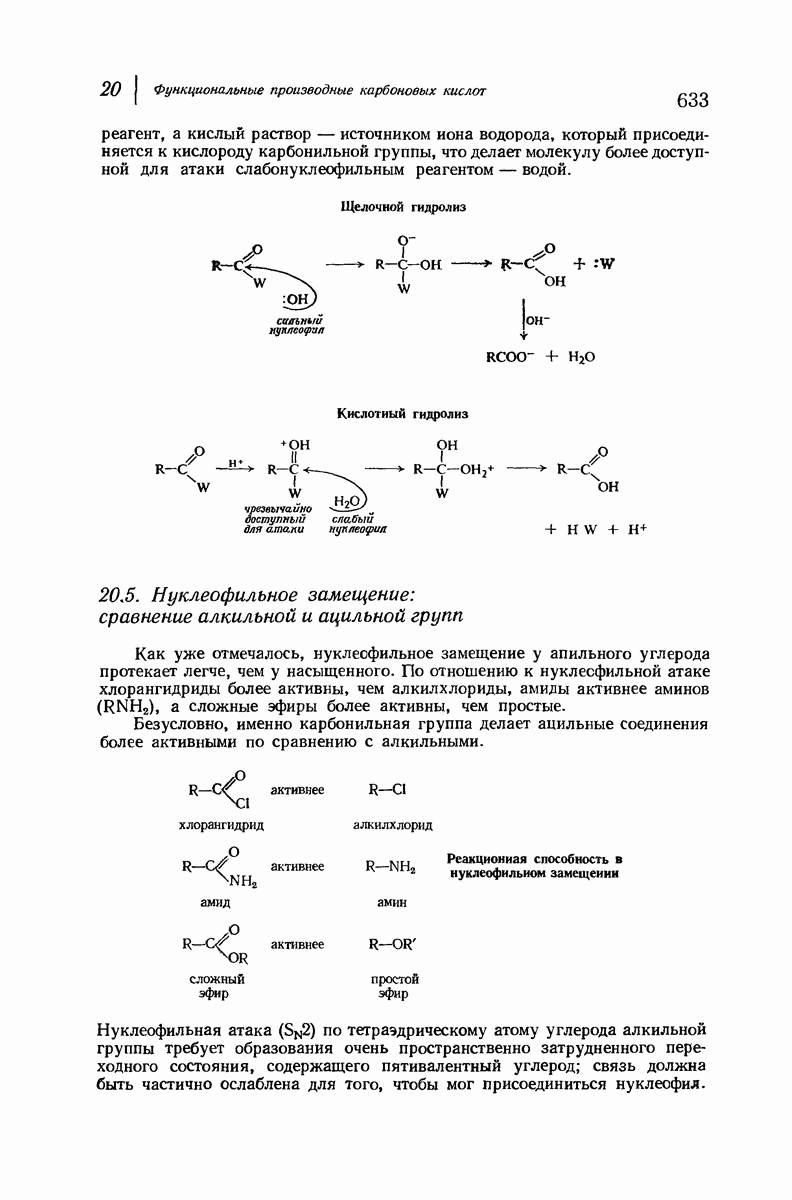
- 20.5. Нуклеофилъное замещение: сравнение алкильной и ацильной групп
- ХЛОРАНГИДРИДЫ
- 20.6. Получение хлорангидридов
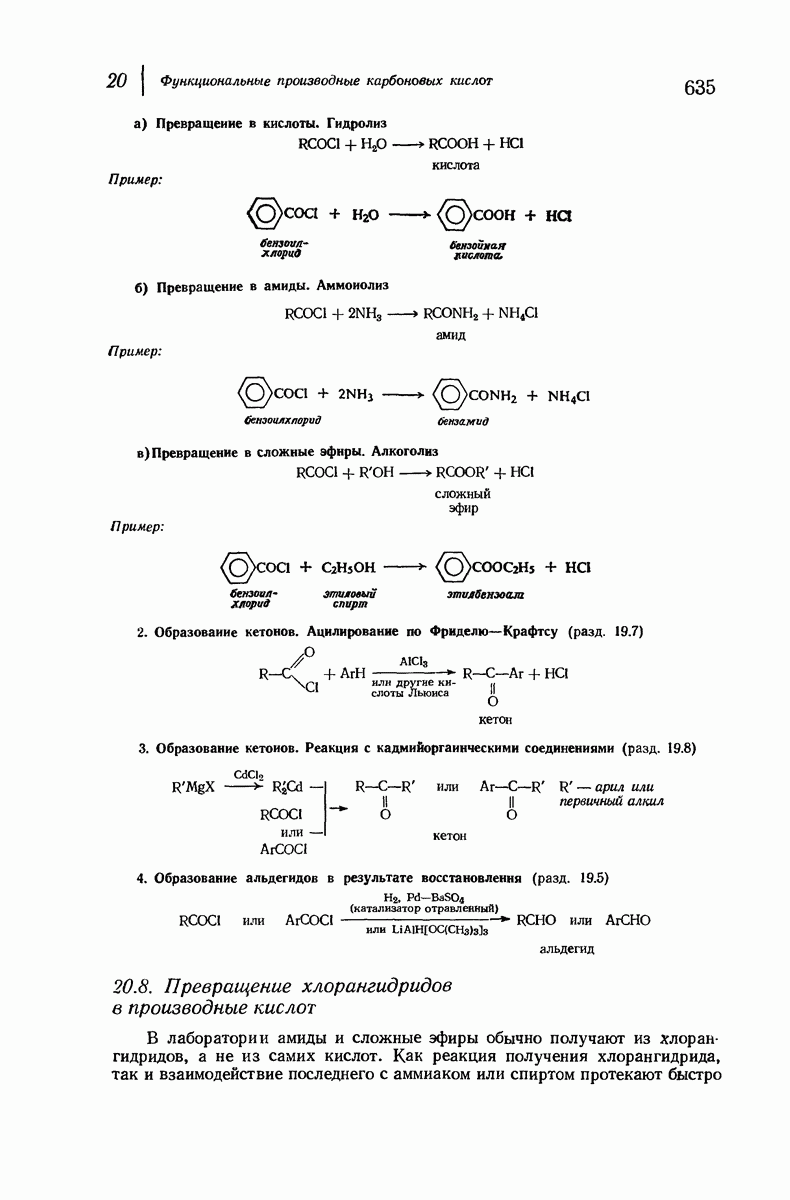
- 20.8. Превращение хлорангидридов в производные кислот
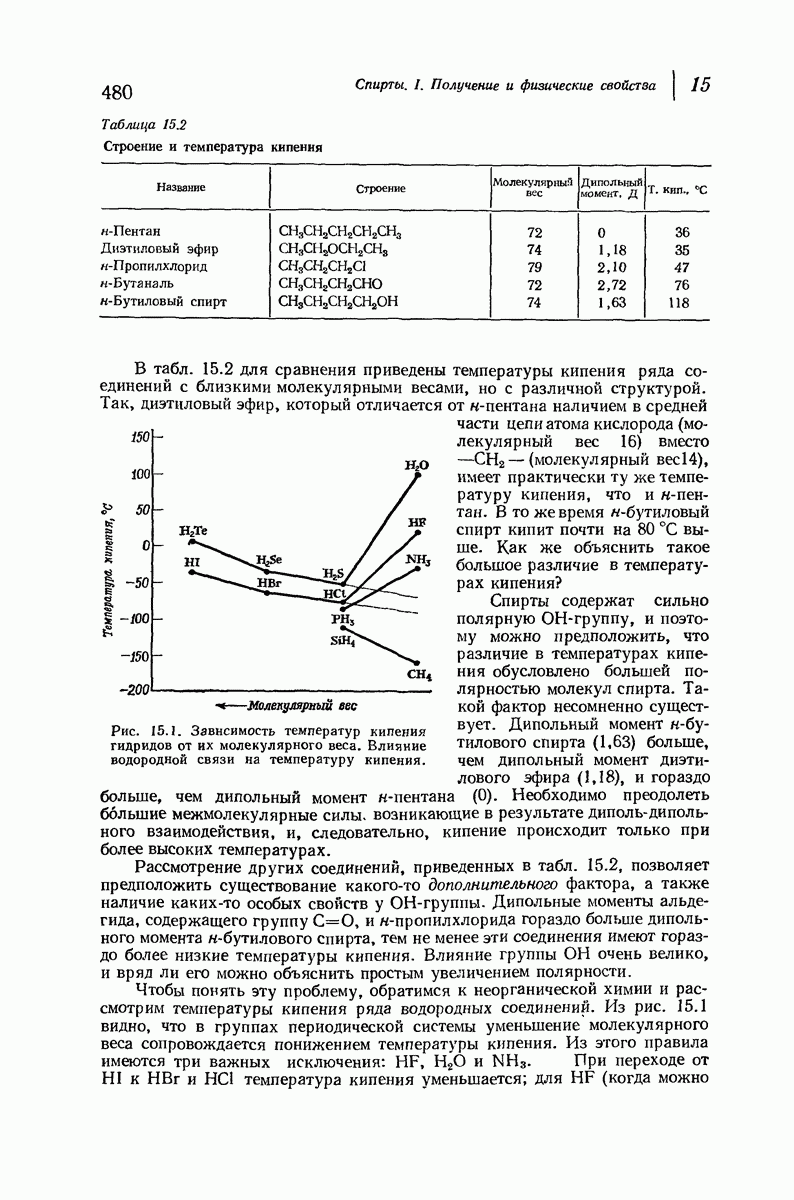
- АНГИДРИДЫ КИСЛОТ
- 20.9. Методы синтеза уксусного ангидрида
- 20.10. Реакции ангидридов кислот
- АМИДЫ
- СЛОЖНЫЕ ЭФИРЫ
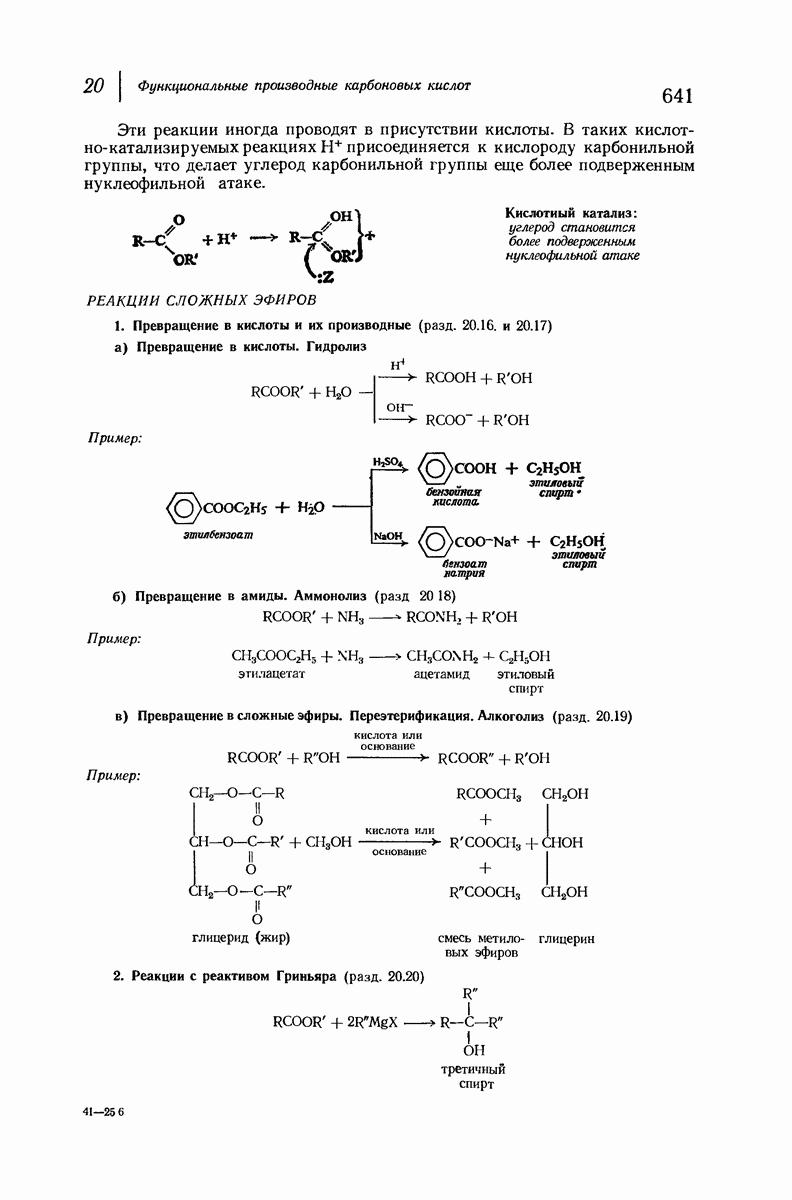
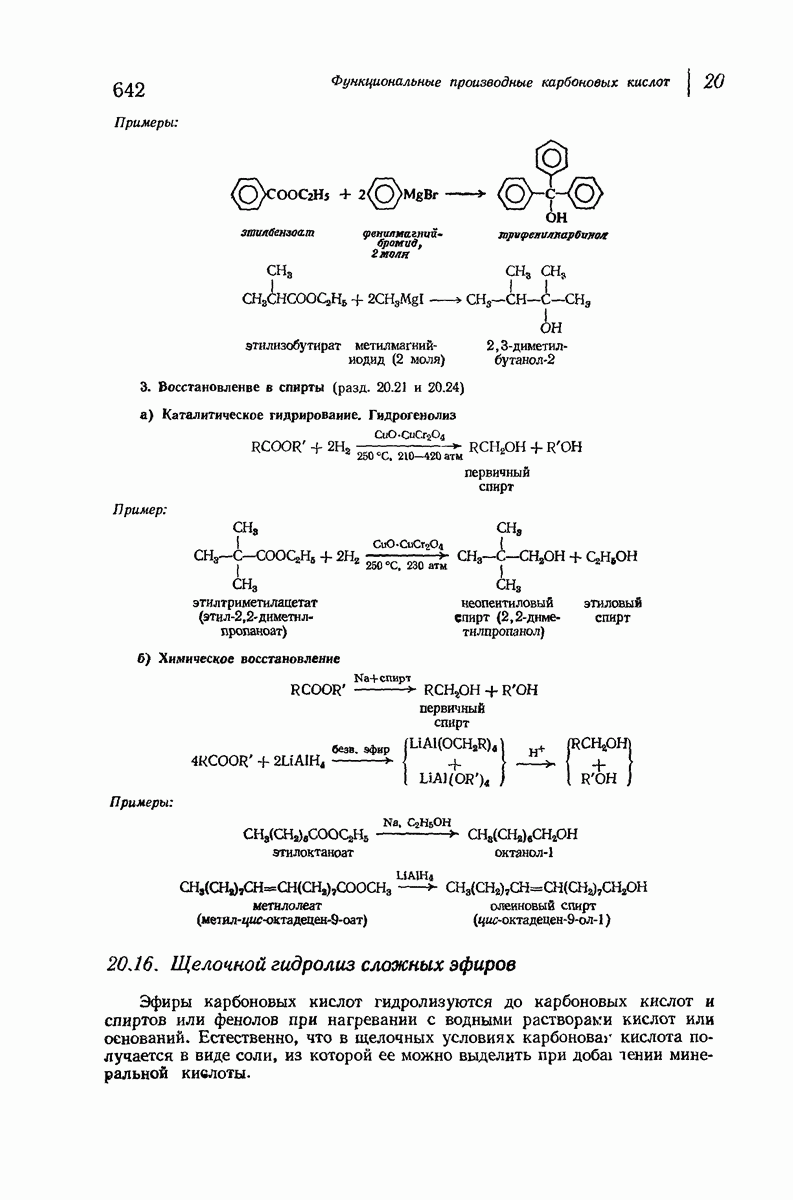
- 20.16. Щелочной гидролиз сложных эфиров
- 20.17. Кислотный гидролиз сложных эфиров
- 20.18. Аммонолиз сложных эфиров
- 20.19. Переэтерификация
- 20.20. Реакции сложных эфиров с реактивом Гриньяра
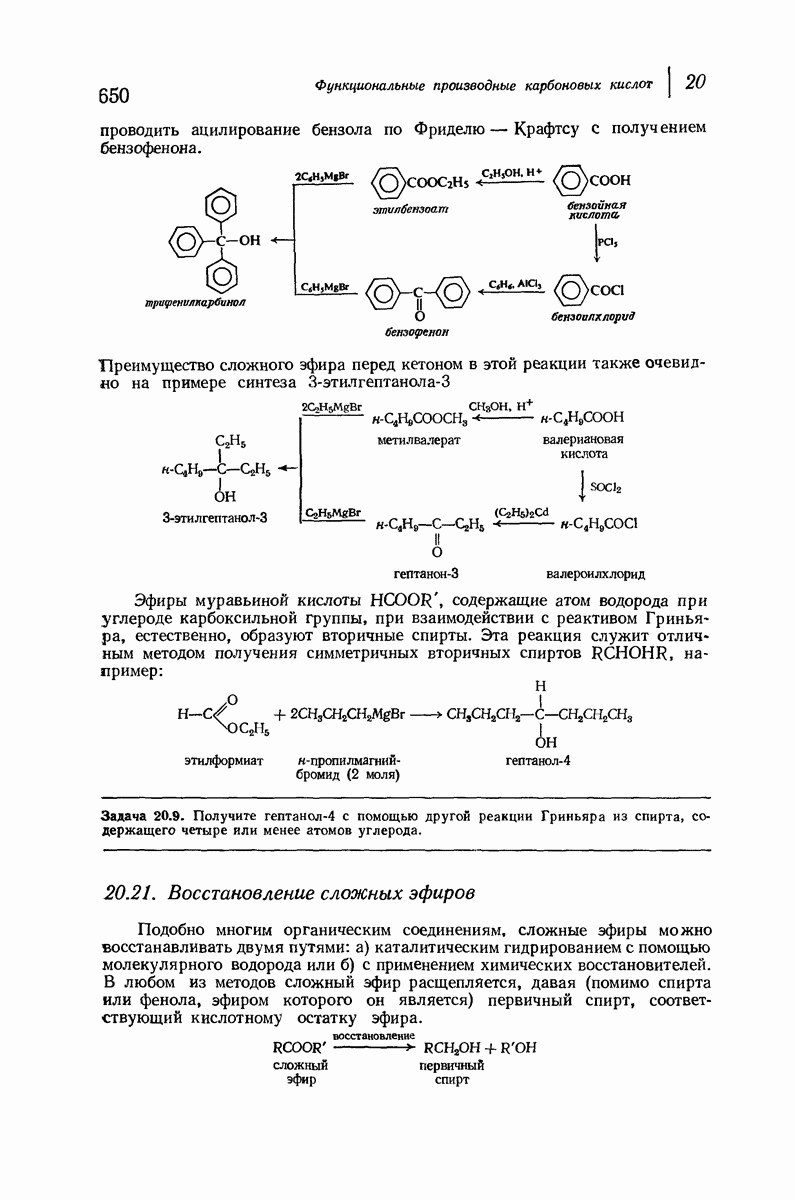
- 20.21. Восстановление сложных эфиров
- ЖИРЫ
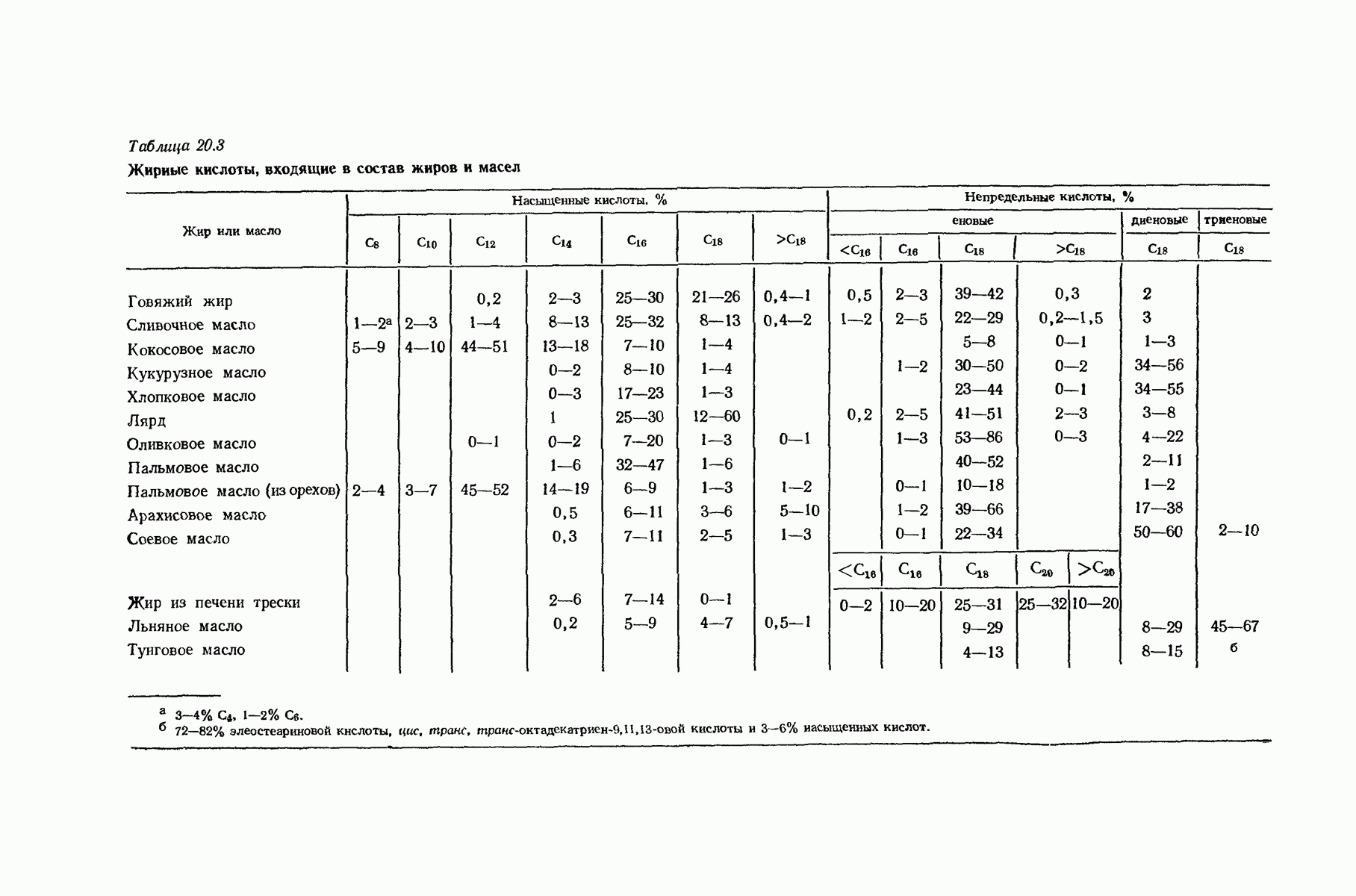
- 20.22. Нахождение жиров в природе и их состав
- 20.23. Гидролиз жиров. Омыление. Мыло
- 20.24. Жиры как источники чистых кислот и спиртов
- 20.25. Детергенты
- 20.26. Непредельные жиры. Отвердение жиров. Высыхающие масла
- 20.27. Анализ производных карбоновых кислот. Эквивалент омыления
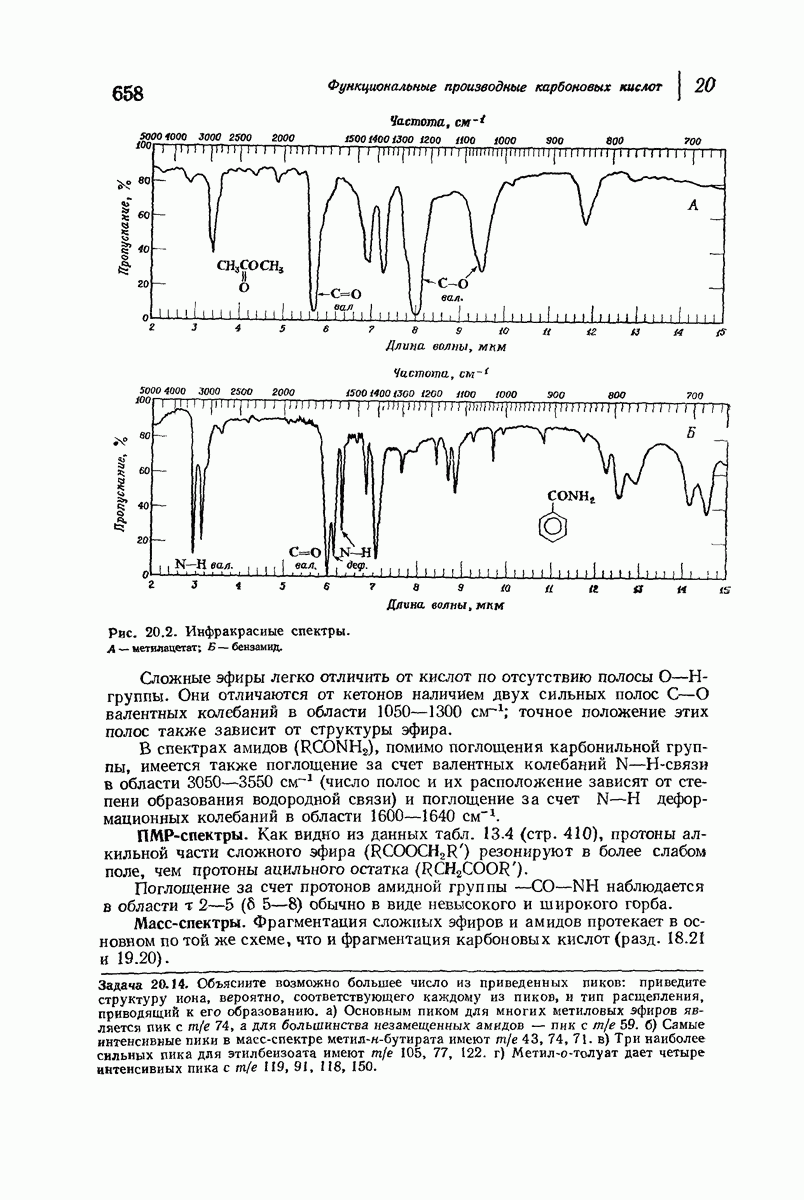
- 20.28. Спектральный анализ производных карбоновых кислот
- 21. Сульфокислоты и их производные
- 21.3. Методы синтеза сульфокислот
- 21.4. Реакции сульфокислот
- 21.5. Десульфирование
- 21.6. Сульфохлориды
- 21.7. Амиды сульфокислот
- 21.8. Эфиры сульфокислот
- 21.9. Стереохимическое обращение
- 21.10. Сравнение производных сульфокислот с производными карбоновых кислот
- 21.11. Анализ сульфокислот
- 21.12. Спектральный анализ сульфокислот
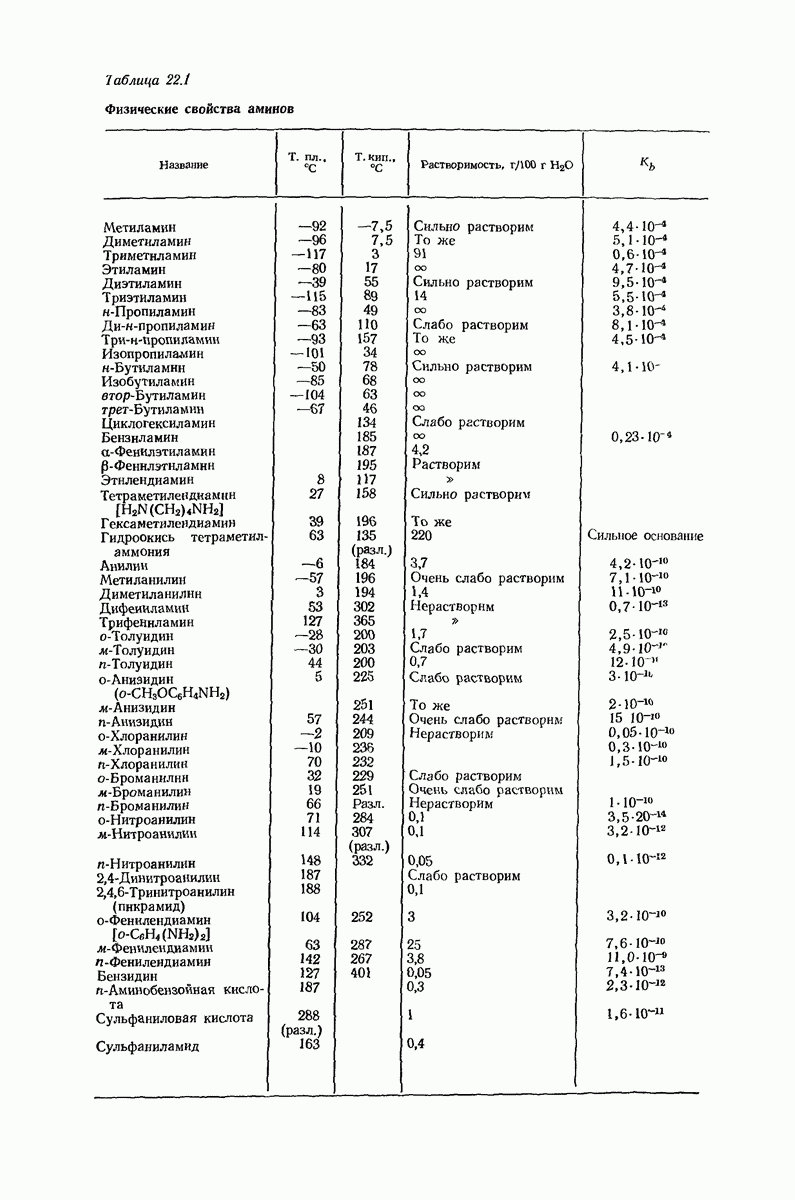
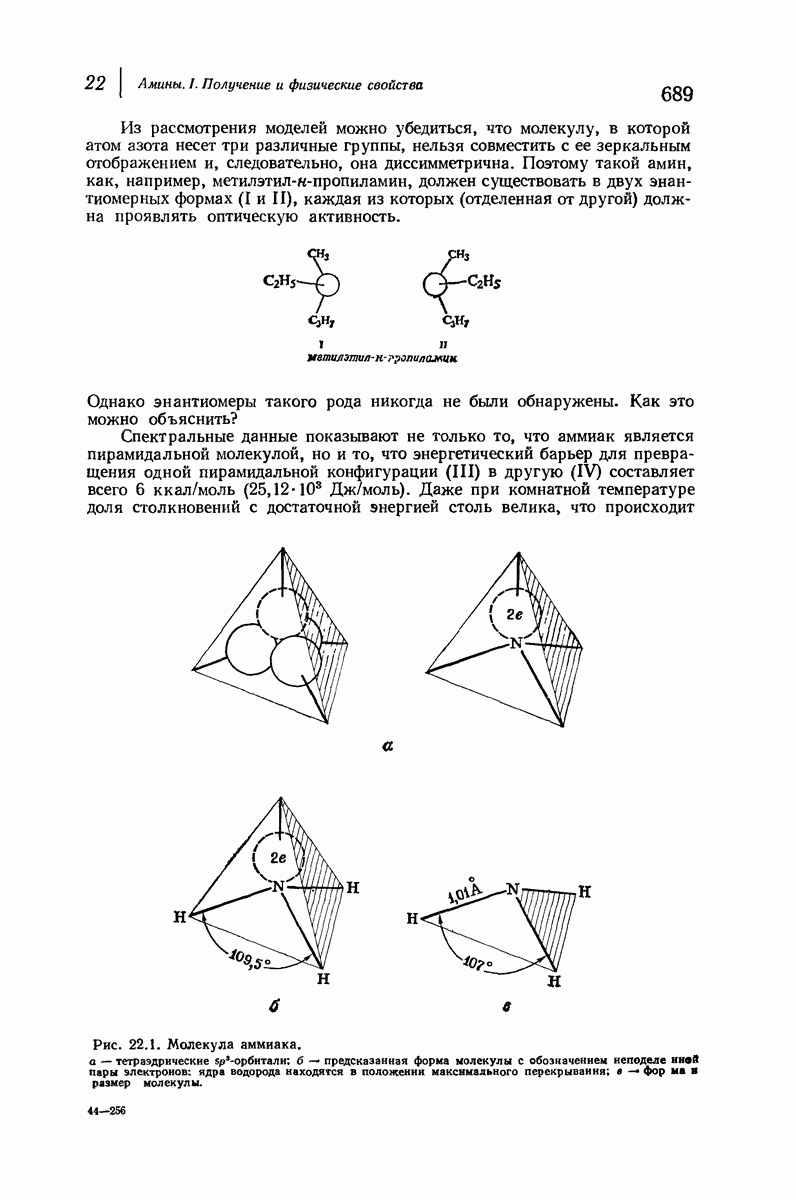
- 22. Амины. I. Получение и физические свойства
- 22.5. Соли аминов
- 22.6. Стереохимия азота
- 22.7. Промышленные источники аминов
- 22.8. Методы синтеза аминов
- 22.9. Восстановление нитросоединений
- 22.10. Аммонолиз галогенпроизводных
- 22.11. Восстановительное аминирование
- 22.12. Методы синтеза вторичных и третичных аминов
- 22.13. Расщепление амидов по Гофману
- 22.14. Стереохимия 1,2-сдвигов. Мигрирующая группа
- 22.15. Миграция арилъных групп
- 23. Амины. II. Реакции
- 23.2. Основность аминов. Константа основности
- 23.3. Структура и основность
- 23.4. Влияние заместителей на основность ароматических аминов
- 23.5. Соли четвертичного аммония. Исчерпывающее метилирование. Элиминирование по Гофману
- 23.6. Превращение аминов в замещенные амиды
- 23.7. Замещение в кольцо ароматических аминов
- 23.8. Галогенирование ароматических аминов
- 23.10. Сульфирование ароматических аминов. Диполярные ионы
- 23.11. Сульфамиды. Сульфамидные препараты
- 23.12. Реакция аминов с азотистой кислотой
- 23.13. Анализ аминов. Проба Хинсберга
- 23.14. Анализ замещенных амидов
- 23.15. Спектральный анализ аминов и замещенных амидов
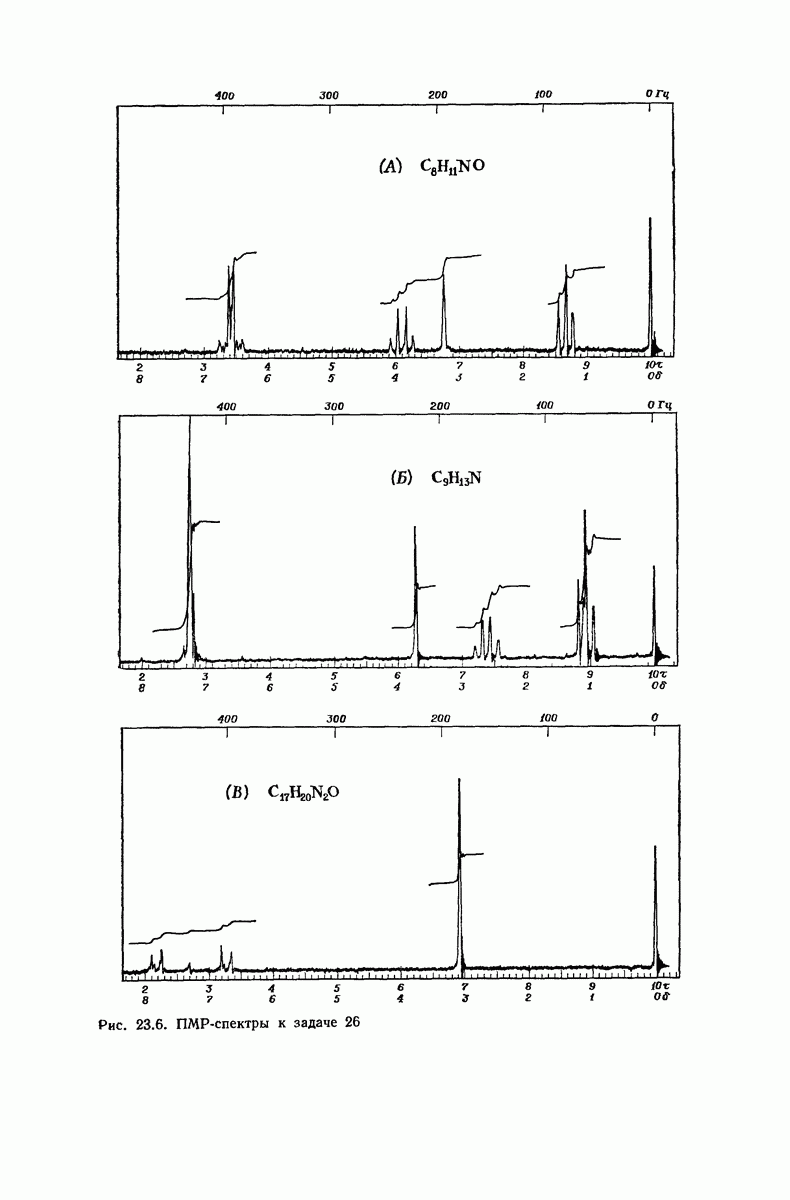
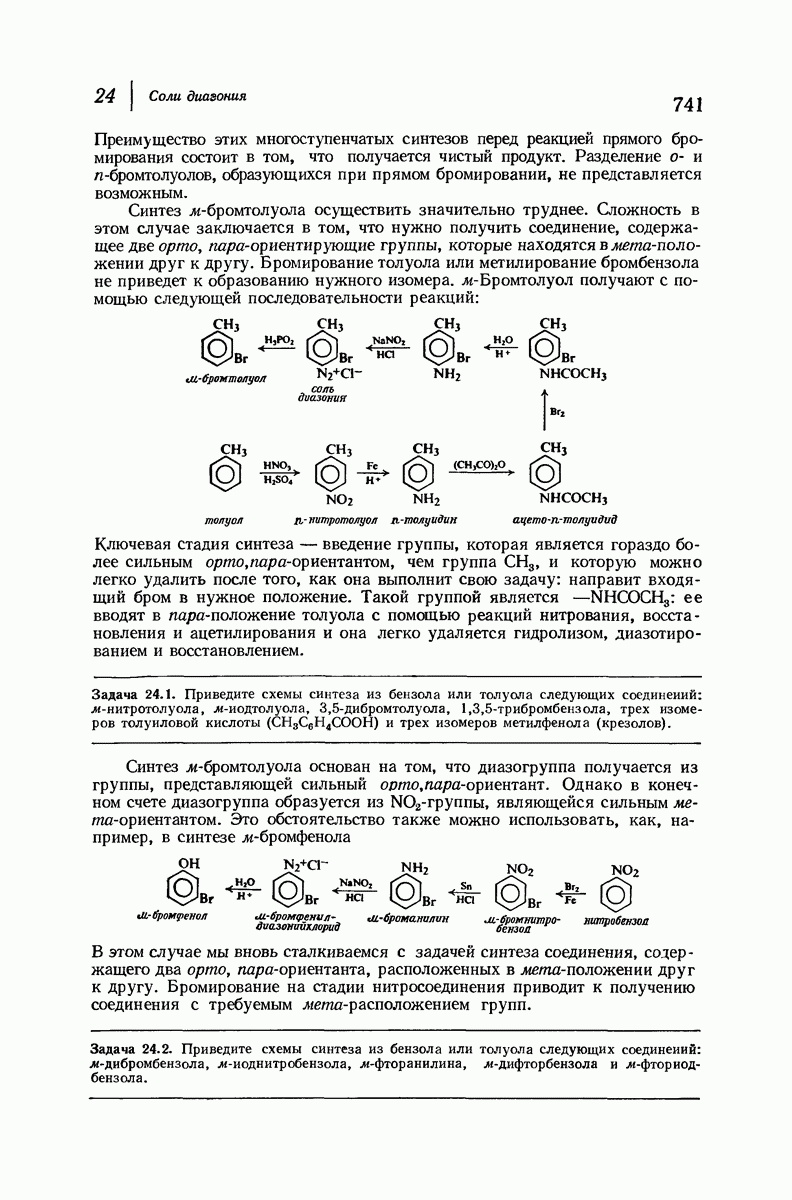
- 24. Соли диазония
- 24.5. Замещение на галоген. Реакция Зандмейера
- 24.6. Замещение на CN. Синтез карбоновых кислот
- 24.7. Замещение на OH. Синтез фенолов
- 24.8. Замещение на Н
- 24.9. Синтезы с использованием солей диазония
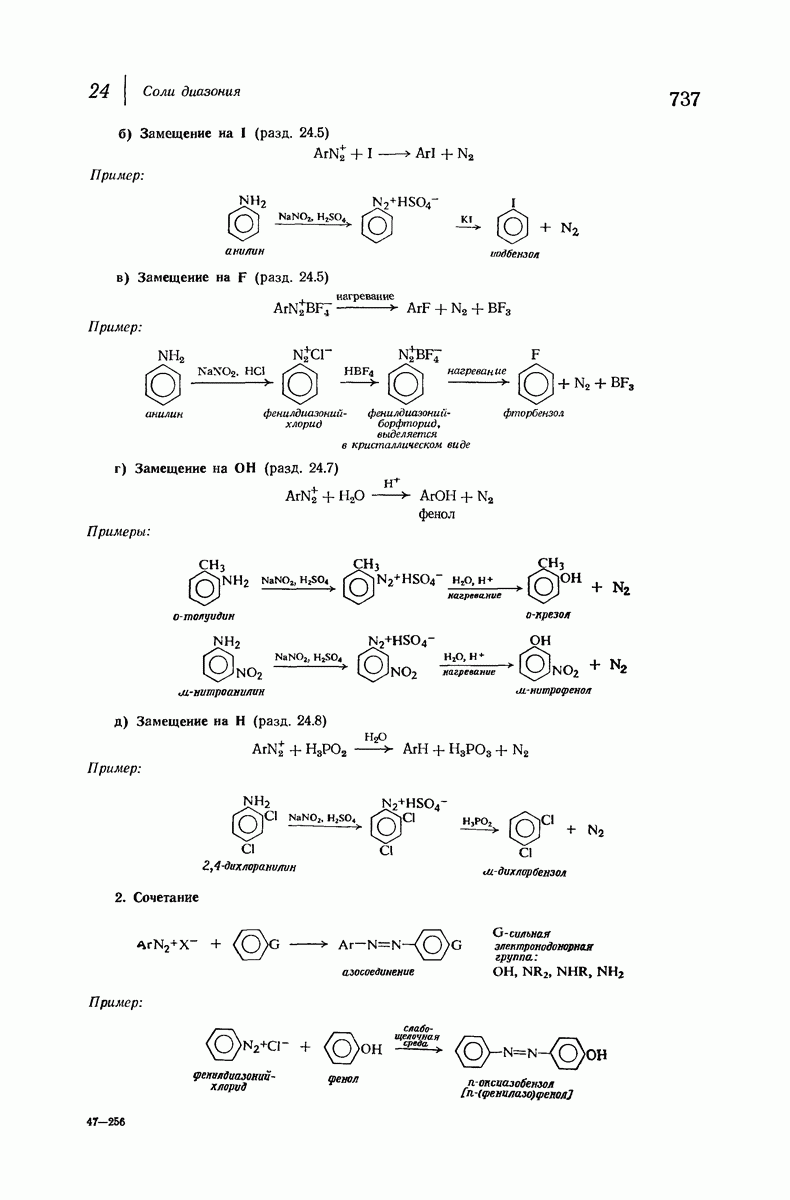
- 24.10. Реакция сочетания. Синтез азосоединений
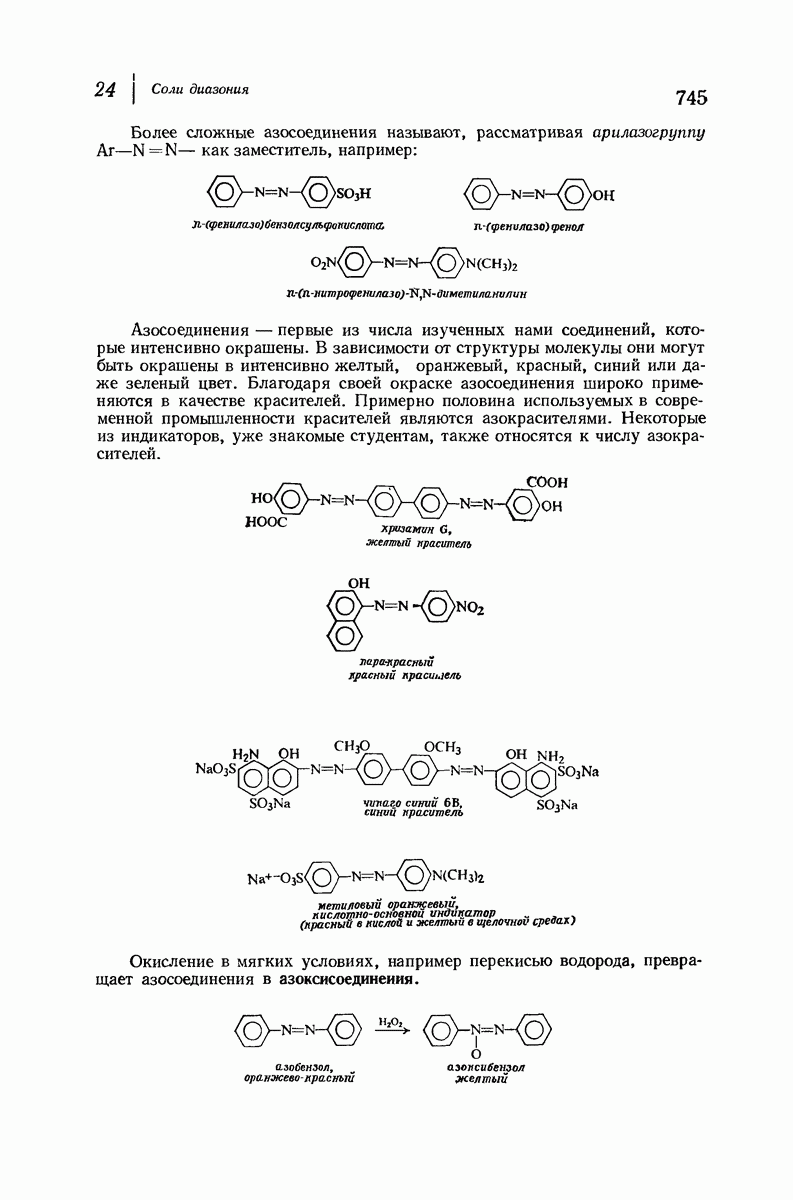
- 24.11. Азосоединения
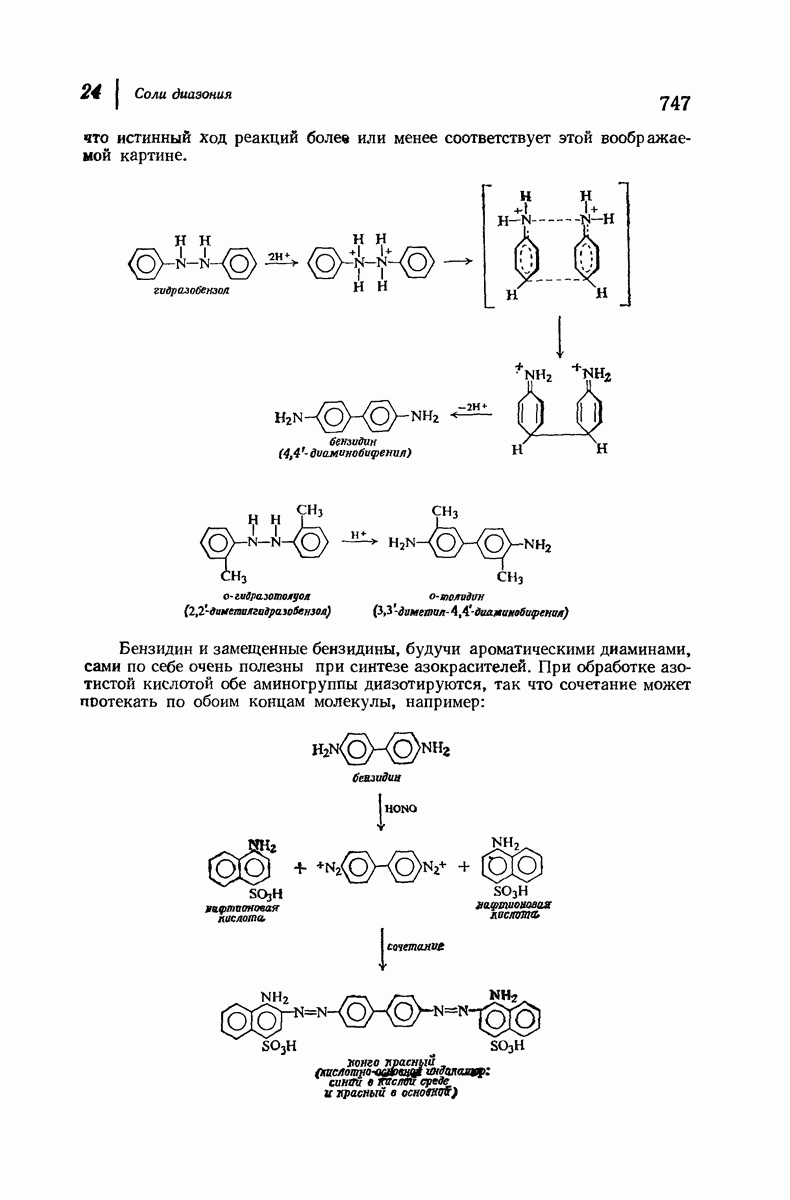
- 24.12. Гидразосоединения. Бензидиновая перегруппировка
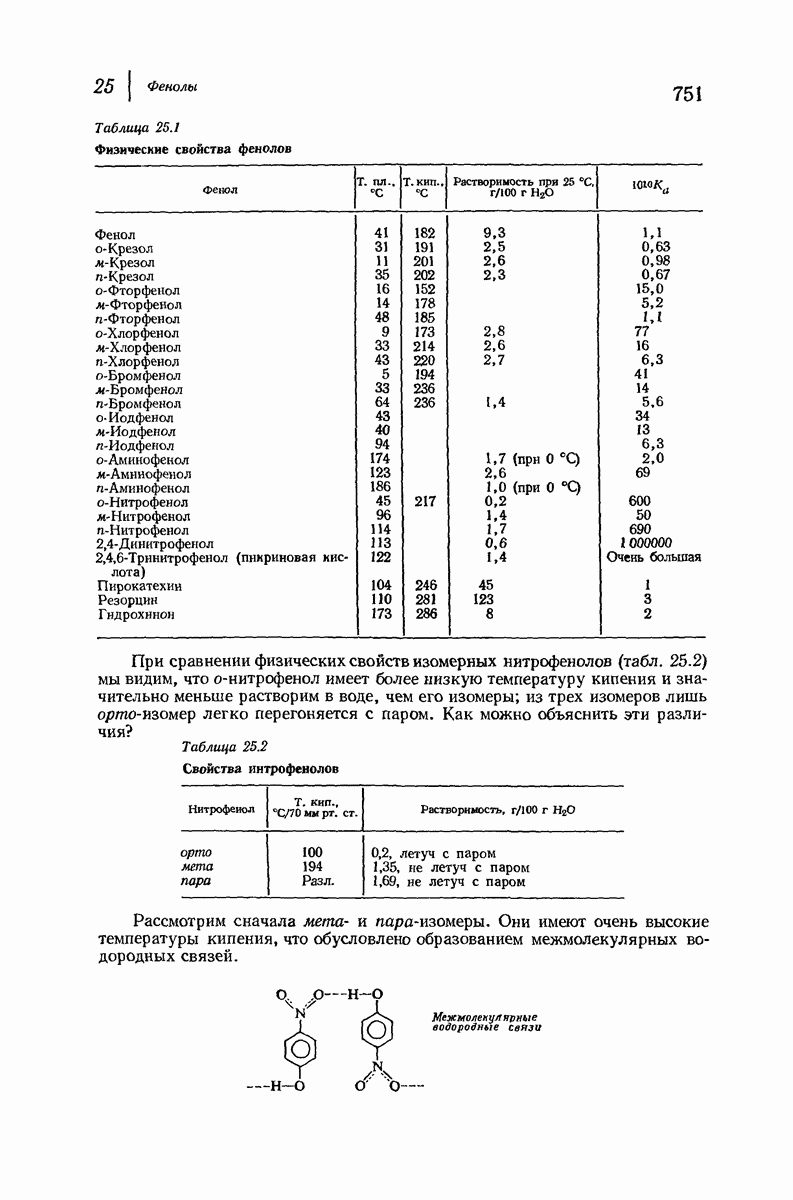
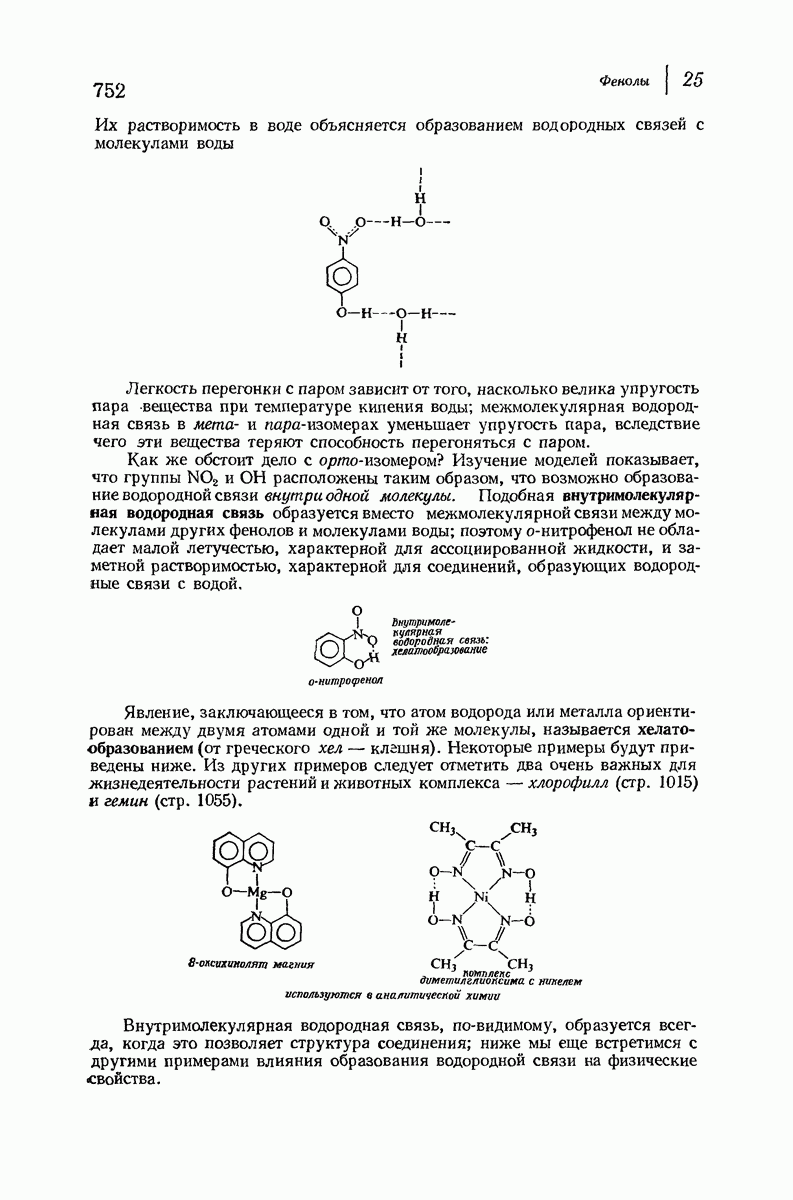
- 25. Фенолы
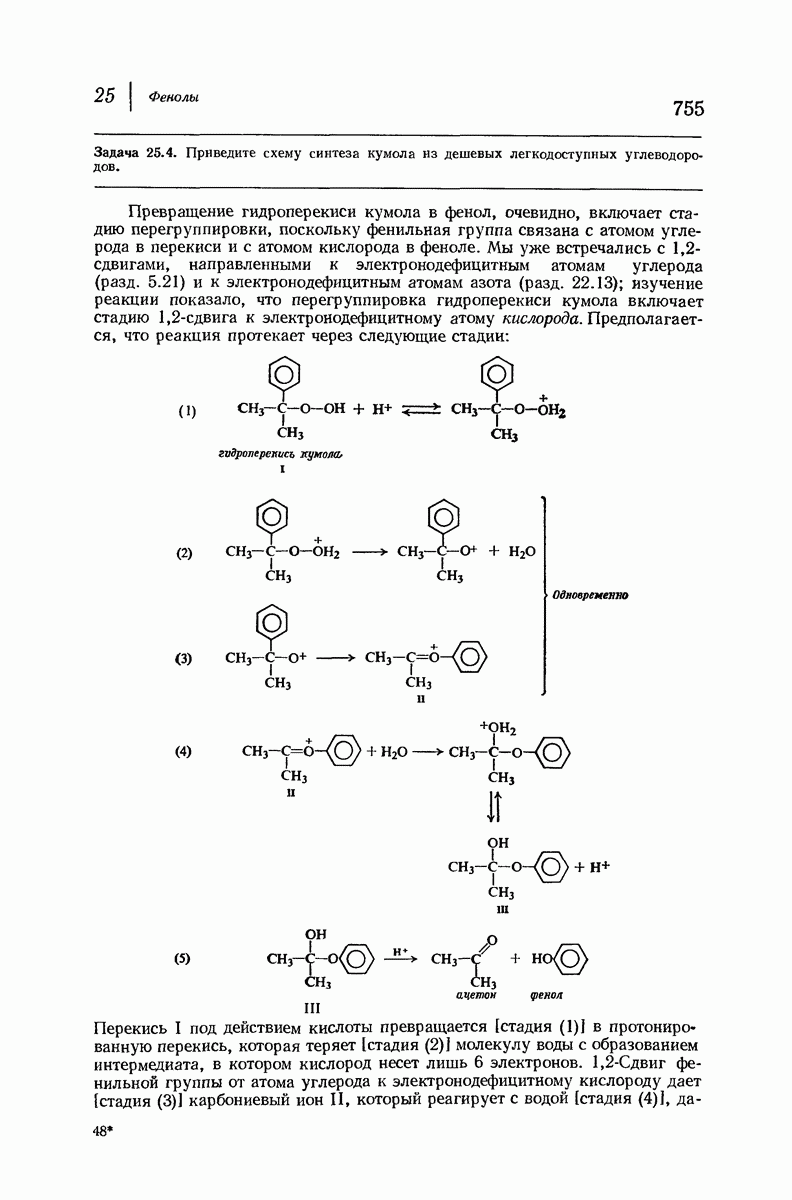
- 25.5. Фенол из гидроперекиси кумола. Миграция к электронодефицитному атому кислорода
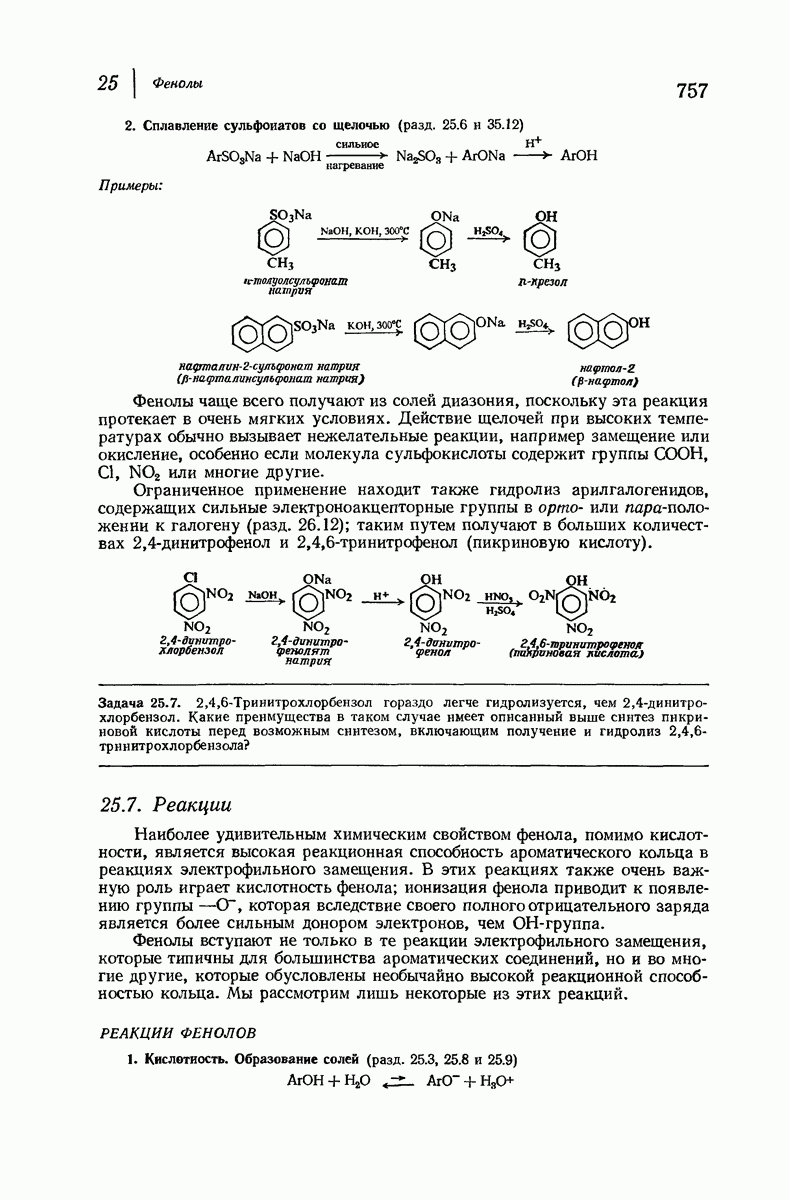
- 25.6. Методы синтеза фенолов
- 25.7. Реакции фенолов
- 25.8. Кислотность фенолов
- 25.9. Влияние заместителей на кислотность
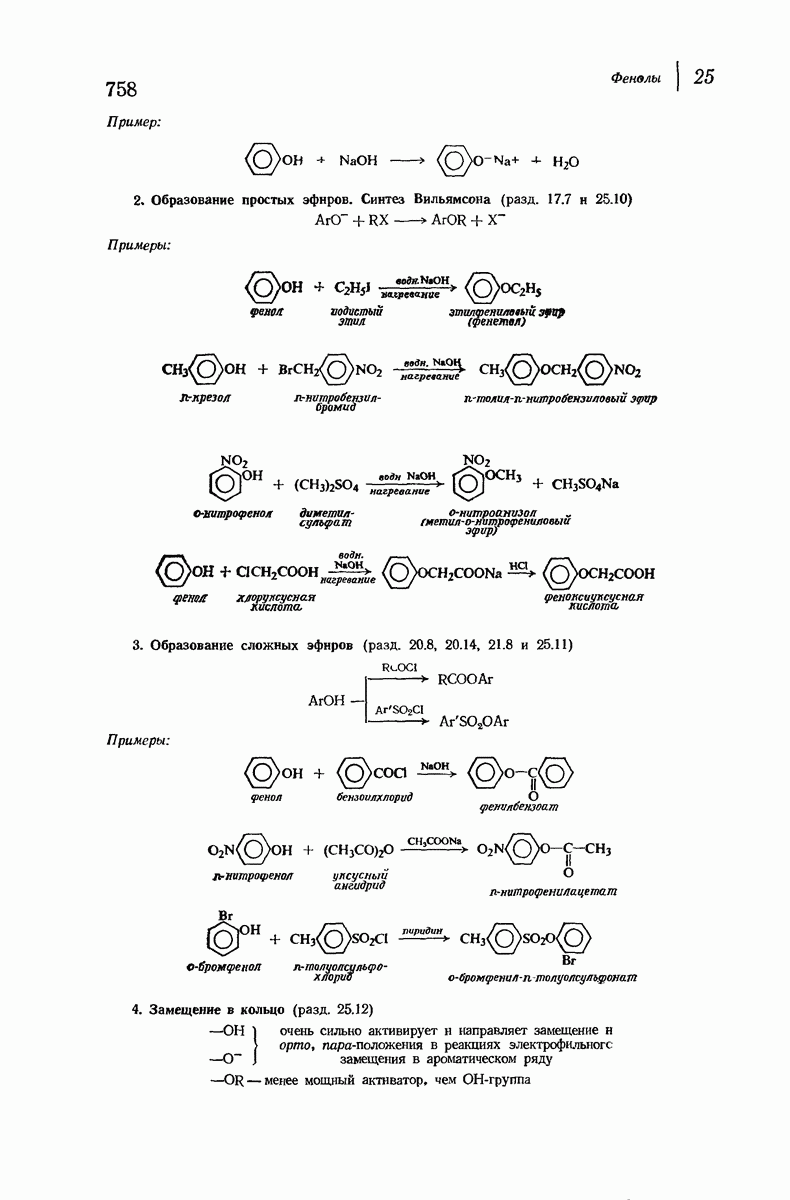
- 25.10. Образование простых эфиров. Синтез Вильямсона
- 25.11. Образование сложных эфиров. Перегруппировка Фриса
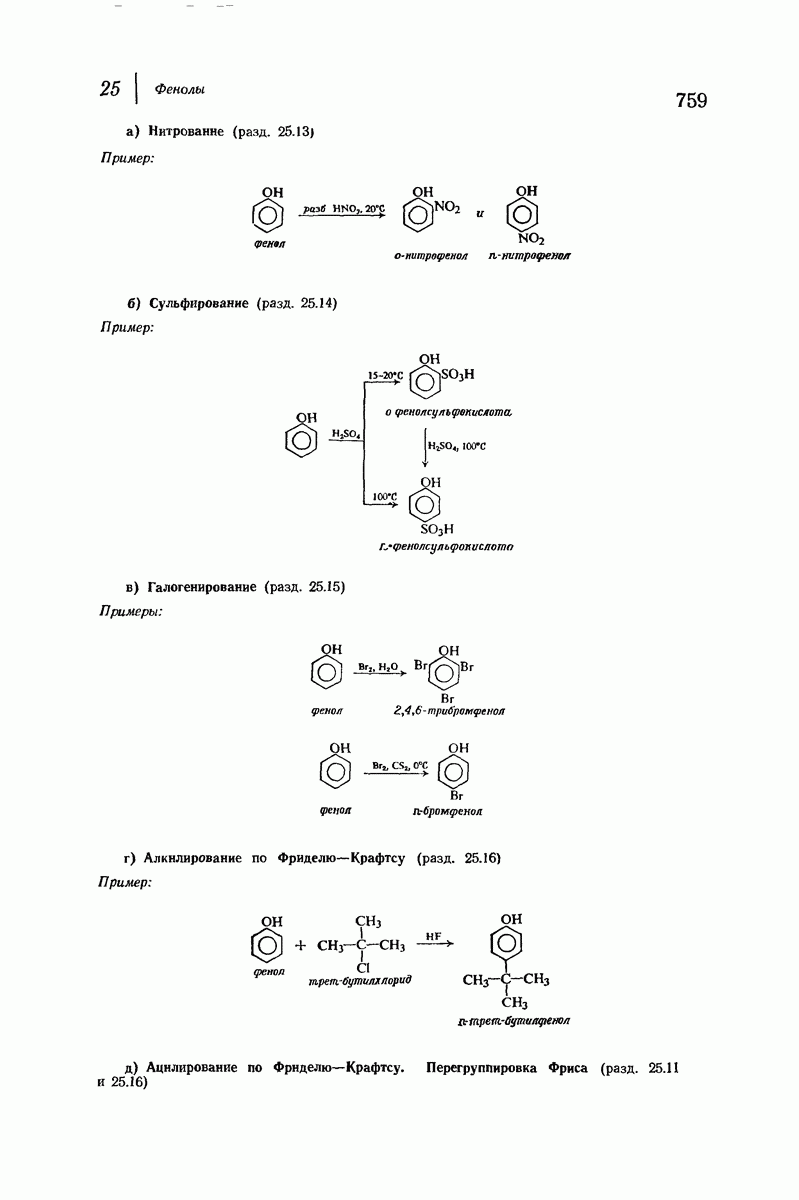
- 25.12. Замещение в кольцо
- 25.13. Нитрование фенолов
- 25.14. Сульфирование фенолов
- 25.15. Галогенирование фенолов
- 25.16. Алкилирование и ацилирование по Фриделю — Крафтсу
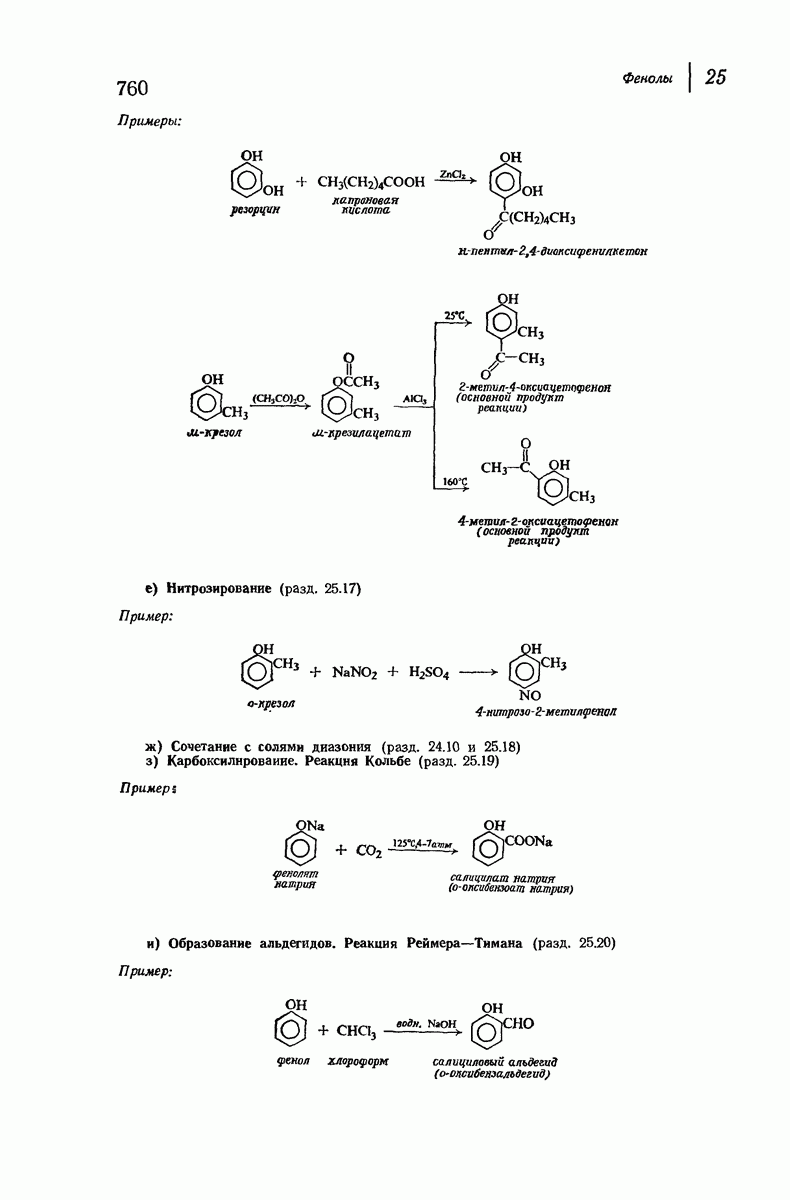
- 25.17. Нитрозирование
- 25.18. Сочетание с солями диазония
- 25.19. Реакция Кольбе. Синтез фенолкарбоновых кислот
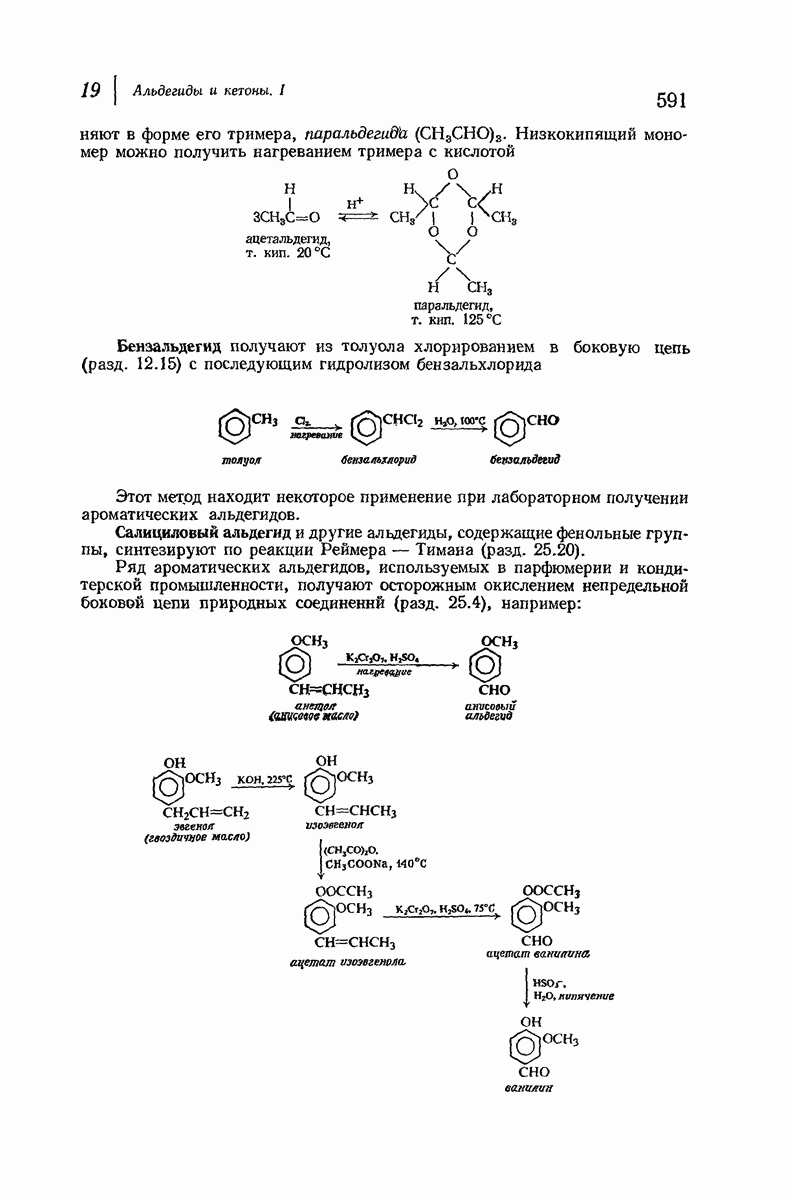
- 25.20. Реакция Реймера — Тимана. Синтез ароматических альдегидов, содержащих ОН-группу. Дихлорметилен
- 25.21. Реакция с формальдегидом. Фенолформальдегидные смолы
- 25.22. Анализ фенолов
- 25.23. Спектральный анализ фенолов
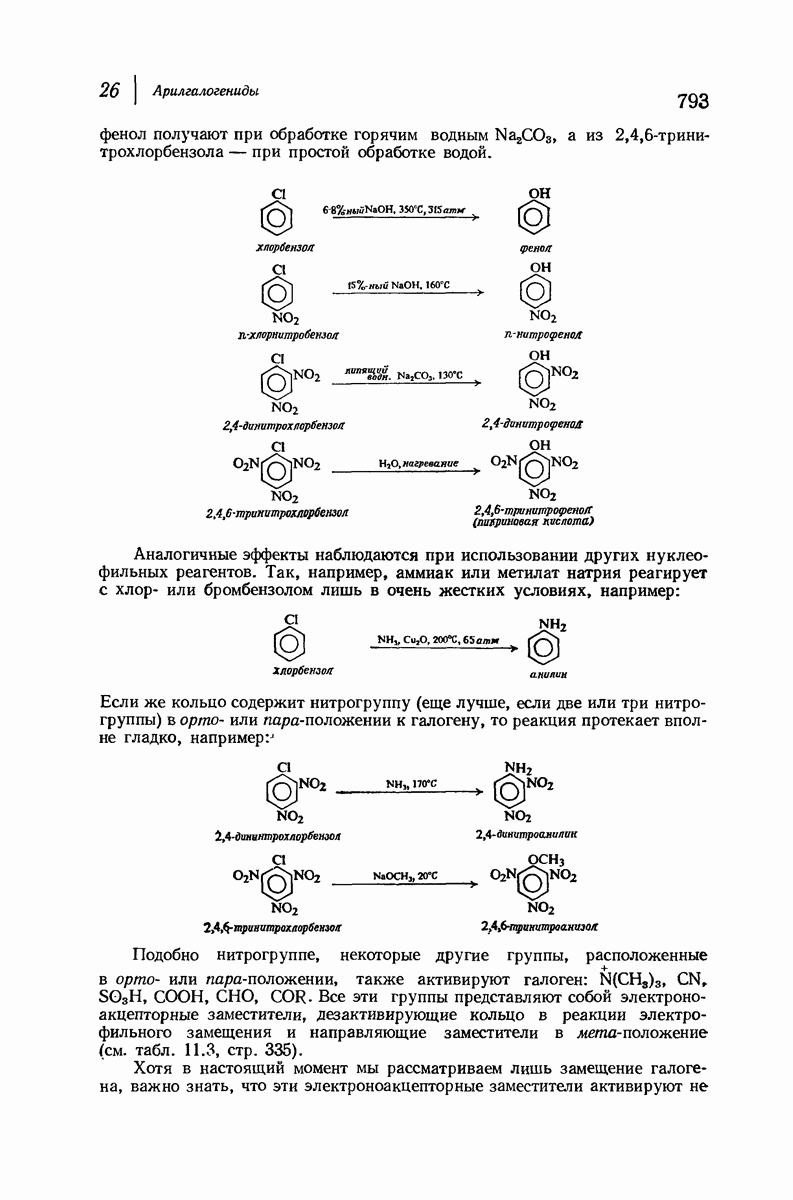
- 26. Арилгалогениды. НУКЛЕОФИЛЬНОЕ ЗАМЕЩЕНИЕ В АРОМАТИЧЕСКОМ РЯДУ
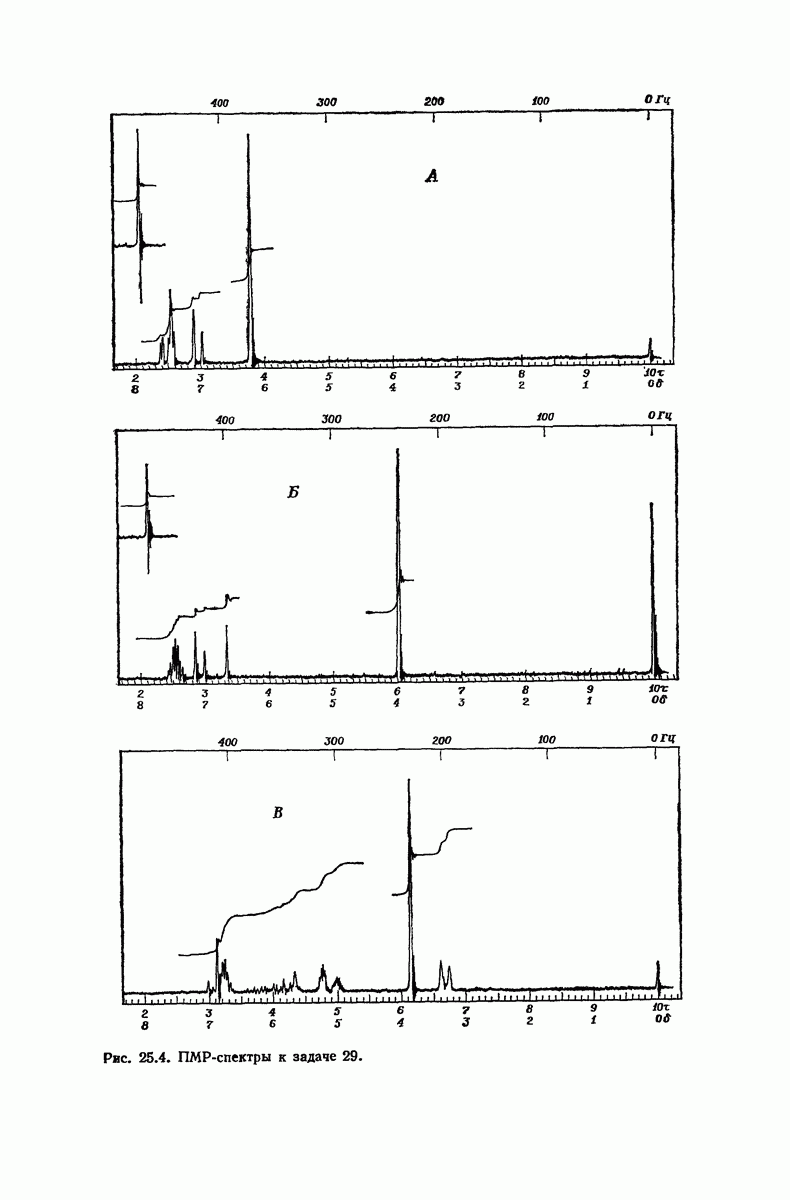
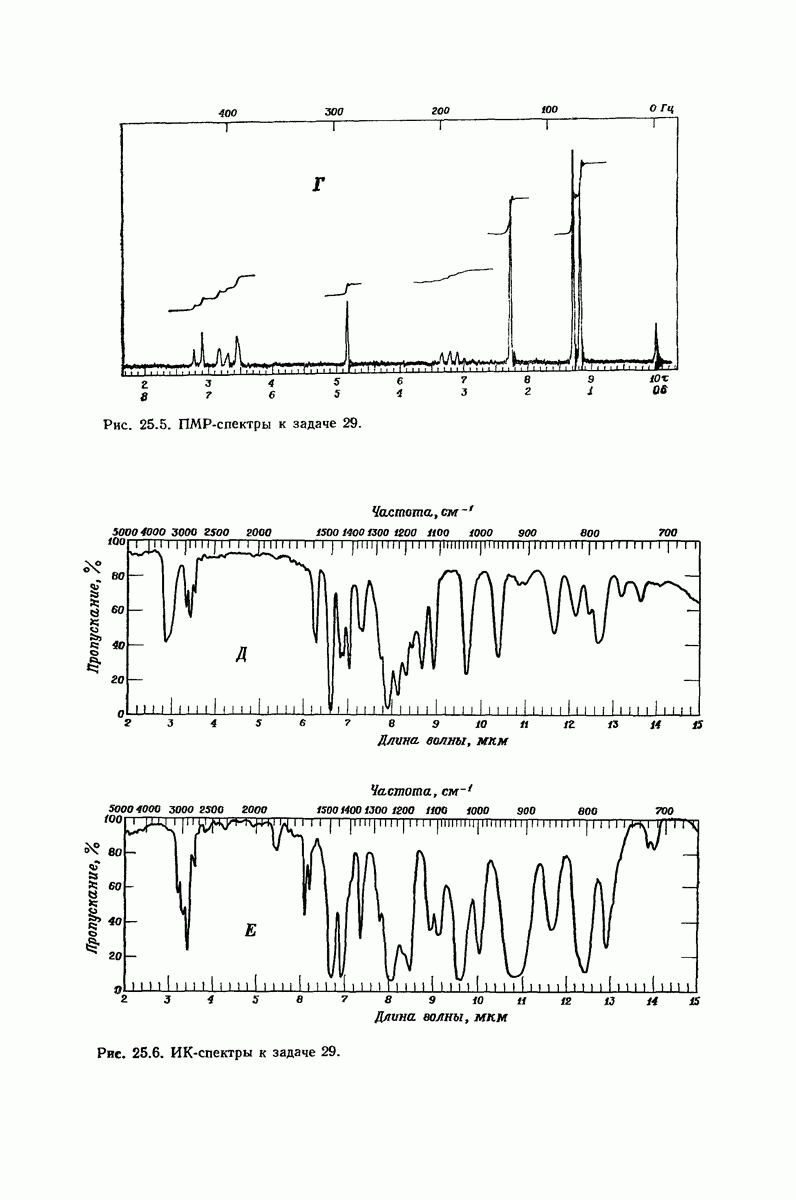
- 26.7. Низкая реакционная способность арил- и винилгалогенидов
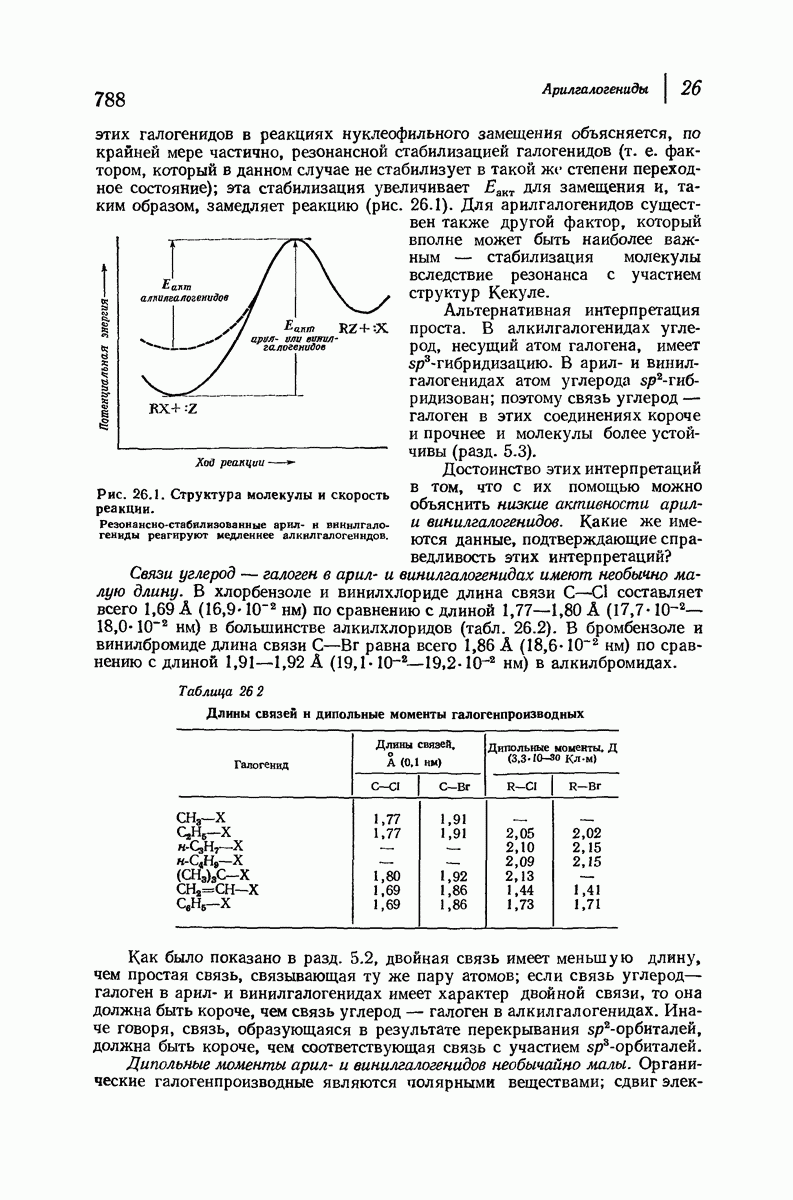
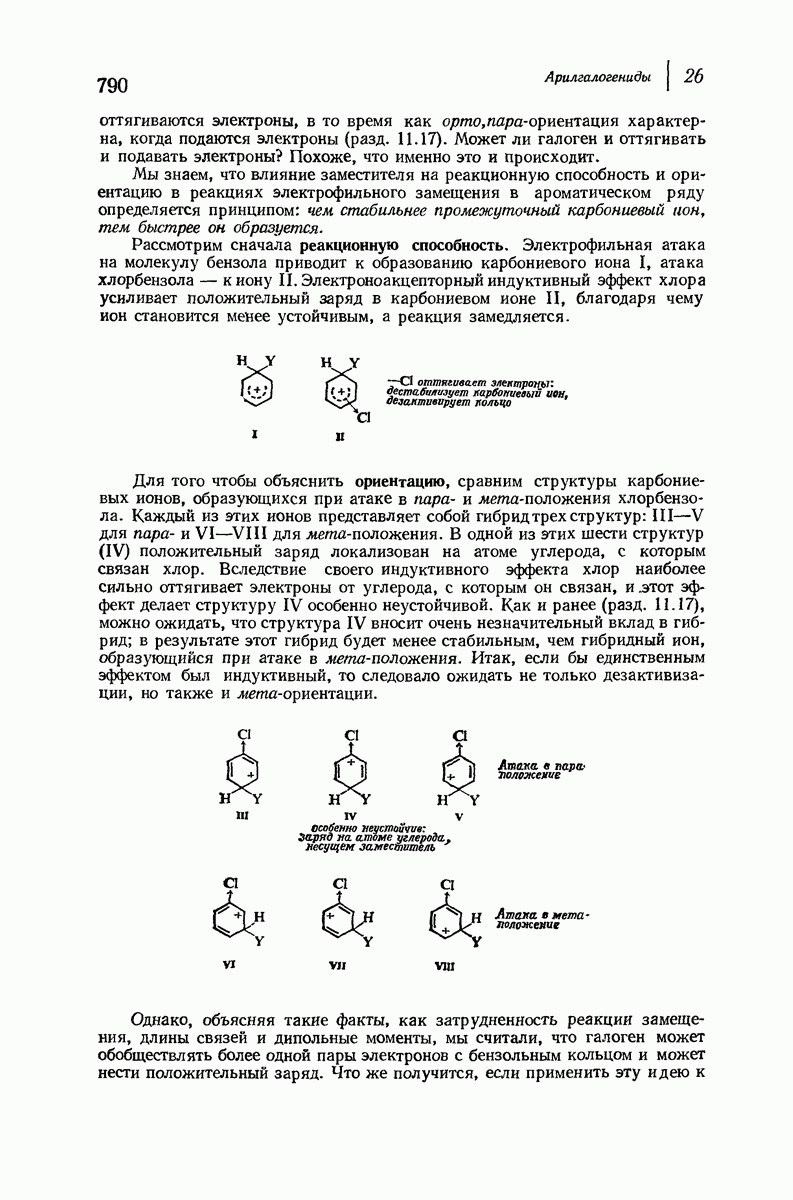
- 26.8. Структура арил- и винилгалогенидов
- 26.9. Влияние галогена на реакцию электрофильного замещения в ароматическом ряду
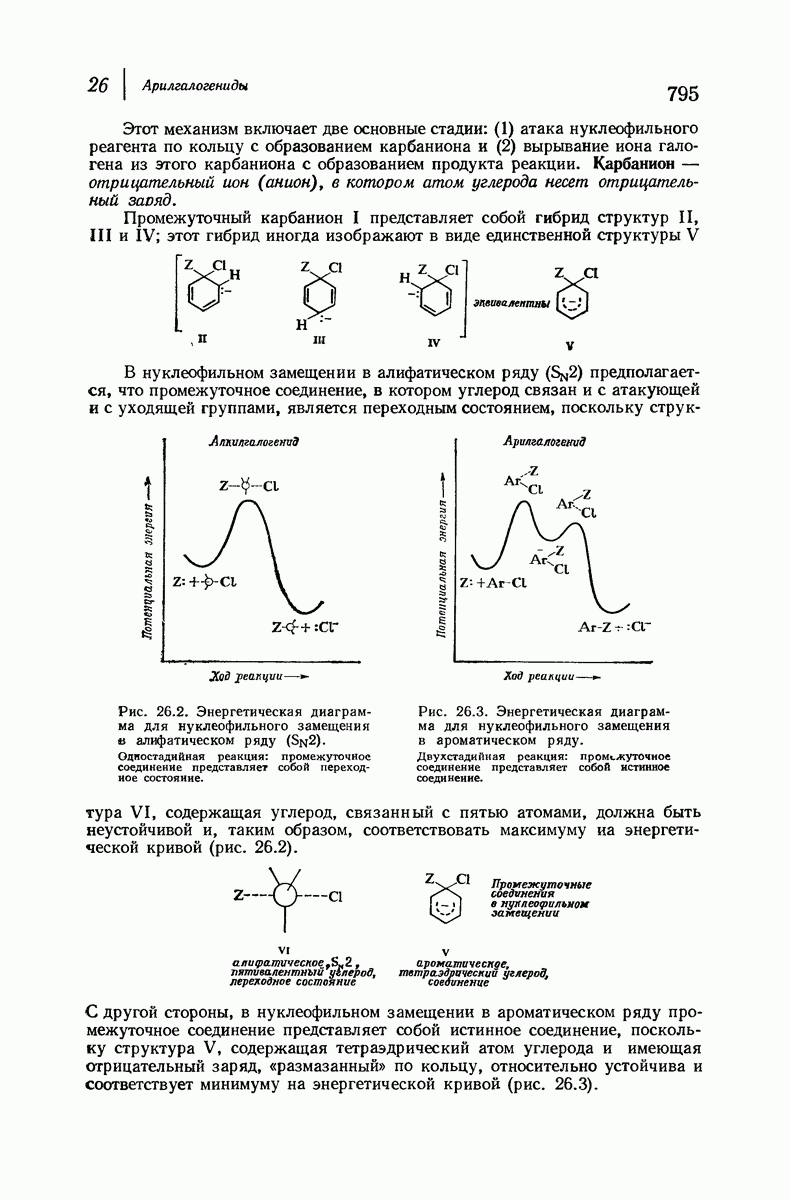
- 26.10. Нуклеофильное замещение в ароматическом ряду: бимолекулярный механизм
- 26.11. Бимолекулярный механизм нуклеофильного замещения, в ароматическом ряду
- 26.12. Реакционная способность при нуклеофильпом замещении в ароматическом ряду
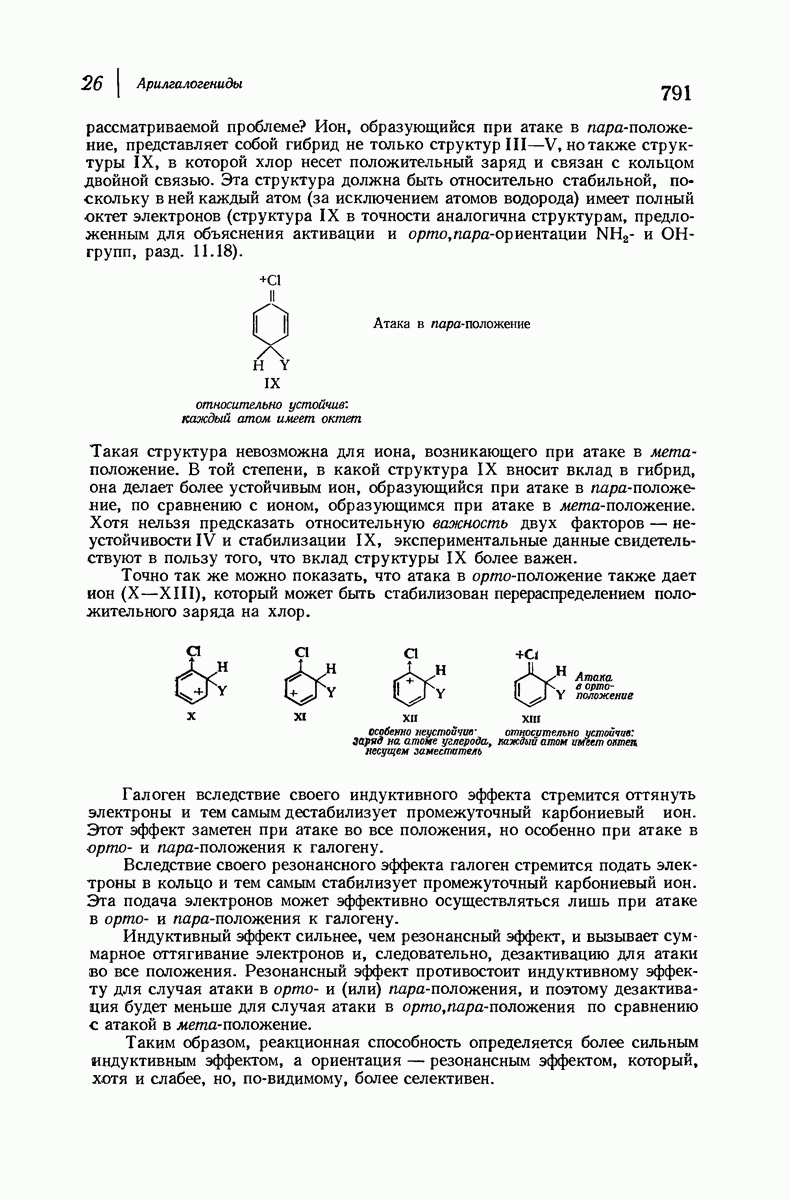
- 26.13. Ориентация при нуклеофильном замещении в ароматическом ряду
- 26.14. Оттягивание электронов за счет резонансного эффекта
- 26.15. Данные в пользу наличия двух стадий в бимолекулярном замещении
- 26.16. Нуклеофильное замещение в алифатическом и ароматическом рядах
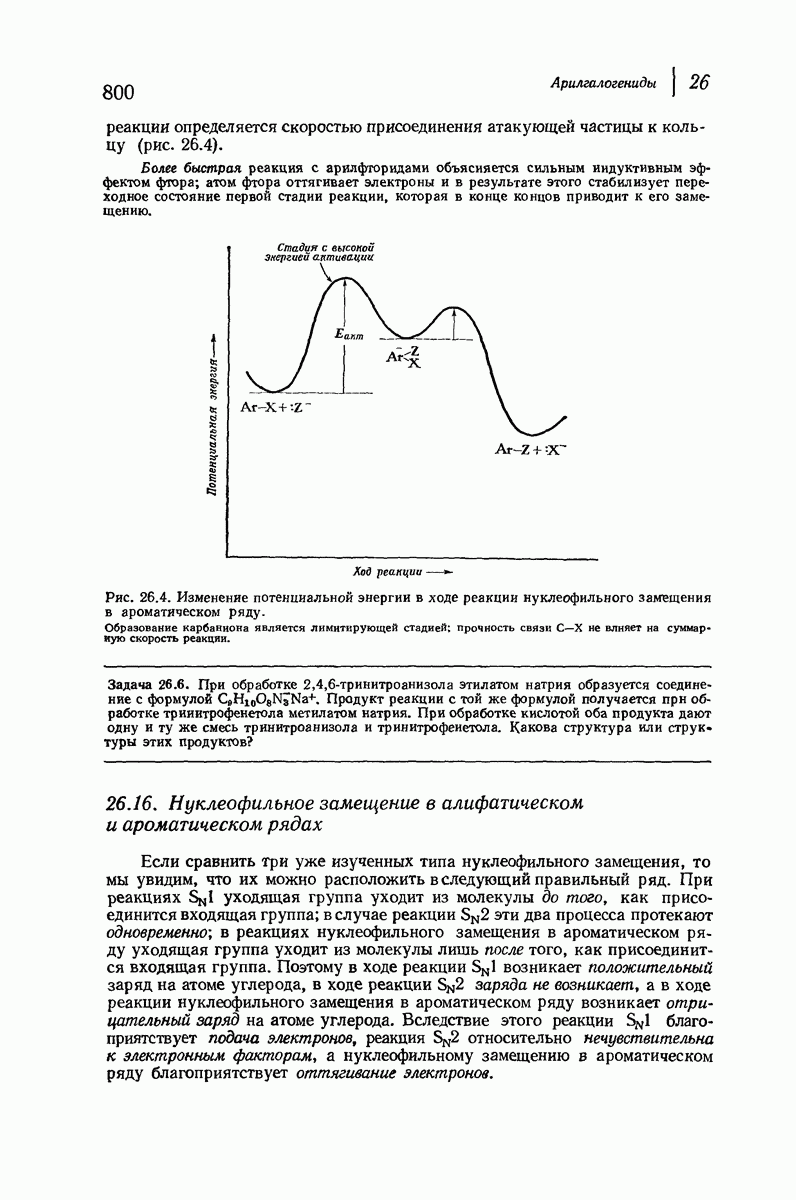
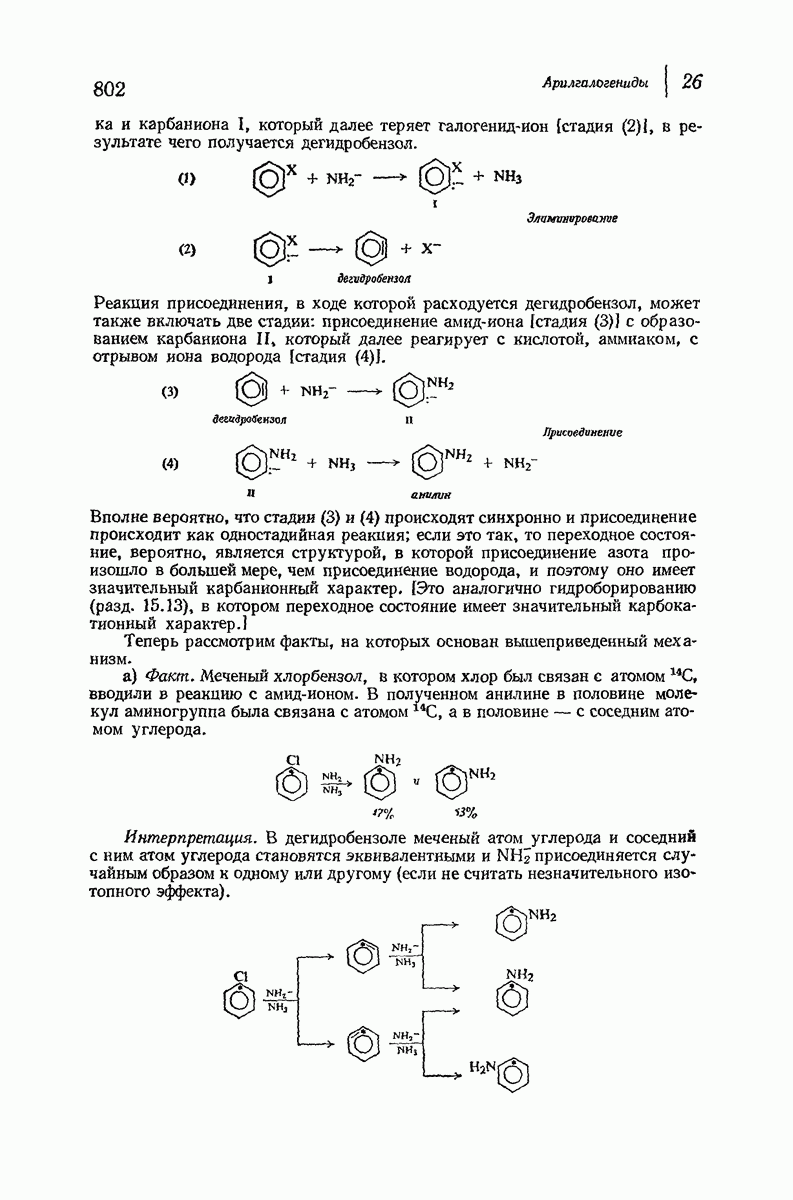
- 26.17. Механизм элиминирования — присоединения при нуклеофильном замещении в ароматическом ряду. Дегидробензол
- 26.18. Анализ арилгалогенидов
- 27. Альдегиды и кетоны. II. Карбанионы
- 27.2. Реакции с участием карбанионов
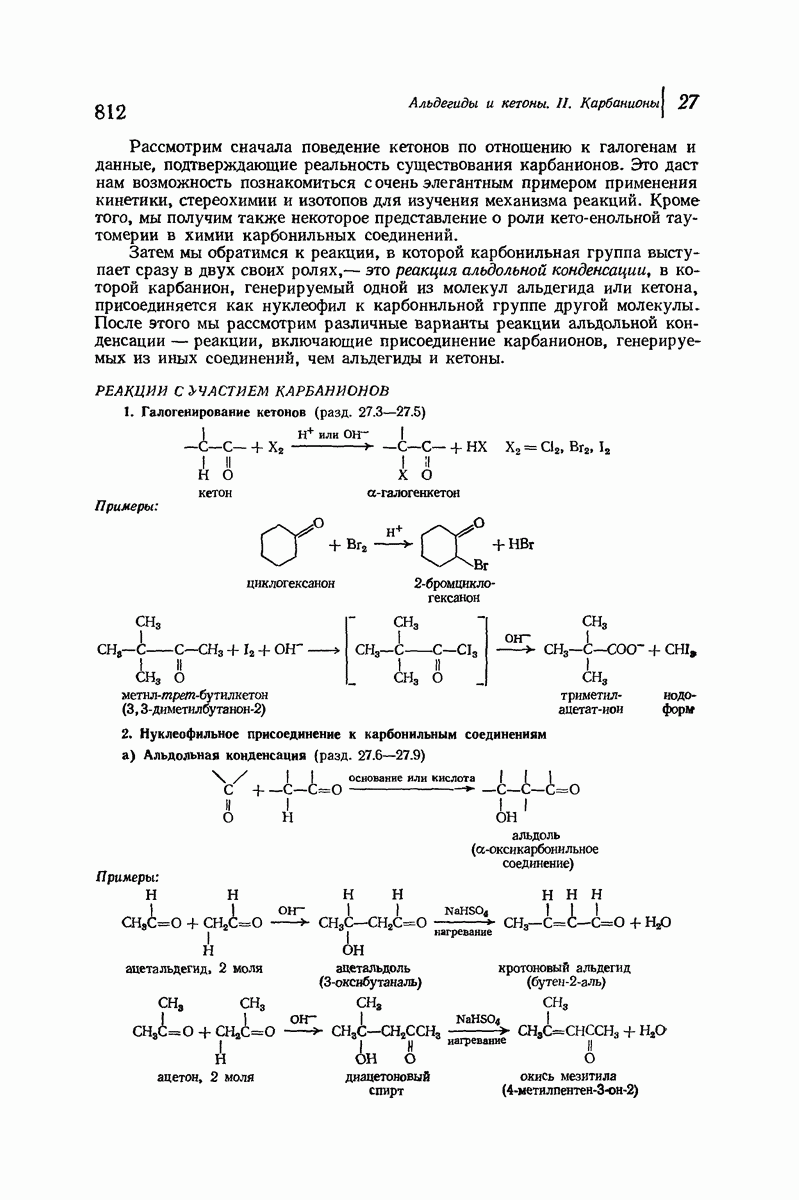
- 27.3. Галогенирование кетонов, промотируемое основаниями
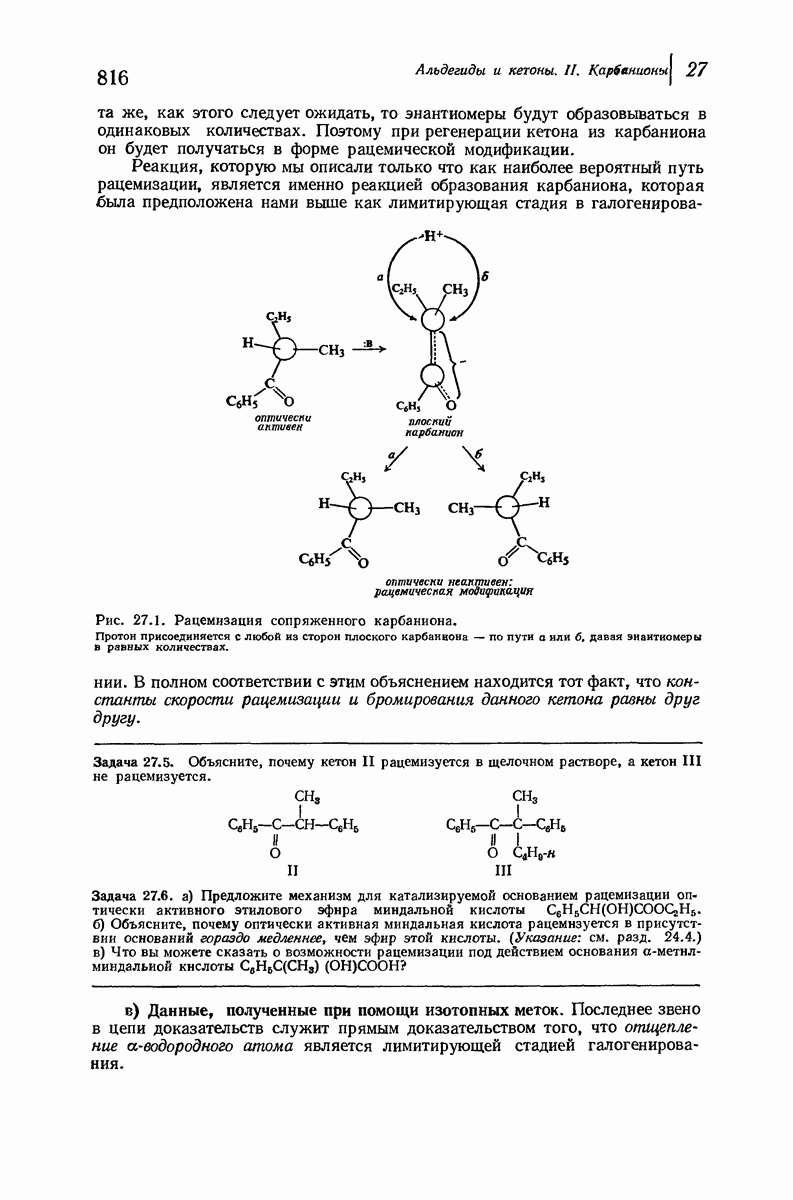
- 27.4. Стереохимия карбанионов
- 27.5. Галогенирование кетонов, катализируемое кислотами. Енолизация
- 27.6. Альдольная конденсация. Присоединение альдегидов и кетонов
- 27.7. Дегидратация продуктов альдольной конденсации
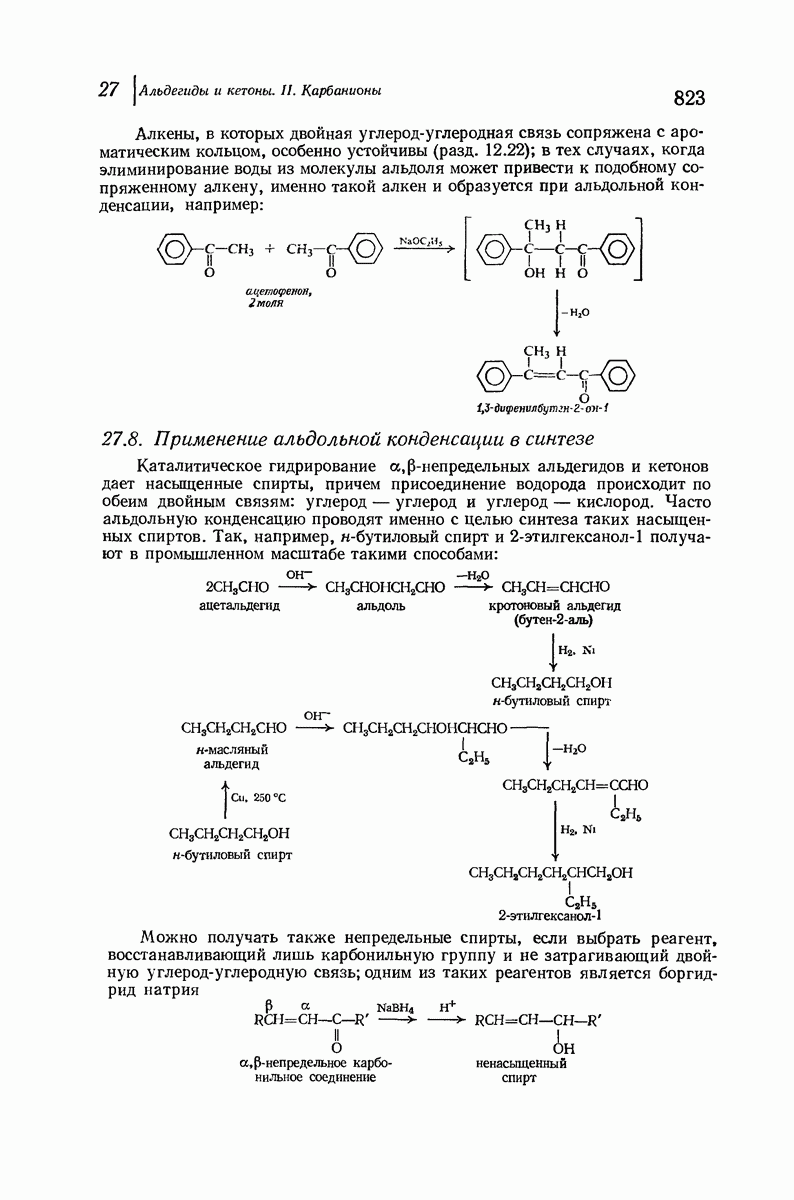
- 27.8. Применение альдольной конденсации в синтезе
- 27.9. Перекрестная альдольная конденсация
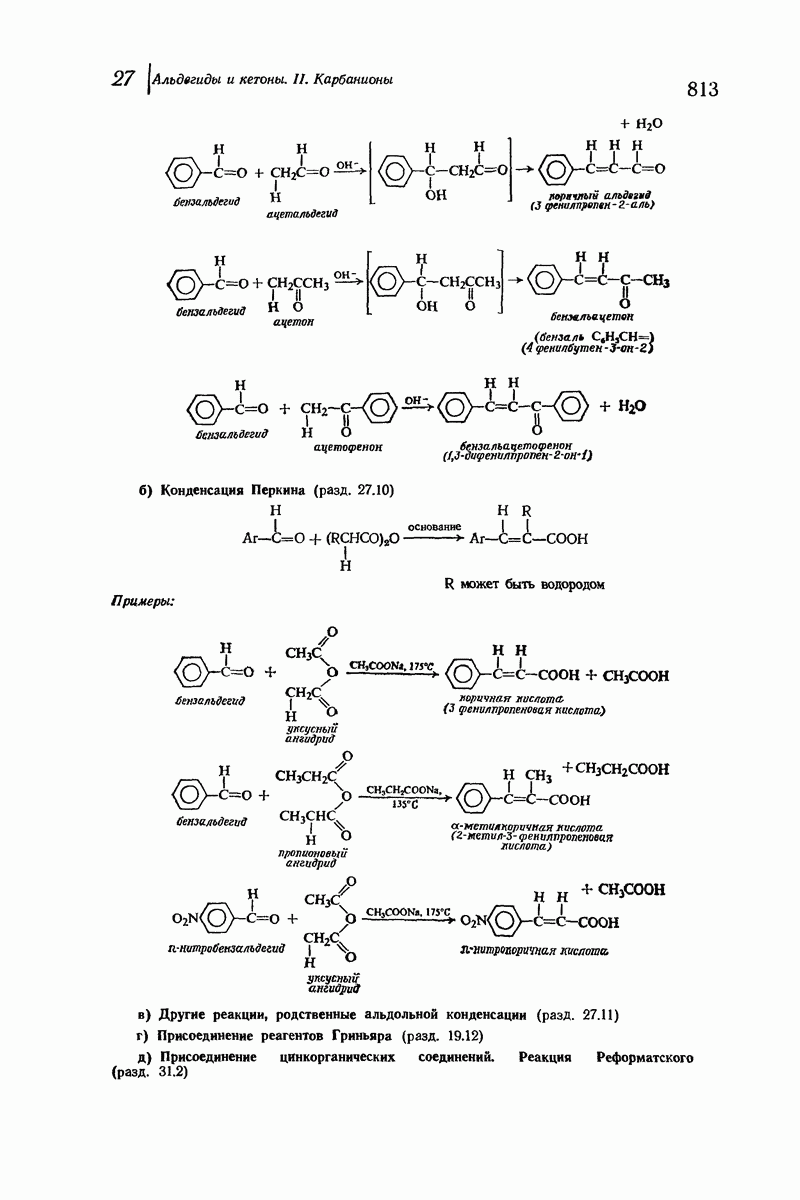
- 27.10. Конденсация Перкина. Присоединение ангидридов
- 27.11. Реакции, родственные альдольной конденсации
- 27.12. Реакция Виттига
- 28. Гликоли и эпокиси
- 28.6. Окисление гликолей йодной кислоты
- 28.7. Пинаколиновая перегруппировка
- 28.8. Стереохимия 1,2-сдвигов: центр, к которому осуществляется миграция
- 28.9. Стереохимия 1,2-сдвигов: конформационные эффекты
- ЭПОКИСИ
- 28.10. Методы синтеза эпокисей
- 28.11. Реакции эпокисей
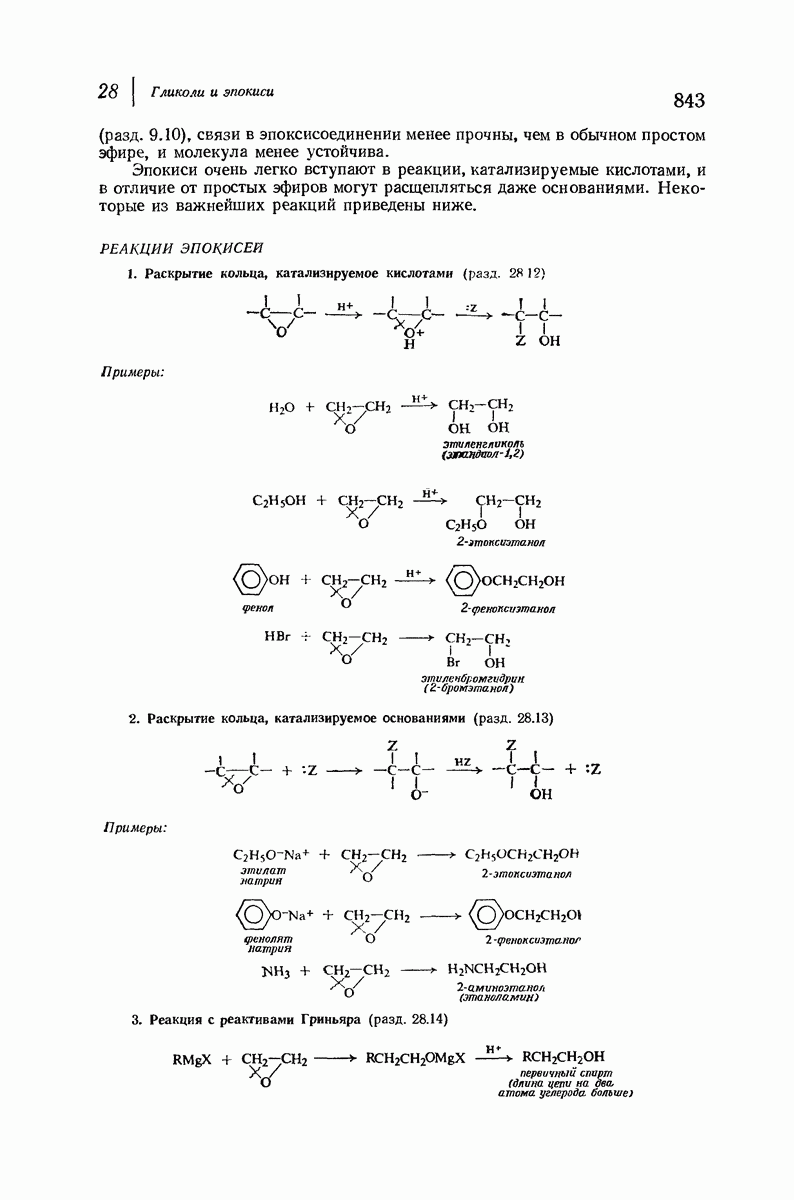
- 28.12. Раскрытие кольца эпокисей, катализируемое кислотами
- 28.13. Раскрытие кольца эпокисей, катализируемое основаниями
- 28.14. Реакция окиси этилена с реактивом Гриньяра
- 28.15. Направление раскрытия кольца эпокисей
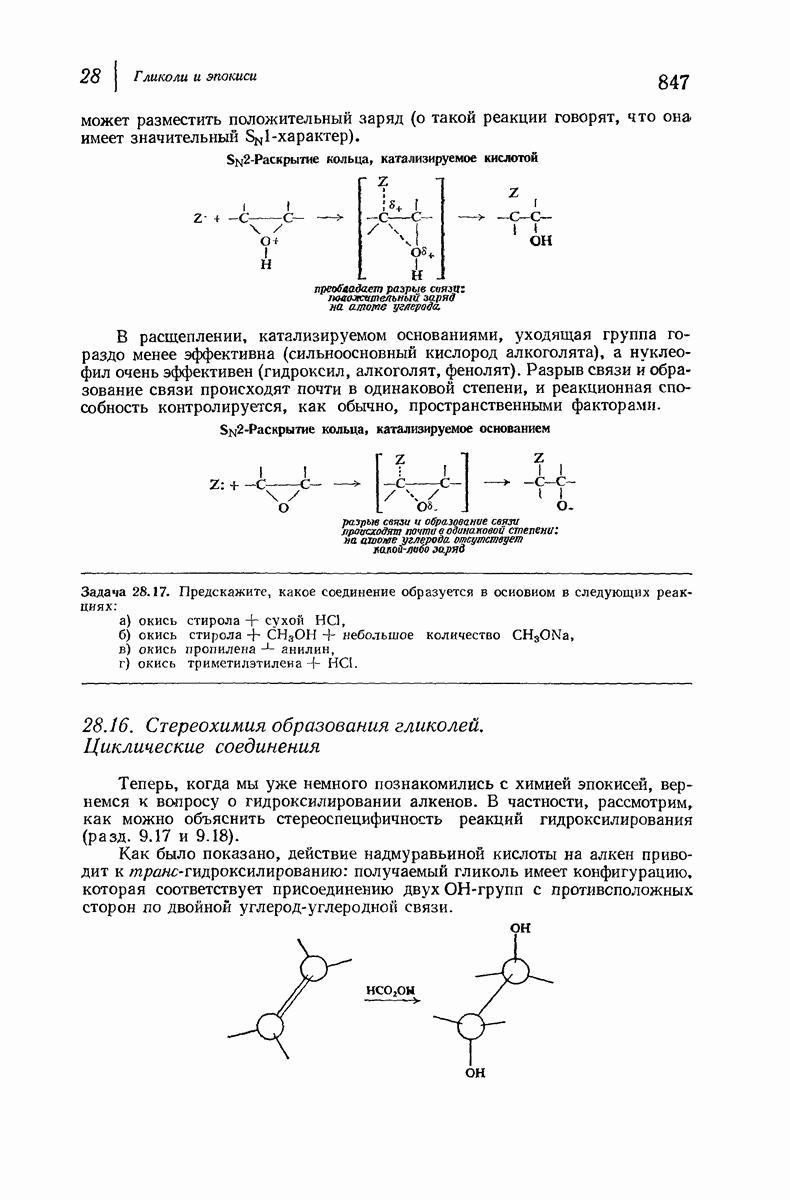
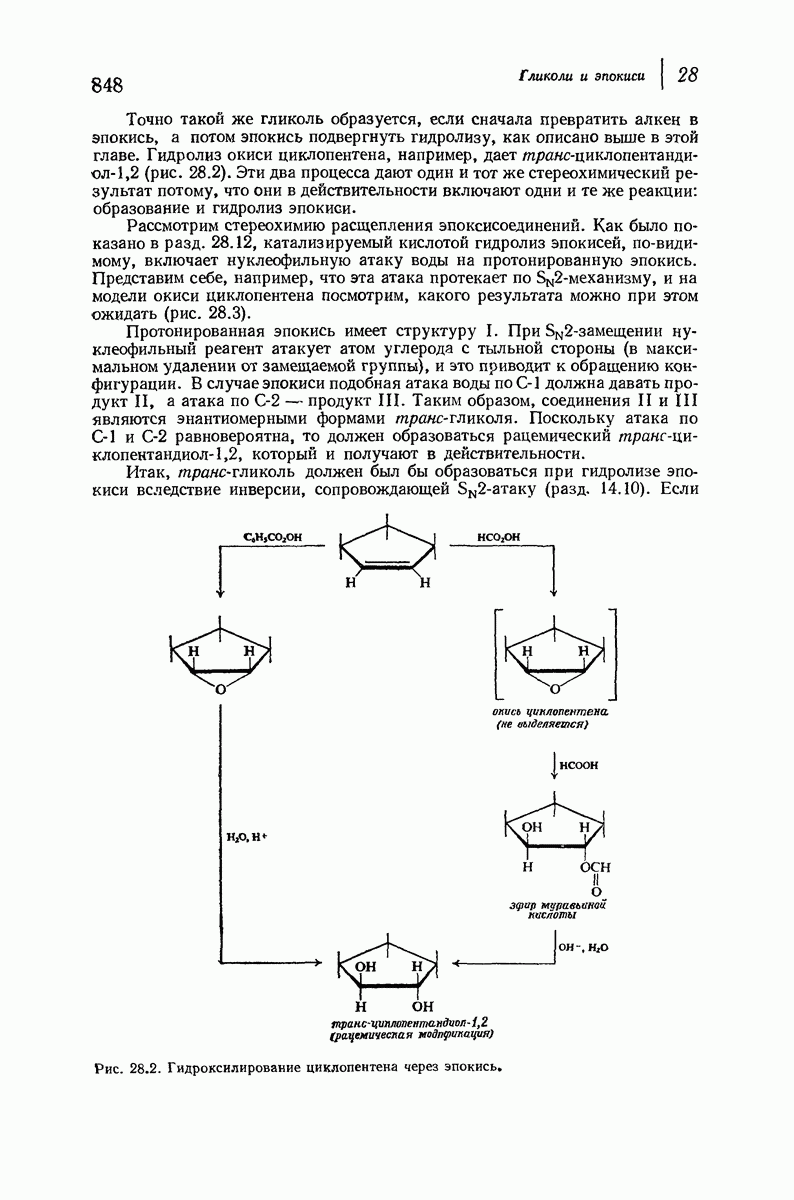
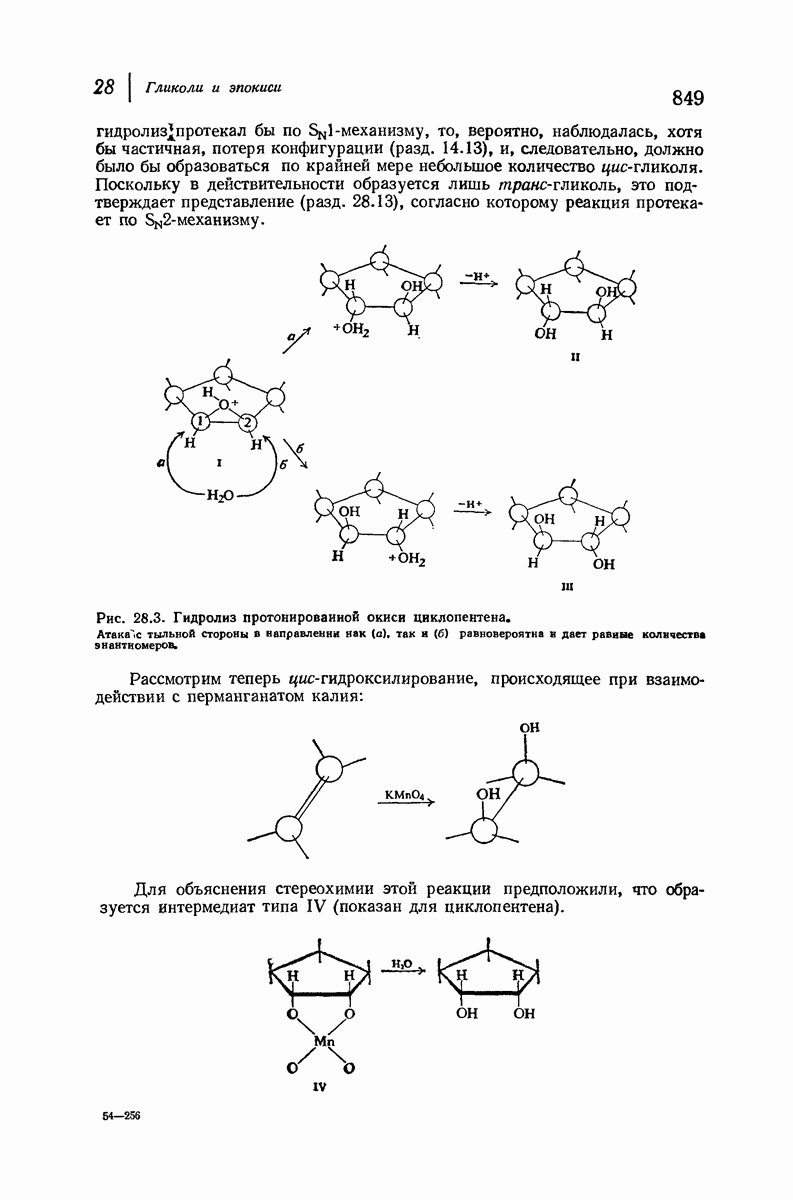
- 28.16. Стереохимия образования гликолей. Циклические соединения
- 28.17. Стереохимия образования гликолей. Ациклические соединения
- 28.18. Стереохимия присоединения галогена
- 29. Дикарбоновые кислоты
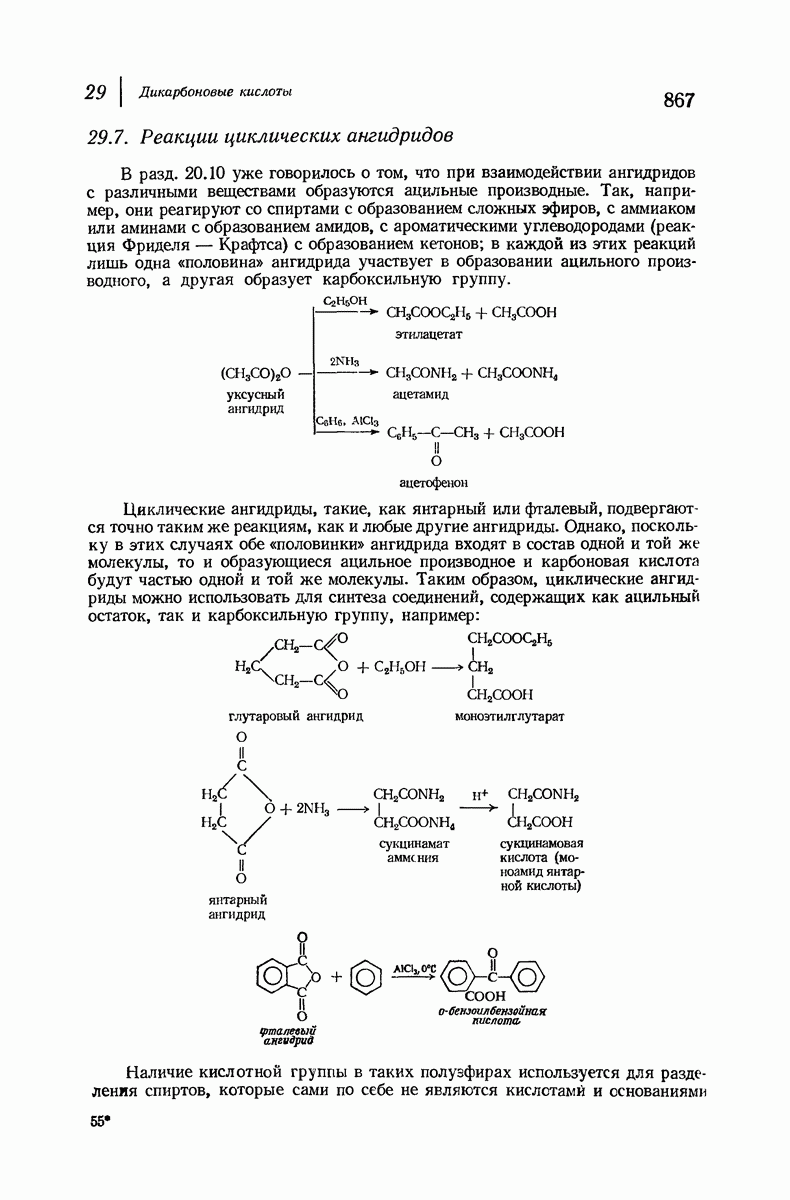
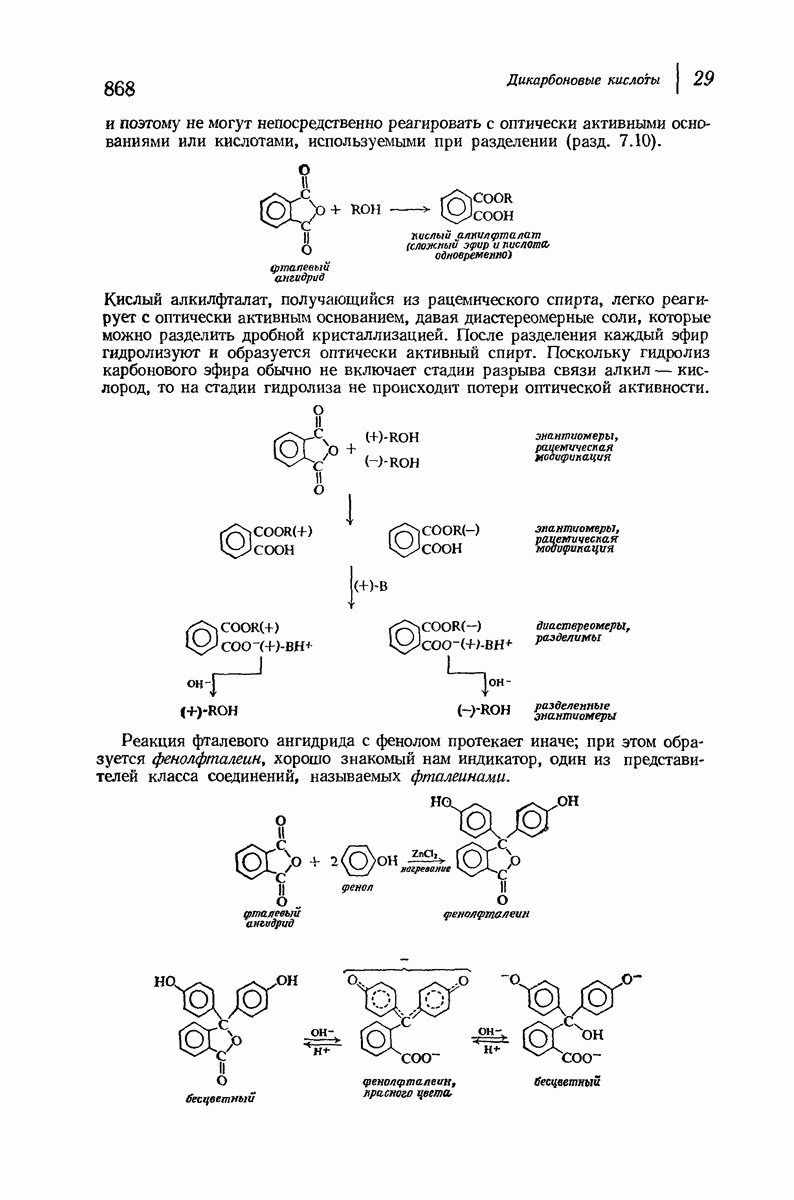
- 29.7. Реакции циклических ангидридов
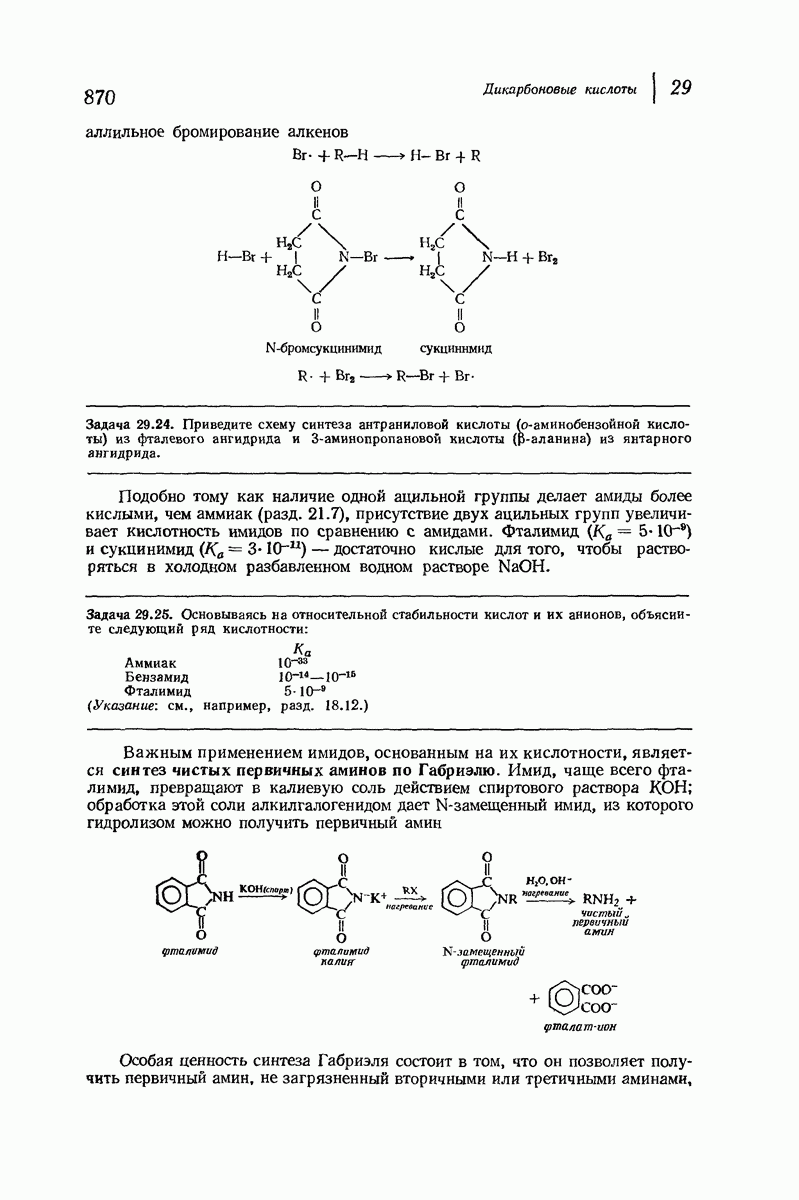
- 29.8. Имиды. Синтез чистых первичных аминов по Габриэлю
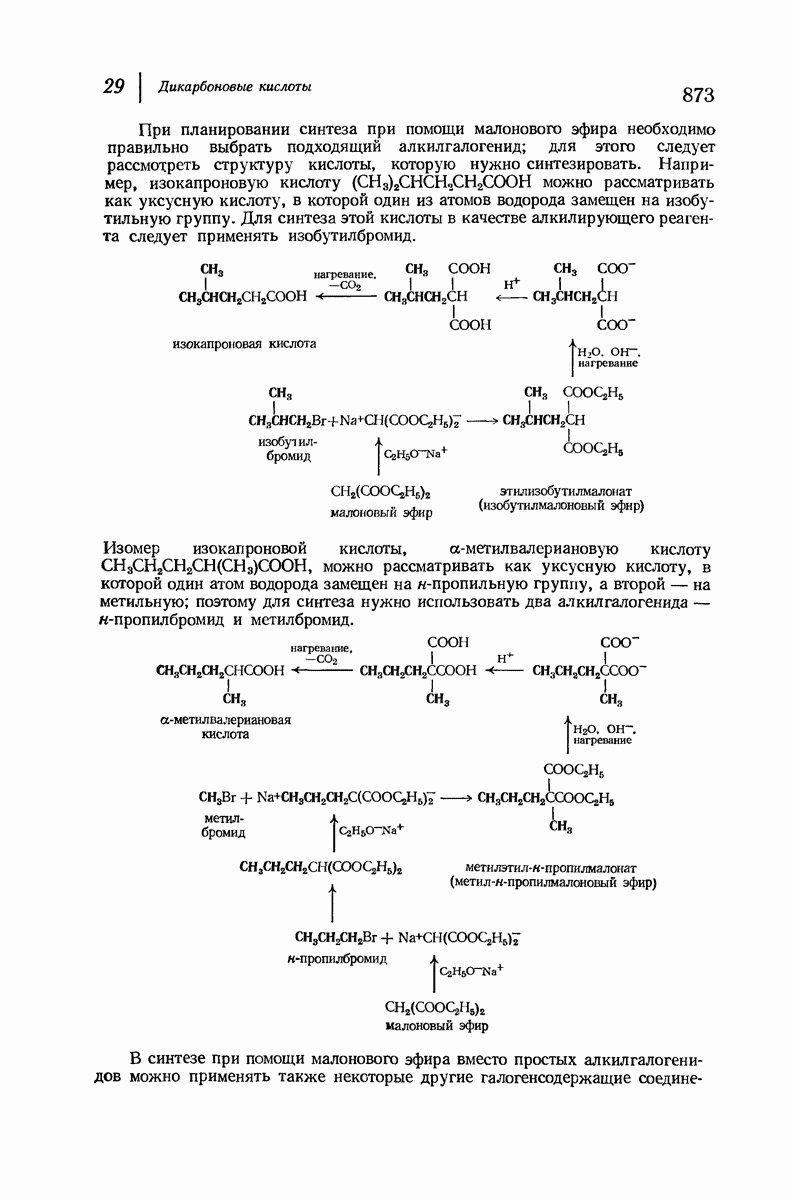
- 29.9. Синтез карбоновых кислот при помощи малонового эфира
- УГОЛЬНАЯ КИСЛОТА И РОДСТВЕННЫЕ СОЕДИНЕНИЯ
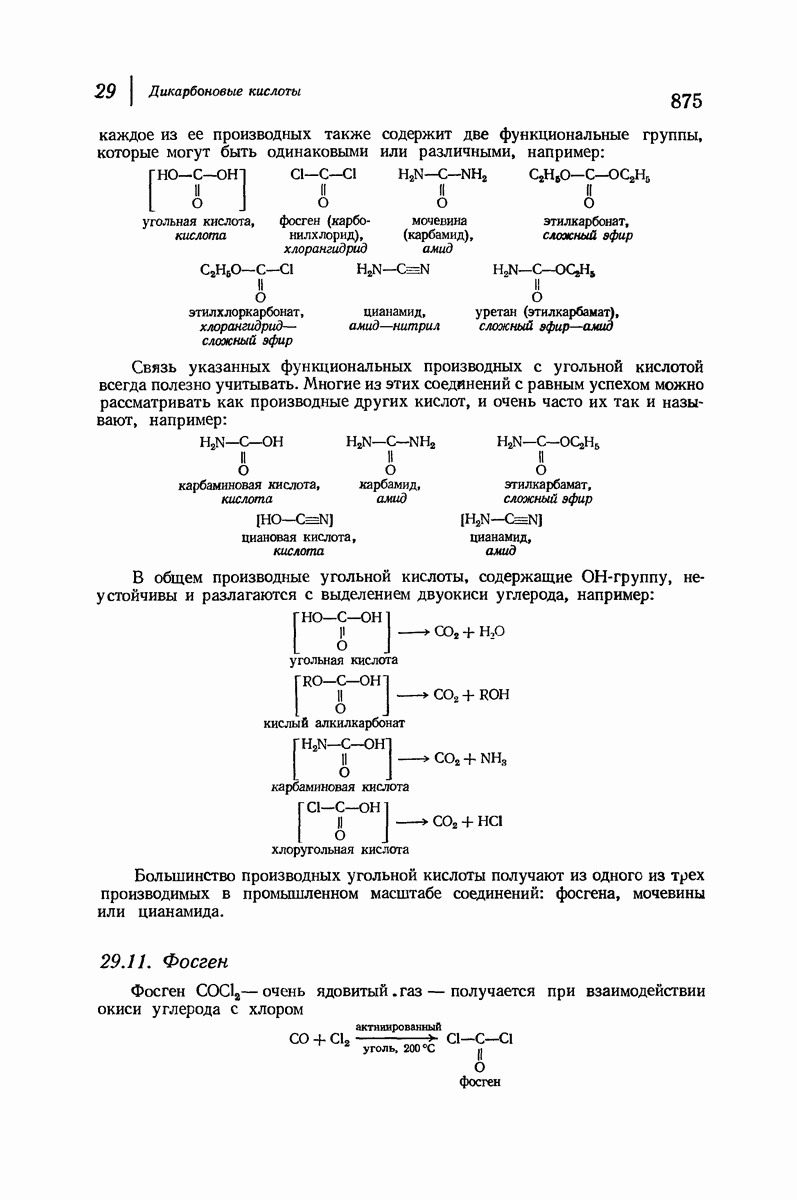
- 29.10. Функциональные производные угольной кислоты
- 29.11. Фосген
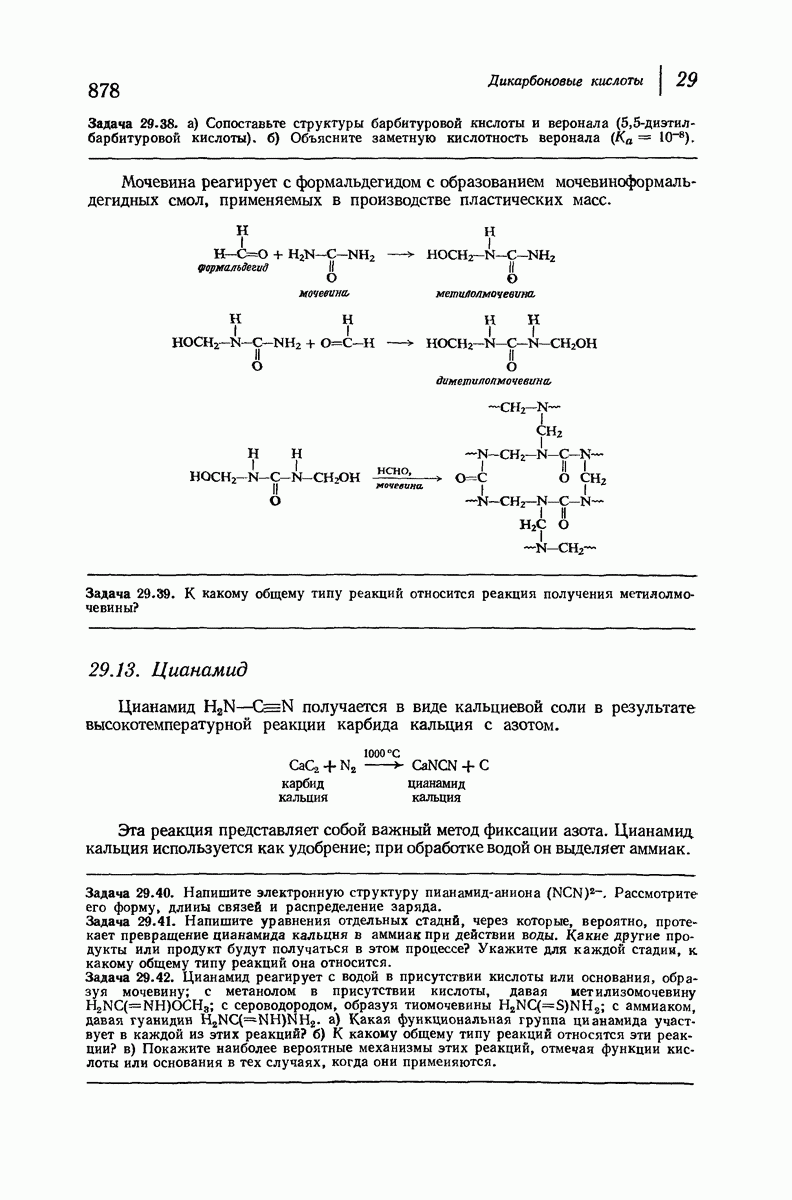
- 29.12. Мочевина. Барбитураты
- 29.13. Цианамид
- 29.14. Изоцианаты
- 30. Кетокислоты
- 30.2. Получение b-кетоэфиров. Конденсация Клайзена
- 30.3. Перекрестная конденсация Клайзена
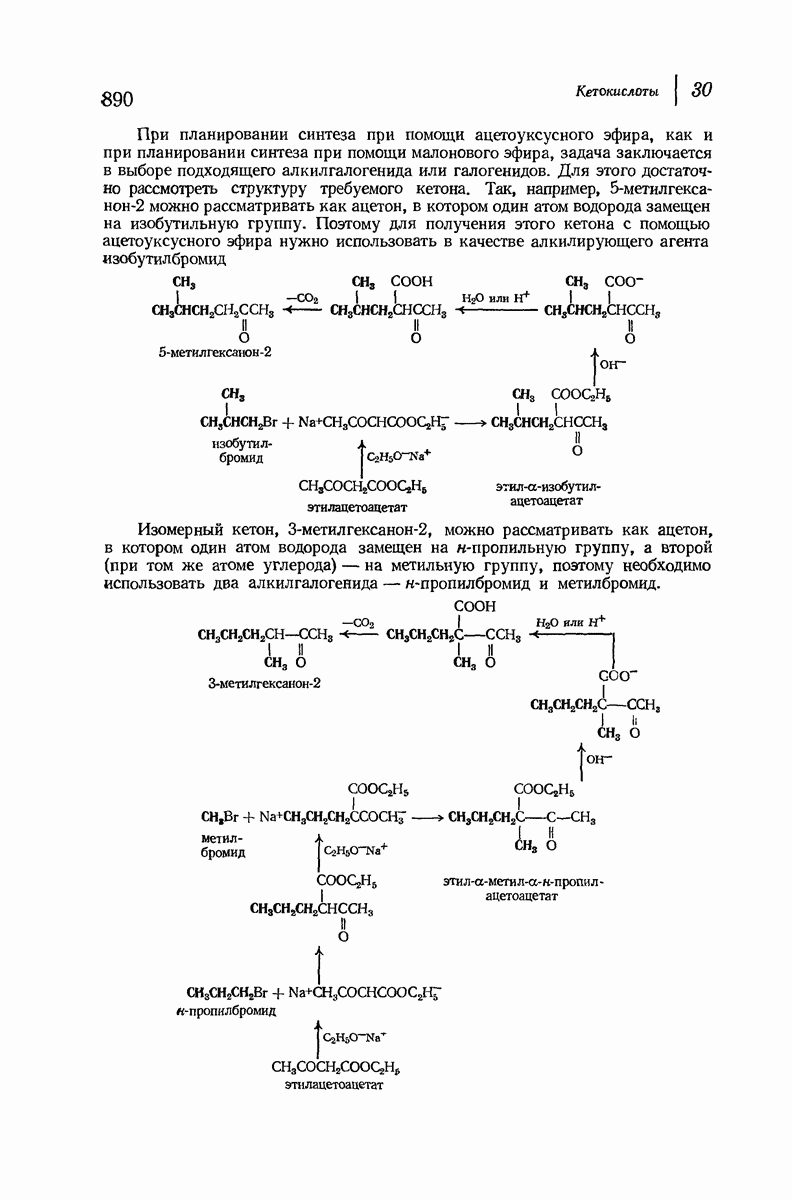
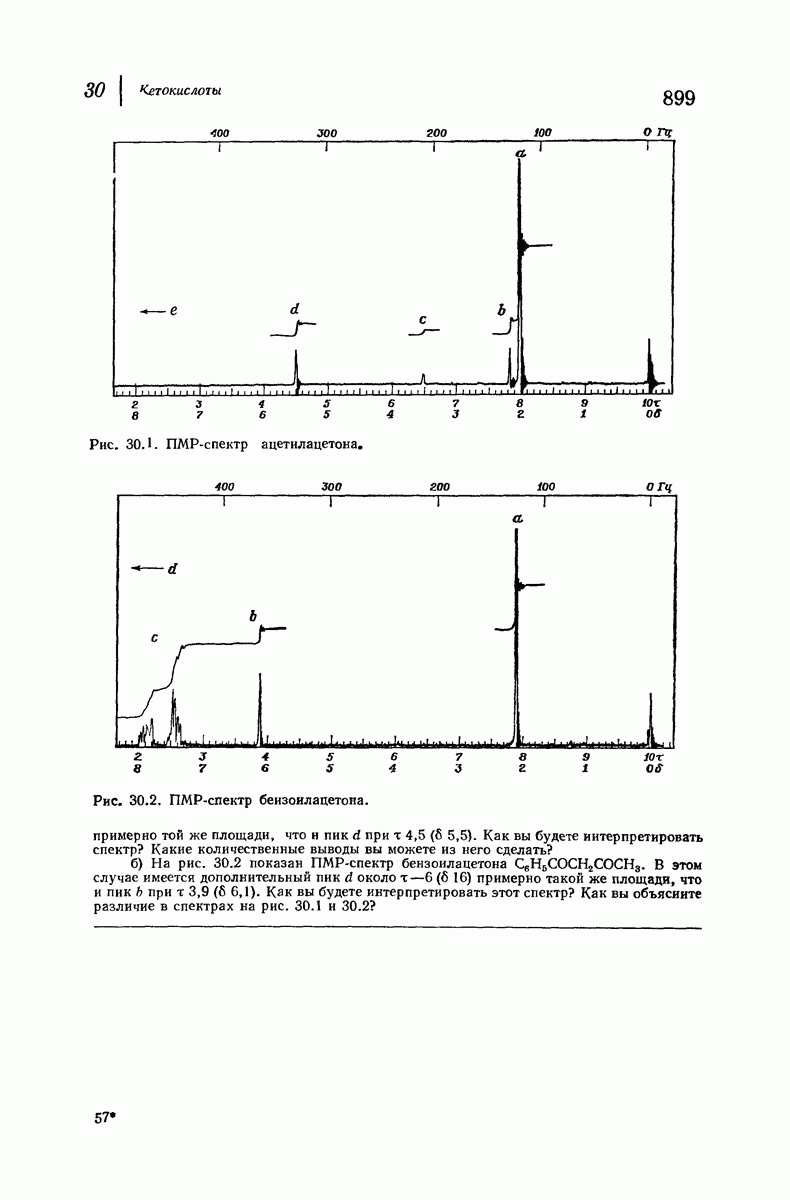
- 30.4. Синтез кетонов при помощи ацетоуксусного эфира
- 30.5. Декарбоксилирование кетокислот
- 30.6. Синтез кислот при помощи ацетоуксусного эфира
- 30.7. Кето-енольная таутомерия и ацетоуксусный эфир
- 30.8. Состав кето-енольных смесей
- 30.9. Кислоты и основания и кето-енольная таутомерия
- 31. Оксикислоты
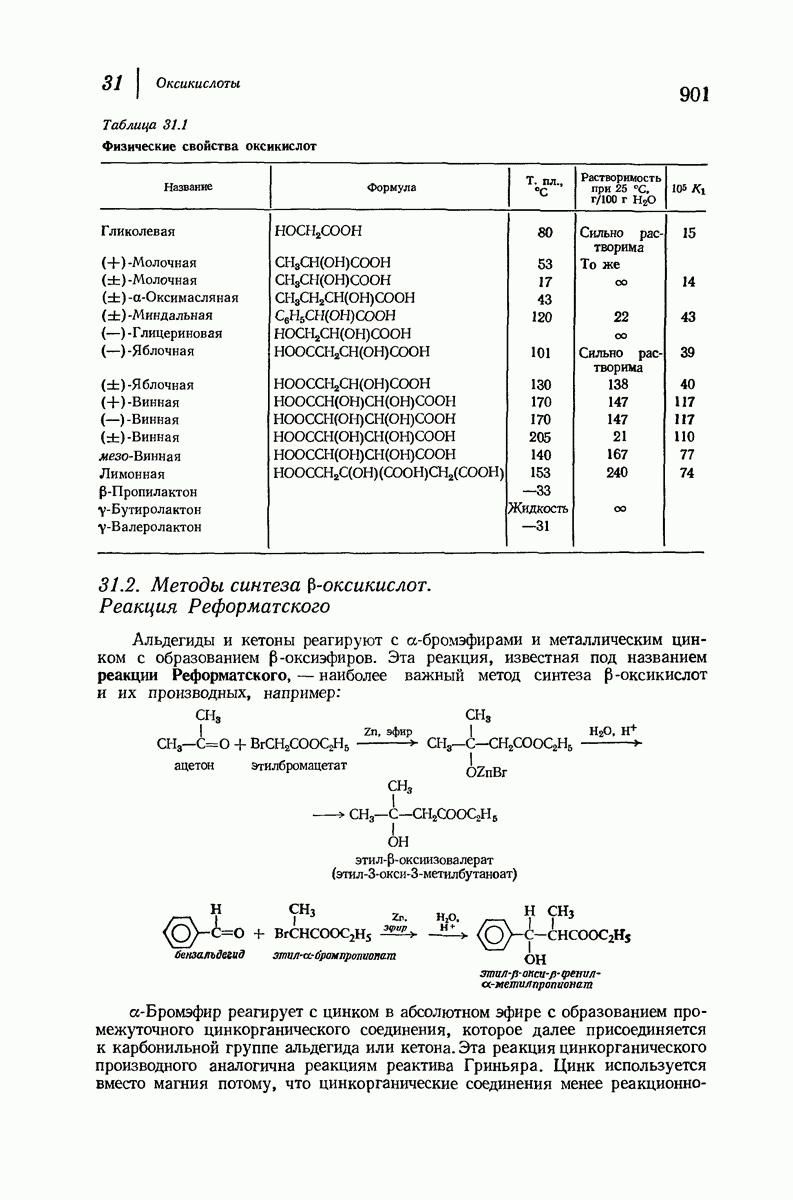
- 31.2. Методы синтеза b-оксикислот. Реакция Реформатского
- 31.3. Дегидратация. Образование лактона
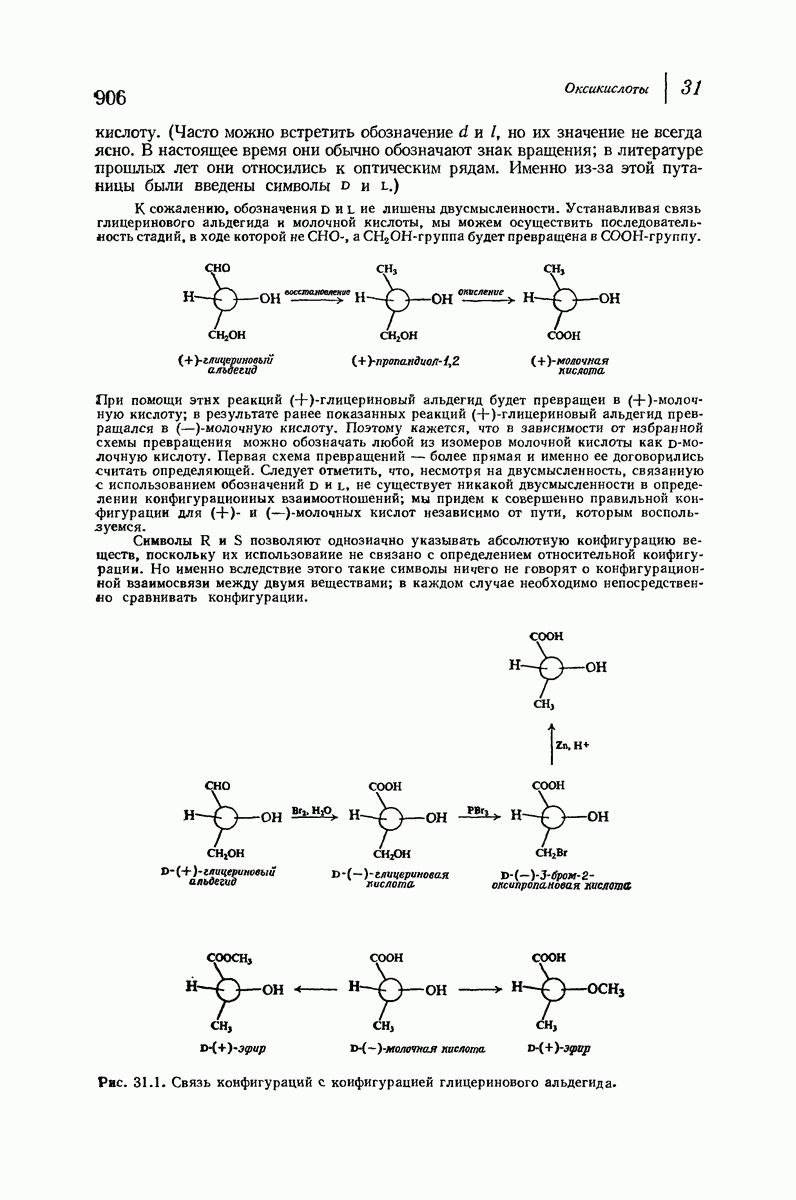
- 31.4. Стереохимия оксикислот
- 31.5. Оптические ряды. Глицериновый альдегид
- 31.6. Винная кислота. Относительные конфигурации
- 32 a,b-Непредельные карбонильные соединения
- 32.5. Электрофильное присоединение
- 32.6. Нуклеофильное присоединение
- 32.7. Сравнение реакций нуклеофильного и электрофильного присоединения
- 32.8. Присоединение по Михаэлю
- 32.9 Реакция Дильса-Альдера
- 32.10. Хиноны
- 33. Углеводы. I. Моносахариды
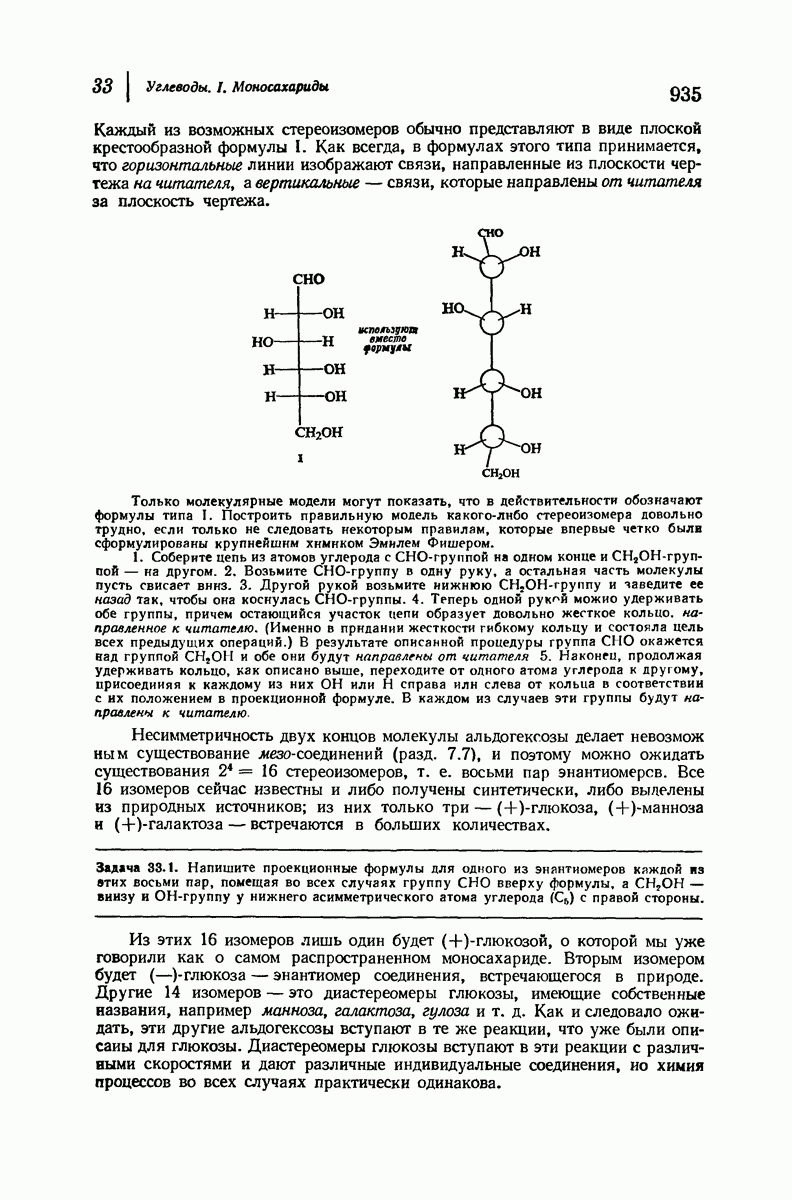
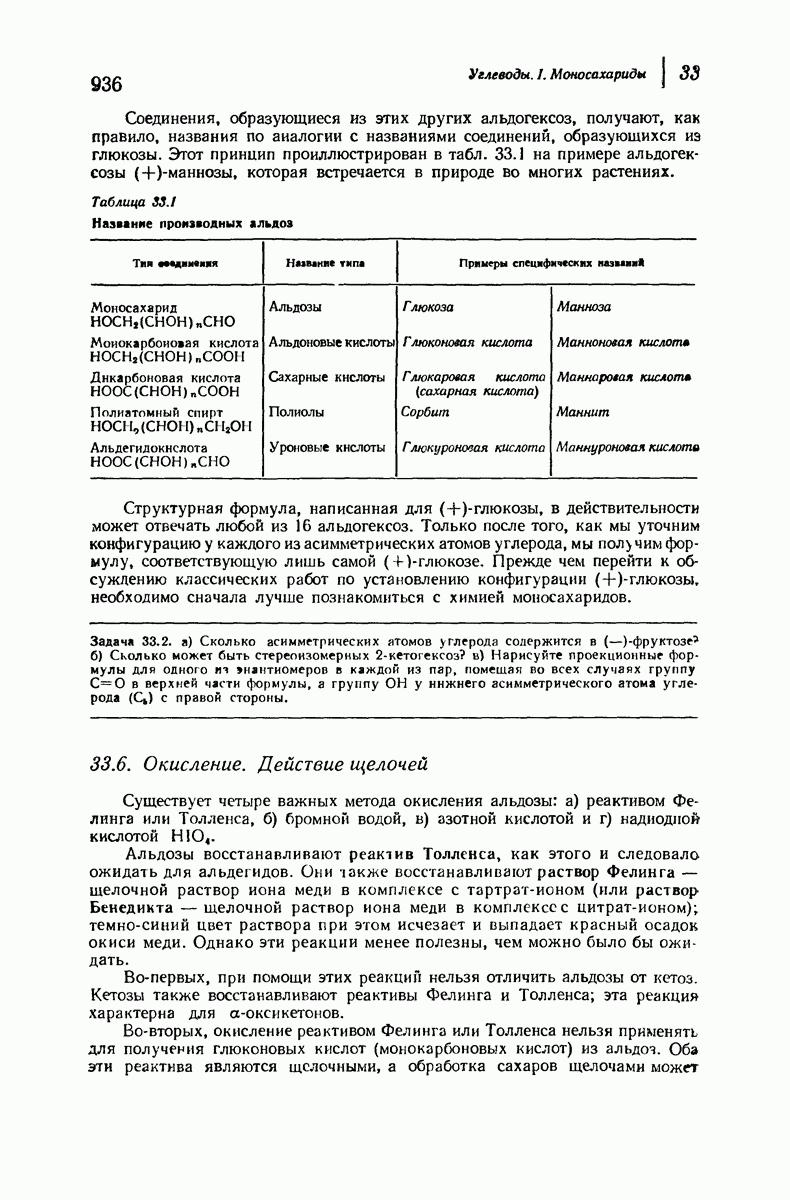
- 33.5. Стереоизомеры (+)-глюкозы. Номенклатура производных альдоз
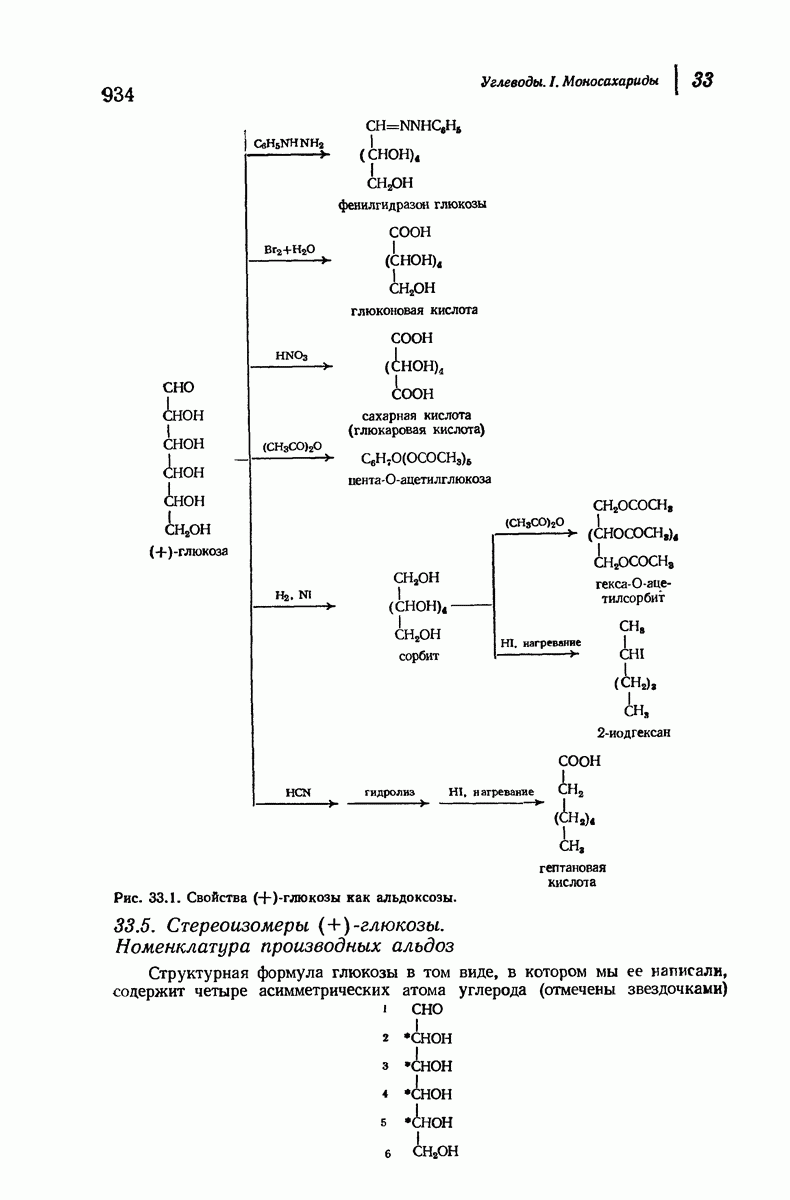
- 33.6. Окисление. Действие щелочей
- 33.7. Образование озазона. Эпимеры
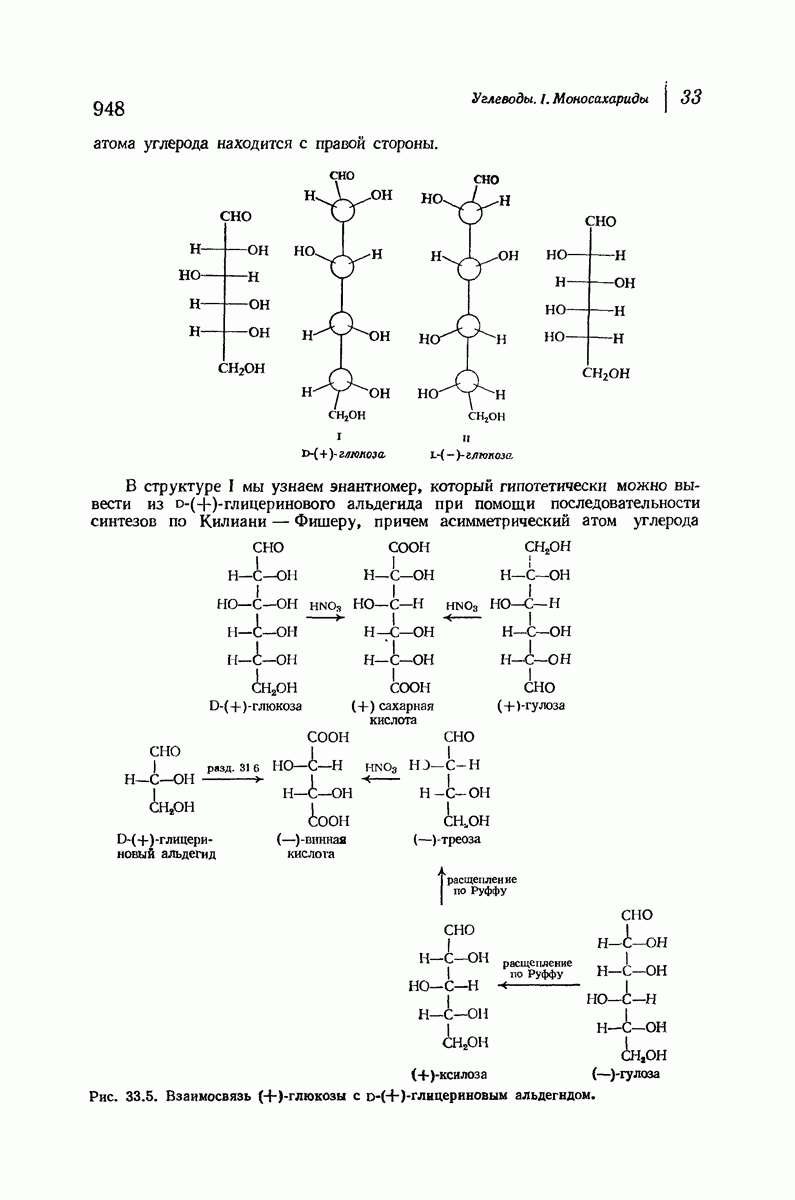
- 33.8. Увеличение длины углеродной цепи альдоз. Синтез Килиани — Фишера
- 33.9. Уменьшение длины цепи альдоз. Расщепление по Руффу
- 33.10. Превращение альдозы в ее эпимер
- 33.11. Конфигурация (+)-глюкозы. Доказательство Фишера
- 33.12. Конфигурации альдоз
- 33.13. Семейство альдоз. Абсолютная конфигурация
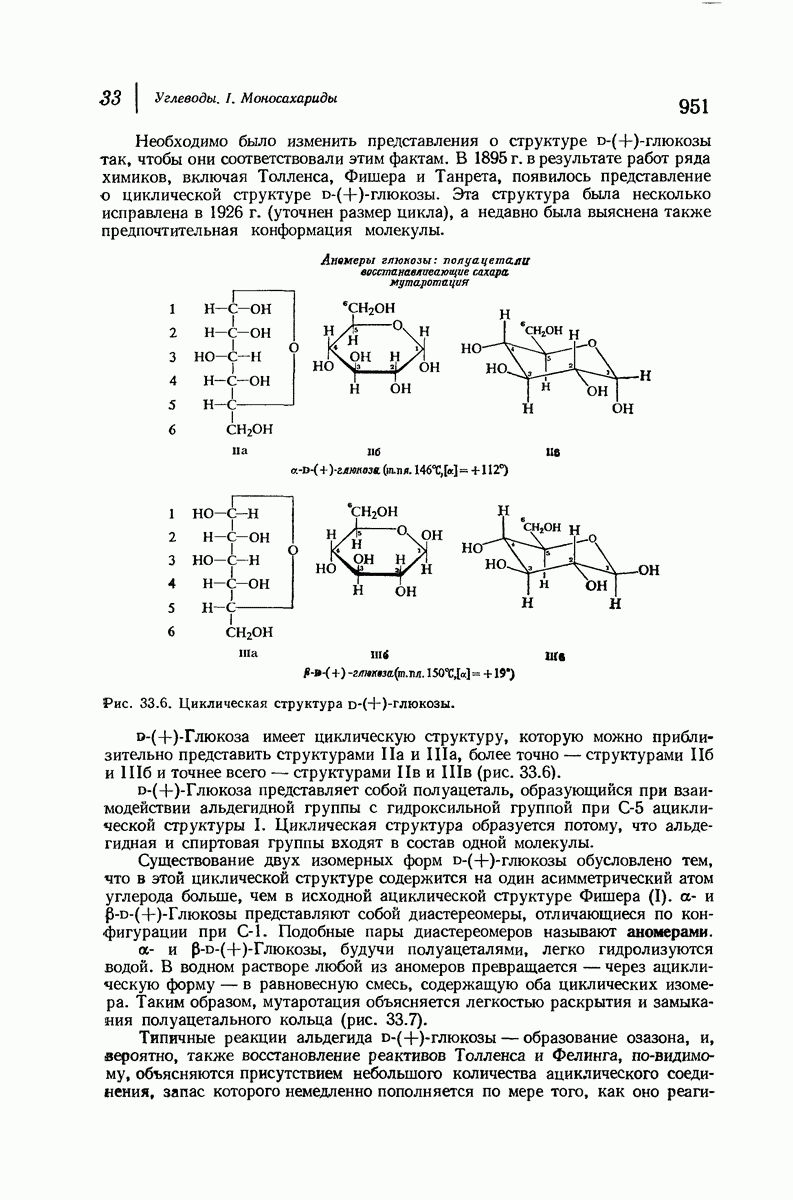
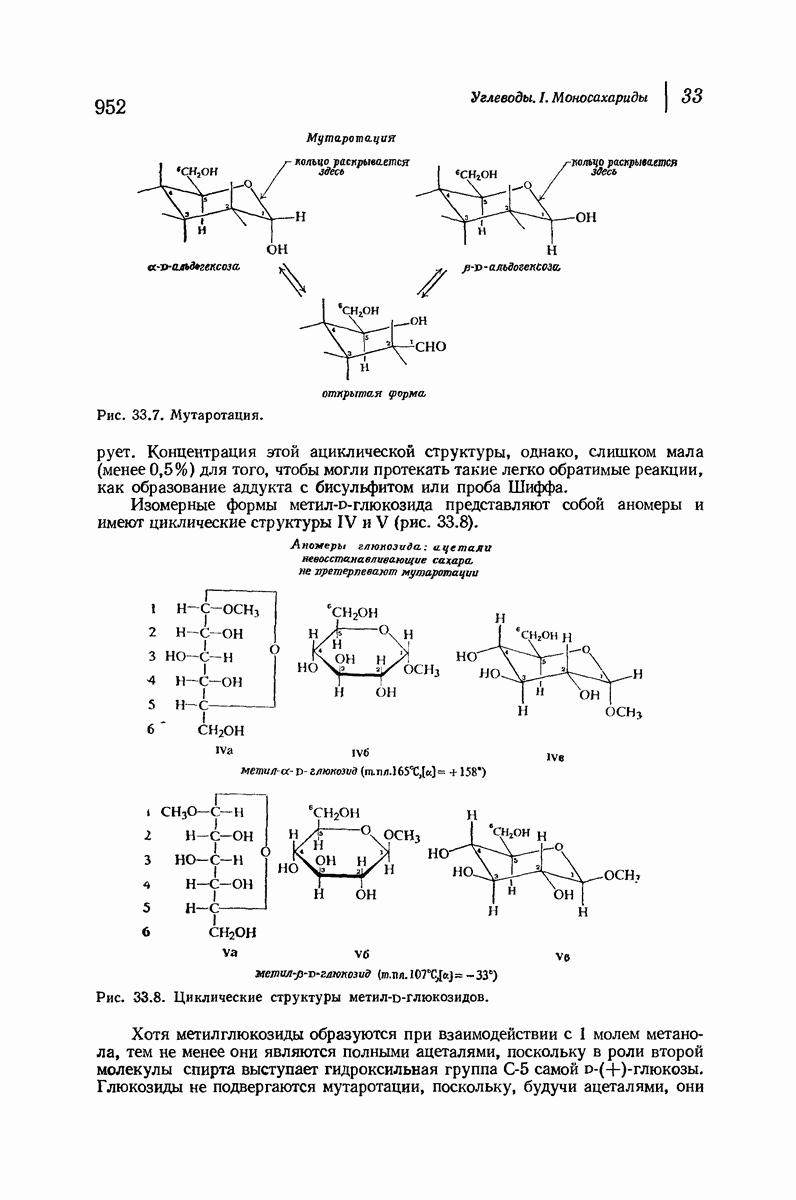
- 33.14. Циклическая структура D-(+)-глюкозы. Образование глюкозидов
- 38.15. Конфигурация при С-1
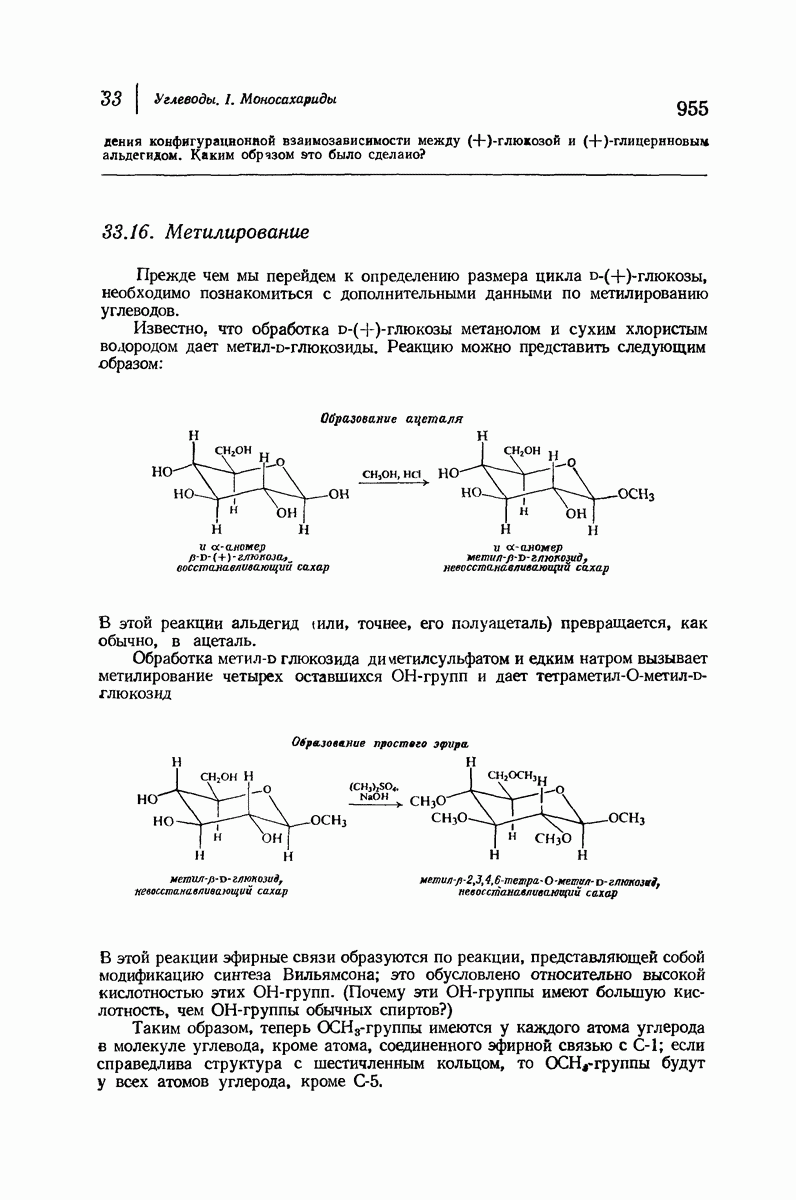
- 33.16. Метилирование
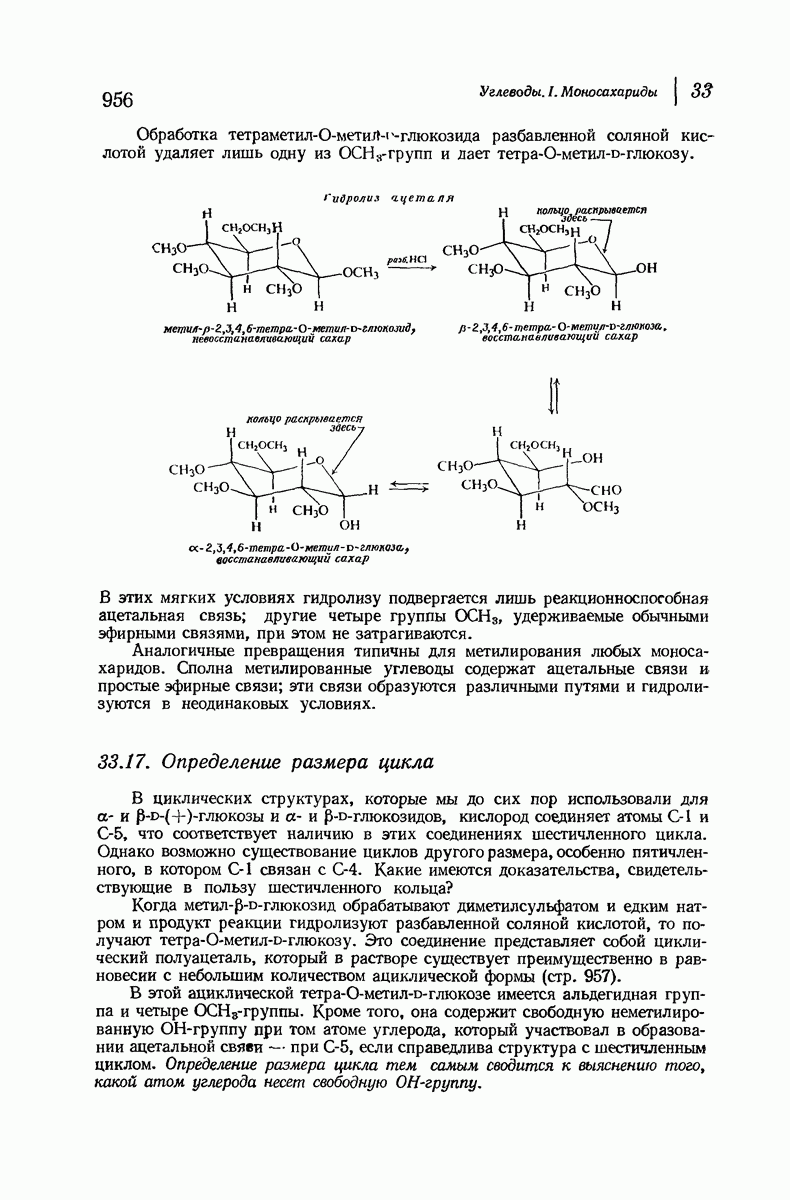
- 33.17. Определение размера цикла
- 33.18. Конформация
- 34. Углеводы. II. Дисахариды и полисахариды
- 34.3. (+)-Целлобиоза
- 34.4. (+)-Лактоза
- 34.4. (+)-Сахароза
- 34.6. Полисахариды
- 34.7. Крахмал
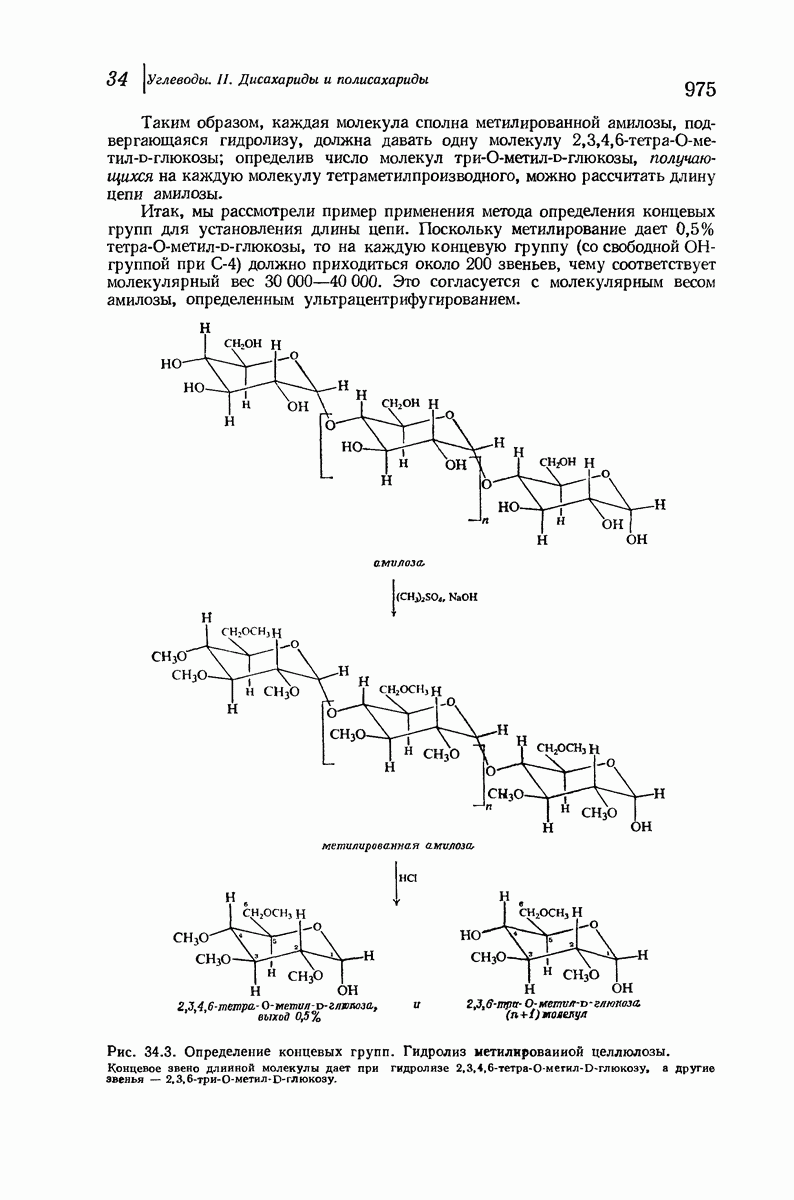
- 34.8. Структура амилозы. Определение концевых групп
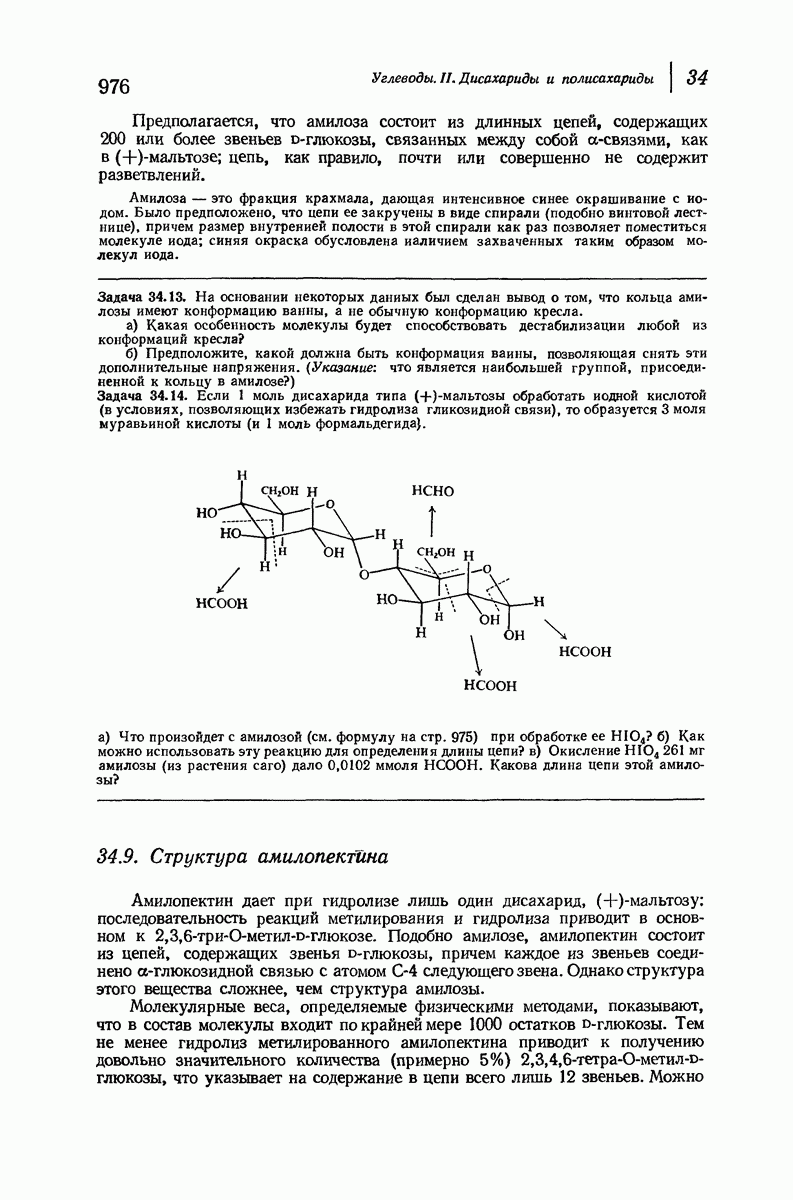
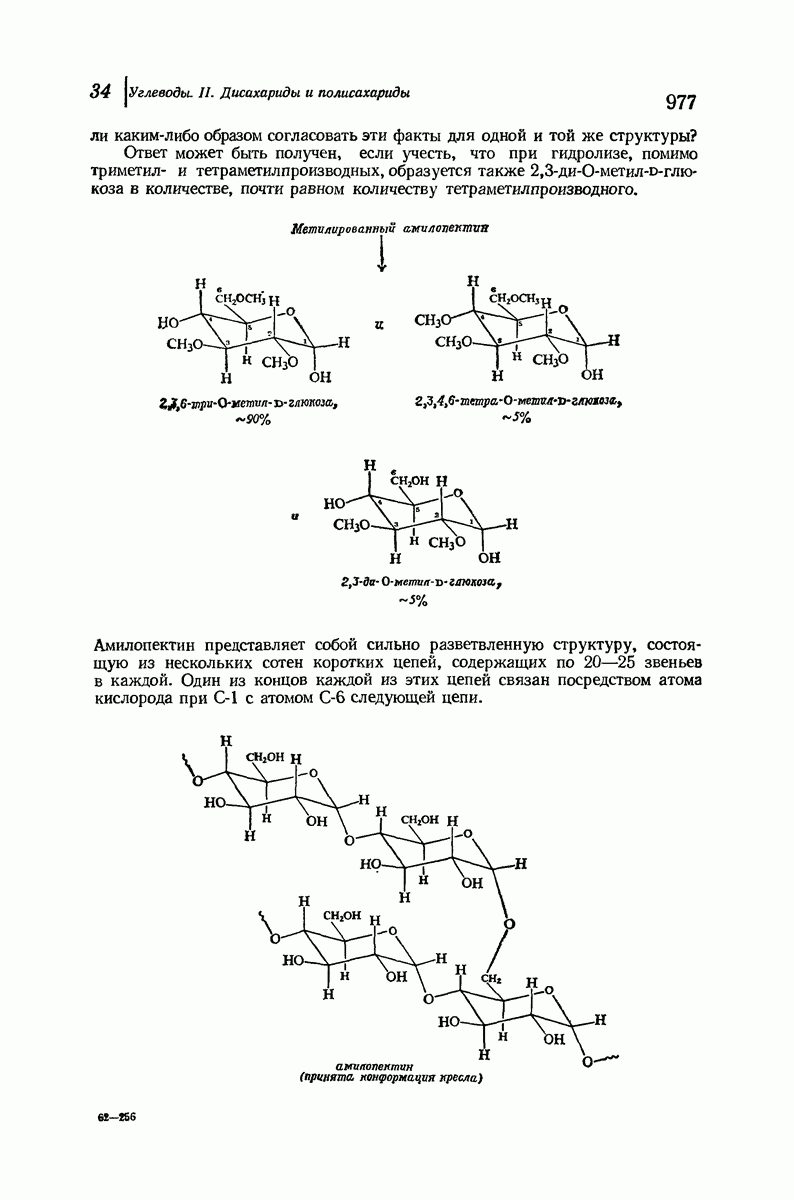
- 34.9. Структура амилопектина
- 34.10. Структура целлюлозы
- 34.11. Реакции целлюлозы
- 34.12. Нитрат целлюлозы
- 34.13. Ацетат целлюлозы
- 34.14. Искусственный шелк. Целлофан
- 34.15. Простые эфиры целлюлозы
- 35. Многоядерные ароматические соединения
- НАФТАЛИН
- 35.2. Номенклатура производных нафталина
- 35.3. Структура нафталина
- 35.4. Реакции нафталина
- 35.5. Окисление нафталина
- 35.6. Восстановление нафталина
- 35.7. Дегидрирование гидроароматических соединений. Ароматизация
- 35.8. Нитрование и галогенирование нафталина
- 35.9. Ориентация электрофильного замещения в нафталине
- 35.10. Ацилирование нафталина по Фриделю-Крафтсу
- 35.11. Сульфирование нафталина
- 35.12. Нафтолы
- 35.13. Ориентация в реакциях электрофильного замещения производных нафталина
- 35.14. Синтез производных нафталина циклизацией. Синтез Хеуорса
- АНТРАЦЕН И ФЕНАНТРЕН
- 35.15. Номенклатура производных антрацена и фенантрена
- 35.18. Получение антрацена циклизацией. Антрахиноны
- 35.19. Получение производных фенантрена циклизацией
- 35.20. Канцерогенные углеводороды
- 36. Гетероциклические соединения
- ПЯТИЧЛЕННЫЕ ЦИКЛЫ
- 36.2. Структура пиррола, фурана и тиофена
- 36.3. Источники получения пиррола, фурана и тиофена
- 36.4. Электрофильное замещение в пирроле, фуране и тиофене. Реакционная способность и ориентация
- 36.5. Насыщенные пятичленные гетероциклы
- ШЕСТИЧЛЕННЫЕ ЦИКЛЫ
- 36.6. Структура пиридина
- 36.10. Нуклеофильное замещение в пиридине
- 36.11. Основность пиридина
- 36.12. Восстановление пиридина
- КОНДЕНСИРОВАННЫЕ КОЛЬЦА
- 36.13. Хинолин. Синтез Скраупа
- 36.14. Изохинолин. Синтез Бишлера — Напиральского
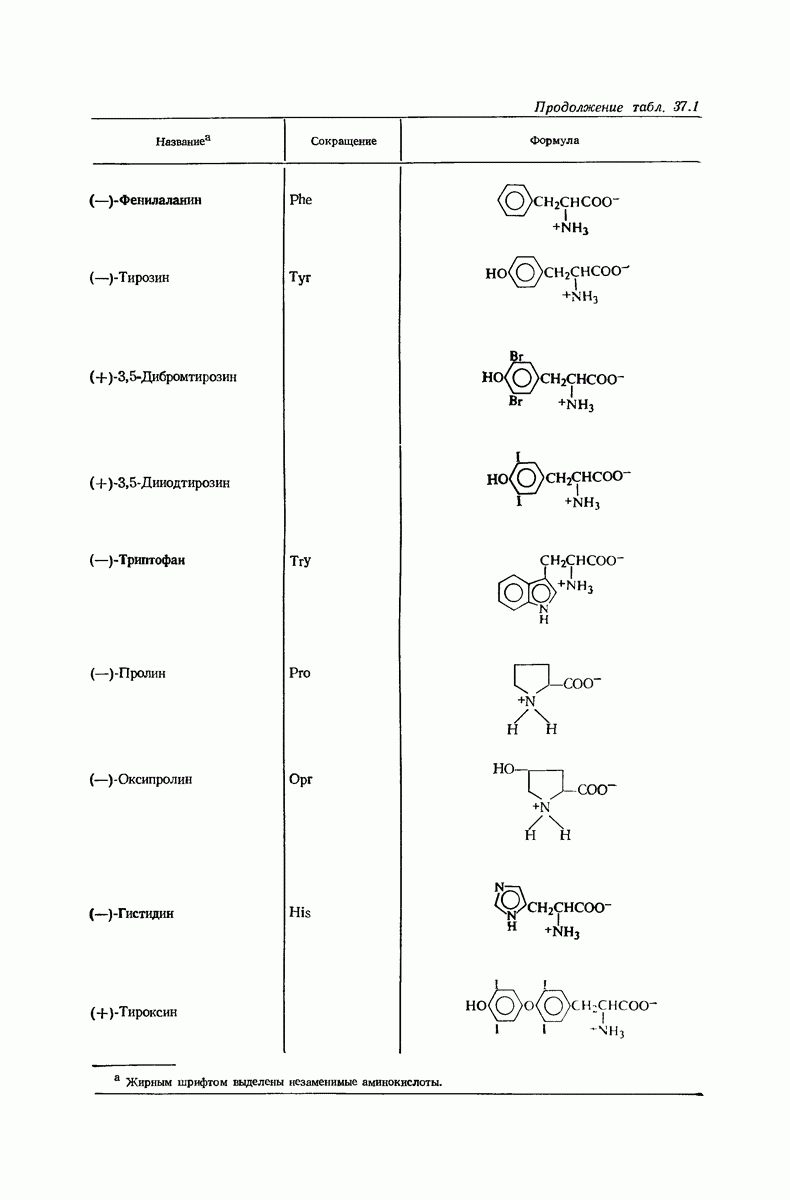
- 37. Аминокислоты и белки
- 37.3. Аминокислоты как биполярные ионы
- 37.4. Изоэлектрическая точка аминокислот
- 37.5. Конфигурация природных аминокислот
- 37.6. Синтез аминокислот
- 37.7. Реакции аминокислот
- 37.8. Пептиды. Геометрия пептидной связи
- 37.9. Определение структуры пептидов. Определение концевых групп. Частичный гидролиз
- 37.10. Синтез пептидов
- 37.11. Белки. Классификация и функция. Денатурация
- 37.12. Структура белков
- 37.13. Пептидная цепь
- 37.14. Боковые цепи. Изоэлектрическая точка. Электрофорез
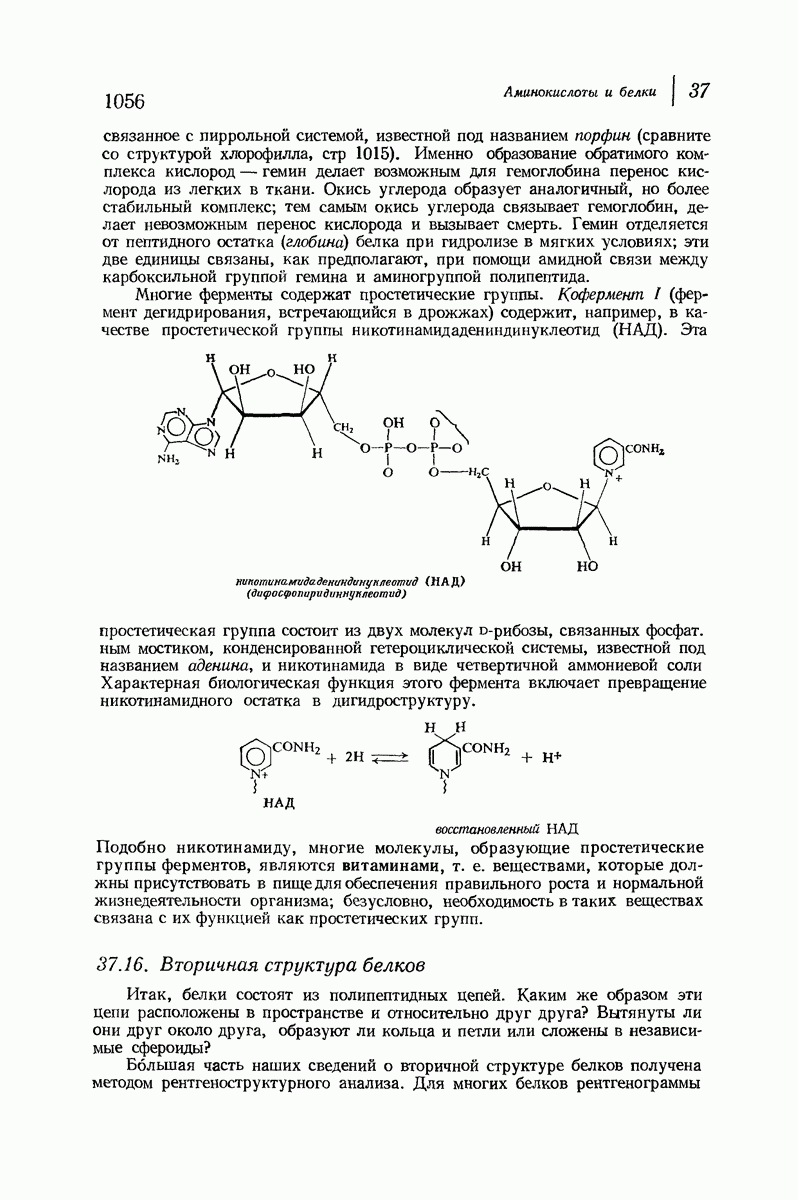
- 37.15. Сложные белки. Простетические группы
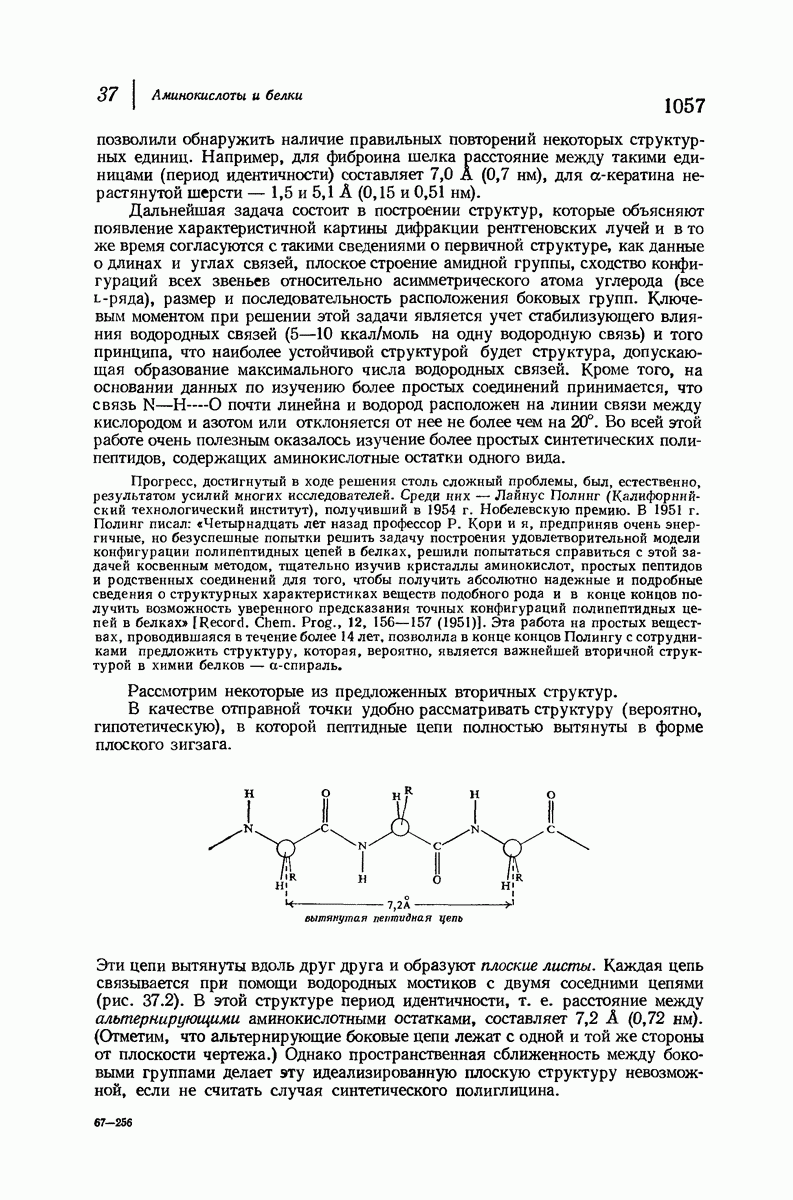
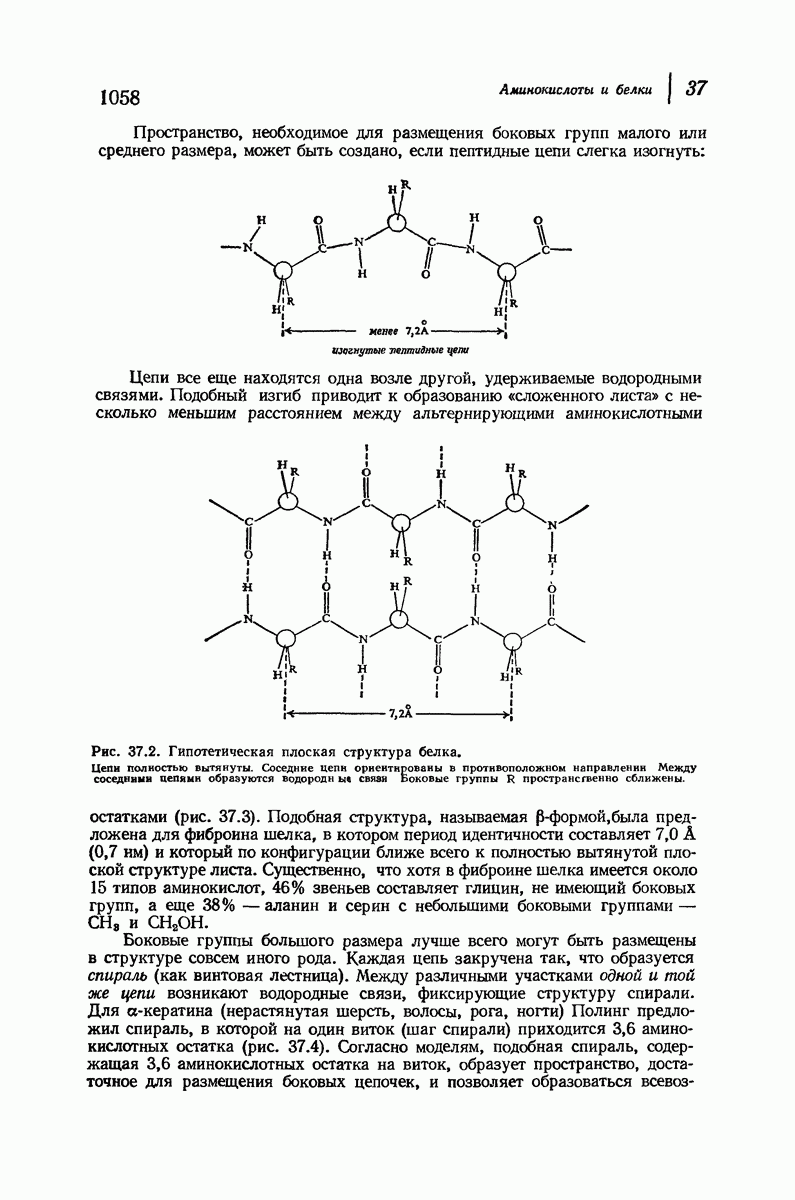
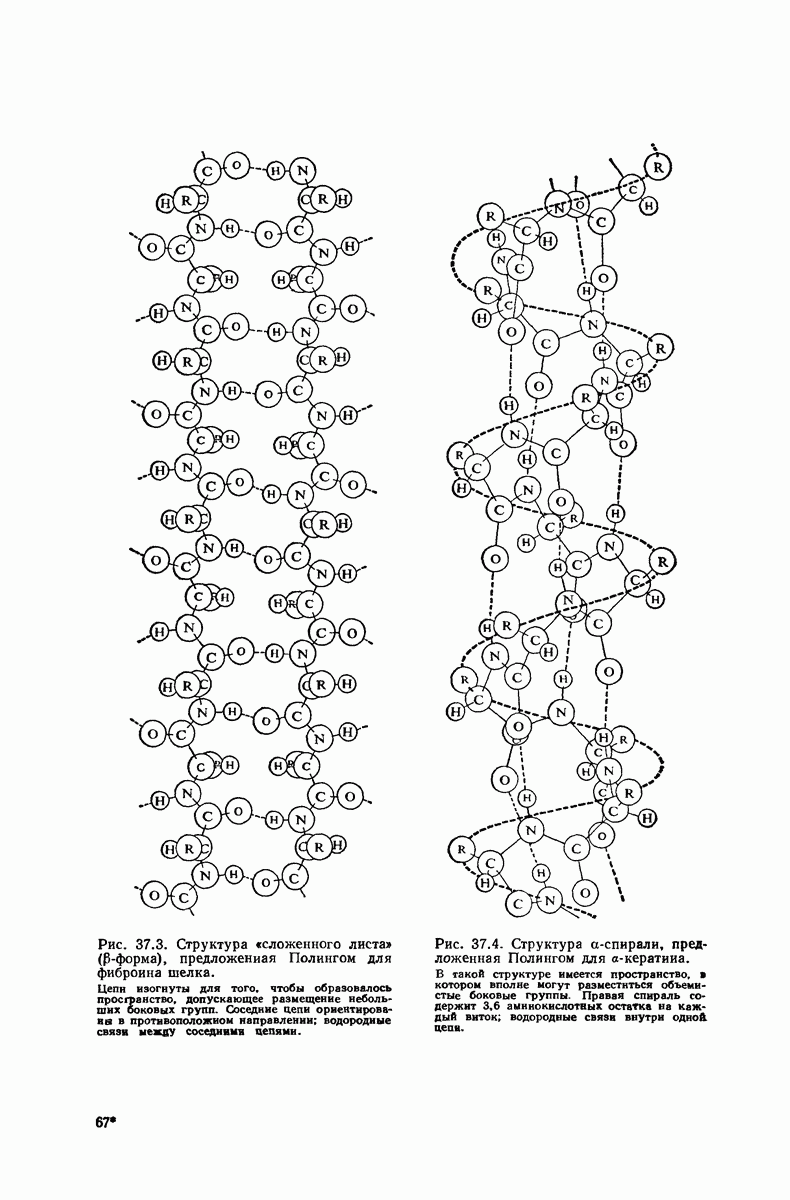
- 37.16. Вторичная структура белков
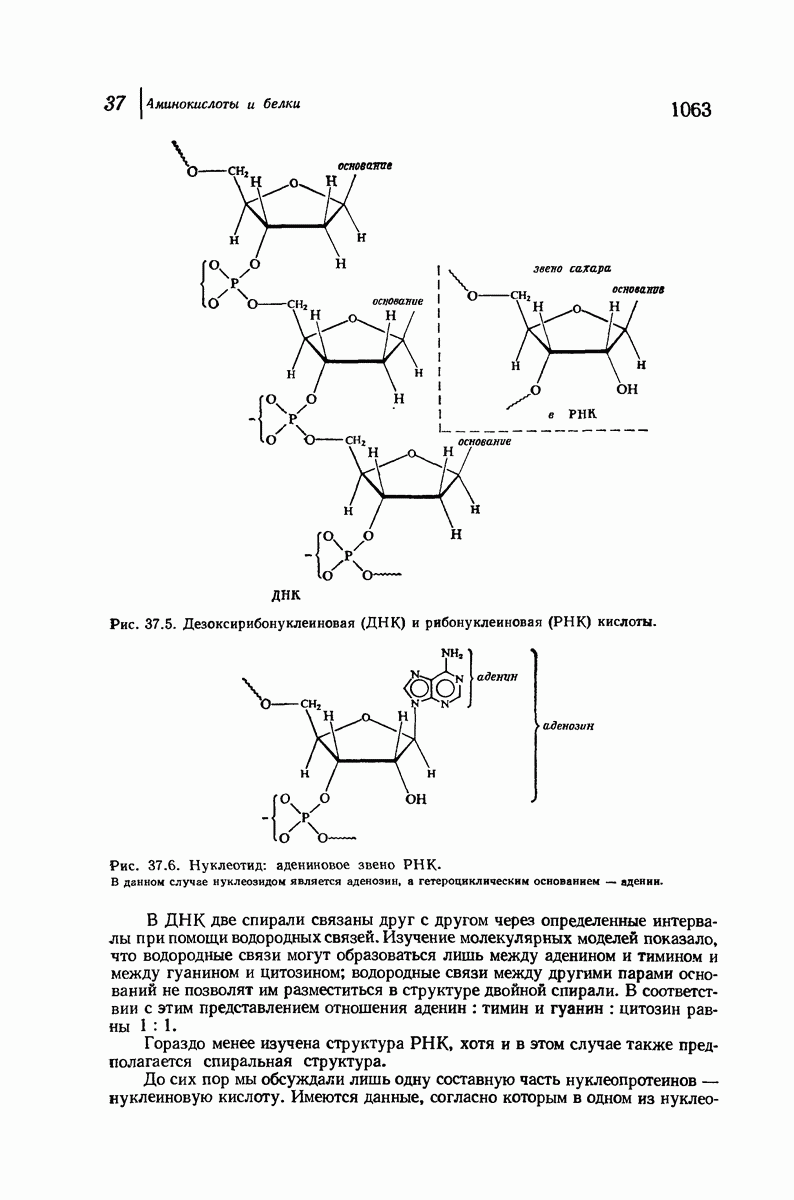
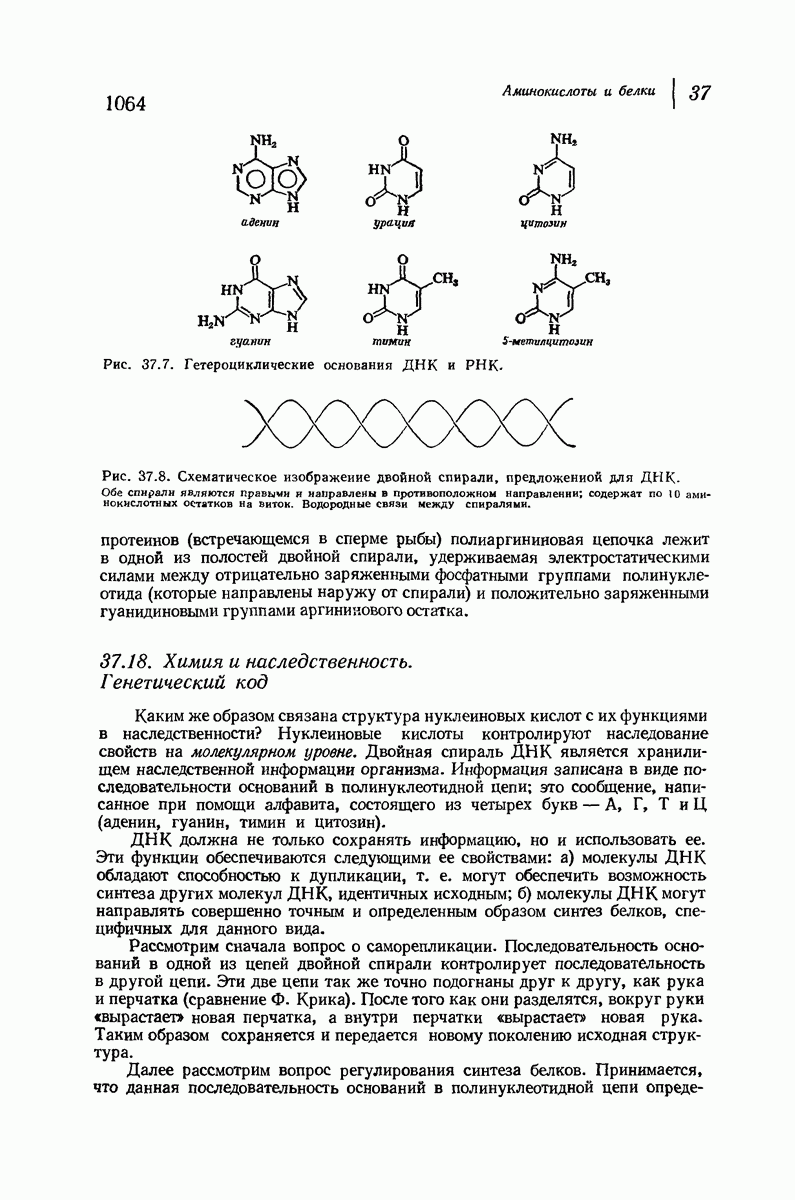
- 37.17. Нуклеопротеиды и нуклеиновые кислоты
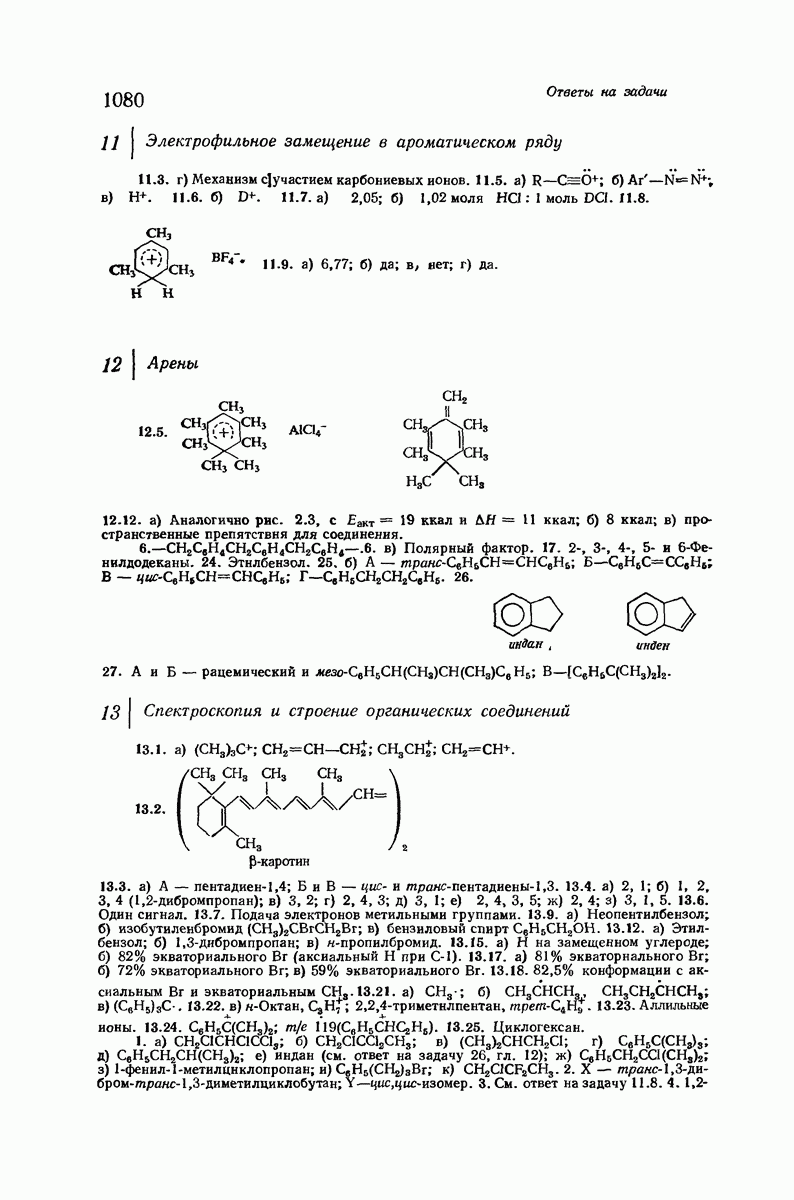
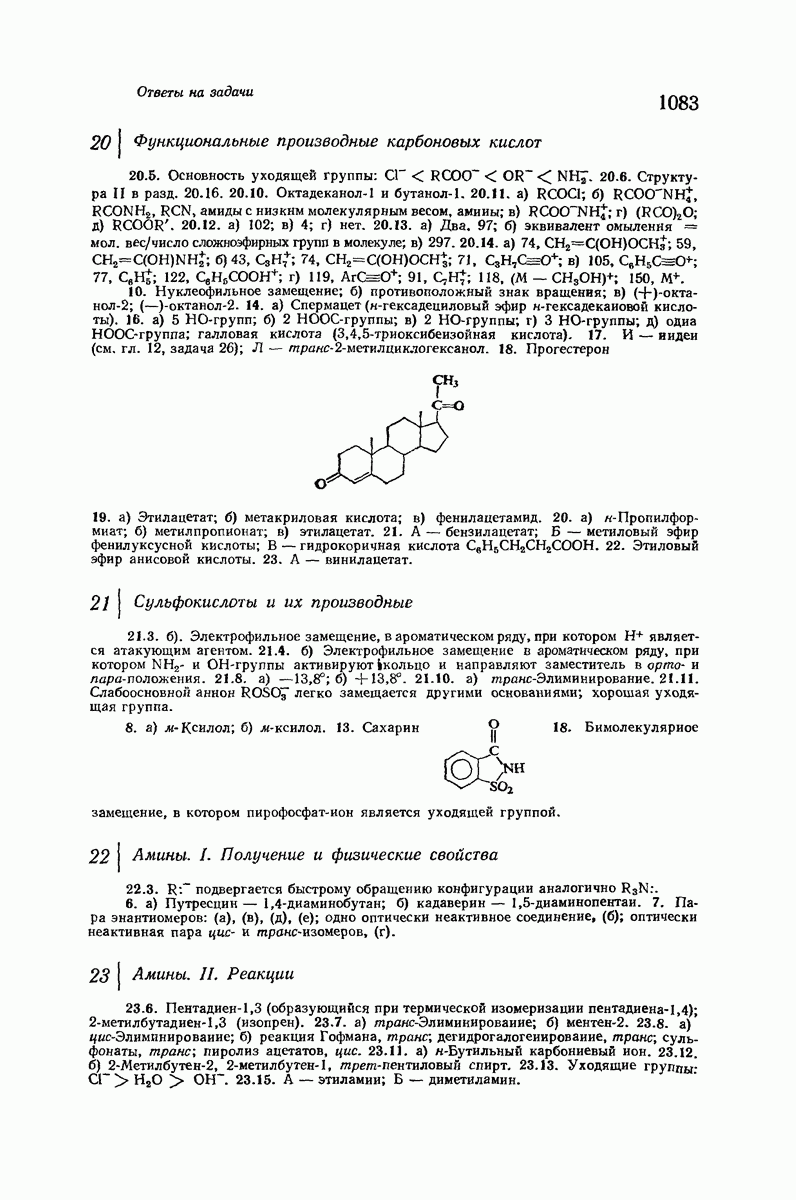
- 37.18. Химия и наследственность. Генетический код
- Список литературы для углубленного изучения