| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 15. Плоские волны вдоль идеально проводящих цилиндрических проводников.
Плоские волны могут распространяться не только в свободном пространстве пли в бесконечно протяженной диэлектрической среде с плоскими границами, но и вдоль системы идеально проводящих цилиндрических проводников, т. е. в некотором направлении z, вдоль которого поперечные сечения проводников не меняются. Согласно § 3 гл. XI, электромагнитное поле не проникает внутрь идеального проводника,  -токи текут лишь в бесконечно тонком слое по его поверхности, поэтому с идеальным проводником не связано никаких потерь энергии. Интересующую нас задачу можно решить несколькими способами. При получении результатов § 26 гл. VII считалось, что вектор-потенциал, а следовательно, согласно § 2, и вектор Герца ориентированы вдоль направления z, т. е. параллельно токам. Решение волнового уравнения для вектора Герца дает и скалярный потенциал и вектор-потенциал. Если, воспользовавшись уравнением (13.16), исключить скалярный потенциал,
-токи текут лишь в бесконечно тонком слое по его поверхности, поэтому с идеальным проводником не связано никаких потерь энергии. Интересующую нас задачу можно решить несколькими способами. При получении результатов § 26 гл. VII считалось, что вектор-потенциал, а следовательно, согласно § 2, и вектор Герца ориентированы вдоль направления z, т. е. параллельно токам. Решение волнового уравнения для вектора Герца дает и скалярный потенциал и вектор-потенциал. Если, воспользовавшись уравнением (13.16), исключить скалярный потенциал,  полученный вектор-потенциал будет лежать в плоскости, нормальной z. Тот же результат можно получить
полученный вектор-потенциал будет лежать в плоскости, нормальной z. Тот же результат можно получить
непосредственно, решая скалярное волновое уравнение

Решение получается, если каждую из скобок по отдельности приравнять нулюх). Это решение имеет вид

где  решения двухмерного уравнения Лапласа. Пусть
решения двухмерного уравнения Лапласа. Пусть  комплексные потенциальные функции, рассмотренные в гл. IV, тогда
комплексные потенциальные функции, рассмотренные в гл. IV, тогда

Если  определен как
определен как  , то из § 11 гл. IV мы имеем
, то из § 11 гл. IV мы имеем

Из соотношения (11.11) вектор-потенциал поперечного электрического поля равен

Очевидно, что первый член соответствует волне, распространяющейся в положительном направлении оси z, а второй — в отрицательном направлении оси z. Поля определяются по формулам

Верхний знак относится к волне, распространяющейся в положительном направлении. Из уравнений (13.117), (13.119) и (13.120) имеем

Будем различать две группы проводников, предполагая, что токи втекают в проводники одной группы и возвращаются по проводникам другой группы. Тогда из уравнения (13.120) с очевидностью следует, что если при некотором значении z потенциалы проводников, относящихся к одной и той же группе, одинаковы, то они останутся одинаковыми и при любых других значениях z. Для нахождения соотношения между полным током и суммарным зарядом в любой из групп, состоящей из  проводников, нужно воспользоваться формулой (13.121), уравнением (7.2), а также привлечь теорему Гаусса (1.40). В результате получим
проводников, нужно воспользоваться формулой (13.121), уравнением (7.2), а также привлечь теорему Гаусса (1.40). В результате получим

Обозначим через  самоиндукцию на единицу длины, через С — емкость на единицу длины, а через
самоиндукцию на единицу длины, через С — емкость на единицу длины, а через  -площадь поперечного сечения
-площадь поперечного сечения  не занимаемую проводниками. Тогда из соотношений (2.15), (2.47) и (8.35) имеем
не занимаемую проводниками. Тогда из соотношений (2.15), (2.47) и (8.35) имеем

Таким образом,  оказываются связанными между собой соотношением
оказываются связанными между собой соотношением

Произведение  равно величине, обратной квадрату скорости распространения электромагнитной волны в окружающей проводники среде.
равно величине, обратной квадрату скорости распространения электромагнитной волны в окружающей проводники среде.
Если в некоторой плоскости  задана зависимость векторов
задана зависимость векторов  от времени, то, пользуясь уравнением (13.118), легко получить выражение для А, пригодное при любых z,
от времени, то, пользуясь уравнением (13.118), легко получить выражение для А, пригодное при любых z,

Пусть  даются формулой (13.116), тогда выражение (13.125) приводит к следующим значениям полей в сечении
даются формулой (13.116), тогда выражение (13.125) приводит к следующим значениям полей в сечении  у
у

Столь же просто, пользуясь уравнением (13.118), написать выражение для А, если в момент  векторы
векторы  заданы в виде функции от
заданы в виде функции от 

Пусть  определены но формуле (13.116), тогда из выражения (13.127) для А получим следующие значения полей в момент времени
определены но формуле (13.116), тогда из выражения (13.127) для А получим следующие значения полей в момент времени 

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ ПЕРЕВОДЧИКОВ
- ОБОЗНАЧЕНИЯ
- Глава I. ОСНОВНЫЕ ПОЛОЖЕНИЯ ЭЛЕКТРОСТАТИКИ
- § 4. Электростатическая индукция.
- § 5. Элементарные электрические заряды.
- § 6. Напряженность электрического поля.
- § 7. Электростатический потенциал.
- § 8а. Электрические диполи и мультиполи.
- § 9. Силовые линии.
- § 10. Эквипотенциальные поверхности.
- § 11а. Теорема Гаусса о потоке электрической индукции.
- § 11б. Силовые линии системы коллинеарных зарядов.
- § 11в. Силовые линии на бесконечности.
- § 12. Максимумы и минимумы потенциала. Теорема Ирншоу.
- § 13. Потенциал двойного электрического слоя.
- § 14. Вектор электрической индукции и силовые трубки.
- § 15. Натяжения в электрическом поле.
- § 16. Теорема Гаусса о потоке электрической индукции для неоднородных сред.
- § 17. Граничные условия и натяжения на поверхности проводников.
- § 18. Граничные условия и натяжения на поверхности диэлектрика.
- § 19. Электрическая индукция и напряженность поля в твердых диэлектриках.
- § 20. Кристаллические диэлектрики.
- Глава II. КОНДЕНСАТОРЫ, ДИЭЛЕКТРИКИ, СИСТЕМЫ ПРОВОДНИКОВ
- § 2. Емкость.
- § 3. Последовательное и параллельное соединение конденсаторов.
- § 4. Сферический конденсатор.
- § 5. Цилиндрический конденсатор.
- § 6. Плоский конденсатор.
- § 7. Защитные кольца.
- § 8. Энергия заряженного конденсатора.
- § 9а. Энергия электрического поля.
- § 9б. Плоский конденсатор с кристаллическим диэлектриком.
- § 10. Натяжения в случае зависимости диэлектрической проницаемости от плотности среды.
- § 11. Электрострикция в жидких диэлектриках.
- § 12. Силы, действующие на проводник в диэлектрике.
- § 13. Теорема взаимности Грина.
- § 14. Суперпозиция полей.
- § 15. Индуцированные заряды на заземленных проводниках.
- § 16. Потенциальные коэффициенты.
- § 17. Собственная и взаимная емкости.
- § 18. Электростатическая экранировка.
- § 19. Потенциальные и емкостные коэффициенты в случае двух отдаленных проводников.
- § 20. Энергия системы зарядов.
- § 21. Силы и моменты сил, действующие на заряженные проводники.
- Глава III. ОБЩИЕ ТЕОРЕМЫ
- § 1. Теорема Остроградского-Гаусса.
- § 2. Теорема Стокса.
- § 3. Уравнения Пуассона и Лапласа.
- § 4. Ортогональные криволинейные координаты.
- § 5. Представление ротора в ортогональных криволинейных координатах.
- § 6. Представление оператора … в различных системах координат.
- § 7. Теорема Грина.
- § 8. Теорема взаимности Грина для диэлектрических сред.
- § 9. Функция Грина.
- § 10. Решение уравнения Пуассона.
- § 11. Теорема единственности при наличии диэлектрических сред.
- § 12. Внесение нового проводника.
- § 13. Эквивалентный слой Грина.
- § 14. Энергия диэлектрического тела в электрическом поле.
- § 15. Изменение электрической энергии системы при увеличении диэлектрической проницаемости.
- § 16. Потенциал аксиально-симметричного поля.
- Глава IV. ДВУХМЕРНОЕ РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА
- § 1. Двухмерные поля и потенциалы.
- § 2. Круговые гармоники.
- § 3. Представление потенциала поля линейного заряда в виде ряда по гармоникам.
- § 4. Проводящий или диэлектрический цилиндр в однородном поле.
- § 5. Диэлектрический цилиндр.
- § 6. Изображение в проводящем цилиндре.
- § 7. Изображение в плоской поверхности проводника или диэлектрика.
- § 8. Задача о диэлектрическом клине.
- § 9. Комплексные величины.
- § 10. Сопряженные функции.
- § 11. Функции потока.
- § 12. Напряженность электрического поля.
- § 13. Функции U и V для поля линейного заряда.
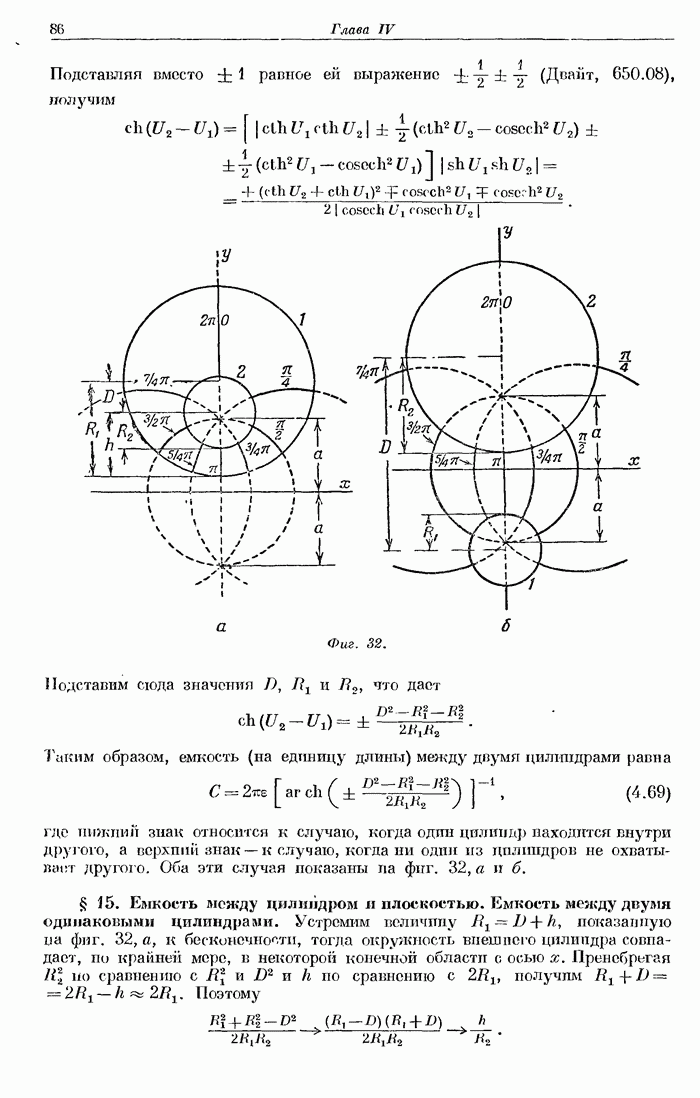
- § 14. Емкость между двумя круглыми цилиндрами.
- § 15. Емкость между цилиндром и плоскостью.
- § 16. Конформные преобразования.
- § 17. Уравнение границы в параметрической форме.
- § 18. Нахождение сопряженных функций.
- § 19. Преобразование Шварца.
- § 20. Многоугольники с одним положительным углом.
- § 21. Многоугольник с углом, равным нулю.
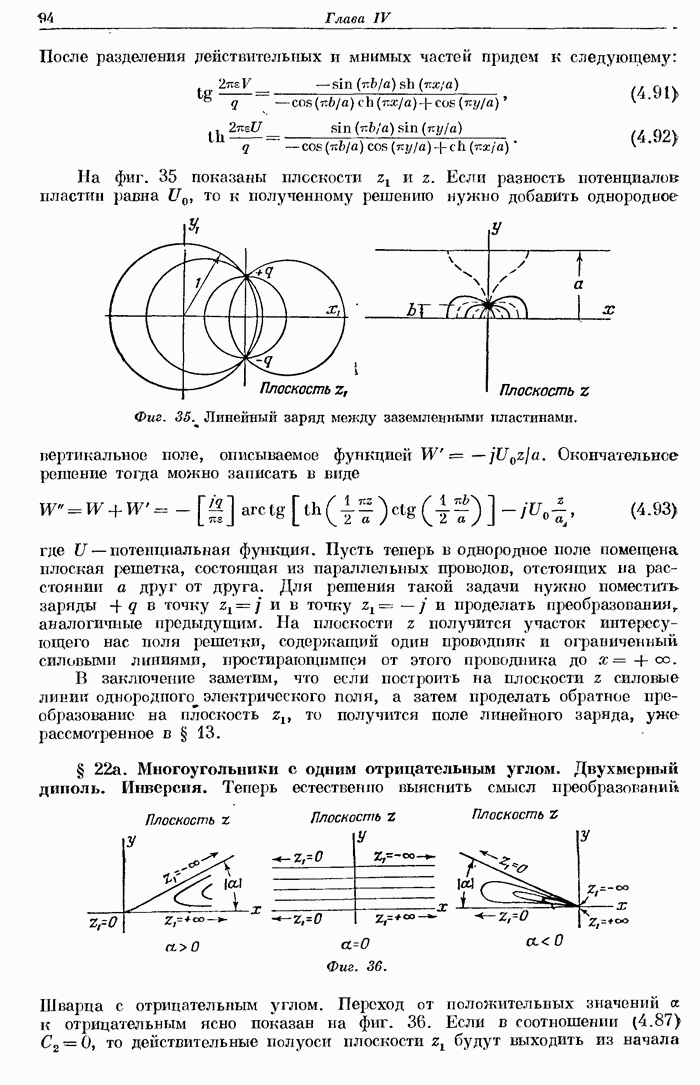
- § 22а. Многоугольники с одним отрицательным углом. Двухмерный диполь. Инверсия.
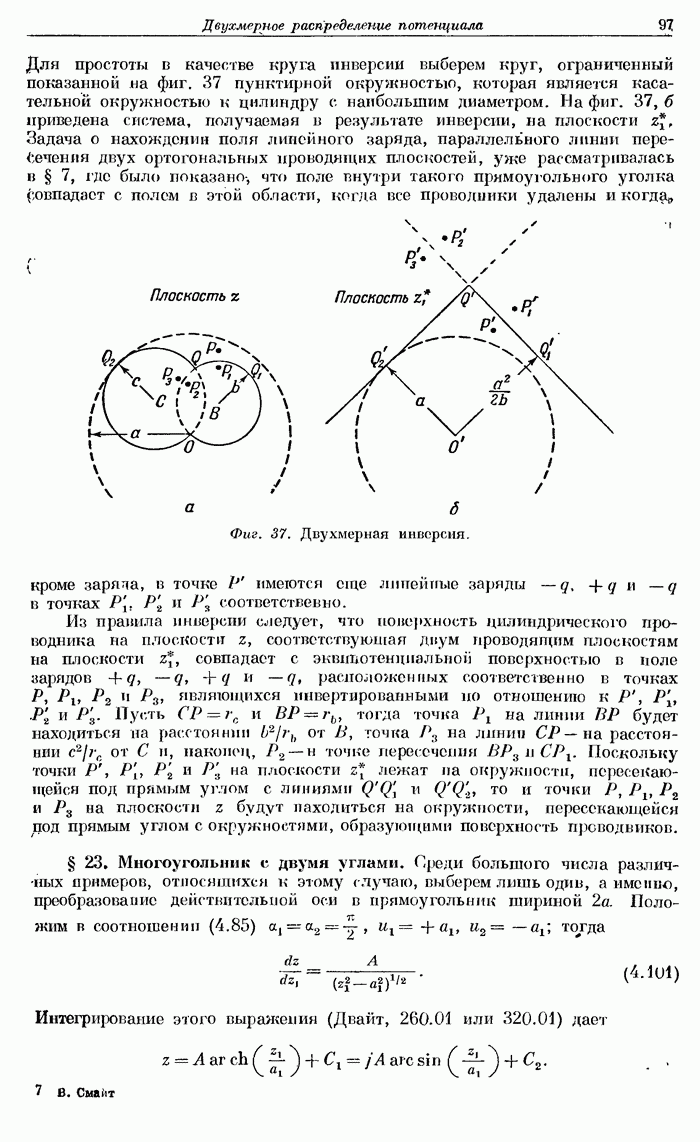
- § 22б. Изображения при двухмерной инверсии.
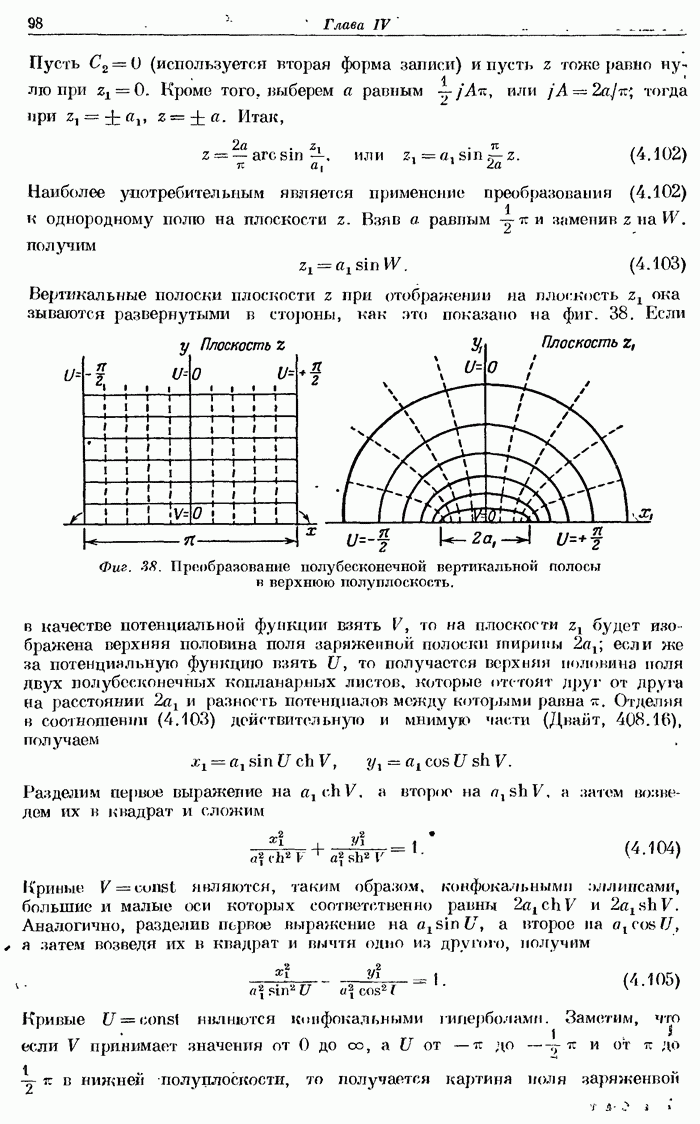
- § 23. Многоугольник с двумя углами.
- § 24. Щель, прорезанная в бесконечной плоскости.
- § 25. Римановы поверхности.
- § 26. Задача о круглом цилиндре, расположенном внутри эллиптического.
- § 27а. Условия на границе раздела двух диэлектриков.
- § 27б. Эллиптический диэлектрический цилиндр.
- § 27в. Момент, действующий на диэлектрический цилиндр.
- § 28. Многоугольник с закругленным углом.
- § 29. Плоская решетка из цилиндрических проводов большого диаметра.
- § 30. Случай углов, нецелократных pi/2.
- Глава V. ТРЕХМЕРНОЕ РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛА
- § 1. При каких условиях поверхности некоторого семейства могут быть эквипотенциальными?
- § 2. Потенциал поверхностей второго порядка, определяемых уравнением …
- § 3. Заряженный проводящий эллипсоид.
- § 4. Эллиптический и круглый диски.
- § 5. Метод изображений. Проводящие плоскости.
- § 6. Плоская граница двух диэлектриков.
- § 7. Изображение в сферическом проводнике.
- § 8. Пример применения метода изображений для нахождения поля точечного заряда.
- § 9а. Бесконечная система изображений. Задача о двух сферах.
- § 9б. Уравнения в конечных разностях. Задача о двух сферах.
- § 9в. Сфера над плоскостью и две одинаковые сферы.
- § 10. Инверсия в пространстве трех измерений. Геометрические свойства.
- § 11а. Инверсия потенциала и зарядов-изображений.
- § 11б. Пример инверсии изображений.
- § 11в. Инверсия заряженной проводящей поверхности.
- § 11г. Преобразование емкости при инверсии.
- § 12а. Пространствешпле гармоники.
- § 12б. Задача о клипе, ортогонально пересекающемся с поверхностью вращения.
- § 13. Сферические гармоники.
- § 14a. Общие свойства поверхностных гармоник.
- § 14б. Потенциал гармонического распределения заряда.
- § 15. Дифференциальные уравнения поверхностных гармоник.
- § 16а. Зональные гармоники. Уравнение Лежандра.
- § 16в. Полиномы Лежандра. Формула Родрига.
- § 16г. Коэффициенты Лежандра. Обратное расстояние.
- § 16д. Рекуррентные формулы для полиномов Лежандра.
- § 16е. Интеграл от произведения полиномов Лежандра.
- § 16ж. Разложение функций по полиномам Лежандра.
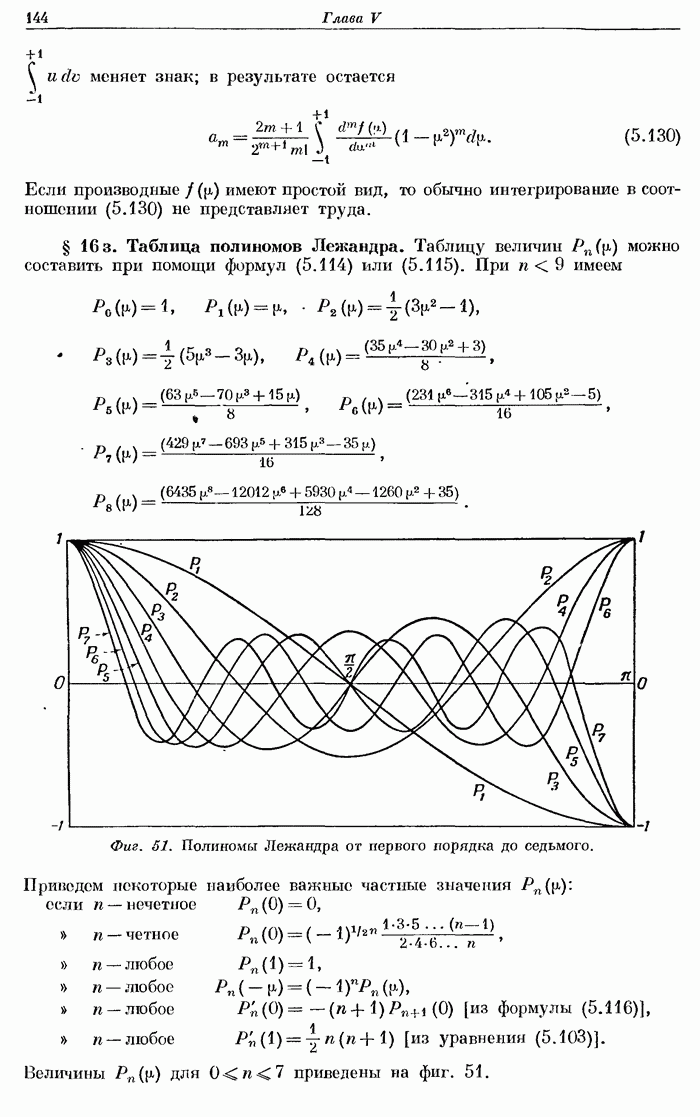
- § 16з. Таблица полиномов Лежандра.
- § 16и. Полиномы Лежандра мнимого аргумента.
- § 17. Потенциал заряженного кольца.
- § 18. Заряженное кольцо в проводящей сфере.
- § 19. Сферическая диэлектрическая оболочка в однородном поле.
- § 20. Сферический конденсатор с малым расстоянием между центрами внутренней и внешней обкладок.
- § 21. Задачи с простой конической границей.
- § 22а. Зональные гармоники второго рода.
- § 22б. Рекуррентные формулы для функций Лежандра второго рода.
- § 22в. Выражение функций Лежандра второго рода через полиномы Лежандра.
- § 22г. Некоторые значения функций Лежандра второго рода.
- § 22д. Функции Лежандра второго рода мнимого аргумента.
- § 22е. Применение функций Лежандра второго рода в теории потенциала.
- § 23. Зональные гармоники нецелого порядка.
- § 24а. Присоединенные функции Лежандра.
- § 24б. Интегралы от произведений присоединенных функции.
- § 24в. Присоединенные функции от мнимого аргумента.
- § 24г. Рекуррентные формулы для присоединенных функций Лежандра.
- § 24д. Некоторые значения присоединенных функций Лежандра.
- § 24е. Равновесные (нейтральные) точки и линии.
- § 25. Биаксиальные гармоники.
- § 26. Конические границы.
- § 27а. Присоединенные функции Лежандра нецелого порядка.
- § 27б. Функция Грина для конуса.
- § 27в. Функция Грина для конической полости.
- § 28а. «Сплюснутые» сфероидальные координаты.
- § 28б. Гармоники сплюснутого сфероида.
- § 28в. Проводящий лист с круглым отверстием.
- § 28г. Момент, действующий на диск в однородном ноле.
- § 28д. Потенциал заряда, распределенного по поверхности сфероида.
- § 28е. Представление потенциала точечного заряда через гармоники сплюснутого сфероида.
- § 29а. Гармоники вытянутого сфероида.
- § 29б. Вытянутый сфероид в однородном поле.
- § 30а. Уравнение Лапласа в цилиндрических координатах.
- § 30б. Уравнение Бесселя и функции Бесселя.
- § 30в. Модифицированное уравнение Бесселя и модифицированные функции Бесселя.
- § 30г. Решение уравнения Бесселя.
- § 30д. Рекуррентные формулы для функций Бесселя
- § 30е. Значения функций Бесееля на бесконечности.
- § 30ж. Интегралы от бесселевых функций.
- § 30з. Разложение в ряд по функциям Бесселя.
- § 30и. Функция Грина для цилиндра. Обратное расстояние.
- § 30к. Функция Грина для цилиндрической полости.
- § 31а. Функции Бесселя нулевого порядка.
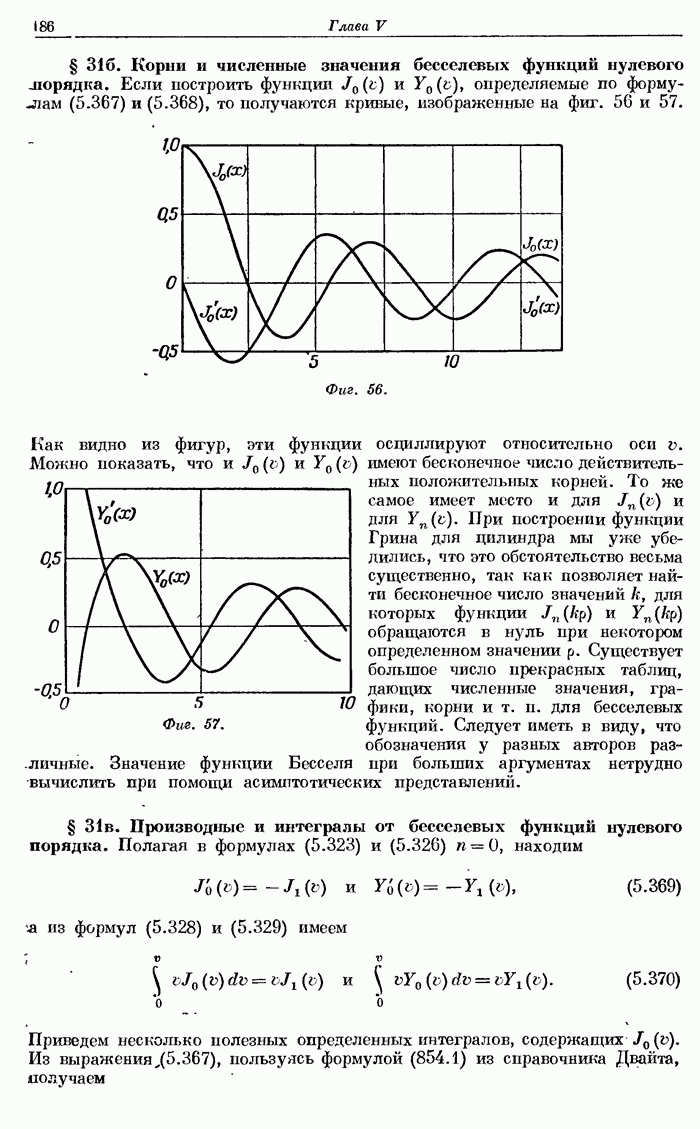
- § 31б. Корни и численные значения бесселевых функций нулевого порядка.
- § 31в. Производные и интегралы от бесселевых функций нулевого порядка.
- § 31г. Поле точечного заряда, расположенного над диэлектрической пластинкой.
- § 31д. Потенциал внутри полого цилиндрического кольца.
- § 32. Функция Бесселя нецелого порядка. Сферические функции Бесселя.
- § 33а. Модифицированные бесселевы функции.
- § 33б. Рекуррентные формулы для модифицированных бесселевых функций.
- § 33в. Значение модифицированных бесселевых функций на бесконечности.
- § 33г. Интеграл от произведения модифицированных бесселевых функций комплексного аргумента.
- § 33д. Функция Грина для кольцевой цилиндрической полости.
- § 34а. Модифицированные бесселевы функции нулевого порядка.
- § 34б. Интегральное представление модифицированных бесселевых функций второго рода.
- § 35. Интегральное представление бесселевых функций пулевого порядка.
- § 36а. Представление обратного расстояния через модифицированные бесселевы функции.
- § 36б. Цилиндрические границы раздела двух диэлектрических сред.
- § 37. Потенциал внутри кольцевой цилиндрической полости.
- § 38. Модифицированные бесселевы функции нецелого порядка.
- § 39. Приближеиные решения. Электростатические линзы.
- § 40. Функции клина.
- Глава VI. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 1. Плотность электрического тока. Уравнение непрерывности.
- § 2. Электродвижущая сила.
- § 3. Закон Ома. Удельное сопротивление.
- § 4. Тепловое действие электрического тока.
- § 5. Линейные проводники. Законы Кирхгофа. Последовательные и параллельные соединения проводников.
- § 6. Расчет электрических цепей. Контурные токи. Мост Уитстона.
- § 7. Цепи из одинаковых звеньев.
- § 8. Линия с непрерывно распределенной утечкой.
- § 9. Общая теория цепей.
- § 10. Сопряженные проводники. Двойной мост Кельвина.
- § 11. Постоянные токи в проводящих средах.
- § 12. Общие теоремы.
- § 13. Двухмерный ток.
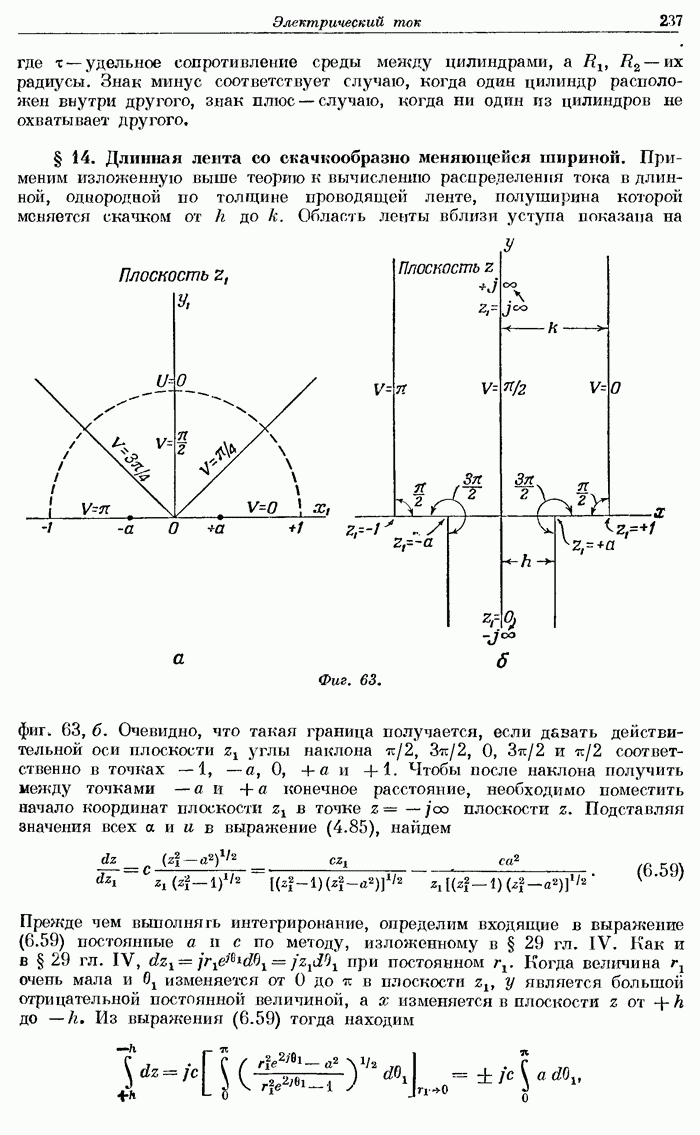
- § 14. Длинная лента со скачкообразно меняющейся шириной.
- § 15. Трехмерное распределение тока.
- § 16. Системы электродов. Две сферы. Удаленные электроды.
- § 17. Задача о проводящем шаре.
- § 18. Задача о сплошном проводящем цилиндре.
- § 19. Сопротивление земли.
- § 20. Токи в тонких изогнутых пленках.
- § 21. Распределение тока в сферической пленке.
- § 22. Поверхность вращения.
- § 23. Предельные значения сопротивления.
- § 24. Токи в анизотропных средах. Слои в земной коре.
- § 25. Ток, обусловленный движением пространственного заряда. Уравнение Чайльда.
- Глава VII. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ТОКОВ
- § 1. Определение единицы силы тока (ампера) через величину магнитного момента.
- § 2. Магнитная индукция и магнитная проницаемость.
- § 3. Магнитный вектор-потенциал. Однородное поле.
- § 4. Теоремы единственности в магнитостатике.
- § 5. Разложение вектор-потенциала но ортогональным функциям.
- § 6. Вектор-потенциал в цилиндрических координатах.
- § 7. Вектор-потенциал в сферических координатах.
- § 8. Выражение для вектор-потенциала через значение магнитной индукции на оси.
- § 9. Уравнение аксиально симметричных трубок магнитной индукции.
- § 10. Вектор-потенциал и поле двухпроводной линии.
- § 11. Вектор-потенциал и поле круглой петли.
- § 12. Поле токов, текущих по сферической пленке.
- § 13. Зональные токи в сферической пленке.
- § 14. Представление поля круглой петли через сферические, гармоники.
- § 15. Закон Био и Савара. Поле прямолинейного провода.
- § 16. Поле соленоида с произвольным шагом намотки.
- § 17. Поле в цилиндрической полости внутри проводящего круглого стержня.
- § 18. Поле токов, текущих вдоль цилиндрической проводящей пленки.
- § 19. Сила, действующая на электрический контур в магнитном ноле.
- § 20. Примеры на вычисление сил взаимодействия между электрическими контурами.
- § 21. Вектор-потенциал и вектор намагниченности.
- § 22. Граничные условия для магнитных полей и для вектор-потенциалов.
- § 23. Пример использования векторов a и A.
- § 24. Метод изображений для токов в случае плоской границы.
- § 25. Магнитная индукция и магнитная проницаемость в кристаллах.
- § 26. Двухмерные магнитные поля.
- § 27. Магнитное экранирование двухпроводной линии.
- § 28. Метод изображений для токов в двухмерных системах.
- § 29. Магнитодвижущая сила и напряженность магнитного поля.
- § 30. Магнитный контур. Тор.
- § 31. Магнитный контур с воздушным зазором.
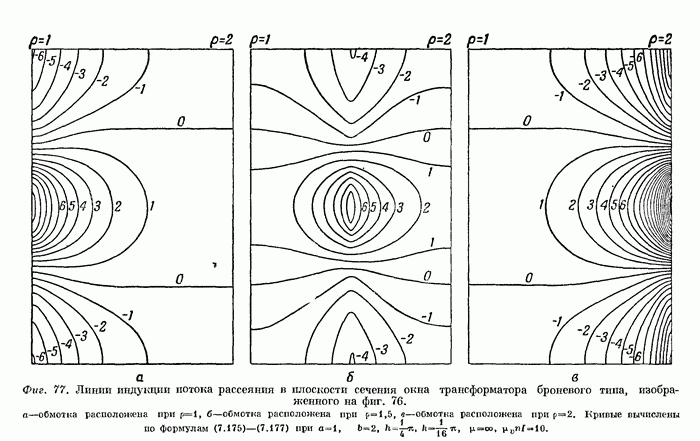
- § 32. Поле в трансформаторе броневого типа.
- § 33. Полюс с расщепленным наконечником. Эффективный воздушный зазор.
- Глава VIII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
- § 1. Закон индукции Фарадея.
- § 2. Взаимная энергия двух контуров.
- § 3. Энергия магнитного поля.
- § 4. Коэффициент взаимной индукции.
- § 5. Граничные условия для a.
- § 6. Коэффициент взаимной индукции простейших контуров.
- § 7. Коэффициент взаимной индукции двух колец.
- § 8. Переменная взаимная индукция.
- § 9. Самоиндукция.
- § 10. Вычисление самоиндукции. Тонкий провод.
- § 11. Самоиндукция круглой петли.
- § 12. Самоиндукция соленоида.
- § 13. Самоиндукция двухпроводной линии.
- § 14. Энергия n контуров.
- § 15. Натяжения в магнитном поле.
- § 16. Энергия магнетика в статическом магнитном поле.
- Глава IX. ПЕРЕХОДНЫЕ ЯВЛЕНИЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 1. Неустановившиеся электрические процессы.
- § 2. Энергетические соотношевия в электрической цепи.
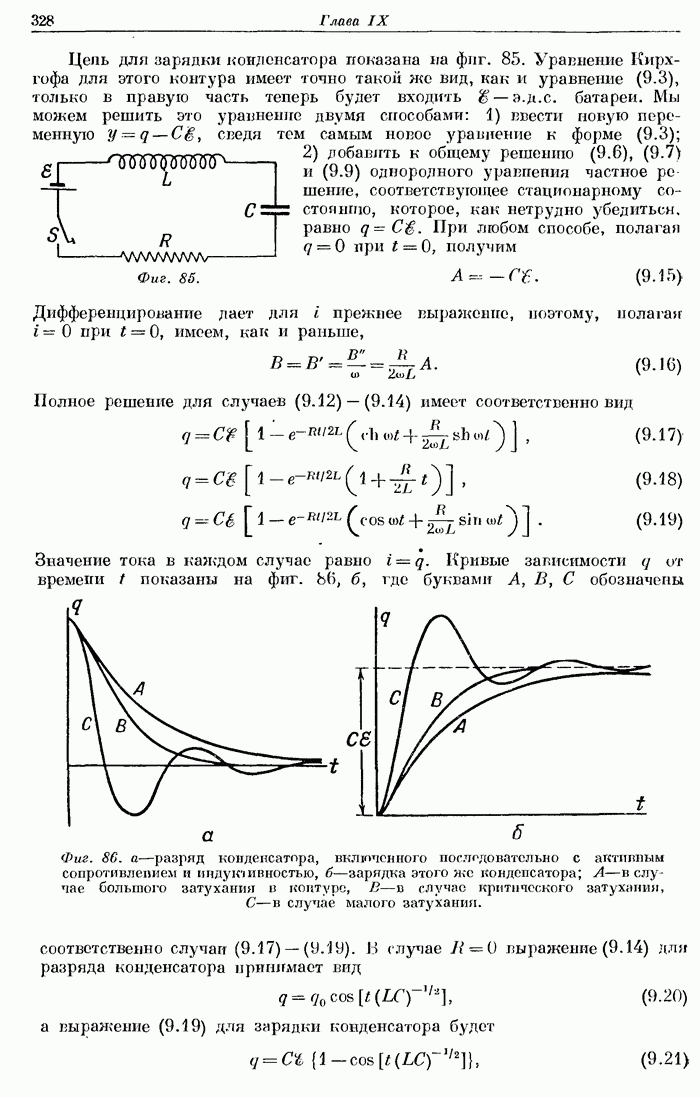
- § 3. Контур, состоящий из емкости, индуктивности и сопротивления.
- § 4. Зарядка и разряд конденсатора.
- § 5а. Нарастание и спадание тока в катушке индуктивности.
- § 5б. Индуктивно связанные контуры.
- § 6. Кинетическая энергия и электрокинетический импульс.
- § 7. Общий вид уравнений переходных процессов в цепях.
- § 8. Решение для цепей общего вида.
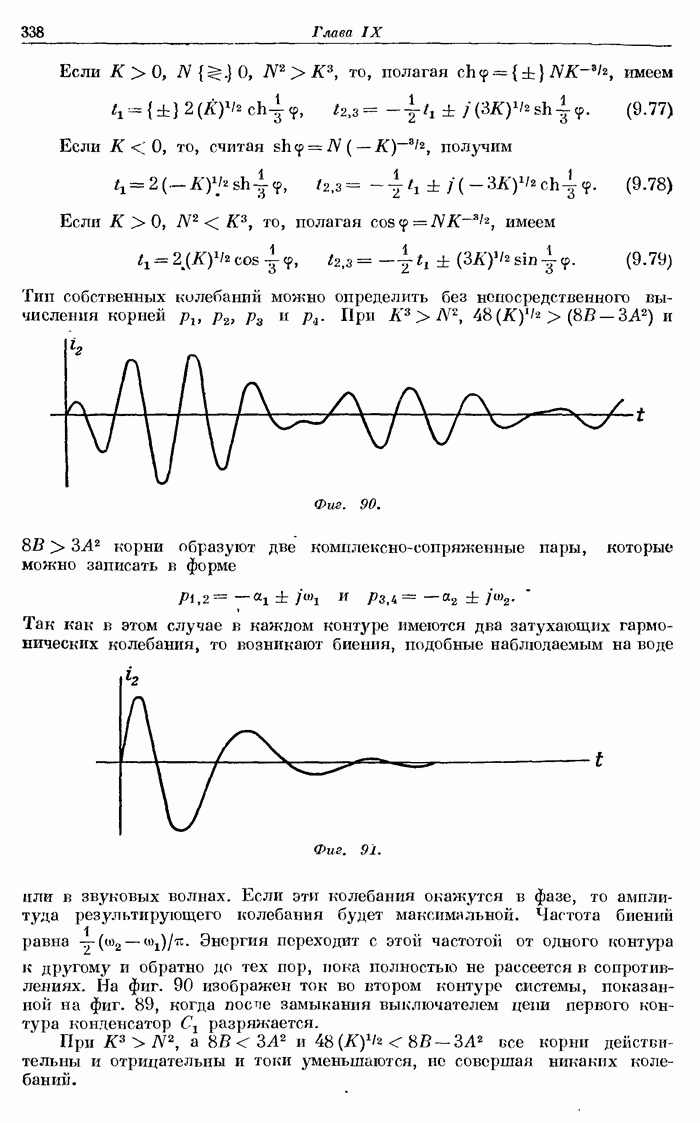
- § 9. Типы собственных колебаний.
- § 10. Цепь, содержащая постоянную э.д.с.
- § 11. Собственные частоты двух индуктивно связанных контуров.
- § 12. Амплитуды колебаний в двух связанных контурах.
- § 13. Колебательный режим.
- § 14. Индуктивно связанные контуры, обладающие малым активным сопротивлением.
- § 15. Настроенные индуктивно связанные контуры, обладающие малым активным сопротивлением.
- § 16. Цепи из одинаковых звеньев.
- § 17. Интегральный эффект переходного процесса.
- § 18. Переходные явления при импульсах конечной продолжительности.
- Глава X. ПЕРЕМЕННЫЕ ТОКИ
- § 1. Гармонические электродвижущие силы. Частное решение.
- § 2. Контур, содержащий сопротивление, емкость и индуктивность.
- § 3. Мощность, эффективные значения, резонанс.
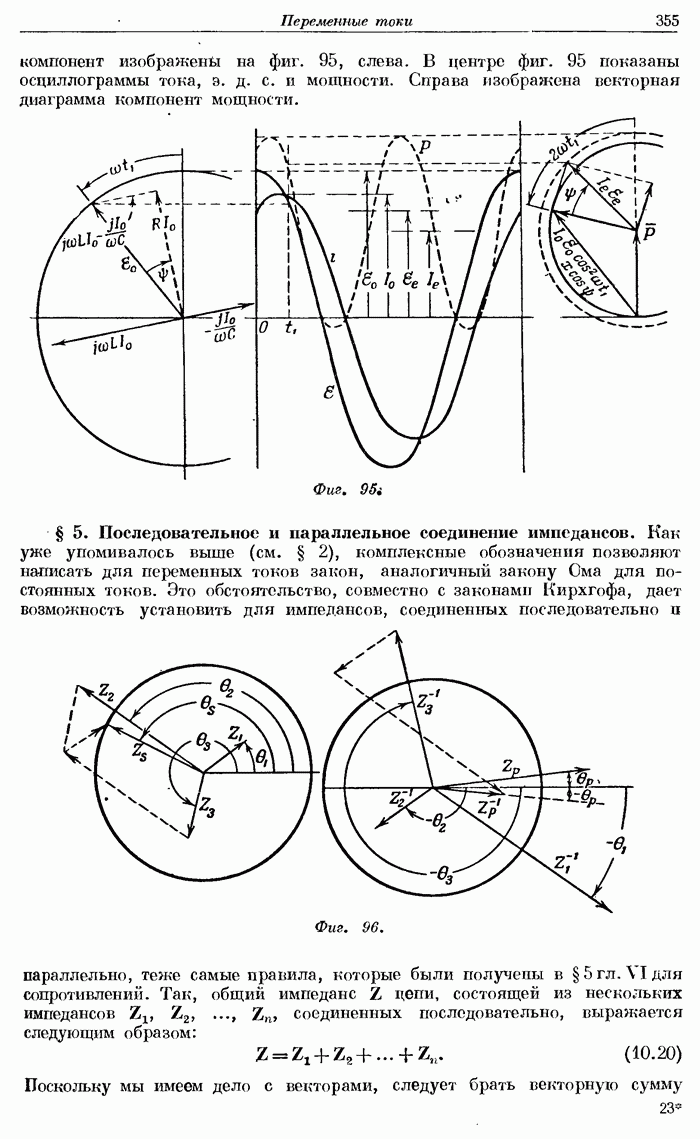
- § 4. Графическое представление. Векторная диаграмма.
- § 5. Последовательное и параллельное соединение импедансов.
- § 6. Передача мощности.
- § 7. Мостик импедансов.
- § 8. Цепь переменного тока в общем случае.
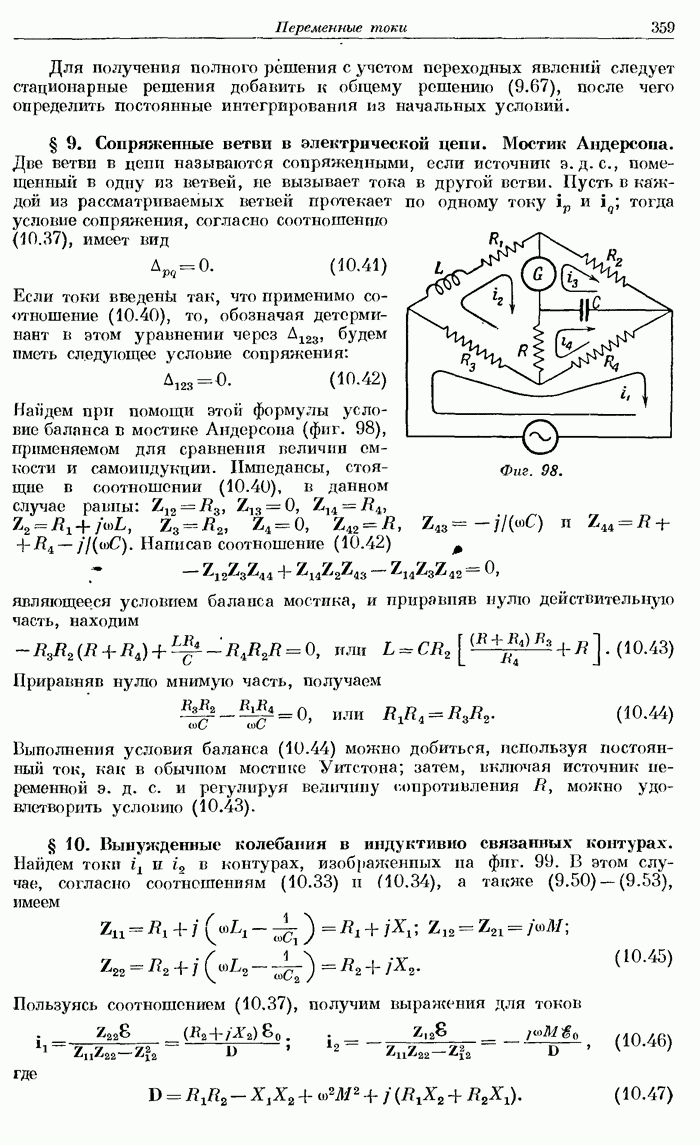
- § 9. Сопряженные ветви в электрической цепи. Мостик Андерсона.
- § 10. Вынужденные колебания в индуктивно связанных контурах.
- § 11. Индуктивно связанные контуры, обладающие малым активным сопротивлением.
- § 12. Настроенные индуктивно связанные контуры, обладающие малым активным сопротивлением.
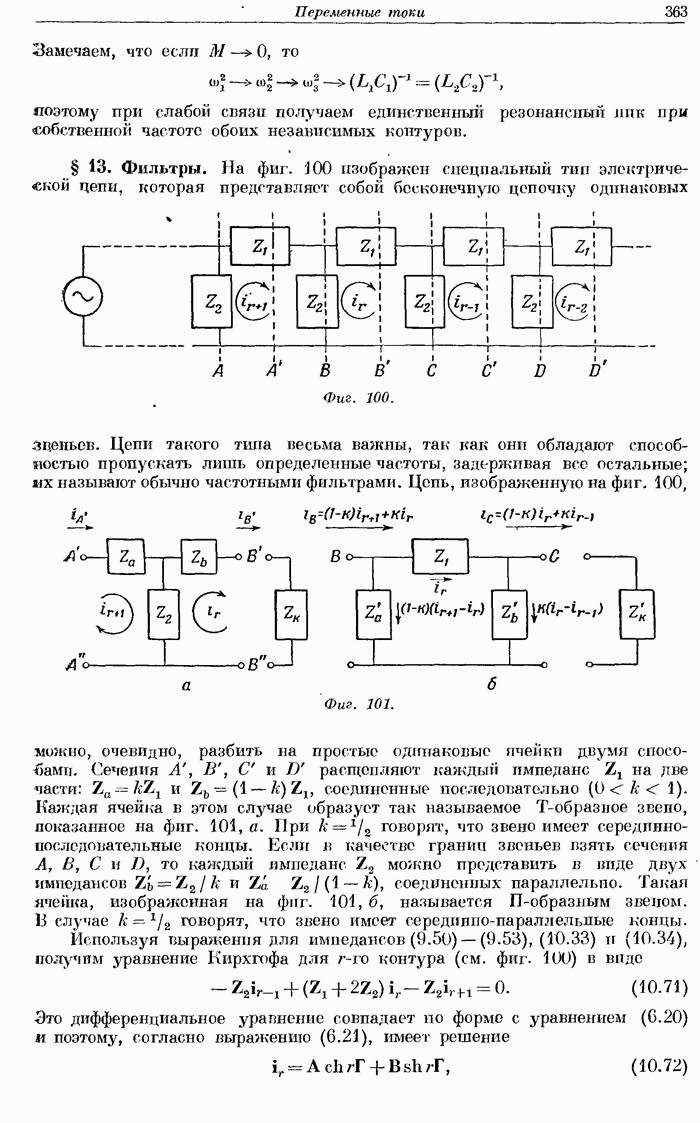
- § 13. Фильтры.
- § 14. Условия на концах в частотных фильтрах.
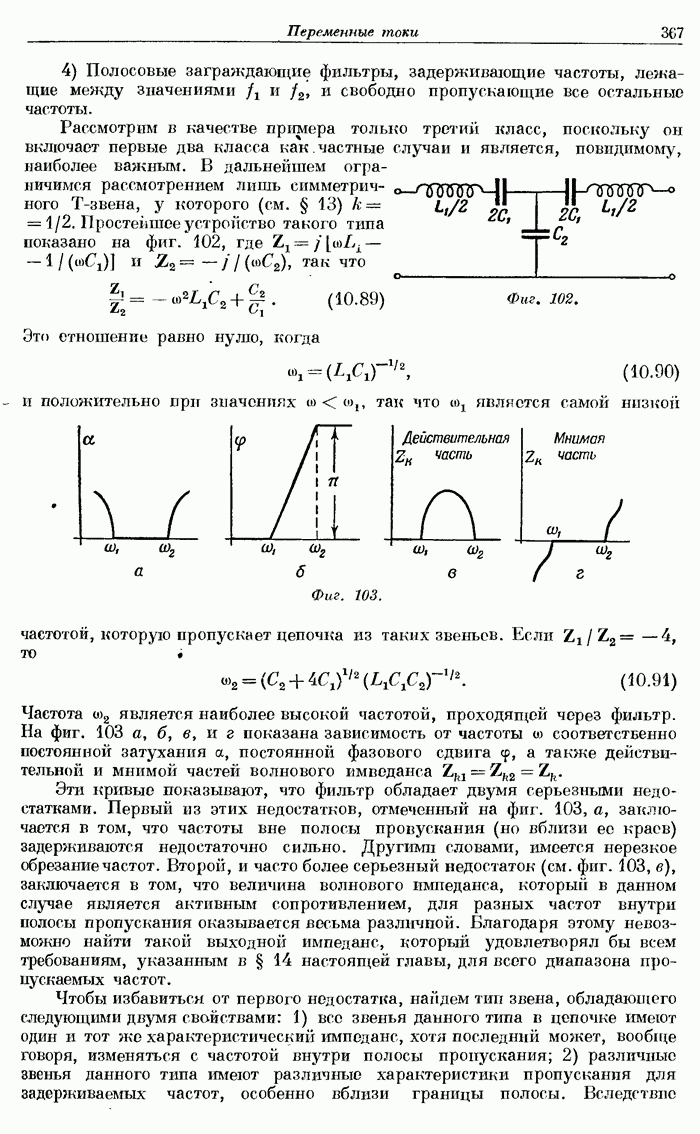
- § 15. Частотные характеристики фильтров.
- § 16. Полосовой фильтр.
- § 17. Производные звенья типа M.
- § 18. Выходное устройство фильтра.
- § 19. Линии передачи.
- § 20. Электродвижущие силы несинусоидальной формы. Метод рядов Фурье.
- § 21. Электродвижущие силы несинусоидальной формы. Метод повторяющегося переходного режима.
- § 22. Контур с отрицательным активным сопротивлением.
- Глава XI. ВИХРЕВЫЕ ТОКИ
- § 1. Индуцированные токи в объемных проводниках.
- § 2. Решение уравнения для вектор-потенциала вихревых токов.
- § 3. Скин-эффект в стационарном случае.
- § 4. Скин-эффект в случае полого цилиндрического проводника.
- § 5. Скин-эффект в сплошном цилиндрическом проводнике.
- § 6. Решение в сферических координатах при аксиальной симметрии.
- § 7. Проводящий шар в переменном поле.
- § 8. Мощность, поглощаемая шаром в переменном магнитном поле.
- § 9. Переходные явления в проводящем шаре.
- § 10. Вихревые токи в плоских пластинках.
- § 11. Решение задачи о вихревых токах в плоской бесконечной пластинке методом изображений.
- § 12. Момент, действующий на вращающуюся петлю с током или магнитный диполь.
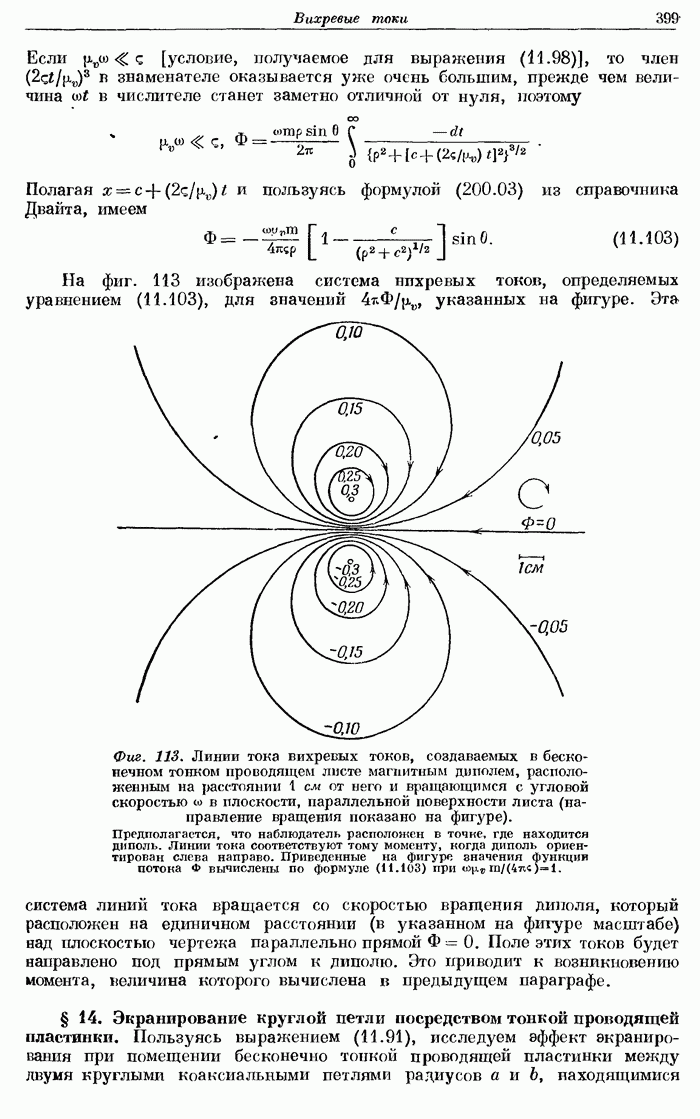
- § 13. Вихревые токи, возбуждаемые вращающимся диполем.
- § 14. Экранирование круглой петли посредством тонкой проводящей пластинки.
- § 15. Зональные вихревые токи в сферической пленке.
- § 16. Вихревые токи в тонкой цилиндрической пленке.
- § 17. Переходные явления при экранировании с помощью толстой цилиндрической оболочки.
- Глава XII. МАГНЕТИЗМ
- § 1. Парамагнетизм и диамагнетизм.
- § 2. Магнитная восприимчивость.
- § 3. Магнитные свойства кристаллов.
- § 4. Кристаллический шар в однородном магнитном поле.
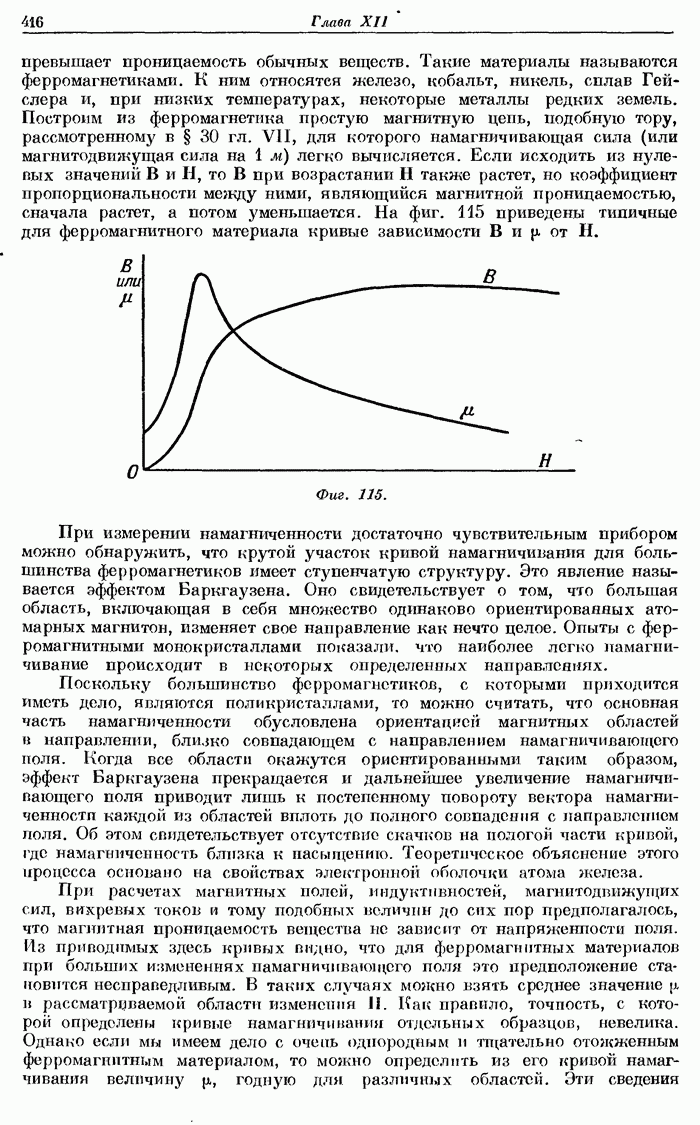
- § 5. Ферромагнетизм.
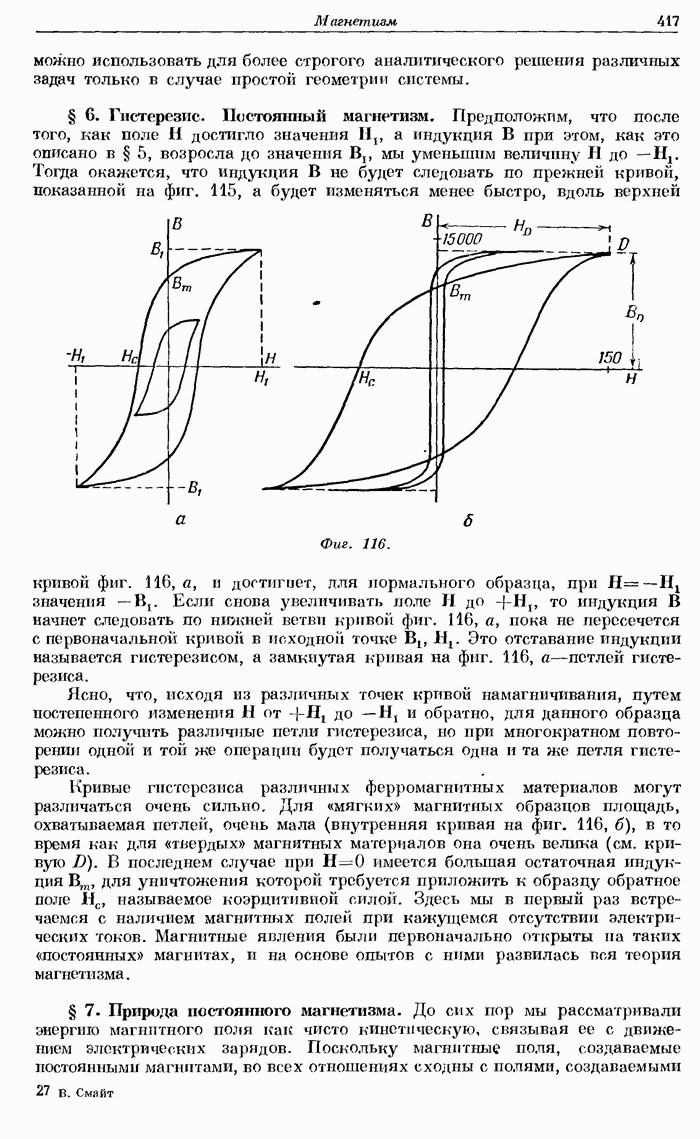
- § 6. Гистерезис. Постоянный магнетизм.
- § 7. Природа постоянного магнетизма.
- § 8. Равномерное намагничивание. Эквивалентный поверхностный ток.
- § 9. Намагниченный шар и цилиндр. Магнитные полюсы.
- § 10. Условия на границе с постоянным магнитом.
- § 11. Сферический постоянный магнит в однородном поле.
- § 12а. Подъемная сила подковообразного магнита.
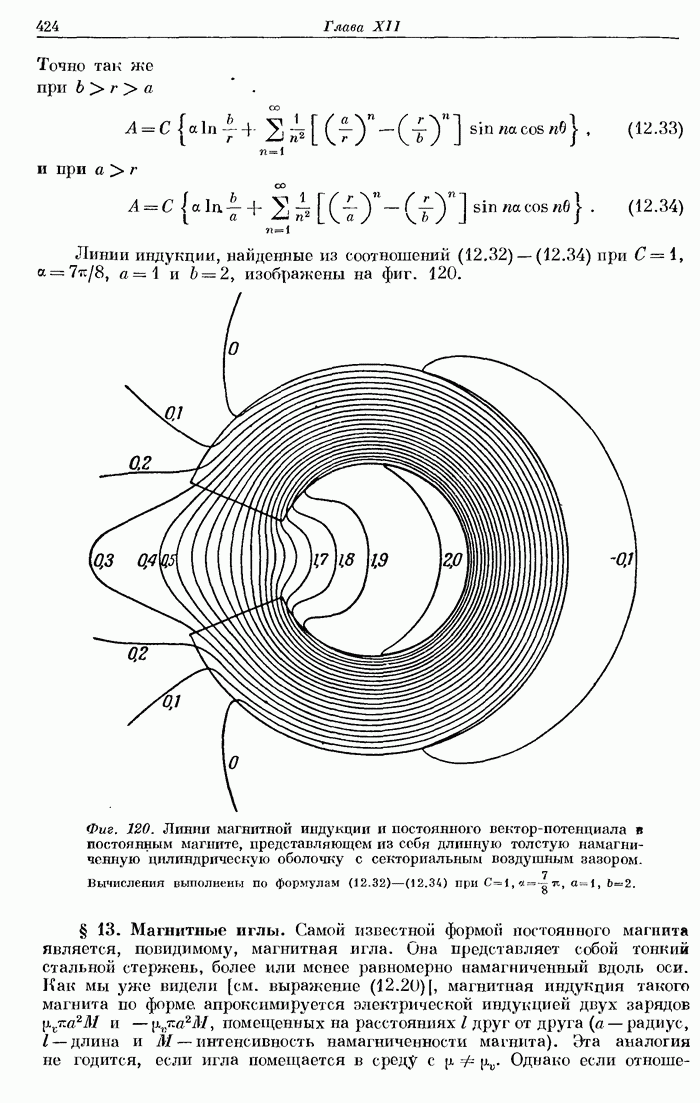
- § 12б. Поле цилиндрического магнита.
- § 13. Магнитные иглы.
- Глава XIII. ПЛОСКИЕ ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- § 2. Волновое уравнение. Электромагнитные потенциалы. Вектор Герца.
- § 3. Вектор Умова-Пойнтинга.
- § 4. Плоские волны в однородном незаряженном диэлектрике.
- § 5. Скорость распространения волны в анизотропных средах.
- § 6. Поверхность, образованная, лучом, и поляризация в анизотропных средах.
- § 7. Энергия, давление и импульс плоской волны.
- § 8. Отражение и преломление плоских волн.
- § 9. Интенсивности отраженной и преломленной волн.
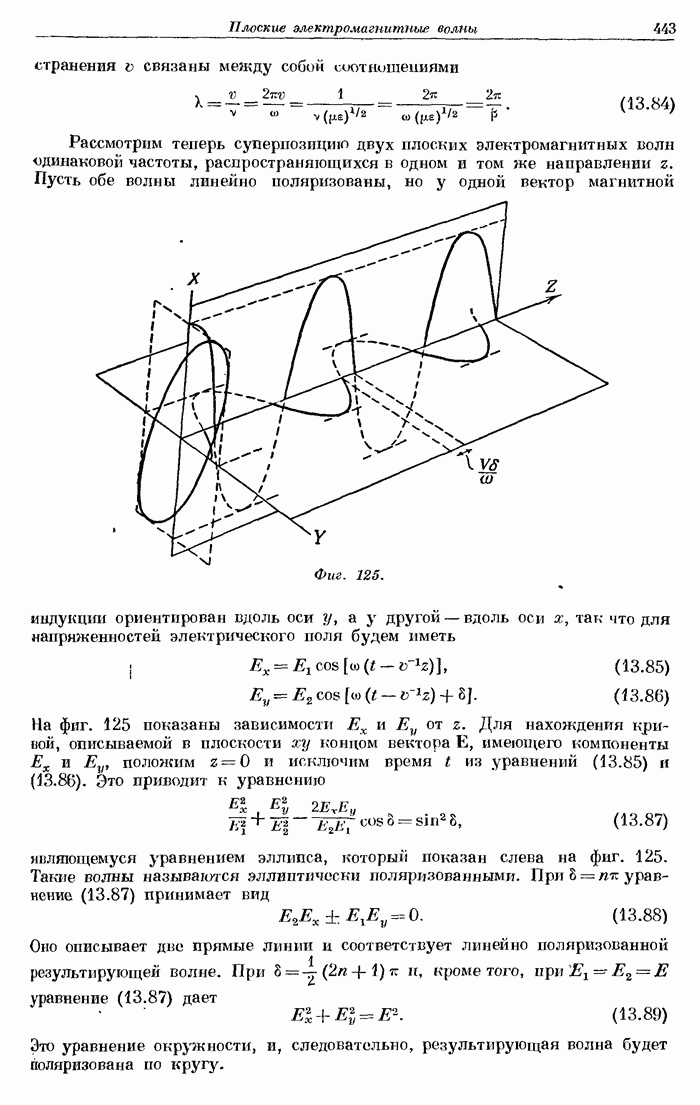
- § 10. Частота. Длина волны. Эллиптическая поляризация.
- § 11. Полное отражение.
- § 12. Электромагнитные волны в однородных проводниках.
- § 13. Плоские волны в однородных изотропных проводниках.
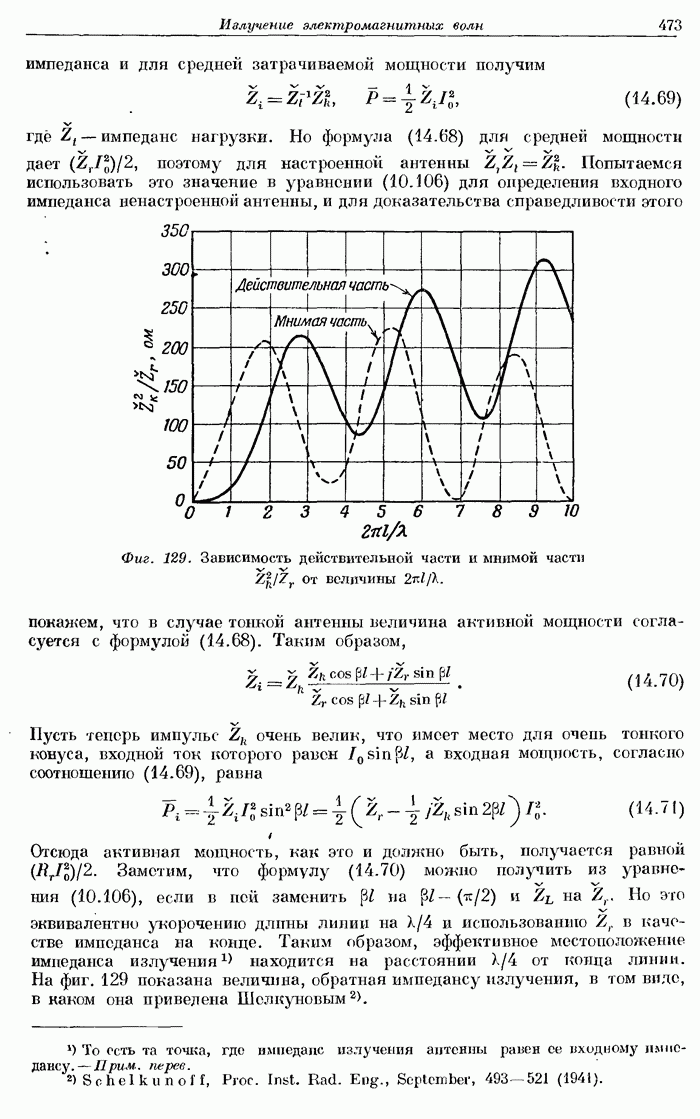
- § 14. Отражение от проводящей поверхности.
- § 15. Плоские волны вдоль идеально проводящих цилиндрических проводников.
- § 16. Характеристический импеданс среды
- § 17. Отражения от иеоднородностей. Согласующие секции.
- § 18. Комплексный вектор Умова-Пойнтинга.
- § 19. Квазиплоские волны вдоль неидеальных проводников. Двухпроводная линия Лехера.
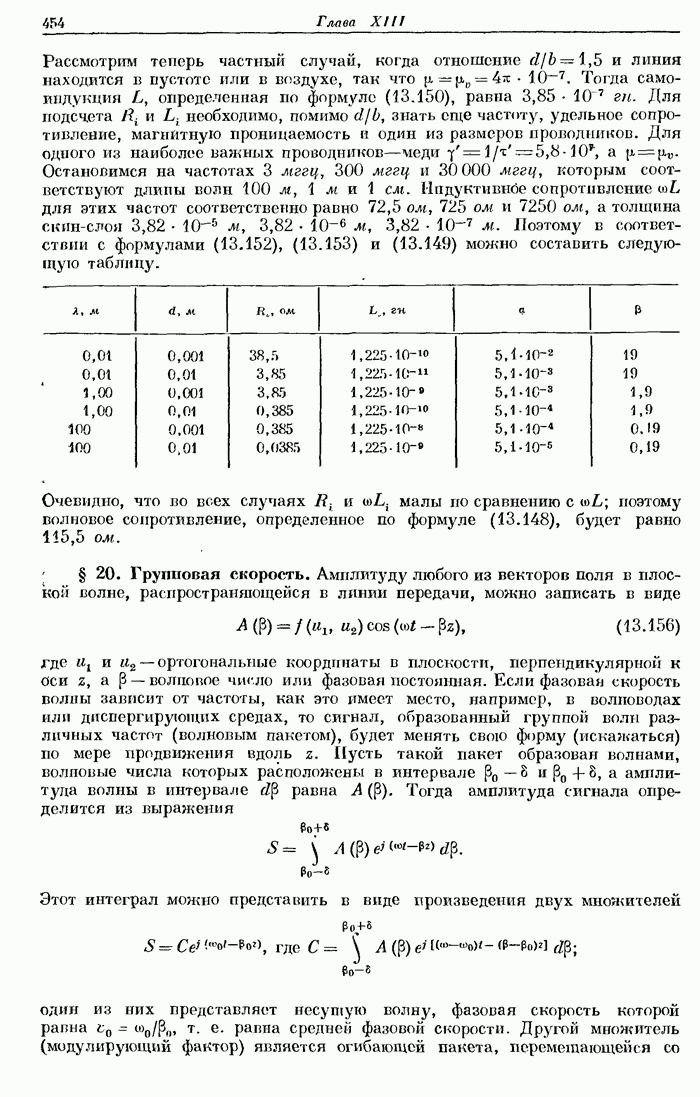
- § 20. Групповая скорость.
- Глава XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
- § 2. Два типа вектор-потенциалов.
- § 3. Сферические электромагнитные волны. Диполь.
- § 4. Запаздывающие потенциалы.
- § 5. Излучение линейной антенны.
- § 6. Поля на больших расстояниях от линейной антенны.
- § 7. Излучение бегущей волны.
- § 8. Коническая линия передачи.
- § 9. Биконическая антенна.
- § 10. Сложные антенны.
- § 11. Влияние земли.
- § 12. Единственность решения.
- § 13. Решения волнового уравнения в сферических координатах.
- § 14. Разложение плоской волны по полиномам Лежандра.
- § 15. Излучение кольцевого тока. Магнитный диполь.
- § 16. Свободные колебания проводящей сферы.
- § 17. Вынужденные колебания диэлектрического или проводящего шара.
- § 18. Решения волнового уравнения в цилиндрических координатах.
- § 19. Разложение плоской волны по цилиндрическим гармоникам
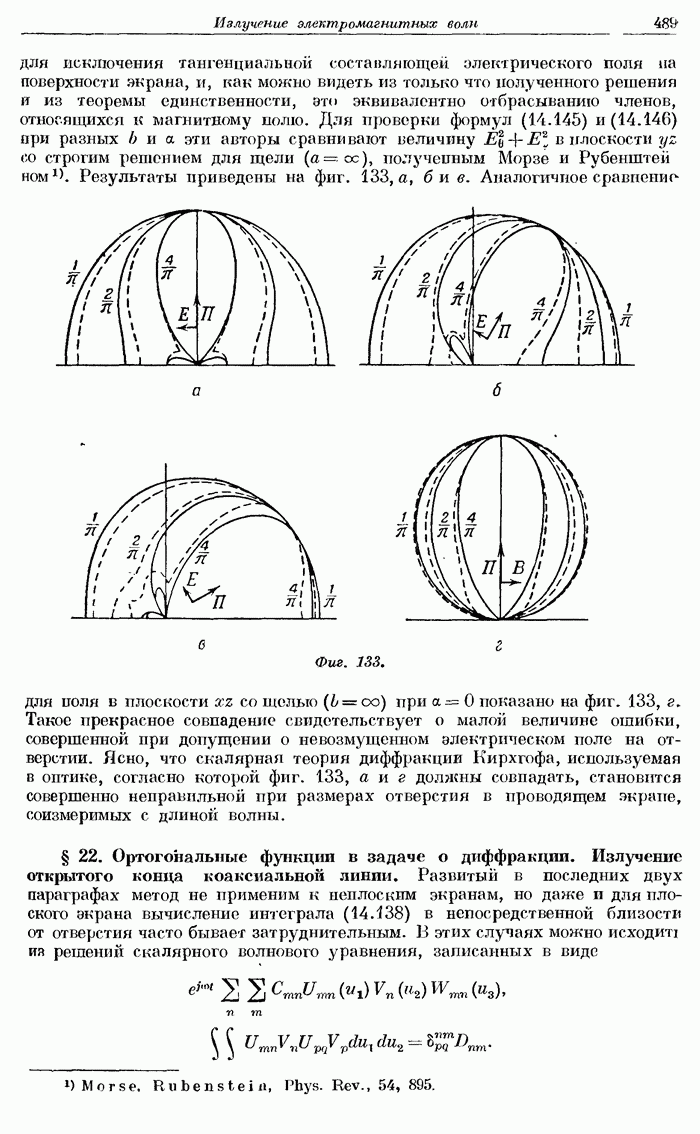
- § 20. Излучение из отверстий в плоском проводящем экране.
- § 21. Диффракция на прямоугольном отверстии в проводящем плоском экране.
- § 22. Ортогональные функции в задаче о диффракции. Излучение открытого конца коаксиальной линии.
- Глава XV. ВОЛНОВОДЫ И ПОЛЫЕ РЕЗОНАТОРЫ
- § 1. Волны в полых цилиндрических трубах.
- § 2. Учет затухания в волноводах.
- § 3. Прямоугольный волновод.
- § 4. Круглый волновод.
- § 5. Коаксиальный волновод.
- § 6. Плоские неоднородности в коаксиальной линии.
- § 7. Возбуждение волноводов.
- § 8. Возбуждение круглого волновода элементом тока.
- § 9. Возбуждение круглого волновода петлей с током.
- § 10. Возбуждение круглого волновода через отверстие.
- § 11. Плоские неоднородности в прямоугольных волноводах.
- § 12. Полые резонаторы. Собственные колебания.
- § 13. Типы независимых собственных колебаний полости.
- § 14. Емкость и индуктивность цилиндрической полости.
- § 15. Затухание собственных колебаний. Активное сопротивление полости.
- § 16. Собственные колебания цилиндрической полости.
- § 17. Свойства прямоугольного резонатора.
- § 18. Свойства резонатора, имеющего форму круглого цилиндра.
- § 19. Многосвязные цилиндрические полые резонаторы.
- § 20. Отрезок коаксиального кабеля как резонатор.
- § 21. Собственные колебания сферической полости.
- § 22. Собственные колебания реальных полых резонаторов.
- § 23. Полые резонаторы сложной формы.
- § 24. Возбуждение полого резонатора петлей с током.
- § 25. Возбуждение круглого цилиндрического резонатора петлей с током.
- § 26. Возбуждение полого резонатора при помощи электрода.
- § 27. Возбуждение полого резонатора через отверстие.
- Глава XVI. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ И ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ
- § 1. Постулаты специальной теории относительности.
- § 2. Преобразование Лоренца.
- § 3. Преобразование скорости и ускорения.
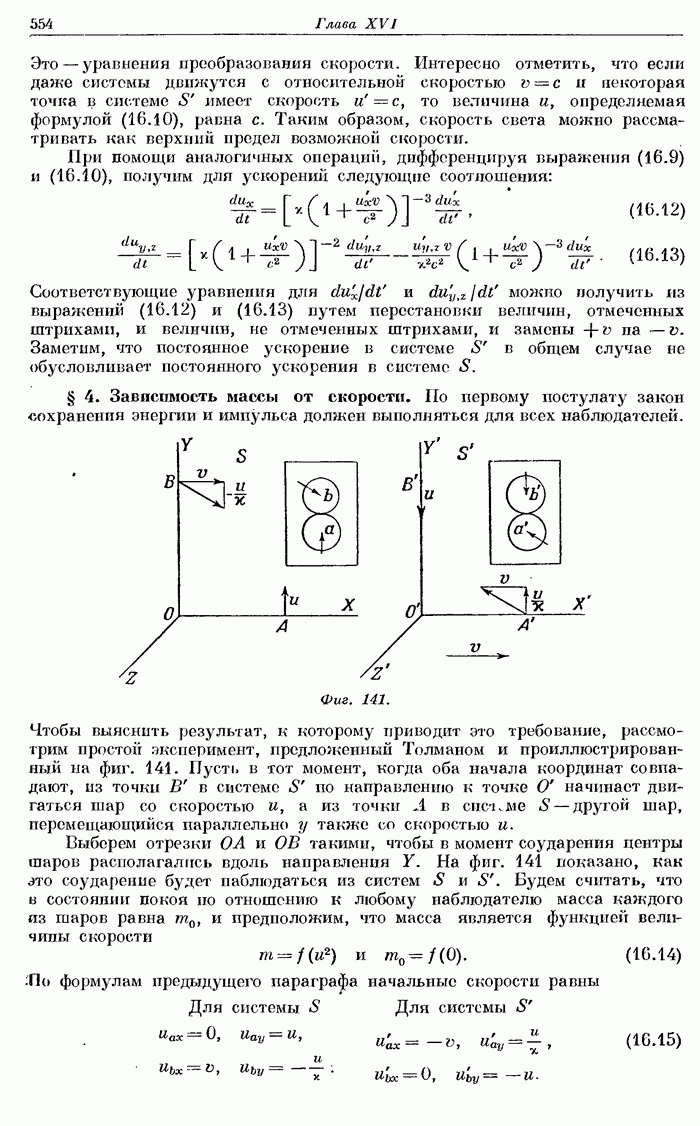
- § 4. Зависимость массы от скорости.
- § 5. Преобразование сил.
- § 6. Сила, действующая на заряд, движущийся в магнитном поле.
- § 7. Движение зарядов в однородном магнитном поле.
- § 8. Энергия движущейся заряженной частицы.
- § 9. Критическое магнитное поле в магнетроне.
- § 10. Траектория космической частицы в однородном поле.
- § 11. Магнитное поле движущегося заряда.
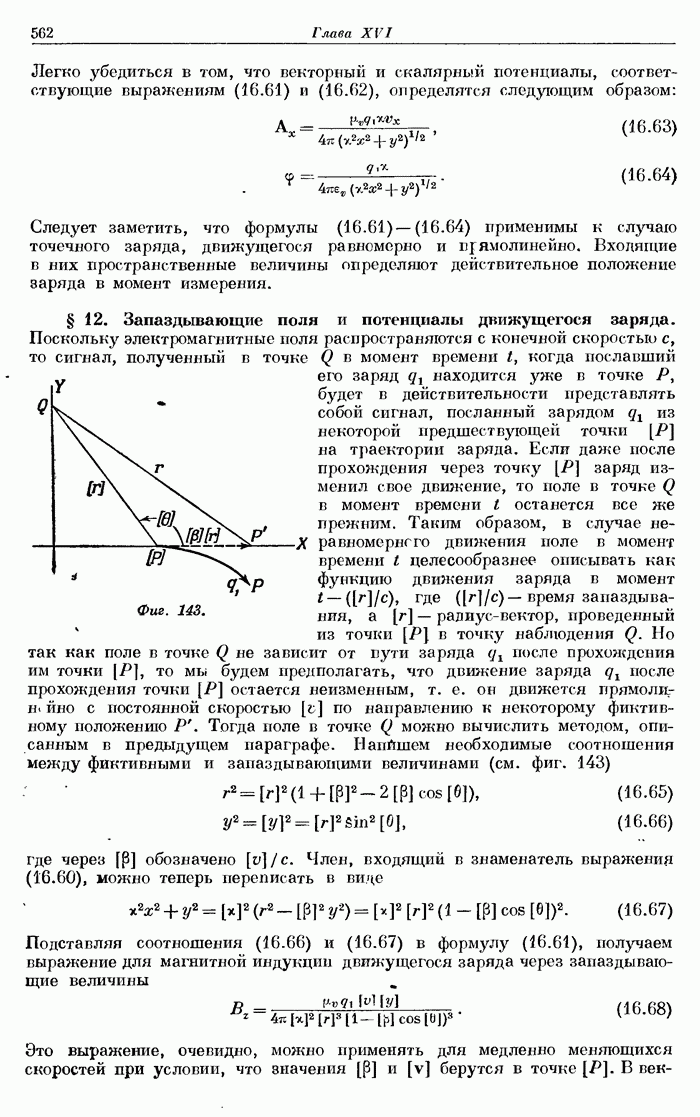
- § 12. Запаздывающие поля и потенциалы движущегося заряда.
- § 13. Излучение равномерно ускоренного, прямолинейно движущегося электрона.
- § 14. Преобразование уравнений Максвелла.
- § 15. Определение скорости самолета относительно земли.
- § 16. Движение заряженной частицы в перекрещивающихся электрическом и магнитном полях.
- § 17. Аберрация и эффект Допплера.
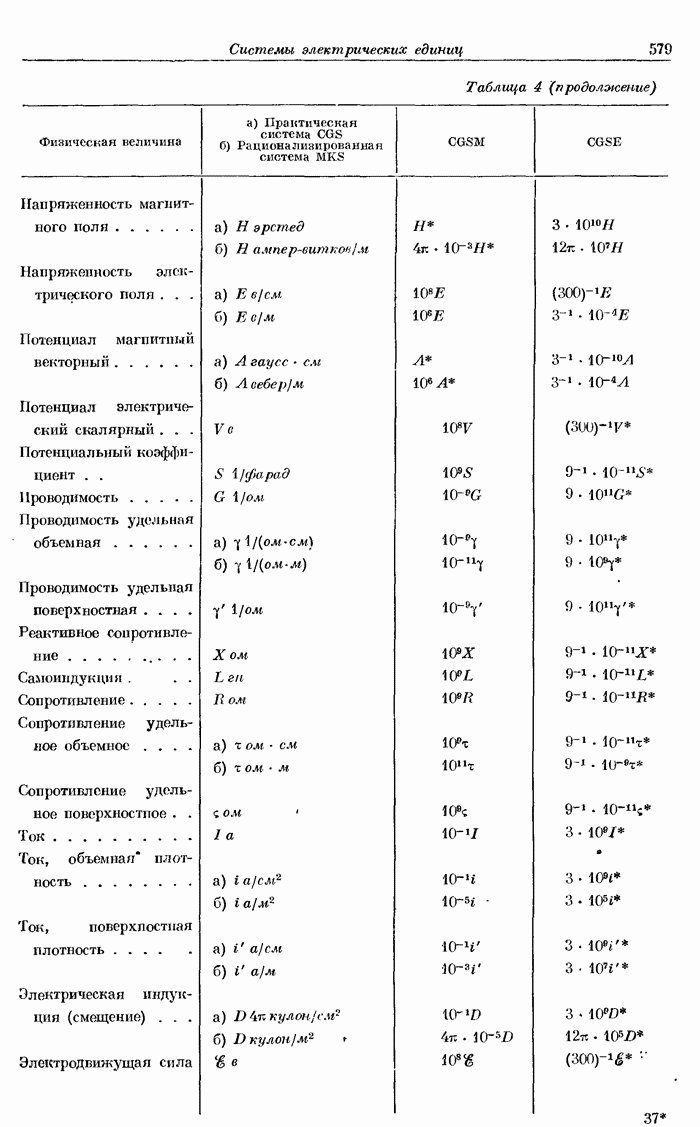
- ПРИЛОЖЕНИЕ. СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ ЕДИНИЦ