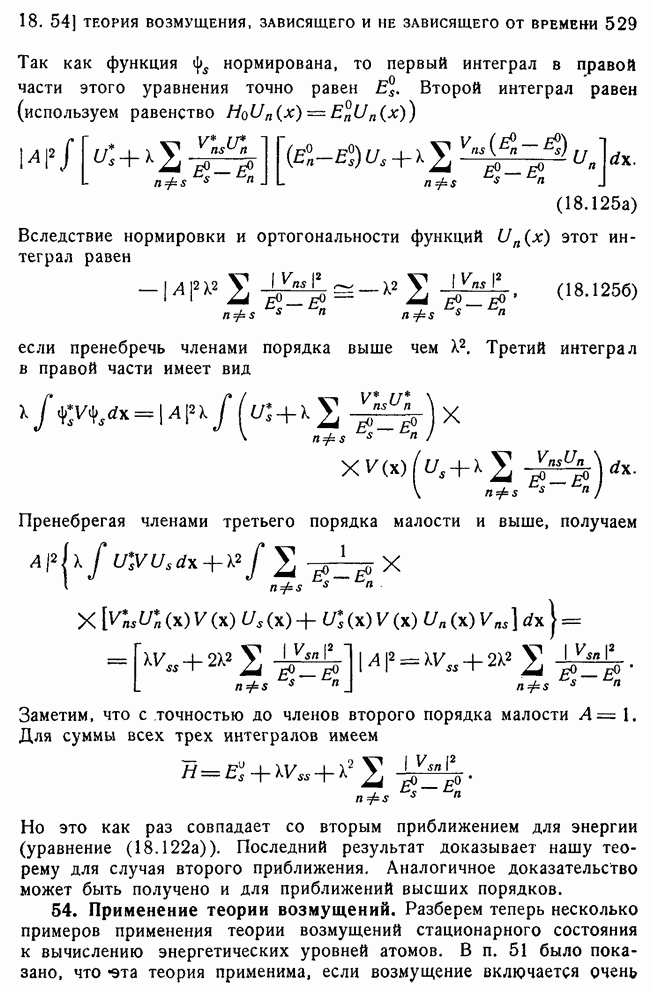| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Матричное выражение операторов момента количества движения.
В этой главе удобно воспользоваться матричным представлением операторов момента количества движения. В соответствии с уравнением (14.35) собственные функции операторов момента количества движения можно определить с помощью двух квантовых чисел  тогда
тогда

В представлении, в котором  диагональны, получаем для матричных элементов вышеприведенных операторов
диагональны, получаем для матричных элементов вышеприведенных операторов

Произвольную волновую функцию можно разложить в ряд

а  — обобщение выражения волновой функции в виде столбца (см. гл. 16, п. 9), при этом собственные векторы можно рассматривать как прямоугольную таблицу, а не простой столбец. Здесь матричные элементы имеют четыре индекса:
— обобщение выражения волновой функции в виде столбца (см. гл. 16, п. 9), при этом собственные векторы можно рассматривать как прямоугольную таблицу, а не простой столбец. Здесь матричные элементы имеют четыре индекса:  как видно из уравнений (17.1а) и (17.16). Нетрудно обобщить матричное умножение и на этот случай.
как видно из уравнений (17.1а) и (17.16). Нетрудно обобщить матричное умножение и на этот случай.
Остается задача определения матриц для  Для решения ее удобно воспользоваться выражениями
Для решения ее удобно воспользоваться выражениями  . В соответствии с уравнениями (14.27) и (14.28) имеем
. В соответствии с уравнениями (14.27) и (14.28) имеем

где  некоторые постоянные, которые будут определены позже. Чтобы найти матричные элементы
некоторые постоянные, которые будут определены позже. Чтобы найти матричные элементы  воспользуемся
воспользуемся
уравнением (16.2):

Аналогично

Это означает, что операторы  представляются диагональными по I матрицами, все элементы которых сдвинуты на одно место от диагонали по
представляются диагональными по I матрицами, все элементы которых сдвинуты на одно место от диагонали по 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. ФИЗИЧЕСКОЕ СОДЕРЖАНИЕ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА I. ВОЗНИКНОВЕНИЕ КВАНТОВОЙ ТЕОРИИ
- 1. Равновесное излучение абсолютно черного тела.
- 2. Электромагнитная энергия.
- 3. Электромагнитные потенциалы.
- 4. Граничные условия.
- 5. Разложение полей в ряд Фурье.
- 6. Поляризация волн.
- 7. Вычисление электромагнитной энергии.
- 8. Анализ полученного выражения электромагнитной энергии.
- 9. Число осцилляторов.
- 10. Закон равномерного распределения энергии по степеням свободы.
- Гипотеза Планка
- 12. Обсуждение результатов.
- 13. Осцилляторы вещества и излучение.
- 14. Квантование осцилляторов вещества.
- 15. Основные выводы гл. 1.
- ГЛАВА 2. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ СТАРОЙ КВАНТОВОЙ ТЕОРИИ
- 1. Фотоэлектрический эффект.
- 2. Различия между классическими и квантовыми законами физики.
- 3. Дискретность квантовых процессов.
- 4. Вероятностный характер и неполный механический детерминизм законов квантовой теории.
- 5. Непригодность классических динамических законов в области элементарных явлений.
- 6. Принцип соответствия.
- 7. Корпускулярные свойства света.
- 8. Эффект Комптона. Рассеяние электромагнитного излучения.
- 9. Анализ эффекта Комптона.
- Квантование атомных систем
- 10. Доказательство квантования всех атомных систем.
- 11. Определение энергетических уровней.
- 12. Переменная действия.
- 13. Квантование момента количества движения.
- 14. Атом водорода.
- 15. Опыты Франка и Герца.
- Теория излучения в рамках принципа соответствия
- 17. Испускание излучения.
- ГЛАВА 3. ВОЛНОВЫЕ ПАКЕТЫ И ВОЛНЫ ДЕ БРОЙЛЯ
- 2. Движение импульсов света.
- 3. Ширина волнового пакета.
- 4. Групповая скорость.
- 5. Расплывание волновых пакетов.
- 6. Более общий критерий для определения ширины волновых пакетов.
- 7. Обобщение на трехмерный случай.
- Электронные волны
- 8. Движение электронных волновых пакетов.
- 9. Учет действия внешних сил.
- 10. Эффекты квантования.
- 11. Опыт Дэвиссона-Джермера.
- 12. Предсказание дифракции электронов теорией Бора — Зоммерфельда.
- 13. Вероятностная трактовка волновой функции.
- 14. Сравнение электронных и электромагнитных волн.
- 15. Более детальная картина электронных волн.
- 16. Переходы между орбитами.
- Волновое уравнение
- 18. Волна для свободной частицы.
- 19. Волновое уравнение для свободной частицы.
- ГЛАВА 4. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- 3. Доказательство сохранения вероятности.
- 4. Ток вероятности.
- 5. Является ли приведенная формулировка наиболее общей?
- 6. Релятивистские теории.
- 7. Плотность вероятности для кванта света.
- 8. Вероятность определения значений импульса.
- 9. Связь между функциями Р(х) и P(k).
- 10. Нормировочный фактор функции P(k).
- Сводка основных сведений о вероятностях
- ГЛАВА 5. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- 2. Вывод соотношения неопределенностей для случая электронов.
- 3. О трактовке соотношений неопределенностей.
- 4. Связь явления расплывания волнового пакета с со отношением неопределенностей.
- 5. Связь устойчивости атомов с соотношением неопределенностей.
- 6. Теория измерений.
- 7. Влияние на измерение квантовых эффектов.
- 8. Микроскоп.
- 9. Измерение импульса.
- 10. Соотношение неопределенностей для энергии и времени.
- 11. Применение соотношения неопределенностей к квантам света.
- 12. Наблюдения кванта света при помощи электронного микроскопа.
- 13. Локализация электромагнитной энергии и импульса при помощи щелей и затворов.
- 14. Применение соотношения неопределенностей к задаче определения орбит в атомах.
- 15. Более общее применение соотношения неопределенностей.
- 16. Внутренняя непротиворечивость квантовой теории.
- 17. Существуют ли скрытые параметры, лежащие в основе квантовой теории?
- ГЛАВА 6. ВОЛНОВЫЕ И КОРПУСКУЛЯРНЫЕ СВОЙСТВА МАТЕРИИ
- 1. Явление интерференции и корпускулярно-волновая природа материи.
- 2. Невозможность одновременного наблюдения волновых и корпускулярных свойств материи.
- 3. Влияние процесса наблюдения на волновую функцию.
- 4. Нарушение интерференции и непротиворечивость корпускулярно-волнового дуализма.
- 5. Обобщение предыдущих результатов.
- 6. Измерение импульса.
- 7. Связь изменений фазы с соотношением неопределенностей.
- 8. Значение фазовых соотношений.
- 9. Квантовые свойства материи как возможность.
- 10. Рассмотрение более общих взаимодействий.
- 11. О реальности волновых свойств материи.
- 12. Волномеханическое объяснение следов в камере Вильсона.
- 13. Качественная картина квантовых свойств материи.
- ГЛАВА 7. СВОДКА ОСНОВНЫХ КВАНТОВЫХ ПРЕДСТАВЛЕНИЙ
- ГЛАВА 8. ПОПЫТКА ПОСТРОЕНИЯ ФИЗИЧЕСКОЙ КАРТИНЫ КВАНТОВОЙ ПРИРОДЫ МАТЕРИИ
- 3. Простое и наглядное описание непрерывного движения.
- 4. Аналогия простых и квантовых представлений о движении.
- 5. Аналогия простых и квантовых представлений о фиксированном положении.
- 6. Более сложные представления, включающие понятие непрерывной траектории.
- 7. Причина и следствие.
- 8. Ранние представления о причине и следствии.
- 9. Полный механический детерминизм и причинность как тенденция.
- 10. Классическая теория как предписывающая, а не причинная.
- 11. Новые свойства квантовых представлений: приближенная и статистическая причинность.
- 12. Энергия и импульс в классической и квантовой теориях.
- 13. Импульс и энергия, и причинная форма описания материи.
- 14. Связь между пространственно-временным и причинным описанием материи.
- 15. Принцип дополнительности.
- 16. Неделимое единство мира.
- 17. Различие между объектом и окружающей средой в классической теории.
- 18. Роль непрерывности.
- 19. Роль причинных законов.
- 20. Анализ и синтез.
- 21. Применимость анализа и синтеза в классической теории.
- 22. Системы, описываемые классически, и существенно квантовомеханические системы.
- 23. Попытка разложения квантовой системы на отдельные части.
- 24. Неделимое единство квантовых систем.
- 26. Пример: атом водорода.
- 26. Необходимость немеханического описания.
- Сводка новых понятий квантовой теории
- Аналогии с квантовыми процессами
- 28. Возможные причины для аналогий между мышлением и квантовыми процессами.
- Примечание редактора к гл. 8
- ЧАСТЬ II. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА 9. ВОЛНОВЫЕ ФУНКЦИИ, ОПЕРАТОРЫ И УРАВНЕНИЕ ШРЁДИНГЕРА
- 2. Гипотеза линейной суперпозиции.
- 3. Понятие состояния системы в квантовой теории.
- 4. Статистический смысл понятия квантового состояния.
- 5. Математическое выражение для средних величин.
- 6. Операторы для вычисления средних значений импульса из интегралов в пространстве координат.
- 7. Функции импульса.
- 8. Операторы в пространстве импульсов. Импульсное представление.
- 9. Линейность операторов.
- 10. Координата x как оператор.
- 11. Умножение операторов. Коммутаторы.
- 12. Операторная форма функций общего вида.
- 13. Вещественность средних значений и порядок сомножителей.
- 14. Эрмитовские операторы.
- 15. Видоизмененное правило вычисления средних значений f(x, р).
- 16. Эрмитовски сопряженные операторы.
- 17. Обобщенное определение эрмитовского оператора.
- 18. Обобщенное определение эрмитовски сопряженных операторов.
- 19. Определение оператора, эрмитовски сопряженного произведению двух операторов.
- 20. Применение к коммутаторам.
- 21. Теорема для эрмитовских операторов.
- Вывод уравнения Шрёдингера
- 26. Задача вычисления среднего движения волнового пакета.
- 27. Общее правило для вычисления Н.
- 28. Является ли вышеприведенное уравнение наиболее общим из всех возможных?
- 29. Значение волнового уравнения.
- 30. Общее определение тока вероятности.
- 31. Истолкование величины Н как средней энергии.
- 32. Закон сохранения энергии.
- ГЛАВА 10. ФЛУКТУАЦИИ, КОРРЕЛЯЦИИ И СОБСТВЕННЫЕ ФУНКЦИИ
- 4. Количественная мера корреляции в классической теории.
- 5. Классификация классических статистических систем по средним значениям произведения.
- 6. Квантовое определение корреляций.
- 7. Применение к задаче о расплывании волнового пакета для свободной частицы.
- 8. Полуклассическое описание частицы с неопределенными координатой и импульсом.
- 9. Общий вывод соотношений неопределенностей.
- 10. Особые свойства гауссовской волновой функции.
- 11. Задача многих частиц.
- 12. Собственные значения и собственные функции операторов.
- 13. Примеры собственных функций и собственных значений в координатном пространстве.
- 14. Вырожденные операторы.
- 15. Дельта-функция Дирака.
- 16. Собственные функции оператора импульса в пространстве импульсов.
- 17. Собственные функции оператора х в импульсном представлении.
- 18. Связь между собственными функциями оператора х в координатном пространстве и в пространстве импульсов.
- 19. Дифференцирование дельта-функции.
- 20. Дискретный и непрерывный спектр собственных значений операторов.
- 21. Разложение произвольной функции в ряд по собственным функциям.
- 22. Постулат разложения.
- 23. Теорема о вещественности собственных значений эрмитовского оператора.
- 24. Ортогональность собственных функций эрмитовского оператора.
- 25. Вычисление коэффициентов разложения.
- 26. Разложение дельта-функции Дирака в ряд по собственным функциям произвольного эрмитовского оператора.
- 27. Представление оператора через его собственные функции.
- 28. Выражение среднего значения функции f(A) в методе разложения по собственным функциям А.
- 29. Физическая интерпретация коэффициентов разложения с помощью вероятностей.
- Дальнейшее истолкование вероятностей в квантовой теории
- 30. Интерференция вероятностей.
- 31. Собственные функции оператора Гамильтона.
- 32. Изменение собственных функций Н со временем.
- 33. Изменение вероятности со временем. Стационарные состояния.
- 34. Связь вероятностей, зависящих от времени, с соотношением неопределенностей.
- 35. Важность собственных функций гамильтоновского оператора Н.
- 36. Изменение вероятности со временем для общей волновой функции.
- ЧАСТЬ III. ПРИЛОЖЕНИЯ К ПРОСТЫМ СИСТЕМАМ. ДАЛЬНЕЙШИЕ ОБОБЩЕНИЯ ФОРМУЛИРОВКИ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА 11. РЕШЕНИЕ ВОЛНОВОГО УРАВНЕНИЯ ДЛЯ ПРЯМОУГОЛЬНЫХ ПОТЕНЦИАЛОВ
- 2. Собственные функции оператора энергии.
- 3. Прямоугольные потенциальные барьеры.
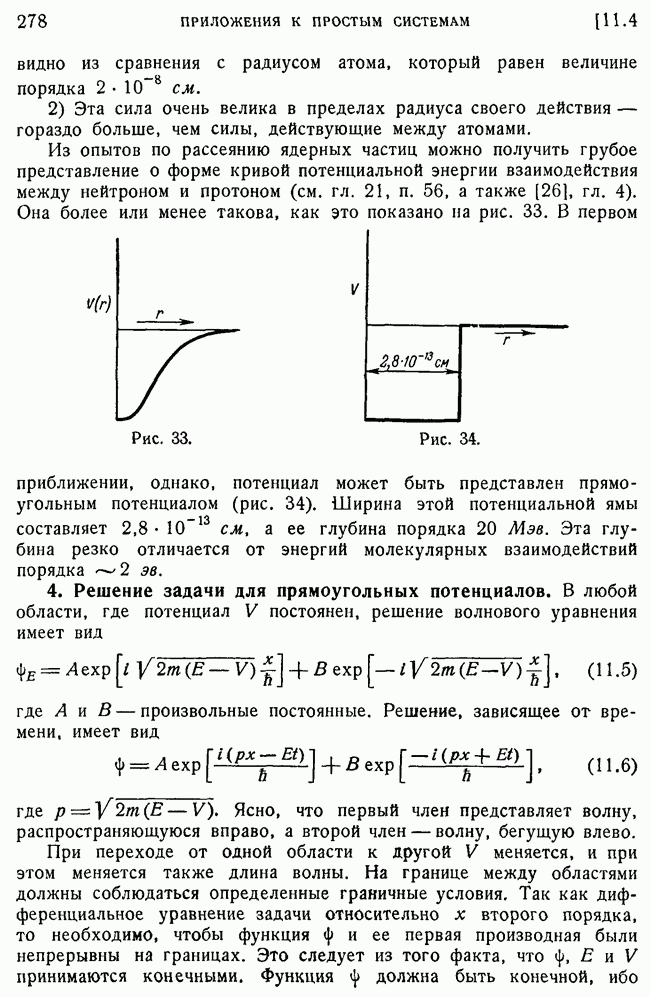
- 4. Решение задачи для прямоугольных потенциалов.
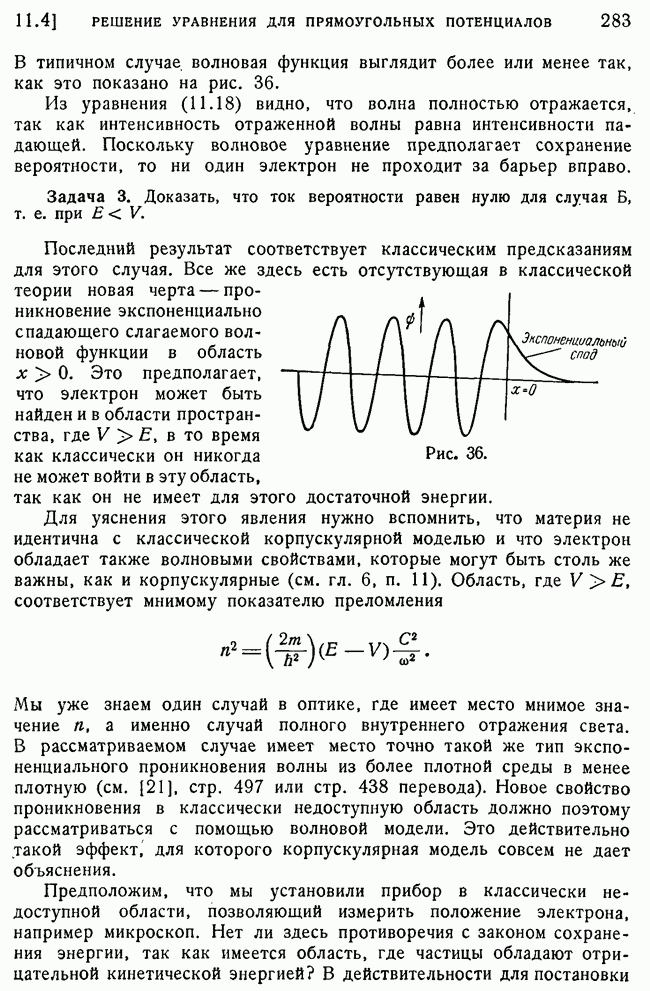
- 5. Проникновение через барьер.
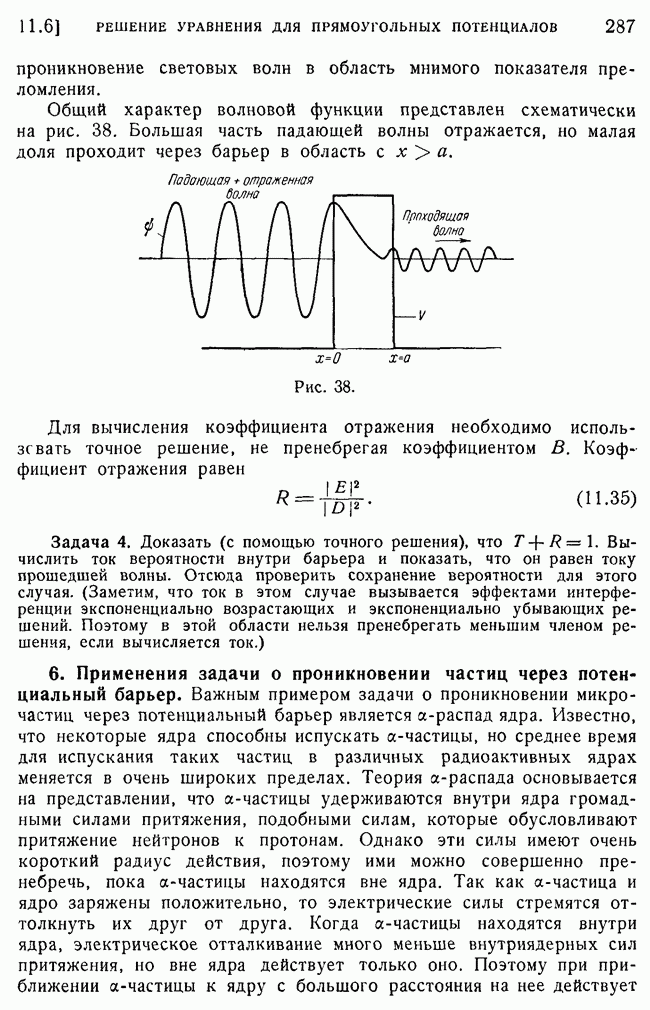
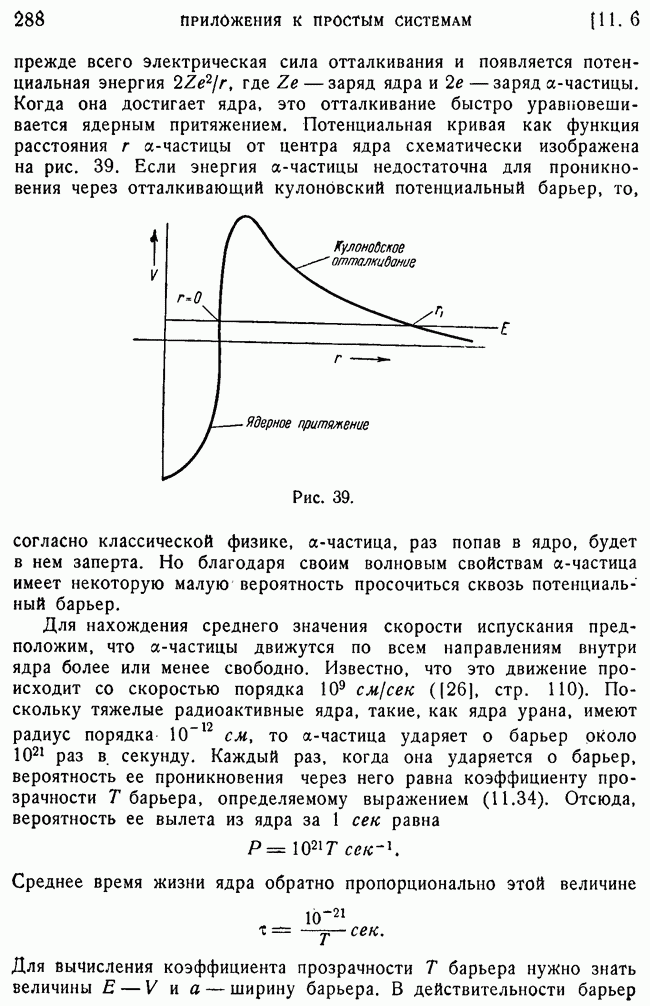
- 6. Применения задачи о проникновении частиц через потенциальный барьер.
- 7. Прямоугольная потенциальная яма.
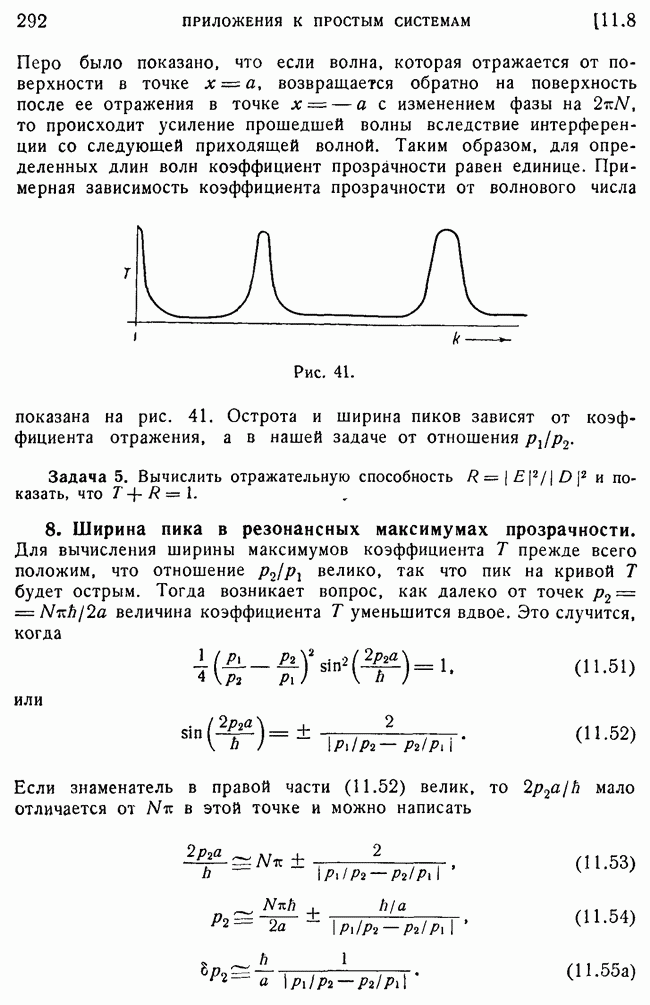
- 8. Ширина пика в резонансных максимумах прозрачности.
- 9. Эффект Рамзауера.
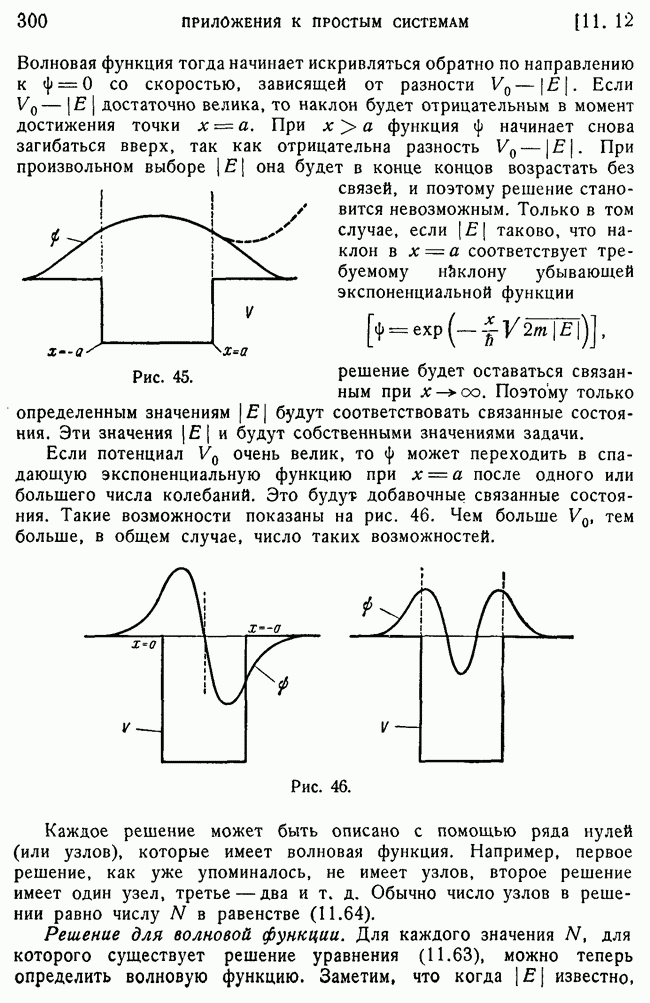
- 10. Связанные состояния.
- 11. Предельный случай бесконечно глубокой ямы.
- 12. Графическая интерпретация решений.
- 13. Применение теоремы разложения.
- 14. Применение к дейтрону.
- 16. Объяснение энергетических уровней с помощью соотношения неопределенностей.
- 16. Использование наблюдаемых энергетических уровней для получения сведений о потенциале.
- 17. Волновые пакеты как континуум собственных функций.
- 18. Волновой пакет для прошедшей волны.
- 19. Время замедления волны при прохождении потенциальной ямы.
- 20. Метастабильные (или виртуальные) состояния микрочастицы в потенциальной яме.
- 21. Метастабильное синглетное состояние дейтрона.
- ГЛАВА 12. КЛАССИЧЕСКИЙ ПРЕДЕЛ КВАНТОВОЙ ТЕОРИИ. ПРИБЛИЖЕНИЕ ВКБ
- 4. Физическая интерпретация решений с помощью классического распределения частиц.
- 5. Волновые пакеты. Решение, зависящее от времени.
- 6. Приближение ВКБ, зависящее от времени, в трехмерном случае.
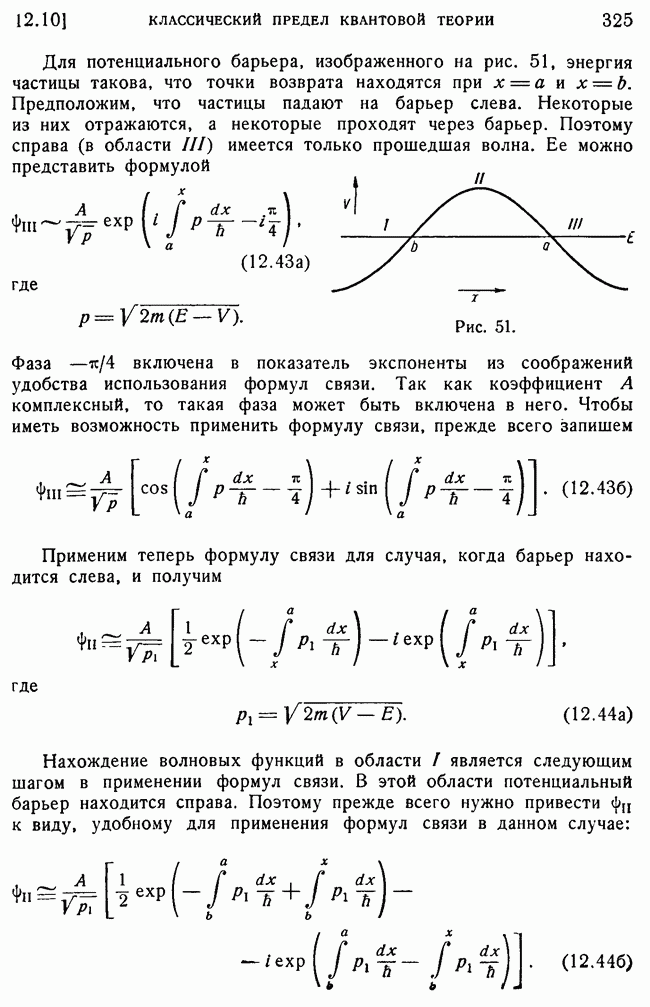
- 7. Проникновение через барьер.
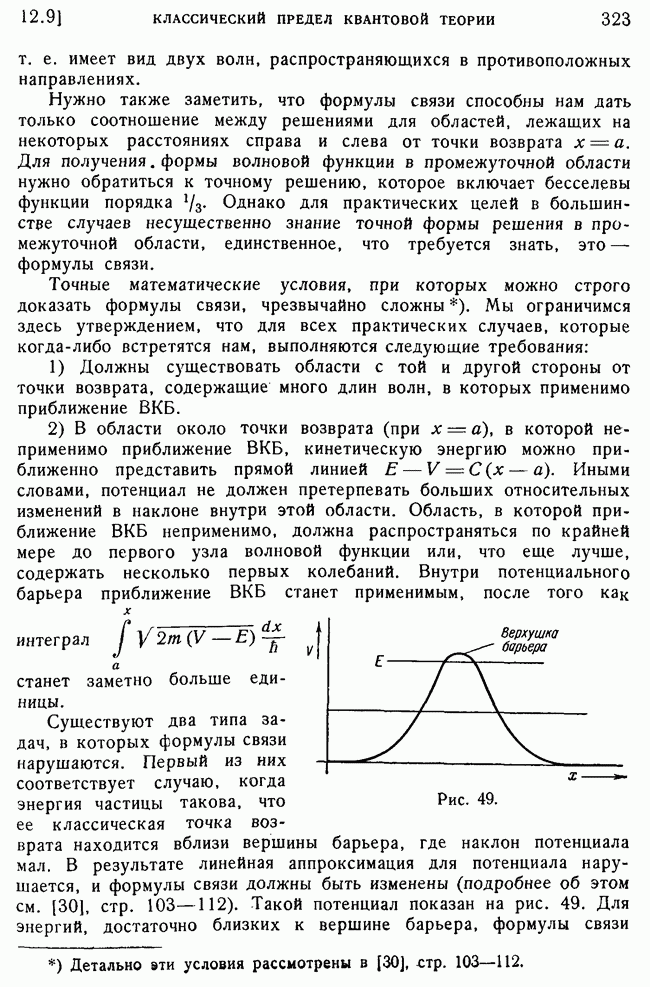
- 8. Формулы связи.
- 9. Формулы связи.
- 10. Вероятность проникновения через барьер.
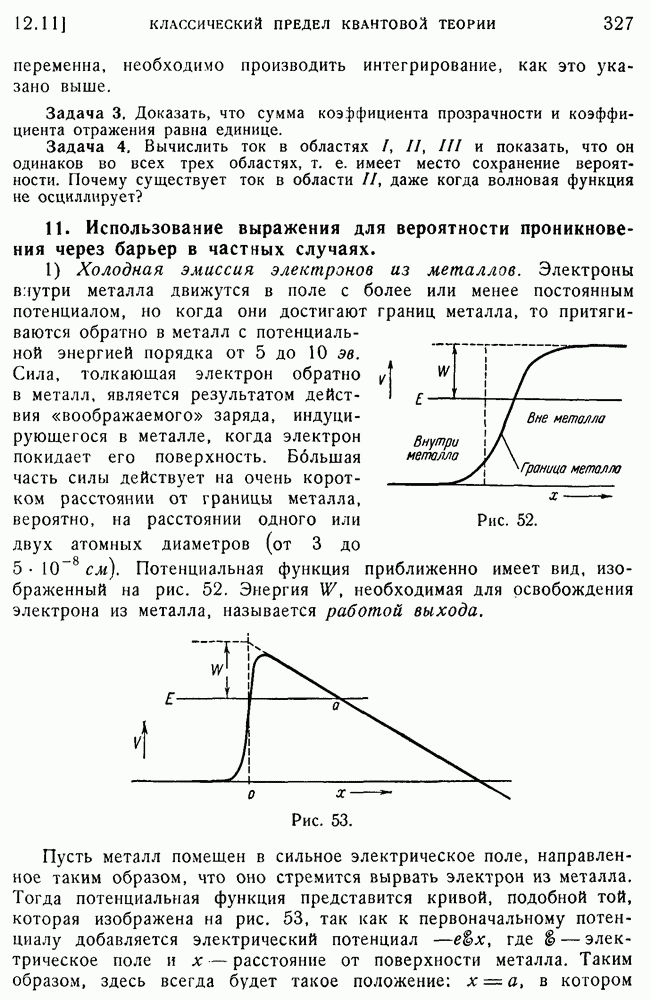
- 11. Использование выражения для вероятности проникновения через барьер в частных случаях.
- 12. Вероятность проникновения частиц внутрь ядра.
- 13. Связанные состояния потенциальной ямы.
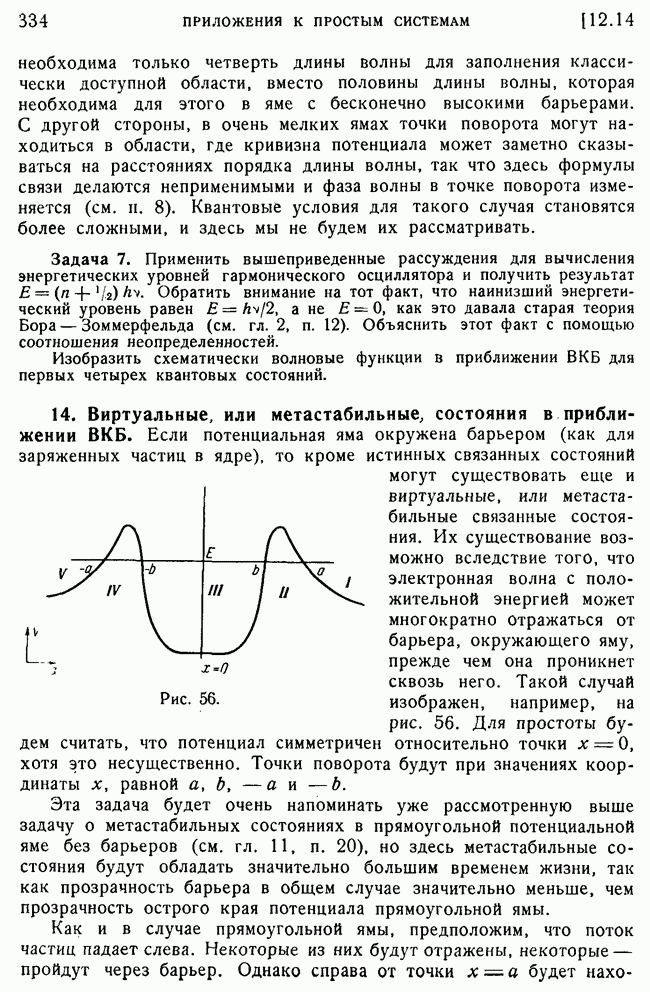
- 14. Виртуальные, или метастабильные, состояния в приближении ВКБ.
- 15. Обсуждение выражения (12.64) для коэффициента прозрачности.
- 16. Ширина резонанса. Коэффициент прозрачности вблизи резонанса.
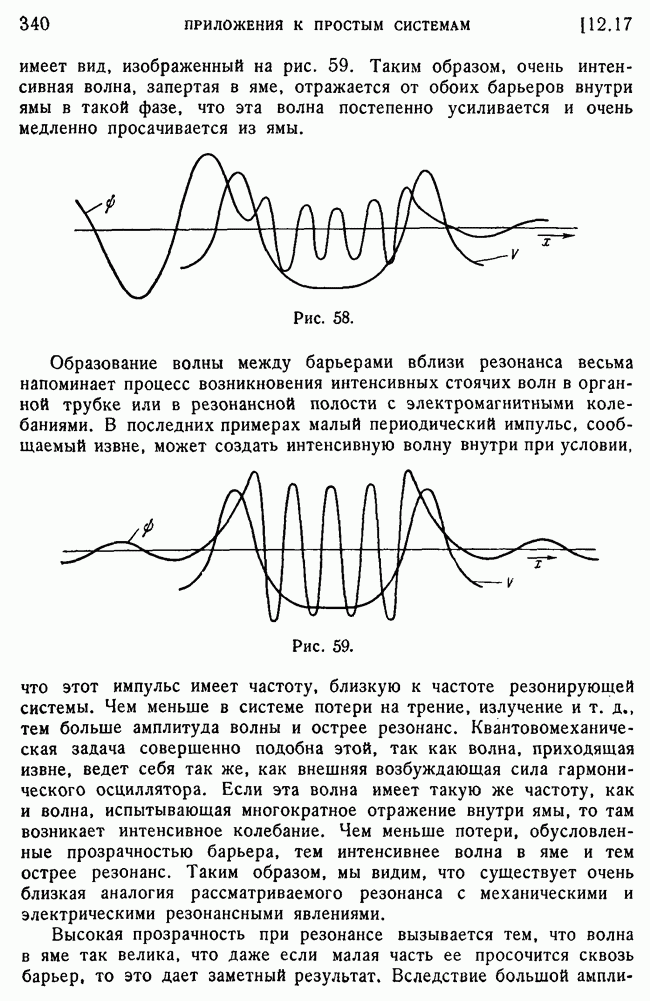
- 17. Интенсивность волны внутри ямы.
- 18. Образование волновых пакетов. Время жизни виртуальных состояний.
- 19. Волновой пакет внутри потенциальной ямы (вблизи резонанса).
- 20. Соотношение неопределенностей.
- 21. Применение к радиоактивным системам.
- 22. Применение к ядерным реакциям.
- ГЛАВА 13. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- 5. Шрёдингеровский метод факторизации.
- 6. Решение для волновых функций.
- 7. Полиномы Эрмита — Чебышева.
- 8. Нормирующий множитель.
- 9. Порождающая функция.
- 10. Рекуррентные соотношения.
- 11. Некоторые вспомогательные математические соотношения.
- 13. Свойства ортогональности полиномов Эрмита — Чебышева.
- 15. Волновые пакеты.
- 16. Средние значения кинетической и потенциальной энергий.
- ГЛАВА 14. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ И ВОЛНОВОЕ УРАВНЕНИЕ В ТРЕХ ИЗМЕРЕНИЯХ
- 2. Момент количества движения.
- 3. Перестановочные соотношения для операторов момента количества движения.
- 4. Полный момент количества движения.
- 5. Слагающие момента количества движения в полярных координатах.
- 6. Константы движения.
- 7. Собственные значения Lz.
- 9. Совместные собственные функции операторов Lz и L2.
- 10. Одновременное определение собственных функций и собственных значений Lz и L2.
- 11. Векторное изображение возможных значений моментов количества движения.
- 12. Флуктуации в ориентациях вектора L.
- 13. Собственные функции операторов L2 и Lz.
- 14. Полиномы Лежандра.
- 15. Присоединенные функции Лежандра.
- 16. Измерение момента количества движения. Опыт Штерна и Герлаха.
- 17. Преобразование к вращающейся системе осей.
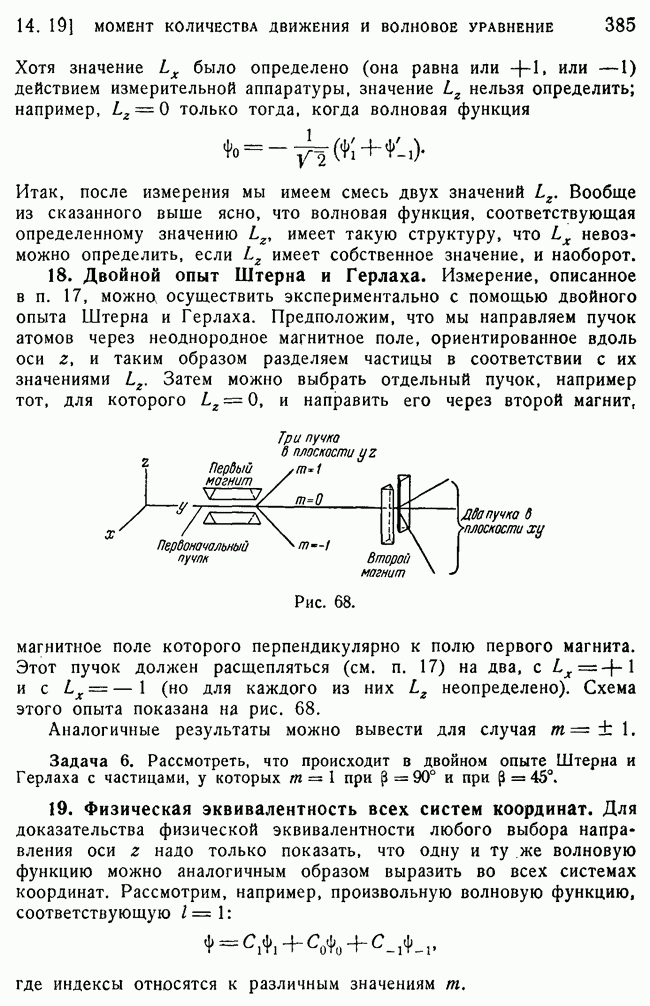
- 18. Двойной опыт Штерна и Герлаха.
- 19. Физическая эквивалентность всех систем координат.
- 20. Обобщение на произвольные повороты и произвольное l.
- 21. Применение к построению орбит.
- ГЛАВА 15. РЕШЕНИЕ РАДИАЛЬНОГО УРАВНЕНИЯ; АТОМ ВОДОРОДА; ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- 4. Центробежный потенциал.
- 5. Разделение переменных в относительных координатах.
- 6. Предварительное обсуждение общей формы решения для атома водорода.
- 7. Общая форма решения для s-волн.
- 8. Общий вид решения при l > 0.
- 9. Определение квантовых чисел.
- 10. Физическая интерпретация волновых функций при различных n, l, m.
- 11. Образование волновых пакетов.
- 12. Точное решение для атома водорода.
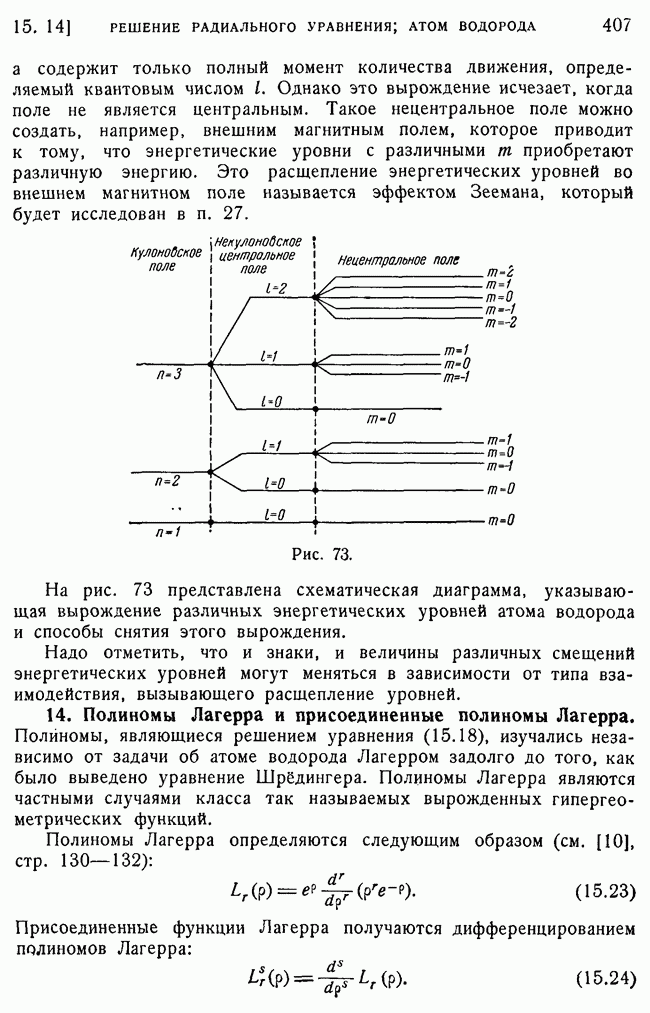
- 13. Вырождение энергетических уровней атома водорода.
- 14. Полиномы Лагерра и присоединенные полиномы Лагерра.
- 15. Трехмерный гармонический осциллятор.
- 16. Возможность вырождения энергетических уровней.
- 17. Случай сферической симметрии.
- 18. Вид волновой функции в случае сферической симметрии.
- 19. Важное свойство вырожденных собственных функций.
- 20. Связь полиномов Эрмита — Чебышева со сферическими гармониками.
- 21. Гамильтониан заряженной частицы в заданном электромагнитном поле.
- 22. Квантовомеханический гамильтониан.
- 23. Сохранение вероятности. Ток вероятности.
- 24. Классический предел.
- 25. Градиентная (калибровочная) инвариантность.
- 26. Частный случай: однородное магнитное поле.
- 27. Зеемановское расщепление энергетических уровней с различными квантовыми числами m.
- ГЛАВА 16. МАТРИЧНАЯ ФОРМУЛИРОВКА КВАНТОВОЙ ТЕОРИИ
- 3. Обоснование матричного представления квантовомеханических операторов.
- 4. Пример: волновые функции гармонического осциллятора.
- 5. Эрмитовские матрицы и эрмитовски сопряженные матрицы.
- 6. Диагональное представление операторов.
- 7. Коммутативность диагональных матриц.
- 8. Непрерывные матрицы.
- 9. Матричное представление волновой функции в виде столбца.
- 10. Нормировка и ортогональность волновых функций, выраженных в виде столбцов.
- 11. Среднее значение оператора.
- 12. Собственные значения и собственные векторы матриц.
- 13. Изменение представления.
- 14. Важное свойство матриц преобразования (a-матриц).
- 15. Значение унитарного преобразования.
- 16. След, или шпур, матрицы.
- 17. Совместные собственные функции коммутирующих операторов.
- 18. Определение произвольного оператора при помощи его коммутаторов с полной системой коммутирующих операторов.
- 19. Уравнение Шредингера в произвольном представлении.
- 20. Гамильтоновское представление.
- 21. Гейзенберговское представление.
- 22. Изменение операторов со временем в гейзенберговском представлении.
- 23. Скобки Пуассона.
- 24. Формулировка квантовой теории по Гейзенбергу.
- 25. Физическое истолкование матричного представления и теории преобразования.
- ГЛАВА 17. СПИН И МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- 1. Спин электрона.
- 2. Матричное выражение операторов момента количества движения.
- 3. Возможные значения l и m; полуцелые квантовые числа момента количества движения.
- 4. Матрицы для операторов …
- 5. Собственные функции операторов «сигма».
- 6. Собственные функции …
- 7. Преобразования спиноров.
- 8. Сложение моментов количества движения.
- 9. Сложение спинов двух различных частиц.
- 10. Распределение вероятности состояний спина в статистическом ансамбле.
- 11. Сложение орбитального и спинового моментов частицы.
- 12. Общая задача сложения моментов количества движения.
- 13. Энергия электрона со спином.
- ЧАСТЬ IV. МЕТОДЫ ПРИБЛИЖЕННОГО РЕШЕНИЯ УРАВНЕНИЯ ШРЁДИНГЕРА
- ГЛАВА 18. ТЕОРИЯ ВОЗМУЩЕНИЯ, ЗАВИСЯЩЕГО И НЕ ЗАВИСЯЩЕГО ОТ ВРЕМЕНИ
- 8. Возмущение вырожденных состояний.
- 9. Описание переходов с помощью квантовых флуктуаций.
- 10. Микроскопическая обратимость процессов перехода.
- 11. Сохранение вероятности.
- 12. Случай б: гармоническое изменение матричных элементов со временем, задача поглощения и испускания света.
- 13. Применение к случаю плоской волны.
- 15. Квазиклассическое описание поля излучения.
- 16. Вычисление вероятности перехода.
- 17. Связь между векторным потенциалом и интенсивностью излучения.
- 18. Влияние распределения частот падающего света.
- 19. Обсуждение результатов.
- 20. Индуцированное испускание квантов.
- 21. Классическая аналогия индуцированного излучения.
- 22. Самопроизвольное излучение.
- 23. Трактовка самопроизвольного излучения по Эйнштейну.
- 24. Применения теории переходов.
- 25. Приближение электрического диполя.
- 26. Вычисление величин для изотропного гармонического осциллятора.
- 27. Правила отбора для гармонического осциллятора.
- 28. Связь правил отбора с принципом соответствия.
- 29. Введение четности.
- 30. Правила отбора для четности.
- 31. Правила отбора для сферически симметричного потенциала без учета спина.
- 32. Запрещенные переходы, электрическое квадрупольное излучение.
- 33. Магнитное дипольное излучение.
- 34. Правила отбора для электрического квадрупольного излучения.
- 35. Правила отбора для магнитного дипольного излучения.
- 36. Переходы более высокого порядка.
- 37. Полностью запрещенные переходы между состояниями с l = 0.
- 38. Полная вероятность излучения.
- 39. Сравнение с классической теорией.
- 40. Правила сумм для вычисления матричных элементов.
- 41. Круговая поляризация.
- 42. Эллиптическая поляризация.
- 43. Квантовая трактовка.
- 44. Правила отбора.
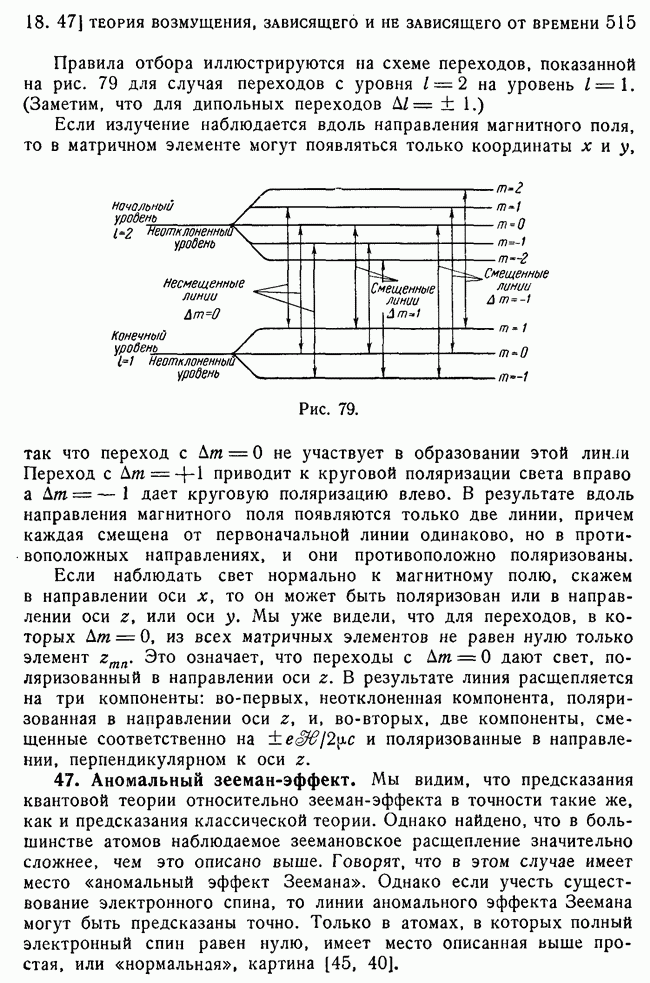
- 45. Применение к случаю нормального зееман-эффекта.
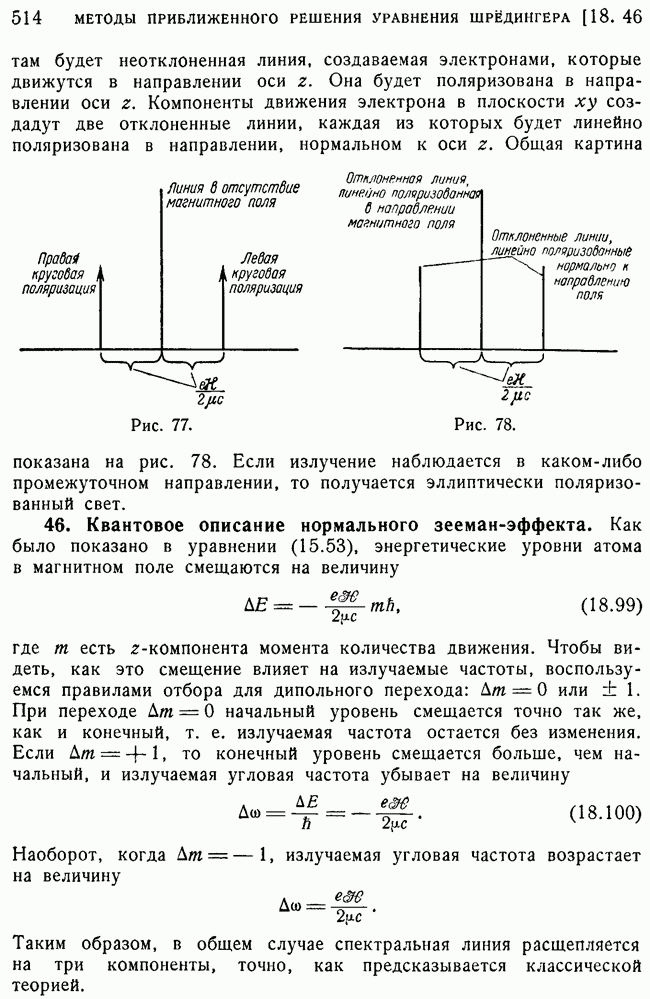
- 46. Квантовое описание нормального зееман-эффекта.
- 47. Аномальный зееман-эффект.
- 48. Общие методы вычисления вероятностей переходов.
- 49. Влияние спина электрона на вероятности переходов.
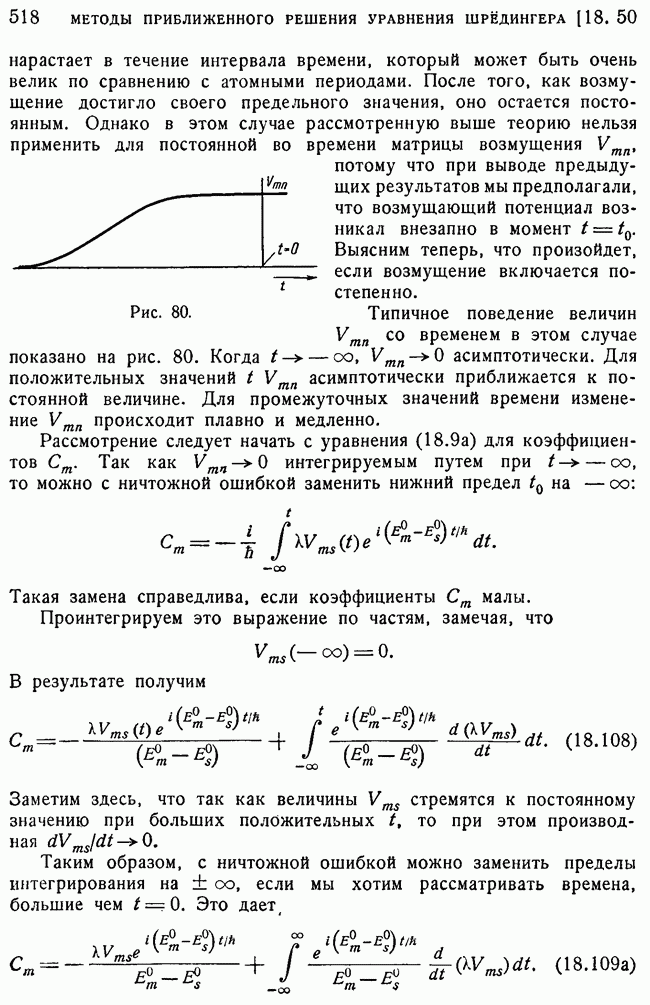
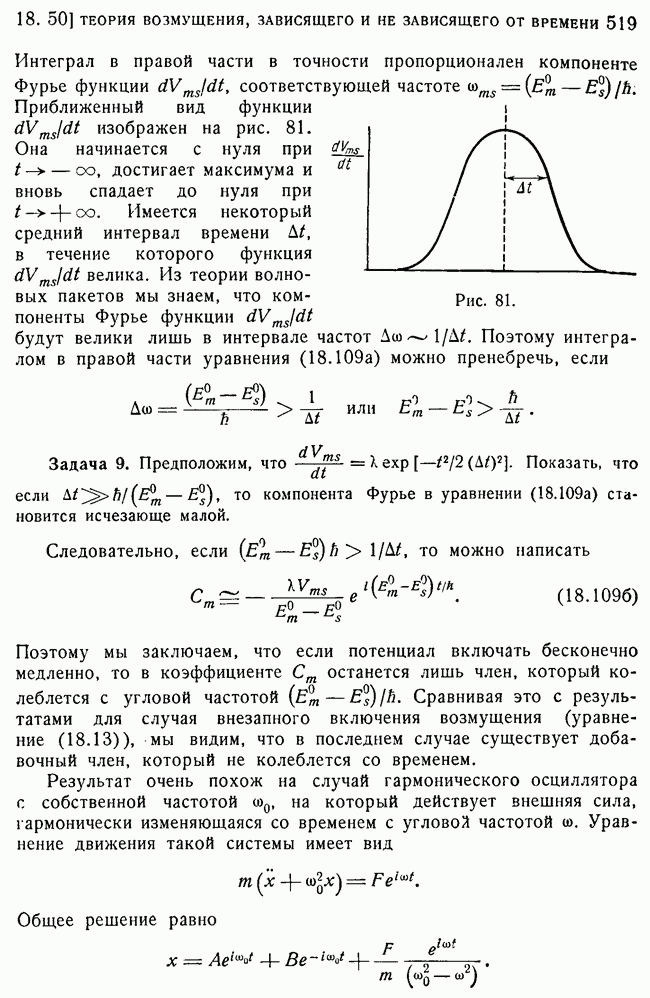
- 50. Случай в: возмущение Vmn медленно изменяющееся со временем (адиабатический случай).
- 51. Адиабатическое включение потенциала, приводящее к возмущению стационарного состояния.
- 52. Возмущение волновых функций стационарного состояния.
- 53. Интерпретация формул второго приближения для энергии.
- 54. Применение теории возмущений.
- ГЛАВА 19. ВОЗМУЩЕНИЯ В СЛУЧАЕ ВЫРОЖДЕННЫХ СИСТЕМ
- 9. Кваитовомеханический «резонанс».
- 10. Аналогия задачи возмущения вырожденных состояний с преобразованием к главным осям.
- Приложения теории возмущений вырожденных состояний
- 11. Эффект Штарка первого порядка.
- 12. Классическая интерпретация линейного эффекта Штарка.
- 13. Межатомные ван-дер-ваальсовские силы.
- 14. Квантовомеханическая аналогия фазы осциллятора.
- 16. Обменное вырождение.
- 18. Симметричные и антисимметричные функции.
- 19. Вычисление энергии.
- 20. Приближения высших порядков.
- 21. Влияние спина.
- 22. Антисимметричность волновых функций электронов.
- 23. Связь между обменной энергией и спином электрона, обусловленная свойством антисимметричности волновых функций.
- 24. Формальное выражение обменной энергии при помощи спиновых операторов.
- 25. Система из многих электронов.
- 26. Принцип запрета Паули.
- 28. Полностью симметричные волновые функции.
- 29. Неразличимость эквивалентных частиц.
- ГЛАВА 20. ВНЕЗАПНЫЕ И АДИАБАТИЧЕСКИЕ ВОЗМУЩЕНИЯ
- 1. Общая форма адиабатического возмущения.
- 3. Примеры адиабатических возмущений.
- 4. Внезапное изменение возмущающего потенциала.
- 5. Приложения. Испускание электронов из ядра при «бета»-pacпаде.
- 6. Связь между теорией возмущений и теорией внезапных переходов.
- ЧАСТЬ V. ТЕОРИЯ РАССЕЯНИЯ
- ГЛАВА 21. ТЕОРИЯ РАССЕЯНИЯ
- 4. Распределение длин свободного пробега.
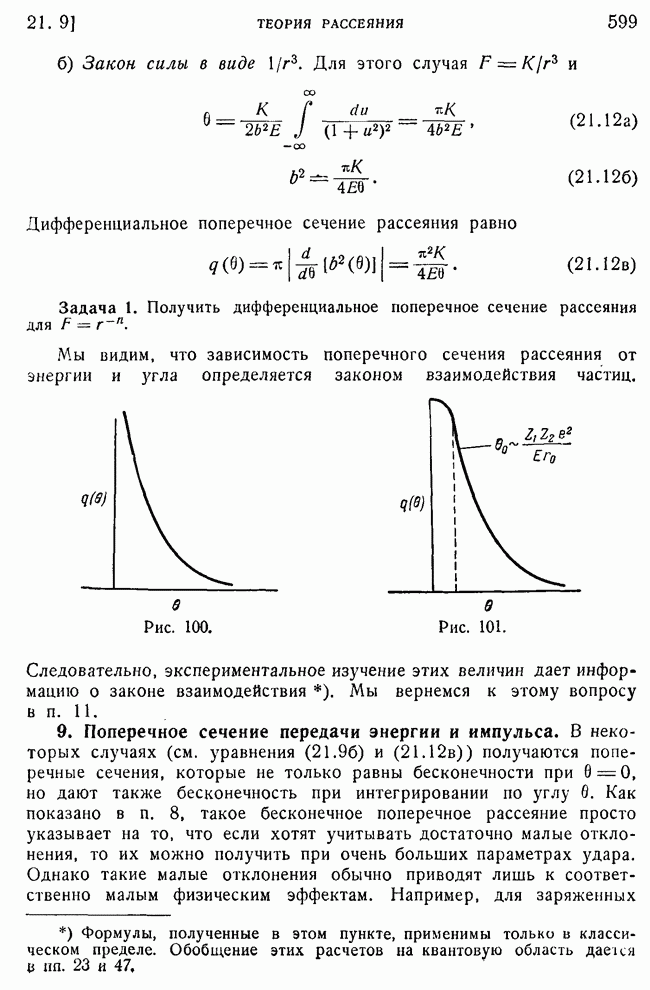
- 5. Зависимость поперечного сечения от угла рассеяния.
- 6. Дифференциальные поперечные сечения.
- 7. Более общая теория рассеяния.
- 8. Приближение малых отклонений. Классическая теория возмущений.
- 9. Поперечное сечение передачи энергии и импульса.
- 10. Точное решение задачи рассеяния.
- 11. Использование поперечных сечений рассеяния для исследования вида взаимодействия между частицами.
- 12. Переход от системы координат центра инерции к лабораторной системе координат.
- 14. Столкновение тождественных частиц.
- 15. Квантовая теория рассеяния.
- 17. Квантовое описание процесса рассеяния.
- 18. Рассеяние как процесс перехода между различными состояниями в пространстве импульсов.
- 19. Борновское приближение. Теория возмущений.
- 21. Конкретный пример рассеяния на экранированном кулоновском потенциале.
- 22. Связь между борновским приближением и коэффициентами разложения потенциала в ряд Фурье.
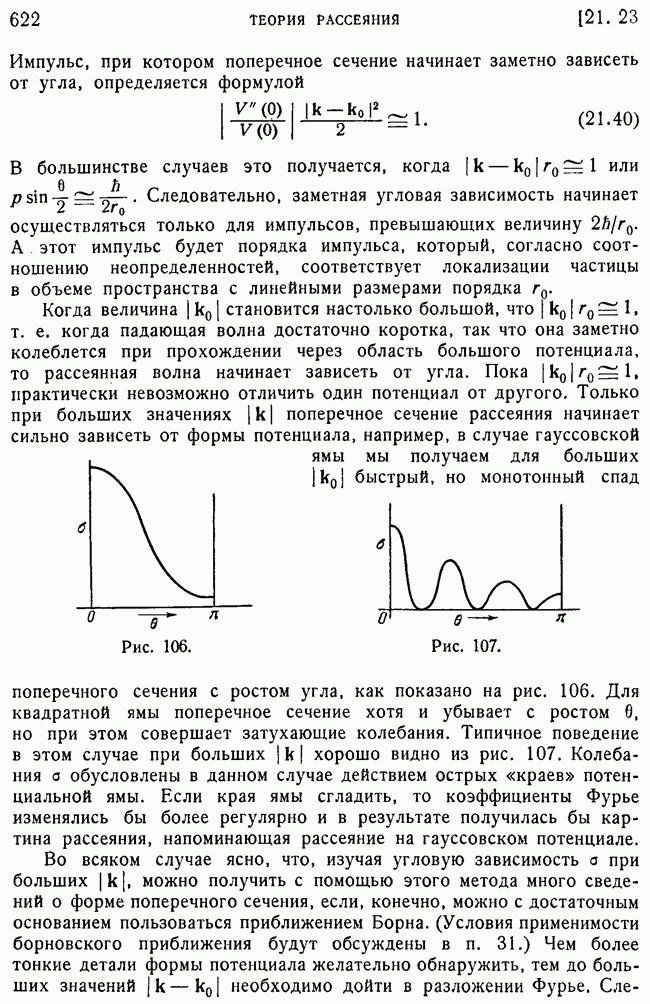
- 23. Примеры: сравнение поперечных сечений для гауссовского потенциала и прямоугольной ямы.
- 24. Исследование процесса рассеяния в координатном представлении.
- 25. Новая форма уравнения Шредингера.
- 27. Борновское приближение.
- 28. Связь между описанием процессов рассеяния в координатном и импульсном представлениях.
- 29. Связь между методом стационарных состояний и временным описанием процессов рассеяния.
- 30. Другое применение борновского приближения: рассеяние от кристаллической решетки.
- 31. Условия применимости борновского приближения.
- 32. Применение к случаю экранированного кулоновского рассеяния.
- 33. Другой критерий применимости борновского приближения.
- 34. Связь условия применимости классического приближения с условием нарушения критерия применимости борновского приближения.
- 35. Сравнение классического и борновского приближений для случая кулоновского потенциала.
- 36. Специфические свойства кулоновского потенциала.
- 37. Неприменимость борновского приближения при рассеянии на ядрах.
- 38. Применение к случаю экранированного кулоновского потенциала.
- 39. Метод парциальных волн (Рэлей, Факсен и Хольтсмарк).
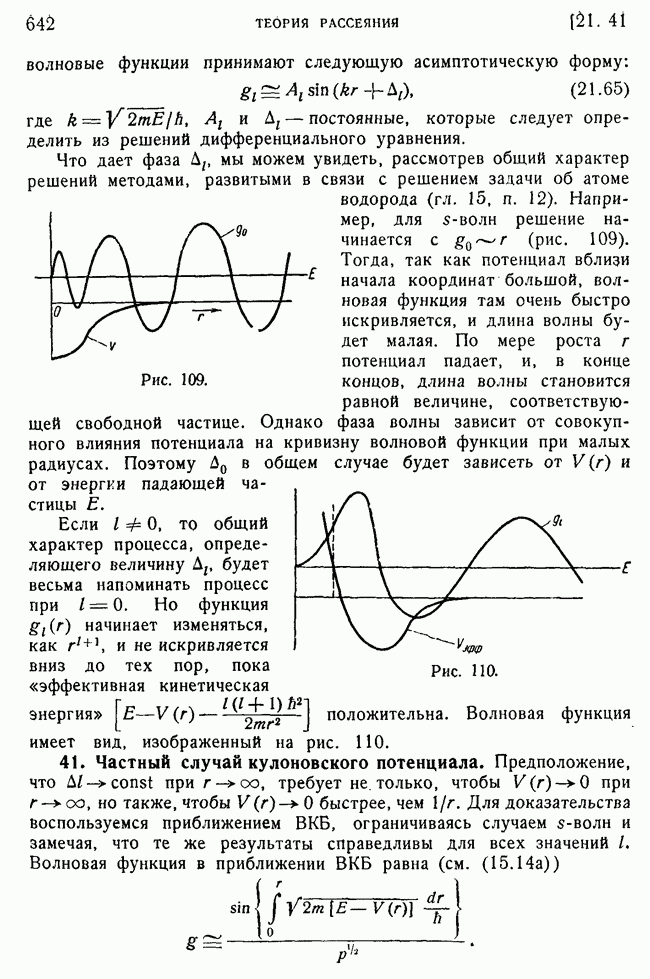
- 40. Общий характер решений.
- 41. Частный случай кулоновского потенциала.
- 42. Парциальные волны для свободной частицы.
- 43. Асимптотическая форма функций Бесселя.
- 44. Интерпретация парциальных волн.
- 45. Граничные условия для парциальных волн в случае свободной частицы.
- 46. Учет граничных условий в присутствии потенциала.
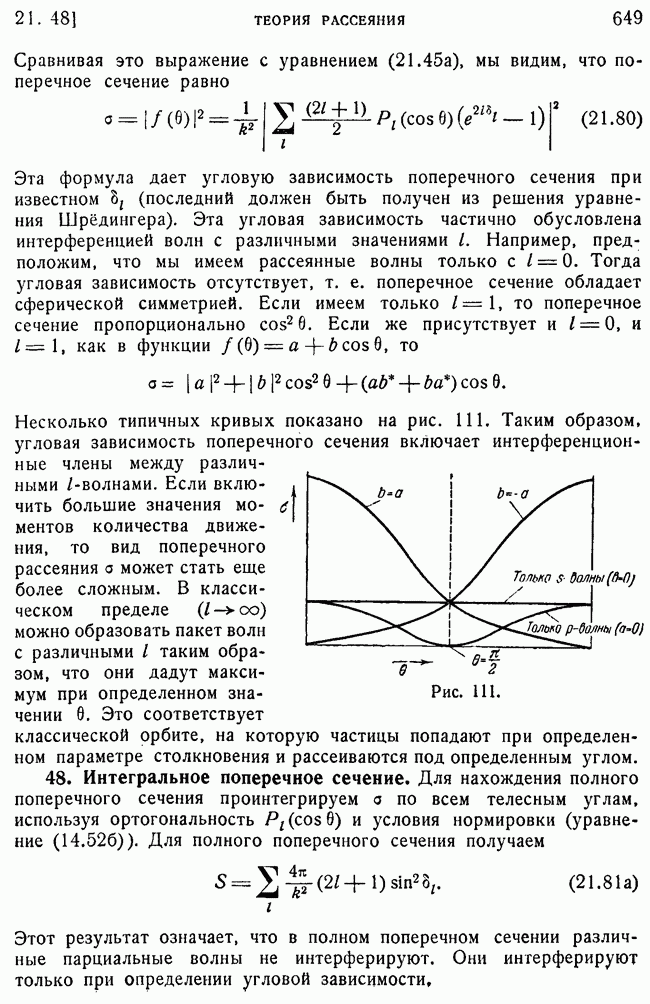
- 47. Формула для поперечного сечения рассеяния.
- 48. Интегральное поперечное сечение.
- 49. Вычисление фазы для непроницаемой сферы.
- 50. Применение точного метода к задаче рассеяния от прямоугольной ямы для случая s-волн.
- 51. Эффект Рамзауера.
- 52. Приближение для случая малых k.
- 53. Применение для случая ядерного рассеяния.
- 54. Приближенная зависимость поперечного сечения рассеяния от энергии связи дейтрона при малых значениях энергии.
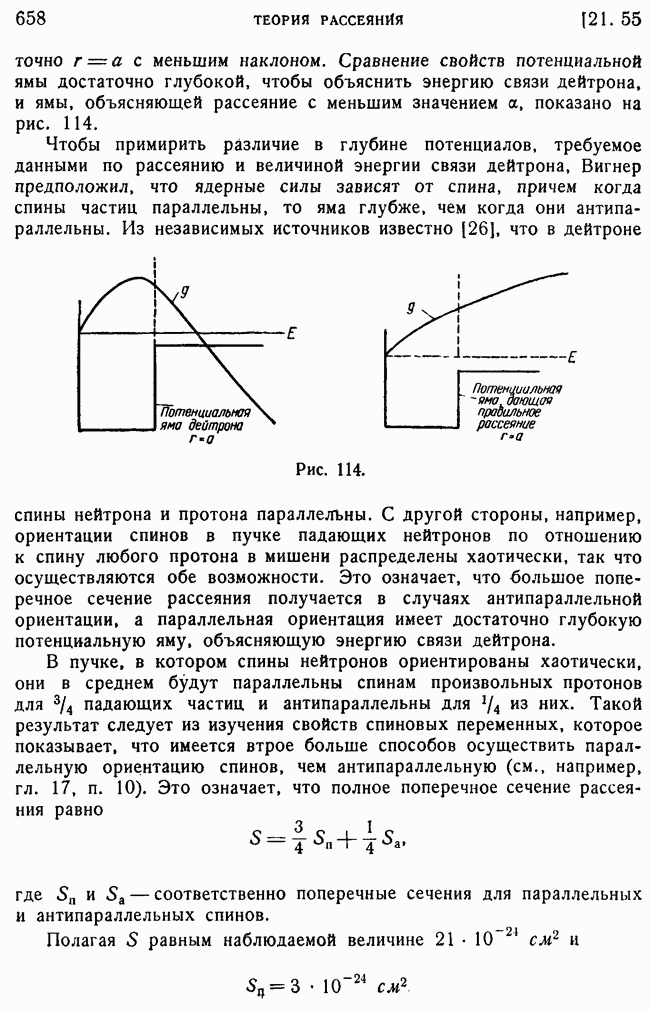
- 55. Учет спиновых сил.
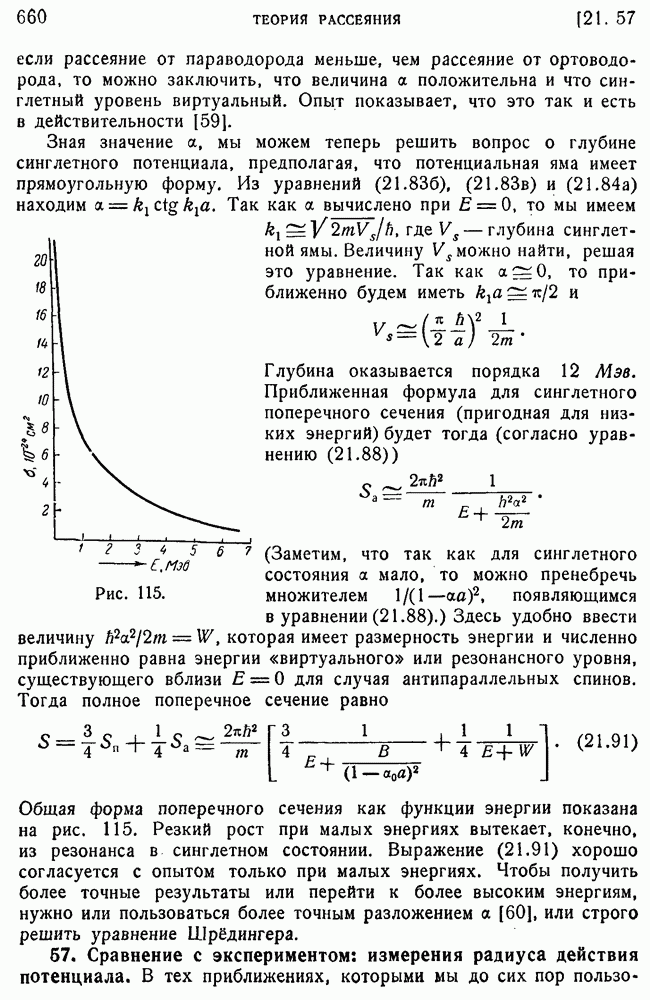
- 56. Определение глубины потенциальной ямы.
- 57. Сравнение с экспериментом: измерения радиуса действия потенциала.
- 58. Кулоновское рассеяние.
- 59. Интерпретация полученных результатов.
- 60. Обменные эффекты при кулоновском рассеянии.
- ЧАСТЬ VI. КВАНТОВАЯ ТЕОРИЯ ПРОЦЕССА ИЗМЕРЕНИЯ
- ГЛАВА 22. КВАНТОВАЯ ТЕОРИЯ ПРОЦЕССА ИЗМЕРЕНИЯ
- 5. Математическая трактовка процесса наблюдения.
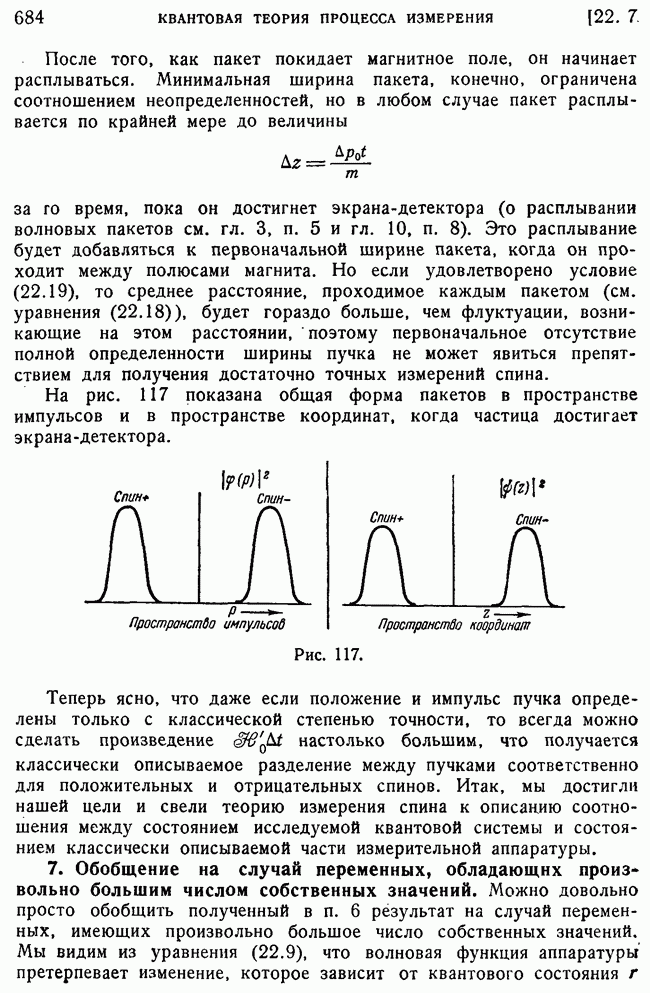
- 6. Измерение спина атома.
- 7. Обобщение на случай переменных, обладающих произвольно большим числом собственных значений.
- 8. Разрушение интерференционной картины в процессе измерения.
- 9. Появление случайных фазовых множителей.
- 10. Интерпретация полной волновой функции с помощью статистического ансамбля волновых функций только одного спина.
- 11. Включение координат аппаратуры.
- 12. Необратимость процесса измерения и фундаментальная роль этого явления в квантовой теории.
- 13. Волновые и корпускулярные свойства вещества как потенциальные возможности.
- 14. О связи между непрерывностью и дискретностью квантовых представлений.
- 15. Парадокс Эйнштейна, Розена и Подольского.
- 16. Мысленный эксперимент Эйнштейна, Розена и Подольского.
- 17. Математический анализ опыта по квантовой теории.
- 18. Физическое описание причин корреляции.
- 19. Доказательство несовместимости квантовой теории с понятием скрытых параметров.
- ГЛАВА 23. СООТНОШЕНИЕ МЕЖДУ КВАНТОВЫМ И КЛАССИЧЕСКИМ ПРЕДСТАВЛЕНИЯМИ
- ЛИТЕРАТУРА