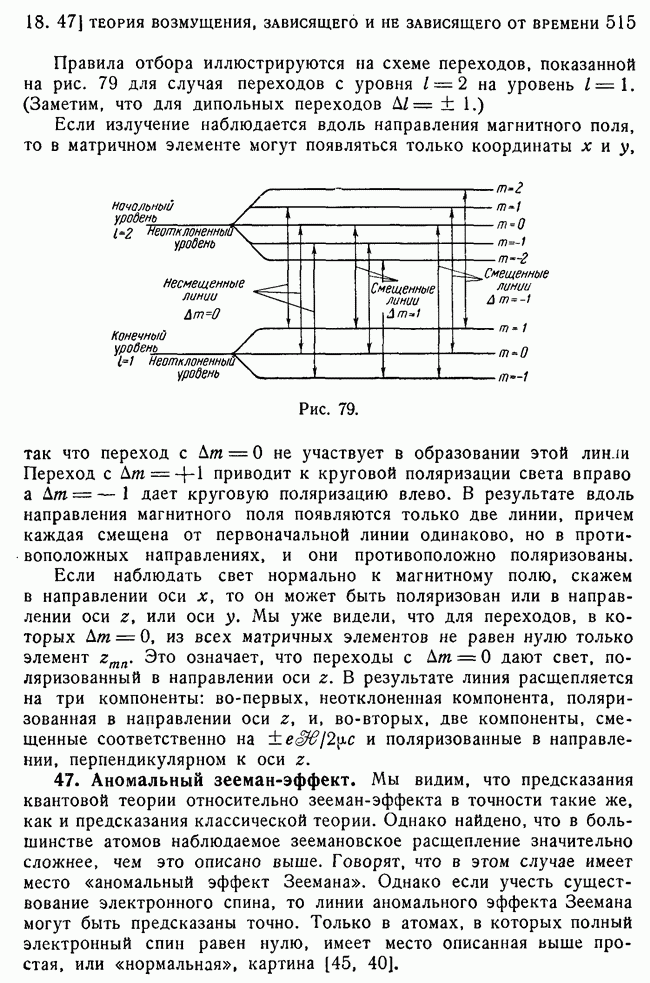
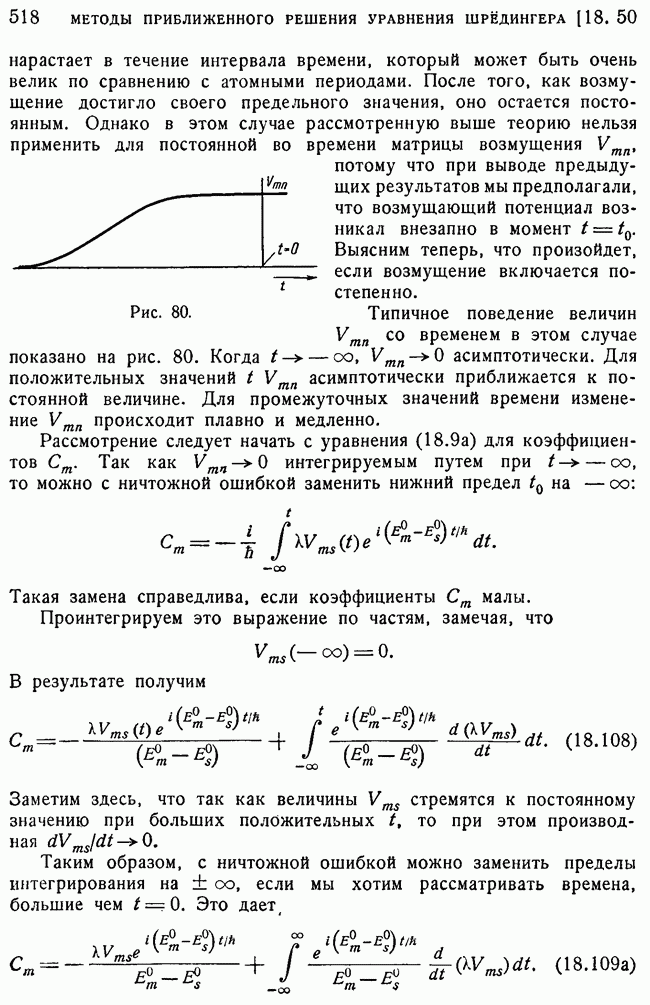
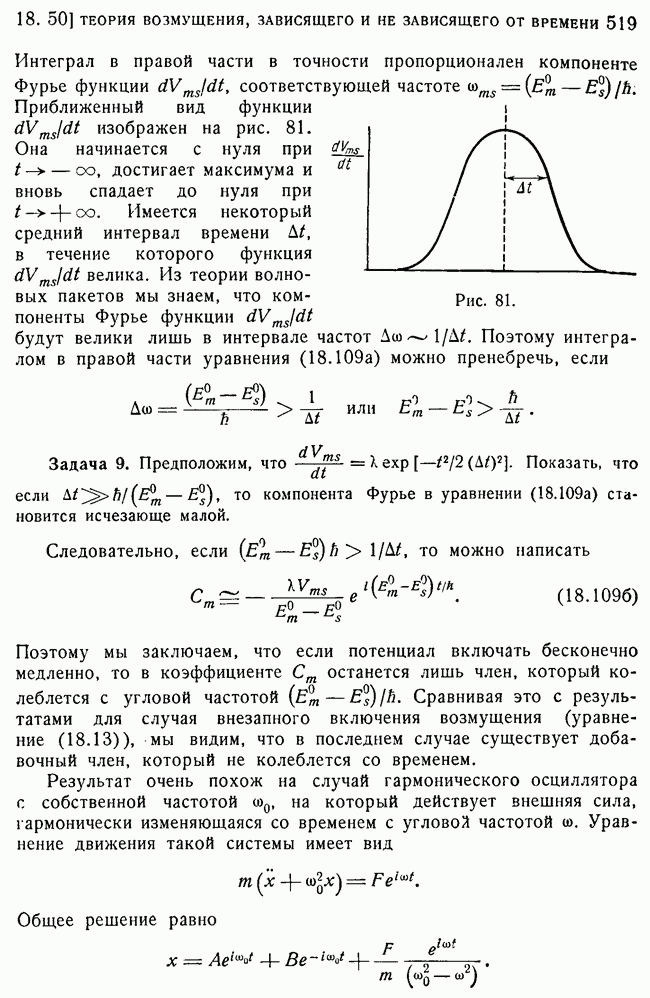
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
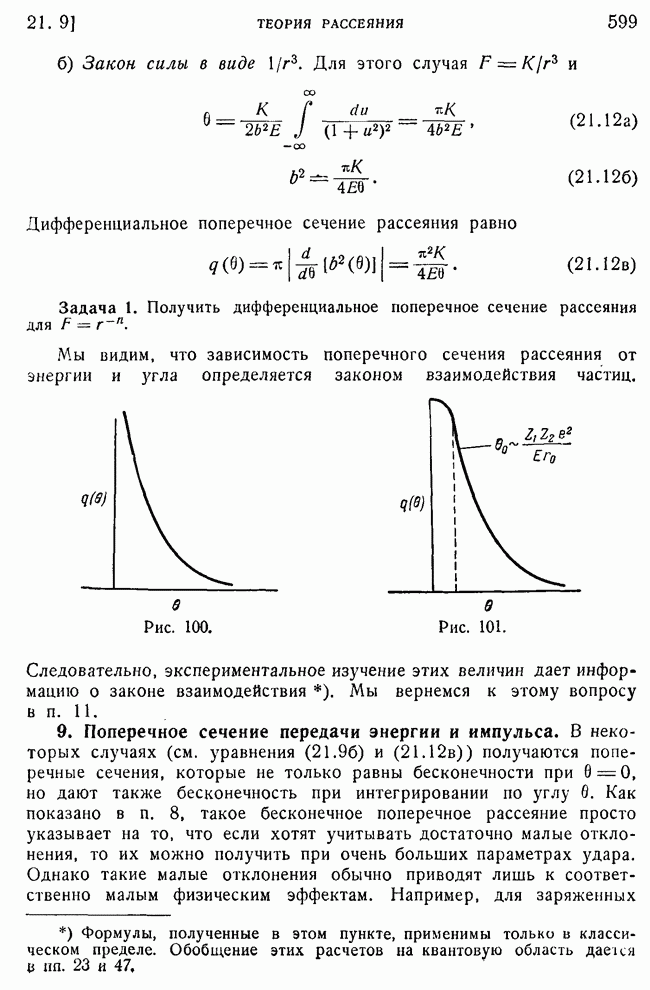
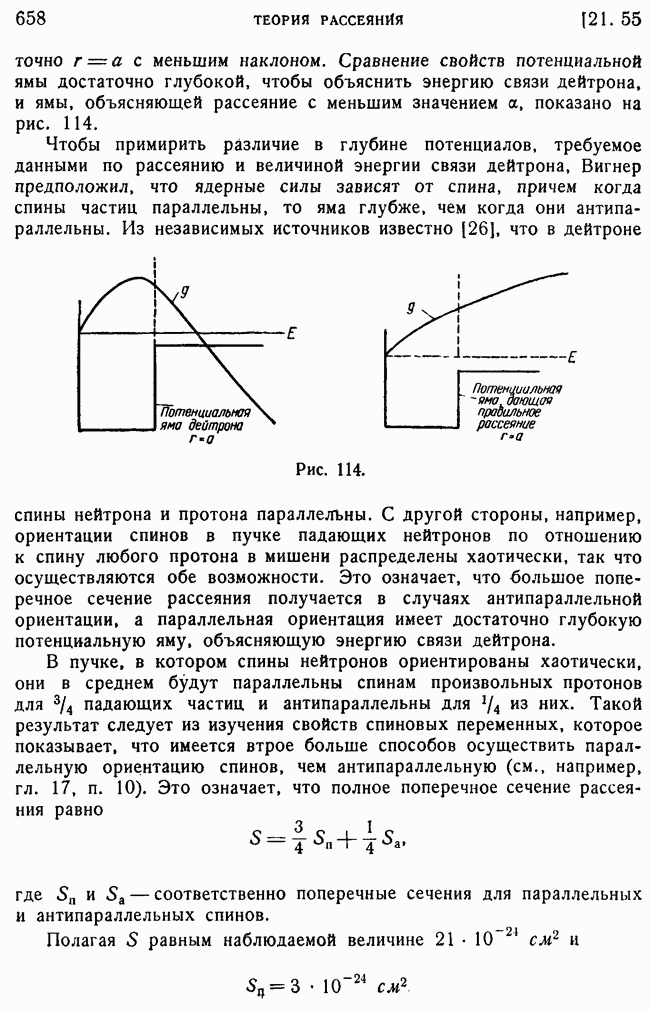
4. Нарушение интерференции и непротиворечивость корпускулярно-волнового дуализма.
Здесь будет показано, что статистическая интерпретация волновой функции вместе с явлением нарушения интерференции, обусловленного взаимодействием электрона с измерительным прибором, позволяют получить непротиворечивую формулировку корпускулярно-волнового дуализма. Предположим, например, что результаты измерения положения электрона под микроскопом автоматически регистрируются на фотопластинке. Положение пятна, появляющегося на фотопластинке, будет зависеть от того, через какую щель А или В прошел электрон. Если прибор работает правильно, то наблюдатель, рассматривая пластинку, может определить, через какую щель прошел электрон. Однако, даже не глядя на фотопластинку, наблюдатель знает, что прибор покажет прохождение электрона через одну из двух щелей (как если бы он был частицей), а не через обе сразу (как если бы он был волной).
Разберем теперь, как следует описать эти результаты с помощью волновой функции электрона. До взаимодействия прибора с электроном волновая функция имела вид  после же взаимодействия она определяется выражением
после же взаимодействия она определяется выражением  Вследствие неконтролируемых изменений в фазах
Вследствие неконтролируемых изменений в фазах  интерференция между волнами
интерференция между волнами  нарушается, и в результате вероятность обнаружения частицы в точке х оказывается равной (см. п. 3)
нарушается, и в результате вероятность обнаружения частицы в точке х оказывается равной (см. п. 3)

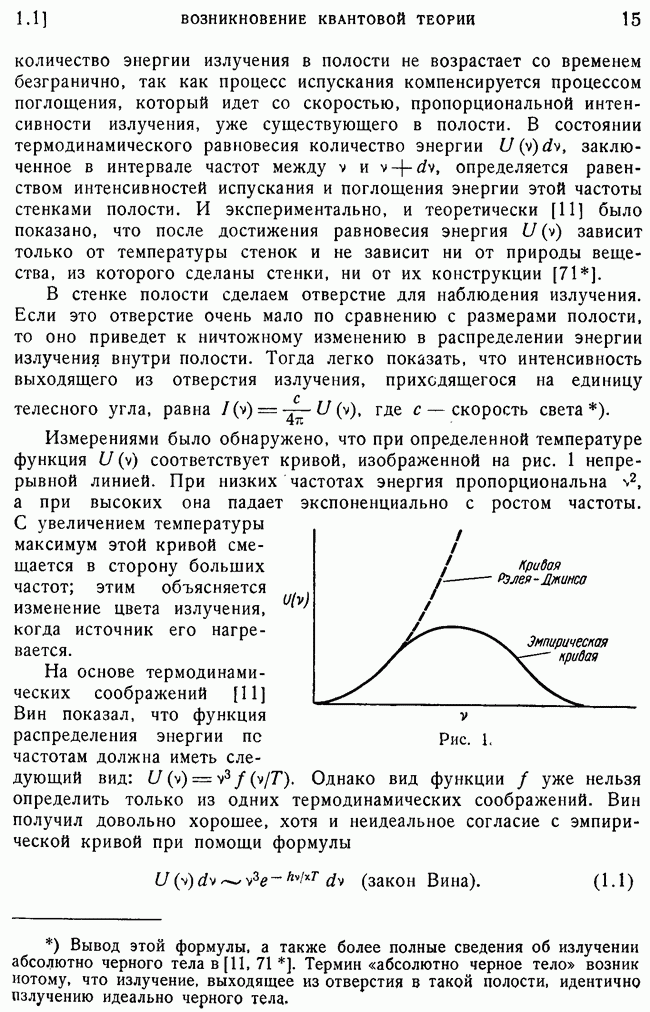
Но эта функция как раз такая, какая получилась бы для распределения классических частиц, проходящих через каждую щель в отдельности. Следовательно, электрон во всех отношениях ведет себя так, как если бы он, подобно частице, проходил через одну определенную, но неизвестно какую щель с вероятностью

что это будет щель  и с вероятностью
и с вероятностью

что это будет щель В. (Интегрирование проводится только по области пространства, расположенной вправо от щелей.) Однако перед взаимодействием электрона с измерительным прибором можно
было бы наблюдать эффекты интерференции, которые для своего объяснения требуют, чтобы электрон, подобно волне, мог проходить одновременно через обе щели. Таким образом, если принять во внимание влияние измерительного прибора на волновую функцию, мы получаем эффективное превращение электрона из образования типа волны в образование типа частицы. Такое превращение было получено также в п. 2 в связи с мысленным опытом, в котором мы пытались наблюдать, через какую щель проходил электрон в процессе дифракции.
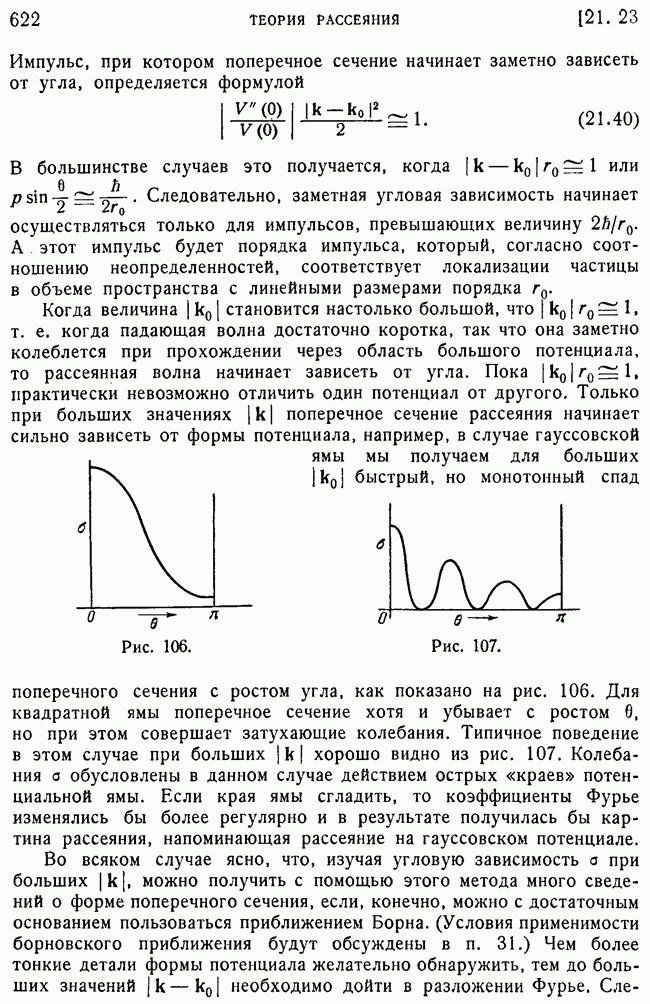
Покажем теперь, как нарушение интерференционной картины приводит к последовательному объяснению того, что происходит с волновой функцией, когда наблюдатель смотрит на фотопластинку и определяет ту из щелей, через которую в действительности прошел электрон. Как мы видели, те же результаты для всех физических процессов можно предсказать и по волновой функции

и по волновой функции, которая равна либо только  либо только
либо только  но с соответствующими вероятностями
но с соответствующими вероятностями  и
и  что каждая из них действительно является правильной волновой функцией. Когда наблюдатель находит, через которую из щелей прошел электрон, он заменяет
что каждая из них действительно является правильной волновой функцией. Когда наблюдатель находит, через которую из щелей прошел электрон, он заменяет  или на
или на  или на
или на  в зависимости от результатов эксперимента. Таким образом, получается редукция волновой функции, о которой шла речь в начале п. 3. Вследствие нарушения интерференционной картины такая редукция соответствовала выбору только одной из двух возможных альтернатив для действительной волновой функции, а не каким-то реальным физическим изменениям в состоянии самого электрона.
в зависимости от результатов эксперимента. Таким образом, получается редукция волновой функции, о которой шла речь в начале п. 3. Вследствие нарушения интерференционной картины такая редукция соответствовала выбору только одной из двух возможных альтернатив для действительной волновой функции, а не каким-то реальным физическим изменениям в состоянии самого электрона.
Хотя разрушение определенных фазовых соотношений вытекает из основ квантовой теории (см. гл. 22), но мы хотим здесь показать, что этот результат существен для последовательной вероятностной трактовки волновой функции.
Предположим, что в мысленном опыте, описанном в п. 1, интерференция между  не была бы полностью нарушена действием измерительного прибора, применявшегося для обнаружения, через какую щель фактически прошел каждый электрон. Тогда, согласно этому предположению, на экране справа от щелей должны появиться интерференционные полосы. Но как только наблюдатель прибегает к помощи измерительного прибора (например, фотопластинки, на которой регистрируется изображение электрона в
не была бы полностью нарушена действием измерительного прибора, применявшегося для обнаружения, через какую щель фактически прошел каждый электрон. Тогда, согласно этому предположению, на экране справа от щелей должны появиться интерференционные полосы. Но как только наблюдатель прибегает к помощи измерительного прибора (например, фотопластинки, на которой регистрируется изображение электрона в
микроскопе), он может обнаружить, через какую щель прошел каждый электрон. Поскольку при этом можно показать, что каждый электрон несомненно прошел через определенную щель, то его последующее поведение не должно зависеть от того, была ли открыта другая щель в это время или нет. Поэтому вероятность появления данного электрона в какой-либо точке экрана должна быть пропорциональна одной из плотностей вероятности «отдельной щели», т. е. или  или
или  в зависимости от того, прошел ли этот электрон через щель А или щель В. Так как равновероятно, что данный электрон пройдет через любую щель, то, следовательно, после того как через систему пройдет много электронов, интенсивность полос на экране определяется суммой плотностей вероятностей отдельных щелей и не зависит от интерференционных членов
в зависимости от того, прошел ли этот электрон через щель А или щель В. Так как равновероятно, что данный электрон пройдет через любую щель, то, следовательно, после того как через систему пройдет много электронов, интенсивность полос на экране определяется суммой плотностей вероятностей отдельных щелей и не зависит от интерференционных членов  Таким образом, мы показали, что если наблюдатель пользуется фотопластинкой, то на экране не будет получено никаких интерференционных полос. Если интерференция между и
Таким образом, мы показали, что если наблюдатель пользуется фотопластинкой, то на экране не будет получено никаких интерференционных полос. Если интерференция между и  была бы не полностью нарушена действием измерительного прибора, то мы пришли бы к теории, в которой статистически получающиеся полосы от электронов, попадающих на экран, должны были бы зависеть от того, взглянет или нет наблюдатель на регистрирующую часть измерительного прибора (в данном случае фотопластинку). Такая теория, очевидно, не имеет смысла. В итоге мы приходим к выводу, что полное нарушение интерференции между
была бы не полностью нарушена действием измерительного прибора, то мы пришли бы к теории, в которой статистически получающиеся полосы от электронов, попадающих на экран, должны были бы зависеть от того, взглянет или нет наблюдатель на регистрирующую часть измерительного прибора (в данном случае фотопластинку). Такая теория, очевидно, не имеет смысла. В итоге мы приходим к выводу, что полное нарушение интерференции между  необходимо для последовательной интерпретации
необходимо для последовательной интерпретации  соответственно как вероятностей прохождения электрона или через щель А, или через щель В. Следовательно, для электрона, проходящего через систему щелей без взаимодействия с устройством, которое способно определить его положение, нельзя считать, что волновая функция претерпевает редукцию до значений
соответственно как вероятностей прохождения электрона или через щель А, или через щель В. Следовательно, для электрона, проходящего через систему щелей без взаимодействия с устройством, которое способно определить его положение, нельзя считать, что волновая функция претерпевает редукцию до значений  или
или  так как интерференция между этими функциями по-прежнему существует.
так как интерференция между этими функциями по-прежнему существует.
Резкие изменения математических величин, аналогичные описанной выше редукции волновой функции, часто встречаются и в классических вероятностных функциях всякий раз, когда получаются новые сведения. Так, на основе статистики страхований можно предсказать некоторую ожидаемую продолжительность жизни человека, о котором известно только, что ему больше 21 года. Пусть затем мы внезапно узнали, что ему в действительности 70 лет. С этого момента мы немедленно предскажем ему значительно более короткую продолжительность жизни. Внезапное изменение предсказываемой длительности жизни не вызвано изменением в состоянии человека, а лишь уточнением информации о нем. Резкие изменения такого рода допустимы, так как продолжительность жизни выражается только
с помощью табличных статистических данных и поэтому непосредственно не соответствует ее действительной длине у конкретного человека. Такую статистическую теорию можно противопоставить полной динамической теории, например классической механике, которая принципиально должна иметь возможность предсказать продолжительность жизни конкретного человека на основе движения всех составляющих его атомов и молекул. В теории такого типа динамические переменные должны быть в однозначном соответствии с описываемой ими системой. Поэтому с этими переменными не может произойти никаких изменений, если только последние не отражают соответствующих физических изменений в описываемой системе и просто являются уточнениями каких-либо сведений о ней.
Переменные в квантовой теории имеют некоторое сходство с классическими статистическими функциями типа ожидаемой продолжительности жизни, но, как будет видно, имеются весьма существенные различия между ними. Аналогия заключается в том, что волновая функция предсказывает только вероятности действительных событий, т. е. она не находится в однозначном соответствии с описываемой системой, как и классическая статистическая функция. Поэтому внезапная редукция волновой функции, наступающая, когда наблюдатель пользуется измерительным прибором (например, фотопластинкой), отражает не изменения в наблюдаемом, объекте, а просто изменение статистической функции, дающей наблюдателю сведения об этой системе. С другой стороны, волновая функция весьма существенно отличается от классической вероятностной функции, поскольку до нарушения интерференции действием соответствующего измерительного прибора волновая функция не может быть последовательно выражена через простую вероятность. Это происходит потому, что фазовые соотношения между различными частями волновой функции, так же как и амплитуды, имеют физический смысл. Так, например, в мысленном опыте, где электрон проходит через систему двух щелей, фазовые соотношения между функциями  определяют интерференционные полосы, которые можно обнаружить
определяют интерференционные полосы, которые можно обнаружить  экране, расположенном вправо от щелей. Пока существуют определенные фазовые соотношения между
экране, расположенном вправо от щелей. Пока существуют определенные фазовые соотношения между  электрон способен проявлять интерференционные эффекты (действовать так, как будто он, подобно волне, проходит одновременно через обе щели). Поэтому внезапная редукция волновой функции в момент наблюдения представляет реальное изменение в физическом состоянии электрона (от поведения, подобного волне, к поведению, подобному частице). Как мы уже видели, интерпретация такого внезапного изменения волновой функции просто уточнением сведений наблюдателя об электроне привела бы к бессмысленным результатам. И лишь после того, как определенные фазовые соотношения между
электрон способен проявлять интерференционные эффекты (действовать так, как будто он, подобно волне, проходит одновременно через обе щели). Поэтому внезапная редукция волновой функции в момент наблюдения представляет реальное изменение в физическом состоянии электрона (от поведения, подобного волне, к поведению, подобному частице). Как мы уже видели, интерпретация такого внезапного изменения волновой функции просто уточнением сведений наблюдателя об электроне привела бы к бессмысленным результатам. И лишь после того, как определенные фазовые соотношения между 
нарушены вследствие действия измерительного прибора, редукция волновой функции перестает отражать соответствующее физическое изменение в состоянии электрона. Это означает, что когда между  существует определенное фазовое соотношение, то волновая функция находится в большем соответствии с состоянием электрона, чем это было бы в случае простой классической функции, определяющей вероятность прохождения электрона через какую-нибудь из щелей. Несмотря на это, степень соответствля между волновой функцией и действительным поведением электрона всегда меньше, чем та, которая имеет место для динамических переменных классической механики. В пп. 9 и 13 мы увидим, что эта вспомогательная степень соответствия волновор функции с поведением электрона может быть положена в основу новой физической картины квантовой природы материи.
существует определенное фазовое соотношение, то волновая функция находится в большем соответствии с состоянием электрона, чем это было бы в случае простой классической функции, определяющей вероятность прохождения электрона через какую-нибудь из щелей. Несмотря на это, степень соответствля между волновой функцией и действительным поведением электрона всегда меньше, чем та, которая имеет место для динамических переменных классической механики. В пп. 9 и 13 мы увидим, что эта вспомогательная степень соответствия волновор функции с поведением электрона может быть положена в основу новой физической картины квантовой природы материи.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. ФИЗИЧЕСКОЕ СОДЕРЖАНИЕ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА I. ВОЗНИКНОВЕНИЕ КВАНТОВОЙ ТЕОРИИ
- 1. Равновесное излучение абсолютно черного тела.
- 2. Электромагнитная энергия.
- 3. Электромагнитные потенциалы.
- 4. Граничные условия.
- 5. Разложение полей в ряд Фурье.
- 6. Поляризация волн.
- 7. Вычисление электромагнитной энергии.
- 8. Анализ полученного выражения электромагнитной энергии.
- 9. Число осцилляторов.
- 10. Закон равномерного распределения энергии по степеням свободы.
- Гипотеза Планка
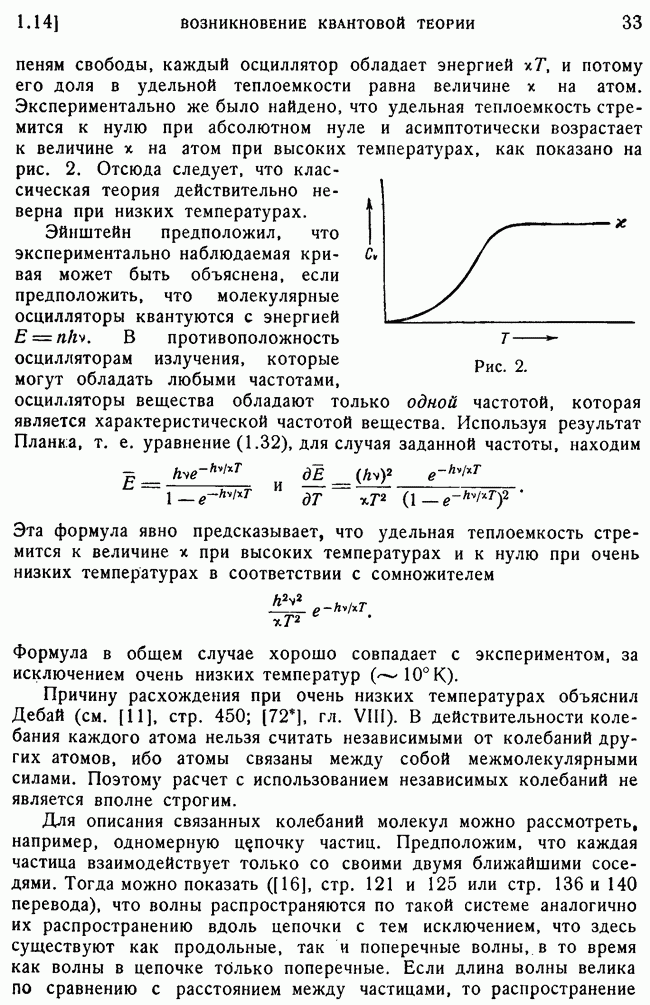
- 12. Обсуждение результатов.
- 13. Осцилляторы вещества и излучение.
- 14. Квантование осцилляторов вещества.
- 15. Основные выводы гл. 1.
- ГЛАВА 2. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ СТАРОЙ КВАНТОВОЙ ТЕОРИИ
- 1. Фотоэлектрический эффект.
- 2. Различия между классическими и квантовыми законами физики.
- 3. Дискретность квантовых процессов.
- 4. Вероятностный характер и неполный механический детерминизм законов квантовой теории.
- 5. Непригодность классических динамических законов в области элементарных явлений.
- 6. Принцип соответствия.
- 7. Корпускулярные свойства света.
- 8. Эффект Комптона. Рассеяние электромагнитного излучения.
- 9. Анализ эффекта Комптона.
- Квантование атомных систем
- 10. Доказательство квантования всех атомных систем.
- 11. Определение энергетических уровней.
- 12. Переменная действия.
- 13. Квантование момента количества движения.
- 14. Атом водорода.
- 15. Опыты Франка и Герца.
- Теория излучения в рамках принципа соответствия
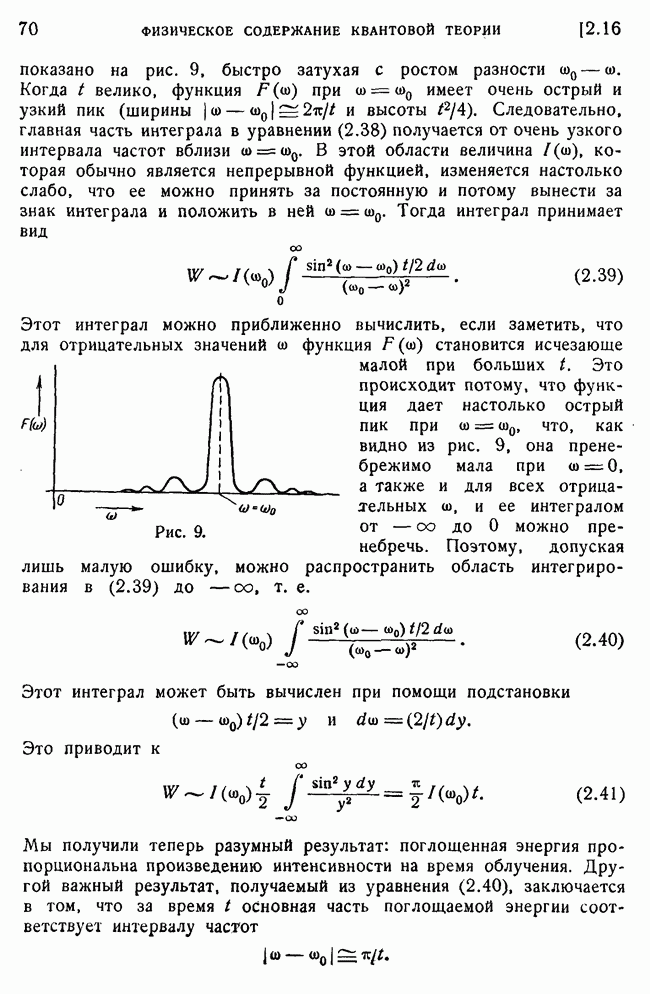
- 17. Испускание излучения.
- ГЛАВА 3. ВОЛНОВЫЕ ПАКЕТЫ И ВОЛНЫ ДЕ БРОЙЛЯ
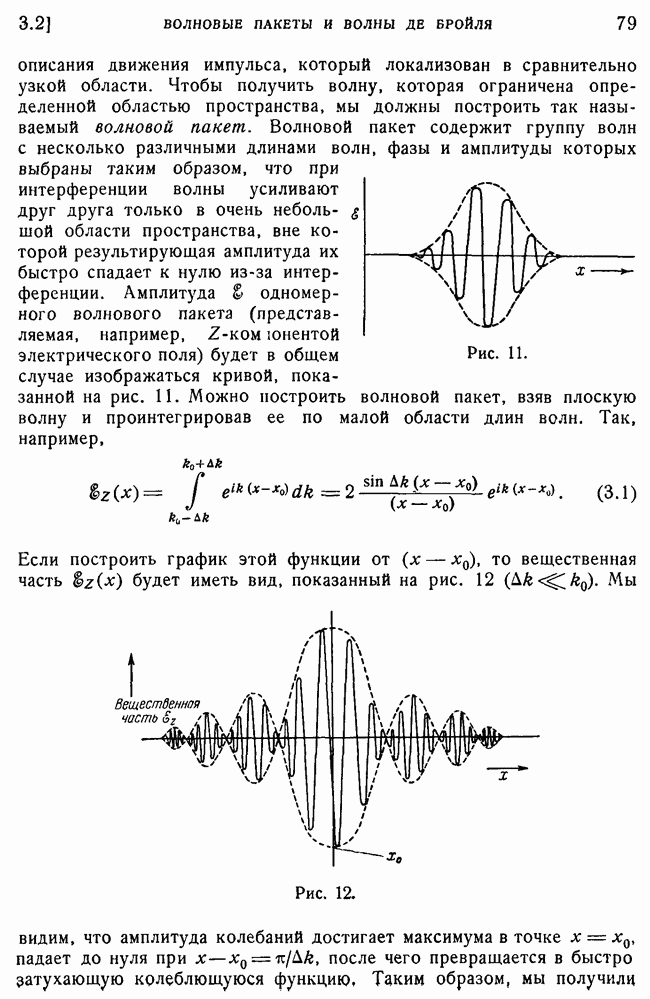
- 2. Движение импульсов света.
- 3. Ширина волнового пакета.
- 4. Групповая скорость.
- 5. Расплывание волновых пакетов.
- 6. Более общий критерий для определения ширины волновых пакетов.
- 7. Обобщение на трехмерный случай.
- Электронные волны
- 8. Движение электронных волновых пакетов.
- 9. Учет действия внешних сил.
- 10. Эффекты квантования.
- 11. Опыт Дэвиссона-Джермера.
- 12. Предсказание дифракции электронов теорией Бора — Зоммерфельда.
- 13. Вероятностная трактовка волновой функции.
- 14. Сравнение электронных и электромагнитных волн.
- 15. Более детальная картина электронных волн.
- 16. Переходы между орбитами.
- Волновое уравнение
- 18. Волна для свободной частицы.
- 19. Волновое уравнение для свободной частицы.
- ГЛАВА 4. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- 3. Доказательство сохранения вероятности.
- 4. Ток вероятности.
- 5. Является ли приведенная формулировка наиболее общей?
- 6. Релятивистские теории.
- 7. Плотность вероятности для кванта света.
- 8. Вероятность определения значений импульса.
- 9. Связь между функциями Р(х) и P(k).
- 10. Нормировочный фактор функции P(k).
- Сводка основных сведений о вероятностях
- ГЛАВА 5. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- 2. Вывод соотношения неопределенностей для случая электронов.
- 3. О трактовке соотношений неопределенностей.
- 4. Связь явления расплывания волнового пакета с со отношением неопределенностей.
- 5. Связь устойчивости атомов с соотношением неопределенностей.
- 6. Теория измерений.
- 7. Влияние на измерение квантовых эффектов.
- 8. Микроскоп.
- 9. Измерение импульса.
- 10. Соотношение неопределенностей для энергии и времени.
- 11. Применение соотношения неопределенностей к квантам света.
- 12. Наблюдения кванта света при помощи электронного микроскопа.
- 13. Локализация электромагнитной энергии и импульса при помощи щелей и затворов.
- 14. Применение соотношения неопределенностей к задаче определения орбит в атомах.
- 15. Более общее применение соотношения неопределенностей.
- 16. Внутренняя непротиворечивость квантовой теории.
- 17. Существуют ли скрытые параметры, лежащие в основе квантовой теории?
- ГЛАВА 6. ВОЛНОВЫЕ И КОРПУСКУЛЯРНЫЕ СВОЙСТВА МАТЕРИИ
- 1. Явление интерференции и корпускулярно-волновая природа материи.
- 2. Невозможность одновременного наблюдения волновых и корпускулярных свойств материи.
- 3. Влияние процесса наблюдения на волновую функцию.
- 4. Нарушение интерференции и непротиворечивость корпускулярно-волнового дуализма.
- 5. Обобщение предыдущих результатов.
- 6. Измерение импульса.
- 7. Связь изменений фазы с соотношением неопределенностей.
- 8. Значение фазовых соотношений.
- 9. Квантовые свойства материи как возможность.
- 10. Рассмотрение более общих взаимодействий.
- 11. О реальности волновых свойств материи.
- 12. Волномеханическое объяснение следов в камере Вильсона.
- 13. Качественная картина квантовых свойств материи.
- ГЛАВА 7. СВОДКА ОСНОВНЫХ КВАНТОВЫХ ПРЕДСТАВЛЕНИЙ
- ГЛАВА 8. ПОПЫТКА ПОСТРОЕНИЯ ФИЗИЧЕСКОЙ КАРТИНЫ КВАНТОВОЙ ПРИРОДЫ МАТЕРИИ
- 3. Простое и наглядное описание непрерывного движения.
- 4. Аналогия простых и квантовых представлений о движении.
- 5. Аналогия простых и квантовых представлений о фиксированном положении.
- 6. Более сложные представления, включающие понятие непрерывной траектории.
- 7. Причина и следствие.
- 8. Ранние представления о причине и следствии.
- 9. Полный механический детерминизм и причинность как тенденция.
- 10. Классическая теория как предписывающая, а не причинная.
- 11. Новые свойства квантовых представлений: приближенная и статистическая причинность.
- 12. Энергия и импульс в классической и квантовой теориях.
- 13. Импульс и энергия, и причинная форма описания материи.
- 14. Связь между пространственно-временным и причинным описанием материи.
- 15. Принцип дополнительности.
- 16. Неделимое единство мира.
- 17. Различие между объектом и окружающей средой в классической теории.
- 18. Роль непрерывности.
- 19. Роль причинных законов.
- 20. Анализ и синтез.
- 21. Применимость анализа и синтеза в классической теории.
- 22. Системы, описываемые классически, и существенно квантовомеханические системы.
- 23. Попытка разложения квантовой системы на отдельные части.
- 24. Неделимое единство квантовых систем.
- 26. Пример: атом водорода.
- 26. Необходимость немеханического описания.
- Сводка новых понятий квантовой теории
- Аналогии с квантовыми процессами
- 28. Возможные причины для аналогий между мышлением и квантовыми процессами.
- Примечание редактора к гл. 8
- ЧАСТЬ II. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА 9. ВОЛНОВЫЕ ФУНКЦИИ, ОПЕРАТОРЫ И УРАВНЕНИЕ ШРЁДИНГЕРА
- 2. Гипотеза линейной суперпозиции.
- 3. Понятие состояния системы в квантовой теории.
- 4. Статистический смысл понятия квантового состояния.
- 5. Математическое выражение для средних величин.
- 6. Операторы для вычисления средних значений импульса из интегралов в пространстве координат.
- 7. Функции импульса.
- 8. Операторы в пространстве импульсов. Импульсное представление.
- 9. Линейность операторов.
- 10. Координата x как оператор.
- 11. Умножение операторов. Коммутаторы.
- 12. Операторная форма функций общего вида.
- 13. Вещественность средних значений и порядок сомножителей.
- 14. Эрмитовские операторы.
- 15. Видоизмененное правило вычисления средних значений f(x, р).
- 16. Эрмитовски сопряженные операторы.
- 17. Обобщенное определение эрмитовского оператора.
- 18. Обобщенное определение эрмитовски сопряженных операторов.
- 19. Определение оператора, эрмитовски сопряженного произведению двух операторов.
- 20. Применение к коммутаторам.
- 21. Теорема для эрмитовских операторов.
- Вывод уравнения Шрёдингера
- 26. Задача вычисления среднего движения волнового пакета.
- 27. Общее правило для вычисления Н.
- 28. Является ли вышеприведенное уравнение наиболее общим из всех возможных?
- 29. Значение волнового уравнения.
- 30. Общее определение тока вероятности.
- 31. Истолкование величины Н как средней энергии.
- 32. Закон сохранения энергии.
- ГЛАВА 10. ФЛУКТУАЦИИ, КОРРЕЛЯЦИИ И СОБСТВЕННЫЕ ФУНКЦИИ
- 4. Количественная мера корреляции в классической теории.
- 5. Классификация классических статистических систем по средним значениям произведения.
- 6. Квантовое определение корреляций.
- 7. Применение к задаче о расплывании волнового пакета для свободной частицы.
- 8. Полуклассическое описание частицы с неопределенными координатой и импульсом.
- 9. Общий вывод соотношений неопределенностей.
- 10. Особые свойства гауссовской волновой функции.
- 11. Задача многих частиц.
- 12. Собственные значения и собственные функции операторов.
- 13. Примеры собственных функций и собственных значений в координатном пространстве.
- 14. Вырожденные операторы.
- 15. Дельта-функция Дирака.
- 16. Собственные функции оператора импульса в пространстве импульсов.
- 17. Собственные функции оператора х в импульсном представлении.
- 18. Связь между собственными функциями оператора х в координатном пространстве и в пространстве импульсов.
- 19. Дифференцирование дельта-функции.
- 20. Дискретный и непрерывный спектр собственных значений операторов.
- 21. Разложение произвольной функции в ряд по собственным функциям.
- 22. Постулат разложения.
- 23. Теорема о вещественности собственных значений эрмитовского оператора.
- 24. Ортогональность собственных функций эрмитовского оператора.
- 25. Вычисление коэффициентов разложения.
- 26. Разложение дельта-функции Дирака в ряд по собственным функциям произвольного эрмитовского оператора.
- 27. Представление оператора через его собственные функции.
- 28. Выражение среднего значения функции f(A) в методе разложения по собственным функциям А.
- 29. Физическая интерпретация коэффициентов разложения с помощью вероятностей.
- Дальнейшее истолкование вероятностей в квантовой теории
- 30. Интерференция вероятностей.
- 31. Собственные функции оператора Гамильтона.
- 32. Изменение собственных функций Н со временем.
- 33. Изменение вероятности со временем. Стационарные состояния.
- 34. Связь вероятностей, зависящих от времени, с соотношением неопределенностей.
- 35. Важность собственных функций гамильтоновского оператора Н.
- 36. Изменение вероятности со временем для общей волновой функции.
- ЧАСТЬ III. ПРИЛОЖЕНИЯ К ПРОСТЫМ СИСТЕМАМ. ДАЛЬНЕЙШИЕ ОБОБЩЕНИЯ ФОРМУЛИРОВКИ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА 11. РЕШЕНИЕ ВОЛНОВОГО УРАВНЕНИЯ ДЛЯ ПРЯМОУГОЛЬНЫХ ПОТЕНЦИАЛОВ
- 2. Собственные функции оператора энергии.
- 3. Прямоугольные потенциальные барьеры.
- 4. Решение задачи для прямоугольных потенциалов.
- 5. Проникновение через барьер.
- 6. Применения задачи о проникновении частиц через потенциальный барьер.
- 7. Прямоугольная потенциальная яма.
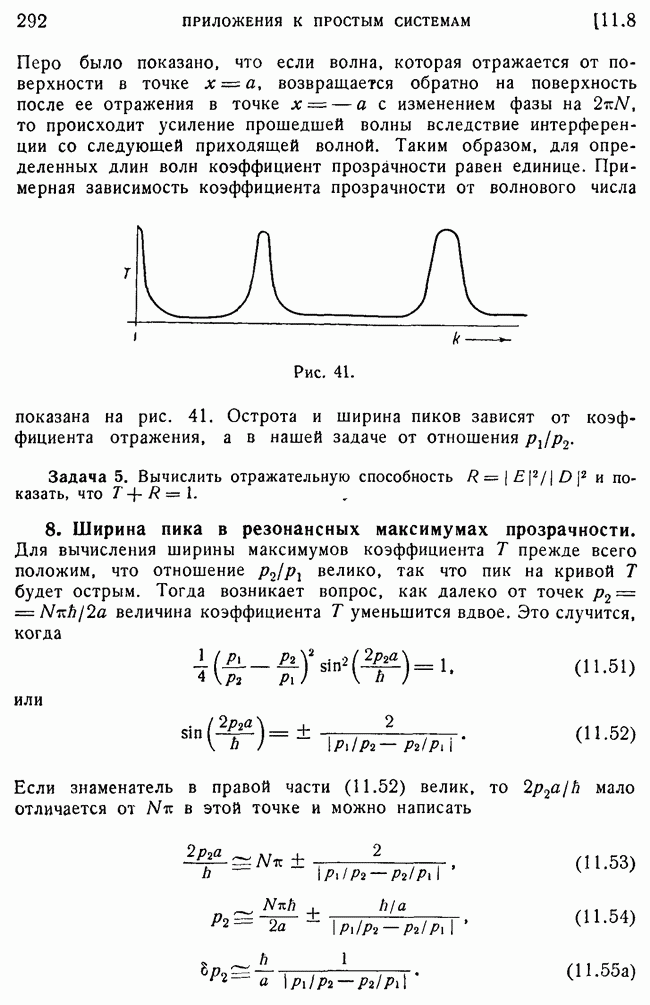
- 8. Ширина пика в резонансных максимумах прозрачности.
- 9. Эффект Рамзауера.
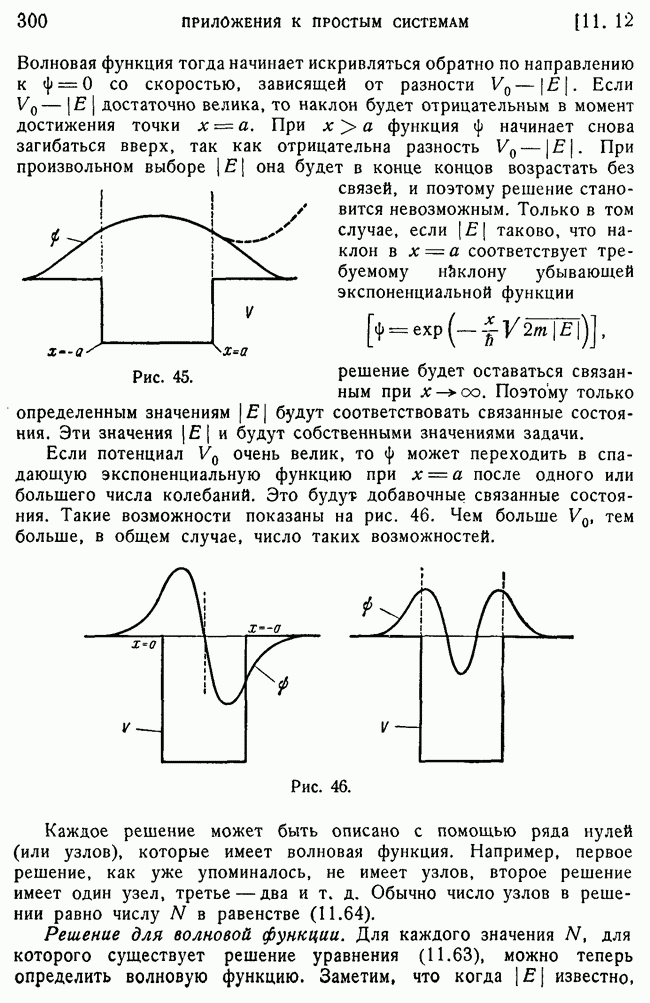
- 10. Связанные состояния.
- 11. Предельный случай бесконечно глубокой ямы.
- 12. Графическая интерпретация решений.
- 13. Применение теоремы разложения.
- 14. Применение к дейтрону.
- 16. Объяснение энергетических уровней с помощью соотношения неопределенностей.
- 16. Использование наблюдаемых энергетических уровней для получения сведений о потенциале.
- 17. Волновые пакеты как континуум собственных функций.
- 18. Волновой пакет для прошедшей волны.
- 19. Время замедления волны при прохождении потенциальной ямы.
- 20. Метастабильные (или виртуальные) состояния микрочастицы в потенциальной яме.
- 21. Метастабильное синглетное состояние дейтрона.
- ГЛАВА 12. КЛАССИЧЕСКИЙ ПРЕДЕЛ КВАНТОВОЙ ТЕОРИИ. ПРИБЛИЖЕНИЕ ВКБ
- 4. Физическая интерпретация решений с помощью классического распределения частиц.
- 5. Волновые пакеты. Решение, зависящее от времени.
- 6. Приближение ВКБ, зависящее от времени, в трехмерном случае.
- 7. Проникновение через барьер.
- 8. Формулы связи.
- 9. Формулы связи.
- 10. Вероятность проникновения через барьер.
- 11. Использование выражения для вероятности проникновения через барьер в частных случаях.
- 12. Вероятность проникновения частиц внутрь ядра.
- 13. Связанные состояния потенциальной ямы.
- 14. Виртуальные, или метастабильные, состояния в приближении ВКБ.
- 15. Обсуждение выражения (12.64) для коэффициента прозрачности.
- 16. Ширина резонанса. Коэффициент прозрачности вблизи резонанса.
- 17. Интенсивность волны внутри ямы.
- 18. Образование волновых пакетов. Время жизни виртуальных состояний.
- 19. Волновой пакет внутри потенциальной ямы (вблизи резонанса).
- 20. Соотношение неопределенностей.
- 21. Применение к радиоактивным системам.
- 22. Применение к ядерным реакциям.
- ГЛАВА 13. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- 5. Шрёдингеровский метод факторизации.
- 6. Решение для волновых функций.
- 7. Полиномы Эрмита — Чебышева.
- 8. Нормирующий множитель.
- 9. Порождающая функция.
- 10. Рекуррентные соотношения.
- 11. Некоторые вспомогательные математические соотношения.
- 13. Свойства ортогональности полиномов Эрмита — Чебышева.
- 15. Волновые пакеты.
- 16. Средние значения кинетической и потенциальной энергий.
- ГЛАВА 14. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ И ВОЛНОВОЕ УРАВНЕНИЕ В ТРЕХ ИЗМЕРЕНИЯХ
- 2. Момент количества движения.
- 3. Перестановочные соотношения для операторов момента количества движения.
- 4. Полный момент количества движения.
- 5. Слагающие момента количества движения в полярных координатах.
- 6. Константы движения.
- 7. Собственные значения Lz.
- 9. Совместные собственные функции операторов Lz и L2.
- 10. Одновременное определение собственных функций и собственных значений Lz и L2.
- 11. Векторное изображение возможных значений моментов количества движения.
- 12. Флуктуации в ориентациях вектора L.
- 13. Собственные функции операторов L2 и Lz.
- 14. Полиномы Лежандра.
- 15. Присоединенные функции Лежандра.
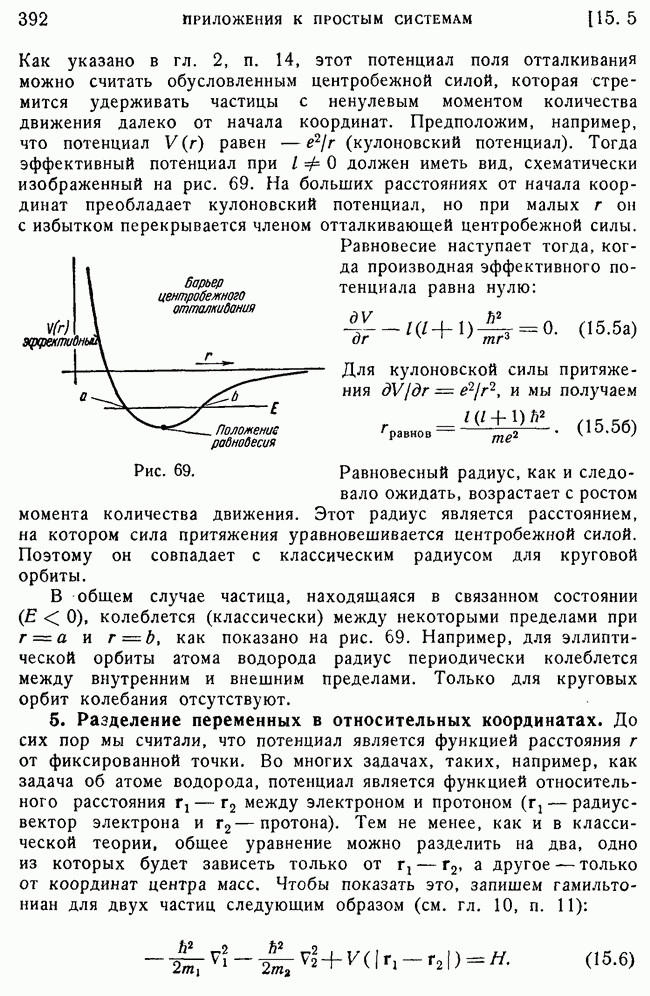
- 16. Измерение момента количества движения. Опыт Штерна и Герлаха.
- 17. Преобразование к вращающейся системе осей.
- 18. Двойной опыт Штерна и Герлаха.
- 19. Физическая эквивалентность всех систем координат.
- 20. Обобщение на произвольные повороты и произвольное l.
- 21. Применение к построению орбит.
- ГЛАВА 15. РЕШЕНИЕ РАДИАЛЬНОГО УРАВНЕНИЯ; АТОМ ВОДОРОДА; ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
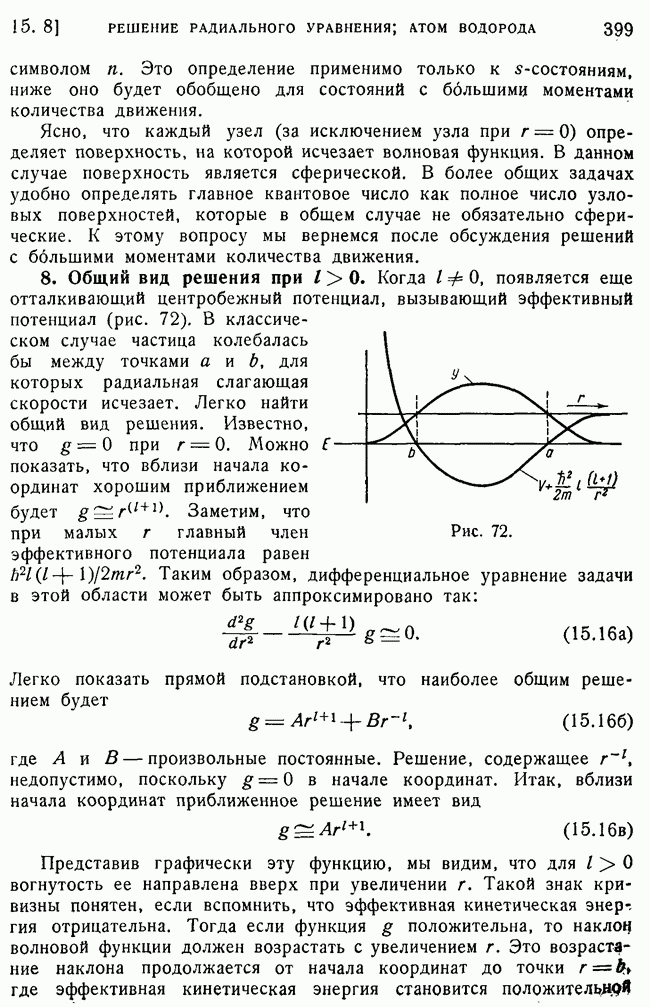
- 4. Центробежный потенциал.
- 5. Разделение переменных в относительных координатах.
- 6. Предварительное обсуждение общей формы решения для атома водорода.
- 7. Общая форма решения для s-волн.
- 8. Общий вид решения при l > 0.
- 9. Определение квантовых чисел.
- 10. Физическая интерпретация волновых функций при различных n, l, m.
- 11. Образование волновых пакетов.
- 12. Точное решение для атома водорода.
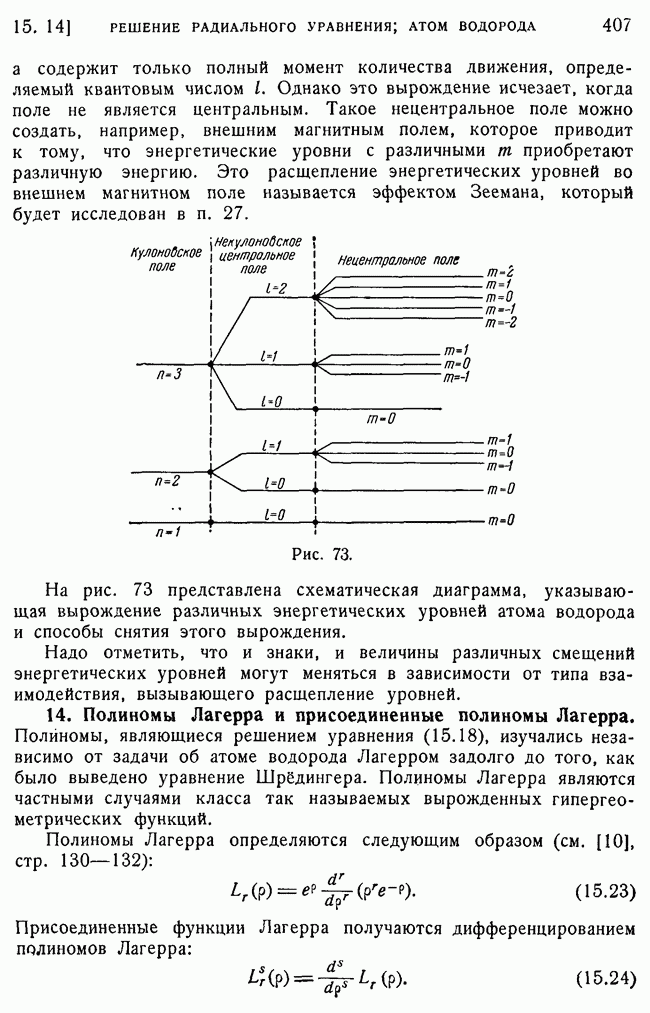
- 13. Вырождение энергетических уровней атома водорода.
- 14. Полиномы Лагерра и присоединенные полиномы Лагерра.
- 15. Трехмерный гармонический осциллятор.
- 16. Возможность вырождения энергетических уровней.
- 17. Случай сферической симметрии.
- 18. Вид волновой функции в случае сферической симметрии.
- 19. Важное свойство вырожденных собственных функций.
- 20. Связь полиномов Эрмита — Чебышева со сферическими гармониками.
- 21. Гамильтониан заряженной частицы в заданном электромагнитном поле.
- 22. Квантовомеханический гамильтониан.
- 23. Сохранение вероятности. Ток вероятности.
- 24. Классический предел.
- 25. Градиентная (калибровочная) инвариантность.
- 26. Частный случай: однородное магнитное поле.
- 27. Зеемановское расщепление энергетических уровней с различными квантовыми числами m.
- ГЛАВА 16. МАТРИЧНАЯ ФОРМУЛИРОВКА КВАНТОВОЙ ТЕОРИИ
- 3. Обоснование матричного представления квантовомеханических операторов.
- 4. Пример: волновые функции гармонического осциллятора.
- 5. Эрмитовские матрицы и эрмитовски сопряженные матрицы.
- 6. Диагональное представление операторов.
- 7. Коммутативность диагональных матриц.
- 8. Непрерывные матрицы.
- 9. Матричное представление волновой функции в виде столбца.
- 10. Нормировка и ортогональность волновых функций, выраженных в виде столбцов.
- 11. Среднее значение оператора.
- 12. Собственные значения и собственные векторы матриц.
- 13. Изменение представления.
- 14. Важное свойство матриц преобразования (a-матриц).
- 15. Значение унитарного преобразования.
- 16. След, или шпур, матрицы.
- 17. Совместные собственные функции коммутирующих операторов.
- 18. Определение произвольного оператора при помощи его коммутаторов с полной системой коммутирующих операторов.
- 19. Уравнение Шредингера в произвольном представлении.
- 20. Гамильтоновское представление.
- 21. Гейзенберговское представление.
- 22. Изменение операторов со временем в гейзенберговском представлении.
- 23. Скобки Пуассона.
- 24. Формулировка квантовой теории по Гейзенбергу.
- 25. Физическое истолкование матричного представления и теории преобразования.
- ГЛАВА 17. СПИН И МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- 1. Спин электрона.
- 2. Матричное выражение операторов момента количества движения.
- 3. Возможные значения l и m; полуцелые квантовые числа момента количества движения.
- 4. Матрицы для операторов …
- 5. Собственные функции операторов «сигма».
- 6. Собственные функции …
- 7. Преобразования спиноров.
- 8. Сложение моментов количества движения.
- 9. Сложение спинов двух различных частиц.
- 10. Распределение вероятности состояний спина в статистическом ансамбле.
- 11. Сложение орбитального и спинового моментов частицы.
- 12. Общая задача сложения моментов количества движения.
- 13. Энергия электрона со спином.
- ЧАСТЬ IV. МЕТОДЫ ПРИБЛИЖЕННОГО РЕШЕНИЯ УРАВНЕНИЯ ШРЁДИНГЕРА
- ГЛАВА 18. ТЕОРИЯ ВОЗМУЩЕНИЯ, ЗАВИСЯЩЕГО И НЕ ЗАВИСЯЩЕГО ОТ ВРЕМЕНИ
- 8. Возмущение вырожденных состояний.
- 9. Описание переходов с помощью квантовых флуктуаций.
- 10. Микроскопическая обратимость процессов перехода.
- 11. Сохранение вероятности.
- 12. Случай б: гармоническое изменение матричных элементов со временем, задача поглощения и испускания света.
- 13. Применение к случаю плоской волны.
- 15. Квазиклассическое описание поля излучения.
- 16. Вычисление вероятности перехода.
- 17. Связь между векторным потенциалом и интенсивностью излучения.
- 18. Влияние распределения частот падающего света.
- 19. Обсуждение результатов.
- 20. Индуцированное испускание квантов.
- 21. Классическая аналогия индуцированного излучения.
- 22. Самопроизвольное излучение.
- 23. Трактовка самопроизвольного излучения по Эйнштейну.
- 24. Применения теории переходов.
- 25. Приближение электрического диполя.
- 26. Вычисление величин для изотропного гармонического осциллятора.
- 27. Правила отбора для гармонического осциллятора.
- 28. Связь правил отбора с принципом соответствия.
- 29. Введение четности.
- 30. Правила отбора для четности.
- 31. Правила отбора для сферически симметричного потенциала без учета спина.
- 32. Запрещенные переходы, электрическое квадрупольное излучение.
- 33. Магнитное дипольное излучение.
- 34. Правила отбора для электрического квадрупольного излучения.
- 35. Правила отбора для магнитного дипольного излучения.
- 36. Переходы более высокого порядка.
- 37. Полностью запрещенные переходы между состояниями с l = 0.
- 38. Полная вероятность излучения.
- 39. Сравнение с классической теорией.
- 40. Правила сумм для вычисления матричных элементов.
- 41. Круговая поляризация.
- 42. Эллиптическая поляризация.
- 43. Квантовая трактовка.
- 44. Правила отбора.
- 45. Применение к случаю нормального зееман-эффекта.
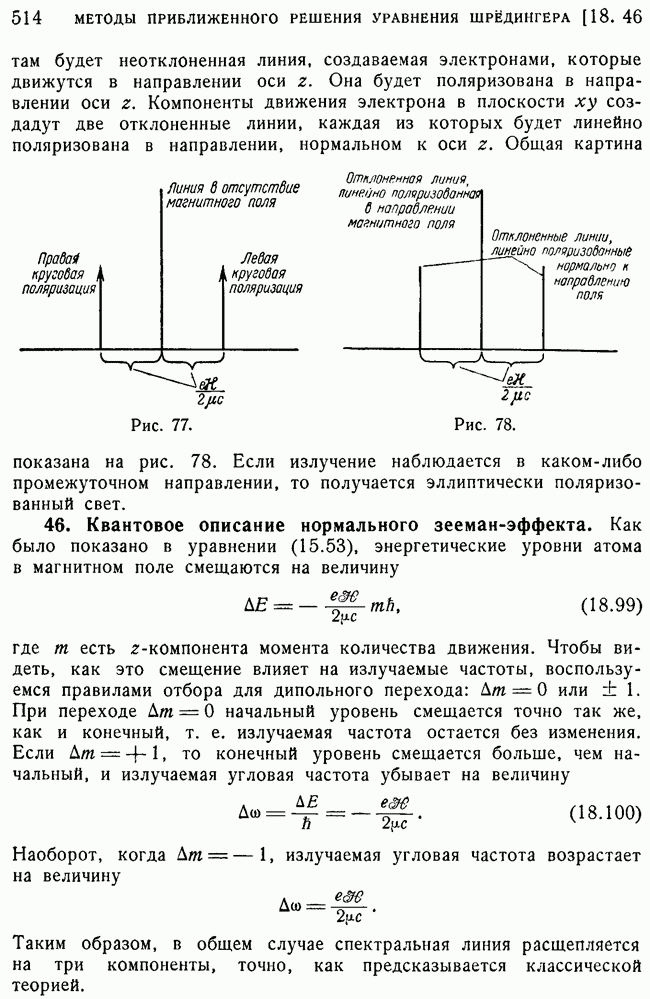
- 46. Квантовое описание нормального зееман-эффекта.
- 47. Аномальный зееман-эффект.
- 48. Общие методы вычисления вероятностей переходов.
- 49. Влияние спина электрона на вероятности переходов.
- 50. Случай в: возмущение Vmn медленно изменяющееся со временем (адиабатический случай).
- 51. Адиабатическое включение потенциала, приводящее к возмущению стационарного состояния.
- 52. Возмущение волновых функций стационарного состояния.
- 53. Интерпретация формул второго приближения для энергии.
- 54. Применение теории возмущений.
- ГЛАВА 19. ВОЗМУЩЕНИЯ В СЛУЧАЕ ВЫРОЖДЕННЫХ СИСТЕМ
- 9. Кваитовомеханический «резонанс».
- 10. Аналогия задачи возмущения вырожденных состояний с преобразованием к главным осям.
- Приложения теории возмущений вырожденных состояний
- 11. Эффект Штарка первого порядка.
- 12. Классическая интерпретация линейного эффекта Штарка.
- 13. Межатомные ван-дер-ваальсовские силы.
- 14. Квантовомеханическая аналогия фазы осциллятора.
- 16. Обменное вырождение.
- 18. Симметричные и антисимметричные функции.
- 19. Вычисление энергии.
- 20. Приближения высших порядков.
- 21. Влияние спина.
- 22. Антисимметричность волновых функций электронов.
- 23. Связь между обменной энергией и спином электрона, обусловленная свойством антисимметричности волновых функций.
- 24. Формальное выражение обменной энергии при помощи спиновых операторов.
- 25. Система из многих электронов.
- 26. Принцип запрета Паули.
- 28. Полностью симметричные волновые функции.
- 29. Неразличимость эквивалентных частиц.
- ГЛАВА 20. ВНЕЗАПНЫЕ И АДИАБАТИЧЕСКИЕ ВОЗМУЩЕНИЯ
- 1. Общая форма адиабатического возмущения.
- 3. Примеры адиабатических возмущений.
- 4. Внезапное изменение возмущающего потенциала.
- 5. Приложения. Испускание электронов из ядра при «бета»-pacпаде.
- 6. Связь между теорией возмущений и теорией внезапных переходов.
- ЧАСТЬ V. ТЕОРИЯ РАССЕЯНИЯ
- ГЛАВА 21. ТЕОРИЯ РАССЕЯНИЯ
- 4. Распределение длин свободного пробега.
- 5. Зависимость поперечного сечения от угла рассеяния.
- 6. Дифференциальные поперечные сечения.
- 7. Более общая теория рассеяния.
- 8. Приближение малых отклонений. Классическая теория возмущений.
- 9. Поперечное сечение передачи энергии и импульса.
- 10. Точное решение задачи рассеяния.
- 11. Использование поперечных сечений рассеяния для исследования вида взаимодействия между частицами.
- 12. Переход от системы координат центра инерции к лабораторной системе координат.
- 14. Столкновение тождественных частиц.
- 15. Квантовая теория рассеяния.
- 17. Квантовое описание процесса рассеяния.
- 18. Рассеяние как процесс перехода между различными состояниями в пространстве импульсов.
- 19. Борновское приближение. Теория возмущений.
- 21. Конкретный пример рассеяния на экранированном кулоновском потенциале.
- 22. Связь между борновским приближением и коэффициентами разложения потенциала в ряд Фурье.
- 23. Примеры: сравнение поперечных сечений для гауссовского потенциала и прямоугольной ямы.
- 24. Исследование процесса рассеяния в координатном представлении.
- 25. Новая форма уравнения Шредингера.
- 27. Борновское приближение.
- 28. Связь между описанием процессов рассеяния в координатном и импульсном представлениях.
- 29. Связь между методом стационарных состояний и временным описанием процессов рассеяния.
- 30. Другое применение борновского приближения: рассеяние от кристаллической решетки.
- 31. Условия применимости борновского приближения.
- 32. Применение к случаю экранированного кулоновского рассеяния.
- 33. Другой критерий применимости борновского приближения.
- 34. Связь условия применимости классического приближения с условием нарушения критерия применимости борновского приближения.
- 35. Сравнение классического и борновского приближений для случая кулоновского потенциала.
- 36. Специфические свойства кулоновского потенциала.
- 37. Неприменимость борновского приближения при рассеянии на ядрах.
- 38. Применение к случаю экранированного кулоновского потенциала.
- 39. Метод парциальных волн (Рэлей, Факсен и Хольтсмарк).
- 40. Общий характер решений.
- 41. Частный случай кулоновского потенциала.
- 42. Парциальные волны для свободной частицы.
- 43. Асимптотическая форма функций Бесселя.
- 44. Интерпретация парциальных волн.
- 45. Граничные условия для парциальных волн в случае свободной частицы.
- 46. Учет граничных условий в присутствии потенциала.
- 47. Формула для поперечного сечения рассеяния.
- 48. Интегральное поперечное сечение.
- 49. Вычисление фазы для непроницаемой сферы.
- 50. Применение точного метода к задаче рассеяния от прямоугольной ямы для случая s-волн.
- 51. Эффект Рамзауера.
- 52. Приближение для случая малых k.
- 53. Применение для случая ядерного рассеяния.
- 54. Приближенная зависимость поперечного сечения рассеяния от энергии связи дейтрона при малых значениях энергии.
- 55. Учет спиновых сил.
- 56. Определение глубины потенциальной ямы.
- 57. Сравнение с экспериментом: измерения радиуса действия потенциала.
- 58. Кулоновское рассеяние.
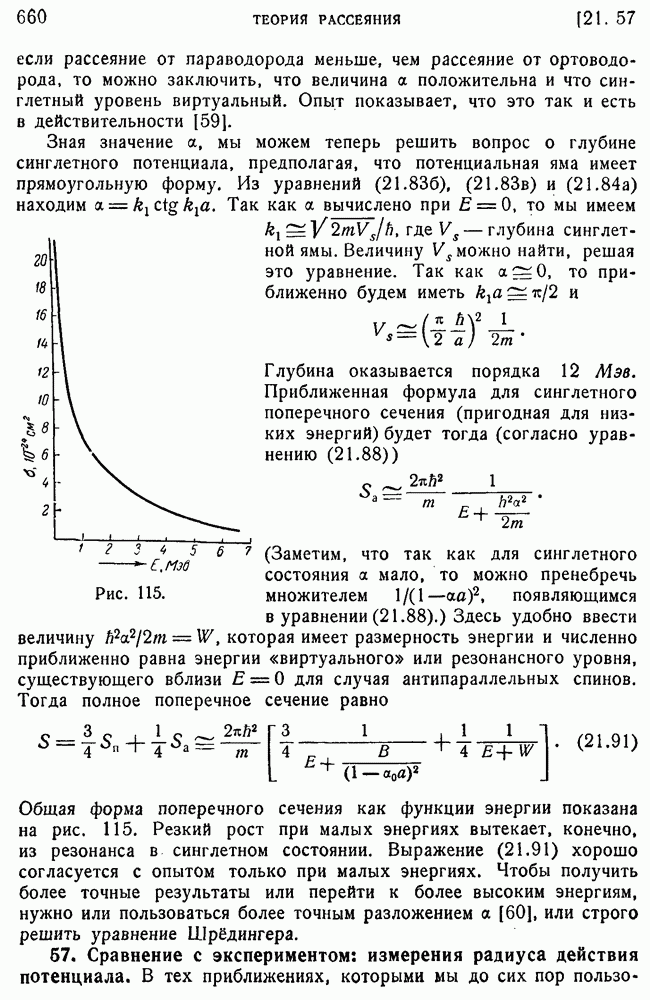
- 59. Интерпретация полученных результатов.
- 60. Обменные эффекты при кулоновском рассеянии.
- ЧАСТЬ VI. КВАНТОВАЯ ТЕОРИЯ ПРОЦЕССА ИЗМЕРЕНИЯ
- ГЛАВА 22. КВАНТОВАЯ ТЕОРИЯ ПРОЦЕССА ИЗМЕРЕНИЯ
- 5. Математическая трактовка процесса наблюдения.
- 6. Измерение спина атома.
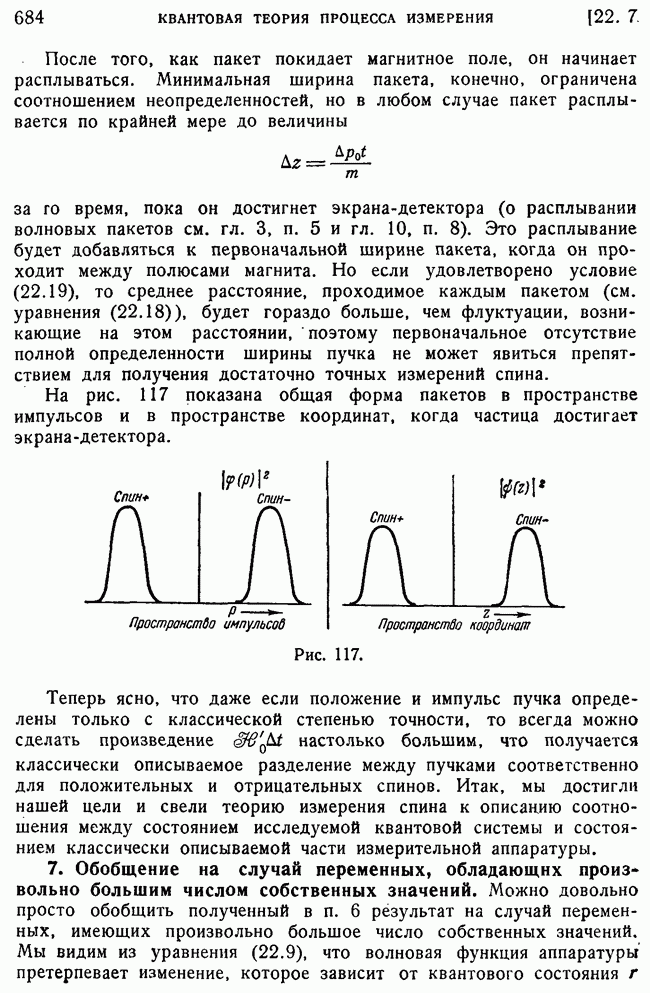
- 7. Обобщение на случай переменных, обладающих произвольно большим числом собственных значений.
- 8. Разрушение интерференционной картины в процессе измерения.
- 9. Появление случайных фазовых множителей.
- 10. Интерпретация полной волновой функции с помощью статистического ансамбля волновых функций только одного спина.
- 11. Включение координат аппаратуры.
- 12. Необратимость процесса измерения и фундаментальная роль этого явления в квантовой теории.
- 13. Волновые и корпускулярные свойства вещества как потенциальные возможности.
- 14. О связи между непрерывностью и дискретностью квантовых представлений.
- 15. Парадокс Эйнштейна, Розена и Подольского.
- 16. Мысленный эксперимент Эйнштейна, Розена и Подольского.
- 17. Математический анализ опыта по квантовой теории.
- 18. Физическое описание причин корреляции.
- 19. Доказательство несовместимости квантовой теории с понятием скрытых параметров.
- ГЛАВА 23. СООТНОШЕНИЕ МЕЖДУ КВАНТОВЫМ И КЛАССИЧЕСКИМ ПРЕДСТАВЛЕНИЯМИ
- ЛИТЕРАТУРА