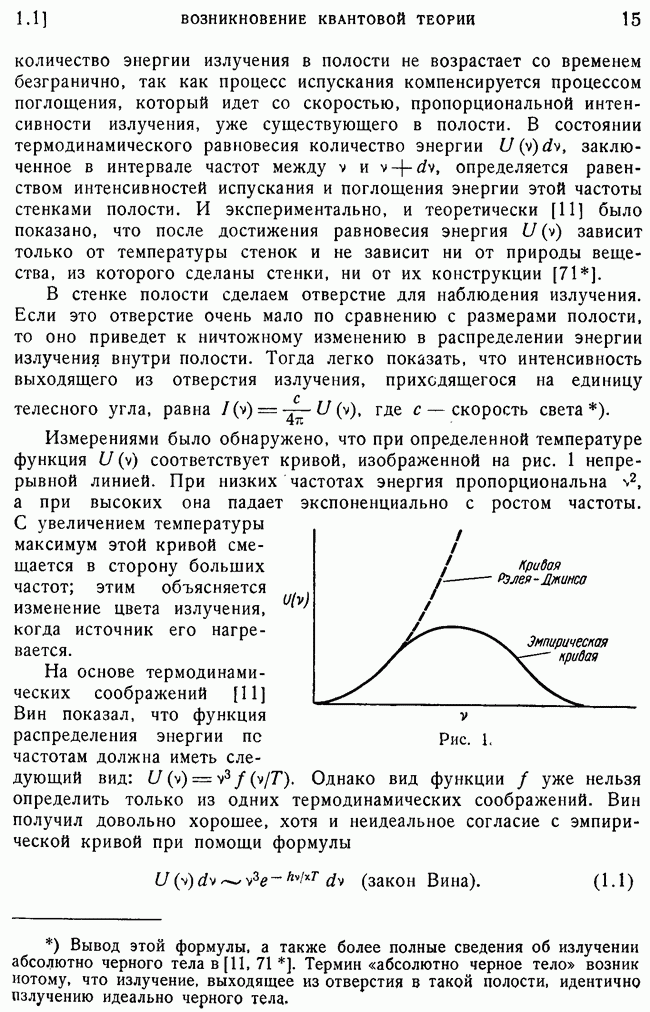
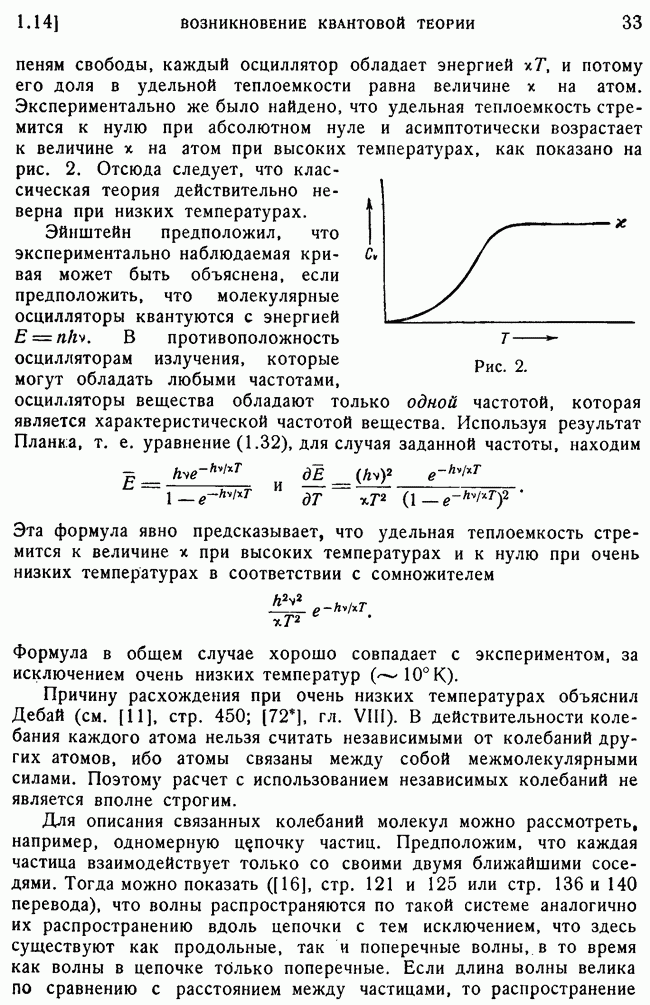
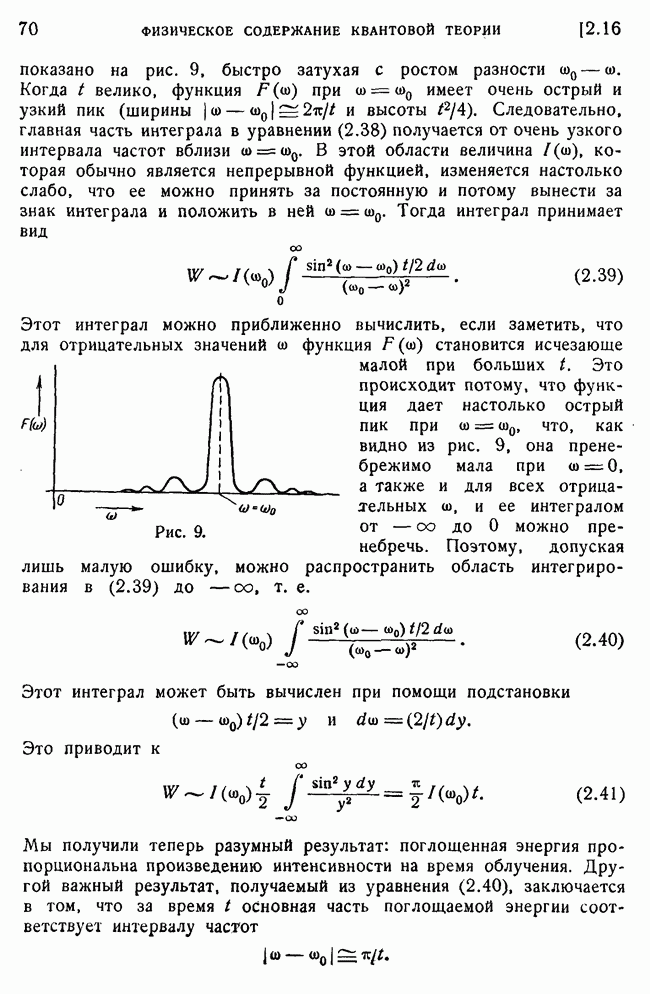
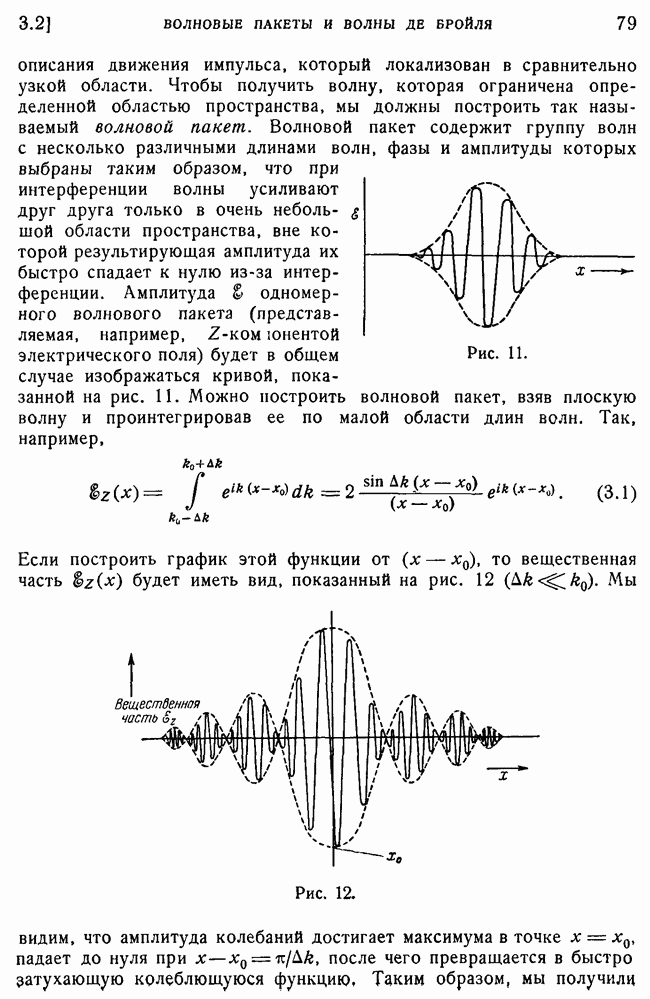
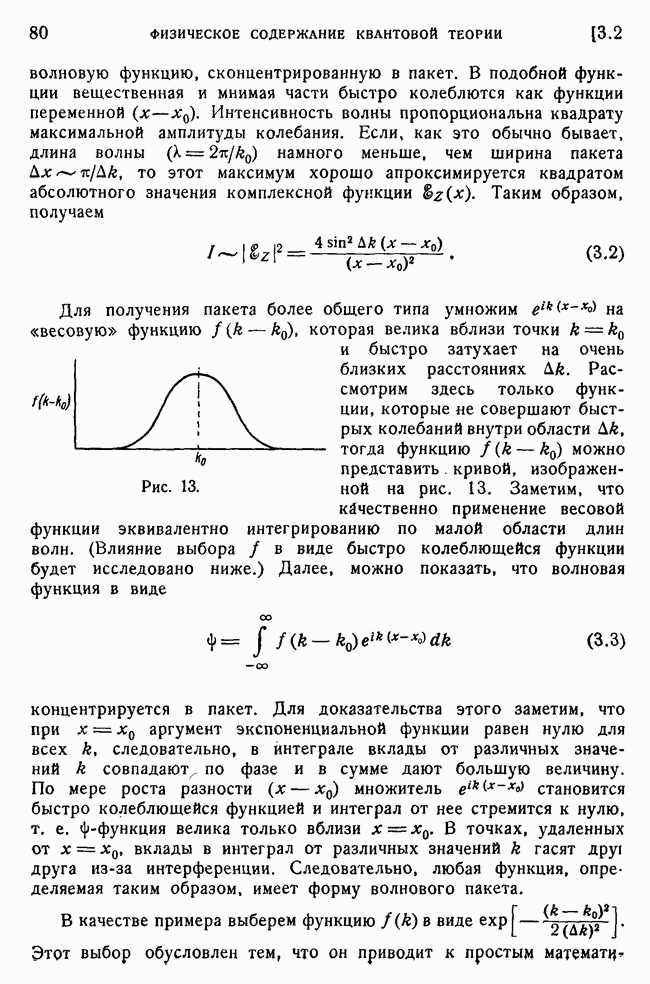
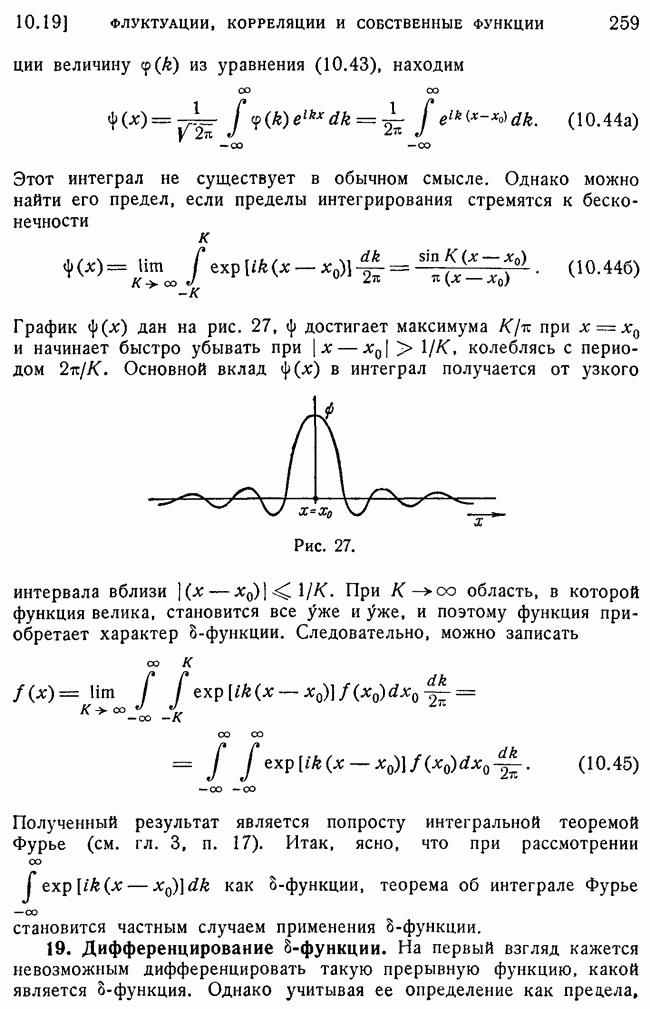
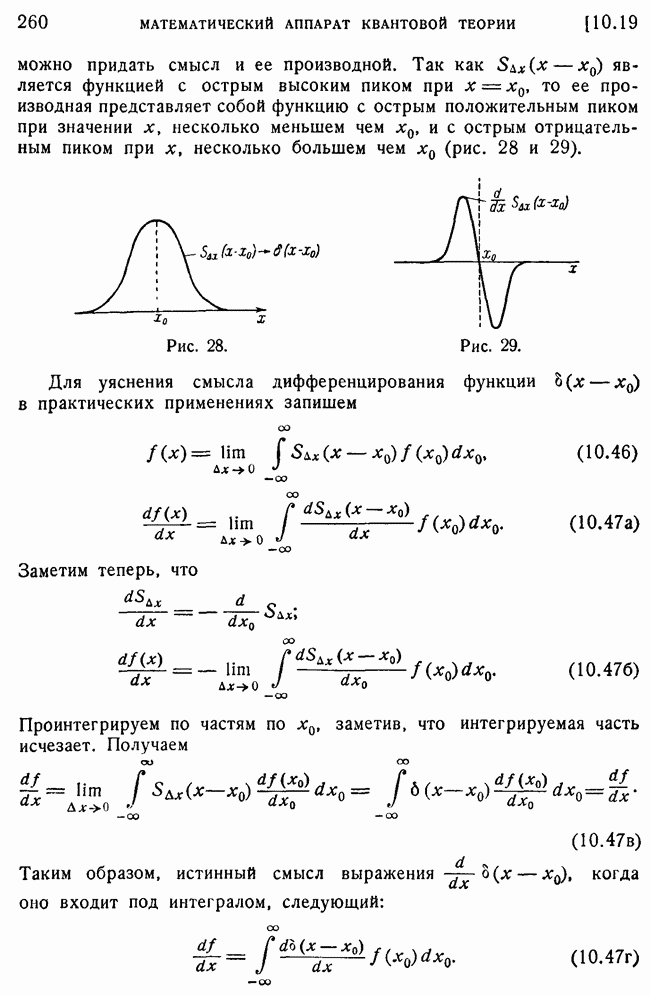
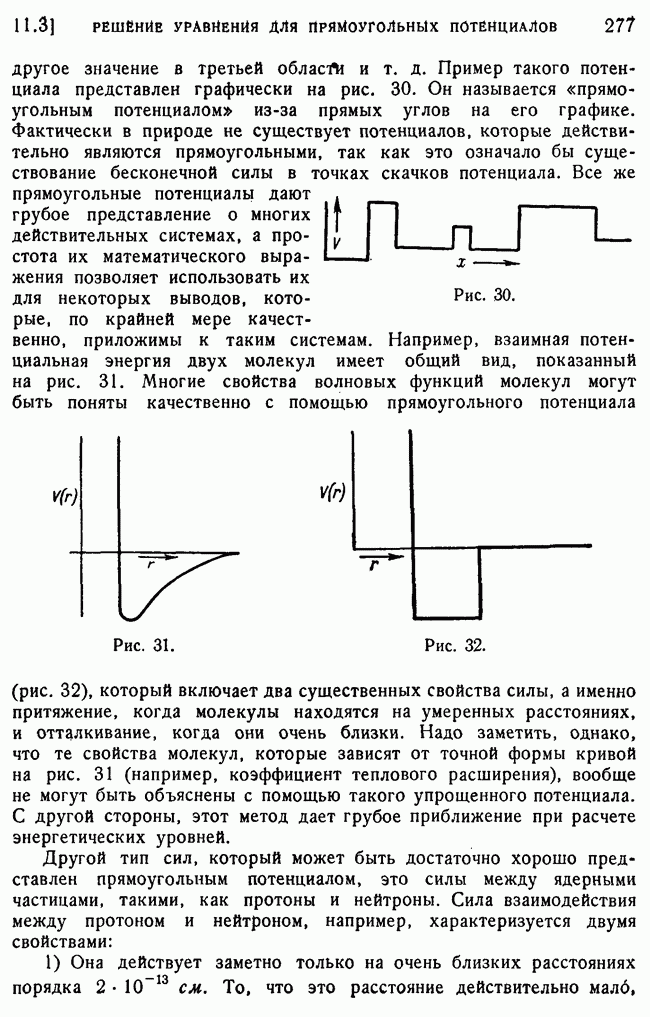
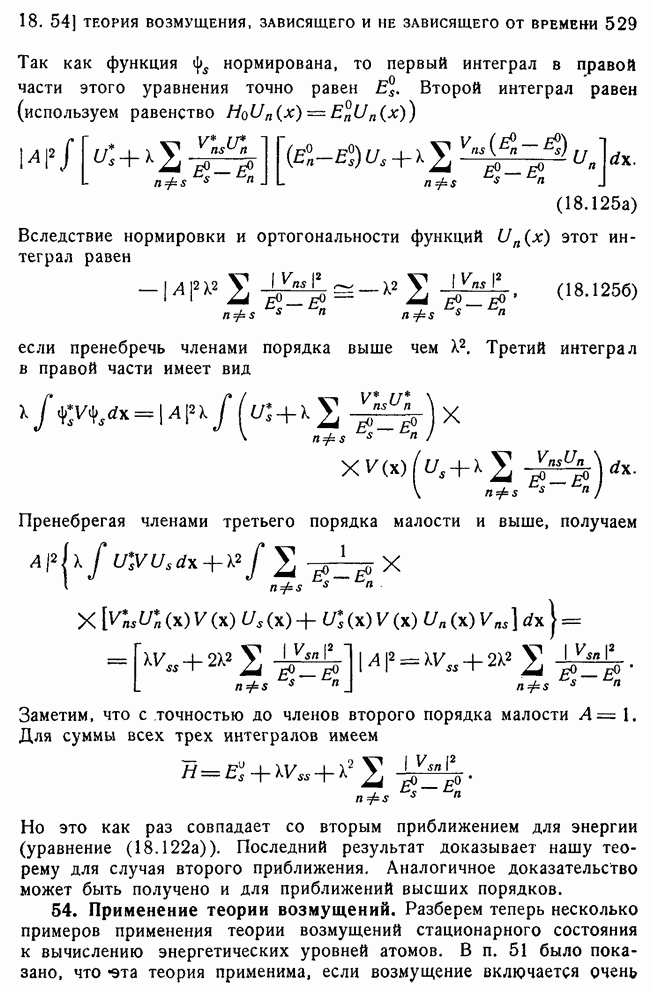| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
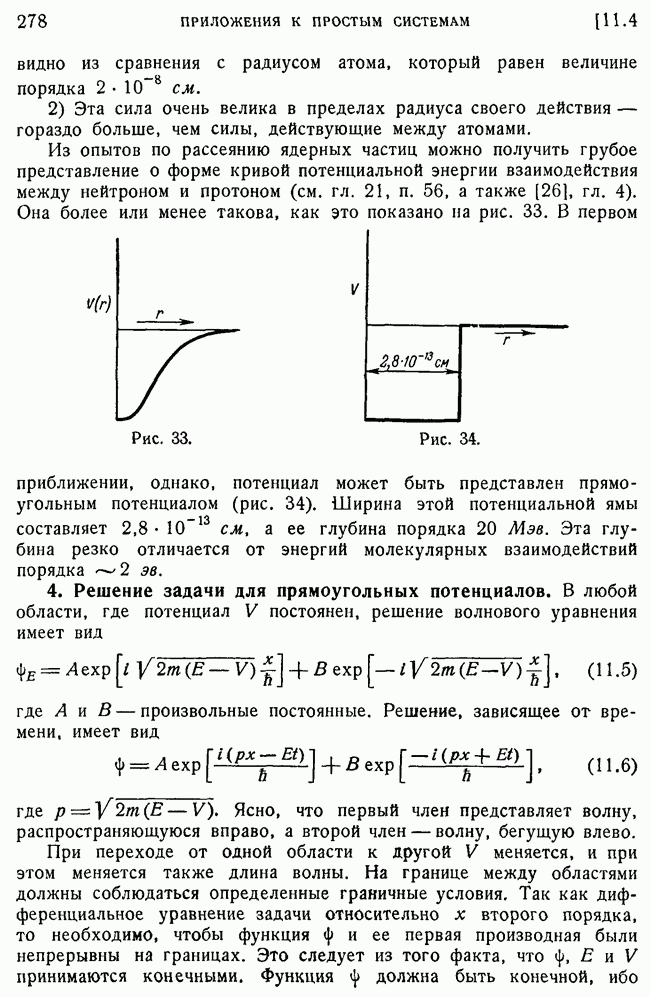
278
279
280
281
282
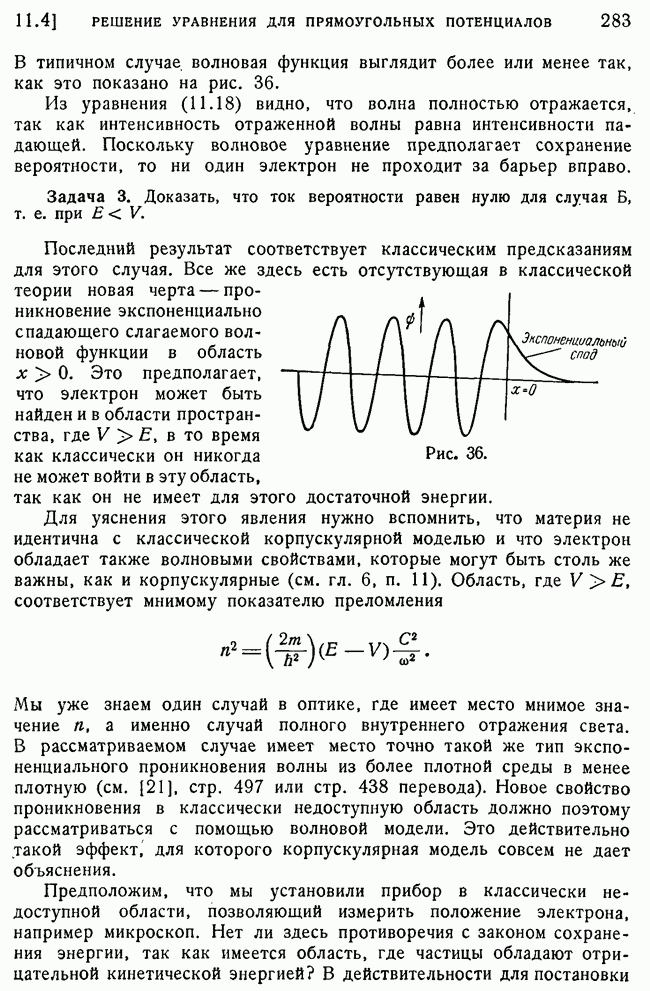
283
284
285
286
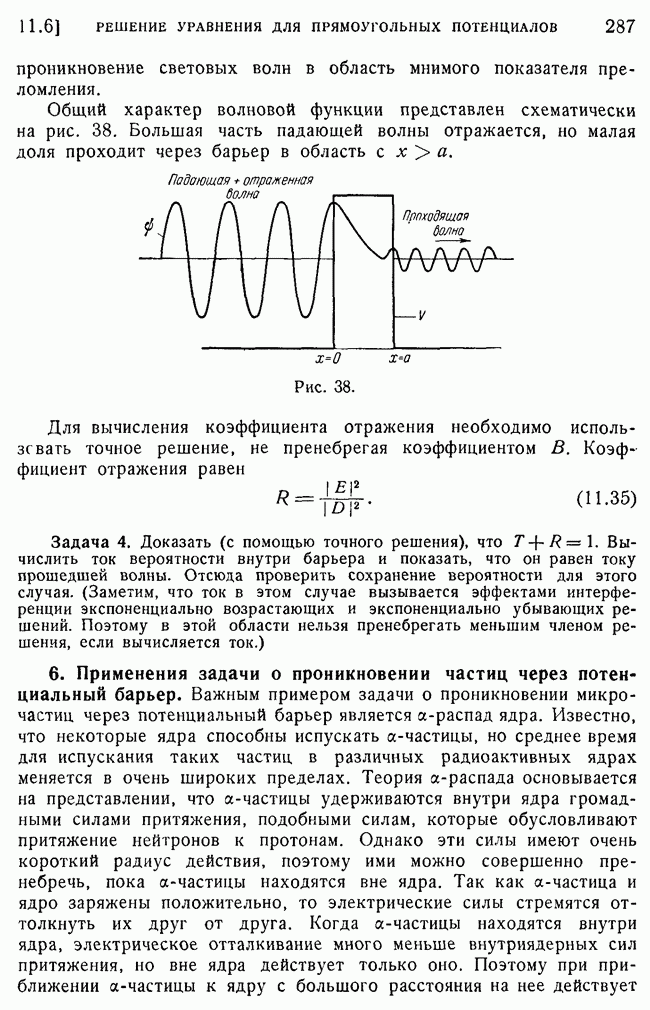
287
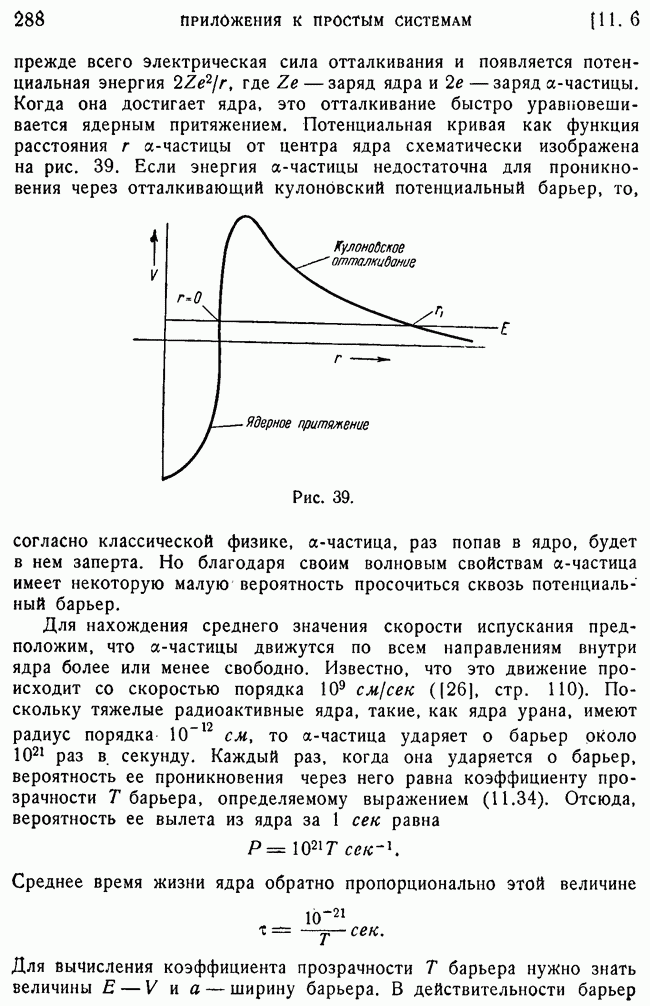
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
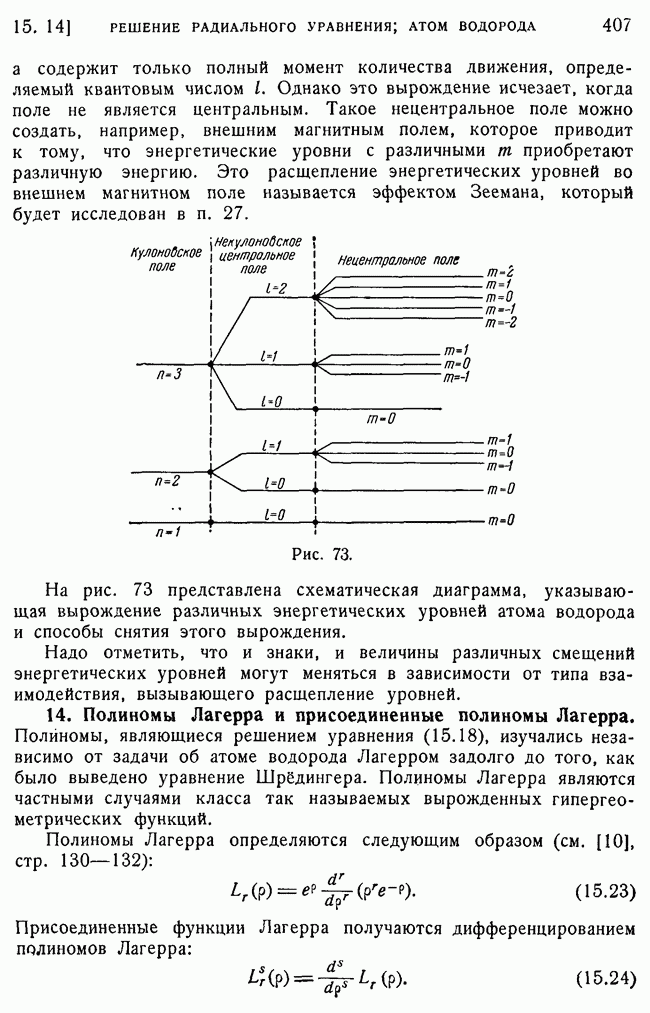
407
408
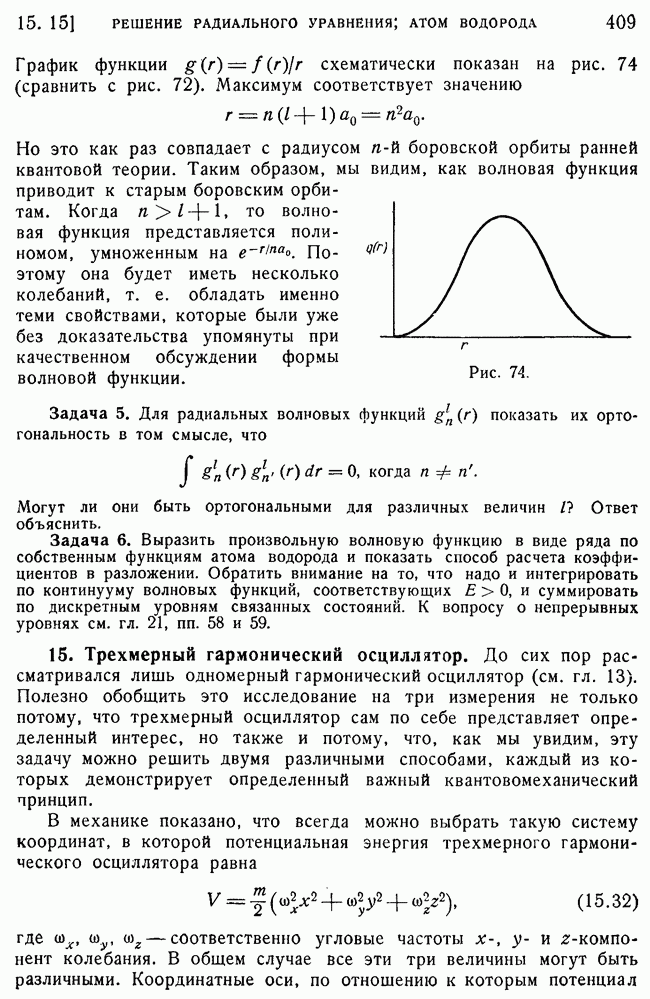
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
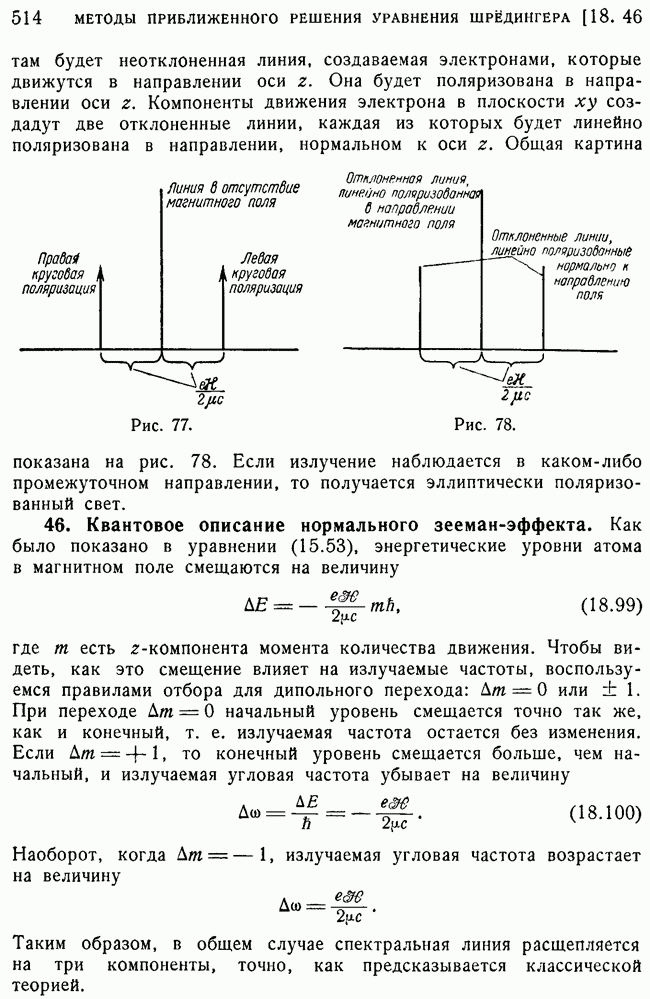
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
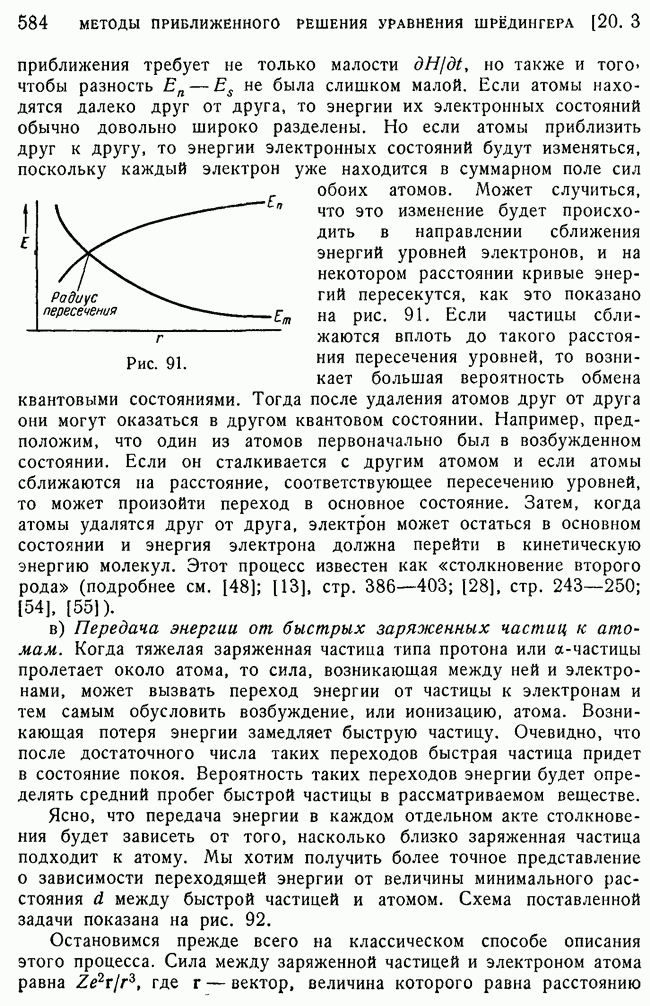
584
585
586
587
588
589
590
591
592
593
594
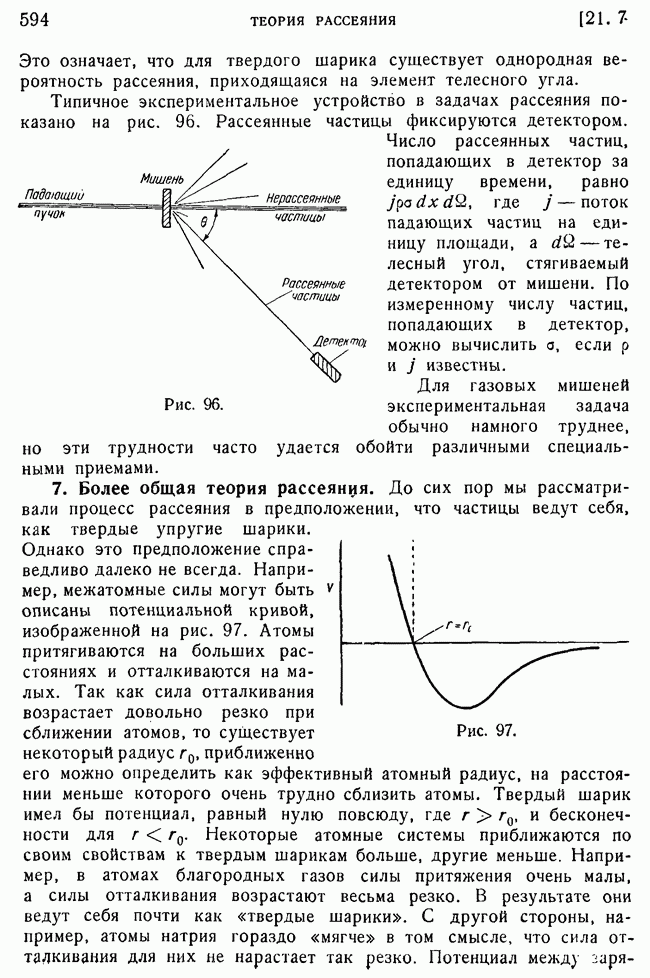
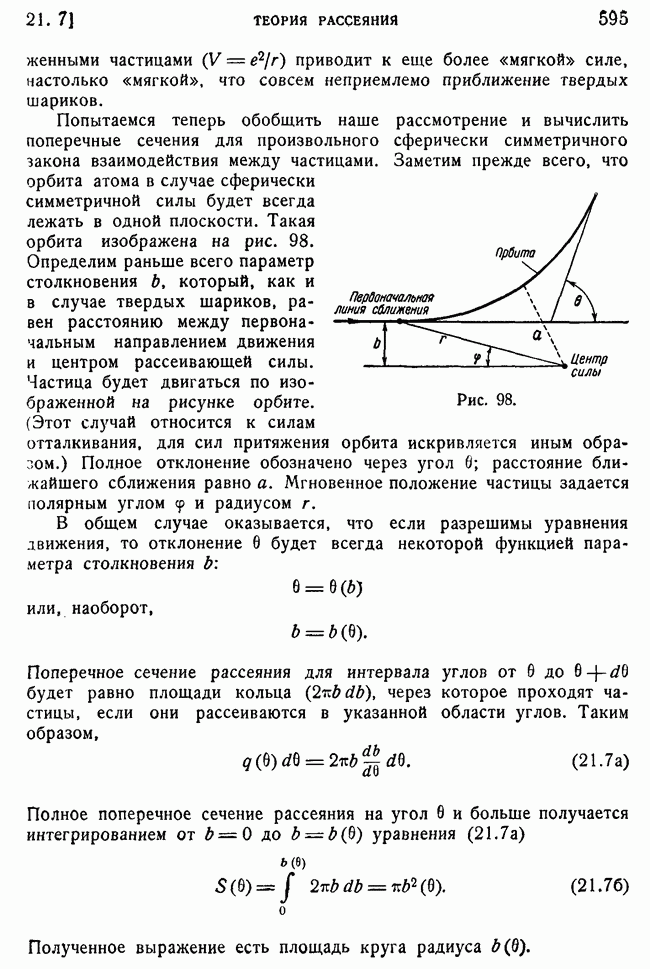
595
596
597
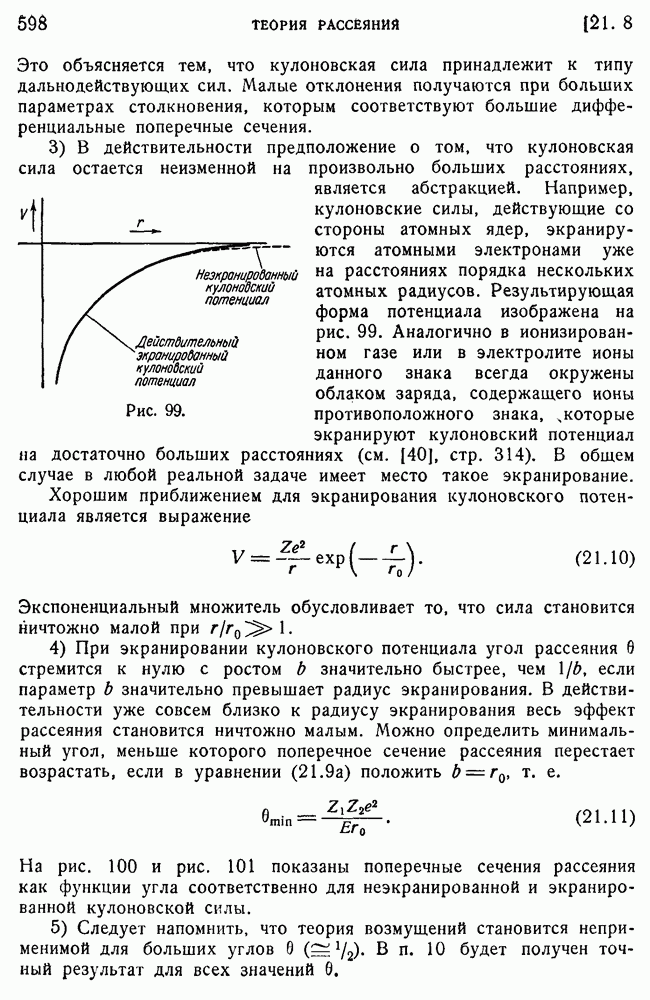
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
9. Число осцилляторов.
Теперь нам надо найти число осцилляторов с частотами, лежащими в интервале от  до
до  Так как
Так как  то задача эквивалентна определению числа осцилляторов в интервале от
то задача эквивалентна определению числа осцилляторов в интервале от  до
до 
Для любого разумного значения  число волн, находящихся в полости, обычно очень велико. Например, при средних температурах большая часть излучения находится в инфракрасной области с
число волн, находящихся в полости, обычно очень велико. Например, при средних температурах большая часть излучения находится в инфракрасной области с
длинами волн  Поэтому, когда
Поэтому, когда  изменяется таким образом, что в полости укладывается на одну длину волны больше, то в результате происходит лишь ничтожное изменение величины
изменяется таким образом, что в полости укладывается на одну длину волны больше, то в результате происходит лишь ничтожное изменение величины  Это позволяет выбрать интервал
Это позволяет выбрать интервал  столь малым, чтобы ни одна существенная физическая величина (как, например, средняя энергия) не изменялась заметно внутри этого интервала, и вместе с тем выбрать этот интервал все же достаточно большим, чтобы он включал очень много осцилляторов излучения. Это означает, что число осцилляторов можно считать условно непрерывным и ввести для него функцию плотности.
столь малым, чтобы ни одна существенная физическая величина (как, например, средняя энергия) не изменялась заметно внутри этого интервала, и вместе с тем выбрать этот интервал все же достаточно большим, чтобы он включал очень много осцилляторов излучения. Это означает, что число осцилляторов можно считать условно непрерывным и ввести для него функцию плотности.
Найдем теперь число осцилляторов, заключенных в объеме  Если вообразить пространство координат
Если вообразить пространство координат  то каждому набору целочисленных значений
то каждому набору целочисленных значений  будет соответствовать один осциллятор. Следовательно, в единичном кубике пространства
будет соответствовать один осциллятор. Следовательно, в единичном кубике пространства  находится один осциллятор, и поэтому плотность осцилляторов в этом пространстве равна единице. Чтобы перейти к k-пространству, воспользуемся уравнением (1.18); это дает
находится один осциллятор, и поэтому плотность осцилляторов в этом пространстве равна единице. Чтобы перейти к k-пространству, воспользуемся уравнением (1.18); это дает

Для дальнейшего удобнее ввести полярные координаты в k-пространстве. Если написать  то элемент объема запишется в виде
то элемент объема запишется в виде  где
где  элемент телесного угла. Так как мы не интересуемся направлением вектора к, то проинтегрируем по
элемент телесного угла. Так как мы не интересуемся направлением вектора к, то проинтегрируем по  и получим для элемента объема
и получим для элемента объема  тогда
тогда

Заменяя  получаем
получаем

Это выражение дает число возможных значений к в интервале от  до
до  Как показано в
Как показано в  где обсуждался смысл коэффициентов а и
где обсуждался смысл коэффициентов а и  существует две независимые координаты для каждого к в соответствии с двумя направлениями поляризации. Следовательно, для полного числа осцилляторов, находящихся в интервале от
существует две независимые координаты для каждого к в соответствии с двумя направлениями поляризации. Следовательно, для полного числа осцилляторов, находящихся в интервале от  до
до  получаем
получаем

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА КО ВТОРОМУ ИЗДАНИЮ
- ЧАСТЬ I. ФИЗИЧЕСКОЕ СОДЕРЖАНИЕ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА I. ВОЗНИКНОВЕНИЕ КВАНТОВОЙ ТЕОРИИ
- 1. Равновесное излучение абсолютно черного тела.
- 2. Электромагнитная энергия.
- 3. Электромагнитные потенциалы.
- 4. Граничные условия.
- 5. Разложение полей в ряд Фурье.
- 6. Поляризация волн.
- 7. Вычисление электромагнитной энергии.
- 8. Анализ полученного выражения электромагнитной энергии.
- 9. Число осцилляторов.
- 10. Закон равномерного распределения энергии по степеням свободы.
- Гипотеза Планка
- 12. Обсуждение результатов.
- 13. Осцилляторы вещества и излучение.
- 14. Квантование осцилляторов вещества.
- 15. Основные выводы гл. 1.
- ГЛАВА 2. ДАЛЬНЕЙШЕЕ РАЗВИТИЕ СТАРОЙ КВАНТОВОЙ ТЕОРИИ
- 1. Фотоэлектрический эффект.
- 2. Различия между классическими и квантовыми законами физики.
- 3. Дискретность квантовых процессов.
- 4. Вероятностный характер и неполный механический детерминизм законов квантовой теории.
- 5. Непригодность классических динамических законов в области элементарных явлений.
- 6. Принцип соответствия.
- 7. Корпускулярные свойства света.
- 8. Эффект Комптона. Рассеяние электромагнитного излучения.
- 9. Анализ эффекта Комптона.
- Квантование атомных систем
- 10. Доказательство квантования всех атомных систем.
- 11. Определение энергетических уровней.
- 12. Переменная действия.
- 13. Квантование момента количества движения.
- 14. Атом водорода.
- 15. Опыты Франка и Герца.
- Теория излучения в рамках принципа соответствия
- 17. Испускание излучения.
- ГЛАВА 3. ВОЛНОВЫЕ ПАКЕТЫ И ВОЛНЫ ДЕ БРОЙЛЯ
- 2. Движение импульсов света.
- 3. Ширина волнового пакета.
- 4. Групповая скорость.
- 5. Расплывание волновых пакетов.
- 6. Более общий критерий для определения ширины волновых пакетов.
- 7. Обобщение на трехмерный случай.
- Электронные волны
- 8. Движение электронных волновых пакетов.
- 9. Учет действия внешних сил.
- 10. Эффекты квантования.
- 11. Опыт Дэвиссона-Джермера.
- 12. Предсказание дифракции электронов теорией Бора — Зоммерфельда.
- 13. Вероятностная трактовка волновой функции.
- 14. Сравнение электронных и электромагнитных волн.
- 15. Более детальная картина электронных волн.
- 16. Переходы между орбитами.
- Волновое уравнение
- 18. Волна для свободной частицы.
- 19. Волновое уравнение для свободной частицы.
- ГЛАВА 4. ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ
- 3. Доказательство сохранения вероятности.
- 4. Ток вероятности.
- 5. Является ли приведенная формулировка наиболее общей?
- 6. Релятивистские теории.
- 7. Плотность вероятности для кванта света.
- 8. Вероятность определения значений импульса.
- 9. Связь между функциями Р(х) и P(k).
- 10. Нормировочный фактор функции P(k).
- Сводка основных сведений о вероятностях
- ГЛАВА 5. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
- 2. Вывод соотношения неопределенностей для случая электронов.
- 3. О трактовке соотношений неопределенностей.
- 4. Связь явления расплывания волнового пакета с со отношением неопределенностей.
- 5. Связь устойчивости атомов с соотношением неопределенностей.
- 6. Теория измерений.
- 7. Влияние на измерение квантовых эффектов.
- 8. Микроскоп.
- 9. Измерение импульса.
- 10. Соотношение неопределенностей для энергии и времени.
- 11. Применение соотношения неопределенностей к квантам света.
- 12. Наблюдения кванта света при помощи электронного микроскопа.
- 13. Локализация электромагнитной энергии и импульса при помощи щелей и затворов.
- 14. Применение соотношения неопределенностей к задаче определения орбит в атомах.
- 15. Более общее применение соотношения неопределенностей.
- 16. Внутренняя непротиворечивость квантовой теории.
- 17. Существуют ли скрытые параметры, лежащие в основе квантовой теории?
- ГЛАВА 6. ВОЛНОВЫЕ И КОРПУСКУЛЯРНЫЕ СВОЙСТВА МАТЕРИИ
- 1. Явление интерференции и корпускулярно-волновая природа материи.
- 2. Невозможность одновременного наблюдения волновых и корпускулярных свойств материи.
- 3. Влияние процесса наблюдения на волновую функцию.
- 4. Нарушение интерференции и непротиворечивость корпускулярно-волнового дуализма.
- 5. Обобщение предыдущих результатов.
- 6. Измерение импульса.
- 7. Связь изменений фазы с соотношением неопределенностей.
- 8. Значение фазовых соотношений.
- 9. Квантовые свойства материи как возможность.
- 10. Рассмотрение более общих взаимодействий.
- 11. О реальности волновых свойств материи.
- 12. Волномеханическое объяснение следов в камере Вильсона.
- 13. Качественная картина квантовых свойств материи.
- ГЛАВА 7. СВОДКА ОСНОВНЫХ КВАНТОВЫХ ПРЕДСТАВЛЕНИЙ
- ГЛАВА 8. ПОПЫТКА ПОСТРОЕНИЯ ФИЗИЧЕСКОЙ КАРТИНЫ КВАНТОВОЙ ПРИРОДЫ МАТЕРИИ
- 3. Простое и наглядное описание непрерывного движения.
- 4. Аналогия простых и квантовых представлений о движении.
- 5. Аналогия простых и квантовых представлений о фиксированном положении.
- 6. Более сложные представления, включающие понятие непрерывной траектории.
- 7. Причина и следствие.
- 8. Ранние представления о причине и следствии.
- 9. Полный механический детерминизм и причинность как тенденция.
- 10. Классическая теория как предписывающая, а не причинная.
- 11. Новые свойства квантовых представлений: приближенная и статистическая причинность.
- 12. Энергия и импульс в классической и квантовой теориях.
- 13. Импульс и энергия, и причинная форма описания материи.
- 14. Связь между пространственно-временным и причинным описанием материи.
- 15. Принцип дополнительности.
- 16. Неделимое единство мира.
- 17. Различие между объектом и окружающей средой в классической теории.
- 18. Роль непрерывности.
- 19. Роль причинных законов.
- 20. Анализ и синтез.
- 21. Применимость анализа и синтеза в классической теории.
- 22. Системы, описываемые классически, и существенно квантовомеханические системы.
- 23. Попытка разложения квантовой системы на отдельные части.
- 24. Неделимое единство квантовых систем.
- 26. Пример: атом водорода.
- 26. Необходимость немеханического описания.
- Сводка новых понятий квантовой теории
- Аналогии с квантовыми процессами
- 28. Возможные причины для аналогий между мышлением и квантовыми процессами.
- Примечание редактора к гл. 8
- ЧАСТЬ II. МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА 9. ВОЛНОВЫЕ ФУНКЦИИ, ОПЕРАТОРЫ И УРАВНЕНИЕ ШРЁДИНГЕРА
- 2. Гипотеза линейной суперпозиции.
- 3. Понятие состояния системы в квантовой теории.
- 4. Статистический смысл понятия квантового состояния.
- 5. Математическое выражение для средних величин.
- 6. Операторы для вычисления средних значений импульса из интегралов в пространстве координат.
- 7. Функции импульса.
- 8. Операторы в пространстве импульсов. Импульсное представление.
- 9. Линейность операторов.
- 10. Координата x как оператор.
- 11. Умножение операторов. Коммутаторы.
- 12. Операторная форма функций общего вида.
- 13. Вещественность средних значений и порядок сомножителей.
- 14. Эрмитовские операторы.
- 15. Видоизмененное правило вычисления средних значений f(x, р).
- 16. Эрмитовски сопряженные операторы.
- 17. Обобщенное определение эрмитовского оператора.
- 18. Обобщенное определение эрмитовски сопряженных операторов.
- 19. Определение оператора, эрмитовски сопряженного произведению двух операторов.
- 20. Применение к коммутаторам.
- 21. Теорема для эрмитовских операторов.
- Вывод уравнения Шрёдингера
- 26. Задача вычисления среднего движения волнового пакета.
- 27. Общее правило для вычисления Н.
- 28. Является ли вышеприведенное уравнение наиболее общим из всех возможных?
- 29. Значение волнового уравнения.
- 30. Общее определение тока вероятности.
- 31. Истолкование величины Н как средней энергии.
- 32. Закон сохранения энергии.
- ГЛАВА 10. ФЛУКТУАЦИИ, КОРРЕЛЯЦИИ И СОБСТВЕННЫЕ ФУНКЦИИ
- 4. Количественная мера корреляции в классической теории.
- 5. Классификация классических статистических систем по средним значениям произведения.
- 6. Квантовое определение корреляций.
- 7. Применение к задаче о расплывании волнового пакета для свободной частицы.
- 8. Полуклассическое описание частицы с неопределенными координатой и импульсом.
- 9. Общий вывод соотношений неопределенностей.
- 10. Особые свойства гауссовской волновой функции.
- 11. Задача многих частиц.
- 12. Собственные значения и собственные функции операторов.
- 13. Примеры собственных функций и собственных значений в координатном пространстве.
- 14. Вырожденные операторы.
- 15. Дельта-функция Дирака.
- 16. Собственные функции оператора импульса в пространстве импульсов.
- 17. Собственные функции оператора х в импульсном представлении.
- 18. Связь между собственными функциями оператора х в координатном пространстве и в пространстве импульсов.
- 19. Дифференцирование дельта-функции.
- 20. Дискретный и непрерывный спектр собственных значений операторов.
- 21. Разложение произвольной функции в ряд по собственным функциям.
- 22. Постулат разложения.
- 23. Теорема о вещественности собственных значений эрмитовского оператора.
- 24. Ортогональность собственных функций эрмитовского оператора.
- 25. Вычисление коэффициентов разложения.
- 26. Разложение дельта-функции Дирака в ряд по собственным функциям произвольного эрмитовского оператора.
- 27. Представление оператора через его собственные функции.
- 28. Выражение среднего значения функции f(A) в методе разложения по собственным функциям А.
- 29. Физическая интерпретация коэффициентов разложения с помощью вероятностей.
- Дальнейшее истолкование вероятностей в квантовой теории
- 30. Интерференция вероятностей.
- 31. Собственные функции оператора Гамильтона.
- 32. Изменение собственных функций Н со временем.
- 33. Изменение вероятности со временем. Стационарные состояния.
- 34. Связь вероятностей, зависящих от времени, с соотношением неопределенностей.
- 35. Важность собственных функций гамильтоновского оператора Н.
- 36. Изменение вероятности со временем для общей волновой функции.
- ЧАСТЬ III. ПРИЛОЖЕНИЯ К ПРОСТЫМ СИСТЕМАМ. ДАЛЬНЕЙШИЕ ОБОБЩЕНИЯ ФОРМУЛИРОВКИ КВАНТОВОЙ ТЕОРИИ
- ГЛАВА 11. РЕШЕНИЕ ВОЛНОВОГО УРАВНЕНИЯ ДЛЯ ПРЯМОУГОЛЬНЫХ ПОТЕНЦИАЛОВ
- 2. Собственные функции оператора энергии.
- 3. Прямоугольные потенциальные барьеры.
- 4. Решение задачи для прямоугольных потенциалов.
- 5. Проникновение через барьер.
- 6. Применения задачи о проникновении частиц через потенциальный барьер.
- 7. Прямоугольная потенциальная яма.
- 8. Ширина пика в резонансных максимумах прозрачности.
- 9. Эффект Рамзауера.
- 10. Связанные состояния.
- 11. Предельный случай бесконечно глубокой ямы.
- 12. Графическая интерпретация решений.
- 13. Применение теоремы разложения.
- 14. Применение к дейтрону.
- 16. Объяснение энергетических уровней с помощью соотношения неопределенностей.
- 16. Использование наблюдаемых энергетических уровней для получения сведений о потенциале.
- 17. Волновые пакеты как континуум собственных функций.
- 18. Волновой пакет для прошедшей волны.
- 19. Время замедления волны при прохождении потенциальной ямы.
- 20. Метастабильные (или виртуальные) состояния микрочастицы в потенциальной яме.
- 21. Метастабильное синглетное состояние дейтрона.
- ГЛАВА 12. КЛАССИЧЕСКИЙ ПРЕДЕЛ КВАНТОВОЙ ТЕОРИИ. ПРИБЛИЖЕНИЕ ВКБ
- 4. Физическая интерпретация решений с помощью классического распределения частиц.
- 5. Волновые пакеты. Решение, зависящее от времени.
- 6. Приближение ВКБ, зависящее от времени, в трехмерном случае.
- 7. Проникновение через барьер.
- 8. Формулы связи.
- 9. Формулы связи.
- 10. Вероятность проникновения через барьер.
- 11. Использование выражения для вероятности проникновения через барьер в частных случаях.
- 12. Вероятность проникновения частиц внутрь ядра.
- 13. Связанные состояния потенциальной ямы.
- 14. Виртуальные, или метастабильные, состояния в приближении ВКБ.
- 15. Обсуждение выражения (12.64) для коэффициента прозрачности.
- 16. Ширина резонанса. Коэффициент прозрачности вблизи резонанса.
- 17. Интенсивность волны внутри ямы.
- 18. Образование волновых пакетов. Время жизни виртуальных состояний.
- 19. Волновой пакет внутри потенциальной ямы (вблизи резонанса).
- 20. Соотношение неопределенностей.
- 21. Применение к радиоактивным системам.
- 22. Применение к ядерным реакциям.
- ГЛАВА 13. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
- 5. Шрёдингеровский метод факторизации.
- 6. Решение для волновых функций.
- 7. Полиномы Эрмита — Чебышева.
- 8. Нормирующий множитель.
- 9. Порождающая функция.
- 10. Рекуррентные соотношения.
- 11. Некоторые вспомогательные математические соотношения.
- 13. Свойства ортогональности полиномов Эрмита — Чебышева.
- 15. Волновые пакеты.
- 16. Средние значения кинетической и потенциальной энергий.
- ГЛАВА 14. МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ И ВОЛНОВОЕ УРАВНЕНИЕ В ТРЕХ ИЗМЕРЕНИЯХ
- 2. Момент количества движения.
- 3. Перестановочные соотношения для операторов момента количества движения.
- 4. Полный момент количества движения.
- 5. Слагающие момента количества движения в полярных координатах.
- 6. Константы движения.
- 7. Собственные значения Lz.
- 9. Совместные собственные функции операторов Lz и L2.
- 10. Одновременное определение собственных функций и собственных значений Lz и L2.
- 11. Векторное изображение возможных значений моментов количества движения.
- 12. Флуктуации в ориентациях вектора L.
- 13. Собственные функции операторов L2 и Lz.
- 14. Полиномы Лежандра.
- 15. Присоединенные функции Лежандра.
- 16. Измерение момента количества движения. Опыт Штерна и Герлаха.
- 17. Преобразование к вращающейся системе осей.
- 18. Двойной опыт Штерна и Герлаха.
- 19. Физическая эквивалентность всех систем координат.
- 20. Обобщение на произвольные повороты и произвольное l.
- 21. Применение к построению орбит.
- ГЛАВА 15. РЕШЕНИЕ РАДИАЛЬНОГО УРАВНЕНИЯ; АТОМ ВОДОРОДА; ВЛИЯНИЕ МАГНИТНОГО ПОЛЯ
- 4. Центробежный потенциал.
- 5. Разделение переменных в относительных координатах.
- 6. Предварительное обсуждение общей формы решения для атома водорода.
- 7. Общая форма решения для s-волн.
- 8. Общий вид решения при l > 0.
- 9. Определение квантовых чисел.
- 10. Физическая интерпретация волновых функций при различных n, l, m.
- 11. Образование волновых пакетов.
- 12. Точное решение для атома водорода.
- 13. Вырождение энергетических уровней атома водорода.
- 14. Полиномы Лагерра и присоединенные полиномы Лагерра.
- 15. Трехмерный гармонический осциллятор.
- 16. Возможность вырождения энергетических уровней.
- 17. Случай сферической симметрии.
- 18. Вид волновой функции в случае сферической симметрии.
- 19. Важное свойство вырожденных собственных функций.
- 20. Связь полиномов Эрмита — Чебышева со сферическими гармониками.
- 21. Гамильтониан заряженной частицы в заданном электромагнитном поле.
- 22. Квантовомеханический гамильтониан.
- 23. Сохранение вероятности. Ток вероятности.
- 24. Классический предел.
- 25. Градиентная (калибровочная) инвариантность.
- 26. Частный случай: однородное магнитное поле.
- 27. Зеемановское расщепление энергетических уровней с различными квантовыми числами m.
- ГЛАВА 16. МАТРИЧНАЯ ФОРМУЛИРОВКА КВАНТОВОЙ ТЕОРИИ
- 3. Обоснование матричного представления квантовомеханических операторов.
- 4. Пример: волновые функции гармонического осциллятора.
- 5. Эрмитовские матрицы и эрмитовски сопряженные матрицы.
- 6. Диагональное представление операторов.
- 7. Коммутативность диагональных матриц.
- 8. Непрерывные матрицы.
- 9. Матричное представление волновой функции в виде столбца.
- 10. Нормировка и ортогональность волновых функций, выраженных в виде столбцов.
- 11. Среднее значение оператора.
- 12. Собственные значения и собственные векторы матриц.
- 13. Изменение представления.
- 14. Важное свойство матриц преобразования (a-матриц).
- 15. Значение унитарного преобразования.
- 16. След, или шпур, матрицы.
- 17. Совместные собственные функции коммутирующих операторов.
- 18. Определение произвольного оператора при помощи его коммутаторов с полной системой коммутирующих операторов.
- 19. Уравнение Шредингера в произвольном представлении.
- 20. Гамильтоновское представление.
- 21. Гейзенберговское представление.
- 22. Изменение операторов со временем в гейзенберговском представлении.
- 23. Скобки Пуассона.
- 24. Формулировка квантовой теории по Гейзенбергу.
- 25. Физическое истолкование матричного представления и теории преобразования.
- ГЛАВА 17. СПИН И МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ
- 1. Спин электрона.
- 2. Матричное выражение операторов момента количества движения.
- 3. Возможные значения l и m; полуцелые квантовые числа момента количества движения.
- 4. Матрицы для операторов …
- 5. Собственные функции операторов «сигма».
- 6. Собственные функции …
- 7. Преобразования спиноров.
- 8. Сложение моментов количества движения.
- 9. Сложение спинов двух различных частиц.
- 10. Распределение вероятности состояний спина в статистическом ансамбле.
- 11. Сложение орбитального и спинового моментов частицы.
- 12. Общая задача сложения моментов количества движения.
- 13. Энергия электрона со спином.
- ЧАСТЬ IV. МЕТОДЫ ПРИБЛИЖЕННОГО РЕШЕНИЯ УРАВНЕНИЯ ШРЁДИНГЕРА
- ГЛАВА 18. ТЕОРИЯ ВОЗМУЩЕНИЯ, ЗАВИСЯЩЕГО И НЕ ЗАВИСЯЩЕГО ОТ ВРЕМЕНИ
- 8. Возмущение вырожденных состояний.
- 9. Описание переходов с помощью квантовых флуктуаций.
- 10. Микроскопическая обратимость процессов перехода.
- 11. Сохранение вероятности.
- 12. Случай б: гармоническое изменение матричных элементов со временем, задача поглощения и испускания света.
- 13. Применение к случаю плоской волны.
- 15. Квазиклассическое описание поля излучения.
- 16. Вычисление вероятности перехода.
- 17. Связь между векторным потенциалом и интенсивностью излучения.
- 18. Влияние распределения частот падающего света.
- 19. Обсуждение результатов.
- 20. Индуцированное испускание квантов.
- 21. Классическая аналогия индуцированного излучения.
- 22. Самопроизвольное излучение.
- 23. Трактовка самопроизвольного излучения по Эйнштейну.
- 24. Применения теории переходов.
- 25. Приближение электрического диполя.
- 26. Вычисление величин для изотропного гармонического осциллятора.
- 27. Правила отбора для гармонического осциллятора.
- 28. Связь правил отбора с принципом соответствия.
- 29. Введение четности.
- 30. Правила отбора для четности.
- 31. Правила отбора для сферически симметричного потенциала без учета спина.
- 32. Запрещенные переходы, электрическое квадрупольное излучение.
- 33. Магнитное дипольное излучение.
- 34. Правила отбора для электрического квадрупольного излучения.
- 35. Правила отбора для магнитного дипольного излучения.
- 36. Переходы более высокого порядка.
- 37. Полностью запрещенные переходы между состояниями с l = 0.
- 38. Полная вероятность излучения.
- 39. Сравнение с классической теорией.
- 40. Правила сумм для вычисления матричных элементов.
- 41. Круговая поляризация.
- 42. Эллиптическая поляризация.
- 43. Квантовая трактовка.
- 44. Правила отбора.
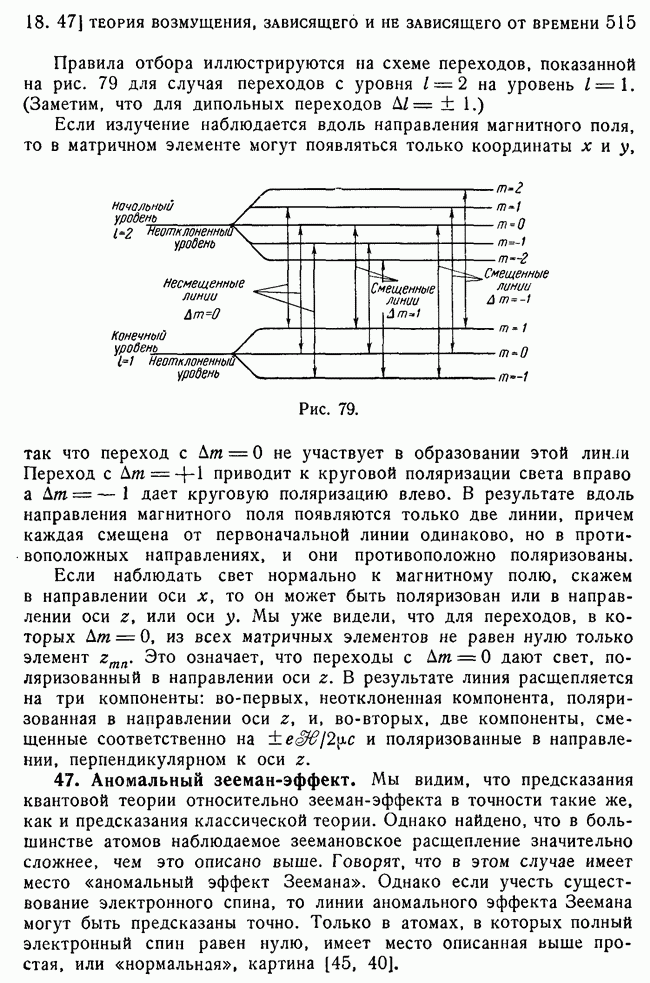
- 45. Применение к случаю нормального зееман-эффекта.
- 46. Квантовое описание нормального зееман-эффекта.
- 47. Аномальный зееман-эффект.
- 48. Общие методы вычисления вероятностей переходов.
- 49. Влияние спина электрона на вероятности переходов.
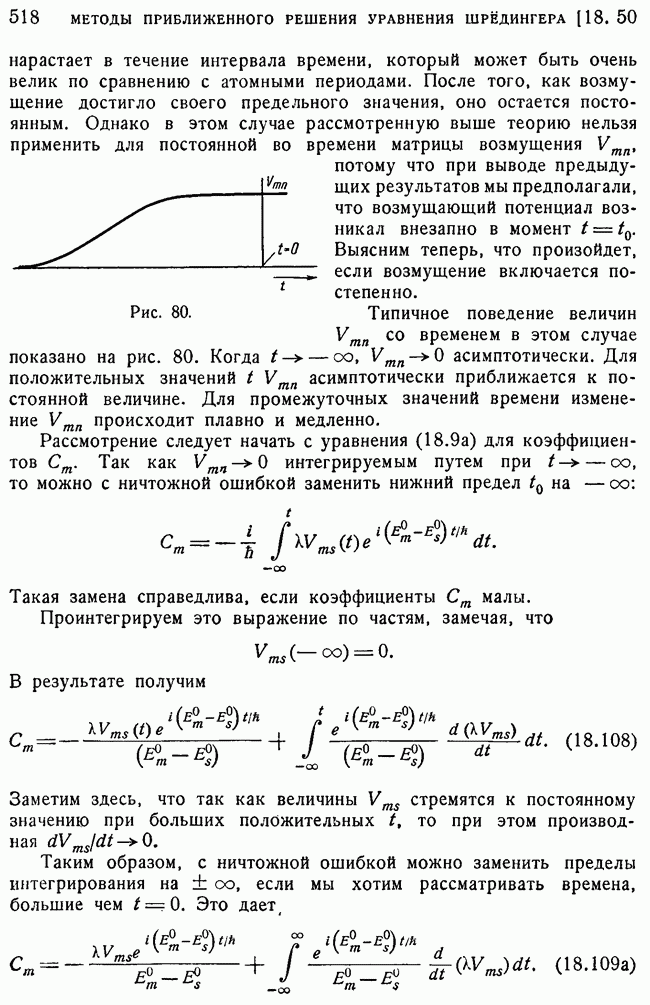
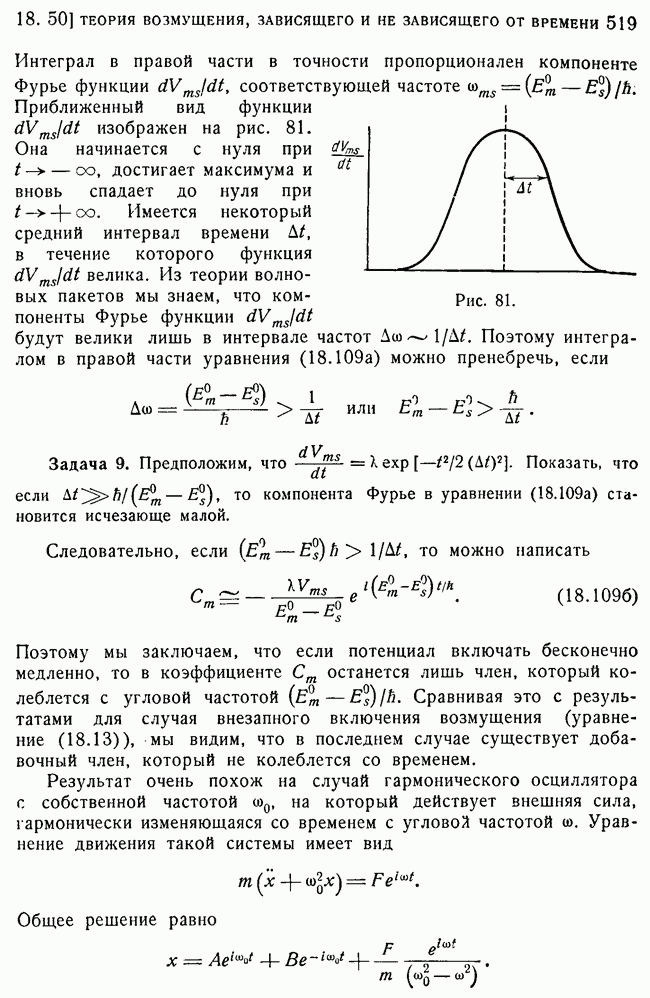
- 50. Случай в: возмущение Vmn медленно изменяющееся со временем (адиабатический случай).
- 51. Адиабатическое включение потенциала, приводящее к возмущению стационарного состояния.
- 52. Возмущение волновых функций стационарного состояния.
- 53. Интерпретация формул второго приближения для энергии.
- 54. Применение теории возмущений.
- ГЛАВА 19. ВОЗМУЩЕНИЯ В СЛУЧАЕ ВЫРОЖДЕННЫХ СИСТЕМ
- 9. Кваитовомеханический «резонанс».
- 10. Аналогия задачи возмущения вырожденных состояний с преобразованием к главным осям.
- Приложения теории возмущений вырожденных состояний
- 11. Эффект Штарка первого порядка.
- 12. Классическая интерпретация линейного эффекта Штарка.
- 13. Межатомные ван-дер-ваальсовские силы.
- 14. Квантовомеханическая аналогия фазы осциллятора.
- 16. Обменное вырождение.
- 18. Симметричные и антисимметричные функции.
- 19. Вычисление энергии.
- 20. Приближения высших порядков.
- 21. Влияние спина.
- 22. Антисимметричность волновых функций электронов.
- 23. Связь между обменной энергией и спином электрона, обусловленная свойством антисимметричности волновых функций.
- 24. Формальное выражение обменной энергии при помощи спиновых операторов.
- 25. Система из многих электронов.
- 26. Принцип запрета Паули.
- 28. Полностью симметричные волновые функции.
- 29. Неразличимость эквивалентных частиц.
- ГЛАВА 20. ВНЕЗАПНЫЕ И АДИАБАТИЧЕСКИЕ ВОЗМУЩЕНИЯ
- 1. Общая форма адиабатического возмущения.
- 3. Примеры адиабатических возмущений.
- 4. Внезапное изменение возмущающего потенциала.
- 5. Приложения. Испускание электронов из ядра при «бета»-pacпаде.
- 6. Связь между теорией возмущений и теорией внезапных переходов.
- ЧАСТЬ V. ТЕОРИЯ РАССЕЯНИЯ
- ГЛАВА 21. ТЕОРИЯ РАССЕЯНИЯ
- 4. Распределение длин свободного пробега.
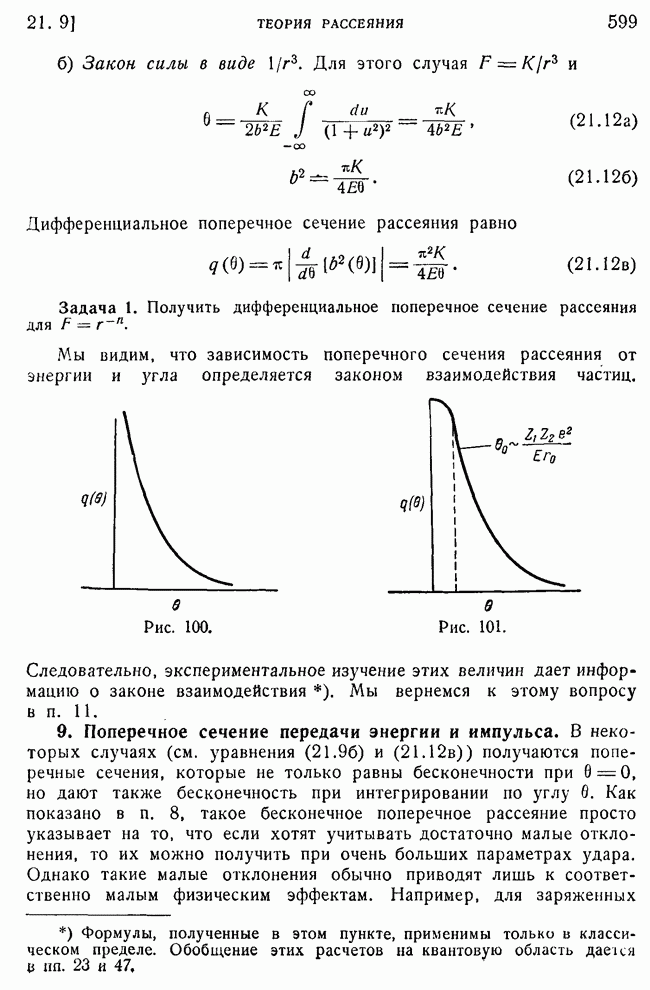
- 5. Зависимость поперечного сечения от угла рассеяния.
- 6. Дифференциальные поперечные сечения.
- 7. Более общая теория рассеяния.
- 8. Приближение малых отклонений. Классическая теория возмущений.
- 9. Поперечное сечение передачи энергии и импульса.
- 10. Точное решение задачи рассеяния.
- 11. Использование поперечных сечений рассеяния для исследования вида взаимодействия между частицами.
- 12. Переход от системы координат центра инерции к лабораторной системе координат.
- 14. Столкновение тождественных частиц.
- 15. Квантовая теория рассеяния.
- 17. Квантовое описание процесса рассеяния.
- 18. Рассеяние как процесс перехода между различными состояниями в пространстве импульсов.
- 19. Борновское приближение. Теория возмущений.
- 21. Конкретный пример рассеяния на экранированном кулоновском потенциале.
- 22. Связь между борновским приближением и коэффициентами разложения потенциала в ряд Фурье.
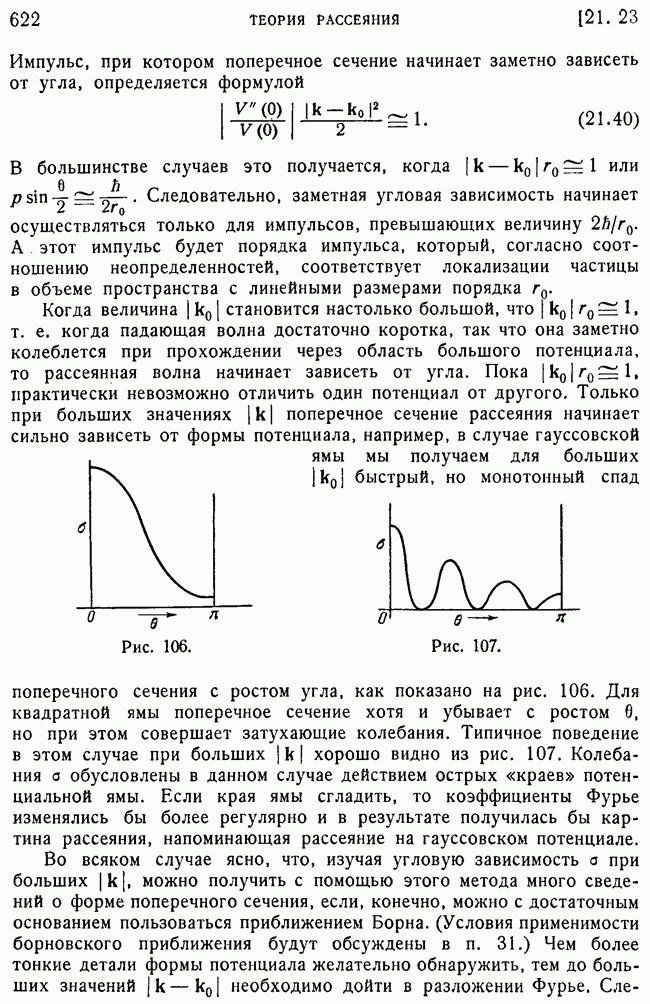
- 23. Примеры: сравнение поперечных сечений для гауссовского потенциала и прямоугольной ямы.
- 24. Исследование процесса рассеяния в координатном представлении.
- 25. Новая форма уравнения Шредингера.
- 27. Борновское приближение.
- 28. Связь между описанием процессов рассеяния в координатном и импульсном представлениях.
- 29. Связь между методом стационарных состояний и временным описанием процессов рассеяния.
- 30. Другое применение борновского приближения: рассеяние от кристаллической решетки.
- 31. Условия применимости борновского приближения.
- 32. Применение к случаю экранированного кулоновского рассеяния.
- 33. Другой критерий применимости борновского приближения.
- 34. Связь условия применимости классического приближения с условием нарушения критерия применимости борновского приближения.
- 35. Сравнение классического и борновского приближений для случая кулоновского потенциала.
- 36. Специфические свойства кулоновского потенциала.
- 37. Неприменимость борновского приближения при рассеянии на ядрах.
- 38. Применение к случаю экранированного кулоновского потенциала.
- 39. Метод парциальных волн (Рэлей, Факсен и Хольтсмарк).
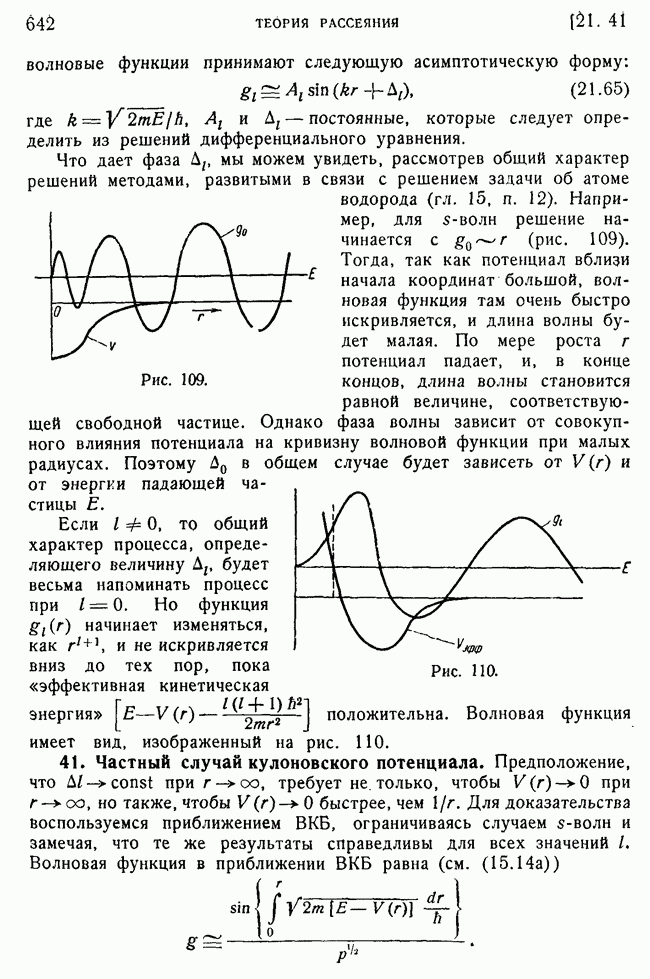
- 40. Общий характер решений.
- 41. Частный случай кулоновского потенциала.
- 42. Парциальные волны для свободной частицы.
- 43. Асимптотическая форма функций Бесселя.
- 44. Интерпретация парциальных волн.
- 45. Граничные условия для парциальных волн в случае свободной частицы.
- 46. Учет граничных условий в присутствии потенциала.
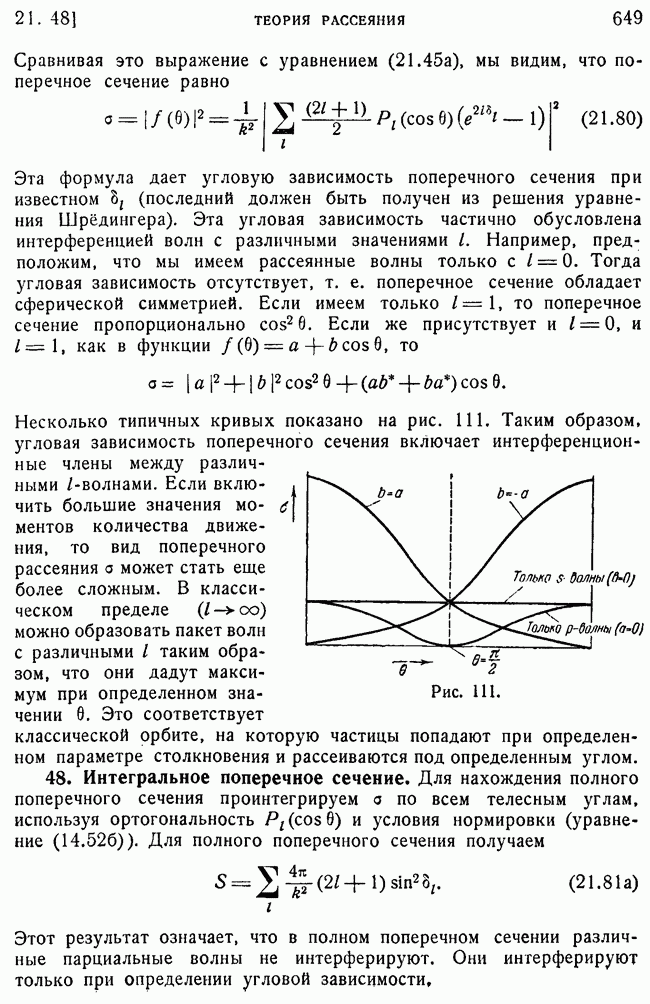
- 47. Формула для поперечного сечения рассеяния.
- 48. Интегральное поперечное сечение.
- 49. Вычисление фазы для непроницаемой сферы.
- 50. Применение точного метода к задаче рассеяния от прямоугольной ямы для случая s-волн.
- 51. Эффект Рамзауера.
- 52. Приближение для случая малых k.
- 53. Применение для случая ядерного рассеяния.
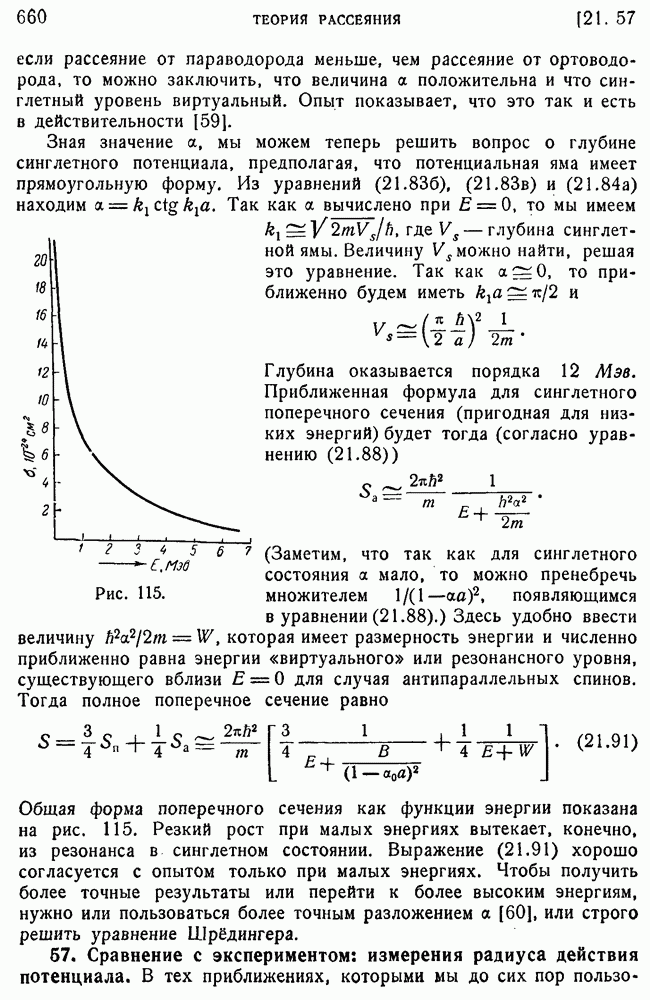
- 54. Приближенная зависимость поперечного сечения рассеяния от энергии связи дейтрона при малых значениях энергии.
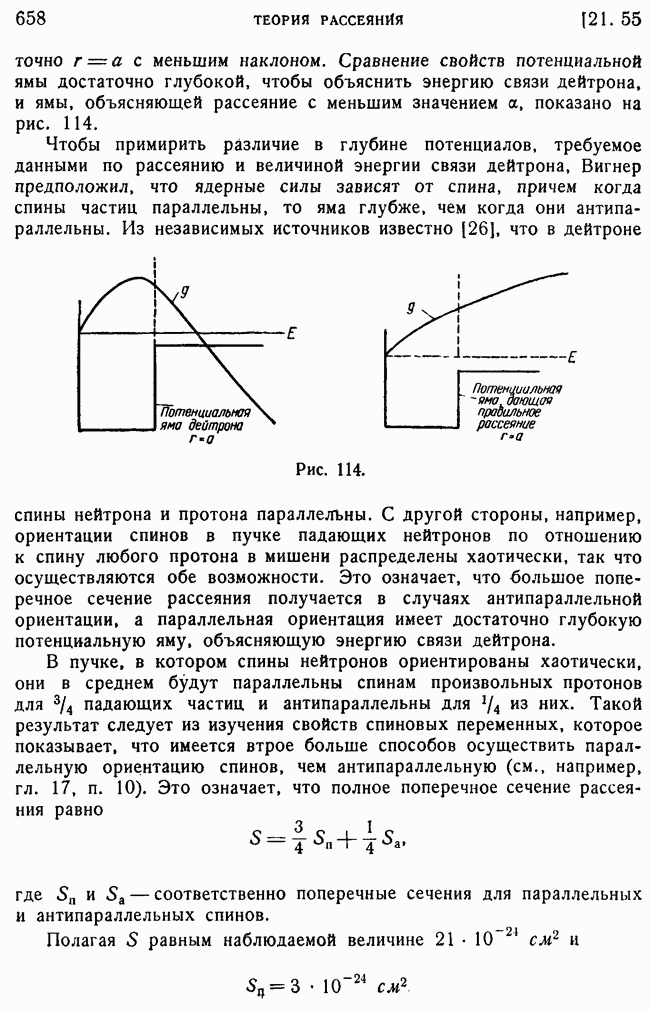
- 55. Учет спиновых сил.
- 56. Определение глубины потенциальной ямы.
- 57. Сравнение с экспериментом: измерения радиуса действия потенциала.
- 58. Кулоновское рассеяние.
- 59. Интерпретация полученных результатов.
- 60. Обменные эффекты при кулоновском рассеянии.
- ЧАСТЬ VI. КВАНТОВАЯ ТЕОРИЯ ПРОЦЕССА ИЗМЕРЕНИЯ
- ГЛАВА 22. КВАНТОВАЯ ТЕОРИЯ ПРОЦЕССА ИЗМЕРЕНИЯ
- 5. Математическая трактовка процесса наблюдения.
- 6. Измерение спина атома.
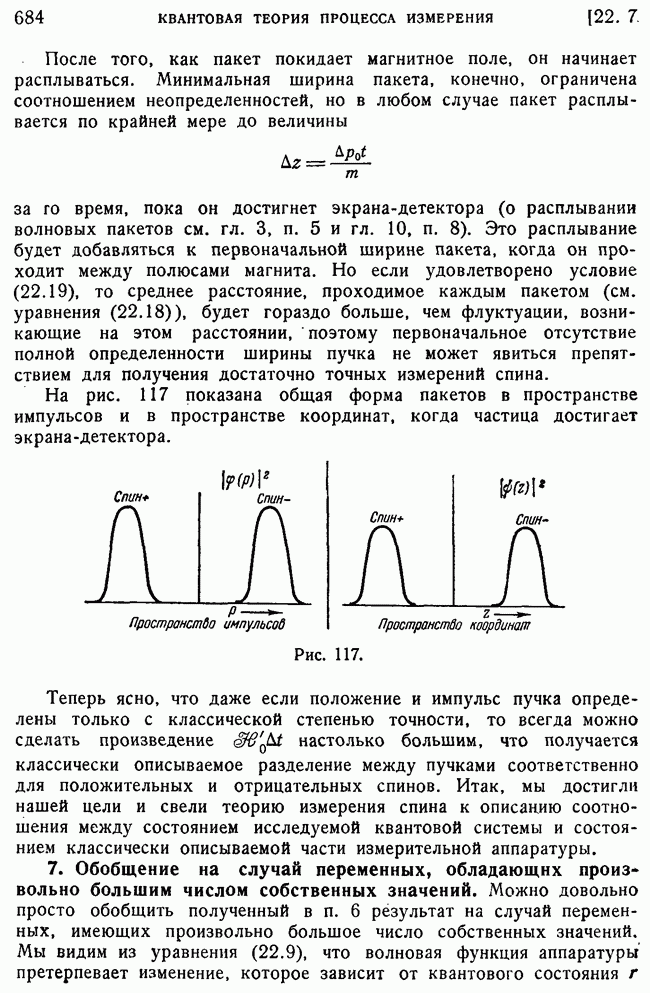
- 7. Обобщение на случай переменных, обладающих произвольно большим числом собственных значений.
- 8. Разрушение интерференционной картины в процессе измерения.
- 9. Появление случайных фазовых множителей.
- 10. Интерпретация полной волновой функции с помощью статистического ансамбля волновых функций только одного спина.
- 11. Включение координат аппаратуры.
- 12. Необратимость процесса измерения и фундаментальная роль этого явления в квантовой теории.
- 13. Волновые и корпускулярные свойства вещества как потенциальные возможности.
- 14. О связи между непрерывностью и дискретностью квантовых представлений.
- 15. Парадокс Эйнштейна, Розена и Подольского.
- 16. Мысленный эксперимент Эйнштейна, Розена и Подольского.
- 17. Математический анализ опыта по квантовой теории.
- 18. Физическое описание причин корреляции.
- 19. Доказательство несовместимости квантовой теории с понятием скрытых параметров.
- ГЛАВА 23. СООТНОШЕНИЕ МЕЖДУ КВАНТОВЫМ И КЛАССИЧЕСКИМ ПРЕДСТАВЛЕНИЯМИ
- ЛИТЕРАТУРА