| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
8. Пространственные струи.
Методы теории функций комплексного переменного не пригодны для изучения пространственных форм струй. Соответствующие методы теории потенциала очень сложны и, кроме того, пригодны только для получения последовательных приближений. Поэтому о пространственных струях, за исключением тривиальных случаев, нам известно мало.
В том случае, когда внешними силами, в особенности силой тяжести, можно пренебречь, скорость на свободной поверхности будет оставаться,  уравнению Вернулли, постоянной, если под внешним давлением разуметь постоянное давление атмосферы. Ряд общих теорем был установлен Моленбруком и другими авторами. Линии тока на поверхности струи суть, геодезические линии: линии пересечения поверхности струи с поверхностями уровня потенциала скоростей геодезически параллельны; в точках этих линий пересечения средняя кривизна самых поверхностей уровня равна нулю.
уравнению Вернулли, постоянной, если под внешним давлением разуметь постоянное давление атмосферы. Ряд общих теорем был установлен Моленбруком и другими авторами. Линии тока на поверхности струи суть, геодезические линии: линии пересечения поверхности струи с поверхностями уровня потенциала скоростей геодезически параллельны; в точках этих линий пересечения средняя кривизна самых поверхностей уровня равна нулю.
Точное решение не известно даже для струй, имеющих аксиальную симметрию. Треффц, пренебрегая влиянием силы тяжести, привел задачу нахождения поверхности аксиально-симметричной струи, вытекающей из бесконечно большого сосуда, к линейному однородному интегральному уравнению. Главная трудность состоит здесь в том, что ядро втого интегрального уравнения зависит от вида меридиональной кривой струи, так что оно неизвестно и должно быть получено путем последовательных приближений одновременно с этой меридиональной кривой, на основании требования постоянства скорости поверхности струи.
Для тяжелой струи о аксиальной симметрией часто приводят грубую приближенную формулу, выведенную из предположения, что скорость во всех точках горизонтального поперечного сечения струи одинакова и направлена вертикально. Ферстер пытался получить, с помощью разложения в ряд, меридиональную кривую струи для случая произвольных внешних сил. Ряды эти годятся, однако, только для определения асимптотического приближения струи в форме кругового цилиндра и не позволяют сделать каких-либо заключений о форме струи вблизи места ее выхода  сосуда.
сосуда.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ ИЗДАТЕЛЯ К ПЕРВОМУ НЕМЕЦКОМУ ИЗДАНИЮ
- ЧАСТЬ ПЕРВАЯ. КЛАССИЧЕСКАЯ МЕХАНИКА И ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 1. Световые лучи и волновые поверхности в любых телах
- 2. Принцип Ферма и световые лучи.
- 3. Световые лучи и волновые поверхности.
- 4. Дифференциальное уравнение волновых поверхностей и световых лучей.
- § 2. Оптическое отображение в общей случае анизотропной среды
- 2. Отображение элеиентов линии и элеиентов поверхности.
- 3. Нахождение световых лучей при помощи эйконала, касательные преобразования.
- § 3. Ход луча в различных средах
- 2. Изотропные среды.
- 3. Одноосные кристаллы.
- 4. Движущиеся тела
- 5. Электронный микроскоп.
- § 4. Отображение посредством симметричных оптических приборов
- 2. Диоптрика Гаусса.
- 3. Диоптрика электронных лучей.
- ГЛАВА II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ В ОБЩЕМ СЛУЧАЕ
- § 1. Уравнения движения в прямоугольных координатах
- 2. Пример: влияние сопротивления воздуха на движение точки под влиянием силы тяжести.
- 3. Уравнения движения системы свободных материальных точек и их интегралы.
- 4. Положения равновесия как особые точки.
- 5. Принцип Даламбера.
- § 2. Уравнения движения Лагранжа и Гамильтона
- 2. Примеры.
- 3. Законы энергии и импульса.
- 4. Связь с вариационным исчислением.
- 5. Уравнения движения в форме Гамильтона и Рауза.
- 6. Интегралы уравнений движения Гамильтона.
- § 3. Дифференциальные уравнения траекторий
- 2. Траектории механических систем в общем случае.
- 3. Различные виды траекторий.
- 4. Примеры.
- § 4. Теория преобразований дифференциальных уравнений Гамильтона
- 2. Касательное преобразование, канонические переменные.
- 3. Соответствующие канонические перепенные.
- 4. К интегрированию уравнения Гамильтона-Якоби в частных производных.
- 5. Введение волн, соответствующих движению точки.
- § 5. Метод разделения переменных
- 2. Критерий его применимости.
- 3. Выполнение вычисления.
- 4. Цримеры.
- 5. Свойства периодичности разделяющихся переменных.
- 6. Угловые переменные и переменные действия.
- § 6. Многократно-периодические системы
- 2. Введение общих многократно-периодических систем.
- 3. Вырождение.
- 4. Примеры.
- § 7. Однозначные интегралы и траектории, заполняющие объем
- 2. Системы однозначных интегралов; импримитивные системы.
- 3. Приближенные периоды n-кратно периодических систем.
- § 8. Некоторые сведения из статистической механики
- 2. Вычисление объемов в фазовом пространстве.
- 3. Теорема Лиувилля.
- 4. Теорема Больцмана.
- 5. Время пребывания n-кратно периодической системы.
- 6. Квазиэргодическая система, микрокаяоническое множество.
- ГЛАВА III. УСТОЙЧИВОСТЬ И МАЛЫЕ КОЛЕБАНИЯ
- § 1. Квазистатические движения
- 2. Квазистатическио движения по Раузу.
- 3. Обобщение понятна квазистатического движения по Леви-Чивита.
- § 2. Устойчивость и энергия
- 2. Энергетический критерий устойчивости Рауза.
- 3. Примеры.
- § 3. Малые колебания системы около положения равновесия, или установившегося движения
- 2. Интегрирование дифференциальных уравнений свободных колебаний.
- 3. Частные случаи колебания системы. Колебания около положений равновесия.
- § 4. Вынужденные колебания
- 2. Система с одной степенью свободы.
- § 5. Малые колебания и устойчивость
- 2. Примеры.
- 3. Центробежный регулятор.
- ГЛАВА IV. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДЫХ ТЕЛ
- 2. Скоростные координаты.
- 3. Законы движения твердого тела.
- 4. Уравнения движении Эйлера.
- 5. Формальное обобщение математических выражений (исчисление моторов).
- 6. Уравнения движения Лагранжа.
- § 2. Свободное движение твердого тела
- 2. Явный вид решений в случае периодического движения.
- 3. Квазистатические движения.
- 4. Симмеричный волчок.
- § 3. Движение в поле тяжести
- 2. Симметричный волчок. Квазистатическое движение.
- 3. Симметричный волчок. Самое общее движение.
- 4. Колебательные движения с конечной амплитудой.
- § 4. Движение самолета
- 2. Дифференциальные уравнения продольного движения.
- 3. Постоянные (перманентные) движения и малые колебания.
- 4. Продольная устойчивость горизонтального полета.
- 5. Фигондное движение.
- ГЛАВА V. МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 1. Основные понятия теории возмущений
- 2. Многократно-периодические системы.
- 3. Вырожденные системы.
- 4. Дифференциальные уравнения вековых возмущений.
- § 2. Возмущения упругих колебаний
- 2. Возмущающая сила пропорциональна кубу отклонения.
- 3. Возмущающая сила содержит члены связи.
- 4. Возмущения просто-пориодических траекторий.
- § 3. Выражение энергии для возмущенных систем
- 2. Вычисление выражения энергии.
- 3. Невозмущенная система вырождена.
- § 4. Выражение энергии для негармонических колебаний
- 2. Просто-периодическое основное движение.
- ГЛАВА VI. ЗАДАЧИ НЕБЕСНОЙ И АТОМНОЙ МЕХАНИКИ
- § 1. Движение Кеплера
- 2. Введение угловых переменных и переиенпых действия.
- 3. Вычисление координат положения.
- § 2. Возмущенное движение Кеплера
- § 3. Некоторые введения, касающиеся задачи трех тел
- 2. Приведение задачи трех тел.
- 3. Квазнстатические орбиты в случае плоской задачи трех тел.
- § 4. О касательных преобразованиях (Дополнение редактора)
- ЧАСТЬ ВТОРАЯ. МЕХАНИКА СПЛОШНЫХ СРЕД
- ГЛАВА VII. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ УПРУГОСТИ
- § 2. Анализ напряжений и деформаций
- 2. Тензор нанряженнй.
- 3. Тензор деформации.
- § 3. Закон Гука и основные уравнения теорнн упругости
- 2. Основные уравнения теории упругости.
- 3. Вычисление смещений но данный напряжениям.
- § 4. Минимальные принципы. Теоремы единственности
- 2. Принцип минимума для смещений. Принцип возможных перемещений.
- 3. Принцип минимума для напряжений.
- 4. Единственность решения.
- § 6. Уравнения движения. Единственность решения
- ГЛАВА VIII. ЗАДАЧИ НА УПРУГОЕ РАВНОВЕСИЕ
- § 1. Элементарные решения с лннейныи распределением напряжений
- 2. Растягивающая нагрузка, равномерно распределенная на концах цилиндра.
- 3. Изгиб стержня приложенными на концах его моментами.
- § 2. Кручение призматических стержней
- 2. Простейшие примеры.
- 3. Прямоугольник. Метод разложения в ряды.
- 4. Сечение, ограниченное многоугольником. Применение метода теории функций комплексной переменной.
- 5. Кручение призм, составленных из различных материалов
- § 3. Плоская пластинка, к которой приложены силы, расположенные в этой же плоскости
- 1а. Комплексное представление функции напряжений.
- 2. Сосредоточенная сила, приложенная на границе полуплоскости.
- 3. Круглая шайба (диск) под действием: нормальных: сил, приложенных к ее границе.
- 4. Растяжение полосы с отверстием.
- § 4. Пространственные задачи
- 1. Равновесие тела, ограниченного бесконечной плоскостью.
- 2. Вдавливание цилиндра в горизонтальную плоскость.
- ГЛАВА IX. ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- 1. Дифференциальное уравнение колебаний струны.
- 2. Метод разложения в ряд.
- 3. Определение постоянных по начальному состоянию струны.
- 4. Решение в форме Даламбера.
- 5. Бесконечная струна.
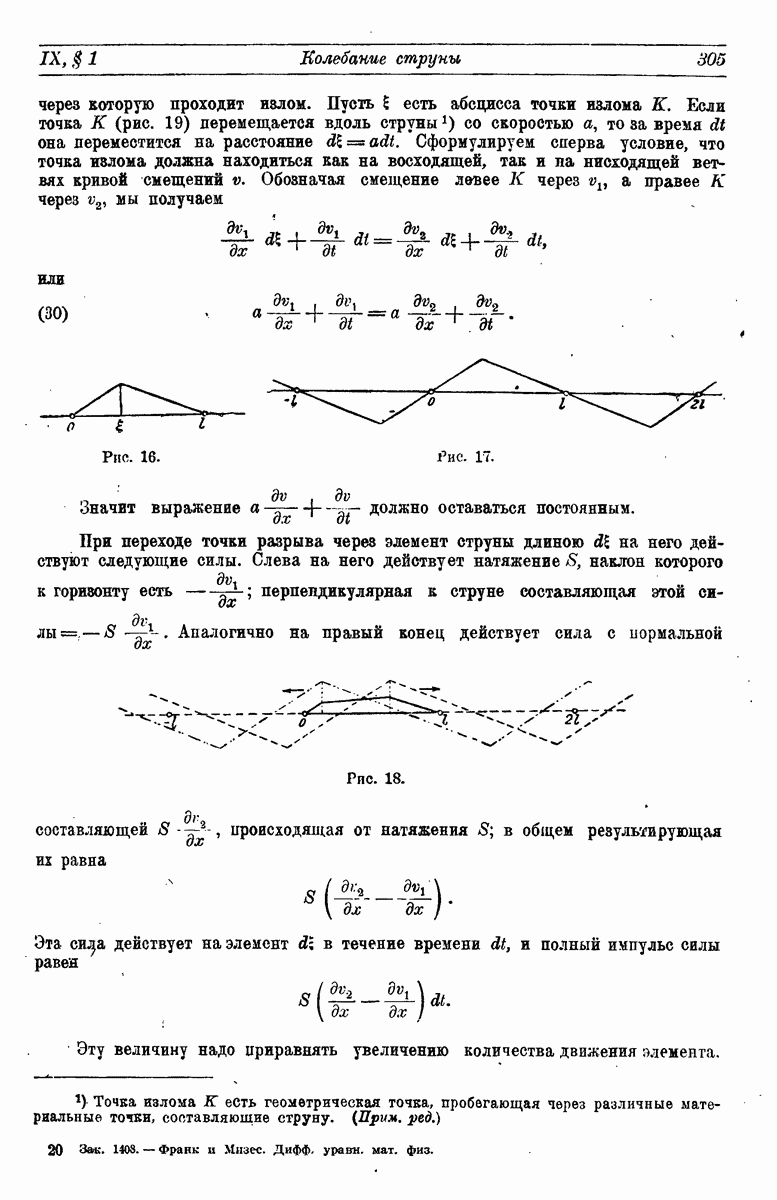
- 6. Разрывы.
- § 2. Приложение интегральных уравнений к задаче колебания
- 2. Потенциальная и кинетическая энергия.
- 3. Решение при данных начальных условиях.
- 4. Вынужденные колебания.
- 5. Колебания стержня.
- § 3. Колебания мембраны
- 1. Дифференциальное уравнение колебаний мембраны.
- 2. Прямоугольная мембрана.
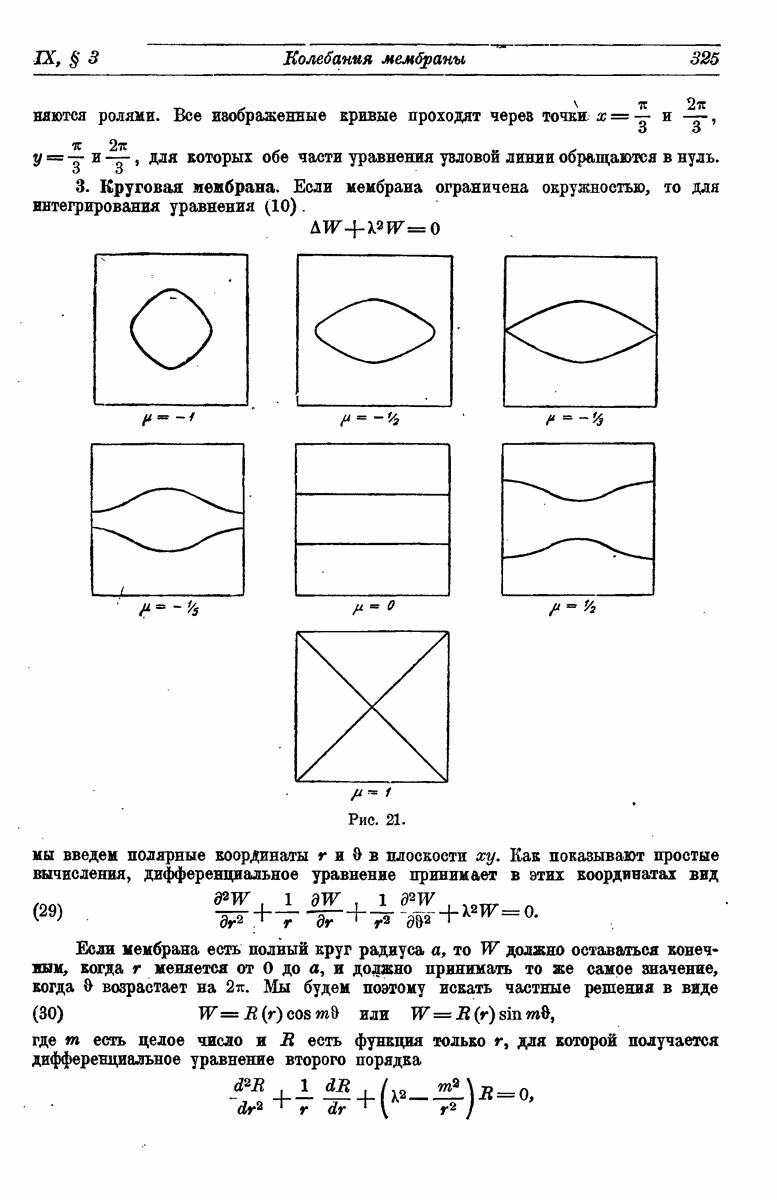
- 3. Круговая мембрана.
- 4. Аналитические свойства решений.
- 5. Интегральное уравнение колебания мембраны.
- § 4. Граничная задача колеблющейся мембраны как задача вариационного исчисления
- 2. Высшие характеристические числа.
- 3. Следствия из минимальных свойств.
- 4. Метод Ритца. Эллиптическая мембрана.
- 5. Асимптотическое распределение характеристических чисел.
- ГЛАВА X. ИДЕАЛЬНЫЕ ЖИДКОСТИ
- 1. Определение идеальной жидкости.
- 2. Поле скоростей.
- 3. Уравнение неразрывности.
- 4. Теорема Гаусса; поток.
- 5. Деформация частицы жидкости.
- 6. Безвихревое движение; потенциал скоростей.
- 7. Примеры
- 8. Уравнения Эйлера.
- 9. Уравнения Лагранжа.
- 10. Гидростатика; плавание.
- 11. Свободная поверхность вращающейся жидкости. Фигуры равновесия.
- 12. Уравнение для давления; уравнение энергии.
- 13. Теоремы о количестве движения для стационарного течения жидкости. Истечение из сосуда.
- 14. Теоремы о количестве движения. Общая формулировка.
- 15. Ток и циркуляция.
- 16. Теорема Стовса. Поток вихря.
- 17. Сохранение циркуляции.
- 18. Теоремы Гельягольца о вихрях.
- 19. Стационарное вихревое движение.
- § 2 Общие методы
- 1. Потенциальное движение; теорема Грина.
- 2. Следствия из теоремы Грина.
- 3. Источники.
- 4. Двойной источник (диполь).
- 5. Поверхностное распределение источников; слои источников.
- 6. Задачи с граничными условиями; функция Грина.
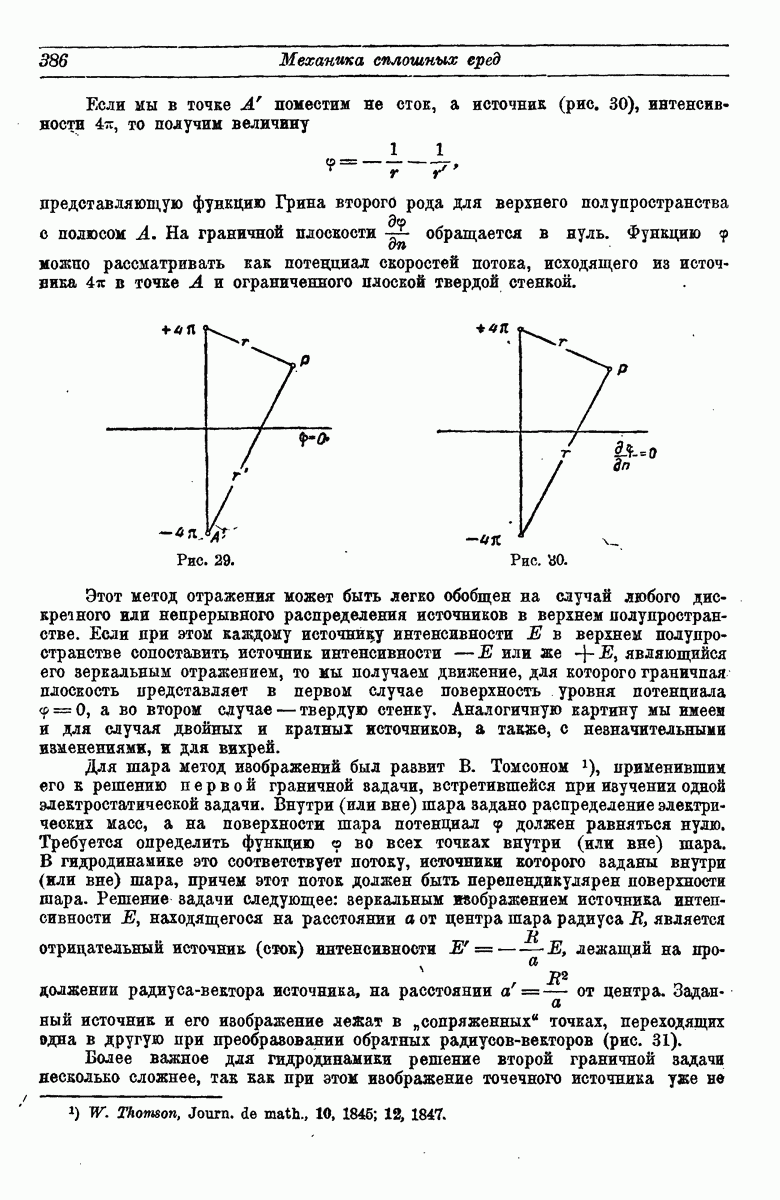
- 7. Метод изображений.
- 8. Вихревое поле; вихревые линии; закон Био-Савара.
- 9. Вихревые слои.
- 10. Представление потока с помощью источников и вихрей.
- 11. Кинетическая энергия потока.
- 12. Геометрические свойства; слои тока.
- 13. Давление в потоке.
- 14. Движение твердых тел в идеальной жидкости.
- § 3. Частные задачи и методы
- 2. Конформное отображение.
- b) ОБРАЗОВАНИЕ СТРУЙ
- 3. Струя в покоящейся («мертвой») воде.
- 4. Плоские струи. Методы Гельмгольца и Кирхгофа.
- 5. Метод Леви-Чивита.
- 6. Учет силы тяжести. Переливание жидкости через плотину.
- 7. Функциональное уравнение для свободной границы струи; перманентные волны.
- 8. Пространственные струи.
- с) ВОЛНЫ
- 9. Общие соображения о волнах жидкости.
- 10. Периодические волны в канале.
- 11. Наложение (суперпозиция) волн в каналах.
- 12. Волны Герстнера.
- 13. Корабельные волны.
- 14. Волны прилива и отлива.
- d) ВИХРИ
- 15. Вихревые точки в неограниченной плоскости.
- 16. Вихревые точки в ограниченной области.
- 17. Вихри Кармана.
- 18. Возникновение вихрей Кармана.
- 19. Вихревые кольца.
- 20. Другие вихревые образования.
- е) ЦИРКУЛЯЦИЯ И ПОДЪЕМНАЯ СИЛА
- 21. Гидродинамическая подъемная сила.
- 22. Теорема Кутта-Жуковского.
- 23. Техническое значение гидродинамической подъемной силы.
- 24. Прандтлевская теория несущего крыла.
- ГЛАВА XI. ДВИЖЕНИЕ ЖИДКОСТЕЙ С ТРЕНИЕМ
- 2. Закон Пуазейля.
- 3. Обозначения.
- 4. Связь между напряжениями и скоростью деформаций.
- 5. Полные дифференциальные уравнения.
- 6. Составляющие напряжения на поверхности покоящегося тела.
- 7. Линеаризованные дифференциальные уравнения.
- § 2. Фундаментальные интегралы линеаризованных дифференциальных уравнений
- 2. Линеаризованные уравнения пространственного движения для случая, когда система координат ииеет постоянную поступательную скорость.
- 3. Линеаризованные уравнения плоского движения для случая, когда система координат имеет постоянную поступательную скорость.
- 4. Движение твердого тела.
- 5. Наиболее общие линеаризованные дифференциальные уравнения.
- § 3. Стоксова формула сопротивления и связанные с ней формулы
- 2. Более точное вычисление потока вокруг шара.
- 3. Поступательное движение тонкого кругового цилиндра в вязкой жидкости.
- § 4. Точные решении уравнений движения вязкой иесжииаеиой жидкости
- § 5. Теория пограничного слоя
- 2. Уравнение движения пограничного слоя.
- 3. Отрыв пограничного слоя.
- 4. Пограничный слой в точной теории Гамеля.
- ГЛАВА XII. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ РАСПРОСТРАНЕНИЯ КОЛЕБАНИЙ
- § 1. Задача об отражении плоских упругих волн
- 2. Плоская задача.
- 3. Граничные (краевые) условия. Полупространство.
- 4. Линейно-поляризованные поперечные волны.
- 5. Звуковые волны.
- 6. Класс комплексных решений волнового уравнения.
- 7. Плоские волны. Отражение плоских продольных волн.
- 8. Отражение поперечных волн.
- 9. Поверхностные волны Рэлея.
- 10. Общие формулы комплексной теории отражения.
- § 2. Общий анализ комплексных решений
- 1. Однородные комплексные решения волнового уравнения. Внутренность основного конуса.
- 2. Внешность основного конуса.
- 3. Кинематические и динамические условия совместности. Характеристики.
- 4. Условия правильности однородных, комплексных решений.
- 5. Анализ комплексных решений общего типа.
- § 3. Задача об источниках колебаний для полупространства
- 2. Задача с однородными смещениями.
- 3. Конформное преобразование типа …
- 4. Задача об отражении продольных волн. Случай комплексных потенциалов.
- 5. Задача об отражении продольных волн. Случай комплексных смещений.
- 6. Принцип Ферма.
- 7. Отражение поперечных волн. Случай комплексных потенциалов.
- 8. Отражение поперечных волн. Случай комплексных смещений.
- 9. Принцип Ферма.
- 10. Волны Рэлея.
- § 4. Задача Коши для упругого полупространства в двух измерениях
- 2. Фундаментальное решение Вольтерра.
- 4. Решение задачи Коши по методу Вольтерра.
- 4. Формула Грнна-Вольтерра.
- 5. Кинематические и динамические условии совместности для уравнений упругости.
- 6. Постановка плоской задачи теории упругости для полупространства.
- 7. Фундаментальные решения.
- 8. Решение общей задачи теории упругости для полупространства в плоском случае.
- 9. Теория точечных источников.
- 10. Задача Лэмба.
- 11. Волны Рэлея.
- § 5. Основы решения трехмерных: задач распространении колебаний методом комплексной переменной
- 2. Отражение упругих примитивных волн.
- 3. Полное внутреннее отражение поперечной волны при …
- 4. Волны Рэлея.
- 5. Принцип наложения.
- 6. Построение первого фундаментального решения для трехмерной задачи теории упругости.
- 7. Задачи с осевой симметрией.
- 8. Построение других фундаментальных решений.
- 9. Основные свойства наложения общих комплексных решений.
- 10. Отражение фундаментальных решений.
- § 6. Задача Коши в трехмерном пространстве
- 2. Формула Грина для волнового уравнения.
- 3. Фундаментальное решение волнового уравнения.
- 4. Решение волнового уравнения.
- 5. Формула Грина для уравнений теории упругости.
- 6. Фундаментальные решения уравнений упругости для полупространства.
- 7. Решение задачи Коши для упругого полупространства.
- 8. Анализ полученных результатов.
- § 7. Обобщение решения волнового уравнения
- 2. Обобщенные решения волнового уравнения.
- 3. Связь с условиями совместности.
- 4. Теорема интегрирования.
- 5. Обобщенные комплексные решения.
- 6. Обобщенные комплексные решения во всей области существования.
- §. 8. Задача о диффракции плоских волн
- 2. Разветвляющиеся комплексные решения волнового уравнения.
- 3. Элементарные плоские волны логарифмической поверхности.
- 4. Диффракция произвольной плоской волны.
- 5. Периодические решения.
- 6. Диффракция относительно угла.
- 7. Трехмерная задача диффракции плоских волн.
- 8. Общая задача диффракции для двухмерного пространства.
- ЧАСТЬ ТРЕТЬЯ. ТЕПЛОПРОВОДНОСТЬ И ДИФФУЗИЯ
- 1. Основные понятия теплопроводности в твердых телах.
- 2. Дифференциальное уравнение теплопроводности.
- 3. Основные понятия диффузии при отсутствии внешних сил.
- 4. Дифференциальное уравнение диффузии.
- § 2. Теплопроводность и диффузия в неограниченных телах
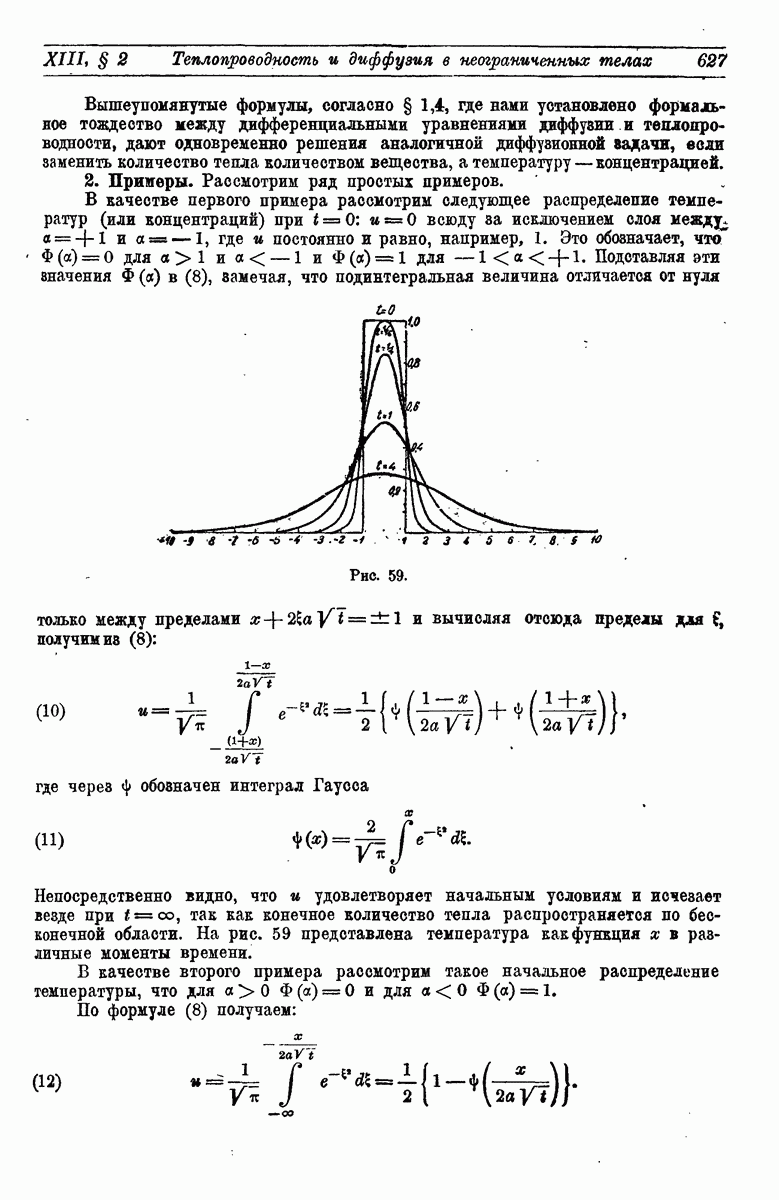
- 2. Примеры.
- 3. Применение к броуновскому движению одной частицы.
- 4. Тела, бесконечно протяженные в двух измерениях.
- 5. Тела, бесконечно протяженные в трех измерениях.
- 6. Интегральное уравнение теплопроводности и диффузии.
- § 3. Теплопроводность и диффузия в ограниченных телах
- 2. Диффузнонный опыт Бриллуэпа и «первые прохождения» при броуновском движении.
- 3. Тело, ограниченное двумя плоскостями.
- 4. «Двухсторонние первые прохождения» при броуновском движении.
- 5. Слоистые тела.
- 6. Теплопроводность в цилиндре.
- 7. Теплопроводность в шаре.
- 8. Распространение холода.
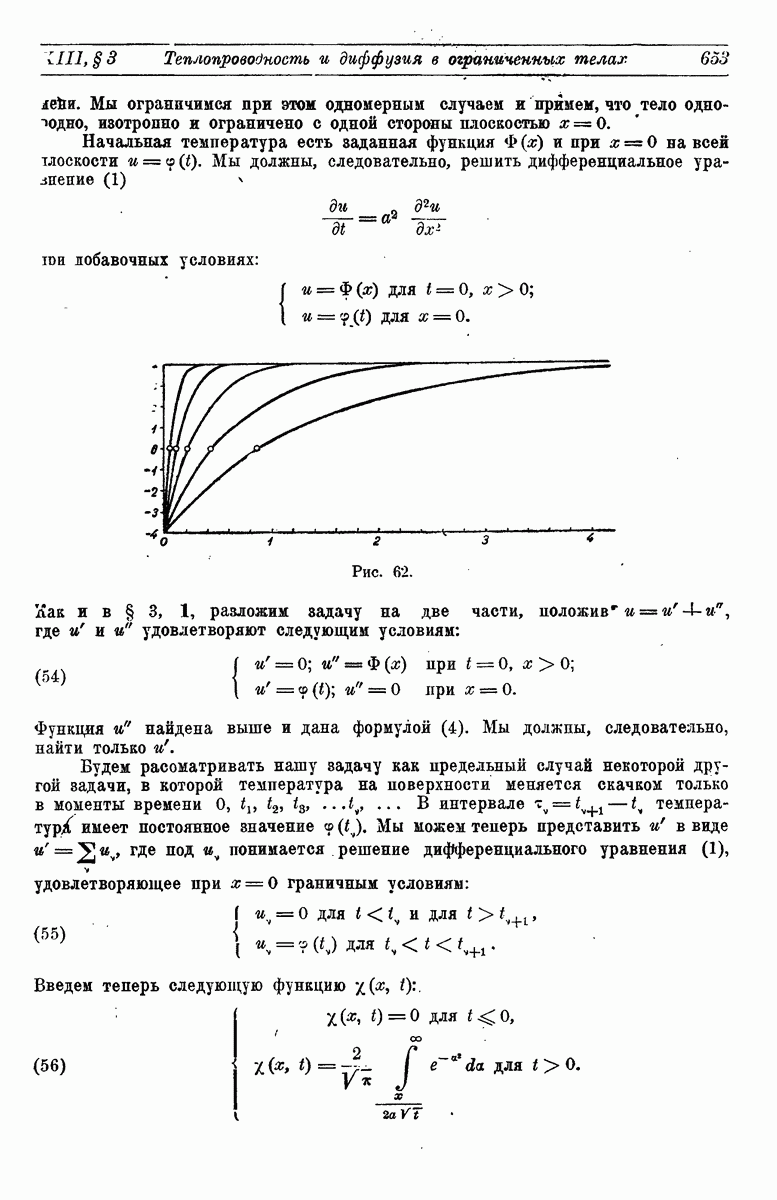
- 9. Температура (концентрация) граничной поверхности есть заданная функция времени.
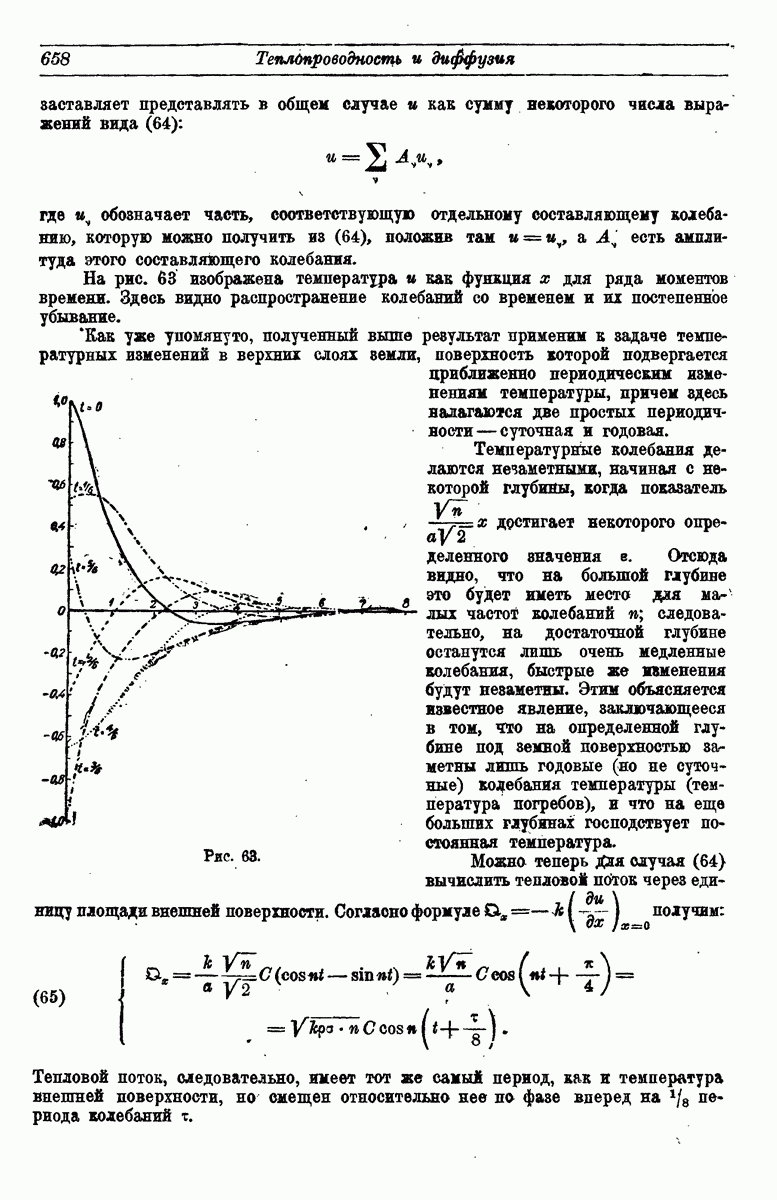
- 10. Тепловые волны.
- 11. Внешняя поверхность — изолятор.
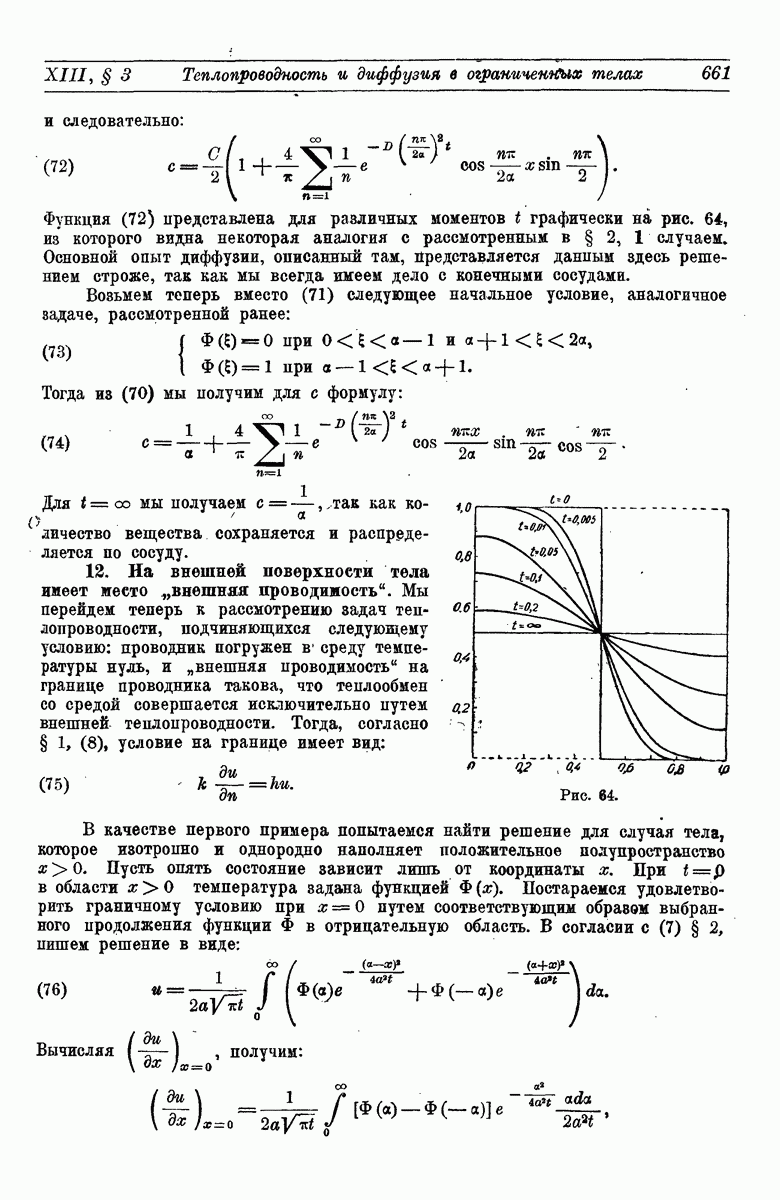
- 12. На внешней поверхности тела имеет место «внешняя проводимость».
- 13. Диффузия сквозь диафрагму.
- 14. Задача внешней теплопроводности в двух измерениях.
- 15. Теплопроводность стержня.
- ГЛАВА XIV. ВЫНУЖДЕННАЯ ТЕПЛОПРОВОДНОСТЬ И ДИФФУЗИЯ
- 2. Дифференциальное уравнение диффузии при действии внешних сил.
- 3. Интегральное уравнение диффузии и его связь со статистикой.
- § 2. Теплопроводность и диффузия при вынужденной конвекции
- 2. Конечный коэффициент теплопередачи.
- 3. Течение сквозь узкие трубы. Холодильник.
- 4. Диффузия в текущих газах и под действием заданных внешних сил.
- 5. Седиментация и броуновское движение в поле силы тяжести.
- 6. Связь с одной теоремой статистической механики.
- 7. Диффузия электролитов.
- 7. Диффузия ионов в газах.
- § 3. Спонтанное конвекционное течение под действием внешних сил
- § 4. Связь между теорией диффузии и волновой механикой
- 2. Движение системы частиц под действием внешних сил.
- 3. Движение по инерции.
- 4. Связь с соотношением неопределенности.
- ЧАСТЬ ЧЕТВЕРТАЯ. СТАЦИОНАРНОЕ (И КВАЗИСТАЦИОНАРНОЕ) ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- ГЛАВА XV. ЭЛЕКТРОСТАТИКА
- 2. Математические уравнения поля.
- § 2. Основные задачи; метод отражений и электрических изображений
- 2. Распределение электричества на эллипсоиде.
- 4. Отражение и электрические изображения.
- § 3. Электростатическое равновесие на двух заряженных сферах
- § 4. Цилиндрические поля. Представление посредством функций комплексной переменной
- 2. Отражение, эксцентрические круговые цилиндры.
- 3. Представление поля посредством функций комплексной переменной.
- § 5. Поле призматических проводников
- 2. Два бесконечных призматических проводника.
- 3. Поле между двумя конечными ограниченными проводниками.
- § 6. Применение электростатики к теории катодных ламп
- ГЛАВА XVI. СТАЦИОНАРНЫЕ ЭЛЕКТРИЧЕСКИЕ ТОКИ
- § 1. Формулировка уравнений поля и простые задачи
- 2. Простые задачи о стационарных полях тока.
- § 2. Прохождение тока между землей и металлическими проводниками
- 3. Решение интегрального уравнения для распределения тока.
- 4. Решение интегродифференциального уравнения для выхода тока.
- § 3. Слой жидкости с металлической границей. Цветные кольца Нобили
- 2. Учет поляризации.
- 3. Однородная вспомогательная задача.
- 4. Общее решение неоднородной задачи.
- 5. Решение в случае тока.
- ГЛАВА XVII. МАГНИТОСТАТИКА
- § 1. Образование магнитных полей
- 2. Постоянный магнит и магнитный момент.
- 3. Стационарное электромагнитное поле.
- § 2. Парамагнитные тела в магнитном поло
- 2. Шар в однородном поле
- 3. Эллипсоид в однородном поле.
- § 3. Силы, испытываемые материальными телами в электрическом или магнитном поле
- 2. Вспомогательная теорема.
- 3. Энергия диэлектрического тела в электрической поле.
- 4. Энергия пара- или диаиагнитиого тела в магнитнои поле.
- 5. Применение в эллипсоиду.
- ГЛАВА XVIII. КВАЗИСТАЦИОНАРНЫЕ ТОКИ И ВОЛНЫ
- § 1. Квазистационарные контуры тока
- 2. Механическое представление системы. Закон индукции Фарадея.
- 3. Колебание цепей. Сопротивление при переменном токе.
- § 2. Квазистационарные волны в проводниках
- 2. Стоячие волны. Свободные колебания.
- 3. Вынужденные колебания.
- 4. Бегущие волны произвольной формы.
- § 3. Квазистационарные волны в катушках
- 2. Гармонические волны.
- 3. Образование преломленных волн.
- ЧАСТЬ ПЯТАЯ. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ И МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Закон сохранения энергии и однозначность решений.
- 3. Замечание о математической трактовке колебательных процессов.
- 4. Электронная теория.
- § 2. Инвариантность уравнений Максвелла по отношению к преобразованию Лоренца
- 2. Антисимметричный тензор поля.
- 3. Группа ортогональных преобразований.
- 4. Частное преобразование Лоренца.
- § 3. Запаздывающие потенциалы и поле ускоренно движущегося заряда
- 2. Запаздывающие потенциалы и приближение Льенарда-Вихерта.
- 3. Поле произвольно движущегося заряда.
- § 4. Вектор Герца и излучение колеблющегося диполя
- 1. Непосредственное рассмотрение электрического диполя.
- 2. Поле линейного гармонического вибратора.
- 3. Излучение энергии.
- 4. Обобщения.
- 5. Вычисление оптической интенсивности по вектору Герца.
- § 5. Условия излучениях). Собственные функции и собственные значения
- ГЛАВА XX. ТЕОРИЯ ДИФФРАКЦИИ
- § 1. Разветвленные решения уравнения колебаний
- 2. Понятие пространства Римана.
- 3. Функция плоской волны, однозначная на поверхности Римана.
- 4. Решения для пространства Римана.
- 5. Приложения и дополнения.
- § 2. Сходящиеся и полусходящиеся разложения разветвленных решений.
- 2. Выражение для разветвленной функции плоской волны в виде сходящихся рядов по Бесселевым функциям.
- 3. Асимптотическое выражение разветвленной функции плоской волны.
- 4. Частный случай n=2.
- § 3. Сравнение с классической теорией диффракции (Френель-Кирхгоф)
- 2. Принцип Гюйгенса.
- 3. Прямоугольное отверстие, щель и полуплоскость.
- 4. Связь между геометрической и волновой оптикой.
- § 4. Диффракция от шара и от других тел. Метод разложения в ряды
- 2. Теоремы сложения.
- 3. Диффракции от цилиндра.
- 4. Диффракции от шара. Коллоидальные частицы.
- ГЛАВА XXI. СОПРОТИВЛЕНИЕ ДЛЯ ПЕРЕМЕННЫХ ТОКОВ И СКИН-ЭФФЕКТ
- § 1. Распределение в проводящей плоскости
- 2. Исследование поля.
- 3. Сопротивление переменному току.
- § 2. Провод с круговым сечением при низких и высоких частотах
- 2. Исследование поля.
- 3. Сопротивление и самоиндукция провода.
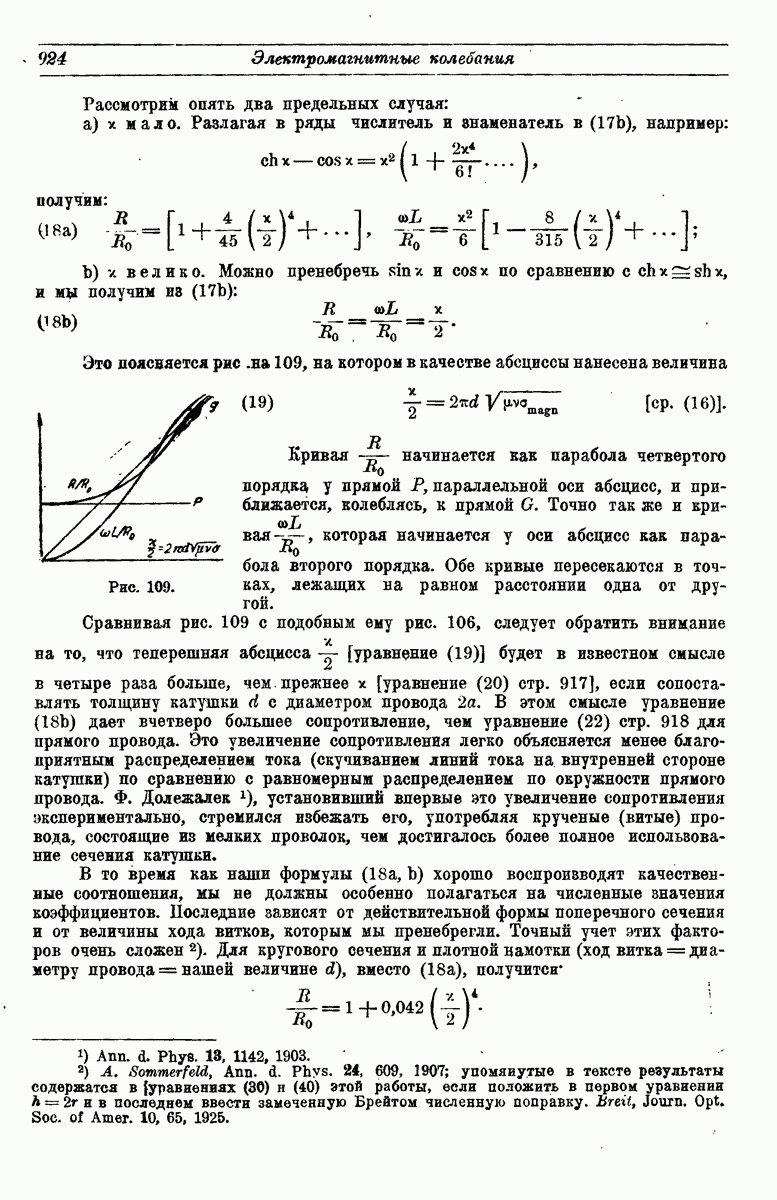
- § 3. Катушка с переменным током
- 2. Исследование поля.
- 3. Сопротивление и самоиндукция катушки.
- ГЛАВА XXII. ВОЛНЫ ВДОЛЬ ПРОВОДОВ
- § 1. Поле и распространение волн вдоль проводов
- 2. Численный пример для одного типичного случая.
- 3. Очень тонкий провод. Аномальный случай распространения и затухания.
- 4. Поток энергии на бесконечности.
- 5. Структура поля.
- § 2. Дополнения
- 1. Побочные волны электрического и магнитного типов. Несимметричные волны.
- 2. Поверхностные волны на непроводниках.
- 3. Случай металлического обратного провода.
- ГЛАВА XXIII. БЕСПРОВОЛОЧНАЯ ТЕЛЕГРАФИЯ
- § 1. Вертикальная антенна на плоской земле
- 2. Преобразование первичного возбуждения.
- 3. Выполнение граничных условий.
- 4. Другие формы решения.
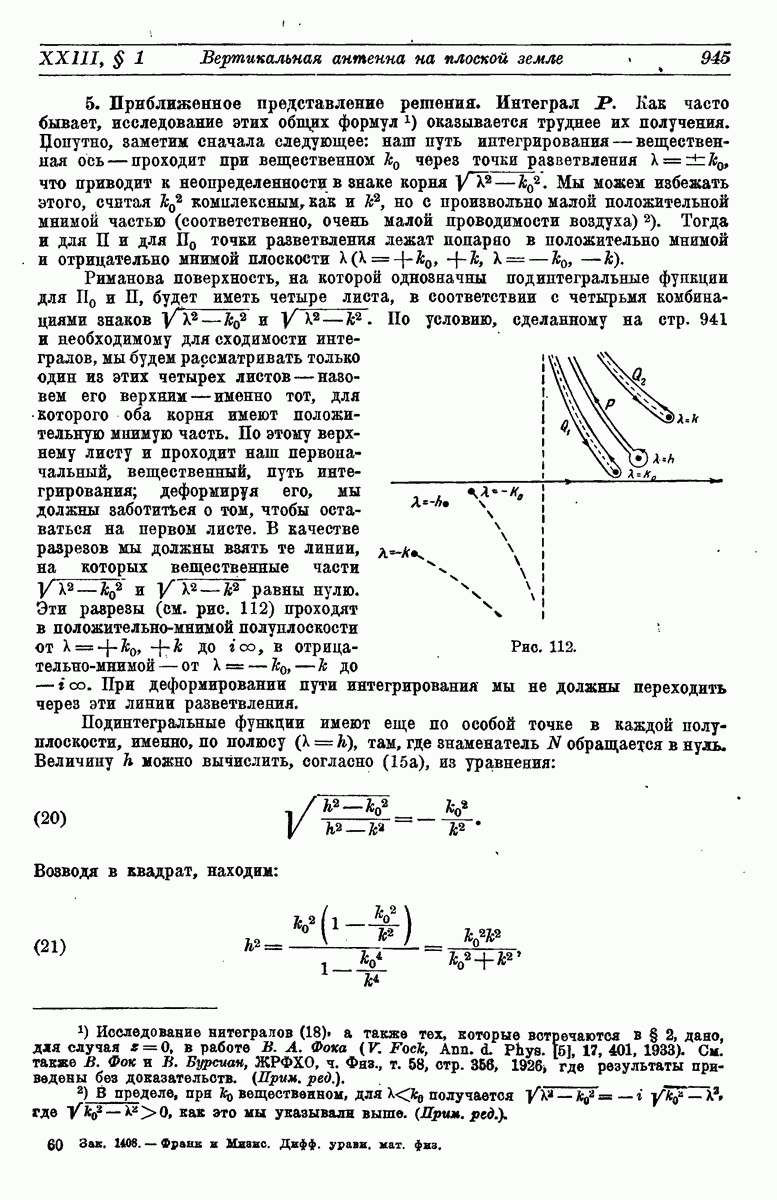
- 5. Приближенное представление решения.
- 6. Приближенное представление решения.
- 7. Вывод приближенной формулы для точек вблизи поверхности земли.
- § 2. Горизонтальная и рамочная антенны
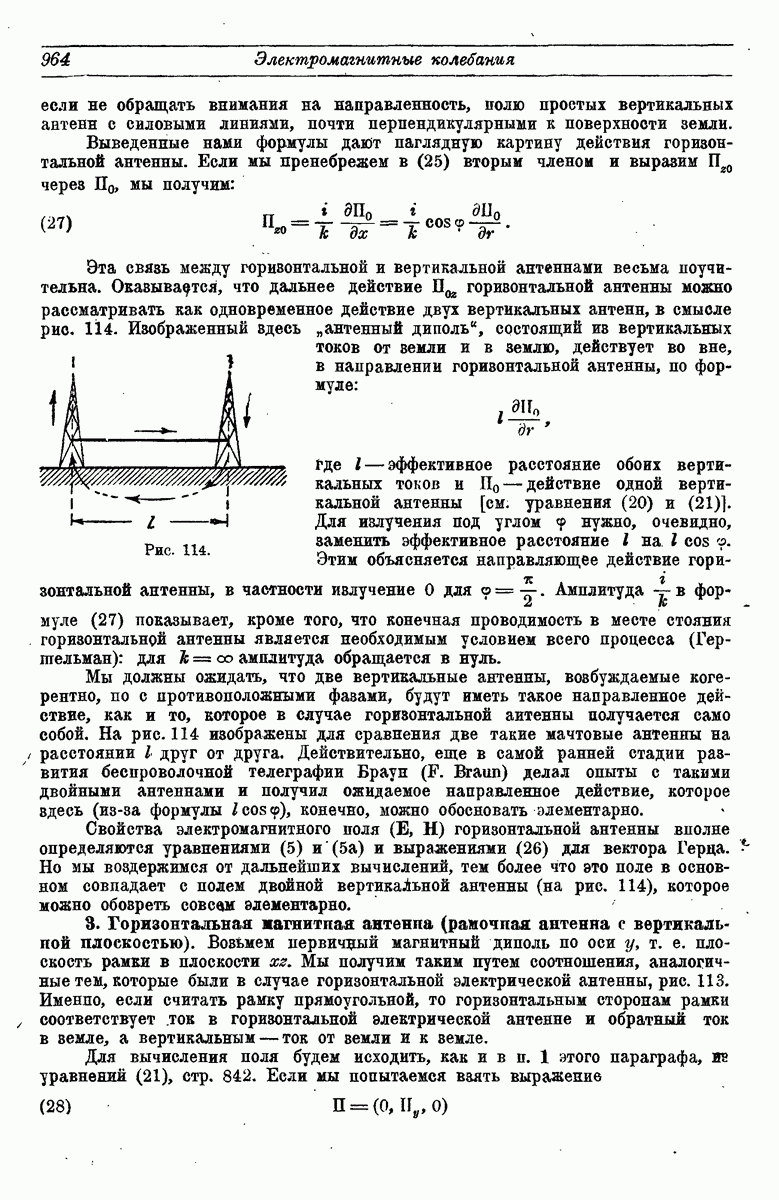
- 2. Горизонтальная электрическая антенна.
- 3. Горизонтальная магнитная антенна (рамочная антенна с вертикальной плоскостью).
- ПРИМЕЧАНИЕ
- § 3. Теорема взаимности в беспроволочной телеграфии
- 2. Две линейные электрические антенны.
- 3. Две магнитные антенны или одна электрическая и одна магнитная антенны.
- § 4. Беспроволочная телеграфия вокруг земли