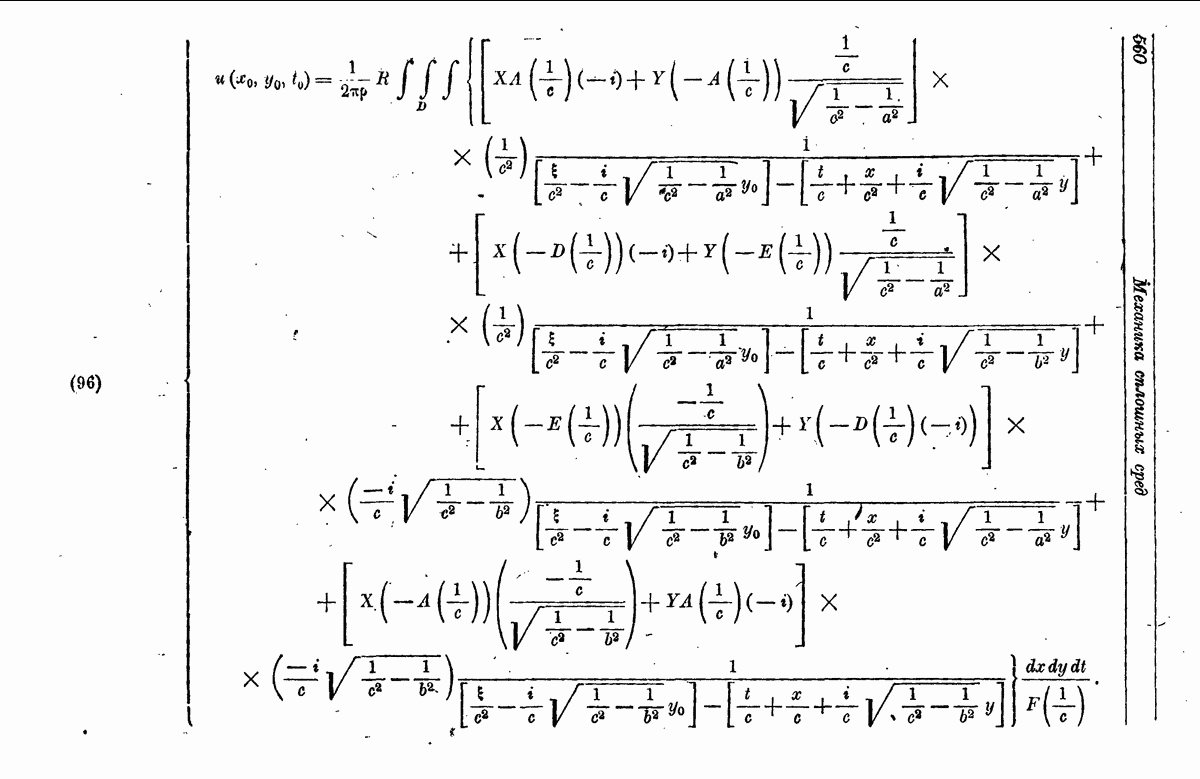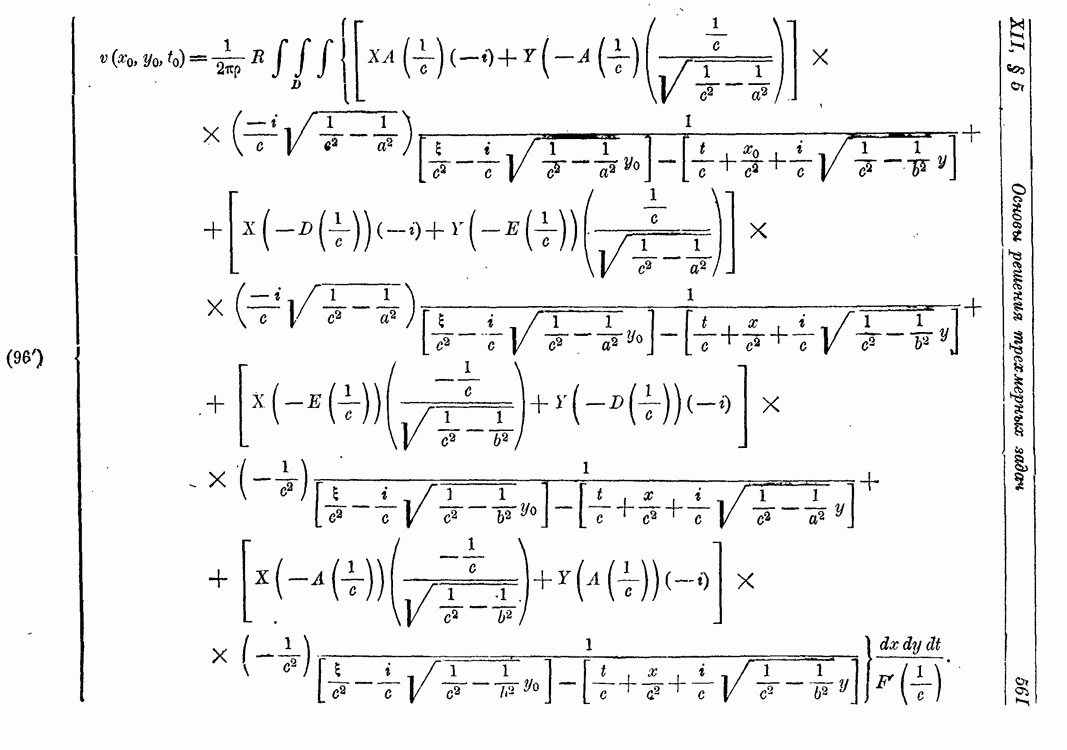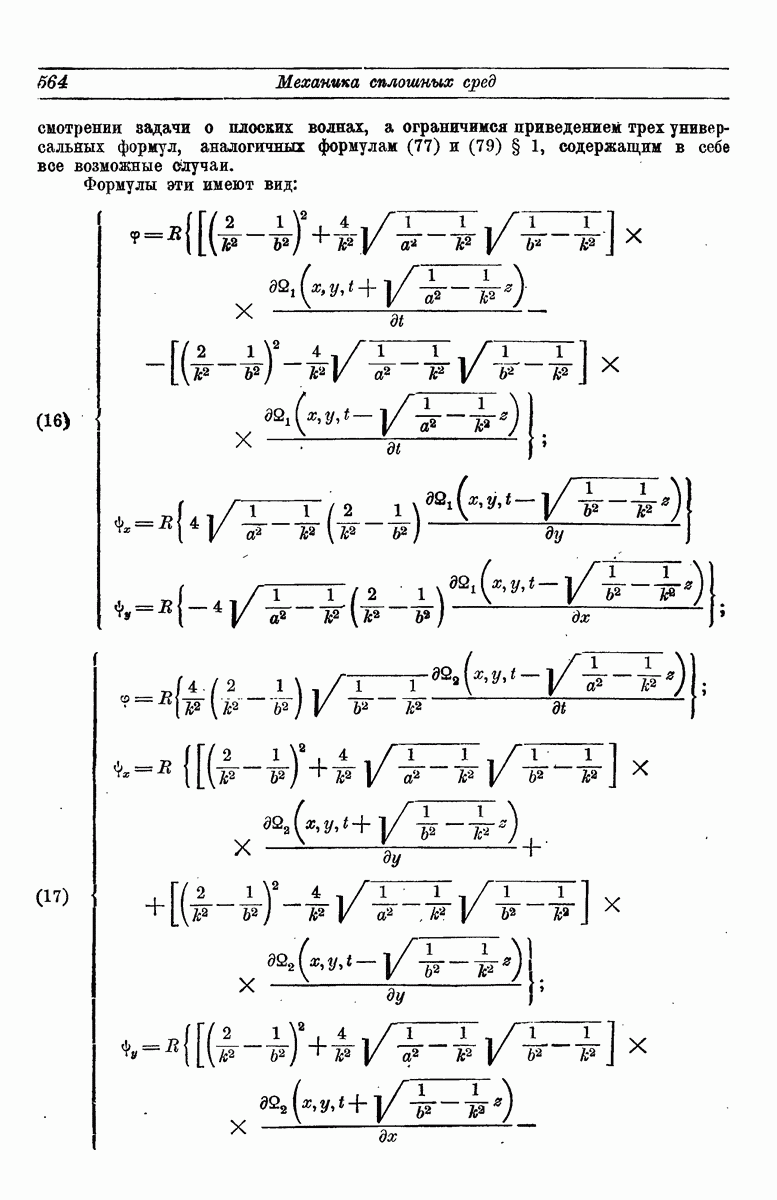| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
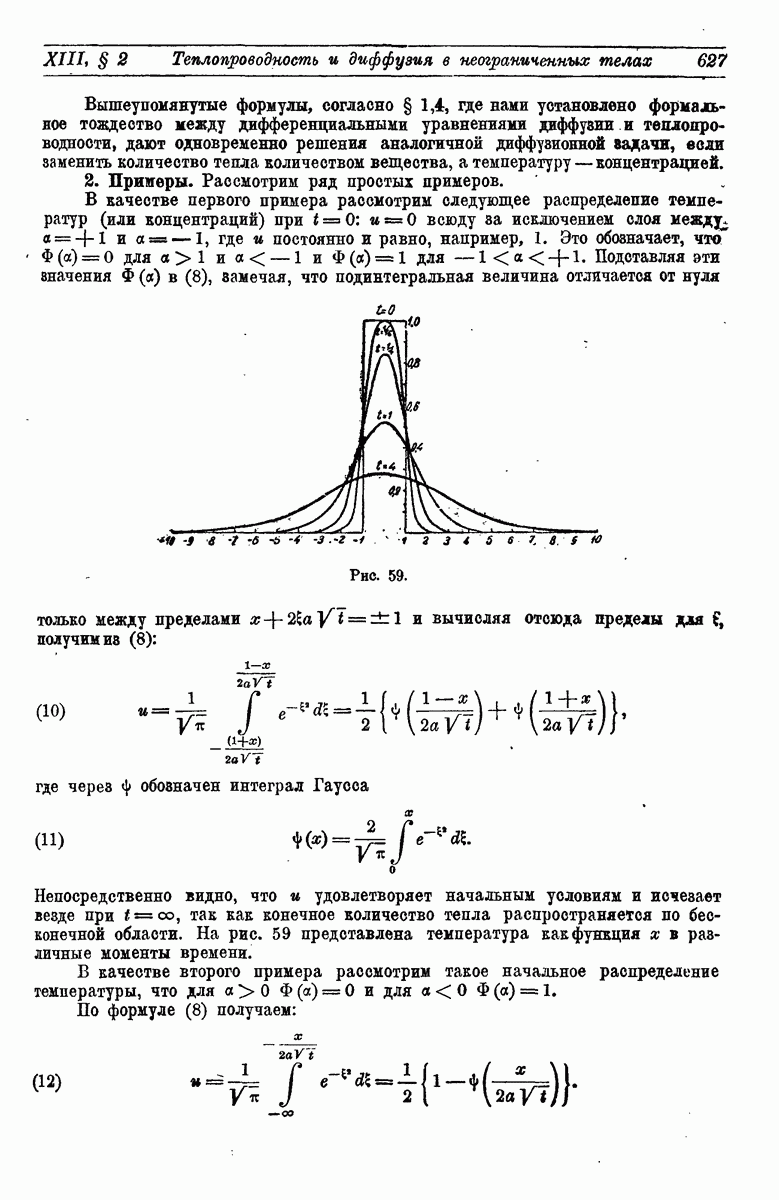
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
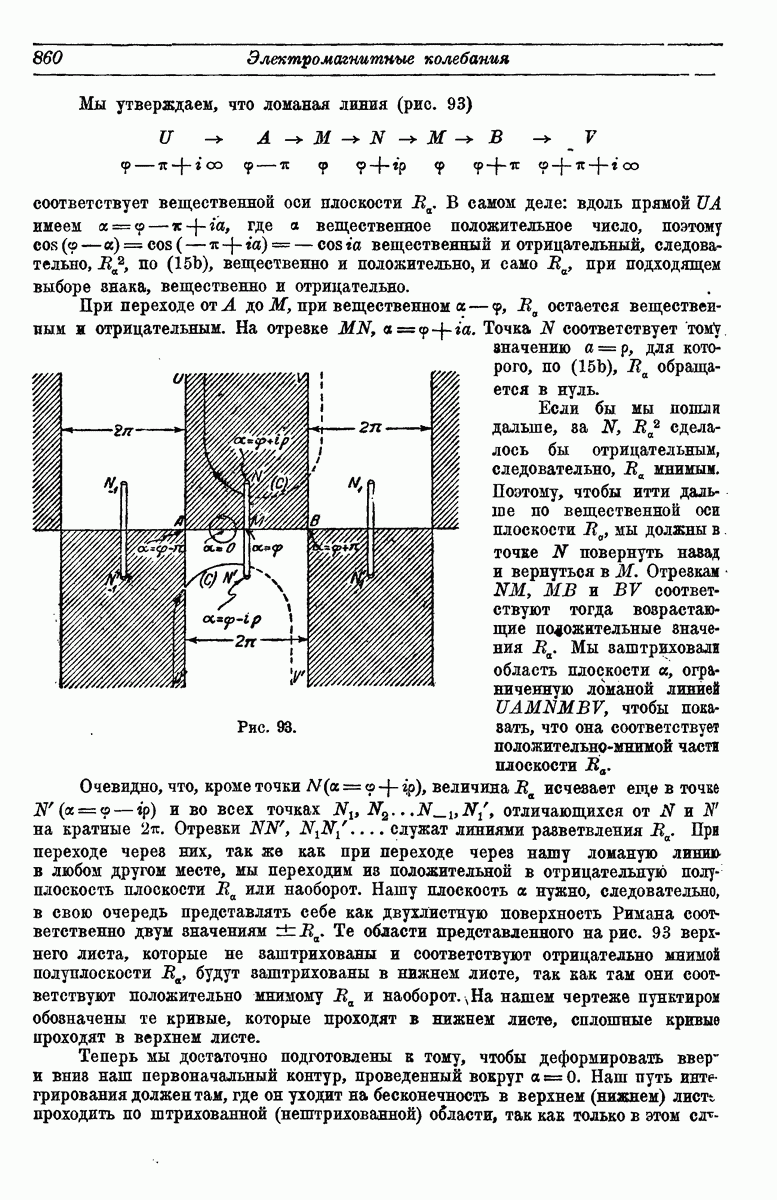
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
955
956
957
958
959
960
961
962
963
964
965
966
967
968
969
970
971
972
973
974
975
976
977
978
979
980
981
982
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. Нахождение световых лучей при помощи эйконала, касательные преобразования.
Если радиус-вектор  и нормальный вектор
и нормальный вектор  удовлетворяют уравнению (47) §
удовлетворяют уравнению (47) §  то они определяют некоторый световой луч. Если крез
то они определяют некоторый световой луч. Если крез  обозначить радиус-вектор и нормальный вектор в какой-либо точке
обозначить радиус-вектор и нормальный вектор в какой-либо точке  то эти величины удовлетворяют уравнениям (8) и (5). Поэтому при заданных
то эти величины удовлетворяют уравнениям (8) и (5). Поэтому при заданных  По выражения
По выражения

южно рассматривать как уравнения радиуса-вектора и нормального вектора  некоторого светового луча. Так как функция
некоторого светового луча. Так как функция  удовлетворяет уравнению йконала
удовлетворяет уравнению йконала  , и, следовательно, векторы
, и, следовательно, векторы  удовлетворяют уравнению (47) § 1, то уравнения (27) дают только пять соотношений между шестью оставляющими векторов
удовлетворяют уравнению (47) § 1, то уравнения (27) дают только пять соотношений между шестью оставляющими векторов  Таким образом, из этих уравнений можно получать
Таким образом, из этих уравнений можно получать  как функции от
как функции от  и одного параметра. Уравнения (26) можно
и одного параметра. Уравнения (26) можно
рассматривать как каноническое преобразование от переменных  к переменным
к переменным  и наоборот. С помощью такого преобразования система канонических уравнений световых лучей [см. § 1, (66), (67)] переходит в систему уравнений того же вида для переменных
и наоборот. С помощью такого преобразования система канонических уравнений световых лучей [см. § 1, (66), (67)] переходит в систему уравнений того же вида для переменных  ,
,

причем

В случае, если переменные  связаны преобразованием (26), причем величина
связаны преобразованием (26), причем величина  удовлетворяет уравнению эйконала
удовлетворяет уравнению эйконала  то
то

следовательно, уравнения (27) можно легко проинтегрировать. Интегрирование  показывает, что векторы
показывает, что векторы  , вдоль светового луча постоянны. Таким образом, при постоянных
, вдоль светового луча постоянны. Таким образом, при постоянных  уравнение (27) действительно является уравнением световых лучей. Если мы нашли решение уравнения эйконала, которое не есть точечный эйконал, но так же как и последний зависит от трех постоянных
уравнение (27) действительно является уравнением световых лучей. Если мы нашли решение уравнения эйконала, которое не есть точечный эйконал, но так же как и последний зависит от трех постоянных  т. е. имеет вид
т. е. имеет вид  то формулы
то формулы

определяют каноническое преобразование, и уравнения (30) на основании тех же соображений представляют собой при постоянных  уравнения светового луча.
уравнения светового луча.
Уравнения (27) можно также рассматривать как частный случай касательного преобразования. В этом случае преобразуемый элемент представляет собой элемент поверхности в четырехмерном пространстве  Координаты элемента тогда равны
Координаты элемента тогда равны  или в векторных обозначениях:
или в векторных обозначениях:  в.
в.
Касательное преобразование определяется тем, что "объединенные" элементы преобразуются в такие же. Два элемента  называются "объединенными", если удовлетворяется условие
называются "объединенными", если удовлетворяется условие

Но так как  [см. § 1, (56) и (44)], то это означает, что
[см. § 1, (56) и (44)], то это означает, что

Если  то
то  и элементы представляют собой смежные элементы одной и той же волновой поверхности
и элементы представляют собой смежные элементы одной и той же волновой поверхности  Если же
Если же  то равенство (32) означает, что оба элемента при распространении света в рассматриваемой среде переходят друг в друга за время
то равенство (32) означает, что оба элемента при распространении света в рассматриваемой среде переходят друг в друга за время  Они являются соседними элементами одноге и того же светового луча. Совокупность
Они являются соседними элементами одноге и того же светового луча. Совокупность  элементов, т. е. гиперповерхность четырехмерного пространства, образуется из элементов волновой последовательности.
элементов, т. е. гиперповерхность четырехмерного пространства, образуется из элементов волновой последовательности.
Легко видеть, что равенства (27) определяют касательное преобразование. В самом деле мы, имеем тождество:

и вследствие (27):

Но это равенство является условием касательного преобразования в том случае, когда переменная  не входит в уравнения преобразования, а это обстоятельство как раз и имеет место в уравнениях преобразования (27).
не входит в уравнения преобразования, а это обстоятельство как раз и имеет место в уравнениях преобразования (27).
Мы уже имели случай убедиться в том, что уравнения (27) преобразуют начальный элемент  и светового луча в некоторый другой элемент того же луча. Мы можем для нашего касательного преобразования ввести понятие бесконечно малого преобразования, которое преобразует некоторый элемент в соседний элемент; например, элемент
и светового луча в некоторый другой элемент того же луча. Мы можем для нашего касательного преобразования ввести понятие бесконечно малого преобразования, которое преобразует некоторый элемент в соседний элемент; например, элемент  светового луча преобразует в соседний элемент
светового луча преобразует в соседний элемент  Если значения параметра
Если значения параметра  в двух таких соседних точках светового луча отличаются друг от друга на величину
в двух таких соседних точках светового луча отличаются друг от друга на величину  то переход между этими двумя элементами совершается с помощью канонических уравнений (71) § 1. Если параметром служит длина дуги о, то будут иметь место уравнения (73), которые, следовательно, представляют собой бесконечно малое касательное преобразование. Поэтому мы можем при помощи повторного применения бесконечно малого преобразования получить группу касательных преобразований, зависящую от одного параметра. Эта группа в нашем случае состоит из всех касательных преобразований, которые преобразуют каждый элемент светового луча в элемент
то переход между этими двумя элементами совершается с помощью канонических уравнений (71) § 1. Если параметром служит длина дуги о, то будут иметь место уравнения (73), которые, следовательно, представляют собой бесконечно малое касательное преобразование. Поэтому мы можем при помощи повторного применения бесконечно малого преобразования получить группу касательных преобразований, зависящую от одного параметра. Эта группа в нашем случае состоит из всех касательных преобразований, которые преобразуют каждый элемент светового луча в элемент  того же луча.
того же луча.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ ИЗДАТЕЛЯ К ПЕРВОМУ НЕМЕЦКОМУ ИЗДАНИЮ
- ЧАСТЬ ПЕРВАЯ. КЛАССИЧЕСКАЯ МЕХАНИКА И ГЕОМЕТРИЧЕСКАЯ ОПТИКА
- § 1. Световые лучи и волновые поверхности в любых телах
- 2. Принцип Ферма и световые лучи.
- 3. Световые лучи и волновые поверхности.
- 4. Дифференциальное уравнение волновых поверхностей и световых лучей.
- § 2. Оптическое отображение в общей случае анизотропной среды
- 2. Отображение элеиентов линии и элеиентов поверхности.
- 3. Нахождение световых лучей при помощи эйконала, касательные преобразования.
- § 3. Ход луча в различных средах
- 2. Изотропные среды.
- 3. Одноосные кристаллы.
- 4. Движущиеся тела
- 5. Электронный микроскоп.
- § 4. Отображение посредством симметричных оптических приборов
- 2. Диоптрика Гаусса.
- 3. Диоптрика электронных лучей.
- ГЛАВА II. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ В ОБЩЕМ СЛУЧАЕ
- § 1. Уравнения движения в прямоугольных координатах
- 2. Пример: влияние сопротивления воздуха на движение точки под влиянием силы тяжести.
- 3. Уравнения движения системы свободных материальных точек и их интегралы.
- 4. Положения равновесия как особые точки.
- 5. Принцип Даламбера.
- § 2. Уравнения движения Лагранжа и Гамильтона
- 2. Примеры.
- 3. Законы энергии и импульса.
- 4. Связь с вариационным исчислением.
- 5. Уравнения движения в форме Гамильтона и Рауза.
- 6. Интегралы уравнений движения Гамильтона.
- § 3. Дифференциальные уравнения траекторий
- 2. Траектории механических систем в общем случае.
- 3. Различные виды траекторий.
- 4. Примеры.
- § 4. Теория преобразований дифференциальных уравнений Гамильтона
- 2. Касательное преобразование, канонические переменные.
- 3. Соответствующие канонические перепенные.
- 4. К интегрированию уравнения Гамильтона-Якоби в частных производных.
- 5. Введение волн, соответствующих движению точки.
- § 5. Метод разделения переменных
- 2. Критерий его применимости.
- 3. Выполнение вычисления.
- 4. Цримеры.
- 5. Свойства периодичности разделяющихся переменных.
- 6. Угловые переменные и переменные действия.
- § 6. Многократно-периодические системы
- 2. Введение общих многократно-периодических систем.
- 3. Вырождение.
- 4. Примеры.
- § 7. Однозначные интегралы и траектории, заполняющие объем
- 2. Системы однозначных интегралов; импримитивные системы.
- 3. Приближенные периоды n-кратно периодических систем.
- § 8. Некоторые сведения из статистической механики
- 2. Вычисление объемов в фазовом пространстве.
- 3. Теорема Лиувилля.
- 4. Теорема Больцмана.
- 5. Время пребывания n-кратно периодической системы.
- 6. Квазиэргодическая система, микрокаяоническое множество.
- ГЛАВА III. УСТОЙЧИВОСТЬ И МАЛЫЕ КОЛЕБАНИЯ
- § 1. Квазистатические движения
- 2. Квазистатическио движения по Раузу.
- 3. Обобщение понятна квазистатического движения по Леви-Чивита.
- § 2. Устойчивость и энергия
- 2. Энергетический критерий устойчивости Рауза.
- 3. Примеры.
- § 3. Малые колебания системы около положения равновесия, или установившегося движения
- 2. Интегрирование дифференциальных уравнений свободных колебаний.
- 3. Частные случаи колебания системы. Колебания около положений равновесия.
- § 4. Вынужденные колебания
- 2. Система с одной степенью свободы.
- § 5. Малые колебания и устойчивость
- 2. Примеры.
- 3. Центробежный регулятор.
- ГЛАВА IV. УРАВНЕНИЯ ДВИЖЕНИЯ ТВЕРДЫХ ТЕЛ
- 2. Скоростные координаты.
- 3. Законы движения твердого тела.
- 4. Уравнения движении Эйлера.
- 5. Формальное обобщение математических выражений (исчисление моторов).
- 6. Уравнения движения Лагранжа.
- § 2. Свободное движение твердого тела
- 2. Явный вид решений в случае периодического движения.
- 3. Квазистатические движения.
- 4. Симмеричный волчок.
- § 3. Движение в поле тяжести
- 2. Симметричный волчок. Квазистатическое движение.
- 3. Симметричный волчок. Самое общее движение.
- 4. Колебательные движения с конечной амплитудой.
- § 4. Движение самолета
- 2. Дифференциальные уравнения продольного движения.
- 3. Постоянные (перманентные) движения и малые колебания.
- 4. Продольная устойчивость горизонтального полета.
- 5. Фигондное движение.
- ГЛАВА V. МЕТОДЫ ТЕОРИИ ВОЗМУЩЕНИЙ
- § 1. Основные понятия теории возмущений
- 2. Многократно-периодические системы.
- 3. Вырожденные системы.
- 4. Дифференциальные уравнения вековых возмущений.
- § 2. Возмущения упругих колебаний
- 2. Возмущающая сила пропорциональна кубу отклонения.
- 3. Возмущающая сила содержит члены связи.
- 4. Возмущения просто-пориодических траекторий.
- § 3. Выражение энергии для возмущенных систем
- 2. Вычисление выражения энергии.
- 3. Невозмущенная система вырождена.
- § 4. Выражение энергии для негармонических колебаний
- 2. Просто-периодическое основное движение.
- ГЛАВА VI. ЗАДАЧИ НЕБЕСНОЙ И АТОМНОЙ МЕХАНИКИ
- § 1. Движение Кеплера
- 2. Введение угловых переменных и переиенпых действия.
- 3. Вычисление координат положения.
- § 2. Возмущенное движение Кеплера
- § 3. Некоторые введения, касающиеся задачи трех тел
- 2. Приведение задачи трех тел.
- 3. Квазнстатические орбиты в случае плоской задачи трех тел.
- § 4. О касательных преобразованиях (Дополнение редактора)
- ЧАСТЬ ВТОРАЯ. МЕХАНИКА СПЛОШНЫХ СРЕД
- ГЛАВА VII. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ УПРУГОСТИ
- § 2. Анализ напряжений и деформаций
- 2. Тензор нанряженнй.
- 3. Тензор деформации.
- § 3. Закон Гука и основные уравнения теорнн упругости
- 2. Основные уравнения теории упругости.
- 3. Вычисление смещений но данный напряжениям.
- § 4. Минимальные принципы. Теоремы единственности
- 2. Принцип минимума для смещений. Принцип возможных перемещений.
- 3. Принцип минимума для напряжений.
- 4. Единственность решения.
- § 6. Уравнения движения. Единственность решения
- ГЛАВА VIII. ЗАДАЧИ НА УПРУГОЕ РАВНОВЕСИЕ
- § 1. Элементарные решения с лннейныи распределением напряжений
- 2. Растягивающая нагрузка, равномерно распределенная на концах цилиндра.
- 3. Изгиб стержня приложенными на концах его моментами.
- § 2. Кручение призматических стержней
- 2. Простейшие примеры.
- 3. Прямоугольник. Метод разложения в ряды.
- 4. Сечение, ограниченное многоугольником. Применение метода теории функций комплексной переменной.
- 5. Кручение призм, составленных из различных материалов
- § 3. Плоская пластинка, к которой приложены силы, расположенные в этой же плоскости
- 1а. Комплексное представление функции напряжений.
- 2. Сосредоточенная сила, приложенная на границе полуплоскости.
- 3. Круглая шайба (диск) под действием: нормальных: сил, приложенных к ее границе.
- 4. Растяжение полосы с отверстием.
- § 4. Пространственные задачи
- 1. Равновесие тела, ограниченного бесконечной плоскостью.
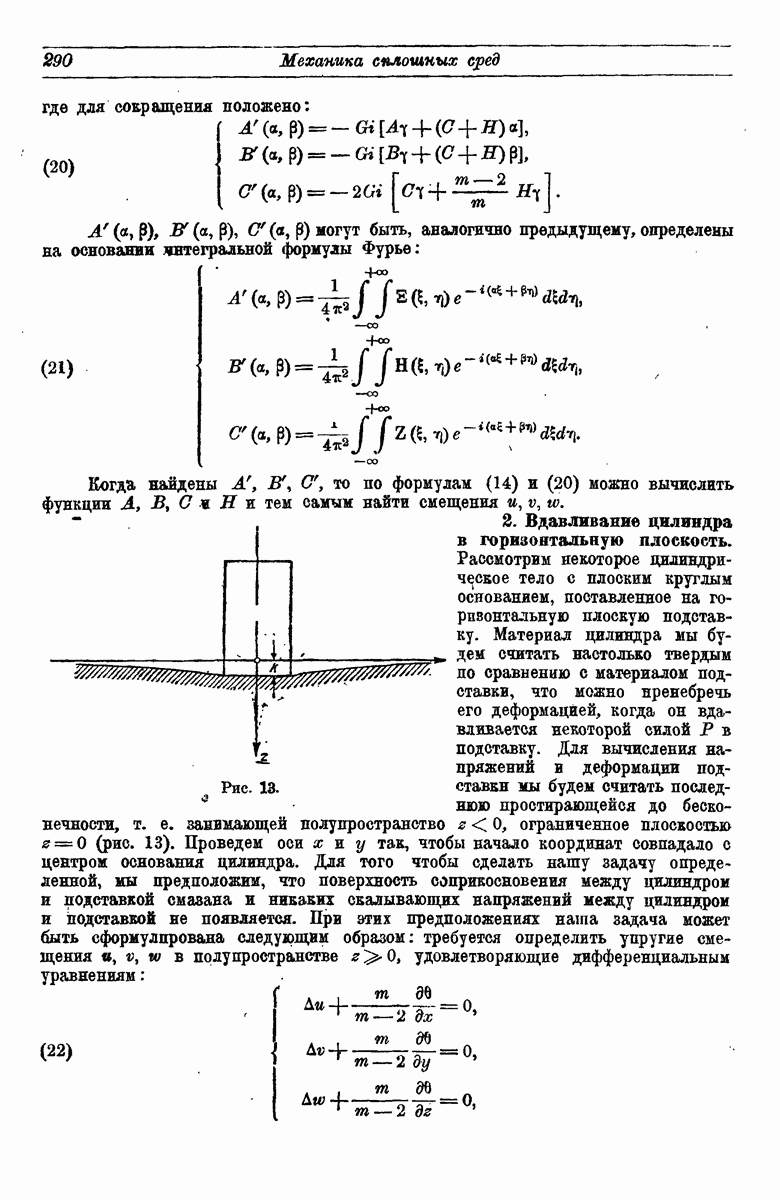
- 2. Вдавливание цилиндра в горизонтальную плоскость.
- ГЛАВА IX. ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
- 1. Дифференциальное уравнение колебаний струны.
- 2. Метод разложения в ряд.
- 3. Определение постоянных по начальному состоянию струны.
- 4. Решение в форме Даламбера.
- 5. Бесконечная струна.
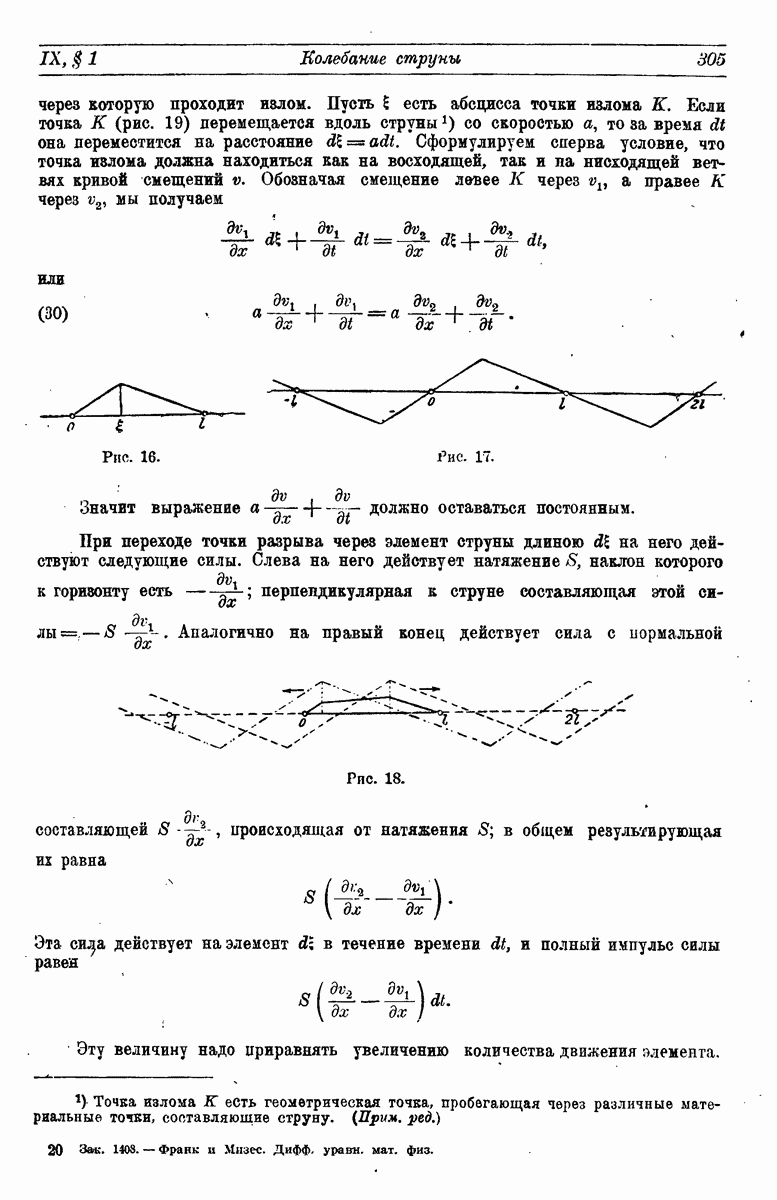
- 6. Разрывы.
- § 2. Приложение интегральных уравнений к задаче колебания
- 2. Потенциальная и кинетическая энергия.
- 3. Решение при данных начальных условиях.
- 4. Вынужденные колебания.
- 5. Колебания стержня.
- § 3. Колебания мембраны
- 1. Дифференциальное уравнение колебаний мембраны.
- 2. Прямоугольная мембрана.
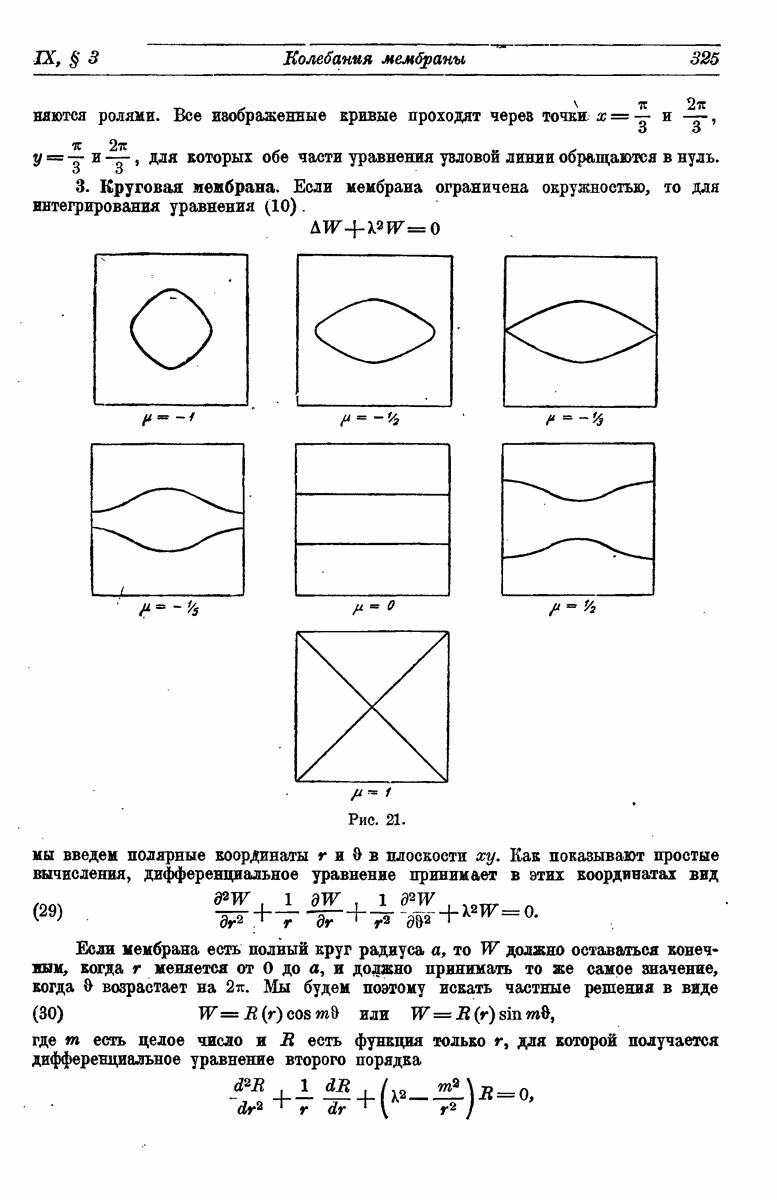
- 3. Круговая мембрана.
- 4. Аналитические свойства решений.
- 5. Интегральное уравнение колебания мембраны.
- § 4. Граничная задача колеблющейся мембраны как задача вариационного исчисления
- 2. Высшие характеристические числа.
- 3. Следствия из минимальных свойств.
- 4. Метод Ритца. Эллиптическая мембрана.
- 5. Асимптотическое распределение характеристических чисел.
- ГЛАВА X. ИДЕАЛЬНЫЕ ЖИДКОСТИ
- 1. Определение идеальной жидкости.
- 2. Поле скоростей.
- 3. Уравнение неразрывности.
- 4. Теорема Гаусса; поток.
- 5. Деформация частицы жидкости.
- 6. Безвихревое движение; потенциал скоростей.
- 7. Примеры
- 8. Уравнения Эйлера.
- 9. Уравнения Лагранжа.
- 10. Гидростатика; плавание.
- 11. Свободная поверхность вращающейся жидкости. Фигуры равновесия.
- 12. Уравнение для давления; уравнение энергии.
- 13. Теоремы о количестве движения для стационарного течения жидкости. Истечение из сосуда.
- 14. Теоремы о количестве движения. Общая формулировка.
- 15. Ток и циркуляция.
- 16. Теорема Стовса. Поток вихря.
- 17. Сохранение циркуляции.
- 18. Теоремы Гельягольца о вихрях.
- 19. Стационарное вихревое движение.
- § 2 Общие методы
- 1. Потенциальное движение; теорема Грина.
- 2. Следствия из теоремы Грина.
- 3. Источники.
- 4. Двойной источник (диполь).
- 5. Поверхностное распределение источников; слои источников.
- 6. Задачи с граничными условиями; функция Грина.
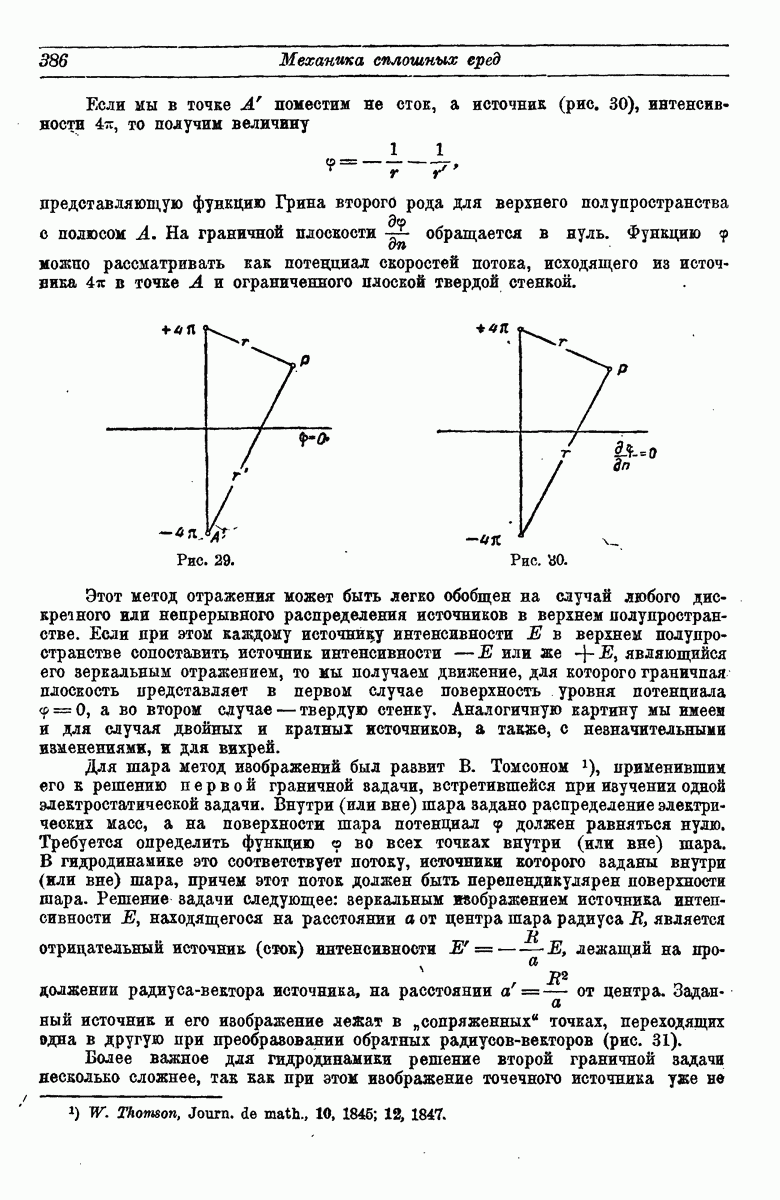
- 7. Метод изображений.
- 8. Вихревое поле; вихревые линии; закон Био-Савара.
- 9. Вихревые слои.
- 10. Представление потока с помощью источников и вихрей.
- 11. Кинетическая энергия потока.
- 12. Геометрические свойства; слои тока.
- 13. Давление в потоке.
- 14. Движение твердых тел в идеальной жидкости.
- § 3. Частные задачи и методы
- 2. Конформное отображение.
- b) ОБРАЗОВАНИЕ СТРУЙ
- 3. Струя в покоящейся («мертвой») воде.
- 4. Плоские струи. Методы Гельмгольца и Кирхгофа.
- 5. Метод Леви-Чивита.
- 6. Учет силы тяжести. Переливание жидкости через плотину.
- 7. Функциональное уравнение для свободной границы струи; перманентные волны.
- 8. Пространственные струи.
- с) ВОЛНЫ
- 9. Общие соображения о волнах жидкости.
- 10. Периодические волны в канале.
- 11. Наложение (суперпозиция) волн в каналах.
- 12. Волны Герстнера.
- 13. Корабельные волны.
- 14. Волны прилива и отлива.
- d) ВИХРИ
- 15. Вихревые точки в неограниченной плоскости.
- 16. Вихревые точки в ограниченной области.
- 17. Вихри Кармана.
- 18. Возникновение вихрей Кармана.
- 19. Вихревые кольца.
- 20. Другие вихревые образования.
- е) ЦИРКУЛЯЦИЯ И ПОДЪЕМНАЯ СИЛА
- 21. Гидродинамическая подъемная сила.
- 22. Теорема Кутта-Жуковского.
- 23. Техническое значение гидродинамической подъемной силы.
- 24. Прандтлевская теория несущего крыла.
- ГЛАВА XI. ДВИЖЕНИЕ ЖИДКОСТЕЙ С ТРЕНИЕМ
- 2. Закон Пуазейля.
- 3. Обозначения.
- 4. Связь между напряжениями и скоростью деформаций.
- 5. Полные дифференциальные уравнения.
- 6. Составляющие напряжения на поверхности покоящегося тела.
- 7. Линеаризованные дифференциальные уравнения.
- § 2. Фундаментальные интегралы линеаризованных дифференциальных уравнений
- 2. Линеаризованные уравнения пространственного движения для случая, когда система координат ииеет постоянную поступательную скорость.
- 3. Линеаризованные уравнения плоского движения для случая, когда система координат имеет постоянную поступательную скорость.
- 4. Движение твердого тела.
- 5. Наиболее общие линеаризованные дифференциальные уравнения.
- § 3. Стоксова формула сопротивления и связанные с ней формулы
- 2. Более точное вычисление потока вокруг шара.
- 3. Поступательное движение тонкого кругового цилиндра в вязкой жидкости.
- § 4. Точные решении уравнений движения вязкой иесжииаеиой жидкости
- § 5. Теория пограничного слоя
- 2. Уравнение движения пограничного слоя.
- 3. Отрыв пограничного слоя.
- 4. Пограничный слой в точной теории Гамеля.
- ГЛАВА XII. НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ РАСПРОСТРАНЕНИЯ КОЛЕБАНИЙ
- § 1. Задача об отражении плоских упругих волн
- 2. Плоская задача.
- 3. Граничные (краевые) условия. Полупространство.
- 4. Линейно-поляризованные поперечные волны.
- 5. Звуковые волны.
- 6. Класс комплексных решений волнового уравнения.
- 7. Плоские волны. Отражение плоских продольных волн.
- 8. Отражение поперечных волн.
- 9. Поверхностные волны Рэлея.
- 10. Общие формулы комплексной теории отражения.
- § 2. Общий анализ комплексных решений
- 1. Однородные комплексные решения волнового уравнения. Внутренность основного конуса.
- 2. Внешность основного конуса.
- 3. Кинематические и динамические условия совместности. Характеристики.
- 4. Условия правильности однородных, комплексных решений.
- 5. Анализ комплексных решений общего типа.
- § 3. Задача об источниках колебаний для полупространства
- 2. Задача с однородными смещениями.
- 3. Конформное преобразование типа …
- 4. Задача об отражении продольных волн. Случай комплексных потенциалов.
- 5. Задача об отражении продольных волн. Случай комплексных смещений.
- 6. Принцип Ферма.
- 7. Отражение поперечных волн. Случай комплексных потенциалов.
- 8. Отражение поперечных волн. Случай комплексных смещений.
- 9. Принцип Ферма.
- 10. Волны Рэлея.
- § 4. Задача Коши для упругого полупространства в двух измерениях
- 2. Фундаментальное решение Вольтерра.
- 4. Решение задачи Коши по методу Вольтерра.
- 4. Формула Грнна-Вольтерра.
- 5. Кинематические и динамические условии совместности для уравнений упругости.
- 6. Постановка плоской задачи теории упругости для полупространства.
- 7. Фундаментальные решения.
- 8. Решение общей задачи теории упругости для полупространства в плоском случае.
- 9. Теория точечных источников.
- 10. Задача Лэмба.
- 11. Волны Рэлея.
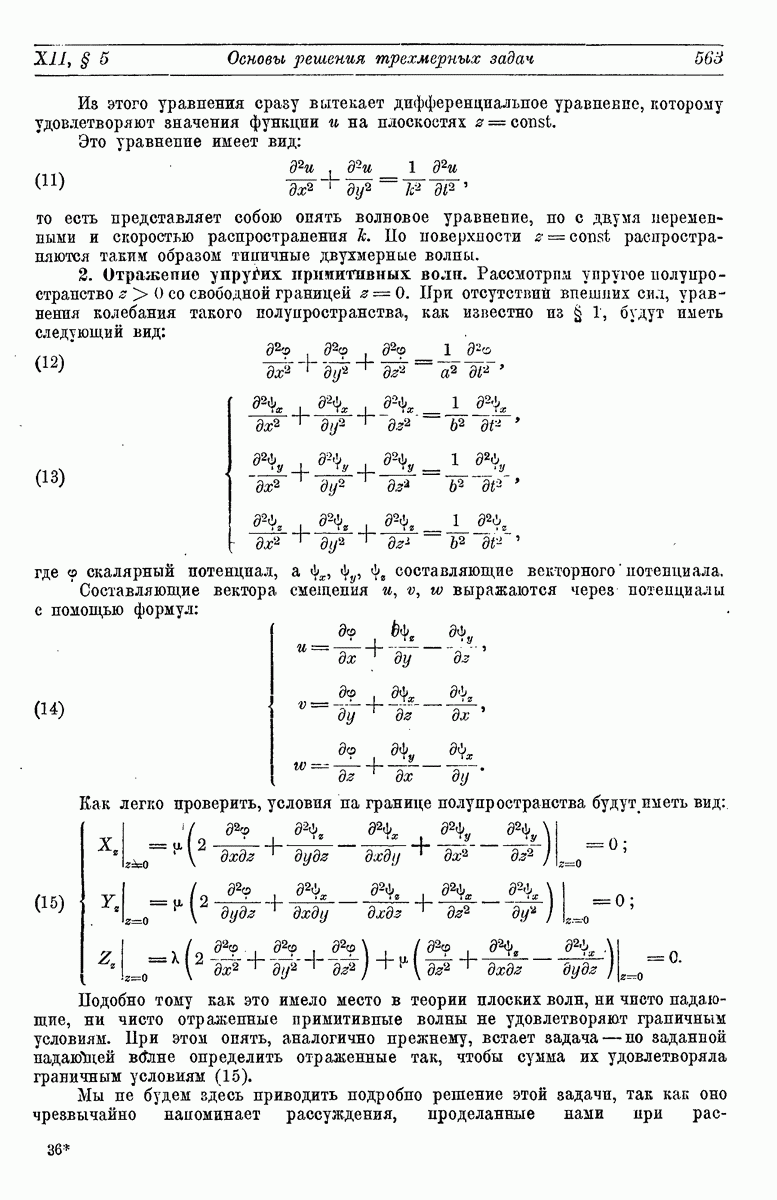
- § 5. Основы решения трехмерных: задач распространении колебаний методом комплексной переменной
- 2. Отражение упругих примитивных волн.
- 3. Полное внутреннее отражение поперечной волны при …
- 4. Волны Рэлея.
- 5. Принцип наложения.
- 6. Построение первого фундаментального решения для трехмерной задачи теории упругости.
- 7. Задачи с осевой симметрией.
- 8. Построение других фундаментальных решений.
- 9. Основные свойства наложения общих комплексных решений.
- 10. Отражение фундаментальных решений.
- § 6. Задача Коши в трехмерном пространстве
- 2. Формула Грина для волнового уравнения.
- 3. Фундаментальное решение волнового уравнения.
- 4. Решение волнового уравнения.
- 5. Формула Грина для уравнений теории упругости.
- 6. Фундаментальные решения уравнений упругости для полупространства.
- 7. Решение задачи Коши для упругого полупространства.
- 8. Анализ полученных результатов.
- § 7. Обобщение решения волнового уравнения
- 2. Обобщенные решения волнового уравнения.
- 3. Связь с условиями совместности.
- 4. Теорема интегрирования.
- 5. Обобщенные комплексные решения.
- 6. Обобщенные комплексные решения во всей области существования.
- §. 8. Задача о диффракции плоских волн
- 2. Разветвляющиеся комплексные решения волнового уравнения.
- 3. Элементарные плоские волны логарифмической поверхности.
- 4. Диффракция произвольной плоской волны.
- 5. Периодические решения.
- 6. Диффракция относительно угла.
- 7. Трехмерная задача диффракции плоских волн.
- 8. Общая задача диффракции для двухмерного пространства.
- ЧАСТЬ ТРЕТЬЯ. ТЕПЛОПРОВОДНОСТЬ И ДИФФУЗИЯ
- 1. Основные понятия теплопроводности в твердых телах.
- 2. Дифференциальное уравнение теплопроводности.
- 3. Основные понятия диффузии при отсутствии внешних сил.
- 4. Дифференциальное уравнение диффузии.
- § 2. Теплопроводность и диффузия в неограниченных телах
- 2. Примеры.
- 3. Применение к броуновскому движению одной частицы.
- 4. Тела, бесконечно протяженные в двух измерениях.
- 5. Тела, бесконечно протяженные в трех измерениях.
- 6. Интегральное уравнение теплопроводности и диффузии.
- § 3. Теплопроводность и диффузия в ограниченных телах
- 2. Диффузнонный опыт Бриллуэпа и «первые прохождения» при броуновском движении.
- 3. Тело, ограниченное двумя плоскостями.
- 4. «Двухсторонние первые прохождения» при броуновском движении.
- 5. Слоистые тела.
- 6. Теплопроводность в цилиндре.
- 7. Теплопроводность в шаре.
- 8. Распространение холода.
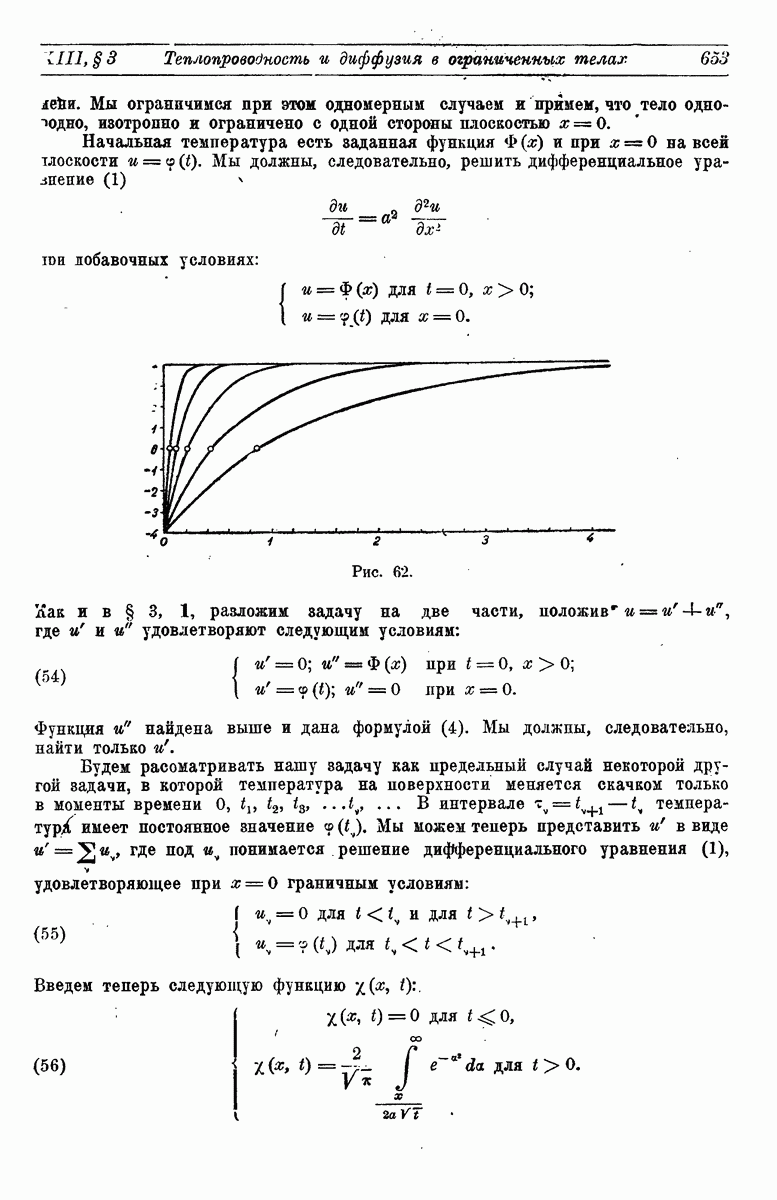
- 9. Температура (концентрация) граничной поверхности есть заданная функция времени.
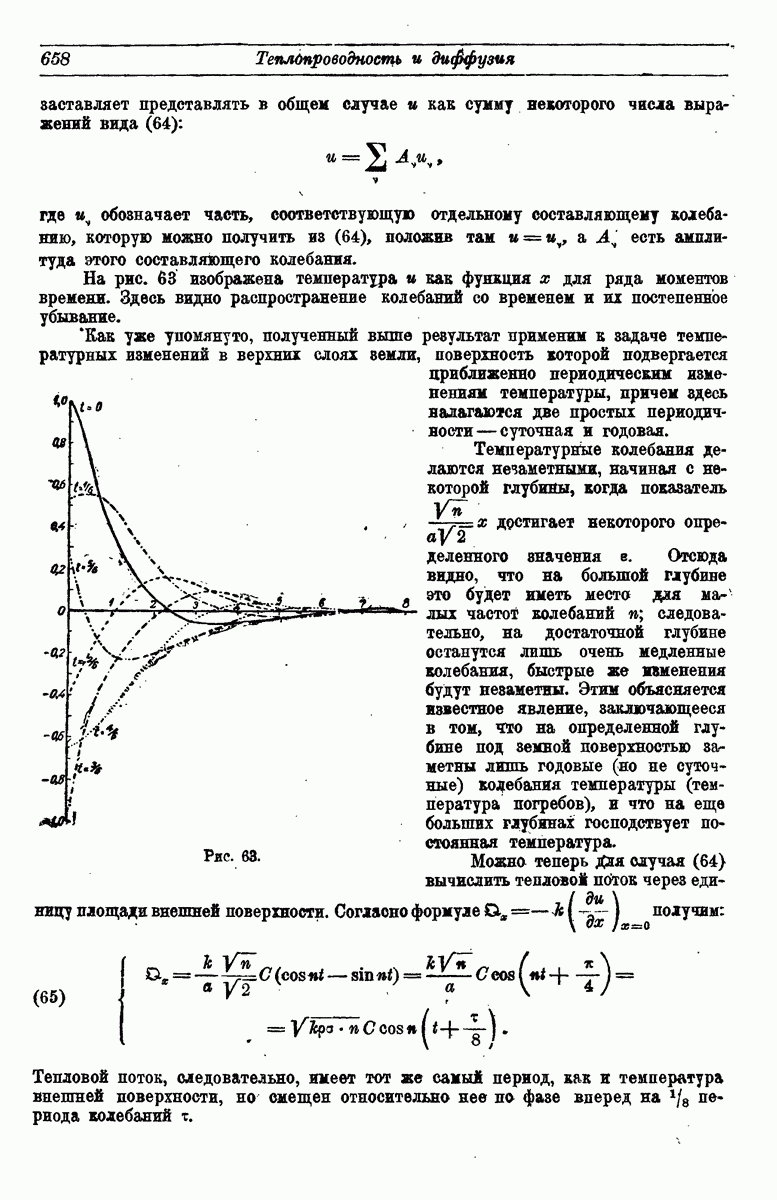
- 10. Тепловые волны.
- 11. Внешняя поверхность — изолятор.
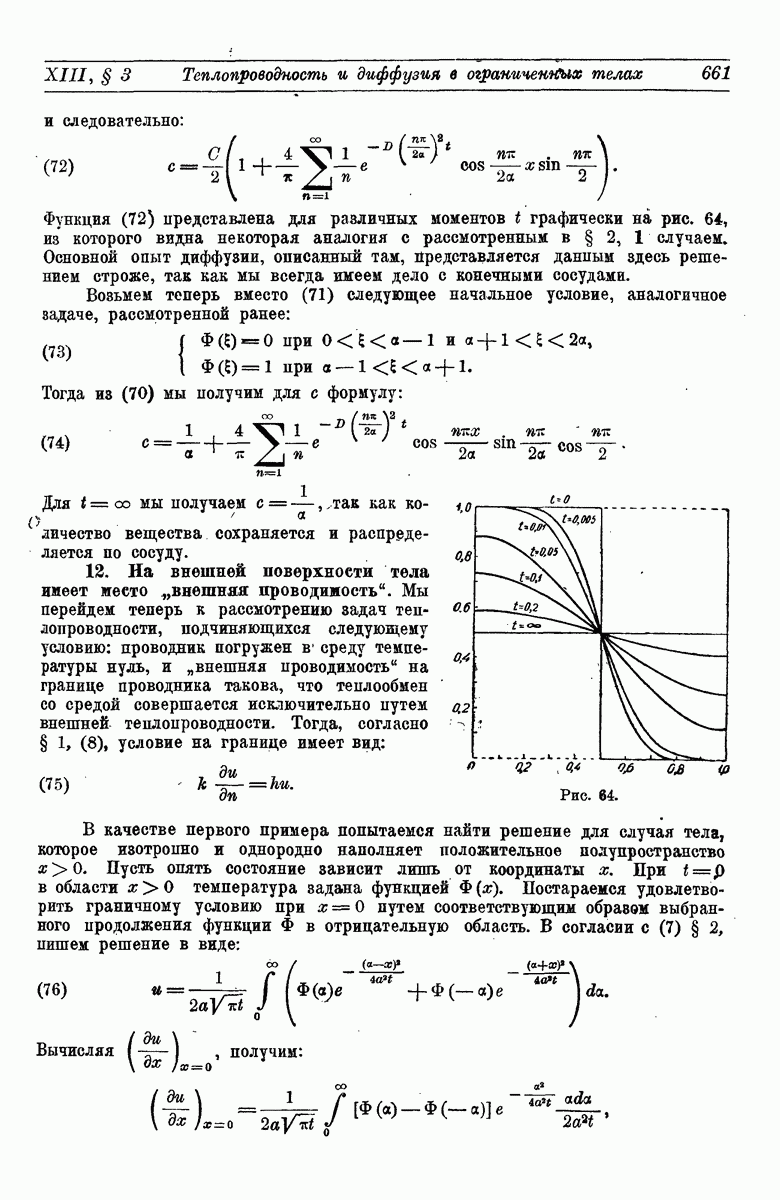
- 12. На внешней поверхности тела имеет место «внешняя проводимость».
- 13. Диффузия сквозь диафрагму.
- 14. Задача внешней теплопроводности в двух измерениях.
- 15. Теплопроводность стержня.
- ГЛАВА XIV. ВЫНУЖДЕННАЯ ТЕПЛОПРОВОДНОСТЬ И ДИФФУЗИЯ
- 2. Дифференциальное уравнение диффузии при действии внешних сил.
- 3. Интегральное уравнение диффузии и его связь со статистикой.
- § 2. Теплопроводность и диффузия при вынужденной конвекции
- 2. Конечный коэффициент теплопередачи.
- 3. Течение сквозь узкие трубы. Холодильник.
- 4. Диффузия в текущих газах и под действием заданных внешних сил.
- 5. Седиментация и броуновское движение в поле силы тяжести.
- 6. Связь с одной теоремой статистической механики.
- 7. Диффузия электролитов.
- 7. Диффузия ионов в газах.
- § 3. Спонтанное конвекционное течение под действием внешних сил
- § 4. Связь между теорией диффузии и волновой механикой
- 2. Движение системы частиц под действием внешних сил.
- 3. Движение по инерции.
- 4. Связь с соотношением неопределенности.
- ЧАСТЬ ЧЕТВЕРТАЯ. СТАЦИОНАРНОЕ (И КВАЗИСТАЦИОНАРНОЕ) ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- ГЛАВА XV. ЭЛЕКТРОСТАТИКА
- 2. Математические уравнения поля.
- § 2. Основные задачи; метод отражений и электрических изображений
- 2. Распределение электричества на эллипсоиде.
- 4. Отражение и электрические изображения.
- § 3. Электростатическое равновесие на двух заряженных сферах
- § 4. Цилиндрические поля. Представление посредством функций комплексной переменной
- 2. Отражение, эксцентрические круговые цилиндры.
- 3. Представление поля посредством функций комплексной переменной.
- § 5. Поле призматических проводников
- 2. Два бесконечных призматических проводника.
- 3. Поле между двумя конечными ограниченными проводниками.
- § 6. Применение электростатики к теории катодных ламп
- ГЛАВА XVI. СТАЦИОНАРНЫЕ ЭЛЕКТРИЧЕСКИЕ ТОКИ
- § 1. Формулировка уравнений поля и простые задачи
- 2. Простые задачи о стационарных полях тока.
- § 2. Прохождение тока между землей и металлическими проводниками
- 3. Решение интегрального уравнения для распределения тока.
- 4. Решение интегродифференциального уравнения для выхода тока.
- § 3. Слой жидкости с металлической границей. Цветные кольца Нобили
- 2. Учет поляризации.
- 3. Однородная вспомогательная задача.
- 4. Общее решение неоднородной задачи.
- 5. Решение в случае тока.
- ГЛАВА XVII. МАГНИТОСТАТИКА
- § 1. Образование магнитных полей
- 2. Постоянный магнит и магнитный момент.
- 3. Стационарное электромагнитное поле.
- § 2. Парамагнитные тела в магнитном поло
- 2. Шар в однородном поле
- 3. Эллипсоид в однородном поле.
- § 3. Силы, испытываемые материальными телами в электрическом или магнитном поле
- 2. Вспомогательная теорема.
- 3. Энергия диэлектрического тела в электрической поле.
- 4. Энергия пара- или диаиагнитиого тела в магнитнои поле.
- 5. Применение в эллипсоиду.
- ГЛАВА XVIII. КВАЗИСТАЦИОНАРНЫЕ ТОКИ И ВОЛНЫ
- § 1. Квазистационарные контуры тока
- 2. Механическое представление системы. Закон индукции Фарадея.
- 3. Колебание цепей. Сопротивление при переменном токе.
- § 2. Квазистационарные волны в проводниках
- 2. Стоячие волны. Свободные колебания.
- 3. Вынужденные колебания.
- 4. Бегущие волны произвольной формы.
- § 3. Квазистационарные волны в катушках
- 2. Гармонические волны.
- 3. Образование преломленных волн.
- ЧАСТЬ ПЯТАЯ. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ
- ГЛАВА XIX. ОБЩИЕ ТЕОРЕМЫ И МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Закон сохранения энергии и однозначность решений.
- 3. Замечание о математической трактовке колебательных процессов.
- 4. Электронная теория.
- § 2. Инвариантность уравнений Максвелла по отношению к преобразованию Лоренца
- 2. Антисимметричный тензор поля.
- 3. Группа ортогональных преобразований.
- 4. Частное преобразование Лоренца.
- § 3. Запаздывающие потенциалы и поле ускоренно движущегося заряда
- 2. Запаздывающие потенциалы и приближение Льенарда-Вихерта.
- 3. Поле произвольно движущегося заряда.
- § 4. Вектор Герца и излучение колеблющегося диполя
- 1. Непосредственное рассмотрение электрического диполя.
- 2. Поле линейного гармонического вибратора.
- 3. Излучение энергии.
- 4. Обобщения.
- 5. Вычисление оптической интенсивности по вектору Герца.
- § 5. Условия излучениях). Собственные функции и собственные значения
- ГЛАВА XX. ТЕОРИЯ ДИФФРАКЦИИ
- § 1. Разветвленные решения уравнения колебаний
- 2. Понятие пространства Римана.
- 3. Функция плоской волны, однозначная на поверхности Римана.
- 4. Решения для пространства Римана.
- 5. Приложения и дополнения.
- § 2. Сходящиеся и полусходящиеся разложения разветвленных решений.
- 2. Выражение для разветвленной функции плоской волны в виде сходящихся рядов по Бесселевым функциям.
- 3. Асимптотическое выражение разветвленной функции плоской волны.
- 4. Частный случай n=2.
- § 3. Сравнение с классической теорией диффракции (Френель-Кирхгоф)
- 2. Принцип Гюйгенса.
- 3. Прямоугольное отверстие, щель и полуплоскость.
- 4. Связь между геометрической и волновой оптикой.
- § 4. Диффракция от шара и от других тел. Метод разложения в ряды
- 2. Теоремы сложения.
- 3. Диффракции от цилиндра.
- 4. Диффракции от шара. Коллоидальные частицы.
- ГЛАВА XXI. СОПРОТИВЛЕНИЕ ДЛЯ ПЕРЕМЕННЫХ ТОКОВ И СКИН-ЭФФЕКТ
- § 1. Распределение в проводящей плоскости
- 2. Исследование поля.
- 3. Сопротивление переменному току.
- § 2. Провод с круговым сечением при низких и высоких частотах
- 2. Исследование поля.
- 3. Сопротивление и самоиндукция провода.
- § 3. Катушка с переменным током
- 2. Исследование поля.
- 3. Сопротивление и самоиндукция катушки.
- ГЛАВА XXII. ВОЛНЫ ВДОЛЬ ПРОВОДОВ
- § 1. Поле и распространение волн вдоль проводов
- 2. Численный пример для одного типичного случая.
- 3. Очень тонкий провод. Аномальный случай распространения и затухания.
- 4. Поток энергии на бесконечности.
- 5. Структура поля.
- § 2. Дополнения
- 1. Побочные волны электрического и магнитного типов. Несимметричные волны.
- 2. Поверхностные волны на непроводниках.
- 3. Случай металлического обратного провода.
- ГЛАВА XXIII. БЕСПРОВОЛОЧНАЯ ТЕЛЕГРАФИЯ
- § 1. Вертикальная антенна на плоской земле
- 2. Преобразование первичного возбуждения.
- 3. Выполнение граничных условий.
- 4. Другие формы решения.
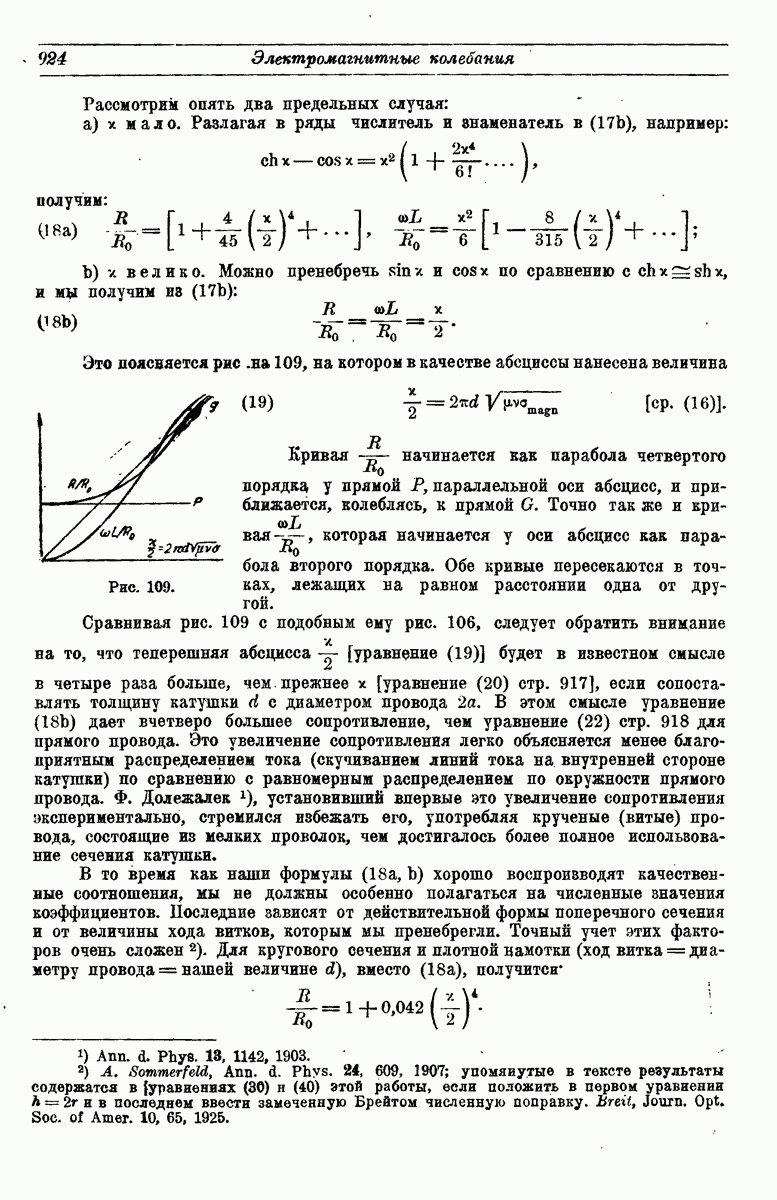
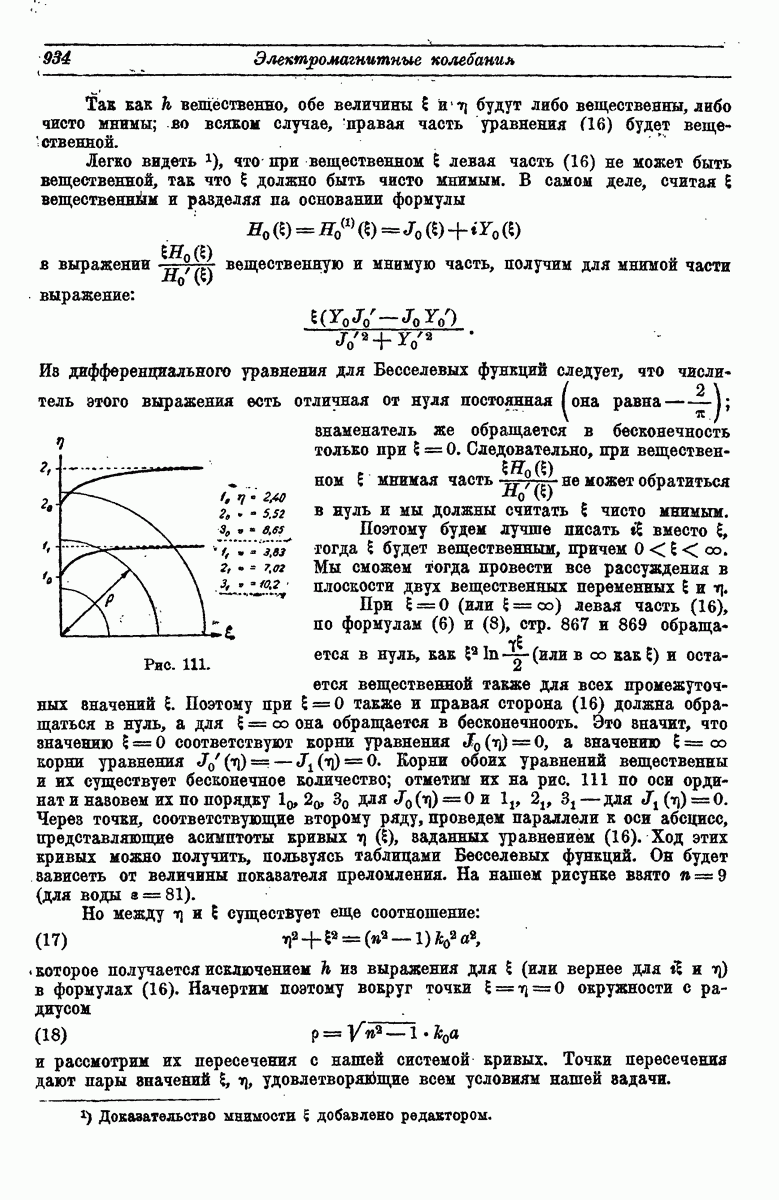
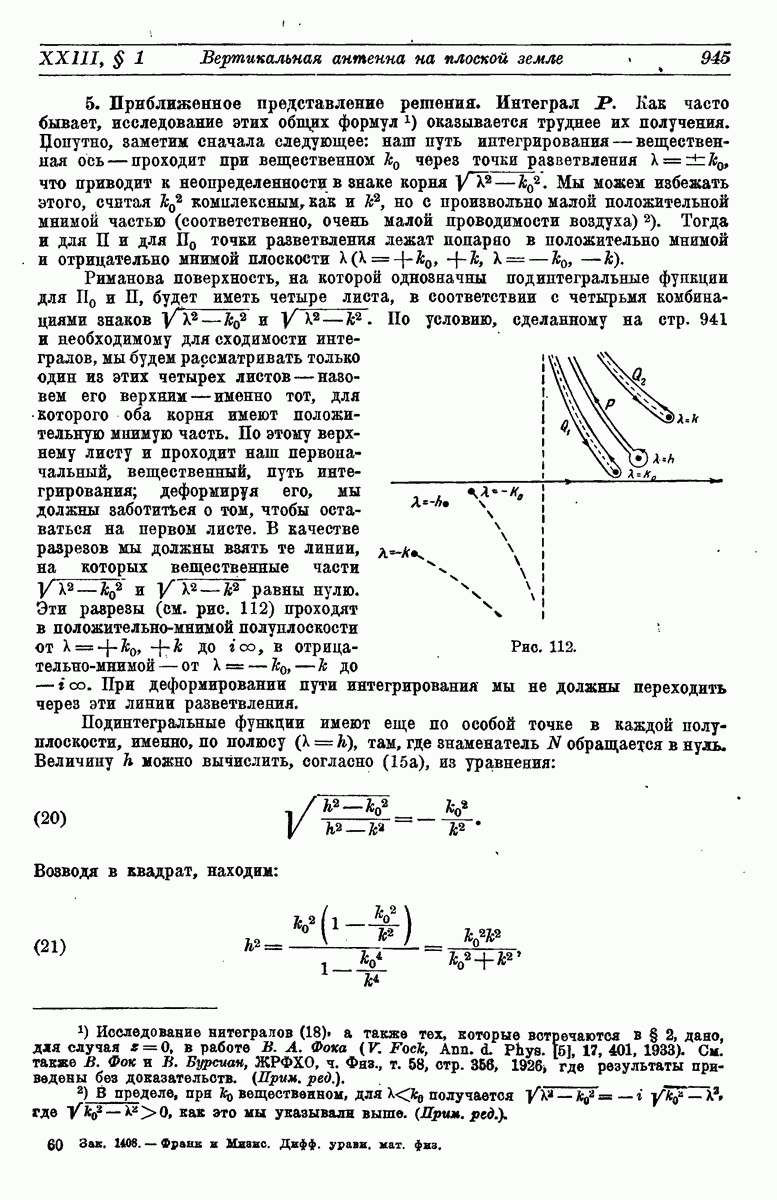
- 5. Приближенное представление решения.
- 6. Приближенное представление решения.
- 7. Вывод приближенной формулы для точек вблизи поверхности земли.
- § 2. Горизонтальная и рамочная антенны
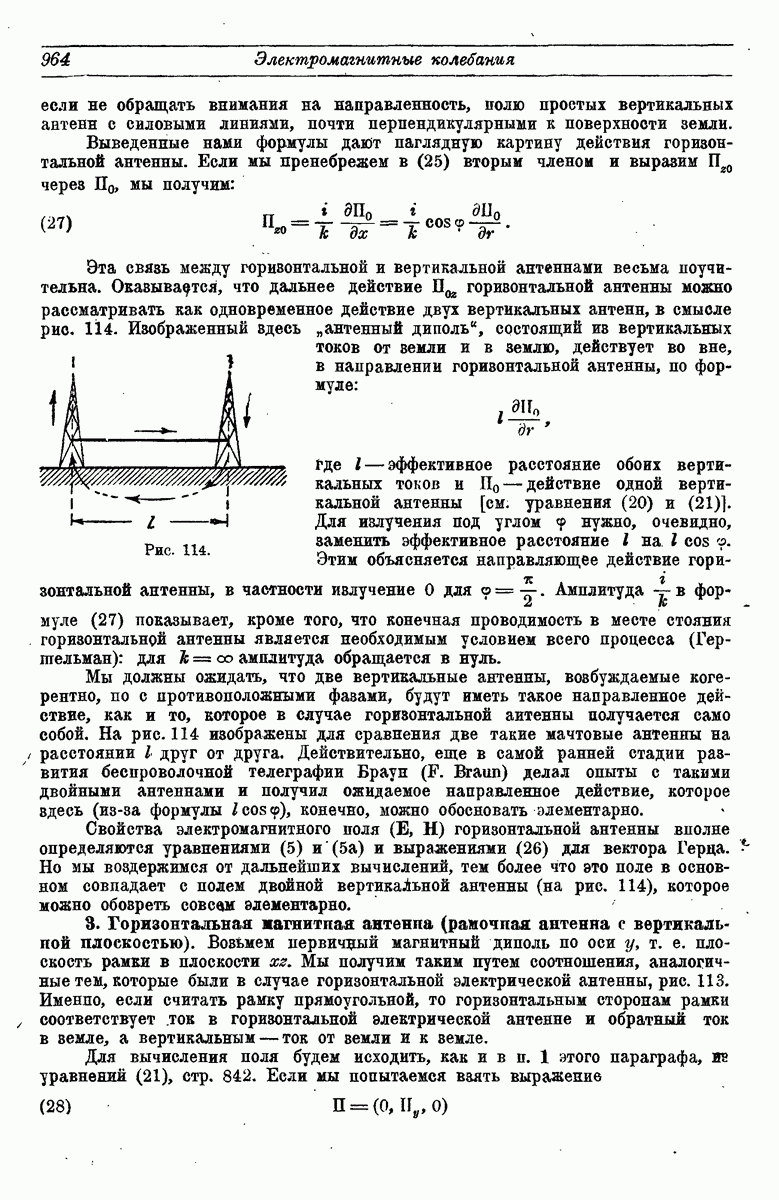
- 2. Горизонтальная электрическая антенна.
- 3. Горизонтальная магнитная антенна (рамочная антенна с вертикальной плоскостью).
- ПРИМЕЧАНИЕ
- § 3. Теорема взаимности в беспроволочной телеграфии
- 2. Две линейные электрические антенны.
- 3. Две магнитные антенны или одна электрическая и одна магнитная антенны.
- § 4. Беспроволочная телеграфия вокруг земли