| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
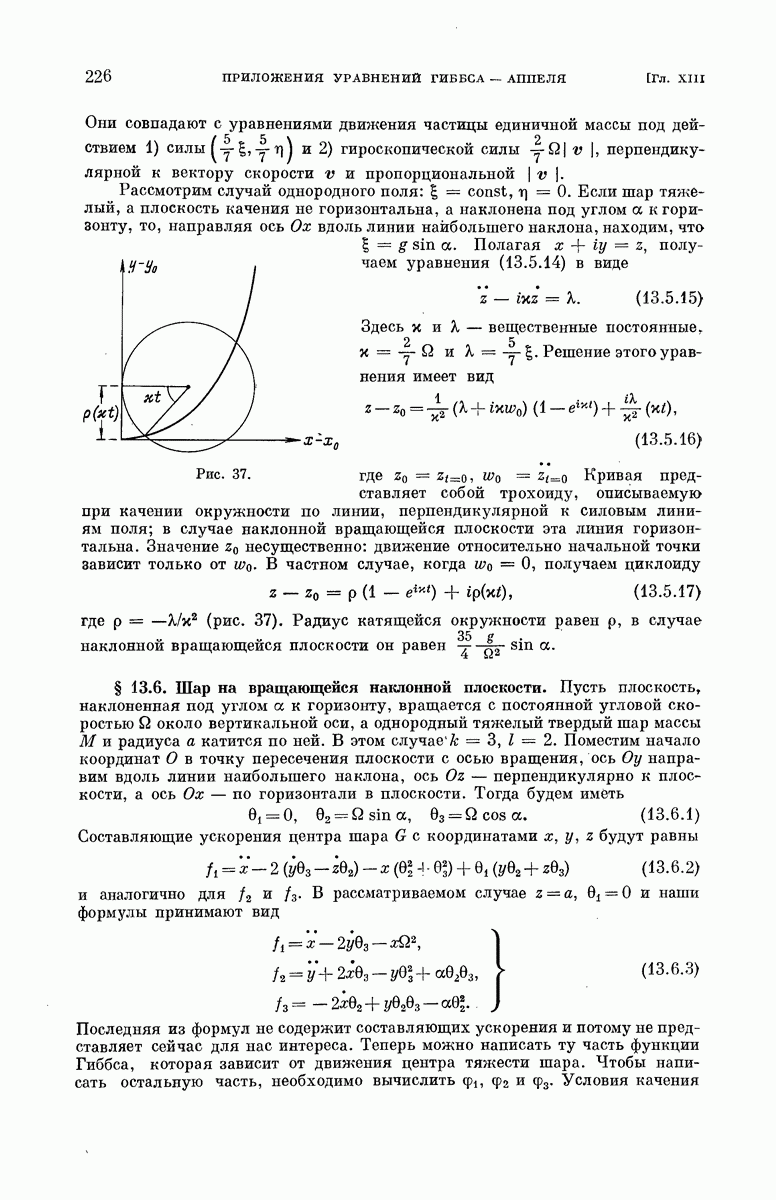
§ 9.8. Гироскоп Фуко.
Рассмотрим вращающийся волчок, подвешенный к неподвижной точке  пусть центр тяжести его
пусть центр тяжести его  находится на одной вертикали с точкой О и вращение происходит около его оси. Если волчку сообщить малое возмущение, то его ось
находится на одной вертикали с точкой О и вращение происходит около его оси. Если волчку сообщить малое возмущение, то его ось  сохранит направление, близкое к вертикальному. Это имеет место независимо от скорости вращения и следует из уравнения энергии, которое можно записать в форме, аналогичной (8.6.8):
сохранит направление, близкое к вертикальному. Это имеет место независимо от скорости вращения и следует из уравнения энергии, которое можно записать в форме, аналогичной (8.6.8):

Когда ось стационарна,  если эту величину немного изменить, положив
если эту величину немного изменить, положив  где а — малая величина, то для возмущенного движения получим
где а — малая величина, то для возмущенного движения получим

и во все время движения будем иметь 
При изучении возмущенного движения в окрестности направленной вниз вертикали удобно ось  направить вертикально вниз и избежать, таким образом, неприятностей, связанных с неопределенностью
направить вертикально вниз и избежать, таким образом, неприятностей, связанных с неопределенностью  в состоянии покоя, возникающей, когда ось
в состоянии покоя, возникающей, когда ось  направлена вертикально. Тогда будем иметь
направлена вертикально. Тогда будем иметь

Полагая, как обычно,

и используя это равенство при составлении уравнений Лагранжа для  и
и  получаем
получаем

Во втором из этих уравнений произведено сокращение на множитель  он отличен от нуля
он отличен от нуля  близок к единице).
близок к единице).
Чтобы рассмотреть возмущенное движение в окрестности вертикали, направленной вниз, положим  Тогда с точностью до величин первого порядка относительно
Тогда с точностью до величин первого порядка относительно  направляющие косинусы оси волчка будут равны
направляющие косинусы оси волчка будут равны  Приближенные уравнения движения, составленные с такой же точностью, будут иметь вид
Приближенные уравнения движения, составленные с такой же точностью, будут иметь вид

Эти уравнения совпадают с уравнениями движения частицы в плоскости  под действием линейно изменяющейся притягивающей силы и гироскопической силы (§ 8.8). Полагая
под действием линейно изменяющейся притягивающей силы и гироскопической силы (§ 8.8). Полагая  и обозначая, как и ранее,
и обозначая, как и ранее,  находим, что
находим, что  удовлетворяет дифференциальному уравнению
удовлетворяет дифференциальному уравнению

Решение этого уравнения имеет вид

где

а коэффициенты  вообще говоря, комплексные. При малом возмущении, когда
вообще говоря, комплексные. При малом возмущении, когда  в начальный момент малы,
в начальный момент малы,  все время остается малым и линейное приближение достаточно хорошо аппроксимирует действительное движение, по крайней мере для не слишком больших значений t.
все время остается малым и линейное приближение достаточно хорошо аппроксимирует действительное движение, по крайней мере для не слишком больших значений t.
Уравнения (9.8.6) можно очень просто получить с помощью метода, описанного в § 8.7. Имеем

Поскольку вектор  имеет теперь компоненты (
имеет теперь компоненты ( векторное уравнение (8.7.2) эквивалентно трем скалярным уравнениям
векторное уравнение (8.7.2) эквивалентно трем скалярным уравнениям

где и есть вектор  В нашей задаче у и z малы, а х близок к единице; учитывая это, мы приходим к уравнениям (9.8.6).
В нашей задаче у и z малы, а х близок к единице; учитывая это, мы приходим к уравнениям (9.8.6).
Рассмотрим решение уравнения (9.8.7) в двух частных случаях; начальные значения  обозначим соответственно через
обозначим соответственно через 
1)  вещественно и положительно (и, разумеется, мало); в момент
вещественно и положительно (и, разумеется, мало); в момент  ось волчка имеет вертикальное направление. Решение имеет вид
ось волчка имеет вертикальное направление. Решение имеет вид

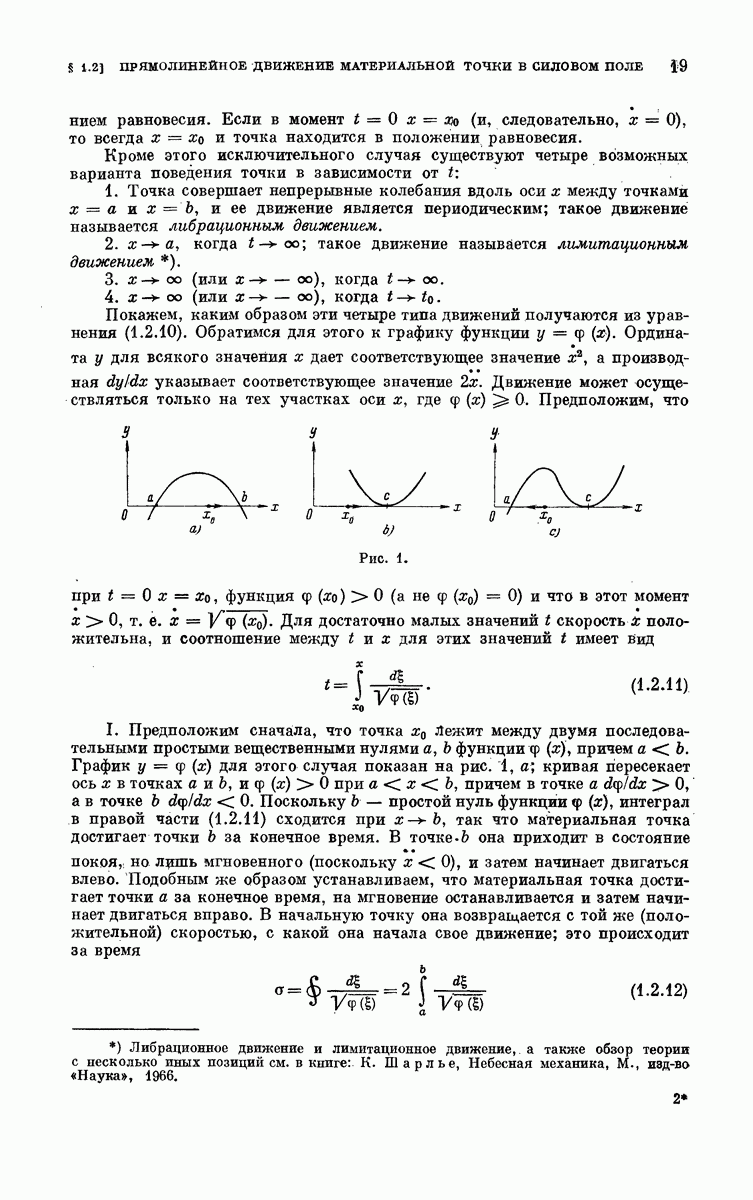
Траектория имеет форму розетки и в полярных координатах описывается уравнением

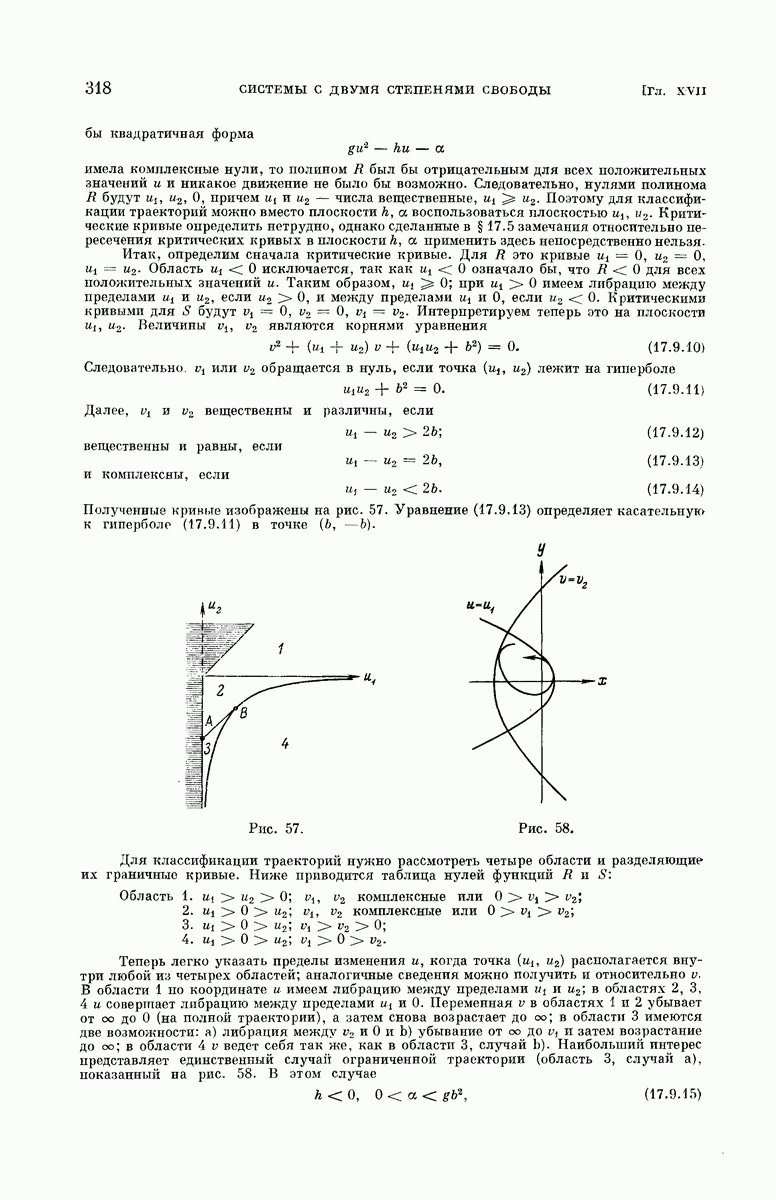
где  Траектория изображена на рис. 25, она построена для случая, когда скорость вращения мала и X, следовательно, велико.
Траектория изображена на рис. 25, она построена для случая, когда скорость вращения мала и X, следовательно, велико.

Рис. 25.

Рис. 26.
Если скорость вращения велика и X лишь немного превышает единицу, то форма траектории близка к окружности.
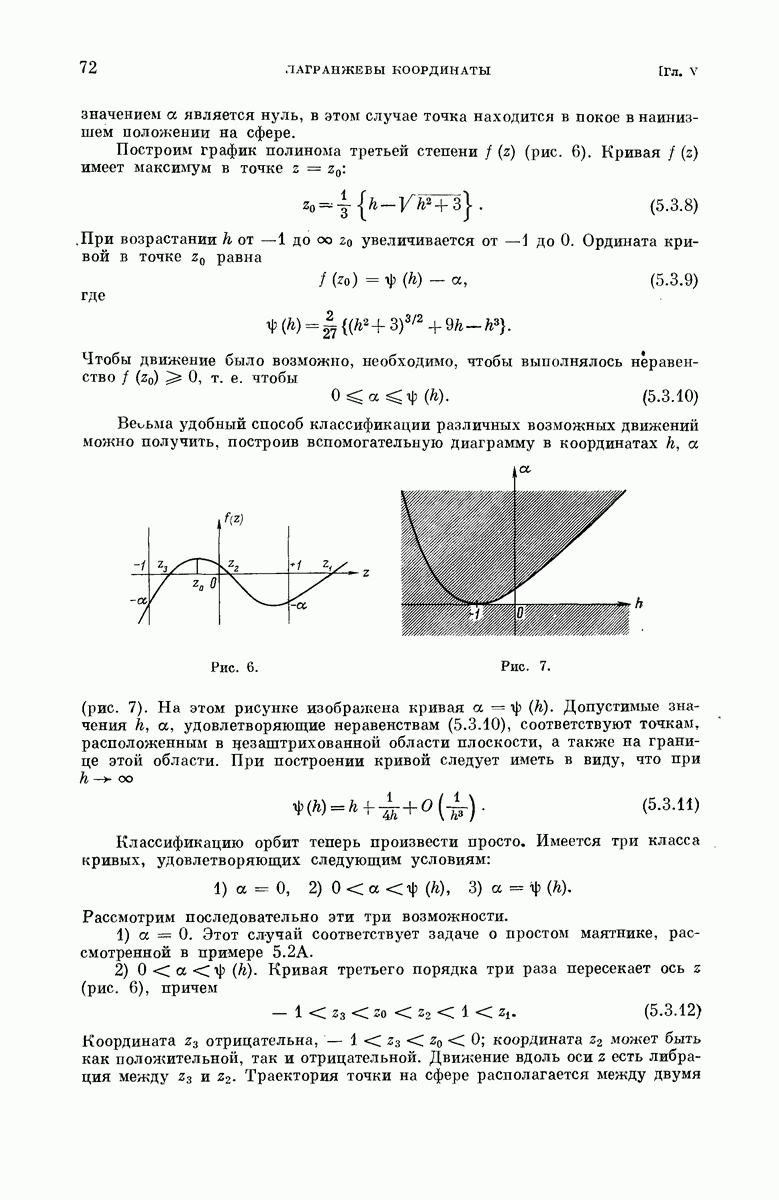
2)  , причем а вещественно и положительно; ось волчка начинает движение из состояния покоя вблизи вертикали. Решение имеет вид
, причем а вещественно и положительно; ось волчка начинает движение из состояния покоя вблизи вертикали. Решение имеет вид

и траектория представляет собой гипоциклоиду. Такую кривую описывает точка окружности радиуса  катящаяся внутри окружности радиуса а (рис. 26). В обозначениях, указанных на рисунке, можем написать
катящаяся внутри окружности радиуса а (рис. 26). В обозначениях, указанных на рисунке, можем написать

Если положить здесь

то мы получим формулу (9.8.13).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1.1. Свободная материальная точка.
- § 1.2. Прямолинейное движение материальной точки в силовом поле.
- § 1.3. Либрационное движение.
- § 1.4. Заданная сила не может быть функцией от ускорения.
- § 1.5. Несвободная материальная точка (случай I).
- § 1.6. Несвободная материальная точка (случай II).
- § 1.7. Несвободная материальная точка (случай III).
- § 1.8. Голономные и неголономные системы.
- Глава II. МЕХАНИЧЕСКИЕ СИСТЕМЫ
- § 2.1. Система двух материальных точек.
- § 2.2. Система материальных точек.
- § 2.3. Катастатическая система.
- § 2.4. Реакции связей.
- § 2.5. К понятию о механической системе.
- Глава III. ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 3.2. Сохранение импульса.
- § 3.3. Катастатическая система и первая форма уравнения энергии.
- § 3.4. Консервативные силы и вторая форма уравнения энергии.
- § 3.5. Третья форма уравнения энергии.
- § 3.6. Сохранение энергии.
- § 3.7. Принцип Гамильтона.
- § 3.8. Варьированный путь.
- § 3.9. Распределенные системы.
- Глава IV. ВТОРАЯ И ТРЕТЬЯ ФОРМЫ ОСНОВНОГО УРАВНЕНИЯ
- § 4.1. Вторая форма основного уравнения.
- § 4.2. Третья форма основного уравнения.
- § 4.3. Принцип Гаусса наименьшего принуждения.
- § 4.4. Приложения принципа Гаусса.
- § 4.5. Физический смысл принципа Гаусса.
- Глава V. ЛАГРАНЖЕВЫ КООРДИНАТЫ
- § 5.2. Некоторые классические задачи.
- § 5.3. Сферический маятник.
- § 5.4. Задача двух тел.
- § 5.5. Уравнение Кеплера.
- § 5.6. Столкновение.
- § 5.7. Лагранжевы координаты для голономной системы.
- § 5.8. Лагранжевы координаты для неголономной системы.
- § 5.9. Качение тела.
- § 5.10. Достижимость.
- § 5.11. Варьированный путь в принципе Гамильтона.
- § 5.12. Обзор полученных результатов.
- Глава VI. УРАВНЕНИЯ ЛАГРАНЖА
- § 6.1. Четвертая форма основного уравнения. Лагранжевы координаты.
- § 6.2. Уравнения Лагранжа.
- § 6.3. Вывод уравнений Лагранжа из принципа Гамильтона.
- § 6.4. Форма уравнений Лагранжа.
- § 6.5. Консервативные системы и другие системы, обладающие потенциальной функцией.
- § 6.6. Функция Лагранжа.
- § 6.7. Интеграл Якоби.
- § 6.8. Явная форма интеграла Якоби.
- § 6.9. Об одной ошибке.
- § 6.11. Циклические координаты.
- § 6.12. Инвариантность уравнений Лагранжа.
- Глава VII. ТЕОРИЯ ПОВОРОТОВ
- § 7.2. Теорема Эйлера.
- § 7.3. Матрица l и вектор Т.
- § 7.4. Обобщение теоремы Эйлера.
- § 7.5. Теорема Шаля.
- § 7.6. Формула поворота.
- § 7.7. Полуобороты и отражения.
- § 7.8. Кватернионная форма записи формулы поворота.
- § 7.9. Сложение вращений.
- § 7.10. Угловая скорость.
- § 7.11. Ориентация твердого тела в пространстве. Углы Эйлера.
- § 7.12. Ориентация твердого тела в пространстве. Углы …
- § 7.13. Повороты около движущихся осей.
- § 7.14. Повороты около неподвижных осей.
- § 7.15. Определение угловой скорости с помощью матриц
- § 7.16. Составляющие вектора угловой скорости.
- Глава VIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 8.1. Дифференциальные уравнения.
- § 8.2. Формулы ускорения в ортогональных координатах.
- § 8.3. Обезьяна и противовес.
- § 8.4. Кинетическая энергия твердого тела.
- § 8.5. Задача о движении в двух измерениях.
- § 8.6. Вращающийся волчок; основные уравнения.
- § 8.7. Вращающийся волчок; другое решение.
- § 8.8. Гироскопические силы.
- § 8.9. Вращающийся волчок; исследование движения.
- § 8.10. Численный пример.
- § 8.11. Стержень во вращающейся плоскости.
- § 8.12. Качение диска.
- Глава IX. ТЕОРИЯ КОЛЕБАНИЙ
- § 9.1. Колебания около положения равновесия.
- § 9.2. Теория преобразования к главным координатам.
- § 9.3. Приложение теории.
- § 9.4. Наложение связи.
- § 9.5. Принцип Релея.
- § 9.6. Устойчивость установившегося движения.
- § 9.7. Колебания в окрестности установившегося движения.
- § 9.8. Гироскоп Фуко.
- § 9.9. Спящий волчок.
- § 9.10. Вынужденные колебания.
- Глава X. ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 10.2. Исключение одной координаты.
- § 10.3. Гироскопическая устойчивость.
- § 10.4. Явное выражение для R в общем случае.
- § 10.5. Вращающийся волчок.
- § 10.6. Линейные члены в функции L.
- § 10.7. Движение относительно подвижной системы отсчета.
- § 10.8. Движение частицы вблизи заданной точки на поверхности Земли.
- § 10.9. Маятник Фуко.
- § 10.10. Движение снаряда.
- § 10.11. Диссипативная функция Релея.
- § 10.12. Гироскопическая система с диссипацией.
- § 10.13. Уравнения Гамильтона.
- § 10.14. Уравнение энергии и явное выражение для Н.
- § 10.15. Главный триэдр.
- Глава XI. ПЕРЕМЕННАЯ МАССА
- § 11.1. Частица переменной массы. Функция Лагранжа.
- § 11.2. Кинетическая энергия.
- § 11.3. Функция Гамильтона.
- § 11.4. Движущийся электрон.
- § 11.2. Кинетическая энергия.
- § 11.5. Электрон в электромагнитном поле.
- Глава XII. УРАВНЕНИЯ ГИББСА-АППЕЛЯ
- § 12.3. Пятая форма основного уравнения.
- § 12.5. Уравнения Гиббса — Аппеля.
- Глава XIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА-АППЕЛЯ
- § 13.2. Аналог теоремы Кёнига.
- § 13.3. Плоское движение.
- § 13.4. Движение твердого тела.
- § 13.5. Шар на вращающейся плоскости.
- § 13.6. Шар на вращающейся наклонной плоскости.
- § 13.7. Качение шара по неподвижной поверхности.
- § 13.8. Вращающийся волчок.
- § 13.9. Качение монеты (тонкого диска).
- § 13.10. Уравнения Эйлера.
- § 13.11. Свободное тело; случай осевой симметрии.
- § 13.12. Свободное тело; общий случай.
- § 13.13. Ориентация свободного тела.
- § 13.14. Теоремы Пуансо и Сильвестра.
- § 13.15. Качение эллипсоида по шероховатой горизонтальной плоскости.
- § 13.16. Устойчивость вращающегося эллипсоида.
- Глава XIV. ТЕОРИЯ УДАРА
- § 14.1. Ударный импульс.
- § 14.2. Импульсные связи.
- § 14.3. Движение системы, на которую действуют ударные импульсы. Основное уравнение теории удара.
- § 14.4. Катастатическая система.
- § 14.5. Принцип наименьшего принуждения в теории удара.
- § 14.6. Катастатическая система. Теорема о суперпозиции.
- § 14.7. Катастатическая система. Шесть теорем об энергии.
- § 14.8. Лагранжевы координаты и квазикоординаты.
- § 14.9. Лагранжева форма уравнений движения в теории удара.
- § 14.10. Другие доказательства теорем об энергии.
- § 14.11. Приложения теории удара.
- § 14.12. Импульсивное движение непрерывных систем.
- Глава XV. ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 15.1. Шестая форма основного уравнения.
- § 15.2. Непосредственные выводы.
- § 15.3. Функция Рауса.
- § 15.4. Теорема …
- § 15.5. Главная функция.
- § 15.6. Примеры использования главной функции.
- § 15.7. Доказательство равенства …
- § 15.8. Свойства главной функции.
- § 15.9. Примеры непосредственного вычисления главной функции.
- Глава XVI. ТЕОРЕМА ГАМИЛЬТОНА—ЯКОБИ
- § 16.1. Уравнение Гамильтона в частных производных.
- § 16.2. Теорема Гамильтона — Якоби (доказательство первое).
- § 16.3. Теорема об эквивалентности.
- § 16.4. Теорема Гамильтона — Якоби (доказательство второе).
- § 16.5. Замечания по теореме Гамильтона — Якоби.
- § 16.6. Однородное поле.
- § 16.7. Гармонический осциллятор.
- § 16.8 Частица в переменном поле At.
- § 16.9. Центральная орбита.
- § 16.10. Сферический маятник.
- § 16.11. Вращающийся волчок.
- § 16.12. Стержень на вращающейся плоскости.
- § 16.13. Электрон в центральном поле.
- § 16.14. Пфаффова форма
- Глава XVII. СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 17.2. Условия разделимости переменных в системах с двумя степенями свободы.
- § 17.3. Изучение движения системы.
- § 17.4. Классификация траекторий.
- § 17.5. Устойчивость.
- § 17.6. Приложения теории.
- § 17.7. Притяжение к центру по закону …
- § 17.8. Притяжение к центру по закону …
- § 17.9. Ньютоновское притяжение и однородное поле.
- § 17.10. Два неподвижных притягивающих центра
- § 17.11. Ограниченные траектории.
- § 17.12. Уравнения орбит.
- § 17.13. Неограниченные орбиты.
- § 17.14. Системы, допускающие разделение переменных более чем одним способом.
- Глава XVIII. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 18.1. Система Лиувилля
- § 18.2. Теорема Штеккеля.
- § 18.3. Исследование интегралов.
- § 18.4. Дополнительные замечания к теореме Штеккеля.
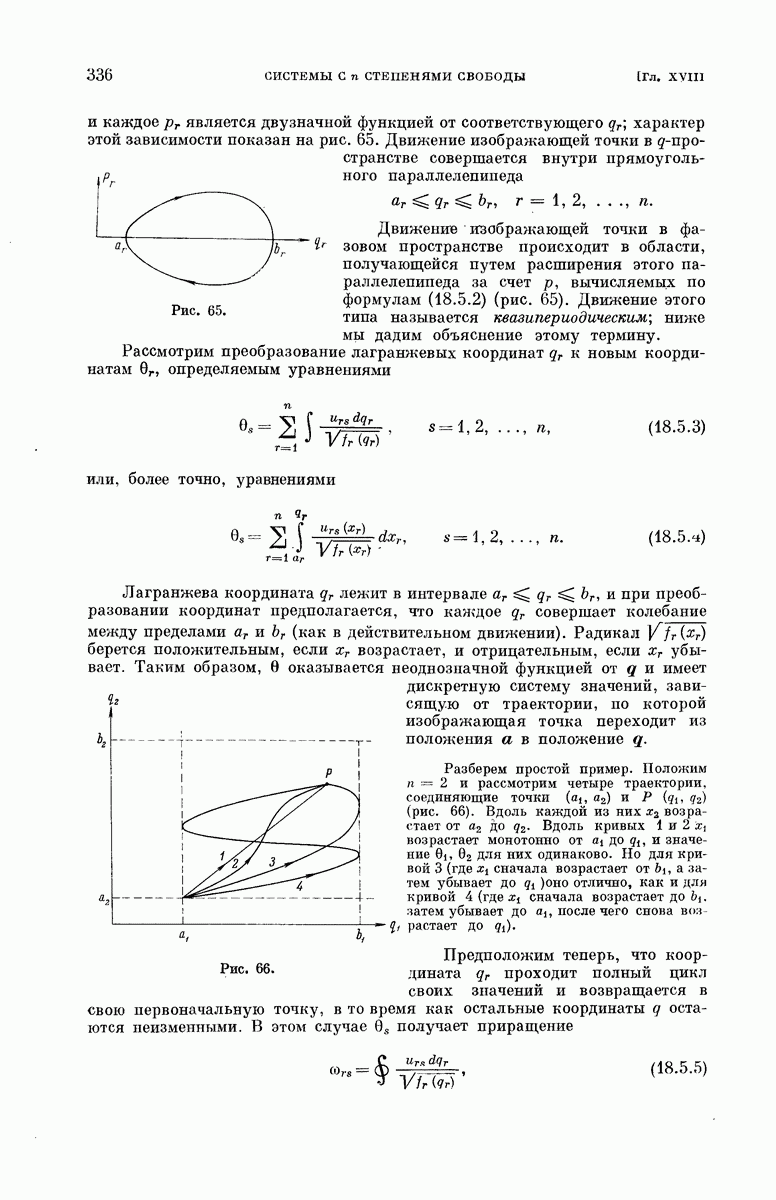
- § 18.5. Квазипериодические движения.
- § 18.6. Угловые переменные.
- § 18.7. Стандартный куб.
- § 18.8. Постоянные …
- § 18.9. Соотношения между q и v.
- § 18.10. Малые колебания.
- § 18.11. Сферический маятник.
- § 18.12. Задача двух тел.
- § 18.13. Интерпретация параметров a и b.
- § 18.14. Выражение r как функции от t.
- § 18.15. Угловые переменные.
- § 18.16. Постоянные …
- § 18.17. Возмущения.
- § 18.18. Неортогональные и ненатуральные разделимые системы.
- Глава XIX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ, ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ
- § 19.2. Движение частицы по прямой.
- § 19.3. Система с одной степенью свободы.
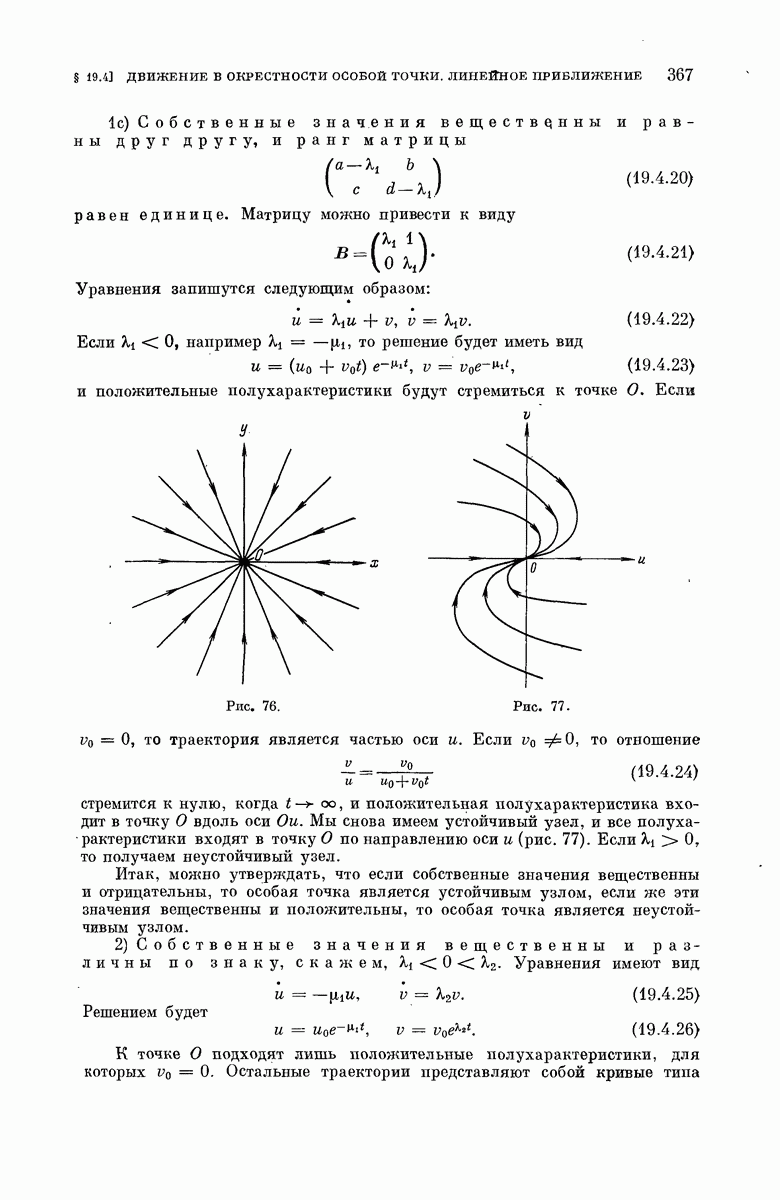
- § 19.4. Движение в окрестности особой точки. Линейное приближение.
- § 19.5. Устойчивость равновесия. Асимптотическая устойчивость и неустойчивость.
- § 19.6. Движение в окрестности особой точки. Общая теория.
- § 19.7. Движение в окрестности узла.
- § 19.8. Движение в окрестности седловой точки.
- § 19.9. Движение в окрестности фокуса.
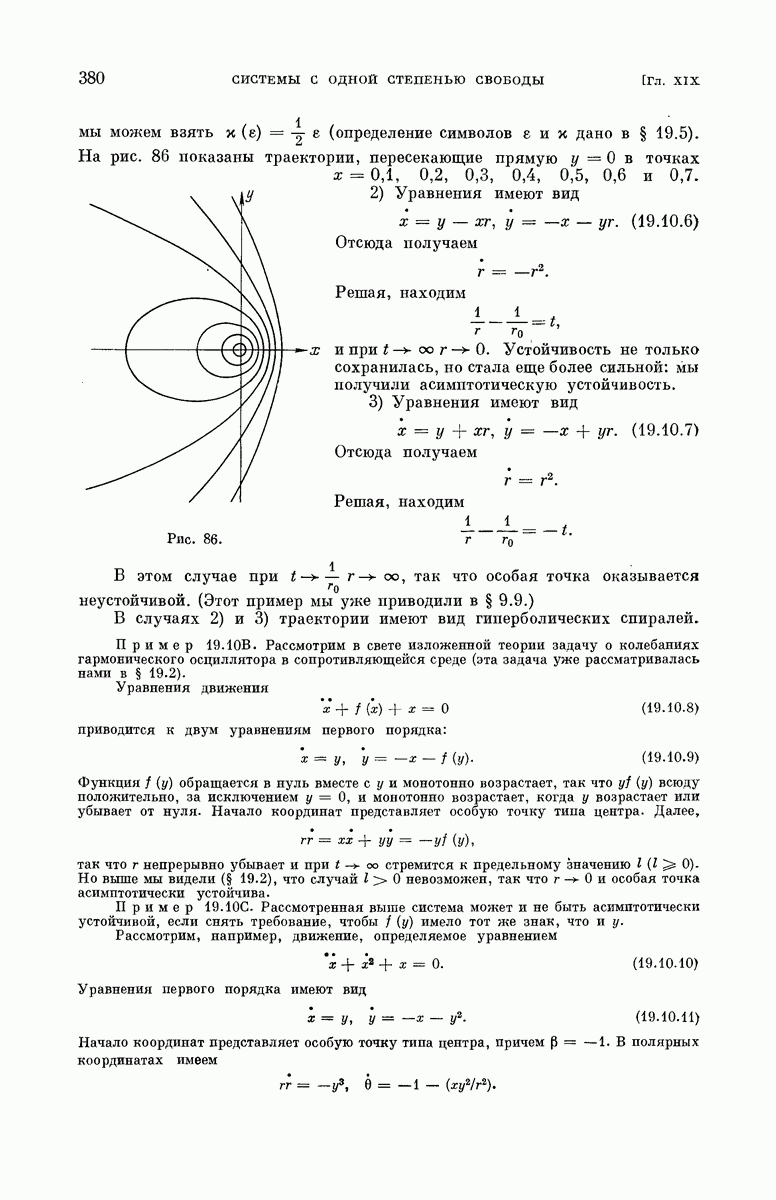
- § 19.10. Движение в окрестности центра.
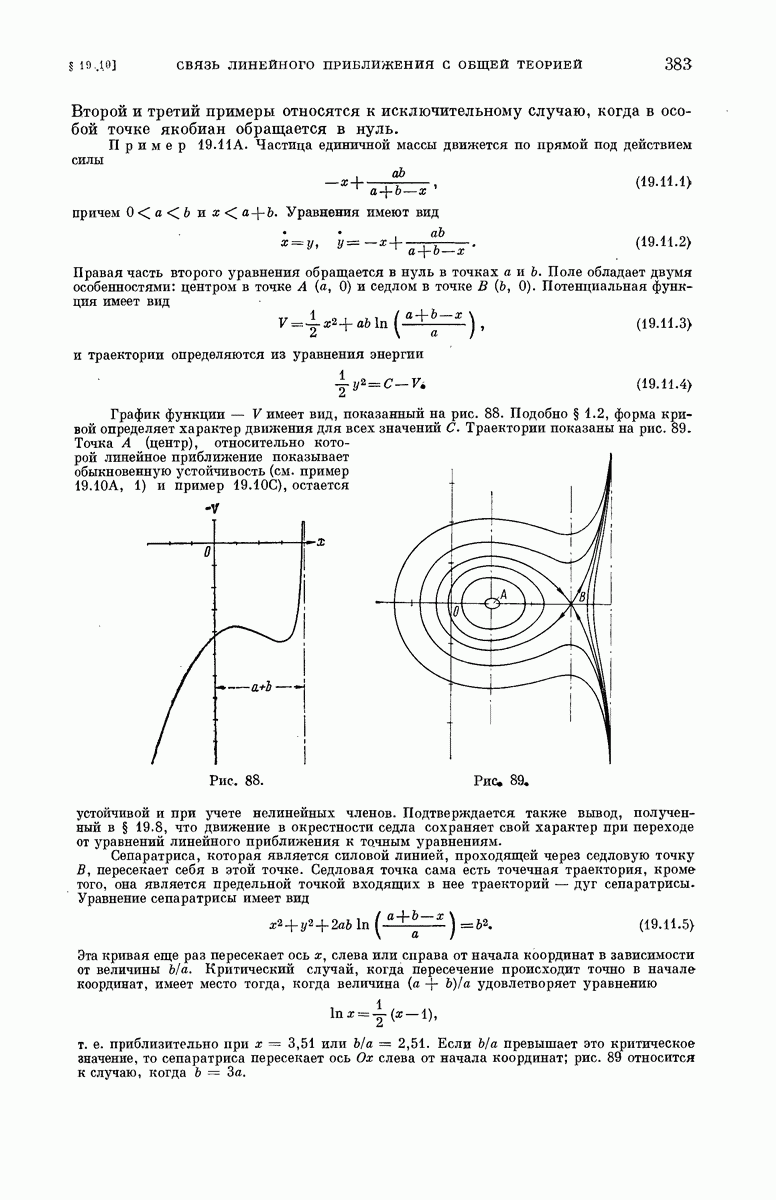
- § 19.11. Связь линейного приближения с общей теорией.
- Глава XX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- § 20.2. Положительное предельное множество.
- § 20.3. Отрезок без контакта.
- § 20.4. Отрезок без контакта, проходящий через точку множества A.
- § 20.5. Структура множества A.
- § 20.6. Теорема Пуанкаре — Бендиксона.
- § 20.7. Приложение к системе частного вида.
- § 20.8. Существование предельного цикла.
- § 20.9. Уравнение Ван-дер-Поля.
- Глава XXI. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК
- § 21.2. Преобразование к новым координатам.
- § 21.3. Оператор Tt
- § 21.4. Решение в форме степенных рядов.
- § 21.5. Формула для X(x)-X(a)
- § 21.6. Интегральные инварианты.
- § 21.7. Интегральные инварианты порядка m.
- § 21.8. Свойства множителей.
- § 21.9. Последний множитель Якоби.
- § 21.10. Линейная система.
- § 21.11. Устойчивость равновесия.
- § 21.12. Дискретная устойчивость.
- § 21.13. Устойчивость преобразований.
- § 21.14. Приложение к дифференциальным уравнениям.
- § 21.15. Теорема Пуанкаре — Ляпунова.
- § 21.16. Критический случай.
- Глава XXII. УРАВНЕНИЯ ГАМИЛЬТОНА
- § 22.1. Уравнения Гамильтона.
- § 22.2. Скобки Пуассона.
- § 22.3. Теорема Пуассона.
- § 22.4. Использование известного интеграла.
- § 22.5. Линейный интегральный инвариант Пуанкаре.
- § 22.6. Теорема Лиувилля.
- § 22.7. Теорема возвращения (теорема Пуанкаре).
- § 22.8. Примеры инвариантных областей.
- § 22.9. Эргодические теоремы.
- § 22.10. Конкретные примеры.
- § 22.11. Множество …
- § 22.12. Собственные отрезки.
- § 22.13. Доказательство эргодической теоремы; первый этап.
- § 22.14. Доказательство эргодической теоремы; второй этап.
- § 22.15. Метрическая неразложимость.
- § 22.16. Интегралы уравнений движения.
- § 22.17. Следствие теоремы Лиувилля.
- § 22.18. Последний множитель.
- Глава XXIII. ДВИЖЕНИЕ В ОКРЕСТНОСТИ ЗАДАННОГО ДВИЖЕНИЯ. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- § 23.2. Решение уравнений в вариациях.
- § 23.3. Случай постоянных коэффициентов.
- § 23.4. Случай периодических коэффициентов.
- § 23.5. Нулевые показатели.
- § 23.6. Уравнения в вариациях для системы Гамильтона.
- § 23.7. Устойчивость траекторий (1).
- § 23.8. Устойчивость траекторий (2).
- § 23.9. Устойчивость периодических орбит.
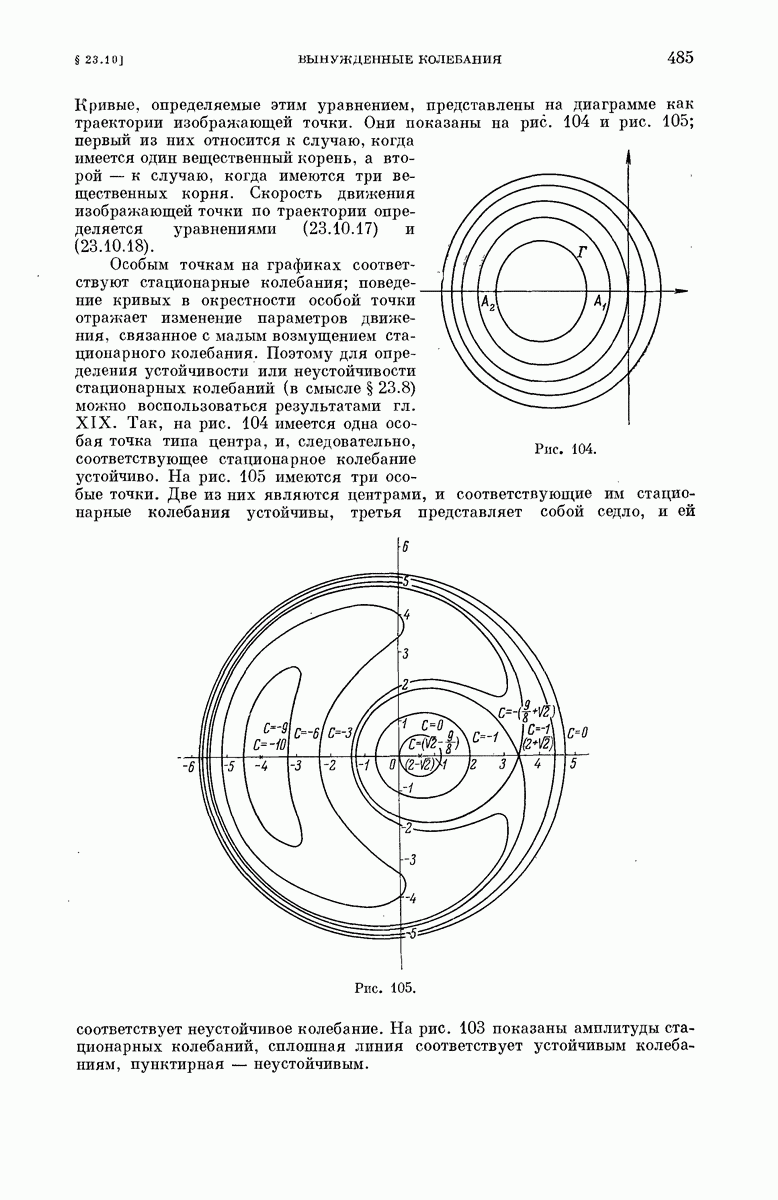
- § 23.10. Вынужденные колебания.
- Глава XXIV. КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ
- § 24.1. Контактные преобразования.
- § 24.2. Формулы контактного преобразования.
- § 24.3. Другие формулы.
- § 24.4. Обобщенное точечное преобразование и другие однородные контактные преобразования.
- § 24.5. Специальная форма уравнений преобразований. Бесконечно малые контактные преобразования.
- § 24.6. Обобщение теоремы Лиувилля.
- § 24.7. Условия контактности преобразования, скобки Лагранжа.
- § 24.8. Соотношения между двумя системами производных.
- § 24.9. Условия контактности преобразования, выраженные с помощью скобок Пуассона.
- § 24.10. Соотношения между скобками Лагранжа и скобками Пуассона.
- § 24.11. Приложение к контактному преобразованию.
- § 24.12. Инвариантность скобки Пуассона.
- § 24.13. Другая форма условий контактности преобразования.
- § 24.14. Функции, находящиеся в инволюции.
- § 24.15. Некоторые примеры.
- Глава XXV. ТЕОРИЯ ПРЕОБРАЗОВАНИЙ
- § 25.1. Уравнения движения после контактных преобразований.
- § 25.2. Вариация элементов траектории.
- § 25.3. Вариация эллиптических элементов.
- § 25.4. Другие доказательства теоремы Якоби.
- § 25.5. Постоянство скобок Лагранжа.
- § 25.6. Бесконечно малые контактные преобразования.
- § 25.7. Интегралы в инволюции.
- § 25.8. Теорема Ли о системах в инволюции.
- § 25.9. Интегралы, линейные относительно импульсов.
- § 25.10. Случай, когда функция Гамильтона является однородной квадратичной формой
- Глава XXVI. ВАРИАЦИОННЫЕ ПРИНЦИПЫ
- § 26.2. Теорема Ливенса.
- § 26.3. Точки минимума и седловые точки.
- § 26.4. Асинхронное варьирование. Принцип Гёльдера.
- § 26.5. Принцип Фосса.
- § 26.6. Обобщение принципа Гамильтона.
- § 26.7. Замена независимой переменной.
- § 26.8. Нормальная форма системы с двумя степенями свободы.
- § 26.9. Система Лиувилля.
- § 26.10. Конформные преобразования.
- Глава XXVII. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- § 27.3. Принцип наименьшего действия в форме Якоби.
- § 27.4. Теорема Уиттекера.
- § 27.5. Исключение координат.
- § 27.6. Характеристическая функция.
- § 27.7. Пространство конфигураций.
- § 27.8. Система с двумя степенями свободы.
- § 27.9. Теорема Кельвина.
- § 27.10. Однородное поле.
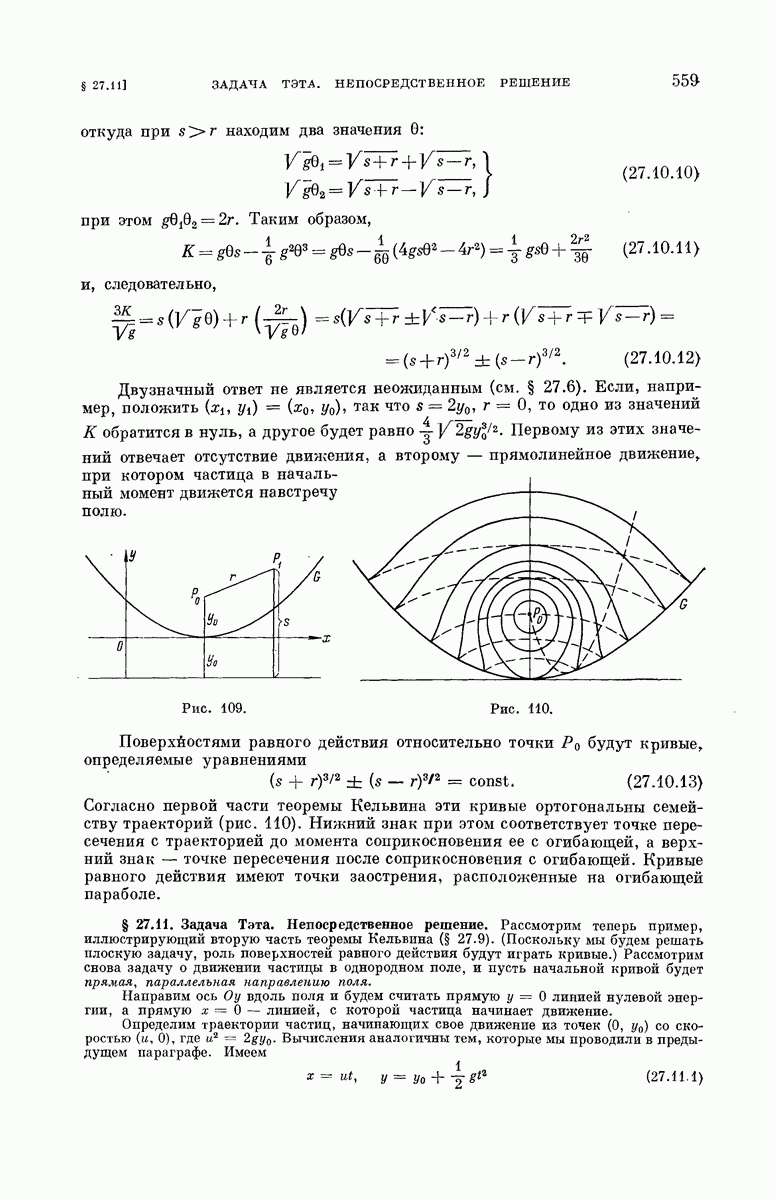
- § 27.11. Задача Тэта. Непосредственное решение.
- § 27.12. Задача Тэта. Теория огибающих.
- Глава XXVIII. ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 28.2. Ограниченная задача. Уравнения движения.
- § 28.3. Положения равновесия.
- § 28.4. Положения равновесия на прямой АВ.
- § 28.5. Положения равновесия, не лежащие на прямой АВ
- § 28.6. Поверхность z=U.
- § 28.7. Движение вблизи положения равновесия.
- § 28.8. Теория движения Луны.
- Глава XXIX. ЗАДАЧА ТРЕХ ТЕЛ
- § 29.2. Случай, когда вектор момента количеств движения равен нулю.
- § 29.3. Три точки Лагранжа.
- § 29.4. Решения, для которых треугольник Лагранжа сохраняет свою форму.
- § 29.5. Случай плоского движения.
- § 29.6. Координаты относительно частицы Az
- § 29.7. Движение в окрестности равновесного решения.
- § 29.8. Сведение к системе шести уравнений.
- § 29.9. Устойчивость трех точек Лагранжа.
- § 29.10. Преобразованная форма уравнений движения.
- § 29.11. Другой подход к задаче трех точек Лагранжа.
- § 29.12. Сведение к системе восьми уравнений.
- § 29.13. Невозможность тройных столкновений.
- § 29.14. Плоское движение. Другой способ приведения к системе шестого порядка.
- § 29.15. Равновесные решения.
- Глава XXX. ПЕРИОДИЧЕСКИЕ ОРБИТЫ
- § 30.1. Периодические орбиты.
- § 30.3. Условия вещественности.
- § 30.4. Уравнения Гамильтона.
- § 30.5. Сходимость.
- § 30.6. Три точки Лагранжа.
- § 30.7. Системы, содержащие параметр.
- § 30.8. Приложение к ограниченной задаче трех тел.
- § 30.9. Метод неподвижной точки.
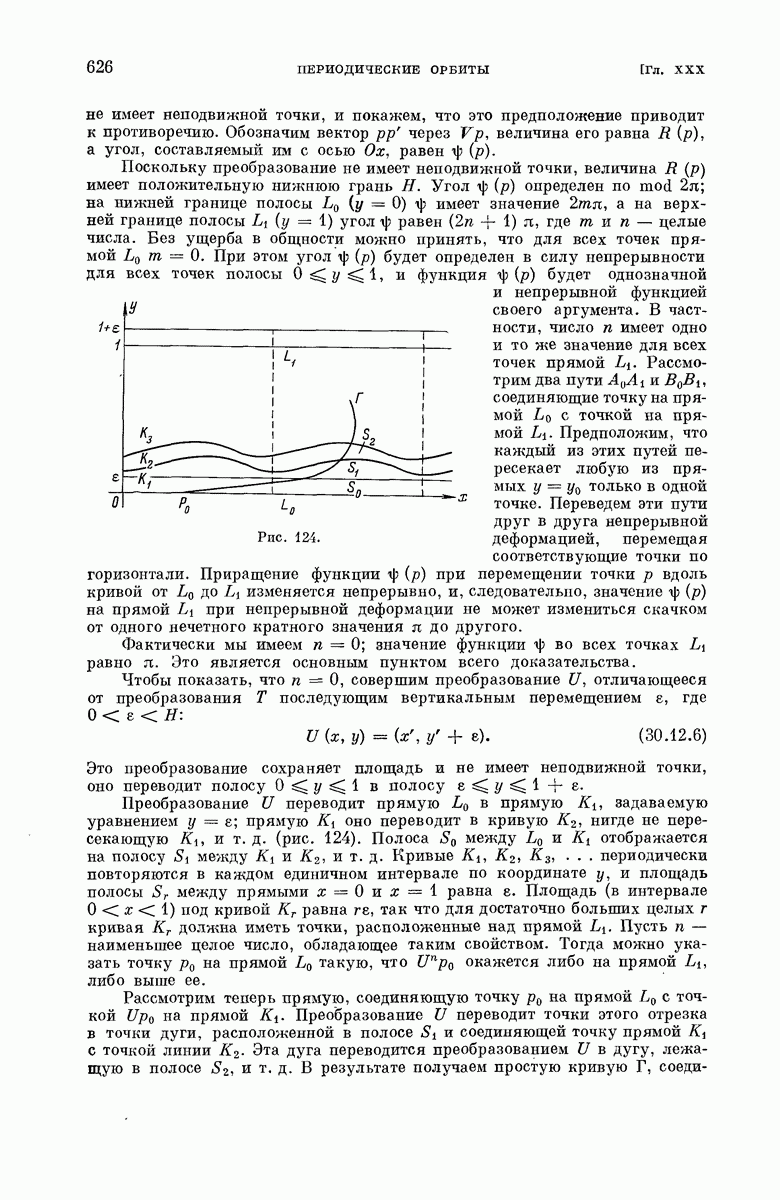
- § 30.11. Периодические орбиты и теорема о кольце.
- § 30.12. Доказательство теоремы Пуанкаре о кольце.