Глава IX. ТЕОРИЯ КОЛЕБАНИЙ

§ 9.1. Колебания около положения равновесия.

Свой метод Лагранж с особо выдающимся успехом применил к теории малых колебаний механической системы около положения устойчивого равновесия. Правда, применяемые там уравнения описывают, движение приближенно, но, несмотря на это. представляют большой интерес, поскольку, как уже отмечалось ранее в § 8.1. эти уравнения относятся к числу полностью разрешимых: задаваясь значениями при можно получить явные формулы, дающие решения уравнений для всех последующих значений t.

Рассмотрим натуральную систему (§ 6.5) с функцией кинетической энергии

и функцией потенциальной энергии

В точке в которой функция V имеет минимум, система может находиться в состоянии устойчивого равновесия. Отсчет координат удобно производить от этой точки, тогда положению равновесия будет соответствовать точка О, где Без потери общности можно принять, что в ней Повсюду в окрестности О, за исключением самой этой точки, Уравнение для достаточно малых значений С представляет замкнутое -мерное многообразие внутренность которого, -область, характеризуется неравенством и расположена в малой окрестности точки О. Если функцию V разложить в ряд Тейлора в окрестности начала координат, то главные члены разложения

образуют определенно-положительную квадратичную форму. Для достаточно малых значений С многообразие мало отличается от эллипсоида с центром в точке О.

Имеем интеграл энергии

Если система начинает свое движение в непосредственной близости от точки О с малой начальной скоростью, то постоянная С мала. В этом случае во все время движения будут, оставаться малыми и равновесие в точке О будет устойчивым. В самом деле, поскольку движение происходит в области

Изображающая точка располагается в области или в исключительном случае (если во время движения эта точка останавливается) — на поверхности Это указывает на то, что значения остаются

малыми в процессе всего движения. Далее, поскольку во время движения

V О, справедливо неравенство

и, следовательно, величины также остаются малыми. Поэтому достаточно хорошее приближение к действительному движению мояшо получить, сохранив в уравнениях движения лишь слагаемые первого порядка относительно . В этом заключается так называемое линейное приближение. Определяемое этим приближением движение тем ближе к точному, чем меньше значение С.

уравнение Лагранжа может быть записано в следующей форме (см. (6.4.5)):

Мы сохраним лишь члены первого порядка относительно Тогда в левой части уравнения (9.1.7) будем иметь

Кроме того, можно считать, что коэффициенты в этом выражении имеют постоянные значения, равные их значениям в положении равновесия. В правой части уравнения (9.1.7) мы оставим лишь члены первого порядка в разложении в ряд Тейлора по

Таким образом, для получения линейного приближения можно составить уравнения Лагранжа по выражениям каждое из которых представляет квадратичную форму с постоянными коэффициентами. Коэффициенты в выражении для можно взять равными их значениям в положении равновесия; иными словами, для наших целей достаточно найти выражение для в момент, когда система проходит положение равновесия. Функцию V можно представить членами второго порядка в разложении Тейлора в окрестности точки О, т. е. квадратичной формой вида (9.1.3). Таким образом, теория колебаний будет основываться на уравнениях Лагранжа, когда задаются определенно-положительными квадратичными формами с постоянными коэффициентами. Мы будем пользоваться теми же обозначениями, что и ранее, а именно:

причем, как уже говорилось, коэффициенты постоянны. Для функции V примем приближенное выражение (9.1.3):

в котором коэффициенты постоянны. В результате мы приходим к системе линейных уравнений с постоянными коэффициентами

Если матрицу обозначить через А, матрицу через и вектор (матрицу-столбец) через то уравнения (9.1.11) можно записать в матричной форме:

С помощью действительного неособого линейного преобразования квадратичные формы (9.1.9) и (9.1.10) можно одновременно привести к суммам квадратов с положительными коэффициентами. Одновременное приведение двух квадратичных форм к суммам квадратов всегда возможно, если по крайней мере одна из форм определенно-положительная. (То обстоятельство, что в нашем случае одна из форм содержит а другая несущественно, так как линейное преобразование влечет за собой такое же преобразование Можно найти новые координаты связанные с линейными соотношениями, такие, что

Коэффициенты в этих формулах суть вещественные положительные постоянные. При желании можно было бы пойти еще дальше и представить в виде квадратичной формы, все коэффициенты которой равны единице, однако для динамической задачи это несущественно.

В координатах уравнение движения имеет вид

Оно содержит только одну координату Таким образом, система уравнений распадается на полностью независимых систем.

Если в момент равно равно то

Это решение получено совершенно независимо от остальных

Координаты называются главными или нормальными координатами колебательной системы; колебание, при котором изменяется лишь одна главная координата, а остальные все время равны нулю, называется главным колебанием. Мы говорим, что в главном колебании соответствующая главная координата возбуждена, а остальные координаты находятся в покое. Как видно из формулы (9.1.14), в главном колебании координата изменяется по гармоническому закону с периодом Всего имеется таких периодов, не обязательно различных; их называют собственными периодами или периодами свободных колебаний системы. Периоды свободных колебаний являются инвариантами системы и не зависят от лагранжевых координат, выбранных первоначально для описания системы. Главное колебание с наибольшим периодом и, стало быть, с наименьшей частотой, т. е. колебание с наименьшим называется основным колебанием. Поскольку зависят от линейно, любое колебание может быть представлено как суперпозиция главных колебаний.

Движение системы в общем случае, в противоположность описанному выше, обычно не является периодическим, однако в одном случае движение всегда будет периодическим независимо от начальных условий. Это имеет место тогда, когда отношение любой пары величин представляет собой рациональное число. Если существуют целые числа (не имеющие общего множителя) такие, что

то любое колебание системы является периодическим с периодом Если, однако, отношение одной пары величин скажем иррационально,

то любое движение, в котором возбуждаются главные колебания t не может быть периодическим. Но можно, однако, всегда указать целые числа ту, такие, что равенство (9.1.16) будет выполнено приближенно, и, таким образом, в широком смысле каждое движение приближенно является периодическим. В самом деле, каждая переменная представляет собой почти периодическую функцию от t. Для того чтобы приближение к периодическому движению было достаточно хорошим, приближенный период может оказаться весьма большим.

В главном колебании, скажем в первом главном колебании, координаты время равны нулю; отсюда следует, что отношения постоянны. В самом деле, если связаны соотношениями

то в первом главном колебании

и каждая координата изменяется по гармоническому закону с периодом

В главном колебании наблюдаемая конфигурация системы, определяемая отношениями остается неизменной, а сами координаты изменяются по гармоническому закону с периодом соответствующего главного колебания.

Преобразование (9.1.17) можно записать в следующей форме:

Здесь вектор (матрица-столбец) вектор квадратная матрица

Решение конкретных задач, по крайней мере в тех случаях, когда периоды главных колебаний различны, не вызывает особых затруднений. Один из возможных путей решения используется ниже в примере 9.1 А. Он состоит в следующем. Сначала определяют периоды главных колебаний и отношения для каждого такого колебания. Таким образом находят элементы матрицы и с помощью преобразования (9.1.17) приводят уравнения движения к форме (9.1.14). После этого, можно выразить решение через переменные если знать начальные значения последние можно определить из начальных значений Итак, для любого момента времени можно найти значения зависящие линейным образом от если известны начальные значения Таким образом, задача полностью решается при любых начальных условиях.

Значения коэффициентов к, входящих в (9.1.13), не определяются описанной выше процедурой, так как мы нашли лишь отношения элементов в каждом столбце матрицы . Соответствующая неопределенность имеет место и в отношении переменных Это обстоятельство, однако, совершенно несущественно с практической точки зрения. Преобразование

в котором постоянные, а главные координаты, при надлежащем выборе приводит выражения для к виду

Этой формой часто пользуются при теоретических исследованиях, но практически можно обойтись без перехода от (9.1.13) к (9.1.22). Входящие в выражения (9.1.22) главные координаты определяются единственным образом (с точностью до знака), если все различны.

Сделаем еще одно существенное замечание. Форма (9.1.10) должна быть определенно-положительной; если V — лишь знакопостоянная (полуопределенная) форма, то изложенная выше теория теряет силу. Например, если одна из переменных скажем не входит в V, то соответствующее уравнение движения имеет вид Отсюда следует, что — и переменная в общем случае не остается малой в течение всего движения.

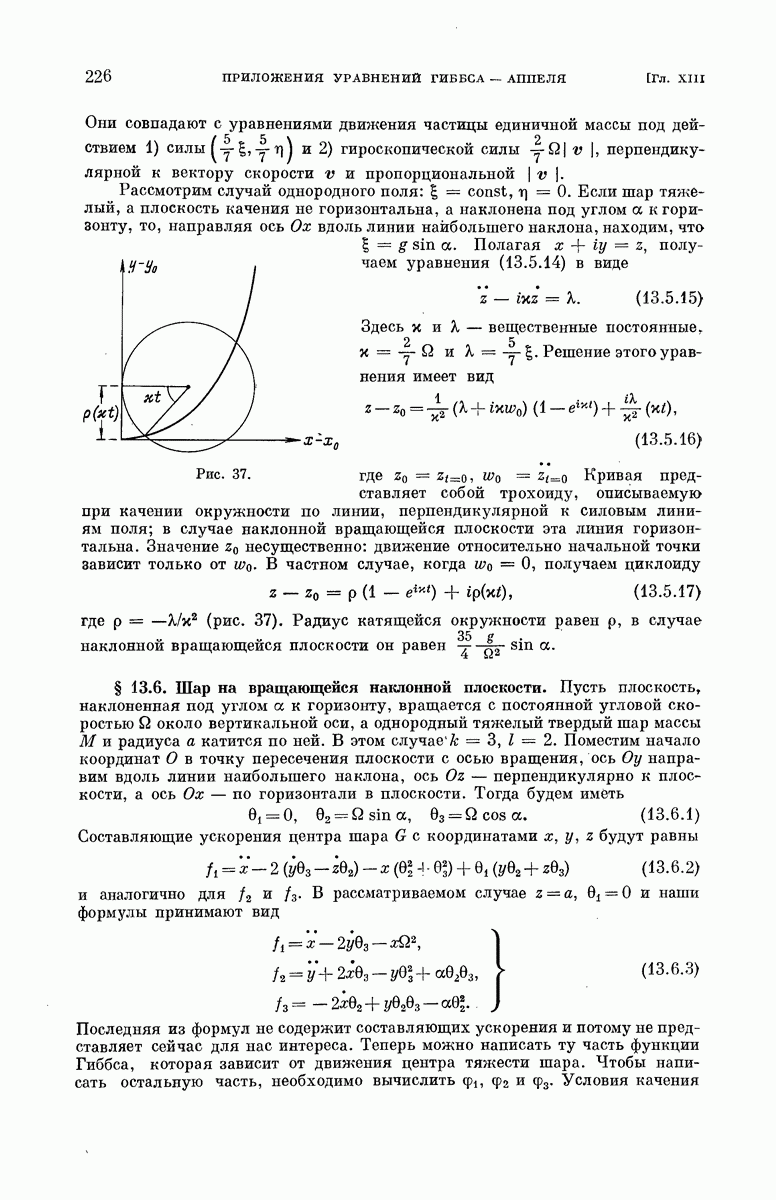
Рассмотрим теперь два конкретных примера; во втором из них система имеет лишь две степени свободы и решение поэтому значительно упрощается. Пример 9.1А. Невесомая струна длиной натянута силой между двумя фиксированными точками. На струне закреплены точечные массы на равных расстояниях друг от друга и от концов струны (рис. 23).

Рис. 23.

Система совершает поперечные колебания в своей плоскости. Требуется найти движение системы.

Представим себе, что движение совершается на гладкой поверхности стола. Натяжение будем считать большим и изменением его будем пренебрегать.

Пусть х, у, z обозначают смещения частиц в некоторый момент t. Уравнения движения частиц с точностью до величин первого порядка относительно х, у. z запишутся в виде

Эти уравнения можно переписать в следующей эквивалентной форме:

где

Можно, конечно, получить уравнения движения и с помощью метода Лагранжа. Удлинение первого участка струны с точностью до величин второго порядка относительно равно Учитывая аналогичным образом

удлинения остальных участков струны, получаем

Кроме того,

Если составить теперь уравнения Лагранжа, то легко убедиться, что они совпадают с уравнениями движения (9.1.23).

Рис. 24.

Для главного колебания с периодом имеем

Подставляя х, у, z в уравнения движения, получаем

Эти уравнения будут совместны, если

Отсюда, как и следовало ожидать, получаем три положительных значения

Для первого, или основного, главного колебания и уравнения (9.1.25) для отношений образуют (совместную) систему

так что для первого главного колебания

Аналогично, для второго главного колебания а для третьего Формы всех трех колебаний (несколько напоминающие формы первых трех колебаний однородной непрерывной струны) показаны на рис. 24.

Любое движение, в котором третье главное колебание отсутствует, является периодическим с периодом

Преобразование к главным координатам имеет вид

Отсюда

Легко проверить, что выраженные через имеют вид суммы квадратов:

Теперь можно дать полное решение задачи линейного приближения при любых заданных начальных условиях. Значение в некоторый момент t дается, например, формулой

где значения при

Для конкретности предположим, что в начальный момент система находится в покое в положении равновесия и движение вызывается малым поперечным импульсом величиной приложенным к первой частице. В начальный момент имеем

В любой последующий момент времени будем иметь

и окончательное решение будет иметь вид

где

Пример Невесомая струна длиной натянута силой между двумя фиксированными точками. В середине струны В укреплена точечная масса другая точечная масса укреплена в точке С, делящей

пополам отрезок между Система совершает малые поперечные колебания в плоскости, проходящей через точки

Доказать, что движение системы является периодическим с периодом где и найти ее движение при условии, что в момент каждая частица получает отклонение от прямой а начальные скорости равны нулю.

Обозначим смещение частицы В через х, а смещение частицы С через у. Уравнения движения имеют вид

Как и в предыдущем примере, эти уравнения легко получить из уравнений Лагранжа; с принятой точностью приближения имеем

где Уравнения Лагранжа имеют вид

Система имеет всего лишь две степени свободы, что упрощает решение. Рассмотрим два способа решения этой задачи.

1) Как в предыдущем примере, для главного колебания имеем Подставляя эти значения х и у в уравнения движения, находим

Этим уравнениям удовлетворяет ненулевой вектор при условии, что

Значения в двух главных колебаниях равны

В первом главном колебании — а во втором Можно было бы, аналогично предыдущему примеру, перейти к главным координатам, однако в этом нет необходимости, поскольку в случае двух степеней свободы результат очевиден. Когда система совершает первое главное колебание, вторая главная координата равна нулю, а когда система совершает второе главное колебание, первая главная координата равна нулю. Поэтому первая и вторая главные координаты и могут быть взяты в форме

откуда

Как легко проверить, в этих координатах представляются суммами квадратов:

2) Умножая второе уравнение движения на А, и складывая с первым, получаем

Это равенство принимает вид при

Следовательно, или —1, Если то получаем уравнение

вели же к получаем уравнение

Таким образом, мы находим как главные координаты, так и соответствующие периоды. Главные координаты равны . Имеем

Периоды главных колебаний равны поскольку первый из них в два раза больше второго, любое движение системы является периодическим с периодом

В начальный момент имеем

Или

Следовательно,

и

Пример Связанные системы. Пусть на стене висят двое маятниковых часов. Приведем один из маятников в колебание с амплитудой а. Тогда может случиться, что спустя некоторое время амплитуда колебаний этого маятника уменьшится почти до нуля, а второй маятник придет в колебание с амплитудой а. Спустя еще период времени второй маятник остановится, а первый придет в колебание с первоначальной амплитудой а. Таким образом, колебание будет поочередно передаваться от одного маятника к другому. Аналогичное явление происходит в рассматриваемом ниже примере.

Тяжелый стержень массы подвешен в горизонтальном положении да концы на двух невесомых нитях длиной а каждая. К точке А подвешена на невесомой нити длиной а частица С массы такая же частица на такой же нити подвешена к точке В. Система совершает малые колебания в вертикальной плоскости около положения равновесия.

Если угол, который нити, удерживающие стержень, составляют с вертикалью, обозначить через , а углы отклонения маятников от вертикали — через то с принятой точностью приближения можно написать

Уравнения движения запишутся в виде

где Отсюда

так что одна из главных координат равна Если второе и третье уравнения сложить и умножить на и прибавить или вычесть первое уравнение, то получим

Эти формулы определяют две другие главные координаты. Таким образом, главными координатами будут

Кроме того, Нас будет интересовать случай, когда отношение велико (и, следовательно, к велико); в этом случае, как и следовало ожидать, все три периода почти одинаковы. Разрешая уравнения (9.1.56) относительно получаем

Рассмотрим теперь движение, определяемое следующими начальными условиями:

При

и, следовательно,

Предположим теперь, что отношение велико. Тогда несколько меньше, чем запишем его в виде где малая величина. Переменные можно представить в форме

Движение по координате можно считать гармоническим с периодом (который мало отличается от периода свободных колебаний каждого из маятников, когда стержень А В находится в покое) и медленно изменяющейся амплитудой с большим периодом Движение по координате принадлежит к тому же типу. При этом, однако, амплитуда -колебаний максимальна тогда когда амплитуда -колебания минимальна, и наоборот. Колебание медленно передается от первого маятника ко второму, затем обратно — от второго к первому и т. д.