| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
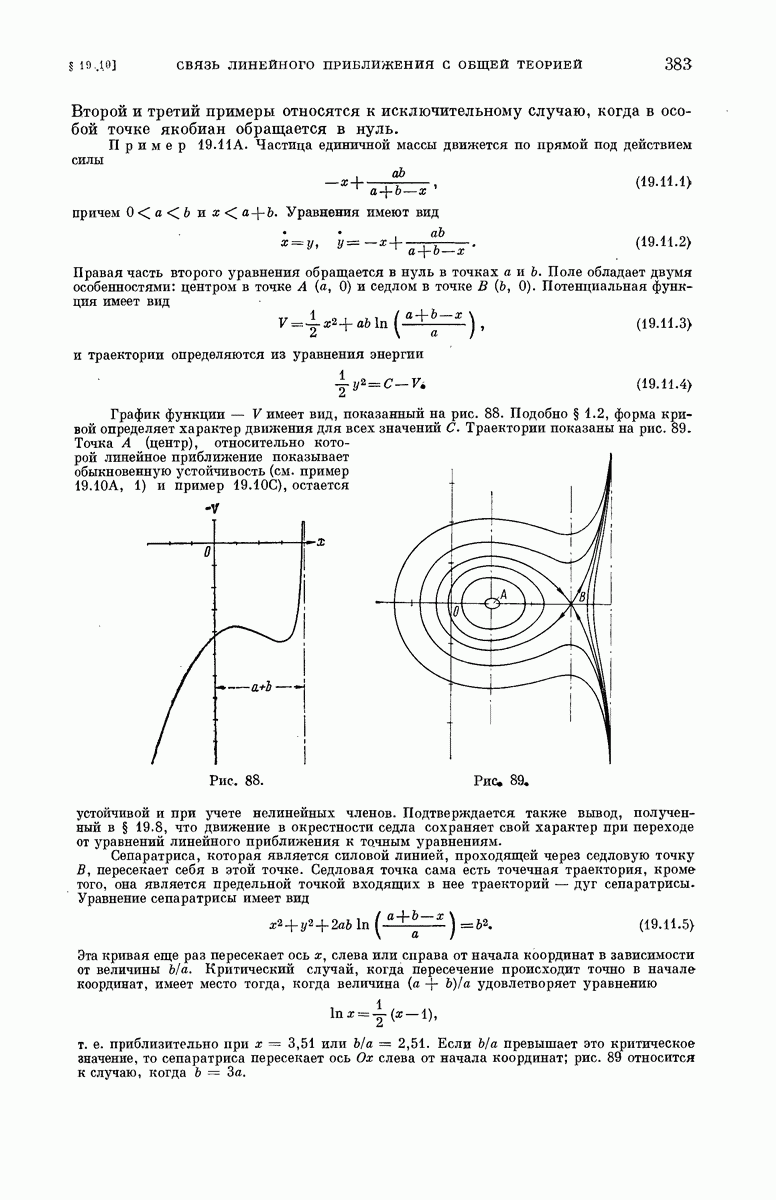
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
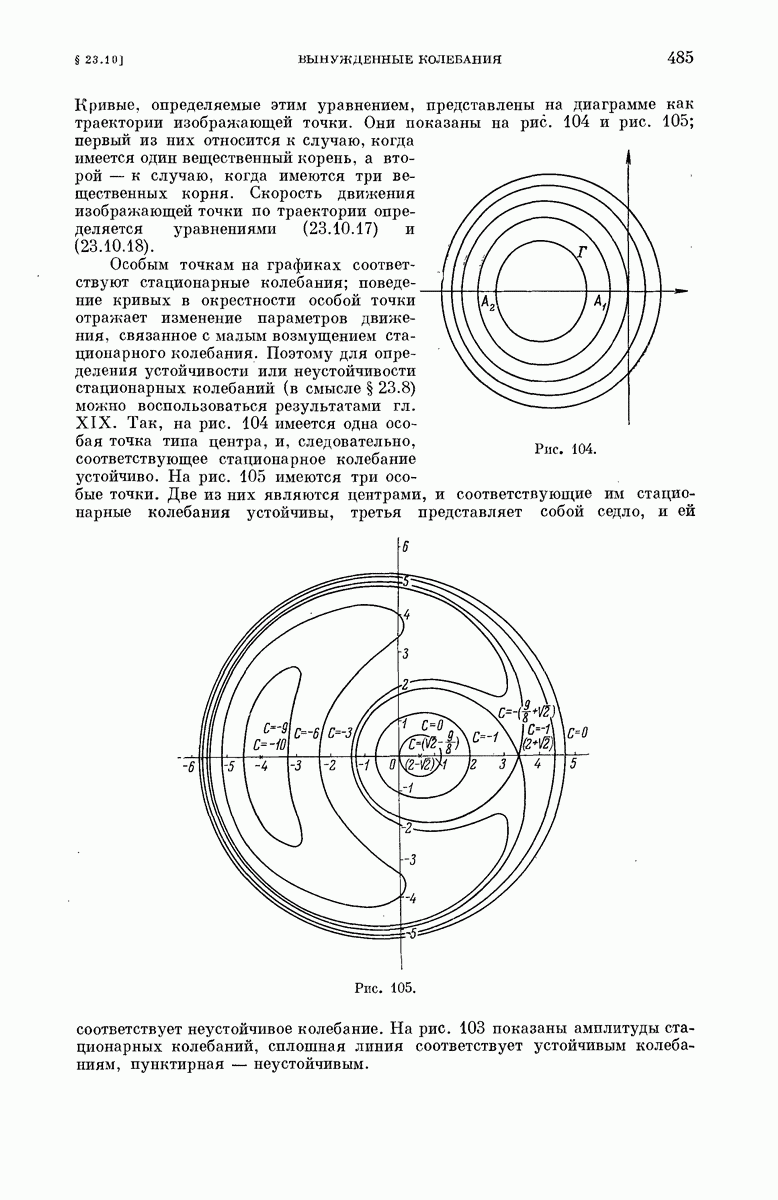
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
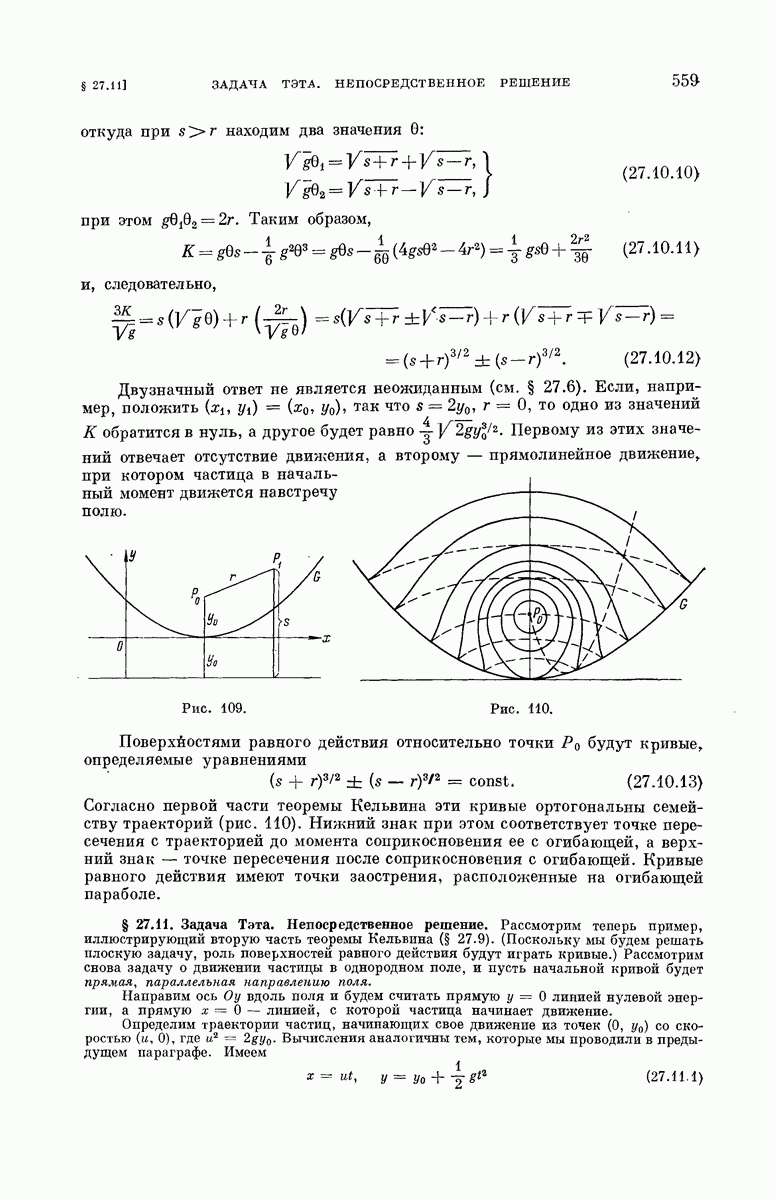
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
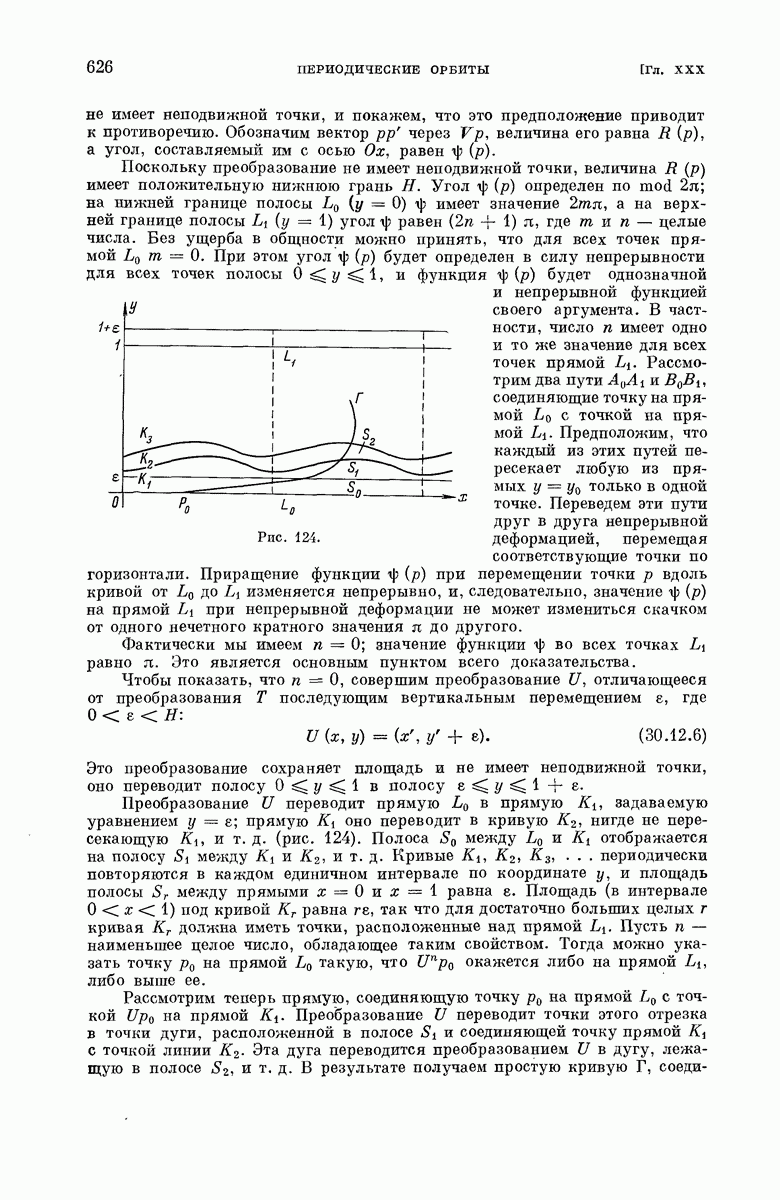
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 14.12. Импульсивное движение непрерывных систем.
Мы уже высказывали точку зрения, что основное уравнение для случая конечных сил приложимо к непрерывным системам; в § 3.9 это положение было проиллюстрировано на конкретных примерах. Эта точка зрения основывалась на физических соображениях.
Здесь мы выскажем аналогичное предположение о том, что основное уравнение (14.3.6) теории удара сохраняет силу и для непрерывных систем,
с той лишь разницей, что там, где это нужно, суммирование заменяется интегриров анием.
Рассмотрим некоторые примеры.
1) Несжимаемая жидкость. Рассмотрим однородную идеальную несжимаемую жидкость. Пусть имеются внутренние и внешние границы. Границы либо представляют собой твердые поверхности, либо являются деформируемыми; в последнем случае изменение их должно происходить таким образом, чтобы ограничиваемый ими объем оставался неизменным. Если движение границ в некоторый момент  претерпевает разрыв (например, если жидкость находится в покое в замкнутом сосуде и этому сосуду внезапно сообщается резкий толчок), то движение жидкости также будет разрывным. Задача заключается в том, чтобы определить мгновенное изменение движения.
претерпевает разрыв (например, если жидкость находится в покое в замкнутом сосуде и этому сосуду внезапно сообщается резкий толчок), то движение жидкости также будет разрывным. Задача заключается в том, чтобы определить мгновенное изменение движения.
Обозначим составляющие вектора скорости  относительно неподвижной прямоугольной системы координат через
относительно неподвижной прямоугольной системы координат через  а (постоянную) плотность жидкости
а (постоянную) плотность жидкости  через
через  . В жидкости устанавливается импульсивное давление
. В жидкости устанавливается импульсивное давление  , подобно тому как в системе с конечным числом степеней свободы возникают импульсы связей. Основное уравнение (14.3.6) принимает вид
, подобно тому как в системе с конечным числом степеней свободы возникают импульсы связей. Основное уравнение (14.3.6) принимает вид

Объемный интеграл берется по всему пространству, занятому жидкостью, а поверхностный интеграл — по ограничивающим поверхностям. Через  обозначена составляющая скорости вдоль внешней нормали. Символ А обозначает конечное (не бесконечно малое) приращение, возможное в момент
обозначена составляющая скорости вдоль внешней нормали. Символ А обозначает конечное (не бесконечно малое) приращение, возможное в момент  Если направляющие косинусы внешней нормали обозначить через
Если направляющие косинусы внешней нормали обозначить через  то правую часть уравнения (14.12.1) можно представить в виде
то правую часть уравнения (14.12.1) можно представить в виде

Второй член правой части равенства равен нулю, так как  Из уравнений (14.12.1) и (14.12.2) получаем
Из уравнений (14.12.1) и (14.12.2) получаем

Это равенство справедливо для произвольных значений  удовлетворяющих условиям
удовлетворяющих условиям  Таким образом,
Таким образом,

Мы получили уравнения импульсивного движения жидкости. Если в момент  движение было безвихревое, то оно будет безвихревое и в момент
движение было безвихревое, то оно будет безвихревое и в момент  Движение, начинающееся из состояния покоя, является безвихревым, так что
Движение, начинающееся из состояния покоя, является безвихревым, так что  Импульсивное давление
Импульсивное давление  связано с потенциалом скоростей возникшего движения соотношением
связано с потенциалом скоростей возникшего движения соотношением

Все эти выводы справедливы лишь для классического случая идеальной несжимаемой жидкости.
Некоторые хорошо известные теоремы классической гидродинамики, доказываемые обычно с помощью формулы Грина, легко могут быть получены из общих теорем теории удара. Предположим, что движение начинается из состояния покоя от резкого толчка жестких границ. Энергия системы при этом будет равна (§ 14.7, п. 1)

Интегралы здесь берутся по граничным поверхностям, а индекс  относится к внешней нормали. Сообщенная энергия является наименьшей из всех возможных при заданных значениях нормальной скорости в точках границы. Это следует из замечания 1 к теореме Кельвина (§ 14.7, п. 5), так как в каждой точке границы задано как направление импульса, так и составляющая скорости в этом направлении.
относится к внешней нормали. Сообщенная энергия является наименьшей из всех возможных при заданных значениях нормальной скорости в точках границы. Это следует из замечания 1 к теореме Кельвина (§ 14.7, п. 5), так как в каждой точке границы задано как направление импульса, так и составляющая скорости в этом направлении.
2) Неупругая струна (нить). Неупругая струна  лежащая на гладкой горизонтальной плоскости, приводится в движение импульсом
лежащая на гладкой горизонтальной плоскости, приводится в движение импульсом  направленным по касательной к струне в точке В. Найти движение струны после приложения импульса.
направленным по касательной к струне в точке В. Найти движение струны после приложения импульса.

Рис. 47.
Пусть  длина струны между точками
длина струны между точками  а
а  угол между касательными к струне в этих точках. Будем предполагать, что радиус кривизны
угол между касательными к струне в этих точках. Будем предполагать, что радиус кривизны  положителен и конечен и представляет собой дифференцируемую функцию от во всех точках дуги
положителен и конечен и представляет собой дифференцируемую функцию от во всех точках дуги  Обозначим через
Обозначим через  тангенциальную и нормальную составляющие скорости точки
тангенциальную и нормальную составляющие скорости точки  (рис. 47). Если
(рис. 47). Если  — линейная плотность струны в точке
— линейная плотность струны в точке  то основное уравнение (14.3.6) запишется в форме
то основное уравнение (14.3.6) запишется в форме

где символ А, как обычно, обозначает конечную (не бесконечно малую) вариацию, а  значение и в точке В.
значение и в точке В.
Поскольку струна нерастяжима, имеем

и уравнение (14.12.7) записывается в виде

Здесь а обозначает величину угла  в точке В. Интегрируя по частям, находим
в точке В. Интегрируя по частям, находим

На концах струны выполняются следующие условия:

и так как равенство (14.12.10) выполняется для произвольных А и, то можем написать

Функция и удовлетворяет дифференциальному уравнению

Что же касается функции  то для нее имеем дифференциальное соотношение
то для нее имеем дифференциальное соотношение

эквивалентное однородному линейному уравнению

где  заданная функция от
заданная функция от  штрихом обозначено дифференцирование по
штрихом обозначено дифференцирование по  Нас интересует решение уравнения (14.12.15), удовлетворяющее условиям на концах (14.12.11). Заметим, что если радиус кривизны струны в точке В равен нулю, например, когда В является точкой заострения дуги циклоиды, это решение не имеет места.
Нас интересует решение уравнения (14.12.15), удовлетворяющее условиям на концах (14.12.11). Заметим, что если радиус кривизны струны в точке В равен нулю, например, когда В является точкой заострения дуги циклоиды, это решение не имеет места.
Другой случай мы имеем, когда конец А не свободен, а вынужден двигаться в направлении нормали к, кривой в точке А (другие направления невозможны). Условиями на концах тогда будут

Рассмотрим два конкретных примера движения однородной струны, когда 
а) Струна имеет форму дуги окружности, и угол  изменяется от
изменяется от  до
до  Уравнение для
Уравнение для  запишется в виде
запишется в виде

Решение его будет иметь вид

где  масса струны. Из (14.12.12) находим
масса струны. Из (14.12.12) находим

Энергия струны будет равна

Интересно отметить, что это значение больше, чем —  что и следовало ожидать на основании теоремы Бертрана; мы должны были бы наложить на движение связь, ваставив струну двигаться внутри гладкой трубы; тогда ее энергия была бы равна
что и следовало ожидать на основании теоремы Бертрана; мы должны были бы наложить на движение связь, ваставив струну двигаться внутри гладкой трубы; тогда ее энергия была бы равна 
Если конец А не свободен, а принужден двигаться в направлении нормали к струне, то решение записывается в виде

и

В этом случае энергия струны равна

и она меньше того значения, которое дает формула (14.12.20). Таким образом, мы еще раз проиллюстрировали теорему Бертрана.
b) Струна имеет форму дуги денной линии

где угол  изменяется от
изменяется от  до
до  В этом случае
В этом случае  и дифференциальное уравнение для
и дифференциальное уравнение для  принимает вид
принимает вид

Решением его будет

Из условия (14.12.12) получаем

В случае свободной струны условия на концах (14.12.11) принимают вид

Если же точка А принуждена двигаться по нормали, то условия на концах (14.12.16) дают

В этом случае

и все точки струны движутся с одинаковой скоростью С в одном направлении — в направлении нормали к кривой в точке А.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1.1. Свободная материальная точка.
- § 1.2. Прямолинейное движение материальной точки в силовом поле.
- § 1.3. Либрационное движение.
- § 1.4. Заданная сила не может быть функцией от ускорения.
- § 1.5. Несвободная материальная точка (случай I).
- § 1.6. Несвободная материальная точка (случай II).
- § 1.7. Несвободная материальная точка (случай III).
- § 1.8. Голономные и неголономные системы.
- Глава II. МЕХАНИЧЕСКИЕ СИСТЕМЫ
- § 2.1. Система двух материальных точек.
- § 2.2. Система материальных точек.
- § 2.3. Катастатическая система.
- § 2.4. Реакции связей.
- § 2.5. К понятию о механической системе.
- Глава III. ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 3.2. Сохранение импульса.
- § 3.3. Катастатическая система и первая форма уравнения энергии.
- § 3.4. Консервативные силы и вторая форма уравнения энергии.
- § 3.5. Третья форма уравнения энергии.
- § 3.6. Сохранение энергии.
- § 3.7. Принцип Гамильтона.
- § 3.8. Варьированный путь.
- § 3.9. Распределенные системы.
- Глава IV. ВТОРАЯ И ТРЕТЬЯ ФОРМЫ ОСНОВНОГО УРАВНЕНИЯ
- § 4.1. Вторая форма основного уравнения.
- § 4.2. Третья форма основного уравнения.
- § 4.3. Принцип Гаусса наименьшего принуждения.
- § 4.4. Приложения принципа Гаусса.
- § 4.5. Физический смысл принципа Гаусса.
- Глава V. ЛАГРАНЖЕВЫ КООРДИНАТЫ
- § 5.2. Некоторые классические задачи.
- § 5.3. Сферический маятник.
- § 5.4. Задача двух тел.
- § 5.5. Уравнение Кеплера.
- § 5.6. Столкновение.
- § 5.7. Лагранжевы координаты для голономной системы.
- § 5.8. Лагранжевы координаты для неголономной системы.
- § 5.9. Качение тела.
- § 5.10. Достижимость.
- § 5.11. Варьированный путь в принципе Гамильтона.
- § 5.12. Обзор полученных результатов.
- Глава VI. УРАВНЕНИЯ ЛАГРАНЖА
- § 6.1. Четвертая форма основного уравнения. Лагранжевы координаты.
- § 6.2. Уравнения Лагранжа.
- § 6.3. Вывод уравнений Лагранжа из принципа Гамильтона.
- § 6.4. Форма уравнений Лагранжа.
- § 6.5. Консервативные системы и другие системы, обладающие потенциальной функцией.
- § 6.6. Функция Лагранжа.
- § 6.7. Интеграл Якоби.
- § 6.8. Явная форма интеграла Якоби.
- § 6.9. Об одной ошибке.
- § 6.11. Циклические координаты.
- § 6.12. Инвариантность уравнений Лагранжа.
- Глава VII. ТЕОРИЯ ПОВОРОТОВ
- § 7.2. Теорема Эйлера.
- § 7.3. Матрица l и вектор Т.
- § 7.4. Обобщение теоремы Эйлера.
- § 7.5. Теорема Шаля.
- § 7.6. Формула поворота.
- § 7.7. Полуобороты и отражения.
- § 7.8. Кватернионная форма записи формулы поворота.
- § 7.9. Сложение вращений.
- § 7.10. Угловая скорость.
- § 7.11. Ориентация твердого тела в пространстве. Углы Эйлера.
- § 7.12. Ориентация твердого тела в пространстве. Углы …
- § 7.13. Повороты около движущихся осей.
- § 7.14. Повороты около неподвижных осей.
- § 7.15. Определение угловой скорости с помощью матриц
- § 7.16. Составляющие вектора угловой скорости.
- Глава VIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 8.1. Дифференциальные уравнения.
- § 8.2. Формулы ускорения в ортогональных координатах.
- § 8.3. Обезьяна и противовес.
- § 8.4. Кинетическая энергия твердого тела.
- § 8.5. Задача о движении в двух измерениях.
- § 8.6. Вращающийся волчок; основные уравнения.
- § 8.7. Вращающийся волчок; другое решение.
- § 8.8. Гироскопические силы.
- § 8.9. Вращающийся волчок; исследование движения.
- § 8.10. Численный пример.
- § 8.11. Стержень во вращающейся плоскости.
- § 8.12. Качение диска.
- Глава IX. ТЕОРИЯ КОЛЕБАНИЙ
- § 9.1. Колебания около положения равновесия.
- § 9.2. Теория преобразования к главным координатам.
- § 9.3. Приложение теории.
- § 9.4. Наложение связи.
- § 9.5. Принцип Релея.
- § 9.6. Устойчивость установившегося движения.
- § 9.7. Колебания в окрестности установившегося движения.
- § 9.8. Гироскоп Фуко.
- § 9.9. Спящий волчок.
- § 9.10. Вынужденные колебания.
- Глава X. ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 10.2. Исключение одной координаты.
- § 10.3. Гироскопическая устойчивость.
- § 10.4. Явное выражение для R в общем случае.
- § 10.5. Вращающийся волчок.
- § 10.6. Линейные члены в функции L.
- § 10.7. Движение относительно подвижной системы отсчета.
- § 10.8. Движение частицы вблизи заданной точки на поверхности Земли.
- § 10.9. Маятник Фуко.
- § 10.10. Движение снаряда.
- § 10.11. Диссипативная функция Релея.
- § 10.12. Гироскопическая система с диссипацией.
- § 10.13. Уравнения Гамильтона.
- § 10.14. Уравнение энергии и явное выражение для Н.
- § 10.15. Главный триэдр.
- Глава XI. ПЕРЕМЕННАЯ МАССА
- § 11.1. Частица переменной массы. Функция Лагранжа.
- § 11.2. Кинетическая энергия.
- § 11.3. Функция Гамильтона.
- § 11.4. Движущийся электрон.
- § 11.2. Кинетическая энергия.
- § 11.5. Электрон в электромагнитном поле.
- Глава XII. УРАВНЕНИЯ ГИББСА-АППЕЛЯ
- § 12.3. Пятая форма основного уравнения.
- § 12.5. Уравнения Гиббса — Аппеля.
- Глава XIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА-АППЕЛЯ
- § 13.2. Аналог теоремы Кёнига.
- § 13.3. Плоское движение.
- § 13.4. Движение твердого тела.
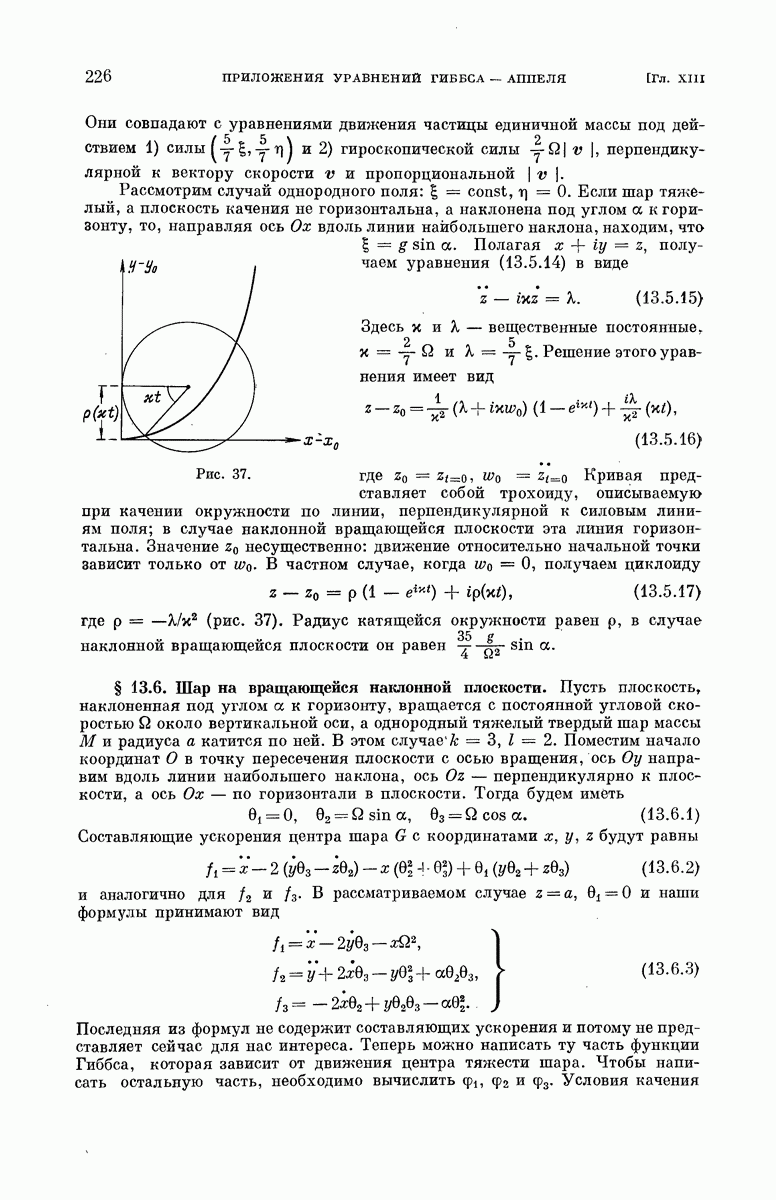
- § 13.5. Шар на вращающейся плоскости.
- § 13.6. Шар на вращающейся наклонной плоскости.
- § 13.7. Качение шара по неподвижной поверхности.
- § 13.8. Вращающийся волчок.
- § 13.9. Качение монеты (тонкого диска).
- § 13.10. Уравнения Эйлера.
- § 13.11. Свободное тело; случай осевой симметрии.
- § 13.12. Свободное тело; общий случай.
- § 13.13. Ориентация свободного тела.
- § 13.14. Теоремы Пуансо и Сильвестра.
- § 13.15. Качение эллипсоида по шероховатой горизонтальной плоскости.
- § 13.16. Устойчивость вращающегося эллипсоида.
- Глава XIV. ТЕОРИЯ УДАРА
- § 14.1. Ударный импульс.
- § 14.2. Импульсные связи.
- § 14.3. Движение системы, на которую действуют ударные импульсы. Основное уравнение теории удара.
- § 14.4. Катастатическая система.
- § 14.5. Принцип наименьшего принуждения в теории удара.
- § 14.6. Катастатическая система. Теорема о суперпозиции.
- § 14.7. Катастатическая система. Шесть теорем об энергии.
- § 14.8. Лагранжевы координаты и квазикоординаты.
- § 14.9. Лагранжева форма уравнений движения в теории удара.
- § 14.10. Другие доказательства теорем об энергии.
- § 14.11. Приложения теории удара.
- § 14.12. Импульсивное движение непрерывных систем.
- Глава XV. ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 15.1. Шестая форма основного уравнения.
- § 15.2. Непосредственные выводы.
- § 15.3. Функция Рауса.
- § 15.4. Теорема …
- § 15.5. Главная функция.
- § 15.6. Примеры использования главной функции.
- § 15.7. Доказательство равенства …
- § 15.8. Свойства главной функции.
- § 15.9. Примеры непосредственного вычисления главной функции.
- Глава XVI. ТЕОРЕМА ГАМИЛЬТОНА—ЯКОБИ
- § 16.1. Уравнение Гамильтона в частных производных.
- § 16.2. Теорема Гамильтона — Якоби (доказательство первое).
- § 16.3. Теорема об эквивалентности.
- § 16.4. Теорема Гамильтона — Якоби (доказательство второе).
- § 16.5. Замечания по теореме Гамильтона — Якоби.
- § 16.6. Однородное поле.
- § 16.7. Гармонический осциллятор.
- § 16.8 Частица в переменном поле At.
- § 16.9. Центральная орбита.
- § 16.10. Сферический маятник.
- § 16.11. Вращающийся волчок.
- § 16.12. Стержень на вращающейся плоскости.
- § 16.13. Электрон в центральном поле.
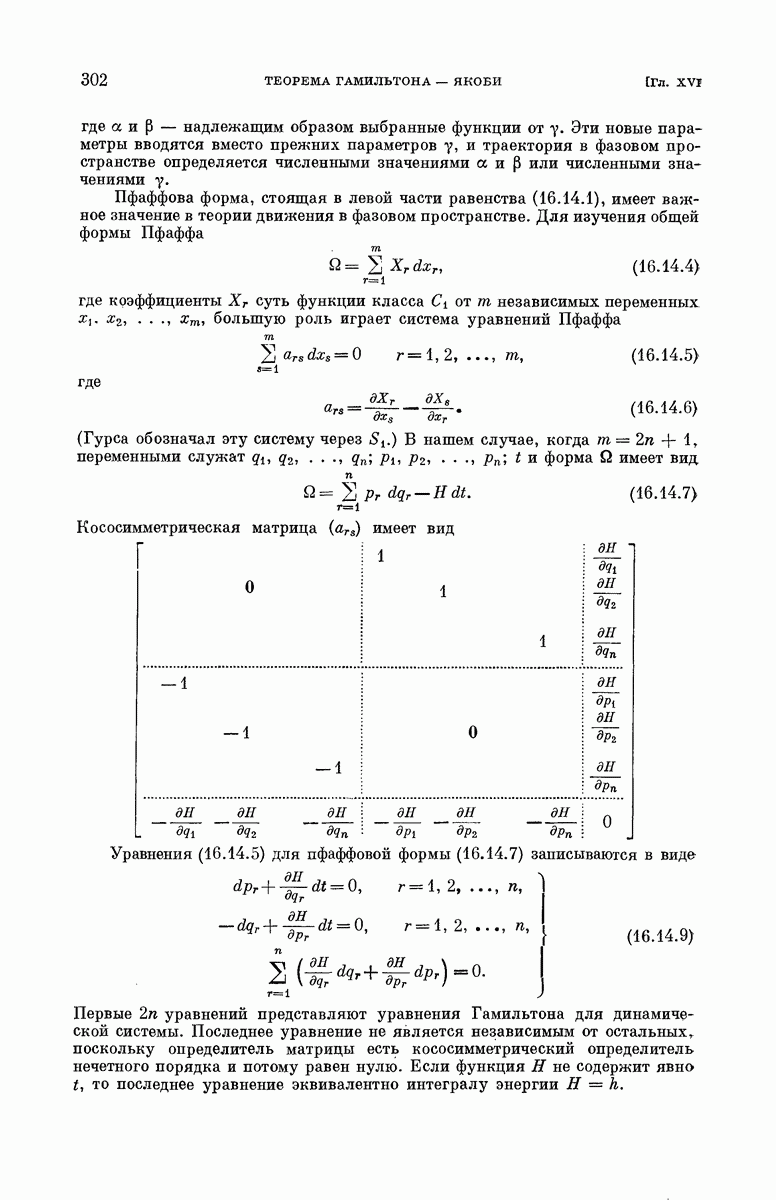
- § 16.14. Пфаффова форма
- Глава XVII. СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 17.2. Условия разделимости переменных в системах с двумя степенями свободы.
- § 17.3. Изучение движения системы.
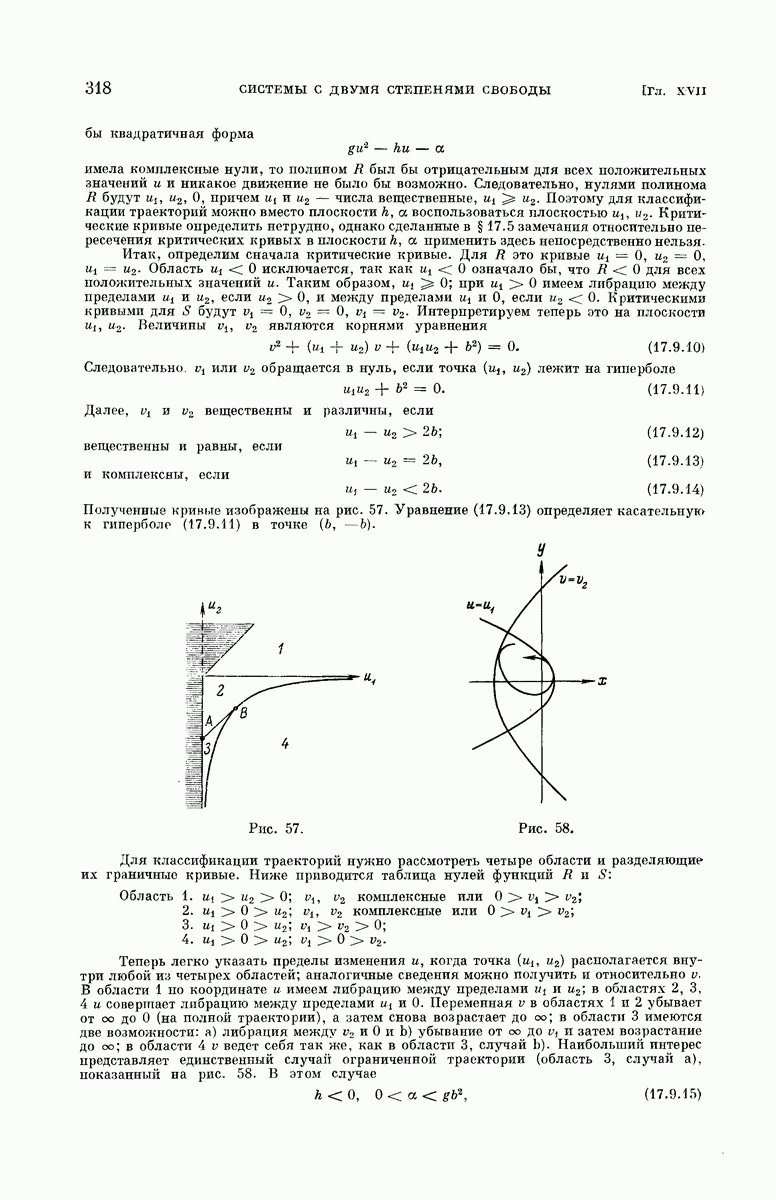
- § 17.4. Классификация траекторий.
- § 17.5. Устойчивость.
- § 17.6. Приложения теории.
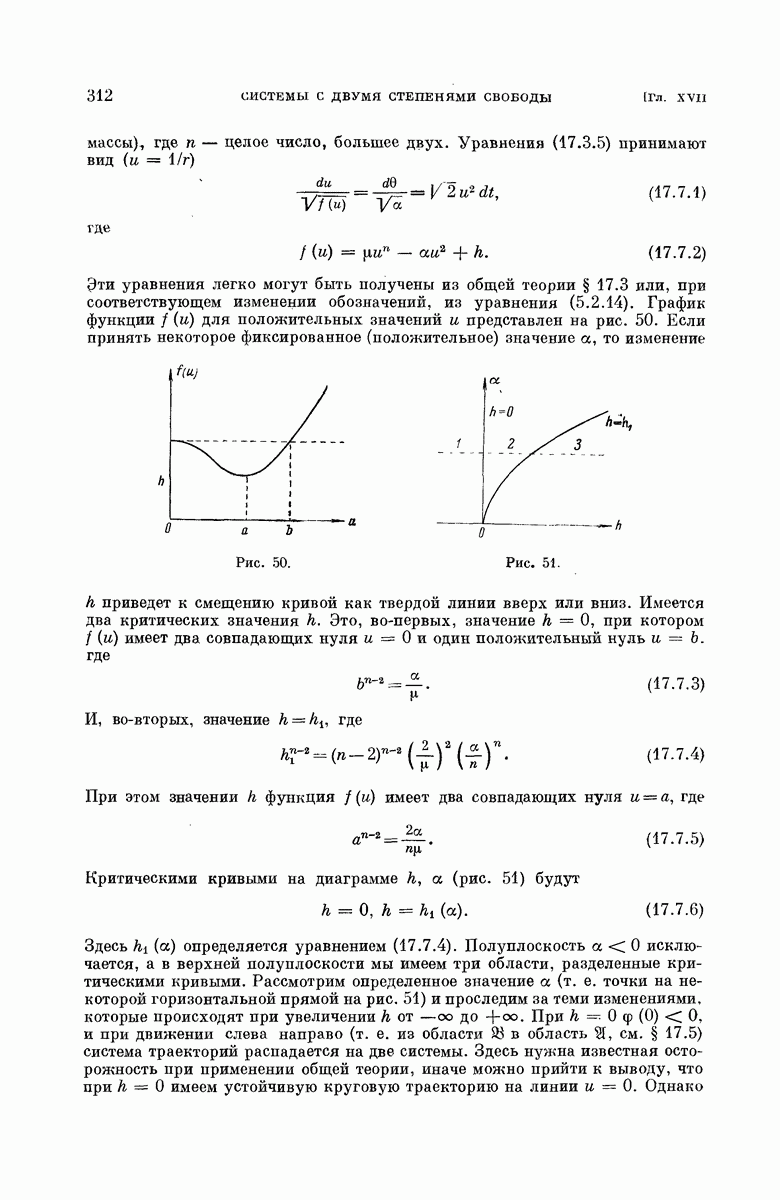
- § 17.7. Притяжение к центру по закону …
- § 17.8. Притяжение к центру по закону …
- § 17.9. Ньютоновское притяжение и однородное поле.
- § 17.10. Два неподвижных притягивающих центра
- § 17.11. Ограниченные траектории.
- § 17.12. Уравнения орбит.
- § 17.13. Неограниченные орбиты.
- § 17.14. Системы, допускающие разделение переменных более чем одним способом.
- Глава XVIII. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 18.1. Система Лиувилля
- § 18.2. Теорема Штеккеля.
- § 18.3. Исследование интегралов.
- § 18.4. Дополнительные замечания к теореме Штеккеля.
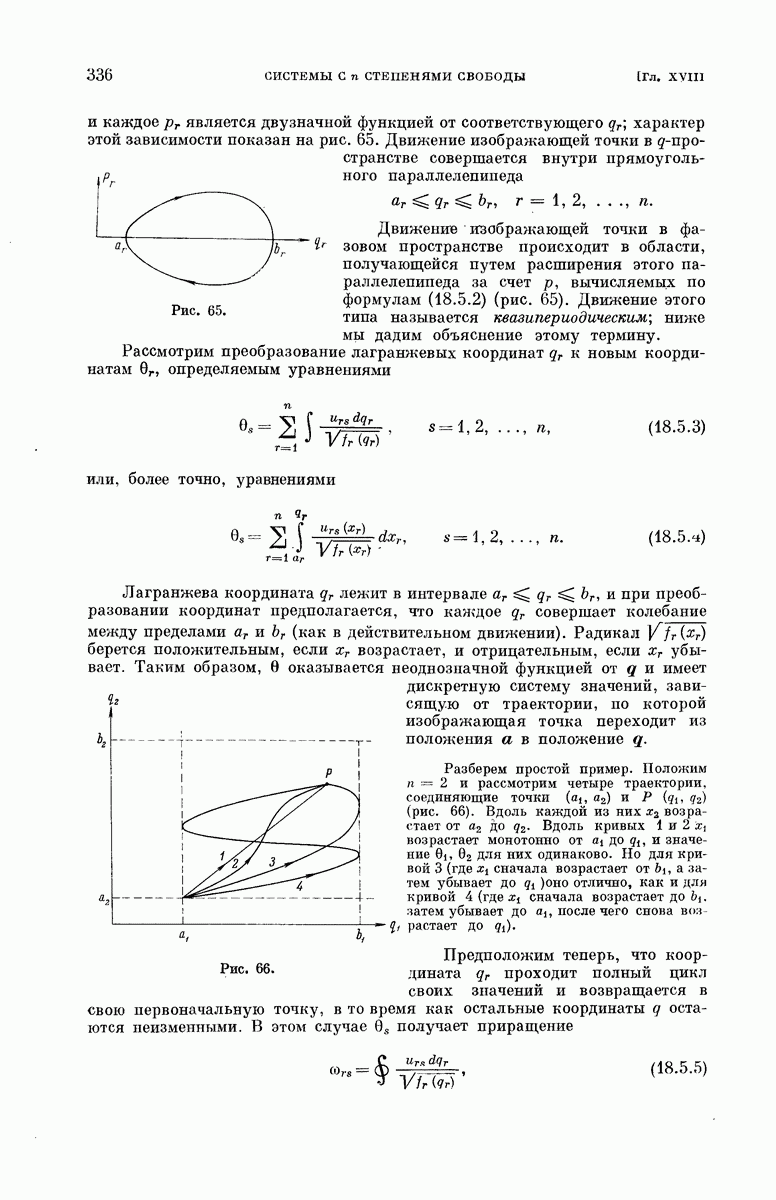
- § 18.5. Квазипериодические движения.
- § 18.6. Угловые переменные.
- § 18.7. Стандартный куб.
- § 18.8. Постоянные …
- § 18.9. Соотношения между q и v.
- § 18.10. Малые колебания.
- § 18.11. Сферический маятник.
- § 18.12. Задача двух тел.
- § 18.13. Интерпретация параметров a и b.
- § 18.14. Выражение r как функции от t.
- § 18.15. Угловые переменные.
- § 18.16. Постоянные …
- § 18.17. Возмущения.
- § 18.18. Неортогональные и ненатуральные разделимые системы.
- Глава XIX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ, ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ
- § 19.2. Движение частицы по прямой.
- § 19.3. Система с одной степенью свободы.
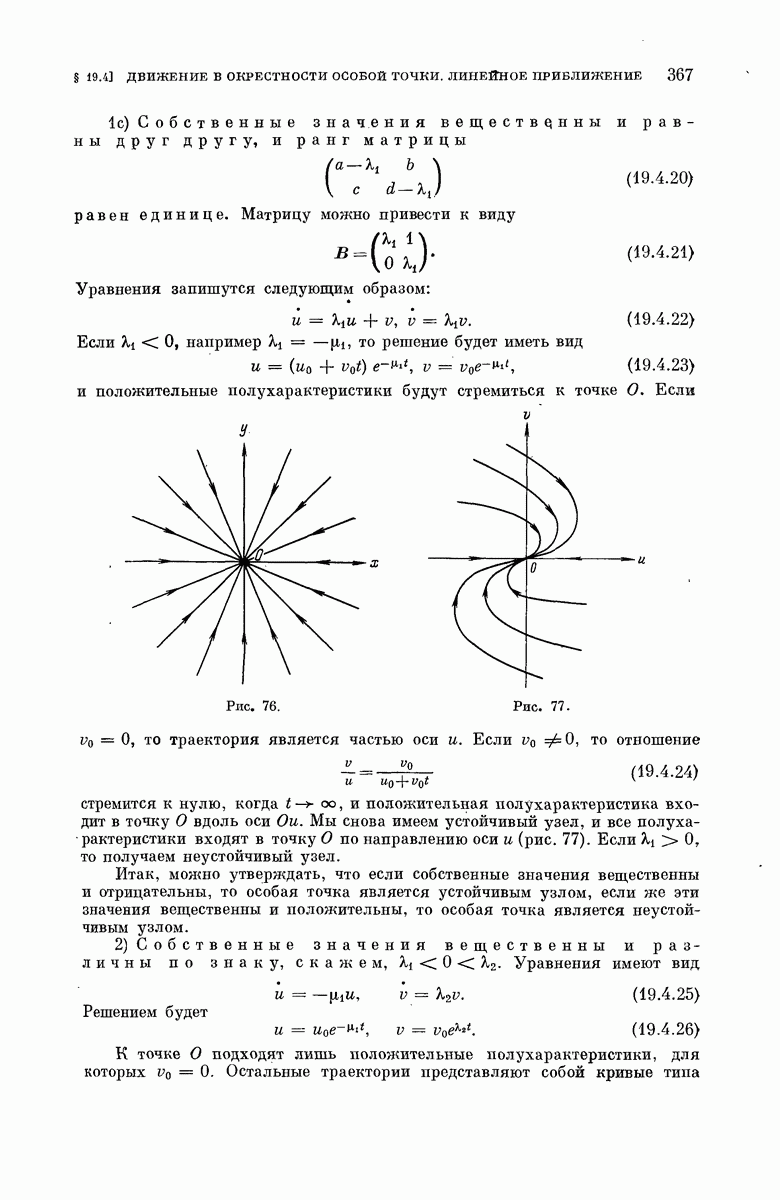
- § 19.4. Движение в окрестности особой точки. Линейное приближение.
- § 19.5. Устойчивость равновесия. Асимптотическая устойчивость и неустойчивость.
- § 19.6. Движение в окрестности особой точки. Общая теория.
- § 19.7. Движение в окрестности узла.
- § 19.8. Движение в окрестности седловой точки.
- § 19.9. Движение в окрестности фокуса.
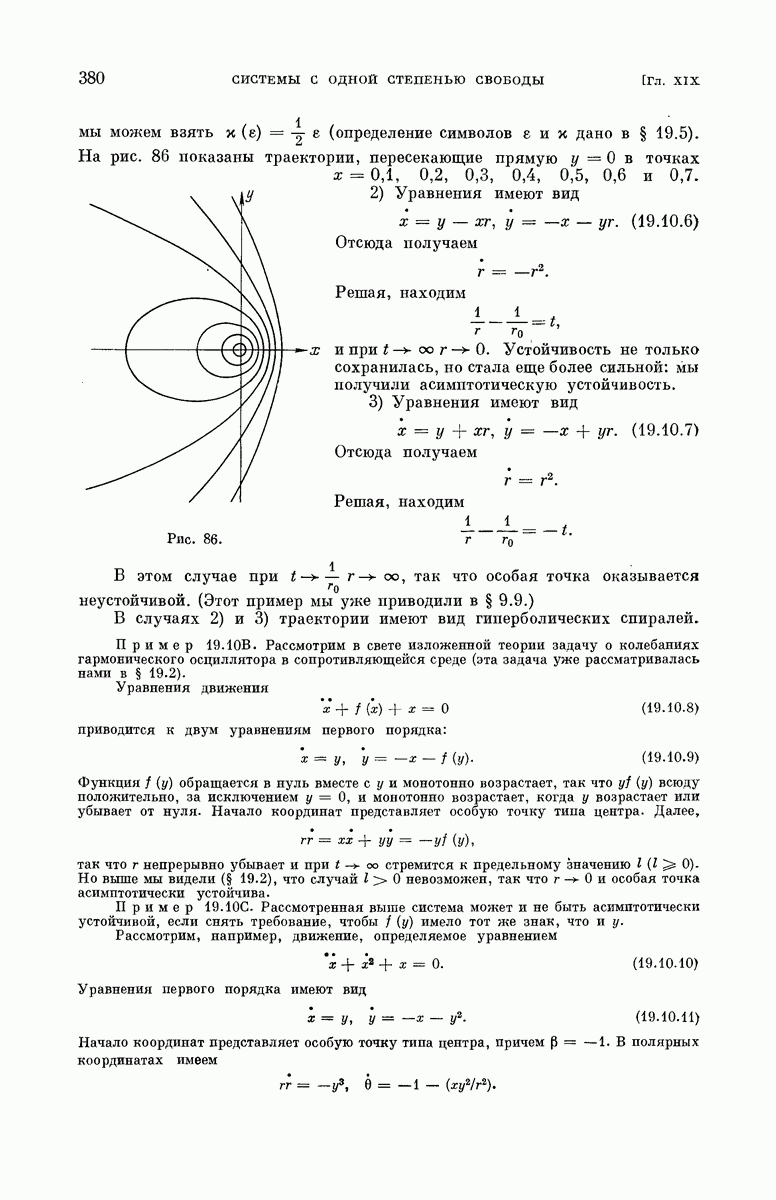
- § 19.10. Движение в окрестности центра.
- § 19.11. Связь линейного приближения с общей теорией.
- Глава XX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- § 20.2. Положительное предельное множество.
- § 20.3. Отрезок без контакта.
- § 20.4. Отрезок без контакта, проходящий через точку множества A.
- § 20.5. Структура множества A.
- § 20.6. Теорема Пуанкаре — Бендиксона.
- § 20.7. Приложение к системе частного вида.
- § 20.8. Существование предельного цикла.
- § 20.9. Уравнение Ван-дер-Поля.
- Глава XXI. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК
- § 21.2. Преобразование к новым координатам.
- § 21.3. Оператор Tt
- § 21.4. Решение в форме степенных рядов.
- § 21.5. Формула для X(x)-X(a)
- § 21.6. Интегральные инварианты.
- § 21.7. Интегральные инварианты порядка m.
- § 21.8. Свойства множителей.
- § 21.9. Последний множитель Якоби.
- § 21.10. Линейная система.
- § 21.11. Устойчивость равновесия.
- § 21.12. Дискретная устойчивость.
- § 21.13. Устойчивость преобразований.
- § 21.14. Приложение к дифференциальным уравнениям.
- § 21.15. Теорема Пуанкаре — Ляпунова.
- § 21.16. Критический случай.
- Глава XXII. УРАВНЕНИЯ ГАМИЛЬТОНА
- § 22.1. Уравнения Гамильтона.
- § 22.2. Скобки Пуассона.
- § 22.3. Теорема Пуассона.
- § 22.4. Использование известного интеграла.
- § 22.5. Линейный интегральный инвариант Пуанкаре.
- § 22.6. Теорема Лиувилля.
- § 22.7. Теорема возвращения (теорема Пуанкаре).
- § 22.8. Примеры инвариантных областей.
- § 22.9. Эргодические теоремы.
- § 22.10. Конкретные примеры.
- § 22.11. Множество …
- § 22.12. Собственные отрезки.
- § 22.13. Доказательство эргодической теоремы; первый этап.
- § 22.14. Доказательство эргодической теоремы; второй этап.
- § 22.15. Метрическая неразложимость.
- § 22.16. Интегралы уравнений движения.
- § 22.17. Следствие теоремы Лиувилля.
- § 22.18. Последний множитель.
- Глава XXIII. ДВИЖЕНИЕ В ОКРЕСТНОСТИ ЗАДАННОГО ДВИЖЕНИЯ. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- § 23.2. Решение уравнений в вариациях.
- § 23.3. Случай постоянных коэффициентов.
- § 23.4. Случай периодических коэффициентов.
- § 23.5. Нулевые показатели.
- § 23.6. Уравнения в вариациях для системы Гамильтона.
- § 23.7. Устойчивость траекторий (1).
- § 23.8. Устойчивость траекторий (2).
- § 23.9. Устойчивость периодических орбит.
- § 23.10. Вынужденные колебания.
- Глава XXIV. КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ
- § 24.1. Контактные преобразования.
- § 24.2. Формулы контактного преобразования.
- § 24.3. Другие формулы.
- § 24.4. Обобщенное точечное преобразование и другие однородные контактные преобразования.
- § 24.5. Специальная форма уравнений преобразований. Бесконечно малые контактные преобразования.
- § 24.6. Обобщение теоремы Лиувилля.
- § 24.7. Условия контактности преобразования, скобки Лагранжа.
- § 24.8. Соотношения между двумя системами производных.
- § 24.9. Условия контактности преобразования, выраженные с помощью скобок Пуассона.
- § 24.10. Соотношения между скобками Лагранжа и скобками Пуассона.
- § 24.11. Приложение к контактному преобразованию.
- § 24.12. Инвариантность скобки Пуассона.
- § 24.13. Другая форма условий контактности преобразования.
- § 24.14. Функции, находящиеся в инволюции.
- § 24.15. Некоторые примеры.
- Глава XXV. ТЕОРИЯ ПРЕОБРАЗОВАНИЙ
- § 25.1. Уравнения движения после контактных преобразований.
- § 25.2. Вариация элементов траектории.
- § 25.3. Вариация эллиптических элементов.
- § 25.4. Другие доказательства теоремы Якоби.
- § 25.5. Постоянство скобок Лагранжа.
- § 25.6. Бесконечно малые контактные преобразования.
- § 25.7. Интегралы в инволюции.
- § 25.8. Теорема Ли о системах в инволюции.
- § 25.9. Интегралы, линейные относительно импульсов.
- § 25.10. Случай, когда функция Гамильтона является однородной квадратичной формой
- Глава XXVI. ВАРИАЦИОННЫЕ ПРИНЦИПЫ
- § 26.2. Теорема Ливенса.
- § 26.3. Точки минимума и седловые точки.
- § 26.4. Асинхронное варьирование. Принцип Гёльдера.
- § 26.5. Принцип Фосса.
- § 26.6. Обобщение принципа Гамильтона.
- § 26.7. Замена независимой переменной.
- § 26.8. Нормальная форма системы с двумя степенями свободы.
- § 26.9. Система Лиувилля.
- § 26.10. Конформные преобразования.
- Глава XXVII. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- § 27.3. Принцип наименьшего действия в форме Якоби.
- § 27.4. Теорема Уиттекера.
- § 27.5. Исключение координат.
- § 27.6. Характеристическая функция.
- § 27.7. Пространство конфигураций.
- § 27.8. Система с двумя степенями свободы.
- § 27.9. Теорема Кельвина.
- § 27.10. Однородное поле.
- § 27.11. Задача Тэта. Непосредственное решение.
- § 27.12. Задача Тэта. Теория огибающих.
- Глава XXVIII. ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 28.2. Ограниченная задача. Уравнения движения.
- § 28.3. Положения равновесия.
- § 28.4. Положения равновесия на прямой АВ.
- § 28.5. Положения равновесия, не лежащие на прямой АВ
- § 28.6. Поверхность z=U.
- § 28.7. Движение вблизи положения равновесия.
- § 28.8. Теория движения Луны.
- Глава XXIX. ЗАДАЧА ТРЕХ ТЕЛ
- § 29.2. Случай, когда вектор момента количеств движения равен нулю.
- § 29.3. Три точки Лагранжа.
- § 29.4. Решения, для которых треугольник Лагранжа сохраняет свою форму.
- § 29.5. Случай плоского движения.
- § 29.6. Координаты относительно частицы Az
- § 29.7. Движение в окрестности равновесного решения.
- § 29.8. Сведение к системе шести уравнений.
- § 29.9. Устойчивость трех точек Лагранжа.
- § 29.10. Преобразованная форма уравнений движения.
- § 29.11. Другой подход к задаче трех точек Лагранжа.
- § 29.12. Сведение к системе восьми уравнений.
- § 29.13. Невозможность тройных столкновений.
- § 29.14. Плоское движение. Другой способ приведения к системе шестого порядка.
- § 29.15. Равновесные решения.
- Глава XXX. ПЕРИОДИЧЕСКИЕ ОРБИТЫ
- § 30.1. Периодические орбиты.
- § 30.3. Условия вещественности.
- § 30.4. Уравнения Гамильтона.
- § 30.5. Сходимость.
- § 30.6. Три точки Лагранжа.
- § 30.7. Системы, содержащие параметр.
- § 30.8. Приложение к ограниченной задаче трех тел.
- § 30.9. Метод неподвижной точки.
- § 30.11. Периодические орбиты и теорема о кольце.
- § 30.12. Доказательство теоремы Пуанкаре о кольце.