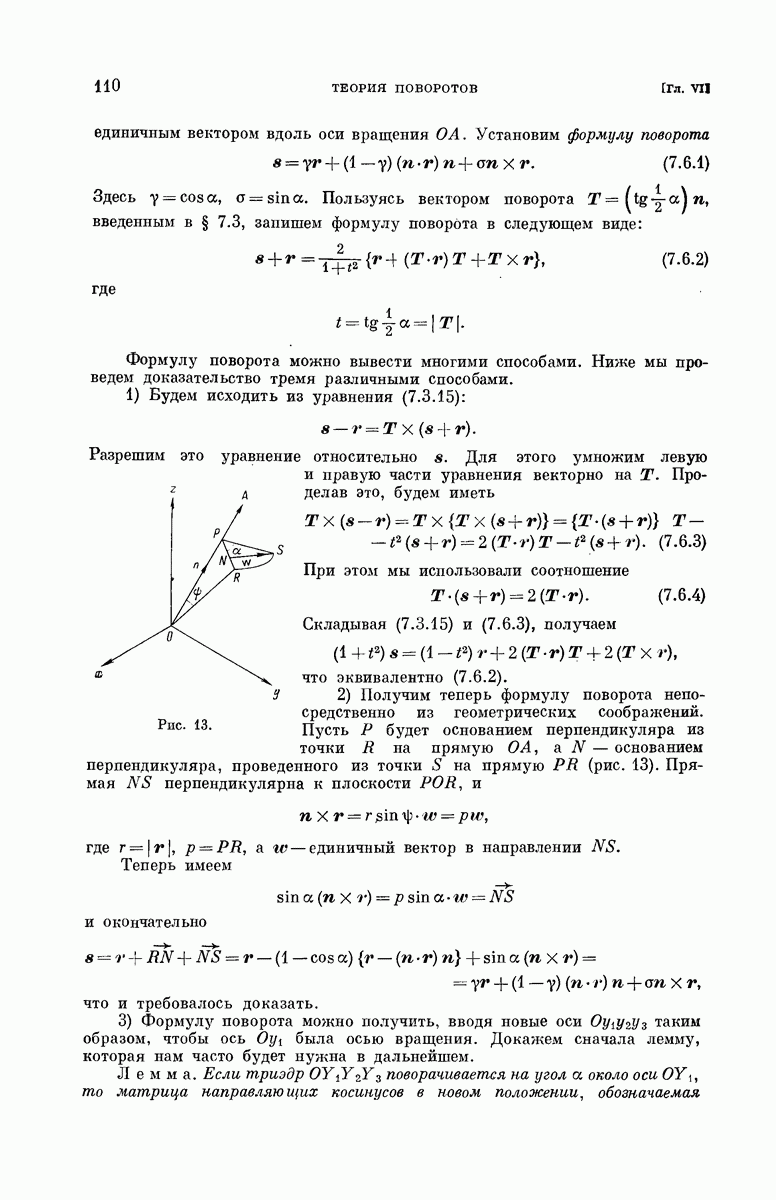
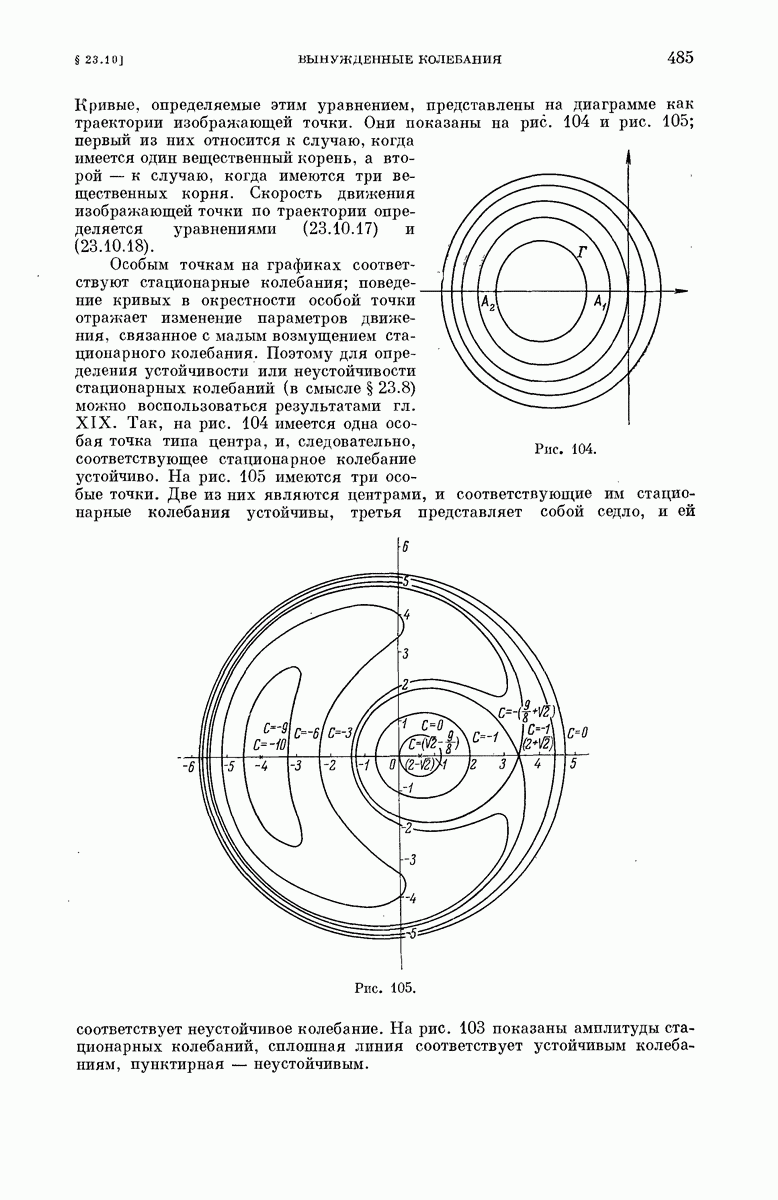
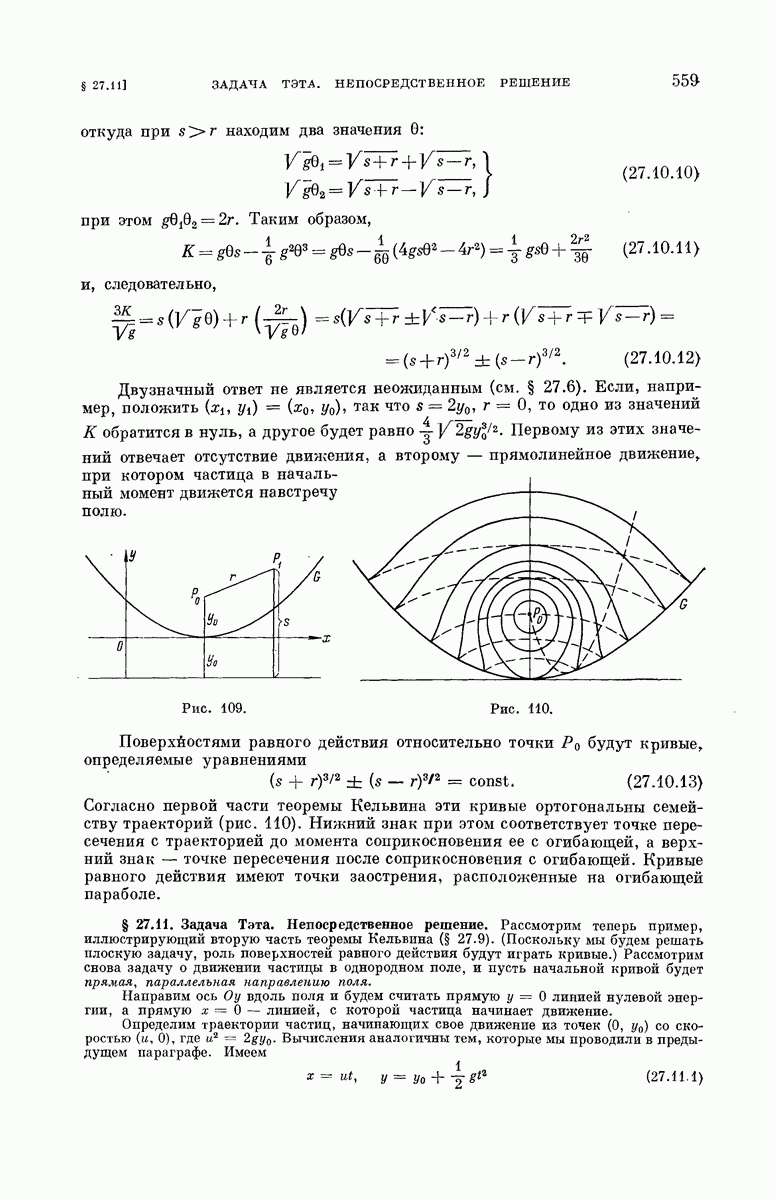
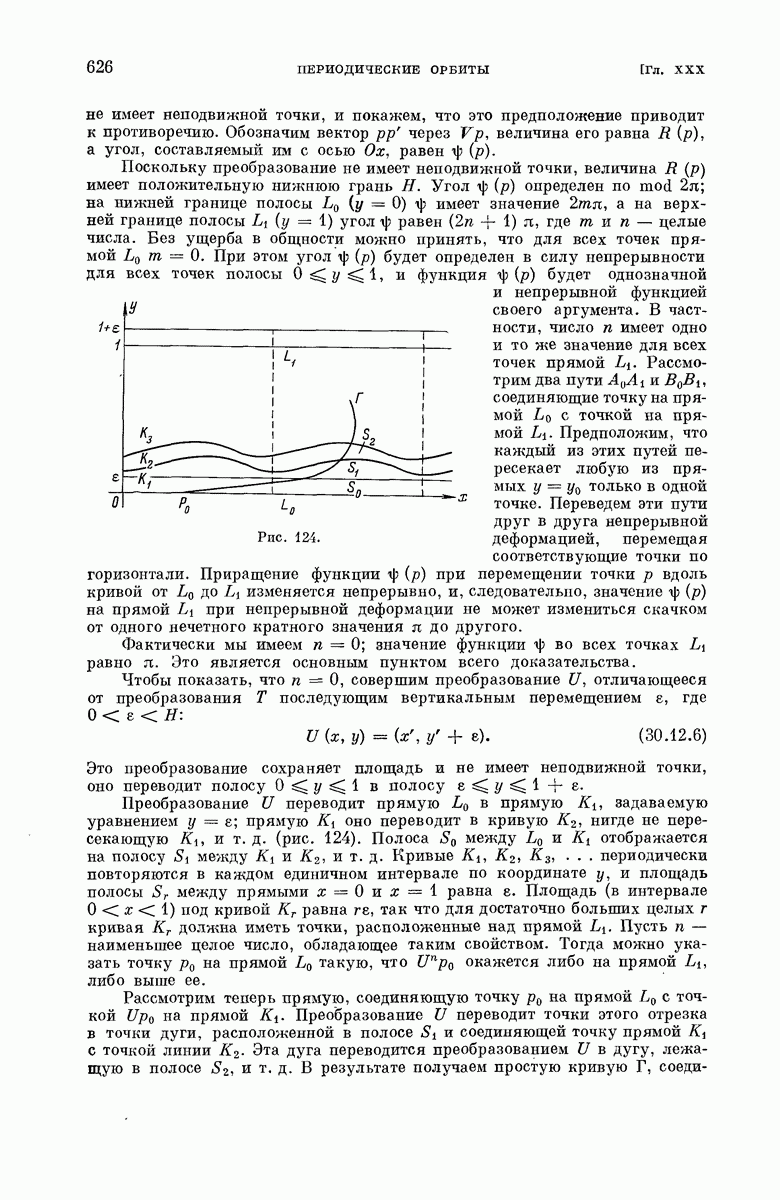
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5.2. Некоторые классические задачи.
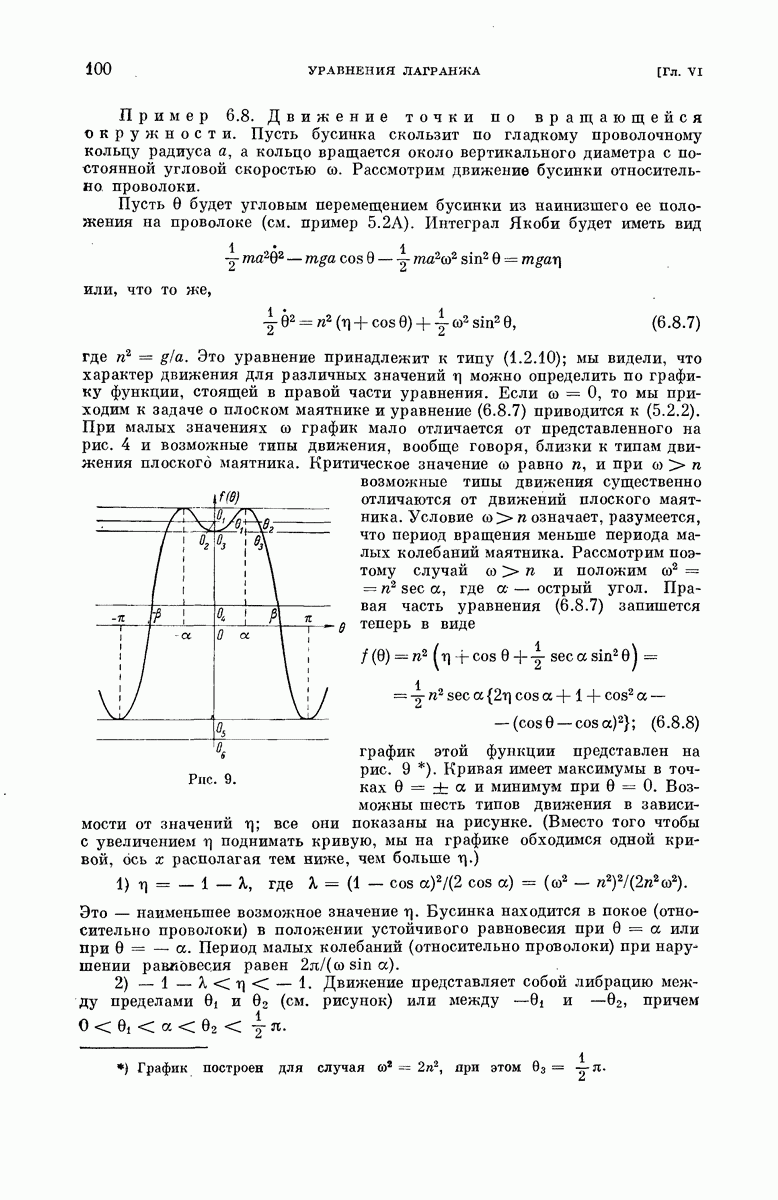
Позже (в § 6.2) мы выведем уравнения Лагранжа, описывающие движение механической системы в лагранжевых координатах. Однако уже сейчас мы можем решить некоторые важные задачи, не пользуясь уравнениями Лагранжа. Рассмотрим пять задач. Четыре из них (примеры 5.2А, 5.2В, 5.2С и § 5.3) могут быть решены с помощью одних только законов сохранения энергии (3.4.5) и сохранения момента количества движения (3.2.12). В последней задаче (§§ 5.4, 5.5, 5.6) мы используем также уравнения движения в декартовых координатах.
Пример 5.2А. Простой маятник. Тяжелая точка движется без трения по окружности радиуса а в вертикальной плоскости. Система голономна с одной степенью свободы. В качестве лагранжевой координаты возьмем угол 9, отсчитываемый от наинизшей точки окружности. Заданной силой здесь является вес частицы, а реакцией связи — нормальная реакция проволоки (если представить, что бусинка скользит по гладкой проволоке) или натяжение стержня (если считать, что частица закреплена на конце невесомого стержня, другой конец которого шарнирно закреплен в неподвижной точке). Потенциальная энергия равна  где
где  высота частицы относительно центра окружности. Уравнение энергии имеет вид
высота частицы относительно центра окружности. Уравнение энергии имеет вид

Положим  где
где  безразмерная величина, а
безразмерная величина, а  высота энергетического уровня
высота энергетического уровня  над центром окружности (рис. 3). В этих обозначениях уравнение (5.2.1) переписывается в виде
над центром окружности (рис. 3). В этих обозначениях уравнение (5.2.1) переписывается в виде

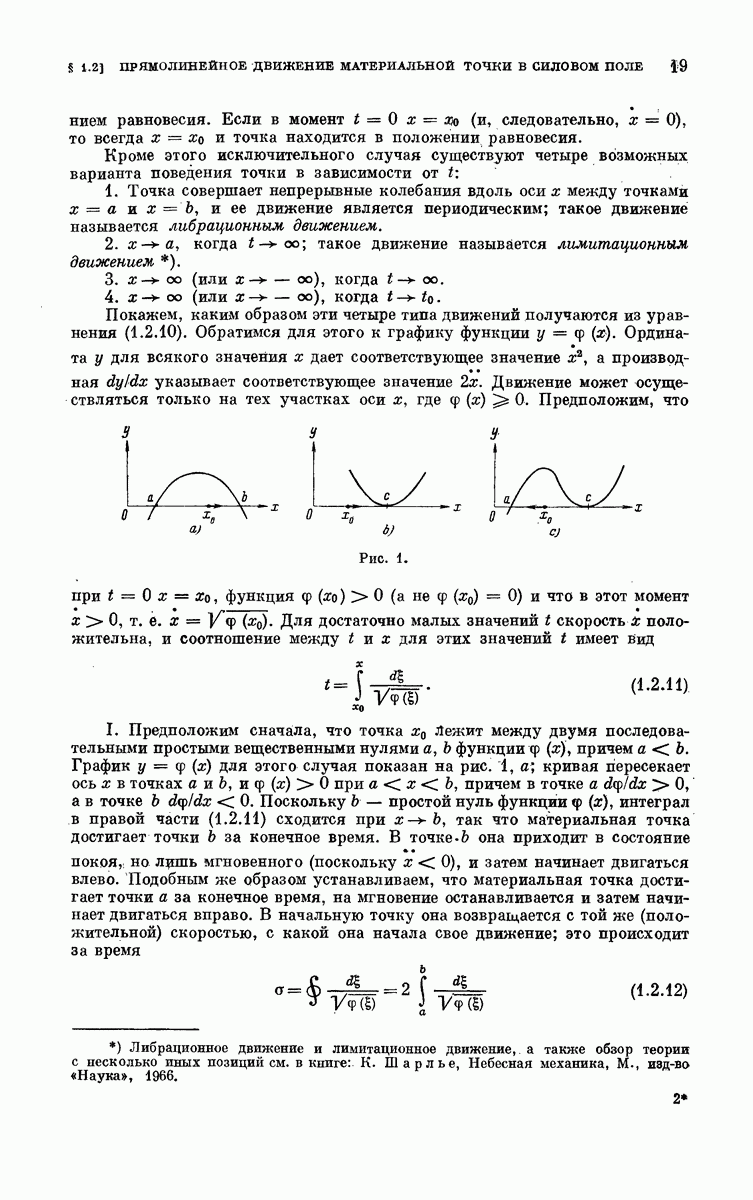
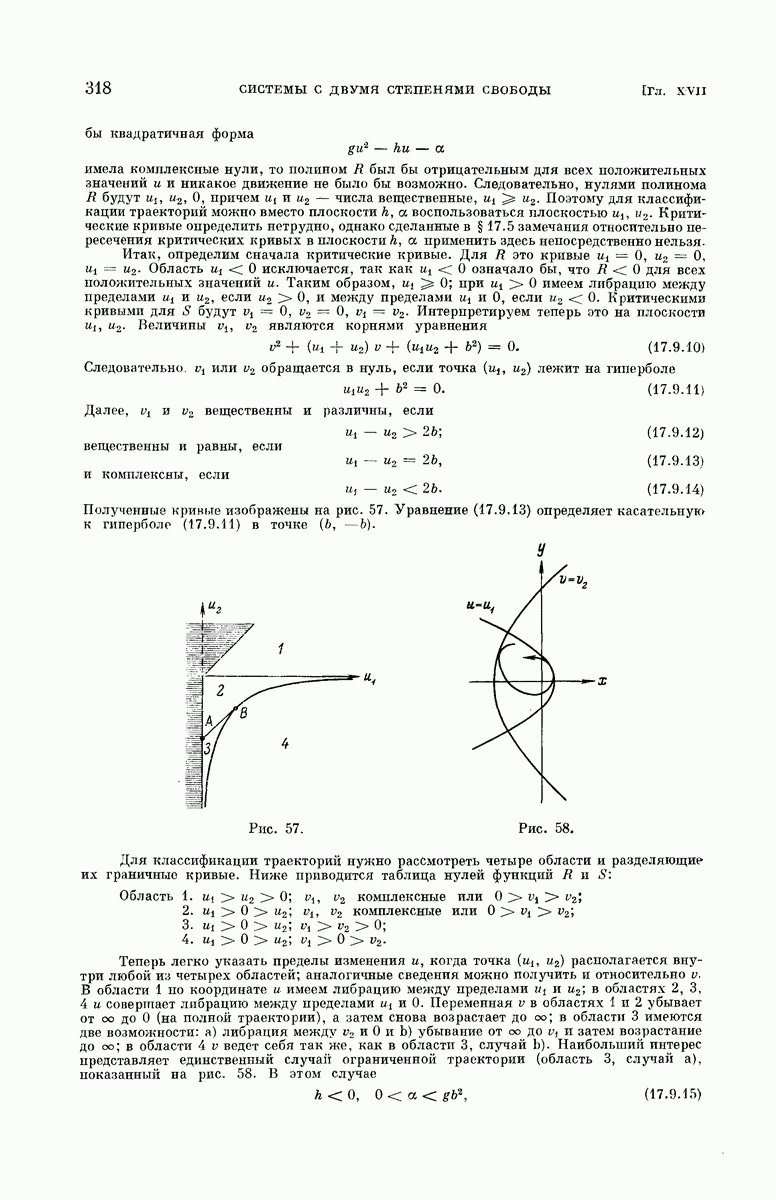
Это уравнение принадлежит к типу (1.2.10), и решение его уже было нами исследовано. Если  то движение невозможно. График правой части уравнения (5.2.2), приведенный на рис. 4, показывает, что могут иметь место четыре следующих случая:
то движение невозможно. График правой части уравнения (5.2.2), приведенный на рис. 4, показывает, что могут иметь место четыре следующих случая:
1)  ; частица находится в покое в положении устойчивого равновесия при
; частица находится в покое в положении устойчивого равновесия при 
2)  ; частица совершает либрационное движение в пределах от —а до а, т. е. совершает типичное для маятника движение;
; частица совершает либрационное движение в пределах от —а до а, т. е. совершает типичное для маятника движение;
3)  ; частица находится в покое в положении неустойчивого равновесия при
; частица находится в покое в положении неустойчивого равновесия при  или совершает лимитационное движение, при котором
или совершает лимитационное движение, при котором  (или —я), когда
(или —я), когда 

Рис. 3.

Рис. 4.
4)  ; угол
; угол  непрерывно возрастает вместе с t (если в начальный момент
непрерывно возрастает вместе с t (если в начальный момент 
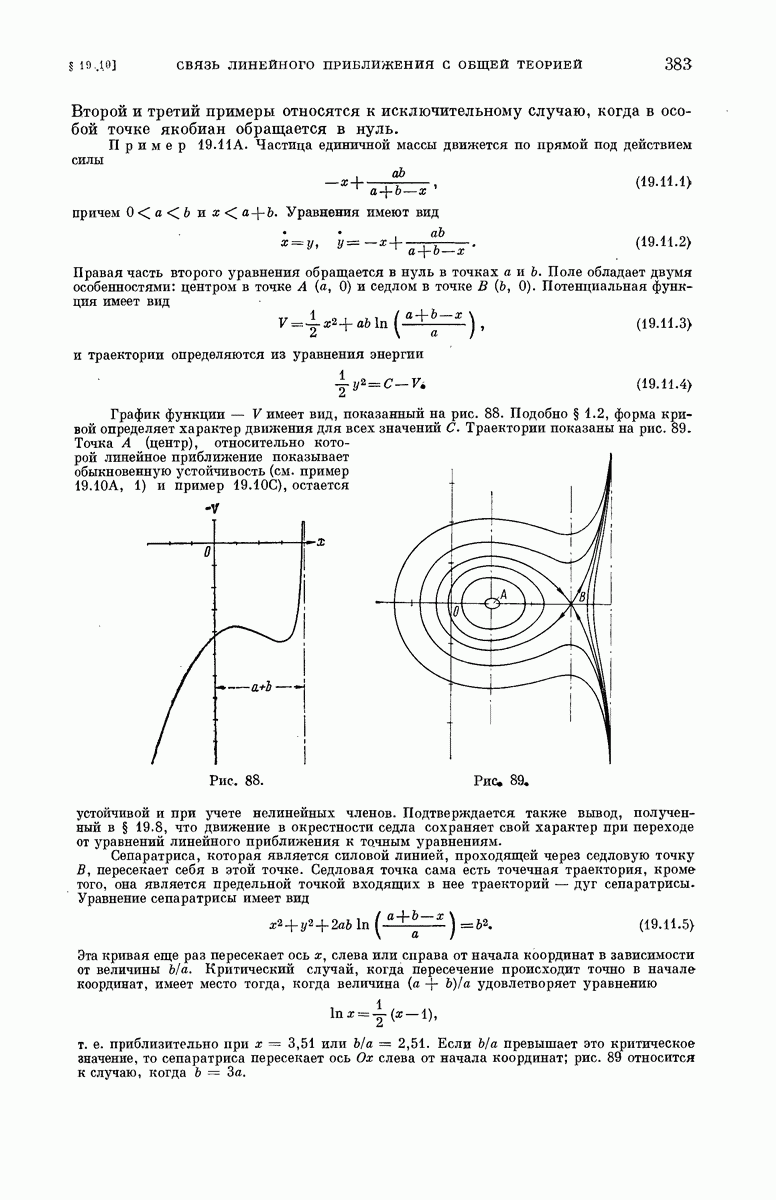
Рассмотрим эти случаи более подробно.
1) При изменении  от —1 до
от —1 до  имеют место малые колебания около положения
имеют место малые колебания около положения  с периодом
с периодом  и амплитудой
и амплитудой  (см. пример 1.2А).
(см. пример 1.2А).

Полагая

находим

Решение, удовлетворяющее условию  при
при  имеет вид
имеет вид

Таким образом, окончательно получаем

где  а
а  обозначает угловую скорость в момент, когда
обозначает угловую скорость в момент, когда  Период
Период  равен
равен  Заметим, что с ростом а от
Заметим, что с ростом а от  до
до  период
период  монотонно возрастает от
монотонно возрастает от  до
до 
Рассмотрим лимитационное движение, приняв  в момент
в момент  Имеем
Имеем

Отсюда

Этот результат можно представить в более удобной форме. Пользуясь равенством

находим

откуда

и окончательно

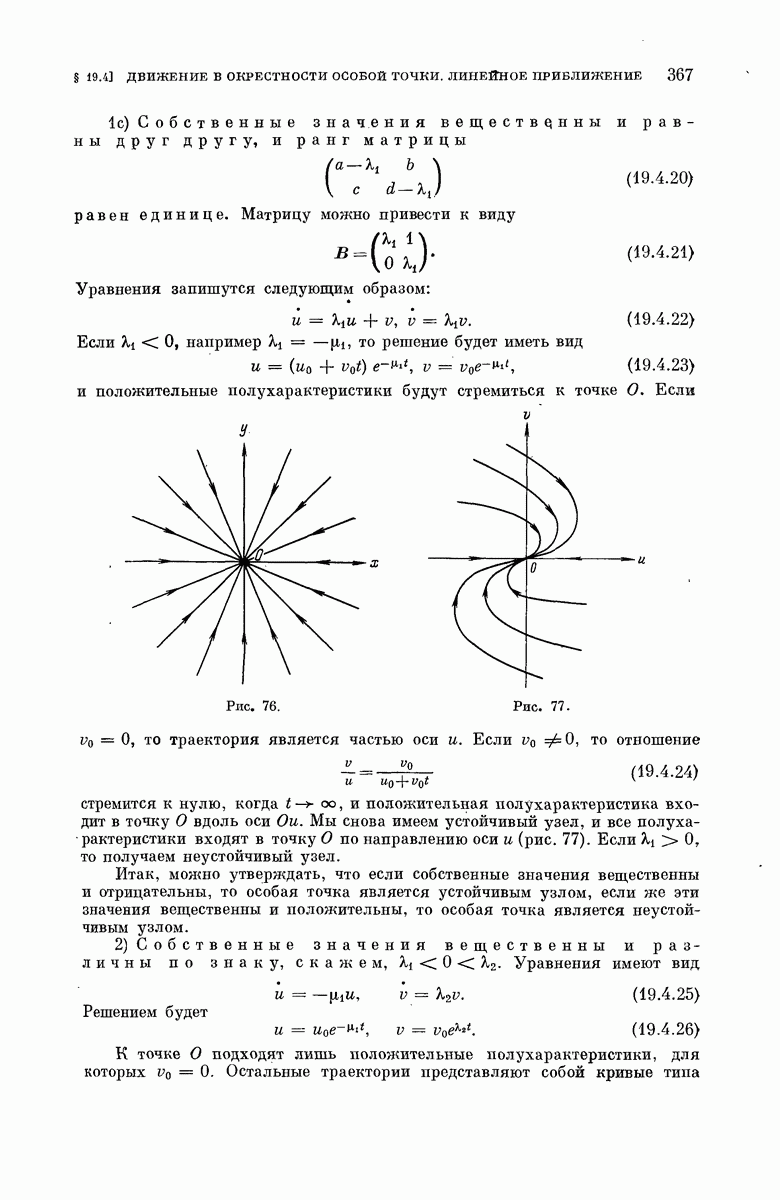
Последняя форма (5.2.7), по-видимому, наиболее удобна. Заметим, что (как уже известно из общей теории)  и при
и при 
Если положить  то
то  и приближенно
и приближенно  . В этом случае имеем
. В этом случае имеем  где
где  и окончательно
и окончательно

При этом, как и ранее, предполагалось, что  при
при 
Движение является периодическим.  непрерывно возрастает, но является циклической координатой: значения
непрерывно возрастает, но является циклической координатой: значения  эквивалентны, поскольку соответствуют одному и тому же положению системы. Период равен
эквивалентны, поскольку соответствуют одному и тому же положению системы. Период равен 
Таким образом, для трех последних случаев имеем

В заключение напишем дифференциальное уравнение, описывающее рассматриваемое движение:

Его можно вывести из уравнения (5.2.1) или получить непосредственно. И обратно, из уравнения (5.2.10) легко вывести уравнение (5.2.1). Если рассматривать малые колебания около положения устойчивого рановесия  то приближенная форма уравнения совпадает с уравнением гармонического движения
то приближенная форма уравнения совпадает с уравнением гармонического движения

Период колебаний, как уже отмечалось, приближенно равен 
Зависимость  от
от  получаемая в результате решения уравнения (5.2.10), представлена графически на рис. 5 для различных положительных значений
получаемая в результате решения уравнения (5.2.10), представлена графически на рис. 5 для различных положительных значений  . При
. При  , превышающих критическое значение
, превышающих критическое значение  переменная
переменная  всегда возрастает с ростом t. В этом случае вместо значения
всегда возрастает с ростом t. В этом случае вместо значения  в промежутке
в промежутке
 можно взять соответствующее значение
можно взять соответствующее значение  в промежутке
в промежутке  представляющее ту же самую точку окружности, что и делалось при построении графика.
представляющее ту же самую точку окружности, что и делалось при построении графика.

Рис. 5
Приближенное вычисление периода. В случае 2), когда маятник совершает колебания с амплитудой а, период равен  . Этот результат является точным, однако существуют различные приближенные способы вычисления периода, в которых не используются эллиптические функции.
. Этот результат является точным, однако существуют различные приближенные способы вычисления периода, в которых не используются эллиптические функции.
Прежде всего заметим, что для малых колебаний хорошим приближением для периода служит  если а достаточно мало. Если а представляет собой острый угол, то
если а достаточно мало. Если а представляет собой острый угол, то

Рассмотрим ту четверть периода, в которой значения  и
и  положительны. Когда х увеличивается от
положительны. Когда х увеличивается от  до а, отношение
до а, отношение  монотонно убывает от 1 до
монотонно убывает от 1 до  так что при заданном
так что при заданном  имеем
имеем

и

Таким образом, величина четверти периода

заключена между пределами

а значение а — между пределами

Если амплитуда составляет 5°, то значение приближенно равно 1,0007 и классическое значение  отличается от точного менее чем на одну десятую процента.
отличается от точного менее чем на одну десятую процента.
Можно получить более точную оценку периода, если воспользоваться одной теоремой, относящейся к арифметическому и геометрическому средним значениям. Пусть  два заданных положительных числа, таких, что
два заданных положительных числа, таких, что  Образуем две бесконечные последовательности
Образуем две бесконечные последовательности  по следующему правилу:
по следующему правилу:  при
при  представляет собой среднее арифметическое чисел
представляет собой среднее арифметическое чисел  среднее геометрическое этих же чисел. Последовательность
среднее геометрическое этих же чисел. Последовательность  тогда будет монотонно убывающей, а
тогда будет монотонно убывающей, а  монотонно возрастающей, и при
монотонно возрастающей, и при  обе эти последовательности стремятся к одному и тому же пределу
обе эти последовательности стремятся к одному и тому же пределу  Для каждого значения
Для каждого значения  справедливы неравенства
справедливы неравенства  и величина
и величина  аппроксимирует
аппроксимирует  с ошибкой, меньшей чем
с ошибкой, меньшей чем  Рассмотрим теперь интеграл
Рассмотрим теперь интеграл

С помощью подстановки

докажем, что

Продолжая этот процесс, убедимся, что для всех значений 

Значение  лежит между пределами и
лежит между пределами и  каждый из которых стремится к значению
каждый из которых стремится к значению  таким образом,
таким образом,

Для того чтобы оценить быстроту сходимости, можно воспользоваться равенствами

и

Первое из них получается сразу, если заметить, что левая и правая части порознь равны 
Пользуясь этими результатами, найдем приближенное значение периода  соответствующего амплитуде а
соответствующего амплитуде а  Обозначая через
Обозначая через 
период малых колебаний, получаем из (5.2.3)

где  следовательно,
следовательно,

причем  а. Первые несколько членов последовательностей
а. Первые несколько членов последовательностей  имеют следующий вид:
имеют следующий вид:

В качестве приближенного значения для  можно взять
можно взять  или
или  Чтобы оценить величину относительной ошибки, введем параметры
Чтобы оценить величину относительной ошибки, введем параметры 

Тогда, учитывая соотношения  находим
находим

Полагая  и пользуясь (5.2.23), можем написать
и пользуясь (5.2.23), можем написать

Здесь

Кроме того,

и, следовательно,

Обозначим правую часть последнего неравенства через  . Это неравенство справедливо для
. Это неравенство справедливо для  но при а, слишком близких к
но при а, слишком близких к  , оно становится бесполезным. Если же что представляет наиболее интересный случай, то правая часть неравенства (5.2.33) будет максимальной
, оно становится бесполезным. Если же что представляет наиболее интересный случай, то правая часть неравенства (5.2.33) будет максимальной
при  в этом случае
в этом случае

и

поскольку  Окончательно будем иметь
Окончательно будем иметь

Здесь

Для большей части приложений такая точность вполне достаточна, но если требуется более высокая точность, можно взять  что даст ошибку
что даст ошибку

Пример 5.2В. Центральная орбита. Выберем центр притяжения за начало координат, а в качестве лагранжевых координат возьмем полярные координаты точки  Силовыми линиями здесь будут радиусы, а эквипотенциальными линиями (ортогональными семейству силовых линий) — окружности
Силовыми линиями здесь будут радиусы, а эквипотенциальными линиями (ортогональными семейству силовых линий) — окружности  Потенциальная функция будет зависеть поэтому только от
Потенциальная функция будет зависеть поэтому только от  обозначим ее через
обозначим ее через  так что 93 будет потенциальной энергией единицы массы. Сила притяжения
так что 93 будет потенциальной энергией единицы массы. Сила притяжения  также будет зависеть только от
также будет зависеть только от  Если мы имеем поле сил притяжения к точке О, то
Если мы имеем поле сил притяжения к точке О, то  является монотонно возрастающей функцией от
является монотонно возрастающей функцией от 
Имеем интеграл энергии и интеграл момента количества движения:

Предположим для определенности, что  положительное число, так что
положительное число, так что  возрастает вместе с t. В поле сил притяжения орбита располагается внутри окружности
возрастает вместе с t. В поле сил притяжения орбита располагается внутри окружности  если такая окружность существует. Исключая 0, находим
если такая окружность существует. Исключая 0, находим

Это уравнение принадлежит к типу (1.2.10), и решение его нами уже изучалось. В простейших случаях начальное значение  лежит между последовательными простыми вещественными нулями
лежит между последовательными простыми вещественными нулями  функции
функции  где через
где через  обозначена правая часть уравнения
обозначена правая часть уравнения  В радиальном направлении движение представляет собой либрацию между пределами
В радиальном направлении движение представляет собой либрацию между пределами  называемыми апсидалъными расстояниями, и орбита попеременно касается окружностей радиусов
называемыми апсидалъными расстояниями, и орбита попеременно касается окружностей радиусов  Точки касания, в которых
Точки касания, в которых  достигает минимального и максимального значений, называются апсидами; та из них, в которой
достигает минимального и максимального значений, называются апсидами; та из них, в которой  называется перигелием, а та,
называется перигелием, а та,
в которой  называется афелием. Угловая скорость
называется афелием. Угловая скорость  изменяется от наименьшего значения
изменяется от наименьшего значения  афелии) до наибольшего значения
афелии) до наибольшего значения  перигелии). Угол, на который поворачивается радиус-вектор между двумя последовательными апсидами, называется апсидалъным углом.
перигелии). Угол, на который поворачивается радиус-вектор между двумя последовательными апсидами, называется апсидалъным углом.
Связь между  выражается следующим соотношением:
выражается следующим соотношением:

Знак здесь выбирается согласно правилу, указанному в § 1.3. Таким образом, если частицы в момент  находится в перигелии, то
находится в перигелии, то

(знак в правой части для краткости записи опущен).
Связь между  и
и  может быть представлена в форме
может быть представлена в форме

причем знак перед корнем определяется так, как указывалось выше. Если в перигелии  то уравнение орбиты будет иметь вид
то уравнение орбиты будет иметь вид

Апсидальный угол равен

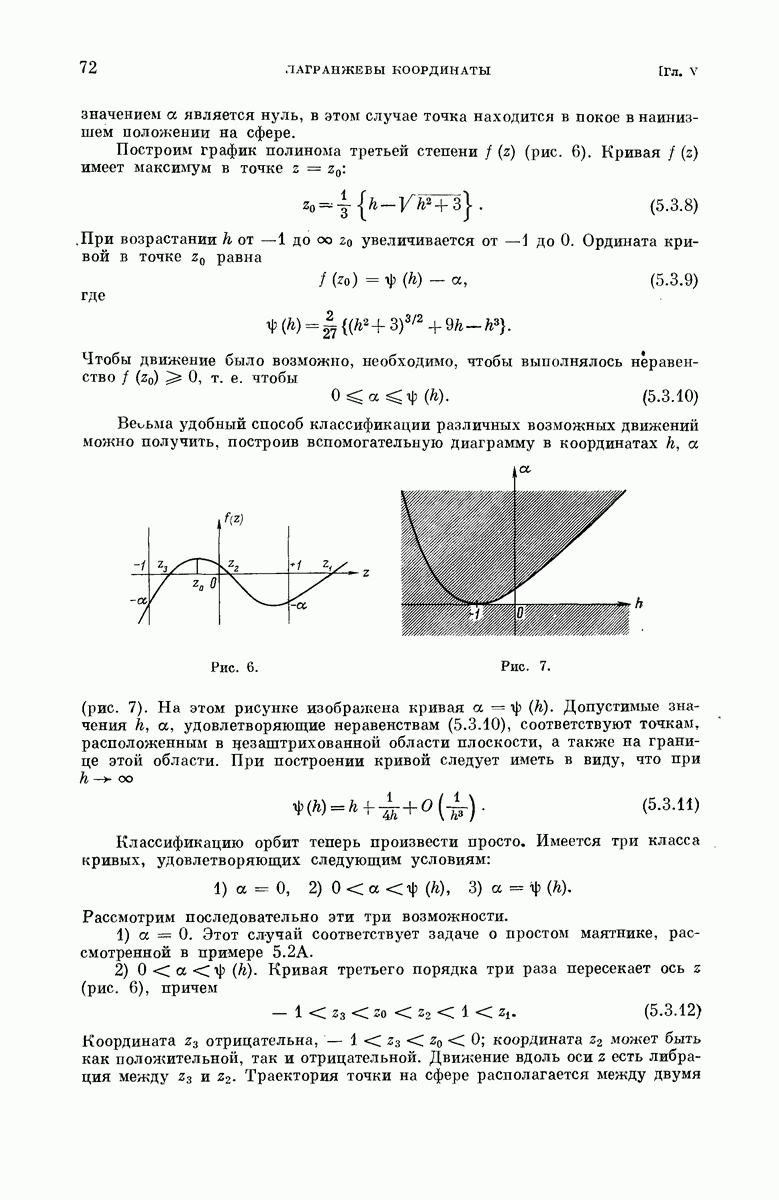
Орбита представляет собой простую замкнутую кривую С одним перигелием и одним афелием, если  Если отношение
Если отношение  есть число рациональное, т. е.
есть число рациональное, т. е.

где  целые числа, не имеющие общего множителя, то орбита является периодической с периодом
целые числа, не имеющие общего множителя, то орбита является периодической с периодом

Особый интерес представляют два частных случая. В изотропном осцилляторе притяжение пропорционально расстоянию от точки О, функция  имеет вид
имеет вид  и орбита представляет собой эллипс с центром в точке О. Апсидальный угол равен
и орбита представляет собой эллипс с центром в точке О. Апсидальный угол равен  В случае же притяжения точки по закону Ньютона сила обратно пропорциональна квадрату расстояния от точки
В случае же притяжения точки по закону Ньютона сила обратно пропорциональна квадрату расстояния от точки  Орбитой является коническое сечение, один из фокусов которого расположен в точке О. Если начальная скорость не превышает величины
Орбитой является коническое сечение, один из фокусов которого расположен в точке О. Если начальная скорость не превышает величины  где
где  начальное расстояние от точки О, то это сечение есть эллипс. Апсидальный угол равен
начальное расстояние от точки О, то это сечение есть эллипс. Апсидальный угол равен  . Особенностью обеих задач — задачи об изотропном осцилляторе и задачи о движении в гравитационном поле по эллиптической орбите — является то, что орбита всегда периодическая, каковы бы ни были начальные условия.
. Особенностью обеих задач — задачи об изотропном осцилляторе и задачи о движении в гравитационном поле по эллиптической орбите — является то, что орбита всегда периодическая, каковы бы ни были начальные условия.
Остановимся на этих задачах немного подробнее.
1) Изотропный осциллятор. Имеем

Здесь расстояние до афелия  обозначено через а, а расстояние до перигелия
обозначено через а, а расстояние до перигелия  через
через  Дифференциальное уравнение орбиты имеет вид
Дифференциальное уравнение орбиты имеет вид

Полагая  получаем его в виде
получаем его в виде

где  Если положить
Если положить

то найдем, что  , и уравнение орбиты перепишется в виде
, и уравнение орбиты перепишется в виде

Осуществляя поворот осей на угол  ему можно придать форму уравнения эллипса с центром в точке О:
ему можно придать форму уравнения эллипса с центром в точке О:

Имеем

Отсюда

Эксцентрический угол  точки на эллипсе, в которой находится частица, возрастает пропорционально времени
точки на эллипсе, в которой находится частица, возрастает пропорционально времени 
Вычисление в декартовых координатах в этой задаче было бы проще, чем в полярных. 
2) Движение точки в гравитационном поле. В этом случае

 движение представляет собой либрацию между
движение представляет собой либрацию между  где
где  нули выражения
нули выражения  Дифференциальное уравнение орбиты (если отношение
Дифференциальное уравнение орбиты (если отношение  заменить на
заменить на  будет иметь вид
будет иметь вид

Чтобы проинтегрировать это уравнение, введем параметр  определив его следующим соотношением:
определив его следующим соотношением:

Находим  Орбитой, таки,
Орбитой, таки,  служит кривая
служит кривая

причем угол  отсчитывается от перигелия. Если, как обычно, написать
отсчитывается от перигелия. Если, как обычно, написать

то уравнение примет вид

где  Мы получили уравнение эллипса с эксцентриситетом
Мы получили уравнение эллипса с эксцентриситетом  и фокальным параметром
и фокальным параметром  Поскольку
Поскольку  постоянная энергии
постоянная энергии  равна
равна

Координата  определяется из уравнения
определяется из уравнения

Введем параметр 

так что  есть эксцентрический угол, отсчитываемый от перигелия. Имеем
есть эксцентрический угол, отсчитываемый от перигелия. Имеем

Интегрируя, получаем

где через  обозначена величина
обозначена величина  среднее движение. Соотношение (5.2.65) известно как уравнение Кеплера; оно выражает связь между положением тела на эллиптической орбите и временем.
среднее движение. Соотношение (5.2.65) известно как уравнение Кеплера; оно выражает связь между положением тела на эллиптической орбите и временем.
Пример  Теорема Ньютона о вращении орбиты. Рассмотрим теперь движение, возникающее при наложении на гравитационное поле дополнительного притяжения
Теорема Ньютона о вращении орбиты. Рассмотрим теперь движение, возникающее при наложении на гравитационное поле дополнительного притяжения  Чтобы решить эту задачу, заменим функцию
Чтобы решить эту задачу, заменим функцию  на функцию
на функцию

а функцию  на функцию
на функцию 

где  а у — постоянные энергии и момента количества движения в новом движении. Если положить
а у — постоянные энергии и момента количества движения в новом движении. Если положить

то функции  окажутся одинаковыми. Чтобы убедиться в том, что движение с такими значениями
окажутся одинаковыми. Чтобы убедиться в том, что движение с такими значениями  и возможно, рассмотрим апсиду первоначальной орбиты, в которой
и возможно, рассмотрим апсиду первоначальной орбиты, в которой  и скорость равна и.
и скорость равна и.
Если в той же начальной точке сообщить частице под прямым углом к радиус-вектору скорость, равную 

то будем иметь

и условия (5.2.68) будут удовлетворяться.
Если в обеих задачах при  принять
принять  то связь между
то связь между  будет одной и той же. Если в первоначальной задаче орбита задается уравнением
будет одной и той же. Если в первоначальной задаче орбита задается уравнением

то в новой задаче она будет описываться соотношением

где  Чтобы достигнуть значения
Чтобы достигнуть значения  соответствующего
соответствующего  в первой орбите, радиус-вектор во второй орбите должен повернуться на больший угол:
в первой орбите, радиус-вектор во второй орбите должен повернуться на больший угол:  Поэтому влияние дополнительного притяжения можно представить как вращение первоначальной орбиты.
Поэтому влияние дополнительного притяжения можно представить как вращение первоначальной орбиты.
| << Предыдущий параграф | Следующий параграф >> |
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
- § 1.1. Свободная материальная точка.
- § 1.2. Прямолинейное движение материальной точки в силовом поле.
- § 1.3. Либрационное движение.
- § 1.4. Заданная сила не может быть функцией от ускорения.
- § 1.5. Несвободная материальная точка (случай I).
- § 1.6. Несвободная материальная точка (случай II).
- § 1.7. Несвободная материальная точка (случай III).
- § 1.8. Голономные и неголономные системы.
- Глава II. МЕХАНИЧЕСКИЕ СИСТЕМЫ
- § 2.1. Система двух материальных точек.
- § 2.2. Система материальных точек.
- § 2.3. Катастатическая система.
- § 2.4. Реакции связей.
- § 2.5. К понятию о механической системе.
- Глава III. ПЕРВАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 3.2. Сохранение импульса.
- § 3.3. Катастатическая система и первая форма уравнения энергии.
- § 3.4. Консервативные силы и вторая форма уравнения энергии.
- § 3.5. Третья форма уравнения энергии.
- § 3.6. Сохранение энергии.
- § 3.7. Принцип Гамильтона.
- § 3.8. Варьированный путь.
- § 3.9. Распределенные системы.
- Глава IV. ВТОРАЯ И ТРЕТЬЯ ФОРМЫ ОСНОВНОГО УРАВНЕНИЯ
- § 4.1. Вторая форма основного уравнения.
- § 4.2. Третья форма основного уравнения.
- § 4.3. Принцип Гаусса наименьшего принуждения.
- § 4.4. Приложения принципа Гаусса.
- § 4.5. Физический смысл принципа Гаусса.
- Глава V. ЛАГРАНЖЕВЫ КООРДИНАТЫ
- § 5.2. Некоторые классические задачи.
- § 5.3. Сферический маятник.
- § 5.4. Задача двух тел.
- § 5.5. Уравнение Кеплера.
- § 5.6. Столкновение.
- § 5.7. Лагранжевы координаты для голономной системы.
- § 5.8. Лагранжевы координаты для неголономной системы.
- § 5.9. Качение тела.
- § 5.10. Достижимость.
- § 5.11. Варьированный путь в принципе Гамильтона.
- § 5.12. Обзор полученных результатов.
- Глава VI. УРАВНЕНИЯ ЛАГРАНЖА
- § 6.1. Четвертая форма основного уравнения. Лагранжевы координаты.
- § 6.2. Уравнения Лагранжа.
- § 6.3. Вывод уравнений Лагранжа из принципа Гамильтона.
- § 6.4. Форма уравнений Лагранжа.
- § 6.5. Консервативные системы и другие системы, обладающие потенциальной функцией.
- § 6.6. Функция Лагранжа.
- § 6.7. Интеграл Якоби.
- § 6.8. Явная форма интеграла Якоби.
- § 6.9. Об одной ошибке.
- § 6.11. Циклические координаты.
- § 6.12. Инвариантность уравнений Лагранжа.
- Глава VII. ТЕОРИЯ ПОВОРОТОВ
- § 7.2. Теорема Эйлера.
- § 7.3. Матрица l и вектор Т.
- § 7.4. Обобщение теоремы Эйлера.
- § 7.5. Теорема Шаля.
- § 7.6. Формула поворота.
- § 7.7. Полуобороты и отражения.
- § 7.8. Кватернионная форма записи формулы поворота.
- § 7.9. Сложение вращений.
- § 7.10. Угловая скорость.
- § 7.11. Ориентация твердого тела в пространстве. Углы Эйлера.
- § 7.12. Ориентация твердого тела в пространстве. Углы …
- § 7.13. Повороты около движущихся осей.
- § 7.14. Повороты около неподвижных осей.
- § 7.15. Определение угловой скорости с помощью матриц
- § 7.16. Составляющие вектора угловой скорости.
- Глава VIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 8.1. Дифференциальные уравнения.
- § 8.2. Формулы ускорения в ортогональных координатах.
- § 8.3. Обезьяна и противовес.
- § 8.4. Кинетическая энергия твердого тела.
- § 8.5. Задача о движении в двух измерениях.
- § 8.6. Вращающийся волчок; основные уравнения.
- § 8.7. Вращающийся волчок; другое решение.
- § 8.8. Гироскопические силы.
- § 8.9. Вращающийся волчок; исследование движения.
- § 8.10. Численный пример.
- § 8.11. Стержень во вращающейся плоскости.
- § 8.12. Качение диска.
- Глава IX. ТЕОРИЯ КОЛЕБАНИЙ
- § 9.1. Колебания около положения равновесия.
- § 9.2. Теория преобразования к главным координатам.
- § 9.3. Приложение теории.
- § 9.4. Наложение связи.
- § 9.5. Принцип Релея.
- § 9.6. Устойчивость установившегося движения.
- § 9.7. Колебания в окрестности установившегося движения.
- § 9.8. Гироскоп Фуко.
- § 9.9. Спящий волчок.
- § 9.10. Вынужденные колебания.
- Глава X. ДАЛЬНЕЙШИЕ ПРИЛОЖЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА
- § 10.2. Исключение одной координаты.
- § 10.3. Гироскопическая устойчивость.
- § 10.4. Явное выражение для R в общем случае.
- § 10.5. Вращающийся волчок.
- § 10.6. Линейные члены в функции L.
- § 10.7. Движение относительно подвижной системы отсчета.
- § 10.8. Движение частицы вблизи заданной точки на поверхности Земли.
- § 10.9. Маятник Фуко.
- § 10.10. Движение снаряда.
- § 10.11. Диссипативная функция Релея.
- § 10.12. Гироскопическая система с диссипацией.
- § 10.13. Уравнения Гамильтона.
- § 10.14. Уравнение энергии и явное выражение для Н.
- § 10.15. Главный триэдр.
- Глава XI. ПЕРЕМЕННАЯ МАССА
- § 11.1. Частица переменной массы. Функция Лагранжа.
- § 11.2. Кинетическая энергия.
- § 11.3. Функция Гамильтона.
- § 11.4. Движущийся электрон.
- § 11.2. Кинетическая энергия.
- § 11.5. Электрон в электромагнитном поле.
- Глава XII. УРАВНЕНИЯ ГИББСА-АППЕЛЯ
- § 12.3. Пятая форма основного уравнения.
- § 12.5. Уравнения Гиббса — Аппеля.
- Глава XIII. ПРИЛОЖЕНИЯ УРАВНЕНИЙ ГИББСА-АППЕЛЯ
- § 13.2. Аналог теоремы Кёнига.
- § 13.3. Плоское движение.
- § 13.4. Движение твердого тела.
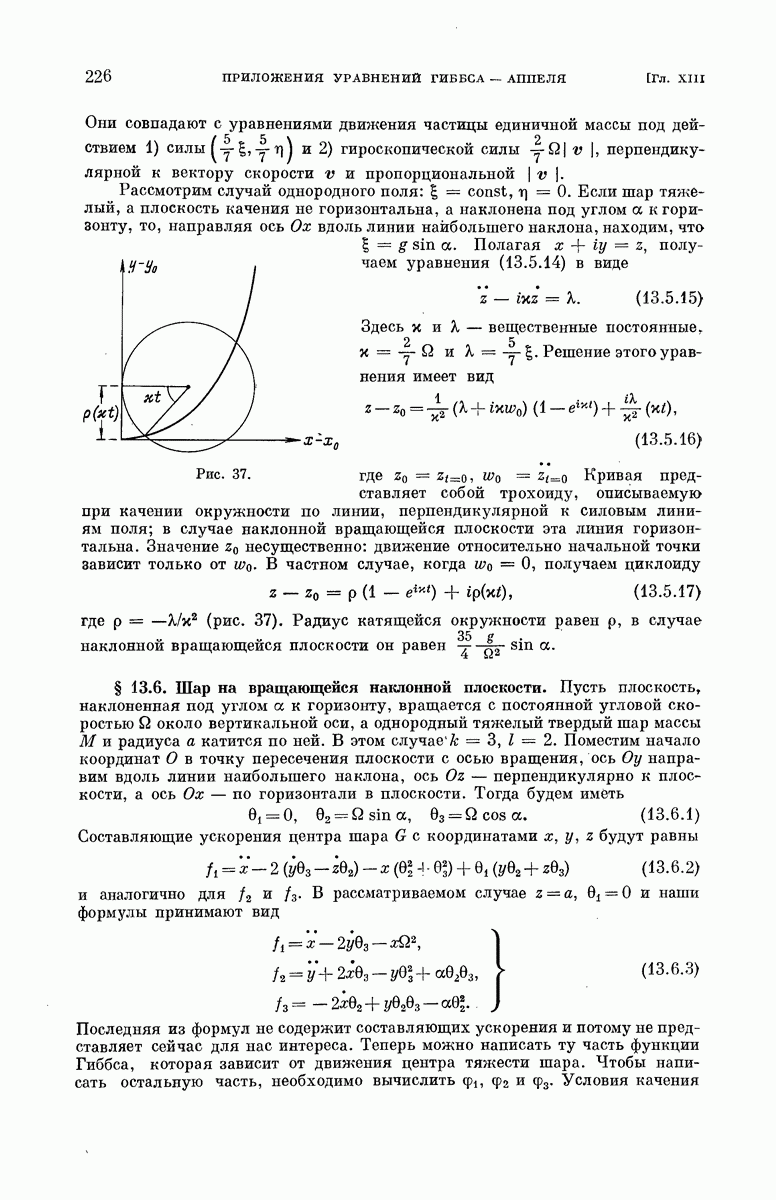
- § 13.5. Шар на вращающейся плоскости.
- § 13.6. Шар на вращающейся наклонной плоскости.
- § 13.7. Качение шара по неподвижной поверхности.
- § 13.8. Вращающийся волчок.
- § 13.9. Качение монеты (тонкого диска).
- § 13.10. Уравнения Эйлера.
- § 13.11. Свободное тело; случай осевой симметрии.
- § 13.12. Свободное тело; общий случай.
- § 13.13. Ориентация свободного тела.
- § 13.14. Теоремы Пуансо и Сильвестра.
- § 13.15. Качение эллипсоида по шероховатой горизонтальной плоскости.
- § 13.16. Устойчивость вращающегося эллипсоида.
- Глава XIV. ТЕОРИЯ УДАРА
- § 14.1. Ударный импульс.
- § 14.2. Импульсные связи.
- § 14.3. Движение системы, на которую действуют ударные импульсы. Основное уравнение теории удара.
- § 14.4. Катастатическая система.
- § 14.5. Принцип наименьшего принуждения в теории удара.
- § 14.6. Катастатическая система. Теорема о суперпозиции.
- § 14.7. Катастатическая система. Шесть теорем об энергии.
- § 14.8. Лагранжевы координаты и квазикоординаты.
- § 14.9. Лагранжева форма уравнений движения в теории удара.
- § 14.10. Другие доказательства теорем об энергии.
- § 14.11. Приложения теории удара.
- § 14.12. Импульсивное движение непрерывных систем.
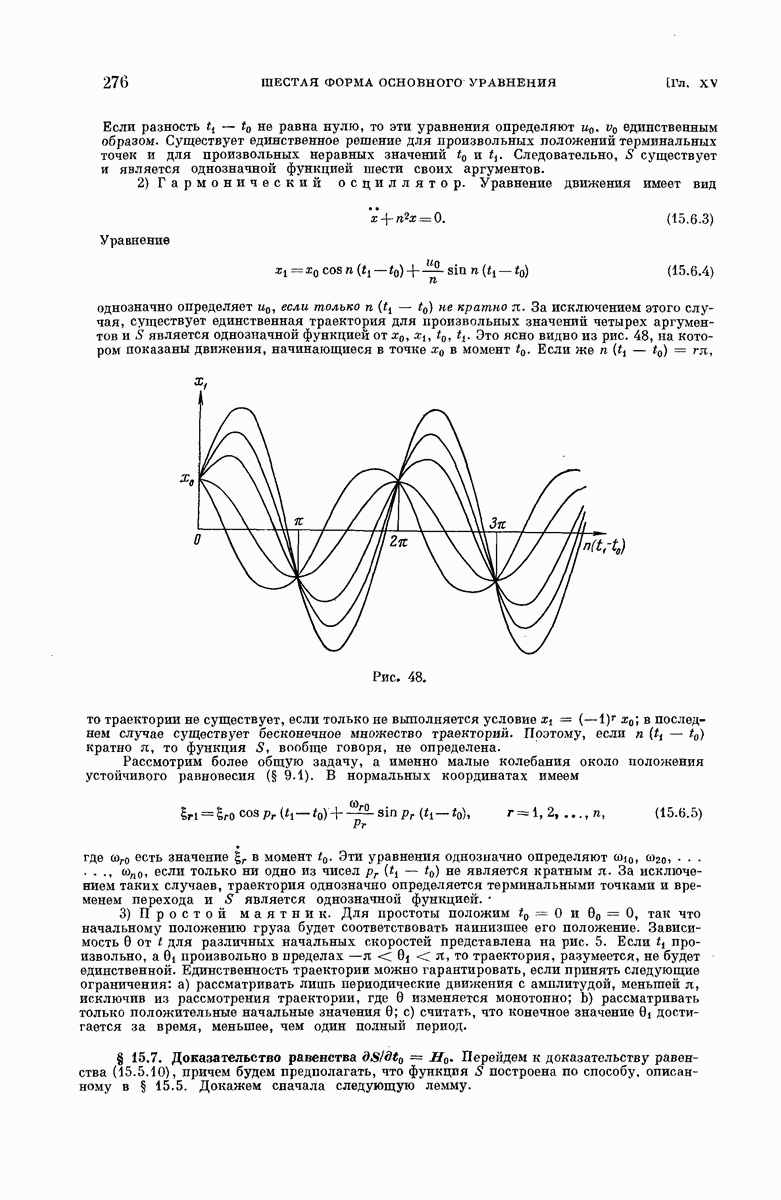
- Глава XV. ШЕСТАЯ ФОРМА ОСНОВНОГО УРАВНЕНИЯ
- § 15.1. Шестая форма основного уравнения.
- § 15.2. Непосредственные выводы.
- § 15.3. Функция Рауса.
- § 15.4. Теорема …
- § 15.5. Главная функция.
- § 15.6. Примеры использования главной функции.
- § 15.7. Доказательство равенства …
- § 15.8. Свойства главной функции.
- § 15.9. Примеры непосредственного вычисления главной функции.
- Глава XVI. ТЕОРЕМА ГАМИЛЬТОНА—ЯКОБИ
- § 16.1. Уравнение Гамильтона в частных производных.
- § 16.2. Теорема Гамильтона — Якоби (доказательство первое).
- § 16.3. Теорема об эквивалентности.
- § 16.4. Теорема Гамильтона — Якоби (доказательство второе).
- § 16.5. Замечания по теореме Гамильтона — Якоби.
- § 16.6. Однородное поле.
- § 16.7. Гармонический осциллятор.
- § 16.8 Частица в переменном поле At.
- § 16.9. Центральная орбита.
- § 16.10. Сферический маятник.
- § 16.11. Вращающийся волчок.
- § 16.12. Стержень на вращающейся плоскости.
- § 16.13. Электрон в центральном поле.
- § 16.14. Пфаффова форма
- Глава XVII. СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 17.2. Условия разделимости переменных в системах с двумя степенями свободы.
- § 17.3. Изучение движения системы.
- § 17.4. Классификация траекторий.
- § 17.5. Устойчивость.
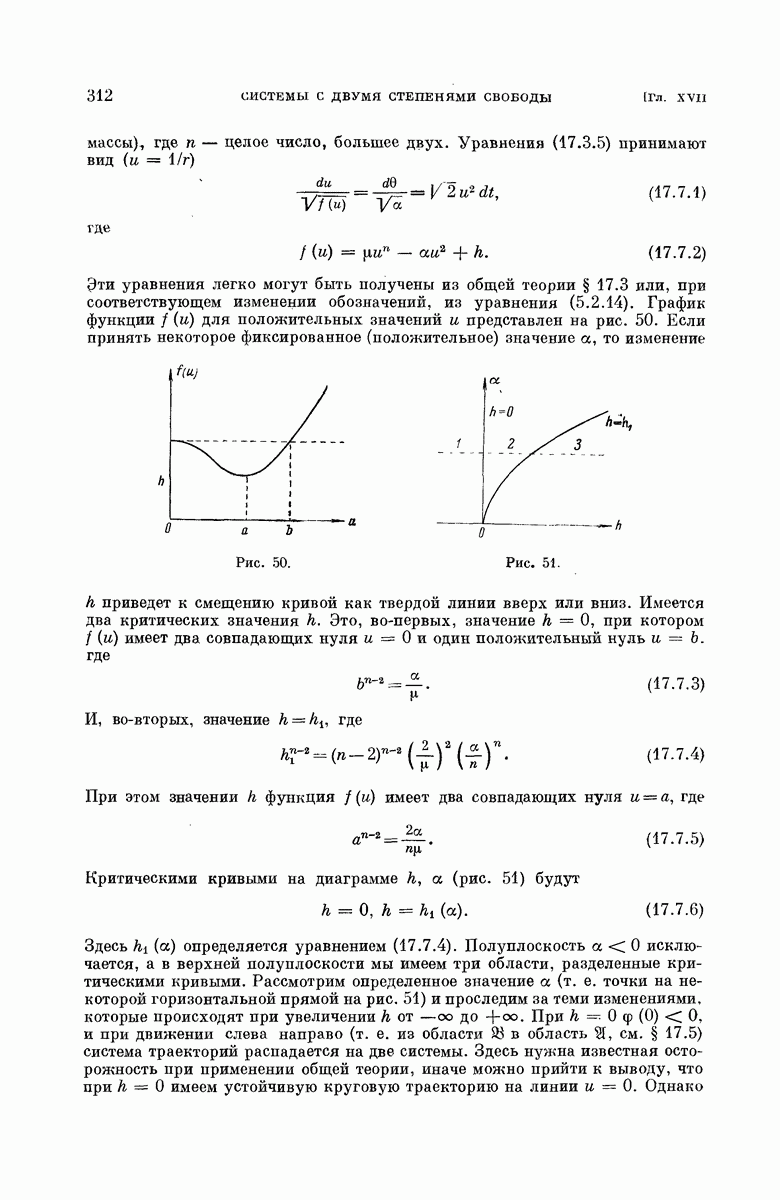
- § 17.6. Приложения теории.
- § 17.7. Притяжение к центру по закону …
- § 17.8. Притяжение к центру по закону …
- § 17.9. Ньютоновское притяжение и однородное поле.
- § 17.10. Два неподвижных притягивающих центра
- § 17.11. Ограниченные траектории.
- § 17.12. Уравнения орбит.
- § 17.13. Неограниченные орбиты.
- § 17.14. Системы, допускающие разделение переменных более чем одним способом.
- Глава XVIII. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ, ДОПУСКАЮЩИЕ РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ
- § 18.1. Система Лиувилля
- § 18.2. Теорема Штеккеля.
- § 18.3. Исследование интегралов.
- § 18.4. Дополнительные замечания к теореме Штеккеля.
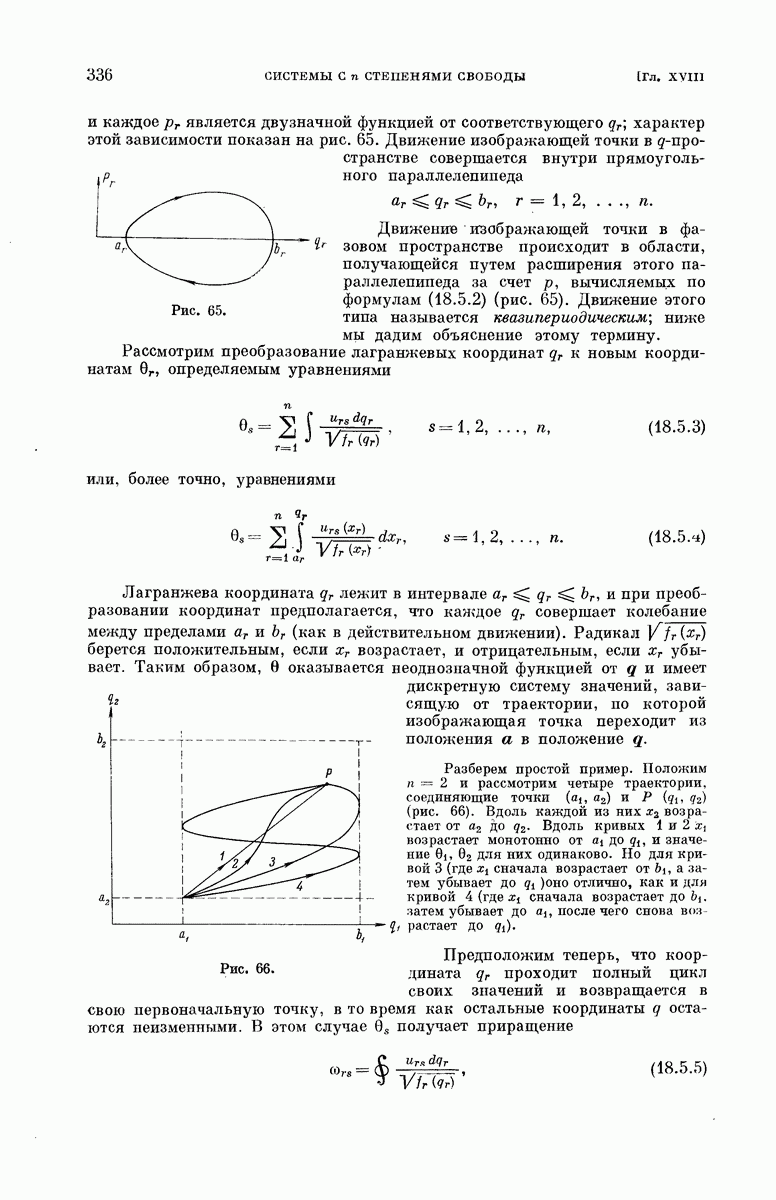
- § 18.5. Квазипериодические движения.
- § 18.6. Угловые переменные.
- § 18.7. Стандартный куб.
- § 18.8. Постоянные …
- § 18.9. Соотношения между q и v.
- § 18.10. Малые колебания.
- § 18.11. Сферический маятник.
- § 18.12. Задача двух тел.
- § 18.13. Интерпретация параметров a и b.
- § 18.14. Выражение r как функции от t.
- § 18.15. Угловые переменные.
- § 18.16. Постоянные …
- § 18.17. Возмущения.
- § 18.18. Неортогональные и ненатуральные разделимые системы.
- Глава XIX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ, ДВИЖЕНИЕ В ОКРЕСТНОСТИ ОСОБОЙ ТОЧКИ
- § 19.2. Движение частицы по прямой.
- § 19.3. Система с одной степенью свободы.
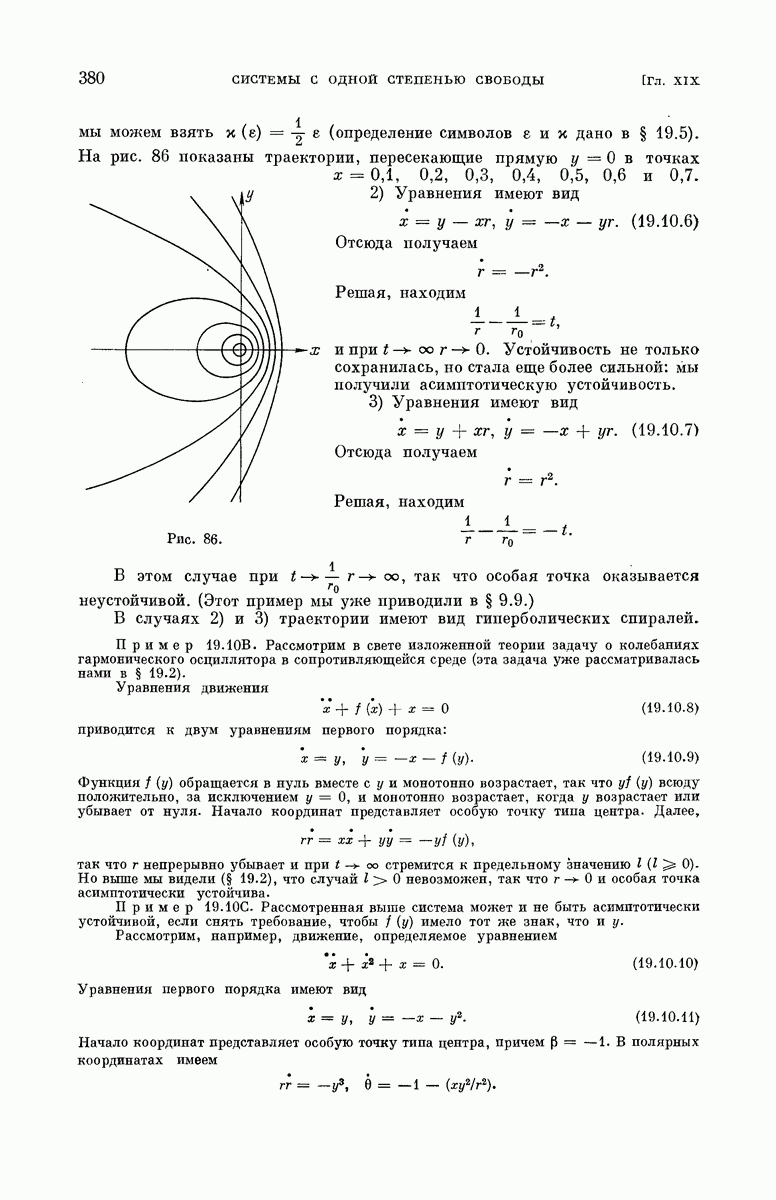
- § 19.4. Движение в окрестности особой точки. Линейное приближение.
- § 19.5. Устойчивость равновесия. Асимптотическая устойчивость и неустойчивость.
- § 19.6. Движение в окрестности особой точки. Общая теория.
- § 19.7. Движение в окрестности узла.
- § 19.8. Движение в окрестности седловой точки.
- § 19.9. Движение в окрестности фокуса.
- § 19.10. Движение в окрестности центра.
- § 19.11. Связь линейного приближения с общей теорией.
- Глава XX. СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. ЦИКЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- § 20.2. Положительное предельное множество.
- § 20.3. Отрезок без контакта.
- § 20.4. Отрезок без контакта, проходящий через точку множества A.
- § 20.5. Структура множества A.
- § 20.6. Теорема Пуанкаре — Бендиксона.
- § 20.7. Приложение к системе частного вида.
- § 20.8. Существование предельного цикла.
- § 20.9. Уравнение Ван-дер-Поля.
- Глава XXI. СИСТЕМЫ С n СТЕПЕНЯМИ СВОБОДЫ. СВОЙСТВА ХАРАКТЕРИСТИК
- § 21.2. Преобразование к новым координатам.
- § 21.3. Оператор Tt
- § 21.4. Решение в форме степенных рядов.
- § 21.5. Формула для X(x)-X(a)
- § 21.6. Интегральные инварианты.
- § 21.7. Интегральные инварианты порядка m.
- § 21.8. Свойства множителей.
- § 21.9. Последний множитель Якоби.
- § 21.10. Линейная система.
- § 21.11. Устойчивость равновесия.
- § 21.12. Дискретная устойчивость.
- § 21.13. Устойчивость преобразований.
- § 21.14. Приложение к дифференциальным уравнениям.
- § 21.15. Теорема Пуанкаре — Ляпунова.
- § 21.16. Критический случай.
- Глава XXII. УРАВНЕНИЯ ГАМИЛЬТОНА
- § 22.1. Уравнения Гамильтона.
- § 22.2. Скобки Пуассона.
- § 22.3. Теорема Пуассона.
- § 22.4. Использование известного интеграла.
- § 22.5. Линейный интегральный инвариант Пуанкаре.
- § 22.6. Теорема Лиувилля.
- § 22.7. Теорема возвращения (теорема Пуанкаре).
- § 22.8. Примеры инвариантных областей.
- § 22.9. Эргодические теоремы.
- § 22.10. Конкретные примеры.
- § 22.11. Множество …
- § 22.12. Собственные отрезки.
- § 22.13. Доказательство эргодической теоремы; первый этап.
- § 22.14. Доказательство эргодической теоремы; второй этап.
- § 22.15. Метрическая неразложимость.
- § 22.16. Интегралы уравнений движения.
- § 22.17. Следствие теоремы Лиувилля.
- § 22.18. Последний множитель.
- Глава XXIII. ДВИЖЕНИЕ В ОКРЕСТНОСТИ ЗАДАННОГО ДВИЖЕНИЯ. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ
- § 23.2. Решение уравнений в вариациях.
- § 23.3. Случай постоянных коэффициентов.
- § 23.4. Случай периодических коэффициентов.
- § 23.5. Нулевые показатели.
- § 23.6. Уравнения в вариациях для системы Гамильтона.
- § 23.7. Устойчивость траекторий (1).
- § 23.8. Устойчивость траекторий (2).
- § 23.9. Устойчивость периодических орбит.
- § 23.10. Вынужденные колебания.
- Глава XXIV. КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ
- § 24.1. Контактные преобразования.
- § 24.2. Формулы контактного преобразования.
- § 24.3. Другие формулы.
- § 24.4. Обобщенное точечное преобразование и другие однородные контактные преобразования.
- § 24.5. Специальная форма уравнений преобразований. Бесконечно малые контактные преобразования.
- § 24.6. Обобщение теоремы Лиувилля.
- § 24.7. Условия контактности преобразования, скобки Лагранжа.
- § 24.8. Соотношения между двумя системами производных.
- § 24.9. Условия контактности преобразования, выраженные с помощью скобок Пуассона.
- § 24.10. Соотношения между скобками Лагранжа и скобками Пуассона.
- § 24.11. Приложение к контактному преобразованию.
- § 24.12. Инвариантность скобки Пуассона.
- § 24.13. Другая форма условий контактности преобразования.
- § 24.14. Функции, находящиеся в инволюции.
- § 24.15. Некоторые примеры.
- Глава XXV. ТЕОРИЯ ПРЕОБРАЗОВАНИЙ
- § 25.1. Уравнения движения после контактных преобразований.
- § 25.2. Вариация элементов траектории.
- § 25.3. Вариация эллиптических элементов.
- § 25.4. Другие доказательства теоремы Якоби.
- § 25.5. Постоянство скобок Лагранжа.
- § 25.6. Бесконечно малые контактные преобразования.
- § 25.7. Интегралы в инволюции.
- § 25.8. Теорема Ли о системах в инволюции.
- § 25.9. Интегралы, линейные относительно импульсов.
- § 25.10. Случай, когда функция Гамильтона является однородной квадратичной формой
- Глава XXVI. ВАРИАЦИОННЫЕ ПРИНЦИПЫ
- § 26.2. Теорема Ливенса.
- § 26.3. Точки минимума и седловые точки.
- § 26.4. Асинхронное варьирование. Принцип Гёльдера.
- § 26.5. Принцип Фосса.
- § 26.6. Обобщение принципа Гамильтона.
- § 26.7. Замена независимой переменной.
- § 26.8. Нормальная форма системы с двумя степенями свободы.
- § 26.9. Система Лиувилля.
- § 26.10. Конформные преобразования.
- Глава XXVII. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ
- § 27.3. Принцип наименьшего действия в форме Якоби.
- § 27.4. Теорема Уиттекера.
- § 27.5. Исключение координат.
- § 27.6. Характеристическая функция.
- § 27.7. Пространство конфигураций.
- § 27.8. Система с двумя степенями свободы.
- § 27.9. Теорема Кельвина.
- § 27.10. Однородное поле.
- § 27.11. Задача Тэта. Непосредственное решение.
- § 27.12. Задача Тэта. Теория огибающих.
- Глава XXVIII. ОГРАНИЧЕННАЯ ЗАДАЧА ТРЕХ ТЕЛ
- § 28.2. Ограниченная задача. Уравнения движения.
- § 28.3. Положения равновесия.
- § 28.4. Положения равновесия на прямой АВ.
- § 28.5. Положения равновесия, не лежащие на прямой АВ
- § 28.6. Поверхность z=U.
- § 28.7. Движение вблизи положения равновесия.
- § 28.8. Теория движения Луны.
- Глава XXIX. ЗАДАЧА ТРЕХ ТЕЛ
- § 29.2. Случай, когда вектор момента количеств движения равен нулю.
- § 29.3. Три точки Лагранжа.
- § 29.4. Решения, для которых треугольник Лагранжа сохраняет свою форму.
- § 29.5. Случай плоского движения.
- § 29.6. Координаты относительно частицы Az
- § 29.7. Движение в окрестности равновесного решения.
- § 29.8. Сведение к системе шести уравнений.
- § 29.9. Устойчивость трех точек Лагранжа.
- § 29.10. Преобразованная форма уравнений движения.
- § 29.11. Другой подход к задаче трех точек Лагранжа.
- § 29.12. Сведение к системе восьми уравнений.
- § 29.13. Невозможность тройных столкновений.
- § 29.14. Плоское движение. Другой способ приведения к системе шестого порядка.
- § 29.15. Равновесные решения.
- Глава XXX. ПЕРИОДИЧЕСКИЕ ОРБИТЫ
- § 30.1. Периодические орбиты.
- § 30.3. Условия вещественности.
- § 30.4. Уравнения Гамильтона.
- § 30.5. Сходимость.
- § 30.6. Три точки Лагранжа.
- § 30.7. Системы, содержащие параметр.
- § 30.8. Приложение к ограниченной задаче трех тел.
- § 30.9. Метод неподвижной точки.
- § 30.11. Периодические орбиты и теорема о кольце.
- § 30.12. Доказательство теоремы Пуанкаре о кольце.