| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Апостериорные оценки для нормальных матриц
53. Предположим, что мы имеем приближенное собственное значение  и соответствующий собственный вектор
и соответствующий собственный вектор  матрицы А. Тогда рассмотрим вектор
матрицы А. Тогда рассмотрим вектор  определенный равенством
определенный равенством

Обычно он называется вектором-невязкой, соответствующим  Если
Если  точные, то
точные, то  должен быть нулевым. Следовательно, если
должен быть нулевым. Следовательно, если  мал, мы могли бы ожидать, что
мал, мы могли бы ожидать, что  будет хорошим приближением к собственному значению.
будет хорошим приближением к собственному значению.
Если А имеет линейные делители, то существует  такая, что
такая, что

Итак, из (53.1)

Возможны два случая:
(i)  для некоторого i;
для некоторого i;
(ii)  для любого
для любого  при этом (53.2) дает
при этом (53.2) дает

и, следовательно,

для любой нормы такой, что норма диагональной матрицы равна модулю наибольшего ее элемента.
Таким образом, используя  -норму,
-норму,

где к такое же, как в § 51. Соотношение (53.5), очевидно, удовлетворяется в случае  следовательно, мы можем заключить, что всегда существует по крайней мере одно собственное значение матрицы А в круге с центром
следовательно, мы можем заключить, что всегда существует по крайней мере одно собственное значение матрицы А в круге с центром  и радиусом к
и радиусом к  Очевидно, что не теряется никакой общности в предположении, что
Очевидно, что не теряется никакой общности в предположении, что  и мы будем делать его в дальнейшем. Так как, вообще говоря, мы не имеем априорной оценки к, то этот результат обычно практически не очень важен, если только у нас нет больше информации о собственной системе. Однако если А — нормальная, то мы знаем, что к — 1, и тогда наш результат показывает, что существует по крайней мере одно собственное значение в круге с центром
и мы будем делать его в дальнейшем. Так как, вообще говоря, мы не имеем априорной оценки к, то этот результат обычно практически не очень важен, если только у нас нет больше информации о собственной системе. Однако если А — нормальная, то мы знаем, что к — 1, и тогда наш результат показывает, что существует по крайней мере одно собственное значение в круге с центром  и радиусом
и радиусом 
Существует другой путь рассмотрения уравнения (53.1), который связывает этот результат с результатом главы 2. Уравнение (53.1) означает, что

и,следовательно,  будут точным собственным значением и собственным вектором матрицы
будут точным собственным значением и собственным вектором матрицы  Из гл. 2, § 30 мы знаем, что все собственные значения
Из гл. 2, § 30 мы знаем, что все собственные значения  лежат в кругах
лежат в кругах

и это приводит к тому же самому результату, который мы только что получили.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА
- ГЛАВА 1. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
- Собственные значения и собственные векторы транспонированной матрицы
- Различные собственные значения
- Преобразования подобия
- Кратные собственные значения и канонические формы матриц общего вида
- Неполная система собственных векторов
- Жорданова (классическая) каноническая форма
- Элементарные делители
- Сопровождающая матрица характеристического полинома
- Полные матрицы
- Каноническая (рациональная) форма Фробениуса
- Связь между жордановой и фробениусовой каноническими формами
- Преобразования эквивалентности
- лямбда-матрицы
- Элементарные операции
- Каноническая форма Смита
- Наибольший общий делитель k-строчных миноров лямбда-матрицы
- Инвариантные множители
- Треугольная каноническая форма
- Эрмитовы и симметричные матрицы
- Элементарные свойства эрмитовых матриц
- Комплексные симметричные матрицы
- Приведение к треугольной форме унитарными преобразованиями
- Квадратичные формы
- Необходимые и достаточные условия положительной определенности
- Дифференциальные уравнения с постоянными коэффициентами
- Решения, соответствующие нелинейным элементарным делителям
- Дифференциальные уравнения высшего порядка
- Уравнения второго порядка специального вида
- Явное решение уравнения …
- Уравнения вида (AB — lI)x = 0
- Минимальный полином вектора
- Минимальный полином матрицы
- Теорема Кэли — Гамильтона
- Соотношения между минимальным полиномом и каноническими формами
- Корневые векторы
- Элементарные преобразования подобия
- Свойства элементарных матриц
- Приведение к треугольной канонической форме элементарными преобразованиями подобия
- Элементарные унитарные преобразования
- Элементарные унитарные эрмитовы матрицы (матрицы отражения)
- Приведение к треугольному виду элементарными унитарными преобразованиями
- Нормальные матрицы
- Коммутирующие матрицы
- Собственные значения АВ
- Векторные и матричные нормы
- Подчиненные матричные нормы
- Евклидова и спектральная нормы
- Нормы и пределы
- Некоторые оценки без использования бесконечных матричных рядов
- ГЛАВА 2. ТЕОРИЯ ВОЗМУЩЕНИЙ
- Теорема Островского о непрерывности собственных значений
- Алгебраические функции
- Численные примеры
- Теория возмущений для простых собственных значений
- Возмущение соответствующих собственных векторов
- Матрица с линейными элементарными делителями
- Возмущения первого порядка собственных значений
- Возмущения первого порядка собственных векторов
- Возмущения высоких порядков
- Кратные собственные значения
- Теоремы Гершгорина
- Теория возмущений, основанная на теоремах Гершгорина
- Возмущения, соответствующие общему распределению нелинейных делителей
- Теория возмущений для собственных векторов матриц, основанная на исследовании жордановой канонической формы
- Возмещения собственных векторов, соответствующих кратным собственным значениям (линейные элементарные делители)
- Ограничения теории возмущений
- Соотношения между …
- Обусловленность вычислительных проблем
- Числа обусловленности
- Спектральное число обусловленности матрицы по отношению к проблеме собственных значений
- Свойства спектрального числа обусловленности
- Инвариантные свойства чисел обусловленности
- Очень плохо обусловленные матрицы
- Теория возмущений для вещественных симметричных матриц
- Несимметричные возмущения
- Симметричные возмущения
- Классическая техника
- Симметричная матрица с рангом единица
- Экстремальные свойства собственных значений
- Минимаксные свойства собственных значений
- Собственные значения суммы двух симметричных матриц
- Практические применения
- Дальнейшие применения принципа минимакса
- Теорема разделения
- Теорема Виландта — Гофмана
- Дополнительные замечания
- ГЛАВА 3. АНАЛИЗ ОШИБОК
- Операции с фиксированной запятой
- Накопление скалярного произведения
- Операции с плавающей запятой
- Упрощенные выражения для границ ошибок
- Оценки ошибок для некоторых основных вычислений с плавающей запятой
- Накопление скалярных произведений в арифметике с плавающей запятой
- Оценки ошибок для некоторых основных вычислений с двойным числом разрядов
- Вычисление квадратных корней
- Блочно-плавающие векторы и матрицы
- Основные ограничения t-разрядных вычислений
- Методы определения собственных значений, основанные на подобных преобразованиях
- Анализ ошибок методов, основанных на элементарных неунитарных преобразованиях
- Анализ ошибок методов, основанных на элементарных унитарных преобразованиях
- Преимущество унитарных преобразований
- Вещественные симметричные матрицы
- Ограничения унитарных преобразований
- Анализ ошибок вычисления плоских вращений с плавающей запятой
- Умножение на плоское вращение
- Умножение на последовательность плоских вращений
- Ошибка в произведении приближенных плоских вращений
- Ошибки в подобных преобразованиях
- Симметричные матрицы
- Плоские вращения в арифметике с фиксированной запятой
- Другое вычисление sin a и cos a
- Левое умножение на приближенное вращение с фиксированной запятой
- Умножение на последовательность плоских вращений (фиксированная запятая)
- Вычисленное произведение приближенной последовательности плоских вращений
- Ошибки в подобных преобразованиях
- Общее замечание об оценках ошибки
- Матрицы отражения с плавающей запятой
- Анализ ошибок вычисления матрицы отражения
- Численный пример
- Левое умножение на приближенную матрицу отражения
- Умножение на последовательность приближенных матриц отражения
- Неунитарные элементарные матрицы, аналогичные плоским вращениям
- Неунитарные элементарные матрицы, аналогичные матрицам отражения
- Левые умножения на последовательность неунитарных матриц
- Априорные оценки ошибок
- Отклонение от нормальности
- Простые примеры
- Апостериорные оценки
- Апостериорные оценки для нормальных матриц
- Отношение Релея
- Ошибка в отношении Релея
- Эрмитовы матрицы
- Патологически близкие собственные значения
- Ненормальные матрицы
- Анализ ошибок для полной собственной системы
- Численный пример
- Условия, ограничивающие достижимую точность
- Нелинейные элементарные делители
- Приближенные инвариантные подпространства
- Почти нормальные матрицы
- Дополнительные замечания
- ГЛАВА 4. РЕШЕНИЕ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- Числа обусловленности
- Уравновешенные матрицы
- Простые практические примеры
- Обусловленность матрицы собственных векторов
- Явное решение
- Общие замечания об обусловленности матриц
- Связь плохой обусловленности и почти вырожденности
- Ограничения, накладываемые t-разрядной арифметикой
- Алгорифмы решения линейных уравнений
- Метод Гаусса
- Треугольное разложение
- Структура матриц треугольного разложения
- Явные выражения для элементов треугольных матриц
- Несостоятельность метода Гаусса
- Численная устойчивость
- Значение перестановок
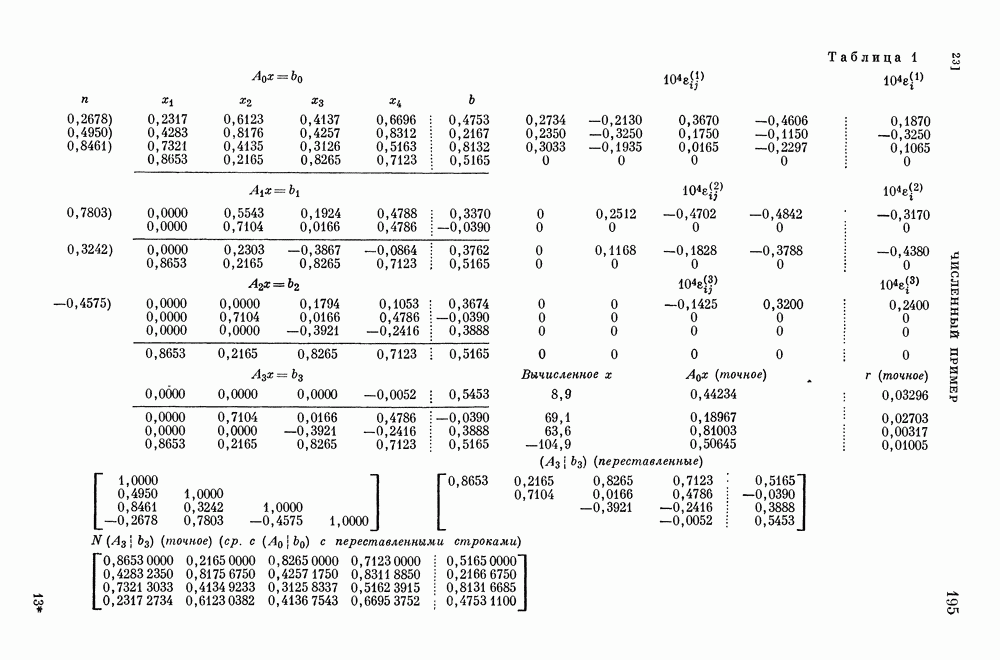
- Численный пример
- Анализ ошибок метода Гаусса
- Верхние оценки матриц возмущения для арифметики с фиксированной запятой
- Верхняя оценка для элементов преобразованных матриц
- Выбор главного элемента по всей матрице
- Практический процесс с выбором главного элемента по столбцу
- Анализ ошибок с плавающей запятой
- Разложение с плавающей запятой без выбора главного элемента
- Потеря верных знаков
- Общераспространенная ошибка
- Матрицы специального вида
- Метод Гаусса на быстродействующей вычислительной машине
- Решения, соответствующие различным правым частям
- Прямое треугольное разложение
- Связь метода Гаусса с прямым треугольным разложением
- Примеры несостоятельности и неединственности разложения
- Треугольное разложение с перестановкой строк
- Анализ ошибок треугольного разложения
- Вычисление определителей
- Разложение Холецкого
- Произвольные симметричные матрицы
- Анализ ошибок разложения Холецкого в арифметике с фиксированной запятой
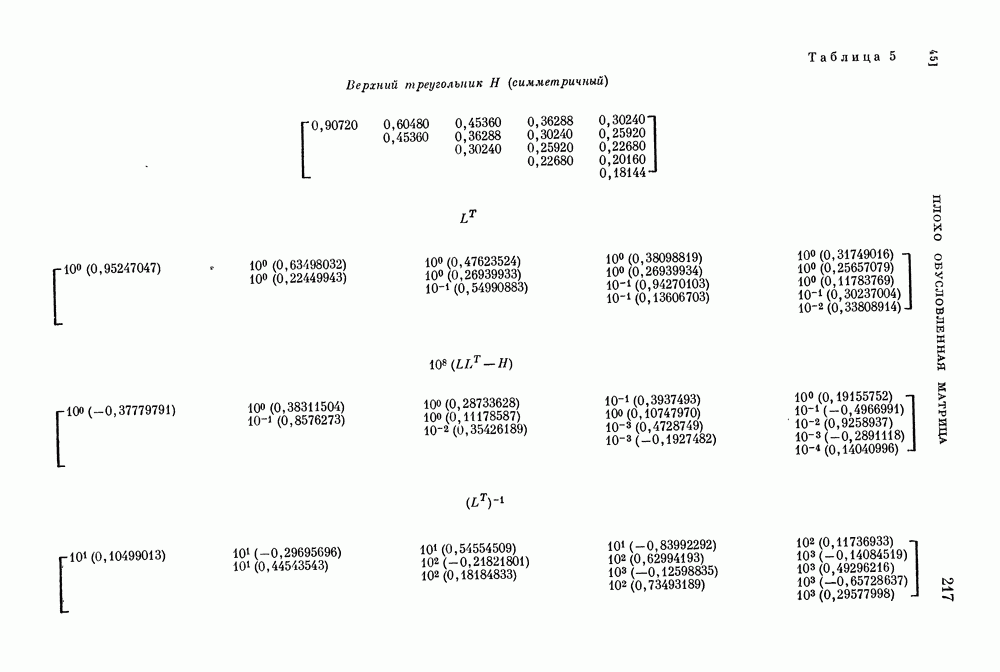
- Плохо обусловленная матрица
- Триангуляризация, использующая матрицы отражения
- Анализ ошибок триангуляризации Хаусхолдера
- Триангуляризации элементарными устойчивыми матрицами типа М
- Вычисление главных миноров
- Триангуляризация плоскими вращениями
- Анализ ошибок преобразования Гивенса
- Единственность ортогональной триангуляризации
- Ортогонализация Шмидта
- Сравнение методов триангуляризации
- Обратная подстановка
- Высокая точность вычисленного решения треугольной системы уравнений
- Решение общей системы уравнений
- Вычисление общей обратной матрицы
- Точность вычисленных решений
- Плохо обусловленные матрицы, которые дают немалые ведущие элементы
- Итерационное улучшение приближенного решения
- Влияние ошибок округления на итерационный процесс
- Итерационный процесс в вычислении с фиксированной запятой
- Простой пример итерационного процесса
- Общие замечания по итерационному процессу
- Родственные итерационные процессы
- Ограниченность итерационного процесса
- Строгое обоснование итерационного метода
- Дополнительные замечания
- ГЛАВА 5. ЭРМИТОВЫ МАТРИЦЫ
- Классический метод Якоби для вещественных симметричных матриц
- Быстрота сходимости
- Сходимость к фиксированной диагональной матрице
- Циклический метод Якоби
- Круги Гершгорина
- Асимптотическая квадратичная сходимость методов Якоби
- Близкие и кратные собственные значения
- Численные примеры
- Вычисление cos a и sin a
- Более простое определение углов вращения
- Циклический метод Якоби с преградами
- Вычисление собственных векторов
- Численный пример
- Анализ ошибок метода Якоби
- Точность вычисленных собственных векторов
- Оценки ошибок для вычислений с фиксированной запятой
- Организационные проблемы
- Метод Гивенса
- Процесс Гивенса на вычислительной машине с двухступенчатой памятью
- Анализ ошибок процесса Гивенса в арифметике с плавающей запятой
- Анализ ошибок в арифметике с фиксированной запятой
- Численный пример
- Метод Хаусхолдера
- Использование симметрии
- Некоторые соображения о необходимой величине памяти
- Процесс Хаусхолдера на вычислительной машине с двухступенчатой памятью
- Метод Хаусхолдера в арифметике с фиксированной запятой
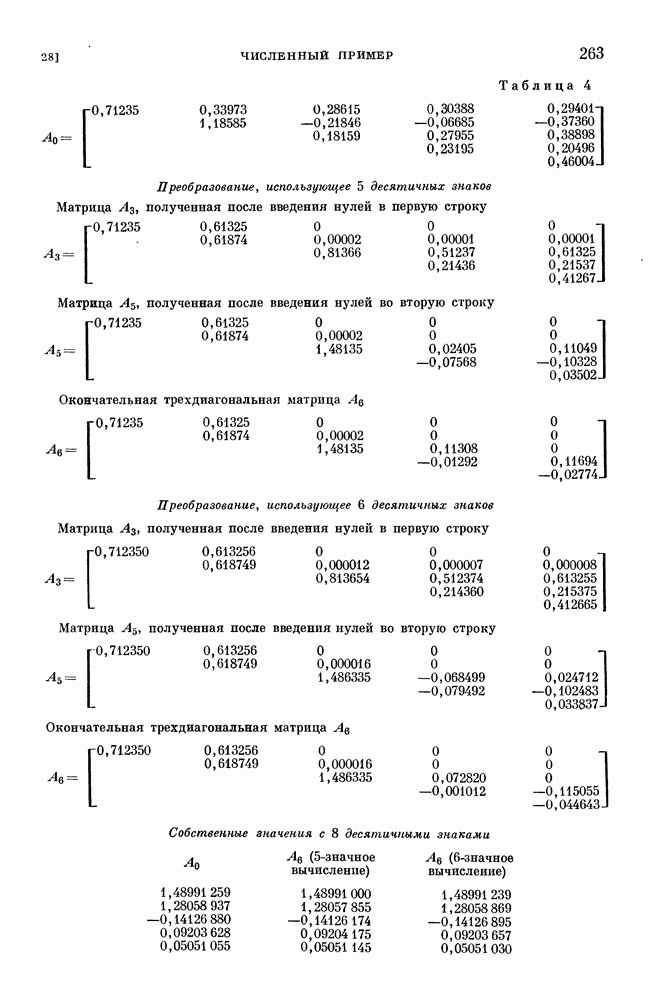
- Численный пример
- Анализ ошибок метода Хаусхолдера
- Собственные значения симметричной трехдиагональной матрицы
- Свойство последовательности Штурма
- Метод деления пополам
- Численная устойчивость метода деления пополам
- Численный пример
- Общие замечания о методе деления пополам
- Малые собственные значения
- Близкие собственные значения и малые
- Вычисление собственных значений в арифметике с фиксированной запятой
- Вычисление собственных векторов трехдиагональной матрицы
- Неустойчивость явного выражения для собственного вектора
- Численные примеры
- Обратная итерация
- Выбор начального вектора b
- Анализ ошибок
- Численный пример
- Близкие собственные значения и малые
- Линейно независимые векторы, соответствующие совпадающим собственным значениям
- Другой метод вычисления собственных векторов
- Численный пример
- Замечания о проблеме собственных значений для трехдиагональных матриц
- Завершение методов Гивенса и Хаусхолдера
- Сравнение методов
- Квазисимметричные трехдиагональные матрицы
- Вычисление собственных векторов
- Уравнения вида Ах = lВх и АВх = lх
- Численный пример
- Одновременное приведение A и B к диагональному виду
- Трехдиагональные A и B
- Комплексные эрмитовы матрицы
- Дополнительные замечания
- ГЛАВА 6. ПРИВЕДЕНИЕ ОБЩИХ МАТРИЦ К МАТРИЦАМ СПЕЦИАЛЬНОГО ВИДА
- Метод Гивенса
- Метод Хаусхолдера
- Соображения о необходимой величине памяти
- Анализ ошибок
- Связь методов Гивенса и Хаусхолдера
- Элементарные устойчивые преобразования
- Значение перестановок
- Прямое приведение к форме Хессенберга
- Введение перестановок
- Численный пример
- Анализ ошибок
- Дальнейший анализ ошибок
- Плохая определимость матрицы Хессенберга
- Приведение к форме Хессенберга матрицами типа …
- Метод Крылова
- Метод Гаусса с исключением по столбцам
- Практические трудности
- Обусловленность С для некоторых стандартных расположений собственных значений
- Начальный вектор высоты, меньшей чем n
- Практическое применение
- Обобщенные процессы Хессенберга
- Срыв обобщенного процесса Хессенберга
- Метод Хессенберга
- Практическая процедура
- Связь метода Хессенберга и предыдущих методов
- Метод Арнольди
- Практические рассмотрения
- Значение переортогонализации
- Метод Ланцоша
- Срыв процесса
- Численный пример
- Практический процесс Ланцоша
- Численный пример
- Общие замечания к несимметричному процессу Ланцоша
- Симметричный процесс Ланцоша
- Приведение матриц Хессенберга к более компактному виду
- Приведение нижней матрицы Хессенберга к трехдиагональному виду
- Использование перестановок
- Влияние малого ведущего элемента
- Анализ ошибок
- Процесс Хессенберга в применении к нижней матрице Хессенберга
- Связь процесса Хессенберга и процесса Ланцоша
- Приведение матрицы общего вида к трехдиагональному виду
- Сравнение с методом Ланцоша
- Повторное исследование приведения к трехдиагональному виду
- Приведение матриц в верхней форме Хессенберга к форме Фробениуса
- Влияние малых ведущих элементов
- Численный пример
- Общие замечания об устойчивости
- Специальная верхняя форма Хессенберга
- Прямое определение характеристического полинома
- Дополнительные замечания
- ГЛАВА 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦ СПЕЦИАЛЬНОГО ВИДА
- Числа обусловленности явно заданных полиномов
- Несколько типичных расположений корней
- Окончательная оценка метода Крылова
- Общие замечания о явно заданных полиномах
- Трехдиагональные матрицы
- Определители матриц Хессенберга
- Влияние ошибок округления
- Накопление с плавающей запятой
- Вычисление при помощи ортогональных преобразований
- Вычисление определителей матриц общего вида
- Обобщенная проблема собственных значений
- Косвенное определение характеристического полинома
- Метод Леверье
- Итерационные методы, основанные на интерполяции
- Асимптотическая скорость сходимости
- Кратные корни
- Обращение функционального соотношения
- Метод деления отрезка пополам
- Метод Ньютона
- Сравнение метода Ньютона с методом интерполяции
- Методы, дающие кубическую сходимость
- Метод Лагерра
- Комплексные корни
- Комплексно сопряженные корни
- Метод Берстоу
- Обобщенный метод Берстоу
- Практические рассмотрения
- Влияние ошибок округления на асимптотическую сходимость
- Метод деления отрезка пополам
- Последовательная линейная интерполяция
- Кратные и патологически близкие собственные значения
- Другие интерполяционные методы
- Методы, в которых используются производные
- Критерий достижения корня
- Влияние ошибок округления
- Удаление вычисленных корней
- Исчерпывание для матриц Хессенберга
- Исчерпывание для трехдиагональной матрицы
- Исчерпывание при помощи вращений или устойчивых элементарных преобразований
- Устойчивость исчерпывания
- Общие замечания об исчерпывании
- Удаление вычисленных нулей
- Удаление вычисленного квадратичного множителя
- Общие комментарии о методах удаления
- Асимптотическая скорость сходимости
- Сходимость в целом
- Комплексные корни
- Рекомендации
- Комплексные матрицы
- Матрицы, содержащие независимый параметр
- Дополнительные замечания
- ГЛАВА 8. LR- и QR-алгоритмы
- Вещественные матрицы с комплексными собственными значениями
- LR-алгоритм
- Доказательство сходимости последовательности As
- Положительно определенные эрмитовы матрицы
- Комплексно сопряженные собственные значения
- Введение перестановок
- Численный пример
- Сходимость модифицированного процесса
- Предварительная подготовка исходной матрицы
- Инвариантность верхней формы Хессенберга
- Одновременное действие со строками и столбцами
- Ускорение сходимости
- Объединение сдвигов
- Выбор сдвига
- Исчерпывание матрицы
- Экспериментальная проверка сходимости
- Улучшенный выбор сдвига
- Комплексно сопряженные собственные значения
- Критика модифицированного LR-алгорифма
- QR-алгорифм
- Сходимость QR-алгорифма
- Формальное доказательство сходимости
- Нарушение порядка собственных значений
- Равные по модулю собственные значения
- Другое доказательство для LR-метода
- Практическое применение QR-алгорифма
- Сдвиг
- Разложение матриц As
- Численный пример
- Практическая процедура
- Устранение комплексно сопряженных сдвигов
- Двойной QR-шаг с использованием матриц отражения
- Вычислительные детали
- Разложение матриц As
- Прием двойного сдвига для LR
- Сравнение LR- и QR-алгорифмов
- Кратные собственные значения
- Специальное использование процесса исчерпывания
- Симметричные матрицы
- Связь между LR- и QR-алгорифмами
- Сходимость LR-алгорифма Холецкого
- Кубическая сходимость QR-алгорифма
- Сдвиг в LR-алгорифме Холецкого
- Срыв факторизации Холецкого
- Кубически сходящийся LR-процесс
- Ленточные матрицы
- QR-разложение ленточной матрицы
- Анализ ошибок
- Несимметричные ленточные матрицы
- Одновременное разложение и переумпожение в QR-алгорифме
- Уменьшение ширины ленточной матрицы
- Дополнительные замечания
- ГЛАВА 9. ИТЕРАЦИОННЫЕ МЕТОДЫ
- Степенной метод
- Прямые итерации одного вектора
- Сдвиг начала
- Влияние ошибок округления
- Процесс ускорения Эйткена
- Комплексно сопряженные собственные значения
- Вычисление комплексного собственного вектора
- Сдвиг начала
- Нелинейные делители
- Одновременное определение нескольких собственных значений
- Комплексные матрицы
- Исчерпывание
- Исчерпывание, основанное на преобразованиях подобия
- Исчерпывание, использующее инвариантные подпространства
- Исчерпывание при помощи устойчивых элементарных преобразований
- Исчерпывание при помощи унитарных преобразований
- Численная устойчивость
- Численный пример
- Устойчивость унитарных преобразований
- Исчерпывание при помощи неподобных преобразований
- Общее приведение, использующее инвариантные подпространства
- Практическое приложение
- Ступенчатые итерации
- Точное определение комплексно сопряженных собственных значений
- Очень близкие собственные значения
- Метод ортогонализации
- Аналог ступенчатых итераций, использующий ортогонализацию
- Биортогонализация
- Численный пример
- Процесс уточнения Ричардсона
- Возведение матрицы в степень
- Численная стабильность
- Использование полиномов Чебышева
- Общая оценка методов, основанных на прямых итерациях
- Обратные итерации
- Анализ ошибок при обратных итерациях
- Общие комментарии к анализу
- Дальнейшее уточнение собственных векторов
- Нелинейные элементарные делители
- Обратные итерации с матрицами Хессенберга
- Вырожденные случаи
- Обратные итерации с ленточными матрицами
- Комплексно сопряженные собственные векторы
- Анализ ошибок
- Численный пример
- Обобщенная проблема собственных значений
- Изменение приближенных собственных значений
- Уточнение системы собственных значений
- Численный пример
- Уточнение собственных векторов
- Комплексно сопряженные собственные значения
- Совпадающие и патологически близкие собственные значения
- Замечания о программах на АСЕ
- Дополнительные замечания