| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Треугольная каноническая форма
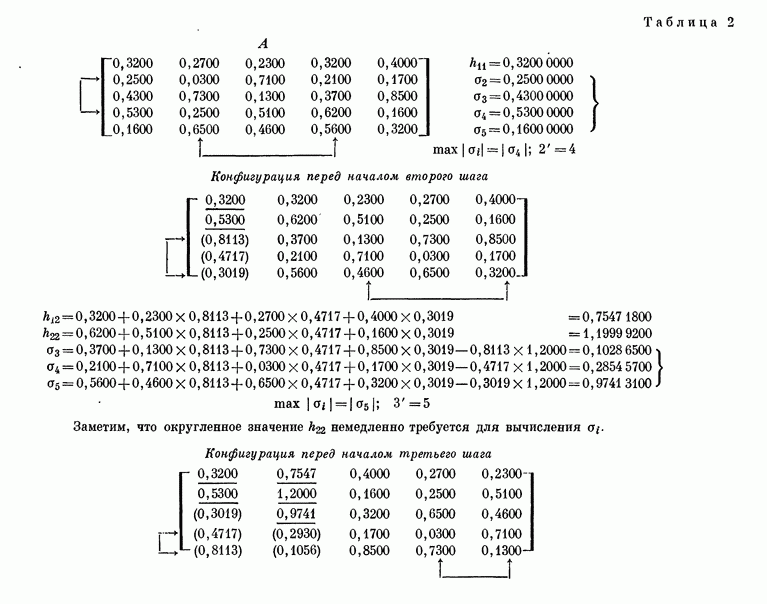
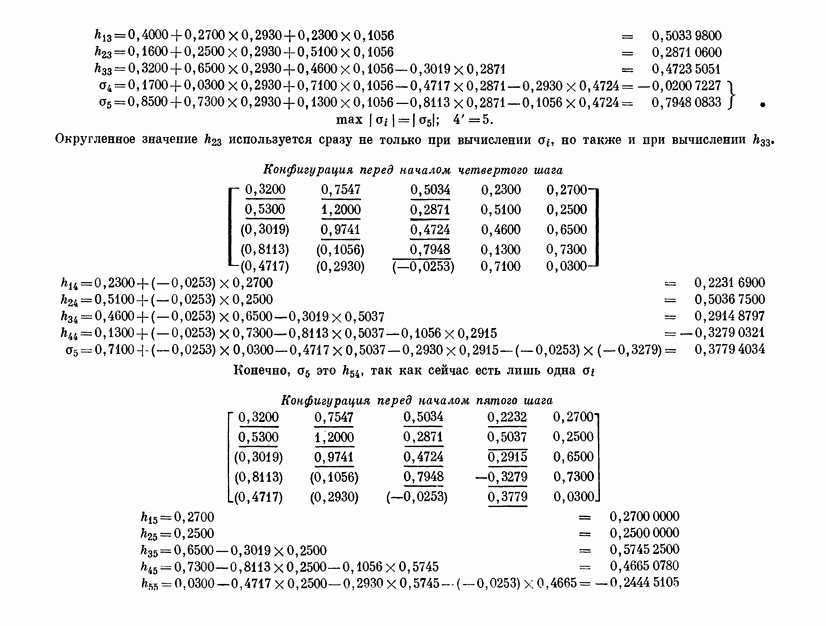
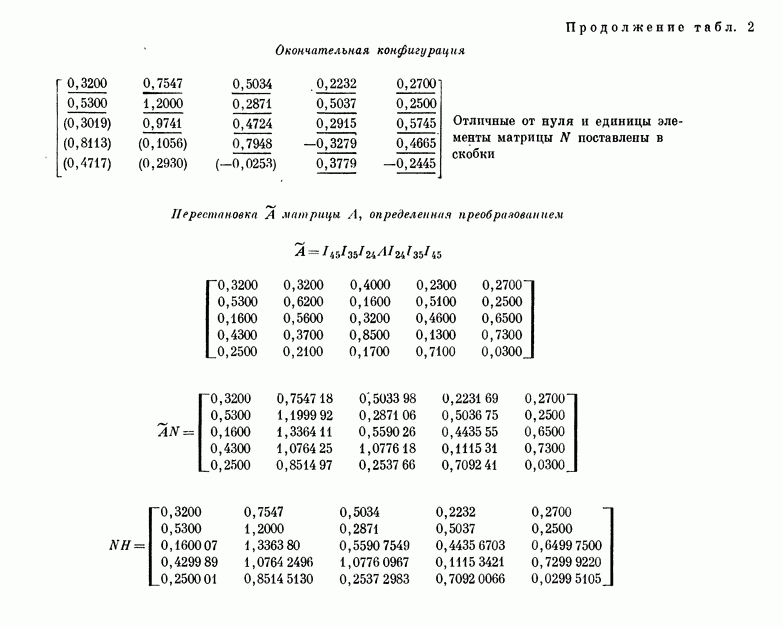
21. Приведение к жордановой канонической форме требует полной информации о всех собственных значениях и собственных векторах. Эта форма является частным случаем треугольной канонической формы. Последняя значительно более проста как с теоретической точки зрения, так и с точки зрения вычислительной практики. Ее важность вытекает из следующей теоремы и из теоремы § 25.
Каждая матрица подобна треугольной матрице, т. е. матрице, у которой все элементы над диагональю равны нулю. Мы будем называть такие
матрицы нижними треугольными матрицами. Как и в случае жордановой формы, существует также преобразование, приводящее к матрице с нулями под диагональю (верхней треугольной). Доказательство, сравнительно элементарное, мы отложим до § 42, где будут введены соответствующие матрицы преобразования.
Очевидно, что диагональные элементы треугольной матрицы суть собственные значения с соответствующими кратностями подобной ей исходной матрицы. Действительно, если это элементы  то характеристический полином треугольной матрицы равен
то характеристический полином треугольной матрицы равен  а мы видели, что характеристический полином инвариантен при преобразованиях подобия.
а мы видели, что характеристический полином инвариантен при преобразованиях подобия.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АВТОРА
- ГЛАВА 1. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
- Собственные значения и собственные векторы транспонированной матрицы
- Различные собственные значения
- Преобразования подобия
- Кратные собственные значения и канонические формы матриц общего вида
- Неполная система собственных векторов
- Жорданова (классическая) каноническая форма
- Элементарные делители
- Сопровождающая матрица характеристического полинома
- Полные матрицы
- Каноническая (рациональная) форма Фробениуса
- Связь между жордановой и фробениусовой каноническими формами
- Преобразования эквивалентности
- лямбда-матрицы
- Элементарные операции
- Каноническая форма Смита
- Наибольший общий делитель k-строчных миноров лямбда-матрицы
- Инвариантные множители
- Треугольная каноническая форма
- Эрмитовы и симметричные матрицы
- Элементарные свойства эрмитовых матриц
- Комплексные симметричные матрицы
- Приведение к треугольной форме унитарными преобразованиями
- Квадратичные формы
- Необходимые и достаточные условия положительной определенности
- Дифференциальные уравнения с постоянными коэффициентами
- Решения, соответствующие нелинейным элементарным делителям
- Дифференциальные уравнения высшего порядка
- Уравнения второго порядка специального вида
- Явное решение уравнения …
- Уравнения вида (AB — lI)x = 0
- Минимальный полином вектора
- Минимальный полином матрицы
- Теорема Кэли — Гамильтона
- Соотношения между минимальным полиномом и каноническими формами
- Корневые векторы
- Элементарные преобразования подобия
- Свойства элементарных матриц
- Приведение к треугольной канонической форме элементарными преобразованиями подобия
- Элементарные унитарные преобразования
- Элементарные унитарные эрмитовы матрицы (матрицы отражения)
- Приведение к треугольному виду элементарными унитарными преобразованиями
- Нормальные матрицы
- Коммутирующие матрицы
- Собственные значения АВ
- Векторные и матричные нормы
- Подчиненные матричные нормы
- Евклидова и спектральная нормы
- Нормы и пределы
- Некоторые оценки без использования бесконечных матричных рядов
- ГЛАВА 2. ТЕОРИЯ ВОЗМУЩЕНИЙ
- Теорема Островского о непрерывности собственных значений
- Алгебраические функции
- Численные примеры
- Теория возмущений для простых собственных значений
- Возмущение соответствующих собственных векторов
- Матрица с линейными элементарными делителями
- Возмущения первого порядка собственных значений
- Возмущения первого порядка собственных векторов
- Возмущения высоких порядков
- Кратные собственные значения
- Теоремы Гершгорина
- Теория возмущений, основанная на теоремах Гершгорина
- Возмущения, соответствующие общему распределению нелинейных делителей
- Теория возмущений для собственных векторов матриц, основанная на исследовании жордановой канонической формы
- Возмещения собственных векторов, соответствующих кратным собственным значениям (линейные элементарные делители)
- Ограничения теории возмущений
- Соотношения между …
- Обусловленность вычислительных проблем
- Числа обусловленности
- Спектральное число обусловленности матрицы по отношению к проблеме собственных значений
- Свойства спектрального числа обусловленности
- Инвариантные свойства чисел обусловленности
- Очень плохо обусловленные матрицы
- Теория возмущений для вещественных симметричных матриц
- Несимметричные возмущения
- Симметричные возмущения
- Классическая техника
- Симметричная матрица с рангом единица
- Экстремальные свойства собственных значений
- Минимаксные свойства собственных значений
- Собственные значения суммы двух симметричных матриц
- Практические применения
- Дальнейшие применения принципа минимакса
- Теорема разделения
- Теорема Виландта — Гофмана
- Дополнительные замечания
- ГЛАВА 3. АНАЛИЗ ОШИБОК
- Операции с фиксированной запятой
- Накопление скалярного произведения
- Операции с плавающей запятой
- Упрощенные выражения для границ ошибок
- Оценки ошибок для некоторых основных вычислений с плавающей запятой
- Накопление скалярных произведений в арифметике с плавающей запятой
- Оценки ошибок для некоторых основных вычислений с двойным числом разрядов
- Вычисление квадратных корней
- Блочно-плавающие векторы и матрицы
- Основные ограничения t-разрядных вычислений
- Методы определения собственных значений, основанные на подобных преобразованиях
- Анализ ошибок методов, основанных на элементарных неунитарных преобразованиях
- Анализ ошибок методов, основанных на элементарных унитарных преобразованиях
- Преимущество унитарных преобразований
- Вещественные симметричные матрицы
- Ограничения унитарных преобразований
- Анализ ошибок вычисления плоских вращений с плавающей запятой
- Умножение на плоское вращение
- Умножение на последовательность плоских вращений
- Ошибка в произведении приближенных плоских вращений
- Ошибки в подобных преобразованиях
- Симметричные матрицы
- Плоские вращения в арифметике с фиксированной запятой
- Другое вычисление sin a и cos a
- Левое умножение на приближенное вращение с фиксированной запятой
- Умножение на последовательность плоских вращений (фиксированная запятая)
- Вычисленное произведение приближенной последовательности плоских вращений
- Ошибки в подобных преобразованиях
- Общее замечание об оценках ошибки
- Матрицы отражения с плавающей запятой
- Анализ ошибок вычисления матрицы отражения
- Численный пример
- Левое умножение на приближенную матрицу отражения
- Умножение на последовательность приближенных матриц отражения
- Неунитарные элементарные матрицы, аналогичные плоским вращениям
- Неунитарные элементарные матрицы, аналогичные матрицам отражения
- Левые умножения на последовательность неунитарных матриц
- Априорные оценки ошибок
- Отклонение от нормальности
- Простые примеры
- Апостериорные оценки
- Апостериорные оценки для нормальных матриц
- Отношение Релея
- Ошибка в отношении Релея
- Эрмитовы матрицы
- Патологически близкие собственные значения
- Ненормальные матрицы
- Анализ ошибок для полной собственной системы
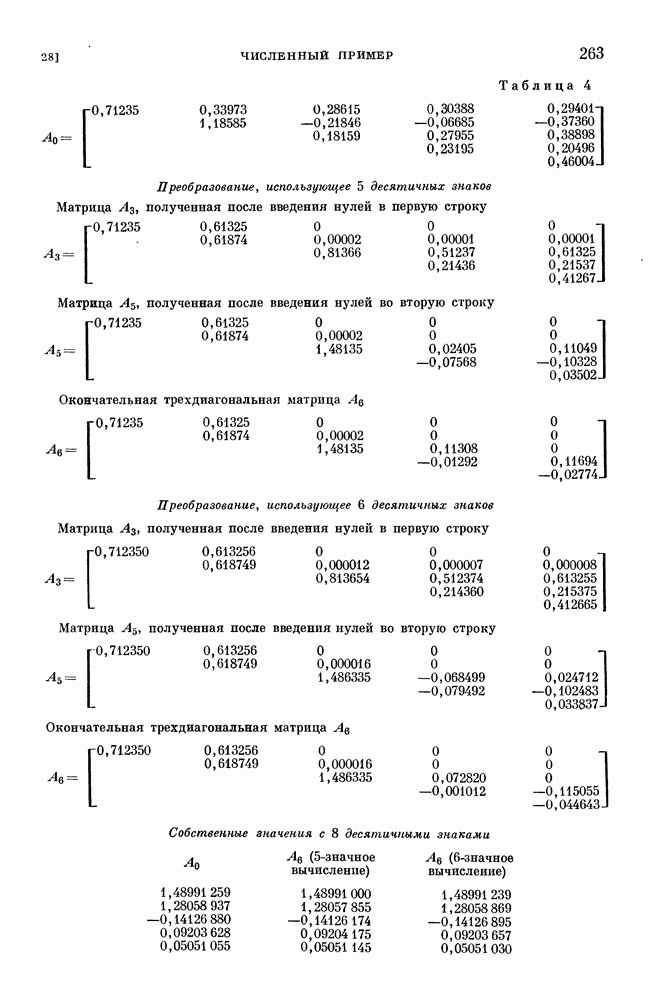
- Численный пример
- Условия, ограничивающие достижимую точность
- Нелинейные элементарные делители
- Приближенные инвариантные подпространства
- Почти нормальные матрицы
- Дополнительные замечания
- ГЛАВА 4. РЕШЕНИЕ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- Числа обусловленности
- Уравновешенные матрицы
- Простые практические примеры
- Обусловленность матрицы собственных векторов
- Явное решение
- Общие замечания об обусловленности матриц
- Связь плохой обусловленности и почти вырожденности
- Ограничения, накладываемые t-разрядной арифметикой
- Алгорифмы решения линейных уравнений
- Метод Гаусса
- Треугольное разложение
- Структура матриц треугольного разложения
- Явные выражения для элементов треугольных матриц
- Несостоятельность метода Гаусса
- Численная устойчивость
- Значение перестановок
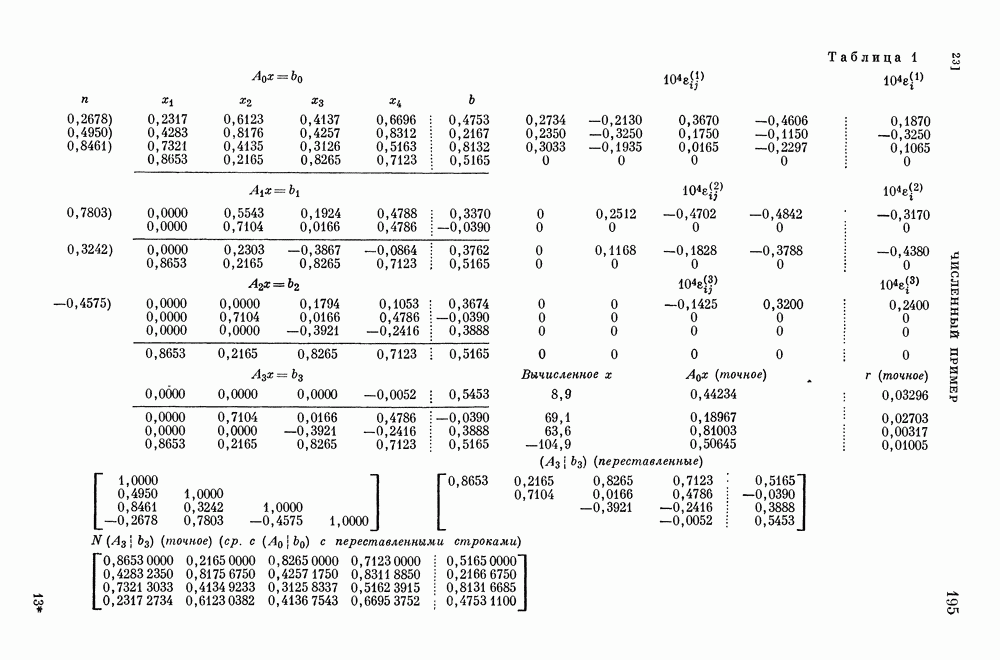
- Численный пример
- Анализ ошибок метода Гаусса
- Верхние оценки матриц возмущения для арифметики с фиксированной запятой
- Верхняя оценка для элементов преобразованных матриц
- Выбор главного элемента по всей матрице
- Практический процесс с выбором главного элемента по столбцу
- Анализ ошибок с плавающей запятой
- Разложение с плавающей запятой без выбора главного элемента
- Потеря верных знаков
- Общераспространенная ошибка
- Матрицы специального вида
- Метод Гаусса на быстродействующей вычислительной машине
- Решения, соответствующие различным правым частям
- Прямое треугольное разложение
- Связь метода Гаусса с прямым треугольным разложением
- Примеры несостоятельности и неединственности разложения
- Треугольное разложение с перестановкой строк
- Анализ ошибок треугольного разложения
- Вычисление определителей
- Разложение Холецкого
- Произвольные симметричные матрицы
- Анализ ошибок разложения Холецкого в арифметике с фиксированной запятой
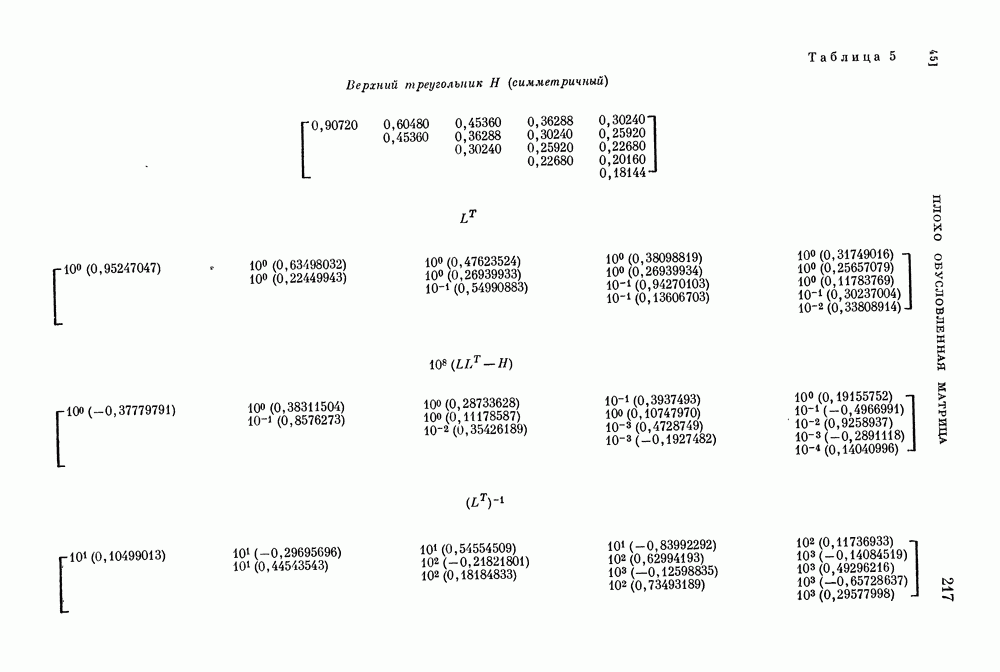
- Плохо обусловленная матрица
- Триангуляризация, использующая матрицы отражения
- Анализ ошибок триангуляризации Хаусхолдера
- Триангуляризации элементарными устойчивыми матрицами типа М
- Вычисление главных миноров
- Триангуляризация плоскими вращениями
- Анализ ошибок преобразования Гивенса
- Единственность ортогональной триангуляризации
- Ортогонализация Шмидта
- Сравнение методов триангуляризации
- Обратная подстановка
- Высокая точность вычисленного решения треугольной системы уравнений
- Решение общей системы уравнений
- Вычисление общей обратной матрицы
- Точность вычисленных решений
- Плохо обусловленные матрицы, которые дают немалые ведущие элементы
- Итерационное улучшение приближенного решения
- Влияние ошибок округления на итерационный процесс
- Итерационный процесс в вычислении с фиксированной запятой
- Простой пример итерационного процесса
- Общие замечания по итерационному процессу
- Родственные итерационные процессы
- Ограниченность итерационного процесса
- Строгое обоснование итерационного метода
- Дополнительные замечания
- ГЛАВА 5. ЭРМИТОВЫ МАТРИЦЫ
- Классический метод Якоби для вещественных симметричных матриц
- Быстрота сходимости
- Сходимость к фиксированной диагональной матрице
- Циклический метод Якоби
- Круги Гершгорина
- Асимптотическая квадратичная сходимость методов Якоби
- Близкие и кратные собственные значения
- Численные примеры
- Вычисление cos a и sin a
- Более простое определение углов вращения
- Циклический метод Якоби с преградами
- Вычисление собственных векторов
- Численный пример
- Анализ ошибок метода Якоби
- Точность вычисленных собственных векторов
- Оценки ошибок для вычислений с фиксированной запятой
- Организационные проблемы
- Метод Гивенса
- Процесс Гивенса на вычислительной машине с двухступенчатой памятью
- Анализ ошибок процесса Гивенса в арифметике с плавающей запятой
- Анализ ошибок в арифметике с фиксированной запятой
- Численный пример
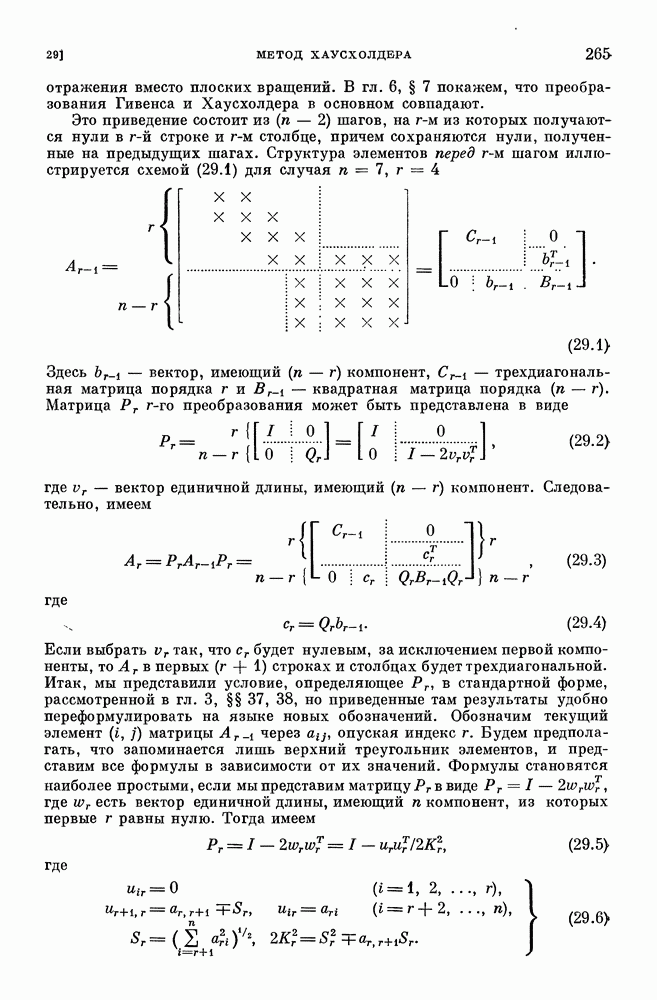
- Метод Хаусхолдера
- Использование симметрии
- Некоторые соображения о необходимой величине памяти
- Процесс Хаусхолдера на вычислительной машине с двухступенчатой памятью
- Метод Хаусхолдера в арифметике с фиксированной запятой
- Численный пример
- Анализ ошибок метода Хаусхолдера
- Собственные значения симметричной трехдиагональной матрицы
- Свойство последовательности Штурма
- Метод деления пополам
- Численная устойчивость метода деления пополам
- Численный пример
- Общие замечания о методе деления пополам
- Малые собственные значения
- Близкие собственные значения и малые
- Вычисление собственных значений в арифметике с фиксированной запятой
- Вычисление собственных векторов трехдиагональной матрицы
- Неустойчивость явного выражения для собственного вектора
- Численные примеры
- Обратная итерация
- Выбор начального вектора b
- Анализ ошибок
- Численный пример
- Близкие собственные значения и малые
- Линейно независимые векторы, соответствующие совпадающим собственным значениям
- Другой метод вычисления собственных векторов
- Численный пример
- Замечания о проблеме собственных значений для трехдиагональных матриц
- Завершение методов Гивенса и Хаусхолдера
- Сравнение методов
- Квазисимметричные трехдиагональные матрицы
- Вычисление собственных векторов
- Уравнения вида Ах = lВх и АВх = lх
- Численный пример
- Одновременное приведение A и B к диагональному виду
- Трехдиагональные A и B
- Комплексные эрмитовы матрицы
- Дополнительные замечания
- ГЛАВА 6. ПРИВЕДЕНИЕ ОБЩИХ МАТРИЦ К МАТРИЦАМ СПЕЦИАЛЬНОГО ВИДА
- Метод Гивенса
- Метод Хаусхолдера
- Соображения о необходимой величине памяти
- Анализ ошибок
- Связь методов Гивенса и Хаусхолдера
- Элементарные устойчивые преобразования
- Значение перестановок
- Прямое приведение к форме Хессенберга
- Введение перестановок
- Численный пример
- Анализ ошибок
- Дальнейший анализ ошибок
- Плохая определимость матрицы Хессенберга
- Приведение к форме Хессенберга матрицами типа …
- Метод Крылова
- Метод Гаусса с исключением по столбцам
- Практические трудности
- Обусловленность С для некоторых стандартных расположений собственных значений
- Начальный вектор высоты, меньшей чем n
- Практическое применение
- Обобщенные процессы Хессенберга
- Срыв обобщенного процесса Хессенберга
- Метод Хессенберга
- Практическая процедура
- Связь метода Хессенберга и предыдущих методов
- Метод Арнольди
- Практические рассмотрения
- Значение переортогонализации
- Метод Ланцоша
- Срыв процесса
- Численный пример
- Практический процесс Ланцоша
- Численный пример
- Общие замечания к несимметричному процессу Ланцоша
- Симметричный процесс Ланцоша
- Приведение матриц Хессенберга к более компактному виду
- Приведение нижней матрицы Хессенберга к трехдиагональному виду
- Использование перестановок
- Влияние малого ведущего элемента
- Анализ ошибок
- Процесс Хессенберга в применении к нижней матрице Хессенберга
- Связь процесса Хессенберга и процесса Ланцоша
- Приведение матрицы общего вида к трехдиагональному виду
- Сравнение с методом Ланцоша
- Повторное исследование приведения к трехдиагональному виду
- Приведение матриц в верхней форме Хессенберга к форме Фробениуса
- Влияние малых ведущих элементов
- Численный пример
- Общие замечания об устойчивости
- Специальная верхняя форма Хессенберга
- Прямое определение характеристического полинома
- Дополнительные замечания
- ГЛАВА 7. СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦ СПЕЦИАЛЬНОГО ВИДА
- Числа обусловленности явно заданных полиномов
- Несколько типичных расположений корней
- Окончательная оценка метода Крылова
- Общие замечания о явно заданных полиномах
- Трехдиагональные матрицы
- Определители матриц Хессенберга
- Влияние ошибок округления
- Накопление с плавающей запятой
- Вычисление при помощи ортогональных преобразований
- Вычисление определителей матриц общего вида
- Обобщенная проблема собственных значений
- Косвенное определение характеристического полинома
- Метод Леверье
- Итерационные методы, основанные на интерполяции
- Асимптотическая скорость сходимости
- Кратные корни
- Обращение функционального соотношения
- Метод деления отрезка пополам
- Метод Ньютона
- Сравнение метода Ньютона с методом интерполяции
- Методы, дающие кубическую сходимость
- Метод Лагерра
- Комплексные корни
- Комплексно сопряженные корни
- Метод Берстоу
- Обобщенный метод Берстоу
- Практические рассмотрения
- Влияние ошибок округления на асимптотическую сходимость
- Метод деления отрезка пополам
- Последовательная линейная интерполяция
- Кратные и патологически близкие собственные значения
- Другие интерполяционные методы
- Методы, в которых используются производные
- Критерий достижения корня
- Влияние ошибок округления
- Удаление вычисленных корней
- Исчерпывание для матриц Хессенберга
- Исчерпывание для трехдиагональной матрицы
- Исчерпывание при помощи вращений или устойчивых элементарных преобразований
- Устойчивость исчерпывания
- Общие замечания об исчерпывании
- Удаление вычисленных нулей
- Удаление вычисленного квадратичного множителя
- Общие комментарии о методах удаления
- Асимптотическая скорость сходимости
- Сходимость в целом
- Комплексные корни
- Рекомендации
- Комплексные матрицы
- Матрицы, содержащие независимый параметр
- Дополнительные замечания
- ГЛАВА 8. LR- и QR-алгоритмы
- Вещественные матрицы с комплексными собственными значениями
- LR-алгоритм
- Доказательство сходимости последовательности As
- Положительно определенные эрмитовы матрицы
- Комплексно сопряженные собственные значения
- Введение перестановок
- Численный пример
- Сходимость модифицированного процесса
- Предварительная подготовка исходной матрицы
- Инвариантность верхней формы Хессенберга
- Одновременное действие со строками и столбцами
- Ускорение сходимости
- Объединение сдвигов
- Выбор сдвига
- Исчерпывание матрицы
- Экспериментальная проверка сходимости
- Улучшенный выбор сдвига
- Комплексно сопряженные собственные значения
- Критика модифицированного LR-алгорифма
- QR-алгорифм
- Сходимость QR-алгорифма
- Формальное доказательство сходимости
- Нарушение порядка собственных значений
- Равные по модулю собственные значения
- Другое доказательство для LR-метода
- Практическое применение QR-алгорифма
- Сдвиг
- Разложение матриц As
- Численный пример
- Практическая процедура
- Устранение комплексно сопряженных сдвигов
- Двойной QR-шаг с использованием матриц отражения
- Вычислительные детали
- Разложение матриц As
- Прием двойного сдвига для LR
- Сравнение LR- и QR-алгорифмов
- Кратные собственные значения
- Специальное использование процесса исчерпывания
- Симметричные матрицы
- Связь между LR- и QR-алгорифмами
- Сходимость LR-алгорифма Холецкого
- Кубическая сходимость QR-алгорифма
- Сдвиг в LR-алгорифме Холецкого
- Срыв факторизации Холецкого
- Кубически сходящийся LR-процесс
- Ленточные матрицы
- QR-разложение ленточной матрицы
- Анализ ошибок
- Несимметричные ленточные матрицы
- Одновременное разложение и переумпожение в QR-алгорифме
- Уменьшение ширины ленточной матрицы
- Дополнительные замечания
- ГЛАВА 9. ИТЕРАЦИОННЫЕ МЕТОДЫ
- Степенной метод
- Прямые итерации одного вектора
- Сдвиг начала
- Влияние ошибок округления
- Процесс ускорения Эйткена
- Комплексно сопряженные собственные значения
- Вычисление комплексного собственного вектора
- Сдвиг начала
- Нелинейные делители
- Одновременное определение нескольких собственных значений
- Комплексные матрицы
- Исчерпывание
- Исчерпывание, основанное на преобразованиях подобия
- Исчерпывание, использующее инвариантные подпространства
- Исчерпывание при помощи устойчивых элементарных преобразований
- Исчерпывание при помощи унитарных преобразований
- Численная устойчивость
- Численный пример
- Устойчивость унитарных преобразований
- Исчерпывание при помощи неподобных преобразований
- Общее приведение, использующее инвариантные подпространства
- Практическое приложение
- Ступенчатые итерации
- Точное определение комплексно сопряженных собственных значений
- Очень близкие собственные значения
- Метод ортогонализации
- Аналог ступенчатых итераций, использующий ортогонализацию
- Биортогонализация
- Численный пример
- Процесс уточнения Ричардсона
- Возведение матрицы в степень
- Численная стабильность
- Использование полиномов Чебышева
- Общая оценка методов, основанных на прямых итерациях
- Обратные итерации
- Анализ ошибок при обратных итерациях
- Общие комментарии к анализу
- Дальнейшее уточнение собственных векторов
- Нелинейные элементарные делители
- Обратные итерации с матрицами Хессенберга
- Вырожденные случаи
- Обратные итерации с ленточными матрицами
- Комплексно сопряженные собственные векторы
- Анализ ошибок
- Численный пример
- Обобщенная проблема собственных значений
- Изменение приближенных собственных значений
- Уточнение системы собственных значений
- Численный пример
- Уточнение собственных векторов
- Комплексно сопряженные собственные значения
- Совпадающие и патологически близкие собственные значения
- Замечания о программах на АСЕ
- Дополнительные замечания