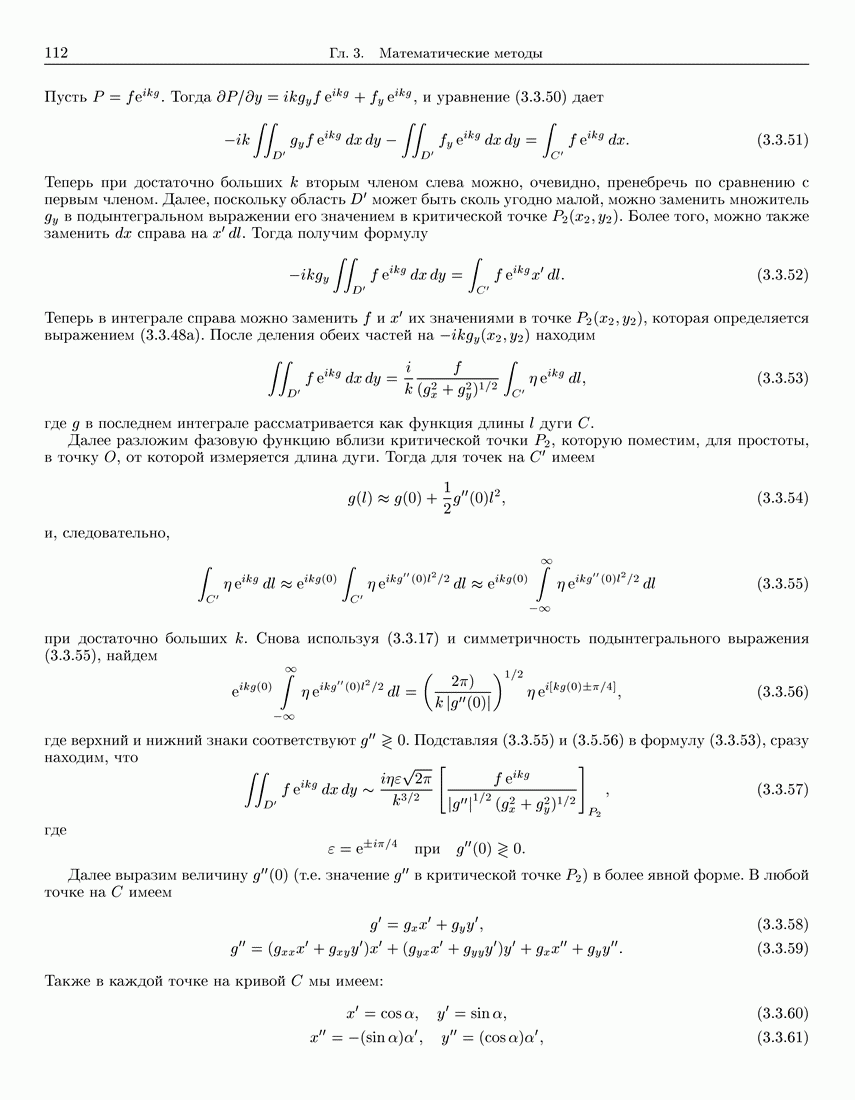| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
11.8. Диагональное представление оператора плотности по когерентным состояниям (Р-представление Глаубера — Сударшана)
В предыдущем разд. 11.7 было показано, что оператор с конечным следом, такой как оператор плотности  описывающий состояние системы, можно представить целиком в виде разложения по проекционным операторам
описывающий состояние системы, можно представить целиком в виде разложения по проекционным операторам  на когерентные состояния, не прибегая к слишком длинному выражению (11.6.10). Таким образом, можно записать
на когерентные состояния, не прибегая к слишком длинному выражению (11.6.10). Таким образом, можно записать

где  некоторая действительная функция
некоторая действительная функция  Поскольку
Поскольку  данное представление все еще задается двойным интегралом, но оно содержит только проекционные операторы и существенно проще представления (11.6.10) через четырехкратный интеграл. Формальный вывод (11.8.1) будет сделан ниже, в разд. 11.8.4 и 11.10.
данное представление все еще задается двойным интегралом, но оно содержит только проекционные операторы и существенно проще представления (11.6.10) через четырехкратный интеграл. Формальный вывод (11.8.1) будет сделан ниже, в разд. 11.8.4 и 11.10.
Данное представление впервые было введено независимо Сударшаном (Sudarshan, 1963) и Глаубером (Glauber, 1963с, 1970) и позже было сформулировано в математически строгом виде Клаудером с коллегами (Klauder, МсКеппа and Currie, 1965; Klauder, 1966; см. также Rocca, 1966; Miller and Mishkin, 1967; Klauder and Sudarshan, 1968). Элемент поверхности  иногда называют элементом фазового пространства. При этом интеграл в (11.8.1) становится интегралом по всему фазовому пространству, где
иногда называют элементом фазового пространства. При этом интеграл в (11.8.1) становится интегралом по всему фазовому пространству, где  играет роль плотности вероятности в фазовом пространстве или весовой функции. Выражение (11.8.1) также называют
играет роль плотности вероятности в фазовом пространстве или весовой функции. Выражение (11.8.1) также называют  -представлением состояния
-представлением состояния  и весовая функция в этом случае обозначается через
и весовая функция в этом случае обозначается через  Данное представление предполагает, что состояние электромагнитного поля можно рассматривать как смесь когерентных состояний с относительным весом
Данное представление предполагает, что состояние электромагнитного поля можно рассматривать как смесь когерентных состояний с относительным весом  или
или  Поскольку
Поскольку  эрмитов оператор, то
эрмитов оператор, то  действительная величина. Требование, что
действительная величина. Требование, что  имеет след, равный единице, означает, что
имеет след, равный единице, означает, что  нормирована на единицу, так как
нормирована на единицу, так как

Оба этих свойства согласуются с интуитивным представлением о том, что  играет роль плотности вероятности в фазовом пространстве.
играет роль плотности вероятности в фазовом пространстве.
Определим классическое состояние света как состояние, в котором  является плотностью вероятности. Однако, интерпретация
является плотностью вероятности. Однако, интерпретация  в общем случае более сложная. Прежде всего, различные когерентные состояния не ортогональны, так что даже если
в общем случае более сложная. Прежде всего, различные когерентные состояния не ортогональны, так что даже если  вела бы себя, как истинная плотность вероятности, она не могла бы описывать вероятности взаимоисключающих состояний. В действительности, существуют состояния поля, называемые неклассическими состояниями, для которых
вела бы себя, как истинная плотность вероятности, она не могла бы описывать вероятности взаимоисключающих состояний. В действительности, существуют состояния поля, называемые неклассическими состояниями, для которых  менее регулярна, чем плотность вероятности, которая должна быть неотрицательной и не может быть более сингулярной, чем дельта-функция. Далее мы увидим, что нетрудно найти примеры, когда
менее регулярна, чем плотность вероятности, которая должна быть неотрицательной и не может быть более сингулярной, чем дельта-функция. Далее мы увидим, что нетрудно найти примеры, когда  принимает отрицательные значения и становится более сингулярной, чем дельта-функция. В качестве примера весовой функции, которая не всегда является плотностью вероятности, рассмотрим распределение Вигнера (Wigner, 1932).
принимает отрицательные значения и становится более сингулярной, чем дельта-функция. В качестве примера весовой функции, которая не всегда является плотностью вероятности, рассмотрим распределение Вигнера (Wigner, 1932).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 1.2. Свойства вероятностей
- 1.2.1. Совместные вероятности
- 1.2.2. Условные вероятности
- 1.2.3. Теорема Байеса для апостериорных вероятностей
- 1.3. Случайные переменные и распределение вероятностей
- 1.3.1. Преобразования случайных переменных
- 1.3.2. Математические ожидания и моменты
- 1.3.3. Неравенство Чебышева
- 1.4. Производящие функции
- 1.4.1. Производящая функция моментов
- 1.4.2. Характеристическая функция
- 1.4.3. Кумулянты
- 1.5. Некоторые примеры распределений вероятности
- 1.5.1. Распределение Бернулли или биноминальное распределение
- 1.5.2. Пуассоновское распределение
- 1.5.3. Распределение Бозе — Эйнштейна
- 1.5.4. Закон больших чисел
- 1.5.5. Нормальное, или гауссовское распределение
- 1.5.6. Центральная предельная теорема
- 1.5.7. Гамма-распределение
- 1.6. Многомерное гауссовское распределение
- 1.6.1. Теорема о гауссовском моменте
- 1.6.2. Производящая функция моментов и характеристическая функция
- 1.6.3. Многократные комплексные гауссовские случайные переменные
- Глава 2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. Введение в статистические ансамбли
- 2.1.2. Совместные вероятности и корреляции
- 2.1.3. Функционал вероятности
- 2.2. Стационарность и эргодичность
- 2.2.1. Среднее по времени стационарного процесса
- 2.2.2. Эргодичность
- 2.2.3. Примеры случайных процессов
- 2.3. Свойства автокорреляционной функции
- 2.4. Спектральные свойства стационарного случайного процесса
- 2.4.1. Спектральная плотность и теорема Винера — Хинчина
- 2.4.2. Сингулярности спектральной плотности
- 2.4.3. Нормированные корреляции и нормированные спектральные плотности
- 2.4.4. Взаимные корреляции и взаимные спектральные плотности
- 2.5. Ортогональное представление случайного процесса
- 2.5.2. Предел … другой подход к теореме Винера — Хинчина
- 2.6. Временная эволюция и классификация случайных процессов
- 2.6.2. Абсолютно случайные или сепарабельные процессы
- 2.6.3. Марковский процесс первого порядка
- 2.6.4. Марковский процесс высшего порядка
- 2.7. Основные уравнения в интегро-дифференциальной форме
- 2.8. Основные уравнения в дифференциальной форме
- 2.8.1. Дифференциальное уравнение Крамерса — Мояля
- 2.8.2. Векторный случайный процесс
- 2.8.3. Порядок дифференциального уравнения Крамерса — Мояля
- 2.9. Уравнение Ланжевена и уравнение Фоккера — Планка
- 2.9.1. Моменты перехода для процесса Ланжевена
- 2.9.2. Стационарное решение уравнения Фоккера — Планка
- 2.9.3. Зависящее от времени решение уравнения Фоккера — Планка
- 2.10. Процесс Винера (или одномерное случайное блуждание)
- 2.10.2. Совместные вероятности и автокорреляция
- Глава 3. МАТЕМАТИЧЕСКИЕ МЕТОДЫ
- 3.1. Комплексный аналитический сигнал
- 3.1.2. Квази-монохроматические сигналы и их огибающие
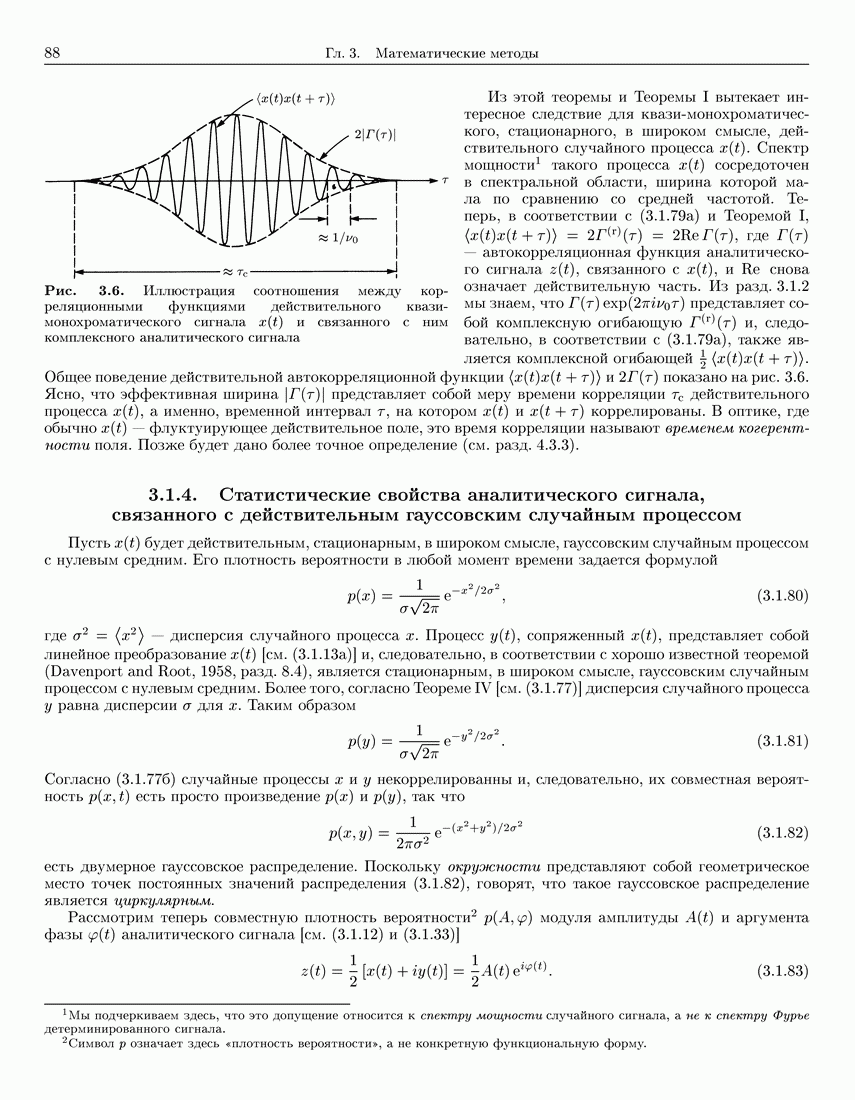
- 3.1.3. Соотношения между корреляционными функциями действительного и связанного с ним комплексного аналитических случайных процессов
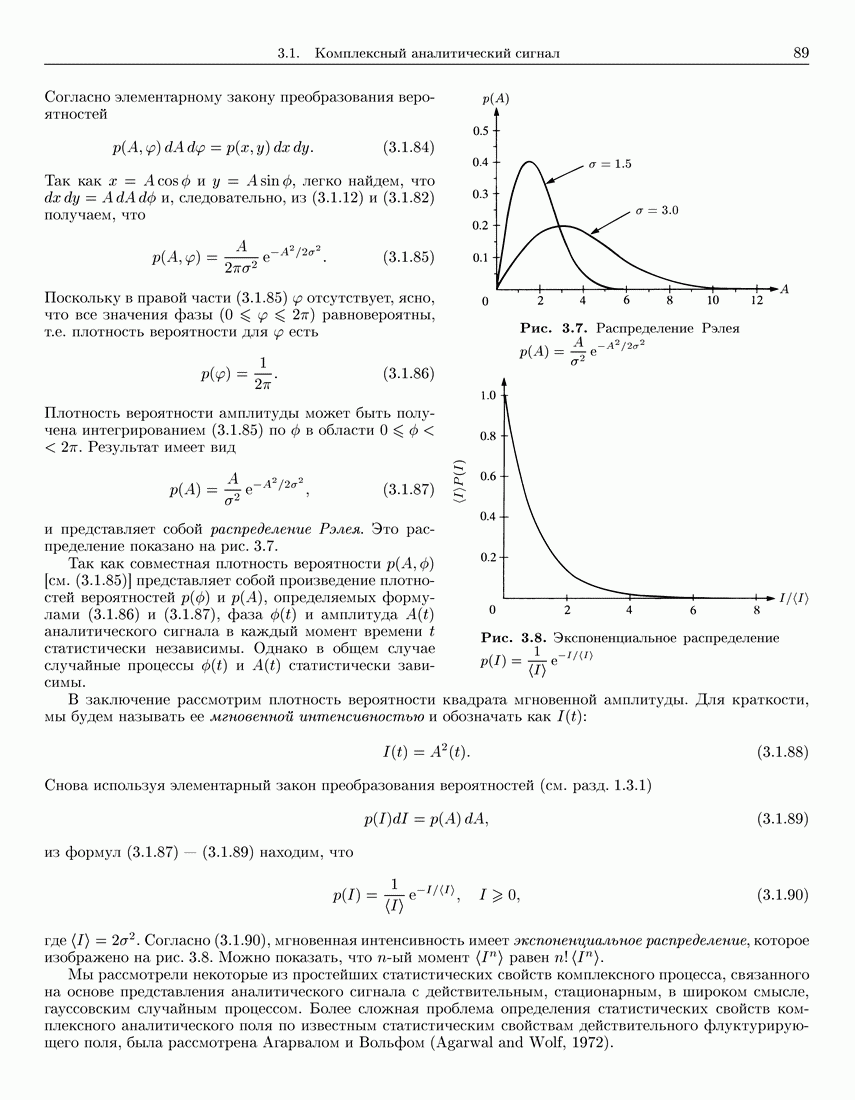
- 3.1.4. Статистические свойства аналитического сигнала, связанного с действительным гауссовским случайным процессом
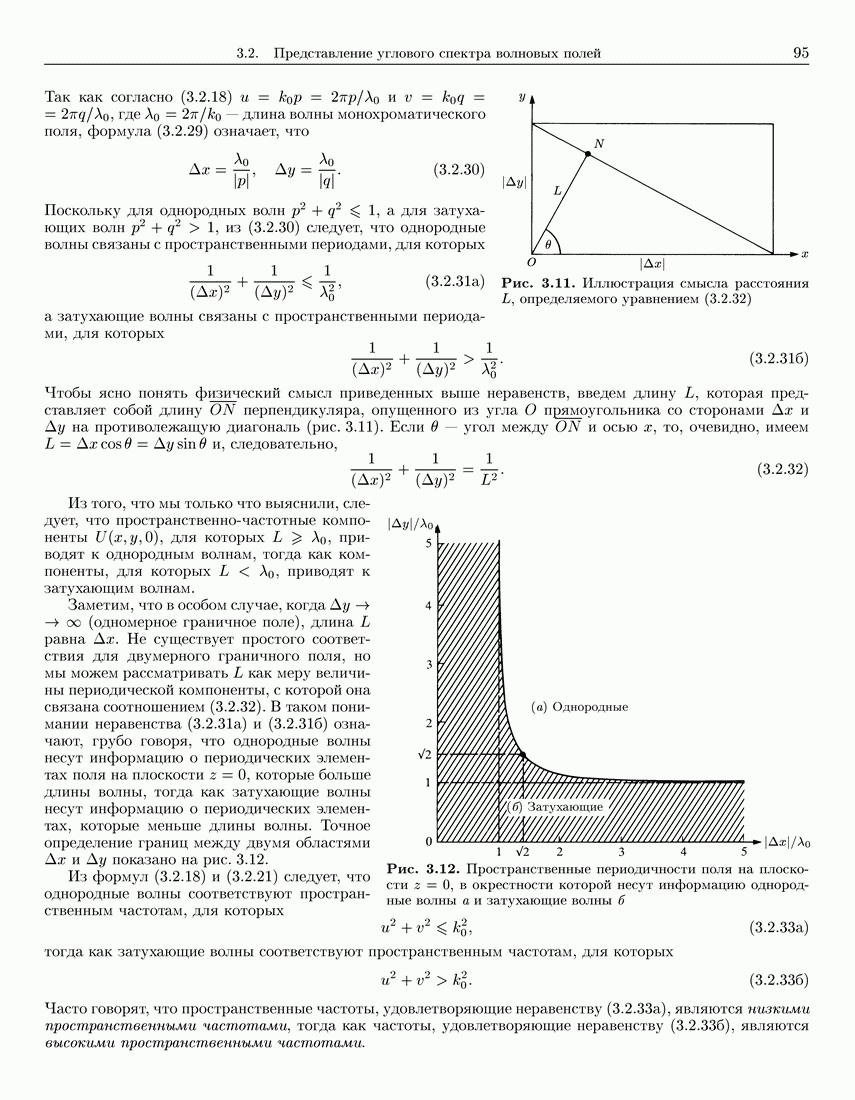
- 3.2. Представление углового спектра волновых полей
- 3.2.1. Угловой спектр волнового поля в плоско-параллельном слое
- 3.2.2. Угловой спектр волнового поля в полупространстве
- 3.2.3. Пример: дифракция на полупрозрачном объекте
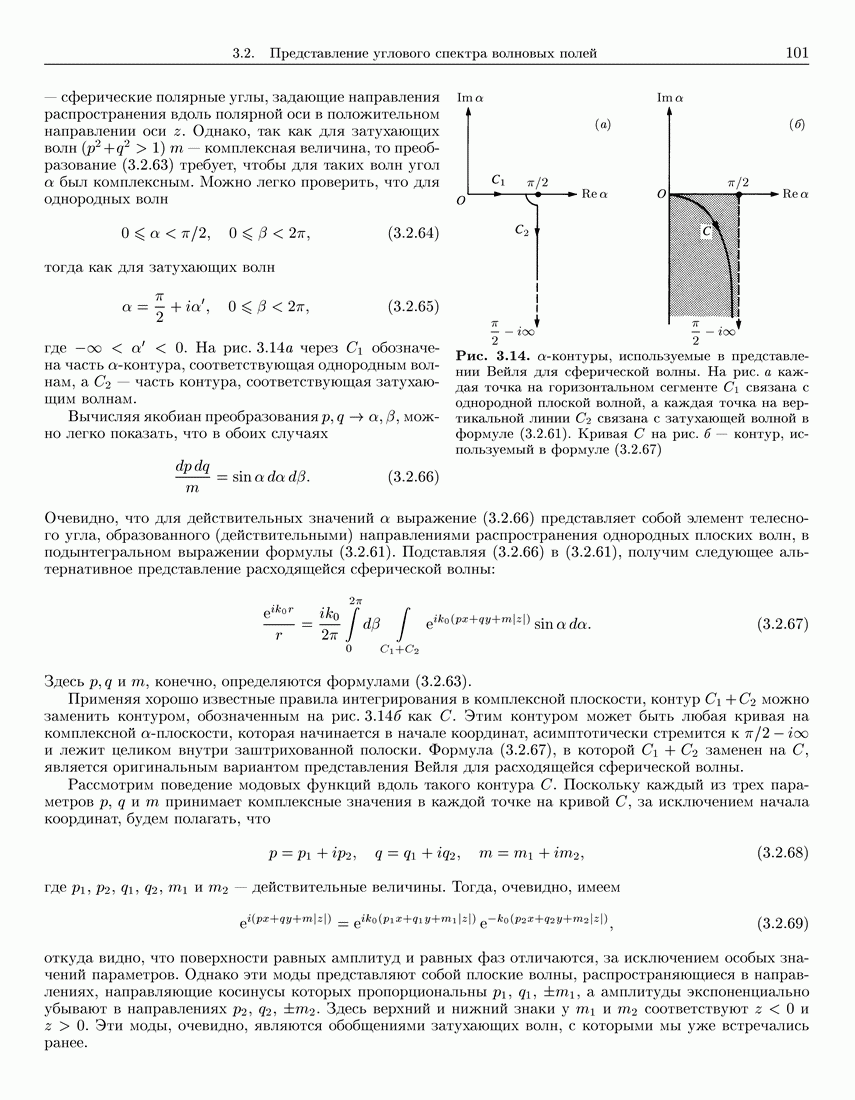
- 3.2.4. Представление Вейля для сферической волны
- 3.2.5. Дифракционные формулы Рэлея
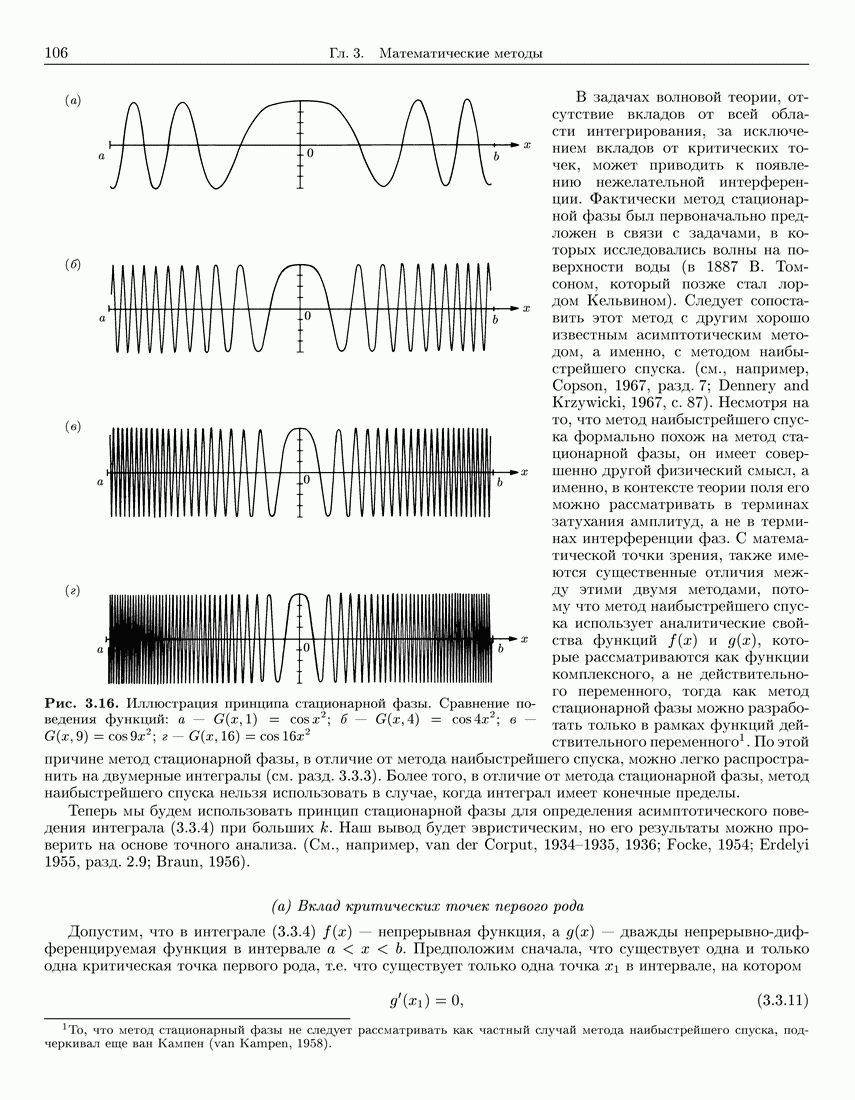
- 3.3. Метод стационарной фазы
- 3.3.2. Метод стационарной фазы для однократных интегралов
- 3.3.3. Метод стационарной фазы для двойных интегралов
- 3.3.4. Пример: поведение представления углового спектра для волновых полей в дальней зоне
- Глава 4. ТЕОРИЯ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА СКАЛЯРНЫХ ВОЛНОВЫХ ПОЛЕЙ
- 4.2. Некоторые элементарные представления и определения
- 4.2.1. Временная когерентность и время когерентности
- 4.2.2. Пространственная когерентность и площадь когерентности
- 4.2.3. Объем когерентности и параметр вырождения
- 4.3. Интерференция двух стационарных световых пучков как проявление корреляции второго порядка
- 4.3.2. Корреляции второго порядка в пространственно-частотной области. Взаимная спектральная плотность и спектральная степень когерентности
- 4.3.3. Время когерентности и ширина спектра
- 4.4. Распространение корреляций
- 4.4.2. Распространение корреляций от плоскости
- 4.4.3. Распространение корреляций от ограниченных поверхностей
- 4.4.4. Теорема Ван Циттерта — Цернике
- 4.4.5. Распространение корреляций от первичных источников
- 4.5. Специальные типы полей
- 4.5.1. Взаимно спектрально чистый свет
- 4.5.2. Когерентный свет в пространственно-временной области
- 4.5.3. Когерентный свет в пространственно-частотной области
- 4.6. Свободные поля с произвольной степенью когерентности
- 4.6.1. Уравнения Сударшана для распространения корреляционных функций второго порядка свободных полей
- 4.6.2. Временная эволюция корреляционных функций второго порядка свободных полей
- 4.6.3. Взаимосвязь между свойствами временной и пространственной когерентности свободных полей
- 4.6.4. Взаимосвязь спектральных свойств и свойств пространственной когерентности свободных полей
- 4.7. Представление по когерентным модам и представление по ансамблю для источников и полей в пространственно-частотной области
- 4.7.1. Представление по когерентным модам частично когерентных полей в свободном пространстве
- 4.7.2. Строгое представление взаимной спектральной плотности в виде корреляционной функции
- 4.7.3. Нормальные моды колебаний частично когерентных первичных источников и представление их взаимной спектральной плотности в виде корреляционной функции
- Приложение 4.1. Ядро H(R) оператора … в представлении интегрального преобразования
- Приложение 4.2. Функция Грина G(R, Т) для временной эволюции аналитического сигнала свободного поля и ее фурье-образ …
- Глава 5. ИЗЛУЧЕНИЕ ИСТОЧНИКОВ ЛЮБОЙ СТЕПЕНИ КОГЕРЕНТНОСТИ
- 5.2. Излучение трехмерных первичных источников
- 5.2.2. Излучение от некоторых модельных источников
- 5.3. Излучение плоских вторичных источников
- 5.3.2. Излучение плоских, вторичных, квазиоднородных источников
- 5.3.3. Обратная задача для плоских, вторичных, квазиоднородных источников
- 5.4. Теоремы эквивалентности для плоских источников, генерирующих одинаковую интенсивность излучения
- 5.4.1. Теорема эквивалентности для плоских источников
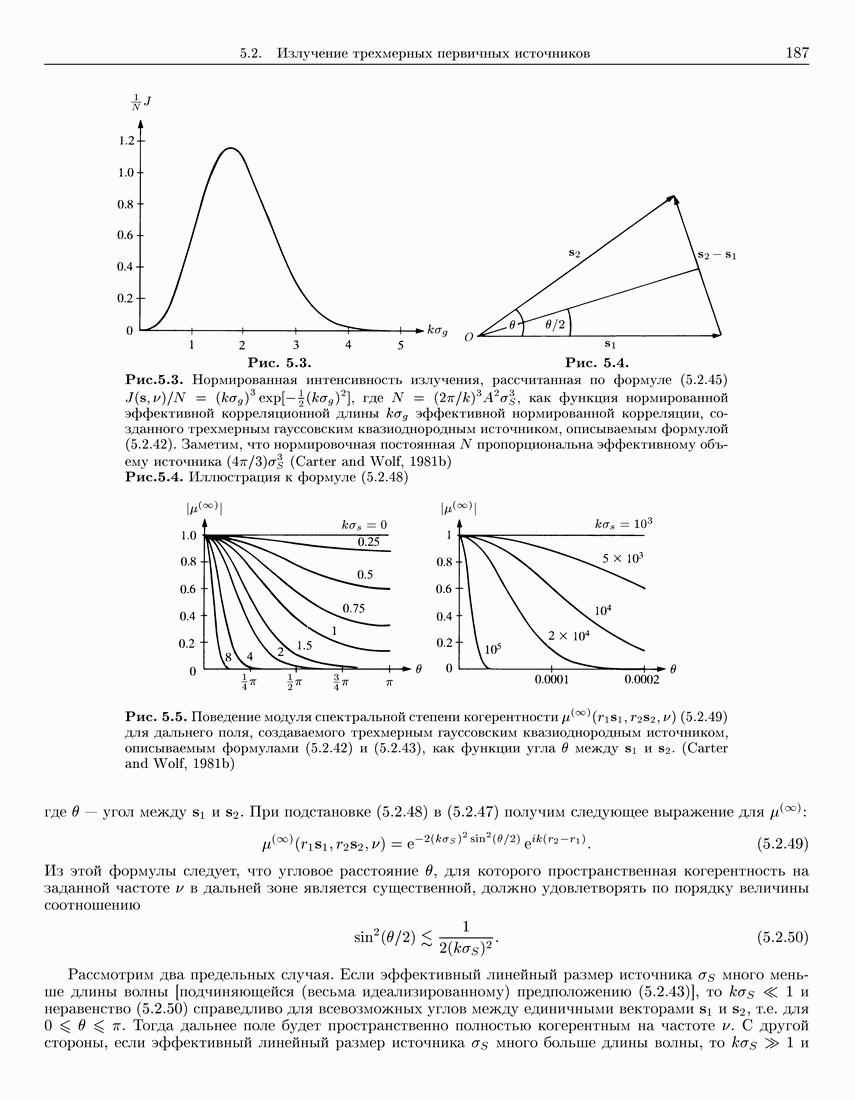
- 5.4.2. Пример: эквивалентные гауссовские источники модели Шелла
- 5.4.3. Экспериментальная проверка теоремы эквивалентности
- 5.5. Представление по когерентным модам для гауссовскнх источников модели Шелла
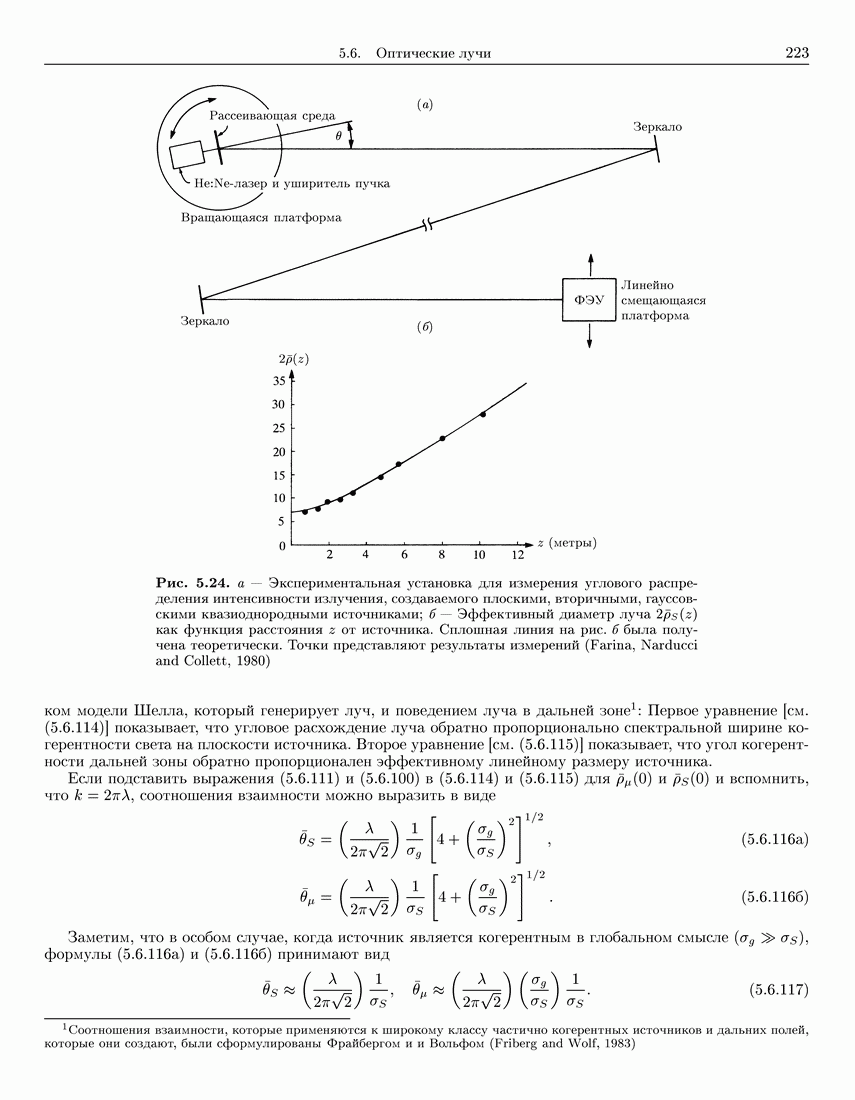
- 5.6. Оптические лучи
- 5.6.1. Монохроматические лучи
- 5.6.2. Пример: монохроматические гауссовские лучи
- 5.6.3. Частично когерентные лучи
- 5.6.4. Гауссовские лучи модели Шелла
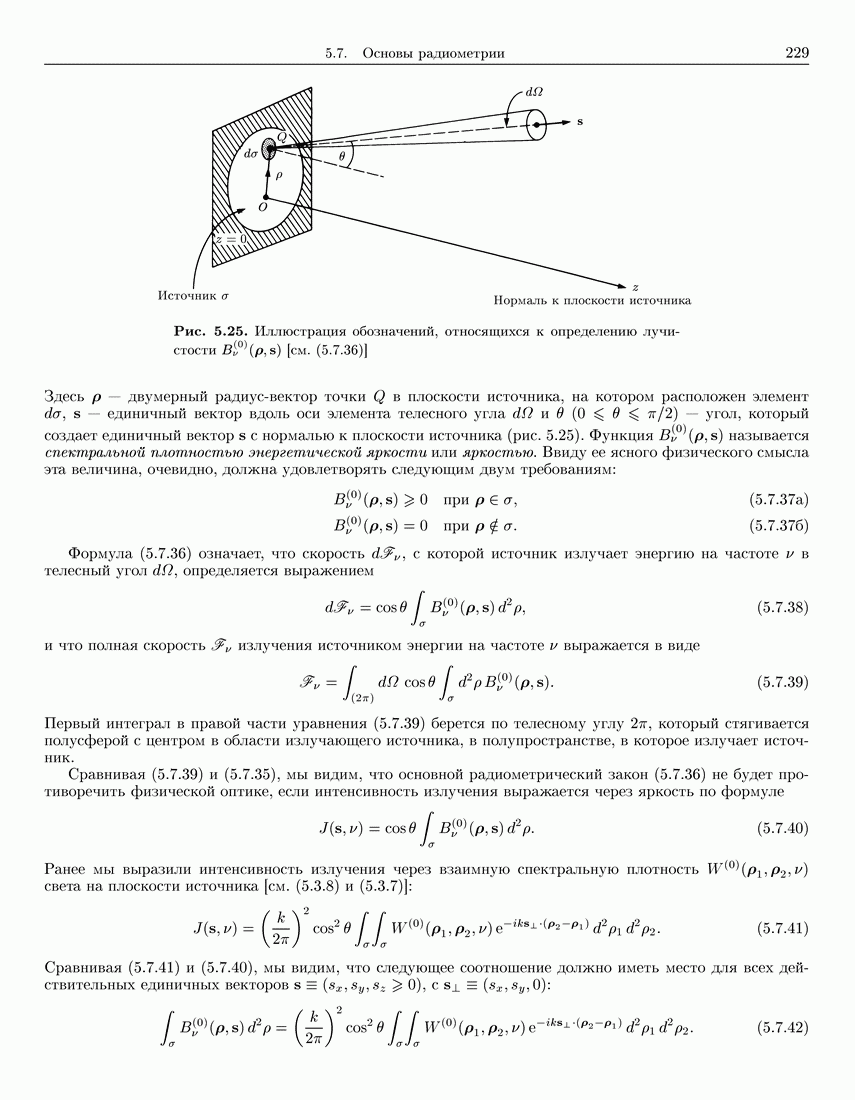
- 5.7. Основы радиометрии
- 5.7.1. Плотность энергии, поток энергии и закон сохранения энергии в скалярных волновых полях
- 5.7.2. Основные понятия радиометрии
- 5.7.3. Функция энергетической яркости от плоских вторичных квазиоднородных источников
- 5.7.4. Модель переноса энергии излучения
- 5.7.5. Радиометрия как коротковолновой предел статистической волновой теории с квазиоднородными источниками
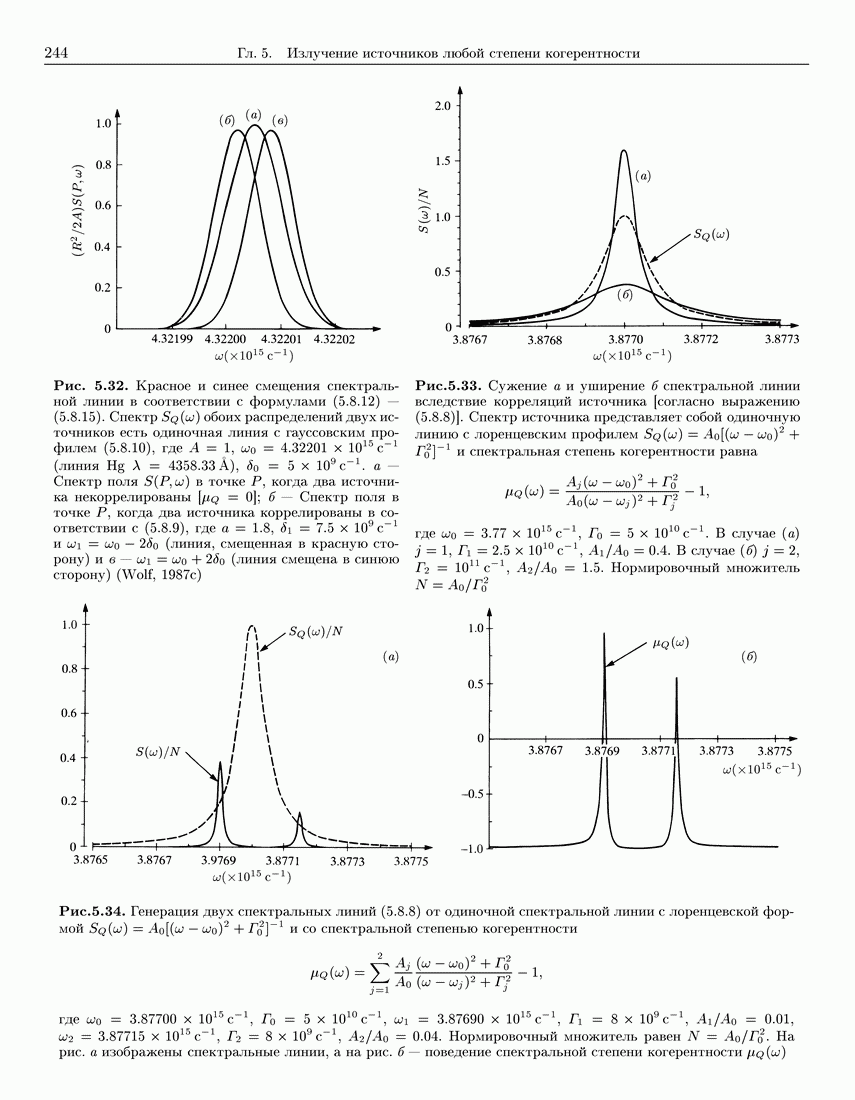
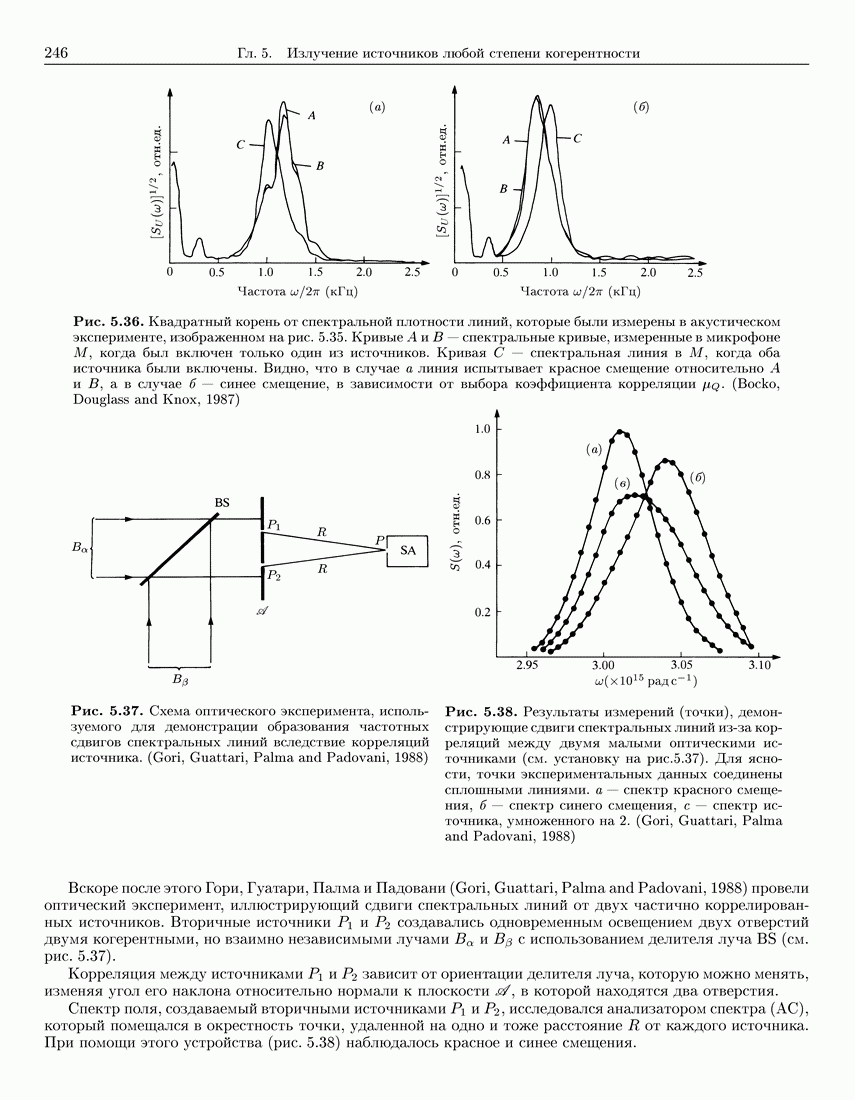
- 5.8. Влияние пространственной когерентности источника на спектр излучаемых полей
- 5.8.2. Спектр дальнего поля, образуемого плоскими вторичными квазиоднородными источниками
- 5.8.3. Условие для спектральной инвариантности: закон скейлинга для плоских вторичных квазиоднородных источников
- Приложение 5.1 Вывод асимптотического приближения (5.7.103)
- Приложение 5.2 Теорема произведения для гауссовских функций
- Глава 6. ТЕОРИЯ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА ВЕКТОРНЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
- 6.2. Равновременная 2×2-матрица когерентности хорошо коллимированного, однородного, квазимонохроматического светового луча
- 6.3. Полностью неполяризованный и полностью поляризованный свет. Степень поляризации
- 6.3.2. Полностью поляризованный свет
- 6.3.3. Степень поляризации
- 6.4. Прохождение квазимонохроматического луча через линейные, не формирующие изображения устройства
- 6.5. Обобщенные матрицы когерентности второго порядка и тензоры когерентности стационарного электромагнитного поля
- 6.5.2. Дифференциальные уравнения первого порядка для распространения тензоров когерентности
- 6.5.3. Волновые уравнения для распространения тензоров когерентности
- 6.6. Тензоры взаимной спектральной плотности второго порядка стационарного электромагнитного поля
- 6.6.1. Электрический, магнитный и смешанный тензоры взаимной спектральной плотности
- 6.6.2. Дифференциальные уравнения первого порядка для распространения тензоров взаимной спектральной плотности
- 6.6.3. Уравнения Гельмгольца для распространения тензоров взаимной спектральной плотности
- Глава 7. ПРИМЕНЕНИЯ ТЕОРИИ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА
- 7.2. Звездная интерферометрия
- 7.3. Интерференционная спектроскопия
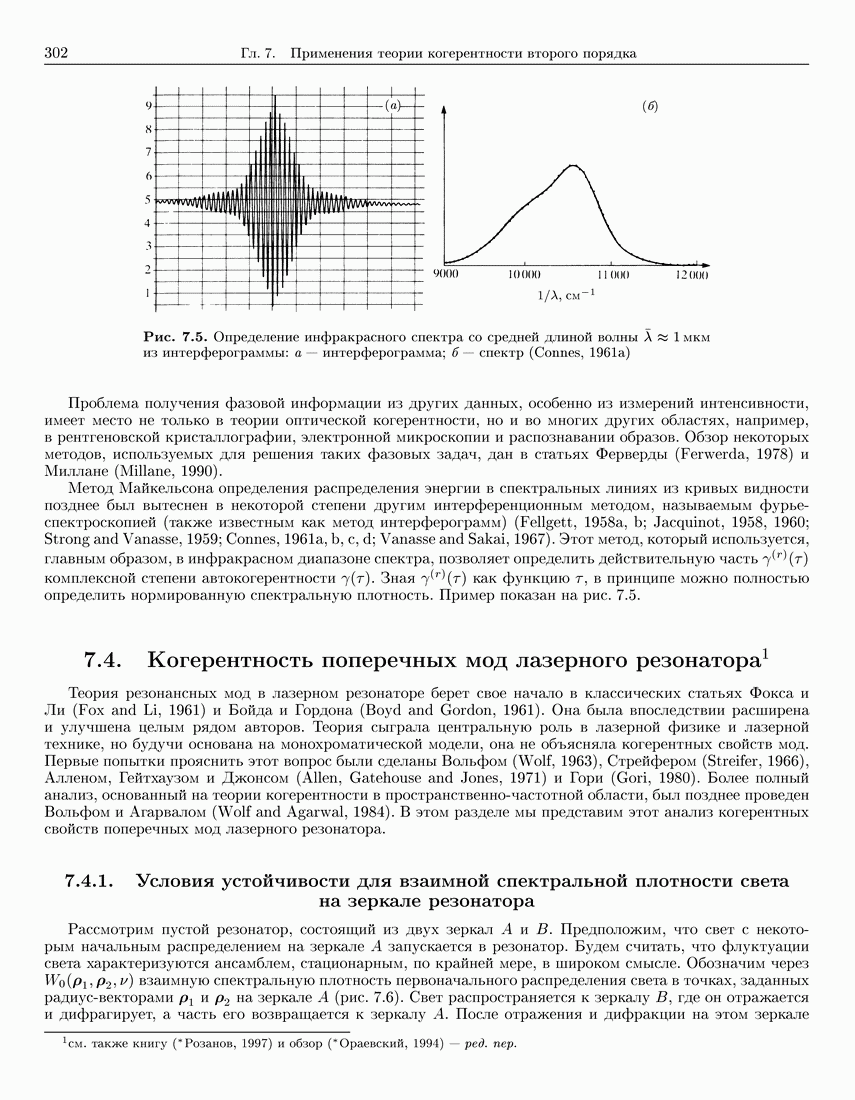
- 7.3.2. Проблема фазы
- 7.4. Когерентность поперечных мод лазерного резонатора
- 7.4.1. Условия устойчивости для взаимной спектральной плотности света на зеркале резонатора
- 7.4.2. Природа решений интегрального уравнения (7.4.7)
- 7.5. Диэлектрический отклик и спектр индуцированной поляризации во флуктуирующей среде
- 7.5.1. Среда, макроскопические свойства которой не изменяются со временем
- 7.5.2. Среда, макроскопические свойства которой зависят от времени детерминированным образом
- 7.5.3. Среда, макроскопические свойства которой случайным образом меняются во времени
- 7.6. Рассеяние от случайных сред
- 7.6.1. Основные уравнения для детерминированного рассеяния
- 7.6.2. Рассеяние на детерминированной среде в приближении Борна первого порядка
- 7.6.3. Рассеяние случайной средой в приближении Борна первого порядка
- 7.6.4. Некоторые частные случаи
- 7.6.5. Рассеяние от простой жидкости
- Приложение 7.1 Вычисление среднего значения … (выражение (7.6.36))
- Глава 8. КОРРЕЛЯЦИИ ОПТИЧЕСКИХ ПОЛЕЙ ВЫСШЕГО ПОРЯДКА
- 8.2. Пространственно-временные корреляционные функции произвольного порядка
- 8.3. Пространственно-частотные корреляционные функции произвольного порядка
- 8.4. Корреляционные функции полей, подчиняющихся гауссовской статистике
- 8.5. Представление по когерентным модам взаимных спектральных плотностей произвольного порядка
- 8.5.2. Одномодовое поле
- 8.5.3. Поля, подчиняющиеся гауссовской статистике
- Глава 9. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ФОТОДЕТЕКТИРОВАНИЯ
- 9.2. Обзор элементарной квантовой механики
- 9.3. Дифференциальная вероятность фотодетектирования
- 9.4. Совместные вероятности многократного фотодетектирования
- 9.5. Интегральные вероятности детектирования
- 9.6. Фотоэлектрическое детектирование во флуктуирующих полях
- 9.6.1. Фотоэлектрическая группировка
- 9.7. Статистика фотоэлектрических отсчетов флуктуирующего поля
- 9.8. Флуктуации фотоэлектрического тока
- 9.8.2. Свет от теплового источника
- 9.8.3. Спектральная плотность фототока
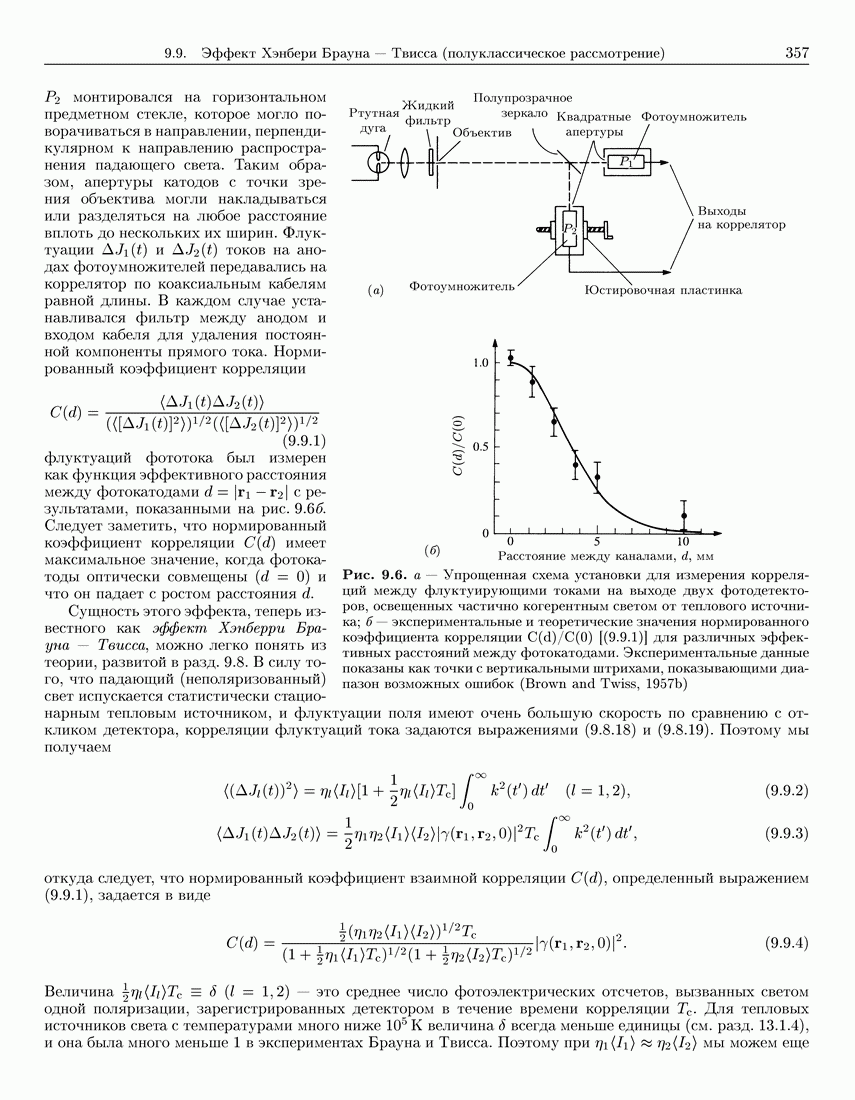
- 9.9. Эффект Хэнбери Брауна — Твисса (полуклассическое рассмотрение)
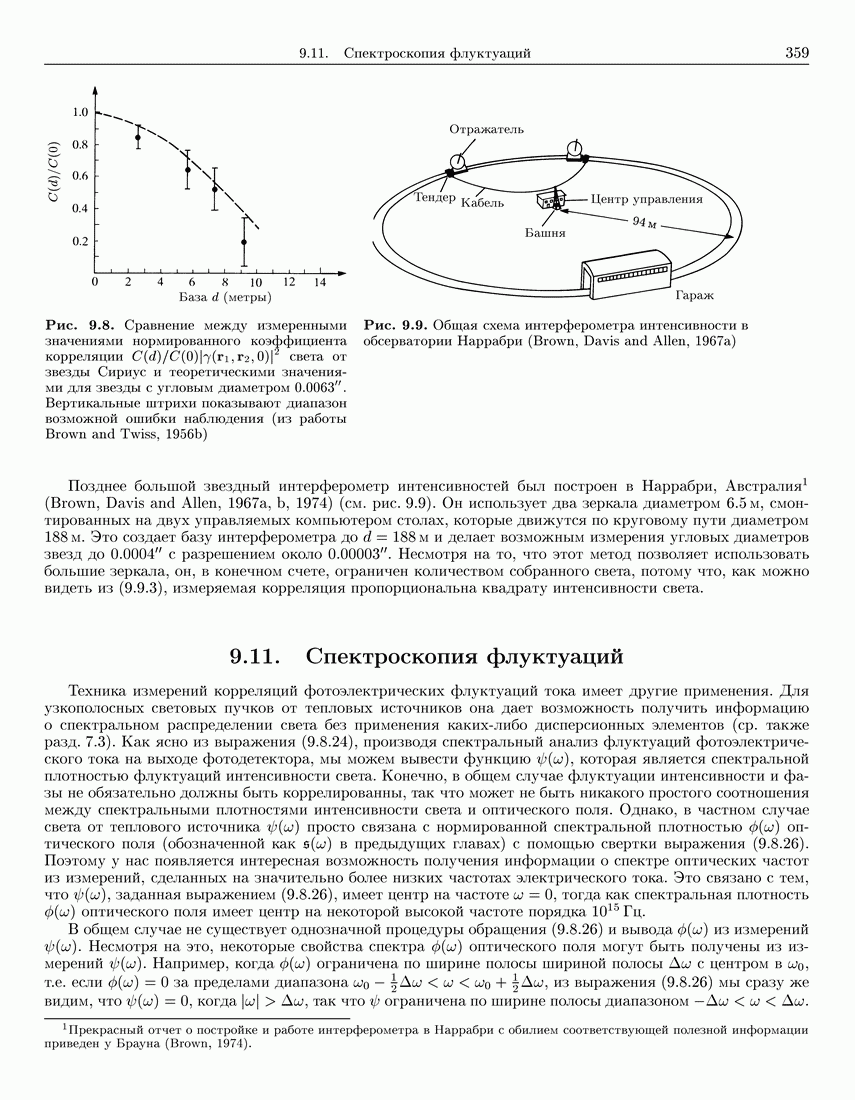
- 9.10. Звездная интерферометрия интенсивностей
- 9.11. Спектроскопия флуктуаций
- Глава 10. КВАНТОВАНИЕ СВОБОДНОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 10.2. Гамильтониан классического поля и канонические уравнения движения
- 10.2.2. Единичные векторы поляризации
- 10.2.3. Энергия электромагнитного поля
- 10.3. Каноническое квантование поперечного поля
- 10.4. Энергетический спектр; фотоны
- 10.4.1. Фоковские состояния
- 10.4.2. Псевдолокализованные фотоны
- 10.4.3. Базис фоковских состояний
- 10.4.4. q-представление фоковских состояний
- 10.4.5. Зависимость операторов поля от времени
- 10.5. Импульс квантованного поля
- 10.6. Момент количества движения квантованного поля.
- 10.6.2. Разложение полного момента количества движения
- 10.6.3. Собственный (спиновый) момент количества движения
- 10.6.4. Орбитальный момент количества движения
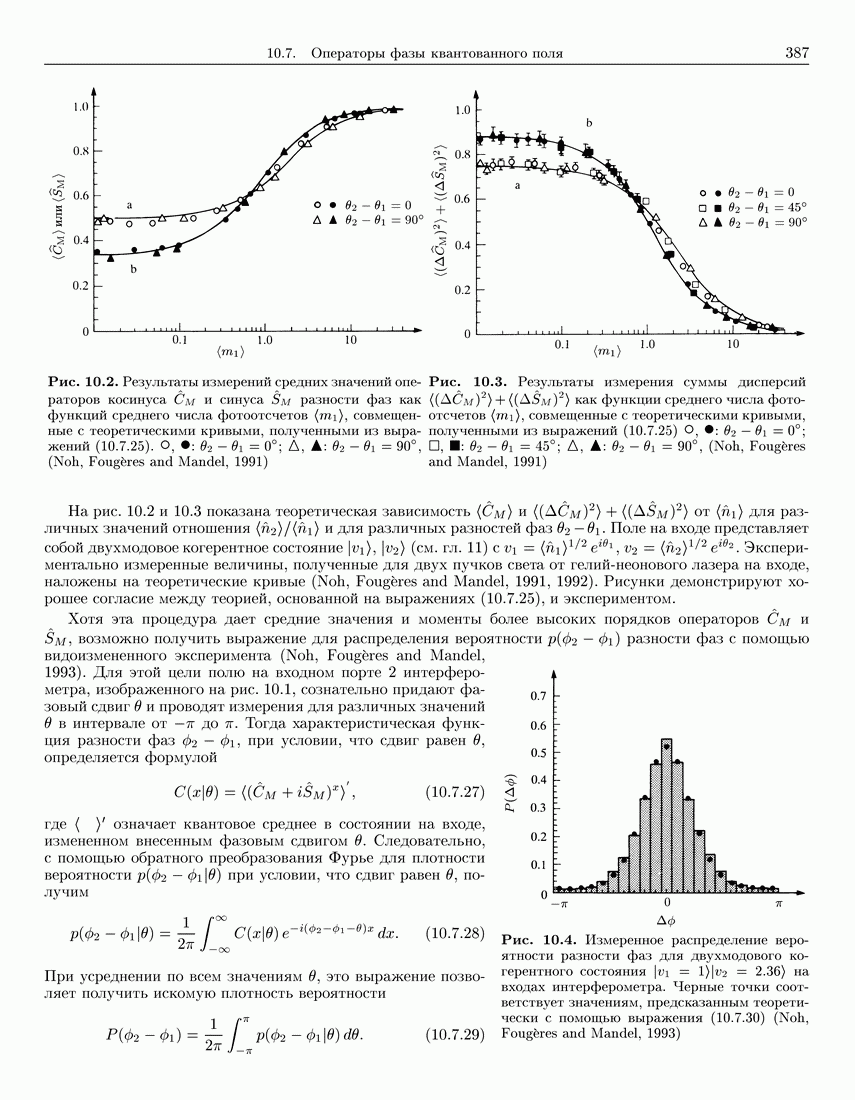
- 10.7. Операторы фазы квантованного поля
- 10.7.2. Операторы косинуса и синуса
- 10.7.3. Оператор фазы на основе проекционного оператора на фазовые состояния
- 10.7.4. Операционно определенные фазовые операторы
- 10.8. Пространственно-временные коммутационные соотношения
- 10.9. Вакуумные флуктуации
- 10.9.1. Флуктуации локально усредненных полей
- 10.9.2. Порядок величины вакуумных флуктуаций
- 10.9.3. Сила Казимира между проводниками
- 10.9.4. Лэмбовский сдвиг
- 10.9.5. Вакуумные эффекты в делителе пучка
- 10.10. Непрерывное фоковское пространство
- 10.11. Некоторые теоремы операторной алгебры
- 10.11.2. Теоремы о преобразовании подобия
- 10.11.3. Теоремы о производных
- 10.11.4. Нормальный и антинормальный порядок
- 10.11.5. Теорема Кемпбелла — Бейкера — Хаусдорфа.
- Глава 11. КОГЕРЕНТНЫЕ СОСТОЯНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 11.2. Фоковское представление когерентных состояний
- 11.3. Когерентное состояние как смещенное вакуумное состояние. Оператор смещения
- 11.3.1. Свойства оператора смещения
- 11.4. q-представление когерентных состояний
- 11.5. Эволюция во времени и соотношения неопределенностей
- 11.5.1. Произведение канонических неопределенностей
- 11.5.2. Более общие состояния с минимальной неопределенностью
- 11.6. Когерентные состояния как базис. Неортогональность и переполненность
- 11.6.1. Линейная зависимость когерентных состояний
- 11.6.2. Переполненность
- 11.6.3. Представление операторов по когерентным состояниям
- 11.6.4. Вычисление матричных элементов нормально упорядоченных операторов
- 11.7. Представление состояний и операторов целыми функциями
- 11.8. Диагональное представление оператора плотности по когерентным состояниям (Р-представление Глаубера — Сударшана)
- 11.8.1. Плотности квазивероятности. Распределение Вигнера
- 11.8.2. Два достоинства диагонального представления
- 11.8.3. Диагональное представление p с помощью последовательности функций
- 11.8.4. Диагональное представление антинормально упорядоченного оператора плотности
- 11.8.5. Интегральное представление функции …
- 11.8.6. Примеры
- 11.9. Оптическая теорема эквивалентности для нормально упорядоченных операторов
- 11.9.1. Квантовые характеристические функции
- 11.10. Более общие представления в фазовом пространстве
- 11.10.2. Упорядочение операторов
- 11.10.3. Приложение к квантовым средним и диагональному представлению по когерентным состояниям
- 11.11. Многомодовые поля
- 11.11.1. Когерентные состояния в непрерывном представлении
- 11.12. Положительно- и отрицательно-частотные операторы поля
- 11.12.1. Коммутационные соотношения
- 11.12.2. Нормально упорядоченные корреляционные функции
- 11.13. Поле, создаваемое классическим током
- Глава 12. КВАНТОВЫЕ КОРРЕЛЯЦИИ И ФОТОННАЯ СТАТИСТИКА
- 12.2. Фотоэлектрическое измерение оптического поля; нормальное упорядочение
- 12.2.1. Детектирование нескольких фотонов; корреляционные функции высшего порядка
- 12.2.2. Символы и операторы упорядочения
- 12.3. Оператор фотонной плотности
- 12.4. Интерференционные эксперименты; корреляционные функции второго порядка
- 12.5. Корреляционные функции и взаимные спектральные плотности произвольного порядка
- 12.5.1. Свойства корреляционных функций
- 12.5.2. Взаимные спектральные плотности произвольного порядка
- 12.5.3. Независящие от фазы весовые функции
- 12.6. Степень и порядок когерентности
- 12.7. Значение когерентности второго порядка
- 12.7.2. Корреляции произвольного порядка
- 12.7.3. Оператор плотности для поля
- 12.7.4. Волновые пакеты в качестве мод
- 12.8. Стационарность, однородность, изотропность
- 12.8.2. Условие для оператора плотности
- 12.8.3. Свойства взаимных спектральных плотностей в случае стационарных полей
- 12.8.4. Однородность
- 12.8.5. Изотропность
- 12.9. Антинормально упорядоченные корреляционные функции
- 12.9.2. Замена дифференциальными операторами
- 12.9.3. Весовой функционал для антинормально упорядоченных корреляционных функций
- 12.10. Фотонная статистика
- 12.10.2. Условия для неклассических состояний
- 12.10.3. Моменты n
- 12.10.4. Производящие функции для числа фотонов при нормальном и антинормальном порядке
- 12.11. Проблема локализации фотонов
- 12.11.1. Оператор числа фотонов, определяемый в конфигурационном пространстве
- 12.11.2. Коммутационные соотношения
- 12.11.3. Собственные состояния …
- 12.11.4. Статистика фотона в конечном объеме
- 12.11.5. Полихроматические фотоны и не локальность
- 12.12. Влияние аттенюатора или делителя пучка на квантовое поле
- 12.12.2. Корреляции фотонов
- 12.12.3. Интерферометр Майкельсона
- 12.12.4. Связь между входными и выходными состояниями для делителя пучка
- 12.13. Влияние поляризатора на поле
- 12.14. Локальность Эйнштейна и корреляции фотонов
- 12.14.1. Парадокс Эйнштейна — Подольского — Розена для перепутанного двухфотонного состояния
- 12.14.2. Неравенства Белла
- 12.14.3. Форма Клаузера — Хорна неравенства Белла
- 12.14.4. Экспериментальное подтверждение
- 12.14.5. Неклассические состояния и неравенства Белла
- Глава 13. ИЗЛУЧЕНИЕ ИСТОЧНИКОВ, НАХОДЯЩИХСЯ В СОСТОЯНИИ ТЕПЛОВОГО РАВНОВЕСИЯ
- 13.1. Излучение черного тела
- 13.1.2. Статистика фотонов
- 13.1.3. Поляризация
- 13.1.4. Спектральные распределения
- 13.1.5. Диагональное представление p по когерентным состояниям
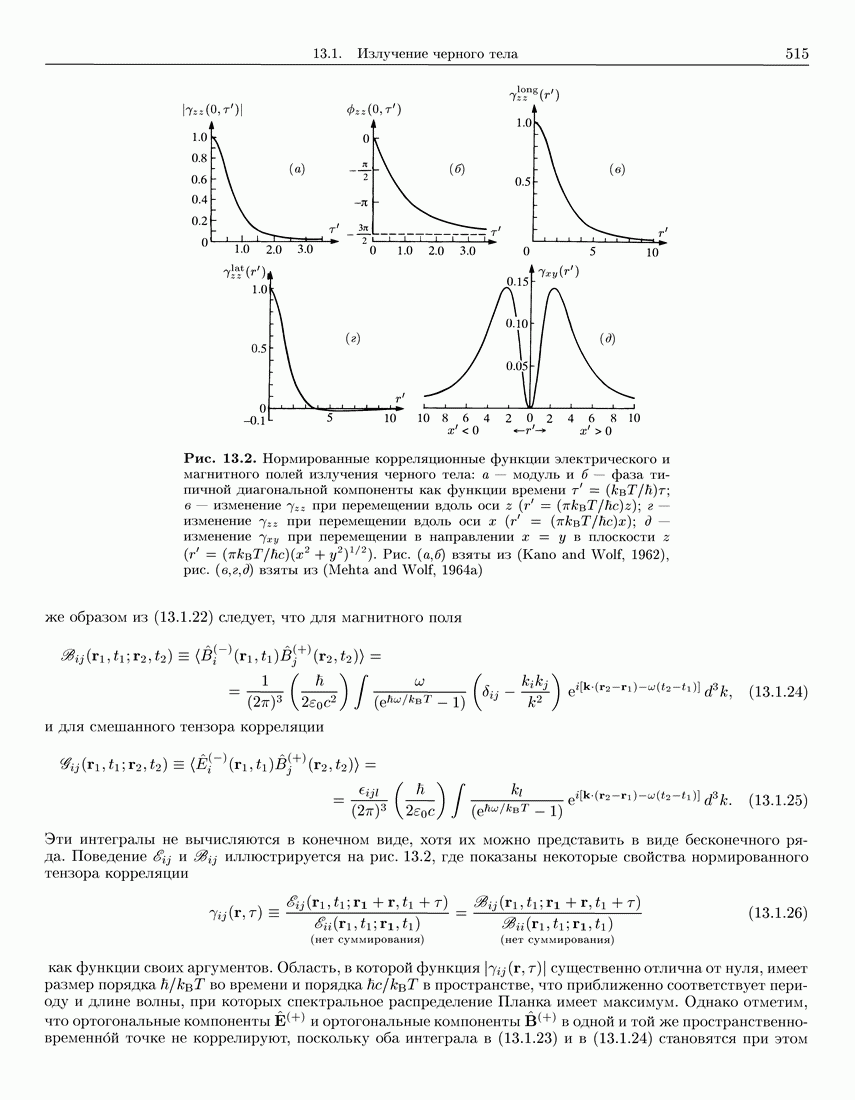
- 13.1.6. Корреляционные функции излучения черного тела
- 13.1.7. Функции корреляции высокого порядка
- 13.1.8. Изотропность излучения черного тела
- 13.1.9. Флуктуации интенсивности излучения черного тела
- 13.2. Свет от теплового источника
- 13.3. Пучки стационарного света от теплового источника
- 13.3.2. Статистика фотонов при одинаковых средних числах заполнения
- Глава 14. КВАНТОВАЯ ТЕОРИЯ ФОТОДЕТЕКТИРОВАНИЯ
- 14.1. Взаимодействия квантованного электромагнитного поля
- 14.1.1. Решение по теории возмущений в картине взаимодействия
- 14.1.2. Электромагнитное взаимодействие между полями и зарядами
- 14.1.3. Многополюсный гамильтониан
- 14.2. Вероятность одноэлектронного фотодетектирования
- 14.2.1. Применение к чистому когерентному состоянию
- 14.2.2. Вычисление вероятности в квазимонохроматическом приближении
- 14.2.3. Вычисление электронного матричного элемента
- 14.2.4. Вычисление вероятности детектирования для аксиально симметричного детектора
- 14.3. N-электронный фотодетектор
- 14.4. Вероятность многократного фотоэлектрического детектирования
- 14.5. Вероятность многократного детектирования при произвольном начальном состоянии поля
- 14.6. Фотоэлектрические корреляции
- 14.6.1. Эффект Хэнбери Брауна — Твисса (квантовая трактовка)
- 14.6.2. Корреляции фототоков
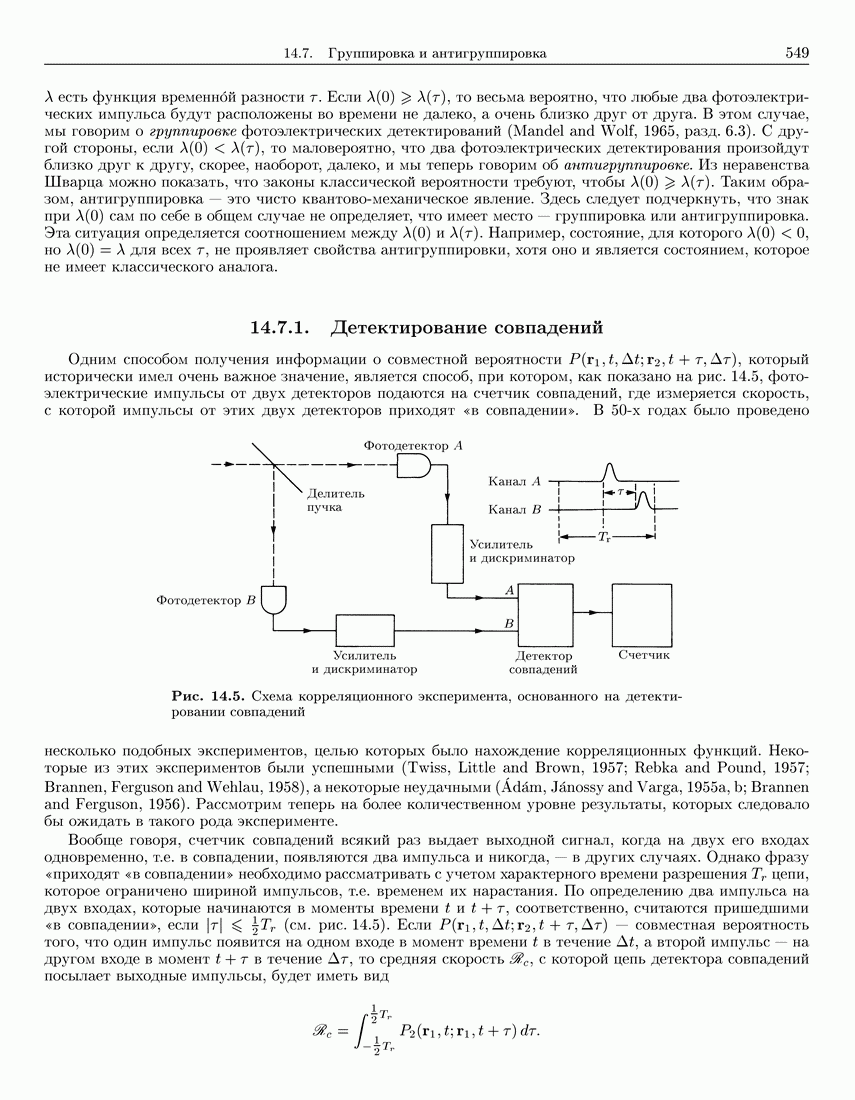
- 14.7. Группировка и антигруппировка
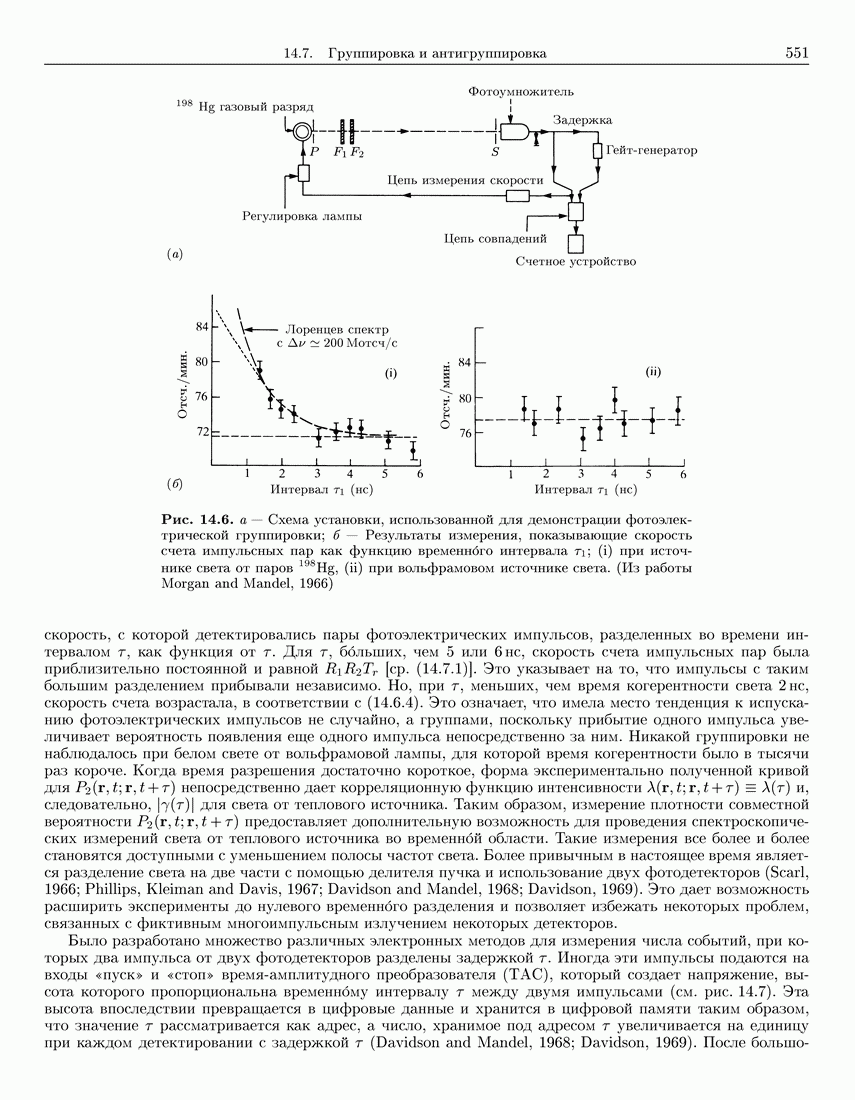
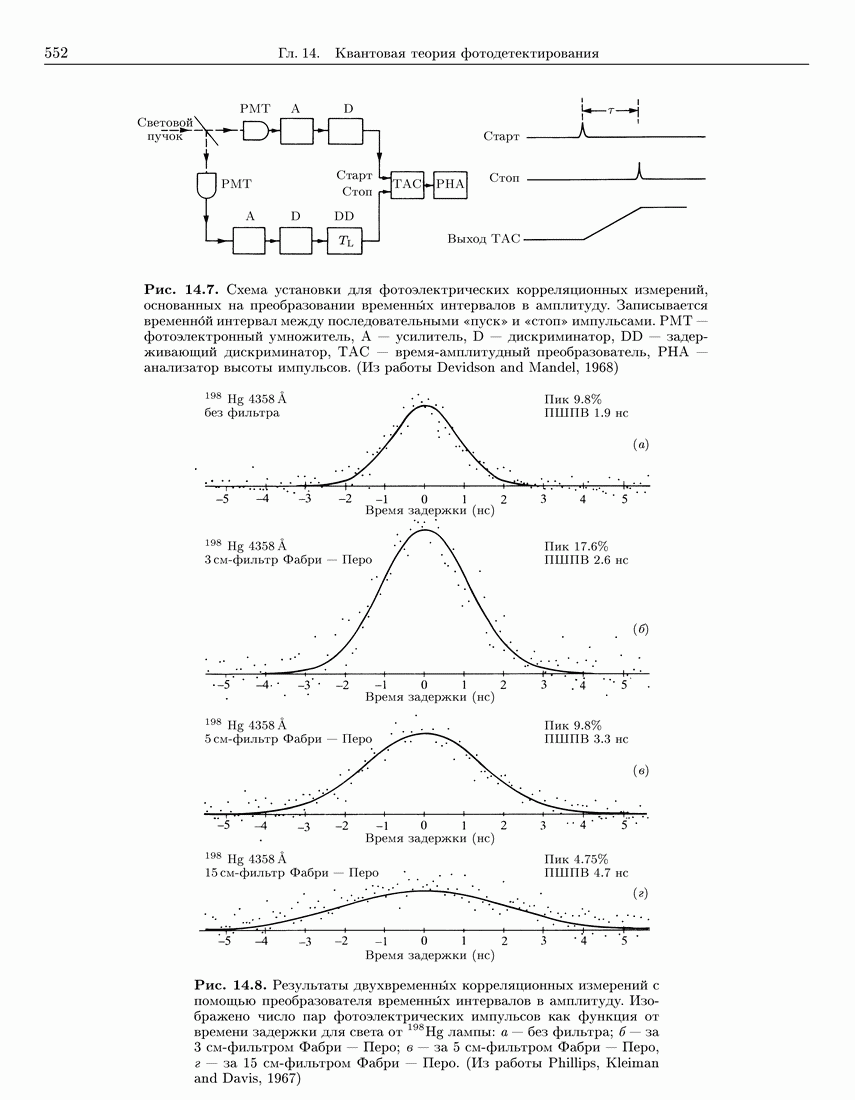
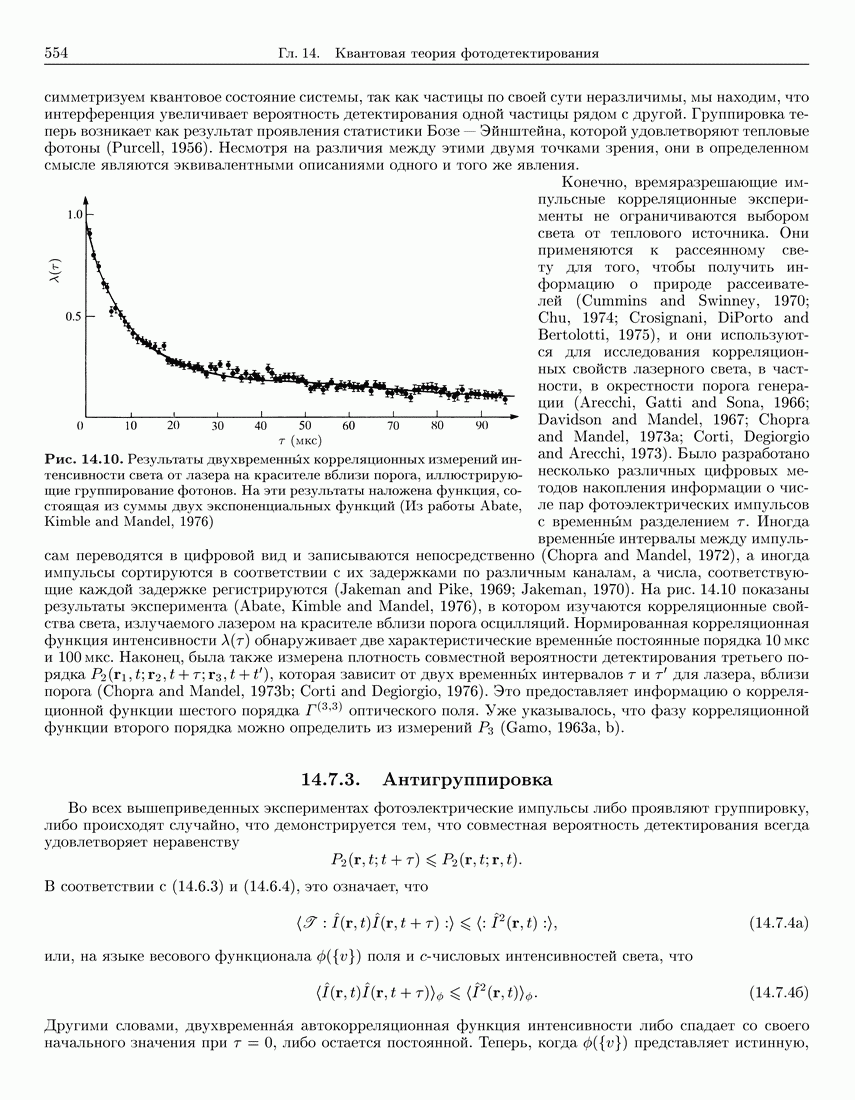
- 14.7.2. Двухвременные импульсные корреляционные измерения
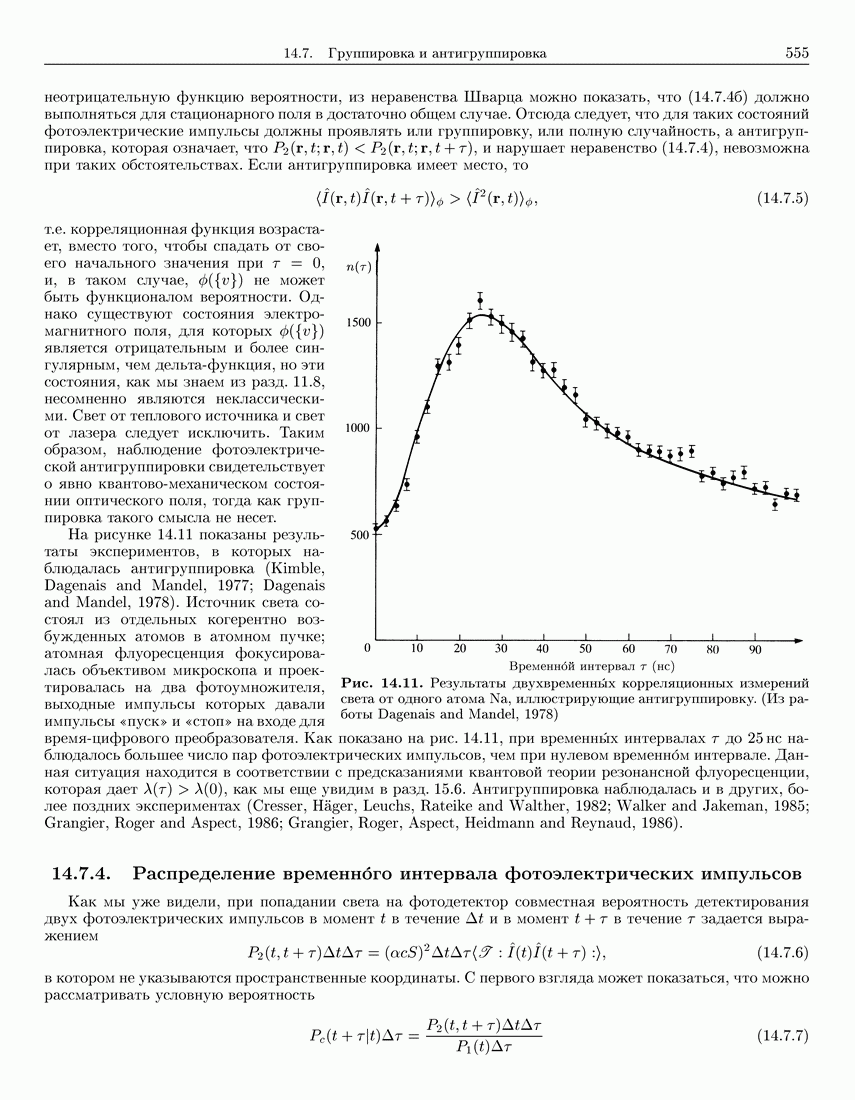
- 14.7.3. Антигруппировка
- 14.7.4. Распределение временного интервала фотоэлектрических импульсов
- 14.8. Статистика фотоэлектрического счета
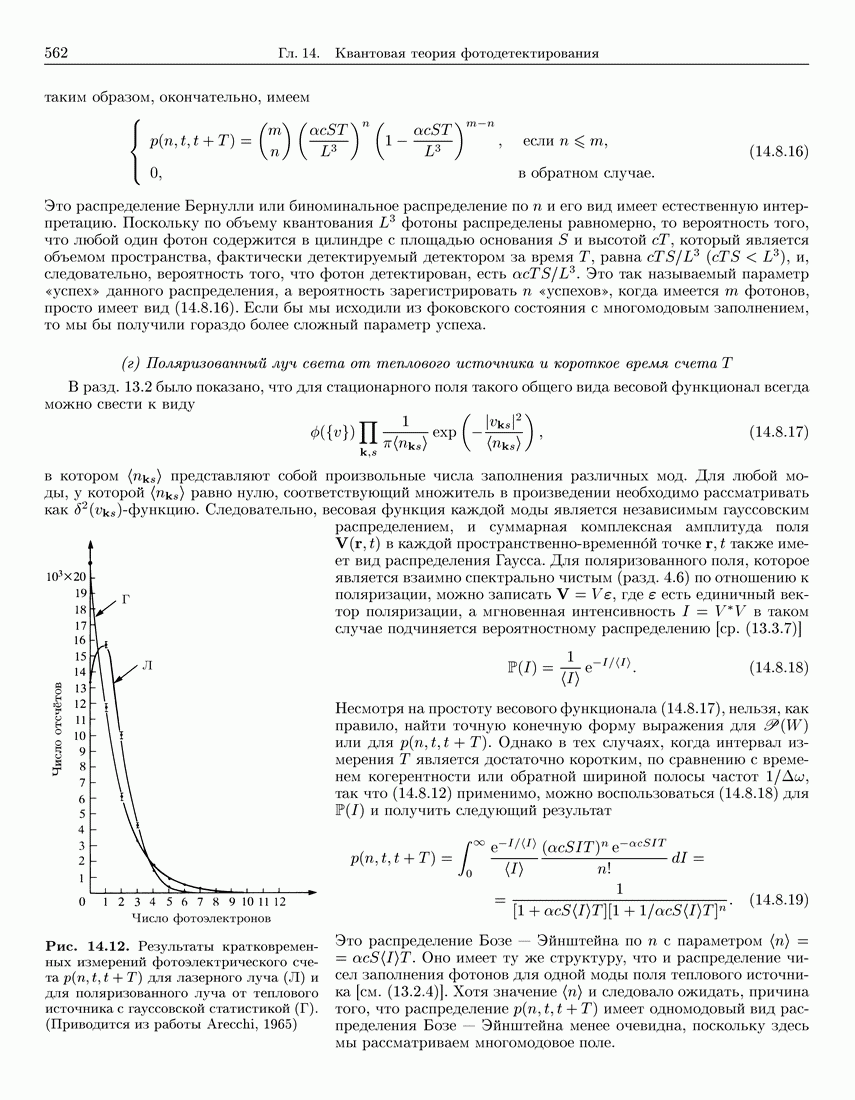
- 14.8.2. Примеры вероятности детектирования
- 14.8.3. Естественная мера времени когерентности
- 14.9. Свойства вероятности детектирования …
- 14.9.1. Производящие функции и проблема обратного преобразования
- 14.9.2. Второй момент и субпуассоновская статистика счета
- 14.9.3. Получение корреляционных функций из статистики счета
- Глава 15. ВЗАИМОДЕЙСТВИЕ СВЕТА И ДВУХУРОВНЕГО АТОМА
- 15.1. Динамические переменные для двухуровневого атома
- 15.1.1. Атомная энергия и атомный дипольный момент
- 15.2. Блоховское представление
- 15.2.1. Средние значения спиновых операторов
- 15.3. Взаимодействие атома с классическим полем
- 15.3.1. Уравнения Блоха
- 15.3.2. Уравнения Блоха во вращающейся системе координат
- 15.3.3. Задача Раби
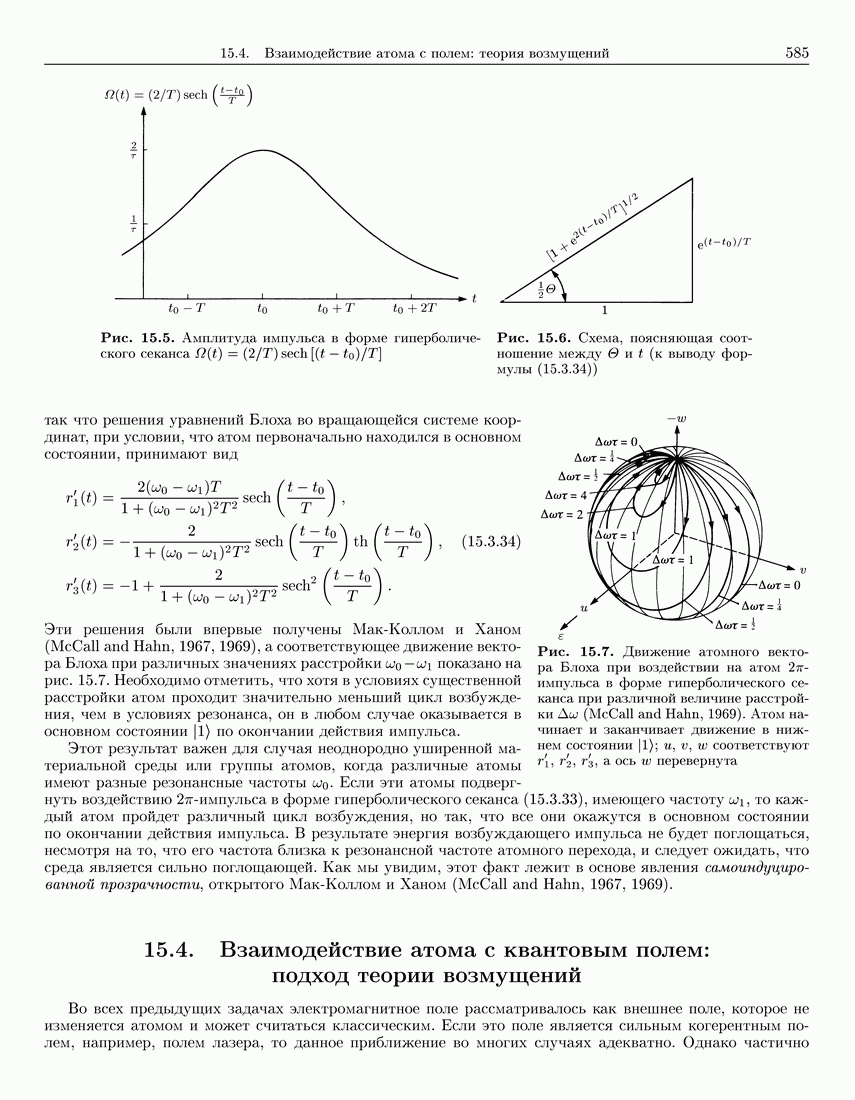
- 15.3.4. Отклик атома на воздействие лазерного импульса
- 15.3.5. 2«пи»-импульс в форме гиперболического секанса
- 15.4. Взаимодействие атома с квантовым полем: подход теории возмущений
- 15.4.1. Поглощение и излучение фотонов
- 15.5. Взаимодействие атома с квантовым полем: общее рассмотрение
- 15.5.1. Гейзенберговские уравнения движения
- 15.5.2. Приближенное решение — коэффициент Эйнштейна A и лэмбовский сдвиг
- 15.5.3. Интегральные уравнения движения
- 15.5.4. Спонтанное излучение
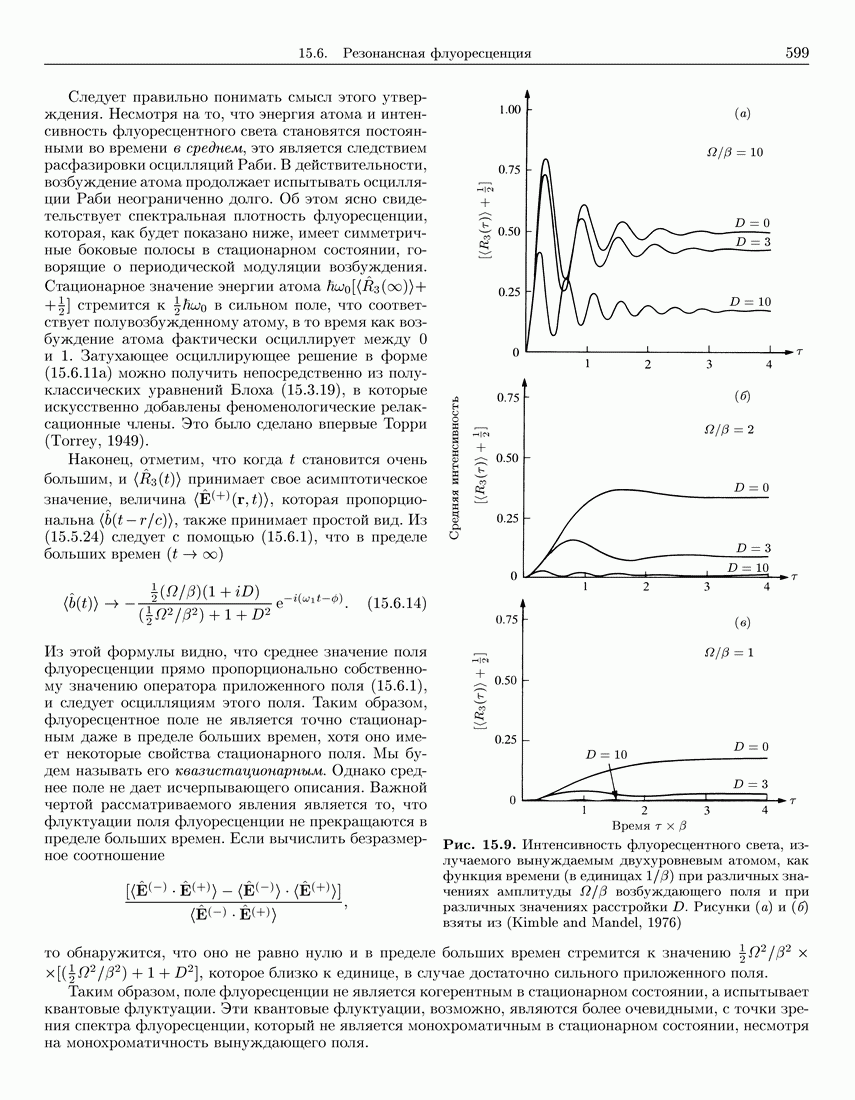
- 15.6. Резонансная флуоресценция
- 15.6.2. Сечение рассеяния атомов
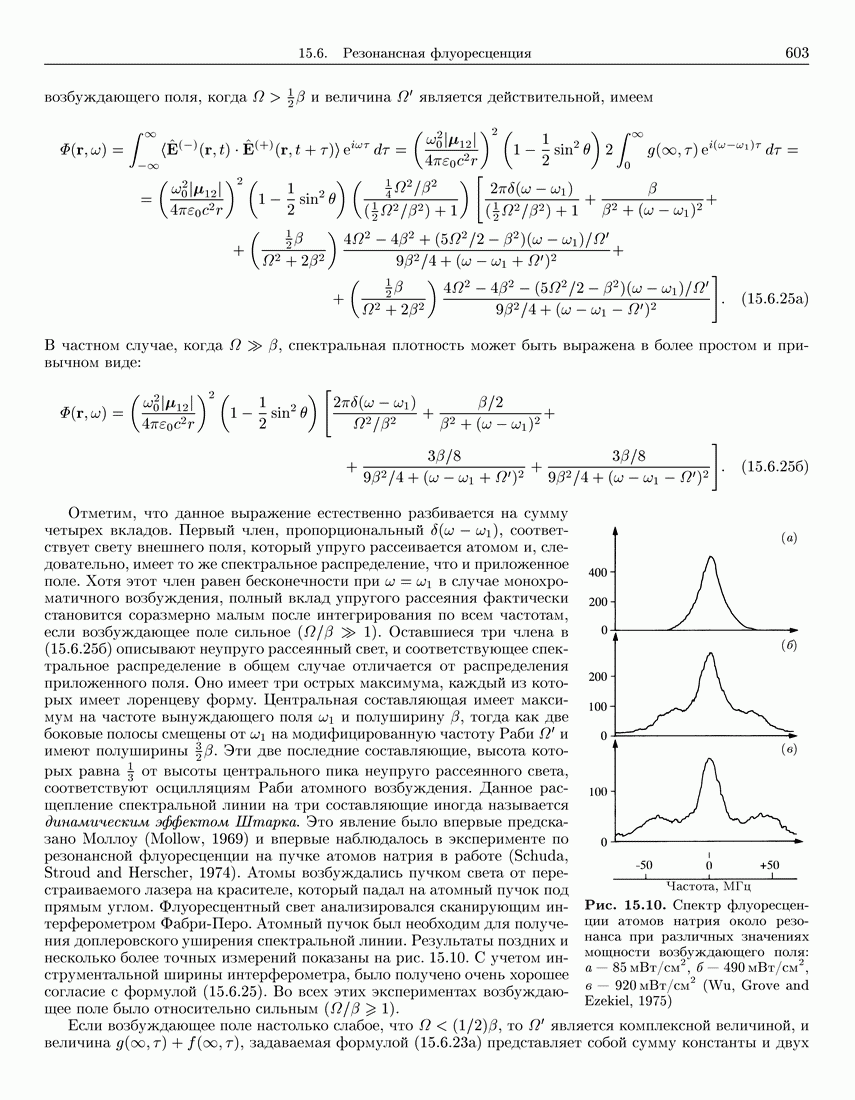
- 15.6.3. Спектр флуоресценции
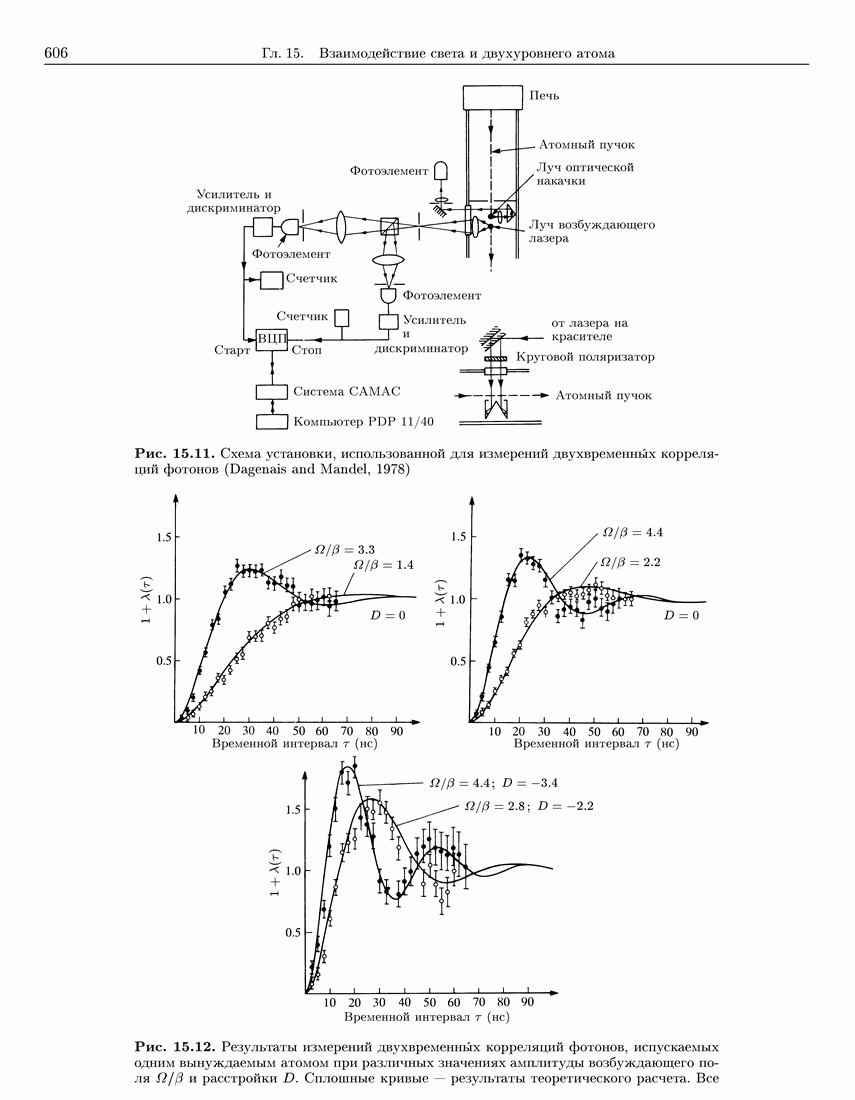
- 15.6.4. Корреляция интенсивности флуоресценции
- 15.6.5. Измерения антигруппировки фотонов
- 15.6.6. Субпуассоновская статистика фотонов
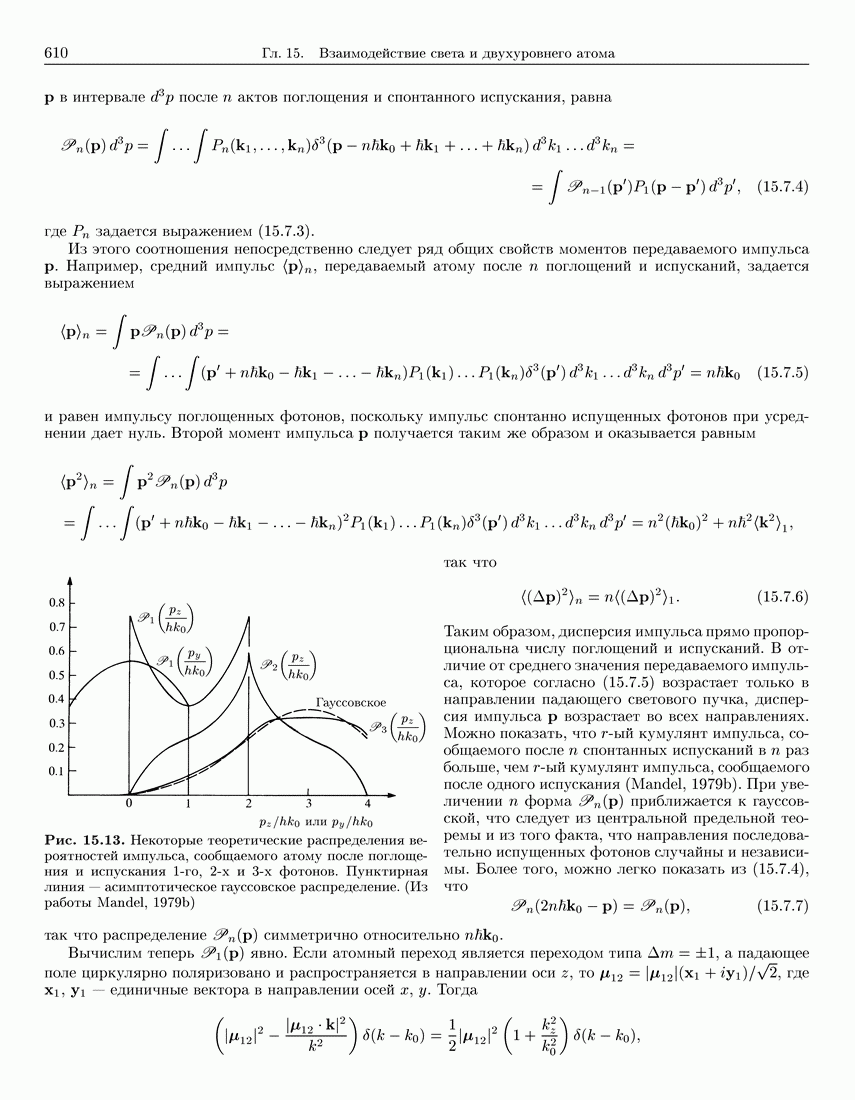
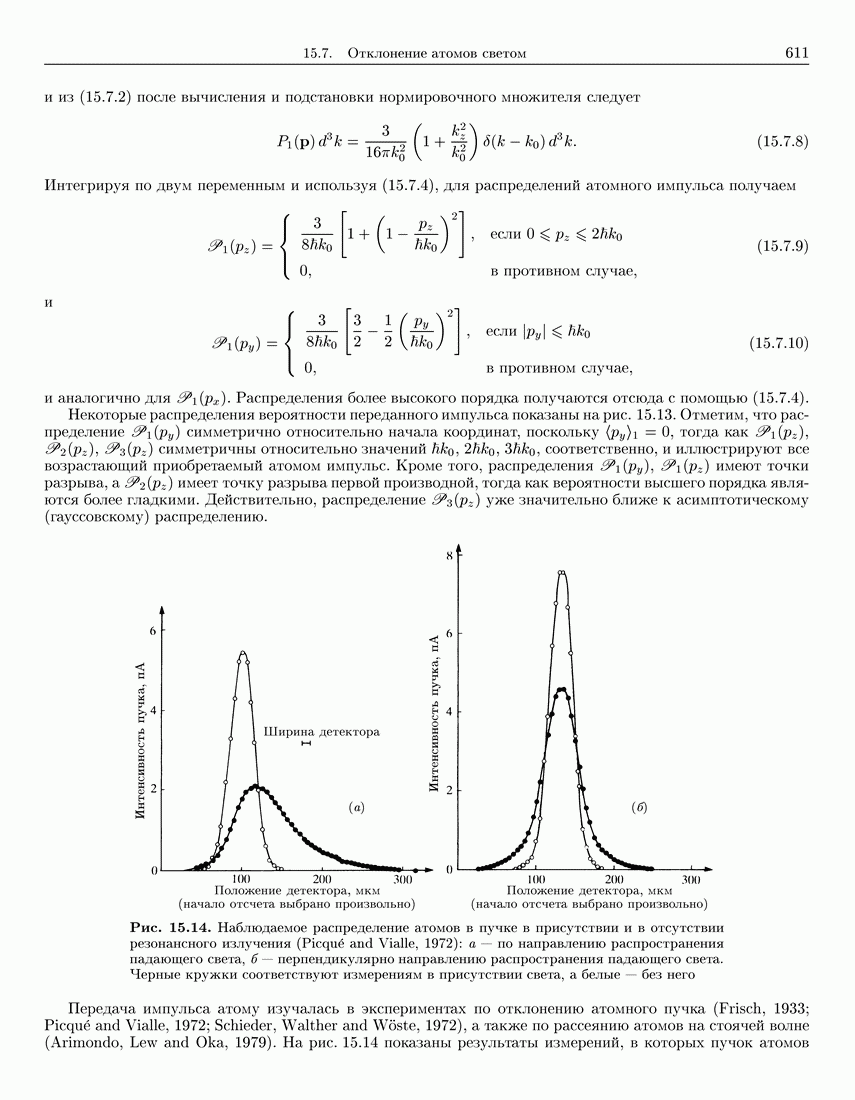
- 15.7. Отклонение атомов светом
- 15.7.1. Передача импульса после n спонтанных испусканий
- 15.7.2. Передача импульса при вынужденном излучении или градиентные силы в сильном поле
- 15.8. Охлаждение и пленение атомов
- 15.8.2. Оценка наименьшей достижимой температуры, основанная на балансе энергии
- Глава 16. КОЛЛЕКТИВНЫЕ АТОМНЫЕ ВЗАИМОДЕЙСТВИЯ
- 16.1. Затухание оптической свободной индукции
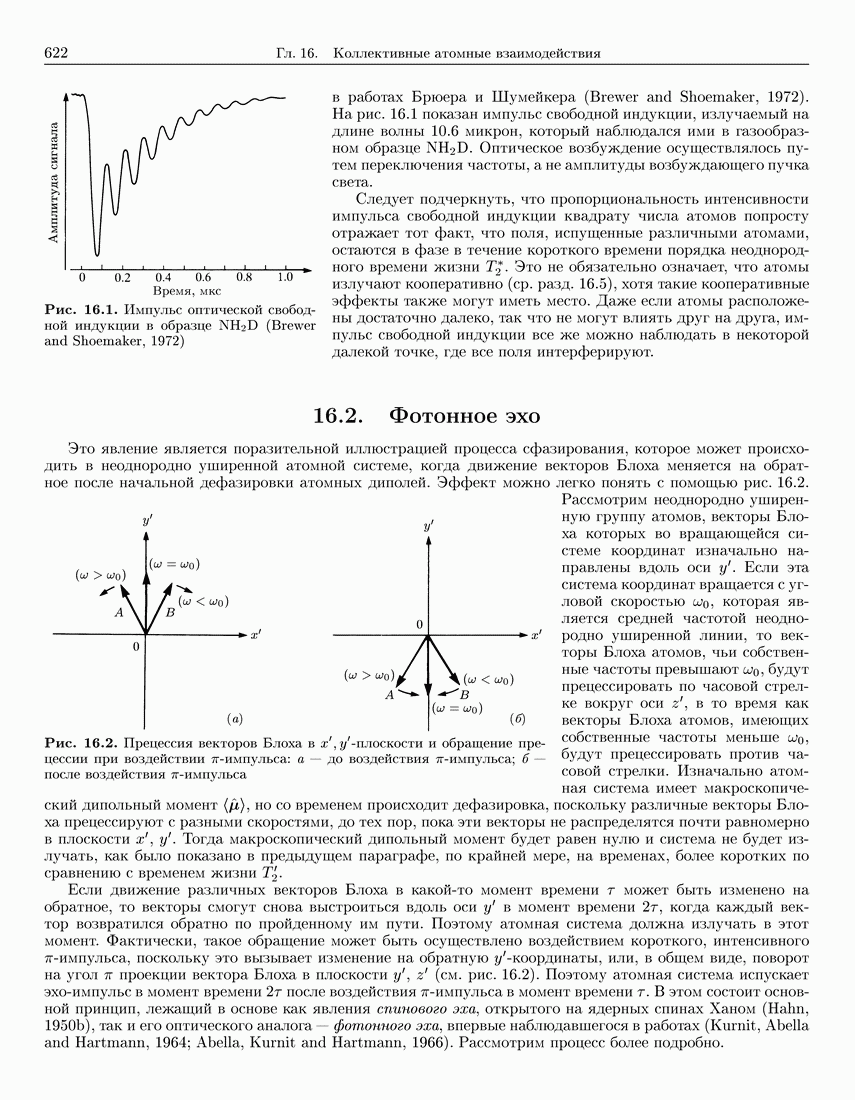
- 16.2. Фотонное эхо
- 16.3. Самоиндуцированная прозрачность
- 16.3.1. Уравнение движения для огибающей импульса
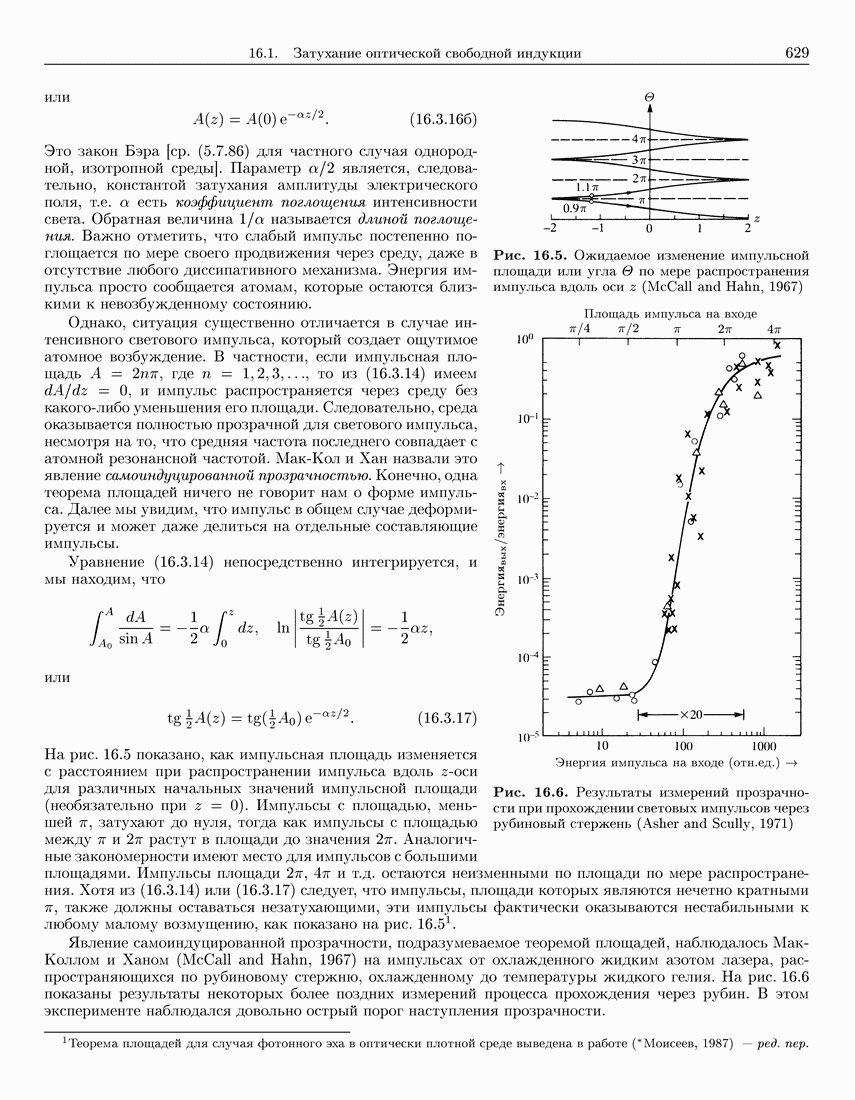
- 16.3.2. Теорема площадей Мак-Колла и Хана
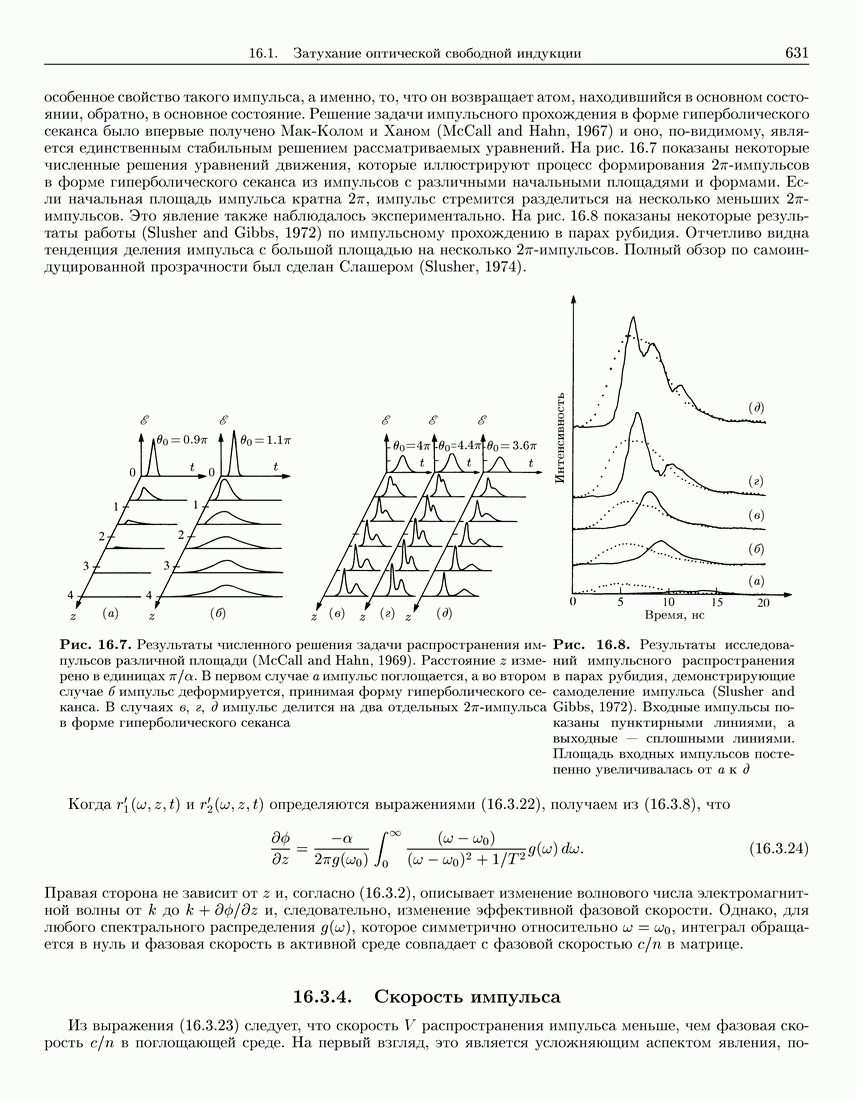
- 16.3.3. Форма импульса
- 16.3.4. Скорость импульса
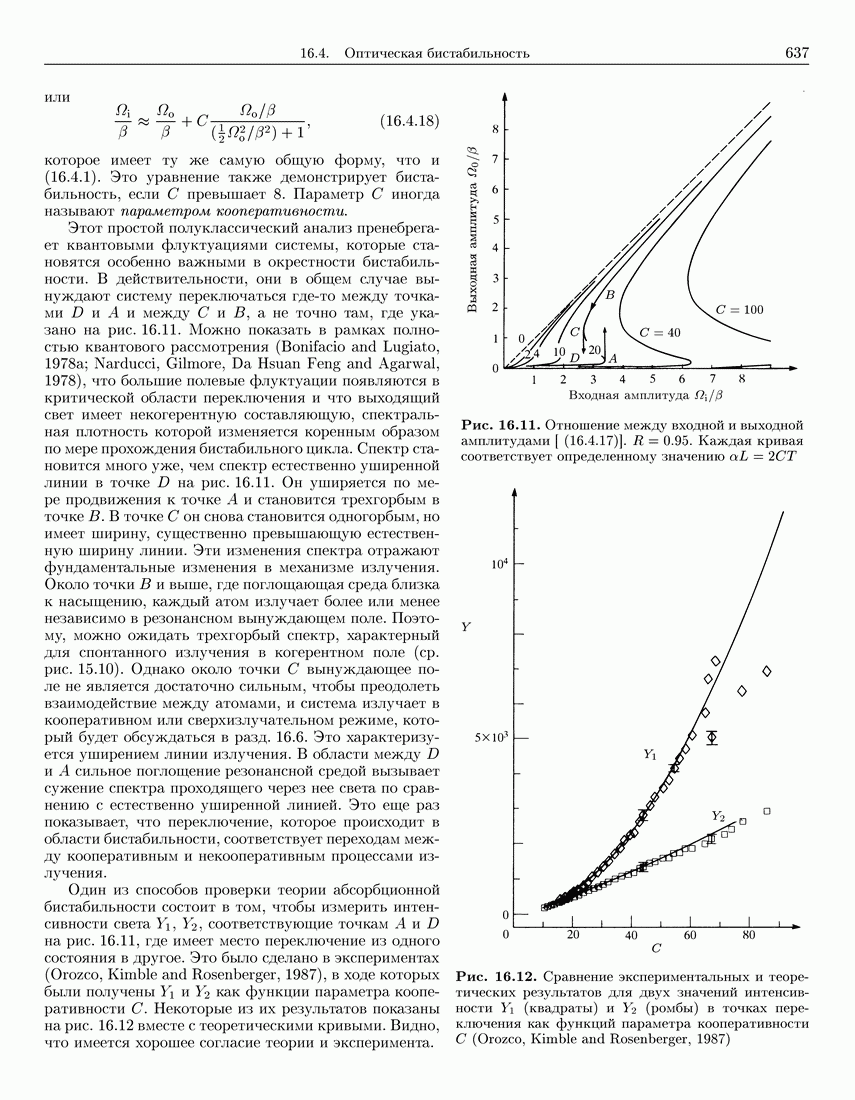
- 16.4. Оптическая бистабильность
- 16.4.1. Абсорбционная бистабильность в кольцевом резонаторе
- 16.4.2. Дисперсионная бистабильность
- 16.4.3. Хаос в оптической бистабильности
- 16.5. Коллективные атомные состояния и коллективные динамические переменные
- 16.5.1. Состояния Дике
- 16.5.2. Вырождение состояний Дике
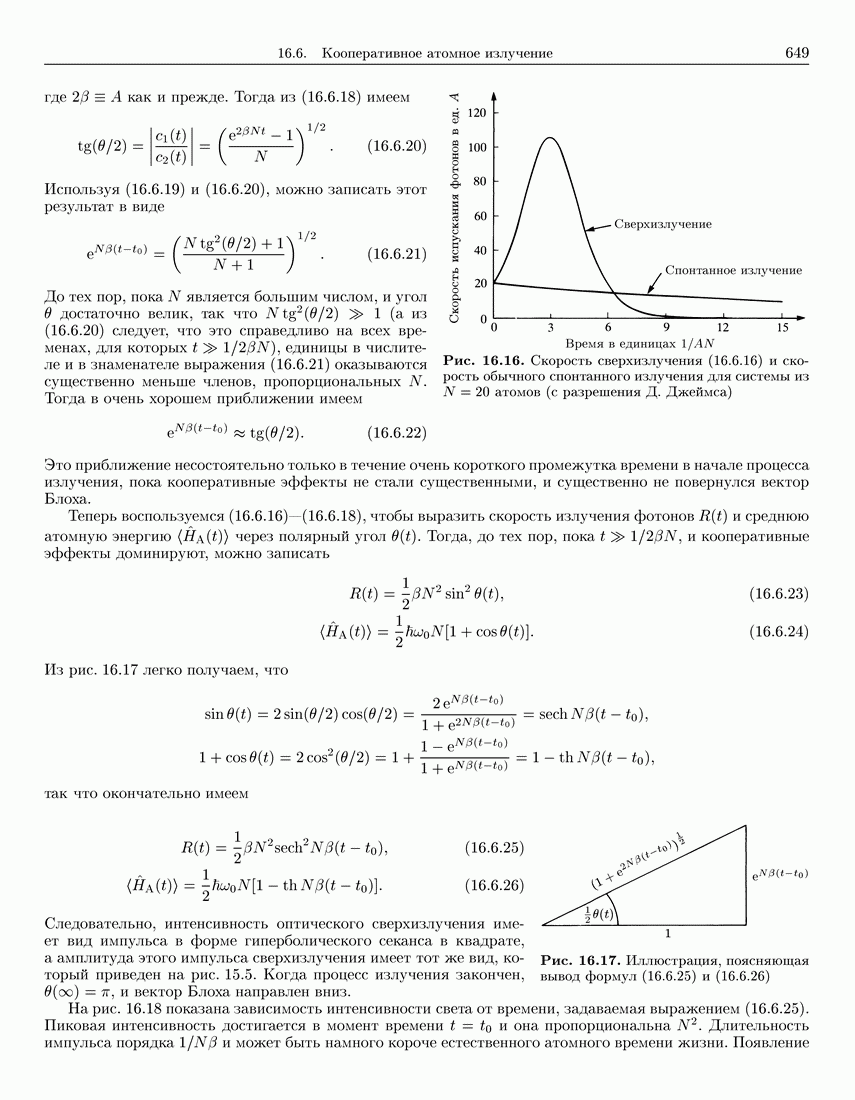
- 16.6. Кооперативное атомное излучение
- 16.6.2. Кооперативное излучение атомов, находящихся в факторизованном состоянии
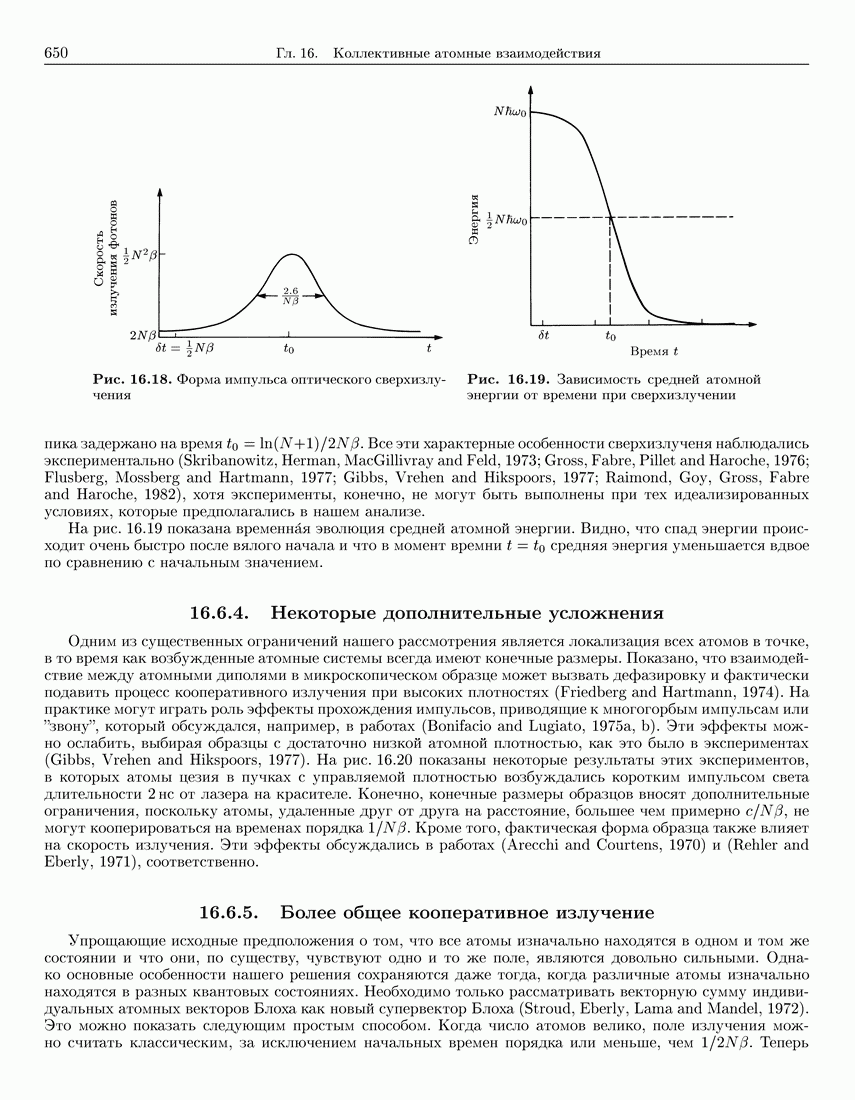
- 16.6.3. Временная эволюция сверхизлучения
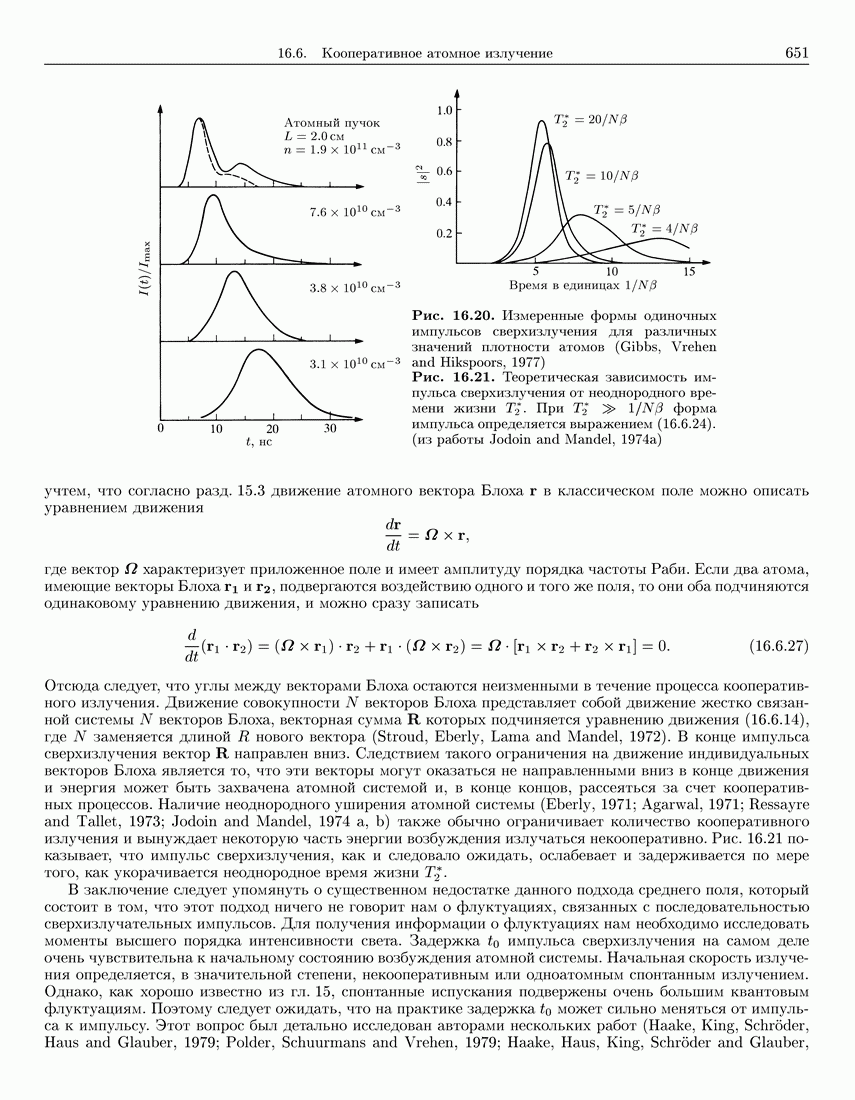
- 16.6.4. Некоторые дополнительные усложнения
- 16.6.5. Более общее кооперативное излучение
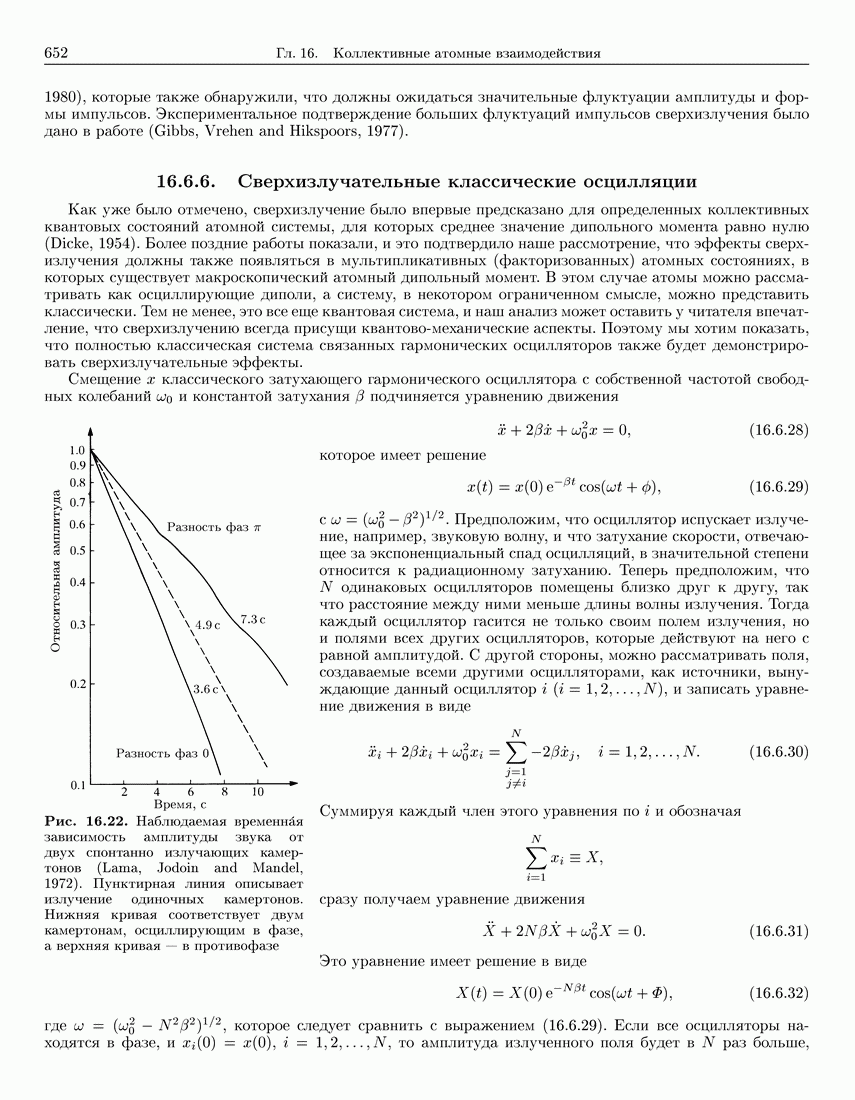
- 16.6.6. Сверхизлучательные классические осцилляции
- 16.7. Атомные когерентные состояния
- 16.7.1. Блоховское представление атомного когерентного состояния
- 16.7.2. Неортогональность и переполненность
- 16.7.3. Атомные состояния, создаваемые классическим полем
- Глава 17. ОБЩИЕ МЕТОДЫ ИЗУЧЕНИЯ ВЗАИМОДЕЙСТВУЮЩИХ СИСТЕМ
- 17.1. Квантовая теорема регрессии
- 17.1.1. Одновременные средние значения
- 17.1.2. Многовременные средние значения
- 17.1.3. Спонтанное излучение атома
- 17.1.4. Резонансная флуоресценция двухуровневого атома
- 17.1.5. Квантовая теорема регрессии для нормально упорядоченных операторов поля
- 17.2. Флуктуационно-диссипационная теорема
- 17.2.2. Квантово-механическая линейная диссипативная система
- 17.2.3. Мощность рассеяния
- 17.2.4. Флуктуации тока в состоянии теплового равновесия
- 17.2.5. Спектральная плотность флуктуаций
- 17.2.6. Броуновское движение частицы
- 17.2.7. Флуктуации поля в излучении черного тела
- 17.3. Основные кинетические уравнения
- 17.3.2. Обобщенное основное кинетическое уравнение Цванцига
- 17.3.3. Применение к кинетическому уравнению Паули
- 17.3.4. Применение к задаче Дике
- 17.4. Источники квантового шума и квантовые уравнения Ланжевена
- 17.4.2. Уравнения движения квантовой системы
- 17.4.3. Коммутационные соотношения
- 17.4.4. Двухвременные корреляционные функции
- 17.4.5. Уравнение Ланжевена для возбужденной системы осцилляторов
- 17.4.6. Необратимость и стрела времени
- Глава 18. ОДНОМОДОВЫЙ ЛАЗЕР
- 18.1.1. Условие лазерной генерации
- 18.2. Полуклассическая теория лазера
- 18.2.1. Нормальные моды резонатора
- 18.2.2. Уравнение движения для лазерного поля
- 18.2.3. Аналогия с фазовым переходом
- 18.3. Полуклассическая теория лазера с учетом шума спонтанного излучения
- 18.3.1. Уравнение Фоккера — Планка
- 18.3.2. Стационарное решение
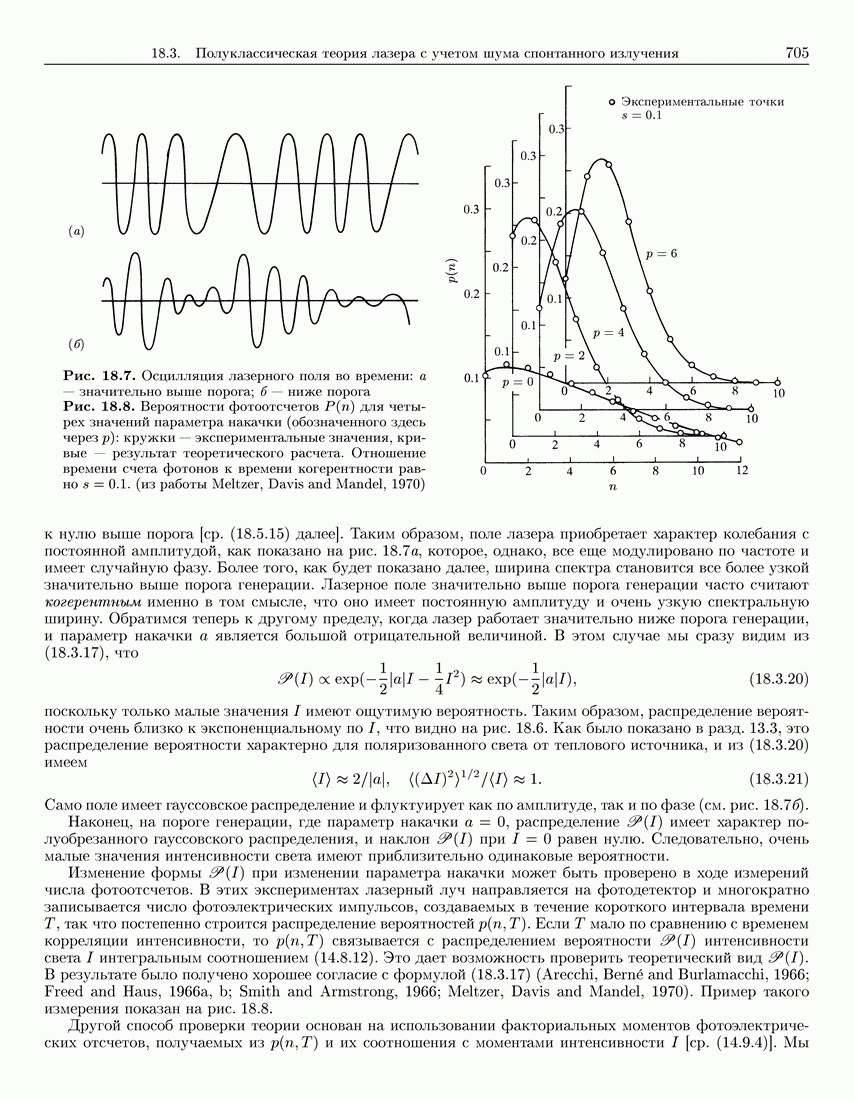
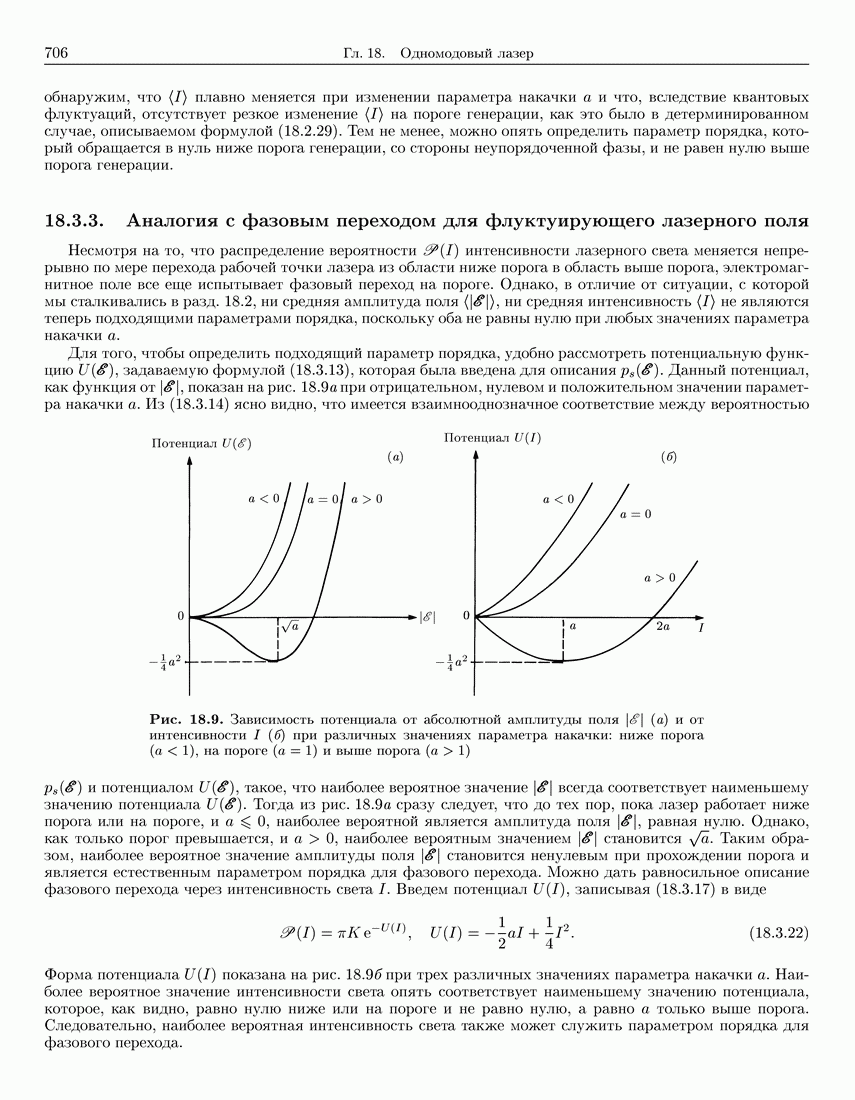
- 18.3.3. Аналогия с фазовым переходом для флуктуирующего лазерного поля
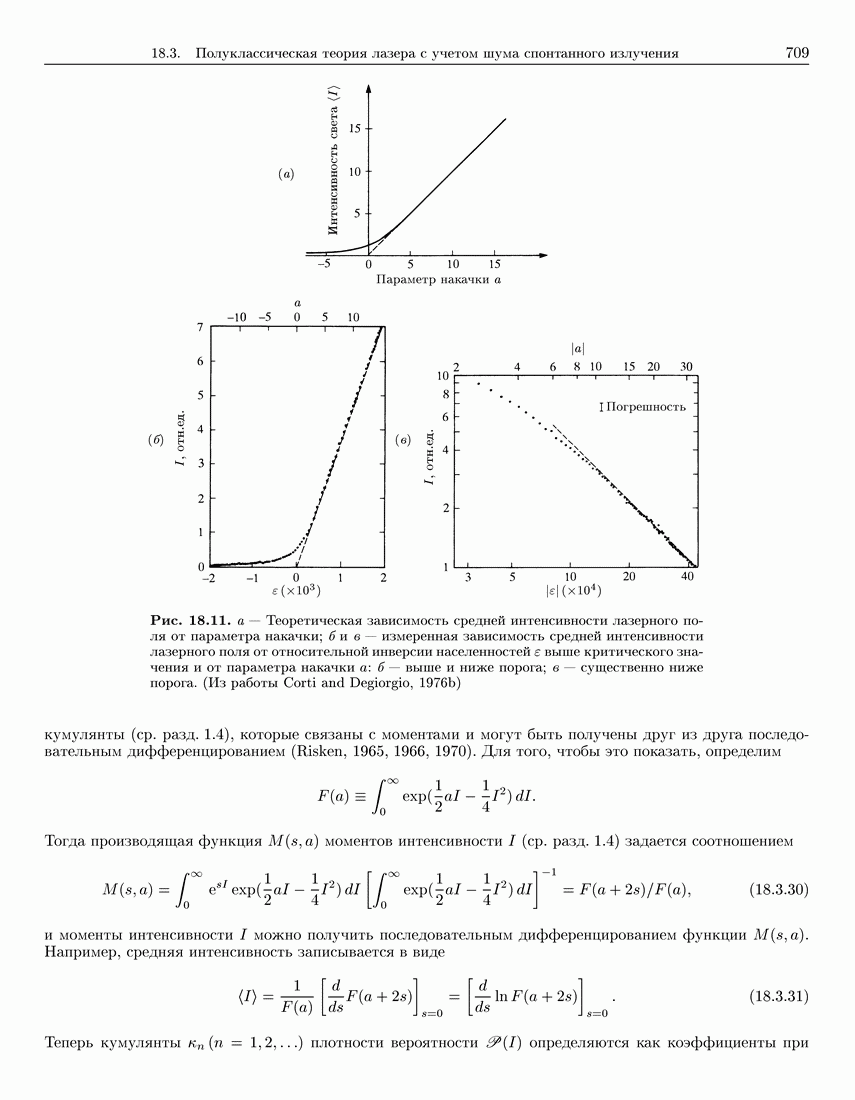
- 18.3.4. Моменты интенсивности света
- 18.4. Квантовая теория лазера
- 18.4.1. Основное кинетическое уравнение для лазерного поля
- 18.4.2. Статистика фотонов
- 18.4.3. Стационарная вероятность
- 18.5. Взаимосвязь между квантовой и полуклассической теориями лазера
- 18.5.2. Стационарное решение основного кинетического уравнения
- 18.6. Решение зависящего от времени уравнения движения
- 18.6.1. Развитие лазерного поля из вакуумного состояния
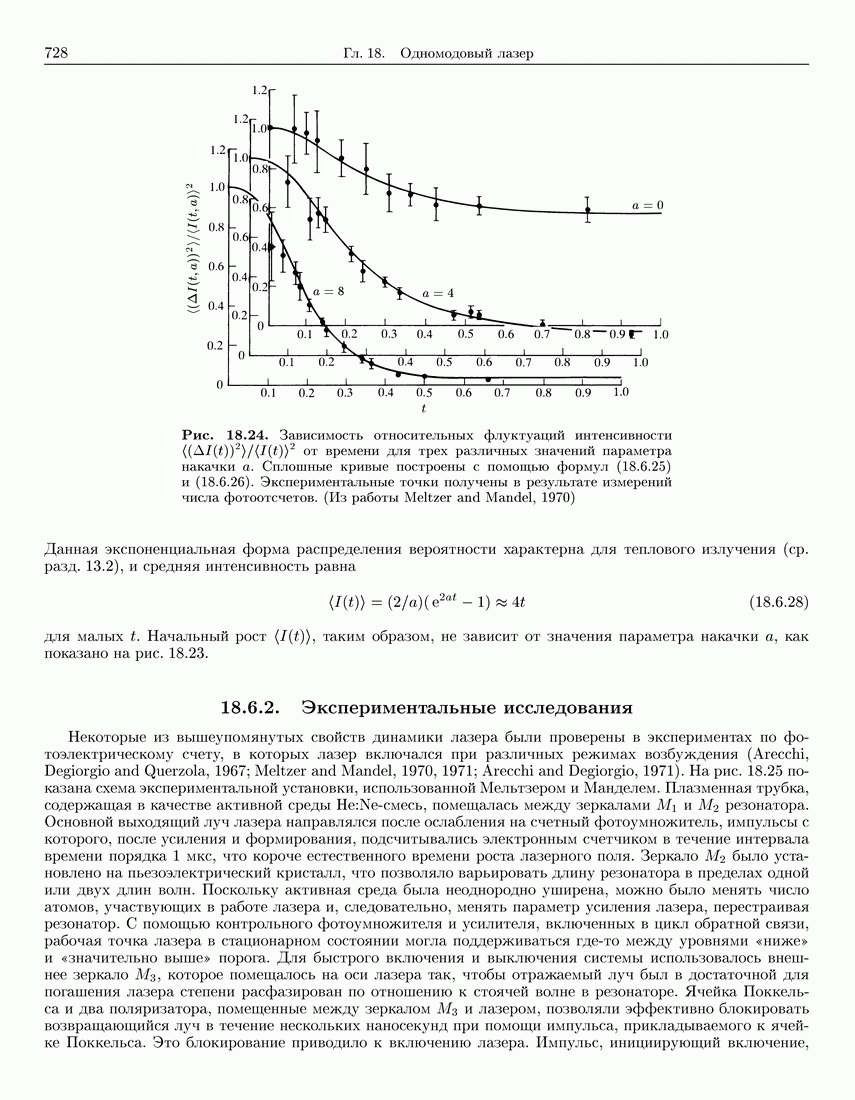
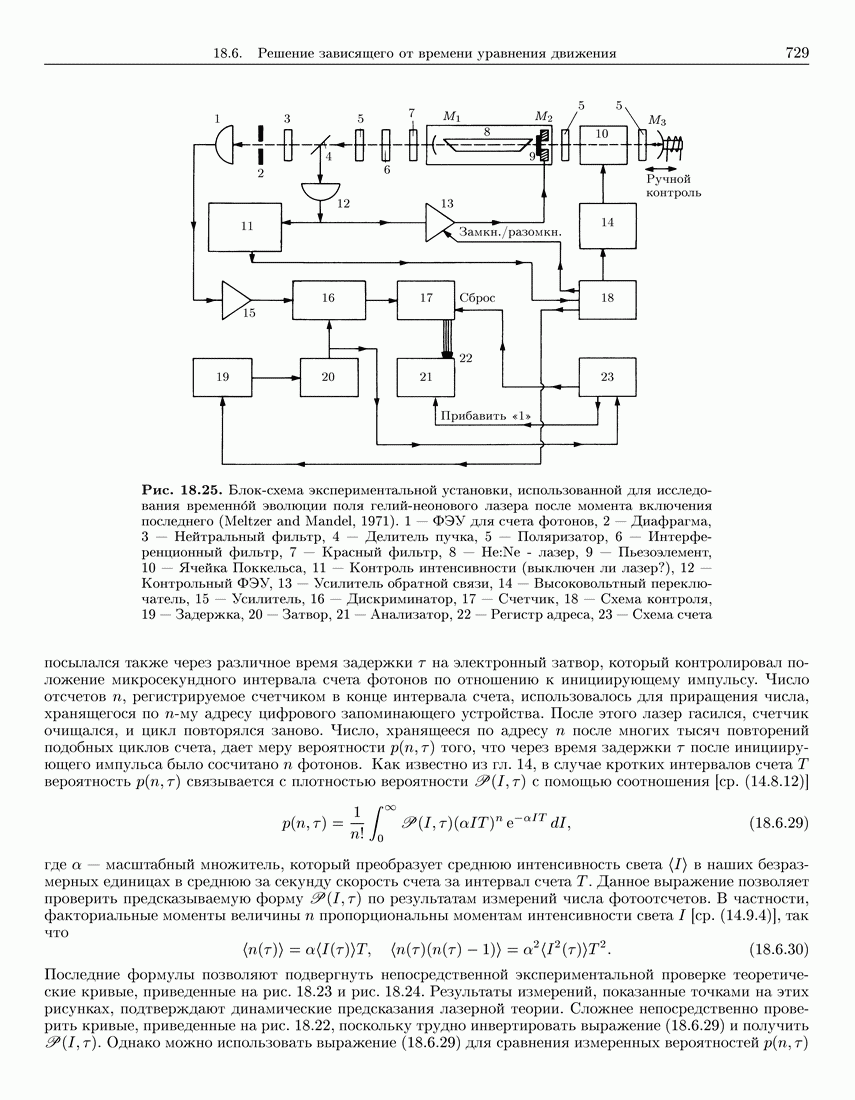
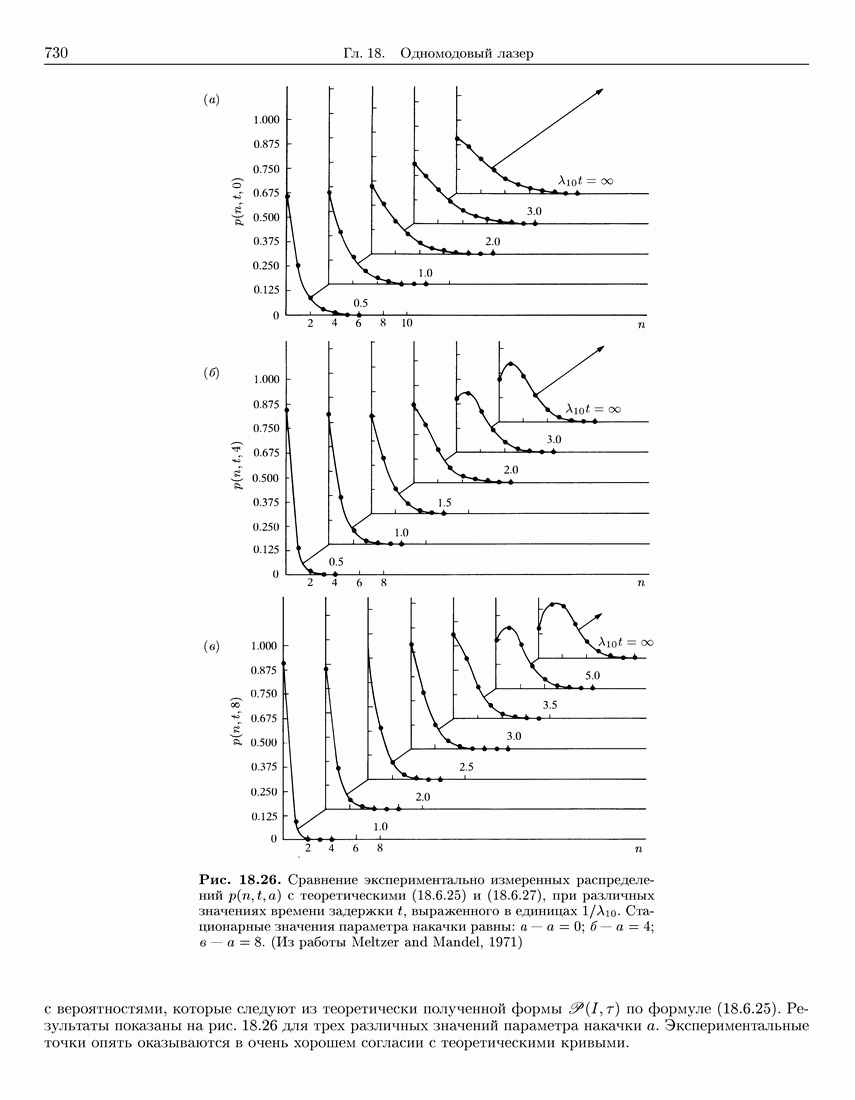
- 18.6.2. Экспериментальные исследования
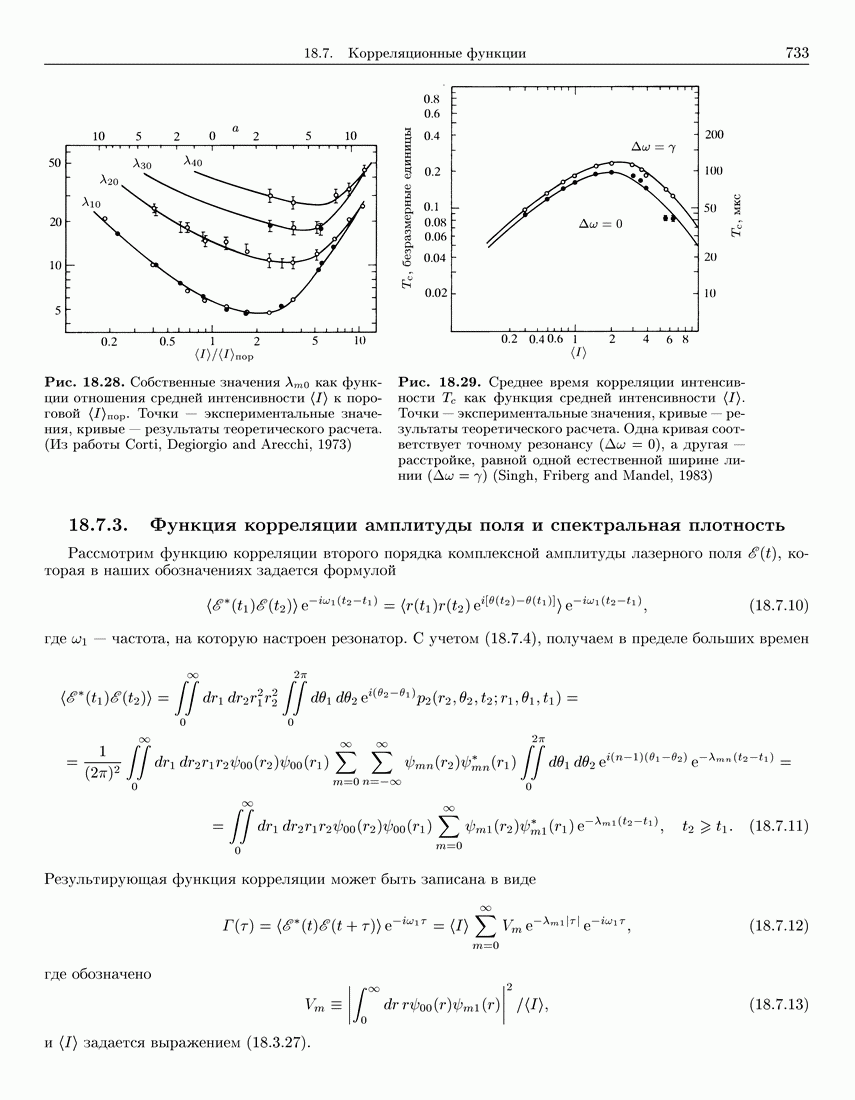
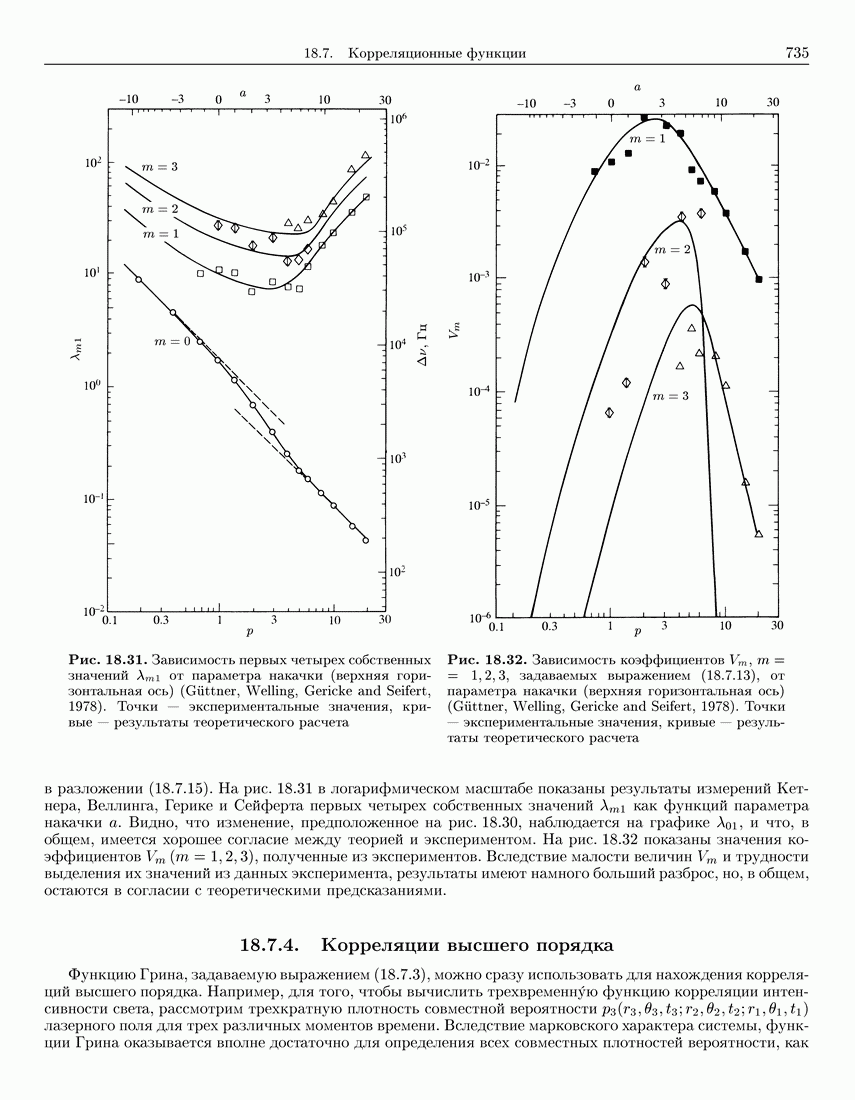
- 18.7. Корреляционные функции
- 18.7.1. Функции Грина
- 18.7.2. Корреляция интенсивности
- 18.7.3. Функция корреляции амплитуды поля и спектральная плотность
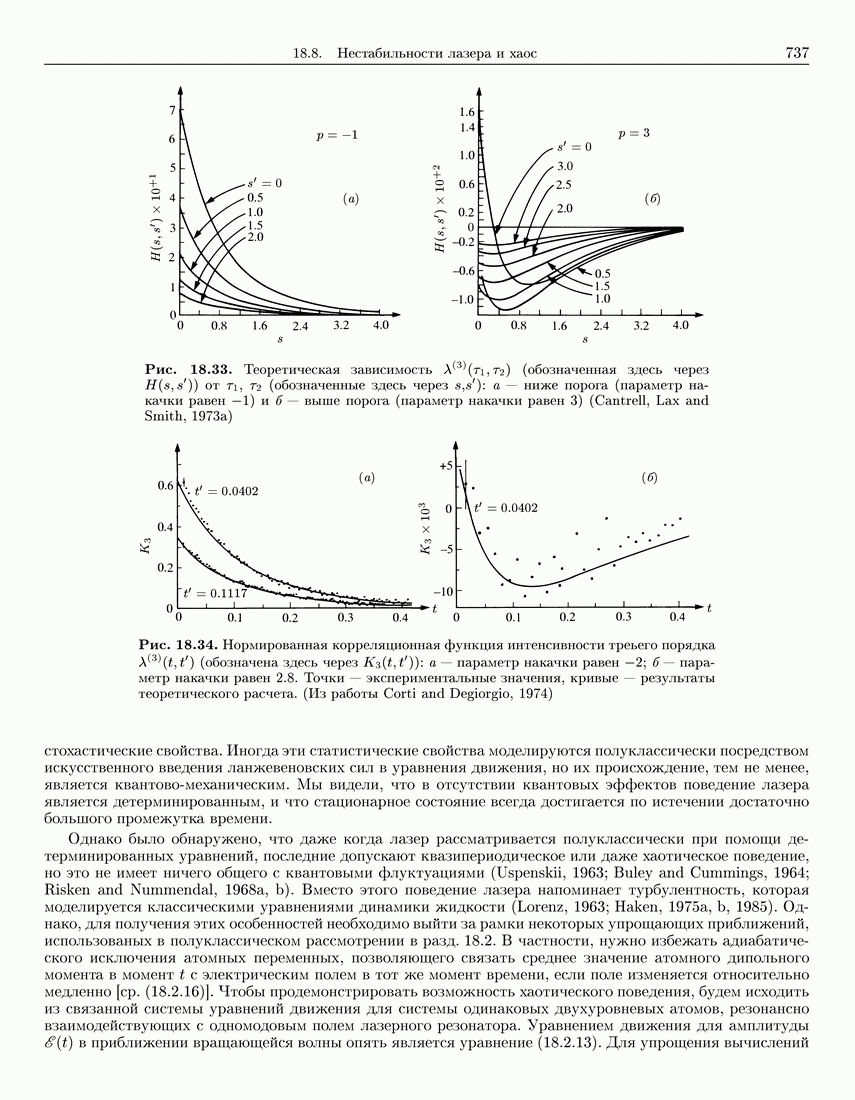
- 18.7.4. Корреляции высшего порядка
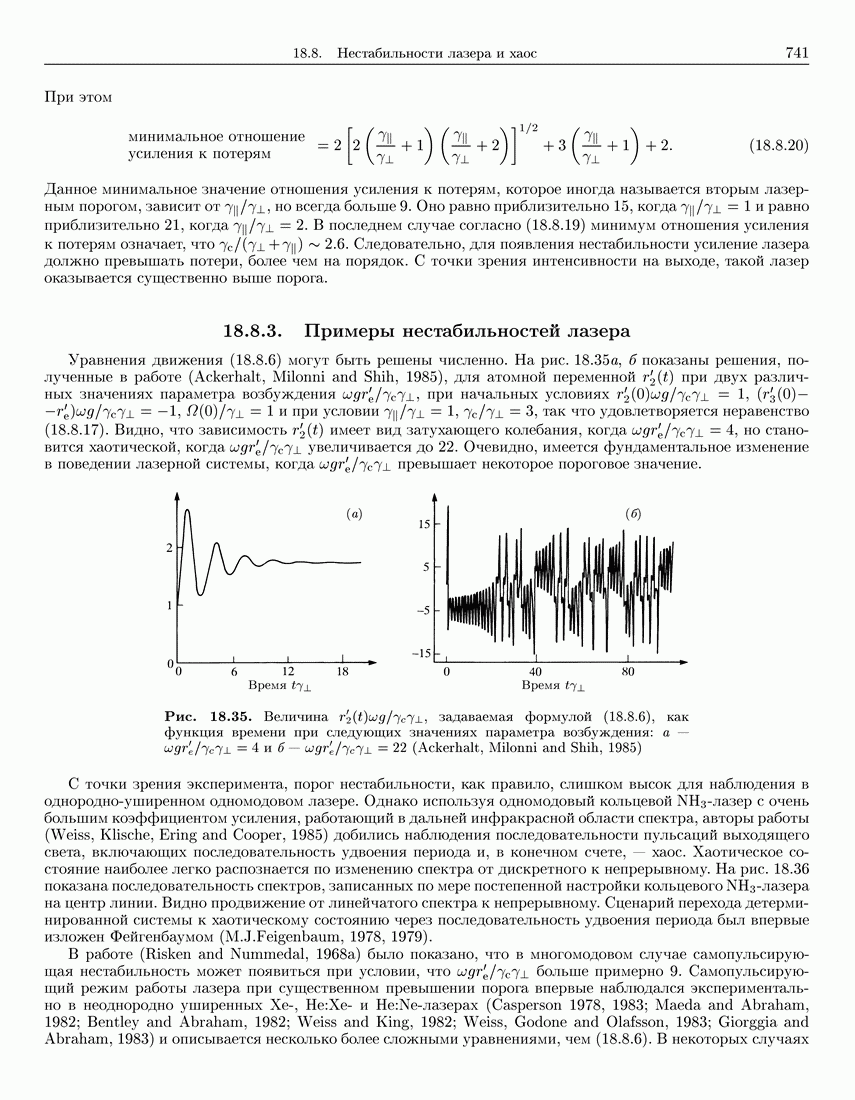
- 18.8. Нестабильности лазера и хаос
- 18.8.2. Линейный анализ устойчивости
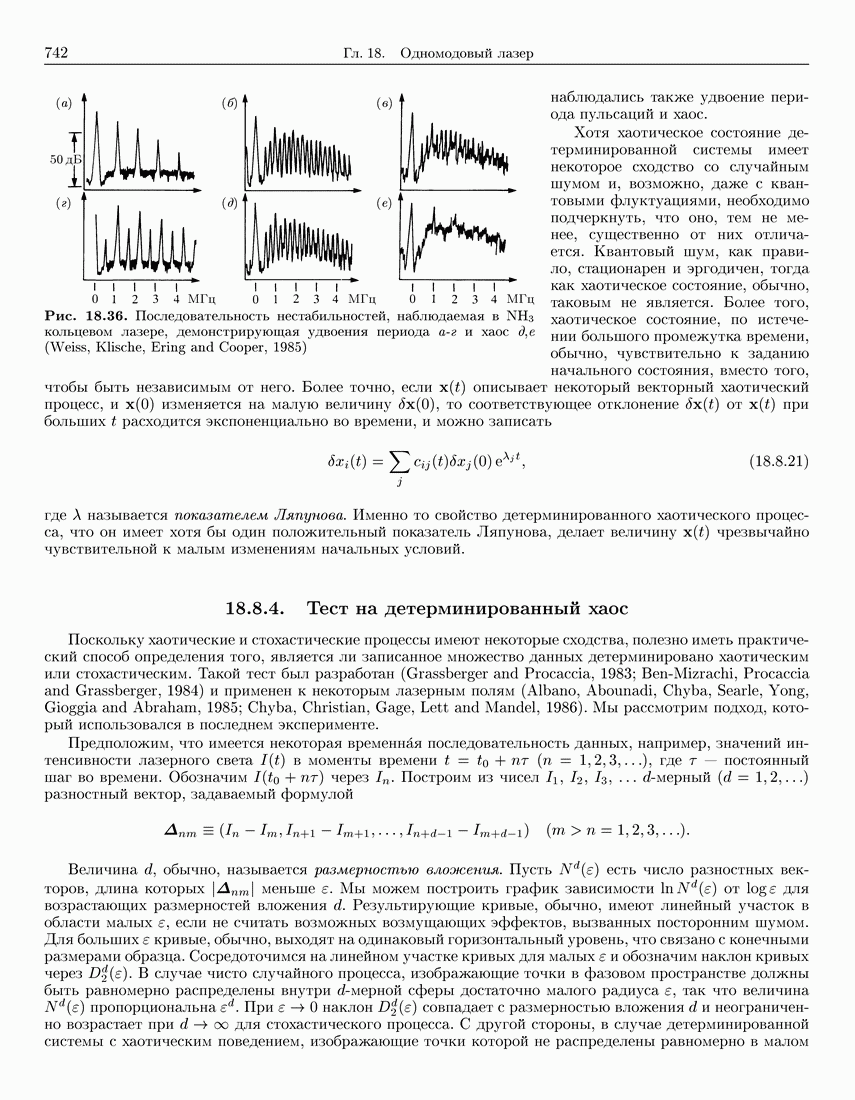
- 18.8.3. Примеры нестабильностей лазера
- 18.8.4. Тест на детерминированный хаос
- Глава 19. ДВУХМОДОВЫЙ КОЛЬЦЕВОЙ ЛАЗЕР
- 19.1.1. Учет флуктуаций спонтанного излучения
- 19.2. Стационарное решение
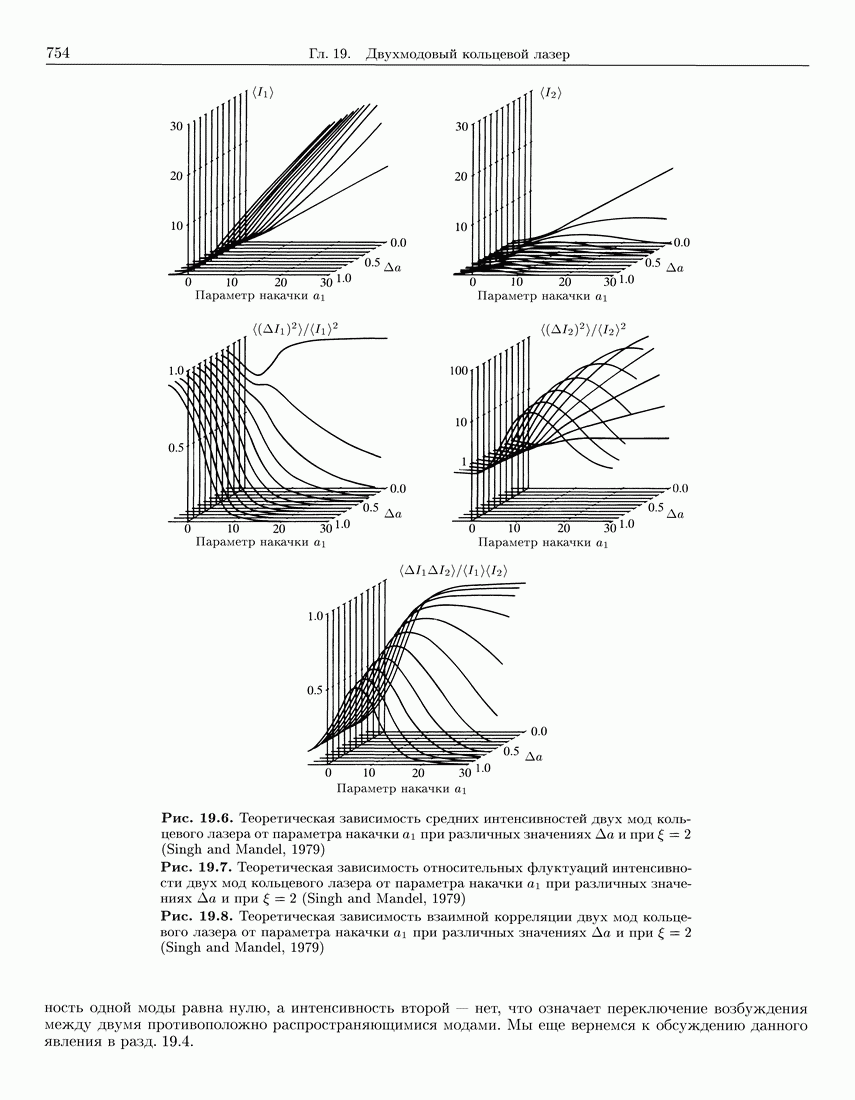
- 19.2.1. Моменты интенсивности света
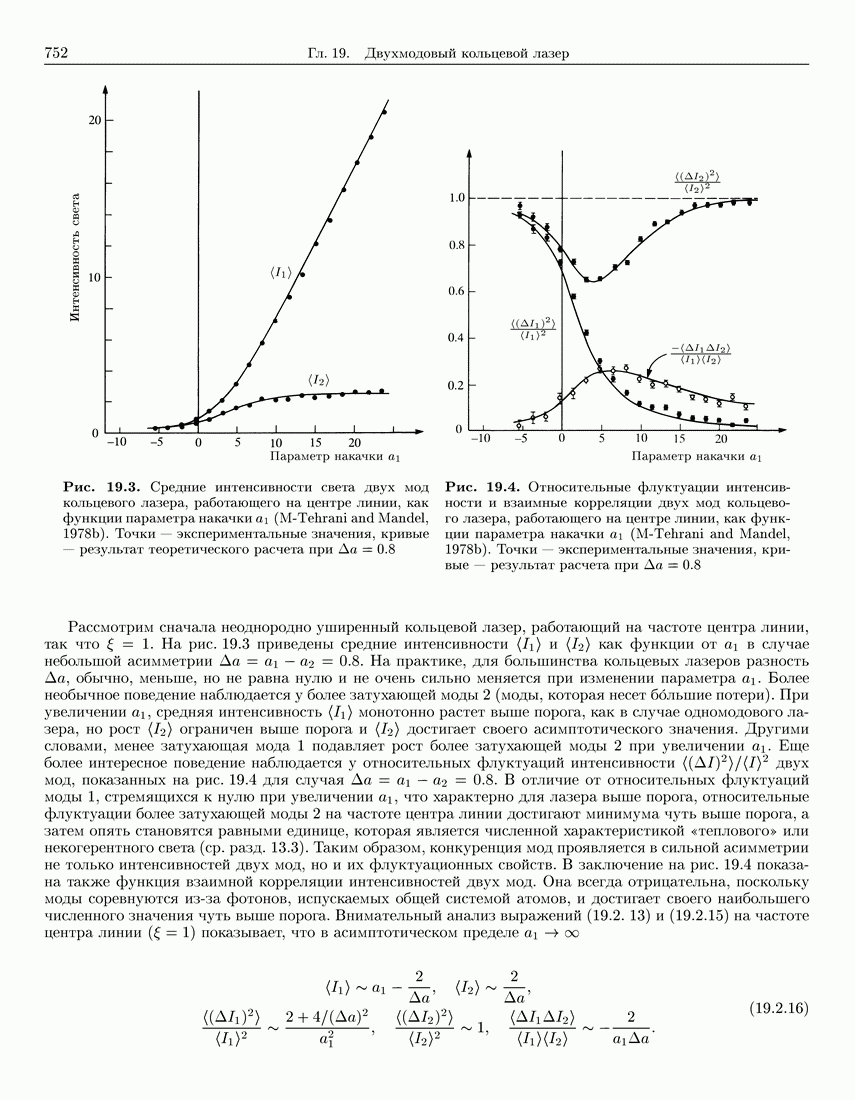
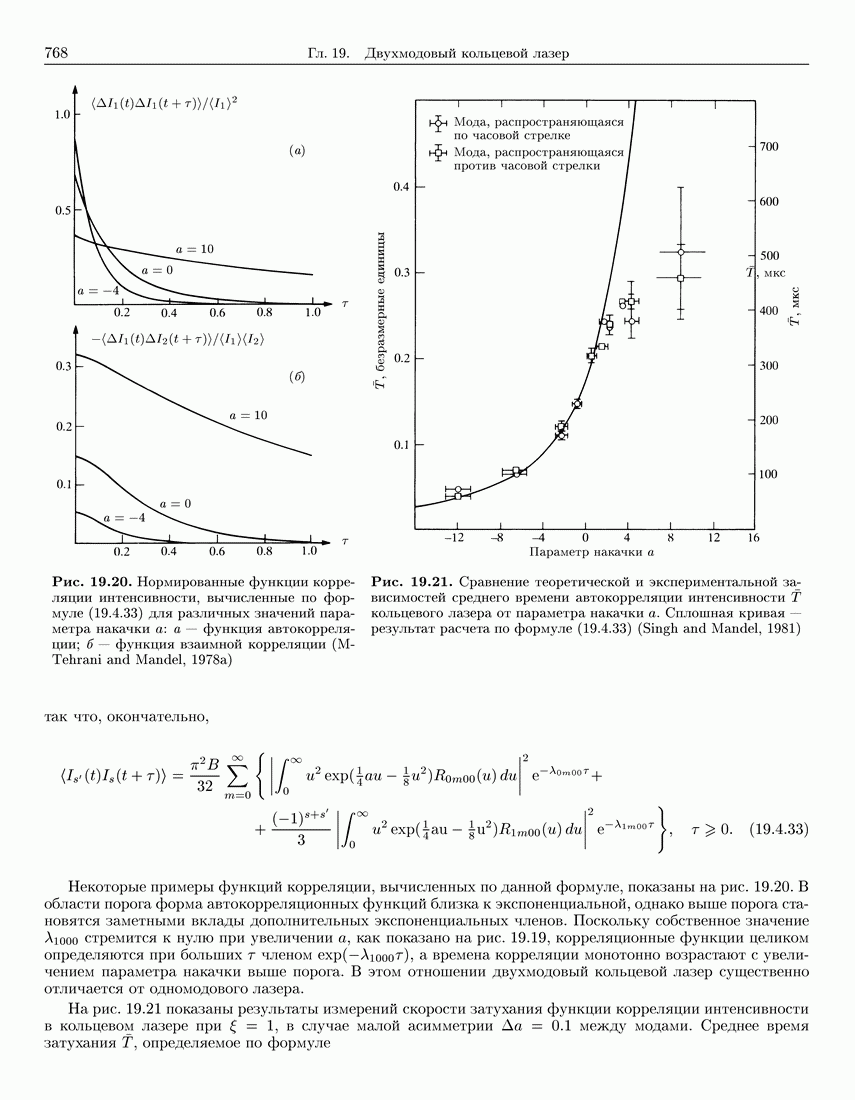
- 19.2.2. Сравнение с экспериментом
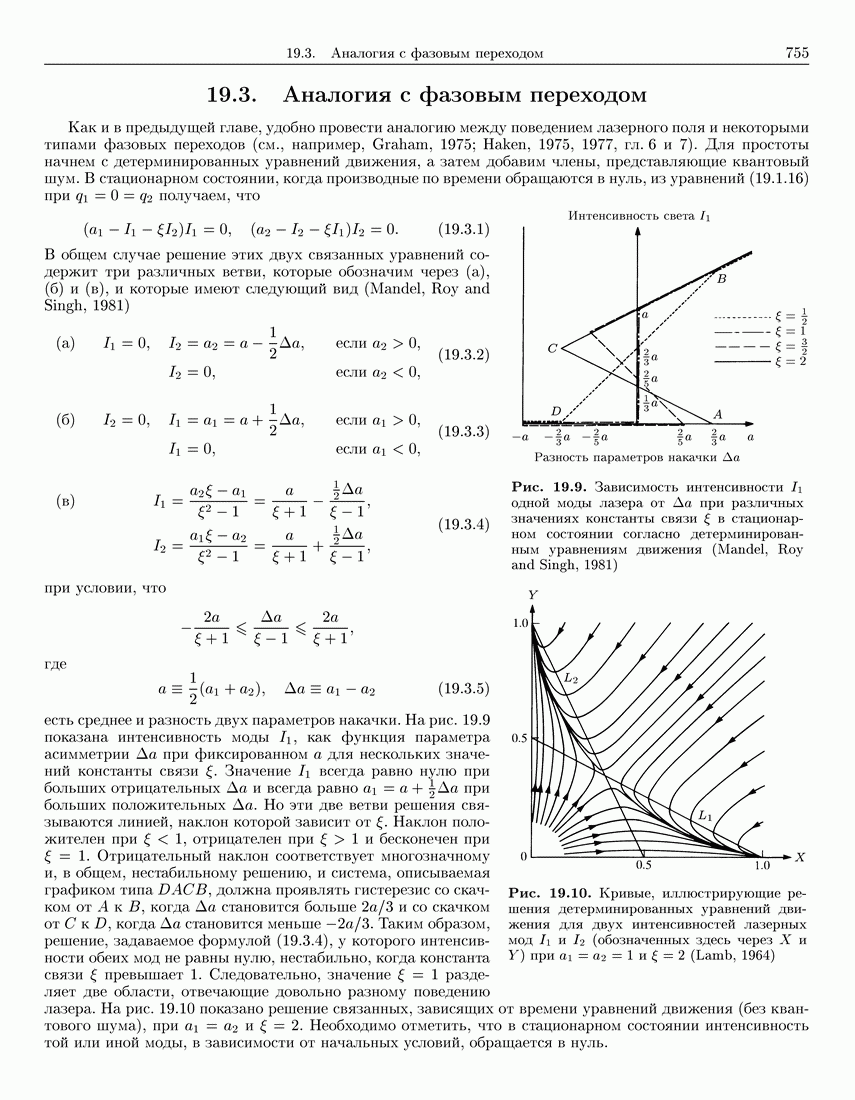
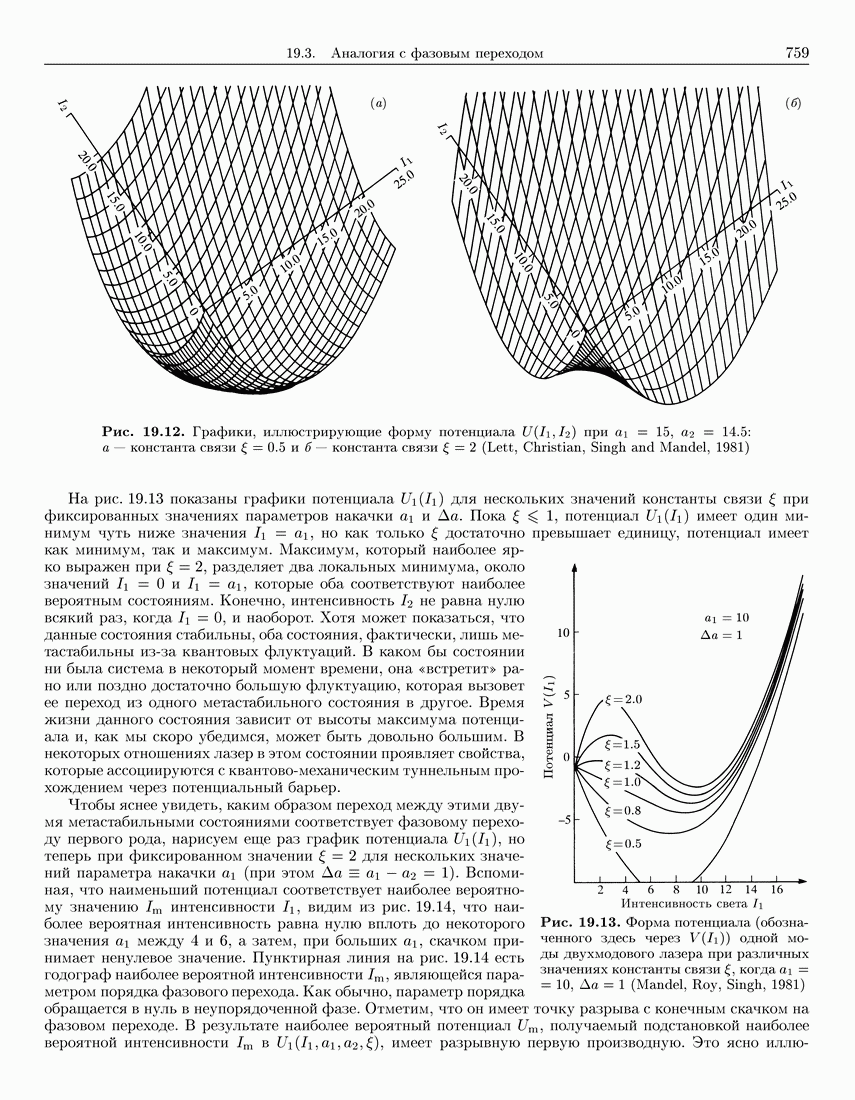
- 19.3. Аналогия с фазовым переходом
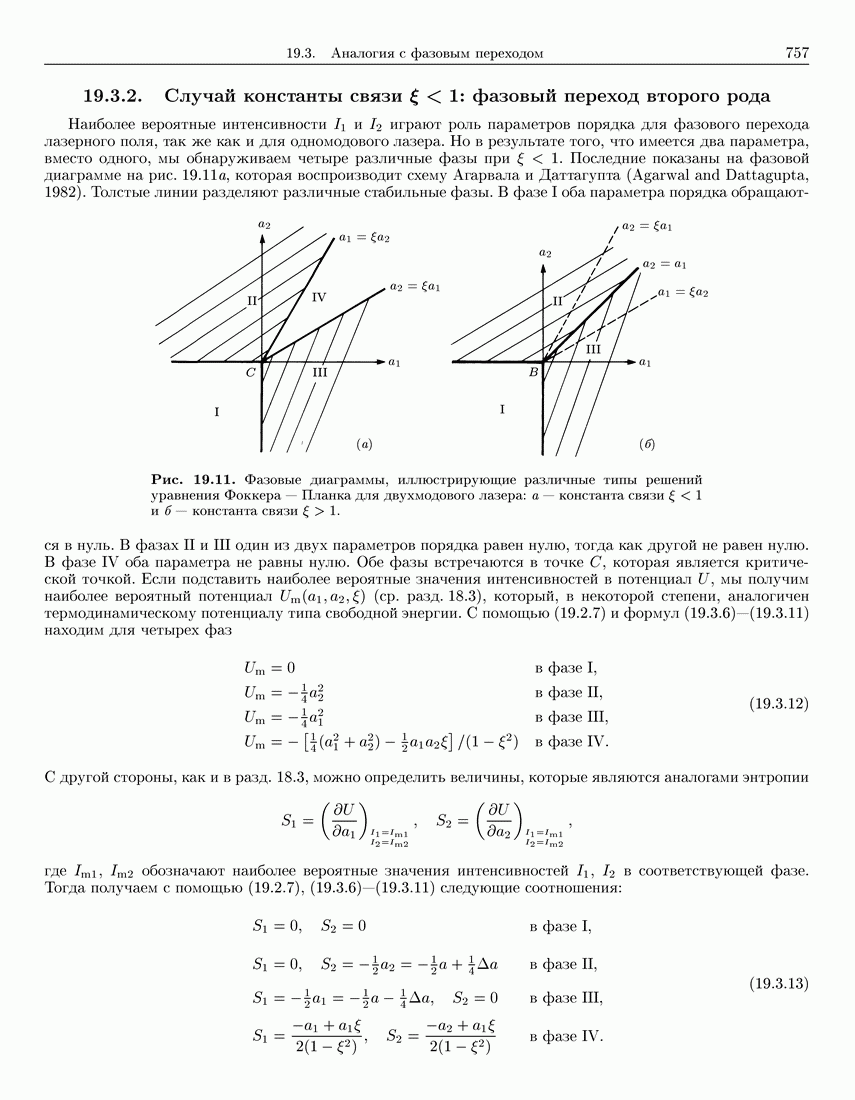
- 19.3.2. Случай константы связи …: фазовый переход второго рода
- 19.3.3. Случай константы связи …: фазовый переход первого рода
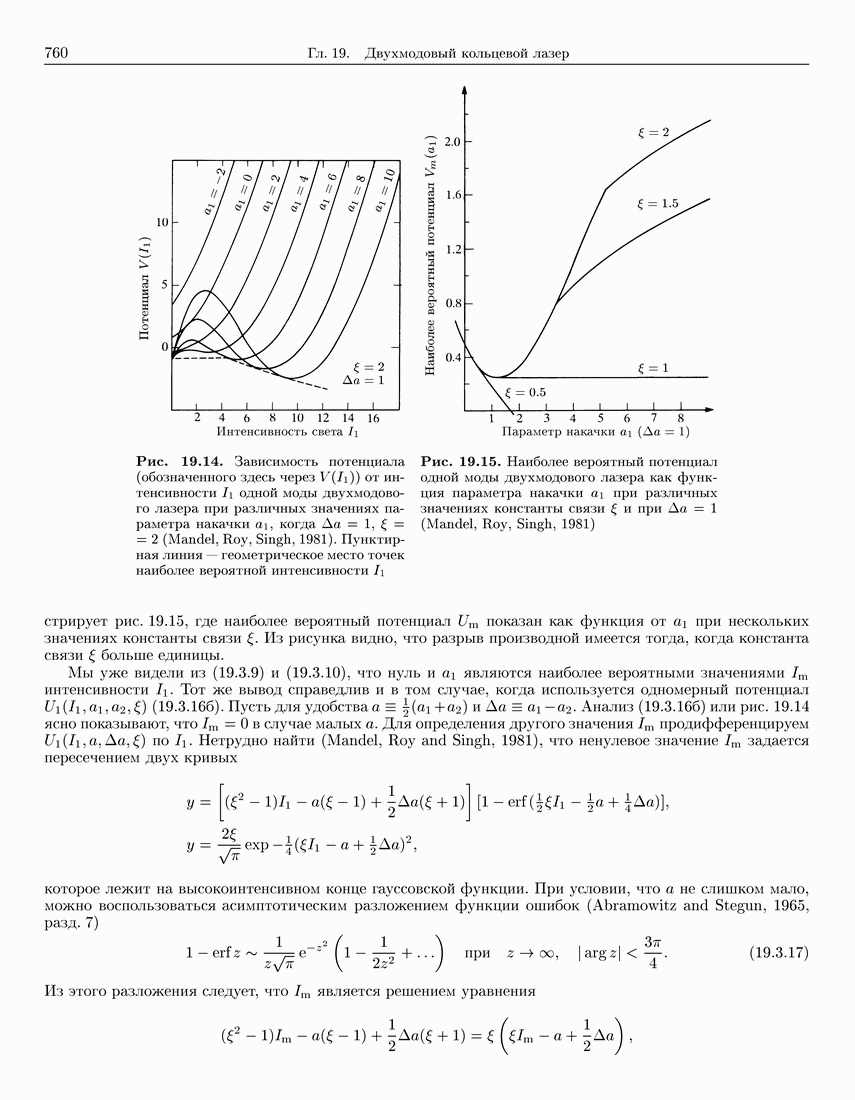
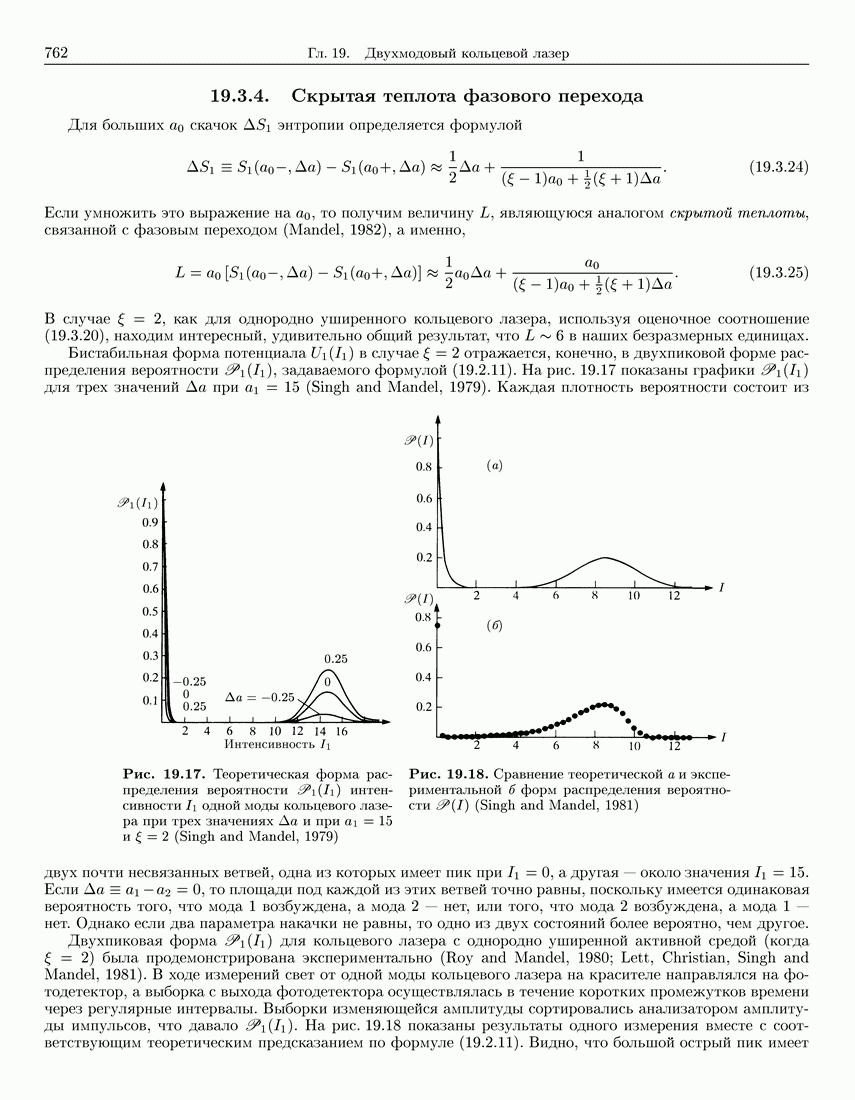
- 19.3.4. Скрытая теплота фазового перехода
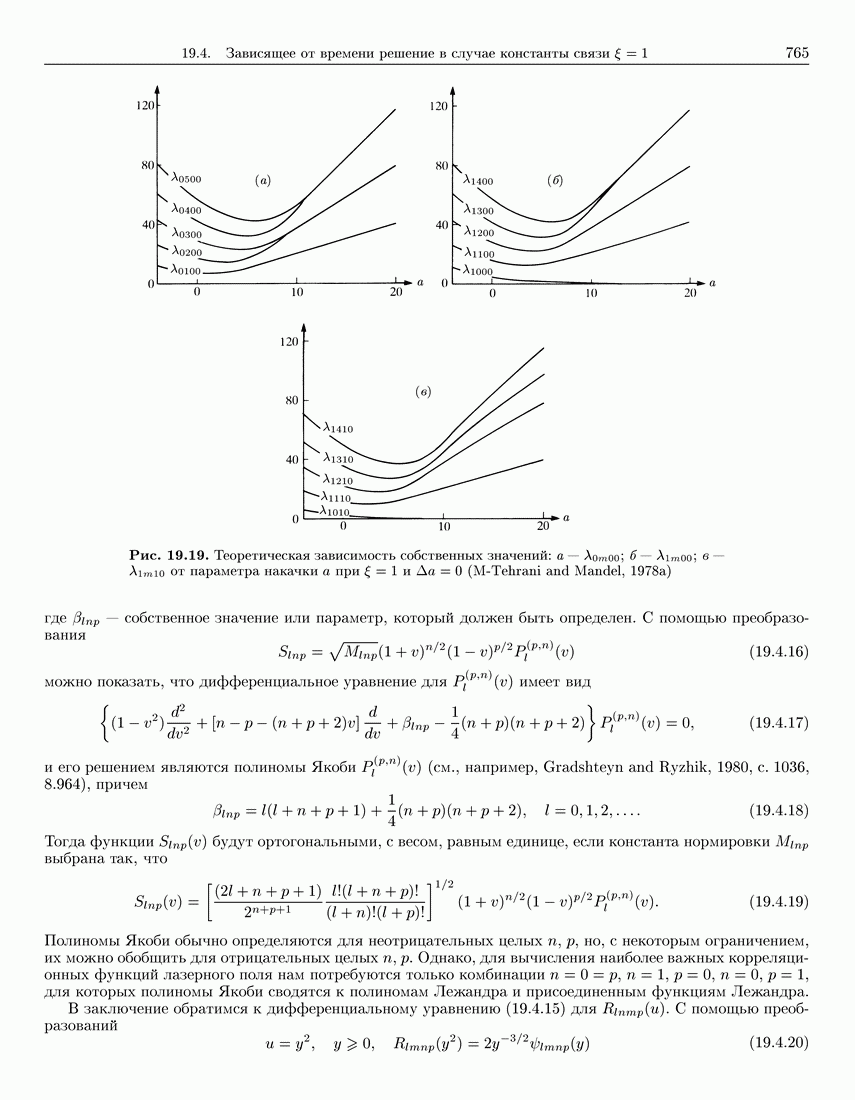
- 19.4. Зависящее от времени решение в случае константы связи …
- 19.5. Зависящее от времени решение в более общем случае взаимодействия между модами …
- 19.5.1. Переключение мод и времена первого прохождения
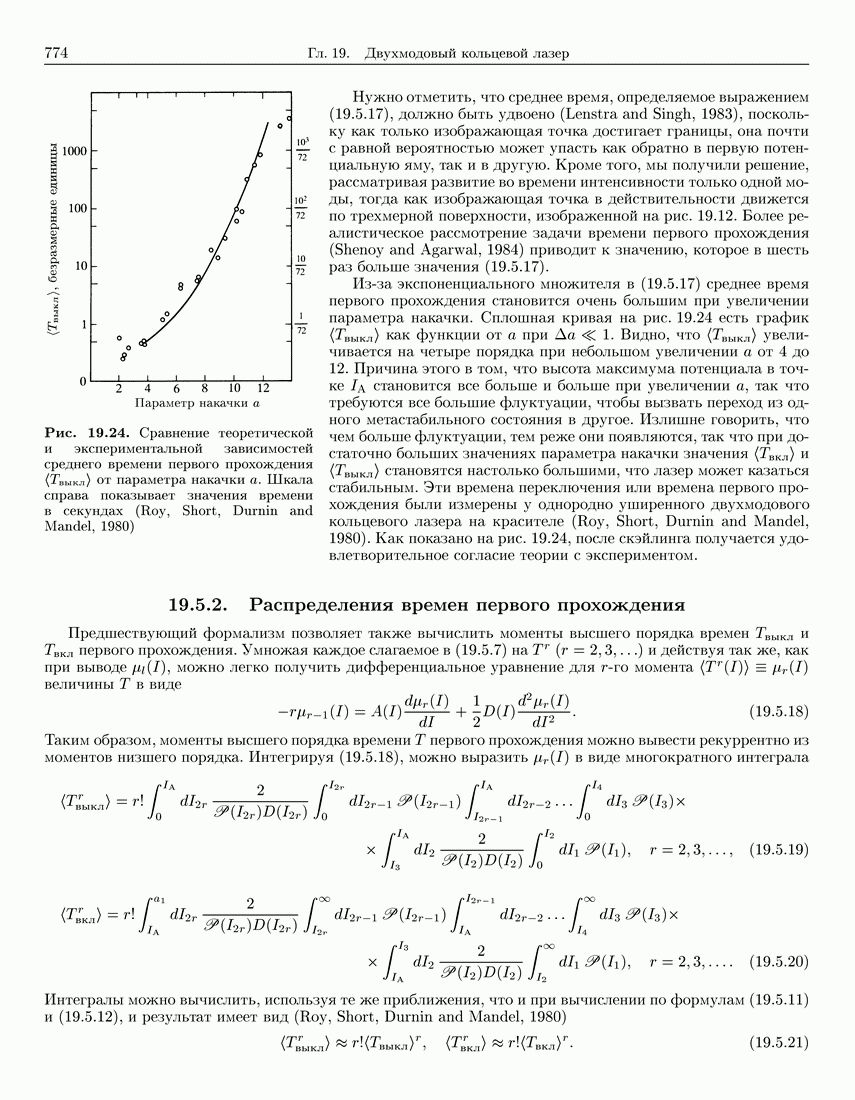
- 19.5.2. Распределения времен первого прохождения
- Глава 20. ЛИНЕЙНЫЙ УСИЛИТЕЛЬ СВЕТА
- 20.2. Основное кинетическое уравнения для поля усилителя
- 20.3. Решение основного кинетического уравнения
- 20.4. Статистика фотонов
- 20.4.2. Полностью инвертированный усилитель света
- 20.5. Сжатый свет
- 20.6. Условие, при котором поле на выходе усилителя является классическим
- Глава 21. СЖАТЫЕ СОСТОЯНИЯ СВЕТА
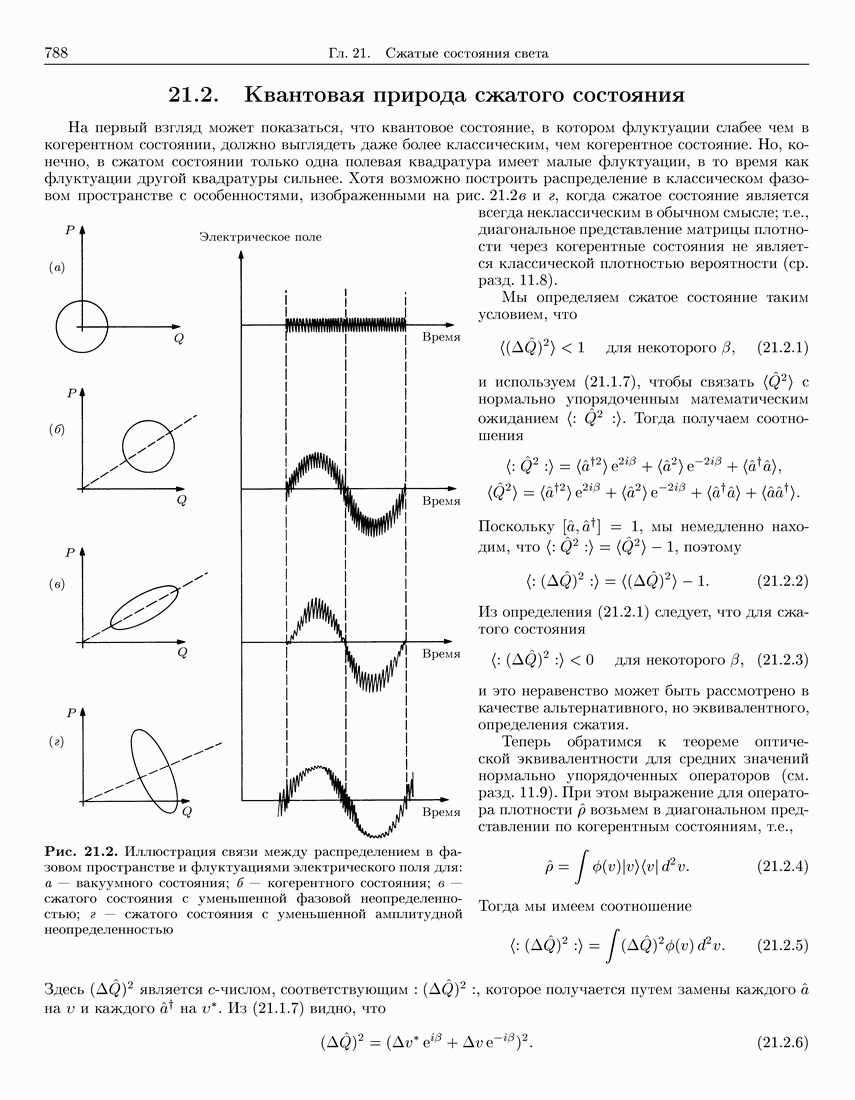
- 21.2. Квантовая природа сжатого состояния
- 21.3. Унитарный оператор сжатия
- 21.3.1. Сжатие двухфотонного когерентного состояния
- 21.3.2. Действие оператора сжатия на произвольное состояние
- 21.4. Идеальное сжатое состояние
- 21.5. Двухфотонное когерентное состояние
- 21.5.1. Преобразованные фоковские состояния
- 21.5.2. Представление по когерентным состояниям двухфотонного когерентного состояния
- 21.5.3. Фотонная статистика двухфотонного когерентного состояния
- 21.6. Детектирование сжатия гомодинированием с когерентным светом
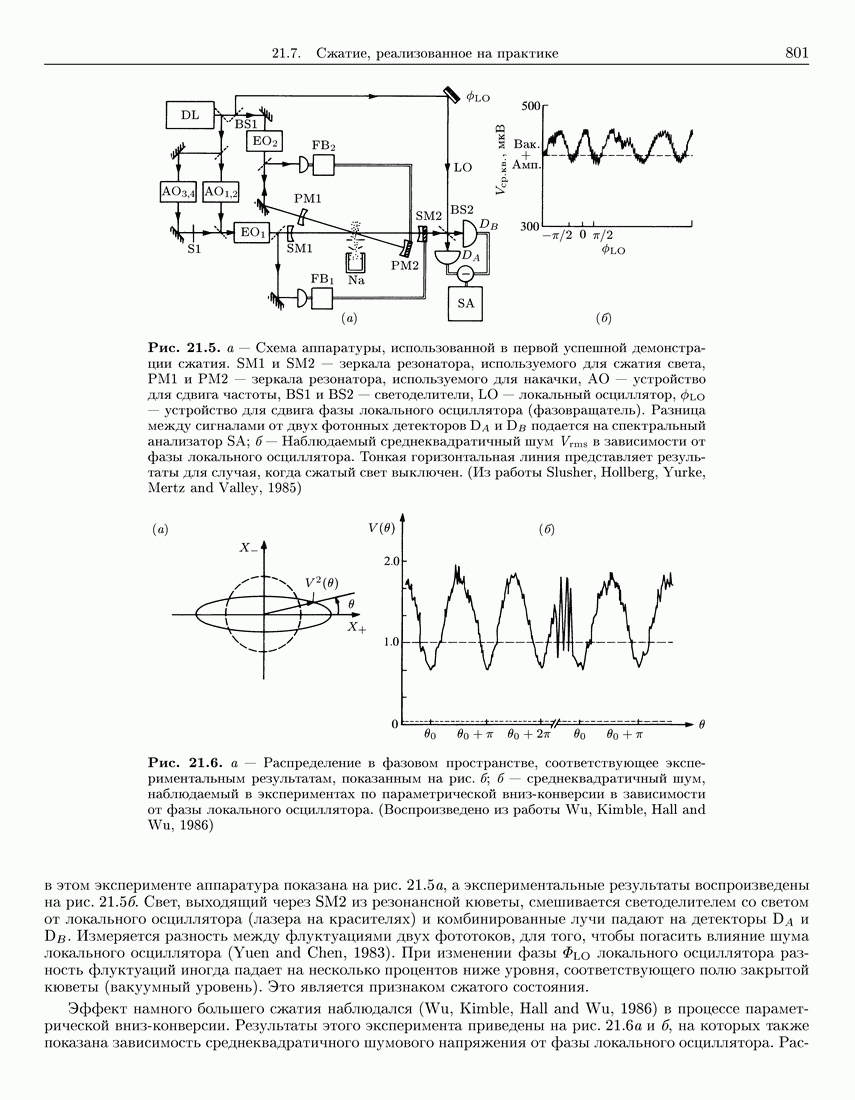
- 21.7. Сжатие, реализованное на практике: вырожденная параметрическая вниз-конверсия
- 21.7.1. Создание сжатого состояния при вырожденной параметрической вниз-конверсии
- 21.8. Широкополосный сжатый свет
- 21.8.1. Гомодинирование и корреляционные функции
- 21.8.2. Квадратурные корреляции
- 21.8.3. Спектральные корреляции
- 21.8.4. Спектрально-компонентное сжатие и степень сжатия
- 21.8.5. Примеры степени сжатия Q(w)
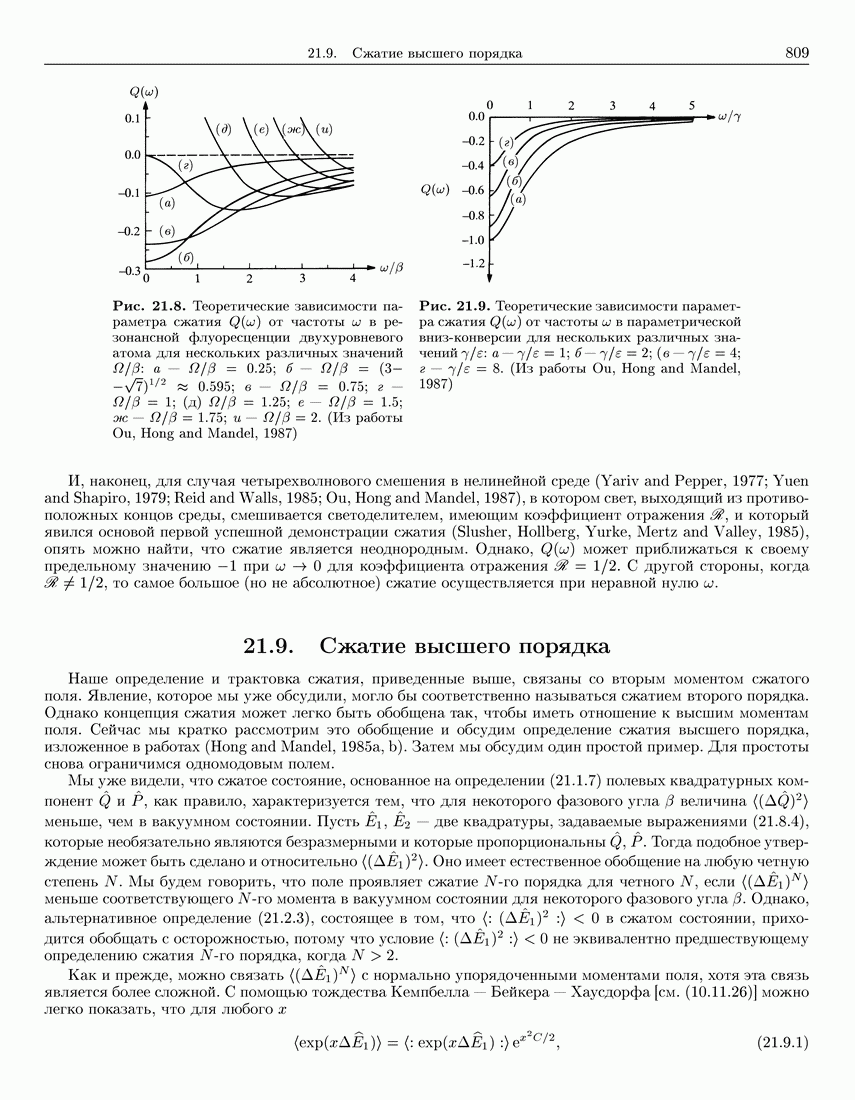
- 21.9. Сжатие высшего порядка
- 21.9.1. Сжатие N-ого порядка двухфотонного когерентного состояния
- 21.9.2. Амплитудно-квадратичное сжатие
- Глава 22. НЕКОТОРЫЕ КВАНТОВЫЕ ЭФФЕКТЫ В НЕЛИНЕЙНОЙ ОПТИКЕ
- 22.2. Энергия поля в диэлектрике
- 22.3. Генерация оптических гармоник
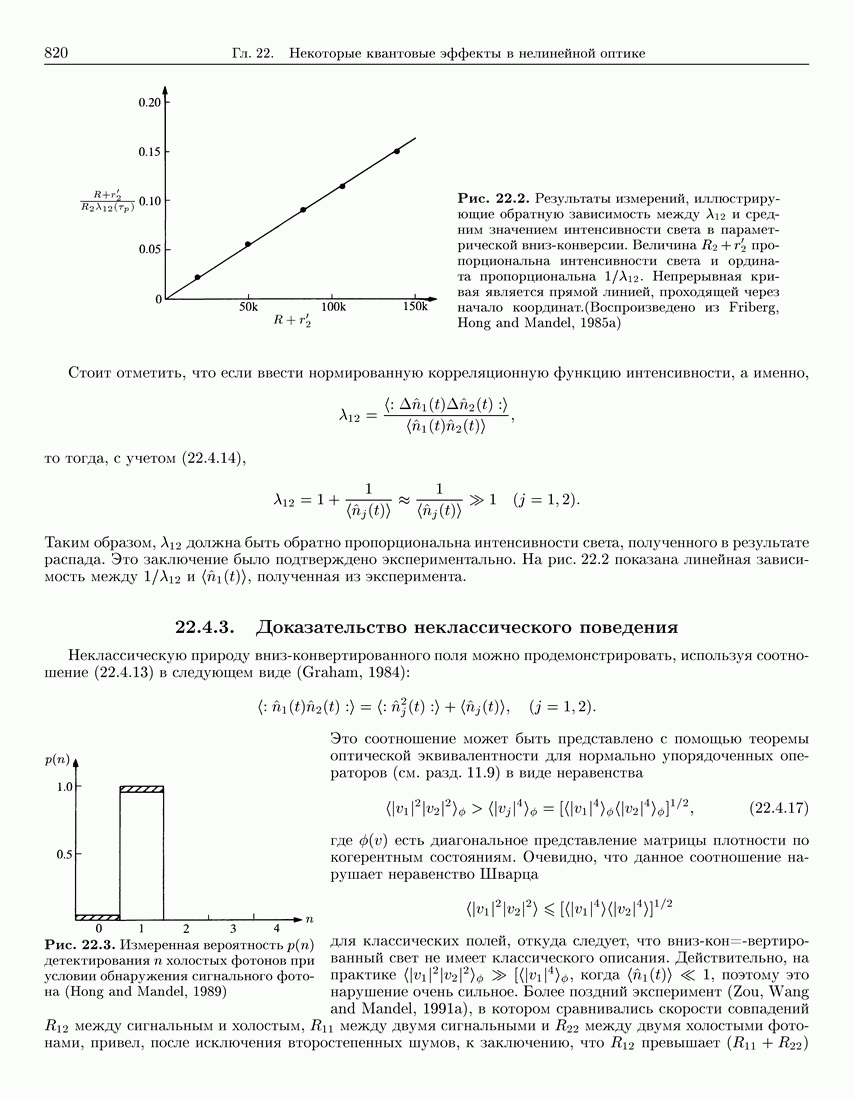
- 22.4. Параметрическая вниз-конверсия
- 22.4.2. Статистика фотонов
- 22.4.3. Доказательство неклассического поведения
- 22.4.4. Многомодовая теория возмущений процесса параметрического распада
- 22.4.5. Перепутанное квантовое состояние
- 22.4.6. Скорость вниз-конверсии
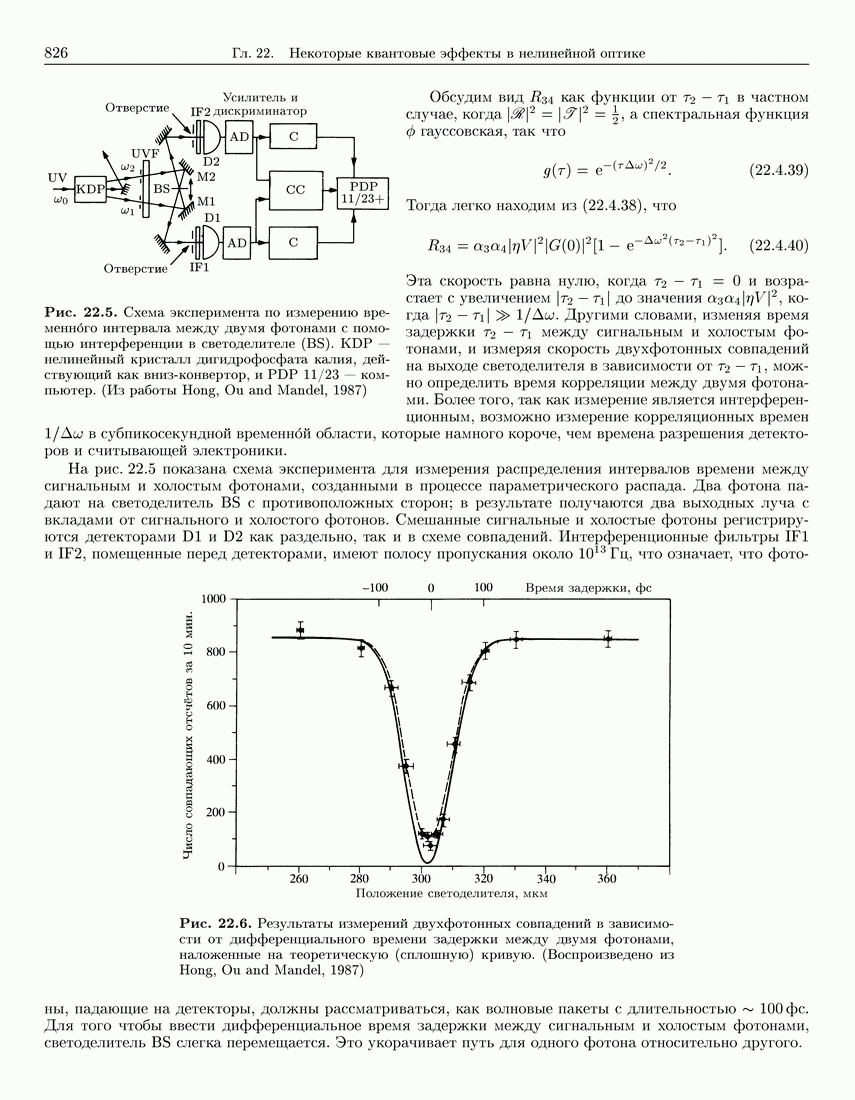
- 22.4.7. Временной интервал между сигнальным и холостым фотонами
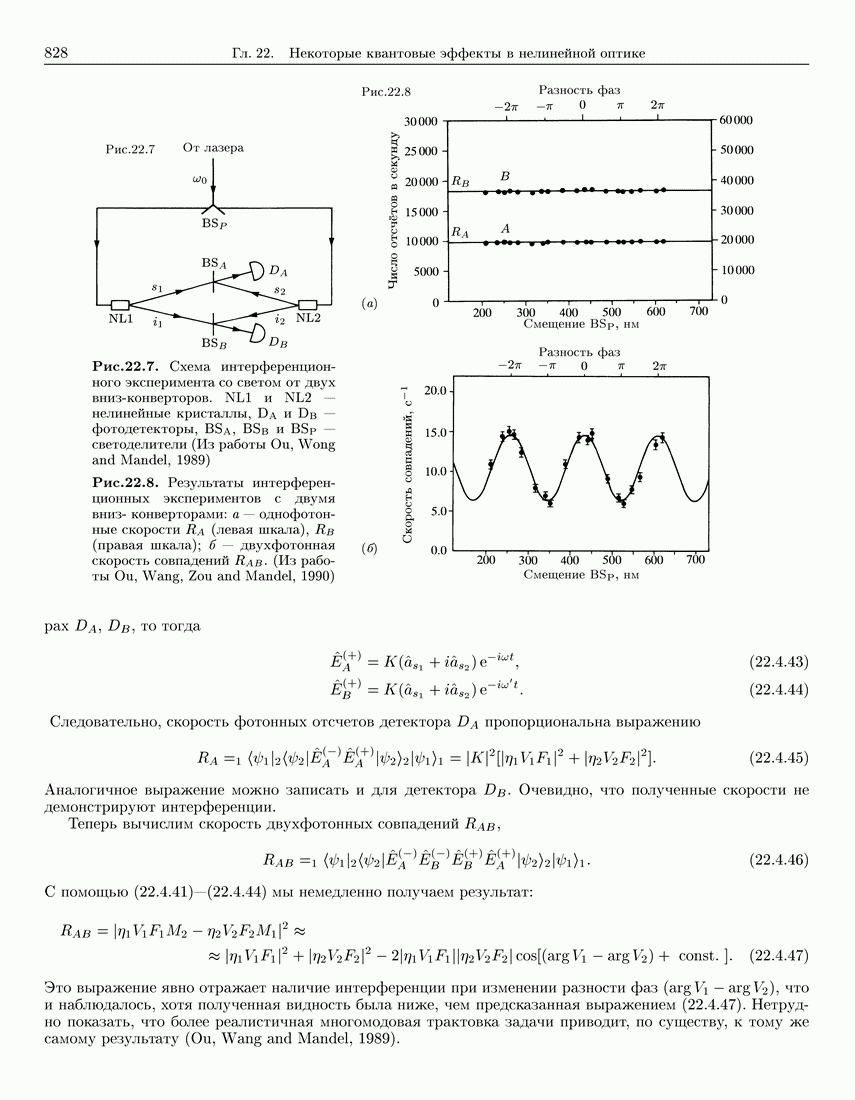
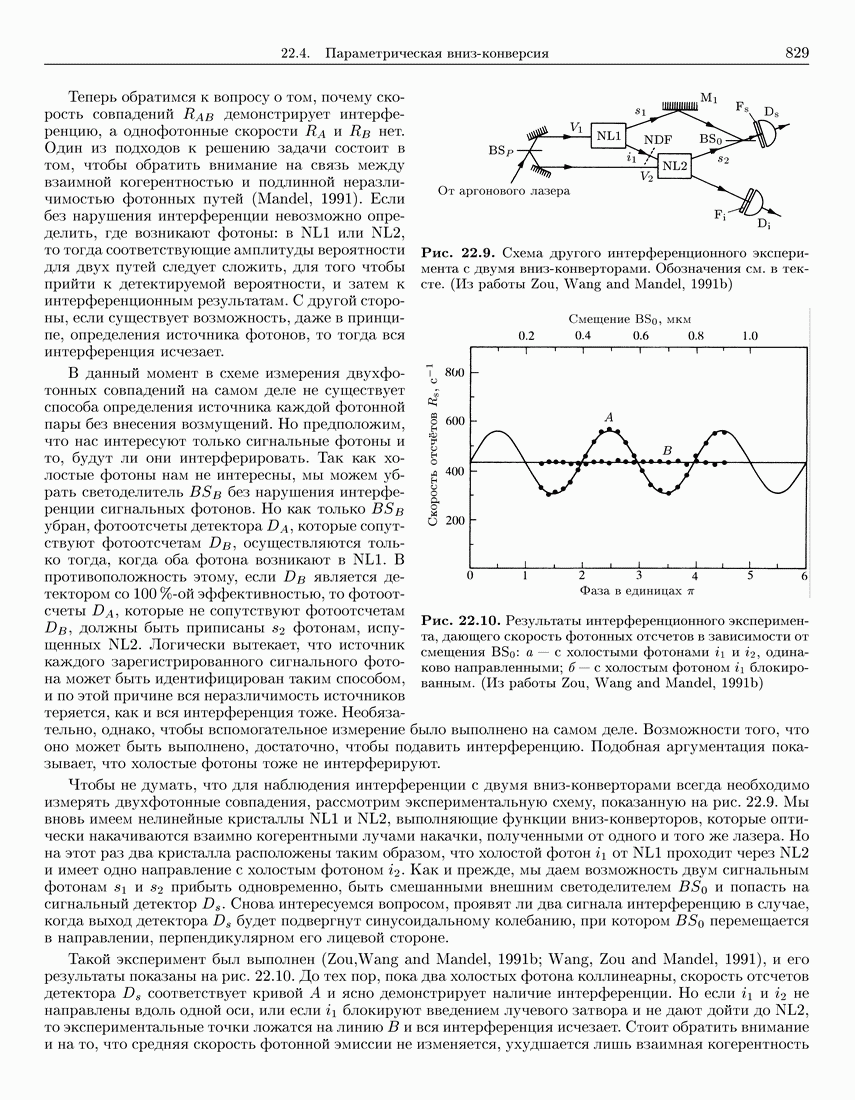
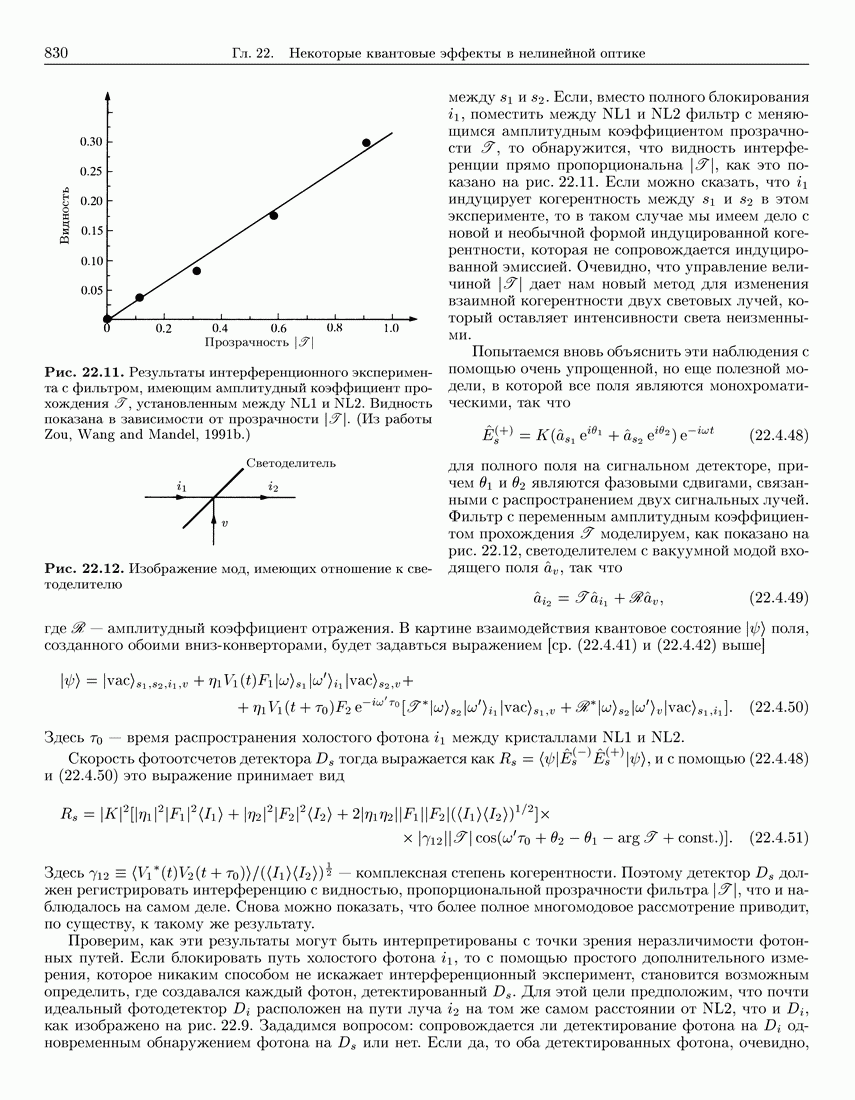
- 22.4.8. Интерференционные эксперименты с двумя вниз-конверторами
- 22.5. Вырожденное четырехволновое смешение
- 22.5.2. Применение к когерентному состоянию
- 22.5.3. Сжатие в четырехволновом смешении
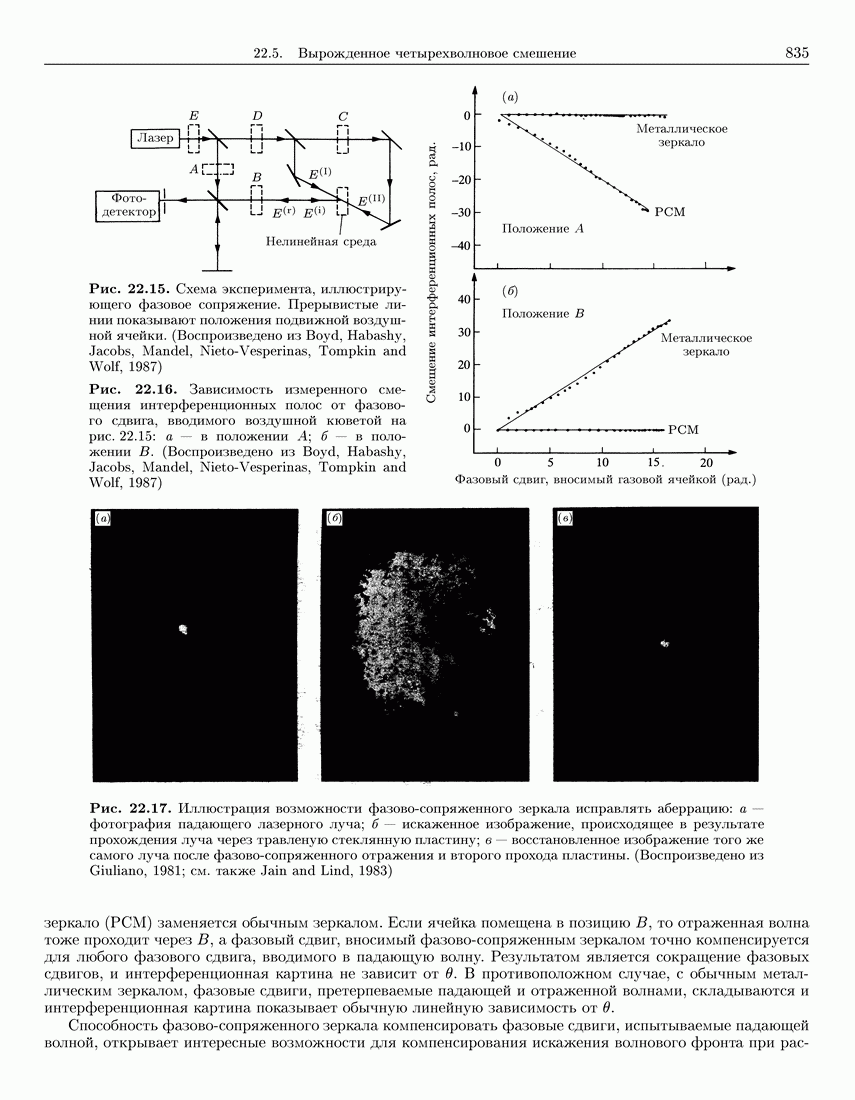
- 22.5.4. Фазовое сопряжение
- 22.6. Квантовые неразрушающие измерения
- 22.6.1. Эффект Керра — пример QND-переменной
- 22.6.2. Анализ интерференционного эксперимента
- 22.6.3. Вычисление видности интерференционных полос
- 22.6.4. Фазовый сдвиг зондирующей волны
- 22.6.5. Дополнительность