| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
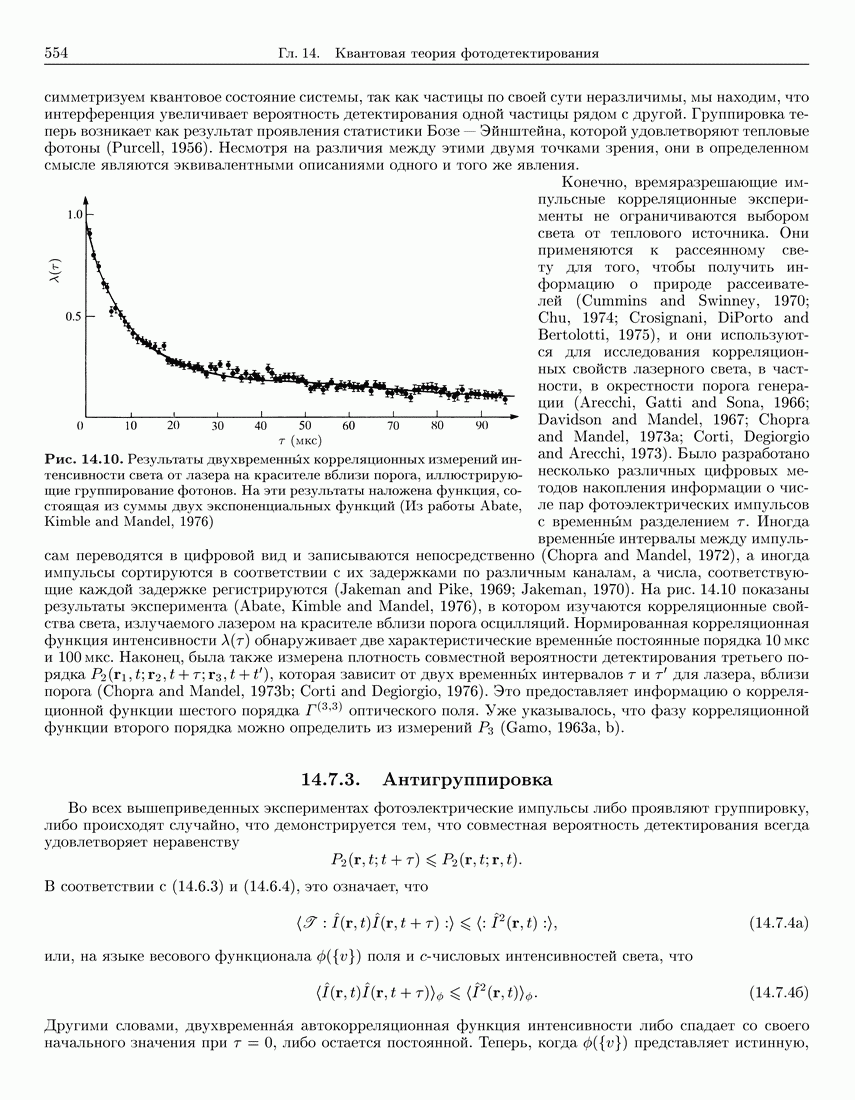
544
545
546
547
548
549
550
551
552
553
554
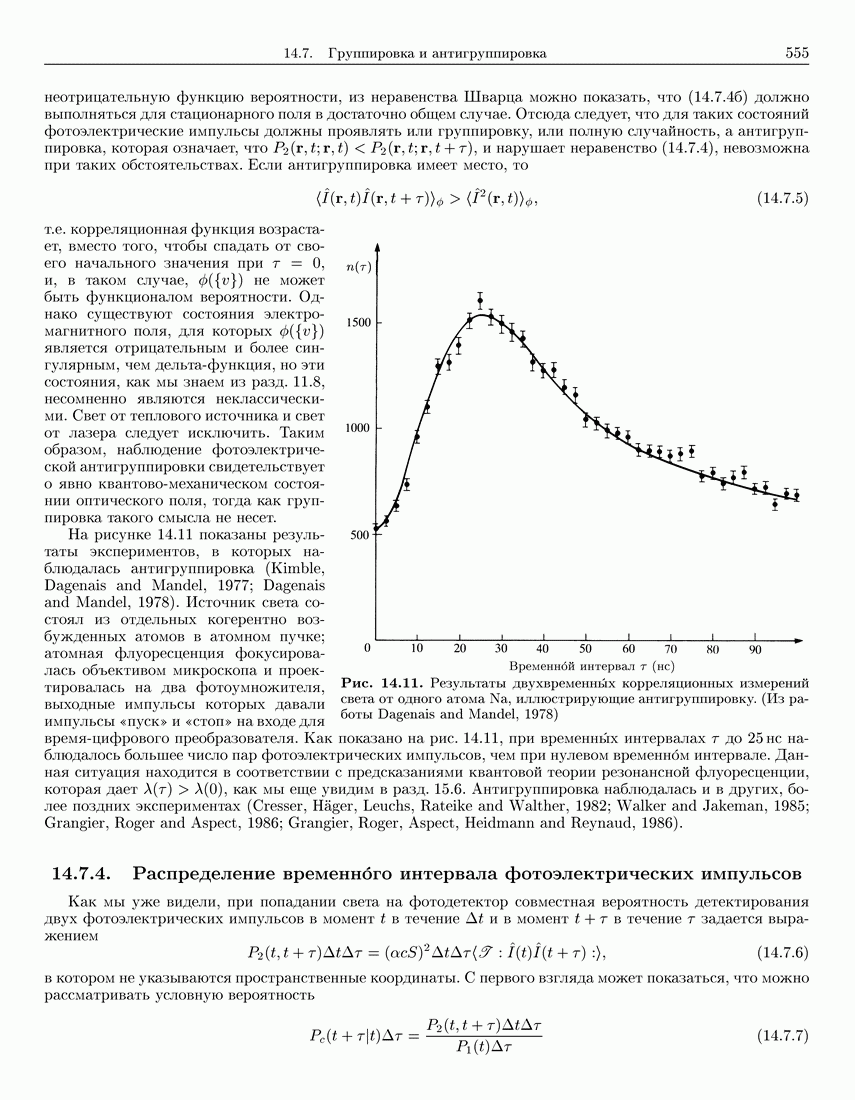
555
556
557
558
559
560
561
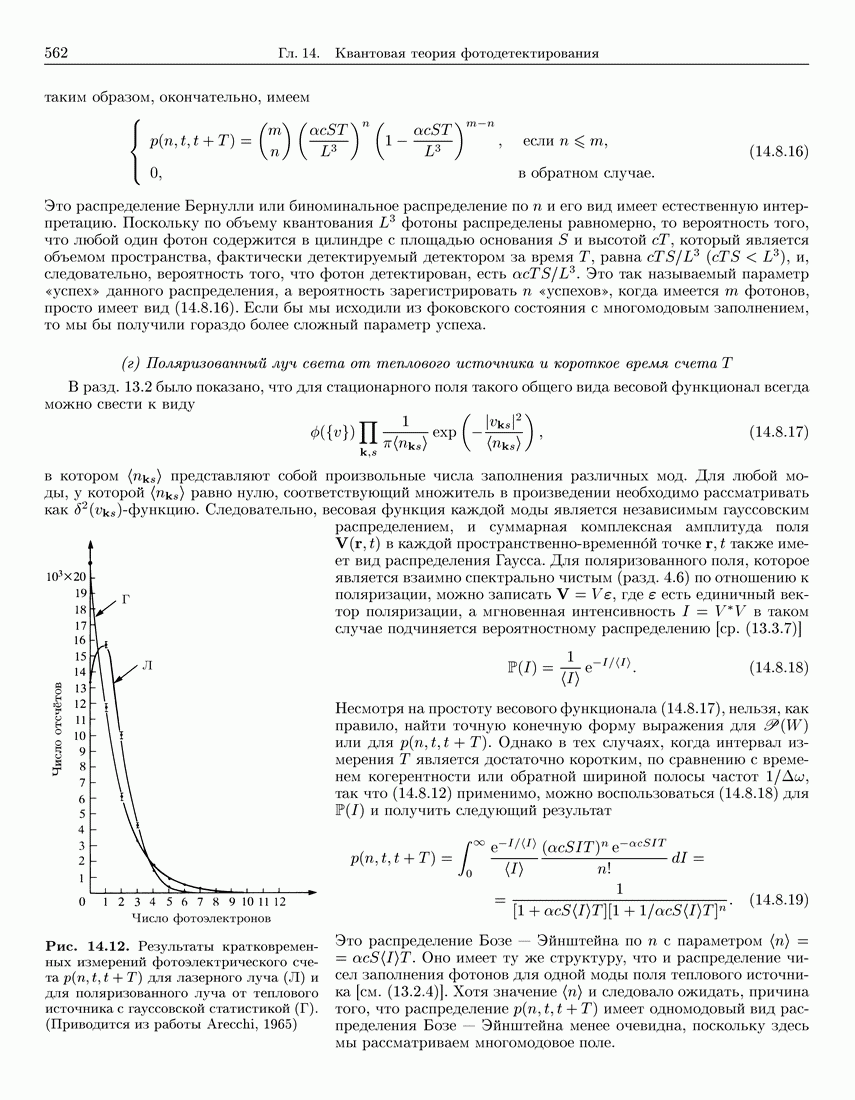
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
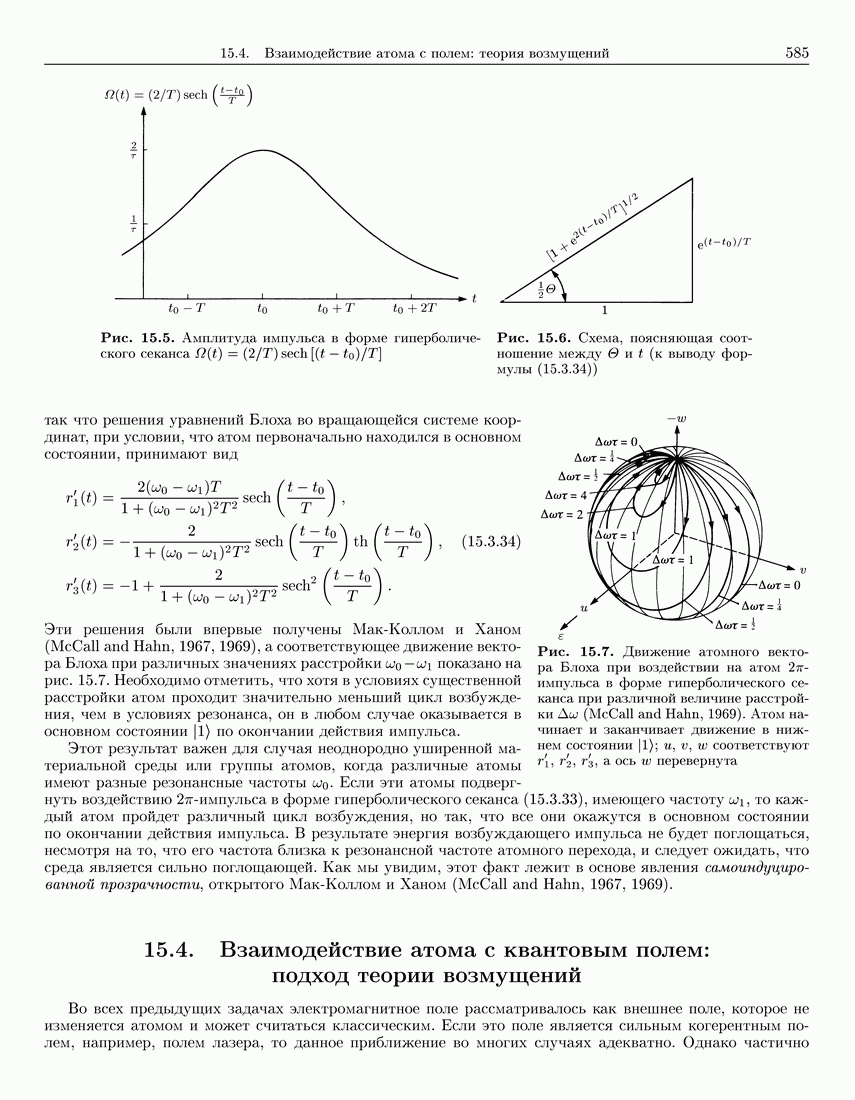
585
586
587
588
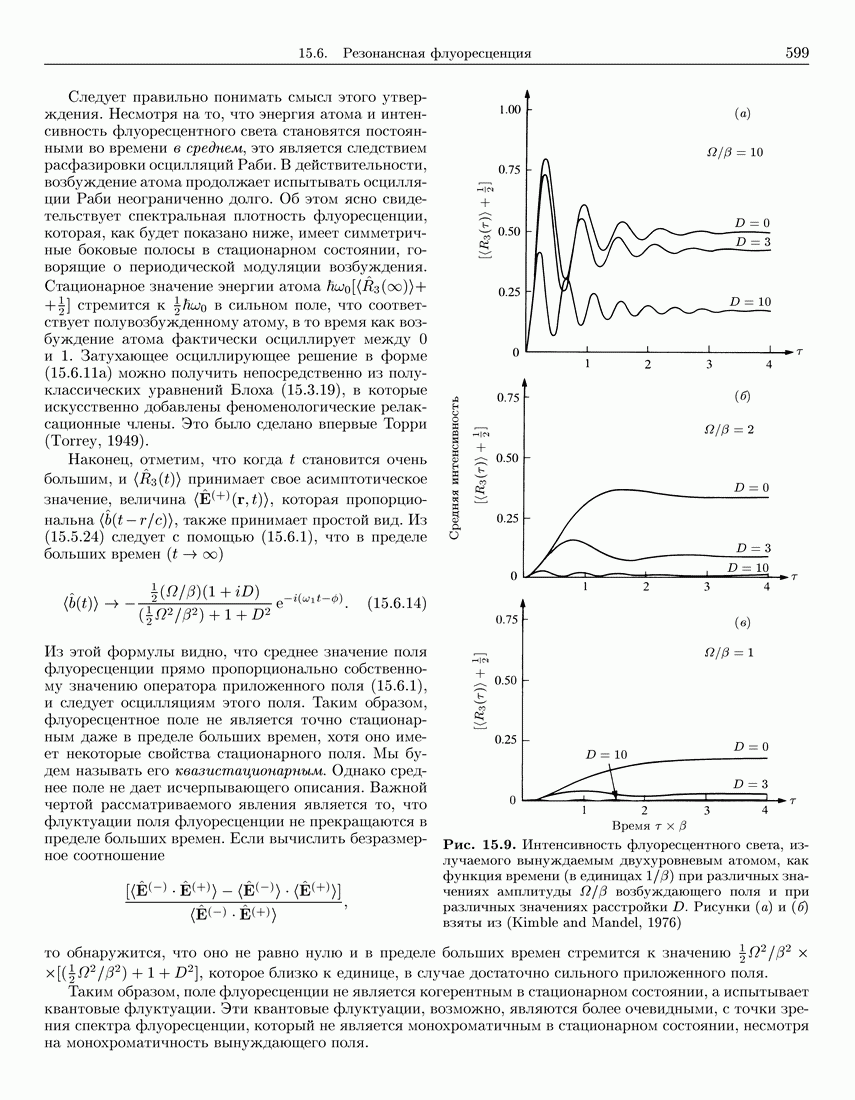
589
590
591
592
593
594
595
596
597
598
599
600
601
602
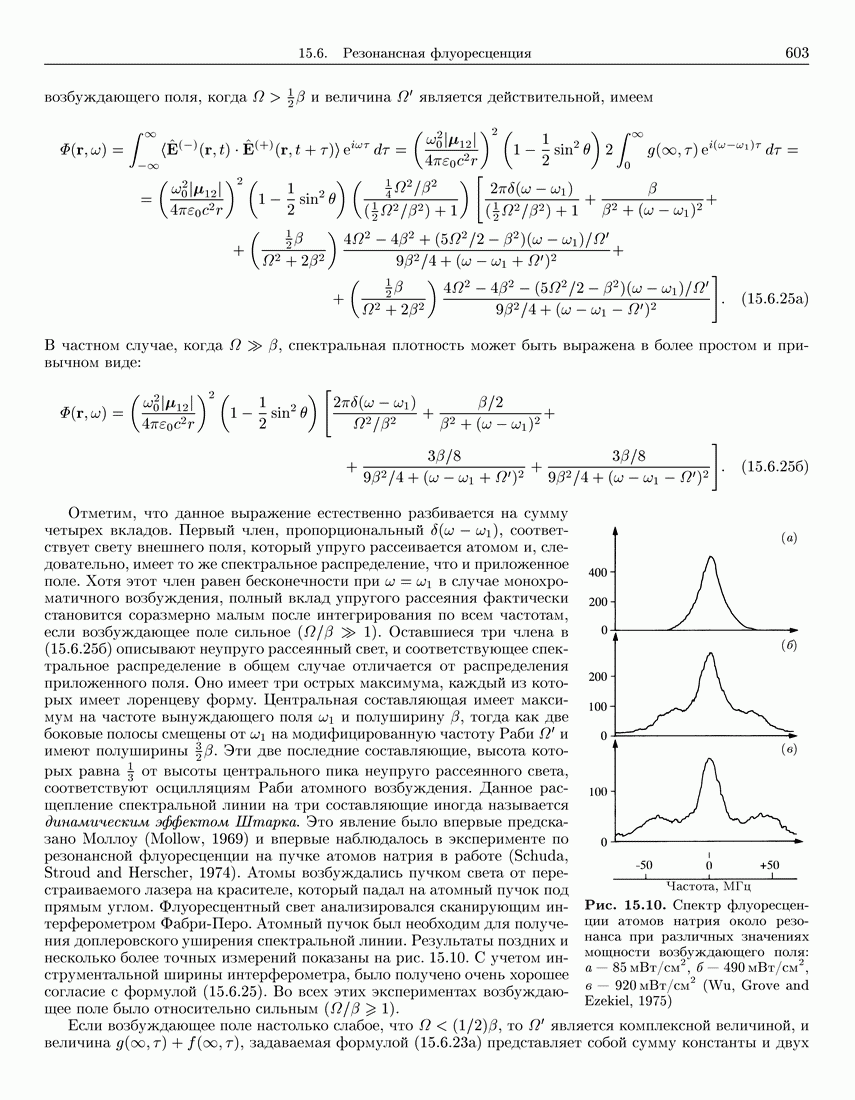
603
604
605
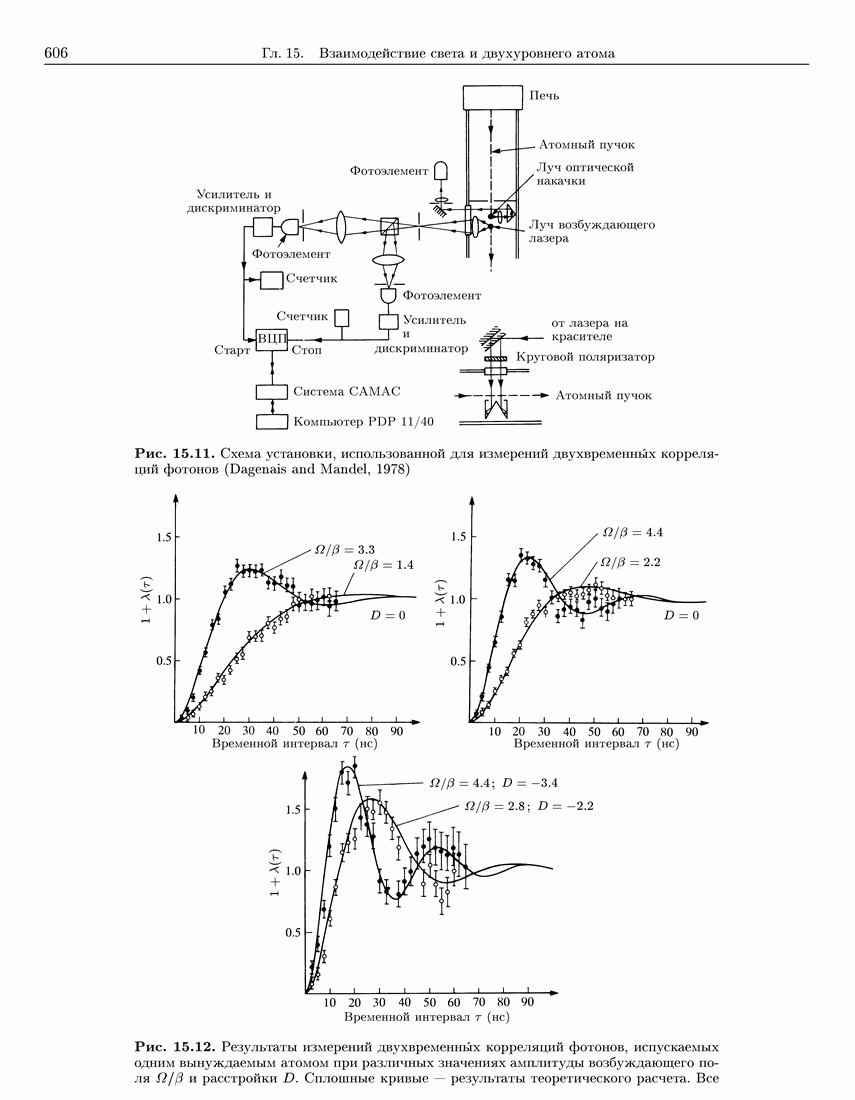
606
607
608
609
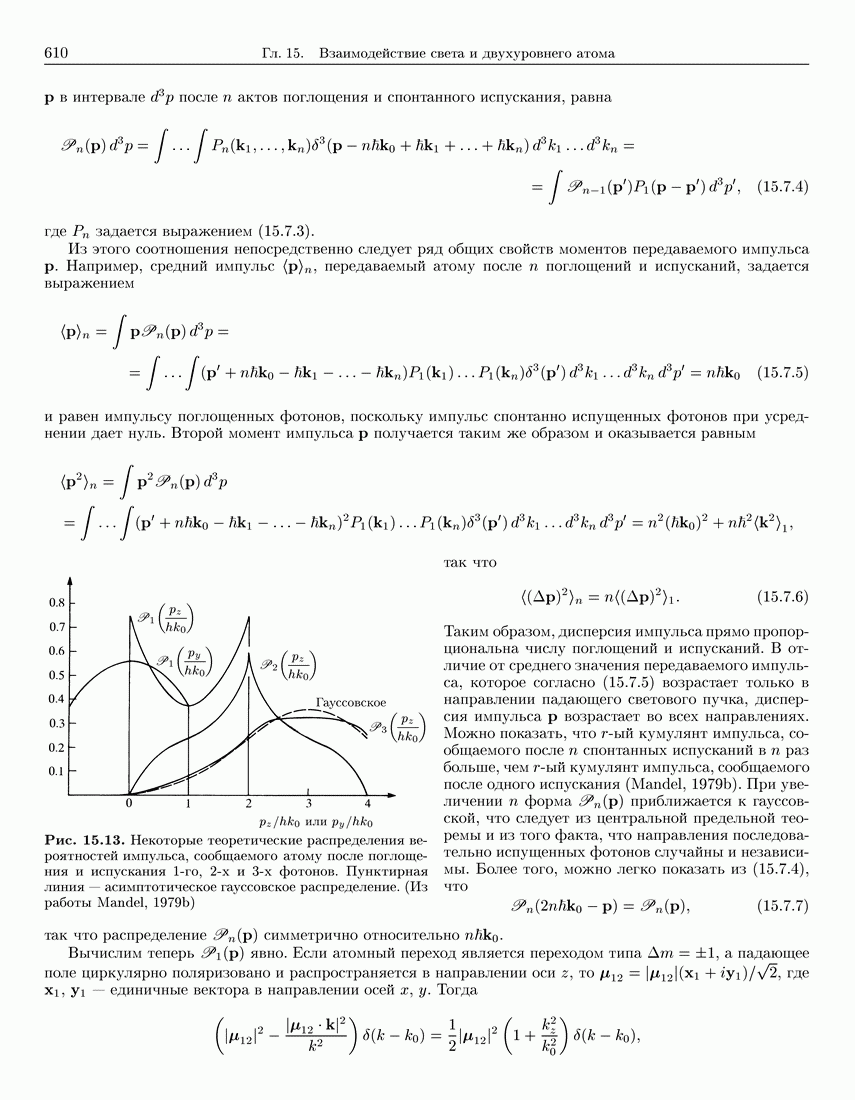
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
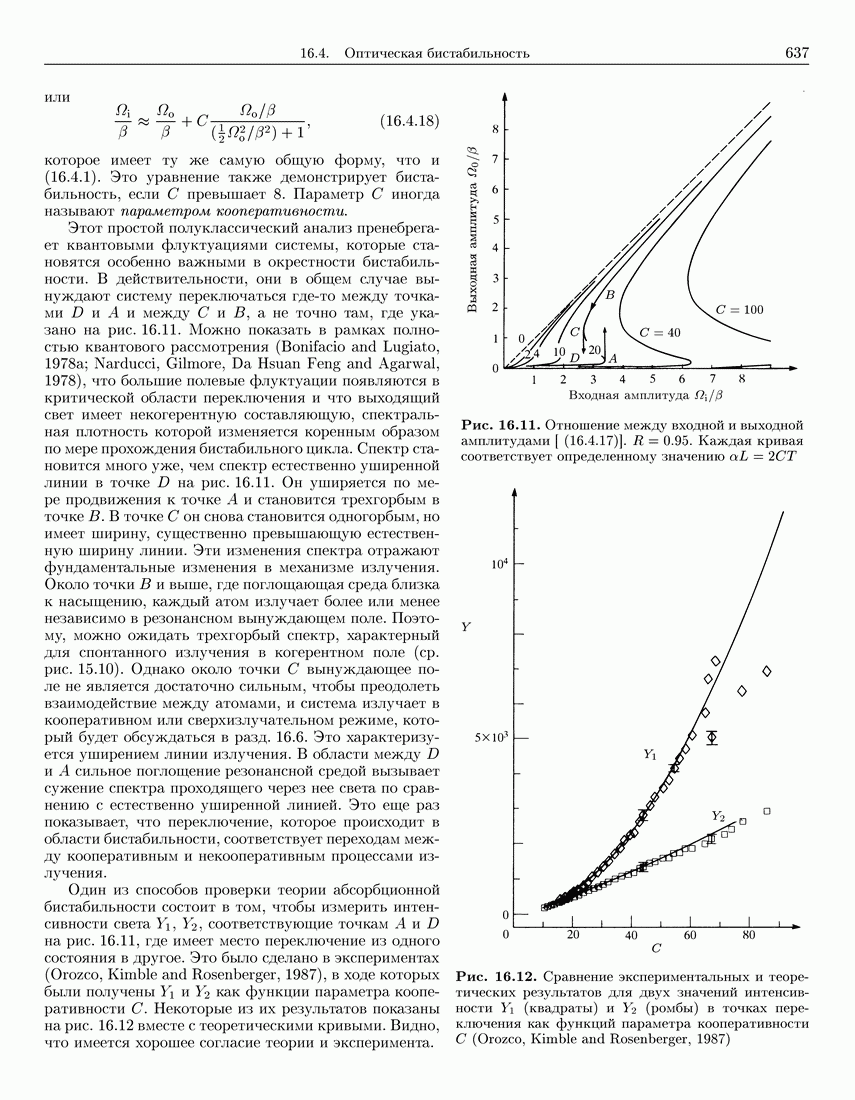
627
628
629
630
631
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
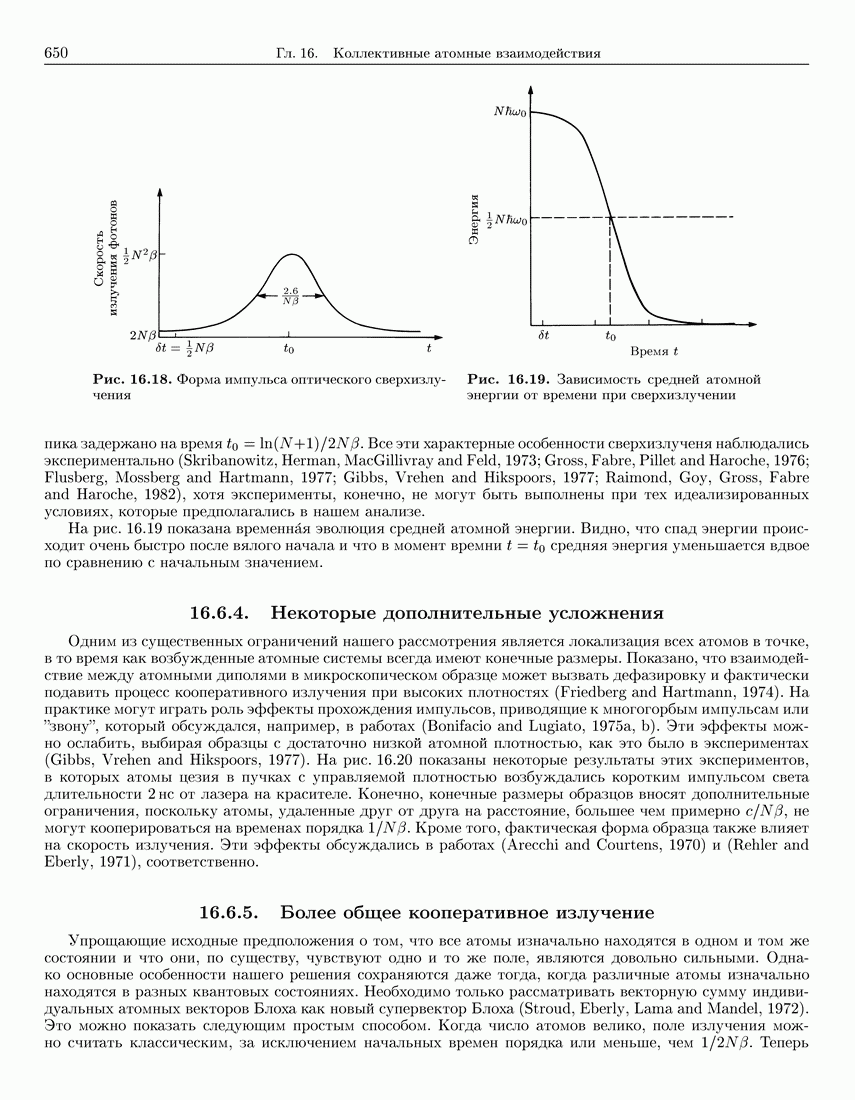
650
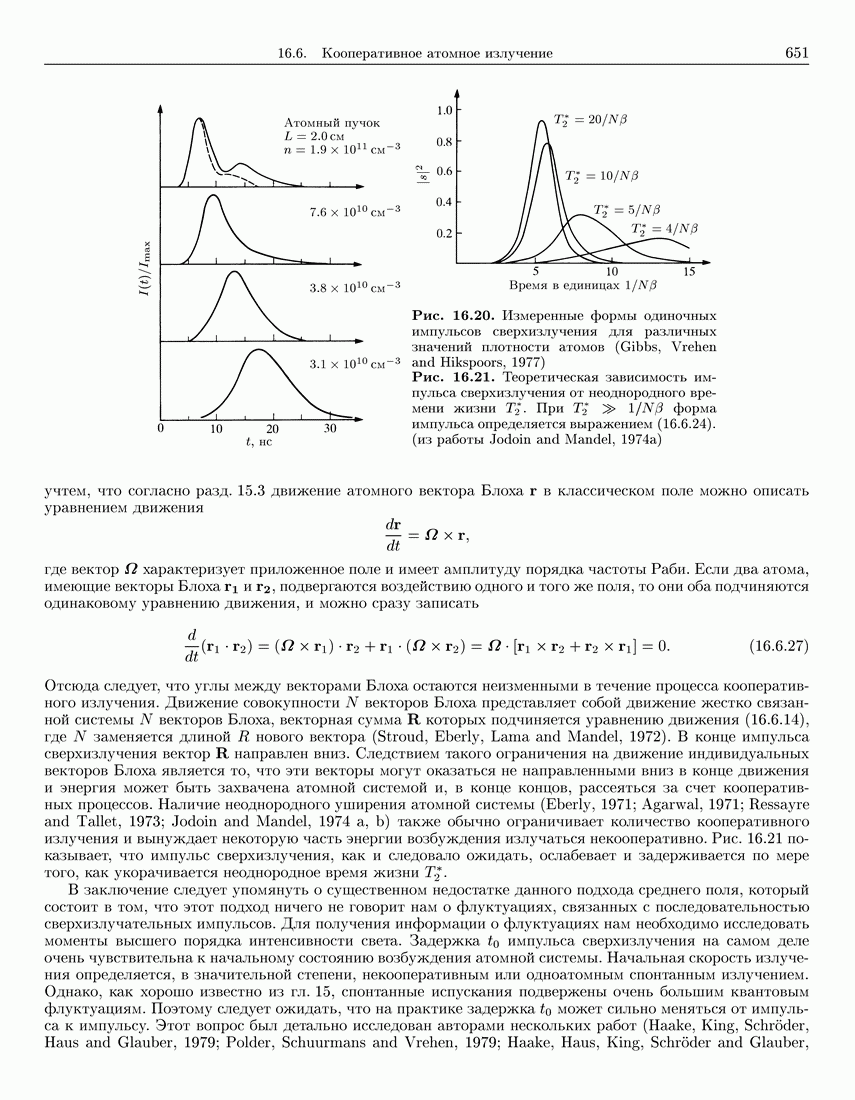
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
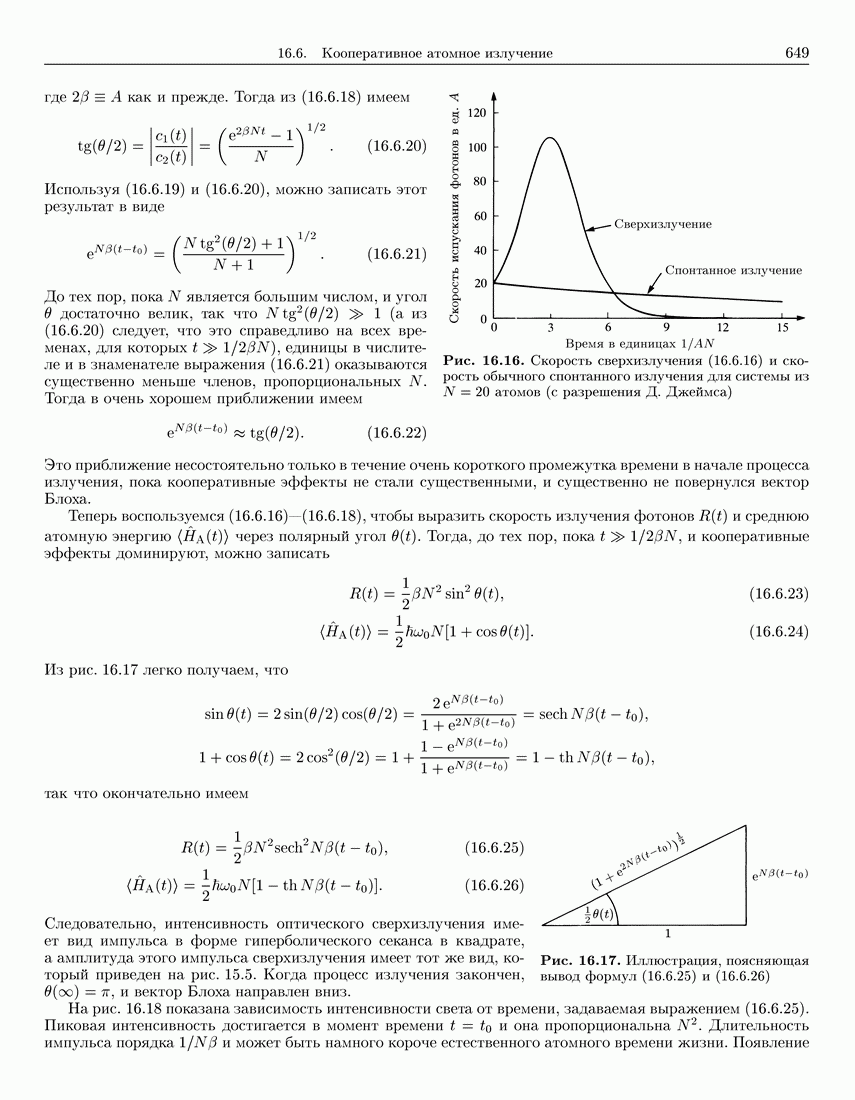
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
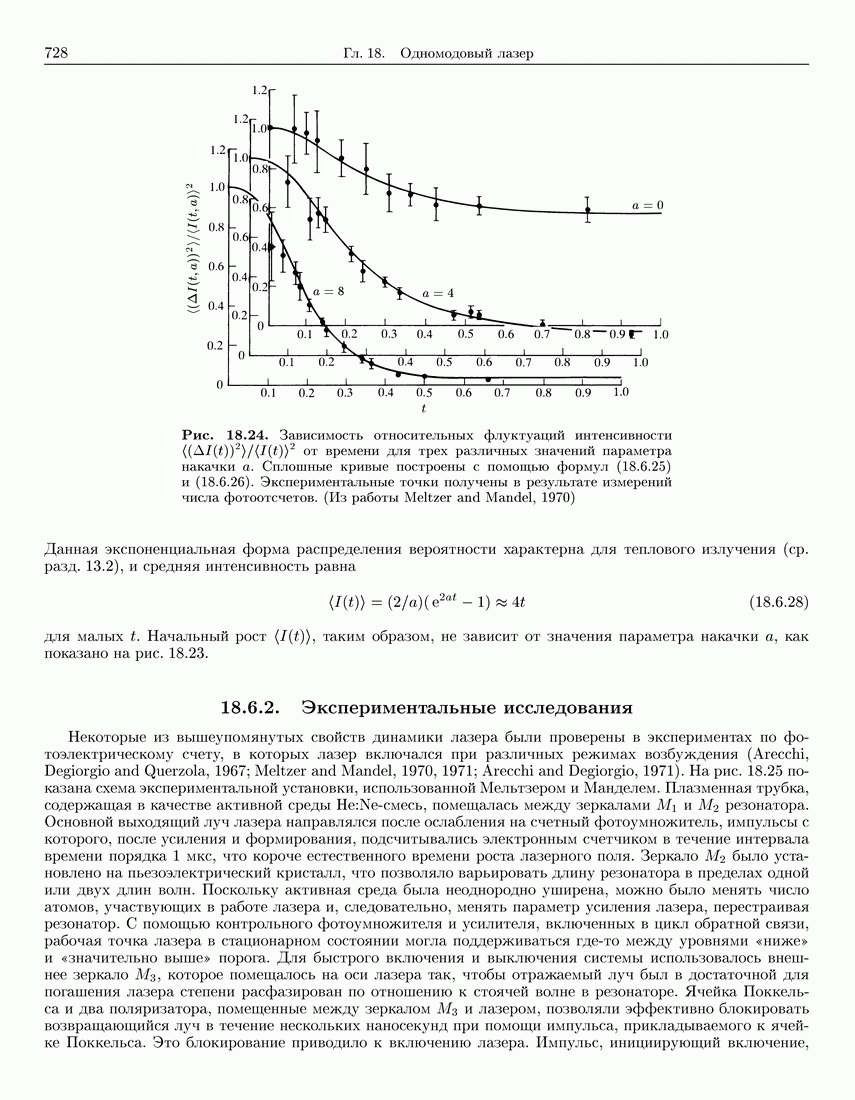
728
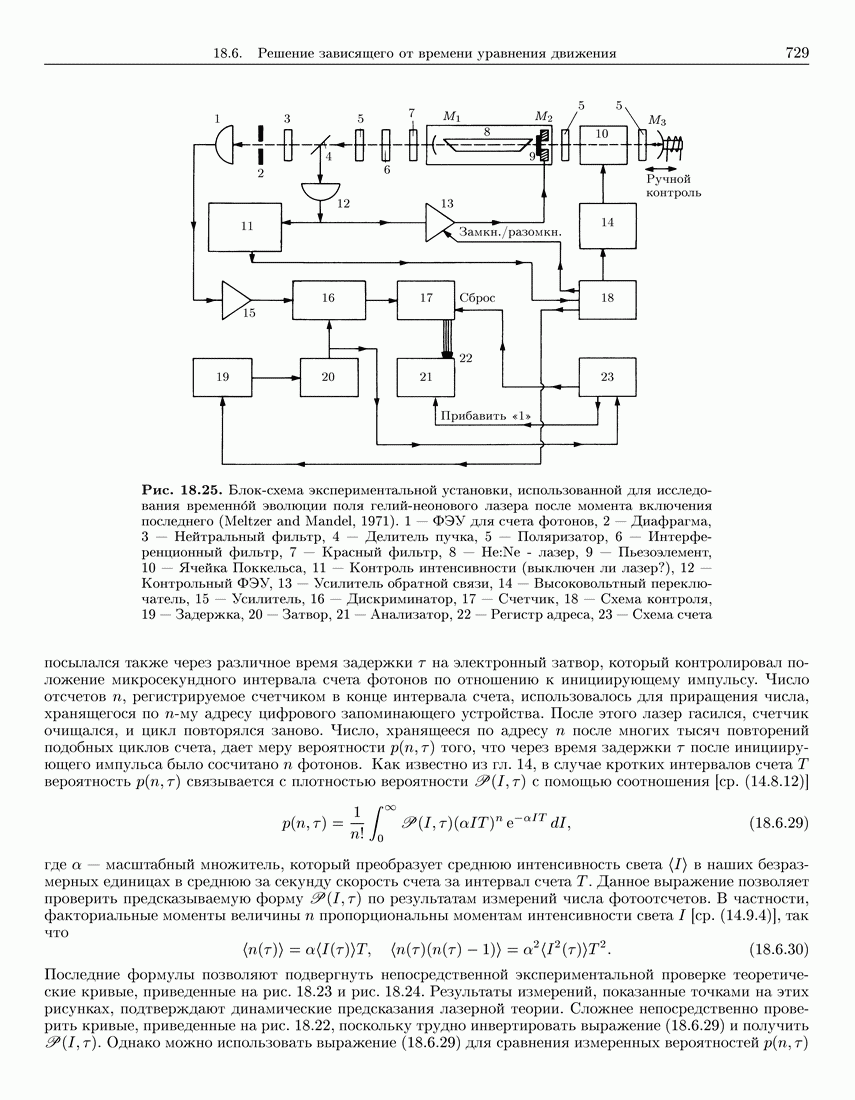
729
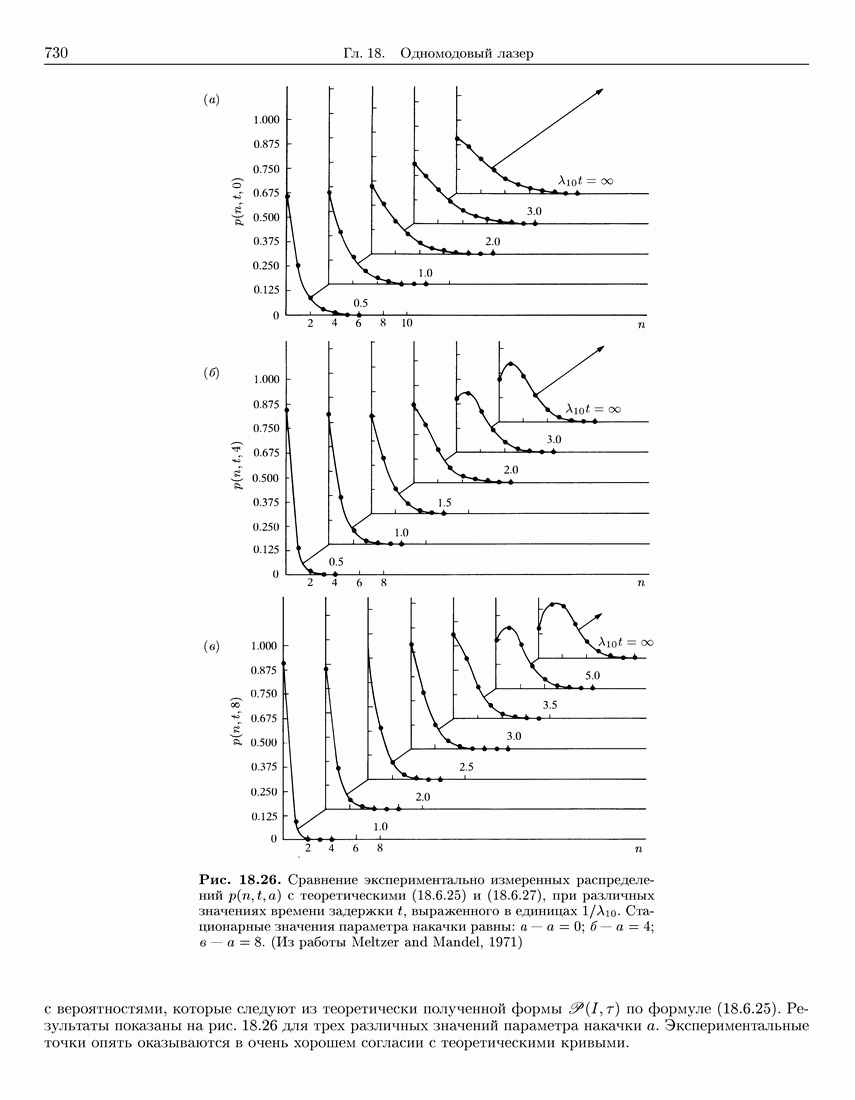
730
731
732
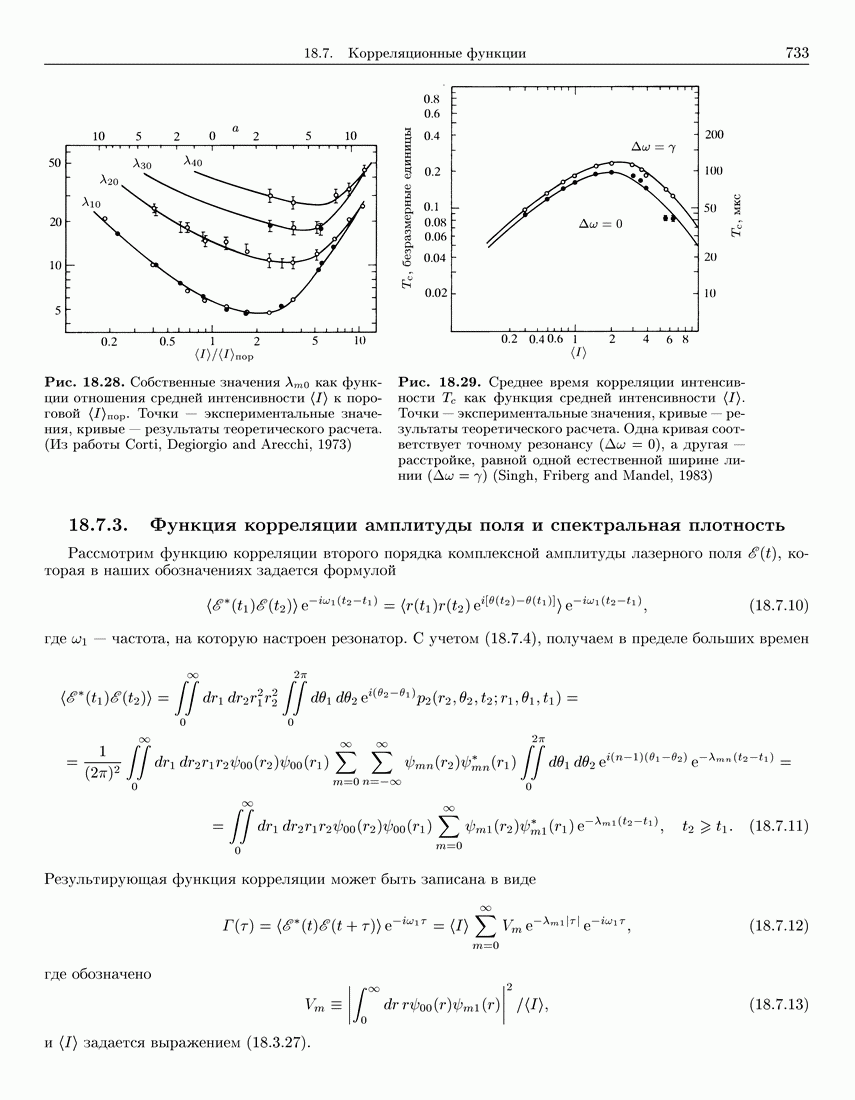
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
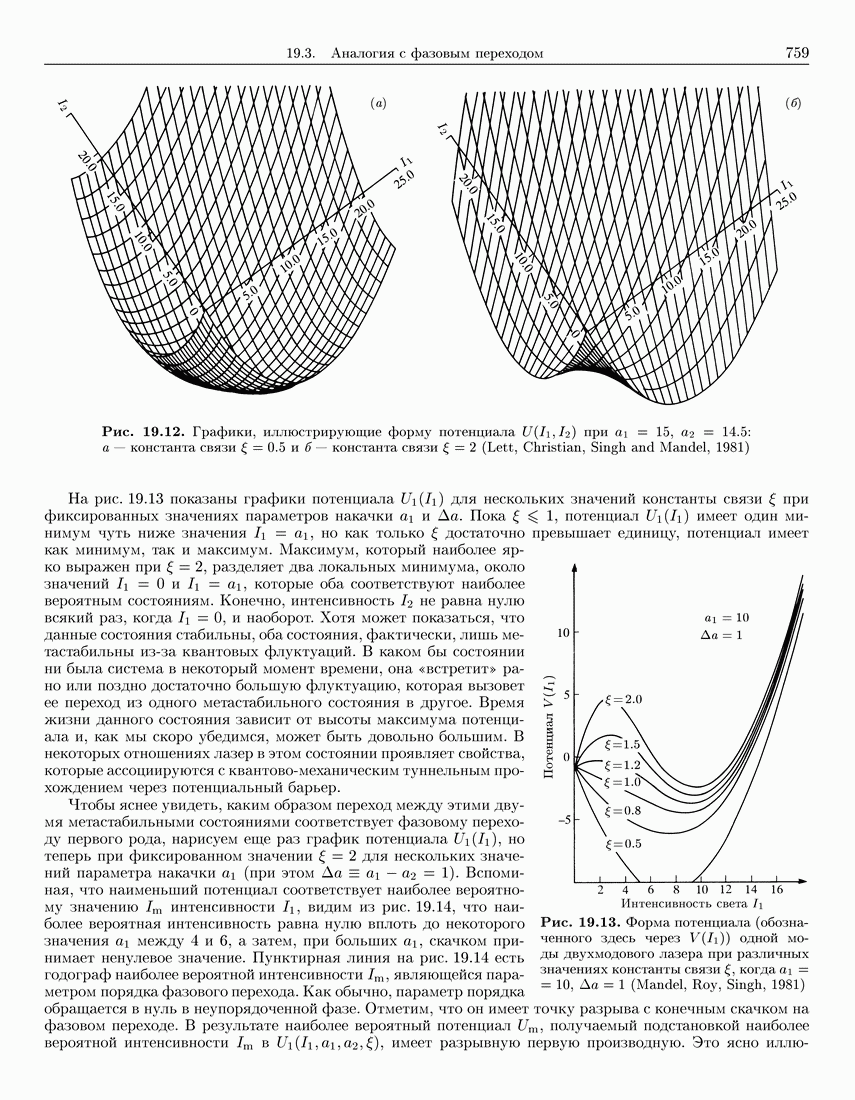
759
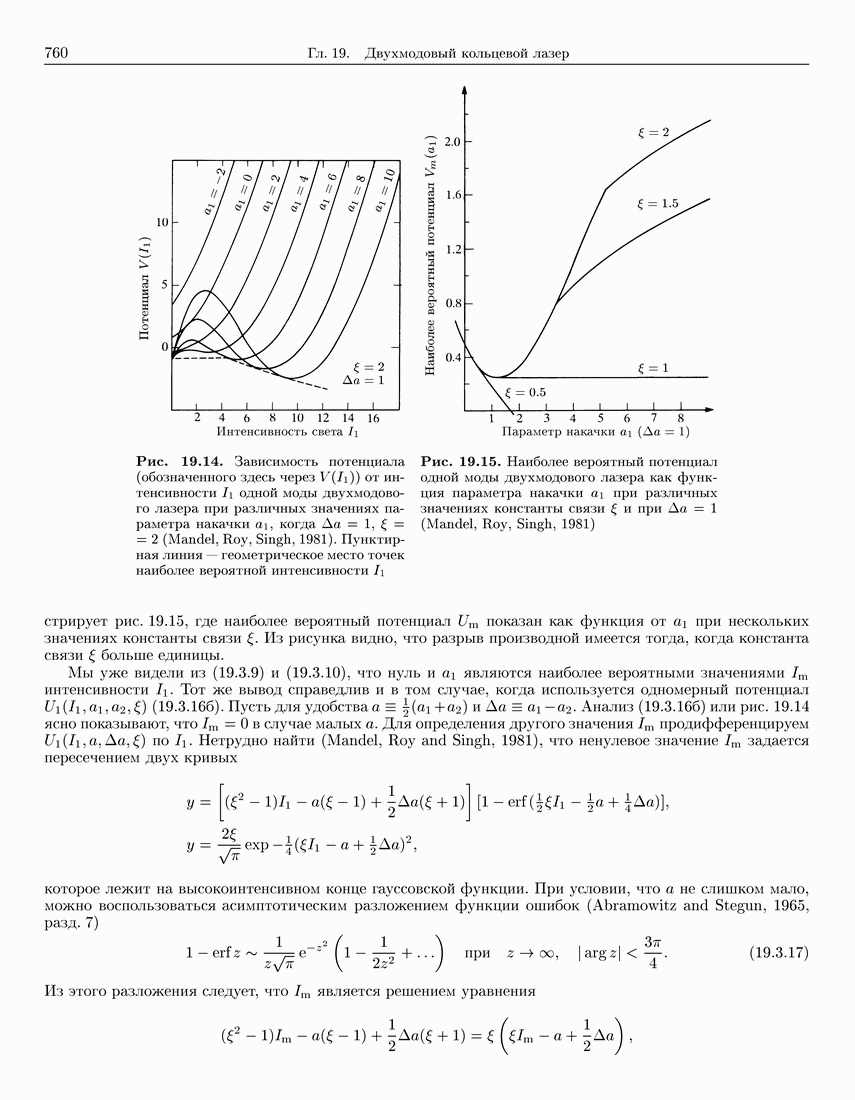
760
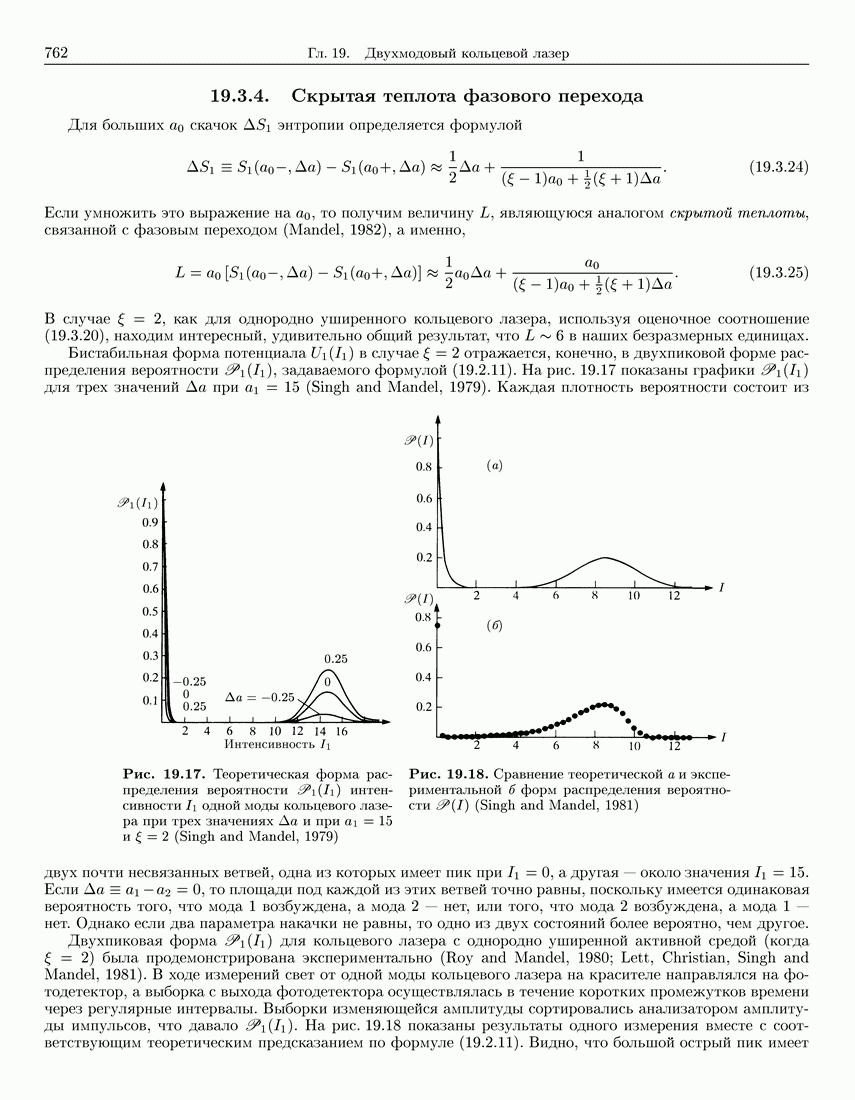
761
762
763
764
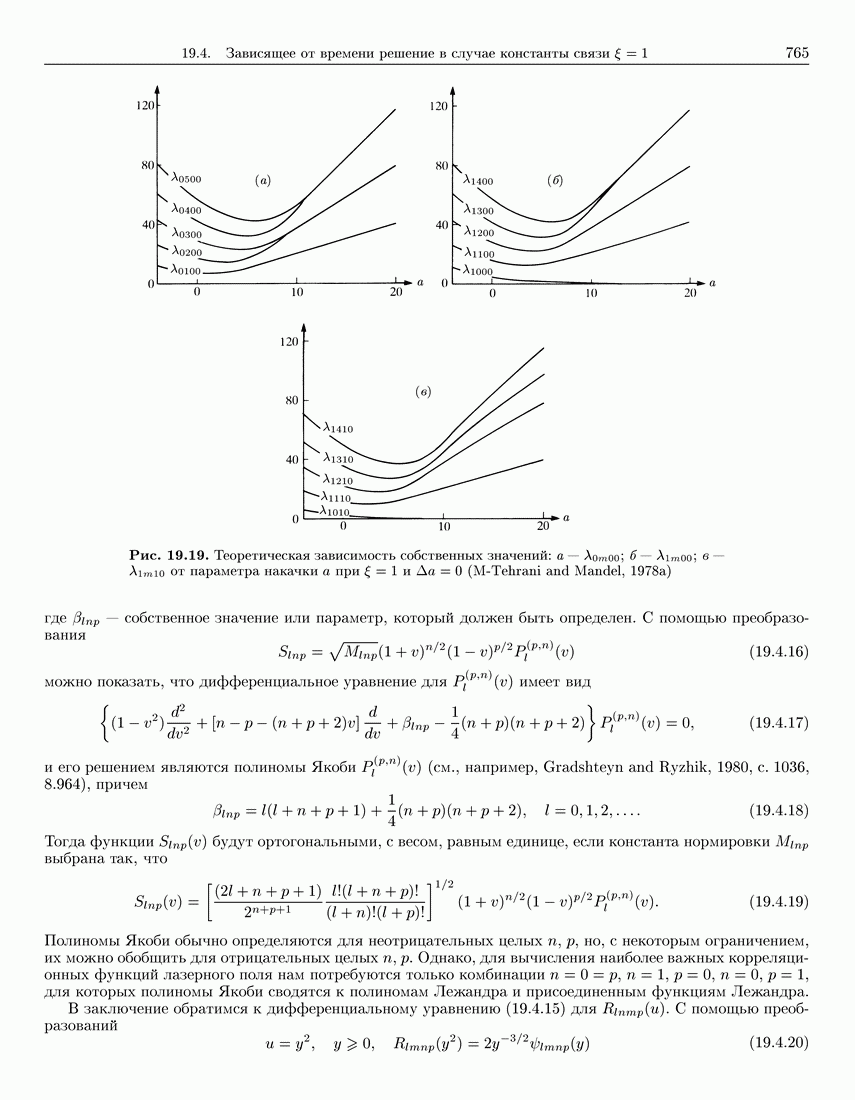
765
766
767
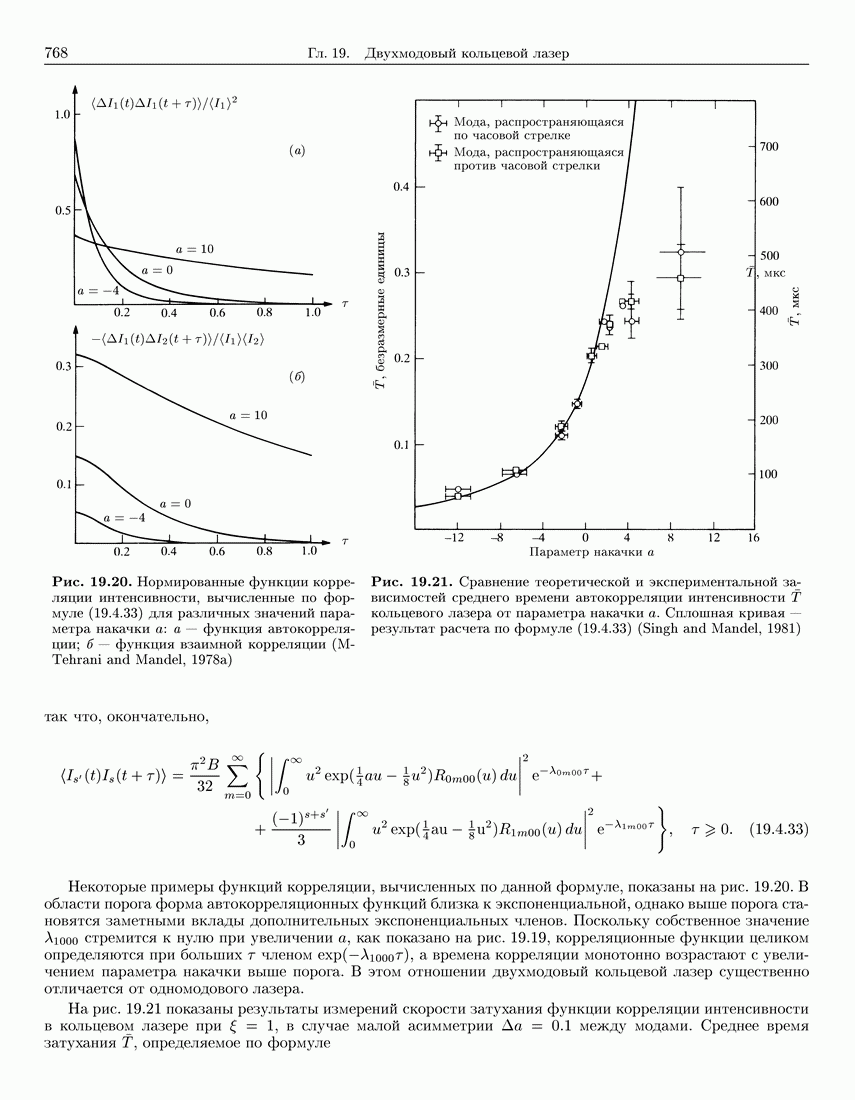
768
769
770
771
772
773
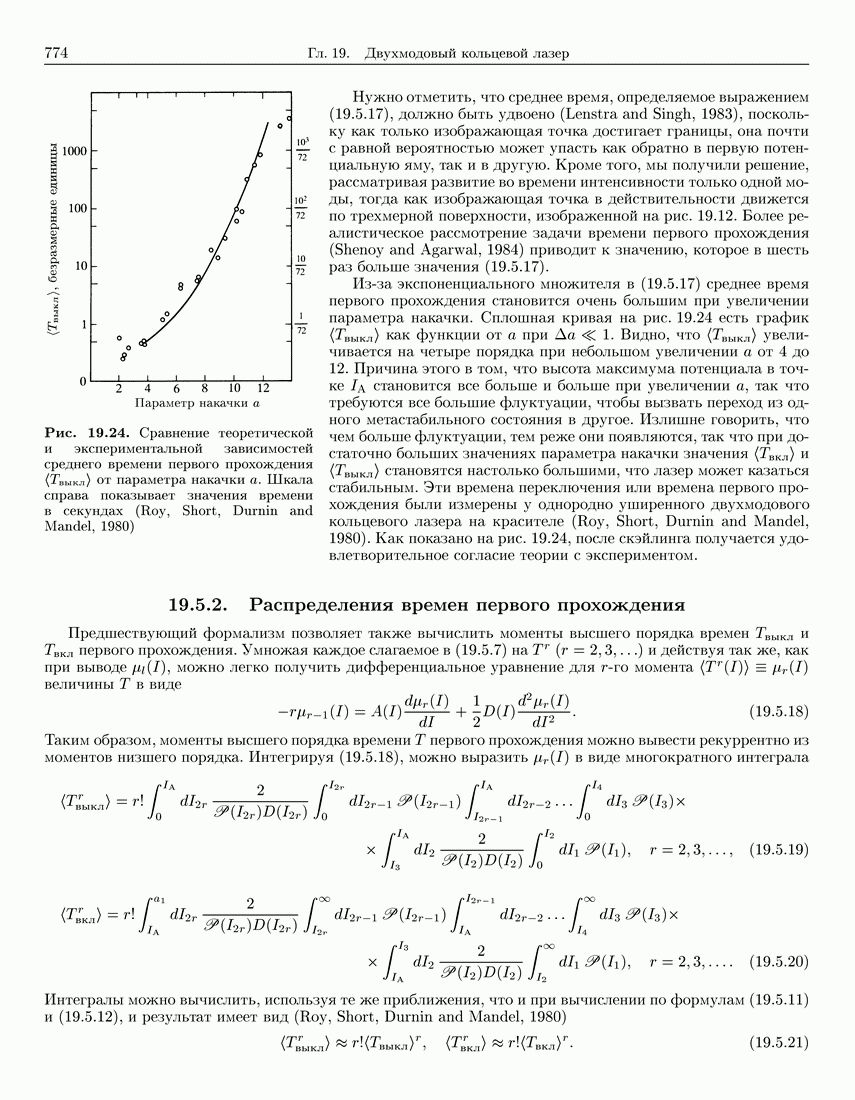
774
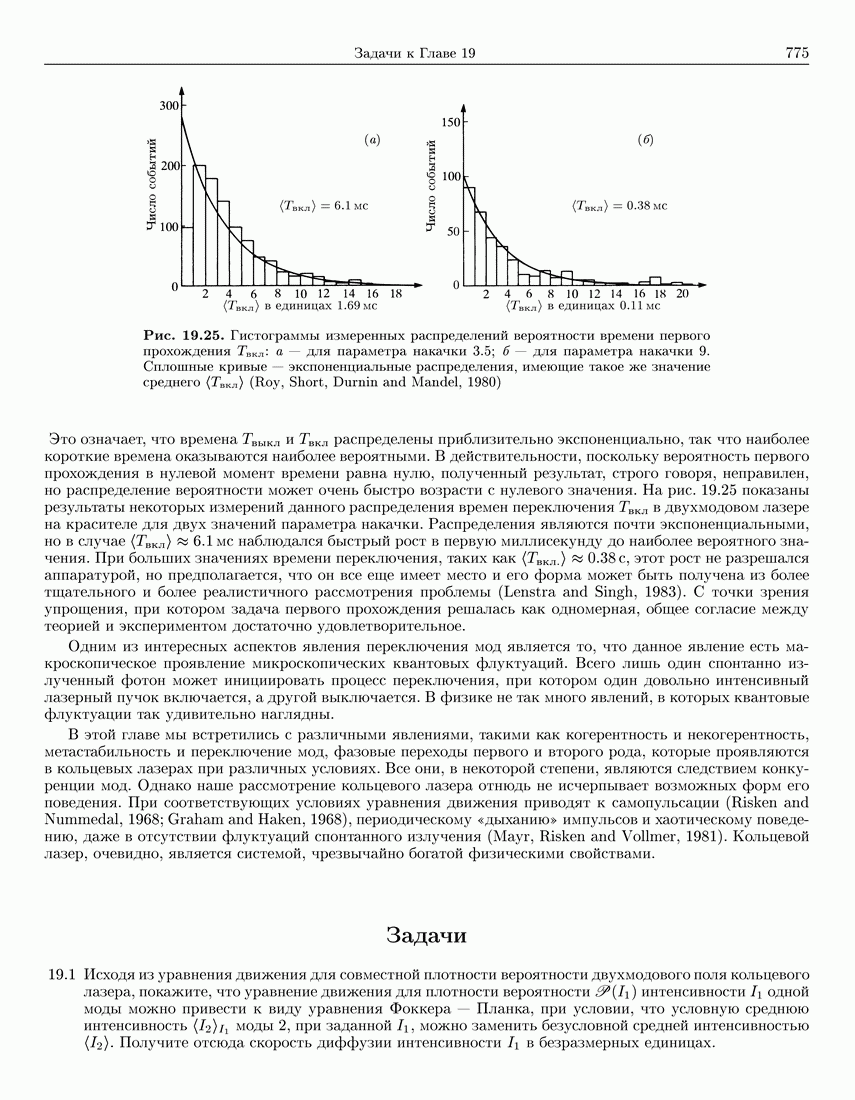
775
776
777
778
779
780
781
782
783
784
785
786
787
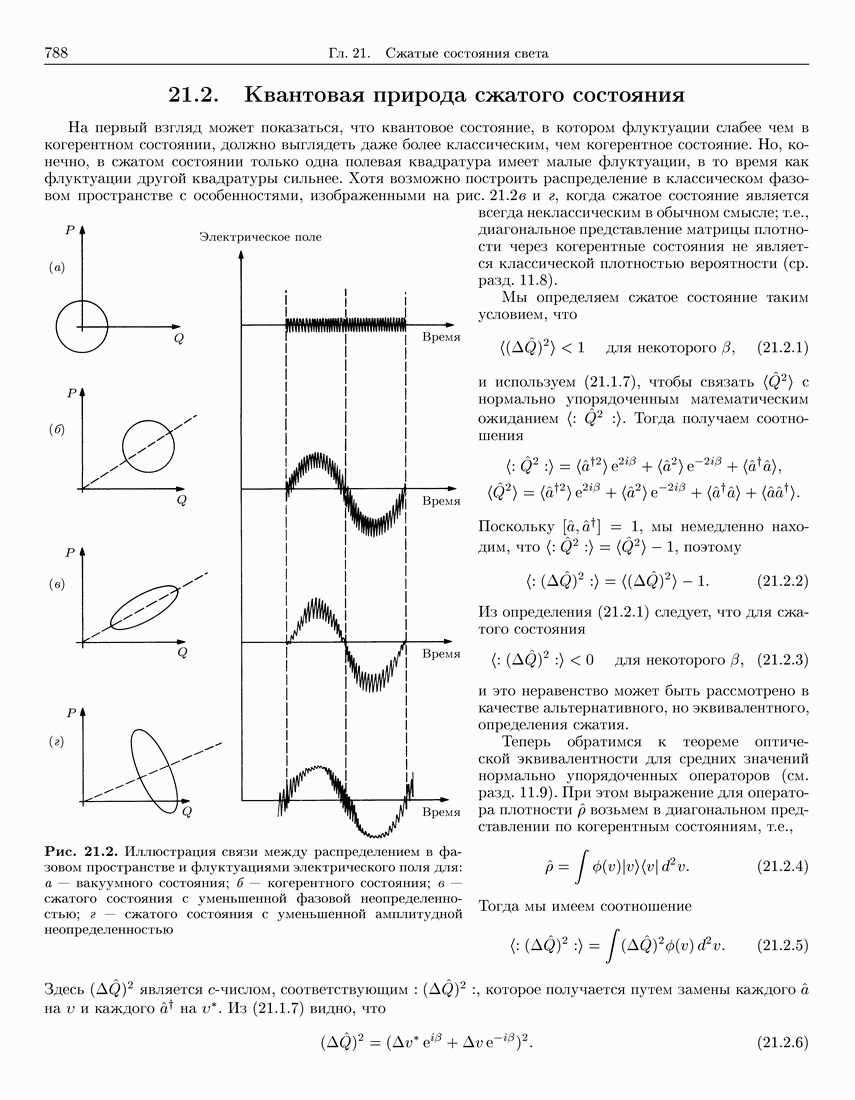
788
789
790
791
792
793
794
795
796
797
798
799
800
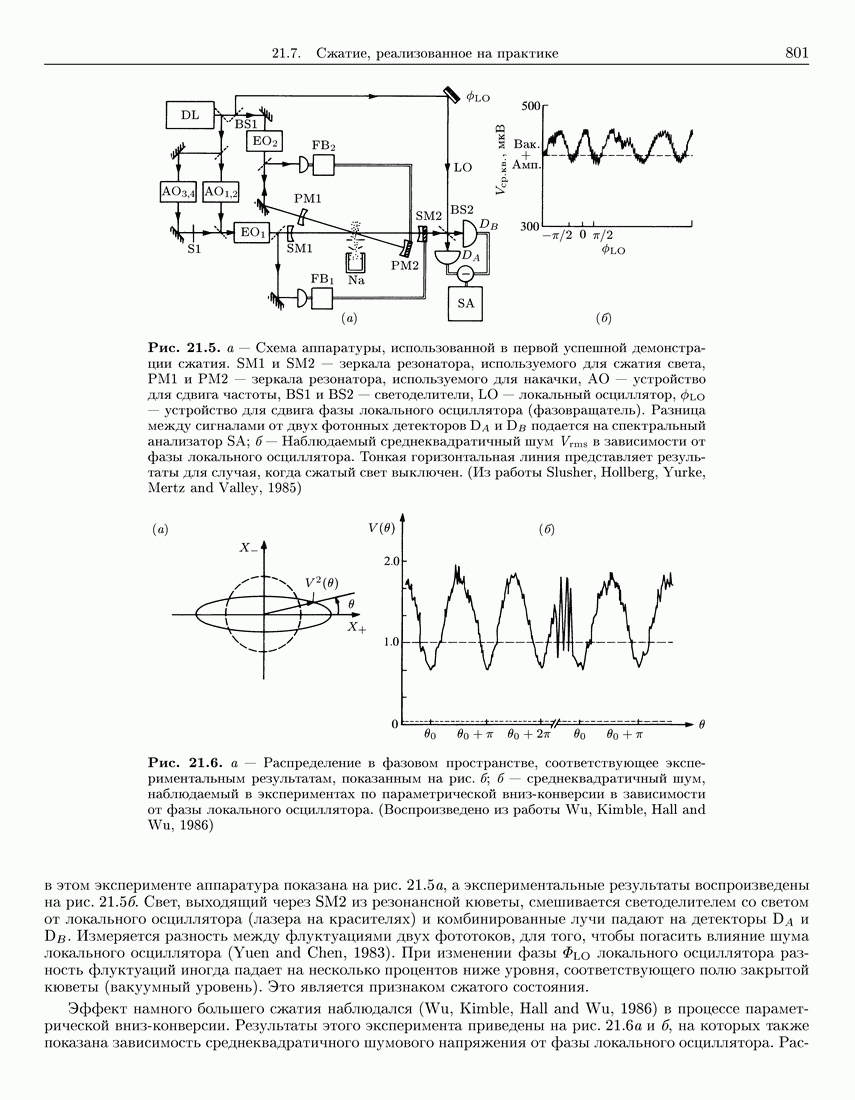
801
802
803
804
805
806
807
808
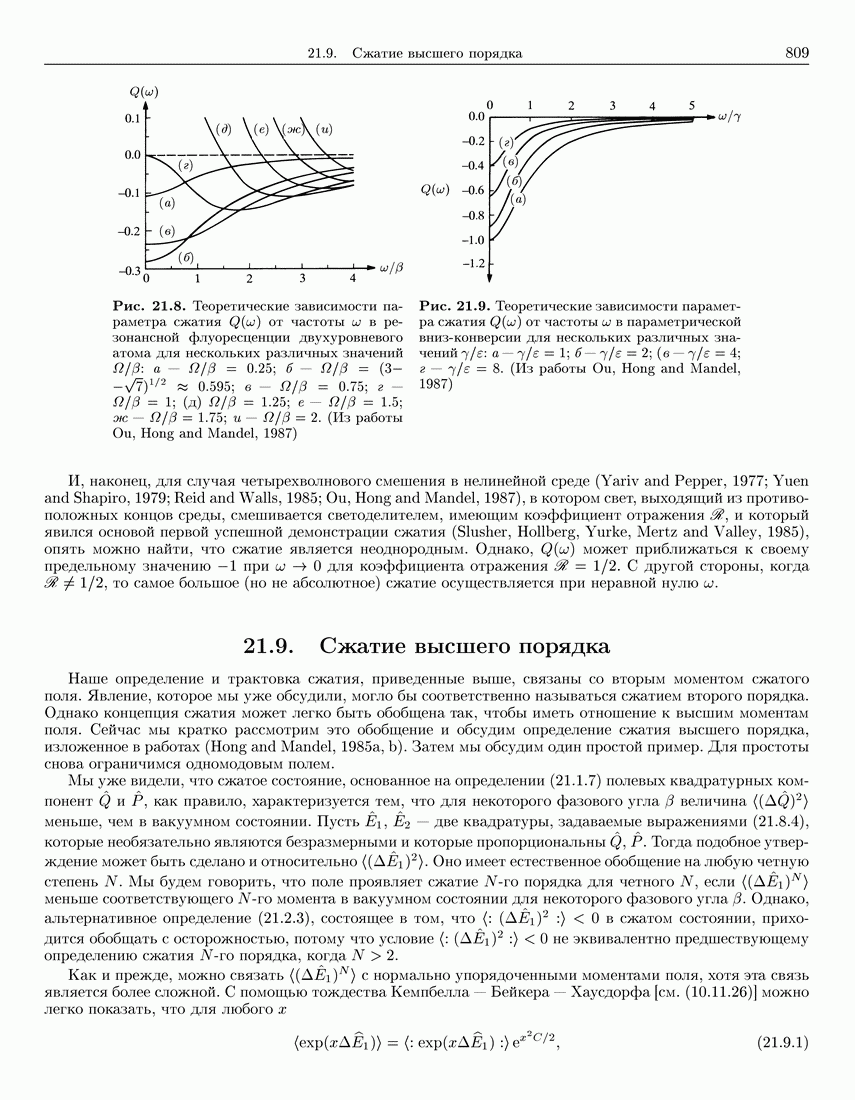
809
810
811
812
813
814
815
816
817
818
819
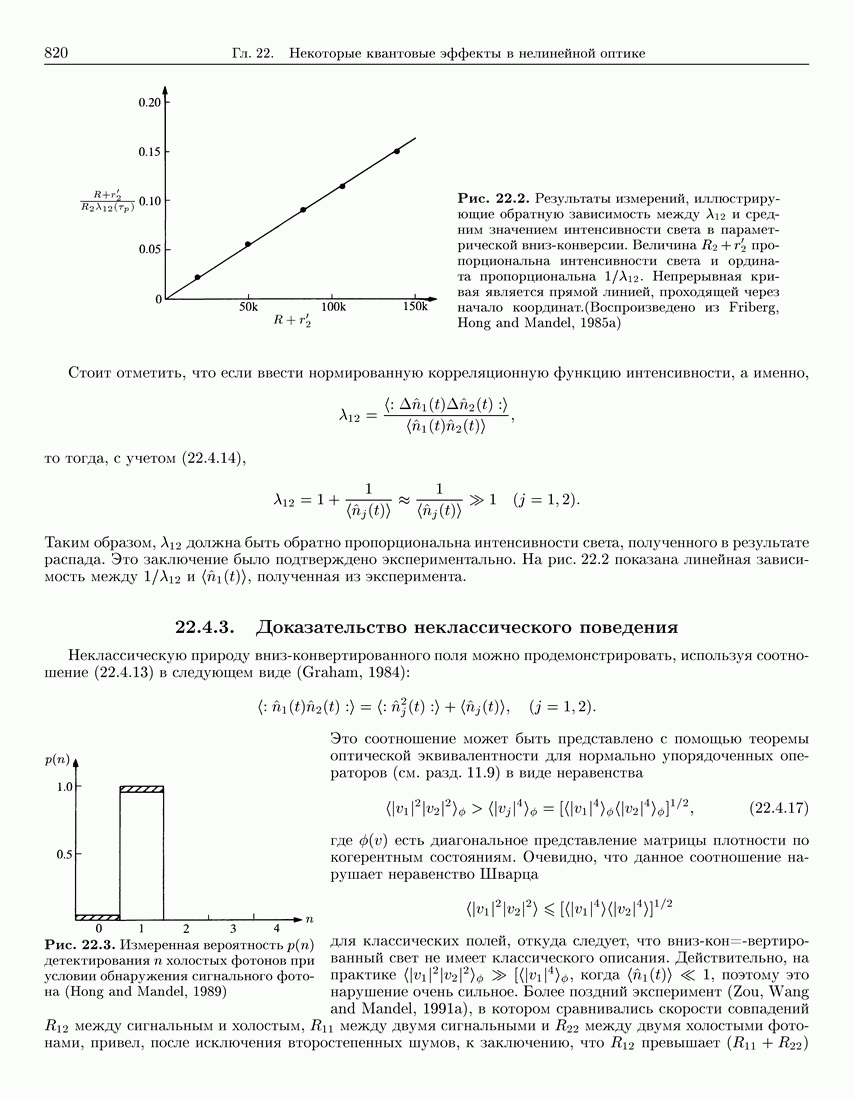
820
821
822
823
824
825
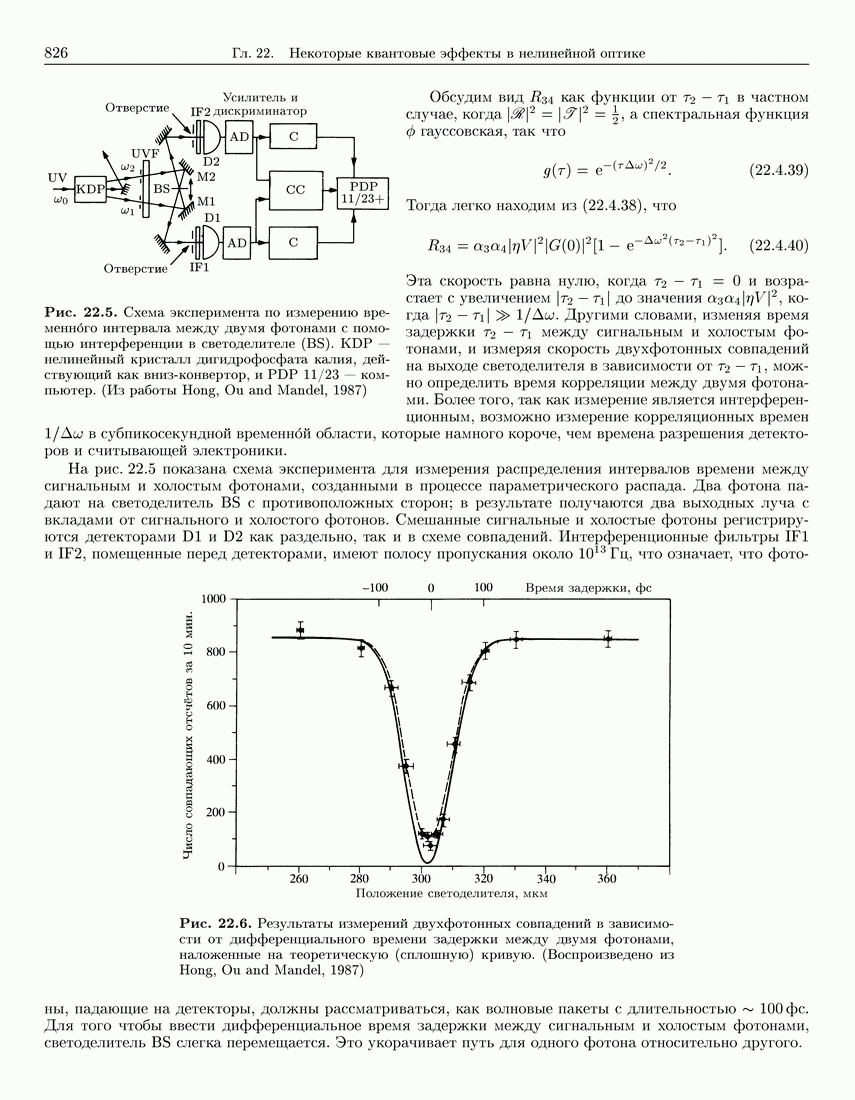
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
12.6. Степень и порядок когерентности
При обсуждении в разд. 4.3 и 12.4 интерференции двух световых лучей мы естественным образом пришли к нормированной корреляционной функции второго порядка

при условии, что и не обращаются в нуль. Величина  обеспечивает естественную меру степени когерентности определенных декартовых компонент в пространственно-временных точках х и у, которая, в контексте корреляциий второго порядка, просто связана к видностью сформированных интерференционных полос. В силу неравенства
обеспечивает естественную меру степени когерентности определенных декартовых компонент в пространственно-временных точках х и у, которая, в контексте корреляциий второго порядка, просто связана к видностью сформированных интерференционных полос. В силу неравенства  автоматически является нормированной так, что
автоматически является нормированной так, что

Более того, как мы уже обнаружили при классическом рассмотрении когерентности в разд. 4.5 и как будет показано в разд. 12.7, условие  означает возможность представления Г11х,у) в виде произведения
означает возможность представления Г11х,у) в виде произведения  и поэтому оно согласуется с интуитивным понятием о том, что подразумевается под когерентностью.
и поэтому оно согласуется с интуитивным понятием о том, что подразумевается под когерентностью.
Было сделано несколько попыток ввести нормированные корреляционные функции высшего порядка и, опосредованным образом, определить степень когерентности произвольного порядка  Когда нормированная функция является унимодулярной, это означает, что поле обладает степенью когерентности «единица» для порядка
Когда нормированная функция является унимодулярной, это означает, что поле обладает степенью когерентности «единица» для порядка  Но ни одна из этих нормированных корреляционных функций не содержит такой важной интерпретации, которую содержит корреляционная функция второго порядка. Рассмотрим некоторые из этих функций.
Но ни одна из этих нормированных корреляционных функций не содержит такой важной интерпретации, которую содержит корреляционная функция второго порядка. Рассмотрим некоторые из этих функций.
Для корреляционных функций четного порядка типа  Глаубер (Glauber, 1963а) расширил определение
Глаубер (Glauber, 1963а) расширил определение  Он ввел нормированную величину
Он ввел нормированную величину

Откладывая пока в сторону математическую значимость данной величины, мы видим, что, если бы равнялась единице при  то
то  представлялась бы в виде
представлялась бы в виде
произведения  Но
Но  является нормально упорядоченной корреляционной функцией интенсивности, которая пропорциональна совместной вероятности фотодетектирования в
является нормально упорядоченной корреляционной функцией интенсивности, которая пропорциональна совместной вероятности фотодетектирования в  пространственно-временных точках [ср. (12.2.14)]. Поэтому представление в виде произведения означает, что совместная вероятность
пространственно-временных точках [ср. (12.2.14)]. Поэтому представление в виде произведения означает, что совместная вероятность  -кратного детектирования сводится к произведению
-кратного детектирования сводится к произведению  отдельных вероятностей детектирования и, таким образом, события фотодетектирования являются независимыми. Условие
отдельных вероятностей детектирования и, таким образом, события фотодетектирования являются независимыми. Условие  другими словами, гарантирует, что не существует никаких фотоэлектрических корреляций интенсивностей порядка
другими словами, гарантирует, что не существует никаких фотоэлектрических корреляций интенсивностей порядка  пространственно-временных точках.
пространственно-временных точках.
Представляется заманчивым попытаться интерпретировать  по аналогии с
по аналогии с  как степень когерентности порядка
как степень когерентности порядка  Тогда про поле можно было бы сказать, что оно когерентно до порядка
Тогда про поле можно было бы сказать, что оно когерентно до порядка  если
если  равно единице для всех
равно единице для всех  в том смысле, что не существует никаких корреляций интенсивности до
в том смысле, что не существует никаких корреляций интенсивности до  порядка. Когерентность при любом порядке
порядка. Когерентность при любом порядке  тогда автоматически означала бы когерентность при любом меньшем порядке
тогда автоматически означала бы когерентность при любом меньшем порядке  для
для  К сожалению, в общем случае не удовлетворяет неравенству типа (12.6.2), за исключением случая, когда
К сожалению, в общем случае не удовлетворяет неравенству типа (12.6.2), за исключением случая, когда  таким образом, интерпретация в качестве степени когерентности порядка
таким образом, интерпретация в качестве степени когерентности порядка  не имеет основания. Более того, условие
не имеет основания. Более того, условие  в общем случае, не означает, что корреляционная функция может быть представлена в виде произведения комплексных сомножителей, как это имеет место при
в общем случае, не означает, что корреляционная функция может быть представлена в виде произведения комплексных сомножителей, как это имеет место при  равно, как
равно, как  в общем случае, не равна единице. Тем не менее, мы можем считать, что представление
в общем случае, не равна единице. Тем не менее, мы можем считать, что представление  в виде следующего произведения
в виде следующего произведения

является условием когерентности до порядка  и это автоматически подразумевает, что
и это автоматически подразумевает, что 
В разд. 13.3 будет показано (соответствующий классический результат также может быть получен — см. разд. 8.4), что для поляризованного света от всех тепловых источников имеем

так, что

На основе этого определения когерентности порядка  следует, что никакое поле теплового излучения не может быть когерентным выше второго порядка.
следует, что никакое поле теплового излучения не может быть когерентным выше второго порядка.
Другая попытка введения нормированной корреляционной функции произвольного порядка  которая удовлетворяла бы тому же неравентству, что и
которая удовлетворяла бы тому же неравентству, что и  была предпринята Метой (Mehta, 1966, 1967). Он определил
была предпринята Метой (Mehta, 1966, 1967). Он определил

при условии, что корреляционные функции в знаменателе отличны от нуля. Очевидно, что эта функция удовлетворяет соотношению

Более того, можно показать, что при  функция
функция  может быть представлена в виде произведения вида (12.6.4) так, что условие
может быть представлена в виде произведения вида (12.6.4) так, что условие  действительно, представляется в интуитивно приемлемом смысле условием когерентности порядка
действительно, представляется в интуитивно приемлемом смысле условием когерентности порядка  Доказательство возможности представления в виде произведения, в основе которого лежат рассуждения Титулайра и Глаубера (Titulaer and Glauber, 1965), приводится в разд. 12.7. Для полей, у которых весовой функционал
Доказательство возможности представления в виде произведения, в основе которого лежат рассуждения Титулайра и Глаубера (Titulaer and Glauber, 1965), приводится в разд. 12.7. Для полей, у которых весовой функционал  в диагональном представлении по когерентным состояниям является неотрицательным и ведет себя как классическая плотность вероятности, также можно показать, что
в диагональном представлении по когерентным состояниям является неотрицательным и ведет себя как классическая плотность вероятности, также можно показать, что

так что  можно, в определенном смысле, интерпретировать как степень когерентности порядка
можно, в определенном смысле, интерпретировать как степень когерентности порядка 
К сожалению, это неравенство не удовлетворяется в общем случае квантованного поля, когда, по-видимому, не существует верхней границы для Более того, когерентность при любом четном порядке  автоматически подразумевает когерентность во всех высших четных порядках в том случае, когда нет ограничения на число фотонов и во всех высших четных порядках до
автоматически подразумевает когерентность во всех высших четных порядках в том случае, когда нет ограничения на число фотонов и во всех высших четных порядках до  при
при  когда имеется
когда имеется  фотонов (в таком случае обращается в нуль и
фотонов (в таком случае обращается в нуль и  не определена при
не определена при  При таком определении когерентности высших порядков, когерентность второго порядка является наиболее сильной формой когерентности, которая имеет значение для когерентности высших порядков, а не наоборот. Как мы покажем в следующем разделе, когерентность второго порядка действительно имеет важное значение для корреляционных функций высшего порядка.
При таком определении когерентности высших порядков, когерентность второго порядка является наиболее сильной формой когерентности, которая имеет значение для когерентности высших порядков, а не наоборот. Как мы покажем в следующем разделе, когерентность второго порядка действительно имеет важное значение для корреляционных функций высшего порядка.
Еще одна нормированная корреляционная функция рассматривалась Сударшаном (Sudarshan, 1969; см. также Klauder and Sudarshan, 1968, гл. 8, выражение (8-84), который ввел

при условии, что корреляционные функции, входящие в знаменатель, не обращаются в нуль. Эти функции удовлетворяют условию

и неравенству

для всех полей. Кроме того, они демонстрируют свойство состоящее в том, что  означает, что
означает, что  для всех
для всех  при условии, что число фотонов не ограничено.
при условии, что число фотонов не ограничено.
Однако, конечно, условие  делает интерпретации
делает интерпретации  в целом, различными.
в целом, различными.
Следует сказать, что хотя, без всякого сомнения, корреляционные функции высших порядков являются важными для полного описания электромагнитного поля и его когерентных свойств, полезность введения понятия когерентности высшего порядка и степени когерентности высшего порядка можно оспорить. Общепризнано, что когерентное состояние поля когерентно во всех порядках и нормированные корреляционные функции являются унимодулярными практически при всех определениях. Однако не известно никаких примеров полей, которые были бы когерентными только для каких-то некоторых порядков (за исключением второго), а не для других. Вызывает сомнение, что такие поля когда-нибудь могут быть встречены на практике, и что они вообще существуют. Вполне может быть, что представление о когерентности второго порядка, которое было отправной точкой при развитии теории когерентности, является, в конечном счете, единственно реально значимым представлением.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 1.2. Свойства вероятностей
- 1.2.1. Совместные вероятности
- 1.2.2. Условные вероятности
- 1.2.3. Теорема Байеса для апостериорных вероятностей
- 1.3. Случайные переменные и распределение вероятностей
- 1.3.1. Преобразования случайных переменных
- 1.3.2. Математические ожидания и моменты
- 1.3.3. Неравенство Чебышева
- 1.4. Производящие функции
- 1.4.1. Производящая функция моментов
- 1.4.2. Характеристическая функция
- 1.4.3. Кумулянты
- 1.5. Некоторые примеры распределений вероятности
- 1.5.1. Распределение Бернулли или биноминальное распределение
- 1.5.2. Пуассоновское распределение
- 1.5.3. Распределение Бозе — Эйнштейна
- 1.5.4. Закон больших чисел
- 1.5.5. Нормальное, или гауссовское распределение
- 1.5.6. Центральная предельная теорема
- 1.5.7. Гамма-распределение
- 1.6. Многомерное гауссовское распределение
- 1.6.1. Теорема о гауссовском моменте
- 1.6.2. Производящая функция моментов и характеристическая функция
- 1.6.3. Многократные комплексные гауссовские случайные переменные
- Глава 2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. Введение в статистические ансамбли
- 2.1.2. Совместные вероятности и корреляции
- 2.1.3. Функционал вероятности
- 2.2. Стационарность и эргодичность
- 2.2.1. Среднее по времени стационарного процесса
- 2.2.2. Эргодичность
- 2.2.3. Примеры случайных процессов
- 2.3. Свойства автокорреляционной функции
- 2.4. Спектральные свойства стационарного случайного процесса
- 2.4.1. Спектральная плотность и теорема Винера — Хинчина
- 2.4.2. Сингулярности спектральной плотности
- 2.4.3. Нормированные корреляции и нормированные спектральные плотности
- 2.4.4. Взаимные корреляции и взаимные спектральные плотности
- 2.5. Ортогональное представление случайного процесса
- 2.5.2. Предел … другой подход к теореме Винера — Хинчина
- 2.6. Временная эволюция и классификация случайных процессов
- 2.6.2. Абсолютно случайные или сепарабельные процессы
- 2.6.3. Марковский процесс первого порядка
- 2.6.4. Марковский процесс высшего порядка
- 2.7. Основные уравнения в интегро-дифференциальной форме
- 2.8. Основные уравнения в дифференциальной форме
- 2.8.1. Дифференциальное уравнение Крамерса — Мояля
- 2.8.2. Векторный случайный процесс
- 2.8.3. Порядок дифференциального уравнения Крамерса — Мояля
- 2.9. Уравнение Ланжевена и уравнение Фоккера — Планка
- 2.9.1. Моменты перехода для процесса Ланжевена
- 2.9.2. Стационарное решение уравнения Фоккера — Планка
- 2.9.3. Зависящее от времени решение уравнения Фоккера — Планка
- 2.10. Процесс Винера (или одномерное случайное блуждание)
- 2.10.2. Совместные вероятности и автокорреляция
- Глава 3. МАТЕМАТИЧЕСКИЕ МЕТОДЫ
- 3.1. Комплексный аналитический сигнал
- 3.1.2. Квази-монохроматические сигналы и их огибающие
- 3.1.3. Соотношения между корреляционными функциями действительного и связанного с ним комплексного аналитических случайных процессов
- 3.1.4. Статистические свойства аналитического сигнала, связанного с действительным гауссовским случайным процессом
- 3.2. Представление углового спектра волновых полей
- 3.2.1. Угловой спектр волнового поля в плоско-параллельном слое
- 3.2.2. Угловой спектр волнового поля в полупространстве
- 3.2.3. Пример: дифракция на полупрозрачном объекте
- 3.2.4. Представление Вейля для сферической волны
- 3.2.5. Дифракционные формулы Рэлея
- 3.3. Метод стационарной фазы
- 3.3.2. Метод стационарной фазы для однократных интегралов
- 3.3.3. Метод стационарной фазы для двойных интегралов
- 3.3.4. Пример: поведение представления углового спектра для волновых полей в дальней зоне
- Глава 4. ТЕОРИЯ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА СКАЛЯРНЫХ ВОЛНОВЫХ ПОЛЕЙ
- 4.2. Некоторые элементарные представления и определения
- 4.2.1. Временная когерентность и время когерентности
- 4.2.2. Пространственная когерентность и площадь когерентности
- 4.2.3. Объем когерентности и параметр вырождения
- 4.3. Интерференция двух стационарных световых пучков как проявление корреляции второго порядка
- 4.3.2. Корреляции второго порядка в пространственно-частотной области. Взаимная спектральная плотность и спектральная степень когерентности
- 4.3.3. Время когерентности и ширина спектра
- 4.4. Распространение корреляций
- 4.4.2. Распространение корреляций от плоскости
- 4.4.3. Распространение корреляций от ограниченных поверхностей
- 4.4.4. Теорема Ван Циттерта — Цернике
- 4.4.5. Распространение корреляций от первичных источников
- 4.5. Специальные типы полей
- 4.5.1. Взаимно спектрально чистый свет
- 4.5.2. Когерентный свет в пространственно-временной области
- 4.5.3. Когерентный свет в пространственно-частотной области
- 4.6. Свободные поля с произвольной степенью когерентности
- 4.6.1. Уравнения Сударшана для распространения корреляционных функций второго порядка свободных полей
- 4.6.2. Временная эволюция корреляционных функций второго порядка свободных полей
- 4.6.3. Взаимосвязь между свойствами временной и пространственной когерентности свободных полей
- 4.6.4. Взаимосвязь спектральных свойств и свойств пространственной когерентности свободных полей
- 4.7. Представление по когерентным модам и представление по ансамблю для источников и полей в пространственно-частотной области
- 4.7.1. Представление по когерентным модам частично когерентных полей в свободном пространстве
- 4.7.2. Строгое представление взаимной спектральной плотности в виде корреляционной функции
- 4.7.3. Нормальные моды колебаний частично когерентных первичных источников и представление их взаимной спектральной плотности в виде корреляционной функции
- Приложение 4.1. Ядро H(R) оператора … в представлении интегрального преобразования
- Приложение 4.2. Функция Грина G(R, Т) для временной эволюции аналитического сигнала свободного поля и ее фурье-образ …
- Глава 5. ИЗЛУЧЕНИЕ ИСТОЧНИКОВ ЛЮБОЙ СТЕПЕНИ КОГЕРЕНТНОСТИ
- 5.2. Излучение трехмерных первичных источников
- 5.2.2. Излучение от некоторых модельных источников
- 5.3. Излучение плоских вторичных источников
- 5.3.2. Излучение плоских, вторичных, квазиоднородных источников
- 5.3.3. Обратная задача для плоских, вторичных, квазиоднородных источников
- 5.4. Теоремы эквивалентности для плоских источников, генерирующих одинаковую интенсивность излучения
- 5.4.1. Теорема эквивалентности для плоских источников
- 5.4.2. Пример: эквивалентные гауссовские источники модели Шелла
- 5.4.3. Экспериментальная проверка теоремы эквивалентности
- 5.5. Представление по когерентным модам для гауссовскнх источников модели Шелла
- 5.6. Оптические лучи
- 5.6.1. Монохроматические лучи
- 5.6.2. Пример: монохроматические гауссовские лучи
- 5.6.3. Частично когерентные лучи
- 5.6.4. Гауссовские лучи модели Шелла
- 5.7. Основы радиометрии
- 5.7.1. Плотность энергии, поток энергии и закон сохранения энергии в скалярных волновых полях
- 5.7.2. Основные понятия радиометрии
- 5.7.3. Функция энергетической яркости от плоских вторичных квазиоднородных источников
- 5.7.4. Модель переноса энергии излучения
- 5.7.5. Радиометрия как коротковолновой предел статистической волновой теории с квазиоднородными источниками
- 5.8. Влияние пространственной когерентности источника на спектр излучаемых полей
- 5.8.2. Спектр дальнего поля, образуемого плоскими вторичными квазиоднородными источниками
- 5.8.3. Условие для спектральной инвариантности: закон скейлинга для плоских вторичных квазиоднородных источников
- Приложение 5.1 Вывод асимптотического приближения (5.7.103)
- Приложение 5.2 Теорема произведения для гауссовских функций
- Глава 6. ТЕОРИЯ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА ВЕКТОРНЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
- 6.2. Равновременная 2×2-матрица когерентности хорошо коллимированного, однородного, квазимонохроматического светового луча
- 6.3. Полностью неполяризованный и полностью поляризованный свет. Степень поляризации
- 6.3.2. Полностью поляризованный свет
- 6.3.3. Степень поляризации
- 6.4. Прохождение квазимонохроматического луча через линейные, не формирующие изображения устройства
- 6.5. Обобщенные матрицы когерентности второго порядка и тензоры когерентности стационарного электромагнитного поля
- 6.5.2. Дифференциальные уравнения первого порядка для распространения тензоров когерентности
- 6.5.3. Волновые уравнения для распространения тензоров когерентности
- 6.6. Тензоры взаимной спектральной плотности второго порядка стационарного электромагнитного поля
- 6.6.1. Электрический, магнитный и смешанный тензоры взаимной спектральной плотности
- 6.6.2. Дифференциальные уравнения первого порядка для распространения тензоров взаимной спектральной плотности
- 6.6.3. Уравнения Гельмгольца для распространения тензоров взаимной спектральной плотности
- Глава 7. ПРИМЕНЕНИЯ ТЕОРИИ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА
- 7.2. Звездная интерферометрия
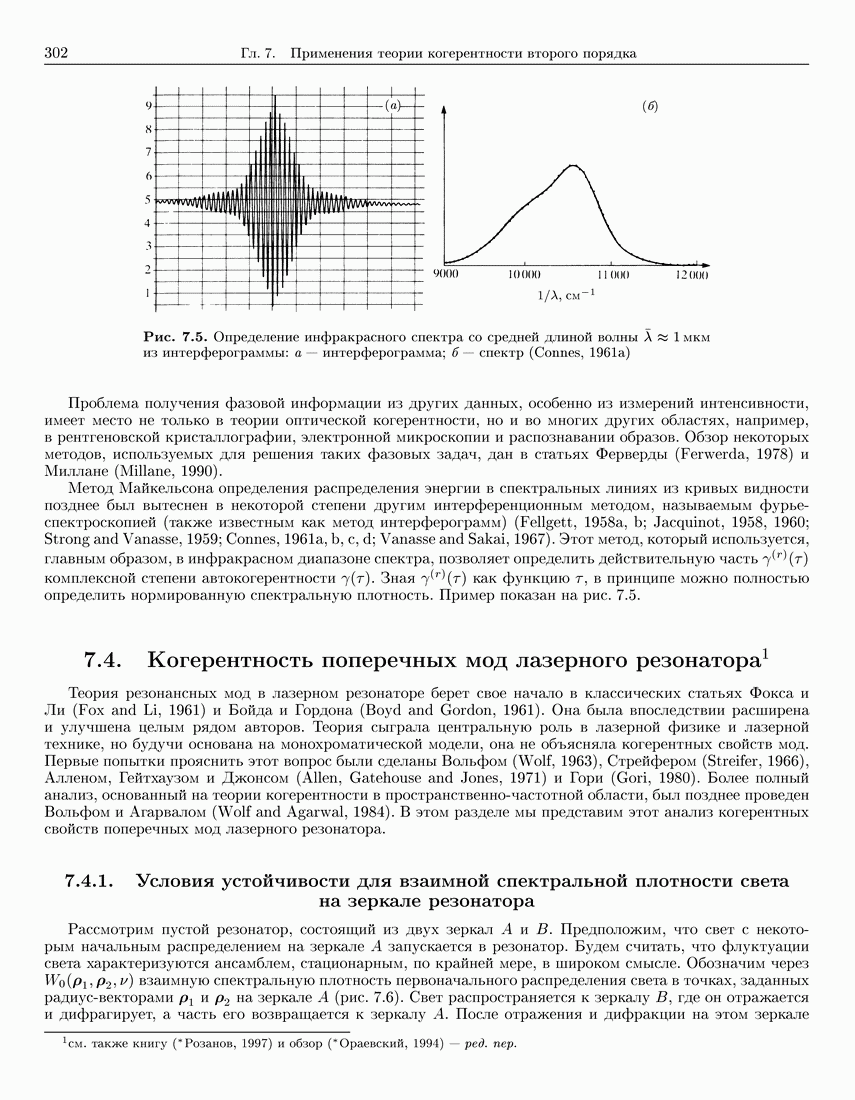
- 7.3. Интерференционная спектроскопия
- 7.3.2. Проблема фазы
- 7.4. Когерентность поперечных мод лазерного резонатора
- 7.4.1. Условия устойчивости для взаимной спектральной плотности света на зеркале резонатора
- 7.4.2. Природа решений интегрального уравнения (7.4.7)
- 7.5. Диэлектрический отклик и спектр индуцированной поляризации во флуктуирующей среде
- 7.5.1. Среда, макроскопические свойства которой не изменяются со временем
- 7.5.2. Среда, макроскопические свойства которой зависят от времени детерминированным образом
- 7.5.3. Среда, макроскопические свойства которой случайным образом меняются во времени
- 7.6. Рассеяние от случайных сред
- 7.6.1. Основные уравнения для детерминированного рассеяния
- 7.6.2. Рассеяние на детерминированной среде в приближении Борна первого порядка
- 7.6.3. Рассеяние случайной средой в приближении Борна первого порядка
- 7.6.4. Некоторые частные случаи
- 7.6.5. Рассеяние от простой жидкости
- Приложение 7.1 Вычисление среднего значения … (выражение (7.6.36))
- Глава 8. КОРРЕЛЯЦИИ ОПТИЧЕСКИХ ПОЛЕЙ ВЫСШЕГО ПОРЯДКА
- 8.2. Пространственно-временные корреляционные функции произвольного порядка
- 8.3. Пространственно-частотные корреляционные функции произвольного порядка
- 8.4. Корреляционные функции полей, подчиняющихся гауссовской статистике
- 8.5. Представление по когерентным модам взаимных спектральных плотностей произвольного порядка
- 8.5.2. Одномодовое поле
- 8.5.3. Поля, подчиняющиеся гауссовской статистике
- Глава 9. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ФОТОДЕТЕКТИРОВАНИЯ
- 9.2. Обзор элементарной квантовой механики
- 9.3. Дифференциальная вероятность фотодетектирования
- 9.4. Совместные вероятности многократного фотодетектирования
- 9.5. Интегральные вероятности детектирования
- 9.6. Фотоэлектрическое детектирование во флуктуирующих полях
- 9.6.1. Фотоэлектрическая группировка
- 9.7. Статистика фотоэлектрических отсчетов флуктуирующего поля
- 9.8. Флуктуации фотоэлектрического тока
- 9.8.2. Свет от теплового источника
- 9.8.3. Спектральная плотность фототока
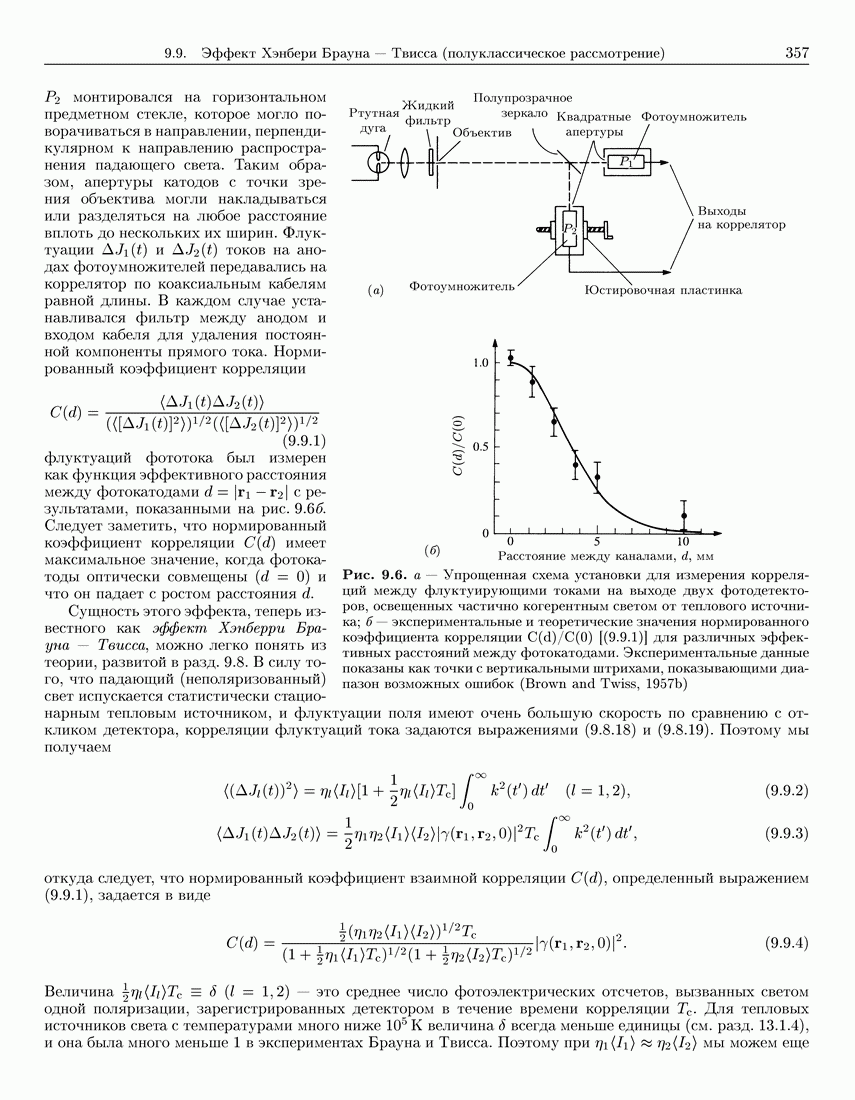
- 9.9. Эффект Хэнбери Брауна — Твисса (полуклассическое рассмотрение)
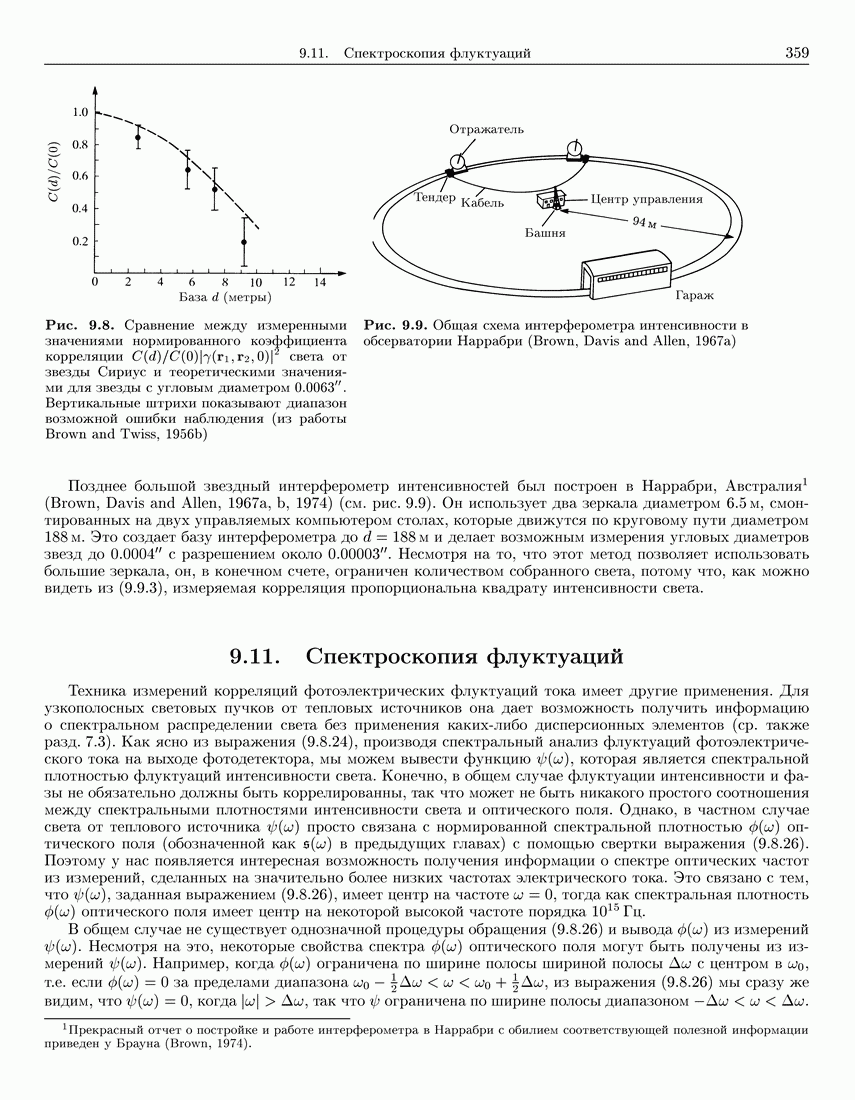
- 9.10. Звездная интерферометрия интенсивностей
- 9.11. Спектроскопия флуктуаций
- Глава 10. КВАНТОВАНИЕ СВОБОДНОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 10.2. Гамильтониан классического поля и канонические уравнения движения
- 10.2.2. Единичные векторы поляризации
- 10.2.3. Энергия электромагнитного поля
- 10.3. Каноническое квантование поперечного поля
- 10.4. Энергетический спектр; фотоны
- 10.4.1. Фоковские состояния
- 10.4.2. Псевдолокализованные фотоны
- 10.4.3. Базис фоковских состояний
- 10.4.4. q-представление фоковских состояний
- 10.4.5. Зависимость операторов поля от времени
- 10.5. Импульс квантованного поля
- 10.6. Момент количества движения квантованного поля.
- 10.6.2. Разложение полного момента количества движения
- 10.6.3. Собственный (спиновый) момент количества движения
- 10.6.4. Орбитальный момент количества движения
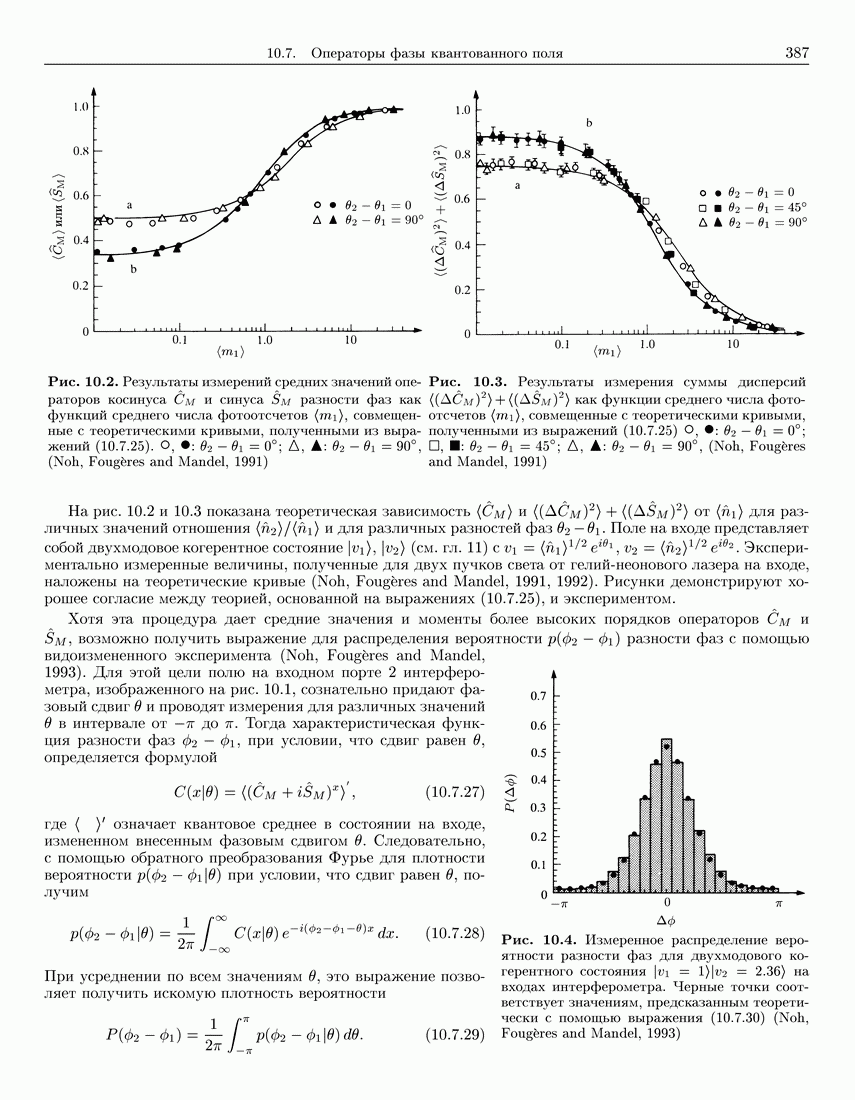
- 10.7. Операторы фазы квантованного поля
- 10.7.2. Операторы косинуса и синуса
- 10.7.3. Оператор фазы на основе проекционного оператора на фазовые состояния
- 10.7.4. Операционно определенные фазовые операторы
- 10.8. Пространственно-временные коммутационные соотношения
- 10.9. Вакуумные флуктуации
- 10.9.1. Флуктуации локально усредненных полей
- 10.9.2. Порядок величины вакуумных флуктуаций
- 10.9.3. Сила Казимира между проводниками
- 10.9.4. Лэмбовский сдвиг
- 10.9.5. Вакуумные эффекты в делителе пучка
- 10.10. Непрерывное фоковское пространство
- 10.11. Некоторые теоремы операторной алгебры
- 10.11.2. Теоремы о преобразовании подобия
- 10.11.3. Теоремы о производных
- 10.11.4. Нормальный и антинормальный порядок
- 10.11.5. Теорема Кемпбелла — Бейкера — Хаусдорфа.
- Глава 11. КОГЕРЕНТНЫЕ СОСТОЯНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 11.2. Фоковское представление когерентных состояний
- 11.3. Когерентное состояние как смещенное вакуумное состояние. Оператор смещения
- 11.3.1. Свойства оператора смещения
- 11.4. q-представление когерентных состояний
- 11.5. Эволюция во времени и соотношения неопределенностей
- 11.5.1. Произведение канонических неопределенностей
- 11.5.2. Более общие состояния с минимальной неопределенностью
- 11.6. Когерентные состояния как базис. Неортогональность и переполненность
- 11.6.1. Линейная зависимость когерентных состояний
- 11.6.2. Переполненность
- 11.6.3. Представление операторов по когерентным состояниям
- 11.6.4. Вычисление матричных элементов нормально упорядоченных операторов
- 11.7. Представление состояний и операторов целыми функциями
- 11.8. Диагональное представление оператора плотности по когерентным состояниям (Р-представление Глаубера — Сударшана)
- 11.8.1. Плотности квазивероятности. Распределение Вигнера
- 11.8.2. Два достоинства диагонального представления
- 11.8.3. Диагональное представление p с помощью последовательности функций
- 11.8.4. Диагональное представление антинормально упорядоченного оператора плотности
- 11.8.5. Интегральное представление функции …
- 11.8.6. Примеры
- 11.9. Оптическая теорема эквивалентности для нормально упорядоченных операторов
- 11.9.1. Квантовые характеристические функции
- 11.10. Более общие представления в фазовом пространстве
- 11.10.2. Упорядочение операторов
- 11.10.3. Приложение к квантовым средним и диагональному представлению по когерентным состояниям
- 11.11. Многомодовые поля
- 11.11.1. Когерентные состояния в непрерывном представлении
- 11.12. Положительно- и отрицательно-частотные операторы поля
- 11.12.1. Коммутационные соотношения
- 11.12.2. Нормально упорядоченные корреляционные функции
- 11.13. Поле, создаваемое классическим током
- Глава 12. КВАНТОВЫЕ КОРРЕЛЯЦИИ И ФОТОННАЯ СТАТИСТИКА
- 12.2. Фотоэлектрическое измерение оптического поля; нормальное упорядочение
- 12.2.1. Детектирование нескольких фотонов; корреляционные функции высшего порядка
- 12.2.2. Символы и операторы упорядочения
- 12.3. Оператор фотонной плотности
- 12.4. Интерференционные эксперименты; корреляционные функции второго порядка
- 12.5. Корреляционные функции и взаимные спектральные плотности произвольного порядка
- 12.5.1. Свойства корреляционных функций
- 12.5.2. Взаимные спектральные плотности произвольного порядка
- 12.5.3. Независящие от фазы весовые функции
- 12.6. Степень и порядок когерентности
- 12.7. Значение когерентности второго порядка
- 12.7.2. Корреляции произвольного порядка
- 12.7.3. Оператор плотности для поля
- 12.7.4. Волновые пакеты в качестве мод
- 12.8. Стационарность, однородность, изотропность
- 12.8.2. Условие для оператора плотности
- 12.8.3. Свойства взаимных спектральных плотностей в случае стационарных полей
- 12.8.4. Однородность
- 12.8.5. Изотропность
- 12.9. Антинормально упорядоченные корреляционные функции
- 12.9.2. Замена дифференциальными операторами
- 12.9.3. Весовой функционал для антинормально упорядоченных корреляционных функций
- 12.10. Фотонная статистика
- 12.10.2. Условия для неклассических состояний
- 12.10.3. Моменты n
- 12.10.4. Производящие функции для числа фотонов при нормальном и антинормальном порядке
- 12.11. Проблема локализации фотонов
- 12.11.1. Оператор числа фотонов, определяемый в конфигурационном пространстве
- 12.11.2. Коммутационные соотношения
- 12.11.3. Собственные состояния …
- 12.11.4. Статистика фотона в конечном объеме
- 12.11.5. Полихроматические фотоны и не локальность
- 12.12. Влияние аттенюатора или делителя пучка на квантовое поле
- 12.12.2. Корреляции фотонов
- 12.12.3. Интерферометр Майкельсона
- 12.12.4. Связь между входными и выходными состояниями для делителя пучка
- 12.13. Влияние поляризатора на поле
- 12.14. Локальность Эйнштейна и корреляции фотонов
- 12.14.1. Парадокс Эйнштейна — Подольского — Розена для перепутанного двухфотонного состояния
- 12.14.2. Неравенства Белла
- 12.14.3. Форма Клаузера — Хорна неравенства Белла
- 12.14.4. Экспериментальное подтверждение
- 12.14.5. Неклассические состояния и неравенства Белла
- Глава 13. ИЗЛУЧЕНИЕ ИСТОЧНИКОВ, НАХОДЯЩИХСЯ В СОСТОЯНИИ ТЕПЛОВОГО РАВНОВЕСИЯ
- 13.1. Излучение черного тела
- 13.1.2. Статистика фотонов
- 13.1.3. Поляризация
- 13.1.4. Спектральные распределения
- 13.1.5. Диагональное представление p по когерентным состояниям
- 13.1.6. Корреляционные функции излучения черного тела
- 13.1.7. Функции корреляции высокого порядка
- 13.1.8. Изотропность излучения черного тела
- 13.1.9. Флуктуации интенсивности излучения черного тела
- 13.2. Свет от теплового источника
- 13.3. Пучки стационарного света от теплового источника
- 13.3.2. Статистика фотонов при одинаковых средних числах заполнения
- Глава 14. КВАНТОВАЯ ТЕОРИЯ ФОТОДЕТЕКТИРОВАНИЯ
- 14.1. Взаимодействия квантованного электромагнитного поля
- 14.1.1. Решение по теории возмущений в картине взаимодействия
- 14.1.2. Электромагнитное взаимодействие между полями и зарядами
- 14.1.3. Многополюсный гамильтониан
- 14.2. Вероятность одноэлектронного фотодетектирования
- 14.2.1. Применение к чистому когерентному состоянию
- 14.2.2. Вычисление вероятности в квазимонохроматическом приближении
- 14.2.3. Вычисление электронного матричного элемента
- 14.2.4. Вычисление вероятности детектирования для аксиально симметричного детектора
- 14.3. N-электронный фотодетектор
- 14.4. Вероятность многократного фотоэлектрического детектирования
- 14.5. Вероятность многократного детектирования при произвольном начальном состоянии поля
- 14.6. Фотоэлектрические корреляции
- 14.6.1. Эффект Хэнбери Брауна — Твисса (квантовая трактовка)
- 14.6.2. Корреляции фототоков
- 14.7. Группировка и антигруппировка
- 14.7.2. Двухвременные импульсные корреляционные измерения
- 14.7.3. Антигруппировка
- 14.7.4. Распределение временного интервала фотоэлектрических импульсов
- 14.8. Статистика фотоэлектрического счета
- 14.8.2. Примеры вероятности детектирования
- 14.8.3. Естественная мера времени когерентности
- 14.9. Свойства вероятности детектирования …
- 14.9.1. Производящие функции и проблема обратного преобразования
- 14.9.2. Второй момент и субпуассоновская статистика счета
- 14.9.3. Получение корреляционных функций из статистики счета
- Глава 15. ВЗАИМОДЕЙСТВИЕ СВЕТА И ДВУХУРОВНЕГО АТОМА
- 15.1. Динамические переменные для двухуровневого атома
- 15.1.1. Атомная энергия и атомный дипольный момент
- 15.2. Блоховское представление
- 15.2.1. Средние значения спиновых операторов
- 15.3. Взаимодействие атома с классическим полем
- 15.3.1. Уравнения Блоха
- 15.3.2. Уравнения Блоха во вращающейся системе координат
- 15.3.3. Задача Раби
- 15.3.4. Отклик атома на воздействие лазерного импульса
- 15.3.5. 2«пи»-импульс в форме гиперболического секанса
- 15.4. Взаимодействие атома с квантовым полем: подход теории возмущений
- 15.4.1. Поглощение и излучение фотонов
- 15.5. Взаимодействие атома с квантовым полем: общее рассмотрение
- 15.5.1. Гейзенберговские уравнения движения
- 15.5.2. Приближенное решение — коэффициент Эйнштейна A и лэмбовский сдвиг
- 15.5.3. Интегральные уравнения движения
- 15.5.4. Спонтанное излучение
- 15.6. Резонансная флуоресценция
- 15.6.2. Сечение рассеяния атомов
- 15.6.3. Спектр флуоресценции
- 15.6.4. Корреляция интенсивности флуоресценции
- 15.6.5. Измерения антигруппировки фотонов
- 15.6.6. Субпуассоновская статистика фотонов
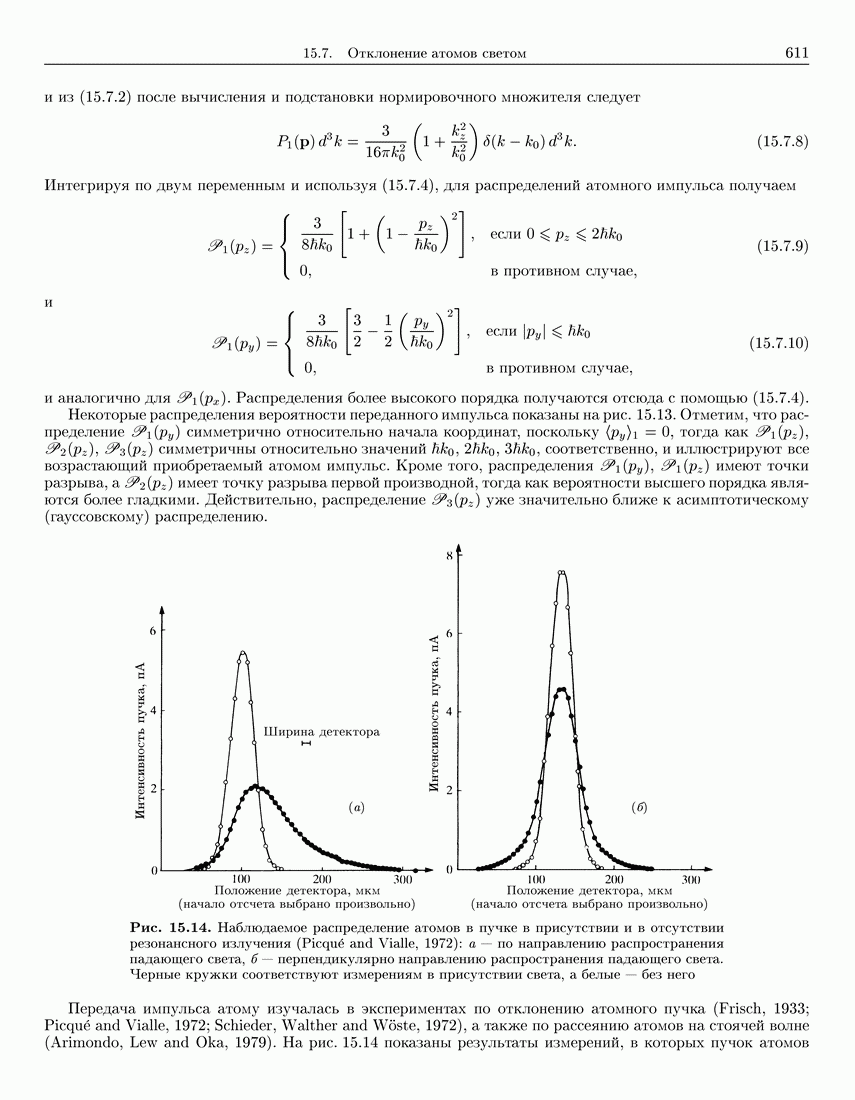
- 15.7. Отклонение атомов светом
- 15.7.1. Передача импульса после n спонтанных испусканий
- 15.7.2. Передача импульса при вынужденном излучении или градиентные силы в сильном поле
- 15.8. Охлаждение и пленение атомов
- 15.8.2. Оценка наименьшей достижимой температуры, основанная на балансе энергии
- Глава 16. КОЛЛЕКТИВНЫЕ АТОМНЫЕ ВЗАИМОДЕЙСТВИЯ
- 16.1. Затухание оптической свободной индукции
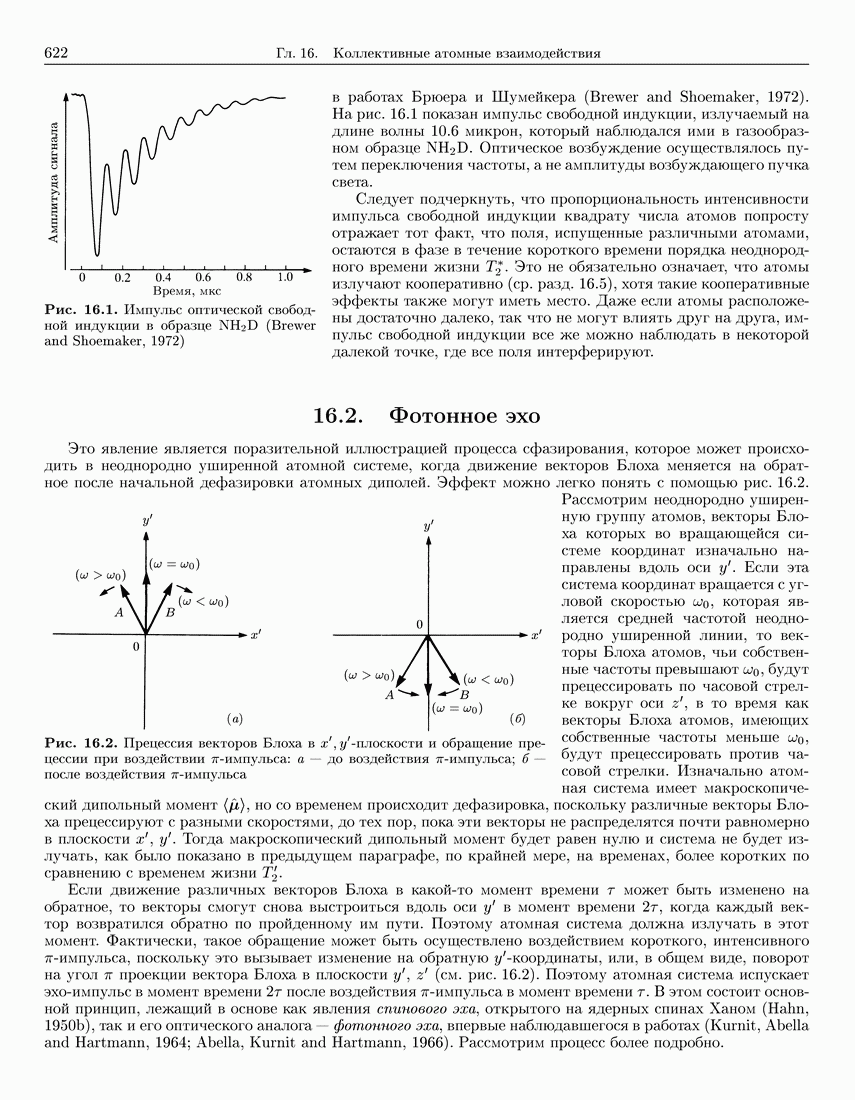
- 16.2. Фотонное эхо
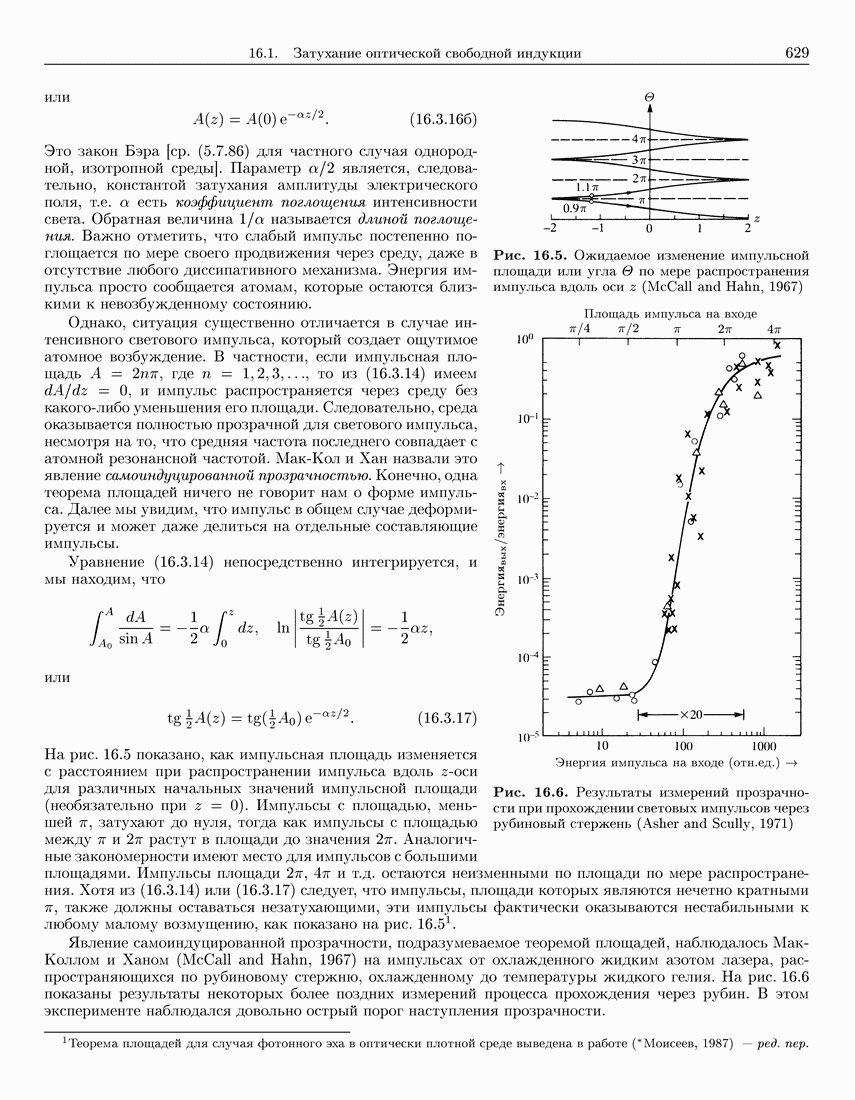
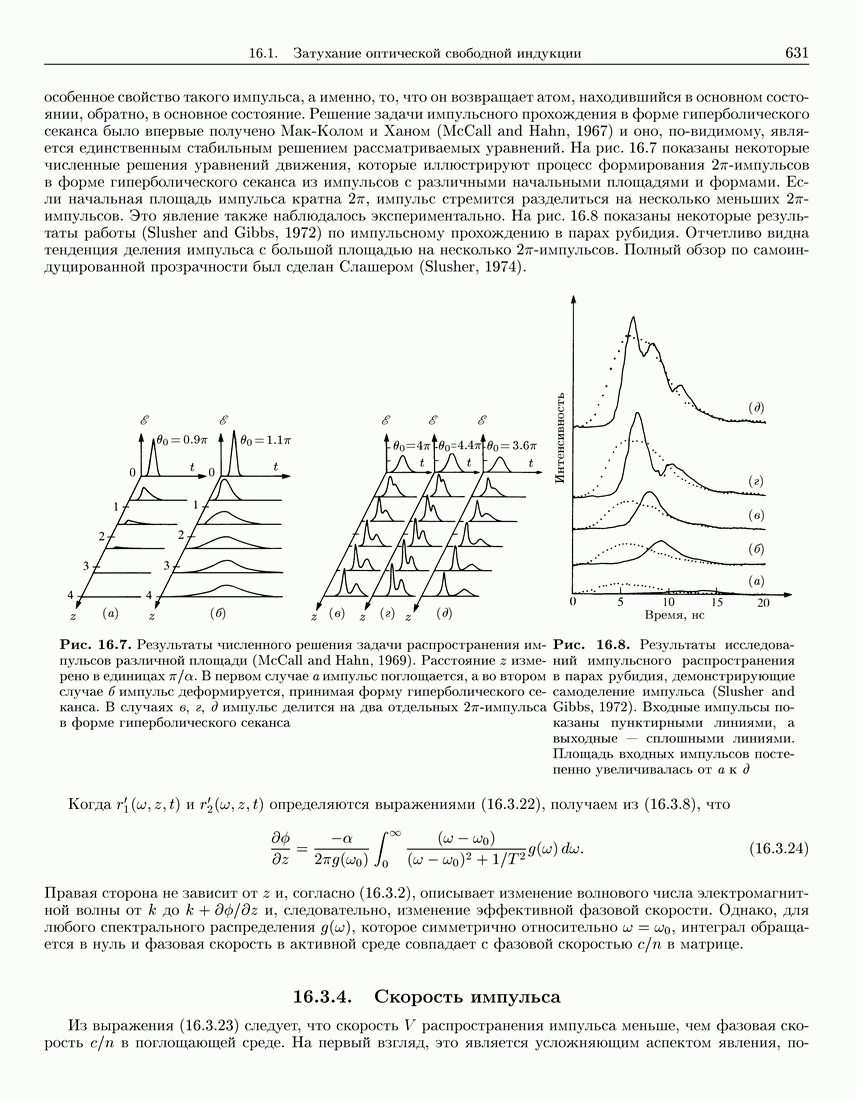
- 16.3. Самоиндуцированная прозрачность
- 16.3.1. Уравнение движения для огибающей импульса
- 16.3.2. Теорема площадей Мак-Колла и Хана
- 16.3.3. Форма импульса
- 16.3.4. Скорость импульса
- 16.4. Оптическая бистабильность
- 16.4.1. Абсорбционная бистабильность в кольцевом резонаторе
- 16.4.2. Дисперсионная бистабильность
- 16.4.3. Хаос в оптической бистабильности
- 16.5. Коллективные атомные состояния и коллективные динамические переменные
- 16.5.1. Состояния Дике
- 16.5.2. Вырождение состояний Дике
- 16.6. Кооперативное атомное излучение
- 16.6.2. Кооперативное излучение атомов, находящихся в факторизованном состоянии
- 16.6.3. Временная эволюция сверхизлучения
- 16.6.4. Некоторые дополнительные усложнения
- 16.6.5. Более общее кооперативное излучение
- 16.6.6. Сверхизлучательные классические осцилляции
- 16.7. Атомные когерентные состояния
- 16.7.1. Блоховское представление атомного когерентного состояния
- 16.7.2. Неортогональность и переполненность
- 16.7.3. Атомные состояния, создаваемые классическим полем
- Глава 17. ОБЩИЕ МЕТОДЫ ИЗУЧЕНИЯ ВЗАИМОДЕЙСТВУЮЩИХ СИСТЕМ
- 17.1. Квантовая теорема регрессии
- 17.1.1. Одновременные средние значения
- 17.1.2. Многовременные средние значения
- 17.1.3. Спонтанное излучение атома
- 17.1.4. Резонансная флуоресценция двухуровневого атома
- 17.1.5. Квантовая теорема регрессии для нормально упорядоченных операторов поля
- 17.2. Флуктуационно-диссипационная теорема
- 17.2.2. Квантово-механическая линейная диссипативная система
- 17.2.3. Мощность рассеяния
- 17.2.4. Флуктуации тока в состоянии теплового равновесия
- 17.2.5. Спектральная плотность флуктуаций
- 17.2.6. Броуновское движение частицы
- 17.2.7. Флуктуации поля в излучении черного тела
- 17.3. Основные кинетические уравнения
- 17.3.2. Обобщенное основное кинетическое уравнение Цванцига
- 17.3.3. Применение к кинетическому уравнению Паули
- 17.3.4. Применение к задаче Дике
- 17.4. Источники квантового шума и квантовые уравнения Ланжевена
- 17.4.2. Уравнения движения квантовой системы
- 17.4.3. Коммутационные соотношения
- 17.4.4. Двухвременные корреляционные функции
- 17.4.5. Уравнение Ланжевена для возбужденной системы осцилляторов
- 17.4.6. Необратимость и стрела времени
- Глава 18. ОДНОМОДОВЫЙ ЛАЗЕР
- 18.1.1. Условие лазерной генерации
- 18.2. Полуклассическая теория лазера
- 18.2.1. Нормальные моды резонатора
- 18.2.2. Уравнение движения для лазерного поля
- 18.2.3. Аналогия с фазовым переходом
- 18.3. Полуклассическая теория лазера с учетом шума спонтанного излучения
- 18.3.1. Уравнение Фоккера — Планка
- 18.3.2. Стационарное решение
- 18.3.3. Аналогия с фазовым переходом для флуктуирующего лазерного поля
- 18.3.4. Моменты интенсивности света
- 18.4. Квантовая теория лазера
- 18.4.1. Основное кинетическое уравнение для лазерного поля
- 18.4.2. Статистика фотонов
- 18.4.3. Стационарная вероятность
- 18.5. Взаимосвязь между квантовой и полуклассической теориями лазера
- 18.5.2. Стационарное решение основного кинетического уравнения
- 18.6. Решение зависящего от времени уравнения движения
- 18.6.1. Развитие лазерного поля из вакуумного состояния
- 18.6.2. Экспериментальные исследования
- 18.7. Корреляционные функции
- 18.7.1. Функции Грина
- 18.7.2. Корреляция интенсивности
- 18.7.3. Функция корреляции амплитуды поля и спектральная плотность
- 18.7.4. Корреляции высшего порядка
- 18.8. Нестабильности лазера и хаос
- 18.8.2. Линейный анализ устойчивости
- 18.8.3. Примеры нестабильностей лазера
- 18.8.4. Тест на детерминированный хаос
- Глава 19. ДВУХМОДОВЫЙ КОЛЬЦЕВОЙ ЛАЗЕР
- 19.1.1. Учет флуктуаций спонтанного излучения
- 19.2. Стационарное решение
- 19.2.1. Моменты интенсивности света
- 19.2.2. Сравнение с экспериментом
- 19.3. Аналогия с фазовым переходом
- 19.3.2. Случай константы связи …: фазовый переход второго рода
- 19.3.3. Случай константы связи …: фазовый переход первого рода
- 19.3.4. Скрытая теплота фазового перехода
- 19.4. Зависящее от времени решение в случае константы связи …
- 19.5. Зависящее от времени решение в более общем случае взаимодействия между модами …
- 19.5.1. Переключение мод и времена первого прохождения
- 19.5.2. Распределения времен первого прохождения
- Глава 20. ЛИНЕЙНЫЙ УСИЛИТЕЛЬ СВЕТА
- 20.2. Основное кинетическое уравнения для поля усилителя
- 20.3. Решение основного кинетического уравнения
- 20.4. Статистика фотонов
- 20.4.2. Полностью инвертированный усилитель света
- 20.5. Сжатый свет
- 20.6. Условие, при котором поле на выходе усилителя является классическим
- Глава 21. СЖАТЫЕ СОСТОЯНИЯ СВЕТА
- 21.2. Квантовая природа сжатого состояния
- 21.3. Унитарный оператор сжатия
- 21.3.1. Сжатие двухфотонного когерентного состояния
- 21.3.2. Действие оператора сжатия на произвольное состояние
- 21.4. Идеальное сжатое состояние
- 21.5. Двухфотонное когерентное состояние
- 21.5.1. Преобразованные фоковские состояния
- 21.5.2. Представление по когерентным состояниям двухфотонного когерентного состояния
- 21.5.3. Фотонная статистика двухфотонного когерентного состояния
- 21.6. Детектирование сжатия гомодинированием с когерентным светом
- 21.7. Сжатие, реализованное на практике: вырожденная параметрическая вниз-конверсия
- 21.7.1. Создание сжатого состояния при вырожденной параметрической вниз-конверсии
- 21.8. Широкополосный сжатый свет
- 21.8.1. Гомодинирование и корреляционные функции
- 21.8.2. Квадратурные корреляции
- 21.8.3. Спектральные корреляции
- 21.8.4. Спектрально-компонентное сжатие и степень сжатия
- 21.8.5. Примеры степени сжатия Q(w)
- 21.9. Сжатие высшего порядка
- 21.9.1. Сжатие N-ого порядка двухфотонного когерентного состояния
- 21.9.2. Амплитудно-квадратичное сжатие
- Глава 22. НЕКОТОРЫЕ КВАНТОВЫЕ ЭФФЕКТЫ В НЕЛИНЕЙНОЙ ОПТИКЕ
- 22.2. Энергия поля в диэлектрике
- 22.3. Генерация оптических гармоник
- 22.4. Параметрическая вниз-конверсия
- 22.4.2. Статистика фотонов
- 22.4.3. Доказательство неклассического поведения
- 22.4.4. Многомодовая теория возмущений процесса параметрического распада
- 22.4.5. Перепутанное квантовое состояние
- 22.4.6. Скорость вниз-конверсии
- 22.4.7. Временной интервал между сигнальным и холостым фотонами
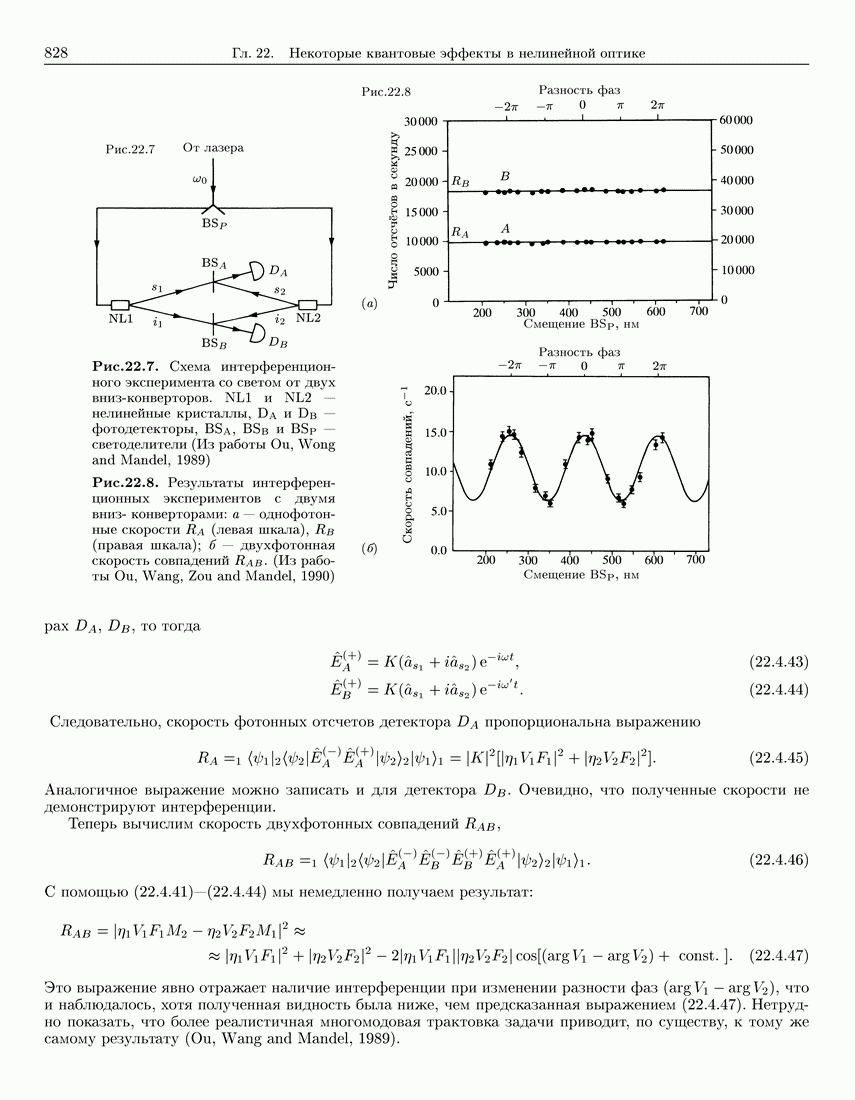
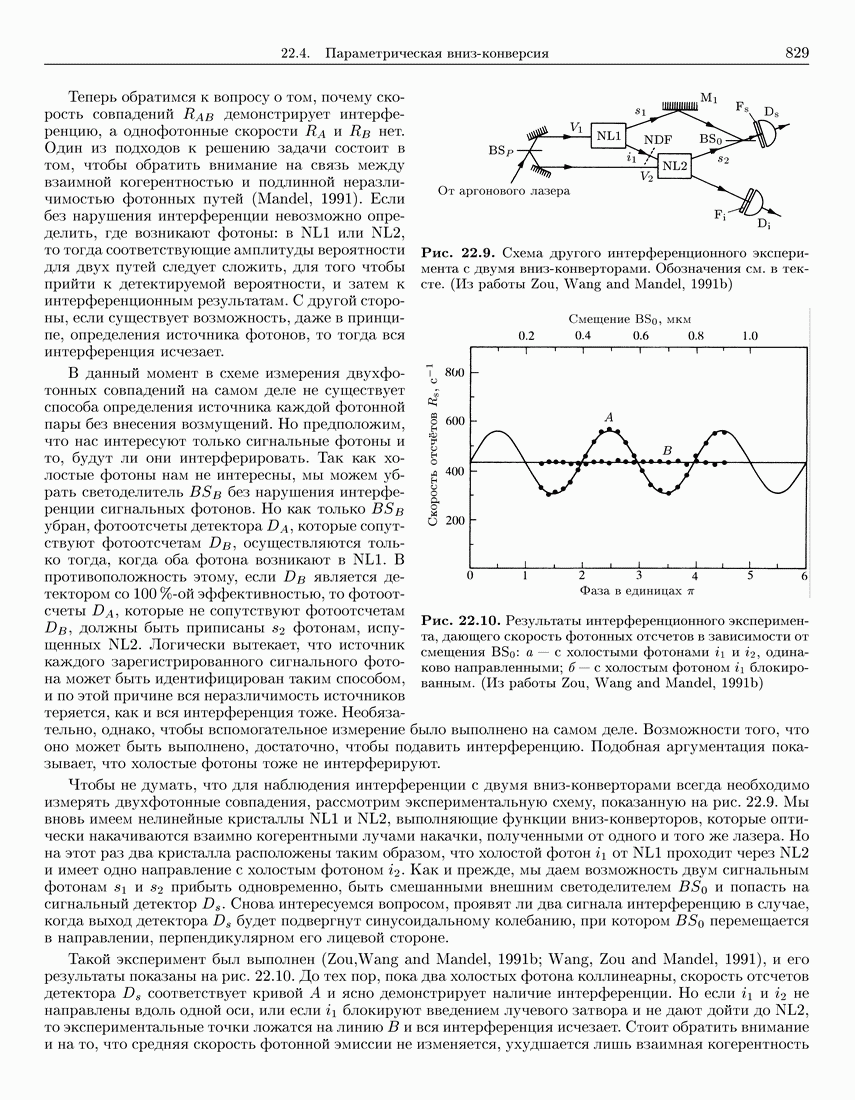
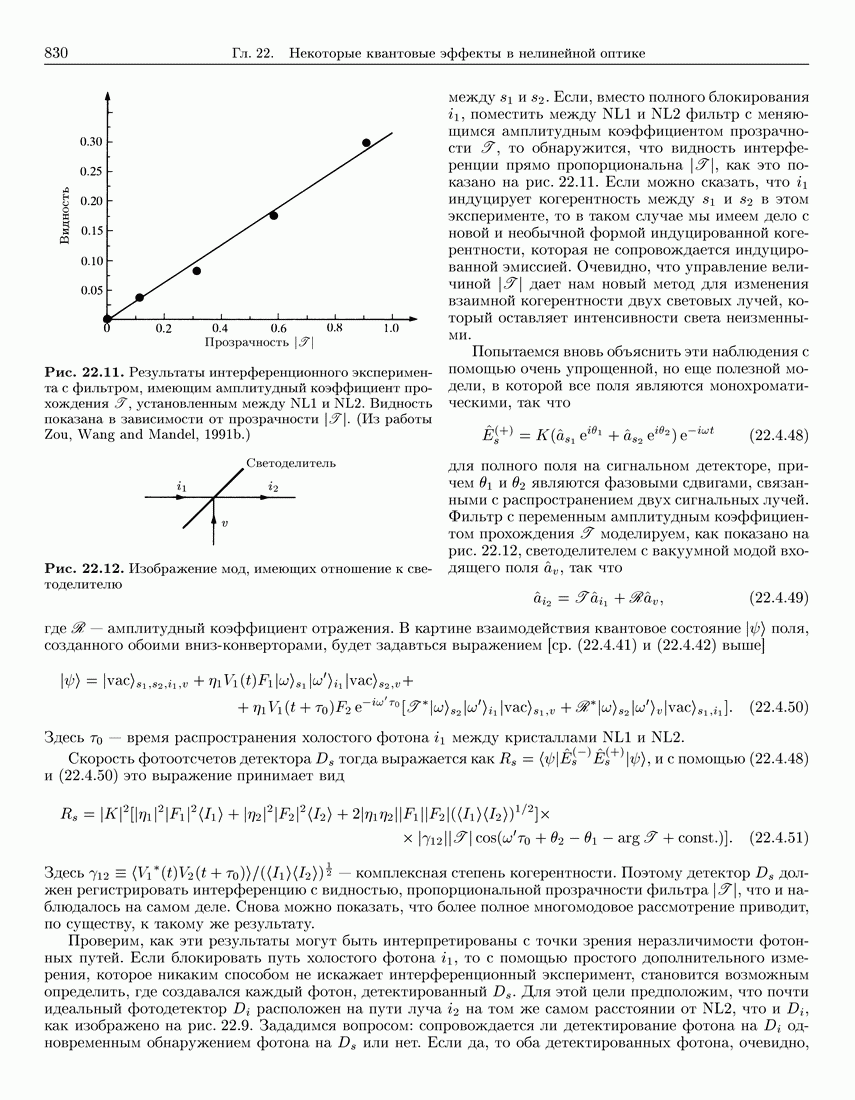
- 22.4.8. Интерференционные эксперименты с двумя вниз-конверторами
- 22.5. Вырожденное четырехволновое смешение
- 22.5.2. Применение к когерентному состоянию
- 22.5.3. Сжатие в четырехволновом смешении
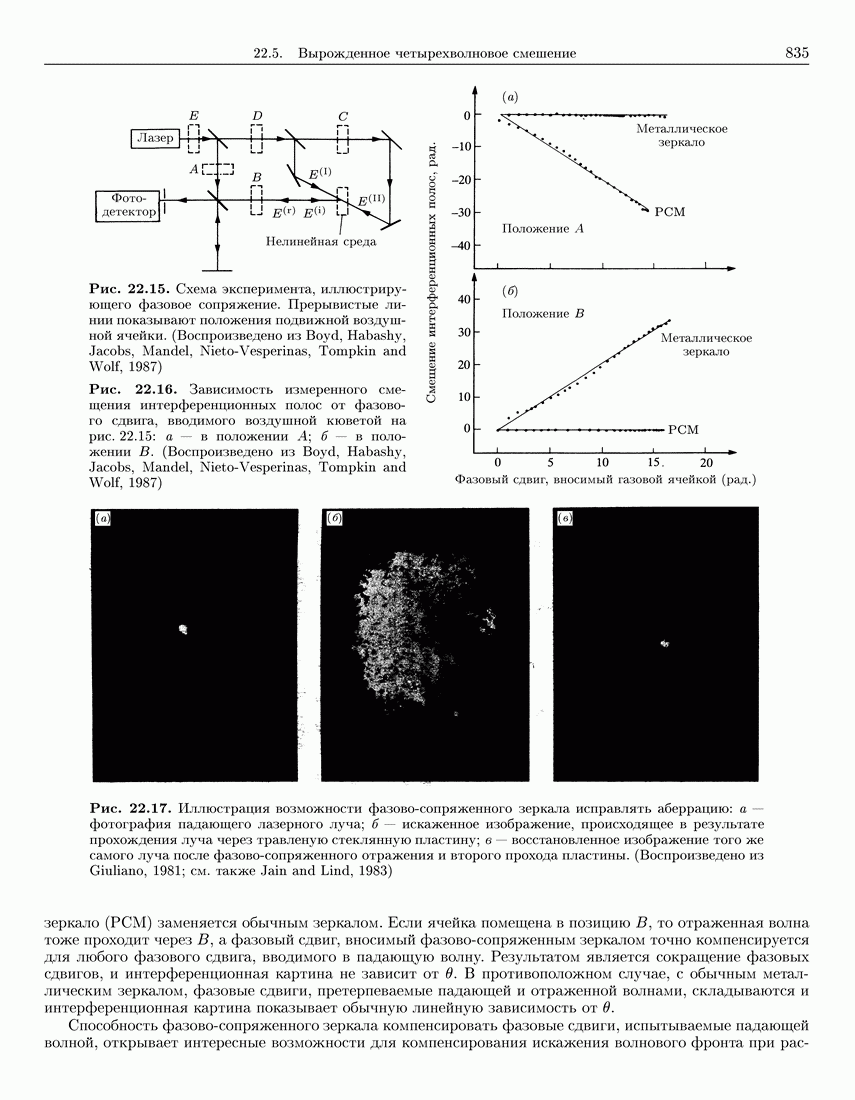
- 22.5.4. Фазовое сопряжение
- 22.6. Квантовые неразрушающие измерения
- 22.6.1. Эффект Керра — пример QND-переменной
- 22.6.2. Анализ интерференционного эксперимента
- 22.6.3. Вычисление видности интерференционных полос
- 22.6.4. Фазовый сдвиг зондирующей волны
- 22.6.5. Дополнительность