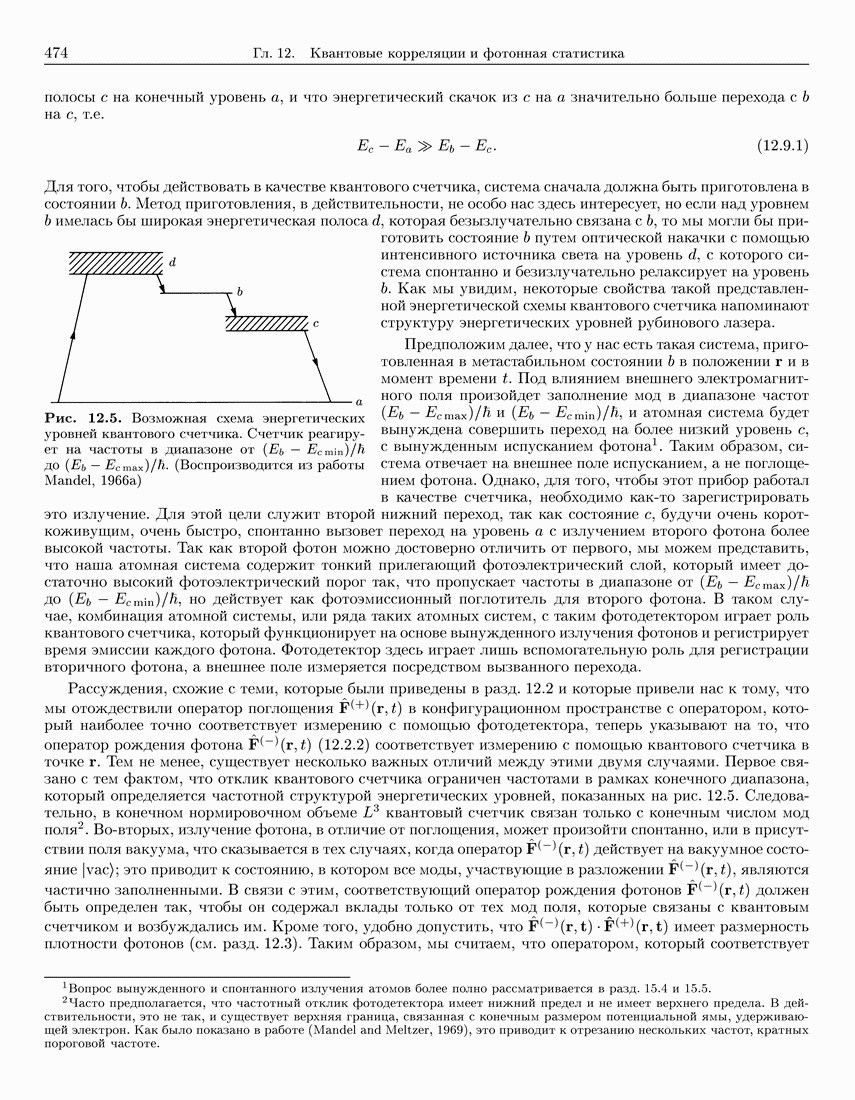
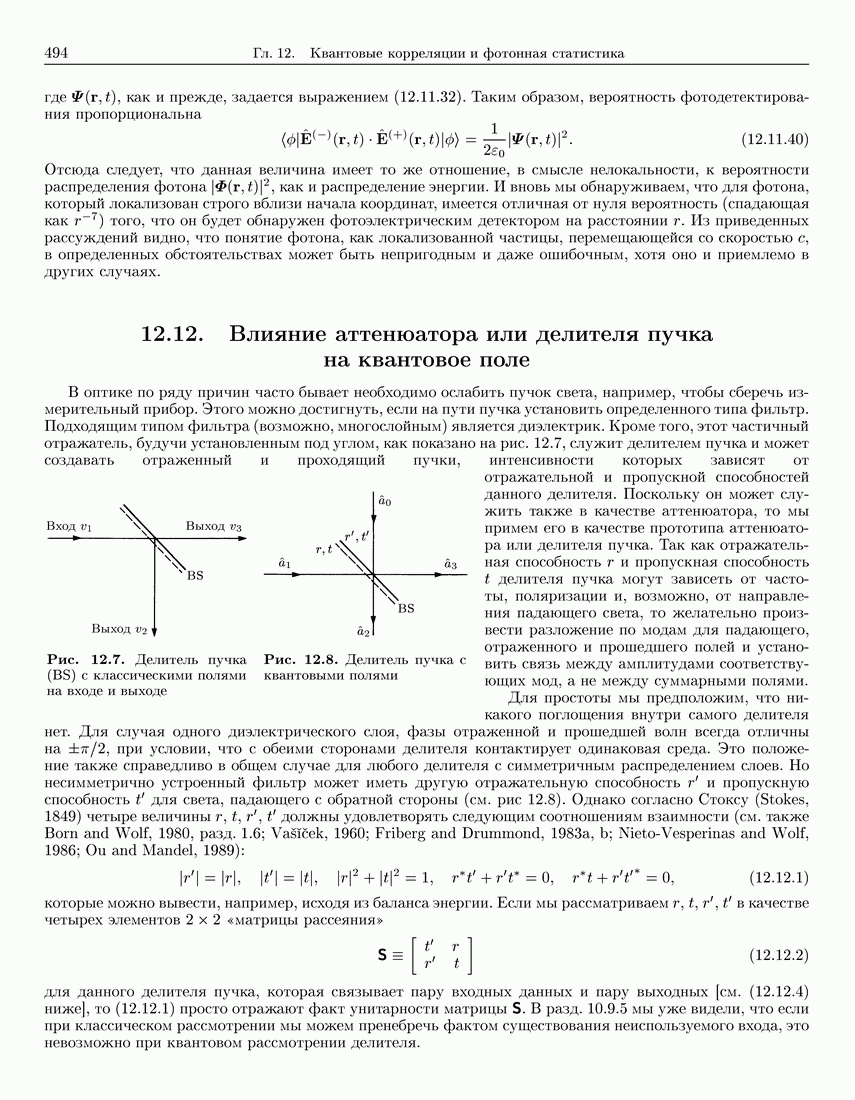
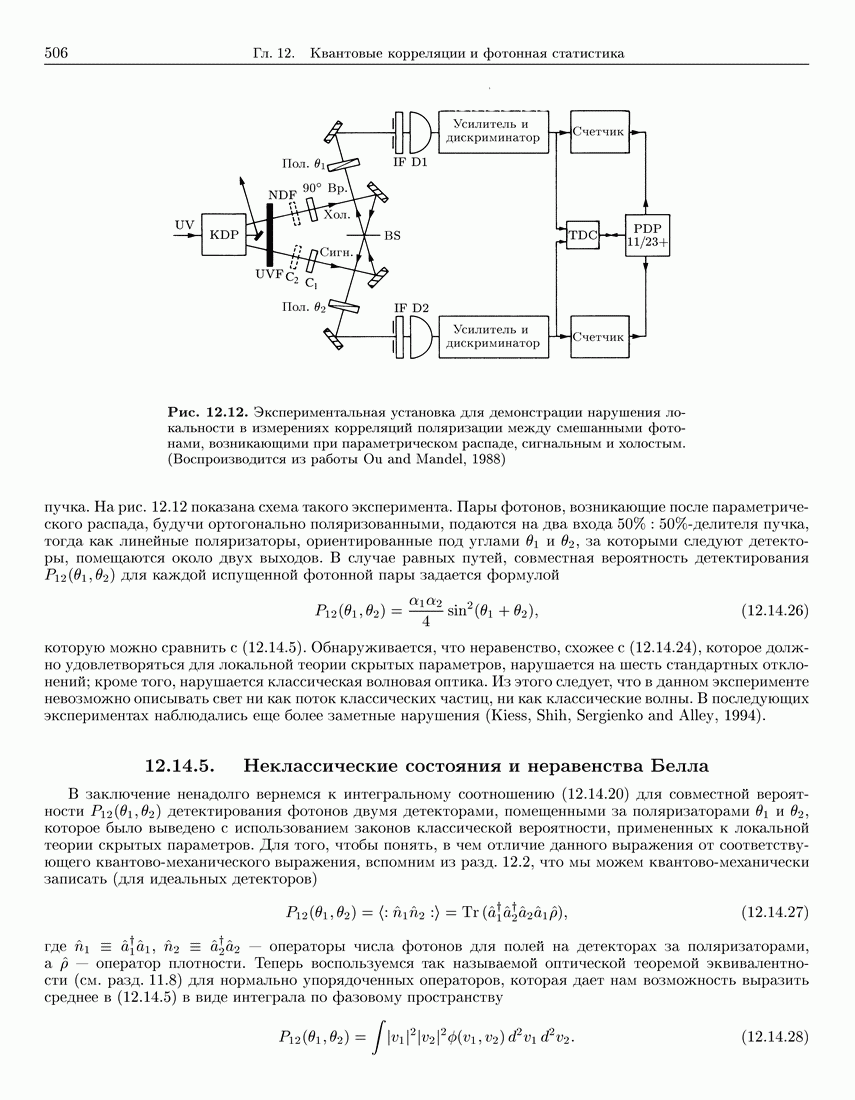
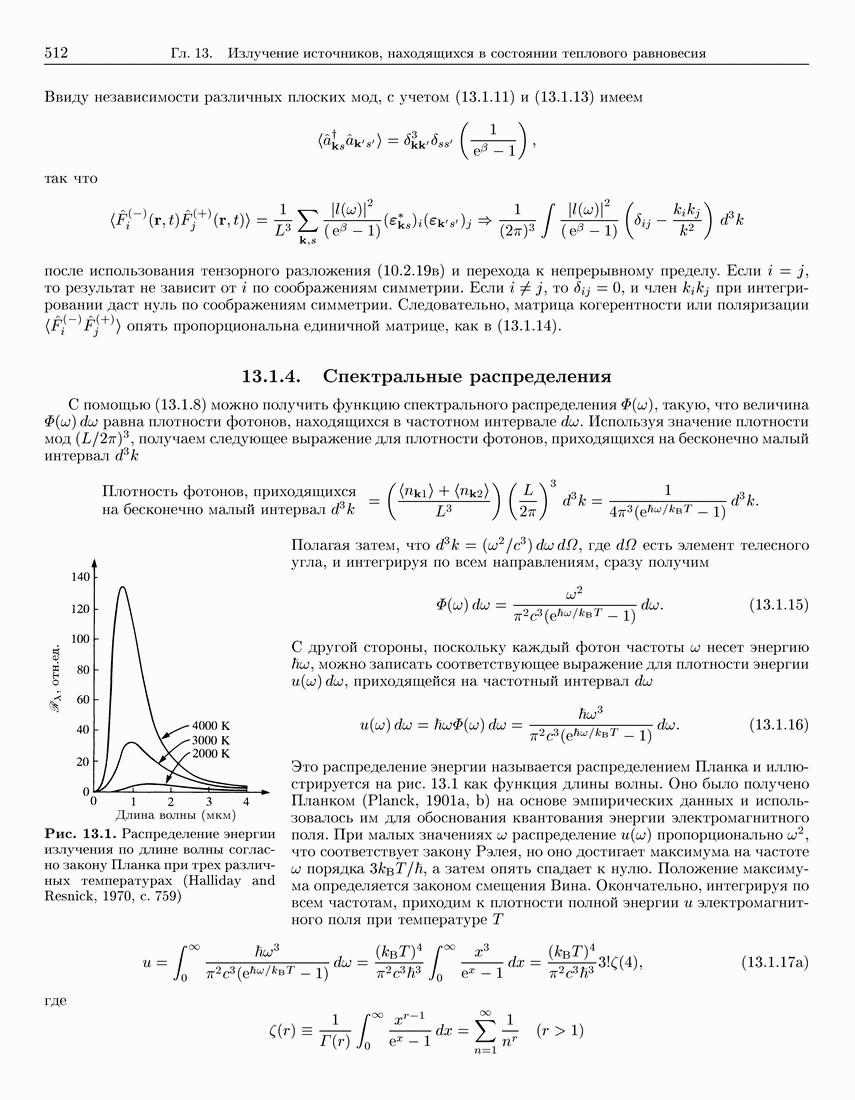
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
17.1.3. Спонтанное излучение атома
Рассмотрим квантовую систему  в виде двухуровневого атома, взаимодействующего с электромагнитным полем, которое находится первоначально в вакуумном состоянии и которое следует рассматривать как резервуар
в виде двухуровневого атома, взаимодействующего с электромагнитным полем, которое находится первоначально в вакуумном состоянии и которое следует рассматривать как резервуар  Два энергетических собственных состояния атома
Два энергетических собственных состояния атома  образуют базис. Основными динамическими переменными являются атомные понижающий и повышающий операторы
образуют базис. Основными динамическими переменными являются атомные понижающий и повышающий операторы  а так же оператор возбуждения
а так же оператор возбуждения  Они имеют следующие матричные элементы (ср. разд. 15.1)
Они имеют следующие матричные элементы (ср. разд. 15.1)

и начальные средние значения

Для более позднего момента времени  получаем из (17.1.12), после отождествления
получаем из (17.1.12), после отождествления  что
что

Однако из обсуждения, сделанного в разд. 15.5, мы уже знаем  что
что

и сравнение выражений (17.1.19) и (17.1.20) позволяет установить четыре элемента функции Грина

Воспользуемся теперь этими результатами для вычисления двухвременнбй атомной корреляционной функции  из теоремы регрессии. Если предположение о факторизации справедливо, то из (17.1.6), полагая
из теоремы регрессии. Если предположение о факторизации справедливо, то из (17.1.6), полагая  получим
получим

и, с учетом формулы (17.1.21),

Этот результат согласуется с результатом, полученным в разд. 15.5. Необходимо отметить, что хотя, строго говоря, атом и электромагнитное поле взаимодействуют в момент времени тем не менее, состояние поля слабо изменяется атомом, в том смысле, что почти все моды остаются незаполненными. Пока наш интерес сосредоточен на атоме, а не на излученном фотоне, мы можем считать, что состояние поля почти не отличается от вакуумного.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
- 1.2. Свойства вероятностей
- 1.2.1. Совместные вероятности
- 1.2.2. Условные вероятности
- 1.2.3. Теорема Байеса для апостериорных вероятностей
- 1.3. Случайные переменные и распределение вероятностей
- 1.3.1. Преобразования случайных переменных
- 1.3.2. Математические ожидания и моменты
- 1.3.3. Неравенство Чебышева
- 1.4. Производящие функции
- 1.4.1. Производящая функция моментов
- 1.4.2. Характеристическая функция
- 1.4.3. Кумулянты
- 1.5. Некоторые примеры распределений вероятности
- 1.5.1. Распределение Бернулли или биноминальное распределение
- 1.5.2. Пуассоновское распределение
- 1.5.3. Распределение Бозе — Эйнштейна
- 1.5.4. Закон больших чисел
- 1.5.5. Нормальное, или гауссовское распределение
- 1.5.6. Центральная предельная теорема
- 1.5.7. Гамма-распределение
- 1.6. Многомерное гауссовское распределение
- 1.6.1. Теорема о гауссовском моменте
- 1.6.2. Производящая функция моментов и характеристическая функция
- 1.6.3. Многократные комплексные гауссовские случайные переменные
- Глава 2. СЛУЧАЙНЫЕ ПРОЦЕССЫ
- 2.1. Введение в статистические ансамбли
- 2.1.2. Совместные вероятности и корреляции
- 2.1.3. Функционал вероятности
- 2.2. Стационарность и эргодичность
- 2.2.1. Среднее по времени стационарного процесса
- 2.2.2. Эргодичность
- 2.2.3. Примеры случайных процессов
- 2.3. Свойства автокорреляционной функции
- 2.4. Спектральные свойства стационарного случайного процесса
- 2.4.1. Спектральная плотность и теорема Винера — Хинчина
- 2.4.2. Сингулярности спектральной плотности
- 2.4.3. Нормированные корреляции и нормированные спектральные плотности
- 2.4.4. Взаимные корреляции и взаимные спектральные плотности
- 2.5. Ортогональное представление случайного процесса
- 2.5.2. Предел … другой подход к теореме Винера — Хинчина
- 2.6. Временная эволюция и классификация случайных процессов
- 2.6.2. Абсолютно случайные или сепарабельные процессы
- 2.6.3. Марковский процесс первого порядка
- 2.6.4. Марковский процесс высшего порядка
- 2.7. Основные уравнения в интегро-дифференциальной форме
- 2.8. Основные уравнения в дифференциальной форме
- 2.8.1. Дифференциальное уравнение Крамерса — Мояля
- 2.8.2. Векторный случайный процесс
- 2.8.3. Порядок дифференциального уравнения Крамерса — Мояля
- 2.9. Уравнение Ланжевена и уравнение Фоккера — Планка
- 2.9.1. Моменты перехода для процесса Ланжевена
- 2.9.2. Стационарное решение уравнения Фоккера — Планка
- 2.9.3. Зависящее от времени решение уравнения Фоккера — Планка
- 2.10. Процесс Винера (или одномерное случайное блуждание)
- 2.10.2. Совместные вероятности и автокорреляция
- Глава 3. МАТЕМАТИЧЕСКИЕ МЕТОДЫ
- 3.1. Комплексный аналитический сигнал
- 3.1.2. Квази-монохроматические сигналы и их огибающие
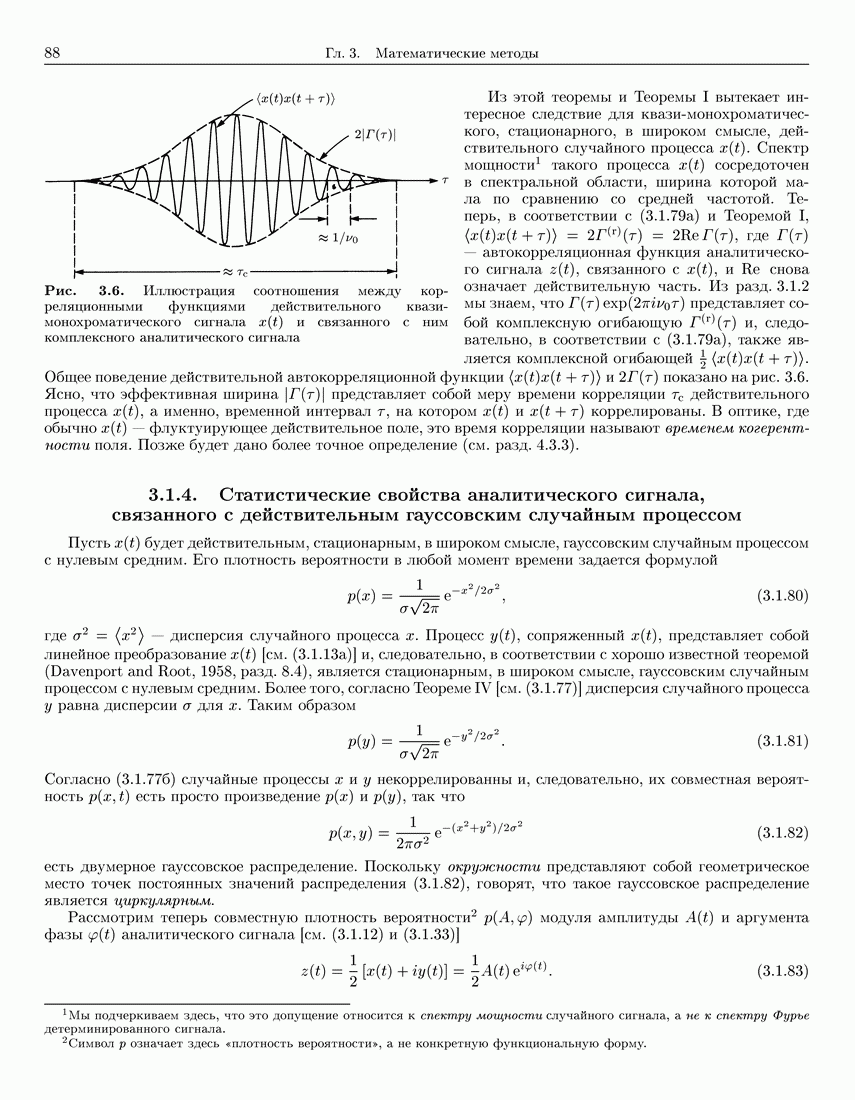
- 3.1.3. Соотношения между корреляционными функциями действительного и связанного с ним комплексного аналитических случайных процессов
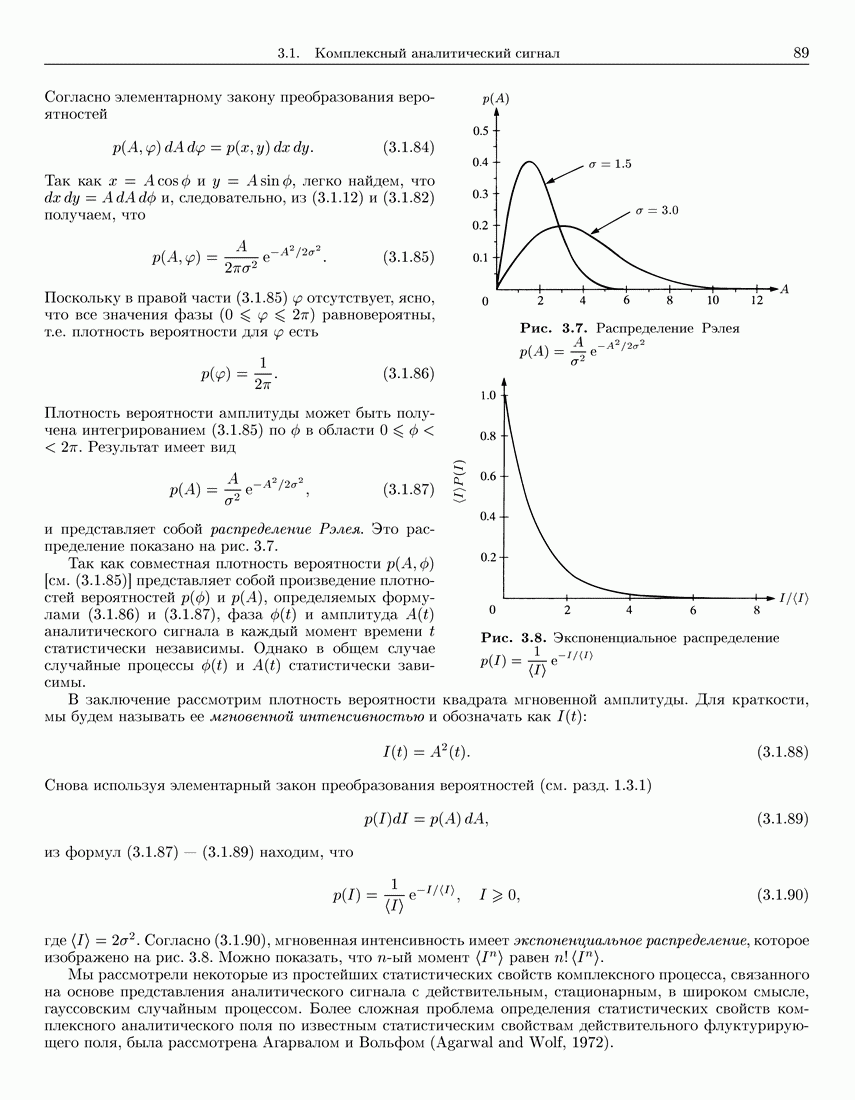
- 3.1.4. Статистические свойства аналитического сигнала, связанного с действительным гауссовским случайным процессом
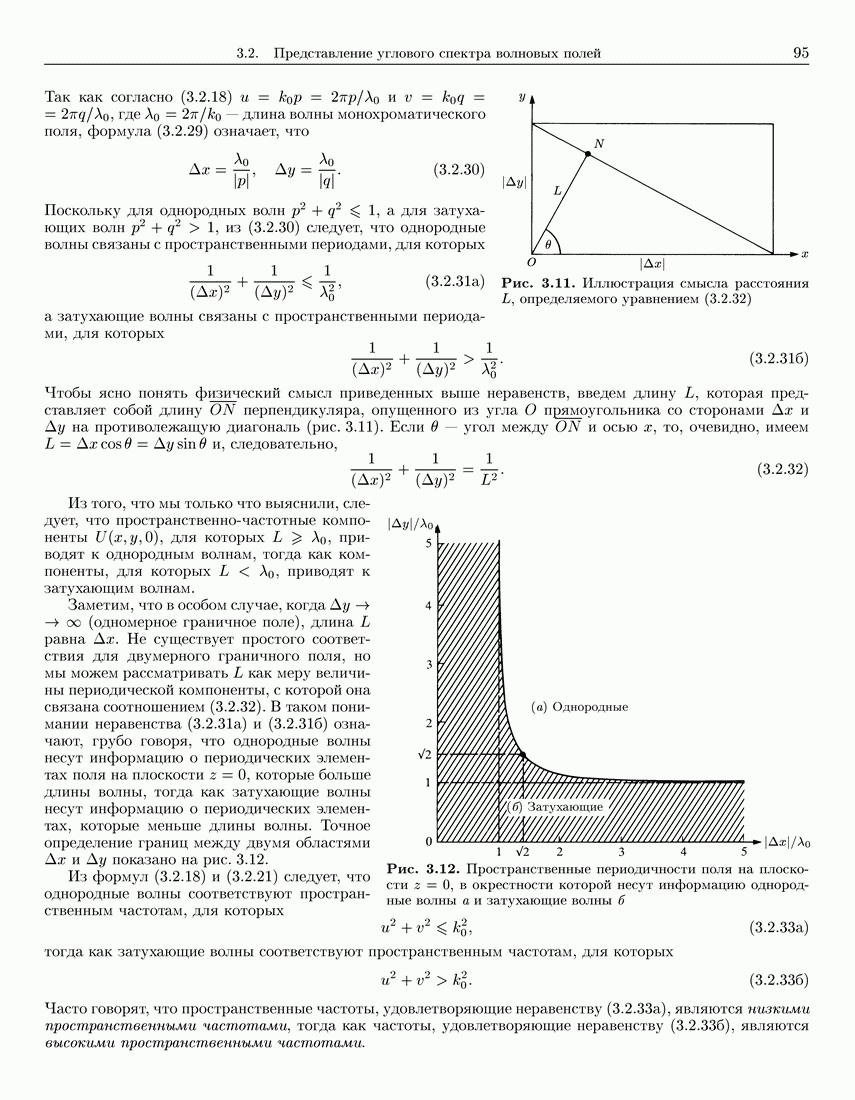
- 3.2. Представление углового спектра волновых полей
- 3.2.1. Угловой спектр волнового поля в плоско-параллельном слое
- 3.2.2. Угловой спектр волнового поля в полупространстве
- 3.2.3. Пример: дифракция на полупрозрачном объекте
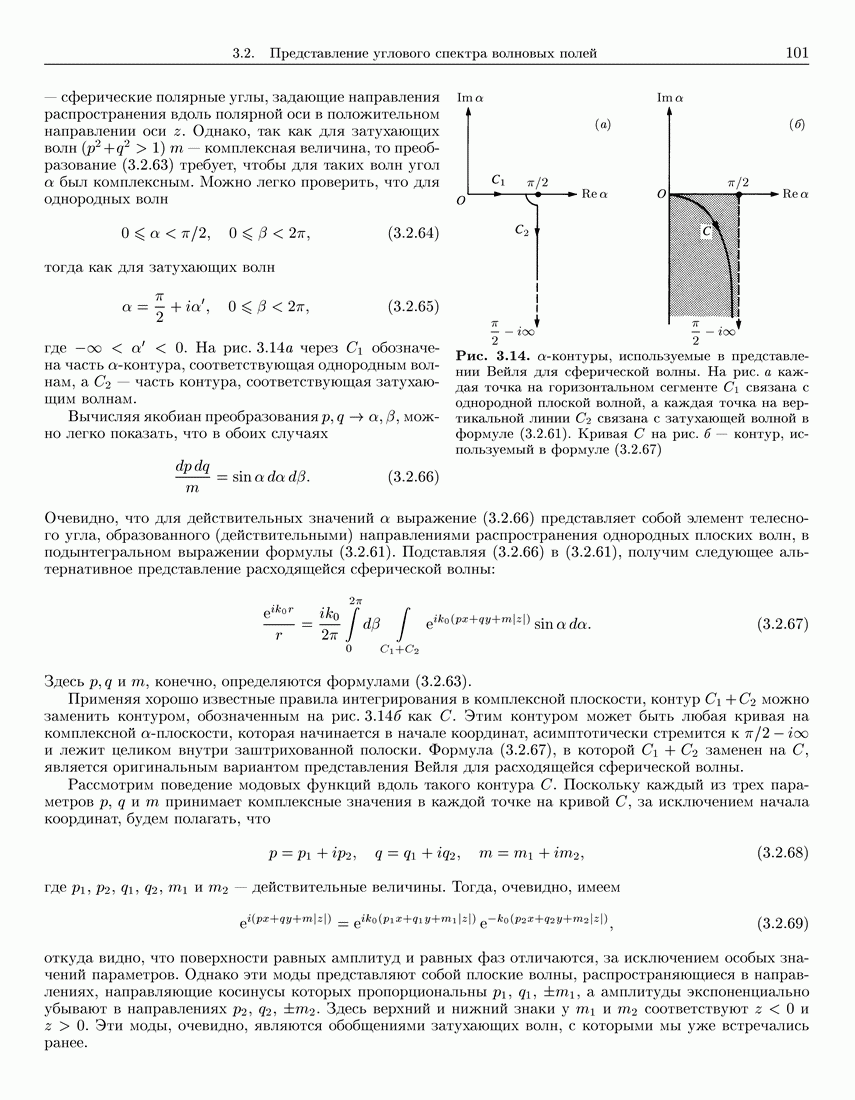
- 3.2.4. Представление Вейля для сферической волны
- 3.2.5. Дифракционные формулы Рэлея
- 3.3. Метод стационарной фазы
- 3.3.2. Метод стационарной фазы для однократных интегралов
- 3.3.3. Метод стационарной фазы для двойных интегралов
- 3.3.4. Пример: поведение представления углового спектра для волновых полей в дальней зоне
- Глава 4. ТЕОРИЯ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА СКАЛЯРНЫХ ВОЛНОВЫХ ПОЛЕЙ
- 4.2. Некоторые элементарные представления и определения
- 4.2.1. Временная когерентность и время когерентности
- 4.2.2. Пространственная когерентность и площадь когерентности
- 4.2.3. Объем когерентности и параметр вырождения
- 4.3. Интерференция двух стационарных световых пучков как проявление корреляции второго порядка
- 4.3.2. Корреляции второго порядка в пространственно-частотной области. Взаимная спектральная плотность и спектральная степень когерентности
- 4.3.3. Время когерентности и ширина спектра
- 4.4. Распространение корреляций
- 4.4.2. Распространение корреляций от плоскости
- 4.4.3. Распространение корреляций от ограниченных поверхностей
- 4.4.4. Теорема Ван Циттерта — Цернике
- 4.4.5. Распространение корреляций от первичных источников
- 4.5. Специальные типы полей
- 4.5.1. Взаимно спектрально чистый свет
- 4.5.2. Когерентный свет в пространственно-временной области
- 4.5.3. Когерентный свет в пространственно-частотной области
- 4.6. Свободные поля с произвольной степенью когерентности
- 4.6.1. Уравнения Сударшана для распространения корреляционных функций второго порядка свободных полей
- 4.6.2. Временная эволюция корреляционных функций второго порядка свободных полей
- 4.6.3. Взаимосвязь между свойствами временной и пространственной когерентности свободных полей
- 4.6.4. Взаимосвязь спектральных свойств и свойств пространственной когерентности свободных полей
- 4.7. Представление по когерентным модам и представление по ансамблю для источников и полей в пространственно-частотной области
- 4.7.1. Представление по когерентным модам частично когерентных полей в свободном пространстве
- 4.7.2. Строгое представление взаимной спектральной плотности в виде корреляционной функции
- 4.7.3. Нормальные моды колебаний частично когерентных первичных источников и представление их взаимной спектральной плотности в виде корреляционной функции
- Приложение 4.1. Ядро H(R) оператора … в представлении интегрального преобразования
- Приложение 4.2. Функция Грина G(R, Т) для временной эволюции аналитического сигнала свободного поля и ее фурье-образ …
- Глава 5. ИЗЛУЧЕНИЕ ИСТОЧНИКОВ ЛЮБОЙ СТЕПЕНИ КОГЕРЕНТНОСТИ
- 5.2. Излучение трехмерных первичных источников
- 5.2.2. Излучение от некоторых модельных источников
- 5.3. Излучение плоских вторичных источников
- 5.3.2. Излучение плоских, вторичных, квазиоднородных источников
- 5.3.3. Обратная задача для плоских, вторичных, квазиоднородных источников
- 5.4. Теоремы эквивалентности для плоских источников, генерирующих одинаковую интенсивность излучения
- 5.4.1. Теорема эквивалентности для плоских источников
- 5.4.2. Пример: эквивалентные гауссовские источники модели Шелла
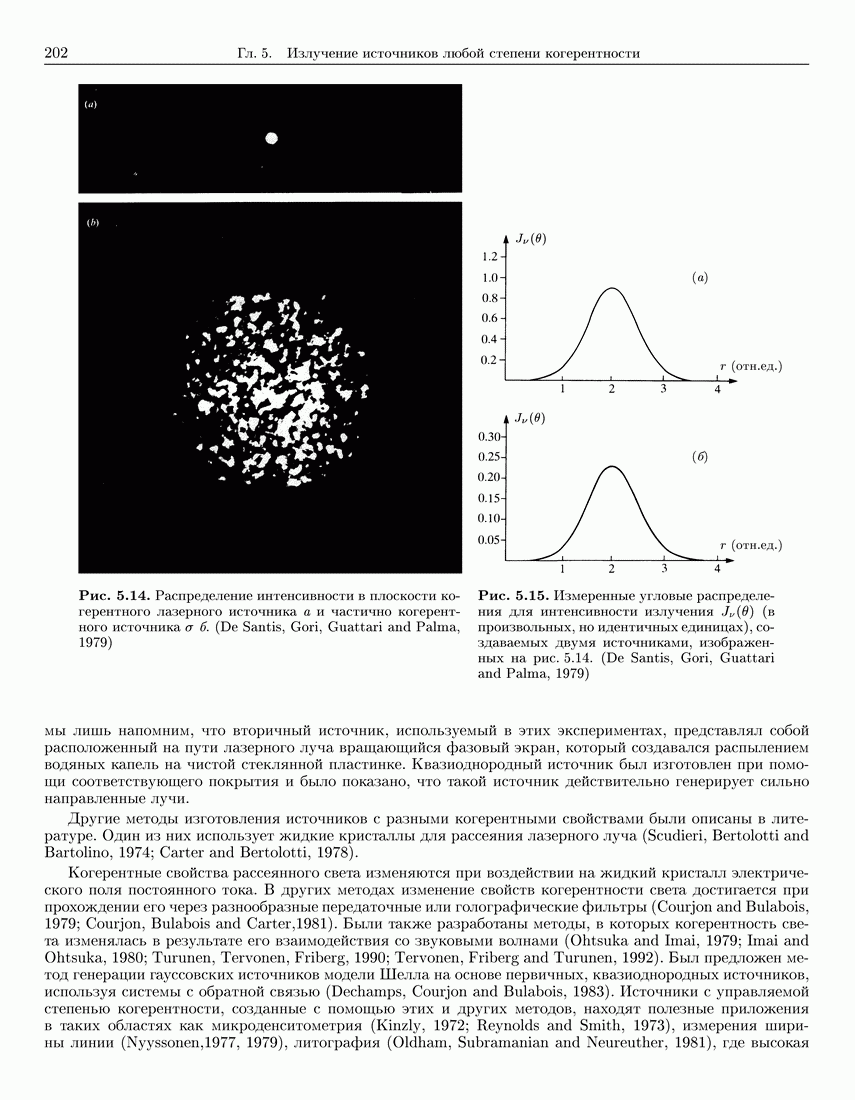
- 5.4.3. Экспериментальная проверка теоремы эквивалентности
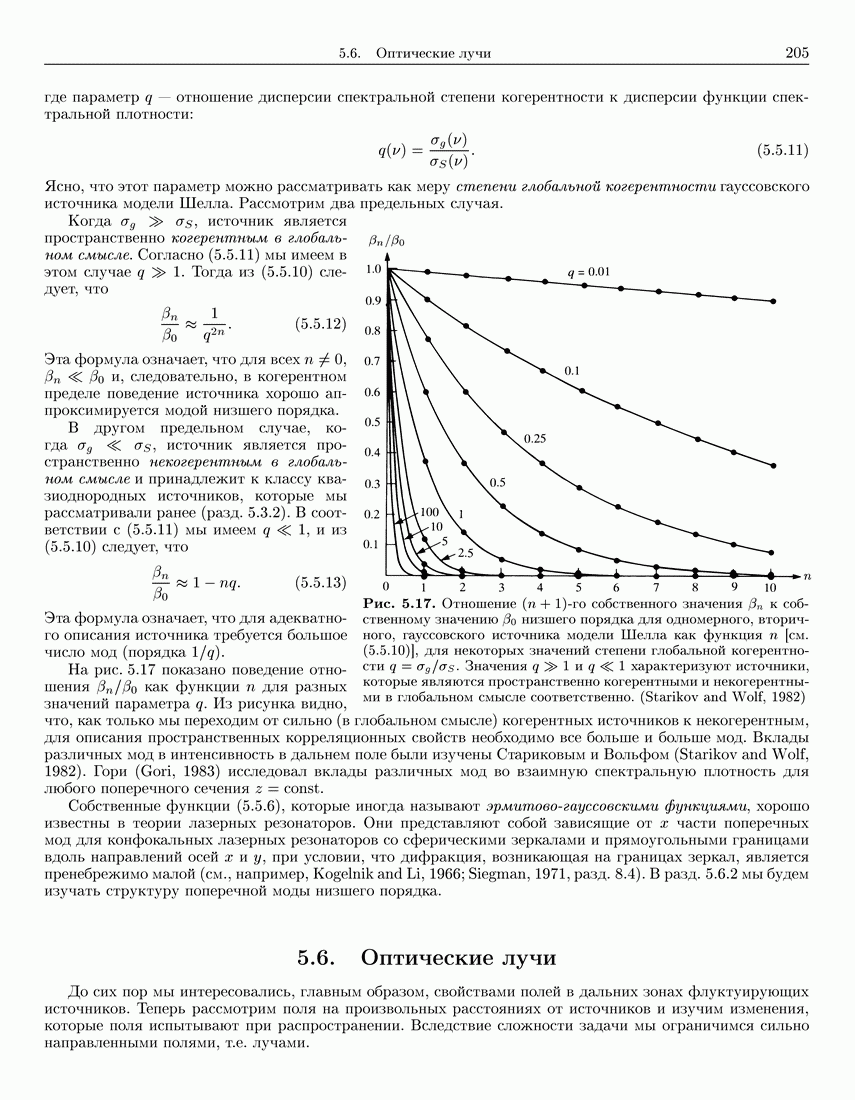
- 5.5. Представление по когерентным модам для гауссовскнх источников модели Шелла
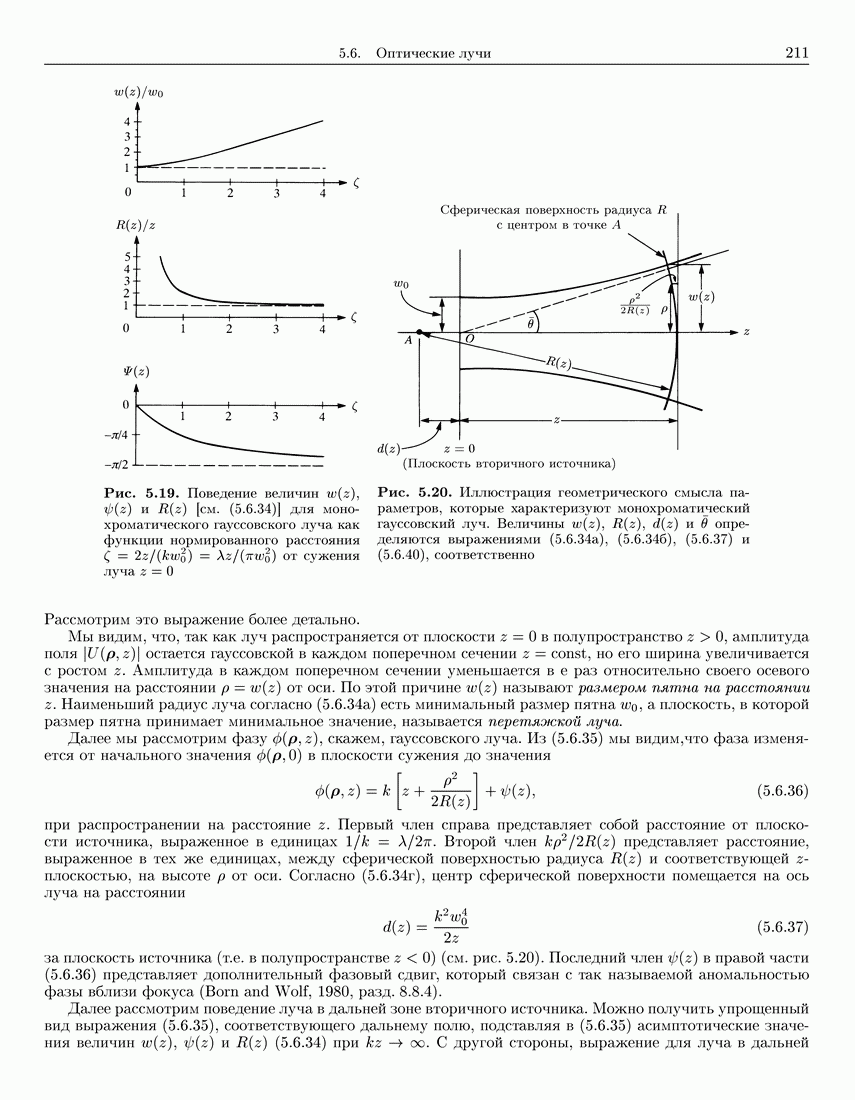
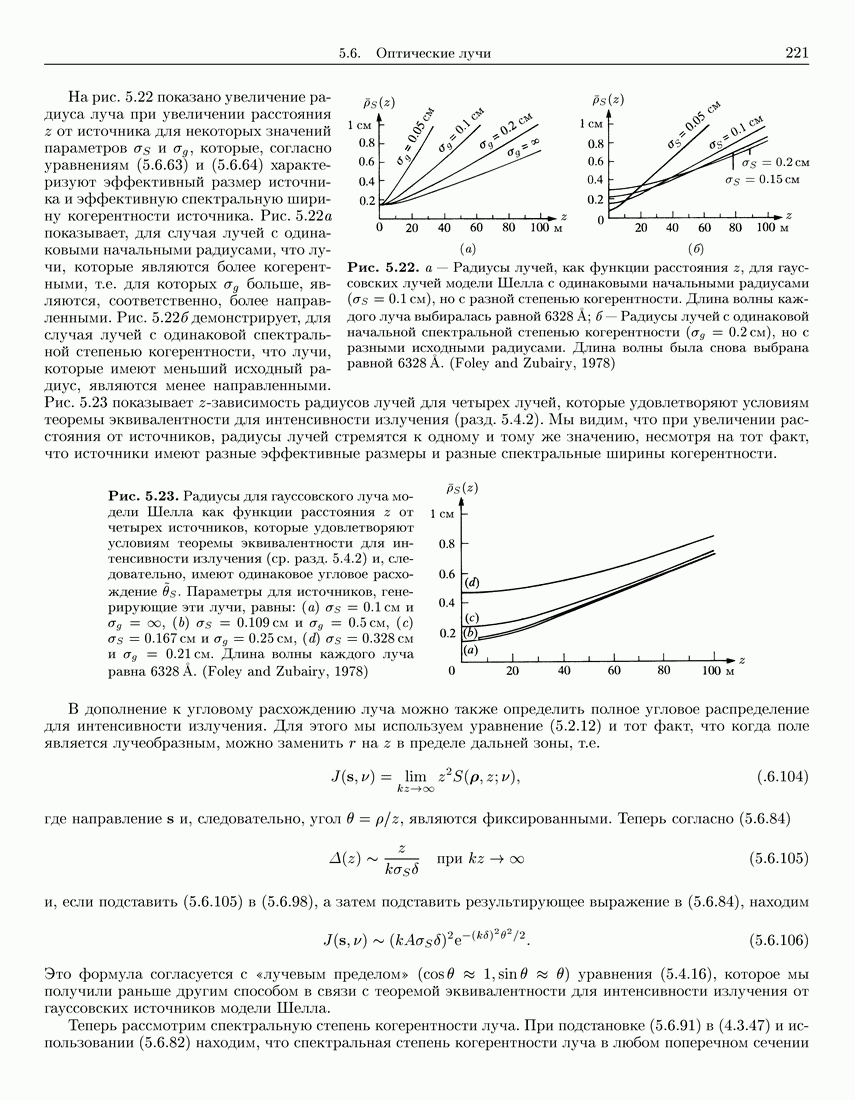
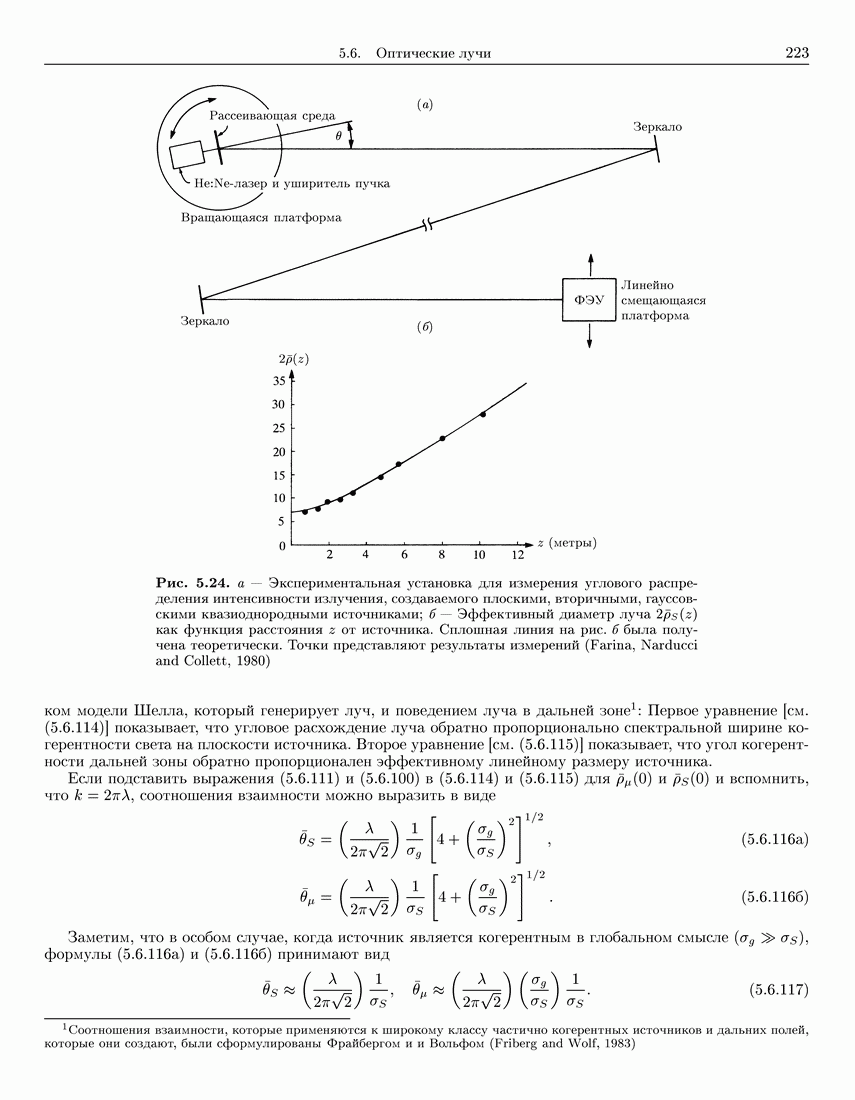
- 5.6. Оптические лучи
- 5.6.1. Монохроматические лучи
- 5.6.2. Пример: монохроматические гауссовские лучи
- 5.6.3. Частично когерентные лучи
- 5.6.4. Гауссовские лучи модели Шелла
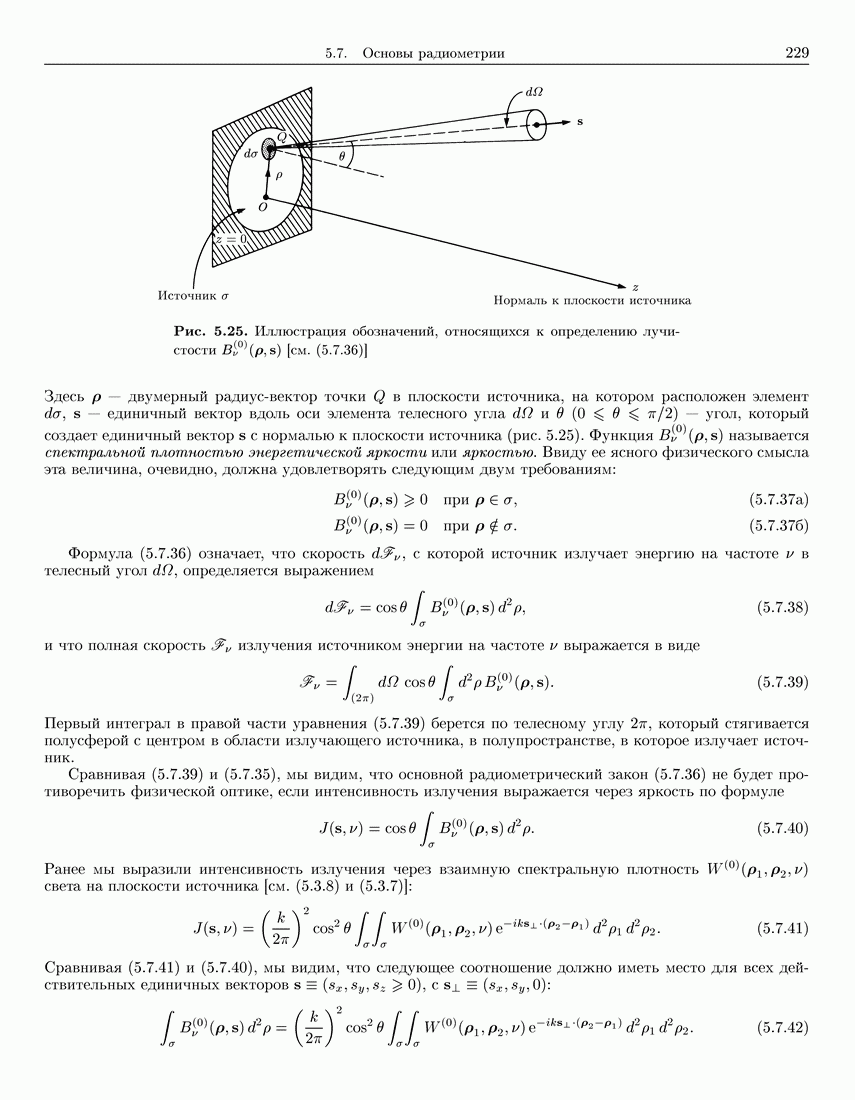
- 5.7. Основы радиометрии
- 5.7.1. Плотность энергии, поток энергии и закон сохранения энергии в скалярных волновых полях
- 5.7.2. Основные понятия радиометрии
- 5.7.3. Функция энергетической яркости от плоских вторичных квазиоднородных источников
- 5.7.4. Модель переноса энергии излучения
- 5.7.5. Радиометрия как коротковолновой предел статистической волновой теории с квазиоднородными источниками
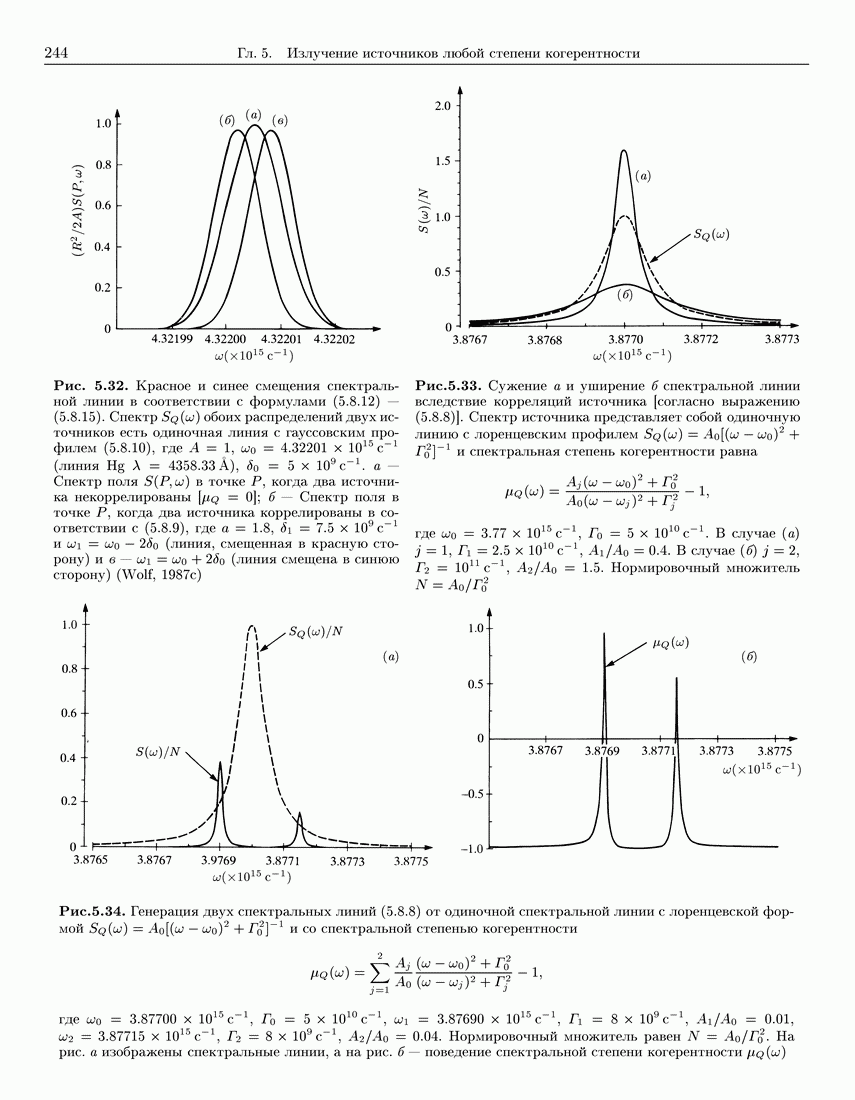
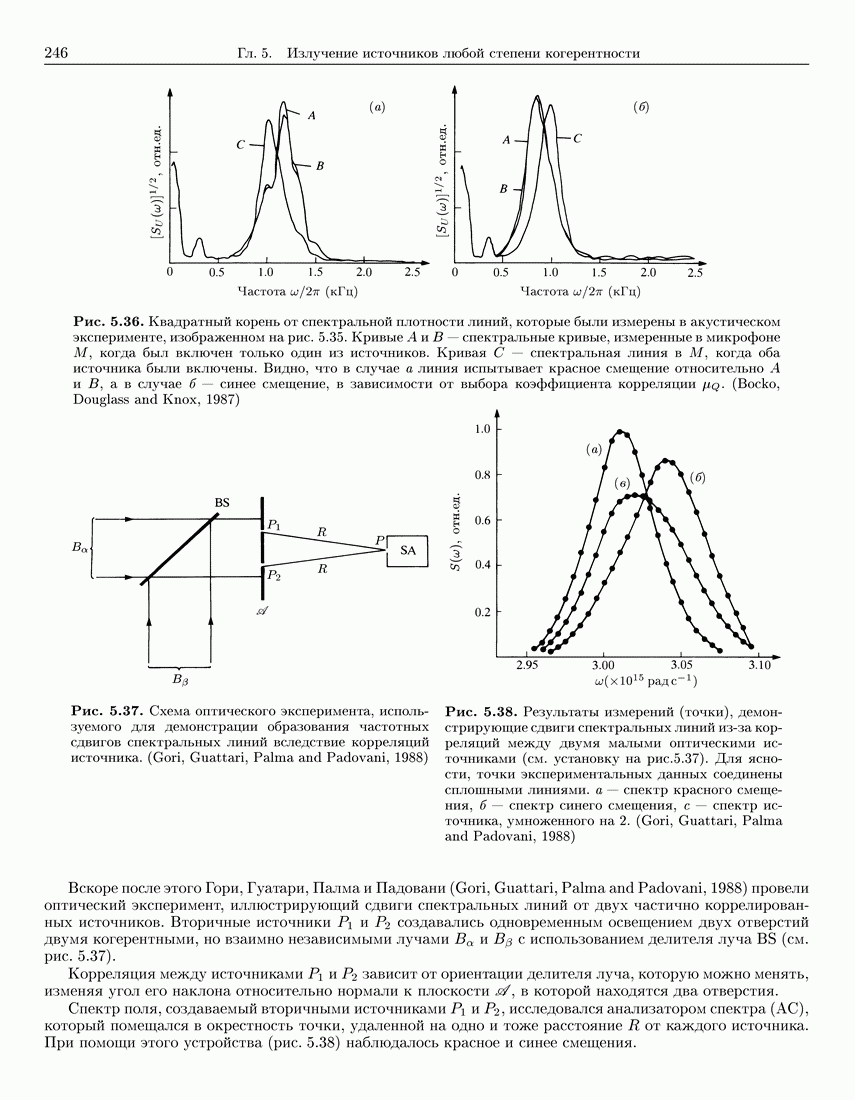
- 5.8. Влияние пространственной когерентности источника на спектр излучаемых полей
- 5.8.2. Спектр дальнего поля, образуемого плоскими вторичными квазиоднородными источниками
- 5.8.3. Условие для спектральной инвариантности: закон скейлинга для плоских вторичных квазиоднородных источников
- Приложение 5.1 Вывод асимптотического приближения (5.7.103)
- Приложение 5.2 Теорема произведения для гауссовских функций
- Глава 6. ТЕОРИЯ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА ВЕКТОРНЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
- 6.2. Равновременная 2×2-матрица когерентности хорошо коллимированного, однородного, квазимонохроматического светового луча
- 6.3. Полностью неполяризованный и полностью поляризованный свет. Степень поляризации
- 6.3.2. Полностью поляризованный свет
- 6.3.3. Степень поляризации
- 6.4. Прохождение квазимонохроматического луча через линейные, не формирующие изображения устройства
- 6.5. Обобщенные матрицы когерентности второго порядка и тензоры когерентности стационарного электромагнитного поля
- 6.5.2. Дифференциальные уравнения первого порядка для распространения тензоров когерентности
- 6.5.3. Волновые уравнения для распространения тензоров когерентности
- 6.6. Тензоры взаимной спектральной плотности второго порядка стационарного электромагнитного поля
- 6.6.1. Электрический, магнитный и смешанный тензоры взаимной спектральной плотности
- 6.6.2. Дифференциальные уравнения первого порядка для распространения тензоров взаимной спектральной плотности
- 6.6.3. Уравнения Гельмгольца для распространения тензоров взаимной спектральной плотности
- Глава 7. ПРИМЕНЕНИЯ ТЕОРИИ КОГЕРЕНТНОСТИ ВТОРОГО ПОРЯДКА
- 7.2. Звездная интерферометрия
- 7.3. Интерференционная спектроскопия
- 7.3.2. Проблема фазы
- 7.4. Когерентность поперечных мод лазерного резонатора
- 7.4.1. Условия устойчивости для взаимной спектральной плотности света на зеркале резонатора
- 7.4.2. Природа решений интегрального уравнения (7.4.7)
- 7.5. Диэлектрический отклик и спектр индуцированной поляризации во флуктуирующей среде
- 7.5.1. Среда, макроскопические свойства которой не изменяются со временем
- 7.5.2. Среда, макроскопические свойства которой зависят от времени детерминированным образом
- 7.5.3. Среда, макроскопические свойства которой случайным образом меняются во времени
- 7.6. Рассеяние от случайных сред
- 7.6.1. Основные уравнения для детерминированного рассеяния
- 7.6.2. Рассеяние на детерминированной среде в приближении Борна первого порядка
- 7.6.3. Рассеяние случайной средой в приближении Борна первого порядка
- 7.6.4. Некоторые частные случаи
- 7.6.5. Рассеяние от простой жидкости
- Приложение 7.1 Вычисление среднего значения … (выражение (7.6.36))
- Глава 8. КОРРЕЛЯЦИИ ОПТИЧЕСКИХ ПОЛЕЙ ВЫСШЕГО ПОРЯДКА
- 8.2. Пространственно-временные корреляционные функции произвольного порядка
- 8.3. Пространственно-частотные корреляционные функции произвольного порядка
- 8.4. Корреляционные функции полей, подчиняющихся гауссовской статистике
- 8.5. Представление по когерентным модам взаимных спектральных плотностей произвольного порядка
- 8.5.2. Одномодовое поле
- 8.5.3. Поля, подчиняющиеся гауссовской статистике
- Глава 9. ПОЛУКЛАССИЧЕСКАЯ ТЕОРИЯ ФОТОДЕТЕКТИРОВАНИЯ
- 9.2. Обзор элементарной квантовой механики
- 9.3. Дифференциальная вероятность фотодетектирования
- 9.4. Совместные вероятности многократного фотодетектирования
- 9.5. Интегральные вероятности детектирования
- 9.6. Фотоэлектрическое детектирование во флуктуирующих полях
- 9.6.1. Фотоэлектрическая группировка
- 9.7. Статистика фотоэлектрических отсчетов флуктуирующего поля
- 9.8. Флуктуации фотоэлектрического тока
- 9.8.2. Свет от теплового источника
- 9.8.3. Спектральная плотность фототока
- 9.9. Эффект Хэнбери Брауна — Твисса (полуклассическое рассмотрение)
- 9.10. Звездная интерферометрия интенсивностей
- 9.11. Спектроскопия флуктуаций
- Глава 10. КВАНТОВАНИЕ СВОБОДНОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 10.2. Гамильтониан классического поля и канонические уравнения движения
- 10.2.2. Единичные векторы поляризации
- 10.2.3. Энергия электромагнитного поля
- 10.3. Каноническое квантование поперечного поля
- 10.4. Энергетический спектр; фотоны
- 10.4.1. Фоковские состояния
- 10.4.2. Псевдолокализованные фотоны
- 10.4.3. Базис фоковских состояний
- 10.4.4. q-представление фоковских состояний
- 10.4.5. Зависимость операторов поля от времени
- 10.5. Импульс квантованного поля
- 10.6. Момент количества движения квантованного поля.
- 10.6.2. Разложение полного момента количества движения
- 10.6.3. Собственный (спиновый) момент количества движения
- 10.6.4. Орбитальный момент количества движения
- 10.7. Операторы фазы квантованного поля
- 10.7.2. Операторы косинуса и синуса
- 10.7.3. Оператор фазы на основе проекционного оператора на фазовые состояния
- 10.7.4. Операционно определенные фазовые операторы
- 10.8. Пространственно-временные коммутационные соотношения
- 10.9. Вакуумные флуктуации
- 10.9.1. Флуктуации локально усредненных полей
- 10.9.2. Порядок величины вакуумных флуктуаций
- 10.9.3. Сила Казимира между проводниками
- 10.9.4. Лэмбовский сдвиг
- 10.9.5. Вакуумные эффекты в делителе пучка
- 10.10. Непрерывное фоковское пространство
- 10.11. Некоторые теоремы операторной алгебры
- 10.11.2. Теоремы о преобразовании подобия
- 10.11.3. Теоремы о производных
- 10.11.4. Нормальный и антинормальный порядок
- 10.11.5. Теорема Кемпбелла — Бейкера — Хаусдорфа.
- Глава 11. КОГЕРЕНТНЫЕ СОСТОЯНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
- 11.2. Фоковское представление когерентных состояний
- 11.3. Когерентное состояние как смещенное вакуумное состояние. Оператор смещения
- 11.3.1. Свойства оператора смещения
- 11.4. q-представление когерентных состояний
- 11.5. Эволюция во времени и соотношения неопределенностей
- 11.5.1. Произведение канонических неопределенностей
- 11.5.2. Более общие состояния с минимальной неопределенностью
- 11.6. Когерентные состояния как базис. Неортогональность и переполненность
- 11.6.1. Линейная зависимость когерентных состояний
- 11.6.2. Переполненность
- 11.6.3. Представление операторов по когерентным состояниям
- 11.6.4. Вычисление матричных элементов нормально упорядоченных операторов
- 11.7. Представление состояний и операторов целыми функциями
- 11.8. Диагональное представление оператора плотности по когерентным состояниям (Р-представление Глаубера — Сударшана)
- 11.8.1. Плотности квазивероятности. Распределение Вигнера
- 11.8.2. Два достоинства диагонального представления
- 11.8.3. Диагональное представление p с помощью последовательности функций
- 11.8.4. Диагональное представление антинормально упорядоченного оператора плотности
- 11.8.5. Интегральное представление функции …
- 11.8.6. Примеры
- 11.9. Оптическая теорема эквивалентности для нормально упорядоченных операторов
- 11.9.1. Квантовые характеристические функции
- 11.10. Более общие представления в фазовом пространстве
- 11.10.2. Упорядочение операторов
- 11.10.3. Приложение к квантовым средним и диагональному представлению по когерентным состояниям
- 11.11. Многомодовые поля
- 11.11.1. Когерентные состояния в непрерывном представлении
- 11.12. Положительно- и отрицательно-частотные операторы поля
- 11.12.1. Коммутационные соотношения
- 11.12.2. Нормально упорядоченные корреляционные функции
- 11.13. Поле, создаваемое классическим током
- Глава 12. КВАНТОВЫЕ КОРРЕЛЯЦИИ И ФОТОННАЯ СТАТИСТИКА
- 12.2. Фотоэлектрическое измерение оптического поля; нормальное упорядочение
- 12.2.1. Детектирование нескольких фотонов; корреляционные функции высшего порядка
- 12.2.2. Символы и операторы упорядочения
- 12.3. Оператор фотонной плотности
- 12.4. Интерференционные эксперименты; корреляционные функции второго порядка
- 12.5. Корреляционные функции и взаимные спектральные плотности произвольного порядка
- 12.5.1. Свойства корреляционных функций
- 12.5.2. Взаимные спектральные плотности произвольного порядка
- 12.5.3. Независящие от фазы весовые функции
- 12.6. Степень и порядок когерентности
- 12.7. Значение когерентности второго порядка
- 12.7.2. Корреляции произвольного порядка
- 12.7.3. Оператор плотности для поля
- 12.7.4. Волновые пакеты в качестве мод
- 12.8. Стационарность, однородность, изотропность
- 12.8.2. Условие для оператора плотности
- 12.8.3. Свойства взаимных спектральных плотностей в случае стационарных полей
- 12.8.4. Однородность
- 12.8.5. Изотропность
- 12.9. Антинормально упорядоченные корреляционные функции
- 12.9.2. Замена дифференциальными операторами
- 12.9.3. Весовой функционал для антинормально упорядоченных корреляционных функций
- 12.10. Фотонная статистика
- 12.10.2. Условия для неклассических состояний
- 12.10.3. Моменты n
- 12.10.4. Производящие функции для числа фотонов при нормальном и антинормальном порядке
- 12.11. Проблема локализации фотонов
- 12.11.1. Оператор числа фотонов, определяемый в конфигурационном пространстве
- 12.11.2. Коммутационные соотношения
- 12.11.3. Собственные состояния …
- 12.11.4. Статистика фотона в конечном объеме
- 12.11.5. Полихроматические фотоны и не локальность
- 12.12. Влияние аттенюатора или делителя пучка на квантовое поле
- 12.12.2. Корреляции фотонов
- 12.12.3. Интерферометр Майкельсона
- 12.12.4. Связь между входными и выходными состояниями для делителя пучка
- 12.13. Влияние поляризатора на поле
- 12.14. Локальность Эйнштейна и корреляции фотонов
- 12.14.1. Парадокс Эйнштейна — Подольского — Розена для перепутанного двухфотонного состояния
- 12.14.2. Неравенства Белла
- 12.14.3. Форма Клаузера — Хорна неравенства Белла
- 12.14.4. Экспериментальное подтверждение
- 12.14.5. Неклассические состояния и неравенства Белла
- Глава 13. ИЗЛУЧЕНИЕ ИСТОЧНИКОВ, НАХОДЯЩИХСЯ В СОСТОЯНИИ ТЕПЛОВОГО РАВНОВЕСИЯ
- 13.1. Излучение черного тела
- 13.1.2. Статистика фотонов
- 13.1.3. Поляризация
- 13.1.4. Спектральные распределения
- 13.1.5. Диагональное представление p по когерентным состояниям
- 13.1.6. Корреляционные функции излучения черного тела
- 13.1.7. Функции корреляции высокого порядка
- 13.1.8. Изотропность излучения черного тела
- 13.1.9. Флуктуации интенсивности излучения черного тела
- 13.2. Свет от теплового источника
- 13.3. Пучки стационарного света от теплового источника
- 13.3.2. Статистика фотонов при одинаковых средних числах заполнения
- Глава 14. КВАНТОВАЯ ТЕОРИЯ ФОТОДЕТЕКТИРОВАНИЯ
- 14.1. Взаимодействия квантованного электромагнитного поля
- 14.1.1. Решение по теории возмущений в картине взаимодействия
- 14.1.2. Электромагнитное взаимодействие между полями и зарядами
- 14.1.3. Многополюсный гамильтониан
- 14.2. Вероятность одноэлектронного фотодетектирования
- 14.2.1. Применение к чистому когерентному состоянию
- 14.2.2. Вычисление вероятности в квазимонохроматическом приближении
- 14.2.3. Вычисление электронного матричного элемента
- 14.2.4. Вычисление вероятности детектирования для аксиально симметричного детектора
- 14.3. N-электронный фотодетектор
- 14.4. Вероятность многократного фотоэлектрического детектирования
- 14.5. Вероятность многократного детектирования при произвольном начальном состоянии поля
- 14.6. Фотоэлектрические корреляции
- 14.6.1. Эффект Хэнбери Брауна — Твисса (квантовая трактовка)
- 14.6.2. Корреляции фототоков
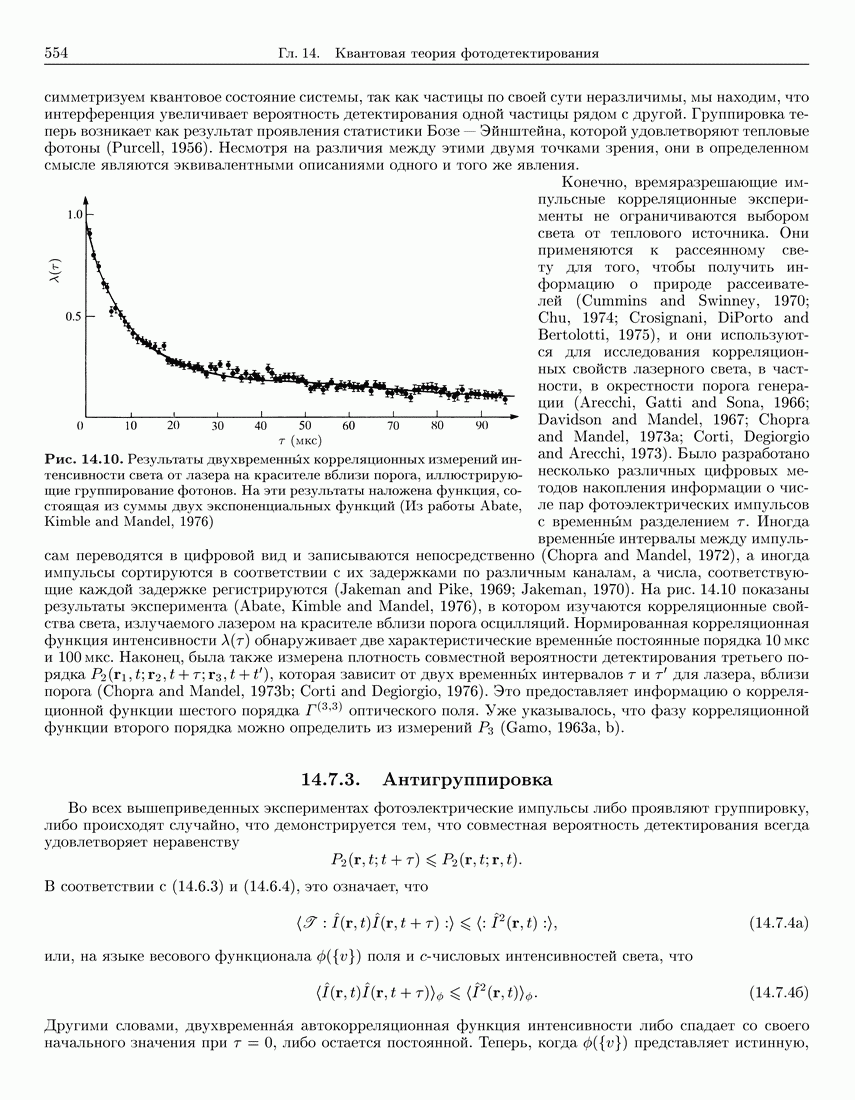
- 14.7. Группировка и антигруппировка
- 14.7.2. Двухвременные импульсные корреляционные измерения
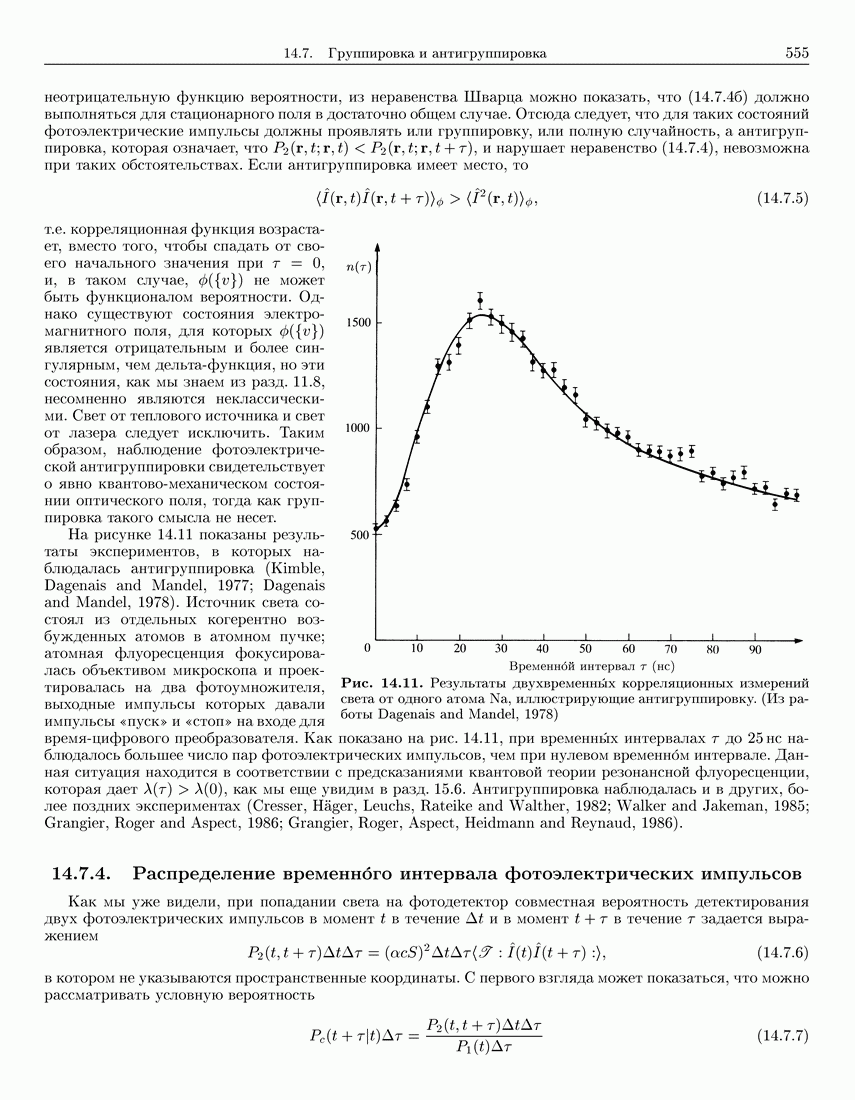
- 14.7.3. Антигруппировка
- 14.7.4. Распределение временного интервала фотоэлектрических импульсов
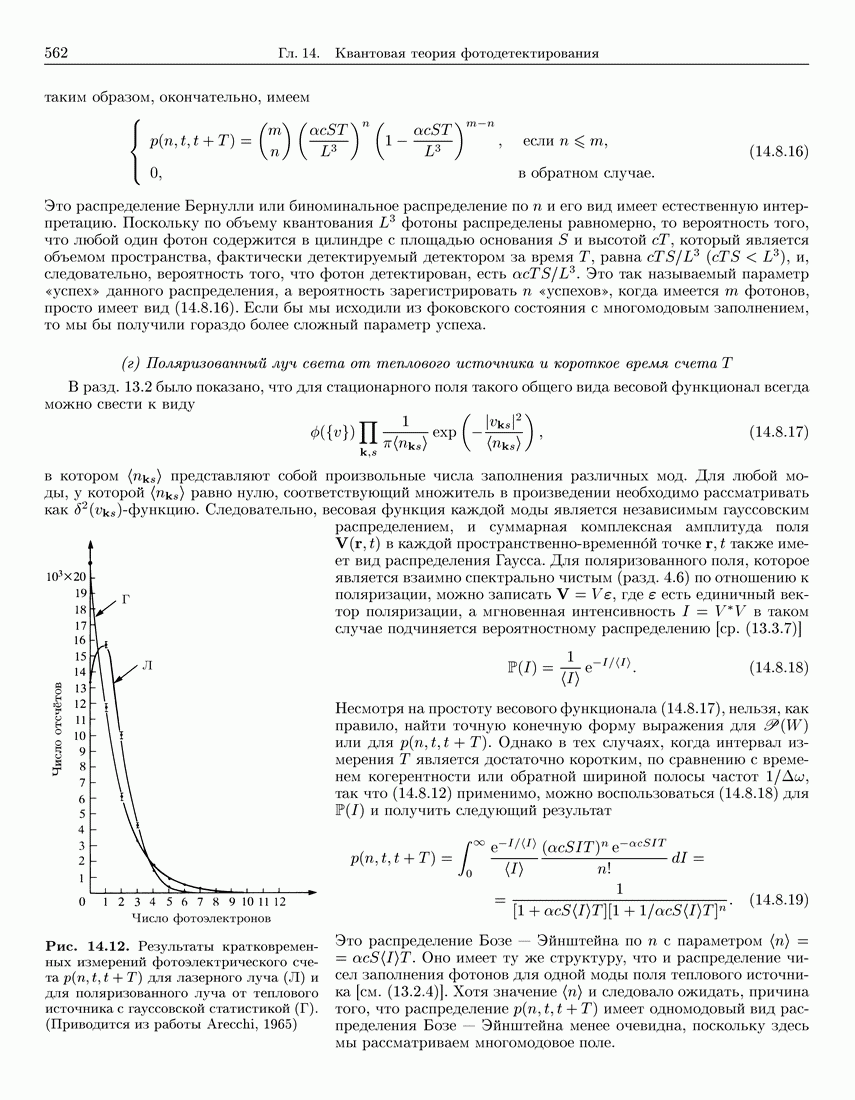
- 14.8. Статистика фотоэлектрического счета
- 14.8.2. Примеры вероятности детектирования
- 14.8.3. Естественная мера времени когерентности
- 14.9. Свойства вероятности детектирования …
- 14.9.1. Производящие функции и проблема обратного преобразования
- 14.9.2. Второй момент и субпуассоновская статистика счета
- 14.9.3. Получение корреляционных функций из статистики счета
- Глава 15. ВЗАИМОДЕЙСТВИЕ СВЕТА И ДВУХУРОВНЕГО АТОМА
- 15.1. Динамические переменные для двухуровневого атома
- 15.1.1. Атомная энергия и атомный дипольный момент
- 15.2. Блоховское представление
- 15.2.1. Средние значения спиновых операторов
- 15.3. Взаимодействие атома с классическим полем
- 15.3.1. Уравнения Блоха
- 15.3.2. Уравнения Блоха во вращающейся системе координат
- 15.3.3. Задача Раби
- 15.3.4. Отклик атома на воздействие лазерного импульса
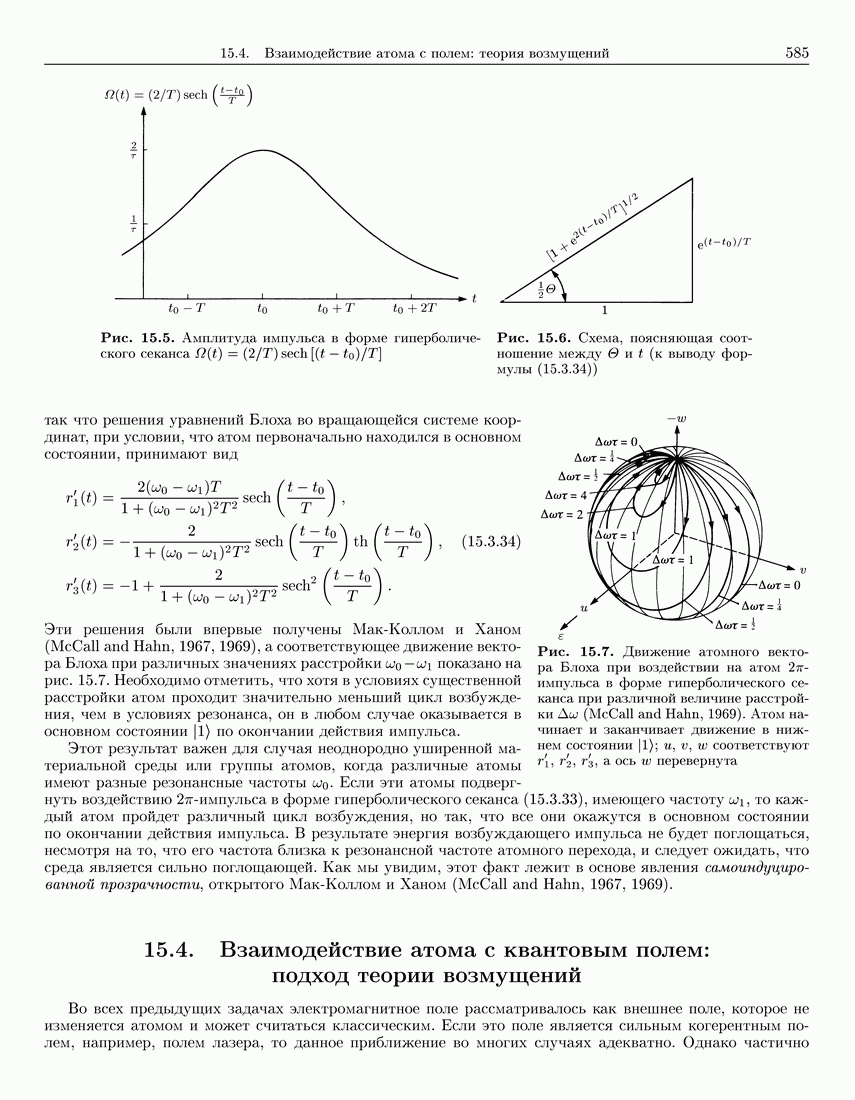
- 15.3.5. 2«пи»-импульс в форме гиперболического секанса
- 15.4. Взаимодействие атома с квантовым полем: подход теории возмущений
- 15.4.1. Поглощение и излучение фотонов
- 15.5. Взаимодействие атома с квантовым полем: общее рассмотрение
- 15.5.1. Гейзенберговские уравнения движения
- 15.5.2. Приближенное решение — коэффициент Эйнштейна A и лэмбовский сдвиг
- 15.5.3. Интегральные уравнения движения
- 15.5.4. Спонтанное излучение
- 15.6. Резонансная флуоресценция
- 15.6.2. Сечение рассеяния атомов
- 15.6.3. Спектр флуоресценции
- 15.6.4. Корреляция интенсивности флуоресценции
- 15.6.5. Измерения антигруппировки фотонов
- 15.6.6. Субпуассоновская статистика фотонов
- 15.7. Отклонение атомов светом
- 15.7.1. Передача импульса после n спонтанных испусканий
- 15.7.2. Передача импульса при вынужденном излучении или градиентные силы в сильном поле
- 15.8. Охлаждение и пленение атомов
- 15.8.2. Оценка наименьшей достижимой температуры, основанная на балансе энергии
- Глава 16. КОЛЛЕКТИВНЫЕ АТОМНЫЕ ВЗАИМОДЕЙСТВИЯ
- 16.1. Затухание оптической свободной индукции
- 16.2. Фотонное эхо
- 16.3. Самоиндуцированная прозрачность
- 16.3.1. Уравнение движения для огибающей импульса
- 16.3.2. Теорема площадей Мак-Колла и Хана
- 16.3.3. Форма импульса
- 16.3.4. Скорость импульса
- 16.4. Оптическая бистабильность
- 16.4.1. Абсорбционная бистабильность в кольцевом резонаторе
- 16.4.2. Дисперсионная бистабильность
- 16.4.3. Хаос в оптической бистабильности
- 16.5. Коллективные атомные состояния и коллективные динамические переменные
- 16.5.1. Состояния Дике
- 16.5.2. Вырождение состояний Дике
- 16.6. Кооперативное атомное излучение
- 16.6.2. Кооперативное излучение атомов, находящихся в факторизованном состоянии
- 16.6.3. Временная эволюция сверхизлучения
- 16.6.4. Некоторые дополнительные усложнения
- 16.6.5. Более общее кооперативное излучение
- 16.6.6. Сверхизлучательные классические осцилляции
- 16.7. Атомные когерентные состояния
- 16.7.1. Блоховское представление атомного когерентного состояния
- 16.7.2. Неортогональность и переполненность
- 16.7.3. Атомные состояния, создаваемые классическим полем
- Глава 17. ОБЩИЕ МЕТОДЫ ИЗУЧЕНИЯ ВЗАИМОДЕЙСТВУЮЩИХ СИСТЕМ
- 17.1. Квантовая теорема регрессии
- 17.1.1. Одновременные средние значения
- 17.1.2. Многовременные средние значения
- 17.1.3. Спонтанное излучение атома
- 17.1.4. Резонансная флуоресценция двухуровневого атома
- 17.1.5. Квантовая теорема регрессии для нормально упорядоченных операторов поля
- 17.2. Флуктуационно-диссипационная теорема
- 17.2.2. Квантово-механическая линейная диссипативная система
- 17.2.3. Мощность рассеяния
- 17.2.4. Флуктуации тока в состоянии теплового равновесия
- 17.2.5. Спектральная плотность флуктуаций
- 17.2.6. Броуновское движение частицы
- 17.2.7. Флуктуации поля в излучении черного тела
- 17.3. Основные кинетические уравнения
- 17.3.2. Обобщенное основное кинетическое уравнение Цванцига
- 17.3.3. Применение к кинетическому уравнению Паули
- 17.3.4. Применение к задаче Дике
- 17.4. Источники квантового шума и квантовые уравнения Ланжевена
- 17.4.2. Уравнения движения квантовой системы
- 17.4.3. Коммутационные соотношения
- 17.4.4. Двухвременные корреляционные функции
- 17.4.5. Уравнение Ланжевена для возбужденной системы осцилляторов
- 17.4.6. Необратимость и стрела времени
- Глава 18. ОДНОМОДОВЫЙ ЛАЗЕР
- 18.1.1. Условие лазерной генерации
- 18.2. Полуклассическая теория лазера
- 18.2.1. Нормальные моды резонатора
- 18.2.2. Уравнение движения для лазерного поля
- 18.2.3. Аналогия с фазовым переходом
- 18.3. Полуклассическая теория лазера с учетом шума спонтанного излучения
- 18.3.1. Уравнение Фоккера — Планка
- 18.3.2. Стационарное решение
- 18.3.3. Аналогия с фазовым переходом для флуктуирующего лазерного поля
- 18.3.4. Моменты интенсивности света
- 18.4. Квантовая теория лазера
- 18.4.1. Основное кинетическое уравнение для лазерного поля
- 18.4.2. Статистика фотонов
- 18.4.3. Стационарная вероятность
- 18.5. Взаимосвязь между квантовой и полуклассической теориями лазера
- 18.5.2. Стационарное решение основного кинетического уравнения
- 18.6. Решение зависящего от времени уравнения движения
- 18.6.1. Развитие лазерного поля из вакуумного состояния
- 18.6.2. Экспериментальные исследования
- 18.7. Корреляционные функции
- 18.7.1. Функции Грина
- 18.7.2. Корреляция интенсивности
- 18.7.3. Функция корреляции амплитуды поля и спектральная плотность
- 18.7.4. Корреляции высшего порядка
- 18.8. Нестабильности лазера и хаос
- 18.8.2. Линейный анализ устойчивости
- 18.8.3. Примеры нестабильностей лазера
- 18.8.4. Тест на детерминированный хаос
- Глава 19. ДВУХМОДОВЫЙ КОЛЬЦЕВОЙ ЛАЗЕР
- 19.1.1. Учет флуктуаций спонтанного излучения
- 19.2. Стационарное решение
- 19.2.1. Моменты интенсивности света
- 19.2.2. Сравнение с экспериментом
- 19.3. Аналогия с фазовым переходом
- 19.3.2. Случай константы связи …: фазовый переход второго рода
- 19.3.3. Случай константы связи …: фазовый переход первого рода
- 19.3.4. Скрытая теплота фазового перехода
- 19.4. Зависящее от времени решение в случае константы связи …
- 19.5. Зависящее от времени решение в более общем случае взаимодействия между модами …
- 19.5.1. Переключение мод и времена первого прохождения
- 19.5.2. Распределения времен первого прохождения
- Глава 20. ЛИНЕЙНЫЙ УСИЛИТЕЛЬ СВЕТА
- 20.2. Основное кинетическое уравнения для поля усилителя
- 20.3. Решение основного кинетического уравнения
- 20.4. Статистика фотонов
- 20.4.2. Полностью инвертированный усилитель света
- 20.5. Сжатый свет
- 20.6. Условие, при котором поле на выходе усилителя является классическим
- Глава 21. СЖАТЫЕ СОСТОЯНИЯ СВЕТА
- 21.2. Квантовая природа сжатого состояния
- 21.3. Унитарный оператор сжатия
- 21.3.1. Сжатие двухфотонного когерентного состояния
- 21.3.2. Действие оператора сжатия на произвольное состояние
- 21.4. Идеальное сжатое состояние
- 21.5. Двухфотонное когерентное состояние
- 21.5.1. Преобразованные фоковские состояния
- 21.5.2. Представление по когерентным состояниям двухфотонного когерентного состояния
- 21.5.3. Фотонная статистика двухфотонного когерентного состояния
- 21.6. Детектирование сжатия гомодинированием с когерентным светом
- 21.7. Сжатие, реализованное на практике: вырожденная параметрическая вниз-конверсия
- 21.7.1. Создание сжатого состояния при вырожденной параметрической вниз-конверсии
- 21.8. Широкополосный сжатый свет
- 21.8.1. Гомодинирование и корреляционные функции
- 21.8.2. Квадратурные корреляции
- 21.8.3. Спектральные корреляции
- 21.8.4. Спектрально-компонентное сжатие и степень сжатия
- 21.8.5. Примеры степени сжатия Q(w)
- 21.9. Сжатие высшего порядка
- 21.9.1. Сжатие N-ого порядка двухфотонного когерентного состояния
- 21.9.2. Амплитудно-квадратичное сжатие
- Глава 22. НЕКОТОРЫЕ КВАНТОВЫЕ ЭФФЕКТЫ В НЕЛИНЕЙНОЙ ОПТИКЕ
- 22.2. Энергия поля в диэлектрике
- 22.3. Генерация оптических гармоник
- 22.4. Параметрическая вниз-конверсия
- 22.4.2. Статистика фотонов
- 22.4.3. Доказательство неклассического поведения
- 22.4.4. Многомодовая теория возмущений процесса параметрического распада
- 22.4.5. Перепутанное квантовое состояние
- 22.4.6. Скорость вниз-конверсии
- 22.4.7. Временной интервал между сигнальным и холостым фотонами
- 22.4.8. Интерференционные эксперименты с двумя вниз-конверторами
- 22.5. Вырожденное четырехволновое смешение
- 22.5.2. Применение к когерентному состоянию
- 22.5.3. Сжатие в четырехволновом смешении
- 22.5.4. Фазовое сопряжение
- 22.6. Квантовые неразрушающие измерения
- 22.6.1. Эффект Керра — пример QND-переменной
- 22.6.2. Анализ интерференционного эксперимента
- 22.6.3. Вычисление видности интерференционных полос
- 22.6.4. Фазовый сдвиг зондирующей волны
- 22.6.5. Дополнительность