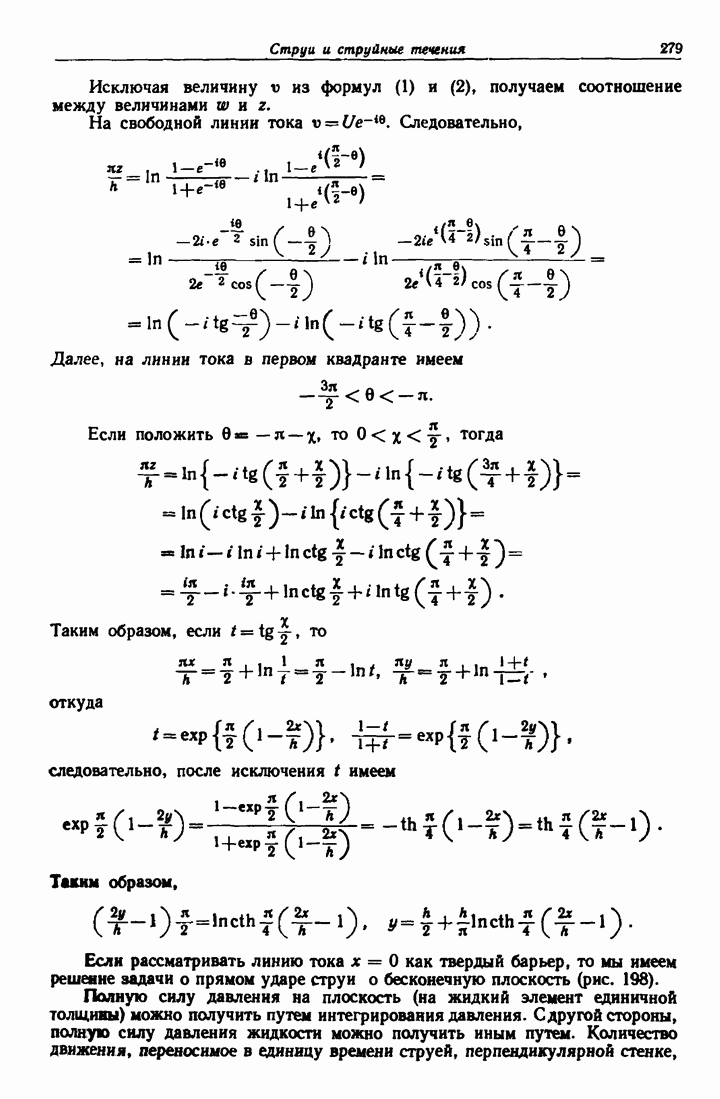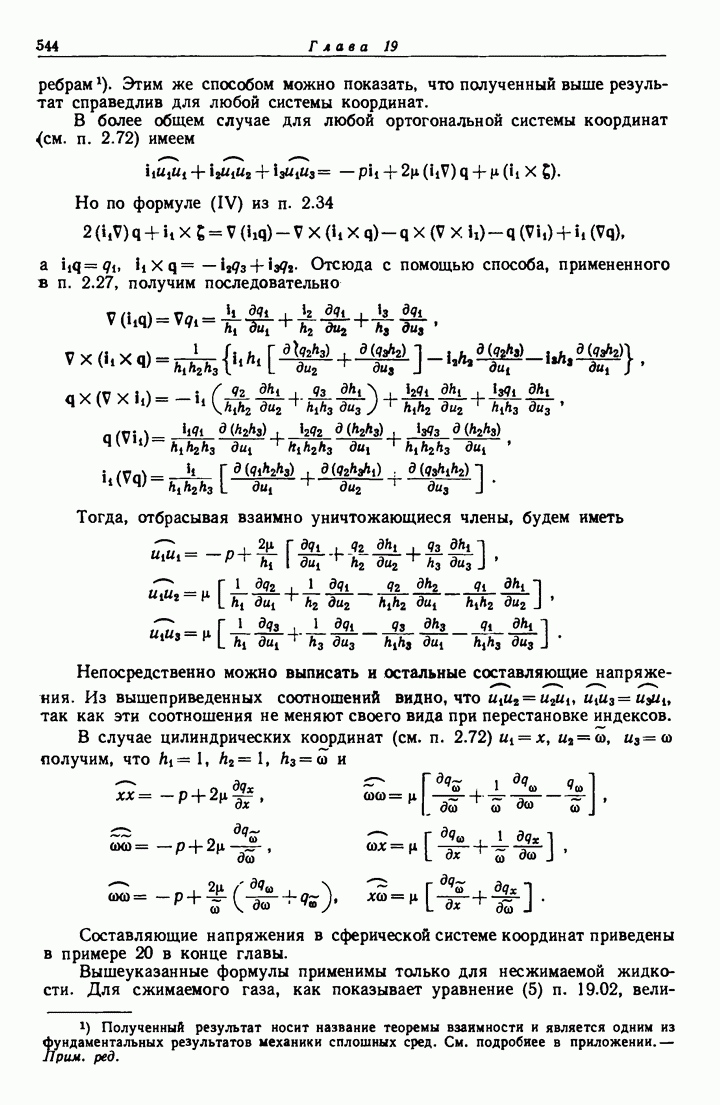| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
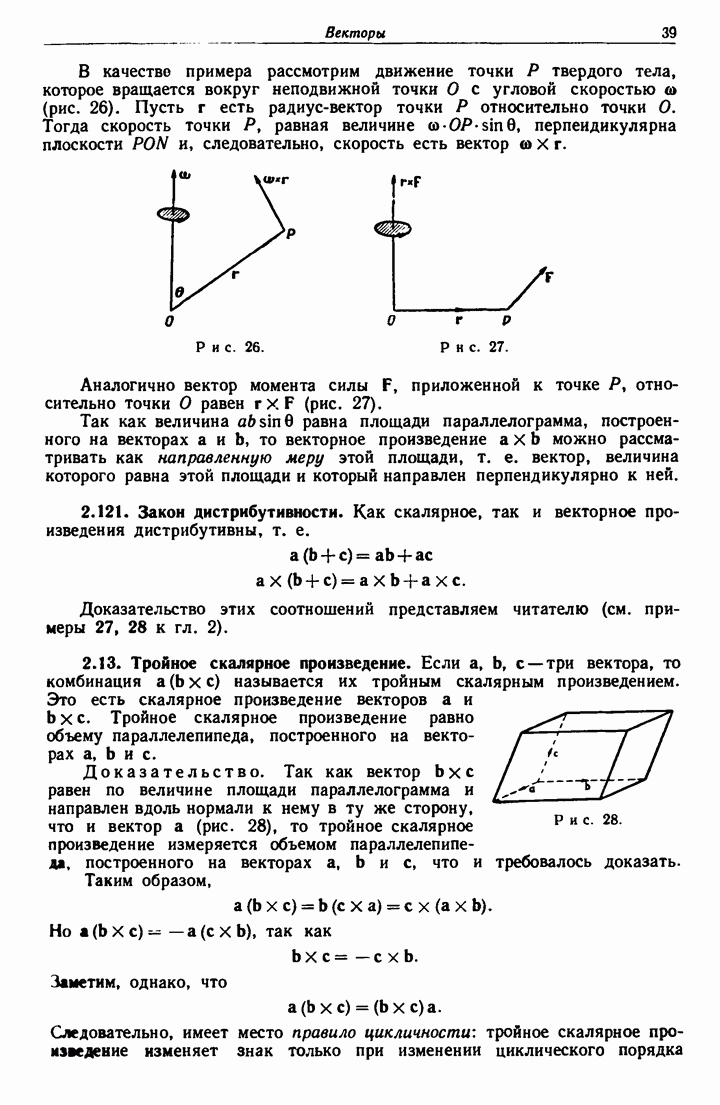
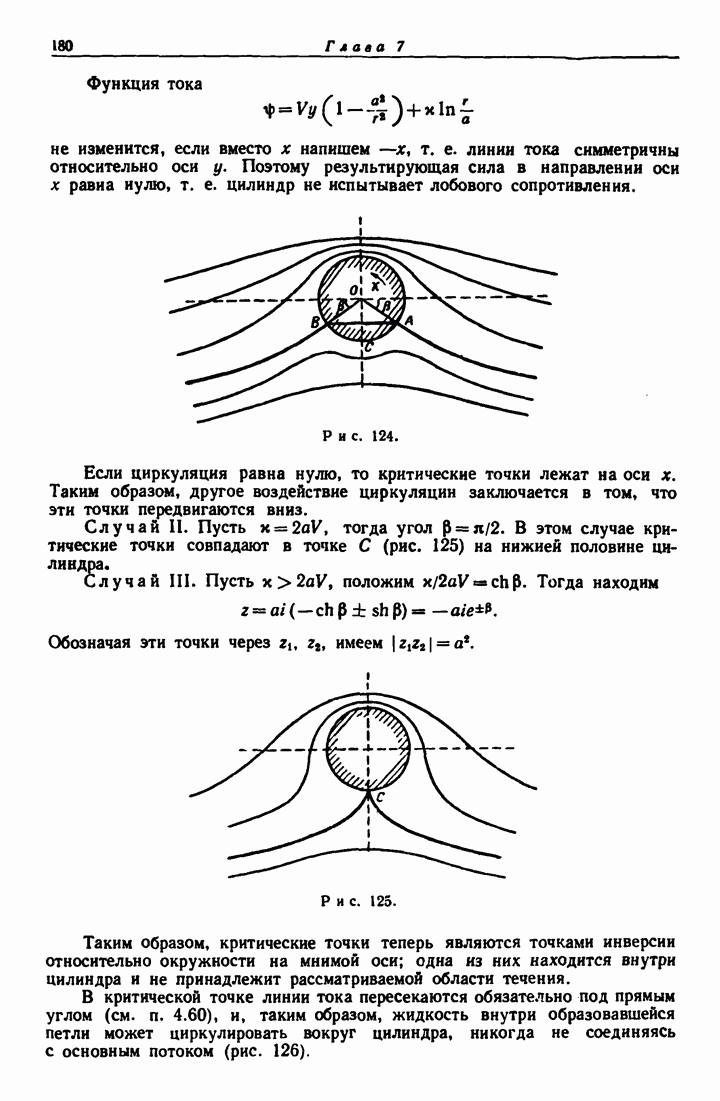
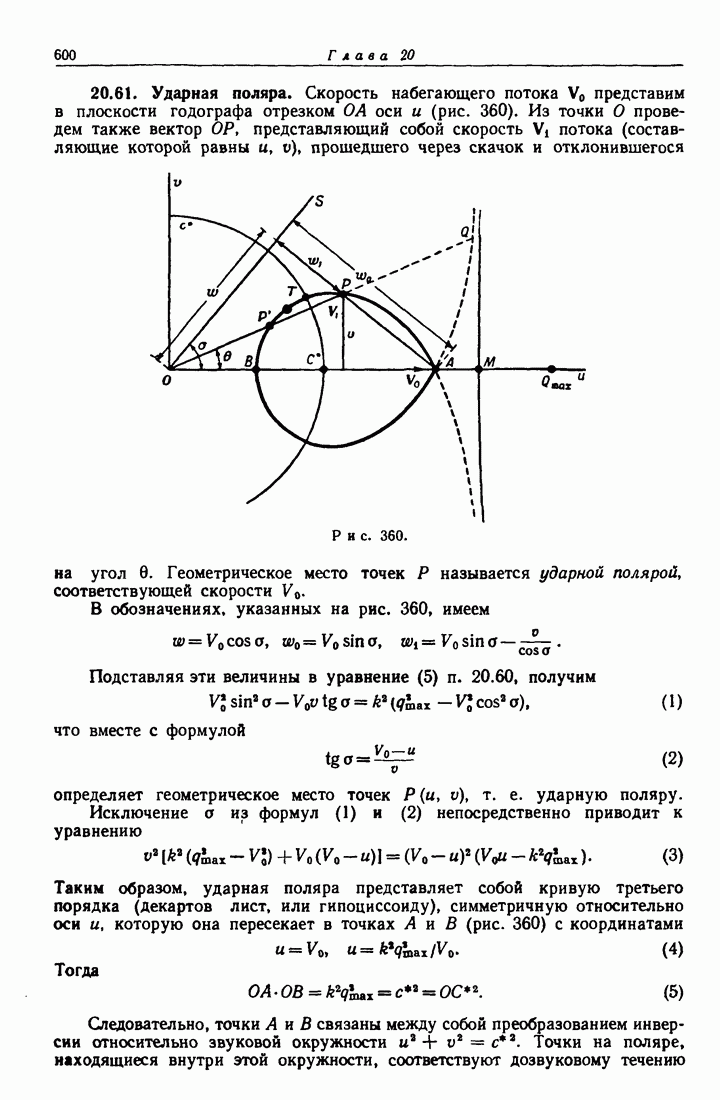
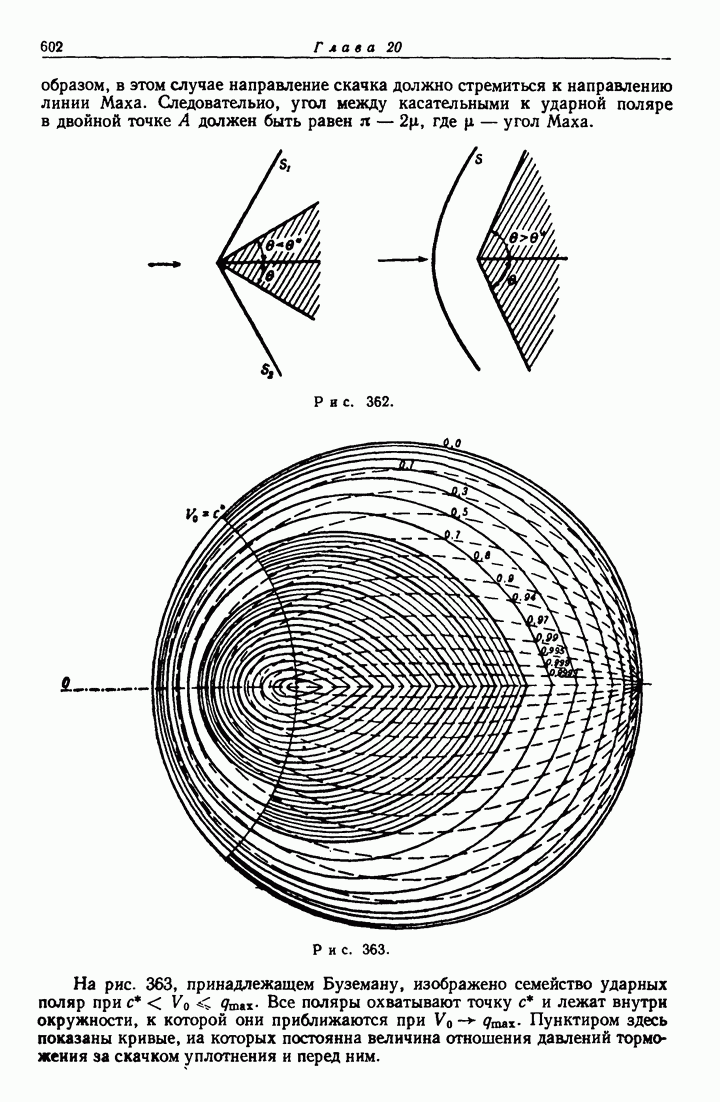
18.41. Круговая вихревая нить.
Рассмотрим круговую вихревую трубку С (см. рис. 329) весьма малого поперечного сечения а (вихревую нить). Тогда интенсивность этой нити будет, скажем,  Пусть
Пусть  некоторая точка на окружности С с центром
некоторая точка на окружности С с центром  причем
причем  Проведем отрезок
Проведем отрезок  равный и параллельный
равный и параллельный  Пусть угол
Пусть угол  равен
равен  и пусть
и пусть  Тогда элемент дуги в точке
Тогда элемент дуги в точке  будет
будет  а вектор вихря в
а вектор вихря в  будет направлен по касательной к С. Таким образом, вихрь в точке
будет направлен по касательной к С. Таким образом, вихрь в точке  равен
равен  где и
где и  единичные векторы оси со и перпендикуляра к меридиональной плоскости соответственно. Следовательно, по п. 18.22
единичные векторы оси со и перпендикуляра к меридиональной плоскости соответственно. Следовательно, по п. 18.22

Коэффициент при обращается в нуль по вышеуказанным причинам; в данном случае в этом легко убедиться непосредственно, выполнив интегрирование; коэффициент же при представляет собой модуль вектора В, и, следовательно, функция тока будет равна

Детальное исследование такого движения требует применения эллиптических функций. Можно, однако, заметить, что для точек, расположенных в плоскости кольца (которое рассматривается как кольцо с бесконечно малым поперечным сечением), радиальные скорости будут равны нулю. Это вытекает сразу из закона  Савара, упомянутого в п. 18.23. Таким образом, отсюда следует, что радиус кольца будет оставаться постоянным, а кольцо будет двигаться со скоростью, которая также должна быть постоянной, поскольку движение относительно кольца должно быть установившимся.
Савара, упомянутого в п. 18.23. Таким образом, отсюда следует, что радиус кольца будет оставаться постоянным, а кольцо будет двигаться со скоростью, которая также должна быть постоянной, поскольку движение относительно кольца должно быть установившимся.
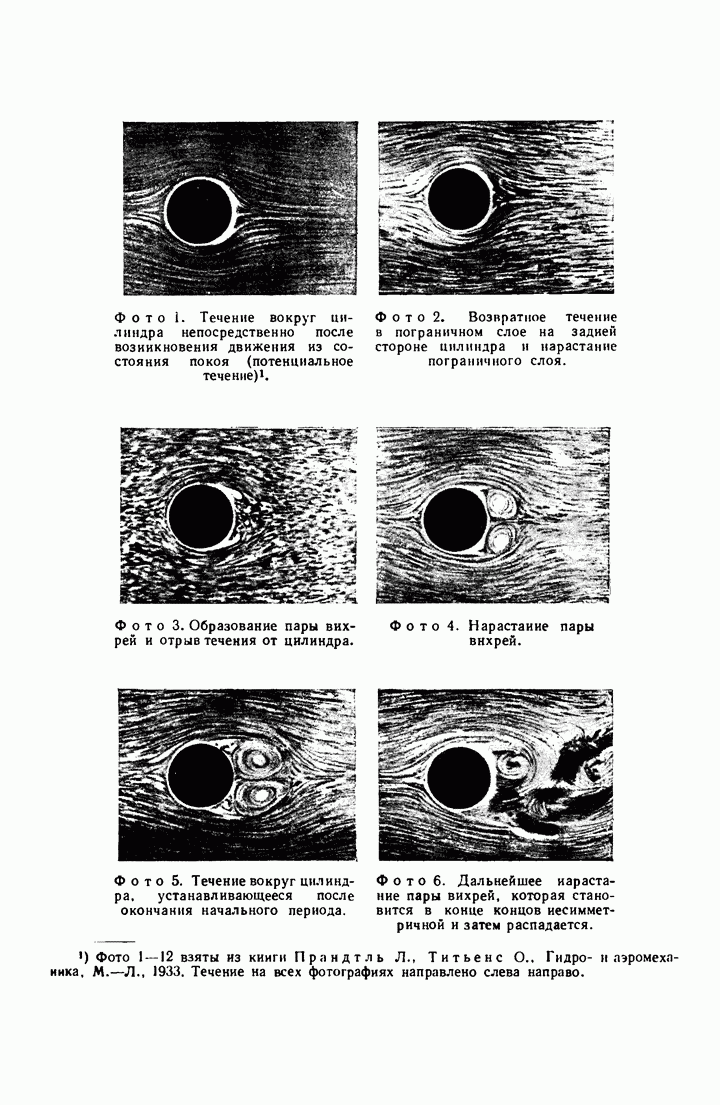
Если два таких вихревых кольца с одной и той же осью и одинаковым направлением вращения движутся одно за другим, то действие индуцированной скорости приводит к увеличению диаметра движущегося впереди кольца и уменьшению диаметра другого кольца. Второе кольцо может в конце концов пройти через первое, и тогда они поменяются ролями.
Если два одинаковых вихревых кольца с противоположными направлениями вращения сближаются, то индуцированная скорость будет стремиться увеличить каждое из этих колец, а на плоскости, проходящей посредине между кольцами, скорость будет перпендикулярна оси. Значит, если вихревое кольцо движется по направлению к стенке, которая параллельна плоскости этого кольца, то диаметр кольца будет непрерывно увеличиваться, а его скорость будет непрерывно уменьшаться.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава 1. УРАВНЕНИЕ БЕРНУЛЛИ
- 1.01. Размерности физических величин.
- 1.10. Скорость.
- 1.11. Линии тока и траектории частиц.
- 1.12. Трубки тока и струйки тока.
- 1.20. Плотность.
- 1.30. Давление.
- 1.40. Теорема Бернулли (специальная форма).
- 1.41. Поток в канале.
- 1.42. Замечания о теореме Бернулли.
- 1.43. Константа в теореме Бернулли.
- 1.44. Гидродинамическое давление.
- 1.50. Трубка Пито.
- 1.60. Работа газа при расширении.
- 1.61. Теорема Бернулли для сжимаемой жидкости.
- 1.62. Применение теоремы Бернулли к адиабатическому расширению.
- 1.63. Дозвуковой и сверхзвуковой потоки.
- 1.64. Газовый поток в сужающейся трубке.
- 1.70. Трубка Вентури.
- 1.71. Измерение скорости течения газа трубкой Вентури.
- 1.80. Истечение из отверстия.
- 1.82. Коэффициент сжатия.
- 1.90. Теорема Эйлера о количестве движения.
- 1.91. Сила, действующая на стенки тонкой трубки.
- 1.92. Парадокс Даламбера.
- 1.93. Поток за препятствием.
- Глава 2. ВЕКТОРЫ
- 2.10. Скаляры и векторы.
- 2.11. Скалярное произведение двух векторов.
- 2.12. Векторное произведение двух векторов.
- 2.13. Тройное скалярное произведение.
- 2.14. Тройное векторное произведение.
- 2.15. Разложение вектора.
- 2.16. Индефинитное, или диадное, произведение.
- 2.19. Скалярные и векторные поля.
- 2.20. Криволинейные, поверхностные и объемные интегралы.
- 2.22. Изменение скалярной функции координат.
- 2.23. Другое выражение для градиента функции.
- 2.24. Обобщенное определение оператора V.
- 2.32. Некоторые дифференциальные операции над одним вектором или скаляром.
- 2.33. Некоторые операции над произведением величин.
- 2.34. Применение оператора V к некоторым произведениям.
- 2.40. Анализ движения элемента жидкости.
- 2.41. Вихрь.
- 2.42. Циркуляция.
- 2.50. Теорема Стокса.
- 2.51. Следствия из теоремы Стокса.
- 2.52. Безвихревое движение.
- 2.53. Консервативное поле сил.
- 2.60. Теорема Гаусса.
- 2.61. Следствия из теоремы Гаусса.
- 2.62. Теорема Грина.
- 2.63. Приложения теоремы Грина.
- 2.70. Декартовы координаты.
- 2.71. Другое обозначение для оператора d/dr
- 2.72. Криволинейные ортогональные координаты.
- 2.73. Скорость изменения единичных векторов.
- Глава 3. УРАВНЕНИЯ ДВИЖЕНИЯ
- 3.20. Уравнение неразрывности.
- 3.30. Граничные условия (кинематические).
- 3.31. Граничные условия (физические).
- 3.32. Истечение из отверстия.
- 3.40. Скорость изменения количества движения.
- 3.41. Уравнение движения невязкой жидкости.
- 3.42. Теорема Эйлера о количестве движения.
- 3.43. Консервативные силы.
- 3.44. Уравнение движения в форме Лаграижа.
- 3.45. Установившееся движение.
- 3.50. Уравнение энергии.
- 3.51. Скорость изменения циркуляции.
- 3.52. Вихревое движение.
- 3.53. Сохраняемость вихревого движения.
- 3.54. Сохраняемость вихревых линий.
- 3.55. Относительное движение.
- 3.60. Безвихревое движение.
- 3.61. Уравнение для давления относительно подвижных осей.
- 3.62. Давление жидкости на препятствие.
- 3.64. Импульсивное движение.
- 3.70. Связность. Определение.
- 3.71. Ациклическое и циклическое безвихревые движения.
- 3.72. Кинетическая энергия жидкости.
- 3.73. Теорема Кельвина о минимуме энергии.
- 3.74. Среднее значение потенциала скоростей.
- 3.75. Среднее значение потенциала скоростей в перифрактической области.
- 3.76. Кинетическая энергия жидкости, занимающей бесконечную область.
- 3.77. Теоремы единственности.
- Глава 4. ДВУМЕРНОЕ ДВИЖЕНИЕ
- 4.10. Двумерное движение.
- 4.20. Двумерное установившееся движение жидкости.
- 4.21. Безвихревое движение.
- 4.22. Движение без деформации.
- 4.23. Вихрь.
- 4.24. Уравнения установившегося движения.
- 4.30. Функция тока.
- 4.31. Выражение скорости через функцию тока.
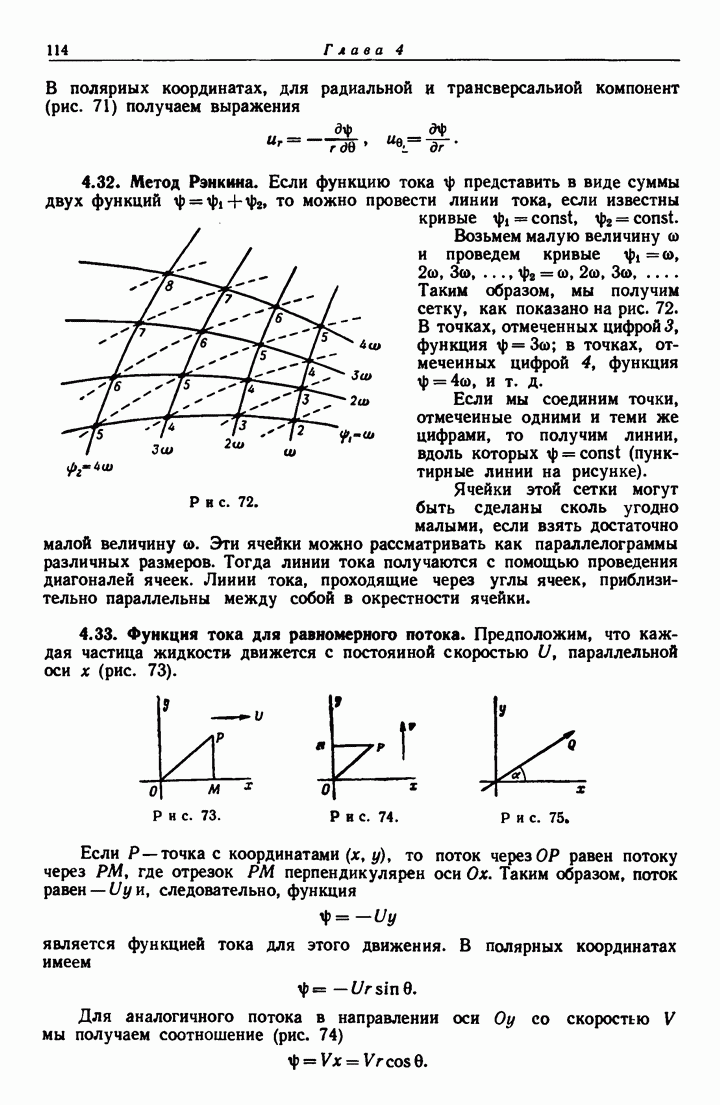
- 4.32. Метод Рэнкина.
- 4.33. Функция тока для равномерного потока.
- 4.40. Векторные соотношения, связывающие скорость и вихрь.
- 4.41. Уравнение для функции …
- 4.60. Критические точки.
- 4.70. Потенциал скоростей жидкости.
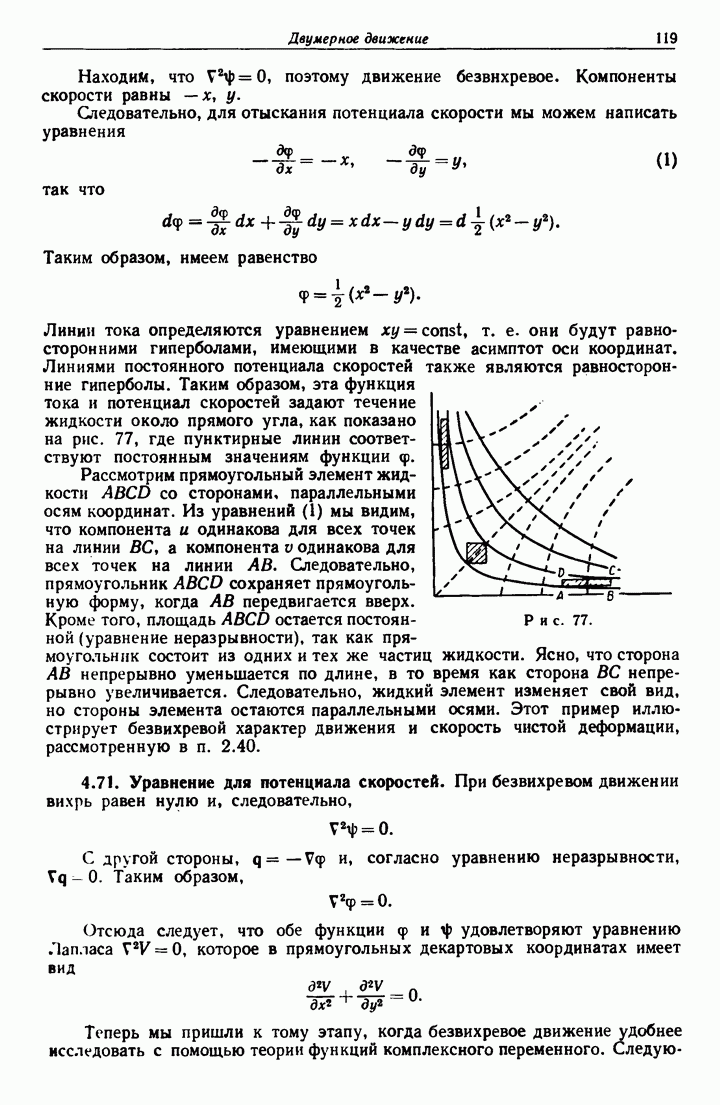
- 4.71. Уравнение для потенциала скоростей.
- Глава 5. КОМПЛЕКСНОЕ ПЕРЕМЕННОЕ
- 5.01. Комплексные числа.
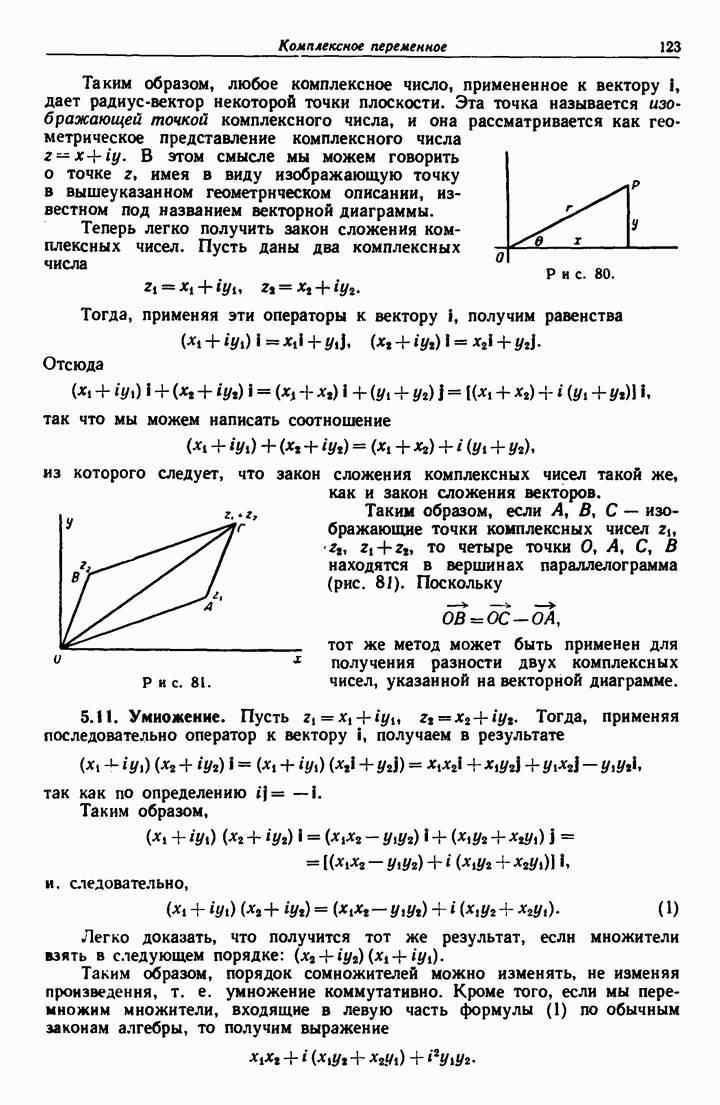
- 5.10. Векторная диаграмма.
- 5.11. Умножение.
- 5.12. Равенство комплексных чисел.
- 5.13. Теорема Эйлера.
- 5.14. Сопряженные комплексные числа.
- 5.15. Число, обратное комплексному числу.
- 5.16. Векторные свойства комплексных чисел.
- 5.17. Поворот координатных осей.
- 5.20. Логарифмы.
- 5.21. Действительная и мнимая части.
- 5.30. Определение аналитической функции от z.
- 5.31. Сопряженные функции.
- 5.32. О связи сопряженных функций с f(z).
- 5.33. Решение уравнения Лапласа.
- 5.40. Направление обхода контура.
- 5.43. Теорема Стокса в комплексной форме.
- 5.50. Интегральная теорема Коши.
- 5.51. Теорема Морера.
- 5.52. Аналитическое продолжение.
- 5.53. Принцип симметрии.
- 5.54. Деформация контура.
- 5.55. Случай, когда функция не аналитична в некоторых точках.
- 5.56. Особенности.
- 5.57. Вычеты.
- 5.58. Теорема Коши о вычетах.
- 5.59. Формула Коши.
- 5.60. Нули.
- 5.61. Принцип аргумента.
- 5.62. Отображение.
- 5.63. Контуры с нулями функции f(z).
- 5.70. Конформное отображение.
- 5.71. Отображение бесконечных областей.
- Глава 6. ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ
- 6.01. Комплексная скорость.
- 6.02. Критические точки.
- 6.03. Скорость.
- 6.04. Уравнения линий тока.
- 6.10. Течение через отверстие.
- 6.11. Течение вокруг эллиптического цилиндра.
- 6.21. Теорема об окружности.
- 6.22. Потенциальное обтекание кругового цилиндра.
- 6.23. Разветвляющаяся линия тока.
- 6.24. Распределение давления на цилиндре.
- 6.25. Кавитация.
- 6.29. Применение конформного отображения.
- 6.30. Преобразование Жуковского.
- 6.31. Обтекание эллиптического цилиндра.
- 6.32. Эллиптические координаты.
- 6.33. Применение эллиптических координат к изучению обтекания эллипса.
- 6.34. Обтекание пластины.
- 6.35. Общий метод.
- 6.41. Теорема Блазиуса.
- 6.42. Действие равномерного потока на эллиптический цилиндр.
- 6.50. Коаксиальные координаты.
- 6.51. Обтекание впадины или выступа дна.
- 6.52. Обтекание цилиндрического тела.
- 6.53. Цилиндр в тоннеле.
- Глава 7. ПРОФИЛИ КРЫЛЬЕВ
- 7.11. Циркуляционное движение жидкости между концентрическими цилиндрами.
- 7.12. Обтекание кругового цилиндра с циркуляцией и без циркуляции.
- 7.13. Равномерное течение с поперечным градиентом скорости.
- 7.20. Профиль крыла.
- 7.30. Дальнейшее исследование преобразования Жуковского.
- 7.31. Геометрическое построение преобразования.
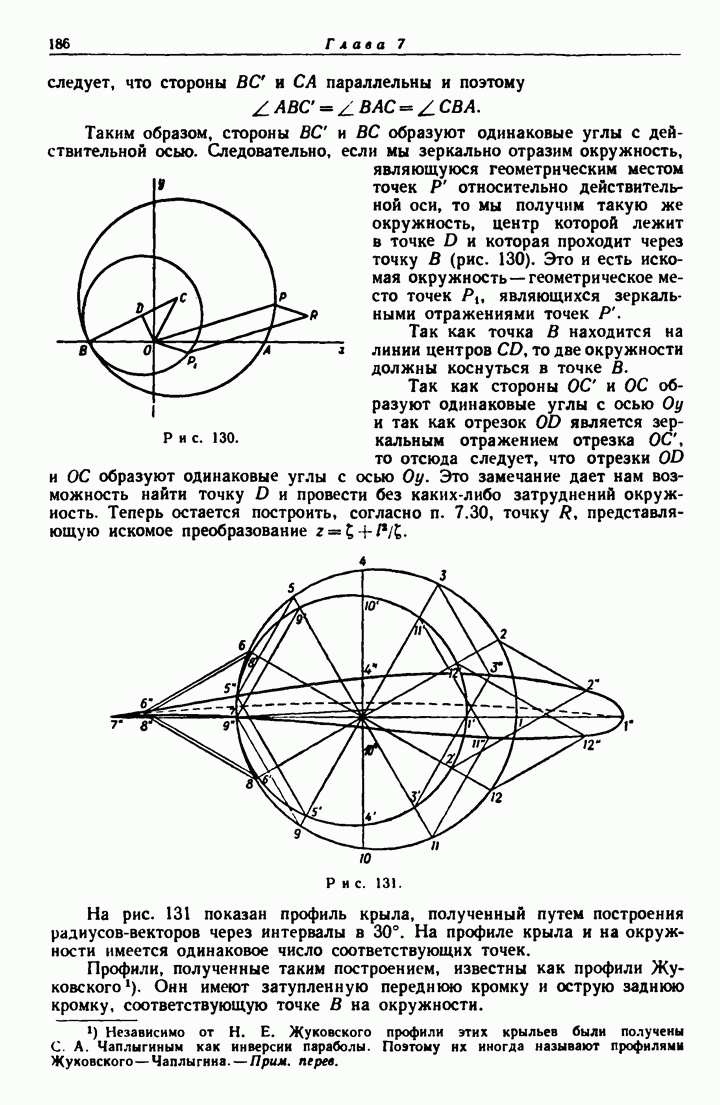
- 7.32. Характер задней кромки крыла.
- 7.40. Постулат Жуковского.
- 7.45. Теорема Кутта—Жуковского.
- 7.50. Подъемная сила крыла в равномерном потоке.
- 7.51. Оси профиля.
- 7.52. Фокус профиля.
- 7.53. Парабола метацентров.
- Глава 8. ИСТОЧНИКИ И СТОКИ
- 8.12. Комплексный потенциал для простого источника.
- 8.20. Комбинация источника и стока.
- 8.21. Источник в равномерном потоке.
- 8.22. Источник и сток одинаковой мощности.
- 8.23. Диполь, или двойной источник.
- 8.24. Эквивалентный слой диполей по Грину.
- 8.30. Источник и сток в равномерном потоке.
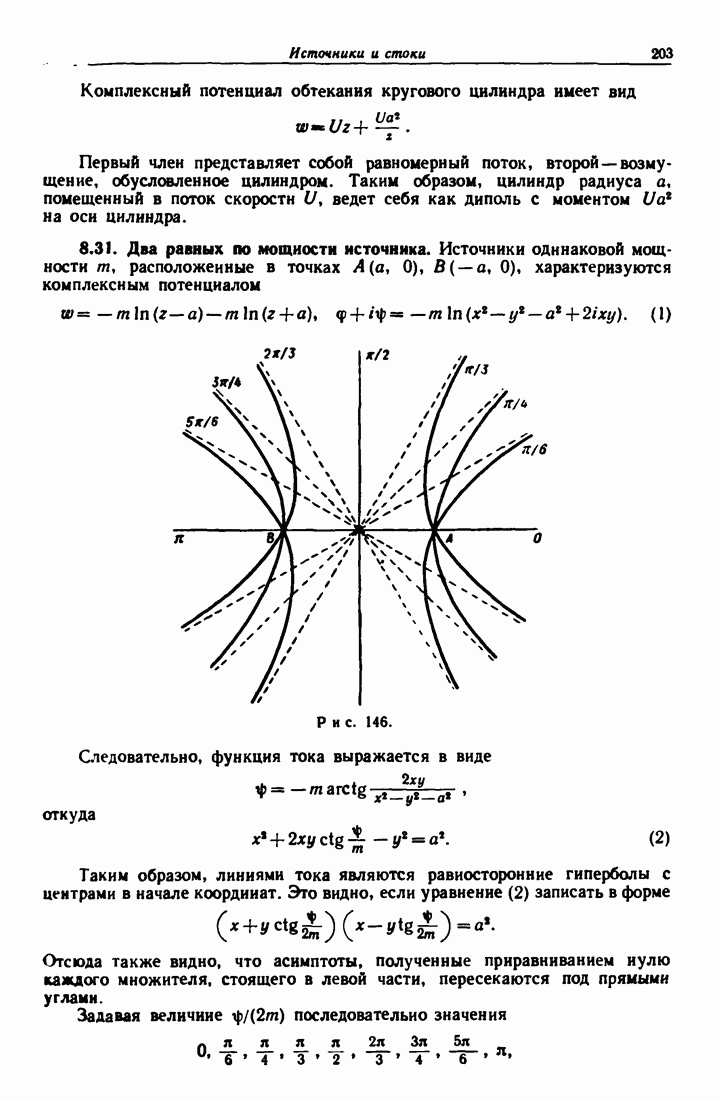
- 8.31. Два равных по мощности источника.
- 8.40. Метод отображений.
- 8.41. Действие на стенку точечного источника.
- 8.42. Общий метод отображений относительно плоскости.
- 8.43. Отображение диполя относительно плоскости.
- 8.50. Источники при конформном преобразовании.
- 8.51. Источник, расположенный в углу между двумя стенками.
- 8.60. Источник вне кругового цилиндра.
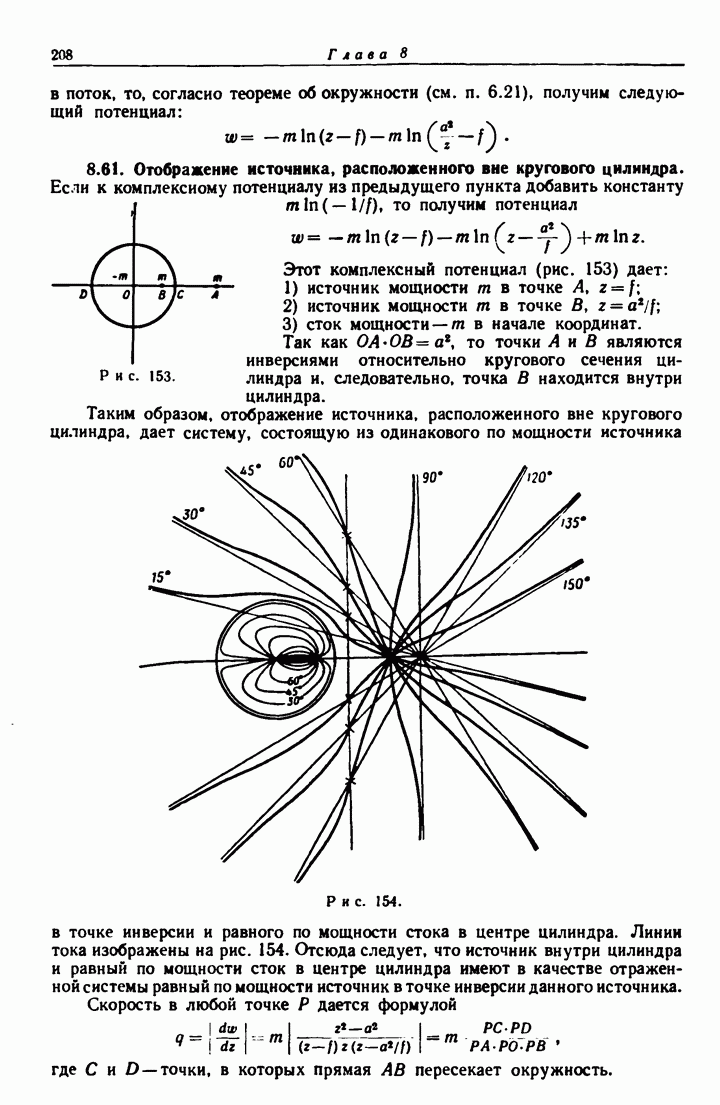
- 8.61. Отображение источника, расположенного вне кругового цилиндра.
- 8.62. Сила, действующая на круговой цилиндр от источника.
- 8.63. Теорема Лагалли.
- 8.64. Источник вне эллиптического цилиндра.
- 8.70. Отображение на единичный круг.
- 8.71. Источники вне цилиндра.
- 8.72. Сила, действующая на цилиндр.
- 8.80. Источник и сток вне кругового цилиндра.
- 8.81. Отображение диполя относительно кругового цилиндра.
- 8.82. Сила, действующая на цилиндр, обусловленная диполем.
- 8.83. Распространение теоремы Лагалли на диполи.
- 8.90. Источник в сжимаемом потоке.
- Глава 9. ДВИЖЕНИЕ ЦИЛИНДРОВ
- 9.10. Кинетическая энергия ациклического безвихревого движения.
- 9.20. Круговой цилиндр, движущийся поступательно.
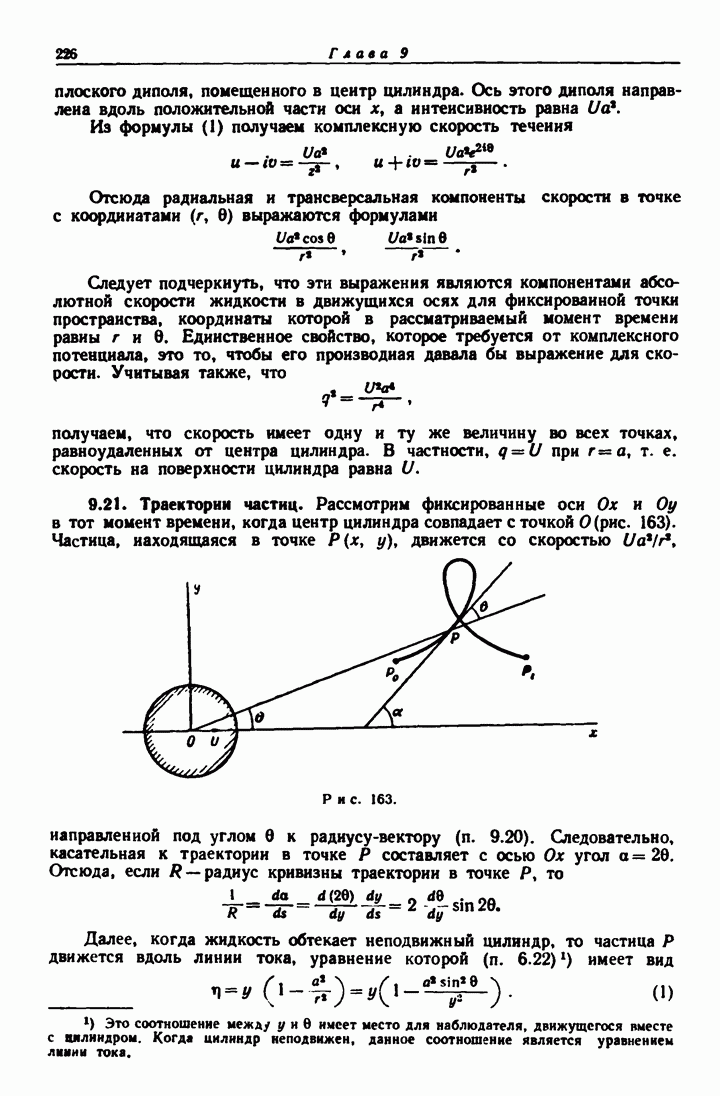
- 9.21. Траектории частиц.
- 9.22. Кинетическая энергия.
- 9.23. Круговой цилиндр, падающий под действием силы тяжести.
- 9.24. Круговой цилиндр с циркуляцией.
- 9.25. Цилиндр с циркуляцией, движущийся под действием силы тяжести.
- 9.30. Уравнение для давления в движущейся системе координат.
- 9.40. Функция тока на границе.
- 9.50. Сила, действующая на движущийся цилиндр.
- 9.52. Обобщение теоремы Чаплыгина-Блазиуса.
- 9.53. Цилиндр, движущийся в безграничной жидкости.
- 9.62. Общий случай движения цилиндра.
- 9.63. Комплексный потенциал движущегося цилиндра.
- 9.64. Круговой цилиндр (общий метод).
- 9.65. Эллиптический цилиндр.
- 9.66. Цилиндр с циркуляцией.
- 9.70. Вращающийся цилиндр.
- 9.71. Вращающийся эллиптический цилиндр, содержащий жидкость.
- 9.72. Вращающаяся равносторонняя призма, содержащая жидкость.
- 9.73. Круговой цилиндр с вырезом.
- 9.74. Метод конформного отображения для комплексного потенциала.
- 9.75. Криволинейная многоугольная граница.
- 9.76. Вращение вокруг эксцентрической точки.
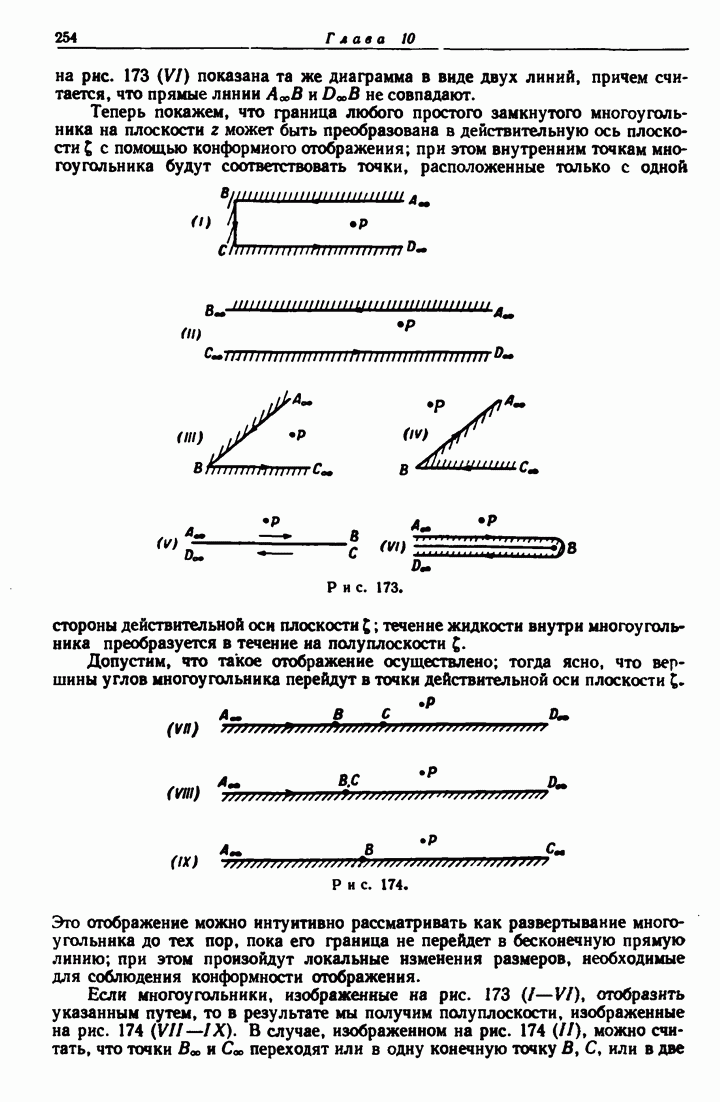
- Глава 10. ТЕОРЕМА ШВАРЦА — КРИСТОФФЕЛЯ
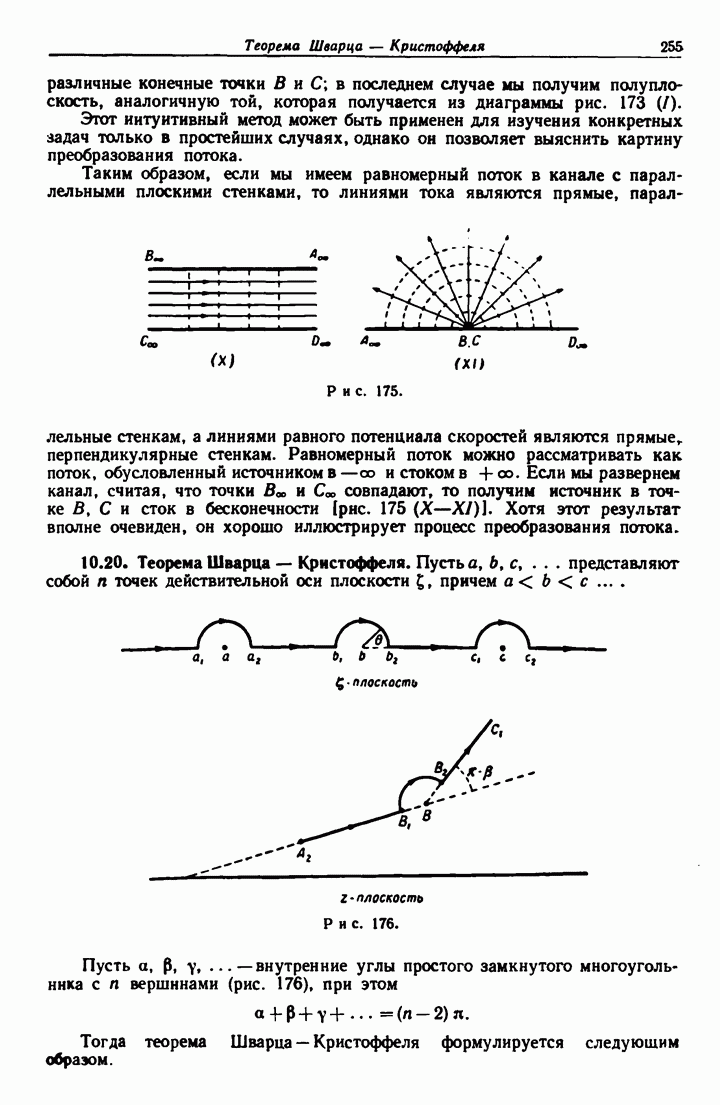
- 10.20. Теорема Шварца — Кристоффеля.
- 10.31. Отображение полубесконечной полосы.
- 10.32. Отображение бесконечной полосы.
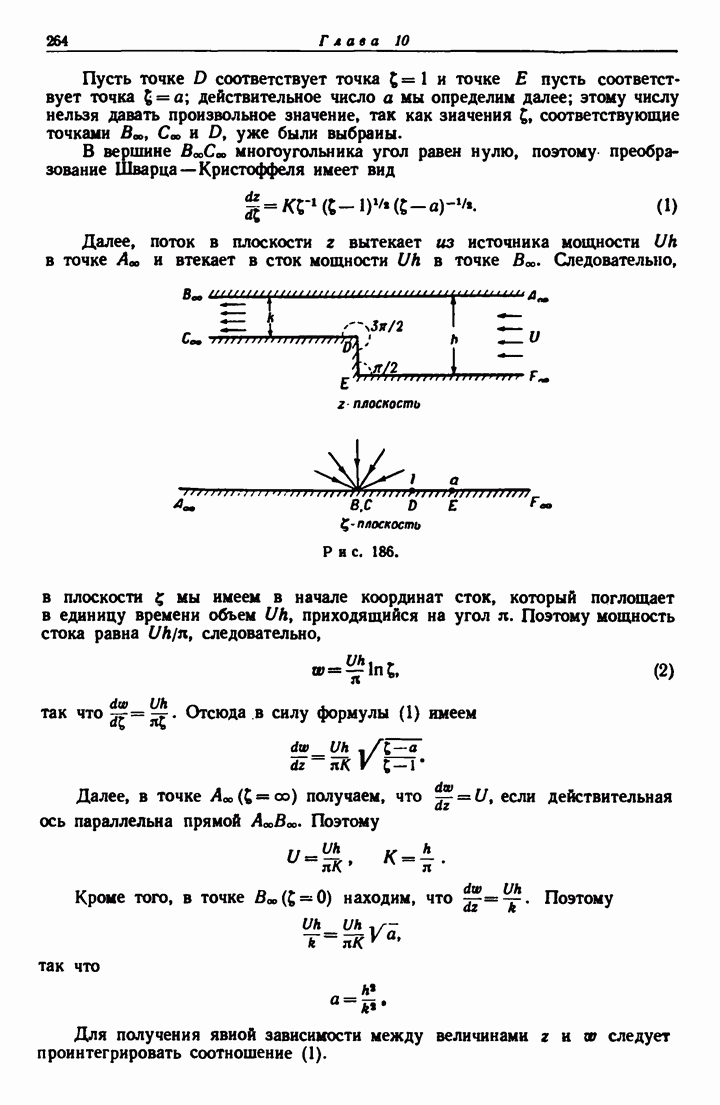
- 10.40. Источник, расположенный в стенке канала (рис. 180).
- 10.50. Источник, расположенный посередине между двумя плоскостями.
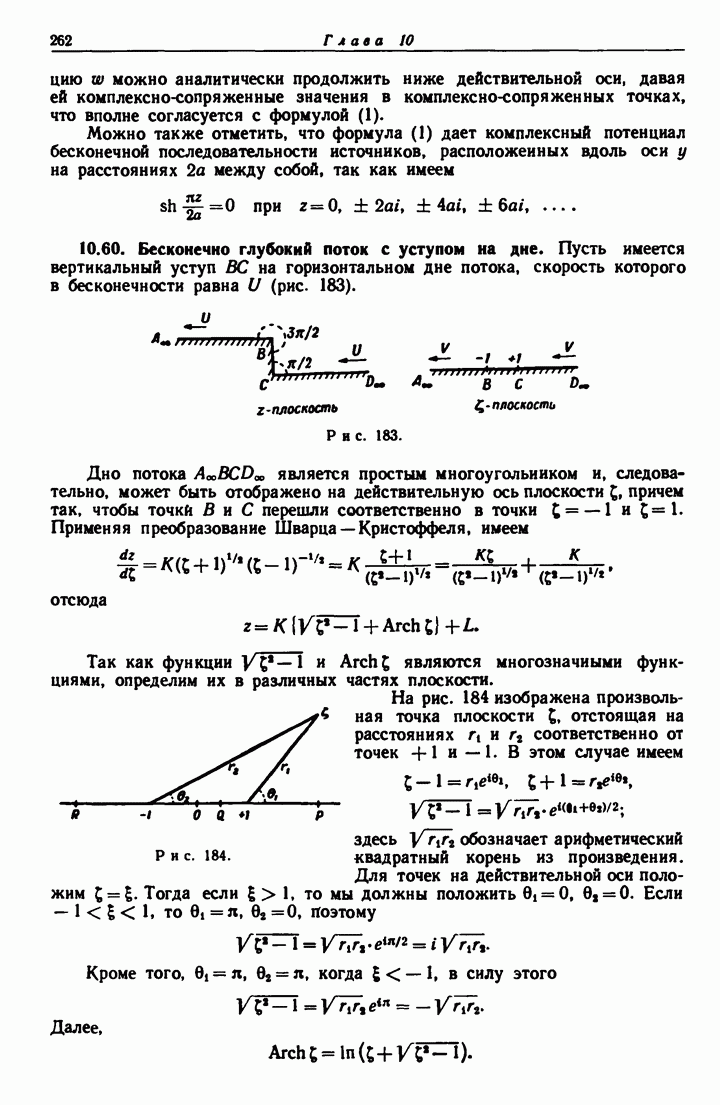
- 10.60. Бесконечно глубокий поток с уступом на дне.
- 10.70. Канал с резко изменяющейся шириной.
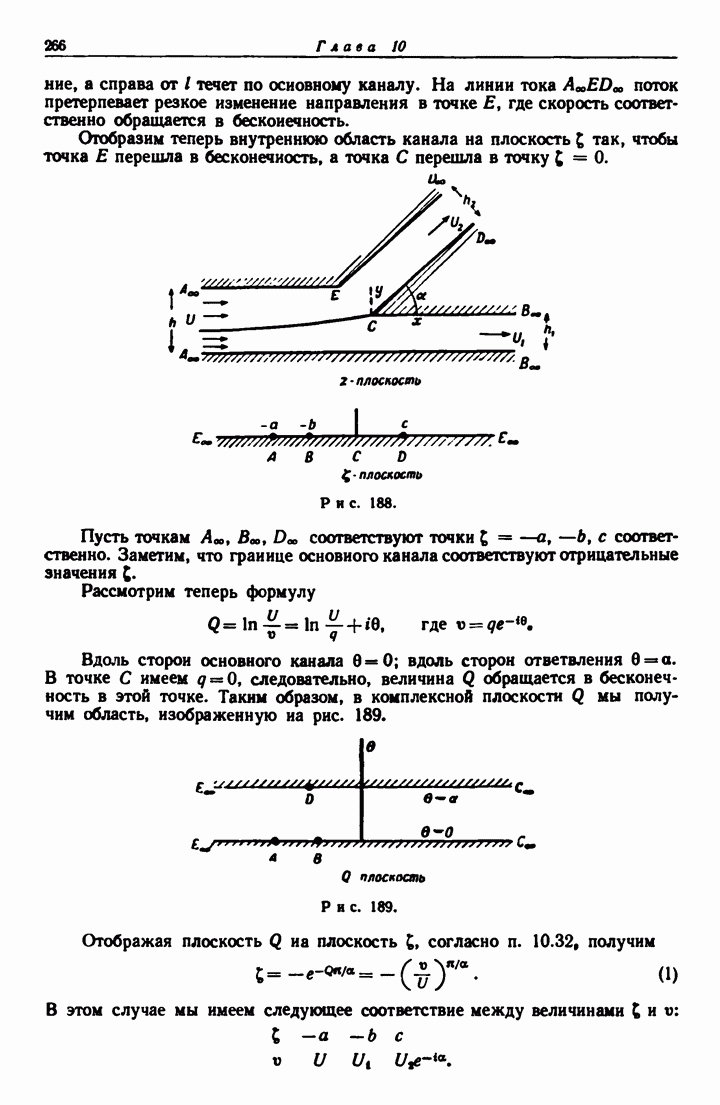
- 10.80. Канал с разветвляющимся руслом.
- Глава 11. СТРУИ И СТРУЙНЫЕ ТЕЧЕНИЯ
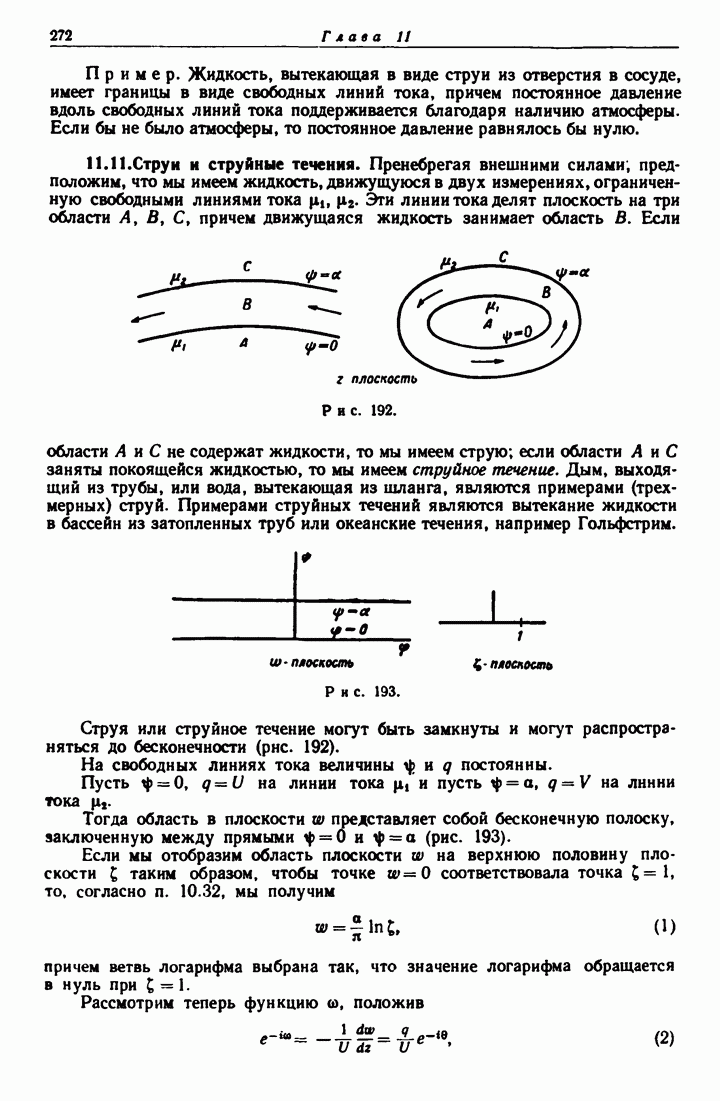
- 11.11. Струи и струйные течения.
- 11.20. Формула Шварца.
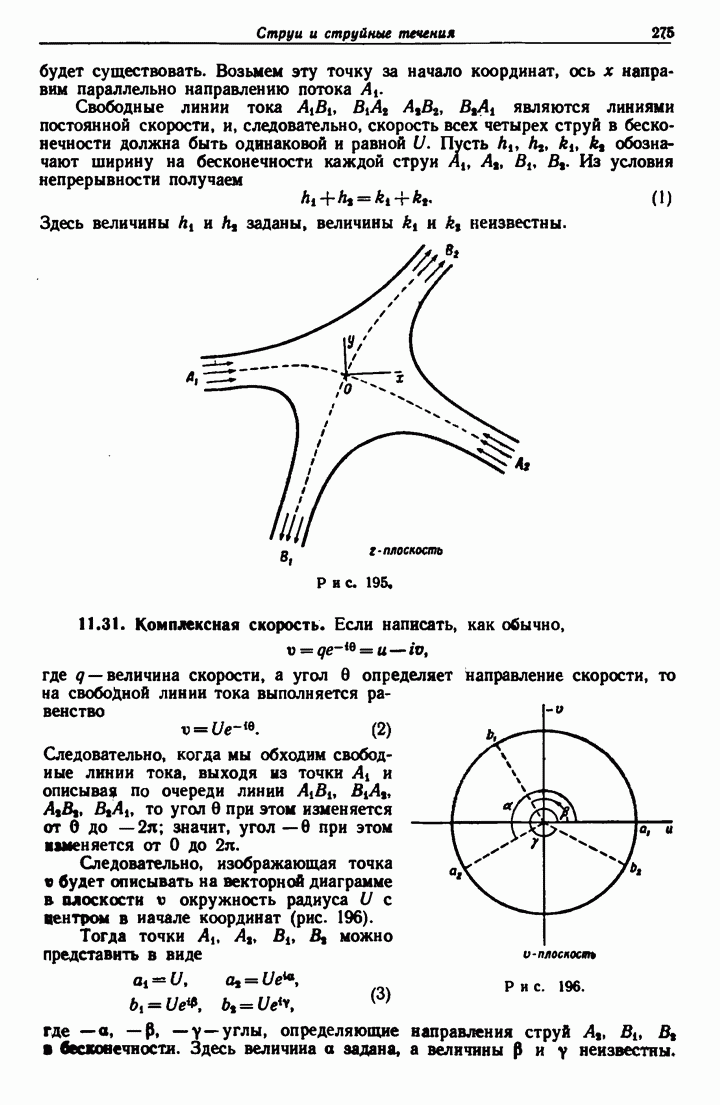
- 11.30. Соударяющиеся струи.
- 11.31. Комплексная скорость.
- 11.32. Выражение комплексного потенциала через комплексную скорость v.
- 11.33. Соотношения между шириной и направлением струй.
- 11.34. Выражение величины z через комплексную скорость v.
- 11.35. Уравнения свободных линий тока.
- 11.40. Неопределенность задачи.
- 11.41. Прямой удар двух одинаковых струй.
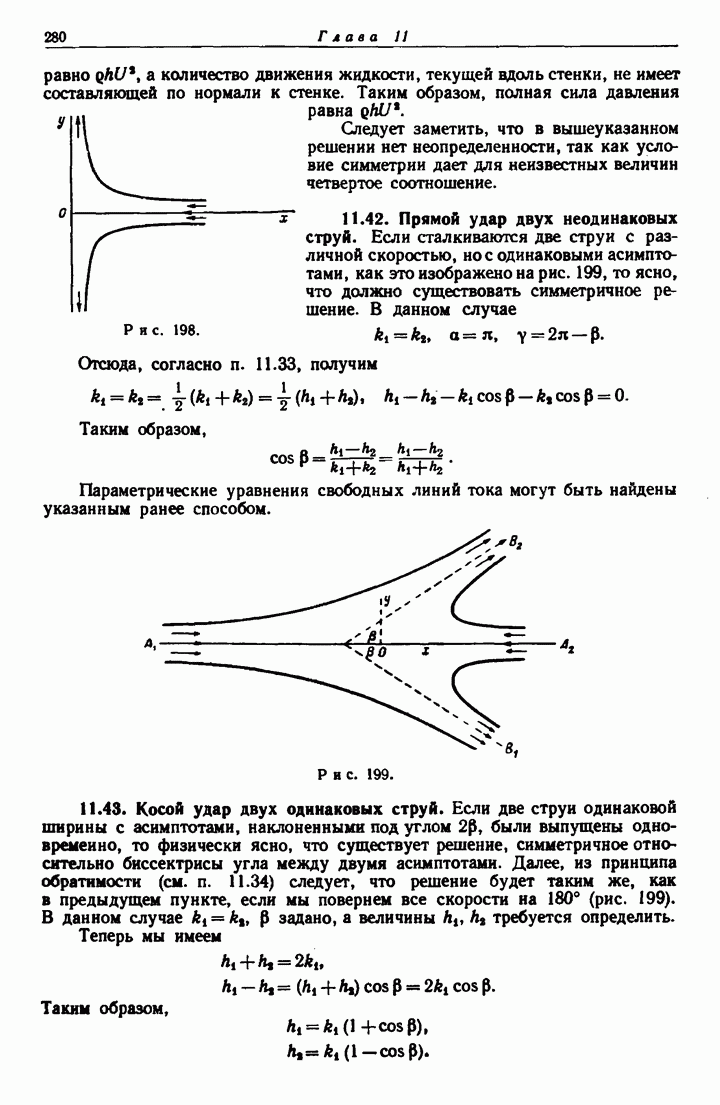
- 11.42. Прямой удар двух неодинаковых струй.
- 11.43. Косой удар двух одинаковых струй.
- 11.50. Твердые границы.
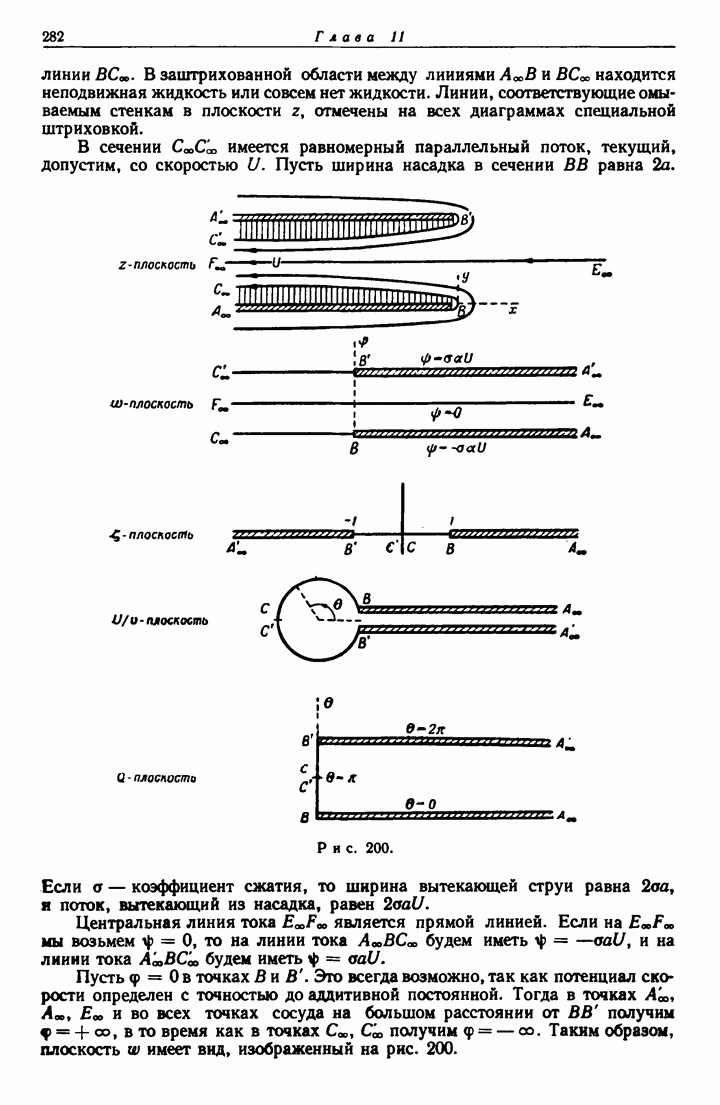
- 11.51. Плоская форма насадка Борда.
- 11.52. Уравнение свободных линий тока.
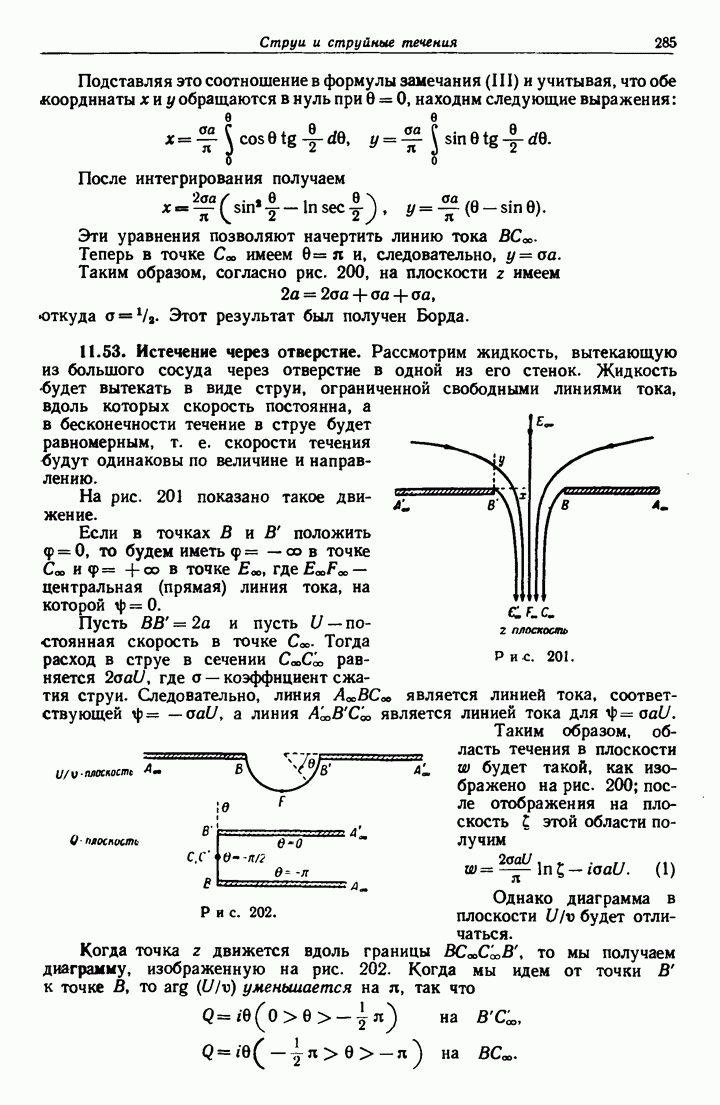
- 11.53. Истечение через отверстие.
- 11.54. Криволинейные границы.
- 11.60. Поток со свободной поверхностью под действием силы тяжести.
- 11.61. Потенциальный поток со свободной поверхностью.
- 11.62. Установившийся поток со свободной поверхностью.
- 11.63. Касательные потоки.
- 11.64. Касательное решение для струи, направленной вертикально вниз.
- Глава 12. ДВИЖЕНИЕ ПО СХЕМЕ ГЕЛЬМГОЛЬЦА
- 12.12. Правильная кавитация.
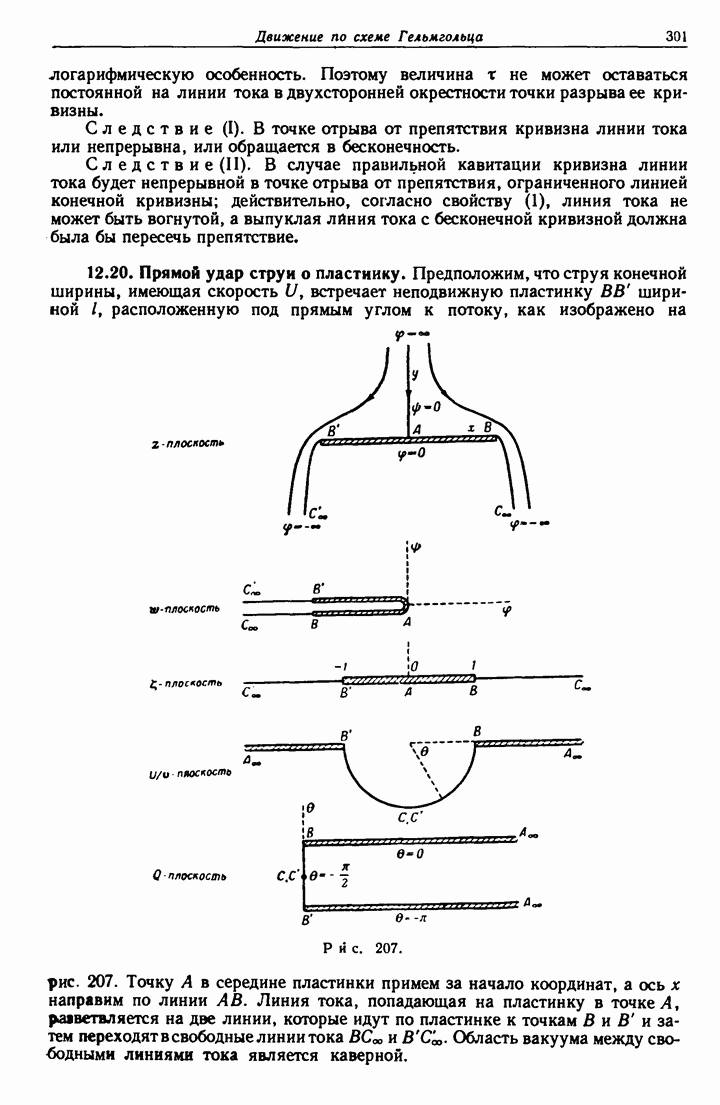
- 12.20. Прямой удар струи о пластинку.
- 12.21. Лобовое сопротивление пластинки.
- 12.22. Коэффициент лобового сопротивления.
- 12.23. Задача Рябушинского.
- 12.25. Скольжение и глиссирование.
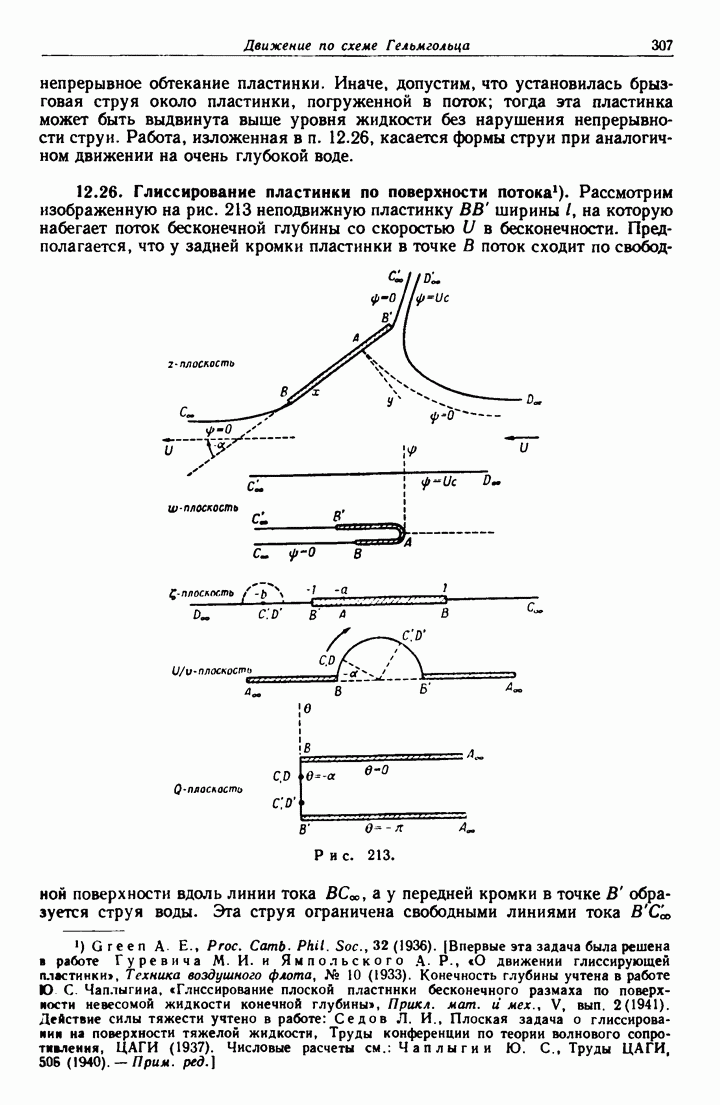
- 12.26. Глиссирование пластинки по поверхности потока.
- 12.30. Отображение относительно свободных линий тока.
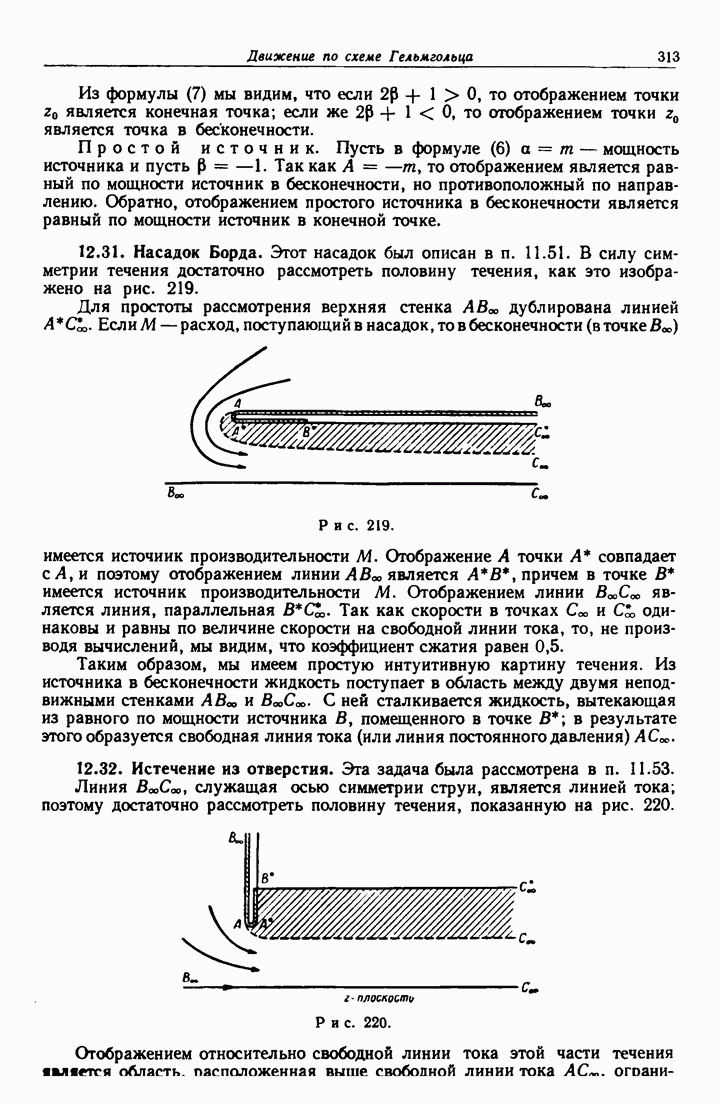
- 12.31. Насадок Борда.
- 12.32. Истечение из отверстия.
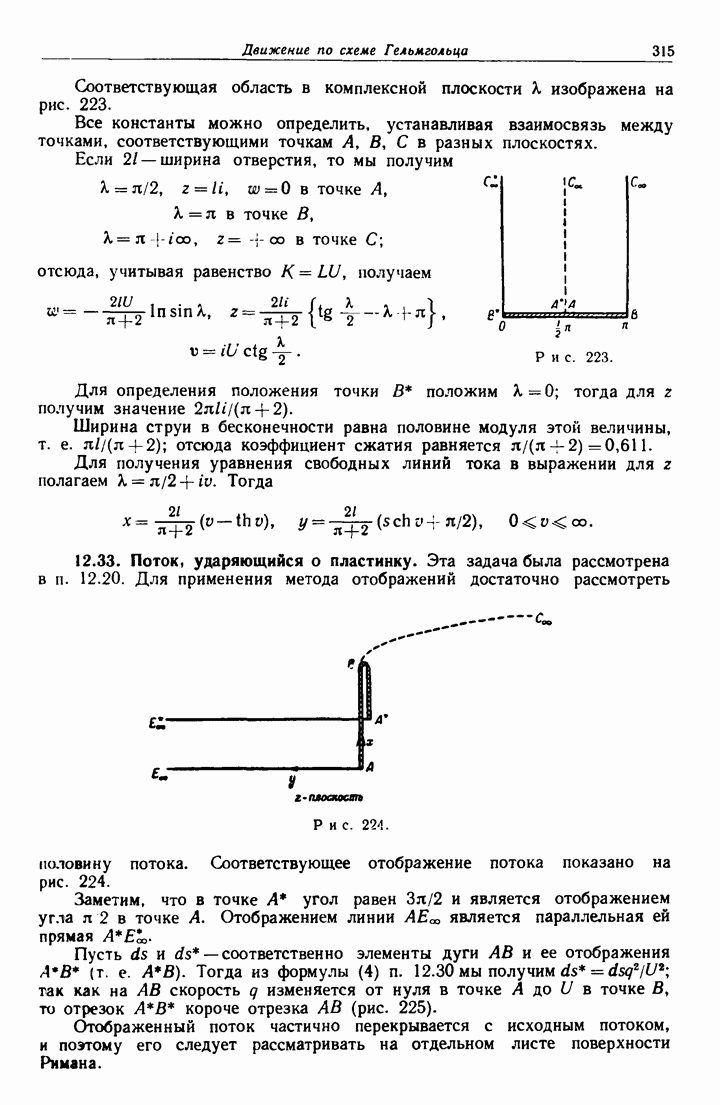
- 12.33. Поток, ударяющийся о пластинку.
- 12.34. Геометрическая интерпретация силы, действующей на препятствие.
- 12.35. Обратная струя.
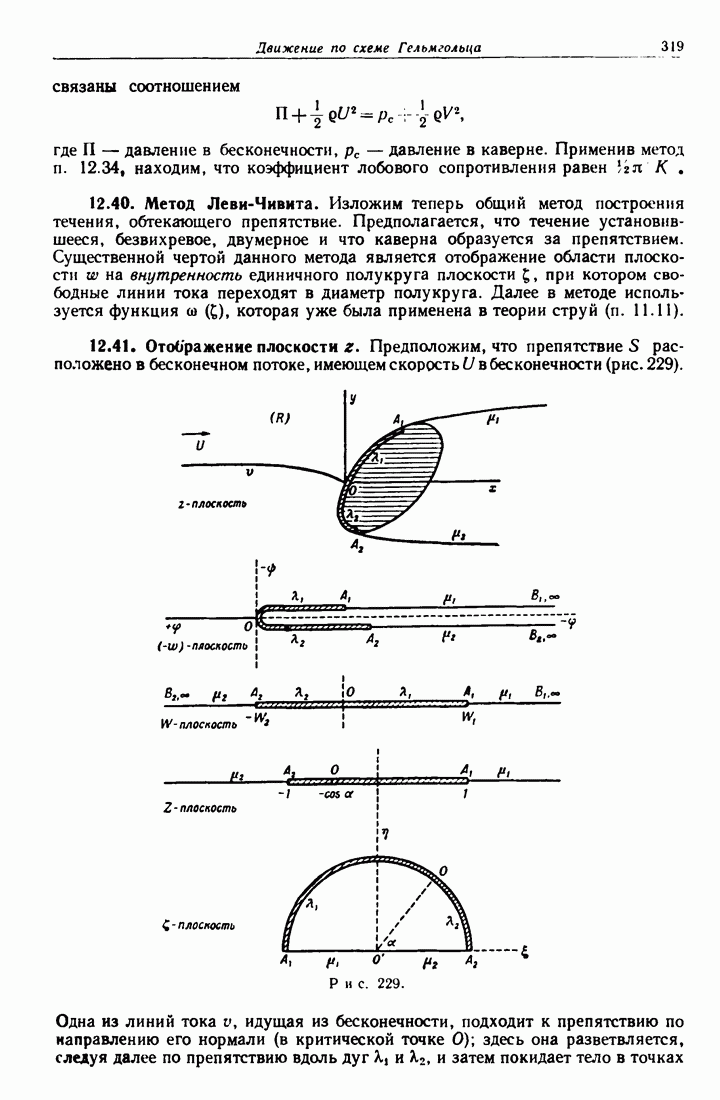
- 12.40. Метод Леви-Чивита.
- 12.46. Лобовое сопротивление, подъемная сила и момент.
- 12.47. Точка разрыва функции w(e).
- 12.50. Решение для случая …
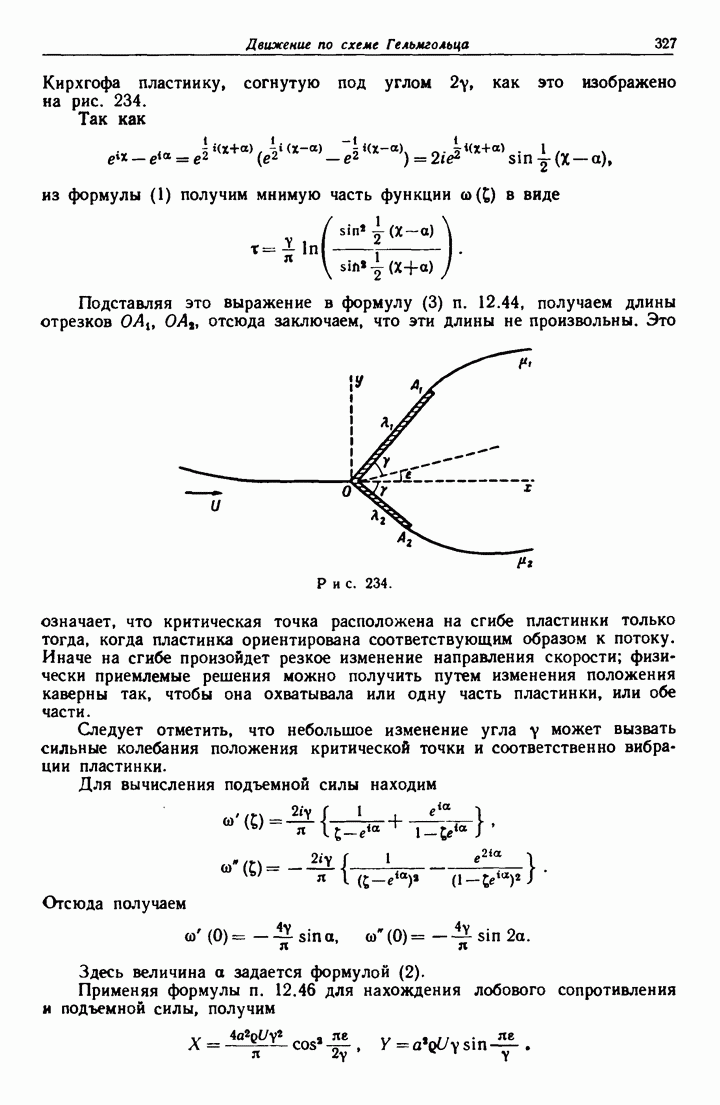
- 12.51. Удар потока о пластинку.
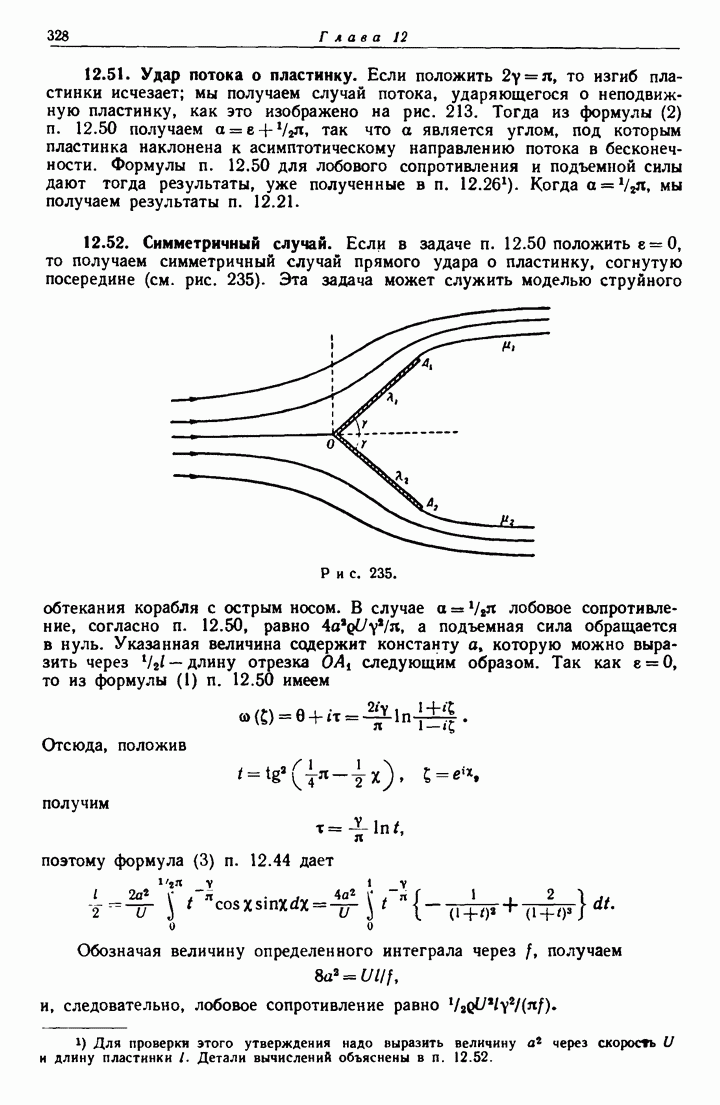
- 12.52. Симметричный случай.
- Глава 13. ПРЯМОЛИНЕЙНЫЕ ВИХРИ
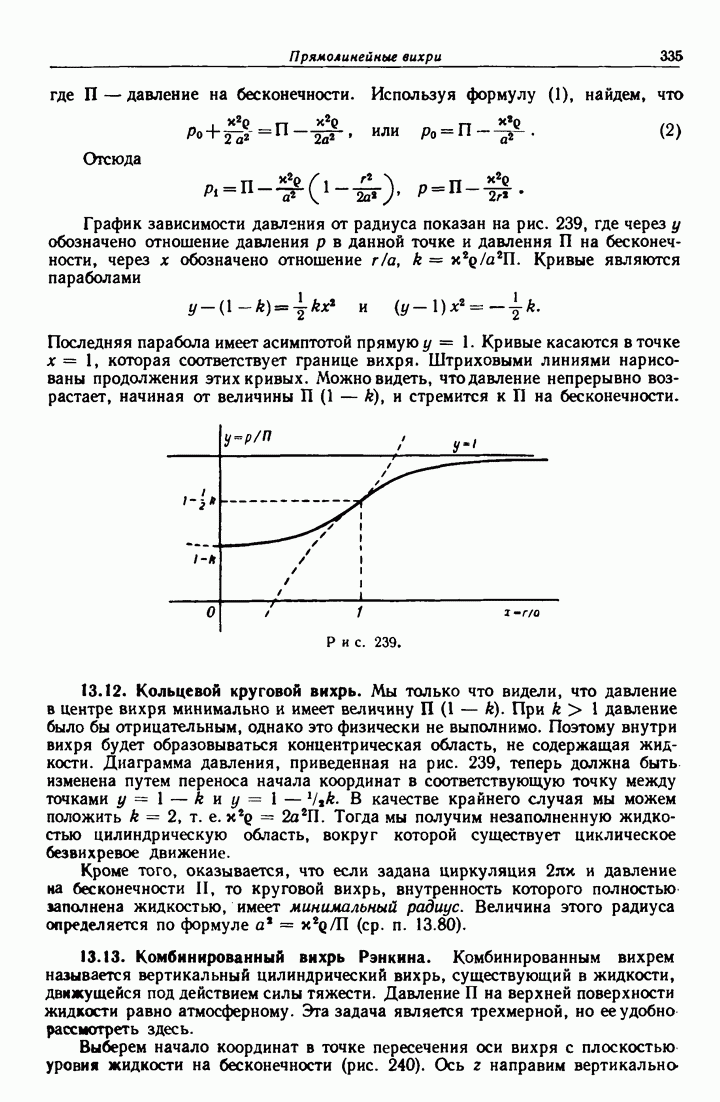
- 13.11. Давление в поле кругового вихря.
- 13.12. Кольцевой круговой вихрь.
- 13.13. Комбинированный вихрь Рэнкина.
- 13.20. Прямолинейная вихревая нить.
- 13.21. Изолированная вихревая нить.
- 13.22. Движение вихревых нитей.
- 13.23. Две вихревые нити.
- 13.24. Движение системы вихревых нитей.
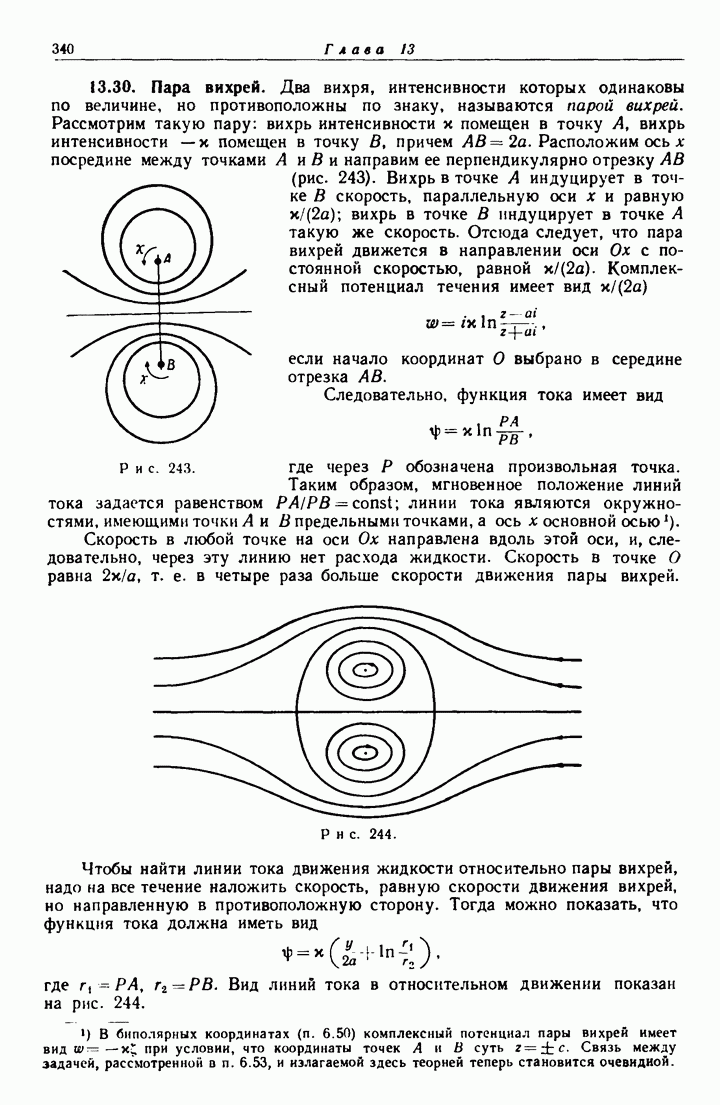
- 13.30. Пара вихрей.
- 13.31. Вихревая нить, параллельная плоскости.
- 13.32. Вихревой диполь.
- 13.33. Вихреисточник.
- 13.40. Вихревая нить, параллельная двум перпендикулярным плоскостям.
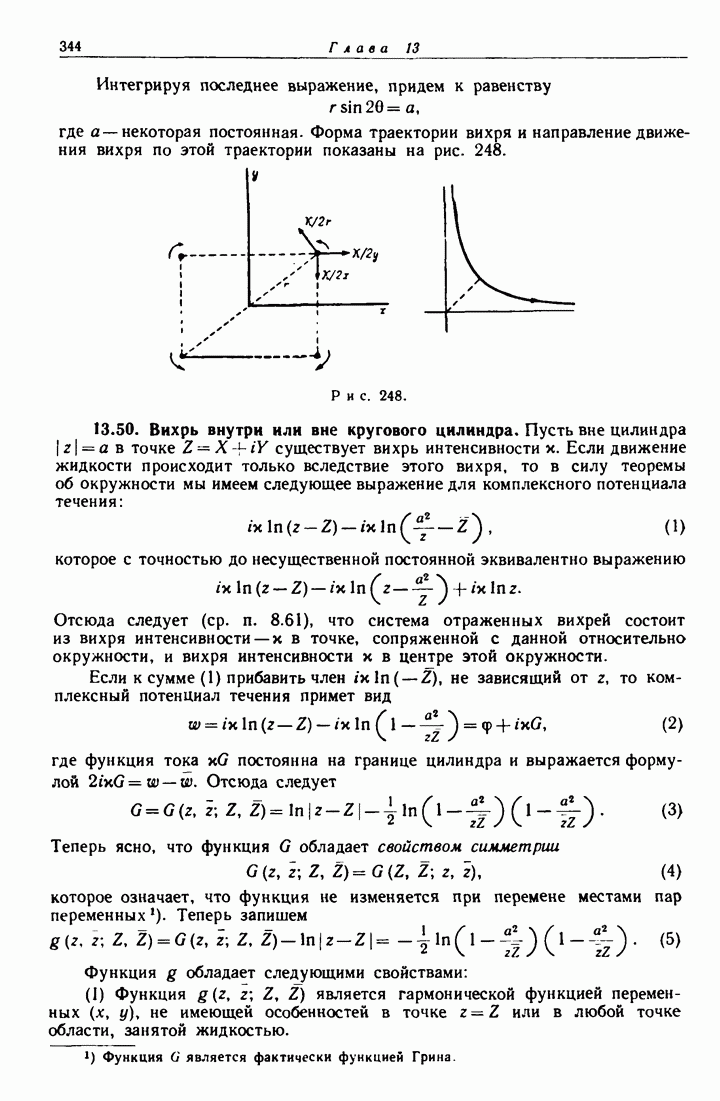
- 13.50. Вихрь внутри или вне кругового цилиндра.
- 13.51. Вихри около кругового цилиндра.
- 13.52. Стационарные вихревые нити около цилиндра.
- 13.60. Конформное отображение.
- 13.61. Вихрь вне произвольного цилиндра.
- 13.62. Эквивалентный слой Грина из источников и вихрей.
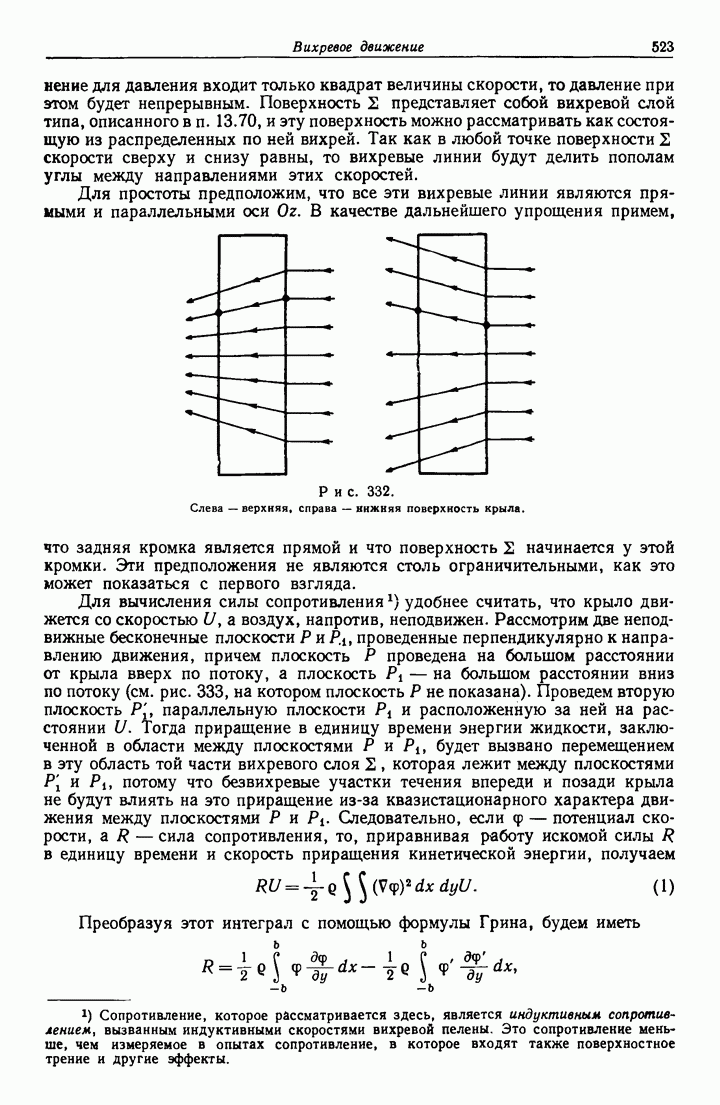
- 13.70. Вихревая пелена.
- 13.71. Одна бесконечная цепочка вихрей.
- 13.72. Вихревая дорожка Кармана.
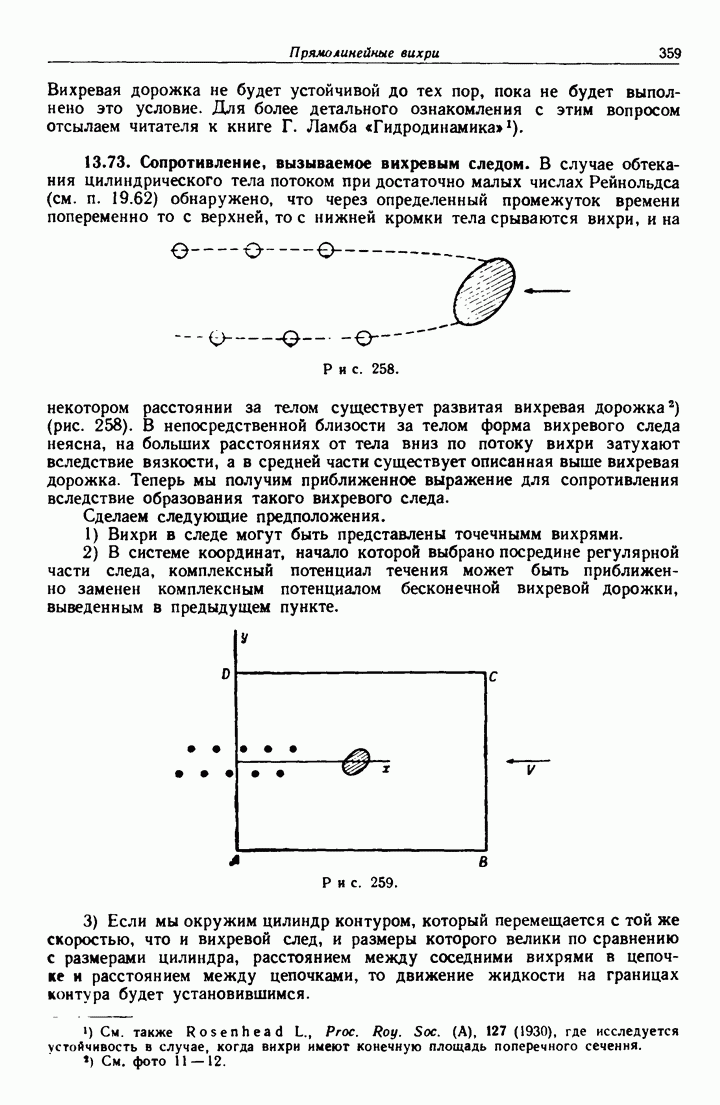
- 13.73. Сопротивление, вызываемое вихревым следом.
- 13.8. Вихрь в сжимаемом газе.
- Глава 14. ВОЛНЫ
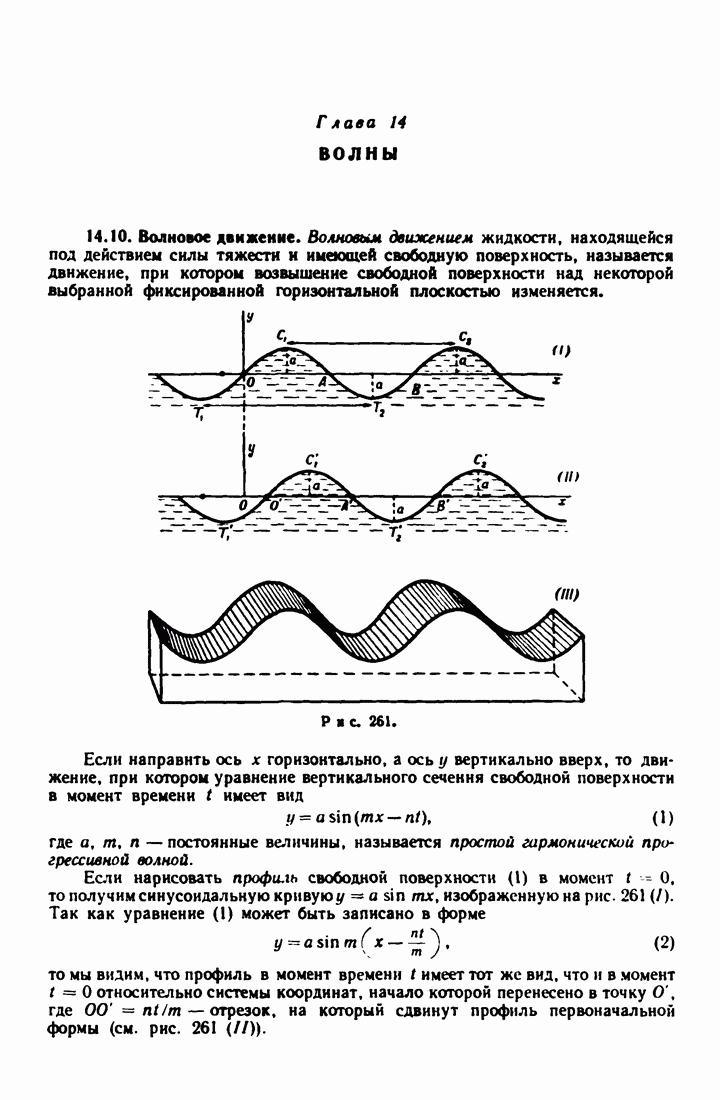
- 14.10. Волновое движение.
- 14.11. Кинематическое условие на свободной поверхности.
- 14.12. Условие для давления на свободной поверхности.
- 14.13. Поверхностные волны.
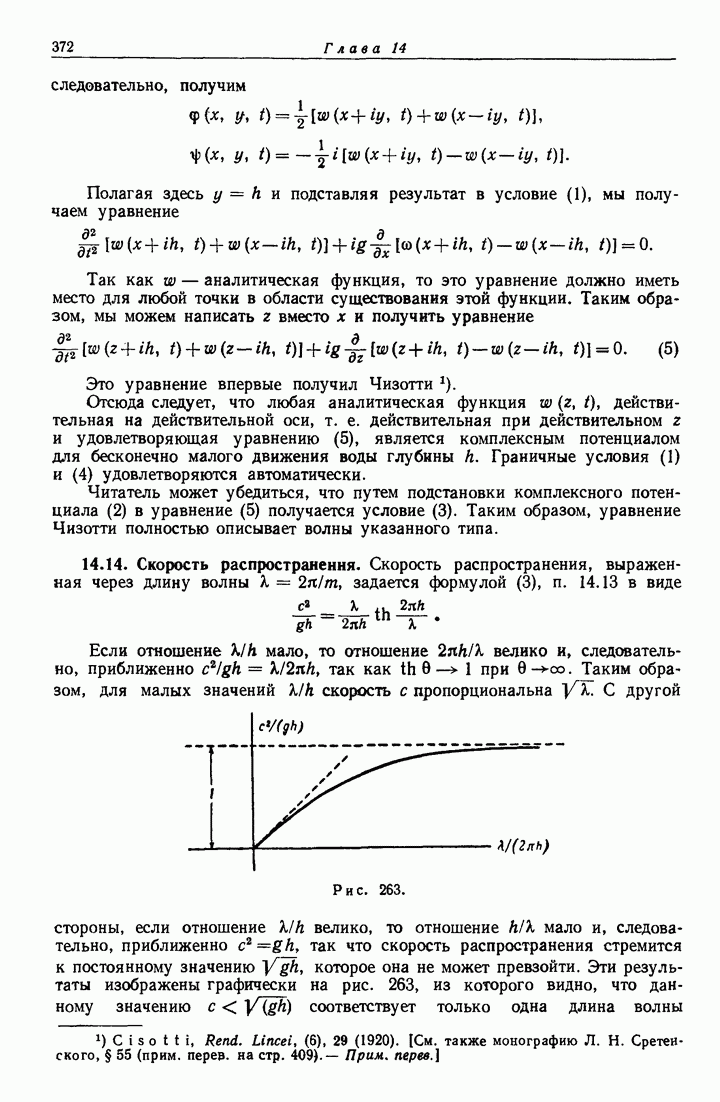
- 14.14. Скорость распространения.
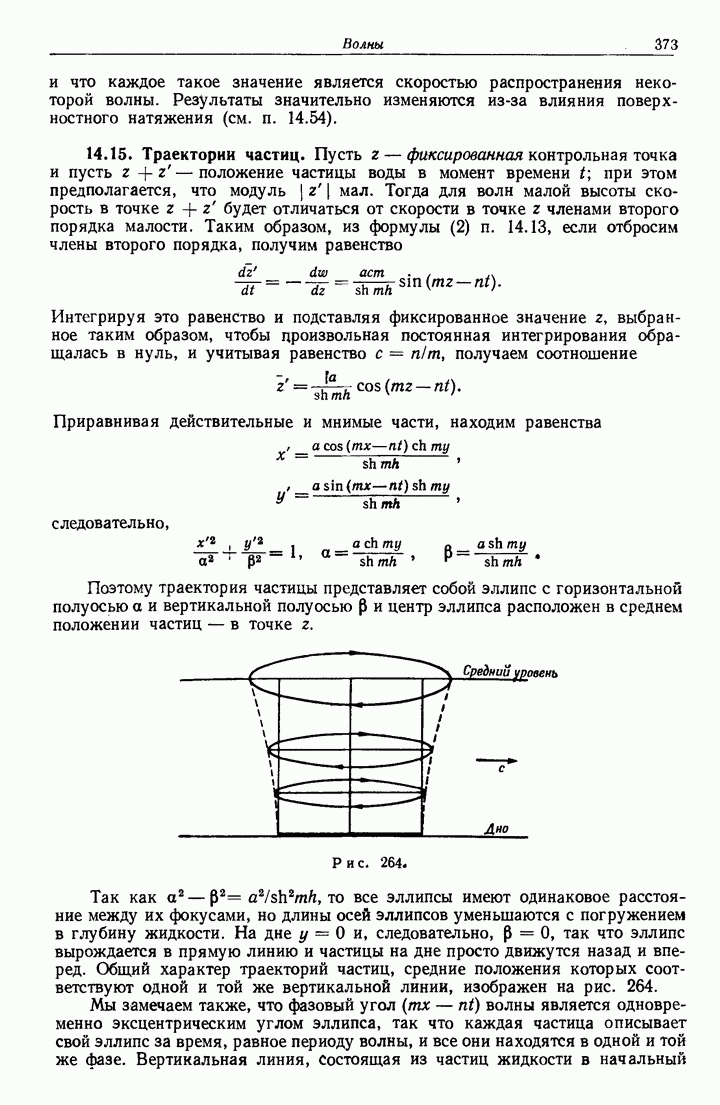
- 14.15. Траектории частиц.
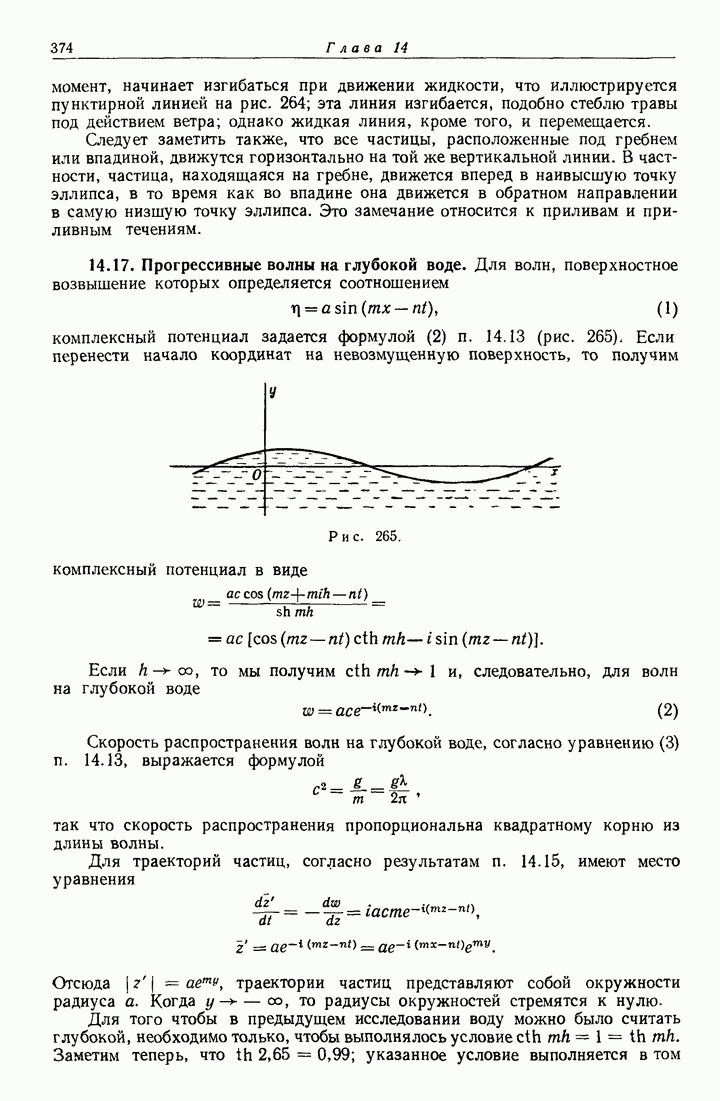
- 14.17. Прогрессивные волны на глубокой воде.
- 14.18. Давление, обусловленное волной на глубокой воде.
- 14.20. Кинетическая энергия прогрессивных волн.
- 14.21. Потенциальная энергия.
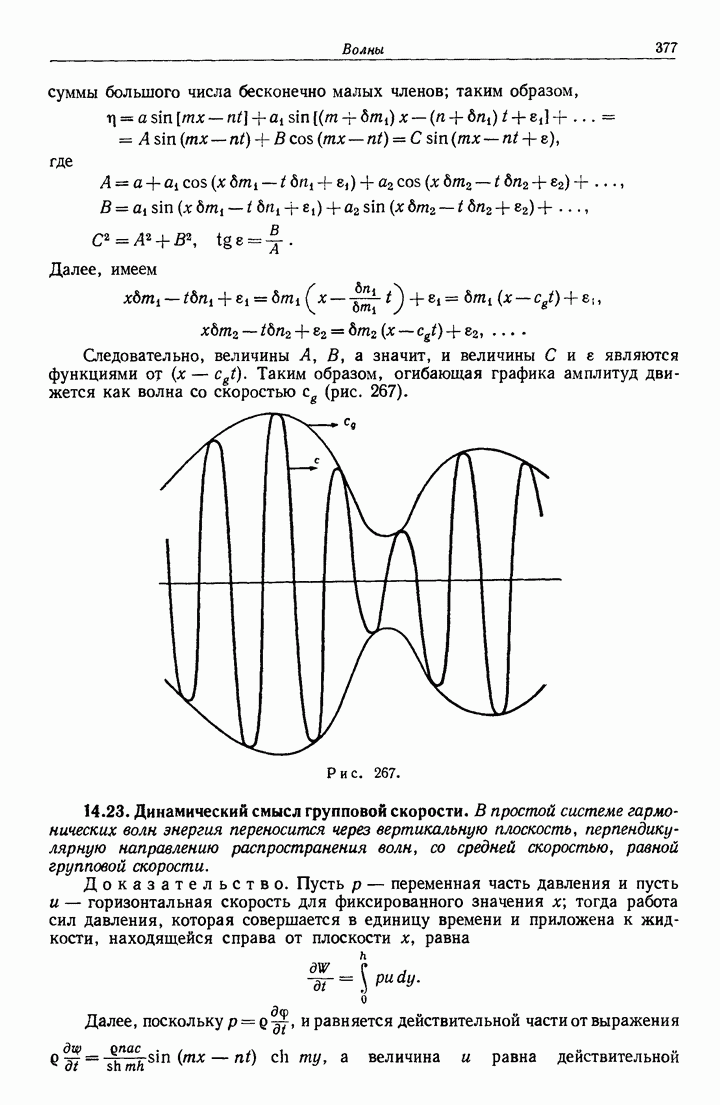
- 14.22. Групповая скорость.
- 14.23. Динамический смысл групповой скорости.
- 14.24. Волновое сопротивление.
- 14.30. Стоячие, или стационарные волны.
- 14.31. Комплексный потенциал стоячих волн.
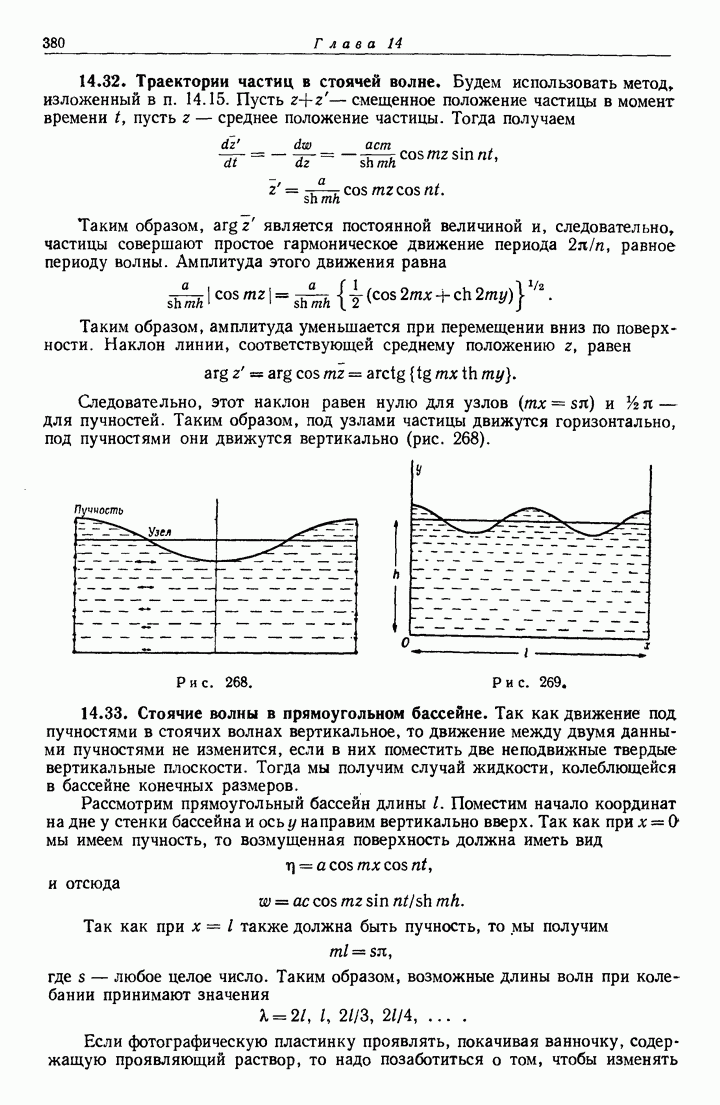
- 14.32. Траектории частиц в стоячей волне.
- 14.33. Стоячие волны в прямоугольном бассейне.
- 14.34. Энергия стоячих волн.
- 14.40. Установившееся движение.
- 14.41. Второе приближение для величины скорости волны.
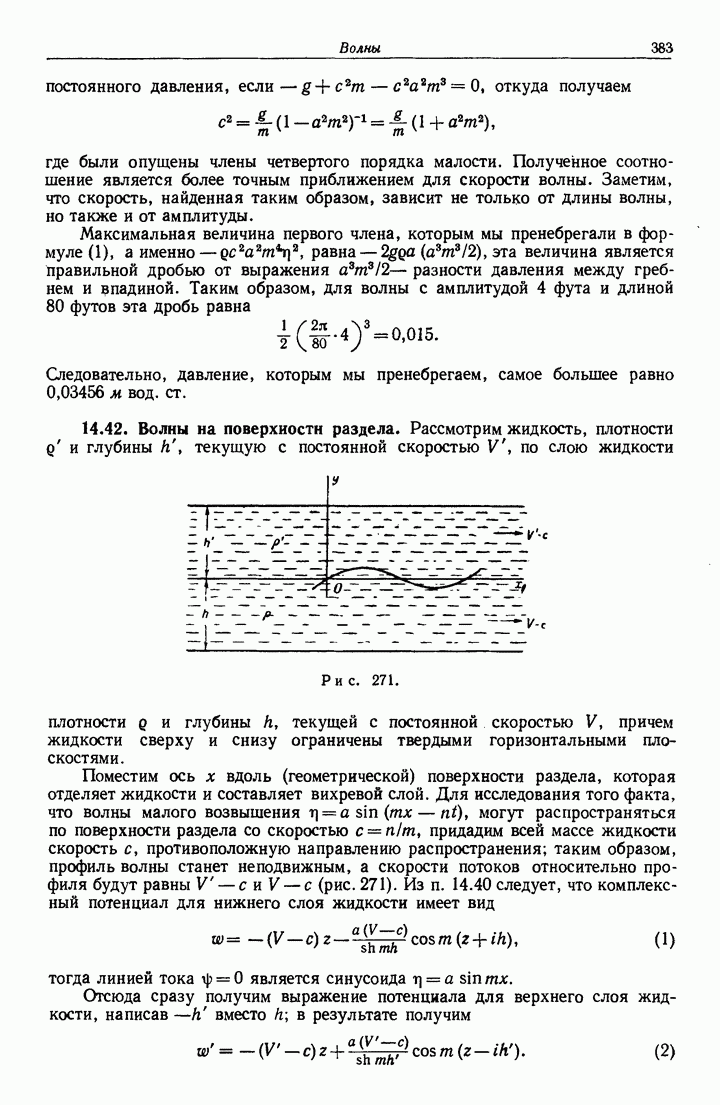
- 14.42. Волны на поверхности раздела.
- 14.43. Установившийся поток над синусоидальным дном.
- 14.44. Волны на поверхности раздела в случае, когда верхний слой имеет свободную поверхность.
- 14.50. Поверхностное натяжение.
- 14.51. Уравнение для комплексного потенциала.
- 14.52. Поверхностные волны.
- 14.53. Влияние капиллярности в случае волн на поверхности раздела.
- 14.54. Скорость распространения.
- 14.55. Действие ветра на глубокой воде.
- 14.58. Условие Леви-Чивита для поверхности жидкости.
- 14.60. Длинные волны.
- 14.61. Давление.
- 14.62. Поверхностное возвышение.
- 14.63. Волны, распространяющиеся только в одном направлении.
- 14.64. Изменение профиля в длинных волнах.
- 14.70. Действие малых возмущающих сил.
- 14.71. Приливы в экваториальном канале.
- 14.80. Трохоидальная волна Герстнера.
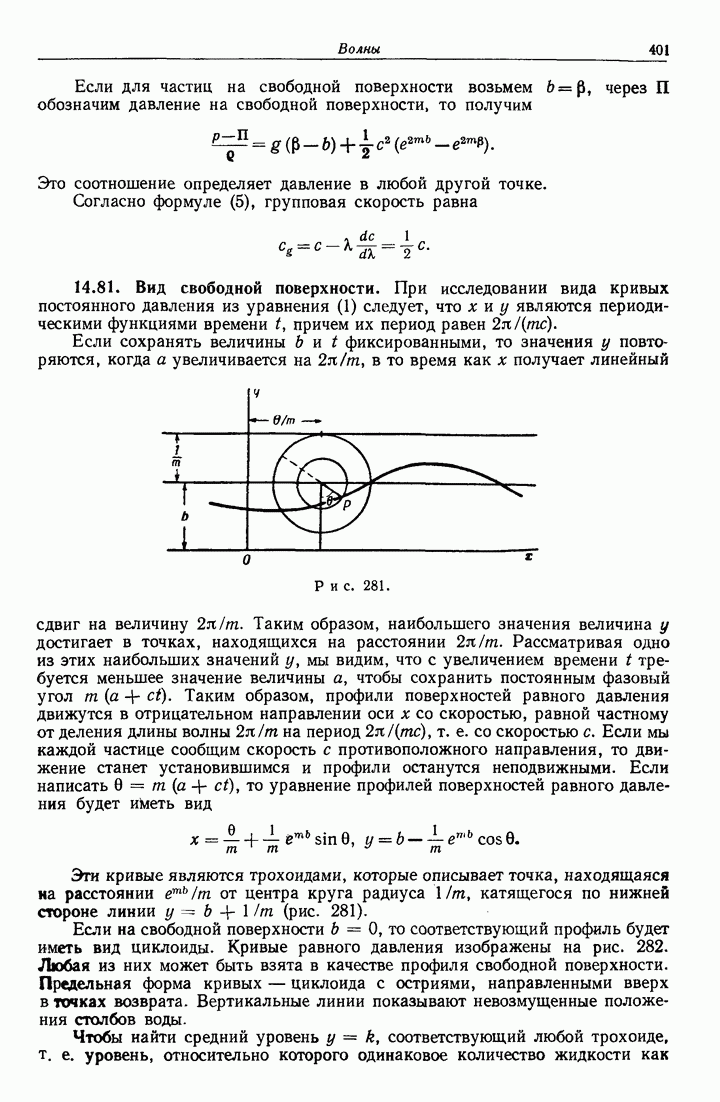
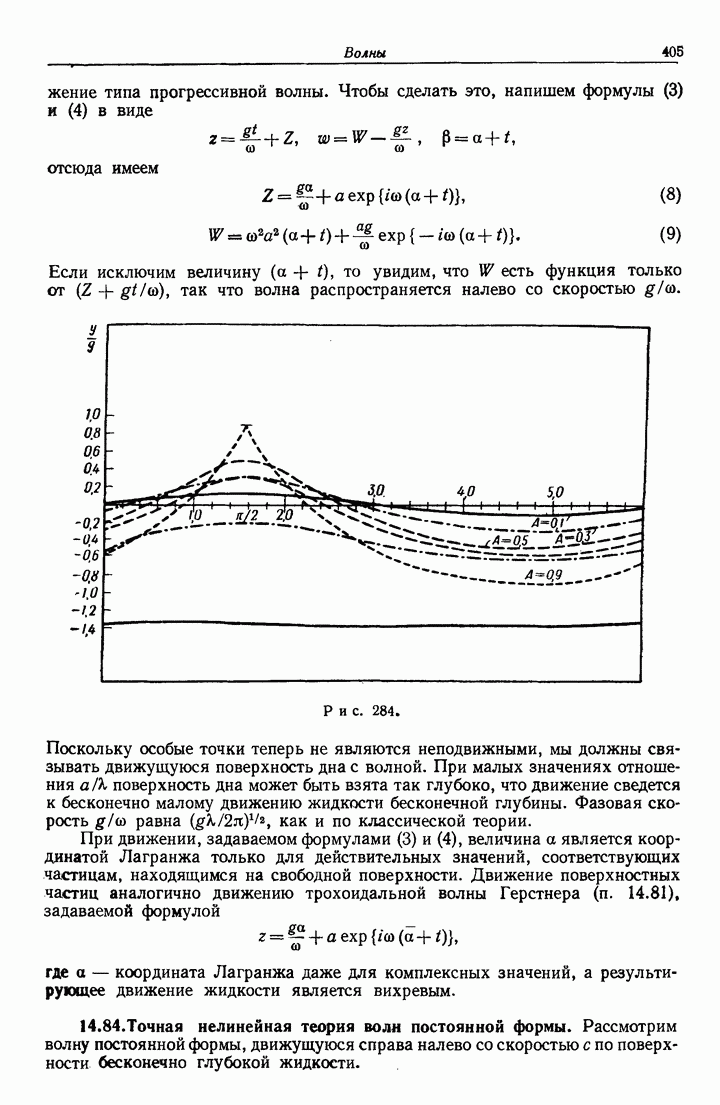
- 14.81. Вид свободной поверхности.
- 14.82. Точное решение для безвихревой волны.
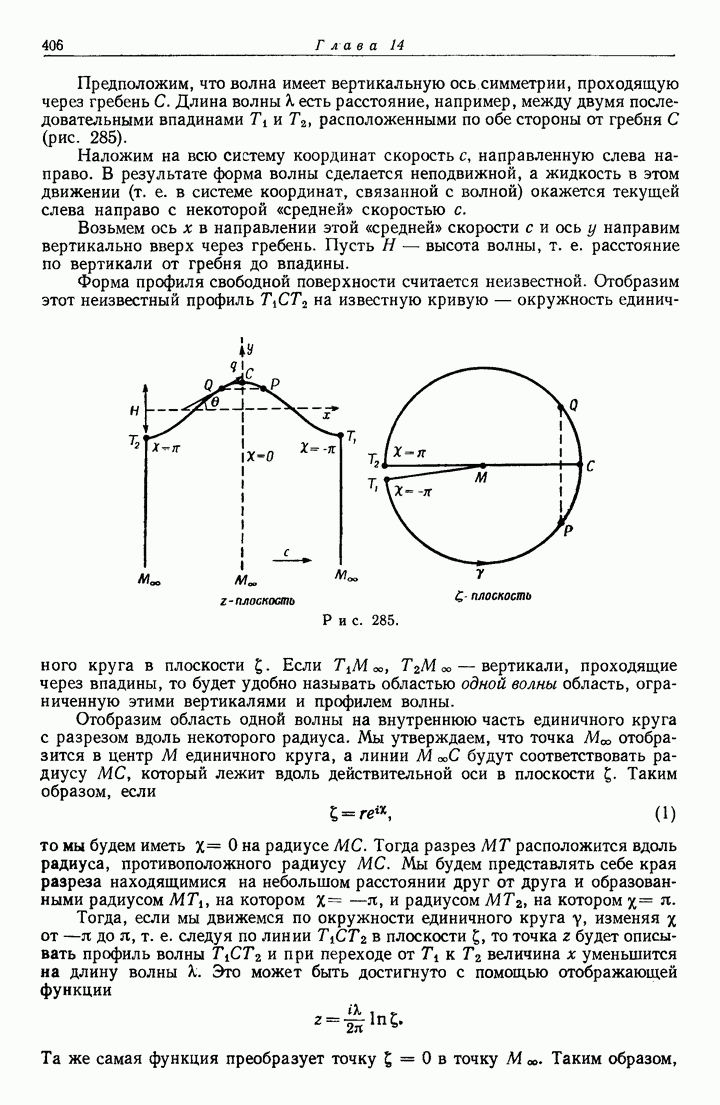
- 14.84. Точная нелинейная теория волн постоянной формы.
- 14.85. Точная линейная теория.
- 14.86. Звуковые волны.
- 14.87. Плоские волны.
- 14.88. Плоские волны в цилиндрической трубе.
- 14.89. Сферические волны.
- Глава 15. ФУНКЦИЯ ТОКА СТОКСА
- 15.21. Подводный взрыв.
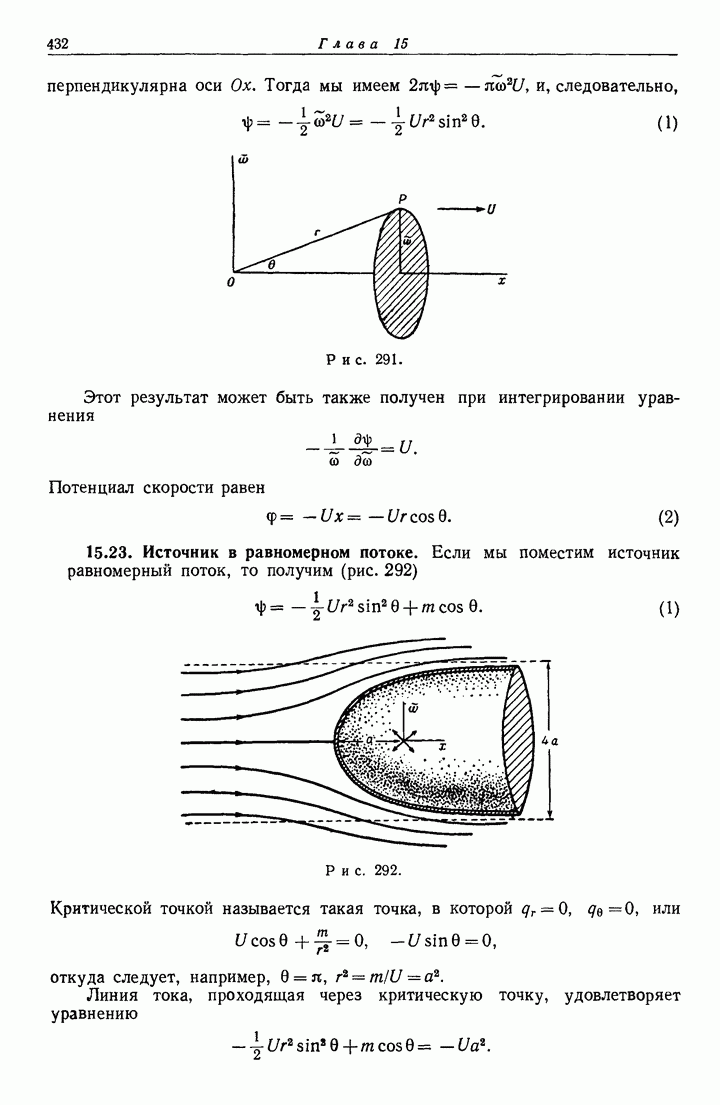
- 15.22. Равномерный поток.
- 15.23. Источник в равномерном потоке.
- 15.24. Линейный источник конечных размеров.
- 15.25. Дирижаблеобразные формы.
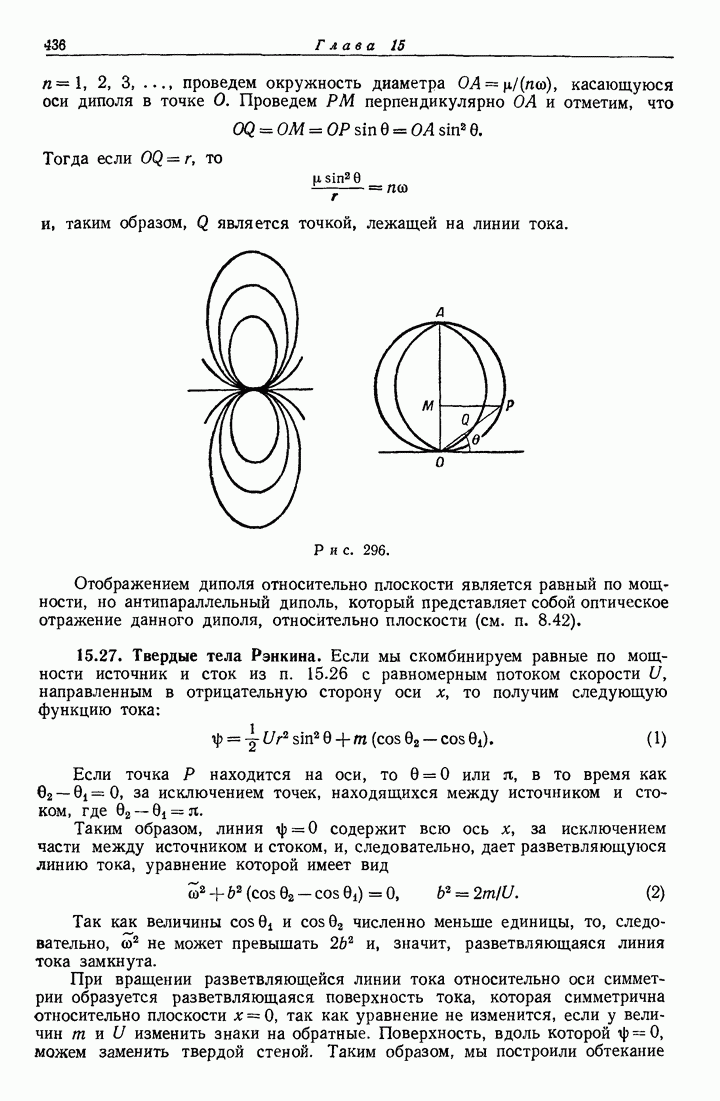
- 15.26. Равные по мощности источник и сток. Диполь.
- 15.27. Твердые тела Рэнкина.
- 15.28. Эквивалентный слой Грина.
- 15.29. Теорема Бутлера для сферы.
- 15.30. Сфера в потоке.
- 15.31. Кинетическая энергия.
- 15.32. Движущаяся сфера.
- 15.33. Давление на движущуюся сферу.
- 15.40. Отображение источника относительно сферы.
- 15.41. Отображение радиального диполя относительно сферы.
- 15.42. Сила, действующая на препятствие.
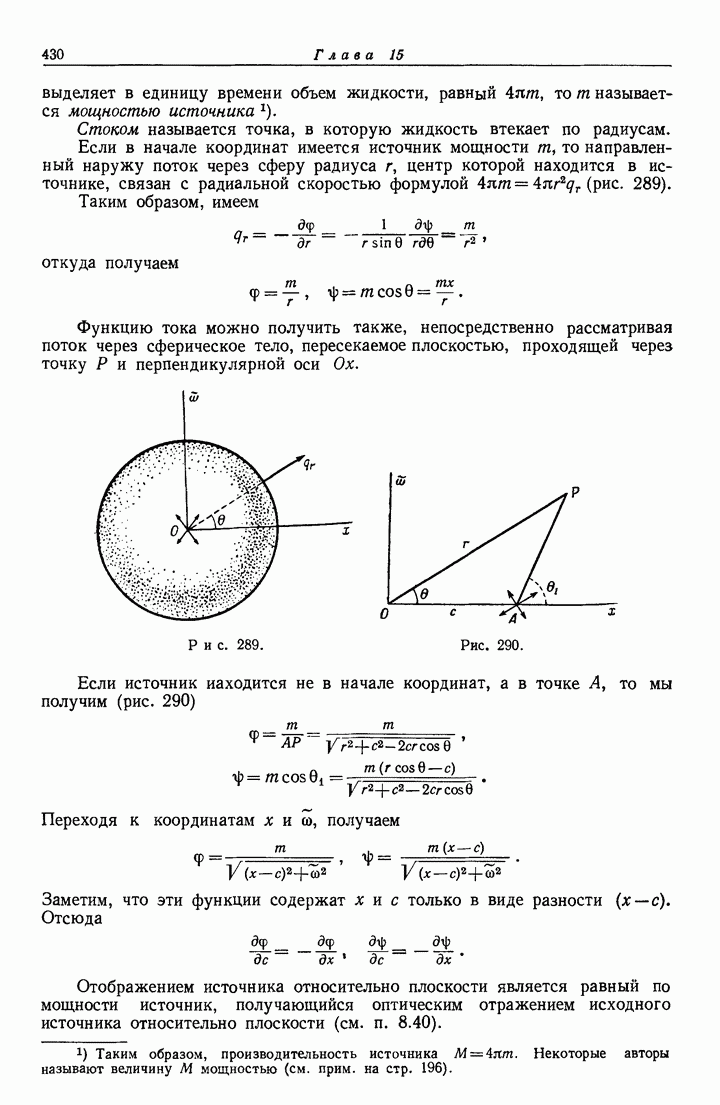
- 15.43. Действие источника на сферу.
- 15.44. Действие радиального диполя на сферу.
- 15.50. Уравнение для функции тока при безвихревом движении.
- 15.51. Скорость.
- 15.52. Граничные условия для функции тока.
- 15.53. Сфера.
- 15.54. Функция тока для сжатого эллипсоида.
- 15.55. Круглый диск.
- 15.56. Трубка Вентури.
- 15.57. Функция тока для вытянутого эллипсоида.
- 15.58. Параболоид вращения.
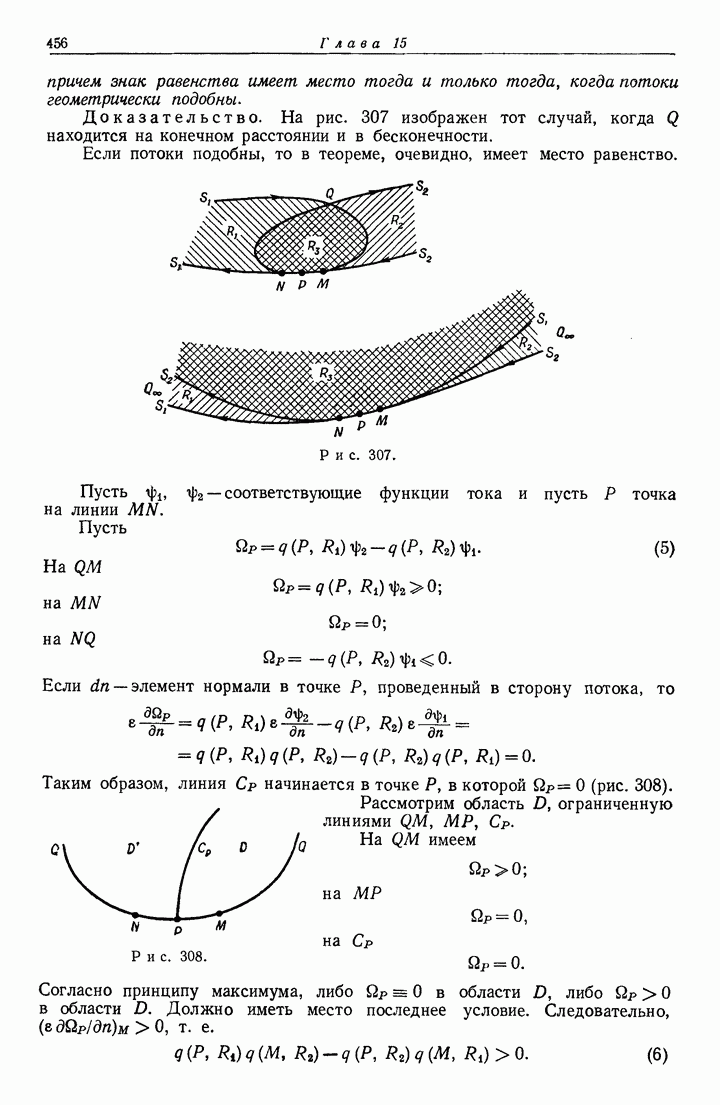
- 15.60. Теоремы сравнения.
- Глава 16. СФЕРЫ И ЭЛЛИПСОИДЫ
- 16.12. Теорема Кельвина об инверсии гармонической функции.
- 16.13. Теорема Вейса для сферы.
- 16.20. Концентрические сферы.
- 16.21. Концентрические сферы, движущиеся в одном направлении.
- 16.22. Неподвижная внешняя сфера.
- 16.30. Две сферы, движущиеся вдоль линии центров.
- 16.31. Сфера, движущаяся перпендикулярно стенке.
- 16.40. Две сферы, движущиеся под прямыми углами к линии центров.
- 16.41. Сфера, движущаяся параллельно стенке.
- 16.50. Эллипсоидальные координаты.
- 16.51. Эллипсоидальные гармонические функции.
- 16.52. Поступательное движение эллипсоида.
- 16.53. Вращающийся эллипсоид.
- 16.54. Вращающаяся эллипсоидальная оболочка.
- Глава 17. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- 17.20. Кинетическая энергия жидкости.
- 17.21. Кинетическая энергия тела.
- 17.30. Динама.
- 17.31. Импульс.
- 17.32. Скорость изменения импульса.
- 17.40. Движущееся начало координат.
- 17.41. Уравнения движения.
- 17.42. Определение импульса через кинетическую энергию.
- 17.43. Уравнения движения, выраженные через кинетическую энергию.
- 17.50. Установившееся поступательное движение.
- 17.52. Тело вращения.
- 17.53. Устойчивость, обусловленная вращением.
- 17.54. Тело, содержащее полость.
- 17.60. Уравнения Лагранжа.
- 17.61. Движение сферы в присутствии стенки.
- 17.70. Тело вращения, ось которого расположена перпендикулярно направлению потока невязкой жидкости.
- Глава 18. ВИХРЕВОЕ ДВИЖЕНИЕ
- 18.20. Выражение скорости через вихрь.
- 18.21. Поток через замкнутый контур.
- 18.22. Неограниченная жидкость.
- 18.23. Вихревая нить.
- 18.24. Электромагнитная аналогия.
- 18.30. Кинетическая энергия.
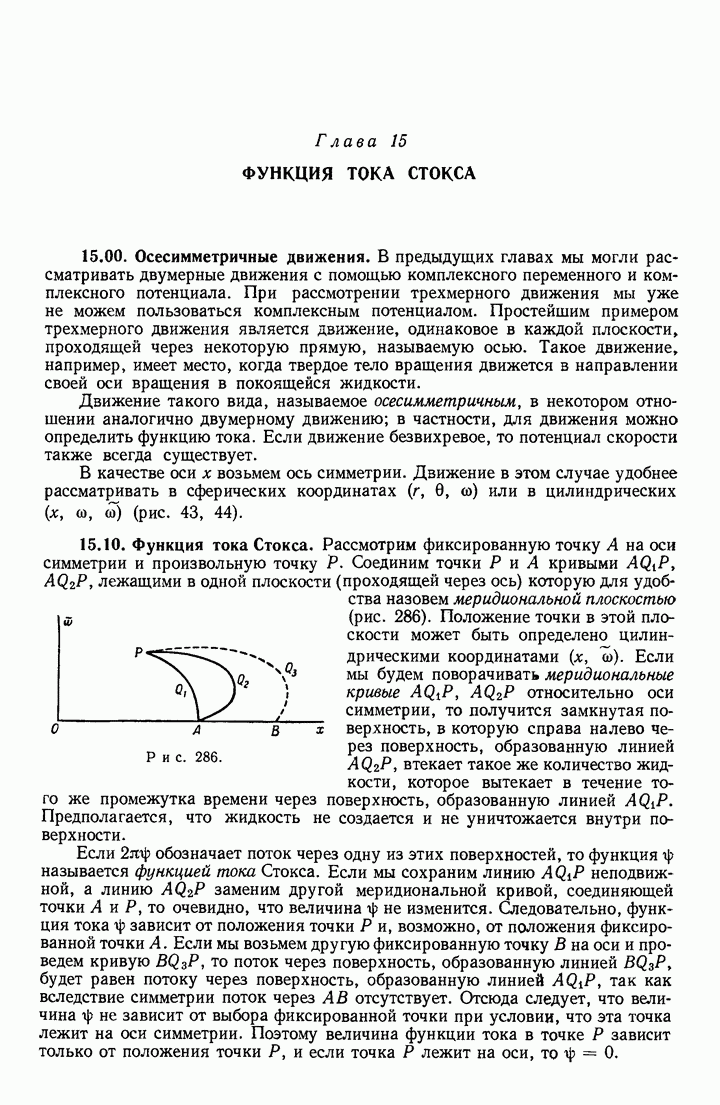
- 18.40. Осесимметричные движения.
- 18.41. Круговая вихревая нить.
- 18.50. Уравнение, которому удовлетворяет функция тока.
- 18.51. Сферический вихрь Хилла.
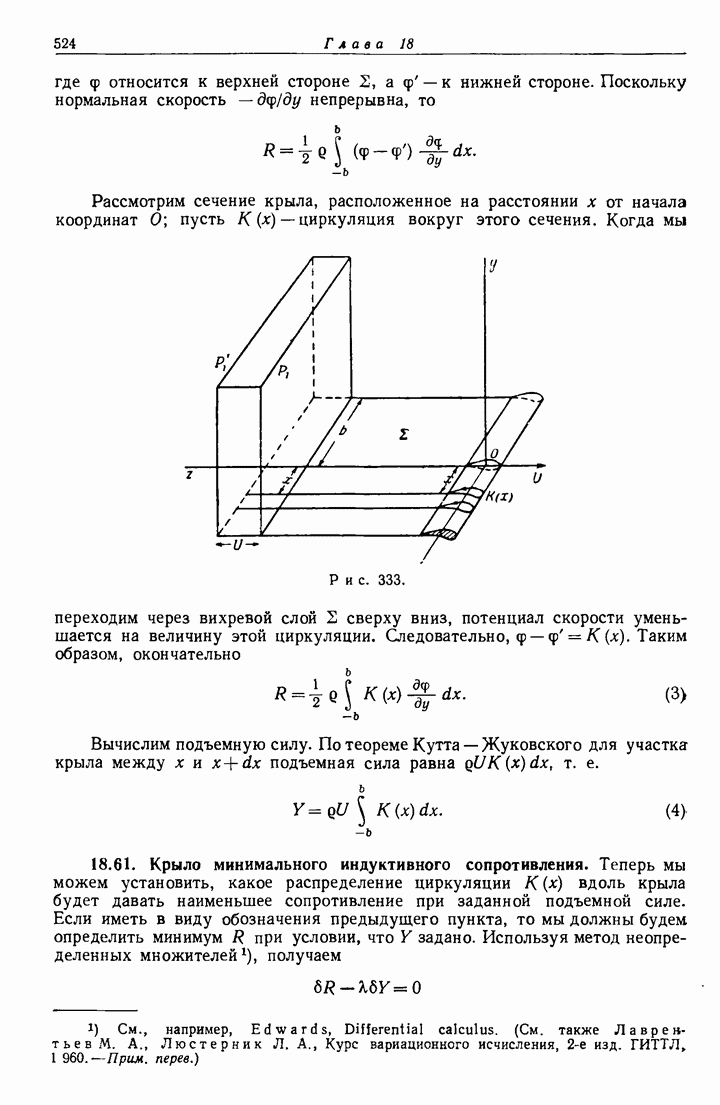
- 18.60. Крыло конечного размаха.
- 18.61. Крыло минимального индуктивного сопротивления.
- Глава 19. ВЯЗКОСТЬ
- 19.02. Гипотеза вязкости.
- 19.03. Уравнение движения.
- 19.04. Установившееся движение; отсутствие внешних сил.
- 19.05. Граничные условия в вязкой жидкости.
- 19.11. Уравнение, которому удовлетворяет вихрь.
- 19.12. Диффузия вихря.
- 19.13. Циркуляция в вязкой жидкости.
- 19.21. Диссипация энергии.
- 19.22. Приток тепла в жидкости.
- 19.31. Течение между двумя параллельными пластинками.
- 19.32. Течение в трубе.
- 19.41. Составляющие напряжения.
- 19.42. Установившееся вращательное движение.
- 19.51. Влияние вязкости на волны в воде.
- 19.61. Осесимметричное движение.
- 19.62. Медленные движения.
- 19.63. Медленное обтекание сферы.
- 19.64. Сопротивление медленно движущейся сферы.
- 19.70. Векторная циркуляция.
- 19.71. Вихревой след.
- 19.72. Суммарный вихрь в кормовом вихревом следе.
- 19.73. Перенос вихрей.
- 19.74. Сила, действующая на крыло.
- 19.75. Приближенное решение Озеена для достаточно больших расстояний от тела.
- 19.76. Подъемная сила и сила сопротивления.
- 19.80. Подобие.
- 19.81. Пограничный слой.
- 19.82. Уравнения в естественных координатах.
- Глава 20. ДОЗВУКОВОЕ И СВЕРХЗВУКОВОЕ ТЕЧЕНИЕ
- 20.10. Уравнение Крокко.
- 20.12. Наложение постоянной скорости.
- 20.13. Установившееся движение.
- 20.20. Установившееся безвихревое движение.
- 20.30. Метод годографа.
- 20.31. Уравнение в плоскости годографа для гомэнтропического течения.
- 20.33. Течение сжимаемого газа внутри сопла, которое сначала сужается, а затем расширяется.
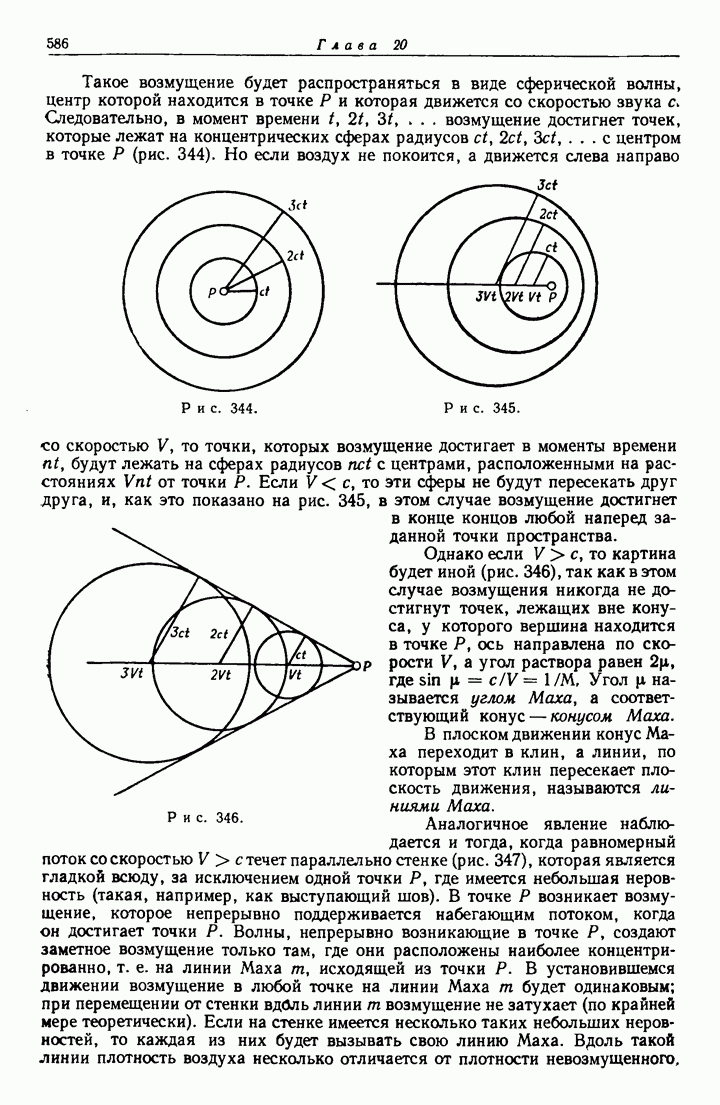
- 20.40. Движущееся возмущение.
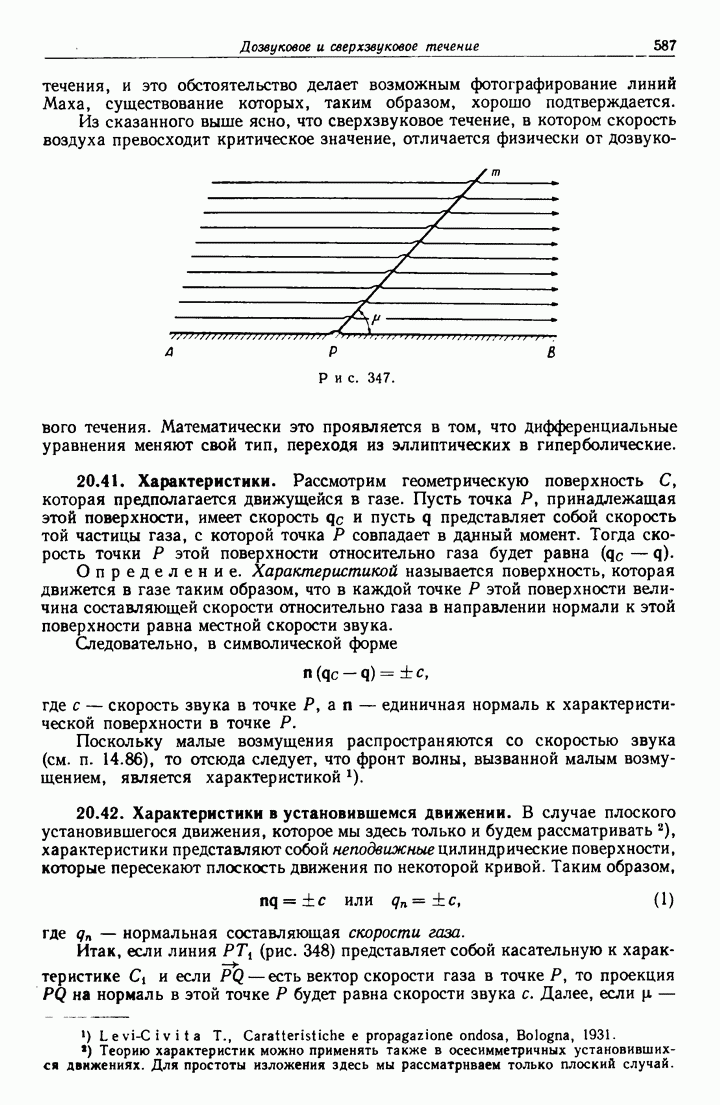
- 20.41. Характеристики.
- 20.42. Характеристики в установившемся движении.
- 20.43. Изменение скорости вдоль характеристики.
- 20.44. Характеристические координаты.
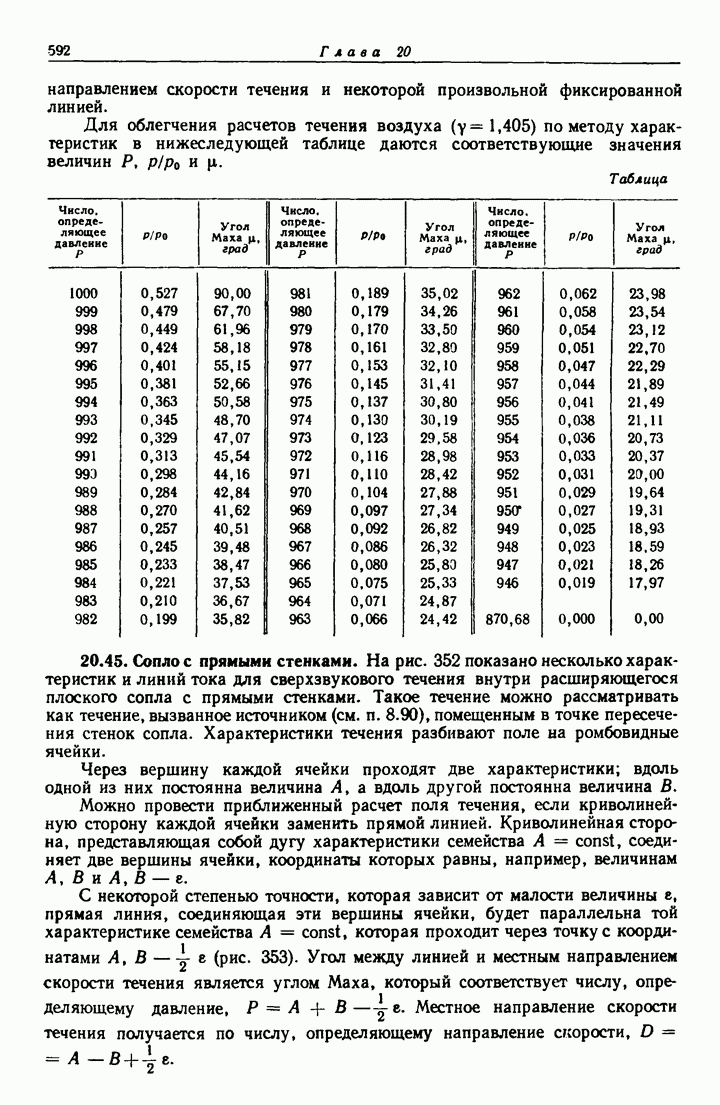
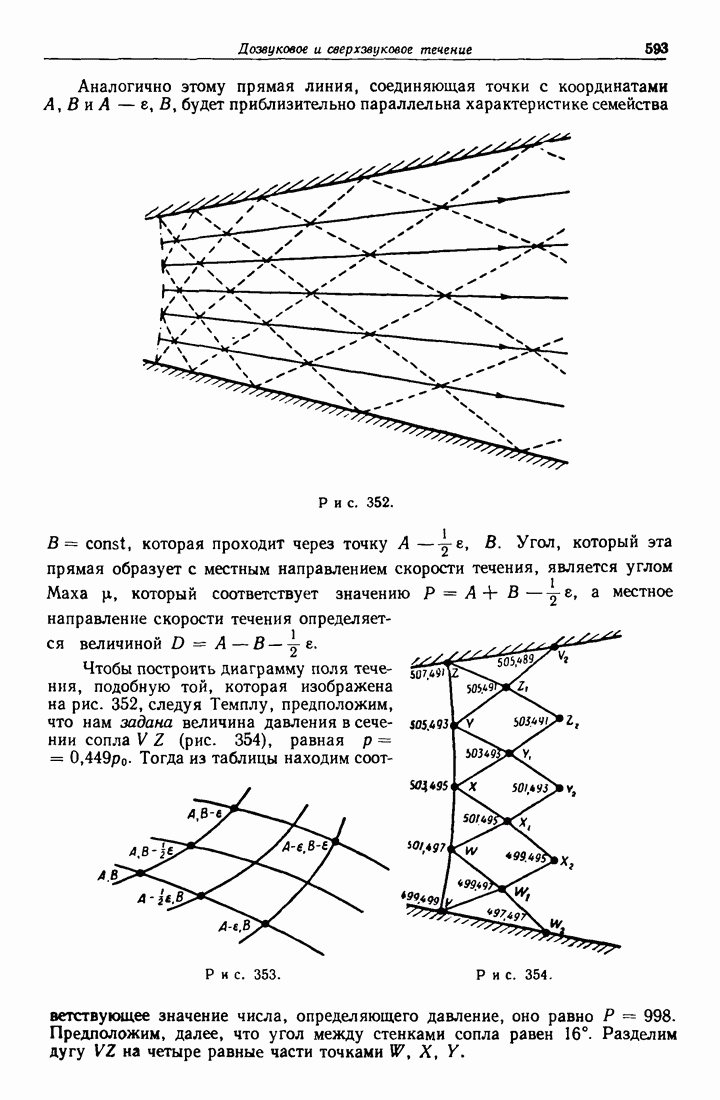
- 20.45. Сопло с прямыми стенками.
- 20.50. Обтекание угла.
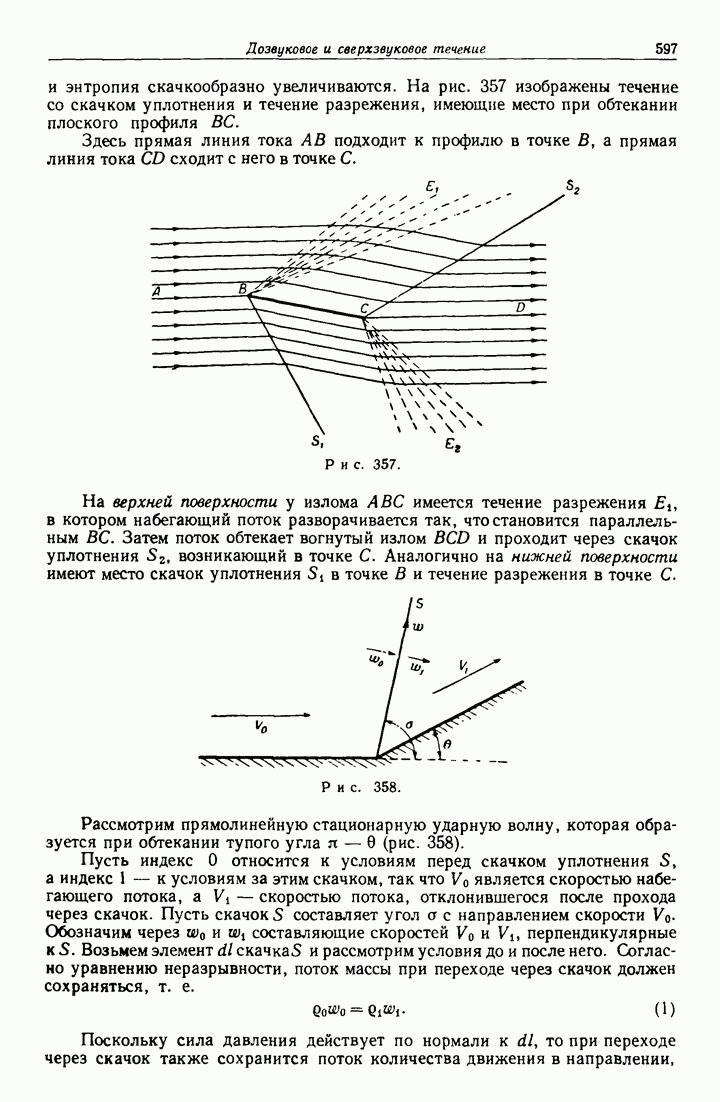
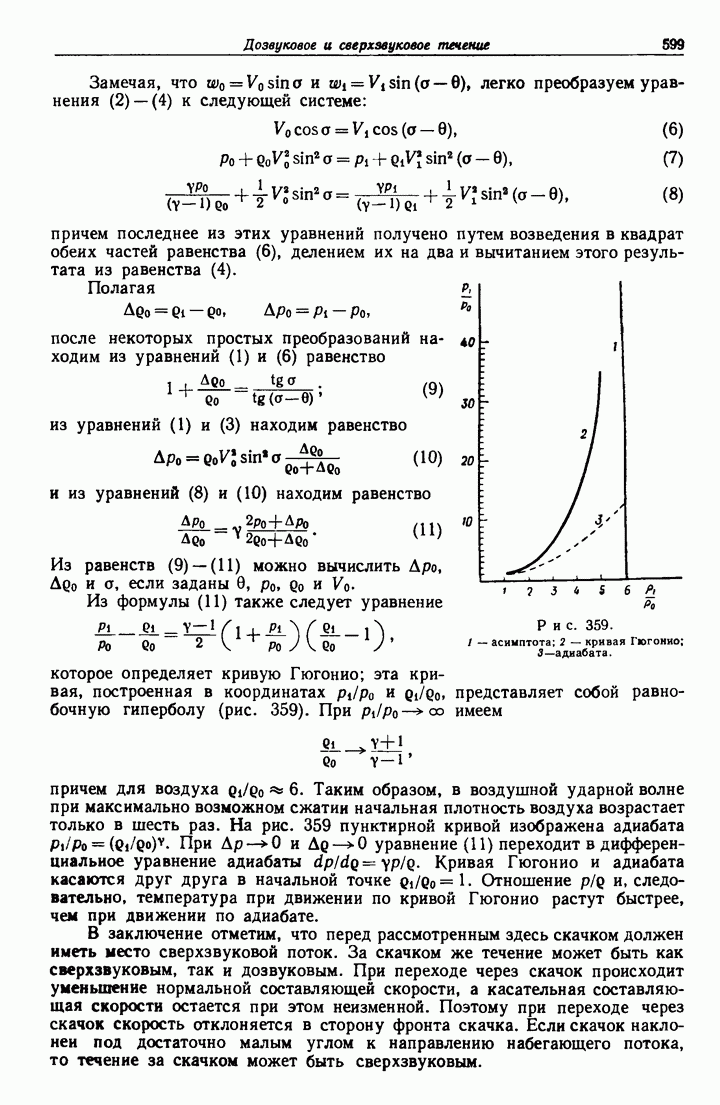
- 20.60. Ударные волны.
- 20.61. Ударная поляра.
- 20.70. Характеристики в изэнтропическом течении.
- 20.71. Теорема единственности.
- 20.80. Течения, зависящие от времени.
- ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К ГЛАВЕ 2. АФИННЫЕ ОРТОГОНАЛЬНЫЕ ТЕНЗОРЫ
- 2. Диады.
- 3. Тензор как оператор.
- 4. Произведение двух тензоров.
- ПРИЛОЖЕНИЕ К ГЛАВЕ 3
- 2. Вывод кинематического условия на свободной поверхности.
- 3. Теоремы о сохраняемости вихревых движений.
- ПРИЛОЖЕНИЕ К ГЛАВЕ 19
- 1. Силы и деформации
- 2. Тензор скоростей деформаций. Теорема Гельмгольца
- 3. Общее уравнение движения сплошной среды
- 4. Вывод уравнений Навье — Стокса
- 5. Уравнение энергии