| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. Тензор как оператор.
Пусть а — вектор, а  некоторая матрица; символом
некоторая матрица; символом  мы будем обозначать тройку чисел
мы будем обозначать тройку чисел  образованную по правилу
образованную по правилу

Тогда имеет место следующая основная теорема. Теорема. Пусть матрица  определена в некоторой системе координат; для того чтобы эта матрица была тензором, необходимо и достаточно, чтобы тройка чисел
определена в некоторой системе координат; для того чтобы эта матрица была тензором, необходимо и достаточно, чтобы тройка чисел  определяемая по формуле
определяемая по формуле  , представляла собой вектор, если тройка чисел
, представляла собой вектор, если тройка чисел  является вектором.
является вектором.
Доказательство. Для доказательства необходимости предположим, что  представляет собой тензор. Обозначим через
представляет собой тензор. Обозначим через  компоненты тензора
компоненты тензора  и вектора а в новой системе координат. Теперь определим в этой системе координат тройку чисел
и вектора а в новой системе координат. Теперь определим в этой системе координат тройку чисел  следующим образом:
следующим образом:

Найдем связь между величинами  Так как по предположению
Так как по предположению  тензор,
тензор,  вектор, то
вектор, то

Следовательно, соотношение  может быть записано в таком виде:
может быть записано в таком виде:

или

но

поэтому

Далее, согласно формуле  ,
,

следовательно,

Таким образом, тройка чисел при переходе от одной системы координат к другой преобразуется по формулам преобразования компонент вектора, т. е. образует вектор.
Для доказательства достаточности возьмем две произвольные системы координат  и в этих системах координат определим матрицы
и в этих системах координат определим матрицы  Пусть, далее, любому вектору а по формуле
Пусть, далее, любому вектору а по формуле  ставится в соответствие ветор
ставится в соответствие ветор  т. е. его компоненты в новой системе координат связаны с компонентами в старой системе координат формулами
т. е. его компоненты в новой системе координат связаны с компонентами в старой системе координат формулами

Докажем, что матрица  определяет некоторый тензор, т. е. что величины
определяет некоторый тензор, т. е. что величины  связаны формулами
связаны формулами

Так как величины  определяются формулами
определяются формулами  , то равенство
, то равенство  может быть записано в виде
может быть записано в виде

Величины  связаны формулами
связаны формулами 

Поэтому соотношение  с учетом формулы
с учетом формулы  можно переписать в виде
можно переписать в виде

Но равенство  имеет место при любых значениях
имеет место при любых значениях  следовательно,
следовательно,

что и требовалось доказать.
Таким образом, тензор можно рассматривать как оператор, который по определенному закону ставит в соответствие каждому вектору а новый вектор. Кроме того, этот оператор является линейным. Итак, выражение  определяет некоторую линейную вектор-функцию вектора а.
определяет некоторую линейную вектор-функцию вектора а.
Доказанная теорема играет большую роль в механике. В самом деле, согласно этой теореме, линейный оператор, действующий в трехмерном евклидовом векторном пространстве, можно рассматривать как аффинный тензор. Это определение, в свою очередь, удобно тем, что позволяет во многих важных случаях ответить на вопрос, является ли данная физическая величина тензором без проверки выполнения условий (5. Например, в динамике твердого тела вводится матрица моментов инерции

где  осевые и центробежные моменты инерции. Составляющие вектора момента количества движения
осевые и центробежные моменты инерции. Составляющие вектора момента количества движения  вычисляются по формуле
вычисляются по формуле

где  компоненты вектора мгновенной угловой скорости. Формула
компоненты вектора мгновенной угловой скорости. Формула  может быть записана более экономно в виде
может быть записана более экономно в виде

Равенство  показывает, что матрица
показывает, что матрица  в любой системе координат ставит в соответствие вектору
в любой системе координат ставит в соответствие вектору  вектор
вектор  Следовательно, матрица
Следовательно, матрица  определяет тензор.
определяет тензор.
Теперь определим умножение тензора на вектор слева. Равенство

означает, что

Формула (17 показывает, что равенство  может быть записано в виде
может быть записано в виде

где  транспонированная матрица, для которой
транспонированная матрица, для которой

Как следствие доказанной теоремы находим, что если  — тензор, то
— тензор, то  — также тензор.
— также тензор.
Рассмотрим теперь произведение диады на вектор. Пользуясь тем, что любая диада есть тензор, найдем компоненты вектора  Эти компоненты записываются в виде
Эти компоненты записываются в виде

т. е.

где  обычное скалярное произведение. Аналогично, если обозначить
обычное скалярное произведение. Аналогично, если обозначить  то
то

т. е.

Пользуясь выведенными формулами, запишем тройное векторное произведение в форме диадного произведения

Легко видеть, что эта запись может быть сделана не единственным способом.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава 1. УРАВНЕНИЕ БЕРНУЛЛИ
- 1.01. Размерности физических величин.
- 1.10. Скорость.
- 1.11. Линии тока и траектории частиц.
- 1.12. Трубки тока и струйки тока.
- 1.20. Плотность.
- 1.30. Давление.
- 1.40. Теорема Бернулли (специальная форма).
- 1.41. Поток в канале.
- 1.42. Замечания о теореме Бернулли.
- 1.43. Константа в теореме Бернулли.
- 1.44. Гидродинамическое давление.
- 1.50. Трубка Пито.
- 1.60. Работа газа при расширении.
- 1.61. Теорема Бернулли для сжимаемой жидкости.
- 1.62. Применение теоремы Бернулли к адиабатическому расширению.
- 1.63. Дозвуковой и сверхзвуковой потоки.
- 1.64. Газовый поток в сужающейся трубке.
- 1.70. Трубка Вентури.
- 1.71. Измерение скорости течения газа трубкой Вентури.
- 1.80. Истечение из отверстия.
- 1.82. Коэффициент сжатия.
- 1.90. Теорема Эйлера о количестве движения.
- 1.91. Сила, действующая на стенки тонкой трубки.
- 1.92. Парадокс Даламбера.
- 1.93. Поток за препятствием.
- Глава 2. ВЕКТОРЫ
- 2.10. Скаляры и векторы.
- 2.11. Скалярное произведение двух векторов.
- 2.12. Векторное произведение двух векторов.
- 2.13. Тройное скалярное произведение.
- 2.14. Тройное векторное произведение.
- 2.15. Разложение вектора.
- 2.16. Индефинитное, или диадное, произведение.
- 2.19. Скалярные и векторные поля.
- 2.20. Криволинейные, поверхностные и объемные интегралы.
- 2.22. Изменение скалярной функции координат.
- 2.23. Другое выражение для градиента функции.
- 2.24. Обобщенное определение оператора V.
- 2.32. Некоторые дифференциальные операции над одним вектором или скаляром.
- 2.33. Некоторые операции над произведением величин.
- 2.34. Применение оператора V к некоторым произведениям.
- 2.40. Анализ движения элемента жидкости.
- 2.41. Вихрь.
- 2.42. Циркуляция.
- 2.50. Теорема Стокса.
- 2.51. Следствия из теоремы Стокса.
- 2.52. Безвихревое движение.
- 2.53. Консервативное поле сил.
- 2.60. Теорема Гаусса.
- 2.61. Следствия из теоремы Гаусса.
- 2.62. Теорема Грина.
- 2.63. Приложения теоремы Грина.
- 2.70. Декартовы координаты.
- 2.71. Другое обозначение для оператора d/dr
- 2.72. Криволинейные ортогональные координаты.
- 2.73. Скорость изменения единичных векторов.
- Глава 3. УРАВНЕНИЯ ДВИЖЕНИЯ
- 3.20. Уравнение неразрывности.
- 3.30. Граничные условия (кинематические).
- 3.31. Граничные условия (физические).
- 3.32. Истечение из отверстия.
- 3.40. Скорость изменения количества движения.
- 3.41. Уравнение движения невязкой жидкости.
- 3.42. Теорема Эйлера о количестве движения.
- 3.43. Консервативные силы.
- 3.44. Уравнение движения в форме Лаграижа.
- 3.45. Установившееся движение.
- 3.50. Уравнение энергии.
- 3.51. Скорость изменения циркуляции.
- 3.52. Вихревое движение.
- 3.53. Сохраняемость вихревого движения.
- 3.54. Сохраняемость вихревых линий.
- 3.55. Относительное движение.
- 3.60. Безвихревое движение.
- 3.61. Уравнение для давления относительно подвижных осей.
- 3.62. Давление жидкости на препятствие.
- 3.64. Импульсивное движение.
- 3.70. Связность. Определение.
- 3.71. Ациклическое и циклическое безвихревые движения.
- 3.72. Кинетическая энергия жидкости.
- 3.73. Теорема Кельвина о минимуме энергии.
- 3.74. Среднее значение потенциала скоростей.
- 3.75. Среднее значение потенциала скоростей в перифрактической области.
- 3.76. Кинетическая энергия жидкости, занимающей бесконечную область.
- 3.77. Теоремы единственности.
- Глава 4. ДВУМЕРНОЕ ДВИЖЕНИЕ
- 4.10. Двумерное движение.
- 4.20. Двумерное установившееся движение жидкости.
- 4.21. Безвихревое движение.
- 4.22. Движение без деформации.
- 4.23. Вихрь.
- 4.24. Уравнения установившегося движения.
- 4.30. Функция тока.
- 4.31. Выражение скорости через функцию тока.
- 4.32. Метод Рэнкина.
- 4.33. Функция тока для равномерного потока.
- 4.40. Векторные соотношения, связывающие скорость и вихрь.
- 4.41. Уравнение для функции …
- 4.60. Критические точки.
- 4.70. Потенциал скоростей жидкости.
- 4.71. Уравнение для потенциала скоростей.
- Глава 5. КОМПЛЕКСНОЕ ПЕРЕМЕННОЕ
- 5.01. Комплексные числа.
- 5.10. Векторная диаграмма.
- 5.11. Умножение.
- 5.12. Равенство комплексных чисел.
- 5.13. Теорема Эйлера.
- 5.14. Сопряженные комплексные числа.
- 5.15. Число, обратное комплексному числу.
- 5.16. Векторные свойства комплексных чисел.
- 5.17. Поворот координатных осей.
- 5.20. Логарифмы.
- 5.21. Действительная и мнимая части.
- 5.30. Определение аналитической функции от z.
- 5.31. Сопряженные функции.
- 5.32. О связи сопряженных функций с f(z).
- 5.33. Решение уравнения Лапласа.
- 5.40. Направление обхода контура.
- 5.43. Теорема Стокса в комплексной форме.
- 5.50. Интегральная теорема Коши.
- 5.51. Теорема Морера.
- 5.52. Аналитическое продолжение.
- 5.53. Принцип симметрии.
- 5.54. Деформация контура.
- 5.55. Случай, когда функция не аналитична в некоторых точках.
- 5.56. Особенности.
- 5.57. Вычеты.
- 5.58. Теорема Коши о вычетах.
- 5.59. Формула Коши.
- 5.60. Нули.
- 5.61. Принцип аргумента.
- 5.62. Отображение.
- 5.63. Контуры с нулями функции f(z).
- 5.70. Конформное отображение.
- 5.71. Отображение бесконечных областей.
- Глава 6. ПОТЕНЦИАЛЬНЫЕ ТЕЧЕНИЯ
- 6.01. Комплексная скорость.
- 6.02. Критические точки.
- 6.03. Скорость.
- 6.04. Уравнения линий тока.
- 6.10. Течение через отверстие.
- 6.11. Течение вокруг эллиптического цилиндра.
- 6.21. Теорема об окружности.
- 6.22. Потенциальное обтекание кругового цилиндра.
- 6.23. Разветвляющаяся линия тока.
- 6.24. Распределение давления на цилиндре.
- 6.25. Кавитация.
- 6.29. Применение конформного отображения.
- 6.30. Преобразование Жуковского.
- 6.31. Обтекание эллиптического цилиндра.
- 6.32. Эллиптические координаты.
- 6.33. Применение эллиптических координат к изучению обтекания эллипса.
- 6.34. Обтекание пластины.
- 6.35. Общий метод.
- 6.41. Теорема Блазиуса.
- 6.42. Действие равномерного потока на эллиптический цилиндр.
- 6.50. Коаксиальные координаты.
- 6.51. Обтекание впадины или выступа дна.
- 6.52. Обтекание цилиндрического тела.
- 6.53. Цилиндр в тоннеле.
- Глава 7. ПРОФИЛИ КРЫЛЬЕВ
- 7.11. Циркуляционное движение жидкости между концентрическими цилиндрами.
- 7.12. Обтекание кругового цилиндра с циркуляцией и без циркуляции.
- 7.13. Равномерное течение с поперечным градиентом скорости.
- 7.20. Профиль крыла.
- 7.30. Дальнейшее исследование преобразования Жуковского.
- 7.31. Геометрическое построение преобразования.
- 7.32. Характер задней кромки крыла.
- 7.40. Постулат Жуковского.
- 7.45. Теорема Кутта—Жуковского.
- 7.50. Подъемная сила крыла в равномерном потоке.
- 7.51. Оси профиля.
- 7.52. Фокус профиля.
- 7.53. Парабола метацентров.
- Глава 8. ИСТОЧНИКИ И СТОКИ
- 8.12. Комплексный потенциал для простого источника.
- 8.20. Комбинация источника и стока.
- 8.21. Источник в равномерном потоке.
- 8.22. Источник и сток одинаковой мощности.
- 8.23. Диполь, или двойной источник.
- 8.24. Эквивалентный слой диполей по Грину.
- 8.30. Источник и сток в равномерном потоке.
- 8.31. Два равных по мощности источника.
- 8.40. Метод отображений.
- 8.41. Действие на стенку точечного источника.
- 8.42. Общий метод отображений относительно плоскости.
- 8.43. Отображение диполя относительно плоскости.
- 8.50. Источники при конформном преобразовании.
- 8.51. Источник, расположенный в углу между двумя стенками.
- 8.60. Источник вне кругового цилиндра.
- 8.61. Отображение источника, расположенного вне кругового цилиндра.
- 8.62. Сила, действующая на круговой цилиндр от источника.
- 8.63. Теорема Лагалли.
- 8.64. Источник вне эллиптического цилиндра.
- 8.70. Отображение на единичный круг.
- 8.71. Источники вне цилиндра.
- 8.72. Сила, действующая на цилиндр.
- 8.80. Источник и сток вне кругового цилиндра.
- 8.81. Отображение диполя относительно кругового цилиндра.
- 8.82. Сила, действующая на цилиндр, обусловленная диполем.
- 8.83. Распространение теоремы Лагалли на диполи.
- 8.90. Источник в сжимаемом потоке.
- Глава 9. ДВИЖЕНИЕ ЦИЛИНДРОВ
- 9.10. Кинетическая энергия ациклического безвихревого движения.
- 9.20. Круговой цилиндр, движущийся поступательно.
- 9.21. Траектории частиц.
- 9.22. Кинетическая энергия.
- 9.23. Круговой цилиндр, падающий под действием силы тяжести.
- 9.24. Круговой цилиндр с циркуляцией.
- 9.25. Цилиндр с циркуляцией, движущийся под действием силы тяжести.
- 9.30. Уравнение для давления в движущейся системе координат.
- 9.40. Функция тока на границе.
- 9.50. Сила, действующая на движущийся цилиндр.
- 9.52. Обобщение теоремы Чаплыгина-Блазиуса.
- 9.53. Цилиндр, движущийся в безграничной жидкости.
- 9.62. Общий случай движения цилиндра.
- 9.63. Комплексный потенциал движущегося цилиндра.
- 9.64. Круговой цилиндр (общий метод).
- 9.65. Эллиптический цилиндр.
- 9.66. Цилиндр с циркуляцией.
- 9.70. Вращающийся цилиндр.
- 9.71. Вращающийся эллиптический цилиндр, содержащий жидкость.
- 9.72. Вращающаяся равносторонняя призма, содержащая жидкость.
- 9.73. Круговой цилиндр с вырезом.
- 9.74. Метод конформного отображения для комплексного потенциала.
- 9.75. Криволинейная многоугольная граница.
- 9.76. Вращение вокруг эксцентрической точки.
- Глава 10. ТЕОРЕМА ШВАРЦА — КРИСТОФФЕЛЯ
- 10.20. Теорема Шварца — Кристоффеля.
- 10.31. Отображение полубесконечной полосы.
- 10.32. Отображение бесконечной полосы.
- 10.40. Источник, расположенный в стенке канала (рис. 180).
- 10.50. Источник, расположенный посередине между двумя плоскостями.
- 10.60. Бесконечно глубокий поток с уступом на дне.
- 10.70. Канал с резко изменяющейся шириной.
- 10.80. Канал с разветвляющимся руслом.
- Глава 11. СТРУИ И СТРУЙНЫЕ ТЕЧЕНИЯ
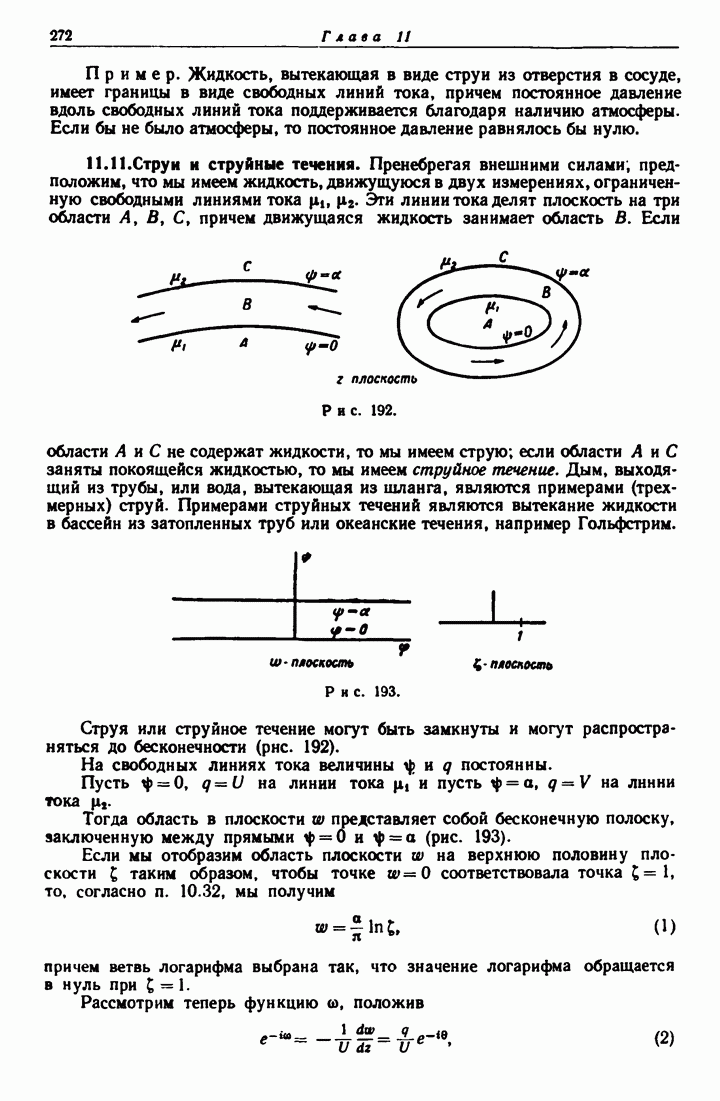
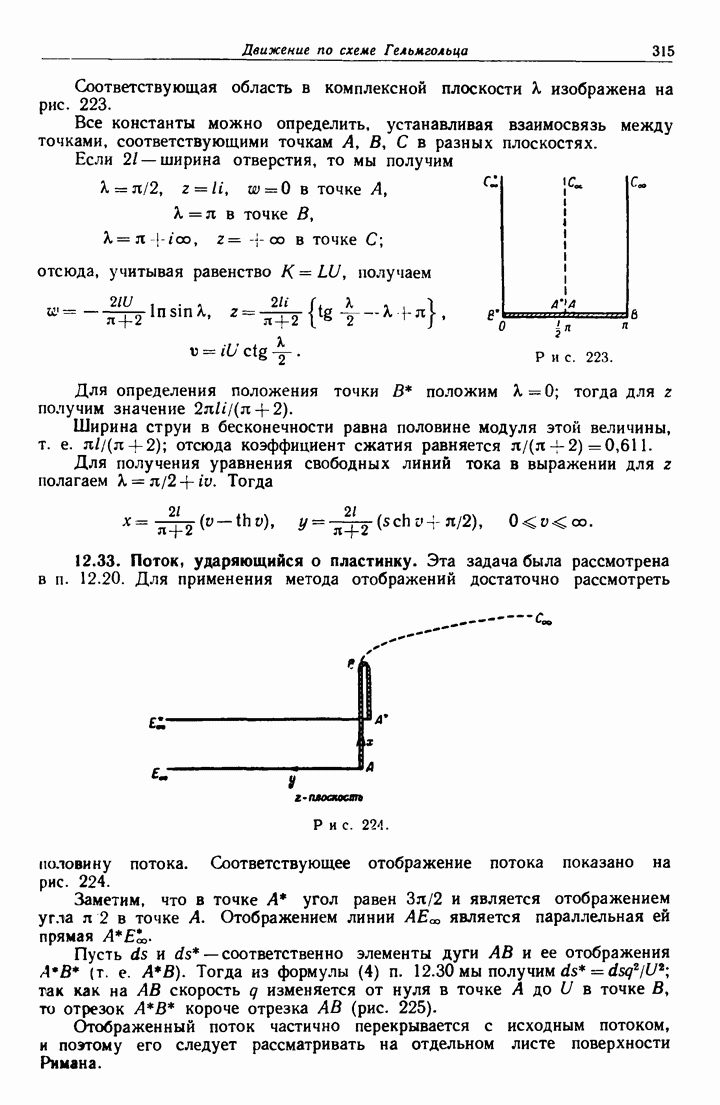
- 11.11. Струи и струйные течения.
- 11.20. Формула Шварца.
- 11.30. Соударяющиеся струи.
- 11.31. Комплексная скорость.
- 11.32. Выражение комплексного потенциала через комплексную скорость v.
- 11.33. Соотношения между шириной и направлением струй.
- 11.34. Выражение величины z через комплексную скорость v.
- 11.35. Уравнения свободных линий тока.
- 11.40. Неопределенность задачи.
- 11.41. Прямой удар двух одинаковых струй.
- 11.42. Прямой удар двух неодинаковых струй.
- 11.43. Косой удар двух одинаковых струй.
- 11.50. Твердые границы.
- 11.51. Плоская форма насадка Борда.
- 11.52. Уравнение свободных линий тока.
- 11.53. Истечение через отверстие.
- 11.54. Криволинейные границы.
- 11.60. Поток со свободной поверхностью под действием силы тяжести.
- 11.61. Потенциальный поток со свободной поверхностью.
- 11.62. Установившийся поток со свободной поверхностью.
- 11.63. Касательные потоки.
- 11.64. Касательное решение для струи, направленной вертикально вниз.
- Глава 12. ДВИЖЕНИЕ ПО СХЕМЕ ГЕЛЬМГОЛЬЦА
- 12.12. Правильная кавитация.
- 12.20. Прямой удар струи о пластинку.
- 12.21. Лобовое сопротивление пластинки.
- 12.22. Коэффициент лобового сопротивления.
- 12.23. Задача Рябушинского.
- 12.25. Скольжение и глиссирование.
- 12.26. Глиссирование пластинки по поверхности потока.
- 12.30. Отображение относительно свободных линий тока.
- 12.31. Насадок Борда.
- 12.32. Истечение из отверстия.
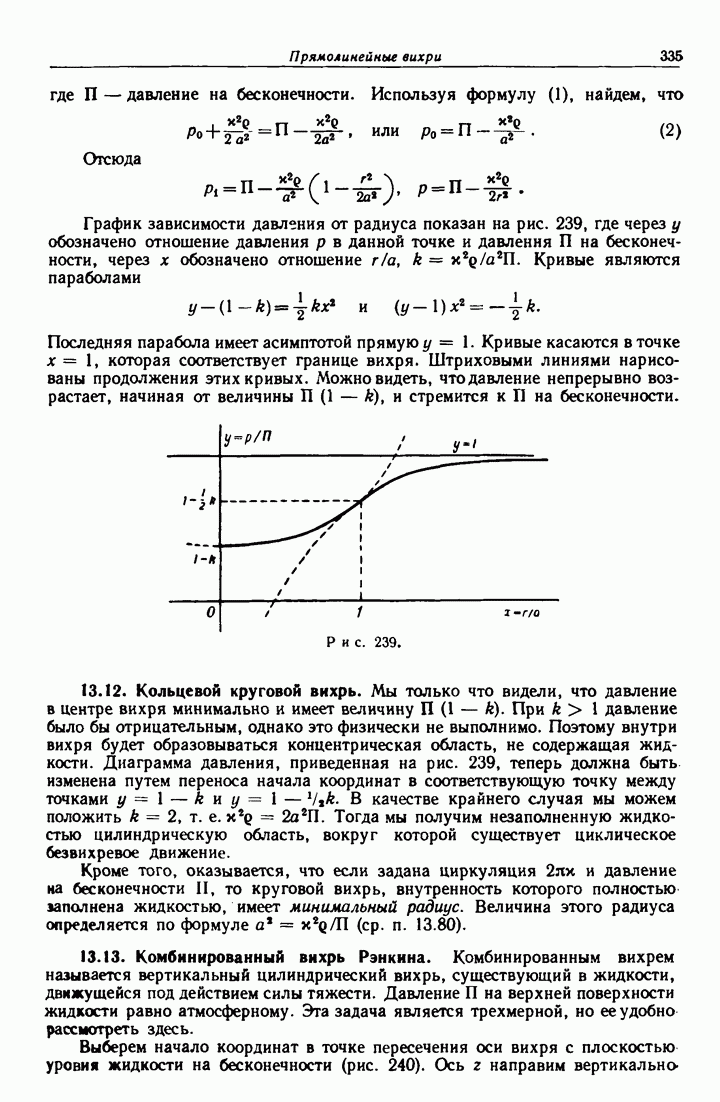
- 12.33. Поток, ударяющийся о пластинку.
- 12.34. Геометрическая интерпретация силы, действующей на препятствие.
- 12.35. Обратная струя.
- 12.40. Метод Леви-Чивита.
- 12.46. Лобовое сопротивление, подъемная сила и момент.
- 12.47. Точка разрыва функции w(e).
- 12.50. Решение для случая …
- 12.51. Удар потока о пластинку.
- 12.52. Симметричный случай.
- Глава 13. ПРЯМОЛИНЕЙНЫЕ ВИХРИ
- 13.11. Давление в поле кругового вихря.
- 13.12. Кольцевой круговой вихрь.
- 13.13. Комбинированный вихрь Рэнкина.
- 13.20. Прямолинейная вихревая нить.
- 13.21. Изолированная вихревая нить.
- 13.22. Движение вихревых нитей.
- 13.23. Две вихревые нити.
- 13.24. Движение системы вихревых нитей.
- 13.30. Пара вихрей.
- 13.31. Вихревая нить, параллельная плоскости.
- 13.32. Вихревой диполь.
- 13.33. Вихреисточник.
- 13.40. Вихревая нить, параллельная двум перпендикулярным плоскостям.
- 13.50. Вихрь внутри или вне кругового цилиндра.
- 13.51. Вихри около кругового цилиндра.
- 13.52. Стационарные вихревые нити около цилиндра.
- 13.60. Конформное отображение.
- 13.61. Вихрь вне произвольного цилиндра.
- 13.62. Эквивалентный слой Грина из источников и вихрей.
- 13.70. Вихревая пелена.
- 13.71. Одна бесконечная цепочка вихрей.
- 13.72. Вихревая дорожка Кармана.
- 13.73. Сопротивление, вызываемое вихревым следом.
- 13.8. Вихрь в сжимаемом газе.
- Глава 14. ВОЛНЫ
- 14.10. Волновое движение.
- 14.11. Кинематическое условие на свободной поверхности.
- 14.12. Условие для давления на свободной поверхности.
- 14.13. Поверхностные волны.
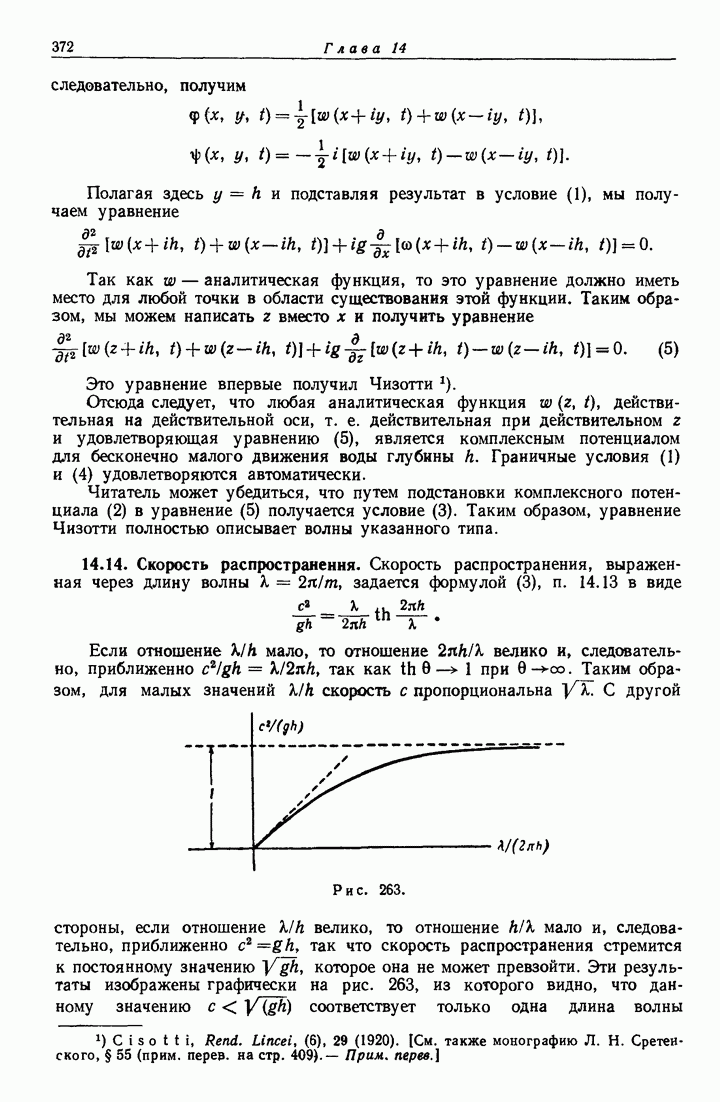
- 14.14. Скорость распространения.
- 14.15. Траектории частиц.
- 14.17. Прогрессивные волны на глубокой воде.
- 14.18. Давление, обусловленное волной на глубокой воде.
- 14.20. Кинетическая энергия прогрессивных волн.
- 14.21. Потенциальная энергия.
- 14.22. Групповая скорость.
- 14.23. Динамический смысл групповой скорости.
- 14.24. Волновое сопротивление.
- 14.30. Стоячие, или стационарные волны.
- 14.31. Комплексный потенциал стоячих волн.
- 14.32. Траектории частиц в стоячей волне.
- 14.33. Стоячие волны в прямоугольном бассейне.
- 14.34. Энергия стоячих волн.
- 14.40. Установившееся движение.
- 14.41. Второе приближение для величины скорости волны.
- 14.42. Волны на поверхности раздела.
- 14.43. Установившийся поток над синусоидальным дном.
- 14.44. Волны на поверхности раздела в случае, когда верхний слой имеет свободную поверхность.
- 14.50. Поверхностное натяжение.
- 14.51. Уравнение для комплексного потенциала.
- 14.52. Поверхностные волны.
- 14.53. Влияние капиллярности в случае волн на поверхности раздела.
- 14.54. Скорость распространения.
- 14.55. Действие ветра на глубокой воде.
- 14.58. Условие Леви-Чивита для поверхности жидкости.
- 14.60. Длинные волны.
- 14.61. Давление.
- 14.62. Поверхностное возвышение.
- 14.63. Волны, распространяющиеся только в одном направлении.
- 14.64. Изменение профиля в длинных волнах.
- 14.70. Действие малых возмущающих сил.
- 14.71. Приливы в экваториальном канале.
- 14.80. Трохоидальная волна Герстнера.
- 14.81. Вид свободной поверхности.
- 14.82. Точное решение для безвихревой волны.
- 14.84. Точная нелинейная теория волн постоянной формы.
- 14.85. Точная линейная теория.
- 14.86. Звуковые волны.
- 14.87. Плоские волны.
- 14.88. Плоские волны в цилиндрической трубе.
- 14.89. Сферические волны.
- Глава 15. ФУНКЦИЯ ТОКА СТОКСА
- 15.21. Подводный взрыв.
- 15.22. Равномерный поток.
- 15.23. Источник в равномерном потоке.
- 15.24. Линейный источник конечных размеров.
- 15.25. Дирижаблеобразные формы.
- 15.26. Равные по мощности источник и сток. Диполь.
- 15.27. Твердые тела Рэнкина.
- 15.28. Эквивалентный слой Грина.
- 15.29. Теорема Бутлера для сферы.
- 15.30. Сфера в потоке.
- 15.31. Кинетическая энергия.
- 15.32. Движущаяся сфера.
- 15.33. Давление на движущуюся сферу.
- 15.40. Отображение источника относительно сферы.
- 15.41. Отображение радиального диполя относительно сферы.
- 15.42. Сила, действующая на препятствие.
- 15.43. Действие источника на сферу.
- 15.44. Действие радиального диполя на сферу.
- 15.50. Уравнение для функции тока при безвихревом движении.
- 15.51. Скорость.
- 15.52. Граничные условия для функции тока.
- 15.53. Сфера.
- 15.54. Функция тока для сжатого эллипсоида.
- 15.55. Круглый диск.
- 15.56. Трубка Вентури.
- 15.57. Функция тока для вытянутого эллипсоида.
- 15.58. Параболоид вращения.
- 15.60. Теоремы сравнения.
- Глава 16. СФЕРЫ И ЭЛЛИПСОИДЫ
- 16.12. Теорема Кельвина об инверсии гармонической функции.
- 16.13. Теорема Вейса для сферы.
- 16.20. Концентрические сферы.
- 16.21. Концентрические сферы, движущиеся в одном направлении.
- 16.22. Неподвижная внешняя сфера.
- 16.30. Две сферы, движущиеся вдоль линии центров.
- 16.31. Сфера, движущаяся перпендикулярно стенке.
- 16.40. Две сферы, движущиеся под прямыми углами к линии центров.
- 16.41. Сфера, движущаяся параллельно стенке.
- 16.50. Эллипсоидальные координаты.
- 16.51. Эллипсоидальные гармонические функции.
- 16.52. Поступательное движение эллипсоида.
- 16.53. Вращающийся эллипсоид.
- 16.54. Вращающаяся эллипсоидальная оболочка.
- Глава 17. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА В ЖИДКОСТИ
- 17.20. Кинетическая энергия жидкости.
- 17.21. Кинетическая энергия тела.
- 17.30. Динама.
- 17.31. Импульс.
- 17.32. Скорость изменения импульса.
- 17.40. Движущееся начало координат.
- 17.41. Уравнения движения.
- 17.42. Определение импульса через кинетическую энергию.
- 17.43. Уравнения движения, выраженные через кинетическую энергию.
- 17.50. Установившееся поступательное движение.
- 17.52. Тело вращения.
- 17.53. Устойчивость, обусловленная вращением.
- 17.54. Тело, содержащее полость.
- 17.60. Уравнения Лагранжа.
- 17.61. Движение сферы в присутствии стенки.
- 17.70. Тело вращения, ось которого расположена перпендикулярно направлению потока невязкой жидкости.
- Глава 18. ВИХРЕВОЕ ДВИЖЕНИЕ
- 18.20. Выражение скорости через вихрь.
- 18.21. Поток через замкнутый контур.
- 18.22. Неограниченная жидкость.
- 18.23. Вихревая нить.
- 18.24. Электромагнитная аналогия.
- 18.30. Кинетическая энергия.
- 18.40. Осесимметричные движения.
- 18.41. Круговая вихревая нить.
- 18.50. Уравнение, которому удовлетворяет функция тока.
- 18.51. Сферический вихрь Хилла.
- 18.60. Крыло конечного размаха.
- 18.61. Крыло минимального индуктивного сопротивления.
- Глава 19. ВЯЗКОСТЬ
- 19.02. Гипотеза вязкости.
- 19.03. Уравнение движения.
- 19.04. Установившееся движение; отсутствие внешних сил.
- 19.05. Граничные условия в вязкой жидкости.
- 19.11. Уравнение, которому удовлетворяет вихрь.
- 19.12. Диффузия вихря.
- 19.13. Циркуляция в вязкой жидкости.
- 19.21. Диссипация энергии.
- 19.22. Приток тепла в жидкости.
- 19.31. Течение между двумя параллельными пластинками.
- 19.32. Течение в трубе.
- 19.41. Составляющие напряжения.
- 19.42. Установившееся вращательное движение.
- 19.51. Влияние вязкости на волны в воде.
- 19.61. Осесимметричное движение.
- 19.62. Медленные движения.
- 19.63. Медленное обтекание сферы.
- 19.64. Сопротивление медленно движущейся сферы.
- 19.70. Векторная циркуляция.
- 19.71. Вихревой след.
- 19.72. Суммарный вихрь в кормовом вихревом следе.
- 19.73. Перенос вихрей.
- 19.74. Сила, действующая на крыло.
- 19.75. Приближенное решение Озеена для достаточно больших расстояний от тела.
- 19.76. Подъемная сила и сила сопротивления.
- 19.80. Подобие.
- 19.81. Пограничный слой.
- 19.82. Уравнения в естественных координатах.
- Глава 20. ДОЗВУКОВОЕ И СВЕРХЗВУКОВОЕ ТЕЧЕНИЕ
- 20.10. Уравнение Крокко.
- 20.12. Наложение постоянной скорости.
- 20.13. Установившееся движение.
- 20.20. Установившееся безвихревое движение.
- 20.30. Метод годографа.
- 20.31. Уравнение в плоскости годографа для гомэнтропического течения.
- 20.33. Течение сжимаемого газа внутри сопла, которое сначала сужается, а затем расширяется.
- 20.40. Движущееся возмущение.
- 20.41. Характеристики.
- 20.42. Характеристики в установившемся движении.
- 20.43. Изменение скорости вдоль характеристики.
- 20.44. Характеристические координаты.
- 20.45. Сопло с прямыми стенками.
- 20.50. Обтекание угла.
- 20.60. Ударные волны.
- 20.61. Ударная поляра.
- 20.70. Характеристики в изэнтропическом течении.
- 20.71. Теорема единственности.
- 20.80. Течения, зависящие от времени.
- ПРИЛОЖЕНИЯ
- ПРИЛОЖЕНИЕ К ГЛАВЕ 2. АФИННЫЕ ОРТОГОНАЛЬНЫЕ ТЕНЗОРЫ
- 2. Диады.
- 3. Тензор как оператор.
- 4. Произведение двух тензоров.
- ПРИЛОЖЕНИЕ К ГЛАВЕ 3
- 2. Вывод кинематического условия на свободной поверхности.
- 3. Теоремы о сохраняемости вихревых движений.
- ПРИЛОЖЕНИЕ К ГЛАВЕ 19
- 1. Силы и деформации
- 2. Тензор скоростей деформаций. Теорема Гельмгольца
- 3. Общее уравнение движения сплошной среды
- 4. Вывод уравнений Навье — Стокса
- 5. Уравнение энергии