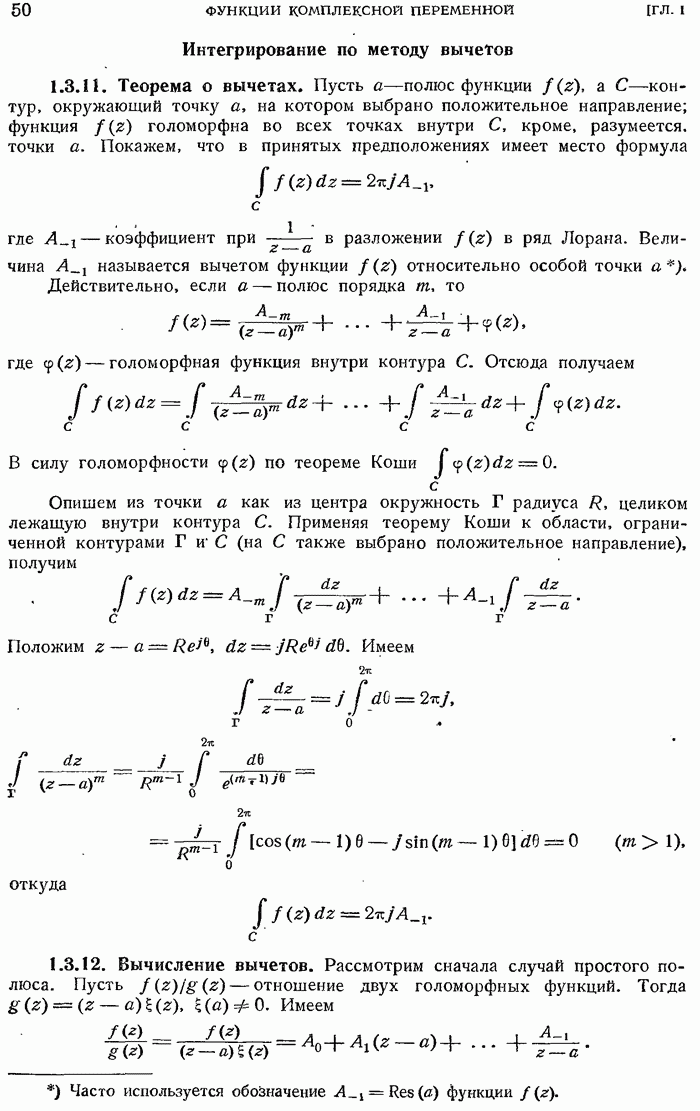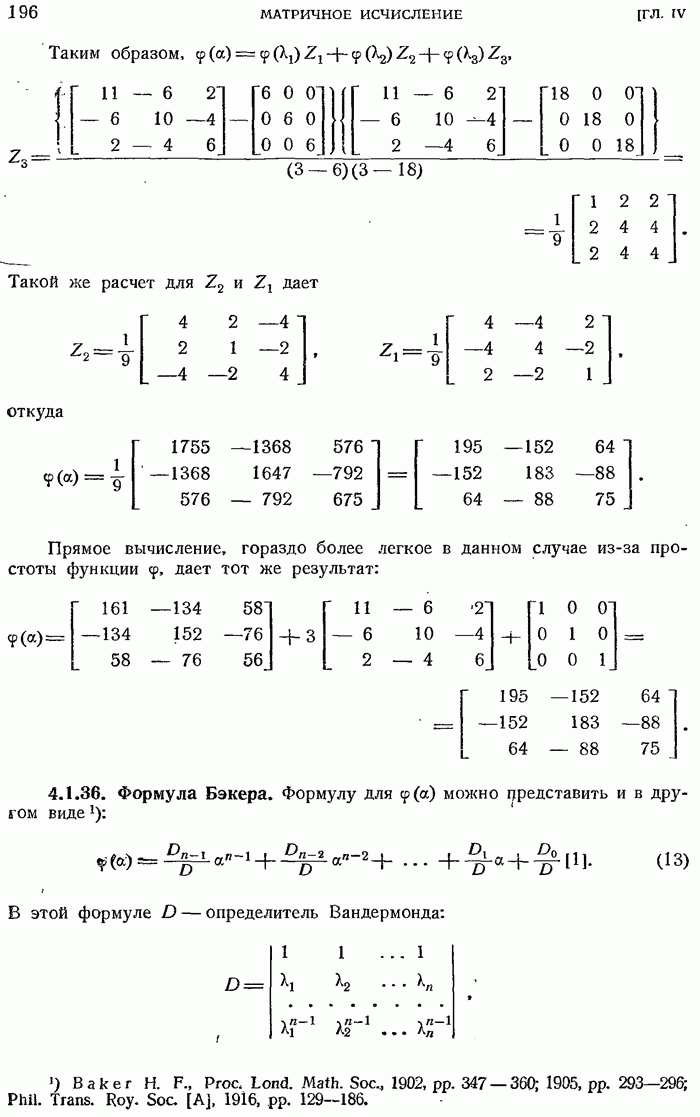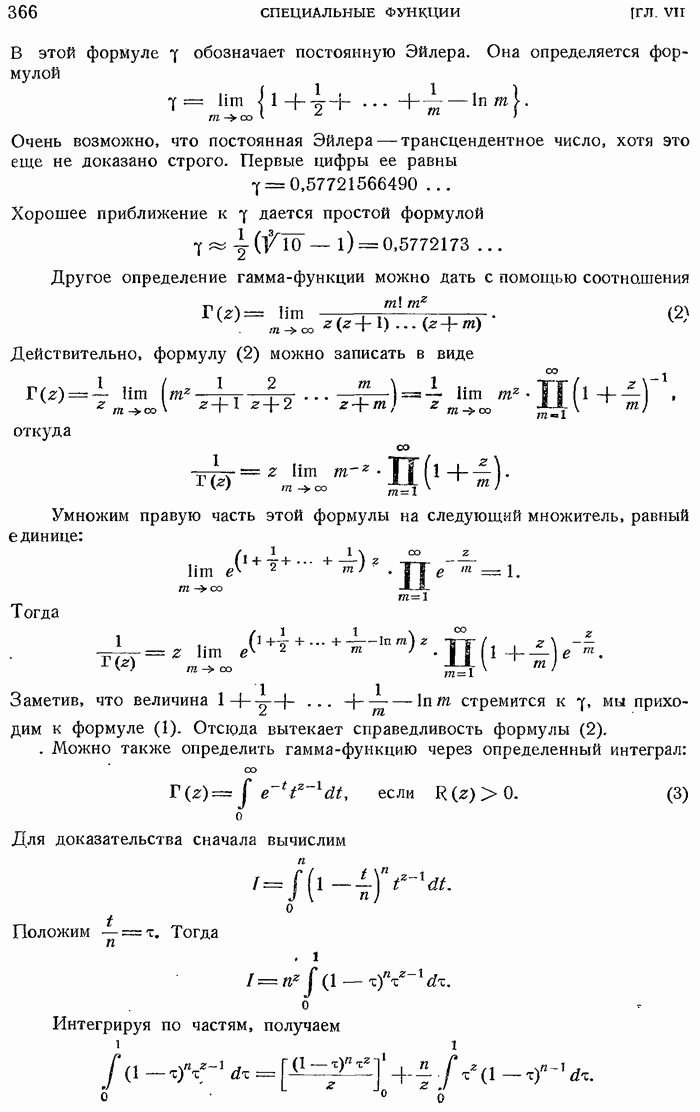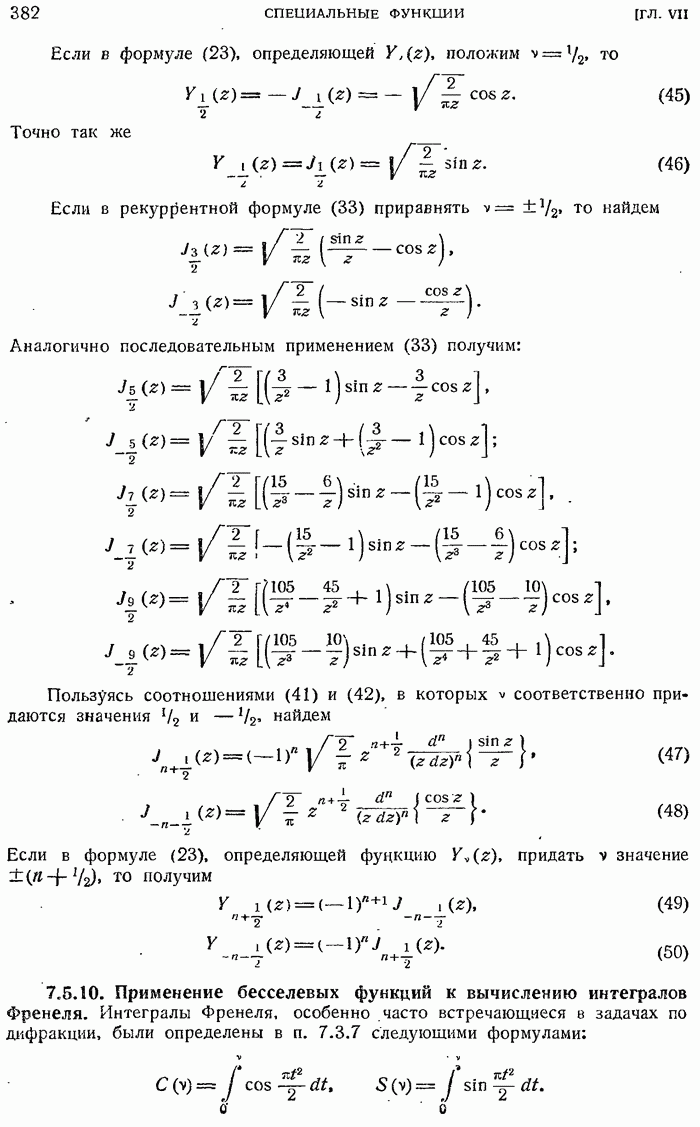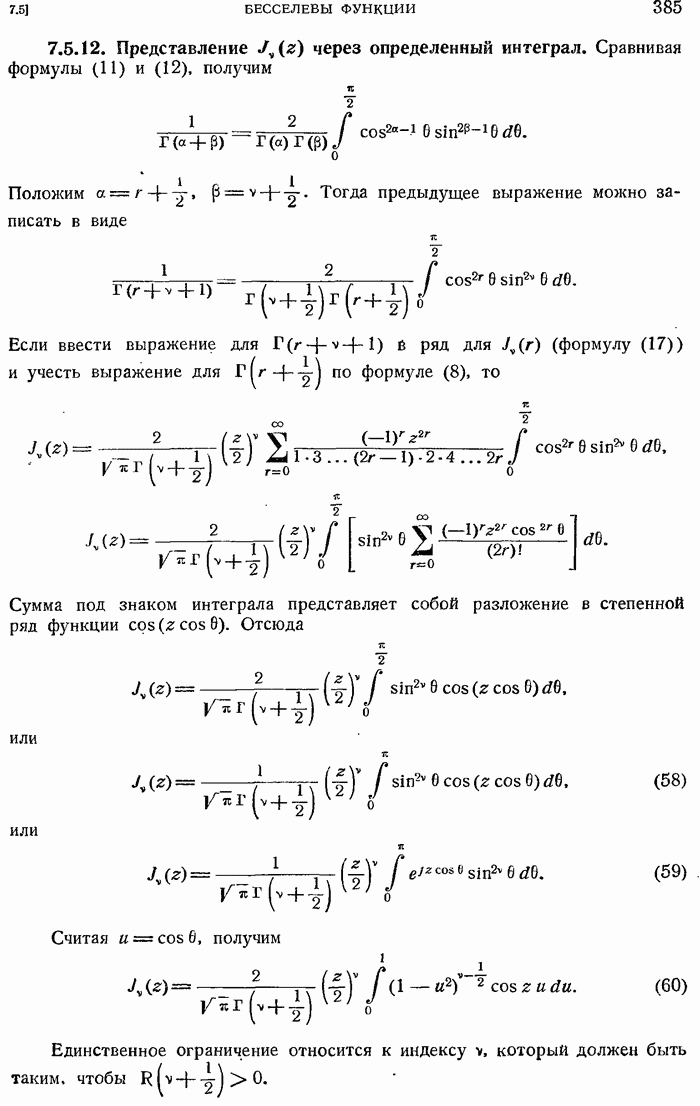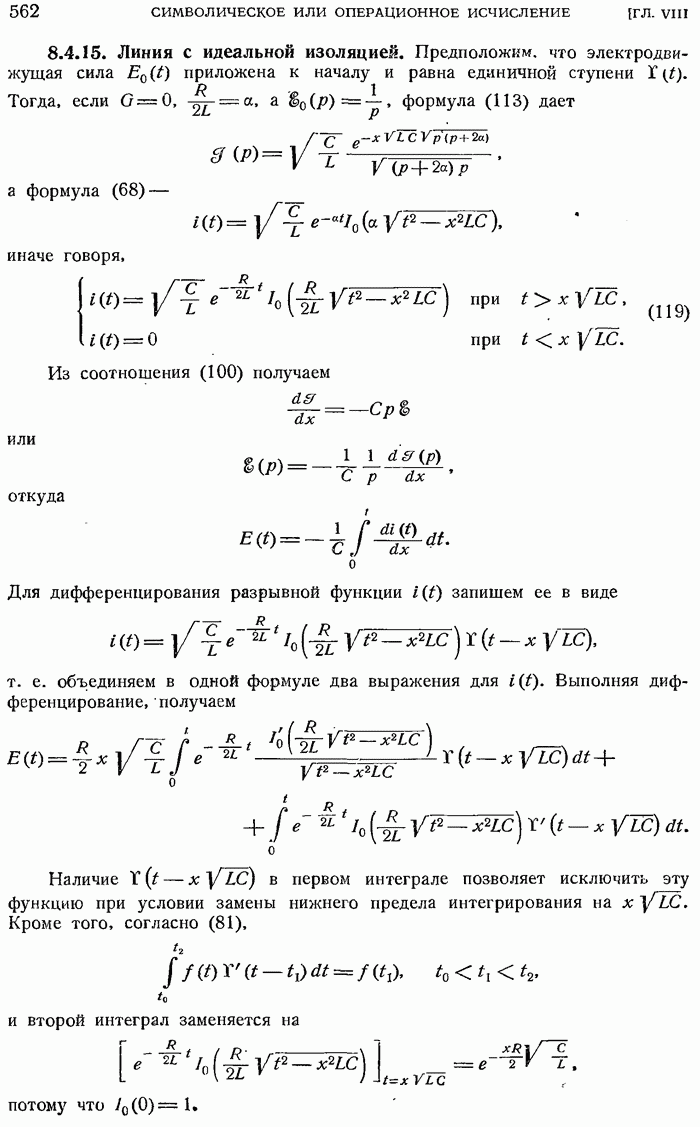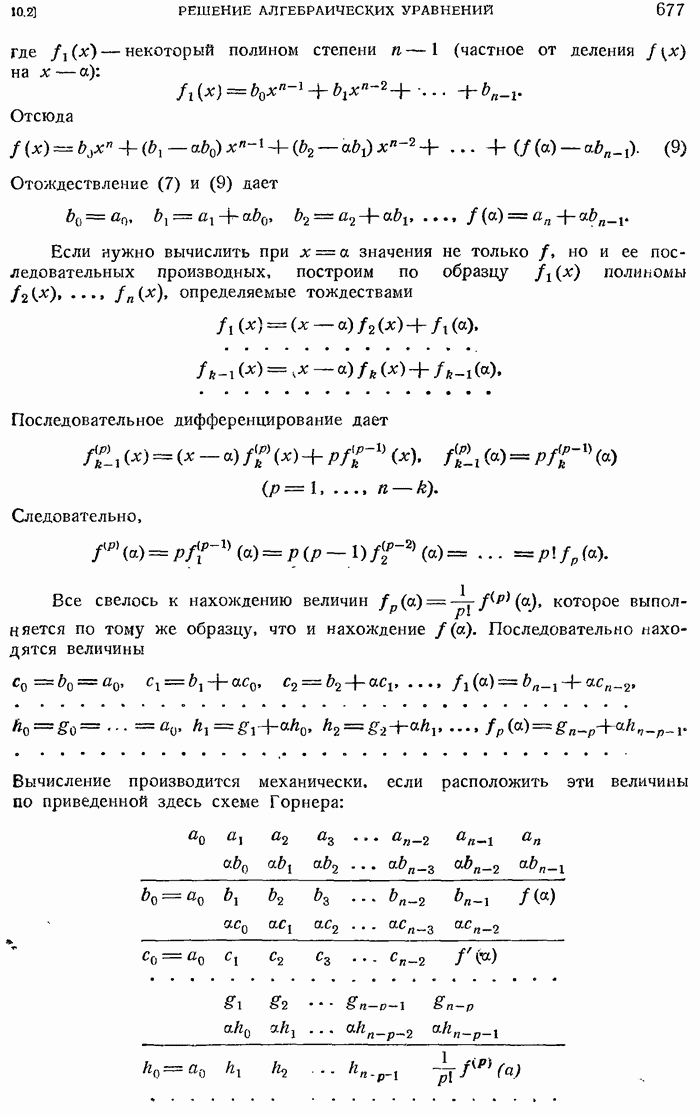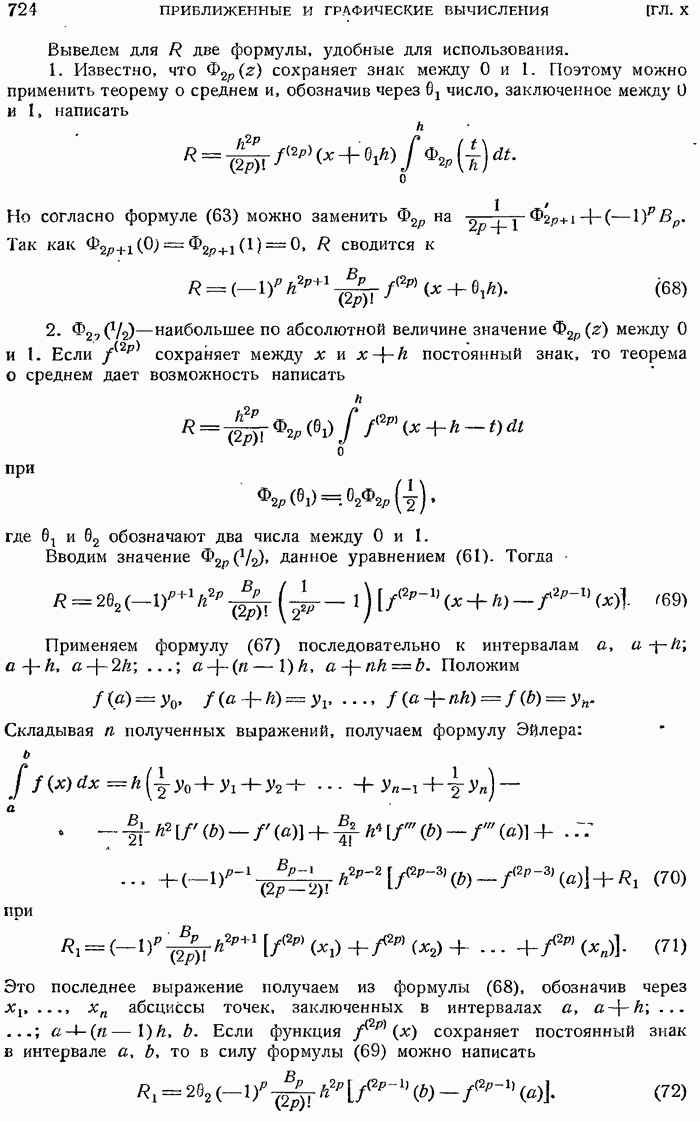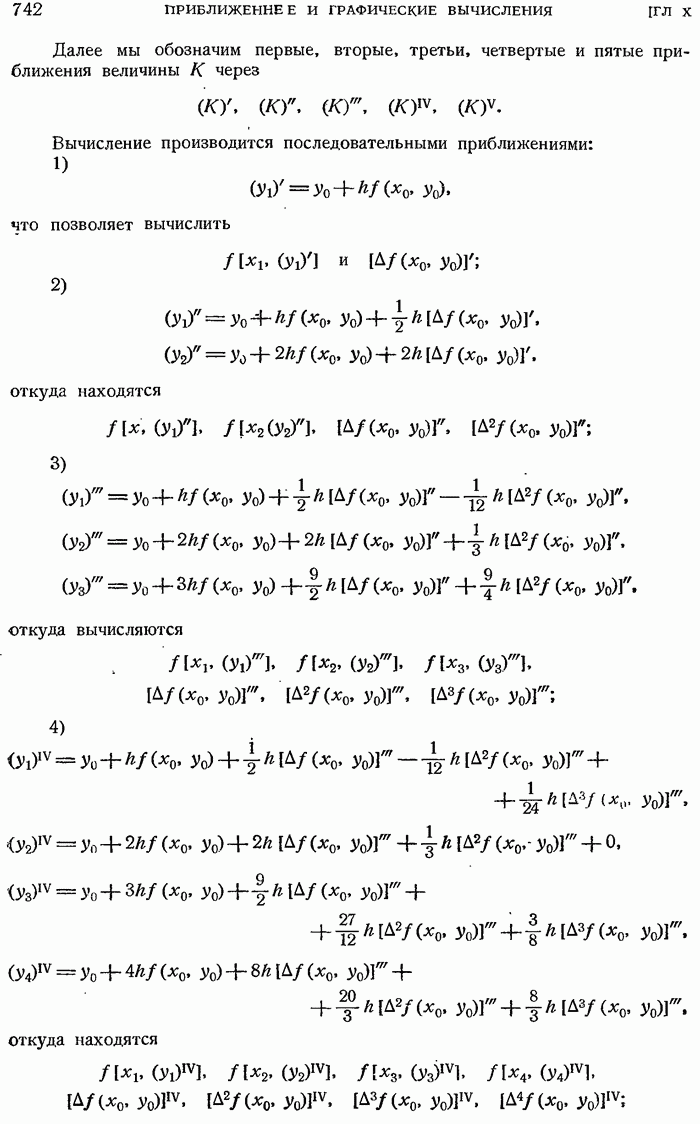| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
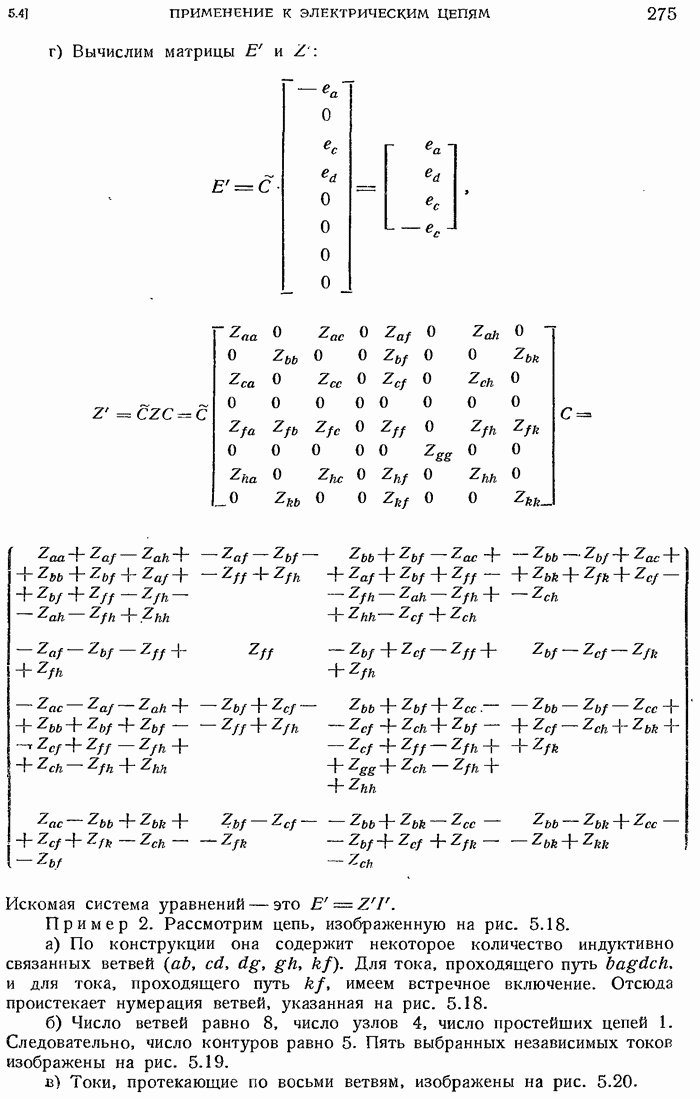
4.1.30. Матрица, отнесенная к собственным направлениям.
Предположим, что характеристическое уравнение  имеет лишь простые корни. Тогда
имеет лишь простые корни. Тогда  собственных направлений различны. Их можно принять за оси координат.
собственных направлений различны. Их можно принять за оси координат.
Пусть  корни уравнения
корни уравнения  Докажем, что в новой системе координат матрица а получит вид
Докажем, что в новой системе координат матрица а получит вид

Это, очевидно, диагональная матрица; она сообщает вектору на I-й оси лишь удлинение или сокращение в  раз. Обозначим через
раз. Обозначим через  проекцию на ось
проекцию на ось  собственного вектора, соответствующего собственному значению
собственного вектора, соответствующего собственному значению  Тогда матрицей преобразования координат о станет матрица
Тогда матрицей преобразования координат о станет матрица  Произведение
Произведение  представит в этом случае преобразование матрицы а в системе координат, оси которой имеют направления собственных векторов а. Это будет, следовательно, матрица (8).
представит в этом случае преобразование матрицы а в системе координат, оси которой имеют направления собственных векторов а. Это будет, следовательно, матрица (8).
Пример. Обратимся к примеру п. 4.1.28. Матрица о и обратная ей матрица  равны, (с точностью до коэффициентов
равны, (с точностью до коэффициентов 

Произведение  будет
будет

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- ГЛАВА I. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- 1.1. КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ
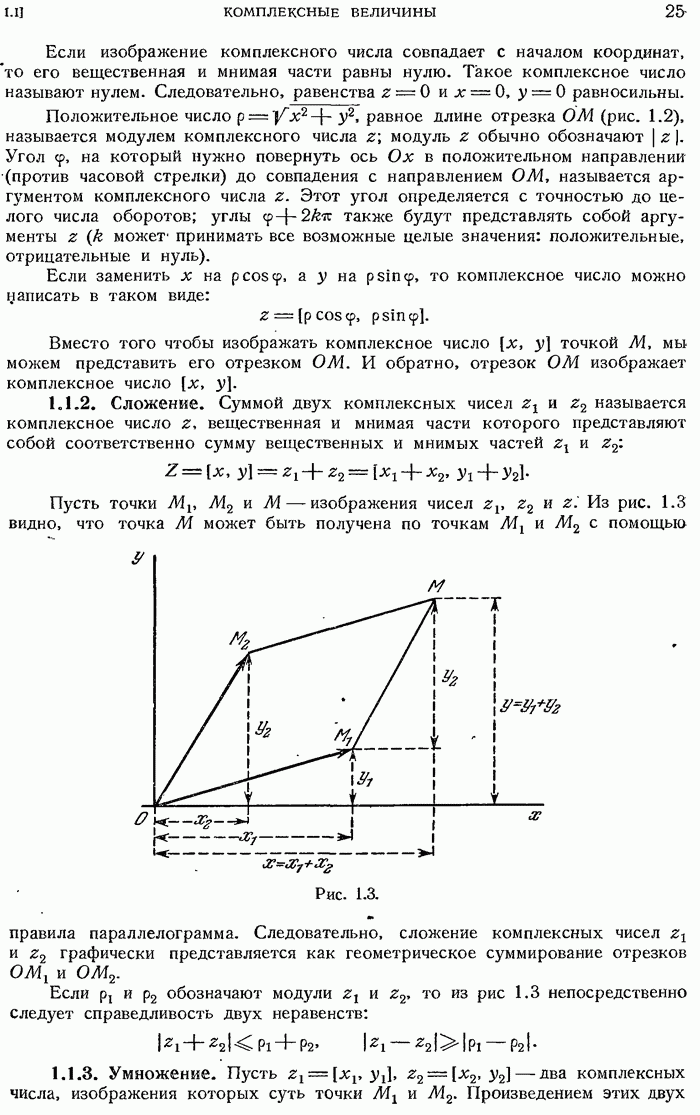
- 1.1.2. Сложение.
- 1.1.3. Умножение.
- 1.1.4. Замена обозначений.
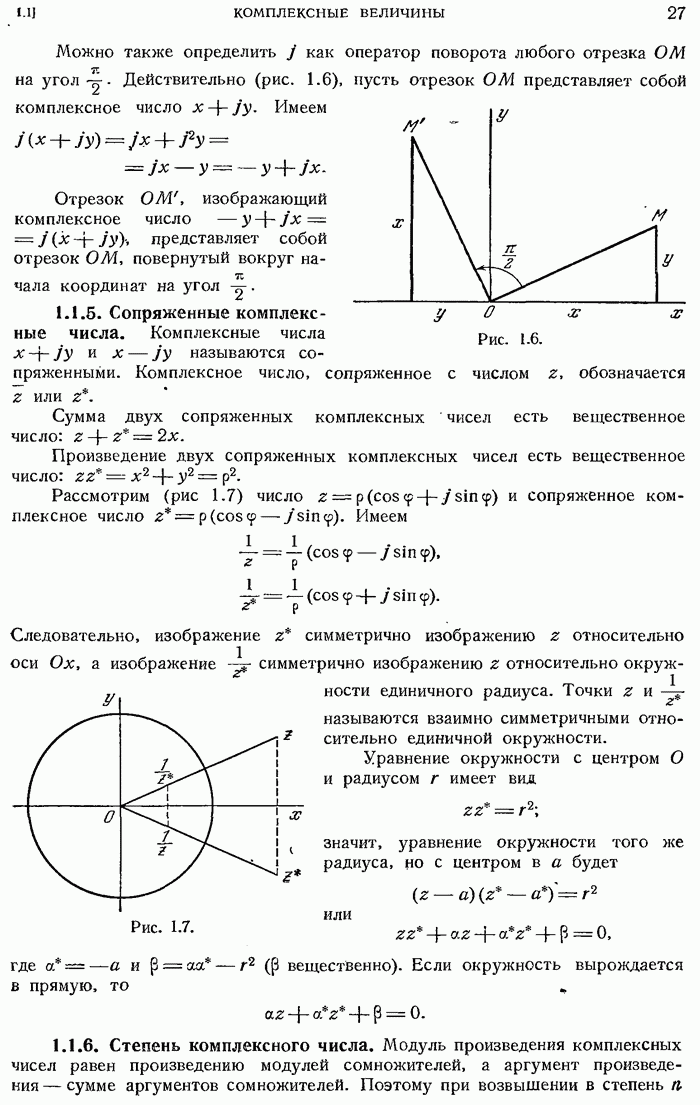
- 1.1.5. Сопряженные комплексные числа.
- 1.1.6. Степень комплексного числа.
- 1.1.7. Корни из комплексного числа.
- 1.1.8. Корни из единицы.
- 1.1.9. Ряды с комплексными членами.
- 1.1.10. Степенные ряды.
- 1.1.11. Экспоненциальная функция и логарифм.
- 1.1.12. Дифференцирование и интегрирование по аргументу.
- 1.1.13. Суммирование тригонометрических функций, аргументы которых составляют арифметическую прогрессию.
- 1.2. ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ВЕЛИЧИН ПРИ РАСЧЕТЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ В СИНУСОИДАЛЬНОМ РЕЖИМЕ
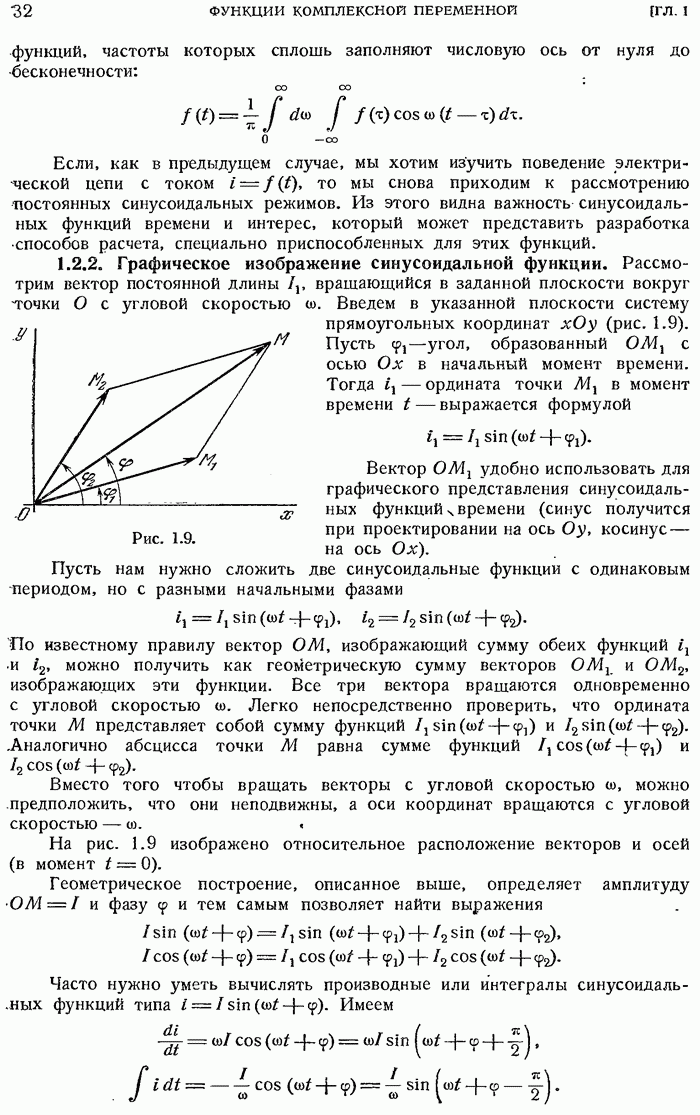
- 1.2.2. Графическое изображение синусоидальной функции.
- 1.2.3. Представление с помощью комплексных чисел.
- 1.2.4. Ограничения метода.
- 1.2.5. Понятие комплексного полного сопротивления.
- 1.2.6. Комплексное полное сопротивление при последовательном и параллельном соединении.
- 1.2.7. Законы Кирхгофа.
- 1.2.8. Обобщение понятия комплексного полного сопротивления.
- 1.2.9. Комплексный вектор.
- 1.3. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- 1.3.5. Криволинейный интеграл от функции комплексной переменной.
- 1.3.6. Теорема Коши.
- 1.3.8. Ряд Тейлора.
- 1.3.9. Особые точки.
- 1.3.10. Разложение в ряд Лорана.
- 1.3.11. Теорема о вычетах.
- 1.3.12. Вычисление вычетов.
- 1.3.13. Вычисление вычетов относительно кратных полюсов с помощью производных.
- 1.3.14. Лемма Жордана.
- 1.3.15. Применение леммы Жордана к единичной функции.
- 1.3.16. Интегрирование при наличии точки разветвления.
- 1.3.17. Контур Бромвича.
- 1.3.18. Интеграл Бромвича — Вагнера.
- 1.3.19. Эквивалентный контур.
- 1.3.20. Теорема о числе полюсов и числе нулей.
- Применение теоремы о вычетах к вычислению некоторых определенных интегралов
- 1.3.25. Применение теоремы о вычетах к суммированию некоторых рядов.
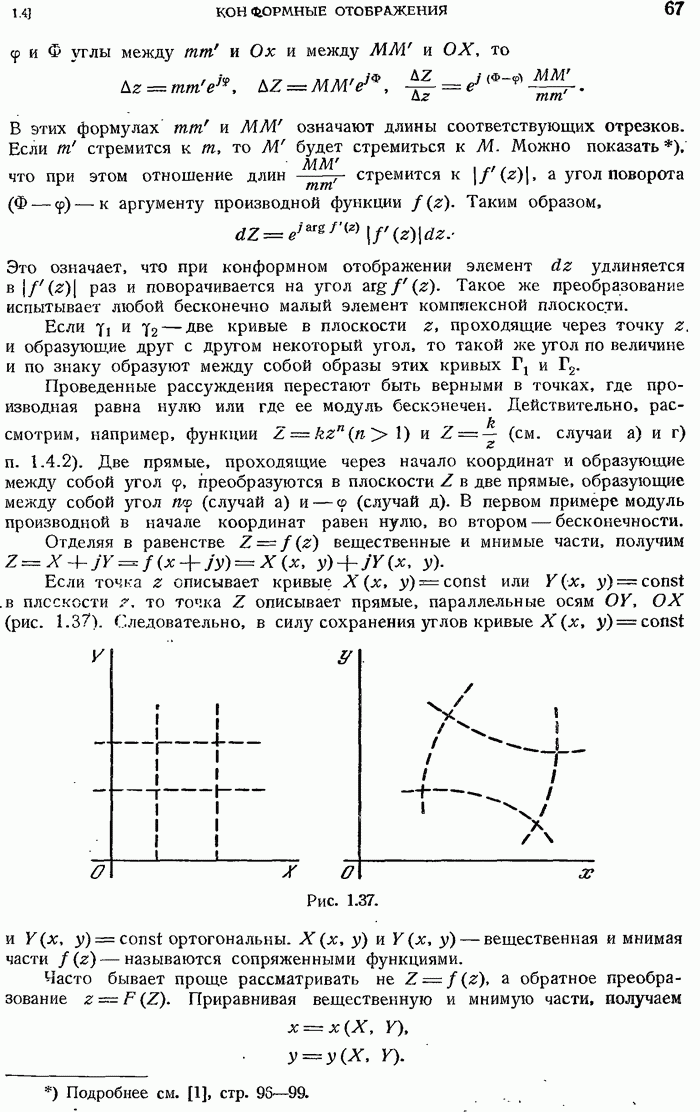
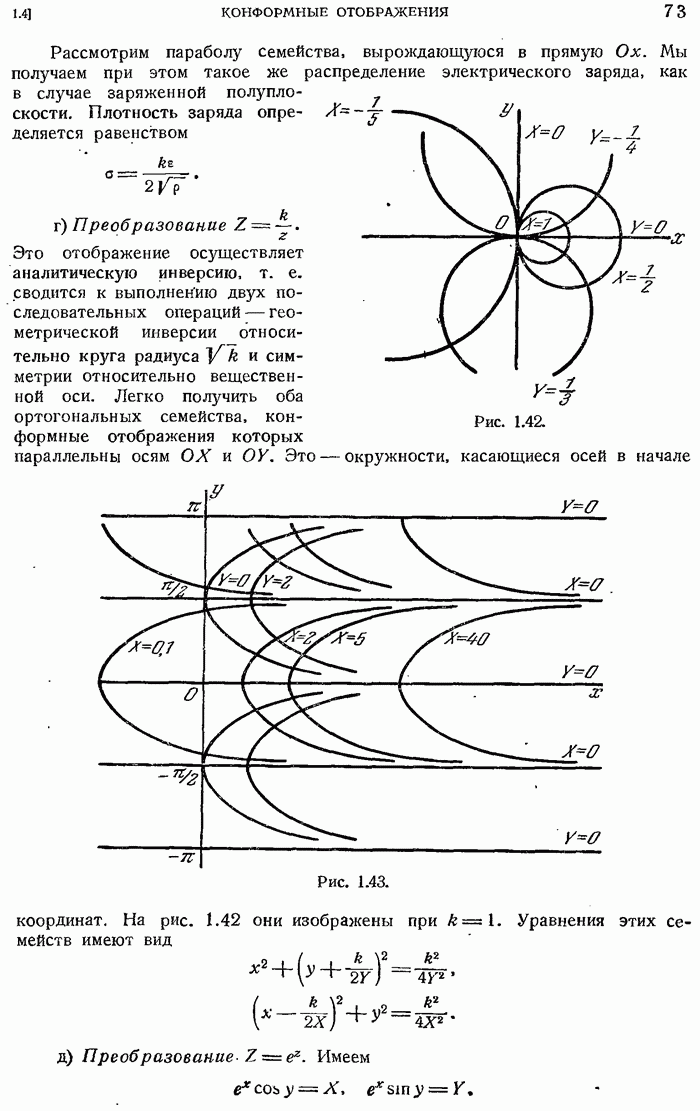
- 1.4. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
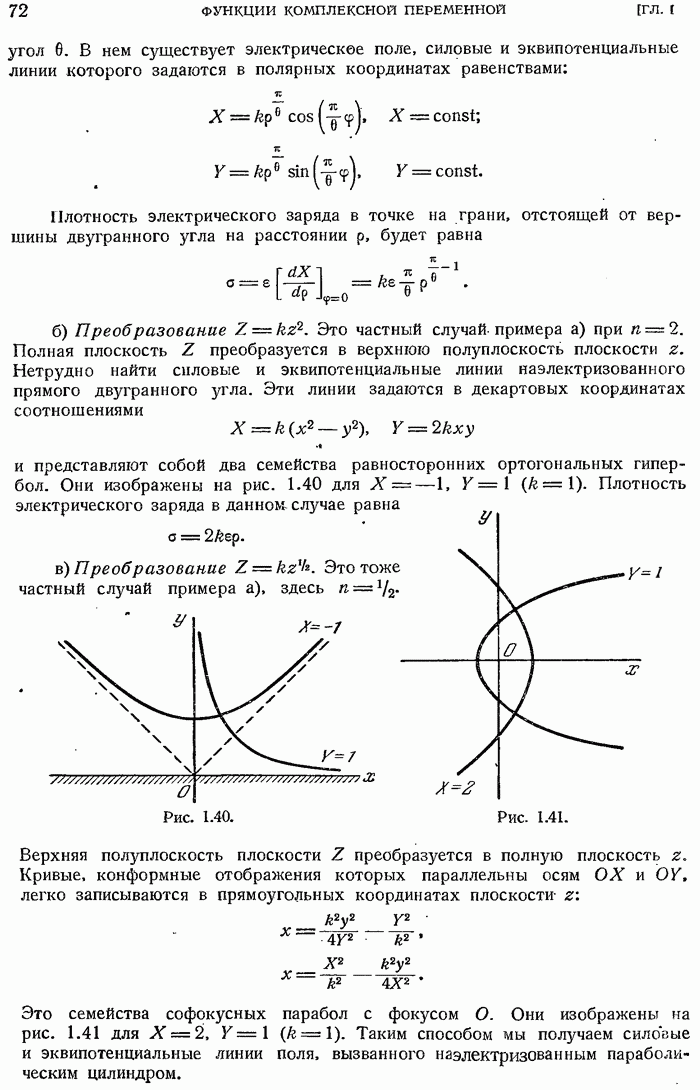
- 1.4.2. Несколько примеров конформных отображений.
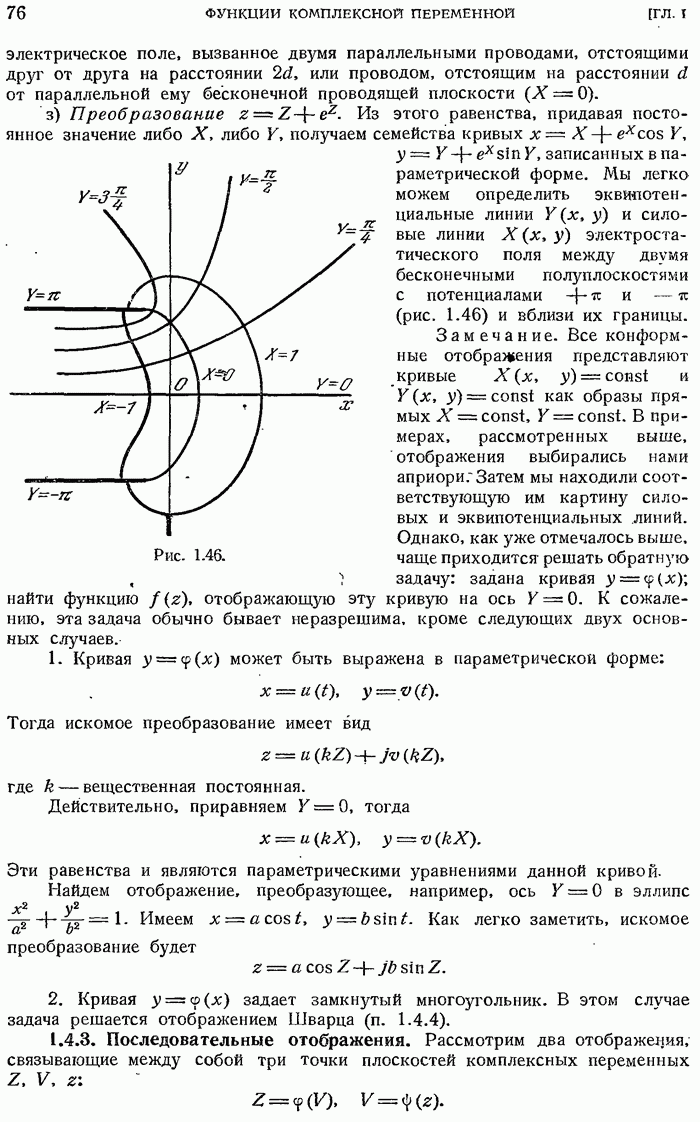
- 1.4.3. Последовательные отображения.
- 1.4.4. Отображение Шварца.
- 1.4.5. Различные применения конформных отображений.
- ГЛАВА II. РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
- 2.1. РЯД ФУРЬЕ
- 2.1.2. Разложение в ряд по ортогональным функциям.
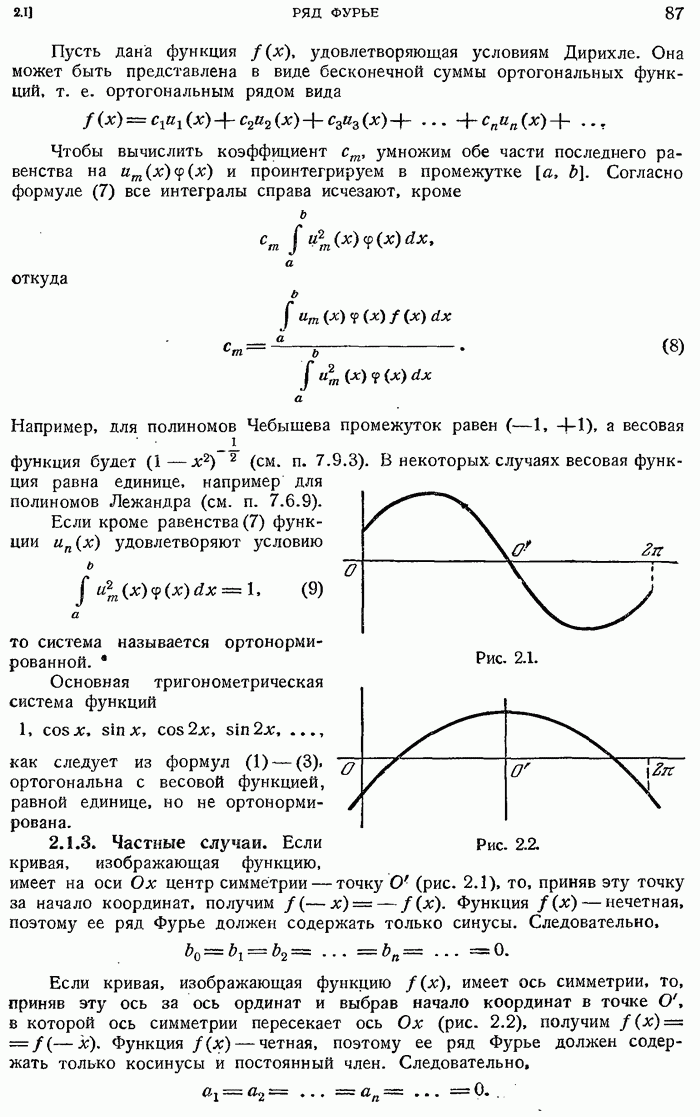
- 2.1.3. Частные случаи.
- 2.1.4. Интегрирование и дифференцирование.
- 2.1.5. Случай, когда разложение в ряд Фурье ограничено первыми n членами.
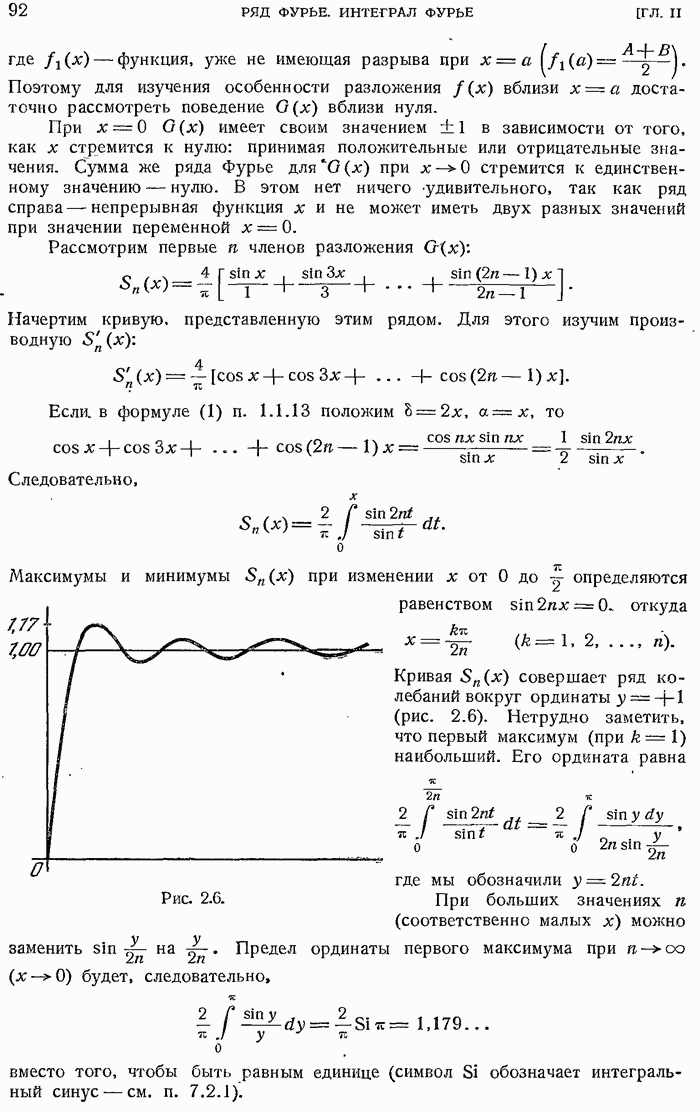
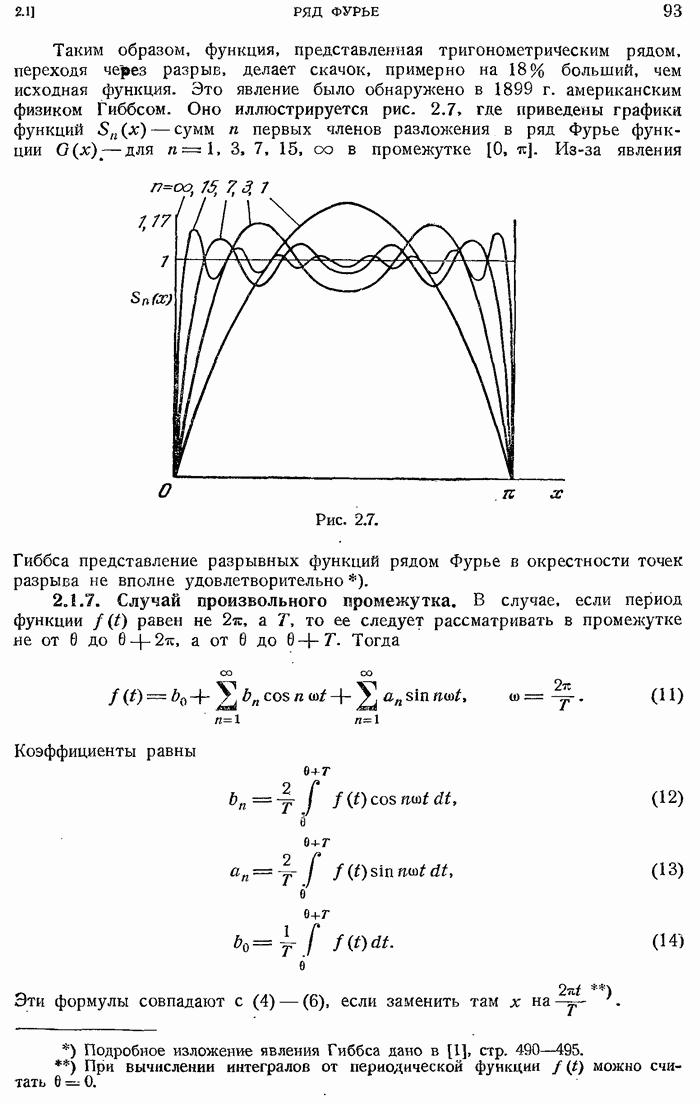
- 2.1.6. Изучение разложения в ряд Фурье вблизи точки разрыва. Явление Гиббса.
- 2.1.7. Случай произвольного промежутка.
- 2.1.8. Ряды с комплексными членами.
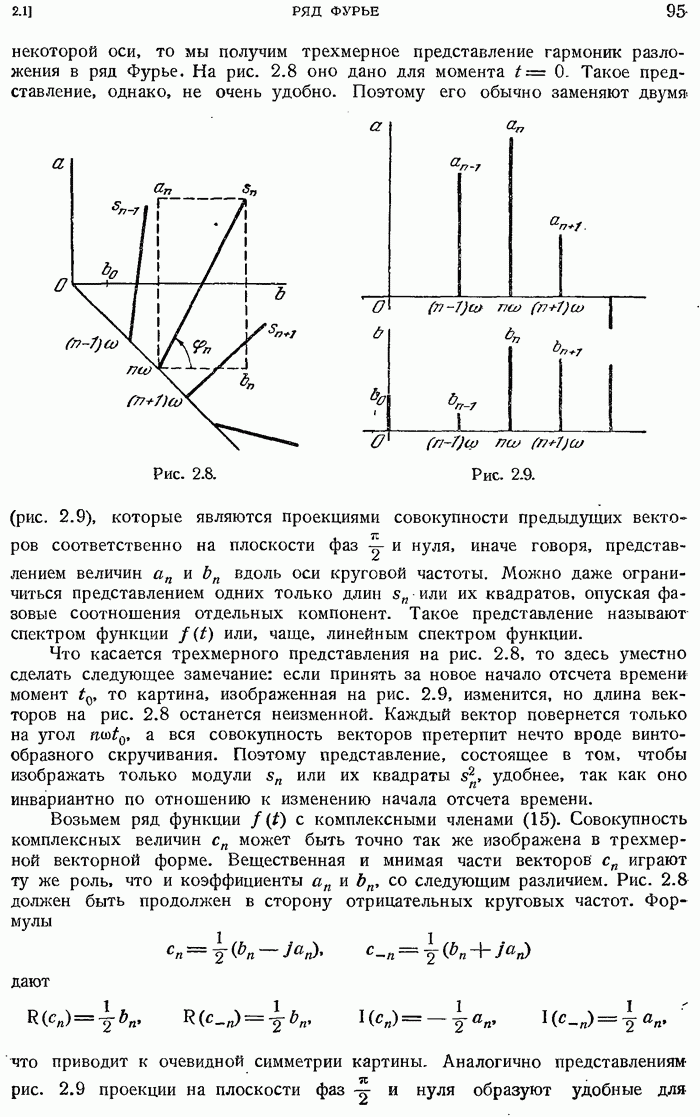
- 2.1.9. Графическое представление. Спектр.
- 2.1.10. Среднее значение произведения двух функций одного периода, разложимых в ряд Фурье.
- 2.1.11. Распространение ряда Фурье на почти периодические функции.
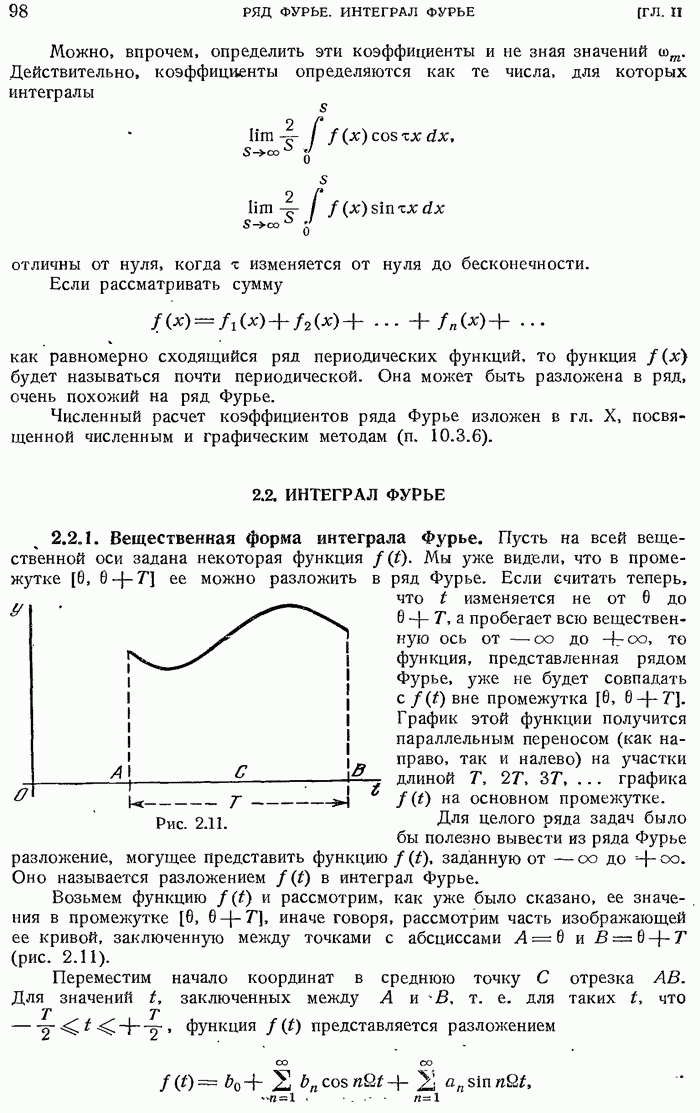
- 2.2. ИНТЕГРАЛ ФУРЬЕ
- 2.2.2. Комплексная форма интеграла Фурье.
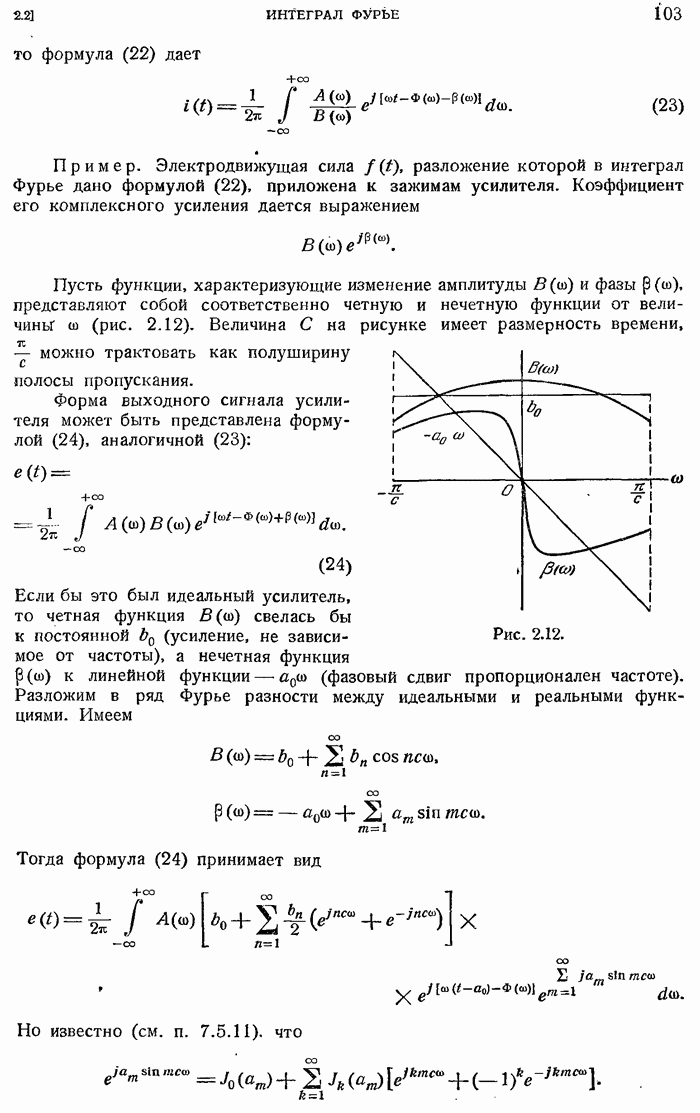
- 2.2.3. Применение к электрическим цепям.
- 2.2.4. Случай незатухающей цепи.
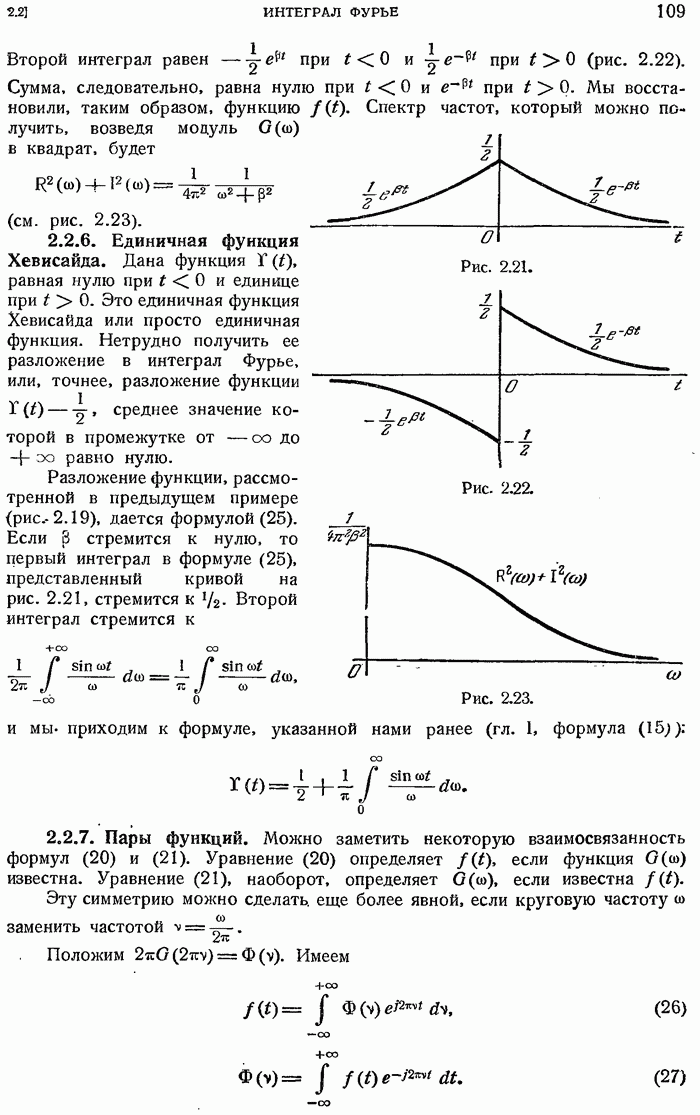
- 2.2.5. Спектр частот.
- 2.2.6. Единичная функция Хевисайда.
- 2.2.7. Пары функций.
- 2.2.8. Преобразование Фурье.
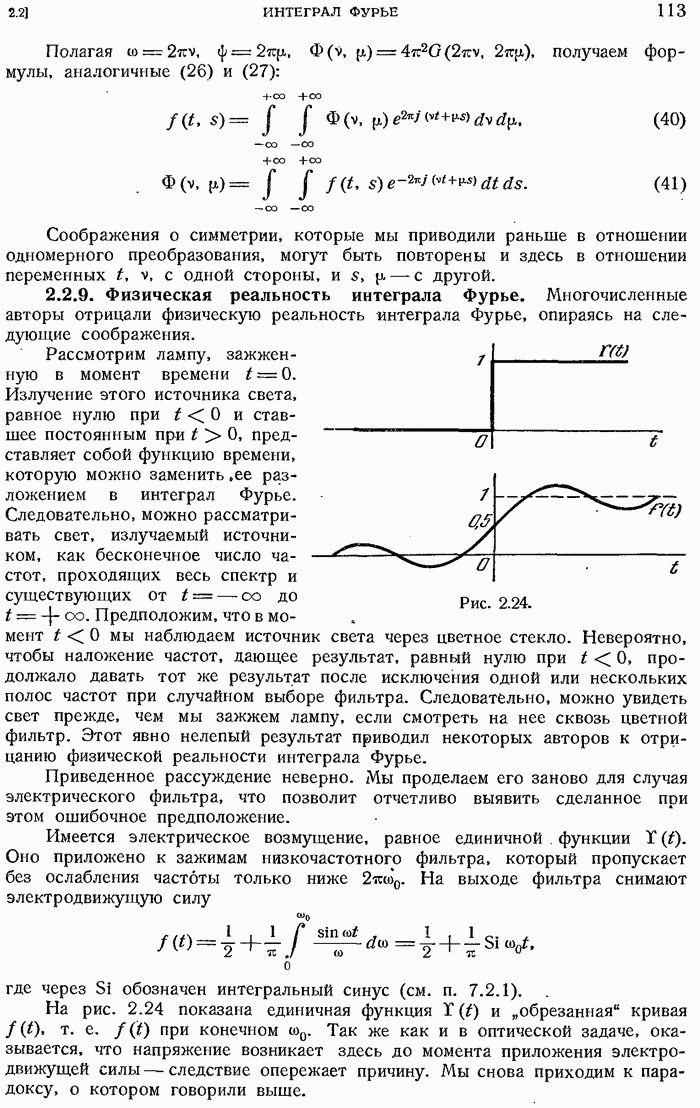
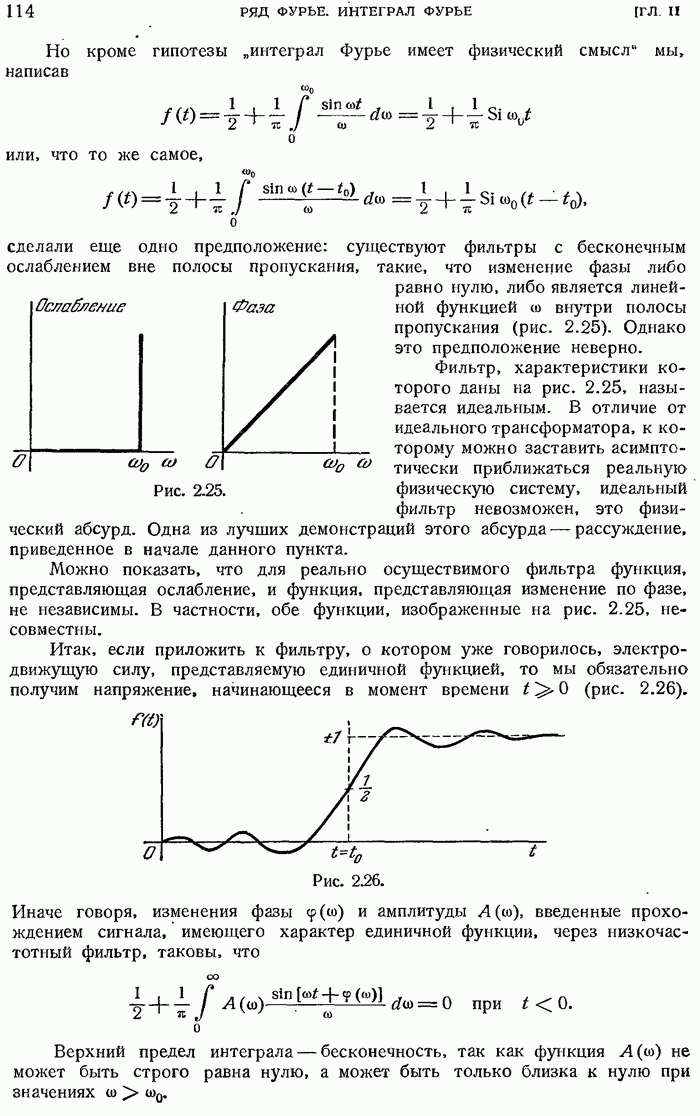
- 2.2.9. Физическая реальность интеграла Фурье.
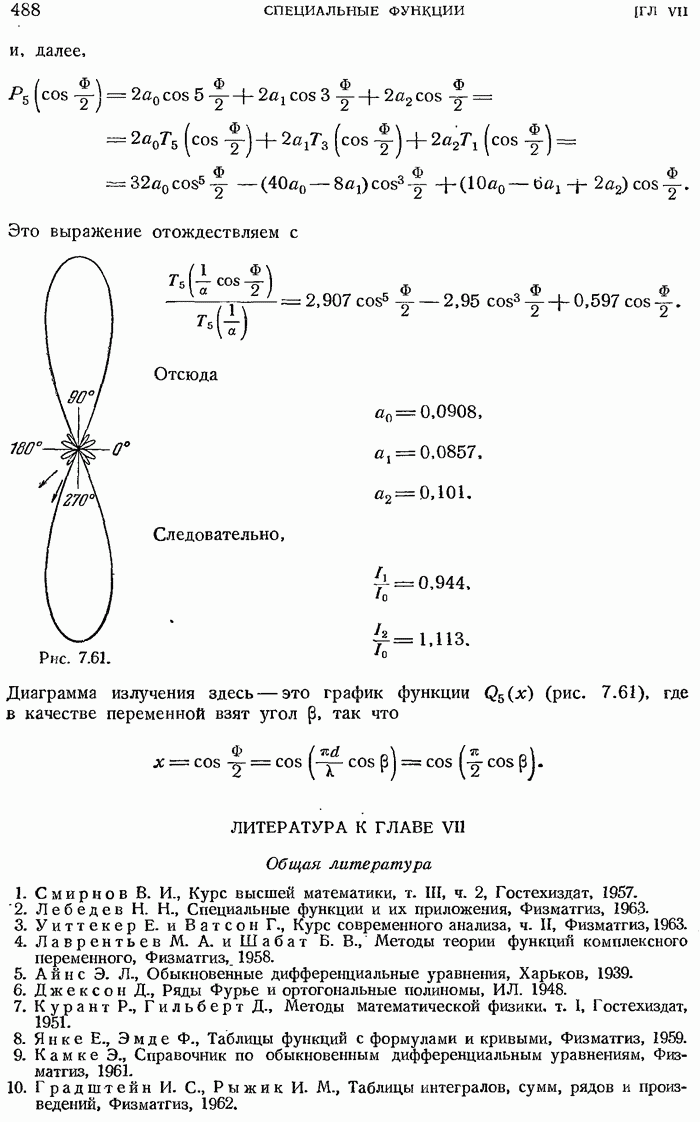
- 2.2.10. Изучение диаграмм направленности.
- ГЛАВА III. ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
- 3.1. СКАЛЯРНЫЕ ВЕЛИЧИНЫ. ВЕКТОРНЫЕ ВЕЛИЧИНЫ. ОПРЕДЕЛЕНИЯ
- 3.1.6. Векторы.
- Операции над векторами
- 3.1.12. Скалярное произведение.
- 3.1.13. Векторное произведение.
- 3.1.14. Смешанное произведение трех векторов.
- 3.1.15. Двойное векторное произведение трех векторов.
- 3.2. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 3.2.2. Производная вектора по другому вектору.
- 3.2.3. Основные формулы дифференцирования.
- 3.2.4. Интеграл от вектора.
- Функции точки
- 3.2.11. Дивергенция и вихрь.
- 3.2.12. Оператор Лапласа.
- 3.2.13. Символический вектор набла (оператор Гамильтона).
- 3.2.14. Наиболее употребительные формулы.
- 3.2.15. Смысл вектора rot a.
- 3.2.16. Скалярный потенциал.
- 3.2.17. Частный случай: вектор проходит через фиксированную точку.
- 3.2.18. Векторный потенциал.
- 3.2.19. Общий случай векторного поля.
- 3.3. ВЕКТОРНЫЕ ИНТЕГРАЛЫ
- 3.3.1. Циркуляция вектора.
- 3.3.2. Поток вектора.
- Основные формулы
- 3.3.3. Теорема Остроградского.
- 3.3.4. Смысл скаляра div a.
- 3.3.5. Формула для градиента.
- 3.3.6. Формула для вихря.
- 3.3.7. Инвариантность градиента, дивергенции, вихря.
- 3.3.8. Формула Грина.
- 3.3.9. Формула Стокса.
- Приложение векторного исчисления к теории электромагнитного поля
- 3.3.10. Электростатическое поле.
- 3.3.11. Магнитное поле постоянных токов.
- 3.3.12. Электромагнитное поле.
- 3.3.13. Закон Фарадея.
- 3.3.14. Закон Ампера.
- 3.3.15. Уравнения Максвелла.
- 3.3.16. Векторный потенциал магнитного поля, возбужденного током.
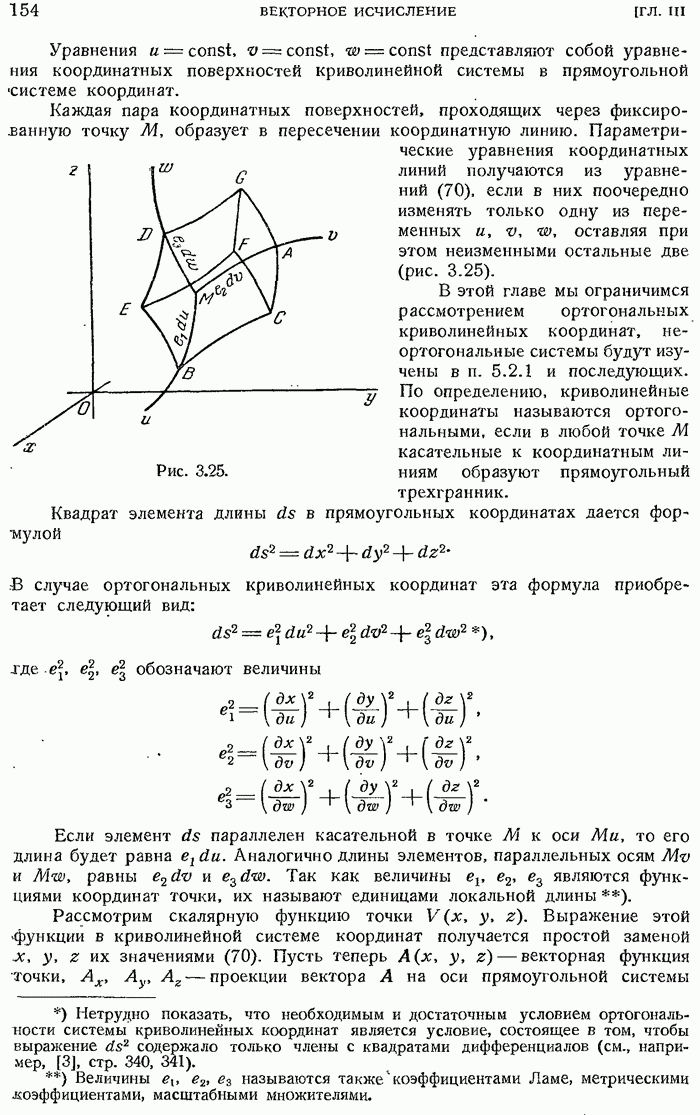
- 3.4. СИСТЕМЫ ОРТОГОНАЛЬНЫХ КРИВОЛИНЕЙНЫХ КООРДИНАТ
- 3.4.2. Дифференциальные операторы в ортогональных криволинейных координатах.
- Важнейшие системы ортогональных криволинейных координат в пространстве
- 3.4.3. Система цилиндрических координат.
- 3.4.4. Система сферических координат.
- 3.4.5. Система параболических цилиндрических координат.
- 3.4.6. Система параболических координат вращения (параболоидальные координаты).
- 3.4.7. Система эллиптических цилиндрических координат.
- 3.4.8. Система вытянутых эллипсоидальных координат (вращения).
- 3.4.9. Система сплюснутых эллипсоидальных координат (вращения).
- 3.4.10. Система бицилиндрических координат.
- 3.4.11. Системы тороидальных и бисферических координат.
- 3.4.12. Система софокусных поверхностей второго порядка (система общих эллипсоидальных координат).
- 3.4.13. Приложение к уравнениям Максвелла. Уравнения Максвелла в ортогональных криволинейных координатах.
- ГЛАВА IV. МАТРИЧНОЕ ИСЧИСЛЕНИЕ
- 4.1. АЛГЕБРА МАТРИЦ
- 4.1.4. Представление плоских преобразований с помощью матриц.
- 4.1.5. Произведение двух матриц.
- 4.1.6. Представление вектора посредством матрицы.
- 4.1.7. Обобщение на n-мерное пространство.
- 4.1.8. Равенство двух матриц.
- 4.1.9. Сложение двух матриц.
- 4.1.10. Умножение матрицы на число.
- 4.1.11. Умножение матриц.
- 4.1.12. Симметричные матрицы.
- 4.1.13. Кососимметричные матрицы.
- 4.1.14. Диагональные матрицы.
- 4.1.15. Единичная матрица. Нулевая матрица.
- 4.1.16. Порядок, ранг матрицы.
- 4.1.17. Необходимые условия равенства нулю произведения двух матриц.
- 4.1.18. Транспонированная матрица.
- 4.1.19. Обратная матрица.
- 4.1.20. Применение матричного исчисления к решению системы линейных уравнений.
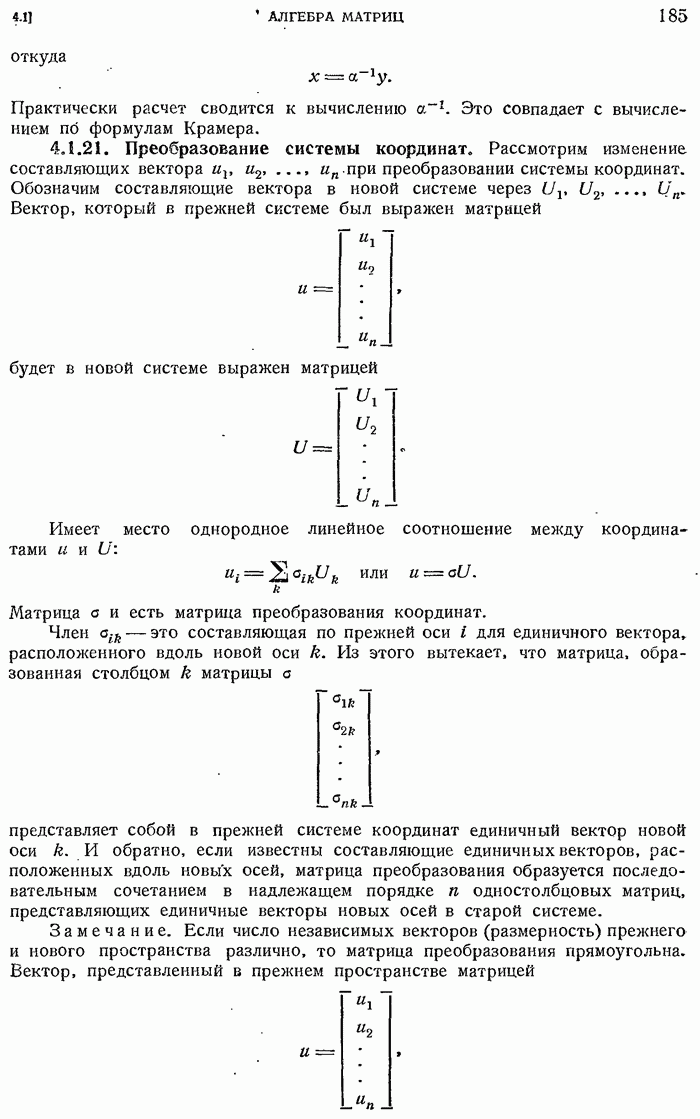
- 4.1.21. Преобразование системы координат.
- 4.1.22. Ортогональное преобразование.
- 4.1.23. Пример ортогональных преобразований. Поворот.
- Обобщение на комплексное пространство
- 4.1.24. Эрмитова матрица.
- 4.1.25. Эрмитово-сопряженная матрица.
- 4.1.26. Модуль и скалярное произведение в комплексном пространстве.
- 4.1.27. Ортогональное преобразование комплексного пространства (унитарное преобразование).
- 4.1.28. Собственные значения, собственные векторы и характеристическое уравнение матрицы.
- 4.1.29. Свойства характеристического уравнения.
- 4.1.30. Матрица, отнесенная к собственным направлениям.
- 4.1.31. Условия коммутативности двух матриц.
- 4.1.32. Собственные значения и собственные направления эрмитовой матрицы.
- Функции от матриц
- 4.1.33. Степень матрицы.
- 4.1.34. Теорема Кэли-Гамильтона.
- 4.1.35. Функции от матриц. Теорема Сильвестра.
- 4.1.36. Формула Бэкера.
- 4.1.37. Высокие степени матрицы.
- 4.1.38. Дробная степень матрицы.
- 4.1.39. Приближенное вычисление собственных значений матрицы.
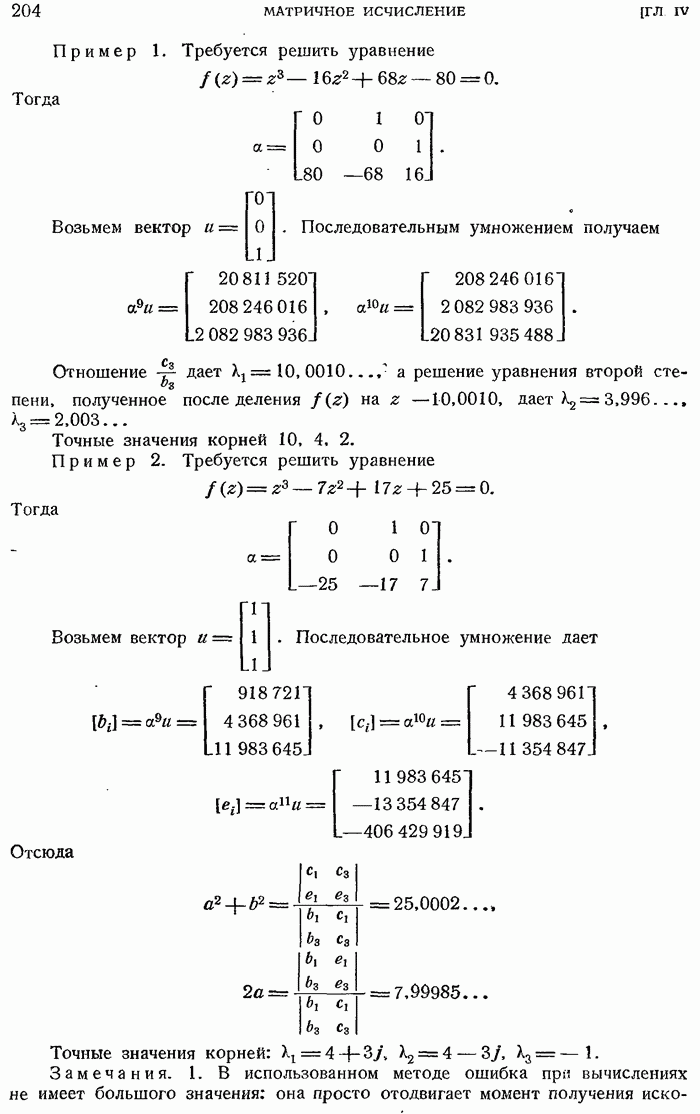
- 4.1.40. Приближенное вычисление корней уравнения n-й степени.
- Дифференциальные операции над матрицами. Применение к решению дифференциальных уравнений
- 4.1.41. Дифференцирование и интегрирование матрицы.
- 4.1.42. Решение системы линейных дифференциальных уравнений первого порядка.
- 4.1.43. Система дифференциальных уравнений первого порядка, с постоянными коэффициентами.
- 4.1.44. Случай линейного дифференциального уравнения n-го порядка.
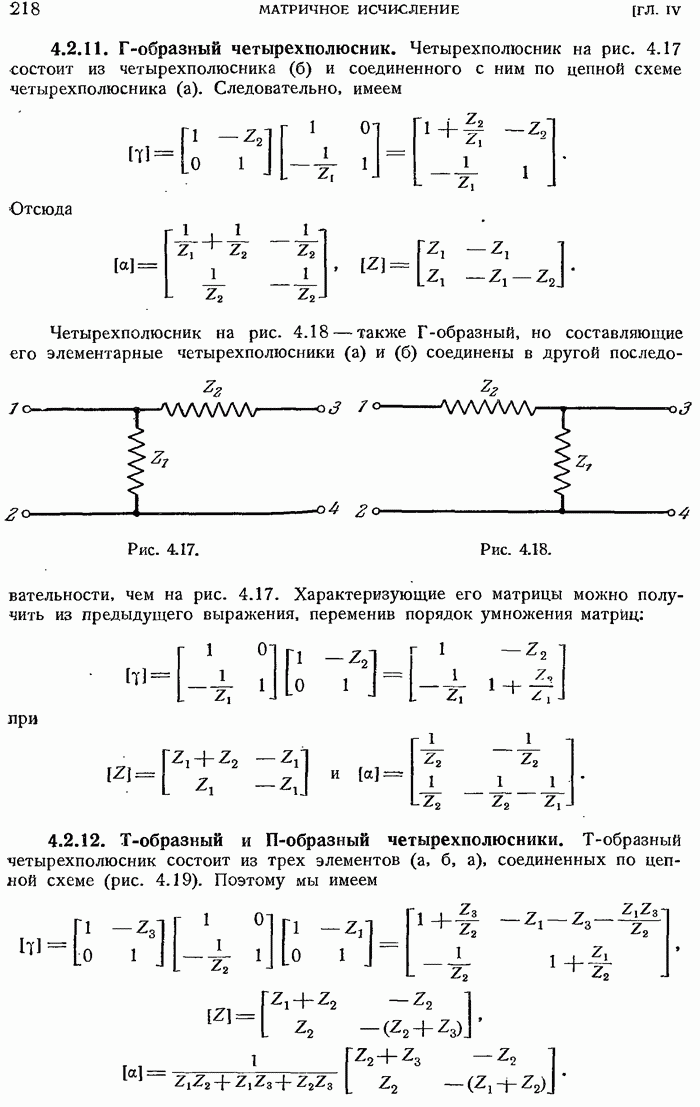
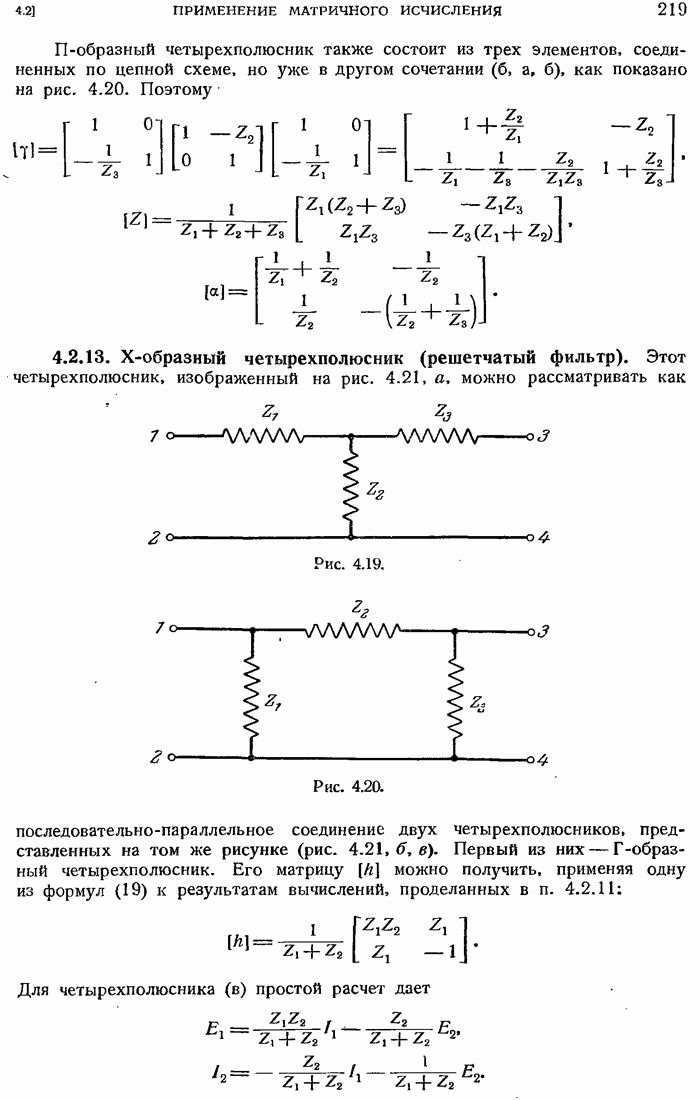
- 4.2. ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ. ИЗУЧЕНИЕ ЧЕТЫРЕХПОЛЮСНИКОВ
- 4.2.2. Соединение четырехполюсников по цепной схеме.
- 4.2.3. Параллельное соединение четырехполюсников.
- 4.2.4. Последовательное соединение четырехполюсников.
- 4.2.5. Последовательно-параллельное и параллельно-последовательное соединение четырехполюсников.
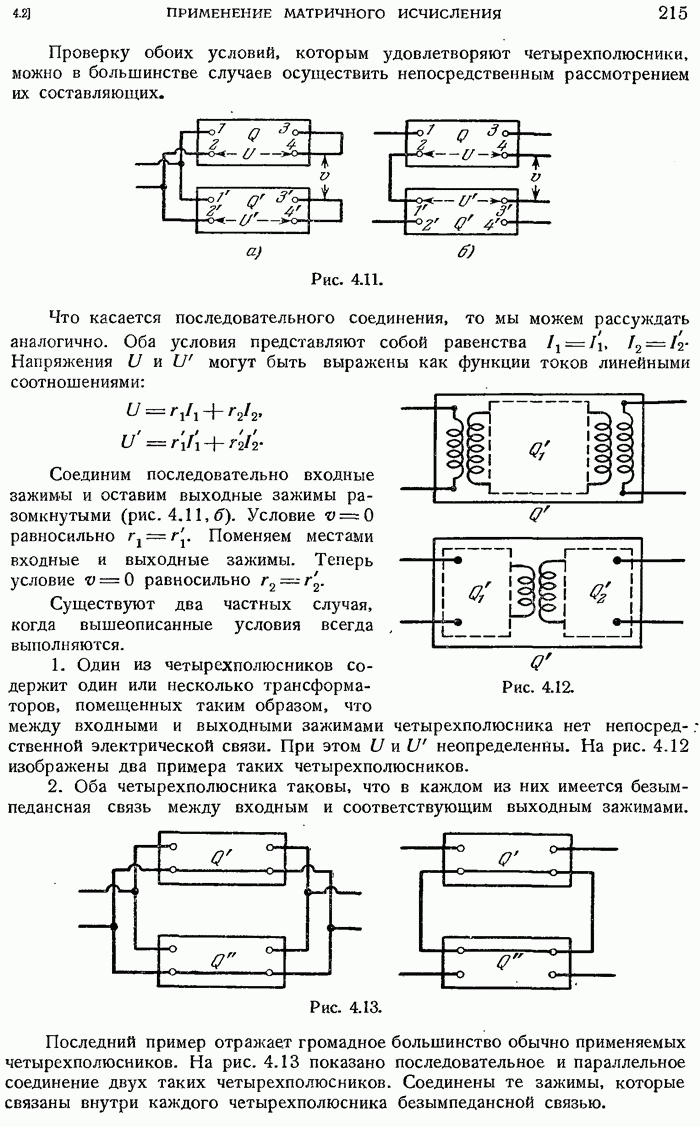
- 4.2.6. Сопротивления холостого хода и короткого замыкания четырехполюсника.
- 4.2.7. Пассивные четырехполюсники.
- 4.2.8. Симметричные четырехполюсники.
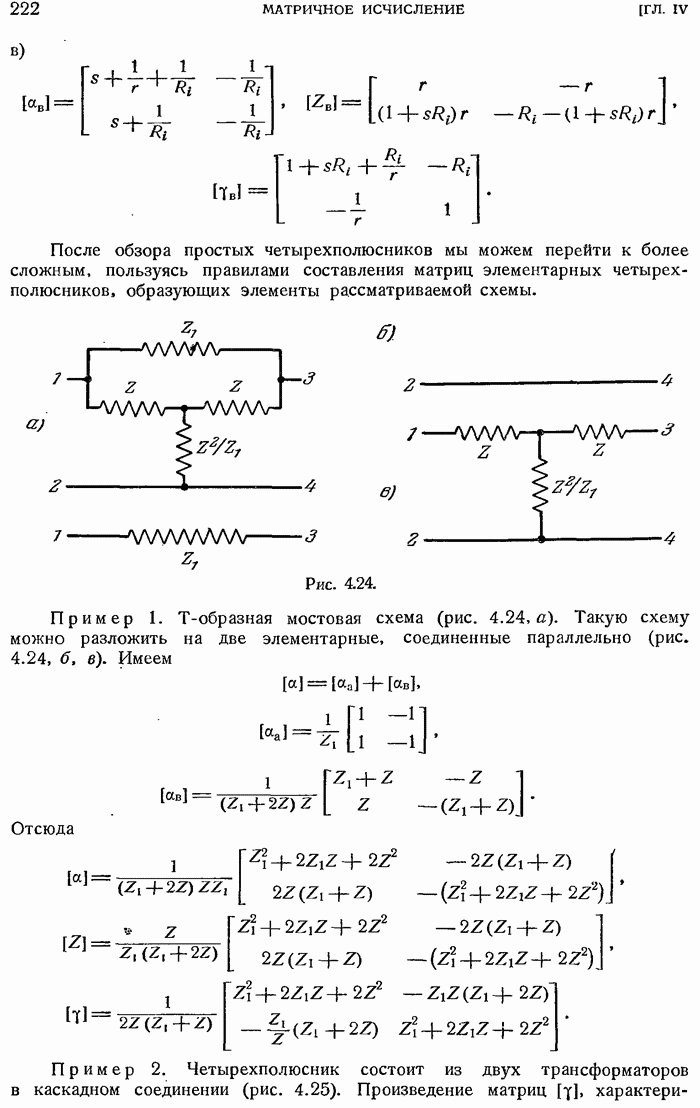
- Примеры простых четырехполюсников
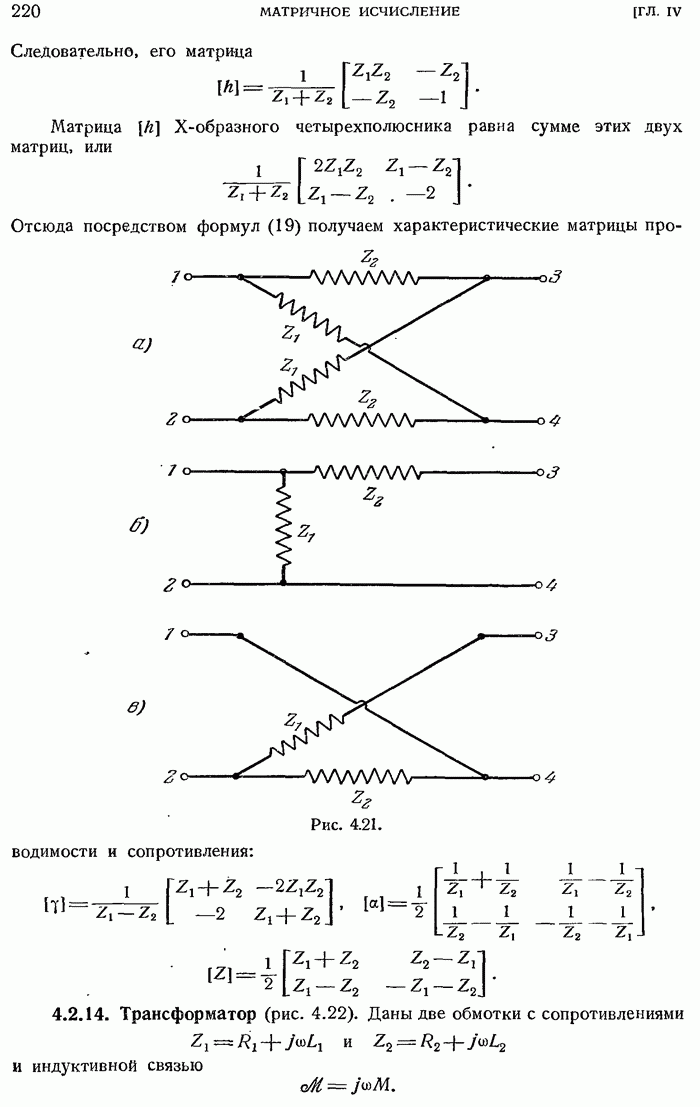
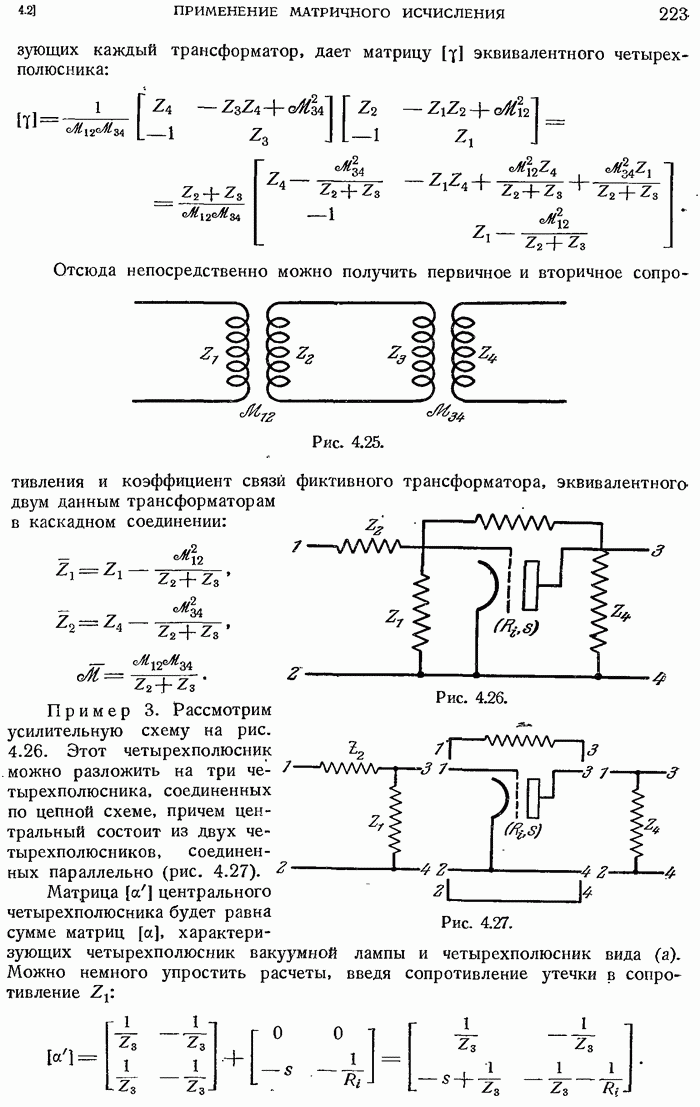
- 4.2.14. Трансформатор
- 4.2.15. Электронная лампа.
- 4.2.16. Повторное сопротивление четырехполюсника.
- 4.2.17. Случай пассивного четырехполюсника.
- 4.2.18. Цепные фильтры.
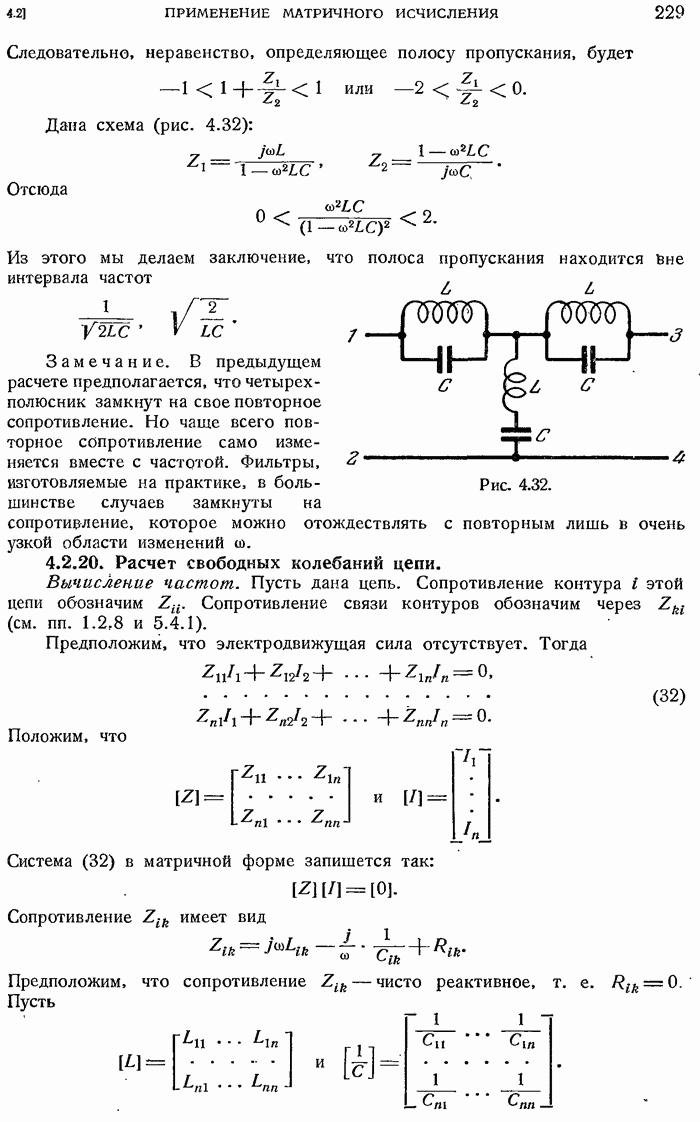
- 4.2.19. Полоса пропускания четырехполюсника.
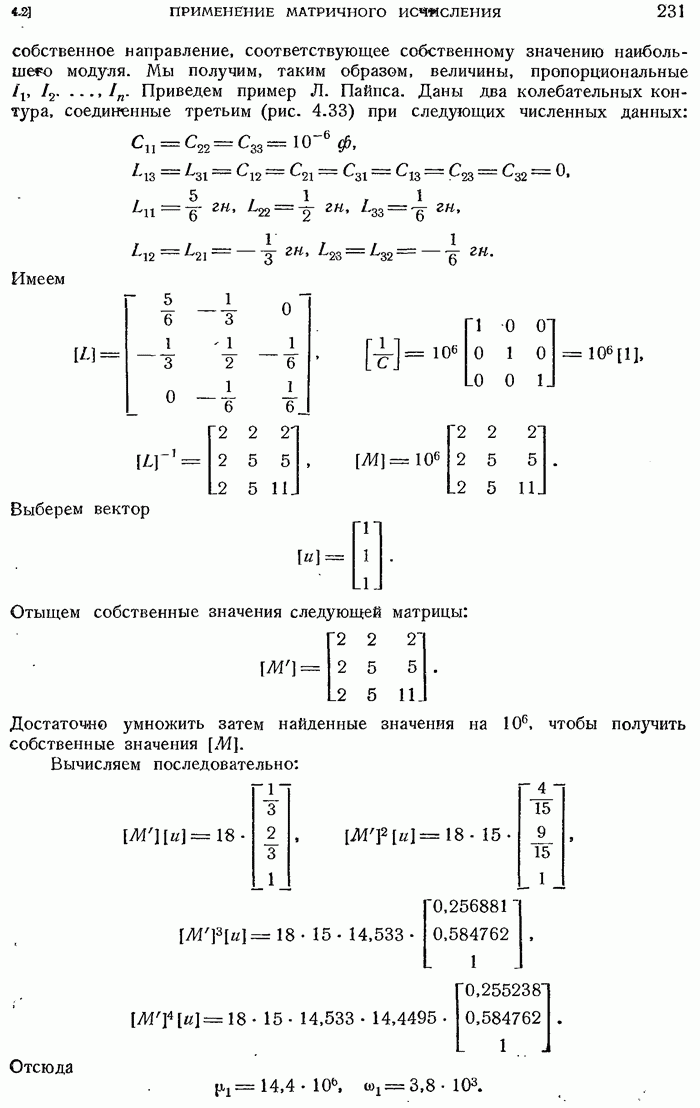
- 4.2.20. Расчет свободных колебаний цепи.
- 4.2.21. Контуры с периодически меняющимися параметрами.
- 4.2.22. Матрицы в квантовой механике.
- ГЛАВА V. ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
- 5.1. ТЕНЗОРНАЯ АЛГЕБРА
- 5.1.3. Ковариантные и контравариантные векторы.
- 5.1.4. Определение тензора.
- 5.1.5. Матричная форма формул преобразования координат.
- 5.1.6. Немой индекс.
- 5.1.7. Симметрия и антисимметрия.
- 5.1.8. Псевдоскаляры. Скалярная плотность и скалярная емкость.
- 5.1.9. Тензорная плотность и тензорная емкость.
- 5.1.10. Антисимметричный тензор второй валентности в трехмерном пространстве.
- Операции над тензорами
- 5.3.11. Сложение двух тензоров.
- 5.1.12. Свертывание тензора.
- 5.1.13. Умножение тензоров.
- 5.1.14. Свертывание произведения.
- 5.1.15. Установление типа тензора.
- 5.2. ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ
- 5.2.2. Фундаментальный метрический тензор.
- 5.2.3. Преобразование определителя g фундаментального метрического тензора при преобразовании координат.
- 5.2.4. Выражение для элемента объема.
- 5.2.5. Косоугольная система координат на плоскости.
- 5.2.6. Ортогональные криволинейные координаты в трехмерном пространстве.
- 5.2.7. Случай произвольных криволинейных координат.
- 5.2.8. Контравариантные или ковариантные компоненты одного и того же вектора.
- 5.2.9. Изменение вариантности тензора.
- 5.2.10. Смешанный фундаментальный метрический тензор.
- 5.2.11. Случай прямолинейной прямоугольной системы координат.
- Геометрическое представление контравариантных и ковариантных компонент вектора
- 5.2.12. Случай прямолинейной косоугольной системы координат.
- 5.2.13. Случай криволинейных координат.
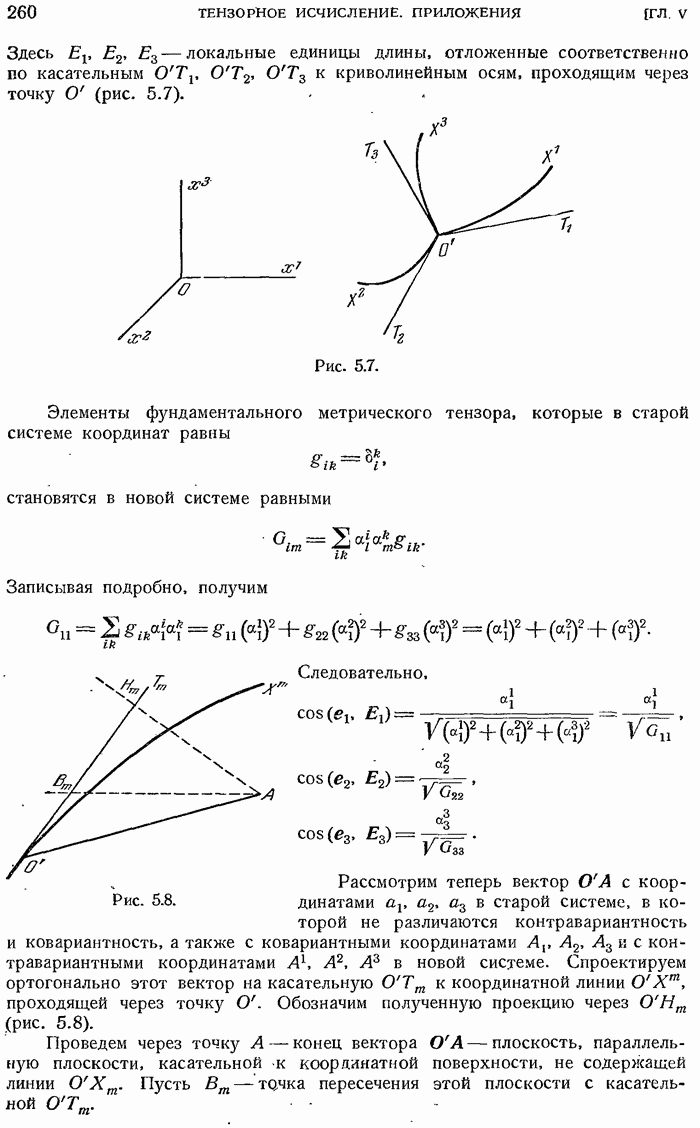
- 5.2.14. Частный случай ортогональных криволинейных координат.
- 5.3. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- Частный случай ортогональных криволинейных координат
- 5.3.9. Тензорная форма уравнений Максвелла.
- 5.4. ПРИМЕНЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 5.4.1. Элементы электрических цепей с сосредоточенными постоянными.
- 5.4.2. Метод составления уравнений для цепи наиболее общего вида.
- 5.4.3. Соединение цепей посредством проводников.
- 5.4.4. Соединение цепей посредством магнитопроводов.
- 5.4.5. Анализ эквивалентных цепей.
- 5.4.6. Цепи с внешним питанием.
- 5.5. ПРИМЕНЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД
- 5.5.2. Диэлектрические свойства кристалла.
- 5.5.3. Матрицы преобразования для некоторых часто встречающихся систем координат.
- Механические свойства кристалла
- 5.5.8. Применение шестимерного пространства.
- 5.5.9. Модуль Юнга.
- Пьезоэлектричество
- 5.5.10. Электрическая поляризация.
- 5.5.11. Закон Кюри.
- 5.5.12. Пьезоэлектрические свойства кварца.
- 5.5.13. Распространение упругих волн в кристаллах.
- 5.5.14. Плоские волны.
- ГЛАВА VI. МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 6.1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 6.1.2. Уравнения с разделяющимися переменными.
- 6.1.3. Однородные уравнения.
- 6.1.4. Уравнение в полных дифференциалах.
- 6.1.5. Линейное уравнение.
- 6.1.6. Уравнение Бернулли.
- 6.1.7. Уравнение Риккати.
- 6.1.8. Уравнение Лагранжа.
- 6.1.9. Уравнение Клеро.
- 6.1.10. Общий случай f(x,y,dy/dx)=0
- 6.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
- Линейное дифференциальное уравнение n-го порядка
- 6.2.9. Уравнение Эйлера.
- 6.2.10. Интегрирование при помощи степенных рядов.
- 6.2.11. Некоторые теоремы о свойствах решений линейного дифференциального уравнения второго порядка.
- Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами
- 6.3. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 6.3.1. Линейное уравнение с постоянными коэффициентами, однородное относительно частных производных.
- 6.3.2. Уравнение с правой частью.
- 6.3.3. Уравнение колебаний струны.
- 6.3.4. Телеграфное уравнение.
- 6.3.5. Уравнение Лапласа.
- 6.3.6. Прямоугольная система координат.
- 6.3.7. Система цилиндрических координат.
- 6.3.8. Система сферических координат.
- 6.3.9. Система эллиптических цилиндрических координат.
- 6.3.10. Система параболических цилиндрических координат.
- 6.3.11. Другие системы координат.
- 6.3.12. Уравнение Пуассона.
- 6.3.13. Решение уравнений Максвелла методом Бромвича.
- 6.3.14. Пример. Электромагнитные колебания в прямоугольной полости.
- ГЛАВА VII. НАИБОЛЕЕ УПОТРЕБИТЕЛЬНЫЕ СПЕЦИАЛЬНЫЕ ФУНКЦИИ
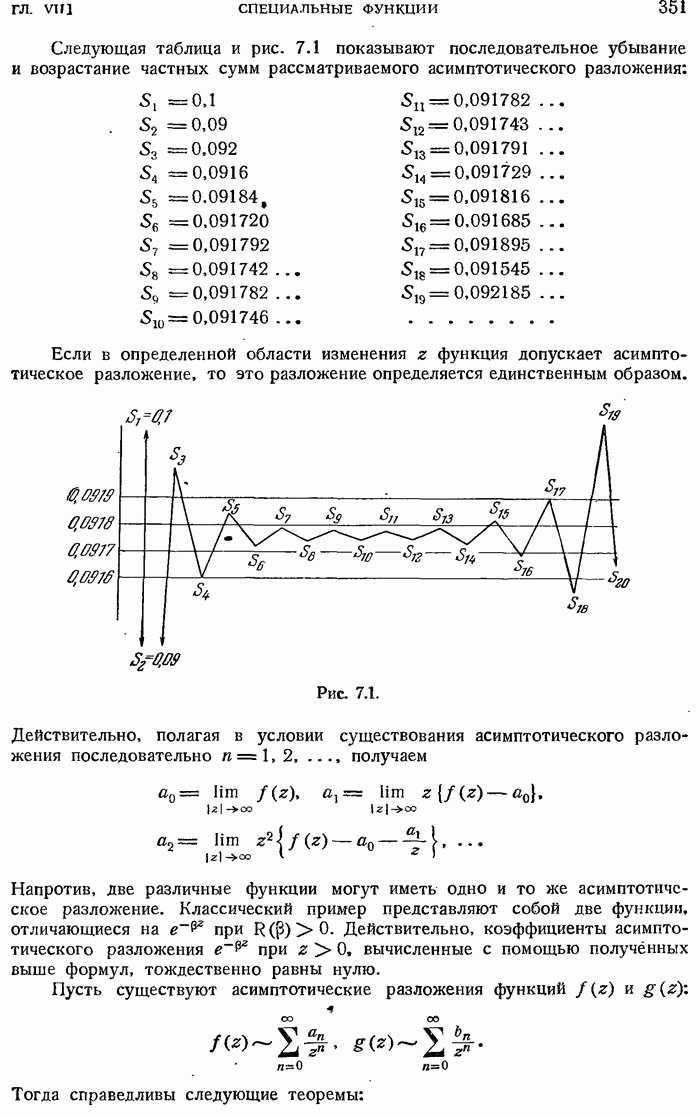
- 7.0.1. Асимптотическое разложение.
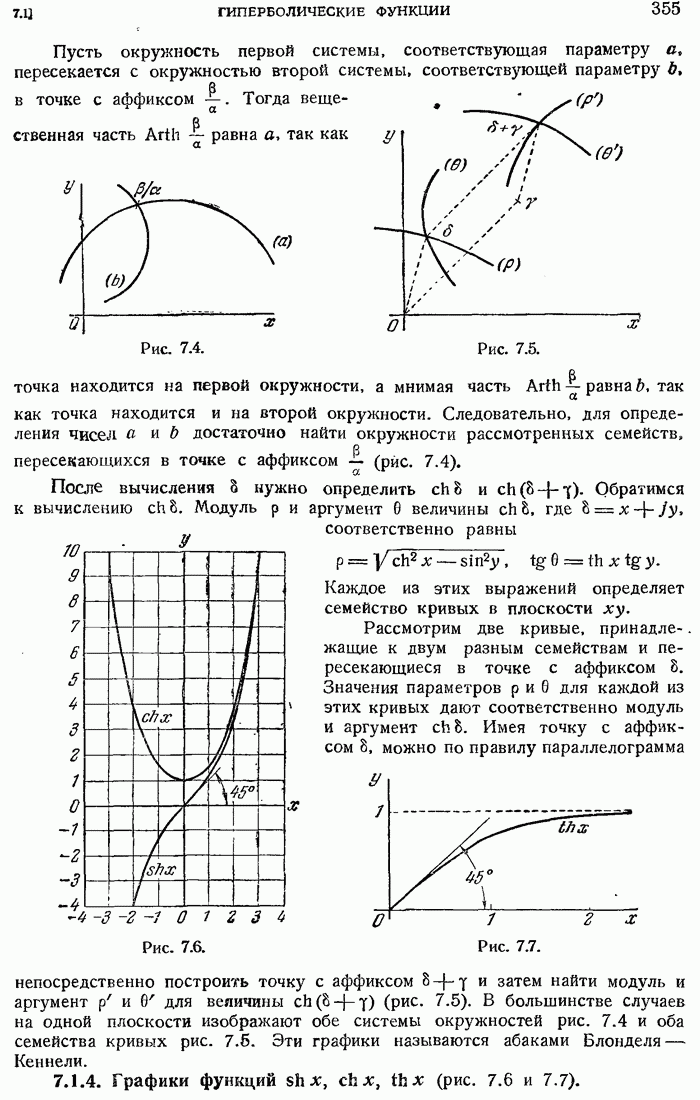
- 7.1. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
- 7.1.2. Обратные гиперболические функции.
- 7.1.3. Приложение гиперболических функций к расчету длинных линий. Метод Броуна. Абаки Блонделя — Кеннеди.
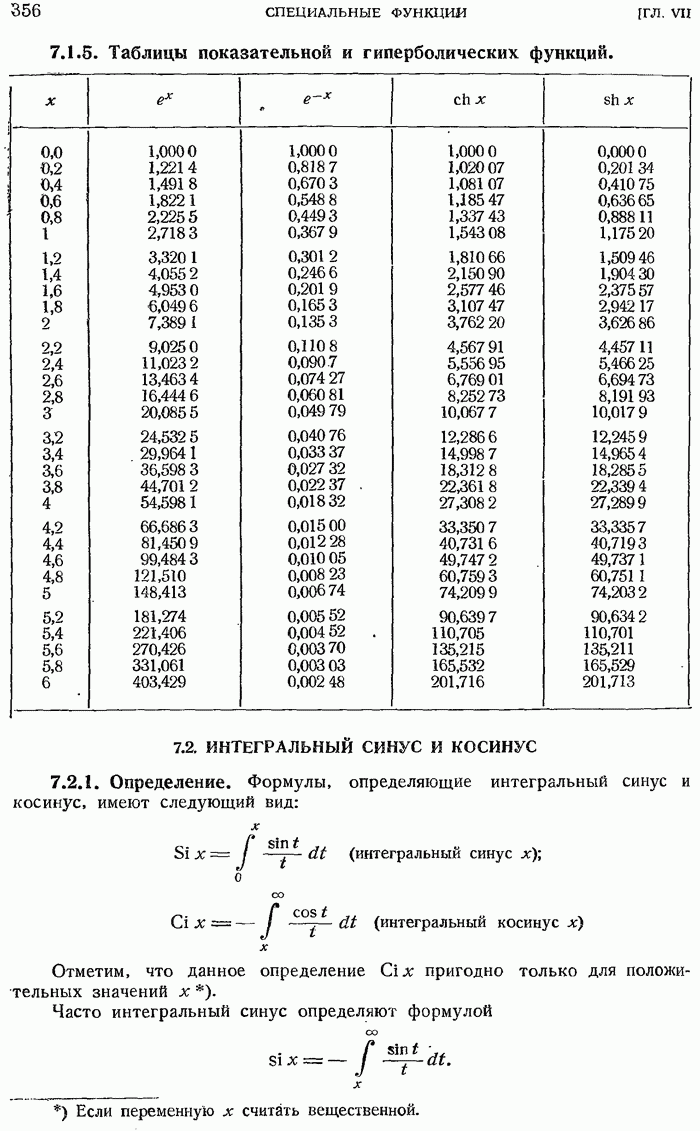
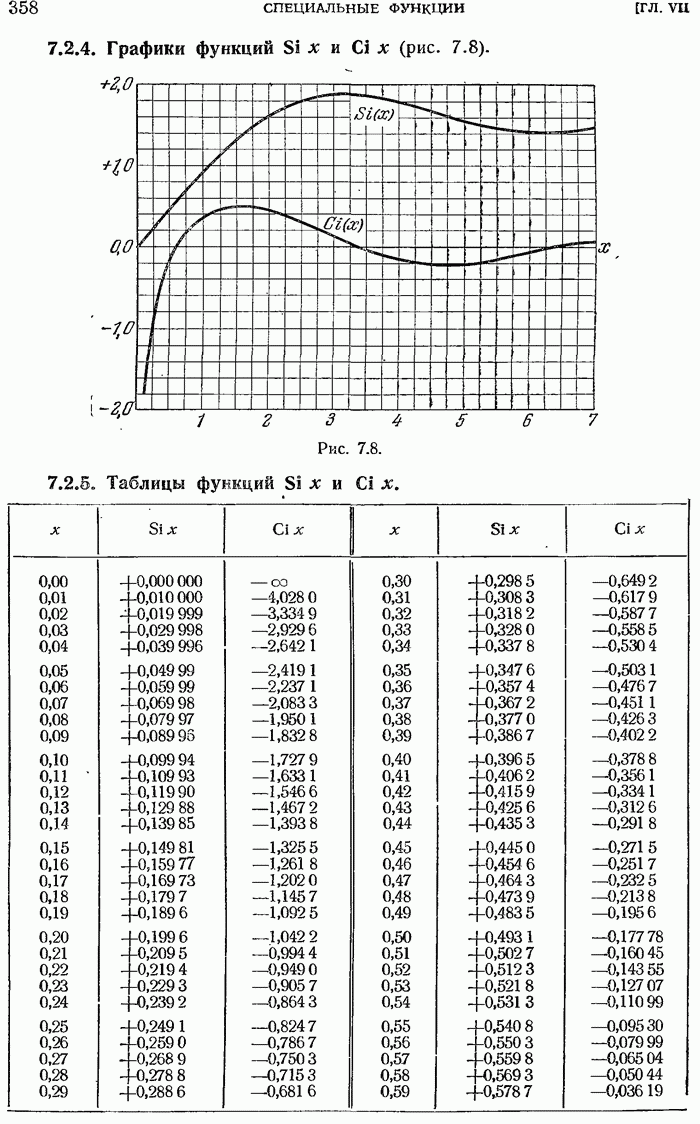
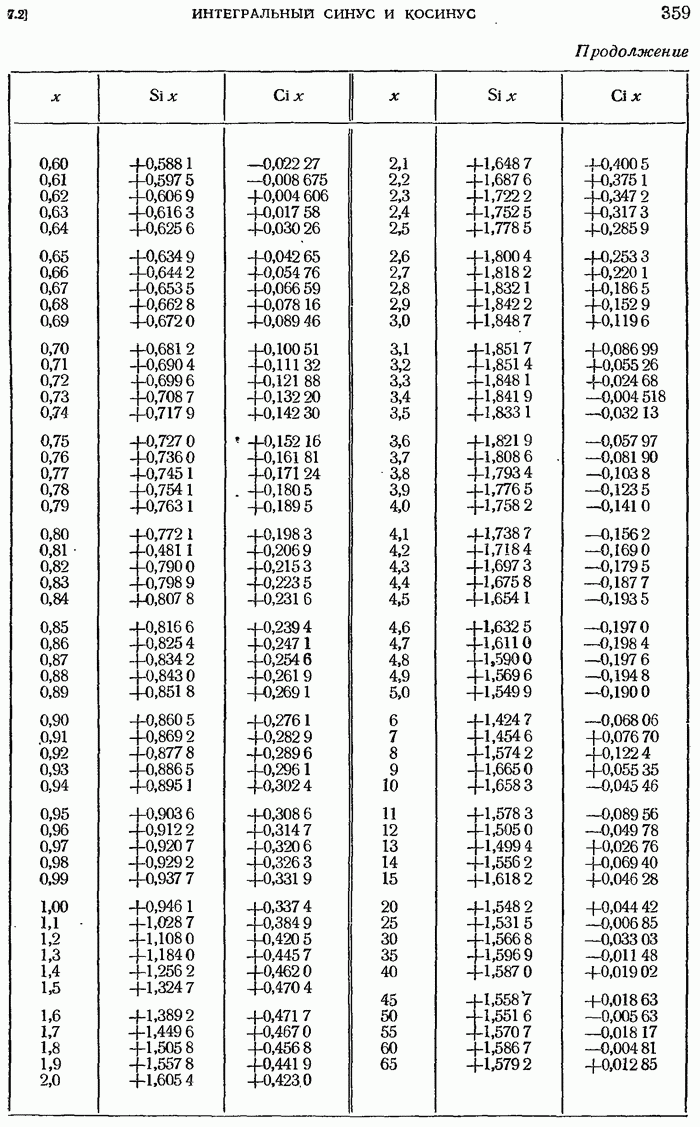
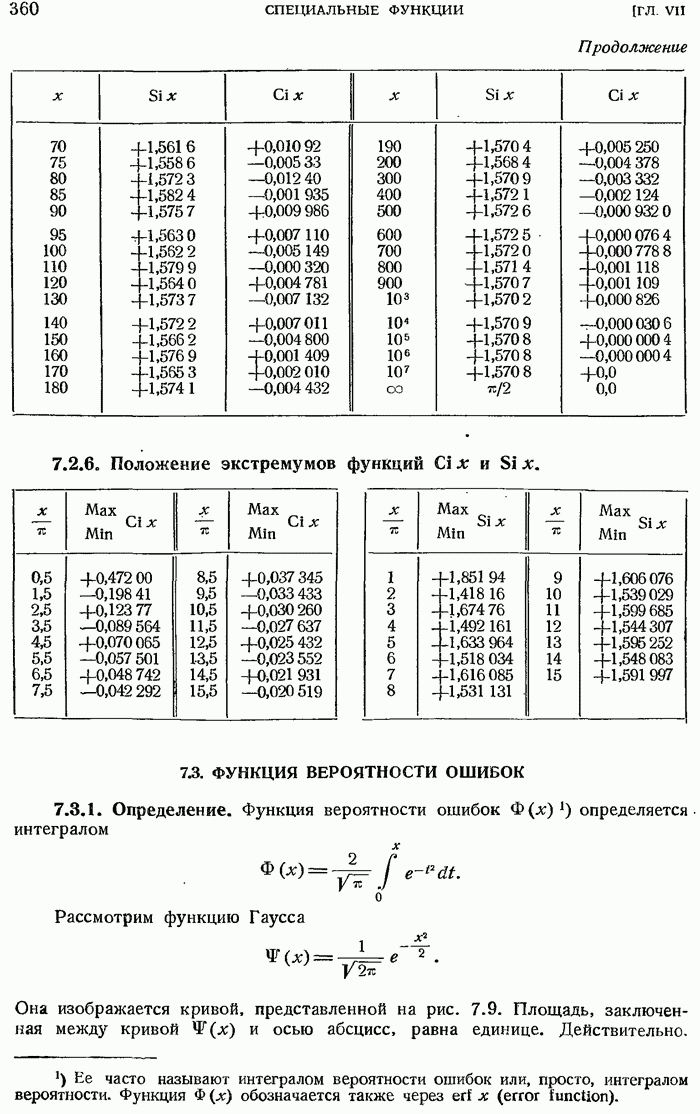
- 7.2. ИНТЕГРАЛЬНЫЙ СИНУС И КОСИНУС
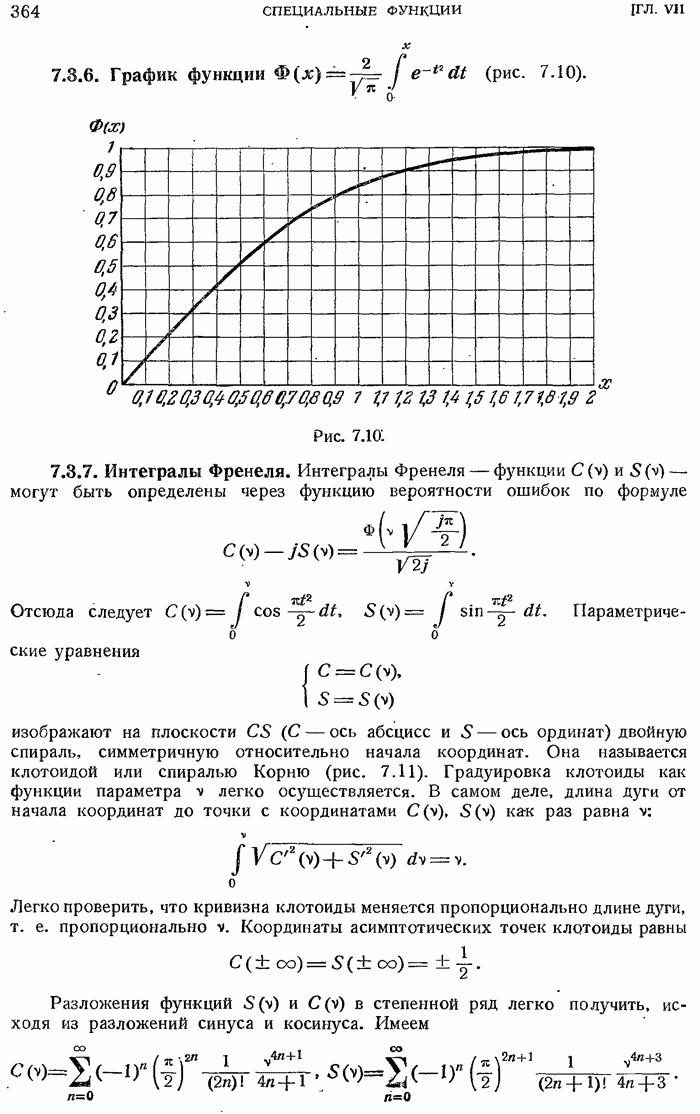
- 7.3. ФУНКЦИЯ ВЕРОЯТНОСТИ ОШИБОК
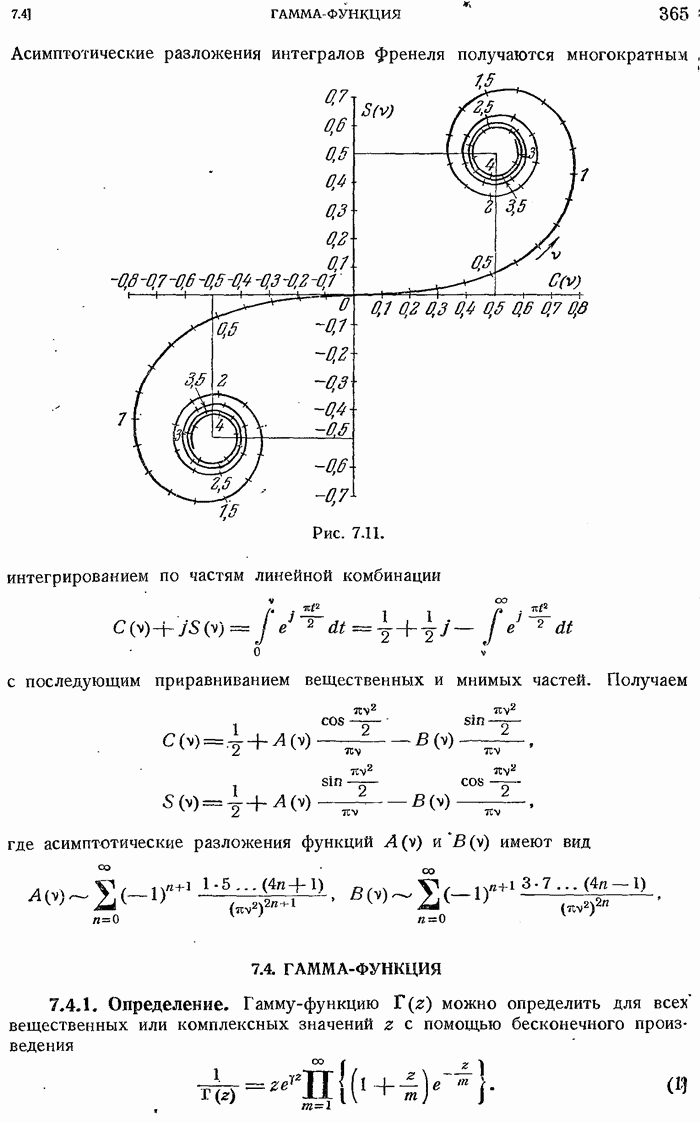
- 7.3.7. Интегралы Френеля.
- 7.4. ГАММА-ФУНКЦИЯ
- 7.4.2. Свойства гамма-функции.
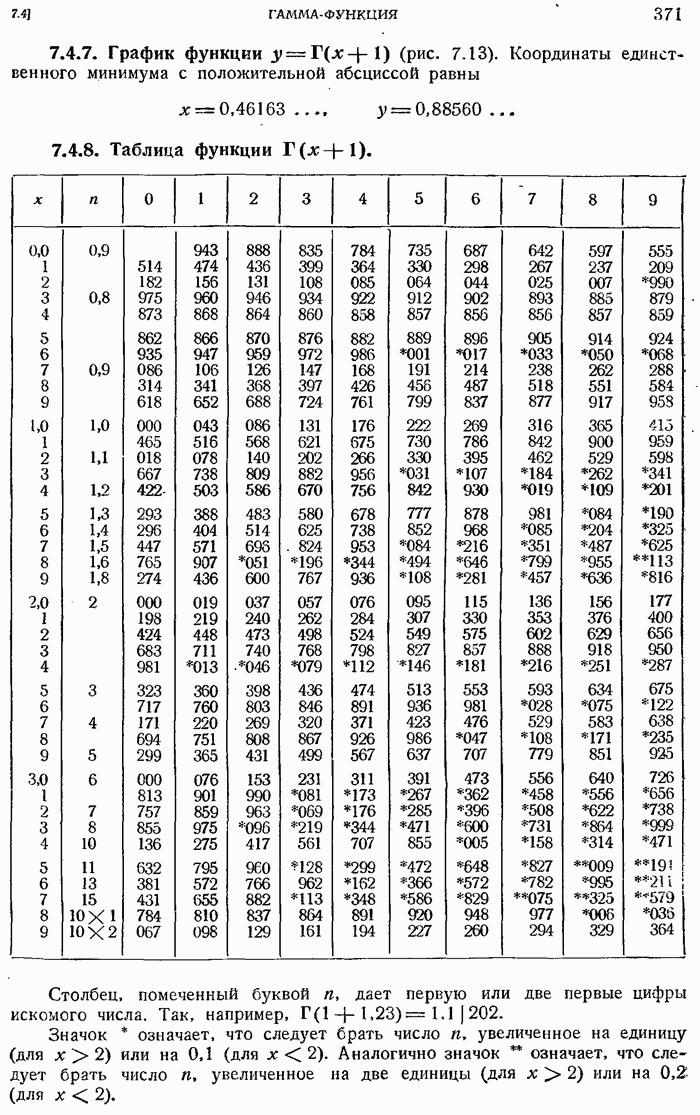
- 7.4.3. Некоторые значения функции Г(z).
- 7.4.4. Логарифмическая производная гамма-функции.
- 7.4.5. Представление гамма-функции через интеграл Коши.
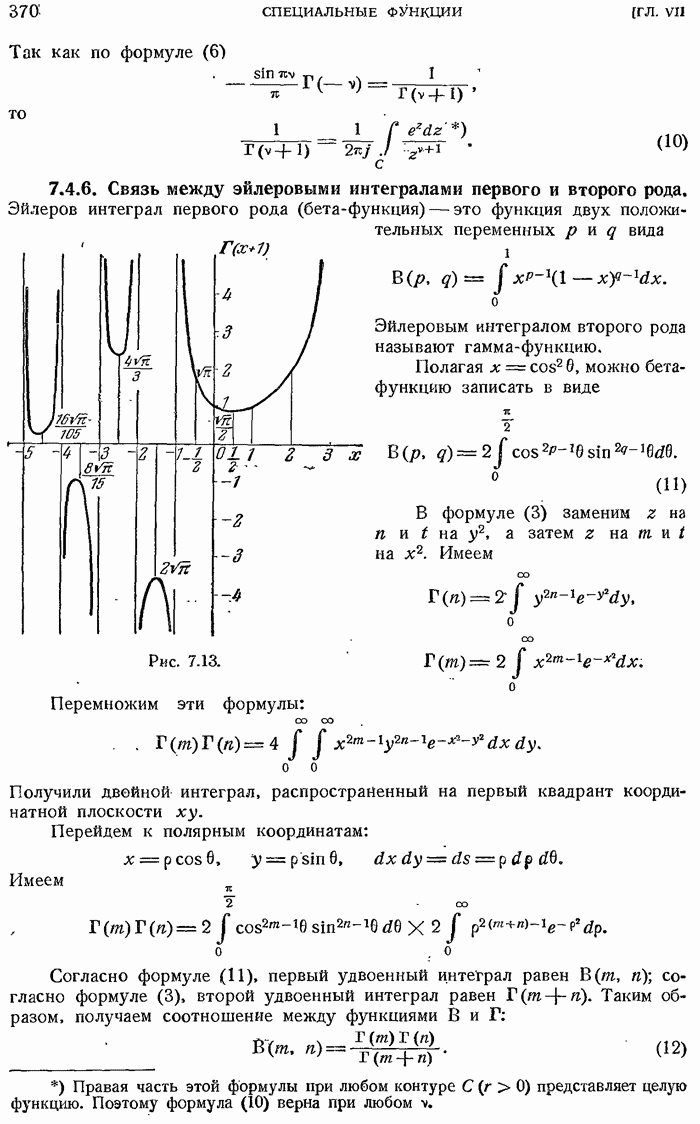
- 7.4.6. Связь между эйлеровыми интегралами первого и второго рода.
- 7.5. ФУНКЦИИ БЕССЕЛЯ
- Функции Бесселя первого и второго рода
- 7.5.6. Интегралы Ломмеля.
- 7.5.7. Соотношение между двумя функциями, индексы которых отличаются на целое число.
- 7.5.8. Применение интегралов Ломмеля к разложению в ряд по бесселевым функциям.
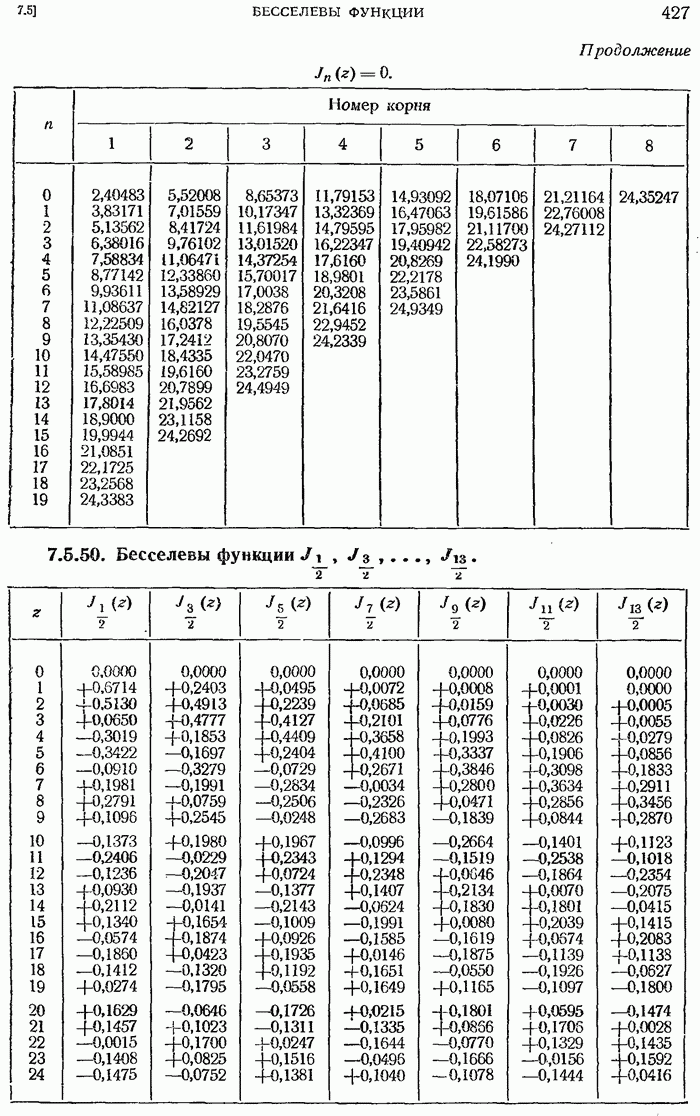
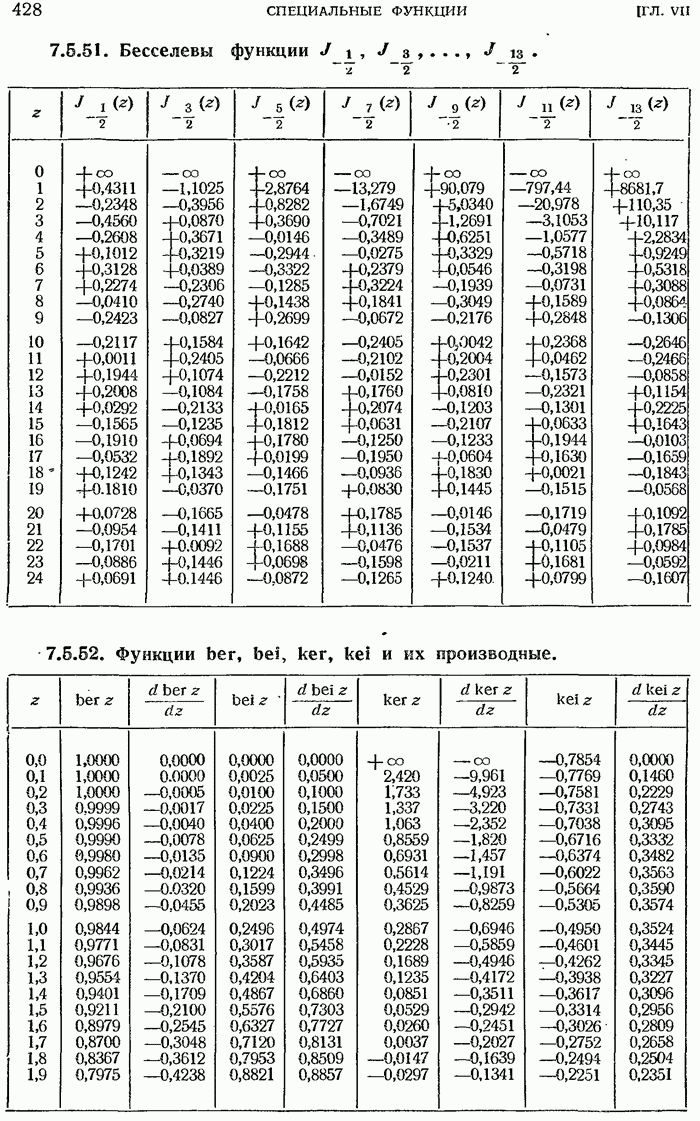
- 7.5.9. Бесселевы функции первого и второго рода с полуцелым индексом.
- 7.5.10. Применение бесселевых функций к вычислению интегралов Френеля.
- 7.5.11. Случай, когда индекс равен целому числу v=n
- 7.5.12. Представление Jv(z) через определенный интеграл.
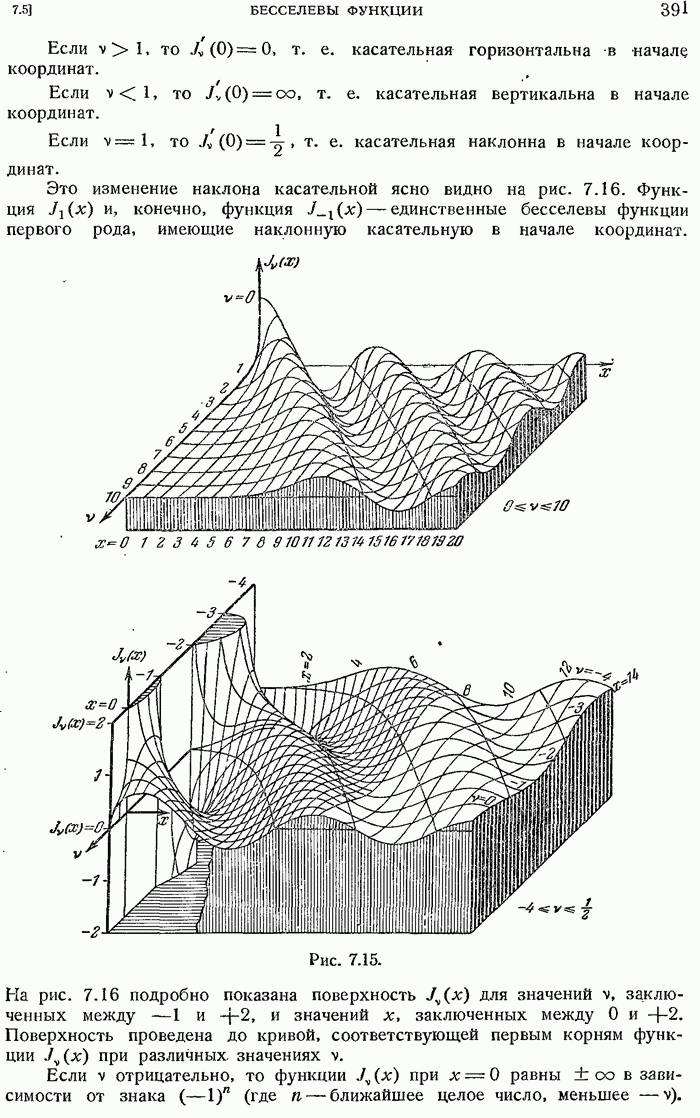
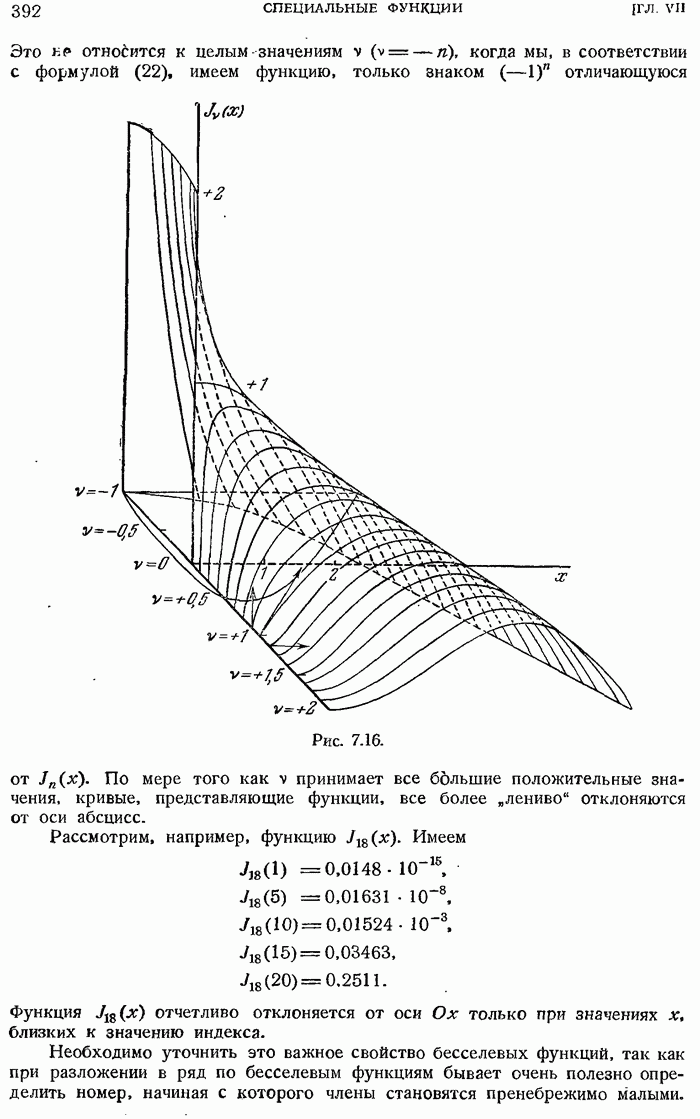
- 7.5.13. Представление Jv(z) с помощью интеграла Коши.
- 7.5.14. Теорема сложения.
- 7.5.15. Бесселевы функции третьего рода или функции Ханкеля. Определение.
- 7.5.17. Нахождение численных значений бесселевых функций.
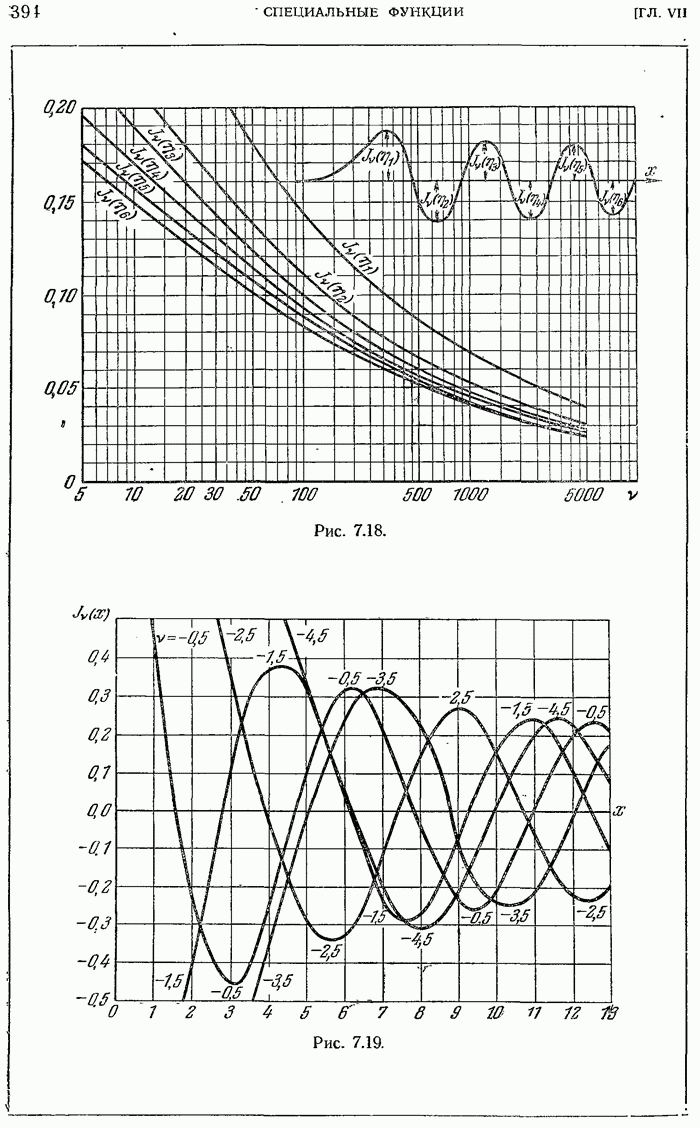
- 7.5.18. Асимптотические выражения для бесселевых функций при больших значениях аргумента.
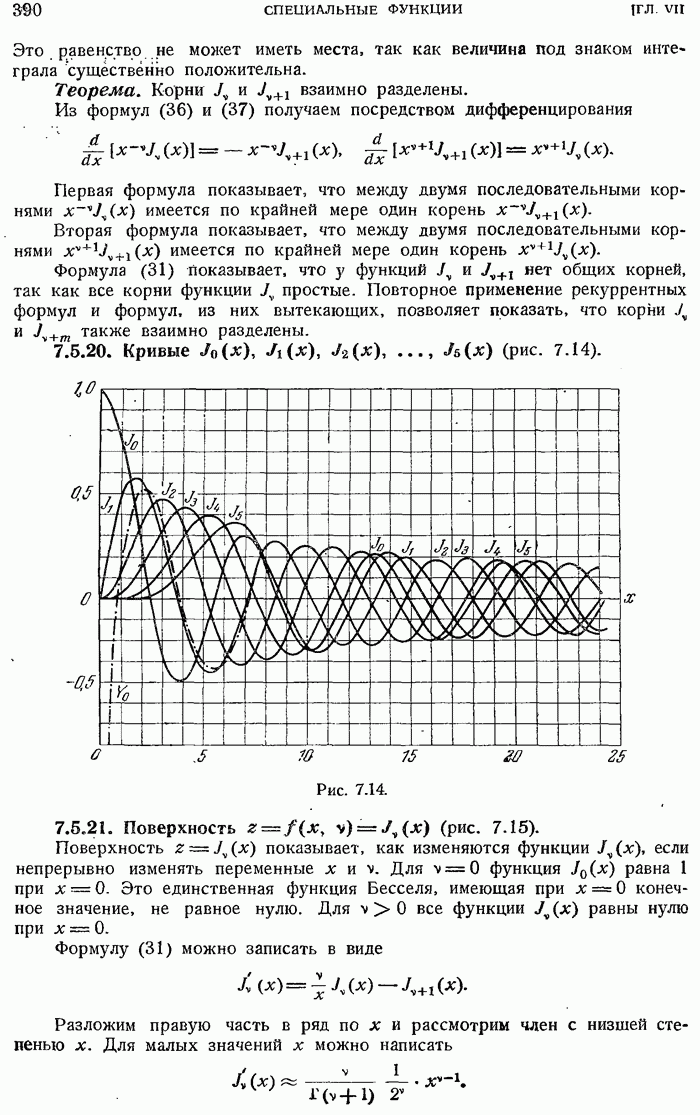
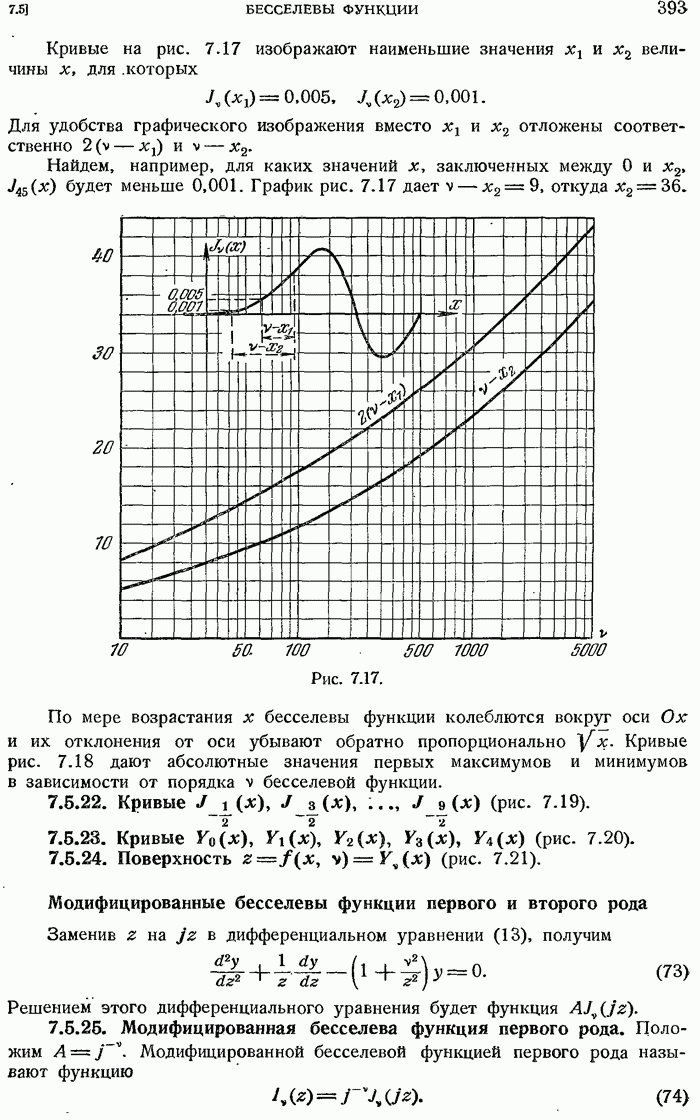
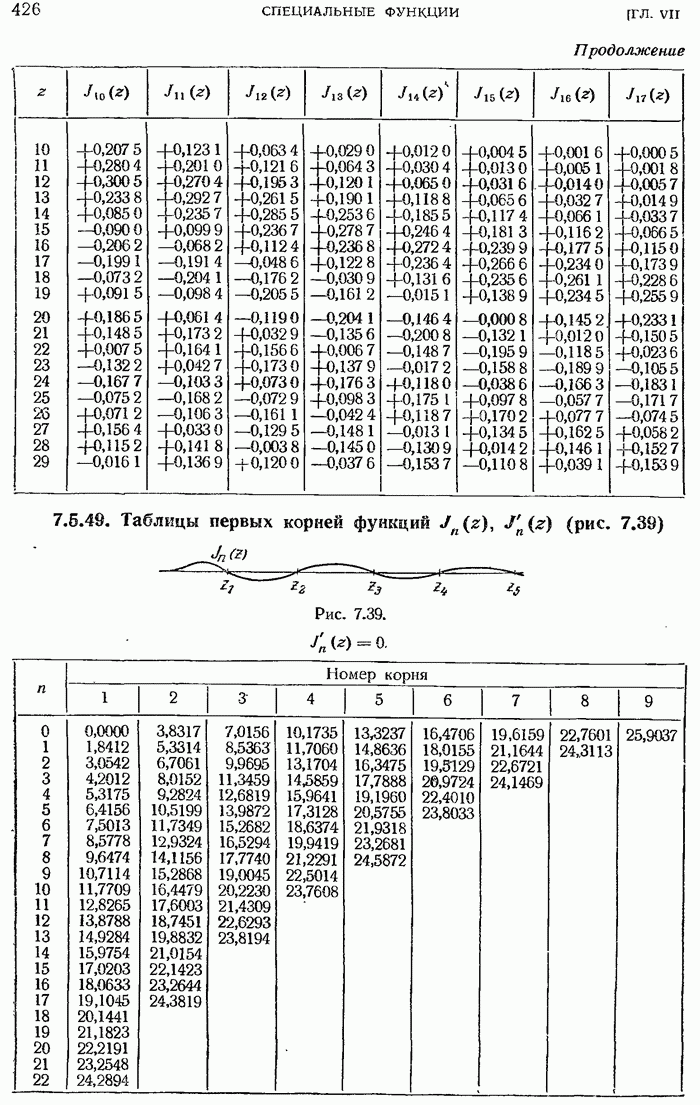
- 7.5.19. Корни бесселевых функций.
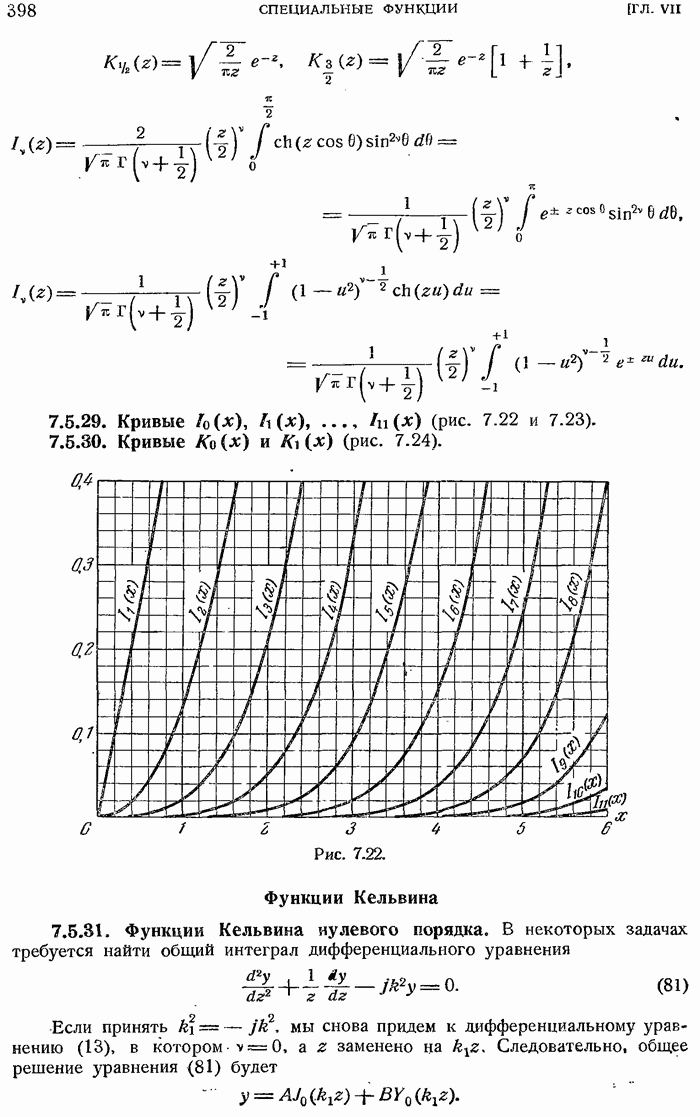
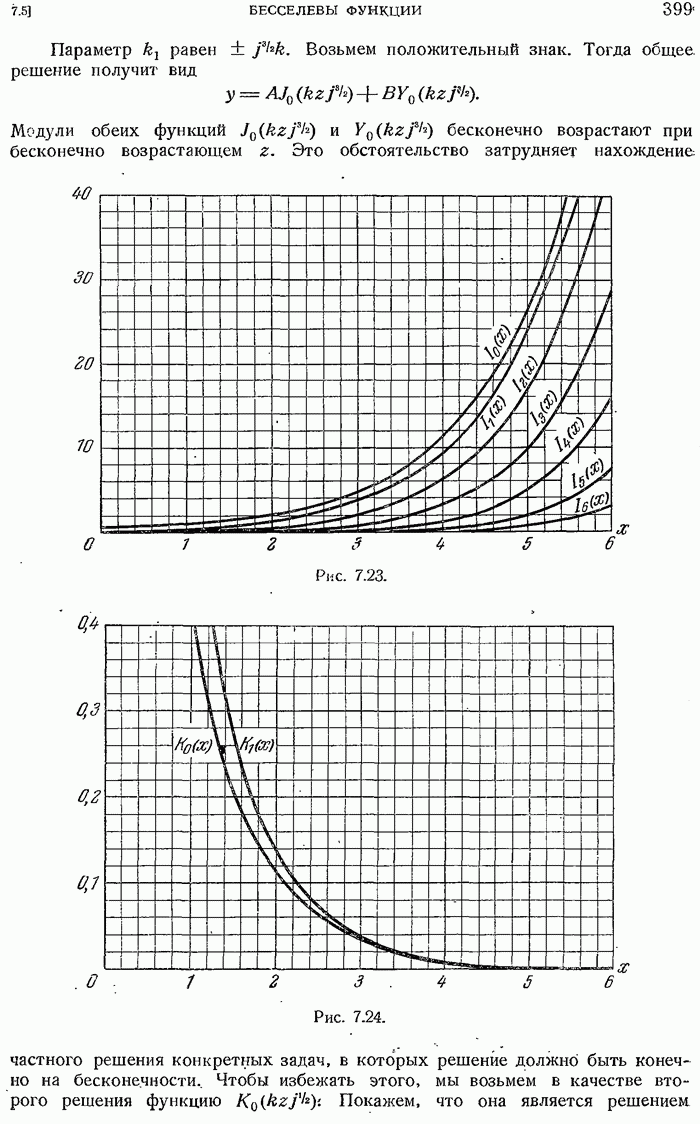
- Модифицированные бесселевы функции первого и второго рода
- 7.5.26. Модифицированная бесселева функция второго рода.
- 7.5.27. Асимптотические разложения.
- 7.5.28. Рекуррентные формулы.
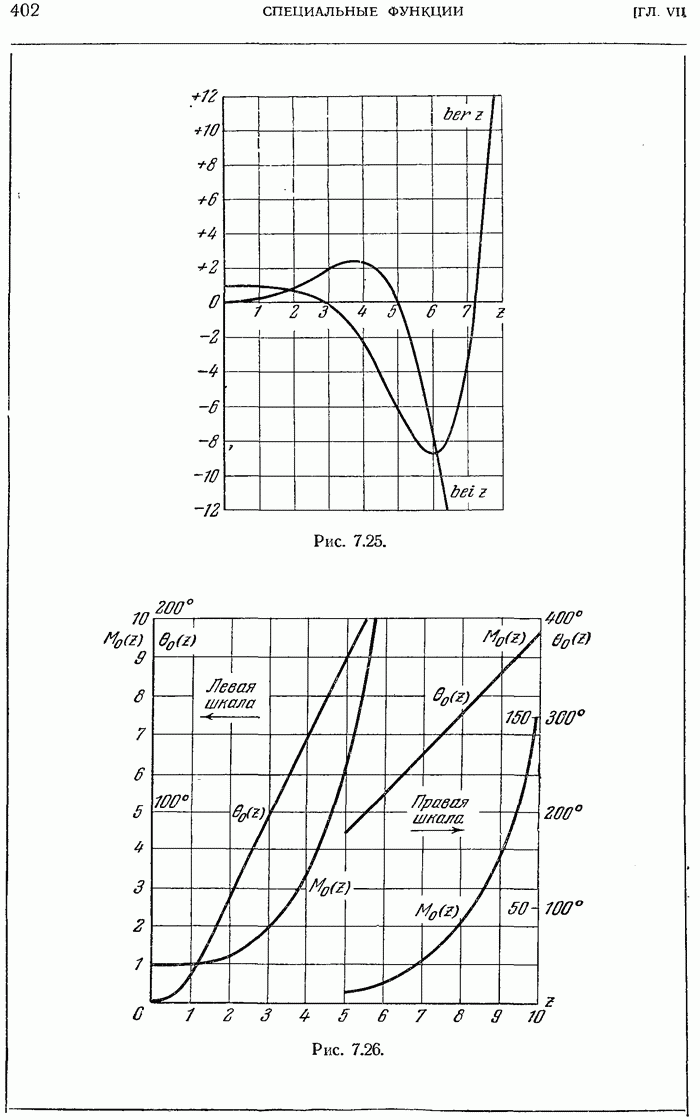
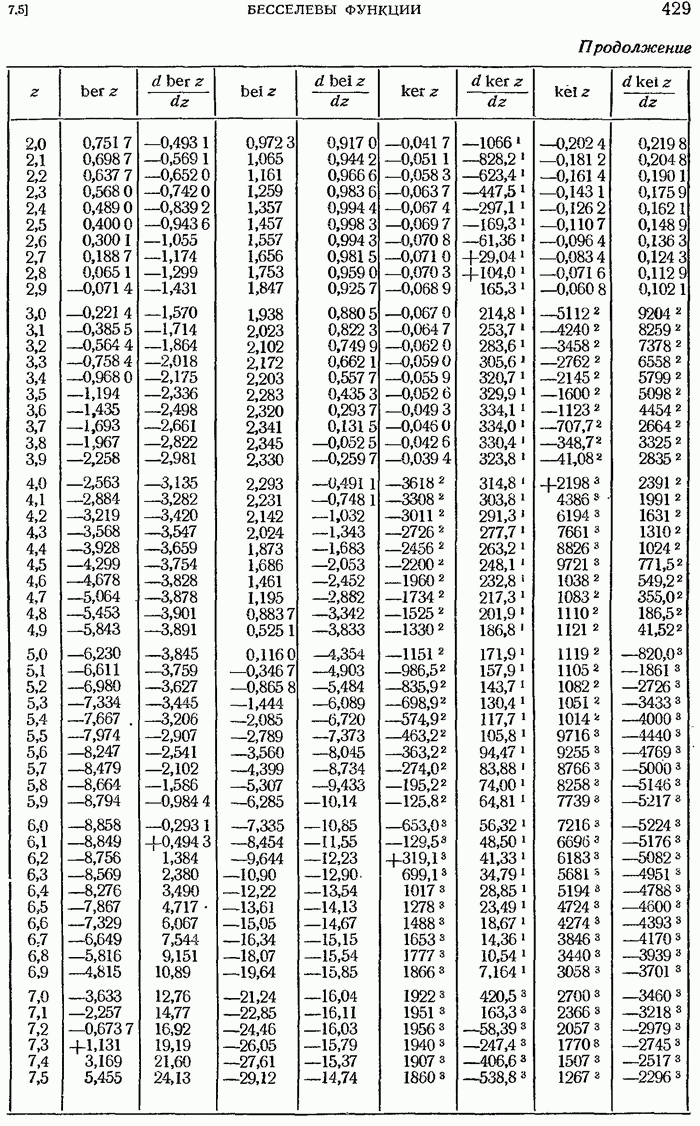
- Функции Кельвина
- 7.5.32. Функция Кельвина v-го порядка.
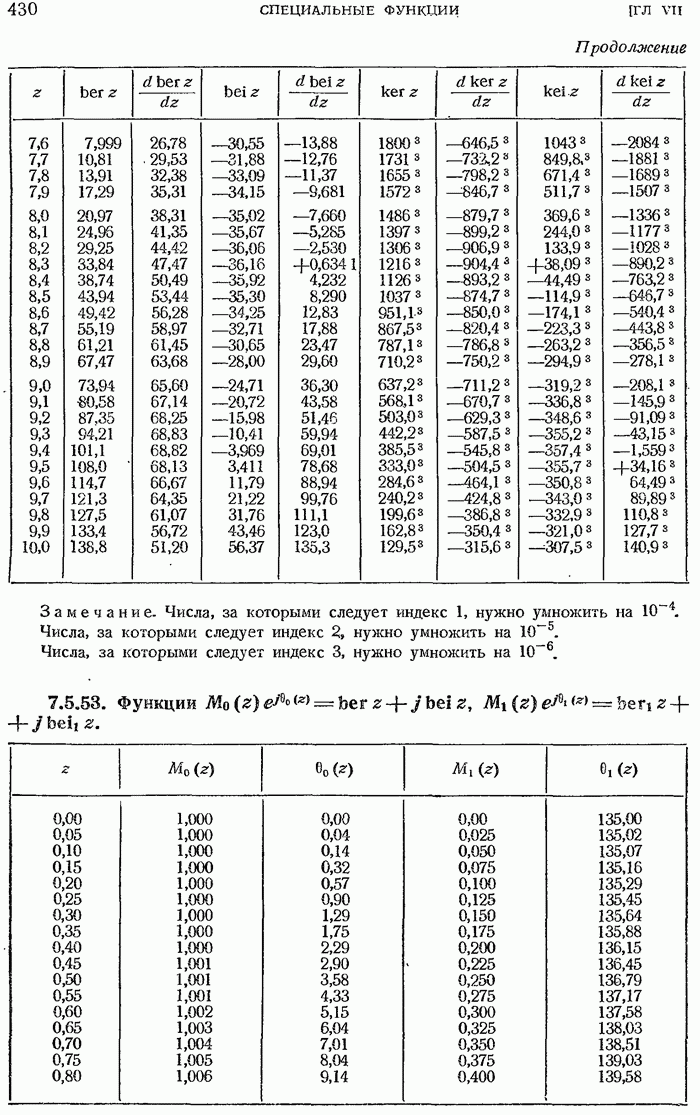
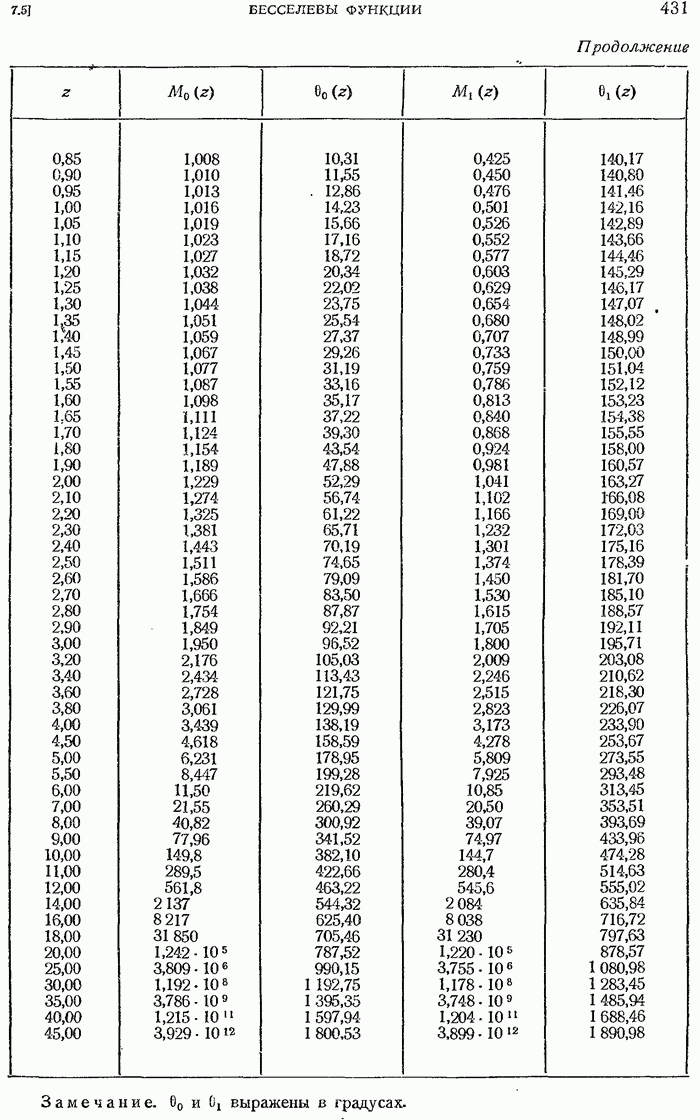
- 7.5.33. Представление функций Кельвина через модуль и аргумент.
- 7.5.34. Производные функций Кельвина.
- Дифференциальные уравнения, решение которых может быть выражено через решение дифференциального уравнения Бесселя
- Некоторые примеры применения бесселевых функций
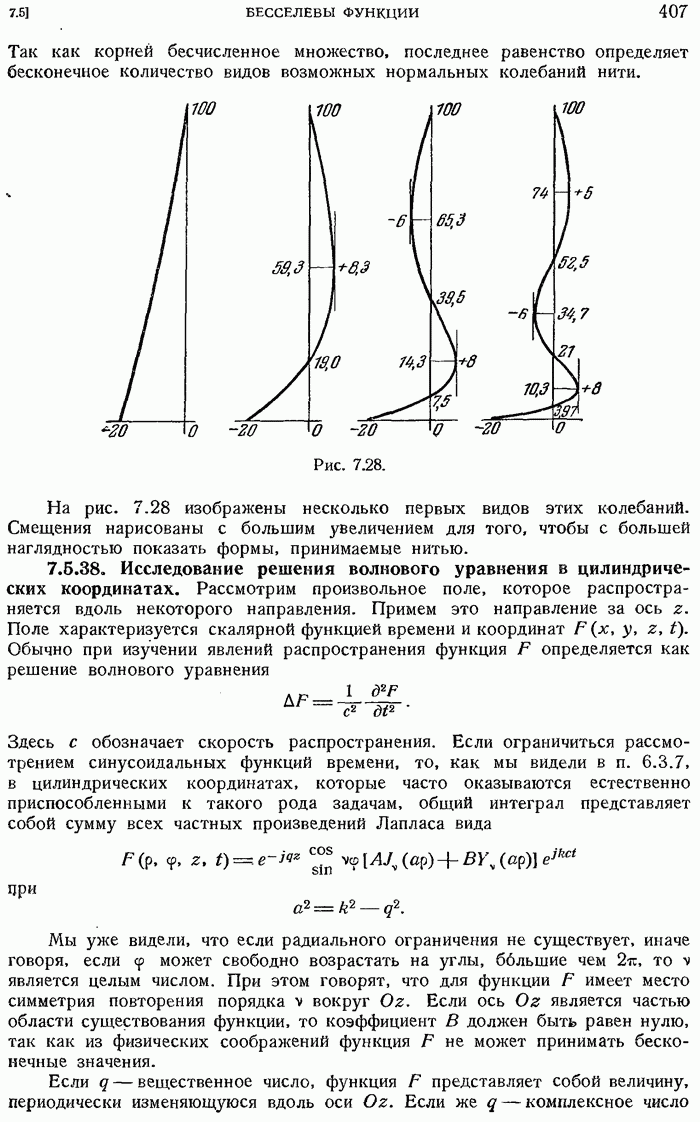
- 7.5.38. Исследование решения волнового уравнения в цилиндрических координатах.
- 7.5.39. Колебания равномерно натянутой мембраны.
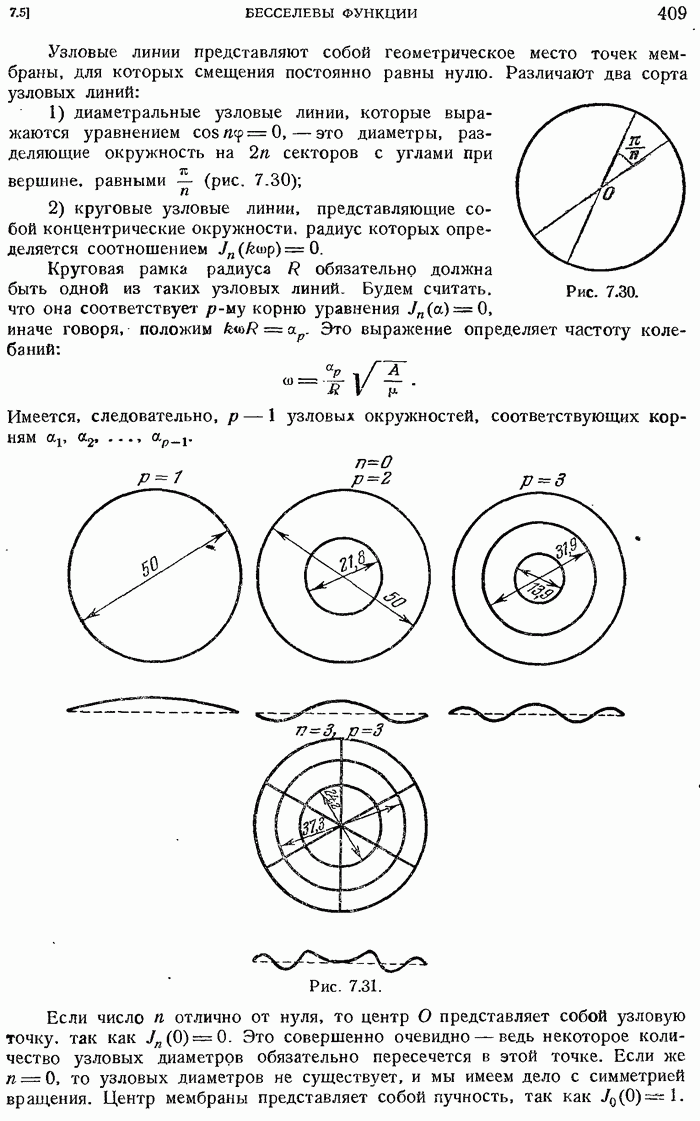
- 7.5.40. Случай круглой мембраны.
- 7.5.41. Собственные электромагнитные колебания резонатора, имеющего форму кругового цилиндра.
- 7.5.42. Распространение электромагнитной волны внутри бесконечного кругового цилиндра.
- 7.5.43. Случай коаксиального проводника.
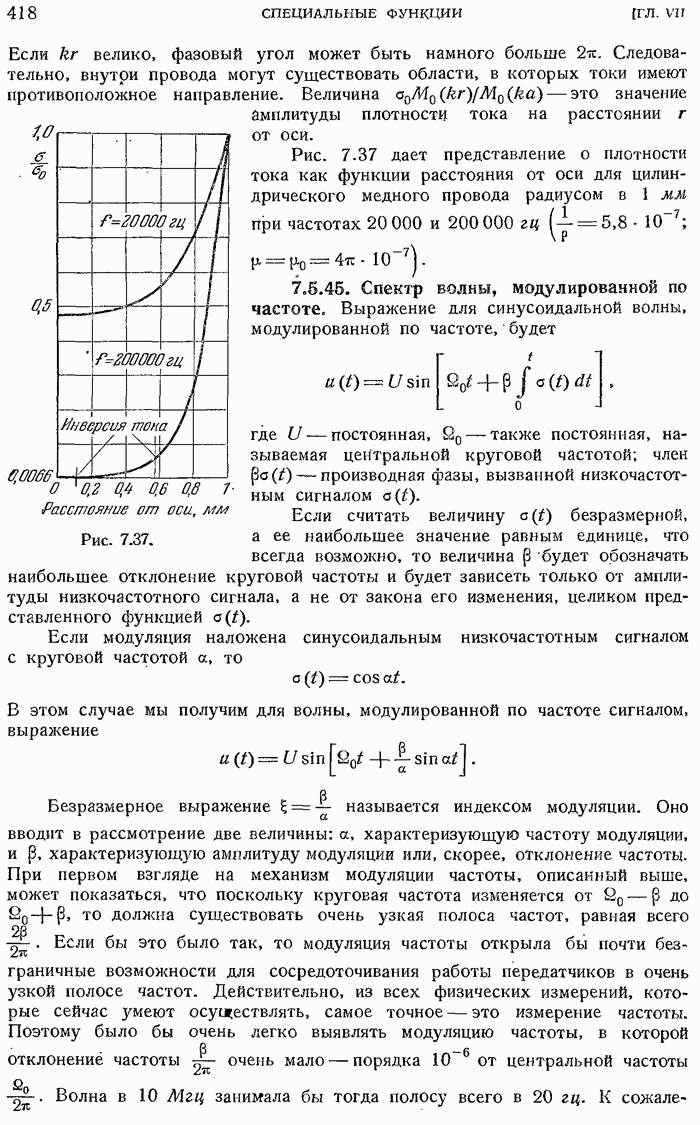
- 7.5.44. Скин-эффект переменных токов, проходящих по цилиндрическому проводнику круглого сечения.
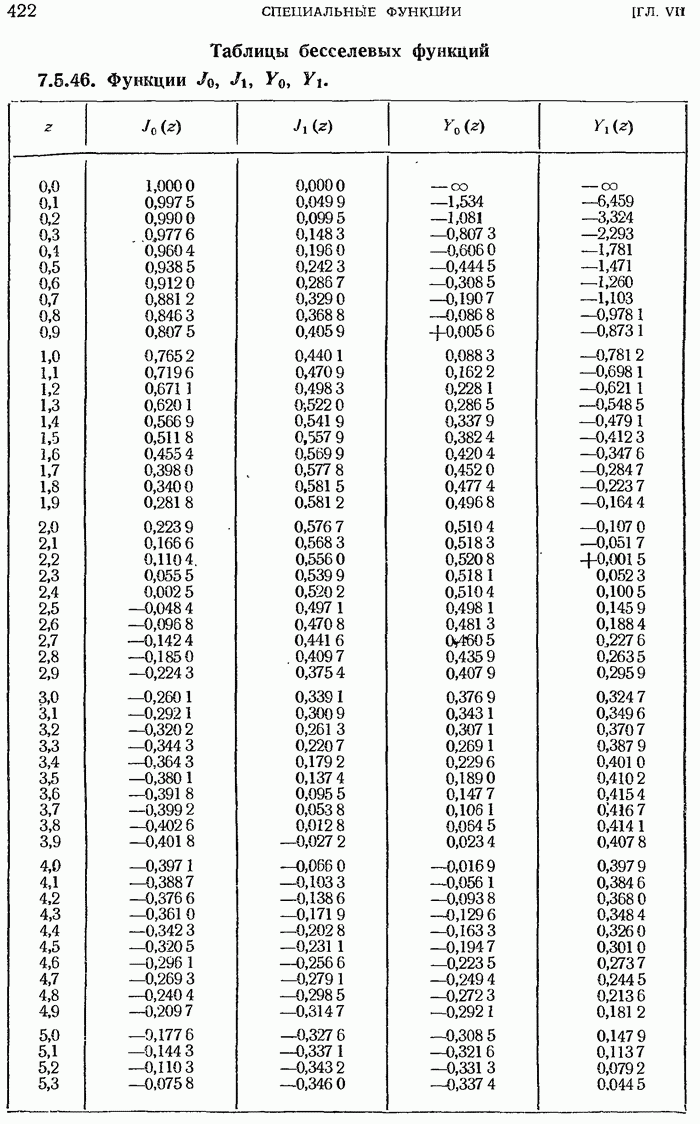
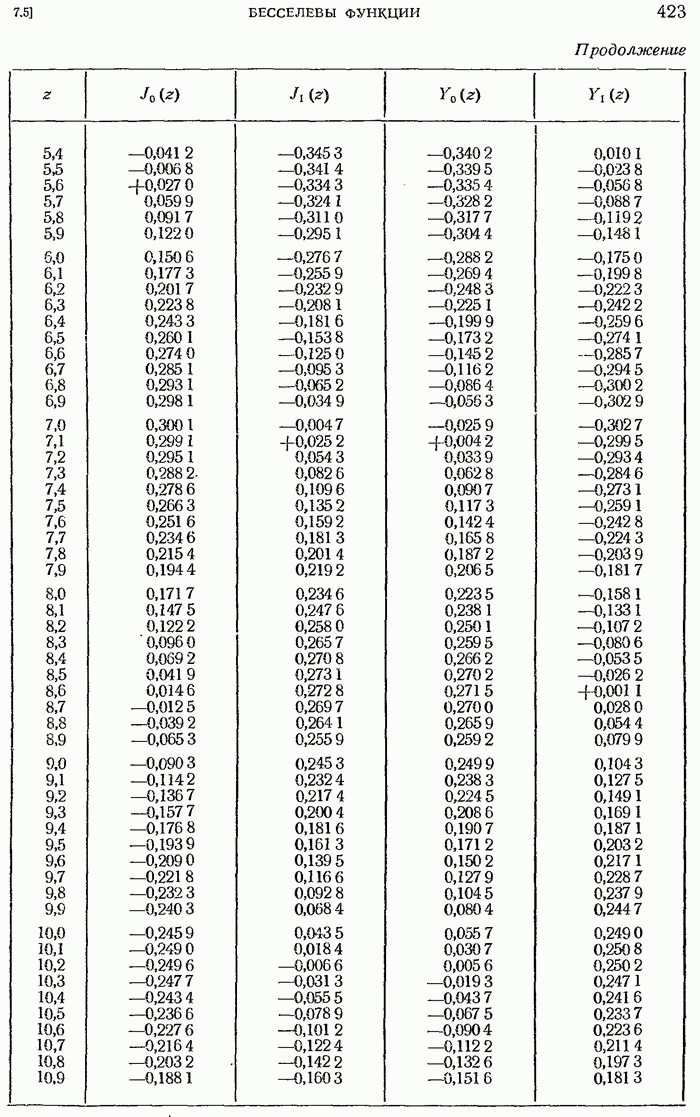
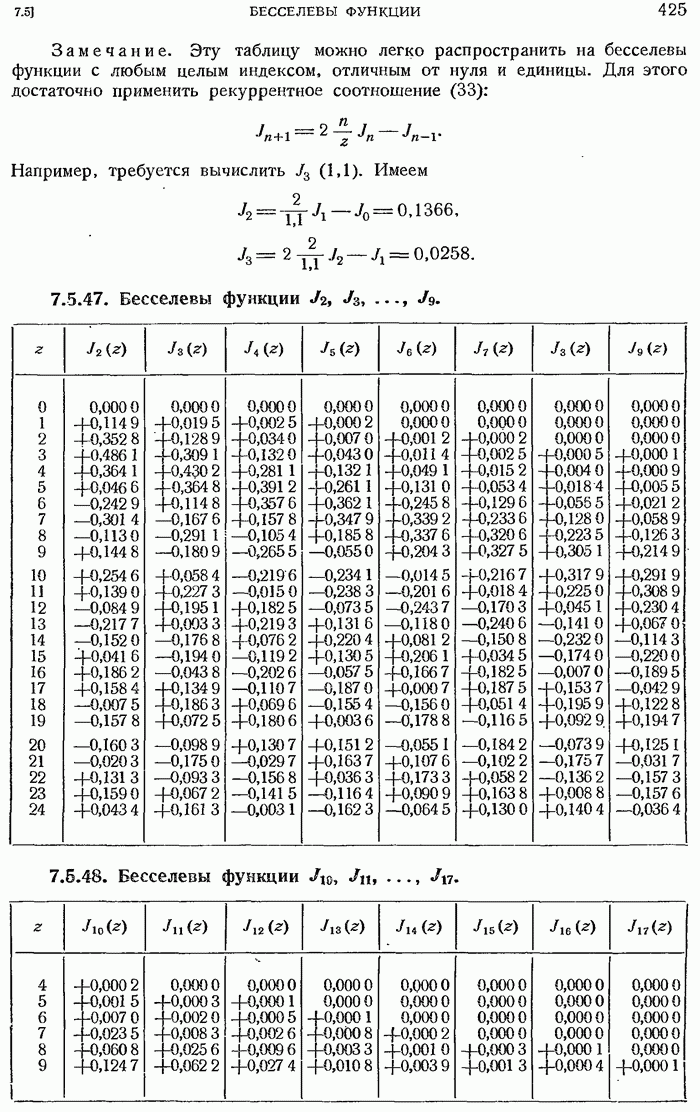
- Таблицы бесселевых функций
- 7.6. ФУНКЦИИ ЛЕЖАНДРА
- 7.6.3. Полиномы Лежандра.
- 7.6.4. Производящая функция полиномов Лежандра.
- 7.6.6. Представление полиномов Лежандра через определенный интеграл. Формула Лапласа.
- 7.6.8. Формула Родрига.
- 7.6.9. Ортогональность полиномов Лежандра.
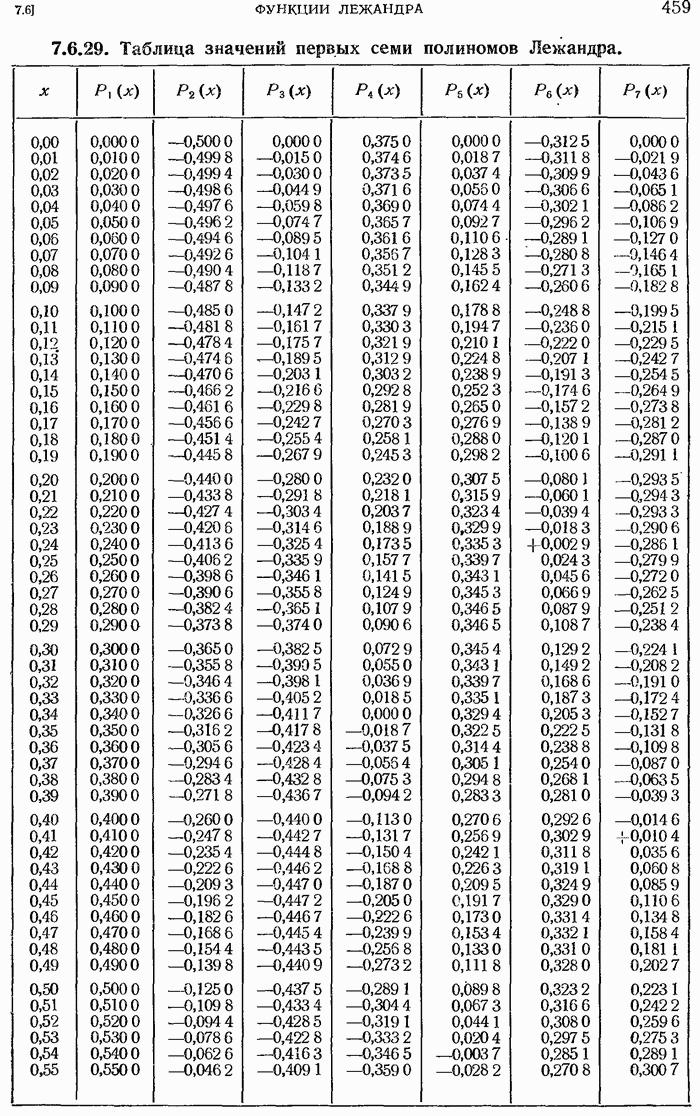
- 7.6.10. Некоторые значения полиномов Лежандра.
- 7.6.11. Корни полиномов Лежандра.
- 7.6.12. Интеграл Шлефли.
- 7.6.13. Обобщение полиномов Лежандра. Полиномы Гегенбауера.
- 7.6.14. Функции Лежандра первого рода.
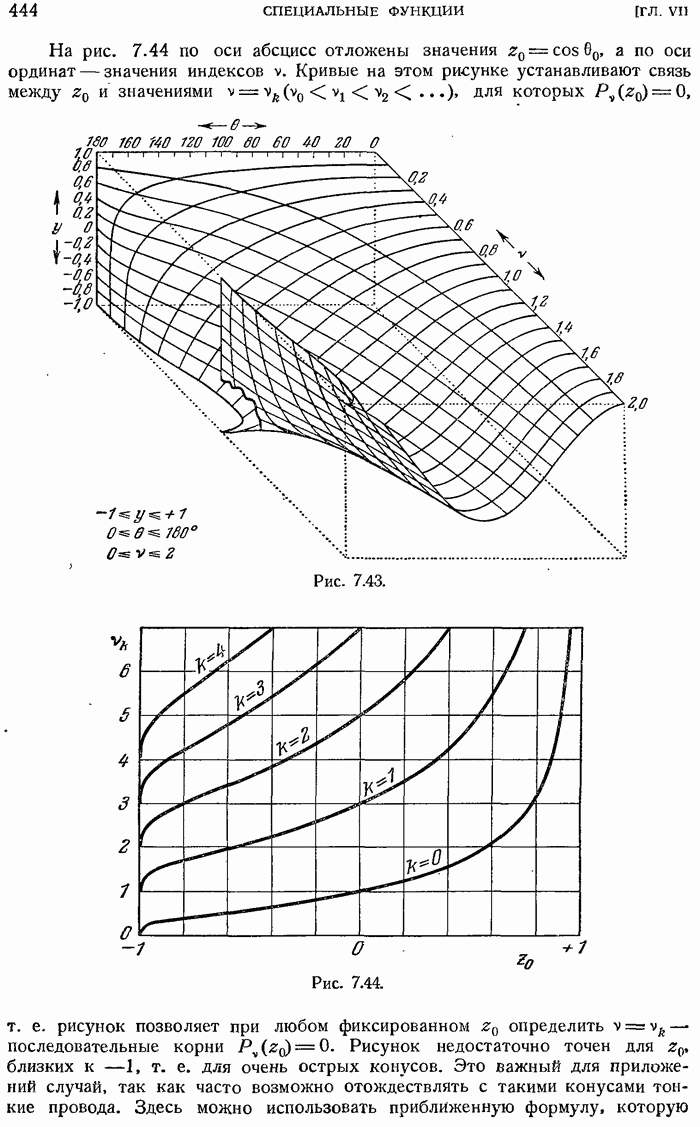
- 7.6.16. Корни функций Лежандра первого рода.
- 7.6.18. Определение функции Лежандра первого рода через интеграл Коши.
- 7.6.19. Функция Лежандра второго рода.
- 7.6.20. Определение функции Лежандра второго рода через интеграл Коши.
- 7.6.21. Присоединенные функции Лежандра.
- 7.6.22. Присоединенные функции Лежандра для целых положительных индексов.
- 7.6.24. Ортогональность присоединенных функций Лежандра.
- 7.6.25. Некоторые значения присоединенных функций Лежандра.
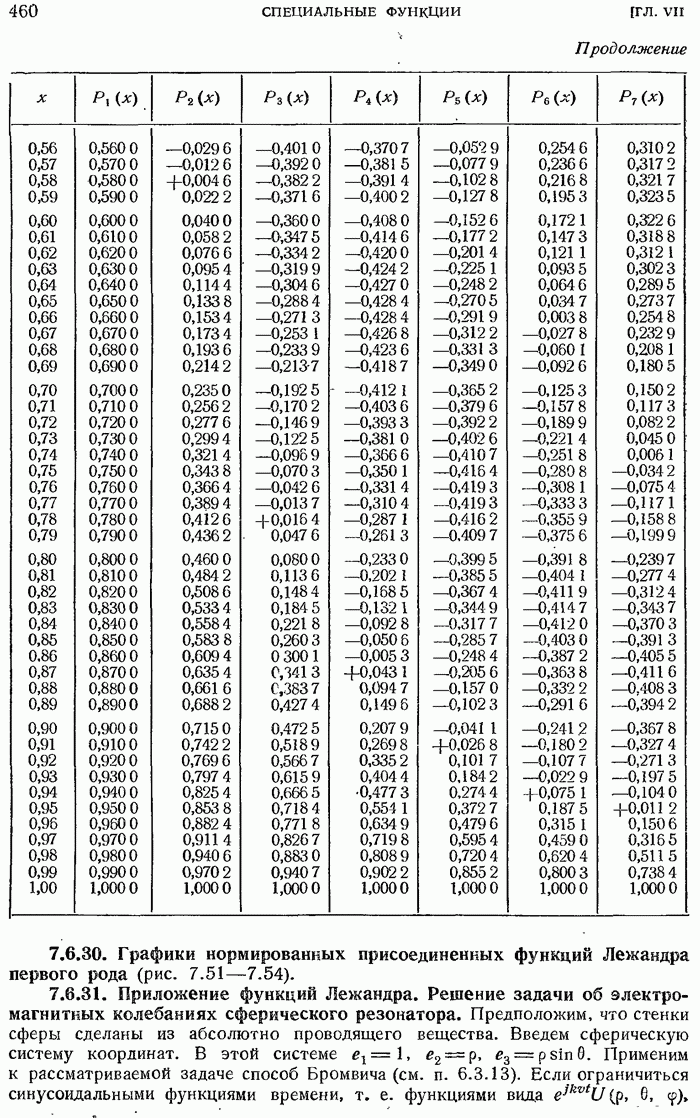
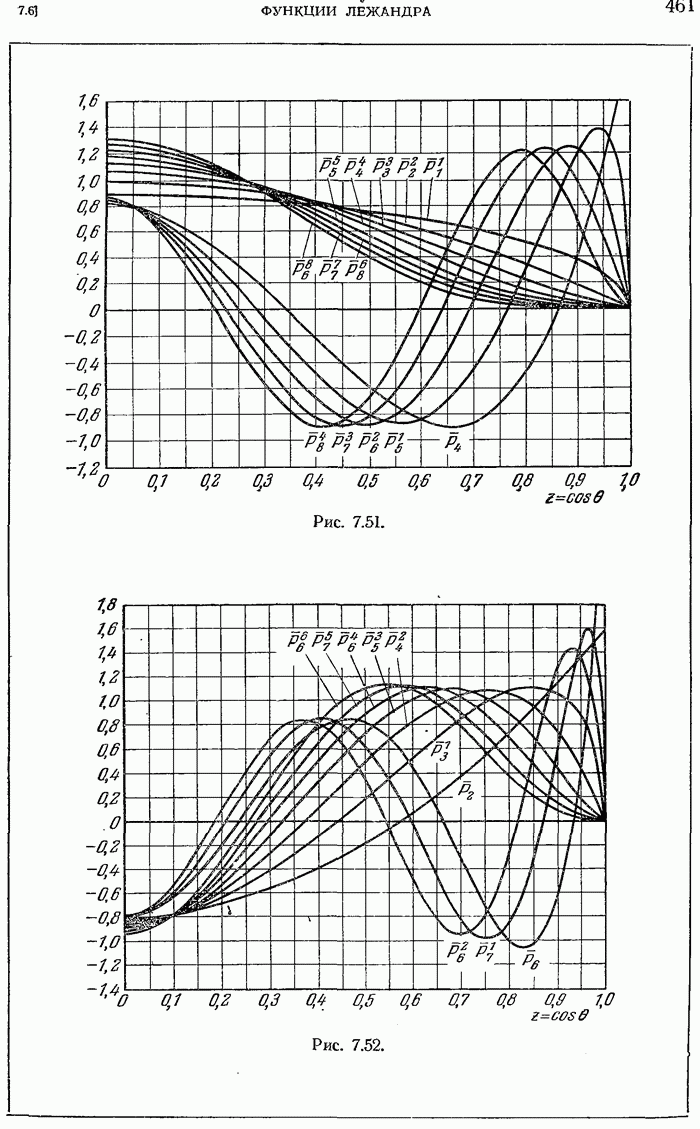
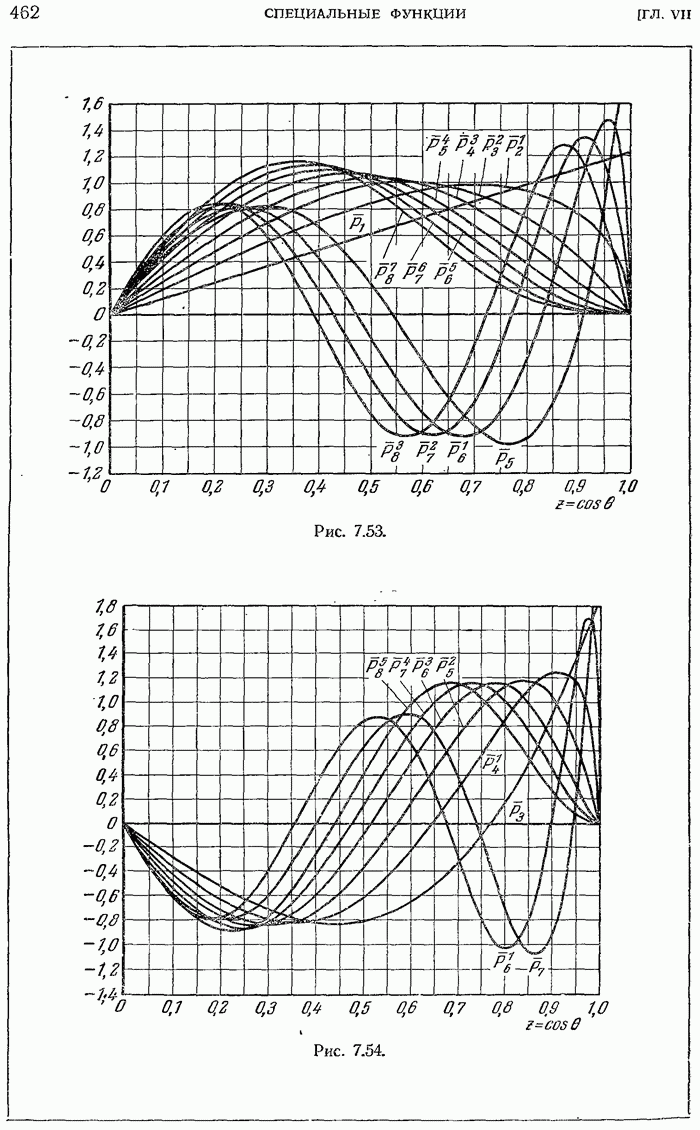
- 7.6.26. Сферические гармоники.
- 7.6.25. Некоторые значения присоединенных функций Лежандра.
- 7.6.31. Приложение функций Лежандра. Решение задачи об электромагнитных колебаниях сферического резонатора.
- 7.7. ФУНКЦИИ МАТЬЕ
- 7.7.2. Ортогональность функций Матье первого рода.
- Функции Матье: 7.7.3. Разложение в ряд Фурье.
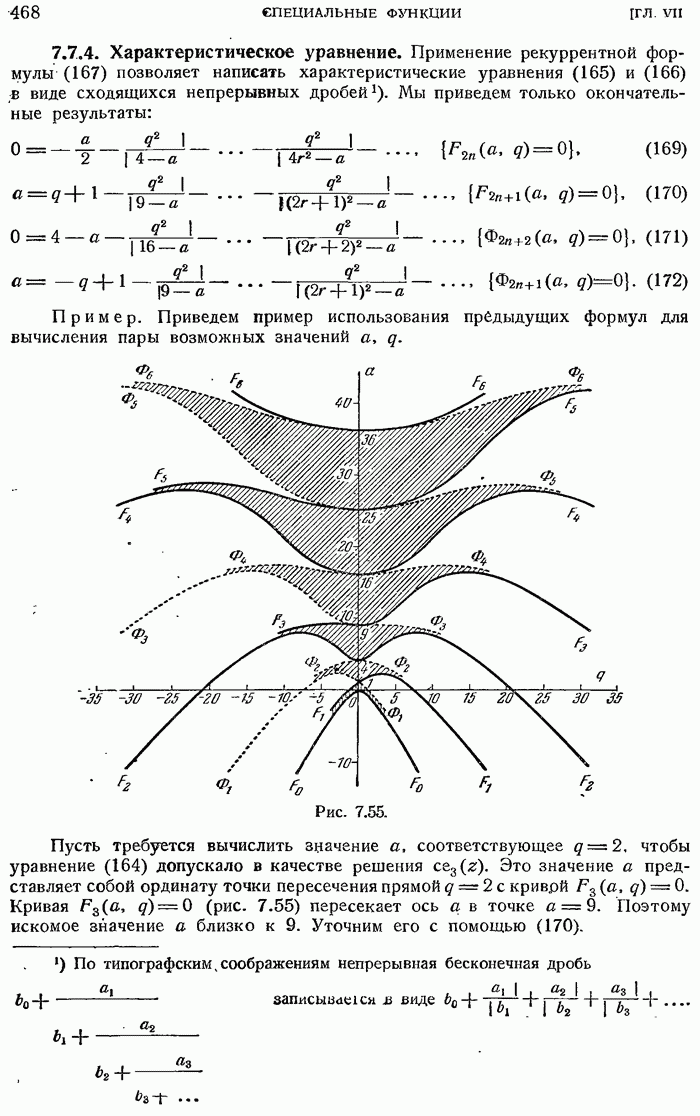
- Функции Матье: 7.7.4. Характеристическое уравнение.
- Функции Матье: 7.7.5. Поведение функций …
- 7.7.6. Присоединенные функции Матье первого рода.
- 7.7.7. Функции Матье для произвольных а и q.
- 7.7.8. Разложение в ряды по бесселевым функциям.
- 7.7.9. Функции Матье второго рода.
- 7.8. ФУНКЦИИ ВЕБЕРА — ЭРМИТА. ПОЛИНОМЫ ЭРМИТА
- 7.8.2. Полиномы Эрмита.
- 7.8.3. Производящая функция и ортогональность полиномов Эрмита.
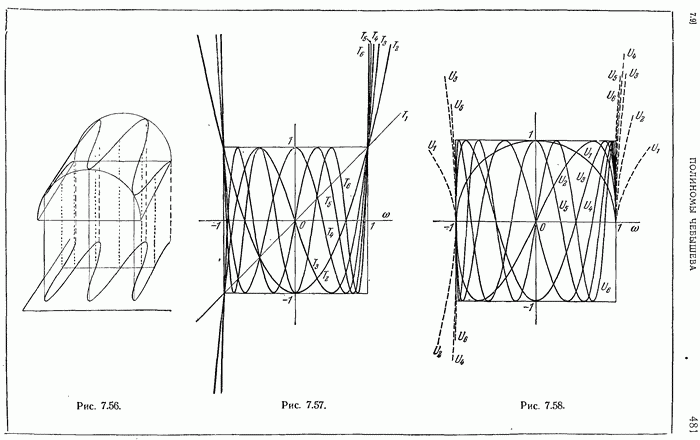
- 7.9. ПОЛИНОМЫ ЧЕБЫШЕВА
- 7.9.3. Основные свойства полиномов Чебышева.
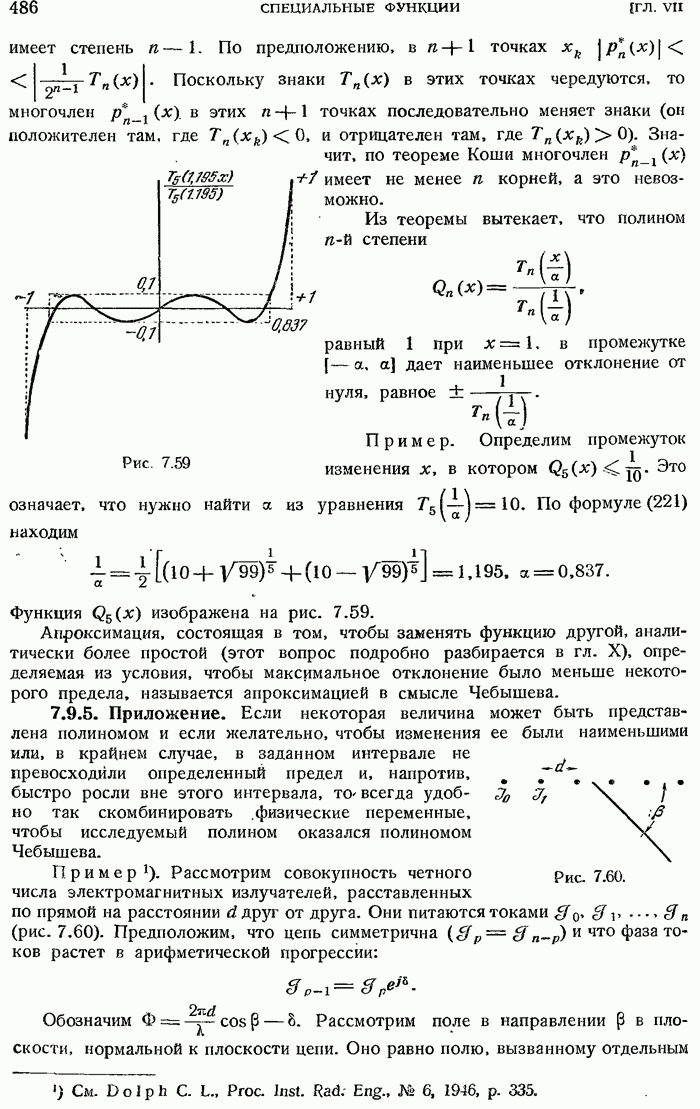
- 7.9.4. Фундаментальное свойство полиномов Чебышева.
- 7.9.5. Приложение.
- ГЛАВА VIII. СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ, ИСЧИСЛЕНИЕ
- 8.1.3. Расчет переходных режимов.
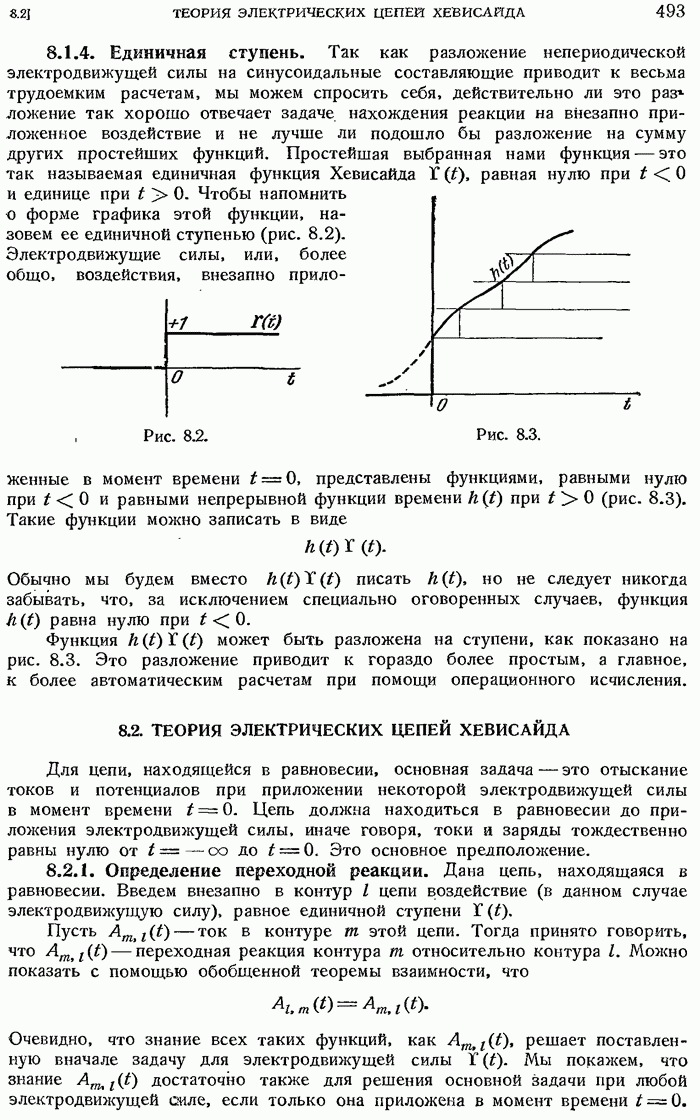
- 8.1.4. Единичная ступень.
- 8.2. ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ХЕВИСАЙДА
- 8.2.2. Вычисление переходной реакции.
- 8.3. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
- Правила операционного исчисления
- 8.3.10. Теорема свертывания, или теорема Бореля.
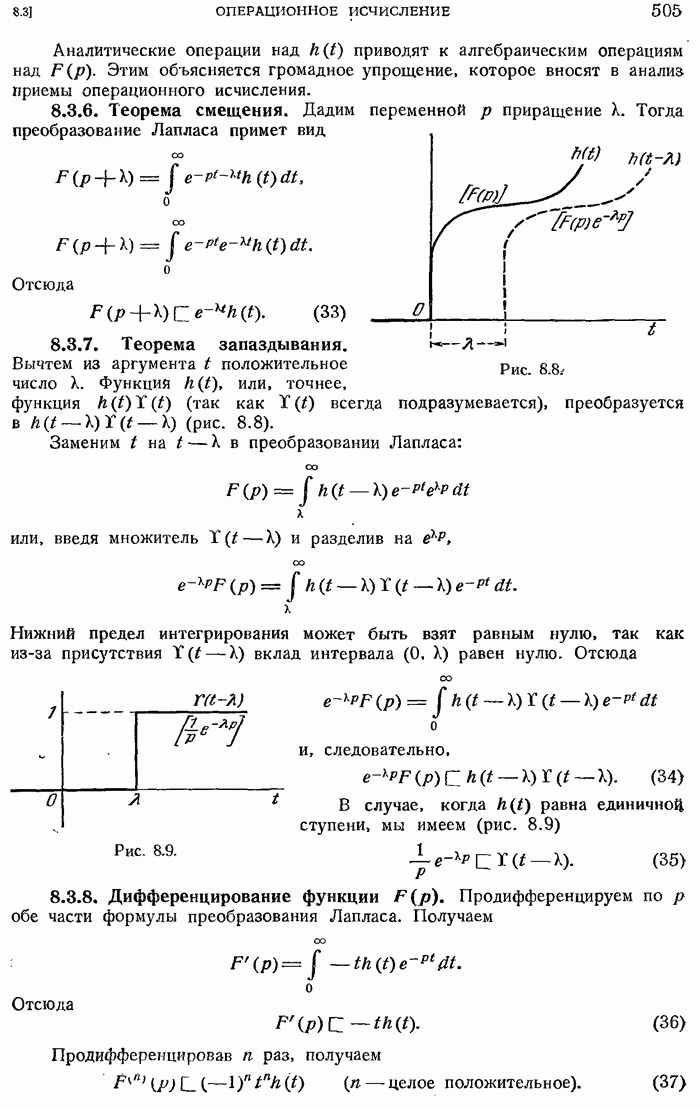
- 8.3.11. Различные формулы.
- 8.3.12. Теорема разложения Хевисайда.
- 8.3.13. Приложение теоремы разложения к электрическим цепям.
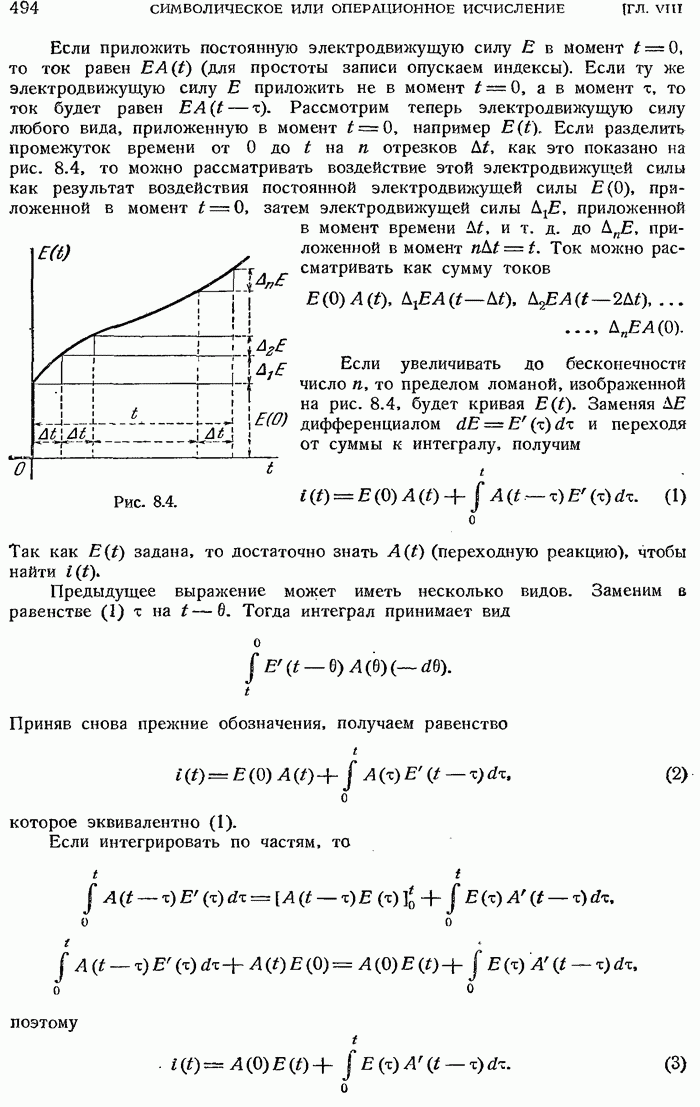
- 8.3.14. Случай переменного напряжения.
- 8.3.15. Случай кратных корней.
- Преобразование некоторых употребительных функций
- 8.3.16. Оригиналы некоторых рациональных функций.
- 8.3.17. Изображения бесселевых функций целого порядка.
- 8.3.18. Изображение ln t.
- 8.3.19. Изображение интегральных косинуса и синуса.
- 8.3.20. Изображение функции ошибок.
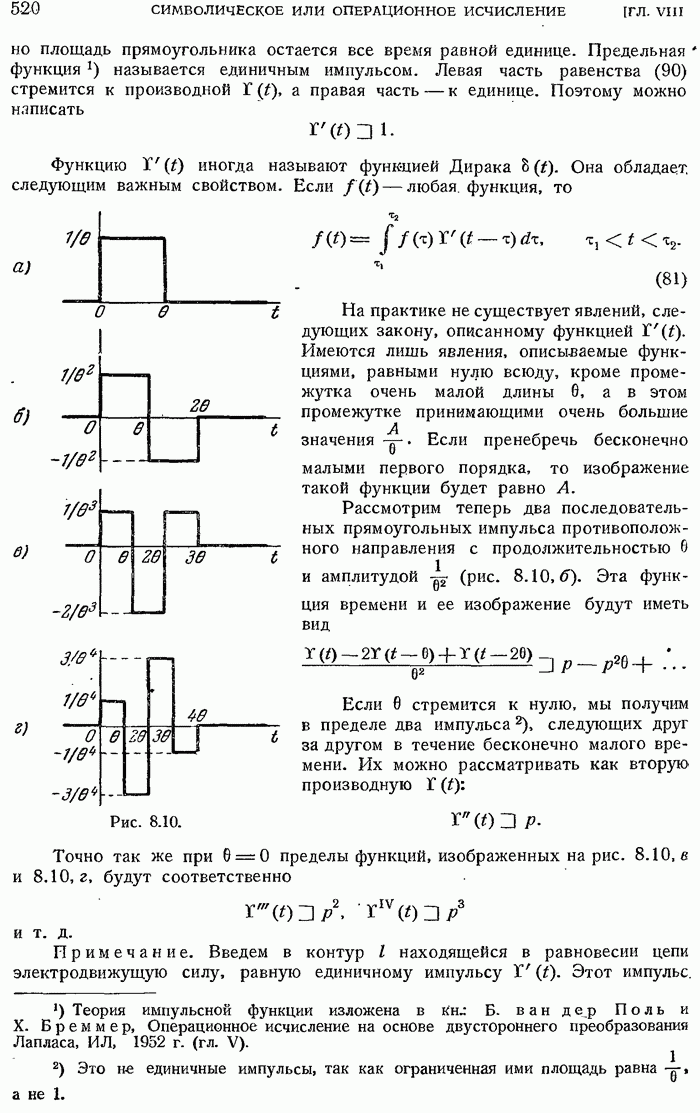
- 8.3.21. Изображение единичного импульса
- Применение формулы обращения
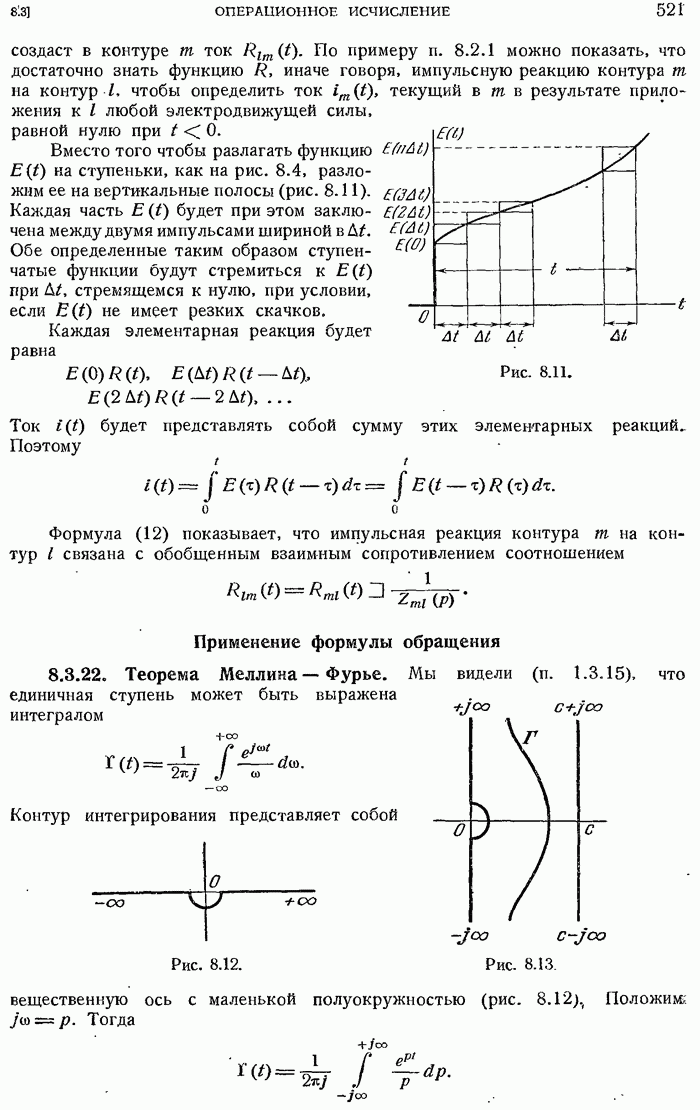
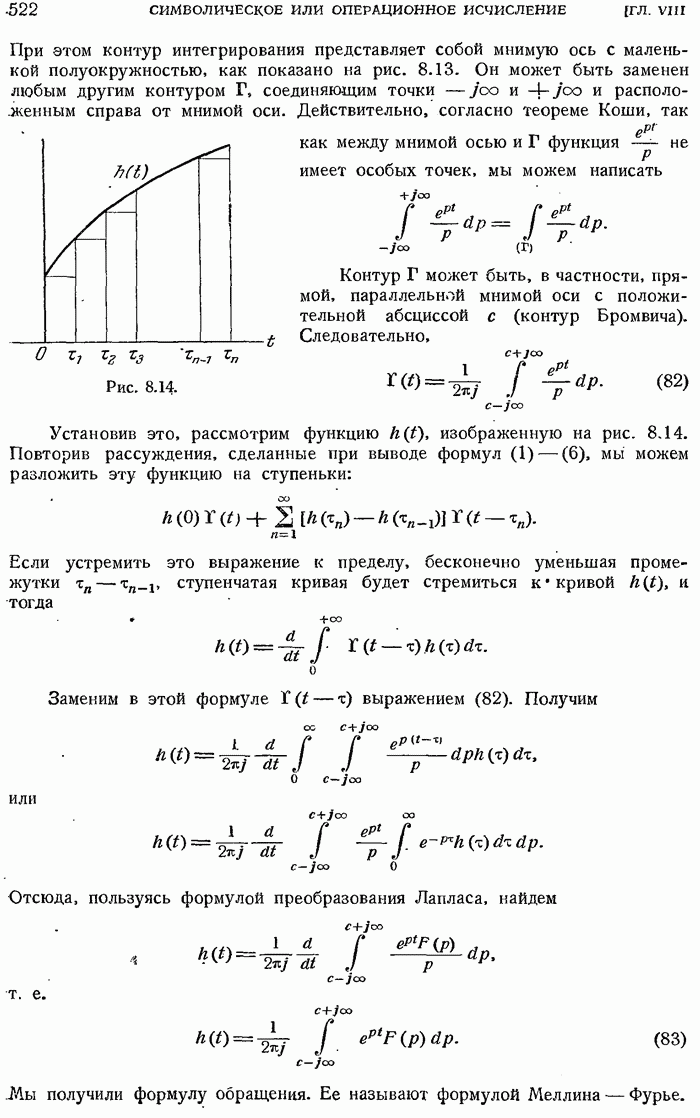
- 8.3.22. Теорема Меллина — Фурье.
- 8.3.23. Замечания о применении формулы обращения.
- 8.3.24. Обобщение теоремы разложения Хевисайда.
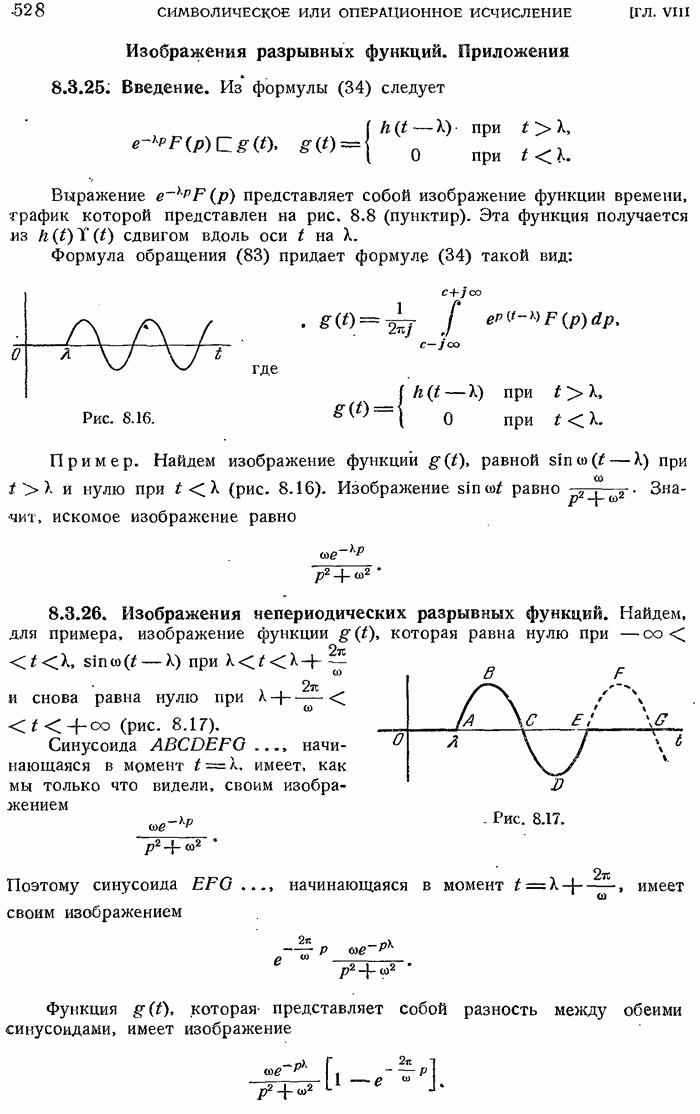
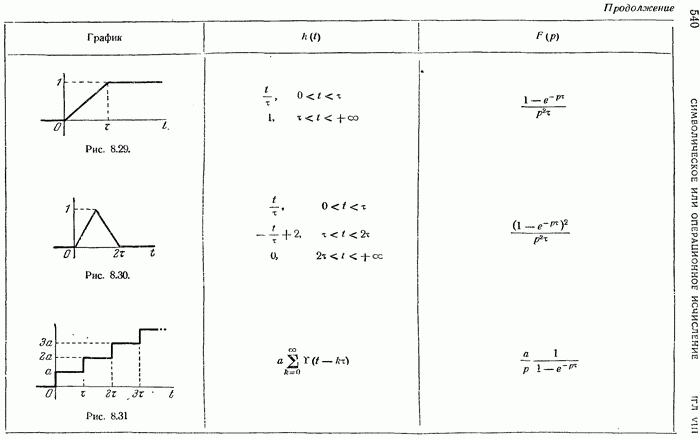
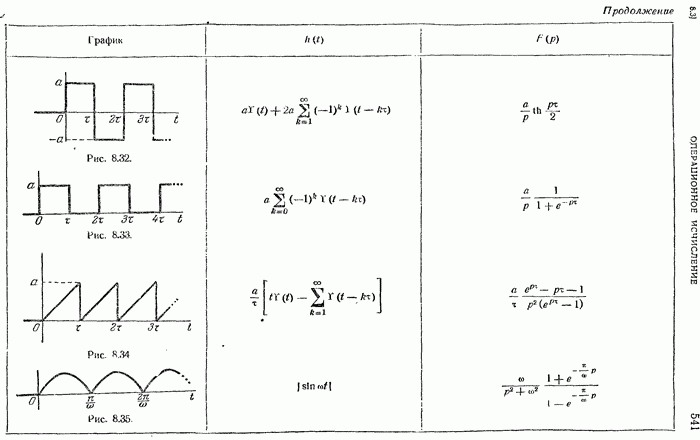
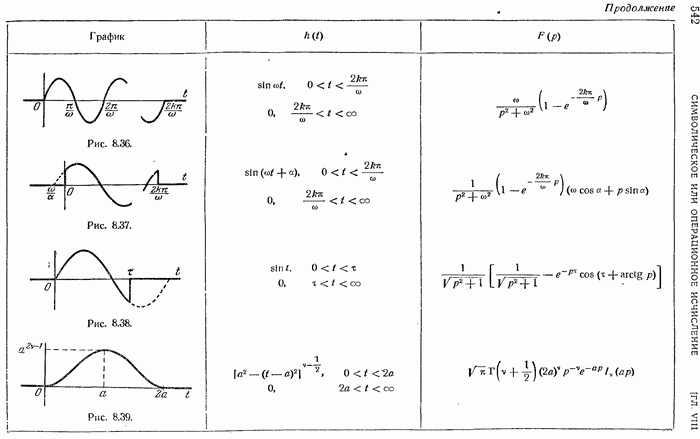
- Изображения разрывных функций. Приложения
- Таблица соответствия
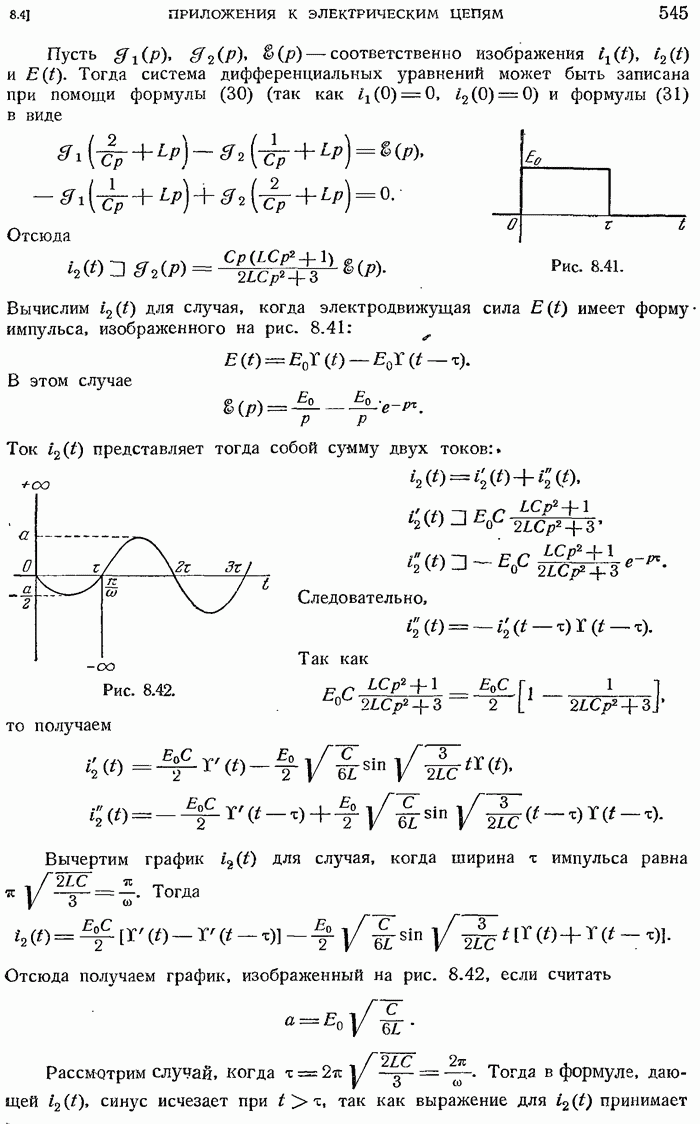
- 8.4. ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
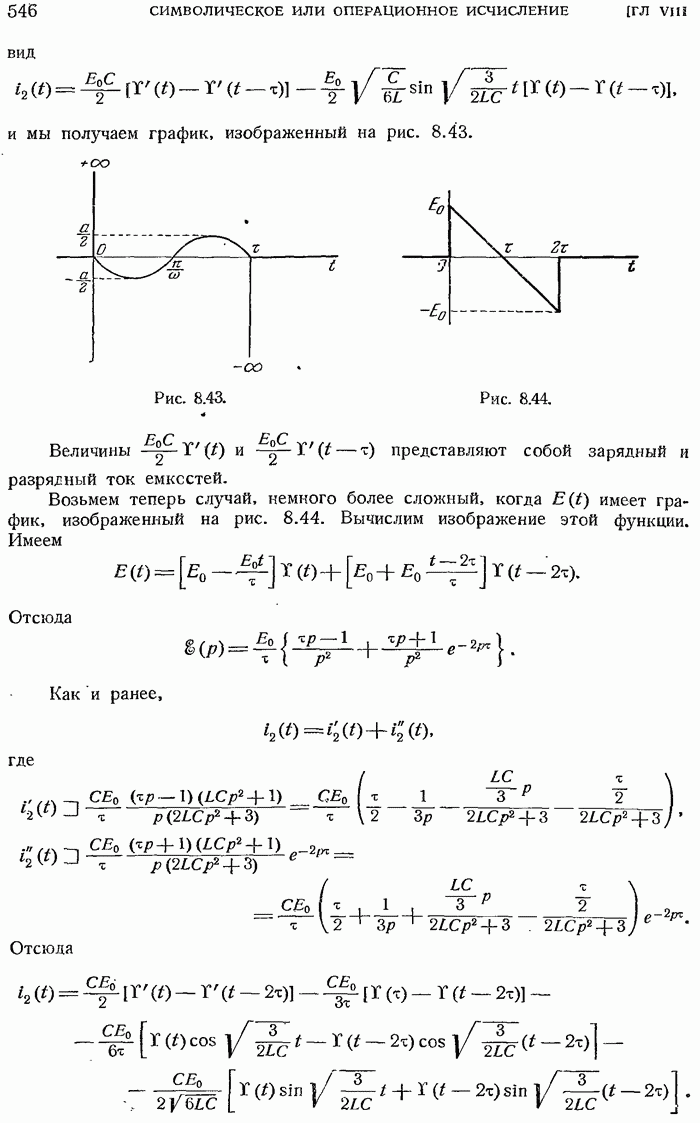
- 8.4.2. Пример применения к системе двух связанных контуров.
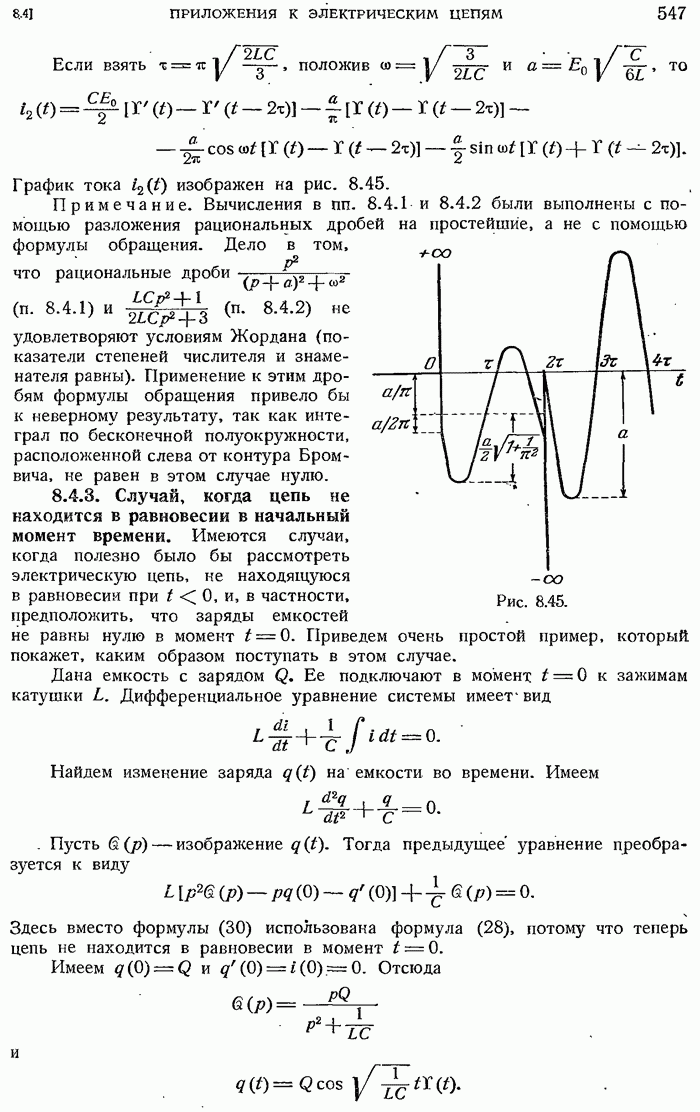
- 8.4.3. Случай, когда цепь не находится в равновесии в начальный момент времени.
- 8.4.4. Электрические фильтры.
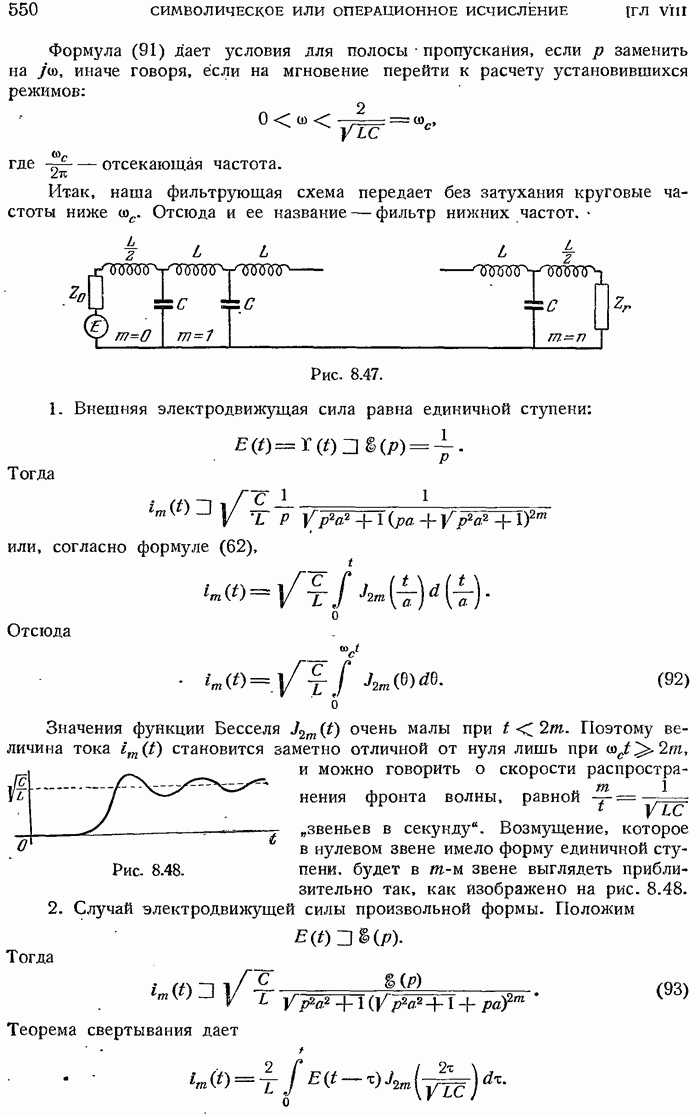
- 8.4.5. Фильтр нижних частот.
- 8.4.6. Фильтр верхних частот.
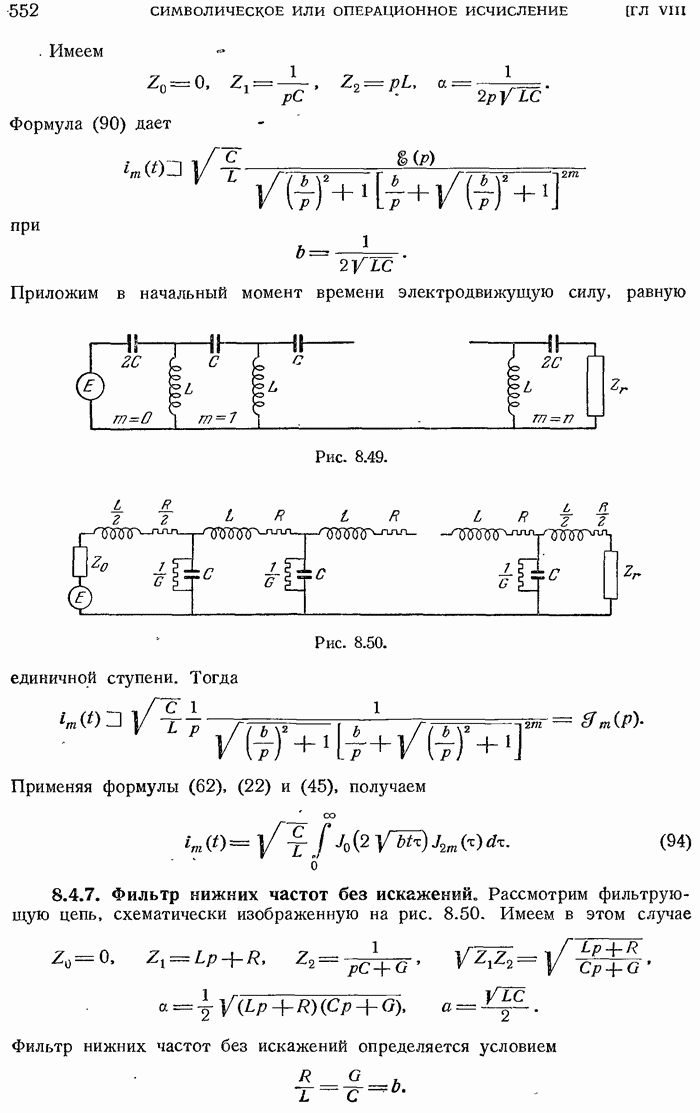
- 8.4.7. Фильтр нижних частот без искажений.
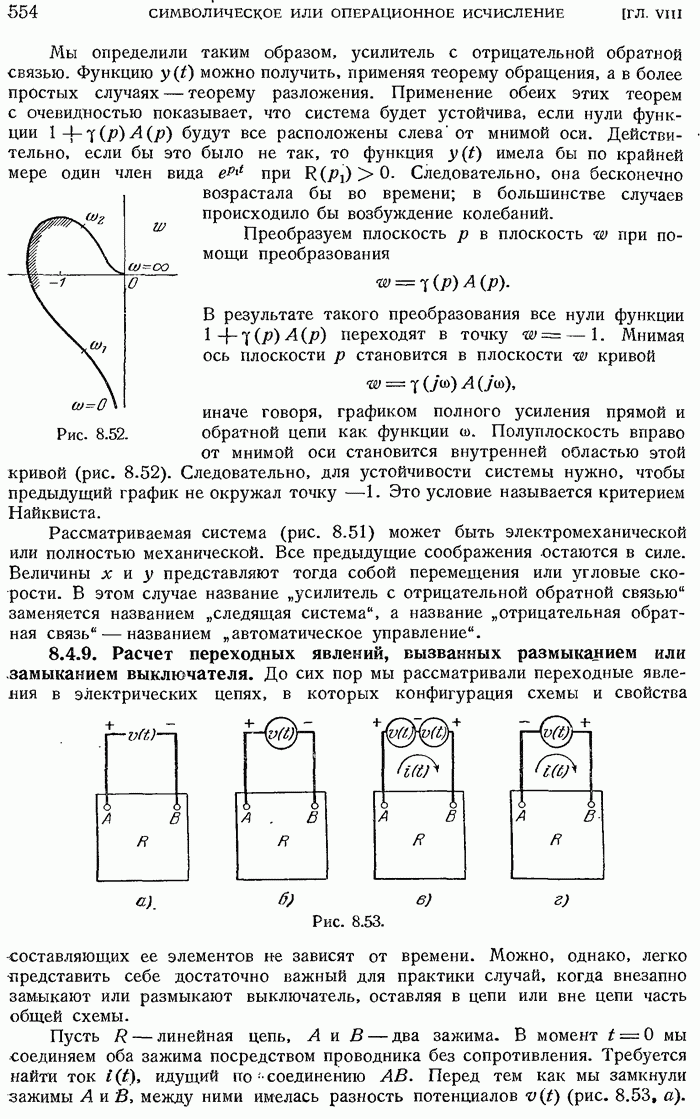
- 8.4.8. Усилители. Отрицательная обратная связь. Критерий Найквиста.
- 8.4.9. Расчет переходных явлений, вызванных размыканием или замыканием выключателя.
- Распространение электрических возмущений вдоль линий передач
- 8.4.11. Бесконечная или замкнутая на волновое сопротивление линия.
- 8.4.12. Линия без потерь.
- 8.4.13. Линия без искажений.
- 8.4.14. Подземный кабель.
- 8.4.15. Линия с идеальной изоляцией.
- 8.4.16. Общий случай. Произвольная линия.
- 8.4.17. Линия передачи конечной длины.
- 8.4.18. Закороченная с одного конца линия с пренебрежимо малыми проводимостью изоляции и индуктивностью (подземный кабель).
- 8.4.19. Линия конечной длины без потерь, замкнутая на сопротивление.
- 8.4.20. Сопротивление, сосредоточенное в начале линии.
- 8.4.21. Повреждение на линии.
- 8.5. МАТЕМАТИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
- Применение операционного исчисления к решению линейных дифференциальных уравнений
- 8.5.3. Линейное дифференциальное уравнение с переменными алгебраическими коэффициентами (метод ван дер Поля).
- Применение операционного исчисления к решению некоторых интегральных уравнений
- 8.5.5. Нелинейные интегральные уравнения.
- 8.5.6. Интегродифференциальные уравнения.
- 8.5.7. Применение операционного исчисления к исследованию функций.
- 8.5.8. Применение операционного исчисления к разложению в асимптотический ряд.
- 8.6. НЕКОТОРЫЕ ЗАМЕЧАНИЯ
- 8.6.1. Замечания об операционном исчислении Хевисайда.
- ГЛАВА IX. ТЕОРИЯ ВЕРОЯТНОСТЕЙ. ПРИЛОЖЕНИЯ
- 9.1.1. Определение вероятности.
- 9.1.2. Независимые события. Теорема умножения вероятностей.
- 9.1.3. Несовместные события. Теорема сложения вероятностей.
- 9.1.4. Формула Стирлинга.
- Законы распределения случайных величин
- 9.1.5. Дискретные случайные величины.
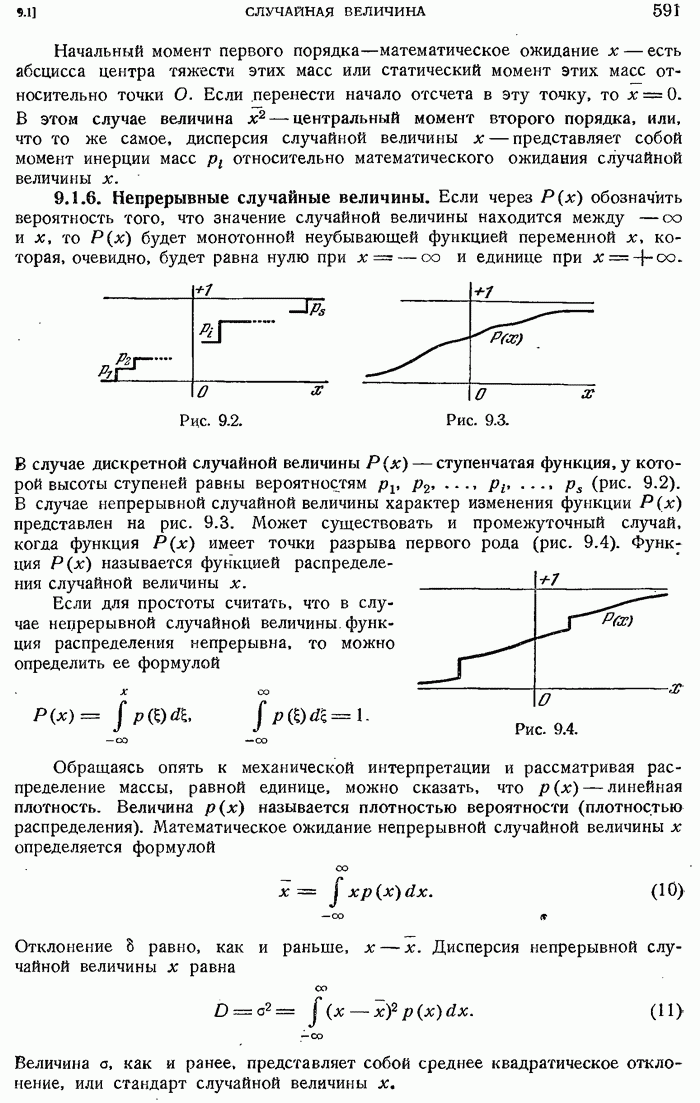
- 9.1.6. Непрерывные случайные величины.
- 9.1.7. Характеристическая функция.
- 9.1.8. Распределение системы двух случайных величин.
- 9.1.9. Характеристическая функция суммы независимых случайных величин.
- Основные законы распределения случайных величин
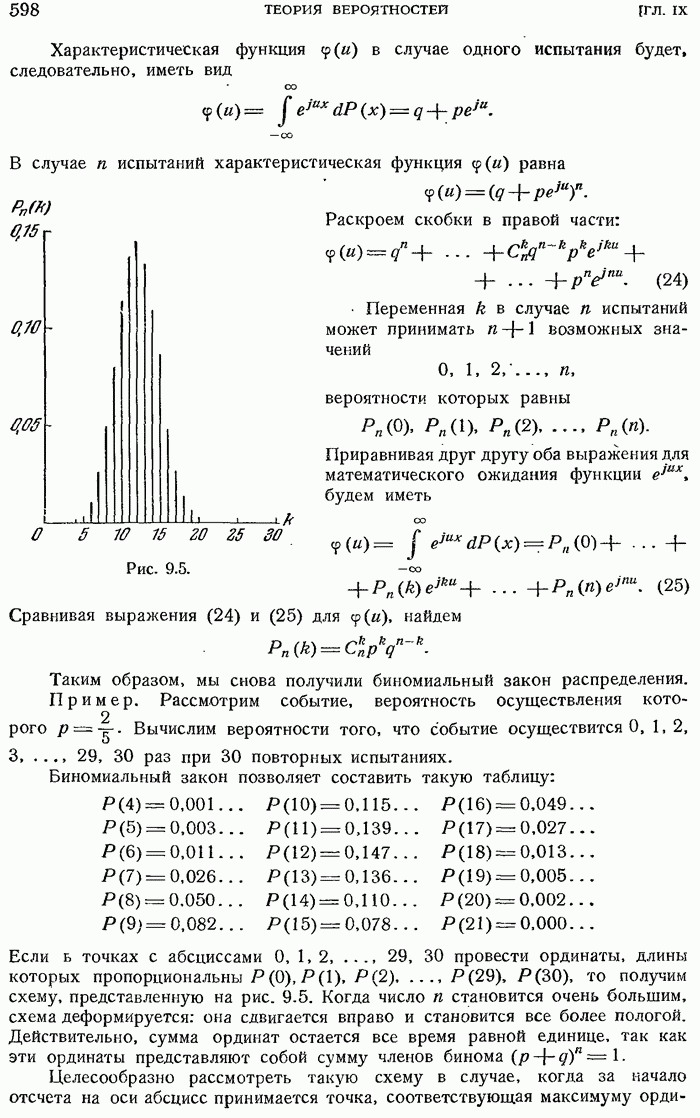
- 9.1.10. Биномиальный закон распределения.
- 9.1.11. Характеристическая функция биномиального закона.
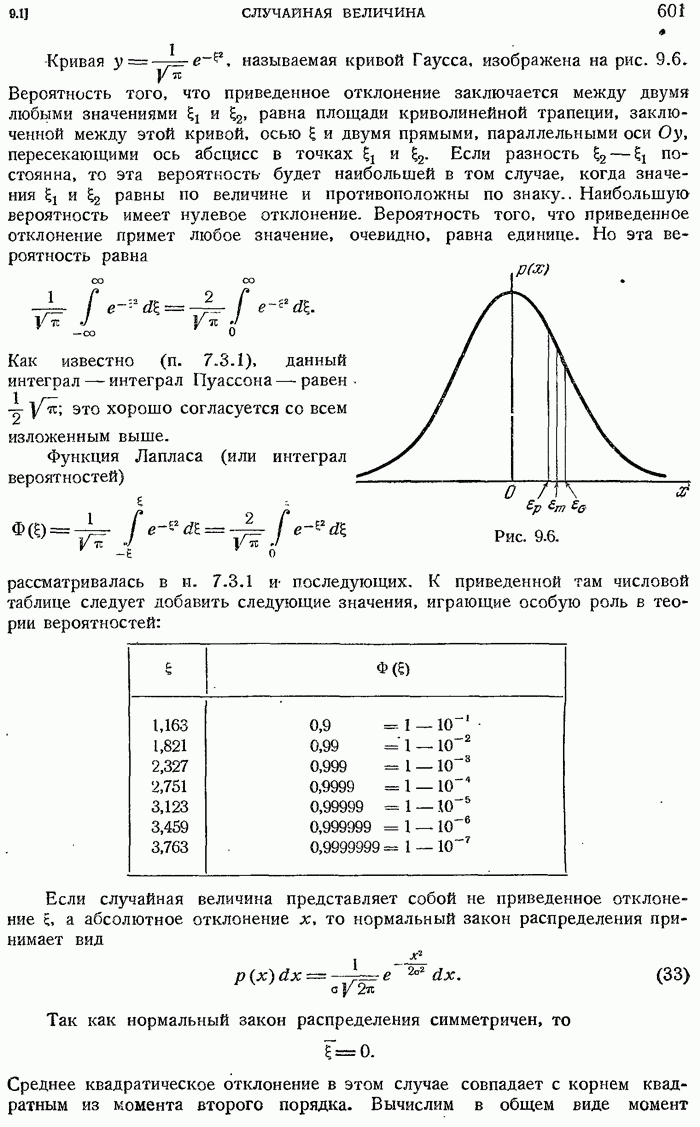
- 9.1.12. Формула Лапласа. Нормальный закон распределения (закон Лапласа — Гаусса).
- 9.1.13. Характеристическая функция нормального закона распределения.
- 9.1.14. Теорема Бернулли.
- 9.1.15. Замечания о переходе от биномиального закона распределения к нормальному.
- 9.1.16. Закон распределения Пуассона.
- 9.1.17. Характеристическая функция и моменты закона распределения Пуассона.
- 9.1.18. Приложение к задачам автоматической телефонии.
- 9.1.19. Согласование наблюденных данных с теоретическим законом распределения.
- 9.1.20. Частный случай нормального закона распределения.
- Ошибки измерений и способ наименьших квадратов
- 9.1.21. Ошибки измерений и нормальный закон распределения.
- 9.1.22. Способ наименьших квадратов.
- 9.1.23. Линейная комбинация ошибок.
- 9.1.24. Точность группы измерений.
- 9.1.25. Наивероятнейшее значение меры точности.
- 9.1.26. «Вес» наблюдения.
- 9.1.27. Критерий ошибочного наблюдения.
- 9.1.28. Срединная (вероятная) ошибка функции.
- 9.1.29. Эмпирические формулы.
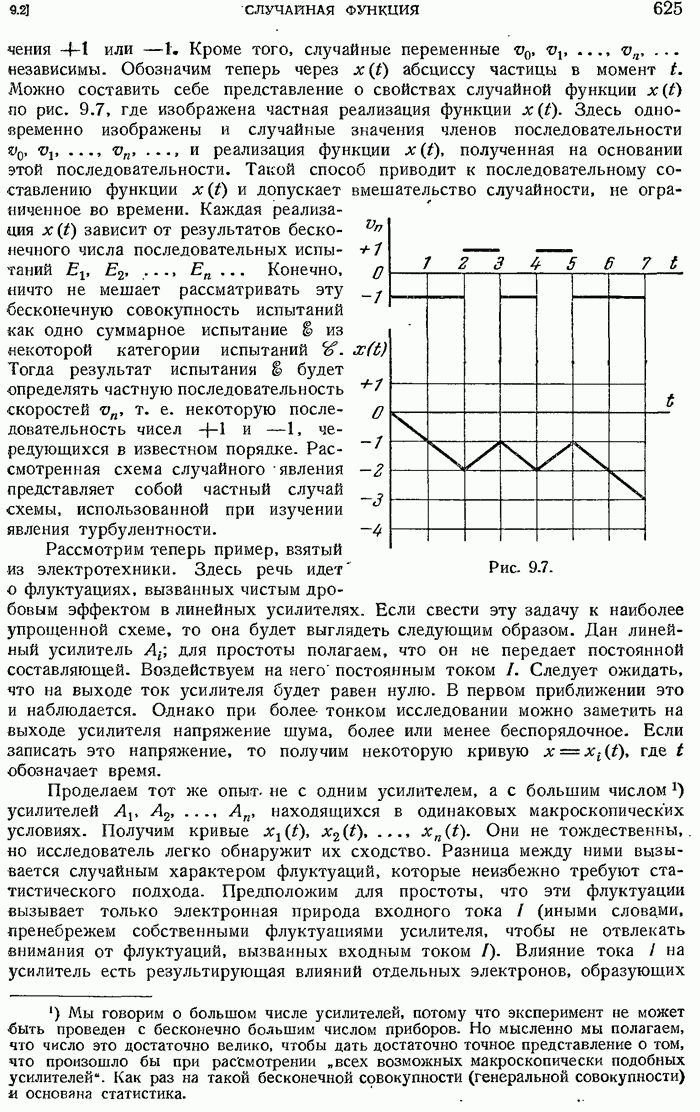
- 9.2. ПОНЯТИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 9.2.2. Функции распределения.
- Проблема сходимости
- 9.2.4. Сходимость в смысле Бернулли.
- 9.2.5. Сходимость по вероятности.
- 9.2.6. Сходимость в среднем квадратическом (сходимость с. к.).
- 9.2.7. Почти достоверная сходимость.
- Стационарные случайные функции. Изучение постоянных режимов
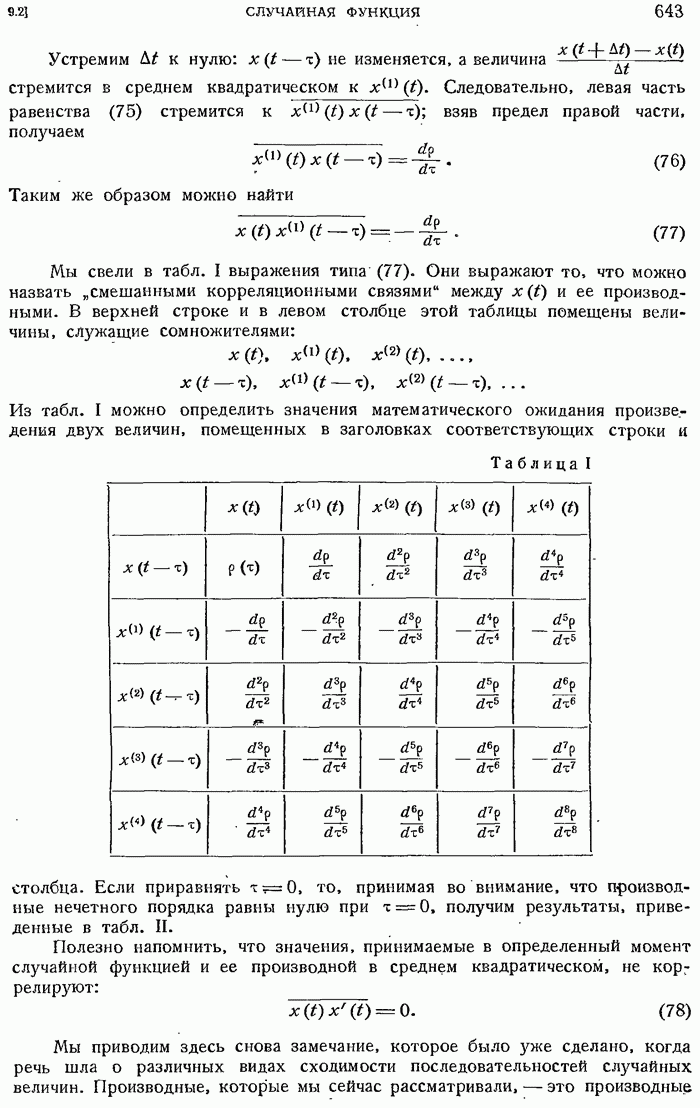
- 9.2.9. Изучение моментов второго порядка. Определение.
- Общие свойства стационарных случайных функций второго порядка
- 9.2.10. Корреляционные функции.
- 9.2.11. Непрерывность. Дифференцируемость.
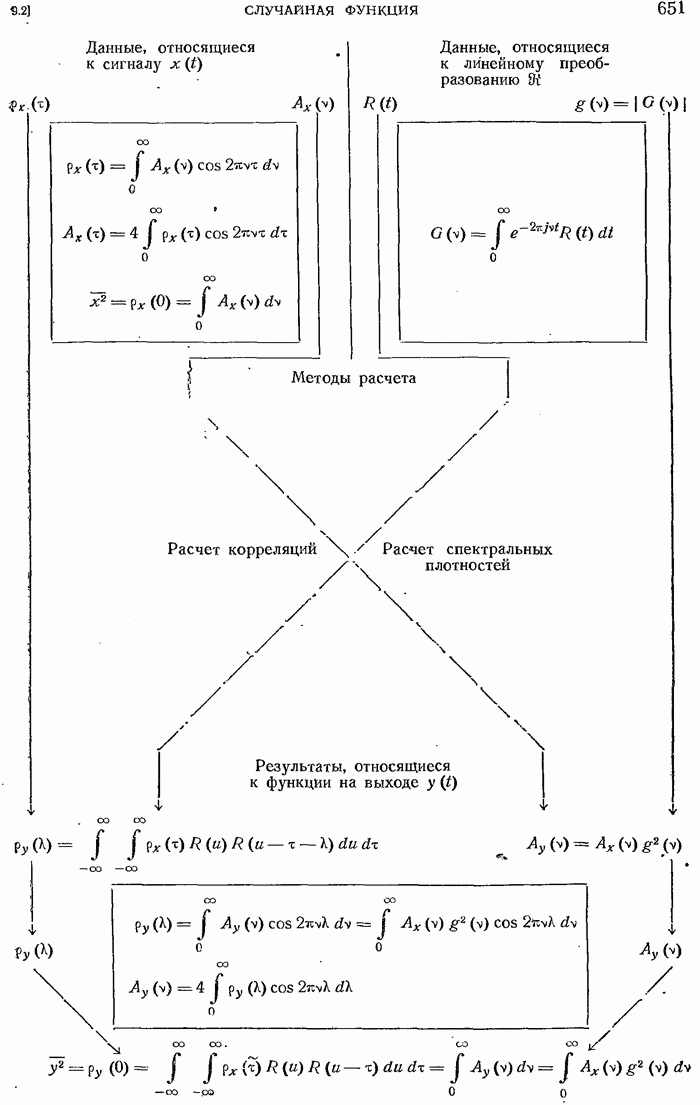
- 9.2.12. Энергетический спектр.
- 9.2.13. Передача энергии стационарной линейной системой.
- 9.2.14. Недостаточность рассмотрения моментов второго порядка и корреляционной функции.
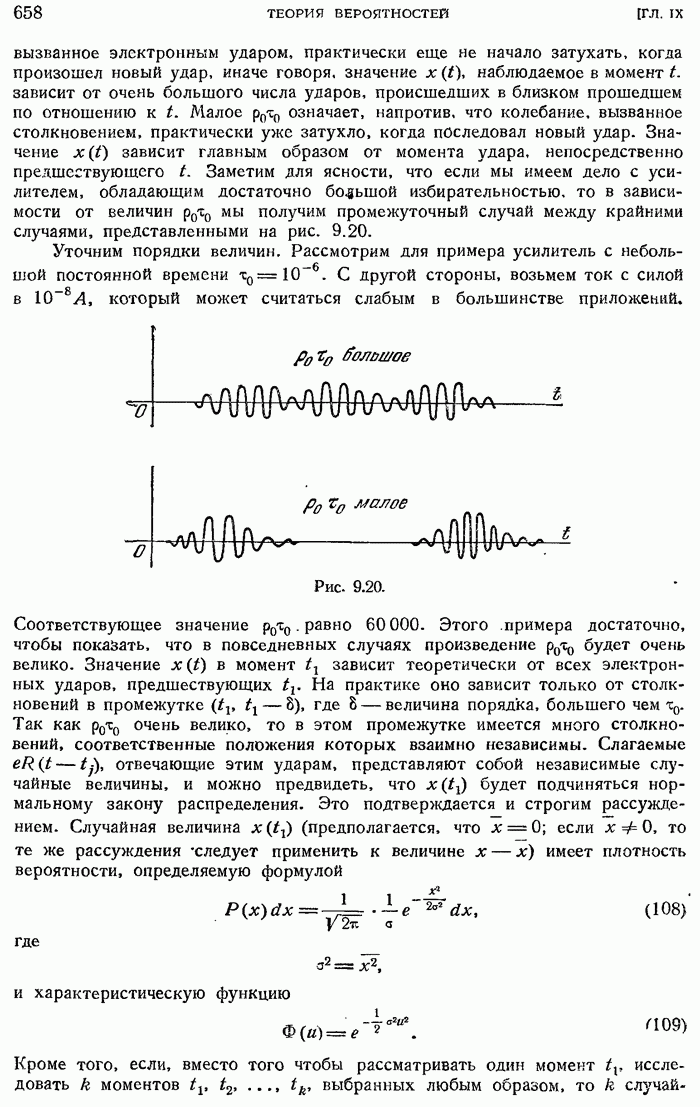
- Стационарные случайные функции Лапласа — Гаусса. Применение к чисто дробовому эффекту
- 9.2.17. Флуктуации в нелинейных системах.
- 9.2.18. Вычисление корреляционной функции на выходе линейного усилителя под действием дробового эффекта постоянного тока.
- ГЛАВА X. ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
- 10.1. РЕШЕНИЕ ЧИСЛЕННЫХ УРАВНЕНИЙ
- 10.1.2. Метод Ньютона и метод пропорциональных частей
- 10.1.3. Метод итерации.
- 10.1.4. Приближенное решение системы двух уравнений.
- 10.2. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- 10.2.1. Численное решение уравнений третьей и четвертой степени.
- 10.2.2. Схема Горнера.
- 10.2.3. Построение Лилла.
- 10.2.4. Способ Лагранжа.
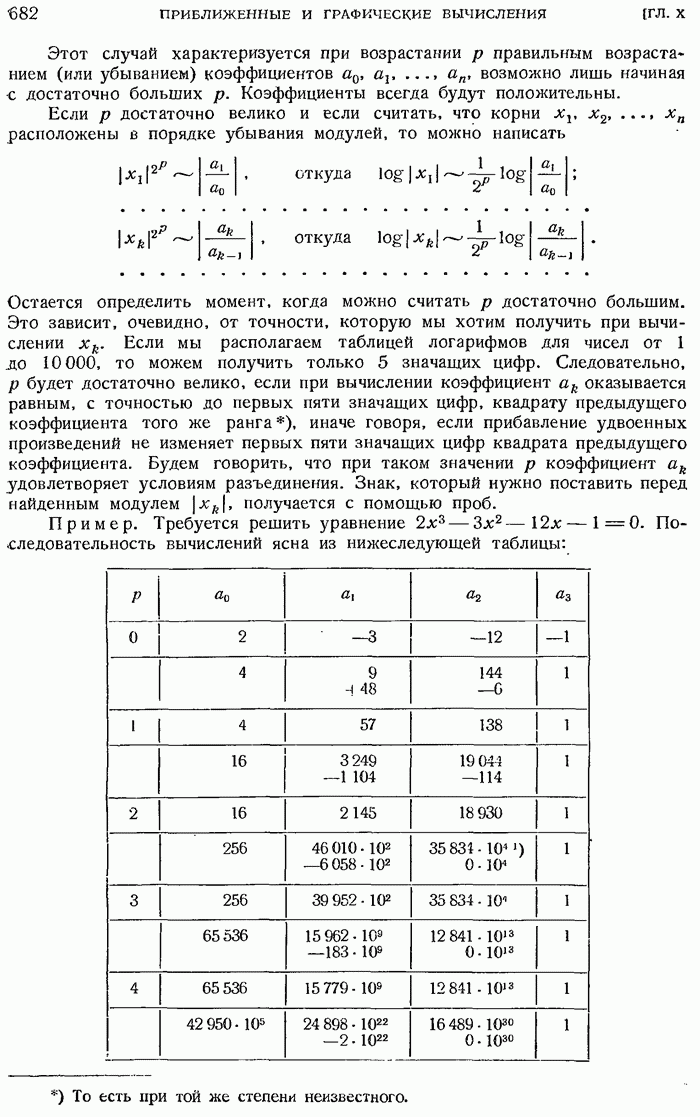
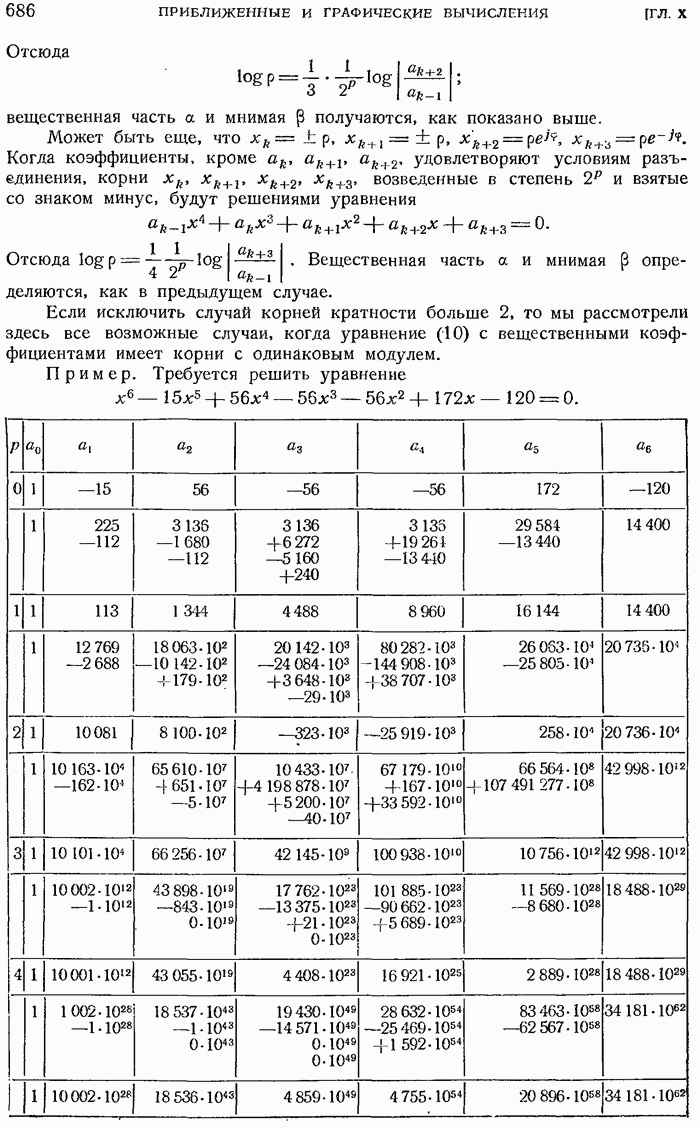
- 10.2.5. Метод Лобачевского — Греффе — Данделена.
- 10.3. ПРИБЛИЖЕНИЕ ФУНКЦИИ
- Приближение функции полиномами
- 10.3.2. Значения аргумента распределены неравномерно. Интерполяционный полином Лагранжа.
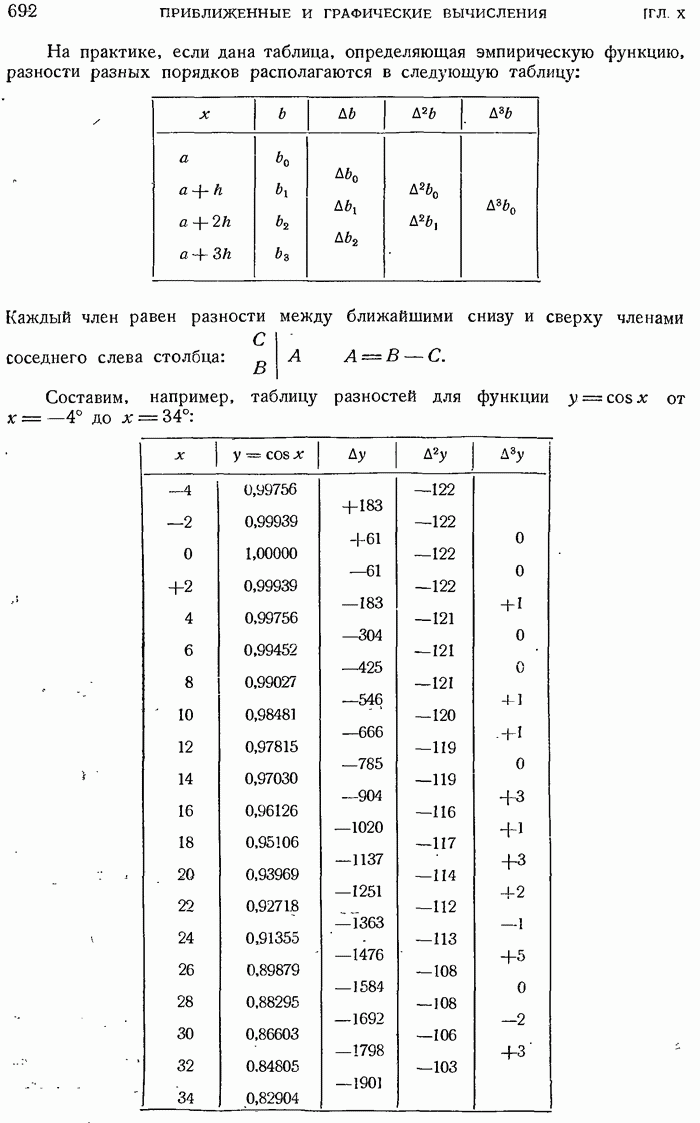
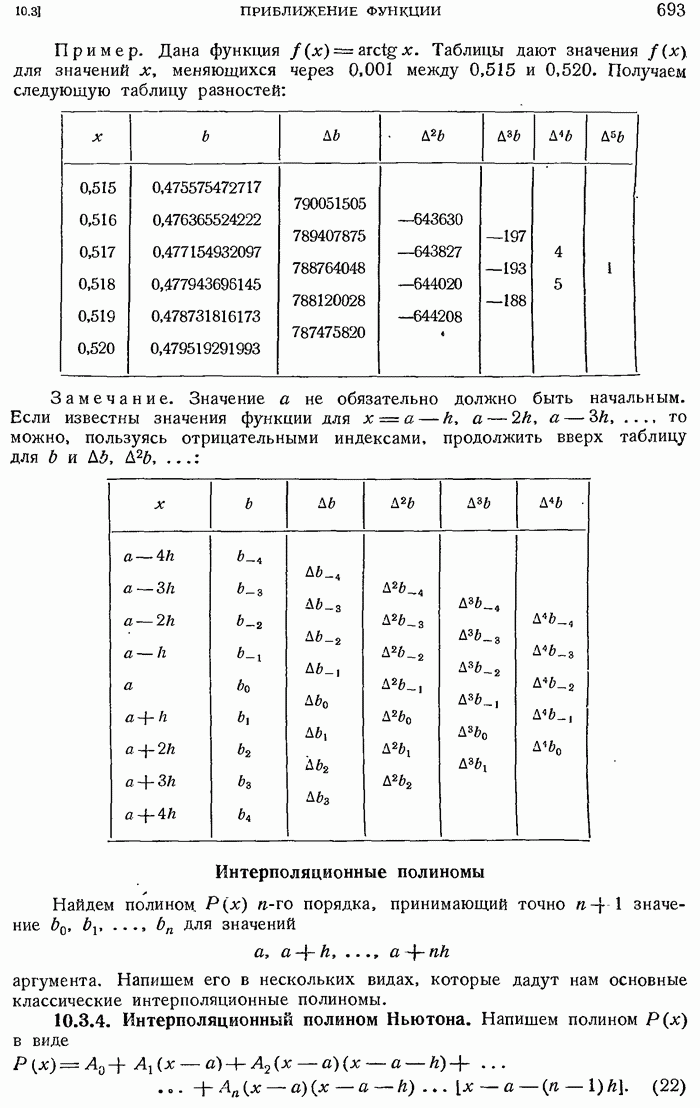
- 10.3.3. Значения переменной находятся в арифметической прогрессии. Таблица разностей.
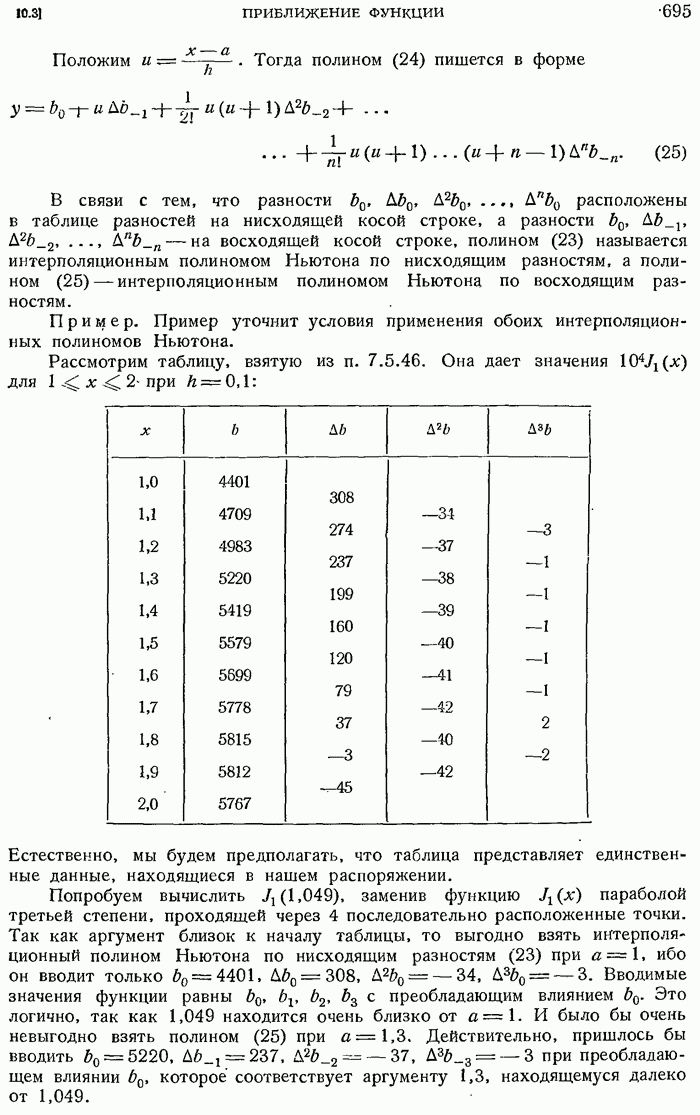
- 10.3.4. Интерполяционный полином Ньютона.
- 10.3.5. Интерполяционный полином Стнрлинга.
- 10.3.6. Интерполяционный полином Бесселя.
- 10.3.7. Области применения интерполяционных полиномов Ньютона, Стирлинга, Бесселя.
- 10.3.8. Верхний предел ошибки, совершаемой при применении интерполяционных формул Ньютона, Стирлинга, Бесселя.
- 10.3.9. Приближение линейной комбинацией функций, определенной с помощью критерия наименьших квадратов.
- 10.3.10. Приближение полиномом, определенным с помощью критерия наименьших квадратов.
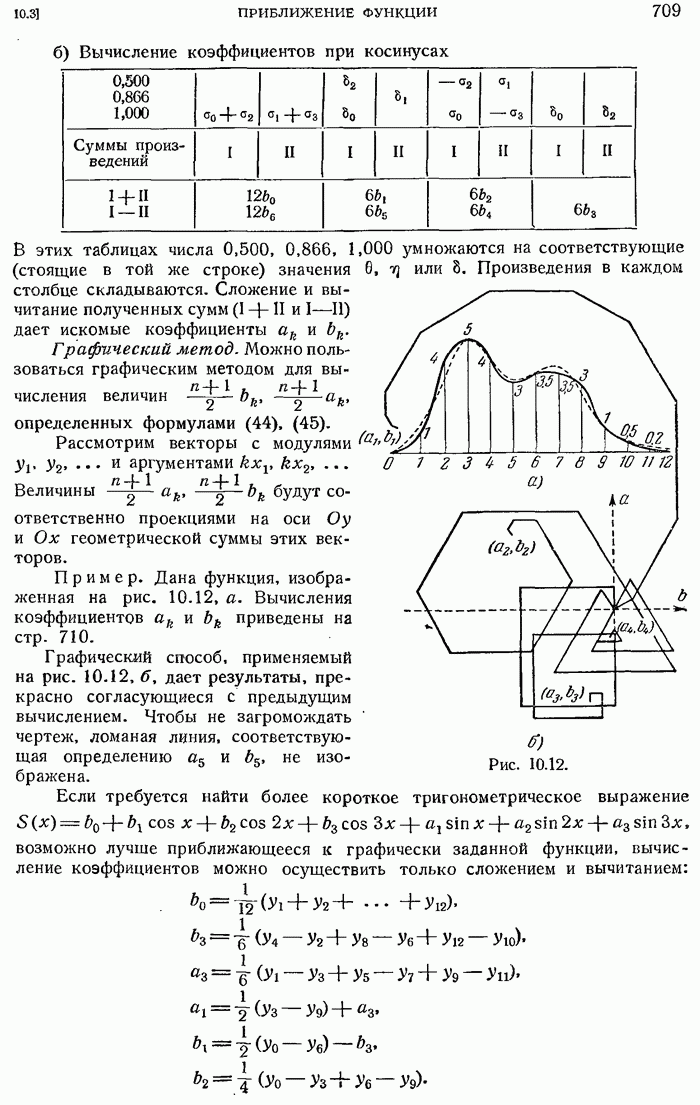
- Приближение отрезком ряда Фурье. Задача гармонического анализа
- 10.3.14. Приближение эмпирической функции линейной комбинацией показательных функций.
- 10.3.15. Приближение функции по Чебышеву.
- 10.3.16. Применение ряда Тейлора.
- 10.4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 10.5. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- 10.5.2. Полином Бернулли.
- 10.5.3. Формула Эйлера.
- 10.5.4. Формула трапеций.
- 10.5.5. Формула Симпсона.
- 10.5.6. Формула Уэддля.
- 10.5.7. Формула Грегори.
- 10.5.8. Введение в методы Ньютона — Котеса, Чебышева, Гаусса.
- 10.5.9. Метод Ньютона — Котеса.
- 10.5.10. Метод Чебышева.
- 10.5.11. Метод Гаусса.
- 10.5.12. Применение интерполяционных полиномов Ньютона.
- 10.5.13. Исключительные случаи.
- 10.6. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 10.6.2. Приближенное интегрирование дифференциального уравнения первого порядка.
- 10.6.3. Решение с помощью ряда Тейлора.
- 10.6.4. Способ Адамса.
- 10.6.5. Сокращенный вариант.
- 10.6.6. Приближенное интегрирование системы дифференциальных уравнений первого порядка.
- 10.6.7. Использование ряда Тейлора.
- 10.6.8. Применение интерполяционного полинома Ньютона с нисходящими разностями.
- 10.6.9. Способ Пикара.
- 10.7. ГРАФИЧЕСКОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 10.7.2. Графическое решение дифференциальных уравнений второго порядка способом радиусов кривизны.
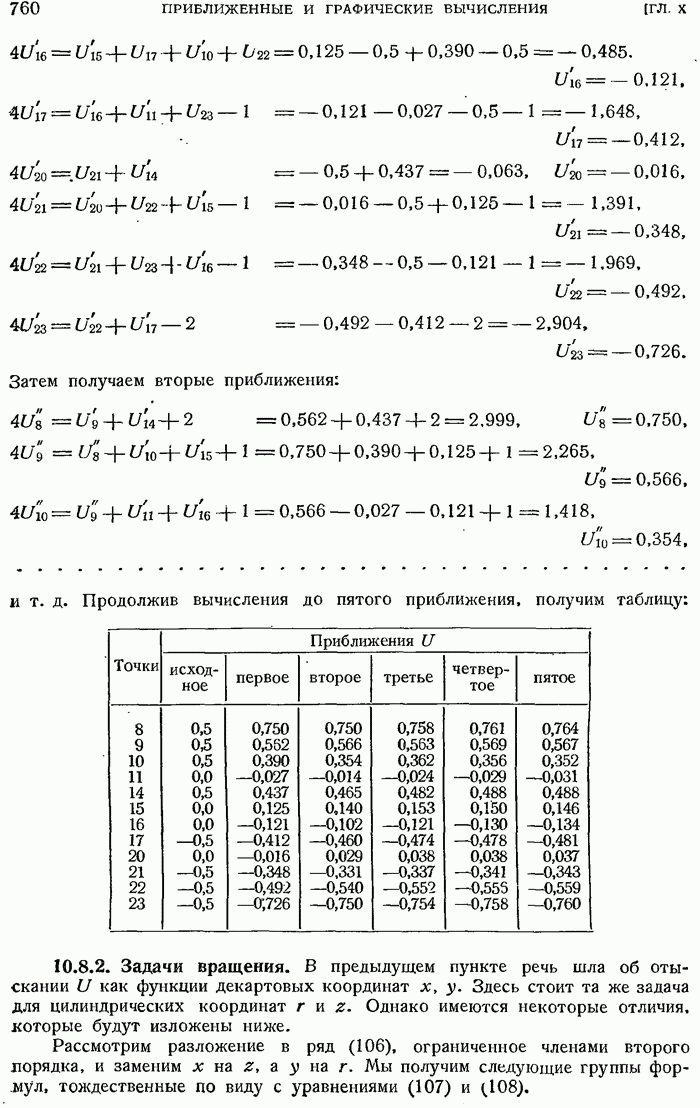
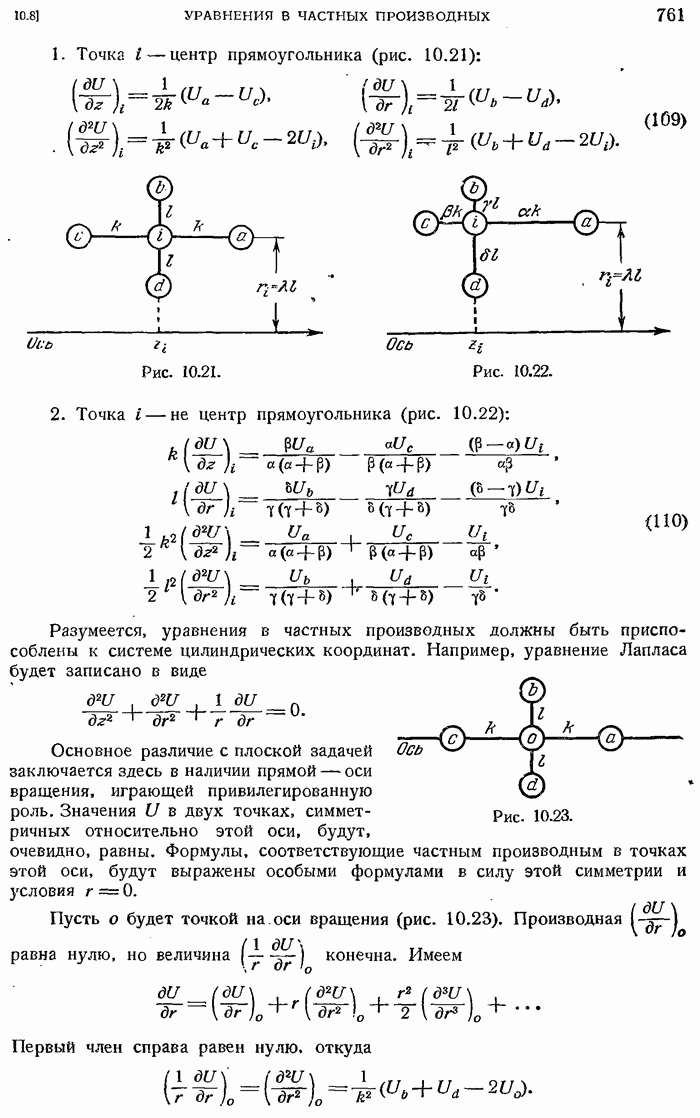
- 10.8. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
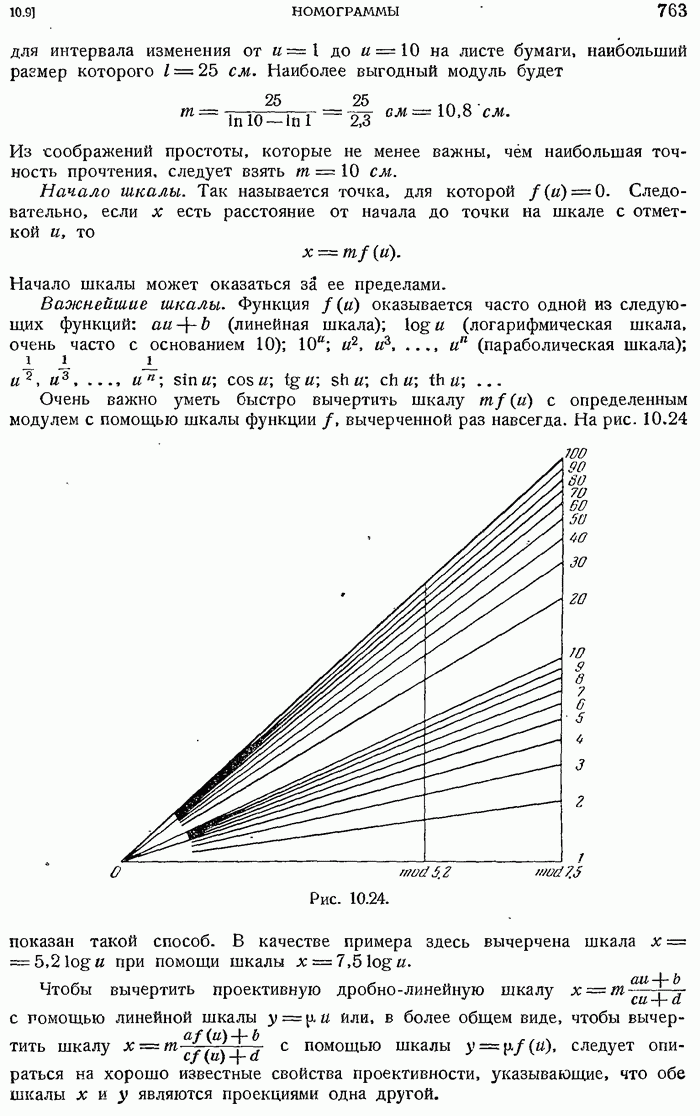
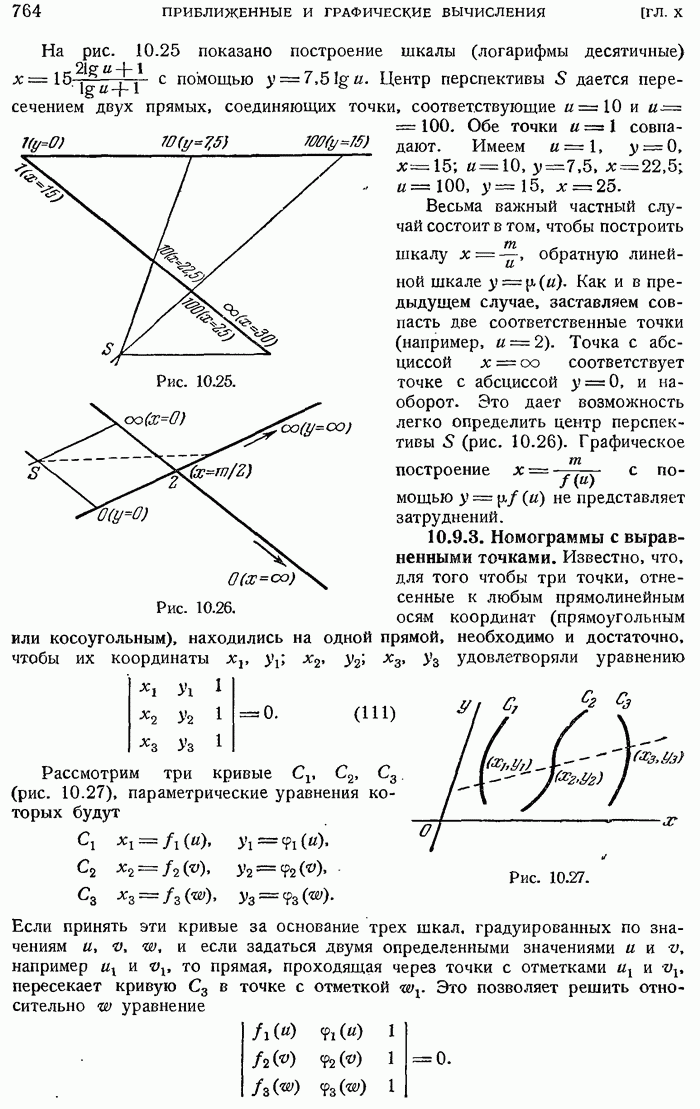
- 10.9. НОМОГРАММЫ
- 10.9.3. Номограммы с выравненными точками.
- 10.9.4. Номограммы с тремя параллельными прямолинейными шкалами.
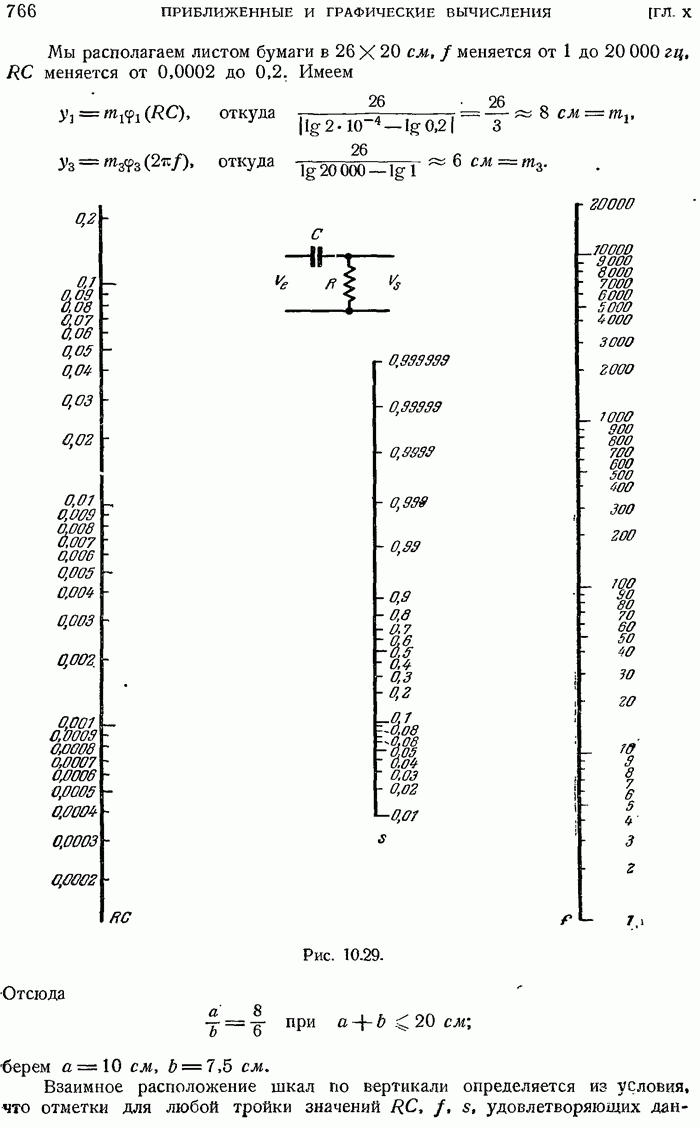
- 10.9.5. Номограммы с двумя параллельными прямолинейными шкалами и одной криволинейной.
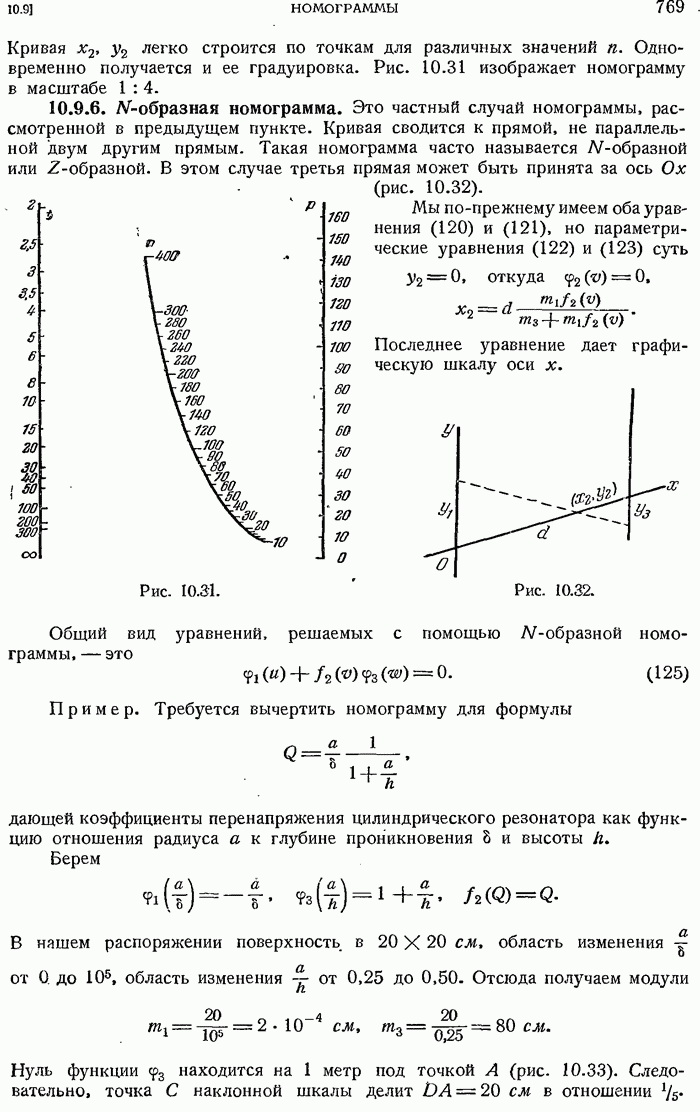
- 10.9.6. N-образная номограмма.
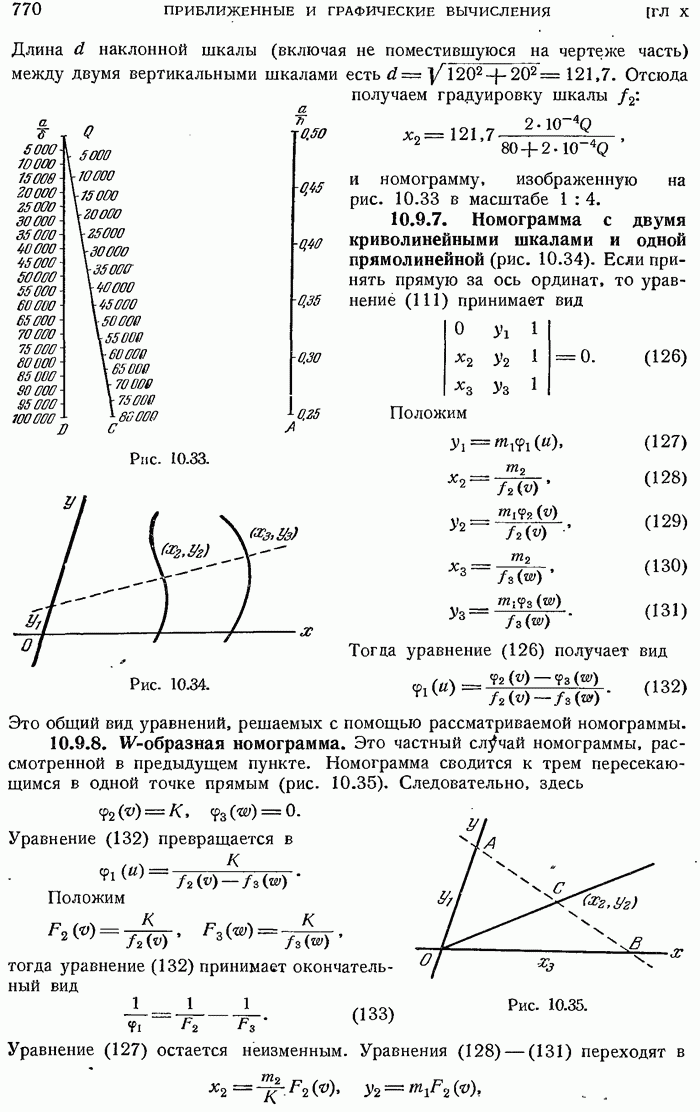
- 10.9.7. Номограмма с двумя криволинейными шкалами и одной прямолинейной
- 10.9.8. W-образная номограмма.
- 10.9.9. Z-образная номограмма.
- 10.9.10. Номограмма с тремя криволинейными шкалами.
- 10.9.11. Сложные номограммы.