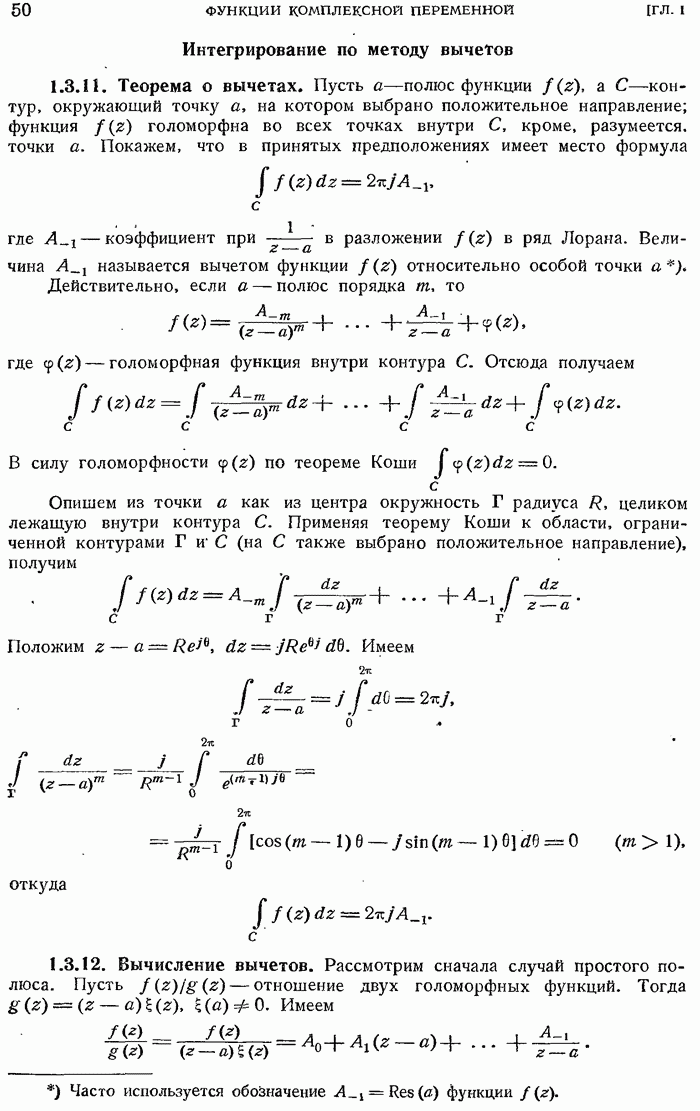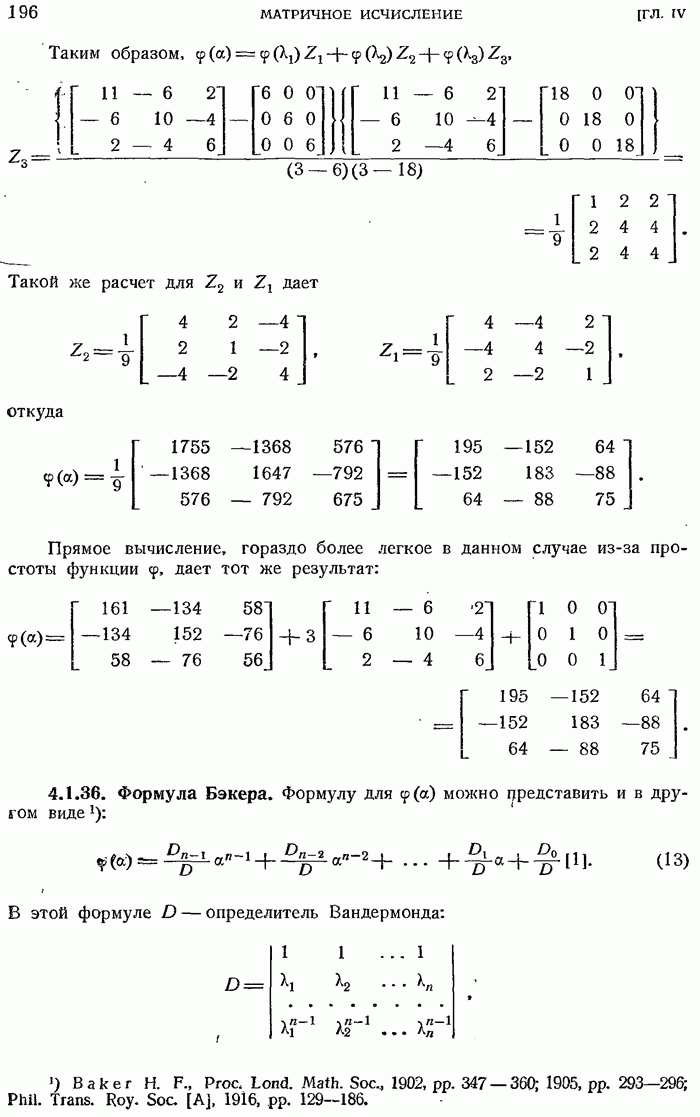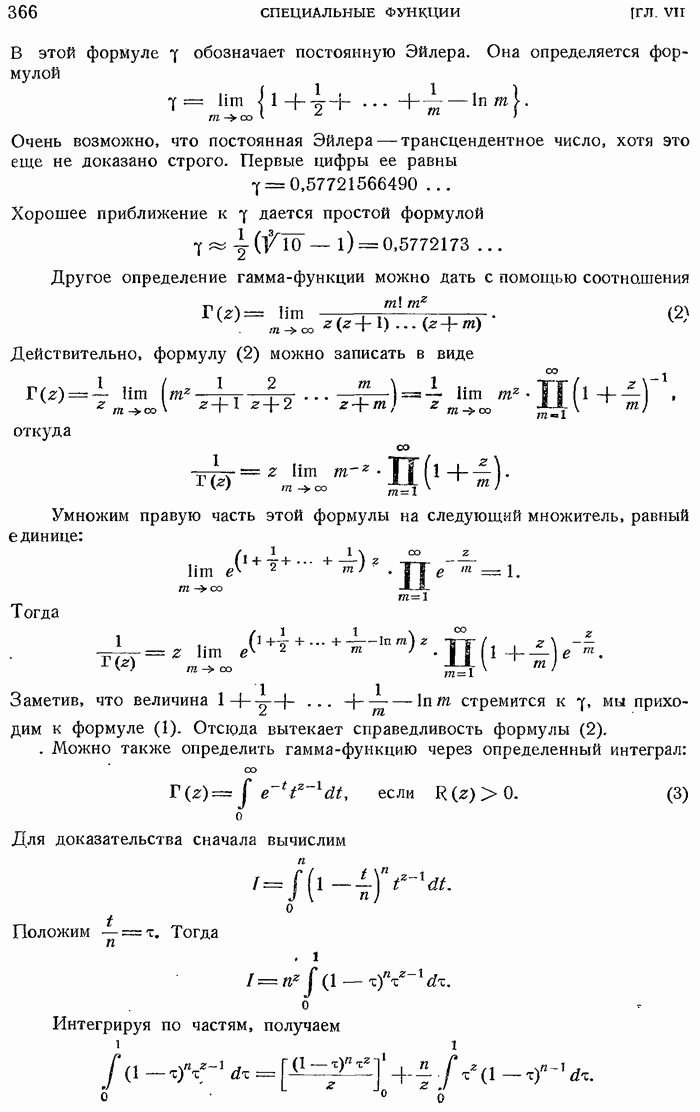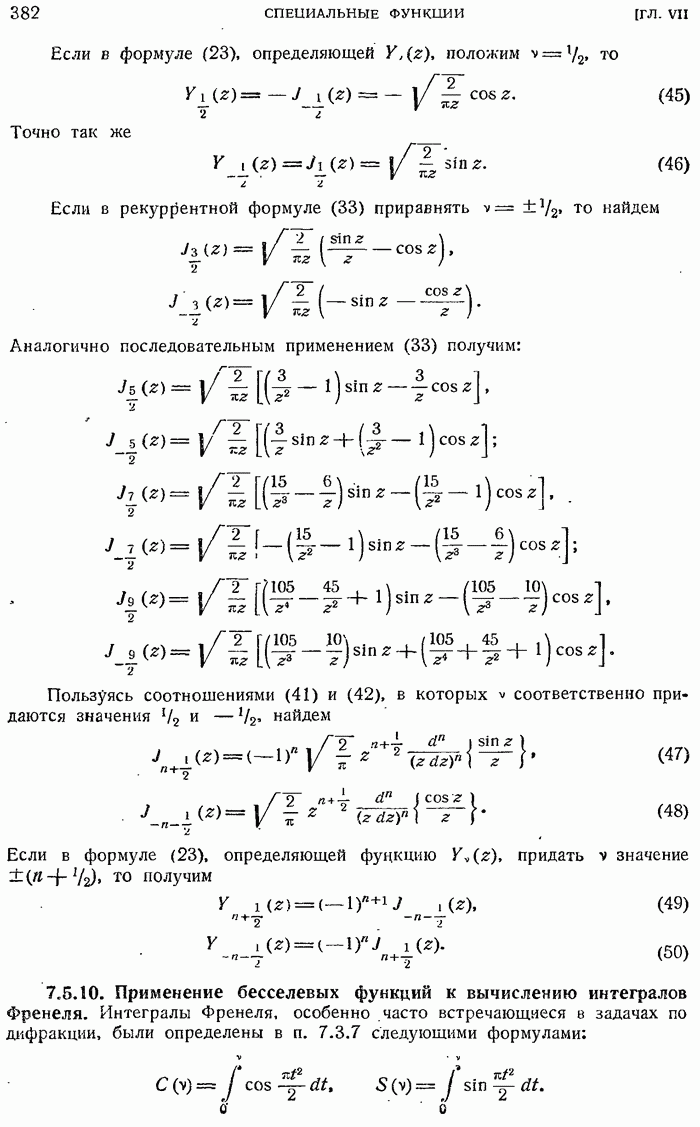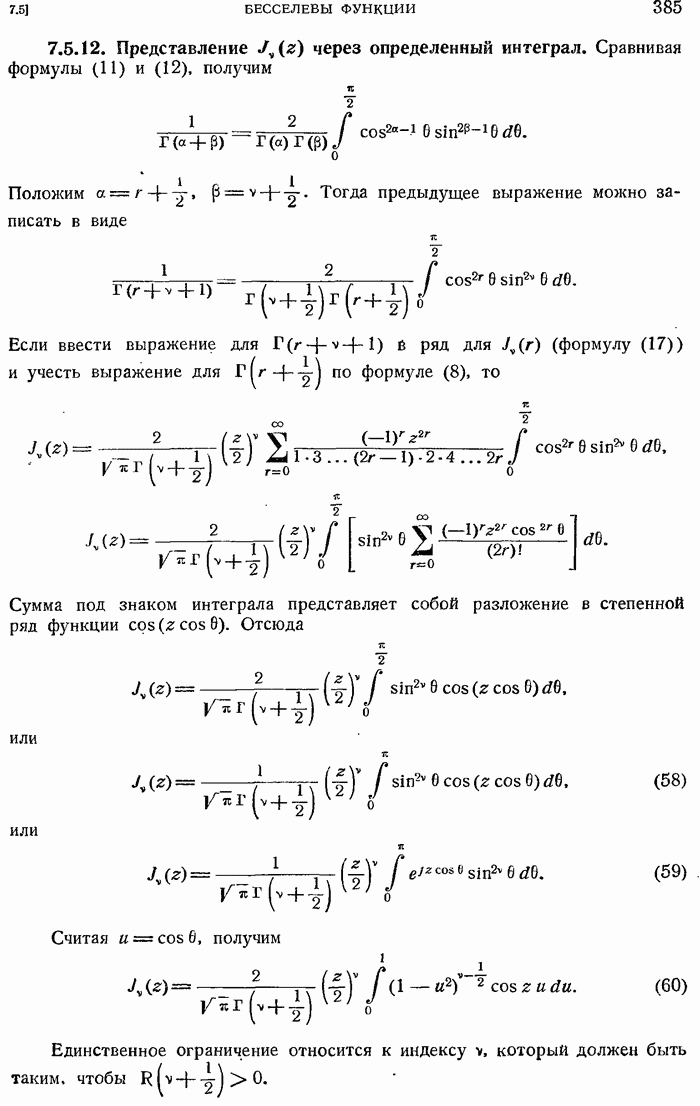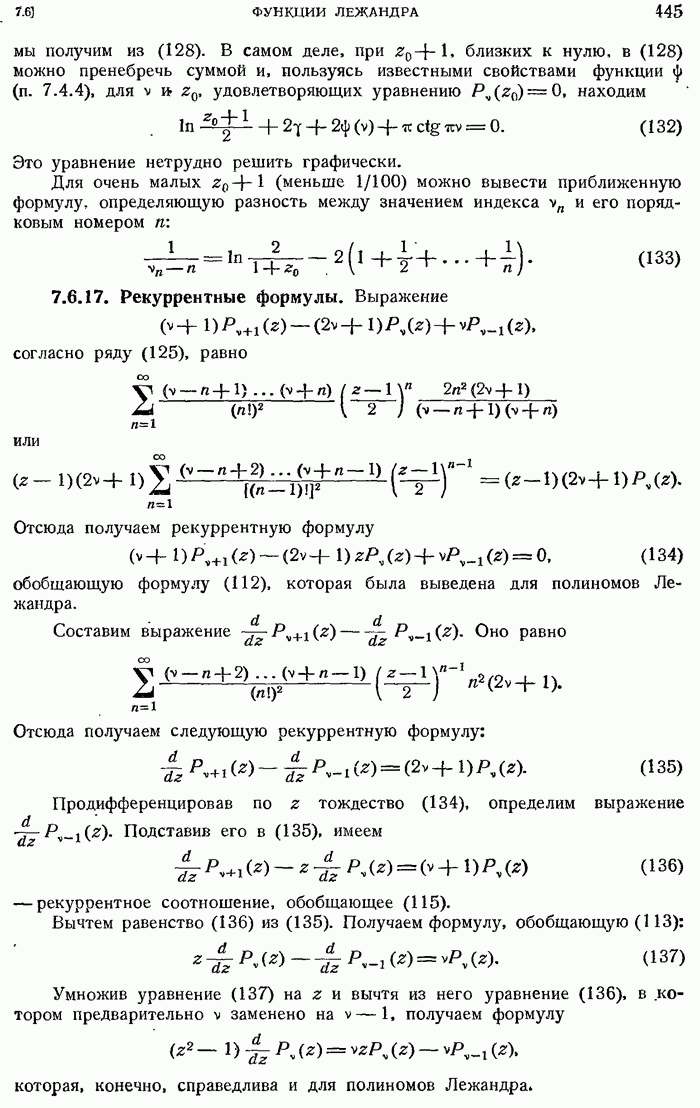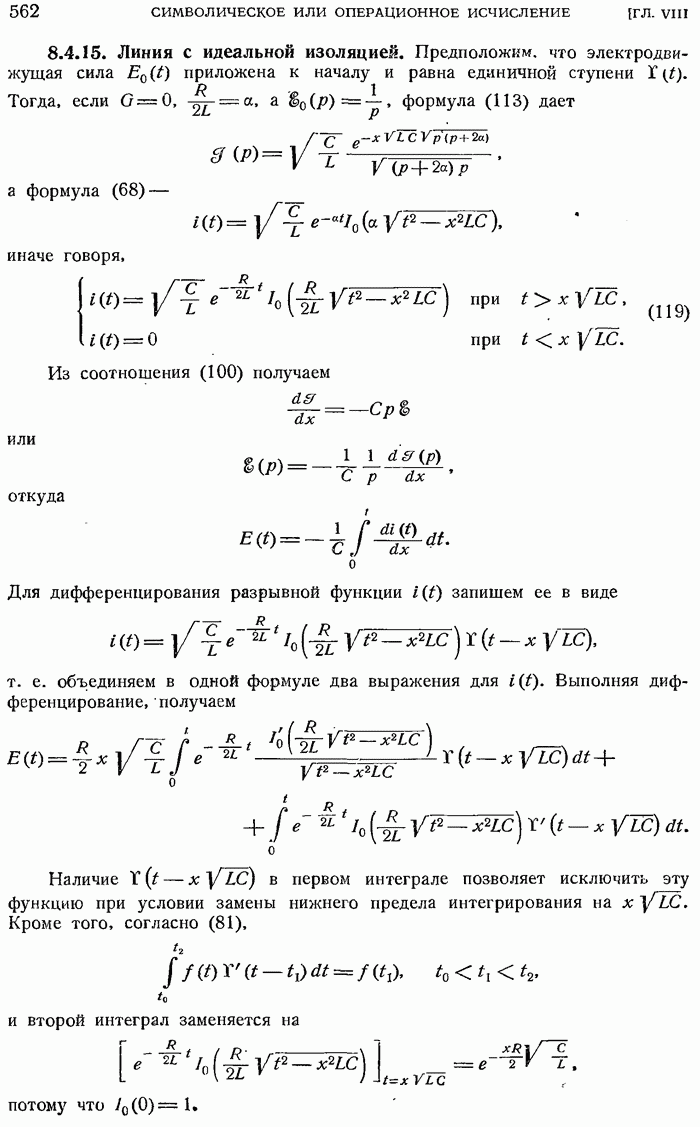| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
10.5.7. Формула Грегори.
Когда функция известна эмпирически, можно составить таблицу разностей. Если в формулу Эйлера ввести значения производных, выраженйых по формулам (48) через разности, то мы получим после некоторых вычислений формулу Грегори:

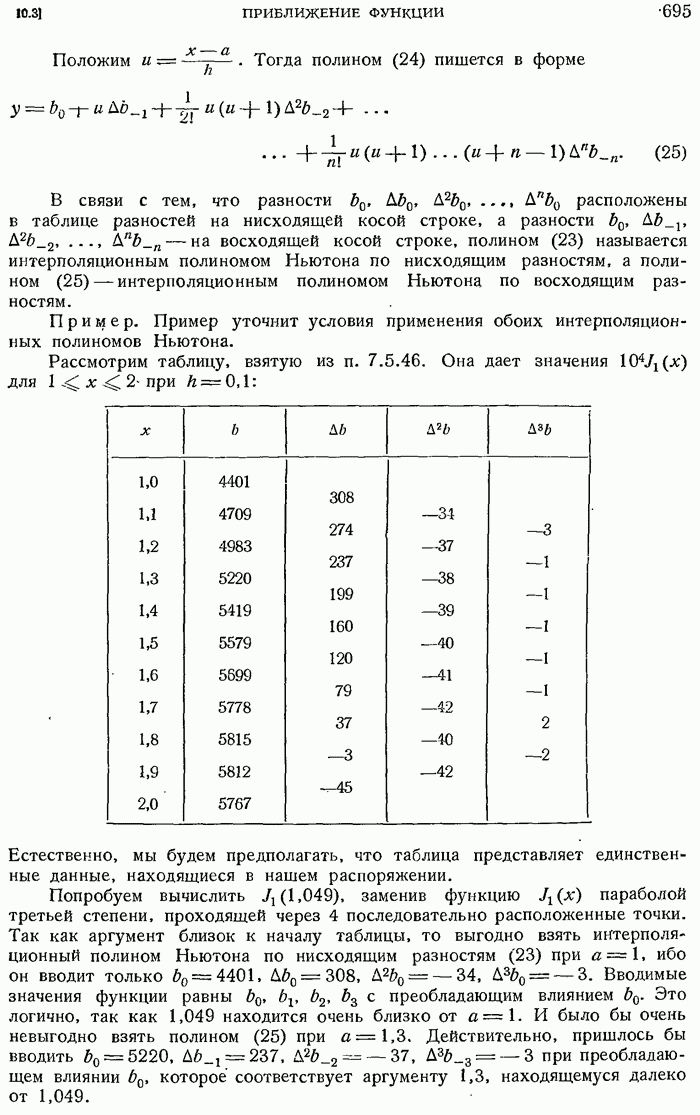
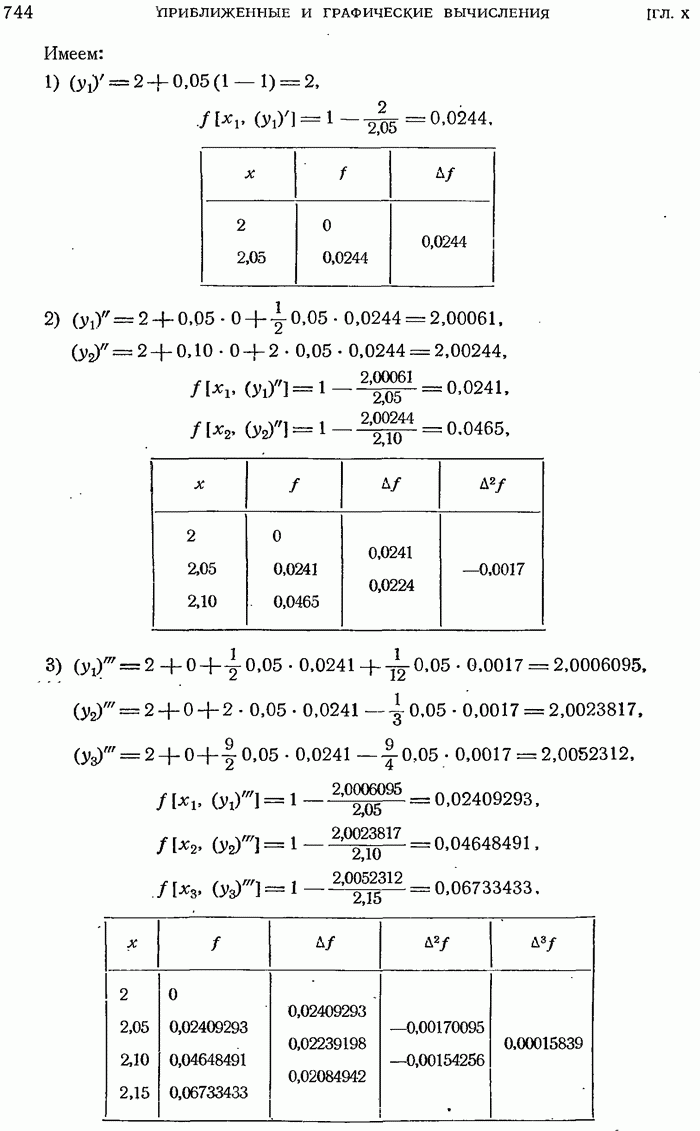
Пример. Вычислить  . Таблица разностей
. Таблица разностей  составленная в п. 10.3.3, дает
составленная в п. 10.3.3, дает

Замечание. Нетрудно вычислить первообразную для функции 

но, несмотря на это, вычисление интеграла посредством нахождения первообразной

гораздо более громоздко и (если пользоваться таблицами арктангенсов и логарифмов с невысокой точностью) дает менее точные результаты, чем прямой подсчет по таблице разностей и формуле Грегори.
Формула Грегори использует разности, помещенные на нисходящей и восходящей диагоналях таблицы разностей, имеющих начало в  Пользуясь при вычислении, подобном предыдущему, выражениями для последовательных производных, данными формулами (50), и произведя подстановку в формуле Эйлера, получаем формулу интегрирования. Она образуется с помощью разностей, находящихся по обе стороны от горизонтальных строк таблицы разностей, имеющих начало в
Пользуясь при вычислении, подобном предыдущему, выражениями для последовательных производных, данными формулами (50), и произведя подстановку в формуле Эйлера, получаем формулу интегрирования. Она образуется с помощью разностей, находящихся по обе стороны от горизонтальных строк таблицы разностей, имеющих начало в 

Пример. Требуется вычислить  Берем таблицу косинусов, приведенную в п. 10.3.3. Интервал 2°, выраженный в радианах,
Берем таблицу косинусов, приведенную в п. 10.3.3. Интервал 2°, выраженный в радианах,
равен 0,0349066. Формула трапеций дает

Ограничимся вычислением первого поправочного члена из-за неправильного поведения третьих разностей. Этот поправочный член равен 0,00005076, откуда

Обращаем внимание на превосходное приближение, полученное несмотря на краткость таблицы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- ГЛАВА I. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- 1.1. КОМПЛЕКСНЫЕ ВЕЛИЧИНЫ
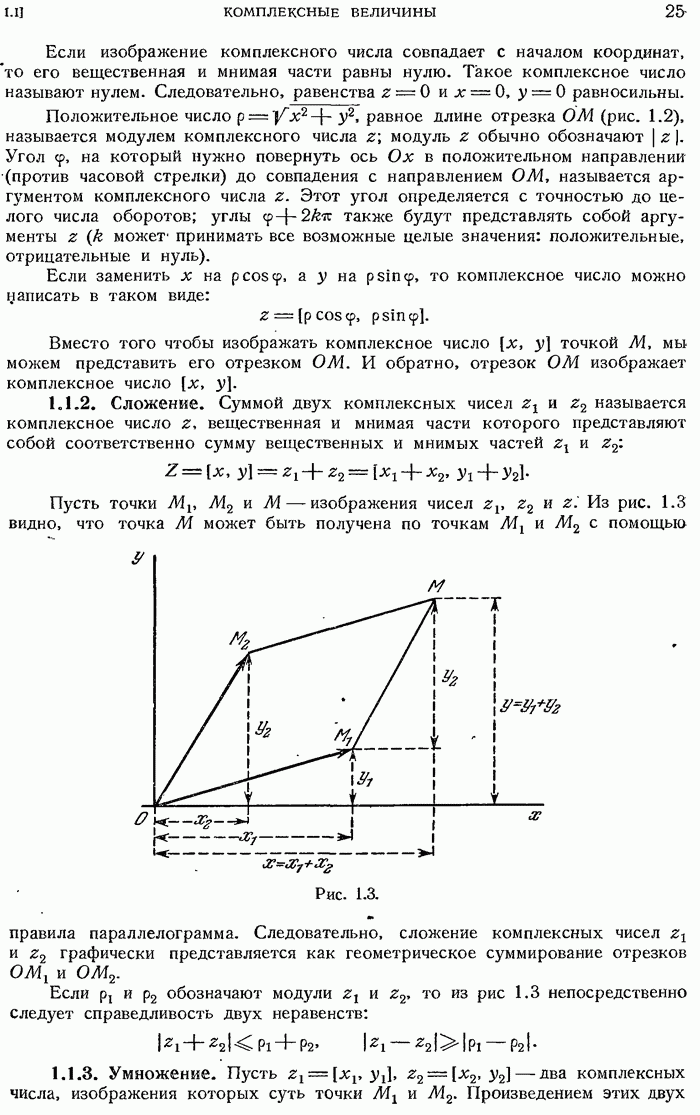
- 1.1.2. Сложение.
- 1.1.3. Умножение.
- 1.1.4. Замена обозначений.
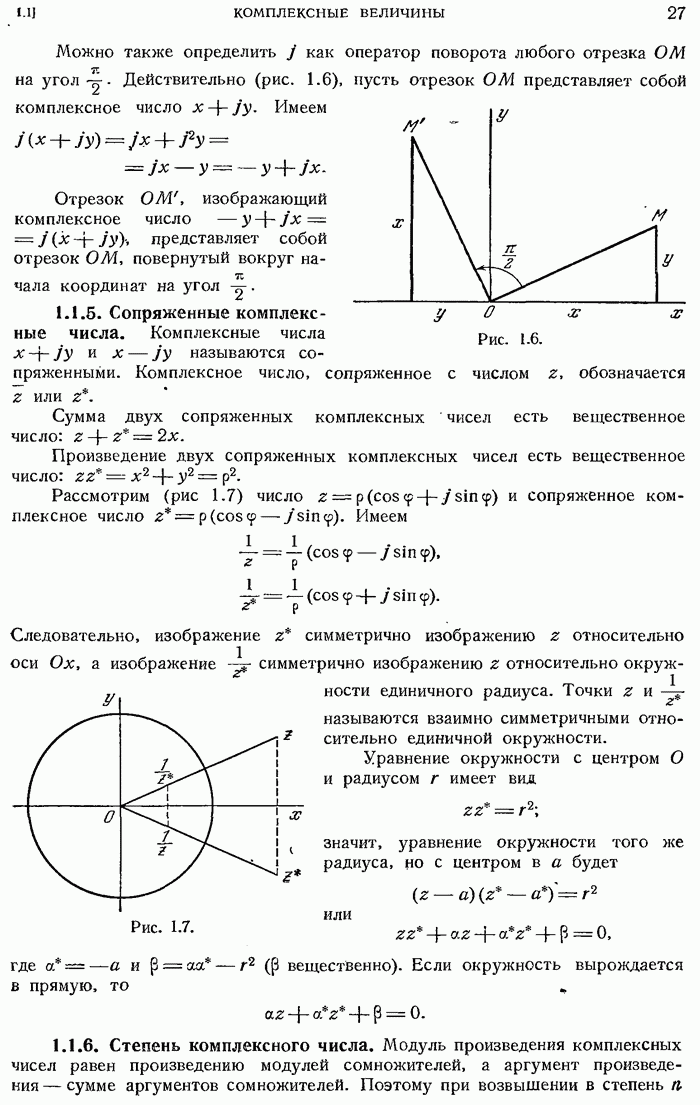
- 1.1.5. Сопряженные комплексные числа.
- 1.1.6. Степень комплексного числа.
- 1.1.7. Корни из комплексного числа.
- 1.1.8. Корни из единицы.
- 1.1.9. Ряды с комплексными членами.
- 1.1.10. Степенные ряды.
- 1.1.11. Экспоненциальная функция и логарифм.
- 1.1.12. Дифференцирование и интегрирование по аргументу.
- 1.1.13. Суммирование тригонометрических функций, аргументы которых составляют арифметическую прогрессию.
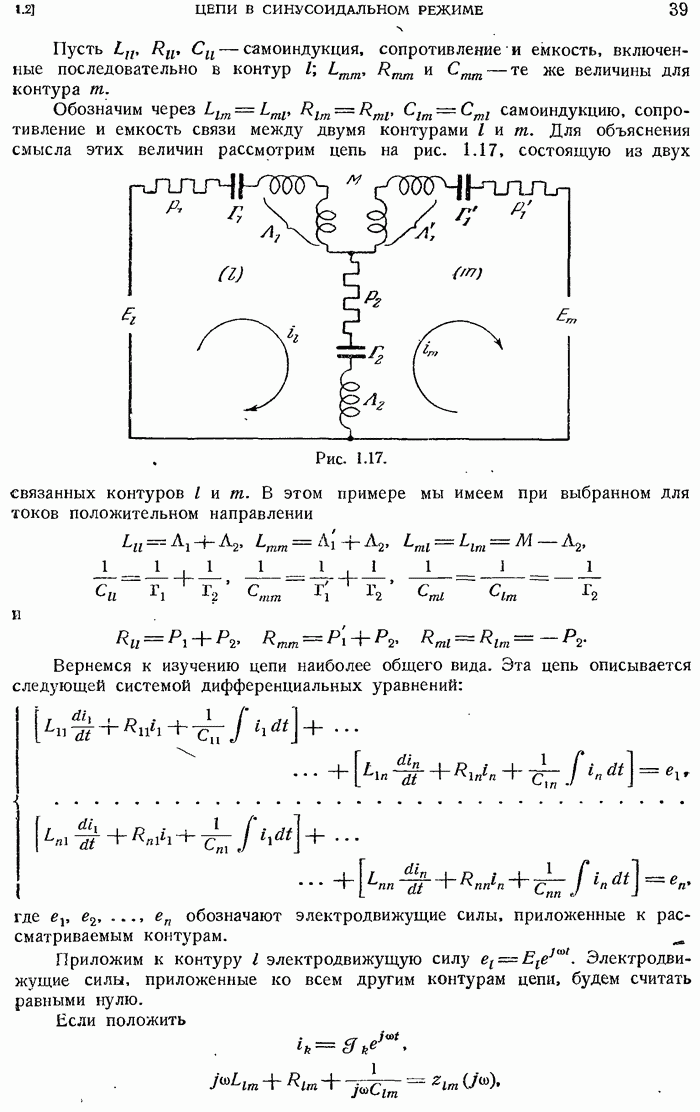
- 1.2. ПРИМЕНЕНИЕ КОМПЛЕКСНЫХ ВЕЛИЧИН ПРИ РАСЧЕТЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ В СИНУСОИДАЛЬНОМ РЕЖИМЕ
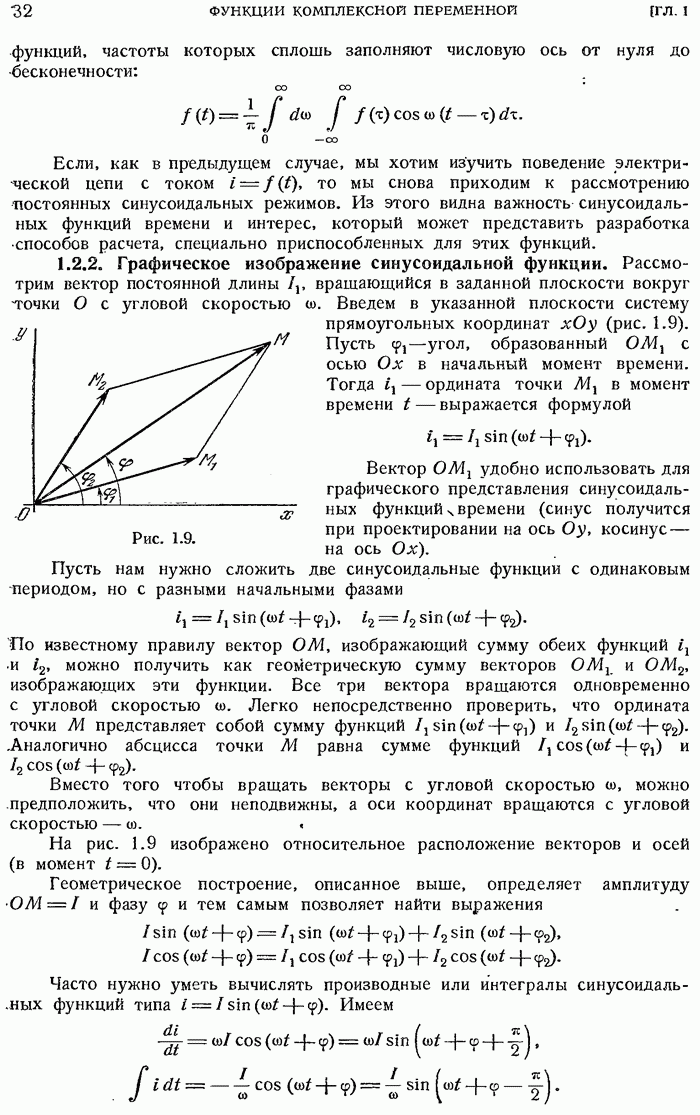
- 1.2.2. Графическое изображение синусоидальной функции.
- 1.2.3. Представление с помощью комплексных чисел.
- 1.2.4. Ограничения метода.
- 1.2.5. Понятие комплексного полного сопротивления.
- 1.2.6. Комплексное полное сопротивление при последовательном и параллельном соединении.
- 1.2.7. Законы Кирхгофа.
- 1.2.8. Обобщение понятия комплексного полного сопротивления.
- 1.2.9. Комплексный вектор.
- 1.3. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
- 1.3.5. Криволинейный интеграл от функции комплексной переменной.
- 1.3.6. Теорема Коши.
- 1.3.8. Ряд Тейлора.
- 1.3.9. Особые точки.
- 1.3.10. Разложение в ряд Лорана.
- 1.3.11. Теорема о вычетах.
- 1.3.12. Вычисление вычетов.
- 1.3.13. Вычисление вычетов относительно кратных полюсов с помощью производных.
- 1.3.14. Лемма Жордана.
- 1.3.15. Применение леммы Жордана к единичной функции.
- 1.3.16. Интегрирование при наличии точки разветвления.
- 1.3.17. Контур Бромвича.
- 1.3.18. Интеграл Бромвича — Вагнера.
- 1.3.19. Эквивалентный контур.
- 1.3.20. Теорема о числе полюсов и числе нулей.
- Применение теоремы о вычетах к вычислению некоторых определенных интегралов
- 1.3.25. Применение теоремы о вычетах к суммированию некоторых рядов.
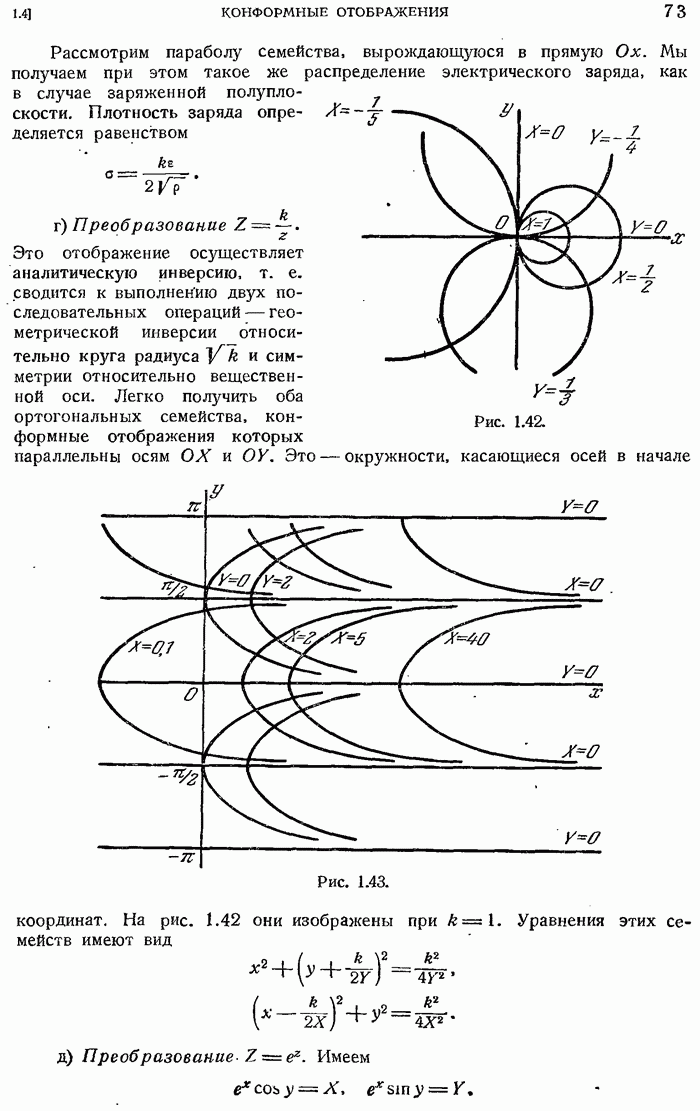
- 1.4. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
- 1.4.2. Несколько примеров конформных отображений.
- 1.4.3. Последовательные отображения.
- 1.4.4. Отображение Шварца.
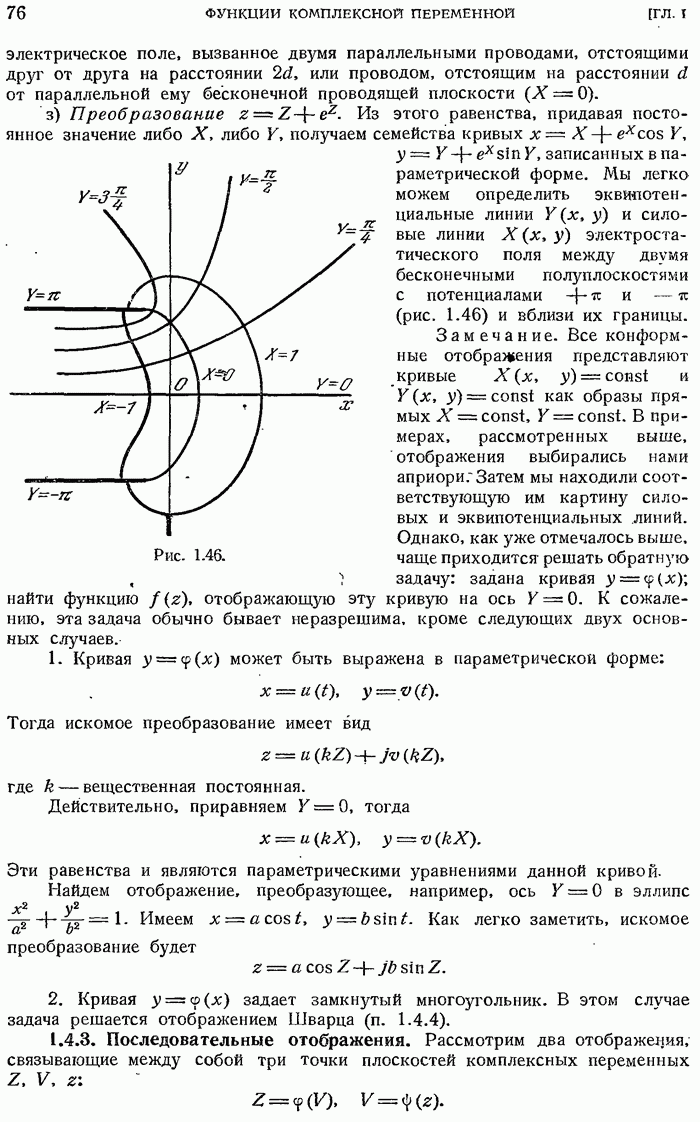
- 1.4.5. Различные применения конформных отображений.
- ГЛАВА II. РЯД ФУРЬЕ. ИНТЕГРАЛ ФУРЬЕ
- 2.1. РЯД ФУРЬЕ
- 2.1.2. Разложение в ряд по ортогональным функциям.
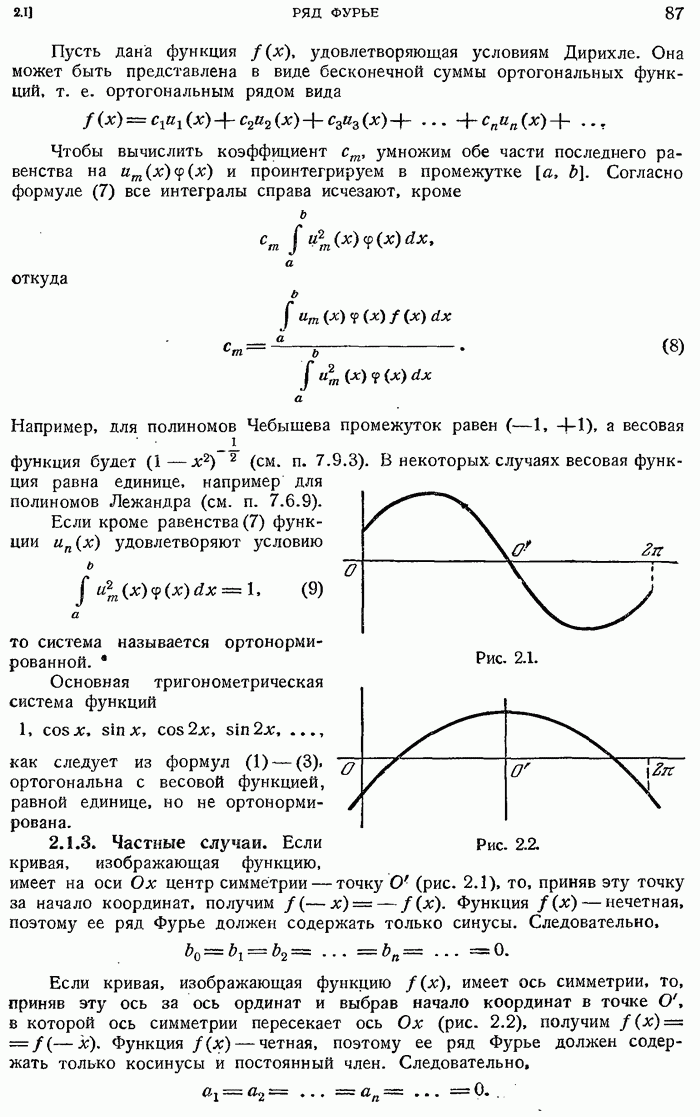
- 2.1.3. Частные случаи.
- 2.1.4. Интегрирование и дифференцирование.
- 2.1.5. Случай, когда разложение в ряд Фурье ограничено первыми n членами.
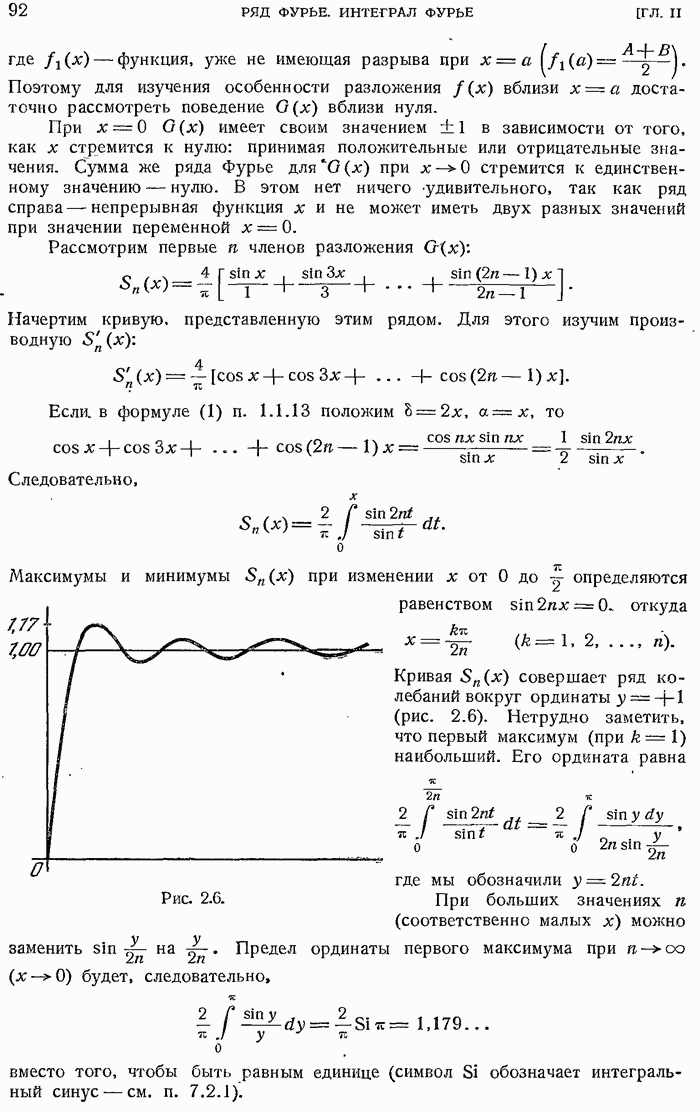
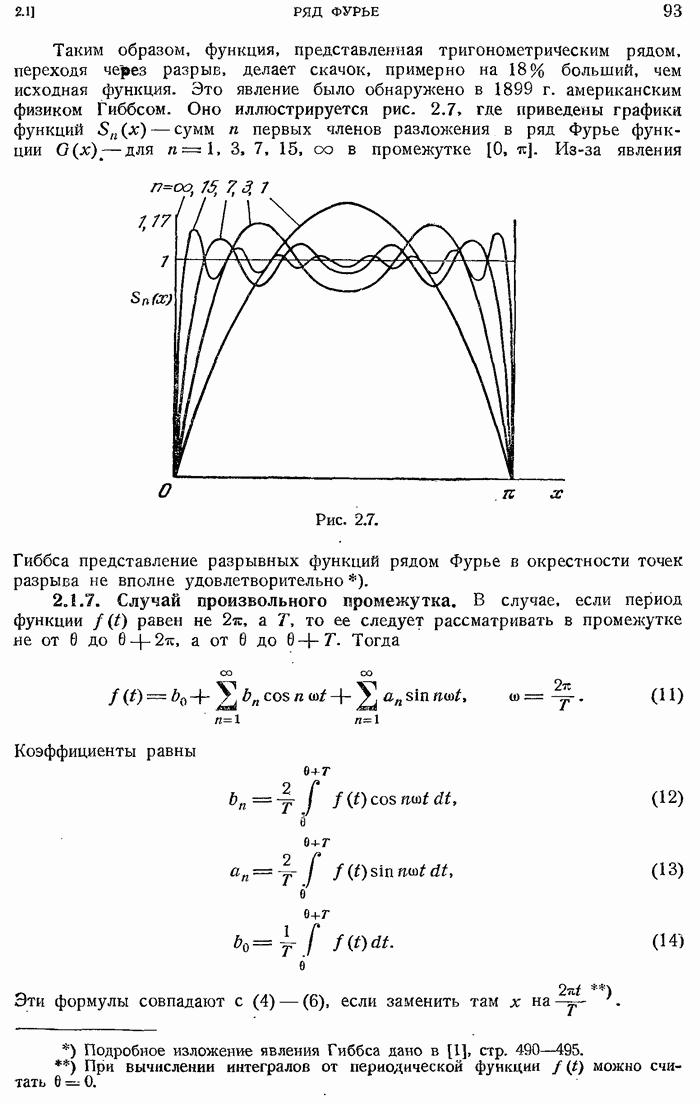
- 2.1.6. Изучение разложения в ряд Фурье вблизи точки разрыва. Явление Гиббса.
- 2.1.7. Случай произвольного промежутка.
- 2.1.8. Ряды с комплексными членами.
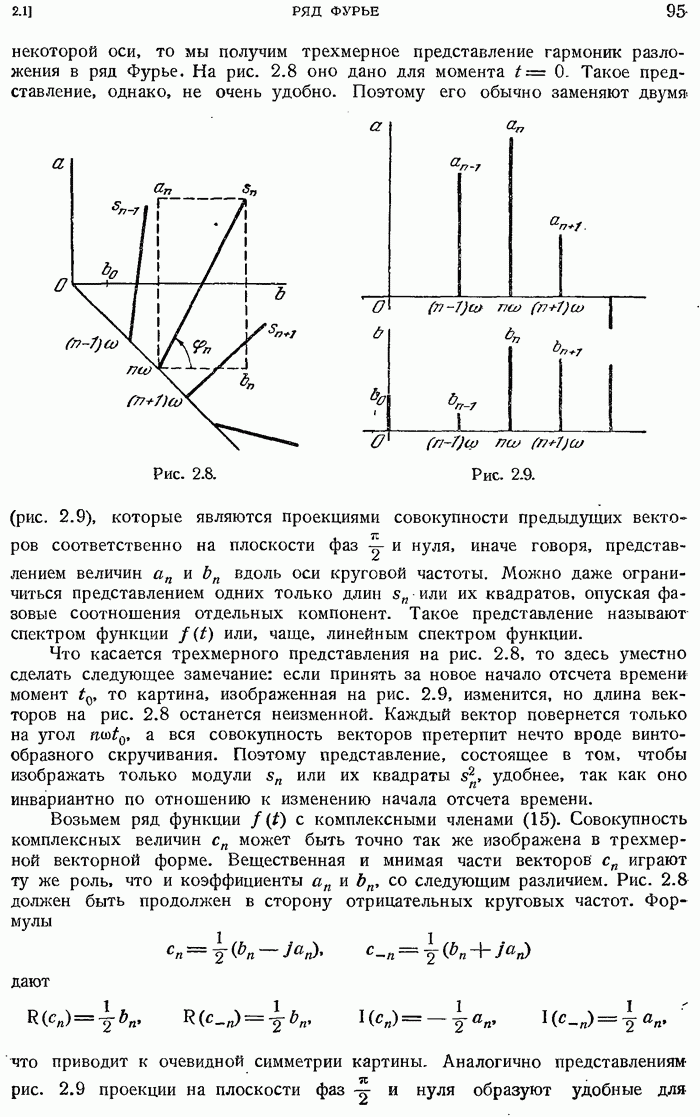
- 2.1.9. Графическое представление. Спектр.
- 2.1.10. Среднее значение произведения двух функций одного периода, разложимых в ряд Фурье.
- 2.1.11. Распространение ряда Фурье на почти периодические функции.
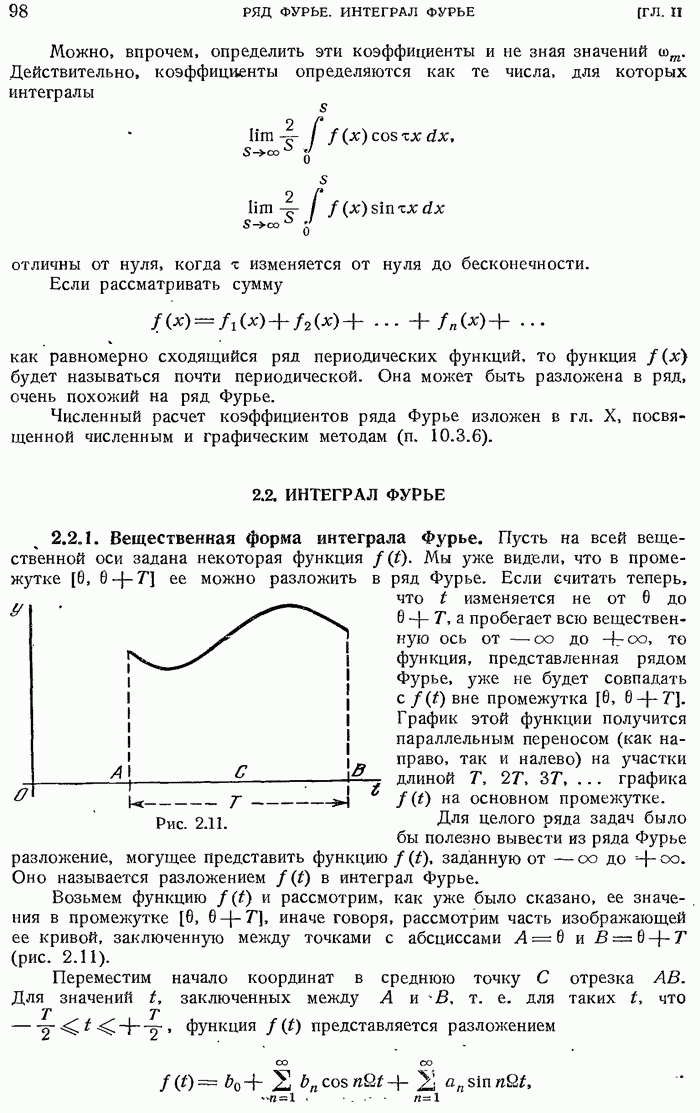
- 2.2. ИНТЕГРАЛ ФУРЬЕ
- 2.2.2. Комплексная форма интеграла Фурье.
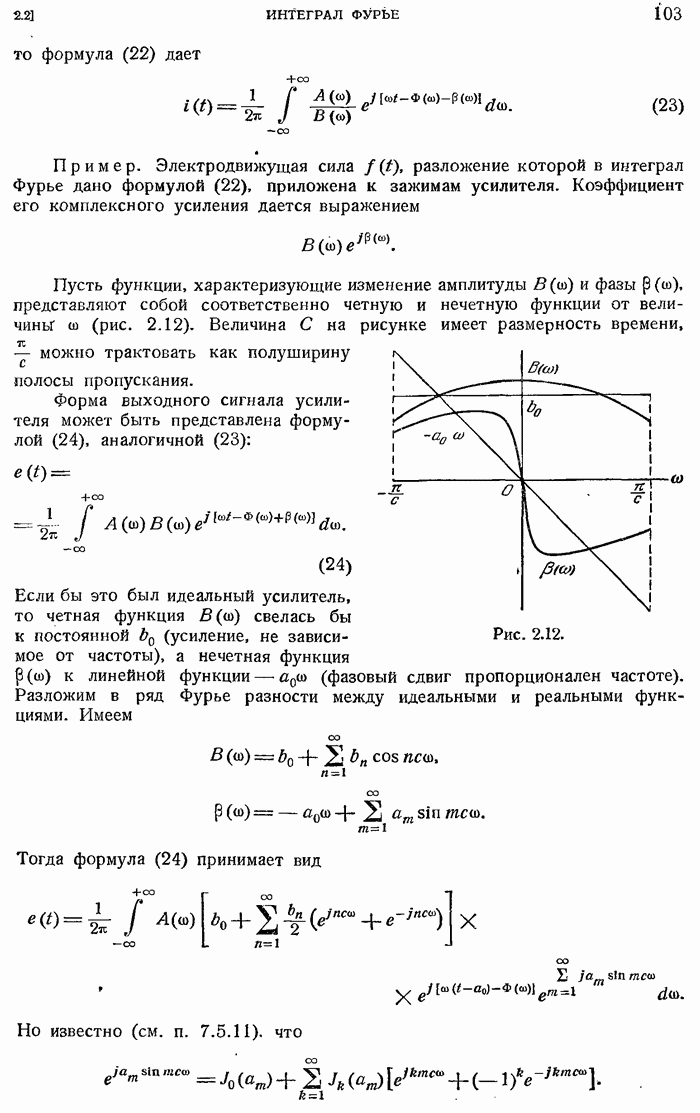
- 2.2.3. Применение к электрическим цепям.
- 2.2.4. Случай незатухающей цепи.
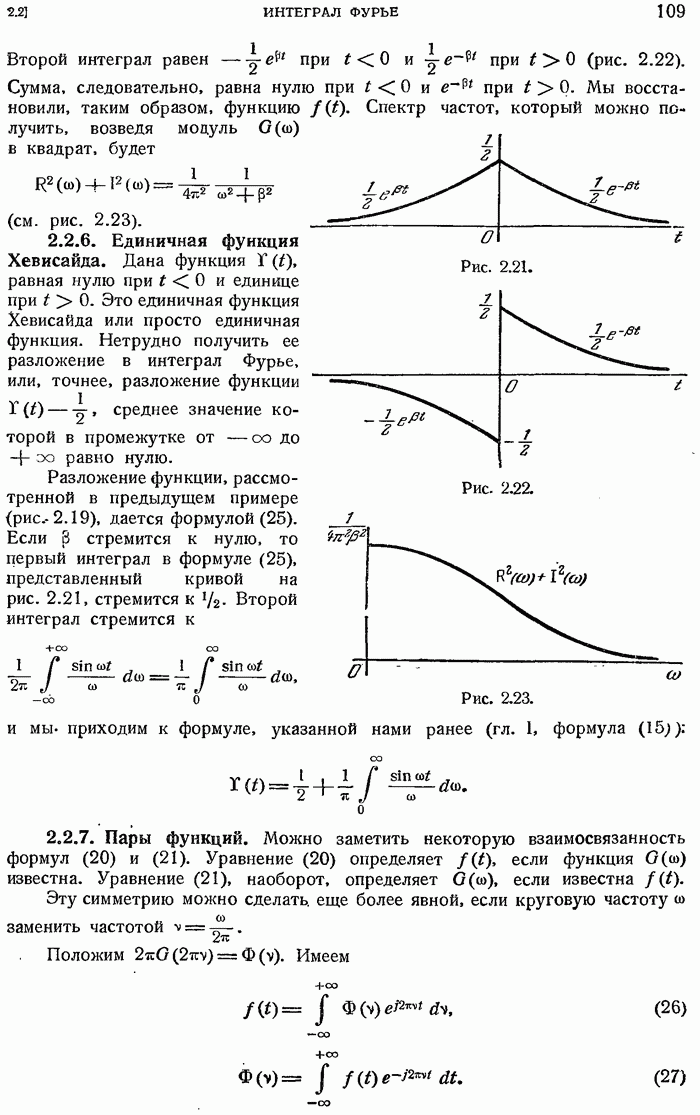
- 2.2.5. Спектр частот.
- 2.2.6. Единичная функция Хевисайда.
- 2.2.7. Пары функций.
- 2.2.8. Преобразование Фурье.
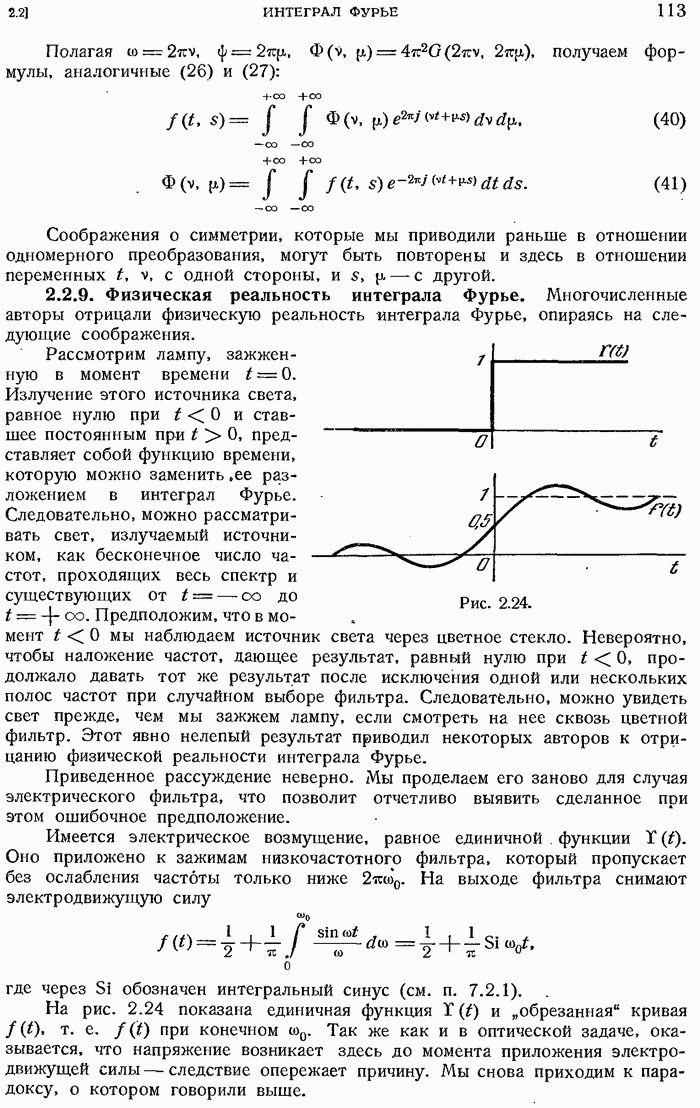
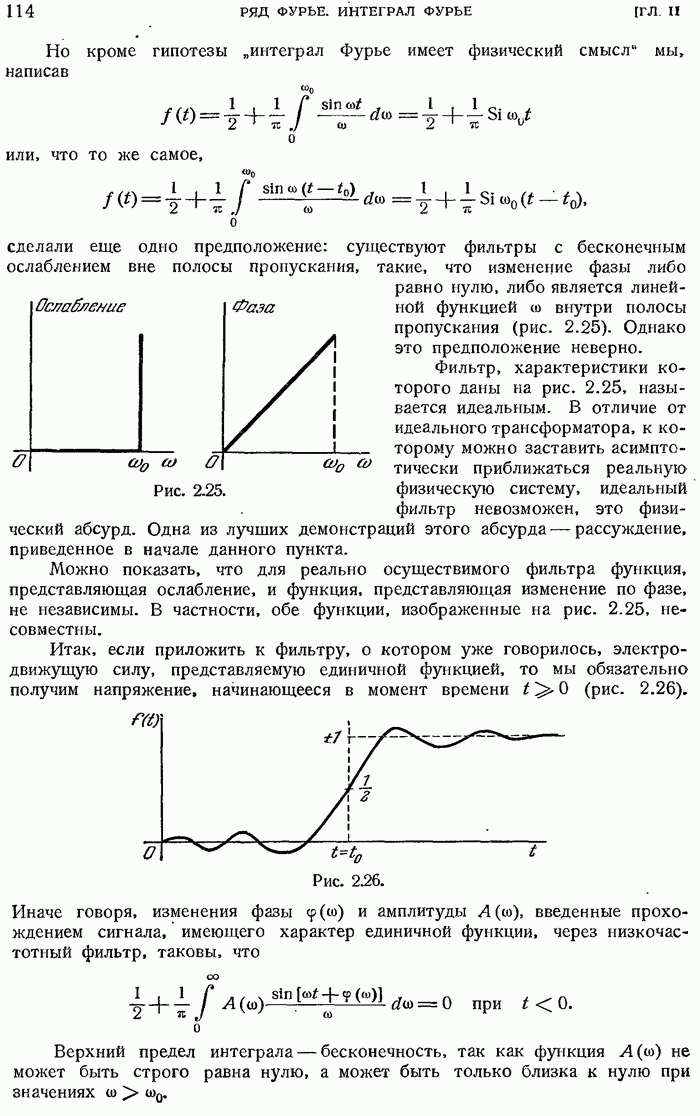
- 2.2.9. Физическая реальность интеграла Фурье.
- 2.2.10. Изучение диаграмм направленности.
- ГЛАВА III. ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
- 3.1. СКАЛЯРНЫЕ ВЕЛИЧИНЫ. ВЕКТОРНЫЕ ВЕЛИЧИНЫ. ОПРЕДЕЛЕНИЯ
- 3.1.6. Векторы.
- Операции над векторами
- 3.1.12. Скалярное произведение.
- 3.1.13. Векторное произведение.
- 3.1.14. Смешанное произведение трех векторов.
- 3.1.15. Двойное векторное произведение трех векторов.
- 3.2. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАЦИИ С ВЕКТОРАМИ
- 3.2.2. Производная вектора по другому вектору.
- 3.2.3. Основные формулы дифференцирования.
- 3.2.4. Интеграл от вектора.
- Функции точки
- 3.2.11. Дивергенция и вихрь.
- 3.2.12. Оператор Лапласа.
- 3.2.13. Символический вектор набла (оператор Гамильтона).
- 3.2.14. Наиболее употребительные формулы.
- 3.2.15. Смысл вектора rot a.
- 3.2.16. Скалярный потенциал.
- 3.2.17. Частный случай: вектор проходит через фиксированную точку.
- 3.2.18. Векторный потенциал.
- 3.2.19. Общий случай векторного поля.
- 3.3. ВЕКТОРНЫЕ ИНТЕГРАЛЫ
- 3.3.1. Циркуляция вектора.
- 3.3.2. Поток вектора.
- Основные формулы
- 3.3.3. Теорема Остроградского.
- 3.3.4. Смысл скаляра div a.
- 3.3.5. Формула для градиента.
- 3.3.6. Формула для вихря.
- 3.3.7. Инвариантность градиента, дивергенции, вихря.
- 3.3.8. Формула Грина.
- 3.3.9. Формула Стокса.
- Приложение векторного исчисления к теории электромагнитного поля
- 3.3.10. Электростатическое поле.
- 3.3.11. Магнитное поле постоянных токов.
- 3.3.12. Электромагнитное поле.
- 3.3.13. Закон Фарадея.
- 3.3.14. Закон Ампера.
- 3.3.15. Уравнения Максвелла.
- 3.3.16. Векторный потенциал магнитного поля, возбужденного током.
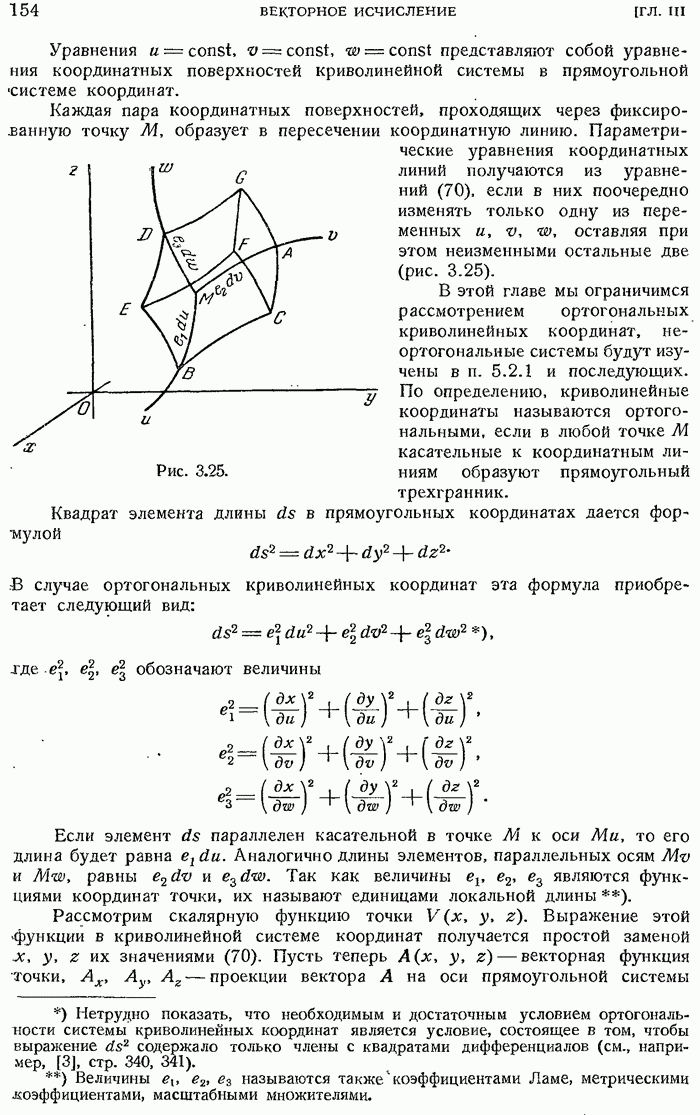
- 3.4. СИСТЕМЫ ОРТОГОНАЛЬНЫХ КРИВОЛИНЕЙНЫХ КООРДИНАТ
- 3.4.2. Дифференциальные операторы в ортогональных криволинейных координатах.
- Важнейшие системы ортогональных криволинейных координат в пространстве
- 3.4.3. Система цилиндрических координат.
- 3.4.4. Система сферических координат.
- 3.4.5. Система параболических цилиндрических координат.
- 3.4.6. Система параболических координат вращения (параболоидальные координаты).
- 3.4.7. Система эллиптических цилиндрических координат.
- 3.4.8. Система вытянутых эллипсоидальных координат (вращения).
- 3.4.9. Система сплюснутых эллипсоидальных координат (вращения).
- 3.4.10. Система бицилиндрических координат.
- 3.4.11. Системы тороидальных и бисферических координат.
- 3.4.12. Система софокусных поверхностей второго порядка (система общих эллипсоидальных координат).
- 3.4.13. Приложение к уравнениям Максвелла. Уравнения Максвелла в ортогональных криволинейных координатах.
- ГЛАВА IV. МАТРИЧНОЕ ИСЧИСЛЕНИЕ
- 4.1. АЛГЕБРА МАТРИЦ
- 4.1.4. Представление плоских преобразований с помощью матриц.
- 4.1.5. Произведение двух матриц.
- 4.1.6. Представление вектора посредством матрицы.
- 4.1.7. Обобщение на n-мерное пространство.
- 4.1.8. Равенство двух матриц.
- 4.1.9. Сложение двух матриц.
- 4.1.10. Умножение матрицы на число.
- 4.1.11. Умножение матриц.
- 4.1.12. Симметричные матрицы.
- 4.1.13. Кососимметричные матрицы.
- 4.1.14. Диагональные матрицы.
- 4.1.15. Единичная матрица. Нулевая матрица.
- 4.1.16. Порядок, ранг матрицы.
- 4.1.17. Необходимые условия равенства нулю произведения двух матриц.
- 4.1.18. Транспонированная матрица.
- 4.1.19. Обратная матрица.
- 4.1.20. Применение матричного исчисления к решению системы линейных уравнений.
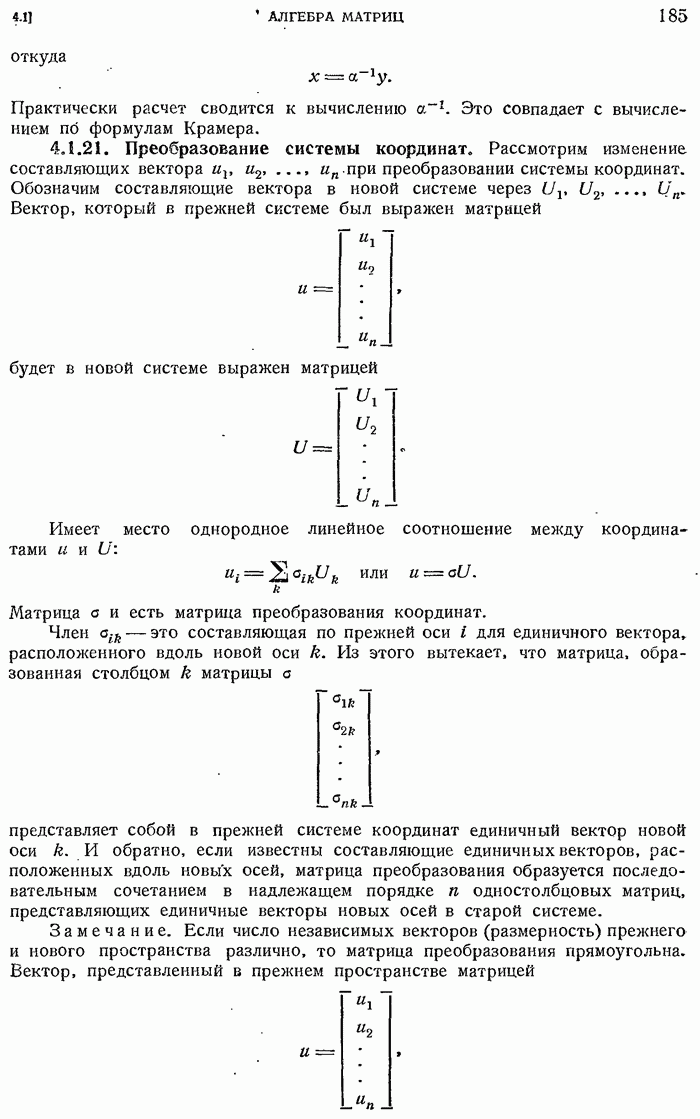
- 4.1.21. Преобразование системы координат.
- 4.1.22. Ортогональное преобразование.
- 4.1.23. Пример ортогональных преобразований. Поворот.
- Обобщение на комплексное пространство
- 4.1.24. Эрмитова матрица.
- 4.1.25. Эрмитово-сопряженная матрица.
- 4.1.26. Модуль и скалярное произведение в комплексном пространстве.
- 4.1.27. Ортогональное преобразование комплексного пространства (унитарное преобразование).
- 4.1.28. Собственные значения, собственные векторы и характеристическое уравнение матрицы.
- 4.1.29. Свойства характеристического уравнения.
- 4.1.30. Матрица, отнесенная к собственным направлениям.
- 4.1.31. Условия коммутативности двух матриц.
- 4.1.32. Собственные значения и собственные направления эрмитовой матрицы.
- Функции от матриц
- 4.1.33. Степень матрицы.
- 4.1.34. Теорема Кэли-Гамильтона.
- 4.1.35. Функции от матриц. Теорема Сильвестра.
- 4.1.36. Формула Бэкера.
- 4.1.37. Высокие степени матрицы.
- 4.1.38. Дробная степень матрицы.
- 4.1.39. Приближенное вычисление собственных значений матрицы.
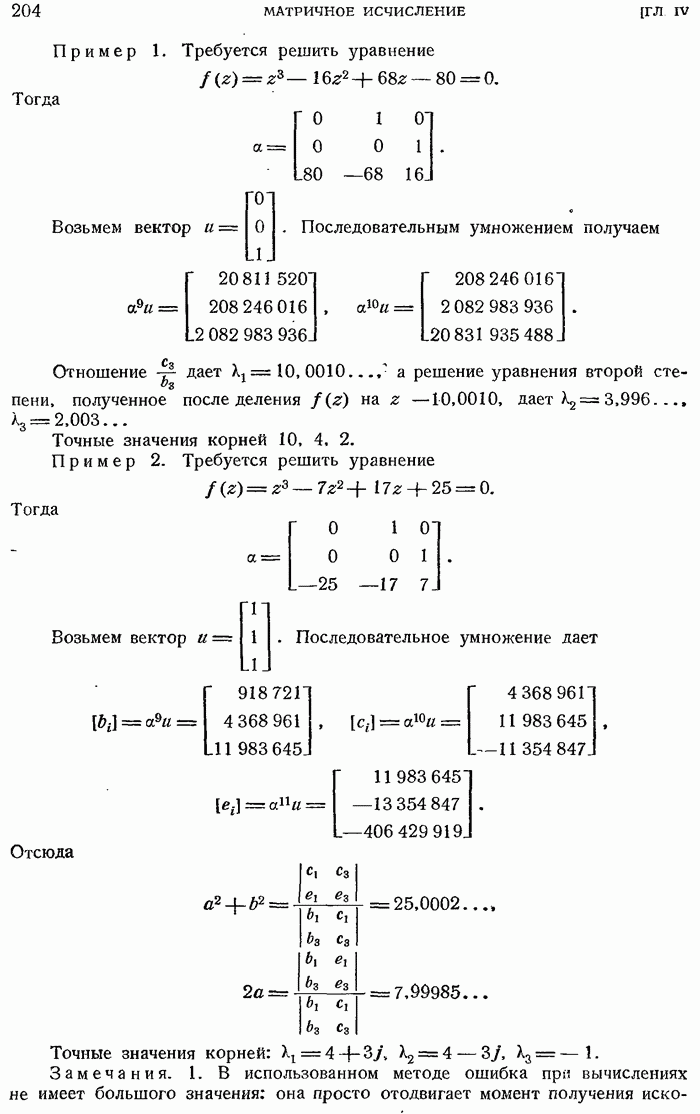
- 4.1.40. Приближенное вычисление корней уравнения n-й степени.
- Дифференциальные операции над матрицами. Применение к решению дифференциальных уравнений
- 4.1.41. Дифференцирование и интегрирование матрицы.
- 4.1.42. Решение системы линейных дифференциальных уравнений первого порядка.
- 4.1.43. Система дифференциальных уравнений первого порядка, с постоянными коэффициентами.
- 4.1.44. Случай линейного дифференциального уравнения n-го порядка.
- 4.2. ПРИМЕНЕНИЕ МАТРИЧНОГО ИСЧИСЛЕНИЯ. ИЗУЧЕНИЕ ЧЕТЫРЕХПОЛЮСНИКОВ
- 4.2.2. Соединение четырехполюсников по цепной схеме.
- 4.2.3. Параллельное соединение четырехполюсников.
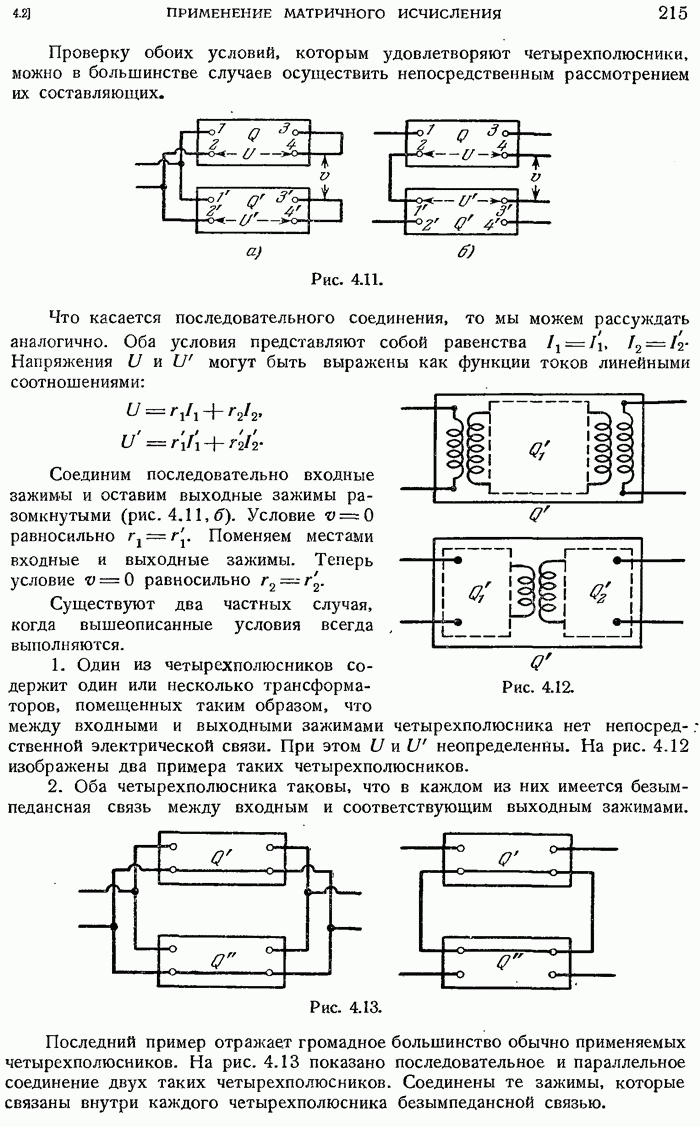
- 4.2.4. Последовательное соединение четырехполюсников.
- 4.2.5. Последовательно-параллельное и параллельно-последовательное соединение четырехполюсников.
- 4.2.6. Сопротивления холостого хода и короткого замыкания четырехполюсника.
- 4.2.7. Пассивные четырехполюсники.
- 4.2.8. Симметричные четырехполюсники.
- Примеры простых четырехполюсников
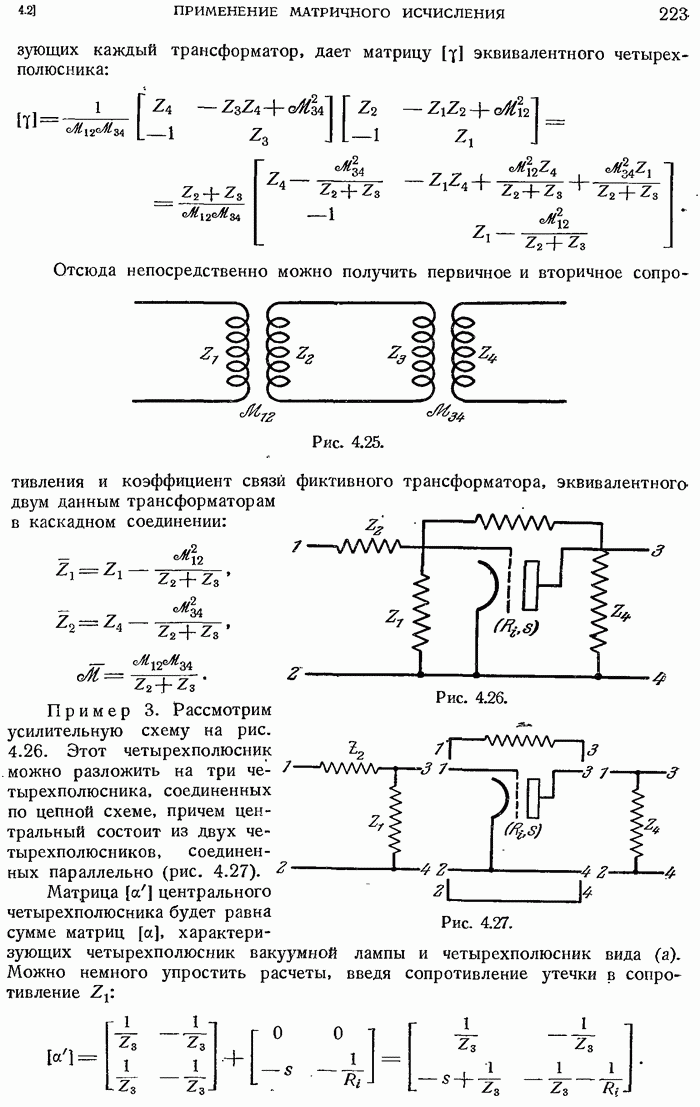
- 4.2.14. Трансформатор
- 4.2.15. Электронная лампа.
- 4.2.16. Повторное сопротивление четырехполюсника.
- 4.2.17. Случай пассивного четырехполюсника.
- 4.2.18. Цепные фильтры.
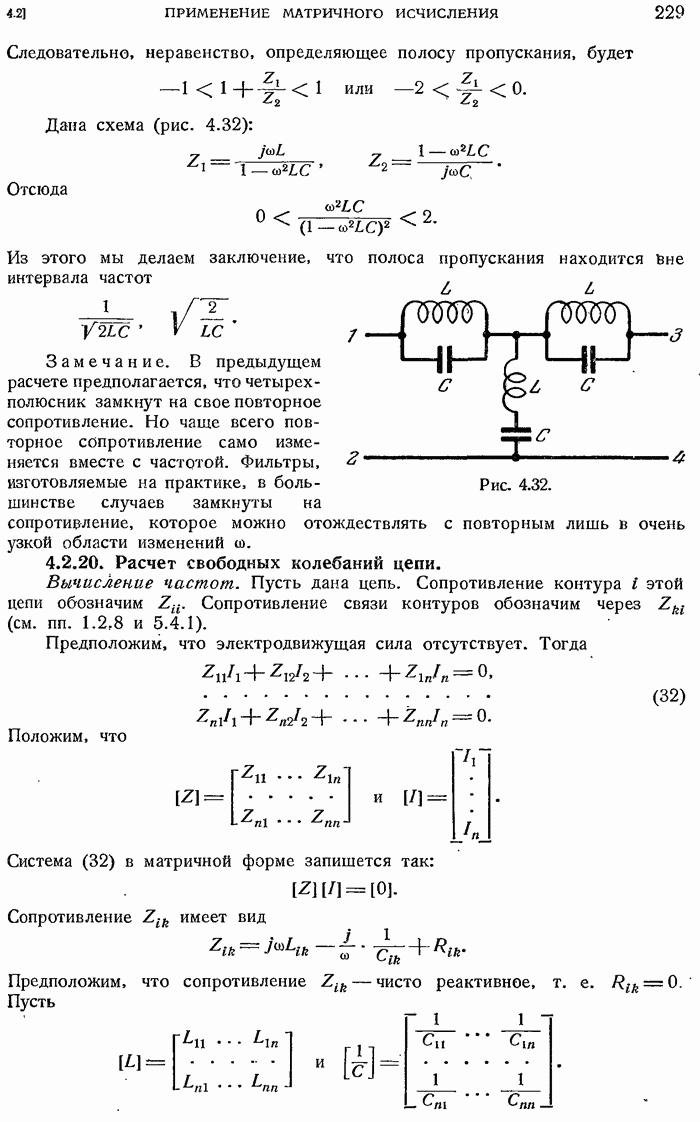
- 4.2.19. Полоса пропускания четырехполюсника.
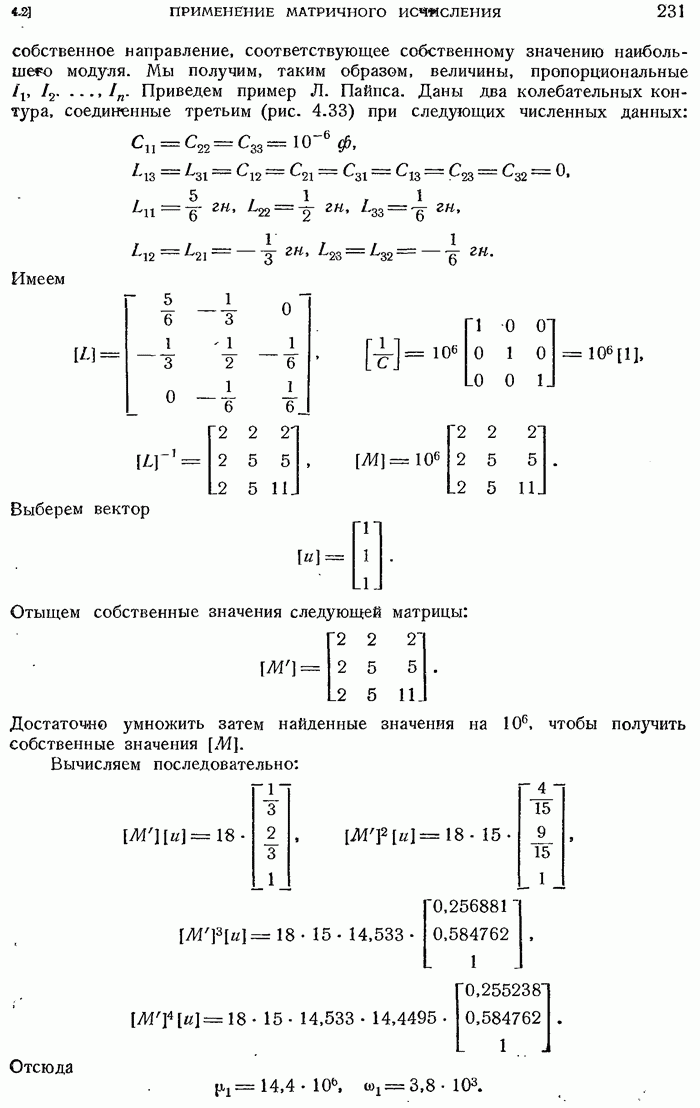
- 4.2.20. Расчет свободных колебаний цепи.
- 4.2.21. Контуры с периодически меняющимися параметрами.
- 4.2.22. Матрицы в квантовой механике.
- ГЛАВА V. ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ. ПРИЛОЖЕНИЯ
- 5.1. ТЕНЗОРНАЯ АЛГЕБРА
- 5.1.3. Ковариантные и контравариантные векторы.
- 5.1.4. Определение тензора.
- 5.1.5. Матричная форма формул преобразования координат.
- 5.1.6. Немой индекс.
- 5.1.7. Симметрия и антисимметрия.
- 5.1.8. Псевдоскаляры. Скалярная плотность и скалярная емкость.
- 5.1.9. Тензорная плотность и тензорная емкость.
- 5.1.10. Антисимметричный тензор второй валентности в трехмерном пространстве.
- Операции над тензорами
- 5.3.11. Сложение двух тензоров.
- 5.1.12. Свертывание тензора.
- 5.1.13. Умножение тензоров.
- 5.1.14. Свертывание произведения.
- 5.1.15. Установление типа тензора.
- 5.2. ТЕНЗОРЫ В КРИВОЛИНЕЙНОЙ СИСТЕМЕ КООРДИНАТ
- 5.2.2. Фундаментальный метрический тензор.
- 5.2.3. Преобразование определителя g фундаментального метрического тензора при преобразовании координат.
- 5.2.4. Выражение для элемента объема.
- 5.2.5. Косоугольная система координат на плоскости.
- 5.2.6. Ортогональные криволинейные координаты в трехмерном пространстве.
- 5.2.7. Случай произвольных криволинейных координат.
- 5.2.8. Контравариантные или ковариантные компоненты одного и того же вектора.
- 5.2.9. Изменение вариантности тензора.
- 5.2.10. Смешанный фундаментальный метрический тензор.
- 5.2.11. Случай прямолинейной прямоугольной системы координат.
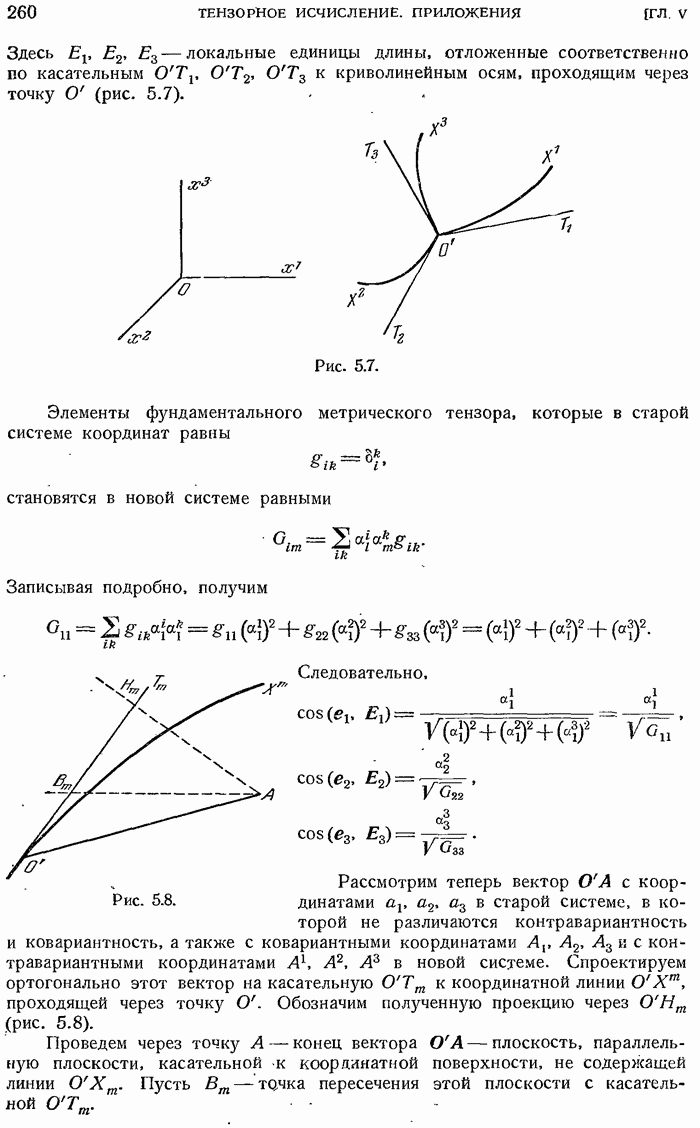
- Геометрическое представление контравариантных и ковариантных компонент вектора
- 5.2.12. Случай прямолинейной косоугольной системы координат.
- 5.2.13. Случай криволинейных координат.
- 5.2.14. Частный случай ортогональных криволинейных координат.
- 5.3. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- Частный случай ортогональных криволинейных координат
- 5.3.9. Тензорная форма уравнений Максвелла.
- 5.4. ПРИМЕНЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К ИССЛЕДОВАНИЮ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- 5.4.1. Элементы электрических цепей с сосредоточенными постоянными.
- 5.4.2. Метод составления уравнений для цепи наиболее общего вида.
- 5.4.3. Соединение цепей посредством проводников.
- 5.4.4. Соединение цепей посредством магнитопроводов.
- 5.4.5. Анализ эквивалентных цепей.
- 5.4.6. Цепи с внешним питанием.
- 5.5. ПРИМЕНЕНИЕ ТЕНЗОРНОГО ИСЧИСЛЕНИЯ К ИЗУЧЕНИЮ АНИЗОТРОПНЫХ СРЕД
- 5.5.2. Диэлектрические свойства кристалла.
- 5.5.3. Матрицы преобразования для некоторых часто встречающихся систем координат.
- Механические свойства кристалла
- 5.5.8. Применение шестимерного пространства.
- 5.5.9. Модуль Юнга.
- Пьезоэлектричество
- 5.5.10. Электрическая поляризация.
- 5.5.11. Закон Кюри.
- 5.5.12. Пьезоэлектрические свойства кварца.
- 5.5.13. Распространение упругих волн в кристаллах.
- 5.5.14. Плоские волны.
- ГЛАВА VI. МЕТОДЫ ИНТЕГРИРОВАНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 6.1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 6.1.2. Уравнения с разделяющимися переменными.
- 6.1.3. Однородные уравнения.
- 6.1.4. Уравнение в полных дифференциалах.
- 6.1.5. Линейное уравнение.
- 6.1.6. Уравнение Бернулли.
- 6.1.7. Уравнение Риккати.
- 6.1.8. Уравнение Лагранжа.
- 6.1.9. Уравнение Клеро.
- 6.1.10. Общий случай f(x,y,dy/dx)=0
- 6.2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПОРЯДКА ВЫШЕ ПЕРВОГО
- Линейное дифференциальное уравнение n-го порядка
- 6.2.9. Уравнение Эйлера.
- 6.2.10. Интегрирование при помощи степенных рядов.
- 6.2.11. Некоторые теоремы о свойствах решений линейного дифференциального уравнения второго порядка.
- Интегрирование линейных дифференциальных уравнений с постоянными коэффициентами
- 6.3. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
- 6.3.1. Линейное уравнение с постоянными коэффициентами, однородное относительно частных производных.
- 6.3.2. Уравнение с правой частью.
- 6.3.3. Уравнение колебаний струны.
- 6.3.4. Телеграфное уравнение.
- 6.3.5. Уравнение Лапласа.
- 6.3.6. Прямоугольная система координат.
- 6.3.7. Система цилиндрических координат.
- 6.3.8. Система сферических координат.
- 6.3.9. Система эллиптических цилиндрических координат.
- 6.3.10. Система параболических цилиндрических координат.
- 6.3.11. Другие системы координат.
- 6.3.12. Уравнение Пуассона.
- 6.3.13. Решение уравнений Максвелла методом Бромвича.
- 6.3.14. Пример. Электромагнитные колебания в прямоугольной полости.
- ГЛАВА VII. НАИБОЛЕЕ УПОТРЕБИТЕЛЬНЫЕ СПЕЦИАЛЬНЫЕ ФУНКЦИИ
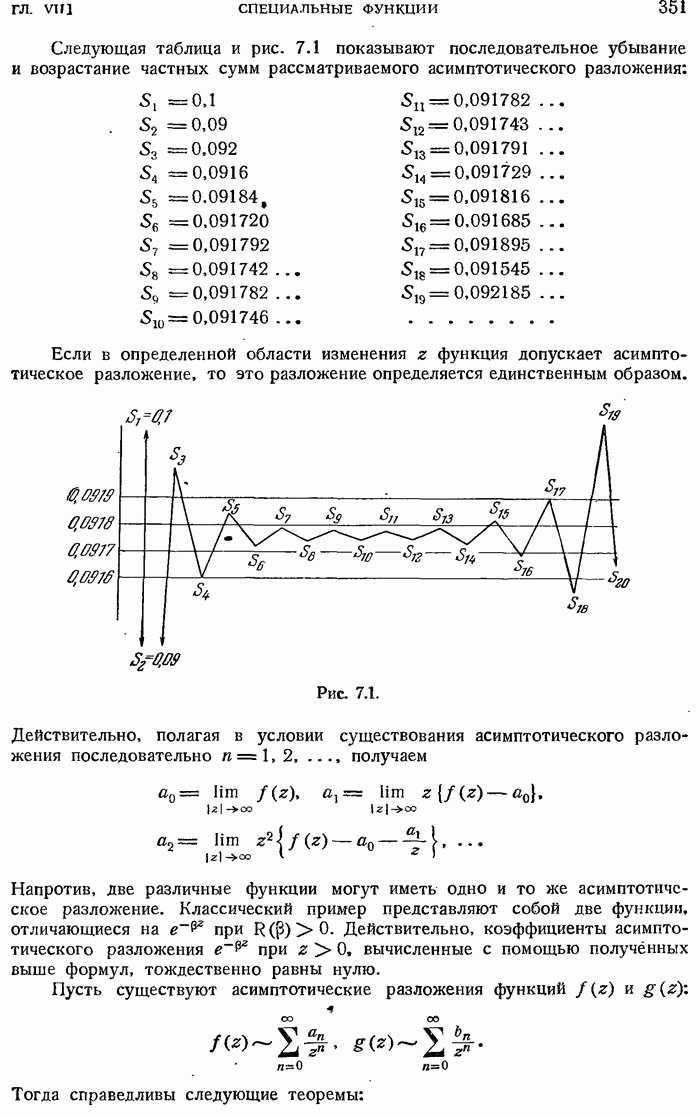
- 7.0.1. Асимптотическое разложение.
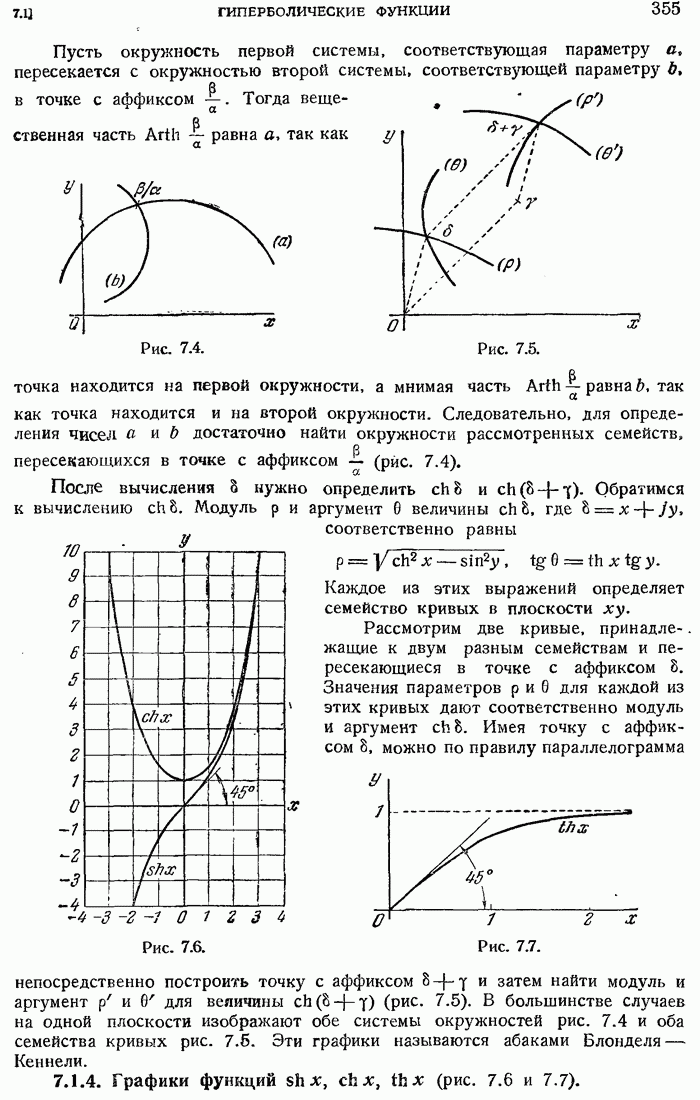
- 7.1. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
- 7.1.2. Обратные гиперболические функции.
- 7.1.3. Приложение гиперболических функций к расчету длинных линий. Метод Броуна. Абаки Блонделя — Кеннеди.
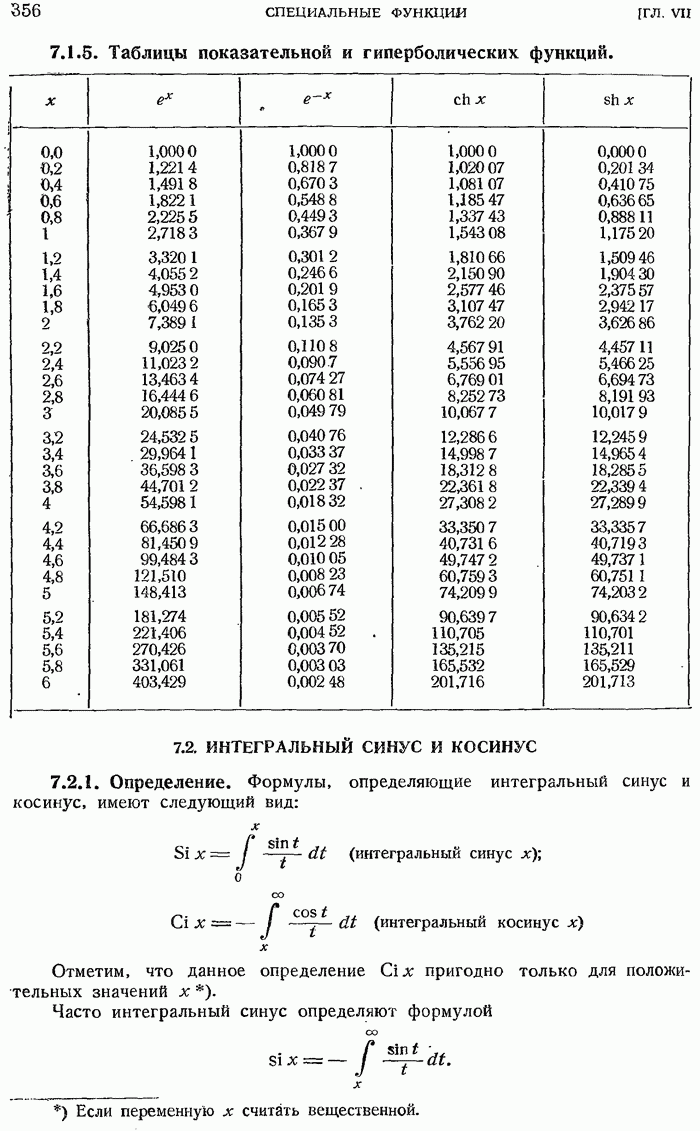
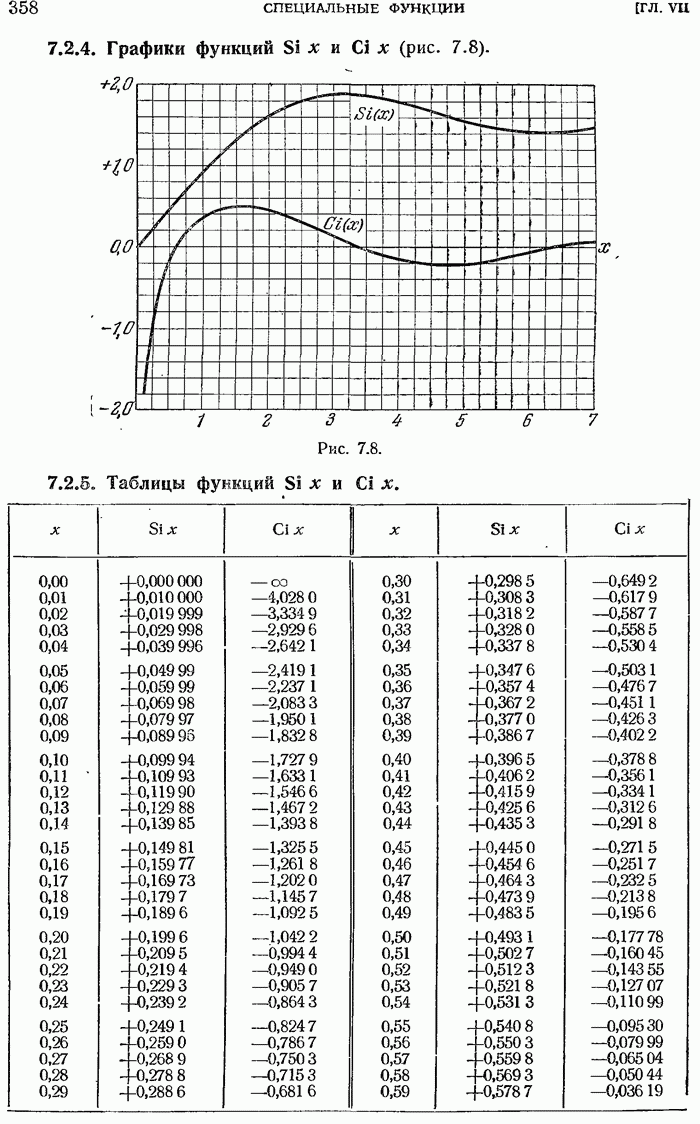
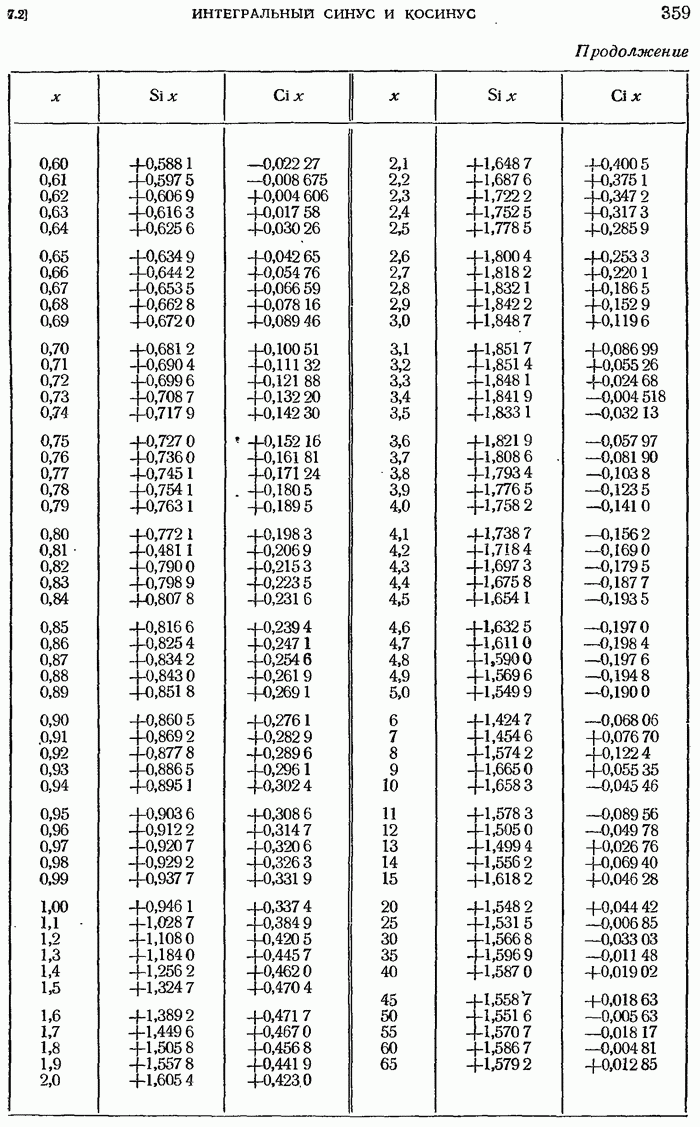
- 7.2. ИНТЕГРАЛЬНЫЙ СИНУС И КОСИНУС
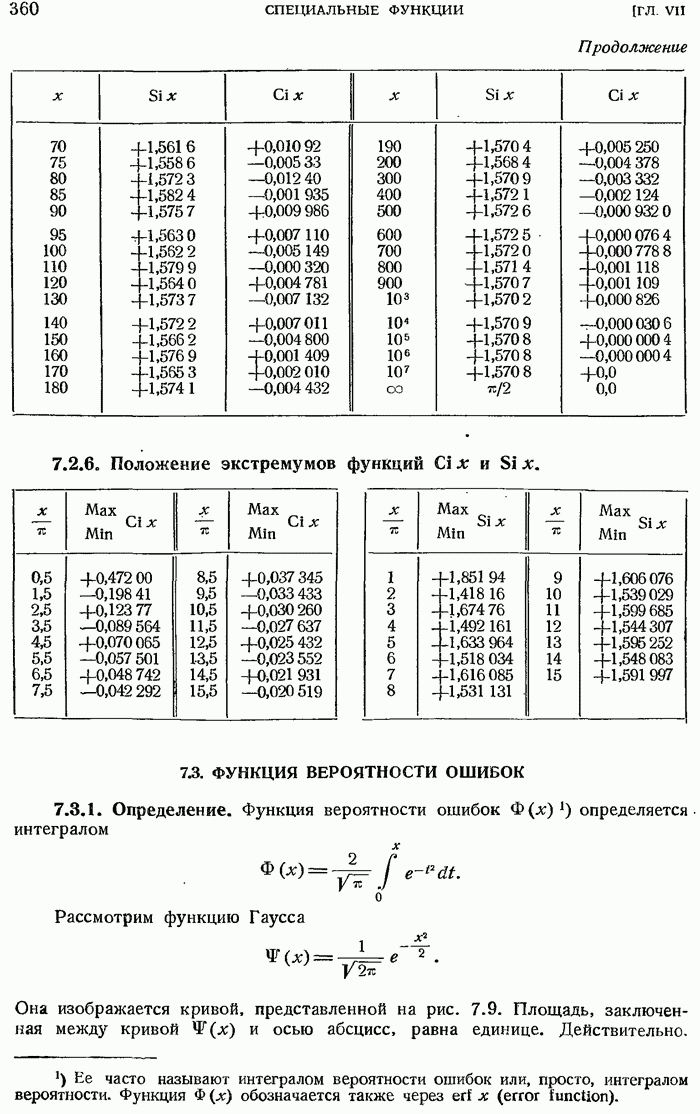
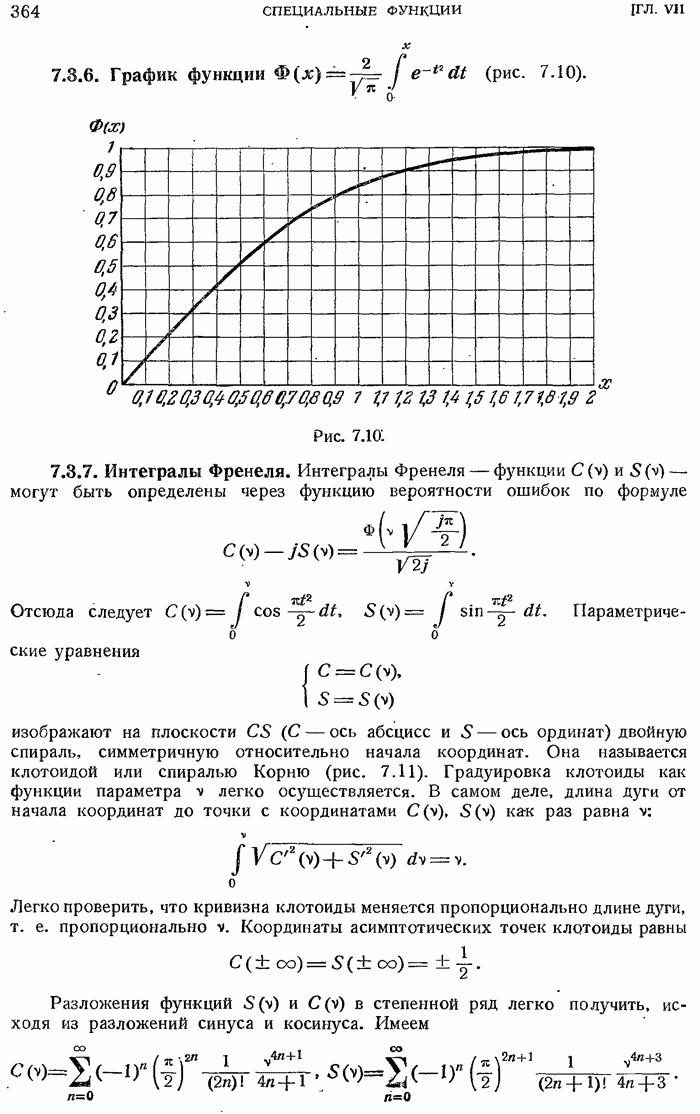
- 7.3. ФУНКЦИЯ ВЕРОЯТНОСТИ ОШИБОК
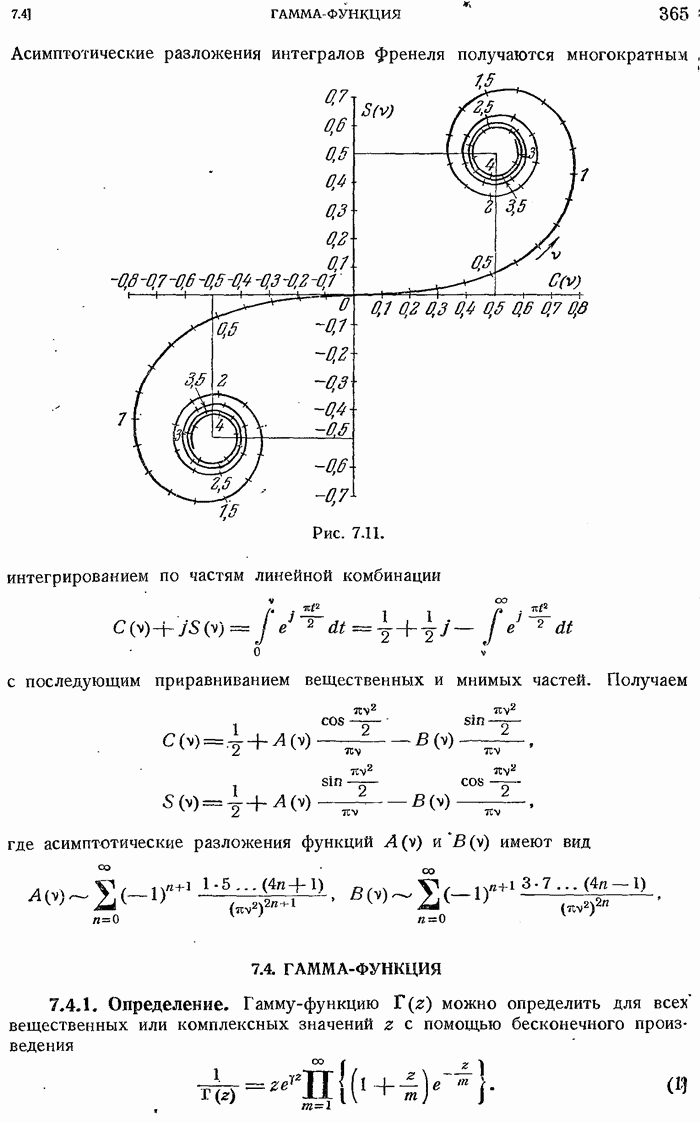
- 7.3.7. Интегралы Френеля.
- 7.4. ГАММА-ФУНКЦИЯ
- 7.4.2. Свойства гамма-функции.
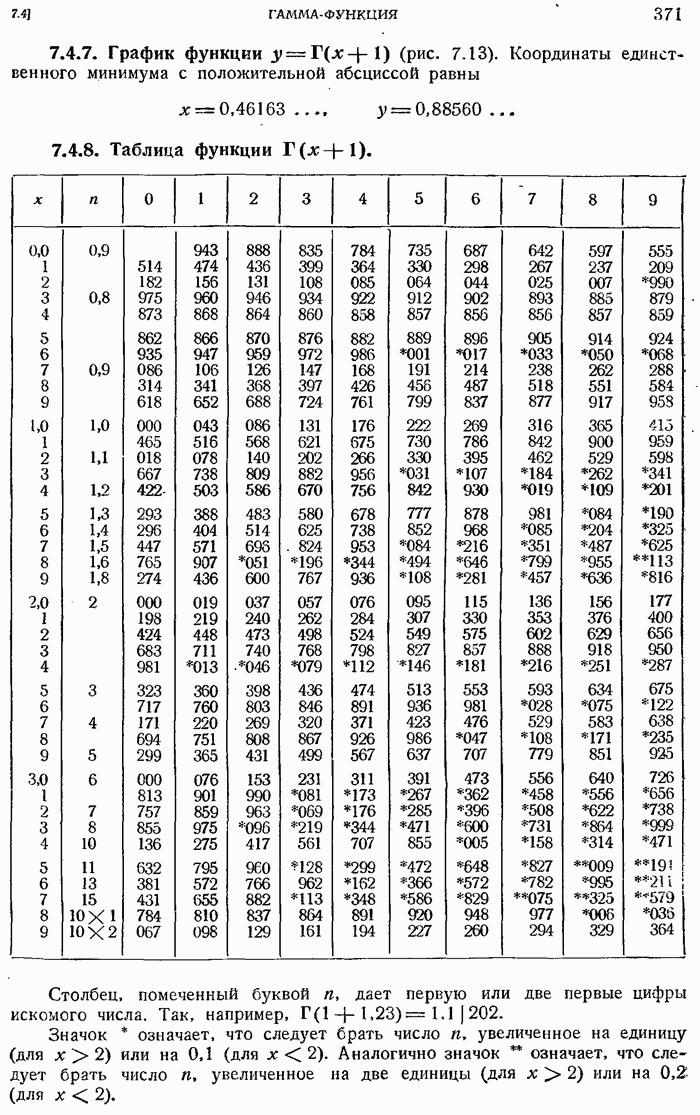
- 7.4.3. Некоторые значения функции Г(z).
- 7.4.4. Логарифмическая производная гамма-функции.
- 7.4.5. Представление гамма-функции через интеграл Коши.
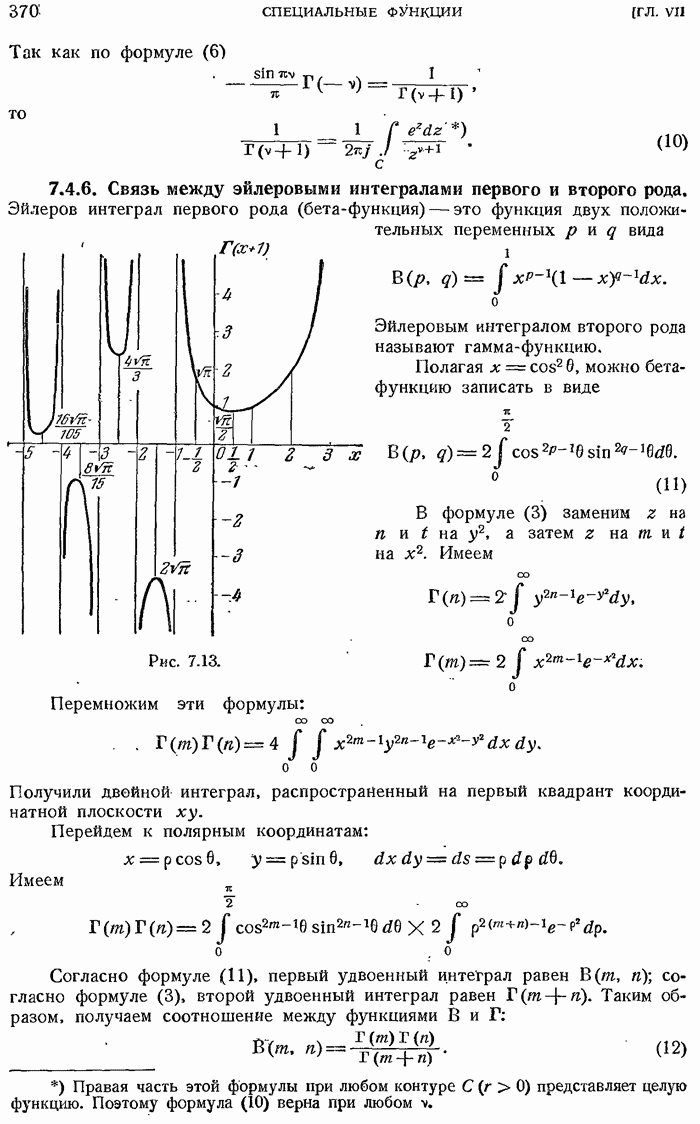
- 7.4.6. Связь между эйлеровыми интегралами первого и второго рода.
- 7.5. ФУНКЦИИ БЕССЕЛЯ
- Функции Бесселя первого и второго рода
- 7.5.6. Интегралы Ломмеля.
- 7.5.7. Соотношение между двумя функциями, индексы которых отличаются на целое число.
- 7.5.8. Применение интегралов Ломмеля к разложению в ряд по бесселевым функциям.
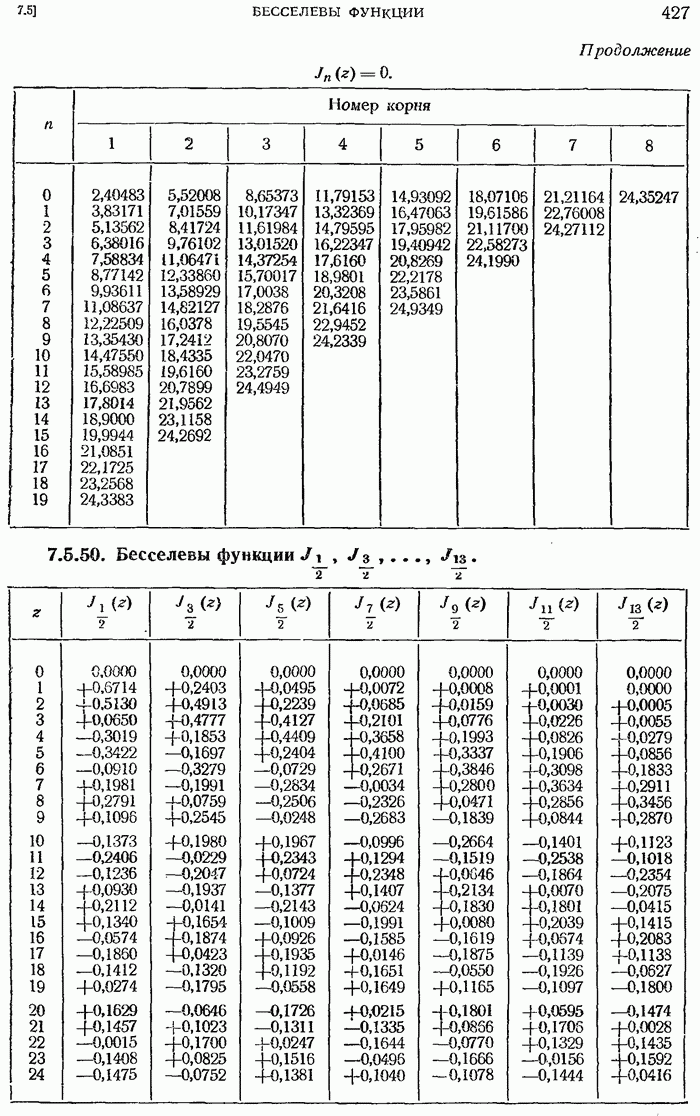
- 7.5.9. Бесселевы функции первого и второго рода с полуцелым индексом.
- 7.5.10. Применение бесселевых функций к вычислению интегралов Френеля.
- 7.5.11. Случай, когда индекс равен целому числу v=n
- 7.5.12. Представление Jv(z) через определенный интеграл.
- 7.5.13. Представление Jv(z) с помощью интеграла Коши.
- 7.5.14. Теорема сложения.
- 7.5.15. Бесселевы функции третьего рода или функции Ханкеля. Определение.
- 7.5.17. Нахождение численных значений бесселевых функций.
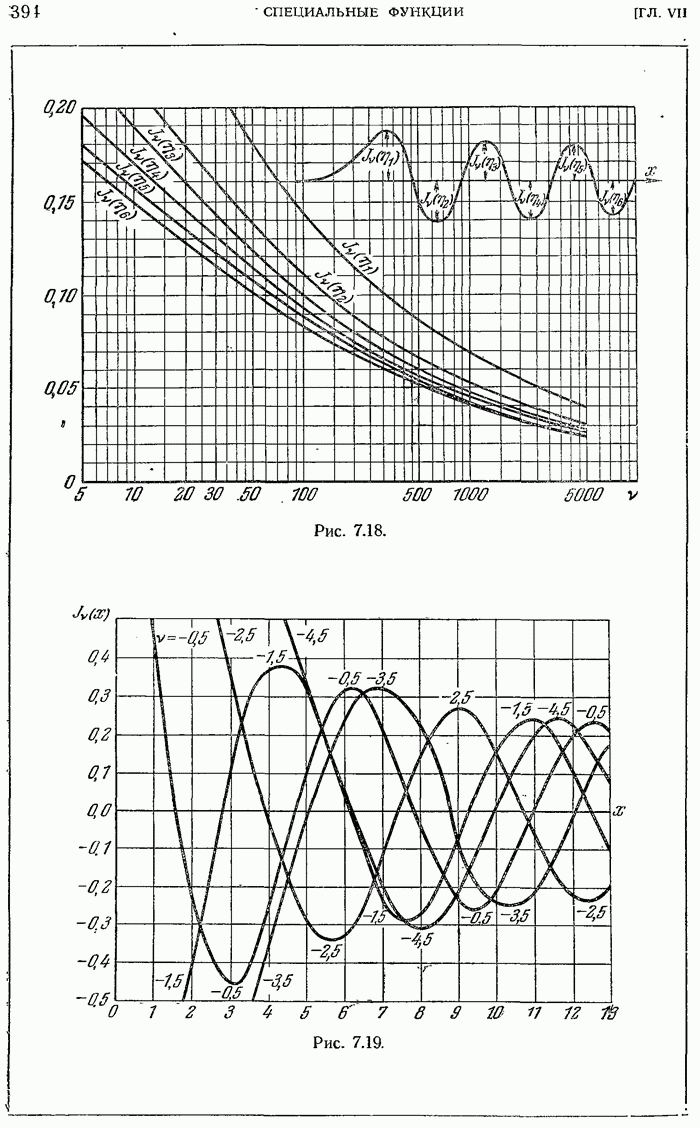
- 7.5.18. Асимптотические выражения для бесселевых функций при больших значениях аргумента.
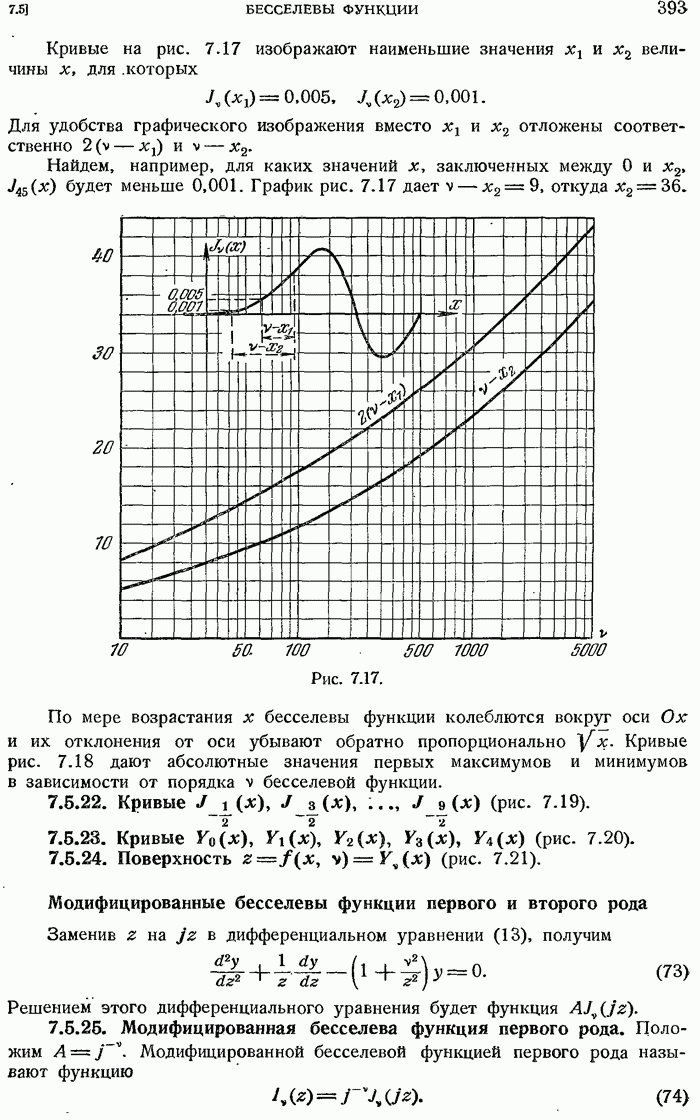
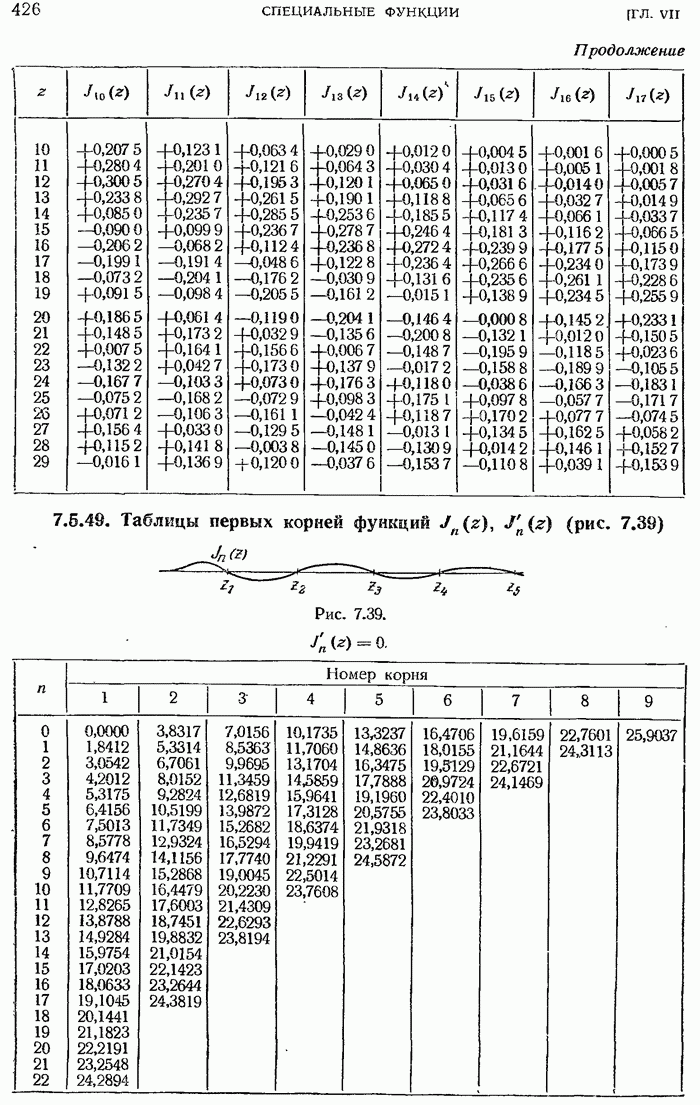
- 7.5.19. Корни бесселевых функций.
- Модифицированные бесселевы функции первого и второго рода
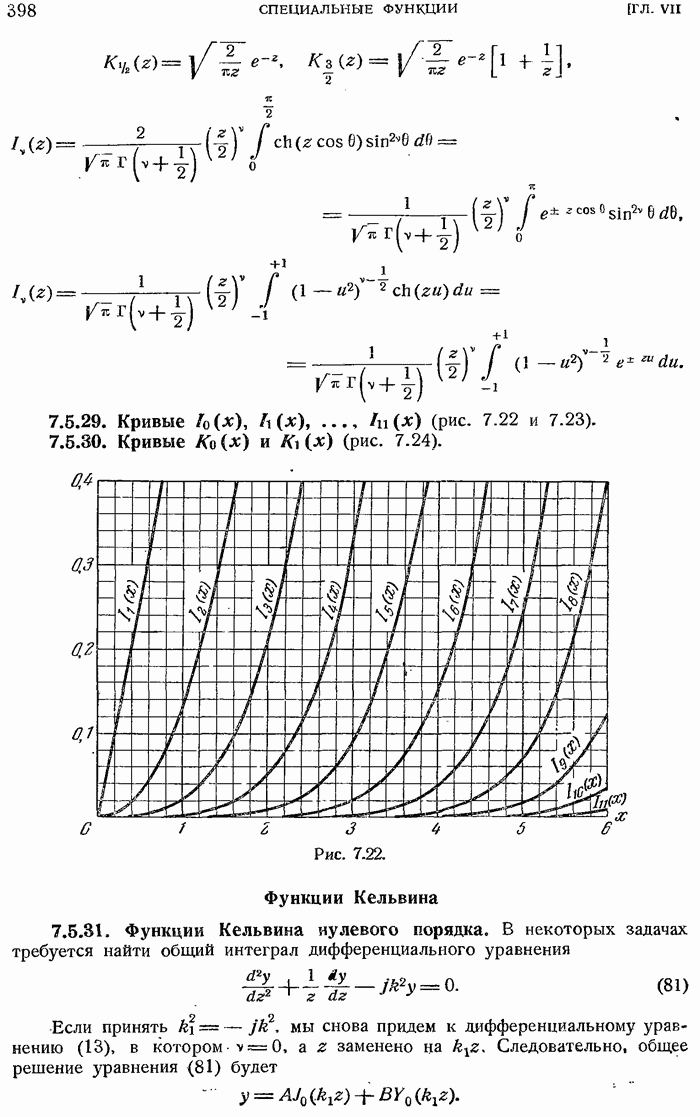
- 7.5.26. Модифицированная бесселева функция второго рода.
- 7.5.27. Асимптотические разложения.
- 7.5.28. Рекуррентные формулы.
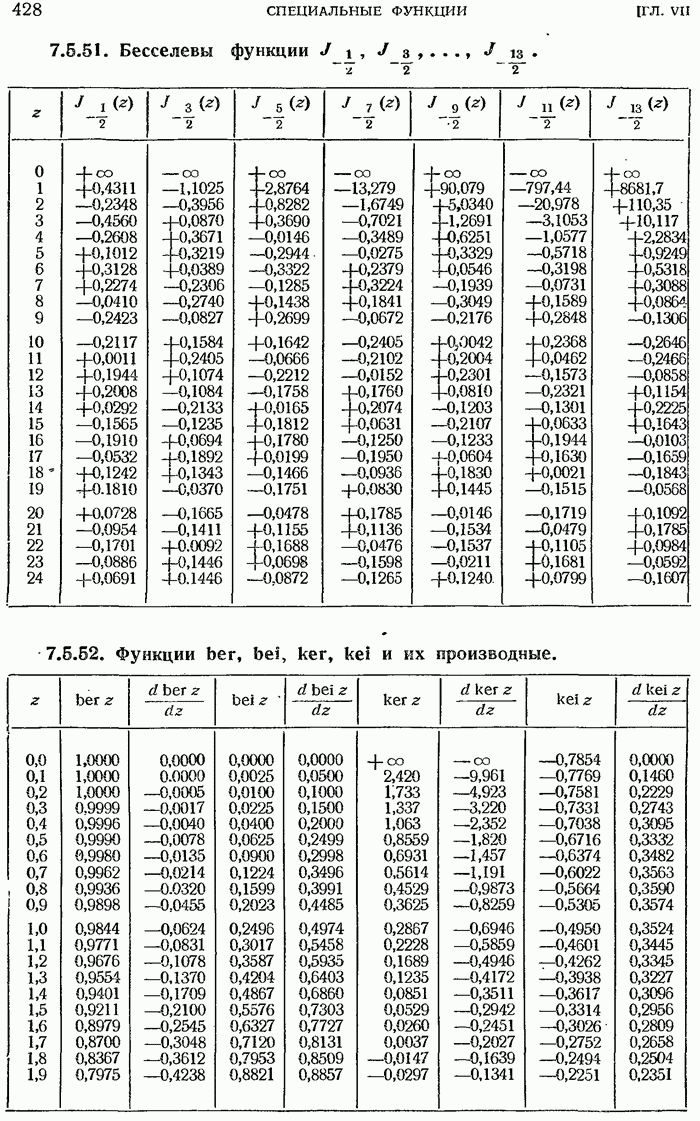
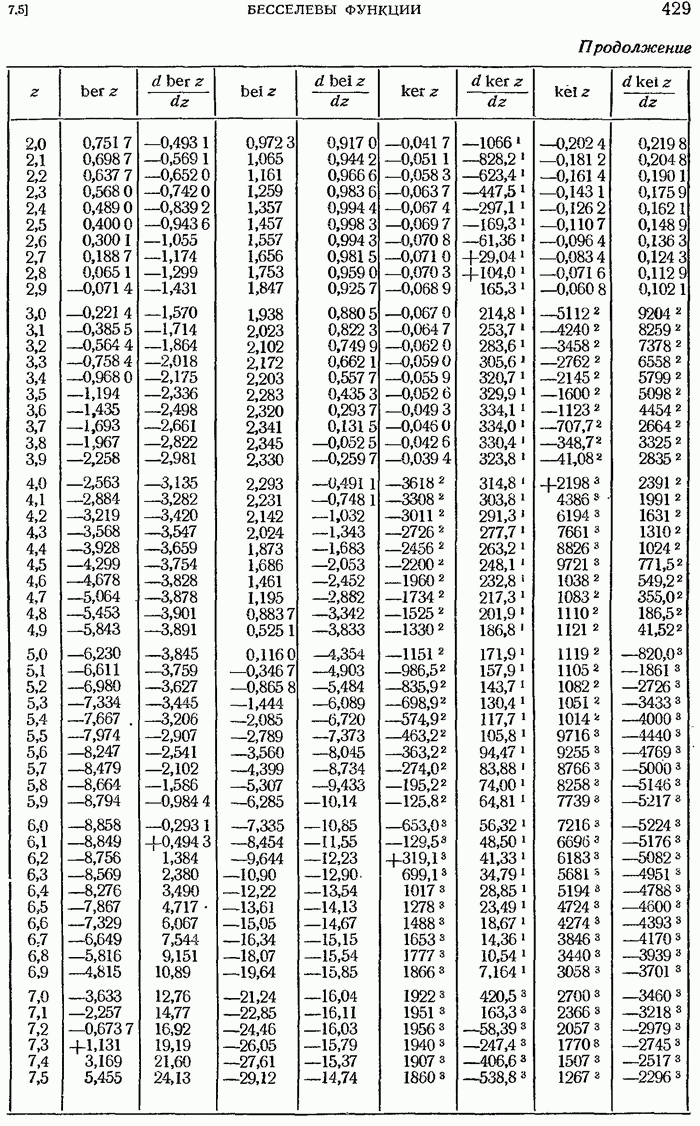
- Функции Кельвина
- 7.5.32. Функция Кельвина v-го порядка.
- 7.5.33. Представление функций Кельвина через модуль и аргумент.
- 7.5.34. Производные функций Кельвина.
- Дифференциальные уравнения, решение которых может быть выражено через решение дифференциального уравнения Бесселя
- Некоторые примеры применения бесселевых функций
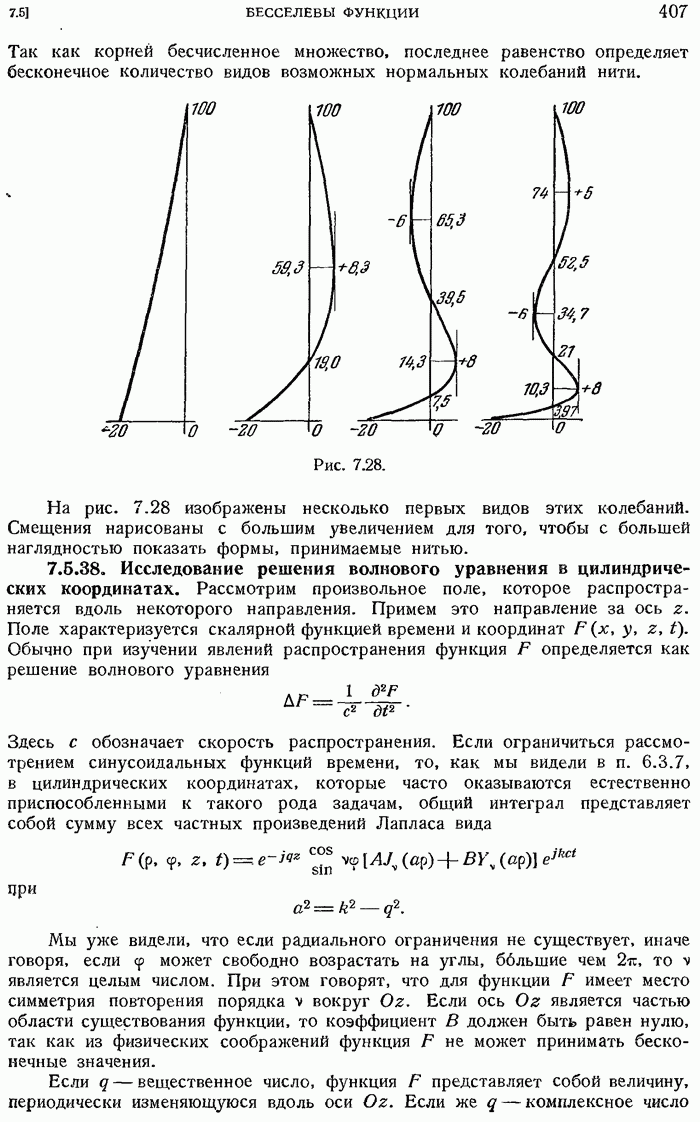
- 7.5.38. Исследование решения волнового уравнения в цилиндрических координатах.
- 7.5.39. Колебания равномерно натянутой мембраны.
- 7.5.40. Случай круглой мембраны.
- 7.5.41. Собственные электромагнитные колебания резонатора, имеющего форму кругового цилиндра.
- 7.5.42. Распространение электромагнитной волны внутри бесконечного кругового цилиндра.
- 7.5.43. Случай коаксиального проводника.
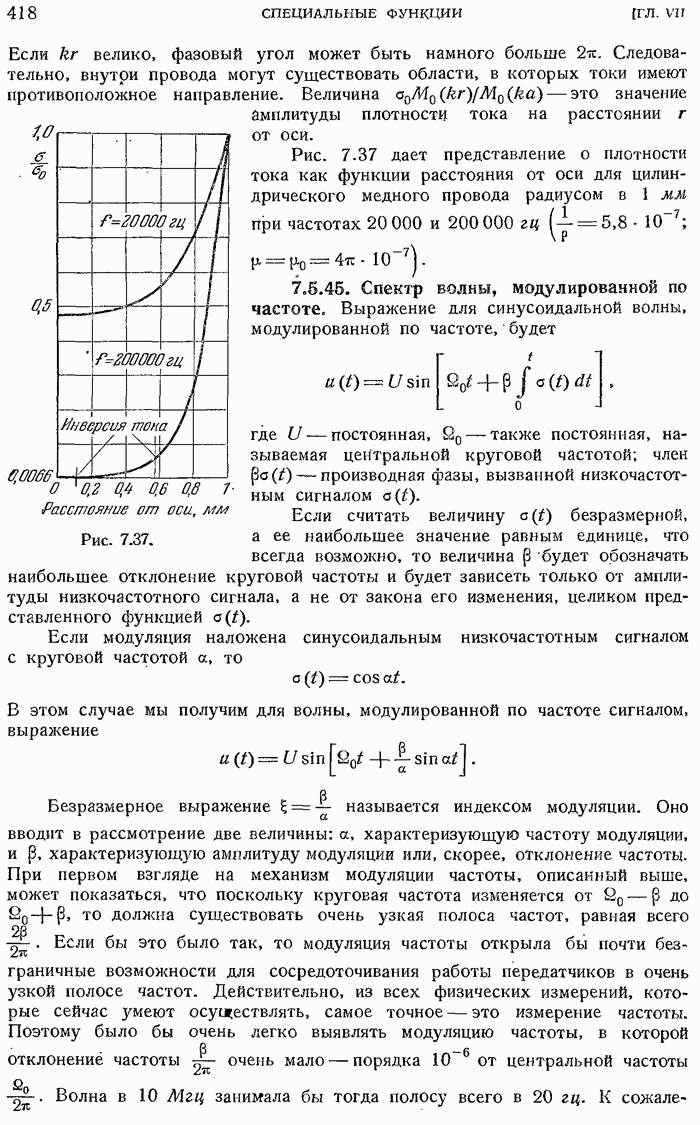
- 7.5.44. Скин-эффект переменных токов, проходящих по цилиндрическому проводнику круглого сечения.
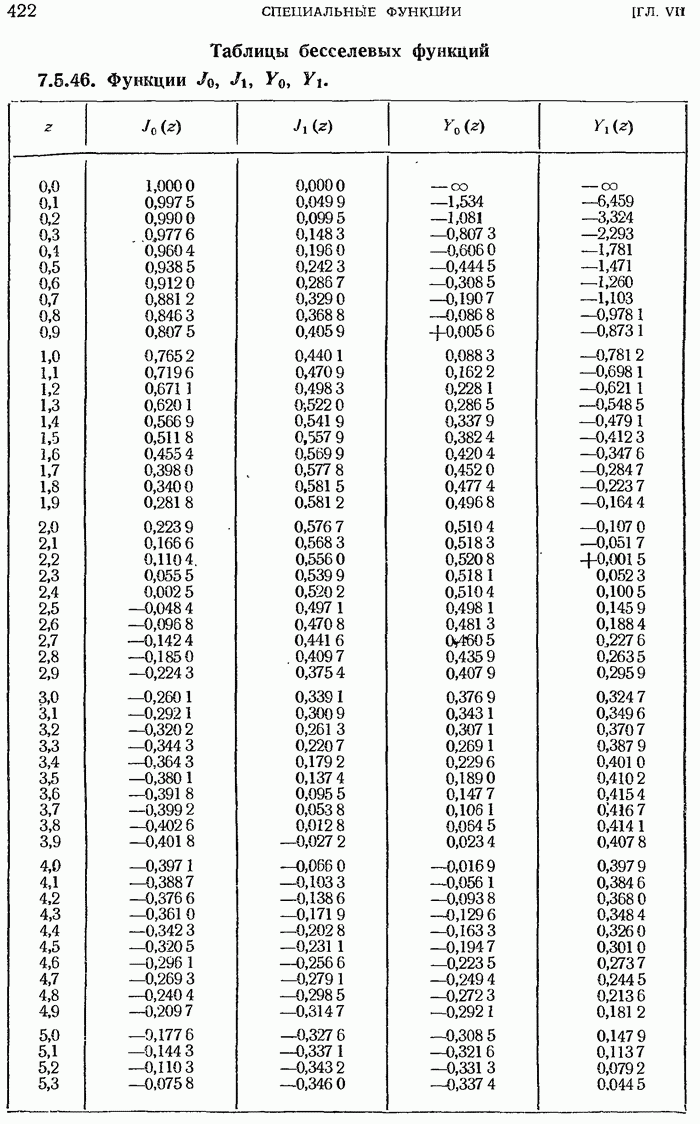
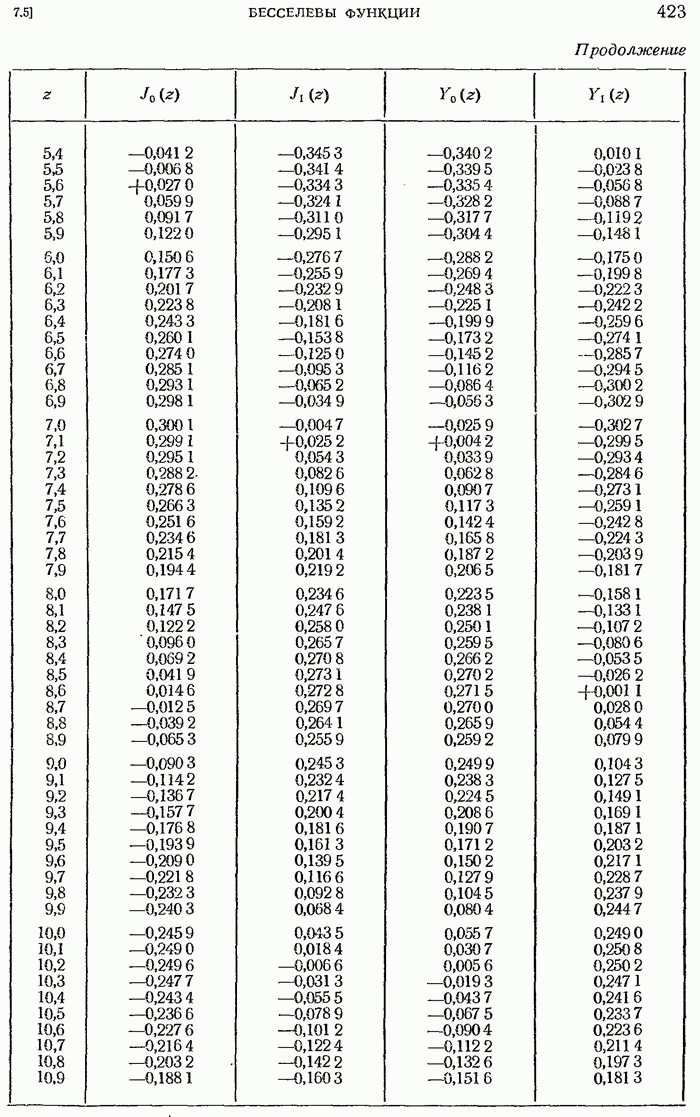
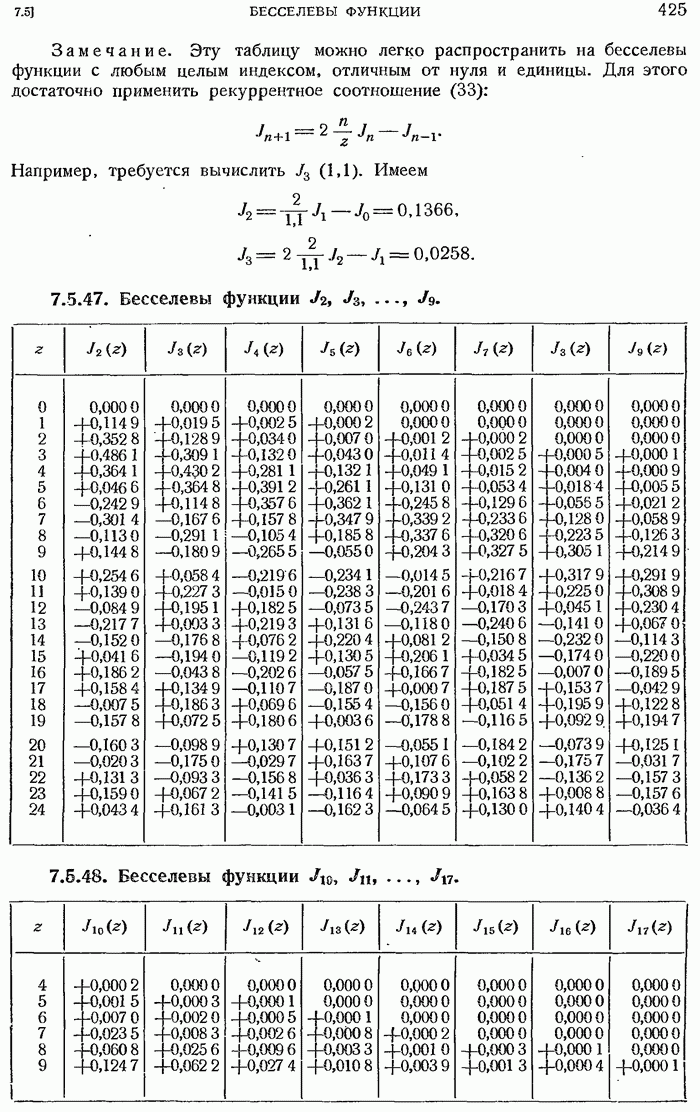
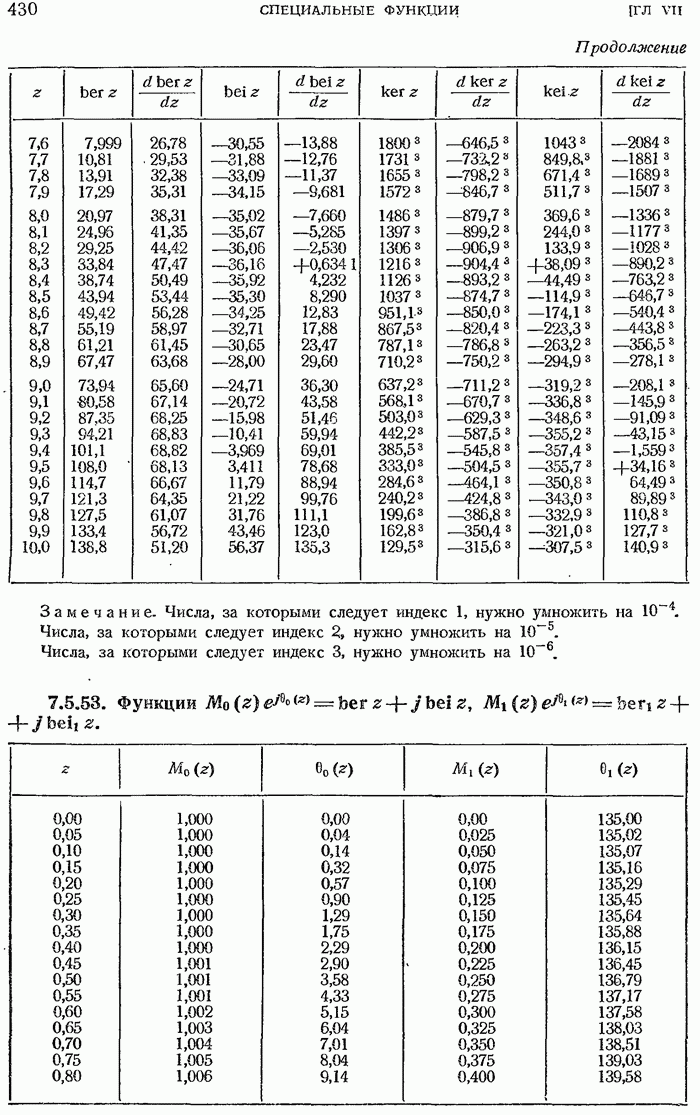
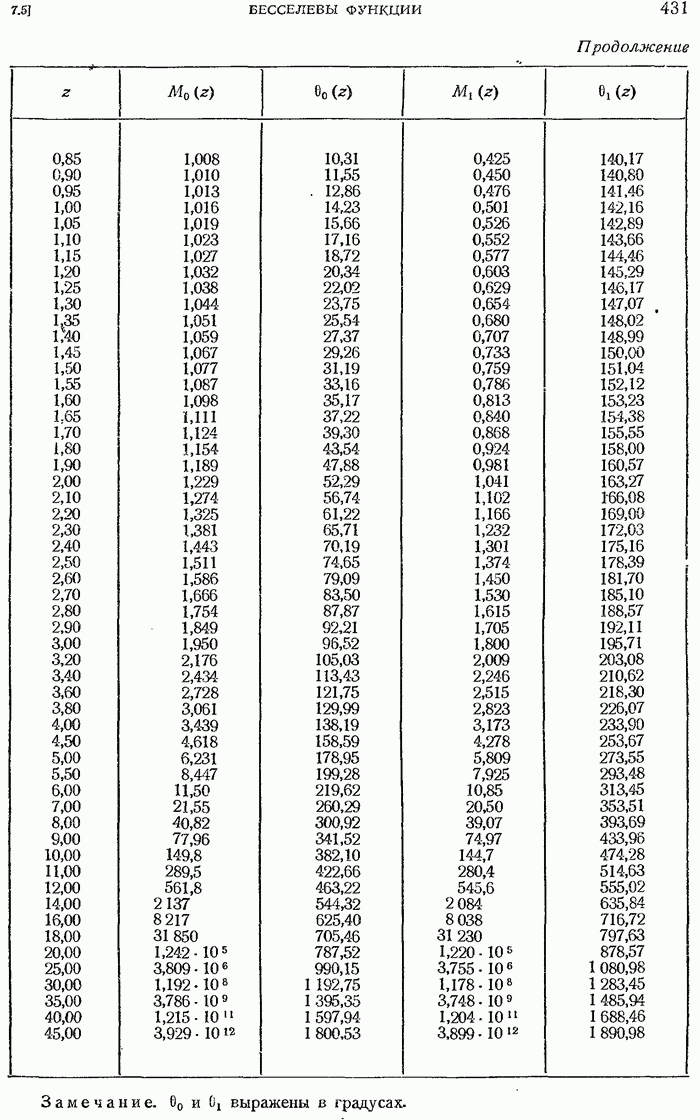
- Таблицы бесселевых функций
- 7.6. ФУНКЦИИ ЛЕЖАНДРА
- 7.6.3. Полиномы Лежандра.
- 7.6.4. Производящая функция полиномов Лежандра.
- 7.6.6. Представление полиномов Лежандра через определенный интеграл. Формула Лапласа.
- 7.6.8. Формула Родрига.
- 7.6.9. Ортогональность полиномов Лежандра.
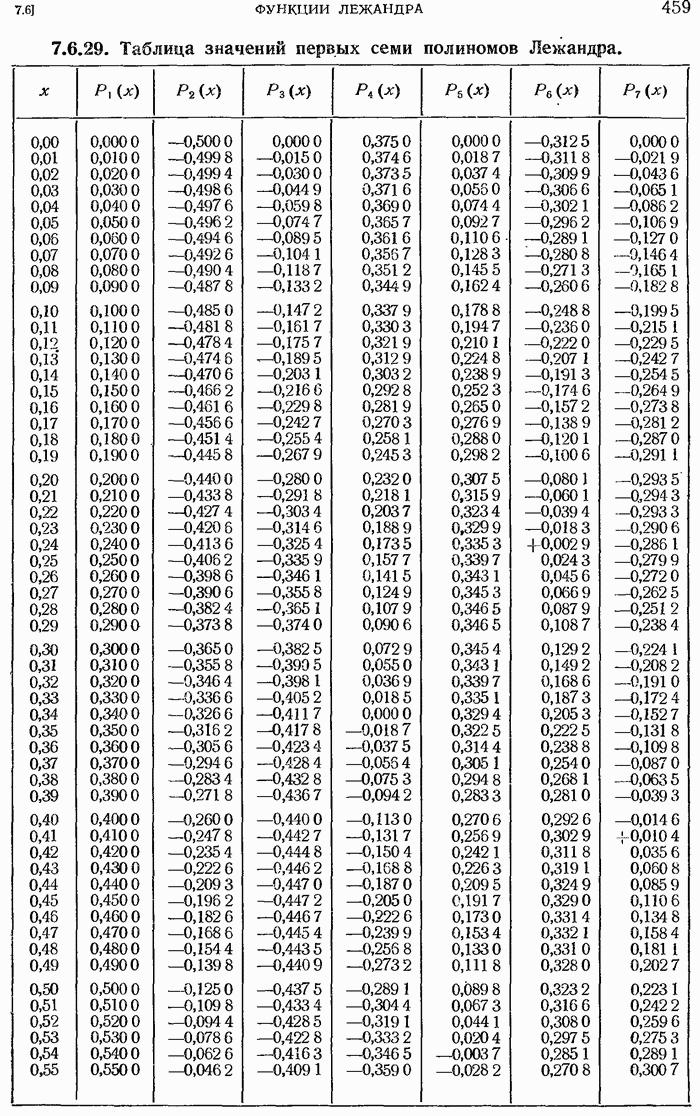
- 7.6.10. Некоторые значения полиномов Лежандра.
- 7.6.11. Корни полиномов Лежандра.
- 7.6.12. Интеграл Шлефли.
- 7.6.13. Обобщение полиномов Лежандра. Полиномы Гегенбауера.
- 7.6.14. Функции Лежандра первого рода.
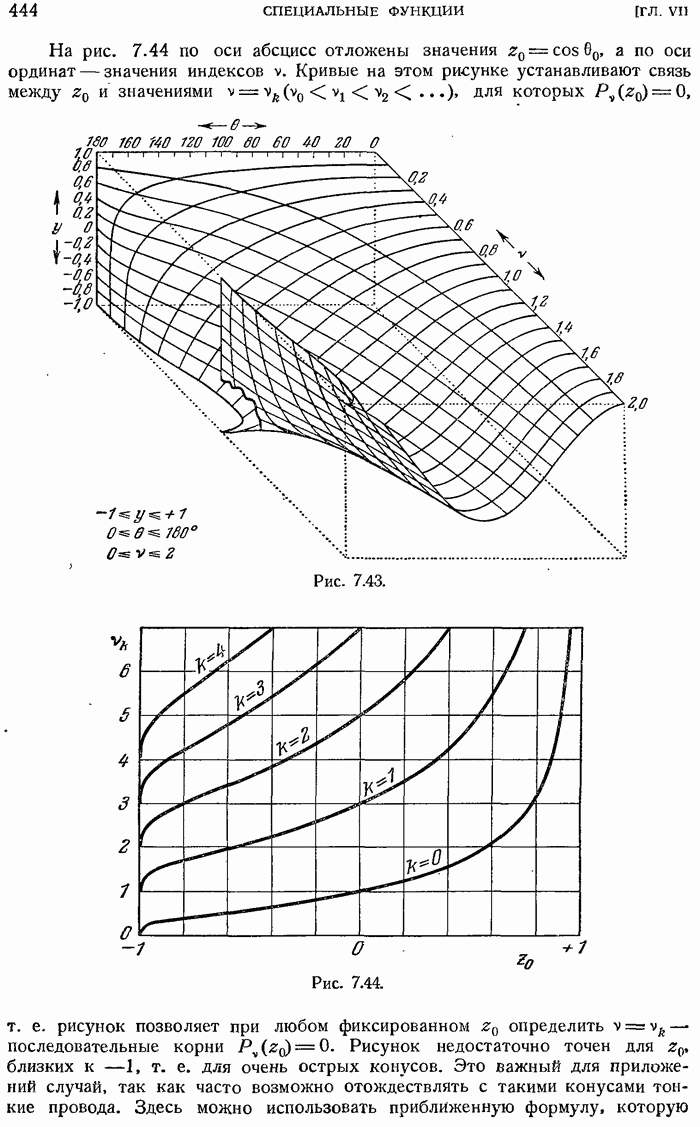
- 7.6.16. Корни функций Лежандра первого рода.
- 7.6.18. Определение функции Лежандра первого рода через интеграл Коши.
- 7.6.19. Функция Лежандра второго рода.
- 7.6.20. Определение функции Лежандра второго рода через интеграл Коши.
- 7.6.21. Присоединенные функции Лежандра.
- 7.6.22. Присоединенные функции Лежандра для целых положительных индексов.
- 7.6.24. Ортогональность присоединенных функций Лежандра.
- 7.6.25. Некоторые значения присоединенных функций Лежандра.
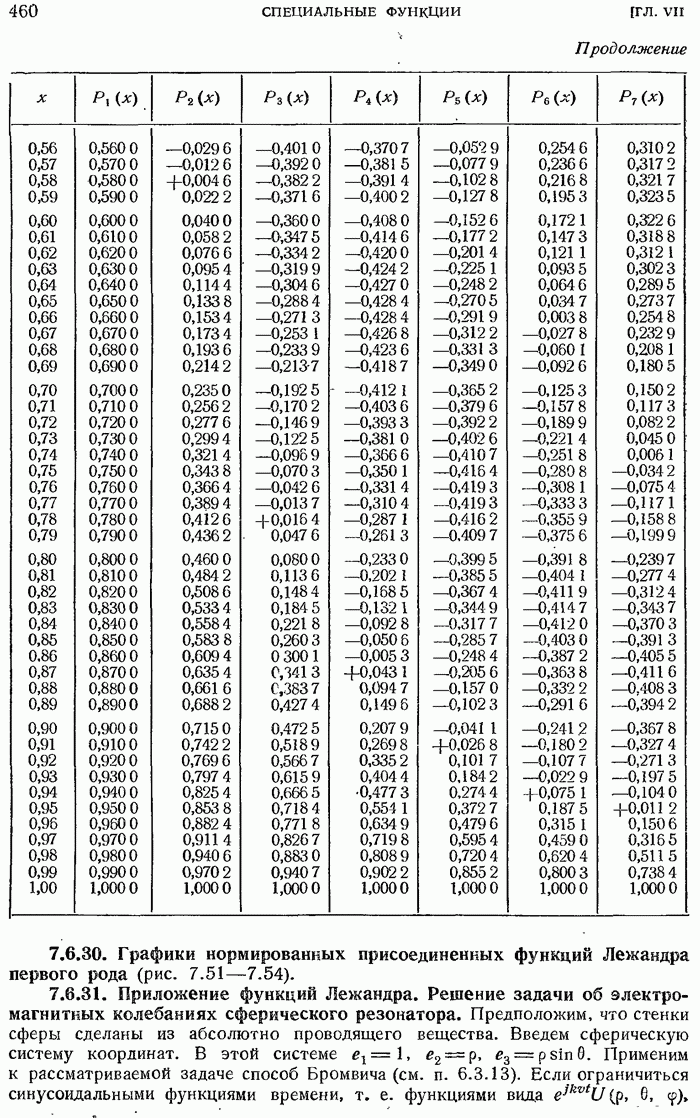
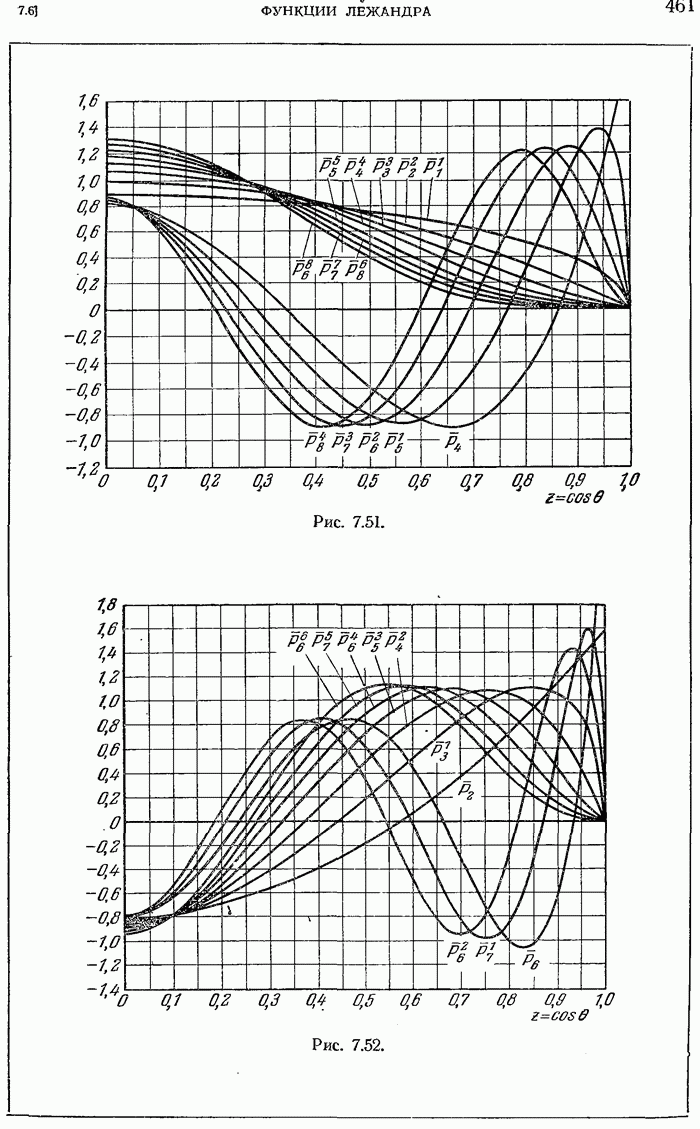
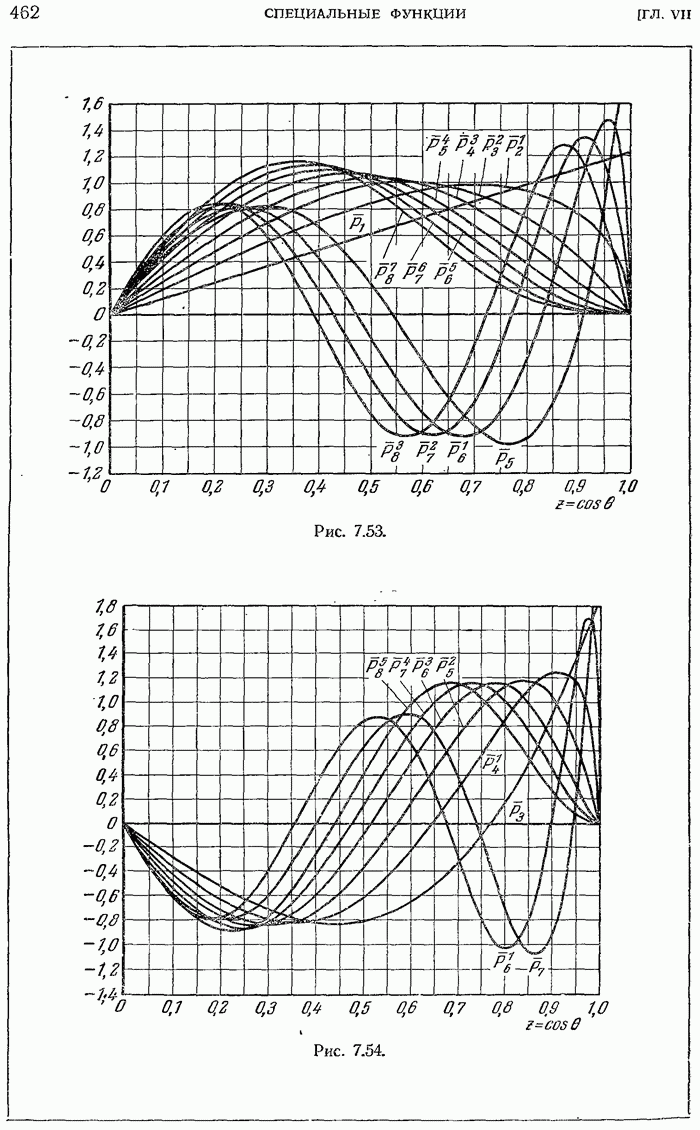
- 7.6.26. Сферические гармоники.
- 7.6.25. Некоторые значения присоединенных функций Лежандра.
- 7.6.31. Приложение функций Лежандра. Решение задачи об электромагнитных колебаниях сферического резонатора.
- 7.7. ФУНКЦИИ МАТЬЕ
- 7.7.2. Ортогональность функций Матье первого рода.
- Функции Матье: 7.7.3. Разложение в ряд Фурье.
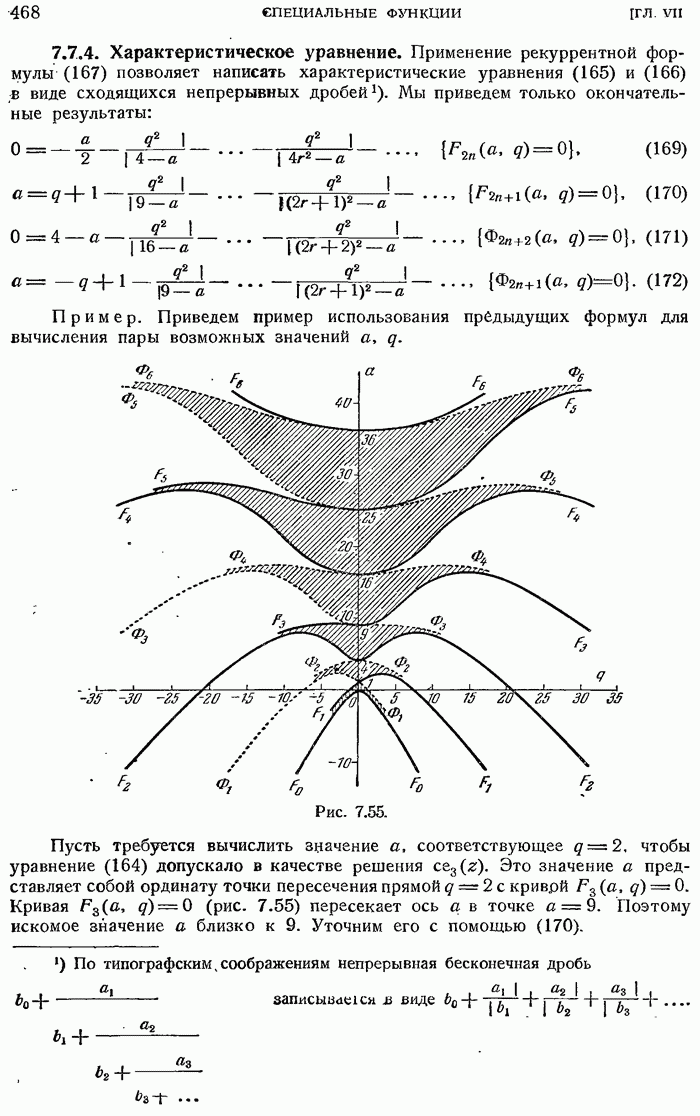
- Функции Матье: 7.7.4. Характеристическое уравнение.
- Функции Матье: 7.7.5. Поведение функций …
- 7.7.6. Присоединенные функции Матье первого рода.
- 7.7.7. Функции Матье для произвольных а и q.
- 7.7.8. Разложение в ряды по бесселевым функциям.
- 7.7.9. Функции Матье второго рода.
- 7.8. ФУНКЦИИ ВЕБЕРА — ЭРМИТА. ПОЛИНОМЫ ЭРМИТА
- 7.8.2. Полиномы Эрмита.
- 7.8.3. Производящая функция и ортогональность полиномов Эрмита.
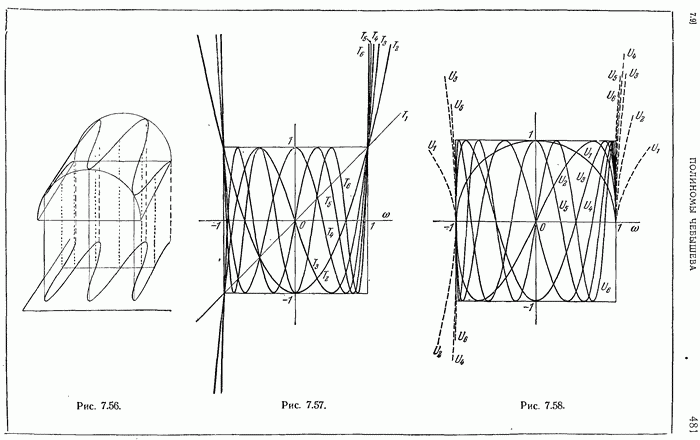
- 7.9. ПОЛИНОМЫ ЧЕБЫШЕВА
- 7.9.3. Основные свойства полиномов Чебышева.
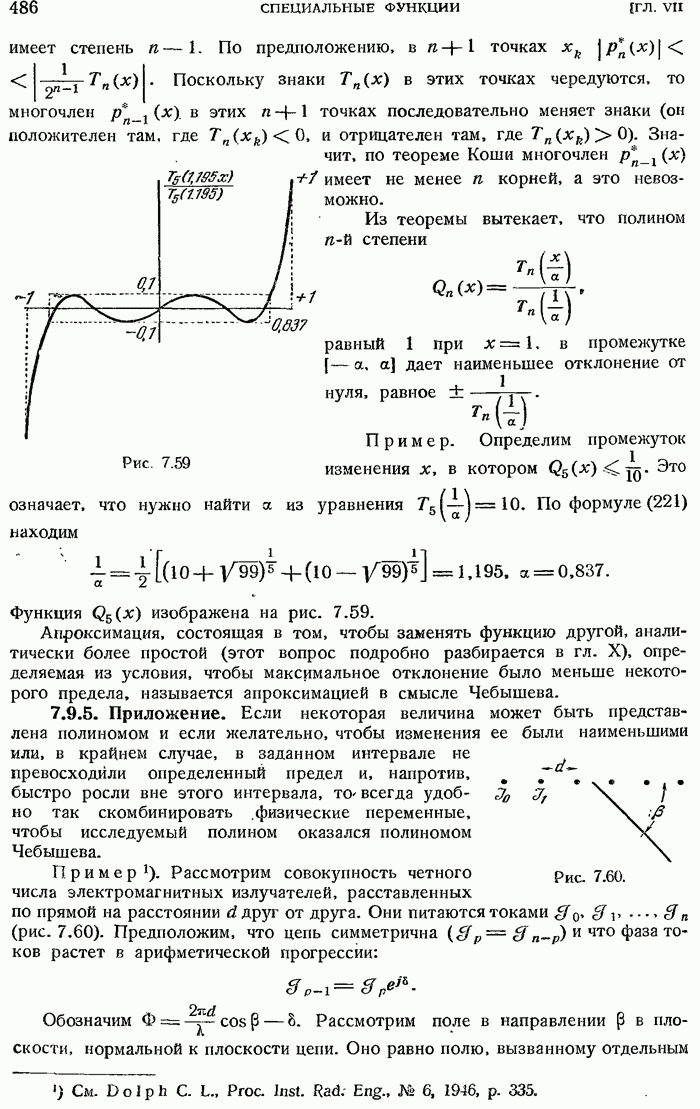
- 7.9.4. Фундаментальное свойство полиномов Чебышева.
- 7.9.5. Приложение.
- ГЛАВА VIII. СИМВОЛИЧЕСКОЕ ИЛИ ОПЕРАЦИОННОЕ, ИСЧИСЛЕНИЕ
- 8.1.3. Расчет переходных режимов.
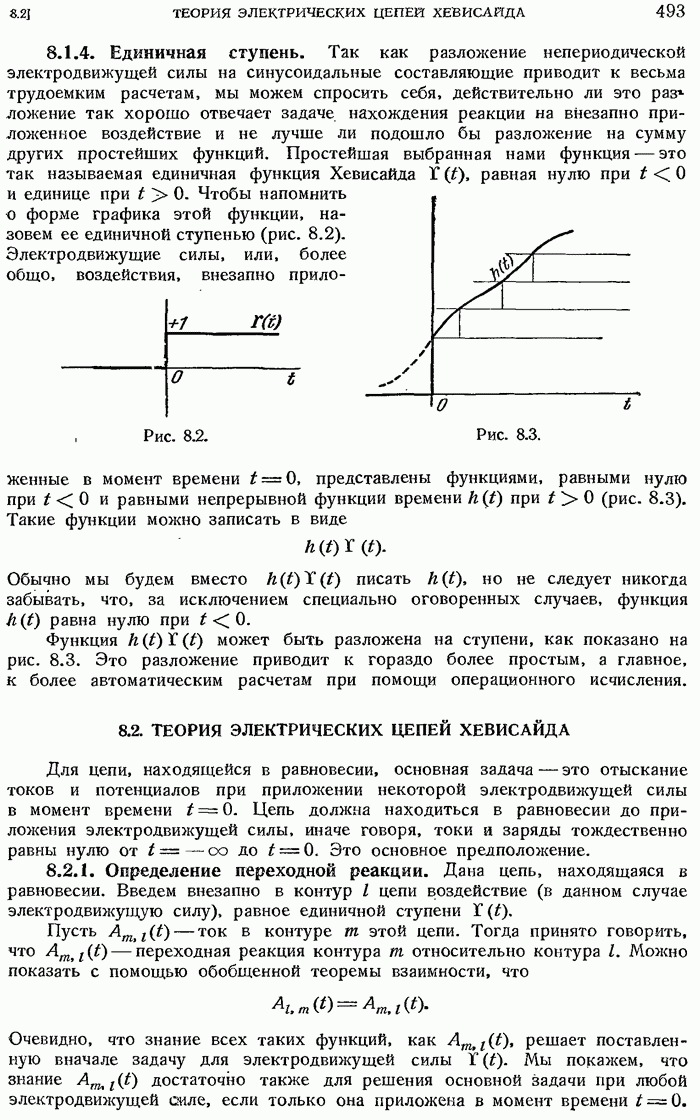
- 8.1.4. Единичная ступень.
- 8.2. ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ХЕВИСАЙДА
- 8.2.2. Вычисление переходной реакции.
- 8.3. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
- Правила операционного исчисления
- 8.3.10. Теорема свертывания, или теорема Бореля.
- 8.3.11. Различные формулы.
- 8.3.12. Теорема разложения Хевисайда.
- 8.3.13. Приложение теоремы разложения к электрическим цепям.
- 8.3.14. Случай переменного напряжения.
- 8.3.15. Случай кратных корней.
- Преобразование некоторых употребительных функций
- 8.3.16. Оригиналы некоторых рациональных функций.
- 8.3.17. Изображения бесселевых функций целого порядка.
- 8.3.18. Изображение ln t.
- 8.3.19. Изображение интегральных косинуса и синуса.
- 8.3.20. Изображение функции ошибок.
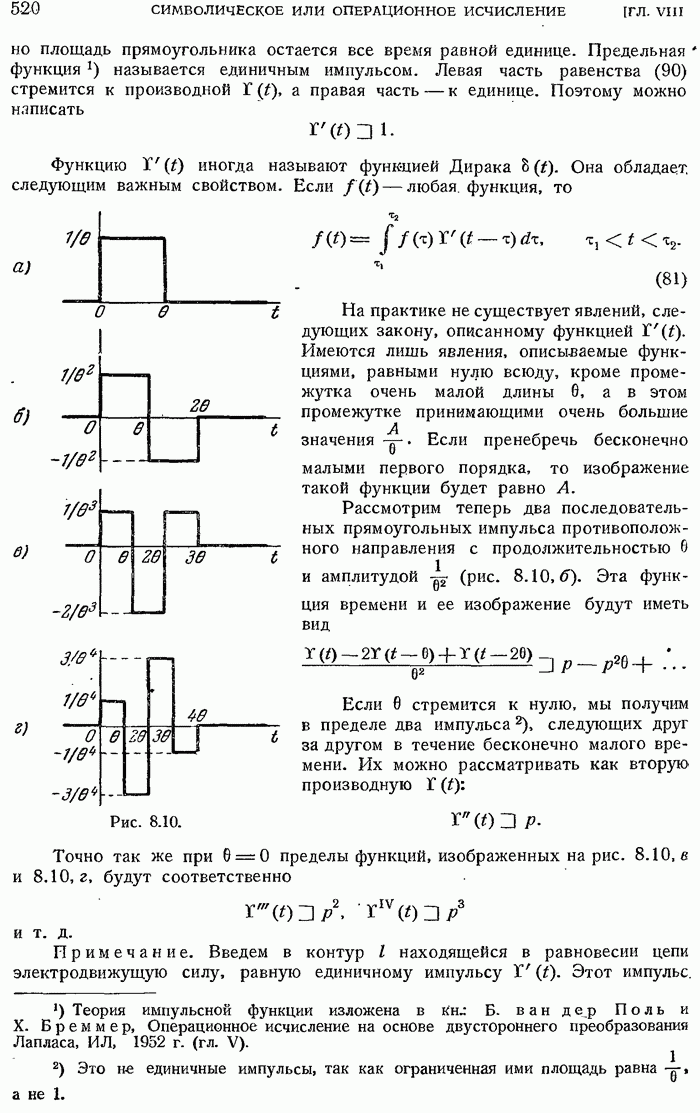
- 8.3.21. Изображение единичного импульса
- Применение формулы обращения
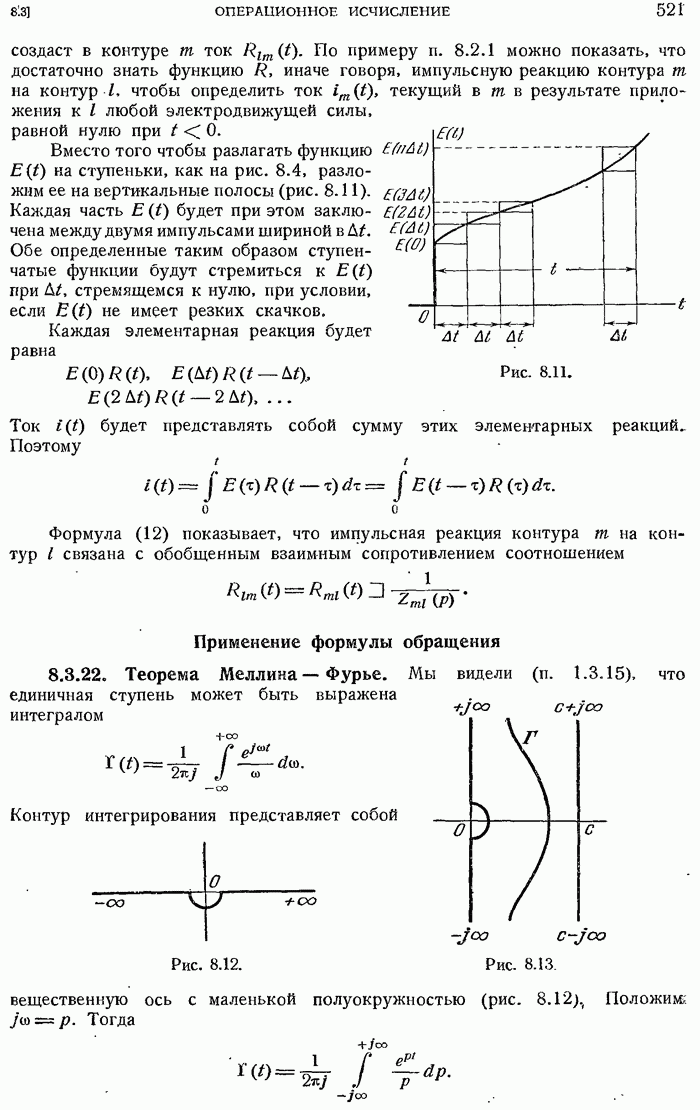
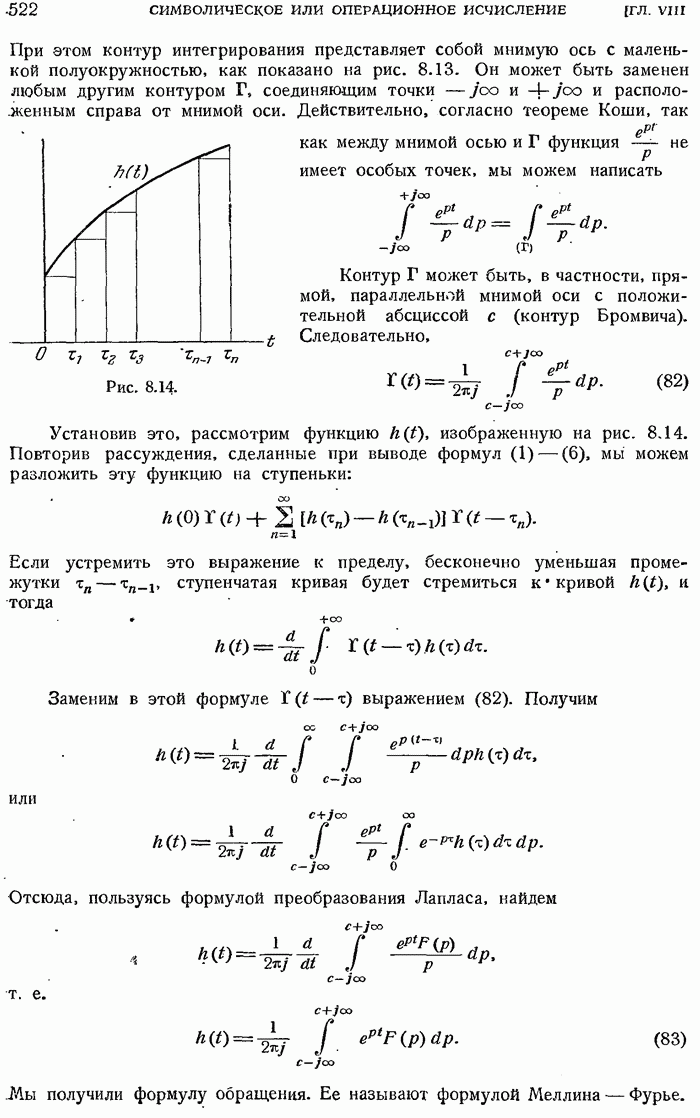
- 8.3.22. Теорема Меллина — Фурье.
- 8.3.23. Замечания о применении формулы обращения.
- 8.3.24. Обобщение теоремы разложения Хевисайда.
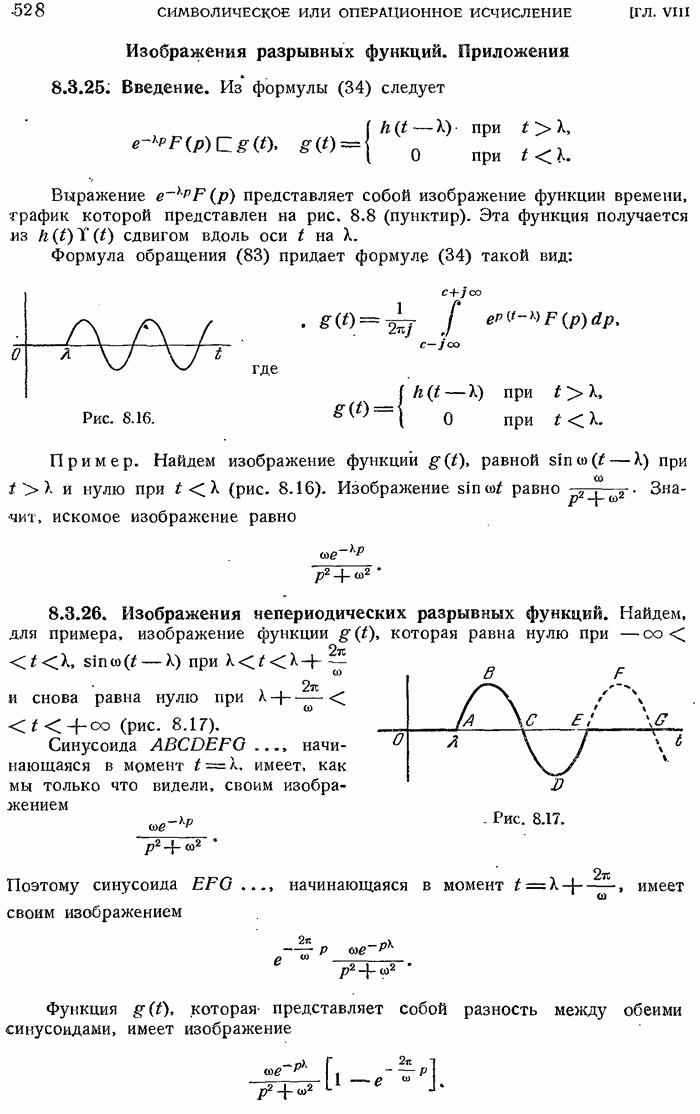
- Изображения разрывных функций. Приложения
- Таблица соответствия
- 8.4. ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ К ЭЛЕКТРИЧЕСКИМ ЦЕПЯМ
- 8.4.2. Пример применения к системе двух связанных контуров.
- 8.4.3. Случай, когда цепь не находится в равновесии в начальный момент времени.
- 8.4.4. Электрические фильтры.
- 8.4.5. Фильтр нижних частот.
- 8.4.6. Фильтр верхних частот.
- 8.4.7. Фильтр нижних частот без искажений.
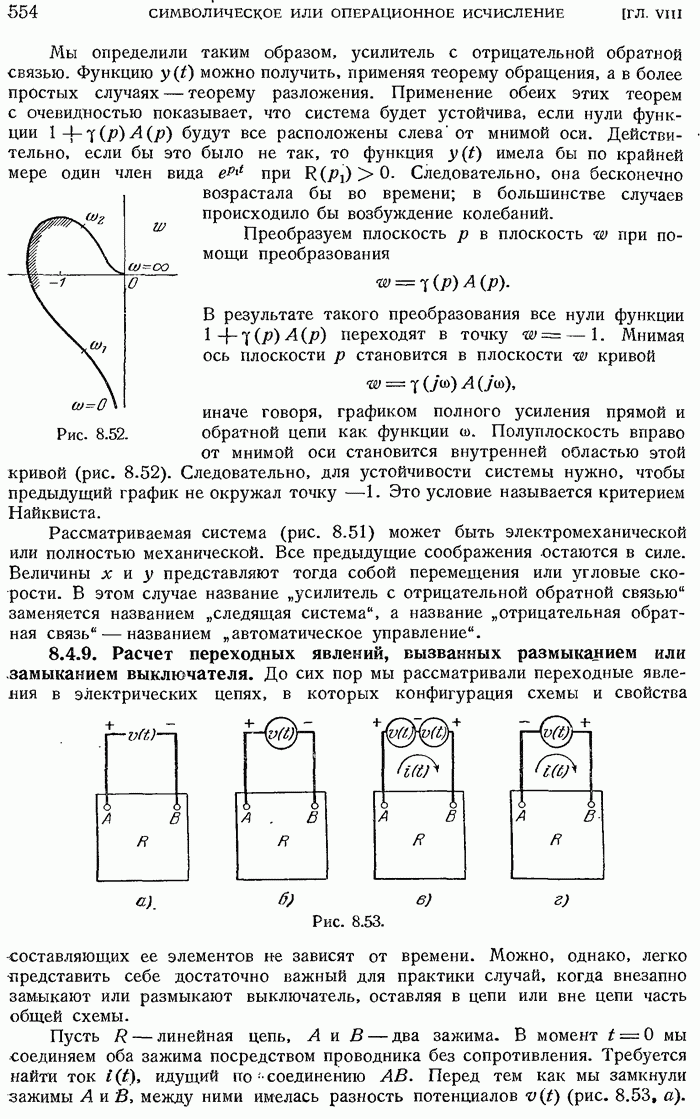
- 8.4.8. Усилители. Отрицательная обратная связь. Критерий Найквиста.
- 8.4.9. Расчет переходных явлений, вызванных размыканием или замыканием выключателя.
- Распространение электрических возмущений вдоль линий передач
- 8.4.11. Бесконечная или замкнутая на волновое сопротивление линия.
- 8.4.12. Линия без потерь.
- 8.4.13. Линия без искажений.
- 8.4.14. Подземный кабель.
- 8.4.15. Линия с идеальной изоляцией.
- 8.4.16. Общий случай. Произвольная линия.
- 8.4.17. Линия передачи конечной длины.
- 8.4.18. Закороченная с одного конца линия с пренебрежимо малыми проводимостью изоляции и индуктивностью (подземный кабель).
- 8.4.19. Линия конечной длины без потерь, замкнутая на сопротивление.
- 8.4.20. Сопротивление, сосредоточенное в начале линии.
- 8.4.21. Повреждение на линии.
- 8.5. МАТЕМАТИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ
- Применение операционного исчисления к решению линейных дифференциальных уравнений
- 8.5.3. Линейное дифференциальное уравнение с переменными алгебраическими коэффициентами (метод ван дер Поля).
- Применение операционного исчисления к решению некоторых интегральных уравнений
- 8.5.5. Нелинейные интегральные уравнения.
- 8.5.6. Интегродифференциальные уравнения.
- 8.5.7. Применение операционного исчисления к исследованию функций.
- 8.5.8. Применение операционного исчисления к разложению в асимптотический ряд.
- 8.6. НЕКОТОРЫЕ ЗАМЕЧАНИЯ
- 8.6.1. Замечания об операционном исчислении Хевисайда.
- ГЛАВА IX. ТЕОРИЯ ВЕРОЯТНОСТЕЙ. ПРИЛОЖЕНИЯ
- 9.1.1. Определение вероятности.
- 9.1.2. Независимые события. Теорема умножения вероятностей.
- 9.1.3. Несовместные события. Теорема сложения вероятностей.
- 9.1.4. Формула Стирлинга.
- Законы распределения случайных величин
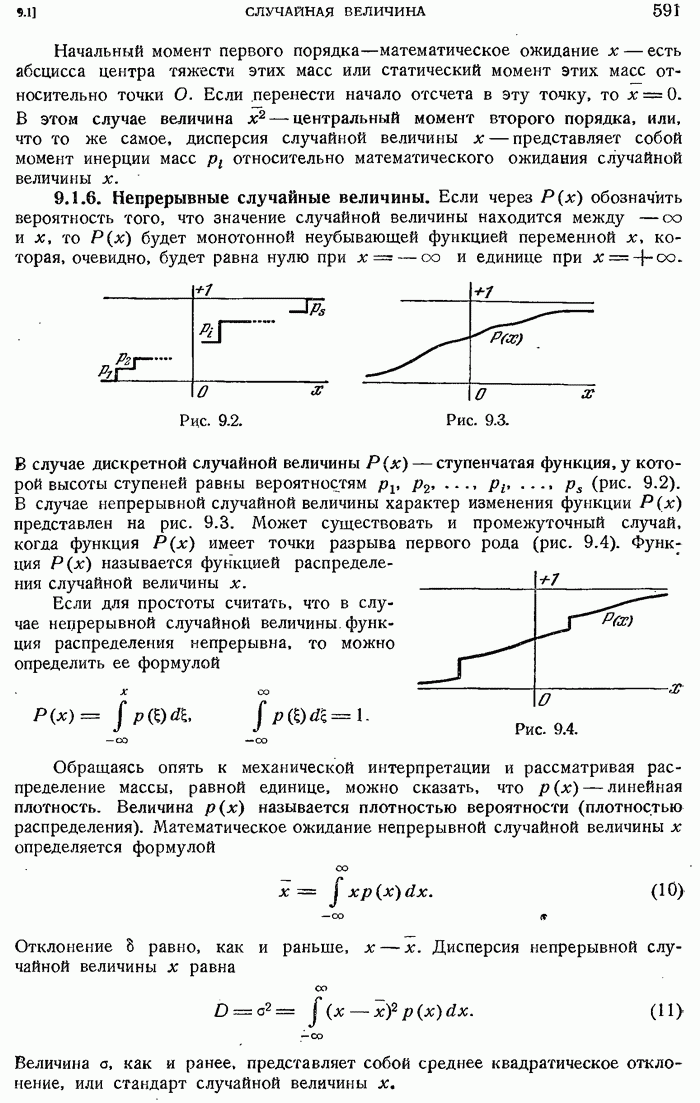
- 9.1.5. Дискретные случайные величины.
- 9.1.6. Непрерывные случайные величины.
- 9.1.7. Характеристическая функция.
- 9.1.8. Распределение системы двух случайных величин.
- 9.1.9. Характеристическая функция суммы независимых случайных величин.
- Основные законы распределения случайных величин
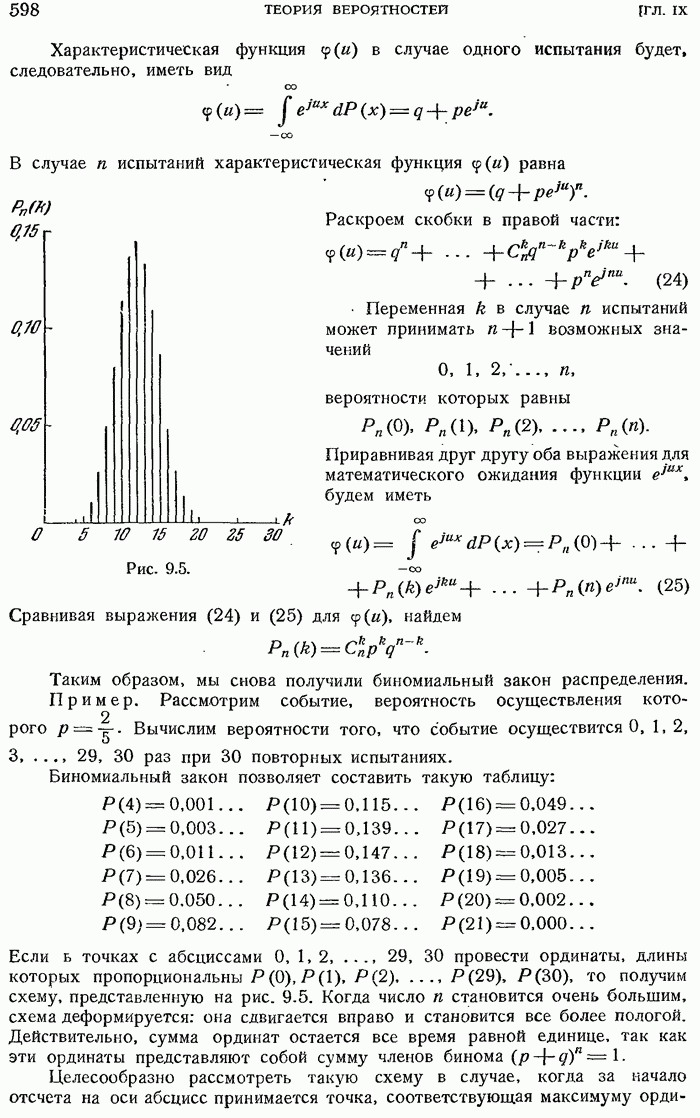
- 9.1.10. Биномиальный закон распределения.
- 9.1.11. Характеристическая функция биномиального закона.
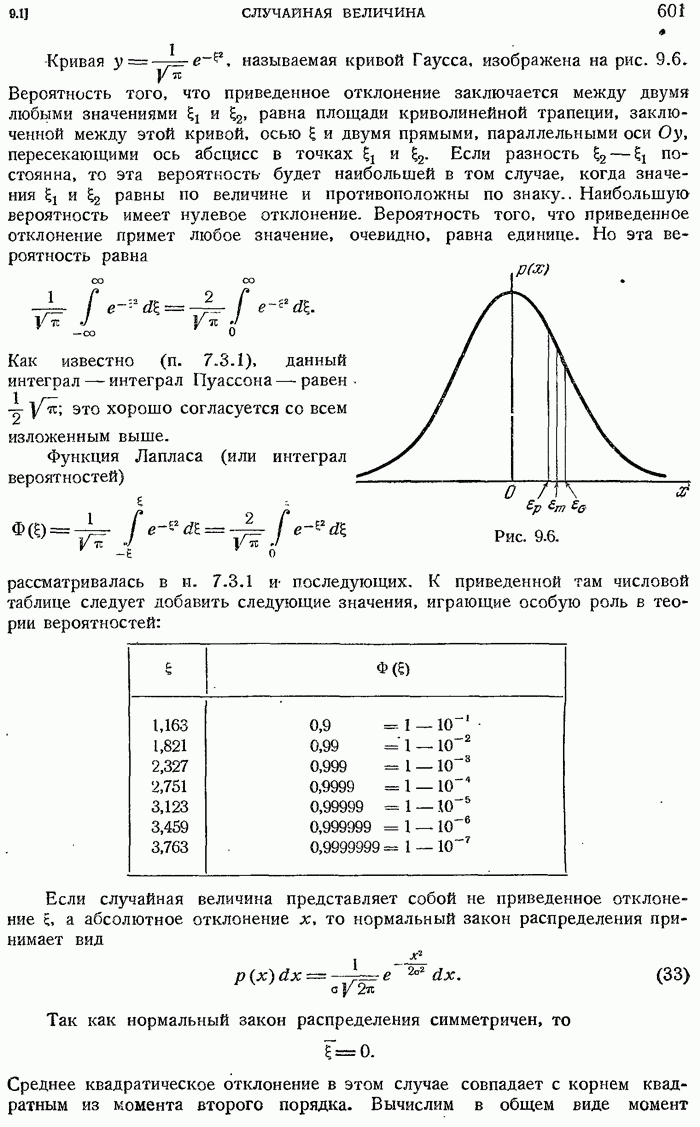
- 9.1.12. Формула Лапласа. Нормальный закон распределения (закон Лапласа — Гаусса).
- 9.1.13. Характеристическая функция нормального закона распределения.
- 9.1.14. Теорема Бернулли.
- 9.1.15. Замечания о переходе от биномиального закона распределения к нормальному.
- 9.1.16. Закон распределения Пуассона.
- 9.1.17. Характеристическая функция и моменты закона распределения Пуассона.
- 9.1.18. Приложение к задачам автоматической телефонии.
- 9.1.19. Согласование наблюденных данных с теоретическим законом распределения.
- 9.1.20. Частный случай нормального закона распределения.
- Ошибки измерений и способ наименьших квадратов
- 9.1.21. Ошибки измерений и нормальный закон распределения.
- 9.1.22. Способ наименьших квадратов.
- 9.1.23. Линейная комбинация ошибок.
- 9.1.24. Точность группы измерений.
- 9.1.25. Наивероятнейшее значение меры точности.
- 9.1.26. «Вес» наблюдения.
- 9.1.27. Критерий ошибочного наблюдения.
- 9.1.28. Срединная (вероятная) ошибка функции.
- 9.1.29. Эмпирические формулы.
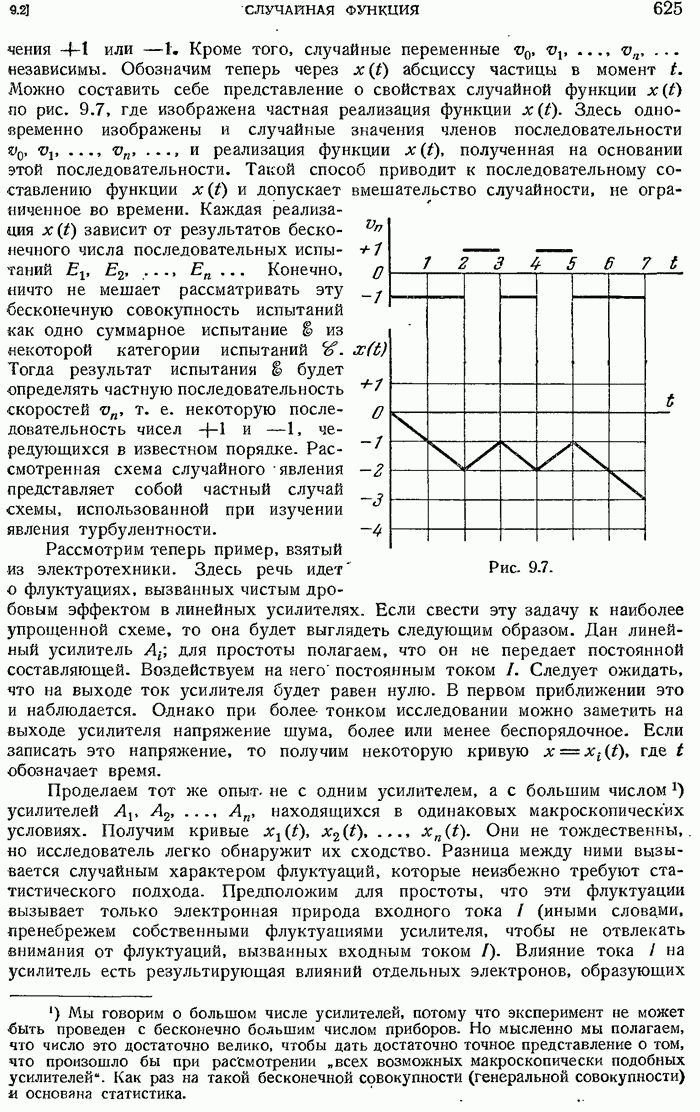
- 9.2. ПОНЯТИЕ СЛУЧАЙНОЙ ФУНКЦИИ
- 9.2.2. Функции распределения.
- Проблема сходимости
- 9.2.4. Сходимость в смысле Бернулли.
- 9.2.5. Сходимость по вероятности.
- 9.2.6. Сходимость в среднем квадратическом (сходимость с. к.).
- 9.2.7. Почти достоверная сходимость.
- Стационарные случайные функции. Изучение постоянных режимов
- 9.2.9. Изучение моментов второго порядка. Определение.
- Общие свойства стационарных случайных функций второго порядка
- 9.2.10. Корреляционные функции.
- 9.2.11. Непрерывность. Дифференцируемость.
- 9.2.12. Энергетический спектр.
- 9.2.13. Передача энергии стационарной линейной системой.
- 9.2.14. Недостаточность рассмотрения моментов второго порядка и корреляционной функции.
- Стационарные случайные функции Лапласа — Гаусса. Применение к чисто дробовому эффекту
- 9.2.17. Флуктуации в нелинейных системах.
- 9.2.18. Вычисление корреляционной функции на выходе линейного усилителя под действием дробового эффекта постоянного тока.
- ГЛАВА X. ПРИБЛИЖЕННЫЕ И ГРАФИЧЕСКИЕ ВЫЧИСЛЕНИЯ
- 10.1. РЕШЕНИЕ ЧИСЛЕННЫХ УРАВНЕНИЙ
- 10.1.2. Метод Ньютона и метод пропорциональных частей
- 10.1.3. Метод итерации.
- 10.1.4. Приближенное решение системы двух уравнений.
- 10.2. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- 10.2.1. Численное решение уравнений третьей и четвертой степени.
- 10.2.2. Схема Горнера.
- 10.2.3. Построение Лилла.
- 10.2.4. Способ Лагранжа.
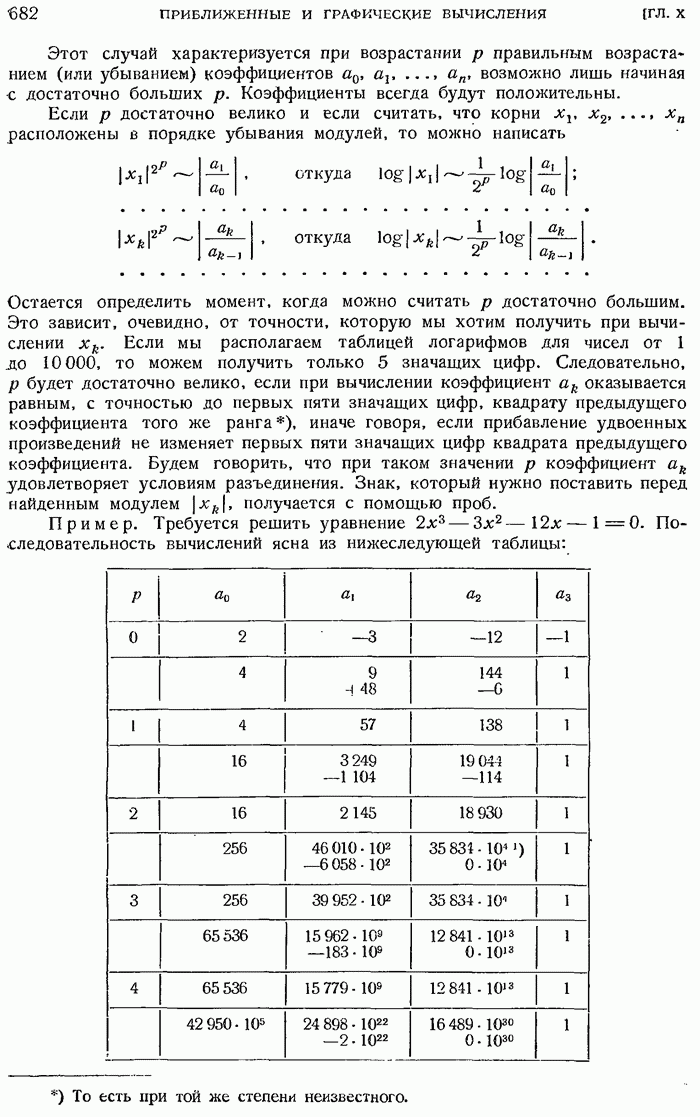
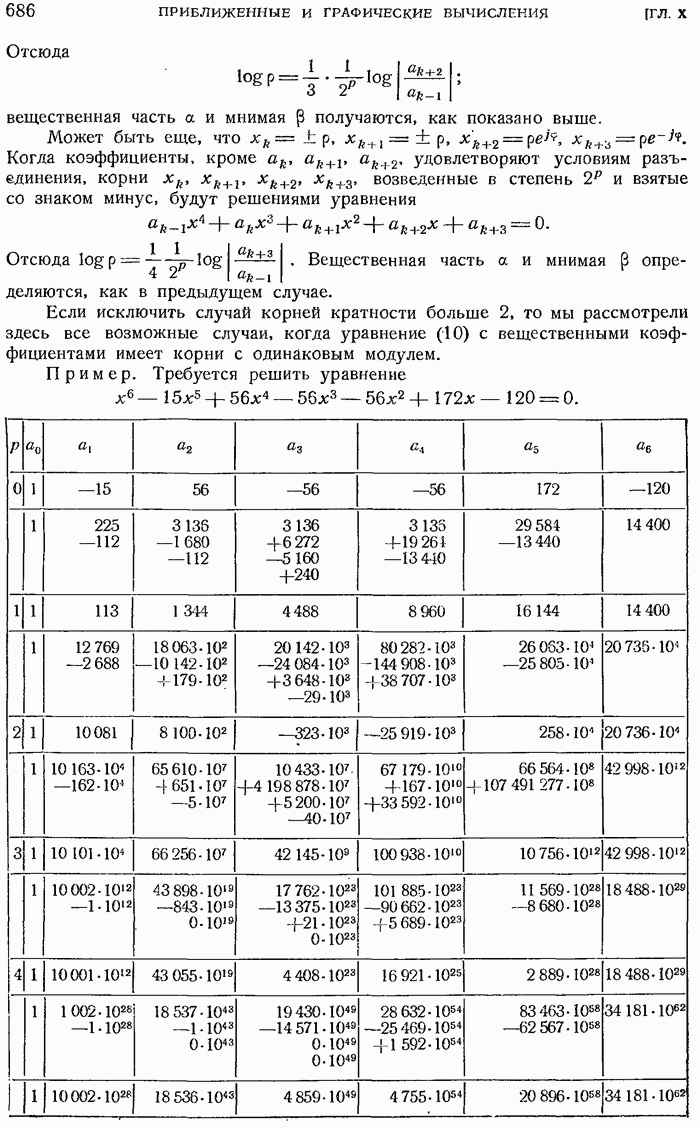
- 10.2.5. Метод Лобачевского — Греффе — Данделена.
- 10.3. ПРИБЛИЖЕНИЕ ФУНКЦИИ
- Приближение функции полиномами
- 10.3.2. Значения аргумента распределены неравномерно. Интерполяционный полином Лагранжа.
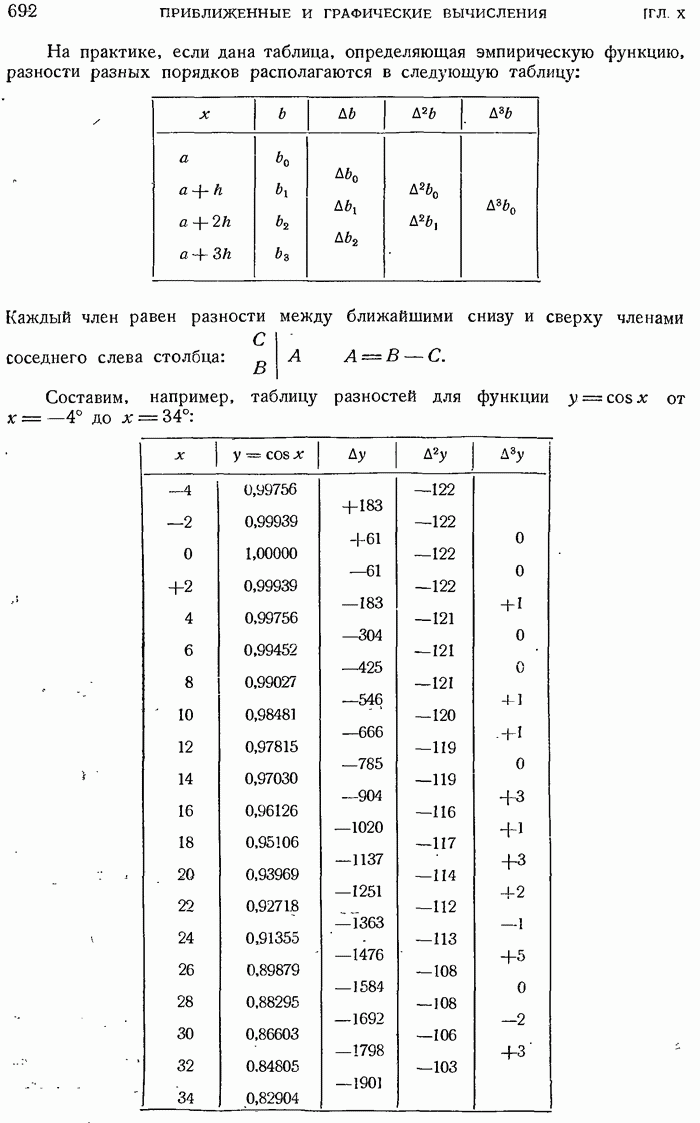
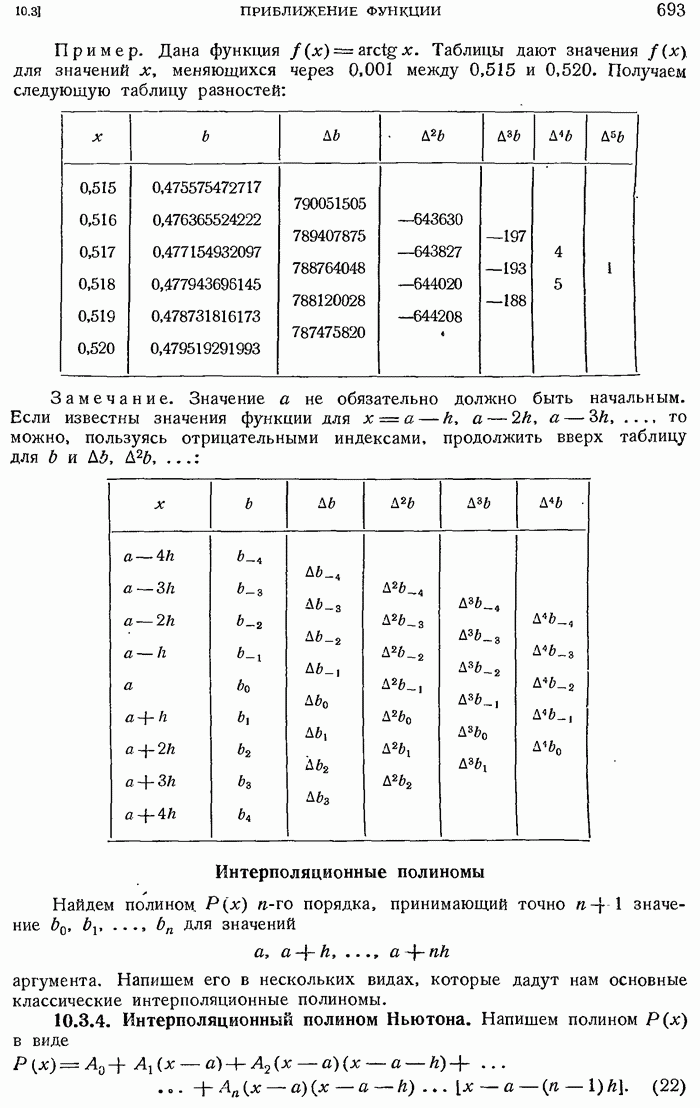
- 10.3.3. Значения переменной находятся в арифметической прогрессии. Таблица разностей.
- 10.3.4. Интерполяционный полином Ньютона.
- 10.3.5. Интерполяционный полином Стнрлинга.
- 10.3.6. Интерполяционный полином Бесселя.
- 10.3.7. Области применения интерполяционных полиномов Ньютона, Стирлинга, Бесселя.
- 10.3.8. Верхний предел ошибки, совершаемой при применении интерполяционных формул Ньютона, Стирлинга, Бесселя.
- 10.3.9. Приближение линейной комбинацией функций, определенной с помощью критерия наименьших квадратов.
- 10.3.10. Приближение полиномом, определенным с помощью критерия наименьших квадратов.
- Приближение отрезком ряда Фурье. Задача гармонического анализа
- 10.3.14. Приближение эмпирической функции линейной комбинацией показательных функций.
- 10.3.15. Приближение функции по Чебышеву.
- 10.3.16. Применение ряда Тейлора.
- 10.4. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
- 10.5. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- 10.5.2. Полином Бернулли.
- 10.5.3. Формула Эйлера.
- 10.5.4. Формула трапеций.
- 10.5.5. Формула Симпсона.
- 10.5.6. Формула Уэддля.
- 10.5.7. Формула Грегори.
- 10.5.8. Введение в методы Ньютона — Котеса, Чебышева, Гаусса.
- 10.5.9. Метод Ньютона — Котеса.
- 10.5.10. Метод Чебышева.
- 10.5.11. Метод Гаусса.
- 10.5.12. Применение интерполяционных полиномов Ньютона.
- 10.5.13. Исключительные случаи.
- 10.6. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 10.6.2. Приближенное интегрирование дифференциального уравнения первого порядка.
- 10.6.3. Решение с помощью ряда Тейлора.
- 10.6.4. Способ Адамса.
- 10.6.5. Сокращенный вариант.
- 10.6.6. Приближенное интегрирование системы дифференциальных уравнений первого порядка.
- 10.6.7. Использование ряда Тейлора.
- 10.6.8. Применение интерполяционного полинома Ньютона с нисходящими разностями.
- 10.6.9. Способ Пикара.
- 10.7. ГРАФИЧЕСКОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 10.7.2. Графическое решение дифференциальных уравнений второго порядка способом радиусов кривизны.
- 10.8. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
- 10.9. НОМОГРАММЫ
- 10.9.3. Номограммы с выравненными точками.
- 10.9.4. Номограммы с тремя параллельными прямолинейными шкалами.
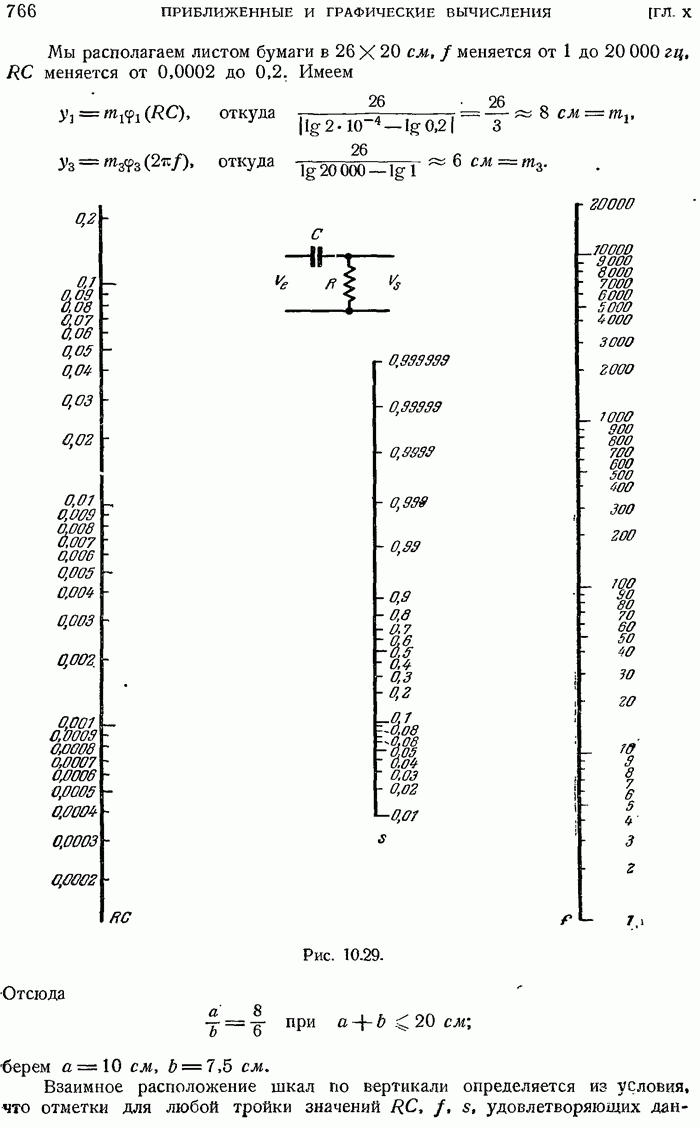
- 10.9.5. Номограммы с двумя параллельными прямолинейными шкалами и одной криволинейной.
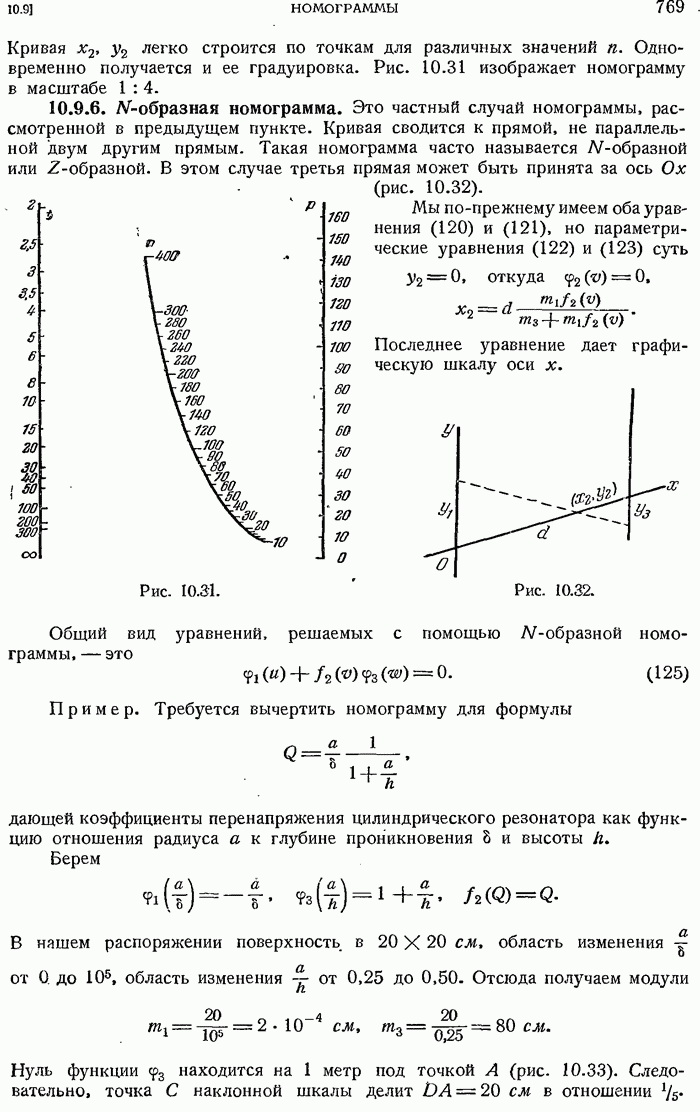
- 10.9.6. N-образная номограмма.
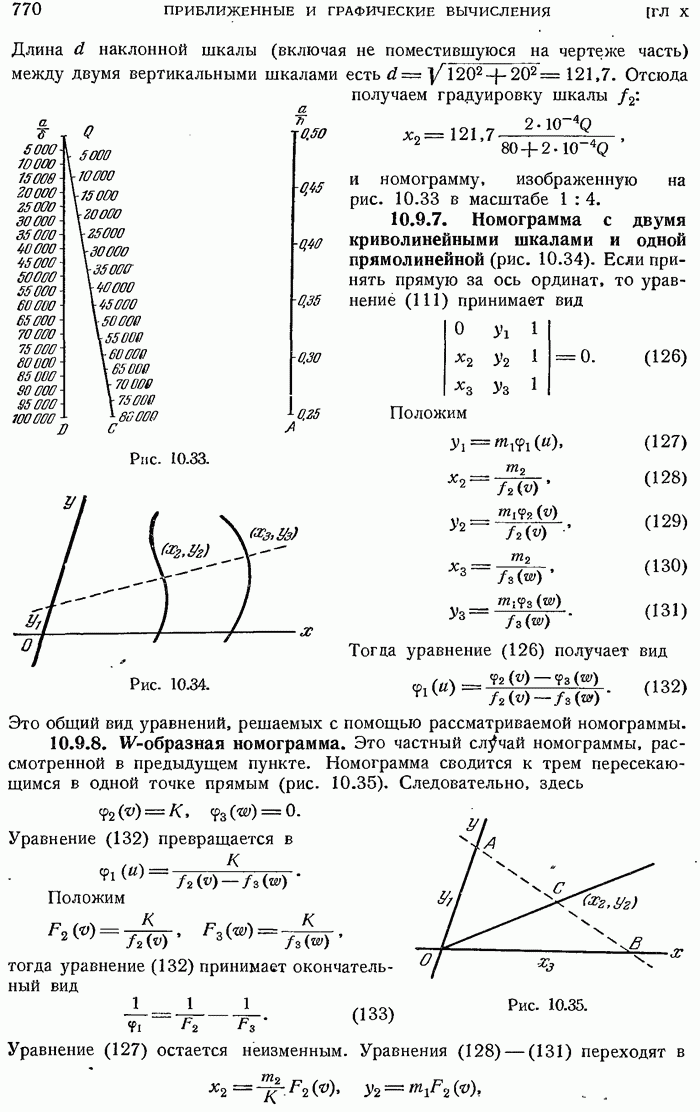
- 10.9.7. Номограмма с двумя криволинейными шкалами и одной прямолинейной
- 10.9.8. W-образная номограмма.
- 10.9.9. Z-образная номограмма.
- 10.9.10. Номограмма с тремя криволинейными шкалами.
- 10.9.11. Сложные номограммы.