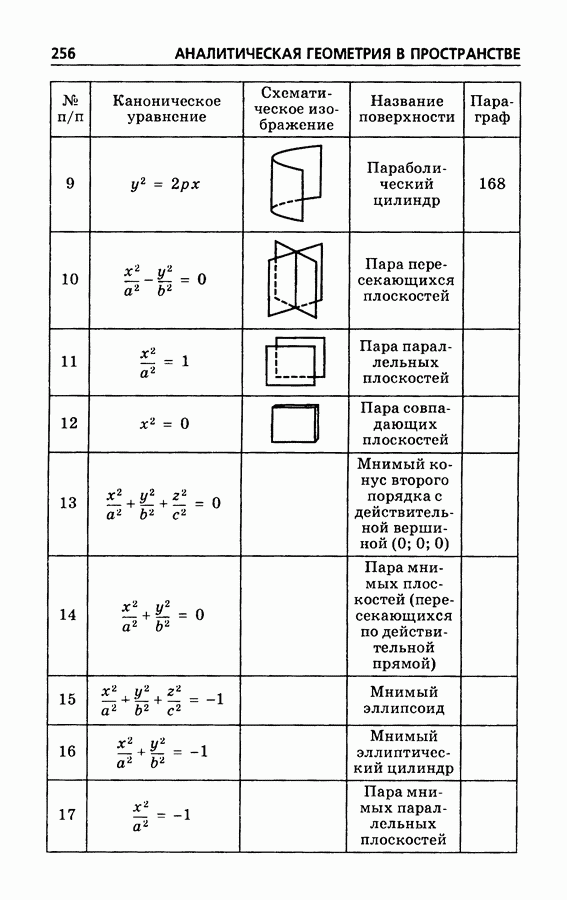
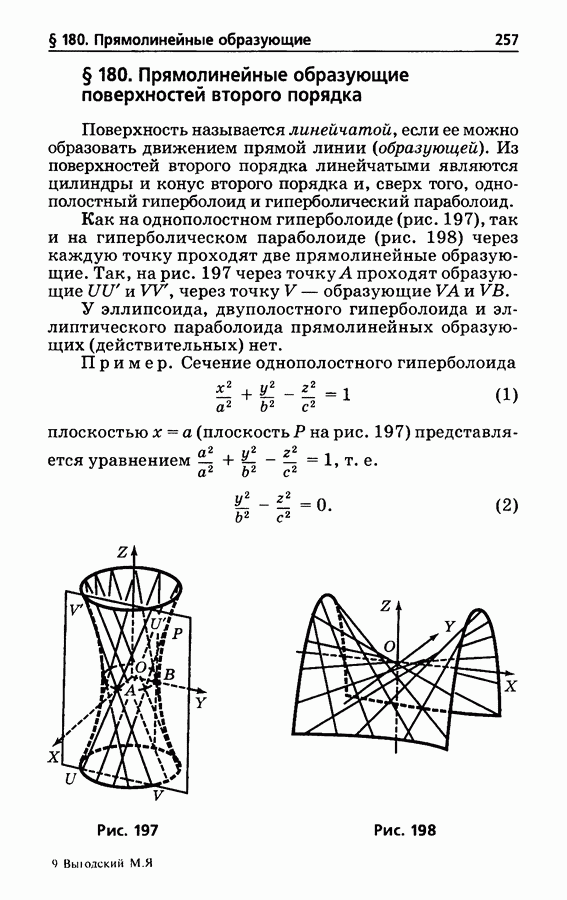
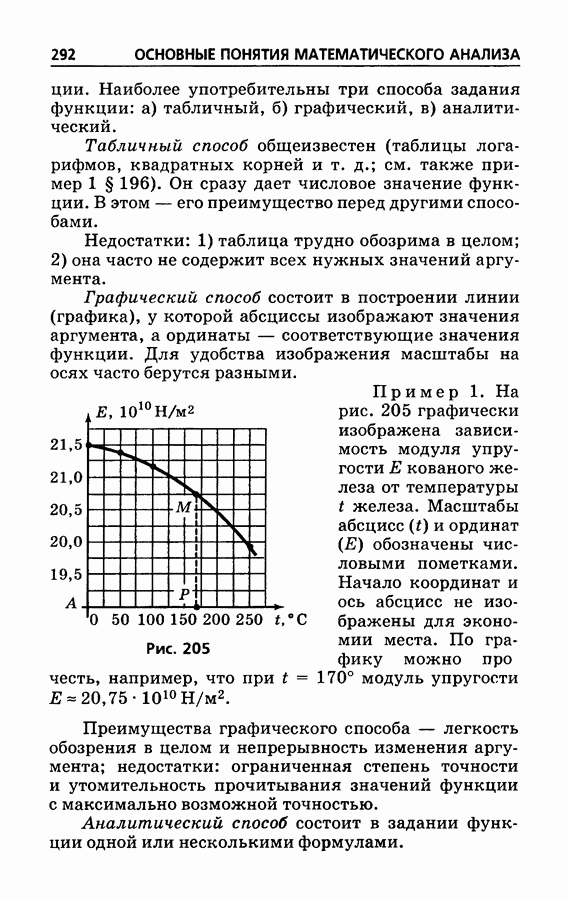
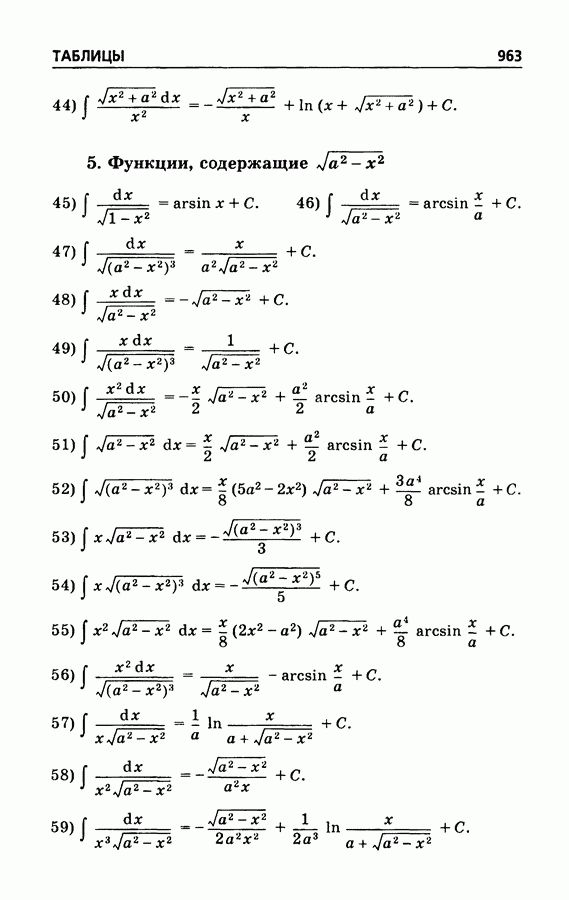| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
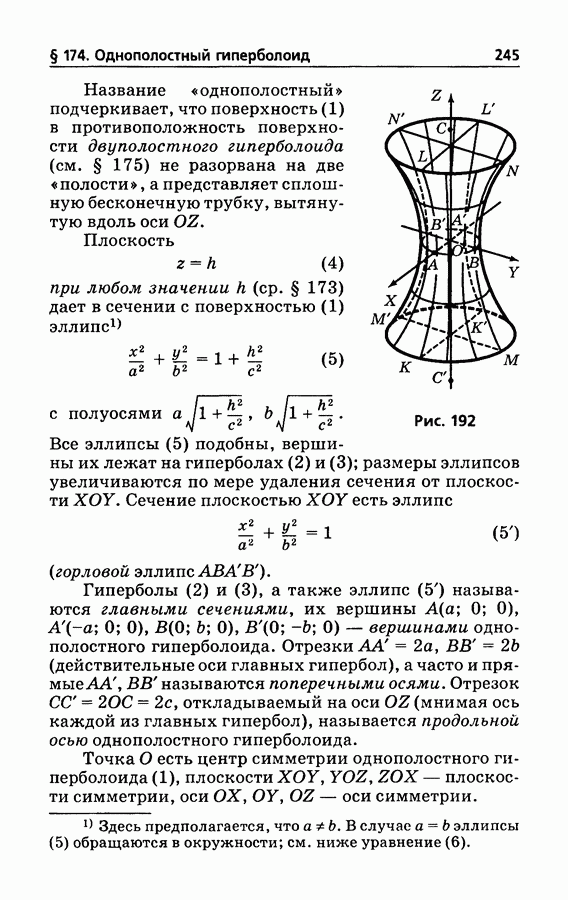
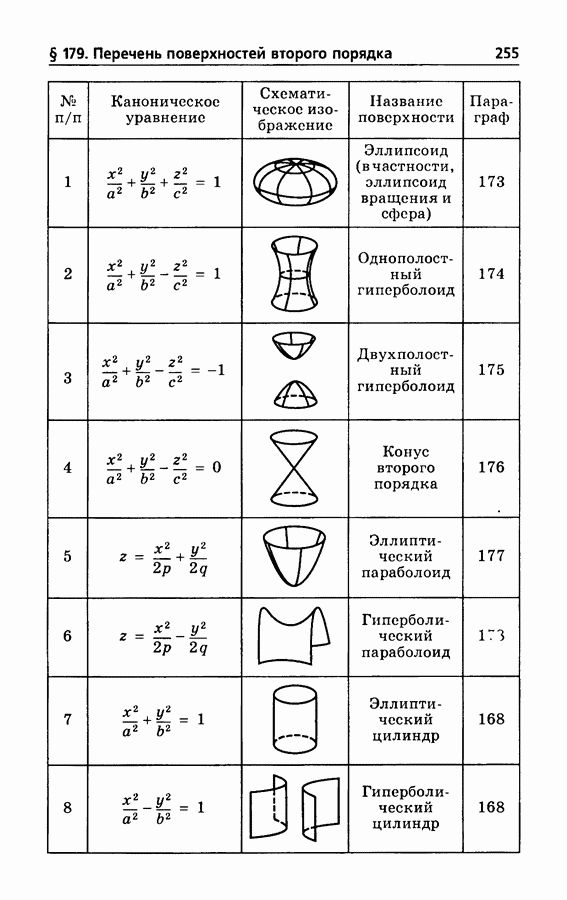
§ 175. Двуполостный гиперболоид
Поверхность, представляемая уравнением

называется двуполостным гиперболоидом (рис. 193).
Сечения плоскостями  и
и  представляются уравнениями
представляются уравнениями

Это — гиперболы  и
и  на рис. 193). Для каждой из них ось
на рис. 193). Для каждой из них ось  является действительной осью (ср. § 174).
является действительной осью (ср. § 174).
Плоскости  не встречаются с гиперболоидом (1) при
не встречаются с гиперболоидом (1) при  (ср. § 174). При
(ср. § 174). При  они касаются гиперболоида в точках
они касаются гиперболоида в точках  . При
. При  в сечении получаются эллипсы
в сечении получаются эллипсы

подобные друг другу ( и др.). Размеры их увеличиваются по мере удаления от плоскости
и др.). Размеры их увеличиваются по мере удаления от плоскости 
Таким образом, поверхность (1) состоит из двух разобщенных полостей, откуда и название двуполостный гиперболоид.
Гиперболы (2) и (3) называются главными сечениями, их общие вершины  вершинами двуполостного гиперболоида, их действительная ось
вершинами двуполостного гиперболоида, их действительная ось  продольной осью двуполостного гиперболоида, мнимые оси
продольной осью двуполостного гиперболоида, мнимые оси  и
и  поперечными осями симметрии.
поперечными осями симметрии.
Двуполостный гиперболоид имеет центр О, оси симметрии  и плоскости симметрии
и плоскости симметрии  Две полости гиперболоида симметричны друг другу относительно плоскости
Две полости гиперболоида симметричны друг другу относительно плоскости 
Двуполостный гиперболоид вращения. Уравнение (1) при  принимает вид
принимает вид


Рис. 193
и представляет поверхность, порождаемую вращением гиперболы около ее действительной оси. Она называется двуполостным гиперболоидом вращения. Двуполостный гиперболоид с неравными поперечными полуосями  называется трехосным.
называется трехосным.
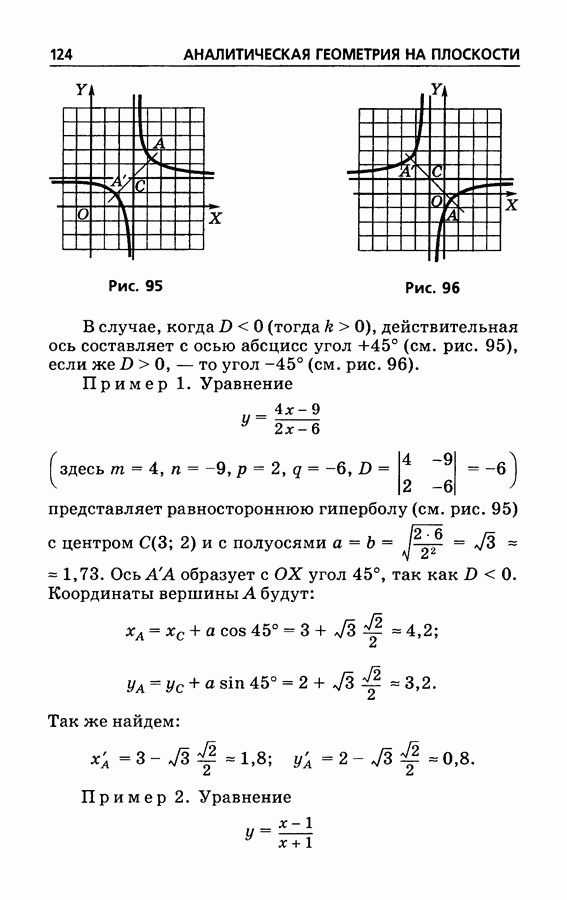
Пример 1. Определить вид поверхности

Решение. Данное уравнение преобразуем к виду

Имеем двуполостный гиперболоид (трехосный). Продольная ось равна  и совпадает с осью
и совпадает с осью  одна поперечная ось равна
одна поперечная ось равна  и направлена по оси
и направлена по оси  другая равна
другая равна  и направлена по оси
и направлена по оси  Пример 2. Уравнение
Пример 2. Уравнение

представляет однополостный (а не двуполостный) гиперболоид (хотя в правой части стоит -1, а не +1, но в левой части два отрицательных слагаемых). Представив данное уравнение в виде  видим, что гиперболоид порожден вращением равносторонней гиперболы около ее мнимой оси (совпадающей с осью
видим, что гиперболоид порожден вращением равносторонней гиперболы около ее мнимой оси (совпадающей с осью 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- § 1. Понятие о предмете аналитической геометрии
- § 2. Координаты
- § 3. Прямоугольная система координат
- § 4. Прямоугольные координаты
- § 5. Координатные углы
- § 6. Косоугольная система координат
- § 7. Уравнение линии
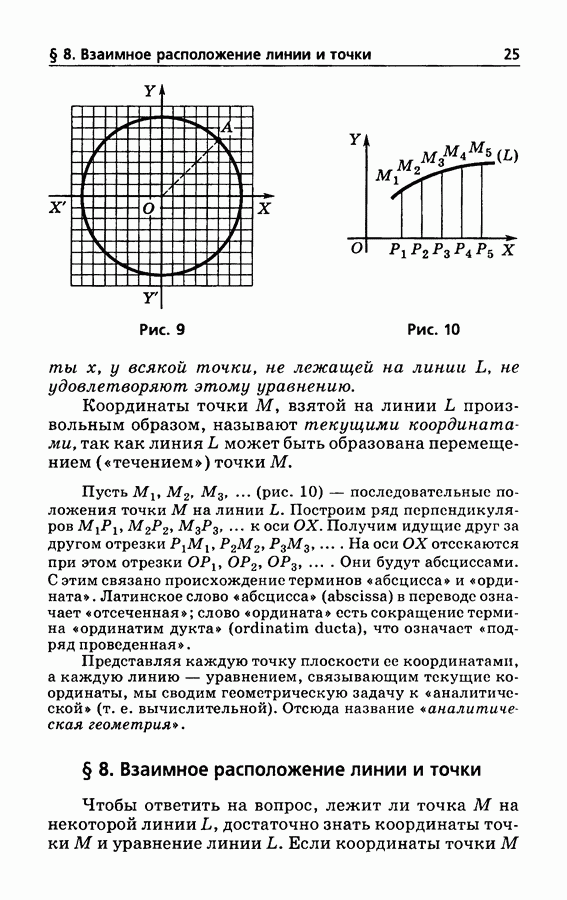
- § 8. Взаимное расположение линии и точки
- § 9. Взаимное расположение двух линий
- § 10. Расстояние между двумя точками
- § 11. Деление отрезка в данном отношении
- § 11а. Деление отрезка пополам
- § 12. Определитель второго порядка
- § 13. Площадь треугольника
- § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом)
- § 15. Прямая, параллельная оси
- § 16. Общее уравнение прямой
- § 17. Построение прямой по ее уравнению
- § 18. Условие параллельности прямых
- § 19. Пересечение прямых
- § 20. Условие перпендикулярности двух прямых
- § 21. Угол между двумя прямыми
- § 22. Условие, при котором три точки лежат на одной прямой
- § 23. Уравнение прямой, проходящей через две точки
- § 24. Пучок прямых
- § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой
- § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- § 27. Взаимное расположение прямой и пары точек
- § 28. Расстояние от точки до прямой
- § 29. Полярные параметры прямой
- § 30. Нормальное уравнение прямой
- § 31. Приведение уравнения прямой к нормальному виду
- § 32. Отрезки на осях
- § 33. Уравнение прямой в отрезках
- § 34. Преобразование координат (постановка вопроса)
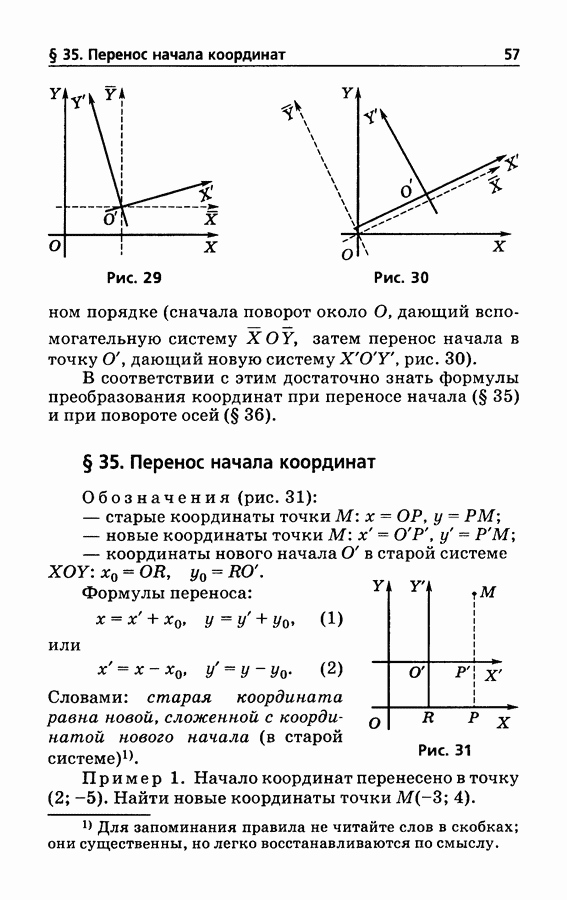
- § 35. Перенос начала координат
- § 36. Поворот осей
- § 37. Алгебраические линии и их порядок
- § 38. Окружность
- § 39. Нахождение центра и радиуса окружности
- § 40. Эллипс как сжатая окружность
- § 41. Другое определение эллипса
- § 42. Построение эллипса по его осям
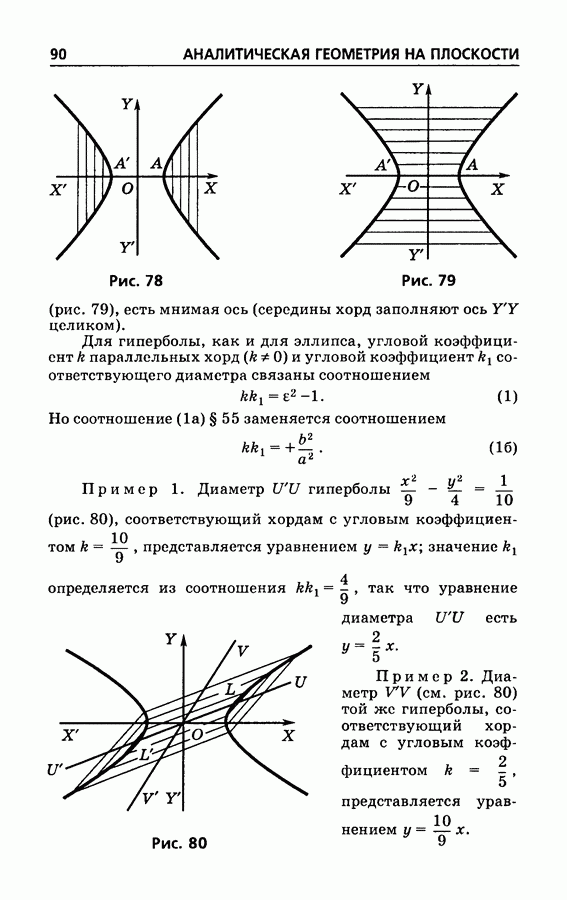
- § 43. Гипербола
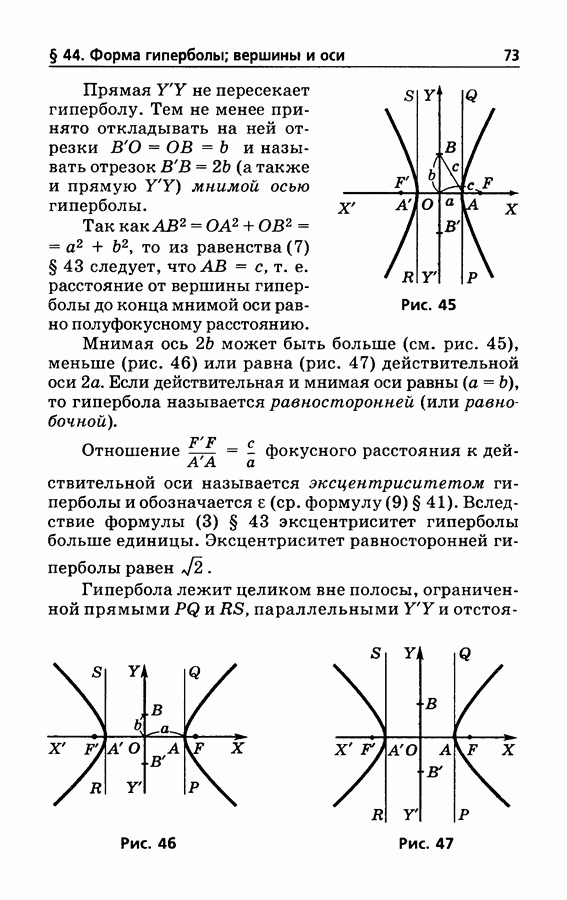
- § 44. Форма гиперболы; вершины и оси
- § 45. Построение гиперболы по ее осям
- § 46. Асимптоты гиперболы
- § 47. Сопряженные гиперболы
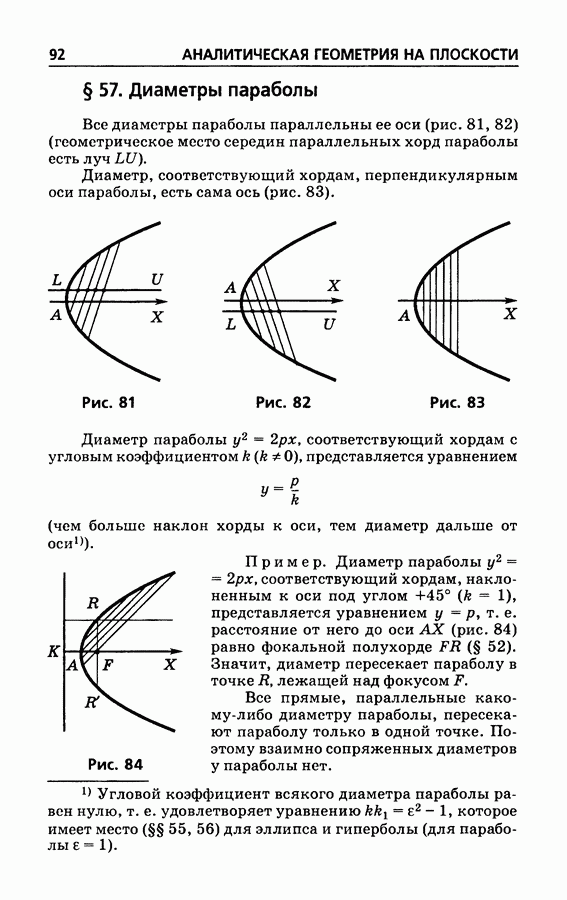
- § 48. Парабола
- § 49. Построение параболы по данному параметру p
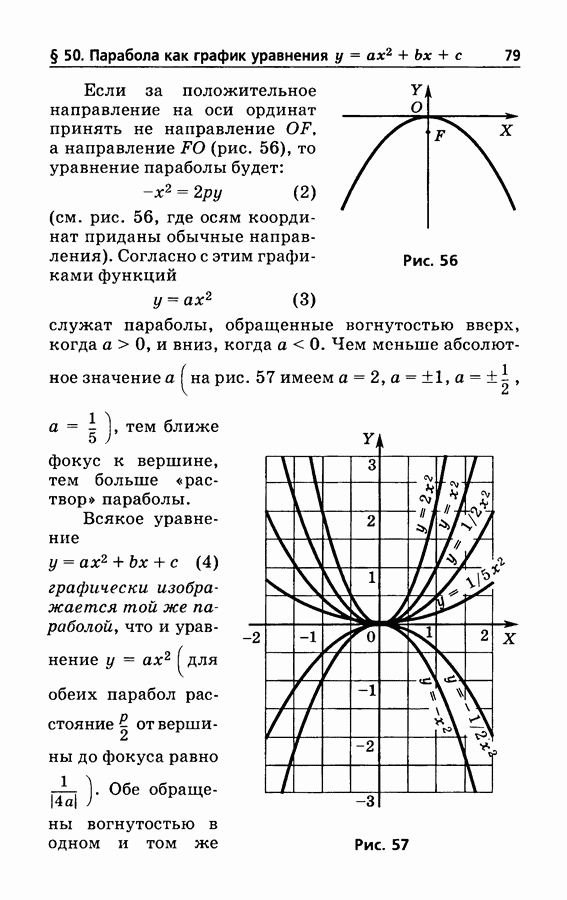
- § 50. Парабола как график уравнения y=ax^2+bx+c
- § 51. Директрисы эллипса и гиперболы
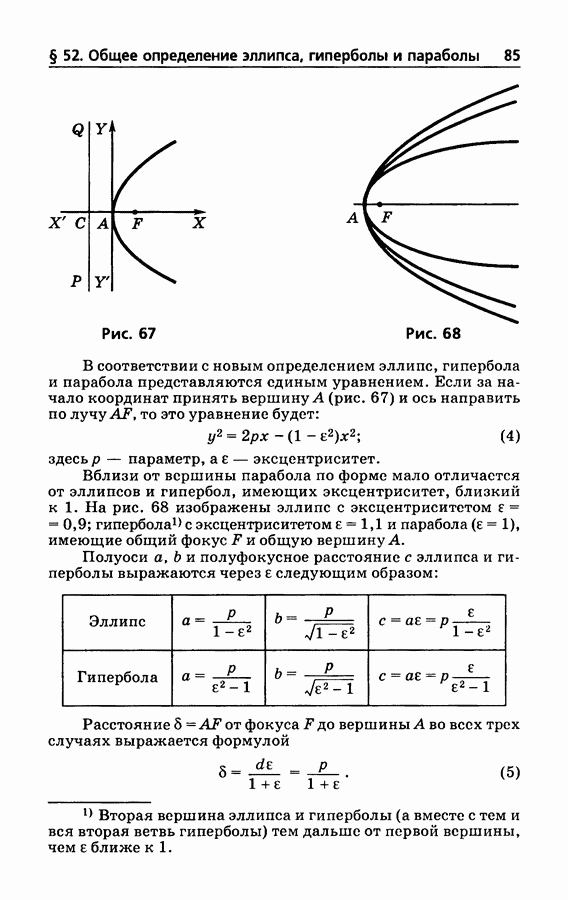
- § 52. Общее определение эллипса, гиперболы и параболы
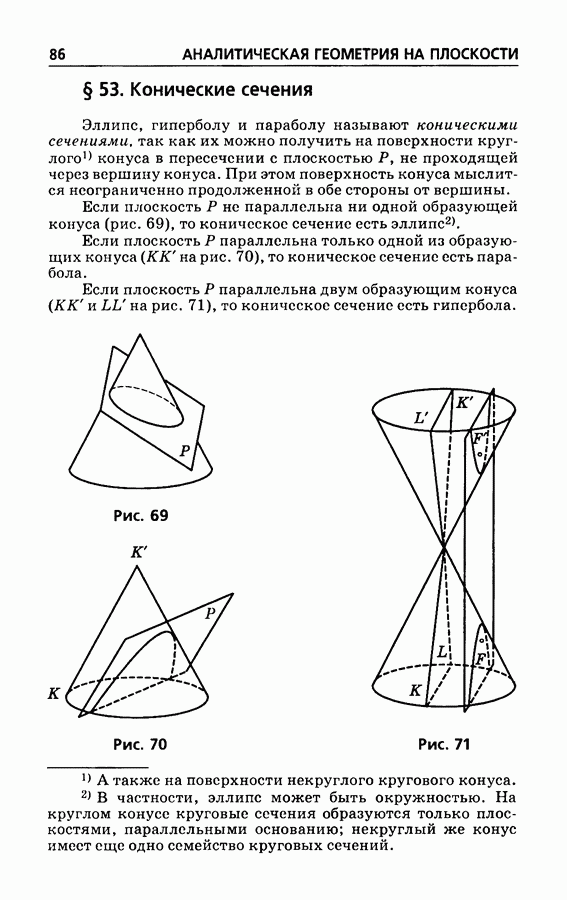
- § 53. Конические сечения
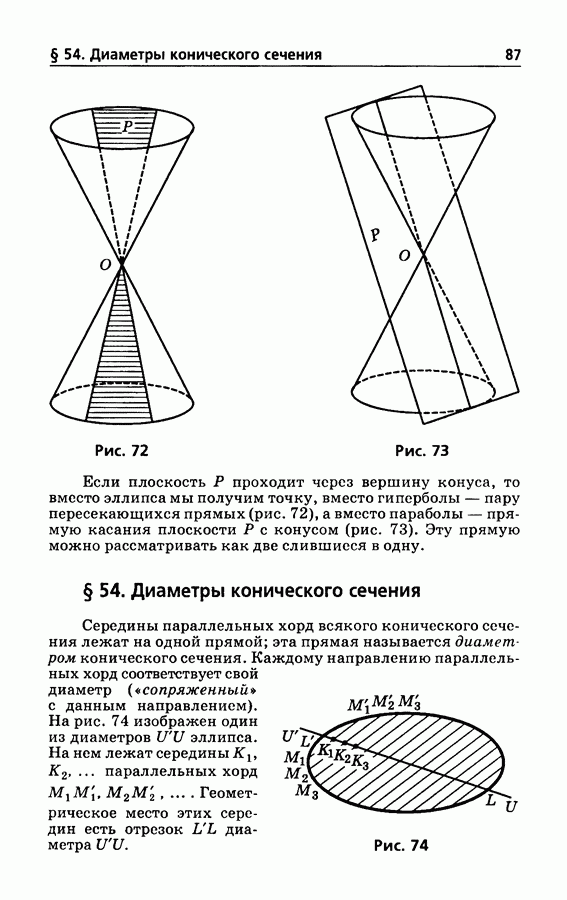
- § 54. Диаметры конического сечения
- § 55. Диаметры эллипса
- § 56. Диаметры гиперболы
- § 57. Диаметры параболы
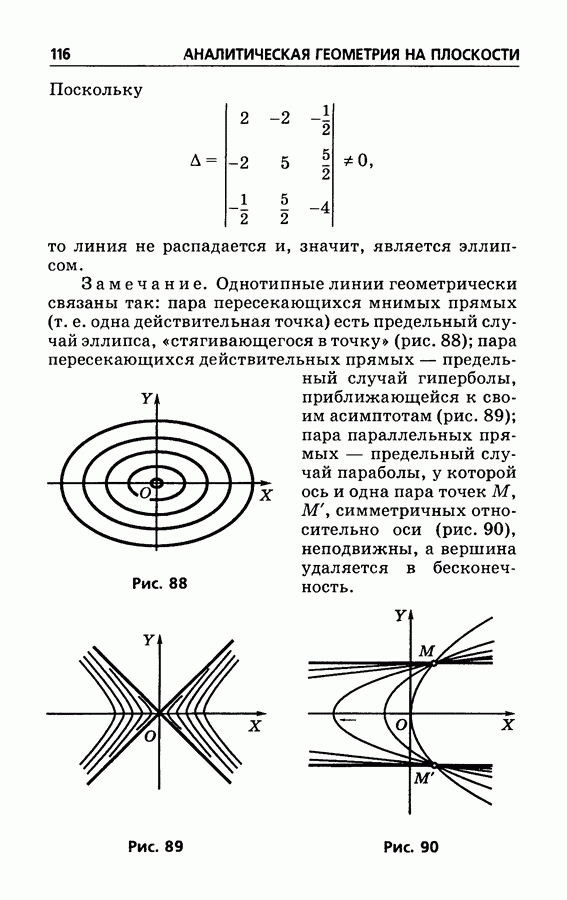
- § 58. Линии второго порядка
- § 59. Запись общего уравнения второй степени
- § 60. Упрощение уравнения второй степени; общие замечания
- § 61. Предварительное преобразование уравнения второй степени
- § 62. Завершающее преобразование уравнения второй степени
- § 63. О приемах, облегчающих упрощение уравнения второй степени
- § 64. Признак распадения линий второго порядка
- § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка
- § 66. Инварианты уравнения второй степени
- § 67. Три типа линий второго порядка
- § 68. Центральные и нецентральные линии второго порядка
- § 69. Нахождение центра центральной линии второго порядка
- § 70. Упрощение уравнения центральной линии второго порядка
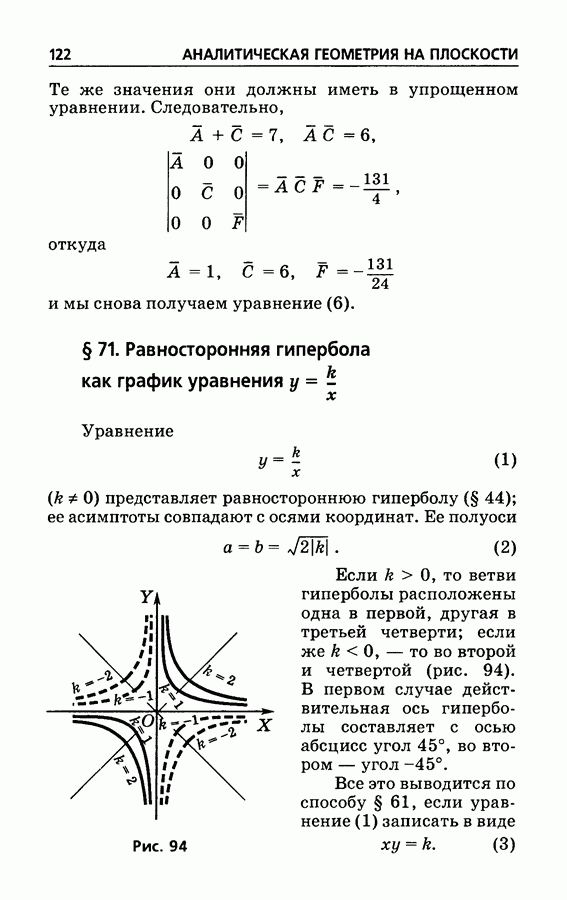
- § 71. Равносторонняя гипербола как график уравнения y=k/x
- § 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q)
- § 73. Полярные координаты
- § 74. Связь между полярными и прямоугольными координатами
- § 75. Архимедова спираль
- § 76. Полярное уравнение прямой
- § 77. Полярное уравнение конического сечения
- АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- § 78. Понятие о векторах и скалярах
- § 79. Вектор в геометрии
- § 80. Векторная алгебра
- § 81. Коллинеарные векторы
- § 82. Нуль-вектор
- § 83. Равенство векторов
- § 84. Приведение векторов к общему началу
- § 85. Противоположные векторы
- § 86. Сложение векторов
- § 87. Сумма нескольких векторов
- § 88. Вычитание векторов
- § 89. Умножение и деление вектора на число
- § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор)
- § 91. Проекция точки на ось
- § 92. Проекция вектора на ось
- § 93. Основные теоремы о проекциях вектора
- § 94. Прямоугольная система координат в пространстве
- § 95. Координаты точки
- § 96. Координаты вектора
- § 97. Выражения вектора через компоненты и через координаты
- § 98. Действия над векторами, заданными своими координатами
- § 99. Выражение вектора через радиусы-векторы его начала и конца
- § 100. Длина вектора. Расстояние между двумя точками
- § 101. Угол между осью координат и вектором
- § 102. Признак коллинеарности (параллельности) векторов
- § 103. Деление отрезка в данном отношении
- § 104. Скалярное произведение двух векторов
- § 104а. Физический смысл скалярного произведения
- § 105. Свойства скалярного произведения
- § 106. Скалярные произведения основных векторов
- § 107. Выражение скалярного произведения через координаты сомножителей
- § 108. Условие перпендикулярности векторов
- § 109. Угол между векторами
- § 110. Правая и левая системы трех векторов
- § 111. Векторное произведение двух векторов
- § 112. Свойства векторного произведения
- § 113. Векторные произведения основных векторов
- § 114. Выражение векторного произведения через координаты сомножителей
- § 115. Компланарные векторы
- § 116. Смешанное произведение
- § 117. Свойства смешанного произведения
- § 118. Определитель третьего порядка
- § 119. Выражение смешанного произведения через координаты сомножителей
- § 120. Признак компланарности в координатной форме
- § 121. Объем параллелепипеда
- § 122. Двойное векторное произведение
- § 123. Уравнение плоскости
- § 124. Особые случаи положения плоскости относительно системы координат
- § 125. Условие параллельности плоскостей
- § 126. Условие перпендикулярности плоскостей
- § 127. Угол между двумя плоскостями
- § 128. Плоскость, проходящая через данную точку параллельно данной плоскости
- § 129. Плоскость, проходящая через три точки
- § 130. Отрезки на осях
- § 131. Уравнение плоскости в отрезках
- § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости
- § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям
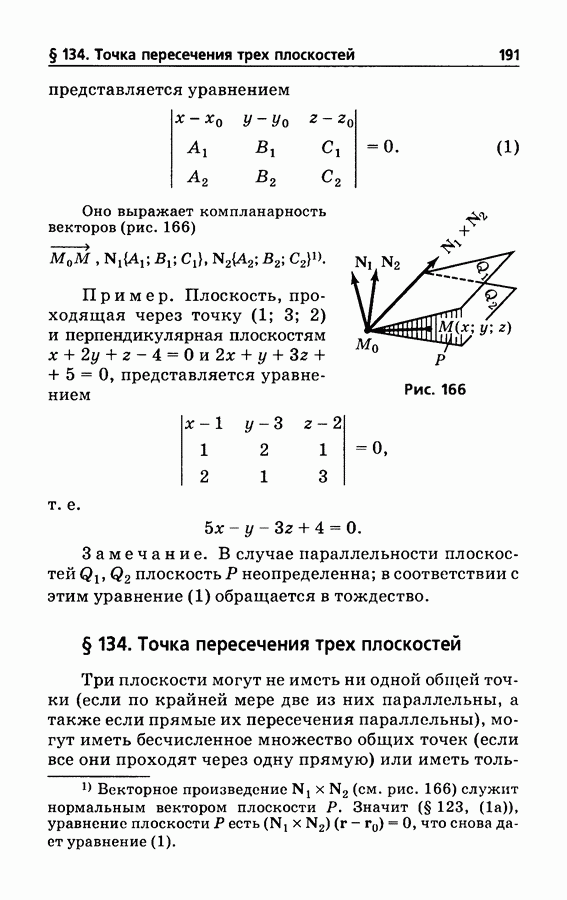
- § 134. Точка пересечения трех плоскостей
- § 135. Взаимное расположение плоскости и пары точек
- § 136. Расстояние от точки до плоскости
- § 137. Полярные параметры плоскости
- § 138. Нормальное уравнение плоскости
- § 139. Приведение уравнения плоскости к нормальному виду
- § 140. Уравнения прямой в пространстве
- § 141. Условие, при котором два уравнения первой степени представляют прямую
- § 142. Пересечение прямой с плоскостью
- § 143. Направляющий вектор
- § 144. Углы между прямой и осями координат
- § 145. Угол между двумя прямыми
- § 146. Угол между прямой и плоскостью
- § 147. Условия параллельности и перпендикулярности прямой и плоскости
- § 148. Пучок плоскостей
- § 149. Проекции прямой на координатные плоскости
- § 150. Симметричные уравнения прямой
- § 151. Приведение уравнений прямой к симметричному виду
- § 152. Параметрические уравнения прямой
- § 153. Пересечение плоскости с прямой, заданной параметрически
- § 154. Уравнения прямой, проходящей через две данные точки
- § 155. Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой
- § 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости
- § 157. Уравнение плоскости, проходящей через данную точку и данную прямую
- § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым
- § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой
- § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости
- § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую
- § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую
- § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости
- § 164. Уравнения общего перпендикуляра к двум данным прямым
- § 165. Кратчайшее расстояние между двумя прямыми
- § 165а. Правые и левые пары прямых
- § 166. Преобразование координат
- § 167. Уравнение поверхности
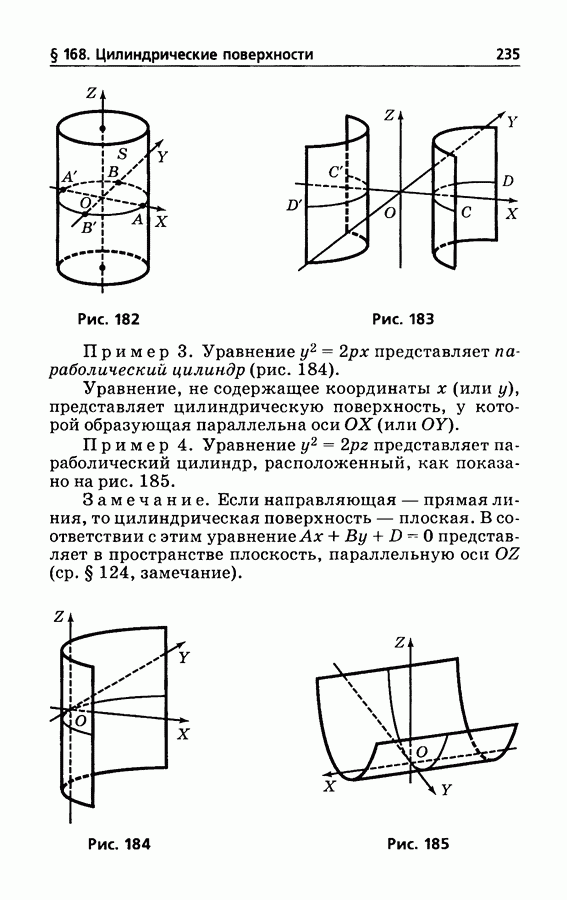
- § 168. Цилиндрические поверхности, у которых образующие параллельны одной из осей координат
- § 169. Уравнения линии
- § 170. Проекция линии на координатную плоскость
- § 171. Алгебраические поверхности и их порядок
- § 172. Сфера
- § 173. Эллипсоид
- § 174. Однополостный гиперболоид
- § 175. Двуполостный гиперболоид
- § 176. Конус второго порядка
- § 177. Эллиптический параболоид
- § 178. Гиперболический параболоид
- § 179. Перечень поверхностей второго порядка
- § 180. Прямолинейные образующие поверхностей второго порядка
- § 181. Поверхности вращения
- § 182. Определители второго и третьего порядков
- § 183. Определители высших порядков
- § 184. Свойства определителей
- § 185. Практический прием вычисления определителей
- § 186. Применение определителей к исследованию и решению системы уравнений
- § 187. Два уравнения с двумя неизвестными
- § 188. Два уравнения с двумя неизвестными
- § 189. Однородная система двух уравнений с тремя неизвестными
- § 190. Два уравнения с двумя неизвестными
- § 190а. Система n уравнений с n неизвестными
- ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- § 192. Рациональные числа
- § 193. Действительные (вещественные) числа
- § 194. Числовая ось
- § 195. Переменные и постоянные величины
- § 196. Функция
- § 197. Способы задания функции
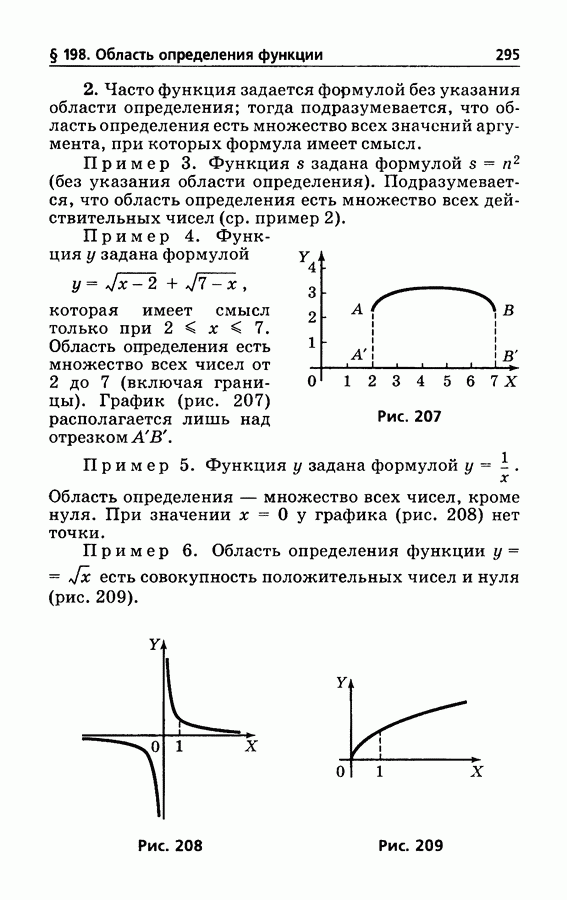
- § 198. Область определения функции
- § 199. Промежуток
- § 200. Классификация функций
- § 201. Основные элементарные функции
- § 202. Обозначение функции
- § 203. Предел последовательности
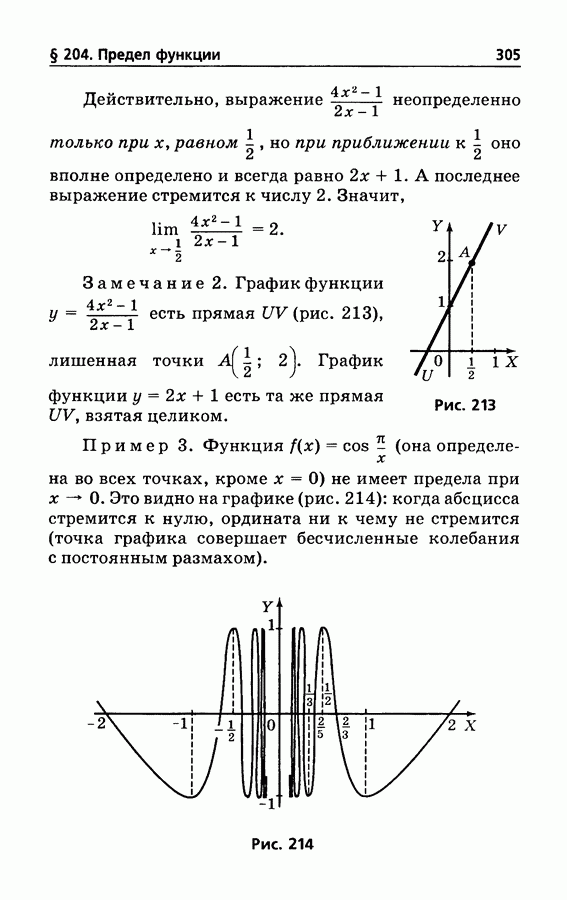
- § 204. Предел функции
- § 205. Определение предела функции
- § 206. Предел постоянной величины
- § 207. Бесконечно малая величина
- § 208. Бесконечно большая величина
- § 209. Связь между бесконечно большими и бесконечно малыми величинами
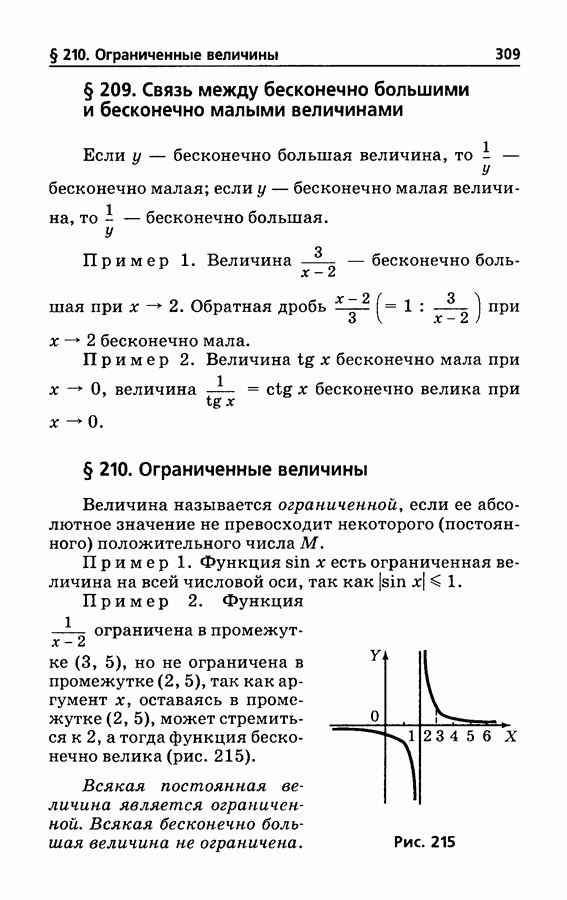
- § 210. Ограниченные величины
- § 211. Расширение понятия предепа
- § 212. Основные свойства бесконечно малых величин
- § 213. Основные теоремы о пределах
- § 214. Число е
- § 215. Предел sinx/x при x стремящемся к 0
- § 216. Эквивалентные бесконечно малые величины
- § 217. Сравнение бесконечно малых величин
- § 217а. Приращение переменной величины
- § 218. Непрерывность функции в точке
- § 219. Свойства функций, непрерывных в точке
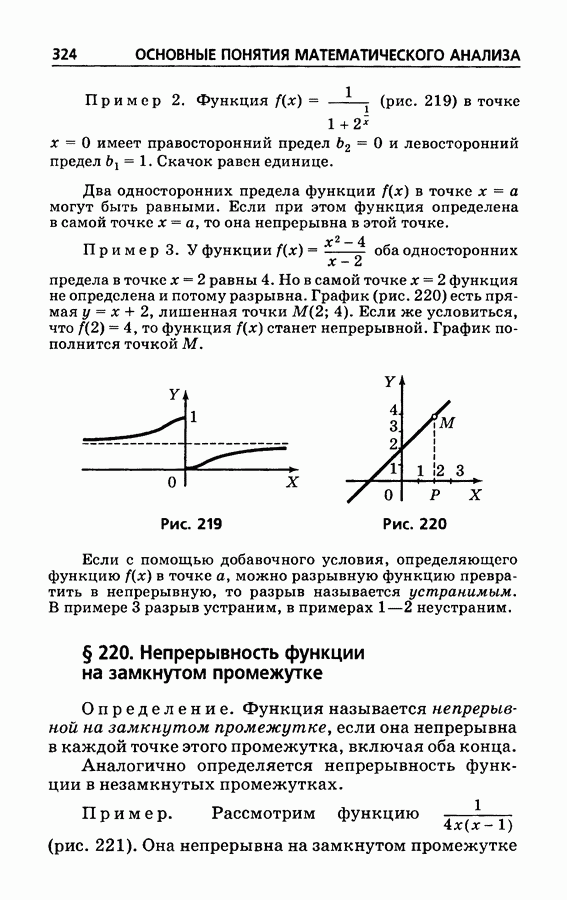
- § 219а. Односторонний предел; скачок функции
- § 220. Непрерывность функции на замкнутом промежутке
- § 221. Свойства функций, непрерывных на замкнутом промежутке
- ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 223. Скорость
- § 224. Определение производной функции
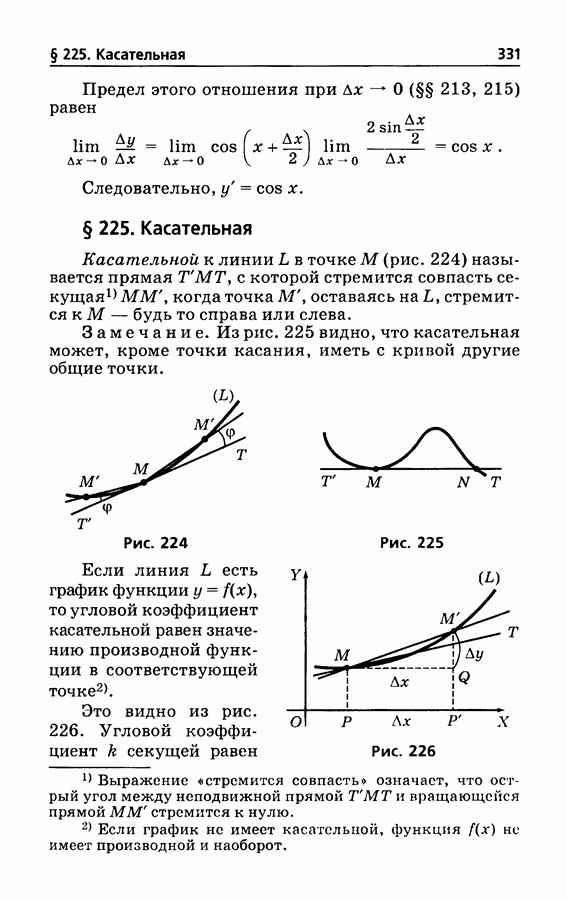
- § 225. Касательная
- § 226. Производные некоторых простейших функций
- § 227. Свойства производной
- § 228. Дифференциал
- § 229. Механический смысл дифференциала
- § 230. Геометрический смысл дифференциала
- § 231. Дифференцируемые функции
- § 232. Дифференциалы некоторых простейших функций
- § 233. Свойства дифференциала
- § 234. Инвариантность выражения f'(x)dx
- § 235. Выражение производной через дифференциалы
- § 236. Функция от функции (сложная функция)
- § 237. Дифференциал сложной функции
- § 238. Производная сложной функции
- § 239. Дифференцирование произведения
- § 240. Дифференцирование частного (дроби)
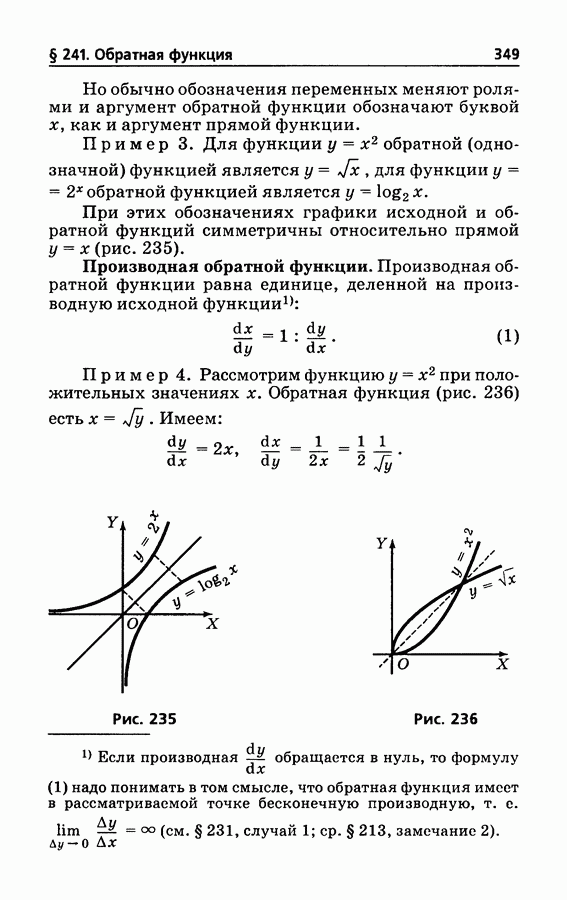
- § 241. Обратная функция
- § 242. Натуральные логарифмы
- § 243. Дифференцирование логарифмической функции
- § 244. Логарифмическое дифференцирование
- § 245. Дифференцирование показательной функции
- § 246. Дифференцирование тригонометрических функций
- § 247. Дифференцирование обратных тригонометрических функций
- § 247а. Некоторые поучительные примеры
- § 248. Дифференциал в приближенных вычислениях
- § 249. Применение дифференциала к оценке погрешности формул
- § 250. Дифференцирование неявных функций
- § 251. Параметрическое задание линии
- § 252. Параметрическое задание функции
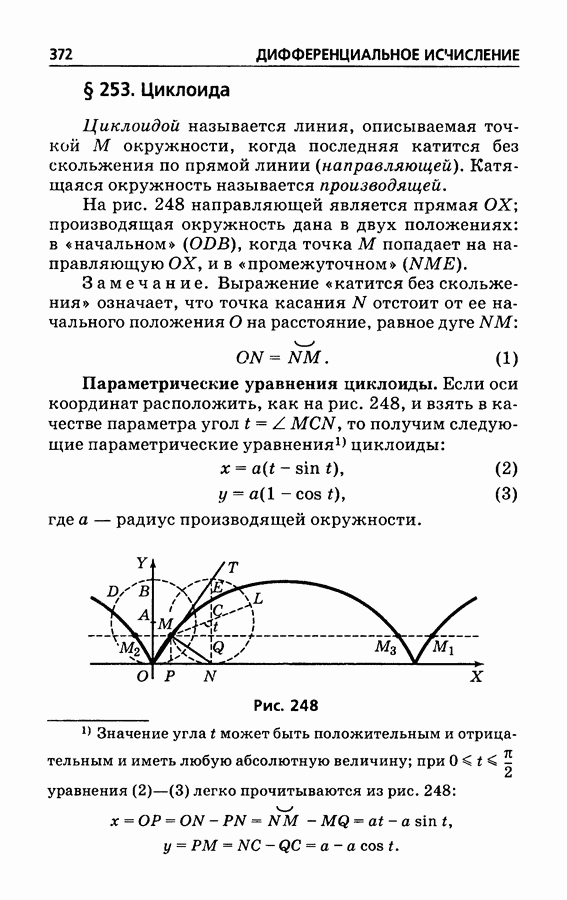
- § 253. Циклоида
- § 254. Уравнение касательной к плоской линии
- § 254а. Касательные к кривым второго порядка
- § 255. Уравнение нормали
- § 256. Производные высших порядков
- § 257. Механический смысл второй производной
- § 258. Дифференциалы высших порядков
- § 259. Выражение высших производных через дифференциалы
- § 260. Высшие производные функций, заданных параметрически
- § 261. Высшие производные неявных функций
- § 262. Правило Лейбница
- § 263. Теорема Ролля
- § 264. Теорема Лагранжа о среднем значении
- § 265. Формула конечных приращений
- § 266. Обобщенная теорема о среднем значении (Коши)
- § 267. Раскрытие неопределенности вида 0/0
- § 268. Раскрытие неопределенности вида бесконесность на бесконечность
- § 269. Неопределенные выражения других видов
- § 270. Исторические сведения о формуле Тейлора
- § 271. Формула Тейлора
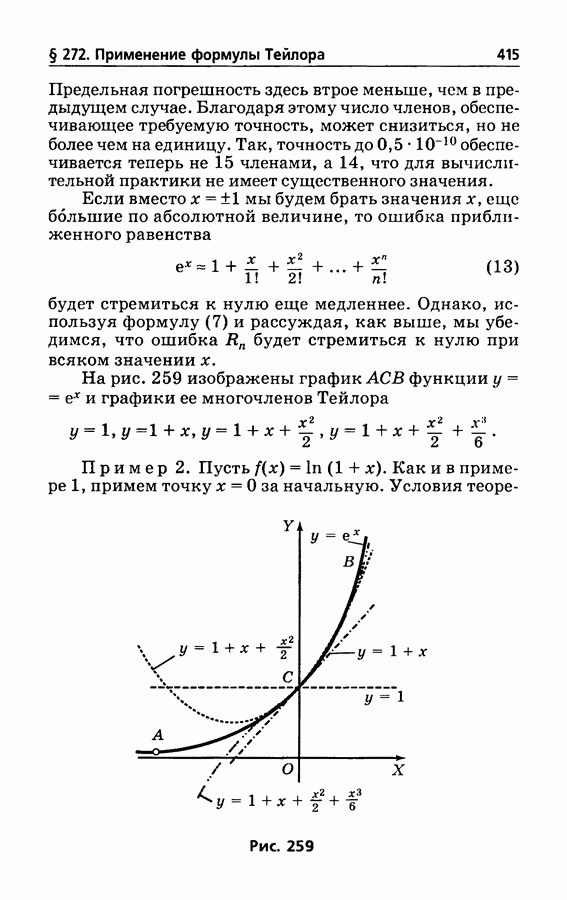
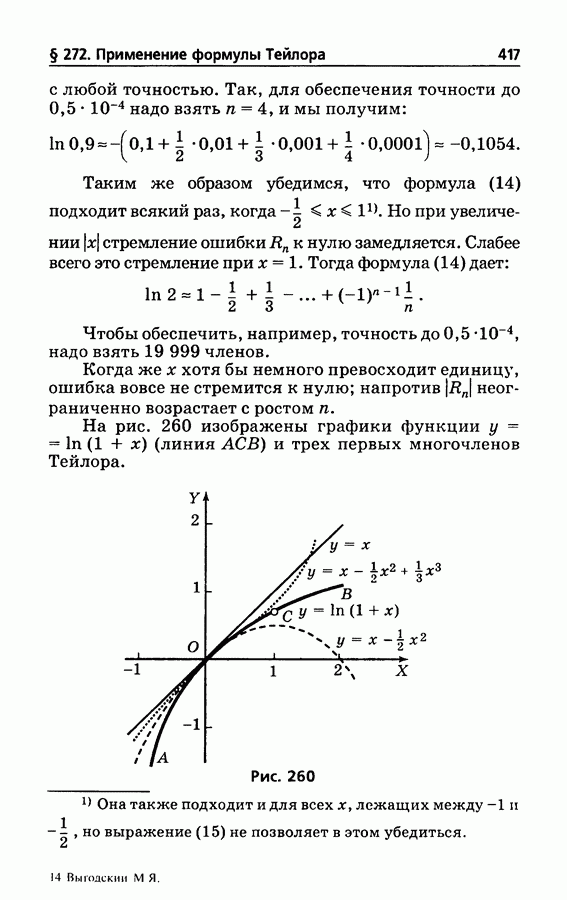
- § 272. Применение формулы Тейлора к вычислению значений функции
- § 273. Возрастание и убывание функции
- § 274. Признаки возрастания и убывания функции в точке
- § 274а. Признаки возрастания и убывания функции в промежутке
- § 275. Максимум и минимум
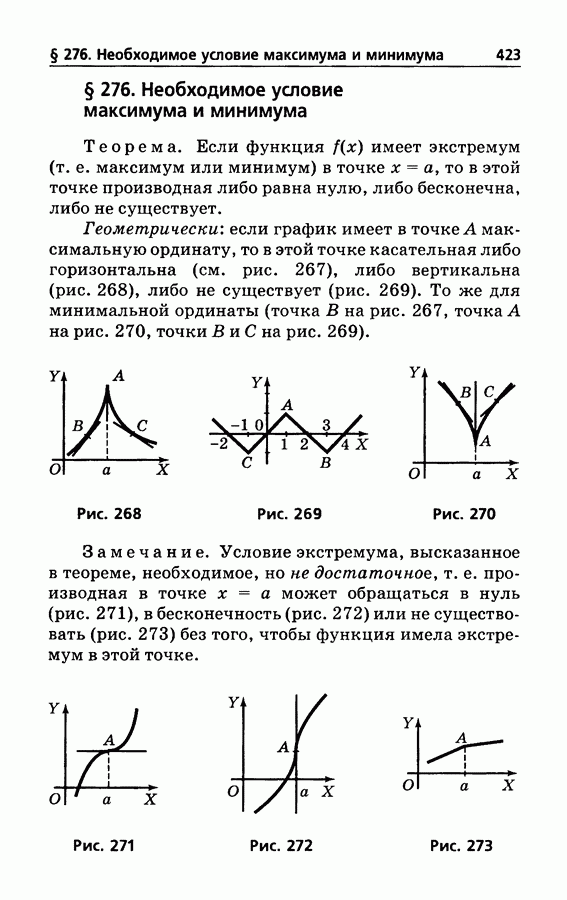
- § 276. Необходимое условие максимума и минимума
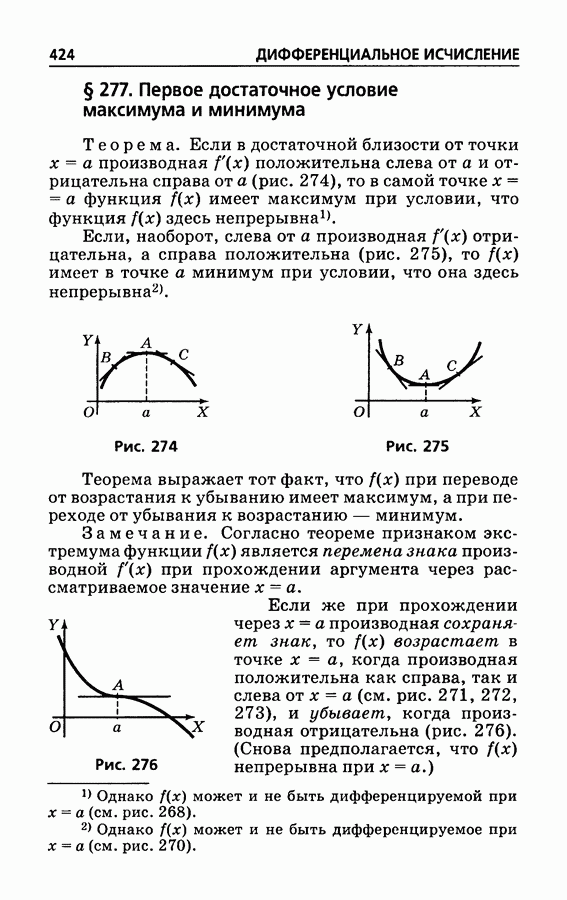
- § 277. Первое достаточное условие максимума и минимума
- § 278. Правило нахождения максимумов и минимумов
- § 279. Второе достаточное условие максимума и минимума
- § 280. Нахождение наибольшего и наименьшего значений функции
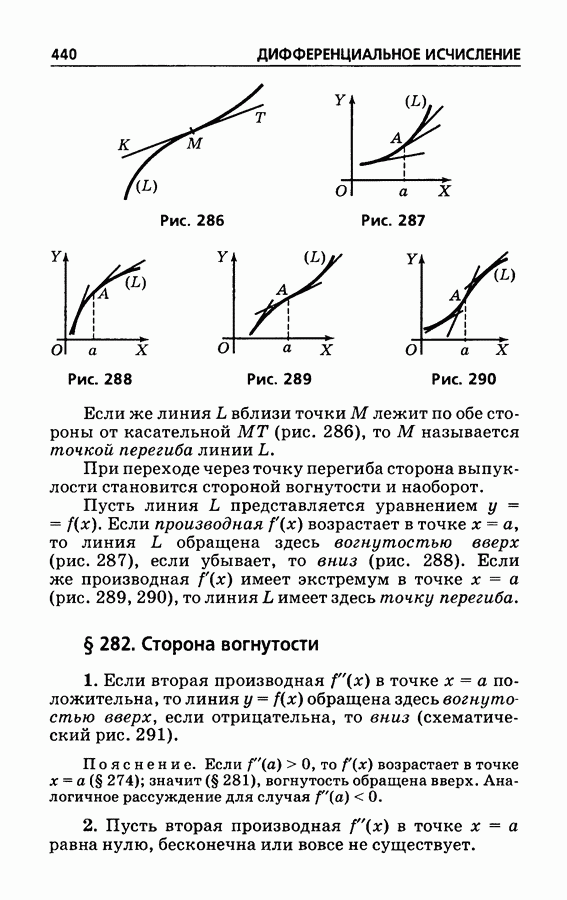
- § 281. Выпуклость плоских кривых; точка перегиба
- § 282. Сторона вогнутости
- § 283. Правило для нахождения точек перегиба
- § 284. Асимптоты
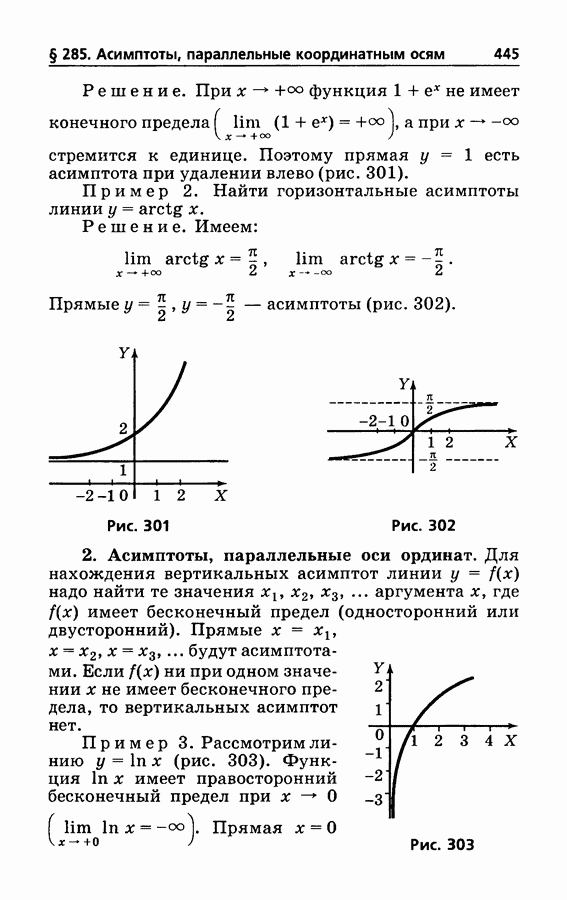
- § 285. Нахождение асимптот, параллельных координатным осям
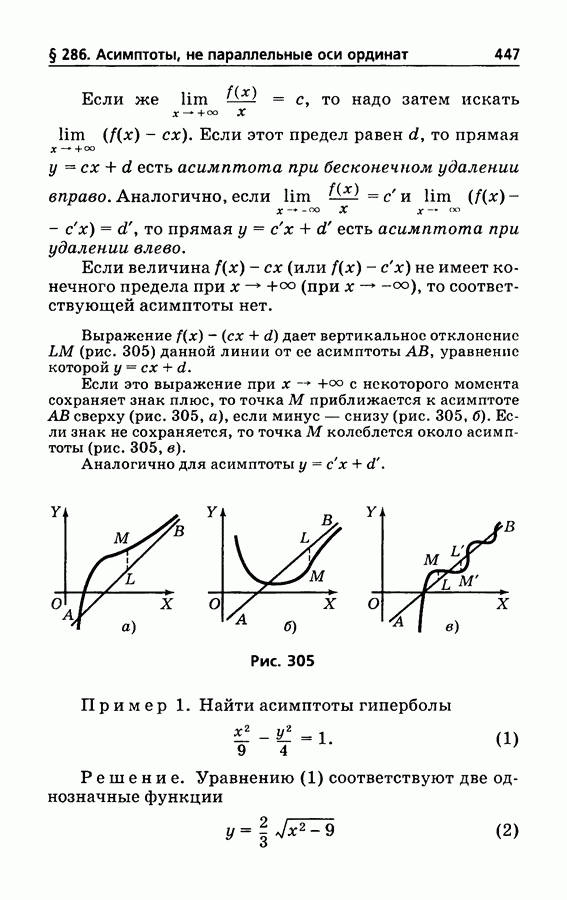
- § 286. Нахождение асимптот, не параллельных оси ординат
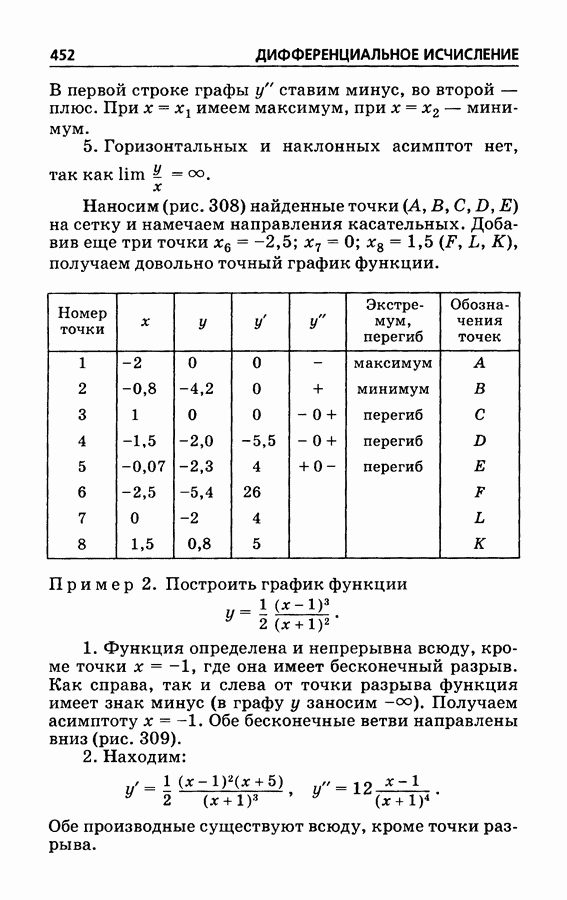
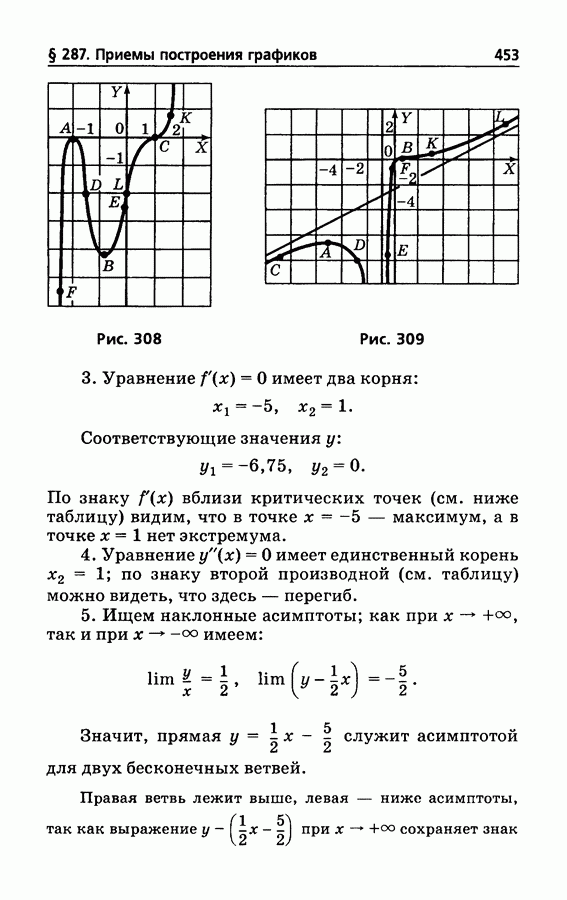
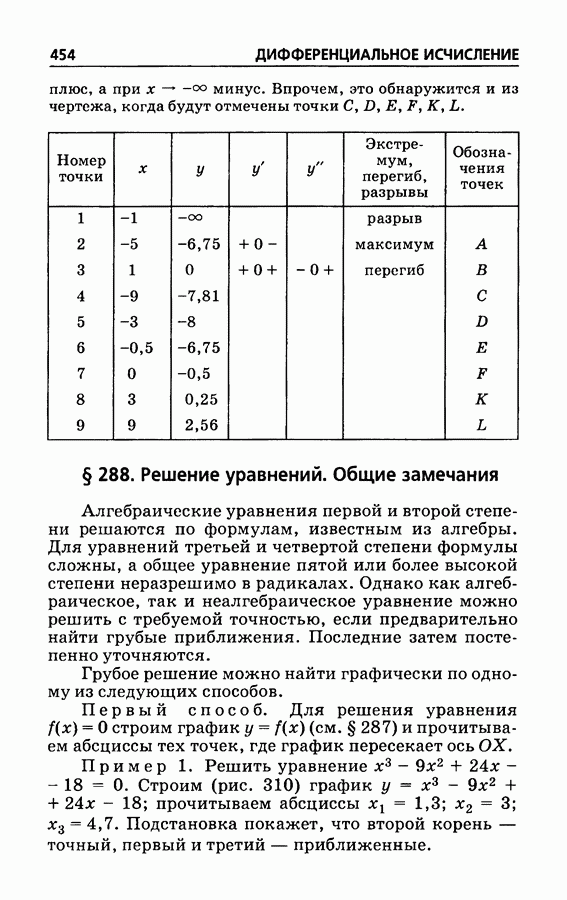
- § 287. Приемы построения графиков
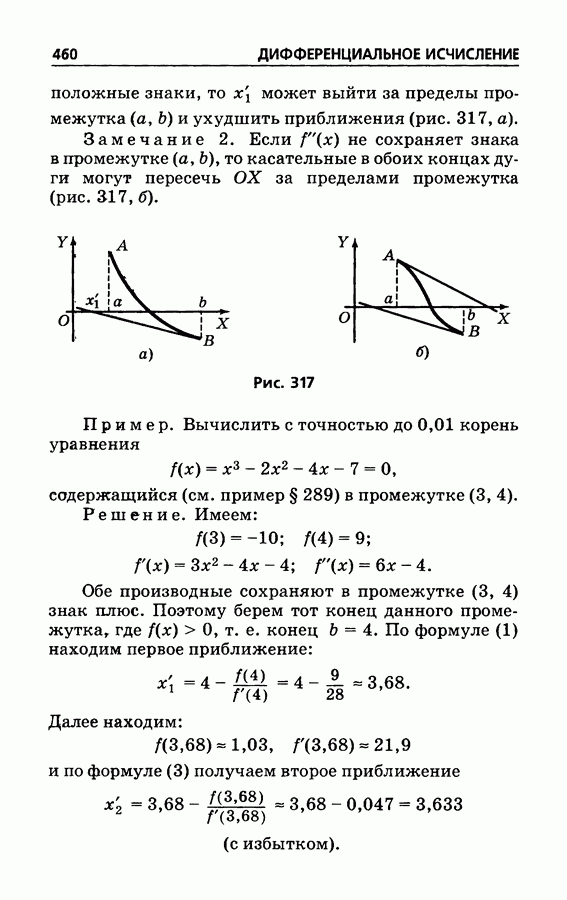
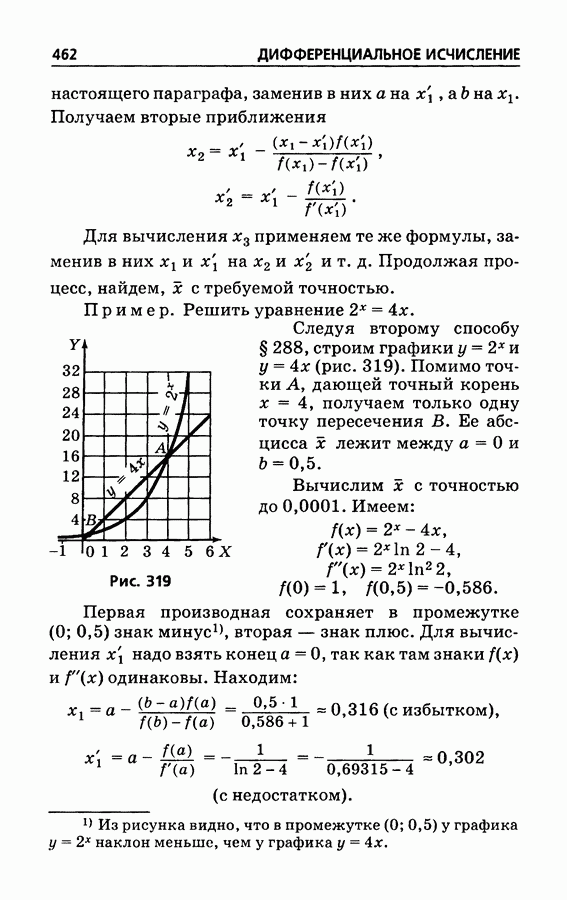
- § 288. Решение уравнений. Общие замечания
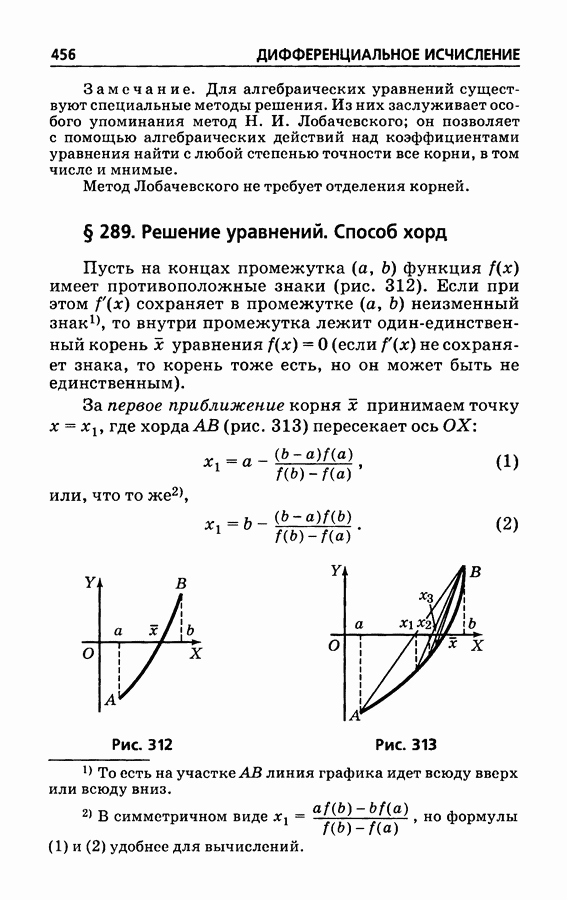
- § 289. Решение уравнений. Способ хорд
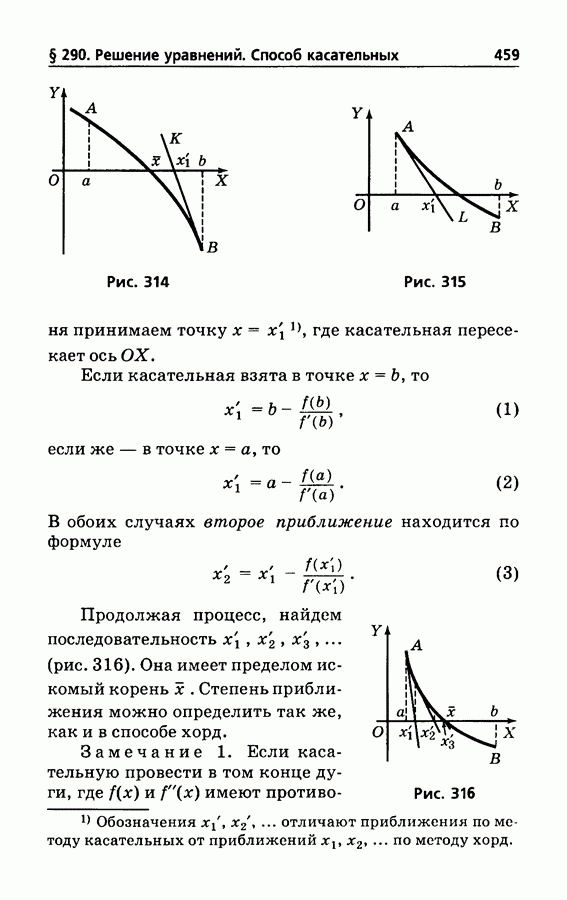
- § 290. Решение уравнений. Способ касательных
- § 291. Комбинированный метод хорд и касательных
- ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 293. Первообразная функция
- § 294. Неопределенный интеграл
- § 295. Геометрический смысл интегрирования
- § 296. Вычисление постоянной интегрирования по начальным данным
- § 297. Свойства неопределенного интеграла
- § 298. Таблица интегралов
- § 299. Непосредственное интегрирование
- § 300. Способ подстановки (интегрирование через вспомогательную переменную)
- § 301. Интегрирование по частям
- § 302. Интегрирование некоторых тригонометрических выражений
- § 303. Тригонометрические подстановки
- § 304. Рациональные функции
- § 304а. Исключение целой части
- § 305. О приемах интегрирования рациональных дробей
- § 306. Интегрирование простейших рациональных дробей
- § 307. Интегрирование рациональных функций (общий метод)
- § 308. О разложении многочлена на множители
- § 309. Об интегрируемости в элементарных функциях
- § 310. Некоторые интегралы, зависящие от радикалов
- § 311. Интеграл от биномиального дифференциала
- § 312. Интегралы вида …
- § 313. Интегралы вида S R(sinx, cosx)dx
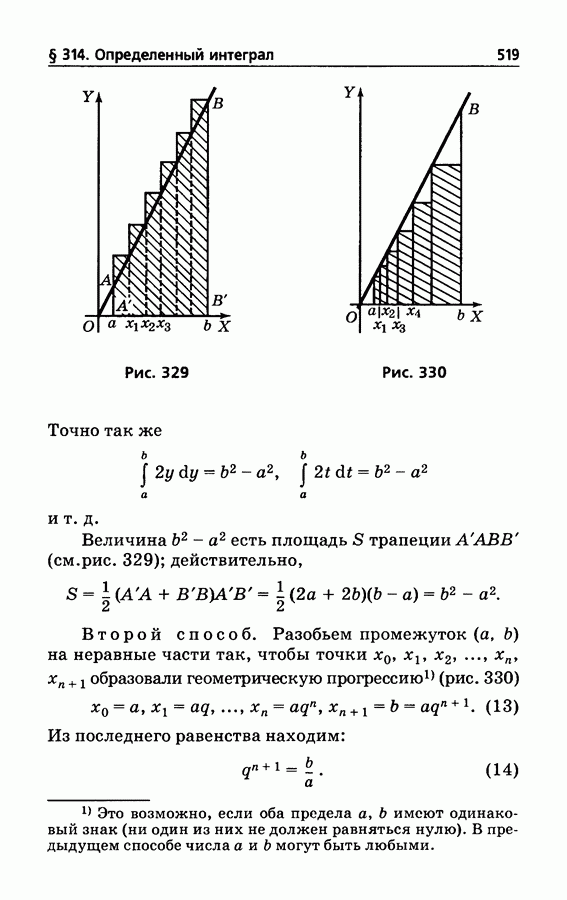
- § 314. Определенный интеграл
- § 315. Свойства определенного интеграла
- § 316. Геометрический смысл определенного интеграла
- § 317. Механический смысл определенного интеграла
- § 318. Оценка определенного интеграла
- § 318а. Неравенство Буняковского
- § 319. Теорема о среднем интегрального исчисления
- § 320. Определенный интеграл как функция верхнего предела
- § 321. Дифференциал интеграла
- § 322. Интеграл дифференциала. Формула Ньютона — Лейбница
- § 323. Вычисление определенного интеграла с помощью неопределенного
- § 324. Определенное интегрирование по частям
- § 325. Способ подстановки в определенном интеграле
- § 326. О несобственных интегралах
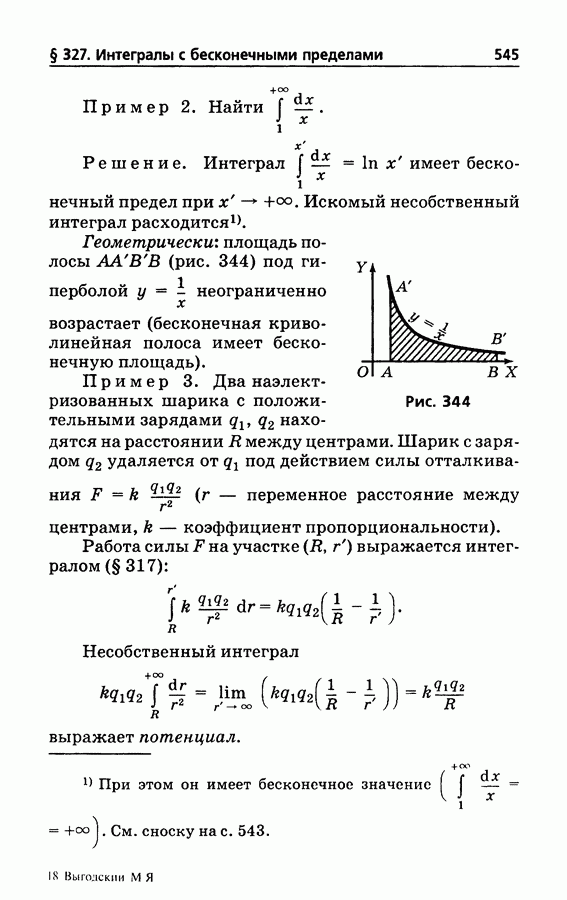
- § 327. Интегралы с бесконечными пределами
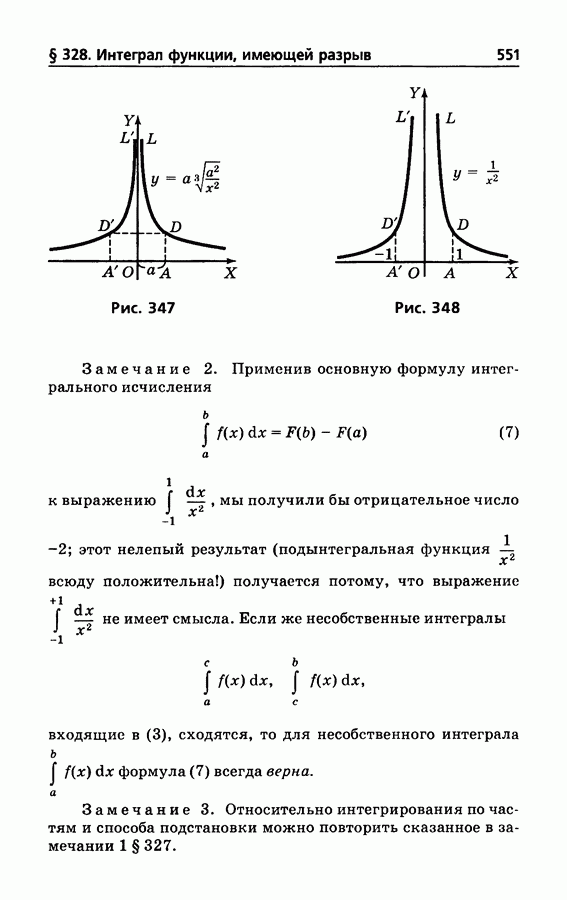
- § 328. Интеграл функции, имеющей разрыв
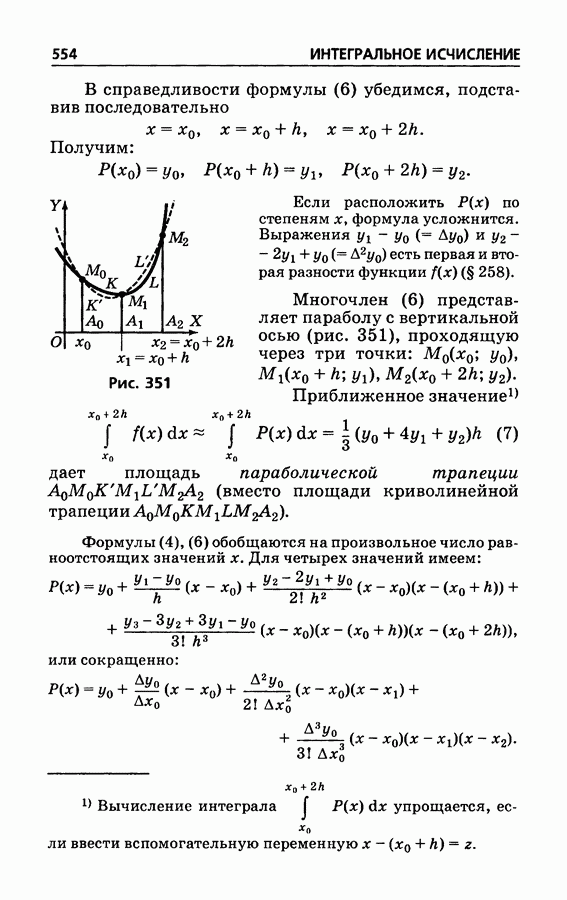
- § 329. О приближенном вычислении интеграла
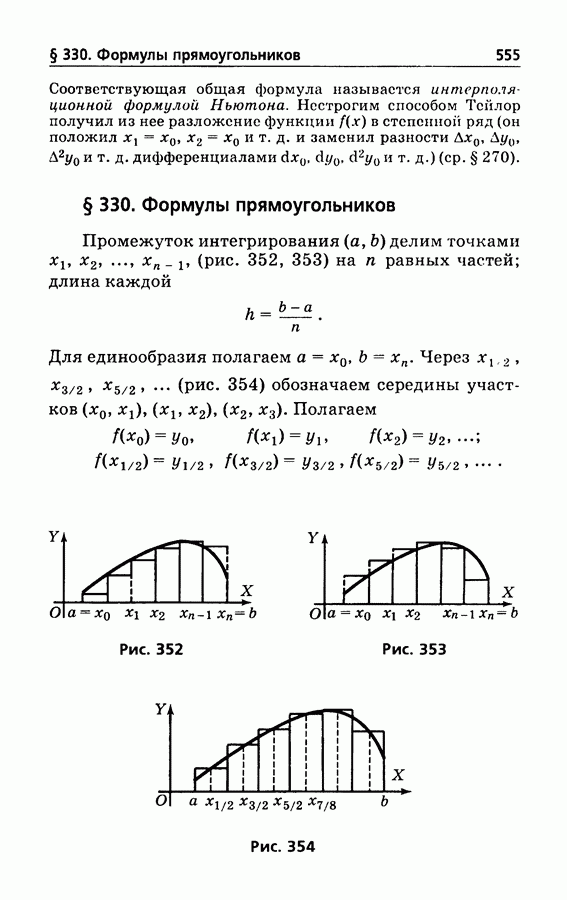
- § 330. Формулы прямоугольников
- § 331. Формула трапеций
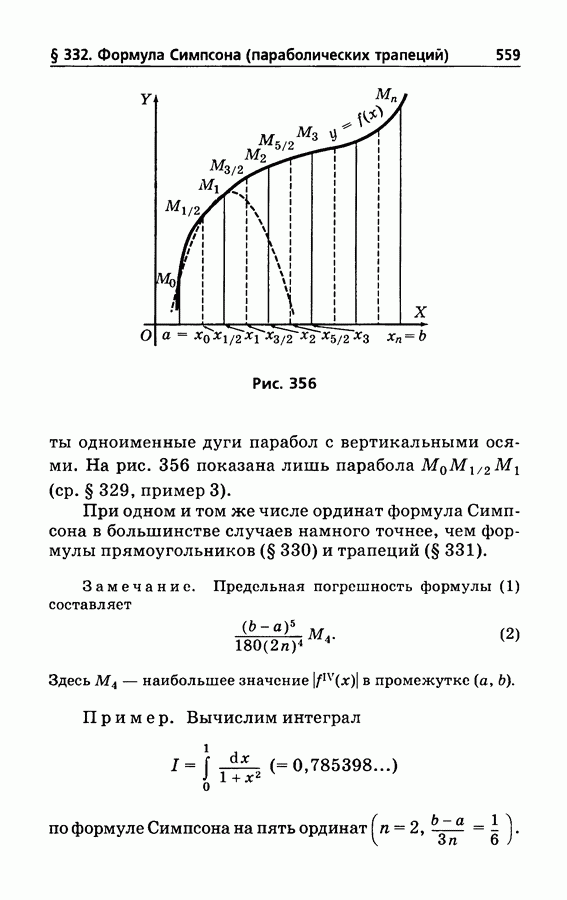
- § 332. Формула Симпсона (параболических трапеций)
- § 333. Площади фигур, отнесенных к прямоугольным координатам
- § 334. Схема применения определенного интеграла
- § 335. Площади фигур, отнесенных к полярным координатам
- § 336. Объем тела по поперечным сечениям
- § 337. Объем тела вращения
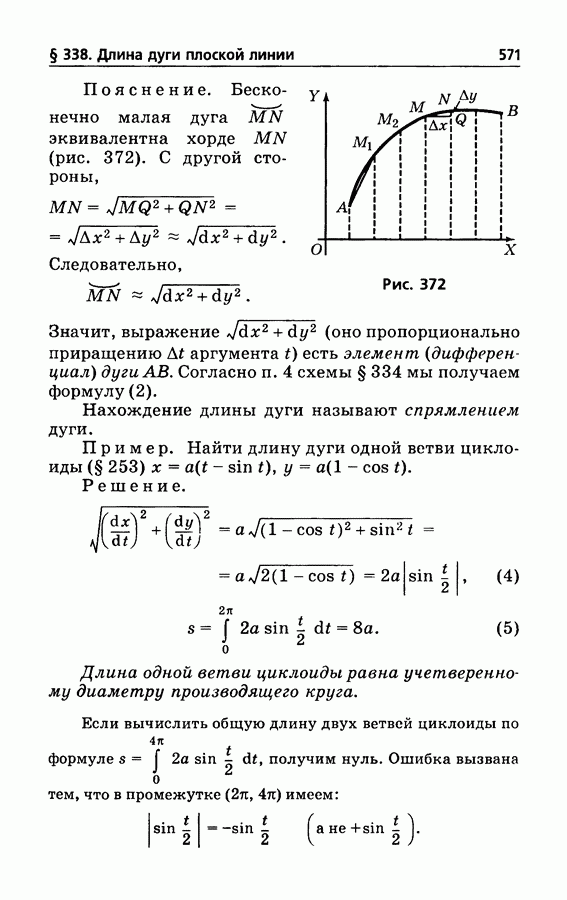
- § 338. Длина дуги плоской линии
- § 339. Дифференциал дуги
- § 340. Длина дуги и ее дифференциал в полярных координатах
- § 341. Площадь поверхности вращения
- ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ
- § 342. Кривизна
- § 343. Центр, радиус и круг кривизны плоской линии
- § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии
- § 345. Эволюта плоской линии
- § 346. Свойства эволюты плоской линии
- § 347. Развертка (эвольвента) плоской линии
- § 348. Параметрическое задание пространственной линии
- § 349. Винтовая линия
- § 350. Длина дуги пространственной линии
- § 351. Касательная к пространственной линии
- § 352. Нормальная плоскость
- § 353. Вектор-функция скалярного аргумента
- § 354. Предел вектор-функции
- § 355. Производная вектор-функции
- § 356. Дифференциал вектор-функции
- § 357. Свойства производной и дифференциала вектор-функции
- § 358. Соприкасающаяся плоскость
- § 359. Главная нормаль. Сопутствующий трехгранник
- § 360. Взаимное расположение линии и плоскости
- § 361. Основные векторы сопутствующего трехгранника
- § 362. Центр, ось и радиус кривизны пространственной линии
- § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии
- § 364. О знаке кривизны
- § 365. Кручение
- РЯДЫ
- § 367. Определение ряда
- § 368. Сходящиеся и расходящиеся ряды
- § 369. Необходимое условие сходимости ряда
- § 370. Остаток ряда
- § 371. Простейшие действия над рядами
- § 372. Положительные ряды
- § 373. Сравнение положительных рядов
- § 374. Признак Даламбера для положительного ряда
- § 375. Интегральный признак сходимости
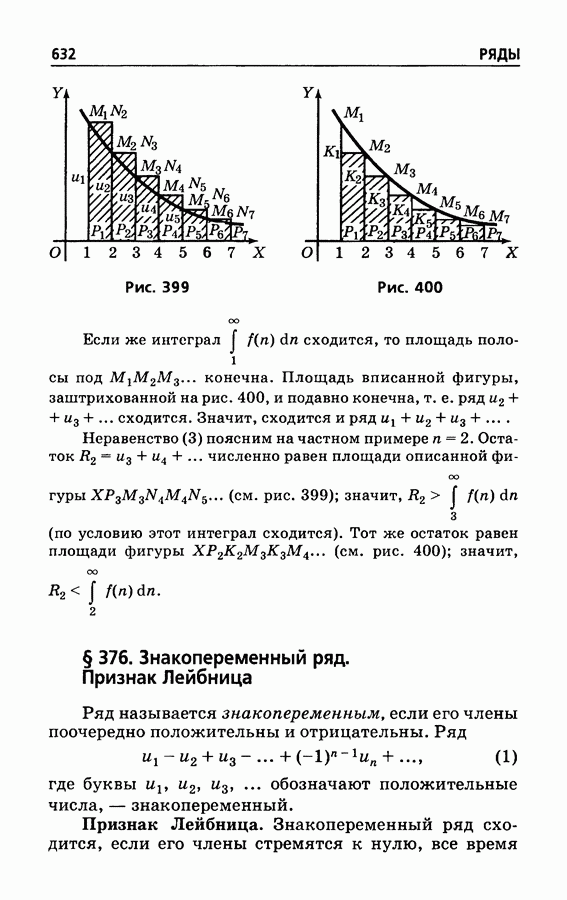
- § 376. Знакопеременный ряд. Признак Лейбница
- § 377. Абсолютная и условная сходимость
- § 378. Признак Даламбера для произвольного ряда
- § 379. Перестановка членов ряда
- § 380. Группировка членов ряда
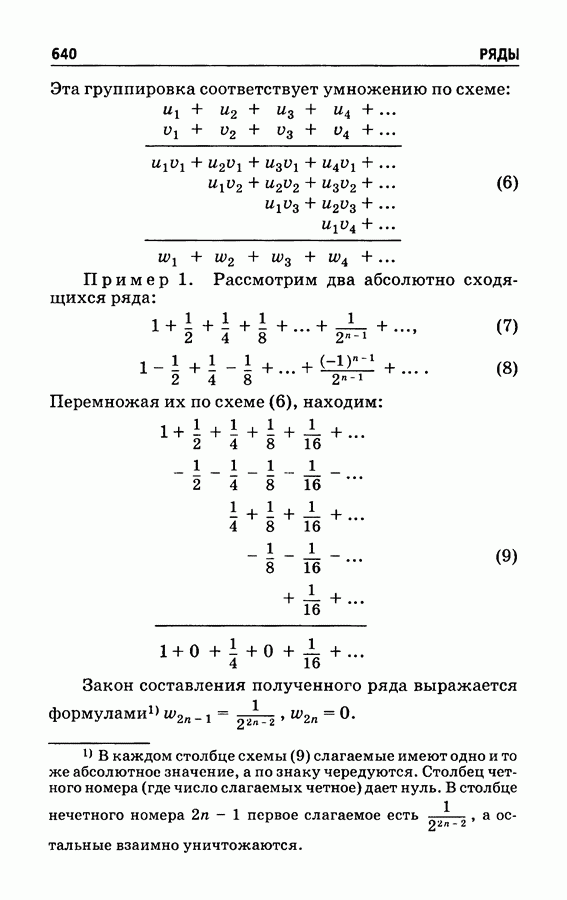
- § 381. Умножение рядов
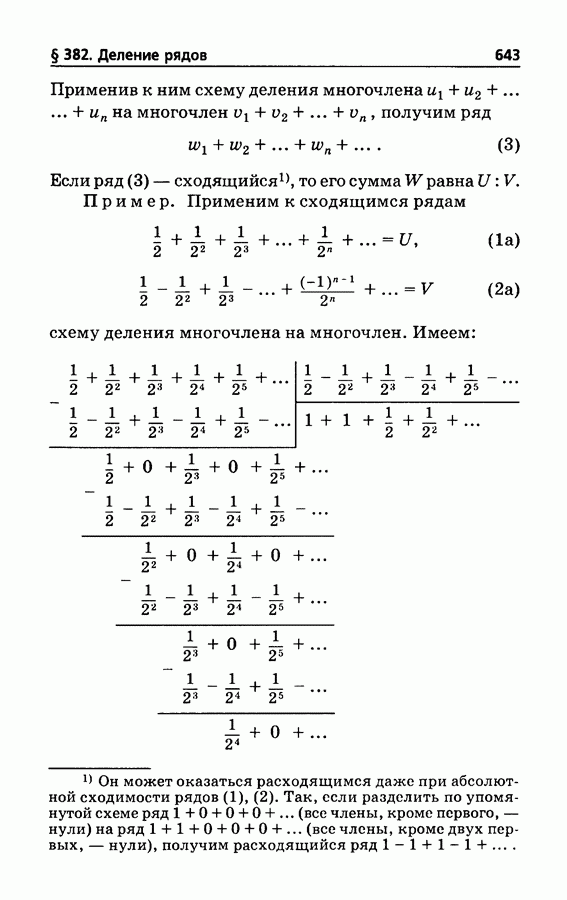
- § 382. Деление рядов
- § 383. Функциональный ряд
- § 384. Область сходимости функционального ряда
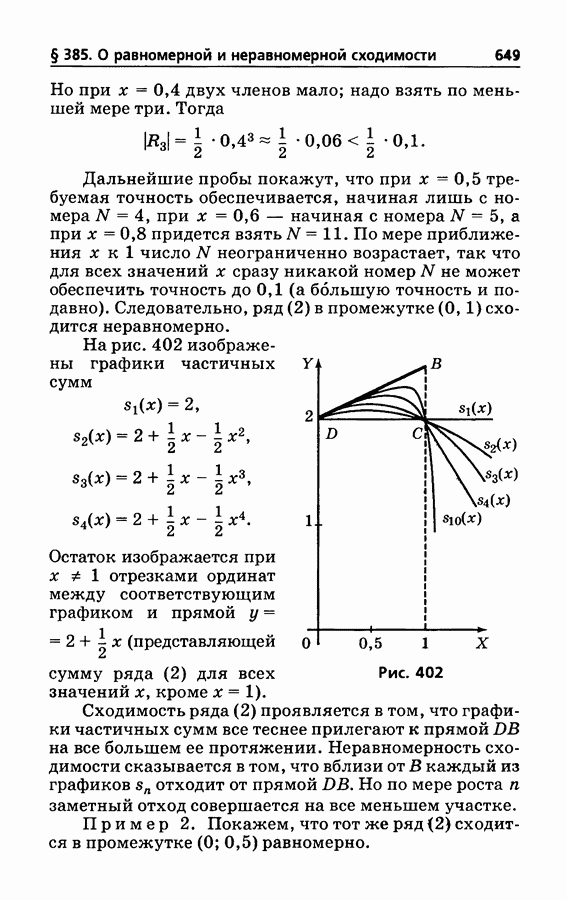
- § 385. О равномерной и неравномерной сходимости
- § 386. Определение равномерной и неравномерной сходимости
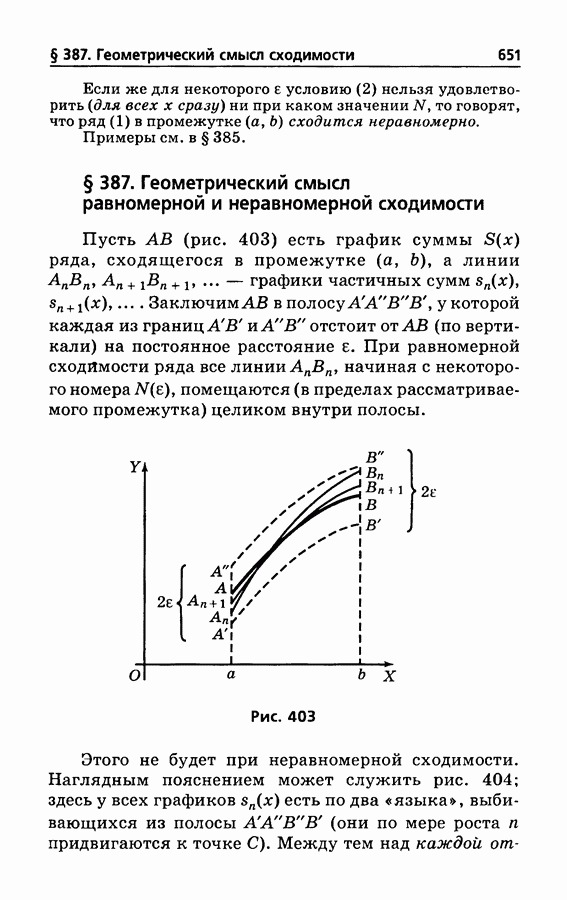
- § 387. Геометрический смысл равномерной и неравномерной сходимости
- § 388. Признак равномерной сходимости; правильные ряды
- § 389. Непрерывность суммы ряда
- § 390. Интегрирование рядов
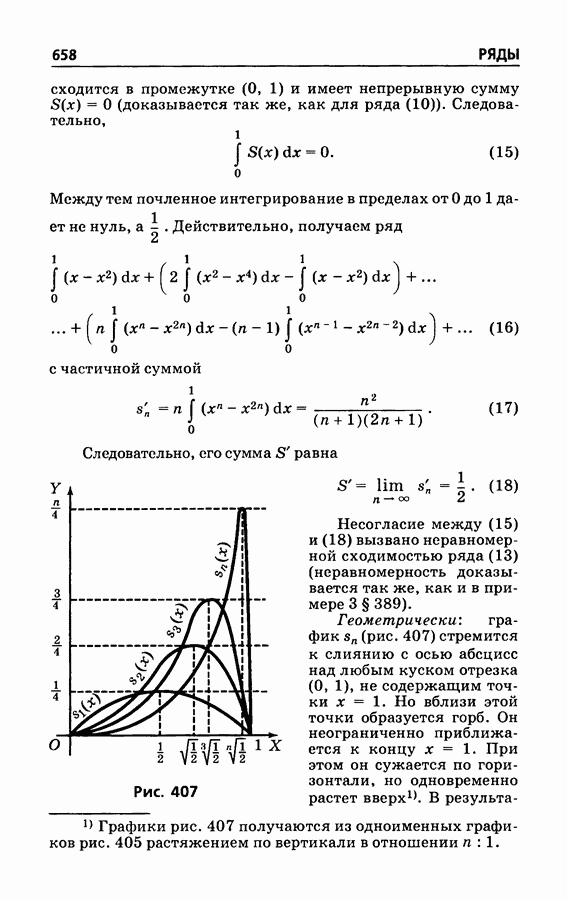
- § 391. Дифференцирование рядов
- § 392. Степенной ряд
- § 393. Промежуток и радиус сходимости степенного ряда
- § 394. Нахождение радиуса сходимости
- § 395. Область сходимости ряда, расположенного по степеням х — х0
- § 396. Теорема Абеля
- § 397. Действия со степенными рядами
- § 398. Дифференцирование и интегрирование степенного ряда
- § 399. Ряд Тейлора
- § 400. Разложение функции в степенной ряд
- § 401. Разложение элементарных функций в степенные ряды
- § 402. Применение рядов к вычислению интегралов
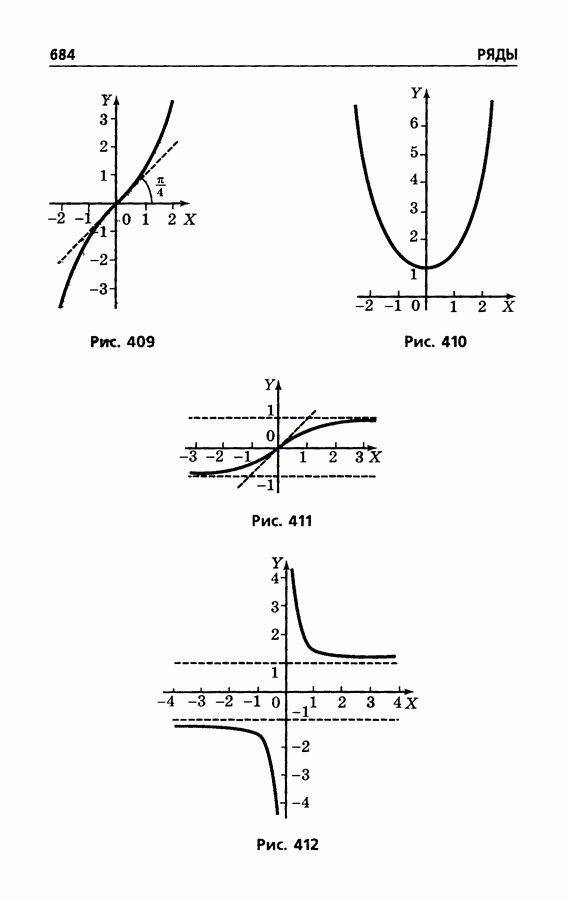
- § 403. Гиперболические функции
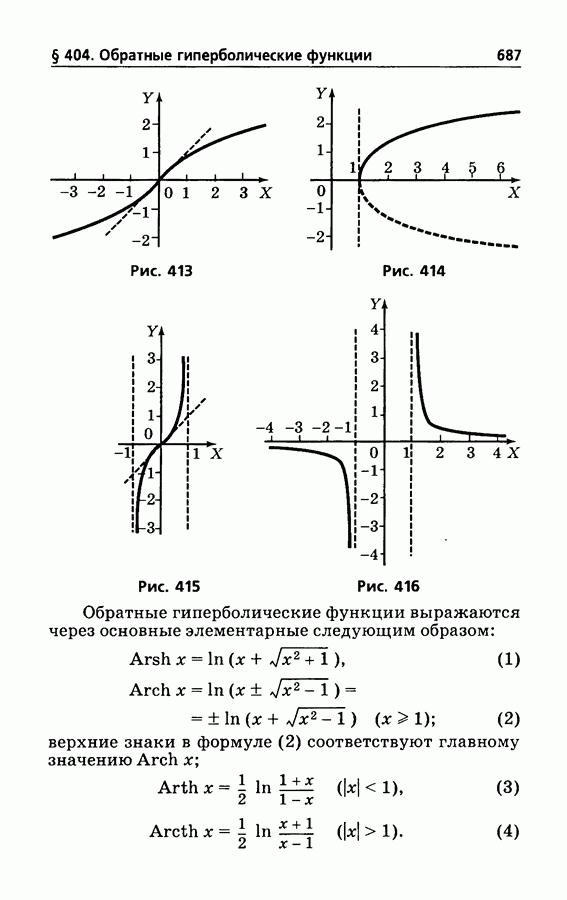
- § 404. Обратные гиперболические функции
- § 405. Происхождение наименований гиперболических функций
- § 406. О комплексных числах
- § 407. Комплексная функция действительного аргумента
- § 408. Производная комплексной функции
- § 409. Возведение положительного числа в комплексную степень
- § 410. Формула Эйлера
- § 411. Тригонометрический ряд
- § 412. Исторические сведения о тригонометрических рядах
- § 413. Ортогональность системы функций cos nx, sin nx
- § 414. Формулы Эйлера-Фурье
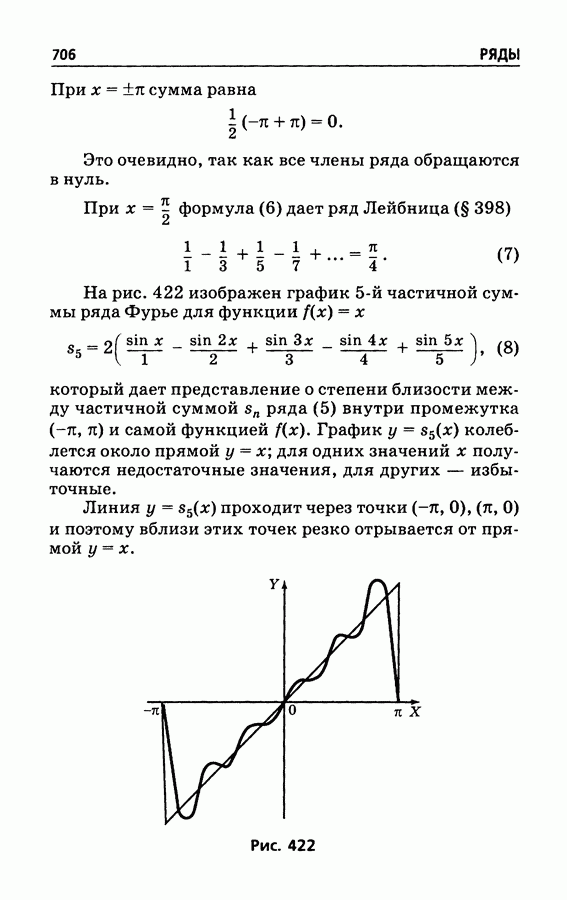
- § 415. Ряд Фурье
- § 416. Ряд Фурье для непрерывной функции
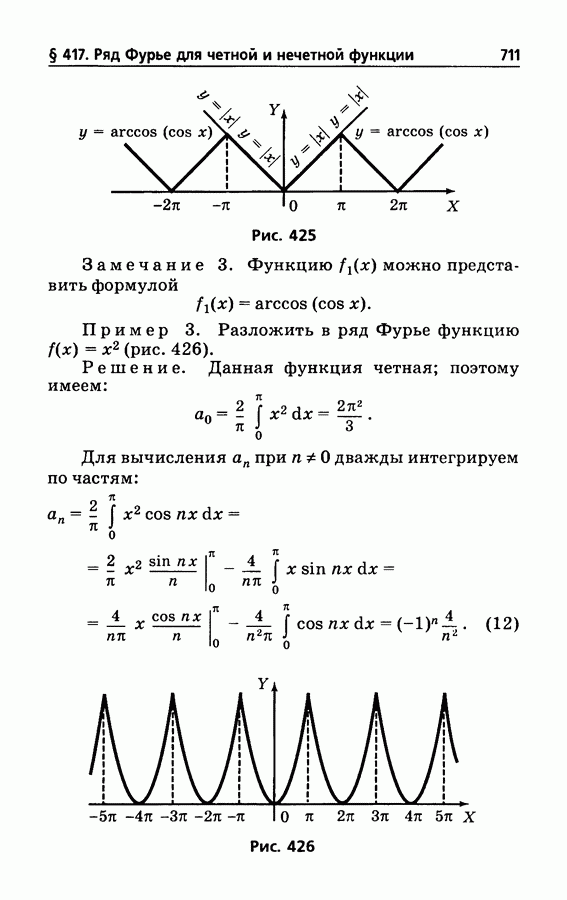
- § 417. Ряд Фурье для четной и нечетной функции
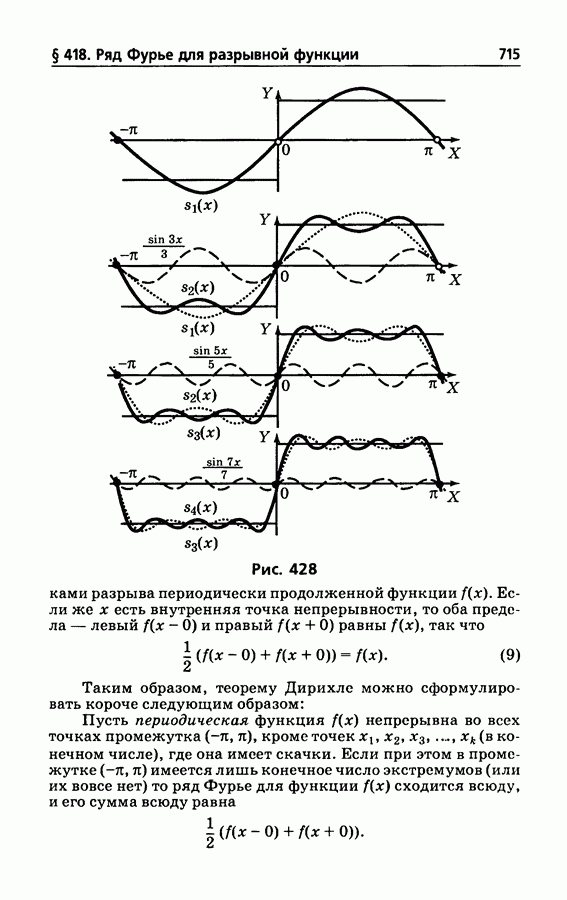
- § 418. Ряд Фурье для разрывной функции
- ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ
- § 420. Функция трех и большего числа аргументов
- § 421. Способы задания функций нескольких аргументов
- § 422. Предел функции нескольких аргументов
- § 424. Непрерывность функции нескольких аргументов
- § 425. Частные производные
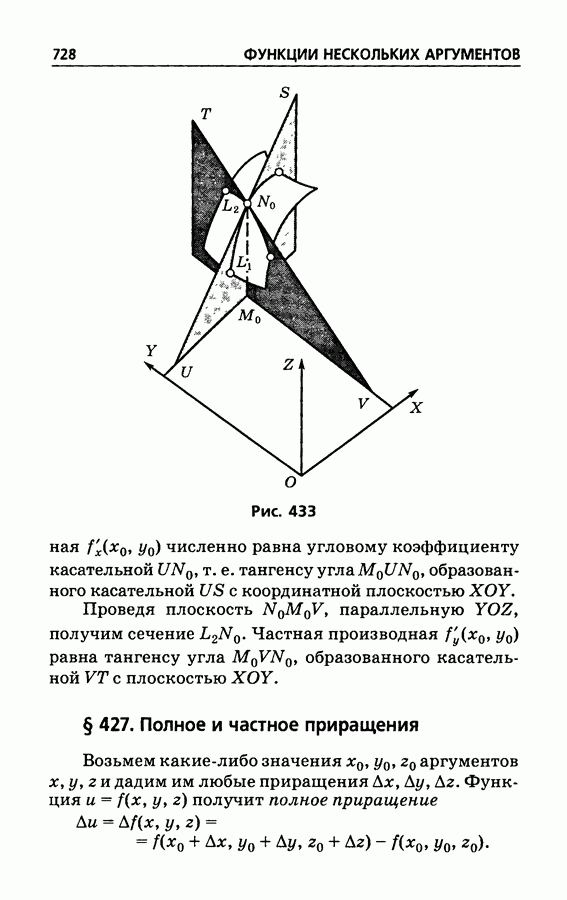
- § 426. Геометрический смысл частных производных для случая двух аргументов
- § 427. Полное и частное приращения
- § 428. Частный дифференциал
- § 429. О выражении частной производной через дифференциал
- § 430. Полный дифференциал
- § 431. Геометрический смысл полного дифференциала (случай двух аргументов)
- § 432. Инвариантность выражения … полного дифференциала
- § 433. Техника дифференцирования
- § 434. Дифференцируемые функции
- § 435. Касательная плоскость и нормаль к поверхности
- § 436. Уравнение касательной плоскости
- § 437. Уравнения нормали
- § 438. Дифференцирование сложной функции
- § 439. Замена прямоугольных координат полярными
- § 440. Формулы для производных сложной функции
- § 441. Полная производная
- § 442. Дифференцирование неявной функции нескольких переменных
- § 443. Частные производные высших порядков
- § 444. Полные дифференциалы высших порядков
- § 445. Техника повторного дифференцирования
- § 446. Условное обозначение дифференциалов
- § 447. Формула Тейлора для функции нескольких аргументов
- § 448. Экстремум (максимум и минимум) функции нескольких аргументов
- § 449. Правило нахождения экстремума
- § 450. Достаточные условия экстремума (случай двух аргументов)
- § 451. Двойной интеграл
- § 452. Геометрический смысл двойного интеграла
- § 453. Свойства двойного интеграла
- § 454. Оценка двойного интеграла
- § 455. Вычисление двойного интеграла (простейший случай)
- § 456. Вычисление двойного интеграла (общий случай)
- § 457. Функция точки
- § 458. Выражение двойного интеграла через полярные координаты
- § 459. Площадь куска поверхности
- § 460. Тройной интеграл
- § 461. Вычисление тройного интеграла (простейший случай)
- § 462. Вычисление тройного интеграла (общий случай)
- § 463. Цилиндрические координаты
- § 464. Выражение тройного интеграла через цилиндрические координаты
- § 465. Сферические координаты
- § 466. Выражение тройного интеграла через сферические координаты
- § 467. Схема применения двойного и тройного интегралов
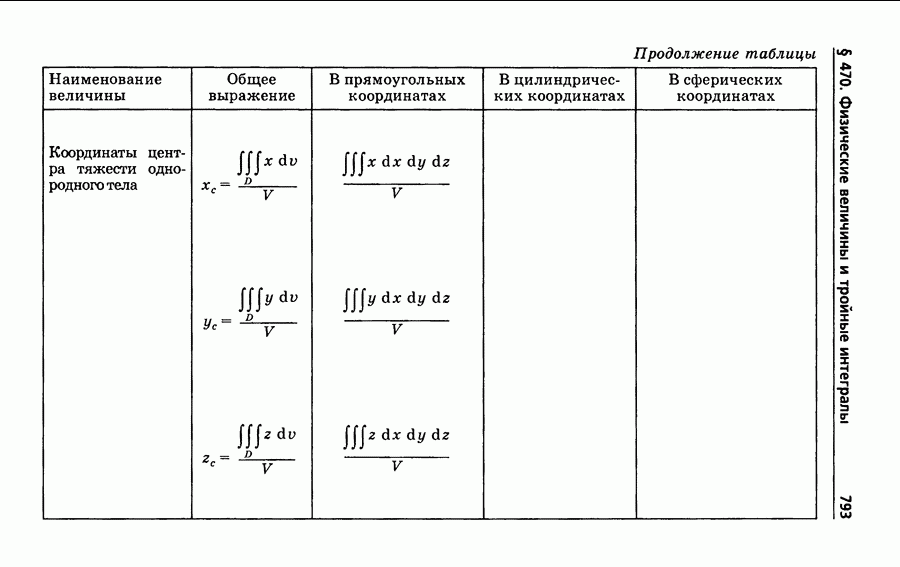
- § 468. Момент инерции
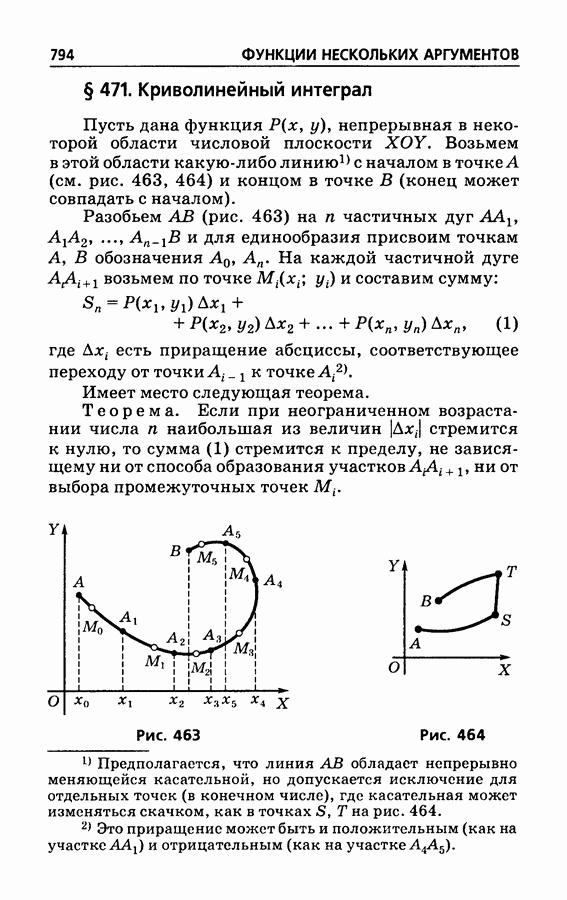
- § 471. Криволинейный интеграл
- § 472. Механический смысл криволинейного интеграла
- § 473. Вычисление криволинейного интеграла
- § 474. Формула Грина
- § 475. Условие, при котором криволинейный интеграл не зависит от пути
- § 476. Другая форма условия предыдущего параграфа
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 478. Уравнение первого порядка
- § 479. Геометрический смысл уравнения первого порядка
- § 480. Изоклины
- § 481. Частное и общее решения уравнения первого порядка
- § 482. Уравнения с разделенными переменными
- § 483. Разделение переменных. Особое решение
- § 484. Уравнение в полных дифференциалах
- § 484а. Интегрирующий множитель
- § 485. Однородное уравнение
- § 486. Линейное уравнение первого порядка
- § 487. Уравнение Клеро
- § 488. Огибающая
- § 489. Об интегрируемости дифференциальных уравнений
- § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера
- § 491. Интегрирование дифференциальных уравнений с помощью рядов
- § 492. О составлении дифференциальных уравнений
- § 493. Уравнение второго порядка
- § 494. Уравнение n-го порядка
- § 495. Случаи понижения порядка
- § 496. Линейное уравнение второго порядка
- § 497. Линейное уравнение второго порядка с постоянными коэффициентами
- § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части
- § 498а. Связь между случаями 1 и 3 § 498
- § 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью
- § 500. Линейные уравнения любого порядка
- § 501. Метод вариации постоянных
- § 502. Системы дифференциальных уравнений. Линейные системы
- НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
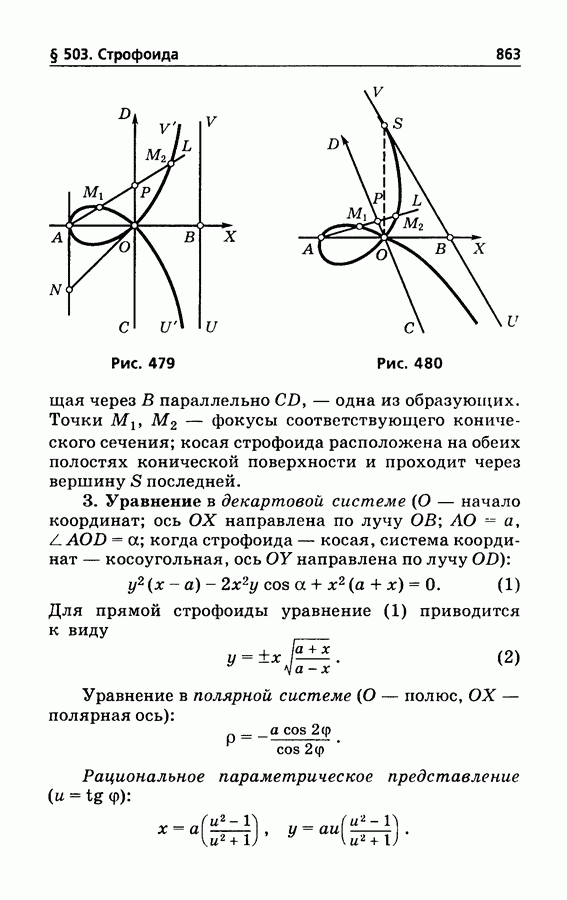
- § 503. Строфоида
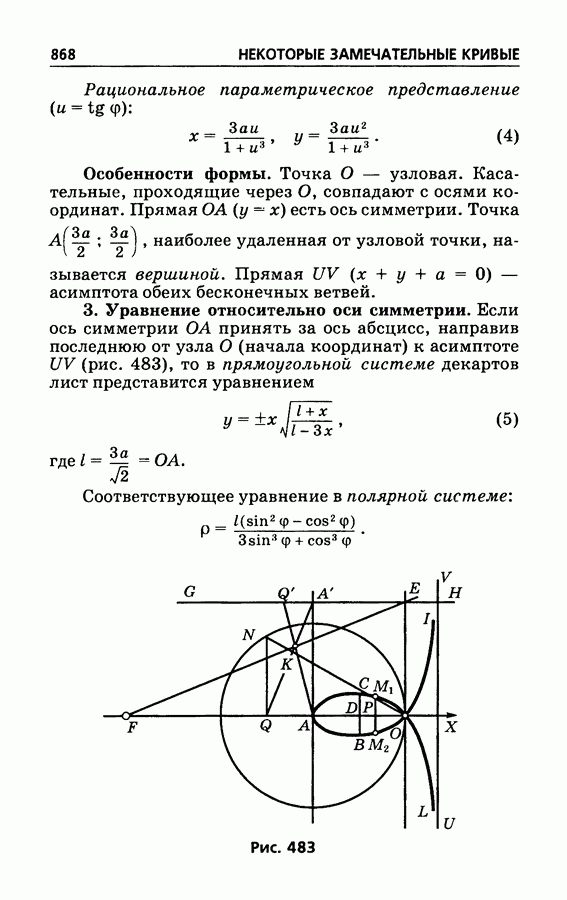
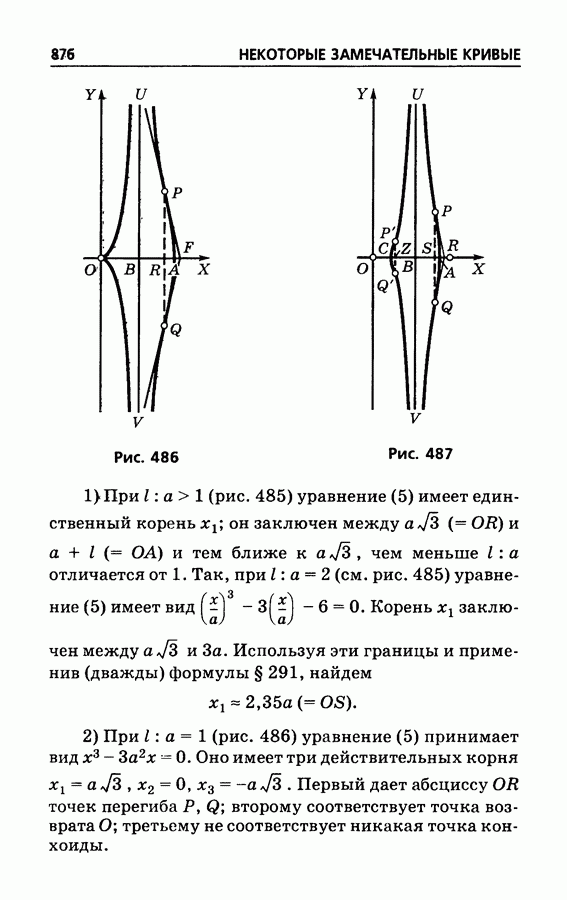
- § 504. Циссоида Диокла
- § 505. Декартов лист
- § 506. Верзьера Аньези
- § 507. Конхоида Никомеда
- § 508. Улитка Паскаля; кардиоида
- § 509. Линия Кассини
- § 510. Лемниската Бернулли
- § 511. Архимедова спираль
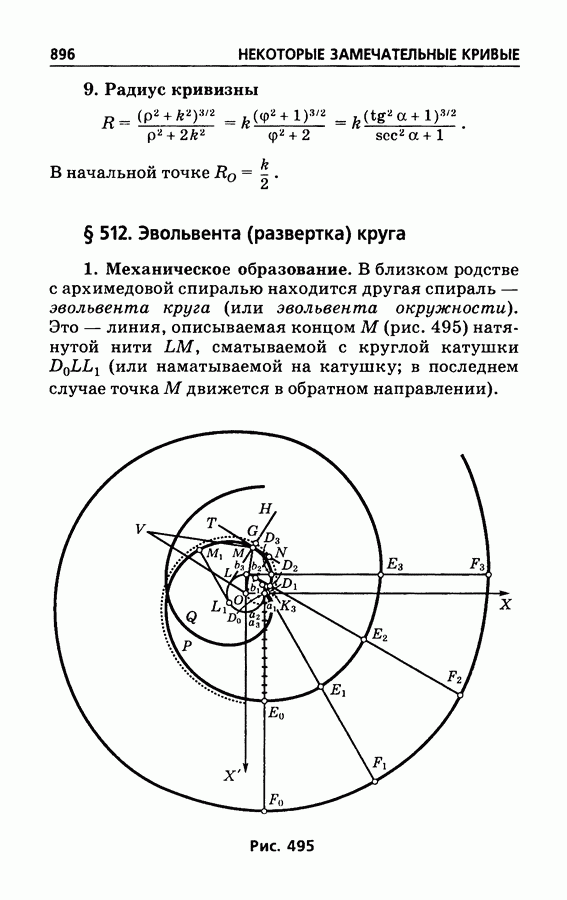
- § 512. Эвольвента (развертка) круга
- § 513. Логарифмическая спираль
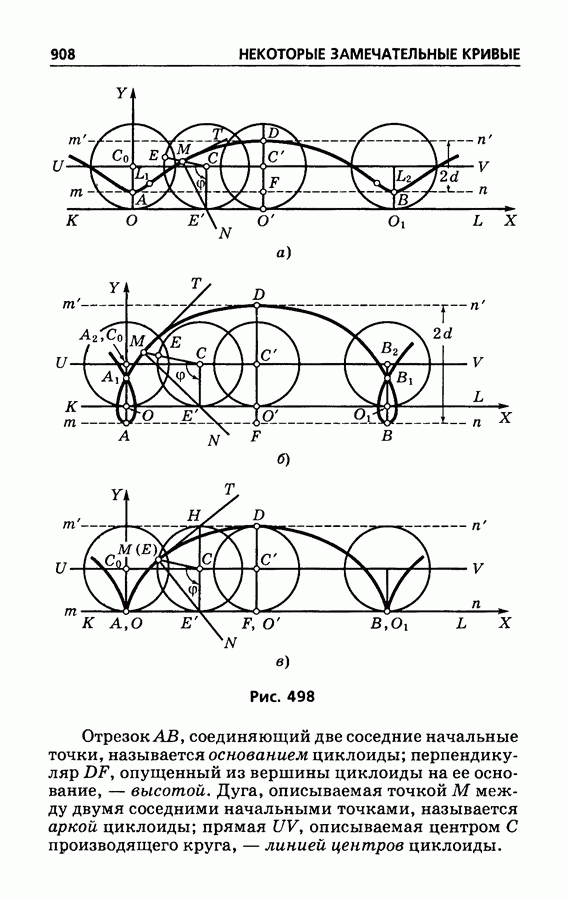
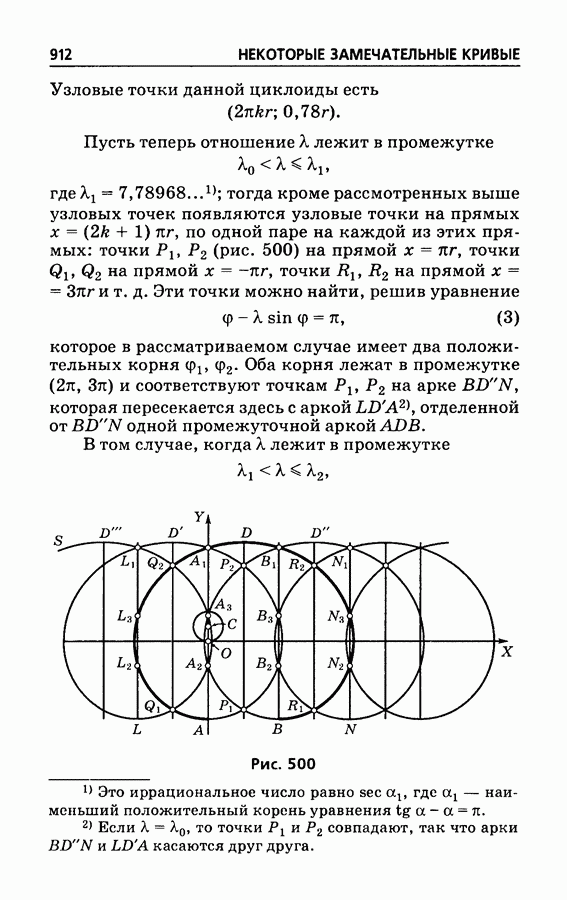
- § 514. Циклоиды
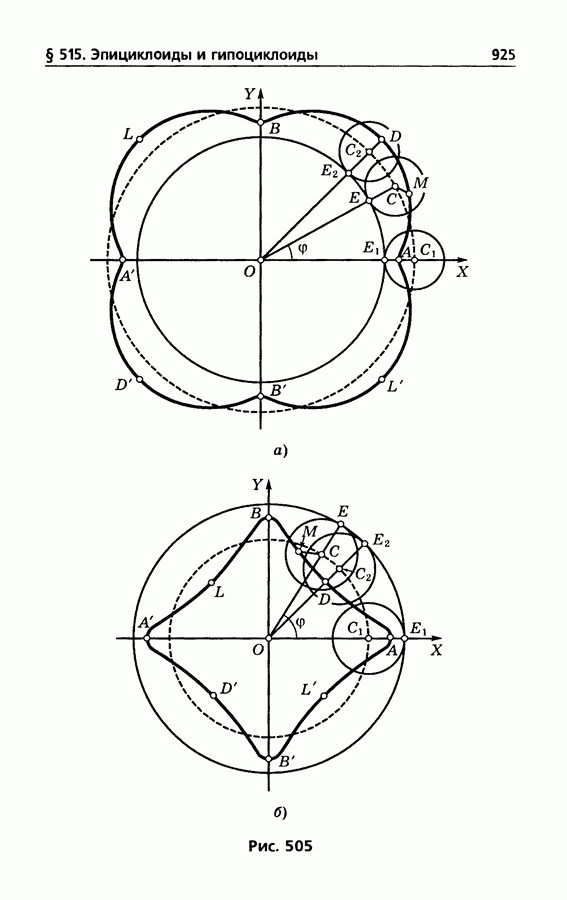
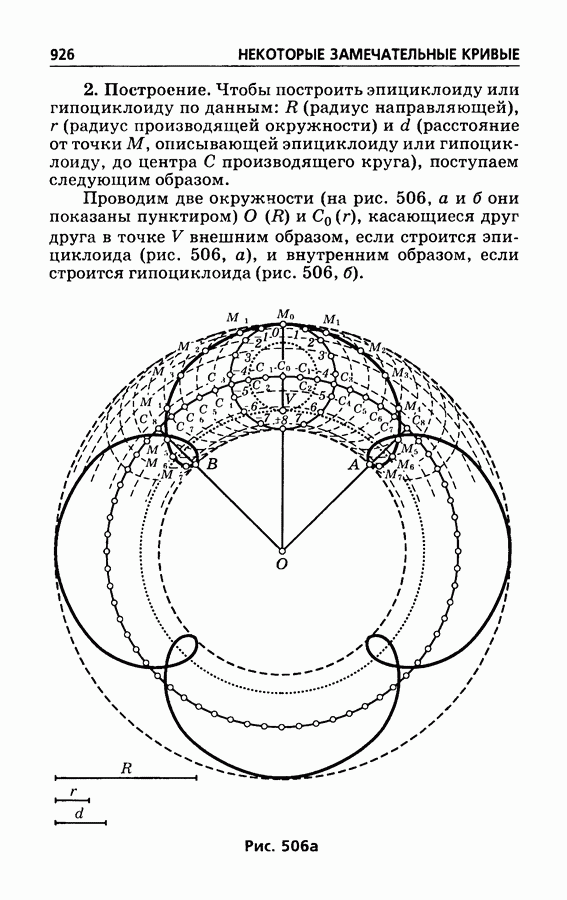
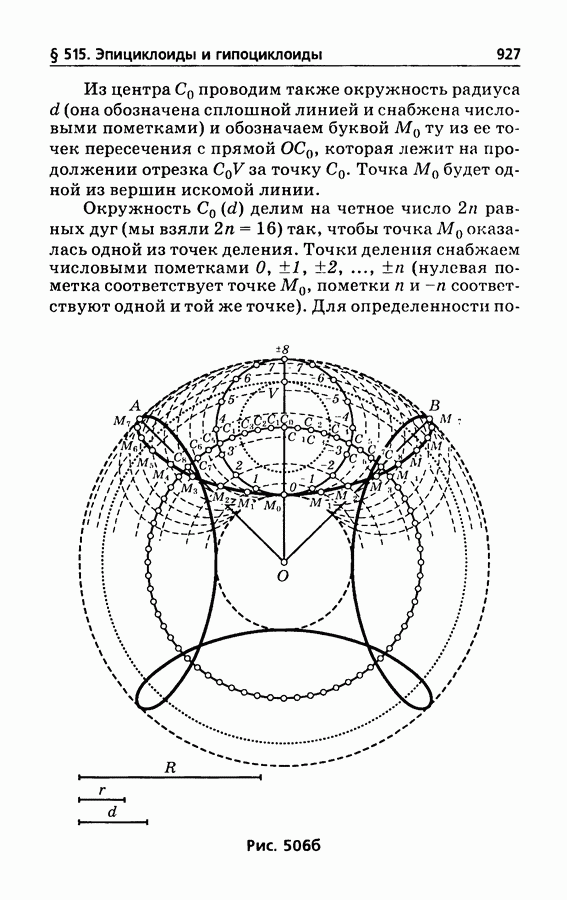
- § 515. Эпициклоиды и гипоциклоиды
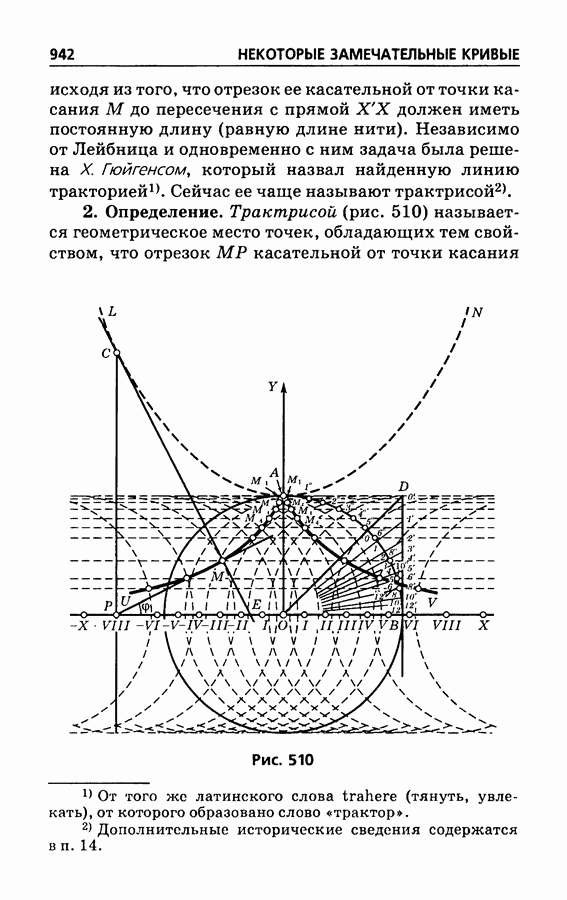
- § 516. Трактриса
- § 517. Цепная линия