| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
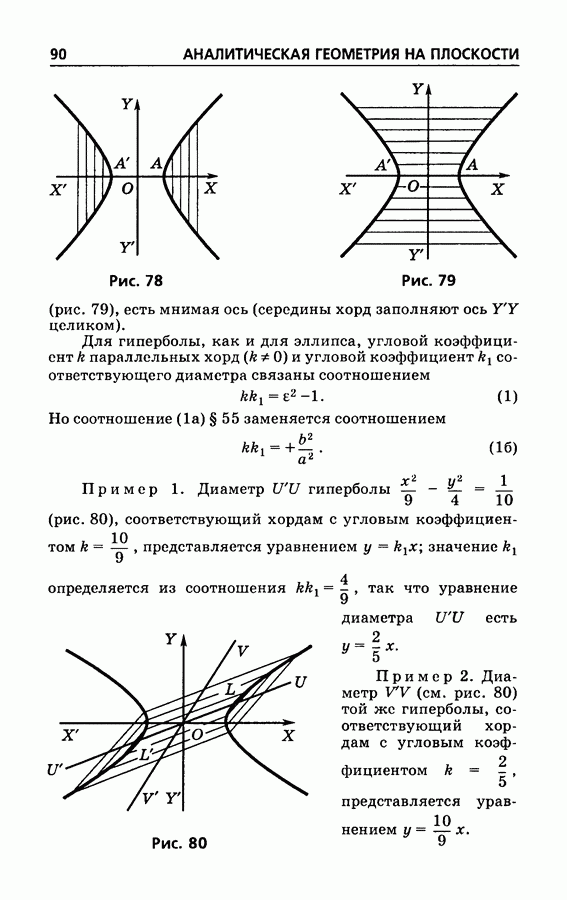
78
79
80
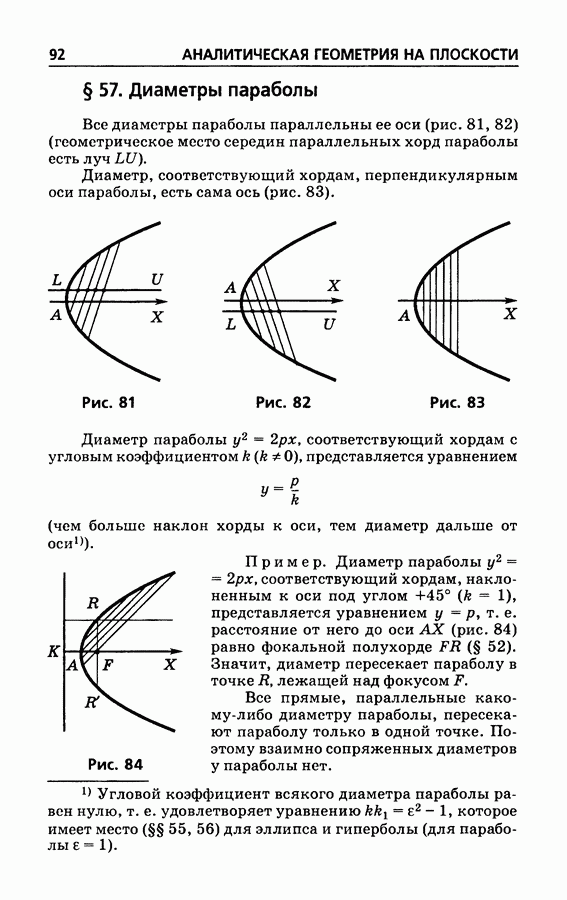
81
82
83
84
85
86
87
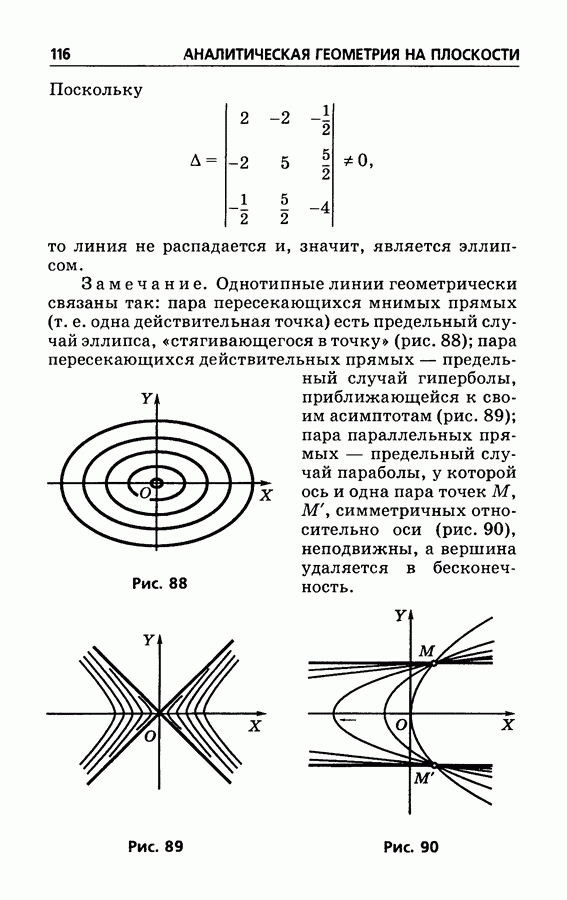
88
89
90
91
92
93
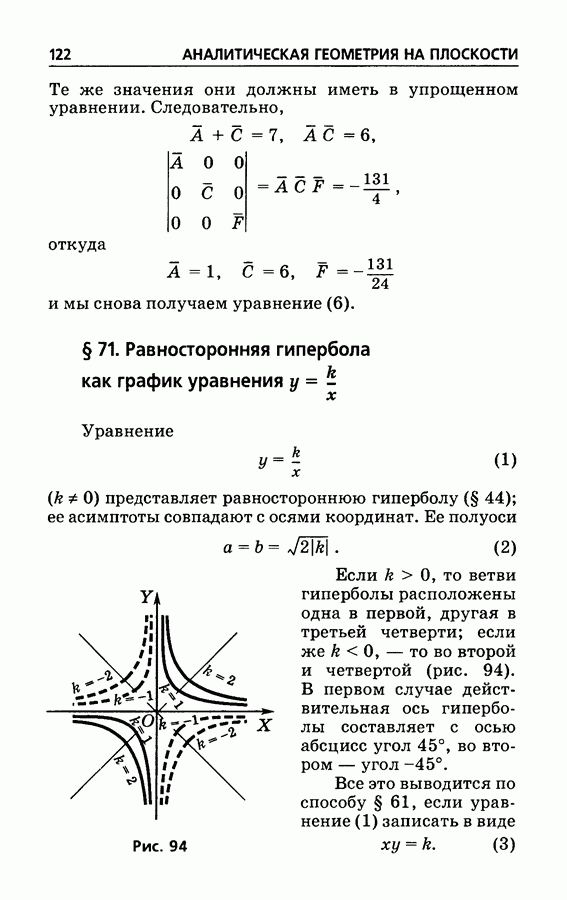
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
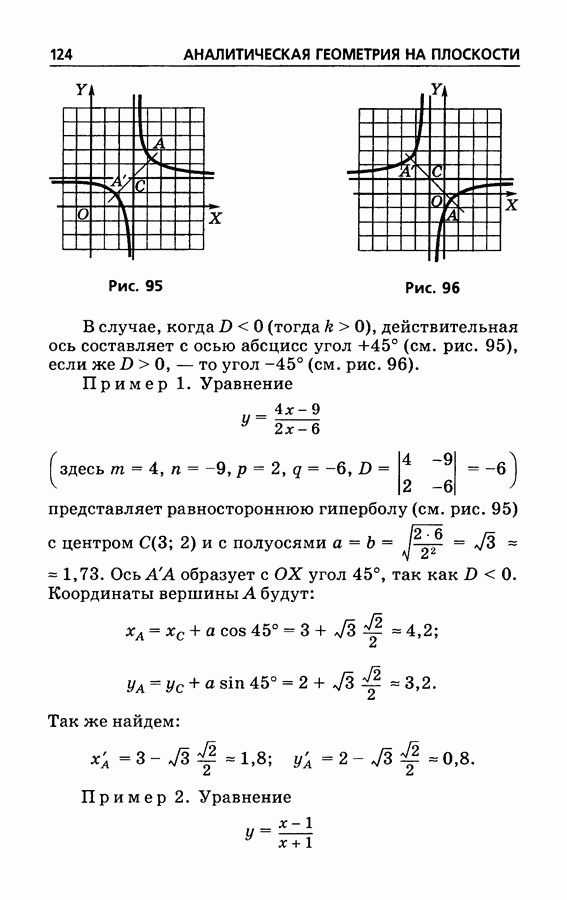
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
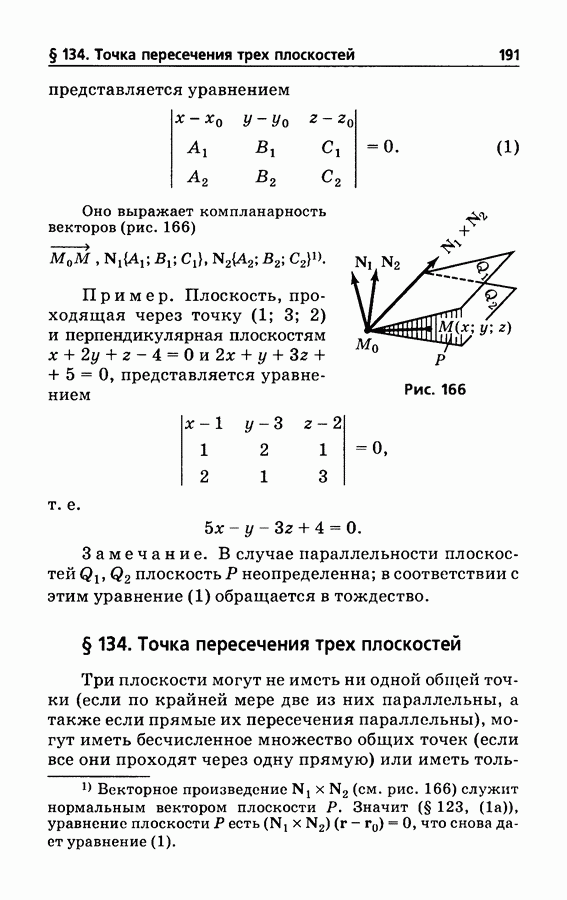
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
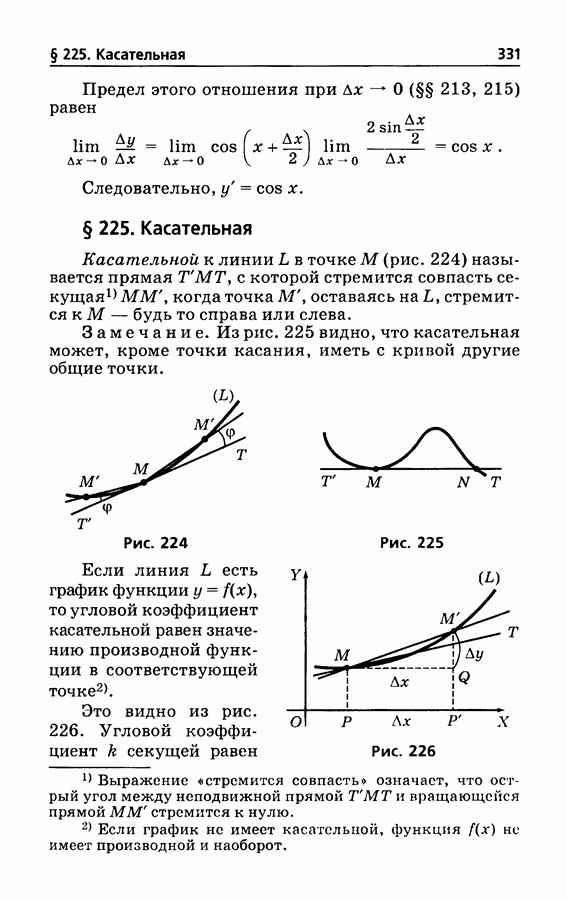
225
226
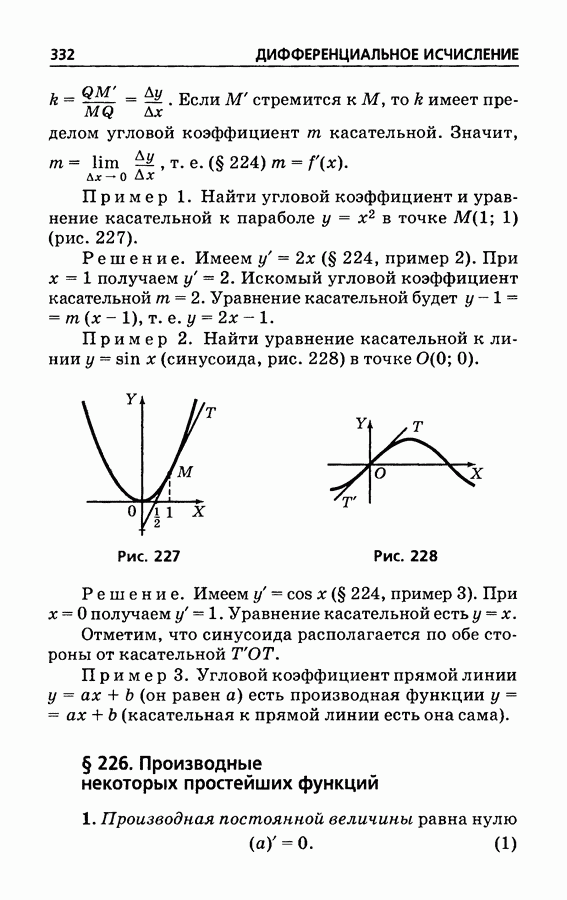
227
228
229
230
231
232
233
234
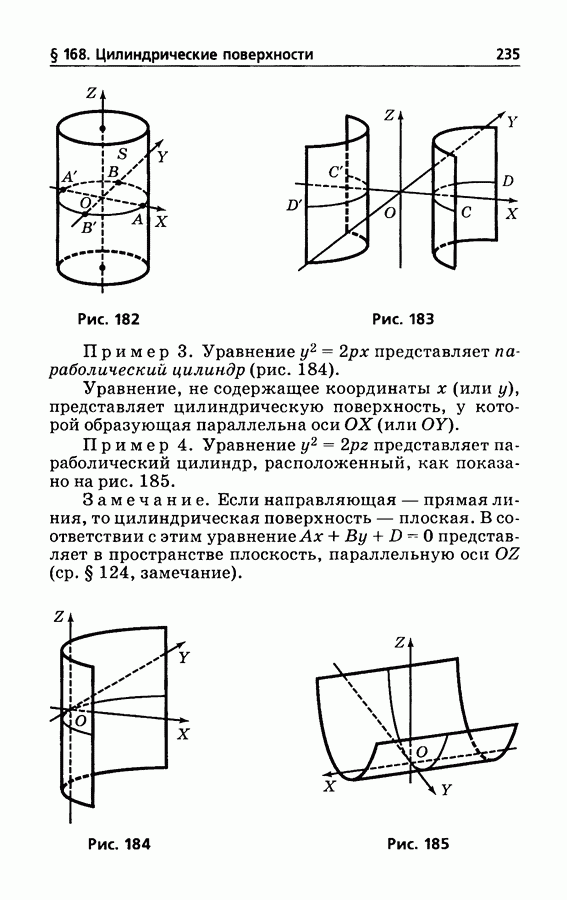
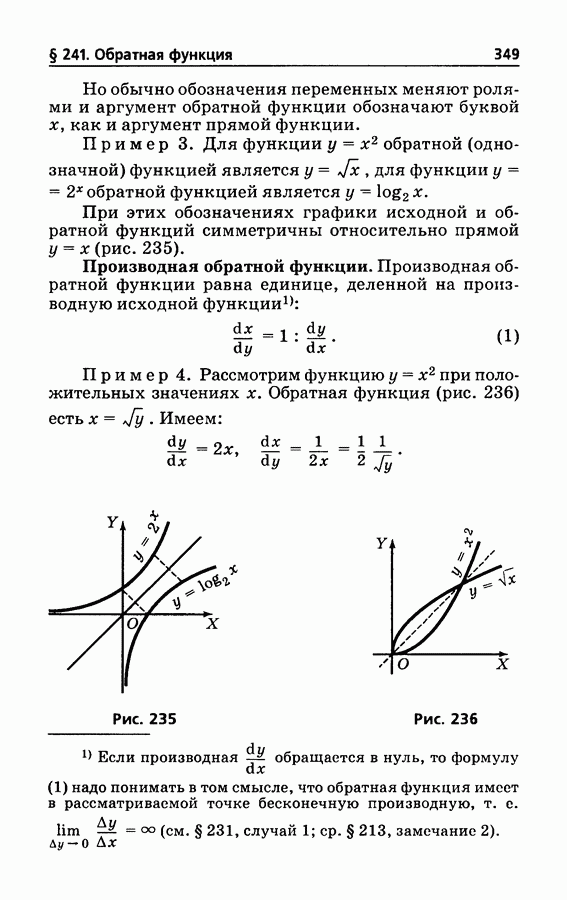
235
236
237
238
239
240
241
242
243
244
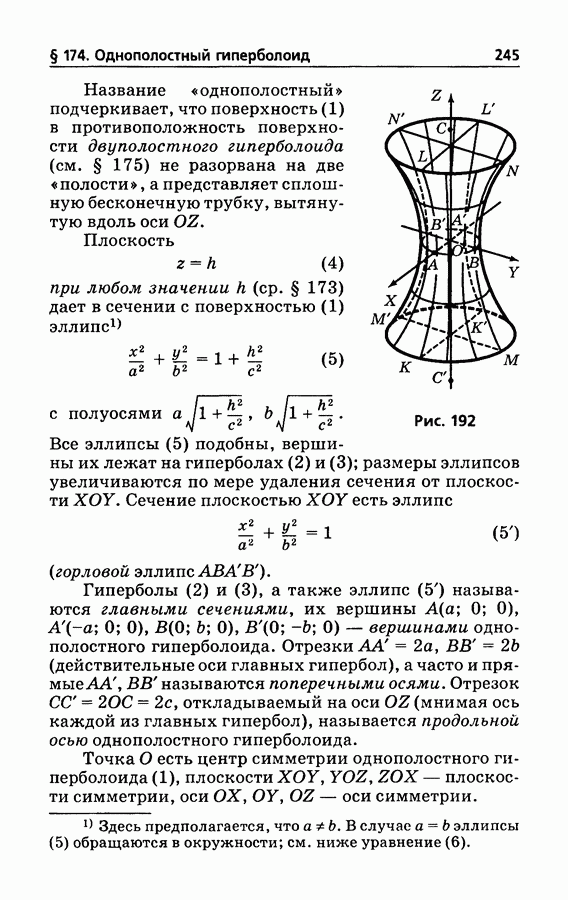
245
246
247
248
249
250
251
252
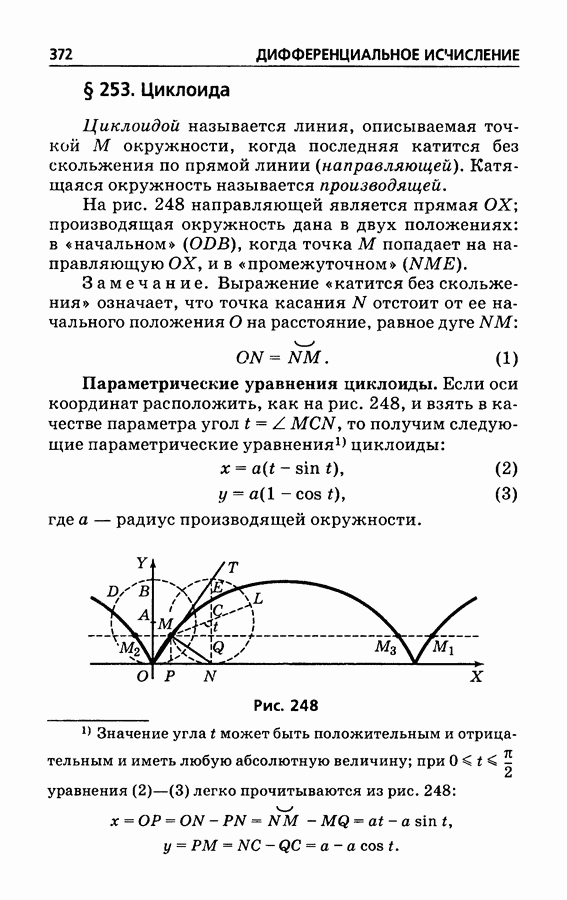
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
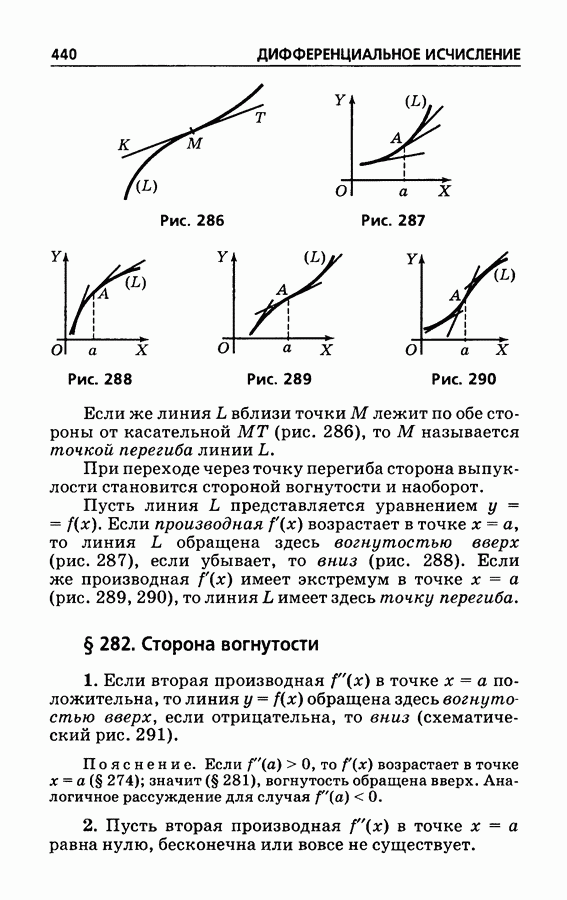
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
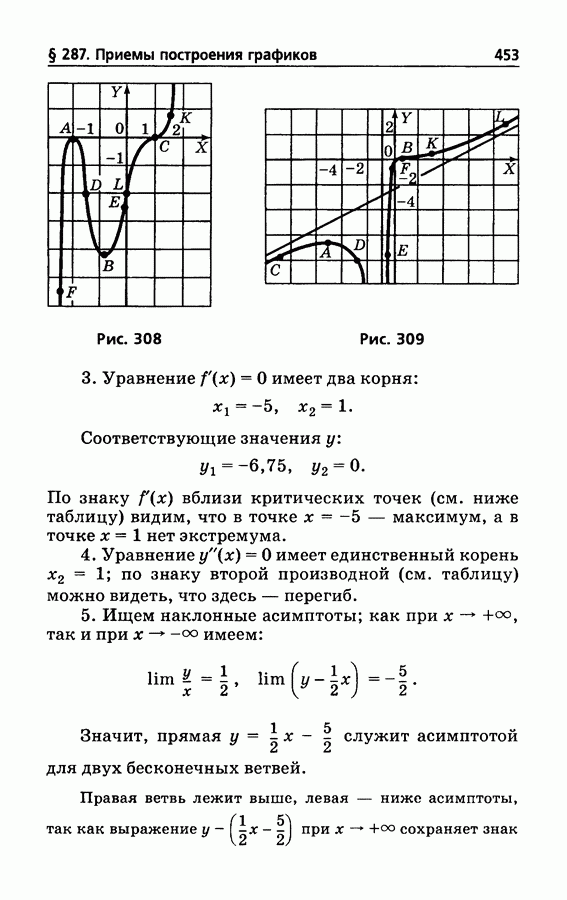
453
454
455
456
457
458
459
460
461
462
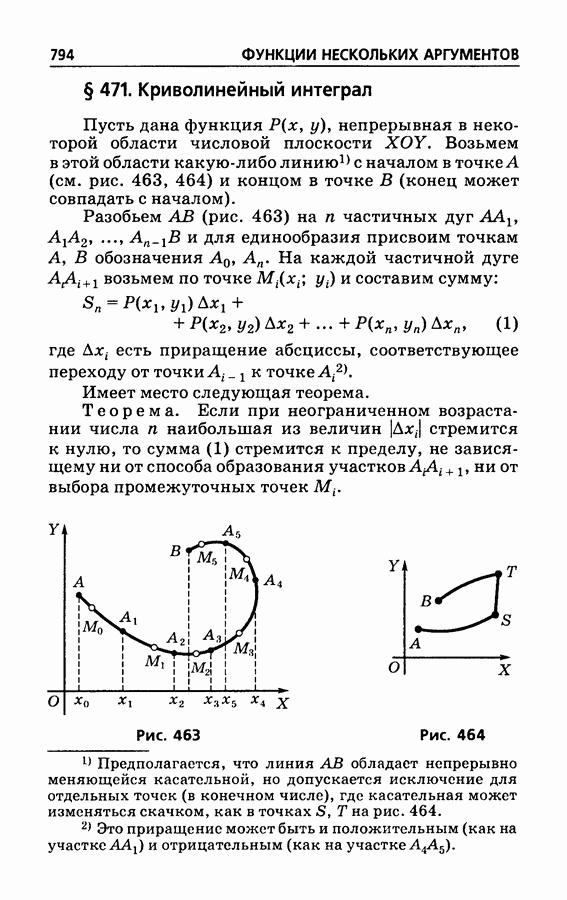
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
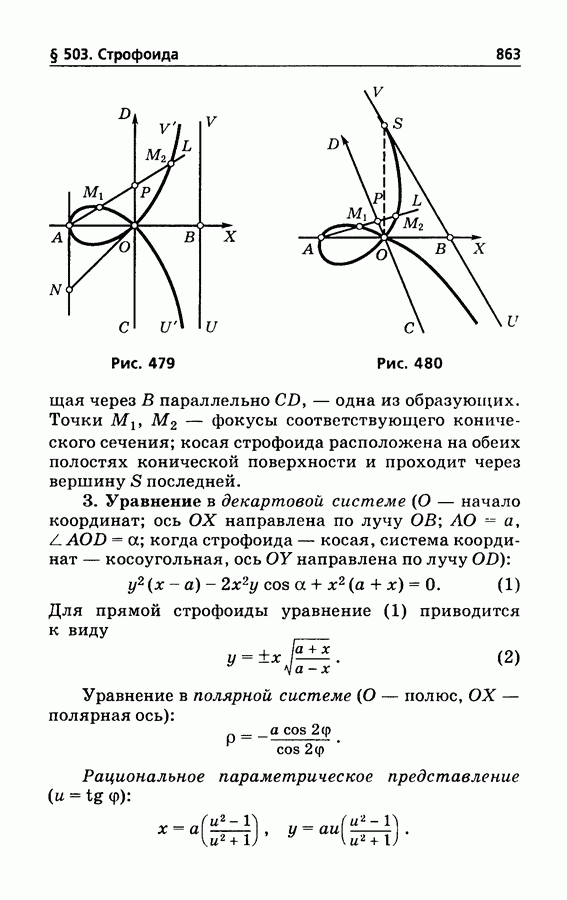
479
480
481
482
483
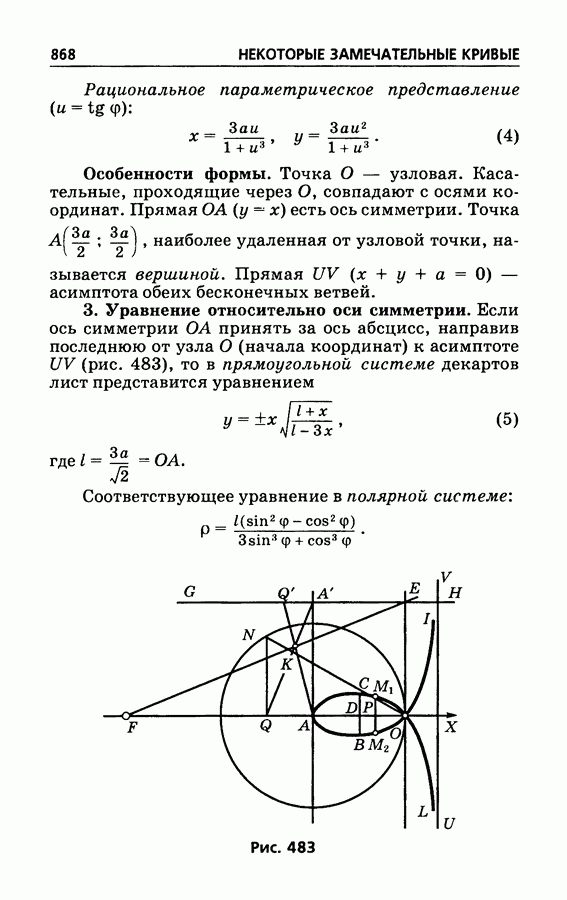
484
485
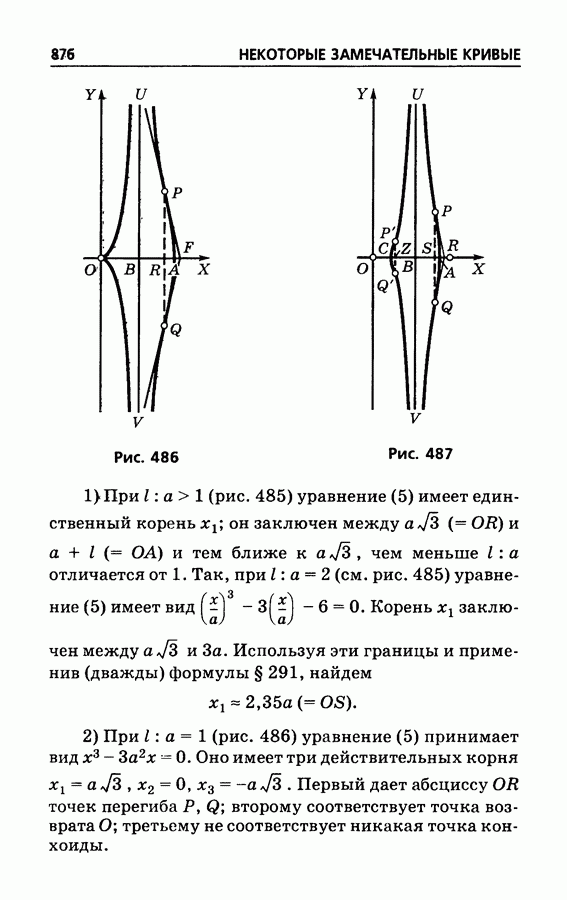
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
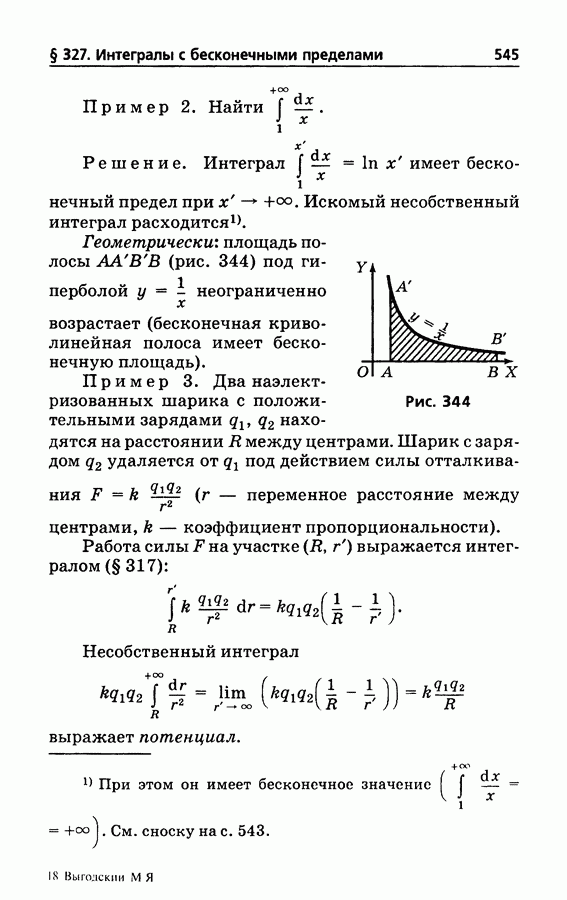
545
546
547
548
549
550
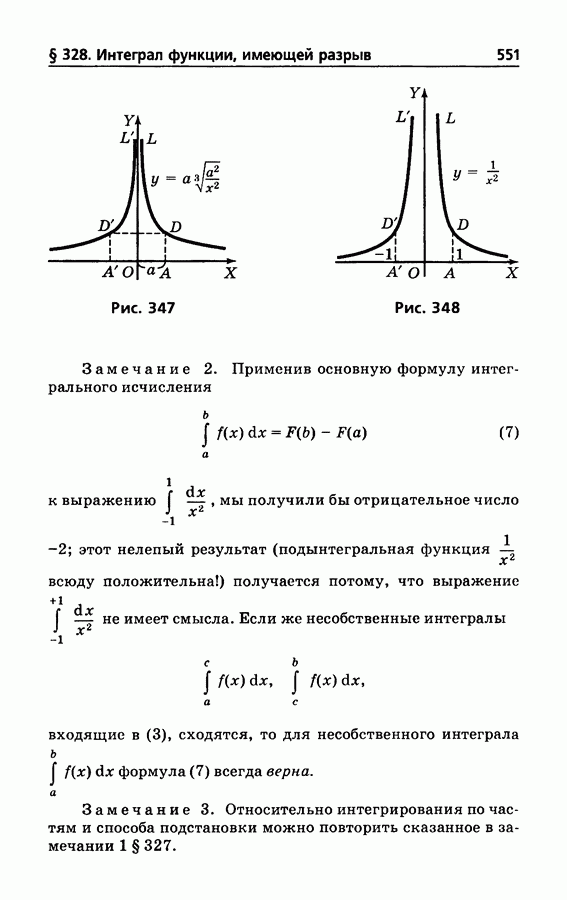
551
552
553
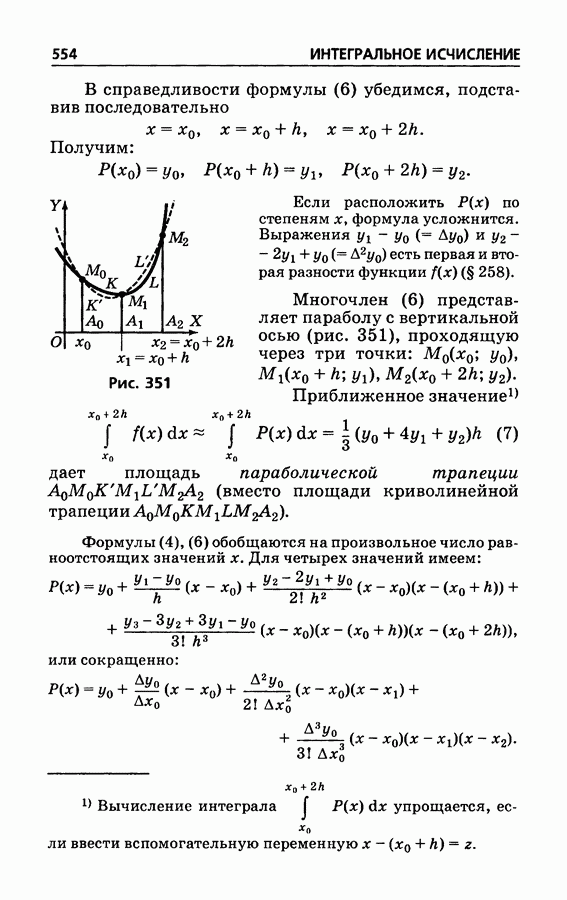
554
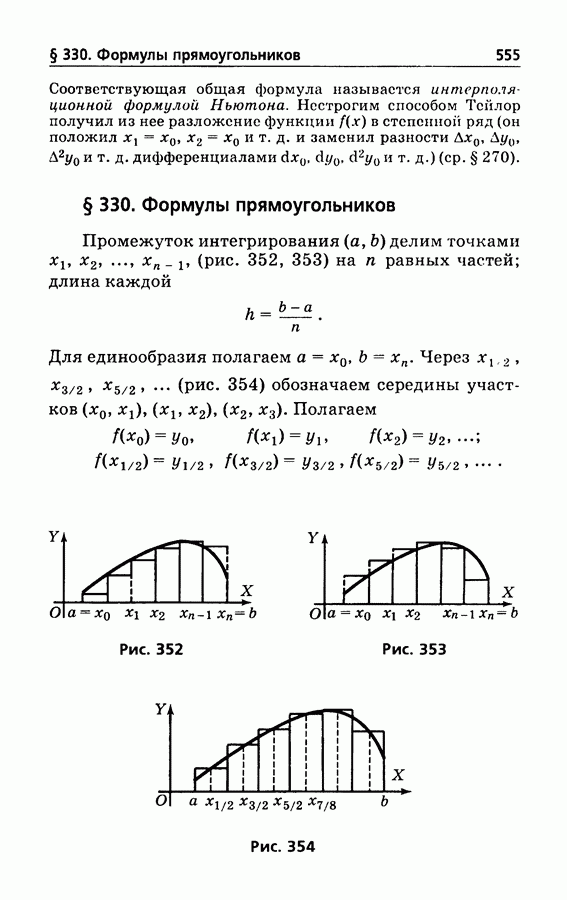
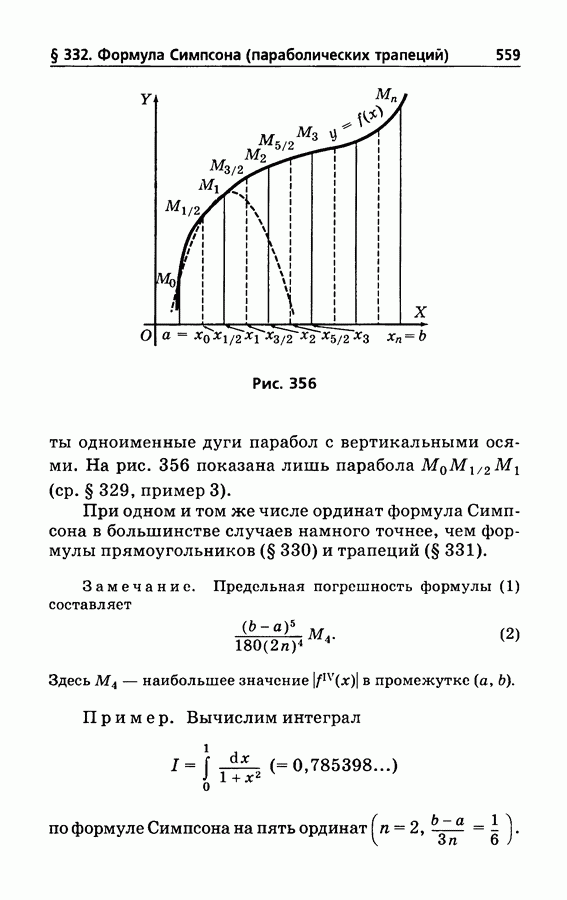
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
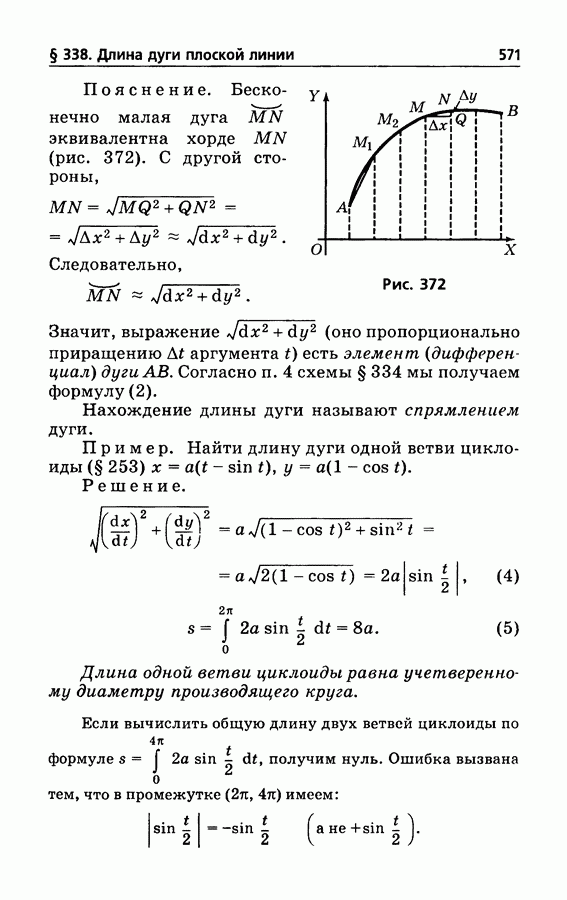
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
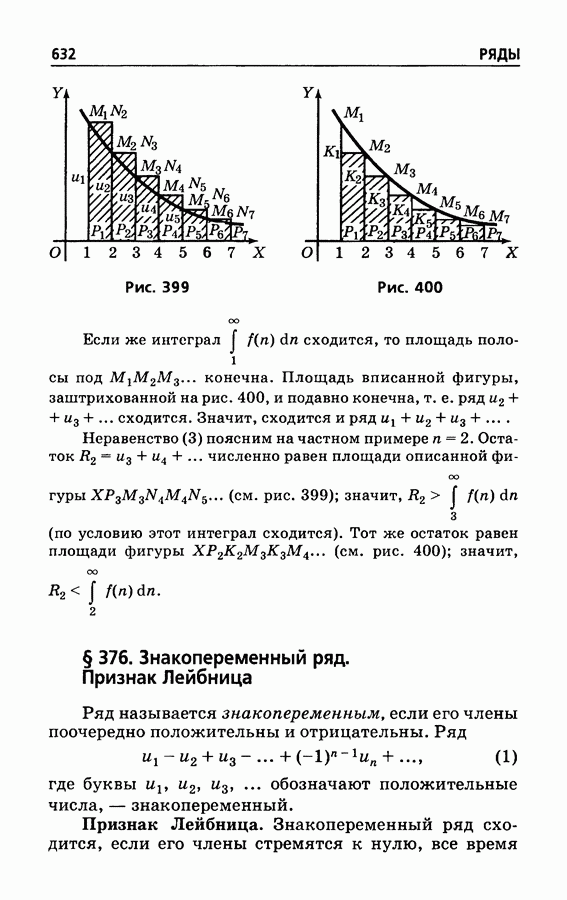
632
633
634
635
636
637
638
639
640
641
642
643
644
645
646
647
648
649
650
651
652
653
654
655
656
657
658
659
660
661
662
663
664
665
666
667
668
669
670
671
672
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
693
694
695
696
697
698
699
700
701
702
703
704
705
706
707
708
709
710
711
712
713
714
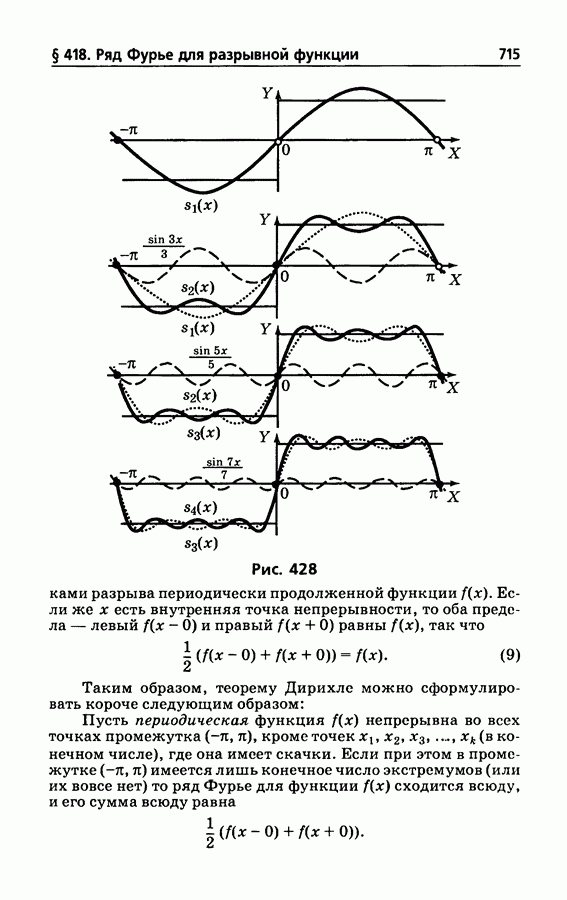
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
735
736
737
738
739
740
741
742
743
744
745
746
747
748
749
750
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
773
774
775
776
777
778
779
780
781
782
783
784
785
786
787
788
789
790
791
792
793
794
795
796
797
798
799
800
801
802
803
804
805
806
807
808
809
810
811
812
813
814
815
816
817
818
819
820
821
822
823
824
825
826
827
828
829
830
831
832
833
834
835
836
837
838
839
840
841
842
843
844
845
846
847
848
849
850
851
852
853
854
855
856
857
858
859
860
861
862
863
864
865
866
867
868
869
870
871
872
873
874
875
876
877
878
879
880
881
882
883
884
885
886
887
888
889
890
891
892
893
894
895
896
897
898
899
900
901
902
903
904
905
906
907
908
909
910
911
912
913
914
915
916
917
918
919
920
921
922
923
924
925
926
927
928
929
930
931
932
933
934
935
936
937
938
939
940
941
942
943
944
945
946
947
948
949
950
951
952
953
954
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 295. Геометрический смысл интегрирования
Пусть  данная непрерывная функция,
данная непрерывная функция,  какая-либо ее первообразная. Если построить график
какая-либо ее первообразная. Если построить график  функции
функции  (рис. 322), то угловой коэффициент касательной
(рис. 322), то угловой коэффициент касательной  будет выражаться данной функцией
будет выражаться данной функцией 
Пусть  другая первообразная той же функции
другая первообразная той же функции  Тогда угловые коэффициенты касательных
Тогда угловые коэффициенты касательных  и
и  (точки касания
(точки касания  имеют одну и ту же абсциссу
имеют одну и ту же абсциссу  ) одинаковы, т. е.
) одинаковы, т. е.  .
.
График первообразной функции  называется интегральной линией функции
называется интегральной линией функции  (или уравнения
(или уравнения  Касательные к двум интегральным линиям в соответствующих точках параллельны. Вместе с тем две интегральные линии отстоят друг от друга (по вертикали) на постоянное расстояние
Касательные к двум интегральным линиям в соответствующих точках параллельны. Вместе с тем две интегральные линии отстоят друг от друга (по вертикали) на постоянное расстояние  на рис. 322), так что, имея одну интегральную линию, легко построить другие.
на рис. 322), так что, имея одну интегральную линию, легко построить другие.
Через каждую точку проходит одна-единственная интегральная линия.
Интегральные линии строятся (приближенно) следующим образом. Из нескольких десятков точек (см. рис. 323, 324, 325), густо покрывающих какую-либо

Рис. 322

Рис. 323

Рис. 324
часть плоскости, проводим короткие отрезки (или стрелки), указывающие направление касательной.
Получаем «поле направлений». Затем проводим на глаз плавную линию так, чтобы она в ряде своих точек касалась стрелок. Получим одну интегральную линию. Таким же образом построим и ряд других.
Пример 1. Найти интегральные линии уравнения

Данная функция  в рассматриваемом примере есть постоянная величина 1. Угловой коэффициент всех стрелок равен единице, т. е. наклон касательной всюду 45°. Интегральные линии (рис. 323) — параллельные прямые. Уравнение каждой из них есть
в рассматриваемом примере есть постоянная величина 1. Угловой коэффициент всех стрелок равен единице, т. е. наклон касательной всюду 45°. Интегральные линии (рис. 323) — параллельные прямые. Уравнение каждой из них есть  т. е.
т. е.  Величина С, постоянная для каждой прямой, меняется от одной прямой к другой.
Величина С, постоянная для каждой прямой, меняется от одной прямой к другой.
Пример 2. Найти интегральные линии для функции  т. е. для уравнения
т. е. для уравнения  .
.
Вдоль оси  берем горизонтальные стрелки
берем горизонтальные стрелки  вдоль ординаты
вдоль ординаты  берем стрелки с угловым коэффициентом
берем стрелки с угловым коэффициентом  Проведя на глаз интегральные линии, получаем «параллельные» параболы
Проведя на глаз интегральные линии, получаем «параллельные» параболы  ; рис. 324 .
; рис. 324 .

Рис. 325
Пример 3. На рис. 325 показаны интегральные линии функции  . Ни одна из них не пересекает ось
. Ни одна из них не пересекает ось  , так как при
, так как при  первообразные функции не определены функция
первообразные функции не определены функция  разрывна при
разрывна при  Вследствие этого лишь те интегральные линии отстоят друг от друга на равные расстояния, которые лежат по одну сторону от оси ординат. Лежащие справа представляются уравнением
Вследствие этого лишь те интегральные линии отстоят друг от друга на равные расстояния, которые лежат по одну сторону от оси ординат. Лежащие справа представляются уравнением  слева — уравнением
слева — уравнением  . Неопределенный интеграл
. Неопределенный интеграл  выражается (для всех
выражается (для всех  кроме
кроме  ) формулой
) формулой

Замечание. Другой геометрический смысл интегрирования получится, если построить график  (рис. 326) данной функции
(рис. 326) данной функции  Пусть дуга
Пусть дуга  целиком лежит выше оси
целиком лежит выше оси  Проведем две ординаты
Проведем две ординаты  Левую ординату
Левую ординату  будем считать неподвижной, а правую
будем считать неподвижной, а правую  подвижной. Площадь
подвижной. Площадь  будет одной из первообразных для функции
будет одной из первообразных для функции  аргумента
аргумента  (ср. § 292, п. 2). Взяв вместо
(ср. § 292, п. 2). Взяв вместо  неподвижную ординату
неподвижную ординату  получим другую первообразную — площадь
получим другую первообразную — площадь  . Эти две первообразные отличаются на постоянную величину
. Эти две первообразные отличаются на постоянную величину 

Рис. 326
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- § 1. Понятие о предмете аналитической геометрии
- § 2. Координаты
- § 3. Прямоугольная система координат
- § 4. Прямоугольные координаты
- § 5. Координатные углы
- § 6. Косоугольная система координат
- § 7. Уравнение линии
- § 8. Взаимное расположение линии и точки
- § 9. Взаимное расположение двух линий
- § 10. Расстояние между двумя точками
- § 11. Деление отрезка в данном отношении
- § 11а. Деление отрезка пополам
- § 12. Определитель второго порядка
- § 13. Площадь треугольника
- § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом)
- § 15. Прямая, параллельная оси
- § 16. Общее уравнение прямой
- § 17. Построение прямой по ее уравнению
- § 18. Условие параллельности прямых
- § 19. Пересечение прямых
- § 20. Условие перпендикулярности двух прямых
- § 21. Угол между двумя прямыми
- § 22. Условие, при котором три точки лежат на одной прямой
- § 23. Уравнение прямой, проходящей через две точки
- § 24. Пучок прямых
- § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой
- § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
- § 27. Взаимное расположение прямой и пары точек
- § 28. Расстояние от точки до прямой
- § 29. Полярные параметры прямой
- § 30. Нормальное уравнение прямой
- § 31. Приведение уравнения прямой к нормальному виду
- § 32. Отрезки на осях
- § 33. Уравнение прямой в отрезках
- § 34. Преобразование координат (постановка вопроса)
- § 35. Перенос начала координат
- § 36. Поворот осей
- § 37. Алгебраические линии и их порядок
- § 38. Окружность
- § 39. Нахождение центра и радиуса окружности
- § 40. Эллипс как сжатая окружность
- § 41. Другое определение эллипса
- § 42. Построение эллипса по его осям
- § 43. Гипербола
- § 44. Форма гиперболы; вершины и оси
- § 45. Построение гиперболы по ее осям
- § 46. Асимптоты гиперболы
- § 47. Сопряженные гиперболы
- § 48. Парабола
- § 49. Построение параболы по данному параметру p
- § 50. Парабола как график уравнения y=ax^2+bx+c
- § 51. Директрисы эллипса и гиперболы
- § 52. Общее определение эллипса, гиперболы и параболы
- § 53. Конические сечения
- § 54. Диаметры конического сечения
- § 55. Диаметры эллипса
- § 56. Диаметры гиперболы
- § 57. Диаметры параболы
- § 58. Линии второго порядка
- § 59. Запись общего уравнения второй степени
- § 60. Упрощение уравнения второй степени; общие замечания
- § 61. Предварительное преобразование уравнения второй степени
- § 62. Завершающее преобразование уравнения второй степени
- § 63. О приемах, облегчающих упрощение уравнения второй степени
- § 64. Признак распадения линий второго порядка
- § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка
- § 66. Инварианты уравнения второй степени
- § 67. Три типа линий второго порядка
- § 68. Центральные и нецентральные линии второго порядка
- § 69. Нахождение центра центральной линии второго порядка
- § 70. Упрощение уравнения центральной линии второго порядка
- § 71. Равносторонняя гипербола как график уравнения y=k/x
- § 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q)
- § 73. Полярные координаты
- § 74. Связь между полярными и прямоугольными координатами
- § 75. Архимедова спираль
- § 76. Полярное уравнение прямой
- § 77. Полярное уравнение конического сечения
- АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- § 78. Понятие о векторах и скалярах
- § 79. Вектор в геометрии
- § 80. Векторная алгебра
- § 81. Коллинеарные векторы
- § 82. Нуль-вектор
- § 83. Равенство векторов
- § 84. Приведение векторов к общему началу
- § 85. Противоположные векторы
- § 86. Сложение векторов
- § 87. Сумма нескольких векторов
- § 88. Вычитание векторов
- § 89. Умножение и деление вектора на число
- § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор)
- § 91. Проекция точки на ось
- § 92. Проекция вектора на ось
- § 93. Основные теоремы о проекциях вектора
- § 94. Прямоугольная система координат в пространстве
- § 95. Координаты точки
- § 96. Координаты вектора
- § 97. Выражения вектора через компоненты и через координаты
- § 98. Действия над векторами, заданными своими координатами
- § 99. Выражение вектора через радиусы-векторы его начала и конца
- § 100. Длина вектора. Расстояние между двумя точками
- § 101. Угол между осью координат и вектором
- § 102. Признак коллинеарности (параллельности) векторов
- § 103. Деление отрезка в данном отношении
- § 104. Скалярное произведение двух векторов
- § 104а. Физический смысл скалярного произведения
- § 105. Свойства скалярного произведения
- § 106. Скалярные произведения основных векторов
- § 107. Выражение скалярного произведения через координаты сомножителей
- § 108. Условие перпендикулярности векторов
- § 109. Угол между векторами
- § 110. Правая и левая системы трех векторов
- § 111. Векторное произведение двух векторов
- § 112. Свойства векторного произведения
- § 113. Векторные произведения основных векторов
- § 114. Выражение векторного произведения через координаты сомножителей
- § 115. Компланарные векторы
- § 116. Смешанное произведение
- § 117. Свойства смешанного произведения
- § 118. Определитель третьего порядка
- § 119. Выражение смешанного произведения через координаты сомножителей
- § 120. Признак компланарности в координатной форме
- § 121. Объем параллелепипеда
- § 122. Двойное векторное произведение
- § 123. Уравнение плоскости
- § 124. Особые случаи положения плоскости относительно системы координат
- § 125. Условие параллельности плоскостей
- § 126. Условие перпендикулярности плоскостей
- § 127. Угол между двумя плоскостями
- § 128. Плоскость, проходящая через данную точку параллельно данной плоскости
- § 129. Плоскость, проходящая через три точки
- § 130. Отрезки на осях
- § 131. Уравнение плоскости в отрезках
- § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости
- § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям
- § 134. Точка пересечения трех плоскостей
- § 135. Взаимное расположение плоскости и пары точек
- § 136. Расстояние от точки до плоскости
- § 137. Полярные параметры плоскости
- § 138. Нормальное уравнение плоскости
- § 139. Приведение уравнения плоскости к нормальному виду
- § 140. Уравнения прямой в пространстве
- § 141. Условие, при котором два уравнения первой степени представляют прямую
- § 142. Пересечение прямой с плоскостью
- § 143. Направляющий вектор
- § 144. Углы между прямой и осями координат
- § 145. Угол между двумя прямыми
- § 146. Угол между прямой и плоскостью
- § 147. Условия параллельности и перпендикулярности прямой и плоскости
- § 148. Пучок плоскостей
- § 149. Проекции прямой на координатные плоскости
- § 150. Симметричные уравнения прямой
- § 151. Приведение уравнений прямой к симметричному виду
- § 152. Параметрические уравнения прямой
- § 153. Пересечение плоскости с прямой, заданной параметрически
- § 154. Уравнения прямой, проходящей через две данные точки
- § 155. Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой
- § 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости
- § 157. Уравнение плоскости, проходящей через данную точку и данную прямую
- § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым
- § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой
- § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости
- § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую
- § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую
- § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости
- § 164. Уравнения общего перпендикуляра к двум данным прямым
- § 165. Кратчайшее расстояние между двумя прямыми
- § 165а. Правые и левые пары прямых
- § 166. Преобразование координат
- § 167. Уравнение поверхности
- § 168. Цилиндрические поверхности, у которых образующие параллельны одной из осей координат
- § 169. Уравнения линии
- § 170. Проекция линии на координатную плоскость
- § 171. Алгебраические поверхности и их порядок
- § 172. Сфера
- § 173. Эллипсоид
- § 174. Однополостный гиперболоид
- § 175. Двуполостный гиперболоид
- § 176. Конус второго порядка
- § 177. Эллиптический параболоид
- § 178. Гиперболический параболоид
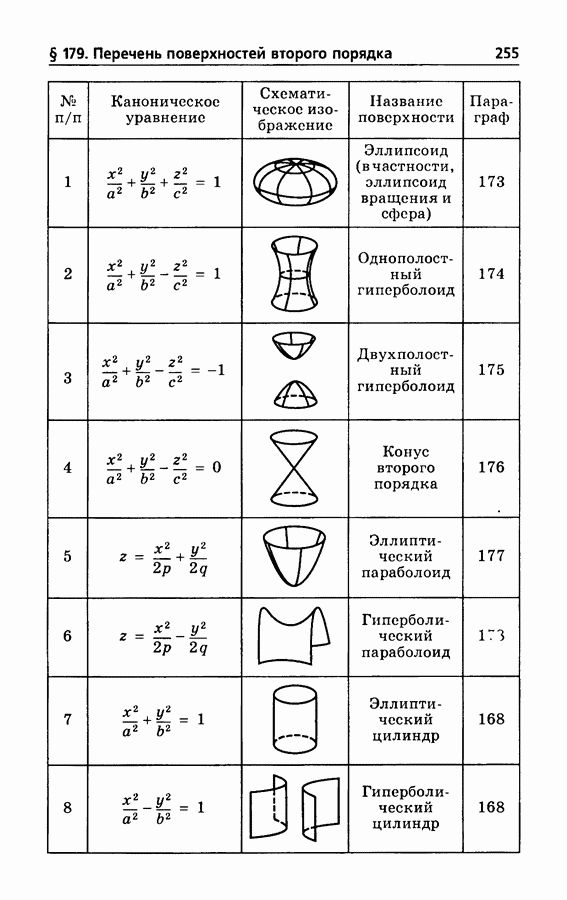
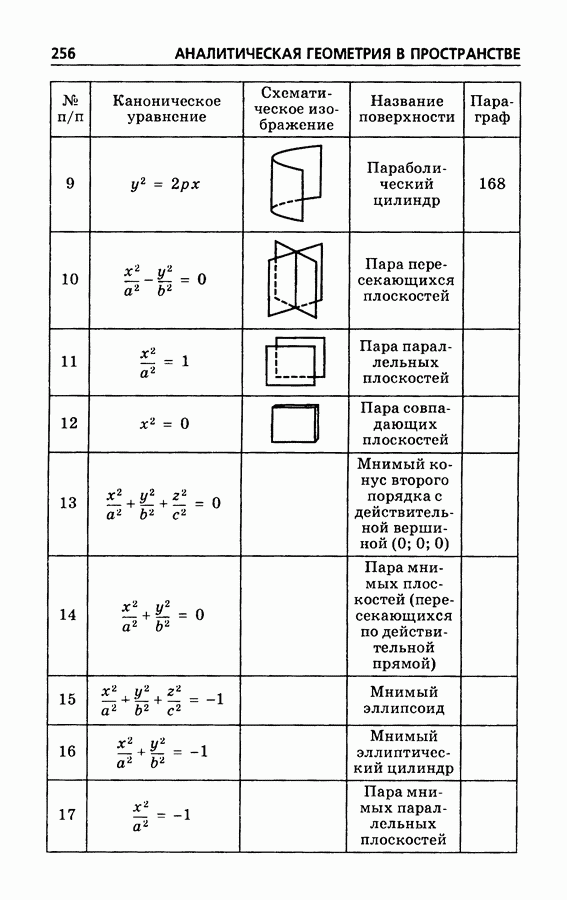
- § 179. Перечень поверхностей второго порядка
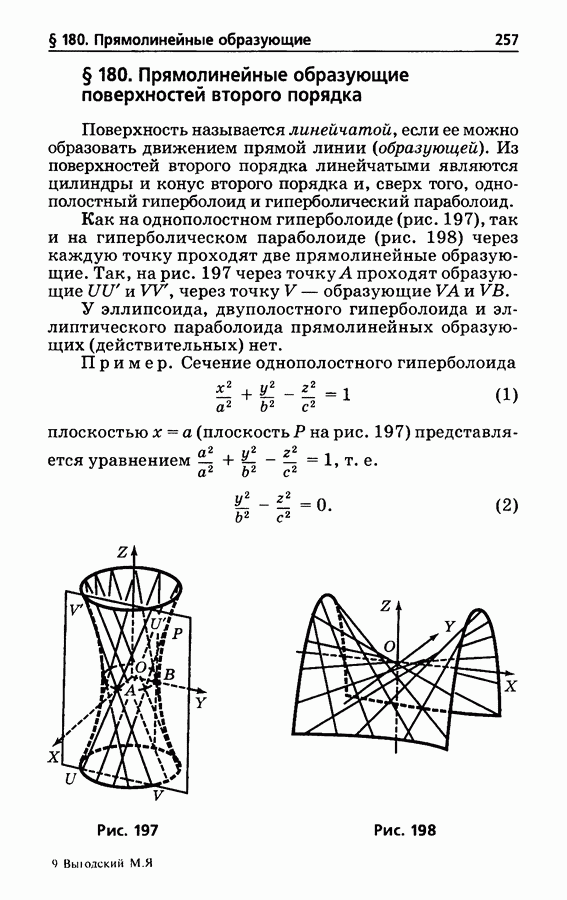
- § 180. Прямолинейные образующие поверхностей второго порядка
- § 181. Поверхности вращения
- § 182. Определители второго и третьего порядков
- § 183. Определители высших порядков
- § 184. Свойства определителей
- § 185. Практический прием вычисления определителей
- § 186. Применение определителей к исследованию и решению системы уравнений
- § 187. Два уравнения с двумя неизвестными
- § 188. Два уравнения с двумя неизвестными
- § 189. Однородная система двух уравнений с тремя неизвестными
- § 190. Два уравнения с двумя неизвестными
- § 190а. Система n уравнений с n неизвестными
- ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
- § 192. Рациональные числа
- § 193. Действительные (вещественные) числа
- § 194. Числовая ось
- § 195. Переменные и постоянные величины
- § 196. Функция
- § 197. Способы задания функции
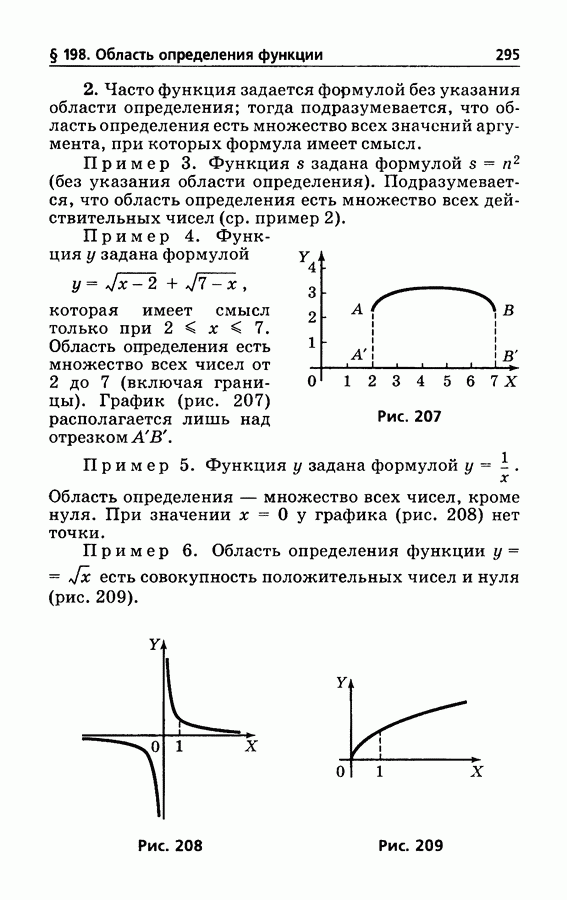
- § 198. Область определения функции
- § 199. Промежуток
- § 200. Классификация функций
- § 201. Основные элементарные функции
- § 202. Обозначение функции
- § 203. Предел последовательности
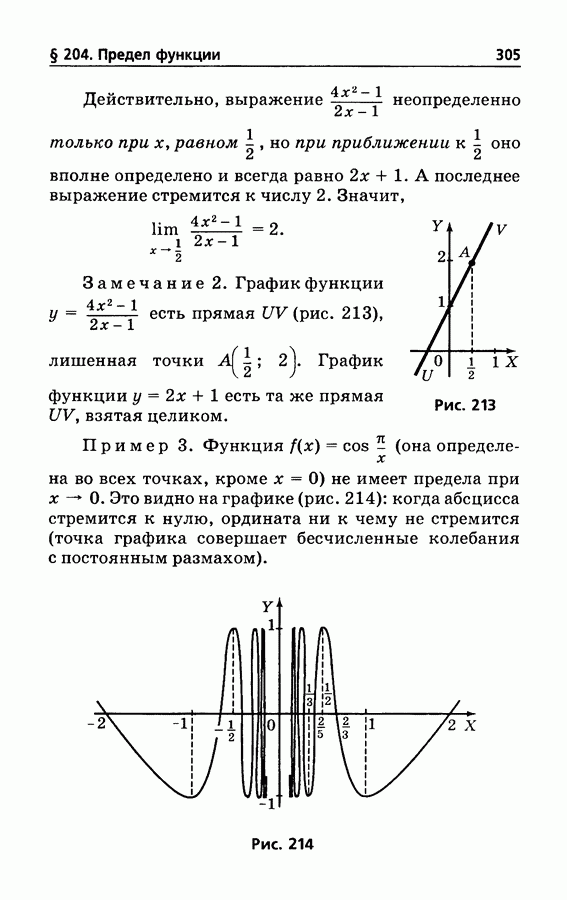
- § 204. Предел функции
- § 205. Определение предела функции
- § 206. Предел постоянной величины
- § 207. Бесконечно малая величина
- § 208. Бесконечно большая величина
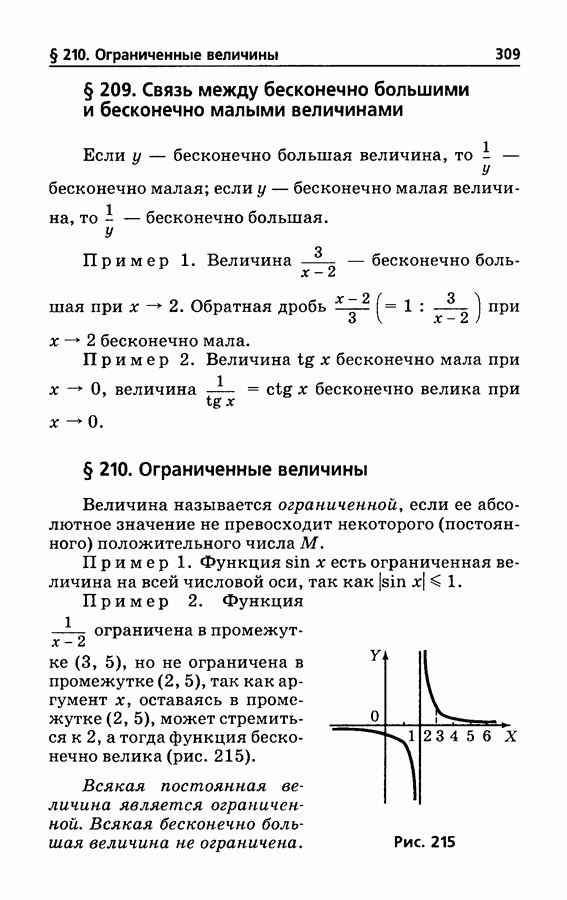
- § 209. Связь между бесконечно большими и бесконечно малыми величинами
- § 210. Ограниченные величины
- § 211. Расширение понятия предепа
- § 212. Основные свойства бесконечно малых величин
- § 213. Основные теоремы о пределах
- § 214. Число е
- § 215. Предел sinx/x при x стремящемся к 0
- § 216. Эквивалентные бесконечно малые величины
- § 217. Сравнение бесконечно малых величин
- § 217а. Приращение переменной величины
- § 218. Непрерывность функции в точке
- § 219. Свойства функций, непрерывных в точке
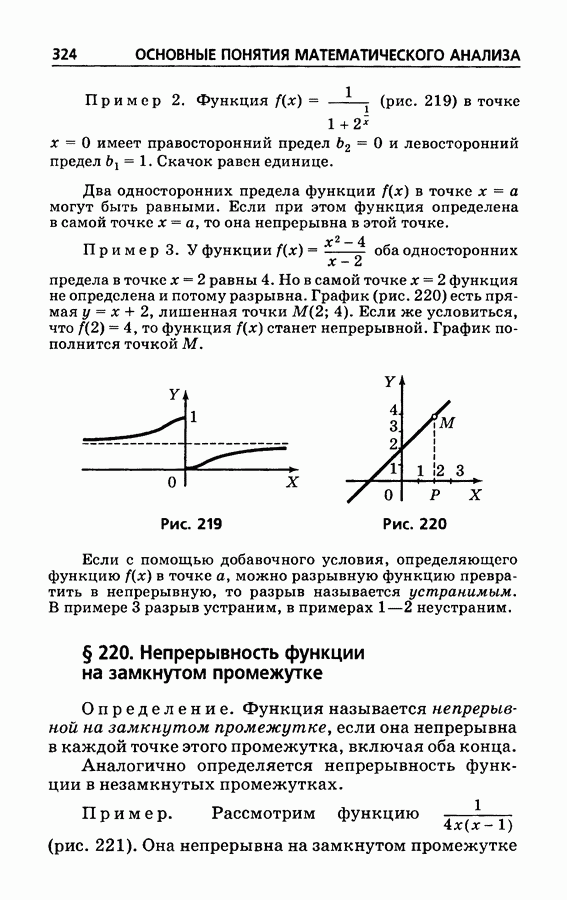
- § 219а. Односторонний предел; скачок функции
- § 220. Непрерывность функции на замкнутом промежутке
- § 221. Свойства функций, непрерывных на замкнутом промежутке
- ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 223. Скорость
- § 224. Определение производной функции
- § 225. Касательная
- § 226. Производные некоторых простейших функций
- § 227. Свойства производной
- § 228. Дифференциал
- § 229. Механический смысл дифференциала
- § 230. Геометрический смысл дифференциала
- § 231. Дифференцируемые функции
- § 232. Дифференциалы некоторых простейших функций
- § 233. Свойства дифференциала
- § 234. Инвариантность выражения f'(x)dx
- § 235. Выражение производной через дифференциалы
- § 236. Функция от функции (сложная функция)
- § 237. Дифференциал сложной функции
- § 238. Производная сложной функции
- § 239. Дифференцирование произведения
- § 240. Дифференцирование частного (дроби)
- § 241. Обратная функция
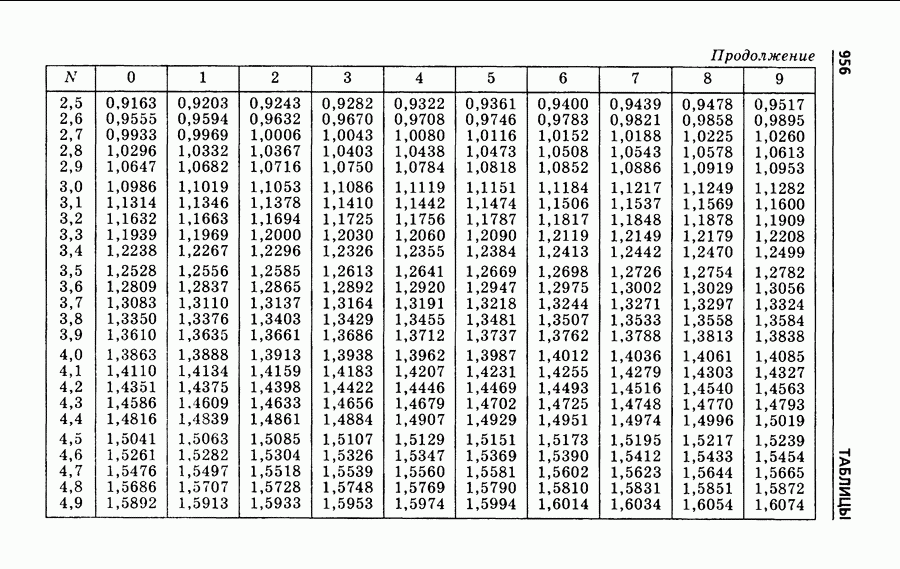
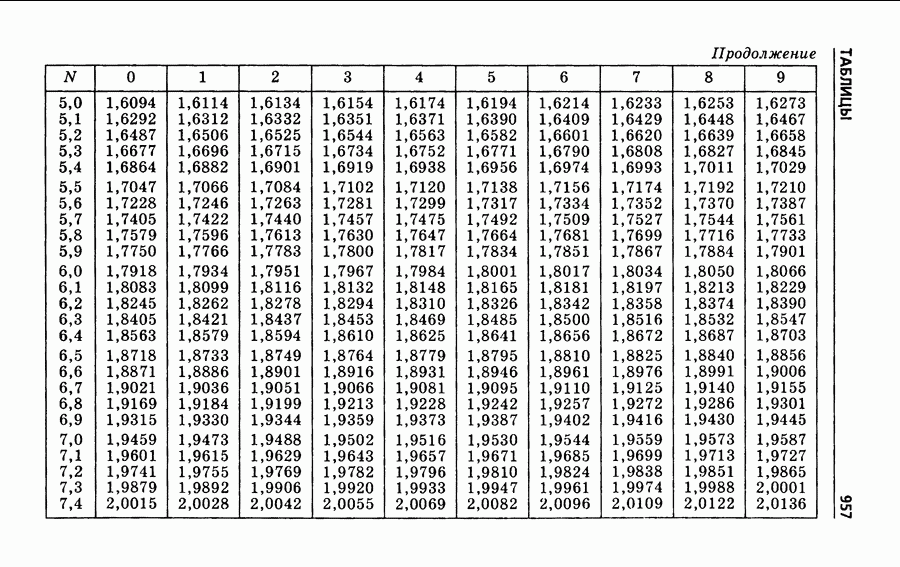
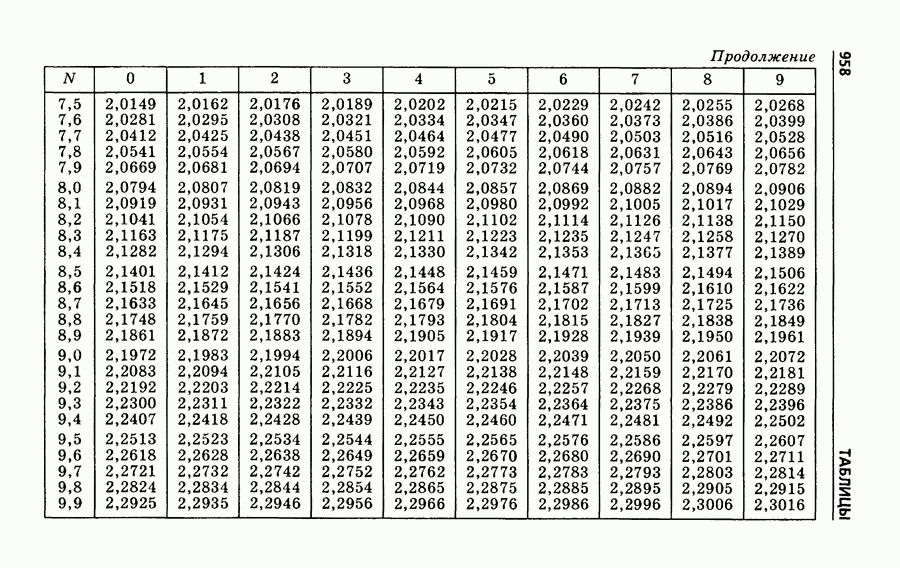
- § 242. Натуральные логарифмы
- § 243. Дифференцирование логарифмической функции
- § 244. Логарифмическое дифференцирование
- § 245. Дифференцирование показательной функции
- § 246. Дифференцирование тригонометрических функций
- § 247. Дифференцирование обратных тригонометрических функций
- § 247а. Некоторые поучительные примеры
- § 248. Дифференциал в приближенных вычислениях
- § 249. Применение дифференциала к оценке погрешности формул
- § 250. Дифференцирование неявных функций
- § 251. Параметрическое задание линии
- § 252. Параметрическое задание функции
- § 253. Циклоида
- § 254. Уравнение касательной к плоской линии
- § 254а. Касательные к кривым второго порядка
- § 255. Уравнение нормали
- § 256. Производные высших порядков
- § 257. Механический смысл второй производной
- § 258. Дифференциалы высших порядков
- § 259. Выражение высших производных через дифференциалы
- § 260. Высшие производные функций, заданных параметрически
- § 261. Высшие производные неявных функций
- § 262. Правило Лейбница
- § 263. Теорема Ролля
- § 264. Теорема Лагранжа о среднем значении
- § 265. Формула конечных приращений
- § 266. Обобщенная теорема о среднем значении (Коши)
- § 267. Раскрытие неопределенности вида 0/0
- § 268. Раскрытие неопределенности вида бесконесность на бесконечность
- § 269. Неопределенные выражения других видов
- § 270. Исторические сведения о формуле Тейлора
- § 271. Формула Тейлора
- § 272. Применение формулы Тейлора к вычислению значений функции
- § 273. Возрастание и убывание функции
- § 274. Признаки возрастания и убывания функции в точке
- § 274а. Признаки возрастания и убывания функции в промежутке
- § 275. Максимум и минимум
- § 276. Необходимое условие максимума и минимума
- § 277. Первое достаточное условие максимума и минимума
- § 278. Правило нахождения максимумов и минимумов
- § 279. Второе достаточное условие максимума и минимума
- § 280. Нахождение наибольшего и наименьшего значений функции
- § 281. Выпуклость плоских кривых; точка перегиба
- § 282. Сторона вогнутости
- § 283. Правило для нахождения точек перегиба
- § 284. Асимптоты
- § 285. Нахождение асимптот, параллельных координатным осям
- § 286. Нахождение асимптот, не параллельных оси ординат
- § 287. Приемы построения графиков
- § 288. Решение уравнений. Общие замечания
- § 289. Решение уравнений. Способ хорд
- § 290. Решение уравнений. Способ касательных
- § 291. Комбинированный метод хорд и касательных
- ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
- § 293. Первообразная функция
- § 294. Неопределенный интеграл
- § 295. Геометрический смысл интегрирования
- § 296. Вычисление постоянной интегрирования по начальным данным
- § 297. Свойства неопределенного интеграла
- § 298. Таблица интегралов
- § 299. Непосредственное интегрирование
- § 300. Способ подстановки (интегрирование через вспомогательную переменную)
- § 301. Интегрирование по частям
- § 302. Интегрирование некоторых тригонометрических выражений
- § 303. Тригонометрические подстановки
- § 304. Рациональные функции
- § 304а. Исключение целой части
- § 305. О приемах интегрирования рациональных дробей
- § 306. Интегрирование простейших рациональных дробей
- § 307. Интегрирование рациональных функций (общий метод)
- § 308. О разложении многочлена на множители
- § 309. Об интегрируемости в элементарных функциях
- § 310. Некоторые интегралы, зависящие от радикалов
- § 311. Интеграл от биномиального дифференциала
- § 312. Интегралы вида …
- § 313. Интегралы вида S R(sinx, cosx)dx
- § 314. Определенный интеграл
- § 315. Свойства определенного интеграла
- § 316. Геометрический смысл определенного интеграла
- § 317. Механический смысл определенного интеграла
- § 318. Оценка определенного интеграла
- § 318а. Неравенство Буняковского
- § 319. Теорема о среднем интегрального исчисления
- § 320. Определенный интеграл как функция верхнего предела
- § 321. Дифференциал интеграла
- § 322. Интеграл дифференциала. Формула Ньютона — Лейбница
- § 323. Вычисление определенного интеграла с помощью неопределенного
- § 324. Определенное интегрирование по частям
- § 325. Способ подстановки в определенном интеграле
- § 326. О несобственных интегралах
- § 327. Интегралы с бесконечными пределами
- § 328. Интеграл функции, имеющей разрыв
- § 329. О приближенном вычислении интеграла
- § 330. Формулы прямоугольников
- § 331. Формула трапеций
- § 332. Формула Симпсона (параболических трапеций)
- § 333. Площади фигур, отнесенных к прямоугольным координатам
- § 334. Схема применения определенного интеграла
- § 335. Площади фигур, отнесенных к полярным координатам
- § 336. Объем тела по поперечным сечениям
- § 337. Объем тела вращения
- § 338. Длина дуги плоской линии
- § 339. Дифференциал дуги
- § 340. Длина дуги и ее дифференциал в полярных координатах
- § 341. Площадь поверхности вращения
- ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ
- § 342. Кривизна
- § 343. Центр, радиус и круг кривизны плоской линии
- § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии
- § 345. Эволюта плоской линии
- § 346. Свойства эволюты плоской линии
- § 347. Развертка (эвольвента) плоской линии
- § 348. Параметрическое задание пространственной линии
- § 349. Винтовая линия
- § 350. Длина дуги пространственной линии
- § 351. Касательная к пространственной линии
- § 352. Нормальная плоскость
- § 353. Вектор-функция скалярного аргумента
- § 354. Предел вектор-функции
- § 355. Производная вектор-функции
- § 356. Дифференциал вектор-функции
- § 357. Свойства производной и дифференциала вектор-функции
- § 358. Соприкасающаяся плоскость
- § 359. Главная нормаль. Сопутствующий трехгранник
- § 360. Взаимное расположение линии и плоскости
- § 361. Основные векторы сопутствующего трехгранника
- § 362. Центр, ось и радиус кривизны пространственной линии
- § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии
- § 364. О знаке кривизны
- § 365. Кручение
- РЯДЫ
- § 367. Определение ряда
- § 368. Сходящиеся и расходящиеся ряды
- § 369. Необходимое условие сходимости ряда
- § 370. Остаток ряда
- § 371. Простейшие действия над рядами
- § 372. Положительные ряды
- § 373. Сравнение положительных рядов
- § 374. Признак Даламбера для положительного ряда
- § 375. Интегральный признак сходимости
- § 376. Знакопеременный ряд. Признак Лейбница
- § 377. Абсолютная и условная сходимость
- § 378. Признак Даламбера для произвольного ряда
- § 379. Перестановка членов ряда
- § 380. Группировка членов ряда
- § 381. Умножение рядов
- § 382. Деление рядов
- § 383. Функциональный ряд
- § 384. Область сходимости функционального ряда
- § 385. О равномерной и неравномерной сходимости
- § 386. Определение равномерной и неравномерной сходимости
- § 387. Геометрический смысл равномерной и неравномерной сходимости
- § 388. Признак равномерной сходимости; правильные ряды
- § 389. Непрерывность суммы ряда
- § 390. Интегрирование рядов
- § 391. Дифференцирование рядов
- § 392. Степенной ряд
- § 393. Промежуток и радиус сходимости степенного ряда
- § 394. Нахождение радиуса сходимости
- § 395. Область сходимости ряда, расположенного по степеням х — х0
- § 396. Теорема Абеля
- § 397. Действия со степенными рядами
- § 398. Дифференцирование и интегрирование степенного ряда
- § 399. Ряд Тейлора
- § 400. Разложение функции в степенной ряд
- § 401. Разложение элементарных функций в степенные ряды
- § 402. Применение рядов к вычислению интегралов
- § 403. Гиперболические функции
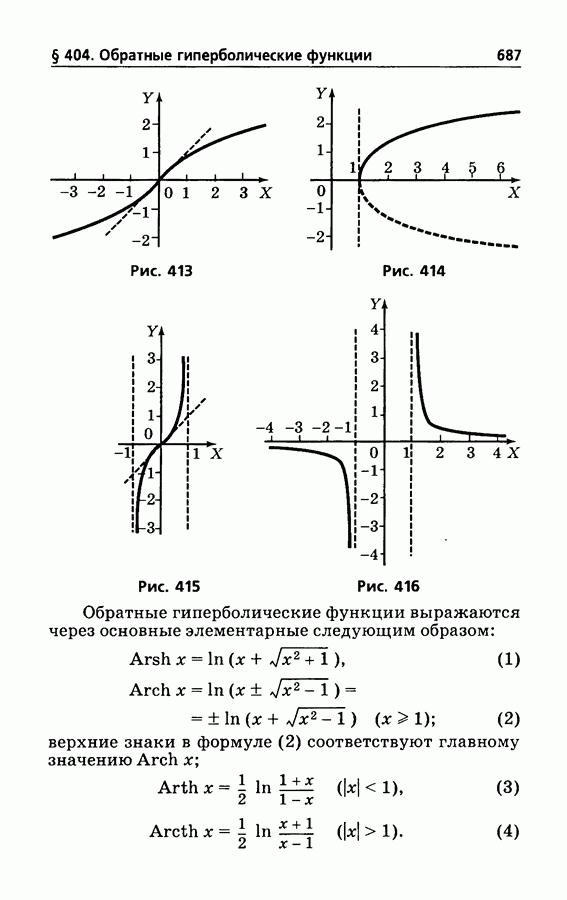
- § 404. Обратные гиперболические функции
- § 405. Происхождение наименований гиперболических функций
- § 406. О комплексных числах
- § 407. Комплексная функция действительного аргумента
- § 408. Производная комплексной функции
- § 409. Возведение положительного числа в комплексную степень
- § 410. Формула Эйлера
- § 411. Тригонометрический ряд
- § 412. Исторические сведения о тригонометрических рядах
- § 413. Ортогональность системы функций cos nx, sin nx
- § 414. Формулы Эйлера-Фурье
- § 415. Ряд Фурье
- § 416. Ряд Фурье для непрерывной функции
- § 417. Ряд Фурье для четной и нечетной функции
- § 418. Ряд Фурье для разрывной функции
- ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ
- § 420. Функция трех и большего числа аргументов
- § 421. Способы задания функций нескольких аргументов
- § 422. Предел функции нескольких аргументов
- § 424. Непрерывность функции нескольких аргументов
- § 425. Частные производные
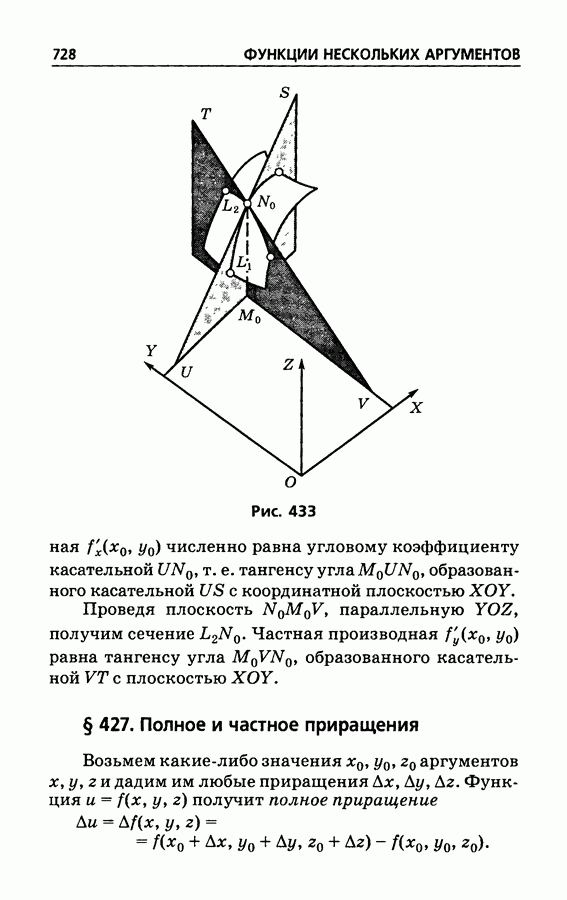
- § 426. Геометрический смысл частных производных для случая двух аргументов
- § 427. Полное и частное приращения
- § 428. Частный дифференциал
- § 429. О выражении частной производной через дифференциал
- § 430. Полный дифференциал
- § 431. Геометрический смысл полного дифференциала (случай двух аргументов)
- § 432. Инвариантность выражения … полного дифференциала
- § 433. Техника дифференцирования
- § 434. Дифференцируемые функции
- § 435. Касательная плоскость и нормаль к поверхности
- § 436. Уравнение касательной плоскости
- § 437. Уравнения нормали
- § 438. Дифференцирование сложной функции
- § 439. Замена прямоугольных координат полярными
- § 440. Формулы для производных сложной функции
- § 441. Полная производная
- § 442. Дифференцирование неявной функции нескольких переменных
- § 443. Частные производные высших порядков
- § 444. Полные дифференциалы высших порядков
- § 445. Техника повторного дифференцирования
- § 446. Условное обозначение дифференциалов
- § 447. Формула Тейлора для функции нескольких аргументов
- § 448. Экстремум (максимум и минимум) функции нескольких аргументов
- § 449. Правило нахождения экстремума
- § 450. Достаточные условия экстремума (случай двух аргументов)
- § 451. Двойной интеграл
- § 452. Геометрический смысл двойного интеграла
- § 453. Свойства двойного интеграла
- § 454. Оценка двойного интеграла
- § 455. Вычисление двойного интеграла (простейший случай)
- § 456. Вычисление двойного интеграла (общий случай)
- § 457. Функция точки
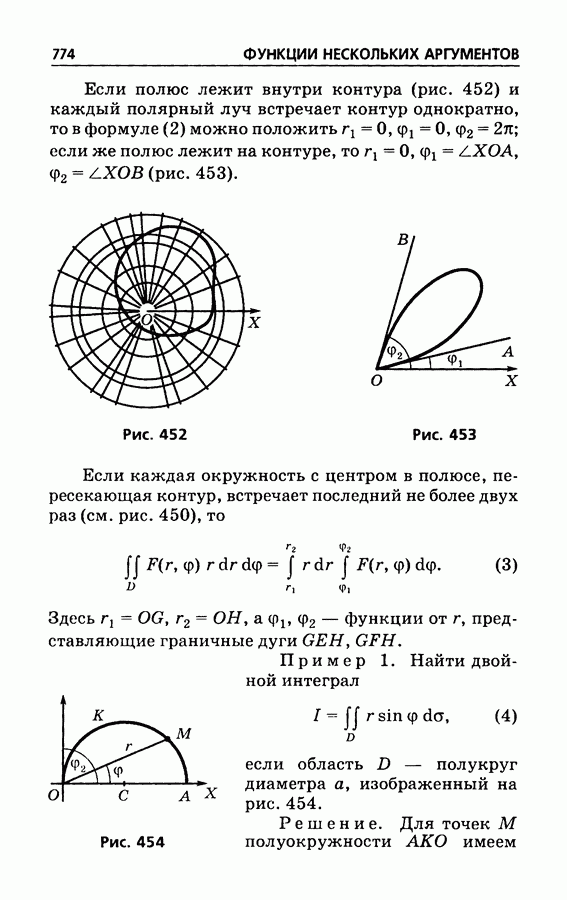
- § 458. Выражение двойного интеграла через полярные координаты
- § 459. Площадь куска поверхности
- § 460. Тройной интеграл
- § 461. Вычисление тройного интеграла (простейший случай)
- § 462. Вычисление тройного интеграла (общий случай)
- § 463. Цилиндрические координаты
- § 464. Выражение тройного интеграла через цилиндрические координаты
- § 465. Сферические координаты
- § 466. Выражение тройного интеграла через сферические координаты
- § 467. Схема применения двойного и тройного интегралов
- § 468. Момент инерции
- § 471. Криволинейный интеграл
- § 472. Механический смысл криволинейного интеграла
- § 473. Вычисление криволинейного интеграла
- § 474. Формула Грина
- § 475. Условие, при котором криволинейный интеграл не зависит от пути
- § 476. Другая форма условия предыдущего параграфа
- ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 478. Уравнение первого порядка
- § 479. Геометрический смысл уравнения первого порядка
- § 480. Изоклины
- § 481. Частное и общее решения уравнения первого порядка
- § 482. Уравнения с разделенными переменными
- § 483. Разделение переменных. Особое решение
- § 484. Уравнение в полных дифференциалах
- § 484а. Интегрирующий множитель
- § 485. Однородное уравнение
- § 486. Линейное уравнение первого порядка
- § 487. Уравнение Клеро
- § 488. Огибающая
- § 489. Об интегрируемости дифференциальных уравнений
- § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера
- § 491. Интегрирование дифференциальных уравнений с помощью рядов
- § 492. О составлении дифференциальных уравнений
- § 493. Уравнение второго порядка
- § 494. Уравнение n-го порядка
- § 495. Случаи понижения порядка
- § 496. Линейное уравнение второго порядка
- § 497. Линейное уравнение второго порядка с постоянными коэффициентами
- § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части
- § 498а. Связь между случаями 1 и 3 § 498
- § 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью
- § 500. Линейные уравнения любого порядка
- § 501. Метод вариации постоянных
- § 502. Системы дифференциальных уравнений. Линейные системы
- НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
- § 503. Строфоида
- § 504. Циссоида Диокла
- § 505. Декартов лист
- § 506. Верзьера Аньези
- § 507. Конхоида Никомеда
- § 508. Улитка Паскаля; кардиоида
- § 509. Линия Кассини
- § 510. Лемниската Бернулли
- § 511. Архимедова спираль
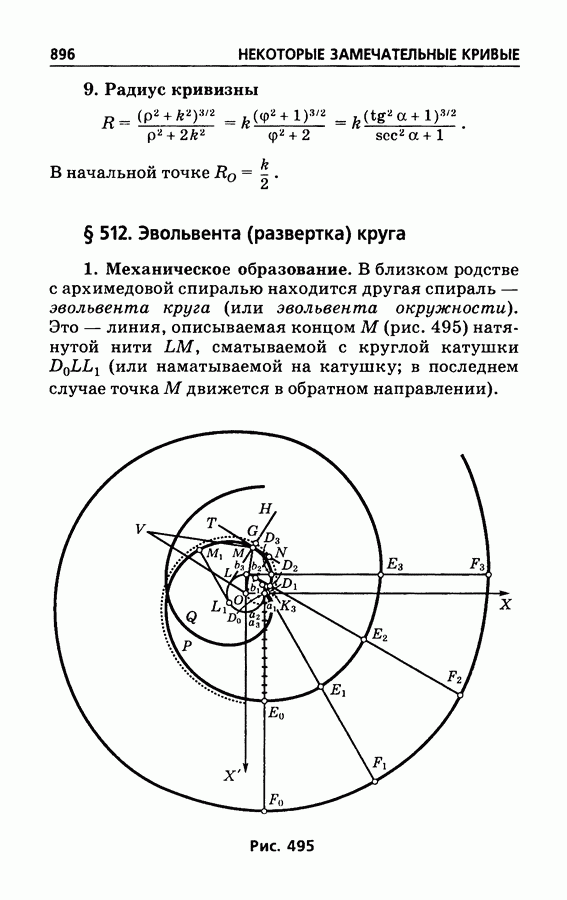
- § 512. Эвольвента (развертка) круга
- § 513. Логарифмическая спираль
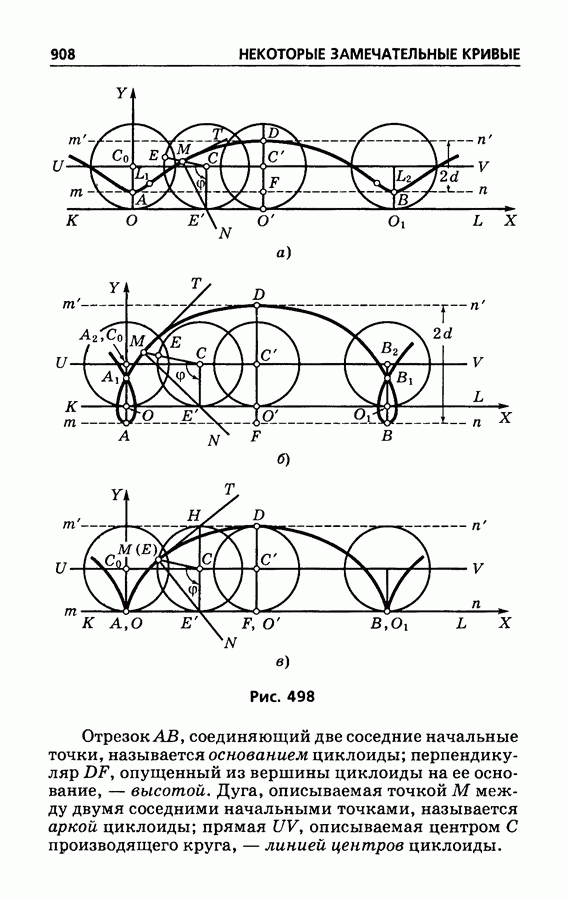
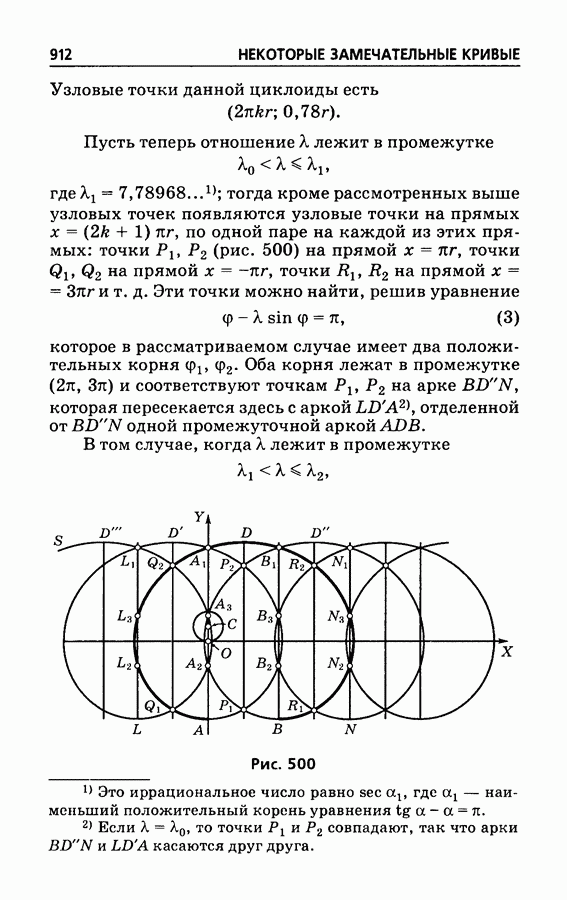
- § 514. Циклоиды
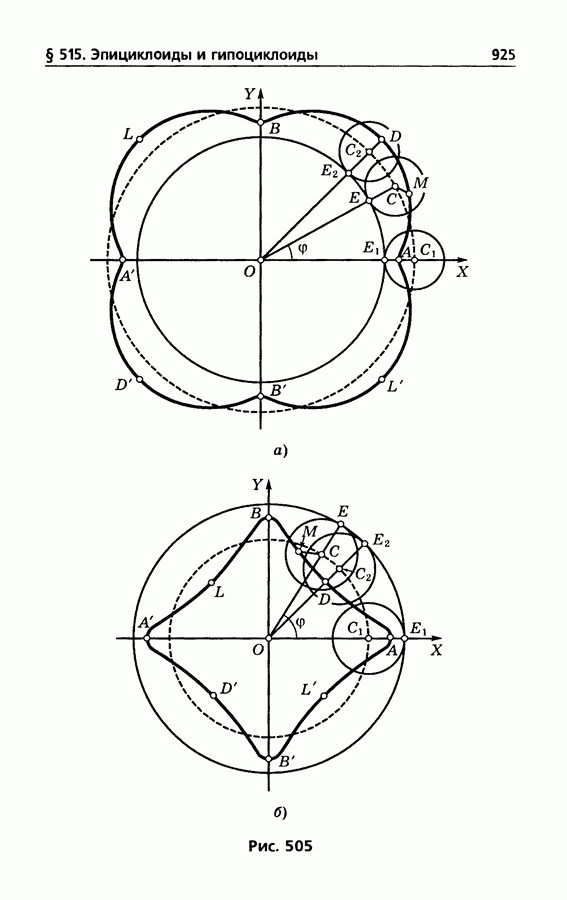
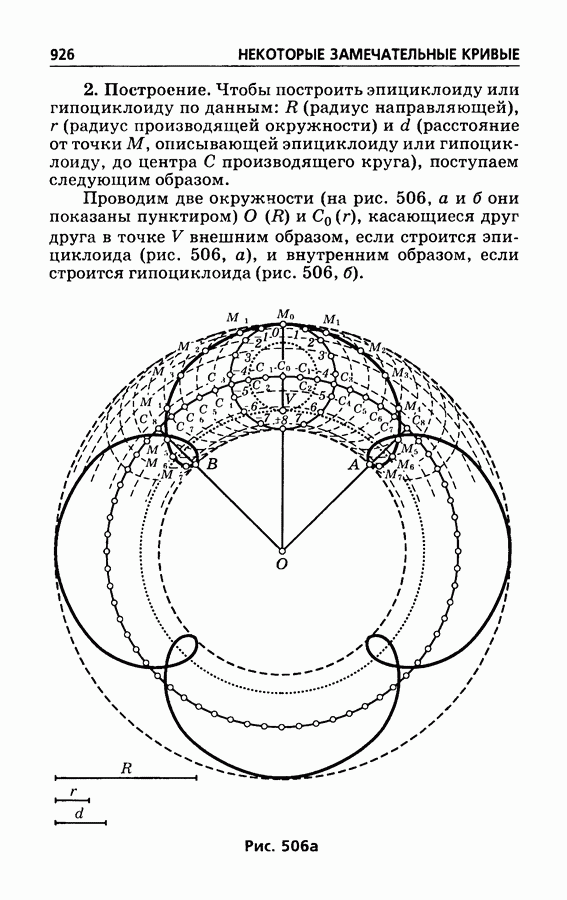
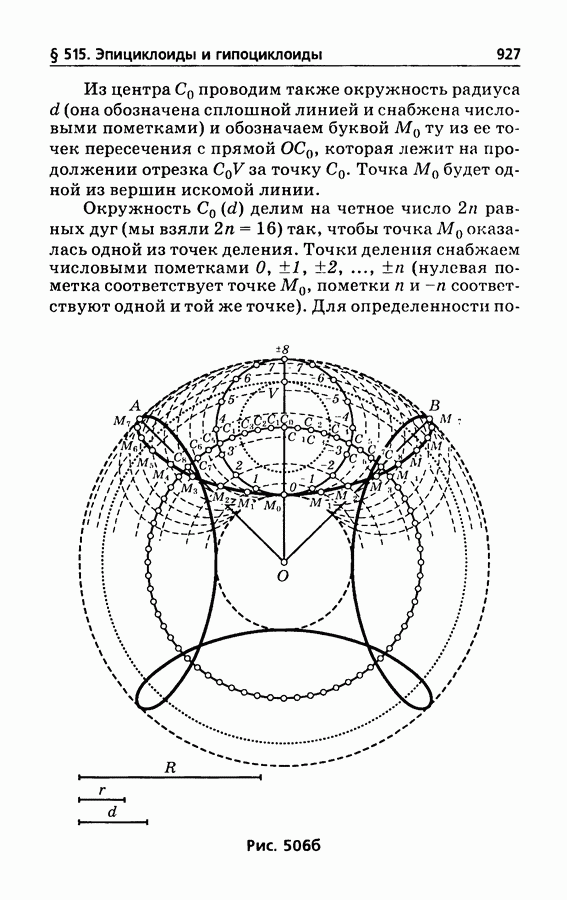
- § 515. Эпициклоиды и гипоциклоиды
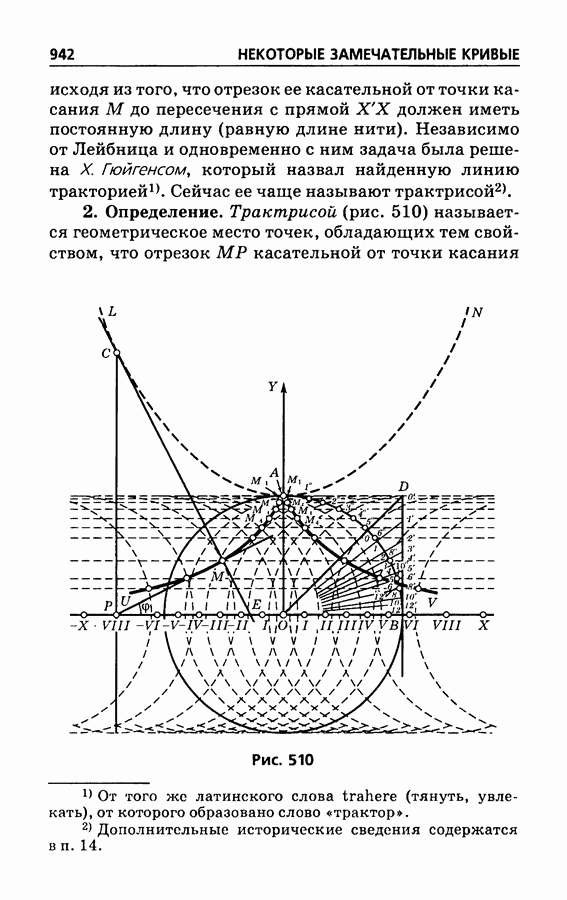
- § 516. Трактриса
- § 517. Цепная линия